2. MODEL EQUATIONS

The OBT in dielectric materials is due to the generation of a sufficiently high free electron density in the material. Breakdown is assumed to occur when the free electron density reaches a critical value n _c. Two critical values are generally admitted in the literature and they correspond to n _n = 10²¹ cm⁻³ or to the density when the laser frequency is equal to the plasma frequency, i.e., $n_c \left({cm^{ - 3} } \right)=1.110^{21} /$${\rm \lambda} _L^2 \left({{\rm \mu} m} \right)$ where λ_L is the laser wavelength. The two breakdown criteria coincide for λ_L ≈ 1 μm. Hence, the threshold laser pulse fluence is defined as the minimal fluence that just creates the critical density. At the critical density, laser light absorption becomes very efficient, so the deposited density of laser energy is extremely high and under these conditions, electrons can cause macroscopic damage in the material. With the advent of the ultra-short laser pulse, the laser induced dielectric breakdown has been extensively studied in the past two decades for various media such as dielectrics (Du et al., Reference Du, Liu and Mourou1996; Lenzner et al., Reference Lenzner, Krüger, Sartania, Cheng, Spielmann, Mourou, Kautek and Krausz1998; Li et al., Reference Li, Menon, Nibarger and Gibson1999; Stuart et al., Reference Stuart, Feit, Rubenchik, Shore and Perry1995; Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry1996; Tien et al., Reference Tien, Backus, Kapteyn, Murnane and Mourou1999), conductors (Eidmann et al., Reference Eidmann, Meyer-Ter-Vehn, Schlegel and Hüller2000; Kirkwood et al., Reference Kirkwood, Tsui, Fedosejevs, Brantov and Bychenkov2009) and semiconductors (Allenspacher et al., Reference Allenspacher, Hüttner and Riede2003; Chen et al., Reference Chen, Tzou and Beraun2005).

In this work, we concentrate on the laser-dielectric interaction and in the following we summarize the main theoretical models reported in the literature. We focus our attention on theoretical models based on the rate equation for free electrons which includes the relevant physical mechanisms, i.e., the photo-ionization and the avalanche source mechanisms together with the loss terms, i.e., the recombination processes.

For ultra-short pulses, Du et al. (Reference Du, Liu and Mourou1996), predicted that the photo-ionization can be described by tunneling effect and that this mechanism is less efficient than the avalanche mechanism. The model is based on the following rate equation that describes the time evolution of the free electron density n in a dielectric material,

(1)$$\displaystyle{{\partial n} \over {\partial t}}=An\left(t \right)\comma \;$$

where the ionization avalanche rate A is described by the Thornber (Reference Thornber1981) formula. We mention that the ultra-short pulse-solid target interaction is characterized by an energy transfer time from free electrons to the lattice by Coulomb collisions typically of few picoseconds, thus longer than the laser pulse duration. As a result the hydrodynamic motion does not occur during the interaction time and the model equations do not account for the spatial effects. Stuart et al. (Reference Stuart, Feit, Rubenchik, Shore and Perry1995; Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry1996) have proposed the following rate equation

(2)$$\displaystyle{{\partial n} \over {\partial t}}={\rm \alpha} I\left(t \right)n+{\rm \sigma} _k I^k \left(t \right)\comma \;$$

where α is the avalanche coefficient and I (t) is the laser pulse intensity. The second term on the right-hand side of Eq. (2) refers to the gain of electron density through the multi-photo-ionization mechanism defined by the following parameters: the k-photon absorption cross section σ_k with the smallest k satisfying $k\hbar {\rm \omega} \geq \Delta $, where ℏ is the reduced Planck's constant, ω is the laser frequency, and Δ is the band gap of the dielectric. The linear scaling law of the avalanche rate with respect to the laser intensity I(t) was modeled through the use of the Fokker-Planck equation. The ionization mechanisms consist to create an important seed of free electrons with the multi-photo-ionization mechanism, and then, these electrons are heated up via the inverse bremsstrahlung mechanism. Once the electron density is sufficiently high, the material is ionized efficiently by means of the avalanche mechanism. The multi-photon contributions to carrier buildup are also present during the cascade phase. A similar rate equation model as the one described by Eq. (2) was proposed by Tien et al. (Reference Tien, Backus, Kapteyn, Murnane and Mourou1999) with the use of the Thornber's (Reference Thornber1981) rate and Keldysh's (Reference Keldysh1965) rate for the avalanche and photo-ionization mechanisms respectively. Li et al. (Reference Li, Menon, Nibarger and Gibson1999) have improved the preceding models with a relaxation term to model the decay process for short pulse duration,

(3)$$\displaystyle{{\partial n} \over {\partial t}}={\rm \alpha} I\left(t \right)n+{\rm \sigma} _k I^k \left(t \right)- \displaystyle{n \over {\rm \tau} }\comma \;$$

where τ is the relaxation constant on the order of 60 fs. We should mention that further models based on the propagation model (Peñano et al., Reference Peñano, Sprangle, Hafizi, Manheimer and Zigler2005) and on the multiple rate equations (Rethfeld et al., Reference Rethfeld2004; Reference Rethfeld, Brenk, Medvedev, Krutsch and Hoffmann2010) have also been reported in the literature.

The model of the present work is based on the rate equation with explicit recombination terms, namely, the three body and exciton recombination terms. In addition, the energy balance equation is also considered. It yields the following model equations

(4)$$\eqalign{& \displaystyle{{dn} \over {dt}}={\rm \alpha} _e n{\rm \theta} \left({{\rm \varepsilon} - 2\Delta } \right)+\displaystyle{{\left({n_a - n} \right)} \over {n_a }} W_{PI} - R_{3C} n^3 - \displaystyle{{dn_{exc} } \over {dt}}\comma \; }$$

(5)$$\eqalign {& \displaystyle{{dn_{exc} } \over {dt}}=- {\rm \alpha} _{exc} n_{exc} \left(t \right){\rm \theta} \left({{\rm \varepsilon} - 2\Delta _{exc} } \right) - \displaystyle{{n_{exc} } \over {n_a }}W_{PI}^{exc}+\displaystyle{n \over {{\rm \tau} _{exc} }}\comma \; }$$

(6)$$\eqalign{ \displaystyle{{d\left({n{\rm \varepsilon} } \right)} \over {dt}}&=\overline {\vec j \cdot \vec E} +\Delta \displaystyle{{\left({n_a - n} \right)} \over {n_a }}W_{PI} +\Delta _{exc} \displaystyle{{n_{exc} } \over {n_a }}W_{PI}^{exc} - 2\Delta {\rm \alpha} _e n \cr & \quad - 2\Delta _{exc} {\rm \alpha} _{exc} n_{exc} - nQ_{ei} \left({T - T_l } \right)\comma \; }$$

where n(t), n _a, and n _exc (t) are the free electron, atomic, and exciton densities, respectively, ɛ is the electron mean energy, $\vec E$ is the electric field, τ_exc = 150 ps is the characteristic trapping time of excitons, T is the free electron temperature, T _l is the lattice temperature, Q _ei = 1 ps is the electron-ion energy coupling parameter,

(7)$$R_{3C} \left({cm^6 s^{ - 1} } \right)=8.75\, 10^{ - 27} T^{ - 9/2} \left({eV} \right)\comma \;$$

is the three-body recombination coefficient (Huba, Reference Huba2000), θ(x) is the theta Heaviside function, α_e and α_exc are the avalanche coefficients, σ_e and σ_exc are the photo-ionization coefficients,

(8)$$\overline {\vec j \cdot \vec E}=\displaystyle{{enI\left(t \right)} \over {{\rm \varepsilon} _0\, cm}}\displaystyle{{\rm \nu} \over {{\rm \nu} ^2+{\rm \omega} ^2 }}\comma \;$$

is the laser energy absorbed by electrons per unit time and volume, where the notation “–”, stands for the average over a laser cycle, I(t) is the pulse intensity, c is the speed of light, m is the effective electron mass, e is the electron charge and ν = ν_ei + ν_en is the electron lattice collision frequency, ν_ei = ν_SHν_ph/(ν_SH + ν_ph) is the electron-ion collision frequency, ν_SH(s ⁻¹) = 310⁻⁶Zn(cm ⁻³)T ^−3/2(eV) ln Λ, is the Spitzer-Härm electron-ion collision frequency (Spitzer & Härm, Reference Spitzer and Härm1953), ν_ph = 4e ²k _BT _L/(ℏ²V _F) is the electron-phonon collision frequency and ν_en(s ⁻¹) = 210⁻⁷n _a(cm ⁻³)T ^1/2 (eV), is the electron-atom collision frequency, where ln Λ is the Coulomb logarithm, Z is the ion charge, V _F = ℏ(3πn)^1/3/m is the de Fermi velocity, ℏ is the reduced Planck's constant and n _a is the atomic density.

We should mention that the interaction of an ultra-short and ultra-intense laser pulse with solid target is a complex physical problem. It is defined by a chain of events which occur on a wide range of length and time scales making the problem even more intractable (Stoian et al., Reference Stoian, Rosenfeld, Ashkenasi, Hertel, Bulgakova and Campbell2002; Perez et al., Reference Perez and Lewis2002; Reference Perez, Beland, Derying, Lewis and Meunier2008). In particular, it is well known that the free electrons created by the ionization mechanisms gain the energy exceeding the threshold energy and escape the solid target during the pulse time. It results a strong electric field due to charge separation. If the electron energy is greater than the binding energy of ions in the lattice this field pulls the ions out of the solid target. Simple scaling laws derived by Gamaly et al. (Reference Gamaly, Rode, Luther-Davies and Tikhonchuk2002), show that below the ablation threshold, the acceleration time of ions is much longer than the pulse duration and when the laser fluence exceeds the ablation threshold this acceleration time could be shorter than the pulse duration. Further manifestations of damage material such as vaporization, melting and crack formation, are also produced after the pulse termination.

It is admitted that ionization by collisions requires an energy greater than the gap energy, Δ. In our model we have used the theta function to model the onset of the avalanche ionization from an energy of about 2Δ, which is the standard value. In addition, we have approximate in Eq. (7), the electron temperature by the mean energy, i.e., ${3 / 2}k_B T \approx {\rm \varepsilon} $, where k _B is the Boltzmann constant.

The photo-ionization rate used in this work is approximated by the Keldysh's (Reference Keldysh1965) expression

(9)$$\eqalign{& w_{PI} \lpar I\rpar =\displaystyle{{2{\rm \omega} } \over {9{\rm \pi} }}\left({\displaystyle{{{\rm \omega} m^\ast } \over {\sqrt {{\rm \gamma} _1 } \hbar }}} \right)^{3/2} Q\lpar {\rm \gamma}\comma \; x\rpar \exp \left\{{ -{\rm \pi} \left\langle {x+1} \right\rangle \displaystyle{{{\rm K}\left({{\rm \gamma} _1 } \right)- {\rm E}\left({{\rm \gamma} _1 } \right)} \over {{\rm E}\left({{\rm \gamma} _2 } \right)}}} \right\}\comma \; }$$

where

$$\eqalign{ Q\lpar {\rm \gamma}\comma \; x\rpar & =\sqrt {\displaystyle{{\rm \pi} \over {2{\rm K}\left({{\rm \gamma} _2 } \right)}}} \times \sum\limits_{n=0}^\infty {\exp \left\{{ - n{\rm \pi} \displaystyle{{{\rm K}\left({{\rm \gamma} _2 } \right)- {\rm E}\left({{\rm \gamma} _2 } \right)} \over {{\rm E}\left({{\rm \gamma} _1 } \right)}}} \right\}} \cr & \quad \times\Phi \left\{{\sqrt {\displaystyle{{{\rm \pi} ^2 \left({2\left\langle {x+1} \right\rangle - 2x+n} \right)} \over {4{\rm K}\left({{\rm \gamma} _2 } \right){\rm E}\left({{\rm \gamma} _2 } \right)}}} } \right\}\comma }\;$$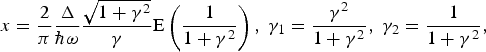

$x=\displaystyle{2 \over {\rm \pi} }\displaystyle{\Delta \over {\hbar {\rm \omega} }}\displaystyle{{\sqrt {1+{\rm \gamma} ^2 } } \over {\rm \gamma} }{\rm E}\left({\displaystyle{1 \over {1+{\rm \gamma} ^2 }}} \right)\comma \; {\rm \gamma} _1=\displaystyle{{{\rm \gamma} ^2 } \over {1+{\rm \gamma} ^2 }}\comma \; {\rm \gamma} _2=\displaystyle{1 \over {1+{\rm \gamma} ^2 }}\comma \; $$ {\rm \gamma}=\displaystyle{{{\rm \omega} \sqrt {m^{\ast} \Delta }} \over {eE}}\comma \; {\rm \omega} $ is the laser frequency, $m^{\ast} =\displaystyle{{mm_h } \over {m+m_h }}$ is the effective reduced electron-hole mass, 〈z〉 is the integer part of the number z, 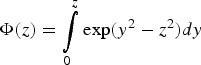$\Phi \lpar z\rpar =\vint\limits_0^z {\exp \lpar y^2 - z^2 \rpar dy} $ is the Dawson integral and, 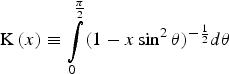${\rm K}\left(x \right)\equiv \vint\limits_0^{{\rm \pi} \over 2} \lpar 1 - x\sin ^2 {\rm \theta} \rpar ^{ - {1 \over 2}} d{\rm \theta} $ and $E\left(x \right)\equiv \vint\limits_0^{{{\rm \pi} \over 2}} {\lpar 1 - x\sin ^2 {\rm \theta} \rpar ^{1 \over 2} } d{\rm \theta} $, are the complete elliptic integrals of the first and second kinds respectively. The subscripts ′e′ and ′exc′ stand for the free electrons and excitons respectively. We just note that the Keldysh's photo-ionization rate is governed by the relevant parameter γ (the so-called Keldysh's parameter). For γ ≫ 1, (typically, I ≪ 10¹³W/cm²), expression (9) tends asymptotically to the multi-photo-ionization rate, w _MPI = σ_kI ^k and for γ ≪ 1 (I ≫ 10¹³W/cm ²), to the tunneling ionization rate.

Otherwise, to our knowledge there is no accurate theoretical model to describe the avalanche ionization in dielectrics. We used the empirical avalanche rate of Thornber (Reference Thornber1981)

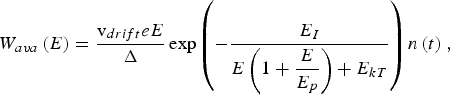(10)$$W_{ava} \left(E \right)=\displaystyle{{{\rm v}_{drift} eE} \over \Delta }\exp \left({ - \displaystyle{{E_I } \over {E\left({1+\displaystyle{E \over {E_p }}} \right)+E_{kT} }}} \right)n\left(t \right)\comma \;$$

where v_drift ≈ 210⁷cm/s is the saturation drift velocity, E _I = 30 MV/cm, E _P = 3.2 MV/cm, and E _kT = 0.01 MV/cm are the electric fields for electrons to overcome the decelerating effects of ionization scattering, optical phonon scattering and thermal scattering in one mean free path, respectively. Eqs. (9) and (10) are valid for arbitrary electric field strengths and thus they are adequate for the description of ultra-short laser pulse-dielectric interaction.

The photo-ionization is a nonlinear mechanism responsible for simultaneous absorption of few photons by electrons in the valance band. It creates a seed of free electrons which are heated by the laser pulse at energy greater than the gap energy. In turn, these electrons collide with bound electrons and create by energy transfer new free electrons in the conduction band: it is the avalanche ionization. The two ionization rates depend strongly on the laser pulse parameters (wavelength and intensity) and on the material parameters (energy gap). As the theoretical models presented above, our model is based on the rate Eq. (4). It includes the ionization and the relaxation mechanisms that are the three-body and exciton recombination. The three-body recombination is often used in ionization models, while the one due to the production of electron-hole pairs is less common and it was suggested by Petite et al. (Reference Petite, Guizard, Martin and Quéré1999) in modeling the interaction of ultra-short laser pulses with dielectrics. We mention that we have checked that radiative recombination mechanism is negligible with respect to the ones used in our model. The excitons are described as a particle population with the energy balance Eq. (5) and their relaxation terms are the photo-ionization and avalanche recombination. Furthermore, our model takes into account the average energy of the free electrons via Eq. (6). The estimate of the electron mean energy is particularly important since it allows the modeling of the interdependence of the two ionization mechanisms with the use of the theta function. Indeed, for free electron energy above the gap (ɛ > 2Δ), the electrons can contribute to the avalanche ionization, otherwise the avalanche mechanism cannot be triggered out. Statistically, there will be also electrons that violate this assumption, but we consider that it is a reasonable approximation.

3. NUMERICAL SOLUTION AND DISCUSSION

The set of Eq. (4)–(6) consists of nonlinear coupled equations which clearly do not admit analytical solutions. We solved numerically this set of equations with the use of standard numerical algorithms. The code input parameters which characterize the incident laser pulse of a Gaussian shape [I(t) = I ₀ exp (−4 ln2(t/τ_p)²)], are the intensity I, the pulse width τ_p, and the wavelength λ_L. The input parameters characterizing the dielectric material are, the atomic density n _a, the band gap energy Δ, the initial free electron density n _in, the initial electron mean energy ɛ_in, the initial exciton density n _{in exc}, and the index of refraction at the wavelength, n _r.

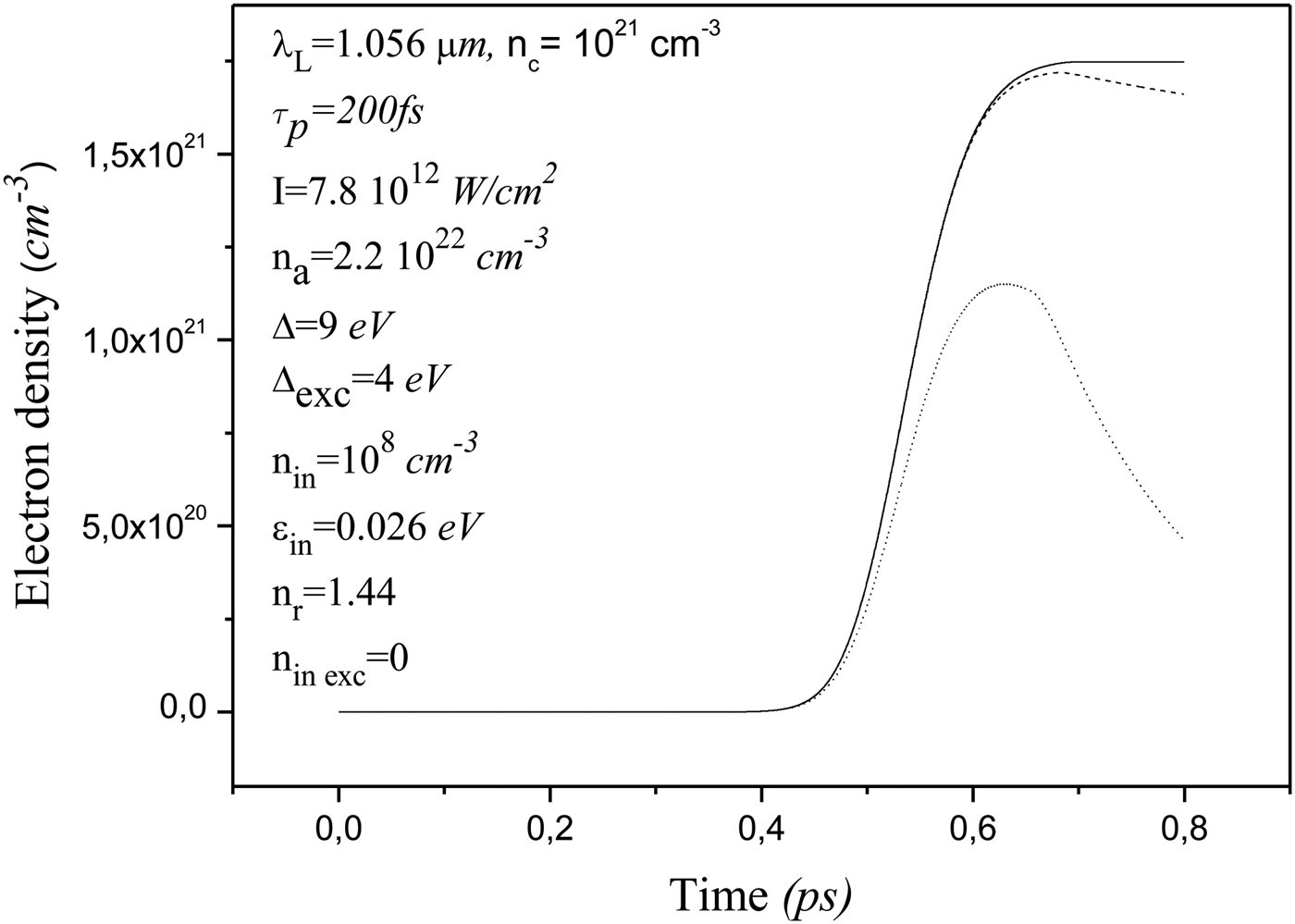
Figure 1 depicts the time evolution of the free electron density in different physical situations with respect to the recombination mechanisms. First, if we drop the recombination terms in Eqs. (4)–(6), the electron density (solid line) tends to a constant value once the ionization becomes negligible. If the recombination mechanisms are accounted for (dashed and dotted lines) we see that the density is less important and the competition between recombination and ionization effects leads to a maximum in the electron density profile. Moreover the exciton recombination (dotted line) is more efficient than the three-body recombination mechanism (dashed line) and therefore, it could play a significant role for the determination of the OBT.

Fig. 1. Free electron density as a function of time. The solid line corresponds to the case without recombination mechanisms, the dotted line to the case with only exciton recombination, and the dashed line to the case with only three-body recombination.

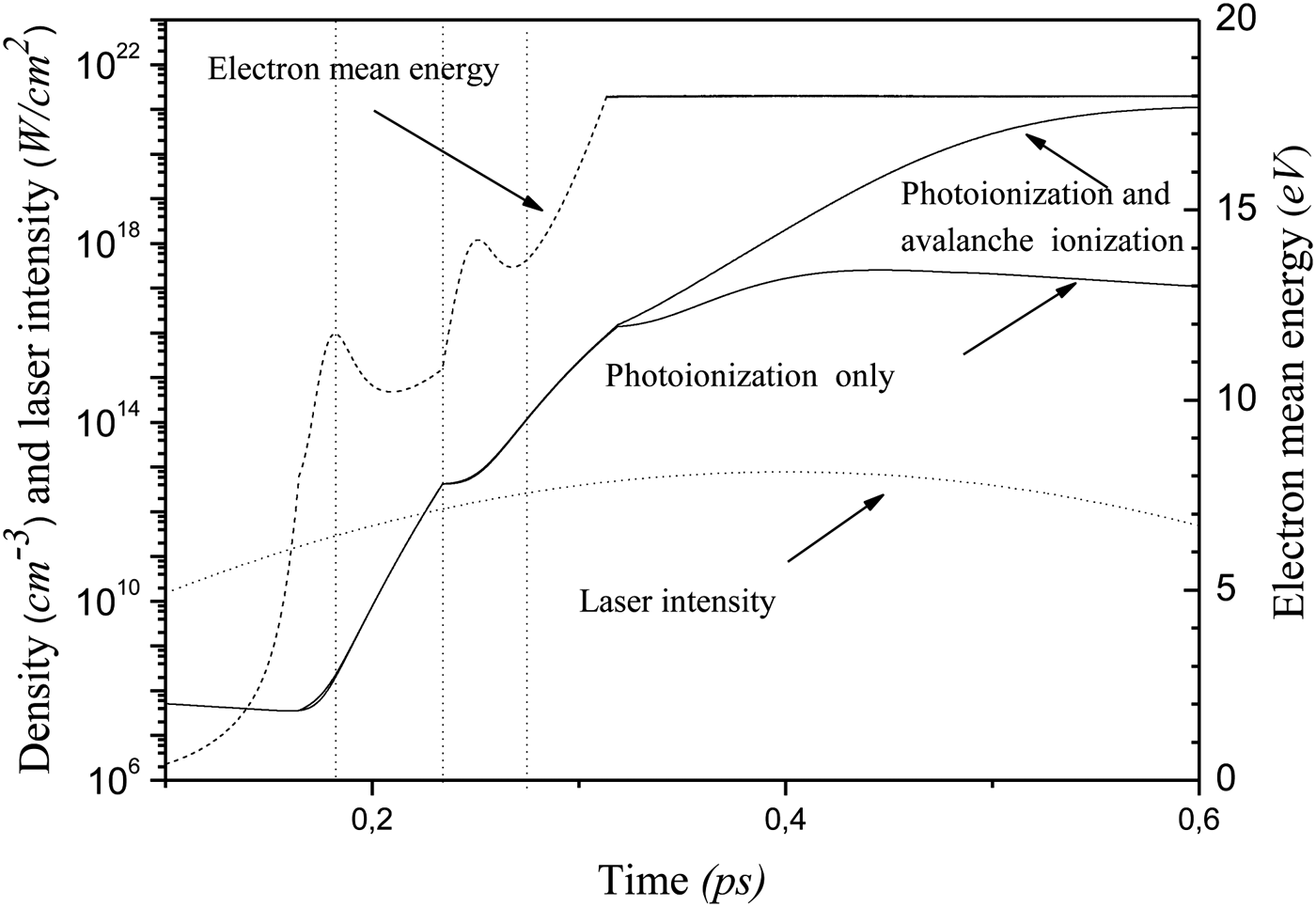
In addition to these recombination mechanisms, let us now investigate the role of the two ionization mechanisms in laser-dielectric interaction. We present in Figure 2 the time evolution of the free electron density in the case where both mechanisms are kept and, in the case where the avalanche ionization is neglected. In addition, we give the time evolution of the electron mean energy and the laser intensity. We can note that the maximum value of the density in the case where we account for the avalanche is four orders of magnitude larger than the one where only the photo-ionization is considered. This large difference implies that the avalanche mechanism plays a crucial role in target ionization. For free electron densities less than 2 × 10¹⁶ cm⁻³, the avalanche ionization is negligible. Thus the photo-ionization has an important contribution, since it generates a seed of free electrons that triggers efficiently the avalanche mechanism. On the other hand, we observe that the thermal energy of free electrons exhibits peak and valley structures. This can be explained by the competition between the rate of change of the electron density (governed by recombination and ionization) and the laser electron heating through an isochoric process. At the beginning of the laser pulse (up to 0.18 ps) the ionization is weak and the laser electron heating is efficient. This leads to a rapid increase in the thermal energy. When the exciton avalanche (threshold energy = 8 eV) is triggered at 0.18 ps, the electron density increases rapidly, the absorption mechanisms are not able to heat the electrons, thus the thermal energy decreases. From 0.24 ps, the electron density increases less rapidly and again the thermal energy increases due to the isochoric heating, and so on. Finally, from 0.32 ps, the temperature reaches its equilibrium value.

Fig. 2. The solid lines correspond to the free electron density in the case with avalanche ionization and without avalanche ionization. The dashed line corresponds to the electron mean energy and the dotted line to the laser intensity. The electron mean energy is calculated with multiphoton and avalanche ionizations. The physical laser and dielectric parameters are the same as in Figure 1.

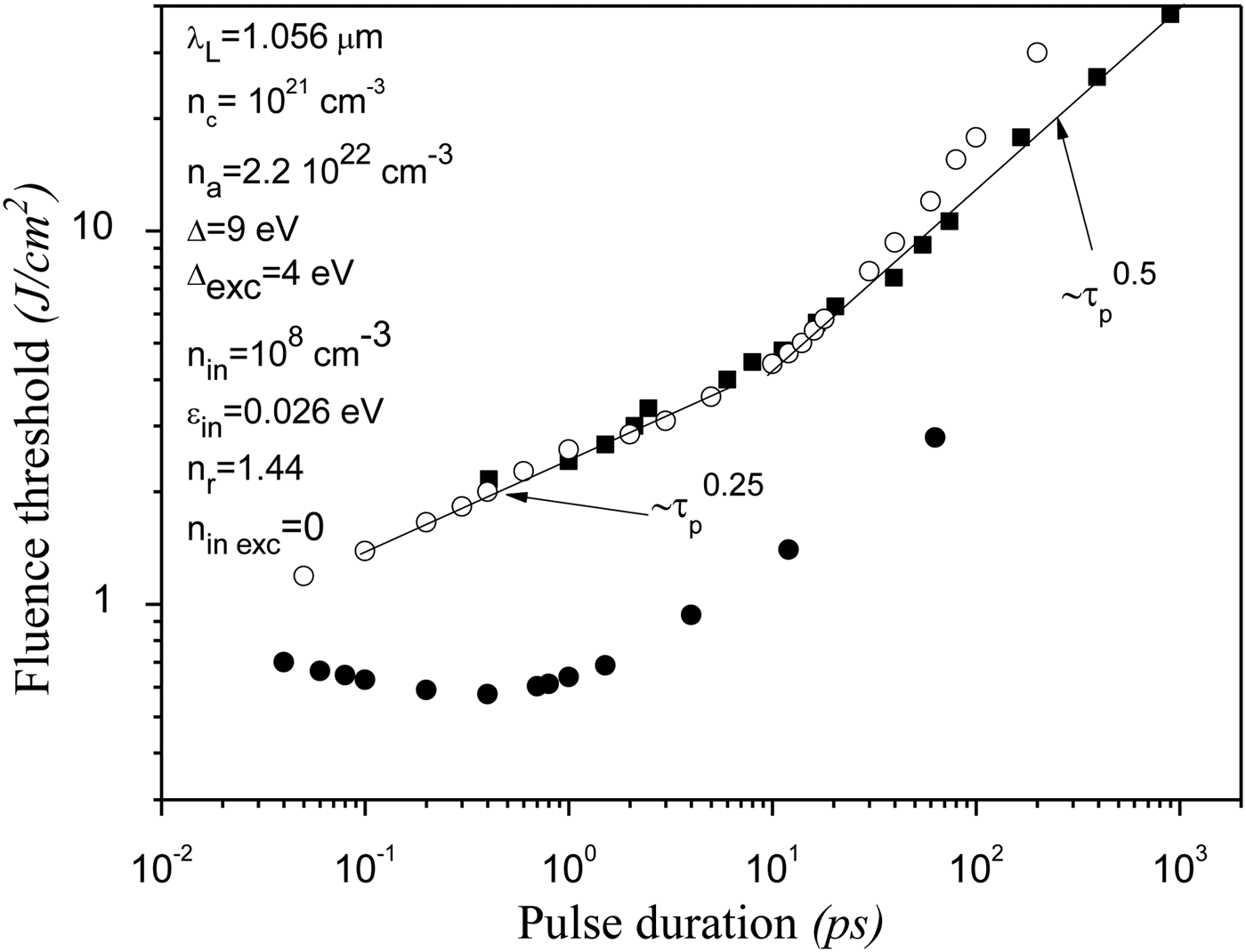
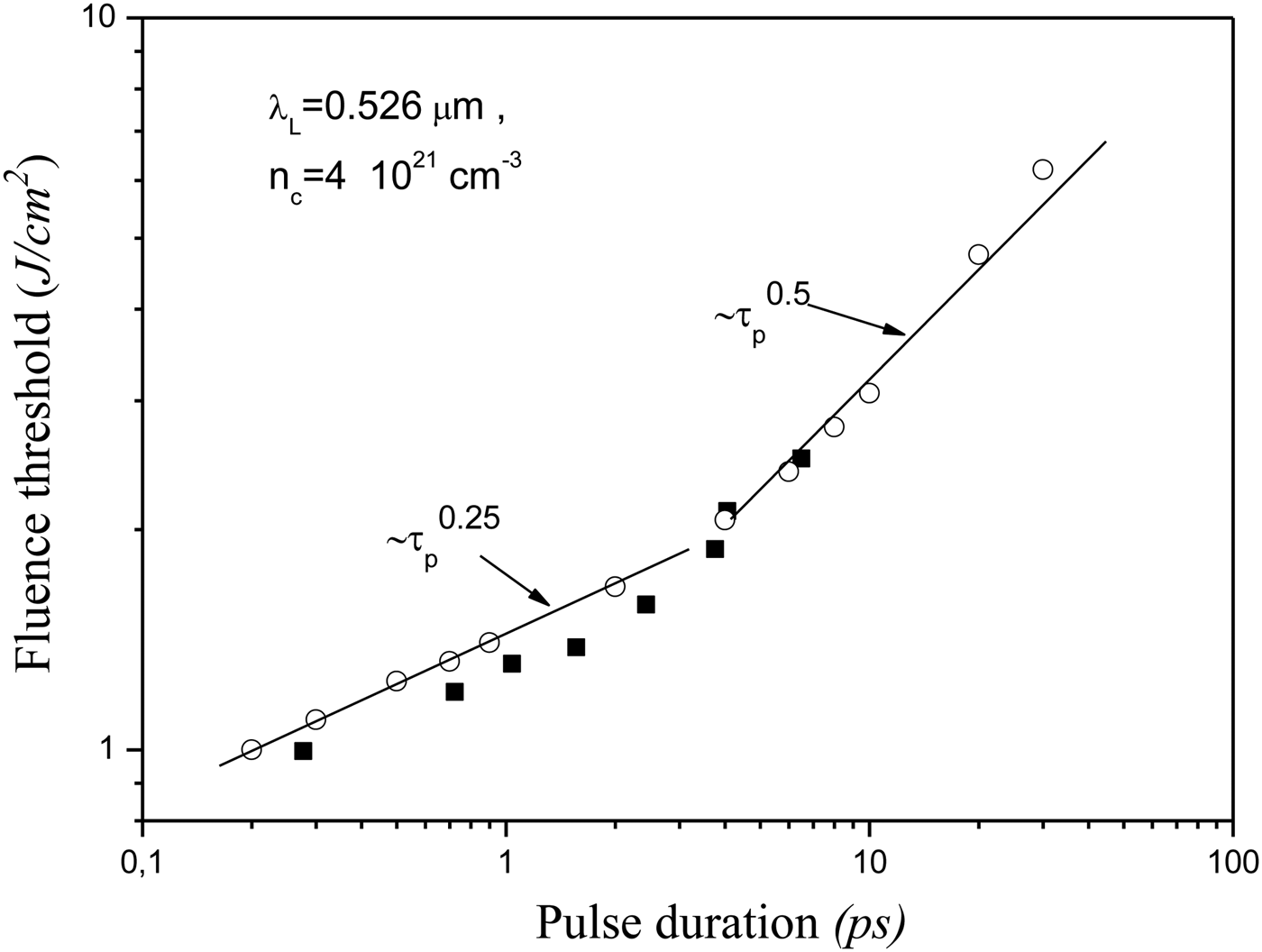
In Figures 3 and 4, we give a comparison of code results to experimentally measured fluence thresholds for breakdown of fused silica (Stuart et al. Reference Stuart, Feit, Rubenchik, Shore and Perry1995; Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry1996). We present the OBT as a function of the pulse duration under 1.056 μm and 0.526 μm laser irradiations respectively. As the experimental results do, the calculated damage threshold increases with increase in pulse duration τ_p and laser wavelength λ_L. For the dependence on τ_p, the longer the pulse duration, the smaller the electric field strength. The ionization mechanisms are thus less efficient and the electron density does not increase rapidly. We mention that this dependence with respect to τ_p was also studied with simple scaling laws by Stuart et al. (Reference Stuart, Feit, Rubenchik, Shore and Perry1995). For the dependence with respect to λ_L, first we remark that the avalanche ionization rate of Thornber (Reference Thornber1981) does not depend on the laser wavelength and that the photo-ionization rate of Keldysh (Reference Keldysh1965) decreases with the increase in the laser wavelength. We deduce that the increase in the electron density is less important and therefore the threshold of the laser fluence is more important for increasing laser wavelength.

Fig. 3. Optical breakdown threshold as a function of the pulse duration. The dark squares correspond to the experimental data, and the open circles to the present results. The dark circles correspond to the code results obtained with the model Eqs. (4) and (5). The straight lines are fits to the model calculations.

Fig. 4. Optical breakdown threshold as a function of the pulse duration. The dark squares correspond to the experimental data and the open circles to the present results. The straight lines are fits to the model calculations. The physical laser and dielectric parameters are the same as in Figure 3.

We can see that the calculated OBT agrees well to experimental data of Stuart et al. (Reference Stuart, Feit, Rubenchik, Shore and Perry1995; Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry1996), for the laser wavelength, λ_L = 1.056 μm but it is slightly larger, for the laser wavelength λ_L = 0.526 μm. Globally, the trend observed for the optical damage threshold is very similar to that observed by Stuart co-workers. There is a gradual decrease of the damage threshold as the pulse duration is reduced down to 1 ps. Below this limit the rate of decrease is less important and the fluence scales roughly as F ~ τ_p^0.25. We should note that the results of Tien et al. (Reference Tien, Backus, Kapteyn, Murnane and Mourou1999) confirm the trend of damage threshold which decays more slowly for short pulse durations. The scaling law F ~ τ_p^0.25 applies approximately to the pulse duration range 0.1 < τ_p (ps) < 1, corresponding in our numerical calculations, to the laser intensity range 2.5 < I ₀ (TW/cm ²) < 13 for the wavelength λ_L = 1.056 μm and 1.5 < I ₀(TW/cm ²) < 9 for λ_L = 0.526 μm. These intensity ranges correspond to the intermediate intensity regime and thus, in the short pulse duration range, both multi-photon and tunneling ionization mechanisms play a relevant part for the estimate of the OBT. On the other hand, for laser pulse duration longer than 40 ps, our results show significant departure with respect to the experimental data which scale as the well-known scaling law ~τ_p^0.5. Actually, this regime is dominated by the thermal diffusion inside the cold material (spatial effects) that our theoretical model does not account for. More precisely, the rate of heating is determined by the rate of laser energy absorption and the rate of energy loss mainly through the electron-lattice energy transfer (typically from few picoseconds) and the thermal conduction away from the focus (typically from few tenth of picoseconds). When the pulse durations are large (greater than one hundred of picosecond) the thermal conduction is the more relevant mechanism. It follows that the OBT is governed by the thermal diffusion length F _th ~ l _th. A simple scaling law of l _th with the use of the balance energy equation (see for instance, Gamaly et al., Reference Gamaly, Rode, Luther-Davies and Tikhonchuk2002), is $l_{th} \sim\sqrt {{\rm \tau} _p }$. Therefore for long pulses the OBT varies with laser pulse duration as $F_{th} \sim\sqrt {{\rm \tau} _p }$, which corresponds to the most experimental results reported in the literature.

One of the significant improvements proposed in our model is the estimate of the free electron mean energy through the energy balance equation and the use of the onset of collisional ionization from an energy threshold. We added in Figure 3, the OBT results keeping only the continuity Eq. (4) and the momentum Eq. (5). The energy Eq. (6) was not taken into account. We have obtained unusual behavior since the curve has a minimum. Moreover the values of the OBT are too low compared to experimental results. For instance, for the laser pulse and dielectric parameters used in Figure 3, and for a pulse duration, τ_p = 200 fs, we obtained the fluence threshold, F = 0.58 J/cm ², instead of $F=1.66\, J/cm^2 $ when the energy equation is accounted for. These results confirm that the energy equation must be taken into account in the theoretical model.

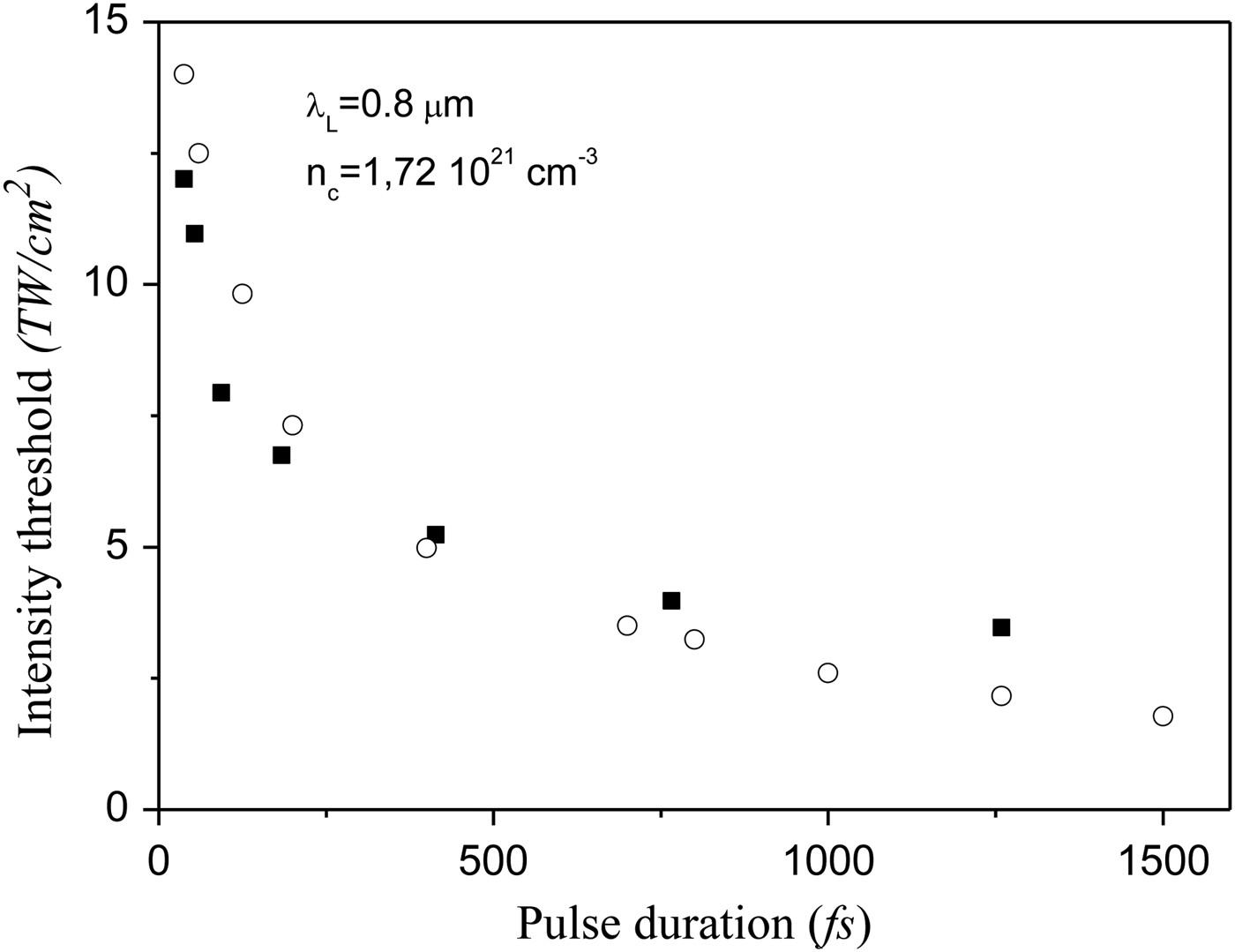
Otherwise, in Figure 5 we compared our results with the experimental data reported more recently by Rajeev et al. (Reference Rajeev, Gertsvolf, Corkum and Rayner2009) on the threshold of the laser intensity as a function of laser pulse width for fused silica. As expected our results again does not fit experimental data for long pulses. On the other hand they are in agreement with the experimental data for pulse durations ranging from 150 fs to 1ps. However they slightly overestimate the experimental data for too short pulses (less than 150 fs). The discrepancy could be due to the field-assisted collisional ionization and to the ejection of electrons from the target that we have not taken into account in our model.

Fig. 5. Laser intensity threshold as a function of the pulse duration. The dark squares correspond to the experimental data of Rajeev et al. (Reference Rajeev, Gertsvolf, Corkum and Rayner2009), and the open circles to the present model results. The physical laser and dielectric parameters are the same as in Figure 3.

4. SUMMARY

A theoretical model has been developed to calculate fluence thresholds for laser induced breakdown in fused silica. The model is mainly an extension of previous models (Du et al., Reference Du, Liu and Mourou1996; Stuart et al., Reference Stuart, Feit, Rubenchik, Shore and Perry1995; Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry1996; Li et al., Reference Li, Menon, Nibarger and Gibson1999) based on the rate equation, with the use of exciton recombination and energy balance equation. Avalanche ionization rate of Thornber (Reference Thornber1981) coupled to photo-ionization rate of Keldysh (Reference Keldysh1965) are used to promote free electron in the conduction band. The numerical results obtained have been compared to experimental data for breakdown of fused silica by ps and fs pulses in the visible and near infrared. Theoretical and experimental values agree fairly well for data with the use of the endpoint n = n _c, where n _c is the critical density. The code has proven useful in explaining trends in the threshold data such as the competition between three-body and exciton recombination mechanisms and the role of the onset of the avalanche ionization with electron mean energy. It may be also useful in the future as part of a more extensive model based on the laser propagation.