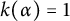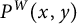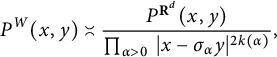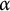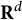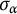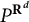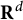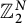1 Introduction
Dunkl differential-difference operators were discovered by Dunkl [Reference Dunkl9] in the late 1980s in the context of a theory of generalized spherical harmonics. Among other applications, they turned out to be very useful in studying Calogero–Moser–Sutherland mechanical particle systems. Since then, Dunkl analysis was intensely developed and its main achievements are gathered in [Reference de Jeu7, Reference Dunkl and Xu11, Reference Rösler31, Reference Rösler, Voit, Graczyk, Rösler and Yor32]. Together with their trigonometric counterparts, which were introduced by Cherednik in 1991 [Reference Cherednik4], Dunkl operators provide an extension of the commuting families of differential operators associated to Riemannian symmetric spaces. They have become an essential tool in the modern analysis associated with root systems.
The main results of the paper are two-sided bounds for the Poisson and Newton kernels (when
![]() $d\ge 3$
) of W-invariant Dunkl Laplacians (also called radial or symmetrized Dunkl Laplacians), in the geometric complex case when the multiplicity
$d\ge 3$
) of W-invariant Dunkl Laplacians (also called radial or symmetrized Dunkl Laplacians), in the geometric complex case when the multiplicity
![]() $k(\alpha )=1$
(i.e., for flat complex symmetric spaces) and in the rank one direct product case
$k(\alpha )=1$
(i.e., for flat complex symmetric spaces) and in the rank one direct product case
![]() $\mathbb {Z}_{2}^{N}$
with any multiplicities. These estimates have an elegant form
$\mathbb {Z}_{2}^{N}$
with any multiplicities. These estimates have an elegant form
 $$ \begin{align*} {\mathcal K}^{W}(x,y)\asymp \frac{{\mathcal K}^{\mathbf{R}^{d}}(x,y)}{\prod_{\alpha> 0 \ }|x-\sigma_{\alpha} y|^{2k(\alpha)}}, \end{align*} $$
$$ \begin{align*} {\mathcal K}^{W}(x,y)\asymp \frac{{\mathcal K}^{\mathbf{R}^{d}}(x,y)}{\prod_{\alpha> 0 \ }|x-\sigma_{\alpha} y|^{2k(\alpha)}}, \end{align*} $$
where
![]() ${\mathcal K}^{\mathbf {R}^{d}}$
is a classical kernel and
${\mathcal K}^{\mathbf {R}^{d}}$
is a classical kernel and
![]() ${\mathcal K}^{W}(x,y)$
its radial Dunkl counterpart. Analogous estimates are conjectured for the general W-invariant Dunkl Laplacians.
${\mathcal K}^{W}(x,y)$
its radial Dunkl counterpart. Analogous estimates are conjectured for the general W-invariant Dunkl Laplacians.
Precise estimates of Poisson and Newton kernels (as well as of the Green function) of local and nonlocal operators have been of interest for many years and constitute an important part of the modern potential theory, see e.g., [Reference Chen and Song3, Reference Cranston and Zhao6, Reference Kulczycki22, Reference Widman35, Reference Zhao37, Reference Zhao38] and references therein. After the work of Dunkl [Reference Dunkl10], expressing the Dunkl Poisson kernel by an integral formula with the intertwining operator, see (2.3), no estimates of the Dunkl Poisson kernel appeared until [Reference Graczyk, Luks and Rösler17], where the case of the root system of rank one was treated. The main difficulty for general root systems is the lack of explicit formulas (or suitable estimates) for the intertwining operator (see Section 2 for its connection with potential kernels). Our methods for the geometric complex case rely on the so-called alternating sums (see Proposition 2.5) and allow us to handle all root systems. In the rank one direct product case, we make use of available formulas for the intertwining operator, see Section 7.
Our results contribute significantly to the further development of the potential theory of Dunkl operators. In particular, they will be essential to study the estimates of the Green function, not treated in this paper. The study of two-sided bounds of potential kernels has motivations and immediate applications in partial differential equations and implies estimates of solutions of important boundary value problems, in particular of Dunkl-harmonic functions (see e.g. [Reference Chrouda5, Reference Gallardo and Rejeb14, Reference Gallardo and Rejeb15, Reference Graczyk, Luks and Rösler17] for the latter).
Our paper is organized as follows. In Section 2, we recall basic facts from Dunkl analysis and we formulate our main results. In Section 3, we prove some useful formulas involving roots. In Section 4, we present results on the Poisson kernel which hold without any restriction on the multiplicity function k. In Sections 5 and 6, we prove our main results for the Poisson and Newton kernel, respectively, in the geometric complex case. In Section 7, we discuss the rank one direct product case. The applications to the important stochastic processes: Dyson Brownian motions and stochastic particle systems are discussed in Section 8.
2 Preliminaries
2.1 Basic facts on root systems and Dunkl operators
Let
![]() $\Phi $
be a root system in
$\Phi $
be a root system in
![]() $\mathbf {R}^{d}$
(equipped with the usual scalar product and Euclidean norm
$\mathbf {R}^{d}$
(equipped with the usual scalar product and Euclidean norm
![]() $|\cdot |$
), and let W be the associated finite reflection group, called Weyl group. We fix a non-negative multiplicity function k on
$|\cdot |$
), and let W be the associated finite reflection group, called Weyl group. We fix a non-negative multiplicity function k on
![]() $\Phi $
, i.e.,
$\Phi $
, i.e.,
![]() $k: \Phi \to [0, \infty )$
is W-invariant, and let
$k: \Phi \to [0, \infty )$
is W-invariant, and let
![]() $\Phi _+$
denote an (arbitrary) positive subsystem of
$\Phi _+$
denote an (arbitrary) positive subsystem of
![]() $\Phi $
.
$\Phi $
.
The root system
![]() $\Phi $
is assumed to be crystallographic (needed in Lemma 3.5) but W is not required to be effective, i.e.,
$\Phi $
is assumed to be crystallographic (needed in Lemma 3.5) but W is not required to be effective, i.e.,
![]() $\text {span}_{\mathbf {R}}\, \Phi $
may be a proper subspace of
$\text {span}_{\mathbf {R}}\, \Phi $
may be a proper subspace of
![]() $\mathbf {R}^{d}$
. The dimension of
$\mathbf {R}^{d}$
. The dimension of
![]() $\text {span}_{\mathbf {R}}\,\Phi $
is called the rank of
$\text {span}_{\mathbf {R}}\,\Phi $
is called the rank of
![]() $\Phi $
.
$\Phi $
.
An important example is
with
![]() $W=S_{r}$
, the symmetric group over r elements. Note that
$W=S_{r}$
, the symmetric group over r elements. Note that
![]() $A_{r-1}$
is also considered on
$A_{r-1}$
is also considered on
![]() $\mathbf {R}^{r-1}=\mathbf {R}^{r}\cap \{ x|\ \sum _{i=1}^{r} x_{i}=0 \}$
.
$\mathbf {R}^{r-1}=\mathbf {R}^{r}\cap \{ x|\ \sum _{i=1}^{r} x_{i}=0 \}$
.
We will assume that
![]() $|\alpha |\geq 1$
for all roots
$|\alpha |\geq 1$
for all roots
![]() $\alpha $
. We denote by
$\alpha $
. We denote by
![]() $A_{\alpha }$
the root vectors, i.e.,
$A_{\alpha }$
the root vectors, i.e.,
![]() $\langle x,A_{\alpha }\rangle =\alpha (x)$
for all
$\langle x,A_{\alpha }\rangle =\alpha (x)$
for all
![]() $x\in \mathfrak {a}$
. We denote
$x\in \mathfrak {a}$
. We denote
![]() $(\alpha _{i})_{i=1,\ldots , r} $
a system of simple positive roots.
$(\alpha _{i})_{i=1,\ldots , r} $
a system of simple positive roots.
The (rational) Dunkl operators associated with
![]() $\Phi $
and k are given by
$\Phi $
and k are given by
 $$ \begin{align*} T_{\xi} f(x) = \partial_{\xi} f(x) + \sum_{\alpha\in \Phi_+} k(\alpha)\,\langle\alpha, \xi\rangle\, \frac{f(x) - f(\sigma_{\alpha} x)}{\langle\alpha, x\rangle}, \quad\xi\in \mathbf{R}^{d} \end{align*} $$
$$ \begin{align*} T_{\xi} f(x) = \partial_{\xi} f(x) + \sum_{\alpha\in \Phi_+} k(\alpha)\,\langle\alpha, \xi\rangle\, \frac{f(x) - f(\sigma_{\alpha} x)}{\langle\alpha, x\rangle}, \quad\xi\in \mathbf{R}^{d} \end{align*} $$
where
![]() $\partial _{\xi }$
is the derivative in the direction of
$\partial _{\xi }$
is the derivative in the direction of
![]() $\xi $
.
$\xi $
.
For fixed
![]() $\Phi $
and k, these operators commute. Moreover, there is a unique linear isomorphism
$\Phi $
and k, these operators commute. Moreover, there is a unique linear isomorphism
![]() $V_{k}$
on the space of polynomial functions in d variables, called the intertwining operator, which preserves the degree of homogeneity, is normalized by
$V_{k}$
on the space of polynomial functions in d variables, called the intertwining operator, which preserves the degree of homogeneity, is normalized by
![]() $V_{k}(1)=1$
and intertwines the Dunkl operators with the usual partial derivatives:
$V_{k}(1)=1$
and intertwines the Dunkl operators with the usual partial derivatives:
The Dunkl Laplacian is defined by
 $$ \begin{align*} \Delta_{k} := \sum_{i=1}^ d T_{\xi_{i}}^{2} \end{align*} $$
$$ \begin{align*} \Delta_{k} := \sum_{i=1}^ d T_{\xi_{i}}^{2} \end{align*} $$
with an arbitrary orthonormal basis
![]() $(\xi _{i})_{ 1\leq i \leq d}$
of
$(\xi _{i})_{ 1\leq i \leq d}$
of
![]() $\mathbf {R}^{d}$
. Then, for
$\mathbf {R}^{d}$
. Then, for
![]() $f\in {\mathcal C}^{2}( \mathbf {R}^{d})$
,
$f\in {\mathcal C}^{2}( \mathbf {R}^{d})$
,
 $$ \begin{align*} \Delta_{k} f(x)=\Delta f(x)+\sum_{\alpha\in \Phi_+}k(\alpha)\left(\frac{\langle\nabla f(x),\alpha\rangle}{\langle\alpha,x\rangle}- \frac{|\alpha|^{2}}{2}\frac{f(x)-f(\sigma_{\alpha} x)}{\langle\alpha,x\rangle^{2}}\right), \end{align*} $$
$$ \begin{align*} \Delta_{k} f(x)=\Delta f(x)+\sum_{\alpha\in \Phi_+}k(\alpha)\left(\frac{\langle\nabla f(x),\alpha\rangle}{\langle\alpha,x\rangle}- \frac{|\alpha|^{2}}{2}\frac{f(x)-f(\sigma_{\alpha} x)}{\langle\alpha,x\rangle^{2}}\right), \end{align*} $$
where
![]() $\Delta $
is the usual Laplacian on
$\Delta $
is the usual Laplacian on
![]() $\mathbf {R}^{d}$
. The restriction of
$\mathbf {R}^{d}$
. The restriction of
![]() $\Delta _{k}$
to W-invariant functions
$\Delta _{k}$
to W-invariant functions
![]() $f\in {\mathcal C}^{2}_{W}( \mathbf {R}^{d})$
is called the W-invariant (or radial) Dunkl Laplacian and is denoted by
$f\in {\mathcal C}^{2}_{W}( \mathbf {R}^{d})$
is called the W-invariant (or radial) Dunkl Laplacian and is denoted by
![]() $\Delta ^{W}$
. We have
$\Delta ^{W}$
. We have
 $$ \begin{align} \Delta^{W} f(x)=\Delta f(x)+\sum_{\alpha\in \Phi_+}k(\alpha)\frac{\langle\nabla f(x),\alpha\rangle}{\langle\alpha,x\rangle},\qquad f\in {\mathcal C}^{2}_{W}( \mathbf{R}^{d}). \end{align} $$
$$ \begin{align} \Delta^{W} f(x)=\Delta f(x)+\sum_{\alpha\in \Phi_+}k(\alpha)\frac{\langle\nabla f(x),\alpha\rangle}{\langle\alpha,x\rangle},\qquad f\in {\mathcal C}^{2}_{W}( \mathbf{R}^{d}). \end{align} $$
For
![]() $x\in \mathbf {R}^{d}$
, denote by
$x\in \mathbf {R}^{d}$
, denote by
![]() $C(x)$
the convex hull of the Weyl group orbit
$C(x)$
the convex hull of the Weyl group orbit
![]() $W\cdot x$
of x in
$W\cdot x$
of x in
![]() $\mathbf {R}^{d}.$
The intertwining operator
$\mathbf {R}^{d}.$
The intertwining operator
![]() $V_{k}$
has the integral representation [Reference Rösler31]
$V_{k}$
has the integral representation [Reference Rösler31]
where
![]() $\mu _{x}^{k}$
is a probability measure on
$\mu _{x}^{k}$
is a probability measure on
![]() $C(x)$
, called Rösler measure, and f is a
$C(x)$
, called Rösler measure, and f is a
![]() ${\mathcal C}^{1}$
function. We put
${\mathcal C}^{1}$
function. We put
and define the weight function
![]() $\omega _{k}$
on
$\omega _{k}$
on
![]() $\mathbf {R}^{d}$
by
$\mathbf {R}^{d}$
by
Let
![]() $\mathfrak {a}^+$
be the positive Weyl chamber associated with
$\mathfrak {a}^+$
be the positive Weyl chamber associated with
![]() $\Phi _+$
. We denote
$\Phi _+$
. We denote
![]() $\pi (x)=\prod _{\alpha \in \Phi _{+}}\langle \alpha ,x\rangle $
.
$\pi (x)=\prod _{\alpha \in \Phi _{+}}\langle \alpha ,x\rangle $
.
2.2 Invariant Poisson and Newton kernels
2.2.1 W-invariant Poisson kernel
For the convenience of the reader, we recall here main facts about the W-invariant Poisson kernel
![]() $P^{W}(x,y)$
of the unit ball, presented in [Reference Graczyk and Sawyer18].
$P^{W}(x,y)$
of the unit ball, presented in [Reference Graczyk and Sawyer18].
We denote by
![]() $B:=B(0,1)$
the unit ball in
$B:=B(0,1)$
the unit ball in
![]() $\mathbf {R}^{d}$
and by
$\mathbf {R}^{d}$
and by
![]() $S:=\partial B$
the unit sphere. Denote
$S:=\partial B$
the unit sphere. Denote
![]() $B^+:=B\cap \overline {\mathfrak {a}^+}$
and
$B^+:=B\cap \overline {\mathfrak {a}^+}$
and
![]() $S^+:=S\cap \overline {\mathfrak {a}^+}$
. First recall the definition of the Dunkl Poisson kernel.
$S^+:=S\cap \overline {\mathfrak {a}^+}$
. First recall the definition of the Dunkl Poisson kernel.
The Dunkl Poisson kernel
![]() $P_{k}(x,y)$
of B is the continuous function on
$P_{k}(x,y)$
of B is the continuous function on
![]() $B\times S$
which solves the Dirichlet problem for the Dunkl Laplacian operator
$B\times S$
which solves the Dirichlet problem for the Dunkl Laplacian operator
![]() $\Delta _{k}$
on
$\Delta _{k}$
on
![]() $\overline B$
namely, for any
$\overline B$
namely, for any
![]() $f\in {\mathcal C}(S)$
,
$f\in {\mathcal C}(S)$
,
is a solution of the equation
![]() $\Delta _{k}\,u(x)=0$
on B, with
$\Delta _{k}\,u(x)=0$
on B, with
![]() $u\in {\mathcal C}^{2}(B)\cap {\mathcal C}(\overline {B})$
and
$u\in {\mathcal C}^{2}(B)\cap {\mathcal C}(\overline {B})$
and
![]() $u(y)=f(y)$
for
$u(y)=f(y)$
for
![]() $y\in S$
. The existence and uniqueness of the Dunkl Poisson kernel
$y\in S$
. The existence and uniqueness of the Dunkl Poisson kernel
![]() $P_{k}(x,y)$
was shown by Dunkl [Reference Dunkl10] for spherical polynomials f and extended in [Reference Maslouhi and Yousffi24] to any continuous f on S.
$P_{k}(x,y)$
was shown by Dunkl [Reference Dunkl10] for spherical polynomials f and extended in [Reference Maslouhi and Yousffi24] to any continuous f on S.
The Dunkl Poisson kernel is given by Dunkl formula (refer to [Reference Dunkl and Xu11])
 $$ \begin{align} P_{k}(x,y)=\frac{2^{2\,\kappa}\,(d/2)_{\kappa}}{\pi(\rho)\,|W|\,w_{d}}\,V_{k}\left[\frac{1-|x|^{2}}{(1-2\langle x,\cdot\rangle +|x|^{2})^{\kappa+ d/2}}\right](y),\ \ x\in B,\ y\in S. \end{align} $$
$$ \begin{align} P_{k}(x,y)=\frac{2^{2\,\kappa}\,(d/2)_{\kappa}}{\pi(\rho)\,|W|\,w_{d}}\,V_{k}\left[\frac{1-|x|^{2}}{(1-2\langle x,\cdot\rangle +|x|^{2})^{\kappa+ d/2}}\right](y),\ \ x\in B,\ y\in S. \end{align} $$
Note that we are using a different normalization from [Reference Dunkl and Xu11] for consistency between (2.3), (2.4) and Remark 2.6.
Remark 2.1 We will use repeatedly the fact that
![]() $\langle x,y\rangle \geq \langle x,w\,y\rangle $
whenever x,
$\langle x,y\rangle \geq \langle x,w\,y\rangle $
whenever x,
![]() $y\in \overline {\mathfrak {a}^+}$
and
$y\in \overline {\mathfrak {a}^+}$
and
![]() $w\in W$
[Reference Helgason20, Theorem 2.12, Chapter VII].
$w\in W$
[Reference Helgason20, Theorem 2.12, Chapter VII].
The following result is well known. We include the proof for convenience.
Lemma 2.2 The map
![]() $\pi _{\mathfrak {a}^+}$
which sends an element
$\pi _{\mathfrak {a}^+}$
which sends an element
![]() $x\in \mathfrak {a}$
to the unique element
$x\in \mathfrak {a}$
to the unique element
![]() $x^+=w\,x\in \overline {\mathfrak {a}^+}$
with
$x^+=w\,x\in \overline {\mathfrak {a}^+}$
with
![]() $w\in W$
is Lipschitz.
$w\in W$
is Lipschitz.
Proof If x,
![]() $y\in \overline {\mathfrak {a}^+}$
and
$y\in \overline {\mathfrak {a}^+}$
and
![]() $w\in W$
then
$w\in W$
then
![]() $|x-w\,y|^{2}=|x-y|^{2}+2\,\langle x,y-w\,y\rangle \geq |x-y|^{2}$
since
$|x-w\,y|^{2}=|x-y|^{2}+2\,\langle x,y-w\,y\rangle \geq |x-y|^{2}$
since
![]() $\langle x,y-w\,y\rangle \geq 0$
. Hence, if
$\langle x,y-w\,y\rangle \geq 0$
. Hence, if
![]() $x^+=w_{1}\,x$
and
$x^+=w_{1}\,x$
and
![]() $y^+=w_{2}\,y$
then
$y^+=w_{2}\,y$
then
▪
Definition 2.3 The W-invariant Poisson kernel
![]() $P^{W}(x,y)$
of B is the
$P^{W}(x,y)$
of B is the
![]() $W\times W$
invariant continuous function on
$W\times W$
invariant continuous function on
![]() $B\times S$
, which solves the Dirichlet problem for the operator
$B\times S$
, which solves the Dirichlet problem for the operator
![]() $\Delta ^{W}$
on B, where
$\Delta ^{W}$
on B, where
![]() $\Delta ^{W}$
is the radial Dunkl Laplacian (2.1). Namely, for any
$\Delta ^{W}$
is the radial Dunkl Laplacian (2.1). Namely, for any
![]() $f\in {\mathcal C}_{W}(S)$
,
$f\in {\mathcal C}_{W}(S)$
,
is a solution of the equation
![]() $\Delta ^{W}\,u(x)=0$
on B, with
$\Delta ^{W}\,u(x)=0$
on B, with
![]() $u\in {\mathcal C}_{W}^{2}(B)\cap {\mathcal C}_{W}(\overline {B})$
and
$u\in {\mathcal C}_{W}^{2}(B)\cap {\mathcal C}_{W}(\overline {B})$
and
![]() $u(y)=f(y)$
for
$u(y)=f(y)$
for
![]() $y\in S$
.
$y\in S$
.
The next proposition will show that the Weyl-invariant Poisson kernel is uniquely determined by the above definition.
Remark 2.4 The proof of the uniqueness of the symmetrized Poisson kernel carries through in the same manner in general.
Proposition 2.5 In the complex case, the Poisson kernel of the open unit ball B is given for
![]() $x\in B$
and
$x\in B$
and
![]() $y\in \partial B$
by
$y\in \partial B$
by
 $$ \begin{align} P^{W}(x,y) =\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\cdot y|^{d}}. \end{align} $$
$$ \begin{align} P^{W}(x,y) =\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\cdot y|^{d}}. \end{align} $$
Proof The derivation of (2.4) is based on the properties of the regular Euclidean Poisson kernel
![]() $\frac {1-|x|^{2}}{w_{d}}\frac {1}{|x-y|^{d}}$
and on the formula
$\frac {1-|x|^{2}}{w_{d}}\frac {1}{|x-y|^{d}}$
and on the formula
(see [Reference Helgason19, Chapter II, Theorem 5.37]).
It is straightforward that this Weyl-invariant kernel solves the Dirichlet problem on the ball B.
Suppose that there is another Weyl-invariant kernel
![]() $\tilde {P}$
which also solves the Dirichlet problem on the ball B. We have
$\tilde {P}$
which also solves the Dirichlet problem on the ball B. We have
for every continuous Weyl-invariant function g on S. There is a one to one correspondence between the continuous Weyl-invariant functions on S and those on
![]() $S^+$
. It suffices to note that the map
$S^+$
. It suffices to note that the map
![]() $x\mapsto \pi _{\mathfrak {a}^+}(x)$
which projects x on the unique
$x\mapsto \pi _{\mathfrak {a}^+}(x)$
which projects x on the unique
![]() $y=w\,x\in \overline {\mathfrak {a}^+}$
is continuous: this is a direct consequence of Lemma 2.2. Hence, for every continuous function g on
$y=w\,x\in \overline {\mathfrak {a}^+}$
is continuous: this is a direct consequence of Lemma 2.2. Hence, for every continuous function g on
![]() $S^+$
and for every
$S^+$
and for every
![]() $x\in B$
, we have
$x\in B$
, we have
By the properties of the Lebesgue integral, we can therefore conclude that
![]() $P^{W}(x,y)-\tilde {P}(x,y)=0$
for every
$P^{W}(x,y)-\tilde {P}(x,y)=0$
for every
![]() $y\in S^+$
and, hence, for every
$y\in S^+$
and, hence, for every
![]() $y\in S$
.▪
$y\in S$
.▪
Remark 2.6 Because of the uniqueness of
![]() $P^{W}$
, we can conclude that
$P^{W}$
, we can conclude that
where
![]() $P_{k}$
is the Dunkl Poisson kernel and
$P_{k}$
is the Dunkl Poisson kernel and
![]() $k=1$
since it satisfies the Definition 2.3.
$k=1$
since it satisfies the Definition 2.3.
Observe that the right hand term in (2.6) is not only Weyl-invariant in y but also in x. This follows from the fact that in proving the uniqueness in Proposition 2.5, we only used Weyl-invariance in y.
2.2.2 W-invariant Newton kernel
Recall that the heat kernel of
![]() $\Delta _{k}$
is given by (see [Reference Rösler30])
$\Delta _{k}$
is given by (see [Reference Rösler30])
where
and
![]() $E_{k}(x,y)=V_{k}(e^{\langle \cdot ,y\rangle })(x)$
denotes the Dunkl kernel. The Newton kernel of
$E_{k}(x,y)=V_{k}(e^{\langle \cdot ,y\rangle })(x)$
denotes the Dunkl kernel. The Newton kernel of
![]() $\Delta _{k}$
is defined by
$\Delta _{k}$
is defined by
A general formula for
![]() $N_{k}(x,y)$
involving the intertwining operator, analogous to (2.3), was proven in [Reference Gallardo and Rejeb15]. It is given by
$N_{k}(x,y)$
involving the intertwining operator, analogous to (2.3), was proven in [Reference Gallardo and Rejeb15]. It is given by
 $$ \begin{align} N_{k}(x,y) &=\frac{2^{2\,\gamma}\,((d-2)/2)_{\gamma}}{|W|\,(d-2)\,w_{d}\,\pi(\rho)}\,V_{k}\left({(|y|^{2}-2\,\langle x,\cdot\rangle+| x|^{2})^{(2-d-2\,\gamma)/2}} \right)(y) \end{align} $$
$$ \begin{align} N_{k}(x,y) &=\frac{2^{2\,\gamma}\,((d-2)/2)_{\gamma}}{|W|\,(d-2)\,w_{d}\,\pi(\rho)}\,V_{k}\left({(|y|^{2}-2\,\langle x,\cdot\rangle+| x|^{2})^{(2-d-2\,\gamma)/2}} \right)(y) \end{align} $$
(as in the case of the Poisson kernel, we are using a slightly different normalization).
The W-invariant Newton kernel serves as the inverse of the operator
![]() $\Delta ^{W}$
. It solves the problem
$\Delta ^{W}$
. It solves the problem
![]() $\Delta ^{W}\,u=f$
, where f is given and
$\Delta ^{W}\,u=f$
, where f is given and
![]() $|u(x)|\to 0$
as
$|u(x)|\to 0$
as
![]() $x\to \infty $
. It is defined by
$x\to \infty $
. It is defined by
where
is the heat kernel of
![]() $\Delta ^{W}$
. We then have
$\Delta ^{W}$
. We then have
Using similar arguments as for the Poisson kernel, we also have the alternating formulas
 $$ \begin{align*} N^{W}(x,y)&=\frac{1}{4\,\pi\,\pi(x)\,\pi(y)}\,\sum_{w\in W}\,\epsilon(w)\,\ln|x-w\cdot y|\ \ \mbox{when }d=2,\\ N^{W}(x,y)&=\frac{1}{|W|\,(2-d)\,w_{d}\,\pi(x)\,\pi(y)} \,\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\, y|^{d-2}}\ \ \mbox{when }d\geq3,\nonumber \end{align*} $$
$$ \begin{align*} N^{W}(x,y)&=\frac{1}{4\,\pi\,\pi(x)\,\pi(y)}\,\sum_{w\in W}\,\epsilon(w)\,\ln|x-w\cdot y|\ \ \mbox{when }d=2,\\ N^{W}(x,y)&=\frac{1}{|W|\,(2-d)\,w_{d}\,\pi(x)\,\pi(y)} \,\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\, y|^{d-2}}\ \ \mbox{when }d\geq3,\nonumber \end{align*} $$
in the geometric complex case. In particular,
 $$ \begin{align} N^{W}(x,0)&=\int_{0}^{\infty}\,p^{W}_{t}(x,0)\,dt =\frac{1}{|W|\,2^{d} \,\pi^{d/2}\,\pi(\rho)} \,\int_{0}^{\infty}\,t^{-\frac{d}2-\gamma} \,e^{-|x|^{2}/(4\,t)}\,dt\nonumber\\ &=\frac{\int_{0}^{\infty}\,u^{-\frac{d}{2}-\gamma} \,e^{-1/(4\,u)}\,du}{|W|\,2^{d} \,\pi^{d/2}\,\pi(\rho)} \,\frac{1}{|x|^{d-2+2\,\gamma}}=\frac{2^{2\,\gamma-2}\,\Gamma(d/2+\gamma-1)}{|W|\,\pi^{d/2}\,\pi(\rho)} \,\frac{1}{|x|^{d-2+2\,\gamma}}. \end{align} $$
$$ \begin{align} N^{W}(x,0)&=\int_{0}^{\infty}\,p^{W}_{t}(x,0)\,dt =\frac{1}{|W|\,2^{d} \,\pi^{d/2}\,\pi(\rho)} \,\int_{0}^{\infty}\,t^{-\frac{d}2-\gamma} \,e^{-|x|^{2}/(4\,t)}\,dt\nonumber\\ &=\frac{\int_{0}^{\infty}\,u^{-\frac{d}{2}-\gamma} \,e^{-1/(4\,u)}\,du}{|W|\,2^{d} \,\pi^{d/2}\,\pi(\rho)} \,\frac{1}{|x|^{d-2+2\,\gamma}}=\frac{2^{2\,\gamma-2}\,\Gamma(d/2+\gamma-1)}{|W|\,\pi^{d/2}\,\pi(\rho)} \,\frac{1}{|x|^{d-2+2\,\gamma}}. \end{align} $$
2.3 Main results of the paper
We write
![]() $f\asymp g$
when there are constants
$f\asymp g$
when there are constants
![]() $0<C_{1}\leq C_{2}$
depending only on the dimension, on the choice of the root system and of the multiplicity function k, such that, on the common domain of f and g, we have
$0<C_{1}\leq C_{2}$
depending only on the dimension, on the choice of the root system and of the multiplicity function k, such that, on the common domain of f and g, we have
![]() $C_{1}\,f\leq g\leq C_{2}\,f$
.
$C_{1}\,f\leq g\leq C_{2}\,f$
.
Conjecture 1 For
![]() $x\in B^+$
and
$x\in B^+$
and
![]() $y\in S^+$
we have
$y\in S^+$
we have
 $$ \begin{align*} P^{W}(x,y)\asymp \Omega(x,y):=\frac{1-|x|^{2}}{|x-y|^{d}\prod_{\alpha\in \Phi_+} |x-\sigma_{\alpha} y|^{2k(\alpha) }}. \end{align*} $$
$$ \begin{align*} P^{W}(x,y)\asymp \Omega(x,y):=\frac{1-|x|^{2}}{|x-y|^{d}\prod_{\alpha\in \Phi_+} |x-\sigma_{\alpha} y|^{2k(\alpha) }}. \end{align*} $$
In the case of the Newton kernel, the conjecture is the following.
Conjecture 2 For
![]() $x, y\in \overline {\mathfrak {a}^+}$
and
$x, y\in \overline {\mathfrak {a}^+}$
and
![]() $d\geq 3$
, we have
$d\geq 3$
, we have
We now formulate our main results.
We also give some results supporting the conjectures in the general Dunkl setting in Section 4. Note also that (2.8) is consistent with Conjecture 2.
3 Analysis with roots
3.1 Some simple formulas
In this section, we give some simple and useful formulas involving roots.
For
![]() $\alpha \in \Phi $
define
$\alpha \in \Phi $
define
where
![]() $H_{\alpha }$
denotes the hyperplane perpendicular to
$H_{\alpha }$
denotes the hyperplane perpendicular to
![]() $\alpha $
and d is the usual Euclidean distance. The following simple properties will be often used.
$\alpha $
and d is the usual Euclidean distance. The following simple properties will be often used.
Lemma 3.1
-
(i) Let
 $y\in \overline {\mathfrak {a}^+}$
and
$y\in \overline {\mathfrak {a}^+}$
and
 $\alpha $
be a positive root. Then
$\alpha $
be a positive root. Then  $$ \begin{align*} d(y,H_{\alpha})=\alpha(y)/|\alpha|. \end{align*} $$
$$ \begin{align*} d(y,H_{\alpha})=\alpha(y)/|\alpha|. \end{align*} $$
-
(ii) For any
 $x,y\in {\mathfrak {a}}$
we have where
$x,y\in {\mathfrak {a}}$
we have where $$ \begin{align*} |x-\sigma_{\alpha} y|^{2}=|x-y|^{2}+C\,\alpha(x)\alpha(y), \end{align*} $$
$$ \begin{align*} |x-\sigma_{\alpha} y|^{2}=|x-y|^{2}+C\,\alpha(x)\alpha(y), \end{align*} $$
 $C=4/|\alpha |^{2}$
.
$C=4/|\alpha |^{2}$
.
Proof
-
(i) Write
 $y=y_{0}+b\,A_{\alpha }$
, where
$y=y_{0}+b\,A_{\alpha }$
, where
 $y_{0}\in H_{\alpha }$
and
$y_{0}\in H_{\alpha }$
and
 $\langle x,A_{\alpha }\rangle =\alpha (x)$
for all
$\langle x,A_{\alpha }\rangle =\alpha (x)$
for all
 $x\in \mathfrak {a}$
. Observe that
$x\in \mathfrak {a}$
. Observe that
 $b=\alpha (y)/|\alpha |^{2}$
. Then, for
$b=\alpha (y)/|\alpha |^{2}$
. Then, for
 $z\in H_{\alpha }$
, we have which attends its minimum when
$z\in H_{\alpha }$
, we have which attends its minimum when $$ \begin{align*} |y-z|^{2}=|y_{0}-z|^{2}+b^{2}|A_{\alpha}|^{2} \end{align*} $$
$$ \begin{align*} |y-z|^{2}=|y_{0}-z|^{2}+b^{2}|A_{\alpha}|^{2} \end{align*} $$
 $z=y_{0}$
. Hence,
$z=y_{0}$
. Hence,
 $\displaystyle d(y,H_{\alpha })=b\,|\alpha |= \frac {\alpha (y)}{|\alpha |}$
.
$\displaystyle d(y,H_{\alpha })=b\,|\alpha |= \frac {\alpha (y)}{|\alpha |}$
.
-
(ii) Follows by direct computation.▪
There is an equivalent formulation for
![]() $\phi _{\alpha }(x,y)$
.
$\phi _{\alpha }(x,y)$
.
Lemma 3.2 Let x,
![]() $y\in \overline {\mathfrak {a}^+}$
. We have
$y\in \overline {\mathfrak {a}^+}$
. We have
Proof Indeed,
while
![]() $|x-\sigma _{\alpha } y|^{2}\geq |x-y|^{2}$
and
$|x-\sigma _{\alpha } y|^{2}\geq |x-y|^{2}$
and
(geometric argument: the straight line joining y with
![]() $\sigma _{\alpha } x$
crosses
$\sigma _{\alpha } x$
crosses
![]() $H_{\alpha }$
; if
$H_{\alpha }$
; if
![]() $\ell (t)=ty+(1-t)\,\sigma _{\alpha } x$
then
$\ell (t)=ty+(1-t)\,\sigma _{\alpha } x$
then
![]() $\alpha (\ell (0))=\alpha (y)\geq 0$
while
$\alpha (\ell (0))=\alpha (y)\geq 0$
while
![]() $\alpha (\ell (1))=-\alpha (x)\leq 0$
).▪
$\alpha (\ell (1))=-\alpha (x)\leq 0$
).▪
Remark 3.3
Lemma 3.2 shows that in proving Conjectures 1 and 2, one can replace
![]() $|x-\sigma _{\alpha }\,y|$
by
$|x-\sigma _{\alpha }\,y|$
by
![]() $\phi _{\alpha }(x,y)$
. We will do this without further mention.
$\phi _{\alpha }(x,y)$
. We will do this without further mention.
Remark 3.4 The same argument shows that
so
Proposition 3.5 Let
![]() $\alpha _{i}$
be the simple roots and let
$\alpha _{i}$
be the simple roots and let
![]() $A_{\alpha _{i}}$
be such that
$A_{\alpha _{i}}$
be such that
![]() $\langle x,A_{\alpha _{i}}\rangle =\alpha _{i}(x)$
for
$\langle x,A_{\alpha _{i}}\rangle =\alpha _{i}(x)$
for
![]() $x\in \mathfrak {a}$
. Suppose
$x\in \mathfrak {a}$
. Suppose
![]() $x,y\in \mathfrak {a}^+$
and
$x,y\in \mathfrak {a}^+$
and
![]() $w\in W\setminus \{id\}$
. Then we have
$w\in W\setminus \{id\}$
. Then we have
 $$ \begin{align} y-w\,y=\sum_{i=1}^{r} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}}, \end{align} $$
$$ \begin{align} y-w\,y=\sum_{i=1}^{r} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}}, \end{align} $$
where
![]() $a_{i}^{w}$
is a linear combination of positive simple roots with non-negative integer coefficients for each i.
$a_{i}^{w}$
is a linear combination of positive simple roots with non-negative integer coefficients for each i.
Example 3.6 Let us first illustrate the proposition on an example. Consider
![]() $w=\sigma _{\alpha _{2}}\,\sigma _{\alpha _{1}}$
. We have
$w=\sigma _{\alpha _{2}}\,\sigma _{\alpha _{1}}$
. We have
 $$ \begin{align*} y-w\,y= \frac{2}{|\alpha_{1}|^{2}}\alpha_{1}(y)A_{\alpha_{1}} + \frac{2}{|\alpha_{2}|^{2}}\,\left( \frac{-2\langle \alpha_{1},\alpha_{2}\rangle }{|\alpha_{1}|^{2}}\alpha_{1}(y)+\alpha_{2}(y)\right)\,A_{\alpha_{2}}. \end{align*} $$
$$ \begin{align*} y-w\,y= \frac{2}{|\alpha_{1}|^{2}}\alpha_{1}(y)A_{\alpha_{1}} + \frac{2}{|\alpha_{2}|^{2}}\,\left( \frac{-2\langle \alpha_{1},\alpha_{2}\rangle }{|\alpha_{1}|^{2}}\alpha_{1}(y)+\alpha_{2}(y)\right)\,A_{\alpha_{2}}. \end{align*} $$
In particular, for the
![]() $A_{n}$
root system in
$A_{n}$
root system in
![]() $\mathbf {R}^{d},\ d\ge n$
and the permutation
$\mathbf {R}^{d},\ d\ge n$
and the permutation
![]() $w=(123)\in W$
, we have
$w=(123)\in W$
, we have
![]() $w=\sigma _{\alpha _{2}}\sigma _{\alpha _{1}}$
and, with the normalization
$w=\sigma _{\alpha _{2}}\sigma _{\alpha _{1}}$
and, with the normalization
![]() $|\alpha _{i}|^{2}=2$
, we get
$|\alpha _{i}|^{2}=2$
, we get
Proof We first prove by induction on the length of the minimal representation of w as a product of reflections by simple roots that (3.1) holds where
![]() $a_{i}^{w}(y)$
is a linear combination of simple roots with integer coefficients for each i.
$a_{i}^{w}(y)$
is a linear combination of simple roots with integer coefficients for each i.
If the length of w is 1 then
![]() $w=\sigma _{\alpha _{i}}$
for a simple root
$w=\sigma _{\alpha _{i}}$
for a simple root
![]() $\alpha _{i}$
and
$\alpha _{i}$
and
 $$ \begin{align*} y-\sigma_{\alpha_{i}}\,y=2\,\frac{\alpha_{i}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}} \end{align*} $$
$$ \begin{align*} y-\sigma_{\alpha_{i}}\,y=2\,\frac{\alpha_{i}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}} \end{align*} $$
and the result holds in that case with
![]() $a_{i}^{w}(y)=\alpha _{i}(y)$
.
$a_{i}^{w}(y)=\alpha _{i}(y)$
.
Let us assume that the result holds for
![]() $k\geq 1$
and let
$k\geq 1$
and let
![]() $w=\sigma _{\alpha _{j}}\,w_{0}$
, where
$w=\sigma _{\alpha _{j}}\,w_{0}$
, where
![]() $|w_{0}|=k$
.
$|w_{0}|=k$
.
 $$ \begin{align*} y-\sigma_{\alpha_{j}}\,w_{0}y &=\sigma_{\alpha_{j}}\,(y-w_{0}y)+y-\sigma_{\alpha_{j}}y =\sigma_{\alpha_{j}}\,\Big(\sum_{i=1}^{r}\,a_{i}^{w_{0}}(y)\,\frac{2A_{\alpha_{i}}}{|\alpha_{i}|^{2}}\Big)+2\,\frac{\alpha_{j}(y)}{|\alpha_{j}|^{2}}\,A_{\alpha_{j}}\\ &=\sum_{i=1}^{r}\,a_{i}^{w_{0}}(y)\,\sigma_{\alpha_{j}}\Big(\frac{2A_{\alpha_{i}}}{|\alpha_{i}|^{2}}\Big)+2\,\frac{\alpha_{j}(y)}{|\alpha_{j}|^{2}}\,A_{\alpha_{j}}\\ &=\sum_{i=1}^{r}\,a_{i}^{w_{0}}(y)\,\frac{2A_{\alpha_{i}}}{|\alpha_{i}|^{2}} {-\sum_{i=1}^{r}\,a_{i}^{w_{0}}(y)\,2\,\frac{\langle\alpha_{j},\alpha_{i}\rangle}{|\alpha_{i}|^{2}}\,2\,\frac{A_{\alpha_{j}}}{|\alpha_{j}|^{2}} }+2\,\frac{\alpha_{j}(y)}{|\alpha_{j}|^{2}}\,A_{\alpha_{j}}. \end{align*} $$
$$ \begin{align*} y-\sigma_{\alpha_{j}}\,w_{0}y &=\sigma_{\alpha_{j}}\,(y-w_{0}y)+y-\sigma_{\alpha_{j}}y =\sigma_{\alpha_{j}}\,\Big(\sum_{i=1}^{r}\,a_{i}^{w_{0}}(y)\,\frac{2A_{\alpha_{i}}}{|\alpha_{i}|^{2}}\Big)+2\,\frac{\alpha_{j}(y)}{|\alpha_{j}|^{2}}\,A_{\alpha_{j}}\\ &=\sum_{i=1}^{r}\,a_{i}^{w_{0}}(y)\,\sigma_{\alpha_{j}}\Big(\frac{2A_{\alpha_{i}}}{|\alpha_{i}|^{2}}\Big)+2\,\frac{\alpha_{j}(y)}{|\alpha_{j}|^{2}}\,A_{\alpha_{j}}\\ &=\sum_{i=1}^{r}\,a_{i}^{w_{0}}(y)\,\frac{2A_{\alpha_{i}}}{|\alpha_{i}|^{2}} {-\sum_{i=1}^{r}\,a_{i}^{w_{0}}(y)\,2\,\frac{\langle\alpha_{j},\alpha_{i}\rangle}{|\alpha_{i}|^{2}}\,2\,\frac{A_{\alpha_{j}}}{|\alpha_{j}|^{2}} }+2\,\frac{\alpha_{j}(y)}{|\alpha_{j}|^{2}}\,A_{\alpha_{j}}. \end{align*} $$
Note that
![]() $2\,\frac {\langle \alpha _{j},\alpha _{i}\rangle }{|\alpha _{i}|^{2}}$
is an integer since
$2\,\frac {\langle \alpha _{j},\alpha _{i}\rangle }{|\alpha _{i}|^{2}}$
is an integer since
![]() $\Phi $
is crystallographic.
$\Phi $
is crystallographic.
We now need to prove that
![]() $a_{i}^{w}(y)$
is a linear combination of simple roots with non-negative integer coefficients for each i.
$a_{i}^{w}(y)$
is a linear combination of simple roots with non-negative integer coefficients for each i.
Suppose that this is not the case. To fix matters, we can assume that
![]() $a_{1}$
contains a term, say
$a_{1}$
contains a term, say
![]() $b_{2}\,\alpha _{2}$
, with
$b_{2}\,\alpha _{2}$
, with
![]() $b_{2}<0$
. Choose x,
$b_{2}<0$
. Choose x,
![]() $y\in \overline {\mathfrak {a}^+}$
such that
$y\in \overline {\mathfrak {a}^+}$
such that
![]() $\alpha _{2}(y)=t>0$
,
$\alpha _{2}(y)=t>0$
,
![]() $\alpha _{k}(y)=0$
for
$\alpha _{k}(y)=0$
for
![]() $k\not =2$
and
$k\not =2$
and
![]() $\alpha _{1}(x)=t>0$
,
$\alpha _{1}(x)=t>0$
,
![]() $\alpha _{k}(x)=0$
for
$\alpha _{k}(x)=0$
for
![]() $k\not =1$
. Then using (3.1),
$k\not =1$
. Then using (3.1),
which cannot be true (refer to Remark 2.1). The result follows.▪
Corollary 3.7 There exists
![]() $C>0$
such that for every x,
$C>0$
such that for every x,
![]() $y\in \mathfrak {a}^+$
and
$y\in \mathfrak {a}^+$
and
![]() $w\in W\setminus \{id\}$
$w\in W\setminus \{id\}$
-
(i)
 $|x-w\,y|^{2}\geq |x-y|^{2}+C\,\min _{i}\,\alpha _{i}(x)\,\min _{j}\alpha _{j}(y)$
and
$|x-w\,y|^{2}\geq |x-y|^{2}+C\,\min _{i}\,\alpha _{i}(x)\,\min _{j}\alpha _{j}(y)$
and -
(ii)
 $|x-w\,y|^{2}\geq \max \left \{\min \{d(x,H_{\alpha })^{2}\colon \alpha>0\},\min \{d(y,H_{\alpha })^{2}\colon \alpha >0\}\right \}$
.
$|x-w\,y|^{2}\geq \max \left \{\min \{d(x,H_{\alpha })^{2}\colon \alpha>0\},\min \{d(y,H_{\alpha })^{2}\colon \alpha >0\}\right \}$
.
Proof Let the notation be as in the Proposition 3.5. By (3.1) and (4.3), we have
 $$ \begin{align*} |x-wy|^{2}=|x-y|^{2}+2\,\langle x,y-wy\rangle =|x-y|^{2}+2\sum_{i=1}^{r}\frac{a_{i}^{w}(y)\alpha_{i}(x)}{|\alpha_{i}|^{2}}, \end{align*} $$
$$ \begin{align*} |x-wy|^{2}=|x-y|^{2}+2\,\langle x,y-wy\rangle =|x-y|^{2}+2\sum_{i=1}^{r}\frac{a_{i}^{w}(y)\alpha_{i}(x)}{|\alpha_{i}|^{2}}, \end{align*} $$
and the first inequality follows since not all
![]() $a_{i}^{w}(y)$
are nul.
$a_{i}^{w}(y)$
are nul.
The second inequality follows from a simple geometric argument since x and
![]() $wy$
are not in the same Weyl chamber, the straight line between x and
$wy$
are not in the same Weyl chamber, the straight line between x and
![]() $wy$
must cross a wall of the Weyl chamber (similarly for y and
$wy$
must cross a wall of the Weyl chamber (similarly for y and
![]() $w^{-1}\,{x}$
).▪
$w^{-1}\,{x}$
).▪
Remark 3.8 The linear combination
![]() $a_{i}^{w}$
only depends on
$a_{i}^{w}$
only depends on
![]() $w\in W$
and therefore the largest coefficient M of a root appearing in any
$w\in W$
and therefore the largest coefficient M of a root appearing in any
![]() $a_{j}^{w}$
, for any j or w, is finite.
$a_{j}^{w}$
, for any j or w, is finite.
Corollary 3.9 For
![]() $z\in \mathfrak {a}$
, let
$z\in \mathfrak {a}$
, let
![]() $\Phi _{z}=\{\alpha \in \Phi \colon \alpha (z)=0\}$
. Let x,
$\Phi _{z}=\{\alpha \in \Phi \colon \alpha (z)=0\}$
. Let x,
![]() $y\in \overline {\mathfrak {a}^+}$
such that
$y\in \overline {\mathfrak {a}^+}$
such that
![]() $\Phi _{x}\subseteq \Phi _{y}$
. Suppose that
$\Phi _{x}\subseteq \Phi _{y}$
. Suppose that
![]() $w\not \in W_{y}=\{w\in W\colon w\,y=y\}$
. Then
$w\not \in W_{y}=\{w\in W\colon w\,y=y\}$
. Then
Proof Recall that by Proposition 3.5
 $$ \begin{align*} y-w\,y=\sum_{i=1}^{r} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}}. \end{align*} $$
$$ \begin{align*} y-w\,y=\sum_{i=1}^{r} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}}. \end{align*} $$
We first show that there exists
![]() $i_{0}$
such that
$i_{0}$
such that
![]() $\alpha _{i_{0}}(y)>0$
and
$\alpha _{i_{0}}(y)>0$
and
![]() $a_{i_{0}}^{w}(y)>0$
. Suppose by contradiction that this is not true, so
$a_{i_{0}}^{w}(y)>0$
. Suppose by contradiction that this is not true, so
 $$ \begin{align*} y-w\,y=\sum_{\alpha_{i}(y)=0} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}}. \end{align*} $$
$$ \begin{align*} y-w\,y=\sum_{\alpha_{i}(y)=0} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}}. \end{align*} $$
Then
 $$ \begin{align*} \langle y, y-w\,y \rangle=\sum_{\alpha_{i}(y)=0} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,\alpha_{i}(y)=0, \end{align*} $$
$$ \begin{align*} \langle y, y-w\,y \rangle=\sum_{\alpha_{i}(y)=0} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,\alpha_{i}(y)=0, \end{align*} $$
so
![]() $\langle y, y \rangle =\langle y, w\,y \rangle $
. As
$\langle y, y \rangle =\langle y, w\,y \rangle $
. As
![]() $\|wy\|=\|y\|$
, this is only possible if
$\|wy\|=\|y\|$
, this is only possible if
![]() $y=wy$
.
$y=wy$
.
Since
![]() $\alpha _{i_{0}}\not \in \Phi _{y}\supseteq \Phi _{x}$
, it follows that
$\alpha _{i_{0}}\not \in \Phi _{y}\supseteq \Phi _{x}$
, it follows that
 $$ \begin{align*} \qquad\qquad\quad\langle x, y-w\,y \rangle=\sum_{i=1}^{r} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,\alpha_{i}(x)\ge 2\,\frac{a_{i_{0}}^{w}(y)}{|\alpha_{i_{0}}|^{2}}\,\alpha_{i_{0}}(x)>0. \end{align*} $$
$$ \begin{align*} \qquad\qquad\quad\langle x, y-w\,y \rangle=\sum_{i=1}^{r} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,\alpha_{i}(x)\ge 2\,\frac{a_{i_{0}}^{w}(y)}{|\alpha_{i_{0}}|^{2}}\,\alpha_{i_{0}}(x)>0. \end{align*} $$
▪
Corollary 3.10 Let
![]() $y\in \overline {\mathfrak {a}^+}$
and
$y\in \overline {\mathfrak {a}^+}$
and
![]() $w\in W$
. Consider the decomposition (3.1) of
$w\in W$
. Consider the decomposition (3.1) of
![]() $y-wy$
. If
$y-wy$
. If
![]() $a_{k}^{w}(y)\not = 0$
then
$a_{k}^{w}(y)\not = 0$
then
![]() $\alpha _{k}$
appears in
$\alpha _{k}$
appears in
![]() $a_{k}^{w}$
, i.e.,
$a_{k}^{w}$
, i.e.,
![]() $a_{k}^{w}=\sum _{i=1}^{r} n_{i} \alpha _{i}$
with
$a_{k}^{w}=\sum _{i=1}^{r} n_{i} \alpha _{i}$
with
![]() $n_{k}>0$
.
$n_{k}>0$
.
Proof Suppose that
![]() $a_{k}^{w}=\sum _{i=1}^{r} n_{i} \alpha _{i}$
with
$a_{k}^{w}=\sum _{i=1}^{r} n_{i} \alpha _{i}$
with
![]() $n_{k}=0$
. Consider
$n_{k}=0$
. Consider
![]() $x_{0}$
,
$x_{0}$
,
![]() $y_{0}$
with
$y_{0}$
with
![]() $\Phi _{x_{0}}=\Phi _{y_{0}}$
generated by
$\Phi _{x_{0}}=\Phi _{y_{0}}$
generated by
![]() $\{\alpha _{i}\colon i\not = k\}$
. Then, we have
$\{\alpha _{i}\colon i\not = k\}$
. Then, we have
 $$ \begin{align*} \langle x_{0},y_{0}-w\,y_{0}\rangle=\sum_{i=1}^{r} \,2\,\frac{a_{i}^{w}(y_{0})}{|\alpha_{i}|^{2}}\,\alpha_{i}(x_{0})= 2\,\frac{a_{k}^{w}(y_{0})}{|\alpha_{k}|^{2}}\,\alpha_{k}(x_{0})=0 \end{align*} $$
$$ \begin{align*} \langle x_{0},y_{0}-w\,y_{0}\rangle=\sum_{i=1}^{r} \,2\,\frac{a_{i}^{w}(y_{0})}{|\alpha_{i}|^{2}}\,\alpha_{i}(x_{0})= 2\,\frac{a_{k}^{w}(y_{0})}{|\alpha_{k}|^{2}}\,\alpha_{k}(x_{0})=0 \end{align*} $$
since
![]() $a_{k}^{w}(y_{0})=\sum _{i\not =k} n_{i} \alpha _{i}(y_{0})=0$
. By Corollary 3.9, we see that
$a_{k}^{w}(y_{0})=\sum _{i\not =k} n_{i} \alpha _{i}(y_{0})=0$
. By Corollary 3.9, we see that
![]() $w\in W_{x_{0}}$
with
$w\in W_{x_{0}}$
with
![]() $W_{x_{0}}$
generated by
$W_{x_{0}}$
generated by
![]() $\sigma _{\alpha _{i}}$
,
$\sigma _{\alpha _{i}}$
,
![]() $i\not =k$
. This implies that
$i\not =k$
. This implies that
![]() $A_{\alpha _{k}}$
does not appear in the decomposition (3.1) of
$A_{\alpha _{k}}$
does not appear in the decomposition (3.1) of
![]() $y-wy$
, thus, equivalently, that
$y-wy$
, thus, equivalently, that
![]() $a_{k}^{w}=0$
.▪
$a_{k}^{w}=0$
.▪
Remark 3.11 There exist constants
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
(which are independent of
$C_{2}$
(which are independent of
![]() $\alpha $
, x and w), such that for any two roots
$\alpha $
, x and w), such that for any two roots
![]() $\alpha ,\beta $
, every
$\alpha ,\beta $
, every
![]() $x\in \mathbf {R}^{d}$
and any
$x\in \mathbf {R}^{d}$
and any
![]() $w\in W$
,
$w\in W$
,
3.2 Basic root subsystems
Definition 3.12 A subsystem of a root system is a subset of the root system which is stable under the reflections with respect to the roots in the subset.
We will say that
![]() $\Phi ^{\prime }$
is a root subsystem of
$\Phi ^{\prime }$
is a root subsystem of
![]() $\Phi $
generated by the set
$\Phi $
generated by the set
![]() $S\subseteq \Phi $
if it is the smallest subsystem of
$S\subseteq \Phi $
if it is the smallest subsystem of
![]() $\Phi $
containing S.
$\Phi $
containing S.
We will say that
![]() $\Phi ^{\prime }$
is a basic root subsystem of
$\Phi ^{\prime }$
is a basic root subsystem of
![]() $\Phi $
if it is generated by simple roots of
$\Phi $
if it is generated by simple roots of
![]() $\Phi $
.
$\Phi $
.
The rank of
![]() $\Phi ^{\prime }$
is defined as the number of simple roots in
$\Phi ^{\prime }$
is defined as the number of simple roots in
![]() $\Phi ^{\prime }$
.
$\Phi ^{\prime }$
.
To simplify the exposition, we will automatically associate the following objects to a basic root subsystem
![]() $\Phi ^{\prime }$
of
$\Phi ^{\prime }$
of
![]() $\Phi $
: let
$\Phi $
: let
![]() $W^{\prime }$
be the group generated by
$W^{\prime }$
be the group generated by
![]() $\sigma _{\alpha }$
,
$\sigma _{\alpha }$
,
![]() $\alpha \in \Phi ^{\prime }$
and consider the polynomial
$\alpha \in \Phi ^{\prime }$
and consider the polynomial
![]() $\pi ^{\prime }(x)=\prod _{\alpha \in \Phi ^{\prime }}\,\alpha (x)$
. We also denote
$\pi ^{\prime }(x)=\prod _{\alpha \in \Phi ^{\prime }}\,\alpha (x)$
. We also denote
![]() $W_{0}=W\setminus W^{\prime }$
,
$W_{0}=W\setminus W^{\prime }$
,
![]() $\Phi _{0}=\Phi \setminus \Phi ^{\prime }$
and let
$\Phi _{0}=\Phi \setminus \Phi ^{\prime }$
and let
![]() $\Phi _{0}^+$
stand for the positive roots in
$\Phi _{0}^+$
stand for the positive roots in
![]() $\Phi _{0}$
. When
$\Phi _{0}$
. When
![]() $\Phi ^{\prime }=\emptyset $
, we will set
$\Phi ^{\prime }=\emptyset $
, we will set
![]() $W^{\prime }=\{id\}$
and therefore
$W^{\prime }=\{id\}$
and therefore
![]() $\Phi _{0}=\Phi $
and
$\Phi _{0}=\Phi $
and
![]() $W_{0}=W\setminus \{id\}$
.
$W_{0}=W\setminus \{id\}$
.
As an example, we present now the basic root subsystems in the
![]() $A_{n}$
case.
$A_{n}$
case.
Example 3.13 If
![]() $\Phi ^{\prime }$
is a basic root subsystem of
$\Phi ^{\prime }$
is a basic root subsystem of
![]() $A_{n}$
with simple roots
$A_{n}$
with simple roots
![]() $\alpha _{i}(x)=x_{i}-x_{i+1}$
,
$\alpha _{i}(x)=x_{i}-x_{i+1}$
,
![]() $1\leq i\leq n$
, then the set of simple roots in
$1\leq i\leq n$
, then the set of simple roots in
![]() $\Phi ^{\prime }$
can be written as
$\Phi ^{\prime }$
can be written as
 $$ \begin{align*} \bigcup_{k=1}^{M}\,\{\alpha_{i_{k}},\alpha_{i_{k}+1},\dots,\alpha_{i_{k}+j_{k}-1}\} \end{align*} $$
$$ \begin{align*} \bigcup_{k=1}^{M}\,\{\alpha_{i_{k}},\alpha_{i_{k}+1},\dots,\alpha_{i_{k}+j_{k}-1}\} \end{align*} $$
with
![]() $i_{k}+j_{k}<i_{k+1}$
whenever
$i_{k}+j_{k}<i_{k+1}$
whenever
![]() $1\leq k\leq M-1$
. This means that
$1\leq k\leq M-1$
. This means that
![]() $ \Phi ^{\prime }\simeq \bigoplus _{k=1}^{M}\,A_{j_{k}}. $
The rank of
$ \Phi ^{\prime }\simeq \bigoplus _{k=1}^{M}\,A_{j_{k}}. $
The rank of
![]() $\Phi ^{\prime }$
is
$\Phi ^{\prime }$
is
![]() $\sum _{k=1}^{M}\,j_{k}$
.
$\sum _{k=1}^{M}\,j_{k}$
.
4 Estimates of the Poisson kernel in the Dunkl setting
In this section, we present results that are true in the general invariant Dunkl setting, without any restriction on the multiplicity function k.
4.1 Framing bounds for the Dunkl-Poisson kernel
Observe that, by (2.3), for
![]() $x\in B$
and
$x\in B$
and
![]() $y\in S$
,
$y\in S$
,
 $$ \begin{align} P_{k}(x,y) =C\,V_{k}\left(\frac{1-|x|^{2}}{(|x-y|^{2}+2\,\langle x,y-\cdot\rangle)^{\kappa+d/2}}\right)(y). \end{align} $$
$$ \begin{align} P_{k}(x,y) =C\,V_{k}\left(\frac{1-|x|^{2}}{(|x-y|^{2}+2\,\langle x,y-\cdot\rangle)^{\kappa+d/2}}\right)(y). \end{align} $$
From (4.1) and (2.2), we deduce the following bounds.
Proposition 4.1 Let
![]() $w_{max}\in W$
be such that
$w_{max}\in W$
be such that
![]() $|x-w_{max}y|=\max _{w\in W} |x-wy|$
. There exists
$|x-w_{max}y|=\max _{w\in W} |x-wy|$
. There exists
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $x\in B^+$
,
$x\in B^+$
,
![]() $y\in S^+$
,
$y\in S^+$
,
 $$ \begin{align} \frac{C{(1-|x|^{2})}}{|x-w_{max}y|^{d+2\,\kappa}}\leq P^{W}(x,y)\leq \frac{C{(1-|x|^{2})}}{|x-y|^{d+2\,\kappa}}, \end{align} $$
$$ \begin{align} \frac{C{(1-|x|^{2})}}{|x-w_{max}y|^{d+2\,\kappa}}\leq P^{W}(x,y)\leq \frac{C{(1-|x|^{2})}}{|x-y|^{d+2\,\kappa}}, \end{align} $$
for all
![]() $x\in B^+$
and
$x\in B^+$
and
![]() $y\in S^+$
.
$y\in S^+$
.
Proof The map
![]() $z\mapsto |x-y|^{2}+2\langle x,y-z\rangle $
is linear in
$z\mapsto |x-y|^{2}+2\langle x,y-z\rangle $
is linear in
![]() $z\in C(y)$
, the convex hull of
$z\in C(y)$
, the convex hull of
![]() $W\cdot y$
. Therefore, it attains its maximum and its minimum at points in
$W\cdot y$
. Therefore, it attains its maximum and its minimum at points in
![]() $W\cdot y$
. When
$W\cdot y$
. When
![]() $z=wy$
, the denominator
$z=wy$
, the denominator
![]() $|x-y|^{2}+2\langle x,y-z\rangle $
in (4.1) equals
$|x-y|^{2}+2\langle x,y-z\rangle $
in (4.1) equals
The smallest value is
![]() $|x-y|^{2}$
and the largest is
$|x-y|^{2}$
and the largest is
![]() $|x-w_{max}y|^{2}$
.▪
$|x-w_{max}y|^{2}$
.▪
Remark 4.2 Proposition 4.1 also holds in the general Dunkl noninvariant case. This is due to (2.2) and (4.1). An analogous estimate of the Newton kernel was obtained in [Reference Gallardo and Rejeb15, Proposition 6.3 (6.6)].
Proposition 4.3 Let
![]() $D>0$
. Then there exists
$D>0$
. Then there exists
![]() $C>0$
independent of D such that
$C>0$
independent of D such that
 $$ \begin{align*} C\,(1+4\,r\,MD\,(D+\max_{\alpha>0}\,|\alpha|))^{-d/2-\kappa}\leq \frac{P^{W}(x,y)}{\Omega(x,y)}\leq C\,(1+D)^{2\,\kappa} \end{align*} $$
$$ \begin{align*} C\,(1+4\,r\,MD\,(D+\max_{\alpha>0}\,|\alpha|))^{-d/2-\kappa}\leq \frac{P^{W}(x,y)}{\Omega(x,y)}\leq C\,(1+D)^{2\,\kappa} \end{align*} $$
for all
![]() $x\in B^+$
and
$x\in B^+$
and
![]() $y\in S^+$
with
$y\in S^+$
with
![]() $\alpha (y)\leq D|x-y|$
for every
$\alpha (y)\leq D|x-y|$
for every
![]() $\alpha>0$
.
$\alpha>0$
.
Proof Note that by Lemma 3.1(i),
![]() $\alpha (x)=|\alpha |\,d(x,H_{\alpha })\leq |\alpha |(|x-y|+d(y,H_{\alpha })) =|\alpha ||x-y|+\alpha (y)$
so
$\alpha (x)=|\alpha |\,d(x,H_{\alpha })\leq |\alpha |(|x-y|+d(y,H_{\alpha })) =|\alpha ||x-y|+\alpha (y)$
so
![]() $\alpha (x)\leq |x-y|\,\max _{\alpha>0}|\alpha |+D\,|x-y|=D^{\prime }\,|x-y|$
. Using (4.3), Proposition 3.5 and Remark 3.8,
$\alpha (x)\leq |x-y|\,\max _{\alpha>0}|\alpha |+D\,|x-y|=D^{\prime }\,|x-y|$
. Using (4.3), Proposition 3.5 and Remark 3.8,
 $$ \begin{align*} |x-wy|^{2}&=|x-y|^{2}+2\langle x,y-wy\rangle = |x-y|^{2}+2\sum_{i=1}^{r}2\,a_{i}^{w}(y)\alpha_{i}(x)/|\alpha_{i}|^{2}\\ &\leq |x-y|^{2}+4\,r\,M\,\max_{\alpha>0}\,\alpha(y)\,\max_{\alpha>0}\,\alpha(x) \leq (1+4\,r\,MD\,D^{\prime})|x-y|^{2}. \end{align*} $$
$$ \begin{align*} |x-wy|^{2}&=|x-y|^{2}+2\langle x,y-wy\rangle = |x-y|^{2}+2\sum_{i=1}^{r}2\,a_{i}^{w}(y)\alpha_{i}(x)/|\alpha_{i}|^{2}\\ &\leq |x-y|^{2}+4\,r\,M\,\max_{\alpha>0}\,\alpha(y)\,\max_{\alpha>0}\,\alpha(x) \leq (1+4\,r\,MD\,D^{\prime})|x-y|^{2}. \end{align*} $$
The result then follows from (4.2) in Proposition 4.1, noting that for all
![]() $\alpha>0$
, we have
$\alpha>0$
, we have
![]() $|x-y|\leq \phi _{\alpha }(x,y)\leq (1+D)\,|x-y|$
.▪
$|x-y|\leq \phi _{\alpha }(x,y)\leq (1+D)\,|x-y|$
.▪
Lemma 4.4 Let
![]() $E=\{ (x,y)\in \mathfrak {a}\times \mathfrak {a} \ |\ \alpha (x)\,\alpha (y)>0 \}$
. Consider
$E=\{ (x,y)\in \mathfrak {a}\times \mathfrak {a} \ |\ \alpha (x)\,\alpha (y)>0 \}$
. Consider
 $$ \begin{align*} T_{1}(x,y)=\frac{\frac{1}{|x-y|^{d}}-\frac{1}{|x-\sigma_{\alpha} y|^{d}}}{\alpha(x)\,\alpha(y)} \end{align*} $$
$$ \begin{align*} T_{1}(x,y)=\frac{\frac{1}{|x-y|^{d}}-\frac{1}{|x-\sigma_{\alpha} y|^{d}}}{\alpha(x)\,\alpha(y)} \end{align*} $$
on E. Then, on E, the following estimate holds
Proof Recall that, by Lemma 3.1(ii),
![]() $|x-\sigma _{\alpha } y|^{2}=|x-y|^{2}+C\,\alpha (x)\,\alpha (y)$
, where
$|x-\sigma _{\alpha } y|^{2}=|x-y|^{2}+C\,\alpha (x)\,\alpha (y)$
, where
![]() $C=4/|\alpha |^{2}$
. Using the formula
$C=4/|\alpha |^{2}$
. Using the formula
![]() $a^{d}-b^{d}=(a-b)\,\sum _{k=0}^{d-1}\,a^{k}\,b^{d-1-k}$
, and the fact that
$a^{d}-b^{d}=(a-b)\,\sum _{k=0}^{d-1}\,a^{k}\,b^{d-1-k}$
, and the fact that
![]() $|x-y|^{d}\leq |x-\sigma _{\alpha } y|^{d}$
on E, we have
$|x-y|^{d}\leq |x-\sigma _{\alpha } y|^{d}$
on E, we have
 $$ \begin{align*} T_{1}(x,y)&=\frac{(|x-\sigma_{\alpha} y|^{2})^{d}-(|x-y|^{2})^{d}}{\alpha(x)\,\alpha(y)\,|x-y|^{d}\,|x-\sigma_{\alpha} y|^{d}\,(|x-y|^{d}+|x-\sigma_{\alpha} y|^{d})}\\ &=C\,\frac{\sum_{k=0}^{d-1}\,|x-\sigma_{\alpha} y|^{2\,k}\,|x-y|^{2\,(d-1-k)}}{|x-y|^{d}\,|x-\sigma_{\alpha} y|^{d}\,(|x-y|^{d}+|x-\sigma_{\alpha} y|^{d})}\\ &\asymp \frac{|x-\sigma_{\alpha} y|^{2\,(d-1)}}{|x-y|^{d}\,|x-\sigma_{\alpha} y|^{2\,d}}=\frac{1}{|x-y|^{d}\,|x-\sigma_{\alpha} y|^{2}}. \end{align*} $$
$$ \begin{align*} T_{1}(x,y)&=\frac{(|x-\sigma_{\alpha} y|^{2})^{d}-(|x-y|^{2})^{d}}{\alpha(x)\,\alpha(y)\,|x-y|^{d}\,|x-\sigma_{\alpha} y|^{d}\,(|x-y|^{d}+|x-\sigma_{\alpha} y|^{d})}\\ &=C\,\frac{\sum_{k=0}^{d-1}\,|x-\sigma_{\alpha} y|^{2\,k}\,|x-y|^{2\,(d-1-k)}}{|x-y|^{d}\,|x-\sigma_{\alpha} y|^{d}\,(|x-y|^{d}+|x-\sigma_{\alpha} y|^{d})}\\ &\asymp \frac{|x-\sigma_{\alpha} y|^{2\,(d-1)}}{|x-y|^{d}\,|x-\sigma_{\alpha} y|^{2\,d}}=\frac{1}{|x-y|^{d}\,|x-\sigma_{\alpha} y|^{2}}. \end{align*} $$
▪
5 The conjecture for complex root systems
5.1 Structure of the proof of Conjecture 1
When the root system is complex, i.e., all the multiplicities
![]() $k(\alpha )=1$
, by Proposition 2.5, we have the alternating sum formula for the W-invariant Poisson–Dunkl kernel at our disposal, see also [Reference Graczyk and Sawyer18]. We have, for any
$k(\alpha )=1$
, by Proposition 2.5, we have the alternating sum formula for the W-invariant Poisson–Dunkl kernel at our disposal, see also [Reference Graczyk and Sawyer18]. We have, for any
![]() $x\in B^+$
,
$x\in B^+$
,
![]() $y\in S^+$
,
$y\in S^+$
,
 $$ \begin{align*} \frac{P^{W}(x,y)}{1-|x|^{2}}=\frac1{|W|w_{d}}\frac{1}{\pi(x)\,\pi(y)}\,\left[\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}\right]. \end{align*} $$
$$ \begin{align*} \frac{P^{W}(x,y)}{1-|x|^{2}}=\frac1{|W|w_{d}}\frac{1}{\pi(x)\,\pi(y)}\,\left[\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}\right]. \end{align*} $$
For a fixed basic root subsystem
![]() $\Phi ^{\prime }$
, it is natural to decompose the alternating sum
$\Phi ^{\prime }$
, it is natural to decompose the alternating sum
 $$ \begin{align*} \sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}= \sum_{w\in W^{\prime}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}+ \sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}, \end{align*} $$
$$ \begin{align*} \sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}= \sum_{w\in W^{\prime}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}+ \sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}, \end{align*} $$
and to apply an induction argument to the “main term”
![]() $\sum _{w\in W^{\prime }}\frac {\epsilon (w)}{|x-w\,y|^{d}}$
. This will require a detailed analysis of the remainder term
$\sum _{w\in W^{\prime }}\frac {\epsilon (w)}{|x-w\,y|^{d}}$
. This will require a detailed analysis of the remainder term
![]() $\sum _{w\in W_{0}}\,\frac {\epsilon (w)}{|x-w\,y|^{d}}$
. The choice of the basic root subsystem
$\sum _{w\in W_{0}}\,\frac {\epsilon (w)}{|x-w\,y|^{d}}$
. The choice of the basic root subsystem
![]() $\Phi ^{\prime }$
and further analysis of the main term and the remainder, will be done by considering
$\Phi ^{\prime }$
and further analysis of the main term and the remainder, will be done by considering
![]() $(x,y)$
in the fixed subregions (5.1) defined in Lemma 5.1.
$(x,y)$
in the fixed subregions (5.1) defined in Lemma 5.1.
5.2 Subregions
Let N denote the maximal length of the positive roots in
![]() $\Phi $
. For example, if the root system is
$\Phi $
. For example, if the root system is
![]() $A_{n}$
then
$A_{n}$
then
![]() $N=n$
.
$N=n$
.
Lemma 5.1 Consider a basic root subsystem
![]() $\Phi $
and fix
$\Phi $
and fix
![]() $c>0$
. Then, given x and
$c>0$
. Then, given x and
![]() $y \in \overline {\mathfrak {a}^+}$
, it is possible to build a basic root subsystem
$y \in \overline {\mathfrak {a}^+}$
, it is possible to build a basic root subsystem
![]() $\Phi ^{\prime }$
of
$\Phi ^{\prime }$
of
![]() $\Phi $
and
$\Phi $
and
![]() $c^{\prime }$
with
$c^{\prime }$
with
![]() $c/N^{r}\leq c^{\prime }\leq c$
where r is the rank of
$c/N^{r}\leq c^{\prime }\leq c$
where r is the rank of
![]() $\Phi $
such that
$\Phi $
such that
for every
![]() $\alpha \in \Phi ^{\prime }_+$
and every
$\alpha \in \Phi ^{\prime }_+$
and every
![]() $\beta \in \Phi _{0}^+$
(this includes the possibility that
$\beta \in \Phi _{0}^+$
(this includes the possibility that
![]() $\Phi ^{\prime }=\emptyset $
).
$\Phi ^{\prime }=\emptyset $
).
Proof Let
![]() $c_{0}=\frac {c}{N^{r}}$
and let
$c_{0}=\frac {c}{N^{r}}$
and let
![]() $S_{0}$
be the set of simple roots
$S_{0}$
be the set of simple roots
![]() $\alpha _{i}$
such that such that
$\alpha _{i}$
such that such that
Let
![]() $\Phi ^{\prime }$
be generated by the simple roots such that (5.2) holds (there are at most r such simple roots). If
$\Phi ^{\prime }$
be generated by the simple roots such that (5.2) holds (there are at most r such simple roots). If
![]() $c_{0}\,\alpha (y)< |x-y|$
for every
$c_{0}\,\alpha (y)< |x-y|$
for every
![]() $\alpha \in \Phi ^{\prime }$
then
$\alpha \in \Phi ^{\prime }$
then
![]() $\Phi ^{\prime }$
satisfies the condition (5.1) with
$\Phi ^{\prime }$
satisfies the condition (5.1) with
![]() $c^{\prime }=c_{0}$
except perhaps
$c^{\prime }=c_{0}$
except perhaps
![]() $c_{0}\,\beta (y)=|x-y|$
for some
$c_{0}\,\beta (y)=|x-y|$
for some
![]() $\beta \in \Phi _{0}^+$
. In that case, we choose
$\beta \in \Phi _{0}^+$
. In that case, we choose
![]() $0<\delta <c-c_{0}$
such that the inequalities
$0<\delta <c-c_{0}$
such that the inequalities
![]() $ (c_{0}+\delta )\,\alpha (y)< |x-y|$
hold for every
$ (c_{0}+\delta )\,\alpha (y)< |x-y|$
hold for every
![]() $\alpha \in \Phi ^{\prime }_+$
. We then take
$\alpha \in \Phi ^{\prime }_+$
. We then take
![]() $c^{\prime }=c_{0}+\delta $
.
$c^{\prime }=c_{0}+\delta $
.
Suppose
![]() $c_{0}\,\alpha (y)\geq |x-y|$
for some
$c_{0}\,\alpha (y)\geq |x-y|$
for some
![]() $\alpha \in \Phi ^{\prime }$
. In that case, since
$\alpha \in \Phi ^{\prime }$
. In that case, since
![]() $\alpha $
is not one of the
$\alpha $
is not one of the
![]() $\alpha _{i}$
’s from (5.2), it is not simple and we have
$\alpha _{i}$
’s from (5.2), it is not simple and we have
![]() $c_{0}\,\alpha _{j}>|x-y|/N$
for some
$c_{0}\,\alpha _{j}>|x-y|/N$
for some
![]() $j\in S_{0}$
. We set
$j\in S_{0}$
. We set
![]() $c_{1}=N\,c_{0}$
and repeat the process.
$c_{1}=N\,c_{0}$
and repeat the process.
Let
![]() $S_{1}$
be the set of simple roots
$S_{1}$
be the set of simple roots
![]() $\alpha _{i}$
such that such that
$\alpha _{i}$
such that such that
Let
![]() $\Phi ^{\prime }$
be generated by the simple roots such that (5.3) holds (there are at most
$\Phi ^{\prime }$
be generated by the simple roots such that (5.3) holds (there are at most
![]() $r-1$
such simple roots). If
$r-1$
such simple roots). If
![]() $c_{1}\,\alpha (y)< |x-y|$
for every
$c_{1}\,\alpha (y)< |x-y|$
for every
![]() $\alpha \in \Phi ^{\prime }$
then
$\alpha \in \Phi ^{\prime }$
then
![]() $\Phi ^{\prime }$
satisfies the condition (5.1) with
$\Phi ^{\prime }$
satisfies the condition (5.1) with
![]() $c^{\prime }=c_{1}$
(if
$c^{\prime }=c_{1}$
(if
![]() $c_{1}\,\beta (y)=|x-y|$
for some
$c_{1}\,\beta (y)=|x-y|$
for some
![]() $\beta \in \Phi _{0}$
, we proceed as in the previous step).
$\beta \in \Phi _{0}$
, we proceed as in the previous step).
Suppose
![]() $c_{1}\,\alpha (y)\geq |x-y|$
for some
$c_{1}\,\alpha (y)\geq |x-y|$
for some
![]() $\alpha \in \Phi ^{\prime }$
. In that case, we have
$\alpha \in \Phi ^{\prime }$
. In that case, we have
![]() $c_{1}\,\alpha _{j}(y)>|x-y|/N$
for some
$c_{1}\,\alpha _{j}(y)>|x-y|/N$
for some
![]() $j\in S_{1}$
. We set
$j\in S_{1}$
. We set
![]() $c_{2}=N\,c_{1}$
and repeat the process.
$c_{2}=N\,c_{1}$
and repeat the process.
Since we decrease the number of simple roots involved each time, the process must stop eventually either because we have achieved (5.1) or because we ran out of simple roots.▪
Remark 5.2 In Lemma 5.1, we do not exclude the possibility that
![]() $\Phi ^{\prime }$
might be empty (with
$\Phi ^{\prime }$
might be empty (with
![]() $\Phi _{0}=\Phi $
and
$\Phi _{0}=\Phi $
and
![]() $W_{0}=W\setminus \{id\}$
) or, at the other extreme, that
$W_{0}=W\setminus \{id\}$
) or, at the other extreme, that
![]() $\Phi ^{\prime }=\Phi $
(with
$\Phi ^{\prime }=\Phi $
(with
![]() $\Phi _{0}=\emptyset $
and
$\Phi _{0}=\emptyset $
and
![]() $W_{0}=\emptyset $
).
$W_{0}=\emptyset $
).
The subregions defined in Lemma 5.1 will be denoted by
The subregions
![]() $S_{\Phi ^{\prime },c}$
will play a crucial role in the proof of Conjecture 1.
$S_{\Phi ^{\prime },c}$
will play a crucial role in the proof of Conjecture 1.
5.3 Estimates of the remainder
This subsection is devoted to the estimates of the remainder term
![]() $\sum _{w\in W_{0}}\,\frac {\epsilon (w)}{|x-w\,y|^{d}}$
. We begin with lower estimates of the expressions
$\sum _{w\in W_{0}}\,\frac {\epsilon (w)}{|x-w\,y|^{d}}$
. We begin with lower estimates of the expressions
![]() $|x-w\,y|$
when
$|x-w\,y|$
when
![]() $w\in W_{0}$
.
$w\in W_{0}$
.
Lemma 5.3 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem of
$\Phi ^{\prime }$
be a basic root subsystem of
![]() $\Phi $
with
$\Phi $
with
![]() $\Phi ^{\prime }\not =\Phi $
, x,
$\Phi ^{\prime }\not =\Phi $
, x,
![]() $y\in \overline {\mathfrak {a}^+}$
and
$y\in \overline {\mathfrak {a}^+}$
and
![]() $w_{0}\in W_{0}$
. Then there exists a simple root
$w_{0}\in W_{0}$
. Then there exists a simple root
![]() $\alpha \in \Phi _{0}^+$
such that
$\alpha \in \Phi _{0}^+$
such that
![]() $|x-w\,y|^{2}\geq K_{0}\,\alpha (x)\,\alpha (y)$
where
$|x-w\,y|^{2}\geq K_{0}\,\alpha (x)\,\alpha (y)$
where
![]() $K_{0}=\max \,\{1/|\alpha |^{2}\colon \alpha \in \Phi _+\}$
.
$K_{0}=\max \,\{1/|\alpha |^{2}\colon \alpha \in \Phi _+\}$
.
Proof We use the decomposition (3.1) of
![]() $y-wy$
. Let
$y-wy$
. Let
![]() $\alpha _{i}$
,
$\alpha _{i}$
,
![]() $i=1,\ldots , s=| \Phi ^{\prime }_+|$
be the simple positive roots from
$i=1,\ldots , s=| \Phi ^{\prime }_+|$
be the simple positive roots from
![]() $\Phi ^{\prime }$
and
$\Phi ^{\prime }$
and
![]() $\alpha _{s+j}$
the simple positive roots from
$\alpha _{s+j}$
the simple positive roots from
![]() $\Phi _{0}^+$
. We have
$\Phi _{0}^+$
. We have
 $$ \begin{align} y-w\,y=\sum_{i=1}^{s} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}} + \sum_{j=1}^{r-s} \,2\,\frac{a_{s+j}^{w}(y)}{|\alpha_{s+j}|^{2}}\,A_{\alpha_{s+j}}. \end{align} $$
$$ \begin{align} y-w\,y=\sum_{i=1}^{s} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,A_{\alpha_{i}} + \sum_{j=1}^{r-s} \,2\,\frac{a_{s+j}^{w}(y)}{|\alpha_{s+j}|^{2}}\,A_{\alpha_{s+j}}. \end{align} $$
In order to prove the lemma it is sufficient to show that the second sum does not vanish since by Corollary 3.10, a nonzero function
![]() $a_{s+j}^{w}$
has a nonzero term
$a_{s+j}^{w}$
has a nonzero term
![]() $n\, \alpha _{s+j}$
.
$n\, \alpha _{s+j}$
.
Suppose by contradiction that the second sum vanishes. Choose x and y with
![]() $\Phi _{x}=\Phi _{y}=\Phi ^{\prime }$
. Formula (5.4) implies that
$\Phi _{x}=\Phi _{y}=\Phi ^{\prime }$
. Formula (5.4) implies that
 $$ \begin{align*} \langle x,y-w\,y\rangle=\sum_{i=1}^{s} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,{\alpha_{i}(x)} =0, \end{align*} $$
$$ \begin{align*} \langle x,y-w\,y\rangle=\sum_{i=1}^{s} \,2\,\frac{a_{i}^{w}(y)}{|\alpha_{i}|^{2}}\,{\alpha_{i}(x)} =0, \end{align*} $$
since
![]() $\alpha _{i}(x)=0$
. By Corollary 3.9, we get
$\alpha _{i}(x)=0$
. By Corollary 3.9, we get
![]() $w\in W_{y}=W^{\prime }$
.▪
$w\in W_{y}=W^{\prime }$
.▪
Remark 5.4
Lemma 5.3 holds with the same proof if
![]() $\Phi ^{\prime }=\emptyset $
,
$\Phi ^{\prime }=\emptyset $
,
![]() $\Phi _{0}=\Phi $
, and
$\Phi _{0}=\Phi $
, and
![]() $W_{0}=W\setminus \{id\}$
.
$W_{0}=W\setminus \{id\}$
.
Corollary 5.5 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem of
$\Phi ^{\prime }$
be a basic root subsystem of
![]() $\Phi $
and x,
$\Phi $
and x,
![]() $y\in \bar {\mathfrak {a}}^+$
. Suppose
$y\in \bar {\mathfrak {a}}^+$
. Suppose
![]() $0<c\leq 1/(4\,C_{1})$
, where
$0<c\leq 1/(4\,C_{1})$
, where
![]() $C_{1}$
is as in Remark 3.11 and
$C_{1}$
is as in Remark 3.11 and
for all
![]() $\alpha \in \Phi _{0}^+$
. Then if
$\alpha \in \Phi _{0}^+$
. Then if
![]() $w\in W_{0}$
and
$w\in W_{0}$
and
![]() $K_{0}$
is as in Lemma 5.3, we have
$K_{0}$
is as in Lemma 5.3, we have
and
 $$ \begin{align} \frac{|x-y|}{|x-w\,y|}\leq \frac{c}{\sqrt{K_{0}/2}}. \end{align} $$
$$ \begin{align} \frac{|x-y|}{|x-w\,y|}\leq \frac{c}{\sqrt{K_{0}/2}}. \end{align} $$
Proof By Remark 3.11, if
![]() $\alpha \in \Phi _{0}^+$
then
$\alpha \in \Phi _{0}^+$
then
On the other hand,
![]() $\alpha (y)\geq \alpha (x)-C_{1}\,|x-y|\geq \alpha (x)-C_{1}\,c\,\alpha (y) \geq \alpha (x)-2\,C_{1}\,c\,\alpha (x) =(1-2\,C_{1}\,c)\,\alpha (x)\geq \alpha (x)/2$
. The rest follows from Lemma 5.3.▪
$\alpha (y)\geq \alpha (x)-C_{1}\,|x-y|\geq \alpha (x)-C_{1}\,c\,\alpha (y) \geq \alpha (x)-2\,C_{1}\,c\,\alpha (x) =(1-2\,C_{1}\,c)\,\alpha (x)\geq \alpha (x)/2$
. The rest follows from Lemma 5.3.▪
Lemma 5.6 (Conjecture 1 in the case
![]() $\Phi ^{\prime }=\emptyset $
) If
$\Phi ^{\prime }=\emptyset $
) If
![]() $0<c\leq \min \{\frac {1}{4\,C_{1}},\frac {\sqrt {K_{0}/2}}{\sqrt [d]{2\,|W|}}\},$
where
$0<c\leq \min \{\frac {1}{4\,C_{1}},\frac {\sqrt {K_{0}/2}}{\sqrt [d]{2\,|W|}}\},$
where
![]() $C_{1}$
is as in Remark 3.11,
$C_{1}$
is as in Remark 3.11,
![]() $K_{0}$
is as in Lemma 5.3 and
$K_{0}$
is as in Lemma 5.3 and
![]() $|x-y|\leq c\,\alpha (y)$
for every
$|x-y|\leq c\,\alpha (y)$
for every
![]() $\alpha \in \Phi $
then the Conjecture 1 holds.
$\alpha \in \Phi $
then the Conjecture 1 holds.
Proof In that case,
![]() $\Phi ^{\prime }=\emptyset $
,
$\Phi ^{\prime }=\emptyset $
,
![]() $\Phi _{0}=\Phi $
,
$\Phi _{0}=\Phi $
,
![]() $W_{0}=W\setminus \{id\}$
, and by Corollary 5.5, for every
$W_{0}=W\setminus \{id\}$
, and by Corollary 5.5, for every
![]() $w\in W_{0}$
, equation (5.5) holds and
$w\in W_{0}$
, equation (5.5) holds and
 $$ \begin{align*} \frac{1-|x|^{2}}{w_{d}\,\pi(x)\,\pi(y)} \,\frac{1}{|x-y|^{d}}&\geq P^{W}(x,y)\\ &\geq\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\left[\frac{1}{|x-y|^{d}}-\sum_{w\not=id}\,\frac{1}{|x-w\,y|^{d}} \right]\\ &\geq\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\left[\frac{1}{|x-y|^{d}}-\frac{c^{d}}{(K_{0}/2)^{d/2}}\,\sum_{w\not=id}\,\frac{1}{|x-y|^{d}} \right]\\ &\geq(1-c^{d}\,|W|/(K_{0}/2)^{d/2})\,\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\frac{1}{|x-y|^{d}}\\ &\geq\frac{1}{2}\,\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\frac{1}{|x-y|^{d}}. \end{align*} $$
$$ \begin{align*} \frac{1-|x|^{2}}{w_{d}\,\pi(x)\,\pi(y)} \,\frac{1}{|x-y|^{d}}&\geq P^{W}(x,y)\\ &\geq\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\left[\frac{1}{|x-y|^{d}}-\sum_{w\not=id}\,\frac{1}{|x-w\,y|^{d}} \right]\\ &\geq\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\left[\frac{1}{|x-y|^{d}}-\frac{c^{d}}{(K_{0}/2)^{d/2}}\,\sum_{w\not=id}\,\frac{1}{|x-y|^{d}} \right]\\ &\geq(1-c^{d}\,|W|/(K_{0}/2)^{d/2})\,\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\frac{1}{|x-y|^{d}}\\ &\geq\frac{1}{2}\,\frac{1-|x|^{2}}{|W|\,w_{d}\,\pi(x)\,\pi(y)} \,\frac{1}{|x-y|^{d}}. \end{align*} $$
Hence, the conjecture holds in this case since
![]() $|x-\sigma _{\alpha }\,y|^{2}=|x-y|^{2}+C\,\alpha (x)\,\alpha (y)\asymp \alpha (x)\,\alpha (y)$
by the hypothesis
$|x-\sigma _{\alpha }\,y|^{2}=|x-y|^{2}+C\,\alpha (x)\,\alpha (y)\asymp \alpha (x)\,\alpha (y)$
by the hypothesis
![]() $|x-y|\leq c\,\alpha (y)$
and Corollary 5.5.▪
$|x-y|\leq c\,\alpha (y)$
and Corollary 5.5.▪
In the second part of this subsection devoted to estimates of the remainder
![]() $\sum _{w\in W_{0}}\,\frac {\epsilon (w)}{|x-w\,y|^{d}}$
, we consider all root subsystems
$\sum _{w\in W_{0}}\,\frac {\epsilon (w)}{|x-w\,y|^{d}}$
, we consider all root subsystems
![]() $\Phi ^{\prime \prime }\subseteq \Phi ^{\prime }$
and we deal with the function
$\Phi ^{\prime \prime }\subseteq \Phi ^{\prime }$
and we deal with the function
![]() $R_{\Phi ^{\prime \prime }}(x,y)$
, defined in the following definition. This will be essential for the upper estimates of the remainder on the subregions
$R_{\Phi ^{\prime \prime }}(x,y)$
, defined in the following definition. This will be essential for the upper estimates of the remainder on the subregions
![]() $S_{\Phi ^{\prime },c}$
.
$S_{\Phi ^{\prime },c}$
.
Definition 5.7 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem of
$\Phi ^{\prime }$
be a basic root subsystem of
![]() $\Phi $
,
$\Phi $
,
![]() $\Phi ^{\prime \prime }$
a subsystem of
$\Phi ^{\prime \prime }$
a subsystem of
![]() $\Phi ^{\prime }$
and
$\Phi ^{\prime }$
and
![]() $I=|\Phi ^{\prime \prime }|$
. We define, when
$I=|\Phi ^{\prime \prime }|$
. We define, when
![]() $(x,y)\in D_{0}=\{(x,y) {\in \mathfrak {a}\times \mathfrak {a}} \ |\ \prod _{w\in W_{0}}|x-w\,y|\not = 0 \}$
,
$(x,y)\in D_{0}=\{(x,y) {\in \mathfrak {a}\times \mathfrak {a}} \ |\ \prod _{w\in W_{0}}|x-w\,y|\not = 0 \}$
,
 $$ \begin{align} R_{\Phi^{\prime\prime}}(x,y)=|x-y|^{d+2\,I}\,\sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}. \end{align} $$
$$ \begin{align} R_{\Phi^{\prime\prime}}(x,y)=|x-y|^{d+2\,I}\,\sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}. \end{align} $$
Remark 5.8 When the subsystem
![]() $\Phi ^{\prime \prime }$
is fixed and it does not lead to misunderstanding, in order to simplify the notation, we will write
$\Phi ^{\prime \prime }$
is fixed and it does not lead to misunderstanding, in order to simplify the notation, we will write
even though
![]() $R(x,y)$
depends on
$R(x,y)$
depends on
![]() $\Phi ^{\prime \prime }$
via the factor
$\Phi ^{\prime \prime }$
via the factor
![]() $|x-y|^{d+2\,I}=|x-y|^{d+2\,|\Phi \prime \prime |}$
.
$|x-y|^{d+2\,I}=|x-y|^{d+2\,|\Phi \prime \prime |}$
.
Lemma 5.9 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem of
$\Phi ^{\prime }$
be a basic root subsystem of
![]() $\Phi $
. Let
$\Phi $
. Let
![]() $\Phi ^{\prime \prime }\not =\emptyset $
be a basic root subsystem of
$\Phi ^{\prime \prime }\not =\emptyset $
be a basic root subsystem of
![]() $\Phi ^{\prime }$
. Let
$\Phi ^{\prime }$
. Let
![]() $R(x,y)$
be defined by (5.6). Denote
$R(x,y)$
be defined by (5.6). Denote
![]() $\partial ^{y}(\pi ^{\prime \prime })=\prod _{\alpha \in \Phi ^{\prime \prime }}\,\partial ^{y}_{\alpha }$
. Then there exists a constant K independent of x and y such that for all
$\partial ^{y}(\pi ^{\prime \prime })=\prod _{\alpha \in \Phi ^{\prime \prime }}\,\partial ^{y}_{\alpha }$
. Then there exists a constant K independent of x and y such that for all
![]() $(x,y)\in D_{0}$
$(x,y)\in D_{0}$
 $$ \begin{align*} \left|\partial^{x}(\pi^{\prime\prime})\,\partial^{y}(\pi^{\prime\prime})\,R(x,y)\right|\ \le \ K\,\max_{0\leq i \leq 2\,I, w\in W_{0}}\,\left\{\frac{|x-y|^{d+i}}{|x-w\,y|^{d+i}}\right\}. \end{align*} $$
$$ \begin{align*} \left|\partial^{x}(\pi^{\prime\prime})\,\partial^{y}(\pi^{\prime\prime})\,R(x,y)\right|\ \le \ K\,\max_{0\leq i \leq 2\,I, w\in W_{0}}\,\left\{\frac{|x-y|^{d+i}}{|x-w\,y|^{d+i}}\right\}. \end{align*} $$
Proof First note that
and
 $$ \begin{align} \partial^{x}_{\alpha}\,\left[|x-y|^{d+2\,I}\,|x-w\,y|^{-d}\right] &=(d+2\,I)\,\alpha(x-y)\,|x-y|^{d+2\,I-2}\,|x-w\,y|^{-d}\nonumber \\ &\quad+(-d)\,\alpha(x-w\,y)|x-y|^{d+2\,I}|x-w\,y|^{-d-2}. \end{align} $$
$$ \begin{align} \partial^{x}_{\alpha}\,\left[|x-y|^{d+2\,I}\,|x-w\,y|^{-d}\right] &=(d+2\,I)\,\alpha(x-y)\,|x-y|^{d+2\,I-2}\,|x-w\,y|^{-d}\nonumber \\ &\quad+(-d)\,\alpha(x-w\,y)|x-y|^{d+2\,I}|x-w\,y|^{-d-2}. \end{align} $$
In the computations below, it is helpful to remember that
![]() $|x-w\,y|=|w^{-1}\,x-y|$
. Using formulas (5.7) and (5.8), we obtain for each
$|x-w\,y|=|w^{-1}\,x-y|$
. Using formulas (5.7) and (5.8), we obtain for each
![]() $w\in W_{0}$
,
$w\in W_{0}$
,
 $$ \begin{align*} &{\partial^{y}_{\alpha}\,\partial^{x}_{\alpha}\,|x-y|^{d+2\,I}\,|x-w\,y|^{-d}}\\ &=-2\,(d+2\,I)\,|x-y|^{d+2\,I-2}\,|x-w\,y|^{-d}\\ &\quad+{(d+2\,I-2)}\,(d+2\,I)\,\alpha(x-y)\,\alpha(y-x)\,|x-y|^{d+2\,I-4}\,|x-w\,y|^{-d}\\ &\quad-d\,(d+2\,I)\,\alpha(x-y)\,\alpha(y-w^{-1}\,x)\,|x-y|^{d+2\,I-2}\,|x-w\,y|^{-d-2}\\ &\quad-{(d+2\,I-2)}\,(d+2\,I)\,\alpha(y-x)\,\alpha(x-w\,y)\,|x-y|^{d +2\,I-2}\,|x-w\,y|^{-d-2}\\ &\quad-{(d+2\,I-2)}\,(d+2\,I)\,\alpha(y-x)\,\alpha(x-w\,y)\,|x-y|^{d+2\,I-2}\,|x-w\,y|^{-d-2}\\ &\quad+d\,\partial_{\alpha}^{y}(\alpha(w\,y))\, |x-y|^{d+2\,I}\,|x-w\,y|^{-d-2}\\ &\quad+d\,(d+2)\,\alpha(x-w\,y)\,\alpha(y-w^{-1}\,x)\,|x-y|^{d+2\,I}\,|x-w\,y|^{-d-4}. \end{align*} $$
$$ \begin{align*} &{\partial^{y}_{\alpha}\,\partial^{x}_{\alpha}\,|x-y|^{d+2\,I}\,|x-w\,y|^{-d}}\\ &=-2\,(d+2\,I)\,|x-y|^{d+2\,I-2}\,|x-w\,y|^{-d}\\ &\quad+{(d+2\,I-2)}\,(d+2\,I)\,\alpha(x-y)\,\alpha(y-x)\,|x-y|^{d+2\,I-4}\,|x-w\,y|^{-d}\\ &\quad-d\,(d+2\,I)\,\alpha(x-y)\,\alpha(y-w^{-1}\,x)\,|x-y|^{d+2\,I-2}\,|x-w\,y|^{-d-2}\\ &\quad-{(d+2\,I-2)}\,(d+2\,I)\,\alpha(y-x)\,\alpha(x-w\,y)\,|x-y|^{d +2\,I-2}\,|x-w\,y|^{-d-2}\\ &\quad-{(d+2\,I-2)}\,(d+2\,I)\,\alpha(y-x)\,\alpha(x-w\,y)\,|x-y|^{d+2\,I-2}\,|x-w\,y|^{-d-2}\\ &\quad+d\,\partial_{\alpha}^{y}(\alpha(w\,y))\, |x-y|^{d+2\,I}\,|x-w\,y|^{-d-2}\\ &\quad+d\,(d+2)\,\alpha(x-w\,y)\,\alpha(y-w^{-1}\,x)\,|x-y|^{d+2\,I}\,|x-w\,y|^{-d-4}. \end{align*} $$
Observe that after each application of an operator
![]() $\partial ^{y}_{\alpha }\,\partial ^{x}_{\alpha }$
, where
$\partial ^{y}_{\alpha }\,\partial ^{x}_{\alpha }$
, where
![]() $\alpha $
is a root from
$\alpha $
is a root from
![]() $\Phi ^{\prime \prime }$
, we get a sum of terms which are products of constants times terms in
$\Phi ^{\prime \prime }$
, we get a sum of terms which are products of constants times terms in
![]() $\alpha (x-y)$
,
$\alpha (x-y)$
,
![]() $\alpha (w^{-1}\,x-y)$
,
$\alpha (w^{-1}\,x-y)$
,
![]() $\alpha (x-w\,y)$
,
$\alpha (x-w\,y)$
,
![]() $|x-y|^{d+2\,I-2\,{k}}$
, and
$|x-y|^{d+2\,I-2\,{k}}$
, and
![]() $|x-w\,y|^{-d-{2l}}$
. We used the fact that a directional derivative of a linear term such as
$|x-w\,y|^{-d-{2l}}$
. We used the fact that a directional derivative of a linear term such as
![]() $\alpha (x-y)$
is a constant.
$\alpha (x-y)$
is a constant.
By applying for the first time
![]() $\partial ^{y}_{\alpha }\,\partial ^{x}_{\alpha }$
, the degree of homogeneity of the function
$\partial ^{y}_{\alpha }\,\partial ^{x}_{\alpha }$
, the degree of homogeneity of the function
![]() $|x-y|^{d+2\,I}\,|x-w\,y|^{-d}$
went from
$|x-y|^{d+2\,I}\,|x-w\,y|^{-d}$
went from
![]() $2\,I$
to
$2\,I$
to
![]() $2\,I-2$
.
$2\,I-2$
.
Each new application of an operator
![]() $\partial ^{y}_{\alpha }\,\partial ^{x}_{\alpha }$
decreases the degree by 2 until we get the degree of 0 once we have applied
$\partial ^{y}_{\alpha }\,\partial ^{x}_{\alpha }$
decreases the degree by 2 until we get the degree of 0 once we have applied
![]() $\partial ^{x}({\pi ^{\prime \prime }})\,\partial ^{y}({\pi ^{\prime \prime }})$
.
$\partial ^{x}({\pi ^{\prime \prime }})\,\partial ^{y}({\pi ^{\prime \prime }})$
.
We use the estimates (3.2) from Remark 3.11. From the fact that
![]() $|\alpha (x-y)|\leq C_{1}\,|x-y|$
,
$|\alpha (x-y)|\leq C_{1}\,|x-y|$
,
![]() $|\alpha (x-w\,y)|\leq C_{1}\,|x-w\,y|$
,
$|\alpha (x-w\,y)|\leq C_{1}\,|x-w\,y|$
,
![]() $|\alpha (w^{-1}\,x-y)|\leq C_{1}\,|w^{-1}\,x-y|=C_{1}\,|x-w\,y|$
, we note that
$|\alpha (w^{-1}\,x-y)|\leq C_{1}\,|w^{-1}\,x-y|=C_{1}\,|x-w\,y|$
, we note that
![]() $\left |\partial ^{x}({\pi ^{\prime \prime }})\,\partial ^{y}({\pi ^{\prime \prime }})\,R(x,y)\right |$
is bounded by a finite sum of terms of the form
$\left |\partial ^{x}({\pi ^{\prime \prime }})\,\partial ^{y}({\pi ^{\prime \prime }})\,R(x,y)\right |$
is bounded by a finite sum of terms of the form
![]() $C\, |x-y|^{d+2\,I-\,{j}}\,|x-w\,y|^{-d-{(2I-\,j)}}$
, or, equivalently,
$C\, |x-y|^{d+2\,I-\,{j}}\,|x-w\,y|^{-d-{(2I-\,j)}}$
, or, equivalently,
 $$ \begin{align*} C\, \frac{|x-y|^{d+i}}{|x-w\,y|^{d+i}}, \end{align*} $$
$$ \begin{align*} C\, \frac{|x-y|^{d+i}}{|x-w\,y|^{d+i}}, \end{align*} $$
where
![]() $0\leq i\leq 2\,I$
. The rest follows.▪
$0\leq i\leq 2\,I$
. The rest follows.▪
Lemma 5.10 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem and let
$\Phi ^{\prime }$
be a basic root subsystem and let
![]() $\alpha _{1}$
, …,
$\alpha _{1}$
, …,
![]() $\alpha _{M}$
be distinct positive roots of
$\alpha _{M}$
be distinct positive roots of
![]() $\Phi ^{\prime }$
with
$\Phi ^{\prime }$
with
![]() $M\leq |\Phi ^{\prime }|$
and let
$M\leq |\Phi ^{\prime }|$
and let
![]() $\pi ^{\prime }(x)=\prod _{\alpha \in \Phi ^{\prime }_+}\,\langle \alpha ,x\rangle $
. Then
$\pi ^{\prime }(x)=\prod _{\alpha \in \Phi ^{\prime }_+}\,\langle \alpha ,x\rangle $
. Then
 $$ \begin{align} \partial_{\alpha_{M}}\,\cdots\,\partial_{\alpha_{1}}\,\pi^{\prime}(x) =\sum_{\beta_{1},\dots,\beta_{M}}\,\prod_{i=1}^{M}\,\langle\beta_{i},\alpha_{i}\rangle\,\prod_{\alpha\in\Phi^{\prime}_+\setminus\{\beta_{1},\dots,\beta_{M}\}}\,\langle\alpha,x\rangle, \end{align} $$
$$ \begin{align} \partial_{\alpha_{M}}\,\cdots\,\partial_{\alpha_{1}}\,\pi^{\prime}(x) =\sum_{\beta_{1},\dots,\beta_{M}}\,\prod_{i=1}^{M}\,\langle\beta_{i},\alpha_{i}\rangle\,\prod_{\alpha\in\Phi^{\prime}_+\setminus\{\beta_{1},\dots,\beta_{M}\}}\,\langle\alpha,x\rangle, \end{align} $$
where the sum is taken over distinct positive roots and the order of the
![]() $\beta _{i}$
’s is important.
$\beta _{i}$
’s is important.
Proof First note that
![]() $\partial _{\alpha _{k}}\,\langle \alpha ,x\rangle =\langle \alpha ,\alpha _{k}\rangle $
. The result then follows easily using induction on M and Leibnitz rule.▪
$\partial _{\alpha _{k}}\,\langle \alpha ,x\rangle =\langle \alpha ,\alpha _{k}\rangle $
. The result then follows easily using induction on M and Leibnitz rule.▪
Corollary 5.11 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem and let
$\Phi ^{\prime }$
be a basic root subsystem and let
![]() $\alpha _{1}$
, …,
$\alpha _{1}$
, …,
![]() $\alpha _{M}$
be distinct positive roots of
$\alpha _{M}$
be distinct positive roots of
![]() $\Phi ^{\prime }$
with
$\Phi ^{\prime }$
with
![]() $M<|\Phi ^{\prime }_+|$
and let
$M<|\Phi ^{\prime }_+|$
and let
![]() $\pi ^{\prime }(x)=\prod _{\alpha \in \Phi ^{\prime }_+}\,\langle \alpha ,x\rangle $
. Then for any positive root
$\pi ^{\prime }(x)=\prod _{\alpha \in \Phi ^{\prime }_+}\,\langle \alpha ,x\rangle $
. Then for any positive root
![]() $\alpha _{M+1}$
other than one of the
$\alpha _{M+1}$
other than one of the
![]() $\alpha _{k}$
,
$\alpha _{k}$
,
![]() $1\leq k\leq M$
, we have
$1\leq k\leq M$
, we have
on the set
![]() $\{x\colon \alpha _{k}(x)=0,\ k=1,\dots ,M+1\}$
.
$\{x\colon \alpha _{k}(x)=0,\ k=1,\dots ,M+1\}$
.
Proof Setting
![]() $\alpha _{i}(x)=0$
for
$\alpha _{i}(x)=0$
for
![]() $i=1$
, …, M in formula (5.9) gives
$i=1$
, …, M in formula (5.9) gives
 $$ \begin{align*} \partial_{\alpha_{M}}\,\cdots\,\partial_{\alpha_{1}}\,\pi^{\prime}(x) =\left[\sum_{\sigma\in S_{M}}\,\prod_{i=1}^{M}\,\langle\alpha_{\sigma(i)},\alpha_{i}\rangle\right]\,\prod_{\alpha\in\Phi^{\prime}_+\setminus\{\alpha_{1},\dots,\alpha_{M}\}}\,\langle\alpha,x\rangle. \end{align*} $$
$$ \begin{align*} \partial_{\alpha_{M}}\,\cdots\,\partial_{\alpha_{1}}\,\pi^{\prime}(x) =\left[\sum_{\sigma\in S_{M}}\,\prod_{i=1}^{M}\,\langle\alpha_{\sigma(i)},\alpha_{i}\rangle\right]\,\prod_{\alpha\in\Phi^{\prime}_+\setminus\{\alpha_{1},\dots,\alpha_{M}\}}\,\langle\alpha,x\rangle. \end{align*} $$
The rest is straightforward: the last product cancels on S because it contains the term
![]() $ \langle \alpha _{M+1},x\rangle $
.▪
$ \langle \alpha _{M+1},x\rangle $
.▪
Lemma 5.12 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem. Then
$\Phi ^{\prime }$
be a basic root subsystem. Then
![]() $\partial (\pi ^{\prime })\,\pi ^{\prime }(x)$
is a nonzero constant.
$\partial (\pi ^{\prime })\,\pi ^{\prime }(x)$
is a nonzero constant.
Remark 5.13 The exact value of
![]() $\partial (\pi ^{\prime })\,\pi ^{\prime }(x)$
is computed in [Reference Helgason19, Chapter II, Corollary 5.36]. We provide here an elementary proof that
$\partial (\pi ^{\prime })\,\pi ^{\prime }(x)$
is computed in [Reference Helgason19, Chapter II, Corollary 5.36]. We provide here an elementary proof that
![]() $\partial (\pi ^{\prime })\,\pi ^{\prime }(x)\not =0$
.
$\partial (\pi ^{\prime })\,\pi ^{\prime }(x)\not =0$
.
Proof It is clear that
![]() $\partial (\pi ^{\prime })\,\pi ^{\prime }(x)$
is a constant given that the degree of the operator
$\partial (\pi ^{\prime })\,\pi ^{\prime }(x)$
is a constant given that the degree of the operator
![]() $\partial (\pi ^{\prime })$
is equal to the degree of
$\partial (\pi ^{\prime })$
is equal to the degree of
![]() $\pi ^{\prime }(x)$
. Now, let
$\pi ^{\prime }(x)$
. Now, let
 $$ \begin{align*} S_{\lambda}(x)= \frac{\sum_{w\in W}\,\epsilon(w)\,e^{\langle \lambda,w\,x\rangle}}{\pi^{\prime}(x)}=\frac{\sum_{w\in W}\,\epsilon(w)\,e^{\langle w^{-1} \lambda,x\rangle}}{\pi^{\prime}(x)}, \end{align*} $$
$$ \begin{align*} S_{\lambda}(x)= \frac{\sum_{w\in W}\,\epsilon(w)\,e^{\langle \lambda,w\,x\rangle}}{\pi^{\prime}(x)}=\frac{\sum_{w\in W}\,\epsilon(w)\,e^{\langle w^{-1} \lambda,x\rangle}}{\pi^{\prime}(x)}, \end{align*} $$
where W is generated by the reflections
![]() $\sigma _{\alpha }$
,
$\sigma _{\alpha }$
,
![]() $\alpha \in \Phi ^{\prime }$
. Now,
$\alpha \in \Phi ^{\prime }$
. Now,
![]() $S_{\lambda }$
is an analytic function (the numerator is W skew-symmetric and analytic; in fact
$S_{\lambda }$
is an analytic function (the numerator is W skew-symmetric and analytic; in fact
![]() $S_{\lambda }$
is a constant multiple of
$S_{\lambda }$
is a constant multiple of
![]() $\pi (\lambda )$
times a spherical function). If we compute
$\pi (\lambda )$
times a spherical function). If we compute
![]() $\partial (\pi ^{\prime })\,(\pi ^{\prime }(x)\,S_{\lambda }(x))$
and set
$\partial (\pi ^{\prime })\,(\pi ^{\prime }(x)\,S_{\lambda }(x))$
and set
![]() $x=0$
, we get
$x=0$
, we get
The left hand side is equal to
![]() $\partial (\pi ^{\prime })\,(\pi ^{\prime }(x))\,S(0)$
since all terms involving derivatives of
$\partial (\pi ^{\prime })\,(\pi ^{\prime }(x))\,S(0)$
since all terms involving derivatives of
![]() $S_{\lambda }$
are eliminated by one of the roots (a consequence of Corollary 5.11). We can therefore conclude that
$S_{\lambda }$
are eliminated by one of the roots (a consequence of Corollary 5.11). We can therefore conclude that
![]() $\partial (\pi ^{\prime })\,(\pi ^{\prime }(x))\not =0$
.▪
$\partial (\pi ^{\prime })\,(\pi ^{\prime }(x))\not =0$
.▪
Proposition 5.14 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem,
$\Phi ^{\prime }$
be a basic root subsystem,
![]() $\Phi ^{\prime \prime }$
a subsystem of
$\Phi ^{\prime \prime }$
a subsystem of
![]() $\Phi ^{\prime }$
and let
$\Phi ^{\prime }$
and let
![]() $P_{\Phi ^{\prime \prime }}=\bigcup _{\alpha \in \Phi ^{\prime \prime }}\,H_{\alpha }$
and
$P_{\Phi ^{\prime \prime }}=\bigcup _{\alpha \in \Phi ^{\prime \prime }}\,H_{\alpha }$
and
![]() $\pi ^{\prime \prime }(x)=\prod _{\alpha \in \Phi ^{\prime \prime }}\,\alpha (x)$
. Suppose
$\pi ^{\prime \prime }(x)=\prod _{\alpha \in \Phi ^{\prime \prime }}\,\alpha (x)$
. Suppose
![]() $R(x,y)$
is defined as in (5.6). Note that
$R(x,y)$
is defined as in (5.6). Note that
![]() $R(x,y)=Q(x,y)\,\pi ^{\prime \prime }(x)\,\pi ^{\prime \prime }(y)$
, where Q is analytic since R is analytic and skew-symmetric with respect to
$R(x,y)=Q(x,y)\,\pi ^{\prime \prime }(x)\,\pi ^{\prime \prime }(y)$
, where Q is analytic since R is analytic and skew-symmetric with respect to
![]() $W^{\prime \prime }$
(the Weyl subgroup generated by the reflections
$W^{\prime \prime }$
(the Weyl subgroup generated by the reflections
![]() $\sigma _{\alpha }$
,
$\sigma _{\alpha }$
,
![]() $\alpha \in \Phi ^{\prime \prime }$
) in both variables. Then there exists a constant K independent of x and y such that
$\alpha \in \Phi ^{\prime \prime }$
) in both variables. Then there exists a constant K independent of x and y such that
 $$ \begin{align*} \mathop{\text{sup}}\limits_{x,y\in {\mathfrak{a}}^+\setminus P_{\Phi^{\prime\prime}}}\,\frac{|R(x,y)|}{\pi^{\prime\prime}(x)\,\pi^{\prime\prime}(y)} &\le \mathop{\text{sup}}\limits_{x,y\in {\mathfrak{a}}^+\setminus P_{\Phi^{\prime\prime}}}\frac{|\partial^{x}(\pi^{\prime\prime})\,\partial^{y}(\pi^{\prime\prime})\, R(x,y)|} {|\partial^{x}(\pi^{\prime\prime})\,\partial^{y}(\pi^{\prime\prime})\,(\pi^{\prime\prime}(x)\,\pi^{\prime\prime}(y)) |}\\ &= K\,\mathop{\text{sup}}\limits_{x,y\in {\mathfrak{a}}^+\setminus P_{\Phi^{\prime\prime}}}|\partial^{x}(\pi^{\prime\prime})\,\partial^{y}(\pi^{\prime\prime})\, R(x,y)|. \end{align*} $$
$$ \begin{align*} \mathop{\text{sup}}\limits_{x,y\in {\mathfrak{a}}^+\setminus P_{\Phi^{\prime\prime}}}\,\frac{|R(x,y)|}{\pi^{\prime\prime}(x)\,\pi^{\prime\prime}(y)} &\le \mathop{\text{sup}}\limits_{x,y\in {\mathfrak{a}}^+\setminus P_{\Phi^{\prime\prime}}}\frac{|\partial^{x}(\pi^{\prime\prime})\,\partial^{y}(\pi^{\prime\prime})\, R(x,y)|} {|\partial^{x}(\pi^{\prime\prime})\,\partial^{y}(\pi^{\prime\prime})\,(\pi^{\prime\prime}(x)\,\pi^{\prime\prime}(y)) |}\\ &= K\,\mathop{\text{sup}}\limits_{x,y\in {\mathfrak{a}}^+\setminus P_{\Phi^{\prime\prime}}}|\partial^{x}(\pi^{\prime\prime})\,\partial^{y}(\pi^{\prime\prime})\, R(x,y)|. \end{align*} $$
Proof We use the Cauchy Mean Value Theorem several times as in the proof of the multivariate de l’Hospital rule proposed by Lawlor [Reference Lawlor23]. More precisely, if x,
![]() $y\not \in H_{\alpha }$
, then, denoting by
$y\not \in H_{\alpha }$
, then, denoting by
![]() $x_{\alpha }$
and
$x_{\alpha }$
and
![]() $y_{\alpha }$
the projections of x and y on
$y_{\alpha }$
the projections of x and y on
![]() $H_{\alpha }$
,
$H_{\alpha }$
,
 $$ \begin{align*} \frac{R(x,y)}{\alpha(x)\,\alpha(y)}=\frac1{\alpha(y)}\frac{R(x,y)-R(x_{\alpha},y)}{\alpha(x)-\alpha(x_{\alpha})}= \frac1{\alpha(y)}\frac{\partial_{\alpha}^{x}R(x^{\prime},y)}{\partial_{\alpha}^{x}\alpha(x^{\prime})} \end{align*} $$
$$ \begin{align*} \frac{R(x,y)}{\alpha(x)\,\alpha(y)}=\frac1{\alpha(y)}\frac{R(x,y)-R(x_{\alpha},y)}{\alpha(x)-\alpha(x_{\alpha})}= \frac1{\alpha(y)}\frac{\partial_{\alpha}^{x}R(x^{\prime},y)}{\partial_{\alpha}^{x}\alpha(x^{\prime})} \end{align*} $$
for an intermediate point
![]() $x^{\prime }\in \mathfrak {a}^+\setminus H_{\alpha }$
. The same reasoning allows us to repeat the argument with
$x^{\prime }\in \mathfrak {a}^+\setminus H_{\alpha }$
. The same reasoning allows us to repeat the argument with
![]() $\partial _{\alpha }^{y}$
:
$\partial _{\alpha }^{y}$
:
 $$ \begin{align*} \frac{\partial_{\alpha}^{x}\,R(x^{\prime},y)}{\alpha(y)} =\frac{\partial_{\alpha}^{x}\,R(x^{\prime},y)-\partial_{\alpha}^{x}\,R(x^{\prime},y_{\alpha})}{\alpha(y)-\alpha(y_{\alpha})} =\frac{\partial_{\alpha}^{y}\,\partial_{\alpha}^{x}\,R(x^{\prime},y^{\prime})}{\partial_{\alpha}^{y}\alpha(y^{\prime})}. \end{align*} $$
$$ \begin{align*} \frac{\partial_{\alpha}^{x}\,R(x^{\prime},y)}{\alpha(y)} =\frac{\partial_{\alpha}^{x}\,R(x^{\prime},y)-\partial_{\alpha}^{x}\,R(x^{\prime},y_{\alpha})}{\alpha(y)-\alpha(y_{\alpha})} =\frac{\partial_{\alpha}^{y}\,\partial_{\alpha}^{x}\,R(x^{\prime},y^{\prime})}{\partial_{\alpha}^{y}\alpha(y^{\prime})}. \end{align*} $$
This was done for a single
![]() $\alpha $
but we can repeat the process for all the roots
$\alpha $
but we can repeat the process for all the roots
![]() $\alpha $
,
$\alpha $
,
![]() $\alpha \in {\Phi ^{\prime \prime }}$
. This is made possible by Corollary 5.11. Note that
$\alpha \in {\Phi ^{\prime \prime }}$
. This is made possible by Corollary 5.11. Note that
![]() $\partial ^{x}(\pi ^{\prime \prime })\,\partial ^{y}(\pi ^{\prime \prime })\,(\pi ^{\prime \prime }(x)\,\pi ^{\prime \prime }(y))\not =0$
by Lemma 5.12.▪
$\partial ^{x}(\pi ^{\prime \prime })\,\partial ^{y}(\pi ^{\prime \prime })\,(\pi ^{\prime \prime }(x)\,\pi ^{\prime \prime }(y))\not =0$
by Lemma 5.12.▪
Proposition 5.15 Let
![]() $\Phi ^{\prime }$
be a basic root subsystem of
$\Phi ^{\prime }$
be a basic root subsystem of
![]() $\Phi $
and
$\Phi $
and
![]() $\Phi ^{\prime \prime }$
a subsystem of
$\Phi ^{\prime \prime }$
a subsystem of
![]() $\Phi ^{\prime }_+$
. Suppose
$\Phi ^{\prime }_+$
. Suppose
![]() $0<c\leq \min \{1,1/(4\,C_{1})\}$
where
$0<c\leq \min \{1,1/(4\,C_{1})\}$
where
![]() $C_{1}$
is as in Remark 3.11 and let
$C_{1}$
is as in Remark 3.11 and let
Suppose
![]() $R(x,y)$
is defined as in (5.6). Then there exists a constant K independent of x and y such that
$R(x,y)$
is defined as in (5.6). Then there exists a constant K independent of x and y such that
 $$ \begin{align*} \mathop{\text{sup}}\limits_{x,y\in S_{\Phi^{\prime},c}}\,\frac{|R(x,y)|}{\pi^{\prime\prime}(x)\,\pi^{\prime\prime}(y)} \leq K\,c^{d}. \end{align*} $$
$$ \begin{align*} \mathop{\text{sup}}\limits_{x,y\in S_{\Phi^{\prime},c}}\,\frac{|R(x,y)|}{\pi^{\prime\prime}(x)\,\pi^{\prime\prime}(y)} \leq K\,c^{d}. \end{align*} $$
Proof This result follows directly from Corollary 5.5, Lemma 5.9, and Proposition 5.14.
5.4 Proof of Conjecture 1
Theorem 5.16 Conjecture 1 is valid for all complex root systems.
Proof We use induction on the rank r of the root system. The result is true in rank 1 by Lemma 4.4.
Assume that it is true for ranks 1,…,
![]() $r-1$
,
$r-1$
,
![]() $r\geq 2$
. Let
$r\geq 2$
. Let
![]() $\Phi $
be a rank r complex root system. The induction hypothesis means that there exist constants
$\Phi $
be a rank r complex root system. The induction hypothesis means that there exist constants
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{2}$
such that for
$K_{2}$
such that for
![]() $x\in B^+,y\in S^+$
, we have
$x\in B^+,y\in S^+$
, we have
 $$ \begin{align} K_{1}\leq |x-y|^{d}\,\prod_{\alpha\in \Phi^{\prime}_+}\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W^{\prime}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}}{\pi^{\prime}(x)\,\pi^{\prime}(y)}\leq K_{2} \end{align} $$
$$ \begin{align} K_{1}\leq |x-y|^{d}\,\prod_{\alpha\in \Phi^{\prime}_+}\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W^{\prime}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}}{\pi^{\prime}(x)\,\pi^{\prime}(y)}\leq K_{2} \end{align} $$
for every basic root subsystem
![]() $\Phi ^{\prime }$
of
$\Phi ^{\prime }$
of
![]() $\Phi $
which is of lower rank. Since the number of such subsystems is finite, we may assume that
$\Phi $
which is of lower rank. Since the number of such subsystems is finite, we may assume that
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{2}$
are independent from the choice of
$K_{2}$
are independent from the choice of
![]() $\Phi ^{\prime }$
(depend only on
$\Phi ^{\prime }$
(depend only on
![]() $\Phi $
).
$\Phi $
).
Fix c such that
 $$ \begin{align*} 0<c\leq \min\left\{1,\frac{1}{4\,C_{1}},\frac{\sqrt{K_{0}/2}}{\sqrt[d]{2\,|W|}}\right\}, \end{align*} $$
$$ \begin{align*} 0<c\leq \min\left\{1,\frac{1}{4\,C_{1}},\frac{\sqrt{K_{0}/2}}{\sqrt[d]{2\,|W|}}\right\}, \end{align*} $$
where
![]() $C_{1}$
is as in Remark 3.11,
$C_{1}$
is as in Remark 3.11,
![]() $K_{0}$
is as in Lemma 5.3 and such that
$K_{0}$
is as in Lemma 5.3 and such that
where K is as in Proposition 5.14 (we consider all the basic root subsystems
![]() $\Phi ^{\prime \prime }\subseteq \Phi ^{\prime }$
for all possible basic root subsystems
$\Phi ^{\prime \prime }\subseteq \Phi ^{\prime }$
for all possible basic root subsystems
![]() $\Phi ^{\prime } $
of
$\Phi ^{\prime } $
of
![]() $\Phi $
and take the largest corresponding value of K). Recall that N denotes the maximal length of positive roots in
$\Phi $
and take the largest corresponding value of K). Recall that N denotes the maximal length of positive roots in
![]() $\Phi $
and M is the number of all positive roots in
$\Phi $
and M is the number of all positive roots in
![]() $\Phi $
. By Lemma 5.1, if
$\Phi $
. By Lemma 5.1, if
![]() $S_{\Phi ^{\prime },c^{\prime }}$
is as in (5.10), we have
$S_{\Phi ^{\prime },c^{\prime }}$
is as in (5.10), we have
where the union is taken over all basic root subsystems
![]() $\Phi ^{\prime }$
of
$\Phi ^{\prime }$
of
![]() $\Phi $
and
$\Phi $
and
![]() $c^{\prime }$
with
$c^{\prime }$
with
![]() $c/N^{r}\leq c^{\prime }\leq c$
. Since the number of such basic root subsystems is finite, we only have to prove the Conjecture 1 for a specific choice of
$c/N^{r}\leq c^{\prime }\leq c$
. Since the number of such basic root subsystems is finite, we only have to prove the Conjecture 1 for a specific choice of
![]() $\Phi ^{\prime }$
where x, y satisfy
$\Phi ^{\prime }$
where x, y satisfy
for
![]() $\alpha \in \Phi ^{\prime }_+$
,
$\alpha \in \Phi ^{\prime }_+$
,
![]() $\beta \in \Phi _{0}^+$
and any
$\beta \in \Phi _{0}^+$
and any
![]() $c^{\prime }$
such that
$c^{\prime }$
such that
![]() $c/N^{r}\leq c^{\prime }\leq c$
.
$c/N^{r}\leq c^{\prime }\leq c$
.
Recall that c is fixed. We ensure that the constants in the estimates of the Conjecture 1 depend only on c, when
![]() $\Phi ^{\prime }$
is fixed and
$\Phi ^{\prime }$
is fixed and
![]() $c^{\prime }$
varies in the segment
$c^{\prime }$
varies in the segment
![]() $[c/N^{r},c]$
.
$[c/N^{r},c]$
.
We examine three possible cases:
![]() $\underline {\Phi ^{\prime }=\emptyset }$
: in that case, Lemma 5.6 allows us to conclude.
$\underline {\Phi ^{\prime }=\emptyset }$
: in that case, Lemma 5.6 allows us to conclude.
![]() $\underline {\Phi ^{\prime }=\Phi }$
: in that case, the result follows from (5.13) and from Proposition 4.3 (if we refer to the notation of Proposition 4.3,
$\underline {\Phi ^{\prime }=\Phi }$
: in that case, the result follows from (5.13) and from Proposition 4.3 (if we refer to the notation of Proposition 4.3,
![]() $D=1/c^{\prime }$
and the constants depend on D; this is where
$D=1/c^{\prime }$
and the constants depend on D; this is where
![]() $c/N^{r}\leq c^{\prime }\leq c $
comes into play).
$c/N^{r}\leq c^{\prime }\leq c $
comes into play).
![]() $\underline {1\leq \mbox {rank}(\Phi ^{\prime })< \mbox {rank}(\Phi )}$
: We have
$\underline {1\leq \mbox {rank}(\Phi ^{\prime })< \mbox {rank}(\Phi )}$
: We have
![]() $\phi _{\beta }(x,y)=\beta (y)$
and
$\phi _{\beta }(x,y)=\beta (y)$
and
![]() $\beta (x)\,\beta (y)/2\leq \phi _{\beta }^{2}(x,y)\leq 2\,\beta (x)\,\beta (y)$
by Corollary 5.5. Hence,
$\beta (x)\,\beta (y)/2\leq \phi _{\beta }^{2}(x,y)\leq 2\,\beta (x)\,\beta (y)$
by Corollary 5.5. Hence,
We used the fact that
![]() $|\Phi _{0}^+|\leq |\Phi _+|\leq M$
.
$|\Phi _{0}^+|\leq |\Phi _+|\leq M$
.
For a basic subsystem
![]() $\Phi ^{\prime \prime }\subseteq \Phi ^{\prime }$
, let
$\Phi ^{\prime \prime }\subseteq \Phi ^{\prime }$
, let
 $$ \begin{align*} X_{\Phi^{\prime\prime}}&=\{(x,y)\in S_{\Phi^{\prime},c^{\prime}}\colon \alpha(y)\leq 2 N\,C_{1}\,|x-y| \mbox{ for } \alpha\in \Phi^{\prime\prime}_+ \\&\qquad\qquad\qquad\qquad\mbox{ and }\alpha(y)>2\,C_{1}\,|x-y| \mbox{ for } \alpha\in \Phi^{\prime}_+\setminus\Phi^{\prime\prime}\} \end{align*} $$
$$ \begin{align*} X_{\Phi^{\prime\prime}}&=\{(x,y)\in S_{\Phi^{\prime},c^{\prime}}\colon \alpha(y)\leq 2 N\,C_{1}\,|x-y| \mbox{ for } \alpha\in \Phi^{\prime\prime}_+ \\&\qquad\qquad\qquad\qquad\mbox{ and }\alpha(y)>2\,C_{1}\,|x-y| \mbox{ for } \alpha\in \Phi^{\prime}_+\setminus\Phi^{\prime\prime}\} \end{align*} $$
and note that the union of all
![]() $X_{\Phi ^{\prime \prime }}$
for
$X_{\Phi ^{\prime \prime }}$
for
![]() $\Phi ^{\prime \prime }\subseteq \Phi ^{\prime }_+$
gives
$\Phi ^{\prime \prime }\subseteq \Phi ^{\prime }_+$
gives
![]() $S_{\Phi ^{\prime },c^{\prime }}$
. Indeed, for given x and y,
$S_{\Phi ^{\prime },c^{\prime }}$
. Indeed, for given x and y,
![]() $\Phi ^{\prime \prime }$
is generated by the simple roots
$\Phi ^{\prime \prime }$
is generated by the simple roots
![]() $\alpha _{i}$
such that
$\alpha _{i}$
such that
![]() $\alpha _{i}(y)\leq 2 \,C_{1}\,|x-y|$
(it may happen that
$\alpha _{i}(y)\leq 2 \,C_{1}\,|x-y|$
(it may happen that
![]() $\Phi ^{\prime \prime }=\emptyset $
in which case
$\Phi ^{\prime \prime }=\emptyset $
in which case
![]() $X_{\Phi ^{\prime \prime }}=\{(x,y)\in S_{\Phi ^{\prime },c^{\prime }}\colon \alpha (y)>2\,C_{1}\,|x-y|\ \mbox {for }\alpha \in \Phi ^{\prime }_+\}$
).
$X_{\Phi ^{\prime \prime }}=\{(x,y)\in S_{\Phi ^{\prime },c^{\prime }}\colon \alpha (y)>2\,C_{1}\,|x-y|\ \mbox {for }\alpha \in \Phi ^{\prime }_+\}$
).
If
![]() $(x,y)\in X_{\Phi ^{\prime \prime }}$
and
$(x,y)\in X_{\Phi ^{\prime \prime }}$
and
![]() $\alpha \in \Phi ^{\prime \prime }$
then
$\alpha \in \Phi ^{\prime \prime }$
then
If
![]() $(x,y)\in X_{\Phi ^{\prime \prime }}$
and
$(x,y)\in X_{\Phi ^{\prime \prime }}$
and
![]() $\alpha \in \Phi ^{\prime }\setminus \Phi ^{\prime \prime }$
then
$\alpha \in \Phi ^{\prime }\setminus \Phi ^{\prime \prime }$
then
![]() $\alpha (x)\geq \alpha (y)-C_{1}\,|x-y|> \alpha (y)/2$
. Hence,
$\alpha (x)\geq \alpha (y)-C_{1}\,|x-y|> \alpha (y)/2$
. Hence,
![]() $|x-y| < (2\,C_{1})^{-1}\,\alpha (y)\leq 2\,(2\,C_{1})^{-1}\,\alpha (x)$
. Therefore,
$|x-y| < (2\,C_{1})^{-1}\,\alpha (y)\leq 2\,(2\,C_{1})^{-1}\,\alpha (x)$
. Therefore,
Let
 $$ \begin{align*} A&=\frac{|W|w_{d} P^{W}(x,y)}{\Omega(x,y)}=|x-y|^{d}\,\prod_{\gamma\in \Phi_+}\,\phi_{\gamma}(x,y)^{2}\,\frac{\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}}{\pi(x)\,\pi(y)}\\ &=\frac{\prod_{\beta\in \Phi_{0}^+}\,\phi_{\beta}(x,y)^{2}}{\prod_{\beta\in \Phi_{0}^+}\,\beta(x)\,\beta(y)} \,\left[\vphantom{\left. +\underbrace{|x-y|^{d}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{ \sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}} } {\pi^{\prime}(x)\,\pi^{\prime}(y)}}_{\widetilde A}\right]}|x-y|^{d}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W^{\prime}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}}{\pi^{\prime}(x)\,\pi^{\prime}(y)} \right.\\&\qquad\left. +\underbrace{|x-y|^{d}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{ \sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}} } {\pi^{\prime}(x)\,\pi^{\prime}(y)}}_{\widetilde A}\right]. \end{align*} $$
$$ \begin{align*} A&=\frac{|W|w_{d} P^{W}(x,y)}{\Omega(x,y)}=|x-y|^{d}\,\prod_{\gamma\in \Phi_+}\,\phi_{\gamma}(x,y)^{2}\,\frac{\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}}{\pi(x)\,\pi(y)}\\ &=\frac{\prod_{\beta\in \Phi_{0}^+}\,\phi_{\beta}(x,y)^{2}}{\prod_{\beta\in \Phi_{0}^+}\,\beta(x)\,\beta(y)} \,\left[\vphantom{\left. +\underbrace{|x-y|^{d}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{ \sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}} } {\pi^{\prime}(x)\,\pi^{\prime}(y)}}_{\widetilde A}\right]}|x-y|^{d}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W^{\prime}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}}}{\pi^{\prime}(x)\,\pi^{\prime}(y)} \right.\\&\qquad\left. +\underbrace{|x-y|^{d}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{ \sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d}} } {\pi^{\prime}(x)\,\pi^{\prime}(y)}}_{\widetilde A}\right]. \end{align*} $$
Now, using (5.11) and (5.14), we get
Let us fix
![]() $\Phi ^{\prime \prime }\subset \Phi ^{\prime }$
. For
$\Phi ^{\prime \prime }\subset \Phi ^{\prime }$
. For
![]() $(x,y)\in X_{\Phi ^{\prime \prime }}$
, using inequalities (5.15) and (5.16) and next the condition (5.12) on c and Proposition 5.15, we obtain
$(x,y)\in X_{\Phi ^{\prime \prime }}$
, using inequalities (5.15) and (5.16) and next the condition (5.12) on c and Proposition 5.15, we obtain
 $$ \begin{align*} |\widetilde A|&\leq (1+2\,NC_{1})^{2\,|\Phi^{\prime\prime}_+|}\,(2+C_{1}^{-1})^{2\,|\Phi^{\prime}_+\setminus\Phi^{\prime\prime}_+|}\, \left|\frac{R(x,y)}{\pi^{\prime\prime}(x)\,\pi^{\prime\prime}(y)}\right|\\ &\leq (1+2\,NC_{1})^{M}\,(2+C_{1}^{-1})^{M}\,K\,c^{d}\leq K_{1}/2. \end{align*} $$
$$ \begin{align*} |\widetilde A|&\leq (1+2\,NC_{1})^{2\,|\Phi^{\prime\prime}_+|}\,(2+C_{1}^{-1})^{2\,|\Phi^{\prime}_+\setminus\Phi^{\prime\prime}_+|}\, \left|\frac{R(x,y)}{\pi^{\prime\prime}(x)\,\pi^{\prime\prime}(y)}\right|\\ &\leq (1+2\,NC_{1})^{M}\,(2+C_{1}^{-1})^{M}\,K\,c^{d}\leq K_{1}/2. \end{align*} $$
This is enough to conclude from (5.17) that
![]() $A\asymp 1$
.▪
$A\asymp 1$
.▪
6 Newton’s kernel
Theorem 6.1 Conjecture 2 is valid for all complex root systems.
Proof The proof follows the same pattern as the proof of Theorem 5.16 for the Poisson kernel with suitable adjustments. Given that, unlike in the case of the Poisson kernel, the domain of the Newton kernel is unbounded, it is worthwhile to review the “road-map” of the proof.
We first introduce the concept of the basic subalgebra generated by simple roots in Definition 3.1. The crucial step is then given in Lemma 5.1 where it is shown that given a Lie algebra
![]() $\Phi $
and
$\Phi $
and
![]() $c>0$
, a basic subalgebra
$c>0$
, a basic subalgebra
![]() $\Phi ^{\prime }$
can be found that
$\Phi ^{\prime }$
can be found that
![]() $ c^{\prime }\,\alpha (y)< |x-y|<c^{\prime }\,\beta (y)$
for
$ c^{\prime }\,\alpha (y)< |x-y|<c^{\prime }\,\beta (y)$
for
![]() $\alpha \in \Phi ^{\prime }$
and
$\alpha \in \Phi ^{\prime }$
and
![]() $\beta \in \Phi \setminus \Phi ^{\prime }$
with
$\beta \in \Phi \setminus \Phi ^{\prime }$
with
![]() $c^{\prime }$
in an interval bounded above and below by universal multiples of c, namely
$c^{\prime }$
in an interval bounded above and below by universal multiples of c, namely
![]() $c^{\prime }\in [c/N^{r},c]$
.
$c^{\prime }\in [c/N^{r},c]$
.
We start by showing that if
![]() $|x-y|\leq c\,\alpha (y)$
for every positive root
$|x-y|\leq c\,\alpha (y)$
for every positive root
![]() $\alpha $
then Conjecture 2 holds provided c is chosen small enough. The proof is the same as the proof of Proposition 4.3 and it only depends on the formula (2.7) analogous to (2.3). This proof is valid in the general Dunkl case.
$\alpha $
then Conjecture 2 holds provided c is chosen small enough. The proof is the same as the proof of Proposition 4.3 and it only depends on the formula (2.7) analogous to (2.3). This proof is valid in the general Dunkl case.
In the other extreme case, when
![]() $ c\,\alpha (y)\leq |x-y|$
for every positive root
$ c\,\alpha (y)\leq |x-y|$
for every positive root
![]() $\alpha $
, the Conjecture 1 in the complex case holds provided that c is small enough, by Lemma 5.6. Once more, the same proof holds for the Newton kernel in the case
$\alpha $
, the Conjecture 1 in the complex case holds provided that c is small enough, by Lemma 5.6. Once more, the same proof holds for the Newton kernel in the case
![]() $d\geq 3$
.
$d\geq 3$
.
It is important to note that the rank 1 case for
![]() $d\geq 3$
which is handled by Lemma 4.4 in the Poisson kernel case, follows practically the same proof in the case of the Newton kernel.
$d\geq 3$
which is handled by Lemma 4.4 in the Poisson kernel case, follows practically the same proof in the case of the Newton kernel.
The rest of the proof of Conjecture 2 follows the same line as that of Theorem 5.16. Indeed, as for the Poisson kernel, we define the subregions of
![]() $\overline {\mathfrak {a}^+}\times \overline {\mathfrak {a}^+}$
in the case of the Newton kernel by
$\overline {\mathfrak {a}^+}\times \overline {\mathfrak {a}^+}$
in the case of the Newton kernel by
For a fixed value of c, the pair x, y will fall in one of the regions
![]() $S_{\Phi ^{\prime },c^{\prime }}$
where
$S_{\Phi ^{\prime },c^{\prime }}$
where
![]() $c^{\prime }$
is in a range bounded above and below by universal multiples of c. Then there are three cases:
$c^{\prime }$
is in a range bounded above and below by universal multiples of c. Then there are three cases:
![]() $\Phi ^{\prime }=\Phi $
,
$\Phi ^{\prime }=\Phi $
,
![]() $\Phi ^{\prime }=\emptyset $
and the “in between case.” The first two situations are covered by the arguments given above. For the “in between case,” we proceed as in the case of the Poisson kernel and write
$\Phi ^{\prime }=\emptyset $
and the “in between case.” The first two situations are covered by the arguments given above. For the “in between case,” we proceed as in the case of the Poisson kernel and write
 $$ \begin{align*} A&=\frac{|W|\,(2-d)\,w_{d}\,N^{W}(x,y)}{\tilde{\Omega}(x,y)}=|x-y|^{d-2}\,\prod_{\gamma\in \Phi_+}\,\phi_{\gamma}(x,y)^{2}\,\frac{\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\,y|^{d-2}}}{\pi(x)\,\pi(y)}\\ &=\frac{\prod_{\beta\in \Phi_{0}^+}\,\phi_{\beta}(x,y)^{2}}{\prod_{\beta\in \Phi_{0}^+}\,\beta(x)\,\beta(y)} \,\left[\vphantom{\left. +\underbrace{|x-y|^{d-2}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d-2}}} {\pi^{\prime}(x)\,\pi^{\prime}(y)}}_{\widetilde A}\right]}|x-y|^{d-2}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W^{\prime}}\,\frac{\epsilon(w)}{|x-w\,y|^{d-2}}}{\pi^{\prime}(x)\,\pi^{\prime}(y)} \right.\\&\qquad\left. +\underbrace{|x-y|^{d-2}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d-2}}} {\pi^{\prime}(x)\,\pi^{\prime}(y)}}_{\widetilde A}\right], \end{align*} $$
$$ \begin{align*} A&=\frac{|W|\,(2-d)\,w_{d}\,N^{W}(x,y)}{\tilde{\Omega}(x,y)}=|x-y|^{d-2}\,\prod_{\gamma\in \Phi_+}\,\phi_{\gamma}(x,y)^{2}\,\frac{\sum_{w\in W}\,\frac{\epsilon(w)}{|x-w\,y|^{d-2}}}{\pi(x)\,\pi(y)}\\ &=\frac{\prod_{\beta\in \Phi_{0}^+}\,\phi_{\beta}(x,y)^{2}}{\prod_{\beta\in \Phi_{0}^+}\,\beta(x)\,\beta(y)} \,\left[\vphantom{\left. +\underbrace{|x-y|^{d-2}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d-2}}} {\pi^{\prime}(x)\,\pi^{\prime}(y)}}_{\widetilde A}\right]}|x-y|^{d-2}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W^{\prime}}\,\frac{\epsilon(w)}{|x-w\,y|^{d-2}}}{\pi^{\prime}(x)\,\pi^{\prime}(y)} \right.\\&\qquad\left. +\underbrace{|x-y|^{d-2}\,\prod_{\alpha\in \Phi^{\prime}_+}\,\phi_{\alpha}(x,y)^{2}\,\frac{\sum_{w\in W_{0}}\,\frac{\epsilon(w)}{|x-w\,y|^{d-2}}} {\pi^{\prime}(x)\,\pi^{\prime}(y)}}_{\widetilde A}\right], \end{align*} $$
where
![]() $\tilde {\Omega }(x,y)$
refers to the conjectured upper and lower bound for the Newton kernel (as per Conjecture 2). The end of the proof is the same as in the proof of Theorem 5.16 and uses, among others, induction on the rank of a subsystem.▪
$\tilde {\Omega }(x,y)$
refers to the conjectured upper and lower bound for the Newton kernel (as per Conjecture 2). The end of the proof is the same as in the proof of Theorem 5.16 and uses, among others, induction on the rank of a subsystem.▪
6.1 Invariant Newton kernel on
 $\mathbf {R}^{2}$
$\mathbf {R}^{2}$
Theorem 2.7 does not cover the case
![]() $d=2$
. Let us discuss the case of the
$d=2$
. Let us discuss the case of the
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
root systems in
$A_{2}$
root systems in
![]() $\mathbf {R}^{2}$
.
$\mathbf {R}^{2}$
.
We use the normalization
![]() $\|\alpha _{i}\|^{2}=2$
. It will be convenient to use the functions
$\|\alpha _{i}\|^{2}=2$
. It will be convenient to use the functions
Proposition 6.2 In the case
![]() $A_{1}$
in
$A_{1}$
in
![]() $R^{2}$
, we have
$R^{2}$
, we have
 $$ \begin{align*} N^{W}(x,y)=-\frac{1}{2\,\pi} \,\frac{1}{|x-y|^{2}} \,\frac{\ln(1+\psi_{\alpha,\alpha}(x,y))}{\psi_{\alpha,\alpha}(x,y)}. \end{align*} $$
$$ \begin{align*} N^{W}(x,y)=-\frac{1}{2\,\pi} \,\frac{1}{|x-y|^{2}} \,\frac{\ln(1+\psi_{\alpha,\alpha}(x,y))}{\psi_{\alpha,\alpha}(x,y)}. \end{align*} $$
In the case
![]() $A_{2}$
in
$A_{2}$
in
![]() $R^{2}$
, we have
$R^{2}$
, we have
where the logarithmic correction factor is given by
 $$ \begin{align*} L(x,y)= {\ln\frac{(1+\psi_{\alpha,\alpha})\,(1+\psi_{\beta,\beta})(1+\psi_{\alpha+\beta,\alpha+\beta})}{(1+\psi_{\alpha,\alpha}+\psi_{\beta,\beta}+\psi_{\alpha,\beta})\,(1+\psi_{\alpha,\alpha}+\psi_{\beta,\beta}+\psi_{\beta,\alpha})}}. \end{align*} $$
$$ \begin{align*} L(x,y)= {\ln\frac{(1+\psi_{\alpha,\alpha})\,(1+\psi_{\beta,\beta})(1+\psi_{\alpha+\beta,\alpha+\beta})}{(1+\psi_{\alpha,\alpha}+\psi_{\beta,\beta}+\psi_{\alpha,\beta})\,(1+\psi_{\alpha,\alpha}+\psi_{\beta,\beta}+\psi_{\beta,\alpha})}}. \end{align*} $$
Proof In the rank 1 case with
![]() $d=2$
, we have
$d=2$
, we have
 $$ \begin{align*} N^{W}(x,y)&=\frac{1}{2\,\pi}\,\frac{\ln|x-y|-\ln|x-\sigma\,y|} {\alpha(x)\,\alpha(y)} =-\frac{1}{4\,\pi}\,\frac{\ln\frac{|x-\sigma\,y|^{2}}{|x-y|^{2}}}{\alpha(x)\,\alpha(y)}\\ &=-\frac{1}{2\,\pi} \,\frac{1}{|x-y|^{2}} \,\frac{\ln(1+\psi_{\alpha,\alpha}(x,y))}{\psi_{\alpha,\alpha}(x,y)}. \end{align*} $$
$$ \begin{align*} N^{W}(x,y)&=\frac{1}{2\,\pi}\,\frac{\ln|x-y|-\ln|x-\sigma\,y|} {\alpha(x)\,\alpha(y)} =-\frac{1}{4\,\pi}\,\frac{\ln\frac{|x-\sigma\,y|^{2}}{|x-y|^{2}}}{\alpha(x)\,\alpha(y)}\\ &=-\frac{1}{2\,\pi} \,\frac{1}{|x-y|^{2}} \,\frac{\ln(1+\psi_{\alpha,\alpha}(x,y))}{\psi_{\alpha,\alpha}(x,y)}. \end{align*} $$
In the
![]() $A_{2}$
case,
$A_{2}$
case,
 $$ \begin{align*} N^{W}(x,y)&=\frac{1}{2\,\pi}\,\sum_{w\in W}\,\epsilon(w)\,\frac{\ln|x-w\,y|} {\pi(x)\,\pi(y)} =\frac{1}{2\,\pi}\,\frac{\ln\frac{|x-y|\,|x-\sigma_{\alpha}\,\sigma_{\beta}\,y|\,|x-\sigma_{\beta}\,\sigma_{\alpha}\,y|}{|x-\sigma_{\alpha}\,y|\,|x-\sigma_{\beta}\,y|\,|x-\sigma_{\alpha+\beta}|}}{\pi(x)\,\pi(y)}\\ &=-\frac{1}{4\,\pi}\,\frac{\ln\frac{|x-\sigma_{\alpha}\,y|^{2}\,|x-\sigma_{\beta}\,y|^{2}\,|x-\sigma_{\alpha+\beta}|^{2}}{|x-y|^{2}\,|x-\sigma_{\alpha}\,\sigma_{\beta}\,y|^{2}\,|x-\sigma_{\beta}\,\sigma_{\alpha}\,y|^{2}}}{\pi(x)\,\pi(y)}\\ &=-\frac{C^{3}}{4\,\pi}\,\frac{1}{|x-y|^{6}} \frac{L(x,y)}{\prod_{\gamma>0}\,\psi_{\gamma,\gamma}(x,y)} \end{align*} $$
$$ \begin{align*} N^{W}(x,y)&=\frac{1}{2\,\pi}\,\sum_{w\in W}\,\epsilon(w)\,\frac{\ln|x-w\,y|} {\pi(x)\,\pi(y)} =\frac{1}{2\,\pi}\,\frac{\ln\frac{|x-y|\,|x-\sigma_{\alpha}\,\sigma_{\beta}\,y|\,|x-\sigma_{\beta}\,\sigma_{\alpha}\,y|}{|x-\sigma_{\alpha}\,y|\,|x-\sigma_{\beta}\,y|\,|x-\sigma_{\alpha+\beta}|}}{\pi(x)\,\pi(y)}\\ &=-\frac{1}{4\,\pi}\,\frac{\ln\frac{|x-\sigma_{\alpha}\,y|^{2}\,|x-\sigma_{\beta}\,y|^{2}\,|x-\sigma_{\alpha+\beta}|^{2}}{|x-y|^{2}\,|x-\sigma_{\alpha}\,\sigma_{\beta}\,y|^{2}\,|x-\sigma_{\beta}\,\sigma_{\alpha}\,y|^{2}}}{\pi(x)\,\pi(y)}\\ &=-\frac{C^{3}}{4\,\pi}\,\frac{1}{|x-y|^{6}} \frac{L(x,y)}{\prod_{\gamma>0}\,\psi_{\gamma,\gamma}(x,y)} \end{align*} $$
(using Lemma 3.1 repeatedly).▪
It is noteworthy that, in the
![]() $A_{1}$
case, the behavior of
$A_{1}$
case, the behavior of
![]() $N^{W}(x,y)$
for
$N^{W}(x,y)$
for
![]() $\psi _{\alpha ,\alpha }(x,y)\leq 1$
is comparable with
$\psi _{\alpha ,\alpha }(x,y)\leq 1$
is comparable with
![]() $-\frac {C}{4\,\pi }\,\frac {1}{|x-y|^{2}}$
, and the behavior for
$-\frac {C}{4\,\pi }\,\frac {1}{|x-y|^{2}}$
, and the behavior for
![]() $\psi _{\alpha ,\alpha }(x,y)\geq 1$
is comparable with
$\psi _{\alpha ,\alpha }(x,y)\geq 1$
is comparable with
![]() $-\frac {C}{4\,\pi }\,\frac {1}{\alpha (x)\alpha (y)}\,\ln \psi _{\alpha ,\alpha }(x,y)$
.
$-\frac {C}{4\,\pi }\,\frac {1}{\alpha (x)\alpha (y)}\,\ln \psi _{\alpha ,\alpha }(x,y)$
.
In the
![]() $A_{2}$
case, the techniques from Section 4.1 imply that for
$A_{2}$
case, the techniques from Section 4.1 imply that for
![]() $\alpha (x),\beta (x)\le c|x-y|^{2}$
one has
$\alpha (x),\beta (x)\le c|x-y|^{2}$
one has
![]() $N^{W}(x,y)\asymp -\frac {1}{|x-y|^{6}}.$
$N^{W}(x,y)\asymp -\frac {1}{|x-y|^{6}}.$
Note that in the above cases, the estimates
 $$ \begin{align*} N^{W}(x,y)\asymp \frac{N^{\mathbf{R}^{2}}(x,y)}{\prod_{\alpha> 0 \ }|x-\sigma_{\alpha} y|^{2}} \end{align*} $$
$$ \begin{align*} N^{W}(x,y)\asymp \frac{N^{\mathbf{R}^{2}}(x,y)}{\prod_{\alpha> 0 \ }|x-\sigma_{\alpha} y|^{2}} \end{align*} $$
are not true.
7 Rank one direct product case
 $\mathbb {Z}_{2}^{J}$
$\mathbb {Z}_{2}^{J}$
The rank one direct product case
![]() $\mathbb {Z}_{2}^{J}$
is an important case of Dunkl analysis, developed intensely in recent years, see e.g., [Reference Deleaval8, Reference Dziubański13, Reference Nowak and Stempak26–Reference Nowak, Stempak and Szarek28, Reference Thangavelu and Xu34, Reference Xu36]. In these papers, the root systems
$\mathbb {Z}_{2}^{J}$
is an important case of Dunkl analysis, developed intensely in recent years, see e.g., [Reference Deleaval8, Reference Dziubański13, Reference Nowak and Stempak26–Reference Nowak, Stempak and Szarek28, Reference Thangavelu and Xu34, Reference Xu36]. In these papers, the root systems
![]() $B_{1}\times \cdots B_{1}$
are commonly considered. An explicit formula for the intertwining operator in the latter (noninvariant) case was obtained in [Reference Xu36], and generalized in [Reference Maslouhi and Yousffi25] in the case of orthogonal positive root systems. In our approach, we consider equivalently the root systems
$B_{1}\times \cdots B_{1}$
are commonly considered. An explicit formula for the intertwining operator in the latter (noninvariant) case was obtained in [Reference Xu36], and generalized in [Reference Maslouhi and Yousffi25] in the case of orthogonal positive root systems. In our approach, we consider equivalently the root systems
![]() $A_{1}\times \cdots A_{1}$
, and the intertwining operator formula obtained in [Reference Sawyer33] for the
$A_{1}\times \cdots A_{1}$
, and the intertwining operator formula obtained in [Reference Sawyer33] for the
![]() $A_{1}$
root system. This leads to estimates of the
$A_{1}$
root system. This leads to estimates of the
![]() $P^{W}$
and
$P^{W}$
and
![]() $N^{W}$
kernels both in
$N^{W}$
kernels both in
![]() $A_{1}\times \cdots A_{1}$
and
$A_{1}\times \cdots A_{1}$
and
![]() $B_{1}\times \cdots B_{1}$
cases.
$B_{1}\times \cdots B_{1}$
cases.
The dual Abel transform (i.e., the W-invariant intertwining operator) for
![]() $A_{1}$
can be written as
$A_{1}$
can be written as
 $$ \begin{align*} &\mathcal{A}(f)(y)\\ &\quad=\frac{\Gamma(m)}{(\Gamma(m/2))^{2}} \,(y_{1}-y_{2})^{1-m}\,\int_{y_{2}}^{y_{1}}\,f(z,y_{1}+y_{2}-z)\,((y_{1}-z)\,(z-y_{2}))^{m/2-1}\,dz \end{align*} $$
$$ \begin{align*} &\mathcal{A}(f)(y)\\ &\quad=\frac{\Gamma(m)}{(\Gamma(m/2))^{2}} \,(y_{1}-y_{2})^{1-m}\,\int_{y_{2}}^{y_{1}}\,f(z,y_{1}+y_{2}-z)\,((y_{1}-z)\,(z-y_{2}))^{m/2-1}\,dz \end{align*} $$
(see [Reference Sawyer33]).
We now consider J orthogonal roots in
![]() $\mathbf {R}^{d}$
. The dual of the generalized Abel transform
$\mathbf {R}^{d}$
. The dual of the generalized Abel transform
![]() $\overbrace {A_{1}\times \cdots A_{1}}^{J}$
can be written as
$\overbrace {A_{1}\times \cdots A_{1}}^{J}$
can be written as
 $$ \begin{align*} \mathcal{A}^{*}(f)(y)&=\left(\prod_{i=1}^{J}\,\frac{\Gamma(m_{i})}{(\Gamma(m_{i}/2))^{2}}\right) \,\prod_{i=1}^{J}\,(y^{(i)}_{1}-y^{(i)}_{2})^{1-m_{i}} \\&\quad \,\int_{y^{(J)}_{2}}^{y^{(J)}_{1}}\dots\, \int_{y^{(1)}_{2}}^{y^{(1)}_{1}} \,f\left((z^{(i)},y^{(i)}_{1}+y_{2}^{(i)}-z^{(i)})_{i=1,\dots,J}\right) \\&\quad\,\prod_{i=1}^{J}\,((y^{(i)}_{1}-z)\,(z-y^{(i)}_{2}))^{m_{i}/2-1}\,dz^{(1)}\,\cdots\,dz^{(J)}, \end{align*} $$
$$ \begin{align*} \mathcal{A}^{*}(f)(y)&=\left(\prod_{i=1}^{J}\,\frac{\Gamma(m_{i})}{(\Gamma(m_{i}/2))^{2}}\right) \,\prod_{i=1}^{J}\,(y^{(i)}_{1}-y^{(i)}_{2})^{1-m_{i}} \\&\quad \,\int_{y^{(J)}_{2}}^{y^{(J)}_{1}}\dots\, \int_{y^{(1)}_{2}}^{y^{(1)}_{1}} \,f\left((z^{(i)},y^{(i)}_{1}+y_{2}^{(i)}-z^{(i)})_{i=1,\dots,J}\right) \\&\quad\,\prod_{i=1}^{J}\,((y^{(i)}_{1}-z)\,(z-y^{(i)}_{2}))^{m_{i}/2-1}\,dz^{(1)}\,\cdots\,dz^{(J)}, \end{align*} $$
where
![]() $m_{i}$
is the multiplicity of the root acting on
$m_{i}$
is the multiplicity of the root acting on
![]() $y^{(i)}_{1}$
and
$y^{(i)}_{1}$
and
![]() $y^{(i)}_{2}$
.
$y^{(i)}_{2}$
.
Remark 7.1 One may have the root system
![]() $A_{1}$
in
$A_{1}$
in
![]() $\mathbf {R}$
(or in
$\mathbf {R}$
(or in
![]() $\mathbf {R}^{2}$
with
$\mathbf {R}^{2}$
with
![]() $y_{1}+y_{2}=0$
) or in
$y_{1}+y_{2}=0$
) or in
![]() $\mathbf {R}^{d}$
where the roots only act on, say,
$\mathbf {R}^{d}$
where the roots only act on, say,
![]() $y_{1}$
and
$y_{1}$
and
![]() $y_{2}$
. The same comment applies to
$y_{2}$
. The same comment applies to
![]() $\overbrace {A_{1}\times \cdots A_{1}}^{J}$
in
$\overbrace {A_{1}\times \cdots A_{1}}^{J}$
in
![]() $\mathbf {R}^{d}$
. To minimize the notation, we will only indicate the variables on which the roots act.
$\mathbf {R}^{d}$
. To minimize the notation, we will only indicate the variables on which the roots act.
We have
 $$ \begin{align*} &\frac{P^{W}(x,y)}{1-|x|^{2}}\\ &\quad=C\,\mathcal{A}^{*}\left(\frac{1}{(|x-y|^{2}+2\,\langle x,y-\cdot\rangle)^{d/2+(m_{1}+\dots+m_{J})/2}}\right)(y)\\ &\quad=C^{\prime}\,\prod_{i=1}^{J}\,(y^{(i)}_{1}-y^{(i)}_{2})^{1-m}\\ &\quad\,\int_{y^{(J)}_{2}}^{y^{(J)}_{1}}\dots\, \int_{y^{(1)}_{2}}^{y^{(1)}_{1}} \frac{\prod_{i=1}^{J}\,((y^{(i)}_{1}-z^{(i)}))\,(z^{(i)})-y^{(i)}_{2}))^{m_{i}/2-1}\,dz^{(1)}\,\cdots\,dz^{(J)}} {\left(|x-y|^{2}+2\,\sum_{i=1}^{J}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-z^{(i)})\right)^{d/2+(m_{1}+\dots+m_{J})/2}}, \end{align*} $$
$$ \begin{align*} &\frac{P^{W}(x,y)}{1-|x|^{2}}\\ &\quad=C\,\mathcal{A}^{*}\left(\frac{1}{(|x-y|^{2}+2\,\langle x,y-\cdot\rangle)^{d/2+(m_{1}+\dots+m_{J})/2}}\right)(y)\\ &\quad=C^{\prime}\,\prod_{i=1}^{J}\,(y^{(i)}_{1}-y^{(i)}_{2})^{1-m}\\ &\quad\,\int_{y^{(J)}_{2}}^{y^{(J)}_{1}}\dots\, \int_{y^{(1)}_{2}}^{y^{(1)}_{1}} \frac{\prod_{i=1}^{J}\,((y^{(i)}_{1}-z^{(i)}))\,(z^{(i)})-y^{(i)}_{2}))^{m_{i}/2-1}\,dz^{(1)}\,\cdots\,dz^{(J)}} {\left(|x-y|^{2}+2\,\sum_{i=1}^{J}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-z^{(i)})\right)^{d/2+(m_{1}+\dots+m_{J})/2}}, \end{align*} $$
where
![]() $m_{i}>0$
is the root multiplicity for the i-th factor.
$m_{i}>0$
is the root multiplicity for the i-th factor.
With the change of variables,
![]() $v^{(i)}=\frac {y^{(i)}_{1}-z^{(i)}}{y^{(i)}_{1}-y^{(i)}_{2}}$
, we find that
$v^{(i)}=\frac {y^{(i)}_{1}-z^{(i)}}{y^{(i)}_{1}-y^{(i)}_{2}}$
, we find that
 $$ \begin{align} &\frac{P^{W}(x,y)}{1-|x|^{2}}\nonumber\\ &\ \ =C^{\prime}\int_{0}^{1}\dots\,\int_{0}^{1} \frac{\prod_{i=1}^{J}\,(v^{(i)}\,(1-v^{(i)}))^{m_{i}/2-1}\,dv^{(1)}\,\cdots\,dv^{(J)}}{\left(|x-y|^{2}+2\,\sum_{i=1}^{J}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}\right)^{d/2+(m_{1}+\dots+m_{J})/2}}. \end{align} $$
$$ \begin{align} &\frac{P^{W}(x,y)}{1-|x|^{2}}\nonumber\\ &\ \ =C^{\prime}\int_{0}^{1}\dots\,\int_{0}^{1} \frac{\prod_{i=1}^{J}\,(v^{(i)}\,(1-v^{(i)}))^{m_{i}/2-1}\,dv^{(1)}\,\cdots\,dv^{(J)}}{\left(|x-y|^{2}+2\,\sum_{i=1}^{J}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}\right)^{d/2+(m_{1}+\dots+m_{J})/2}}. \end{align} $$
In a similar fashion, for
![]() $d\geq 2$
, we have
$d\geq 2$
, we have
 $$ \begin{align*} &N^{W}(x,y)\\ &\ \ =C\,\mathcal{A}^{*}\left(\frac{1}{(|x-y|^{2}+2\,\langle x,y-\cdot\rangle)^{d/2-1+(m_{1}+\dots+m_{J})/2}}\right)(y)\\ &\ \ =C^{\prime}\int_{0}^{1}\dots\int_{0}^{1} \frac{\prod_{i=1}^{J}\,(v^{(i)}\,(1-v^{(i)}))^{m_{i}/2-1}\,dv^{(1)}\,\cdots\,dv^{(J)}}{\left(|x-y|^{2}+2\,\sum_{i=1}^{J}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}\right)^{d/2-1+(m_{1}+\dots+m_{J})/2}}. \end{align*} $$
$$ \begin{align*} &N^{W}(x,y)\\ &\ \ =C\,\mathcal{A}^{*}\left(\frac{1}{(|x-y|^{2}+2\,\langle x,y-\cdot\rangle)^{d/2-1+(m_{1}+\dots+m_{J})/2}}\right)(y)\\ &\ \ =C^{\prime}\int_{0}^{1}\dots\int_{0}^{1} \frac{\prod_{i=1}^{J}\,(v^{(i)}\,(1-v^{(i)}))^{m_{i}/2-1}\,dv^{(1)}\,\cdots\,dv^{(J)}}{\left(|x-y|^{2}+2\,\sum_{i=1}^{J}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}\right)^{d/2-1+(m_{1}+\dots+m_{J})/2}}. \end{align*} $$
We want to prove Conjectures 1 and 2 for the root system
![]() $\overbrace {A_{1}\times \cdots A_{1}}^{J}$
using induction on
$\overbrace {A_{1}\times \cdots A_{1}}^{J}$
using induction on
![]() $J\geq 1$
. To accomplish this, we will need the following technical result.
$J\geq 1$
. To accomplish this, we will need the following technical result.
Lemma 7.2 Suppose
![]() $A>0$
and
$A>0$
and
![]() $B>0$
. Then
$B>0$
. Then
 $$ \begin{align*} T=\int_{0}^{1}\,\frac{(u\,(1-u))^{m/2-1}\,du}{(A+B\,u)^{M}} \left\lbrace\begin{array}{ll} \asymp \frac{1}{A^{M-m/2}\,(A+B)^{m/2}}&\mbox{if }M>m/2,\\ \asymp\frac{\ln\left(2\,\frac{A+B}{A}\right)}{(A+B)^{m/2}}&\mbox{if }M=m/2. \end{array} \right. \end{align*} $$
$$ \begin{align*} T=\int_{0}^{1}\,\frac{(u\,(1-u))^{m/2-1}\,du}{(A+B\,u)^{M}} \left\lbrace\begin{array}{ll} \asymp \frac{1}{A^{M-m/2}\,(A+B)^{m/2}}&\mbox{if }M>m/2,\\ \asymp\frac{\ln\left(2\,\frac{A+B}{A}\right)}{(A+B)^{m/2}}&\mbox{if }M=m/2. \end{array} \right. \end{align*} $$
Proof If
![]() $A\geq B/4$
then
$A\geq B/4$
then
 $$ \begin{align*} \int_{0}^{1}\,\frac{(u\,(1-u))^{m/2-1}\,du}{(A+B\,u)^{M}} \asymp \int_{0}^{1}\,\frac{(u\,(1-u))^{m/2-1}\,du}{A^{M}} \asymp \frac{1}{A^{M}}. \end{align*} $$
$$ \begin{align*} \int_{0}^{1}\,\frac{(u\,(1-u))^{m/2-1}\,du}{(A+B\,u)^{M}} \asymp \int_{0}^{1}\,\frac{(u\,(1-u))^{m/2-1}\,du}{A^{M}} \asymp \frac{1}{A^{M}}. \end{align*} $$
If
![]() $A\leq B/4$
then
$A\leq B/4$
then
 $$ \begin{align*} T=\int_{0}^{A/B}+\int_{A/B}^{1/2}+\int_{1/2}^{1}=T_{1}+T_{2}+T_{3}. \end{align*} $$
$$ \begin{align*} T=\int_{0}^{A/B}+\int_{A/B}^{1/2}+\int_{1/2}^{1}=T_{1}+T_{2}+T_{3}. \end{align*} $$
Now,
since
![]() $u\leq A/B$
and
$u\leq A/B$
and
![]() $A\leq A+B\,u\leq A+B\,A/B=2\,A$
. Next, we note that
$A\leq A+B\,u\leq A+B\,A/B=2\,A$
. Next, we note that
 $$ \begin{align*} T_{2}\asymp \int_{A/B}^{1/2}\,\frac{u^{m/2-1}\,du}{(B\,u)^{M}} &=\frac{1}{B^{M}}\, \int_{A/B}^{1/2}\,u^{m/2-M-1}\,du\\ &=\frac{1}{(M-m/2)\,B^{M}}\,((A/B)^{m/2-M}-(1/2)^{m/2-M})\\ &=\frac{1}{M-m/2}\,\left(\frac{1}{A^{M-m/2}\,B^{m/2}}-\frac{(1/2)^{m/2-M}}{B^{M}}\right) \end{align*} $$
$$ \begin{align*} T_{2}\asymp \int_{A/B}^{1/2}\,\frac{u^{m/2-1}\,du}{(B\,u)^{M}} &=\frac{1}{B^{M}}\, \int_{A/B}^{1/2}\,u^{m/2-M-1}\,du\\ &=\frac{1}{(M-m/2)\,B^{M}}\,((A/B)^{m/2-M}-(1/2)^{m/2-M})\\ &=\frac{1}{M-m/2}\,\left(\frac{1}{A^{M-m/2}\,B^{m/2}}-\frac{(1/2)^{m/2-M}}{B^{M}}\right) \end{align*} $$
if
![]() $M>m/2$
since
$M>m/2$
since
![]() $A/B\leq u\leq 1/2$
and
$A/B\leq u\leq 1/2$
and
![]() $B\,u\leq A+B\,u\leq 2\,B\,u$
. If
$B\,u\leq A+B\,u\leq 2\,B\,u$
. If
![]() $M=m/2$
then
$M=m/2$
then
 $$ \begin{align*} T_{2}\asymp \int_{A/B}^{1/2}\,\frac{u^{m/2-1}\,du}{(B\,u)^{m/2}} &=\frac{1}{B^{m/2}}\, \int_{A/B}^{1/2}\,u^{-1}\,du =\frac{1}{B^{m/2}}\, \ln((B/A)/2). \end{align*} $$
$$ \begin{align*} T_{2}\asymp \int_{A/B}^{1/2}\,\frac{u^{m/2-1}\,du}{(B\,u)^{m/2}} &=\frac{1}{B^{m/2}}\, \int_{A/B}^{1/2}\,u^{-1}\,du =\frac{1}{B^{m/2}}\, \ln((B/A)/2). \end{align*} $$
Finally,
 $$ \begin{align*} T_{3}\asymp \int_{1/2}^{1}\,\frac{(1-u)^{m/2-1}\,du}{B^{M}} &\asymp\frac{1}{B^{M}} \end{align*} $$
$$ \begin{align*} T_{3}\asymp \int_{1/2}^{1}\,\frac{(1-u)^{m/2-1}\,du}{B^{M}} &\asymp\frac{1}{B^{M}} \end{align*} $$
since
![]() $u\geq 1/2$
and
$u\geq 1/2$
and
![]() $B/2\leq A+B\,u\leq 2\,B$
. The result follows then easily.▪
$B/2\leq A+B\,u\leq 2\,B$
. The result follows then easily.▪
Theorem 7.3 We consider the case
![]() $\overbrace {A_{1}\times \cdots A_{1}}^{J}$
. Suppose x,
$\overbrace {A_{1}\times \cdots A_{1}}^{J}$
. Suppose x,
![]() $y\in \overline {\mathfrak {a}^+}$
. We have
$y\in \overline {\mathfrak {a}^+}$
. We have
 $$ \begin{align*} \frac{P^{W}(x,y)}{1-|x|^{2}} \asymp \frac{1}{|x-y|^{d}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\alpha}\,y|^{m_{i}}}, \end{align*} $$
$$ \begin{align*} \frac{P^{W}(x,y)}{1-|x|^{2}} \asymp \frac{1}{|x-y|^{d}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\alpha}\,y|^{m_{i}}}, \end{align*} $$
where
![]() $\sigma ^{(i)}_{\alpha }$
is the reflection with respect to
$\sigma ^{(i)}_{\alpha }$
is the reflection with respect to
![]() $\alpha $
acting on the variables
$\alpha $
acting on the variables
![]() $y^{(i)}_{1}$
and
$y^{(i)}_{1}$
and
![]() $y^{(i)}_{2}$
.
$y^{(i)}_{2}$
.
Proof We have
![]() $|x-\sigma _{\alpha }\,y|^{2}\asymp |x-y|^{2}+2\,(x_{1}-x_{2})\,(y_{1}-y_{2})$
(refer to Lemma 3.1).
$|x-\sigma _{\alpha }\,y|^{2}\asymp |x-y|^{2}+2\,(x_{1}-x_{2})\,(y_{1}-y_{2})$
(refer to Lemma 3.1).
We use induction on
![]() $J\geq 1$
. When
$J\geq 1$
. When
![]() $J=1$
, the result follows using (7.1), Lemma 7.2 with
$J=1$
, the result follows using (7.1), Lemma 7.2 with
![]() $A=|x-y|^{2}$
,
$A=|x-y|^{2}$
,
![]() $B=2\,(x^{(1)}_{1}-x^{(1)}_{2})\,(y^{(1)}_{1}-y^{(1)}_{2})$
and
$B=2\,(x^{(1)}_{1}-x^{(1)}_{2})\,(y^{(1)}_{1}-y^{(1)}_{2})$
and
![]() $M=d/2+m_{1}/2$
.
$M=d/2+m_{1}/2$
.
Assume that the result holds for
![]() $J-1$
,
$J-1$
,
![]() $J\geq 2$
. There exists j such that
$J\geq 2$
. There exists j such that
![]() $(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2}) \leq (x^{(j)}_{1}-x^{(j)}_{2})\,(y^{(j)}_{1}-y^{(j)}_{2})$
for all i. To fix things, say
$(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2}) \leq (x^{(j)}_{1}-x^{(j)}_{2})\,(y^{(j)}_{1}-y^{(j)}_{2})$
for all i. To fix things, say
![]() $j=J$
.
$j=J$
.
Use (7.1), Lemma 7.2 with
![]() $A=|x-y|^{2}+2\,\sum _{i=1}^{J-1}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}$
,
$A=|x-y|^{2}+2\,\sum _{i=1}^{J-1}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}$
,
![]() $B=2\,(x^{(J)}_{1}-x^{(J)}_{2})\,(y^{(J)}_{1}-y^{(J)}_{2})$
and
$B=2\,(x^{(J)}_{1}-x^{(J)}_{2})\,(y^{(J)}_{1}-y^{(J)}_{2})$
and
![]() $M=d/2+(m_{1}+\dots +m_{J})/2$
, integrating with respect to
$M=d/2+(m_{1}+\dots +m_{J})/2$
, integrating with respect to
![]() $v^{(J)}$
. We find that
$v^{(J)}$
. We find that
 $$ \begin{align*} &{\frac{P^{W}(x,y)}{1-|x|^{2}}}\\ &\asymp\int_{0}^{1}\dots\,\int_{0}^{1} \,\frac{\prod_{i=1}^{J}\,(v^{(i)}\,(1-v^{(i)}))^{m_{i}/2-1}\,dv^{(1)}\,\cdots\,dv^{(J-1)}} {\left(|x-y|^{2}+2\,\sum_{i=1}^{J-1}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}\right)^{d/2+(m_{1}+\dots+m_{J-1})/2}}\\ &\frac{1} {\left(|x-y|^{2}+2\,\sum_{i=1}^{J-1}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}+2\,(x^{(J)}_{1}-x^{(J)}_{2})\,(y^{(J)}_{1}-y^{(J)}_{2})\right)^{m_{J}/2}}\\ &\asymp\frac{1} {\left(|x-y|^{2}+2\,(x^{(J)}_{1}-x^{(J)}_{2})\,(y^{(J)}_{1}-y^{(J)}_{2})\right)^{m_{J}/2}} \\&\int_{0}^{1}\dots\,\int_{0}^{1} \,\frac{\prod_{i=1}^{J}\,(v^{(i)}\,(1-v^{(i)}))^{m_{i}/2-1}\,dv^{(1)}\,\cdots\,dv^{(J-1)}} {\left(|x-y|^{2}+2\,\sum_{i=1}^{J-1}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}\right)^{d/2+(m_{1}+\dots+m_{J-1})/2}}\\ &\asymp \frac{1}{|x-y|^{d}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\alpha}\,y|^{m_{i}}} \end{align*} $$
$$ \begin{align*} &{\frac{P^{W}(x,y)}{1-|x|^{2}}}\\ &\asymp\int_{0}^{1}\dots\,\int_{0}^{1} \,\frac{\prod_{i=1}^{J}\,(v^{(i)}\,(1-v^{(i)}))^{m_{i}/2-1}\,dv^{(1)}\,\cdots\,dv^{(J-1)}} {\left(|x-y|^{2}+2\,\sum_{i=1}^{J-1}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}\right)^{d/2+(m_{1}+\dots+m_{J-1})/2}}\\ &\frac{1} {\left(|x-y|^{2}+2\,\sum_{i=1}^{J-1}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}+2\,(x^{(J)}_{1}-x^{(J)}_{2})\,(y^{(J)}_{1}-y^{(J)}_{2})\right)^{m_{J}/2}}\\ &\asymp\frac{1} {\left(|x-y|^{2}+2\,(x^{(J)}_{1}-x^{(J)}_{2})\,(y^{(J)}_{1}-y^{(J)}_{2})\right)^{m_{J}/2}} \\&\int_{0}^{1}\dots\,\int_{0}^{1} \,\frac{\prod_{i=1}^{J}\,(v^{(i)}\,(1-v^{(i)}))^{m_{i}/2-1}\,dv^{(1)}\,\cdots\,dv^{(J-1)}} {\left(|x-y|^{2}+2\,\sum_{i=1}^{J-1}\,(x^{(i)}_{1}-x^{(i)}_{2})\,(y^{(i)}_{1}-y^{(i)}_{2})\,v^{(i)}\right)^{d/2+(m_{1}+\dots+m_{J-1})/2}}\\ &\asymp \frac{1}{|x-y|^{d}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\alpha}\,y|^{m_{i}}} \end{align*} $$
(the last step follows using the induction hypothesis).▪
Theorem 7.4 We consider the case
![]() $\overbrace {A_{1}\times \cdots A_{1}}^{J}$
. Suppose x,
$\overbrace {A_{1}\times \cdots A_{1}}^{J}$
. Suppose x,
![]() $y\in \overline {\mathfrak {a}^+}$
. For
$y\in \overline {\mathfrak {a}^+}$
. For
![]() $d\geq 3$
we have
$d\geq 3$
we have
 $$ \begin{align*} N^{W}(x,y) \asymp \frac{1}{|x-y|^{d-2}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\alpha}\,y|^{m_{i}}}. \end{align*} $$
$$ \begin{align*} N^{W}(x,y) \asymp \frac{1}{|x-y|^{d-2}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\alpha}\,y|^{m_{i}}}. \end{align*} $$
Proof The proof is basically the same as for Theorem 7.3. ▪
We proceed with handling the case
![]() $d=2$
.
$d=2$
.
Proposition 7.5 The Newton kernel in the case of
![]() $A_{1}$
in
$A_{1}$
in
![]() $\mathbf {R}^{2}$
satisfies
$\mathbf {R}^{2}$
satisfies
 $$ \begin{align} N^{W}(x,y) \asymp \frac{\ln\,\left(2\,\frac{|x-\sigma_{\alpha}\,y|^{2}}{|x-y|^{2}}\right)}{|x-\sigma_{\alpha}\,y|^{m}}. \end{align} $$
$$ \begin{align} N^{W}(x,y) \asymp \frac{\ln\,\left(2\,\frac{|x-\sigma_{\alpha}\,y|^{2}}{|x-y|^{2}}\right)}{|x-\sigma_{\alpha}\,y|^{m}}. \end{align} $$
The Newton kernel in the case of
![]() $A_{1}\times A_{1}$
in
$A_{1}\times A_{1}$
in
![]() $\mathbf {R}^{2}$
satisfies
$\mathbf {R}^{2}$
satisfies
 $$ \begin{align} \frac{\ln\,\left(2\,\frac{|x-\sigma^{(1)}_{\alpha}\,y|\wedge |x-\sigma^{(2)}_{\alpha}\,y|}{|x-y|^{2}}\right)}{|x-\sigma^{(1)}_{\alpha}\,y|^{m_{1}}\,|x-\sigma^{(2)}_{\alpha}\,y|^{m_{2}}}, \end{align} $$
$$ \begin{align} \frac{\ln\,\left(2\,\frac{|x-\sigma^{(1)}_{\alpha}\,y|\wedge |x-\sigma^{(2)}_{\alpha}\,y|}{|x-y|^{2}}\right)}{|x-\sigma^{(1)}_{\alpha}\,y|^{m_{1}}\,|x-\sigma^{(2)}_{\alpha}\,y|^{m_{2}}}, \end{align} $$
where
![]() $a\wedge b=\min \{a,b\}$
.
$a\wedge b=\min \{a,b\}$
.
Proof Equation (7.2) follows directly from Lemma 7.2 with
![]() $M=m_{1}/2$
.
$M=m_{1}/2$
.
To obtain equation (7.3), we can assume without loss of generality that
![]() $(x^{(1)}_{1}-x^{(1)}_{2})\,(y^{(1)}_{1}-y^{(1)}_{2})\leq (x^{(2)}_{1}-x^{(2)}_{2})\,(y^{(2)}_{1}-y^{(2)}_{2})$
. Apply Lemma 7.2 to the integral representing
$(x^{(1)}_{1}-x^{(1)}_{2})\,(y^{(1)}_{1}-y^{(1)}_{2})\leq (x^{(2)}_{1}-x^{(2)}_{2})\,(y^{(2)}_{1}-y^{(2)}_{2})$
. Apply Lemma 7.2 to the integral representing
![]() $N^{W}(x,y)$
with
$N^{W}(x,y)$
with
![]() $M=m_{1}+m_{2}$
,
$M=m_{1}+m_{2}$
,
![]() $A=|x-y|^{2}+2\,(x^{(1)}_{1}-x^{(1)}_{2})\,(y^{(1)}_{1}-y^{(1)}_{2})\,u^{(1)}$
and
$A=|x-y|^{2}+2\,(x^{(1)}_{1}-x^{(1)}_{2})\,(y^{(1)}_{1}-y^{(1)}_{2})\,u^{(1)}$
and
![]() $B=2\,(x^{(2)}_{1}-x^{(2)}_{2})\,(y^{(2)}_{1}-y^{(2)}_{2})$
, integrating with respect to
$B=2\,(x^{(2)}_{1}-x^{(2)}_{2})\,(y^{(2)}_{1}-y^{(2)}_{2})$
, integrating with respect to
![]() $u^{(2)}$
. We obtain
$u^{(2)}$
. We obtain
 $$ \begin{align*} N^{W}(x,y) \asymp\frac{1}{|x-\sigma^{(2)}_{\alpha}\,y|^{m_{2}}} \,\int_{0}^{1}\,\frac{(u^{(1)}\,(1-u^{(1)}))^{m/2-1}\,du^{(1)}}{(|x-y|^{2}+2\,(x^{(1)}_{1}-x^{(1)}_{2})\,(y^{(1)}_{1}-y^{(1)}_{2})\,u^{(1)})^{m/2}}. \end{align*} $$
$$ \begin{align*} N^{W}(x,y) \asymp\frac{1}{|x-\sigma^{(2)}_{\alpha}\,y|^{m_{2}}} \,\int_{0}^{1}\,\frac{(u^{(1)}\,(1-u^{(1)}))^{m/2-1}\,du^{(1)}}{(|x-y|^{2}+2\,(x^{(1)}_{1}-x^{(1)}_{2})\,(y^{(1)}_{1}-y^{(1)}_{2})\,u^{(1)})^{m/2}}. \end{align*} $$
If we apply Lemma 7.2 with
![]() $M=m_{1}$
, we get
$M=m_{1}$
, we get
 $$ \begin{align*} N^{W}(x,y) \asymp\frac{1}{|x-\sigma^{(2)}_{\alpha}\,y|^{m_{2}}} \,\frac{\ln\,\left(2\,\frac{|x-\sigma^{(1)}_{\alpha}\,y|^{2}}{|x-y|^{2}}\right)}{|x-\sigma^{(1)}_{\alpha}\,y|^{m}}. \end{align*} $$
$$ \begin{align*} N^{W}(x,y) \asymp\frac{1}{|x-\sigma^{(2)}_{\alpha}\,y|^{m_{2}}} \,\frac{\ln\,\left(2\,\frac{|x-\sigma^{(1)}_{\alpha}\,y|^{2}}{|x-y|^{2}}\right)}{|x-\sigma^{(1)}_{\alpha}\,y|^{m}}. \end{align*} $$
▪
We end this section by a formulation of the results for the systems
![]() $\overbrace {B_{1}\times \cdots B_{1}}^{J}$
acting on
$\overbrace {B_{1}\times \cdots B_{1}}^{J}$
acting on
![]() $\mathbf {R}^{d},\, d\ge J$
, i.e., the symmetries are
$\mathbf {R}^{d},\, d\ge J$
, i.e., the symmetries are
![]() $\sigma _{\beta }^{(i)}(y)=(y_{1},\ldots ,-y_{i},y_{i+1},\ldots , y_{d})$
for
$\sigma _{\beta }^{(i)}(y)=(y_{1},\ldots ,-y_{i},y_{i+1},\ldots , y_{d})$
for
![]() $i\le J$
.
$i\le J$
.
Corollary 7.6 Consider the case
![]() $\overbrace {B_{1}\times \cdots B_{1}}^{J}$
. Suppose x,
$\overbrace {B_{1}\times \cdots B_{1}}^{J}$
. Suppose x,
![]() $y\in \overline {\mathfrak {a}^+}$
.
$y\in \overline {\mathfrak {a}^+}$
.
-
(1) We have
 $$ \begin{align*} \frac{P^{W}(x,y)}{1-|x|^{2}} \asymp \frac{1}{|x-y|^{d}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\beta}\,y|^{m_{i}}}. \end{align*} $$
$$ \begin{align*} \frac{P^{W}(x,y)}{1-|x|^{2}} \asymp \frac{1}{|x-y|^{d}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\beta}\,y|^{m_{i}}}. \end{align*} $$
-
(2) For
 $d\geq 3$
, we have
$d\geq 3$
, we have  $$ \begin{align*} N^{W}(x,y) \asymp \frac{1}{|x-y|^{d-2}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\beta}\,y|^{m_{i}}}. \end{align*} $$
$$ \begin{align*} N^{W}(x,y) \asymp \frac{1}{|x-y|^{d-2}\,\prod_{i=1}^{J}\,|x-\sigma^{(i)}_{\beta}\,y|^{m_{i}}}. \end{align*} $$
8 Applications to stochastic processes
From a probabilistic point of view, the formula (2.5)
gives the generator of the Doob h-transform (refer to [Reference Revuz and Yor29]) of the Brownian Motion on
![]() $\mathbf {R}^{d}$
with the excessive function
$\mathbf {R}^{d}$
with the excessive function
![]() $h(x)=\pi (x)$
. For the root system
$h(x)=\pi (x)$
. For the root system
![]() $A_{d-1}$
on
$A_{d-1}$
on
![]() $\mathbf {R}^{d}$
, the operator
$\mathbf {R}^{d}$
, the operator
![]() $\Delta ^{W}$
is the generator of the Dyson Brownian Motion on
$\Delta ^{W}$
is the generator of the Dyson Brownian Motion on
![]() $\mathbf {R}^{d}$
([Reference Dyson12]), i.e., the d Brownian independent particles
$\mathbf {R}^{d}$
([Reference Dyson12]), i.e., the d Brownian independent particles
![]() $B^{(1)}_{t},\ldots ,B^{(d)}_{t} $
conditioned not to collide. More generally, for any root system
$B^{(1)}_{t},\ldots ,B^{(d)}_{t} $
conditioned not to collide. More generally, for any root system
![]() $\Phi $
on
$\Phi $
on
![]() $\mathbf {R}^{d}$
, the construction of a Dyson Brownian Motion
$\mathbf {R}^{d}$
, the construction of a Dyson Brownian Motion
![]() $D_{t}^{\Phi }$
as a Brownian Motion conditioned not to touch the walls of the positive Weyl chamber, can be done ([Reference Grabiner16]). It is known that
$D_{t}^{\Phi }$
as a Brownian Motion conditioned not to touch the walls of the positive Weyl chamber, can be done ([Reference Grabiner16]). It is known that
![]() $\pi $
is
$\pi $
is
![]() $\Delta _{\mathbf {R}^{d}}$
-harmonic on
$\Delta _{\mathbf {R}^{d}}$
-harmonic on
![]() $\mathbf {R}^{d}$
([Reference Grabiner16]), so in particular
$\mathbf {R}^{d}$
([Reference Grabiner16]), so in particular
![]() $\pi $
is excessive.
$\pi $
is excessive.
Dyson Brownian Motion
![]() $D_{t}^{\Phi }$
is one of the most important models of noncolliding particles (see e.g., [Reference Andraus, Katori and Miyashita1, Reference Andraus and Voit2, Reference Katori21]). In [Reference Andraus and Voit2], W-invariant Dunkl processes are called multivariate Bessel processes.
$D_{t}^{\Phi }$
is one of the most important models of noncolliding particles (see e.g., [Reference Andraus, Katori and Miyashita1, Reference Andraus and Voit2, Reference Katori21]). In [Reference Andraus and Voit2], W-invariant Dunkl processes are called multivariate Bessel processes.
The only difference with the symmetric flat complex case is that no invariant measure
![]() $\pi ^{2}(y)\,dy$
appears for the integral kernels in the Dyson Brownian Motion case.
$\pi ^{2}(y)\,dy$
appears for the integral kernels in the Dyson Brownian Motion case.
Theorem 2.7 implies estimates for the Poisson kernel
![]() $P^{D}$
and the Newton kernel
$P^{D}$
and the Newton kernel
![]() $N^{D}$
for the Dyson Brownian Motion. These estimates are essential for the potential theory of the process
$N^{D}$
for the Dyson Brownian Motion. These estimates are essential for the potential theory of the process
![]() $D_{t}^{\Phi }$
and, consequently, of noncolliding stochastic particles.
$D_{t}^{\Phi }$
and, consequently, of noncolliding stochastic particles.
Corollary 8.1 1. For
![]() $x\in B^+$
and
$x\in B^+$
and
![]() $y\in S^+$
we have
$y\in S^+$
we have
 $$ \begin{align*} P^{D}(x,y)\asymp \frac{(1-|x|^{2})\pi^{2}(y)}{|x-y|^{d}\prod_{\alpha\in \Phi_+} |x-\sigma_{\alpha} y|^{2 }}. \end{align*} $$
$$ \begin{align*} P^{D}(x,y)\asymp \frac{(1-|x|^{2})\pi^{2}(y)}{|x-y|^{d}\prod_{\alpha\in \Phi_+} |x-\sigma_{\alpha} y|^{2 }}. \end{align*} $$
2. For
![]() $x, y\in \overline {\mathfrak {a}^+}$
and
$x, y\in \overline {\mathfrak {a}^+}$
and
![]() $d\geq 3$
, we have
$d\geq 3$
, we have
 $$ \begin{align*} N^{D}(x,y)\asymp \frac{\pi^{2}(y)}{|x-y|^{d-2}\,\prod_{\alpha\in \Phi_+}|x-\sigma_{\alpha} y|^{2}}. \end{align*} $$
$$ \begin{align*} N^{D}(x,y)\asymp \frac{\pi^{2}(y)}{|x-y|^{d-2}\,\prod_{\alpha\in \Phi_+}|x-\sigma_{\alpha} y|^{2}}. \end{align*} $$