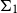1. Introduction
For a countable set
![]() $\mathcal{S}$
, a numbering of
$\mathcal{S}$
, a numbering of
![]() $\mathcal{S}$
is a surjective map
$\mathcal{S}$
is a surjective map
![]() $\nu$
from the set of natural numbers
$\nu$
from the set of natural numbers
![]() $\omega$
onto
$\omega$
onto
![]() $\mathcal{S}$
. Since the 1950s, computable numberings for families of computably enumerable (c.e.) sets have been extensively studied by computability theorists.
$\mathcal{S}$
. Since the 1950s, computable numberings for families of computably enumerable (c.e.) sets have been extensively studied by computability theorists.
Consider a family
![]() $\mathcal{S}$
of c.e. sets. A numbering
$\mathcal{S}$
of c.e. sets. A numbering
![]() $\nu$
of the family
$\nu$
of the family
![]() $\mathcal{S}$
is computable if the set
$\mathcal{S}$
is computable if the set
is c.e. The family
![]() $\mathcal{S}$
is computable if it has a computable numbering. Informally speaking, the computability of
$\mathcal{S}$
is computable if it has a computable numbering. Informally speaking, the computability of
![]() $\mathcal{S}$
means that there is a procedure which provides a uniform enumeration of the family
$\mathcal{S}$
means that there is a procedure which provides a uniform enumeration of the family
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
A measure of relative complexity is provided by the notion of reducibility between numberings: A numbering
![]() $\nu$
is reducible to another numbering
$\nu$
is reducible to another numbering
![]() $\mu$
, denoted by
$\mu$
, denoted by
![]() $\nu\leq \mu$
, if there is total computable function f(x) such that
$\nu\leq \mu$
, if there is total computable function f(x) such that
![]() $\nu(n) = \mu(f(n))$
for all
$\nu(n) = \mu(f(n))$
for all
![]() $n\in\omega$
. In other words, there is an algorithmic procedure which, given a
$n\in\omega$
. In other words, there is an algorithmic procedure which, given a
![]() $\nu$
-index of an object from
$\nu$
-index of an object from
![]() $\mathcal{S}$
, computes a
$\mathcal{S}$
, computes a
![]() $\mu$
-index for the same object.
$\mu$
-index for the same object.
The notion of reducibility induces the Rogers upper semilattice (or Rogers semilattice for short) of a computable family
![]() $\mathcal{S}$
: This semilattice contains the degrees of all computable numberings of
$\mathcal{S}$
: This semilattice contains the degrees of all computable numberings of
![]() $\mathcal{S}$
. As usual, here we assume that two numberings have the same degree if they are reducible to each other. Rogers semilattices are widely used as a tool to classify properties of computable numberings for different families. For known results on computable numberings, the reader is referred to the seminal monograph (Ershov Reference Ershov1977) and the papers (Ershov Reference Ershov1999; Eršov Reference Eršov1973, Reference Eršov1975, Reference Eršov1977).
$\mathcal{S}$
. As usual, here we assume that two numberings have the same degree if they are reducible to each other. Rogers semilattices are widely used as a tool to classify properties of computable numberings for different families. For known results on computable numberings, the reader is referred to the seminal monograph (Ershov Reference Ershov1977) and the papers (Ershov Reference Ershov1999; Eršov Reference Eršov1973, Reference Eršov1975, Reference Eršov1977).
Goncharov and Sorbi (Reference Goncharov and Sorbi1997) started developing the theory of generalized computable numberings. Their approach initiated a fruitful line of research, which is focused on numberings for families of sets which belong to various levels of recursion-theoretic hierarchies: the arithmetical hierarchy (Badaev et al. Reference Badaev, Goncharov and Sorbi2006; Bazhenov et al. Reference Bazhenov, Mustafa and Yamaleev2019c; Podzorov Reference Podzorov2008), the Ershov hierarchy (Badaev and Lempp Reference Badaev and Lempp2009; Goncharov et al. Reference Goncharov, Lempp and Solomon2002; Herbert et al. Reference Herbert, Jain, Lempp, Mustafa and Stephan2019; Ospichev Reference Ospichev2015), the analytical hierarchy (Bazhenov et al. Reference Bazhenov, Ospichev and Yamaleev2019d, 2020b; Dorzhieva Reference Dorzhieva2019), etc. We refer the reader to Badaev and Goncharov (Reference Badaev and Goncharov2008, Reference Badaev and Goncharov2000) for further background on numberings in these hierarchies.
In general, one can say that the theory of numberings is one of the branches of computable or effective mathematics. This research area aims to understand and calibrate the algorithmic content of mathematical objects. The roots of this direction go back to the introduction of non-recursive mathematical methods at the beginning of the 20th century, as discussed in Metakides and Nerode (Reference Metakides and Nerode1982). Working within the framework of effective mathematics, the theory of numberings generally employs the Turing computability model.
This paper is inspired by the recent developments in computable structure theory: Kalimullin et al. (Reference Kalimullin, Melnikov and Ng2017) proposed a general framework for online computations in algebraic and combinatorial structures. The key object of this framework is the notion of a punctual (or fully primitive recursive) structure. An infinite structure
![]() $\mathcal{S}$
in a finite signature is punctual if the domain of
$\mathcal{S}$
in a finite signature is punctual if the domain of
![]() $\mathcal{S}$
is equal to
$\mathcal{S}$
is equal to
![]() $\omega$
, and the basic functions and relations of
$\omega$
, and the basic functions and relations of
![]() $\mathcal{S}$
are primitive recursive.
$\mathcal{S}$
are primitive recursive.
The notion of punctuality essentially eliminates all instances of unbounded search in Turing computable algorithms. This feature allows one to mimic a large class of “on-line” algorithms, that is, algorithms which have to make decisions on the fly. A typical example of such an algorithm is online coloring, say, of a tree: given the n-th vertex of an input tree, you have to decide its color right at the moment (you cannot wait for the
![]() $(n+1)$
-th vertex to appear).
$(n+1)$
-th vertex to appear).
Our paper employs the punctuality paradigm of Kalimullin et al. (Reference Kalimullin, Melnikov and Ng2017) in the studies of numberings.
Definition 1. Let
![]() $\mathcal{S}$
be a family of total functions acting from
$\mathcal{S}$
be a family of total functions acting from
![]() $\omega$
to
$\omega$
to
![]() $\omega$
. We say that a numbering
$\omega$
. We say that a numbering
![]() $\nu$
of the family
$\nu$
of the family
![]() $\mathcal{S}$
is punctual if the function:
$\mathcal{S}$
is punctual if the function:
is primitive recursive. A family
![]() $\mathcal{S}$
is punctual if it has a punctual numbering.
$\mathcal{S}$
is punctual if it has a punctual numbering.
Informally, the punctuality of
![]() $\mathcal{S}$
means that one can promptly (and uniformly) compute every function from
$\mathcal{S}$
means that one can promptly (and uniformly) compute every function from
![]() $\mathcal{S}$
. The punctuality approach requires that we have to modify the notion of the reduction between numberings accordingly:
$\mathcal{S}$
. The punctuality approach requires that we have to modify the notion of the reduction between numberings accordingly:
Definition 2. Let
![]() $\nu$
and
$\nu$
and
![]() $\mu$
be numberings. We say that
$\mu$
be numberings. We say that
![]() $\nu$
is punctually reducible to
$\nu$
is punctually reducible to
![]() $\mu$
, denoted by
$\mu$
, denoted by
![]() $\nu \leq_{pr} \mu$
, if there is a primitive recursive function
$\nu \leq_{pr} \mu$
, if there is a primitive recursive function
![]() $f\colon \omega \to \omega$
such that
$f\colon \omega \to \omega$
such that
In this case, we say that f punctually reduces
![]() $\nu$
to
$\nu$
to
![]() $\mu$
.
$\mu$
.
In a natural way, Definitions 1 and 2 induce the notion of Rogers pr-semilattice for a punctual family
![]() $\mathcal{S}$
, denoted by
$\mathcal{S}$
, denoted by
![]() $\mathcal{R}_{pr}(\mathcal{S})$
, see Section 2.1 for a formal definition.
$\mathcal{R}_{pr}(\mathcal{S})$
, see Section 2.1 for a formal definition.
The paper is arranged as follows. Section 2 provides the necessary preliminaries. In particular, we show that every finite punctual family induces a one-element Rogers pr-semilattice (Proposition 3). So, in the rest of the paper, we work only with infinite punctual families
![]() $\mathcal{S}$
. In Section 3, we introduce the notion of a strongly punctually decidable numbering (Definition 5), which plays a key role in most of our constructions.
$\mathcal{S}$
. In Section 3, we introduce the notion of a strongly punctually decidable numbering (Definition 5), which plays a key role in most of our constructions.
Section 4 gives our first example of a punctual priority construction: we show that below an arbitrary degree from
![]() $\mathcal{R}_{pr}(\mathcal{S})$
, one can find an infinite descending chain (Theorem 16). This fact already provides a contrast with the classical case of computable numberings: for example, the Rogers semilattice of a computable family
$\mathcal{R}_{pr}(\mathcal{S})$
, one can find an infinite descending chain (Theorem 16). This fact already provides a contrast with the classical case of computable numberings: for example, the Rogers semilattice of a computable family
![]() $\mathcal{T}_0 = \{ \emptyset \} \cup \{ \{k\}\,\colon k\in\omega \}$
has a least element.
$\mathcal{T}_0 = \{ \emptyset \} \cup \{ \{k\}\,\colon k\in\omega \}$
has a least element.
Section 5 proves that every non-greatest degree from
![]() $\mathcal{R}_{pr}(\mathcal{S})$
is a part of an infinite antichain (Theorem 20). In Section 6, we consider intervals inside
$\mathcal{R}_{pr}(\mathcal{S})$
is a part of an infinite antichain (Theorem 20). In Section 6, we consider intervals inside
![]() $\mathcal{R}_{pr}(\mathcal{S})$
. We prove that every interval
$\mathcal{R}_{pr}(\mathcal{S})$
. We prove that every interval
![]() $[\mathbf{a} <_{pr} \mathbf{b}]$
inside
$[\mathbf{a} <_{pr} \mathbf{b}]$
inside
![]() $\mathcal{R}_{pr}(\mathcal{S})$
contains an infinite antichain (Theorem 24). Note that the standard recursion-theoretic methods show that the classical Rogers semilattice of the family
$\mathcal{R}_{pr}(\mathcal{S})$
contains an infinite antichain (Theorem 24). Note that the standard recursion-theoretic methods show that the classical Rogers semilattice of the family
![]() $\mathcal{T}_0$
has an initial segment containing precisely two degrees. We also establish that the
$\mathcal{T}_0$
has an initial segment containing precisely two degrees. We also establish that the
![]() $\Sigma_1$
-fragment of the theory
$\Sigma_1$
-fragment of the theory
![]() $Th(\mathcal{R}_{pr}(\mathcal{S}))$
is decidable (Corollary 25).
$Th(\mathcal{R}_{pr}(\mathcal{S}))$
is decidable (Corollary 25).
Section 7 shows that there are infinite Rogers pr-semilattices which are lattices (Theorem 27). This contrasts with the result of Selivanov (Reference Selivanov1976): he established that a classical infinite Rogers semilattice cannot be a lattice. On the other hand, we build a Rogers pr-semilattice which contains a minimal pair (Proposition 29).
Section 8 discusses the existence of greatest elements. We provide examples of Rogers pr-semilattices with greatest element (Lemma 33) and without greatest element (Theorem 31).
In Section 9, Theorem 35 builds an infinite punctual family
![]() $\mathcal{S}$
such that:
$\mathcal{S}$
such that:
-
(a) every punctual numbering
 $\nu$
of
$\nu$
of
 $\mathcal{S}$
is
$\mathcal{S}$
is
 $\equiv_{pr}$
-equivalent to a strongly punctually decidable numbering, and
$\equiv_{pr}$
-equivalent to a strongly punctually decidable numbering, and -
(b)
 $\mathcal{S}$
contains only characteristic functions of one-element sets.
$\mathcal{S}$
contains only characteristic functions of one-element sets.
We conclude our paper with Section 10, which discusses some results on punctual Friedberg numberings.
The paper is an extended version of the conference paper (Bazhenov et al. Reference Bazhenov, Mustafa and Ospichev2020a). New material in this paper includes the following. Subsection 3.1 introduces the notion of a persistently decidable family and discusses its properties. The material of Section 5 is new: it provides a generalization of Theorem 23 of Bazhenov et al. (Reference Bazhenov, Mustafa and Ospichev2020a). Almost everything in Section 8 is new: the only old material is the formulation of Theorem 9 – in Bazhenov et al. (Reference Bazhenov, Mustafa and Ospichev2020a) it was given as Theorem 6.1 (without a proof). In Section 7, Theorem 27 is a generalization of Proposition 5.1 of Bazhenov et al. (Reference Bazhenov, Mustafa and Ospichev2020a). Note that Proposition 29 was given without a proof in Bazhenov et al. (Reference Bazhenov, Mustafa and Ospichev2020a) (see Proposition 5.2 there). Theorem 31 generalizes Proposition 6.1 of Bazhenov et al. (Reference Bazhenov, Mustafa and Ospichev2020a). Sections 9 and 10 are new.
2. Preliminaries
Given a total function
![]() $f\colon \omega \to \omega$
and a nonzero natural number m, by
$f\colon \omega \to \omega$
and a nonzero natural number m, by
![]() $f| m$
we denote the following tuple:
$f| m$
we denote the following tuple:
For a set
![]() $A\subseteq \omega$
, by
$A\subseteq \omega$
, by
![]() $\chi_A$
we denote the characteristic function of A. For a pair of natural numbers
$\chi_A$
we denote the characteristic function of A. For a pair of natural numbers
![]() $(k ,\ell)$
, the value
$(k ,\ell)$
, the value
![]() $\langle k,\ell\rangle$
is its standard Cantor index, that is,
$\langle k,\ell\rangle$
is its standard Cantor index, that is,
2.1 Theory of numberings
Let
![]() $\nu$
be a numbering of a family
$\nu$
be a numbering of a family
![]() $\mathcal{S}_0$
and
$\mathcal{S}_0$
and
![]() $\mu$
be a numbering of a family
$\mu$
be a numbering of a family
![]() $\mathcal{S}_1$
. It is easy to see that the condition
$\mathcal{S}_1$
. It is easy to see that the condition
![]() $\nu \leq \mu$
implies that
$\nu \leq \mu$
implies that
![]() $\mathcal{S}_0$
is a subfamily of
$\mathcal{S}_0$
is a subfamily of
![]() $\mathcal{S}_1$
. Clearly, if
$\mathcal{S}_1$
. Clearly, if
![]() $\nu\leq_{pr} \mu$
, then
$\nu\leq_{pr} \mu$
, then
![]() $\nu\leq \mu$
.
$\nu\leq \mu$
.
Numberings
![]() $\nu$
and
$\nu$
and
![]() $\mu$
are equivalent, denoted by
$\mu$
are equivalent, denoted by
![]() $\nu\equiv \mu$
, if
$\nu\equiv \mu$
, if
![]() $\nu\leq \mu$
and
$\nu\leq \mu$
and
![]() $\mu \leq \nu$
. The punctual equivalence
$\mu \leq \nu$
. The punctual equivalence
![]() $\equiv_{pr}$
is defined in a similar way. The numbering
$\equiv_{pr}$
is defined in a similar way. The numbering
![]() $\nu\oplus\mu$
of the family
$\nu\oplus\mu$
of the family
![]() $\mathcal{S}_0\cup\mathcal{S}_1$
is defined as follows:
$\mathcal{S}_0\cup\mathcal{S}_1$
is defined as follows:
It is not difficult to obtain the following fact (see, e.g., Proposition 3 in Ershov Reference Ershov1977, p. 36). If
![]() $\unlhd \in \{\leq,\leq_{pr}\}$
and
$\unlhd \in \{\leq,\leq_{pr}\}$
and
![]() $\xi$
is an arbitrary numbering, then
$\xi$
is an arbitrary numbering, then
Let
![]() $\mathcal{S}$
be a punctual family of functions. By
$\mathcal{S}$
be a punctual family of functions. By
![]() $Com_{pr}(\mathcal{S})$
, we denote the set of all punctual numberings of
$Com_{pr}(\mathcal{S})$
, we denote the set of all punctual numberings of
![]() $\mathcal{S}$
. Since the relation
$\mathcal{S}$
. Since the relation
![]() $\equiv_{pr}$
is a congruence on the structure
$\equiv_{pr}$
is a congruence on the structure
![]() $(Com_{pr}(\mathcal{S}); \leq_{pr}, \oplus)$
, we use the same symbols
$(Com_{pr}(\mathcal{S}); \leq_{pr}, \oplus)$
, we use the same symbols
![]() $\leq_{pr}$
and
$\leq_{pr}$
and
![]() $\oplus$
on numberings of
$\oplus$
on numberings of
![]() $\mathcal{S}$
and on
$\mathcal{S}$
and on
![]() $\equiv_{pr}$
-equivalence classes of the numberings.
$\equiv_{pr}$
-equivalence classes of the numberings.
The quotient structure
![]() $\mathcal{R}_{pr}(\mathcal{S}) := (Com_{pr}(\mathcal{S}) /_{\displaystyle{\equiv_{pr}}}; \leq_{pr}, \oplus)$
is an upper semilattice. We call the structure
$\mathcal{R}_{pr}(\mathcal{S}) := (Com_{pr}(\mathcal{S}) /_{\displaystyle{\equiv_{pr}}}; \leq_{pr}, \oplus)$
is an upper semilattice. We call the structure
![]() $\mathcal{R}_{pr}(\mathcal{S})$
the Rogers pr-semilattice of the punctual family
$\mathcal{R}_{pr}(\mathcal{S})$
the Rogers pr-semilattice of the punctual family
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
Let
![]() $\mathcal{T}$
be a family of total (Turing) computable functions acting from
$\mathcal{T}$
be a family of total (Turing) computable functions acting from
![]() $\omega$
to
$\omega$
to
![]() $\omega$
. A numbering
$\omega$
. A numbering
![]() $\nu$
of the family
$\nu$
of the family
![]() $\mathcal{T}$
is computable if the function
$\mathcal{T}$
is computable if the function
![]() $g_{\nu}$
from Definition 1 is computable. Note that this definition is consistent with the notion of computable numbering discussed in the introduction: if we identify functions from
$g_{\nu}$
from Definition 1 is computable. Note that this definition is consistent with the notion of computable numbering discussed in the introduction: if we identify functions from
![]() $\mathcal{T}$
with their graphs, then we will get precisely the same notions.
$\mathcal{T}$
with their graphs, then we will get precisely the same notions.
We say that a family
![]() $\mathcal{T}$
is Turing computable if it has a computable numbering. The definition of Rogers semilattice
$\mathcal{T}$
is Turing computable if it has a computable numbering. The definition of Rogers semilattice
![]() $\mathcal{R}_{c}(\mathcal{T})$
is obtained in a similar way to the semilattice
$\mathcal{R}_{c}(\mathcal{T})$
is obtained in a similar way to the semilattice
![]() $\mathcal{R}_{pr}(\mathcal{S})$
, modulo the following modification: one needs to consider all computable numberings of
$\mathcal{R}_{pr}(\mathcal{S})$
, modulo the following modification: one needs to consider all computable numberings of
![]() $\mathcal{T}$
and the standard reducibility
$\mathcal{T}$
and the standard reducibility
![]() $\leq$
between them.
$\leq$
between them.
Another way to look at things is the following. Suppose that
![]() $\mathcal{T}$
is still a Turing computable family of total functions, but our reducibility is punctual. This gives rise to another Rogers semilattice
$\mathcal{T}$
is still a Turing computable family of total functions, but our reducibility is punctual. This gives rise to another Rogers semilattice
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
. In this setting, the semilattices
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
. In this setting, the semilattices
![]() $\mathcal{R}_{pr}(\mathcal{S})$
constitute a special case of
$\mathcal{R}_{pr}(\mathcal{S})$
constitute a special case of
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
. Throughout the paper, we give several comments on how our results on
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
. Throughout the paper, we give several comments on how our results on
![]() $\mathcal{R}_{pr}(\mathcal{S})$
could be extended to a more general case of
$\mathcal{R}_{pr}(\mathcal{S})$
could be extended to a more general case of
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
.
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
.
2.2 The punctuality paradigm
Kalimullin et al. (Reference Kalimullin, Melnikov and Ng2017) noted that many known proofs from polynomial time structure theory (see, e.g., the survey Cenzer and Remmel Reference Cenzer and Remmel1998) are focused on making the operations and relations on a given algebraic structure
![]() $\mathcal{S}$
primitive recursive, and then observing that the obtained presentation of
$\mathcal{S}$
primitive recursive, and then observing that the obtained presentation of
![]() $\mathcal{S}$
is in fact computable in polynomial time.
$\mathcal{S}$
is in fact computable in polynomial time.
Kalimullin et al. (Reference Kalimullin, Melnikov and Ng2017) proposed that a reasonable “online” presentation of a structure must minimally satisfy the following: a countably infinite structure is punctual if its domain equals
![]() $\omega$
and the operations and predicates of the structure are (uniformly) primitive recursive. Roughly speaking, the intuition behind this notion is the following: punctual presentations do not allow any delays – or in other words, there are no instances of truly unbounded search.
$\omega$
and the operations and predicates of the structure are (uniformly) primitive recursive. Roughly speaking, the intuition behind this notion is the following: punctual presentations do not allow any delays – or in other words, there are no instances of truly unbounded search.
Nowadays, the theory of punctual structures is a flourishing research direction. Its intricate constructions have provided a deep insight into the algorithmic complexity of isomorphisms (Downey et al. Reference Downey, Greenberg, Melnikov, Ng and Turetsky2020a,b; Melnikov and Ng Reference Melnikov and Ng2019). The developed techniques found applications in the theory of automatic structures (Bazhenov et al. Reference Bazhenov, Harrison-Trainor, Kalimullin, Melnikov and Ng2019b). For further results on punctual structures, the reader is referred to the surveys (Bazhenov et al. Reference Bazhenov, Downey, Kalimullin and Melnikov2019a; Downey et al. Reference Downey, Melnikov and Ng2021; Melnikov Reference Melnikov2017).
The restricted Church–Turing thesis for primitive recursive functions says the following: A function is primitive recursive if and only if it can be described by an algorithm that uses only bounded loops. Informally speaking, one needs to eliminate all instances of while do, repeat until, and goto in a Pascal-like programming language.
Our proofs will exploit the restricted Church–Turing thesis without an explicit reference.
Let k be a nonzero natural number. We fix a computable list
![]() $(p^{(k)}_e)_{e\in\omega}$
of all k-ary primitive recursive functions. We emphasize that the list is computable, but it cannot be primitive recursive. Nevertheless, the following function can be treated as a punctual object:
$(p^{(k)}_e)_{e\in\omega}$
of all k-ary primitive recursive functions. We emphasize that the list is computable, but it cannot be primitive recursive. Nevertheless, the following function can be treated as a punctual object:
 \begin{align*} p^{(k)}_e[t](\bar x) := \begin{cases} p^{(k)}_e (\bar x), & \text{if the value } p^{(k)}_e(\bar x) \text{ is computed in}\\ & \text{at most } t \text{ computational steps},\\ \text{undefined}, & \text{otherwise}. \end{cases}\end{align*}
\begin{align*} p^{(k)}_e[t](\bar x) := \begin{cases} p^{(k)}_e (\bar x), & \text{if the value } p^{(k)}_e(\bar x) \text{ is computed in}\\ & \text{at most } t \text{ computational steps},\\ \text{undefined}, & \text{otherwise}. \end{cases}\end{align*}
Without loss of generality, one may also assume the following: if
![]() $p^{(k)}_e(\bar x)$
is equal to N, then for any
$p^{(k)}_e(\bar x)$
is equal to N, then for any
![]() $t\leq \max(e,\bar x,N)$
, the value
$t\leq \max(e,\bar x,N)$
, the value
![]() $p^{(k)}_e[t](\bar x)$
is undefined. The formal details can be recovered from Bazhenov et al. (Reference Bazhenov, Downey, Kalimullin and Melnikov2019a, Section 10).
$p^{(k)}_e[t](\bar x)$
is undefined. The formal details can be recovered from Bazhenov et al. (Reference Bazhenov, Downey, Kalimullin and Melnikov2019a, Section 10).
If
![]() $k=1$
, then we omit the superscript – we write
$k=1$
, then we omit the superscript – we write
![]() $p_e$
in place of
$p_e$
in place of
![]() $p^{(1)}_e$
. For
$p^{(1)}_e$
. For
![]() $e\in\omega$
, we define a numbering
$e\in\omega$
, we define a numbering
![]() $\rho_e$
:
$\rho_e$
:
It is clear that
![]() $(\rho_e)_{e\in\omega}$
is a computable list of all punctual numberings.
$(\rho_e)_{e\in\omega}$
is a computable list of all punctual numberings.
2.3 Semilattices for finite families
We note the following – when a punctual family
![]() $\mathcal{S}$
is finite, the situation is very simple:
$\mathcal{S}$
is finite, the situation is very simple:
Proposition 3. Let
![]() $\mathcal{S}$
be a finite punctual family. Then the semilattice
$\mathcal{S}$
be a finite punctual family. Then the semilattice
![]() $\mathcal{R}_{pr}(\mathcal{S})$
contains precisely one element.
$\mathcal{R}_{pr}(\mathcal{S})$
contains precisely one element.
Proof. Suppose that
![]() $\mathcal{S} = \{ f_0,f_1,\dots,f_m\}$
. We fix a natural number N such that the strings
$\mathcal{S} = \{ f_0,f_1,\dots,f_m\}$
. We fix a natural number N such that the strings
![]() $f_i| N$
and
$f_i| N$
and
![]() $i\leq m$
are pairwise different.
$i\leq m$
are pairwise different.
It is sufficient to establish the following fact: for arbitrary punctual numberings
![]() $\nu$
and
$\nu$
and
![]() $\mu$
of
$\mu$
of
![]() $\mathcal{S}$
, one can build a function g, which punctually reduces
$\mathcal{S}$
, one can build a function g, which punctually reduces
![]() $\nu$
to
$\nu$
to
![]() $\mu$
.
$\mu$
.
The desired g is constructed as follows. We fix indices
![]() $a_i$
,
$a_i$
,
![]() $i\leq m$
, such that
$i\leq m$
, such that
![]() $\mu(a_i) = f_i$
. For an arbitrary index
$\mu(a_i) = f_i$
. For an arbitrary index
![]() $k\in\omega$
, we promptly find the number
$k\in\omega$
, we promptly find the number
![]() $j\leq m$
such that
$j\leq m$
such that
![]() $\nu(k)| N = f_j| N$
. Then we define
$\nu(k)| N = f_j| N$
. Then we define
![]() $g(k) := a_j$
.
$g(k) := a_j$
. ![]()
3. Strongly Punctually Decidable Numberings
In this section, we introduce the notion of a strongly punctually decidable numbering and discuss its properties. This notion will play a key role in most of our further constructions.
The background behind the notion comes from some classical results of the theory of numberings. An arbitrary numbering
![]() $\nu$
is traditionally associated with an equivalence relation
$\nu$
is traditionally associated with an equivalence relation
![]() $\eta_{\nu}$
on
$\eta_{\nu}$
on
![]() $\omega$
– the relation
$\omega$
– the relation
![]() $\eta_{\nu}$
is defined as follows:
$\eta_{\nu}$
is defined as follows:
Sometimes, the relation
![]() $\eta_{\nu}$
is called the numeration equivalence of
$\eta_{\nu}$
is called the numeration equivalence of
![]() $\nu$
.
$\nu$
.
A numbering
![]() $\nu$
is called negative if the relation
$\nu$
is called negative if the relation
![]() $\eta_{\nu}$
is co-c.e., that is,
$\eta_{\nu}$
is co-c.e., that is,
![]() $\eta_{\nu}$
is the complement of a c.e. set. A numbering
$\eta_{\nu}$
is the complement of a c.e. set. A numbering
![]() $\nu$
is decidable if the relation
$\nu$
is decidable if the relation
![]() $\eta_{\nu}$
is (Turing) computable. A numbering
$\eta_{\nu}$
is (Turing) computable. A numbering
![]() $\nu$
is Friedberg if
$\nu$
is Friedberg if
![]() $\eta_{\nu}$
is the identity relation.
$\eta_{\nu}$
is the identity relation.
Let
![]() $\mathcal{T}$
be an infinite, Turing computable family of functions. Mal’cev (Reference Mal’cev1965) showed that every computable numbering of
$\mathcal{T}$
be an infinite, Turing computable family of functions. Mal’cev (Reference Mal’cev1965) showed that every computable numbering of
![]() $\mathcal{T}$
is negative. Ershov (Reference Ershov1967) proved that for any computable numbering
$\mathcal{T}$
is negative. Ershov (Reference Ershov1967) proved that for any computable numbering
![]() $\nu$
of
$\nu$
of
![]() $\mathcal{T}$
, there is a computable Friedberg numbering
$\mathcal{T}$
, there is a computable Friedberg numbering
![]() $\mu$
of
$\mu$
of
![]() $\mathcal{T}$
such that
$\mathcal{T}$
such that
![]() $\mu \leq \nu$
.
$\mu \leq \nu$
.
The notion of a strongly punctually decidable numbering comes from a “punctual version” of the results of Mal’cev and Ershov. First, we note the following:
Observation 4. If
![]() $\nu$
is a punctual numbering, then
$\nu$
is a punctual numbering, then
![]() $\nu$
is negative.
$\nu$
is negative.
Indeed, this fact easily follows from the result of Mal’cev (Reference Mal’cev1965). After that, we introduce our new notions:
Definition 5. We say that a numbering
![]() $\nu$
is punctually decidable if the relation
$\nu$
is punctually decidable if the relation
![]() $\eta_{\nu}$
is primitive recursive.
$\eta_{\nu}$
is primitive recursive.
A punctually decidable numbering
![]() $\nu$
is strongly punctually decidable (or spd for short) if every
$\nu$
is strongly punctually decidable (or spd for short) if every
![]() $\eta_{\nu}$
-equivalence class C satisfies the following: either C contains only one element, or
$\eta_{\nu}$
-equivalence class C satisfies the following: either C contains only one element, or
![]() $C = [0]_{\eta_{\nu}}$
.
$C = [0]_{\eta_{\nu}}$
.
Roughly speaking, the intuition behind the notion of an spd numbering is as follows. When one builds a punctual algebraic structure
![]() $\mathcal{P}$
, one of the basic strategies is “time-filling”: while we wait for some Turing computable (not necessarily primitive recursive) process to finish its computations, we still have to promptly construct larger and large finite pieces of
$\mathcal{P}$
, one of the basic strategies is “time-filling”: while we wait for some Turing computable (not necessarily primitive recursive) process to finish its computations, we still have to promptly construct larger and large finite pieces of
![]() $\mathcal{P}$
. Typically, this is achieved via copying some (relatively) simple parts of a given punctual structure
$\mathcal{P}$
. Typically, this is achieved via copying some (relatively) simple parts of a given punctual structure
![]() $\mathcal{A}$
. For example, if
$\mathcal{A}$
. For example, if
![]() $\mathcal{A} = (\omega, s, 0)$
, where s is the successor function, then one could promptly take fresh numbers and declare that inside our
$\mathcal{A} = (\omega, s, 0)$
, where s is the successor function, then one could promptly take fresh numbers and declare that inside our
![]() $\mathcal{P}$
, they are equal to
$\mathcal{P}$
, they are equal to
![]() $0_{\mathcal{P}}$
,
$0_{\mathcal{P}}$
,
![]() $s_{\mathcal{P}}(0_{\mathcal{P}})$
,
$s_{\mathcal{P}}(0_{\mathcal{P}})$
,
![]() $s_{\mathcal{P}}(s_{\mathcal{P}}(0_{\mathcal{P}}))$
,…,
$s_{\mathcal{P}}(s_{\mathcal{P}}(0_{\mathcal{P}}))$
,…,
![]() $s^{(n)}_{\mathcal{P}}(0_{\mathcal{P}})$
,….
$s^{(n)}_{\mathcal{P}}(0_{\mathcal{P}})$
,….
The notion of an spd numbering mirrors the time-filling strategy. In general, the construction of a punctual Friedberg numbering for a given punctual family
![]() $\mathcal{S}$
could be impossible (see Proposition 38 in the last section). Nevertheless, “stalling” the construction process by defining
$\mathcal{S}$
could be impossible (see Proposition 38 in the last section). Nevertheless, “stalling” the construction process by defining
allows to build an spd numbering for
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
We prove the following general result about numberings:
Proposition 6.
-
(i) If
 $\nu$
is a punctually decidable numbering, then any
$\nu$
is a punctually decidable numbering, then any
 $\mu\leq_{pr} \nu$
is also punctually decidable.
$\mu\leq_{pr} \nu$
is also punctually decidable. -
(ii) If
 $\nu$
is a punctually decidable numbering, then there is a spd numbering
$\nu$
is a punctually decidable numbering, then there is a spd numbering
 $\mu$
such that
$\mu$
such that
 $\mu\equiv_{pr} \nu$
.
$\mu\equiv_{pr} \nu$
. -
(iii) If
 $\nu$
is a negative numbering of a family
$\nu$
is a negative numbering of a family
 $\mathcal{S}$
, then there is a spd numbering
$\mathcal{S}$
, then there is a spd numbering
 $\mu$
of the same family such that
$\mu$
of the same family such that
 $\mu \leq_{pr}\nu$
.
$\mu \leq_{pr}\nu$
.
Proof.
-
(i) Suppose that
 $\nu$
is a punctually decidable numbering, and a function f punctually reduces
$\nu$
is a punctually decidable numbering, and a function f punctually reduces
 $\mu$
to
$\mu$
to
 $\nu$
. Then clearly, we have Since
$\nu$
. Then clearly, we have Since \begin{align*} (k ~\eta_{\mu}~ \ell) \ \Leftrightarrow\ (f(k) ~\eta_{\nu}~ f(\ell)). \end{align*}
\begin{align*} (k ~\eta_{\mu}~ \ell) \ \Leftrightarrow\ (f(k) ~\eta_{\nu}~ f(\ell)). \end{align*}
 $\eta_{\nu}$
is primitive recursive, the relation
$\eta_{\nu}$
is primitive recursive, the relation
 $\eta_{\mu}$
is also primitive recursive.
$\eta_{\mu}$
is also primitive recursive.
-
(ii) Let
 $\nu$
be a punctually decidable numbering. We define a new numbering
$\nu$
be a punctually decidable numbering. We define a new numbering
 $\mu$
as follows: Since the relation
$\mu$
as follows: Since the relation \begin{align*} \mu(0) := \nu(0), \quad \mu(k+1) := \begin{cases} \nu(k+1), & \text{if } (\forall i\leq k) \neg [ (i,k+1) \in \eta_{\nu} ],\\ \nu(0), & \text{if } (\exists i \leq k) [ (i,k+1) \in \eta_{\nu} ]. \end{cases} \end{align*}
\begin{align*} \mu(0) := \nu(0), \quad \mu(k+1) := \begin{cases} \nu(k+1), & \text{if } (\forall i\leq k) \neg [ (i,k+1) \in \eta_{\nu} ],\\ \nu(0), & \text{if } (\exists i \leq k) [ (i,k+1) \in \eta_{\nu} ]. \end{cases} \end{align*}
 $\eta_{\nu}$
is primitive recursive, a unary relation is also primitive recursive. Using this fact, it is easy to show that the numbering
$\eta_{\nu}$
is primitive recursive, a unary relation is also primitive recursive. Using this fact, it is easy to show that the numbering \begin{align*} R(k) := (\exists i \leq k) [(i,k+1) \in \eta_{\nu}] \end{align*}
\begin{align*} R(k) := (\exists i \leq k) [(i,k+1) \in \eta_{\nu}] \end{align*}
 $\mu$
is spd, and
$\mu$
is spd, and
 $\mu = \nu\circ f$
for a primitive recursive function f. Moreover, hence,
$\mu = \nu\circ f$
for a primitive recursive function f. Moreover, hence, \begin{align*} \nu(k+1) = \begin{cases} \mu(k+1), & \text{if } (\forall i\leq k) \neg [ (i,k+1) \in \eta_{\nu} ],\\ \mu(0), & \text{otherwise}; \end{cases} \end{align*}
\begin{align*} \nu(k+1) = \begin{cases} \mu(k+1), & \text{if } (\forall i\leq k) \neg [ (i,k+1) \in \eta_{\nu} ],\\ \mu(0), & \text{otherwise}; \end{cases} \end{align*}
 $\nu \leq_{pr} \mu$
. Therefore, we deduce that
$\nu \leq_{pr} \mu$
. Therefore, we deduce that
 $\mu\equiv_{pr}\nu$
.
$\mu\equiv_{pr}\nu$
.
-
(iii) Let
 $\nu$
be a negative numbering of a family
$\nu$
be a negative numbering of a family
 $\mathcal{S}$
. By item (ii), it is sufficient to find a punctually decidable numbering
$\mathcal{S}$
. By item (ii), it is sufficient to find a punctually decidable numbering
 $\mu$
of
$\mu$
of
 $\mathcal{S}$
such that
$\mathcal{S}$
such that
 $\mu \leq_{pr} \nu$
.
$\mu \leq_{pr} \nu$
.
Since the numbering
![]() $\nu$
is negative, the set
$\nu$
is negative, the set
is computably enumerable. Choose a primitive recursive function h(x) such that
![]() $\mathrm{range}(h) = I_{\nu}$
. Then it is not hard to show that the numbering
$\mathrm{range}(h) = I_{\nu}$
. Then it is not hard to show that the numbering
![]() $\mu:= \nu\circ h$
is punctually decidable. Hence,
$\mu:= \nu\circ h$
is punctually decidable. Hence,
![]() $\mu$
has the desired properties.
$\mu$
has the desired properties.
The following consequence of Proposition 6 will play a crucial part in our constructions:
Corollary 7. If
![]() $\nu$
is a punctual numbering of a family
$\nu$
is a punctual numbering of a family
![]() $\mathcal{S}$
, then there is a spd numbering
$\mathcal{S}$
, then there is a spd numbering
![]() $\mu\in Com_{pr}(\mathcal{S})$
such that
$\mu\in Com_{pr}(\mathcal{S})$
such that
![]() $\mu\leq_{pr} \nu$
.
$\mu\leq_{pr} \nu$
.
3.1 Punctual families with spd numberings
After Proposition 6 and Corollary 7 are obtained, it is natural to consider the following problem:
Problem 8. We say that a punctual family
![]() $\mathcal{S}$
is persistently decidable if every punctual numbering of
$\mathcal{S}$
is persistently decidable if every punctual numbering of
![]() $\mathcal{S}$
is punctually decidable. Characterize persistently decidable families.
$\mathcal{S}$
is punctually decidable. Characterize persistently decidable families.
First, we observe the following easy sufficient condition for being persistently decidable.
Definition 9. We say that a punctual family
![]() $\mathcal{S}$
is strongly finitely discrete (or sf-discrete for short) if there exists a natural number N such that for any functions
$\mathcal{S}$
is strongly finitely discrete (or sf-discrete for short) if there exists a natural number N such that for any functions
![]() $f,g\in\mathcal{S}$
, the following conditions are equivalent:
$f,g\in\mathcal{S}$
, the following conditions are equivalent:
Lemma 10. Every sf-discrete punctual family
![]() $\mathcal{S}$
is persistently decidable.
$\mathcal{S}$
is persistently decidable.
Proof. Let
![]() $\nu$
be an arbitrary punctual numbering of
$\nu$
be an arbitrary punctual numbering of
![]() $\mathcal{S}$
. It is clear that we have
$\mathcal{S}$
. It is clear that we have
and this condition is primitive recursive. ![]()
Note that every finite punctual family is sf-discrete.
Example 11. A simple example of an infinite sf-discrete family is the family containing the following functions: for
![]() $i\in\omega$
,
$i\in\omega$
,
Second, we obtain a sufficient condition for being not persistently decidable.
Definition 12. Let
![]() $\nu$
be a punctual numbering of a family
$\nu$
be a punctual numbering of a family
![]() $\mathcal{S}$
. We say that a primitive recursive function f is a quickly spoiling limit point for
$\mathcal{S}$
. We say that a primitive recursive function f is a quickly spoiling limit point for
![]() $\nu$
if it satisfies the following: there is a primitive recursive function sp(n,t) such that for any n,
$\nu$
if it satisfies the following: there is a primitive recursive function sp(n,t) such that for any n,
The intuition behind the definition is as follows. Consider a construction, which promptly defines a function g(x) bit by bit. A default action of this construction is copying the function f – we put
![]() $g(0) := f(0)$
,
$g(0) := f(0)$
,
![]() $g(1) := f(1)$
,
$g(1) := f(1)$
,
![]() $g(2) := f(2)$
,. Then the function sp(n,t) always provides two different opportunities for a quick “diagonalization”: at any stage s, one can abandon copying f and set either
$g(2) := f(2)$
,. Then the function sp(n,t) always provides two different opportunities for a quick “diagonalization”: at any stage s, one can abandon copying f and set either
![]() $g := \nu(sp(s,0))$
or
$g := \nu(sp(s,0))$
or
![]() $g := \nu(sp(s,1))$
.
$g := \nu(sp(s,1))$
.
Observation 13. Let
![]() $\nu$
be a punctual numbering of a family
$\nu$
be a punctual numbering of a family
![]() $\mathcal{S}$
, and let
$\mathcal{S}$
, and let
![]() $\mu$
be a punctual numbering of a family
$\mu$
be a punctual numbering of a family
![]() $\mathcal{T}$
. If f is a quickly spoiling limit point for
$\mathcal{T}$
. If f is a quickly spoiling limit point for
![]() $\nu$
, then f is also quickly spoiling for
$\nu$
, then f is also quickly spoiling for
![]() $\nu\oplus \mu$
.
$\nu\oplus \mu$
.
Example 14. A simple example for Definition 12 can be recovered as follows. Consider a punctual Friedberg numbering:
Then the function
![]() $f := \chi_{\emptyset}$
is a quickly spoiling limit point for
$f := \chi_{\emptyset}$
is a quickly spoiling limit point for
![]() $\nu$
. This is witnessed by a function sp satisfying
$\nu$
. This is witnessed by a function sp satisfying
![]() $sp(n,0) := n+1$
and
$sp(n,0) := n+1$
and
![]() $sp(n,1) := n+2$
. Note that in this example, f is the unique limit point of
$sp(n,1) := n+2$
. Note that in this example, f is the unique limit point of
![]() $\mathcal{S}$
in the Cantor space
$\mathcal{S}$
in the Cantor space
![]() $2^{\omega}$
.
$2^{\omega}$
.
Proposition 15. Suppose that
![]() $\nu$
is a punctual numbering of a family
$\nu$
is a punctual numbering of a family
![]() $\mathcal{S}$
, and f is a quickly spoiling limit point for
$\mathcal{S}$
, and f is a quickly spoiling limit point for
![]() $\nu$
. Then the family
$\nu$
. Then the family
![]() $\mathcal{S}$
is not persistently decidable.
$\mathcal{S}$
is not persistently decidable.
Proof. Choose a primitive recursive function sp(n,t), which witnesses the spoiledness of f. Let A be a computable set which is not primitive recursive. Fix two primitive recursive functions p(x) and q(x) such that
![]() $A = \mathrm{range}(p)$
and
$A = \mathrm{range}(p)$
and
![]() $\overline{A} = \mathrm{range}(q)$
.
$\overline{A} = \mathrm{range}(q)$
.
We define a punctual numbering
![]() $\mu$
of some subfamily
$\mu$
of some subfamily
![]() $\mathcal{S}_0 \subseteq \mathcal{S}$
. An informal idea of the construction is as follows. Consider a number
$\mathcal{S}_0 \subseteq \mathcal{S}$
. An informal idea of the construction is as follows. Consider a number
![]() $k\in\omega$
. We look at two quick listings
$k\in\omega$
. We look at two quick listings
![]() $A = \left\{{}p(0), p(1), p(2), \dots\right\}$
and
$A = \left\{{}p(0), p(1), p(2), \dots\right\}$
and
![]() $\overline{A} = \{ q(0), q(1), q(2), \dots\}$
, and we wait for the first stage
$\overline{A} = \{ q(0), q(1), q(2), \dots\}$
, and we wait for the first stage
![]() $s_0$
, at which we see that k appeared on one of the two lists. At every stage
$s_0$
, at which we see that k appeared on one of the two lists. At every stage
![]() $s< s_0$
, the functions
$s< s_0$
, the functions
![]() $\mu(2k)$
and
$\mu(2k)$
and
![]() $\mu(2k+1)$
just copy (the initial segments of) the limit point f. At the stage
$\mu(2k+1)$
just copy (the initial segments of) the limit point f. At the stage
![]() $s_0$
, we consider two cases:
$s_0$
, we consider two cases:
-
(1). If
 $k \in A$
, then we put
$k \in A$
, then we put
 $\mu(2k) = \mu(2k+1) := \nu( sp(s_0,0))$
.
$\mu(2k) = \mu(2k+1) := \nu( sp(s_0,0))$
. -
(2). If
 $k\not\in A$
, then we set
$k\not\in A$
, then we set
 $\mu(2k) := \nu (sp(s_0,0))$
and
$\mu(2k) := \nu (sp(s_0,0))$
and
 $\mu(2k+1) := \nu (sp(s_0,0))$
.
$\mu(2k+1) := \nu (sp(s_0,0))$
.
The properties of the function sp(n,t) ensure that the described construction builds a punctual numbering, and every function
![]() $\mu(\ell)$
belongs to
$\mu(\ell)$
belongs to
![]() $\mathcal{S}$
. Moreover, we deduce that
$\mathcal{S}$
. Moreover, we deduce that
Since the set A is not primitive recursive, the numbering
![]() $\mu$
cannot be punctually decidable.
$\mu$
cannot be punctually decidable.
For the sake of completeness, we provide a more formal description of the construction. We build the numbering
![]() $\mu$
and auxiliary prompt functions u(k,s) and w(k,s). We put
$\mu$
and auxiliary prompt functions u(k,s) and w(k,s). We put
![]() $\mu(k)(0) = f(0)$
and
$\mu(k)(0) = f(0)$
and
![]() $u(k,0) = w(k,0) = -1$
for all
$u(k,0) = w(k,0) = -1$
for all
![]() $k\in\omega$
.
$k\in\omega$
.
At a stage
![]() $s+1$
, for each k we proceed as follows:
$s+1$
, for each k we proceed as follows:
-
(1). If
 $u(k,s) \geq 0$
, then we put
$u(k,s) \geq 0$
, then we put
 $u(k,s+1) := u(k,s)$
and
$u(k,s+1) := u(k,s)$
and
 $w(k,s+1) := w(k,s)$
. Otherwise, we check the following conditions:
$w(k,s+1) := w(k,s)$
. Otherwise, we check the following conditions:-
– If
 $k\in \{ p(0), p(1),\dots,p(s+1)\}$
, then set
$k\in \{ p(0), p(1),\dots,p(s+1)\}$
, then set
 $u(k,s+1) = w(k,s+1) := sp(s+1, 0)$
.
$u(k,s+1) = w(k,s+1) := sp(s+1, 0)$
. -
– If
 $k \in \{ q(0), q(1), \dots, q(s+1)\}$
, then define
$k \in \{ q(0), q(1), \dots, q(s+1)\}$
, then define
 $u(k,s+1) := sp(s+1,0)$
and
$u(k,s+1) := sp(s+1,0)$
and
 $w(k,s+1) := sp(s+1,1)$
.
$w(k,s+1) := sp(s+1,1)$
. -
– Otherwise, do not change the values of u and v.
-
-
(2). Define
 \begin{gather*} \mu(2k) (s+1) := \begin{cases} \nu(u(k,s+1)) (s+1), & \text{if } u(k,s+1) \geq 0,\\ f (s+1), & \text{if } u(k,s+1) = -1; \end{cases}\\ \mu(2k+1) (s+1) := \begin{cases} \nu(w(k,s+1)) (s+1), & \text{if } w(k,s+1) \geq 0,\\ f (s+1), & \text{if } w(k,s+1) = -1. \end{cases} \end{gather*}
\begin{gather*} \mu(2k) (s+1) := \begin{cases} \nu(u(k,s+1)) (s+1), & \text{if } u(k,s+1) \geq 0,\\ f (s+1), & \text{if } u(k,s+1) = -1; \end{cases}\\ \mu(2k+1) (s+1) := \begin{cases} \nu(w(k,s+1)) (s+1), & \text{if } w(k,s+1) \geq 0,\\ f (s+1), & \text{if } w(k,s+1) = -1. \end{cases} \end{gather*}
This concludes the description of the construction. The argument given before the description shows that
![]() $\mu$
promptly indexes some subfamily
$\mu$
promptly indexes some subfamily
![]() $\mathcal{S}_0$
of
$\mathcal{S}_0$
of
![]() $\mathcal{S}$
, and the numbering
$\mathcal{S}$
, and the numbering
![]() $\mu$
is not punctually decidable. Therefore, the numbering
$\mu$
is not punctually decidable. Therefore, the numbering
![]() $\mu_1 := \nu \oplus \mu$
belongs to
$\mu_1 := \nu \oplus \mu$
belongs to
![]() $Com_{pr}(\mathcal{S})$
, and
$Com_{pr}(\mathcal{S})$
, and
![]() $\mu_1$
is not punctually decidable. Hence, the family
$\mu_1$
is not punctually decidable. Hence, the family
![]() $\mathcal{S}$
is not persistently decidable.
$\mathcal{S}$
is not persistently decidable. ![]()
In general, it seems that Problem 8 is pretty hard to solve. After the reader familiarizes themselves with further punctual constructions, in Section 9, we will build an infinite, persistently decidable family
![]() $\mathcal{S}$
such that:
$\mathcal{S}$
such that:
-
For every function
 $f\in\mathcal{S}$
,
$f\in\mathcal{S}$
,
 $\textrm{range}(f) \subseteq \{ 0,1\}$
. This implies that
$\textrm{range}(f) \subseteq \{ 0,1\}$
. This implies that
 $\mathcal{S}$
is not sf-discrete.
$\mathcal{S}$
is not sf-discrete. -
The family
 $\mathcal{S}$
has a unique limit point f in the Cantor space, and this f is primitive recursive. By Proposition 15, f cannot be quickly spoiling for any punctual numbering
$\mathcal{S}$
has a unique limit point f in the Cantor space, and this f is primitive recursive. By Proposition 15, f cannot be quickly spoiling for any punctual numbering
 $\nu$
of
$\nu$
of
 $\mathcal{S}$
.
$\mathcal{S}$
.
4. Warming Up: Absence of Minimal Elements
The section contains an introduction to punctual priority constructions: we give a detailed proof of the result below, which serves as a good starting point.
Theorem 16. Let
![]() $\mathcal{S}$
be an infinite punctual family. Then the semilattice
$\mathcal{S}$
be an infinite punctual family. Then the semilattice
![]() $\mathcal{R}_{pr}(\mathcal{S})$
does not contain minimal elements. Consequently, the structure
$\mathcal{R}_{pr}(\mathcal{S})$
does not contain minimal elements. Consequently, the structure
![]() $\mathcal{R}_{pr}(\mathcal{S})$
is infinite.
$\mathcal{R}_{pr}(\mathcal{S})$
is infinite.
Proof. Let
![]() $\alpha$
be a punctual numbering of
$\alpha$
be a punctual numbering of
![]() $\mathcal{S}$
. By Corollary 3, there is a spd numbering
$\mathcal{S}$
. By Corollary 3, there is a spd numbering
![]() $\nu\in Com_{pr}(\mathcal{S})$
such that
$\nu\in Com_{pr}(\mathcal{S})$
such that
![]() $\nu\leq_{pr} \alpha$
. In order to prove the theorem, we build a numbering
$\nu\leq_{pr} \alpha$
. In order to prove the theorem, we build a numbering
![]() $\mu\in Com_{pr}(\mathcal{S})$
such that
$\mu\in Com_{pr}(\mathcal{S})$
such that
![]() $\mu\leq_{pr} \nu$
and
$\mu\leq_{pr} \nu$
and
![]() $\nu\not\leq_{pr} \mu$
.
$\nu\not\leq_{pr} \mu$
.
Our construction will satisfy the following series of requirements:
-
 $P_e$
: The function
$P_e$
: The function
 $p_e$
does not punctually reduce
$p_e$
does not punctually reduce
 $\nu$
to
$\nu$
to
 $\mu$
.
$\mu$
.
The key difference between our construction and a typical priority argument (of recursion theory) is the following: our requirements do not injure each other, and we will satisfy only one requirement
![]() $P_e$
at a time.
$P_e$
at a time.
Strategy for
![]() $P_e$
. Suppose that the
$P_e$
. Suppose that the
![]() $P_e$
-strategy starts working at a stage
$P_e$
-strategy starts working at a stage
![]() $s^e$
of the construction, and
$s^e$
of the construction, and
![]() $N^e$
is the least index such that the object
$N^e$
is the least index such that the object
![]() $\mu(N^e)$
is still undefined at the beginning of the stage
$\mu(N^e)$
is still undefined at the beginning of the stage
![]() $s^e$
.
$s^e$
.
We wait until the first stage
![]() $t>s^e$
with the following properties:
$t>s^e$
with the following properties:
-
(a) There is a (least) number
 $w^e\leq t$
such that
$w^e\leq t$
such that
 $w^e \geq e$
,
$w^e \geq e$
,
 $\nu(w^e) \neq \nu(0)$
, and we have not used the object
$\nu(w^e) \neq \nu(0)$
, and we have not used the object
 $\nu(w^e)$
in our definition of
$\nu(w^e)$
in our definition of
 $\mu$
before.
$\mu$
before. -
(b) For this particular
 $w^e$
, the value
$w^e$
, the value
 $p_e[t](w^e)$
is already defined.
$p_e[t](w^e)$
is already defined.
Note that checking whether
![]() $\nu(w^e)$
is equal to
$\nu(w^e)$
is equal to
![]() $\nu(0)$
is a punctual procedure, since the numbering
$\nu(0)$
is a punctual procedure, since the numbering
![]() $\nu$
is spd.
$\nu$
is spd.
While waiting for this t to appear, we should not delay the definition of the numbering
![]() $\mu$
, so, one by one, we put
$\mu$
, so, one by one, we put
When the desired stage t is achieved, we proceed as follows:
-
1. For each
 $k\leq p_e(w^e)$
, if the object
$k\leq p_e(w^e)$
, if the object
 $\mu(k)$
is still undefined, then put
$\mu(k)$
is still undefined, then put
 $\mu(k) := \nu(0)$
.
$\mu(k) := \nu(0)$
. -
2. Let m be the least index such that at this moment,
 $\mu(m)$
is still undefined. Set
$\mu(m)$
is still undefined. Set
 $\mu(m + \ell) := \nu(\ell)$
, for every
$\mu(m + \ell) := \nu(\ell)$
, for every
 $\ell \leq w^e$
.
$\ell \leq w^e$
.
It is clear that the described actions ensure that the requirement
![]() $P_e$
is forever satisfied: our choice of the witness
$P_e$
is forever satisfied: our choice of the witness
![]() $w^e$
guarantees that we have
$w^e$
guarantees that we have
![]() $\nu(w^e)\neq \mu(p_e(w^e))$
.
$\nu(w^e)\neq \mu(p_e(w^e))$
.
The construction is arranged as follows: we start the
![]() $P_0$
-strategy and wait until it is satisfied. When
$P_0$
-strategy and wait until it is satisfied. When
![]() $P_0$
is satisfied, we immediately start the
$P_0$
is satisfied, we immediately start the
![]() $P_1$
-strategy. After
$P_1$
-strategy. After
![]() $P_1$
is satisfied, we start
$P_1$
is satisfied, we start
![]() $P_2$
, etc.
$P_2$
, etc.
Verification. Since the family
![]() $\mathcal{S}$
is infinite, each strategy
$\mathcal{S}$
is infinite, each strategy
![]() $P_e$
will eventually find its witness
$P_e$
will eventually find its witness
![]() $w^e$
, and after that,
$w^e$
, and after that,
![]() $P_e$
will eventually become satisfied. Therefore, we deduce
$P_e$
will eventually become satisfied. Therefore, we deduce
![]() $\nu\not\leq_{pr} \mu$
.
$\nu\not\leq_{pr} \mu$
.
The constructed numbering
![]() $\mu$
is punctual: indeed, for an index
$\mu$
is punctual: indeed, for an index
![]() $k\in\omega$
, one can just look at the stage
$k\in\omega$
, one can just look at the stage
![]() $k+1$
of the described construction. At this stage
$k+1$
of the described construction. At this stage
![]() $k+1$
, we can promptly find an index r(k) such that
$k+1$
, we can promptly find an index r(k) such that
![]() $\mu(k)$
is equal to
$\mu(k)$
is equal to
![]() $\nu(r(k))$
. This shows the punctuality of
$\nu(r(k))$
. This shows the punctuality of
![]() $\mu$
, and furthermore, the function r punctually reduces
$\mu$
, and furthermore, the function r punctually reduces
![]() $\mu$
to
$\mu$
to
![]() $\nu$
.
$\nu$
.
Informally speaking, the punctuality of
![]() $\mu$
is ensured by elimination of unbounded searches: Surely, the
$\mu$
is ensured by elimination of unbounded searches: Surely, the
![]() $P_e$
-strategy wants to “catch” a particularly good stage t, but this quest for t does not delay the construction at all – while doing the t-search, our definition of
$P_e$
-strategy wants to “catch” a particularly good stage t, but this quest for t does not delay the construction at all – while doing the t-search, our definition of
![]() $\mu$
just executes a straightforward filler action (copying
$\mu$
just executes a straightforward filler action (copying
![]() $\nu(0)$
for appropriate
$\nu(0)$
for appropriate
![]() $\mu$
-indices).
$\mu$
-indices).
Now it is enough to show that the numbering
![]() $\mu$
has an index for every element of
$\mu$
has an index for every element of
![]() $\mathcal{S}$
. This is ensured by the assignment
$\mathcal{S}$
. This is ensured by the assignment
![]() $\mu(m + \ell) := \nu(\ell)$
given above – after satisfying
$\mu(m + \ell) := \nu(\ell)$
given above – after satisfying
![]() $P_e$
,
$P_e$
,
![]() $\mu$
copies the long initial segment
$\mu$
copies the long initial segment
![]() $\nu(0),\nu(1),\dots,\nu(w^e)$
.
$\nu(0),\nu(1),\dots,\nu(w^e)$
. ![]()
The classical result of Khutoretskii (Reference Khutoretskii1971) shows that for any computable family
![]() $\mathcal{T}$
, its semilattice
$\mathcal{T}$
, its semilattice
![]() $\mathcal{R}_c(\mathcal{T})$
is either one element or infinite. Proposition 3 and Theorem 16 together imply that the punctual setting exhibits a similar behavior:
$\mathcal{R}_c(\mathcal{T})$
is either one element or infinite. Proposition 3 and Theorem 16 together imply that the punctual setting exhibits a similar behavior:
Corollary 17. For an arbitrary punctual family
![]() $\mathcal{S}$
, its Rogers pr-semilattice is either one element or infinite.
$\mathcal{S}$
, its Rogers pr-semilattice is either one element or infinite.
For a Turing computable family of total functions
![]() $\mathcal{T}$
, we consider the semilattice
$\mathcal{T}$
, we consider the semilattice
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
defined in Section 2.1. A simple analysis of the proof of Theorem 16 shows the following:
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
defined in Section 2.1. A simple analysis of the proof of Theorem 16 shows the following:
Corollary 18. If
![]() $\mathcal{T}$
is a Turing computable infinite family of total functions, then the semilattice
$\mathcal{T}$
is a Turing computable infinite family of total functions, then the semilattice
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
does not contain minimal elements.
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
does not contain minimal elements.
Proof Sketch. In the construction of Theorem 16, one builds a new numbering
![]() $\mu$
only by looking at the
$\mu$
only by looking at the
![]() $\nu$
-indices, that is, we always declare that
$\nu$
-indices, that is, we always declare that
![]() $\mu(k) := \nu(\ell_k)$
for some
$\mu(k) := \nu(\ell_k)$
for some
![]() $\ell_k\in\omega$
, and we never really work with the “internal content” of our functions
$\ell_k\in\omega$
, and we never really work with the “internal content” of our functions
![]() $\nu(\ell_k)$
. By working with the internal content, here we mean the following: say, one can choose to define
$\nu(\ell_k)$
. By working with the internal content, here we mean the following: say, one can choose to define
that is, to copy different finite pieces from different functions
![]() $\nu(\ell_t)$
,
$\nu(\ell_t)$
,
![]() $t\in\omega$
.
$t\in\omega$
.
This observation implies that the constructed new numbering
![]() $\mu$
is a Turing computable numbering of our family
$\mu$
is a Turing computable numbering of our family
![]() $\mathcal{T}$
such that
$\mathcal{T}$
such that
![]() $\mu\leq_{pr} \nu$
and
$\mu\leq_{pr} \nu$
and
![]() $\nu\not\leq_{pr} \mu$
.
$\nu\not\leq_{pr} \mu$
. ![]()
5. Antichains
In this section, we establish that any non-greatest element of a Rogers pr-semilattice is a part of an infinite antichain. First, we prove the following.
Theorem 19. Let
![]() $\mathcal{S}$
be an infinite punctual family. Let
$\mathcal{S}$
be an infinite punctual family. Let
![]() $\alpha$
and
$\alpha$
and
![]() $\mu$
be punctual numberings of
$\mu$
be punctual numberings of
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
![]() $\mu <_{pr} \alpha$
, that is,
$\mu <_{pr} \alpha$
, that is,
![]() $\mu \leq_{pr} \alpha$
and
$\mu \leq_{pr} \alpha$
and
![]() $\alpha\not\leq_{pr} \mu$
. Then there is a numbering
$\alpha\not\leq_{pr} \mu$
. Then there is a numbering
![]() $\nu \in Com_{pr}(\mathcal{S})$
such that
$\nu \in Com_{pr}(\mathcal{S})$
such that
![]() $\nu \leq_{pr} \alpha$
and
$\nu \leq_{pr} \alpha$
and
![]() $\nu$
is
$\nu$
is
![]() $\leq_{pr}$
-incomparable with
$\leq_{pr}$
-incomparable with
![]() $\mu$
.
$\mu$
.
Proof. We apply Corollary 7 and fix a spd numbering
![]() $\tilde\mu$
of the family
$\tilde\mu$
of the family
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
![]() $\tilde\mu \leq_{pr} \mu$
. Our numbering
$\tilde\mu \leq_{pr} \mu$
. Our numbering
![]() $\nu$
will copy different pieces of
$\nu$
will copy different pieces of
![]() $\alpha$
and
$\alpha$
and
![]() $\tilde\mu$
. Choose a function
$\tilde\mu$
. Choose a function
![]() $f_{\tilde\mu}$
, which punctually reduces
$f_{\tilde\mu}$
, which punctually reduces
![]() $\tilde\mu$
to
$\tilde\mu$
to
![]() $\alpha$
.
$\alpha$
.
We satisfy the following series of requirements:
-
 $P_e$
:
$P_e$
:
 $p_e\colon \tilde\mu \not\leq_{pr}\nu$
, that is,
$p_e\colon \tilde\mu \not\leq_{pr}\nu$
, that is,
 $p_e$
does not punctually reduce
$p_e$
does not punctually reduce
 $\tilde\mu$
to
$\tilde\mu$
to
 $\nu$
.
$\nu$
. -
 $Q_i$
:
$Q_i$
:
 $p_i\colon \nu \not\leq_{pr} \mu$
.
$p_i\colon \nu \not\leq_{pr} \mu$
.
The
![]() $P_e$
-requirements ensure that
$P_e$
-requirements ensure that
![]() $\tilde\mu \not\leq_{pr} \nu$
. Since
$\tilde\mu \not\leq_{pr} \nu$
. Since
![]() $\tilde{\mu} \leq_{pr} \mu$
, this implies
$\tilde{\mu} \leq_{pr} \mu$
, this implies
![]() $\mu \not\leq_{pr} \nu$
.
$\mu \not\leq_{pr} \nu$
.
We also have a global requirement
-
R:
 $\nu$
is punctually reducible to
$\nu$
is punctually reducible to
 $\alpha$
.
$\alpha$
.
Informally, this will be satisfied via the following action: at a stage s, we promptly define the value
![]() $f_{\nu}(s)$
such that
$f_{\nu}(s)$
such that
![]() $\nu(s) = \alpha(f_{\nu}(s))$
.
$\nu(s) = \alpha(f_{\nu}(s))$
.
We fix a (punctual) ordering of requirements:
![]() $P_0 < Q_0 < P_1 < Q_1 < \dots$
. This means that we will satisfy
$P_0 < Q_0 < P_1 < Q_1 < \dots$
. This means that we will satisfy
![]() $P_0$
, then
$P_0$
, then
![]() $Q_0$
, then
$Q_0$
, then
![]() $P_1$
, etc.
$P_1$
, etc.
The
![]() $P_e$
-strategy. By the background action of the
$P_e$
-strategy. By the background action of the
![]() $P_e$
-strategy, we mean the following: whenever we are waiting for some object to be found, we do not delay our construction, and we just put
$P_e$
-strategy, we mean the following: whenever we are waiting for some object to be found, we do not delay our construction, and we just put
starting with an appropriate index N. This N is typically clear from the context (recall the
![]() $N^e$
from Theorem 16).
$N^e$
from Theorem 16).
The strategy
![]() $P_e$
waits until the first (large enough) stage t with the following properties:
$P_e$
waits until the first (large enough) stage t with the following properties:
-
(a) There are
 $N+1$
indices
$N+1$
indices
 $a_0,a_1,\dots,a_{N}$
such that
$a_0,a_1,\dots,a_{N}$
such that
 $a_i \leq t$
and the objects
$a_i \leq t$
and the objects
 $\tilde\mu(a_i)$
are pairwise different. Recall that the relation
$\tilde\mu(a_i)$
are pairwise different. Recall that the relation
 $\eta_{\tilde\mu}$
is primitive recursive, so this condition can be verified in a prompt way.
$\eta_{\tilde\mu}$
is primitive recursive, so this condition can be verified in a prompt way. -
(b) For each
 $i\leq N$
, the value
$i\leq N$
, the value
 $p_e(a_i)[t]$
is defined.
$p_e(a_i)[t]$
is defined.
When this t is found, we compute
![]() $M := \max(p_e(a_0),p_e(a_1),\dots,p_e(a_N))$
. For every
$M := \max(p_e(a_0),p_e(a_1),\dots,p_e(a_N))$
. For every
![]() $k\leq M$
, if
$k\leq M$
, if
![]() $\nu(k)$
is still undefined, then we put
$\nu(k)$
is still undefined, then we put
![]() $\nu(k) := \tilde{\mu}(0)$
.
$\nu(k) := \tilde{\mu}(0)$
.
Consider the finite set
![]() $F := \{ j\,\colon j\leq M\}$
. On one hand, it is clear that the family
$F := \{ j\,\colon j\leq M\}$
. On one hand, it is clear that the family
![]() $ \{ \nu(j)\,\colon j\in F\} $
contains at most N different objects. On the other hand, there are
$ \{ \nu(j)\,\colon j\in F\} $
contains at most N different objects. On the other hand, there are
![]() $(N+1)$
different functions
$(N+1)$
different functions
![]() $\tilde{\mu}(a_i)$
,
$\tilde{\mu}(a_i)$
,
![]() $i\leq N$
, and
$i\leq N$
, and
![]() $p_e(a_i) \in F$
for all i.
$p_e(a_i) \in F$
for all i.
Therefore, we deduce that
![]() $p_e$
cannot punctually reduce
$p_e$
cannot punctually reduce
![]() $\tilde\mu$
to our
$\tilde\mu$
to our
![]() $\nu$
, and the
$\nu$
, and the
![]() $P_e$
-requirement is satisfied.
$P_e$
-requirement is satisfied.
The
![]() $Q_i$
-strategy. Suppose that the strategy starts working at a stage
$Q_i$
-strategy. Suppose that the strategy starts working at a stage
![]() $s_0$
of the construction. Let
$s_0$
of the construction. Let
![]() $M_0$
be the least index such that
$M_0$
be the least index such that
![]() $\nu(M_0)$
is still undefined. We put
$\nu(M_0)$
is still undefined. We put
This action ensures that every object from the family
![]() $\mathcal{S}$
eventually obtains a
$\mathcal{S}$
eventually obtains a
![]() $\nu$
-index.
$\nu$
-index.
Put
![]() $N:=M_0+s_0+1$
. The background action of the
$N:=M_0+s_0+1$
. The background action of the
![]() $Q_i$
-strategy is as follows – it defines
$Q_i$
-strategy is as follows – it defines
We wait until the first stage t such that there are an index
![]() $w_0 \leq t$
and a number
$w_0 \leq t$
and a number
![]() $L \leq t$
with the following properties:
$L \leq t$
with the following properties:
-
The value
 $p_i(w_0)[t]$
is defined.
$p_i(w_0)[t]$
is defined. -
The object
 $\nu(w_0)$
is defined.
$\nu(w_0)$
is defined. -
We have
 $\nu(w_0) | L \neq \mu(p_i(w_0)) | L$
.
$\nu(w_0) | L \neq \mu(p_i(w_0)) | L$
.
If these
![]() $w_0$
and L are found, then
$w_0$
and L are found, then
![]() $\nu(w_0) \neq \mu(p_i(w_0))$
. This shows that
$\nu(w_0) \neq \mu(p_i(w_0))$
. This shows that
![]() $p_i$
does not reduce
$p_i$
does not reduce
![]() $\nu$
to
$\nu$
to
![]() $\mu$
, and the
$\mu$
, and the
![]() $Q_i$
-strategy is satisfied.
$Q_i$
-strategy is satisfied.
Now we only need to show that the desired stage t will be eventually reached. Toward a contradiction, assume that there is no such stage t. Then for every w and L, we have
![]() $\nu(w) | L = \mu(p_i(w)) | L$
. In other words, the function
$\nu(w) | L = \mu(p_i(w)) | L$
. In other words, the function
![]() $p_i$
punctually reduces
$p_i$
punctually reduces
![]() $\nu$
to
$\nu$
to
![]() $\mu$
. Then our background actions imply that
$\mu$
. Then our background actions imply that
hence
![]() $\alpha \leq_{pr} \mu$
, which contradicts the conditions of the theorem.
$\alpha \leq_{pr} \mu$
, which contradicts the conditions of the theorem.
The construction is arranged similarly to Theorem 16: our requirements are satisified one by one, according to their priority ordering.
Verification. We have already shown that every requirement will be eventually satisfied; hence, the numberings
![]() $\nu$
and
$\nu$
and
![]() $\mu$
are
$\mu$
are
![]() $\leq_{pr}$
-incomparable. Moreover, our description of a
$\leq_{pr}$
-incomparable. Moreover, our description of a
![]() $Q_i$
-strategy guarantees that
$Q_i$
-strategy guarantees that
![]() $\nu$
provides an index for every element from
$\nu$
provides an index for every element from
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
Note that there is a primitive recursive function
![]() $f_{\nu}(x)$
such that
$f_{\nu}(x)$
such that
![]() $\nu = \alpha \circ f_{\nu}$
. This is ensured by the background actions: at each stage, we promptly set either
$\nu = \alpha \circ f_{\nu}$
. This is ensured by the background actions: at each stage, we promptly set either
![]() $\nu(x) := \tilde{\mu}(0) = \alpha(f_{\tilde\mu}(0))$
or
$\nu(x) := \tilde{\mu}(0) = \alpha(f_{\tilde\mu}(0))$
or
![]() $\nu(x) := \alpha(\ell_x)$
for appropriately chosen index
$\nu(x) := \alpha(\ell_x)$
for appropriately chosen index
![]() $\ell_x$
. Therefore, the numbering
$\ell_x$
. Therefore, the numbering
![]() $\nu$
has desired properties.
$\nu$
has desired properties. ![]()
A not too difficult modification of Theorem 19 provides the following result:
Theorem 20. Let
![]() $\mathcal{S}$
be an infinite punctual family. Let
$\mathcal{S}$
be an infinite punctual family. Let
![]() $\alpha$
and
$\alpha$
and
![]() $\mu$
be punctual numberings of
$\mu$
be punctual numberings of
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
![]() $\mu <_{pr} \alpha$
. Then there is a computable list
$\mu <_{pr} \alpha$
. Then there is a computable list
![]() $(\nu_k)_{k\in\omega}$
of punctual numberings of
$(\nu_k)_{k\in\omega}$
of punctual numberings of
![]() $\mathcal{S}$
such that:
$\mathcal{S}$
such that:
-
(a) for every k,
 $\nu_k \leq_{pr} \alpha$
and
$\nu_k \leq_{pr} \alpha$
and
 $\nu_k$
is
$\nu_k$
is
 $\leq_{pr}$
-incomparable with
$\leq_{pr}$
-incomparable with
 $\mu$
;
$\mu$
; -
(b) the numberings
 $\nu_k$
are pairwise
$\nu_k$
are pairwise
 $\leq_{pr}$
-incomparable.
$\leq_{pr}$
-incomparable.
Corollary 21. If
![]() $\mu$
is a non-greatest element of a Rogers pr-semilattice
$\mu$
is a non-greatest element of a Rogers pr-semilattice
![]() $\mathcal{R}$
, then
$\mathcal{R}$
, then
![]() $\mu$
is a part of an infinite antichain inside
$\mu$
is a part of an infinite antichain inside
![]() $\mathcal{R}$
.
$\mathcal{R}$
.
Proof of Theorem 20. Here we discuss a construction, which builds only two
![]() $\leq_{pr}$
-incomparable punctual numberings
$\leq_{pr}$
-incomparable punctual numberings
![]() $\nu_0$
and
$\nu_0$
and
![]() $\nu_1$
. This construction admits a straightforward generalization to the case of countably many incomparable elements. We use the same notation as in Theorem 19.
$\nu_1$
. This construction admits a straightforward generalization to the case of countably many incomparable elements. We use the same notation as in Theorem 19.
For
![]() $\varepsilon \in\{ 0,1\}$
, we need to satisfy the following requirements:
$\varepsilon \in\{ 0,1\}$
, we need to satisfy the following requirements:
-
 $R^{\varepsilon}$
:
$R^{\varepsilon}$
:
 $\nu_{\varepsilon}$
is punctually reducible to
$\nu_{\varepsilon}$
is punctually reducible to
 $\alpha$
.
$\alpha$
. -
 $P^{\varepsilon}_e$
:
$P^{\varepsilon}_e$
:
 $p_e\colon \tilde\mu \not\leq_{pr}\nu_{\varepsilon}$
.
$p_e\colon \tilde\mu \not\leq_{pr}\nu_{\varepsilon}$
. -
 $Q^{\varepsilon}_i$
:
$Q^{\varepsilon}_i$
:
 $p_i\colon \nu_{\varepsilon} \not\leq_{pr} \mu$
.
$p_i\colon \nu_{\varepsilon} \not\leq_{pr} \mu$
. -
 $N^0_j$
:
$N^0_j$
:
 $p_j\colon \nu_0 \not\leq_{pr} \nu_1$
.
$p_j\colon \nu_0 \not\leq_{pr} \nu_1$
. -
 $N^1_j$
:
$N^1_j$
:
 $p_j\colon \nu_1 \not\leq_{pr} \nu_0$
.
$p_j\colon \nu_1 \not\leq_{pr} \nu_0$
.
The strategies for the requirements
![]() $R^{\varepsilon}$
,
$R^{\varepsilon}$
,
![]() $P^{\varepsilon}_e$
, and
$P^{\varepsilon}_e$
, and
![]() $Q^{\varepsilon}_j$
are essentially the same as those in the proof of Theorem 19. Since
$Q^{\varepsilon}_j$
are essentially the same as those in the proof of Theorem 19. Since
![]() $N^1$
-requirements are similar to
$N^1$
-requirements are similar to
![]() $N^0$
-requirements, it is sufficient to discuss only a
$N^0$
-requirements, it is sufficient to discuss only a
![]() $N^0_j$
-strategy.
$N^0_j$
-strategy.
The
![]() $N^0_j$
-strategy. The background action of the strategy is the following: we put
$N^0_j$
-strategy. The background action of the strategy is the following: we put
Our strategy waits until the first stage t with the following properties:
-
(a) There are
 $N+1$
indices
$N+1$
indices
 $b_0,b_1,\dots,b_{N}$
such that
$b_0,b_1,\dots,b_{N}$
such that
 $N\leq b_i \leq t$
and the objects
$N\leq b_i \leq t$
and the objects
 $\nu_0(b_i)$
are pairwise different. Since the numbering
$\nu_0(b_i)$
are pairwise different. Since the numbering
 $\tilde{\mu}$
is spd and (in the background)
$\tilde{\mu}$
is spd and (in the background)
 $\nu_0(N+x) = \tilde{\mu}(x)$
, these indices will eventually appear.
$\nu_0(N+x) = \tilde{\mu}(x)$
, these indices will eventually appear. -
(b) For each
 $i\leq N$
, the value
$i\leq N$
, the value
 $p_j(b_i)[t]$
is defined.
$p_j(b_i)[t]$
is defined.
When the number t is found, we set
![]() $M:= \max\{ p_j(b_i)\,\colon i\leq N\}$
. For each
$M:= \max\{ p_j(b_i)\,\colon i\leq N\}$
. For each
![]() $k\leq M$
, if the value
$k\leq M$
, if the value
![]() $\nu_0(k)$
is still undefined, then put
$\nu_0(k)$
is still undefined, then put
![]() $\nu_0(k) := \tilde{\mu}(0)$
. We work with
$\nu_0(k) := \tilde{\mu}(0)$
. We work with
![]() $\nu_1(k)$
,
$\nu_1(k)$
,
![]() $k\leq M$
, in a similar way.
$k\leq M$
, in a similar way.
An argument similar to the one given in the description of the
![]() $P_e$
-strategy (Theorem 19) shows that
$P_e$
-strategy (Theorem 19) shows that
![]() $p_j$
does not punctually reduce
$p_j$
does not punctually reduce
![]() $\nu_0$
to
$\nu_0$
to
![]() $\nu_1$
.
$\nu_1$
.
As usual, our construction fixes some punctual ordering of all requirements (except
![]() $R^0$
and
$R^0$
and
![]() $R^1$
) and satisfies these requirements one by one. The requirements
$R^1$
) and satisfies these requirements one by one. The requirements
![]() $R^0$
and
$R^0$
and
![]() $R^1$
are satisfied via “global” actions. The verification proceeds similarly to Theorem 19. This concludes the proof of Theorem 20.
$R^1$
are satisfied via “global” actions. The verification proceeds similarly to Theorem 19. This concludes the proof of Theorem 20.
Similarly to Corollary 18, the proof of Theorem 20 implies the following:
Corollary 22. Let
![]() $\mathcal{T}$
be a Turing computable infinite family of total functions, and let
$\mathcal{T}$
be a Turing computable infinite family of total functions, and let
![]() $\mu$
be a non-greatest element in the semilattice
$\mu$
be a non-greatest element in the semilattice
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
. Then
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
. Then
![]() $\mu$
is a part of an infinite antichain inside
$\mu$
is a part of an infinite antichain inside
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
.
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
.
6. Density
In this section, we consider intervals inside a Rogers pr-semilattice
![]() $\mathcal{R}_{pr}(\mathcal{S})$
. First, we prove that the poset
$\mathcal{R}_{pr}(\mathcal{S})$
. First, we prove that the poset
![]() $\mathcal{R}_{pr}(\mathcal{S})$
is dense:
$\mathcal{R}_{pr}(\mathcal{S})$
is dense:
Theorem 23. Let
![]() $\mathcal{S}$
be an infinite punctual family. Suppose that
$\mathcal{S}$
be an infinite punctual family. Suppose that
![]() $\nu$
and
$\nu$
and
![]() $\mu$
are punctual numberings of
$\mu$
are punctual numberings of
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
![]() $\nu <_{pr} \mu$
. Then there is a numbering
$\nu <_{pr} \mu$
. Then there is a numbering
![]() $\xi \in Com_{pr}(\mathcal{S})$
such that
$\xi \in Com_{pr}(\mathcal{S})$
such that
![]() $\nu <_{pr} \xi <_{pr} \mu$
.
$\nu <_{pr} \xi <_{pr} \mu$
.
Proof. Fix a function f, which provides a punctual reduction
![]() $\nu \leq_{pr} \mu$
. We build a punctual numbering
$\nu \leq_{pr} \mu$
. We build a punctual numbering
![]() $\alpha$
of some subfamily
$\alpha$
of some subfamily
![]() $\mathcal{S}_0 \subseteq \mathcal{S}$
, while satisfying the following requirements:
$\mathcal{S}_0 \subseteq \mathcal{S}$
, while satisfying the following requirements:
-
R:
 $\alpha$
is punctually reducible to
$\alpha$
is punctually reducible to
 $\mu$
.
$\mu$
. -
 $P_e$
:
$P_e$
:
 $p_e\colon \alpha \not\leq_{pr} \nu$
.
$p_e\colon \alpha \not\leq_{pr} \nu$
. -
 $Q_i$
:
$Q_i$
:
 $p_i\colon \mu\not\leq_{pr} \alpha \oplus \nu$
.
$p_i\colon \mu\not\leq_{pr} \alpha \oplus \nu$
.
These requirements are enough for our goals: indeed, assume that all requirements are satisfied and consider the punctual numbering
![]() $\xi:=\alpha \oplus \nu$
of the whole family
$\xi:=\alpha \oplus \nu$
of the whole family
![]() $\mathcal{S}$
. Then clearly, we have
$\mathcal{S}$
. Then clearly, we have
![]() $\nu \leq_{pr} \xi \leq_{pr} \mu$
. The
$\nu \leq_{pr} \xi \leq_{pr} \mu$
. The
![]() $P_e$
-requirements guarantee that
$P_e$
-requirements guarantee that
![]() $\xi \not\leq_{pr} \nu$
. The
$\xi \not\leq_{pr} \nu$
. The
![]() $Q_i$
-requirements ensure
$Q_i$
-requirements ensure
![]() $\mu \not\leq_{pr} \xi$
.
$\mu \not\leq_{pr} \xi$
.
As in Theorem 19, the R-strategy acts globally: at a stage s, we promptly define the value
![]() $g_{\alpha}(s)$
with
$g_{\alpha}(s)$
with
![]() $\alpha(s) = \mu(g_{\alpha}(s))$
.
$\alpha(s) = \mu(g_{\alpha}(s))$
.
The
![]() $P_e$
-strategy. Suppose that the strategy starts working at a stage
$P_e$
-strategy. Suppose that the strategy starts working at a stage
![]() $s_0$
, and N is the least index with
$s_0$
, and N is the least index with
![]() $\alpha(N)$
still being undefined.
$\alpha(N)$
still being undefined.
The background action of the
![]() $P_e$
-strategy is as follows. We propagate
$P_e$
-strategy is as follows. We propagate
We wait for the least stage
![]() $s_1 > s_0$
such that there is a number
$s_1 > s_0$
such that there is a number
![]() $w\leq s_1$
with the following properties:
$w\leq s_1$
with the following properties:
-
The object
 $\alpha(w)$
is already defined, and
$\alpha(w)$
is already defined, and
 $\alpha(w) = \mu(g_{\alpha}(w))$
. The verification will demonstrate that given w, the desired
$\alpha(w) = \mu(g_{\alpha}(w))$
. The verification will demonstrate that given w, the desired
 $\mu$
-index
$\mu$
-index
 $g_{\alpha}(w)$
can be calculated in a prompt way.
$g_{\alpha}(w)$
can be calculated in a prompt way. -
The value
 $p_e[s_1](w)$
is defined.
$p_e[s_1](w)$
is defined. -
By the stage
 $s_1$
, we have already witnessed that
$s_1$
, we have already witnessed that
 $\mu(g_{\alpha}(w)) \neq \mu f(p_e(w))$
.
$\mu(g_{\alpha}(w)) \neq \mu f(p_e(w))$
.
The last item requires a little bit of clarification: How does one check such a condition?
Recall that by Observation 4, the numbering
![]() $\mu$
is negative. In other words, the set
$\mu$
is negative. In other words, the set
![]() $ \left\{ (k,\ell)\,\colon \mu(k) \neq \mu(\ell) \right\} $
is c.e., and hence, it can be enumerated by a punctual function. Thus, if our
$ \left\{ (k,\ell)\,\colon \mu(k) \neq \mu(\ell) \right\} $
is c.e., and hence, it can be enumerated by a punctual function. Thus, if our
![]() $g_{\alpha}(w)$
and
$g_{\alpha}(w)$
and
![]() $f(p_e(w)) $
are
$f(p_e(w)) $
are
![]() $\mu$
-indices of different objects, then we will eventually witness this fact.
$\mu$
-indices of different objects, then we will eventually witness this fact.
We emphasize the following: If the desired stage
![]() $s_1$
is found, then the requirement
$s_1$
is found, then the requirement
![]() $P_e$
will be forever satisfied. Indeed, we know that
$P_e$
will be forever satisfied. Indeed, we know that
![]() $\alpha(w) = \mu(g_{\alpha}(w)) \neq \mu f(p_e(w)) = \nu(p_e(w))$
, and hence,
$\alpha(w) = \mu(g_{\alpha}(w)) \neq \mu f(p_e(w)) = \nu(p_e(w))$
, and hence,
![]() $p_e$
cannot punctually reduce
$p_e$
cannot punctually reduce
![]() $\alpha$
to
$\alpha$
to
![]() $\nu$
. Thus, after the stage
$\nu$
. Thus, after the stage
![]() $s_1$
, one can proceed to working with other requirements.
$s_1$
, one can proceed to working with other requirements.
The
![]() $Q_i$
-strategy. Again, we assume that the strategy starts working at a stage
$Q_i$
-strategy. Again, we assume that the strategy starts working at a stage
![]() $s_0$
, and N is the least index with
$s_0$
, and N is the least index with
![]() $\alpha(N)$
still undefined.
$\alpha(N)$
still undefined.
The background action of
![]() $Q_i$
is propagating the following:
$Q_i$
is propagating the following:
Wait for the least stage
![]() $s_1 > s_0$
such that there is a number
$s_1 > s_0$
such that there is a number
![]() $w\leq s_1$
satisfying:
$w\leq s_1$
satisfying:
-
The value
 $p_i[s_1](w)$
is defined.
$p_i[s_1](w)$
is defined. -
If the value
 $p_i(w)$
is even, then the object
$p_i(w)$
is even, then the object
 $\alpha(p_i(w)/2)$
is already defined. Set Here, again, we assume that
$\alpha(p_i(w)/2)$
is already defined. Set Here, again, we assume that \begin{align*} \ell(w) := \begin{cases} f(\lfloor{}p_i(w)/2 \rfloor), & \text{if } p_i(w) \text{ is odd},\\ g_{\alpha}(p_i(w)/2), & \text{if } p_i(w) \text{ is even}. \end{cases} \end{align*}
\begin{align*} \ell(w) := \begin{cases} f(\lfloor{}p_i(w)/2 \rfloor), & \text{if } p_i(w) \text{ is odd},\\ g_{\alpha}(p_i(w)/2), & \text{if } p_i(w) \text{ is even}. \end{cases} \end{align*}
 $\alpha(k) = \mu(g_{\alpha}(k))$
.
$\alpha(k) = \mu(g_{\alpha}(k))$
.
-
By the stage
 $s_1$
, we have already witnessed that
$s_1$
, we have already witnessed that
 $\mu(w) \neq \mu(\ell(w))$
.
$\mu(w) \neq \mu(\ell(w))$
.
If such a stage
![]() $s_1$
is found, then the requirement
$s_1$
is found, then the requirement
![]() $Q_i$
will be satisfied. Indeed, we witness that
$Q_i$
will be satisfied. Indeed, we witness that
 \begin{align*} \mu(w) \neq \mu(\ell(w)) &= \left\{ \begin{array}{ll} \mu f(\lfloor p_i(w)/2 \rfloor), & \text{if } p_i(w) \text{ is odd},\\ \mu g_{\alpha}(p_i(w)/2), & \text{if } p_i(w) \text{ is even} \end{array} \right\} \\ &= \left\{ \begin{array}{ll} \nu(\lfloor p_i(w)/2 \rfloor), & \text{if } p_i(w) \text{ is odd},\\ \alpha(p_i(w)/2), & \text{if } p_i(w) \text{ is even} \end{array} \right\} = (\alpha \oplus \nu) (p_i(w)). \end{align*}
\begin{align*} \mu(w) \neq \mu(\ell(w)) &= \left\{ \begin{array}{ll} \mu f(\lfloor p_i(w)/2 \rfloor), & \text{if } p_i(w) \text{ is odd},\\ \mu g_{\alpha}(p_i(w)/2), & \text{if } p_i(w) \text{ is even} \end{array} \right\} \\ &= \left\{ \begin{array}{ll} \nu(\lfloor p_i(w)/2 \rfloor), & \text{if } p_i(w) \text{ is odd},\\ \alpha(p_i(w)/2), & \text{if } p_i(w) \text{ is even} \end{array} \right\} = (\alpha \oplus \nu) (p_i(w)). \end{align*}
The construction is arranged as follows. We fix the ordering of our requirements
![]() $P_0 < Q_0 < P_1 < Q_1 < \dots$
, and satisfy them one by one.
$P_0 < Q_0 < P_1 < Q_1 < \dots$
, and satisfy them one by one.
Verification. It is clear that
![]() $\alpha(x) = \mu(g_{\alpha}(x))$
, where
$\alpha(x) = \mu(g_{\alpha}(x))$
, where
![]() $g_{\alpha}$
is a primitive recursive function. This is ensured by our background actions: we always promptly set either
$g_{\alpha}$
is a primitive recursive function. This is ensured by our background actions: we always promptly set either
![]() $\alpha(N) := \mu(\ell_N)$
or
$\alpha(N) := \mu(\ell_N)$
or
![]() $\alpha(N):= \nu(\ell_N) = \mu(f(\ell_N))$
for appropriately chosen index
$\alpha(N):= \nu(\ell_N) = \mu(f(\ell_N))$
for appropriately chosen index
![]() $\ell_N$
. Hence,
$\ell_N$
. Hence,
![]() $\alpha \leq_{pr} \mu$
, and the strategy descriptions above are well defined.
$\alpha \leq_{pr} \mu$
, and the strategy descriptions above are well defined.
In order to finish the proof, we need to establish the following fact: every requirement is eventually satisfied.
Toward a contradiction, assume that there is the least requirement T, which is never satisfied. There are two possible cases.
Case 1. Assume that
![]() $T = P_e$
for some
$T = P_e$
for some
![]() $e\in\omega$
. This implies that the desired stage
$e\in\omega$
. This implies that the desired stage
![]() $s_1$
of the
$s_1$
of the
![]() $P_e$
-strategy is never found. Therefore, for each index w, we have
$P_e$
-strategy is never found. Therefore, for each index w, we have
![]() $\alpha(w) = \mu(g_{\alpha}(w)) = \mu f(p_e(w)) = \nu(p_e(w))$
.
$\alpha(w) = \mu(g_{\alpha}(w)) = \mu f(p_e(w)) = \nu(p_e(w))$
.
Since the
![]() $P_e$
-strategy works forever, for some fixed index N, we have
$P_e$
-strategy works forever, for some fixed index N, we have
![]() $\alpha(N+\ell) = \mu(\ell)$
, for all
$\alpha(N+\ell) = \mu(\ell)$
, for all
![]() $\ell \in \omega$
. Therefore,
$\ell \in \omega$
. Therefore,
This means that
![]() $\mu \leq_{pr} \nu$
, which gives a contradiction.
$\mu \leq_{pr} \nu$
, which gives a contradiction.
Case 2. Suppose that
![]() $T = Q_i$
. The desired
$T = Q_i$
. The desired
![]() $s_1$
of the
$s_1$
of the
![]() $Q_i$
-strategy cannot be found, and this implies that for every index w, we have
$Q_i$
-strategy cannot be found, and this implies that for every index w, we have
![]() $\mu(w) = \mu(\ell(w)) = (\alpha\oplus \nu)(p_i(w))$
.
$\mu(w) = \mu(\ell(w)) = (\alpha\oplus \nu)(p_i(w))$
.
The background actions of the
![]() $Q_i$
-strategy ensure that there is N such that
$Q_i$
-strategy ensure that there is N such that
![]() $\alpha(N + m) = \nu(m)$
, for all
$\alpha(N + m) = \nu(m)$
, for all
![]() $m\in \omega$
. This shows that
$m\in \omega$
. This shows that
![]() $\alpha \leq_{pr} \nu$
, since for each
$\alpha \leq_{pr} \nu$
, since for each
![]() $k<N$
, one can nonuniformly find a
$k<N$
, one can nonuniformly find a
![]() $\nu$
-index of the object
$\nu$
-index of the object
![]() $\alpha(k)$
. Hence, we have
$\alpha(k)$
. Hence, we have
which contradicts the conditions of the theorem.
Therefore, we deduce that every requirement is satisfied. This concludes the proof of Theorem 23. ![]()
With a little bit more work, we obtain the following result.
Theorem 24. Let
![]() $\mathcal{S}$
be an infinite punctual family. Suppose that
$\mathcal{S}$
be an infinite punctual family. Suppose that
![]() $\nu$
and
$\nu$
and
![]() $\mu$
are punctual numberings of
$\mu$
are punctual numberings of
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
![]() $\nu <_{pr} \mu$
. Then there is a computable list
$\nu <_{pr} \mu$
. Then there is a computable list
![]() $(\xi_i)_{i\in\omega}$
of numberings such that:
$(\xi_i)_{i\in\omega}$
of numberings such that:
-
(a)
 $\xi_i \in Com_{pr}(\mathcal{S})$
and
$\xi_i \in Com_{pr}(\mathcal{S})$
and
 $\nu <_{pr} \xi_i <_{pr} \mu$
.
$\nu <_{pr} \xi_i <_{pr} \mu$
. -
(b) For any non-empty finite sets F and G, we have
 \begin{align*} \bigoplus_{i\in F} \xi_i \leq_{pr} \bigoplus_{j\in G} \xi_j\ \Leftrightarrow\ F\subseteq G. \end{align*}
\begin{align*} \bigoplus_{i\in F} \xi_i \leq_{pr} \bigoplus_{j\in G} \xi_j\ \Leftrightarrow\ F\subseteq G. \end{align*}
Proof. First, we give a detailed construction for only two incomparable numberings
![]() $\xi_0$
and
$\xi_0$
and
![]() $\xi_1$
. After that, we discuss the modifications that are needed for the general case.
$\xi_1$
. After that, we discuss the modifications that are needed for the general case.
We use the same notation as in Theorem 23. We build punctual numberings
![]() $\alpha_0 \in Com_{pr}(\mathcal{S}_0)$
and
$\alpha_0 \in Com_{pr}(\mathcal{S}_0)$
and
![]() $\alpha_1 \in Com_{pr}(\mathcal{S}_1)$
for some subfamilies
$\alpha_1 \in Com_{pr}(\mathcal{S}_1)$
for some subfamilies
![]() $\mathcal{S}_0$
and
$\mathcal{S}_0$
and
![]() $\mathcal{S}_1$
of the family
$\mathcal{S}_1$
of the family
![]() $\mathcal{S}$
. We satisfy the following requirements:
$\mathcal{S}$
. We satisfy the following requirements:
-
 $R^0$
:
$R^0$
:
 $\alpha_0 \leq_{pr} \mu$
via a function
$\alpha_0 \leq_{pr} \mu$
via a function
 $g_{\alpha_0}$
.
$g_{\alpha_0}$
. -
 $R^1$
:
$R^1$
:
 $\alpha_1 \leq_{pr} \mu$
via a function
$\alpha_1 \leq_{pr} \mu$
via a function
 $g_{\alpha_1}$
.
$g_{\alpha_1}$
. -
 $N^0_e$
:
$N^0_e$
:
 $p_e\colon \alpha_0\oplus \nu \not\leq_{pr} \alpha_1 \oplus\nu$
.
$p_e\colon \alpha_0\oplus \nu \not\leq_{pr} \alpha_1 \oplus\nu$
. -
 $N^1_i$
:
$N^1_i$
:
 $p_i\colon \alpha_1 \oplus \nu \not\leq_{pr} \alpha_0 \oplus \nu$
.
$p_i\colon \alpha_1 \oplus \nu \not\leq_{pr} \alpha_0 \oplus \nu$
.
Then the numberings
![]() $\xi_0 := \alpha_0 \oplus \nu$
and
$\xi_0 := \alpha_0 \oplus \nu$
and
![]() $\xi_1:= \alpha_1 \oplus \nu$
have all the desired properties. Indeed,
$\xi_1:= \alpha_1 \oplus \nu$
have all the desired properties. Indeed,
![]() $R^0$
ensures that
$R^0$
ensures that
![]() $\xi_0 \leq_{pr}\mu$
. It is obvious that
$\xi_0 \leq_{pr}\mu$
. It is obvious that
![]() $\nu \leq_{pr} \xi_0$
. The
$\nu \leq_{pr} \xi_0$
. The
![]() $N^0_e$
- and
$N^0_e$
- and
![]() $N^1_i$
-requirements guarantee that
$N^1_i$
-requirements guarantee that
![]() $\xi_0$
and
$\xi_0$
and
![]() $\xi_1$
are
$\xi_1$
are
![]() $\leq_{pr}$
-incomparable. Hence, it is clear that
$\leq_{pr}$
-incomparable. Hence, it is clear that
![]() $\nu <_{pr} \xi_j <_{pr} \mu$
for
$\nu <_{pr} \xi_j <_{pr} \mu$
for
![]() $j\in\{ 0,1\}$
.
$j\in\{ 0,1\}$
.
It is sufficient to discuss only an
![]() $N^0_e$
-strategy: The
$N^0_e$
-strategy: The
![]() $R^{j}$
-satisfaction is similar to Theorem 23, and an
$R^{j}$
-satisfaction is similar to Theorem 23, and an
![]() $N^1_i$
-strategy is essentially the same as that for
$N^1_i$
-strategy is essentially the same as that for
![]() $N^0_e$
.
$N^0_e$
.
The
![]() $N^0_e$
-strategy. Suppose that the strategy starts working at a stage
$N^0_e$
-strategy. Suppose that the strategy starts working at a stage
![]() $s_0$
, and M is the least index with both
$s_0$
, and M is the least index with both
![]() $\alpha_0(M)$
and
$\alpha_0(M)$
and
![]() $\alpha_1(M)$
undefined.
$\alpha_1(M)$
undefined.
Our background action defines
We wait for a stage
![]() $s_1 > s_0$
such that there is
$s_1 > s_0$
such that there is
![]() $w\leq s_1$
with the following properties:
$w\leq s_1$
with the following properties:
-
The object
 $\alpha_0(w) = \mu (g_{\alpha_0}(w))$
is already defined.
$\alpha_0(w) = \mu (g_{\alpha_0}(w))$
is already defined. -
The value
 $p_e[s_1](2w)$
is defined.
$p_e[s_1](2w)$
is defined. -
By the stage
 $s_1$
, we have already witnessed that
$s_1$
, we have already witnessed that  \begin{gather*} \mu g_{\alpha_0}(w) \neq \left\{ \begin{array}{ll} \mu g_{\alpha_1} (p_e(2w) / 2), & \text{if } p_e(2w) \text{ is even},\\ \mu f (\lfloor p_e(2w) / 2 \rfloor), & \text{if } p_e(2w) \text{ is odd} \end{array} \right\} = (\alpha_1 \oplus \nu) (p_e(2w)). \end{gather*}
\begin{gather*} \mu g_{\alpha_0}(w) \neq \left\{ \begin{array}{ll} \mu g_{\alpha_1} (p_e(2w) / 2), & \text{if } p_e(2w) \text{ is even},\\ \mu f (\lfloor p_e(2w) / 2 \rfloor), & \text{if } p_e(2w) \text{ is odd} \end{array} \right\} = (\alpha_1 \oplus \nu) (p_e(2w)). \end{gather*}
If this stage
![]() $s_1$
is found, then the
$s_1$
is found, then the
![]() $N^0_e$
-requirement is satisfied: indeed, we have
$N^0_e$
-requirement is satisfied: indeed, we have
We show that
![]() $s_1$
will be eventually reached. Toward a contradiction, assume that there is no such
$s_1$
will be eventually reached. Toward a contradiction, assume that there is no such
![]() $s_1$
. Then we deduce the following:
$s_1$
. Then we deduce the following:
-
1.
 $\mu(x) = \alpha_0(M+x)$
for all
$\mu(x) = \alpha_0(M+x)$
for all
 $x\in\omega$
.
$x\in\omega$
. -
2. The function
 $q(k) := p_e(2k)$
provides a punctual reduction from
$q(k) := p_e(2k)$
provides a punctual reduction from
 $\alpha_0$
to
$\alpha_0$
to
 $(\alpha_1\oplus\nu)$
.
$(\alpha_1\oplus\nu)$
. -
3.
 $\nu(x) = \alpha_1(M+x)$
for all x. By nonuniformly choosing a finite set of
$\nu(x) = \alpha_1(M+x)$
for all x. By nonuniformly choosing a finite set of
 $\nu$
-indices, one can construct a punctual reduction from
$\nu$
-indices, one can construct a punctual reduction from
 $\alpha_1$
to
$\alpha_1$
to
 $\nu$
.
$\nu$
.
These facts together imply that
![]() $\mu \leq_{pr} \alpha_0 \leq_{pr} \alpha_1 \oplus \nu \leq_{pr} \nu$
. Thus,
$\mu \leq_{pr} \alpha_0 \leq_{pr} \alpha_1 \oplus \nu \leq_{pr} \nu$
. Thus,
![]() $\mu$
is punctually reducible to
$\mu$
is punctually reducible to
![]() $\nu$
, which gives a contradiction.
$\nu$
, which gives a contradiction.
The construction is arranged in a straightforward way. It is not hard to prove that the requirements
![]() $R^0$
and
$R^0$
and
![]() $R^1$
are satisfied. We showed above that every
$R^1$
are satisfied. We showed above that every
![]() $N^{\varepsilon}_e$
, where
$N^{\varepsilon}_e$
, where
![]() $\varepsilon \in \{ 0,1\}$
, will be eventually satisfied. This concludes the discussion for the case of two incomparable numberings
$\varepsilon \in \{ 0,1\}$
, will be eventually satisfied. This concludes the discussion for the case of two incomparable numberings
![]() $\xi_0$
and
$\xi_0$
and
![]() $\xi_1$
.
$\xi_1$
.
The general case is obtained as follows. Here, for every
![]() $k\in\omega$
and every non-empty finite set
$k\in\omega$
and every non-empty finite set
![]() $F\subset \omega$
, we need to satisfy the requirements:
$F\subset \omega$
, we need to satisfy the requirements:
-
 $R^k$
:
$R^k$
:
 $\alpha_k \leq_{pr} \mu$
via a function
$\alpha_k \leq_{pr} \mu$
via a function
 $g_{\alpha_k}$
.
$g_{\alpha_k}$
. -
 $N^{k,F}_e$
: If
$N^{k,F}_e$
: If
 $k\not\in F$
, then
$k\not\in F$
, then
 $p_e\colon \alpha_k\oplus \nu \not\leq_{pr} (\bigoplus_{j\in F} \alpha_j) \oplus\nu$
$p_e\colon \alpha_k\oplus \nu \not\leq_{pr} (\bigoplus_{j\in F} \alpha_j) \oplus\nu$
Then one can show that the numberings
![]() $\xi_k := \alpha_k \oplus \nu$
satisfy the theorem.
$\xi_k := \alpha_k \oplus \nu$
satisfy the theorem.
The
![]() $N^{k,F}_e$
-strategy is similar to the
$N^{k,F}_e$
-strategy is similar to the
![]() $N^0_e$
-strategy described above, modulo its background actions. For all
$N^0_e$
-strategy described above, modulo its background actions. For all
![]() $j\in F$
and
$j\in F$
and
![]() $\ell\not\in F\cup\{ k\}$
, here we put
$\ell\not\in F\cup\{ k\}$
, here we put
 \begin{align*} \alpha_k(M) := \mu(0), \ \alpha_k(M+1) := \mu(1),\ \alpha_k(M+2) := \mu(2),\ \dots;\\ \alpha_j(M) := \nu(0), \ \alpha_j(M+1) := \nu(1),\ \alpha_j(M+2) := \nu(2),\ \dots;\\ \alpha_{\ell}(M) := \mu(0),\ \alpha_{\ell}(M+1) := \mu(0), \ \alpha_{\ell}(M+2) := \mu(0),\ \dots. \end{align*}
\begin{align*} \alpha_k(M) := \mu(0), \ \alpha_k(M+1) := \mu(1),\ \alpha_k(M+2) := \mu(2),\ \dots;\\ \alpha_j(M) := \nu(0), \ \alpha_j(M+1) := \nu(1),\ \alpha_j(M+2) := \nu(2),\ \dots;\\ \alpha_{\ell}(M) := \mu(0),\ \alpha_{\ell}(M+1) := \mu(0), \ \alpha_{\ell}(M+2) := \mu(0),\ \dots. \end{align*}
All other modifications are pretty straightforward. This concludes the proof of Theorem 24. ![]()
As a consequence, we obtain the following:
Corollary 25. Let
![]() $\mathcal{S}$
be an infinite punctual family. Suppose that
$\mathcal{S}$
be an infinite punctual family. Suppose that
![]() $\nu$
and
$\nu$
and
![]() $\mu$
are punctual numberings of
$\mu$
are punctual numberings of
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
![]() $\nu <_{pr} \mu$
. Then every finite upper semilattice is isomorphically embeddable into the interval
$\nu <_{pr} \mu$
. Then every finite upper semilattice is isomorphically embeddable into the interval
![]() $[\!\deg_{pr}\!(\nu); \deg_{pr}\!(\mu)]$
inside
$[\!\deg_{pr}\!(\nu); \deg_{pr}\!(\mu)]$
inside
![]() $\mathcal{R}_{pr}(\mathcal{S})$
(this embedding preserves suprema). In particular, this implies that the
$\mathcal{R}_{pr}(\mathcal{S})$
(this embedding preserves suprema). In particular, this implies that the
![]() $\Sigma_1$
-fragment of the theory
$\Sigma_1$
-fragment of the theory
![]() $Th(\mathcal{R}_{pr}(\mathcal{S}))$
(in the signature of upper semilattices) is decidable.
$Th(\mathcal{R}_{pr}(\mathcal{S}))$
(in the signature of upper semilattices) is decidable.
Proof Sketch. It is sufficient to show that every finite Boolean algebra (treated as an upper semilattice) can be isomorphically embedded into the interval
![]() $[\!\deg_{pr}\!(\nu); \deg_{pr}\!(\mu)]$
.
$[\!\deg_{pr}\!(\nu); \deg_{pr}\!(\mu)]$
.
Let B be a finite Boolean algebra with precisely
![]() $n+1$
atoms. Consider the sequence
$n+1$
atoms. Consider the sequence
![]() $(\xi_i)_{i\in\omega}$
constructed in Theorem 24. Then it is not hard to prove that the subsemilattice of
$(\xi_i)_{i\in\omega}$
constructed in Theorem 24. Then it is not hard to prove that the subsemilattice of
![]() $\mathcal{R}_{pr}(\mathcal{S})$
with domain
$\mathcal{R}_{pr}(\mathcal{S})$
with domain
is isomorphic to B. ![]()
Corollary 26. Let
![]() $\mathcal{T}$
be a Turing computable infinite family of total functions, and let
$\mathcal{T}$
be a Turing computable infinite family of total functions, and let
![]() $\nu<_{pr}\mu$
be Turing computable numberings of
$\nu<_{pr}\mu$
be Turing computable numberings of
![]() $\mathcal{T}$
. Then the interval
$\mathcal{T}$
. Then the interval
![]() $[\!\deg_{pr}\!(\nu);\deg_{pr}\!(\mu)]$
inside
$[\!\deg_{pr}\!(\nu);\deg_{pr}\!(\mu)]$
inside
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
contains an infinite antichain.
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
contains an infinite antichain.
Proof Sketch. We follow the proof of Theorem 24. The only nontrivial detail is the following: recall that in Theorem 23, we use the fact that the numbering
![]() $\mu$
is negative. In this corollary, our
$\mu$
is negative. In this corollary, our
![]() $\mu$
is a Turing computable numbering, and it is also negative.
$\mu$
is a Turing computable numbering, and it is also negative. ![]()
7. Lattices
Note that Corollary 25 implies that for arbitrary infinite punctual families
![]() $\mathcal{S}_0$
and
$\mathcal{S}_0$
and
![]() $\mathcal{S}_1$
, the
$\mathcal{S}_1$
, the
![]() $\Sigma_1$
-fragments of the theories
$\Sigma_1$
-fragments of the theories
![]() $Th(\mathcal{R}_{pr}(\mathcal{S}_0))$
and
$Th(\mathcal{R}_{pr}(\mathcal{S}_0))$
and
![]() $Th(\mathcal{R}_{pr}(\mathcal{S}_1))$
are the same. In this section, we witness that this is not the case already for the
$Th(\mathcal{R}_{pr}(\mathcal{S}_1))$
are the same. In this section, we witness that this is not the case already for the
![]() $\Sigma_2$
-fragments. On the one hand, we show that some Rogers pr-semilattices are lattices (Theorem 27). On the other hand, some semilattices contain minimal pairs (Proposition 29).
$\Sigma_2$
-fragments. On the one hand, we show that some Rogers pr-semilattices are lattices (Theorem 27). On the other hand, some semilattices contain minimal pairs (Proposition 29).
Selivanov (Reference Selivanov1976) obtained the following classical result: for any computable family
![]() $\mathcal{T}$
, if the semilattice
$\mathcal{T}$
, if the semilattice
![]() $\mathcal{R}_c(\mathcal{T})$
is infinite, then it cannot be a lattice. This section illustrates that the result of Selivanov cannot be transferred to the punctual setting.
$\mathcal{R}_c(\mathcal{T})$
is infinite, then it cannot be a lattice. This section illustrates that the result of Selivanov cannot be transferred to the punctual setting.
Our first theorem shows that persistently decidable families
![]() $\mathcal{S}$
(see Problem 2) exhibit a pretty tame behavior.
Footnote 1
$\mathcal{S}$
(see Problem 2) exhibit a pretty tame behavior.
Footnote 1
Theorem 27. Let
![]() $\mathcal{S}$
be an infinite persistently decidable family. Then the structure
$\mathcal{S}$
be an infinite persistently decidable family. Then the structure
![]() $\mathcal{R}_{pr}(\mathcal{S})$
is an infinite lattice.
$\mathcal{R}_{pr}(\mathcal{S})$
is an infinite lattice.
Proof. Given two punctual numberings
![]() $\nu$
and
$\nu$
and
![]() $\mu$
of
$\mu$
of
![]() $\mathcal{S}$
, we build their infimum
$\mathcal{S}$
, we build their infimum
![]() $\alpha$
.
$\alpha$
.
First, notice the following: since the family
![]() $\mathcal{S}$
is persistently decidable, the equivalence relation
$\mathcal{S}$
is persistently decidable, the equivalence relation
![]() $\eta_{\nu\oplus \mu}$
is primitive recursive. Therefore, given
$\eta_{\nu\oplus \mu}$
is primitive recursive. Therefore, given
![]() $k,\ell\in\omega$
, one can promptly compute whether the equality
$k,\ell\in\omega$
, one can promptly compute whether the equality
![]() $\nu(k) = \mu(\ell)$
is true: indeed,
$\nu(k) = \mu(\ell)$
is true: indeed,
![]() $\nu(k) = \mu(\ell)$
if and only if
$\nu(k) = \mu(\ell)$
if and only if
![]() $(2k,2\ell+1) \in \eta_{\nu\oplus \mu}$
.
$(2k,2\ell+1) \in \eta_{\nu\oplus \mu}$
.
For each
![]() $s\in\omega$
, at the stage s, we will promptly define an index
$s\in\omega$
, at the stage s, we will promptly define an index
![]() $w_s$
such that
$w_s$
such that
![]() $\alpha(s) = \nu(w_s)$
.
$\alpha(s) = \nu(w_s)$
.
At a stage s of the construction, we find a finite subset of
![]() $\omega$
:
$\omega$
:
It is not hard to show that the procedure of finding I[s] is punctual.
We (punctually) search for the least number
![]() $z\in I[s]$
such that
$z\in I[s]$
such that
![]() $z\not\in \{ w_t\,\colon t<s\}$
. If such a number z exists, then put
$z\not\in \{ w_t\,\colon t<s\}$
. If such a number z exists, then put
![]() $w_s:=z$
and
$w_s:=z$
and
![]() $\alpha(s) := \nu(z)$
. Otherwise, set
$\alpha(s) := \nu(z)$
. Otherwise, set
![]() $w_s:=0$
and
$w_s:=0$
and
![]() $\alpha(s) := \nu(0)$
.
$\alpha(s) := \nu(0)$
.
The construction of
![]() $\alpha$
is described. It is not difficult to prove that the numbering
$\alpha$
is described. It is not difficult to prove that the numbering
![]() $\alpha$
is punctual. Moreover, since we have
$\alpha$
is punctual. Moreover, since we have
![]() $\alpha$
indexes the whole family
$\alpha$
indexes the whole family
![]() $\mathcal{S}$
. In addition, the function
$\mathcal{S}$
. In addition, the function
![]() $s\mapsto w_s$
provides a punctual reduction from
$s\mapsto w_s$
provides a punctual reduction from
![]() $\alpha$
to
$\alpha$
to
![]() $\nu$
.
$\nu$
.
We prove that
![]() $\alpha \leq_{pr} \mu$
. Fix a number
$\alpha \leq_{pr} \mu$
. Fix a number
![]() $a_0$
with
$a_0$
with
![]() $\mu(a_0) = \nu(0)$
. A punctual reduction g from
$\mu(a_0) = \nu(0)$
. A punctual reduction g from
![]() $\alpha$
to
$\alpha$
to
![]() $\mu$
is defined as follows:
$\mu$
is defined as follows:
-
If
 $w_x = 0$
, then put
$w_x = 0$
, then put
 $g(x) := a_0$
.
$g(x) := a_0$
. -
If
 $w_x \neq 0$
, then notice that
$w_x \neq 0$
, then notice that
 $w_x \in I[x]$
, and hence, one can promptly find an index
$w_x \in I[x]$
, and hence, one can promptly find an index
 $\ell\leq x$
with
$\ell\leq x$
with
 $\mu(\ell) = \nu(w_x)$
. We set
$\mu(\ell) = \nu(w_x)$
. We set
 $h(x) := \ell$
.
$h(x) := \ell$
.
In order to finish the proof, we need to establish the following fact: suppose that
![]() $\beta \leq_{pr} \nu$
via a function
$\beta \leq_{pr} \nu$
via a function
![]() $g_0$
, and
$g_0$
, and
![]() $\beta \leq_{pr} \mu$
via a function
$\beta \leq_{pr} \mu$
via a function
![]() $g_1$
. Then
$g_1$
. Then
![]() $\beta$
is punctually reducible to
$\beta$
is punctually reducible to
![]() $\alpha$
.
$\alpha$
.
Since the numbering
![]() $\beta\oplus\nu$
is punctually decidable, we deduce that for
$\beta\oplus\nu$
is punctually decidable, we deduce that for
![]() $k,\ell\in\omega$
, one can quickly compute whether
$k,\ell\in\omega$
, one can quickly compute whether
![]() $\beta(k) = \nu(\ell)$
holds.
$\beta(k) = \nu(\ell)$
holds.
Let
![]() $x\in\omega$
. If
$x\in\omega$
. If
![]() $\beta(x) = \nu(0)$
, then one can nonuniformly choose an
$\beta(x) = \nu(0)$
, then one can nonuniformly choose an
![]() $\alpha$
-index for
$\alpha$
-index for
![]() $\nu(0)$
, and this is enough for us. Assume that
$\nu(0)$
, and this is enough for us. Assume that
![]() $\beta(x) \neq \nu(0)$
. It is clear that there exists k such that
$\beta(x) \neq \nu(0)$
. It is clear that there exists k such that
![]() $k\in \widehat{I}_x := I[\max(g_0(x),g_1(x))]$
and
$k\in \widehat{I}_x := I[\max(g_0(x),g_1(x))]$
and
![]() $\beta(x) = \nu(k)$
. Let M be the greatest element of
$\beta(x) = \nu(k)$
. Let M be the greatest element of
![]() $\widehat{I}_x$
. One can show that there is (the least) index
$\widehat{I}_x$
. One can show that there is (the least) index
![]() $\ell$
such that
$\ell$
such that
![]() $\alpha(\ell) = \nu(k)$
, and
$\alpha(\ell) = \nu(k)$
, and
Thus, this
![]() $\ell$
can be found in a prompt way, and one can construct a punctual reduction from
$\ell$
can be found in a prompt way, and one can construct a punctual reduction from
![]() $\beta$
to
$\beta$
to
![]() $\alpha$
.
$\alpha$
. ![]()
Remark 28. It is unclear whether one can obtain an analog of Theorem 27 for some semilattice
![]() $\mathcal{R}^{(c,pr)}(\mathcal{T})$
, where
$\mathcal{R}^{(c,pr)}(\mathcal{T})$
, where
![]() $\mathcal{T}$
is an infinite Turing computable family of total functions. For such a family
$\mathcal{T}$
is an infinite Turing computable family of total functions. For such a family
![]() $\mathcal{T}$
, one can easily construct a Turing computable numbering
$\mathcal{T}$
, one can easily construct a Turing computable numbering
![]() $\nu$
such that the equivalence
$\nu$
such that the equivalence
![]() $\eta_{\nu}$
is not primitive recursive.
$\eta_{\nu}$
is not primitive recursive.
Indeed, let
![]() $\mu$
be some fixed computable numbering of the family
$\mu$
be some fixed computable numbering of the family
![]() $\mathcal{T}$
such that
$\mathcal{T}$
such that
![]() $\mu(0) \neq \mu(1)$
. Then for an arbitrary computable, not primitive recursive set
$\mu(0) \neq \mu(1)$
. Then for an arbitrary computable, not primitive recursive set
![]() $X\subseteq\omega$
, we define
$X\subseteq\omega$
, we define
 \begin{align*} \nu_X(2k+1) = \mu(k),\quad \nu_X(2k) = \begin{cases} \mu(0), & \text{if } k\not\in X,\\ \mu(1), & \text{if } k\in X. \end{cases} \end{align*}
\begin{align*} \nu_X(2k+1) = \mu(k),\quad \nu_X(2k) = \begin{cases} \mu(0), & \text{if } k\not\in X,\\ \mu(1), & \text{if } k\in X. \end{cases} \end{align*}
The numbering
![]() $\nu_X$
is computable, and
$\nu_X$
is computable, and
![]() $\eta_{\nu_X}$
is not primitive recursive.
$\eta_{\nu_X}$
is not primitive recursive.
Our second result gives an example of a Rogers pr-semilattice, which is not a lattice:
Proposition 29. There exists an infinite punctual family
![]() $\mathcal{S}$
such that the semilattice
$\mathcal{S}$
such that the semilattice
![]() $\mathcal{R}_{pr}(\mathcal{S})$
contains a minimal pair. Consequently,
$\mathcal{R}_{pr}(\mathcal{S})$
contains a minimal pair. Consequently,
![]() $\mathcal{R}_{pr}(\mathcal{S})$
is not a lattice.
$\mathcal{R}_{pr}(\mathcal{S})$
is not a lattice.
Proof. Our family
![]() $\mathcal{S}$
is defined via its punctual Friedberg numbering: for
$\mathcal{S}$
is defined via its punctual Friedberg numbering: for
![]() $k,\ell\in\omega$
, we set
$k,\ell\in\omega$
, we set
![]() $\nu\langle k,0\rangle := \chi_{\{2k\}}$
and
$\nu\langle k,0\rangle := \chi_{\{2k\}}$
and
![]() $\nu \langle k,\ell+1\rangle := \chi_{ \{2k,2\ell+1\} }$
.
$\nu \langle k,\ell+1\rangle := \chi_{ \{2k,2\ell+1\} }$
.
The degree of the numbering
![]() $\nu$
will be one of the components of the minimal pair. Now we build the other component: it will be induced by a Friedberg numbering
$\nu$
will be one of the components of the minimal pair. Now we build the other component: it will be induced by a Friedberg numbering
![]() $\mu$
.
$\mu$
.
Fix a non-computable c.e. set W, and a primitive recursive function q with
![]() $\mathrm{range}(q) = W$
.
$\mathrm{range}(q) = W$
.
For each number
![]() $k\in\omega$
, the construction of the “k-th layer”
$k\in\omega$
, the construction of the “k-th layer”
![]() $\mu \langle k,\cdot\rangle$
proceeds as follows. Beforehand, set the values:
$\mu \langle k,\cdot\rangle$
proceeds as follows. Beforehand, set the values:
for all
![]() $m\neq k$
.
$m\neq k$
.
Consider a stage s of the construction. If
![]() $k\not \in \{ q(0),q(1),\dots,q(s)\}$
, then put
$k\not \in \{ q(0),q(1),\dots,q(s)\}$
, then put
Suppose that
![]() $s_0$
is the least stage with
$s_0$
is the least stage with
![]() $k \in \{ q(0),q(1),\dots,q(s_0)\}$
. Then we set
$k \in \{ q(0),q(1),\dots,q(s_0)\}$
. Then we set
for all
![]() $t\geq s_0$
. After the stage
$t\geq s_0$
. After the stage
![]() $s_0$
, we stop the construction of this particular k-th layer.
$s_0$
, we stop the construction of this particular k-th layer.
It is not hard to show that the constructed
![]() $\mu$
belongs to
$\mu$
belongs to
![]() $Com_{pr}(\mathcal{S})$
, and
$Com_{pr}(\mathcal{S})$
, and
![]() $\mu$
is Friedberg. We need to prove that the degrees of
$\mu$
is Friedberg. We need to prove that the degrees of
![]() $\nu$
and
$\nu$
and
![]() $\mu$
form a minimal pair inside
$\mu$
form a minimal pair inside
![]() $\mathcal{R}_{pr}(\mathcal{S})$
.
$\mathcal{R}_{pr}(\mathcal{S})$
.
Toward a contradiction, assume that there is a punctual numbering
![]() $\alpha$
of
$\alpha$
of
![]() $\mathcal{S}$
with punctual reductions
$\mathcal{S}$
with punctual reductions
![]() $f\colon \alpha \leq_{pr} \nu$
and
$f\colon \alpha \leq_{pr} \nu$
and
![]() $h\colon \alpha \leq_{pr} \mu$
. Consider a c.e. set
$h\colon \alpha \leq_{pr} \mu$
. Consider a c.e. set
Clearly, for a number
![]() $k\in V$
and the corresponding x, we have
$k\in V$
and the corresponding x, we have
![]() $\nu(f(x)) = \mu(h(x)) = \chi_{\{ 2k\}}$
. Since
$\nu(f(x)) = \mu(h(x)) = \chi_{\{ 2k\}}$
. Since
![]() $\mu$
is a Friedberg numbering, the function
$\mu$
is a Friedberg numbering, the function
![]() $\chi_{\{2k\}}$
has a unique
$\chi_{\{2k\}}$
has a unique
![]() $\mu$
-index
$\mu$
-index
![]() $e_k$
.
$e_k$
.
Note that the construction ensures the following:
-
If
 $k\in V$
, then
$k\in V$
, then
 $e_k = \langle k,0\rangle$
and
$e_k = \langle k,0\rangle$
and
 $k\not\in \mathrm{range}(q) = W$
.
$k\not\in \mathrm{range}(q) = W$
. -
If
 $k\not\in V$
, then for every
$k\not\in V$
, then for every
 $x\in\omega$
, the condition
$x\in\omega$
, the condition
 $\alpha(x) = \chi_{\{2k\}}$
implies
$\alpha(x) = \chi_{\{2k\}}$
implies
 $f(x) = \langle k,0\rangle$
and
$f(x) = \langle k,0\rangle$
and
 $h(x) \neq \langle k,0\rangle$
. Hence,
$h(x) \neq \langle k,0\rangle$
. Hence,
 $e_k = \langle k,s_0+1\rangle$
for some
$e_k = \langle k,s_0+1\rangle$
for some
 $s_0\in \omega$
, and
$s_0\in \omega$
, and
 $k\in W$
.
$k\in W$
.
Thus, we deduce that
![]() $V = \overline{W}$
, which contradicts the choice of W.
$V = \overline{W}$
, which contradicts the choice of W. ![]()
Remark 30. Note that the family
![]() $\mathcal{S}$
and its numbering
$\mathcal{S}$
and its numbering
![]() $\nu$
(from the proposition above) have countably many quickly spoiling limit points (in the sense of Definition 12).
$\nu$
(from the proposition above) have countably many quickly spoiling limit points (in the sense of Definition 12).
-
(a) The function
 $\chi_{\emptyset}\not\in\mathcal{S}$
is quickly spoiling – this is witnessed by the function sp(n,t) with
$\chi_{\emptyset}\not\in\mathcal{S}$
is quickly spoiling – this is witnessed by the function sp(n,t) with
 $sp(n,0) = \langle n+1,0\rangle$
and
$sp(n,0) = \langle n+1,0\rangle$
and
 $sp(n,1) = \langle n+2, 0\rangle$
.
$sp(n,1) = \langle n+2, 0\rangle$
. -
(b) For
 $k\in\omega$
, the function
$k\in\omega$
, the function
 $\chi_{ \{2k \} }$
is quickly spoiling. The witness can be defined as follows:
$\chi_{ \{2k \} }$
is quickly spoiling. The witness can be defined as follows:
 $sp(n,0) = \langle k, n+2\rangle$
and
$sp(n,0) = \langle k, n+2\rangle$
and
 $sp(n,1) = \langle k, n+3\rangle$
.
$sp(n,1) = \langle k, n+3\rangle$
.
Therefore, the family
![]() $\mathcal{S}$
is not persistently decidable.
$\mathcal{S}$
is not persistently decidable.
8. Existence of the Greatest Element
In this section, we provide examples of Rogers pr-semilattices with greatest element and without greatest element. This gives another difference in the
![]() $\Sigma_2$
-fragments of the first-order theories.
$\Sigma_2$
-fragments of the first-order theories.
Theorem 31. Let
![]() $\mathcal{S}$
be an infinite punctual family, and let
$\mathcal{S}$
be an infinite punctual family, and let
![]() $\nu$
be its punctual numbering. Suppose that there exists a quickly spoiling limit point f for
$\nu$
be its punctual numbering. Suppose that there exists a quickly spoiling limit point f for
![]() $\nu$
such that
$\nu$
such that
![]() $f\not\in \mathcal{S}$
. Then the semilattice
$f\not\in \mathcal{S}$
. Then the semilattice
![]() $\mathcal{R}_{pr}(\mathcal{S})$
does not have a greatest element.
$\mathcal{R}_{pr}(\mathcal{S})$
does not have a greatest element.
Proof. Fix a primitive recursive function sp(n,t) witnessing the spoiledness of the limit point f.
Let
![]() $\mu$
be an arbitrary punctual numbering of the family
$\mu$
be an arbitrary punctual numbering of the family
![]() $\mathcal{S}$
. In order to prove the theorem, we build a punctual numbering
$\mathcal{S}$
. In order to prove the theorem, we build a punctual numbering
![]() $\alpha$
of some subfamily
$\alpha$
of some subfamily
![]() $\mathcal{S}_0 \subseteq \mathcal{S}$
such that
$\mathcal{S}_0 \subseteq \mathcal{S}$
such that
![]() $\alpha \not\leq_{pr} \mu$
. Indeed, the existence of such
$\alpha \not\leq_{pr} \mu$
. Indeed, the existence of such
![]() $\alpha$
is sufficient for us, since this implies that
$\alpha$
is sufficient for us, since this implies that
![]() $\mu \leq_{pr} \mu \oplus \alpha$
and
$\mu \leq_{pr} \mu \oplus \alpha$
and
![]() $\mu \oplus \alpha \not\leq_{pr} \mu$
.
$\mu \oplus \alpha \not\leq_{pr} \mu$
.
We satisfy the series of requirements:
![]() $P_e$
:
$P_e$
:
![]() $p_e \colon \alpha \not\leq_{pr} \mu$
.
$p_e \colon \alpha \not\leq_{pr} \mu$
.
The
![]() $P_e$
-strategy. Choose the least w such that we have not talked about the object
$P_e$
-strategy. Choose the least w such that we have not talked about the object
![]() $\alpha(w)$
before. Wait for the least stage s such that:
$\alpha(w)$
before. Wait for the least stage s such that:
-
the value
 $p_e[s](w)$
is defined, and
$p_e[s](w)$
is defined, and -
our computations have already provided a number
 $N\leq s$
with
$N\leq s$
with
 $\mu(p_e(w)) | N \neq f | N$
.
$\mu(p_e(w)) | N \neq f | N$
.
Since f does not belong to the family
![]() $\mathcal{S}$
, such a stage s will be eventually reached.
$\mathcal{S}$
, such a stage s will be eventually reached.
While waiting for this s, just propagate
When the stage s and the corresponding N are found, define M as the least number such that
![]() $M\geq N$
and the value
$M\geq N$
and the value
![]() $\alpha(w)(M)$
is still undefined. Using the spoiledness of f, we promptly set
$\alpha(w)(M)$
is still undefined. Using the spoiledness of f, we promptly set
![]() $\alpha(w) := \nu(sp(M,0))$
.
$\alpha(w) := \nu(sp(M,0))$
.
This procedure is well defined, and it satisfies the
![]() $P_e$
-requirement: indeed, we have
$P_e$
-requirement: indeed, we have
The construction is arranged in a straightforward manner. We note that in order to ensure the punctuality of
![]() $\alpha$
, the
$\alpha$
, the
![]() $P_e$
-strategy also has to implement some simple background actions – for example, one by one, we set
$P_e$
-strategy also has to implement some simple background actions – for example, one by one, we set
![]() $\alpha(w+1) := \nu(0)$
,
$\alpha(w+1) := \nu(0)$
,
![]() $\alpha(w+2) := \nu(0)$
.
$\alpha(w+2) := \nu(0)$
.
Clearly,
![]() $\alpha$
indexes a subfamily of
$\alpha$
indexes a subfamily of
![]() $\mathcal{S}$
. Since every
$\mathcal{S}$
. Since every
![]() $P_e$
is eventually satisfied, we have
$P_e$
is eventually satisfied, we have
![]() $\alpha \not\leq_{pr} \mu$
.
$\alpha \not\leq_{pr} \mu$
. ![]()
Remark 32. Note that the family from Example 14 and the family from Proposition 29 both satisfy the conditions of Theorem 31.
We give an example of an infinite punctual family such that its Rogers pr-semilattice has the greatest element.
Lemma 33. Consider the family
![]() $\mathcal{S}$
from Example 11 – it can be defined via its punctual Friedberg numbering: for
$\mathcal{S}$
from Example 11 – it can be defined via its punctual Friedberg numbering: for
![]() $i\in\omega$
,
$i\in\omega$
,
Any punctual numbering
![]() $\mu\in Com_{pr}(\mathcal{S})$
is punctually reducible to
$\mu\in Com_{pr}(\mathcal{S})$
is punctually reducible to
![]() $\nu$
.
$\nu$
.
Proof. Let
![]() $\mu$
be a punctual numbering of
$\mu$
be a punctual numbering of
![]() $\mathcal{S}$
. Then a punctual reduction from
$\mathcal{S}$
. Then a punctual reduction from
![]() $\mu$
to
$\mu$
to
![]() $\nu$
is provided by the function
$\nu$
is provided by the function
![]() $h(k) := \mu(k)(0)$
.
$h(k) := \mu(k)(0)$
. ![]()
We leave the following question open:
Problem 34. Is it true that for any sf-discrete family
![]() $\mathcal{S}$
, the semilattice
$\mathcal{S}$
, the semilattice
![]() $\mathcal{R}_{pr}(\mathcal{S})$
contains the greatest element?
$\mathcal{R}_{pr}(\mathcal{S})$
contains the greatest element?
9. Persistently Decidable Families Revisited
Here we prove the result, which was announced at the end of Subsection 3.1:
Theorem 35. There exists an infinite, persistently decidable family
![]() $\mathcal{S}$
such that for every function
$\mathcal{S}$
such that for every function
![]() $f\in\mathcal{S}$
, there is a number
$f\in\mathcal{S}$
, there is a number
![]() $k\in\omega$
with
$k\in\omega$
with
![]() $f = \chi_{ \{ k\} }$
. Consequently, the family
$f = \chi_{ \{ k\} }$
. Consequently, the family
![]() $\mathcal{S}$
has a unique limit point
$\mathcal{S}$
has a unique limit point
![]() $g = \chi_{\emptyset}$
in the Cantor space.
$g = \chi_{\emptyset}$
in the Cantor space.
Proof. Recall that
![]() $(\rho_e)_{e\in\omega}$
is the computable list of all punctual numberings (see Subsection 2.2). Without loss of generality, we assume that for every e and x,
$(\rho_e)_{e\in\omega}$
is the computable list of all punctual numberings (see Subsection 2.2). Without loss of generality, we assume that for every e and x,
![]() $\mathrm{range}(\rho_e(x)) \subseteq \{ 0,1\}$
.
$\mathrm{range}(\rho_e(x)) \subseteq \{ 0,1\}$
.
The desired family
![]() $\mathcal{S}$
is constructed via its punctual numbering
$\mathcal{S}$
is constructed via its punctual numbering
![]() $\nu$
. Beforehand, we put
$\nu$
. Beforehand, we put
![]() $\nu(0) := \chi_{ \{0\} }$
.
$\nu(0) := \chi_{ \{0\} }$
.
We satisfy the following series of requirements:
![]() $R_e$
: If
$R_e$
: If
![]() $\rho_e$
is a numbering of
$\rho_e$
is a numbering of
![]() $\mathcal{S}$
, then
$\mathcal{S}$
, then
![]() $\eta_{\rho_e}$
is primitive recursive.
$\eta_{\rho_e}$
is primitive recursive.
We fix an ordering of the requirements:
![]() $R_0 < R_1 < R_2 < \dots$
.
$R_0 < R_1 < R_2 < \dots$
.
At a stage s, the
![]() $R_e$
-readiness level is the maximal number
$R_e$
-readiness level is the maximal number
![]() $t\leq s$
such that for every
$t\leq s$
such that for every
![]() $x\leq t$
and every
$x\leq t$
and every
![]() $z\leq t+2$
, the value
$z\leq t+2$
, the value
![]() $\rho_e(x)(z)[s]$
is defined. Note that the
$\rho_e(x)(z)[s]$
is defined. Note that the
![]() $R_e$
-readiness level tends to infinity.
$R_e$
-readiness level tends to infinity.
At a stage s, we define the construction readiness level
![]() $\mathrm{cr}[s] \in \omega$
. We put
$\mathrm{cr}[s] \in \omega$
. We put
![]() $\mathrm{cr}[0] := 1$
. The intuition behind this parameter is as follows. We want to add a fresh element g to the family
$\mathrm{cr}[0] := 1$
. The intuition behind this parameter is as follows. We want to add a fresh element g to the family
![]() $\mathcal{S}$
. This g will be always chosen as either
$\mathcal{S}$
. This g will be always chosen as either
![]() $\chi_{ \{\mathrm{cr}[s]\} }$
or
$\chi_{ \{\mathrm{cr}[s]\} }$
or
![]() $\chi_{ \{ \mathrm{cr}[s]+1\}}$
. The choice of the g is motivated by the following: we want to diagonalize against a requirement
$\chi_{ \{ \mathrm{cr}[s]+1\}}$
. The choice of the g is motivated by the following: we want to diagonalize against a requirement
![]() $R_e$
with the highest priority – this is done via ensuring that
$R_e$
with the highest priority – this is done via ensuring that
![]() $\rho_e$
does not index the family
$\rho_e$
does not index the family
![]() $\mathcal{S}$
(to be elaborated below).
$\mathcal{S}$
(to be elaborated below).
The construction. Consider stage
![]() $s+1$
. We work with the requirements
$s+1$
. We work with the requirements
![]() $R_0,R_1,\dots,R_{\mathrm{cr}[s]}$
. For
$R_0,R_1,\dots,R_{\mathrm{cr}[s]}$
. For
![]() $e\leq \mathrm{cr}[s]$
, let
$e\leq \mathrm{cr}[s]$
, let
![]() $\mathrm{rl}(e)$
be the
$\mathrm{rl}(e)$
be the
![]() $R_e$
-readiness level at the stage
$R_e$
-readiness level at the stage
![]() $s+1$
.
$s+1$
.
If there is
![]() $x\leq \mathrm{rl}(e)$
such that the string
$x\leq \mathrm{rl}(e)$
such that the string
![]() $\rho_e(x)| \mathrm{rl}(e)$
contains at least two ones, then the
$\rho_e(x)| \mathrm{rl}(e)$
contains at least two ones, then the
![]() $R_e$
-requirement is declared inactive. If
$R_e$
-requirement is declared inactive. If
![]() $R_e$
is inactive, then it is forever satisfied: indeed, we have already witnessed that the function
$R_e$
is inactive, then it is forever satisfied: indeed, we have already witnessed that the function
![]() $\rho_e(x)$
cannot be the characteristic function of a one-element set.
$\rho_e(x)$
cannot be the characteristic function of a one-element set.
We compute the parameter:
If
![]() $r<\mathrm{cr}[s]$
, then put
$r<\mathrm{cr}[s]$
, then put
![]() $\nu(s+1) := \nu(0)$
and proceed to the next stage.
$\nu(s+1) := \nu(0)$
and proceed to the next stage.
Suppose that
![]() $r\geq \mathrm{cr}[s]$
. Then, we define
$r\geq \mathrm{cr}[s]$
. Then, we define
![]() $\mathrm{cr}[s+1] := \mathrm{cr}[s]+2$
. We search for the least
$\mathrm{cr}[s+1] := \mathrm{cr}[s]+2$
. We search for the least
![]() $e\leq \mathrm{cr}[s]$
such that there is
$e\leq \mathrm{cr}[s]$
such that there is
![]() $x \leq \mathrm{cr}[s]$
with
$x \leq \mathrm{cr}[s]$
with
If these e and x exist, we put
 \begin{align*} \nu(s+1) := \begin{cases} \chi_{ \{ \mathrm{cr}[s]+1 \} }, & \text{if } \rho_e(x) | (\mathrm{cr}[s]+2) = \chi_{\{\mathrm{cr}[s]\}} | (\mathrm{cr}[s]+2),\\ \chi_{ \{ \mathrm{cr}[s] \} }, & \text{otherwise}. \end{cases} \end{align*}
\begin{align*} \nu(s+1) := \begin{cases} \chi_{ \{ \mathrm{cr}[s]+1 \} }, & \text{if } \rho_e(x) | (\mathrm{cr}[s]+2) = \chi_{\{\mathrm{cr}[s]\}} | (\mathrm{cr}[s]+2),\\ \chi_{ \{ \mathrm{cr}[s] \} }, & \text{otherwise}. \end{cases} \end{align*}
In this case, we say that
![]() $R_e$
is successfully defeated. The requirement
$R_e$
is successfully defeated. The requirement
![]() $R_e$
is declared forever inactive, and
$R_e$
is declared forever inactive, and
![]() $R_e$
is satisfied – our construction ensures that
$R_e$
is satisfied – our construction ensures that
![]() $\rho_e(x)$
does not belong to
$\rho_e(x)$
does not belong to
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
If there are no such e and x, then
![]() $\nu(s+1) := \chi_{\{\mathrm{cr}[s]\}}$
. This concludes the description of the construction.
$\nu(s+1) := \chi_{\{\mathrm{cr}[s]\}}$
. This concludes the description of the construction.
Verification. It is not hard to show that
![]() $\nu$
is a punctual numbering. The construction ensures that for any
$\nu$
is a punctual numbering. The construction ensures that for any
![]() $x\in\omega$
, there is a number k such that
$x\in\omega$
, there is a number k such that
![]() $\nu(x) = \chi_{ \{k\} }$
.
$\nu(x) = \chi_{ \{k\} }$
.
Since for each e, the
![]() $R_e$
-readiness level tends to infinity, we have
$R_e$
-readiness level tends to infinity, we have
![]() $\mathrm{cr}[s] \xrightarrow[s\to\infty]{} \infty$
. This implies that the numbering
$\mathrm{cr}[s] \xrightarrow[s\to\infty]{} \infty$
. This implies that the numbering
![]() $\nu$
indexes an infinite family
$\nu$
indexes an infinite family
![]() $\mathcal{S}$
. Now it is sufficient to establish the following fact.
$\mathcal{S}$
. Now it is sufficient to establish the following fact.
Claim 1. If
![]() $\rho_e$
is a numbering of the family
$\rho_e$
is a numbering of the family
![]() $\mathcal{S}$
, then the equivalence relation
$\mathcal{S}$
, then the equivalence relation
![]() $\eta_{\rho_e}$
is primitive recursive.
$\eta_{\rho_e}$
is primitive recursive.
Proof. Let
![]() $\rho_e \in Com_{pr}(\mathcal{S})$
. It is clear that the requirement
$\rho_e \in Com_{pr}(\mathcal{S})$
. It is clear that the requirement
![]() $R_e$
is never declared inactive. Let
$R_e$
is never declared inactive. Let
![]() $s_0$
be the first stage with the following properties:
$s_0$
be the first stage with the following properties:
-
(a)
 $\mathrm{cr}[s_0] \geq e$
.
$\mathrm{cr}[s_0] \geq e$
. -
(b) If a requirement
 $R_i$
, where
$R_i$
, where
 $i < e$
, is declared inactive at some stage
$i < e$
, is declared inactive at some stage
 $s^{\ast}$
, then this
$s^{\ast}$
, then this
 $s^{\ast}$
is strictly less than
$s^{\ast}$
is strictly less than
 $s_0$
.
$s_0$
.
Given numbers
![]() $x < y$
, we describe a prompt procedure, which checks whether
$x < y$
, we describe a prompt procedure, which checks whether
![]() $\rho_e(x) = \rho_e(y)$
. If
$\rho_e(x) = \rho_e(y)$
. If
![]() $y\leq s_0$
, then this checking is realized nonuniformly.
$y\leq s_0$
, then this checking is realized nonuniformly.
Suppose that
![]() $y>s_0$
. Compute the strings
$y>s_0$
. Compute the strings
![]() $\sigma := \rho_e(x) | y$
and
$\sigma := \rho_e(x) | y$
and
![]() $\tau := \rho_e(y) | y$
. There are two cases:
$\tau := \rho_e(y) | y$
. There are two cases:
Case 1. If one of the strings
![]() $\sigma$
or
$\sigma$
or
![]() $\tau$
contains 1, then it is clear that
$\tau$
contains 1, then it is clear that
Case 2. Otherwise, we have
![]() $\sigma = \tau = \chi_{\emptyset} | y$
. We argue that in this case, our construction ensures that
$\sigma = \tau = \chi_{\emptyset} | y$
. We argue that in this case, our construction ensures that
![]() $\rho_e(x) = \rho_e(y)$
.
$\rho_e(x) = \rho_e(y)$
.
Toward a contradiction, assume that
![]() $\rho_e(x) \neq \rho_e(y)$
. Since
$\rho_e(x) \neq \rho_e(y)$
. Since
![]() $\rho_e$
indexes the family
$\rho_e$
indexes the family
![]() $\mathcal{S}$
, there are numbers
$\mathcal{S}$
, there are numbers
![]() $k,\ell \geq y$
such that
$k,\ell \geq y$
such that
![]() $k\neq \ell$
,
$k\neq \ell$
,
![]() $\rho_e(x) = \chi_{ \{k\} }$
, and
$\rho_e(x) = \chi_{ \{k\} }$
, and
![]() $\rho_e(y) = \chi_{ \{\ell\}}$
. Without loss of generality, one may assume that
$\rho_e(y) = \chi_{ \{\ell\}}$
. Without loss of generality, one may assume that
![]() $k<\ell$
.
$k<\ell$
.
It is not hard to show that there is a unique
![]() $\nu$
-index
$\nu$
-index
![]() $s^{\ast}>0$
such that
$s^{\ast}>0$
such that
![]() $\nu(s^{\ast}) = \chi_{ \{\ell\} }$
. Using the description of the construction, we deduce the following properties (at the stage
$\nu(s^{\ast}) = \chi_{ \{\ell\} }$
. Using the description of the construction, we deduce the following properties (at the stage
![]() $s^{\ast}$
):
$s^{\ast}$
):
-
 $\ell \in \{ \mathrm{cr}[s^{\ast}-1], \mathrm{cr}[s^{\ast}-1]+1\}$
.
$\ell \in \{ \mathrm{cr}[s^{\ast}-1], \mathrm{cr}[s^{\ast}-1]+1\}$
. -
 $s^{\ast} \geq \mathrm{rl}(e) \geq r \geq \mathrm{cr}[s^{\ast}-1] \in \{ \ell, \ell-1\}$
; hence
$s^{\ast} \geq \mathrm{rl}(e) \geq r \geq \mathrm{cr}[s^{\ast}-1] \in \{ \ell, \ell-1\}$
; hence
 $s^{\ast}\geq \ell-1\geq k \geq y >s_0$
.
$s^{\ast}\geq \ell-1\geq k \geq y >s_0$
. -
Since
 $s^{\ast} - 1 \geq s_0$
, we have
$s^{\ast} - 1 \geq s_0$
, we have
 $\mathrm{cr}[s^{\ast}-1] \geq \mathrm{cr}[s_0] \geq e$
.
$\mathrm{cr}[s^{\ast}-1] \geq \mathrm{cr}[s_0] \geq e$
. -
 $\mathrm{cr}[s^{\ast}-1] \geq y$
.
$\mathrm{cr}[s^{\ast}-1] \geq y$
.
Summarizing, at the stage
![]() $s^{\ast} > s_0$
, we have
$s^{\ast} > s_0$
, we have
![]() $e \leq \mathrm{cr}[s^{\ast}-1]$
and
$e \leq \mathrm{cr}[s^{\ast}-1]$
and
![]() $y\leq \mathrm{cr}[s^{\ast} - 1]$
such that
$y\leq \mathrm{cr}[s^{\ast} - 1]$
such that
Recall that after stage
![]() $s_0$
, no additional requirement
$s_0$
, no additional requirement
![]() $R_i$
with
$R_i$
with
![]() $i<e$
can become inactive. Therefore, at the stage
$i<e$
can become inactive. Therefore, at the stage
![]() $s^{\ast}$
, we successfully defeat
$s^{\ast}$
, we successfully defeat
![]() $R_e$
, and
$R_e$
, and
![]() $\rho_e$
does not index
$\rho_e$
does not index
![]() $\mathcal{S}$
. This contradicts the choice of
$\mathcal{S}$
. This contradicts the choice of
![]() $\rho_e$
. Therefore, we deduce that the equality
$\rho_e$
. Therefore, we deduce that the equality
![]() $\sigma = \tau = \chi_{\emptyset} | y$
implies
$\sigma = \tau = \chi_{\emptyset} | y$
implies
![]() $\rho_e(x) = \rho_e(y)$
.
$\rho_e(x) = \rho_e(y)$
.
So, we established that the two discussed cases provide a prompt procedure for checking if
![]() $(x,y) \in \eta_{\rho_e}$
. Therefore, the numbering
$(x,y) \in \eta_{\rho_e}$
. Therefore, the numbering
![]() $\rho_e$
is punctually decidable.
$\rho_e$
is punctually decidable. ![]()
Claim 1 shows that our family
![]() $\mathcal{S}$
is persistently decidable. This concludes the proof of Theorem 35.
$\mathcal{S}$
is persistently decidable. This concludes the proof of Theorem 35. ![]()
After the first version of the paper was submitted, Sergey Goncharov introduced the following simple example of a persistently decidable family which is not sf-discrete.
Example 36
(Goncharov) The family
![]() $\mathcal{S}$
contains the following functions: for each
$\mathcal{S}$
contains the following functions: for each
![]() $k\in\omega$
,
$k\in\omega$
,
 \begin{align*} \begin{array}{l} g^0_{k}(0) = k+1,\ \ g^0_{k}(x+1) = 0 \text{ for all } x;\\ g^1_{k}(0) = k+1, \ \ g^1_{k}(k+1) = 1,\ \ g^1_{k}(x) = 0 \text{ for } x\not\in\{0,k+1\}. \end{array} \end{align*}
\begin{align*} \begin{array}{l} g^0_{k}(0) = k+1,\ \ g^0_{k}(x+1) = 0 \text{ for all } x;\\ g^1_{k}(0) = k+1, \ \ g^1_{k}(k+1) = 1,\ \ g^1_{k}(x) = 0 \text{ for } x\not\in\{0,k+1\}. \end{array} \end{align*}
Since
![]() $g^0_k(k+1) \neq g^1_k(k+1)$
for all k, it is clear that the family
$g^0_k(k+1) \neq g^1_k(k+1)$
for all k, it is clear that the family
![]() $\mathcal{S}$
is not sf-discrete.
$\mathcal{S}$
is not sf-discrete.
On the other hand, let f and h be arbitrary functions from the family
![]() $\mathcal{S}$
. Then
$\mathcal{S}$
. Then
![]() $f = h$
if and only if
$f = h$
if and only if
![]() $f(0) = h(0)$
and
$f(0) = h(0)$
and
![]() $f(f(0)) = h(h(0))$
. This implies that every punctual numbering of
$f(f(0)) = h(h(0))$
. This implies that every punctual numbering of
![]() $\mathcal{S}$
is punctually decidable; hence, the family
$\mathcal{S}$
is punctually decidable; hence, the family
![]() $\mathcal{S}$
is persistently decidable.
$\mathcal{S}$
is persistently decidable.
10. Friedberg Numberings
Recall that a numbering
![]() $\nu$
is Friedberg if
$\nu$
is Friedberg if
![]() $\eta_{\nu}$
equals to the identity relation. Friedberg numberings consitute an important classical object of study. One of the reasons behind this is the following fact: one can show that for any computable family
$\eta_{\nu}$
equals to the identity relation. Friedberg numberings consitute an important classical object of study. One of the reasons behind this is the following fact: one can show that for any computable family
![]() $\mathcal{T}$
, an arbitrary computable Friedberg numbering of
$\mathcal{T}$
, an arbitrary computable Friedberg numbering of
![]() $\mathcal{T}$
induces a minimal element inside the semilattice
$\mathcal{T}$
induces a minimal element inside the semilattice
![]() $\mathcal{R}_c(\mathcal{T})$
.
$\mathcal{R}_c(\mathcal{T})$
.
We have already seen that this fact fails in the punctual setting: recall that an infinite
![]() $\mathcal{R}_{pr}(\mathcal{S})$
is downward dense (Theorem 16). Essentially, the reason behind this is the following fact: the inverse of a primitive recursive function is not necessarily primitive recursive. Furthermore, one can obtain the following:
$\mathcal{R}_{pr}(\mathcal{S})$
is downward dense (Theorem 16). Essentially, the reason behind this is the following fact: the inverse of a primitive recursive function is not necessarily primitive recursive. Furthermore, one can obtain the following:
Proposition 37. Let
![]() $\mathcal{S}$
be a punctual family, and let
$\mathcal{S}$
be a punctual family, and let
![]() $\nu$
be a punctual Friedberg numbering of
$\nu$
be a punctual Friedberg numbering of
![]() $\mathcal{S}$
. Then below the degree of
$\mathcal{S}$
. Then below the degree of
![]() $\nu$
(inside
$\nu$
(inside
![]() $\mathcal{R}_{pr}(\mathcal{S})$
), one can build
$\mathcal{R}_{pr}(\mathcal{S})$
), one can build
-
(a) An infinite descending chain of degrees, such that each of them is induced by a Friedberg numbering.
-
(b) An infinite antichain of degrees, such that each of them is induced by a Friedberg numbering.
Proof Sketch. First, we observe the following simple fact: If
![]() $\nu$
and
$\nu$
and
![]() $\mu$
are Friedberg numberings of
$\mu$
are Friedberg numberings of
![]() $\mathcal{S}$
, and a function f provides a punctual reduction from
$\mathcal{S}$
, and a function f provides a punctual reduction from
![]() $\nu$
to
$\nu$
to
![]() $\mu$
, then f is a primitive recursive permutation of
$\mu$
, then f is a primitive recursive permutation of
![]() $\omega$
.
$\omega$
.
Let
![]() $\alpha$
be a punctual Friedberg numbering of
$\alpha$
be a punctual Friedberg numbering of
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
-
(a) It is known that there is a primitive recursive permutation f of
 $\omega$
such that its inverse
$\omega$
such that its inverse
 $f^{-1}$
is not primitive recursive (Kuznecov Reference Kuznecov1950, a proof sketch in English can be found, for example, in Paolini et al. Reference Paolini, Piccolo and Roversi2016). This implies that the sequence: induces a strictly
$f^{-1}$
is not primitive recursive (Kuznecov Reference Kuznecov1950, a proof sketch in English can be found, for example, in Paolini et al. Reference Paolini, Piccolo and Roversi2016). This implies that the sequence: induces a strictly \begin{align*} \mu_0 := \alpha\circ f,\ \mu_1 := \mu_0 \circ f,\ \dots,\ \mu_{k+1} := \mu_k \circ f,\ \dots \end{align*}
\begin{align*} \mu_0 := \alpha\circ f,\ \mu_1 := \mu_0 \circ f,\ \dots,\ \mu_{k+1} := \mu_k \circ f,\ \dots \end{align*}
 $\leq_{pr}$
-descending chain below
$\leq_{pr}$
-descending chain below
 $\alpha$
.
$\alpha$
.
-
(b) Informally speaking, here one needs to modify the proof of Theorem 20. In the notations of the theorem, we need to build two Friedberg numberings
 $\nu_0$
and
$\nu_0$
and
 $\nu_1$
, while satisfying the requirements
$\nu_1$
, while satisfying the requirements
 $R^{\varepsilon}$
,
$R^{\varepsilon}$
,
 $N^0_j$
, and
$N^0_j$
, and
 $N^1_j$
.
$N^1_j$
.
The numberings
![]() $\nu_i$
, which are being constructed, copy different pieces of the given Friedberg numbering
$\nu_i$
, which are being constructed, copy different pieces of the given Friedberg numbering
![]() $\alpha$
. We modify the
$\alpha$
. We modify the
![]() $N^0_j$
-strategy appropriately.
$N^0_j$
-strategy appropriately.
The new
![]() $N^0_j$
-strategy. Let M be the least index such that the object
$N^0_j$
-strategy. Let M be the least index such that the object
![]() $\alpha(M)$
has not been used in the construction yet. The background action is the following: we put
$\alpha(M)$
has not been used in the construction yet. The background action is the following: we put
Our strategy waits until the first stage t with the following properties: The value
![]() $p_j(N)[t]$
is defined, and the object
$p_j(N)[t]$
is defined, and the object
![]() $\nu_1(p_j(N))$
is also defined.
$\nu_1(p_j(N))$
is also defined.
When the number t is found, it is clear that the
![]() $N^0_j$
-requirement is satisfied: we have
$N^0_j$
-requirement is satisfied: we have
where
![]() $\ell \in \omega\setminus\{ M\}$
.
$\ell \in \omega\setminus\{ M\}$
.
Note that we have a little technical problem here: since we require
![]() $\nu_1\in Com_{pr}(\mathcal{S})$
, we need to provide a unique
$\nu_1\in Com_{pr}(\mathcal{S})$
, we need to provide a unique
![]() $\nu_1$
-index k such that
$\nu_1$
-index k such that
![]() $\nu_1(k) = \alpha(M)$
. Surely, this should be done after the
$\nu_1(k) = \alpha(M)$
. Surely, this should be done after the
![]() $N^0_j$
-requirement is satisfied. It is not difficult to resolve this problem via a careful arrangement of the construction. Proposition 37 is proved.
$N^0_j$
-requirement is satisfied. It is not difficult to resolve this problem via a careful arrangement of the construction. Proposition 37 is proved. ![]()
Recall that below any (Turing) computable negative numbering of an infinite family, one can always find a computable Friedberg numbering (see Section 3). This fact fails in the punctual setting:
Proposition 38. There is an infinite punctual family
![]() $\mathcal{S}$
, which does not have punctual Friedberg numberings.
$\mathcal{S}$
, which does not have punctual Friedberg numberings.
Proof. Choose an infinite c.e. set W, which cannot be the range of a primitive recursive injective function. For the sake of completeness, we sketch the construction of such a set W.
The desired set W is built in stages. Note that these stages have to be arranged in a non-punctual way. At a stage e, we define finite sets W[e] and V[e].
Stage
![]() $e+1$
. Find the least index k such that:
$e+1$
. Find the least index k such that:
-
either the string
 $p_e | k$
witnesses that
$p_e | k$
witnesses that
 $p_e$
is not injective,
$p_e$
is not injective, -
or there are two indices
 $\ell$
and m with
$\ell$
and m with
 $\ell,m\leq k$
and
$\ell,m\leq k$
and
 $\{ p_e(\ell) \neq p_e(m) \} \subseteq \omega \setminus (W[e] \cup V[e])$
.
$\{ p_e(\ell) \neq p_e(m) \} \subseteq \omega \setminus (W[e] \cup V[e])$
.
If these indices are found, then put
![]() $p_e(\ell)$
into W and
$p_e(\ell)$
into W and
![]() $p_e(m)$
into V.
$p_e(m)$
into V.
It is not hard to show that both W and V are infinite,
![]() $W\cap V = \emptyset$
, and for any injective
$W\cap V = \emptyset$
, and for any injective
![]() $p_e$
, we have
$p_e$
, we have
![]() $range(p_e) \neq W$
. This concludes the construction of W.
$range(p_e) \neq W$
. This concludes the construction of W.
Choose a primitive recursive (non-injective) function h with
![]() $\mathrm{range}(h) = W$
. The desired family
$\mathrm{range}(h) = W$
. The desired family
![]() $\mathcal{S}$
is defined via its punctual numbering: for
$\mathcal{S}$
is defined via its punctual numbering: for
![]() $i,x\in\omega$
, set
$i,x\in\omega$
, set
![]() $(\nu(i))(x) := h(i)$
.
$(\nu(i))(x) := h(i)$
.
Assume that
![]() $\mu$
is a punctual Friedberg numbering of
$\mu$
is a punctual Friedberg numbering of
![]() $\mathcal{S}$
. Then the primitive recursive injection
$\mathcal{S}$
. Then the primitive recursive injection
![]() $\psi(i) := (\mu(i))(0)$
satisfies
$\psi(i) := (\mu(i))(0)$
satisfies
![]() $\mathrm{range}(\psi) = W$
, which contradicts the choice of the set W.
$\mathrm{range}(\psi) = W$
, which contradicts the choice of the set W. ![]()
Acknowledgements
Part of the research contained in this paper was carried out while N. Bazhenov and S. Ospichev were visiting the Department of Mathematics of Nazarbayev University, Nur-Sultan. The authors wish to thank Nazarbayev University for its hospitality. N. Bazhenov and S. Ospichev were supported by Mathematical Center in Akademgorodok under agreement No. 075-15-2019-1613 with the Ministry of Science and Higher Education of the Russian Federation. M. Mustafa was supported by NUFDCRG N021220CRP5138 and also partially supported by MESRK grant No. AP08856834. We are grateful to Sergey Goncharov and to the anonymous reviewers for their helpful suggestions.
Conflicts of Interests
The authors declare none.