2. Experimental set-up

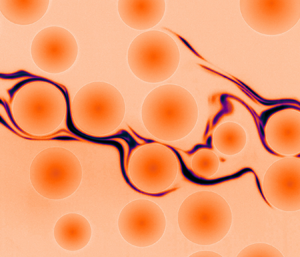
The experimental set-up, sketched in figure 1(a), is similar to the one used in Souzy et al. (Reference Souzy, Zaier, Lhuissier, Le Borgne and Metzger2018). A transparent suspension containing a blob of dyed liquid is deformed in a pure shear flow and the mixing of the dye is measured by monitoring a slice of the suspension perpendicular to the vorticity direction.

Figure 1. (a) Schematic of the experimental set-up. (b) Transverse view of the injection system used to form a thin cylindrical blob of dyed liquid. (c) Picture of the blob cross-section at strains $\gamma =0$ and $\gamma =5$ for . The initial blob size is $2s_0\approx 200\ \mathrm {\mu }\textrm {m}$ by $2l_0\approx 300\ \mathrm {\mu }\textrm {m}$. The intersections of the particles with the light sheet are highlighted in grey.

3. General observations

Figure 2 compares, at equal strains, the typical evolution of the dye concentration field obtained for the two Péclet numbers investigated. On a global scale, the blob of dye is stretched by the mean flow and aligns with the mean flow direction ($x$), while it is dispersed in the transverse direction by the fluctuations of the flow induced by the particles. On a smaller scale, the flow stretches and folds the dyed liquid into thinner lamellar structures, which are eventually blurred by molecular diffusion. At a given strain, the spatial dispersion of the lamellae appears to be similar between the two Péclet numbers. By contrast, the process of mixing is much more advanced for the lowest Pé, consistently with the longest time over which diffusion operates for a smaller shear rate: while most lamellae are still thin and sharp at $\gamma = 30$ for , they are broader and already significantly blurred for .

Figure 2. Blob of dye in the sheared suspension. Dye concentration field for (a) and (b) shown for identical strains $\gamma \equiv \dot {\gamma }t$ (see also supplementary movie 1 available at https://doi.org/10.1017/jfm.2021.270).

Figure 3 presents the evolution of the corresponding concentration distributions, $P(C)$. The concentration distribution is obtained from all the pixels where the concentration level is above the threshold value, ${C_{th}}$, which corresponds to the background noise. The value of $C_{th}$ is adjusted by hand to delineate the lamellae contour. Its value decreases slowly with increasing deformation; however, this does not affect the shape of the distribution above $C_{th}$. Initially, $P(C)$ has the characteristic U-shape of a segregated system, with a peak at the blob initial concentration, $C/C_0=1$. As the blob is stretched and mixes with the surrounding liquid, the probability of the large concentrations decays. At equal strains, the steeper decay of the distributions at large concentration observed at low Péclet number indicates a more advanced mixing. In the following, we provide a theoretical framework to describe the evolution of these concentration distributions.

Figure 3. Evolution of the concentration distribution for (a) and (b) . Symbols: experimental data. Lines: solitary-strip model, $P_{{SS}}(C)$ (4.6), with $f=0.30$ and $g=0.21$. Solid lines highlight strains ($\gamma \leq 18$ and $\gamma \leq 10$ for (a,b), respectively) for which the number of overlaps is expected to be small (${{\mathcal {S}}}/{{\mathcal {A}}}\leq 1$; see text). Dashed lines are used at larger strains. Insets: same in double-logarithmic scales. Each distribution is obtained by averaging seven independent runs.

4. Solitary-strip model

At sufficiently short times, the blob of dye forms thin lamellae, which are essentially isolated from each other and which we call hereafter elementary lamellae. Each elementary lamella results from the stretching induced by the combination of the mean and fluctuating components of the flow. Assuming (in line with the solitary-strip framework (Villermaux Reference Villermaux2019)) that the stretching rate over each lamella cross-section is uniform at each time, the probability distribution of the lamella elongations is set by that of the fluid material lines. In a previous work (Souzy et al. Reference Souzy, Lhuissier, Villermaux and Metzger2017), this elongation distribution has been shown to follow a log-normal statistic given by

(4.1)\begin{equation} P(\rho)=\frac{1}{\sqrt{2{\rm \pi}}\,\sigma\rho} \exp\left({-\frac{(\ln\rho-\mu)^{2}}{2\sigma^{2}}}\right), \end{equation}

where the elongation, $\rho (t)$, is the ratio of the current material line length to its initial length, and both the mean value,

(4.2)\begin{equation} \mu \equiv \langle\ln\rho \rangle=f \gamma, \end{equation}

and the variance,

(4.3)\begin{equation} \sigma^{2} \equiv \langle\ln^{2} \rho\rangle - \langle\ln\rho \rangle^{2} = g \gamma, \end{equation}

of the logarithm of the elongation grow linearly with strain, with coefficients $f\simeq 0.193$ and $g\simeq 0.174$ for $\phi =0.30$ (Souzy et al. Reference Souzy, Lhuissier, Villermaux and Metzger2017).

To compute the concentration distribution of the whole blob of dye, we first derive the concentration distribution of each of its lamellar portions. For a slender portion of lamella with elongation $\rho (\gamma )$, the combined advection and diffusion of the dye transversely to the lamella follows the pure diffusion equation, $\partial _\tau C = \partial _\eta ^{2} C$, in terms of the dimensionless time scale and length scale $\eta = \rho h$, with $h$ the distance to the lamella midplane (Ranz Reference Ranz1979; Rhines & Young Reference Rhines and Young1983; Meunier & Villermaux Reference Meunier and Villermaux2003; Souzy et al. Reference Souzy, Zaier, Lhuissier, Le Borgne and Metzger2018). Assuming that this portion of lamella has an initially Gaussian concentration profile and experiences a constant elongation rate ($\dot {\rho }/\rho =\ln \rho /t= \textrm {const.}$), its profile evolves as $C = {C_{m}}\, \mathrm {e}^{-h^{2}/2s^{2}}$, where the half-width, maximal concentration and dimensionless time follow, respectively,

(4.4a–c)

The concentration probability distribution of this portion of lamella above the threshold concentration ${C_{th}}$ is obtained from the change of variable $P_{G}(C) = |\mathrm {d} h/\mathrm {d} C|/h_{th}$, with $h_{th}$ the distance from the lamella midplane at which $C(h_{th}) = {C_{th}}$. This yields

(4.5)\begin{equation} P_{G}(C,{C_{m}}) = \frac{1}{2C\sqrt{\ln\dfrac{{C_{m}}}{{C_{th}}}}\, \sqrt{\ln\dfrac{{C_{m}}}{C}}},\quad \text{for}\ {C_{th}} \leq C\leq {C_{m}} \end{equation}

(see Souzy et al. (Reference Souzy, Zaier, Lhuissier, Le Borgne and Metzger2018) for details of the calculations).

As long as the different portions of the lamellae do not overlap with each other, the solitary-strip concentration distribution, $P_{{SS}}(C)$, for the whole blob of dye is obtained by summing the contributions of the different lamella portions. It is expressed as $P_{{SS}} \propto \int _0^{\infty } 2h_{th} \rho l_0 P(\rho ) P_{G}(C,{C_{m}})\,\mathrm {d}\rho$, where $2h_{th}\rho l_{0}$ is the area of a portion (in the $xz$-plane) and $P(\rho )$ is the probability, given by (4.1), that a portion has the elongation $\rho$. Using $h_{th}=(s_{0}/\rho ) \sqrt {(1+2\tau )\ln ({C_{m}}/{C_{th}})}$, the concentration distribution becomes

(4.6)\begin{equation} P_{{SS}}(C) = A^{{-}1} \int_0^{\infty}\! \frac{\sqrt{1+2\tau}}{C \sqrt{\ln\dfrac{{C_{m}}}{C}}} \, P(\rho)\,\mathrm{d}\rho, \end{equation}

with $A = 2\int _0^{\infty } \sqrt {1+2\tau } \sqrt {\ln ({C_{m}}/{C_{th}})} P(\rho )\,\mathrm {d}\rho$ a normalizing constant.

Figure 3 compares the solitary-strip prediction (4.6), with $f=0.30\pm 0.03$ and $g=0.21\pm 0.03$ as adjustable parameters, to the experimental results. The fit is performed on the low-Péclet-number data (, for which the minimal lamella width, given by the Batchelor scale , is well resolved), and up to a strain $\gamma =12$ (in order to have a limited influence of coalescence).

The model captures well the shape of the concentration distributions and the progressive decay of the concentration levels, for both Péclet numbers and up to a strain $\gamma \approx 12$ for and $\gamma \approx 16$ for . The fitted values of $f$ and $g$ are also in reasonable agreement with the experimental values determined previously by Souzy et al. (Reference Souzy, Lhuissier, Villermaux and Metzger2017) (i.e. $f\simeq 0.193$ and $g\simeq 0.174$). The difference is possibly related to the fact that the stretching laws measured by Souzy et al. (Reference Souzy, Lhuissier, Villermaux and Metzger2017) were obtained from a two-dimensional section of a three-dimensional flow field, which may have slightly underestimated the actual three-dimensional elongation experienced by the lamellae. Note also that the agreement found at large is somehow unexpected since the minimum lamella width, , is below the spatial resolution of the set-up ($3.3\ \mathrm {\mu }\textrm {m}$). At larger strains, the solitary-strip model fails to describe the concentration distributions. This is better appreciated in the double-logarithmic plots shown in the insets of figure 3, which allow one to compare the concentration distributions at long times. The experimental concentration levels are found to decay much slower than anticipated by $P_{{SS}}$. This is consistent with the increasing interaction between lamellae. The solitary-strip framework no longer applies when lamellae significantly overlap with each other (see figure 2 and Movie 1). Overlapping lamellae add up their concentration levels, which slows down the global concentration decay relative to non-overlapping lamellae. A relevant model of the concentration distributions at high strains thus calls for a description of coalescence.

5. Coalescence model

Overlaps between lamellae necessarily occur because the unfolded area of the blob grows exponentially and eventually becomes larger than the dispersion envelope in which the blob develops. Indeed, the length of the elementary lamellae, $2\langle {\rho }\rangle l _0$, increases exponentially, while, after a short initial contraction, their width $s$ is locked at the Batchelor scale, $s_B\sim \sqrt {D/f\dot {\gamma }}$, at which the transverse compression rate $\sim f\dot {\gamma }$ is balanced by the diffusive broadening rate $\sim D/s^{2}$; see (4.4a–c). The non-overlapping blob area thus increases exponentially as ${{\mathcal {S}}} \sim s_B\,l_0\ \textrm {e}^{f\dot {\gamma } t}$. On the other hand, the dispersion envelope grows from the combined effect of the mean flow and of the Fickian dispersion induced by the fluctuating motion of the particles. for , the area of dispersion, which is illustrated in figure 4(a) by overlaying the concentration fields of seven experiments, increases algebraically with time according to

(5.1)\begin{equation} {{\mathcal{A}}} = {\rm \pi}\sqrt{[l_0^{2}+2\kappa t][s_0^{2}+2\kappa(t+\dot{\gamma}^{2} t^{3}/3)]} \sim \kappa\dot{\gamma} t^{2}, \end{equation}

where $\kappa \approx 0.017 \phi \dot {\gamma } d^{2}$ is the shear-induced dispersion coefficient (Metzger et al. Reference Metzger, Rahli and Yin2013; Souzy et al. Reference Souzy, Lhuissier, Villermaux and Metzger2017). The value of $\kappa$ is obtained from the evolution of the spatial variance of the dye concentration $\sigma ^{2}_z$ in the transverse direction ($z$); see figure 4(b).

Figure 4. (a) Overlay of the concentration fields obtained from seven runs at $\gamma = 7.5$. Each colour corresponds to a run. The dashed line delineates the dispersion envelope of area ${{\mathcal {A}}}$ (5.1). (b) Normalized spatial variance of the dye concentration in the transverse direction, $\Delta \sigma ^{2}_z/d^{2}=(\sigma _z^{2}-\sigma _z^{2}(t=0))/d^{2}$, versus strain. The linear fit (black line) provides the shear-induced dispersion coefficient $\kappa =0.017\phi \dot {\gamma } d^{2}$.

As a result, the typical number of overlaps between elementary lamellae, given by the ratio ${{\mathcal {S}}}/{{\mathcal {A}}}$, eventually becomes very large. For the low-Péclet-number experiments, ${{\mathcal {S}}}/{{\mathcal {A}}} \sim 10$ for $\gamma = 20$ and ${{\mathcal {S}}}/{{\mathcal {A}}}\sim 10^{4}$ for $\gamma = 40$. This estimate for the number of overlaps corroborates the validity range of the solitary-strip model observed in figure 3. Significant deviation from the experimental data is found around $\gamma =12$ (respectively 16) for (respectively 8500), while (4.4a–c) and (5.1) yield ${{\mathcal {S}}}/{{\mathcal {A}}}=1$ at $\gamma \simeq 10$ (respectively 18). However, it must be noted that these estimates are meaningful only in the average sense. In practice, the transition between the solitary-strip and the coalescence regimes is not expected to be sharp, but rather gradual, because of the broad distribution of the stretching and merging statistics, which will be discussed in the following.

As shown in figures 2 and 5(a), these overlaps result from the continuous stretching, folding and fusing of adjacent lamellae into a single portion of lamella. This iterative process continuously creates a new lamella, hereafter called super-lamella, which contains an increasingly large number of folded elementary lamellae, while preserving the essentially lamellar structure of the blob of dye. This super-lamella typically meanders between each pair of neighbouring particles within the dispersion envelope. Hence, its total length $2L$ does not grow exponentially but is limited by the area of the dispersion envelope according to $2L/2l_0 = a {{\mathcal {A}}}/{{\mathcal {A}}}_0$, where $a$ is a constant of order one. Like in (4.4a–c) for the elementary lamellae, this effective stretching dynamics sets the evolution of the super-lamella width $S$ and dimensionless time $T$:

(5.2)

The long-time evolution of is consistent with the experimental observations: the apparent width of the super-lamellae is larger at low and slowly increases with strain (see figure 2).

Figure 5. (a) Coalescence event and corresponding concentration profiles before (blue) and after (red) merging occurs. (b) Sketch of the super-lamella formed by the coalescence of elementary lamellae. (c,d) Comparison between the experimental distributions and the coalescence model $P_{{C}}(C)$ (5.6), for (c) and (d) . The coalescence model is plotted when the number of overlaps becomes significant (${{\mathcal {S}}}/{{\mathcal {A}}}>1$), i.e. when $\gamma >10$ for and when $\gamma >18$ for .

We then assume that the aggregation process forming the super-lamella occurs at random and with a constant rate prescribed by the growth of ${{\mathcal {A}}}$ and $\langle {\rho }\rangle$. As a consequence, the number of elementary lamellae $n$ fused into a super-lamella follows the exponential distribution (Smoluchowski Reference Smoluchowski1917):

(5.3)\begin{equation} P(n) = \frac{1}{\langle{n}\rangle}\,\mathrm{e}^{{-}n/\langle{n}\rangle},\quad \text{with}\ \langle{n}\rangle = \frac{\langle{\rho}\rangle l_0}{L} = \frac{\langle{\rho}\rangle{{\mathcal{A}}}_0}{a{{\mathcal{A}}}}, \end{equation}

which is valid when the mean number of elementary lamellae contained in a super-lamella is large ($\langle {n}\rangle \gg 1$). The expression for $\langle {n}\rangle$ reflects that the length of the elementary lamellae, $2\langle {\rho }\rangle l_0$, must fold entirely over the length $2L$ of the super-lamella. This recovers the exponential increase of $\langle {n}\rangle$ with time discussed above.

As shown in figure 5(a), the super-lamella has a nearly Gaussian concentration profile. Then, owing to the conservation of the dye, the maximum concentration, $C_M$, of a super-lamella is determined by its width $S$ and by the number $n$ of elementary lamellae with maximum concentration ${C_{m}}$ that it contains. This yields

(5.4)\begin{equation} C_M = \frac{1}{S}\sum_{i=1}^{n}\,s_i C_{{m},i} \simeq \frac{n\langle{s{C_{m}}}\rangle}{S} = \frac{s_0C_0}{S\langle{\rho}\rangle}\,n, \end{equation}

where the mean-field approximation (averaging of $s{C_{m}}$) is relevant for the large number of overlaps considered here ($n\gg 1$). The local width $S$ of the super-lamella could possibly correlate with the number $n$ of elementary lamellae it contains locally. However, the variations in $S$ observed in the experiments, which are of the order of a few units, are negligible relative to the orders of magnitude variations in $n$ given by (5.3). We therefore assume that $S$ is independent of $n$ and uniform. The final concentration distribution, accounting for coalescence, is then obtained by summing the contributions of the Gaussian concentration profiles of the super-lamella for all values of $n$, i.e.

(5.5)\begin{equation} P_{{C}}(C) \propto \int_1^{\infty} P(n) {H_{th}} P_G(C,C_M)\,\mathrm{d} n, \end{equation}

where the apparent width of a super-lamella (i.e. where $C>{C_{th}}$) follows ${H_{th}} = S\sqrt {\ln ({{C_{M}}}/{{C_{th}}})}$, which is defined for ${C_{th}}<{C_{M}}$. Introducing $\tilde {n} \equiv n/\langle {n}\rangle$, (5.5) can be recast into

(5.6)\begin{equation} P_{{C}}(C) = \frac{A'^{{-}1}}{2C}\int_{1/\langle{n}\rangle}^{\infty} \frac{\mathrm{e}^{-\tilde{n}}}{\sqrt{\ln\dfrac{\langle{{C_{M}}}\rangle\tilde{n}}{C}}}\,\mathrm{d}\tilde{n}, \quad \text{with}\ \frac{\langle{{C_{M}}}\rangle}{C_0} \equiv \frac{{C_{M}}|_{\tilde{n}=1}}{C_0} = \frac{1}{\sqrt{1+2T}}, \end{equation}

and $A' = \int _{1/\langle {n}\rangle }^{\infty } \mathrm {e}^{-\tilde {n}} \sqrt {\ln (\langle {{C_{M}}}\rangle \tilde {n}/{C_{th}})}\,\mathrm {d}\tilde {n}$ a normalizing constant. Through (5.2)–(5.3) for $T$ and $\langle {n}\rangle$, (5.6) is entirely set by the Péclet number and the kinematic quantities ${{\mathcal {A}}}$ and $\langle {\rho }\rangle$.

The concentration distribution $P_{{C}}$ behaves like $\sim (1/C)\,\mathrm {e}^{-C/\langle {{C_{M}}}\rangle }$ (within logarithmic corrections). It is thus entirely prescribed by the average maximum concentration $\langle {{C_{M}}}\rangle$, below which the distribution decays like $1/C$, and above which the decay is exponential. This prediction is compared with the experimental distributions in figure 5(c,d), with $a$, the proportionality factor between the super-lamellae length $2L/2l_0$ and the dispersion area $A/A_0$, as the only free parameter (its value is set by fitting the model to the low-Péclet-number data, which yields $a=4\pm 1$, consistently with the expectation that $a$ is of order one). For large Péclet number (), the agreement with experiments is slightly improved relative to the solitary-strip model but not quantitative. The coalescence model predicts a larger probability for the intermediate concentration levels and a distribution tail decaying more sharply than observed experimentally. This discrepancy is consistent with the observations in figure 2, which show that for the bundles of lamellae are only partially fused, even at large strains. Their concentration profiles are therefore not well captured by the Gaussian shape assumed in the model. Another potential bias is that, for , the typical thickness $S$ of the super-lamella, which is set by the Batchelor scale, (see 5.2), is comparable with the laser sheet thickness, ${\sim }10\ \mathrm {\mu }\textrm {m}$. For a lamella that is not perpendicular to the laser sheet, this would average the concentration profile and alter the concentration measurements.

By contrast, for moderate Péclet number (), the coalescence model captures quantitatively the shape of the distributions at long times ($\gamma \gtrsim 16$), both for the low-concentration part (${\sim }1/C$) and for the typical concentration $\langle {{C_{M}}}\rangle$ above which the distributions decay sharply. In this case, coalescing lamellae are found to be almost entirely fused, at all times, into a super-lamella with a close to Gaussian concentration profile.