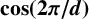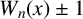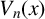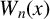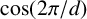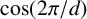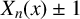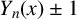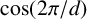1 Introduction
The significance of the widespread applications of Chebyshev and related polynomials in mathematics, engineering and numerical modelling motivates the study of the properties of these polynomials.
In earlier work, Wolfram [Reference Wolfram17] solved an open factorisation problem for Chebyshev polynomials of the second kind
$U_n(x) \pm 1$
and gave a more direct proof of the result for Chebyshev polynomials of the first kind,
$T_n(x) \pm 1$
. We apply this method to solve the analogous factorisation problems for Chebyshev polynomials of the third and fourth kinds. These factorisations are also expressed in terms of the minimal polynomials of
$\cos ({2\pi }/{d})$
. We then show that, in general, there are no factorisations of variants of the Chebyshev polynomials of the fifth and sixth kinds,
$X_n(x) \pm 1$
and
$Y_n(x) \pm 1$
, with these minimal polynomials. Additionally, we give an equation that relates
$U_n(x)$
to the monic form of
$Y_n(x)$
in Theorem 5.1.
Chebyshev polynomials of the first and second kinds,
$T_n(x)$
and
$U_n(x)$
, were introduced by Pafnuty Chebyshev (1821–1894) in 1854. Gautschi [Reference Gautschi8] named the Chebyshev polynomials of the third and fourth kinds
$V_n(x)$
and
$W_n(x)$
in 1992 [Reference Mason and Handscomb13]. They are also called airfoil polynomials [Reference Fromme and Golberg7, Reference Mason and Handscomb13]. They are used in areas such as solving differential equations [Reference Abd-Elhameed and Alkenedri1], numerical integration [Reference Aghigh, Masjed-Jamei and Dehghan5, Reference Fromme and Golberg7, Reference Mason and Handscomb13], approximations [Reference Mason and Handscomb13], interpolation [Reference Gautschi8] and combinatorics [Reference Andrews6].
In 2006, Masjed-Jamei [Reference Masjed-Jamei12] defined orthogonal polynomials called Chebyshev polynomials of the fifth and sixth kinds,
$X_n(x)$
and
$Y_n(x)$
, that satisfy a generalised recurrence equation for monic Chebyshev polynomials (see [Reference Abd-Elhameed and Youssri3, Equations (6)–(7)]) with an exception for
$\bar {T}_2(x)$
where
$A_{1, -1, 0, -1, 1}$
is indeterminate and should equal
$-\tfrac 12$
. Abd-Elhameed and Youssri [Reference Abd-Elhameed and Youssri3] specifically related
$V_n(x)$
and
$W_n(x)$
to the monic form of
$X_n(x)$
.
Chebyshev polynomials of the fifth and sixth kinds are active research areas. In 2018, shifted Chebyshev polynomials of the fifth kind were used to solve problems involving fractional-order differential equations [Reference Abd-Elhameed and Youssri3]. In 2021, connection formulas and other properties of the polynomials of the fifth [Reference Abd-Elhameed and Alkhamisi2] and sixth [Reference Abd-Elhameed and Youssri4] kinds were given. Also, Sadri and Aminikhah defined two-variable shifted Chebyshev polynomials of the sixth kind of the form
$\bar {Y}_i(2x-1) \bar {Y}_j(2t -1)$
in [Reference Sadri and Aminikhah14, Equation (4.7)], and used them to solve fractional-order partial differential equations numerically.
1.1 Chebyshev polynomials of the second kind
Chebyshev polynomials of the second kind can be defined by
$$ \begin{align} U_n(x) = \frac{\sin((n + 1)\theta)}{\sin(\theta)}, \end{align} $$
where
$x = \cos \theta $
and
$n \geq 0$
(see [Reference Mason and Handscomb13, Equation (1.4)]). It follows that
$$ \begin{align} U_n(x)^2 -1 = U_{n-1}(x) U_{n+1}(x), \end{align} $$
where
$n \geq 1$
, by applying the trigonometric identity
$$\begin{align*}\sin^2 A - \sin^2 B = \sin(A + B) \sin(A - B) \quad\mbox{with } A = (n+1)\theta \mbox{ and } B = \theta.\end{align*}$$
These polynomials satisfy the recurrence (see [Reference Mason and Handscomb13, Equations (1.6a)–(1.6b)])
$$ \begin{align} U_0(x) &= 1, \quad U_1(x) = 2x, \quad U_{n}(x) = 2 x U_{n-1}(x) - U_{n-2}(x), \quad \mbox{for } n>1. \end{align} $$
Definition 1.1. The polynomials
$\Psi _d(x)$
are
where
$S_{d/2} =\{k \mid (k, d) = 1, 1 \leq k < d/2\}$
and
$d> 2$
. They have degree
$\phi (d)/2$
where
$\phi $
is Euler’s totient function [Reference Gürtaş9]. The polynomials
$\Psi _1(x) =2(x -1)$
and
$\Psi _2(x) = 2(x+1)$
were defined in Wolfram [Reference Wolfram17, Definition 1]. These are polynomials with roots
$\cos (2 \pi )$
and
$\cos (\pi )$
, respectively.
Gürtaş [Reference Gürtaş9] showed that
Lemma 1.2. The minimal polynomial in
$\mathbb {Q}[x]$
of
$\cos ({2\pi }/{d})$
is
$\bar {\Psi }_d(x) = 2^{-{\phi (d)}/{2}}\Psi _d(x)$
where
$d> 2$
. We also have
$\bar {\Psi }_1(x) = 2^{-1}\Psi _1(x)$
and
$\bar {\Psi }_2(x) = 2^{-1}\Psi _2(x)$
.
Proof. This follows from the proof of [Reference Lehmer11, Theorem 1] and the definition of minimal polynomial.
1.2 Chebyshev polynomials of the third and fourth kinds
Chebyshev polynomials of the third kind can be defined by
$$ \begin{align} V_n(x) = \frac{\cos(n + 1/2)\theta}{\cos {\theta}/2}, \end{align} $$
and of the fourth kind by
$$ \begin{align} W_n(x) = \frac{\sin(n + 1/2)\theta}{\sin {\theta}/2}, \end{align} $$
where
$x = \cos \theta $
and
$n \geq 0$
. They can also be defined with respect to Chebyshev polynomials of the second kind by
$$ \begin{align} V_n(x) = U_n(x) - U_{n-1}(x) \end{align} $$
and
$$ \begin{align} W_n(x) = U_n(x) + U_{n-1}(x), \end{align} $$
where
$n \geq 1$
(see [Reference Mason and Handscomb13, Equations (1.17)–(1.18)]).
2 Solution
The method of solution follows that by Wolfram [Reference Wolfram17]. The first step is to express
$V_n(x)^2 - 1$
and
$W_n(x)^2 -1$
in terms of the polynomials
$\Psi _d(x)$
where
$d \geq 1$
.
Lemma 2.1. For
$n \geq 1$
,
The following theorem solves the factorisation problem for
$V_n(x)^2 -1$
. The second step of the method involves defining the mapping that splits the
$2n$
factors of
$V_n(x)^2 -1$
into the n factors of
$V_n(x) +1$
and the other n factors of
$V_n(x) -1$
. The factorisations are unique up to associativity and commutativity of multiplication.
Theorem 2.2. If
$n \geq 1$
, then
and
Proof. The polynomial
$\Psi _1(x) = 2 (x -1)$
is a factor of
$V_n(x)^2 -1$
from (2.1), and
$\Psi _1(\cos (2 \pi )) = 0$
. It follows from (1.6) that
$V_n(\cos (2 \pi )) = 1$
and so
$\Psi _1(x)$
is a factor of
$V_n(x) -1$
.
If
$d \mid 2n$
and
$d> 2$
, let
$\theta = {2\pi k}/{d}$
where
$(k, d) = 1$
,
$1 \leq k < {d}/2$
and
$a = {2n}/{d}$
. We have
$\theta = {\pi a k }/{n}$
and
$\Psi _d(\cos (\theta )) = 0$
. From (1.6),
$$ \begin{align*} V_n(\cos(\theta)) = \frac{\cos((n + 1/2) {\pi a k}/n )}{\cos({\theta}/2)} = \frac{\cos(\pi a k) \cos({\theta}/2) - \sin(\pi a k) \sin({\theta}/2)}{\cos({\theta}/2)}. \end{align*} $$
The denominator
$\cos ({\theta }/2) \not = 0 $
because
${\theta }/2 = {\pi k}/d$
cannot equal
${\pi }/2$
when
$d> 2$
. The numbers
$a k$
and a have the same parity. This is immediate when a is even. If a is odd, it follows that d is even and k is odd because
$(k, d) = 1$
. We have
$\cos (\pi a k) = \cos (\pi a)$
and
$V_n(\cos (\theta )) = \cos (\pi a)$
.
Hence, if a is even, then
$V_n(\cos (\theta )) = 1$
and
$\Psi _d(x)$
is a factor of
$V_n(x) - 1$
. Similarly, if a is odd, then
$V_n(\cos (\theta )) = -1$
and
$\Psi _d(x)$
is a factor of
$V_n(x) + 1$
.
If
$d \mid 2n+ 2$
and
$d> 2$
, let
$b= {(2n + 2)}/{d}$
. We have
$\theta = {\pi b k}/{(n+ 1)}$
where k is such that
$(k, d) = 1$
and
$1 \leq k < {d}/2$
. From (1.6),
$$ \begin{align*} V_n(\cos(\theta)) &= \frac{\cos((n + 1/2) \theta )}{\cos({\theta}/2)} = \frac{\cos((n +1 ) \theta - {\theta}/2)}{\cos({\theta}/2)}\\[2pt] &= \frac{\cos(\pi b k) \cos({\theta}/2) + \sin(\pi b k) \sin({\theta}/2)}{\cos({\theta}/2)}. \end{align*} $$
Similarly to the previous case, the denominator
$\cos ({\theta }/2) \not = 0$
, the numbers
$b k$
and b have the same parity and
$V_n(\cos (\theta )) = \cos (\pi b)$
. It follows that if b is odd then
$\Psi _d(x)$
is a factor of
$V_n(x) +1$
and if b is even then
$\Psi _d(x)$
is a factor of
$V_n(x) -1$
.
From (1.3) and (1.8),
$V_n(x)$
has degree n. It follows that the right-hand side of (2.1) of the factorisation of
$V_n(x)^2 -1$
has degree
$2n$
. It has
$2n$
factors of the form
$2(x - \cos (\theta ))$
from (1.4) and Definition 1.1, half of which are the factors of
$V_n(x) + 1$
and the other half are the factors of
$V_n(x) -1$
. The mapping defined above maps every such factor of
$V_n(x)^2 - 1$
to either
$V_n(x) + 1$
or
$V_n(x) - 1$
depending on whether
$\cos (\theta )$
is a root of
$V_n(x) + 1$
or
$V_n(x) - 1$
, respectively. The right-hand sides of (2.2) and (2.3) are the products of these mapped factors and so both have degree equal to n.
From (1.3) and (1.8), the leading coefficients of
$V_n(x) \pm 1$
are
$2^n$
. The expansions of the factorisations on the right-hand sides of (2.2) and (2.3) both have
$2^n$
as leading coefficients also. Each is a product of n factors of the form
$2(x - \cos (\theta ))$
.
Corollary 2.3. If
$n \geq 1$
, then the factorisations of
$V_n(x) \pm 1$
in terms of the minimal polynomials of
$\cos ({2\pi }/d)$
are
and
The following theorem solves the factorisation problem for
$W_n(x)^2 -1$
. These factorisations are also unique up to associativity and commutativity of multiplication.
Theorem 2.4. If
$n \geq 1$
, then
and
Proof. The structure of the proof is similar to that of Theorem 2.2. If
$d \mid 2n$
and
$d> 1$
, let
$a = {2n}/{d}$
and k be such that
$(k, d) = 1$
where
$1 \leq k < {d}/2$
. From (1.7),
$$ \begin{align*} W_n(\cos(\theta)) = \frac{\sin((n + 1/2) {\pi a k}/n )}{\sin({\theta}/2)} = \frac{\cos(\pi a k) \sin({\theta}/2) + \sin(\pi a k) \cos({\theta}/2)}{\sin({\theta}/2)}. \end{align*} $$
The denominator
$\sin ({\theta }/2) \not = 0 $
because
${\theta }/2 = {\pi k}/d$
cannot equal
$\pi $
when
$d> 1$
. Similarly,
$a k$
and a have the same parity and
$W_n(\cos (\theta )) = \cos (\pi a)$
. Hence, if a is even, then
$W_n(\cos (\theta )) = 1$
and
$\Psi _d(x)$
is a factor of
$W_n(x) - 1$
. If a is odd, then
$W_n(\cos (\theta )) = -1$
and
$\Psi _d(x)$
is a factor of
$W_n(x) + 1$
.
If
$d \mid 2n+ 2$
and
$d> 2$
, let
$b= {(2n + 2)}/{d}$
and k be such that
$(k, d) = 1$
where
$1 \leq k < {d}/2$
. We have
$\theta = {\pi b k}/{(n+ 1)}$
and
${\theta }/2 = {\pi k}/d$
. From (1.7),
$$ \begin{align*} W_n(\cos(\theta)) &= \frac{\sin((n + 1/2) \theta )}{\sin({\theta}/2)} = \frac{\sin((n +1 ) \theta - {\theta}/2)}{\sin({\theta}/2)}\\[2pt] &= \frac{-\cos(\pi b k) \sin({\theta}/2) + \sin(\pi b k) \cos({\theta}/2)}{\sin({\theta}/2)}. \end{align*} $$
The denominator
$\sin ({\theta }/2) \not = 0 $
and b and
$bk$
have the same parity, as above. Hence, if b is even, then
$W_n(\cos (\theta )) = -1$
and
$\Psi _d(x)$
is a factor of
$W_n(x) + 1$
. If b is odd, then
$W_n(\cos (\theta )) = 1$
and
$\Psi _d(x)$
is a factor of
$W_n(x) - 1$
.
It is straightforward to show that the degrees of the right-hand sides of (2.4) and (2.5) are both n and the leading coefficients of both sides of these equations are
$2^n$
.
Corollary 2.5. If
$n \geq 1$
, then the factorisations of
$W_n(x) \pm 1$
in terms of the minimal polynomials of
$\cos ({2\pi }/d)$
are
and
3 Examples with V
The polynomial
$V_{12}(x)^2 - 1$
has 24 factors, and
$V_{12}(x) + 1$
and
$V_{12}(x) -1$
each are the products of half of these factors. The mapping in the proof of Theorem 2.2 gives
$$ \begin{align*} V_{12}(x) + 1 &= \Psi_8(x) \Psi_{24}(x) \Psi_{26}(x),\\ V_{12}(x) - 1 &= \Psi_1(x) \Psi_3(x)\Psi_4(x)\Psi_6(x)\Psi_{12}(x)\Psi_{13}(x)\\[2pt] &= (2(x -1)) (2x + 1) (2x) (2x -1) (4 x^2 - 3)\\[2pt] &\quad \cdot(64 x^6 + 32 x^5 - 80x^4 - 32 x^3 + 24 x^2 + 6x -1)\\[2pt] &= 2^{12}(x-1)\big(x+ \tfrac12\big)x\big(x-\tfrac12\big)\big(x^2 - \tfrac34\big) \bar{\Psi}_{13}(x). \end{align*} $$
4 Examples with W
The polynomial
$W_{12}(x)^2 - 1$
has 24 factors, and
$W_{12}(x) + 1$
and
$W_{12}(x) -1$
each are the products of half of these factors. The mapping in the proof of Theorem 2.4 gives
$$ \begin{align*} W_{12}(x) + 1 &= \Psi_8(x) \Psi_{24}(x) \Psi_{13}(x),\\ W_{12}(x) - 1 &= \Psi_2(x) \Psi_3(x)\Psi_4(x)\Psi_6(x)\Psi_{12}(x)\Psi_{26}(x)\\[2pt] &= (2(x+1))(2x + 1) (2x) (2x -1) (4 x^2 - 3)\\[2pt] &\quad \cdot (64 x^6 - 32 x^5 - 80x^4 + 32 x^3 + 24 x^2 - 6x -1)\\[2pt] &= 2^{12} (x+1)\big(x+ \tfrac12\big)x\big(x-\tfrac12\big)\big(x^2 - \tfrac34\big)\bar{\Psi}_{26}(x). \end{align*} $$
When n is odd,
$\Psi _2(x)$
is a factor of
$W_n(x) +1$
:
$$ \begin{align*} W_{11}(x) + 1 =& \Psi_2(x) \Psi_{22}(x) \Psi_{3}(x) \Psi_{4}(x)\Psi_6(x) \Psi_{12}(x). \end{align*} $$
5 Chebyshev polynomials of the fifth and sixth kinds
Masjed-Jamei [Reference Masjed-Jamei12] defined the Chebyshev polynomials of the fifth kind,
$X_n(x)$
, and sixth kind,
$Y_n(x)$
. Similarly to the other four kinds of Chebyshev polynomials, they are orthogonal polynomials with integer coefficients. The polynomials
$X_n(x)$
and
$Y_n(x)$
have degree n where
$n \geq 0$
[Reference Abd-Elhameed and Youssri3, Reference Abd-Elhameed and Youssri4], and have definite parity, that is, they have the form
$$ \begin{align*} \sum_{v=0}^{\lfloor {n}/2 \rfloor} a_v x^{n - 2v}. \end{align*} $$
Monic Chebyshev polynomials of the fifth and sixth kinds,
$\bar {X}_n(x)$
and
$\bar {Y}_n(x)$
, can be defined by the following recurrences which we simplify from [Reference Abd-Elhameed and Youssri3]:
$$ \begin{align*} G_{0,m}(x) &= 1, \nonumber\\ G_{1, m}(x) &= x, \nonumber\\ G_{n, m}(x) &= x G_{n -1, m}(x) + A_{n-1, m} \; G_{n-2, m}(x),\; \; { n> 1,} \end{align*} $$
where
$$ \begin{align*} A_{n, m} &= \frac{ (2n + m -2)(-1)^n + (2n -(m -2)) - nm -n^2}{(2 n + m -1)(2n +m -3)}, \end{align*} $$
$$ \begin{align*} \hspace{-8pc} \bar{X}_n(x) &= G_{n, 3}(x), \end{align*} $$
$$ \begin{align*} \hspace{-8pc} \bar{Y}_n(x) &= G_{n, 5}(x). \end{align*} $$
The first seven Chebyshev polynomials of the fifth kind over
$\mathbb {Z}$
are
$$ \begin{align*} X_0(x) &= 1,\\ X_1(x) &= x,\\ X_2(x) &= 4x^2 - 3,\\ X_3(x) &= 6x^3 - 5x,\\ X_4(x) &= 16x^4 - 20x^2 + 5,\\ X_5(x) &= 80x^5 - 112 x^3 + 35 x,\\ X_6(x) &= 64x^6 - 112x^4 + 56x^2 -7. \end{align*} $$
They are orthogonal over
$[-1, 1]$
with weight function
${x^2}/{\sqrt {1-x^2}}$
[Reference Abd-Elhameed and Youssri3]. An interesting property is
$$ \begin{align*} V_n(x) = 2^{2n} \bar{X}_{2n}\bigg(\sqrt{\frac{1+x}2}\bigg), \quad W_n(x) = (-1)^n 2^{2n} \bar{X}_{2n} \bigg(\sqrt{\frac{1-x}2} \bigg) \end{align*} $$
where
$n \geq 0$
[Reference Abd-Elhameed and Youssri3, Section 2.2]. The term
$(-1)^n$
is missing in Abd-Elhameed and Youssri [Reference Abd-Elhameed and Youssri3], but it follows because
$V_n(-x) = (-1)^n W_n(x)$
where
$n \geq 0$
(see [Reference Mason and Handscomb13, Equation (1.19)]).
The first seven Chebyshev polynomials of the sixth kind over
$\mathbb {Z}$
are
$$ \begin{align*} Y_0(x) &= 1,\\ Y_1(x) &= x,\\ Y_2(x) &= 2x^2 - 1,\\ Y_3(x) &= 8x^3 - 5x,\\ Y_4(x) &= 16x^4 - 16x^2 + 3,\\ Y_5(x) &= 24x^5 - 28 x^3 + 7 x,\\ Y_6(x) &= 16x^6 - 24 x^4 + 10x^2 -1. \end{align*} $$
These polynomials are orthogonal over
$[-1, 1]$
with weight function
$x^2\sqrt {1-x^2}$
[Reference Abd-Elhameed and Youssri4]. Their monic forms have been expressed explicitly as sums [Reference Abd-Elhameed and Youssri4, Equations (3) and (4)].
The monic Chebyshev polynomials of the sixth kind can be related to Chebyshev polynomials of the second kind.
Theorem 5.1. We have
$$ \begin{align*} U_n(x) = 2^{2n} \bar{Y}_{2n}\bigg(\sqrt{\frac{1+x}2}\bigg), \quad\mbox{for } n \geq 0. \end{align*} $$
Proof. From [Reference Abd-Elhameed and Youssri4, Equation (3)], the monic form of
$\bar {Y}_{2n}(x)$
is
$$ \begin{align*} \bar{Y}_{2n}(x) = \frac{\Gamma(\frac32 +n)}{(2n+1)!} \sum_{k=0}^n \frac{(-1)^k {n \choose {n-k}} (1 +2n -k)!}{\Gamma(\frac32 + n-k)} x^{2n -2k} \end{align*} $$
where
$n \geq 0$
. After simplifying
$ 2^{2n} \bar {Y}_{2n}(\sqrt {{(1+x)}/2})$
with a computer algebra program, and then substituting
$\cos \theta $
for x and simplifying manually, we find
$$ \begin{align*} 2^{2n} \bar{Y}_{2n}\bigg(\sqrt{\frac{1+x}2}\bigg) = \cos(n \theta) + \cot \theta \; (\sin(n \theta)) = U_n(\cos \theta). \end{align*} $$
The last step follows from the identity
$\sin (A + B) = \sin A \cos B + \cos A \sin B$
, with
$A = n \theta $
and
$B = \theta $
, and (1.1).
Theorem 5.2. In general, the polynomials
$X_n(x) \pm 1$
and
$Y_n(x) \pm 1$
do not have factorisations using the minimal polynomials of
$\cos ({2\pi }/{d})$
.
Proof. The polynomials
$X_5(x) \pm 1$
and
$Y_5(x) \pm 1$
are irreducible over
$\mathbb {Z}$
. We can check this by using a computer algebra program.
It suffices to show that none of them is a polynomial
$\Psi _d(x)$
where
$\Psi _d(x)$
has degree
$5$
. This is because, similarly to
$\Psi _d(x)$
, their coefficients are integers, the greatest common factor of the coefficients in each polynomial is
$1$
and the leading coefficients are positive.
The degree of
$\Psi _d(x) = {\phi (d)}/{2}$
where
$d> 2$
from (1.4), and from Definition 1.1,
$\phi (d) = 1$
when
$d=1$
or
$d=2$
.
From Vaidya [Reference Vaidya16],
$\phi (n) \geq \sqrt {n}$
except for
$n=2$
and
$n=6$
. Therefore, the values of d such that
$\phi (d) = 10$
are in the interval
$3 \leq d \leq 100$
. They are
$d = 11$
and
$d = 22$
by checking an enumeration of
$\phi $
. We have
$$ \begin{align*} \Psi_{11}(x) &= 32 x^5 + 16 x^4 - 32 x^3 - 12 x^2 + 6x + 1,\\ \Psi_{22}(x) &=32 x^5 - 16 x^4 - 32 x^3 + 12 x^2 + 6x - 1. \end{align*} $$
The result follows from these counterexamples.
Remark 5.3. The original paper by Vaidya [Reference Vaidya16] is difficult to find. The result appears in Sándor et al. [Reference Sándor, Mitrinović and Crstici15, Section 1.1, Equation (1)]. A proof of the lower bound depends on finding the conditions for
$(1 - {1}/p) p^{{\alpha }/2} \geq 1$
where p is a prime factor of n with multiplicity
$\alpha $
.
Another lower bound is
$\phi (n)> n^{2/3}$
when
$n> 30$
in Kendall and Osborn [Reference Kendall and Osborn10]. This bound also appears in Sándor et al. [Reference Sándor, Mitrinović and Crstici15, Section 1.1, Equation (2)]. It would have reduced the upper bound of the interval from
$100$
to
$31$
. However, it is not generally correct:
$\phi (42) = 12$
and
$42^{2/3}> 12$
.
Acknowledgement
I am grateful to the College of Engineering and Computer Science at The Australian National University for research support.
