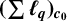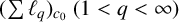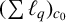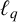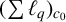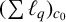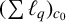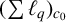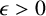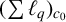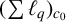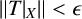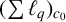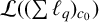1 Introduction
Let X be a Banach space and
$\mathcal {L}(X)$
be the space of bounded linear operators on X. The question of determining maximal ideals of
$\mathcal {L}(X)$
has been studied intensively in the past twenty years. It is well known that the set of compact operators is the unique maximal ideal of
$\mathcal {L}(X)$
when
$X=c_{0}$
or
${\ell }_{p}\ (1\leq p<\infty )$
[Reference Gohberg, Markus and Feldman5]. In these cases, the set of compact operators coincides with the set
$$ \begin{align*} \mathcal{M}_{X}=\{T\in\mathcal{L}(X): I_{X}\ \ \text{does not factor through}\ \ T\}. \end{align*} $$
There are many other Banach spaces X for which
$\mathcal {M}_{X}$
is the unique maximal ideal of
$\mathcal {L}(X)$
, including
$L_{p}(0,1)\ (1\leq p<\infty )$
[Reference Dosev, Johnson and Schechtman4],
${\ell }_{\infty }$
[Reference Dosev and Johnson3],
$(\sum _{n=1}^{\infty } {\ell }_{2}^{n})_{c_{0}}, (\sum _{n=1}^{\infty } {\ell }_{2}^{n})_{{\ell }_{1}}, (\sum _{n=1}^{\infty } {\ell }_{1}^{n})_{c_{0}}$
,
$(\sum _{n=1}^{\infty } {\ell }_{\infty }^{n})_{{\ell }_{1}}, (\sum _{n=1}^{\infty } {\ell }_{\infty }^{n})_{{\ell }_{p}}\ (1{{\kern-2pt}<{\kern-2pt}}p{{\kern-2pt}<{\kern-2pt}}\infty )$
[Reference Leung13, Reference Kania and Laustsen8, Reference Laustsen, Loy and Read10–Reference Laustsen, Schlumprecht and Zsak12],
$(\sum {\ell }_{q})_{{\ell }_{p}}\ (1{{\kern-2pt}\leq{\kern-2pt}}q{{\kern-2pt}<{\kern-2pt}}p{{\kern-2pt}<{\kern-2pt}}\infty )$
[Reference Chen, Johnson and Zheng2],
$(\sum {\ell }_{q})_{{\ell }_{1}} (1<q<\infty )$
[Reference Zheng16],
$d_{w, p}$
[Reference Kaminska, Popov, Spinu, Tcaciuc and Troitsky7] and an Orlicz sequence space which is close to
${\ell }_{p}$
[Reference Lin, Sari and Zheng14].
The main purpose of this paper is to show that
$\mathcal {M}_{X}$
is also the unique maximal ideal in
$\mathcal {L}(X)$
when
$X=(\sum {\ell }_{q})_{c_{0}}\ (1<q<\infty )$
. A key step is to prove that
$(\sum {\ell }_{q})_{c_{0}} (1< q<\infty )$
is complementably homogeneous. Recall that a Banach space X is called complementably homogeneous [Reference Chen, Johnson and Zheng2] if every subspace Y of X that is isomorphic to X contains a further subspace isomorphic to X and complemented in X.
Theorem 1.1. Let
$1<q<\infty $
and let X be a subspace of
$(\sum {\ell }_{q})_{c_{0}}$
which is C-isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
. Then for any
$\epsilon>0$
, there is a subspace Y of X which is
$(C+\epsilon )$
-isomorphic to
$ (\sum {\ell }_{q})_{c_{0}}$
and
$(C+\epsilon )$
-complemented in
$(\sum {\ell }_{q})_{c_{0}}$
.
Our second result is that, for any operator from
$(\sum {\ell }_{q})_{c_{0}}$
into
${\ell }_{q}$
, there is a subspace of
$(\sum {\ell }_{q})_{c_{0}}$
that is isometric to
$(\sum {\ell }_{q})_{c_{0}}$
and the restriction of the operator on this subspace has small norm.
Theorem 1.2. Let
$1<q<\infty $
and let
$T: (\sum {\ell }_{q})_{c_{0}}\rightarrow {\ell }_{q}$
be a bounded linear operator. Then for any
$\epsilon>0$
, there exists a subspace X of
$(\sum {\ell }_{q})_{c_{0}}$
such that X is isometric to
$(\sum {\ell }_{q})_{c_{0}}$
with
$\|T|_{X}\|<\epsilon $
.
A further result follows from Theorems 1.1 and 1.2.
Theorem 1.3. Let
$1<q<\infty $
and let T be a bounded linear operator on
$(\sum {\ell }_{q})_{c_{0}}$
which is
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular. Then for any
$\epsilon>0$
, there is a subspace X of
$(\sum {\ell }_{q})_{c_{0}}$
which is isometric to
$(\sum {\ell }_{q})_{c_{0}}$
and
$\|T|_{X}\|<\epsilon $
.
As an application, we derive the following corollary.
Corollary 1.4. For
$1 < q < \infty $
, the set of all
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operators on
$(\sum {\ell }_{q})_{c_{0}}$
is the unique maximal ideal in the space
$\mathcal {L}((\sum {\ell }_{q})_{c_{0}})$
.
2 Operators on
$(\sum {\ell }_{q})_{c_{0}}$
Let X be a Banach space with a Schauder basis
$(e_{i})$
and let
$S_{X}$
denote the unit sphere of X. A sequence
$(x_{i})$
of nonzero vectors in X is a block basic sequence of
$(e_{i})$
if there exists a sequence of strictly increasing integers
$(N_{i})$
with
$N_{0}=0$
and a sequence of real numbers
$(a_{i})$
so that
$x_{i}= \sum _{j=N_{i-1}+1}^{N_{i}}a_{j}e_{j} \text { for every } i \in \mathbb {N}$
. A block subspace of X is the closed linear span of a block basic sequence in X. A bounded linear operator between two Banach spaces X and Y is an isomorphism if there exists a
$\delta> 0$
such that
$\|Tx\|> \delta $
whenever
$x \in X$
and
$\|x\|=1$
. For
$C\geq 1$
, X and Y are C-isomorphic if there exists an isomorphism T from X onto Y so that
$\|T\|\,\|T^{-1}\|\leq C$
. When the isomorphic constant C is not relevant, we simply say X and Y are isomorphic. Two sequences
$(x_{i}) \subset X$
and
$(y_{i}) \subset Y$
are equivalent if there exists a constant
$C \geq 1$
such that for all sequences of real numbers
$(a_{i})$
,
$$ \begin{align*}C^{-1}\bigg\|\sum a_{i}y_{i}\bigg\| \leq \bigg\|\sum a_{i}x_{i}\bigg\| \leq C\bigg\|\sum a_{i}y_{i}\bigg\|.\end{align*} $$
If
$T : X \rightarrow Y$
is an operator between Banach spaces and Z is a subspace of X, define
$$ \begin{align*}f(T,Z)=\inf \{\|Tz\| : \|z\|=1, z \in Z\} \quad (=\|(T|_{Z})^{-1}\|^{-1}).\end{align*} $$
Then,
$f(T,Z)>0$
if and only if
$T|_{Z}$
is an isomorphism,
$f(T,Z) = \|T\|>0 $
if and only if
$T|_{Z}$
is a multiple of an isometry and
$\|T\| \geq f(T,Z_{1}) \geq f(T,Z_{2})$
if
$Z_{1} \subset Z_{2} \subset X$
.
When
$X = (\sum {\ell }_{q})_{c_{0}}$
, we use
${\ell }_{q}^{(n)}$
to denote the nth
${\ell }_{q}$
in the corresponding direct sum and for
$x=(x_{1},x_{2}, x_{3},\ldots ) \in X$
, we define
$\|x\|= \sup _{i}\{\|x_{i}\|_{{\ell }_{q}}\} $
. Other notations and definitions can be found in [Reference Albiac and Kalton1, Reference Lindenstrauss and Tzafriri15].
Let
$X,Y $
and Z be Banach spaces. A bounded linear operator
$T : X \rightarrow Y$
is Z-strictly singular if there is no subspace
$Z_{0} \subset X$
which is isomorphic to Z and such that
$T|_{Z_{0}}$
is an isomorphism onto its range; T is strictly singular if there is no infinite-dimensional subspace
$Z_{0}\subset X$
such that
$T|_{Z_{0}}$
is an isomorphism onto its range. So an operator is strictly singular if and only if it is Z-strictly singular for every infinite-dimensional space Z. (See [Reference Chen, Johnson and Zheng2–Reference Dosev and Johnson3, Reference Zheng16, Reference Zheng17] for more details on this topic.)
The proof of the next lemma is similar to the proof of Lemma 2.2 in [Reference Chen, Johnson and Zheng2]. An important ingredient is that if X is a subspace of
$(\sum {\ell }_{q})_{c_{0}}$
which is isomorphic to
${\ell }_{q}$
, then there exists a subspace Y of X so that Y is almost isometric to
${\ell }_{q}$
. That is, for any
$\epsilon>0$
, there exists a subspace Y of X which is
$(1+\epsilon )$
-isomorphic to
${\ell }_{q}$
. This fact can be derived using the techniques in [Reference James6, Reference Krivine and Maurey9].
Lemma 2.1. Let
$1 < q < \infty $
and let
$T : {\ell }_{q} \rightarrow (\sum {\ell }_{q})_{c_{0}}$
be a bounded linear operator. Then for any
$\epsilon> 0$
, there exists a block subspace Z of
${\ell }_{q}$
so that
$\|T|_{Z}\|< f(T,Z)+\epsilon .$
Proof. We divide the proof into two parts.
Case 1: T is a strictly singular operator. Then
$f(T,Z) = 0$
for all infinite-dimensional subspaces
$Z\subset {\ell }_{q}$
. Let
$\epsilon>0 $
and choose
$\epsilon _{i}> 0 $
such that
$\sum \epsilon _{i} < \epsilon $
. Let
$(e_{i})_{i=1}^{\infty }$
be the unit vector basis of
${\ell }_{q}$
. Since
$f(T,{\ell }_{q})=0$
, we can pick a norm one element
$x_{1}$
from
${\ell }_{q}$
such that
$\|Tx_{1}\| < \epsilon _{1}/2$
. If
$x_{1} = \sum _{i=1}^{\infty } a_{1,i} e_{i}$
, then we can choose
$n_{1} \in \mathbb {N}$
and define
$y_{1} = \sum _{i=1}^{n_{1}} a_{1,i} e_{i}$
so that
$\|y_{1}\|>1/2$
and
$\|Ty_{1}\|<\epsilon _{1}/2$
. Let
$Z_{1} = [(e_{i})_{i=n_{1}+1}^{\infty }]$
. Since
$f(T,Z_{1}) = 0$
, we can pick a norm one element
$x_{2}$
from
$Z_{1}$
such that
$\|Tx_{2}\| < \epsilon _{2}/2$
. If
$x_{2} = \sum _{i=n_{1}+1}^{\infty } a_{2,i} e_{i}$
, then we can choose
$n_{2} \in \mathbb {N}$
and define
$y_{2} = \sum _{i=n_{1}+1}^{n_{2}} b_{i} e_{i}$
such that
$\|y_{2}\|>1/2$
and
$\|Ty_{2}\|<\epsilon _{2}/2$
. Define
$Z_{2} = [(e_{i})_{i=n_{2}+1}^{\infty }]$
. Continuing in this way, we obtain a block basic sequence
$(y_{i})$
of
$(e_{i})$
such that
$\|y_{i}\|>1/2$
and
$\|Ty_{i}\|<\epsilon _{i}/2$
for all i. Let
$Z=[(y_{i})]$
. Then Z is a block subspace of
${\ell }_{q}$
and hence isometric to
${\ell }_{q}$
. For any
$z=\sum _{i=1}^{\infty }b_{i}({y_{i}}/{\|y_{i}\|})$
in
$S_{Z}$
, we have
$|b_{i}|\leq 1$
and
$$ \begin{align*}\|Tz\| = \bigg\|T\sum_{i=1}^{\infty}b_{i}\bigg(\frac{y_{i}}{\|y_{i}\|}\bigg)\bigg\| = \bigg\|\sum_{i=1}^{\infty}\frac{b_{i}}{\|y_{i}\|}T(y_{i})\bigg\| \leq 2\sum_{i=1}^{\infty}\|Ty_{i}\| < \sum_{i=1}^{\infty}\epsilon_{i} <\epsilon.\end{align*} $$
Since
$f(T,Z) = 0$
, we have
$\|T|_{Z}\|< f(T,Z)+\epsilon .$
Case 2: T is not strictly singular. Then there is an infinite-dimensional subspace
$Z_{1} \subset {\ell }_{q}$
such that
$T|_{Z_{1}}$
is an isomorphism onto its range. By [Reference Albiac and Kalton1, Theorem 2.2.1],
$Z_{1}$
contains a closed subspace
$Z_{2}$
which is isomorphic to
${\ell }_{q}$
. Using the fact that a subspace of
$(\sum {\ell }_{q})_{c_{0}}$
which is isomorphic to
${\ell }_{q}$
contains a smaller subspace almost isometric to
${\ell }_{q}$
, we deduce that
$T(Z_{2})$
contains a subspace
$Z_{3}$
almost isometric to
${\ell }_{q}$
. Since
$\epsilon>0$
, there is enough room for a small perturbation, so the problem reduces to the case where T maps
${\ell }_{q}$
into an isometric copy Y of
${\ell }_{q}$
.
Since T is bounded,
$(Te_{n})^{\infty }_{n=1}$
converges weakly to zero. By passing to a subsequence of
$(e_{n})^{\infty }_{n=1}$
and perturbing, we can assume that
$(Te_{n})^{\infty }_{n=1}$
is disjointly supported in Y. Let
$\liminf _{n\to \infty }\|Te_{n}\|=\delta>0$
. Then by passing to a further subsequence of
$(e_{n})^{\infty }_{n=1}$
and perturbing again, we can assume that
$\lim _{n\to \infty }\|Te_{n}\|=\delta $
and
$\delta -\epsilon /2<||Te_{n}||<\delta +\epsilon /2$
for all n and
$Z=[(e_{n})]$
is a block subspace of
${\ell }_{q}$
.
Let
$x=\sum _{n=1}^{\infty } a_{n} e_{n}\in Z$
with
$\sum ^{\infty }_{n=1}|a_{n}|^{q}=1$
. Then
$$ \begin{align*} \bigg\|T\bigg(\sum^{\infty}_{n=1} a_{n}e_{n}\bigg)\bigg\|=\bigg(\sum\limits^{\infty}_{n=1}|a_{n}|^{q}\|Te_{n}\|^{q}\bigg)^{1/q}>\delta-\epsilon/2. \end{align*} $$
Hence,
$f(T,Z)\geq \delta -\epsilon /2$
and
$\delta \leq f(T,Z)+\epsilon /2$
. However,
$$ \begin{align*} \bigg\|T\bigg(\sum\limits^{\infty}_{n=1} a_{n}e_{n}\bigg)\bigg\|=\bigg(\sum\limits^{\infty}_{n=1}|a_{n}|^{q}||Te_{n}||^{q}\bigg)^{1/q}<\delta+\epsilon/2. \end{align*} $$
So,
$$ \begin{align*} ||T|_{Z}||\leq\delta+\epsilon/2\leq f(T, Z)+\epsilon/2+\epsilon/2= f(T,Z)+\epsilon.\\[-2.8pc] \end{align*} $$
Next we will use Lemma 2.1 to prove Theorem 1.2.
Proof of Theorem 1.2.
First, we prove the theorem for the case when there is an infinite subset
$M\subset \mathbb {N}$
such that
$T|_{{\ell }_{q}^{(n)}}$
is strictly singular for all
$n\in M$
. Hence,
$f(T,Z)=0$
for any infinite-dimensional subspace Z of
${\ell }_{q}^{(n)}$
. In particular,
$f(T,{\ell }_{q}^{(n)})=0$
. Now, let
$\epsilon>0$
and let
$(\delta _{n})^{\infty }_{n=1}$
be a sequence of positive reals decreasing to zero so that
$\sum _{n\in M}\delta _{n}<\epsilon $
. For each
$n\in M$
, choose
$(\epsilon _{n,i})^{\infty }_{i=1}$
converging to zero so fast that
$\sum ^{\infty }_{i=1}\epsilon _{n,i}<\delta _{n}$
. Fix
$n \in M$
and pick a norm one element
$x_{1}=\sum ^{\infty }_{i=1} a_{1,i}e_{n, i}\in {\ell }_{q}^{(n)}$
such that
$||Tx_{1}||<\epsilon _{n,1}/2$
. Choose
$N_{1}\in \mathbb {N}$
and define
$y_{1}=\sum ^{N_{1}}_{i=1} a_{1,i}e_{n, i}$
so that
$\|y_{1}\|>1/2$
and
$||Ty_{1}||<\epsilon _{n,1}/2$
.
Let
$Z_{1} =[(e_{n, i})^{\infty }_{i=N_{1}+1}]$
. Since
$f(T,Z_{1})=0$
, we can pick
$x_{2}=\sum ^{\infty }_{i=N_{1}+1} a_{2,i}e_{n, i}\in Z_{1}$
with norm one such that
$||Tx_{2}||<\epsilon _{n,2}/2$
. Then we can find
$N_{2}\in \mathbb {N}$
such that
$y_{2}=\sum ^{N_{2}}_{i=N_{1}+1} a_{2,i}e_{n, i}$
,
$\|y_{2}\|>1/2$
and
$\|Ty_{2}\|<\epsilon _{n, 2}$
. Let
$Z_{2} = [(e_{n, i})^{\infty }_{i=N_{2}+1}]$
. Continuing in this way, we obtain a block basic sequence
$(y_{i})^{\infty }_{i=1}$
of the canonical basis of
${\ell }_{q}^{(n)}$
. Let
$X_{n}=[(y_{i})]$
. Then
$X_{n}$
is a block subspace of
${\ell }_{q}^{(n)}$
which is isometrically isomorphic to
${\ell }_{q}^{(n)}$
and it is easy to check that
$\|T|_{X_{n}}\| < \delta _{n}$
and
$X=\sum _{n\in M}X_{n}$
is isometrically isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
. Moreover,
$$ \begin{align*} \|T|_{X}\|=\big\|T|_{\sum\limits_{n\in M} X_{n}}\big\|=\bigg\|\sum\limits_{n\in M} T|_{X_{n}}\bigg\|\leq\sum\limits_{n\in M}\|T|_{X_{n}}\|<\sum\limits_{n\in M}\delta_{n}<\epsilon. \end{align*} $$
This completes the proof for the particular case.
Now, suppose that
$T|_{{\ell }_{q}^{(n)}}$
is not strictly singular for all but finitely many
$n\in \mathbb {N}$
. Discarding those finitely many
$n\in \mathbb {N}$
, we get a sequence of operators
$\{T|_{{\ell }_{q}^{(n)}}\}_{n\in I}$
which are not strictly singular. Hence for each
$n\in I$
, there exists an infinite-dimensional subspace
$Z_{n,1}$
of
${\ell }_{q}^{(n)}$
such that
$T|_{Z_{n,1}}$
is an isomorphism. By [Reference Albiac and Kalton1, Theorem 2.2.1],
$Z_{n,1}$
contains a subspace
$Z_{n,2}$
which is isomorphic to
${\ell }_{q}$
. Let
$(x_{i})^{\infty ^{\phantom {l}}}_{i=1}$
be a unit vector basis of
$Z_{n,2}$
equivalent to the canonical basis of
${\ell }_{q}^{(n)}$
. Then,
$(x_{i})^{\infty }_{i=1}$
converges weakly to zero. Passing to a subsequence and doing a small perturbation, without loss of generality, we may assume
$(x_{i})^{\infty }_{i=1}$
is a block basis of
${\ell }_{q}^{(n)}$
. Hence,
$Z_{n,3}=[(x_{i})_{i=1}^{\infty }]$
is a block subspace of
${\ell }_{q}^{(n)}$
which is isometrically isomorphic to
${\ell }_{q}^{(n)}$
. Since
$T|_{Z_{n,3}}$
is an isomorphism, by Lemma 2.1, we get a block subspace
$Z_{n}$
of
$Z_{n,3}$
such that
$$ \begin{align*}\begin{split} \|T|_{Z_{n}}\|<f(T,Z_{n})+2^{-n}(\epsilon/2). \end{split}\end{align*} $$
We claim that
$\lim _{n\to \infty }f(T,Z_{n})=0$
. Suppose this is not the case. Then, there exist a
$\delta>0$
and a sequence
$(n_{k})^{\infty }_{k=1} \subset \mathbb {N}$
such that
$f(T, Z_{n_{k}})>\delta $
. For each
$k\in \mathbb {N}$
, choose
$x_{n_{k}}\in Z_{n_{k}}$
with norm one such that
$\|Tx_{n_{k}}\|\geq \delta $
. Then,
$(x_{n_{k}})^{\infty }_{k=1}$
is
$1$
-equivalent to the canonical basis of
$c_{0}$
. Since T is bounded,
$(T(x_{n_{k}}))^{\infty }_{k=1}$
is weakly null. Passing to a subsequence and doing a small perturbation again, we may assume that
$(Tx_{n_{k}})^{\infty }_{k=1}$
is a block basic sequence which is equivalent to the canonical basis of
${\ell }_{q}$
. This contradicts the boundedness of T. Therefore,
$\lim _{n \to \infty }f(T,Z_{n})=0$
. Choose a subsequence
$(Z_{n_{k}})$
of
$(Z_{n})$
so that
$f(T, Z_{n_{k}})<2^{-(k+1)}\epsilon $
. Let
$X= \sum _{k=1}^{\infty } Z_{n_{k}}$
. Then X is isometric to
$(\sum {\ell }_{q})_{c_{0}}$
and
$$ \begin{align*} \|T|_{X}\|=\|T|_{\sum_{k=1}^{\infty} Z_{n_{k}}}\|\leq\sum_{k=1}^{\infty} \|T|_{Z_{n_{k}}}\|< \sum_{k=1}^{\infty} 2^{-(k+1)}\epsilon+2^{-n_{k}}(\epsilon/2)< \epsilon. \\[-3.8pc] \end{align*} $$
For
$m, n\in \mathbb {N}\cup \{\infty \}$
with
$m\leq n$
, let
$P_{[m, n]}$
denote the natural projection on
$(\sum {\ell }_{q})_{c_{0}}$
so that
$P_{[m, n]}(\sum _{i=1}^{\infty } x_{i})=\sum _{i=m}^{n} x_{i}$
whenever
$\sum _{i=1}^{\infty } x_{i}\in (\sum {\ell }_{q})_{c_{0}}$
with
$x_{i}\in {\ell }_{q}^{(i)}$
for all i.
Lemma 2.2. Let
$1<q<\infty $
and
$T:(\sum {\ell }_{q})_{c_{0}}\rightarrow (\sum {\ell }_{q})_{c_{0}}$
be a bounded linear operator. Then for all
$m\in \mathbb {N}$
,
$$ \begin{align*} \lim\limits_{n\to\infty} \|P_{[1,m]}TP_{[n,\infty)}\|=0. \end{align*} $$
Proof. We will prove this by contradiction. Noting that the sequence of norms is monotone in n, we suppose there exists
$\delta> 0$
and
$m_{0} \in \mathbb {N}$
, such that
$ \|P_{[1,m_{0}]}TP_{[n,\infty )}\|> \delta $
for every
$n \in \mathbb {N}$
. Then there is a sequence
$(x_{n}) \in (\sum l_{q})_{c_{0}}$
with
$\|x_{n}\|=1$
, such that
$$ \begin{align*} \|P_{[1,m_{0}]}TP_{[n,\infty )}x_{k}\|\geq \delta \quad \text{for every } n \in \mathbb {N}. \end{align*} $$
Then, by passing to a subsequence
$(P_{[n_{k},\infty )}x_{k})_{k=1}^{\infty }$
of
$(P_{[n,\infty )}x_{n})_{n=1}^{\infty }$
and doing a truncation, without loss of generality, we can assume
$(P_{[n_{k},\infty )}x_{k})_{k=1}^{\infty }$
is a block basis which converges to zero weakly, but not in norm. Therefore,
$(P_{[n_{k},\infty )}x_{n_{k}})_{k=1}^{\infty }$
is equivalent to the canonical basis of
$c_{0}$
. However,
$(P_{[1,m_{0}]}TP_{[n_{k},\infty )}x_{n_{k}})_{k=1}^{\infty }$
converges to zero weakly in
${\ell }_{q}$
, but not in norm. Hence by passing to a further subsequence, we may assume that
$(P_{[1,m_{0}]}TP_{[n_{k},\infty )}x_{n_{k}})_{k=1}^{\infty }$
is equivalent to the canonical basis of
${\ell }_{q}$
. However, this contradicts the boundedness of T.
Proof of Theorem 1.3.
We will prove the theorem by considering two cases.
Case 1: There is an infinite subset
$M \subset \mathbb {N}$
so that
$T|_{{\ell }_{q}^{(n)}}$
is strictly singular for all
$n\in M$
. Since the proof of the first case of Theorem 1.2 does not use any property of the range space of T, it also works here.
Case 2: For all but finitely many
$n\in \mathbb {N}$
,
$T|_{{\ell }_{q}^{(n)}}$
is not strictly singular.
Discarding finitely many
$n \in \mathbb {N}$
and following the same line of proof as in Theorem 1.2, for each
$n \in \mathbb {N}$
, we can prove the existence of block subspaces
$Z_{n} \subset {\ell }_{q}^{(n)}$
such that
$$ \begin{align*} \|T|_{Z_{n}}\|<f(T,Z_{n})+2^{-n}(\epsilon/2). \end{align*} $$
We claim that
$\lim _{n\to \infty }f(T,Z_{n})=0$
. If not, then there exist a
$\delta>0$
and a sequence of numbers
$(n_{k})$
such that
$f(T, Z_{n_{k}})> \delta $
which implies
$T|_{Z_{n_{k}}}$
is an isomorphism. Consider the operator
$T(\sum Z_{n_{k}})_{c_{0}}\rightarrow (\sum {\ell }_{q})_{c_{0}}$
. By passing to further subspaces of each
$Z_{n_{k}}$
and perturbing, we can assume that
$Tx_{1}$
and
$Tx_{2}$
are disjointly supported in
$(\sum {\ell }_{q})_{c_{0}}$
whenever
$x_{1}\in Z_{n_{k_{1}}}$
,
$x_{2}\in Z_{n_{k_{2}}}$
and
$k_{1}\neq k_{2}$
. Let
$x=\sum _{k} x_{k}\in (\sum Z_{n_{k}})_{c_{0}}$
with
$x_{k}\in Z_{n_{k}}$
and let
$k_{0}\in \mathbb {N}$
be such that
$\|x_{k_{0}}\|\geq \tfrac 12 \|x\|$
. Then
$$ \begin{align*} \|Tx\|=\bigg\|T\bigg(\sum\limits_{k} x_{k}\bigg)\bigg\|=\bigg\|\sum\limits_{k} Tx_{k}\bigg\|\geq\|Tx_{k_{0}}\|\geq\delta\|x_{k_{0}}\|\geq\dfrac{\delta}{2}\|x\|. \end{align*} $$
Thus
$T|_{(\sum Z_{n_{k}})_{c_{0}}}$
is an isomorphism, which contradicts the fact that T is
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular on
$(\sum {\ell }_{q})_{c_{0}}$
.
Since
$f(T, Z_{n})$
converges to zero, by passing to a subsequence of
$(Z_{n})^{\infty }_{n=1}$
and relabelling, we can assume that
$f(T, Z_{n})<2^{-n}(\epsilon /2)$
for all
$n\in \mathbb {N}$
. Thus,
$$ \begin{align*}\|T|_{Z_{n}}\|<2^{-n}(\epsilon/2)+2^{-n}(\epsilon/2).\end{align*} $$
So
$X=(\sum Z_{n})$
is isometrically isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
and
$$ \begin{align*} \|T|_{X}\|=\|T|_{\sum Z_{n}}\|=\bigg\|\sum T|_{Z_{n}}\bigg\|\leq\sum\|T|_{Z_{n}}\|<\sum 2^{-n}\epsilon=\epsilon. \\[-3.4pc] \end{align*} $$
3 Maximal ideal of
$\mathcal {L}((\sum {\ell }_{q})_{c_{0}})$
In this section, we will prove that
$(\sum {\ell }_{q})_{c_{0}}$
is complementably homogeneous. The following two lemmas will be used in the proof.
Lemma 3.1 (Johnson and Schechtman [Reference Chen, Johnson and Zheng2, Lemma 2.5]).
Suppose that X has an unconditionally monotone basis with p-convexity constant one and that
$(x_{k})_{k=1}^{n}$
, for
$n\in \mathbb {N} \cup \{\infty \}$
, is a disjoint sequence in X so that for some
$\theta $
with
$0 < \theta < 1$
and all scalars
$(\alpha _{k})$
,
$$ \begin{align*} \theta\, \bigg(\sum_{k} |\alpha_{k}|^{p}\bigg)^{1/p} \le \bigg\|\sum_{k}\alpha_{k} x_{k}\bigg\| \le \bigg(\sum_{k} |\alpha_{k}|^{p}\bigg)^{1/p}. \end{align*} $$
Then there is an unconditionally monotone norm
$!\cdot !$
on X with p-convexity constant one so that for all scalars
$(\alpha _{k})$
,
-
(1)
$\theta !x! \le \|x\| \le !x!$
for all
$x\in X$
; -
(2)
$(\sum _{k} |\alpha _{k}|^{p})^{1/p} = !\sum _{k}\alpha _{k} x_{k}!$
.
Lemma 3.2 (Johnson and Schechtman [Reference Chen, Johnson and Zheng2, Lemma 2.6]).
Suppose that X has an unconditionally monotone basis with p-convexity constant one (
$1\le p < \infty $
) and
$(x_{k})_{k=1}^{n}$
, for
$n\in \mathbb {N} \cup \{\infty \}$
, is a disjoint sequence of unit vectors in X which is isometrically equivalent to the unit vector basis for
${\ell }_{p}$
. Then
$\overline {\text {span}} \, x_{k}$
is norm one complemented in X.
Proof of Theorem 1.1.
Let
$\epsilon>0$
be given and
$(\epsilon _{j})$
be a sequence of positive real numbers decreasing to
$0$
so fast that
$\epsilon _{j}<\epsilon $
for each j. Write
$X=\sum X_{j}$
, where X is C-isomorphic to
$ (\sum {\ell }_{q})_{c_{0}}$
and each
$X_{j}$
maps onto
${\ell }_{q}$
under this isomorphism. By the stability of
${\ell }_{q}$
, by passing to a subspace for each
$X_{j}$
, we can assume that
$X_{j}$
is
$(1~+~\epsilon _{j})$
-isomorphic to
${\ell }_{q}$
. Let
$(x_{i,j})_{i}$
be a normalised basis of
$X_{j}$
which is
$(1+\epsilon _{j})$
-equivalent to the canonical basis of
${\ell }_{q}$
. Again, by passing to a subspace for each
$X_{j}$
and perturbing, we can assume that
$X_{j}$
is a block subspace of
$(\sum {\ell }_{q})_{c_{0}}$
. By passing to a further subspace and perturbing, we can assume that the
$X_{j}$
subspaces are disjointly supported with respect to the canonical basis of
$(\sum {\ell }_{q})_{c_{0}}$
. Let
$(e_{i,j})_{i,j}$
be the canonical basis of
$(\sum {\ell }_{q})_{c_{0}}$
, where
$(e_{i, j})_{i}$
is the standard basis for
${\ell }_{q}^{(j)}$
and define
$$ \begin{align*}J_{j}=\bigcup^{\infty}_{i=1} \text{Support}(x_{i,j}).\end{align*} $$
Define norm one projections
$$ \begin{align*}P_{J_{j}}: \bigg(\sum{\ell}_{q}\bigg)_{c_{0}}\rightarrow \bigg(\sum{\ell}_{q}\bigg)_{c_{0}} \quad \text{by } P_{J_{j}}(x)=\sum\limits_{(i,j)\in\ J_{j}}a_{i,j}e_{i,j},\end{align*} $$
for all
$x=\sum _{i,j}a_{i,j}e_{i,j}\in (\sum {\ell }_{q})_{c_{0}}$
. Define
$A_{j}=[(e_{i,j})_{(i,j)\in \ J_{j}}]$
which has an unconditionally monotone basis with q-convexity constant one. Since
$\text {Support}(X_{j} )\subset J_{j}$
,
$X_{j}$
is a subspace of
$A_{j}$
. By Lemma 3.1, we can define a new norm
$!\cdot !$
on
$A_{j}$
such that
$!\cdot !$
is
$(1+\epsilon _{j})$
-equivalent to
$\|\cdot \|$
and the sequence
$(x_{i,j})^{\infty }_{i=1}$
under the new norm is
$1$
-equivalent to the canonical basis of
${\ell }_{q}$
. By Lemma 3.2, there exists a projection
$Q_{j}:A_{j}\rightarrow X_{j}$
with
$!Q_{j}! =1$
. Since the formal identity
$I: (A_{j}, !\cdot !)\rightarrow (A_{j}, \|\cdot \|)$
is an onto isomorphism with isomorphism constant
$1+\epsilon _{j}$
, we see that
$X_{j}$
is also complemented in
$A_{j}$
under the original norm
$\|\cdot \|$
and
$\|Q_{j}\|\leq 1+\epsilon _{j}$
. Now, consider the projection
$\sum _{j=1}^{\infty } Q_{j}P_{J_{j}} : (\Sigma {\ell }_{q})_{c_{0}}\rightarrow \Sigma X_{i}$
. We have
$$ \begin{align*} \bigg\|\sum_{j=1}^{\infty} Q_{j}P_{J_{j}}\bigg\| & =\sup\bigg\{\bigg\|\sum_{j=1}^{\infty} Q_{j}P_{J_{j}}x\bigg\| : \|x\|=1\bigg\}\\&=\sup\bigg\{C\sup_{j} \|Q_{j}P_{J_{j}}x\| :\|x\|=1\bigg\}<C(1+\epsilon). \\[-3.6pc] \end{align*} $$
Proof of Corollary 1.4.
First, we show that the set of all
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operators on
$(\sum {\ell }_{q})_{c_{0}}$
is a linear subspace of
$\mathcal {L}((\sum {\ell }_{q})_{c_{0}})$
. Let T and Q be two
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operators on
$(\sum {\ell }_{q})_{c_{0}}$
. If
$T+Q$
is not a
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operator on
$(\sum {\ell }_{q})_{c_{0}}$
, then there exists a subspace X of
$(\sum {\ell }_{q})_{c_{0}}$
, isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
such that
$(T+Q)|_{X}$
is an isomorphism. Thus, there exists a
$\delta>0$
such that
$$ \begin{align*}\|(T+Q)(x)\|\geq\delta\|x\|, \quad\mbox{for all } x\in X.\end{align*} $$
Since T is
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular on
$(\sum {\ell }_{q})_{c_{0}}$
, by Theorem 1.3, there exists a subspace Y of X which is isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
such that
$\|T|_{Y}\|<\delta /2$
. Similarly, there exists a subspace Z of Y which is isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
such that
$\|Q|_{Z}\|<\delta /2$
. Now, for
$z \in Z$
, observe that
$$ \begin{align*}\|(T+Q)(z)\|\leq\|T(z)\|+\|Q(z)\|<\delta\|z\|.\end{align*} $$
This is a contradiction. Therefore,
$T+Q$
is a
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operator on
$(\sum {\ell }_{q})_{c_{0}}$
. It is easy to see that
$\alpha T$
is a
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operator on
$(\sum {\ell }_{q})_{c_{0}}$
for all scalars
$\alpha $
and the ideal property of the set of all
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operators is also trivial.
Next we prove that the set of all
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operators on
$(\sum {\ell }_{q})_{c_{0}}$
is maximal. Let T be an operator in
$\mathcal {L}((\sum {\ell }_{q})_{c_{0}})$
which is not
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular. Then, there exists a subspace X of
$(\sum {\ell }_{q})_{c_{0}}$
, which is isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
such that
$T|_{X}$
is an isomorphism. Hence by Theorem 1.1, the subspace
$TX$
contains a subspace Z which is isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
and complemented in
$(\sum {\ell }_{q})_{c_{0}}$
. Let
$Q_{1}: Z\rightarrow (\sum {\ell }_{q})_{c_{0}}$
be an onto isomorphism and let
$P: (\sum {\ell }_{q})_{c_{0}}\rightarrow Z$
be a continuous projection onto Z. Since Z is isomorphic to
$(\sum {\ell }_{q})_{c_{0}}$
,
$W=X\cap T^{-1}(Z)$
is isomorphic to
$(\Sigma {\ell }_{q})_{c_{0}}$
. Let
$Q_{2} : (\Sigma {\ell }_{q})_{c_{0}}\rightarrow W$
be defined by
$Q_{2}=(T|_{W})^{-1}\circ Q_{1}^{-1}$
. Then
$Q_{2}$
is an onto isomorphism. By the definition of
$Q_{2}$
, the identity map on
$(\sum {\ell }_{q})_{c_{0}}$
is equal to
$(Q_{1}\circ P)\circ T\circ Q_{2}$
. Since
$Q_{2}$
and
$Q_{1}\circ P$
are in
$\mathcal {L}((\sum {\ell }_{q})_{c_{0}})$
, the identity map belongs to in any ideal containing T. Hence, any ideal containing T must coincide with
$\mathcal {L}((\Sigma {\ell }_{q})_{c_{0}})$
. Therefore, the set of all
$(\sum {\ell }_{q})_{c_{0}}$
-strictly singular operators on
$(\sum {\ell }_{q})_{c_{0}}$
is the unique maximal ideal.
