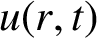1. Introduction and the main results
The axisymmetric diffusion equation is given as [Reference Debnath3, p. 61]
 $$ \begin{align} \kappa \nabla^2u\equiv\kappa\frac{1}{r}\frac{\partial}{\partial r}\bigg(r \frac{\partial u}{\partial r}\bigg)=\kappa\bigg(u_{rr}+\frac{1}{r}u_r\bigg)=\frac{\partial u}{\partial t}, \end{align} $$
$$ \begin{align} \kappa \nabla^2u\equiv\kappa\frac{1}{r}\frac{\partial}{\partial r}\bigg(r \frac{\partial u}{\partial r}\bigg)=\kappa\bigg(u_{rr}+\frac{1}{r}u_r\bigg)=\frac{\partial u}{\partial t}, \end{align} $$
where
![]() $t>0, r\in (0,\infty ), u(r,0)=g(r)$
and
$t>0, r\in (0,\infty ), u(r,0)=g(r)$
and
![]() $\kappa $
is the positive diffusivity constant. The boundary conditions
$\kappa $
is the positive diffusivity constant. The boundary conditions
![]() $u\rightarrow 0,\ \partial u/\partial r\rightarrow 0$
as
$u\rightarrow 0,\ \partial u/\partial r\rightarrow 0$
as
![]() $r\rightarrow \infty $
are also assumed. The Hankel transform of a function
$r\rightarrow \infty $
are also assumed. The Hankel transform of a function
![]() $f(x)$
is defined as [Reference Debnath3, p. 58, equation (1.10.1)]
$f(x)$
is defined as [Reference Debnath3, p. 58, equation (1.10.1)]
 $$ \begin{align*}\mathfrak{H}(f(y))(x):=\int_{0}^{\infty}yJ_0(xy)f(y)\ dy.\end{align*} $$
$$ \begin{align*}\mathfrak{H}(f(y))(x):=\int_{0}^{\infty}yJ_0(xy)f(y)\ dy.\end{align*} $$
We may temporarily drop the integrating variable in denoting integral transforms according to when the context is appropriate throughout. The known explicit solution is obtained by taking Hankel transform of (1.1), which gives
 $$ \begin{align} \frac{\partial}{\partial t}\mathfrak{H}(u(r,t))(x)+x^2\kappa\mathfrak{H}(u(r,t))(x)=0 \end{align} $$
$$ \begin{align} \frac{\partial}{\partial t}\mathfrak{H}(u(r,t))(x)+x^2\kappa\mathfrak{H}(u(r,t))(x)=0 \end{align} $$
with initial condition
![]() $\mathfrak {H}(u(r,0))(x)=\mathfrak {H}(g(r)).$
Applying the inverse Hankel transform
$\mathfrak {H}(u(r,0))(x)=\mathfrak {H}(g(r)).$
Applying the inverse Hankel transform
![]() $\mathfrak {H}^{-1}$
to (1.2) gives the explicit solution [Reference Debnath3, p. 62, equation (1.10.25)]
$\mathfrak {H}^{-1}$
to (1.2) gives the explicit solution [Reference Debnath3, p. 62, equation (1.10.25)]
 $$ \begin{align} u(r,t)=\frac{1}{2\kappa t}e^{-r^2/(4\kappa t)}\int_{0}^{\infty}yg(y)I_0\bigg(\frac{yr}{2\kappa t}\bigg)e^{-y^2/(4\kappa t)}\ dy, \end{align} $$
$$ \begin{align} u(r,t)=\frac{1}{2\kappa t}e^{-r^2/(4\kappa t)}\int_{0}^{\infty}yg(y)I_0\bigg(\frac{yr}{2\kappa t}\bigg)e^{-y^2/(4\kappa t)}\ dy, \end{align} $$
where the modified Bessel function of the first kind is given by
 $$ \begin{align*}I_v(x)=\sum_{n\ge0}\frac{1}{n!\Gamma(v+n+1)}\bigg(\frac{x}{2}\bigg)^{2n+v}.\end{align*} $$
$$ \begin{align*}I_v(x)=\sum_{n\ge0}\frac{1}{n!\Gamma(v+n+1)}\bigg(\frac{x}{2}\bigg)^{2n+v}.\end{align*} $$
Some simple examples include the bell-shaped temperature profile
 $g(r)=e^{-cr^2}$
or the uniform temperature profile
$g(r)=e^{-cr^2}$
or the uniform temperature profile
![]() $g(r)=1$
on
$g(r)=1$
on
![]() $(0,1).$
In both these instances it is a simple task to appeal to the tables for integral transforms.
$(0,1).$
In both these instances it is a simple task to appeal to the tables for integral transforms.
The purpose of this note is to provide further analysis of (1.3) by means of Mellin inversion [Reference Paris and Kaminski6, p. 80]. In applying methods from Olver [Reference Olver5], we can better understand
![]() $u(r,t)$
by providing a method to obtain an infinite series representation involving Laguerre polynomials or a hypergeometric function. One of our motivations for selecting Bessel functions for initial conditions is to apply Watson’s lemma [Reference Olver5, p. 336, equations (6.01) and (6.02)]. Indeed, coefficients for the power series representations of Bessel functions are well known and, as a consequence, we may obtain the asymptotic behaviour related to
$u(r,t)$
by providing a method to obtain an infinite series representation involving Laguerre polynomials or a hypergeometric function. One of our motivations for selecting Bessel functions for initial conditions is to apply Watson’s lemma [Reference Olver5, p. 336, equations (6.01) and (6.02)]. Indeed, coefficients for the power series representations of Bessel functions are well known and, as a consequence, we may obtain the asymptotic behaviour related to
![]() $u(r,t).$
An example of this method will be provided in our last section, which should be compared to our rapidly convergent series obtained in our main theorems. For a general overview of applying Mellin transforms to evaluating integrals involving Bessel functions, see [Reference Titchmarsh8, p. 196]. For a recent example of applying Mellin transforms to analyse partial differential equations, see the paper by Boyadjiev and Luchko [Reference Boyadjiev and Luchko2].
$u(r,t).$
An example of this method will be provided in our last section, which should be compared to our rapidly convergent series obtained in our main theorems. For a general overview of applying Mellin transforms to evaluating integrals involving Bessel functions, see [Reference Titchmarsh8, p. 196]. For a recent example of applying Mellin transforms to analyse partial differential equations, see the paper by Boyadjiev and Luchko [Reference Boyadjiev and Luchko2].
Recall that the Mellin transform [Reference Paris and Kaminski6] is given by
 $$ \begin{align*}\mathfrak{M}(g)(s):=\int_{0}^{\infty}y^{s-1}g(y)\ dy. \end{align*} $$
$$ \begin{align*}\mathfrak{M}(g)(s):=\int_{0}^{\infty}y^{s-1}g(y)\ dy. \end{align*} $$
Parseval’s identity is [Reference Paris and Kaminski6, p. 83, equation (3.1.11)]
 $$ \begin{align} \int_{0}^{\infty}k(y)g(y)\ dy=\frac{1}{2\pi i}\int_{(c)}\mathfrak{M}(k)(s)\mathfrak{M}(g)(1-s)\, ds, \end{align} $$
$$ \begin{align} \int_{0}^{\infty}k(y)g(y)\ dy=\frac{1}{2\pi i}\int_{(c)}\mathfrak{M}(k)(s)\mathfrak{M}(g)(1-s)\, ds, \end{align} $$
where
![]() $(c)$
is the vertical line where the integrand is analytic.
$(c)$
is the vertical line where the integrand is analytic.
Recall from [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 709, equation (6.643),
![]() $\#2$
] (with change of variables
$\#2$
] (with change of variables
![]() $x\rightarrow x^2$
and
$x\rightarrow x^2$
and
![]() $\mu =s/2$
) that
$\mu =s/2$
) that
 $$ \begin{align} \int_{0}^{\infty}y^{s}e^{-\alpha y^2}I_{2v}(2\beta y)\ dy=\frac{\Gamma(s/2+v+1/2)e^{\beta^2/(2\alpha)}}{2\Gamma(2v+1)\beta}\alpha^{-s/2}M_{-s/2,v}\bigg(\frac{\beta^2}{\alpha}\bigg), \end{align} $$
$$ \begin{align} \int_{0}^{\infty}y^{s}e^{-\alpha y^2}I_{2v}(2\beta y)\ dy=\frac{\Gamma(s/2+v+1/2)e^{\beta^2/(2\alpha)}}{2\Gamma(2v+1)\beta}\alpha^{-s/2}M_{-s/2,v}\bigg(\frac{\beta^2}{\alpha}\bigg), \end{align} $$
valid for
![]() $\Re (s/2+v+1/2)>0.$
$\Re (s/2+v+1/2)>0.$
Here
![]() $M_{\mu ,v}(x)$
is the Whittaker hypergeometric function [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1024]
$M_{\mu ,v}(x)$
is the Whittaker hypergeometric function [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1024]
 $$ \begin{align} M_{\mu,v}(x)=x^{v+1/2}e^{-x/2}{}_1F_1\big(v-\mu+\tfrac{1}{2};2v+1;x\big) \end{align} $$
$$ \begin{align} M_{\mu,v}(x)=x^{v+1/2}e^{-x/2}{}_1F_1\big(v-\mu+\tfrac{1}{2};2v+1;x\big) \end{align} $$
and
![]() $_1F_1(a;b;x)$
is the confluent hypergeometric function.
$_1F_1(a;b;x)$
is the confluent hypergeometric function.
Theorem 1.1. If
![]() $\mathfrak {M}(g)(1-s)$
is analytic in a subset S of the region
$\mathfrak {M}(g)(1-s)$
is analytic in a subset S of the region
![]() $\{s\in \mathbb {C}\mid \Re (s)$
$\{s\in \mathbb {C}\mid \Re (s)$
![]() $\,{>}-1\},$
then
$\,{>}-1\},$
then
 $$ \begin{align*}u(x,t)=\frac{1}{r}e^{-(r^2-r^2/2)/(4\kappa t)}\frac{1}{2\pi i}\int_{(c)}\Gamma\bigg(\frac{s}{2}+\frac{1}{2}\bigg) (4\kappa t)^{s/2}M_{-s/2,0}\bigg(\frac{r^2}{4\kappa t}\bigg)\mathfrak{M}(g)(1-s)\, ds,\end{align*} $$
$$ \begin{align*}u(x,t)=\frac{1}{r}e^{-(r^2-r^2/2)/(4\kappa t)}\frac{1}{2\pi i}\int_{(c)}\Gamma\bigg(\frac{s}{2}+\frac{1}{2}\bigg) (4\kappa t)^{s/2}M_{-s/2,0}\bigg(\frac{r^2}{4\kappa t}\bigg)\mathfrak{M}(g)(1-s)\, ds,\end{align*} $$
![]() $c\in S\cap \{s\in \mathbb {C}\mid \Re (s)>-1\}.$
$c\in S\cap \{s\in \mathbb {C}\mid \Re (s)>-1\}.$
Proof. We choose the
![]() $k(y)$
to be the integrand in (1.5) with
$k(y)$
to be the integrand in (1.5) with
![]() $v=0, \alpha =1/4\kappa t, \beta =r/4\kappa t$
and apply (1.4).
$v=0, \alpha =1/4\kappa t, \beta =r/4\kappa t$
and apply (1.4).
Some relevant notes are in order to apply Theorem 1.1. First, Theorem 1.1 requires that
![]() $\mathfrak {M}(g)(s)$
is analytic in the region
$\mathfrak {M}(g)(s)$
is analytic in the region
![]() $\{s\in \mathbb {C}\mid \Re (s)<2\}.$
It is known that
$\{s\in \mathbb {C}\mid \Re (s)<2\}.$
It is known that
![]() $M_{\mu ,v}(x)$
only has simple poles for fixed
$M_{\mu ,v}(x)$
only has simple poles for fixed
![]() $\mu $
and x at
$\mu $
and x at
![]() $v=-(k+1)/2, k\in \mathbb {N}.$
By [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1026, 9.228],
$v=-(k+1)/2, k\in \mathbb {N}.$
By [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1026, 9.228],
 $$ \begin{align*}M_{\mu,v}(x)\sim \frac{1}{\sqrt{\pi}}\Gamma(2v+1)\mu^{-v-1/2}x^{1/4}\cos\bigg(2\sqrt{\mu x}-v\pi-\frac{\pi}{4}\bigg)\end{align*} $$
$$ \begin{align*}M_{\mu,v}(x)\sim \frac{1}{\sqrt{\pi}}\Gamma(2v+1)\mu^{-v-1/2}x^{1/4}\cos\bigg(2\sqrt{\mu x}-v\pi-\frac{\pi}{4}\bigg)\end{align*} $$
as
![]() $|\mu |\rightarrow \infty $
and further we have the functionalrelationship [Reference Debnath3, p. 1026, equation (9.231),
$|\mu |\rightarrow \infty $
and further we have the functionalrelationship [Reference Debnath3, p. 1026, equation (9.231),
![]() $\#2$
],
$\#2$
],
 $$ \begin{align*}x^{-1/2-v}M_{\mu,v}(x)=(-x)^{-1/2-v}M_{-\mu,v}(-x).\end{align*} $$
$$ \begin{align*}x^{-1/2-v}M_{\mu,v}(x)=(-x)^{-1/2-v}M_{-\mu,v}(-x).\end{align*} $$
We now consider three example initial conditions where we choose Bessel functions and products of Bessel functions of various types. It should be mentioned that our choices of initial conditions were due to their following inherent known properties.
-
(i) Mellin transforms of Bessel functions are well known and involve ratios of gamma functions, allowing for easy computation in applying Cauchy’s residue theorem (see [Reference Paris and Kaminski6] for examples).
-
(ii) The power series coefficients for Bessel functions are well known and so power series of products of Bessel functions are also readily computable. Thus, we may apply Watson’s lemma to obtain asymptotic behaviour of our solutions as well.
Example 1.2 In the model with
![]() $u(r,0)=J_0(ar),$
the Bessel function of the first kind, we may proceed in the following way. Note that for
$u(r,0)=J_0(ar),$
the Bessel function of the first kind, we may proceed in the following way. Note that for
![]() $-v<\Re (s)<3/2$
[Reference Paris and Kaminski6, p. 407]
$-v<\Re (s)<3/2$
[Reference Paris and Kaminski6, p. 407]
 $$ \begin{align} \mathfrak{M}(J_v(ay))(s)=\frac{2^{s-1}\Gamma(v/2+s/2)}{\Gamma(1+v/2-s/2)}a^{-s}. \end{align} $$
$$ \begin{align} \mathfrak{M}(J_v(ay))(s)=\frac{2^{s-1}\Gamma(v/2+s/2)}{\Gamma(1+v/2-s/2)}a^{-s}. \end{align} $$
We set
![]() $v=0$
and insert (1.7) into the equation in Theorem 1.1 to obtain for
$v=0$
and insert (1.7) into the equation in Theorem 1.1 to obtain for
![]() $-1/2<\Re (s)=c<1,$
$-1/2<\Re (s)=c<1,$
 $$ \begin{align} u(r,t)=\frac{1}{r}e^{-(r^2-r^2/2)/(4\kappa t)}\frac{1}{2\pi i}\int_{(c)}(4\kappa t)^{s/2}M_{-s/2,0}\bigg(\frac{r^2}{4\kappa t}\bigg)\,2^{-s}\Gamma\bigg(\frac{1-s}{2}\bigg)\,a^{s-1}\,ds. \end{align} $$
$$ \begin{align} u(r,t)=\frac{1}{r}e^{-(r^2-r^2/2)/(4\kappa t)}\frac{1}{2\pi i}\int_{(c)}(4\kappa t)^{s/2}M_{-s/2,0}\bigg(\frac{r^2}{4\kappa t}\bigg)\,2^{-s}\Gamma\bigg(\frac{1-s}{2}\bigg)\,a^{s-1}\,ds. \end{align} $$
It is known that
where
![]() $L_n(x)$
is the Laguerre polynomial [Reference Debnath3]. This can be seen by using [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1001]
$L_n(x)$
is the Laguerre polynomial [Reference Debnath3]. This can be seen by using [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1001]
![]() $L_a(x)={}_1F_1(-a;1;x)$
together with Kummer’s [Reference Abramowitz and Stegun1, p. 509]
$L_a(x)={}_1F_1(-a;1;x)$
together with Kummer’s [Reference Abramowitz and Stegun1, p. 509]
![]() ${}_1F_1(a;b;x)=e^{x}{}_1F_1(1-a;b;-x)$
with
${}_1F_1(a;b;x)=e^{x}{}_1F_1(1-a;b;-x)$
with
![]() $b=1.$
Now (1.6) with (1.8) leads to
$b=1.$
Now (1.6) with (1.8) leads to
 $$ \begin{align*} u(r,t)&=\frac{e^{-r^2/(4\kappa t)}}{\sqrt{4\kappa t}}\frac{1}{2\pi i}\int_{(c)}(4\kappa t)^{s/2}{}_1F_1\bigg(\frac{s}{2}+\frac{1}{2};1;\frac{r^2}{4\kappa t}\bigg)2^{-s}\Gamma\bigg(\frac{1-s}{2}\bigg)a^{s-1}\,ds\nonumber\\[3pt] &=\frac{e^{-r^2/(4\kappa t)}}{\sqrt{4\kappa t}}\frac{1}{2\pi i}\int_{(1-c)}(4\kappa t)^{(1-s)/2}{}_1F_1\bigg(1-\frac{s}{2};1;\frac{r^2}{4\kappa t}\bigg)2^{s-1}\Gamma\bigg(\frac{s}{2}\bigg)a^{-s}\,ds. \end{align*} $$
$$ \begin{align*} u(r,t)&=\frac{e^{-r^2/(4\kappa t)}}{\sqrt{4\kappa t}}\frac{1}{2\pi i}\int_{(c)}(4\kappa t)^{s/2}{}_1F_1\bigg(\frac{s}{2}+\frac{1}{2};1;\frac{r^2}{4\kappa t}\bigg)2^{-s}\Gamma\bigg(\frac{1-s}{2}\bigg)a^{s-1}\,ds\nonumber\\[3pt] &=\frac{e^{-r^2/(4\kappa t)}}{\sqrt{4\kappa t}}\frac{1}{2\pi i}\int_{(1-c)}(4\kappa t)^{(1-s)/2}{}_1F_1\bigg(1-\frac{s}{2};1;\frac{r^2}{4\kappa t}\bigg)2^{s-1}\Gamma\bigg(\frac{s}{2}\bigg)a^{-s}\,ds. \end{align*} $$
Here we made the change of variable
![]() $s\rightarrow 1-s.$
This integrand has simple poles at
$s\rightarrow 1-s.$
This integrand has simple poles at
![]() $s=0$
and the negative even integers
$s=0$
and the negative even integers
![]() $s=-2n.$
We consider a rectangular contour
$s=-2n.$
We consider a rectangular contour
![]() $C_{M,c,T}$
, where
$C_{M,c,T}$
, where
![]() $M=2N+1/2$
with vertices at
$M=2N+1/2$
with vertices at
![]() ${(1-c,iT), (-M, iT), (-M, -iT)}$
and
${(1-c,iT), (-M, iT), (-M, -iT)}$
and
![]() $(1-c,-iT)$
with
$(1-c,-iT)$
with
![]() $T>0.$
Due to Stirling’s formula [Reference Paris and Kaminski6, pp. 31 and 121], the contribution from the horizontal sides tends to zero as
$T>0.$
Due to Stirling’s formula [Reference Paris and Kaminski6, pp. 31 and 121], the contribution from the horizontal sides tends to zero as
![]() $T\rightarrow \infty .$
Noting that these poles are contained within our
$T\rightarrow \infty .$
Noting that these poles are contained within our
![]() $C_{M,c,T}$
and using (1.9) to compute the residues gives
$C_{M,c,T}$
and using (1.9) to compute the residues gives
 $$ \begin{align*}u(r,t)=\sum_{n\ge0}\frac{L_n(-r^2/4\kappa t)}{n!}(-a^2\kappa t)^n=e^{-a^2\kappa t}J_0(ar).\end{align*} $$
$$ \begin{align*}u(r,t)=\sum_{n\ge0}\frac{L_n(-r^2/4\kappa t)}{n!}(-a^2\kappa t)^n=e^{-a^2\kappa t}J_0(ar).\end{align*} $$
Here we have applied the
![]() $\alpha =0$
case of [Reference Szegö7, p. 102, Theorem 5.1 and equation (5.1.16)]
$\alpha =0$
case of [Reference Szegö7, p. 102, Theorem 5.1 and equation (5.1.16)]
 $$ \begin{align*}\sum_{n\ge0}\frac{L^{(\alpha)}_n(x)}{\Gamma(n+\alpha+1)}w^n=e^{w}(xw)^{-\alpha/2}J_{\alpha}(2\sqrt{xw}).\end{align*} $$
$$ \begin{align*}\sum_{n\ge0}\frac{L^{(\alpha)}_n(x)}{\Gamma(n+\alpha+1)}w^n=e^{w}(xw)^{-\alpha/2}J_{\alpha}(2\sqrt{xw}).\end{align*} $$
Next we consider an example of Theorem 1.1 with a function for which it is difficult to evaluate (1.3), and is apparently new.
Theorem 1.3. The solution of (1.1) with
 $u(r,0)=J_0^2(ar)$
is given by
$u(r,0)=J_0^2(ar)$
is given by
 $$ \begin{align*}u(r,t)= \frac{1}{2}\sum_{n\ge0}\frac{(2n)!}{(n!)^3}L_{n}\bigg(-\frac{r^2}{4^2\kappa t}\bigg)(-a^2\kappa t)^{n}.\end{align*} $$
$$ \begin{align*}u(r,t)= \frac{1}{2}\sum_{n\ge0}\frac{(2n)!}{(n!)^3}L_{n}\bigg(-\frac{r^2}{4^2\kappa t}\bigg)(-a^2\kappa t)^{n}.\end{align*} $$
Proof. First, we write down [Reference Paris and Kaminski6, p. 407]
 $$ \begin{align} \mathfrak{M}(J_v^2(ay))(s)=\frac{2^{s-1}\Gamma(s/2+v)\Gamma(1-s)}{\Gamma^2(1-s/2)\Gamma(1+v-s/2)}a^{-s}, \end{align} $$
$$ \begin{align} \mathfrak{M}(J_v^2(ay))(s)=\frac{2^{s-1}\Gamma(s/2+v)\Gamma(1-s)}{\Gamma^2(1-s/2)\Gamma(1+v-s/2)}a^{-s}, \end{align} $$
valid for
![]() $-\Re (v)<\Re (s)=c'<1.$
We set
$-\Re (v)<\Re (s)=c'<1.$
We set
![]() $v=0$
in (1.10) and insert it into the equation in Theorem 1.1 to find for
$v=0$
in (1.10) and insert it into the equation in Theorem 1.1 to find for
![]() $0<c'<1,$
$0<c'<1,$
 $$ \begin{align*}\begin{aligned}u(r,t)&=\frac{1}{r}e^{-r^2/(4\kappa t)}\frac{1}{2\pi i}\int_{(c')}(4\kappa t)^{s/2}M_{-s/2,0}\bigg(\frac{r^2}{4\kappa t}\bigg)\frac{2^{-s}\Gamma((1-s)/2)\Gamma(s)}{\Gamma^2(1/2+s/2)}a^{s-1}\,ds \\[4pt] &=\frac{e^{-r^2/(4\kappa t)}}{\sqrt{4\kappa t}}\frac{1}{2\pi i}\int_{(1-c')}(4\kappa t)^{(1-s)/2}{}_1F_1\bigg(1-s/2;1;\frac{r^2}{4\kappa t}\bigg)\frac{2^{s-1}\Gamma(s/2)\Gamma(1-s)}{\Gamma^2(1-s/2)}a^{-s}\,ds .\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned}u(r,t)&=\frac{1}{r}e^{-r^2/(4\kappa t)}\frac{1}{2\pi i}\int_{(c')}(4\kappa t)^{s/2}M_{-s/2,0}\bigg(\frac{r^2}{4\kappa t}\bigg)\frac{2^{-s}\Gamma((1-s)/2)\Gamma(s)}{\Gamma^2(1/2+s/2)}a^{s-1}\,ds \\[4pt] &=\frac{e^{-r^2/(4\kappa t)}}{\sqrt{4\kappa t}}\frac{1}{2\pi i}\int_{(1-c')}(4\kappa t)^{(1-s)/2}{}_1F_1\bigg(1-s/2;1;\frac{r^2}{4\kappa t}\bigg)\frac{2^{s-1}\Gamma(s/2)\Gamma(1-s)}{\Gamma^2(1-s/2)}a^{-s}\,ds .\end{aligned}\end{align*} $$
The resulting integrand has simple poles at
![]() $s=-2n$
for each integer
$s=-2n$
for each integer
![]() $n\ge 0.$
We consider a rectangular contour
$n\ge 0.$
We consider a rectangular contour
![]() $C_{M,c',T}$
where
$C_{M,c',T}$
where
![]() $M=2N+1/2$
with vertices at
$M=2N+1/2$
with vertices at
![]() ${(1-c',iT), (-M, iT), (-M, -iT)}$
and
${(1-c',iT), (-M, iT), (-M, -iT)}$
and
![]() $(1-c',-iT)$
with
$(1-c',-iT)$
with
![]() $T>0.$
Due to Stirling’s formula, the contribution from the horizontal sides tends to zero as
$T>0.$
Due to Stirling’s formula, the contribution from the horizontal sides tends to zero as
![]() $T\rightarrow \infty .$
Noting that these poles are contained within our
$T\rightarrow \infty .$
Noting that these poles are contained within our
![]() $C_{M,c',T},$
we use (1.9) to compute the residues. Therefore, computing the residues at these poles gives, by Cauchy’s residue theorem and (1.9),
$C_{M,c',T},$
we use (1.9) to compute the residues. Therefore, computing the residues at these poles gives, by Cauchy’s residue theorem and (1.9),
 $$ \begin{align*}u(r,t)=\frac{1}{2}\sum_{n\ge0}\frac{(2n)!}{(n!)^3}L_{n}\bigg(-\frac{r^2}{4^2\kappa t}\bigg)(-a^2\kappa t)^{n}.\\[-48pt]\end{align*} $$
$$ \begin{align*}u(r,t)=\frac{1}{2}\sum_{n\ge0}\frac{(2n)!}{(n!)^3}L_{n}\bigg(-\frac{r^2}{4^2\kappa t}\bigg)(-a^2\kappa t)^{n}.\\[-48pt]\end{align*} $$
It is interesting to note that taking the limit
![]() $r\rightarrow 0$
of Theorem 1.3 gives
$r\rightarrow 0$
of Theorem 1.3 gives
 $$ \begin{align*}\lim_{r\rightarrow0}\bigg(\sum_{n\ge0}\frac{(2n)!}{(n!)^3}L_n\bigg(-\frac{r^2}{4^2\kappa t}\bigg)(-a^2\kappa t)^n\bigg)=e^{-a^2\kappa t}I_0(a^2\kappa t)\end{align*} $$
$$ \begin{align*}\lim_{r\rightarrow0}\bigg(\sum_{n\ge0}\frac{(2n)!}{(n!)^3}L_n\bigg(-\frac{r^2}{4^2\kappa t}\bigg)(-a^2\kappa t)^n\bigg)=e^{-a^2\kappa t}I_0(a^2\kappa t)\end{align*} $$
by means of [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1024, equation (9.215),
![]() $\#3,p=0,z=\mathrm{ix}$
]. Next we consider an initial condition involving the modified Bessel function of the second kind
$\#3,p=0,z=\mathrm{ix}$
]. Next we consider an initial condition involving the modified Bessel function of the second kind
![]() $K_v(x),$
which has the general relationship [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4]
$K_v(x),$
which has the general relationship [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4]
 $$ \begin{align*}K_v(x)=\frac{\pi(I_{-v}(x)-I_v(x))}{2\sin(\pi v)}.\end{align*} $$
$$ \begin{align*}K_v(x)=\frac{\pi(I_{-v}(x)-I_v(x))}{2\sin(\pi v)}.\end{align*} $$
Theorem 1.4. The solution to (1.1) with
![]() $u(r,0)=I_v(ar)K_v(ar)$
is given by
$u(r,0)=I_v(ar)K_v(ar)$
is given by
 $$ \begin{align*} u(r,t)&=e^{-r^2/(4\kappa t)}\frac{(4\kappa t a^2)^{v}}{4\sqrt{\pi}}\bigg[\sum_{n\ge0}{}_1F_1\bigg(1+v+n;1;\frac{r^2}{4\kappa t}\bigg)\\[4pt] &\quad \times\frac{\Gamma(1+v+n)\Gamma(-v-n)\Gamma(1/2+n+v)}{n!\Gamma(2v+1+n)}(-a^24\kappa t)^n \bigg]\\[4pt] &\quad+\frac{e^{-r^2/(4\kappa t)}}{4\sqrt{\pi}}\sum_{n\ge0}{}_1F_1\bigg(1+n;1;\frac{r^2}{4\kappa t}\bigg)\frac{\Gamma(v-n)\Gamma(1/2+n)}{\Gamma(v+1+n)}(-a^24\kappa t)^n, \end{align*} $$
$$ \begin{align*} u(r,t)&=e^{-r^2/(4\kappa t)}\frac{(4\kappa t a^2)^{v}}{4\sqrt{\pi}}\bigg[\sum_{n\ge0}{}_1F_1\bigg(1+v+n;1;\frac{r^2}{4\kappa t}\bigg)\\[4pt] &\quad \times\frac{\Gamma(1+v+n)\Gamma(-v-n)\Gamma(1/2+n+v)}{n!\Gamma(2v+1+n)}(-a^24\kappa t)^n \bigg]\\[4pt] &\quad+\frac{e^{-r^2/(4\kappa t)}}{4\sqrt{\pi}}\sum_{n\ge0}{}_1F_1\bigg(1+n;1;\frac{r^2}{4\kappa t}\bigg)\frac{\Gamma(v-n)\Gamma(1/2+n)}{\Gamma(v+1+n)}(-a^24\kappa t)^n, \end{align*} $$
provided that v is not an integer or equal to
![]() $0.$
$0.$
Proof. From [Reference Titchmarsh8, p. 199, equation (7.10.8)] with
![]() $0<\Re (s)=c'<1,$
$0<\Re (s)=c'<1,$
 $$ \begin{align} \mathfrak{M}(I_v(ay)K_v(ay))(s)=\frac{\Gamma(s/2+v)\Gamma(1/2-s/2)\Gamma(s/2)}{4\sqrt{\pi}\Gamma(v+1-s/2)}a^{-s}. \end{align} $$
$$ \begin{align} \mathfrak{M}(I_v(ay)K_v(ay))(s)=\frac{\Gamma(s/2+v)\Gamma(1/2-s/2)\Gamma(s/2)}{4\sqrt{\pi}\Gamma(v+1-s/2)}a^{-s}. \end{align} $$
Setting
![]() $v=0$
in (1.11) and applying Theorem 1.1, we have that
$v=0$
in (1.11) and applying Theorem 1.1, we have that
![]() $u(r,t)$
is equal to
$u(r,t)$
is equal to
 $$ \begin{align*} u(r,t)&=\frac{1}{r4\sqrt{\pi}}e^{-r^2/(4\kappa t)}\frac{1}{2\pi i} \int_{(c')}\bigg[(4\kappa t)^{s/2}\Gamma\bigg(\frac{1}{2}+\frac{s}{2}\bigg)M_{-s/2,0}\bigg(\frac{r^2}{4\kappa t}\bigg)\\[4pt] &\quad \times \frac{\Gamma((1-s)/2+v)\Gamma(1/2-s/2)\Gamma(s/2)}{\Gamma(v+1/2+s/2)}a^{s-1}\bigg]\,ds \\[4pt] &=\frac{e^{-r^2/(4\kappa t)}}{4\sqrt{\pi}\sqrt{4\kappa t}}\frac{1}{2\pi i} \int_{(1-c')}\bigg[(4\kappa t)^{(1-s)/2}{}_1F_1\bigg(1-\frac{s}{2};1;\frac{r^2}{4\kappa t}\bigg) \\[4pt] &\quad \times \frac{\Gamma(1-s/2)\Gamma(s/2+v)\Gamma(s/2)\Gamma((1-s)/2)}{\Gamma(v+1-s/2)}a^{-s}\bigg]\,ds. \end{align*} $$
$$ \begin{align*} u(r,t)&=\frac{1}{r4\sqrt{\pi}}e^{-r^2/(4\kappa t)}\frac{1}{2\pi i} \int_{(c')}\bigg[(4\kappa t)^{s/2}\Gamma\bigg(\frac{1}{2}+\frac{s}{2}\bigg)M_{-s/2,0}\bigg(\frac{r^2}{4\kappa t}\bigg)\\[4pt] &\quad \times \frac{\Gamma((1-s)/2+v)\Gamma(1/2-s/2)\Gamma(s/2)}{\Gamma(v+1/2+s/2)}a^{s-1}\bigg]\,ds \\[4pt] &=\frac{e^{-r^2/(4\kappa t)}}{4\sqrt{\pi}\sqrt{4\kappa t}}\frac{1}{2\pi i} \int_{(1-c')}\bigg[(4\kappa t)^{(1-s)/2}{}_1F_1\bigg(1-\frac{s}{2};1;\frac{r^2}{4\kappa t}\bigg) \\[4pt] &\quad \times \frac{\Gamma(1-s/2)\Gamma(s/2+v)\Gamma(s/2)\Gamma((1-s)/2)}{\Gamma(v+1-s/2)}a^{-s}\bigg]\,ds. \end{align*} $$
Now we see that if
![]() $v=0$
, then the gamma functions would have a pole of order two at the negative even integers
$v=0$
, then the gamma functions would have a pole of order two at the negative even integers
![]() $s=-2n,$
which we want to avoid due to the lengthy resulting formula. Hence, we restrict v to be a noninteger and
$s=-2n,$
which we want to avoid due to the lengthy resulting formula. Hence, we restrict v to be a noninteger and
![]() $v\neq 0,$
and the poles at
$v\neq 0,$
and the poles at
![]() ${s=-2n-2v}$
and
${s=-2n-2v}$
and
![]() $s=-2n$
are simple. We consider a rectangular contour
$s=-2n$
are simple. We consider a rectangular contour
![]() $C_{M_v,c',T}$
, where
$C_{M_v,c',T}$
, where
![]() $M=2N+2v+1/2$
with vertices at
$M=2N+2v+1/2$
with vertices at
![]() $(1-c',iT), (-M, iT), (-M, -iT)$
and
$(1-c',iT), (-M, iT), (-M, -iT)$
and
![]() $(1-c',-iT)$
with
$(1-c',-iT)$
with
![]() $T>0.$
Due to Stirling’s formula [Reference Paris and Kaminski6, pp. 31 and 121], the contribution from the horizontal sides tends to zero as
$T>0.$
Due to Stirling’s formula [Reference Paris and Kaminski6, pp. 31 and 121], the contribution from the horizontal sides tends to zero as
![]() $T\rightarrow \infty .$
Noting that these poles are contained within our
$T\rightarrow \infty .$
Noting that these poles are contained within our
![]() $C_{M_v,c',T},$
we use the integrand to compute the residues. For the poles at
$C_{M_v,c',T},$
we use the integrand to compute the residues. For the poles at
![]() $s=-2n-2v,$
we have the residue
$s=-2n-2v,$
we have the residue
 $$ \begin{align*}&e^{-r^2/(4\kappa t)}\frac{(4\kappa t a^2)^{v}}{4\sqrt{\pi}}\sum_{n\ge0}{}_1F_1\bigg(1+v+n;1;\frac{r^2}{4\kappa t}\bigg)\\[4pt] &\quad \times\frac{\Gamma(1+v+n)\Gamma(-v-n)\Gamma(1/2+n+v)}{n!\Gamma(2v+1+n)}(-a^24\kappa t)^n\end{align*} $$
$$ \begin{align*}&e^{-r^2/(4\kappa t)}\frac{(4\kappa t a^2)^{v}}{4\sqrt{\pi}}\sum_{n\ge0}{}_1F_1\bigg(1+v+n;1;\frac{r^2}{4\kappa t}\bigg)\\[4pt] &\quad \times\frac{\Gamma(1+v+n)\Gamma(-v-n)\Gamma(1/2+n+v)}{n!\Gamma(2v+1+n)}(-a^24\kappa t)^n\end{align*} $$
and, for the poles at
![]() $s=-2n,$
we have the residue
$s=-2n,$
we have the residue
 $$ \begin{align*}\frac{e^{-r^2/(4\kappa t)}}{4\sqrt{\pi}}\sum_{n\ge0}{}_1F_1\bigg(1+n;1;\frac{r^2}{4\kappa t}\bigg)\frac{\Gamma(v-n)\Gamma(1/2+n)}{\Gamma(v+1+n)}(-a^24\kappa t)^n.\\[-51pt]\end{align*} $$
$$ \begin{align*}\frac{e^{-r^2/(4\kappa t)}}{4\sqrt{\pi}}\sum_{n\ge0}{}_1F_1\bigg(1+n;1;\frac{r^2}{4\kappa t}\bigg)\frac{\Gamma(v-n)\Gamma(1/2+n)}{\Gamma(v+1+n)}(-a^24\kappa t)^n.\\[-51pt]\end{align*} $$
A nice consequence of our series representations of
![]() $u(r,t)$
is that they are rapidly converging and so should be of great interest for numerical calculations. From [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1003, equation (8.978),
$u(r,t)$
is that they are rapidly converging and so should be of great interest for numerical calculations. From [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 1003, equation (8.978),
![]() $\#3,\alpha =0$
], we have the asymptotic expansion for the Laguerre polynomial
$\#3,\alpha =0$
], we have the asymptotic expansion for the Laguerre polynomial
 $$ \begin{align} L_n(x)=\frac{e^{x/2}}{\sqrt{\pi}}(xn)^{-1/4}\cos\bigg(2\sqrt{nx}-\frac{\pi}{4}\bigg)+O(n^{-3/4}) \end{align} $$
$$ \begin{align} L_n(x)=\frac{e^{x/2}}{\sqrt{\pi}}(xn)^{-1/4}\cos\bigg(2\sqrt{nx}-\frac{\pi}{4}\bigg)+O(n^{-3/4}) \end{align} $$
as
![]() $n\rightarrow \infty ,$
uniformly in
$n\rightarrow \infty ,$
uniformly in
![]() $x>0.$
In conjunction with our series involving Laguerre polynomials, (1.12) may be used to obtain approximations for
$x>0.$
In conjunction with our series involving Laguerre polynomials, (1.12) may be used to obtain approximations for
![]() $u(r,t).$
$u(r,t).$
2. Some related observations
We mention a method of evaluating (1.3) when
![]() $g(y)=h(y)\log (y)$
for a suitable function
$g(y)=h(y)\log (y)$
for a suitable function
![]() $h(y).$
It is known [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 919, equation (8.447)] that
$h(y).$
It is known [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 919, equation (8.447)] that
 $$ \begin{align} I_0(x)\log\bigg(\frac{x}{2}\bigg)=-K_0(x)+\sum_{n\ge1}\frac{x^{2n}}{2^{2n}(n!)^2}\psi(n+1), \end{align} $$
$$ \begin{align} I_0(x)\log\bigg(\frac{x}{2}\bigg)=-K_0(x)+\sum_{n\ge1}\frac{x^{2n}}{2^{2n}(n!)^2}\psi(n+1), \end{align} $$
where
![]() $\psi (x)$
is the digamma function [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4]. The formula (2.1) appears to provide an effective way of computing special cases of (1.3). We provide an outline of a method.
$\psi (x)$
is the digamma function [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4]. The formula (2.1) appears to provide an effective way of computing special cases of (1.3). We provide an outline of a method.
Theorem 2.1. Let
![]() $h(y)$
be a suitable function chosen so the series converges. The solution to (1.1) with initial condition
$h(y)$
be a suitable function chosen so the series converges. The solution to (1.1) with initial condition
![]() $u(r,0)=h(r)\log (r)$
satisfies
$u(r,0)=h(r)\log (r)$
satisfies
 $$ \begin{align*} u(r,t)&=\frac{1}{2\kappa t}e^{-r^2/(4\kappa t)}\bigg[\log\bigg(\frac{4\kappa t}{r}\bigg)\mathfrak{Z}_{1}(h) -\int_{0}^{\infty} yh(y)e^{-y^2/(4\kappa t)}K_0\bigg(\frac{yr}{2\kappa t}\bigg)\ dy \\[4pt] &\quad +\sum_{n\ge1}\frac{\psi(n+1)}{2^{2n}(n!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2n}\mathfrak{Z}_{2n+1}(h)\bigg], \end{align*} $$
$$ \begin{align*} u(r,t)&=\frac{1}{2\kappa t}e^{-r^2/(4\kappa t)}\bigg[\log\bigg(\frac{4\kappa t}{r}\bigg)\mathfrak{Z}_{1}(h) -\int_{0}^{\infty} yh(y)e^{-y^2/(4\kappa t)}K_0\bigg(\frac{yr}{2\kappa t}\bigg)\ dy \\[4pt] &\quad +\sum_{n\ge1}\frac{\psi(n+1)}{2^{2n}(n!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2n}\mathfrak{Z}_{2n+1}(h)\bigg], \end{align*} $$
where
 $$ \begin{align*}\mathfrak{Z}_{s}(h):=\mathfrak{M}(yh(y)e^{-y^2/(4\kappa t)})(s)=\int_{0}^{\infty}h(y) y^{s} e^{-y^2/(4\kappa t)}\ dy.\end{align*} $$
$$ \begin{align*}\mathfrak{Z}_{s}(h):=\mathfrak{M}(yh(y)e^{-y^2/(4\kappa t)})(s)=\int_{0}^{\infty}h(y) y^{s} e^{-y^2/(4\kappa t)}\ dy.\end{align*} $$
Proof. Note that equation (2.1) implies that
 $$ \begin{align*}I_0\bigg(\frac{yr}{2\kappa t}\bigg)\log(y) =\log\bigg(\frac{4\kappa t}{r}\bigg)-K_0\bigg(\frac{yr}{2\kappa t}\bigg)+\sum_{n\ge1}\frac{\psi(k+1)}{2^{2k}(k!)^2}\bigg(\frac{yr}{2\kappa t}\bigg)^{2k}.\end{align*} $$
$$ \begin{align*}I_0\bigg(\frac{yr}{2\kappa t}\bigg)\log(y) =\log\bigg(\frac{4\kappa t}{r}\bigg)-K_0\bigg(\frac{yr}{2\kappa t}\bigg)+\sum_{n\ge1}\frac{\psi(k+1)}{2^{2k}(k!)^2}\bigg(\frac{yr}{2\kappa t}\bigg)^{2k}.\end{align*} $$
Hence,
 $$ \begin{align*} \int_{0}^{\infty} yh(y)I_0\bigg(\frac{yr}{2\kappa t}\bigg)\log(y)e^{-y^2/(4\kappa t)}\ dy&=\log\bigg(\frac{4\kappa t}{r}\bigg)\int_{0}^{\infty} yh(y)e^{-y^2/(4\kappa t)}\ dy \\[4pt] &\quad -\int_{0}^{\infty} yh(y)e^{-y^2/(4\kappa t)}K_0\bigg(\frac{yr}{2\kappa t}\bigg)\ dy \\[4pt] &\quad +\sum_{n\ge1}\frac{\psi(k+1)}{2^{2k}(k!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2k}\mathfrak{Z}_{2k}(h(y)), \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty} yh(y)I_0\bigg(\frac{yr}{2\kappa t}\bigg)\log(y)e^{-y^2/(4\kappa t)}\ dy&=\log\bigg(\frac{4\kappa t}{r}\bigg)\int_{0}^{\infty} yh(y)e^{-y^2/(4\kappa t)}\ dy \\[4pt] &\quad -\int_{0}^{\infty} yh(y)e^{-y^2/(4\kappa t)}K_0\bigg(\frac{yr}{2\kappa t}\bigg)\ dy \\[4pt] &\quad +\sum_{n\ge1}\frac{\psi(k+1)}{2^{2k}(k!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2k}\mathfrak{Z}_{2k}(h(y)), \end{align*} $$
provided
![]() $yh(y)\log (y)$
satisfies certain growth conditions. In particular, by [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 920],
$yh(y)\log (y)$
satisfies certain growth conditions. In particular, by [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 920],
![]() $K_{0}(t)=O(e^{-t}/\sqrt {t})$
when
$K_{0}(t)=O(e^{-t}/\sqrt {t})$
when
![]() $t\rightarrow \infty $
in
$t\rightarrow \infty $
in
![]() $|\!\arg (t)|<3\pi /2$
and so we require the very mild necessary condition that for a positive constant
$|\!\arg (t)|<3\pi /2$
and so we require the very mild necessary condition that for a positive constant
![]() $c_1$
and any
$c_1$
and any
![]() $t>0,$
$t>0,$
 $$ \begin{align*}|yh(y)|<c_1e^{y^2/(4\kappa t)}\end{align*} $$
$$ \begin{align*}|yh(y)|<c_1e^{y^2/(4\kappa t)}\end{align*} $$
by the first integral on the right-hand side.
3. Asymptotic analysis of
 $u(r,t)$
$u(r,t)$
First, we write down Watson’s lemma (see [Reference Olver5, p. 336, equations (6.01) and (6.02)] or [Reference Paris and Kaminski6, p. 5, Lemma 1.2]). Suppose that
![]() $f(y)$
has the power series expansion
$f(y)$
has the power series expansion
 $$ \begin{align}f(y) \sim\sum_{n\ge0}a_ny^{(n+\lambda-\mu)/\mu} \end{align} $$
$$ \begin{align}f(y) \sim\sum_{n\ge0}a_ny^{(n+\lambda-\mu)/\mu} \end{align} $$
as
![]() $y\rightarrow 0^{+}.$
Then, if
$y\rightarrow 0^{+}.$
Then, if
![]() $\lambda>0, \mu >0,$
$\lambda>0, \mu >0,$
 $$ \begin{align} \int_{0}^{\infty}e^{-xy}f(y)\ dy\sim\sum_{n\ge0}\Gamma\bigg(\frac{n+\lambda}{\mu}\bigg)\frac{a_n}{x^{(n+\lambda)/\mu}} \end{align} $$
$$ \begin{align} \int_{0}^{\infty}e^{-xy}f(y)\ dy\sim\sum_{n\ge0}\Gamma\bigg(\frac{n+\lambda}{\mu}\bigg)\frac{a_n}{x^{(n+\lambda)/\mu}} \end{align} $$
as
![]() $x\rightarrow \infty ,$
assuming that the integral converges. In this section, we illustrate an attractive aspect of working with Bessel functions for
$x\rightarrow \infty ,$
assuming that the integral converges. In this section, we illustrate an attractive aspect of working with Bessel functions for
![]() $u(r,0).$
Namely, exploiting the power series representation to find an asymptotic formula related to the integral representation of
$u(r,0).$
Namely, exploiting the power series representation to find an asymptotic formula related to the integral representation of
![]() $u(r,t).$
First, in our initial example following Theorem 1.1, with
$u(r,t).$
First, in our initial example following Theorem 1.1, with
![]() $f(r)=J_0(ar),$
we can use the power series formula
$f(r)=J_0(ar),$
we can use the power series formula
 $$ \begin{align} J_{0}(ay)I_0\bigg(\frac{yr}{2\kappa t}\bigg)=\sum_{n\ge0}\bigg(\frac{1}{2^{2n}}\sum_{0\le k\le n}\frac{(-a^2)^k}{(k!)^2((n-k)!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2(n-k)}\bigg)y^{2n}, \end{align} $$
$$ \begin{align} J_{0}(ay)I_0\bigg(\frac{yr}{2\kappa t}\bigg)=\sum_{n\ge0}\bigg(\frac{1}{2^{2n}}\sum_{0\le k\le n}\frac{(-a^2)^k}{(k!)^2((n-k)!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2(n-k)}\bigg)y^{2n}, \end{align} $$
which is easily obtained by equating coefficients after taking the product of power series. Now we replace y by
![]() $\sqrt {y}$
in (3.3), put
$\sqrt {y}$
in (3.3), put
![]() $\mu =\lambda =1$
in (3.1)–(3.2) and make the change of variable
$\mu =\lambda =1$
in (3.1)–(3.2) and make the change of variable
![]() $y\rightarrow y^2$
in (3.2) to obtain the following theorem.
$y\rightarrow y^2$
in (3.2) to obtain the following theorem.
Theorem 3.1. We have
 $$ \begin{align*}2\int_{0}^{\infty}ye^{-xy^2}J_{0}(ay)I_0\bigg(\frac{yr}{2\kappa t}\bigg)\ dy\sim\sum_{n\ge0}\frac{n!b_n}{x^{(n+1)}}\end{align*} $$
$$ \begin{align*}2\int_{0}^{\infty}ye^{-xy^2}J_{0}(ay)I_0\bigg(\frac{yr}{2\kappa t}\bigg)\ dy\sim\sum_{n\ge0}\frac{n!b_n}{x^{(n+1)}}\end{align*} $$
as
![]() $x\rightarrow \infty ,$
where
$x\rightarrow \infty ,$
where
 $$ \begin{align*}b_n=\frac{1}{2^{2n}}\sum_{0\le k\le n}\frac{(-a^2)^k}{(k!)^2((n-k)!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2(n-k)}.\end{align*} $$
$$ \begin{align*}b_n=\frac{1}{2^{2n}}\sum_{0\le k\le n}\frac{(-a^2)^k}{(k!)^2((n-k)!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2(n-k)}.\end{align*} $$
In the example provided in Theorem 1.3, we will need the known power series [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger4, p. 918, equation (8.442),
![]() $\#1,v=\mu =0,z=\mathrm{ay}$
],
$\#1,v=\mu =0,z=\mathrm{ay}$
],
 $$ \begin{align} J_0^2(ay)=\sum_{n\ge0}\frac{(-1)^n(n+1)_n}{(n!)^3}\bigg(\frac{ay}{2}\bigg)^{2n}. \end{align} $$
$$ \begin{align} J_0^2(ay)=\sum_{n\ge0}\frac{(-1)^n(n+1)_n}{(n!)^3}\bigg(\frac{ay}{2}\bigg)^{2n}. \end{align} $$
Proceeding precisely in the same way as we did for Theorem 3.1 but with (3.4), we obtain the following theorem.
Theorem 3.2. We have
 $$ \begin{align*}2\int_{0}^{\infty}ye^{-xy^2}J_{0}^2(ay)I_0\bigg(\frac{yr}{2\kappa t}\bigg)\ dy\sim\sum_{n\ge0}\frac{n! c_n}{x^{(n+1)}}\end{align*} $$
$$ \begin{align*}2\int_{0}^{\infty}ye^{-xy^2}J_{0}^2(ay)I_0\bigg(\frac{yr}{2\kappa t}\bigg)\ dy\sim\sum_{n\ge0}\frac{n! c_n}{x^{(n+1)}}\end{align*} $$
as
![]() $x\rightarrow \infty ,$
where
$x\rightarrow \infty ,$
where
 $$ \begin{align*}c_n=\frac{1}{2^{2n}}\sum_{0\le k\le n}\frac{(-a^2)^k(k+1)_k}{(k!)^3((n-k)!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2(n-k)}.\end{align*} $$
$$ \begin{align*}c_n=\frac{1}{2^{2n}}\sum_{0\le k\le n}\frac{(-a^2)^k(k+1)_k}{(k!)^3((n-k)!)^2}\bigg(\frac{r}{2\kappa t}\bigg)^{2(n-k)}.\end{align*} $$
Acknowledgement
We thank Professor Forbes for helpful suggestions which led to improvements of the manuscript.