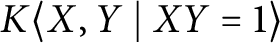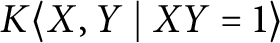1 Introduction
A unital ring A is called directly finite in case, for any
![]() $x,y \in A$
, if
$x,y \in A$
, if
![]() $xy=1$
then
$xy=1$
then
![]() $yx=1$
. It is not hard to show that rings which satisfy various natural conditions (commutativity, some mild chain condition, and so on) are directly finite. On the other hand, examples abound of rings containing elements
$yx=1$
. It is not hard to show that rings which satisfy various natural conditions (commutativity, some mild chain condition, and so on) are directly finite. On the other hand, examples abound of rings containing elements
![]() $x,y$
for which
$x,y$
for which
![]() $xy = 1$
but
$xy = 1$
but
![]() $yx \neq 1$
. Perhaps the most natural ‘concrete’ example is found in the endomorphism ring of a countably-infinite-dimensional vector space V over a field. Here, if
$yx \neq 1$
. Perhaps the most natural ‘concrete’ example is found in the endomorphism ring of a countably-infinite-dimensional vector space V over a field. Here, if
![]() $\{e_i \ | \ i\in {\mathbb N}\}$
is a basis for V, then the right shift transformation y which takes
$\{e_i \ | \ i\in {\mathbb N}\}$
is a basis for V, then the right shift transformation y which takes
![]() $e_i$
to
$e_i$
to
![]() $e_{i+1}$
and the left shift transformation x which takes
$e_{i+1}$
and the left shift transformation x which takes
![]() $e_1$
to
$e_1$
to
![]() $0$
and
$0$
and
![]() $e_{i}$
to
$e_{i}$
to
![]() $e_{i-1}$
for
$e_{i-1}$
for
![]() $i\geq 2$
satisfy
$i\geq 2$
satisfy
![]() $xy=1$
but
$xy=1$
but
![]() $yx\neq 1$
. A moment’s reflection yields that there is an even more natural example of a ring which fails to be directly finite, to wit:
$yx\neq 1$
. A moment’s reflection yields that there is an even more natural example of a ring which fails to be directly finite, to wit:
the free associative K-algebra on two (noncommuting) generators, modulo the single relation
![]() $XY=1$
. A search of the literature suggests that this algebra was first explicitly studied by Jacobson in the late 1940s in [13]. Throughout the article we will refer to this algebra as the Jacobson algebra over K.Footnote
1
While the displayed description of
$XY=1$
. A search of the literature suggests that this algebra was first explicitly studied by Jacobson in the late 1940s in [13]. Throughout the article we will refer to this algebra as the Jacobson algebra over K.Footnote
1
While the displayed description of
![]() $\mathcal {R}$
is quite straightforward, the structure of
$\mathcal {R}$
is quite straightforward, the structure of
![]() $\mathcal {R}$
is anything but.
$\mathcal {R}$
is anything but.
Various ring-theoretic and module-theoretic properties of
![]() $\mathcal {R}$
have been analyzed during the seven decades since Jacobson’s work, including in: Cohn [Reference Cohn10] (1966); Bergman [Reference Bergman8] (1974); Gerritzen [Reference Gerritzen11] (2000); Bavula [Reference Bavula7] (2010); Ara and Rangaswamy [Reference Ara and Rangaswamy6] (2014); Iovanov and Sistko [Reference Iovanov and Sistko12] (2017); and Lu, Wang and Wang [Reference Lu, Wang and Wang15] (2019).
$\mathcal {R}$
have been analyzed during the seven decades since Jacobson’s work, including in: Cohn [Reference Cohn10] (1966); Bergman [Reference Bergman8] (1974); Gerritzen [Reference Gerritzen11] (2000); Bavula [Reference Bavula7] (2010); Ara and Rangaswamy [Reference Ara and Rangaswamy6] (2014); Iovanov and Sistko [Reference Iovanov and Sistko12] (2017); and Lu, Wang and Wang [Reference Lu, Wang and Wang15] (2019).
For the directed graph
 , the Jacobson algebra
, the Jacobson algebra
![]() $\mathcal {R}$
is isomorphic to the Leavitt path algebra
$\mathcal {R}$
is isomorphic to the Leavitt path algebra
![]() $L_K(\mathcal {T})$
(see Proposition 2.1 below). This interpretation guides our investigation. We refer those readers who are unfamiliar with Leavitt path algebras to [Reference Abrams, Ara and Siles Molina1, Chapter 1].
$L_K(\mathcal {T})$
(see Proposition 2.1 below). This interpretation guides our investigation. We refer those readers who are unfamiliar with Leavitt path algebras to [Reference Abrams, Ara and Siles Molina1, Chapter 1].
Following [Reference Ara and Rangaswamy6], there are three classes of Chen simple modules for Leavitt path algebras
![]() $L_K(E)$
of a general (finite) graph E:
$L_K(E)$
of a general (finite) graph E:
-
• simple modules associated to sinks;
-
• simple modules associated to infinite irrational paths, and
-
• simple modules associated to infinite rational paths and irreducible polynomials in
 $K[x]$
with constant term equal to
$K[x]$
with constant term equal to
 $-1$
.
$-1$
.
By [Reference Ara and Rangaswamy6, Corollary 4.6] a complete list of nonisomorphic simple left
![]() $L_K(\mathcal {T})$
-modules is given by
$L_K(\mathcal {T})$
-modules is given by
-
• the Chen simple module
 $L_K(\mathcal {T})w$
associated to the sink w, and
$L_K(\mathcal {T})w$
associated to the sink w, and -
• the Chen simple modules
 $V^f$
associated to the infinite rational path
$V^f$
associated to the infinite rational path
 $c^\infty $
(where c is the loop in
$c^\infty $
(where c is the loop in
 $\mathcal {T}$
), and to irreducible polynomials
$\mathcal {T}$
), and to irreducible polynomials
 $f(x)$
in
$f(x)$
in
 $K[x]$
with
$K[x]$
with
 $f(0)=-1$
.
$f(0)=-1$
.
Among other things, results regarding the
![]() $\text {Ext}^1$
groups of pairs of Chen simple modules, the Bézout property, the construction of “Prüfer-like” modules for Chen simple modules, and the construction of injective envelopes for some of these Chen simples have been achieved in previous collaborative work of the three coauthors ([Reference Abrams, Mantese and Tonolo2], [Reference Abrams, Mantese and Tonolo3], and [Reference Abrams, Mantese and Tonolo4]). In the current work we bundle some of the consequences of these results together with a new type of construction in the specific case where
$\text {Ext}^1$
groups of pairs of Chen simple modules, the Bézout property, the construction of “Prüfer-like” modules for Chen simple modules, and the construction of injective envelopes for some of these Chen simples have been achieved in previous collaborative work of the three coauthors ([Reference Abrams, Mantese and Tonolo2], [Reference Abrams, Mantese and Tonolo3], and [Reference Abrams, Mantese and Tonolo4]). In the current work we bundle some of the consequences of these results together with a new type of construction in the specific case where
![]() $E = \mathcal {T} $
.
$E = \mathcal {T} $
.
Our two main goals of the article are as follows. First, we explicitly construct the injective envelope of each simple left
![]() $L_K(\mathcal {T})$
-module. For modules of the form
$L_K(\mathcal {T})$
-module. For modules of the form
![]() $V^f$
as described above, this is achieved in Corollary 6.3. For the module
$V^f$
as described above, this is achieved in Corollary 6.3. For the module
![]() $L_K(\mathcal {T})w$
this is done in Corollary 6.12. Second, we use the information achieved in the first goal to describe a minimal injective cogenerator for the category
$L_K(\mathcal {T})w$
this is done in Corollary 6.12. Second, we use the information achieved in the first goal to describe a minimal injective cogenerator for the category
![]() $L_K(\mathcal {T})$
-Mod (Theorem 6.14). This is the the first time in the literature that an injective cogenerator for a non-Noetherian Leavitt path algebra is completely described. In particular, the structure of all injective
$L_K(\mathcal {T})$
-Mod (Theorem 6.14). This is the the first time in the literature that an injective cogenerator for a non-Noetherian Leavitt path algebra is completely described. In particular, the structure of all injective
![]() $L_K(\mathcal {T})$
-modules, and hence of all representations of
$L_K(\mathcal {T})$
-modules, and hence of all representations of
![]() $L_K(\mathcal {T})$
, is revealed.
$L_K(\mathcal {T})$
, is revealed.
2 Prerequisites
We set some notation. We denote by
![]() $\mathbb N$
the set of positive integers
$\mathbb N$
the set of positive integers
![]() $\{1,2,3,\dots \}$
, and by
$\{1,2,3,\dots \}$
, and by
![]() $\mathbb Z^+$
the set
$\mathbb Z^+$
the set
![]() $\mathbb N\cup \{0\} = \{0,1,2,\dots \}$
.
$\mathbb N\cup \{0\} = \{0,1,2,\dots \}$
.
The word “module” will always mean “left module”. For
![]() $f(x) \in K[x]$
and
$f(x) \in K[x]$
and
![]() $n\in {\mathbb N}$
we denote
$n\in {\mathbb N}$
we denote
![]() $(f(x))^n$
by
$(f(x))^n$
by
![]() $f^n(x)$
.
$f^n(x)$
.
For any polynomial
![]() $g(x)=\sum _{i=0}^m k_{i}x^{i}\in K[x]$
, and the cycle c in
$g(x)=\sum _{i=0}^m k_{i}x^{i}\in K[x]$
, and the cycle c in
![]() $\mathcal T$
, we denote by
$\mathcal T$
, we denote by
![]() $g(c)$
the element
$g(c)$
the element
Rewritten,
![]() $g(c) = k_0v + k_0w +k_1c+\cdots +k_mc^m\in {{L_K(\mathcal {T})}}$
. This notation is well suited for our purposes, but we note that this definition of
$g(c) = k_0v + k_0w +k_1c+\cdots +k_mc^m\in {{L_K(\mathcal {T})}}$
. This notation is well suited for our purposes, but we note that this definition of
![]() $g(c)$
is different from that used for expressions of the form
$g(c)$
is different from that used for expressions of the form
![]() $g(c)$
elsewhere in the literature. For
$g(c)$
elsewhere in the literature. For
![]() $g(x) = \sum _{i=0}^m k_{i}x^{i}\in K[x]$
we denote by
$g(x) = \sum _{i=0}^m k_{i}x^{i}\in K[x]$
we denote by
 $g\big |_v(c)$
the element
$g\big |_v(c)$
the element
 $$\begin{align*}g \big|_v (c) := k_0v +k_1c+\cdots+k_mc^m\in {{L_K(\mathcal{T})}}.\end{align*}$$
$$\begin{align*}g \big|_v (c) := k_0v +k_1c+\cdots+k_mc^m\in {{L_K(\mathcal{T})}}.\end{align*}$$
So
 $g(c)=k_0w+g \big |_v (c)$
and
$g(c)=k_0w+g \big |_v (c)$
and
 $g \big |_v (c)=vg(c)$
.
$g \big |_v (c)=vg(c)$
.
We denote by
![]() $\mathcal {P}$
the set of polynomials
$\mathcal {P}$
the set of polynomials
and by
![]() $\mathcal {F}\subseteq \mathcal P$
the set of polynomials
$\mathcal {F}\subseteq \mathcal P$
the set of polynomials
We note that the family
![]() $\mathcal {F}$
is a set of pairwise nonassociate representatives of the irreducible elements in the ring of Laurent polynomials
$\mathcal {F}$
is a set of pairwise nonassociate representatives of the irreducible elements in the ring of Laurent polynomials
![]() $K[x,x^{-1}]$
.
$K[x,x^{-1}]$
.
Because the Leavitt path algebra
![]() $L_K(\mathcal {T})$
plays a central role in our investigations, we give a detailed description of it here. For the directed graph
$L_K(\mathcal {T})$
plays a central role in our investigations, we give a detailed description of it here. For the directed graph

we consider the extended graph
![]() $\widehat {\mathcal {T}}$
of
$\widehat {\mathcal {T}}$
of
![]() $\mathcal {T}$
, pictured as:
$\mathcal {T}$
, pictured as:

Then
![]() $L_K(\mathcal {T})$
is defined to be the standard path algebra
$L_K(\mathcal {T})$
is defined to be the standard path algebra
![]() $K\widehat {\mathcal {T}}$
of
$K\widehat {\mathcal {T}}$
of
![]() $\widehat {\mathcal {T}}$
with coefficients in K, modulo these relations:
$\widehat {\mathcal {T}}$
with coefficients in K, modulo these relations:
In particular,
![]() $v+w = 1_{L_K(\mathcal {T})}$
.
$v+w = 1_{L_K(\mathcal {T})}$
.
Proposition 2.1 [Reference Abrams, Ara and Siles Molina1, Proposition 1.3.7] Let K be any field, and let
![]() $\mathcal {T} $
be the graph
$\mathcal {T} $
be the graph
 . Then
. Then
![]() $\mathcal {R}\cong L_K(\mathcal {T})$
as K-algebras.
$\mathcal {R}\cong L_K(\mathcal {T})$
as K-algebras.
Proof In
![]() $L_K(\mathcal {T})$
we have
$L_K(\mathcal {T})$
we have
With this as context, one can show that the map
is an isomorphism of K-algebras.▪
In particular, note that the element c of
![]() $L_K(\mathcal {T})$
corresponds to the element
$L_K(\mathcal {T})$
corresponds to the element
![]() $Y^2X$
of
$Y^2X$
of
![]() $\mathcal {R}$
under this isomorphism.
$\mathcal {R}$
under this isomorphism.
Corollary 2.2 The Jacobson algebra is (left and right) hereditary. Specifically, quotients of injective left
![]() $\mathcal {R}$
-modules are injective.
$\mathcal {R}$
-modules are injective.
Proof By [Reference Abrams, Ara and Siles Molina1, Theorem 3.2.5], the Leavitt path algebra
![]() $L_K(E)$
for any finite graph E is hereditary. But hereditary rings have the specified property by [Reference Lam14, Theorem 3.22]. ▪
$L_K(E)$
for any finite graph E is hereditary. But hereditary rings have the specified property by [Reference Lam14, Theorem 3.22]. ▪
An application of [Reference Abrams, Ara and Siles Molina1, Corollary 1.5.12] yields the following useful description of a K-basis of
![]() $L_K(\mathcal {T})$
.
$L_K(\mathcal {T})$
.
Lemma 2.3 The following set forms a K-basis of
![]() $L_K(\mathcal {T})$
:
$L_K(\mathcal {T})$
:
where
![]() $i, j \geq 1$
.
$i, j \geq 1$
.
We conclude the Prerequisites section by giving some properties of the simple left
![]() $L_K(\mathcal {T})$
-modules of the form
$L_K(\mathcal {T})$
-modules of the form
![]() $V^f$
, where
$V^f$
, where
![]() $f(x)\in \mathcal {F}$
. Some of these properties follow from results which were established in [Reference Ara and Rangaswamy6]. We will develop here some additional information about these simple modules which will be needed in the sequel. Although we will not actually utilize the following piece of information until the final section of the article, we reiterate here that because there is a unique cycle in
$f(x)\in \mathcal {F}$
. Some of these properties follow from results which were established in [Reference Ara and Rangaswamy6]. We will develop here some additional information about these simple modules which will be needed in the sequel. Although we will not actually utilize the following piece of information until the final section of the article, we reiterate here that because there is a unique cycle in
![]() $\mathcal {T}$
, [Reference Ara and Rangaswamy6, Corollary 4.6] applies. This yields that, up to isomorphism, all but one of the simple modules over
$\mathcal {T}$
, [Reference Ara and Rangaswamy6, Corollary 4.6] applies. This yields that, up to isomorphism, all but one of the simple modules over
![]() $L_K(\mathcal {T})$
are of the form
$L_K(\mathcal {T})$
are of the form
![]() $V^f$
, where
$V^f$
, where
![]() $f(x)\in \mathcal {F}$
. The only other simple
$f(x)\in \mathcal {F}$
. The only other simple
![]() $L_K(\mathcal {T})$
-module is
$L_K(\mathcal {T})$
-module is
![]() $L_K(\mathcal {T})w$
.
$L_K(\mathcal {T})w$
.
We now make a detailed presentation of the construction of the modules
![]() $V^f$
. Assume
$V^f$
. Assume
![]() $f(x)\in \mathcal {F}$
has degree n. Denote by
$f(x)\in \mathcal {F}$
has degree n. Denote by
![]() $K'$
the field
$K'$
the field
![]() $K[x]/\langle f(x)\rangle $
and by
$K[x]/\langle f(x)\rangle $
and by
![]() $\overline x$
the element
$\overline x$
the element
![]() $x+\langle f(x)\rangle $
. Clearly
$x+\langle f(x)\rangle $
. Clearly
![]() $\{1, \overline x, \dots , \overline x^{n-1}\}$
is a K-basis of
$\{1, \overline x, \dots , \overline x^{n-1}\}$
is a K-basis of
![]() $K'$
. The class of infinite paths tail equivalent to
$K'$
. The class of infinite paths tail equivalent to
![]() $c^\infty $
consists only of
$c^\infty $
consists only of
![]() $c^\infty $
itself. Let
$c^\infty $
itself. Let
![]() $V^{\overline x}$
be the one dimensional
$V^{\overline x}$
be the one dimensional
![]() $K'$
-vector space generated by
$K'$
-vector space generated by
![]() $c^\infty $
. Setting
$c^\infty $
. Setting
![]() $V^{\overline x}$
becomes a left
$V^{\overline x}$
becomes a left
![]() $L_{K'}(\mathcal {T})$
-module. Consider the linear maps
$L_{K'}(\mathcal {T})$
-module. Consider the linear maps
 $$ \begin{align*}\rho^{\overline x}:K'\to V^{\overline x}, \quad h\mapsto h\cdot c^\infty.\end{align*} $$
$$ \begin{align*}\rho^{\overline x}:K'\to V^{\overline x}, \quad h\mapsto h\cdot c^\infty.\end{align*} $$
Clearly these maps are inverse isomorphisms of one-dimensional
![]() $K'$
-vector spaces.Restricting the scalars to K, the abelian group
$K'$
-vector spaces.Restricting the scalars to K, the abelian group
![]() $V^{\overline x}$
also has a left
$V^{\overline x}$
also has a left
![]() ${{L_K(\mathcal {T})}}$
-module structure: we denote this left
${{L_K(\mathcal {T})}}$
-module structure: we denote this left
![]() ${{L_K(\mathcal {T})}}$
-module by
${{L_K(\mathcal {T})}}$
-module by
![]() $V^{f}$
.
$V^{f}$
.
The set
![]() $\{c^\infty , \overline x c^\infty , \dots , {\overline x}^{ n-1}c^\infty \}$
is a K-basis of
$\{c^\infty , \overline x c^\infty , \dots , {\overline x}^{ n-1}c^\infty \}$
is a K-basis of
![]() $V^{f}$
. Denote by
$V^{f}$
. Denote by
![]() $G^f$
the K-subspace of
$G^f$
the K-subspace of
![]() ${{L_K(\mathcal {T})}}$
generated by
${{L_K(\mathcal {T})}}$
generated by
![]() $\{1, c, \dots , c^{n-1}\}$
. We note that any element in
$\{1, c, \dots , c^{n-1}\}$
. We note that any element in
![]() $G^f$
clearly commutes with
$G^f$
clearly commutes with
![]() $f(c)$
. The linear maps
$f(c)$
. The linear maps
 $$ \begin{align*}\rho^f:G^f \to V^f, \quad c^i\mapsto {\overline x}^{ i}c^\infty\ \end{align*} $$
$$ \begin{align*}\rho^f:G^f \to V^f, \quad c^i\mapsto {\overline x}^{ i}c^\infty\ \end{align*} $$
(for
![]() $0\leq i \leq n-1$
) define inverse isomorphisms of n-dimensional K-vector spaces. The map
$0\leq i \leq n-1$
) define inverse isomorphisms of n-dimensional K-vector spaces. The map
![]() $\rho ^f$
is the restriction to
$\rho ^f$
is the restriction to
![]() $G^f$
of the right multiplication map by
$G^f$
of the right multiplication map by
![]() $c^\infty $
:
$c^\infty $
:
 $$ \begin{align*}\rho:{{L_K(\mathcal{T})}}\to V^f,\ r\mapsto r\star c^\infty.\end{align*} $$
$$ \begin{align*}\rho:{{L_K(\mathcal{T})}}\to V^f,\ r\mapsto r\star c^\infty.\end{align*} $$
Clearly one has
 $$ \begin{align*}\sigma^f({\overline x}^{ i}c^\infty)\star c^\infty=c^i\star c^\infty={\overline x}^{ i}c^\infty=\rho^f(c^i)=\rho(c^i).\end{align*} $$
$$ \begin{align*}\sigma^f({\overline x}^{ i}c^\infty)\star c^\infty=c^i\star c^\infty={\overline x}^{ i}c^\infty=\rho^f(c^i)=\rho(c^i).\end{align*} $$
Lemma 2.4\; [Reference Ara and Rangaswamy6, Lemma 3.3]
Let
![]() $f(x) \in \mathcal {F}$
. Then the left
$f(x) \in \mathcal {F}$
. Then the left
![]() ${{L_K(\mathcal {T})}}$
-module
${{L_K(\mathcal {T})}}$
-module
![]() $V^f$
is simple.
$V^f$
is simple.
Proof Let U be a nonzero
![]() ${{L_K(\mathcal {T})}}$
-submodule of
${{L_K(\mathcal {T})}}$
-submodule of
![]() $V^f$
. Since
$V^f$
. Since
![]() $\{1,\overline x, \dots , {\overline x}^{ n-1}\}$
is a K basis for
$\{1,\overline x, \dots , {\overline x}^{ n-1}\}$
is a K basis for
![]() $K'$
and
$K'$
and
U is also a
![]() $K'$
-space. Since
$K'$
-space. Since
![]() $V^{\overline x}$
is a one-dimensional
$V^{\overline x}$
is a one-dimensional
![]() $K'$
-space, we have
$K'$
-space, we have
![]() $U=V^{\overline x}$
as
$U=V^{\overline x}$
as
![]() $K'$
-spaces and hence
$K'$
-spaces and hence
![]() $U=V^f$
as left
$U=V^f$
as left
![]() ${{L_K(\mathcal {T})}}$
-modules.▪
${{L_K(\mathcal {T})}}$
-modules.▪
Throughout the remainder of the article, we will often denote
![]() $L_K(\mathcal {T})$
simply by R.
$L_K(\mathcal {T})$
simply by R.
3 The Division Algorithm
The goal of this short section is to establish The Division Algorithm, Proposition 3.4. This result will subsequently be used to construct the injective envelope of each simple
![]() ${R}$
-module of the form
${R}$
-module of the form
![]() $V^f$
. We start by showing that each
$V^f$
. We start by showing that each
![]() $V^f$
is finitely presented. We also determine the annihilator of each
$V^f$
is finitely presented. We also determine the annihilator of each
![]() $V^f$
.
$V^f$
.
Lemma 3.1 Let
![]() $f(x) \in \mathcal {F}$
. Denoting by
$f(x) \in \mathcal {F}$
. Denoting by
![]() $\hat {\rho }_{f(c)}:R\to R$
the right multiplication map by
$\hat {\rho }_{f(c)}:R\to R$
the right multiplication map by
![]() $f(c)$
, we have the following short exact sequence of left R-modules:
$f(c)$
, we have the following short exact sequence of left R-modules:
 In particular:
In particular:
-
(1) The kernel of
 $\rho :R\to V^f$
is
$\rho :R\to V^f$
is
 $Rf(c)$
.
$Rf(c)$
. -
(2)
 $Rf(c)$
coincides with the two-sided ideal
$Rf(c)$
coincides with the two-sided ideal
 ${\mathrm {Ann}}_R(V^f)$
.
${\mathrm {Ann}}_R(V^f)$
.
Proof We have already observed that
![]() $\rho ^f$
is surjective, and thus
$\rho ^f$
is surjective, and thus
![]() $\rho $
is surjective as well.
$\rho $
is surjective as well.
For the injectivity of
![]() $\hat {\rho }_{f(c)}$
, we note that any element
$\hat {\rho }_{f(c)}$
, we note that any element
![]() $f(x)\in \mathcal F$
can be written as
$f(x)\in \mathcal F$
can be written as
![]() $f(x)=xg(x)-1$
, and so
$f(x)=xg(x)-1$
, and so
![]() $f(c)=cg(c)-1\in R$
, for a suitable polynomial
$f(c)=cg(c)-1\in R$
, for a suitable polynomial
![]() $g(x)\in K[x]$
. Let
$g(x)\in K[x]$
. Let
![]() $r\in R$
such that
$r\in R$
such that
![]() $\hat {\rho }_{f(c)}(r)=0$
. So
$\hat {\rho }_{f(c)}(r)=0$
. So
![]() $r(cg(c)-1) = 0$
, and thus
$r(cg(c)-1) = 0$
, and thus
![]() $rcg(c) = r$
, which recursively implies
$rcg(c) = r$
, which recursively implies
![]() $r(cg(c))^j = r$
for any
$r(cg(c))^j = r$
for any
![]() $j \geq 1$
. Now write
$j \geq 1$
. Now write
![]() $r=\sum _{i=1}^{n} k_i{\alpha _i}{\beta _i}^*$
, where the
$r=\sum _{i=1}^{n} k_i{\alpha _i}{\beta _i}^*$
, where the
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
are in
$\beta _i$
are in
![]() $ \text {Path}(\mathcal {T})$
. We note that, for any
$ \text {Path}(\mathcal {T})$
. We note that, for any
![]() $\beta \in \text {Path}(\mathcal {T})$
, there exists a suitable
$\beta \in \text {Path}(\mathcal {T})$
, there exists a suitable
![]() $m_{\beta }$
such that
$m_{\beta }$
such that
![]() $\beta ^* (cg(c))^{m_\beta }$
is either
$\beta ^* (cg(c))^{m_\beta }$
is either
![]() $0$
or an element of
$0$
or an element of
![]() $K\mathcal {T}$
. Now let N be the maximum in the set
$K\mathcal {T}$
. Now let N be the maximum in the set
![]() $\{ m_{\beta _1}, m_{\beta _2}, \dots , m_{\beta _n}\}$
. Then the above discussion shows that
$\{ m_{\beta _1}, m_{\beta _2}, \dots , m_{\beta _n}\}$
. Then the above discussion shows that
![]() $r (cg(c))^N$
is an element of R of the form
$r (cg(c))^N$
is an element of R of the form
![]() $\sum _{i=1}^{n} k_i \gamma _i$
, where
$\sum _{i=1}^{n} k_i \gamma _i$
, where
![]() $\gamma _i \in K\mathcal {T}$
for
$\gamma _i \in K\mathcal {T}$
for
![]() $1\leq i \leq n$
. That is,
$1\leq i \leq n$
. That is,
![]() $r (cg(c))^N \in K\mathcal {T}$
. But
$r (cg(c))^N \in K\mathcal {T}$
. But
![]() $r (cg(c))^N = r$
, so that
$r (cg(c))^N = r$
, so that
![]() $r \in K\mathcal {T}$
. However, the equation
$r \in K\mathcal {T}$
. However, the equation
![]() $r(cg(c)) = r$
(i.e.,
$r(cg(c)) = r$
(i.e.,
![]() $rf(c) = 0$
) has only the zero solution in
$rf(c) = 0$
) has only the zero solution in
![]() $K\mathcal {T}$
by a degree argument. So
$K\mathcal {T}$
by a degree argument. So
![]() $r = 0$
.
$r = 0$
.
(1) We now show
![]() ${\mathrm {Ker}} \rho =Rf(c)$
. Using [Reference Ara and Rangaswamy6, Lemma 3.2], we get that the annihilator of
${\mathrm {Ker}} \rho =Rf(c)$
. Using [Reference Ara and Rangaswamy6, Lemma 3.2], we get that the annihilator of
![]() $V^f$
is the two-sided ideal
$V^f$
is the two-sided ideal
 $I=\langle w, f\big |_v(c)\rangle $
. Notice that
$I=\langle w, f\big |_v(c)\rangle $
. Notice that
![]() $w=-w(cg(c)-1)=-wf(c)$
. Therefore, in the notation used herein, we have
$w=-w(cg(c)-1)=-wf(c)$
. Therefore, in the notation used herein, we have
![]() $I=\langle f(c)\rangle $
. Clearly I is contained in the kernel of
$I=\langle f(c)\rangle $
. Clearly I is contained in the kernel of
![]() $\rho $
. Let
$\rho $
. Let
![]() $r\in {\mathrm {Ker}}\rho $
. To prove that
$r\in {\mathrm {Ker}}\rho $
. To prove that
![]() $r\in I$
we have to check that
$r\in I$
we have to check that
![]() $r\star \overline x^{i}c^\infty =0$
for
$r\star \overline x^{i}c^\infty =0$
for
![]() $i=0,\dots , n-1;$
in other words, that left multiplication by r annihilates all the elements of a K-basis of
$i=0,\dots , n-1;$
in other words, that left multiplication by r annihilates all the elements of a K-basis of
![]() $V^f$
. We consider the left
$V^f$
. We consider the left
![]() $L_{K'}(\mathcal {T})$
-module
$L_{K'}(\mathcal {T})$
-module
![]() $V^{\overline x}$
. Since
$V^{\overline x}$
. Since
![]() $\overline x^{ i}$
is a scalar in
$\overline x^{ i}$
is a scalar in
![]() $L_{K'}(\mathcal {T})$
, and
$L_{K'}(\mathcal {T})$
, and
![]() $r\star c^\infty =0$
we have the following equality in
$r\star c^\infty =0$
we have the following equality in
![]() $V^{\overline x}$
:
$V^{\overline x}$
:
Since
![]() $V^{\overline x}=V^f$
as abelian groups, the desired result follows.
$V^{\overline x}=V^f$
as abelian groups, the desired result follows.
(2) We prove now that
![]() $Rf(c)=\langle f(c)\rangle $
. It is sufficient to check that the product of
$Rf(c)=\langle f(c)\rangle $
. It is sufficient to check that the product of
![]() $f(c)$
on the right by each element of the K-basis of
$f(c)$
on the right by each element of the K-basis of
![]() ${R} $
highlighted in Lemma 2.3 belongs to
${R} $
highlighted in Lemma 2.3 belongs to
![]() $Rf(c)$
. First of all observe that
$Rf(c)$
. First of all observe that
Then clearly each of
is in
![]() $ Rf(c).$
Assume
$ Rf(c).$
Assume
![]() $f(c)=-1+k_1c+\cdots +k_nc^n$
. Then
$f(c)=-1+k_1c+\cdots +k_nc^n$
. Then
 $$ \begin{align*} f(c)c^* & = -c^*+k_1cc^*+\cdots+k_nc^nc^* \\ & = -c^*+k_1(1-dd^*)+\cdots+k_nc^{n-1}(1-dd^*) \\ & = (-c^*+k_1+\cdots+k_nc^{n-1})-(k_1d+\cdots+k_nc^{n-1}d)d^* \\ & = c^*f(c)+rd^*\in Rf(c). \end{align*} $$
$$ \begin{align*} f(c)c^* & = -c^*+k_1cc^*+\cdots+k_nc^nc^* \\ & = -c^*+k_1(1-dd^*)+\cdots+k_nc^{n-1}(1-dd^*) \\ & = (-c^*+k_1+\cdots+k_nc^{n-1})-(k_1d+\cdots+k_nc^{n-1}d)d^* \\ & = c^*f(c)+rd^*\in Rf(c). \end{align*} $$
Then, by induction,
![]() $f(c)(c^*)^j\in Rf(c)$
for each
$f(c)(c^*)^j\in Rf(c)$
for each
![]() $j\geq 0$
. Finally,
$j\geq 0$
. Finally,
![]() $f(c)c^i(c^*)^j=c^if(c)(c^*)^j\in Rf(c)$
and
$f(c)c^i(c^*)^j=c^if(c)(c^*)^j\in Rf(c)$
and
![]() $f(c)d^*(c^*)^j=d^*f(c)(c^*)^j\in Rf(c)$
for each
$f(c)d^*(c^*)^j=d^*f(c)(c^*)^j\in Rf(c)$
for each
![]() $j\geq 0$
.▪
$j\geq 0$
.▪
Remark 3.2 As mentioned in the Preliminaries section, for
![]() $f(x) = -1 + \sum _{i=1}^n k_ix^i \text{in }\mathcal {F}$
, we define
$f(x) = -1 + \sum _{i=1}^n k_ix^i \text{in }\mathcal {F}$
, we define
![]() $f(c) = -1_R + \sum _{i=1}^n k_ic^i \in {R} $
. We established in Lemma 3.1(1) that right multiplication by
$f(c) = -1_R + \sum _{i=1}^n k_ic^i \in {R} $
. We established in Lemma 3.1(1) that right multiplication by
![]() $f(c)$
is injective. If one were to instead use the notation for
$f(c)$
is injective. If one were to instead use the notation for
![]() $f(c)$
which appears elsewhere in the literature (namely,
$f(c)$
which appears elsewhere in the literature (namely,
![]() $f(c) := -v + \sum _{i=1}^n k_ic^i$
), then the right multiplication map by
$f(c) := -v + \sum _{i=1}^n k_ic^i$
), then the right multiplication map by
![]() $f(c)$
would not be injective.
$f(c)$
would not be injective.
Lemma 3.3 For any
![]() $f(x)\in \mathcal {F}$
, the intersection of
$f(x)\in \mathcal {F}$
, the intersection of
![]() $Rf(c)$
with
$Rf(c)$
with
![]() $G^f$
is 0.
$G^f$
is 0.
Proof If
![]() $\ell $
belongs to
$\ell $
belongs to
![]() $Rf(c)\cap G^f$
, then
$Rf(c)\cap G^f$
, then
![]() $\rho (\ell )=0$
by Lemma 3.1(1), so that
$\rho (\ell )=0$
by Lemma 3.1(1), so that
 $$\begin{align*}0=\sigma^f(0) = \sigma^f(\rho(\ell))=\sigma^f(\rho^f(\ell)) =\ell\end{align*}$$
$$\begin{align*}0=\sigma^f(0) = \sigma^f(\rho(\ell))=\sigma^f(\rho^f(\ell)) =\ell\end{align*}$$
(using
![]() $\rho ^f(\ell ) = \rho (\ell )$
since
$\rho ^f(\ell ) = \rho (\ell )$
since
![]() $\ell \in G^f$
).▪
$\ell \in G^f$
).▪
Proposition 3.4 (The Division Algorithm)
Let
![]() $f(x) \in \mathcal {F}$
. For any
$f(x) \in \mathcal {F}$
. For any
![]() $\beta \in R$
there exists unique
$\beta \in R$
there exists unique
![]() $q_\beta \in R$
and
$q_\beta \in R$
and
 $r_\beta \in G^f$
such that
$r_\beta \in G^f$
such that
Proof Consider the element
 $r_\beta :=\sigma ^f(\rho (\beta ))$
. Clearly
$r_\beta :=\sigma ^f(\rho (\beta ))$
. Clearly
![]() $r_\beta $
belongs to
$r_\beta $
belongs to
![]() $G^f\subseteq R$
. Let us prove that the difference
$G^f\subseteq R$
. Let us prove that the difference
![]() $\beta -r_\beta $
belongs to
$\beta -r_\beta $
belongs to
![]() ${\mathrm {Ker}}\rho $
. By Lemma 2.3, it is sufficient to prove that
${\mathrm {Ker}}\rho $
. By Lemma 2.3, it is sufficient to prove that
![]() $\beta -r_\beta $
belongs to
$\beta -r_\beta $
belongs to
![]() ${\mathrm {Ker}}\rho $
for
${\mathrm {Ker}}\rho $
for
![]() $\beta \in \{v, w, d, c^i, c^id, c^i (c^*)^j, (c^*)^j, d^*(c^*)^j\}$
. Whenever
$\beta \in \{v, w, d, c^i, c^id, c^i (c^*)^j, (c^*)^j, d^*(c^*)^j\}$
. Whenever
![]() $\rho (\beta )=0$
, then also
$\rho (\beta )=0$
, then also
![]() $r_\beta =0$
and hence
$r_\beta =0$
and hence
![]() $\beta -r_\beta $
belongs to
$\beta -r_\beta $
belongs to
![]() ${\mathrm {Ker}}\rho $
in these cases. So the result immediately holds for
${\mathrm {Ker}}\rho $
in these cases. So the result immediately holds for
![]() $\beta = w, d, c^id,$
and
$\beta = w, d, c^id,$
and
![]() $ d^*(c^*)^j$
. For the others:
$ d^*(c^*)^j$
. For the others:
 $$ \begin{align*}r_v &= \sigma^f(c^\infty)= 1_K,\ r_{c^i}=\sigma^f(\overline x^i c^\infty)=c^i,\\r_{c^i(c^*)^j} &= \sigma^f(\overline x^{i-j} c^\infty)=\begin{cases} c^{i-j} & \text{if}\ i>j\geq 0, \\ 1_K & \text{if}\ i=j\geq 0, \\ (c^*)^{j-i} & \text{if}\ 0\leq i<j, \end{cases}\end{align*} $$
$$ \begin{align*}r_v &= \sigma^f(c^\infty)= 1_K,\ r_{c^i}=\sigma^f(\overline x^i c^\infty)=c^i,\\r_{c^i(c^*)^j} &= \sigma^f(\overline x^{i-j} c^\infty)=\begin{cases} c^{i-j} & \text{if}\ i>j\geq 0, \\ 1_K & \text{if}\ i=j\geq 0, \\ (c^*)^{j-i} & \text{if}\ 0\leq i<j, \end{cases}\end{align*} $$
and clearly
![]() $\ v-1_K$
,
$\ v-1_K$
,
![]() $c^i-r_{c^i}$
(which is
$c^i-r_{c^i}$
(which is
![]() $0$
), and
$0$
), and
![]() $c^i(c^*)^j-c^{i-j}$
for
$c^i(c^*)^j-c^{i-j}$
for
![]() $i>j$
,
$i>j$
,
![]() $c^i(c^*)^i-1_K$
,
$c^i(c^*)^i-1_K$
,
![]() $c^i(c^*)^j-(c^*)^{j-i}$
for
$c^i(c^*)^j-(c^*)^{j-i}$
for
![]() $i<j$
, belong to
$i<j$
, belong to
![]() ${\mathrm {Ker}}\rho $
. By Lemma 3.1,
${\mathrm {Ker}}\rho $
. By Lemma 3.1,
![]() ${\mathrm {Ker}}\rho =Rf(c)$
. Therefore
${\mathrm {Ker}}\rho =Rf(c)$
. Therefore
![]() $\beta -r_\beta =q_\beta f(c)$
for a suitable
$\beta -r_\beta =q_\beta f(c)$
for a suitable
![]() $q_\beta \in R$
.
$q_\beta \in R$
.
We now prove that
![]() $q_\beta \in R$
and
$q_\beta \in R$
and
 $r_\beta \in G^f$
are uniquely determined. Assume
$r_\beta \in G^f$
are uniquely determined. Assume
Then we have
![]() $r_1-r_2=(q_2-q_1)f(c)\in Rf(c)\cap G^f$
, which is 0 by Lemma 3.3. Therefore
$r_1-r_2=(q_2-q_1)f(c)\in Rf(c)\cap G^f$
, which is 0 by Lemma 3.3. Therefore
![]() $r_1=r_2$
and
$r_1=r_2$
and
![]() $(q_1-q_2)f(c)=r_1-r_2=0$
. Since by Lemma 3.1 right multiplication by
$(q_1-q_2)f(c)=r_1-r_2=0$
. Since by Lemma 3.1 right multiplication by
![]() $f(c)$
is injective, we have
$f(c)$
is injective, we have
![]() $q_1=q_2$
.▪
$q_1=q_2$
.▪
4 The Prüfer Modules
 $U^f$
$U^f$
For any simple
![]() ${R} $
-module
${R} $
-module
![]() $V^f$
there exists a uniserial
$V^f$
there exists a uniserial
![]() ${R} $
-module
${R} $
-module
![]() $U^f$
of infinite length, all of whose composition factors are isomorphic to
$U^f$
of infinite length, all of whose composition factors are isomorphic to
![]() $V^f$
. We call
$V^f$
. We call
![]() $U^f$
the Prüfer module associated to
$U^f$
the Prüfer module associated to
![]() $V^f$
. The construction of
$V^f$
. The construction of
![]() $U^f$
is a particular case of a method of building injective modules over general Leavitt path algebras described in [Reference Abrams, Mantese and Tonolo4].
$U^f$
is a particular case of a method of building injective modules over general Leavitt path algebras described in [Reference Abrams, Mantese and Tonolo4].
Lemma 4.1 For any
![]() $f(x)\in \mathcal F$
, the element
$f(x)\in \mathcal F$
, the element
![]() $f(c)\in R$
is neither a right zero divisor nor left-invertible.
$f(c)\in R$
is neither a right zero divisor nor left-invertible.
Proof The element
![]() $f(c)\in R$
is not a right zero divisor, since the right multiplication
$f(c)\in R$
is not a right zero divisor, since the right multiplication
![]() $\hat {\rho }_{f(c)}:R\to R$
is injective by Lemma 3.1. By that same Lemma we also have
$\hat {\rho }_{f(c)}:R\to R$
is injective by Lemma 3.1. By that same Lemma we also have
![]() $f(c)\star c^\infty =0$
in
$f(c)\star c^\infty =0$
in
![]() $V^f$
, and so
$V^f$
, and so
![]() $f(c)$
is not left invertible in R. ▪
$f(c)$
is not left invertible in R. ▪
The upshot of Lemma 4.1 is that we can apply the construction of the Prüfer module described in [Reference Abrams, Mantese and Tonolo4, Section 2] with
![]() $a=f(c)$
. For each natural number
$a=f(c)$
. For each natural number
![]() $n\geq 1$
, set
$n\geq 1$
, set
-
•
 $M_n^f:=R/Rf^n(c)$
, the nonzero cyclic left R-module generated by
$M_n^f:=R/Rf^n(c)$
, the nonzero cyclic left R-module generated by
 $1 + Rf^n(c)$
.
$1 + Rf^n(c)$
. -
•
 $\eta ^f_n:R\to M_n^f$
the canonical projection.
$\eta ^f_n:R\to M_n^f$
the canonical projection. -
•
 $\theta ^f_n:Rf(c)\to M^f_n$
,
$\theta ^f_n:Rf(c)\to M^f_n$
,
 $f(c)\mapsto 1+Rf^n(c)$
.
$f(c)\mapsto 1+Rf^n(c)$
. -
•
 $\psi _{i,\ell }:M_i^f\to M_\ell ^f$
,
$\psi _{i,\ell }:M_i^f\to M_\ell ^f$
,
 $1+Rf^i(c)\mapsto f^{\ell -i}(c)+Rf^\ell (c)$
for each
$1+Rf^i(c)\mapsto f^{\ell -i}(c)+Rf^\ell (c)$
for each
 $i\leq \ell $
; the cokernel of
$i\leq \ell $
; the cokernel of
 $\psi _{i,\ell }$
is isomorphic to
$\psi _{i,\ell }$
is isomorphic to
 $M_{\ell -i}^f$
.
$M_{\ell -i}^f$
.
With this notation, the diagram
 is a pushout diagram. By Lemma 2.4,
is a pushout diagram. By Lemma 2.4,
 $M_1^f\cong V^f$
is a simple R-module.
$M_1^f\cong V^f$
is a simple R-module.
We now establish the key property of the modules
 $\{M_i^f \ | \ i\in {\mathbb N}\}$
which will allow us to further apply additional machinery built in [Reference Abrams, Mantese and Tonolo4].
$\{M_i^f \ | \ i\in {\mathbb N}\}$
which will allow us to further apply additional machinery built in [Reference Abrams, Mantese and Tonolo4].
Lemma 4.2 Let
![]() $f(x) \in \mathcal {F}$
. Then the equation
$f(x) \in \mathcal {F}$
. Then the equation
![]() $f(c)\mathbb X=1+Rf^{n}(c)$
has no solutions in the left R-module
$f(c)\mathbb X=1+Rf^{n}(c)$
has no solutions in the left R-module
 $M^f_{n}$
.
$M^f_{n}$
.
Proof Let
 $m+Rf^n(c)\in M^f_n$
, with
$m+Rf^n(c)\in M^f_n$
, with
![]() $m\in R$
. By a repeated application of Proposition 3.4, we have
$m\in R$
. By a repeated application of Proposition 3.4, we have
where the elements
![]() $g_i$
(
$g_i$
(
![]() $1\leq i \leq n)$
belong to
$1\leq i \leq n)$
belong to
![]() $G^f$
. Therefore
$G^f$
. Therefore
 $$ \begin{align*}m-\big(g_1+g_2f(c)+\cdots+g _nf^{n-1}(c)\big)\in Rf^n(c).\end{align*} $$
$$ \begin{align*}m-\big(g_1+g_2f(c)+\cdots+g _nf^{n-1}(c)\big)\in Rf^n(c).\end{align*} $$
In particular we can assume that the representative m of the coset
![]() $m+Rf^n(c)$
is equal to
$m+Rf^n(c)$
is equal to
![]() $g_1+g_2f(c)+\cdots +g _nf^{n-1}(c)$
. Assume
$g_1+g_2f(c)+\cdots +g _nf^{n-1}(c)$
. Assume
![]() $f(c)m+Rf^n(c)=1+Rf^n(c)$
. Then
$f(c)m+Rf^n(c)=1+Rf^n(c)$
. Then
![]() $f(c)m-1$
belongs to
$f(c)m-1$
belongs to
![]() $Rf^n(c)$
. Therefore
$Rf^n(c)$
. Therefore
 $$ \begin{align*}f(c)\big(g_1+g_2f(c)+\cdots+g _nf^{n-1}(c)\big)-1\end{align*} $$
$$ \begin{align*}f(c)\big(g_1+g_2f(c)+\cdots+g _nf^{n-1}(c)\big)-1\end{align*} $$
belongs to
![]() $Rf^n(c)$
. Since as noted above
$Rf^n(c)$
. Since as noted above
![]() $f(c)g_i=g_if(c)$
for each
$f(c)g_i=g_if(c)$
for each
![]() $1\leq i \leq n$
, we get
$1\leq i \leq n$
, we get
Then
![]() $-1=rf(c)$
for a suitable
$-1=rf(c)$
for a suitable
![]() $r\in R$
and hence
$r\in R$
and hence
![]() $f(c)$
would be left invertible in R, which contradicts Lemma 4.1. ▪
$f(c)$
would be left invertible in R, which contradicts Lemma 4.1. ▪
With Lemma 4.2 established, we may apply [Reference Abrams, Mantese and Tonolo4, Proposition 2.2] to conclude that each left R-module
 $M^f_n$
(
$M^f_n$
(
![]() $n\in {\mathbb N}$
) is uniserial of length n. We define
$n\in {\mathbb N}$
) is uniserial of length n. We define
 $$\begin{align*}U^f:=\varinjlim\left\{M_i^f,\psi_{i,j}\right\}_{i\leq j},\end{align*}$$
$$\begin{align*}U^f:=\varinjlim\left\{M_i^f,\psi_{i,j}\right\}_{i\leq j},\end{align*}$$
and, for each
![]() $i\in {\mathbb N}$
, the induced monomorphism
$i\in {\mathbb N}$
, the induced monomorphism
 $$\begin{align*}\psi_i:M_i^f\to U^f.\end{align*}$$
$$\begin{align*}\psi_i:M_i^f\to U^f.\end{align*}$$
By [Reference Abrams, Mantese and Tonolo4, Proposition 2.4],
![]() $U^f$
is uniserial and artinian.
$U^f$
is uniserial and artinian.
For each
![]() $n\in \mathbb N$
, the element
$n\in \mathbb N$
, the element
is a generator of the submodule
 $\psi _n(M_n^f)$
of
$\psi _n(M_n^f)$
of
![]() $U^f$
. In the sequel, to simplify the notation, we will denote by
$U^f$
. In the sequel, to simplify the notation, we will denote by
 $M_n^f$
the submodule
$M_n^f$
the submodule
 $\psi _n(M_n^f)$
of
$\psi _n(M_n^f)$
of
![]() $U^f$
, in fact identifying
$U^f$
, in fact identifying
 $M_n^f$
with its image in
$M_n^f$
with its image in
![]() $U^f$
through the monomorphism
$U^f$
through the monomorphism
![]() $\psi _n$
. Let
$\psi _n$
. Let
![]() $r\alpha _{n,f}=r+Rf^n(c)$
be a generic element of
$r\alpha _{n,f}=r+Rf^n(c)$
be a generic element of
![]() $U^f$
. Applying the Division Algorithm (Proposition 3.4)
$U^f$
. Applying the Division Algorithm (Proposition 3.4)
![]() $n-1$
times, we get
$n-1$
times, we get
 $$ \begin{align*} r\alpha_{n,f}=r+Rf^n(c)& = g^f_0+g^f_1f(c)+\cdots+g^f_{n-1}f^{n-1}(c)+Rf^n(c) \\ & = \big(g^f_0+g^f_1f(c)+\cdots+g^f_{n-1}f^{n-1}(c)\big)\alpha_{n,f} \end{align*} $$
$$ \begin{align*} r\alpha_{n,f}=r+Rf^n(c)& = g^f_0+g^f_1f(c)+\cdots+g^f_{n-1}f^{n-1}(c)+Rf^n(c) \\ & = \big(g^f_0+g^f_1f(c)+\cdots+g^f_{n-1}f^{n-1}(c)\big)\alpha_{n,f} \end{align*} $$
for suitable
![]() $g^f_0$
, …,
$g^f_0$
, …,
 $g^f_{n-1}\in G^f$
.
$g^f_{n-1}\in G^f$
.
Remark 4.3 As an immediate consequence of Lemma 4.2, we see that any
![]() ${R} $
-module of the form
${R} $
-module of the form
 $M_i^f$
is not injective, because the map
$M_i^f$
is not injective, because the map
 $\psi : R \to M_i^f$
defined by setting
$\psi : R \to M_i^f$
defined by setting
![]() $\psi (1) = 1+ Rf^i(c)$
does not factor through the monomorphism
$\psi (1) = 1+ Rf^i(c)$
does not factor through the monomorphism
![]() $\hat {\rho }_{f(c)}: R\to R$
. In particular, the simple module
$\hat {\rho }_{f(c)}: R\to R$
. In particular, the simple module
 $M_1^f \cong V^f$
is not injective. However, in the next section, we will show that each
$M_1^f \cong V^f$
is not injective. However, in the next section, we will show that each
 $U^f =\varinjlim \{M_i^f\} $
is an injective left
$U^f =\varinjlim \{M_i^f\} $
is an injective left
![]() ${R} $
-module.
${R} $
-module.
5 The Left Ideals in
 ${R}=L_K\mbox{(}\mathcal {T}\mbox{)}$
${R}=L_K\mbox{(}\mathcal {T}\mbox{)}$
In order to test whether a module is injective by applying Baer’s criterion, we must have available a complete description of the left ideals in
![]() ${R} $
. We will show that any ideal of R is either a direct summand of a left ideal of the form
${R} $
. We will show that any ideal of R is either a direct summand of a left ideal of the form
![]() $Rp(c)$
(where
$Rp(c)$
(where
![]() $p(x) \in K[x]$
has
$p(x) \in K[x]$
has
![]() $p(0) = 1$
), or a direct summand of
$p(0) = 1$
), or a direct summand of
![]() $\text {Soc}(R)$
. We recall that
$\text {Soc}(R)$
. We recall that
![]() $\mathcal P$
denotes the set of polynomials
$\mathcal P$
denotes the set of polynomials
![]() $p(x)\in K[x]$
with
$p(x)\in K[x]$
with
![]() $p(0)\not =0$
.
$p(0)\not =0$
.
Remark 5.1 We collect up in this remark some properties of
![]() $J := \text {Soc}({R} )$
, the socle of R. It is well known (or see [Reference Abrams, Ara and Siles Molina1, Theorem 2.6.14]) that
$J := \text {Soc}({R} )$
, the socle of R. It is well known (or see [Reference Abrams, Ara and Siles Molina1, Theorem 2.6.14]) that
![]() $J = \langle w \rangle $
as a two-sided ideal. Further, as left R-ideals,
$J = \langle w \rangle $
as a two-sided ideal. Further, as left R-ideals,
Moreover, each summand of the form
![]() $Rc^idd^* (c^*)^i$
is isomorphic to the simple module
$Rc^idd^* (c^*)^i$
is isomorphic to the simple module
![]() $Rw$
.
$Rw$
.
It has been noted elsewhere in the literature (see e.g. [Reference Rangaswamy16, Example 4.5]) that
![]() $R / J \cong K[x,x^{-1}]$
as K-algebras. This isomorphism is also as left R-modules (and left
$R / J \cong K[x,x^{-1}]$
as K-algebras. This isomorphism is also as left R-modules (and left
![]() $R/J$
-modules), which is not hard to see directly. Indeed, the standard monomials in R end (on the right) with a term having one of the forms
$R/J$
-modules), which is not hard to see directly. Indeed, the standard monomials in R end (on the right) with a term having one of the forms
![]() $v, w, d, d^*, c^i, c^id, c^i (c^*)^j, (c^*)^j, \text{ or } d^*(c^*)^j$
. Moreover, we have
$v, w, d, d^*, c^i, c^id, c^i (c^*)^j, (c^*)^j, \text{ or } d^*(c^*)^j$
. Moreover, we have
So the only terms which survive mod J are powers of c (positive or negative).
The standard bijective correspondence between left ideals of R which contain J and submodules of
![]() $R/J$
, together with the well-known principal ideal structure of
$R/J$
, together with the well-known principal ideal structure of
![]() $K[x,x^{-1}]$
, yields that every left ideal of R which properly contains J is of the form
$K[x,x^{-1}]$
, yields that every left ideal of R which properly contains J is of the form
 $Rp\big |_v(c)$
for some
$Rp\big |_v(c)$
for some
![]() $p(x)\in \mathcal P$
. But
$p(x)\in \mathcal P$
. But
![]() $w\in J$
and
$w\in J$
and
 $J \subseteq Rp\big |_v(c) $
together yield that
$J \subseteq Rp\big |_v(c) $
together yield that
 $Rp\big |_v(c) = Rp(c)$
. The upshot is that every left ideal of R which properly contains J is of the form
$Rp\big |_v(c) = Rp(c)$
. The upshot is that every left ideal of R which properly contains J is of the form
![]() $Rp(c)$
for some
$Rp(c)$
for some
![]() $p(x) \in \mathcal P$
. ▪
$p(x) \in \mathcal P$
. ▪
Proposition 5.2 Let
![]() $f(x)\in \mathcal {F}$
. Then
$f(x)\in \mathcal {F}$
. Then
![]() $\text {Hom}_R(J, U^f) = \{0\}$
.
$\text {Hom}_R(J, U^f) = \{0\}$
.
Proof For any
![]() $f(x)\in \mathcal {F}$
we have
$f(x)\in \mathcal {F}$
we have
![]() $\text {Hom}_R(Rw, V^f) \cong w V^f = \{0\}$
, because
$\text {Hom}_R(Rw, V^f) \cong w V^f = \{0\}$
, because
![]() $V^f $
is generated as a K-space by elements of the form
$V^f $
is generated as a K-space by elements of the form
![]() $\overline {x}^i c^\infty $
(
$\overline {x}^i c^\infty $
(
![]() $0\leq i \leq \text {deg}(f)-1$
), and
$0\leq i \leq \text {deg}(f)-1$
), and
![]() $w \overline {x}^i c^\infty = \overline {x}^i wc^\infty = 0$
.
$w \overline {x}^i c^\infty = \overline {x}^i wc^\infty = 0$
.
By [Reference Abrams, Mantese and Tonolo4, Proposition 2.2], the composition factors of the finitely generated submodules of
![]() $U^f$
are isomorphic to
$U^f$
are isomorphic to
![]() $V^f$
. This together with the previous paragraph implies
$V^f$
. This together with the previous paragraph implies
![]() $\text {Hom}_R(Rw, U^f) = \{0\}$
.
$\text {Hom}_R(Rw, U^f) = \{0\}$
.
As noted in Remark 5.1,
![]() $J = Rw \oplus (\oplus _{i\in \mathbb Z^+} Rc^idd^* (c^*)^i) \cong \oplus _{i\in \mathbb Z^+}Rw.$
Then
$J = Rw \oplus (\oplus _{i\in \mathbb Z^+} Rc^idd^* (c^*)^i) \cong \oplus _{i\in \mathbb Z^+}Rw.$
Then
 $\text {Hom}_R(J, U^f) \cong \text {Hom}_R(\oplus _{i\in \mathbb Z^+}Rw, U^f) \cong \prod _{i\in \mathbb Z^+}\text {Hom}_R(Rw, U^f) = \prod _{i\in \mathbb Z^+}\{0\} = \{0\}$
. ▪
$\text {Hom}_R(J, U^f) \cong \text {Hom}_R(\oplus _{i\in \mathbb Z^+}Rw, U^f) \cong \prod _{i\in \mathbb Z^+}\text {Hom}_R(Rw, U^f) = \prod _{i\in \mathbb Z^+}\{0\} = \{0\}$
. ▪
Proposition 5.3 Let I be a left ideal of R. Then either:
-
1) There exists
 $p(x) \in \mathcal {P}$
for which I is a direct summand of
$p(x) \in \mathcal {P}$
for which I is a direct summand of
 $Rp(c)$
, or
$Rp(c)$
, or -
2) I is a direct summand of
 $J = \mathrm {Soc}(R)$
.
$J = \mathrm {Soc}(R)$
.
Proof Case 1. J is properly contained in I. By Remark 5.1, we have
![]() $I = Rp(c)$
for some
$I = Rp(c)$
for some
![]() $p(x) \in \mathcal P$
, and so we are done in this case.
$p(x) \in \mathcal P$
, and so we are done in this case.
Case 2. Suppose I is not contained in J, and I does not contain J. Consider the left ideal
![]() $A = I+J$
. Then A properly contains J, so we may apply the Case 1 analysis to A, so that
$A = I+J$
. Then A properly contains J, so we may apply the Case 1 analysis to A, so that
![]() $A = Rq(c) $
for some
$A = Rq(c) $
for some
![]() $q(x) \in \mathcal P$
. Since the socle J is a direct sum of simple left R-modules, we have
$q(x) \in \mathcal P$
. Since the socle J is a direct sum of simple left R-modules, we have
![]() $J = (I\cap J) \oplus B$
for some left ideal B of R contained in J. It is straightforward to show that this implies
$J = (I\cap J) \oplus B$
for some left ideal B of R contained in J. It is straightforward to show that this implies
![]() $A = I \oplus B$
. But then I has been shown to be a direct summand of
$A = I \oplus B$
. But then I has been shown to be a direct summand of
![]() $A = Rq(c)$
, as desired.
$A = Rq(c)$
, as desired.
Case 3. Suppose I is contained in J. Then the semisimplicity of J immediately implies that I is a direct summand of J. ▪
Remark 5.4 We note that Gerritzen in [Reference Gerritzen11, Proposition 3.4] established that all one-sided ideals of the Jacobson algebra
![]() $\mathcal {R}$
are either principal, or contained in the socle of
$\mathcal {R}$
are either principal, or contained in the socle of
![]() $\mathcal {R}$
. Similarly, Iovanov and Sistko in [Reference Iovanov and Sistko12, Theorem 2 and Corollary 1] establish the same type of result in
$\mathcal {R}$
. Similarly, Iovanov and Sistko in [Reference Iovanov and Sistko12, Theorem 2 and Corollary 1] establish the same type of result in
![]() $\mathcal {R}$
, in terms of polynomials in the element x of
$\mathcal {R}$
, in terms of polynomials in the element x of
![]() $\mathcal {R}$
. By a previous observation, the element c of
$\mathcal {R}$
. By a previous observation, the element c of
![]() ${R} $
corresponds to the element
${R} $
corresponds to the element
![]() ${Y^2X} $
of
${Y^2X} $
of
![]() $\mathcal {R}$
. The point to be made here is that while these two results from [Reference Gerritzen11] and [Reference Iovanov and Sistko12] are clearly related to the conclusion of Proposition 5.3, Proposition 5.3 yields a more explicit description of these left ideals, in a form which will be quite useful for us in the sequel.
$\mathcal {R}$
. The point to be made here is that while these two results from [Reference Gerritzen11] and [Reference Iovanov and Sistko12] are clearly related to the conclusion of Proposition 5.3, Proposition 5.3 yields a more explicit description of these left ideals, in a form which will be quite useful for us in the sequel.
Corollary 5.5 In order to apply the Baer criterion to determine the injectivity of a left R-module, we need only check injectivity with respect to J, and with respect to left ideals of the form
![]() $Rp(c)$
for
$Rp(c)$
for
![]() $p(x) \in \mathcal P$
.
$p(x) \in \mathcal P$
.
6 A (Minimal) Injective Cogenerator for
 ${R}=L_K\mbox{(}\mathcal {T}\mbox{)}$
${R}=L_K\mbox{(}\mathcal {T}\mbox{)}$
In this final section we use the machinery developed above to achieve the main goal of this article; namely, to identify a minimal injective cogenerator for
![]() ${R} $
. In the first portion of the section we show that the injective envelope of each of the simple modules
${R} $
. In the first portion of the section we show that the injective envelope of each of the simple modules
![]() $V^f$
is the Prüfer module
$V^f$
is the Prüfer module
![]() $U^f$
. We then proceed to construct, using completely different methods, the injective envelope of the simple module
$U^f$
. We then proceed to construct, using completely different methods, the injective envelope of the simple module
![]() $Rw$
. We finish the section by appropriately combining these two types of injective modules.
$Rw$
. We finish the section by appropriately combining these two types of injective modules.
In previous work by the three authors [Reference Abrams, Mantese and Tonolo4], modules of the form
![]() $U^{x-1}$
over general Leavitt path algebras
$U^{x-1}$
over general Leavitt path algebras
![]() $L_K(E)$
were shown to be injective, in case the corresponding cycle c is maximal. Establishing injectivity of such
$L_K(E)$
were shown to be injective, in case the corresponding cycle c is maximal. Establishing injectivity of such
![]() $U^{x-1}$
over the Leavitt path algebra
$U^{x-1}$
over the Leavitt path algebra
![]() $L_K(E)$
of an arbitrary finite graph E required an analysis of the structure of
$L_K(E)$
of an arbitrary finite graph E required an analysis of the structure of
![]() $U^{x-1}$
viewed as a right module over its endomorphism ring. In the present setting, we need not invoke this right module structure, the reason being that in the particular case
$U^{x-1}$
viewed as a right module over its endomorphism ring. In the present setting, we need not invoke this right module structure, the reason being that in the particular case
![]() $R = L_K(\mathcal {T})$
we have a complete description of the left R-ideals, and therefore we are in position to productively use Baer’s criterion to establish injectivity of left R-modules.
$R = L_K(\mathcal {T})$
we have a complete description of the left R-ideals, and therefore we are in position to productively use Baer’s criterion to establish injectivity of left R-modules.
6.1 The injective envelope of
 $V^f$
$V^f$
We start by establishing that
![]() $U^f$
is injective for any
$U^f$
is injective for any
![]() $f(x)\in \mathcal {F}$
. By Proposition 5.2 we have
$f(x)\in \mathcal {F}$
. By Proposition 5.2 we have
![]() $\operatorname {Hom}_R(J,U^f) = 0$
. By Corollary 5.5, in order to check the injectivity of
$\operatorname {Hom}_R(J,U^f) = 0$
. By Corollary 5.5, in order to check the injectivity of
![]() $U^f$
it is enough to check the Baer criterion with respect to left ideals of the form
$U^f$
it is enough to check the Baer criterion with respect to left ideals of the form
![]() $Rp(c)$
for
$Rp(c)$
for
![]() $p(x) \in \mathcal P$
.
$p(x) \in \mathcal P$
.
Lemma 6.1 Let
![]() $f(x)\in \mathcal {F}$
, and let
$f(x)\in \mathcal {F}$
, and let
![]() $g(x) \in K[x]$
which is not divisible by
$g(x) \in K[x]$
which is not divisible by
![]() $f(x)$
. Then there exists a polynomial
$f(x)$
. Then there exists a polynomial
![]() $\beta (x)\in K[x]$
such that
$\beta (x)\in K[x]$
such that
![]() $\beta (c)g(c) \in 1+Rf^n(c)$
. In particular,
$\beta (c)g(c) \in 1+Rf^n(c)$
. In particular,
![]() $g(c)+Rf^n(c)$
is a generator of the uniserial module
$g(c)+Rf^n(c)$
is a generator of the uniserial module
 $M_n^f$
.
$M_n^f$
.
Proof Since
![]() $f(x)$
is irreducible, nondivisibility implies
$f(x)$
is irreducible, nondivisibility implies
![]() $\text {gcd}(f^n(x), g(x))=1$
. Then there exist polynomials
$\text {gcd}(f^n(x), g(x))=1$
. Then there exist polynomials
![]() $\alpha (x)$
,
$\alpha (x)$
,
![]() $\beta (x)\in K[x]$
such that
$\beta (x)\in K[x]$
such that
![]() $1=\alpha (x)f^n(x)+\beta (x)g(x)$
. Therefore
$1=\alpha (x)f^n(x)+\beta (x)g(x)$
. Therefore
![]() $\beta (c)g(c)=1-\alpha (c)f^n(c)$
and hence
$\beta (c)g(c)=1-\alpha (c)f^n(c)$
and hence
![]() $\beta (c)g(c)\in 1+Rf^n(c).$
▪
$\beta (c)g(c)\in 1+Rf^n(c).$
▪
Proposition 6.2 Let
![]() $f(x) \in \mathcal {F}$
. Then the uniserial left R-module
$f(x) \in \mathcal {F}$
. Then the uniserial left R-module
![]() $U^f$
is injective.
$U^f$
is injective.
Proof By Proposition 5.2 and Corollary 5.5, it suffices to show, for any
![]() $p(x)\in \mathcal P$
and
$p(x)\in \mathcal P$
and
![]() $\varphi :Rp(c)\to U^f$
, that
$\varphi :Rp(c)\to U^f$
, that
![]() $\varphi $
extends to a map
$\varphi $
extends to a map
![]() $\overline \varphi :R\to U^f$
. Clearly the zero map extends to R. So suppose
$\overline \varphi :R\to U^f$
. Clearly the zero map extends to R. So suppose
![]() $\varphi \not =0$
. Let
$\varphi \not =0$
. Let
![]() $n\in \mathbb N$
be minimal such that
$n\in \mathbb N$
be minimal such that
 $\operatorname {Im}\varphi \subseteq M_{n}^f$
, and write
$\operatorname {Im}\varphi \subseteq M_{n}^f$
, and write
![]() $\varphi (p(c))=m+Rf^n(c)$
for some
$\varphi (p(c))=m+Rf^n(c)$
for some
![]() $m\in R$
. As noted in the proof of Lemma 4.2, we can choose
$m\in R$
. As noted in the proof of Lemma 4.2, we can choose
where
![]() $g_i \in G^f$
(
$g_i \in G^f$
(
![]() $1\leq i \leq n$
). In particular, m commutes with all polynomials in c.
$1\leq i \leq n$
). In particular, m commutes with all polynomials in c.
By the construction of the direct limit
![]() $U^f$
, for each
$U^f$
, for each
![]() $i\geq 0$
we have
$i\geq 0$
we have
Let
![]() $p(x)=f^\ell (x)p_0(x)$
with
$p(x)=f^\ell (x)p_0(x)$
with
![]() $\ell \geq 0$
and
$\ell \geq 0$
and
![]() $f(x) \nmid p_0(x)$
. By Lemma 6.1 there exists
$f(x) \nmid p_0(x)$
. By Lemma 6.1 there exists
![]() $\beta _0(x)\in K[x]$
such that
$\beta _0(x)\in K[x]$
such that
![]() $\beta _0(c)p_0(c)=p_0(c)\beta _0(c)$
belongs to
$\beta _0(c)p_0(c)=p_0(c)\beta _0(c)$
belongs to
![]() $1+Rf^{n+\ell }(c)$
. Therefore
$1+Rf^{n+\ell }(c)$
. Therefore
 $$ \begin{align*}p(c)(\beta_0(c)m+Rf^{n+\ell}(c))&=f^\ell(c)p_0(c)\beta_0(c)m+Rf^{n+\ell}(c)\\&= f^\ell(c)m+Rf^{n+\ell}(c)=\varphi(p(c)).\end{align*} $$
$$ \begin{align*}p(c)(\beta_0(c)m+Rf^{n+\ell}(c))&=f^\ell(c)p_0(c)\beta_0(c)m+Rf^{n+\ell}(c)\\&= f^\ell(c)m+Rf^{n+\ell}(c)=\varphi(p(c)).\end{align*} $$
Thus the morphism
![]() $\overline {\varphi }: R\to U^f$
defined by setting
$\overline {\varphi }: R\to U^f$
defined by setting
![]() $\overline {\varphi }(1) = \beta _0(c)m+Rf^{n+\ell }(c)$
extends
$\overline {\varphi }(1) = \beta _0(c)m+Rf^{n+\ell }(c)$
extends
![]() $\varphi $
.▪
$\varphi $
.▪
Corollary 6.3 Let
![]() $f(x) \in \mathcal {F}$
. Then
$f(x) \in \mathcal {F}$
. Then
![]() $U^f$
is the injective envelope of
$U^f$
is the injective envelope of
![]() $V^f$
.
$V^f$
.
Proof The simple module
![]() $V^f$
is essential in
$V^f$
is essential in
![]() $U^f$
, since
$U^f$
, since
![]() $U^f$
is uniserial. The injective envelope of any module is an injective module in which the given module sits as an essential submodule. ▪
$U^f$
is uniserial. The injective envelope of any module is an injective module in which the given module sits as an essential submodule. ▪
In general the direct sum of infinitely many injective modules need not be injective. (Over an arbitrary ring S, any infinite direct sum of injectives is injective if and only if S is Noetherian; and clearly
![]() $R = L_K(\mathcal {T})$
is non-Noetherian, because, for example, J is a non-finitely-generated left ideal of R.) This observation notwithstanding, we close this subsection with the following.
$R = L_K(\mathcal {T})$
is non-Noetherian, because, for example, J is a non-finitely-generated left ideal of R.) This observation notwithstanding, we close this subsection with the following.
Proposition 6.4 Let
![]() $U=\oplus _{\lambda \in \Lambda } I_{\lambda }$
where, for each
$U=\oplus _{\lambda \in \Lambda } I_{\lambda }$
where, for each
![]() $\lambda \in \Lambda $
, there exists
$\lambda \in \Lambda $
, there exists
![]() $f(x) \in \mathcal {F}$
such that
$f(x) \in \mathcal {F}$
such that
![]() $I_{\lambda }$
is an injective module isomorphic to
$I_{\lambda }$
is an injective module isomorphic to
![]() $U^f$
. Then U is injective.
$U^f$
. Then U is injective.
Proof We again invoke Corollary 5.5, and so we need only establish two steps.
Step 1: Consider the ideal J and let
![]() $\varphi :J\to U$
. We show that
$\varphi :J\to U$
. We show that
![]() $\varphi =0$
. Suppose otherwise. The image of
$\varphi =0$
. Suppose otherwise. The image of
![]() $\varphi $
is a semisimple module, isomorphic to a direct sum of copies of
$\varphi $
is a semisimple module, isomorphic to a direct sum of copies of
![]() $Rw$
. But each
$Rw$
. But each
![]() $U^f$
has essential socle isomorphic to
$U^f$
has essential socle isomorphic to
![]() $V^f$
and so the socle of U is isomorphic to the direct sum of copies of the
$V^f$
and so the socle of U is isomorphic to the direct sum of copies of the
![]() $V^f$
s. Since
$V^f$
s. Since
![]() $Rw \not \cong V^f$
for any f, we get a contradiction.
$Rw \not \cong V^f$
for any f, we get a contradiction.
Step 2: Let
![]() $p(x)$
be a polynomial in
$p(x)$
be a polynomial in
![]() $\mathcal P$
. If
$\mathcal P$
. If
![]() $\varphi : Rp(c) \rightarrow U$
then the image of
$\varphi : Rp(c) \rightarrow U$
then the image of
![]() $\varphi $
is finitely generated, and so is contained in
$\varphi $
is finitely generated, and so is contained in
 $\hat {U} \cong \oplus _{i=1}^n U^{f_i}$
for some appropriate
$\hat {U} \cong \oplus _{i=1}^n U^{f_i}$
for some appropriate
![]() $f_i$
s. But
$f_i$
s. But
![]() $\hat {U}$
is injective because each
$\hat {U}$
is injective because each
![]() $U^{f_i}$
is (and the sum is finite), and so f extends. ▪
$U^{f_i}$
is (and the sum is finite), and so f extends. ▪
6.2 The injective envelope of
 $Rw$
$Rw$
Having identified the injective envelope of each of the simple modules
![]() $V^f$
(
$V^f$
(
![]() $f(x) \in \mathcal {F}$
), we now turn our attention to identifying the injective envelope of the simple module
$f(x) \in \mathcal {F}$
), we now turn our attention to identifying the injective envelope of the simple module
![]() $Rw$
.
$Rw$
.
Lemma 6.5 The set
![]() $\{w,d,cd,c^2d,\dots , c^id,\dots \}$
is a K-basis of the simple module
$\{w,d,cd,c^2d,\dots , c^id,\dots \}$
is a K-basis of the simple module
![]() $Rw$
. That is, any element of
$Rw$
. That is, any element of
![]() $Rw$
can be written uniquely as
$Rw$
can be written uniquely as
![]() $kw+\sum _{i=0}^n k_ic^id=kw+(\sum _{i=0}^n k_ic^i)d$
, with
$kw+\sum _{i=0}^n k_ic^id=kw+(\sum _{i=0}^n k_ic^i)d$
, with
![]() $k, k_i \in K$
.
$k, k_i \in K$
.
Proof It is easily shown that
![]() $Rw=Rd^*d = Rd$
. By Lemma 2.3, the elements
$Rw=Rd^*d = Rd$
. By Lemma 2.3, the elements
form a K-basis of R. Since
we conclude that a basis of
![]() $Rw=Rd$
is formed by multiplying the remaining elements of the K-basis for R on the right by d, namely
$Rw=Rd$
is formed by multiplying the remaining elements of the K-basis for R on the right by d, namely
which gives the result. ▪
In the following sense, the simple module
![]() $Rw$
behaves similarly to the simple modules
$Rw$
behaves similarly to the simple modules
![]() $V^f$
(see Remark 4.3).
$V^f$
(see Remark 4.3).
Proposition 6.6 The left
![]() ${R} $
-module
${R} $
-module
![]() ${R} w$
is not injective. In particular, the map
${R} w$
is not injective. In particular, the map
![]() $\chi = \rho _d: R \to Rw$
(via
$\chi = \rho _d: R \to Rw$
(via
![]() $1 \mapsto d$
) does not factor through the monomorphism
$1 \mapsto d$
) does not factor through the monomorphism
![]() $\hat {\rho }_{f(c)}: R \to R$
for any
$\hat {\rho }_{f(c)}: R \to R$
for any
![]() $f(x)\in \mathcal {F}$
.
$f(x)\in \mathcal {F}$
.
Proof Write
![]() $f(c)=-1+h_1c+\cdots +h_mc^m$
with
$f(c)=-1+h_1c+\cdots +h_mc^m$
with
![]() $h_m\not =0$
(
$h_m\not =0$
(
![]() $m\geq 1$
). The existence of a map
$m\geq 1$
). The existence of a map
![]() $\xi :R\to Rw$
such that
$\xi :R\to Rw$
such that
![]() $\xi \circ \hat {\rho }_{f(c)}=\chi $
is equivalent to the solvability of the equation
$\xi \circ \hat {\rho }_{f(c)}=\chi $
is equivalent to the solvability of the equation
![]() $f(c)x=d$
in
$f(c)x=d$
in
![]() $Rw$
. We show that no such
$Rw$
. We show that no such
![]() $x\in Rw$
exists. Assume to the contrary that there is such a solution, so necessarily
$x\in Rw$
exists. Assume to the contrary that there is such a solution, so necessarily
![]() $x\neq 0$
. By Lemma 6.5 we may write
$x\neq 0$
. By Lemma 6.5 we may write
![]() $x = kw+\sum _{i=0}^n k_ic^id$
for some (unique)
$x = kw+\sum _{i=0}^n k_ic^id$
for some (unique)
![]() $k, k_0, \dots , k_n \in K$
, where not all of these are
$k, k_0, \dots , k_n \in K$
, where not all of these are
![]() $0$
. Then
$0$
. Then
![]() $f(c)x=d$
implies
$f(c)x=d$
implies
 $$ \begin{align*}f(c)\left(kw+\sum_{i=0}^n k_ic^id\right)=d.\end{align*} $$
$$ \begin{align*}f(c)\left(kw+\sum_{i=0}^n k_ic^id\right)=d.\end{align*} $$
Multiplying both sides of this equation on the left by w we get
![]() $-kw=0$
, so
$-kw=0$
, so
![]() $k=0$
. This yields that there are nonzero terms among the elements
$k=0$
. This yields that there are nonzero terms among the elements
![]() $k_0, k_1, \dots , k_n$
. We may assume
$k_0, k_1, \dots , k_n$
. We may assume
![]() $k_n \neq 0$
. Now we have
$k_n \neq 0$
. Now we have
 $$ \begin{align*}f(c)\left(\sum_{i=0}^n k_ic^id\right)=d.\end{align*} $$
$$ \begin{align*}f(c)\left(\sum_{i=0}^n k_ic^id\right)=d.\end{align*} $$
But this is impossible, as the following shows. Expanding
 $f(c)\big (\sum _{i=0}^n k_ic^id\big )$
, we see the coefficient on the
$f(c)\big (\sum _{i=0}^n k_ic^id\big )$
, we see the coefficient on the
![]() $c^{m+n}d$
term is
$c^{m+n}d$
term is
![]() $h_mk_n$
. But the equation
$h_mk_n$
. But the equation
 $f(c)\big (\sum _{i=0}^n k_ic^id\big ) = d$
implies that the coefficient on the
$f(c)\big (\sum _{i=0}^n k_ic^id\big ) = d$
implies that the coefficient on the
![]() $c^{m+n}d$
term is
$c^{m+n}d$
term is
![]() $0$
. So we get
$0$
. So we get
![]() $0 = h_mk_n$
which, as
$0 = h_mk_n$
which, as
![]() $h_m\neq 0$
, gives
$h_m\neq 0$
, gives
![]() $k_n = 0$
, a contradiction. ▪
$k_n = 0$
, a contradiction. ▪
We seek to describe the injective envelope of
![]() $Rw$
. With Proposition 6.6 in hand, this process will require us to build a module which is strictly larger than
$Rw$
. With Proposition 6.6 in hand, this process will require us to build a module which is strictly larger than
![]() $Rw$
.
$Rw$
.
Definition 6.1 Let
![]() $\hat {W}$
denote the K-space whose elements are “formal series” of the form
$\hat {W}$
denote the K-space whose elements are “formal series” of the form
The K-space
![]() $\hat {W}$
has a natural structure as a left R-module, where for
$\hat {W}$
has a natural structure as a left R-module, where for
![]() $y=k_{-1}w+k_0d+k_1cd+\cdots +k_ic^id+\cdots $
one defines
$y=k_{-1}w+k_0d+k_1cd+\cdots +k_ic^id+\cdots $
one defines
By Lemma 6.5,
![]() $Rw $
is the R-submodule of
$Rw $
is the R-submodule of
![]() $\hat {W}$
consisting of those elements for which
$\hat {W}$
consisting of those elements for which
![]() $k_i = 0$
for all
$k_i = 0$
for all
![]() $i>N$
for some
$i>N$
for some
![]() $N \in {\mathbb N}$
, i.e.,
$N \in {\mathbb N}$
, i.e.,
![]() $Rw$
consists of the “standard polynomials” in
$Rw$
consists of the “standard polynomials” in
![]() $\hat {W}$
.
$\hat {W}$
.
Lemma 6.7 Let
![]() $y = k_{-1}w+k_0d+k_1cd+\cdots +k_ic^id+\cdots \in \hat {W}$
.
$y = k_{-1}w+k_0d+k_1cd+\cdots +k_ic^id+\cdots \in \hat {W}$
.
-
1)
 $wy = k_{-1}w$
.
$wy = k_{-1}w$
. -
2)
 $d^*(c^*)^j y = k_jw$
for all
$d^*(c^*)^j y = k_jw$
for all
 $j\geq 0$
.
$j\geq 0$
.
Proof (1) is obvious, and (2) follows directly from the observation that
![]() $d^*(c^*)^j c^id = w$
if
$d^*(c^*)^j c^id = w$
if
![]() $i=j$
, and is
$i=j$
, and is
![]() $0$
otherwise. ▪
$0$
otherwise. ▪
Lemma 6.8 The simple module
![]() $Rw$
is essential in
$Rw$
is essential in
![]() $\hat {W}$
. In particular,
$\hat {W}$
. In particular,
![]() $Rw = \mathrm {Soc}(\hat {W})$
.
$Rw = \mathrm {Soc}(\hat {W})$
.
Proof Consider an element
![]() $0\not =y=k_{-1}w+k_0d+k_1cd+\cdots +k_ic^id+\cdots \in \hat {W}$
. There exists
$0\not =y=k_{-1}w+k_0d+k_1cd+\cdots +k_ic^id+\cdots \in \hat {W}$
. There exists
![]() $\ell \in \mathbb {Z}^+ \cup \{-1\}$
such that
$\ell \in \mathbb {Z}^+ \cup \{-1\}$
such that
![]() $k_\ell \not =0$
. If
$k_\ell \not =0$
. If
![]() $k_{-1} \neq 0$
, then by Lemma 6.7(1)
$k_{-1} \neq 0$
, then by Lemma 6.7(1)
![]() $wy = k_{-1}w \neq 0$
is in
$wy = k_{-1}w \neq 0$
is in
![]() $ Rw$
. If
$ Rw$
. If
![]() $k_\ell \neq 0$
for
$k_\ell \neq 0$
for
![]() $\ell \geq 0$
, then by Lemma 6.7(2)
$\ell \geq 0$
, then by Lemma 6.7(2)
![]() $d^*(c^*)^{\ell } y=k_{\ell }w \neq 0$
is in
$d^*(c^*)^{\ell } y=k_{\ell }w \neq 0$
is in
![]() $Rw$
. ▪
$Rw$
. ▪
Lemma 6.9 Any R-homomorphism from
![]() $J=Rw\oplus Rd^*\oplus Rd^*c^*\oplus Rd^*(c^*)^2\oplus \cdots $
to
$J=Rw\oplus Rd^*\oplus Rd^*c^*\oplus Rd^*(c^*)^2\oplus \cdots $
to
![]() $\hat {W}$
extends to an R-homomorphism from R to
$\hat {W}$
extends to an R-homomorphism from R to
![]() $\hat {W}$
.
$\hat {W}$
.
Proof Let
![]() $\varphi :J\to \hat {W}$
be a homomorphism of left R-modules. For each
$\varphi :J\to \hat {W}$
be a homomorphism of left R-modules. For each
![]() $i \geq 0$
let
$i \geq 0$
let
![]() $k_i$
denote the K-coefficient of w in the formal power series expression for
$k_i$
denote the K-coefficient of w in the formal power series expression for
![]() $\varphi (d^*(c^*)^i)$
, and let
$\varphi (d^*(c^*)^i)$
, and let
![]() $k_{-1}$
be the K-coefficient of w in
$k_{-1}$
be the K-coefficient of w in
![]() $\varphi (w)$
. Since
$\varphi (w)$
. Since
![]() $\varphi (w) = \varphi (w^2) = w\varphi (w)$
and
$\varphi (w) = \varphi (w^2) = w\varphi (w)$
and
![]() $\varphi (d^*(c^*)^i)= \varphi (wd^*(c^*)^i) = w \varphi (d^*(c^*)^i)$
, Lemma 6.7 implies that
$\varphi (d^*(c^*)^i)= \varphi (wd^*(c^*)^i) = w \varphi (d^*(c^*)^i)$
, Lemma 6.7 implies that
![]() $\varphi (w) = k_{-1}w$
and
$\varphi (w) = k_{-1}w$
and
![]() $\varphi (d^*(c^*)^i) = k_iw$
for all
$\varphi (d^*(c^*)^i) = k_iw$
for all
![]() $i\geq 0$
.
$i\geq 0$
.
Now consider the R-homomorphism
![]() $ \Phi :R\to \hat {W}$
obtained by setting
$ \Phi :R\to \hat {W}$
obtained by setting
Since
![]() $\Phi (w)=w\Phi (1)=k_{-1}w$
and
$\Phi (w)=w\Phi (1)=k_{-1}w$
and
![]() $\Phi (d^*(c^*)^i)=d^*(c^*)^i\Phi (1)=k_iw$
for each
$\Phi (d^*(c^*)^i)=d^*(c^*)^i\Phi (1)=k_iw$
for each
![]() $i\geq 0$
(again by Lemma 6.7),
$i\geq 0$
(again by Lemma 6.7),
![]() $\Phi $
extends
$\Phi $
extends
![]() $\varphi $
.▪
$\varphi $
.▪
It is well known that the invertible elements in the ring of formal power series
![]() $K[[x]]$
are precisely those formal power series
$K[[x]]$
are precisely those formal power series
![]() $\gamma (x) = \sum _{i=0}^\infty k_i x^i$
for which
$\gamma (x) = \sum _{i=0}^\infty k_i x^i$
for which
![]() $k_0 \neq 0$
, i.e., for which
$k_0 \neq 0$
, i.e., for which
![]() $\gamma (0)\neq 0$
.
$\gamma (0)\neq 0$
.
Lemma 6.10 Let
![]() $p(x)=p_0+p_1x+\cdots +p_nx^n \in \mathcal P$
. Any R-homomorphism from
$p(x)=p_0+p_1x+\cdots +p_nx^n \in \mathcal P$
. Any R-homomorphism from
![]() $Rp(c)$
to
$Rp(c)$
to
![]() $\hat {W}$
extends to an R-homomorphism from R to
$\hat {W}$
extends to an R-homomorphism from R to
![]() $\hat {W}$
.
$\hat {W}$
.
Proof Let
![]() $\psi : Rp(c)\to \hat {W}$
be a homomorphism of left R-modules. Let
$\psi : Rp(c)\to \hat {W}$
be a homomorphism of left R-modules. Let
![]() $\psi (p(c))=y$
, where
$\psi (p(c))=y$
, where
![]() $y=k_{-1}w+k_0d+k_1cd+\cdots +k_ic^id+\cdots $
. We need to find an R-homomorphism
$y=k_{-1}w+k_0d+k_1cd+\cdots +k_ic^id+\cdots $
. We need to find an R-homomorphism
![]() $\Psi :R\to \hat {W}$
such that
$\Psi :R\to \hat {W}$
such that
Because
![]() $p_0 \neq 0$
, viewing
$p_0 \neq 0$
, viewing
![]() $p(x) \in K[[x]]$
there exists
$p(x) \in K[[x]]$
there exists
![]() $\alpha (x) \in K[[x]]$
for which
$\alpha (x) \in K[[x]]$
for which
![]() $p(x)\alpha (x) = 1$
in
$p(x)\alpha (x) = 1$
in
![]() $K[[x]]$
. Write
$K[[x]]$
. Write
![]() $\alpha (x) = a_0 + a_1x + a_2x^2 + \cdots .$
Set
$\alpha (x) = a_0 + a_1x + a_2x^2 + \cdots .$
Set
![]() $p(x)=\sum _{i=0}^\infty p_ix^i$
, with
$p(x)=\sum _{i=0}^\infty p_ix^i$
, with
![]() $p_i=0 \forall i>n$
; then
$p_i=0 \forall i>n$
; then
 $$\begin{align*}p_0a_0 = 1, \ \ \mbox{and} \ \ \ \ \sum_{j=0}^N p_ja_{N-j} = 0 \ \ \mbox{for all} \ N\geq 1 \ . \quad\quad\qquad (\star)\end{align*}$$
$$\begin{align*}p_0a_0 = 1, \ \ \mbox{and} \ \ \ \ \sum_{j=0}^N p_ja_{N-j} = 0 \ \ \mbox{for all} \ N\geq 1 \ . \quad\quad\qquad (\star)\end{align*}$$
Now define the following elements of K:
 $$\begin{align*}z_{-1} := a_0k_{-1}, \ \ \mbox{and, for each } M\geq 0, \ z_M := \sum_{i=0}^M a_i k_{M-i}.\end{align*}$$
$$\begin{align*}z_{-1} := a_0k_{-1}, \ \ \mbox{and, for each } M\geq 0, \ z_M := \sum_{i=0}^M a_i k_{M-i}.\end{align*}$$
We construct
![]() $z \in \hat {W}$
by setting
$z \in \hat {W}$
by setting
so that
![]() $p(c)z = (p_0 1_R + p_1c + p_2c^2 + \cdots + p_nc^n) (z_{-1}w + z_0d + z_1cd + z_2c^2d + \cdots )$
. We already know that
$p(c)z = (p_0 1_R + p_1c + p_2c^2 + \cdots + p_nc^n) (z_{-1}w + z_0d + z_1cd + z_2c^2d + \cdots )$
. We already know that
![]() $p_0a_0 = 1$
, so that
$p_0a_0 = 1$
, so that
![]() $p_0z_{-1}=p_0a_0k_{-1}=k_{-1}$
. Moreover, by standard computations and using the previous relations
$p_0z_{-1}=p_0a_0k_{-1}=k_{-1}$
. Moreover, by standard computations and using the previous relations
![]() $(\star )$
, one can show that for any
$(\star )$
, one can show that for any
![]() $i\geq 0$
, the coefficient of the term
$i\geq 0$
, the coefficient of the term
![]() $c^id$
in
$c^id$
in
![]() $p(c)z$
equals the coefficient of the term
$p(c)z$
equals the coefficient of the term
![]() $c^id$
in y. This implies that
$c^id$
in y. This implies that
![]() $p(c)z = y$
in
$p(c)z = y$
in
![]() $\hat {W}$
. (Intuitively, the idea here is to “define informally” the expression
$\hat {W}$
. (Intuitively, the idea here is to “define informally” the expression
![]() $\alpha (c) = a_01_R + a_1c + a_2c^2 + \cdots $
, and subsequently the element
$\alpha (c) = a_01_R + a_1c + a_2c^2 + \cdots $
, and subsequently the element
![]() $z\in \hat {W}$
as
$z\in \hat {W}$
as
![]() $z = \alpha (c)y$
, so that
$z = \alpha (c)y$
, so that
![]() $p(c)\alpha (c)y=1\cdot y=y$
.)
$p(c)\alpha (c)y=1\cdot y=y$
.)
Finally, consider the R-homomorphism
![]() $\Psi :R\to \hat {W}$
obtained by setting
$\Psi :R\to \hat {W}$
obtained by setting
Then
![]() $\Psi (p(c))=p(c)\Psi (1)=p(c)z=y$
, as desired. ▪
$\Psi (p(c))=p(c)\Psi (1)=p(c)z=y$
, as desired. ▪
Proposition 6.11 The left
![]() ${R} $
-module
${R} $
-module
![]() $\hat {W}$
is injective.
$\hat {W}$
is injective.
Proof We use Corollary 5.5 again, which yields that we only need to test the injectivity of
![]() $\hat {W}$
with respect to the two indicated types of left R-ideals. But this is precisely what has been achieved in Lemmas 6.9 and 6.10. ▪
$\hat {W}$
with respect to the two indicated types of left R-ideals. But this is precisely what has been achieved in Lemmas 6.9 and 6.10. ▪
Corollary 6.12
![]() $\hat {W}$
is the injective envelope of
$\hat {W}$
is the injective envelope of
![]() $Rw$
.
$Rw$
.
Proof As noted in Corollary 6.3, the injective envelope of any module is an injective module in which the given module sits as an essential submodule. So the result follows from Lemma 6.8 and Proposition 6.11. ▪
We now describe the quotient
![]() $\hat {W}/Rw$
as an extension of a direct summand of a product of copies of the
$\hat {W}/Rw$
as an extension of a direct summand of a product of copies of the
![]() $U^f$
s by the simple module
$U^f$
s by the simple module
![]() $Rw$
.
$Rw$
.
Proposition 6.13 The module
![]() $\hat {W}/{Rw}$
is a direct summand of a product of copies of the
$\hat {W}/{Rw}$
is a direct summand of a product of copies of the
![]() $U^f$
s.
$U^f$
s.
Proof Consider the short exact sequence
![]() $0\to Rw\to \hat {W}\to \hat {W}/{Rw}\to 0$
. First notice that
$0\to Rw\to \hat {W}\to \hat {W}/{Rw}\to 0$
. First notice that
![]() $\operatorname {Hom}(Rw, \hat {W}/{Rw})=0$
, as follows. To the contrary, suppose there exists
$\operatorname {Hom}(Rw, \hat {W}/{Rw})=0$
, as follows. To the contrary, suppose there exists
![]() $0\neq f: Rw\to \hat {W}/{Rw}$
. Then by the simplicity of
$0\neq f: Rw\to \hat {W}/{Rw}$
. Then by the simplicity of
![]() $Rw$
, the map f must be a monomorphism. Further, since
$Rw$
, the map f must be a monomorphism. Further, since
![]() $Rw$
is projective, there then exists
$Rw$
is projective, there then exists
 $\tilde {f}:Rw\to \hat {W}$
such that
$\tilde {f}:Rw\to \hat {W}$
such that
 $\pi \circ \tilde {f}=f$
. In particular
$\pi \circ \tilde {f}=f$
. In particular
 $\operatorname {Im} \tilde {f}\cap Rw=0$
. But this is a contradiction since
$\operatorname {Im} \tilde {f}\cap Rw=0$
. But this is a contradiction since
![]() $Rw$
is the essential socle of
$Rw$
is the essential socle of
![]() $\hat {W}$
.
$\hat {W}$
.
Now let
![]() $0\neq x\in \hat {W}/{Rw}$
, and consider the cyclic module
$0\neq x\in \hat {W}/{Rw}$
, and consider the cyclic module
![]() $Rx\cong R/{\mathrm {Ann}} (x)$
. Let M be a maximal left ideal of R containing
$Rx\cong R/{\mathrm {Ann}} (x)$
. Let M be a maximal left ideal of R containing
![]() ${\mathrm {Ann}} (x)$
, so that
${\mathrm {Ann}} (x)$
, so that
![]() $Rx\to {R/M}\to 0$
. If
$Rx\to {R/M}\to 0$
. If
![]() $R/M\cong Rw$
, since
$R/M\cong Rw$
, since
![]() $Rw$
is projective we would get that
$Rw$
is projective we would get that
![]() $Rw$
is a summand of
$Rw$
is a summand of
![]() $Rx$
, in particular is a submodule of
$Rx$
, in particular is a submodule of
![]() $Rx$
and thereby also of
$Rx$
and thereby also of
![]() $\hat {W}/{Rw}$
, contrary to the result of the previous paragraph. So
$\hat {W}/{Rw}$
, contrary to the result of the previous paragraph. So
![]() $R/M$
is a simple module of type
$R/M$
is a simple module of type
![]() $V^f$
, and hence it embeds in
$V^f$
, and hence it embeds in
![]() $U^f$
. In such a way, for any
$U^f$
. In such a way, for any
![]() $0\neq x\in \hat {W}/{Rw}$
, there is a suitable
$0\neq x\in \hat {W}/{Rw}$
, there is a suitable
![]() $f(x)\in \mathcal {F}$
and a morphism
$f(x)\in \mathcal {F}$
and a morphism
![]() $\varphi _x:Rx\to U^f$
, such that
$\varphi _x:Rx\to U^f$
, such that
![]() $\varphi _x(x)\neq 0$
. Since
$\varphi _x(x)\neq 0$
. Since
![]() $U^f$
is injective,
$U^f$
is injective,
![]() $\varphi _x$
extends to a morphism
$\varphi _x$
extends to a morphism
![]() $\tilde {\varphi _x}: \hat {W}/{Rw}\to U^f$
. So we get that
$\tilde {\varphi _x}: \hat {W}/{Rw}\to U^f$
. So we get that
![]() $\hat {W}/{Rw}$
embeds in a product of copies of the
$\hat {W}/{Rw}$
embeds in a product of copies of the
![]() $U^f$
(
$U^f$
(
![]() $f(x)\in \mathcal F$
). But
$f(x)\in \mathcal F$
). But
![]() $\hat {W}$
is injective, and so
$\hat {W}$
is injective, and so
![]() $\hat {W}/Rw$
is also injective by Corollary 2.2. Thus
$\hat {W}/Rw$
is also injective by Corollary 2.2. Thus
![]() $\hat {W}/Rw$
is indeed a direct summand of the product of copies of the
$\hat {W}/Rw$
is indeed a direct summand of the product of copies of the
![]() $U^f$
s. ▪
$U^f$
s. ▪
6.3 Consequences of Subsections 6.1 and 6.2
Every ring has (up to isomorphism) a unique minimal injective cogenerator (see e.g. [Reference Anderson and Fuller5, Section 18] for a full description of this concept). Since any representation of the ring embeds in a product of copies of a cogenerator, we can describe the entire category of modules over the ring once we know such a cogenerator. Using the previous results, we are able to determine a minimal injective cogenerator for the algebra
![]() ${R=}L_K(\mathcal {T})$
.
${R=}L_K(\mathcal {T})$
.
Theorem 6.14 The left R-module
 $$\begin{align*}C = \hat{W} \oplus (\oplus_{f(x) \in \mathcal{F}} U^f )\end{align*}$$
$$\begin{align*}C = \hat{W} \oplus (\oplus_{f(x) \in \mathcal{F}} U^f )\end{align*}$$
is a minimal injective cogenerator for
![]() ${R} $
.
${R} $
.
Proof By combining Proposition 6.4 with Proposition 6.12, we directly obtain that C is injective. Because there is a unique cycle in
![]() $\mathcal {T}$
, [Reference Ara and Rangaswamy6, Corollary 4.6] applies, and yields that (up to isomorphism) the set of all the simple modules over
$\mathcal {T}$
, [Reference Ara and Rangaswamy6, Corollary 4.6] applies, and yields that (up to isomorphism) the set of all the simple modules over
![]() ${R} $
consists of
${R} $
consists of
![]() $Rw$
together with the pairwise nonisomorphic modules of the form
$Rw$
together with the pairwise nonisomorphic modules of the form
![]() $\{V^f \ | \ f(x) \in \mathcal {F}\}$
. Thus C contains a copy of every simple left
$\{V^f \ | \ f(x) \in \mathcal {F}\}$
. Thus C contains a copy of every simple left
![]() ${R} $
-module, and so it is a cogenerator for the module category [Reference Anderson and Fuller5, Proposition 18.15]. Since any injective cogenerator has to contain a copy of the injective envelope of any simple module, we get that C is a minimal injective cogenerator for
${R} $
-module, and so it is a cogenerator for the module category [Reference Anderson and Fuller5, Proposition 18.15]. Since any injective cogenerator has to contain a copy of the injective envelope of any simple module, we get that C is a minimal injective cogenerator for
![]() ${R} $
. ▪
${R} $
. ▪
When S is any Noetherian ring, then the minimal injective cogenerator is precisely the direct sum of the injective envelopes of the simple modules. We have reached the same conclusion for the non-Noetherian ring
![]() ${R=}L_K(\mathcal {T})$
in Theorem 6.14. Moreover, we have described each of these injective envelopes explicitly.
${R=}L_K(\mathcal {T})$
in Theorem 6.14. Moreover, we have described each of these injective envelopes explicitly.
With Theorem 6.14 in hand, we achieve a description of all the injective left R-modules.
Corollary 6.15 Let C denote
 $\hat {W} \oplus (\oplus _{f(x) \in \mathcal {F}} U^f )$
. Then a left
$\hat {W} \oplus (\oplus _{f(x) \in \mathcal {F}} U^f )$
. Then a left
![]() ${R} $
-module M is injective if and only if M is isomorphic to a direct summand of a direct product of copies of C.
${R} $
-module M is injective if and only if M is isomorphic to a direct summand of a direct product of copies of C.
Proof This follows immediately from the definition of a cogenerator, together with the facts that direct products and direct summands of injective modules are injective, and an injective submodule of a module is necessarily a direct summand. ▪
Acknowledgment
The authors are quite grateful to the referee for an extremely careful reading of the original version of this manuscript. Part of this work was carried out during a visit of the first author to the University of Padova, Department of Statistical Sciences. The first author is pleased to take this opportunity to express his thanks to the host institution and its faculty for their warm hospitality and travel support by the project of excellence “Statistical methods and models for complex data” (Department of Statistical Sciences) and the grant “Iniziative di cooperazione universitaria Anno 2019” (University of Padova).