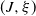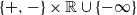1. Introduction and preliminaries
Let ![]() $E\,:\!=\, \{+,-\}$ and suppose
$E\,:\!=\, \{+,-\}$ and suppose ![]() $(\mathcal{F}_t)_{t\geq0}$ is a filtration. A pair of processes
$(\mathcal{F}_t)_{t\geq0}$ is a filtration. A pair of processes ![]() $(J,\xi)$ taking values in
$(J,\xi)$ taking values in ![]() $E\times\mathbb R\cup\{-\infty\}$ with lifetime
$E\times\mathbb R\cup\{-\infty\}$ with lifetime ![]() $\chi$ is a Lamperti–Kiu Markov additive process (MAP) with respect to
$\chi$ is a Lamperti–Kiu Markov additive process (MAP) with respect to ![]() $(\mathcal{F}_t)_{t\geq0}$ if, for any continuous bounded function
$(\mathcal{F}_t)_{t\geq0}$ if, for any continuous bounded function ![]() $f\colon E\times\mathbb R\rightarrow\mathbb R^+$,
$f\colon E\times\mathbb R\rightarrow\mathbb R^+$, ![]() $(z,y)\in E\times\mathbb R$ and
$(z,y)\in E\times\mathbb R$ and ![]() $s,t\geq0$, we have
$s,t\geq0$, we have
where ![]() $\mathbb P_{z,y}$ is the law of
$\mathbb P_{z,y}$ is the law of ![]() $(J,\xi)$ started at (z,y) and
$(J,\xi)$ started at (z,y) and ![]() $\mathbb E_{z,y}$ is the corresponding expectation. For all
$\mathbb E_{z,y}$ is the corresponding expectation. For all ![]() $t>\chi$, the process
$t>\chi$, the process ![]() $\xi$ is in the cemetery state
$\xi$ is in the cemetery state ![]() $-\infty$, whilst J continues as a Markov chain. A detailed account of MAPs is given in [Reference Asmussen2, Chapter XI] whilst a more general definition is given in [Reference Alili, Chaumont, Graczyk and Żak1, Section 3, Definition 1]. Note that
$-\infty$, whilst J continues as a Markov chain. A detailed account of MAPs is given in [Reference Asmussen2, Chapter XI] whilst a more general definition is given in [Reference Alili, Chaumont, Graczyk and Żak1, Section 3, Definition 1]. Note that ![]() $(J_t\exp(\xi_t),t\geq0)$ is a càdlàg multiplicative process taking values in
$(J_t\exp(\xi_t),t\geq0)$ is a càdlàg multiplicative process taking values in ![]() $\mathbb R^*\,:\!=\, \mathbb R\backslash\{0\}$ and so, following [Reference Chaumont, Pantí and Rivero7], we refer to it as a Lamperti–Kiu process.
$\mathbb R^*\,:\!=\, \mathbb R\backslash\{0\}$ and so, following [Reference Chaumont, Pantí and Rivero7], we refer to it as a Lamperti–Kiu process.
There is a well-known construction of a Lamperti–Kiu process given in [Reference Chaumont, Pantí and Rivero7, Theorem 6(i)]. Let ![]() $\xi^\pm$ be two Lévy processes, let
$\xi^\pm$ be two Lévy processes, let ![]() $\zeta^\pm$ be two exponentially distributed random variables with rates
$\zeta^\pm$ be two exponentially distributed random variables with rates ![]() $q^\pm$, and let
$q^\pm$, and let ![]() $U^\pm$ be two random variables taking values in
$U^\pm$ be two random variables taking values in ![]() $\mathbb R$. Then consider sequences
$\mathbb R$. Then consider sequences ![]() $(\xi^{\pm,k})_{k \in \{0, 1, 2, \ldots \}}$,
$(\xi^{\pm,k})_{k \in \{0, 1, 2, \ldots \}}$, ![]() $(\zeta^{\pm,k})_{k\in\mathbb N}$, and
$(\zeta^{\pm,k})_{k\in\mathbb N}$, and ![]() $(U^{\pm,k})_{k\in\mathbb N}$ of independent and identically distributed (i.i.d.) copies of
$(U^{\pm,k})_{k\in\mathbb N}$ of independent and identically distributed (i.i.d.) copies of ![]() $\xi^\pm$,
$\xi^\pm$, ![]() $\zeta^\pm$, and
$\zeta^\pm$, and ![]() $U^\pm$, respectively. Under
$U^\pm$, respectively. Under ![]() $\mathbb P_{\sigma,x}$, i.e. assuming
$\mathbb P_{\sigma,x}$, i.e. assuming ![]() $(J_0,\xi_0)=(\sigma,x)$, for each
$(J_0,\xi_0)=(\sigma,x)$, for each ![]() $k\in\mathbb N$ let
$k\in\mathbb N$ let ![]() $\xi^k=\xi^{\gamma,k}$,
$\xi^k=\xi^{\gamma,k}$, ![]() $\zeta^k=\zeta^{\gamma,k}$, and
$\zeta^k=\zeta^{\gamma,k}$, and ![]() $U^k=U^{\gamma,k}$, where
$U^k=U^{\gamma,k}$, where ![]() $\gamma=\sigma(-1)^k$. Finally, let
$\gamma=\sigma(-1)^k$. Finally, let ![]() $\chi$ be an exponentially distributed random variable of rate
$\chi$ be an exponentially distributed random variable of rate ![]() $q\in[0,\infty)$ independent of the rest of the system, where
$q\in[0,\infty)$ independent of the rest of the system, where ![]() $q=0$ is interpreted to mean
$q=0$ is interpreted to mean ![]() $\chi=\infty$. Then, for
$\chi=\infty$. Then, for ![]() $t\geq0$ and
$t\geq0$ and ![]() $x\in\mathbb R^*\,:\!=\, \mathbb R\backslash\{0\}$, set
$x\in\mathbb R^*\,:\!=\, \mathbb R\backslash\{0\}$, set
with
 \begin{align*}\xi_t &\,:\!=\, \xi^{N_t}_{\pi_t} + \sum_{k=0}^{N_t-1}\bigl( \xi^k_{\zeta^k} + U^k \bigr)\quad \text{and}\quad J_t \,:\!=\, \sigma (-1 )^{N_t}{,} \end{align*}
\begin{align*}\xi_t &\,:\!=\, \xi^{N_t}_{\pi_t} + \sum_{k=0}^{N_t-1}\bigl( \xi^k_{\zeta^k} + U^k \bigr)\quad \text{and}\quad J_t \,:\!=\, \sigma (-1 )^{N_t}{,} \end{align*}
where, for ![]() $n\in\mathbb N$,
$n\in\mathbb N$,
 \begin{align*}T_0 &\,:\!=\, 0, \quad T_n\,:\!=\, \sum_{k=0}^{n-1}\zeta^k, \quad N_t \,:\!=\, \max_{m\in\mathbb N_0} \{T_m \leq t \}\quad \text{and}\quad \pi_t \,:\!=\, t - T_{N_t} \end{align*}
\begin{align*}T_0 &\,:\!=\, 0, \quad T_n\,:\!=\, \sum_{k=0}^{n-1}\zeta^k, \quad N_t \,:\!=\, \max_{m\in\mathbb N_0} \{T_m \leq t \}\quad \text{and}\quad \pi_t \,:\!=\, t - T_{N_t} \end{align*}
using the notation ![]() $\mathbb N_0\,:\!=\{0,1,2\cdots\}$. Then
$\mathbb N_0\,:\!=\{0,1,2\cdots\}$. Then ![]() $(Y_t,t\geq0)$ is a Lamperti–Kiu process and
$(Y_t,t\geq0)$ is a Lamperti–Kiu process and ![]() $(J,\xi)$ is the corresponding MAP. Conversely, any Lamperti–Kiu process has such a decomposition, which we will refer to as the Lamperti–Kiu decomposition. We will refer to
$(J,\xi)$ is the corresponding MAP. Conversely, any Lamperti–Kiu process has such a decomposition, which we will refer to as the Lamperti–Kiu decomposition. We will refer to ![]() $\chi$ as the lifetime of the Lamperti–Kiu process.
$\chi$ as the lifetime of the Lamperti–Kiu process.
We study the standard and signed exponential functionals of ![]() $(Y_t,t\geq0)$ defined, respectively, by
$(Y_t,t\geq0)$ defined, respectively, by
Recall that a perpetuity is a security where a stream of cashflows is paid indefinitely, such as consols issued by the Bank of England. Under the MAP model, we suppose that the cashflows are paid continuously at a rate ![]() $c_t\,:\!=\, \exp(\xi_t+rt)$ at time
$c_t\,:\!=\, \exp(\xi_t+rt)$ at time ![]() $t\geq0$, where r is the rate of interest. Each element of E corresponds to a market state (for example, its states may refer to a bear or bull market), where the state at time
$t\geq0$, where r is the rate of interest. Each element of E corresponds to a market state (for example, its states may refer to a bear or bull market), where the state at time ![]() $t\geq0$ is given by
$t\geq0$ is given by ![]() $J_t$. The value of the perpetuity is given by
$J_t$. The value of the perpetuity is given by ![]() $A_\infty$.
$A_\infty$.
It was shown in [Reference Chaumont, Pantí and Rivero7] that ![]() $A_\infty$ is the first hitting time of zero by an associated self-similar Markov process (ssMp). Indeed, consider the Lamperti–Kiu MAP
$A_\infty$ is the first hitting time of zero by an associated self-similar Markov process (ssMp). Indeed, consider the Lamperti–Kiu MAP ![]() $(J,\xi)$ from (1.1), and for
$(J,\xi)$ from (1.1), and for ![]() $\alpha\in(0,\infty)$ define the time transformation
$\alpha\in(0,\infty)$ define the time transformation
Then the process ![]() $X_t^{(x)}\,:\!=\, J_{\tau(t|x|^{-\alpha})}x\exp(\xi_{\tau(t|x|^{-\alpha})})$, for
$X_t^{(x)}\,:\!=\, J_{\tau(t|x|^{-\alpha})}x\exp(\xi_{\tau(t|x|^{-\alpha})})$, for ![]() $t<|x|^\alpha\int_0^\infty\exp (\alpha\xi_s ) \,{\mathrm{d}} s$ and
$t<|x|^\alpha\int_0^\infty\exp (\alpha\xi_s ) \,{\mathrm{d}} s$ and ![]() $x\in\mathbb R^*$, is a self-similar Markov process of index
$x\in\mathbb R^*$, is a self-similar Markov process of index ![]() $\alpha$ taking values in
$\alpha$ taking values in ![]() $\mathbb R^*$ and started at x. That is, X is a càdlàg Markov process such that, for all
$\mathbb R^*$ and started at x. That is, X is a càdlàg Markov process such that, for all ![]() $c>0$ and
$c>0$ and ![]() $x\in\mathbb R^*$, it satisfies
$x\in\mathbb R^*$, it satisfies
where ![]() $\stackrel{\mathcal{L}}{=}$ means equality in law. Moreover, any self-similar Markov process taking values in
$\stackrel{\mathcal{L}}{=}$ means equality in law. Moreover, any self-similar Markov process taking values in ![]() $\mathbb R^*$ of index
$\mathbb R^*$ of index ![]() $\alpha$ can be constructed in this way. The first hitting time of zero by
$\alpha$ can be constructed in this way. The first hitting time of zero by ![]() $X^{(x)}$ is
$X^{(x)}$ is ![]() $\int_0^\infty\exp(\alpha\xi_s) \,{\mathrm{d}} s$, which equals
$\int_0^\infty\exp(\alpha\xi_s) \,{\mathrm{d}} s$, which equals ![]() $A_\infty$ when
$A_\infty$ when ![]() $\alpha=1$. Many papers are devoted to the study of the Lamperti transform of self-similar Markov processes. For example see [Reference Bertoin and Yor5], [Reference Chaumont, Pantí and Rivero7], [Reference Kiu17], [Reference Lamperti20], and [Reference Lamperti19]. Other applications of MAPs and their exponential functionals include multi-type self-similar fragmentation processes and trees; for example see [Reference Stephenson27].
$\alpha=1$. Many papers are devoted to the study of the Lamperti transform of self-similar Markov processes. For example see [Reference Bertoin and Yor5], [Reference Chaumont, Pantí and Rivero7], [Reference Kiu17], [Reference Lamperti20], and [Reference Lamperti19]. Other applications of MAPs and their exponential functionals include multi-type self-similar fragmentation processes and trees; for example see [Reference Stephenson27].
The focus of this paper is on the finiteness and right tails of ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$. The right tails of a distribution determine which positive moments exist and whether it is a member of the classes of heavy-tailed, long-tailed, or subexponential distributions. These classes of heavy-tailed distribution are of particular interest to us because of their applications in finance, risk theory, and insurance (see e.g. [Reference Ibragimov, Ibragimov and Walden13], [Reference Rachev24], and [Reference Resnick25]). Empirical data often shows realised market returns to be heavy-tailed (see [Reference Cont8] and [Reference Jung and Liesenfeld14]). This motivates both considering Lamperti–Kiu processes with Lamperti–Kiu components that are heavy-tailed and studying
$B_\infty$. The right tails of a distribution determine which positive moments exist and whether it is a member of the classes of heavy-tailed, long-tailed, or subexponential distributions. These classes of heavy-tailed distribution are of particular interest to us because of their applications in finance, risk theory, and insurance (see e.g. [Reference Ibragimov, Ibragimov and Walden13], [Reference Rachev24], and [Reference Resnick25]). Empirical data often shows realised market returns to be heavy-tailed (see [Reference Cont8] and [Reference Jung and Liesenfeld14]). This motivates both considering Lamperti–Kiu processes with Lamperti–Kiu components that are heavy-tailed and studying ![]() $A_\infty$ as an example of a heavy-tailed distribution.
$A_\infty$ as an example of a heavy-tailed distribution.
For Lévy processes, which are MAPs where E is a singleton set, the theory of the exponential functional is well developed. Several results on the moments and tails of the exponential functional, including random affine equations, are collected in the survey [Reference Carmona, Petit and Yor6]. Under Cramér’s condition, with Cramér number ![]() $\theta$, it is shown that the right tails are polynomial with order
$\theta$, it is shown that the right tails are polynomial with order ![]() $-\theta$. More recently, [Reference Patie and Savov23] provided a complete description at the logarithmic level of the asymptotic of the right tail and, under Cramér’s condition, the derivatives of the density. In the heavy-tailed case, Cramér’s condition fails and different methods are needed. In this case, the right tails of
$-\theta$. More recently, [Reference Patie and Savov23] provided a complete description at the logarithmic level of the asymptotic of the right tail and, under Cramér’s condition, the derivatives of the density. In the heavy-tailed case, Cramér’s condition fails and different methods are needed. In this case, the right tails of ![]() $A_\infty$ have been studied in, for example, [Reference Maulik and Zwart21], [Reference Palau, Pardo and Smadi22], [Reference Patie and Savov23], and [Reference Rivero26]. The case of a MAP is studied in [Reference Kuznetsov, Kyprianou, Pardo and Watson18] where, under a Cramér-type condition with Cramér number
$A_\infty$ have been studied in, for example, [Reference Maulik and Zwart21], [Reference Palau, Pardo and Smadi22], [Reference Patie and Savov23], and [Reference Rivero26]. The case of a MAP is studied in [Reference Kuznetsov, Kyprianou, Pardo and Watson18] where, under a Cramér-type condition with Cramér number ![]() $\theta\in(0,1)$, moments of order
$\theta\in(0,1)$, moments of order ![]() $s\in(0,1+\theta)$ are shown to exist and satisfy a recurrence relation. This leads to polynomial tails similar to the Lévy case. The same recurrence relation is shown in [Reference Stephenson27] for the case when the additive component is not increasing. Other properties, including the finiteness and integer moments of the exponential functional of non-increasing MAPs, are also given in [Reference Stephenson27].
$s\in(0,1+\theta)$ are shown to exist and satisfy a recurrence relation. This leads to polynomial tails similar to the Lévy case. The same recurrence relation is shown in [Reference Stephenson27] for the case when the additive component is not increasing. Other properties, including the finiteness and integer moments of the exponential functional of non-increasing MAPs, are also given in [Reference Stephenson27].
We will use the law of large numbers and Erickson’s law of large numbers for when the mean is undefined [Reference Erickson10], to give a characterisation of the finiteness of ![]() $A_\infty$. Then we show that, for a Lamperti–Kiu MAP, both
$A_\infty$. Then we show that, for a Lamperti–Kiu MAP, both ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$ satisfy a random affine equation. Under a Cramér-type condition, we show that the conditions of the implicit renewal theorems of [Reference Goldie12] and [Reference Kesten16] hold, and hence we are able to determine the right tails of
$B_\infty$ satisfy a random affine equation. Under a Cramér-type condition, we show that the conditions of the implicit renewal theorems of [Reference Goldie12] and [Reference Kesten16] hold, and hence we are able to determine the right tails of ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$. In the heavy-tailed cases, when Cramér’s condition does not hold, a different approach to studying the tails of
$B_\infty$. In the heavy-tailed cases, when Cramér’s condition does not hold, a different approach to studying the tails of ![]() $A_\infty$ is required. We define a Lamperti–Kiu process to be of strong subexponential type when
$A_\infty$ is required. We define a Lamperti–Kiu process to be of strong subexponential type when ![]() $Y_{T_2}$ is long-tailed and one of the Lamperti–Kiu components,
$Y_{T_2}$ is long-tailed and one of the Lamperti–Kiu components, ![]() $\xi^{(\pm)}_1$ or
$\xi^{(\pm)}_1$ or ![]() $U^{(\pm)}$, is strong subexponential and has right tails that asymptotically dominate the right tails of the other Lamperti–Kiu components. By careful consideration of an embedded Markov chain, we are able to overcome the lack of independent increments of
$U^{(\pm)}$, is strong subexponential and has right tails that asymptotically dominate the right tails of the other Lamperti–Kiu components. By careful consideration of an embedded Markov chain, we are able to overcome the lack of independent increments of ![]() $\xi$ and provide a generalisation of the subexponential results of [Reference Maulik and Zwart21] to Lamperti–Kiu processes of strong subexponential type. This provides an asymptotic expansion of the right tails of
$\xi$ and provide a generalisation of the subexponential results of [Reference Maulik and Zwart21] to Lamperti–Kiu processes of strong subexponential type. This provides an asymptotic expansion of the right tails of ![]() $A_\infty$ to show that
$A_\infty$ to show that ![]() $A_\infty$ is long-tailed and
$A_\infty$ is long-tailed and ![]() $\log(A_\infty)$ is subexponential.
$\log(A_\infty)$ is subexponential.
This paper is organised as follows. In Section 2 we give necessary and sufficient conditions for the standard and signed exponential functionals ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$, respectively, to be finite. In Section 3 we look at the random affine equation approach to studying the moments and tails of
$B_\infty$, respectively, to be finite. In Section 3 we look at the random affine equation approach to studying the moments and tails of ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$ under Cramér’s condition and the assumption that
$B_\infty$ under Cramér’s condition and the assumption that ![]() $Y_{T_2}$ does not have a lattice distribution. In Section 4 we study the tails of
$Y_{T_2}$ does not have a lattice distribution. In Section 4 we study the tails of ![]() $A_\infty$ when the Lamperti–Kiu process is of strong subexponential type.
$A_\infty$ when the Lamperti–Kiu process is of strong subexponential type.
2. Finiteness of  ${{A}}_{\boldsymbol\infty}$ and
${{A}}_{\boldsymbol\infty}$ and  ${{B}}_{\boldsymbol\infty}$
${{B}}_{\boldsymbol\infty}$
Let us keep the mathematical setting of the Introduction, where ![]() $(Y_t,t\geq0)$ is the Lamperti–Kiu process defined in (1.2) associated with the Lamperti–Kiu MAP
$(Y_t,t\geq0)$ is the Lamperti–Kiu process defined in (1.2) associated with the Lamperti–Kiu MAP ![]() $(J,\xi)$ given, for a fixed
$(J,\xi)$ given, for a fixed ![]() $t\geq0$, by
$t\geq0$, by ![]() $\xi_t\,:\!=\,\log|Y_t|$ and
$\xi_t\,:\!=\,\log|Y_t|$ and ![]() $J_t\,:\!=\,\operatorname{sgn}(Y_t)$.
$J_t\,:\!=\,\operatorname{sgn}(Y_t)$.
If possible, define ![]() $K\in\mathbb R\cup\{-\infty,+\infty\}$ by
$K\in\mathbb R\cup\{-\infty,+\infty\}$ by
where we allow K to take the values ![]() $+\infty$ and
$+\infty$ and ![]() $-\infty$ but if both
$-\infty$ but if both ![]() $\mathbb E[\max(\xi_{T_2},0)]=\infty$ and
$\mathbb E[\max(\xi_{T_2},0)]=\infty$ and ![]() $\mathbb E[\max(-\xi_{T_2}^-,0)]=\infty$ we say that K is undefined.
$\mathbb E[\max(-\xi_{T_2}^-,0)]=\infty$ we say that K is undefined.
A Lamperti–Kiu process Y will be called degenerate if Y is such that ![]() $\limsup_{t\rightarrow\infty} |\xi_t |<\infty$. This can be shown to be equivalent to the case when either Y has a finite lifetime or
$\limsup_{t\rightarrow\infty} |\xi_t |<\infty$. This can be shown to be equivalent to the case when either Y has a finite lifetime or ![]() $\xi^\pm_t\equiv0$ for all
$\xi^\pm_t\equiv0$ for all ![]() $t\geq0$ and
$t\geq0$ and ![]() $U^+=-U^-$ is deterministic, hence
$U^+=-U^-$ is deterministic, hence
 \begin{equation*}Y_t^{(x)} = \begin{cases}x &\text{if $ T_{2k\phantom{+1}}\leq t < T_{2k+1}$ for some $ k\in\mathbb N_0$,}\\[4pt]
x\exp(U^{\operatorname{sgn}(x)}) &\text{if $ T_{2k+1}\leq t
< T_{2k+2}$ for some $ k\in\mathbb N_0$,} \end{cases} \end{equation*}
\begin{equation*}Y_t^{(x)} = \begin{cases}x &\text{if $ T_{2k\phantom{+1}}\leq t < T_{2k+1}$ for some $ k\in\mathbb N_0$,}\\[4pt]
x\exp(U^{\operatorname{sgn}(x)}) &\text{if $ T_{2k+1}\leq t
< T_{2k+2}$ for some $ k\in\mathbb N_0$,} \end{cases} \end{equation*}
for all ![]() $t\geq0$ and
$t\geq0$ and ![]() $x\in\mathbb R^*$.
$x\in\mathbb R^*$.
When K is defined and Y has an infinite lifetime from [Reference Asmussen2, Proposition 2.10] and [Reference Asmussen2, Corollary 2.8], it is known that almost surely ![]() $\lim_{t\rightarrow\infty}t^{-1}\xi_t=K$. Also, if
$\lim_{t\rightarrow\infty}t^{-1}\xi_t=K$. Also, if ![]() $K=0$ and Y is non-degenerate, then
$K=0$ and Y is non-degenerate, then ![]() $\lim_{t\rightarrow\infty}t^{-1}\xi_t=0$,
$\lim_{t\rightarrow\infty}t^{-1}\xi_t=0$, ![]() $\liminf_{t\rightarrow\infty}\xi_t = -\infty$, and
$\liminf_{t\rightarrow\infty}\xi_t = -\infty$, and ![]() $\limsup_{t\rightarrow\infty}\xi_t=\infty$, almost surely.
$\limsup_{t\rightarrow\infty}\xi_t=\infty$, almost surely.
In the case when K is undefined, we will use Erickson’s theorem [Reference Erickson10, Theorem 2], which provides a strong law of large numbers for a random walk with an undefined mean. The following lemma provides an analogous result to Erickson’s theorem for MAPs.
First we define
and
Then the long-term behaviour of ![]() $(\xi_t,t\geq0)$ is described by the following lemma.
$(\xi_t,t\geq0)$ is described by the following lemma.
Lemma 2.1. Suppose that K is undefined. Then at least one of ![]() $I_+$ and
$I_+$ and ![]() $I_-$ equals infinity, and almost surely we have:
$I_-$ equals infinity, and almost surely we have:
(i)
 $\limsup_{t\rightarrow\infty}t^{-1}\xi_t=\infty$ if and only if
$\limsup_{t\rightarrow\infty}t^{-1}\xi_t=\infty$ if and only if  $I_+=\infty$,
$I_+=\infty$,-
(ii)
 $\lim_{t\rightarrow\infty}t^{-1}\xi_t=\infty$ if and only if
$\lim_{t\rightarrow\infty}t^{-1}\xi_t=\infty$ if and only if  $I_+=\infty$ and
$I_+=\infty$ and  $I_-<\infty$,
$I_-<\infty$, -
(iii)
 $\liminf_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ if and only if
$\liminf_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ if and only if  $I_-=\infty$,
$I_-=\infty$, -
(iv)
 $\lim_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ if and only if
$\lim_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ if and only if  $I_+<\infty$ and
$I_+<\infty$ and  $I_-=\infty$.
$I_-=\infty$.
Proof. Consider the sequence ![]() $\{\xi_{T_{2n}}\}_{n\in\mathbb N}$ as the random walk
$\{\xi_{T_{2n}}\}_{n\in\mathbb N}$ as the random walk
and notice that ![]() $\xi_{T_{2n}} - \xi_{T_{2(n-1)}} \stackrel{\mathcal{L}}{=} \xi_{T_2}$ has an undefined mean, for each
$\xi_{T_{2n}} - \xi_{T_{2(n-1)}} \stackrel{\mathcal{L}}{=} \xi_{T_2}$ has an undefined mean, for each ![]() $n\in\mathbb N$. Then Erickson’s theorem for random walks with undefined mean [Reference Erickson10, Theorem 2], and the remark that follows it, states that either
$n\in\mathbb N$. Then Erickson’s theorem for random walks with undefined mean [Reference Erickson10, Theorem 2], and the remark that follows it, states that either ![]() $I_+=\infty$ or
$I_+=\infty$ or ![]() $I_-=\infty$ or both hold, proving the first statement of the lemma. Furthermore, the following statements hold:
$I_-=\infty$ or both hold, proving the first statement of the lemma. Furthermore, the following statements hold:
(1)
 $\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=\infty$ a.s. if and only if
$\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=\infty$ a.s. if and only if  $I_+=\infty$,
$I_+=\infty$,-
(2)
 $\lim_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=\infty$ a.s. if and only if
$\lim_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=\infty$ a.s. if and only if  $I_+=\infty$ and
$I_+=\infty$ and  $I_-<\infty$,
$I_-<\infty$, -
(3)
 $\liminf_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=-\infty$ a.s. if and only if
$\liminf_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=-\infty$ a.s. if and only if  $I_-=\infty$,
$I_-=\infty$, -
(4)
 $\lim_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=-\infty$ a.s. if and only if
$\lim_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=-\infty$ a.s. if and only if  $I_+<\infty$ and
$I_+<\infty$ and  $I_-=\infty$,
$I_-=\infty$,
and similar statements hold for ![]() $\{T_{2n+1}\}_{n\in\mathbb N}$.
$\{T_{2n+1}\}_{n\in\mathbb N}$.
Since ![]() $\mathbb E[T_2]<\infty$, it is immediate that if
$\mathbb E[T_2]<\infty$, it is immediate that if ![]() $\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=\infty$ a.s., then
$\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=\infty$ a.s., then ![]() $\limsup_{t\rightarrow\infty}t^{-1}\xi_t=\infty$ a.s. If
$\limsup_{t\rightarrow\infty}t^{-1}\xi_t=\infty$ a.s. If ![]() $\liminf_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=-\infty$ a.s., then
$\liminf_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=-\infty$ a.s., then ![]() $\liminf_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ a.s., hence the ‘if’ direction of statements (i) and (iii) holds. To prove the ‘only if’ direction of (i) and (iii), we must first prove (ii) and (iv).
$\liminf_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ a.s., hence the ‘if’ direction of statements (i) and (iii) holds. To prove the ‘only if’ direction of (i) and (iii), we must first prove (ii) and (iv).
Consider (iv) and notice that the ‘only if’ direction is an immediate consequence of statement (4) above. Now suppose ![]() $I_+<\infty$ and
$I_+<\infty$ and ![]() $I_-=\infty$. Then
$I_-=\infty$. Then ![]() $\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=-\infty$ a.s. and
$\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_{2n}}=-\infty$ a.s. and ![]() $\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_{2n+1}}=-\infty$ a.s., hence
$\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_{2n+1}}=-\infty$ a.s., hence ![]() $\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_n}=-\infty$ a.s. also. Suppose for a contradiction there exists an
$\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_n}=-\infty$ a.s. also. Suppose for a contradiction there exists an ![]() $R>0$ such that
$R>0$ such that ![]() $\limsup_{t\rightarrow\infty}t^{-1}\xi_t>-R>-\infty$ a.s. Since
$\limsup_{t\rightarrow\infty}t^{-1}\xi_t>-R>-\infty$ a.s. Since ![]() $\lim_{n\rightarrow\infty}n^{-1}T_n = \tfrac{1}{2}\mathbb E[T_2]$ a.s. and
$\lim_{n\rightarrow\infty}n^{-1}T_n = \tfrac{1}{2}\mathbb E[T_2]$ a.s. and ![]() $\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_n}=-\infty$ a.s., there exists some
$\limsup_{n\rightarrow\infty}n^{-1}\xi_{T_n}=-\infty$ a.s., there exists some ![]() $N\in\mathbb N$ such that for all
$N\in\mathbb N$ such that for all ![]() $n>N$ we have
$n>N$ we have ![]() $T_n>1$ and
$T_n>1$ and
Define a sequence ![]() $(\tau_n)_{n\in\mathbb N}$ of times and
$(\tau_n)_{n\in\mathbb N}$ of times and ![]() $(x_n)_{n\in\mathbb N}$ of values such that, for each
$(x_n)_{n\in\mathbb N}$ of values such that, for each ![]() $n\in\mathbb N$, we have
$n\in\mathbb N$, we have
and
Since ![]() $\limsup_{t\rightarrow\infty}t^{-1}\xi_t>-R$ a.s., there is an increasing sequence of times
$\limsup_{t\rightarrow\infty}t^{-1}\xi_t>-R$ a.s., there is an increasing sequence of times ![]() $(s_n)_{n\in\mathbb N}$ such that
$(s_n)_{n\in\mathbb N}$ such that ![]() $s_n^{-1}\xi_{s_n}>-R$ a.s. for each
$s_n^{-1}\xi_{s_n}>-R$ a.s. for each ![]() $n\in\mathbb N$ and
$n\in\mathbb N$ and ![]() $\lim_{n\rightarrow\infty}s_n=\infty$. Then we may take a subsequence
$\lim_{n\rightarrow\infty}s_n=\infty$. Then we may take a subsequence ![]() $(s^{\prime}_n)_{n\in\mathbb N}$ such that there is at most one element of the sequence
$(s^{\prime}_n)_{n\in\mathbb N}$ such that there is at most one element of the sequence ![]() $(s^{\prime}_n)_{n\in\mathbb N}$ in each interval
$(s^{\prime}_n)_{n\in\mathbb N}$ in each interval ![]() $[T_m,T_{m+1}]$ and
$[T_m,T_{m+1}]$ and ![]() $J_{s^{\prime}_n}$ is constant.
$J_{s^{\prime}_n}$ is constant.
Let ![]() $(\tau_{k_n})_{n\in\mathbb N}$ be a subsequence of
$(\tau_{k_n})_{n\in\mathbb N}$ be a subsequence of ![]() $(\tau_{n\in\mathbb N})$ such that
$(\tau_{n\in\mathbb N})$ such that ![]() $k_n>N$ and
$k_n>N$ and ![]() $s^{\prime}_n\in[T_{k_n},T_{{k_n}+1}]$ for each
$s^{\prime}_n\in[T_{k_n},T_{{k_n}+1}]$ for each ![]() $n\in\mathbb N$. Then, for each
$n\in\mathbb N$. Then, for each ![]() $n\in\mathbb N$, we have
$n\in\mathbb N$, we have
whilst ![]() $\xi_{T_{k_n+1}}<-2RT_{k_n+1}$ and
$\xi_{T_{k_n+1}}<-2RT_{k_n+1}$ and ![]() $T_{k_n+1}>1$, therefore
$T_{k_n+1}>1$, therefore
almost surely. However, for each ![]() $n\in\mathbb N$, by the Lamperti–Kiu decomposition,
$n\in\mathbb N$, by the Lamperti–Kiu decomposition,
is a Lévy process, so, by splitting at the last time of the maximum [Reference Bertoin4, Chapter VI, Theorem 5], ![]() $x_{k_n}-\xi_{T_{k_n+1}}$ is independent of
$x_{k_n}-\xi_{T_{k_n+1}}$ is independent of ![]() $x_{k_n}$ and has the same distribution as
$x_{k_n}$ and has the same distribution as ![]() $x_0-\xi_{T_1}$, hence its distribution does not depend on R. This contradicts the fact that it only has support on
$x_0-\xi_{T_1}$, hence its distribution does not depend on R. This contradicts the fact that it only has support on ![]() $(R,\infty)$. Hence
$(R,\infty)$. Hence ![]() $I_+<\infty$ and K undefined imply that
$I_+<\infty$ and K undefined imply that ![]() $\lim_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ a.s. and so the ‘if’ direction of (iv) holds. By applying similar arguments to
$\lim_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ a.s. and so the ‘if’ direction of (iv) holds. By applying similar arguments to ![]() $-\xi_t$, statement (iii) of the lemma also holds.
$-\xi_t$, statement (iii) of the lemma also holds.
To prove the ‘only if’ direction of (i), suppose ![]() $I_+<\infty$. Since K is undefined, by [Reference Erickson10, Theorem 2] and the remark that follows it, we have
$I_+<\infty$. Since K is undefined, by [Reference Erickson10, Theorem 2] and the remark that follows it, we have ![]() $I_-=\infty$. Then, by statement (iv), we have
$I_-=\infty$. Then, by statement (iv), we have ![]() $\lim_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ a.s. Hence
$\lim_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ a.s. Hence ![]() $\limsup_{t\rightarrow\infty}t^{-1}\xi_t=\infty$ a.s. only if
$\limsup_{t\rightarrow\infty}t^{-1}\xi_t=\infty$ a.s. only if ![]() $I_+=\infty$. The argument for (iii) is analogous.
$I_+=\infty$. The argument for (iii) is analogous.
The following theorem shows that in the infinite lifetime case, the convergence and finiteness of ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$ are fully characterised by K when this is defined and by the finiteness of
$B_\infty$ are fully characterised by K when this is defined and by the finiteness of ![]() $I_+$ otherwise.
$I_+$ otherwise.
Theorem 2.1. Suppose Y has an infinite lifetime. Then ![]() $A_\infty$ converges a.s. if and only if
$A_\infty$ converges a.s. if and only if ![]() $B_\infty$ converges a.s. Moreover,
$B_\infty$ converges a.s. Moreover, ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$ converge almost surely if and only if either K is defined and
$B_\infty$ converge almost surely if and only if either K is defined and ![]() $K<0$ or K is undefined and
$K<0$ or K is undefined and ![]() $I_+<\infty.$
$I_+<\infty.$
Before proving Theorem 2.1, we prove the following preliminary lemma.
Lemma 2.2. If ![]() $\limsup_{n\rightarrow\infty}\xi_{T_{2n}}=\infty$ a.s., then both
$\limsup_{n\rightarrow\infty}\xi_{T_{2n}}=\infty$ a.s., then both ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$ diverge a.s.
$B_\infty$ diverge a.s.
Proof. If ![]() $\limsup_{n\rightarrow\infty}\xi_{T_{2n}} = \infty$ a.s., then there exists a strictly increasing sequence
$\limsup_{n\rightarrow\infty}\xi_{T_{2n}} = \infty$ a.s., then there exists a strictly increasing sequence ![]() $ \{\tau_n \}_{n\in\mathbb N}\subset\mathbb N$ such that
$ \{\tau_n \}_{n\in\mathbb N}\subset\mathbb N$ such that ![]() $\exp (\xi_{T_{2\tau_n}} ) \geq 1$ a.s. for all
$\exp (\xi_{T_{2\tau_n}} ) \geq 1$ a.s. for all ![]() $n\in\mathbb N$. First, by considering
$n\in\mathbb N$. First, by considering ![]() $A_\infty$ and using the Markov property for the second inequality, we have
$A_\infty$ and using the Markov property for the second inequality, we have
 \begin{align*} A_\infty &\geq \sum_{n=0}^\infty \exp \big( \xi_{T_{2\tau_n}} \big)\int_{T_{2\tau_n}}^{T_{2\tau_n+2}}\exp\big( \xi_t - \xi_{T_{2\tau_n}}\big) \,{\mathrm{d}} t \geq \sum_{n=0}^\infty \int_{0}^{T_2^{(n)}}\exp\big(\xi_t^{(n)}\big) \,{\mathrm{d}} t.\end{align*}
\begin{align*} A_\infty &\geq \sum_{n=0}^\infty \exp \big( \xi_{T_{2\tau_n}} \big)\int_{T_{2\tau_n}}^{T_{2\tau_n+2}}\exp\big( \xi_t - \xi_{T_{2\tau_n}}\big) \,{\mathrm{d}} t \geq \sum_{n=0}^\infty \int_{0}^{T_2^{(n)}}\exp\big(\xi_t^{(n)}\big) \,{\mathrm{d}} t.\end{align*}
Since the terms of this series form an i.i.d. sequence with strictly positive values, the series must diverge.
Similarly, ![]() $B_\infty$ converges a.s. only if the sum
$B_\infty$ converges a.s. only if the sum ![]() $\sum_{n=0}^\infty \int_{T_{2n}}^{T_{2n+2}}J_t \exp(\xi_t) \,{\mathrm{d}} t$ converges a.s., which implies the a.s. convergence to zero of the subsequence
$\sum_{n=0}^\infty \int_{T_{2n}}^{T_{2n+2}}J_t \exp(\xi_t) \,{\mathrm{d}} t$ converges a.s., which implies the a.s. convergence to zero of the subsequence
 \begin{align*} \biggl|\int_{T_{2\tau_n}}^{T_{2\tau_n+2}}J_t \exp(\xi_t) \,{\mathrm{d}} t\biggr| &= \exp ( \xi_{T_{2\tau_n}} )\biggl|\int_{T_{2\tau_n}}^{T_{2\tau_n+2}} J_t\exp ( \xi_t - \xi_{T_{2\tau_n}} ) \,{\mathrm{d}} t\biggr|\\ &\geq \biggl|\int_{T_{2\tau_n}}^{T_{2\tau_n+2}} J_t\exp ( \xi_t - \xi_{T_{2\tau_n}} ) \,{\mathrm{d}} t\biggr|.\end{align*}
\begin{align*} \biggl|\int_{T_{2\tau_n}}^{T_{2\tau_n+2}}J_t \exp(\xi_t) \,{\mathrm{d}} t\biggr| &= \exp ( \xi_{T_{2\tau_n}} )\biggl|\int_{T_{2\tau_n}}^{T_{2\tau_n+2}} J_t\exp ( \xi_t - \xi_{T_{2\tau_n}} ) \,{\mathrm{d}} t\biggr|\\ &\geq \biggl|\int_{T_{2\tau_n}}^{T_{2\tau_n+2}} J_t\exp ( \xi_t - \xi_{T_{2\tau_n}} ) \,{\mathrm{d}} t\biggr|.\end{align*}
Then, by using the Markov property, ![]() $B_\infty$ converges a.s. only if
$B_\infty$ converges a.s. only if
as ![]() $n\rightarrow\infty$. This convergence is impossible since we are dealing with an i.i.d. sequence that does not converge to zero in distribution.
$n\rightarrow\infty$. This convergence is impossible since we are dealing with an i.i.d. sequence that does not converge to zero in distribution.
Proof of Theorem 2.1. We will consider the cases when K is defined and undefined separately.
1. Suppose that K is defined and ![]() $K<0$. Then recall that
$K<0$. Then recall that ![]() $\lim_{t\rightarrow\infty}t^{-1}\xi_t=K$ a.s. as
$\lim_{t\rightarrow\infty}t^{-1}\xi_t=K$ a.s. as ![]() $t\rightarrow\infty$. If
$t\rightarrow\infty$. If ![]() $-\infty<K<0$ let
$-\infty<K<0$ let ![]() $k=\tfrac{1}{2}K$ and if
$k=\tfrac{1}{2}K$ and if ![]() $K=-\infty$ let
$K=-\infty$ let ![]() $k=-1$. Then a.s. there exists a finite
$k=-1$. Then a.s. there exists a finite ![]() $T\geq0$ such that
$T\geq0$ such that ![]() $\xi_t< kt <0$ for all
$\xi_t< kt <0$ for all ![]() $t>T$. Thus
$t>T$. Thus ![]() $A_\infty\leq \int_0^T\exp(\xi_t) \,{\mathrm{d}} t + k^{-1}\,{\mathrm{e}}^{kT}<\infty$ a.s., and by absolute convergence it is then immediate that
$A_\infty\leq \int_0^T\exp(\xi_t) \,{\mathrm{d}} t + k^{-1}\,{\mathrm{e}}^{kT}<\infty$ a.s., and by absolute convergence it is then immediate that ![]() $B_\infty$ also converges a.s.
$B_\infty$ also converges a.s.
Next we consider the case when either ![]() $K>0$ or both
$K>0$ or both ![]() $K=0$ and Y is non-degenerate. Then, by [Reference Kallenberg15, Proposition 9.14],
$K=0$ and Y is non-degenerate. Then, by [Reference Kallenberg15, Proposition 9.14], ![]() $\limsup_{n\rightarrow\infty}\xi_{T_{2n}} = \infty$ a.s., so the result follows from Lemma 2.2. If
$\limsup_{n\rightarrow\infty}\xi_{T_{2n}} = \infty$ a.s., so the result follows from Lemma 2.2. If ![]() $K=0$ and Y is degenerate, then, since Y has an infinite lifetime, we have
$K=0$ and Y is degenerate, then, since Y has an infinite lifetime, we have
 \begin{equation*} \xi_t = \begin{cases} 0 &\text{if $ T_{2k} \leq t < T_{2k+1}$ for $k\in\mathbb N_0$,}\\[4pt] U^{J_0} &\text{if $ T_{2k+1} \leq t
< T_{2k+2}$ for $k\in\mathbb N_0$.} \end{cases}\end{equation*}
\begin{equation*} \xi_t = \begin{cases} 0 &\text{if $ T_{2k} \leq t < T_{2k+1}$ for $k\in\mathbb N_0$,}\\[4pt] U^{J_0} &\text{if $ T_{2k+1} \leq t
< T_{2k+2}$ for $k\in\mathbb N_0$.} \end{cases}\end{equation*}
Thus, for all ![]() $t\geq0$, we have
$t\geq0$, we have
so ![]() $A_\infty=\infty$ a.s. Also,
$A_\infty=\infty$ a.s. Also, ![]() $B_\infty$ can be written as the sum
$B_\infty$ can be written as the sum
and since ![]() $\zeta^{2n} - \exp(U^{J_0})\zeta^{2n+1} $ does not converge to zero in distribution,
$\zeta^{2n} - \exp(U^{J_0})\zeta^{2n+1} $ does not converge to zero in distribution, ![]() $B_\infty$ must a.s. diverge.
$B_\infty$ must a.s. diverge.
2. Suppose that K is undefined. From [Reference Erickson10, Theorem 2] we know that if ![]() $I_+=\infty$ then
$I_+=\infty$ then ![]() $\limsup_{n\rightarrow\infty}\xi_{T_{2n}}=\infty$ a.s. Hence, by using Lemma 2.2, both
$\limsup_{n\rightarrow\infty}\xi_{T_{2n}}=\infty$ a.s. Hence, by using Lemma 2.2, both ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$ diverge a.s.
$B_\infty$ diverge a.s.
If ![]() $I_+<\infty$, then since K is undefined, as a consequence of [Reference Erickson10, Theorem 2],
$I_+<\infty$, then since K is undefined, as a consequence of [Reference Erickson10, Theorem 2], ![]() $I_-=\infty$ and so by Lemma 2.1 we have
$I_-=\infty$ and so by Lemma 2.1 we have ![]() $\limsup_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ a.s. Then, by the argument of case 1 above, both
$\limsup_{t\rightarrow\infty}t^{-1}\xi_t=-\infty$ a.s. Then, by the argument of case 1 above, both ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$ converge a.s. as desired.
$B_\infty$ converge a.s. as desired.
3. Moments and tail asymptotics of  ${{A}}_\infty$ and
${{A}}_\infty$ and  ${{B}}_\infty$
${{B}}_\infty$
Throughout this section we assume the Lamperti–Kiu process has an infinite lifetime. For ![]() $z\in\mathbb C$ suppose the characteristic exponents
$z\in\mathbb C$ suppose the characteristic exponents ![]() $\psi_\pm(z) \,:\!=\, \log (\mathbb E[\exp(z\xi_1^\pm)] )$ and Laplace transforms
$\psi_\pm(z) \,:\!=\, \log (\mathbb E[\exp(z\xi_1^\pm)] )$ and Laplace transforms ![]() $G^\pm(z)\,:\!=\, \mathbb E[\exp(zU^\pm)]$ exist and are finite. Then the matrix exponent of Y is defined to be
$G^\pm(z)\,:\!=\, \mathbb E[\exp(zU^\pm)]$ exist and are finite. Then the matrix exponent of Y is defined to be
 \begin{equation*}F(z) \,:\!=\, \begin{pmatrix} \psi_+(z) & \quad 0\\[3pt] 0 & \quad \psi_-(z)\end{pmatrix}+ \begin{pmatrix} -q_+& \quad q_+G^+(z) \\[3pt] q_-G^-(z) & \quad -q_-\end{pmatrix}\!, \end{equation*}
\begin{equation*}F(z) \,:\!=\, \begin{pmatrix} \psi_+(z) & \quad 0\\[3pt] 0 & \quad \psi_-(z)\end{pmatrix}+ \begin{pmatrix} -q_+& \quad q_+G^+(z) \\[3pt] q_-G^-(z) & \quad -q_-\end{pmatrix}\!, \end{equation*}
and from [Reference Asmussen2, XI.2b] it is known that, for ![]() $l,j\in\{+,-\}$ and
$l,j\in\{+,-\}$ and ![]() $z\in\mathbb C$,
$z\in\mathbb C$,
Then let ![]() $\lambda(z)$ denote the eigenvalue of F(z) with largest real part. Using Perron–Frobenius theory, it is shown in [Reference Kuznetsov, Kyprianou, Pardo and Watson18, Proposition 3.2] that such an eigenvalue is guaranteed to be simple, real, and continuous as a function of z. From [Reference Kuznetsov, Kyprianou, Pardo and Watson18, Proposition 3.4] we also know that
$\lambda(z)$ denote the eigenvalue of F(z) with largest real part. Using Perron–Frobenius theory, it is shown in [Reference Kuznetsov, Kyprianou, Pardo and Watson18, Proposition 3.2] that such an eigenvalue is guaranteed to be simple, real, and continuous as a function of z. From [Reference Kuznetsov, Kyprianou, Pardo and Watson18, Proposition 3.4] we also know that ![]() $\lambda(z)$ is convex when considered as a map
$\lambda(z)$ is convex when considered as a map ![]() $\lambda\colon \mathbb R\rightarrow\mathbb R$. Provided F exists in a neighbourhood of zero, from [Reference Asmussen2, Corollary 2.9] it is known that
$\lambda\colon \mathbb R\rightarrow\mathbb R$. Provided F exists in a neighbourhood of zero, from [Reference Asmussen2, Corollary 2.9] it is known that ![]() $K=\lambda'(0)\in[-\infty,\infty]$, where the derivative is considered on this restriction.
$K=\lambda'(0)\in[-\infty,\infty]$, where the derivative is considered on this restriction.
It can be shown that the integrals ![]() $A_\infty$ and
$A_\infty$ and ![]() $B_\infty$ are the solutions of random affine equations. We will assume
$B_\infty$ are the solutions of random affine equations. We will assume ![]() $q_+,q_->0$ so that
$q_+,q_->0$ so that ![]() $T_2<\infty$ and note that
$T_2<\infty$ and note that ![]() $T_2$ is independent of
$T_2$ is independent of ![]() $Y_0$. Then, for any
$Y_0$. Then, for any ![]() $T\in[0,\infty]$, define the random variables
$T\in[0,\infty]$, define the random variables
and notice that ![]() $A_\infty=\lim_{T\rightarrow\infty}A_T$ and
$A_\infty=\lim_{T\rightarrow\infty}A_T$ and ![]() $B_\infty=\lim_{T\rightarrow\infty}B_T$. Similarly, due to the result in [Reference Bertoin and Yor5, Section 4.3], by the Markov additive property
$B_\infty=\lim_{T\rightarrow\infty}B_T$. Similarly, due to the result in [Reference Bertoin and Yor5, Section 4.3], by the Markov additive property
where ![]() $\hat{B}_\infty$ is an independent copy of
$\hat{B}_\infty$ is an independent copy of ![]() $B_\infty$.
$B_\infty$.
Notice that ![]() $Y_{T_2}$ has the same sign as
$Y_{T_2}$ has the same sign as ![]() $Y_0$ and that
$Y_0$ and that ![]() $|Y_{T_2}|$ is independent of
$|Y_{T_2}|$ is independent of ![]() $J_0$ because of its symmetry in the components of the decomposition of Y. Similarly
$J_0$ because of its symmetry in the components of the decomposition of Y. Similarly
where ![]() $\hat{A}_\infty$ is an independent but identically distributed copy of
$\hat{A}_\infty$ is an independent but identically distributed copy of ![]() $A_\infty$ and is independent of
$A_\infty$ and is independent of ![]() $Y_{T_2}$ and
$Y_{T_2}$ and ![]() $A_{T_2}$.
$A_{T_2}$.
The following results are generalisations of [Reference Bertoin and Yor5, Corollary 5] to Lamperti–Kiu processes using the implicit renewal theorems given in [Reference Goldie12, Theorem 4.1] and [Reference Kesten16, Theorem 5]. In the case of a Lévy process, it has been shown in [Reference Patie and Savov23] that the coefficient ![]() $c_A$ of the proposition below can be found explicitly by evaluating a Bernstein-gamma function.
$c_A$ of the proposition below can be found explicitly by evaluating a Bernstein-gamma function.
Proposition 3.1. Suppose Y is an infinite lifetime Lamperti–Kiu process with ![]() $K<0$ and there is a
$K<0$ and there is a ![]() $\kappa>0$ such that
$\kappa>0$ such that ![]() $F(\kappa)$ exists,
$F(\kappa)$ exists, ![]() $\lambda(\kappa)=0$ and
$\lambda(\kappa)=0$ and
If ![]() $Y_{T_2}$ does not have a lattice distribution, then there exist constants
$Y_{T_2}$ does not have a lattice distribution, then there exist constants ![]() $c_A,c_B^+,c_B^-\in\mathbb R$ such that
$c_A,c_B^+,c_B^-\in\mathbb R$ such that
and therefore ![]() $A_\infty,B_\infty$ have moments of order
$A_\infty,B_\infty$ have moments of order ![]() $s\in\mathbb C^+\,:\!=\, \{x\in\mathbb C \colon \Re(x)\geq0 \}$ if and only if
$s\in\mathbb C^+\,:\!=\, \{x\in\mathbb C \colon \Re(x)\geq0 \}$ if and only if ![]() ${0\leq \Re(s)<\kappa}$.
${0\leq \Re(s)<\kappa}$.
Proof. Since the proposition assumes (3.2), the result is an immediate consequence of [Reference Goldie12, Theorem 2.3] and [Reference Kesten16, Section 4, Theorem 5] provided that
We now prove that under the conditions of the proposition each of these equations holds.
To show (3.3), we expand ![]() $\log|Y_{T_2}|$ to get
$\log|Y_{T_2}|$ to get
and since ![]() $q_+^{-1} + q_-^{-1}>0$, (3.3) follows from the assumption
$q_+^{-1} + q_-^{-1}>0$, (3.3) follows from the assumption ![]() $K<0$.
$K<0$.
Since ![]() $\det(F(z)) = (\psi^+(z) - q^+)(\psi^-(z) - q^-) - q^+q^-G^+(z)G^-(z)$ and by the assumption that 0 is an eigenvalue of
$\det(F(z)) = (\psi^+(z) - q^+)(\psi^-(z) - q^-) - q^+q^-G^+(z)G^-(z)$ and by the assumption that 0 is an eigenvalue of ![]() $F(\kappa)$, we have
$F(\kappa)$, we have
Let ![]() $\mu(z)$ be the other eigenvalue of F(z). Then, for all real
$\mu(z)$ be the other eigenvalue of F(z). Then, for all real ![]() $z\in(0,\kappa)$, by assumption,
$z\in(0,\kappa)$, by assumption, ![]() $\mu(z)<\lambda(z)<0$ and so
$\mu(z)<\lambda(z)<0$ and so ![]() $0 < \mu(z)\lambda(z) = \det(F(z))$. Rearranging this gives
$0 < \mu(z)\lambda(z) = \det(F(z))$. Rearranging this gives ![]() $(\psi^+(z) - q^+)(\psi^-(z) - q^-) > 0$, so
$(\psi^+(z) - q^+)(\psi^-(z) - q^-) > 0$, so ![]() $\psi^\pm(z) - q^\pm$ has no roots in
$\psi^\pm(z) - q^\pm$ has no roots in ![]() $(0,\kappa)$. Since
$(0,\kappa)$. Since ![]() $\psi^\pm(0)-q^\pm<0$, by continuity,
$\psi^\pm(0)-q^\pm<0$, by continuity, ![]() $\psi^\pm(z)-q^\pm<0$ for all
$\psi^\pm(z)-q^\pm<0$ for all ![]() $z\in(0,\kappa)$. By independence and using (3.7), we get
$z\in(0,\kappa)$. By independence and using (3.7), we get
and hence (3.4) holds.
Using independence and the inequality ![]() $(a+b)^x\leq 2^x(a^x+b^x)$ for
$(a+b)^x\leq 2^x(a^x+b^x)$ for ![]() $a,b,x>0$, we get
$a,b,x>0$, we get
From [Reference Bertoin and Yor5] it is known that
for all ![]() $x\in(0,\infty)$ such that
$x\in(0,\infty)$ such that ![]() $\psi^\pm(x)-q^\pm<0$. This follows from the fact that
$\psi^\pm(x)-q^\pm<0$. This follows from the fact that ![]() $\int_0^{\zeta^\pm}\exp(\xi^\pm_s) \,{\mathrm{d}} s$ is the exponential functional of the Lévy process
$\int_0^{\zeta^\pm}\exp(\xi^\pm_s) \,{\mathrm{d}} s$ is the exponential functional of the Lévy process ![]() $\xi^{(\pm)}$ sent to the cemetery state
$\xi^{(\pm)}$ sent to the cemetery state ![]() $-\infty$ at an independent, exponentially distributed time of rate
$-\infty$ at an independent, exponentially distributed time of rate ![]() $q^\pm$. Then, since we have already seen that
$q^\pm$. Then, since we have already seen that ![]() $\psi^\pm(\kappa)-q^\pm<0$, it follows that
$\psi^\pm(\kappa)-q^\pm<0$, it follows that
By the assumption that ![]() $F(\kappa)$ exists, we have
$F(\kappa)$ exists, we have ![]() $\mathbb E[ \exp(\kappa U^\pm) ]<\infty$, whilst
$\mathbb E[ \exp(\kappa U^\pm) ]<\infty$, whilst ![]() $\mathbb E[ \exp(\kappa\xi_{\zeta_\pm}^\pm) ]<\infty$ follows easily from
$\mathbb E[ \exp(\kappa\xi_{\zeta_\pm}^\pm) ]<\infty$ follows easily from ![]() $ \mathbb E[\exp(\kappa\xi_t^\pm)]=\exp(t\psi_\pm(\kappa))$ for
$ \mathbb E[\exp(\kappa\xi_t^\pm)]=\exp(t\psi_\pm(\kappa))$ for ![]() $t\geq 0$. Hence
$t\geq 0$. Hence ![]() $\mathbb E[|B_{T_2}|^\kappa]\leq\mathbb E[ |A_{T_2}|^\kappa ]<\infty$ and so equations (3.5) and (3.6) hold.
$\mathbb E[|B_{T_2}|^\kappa]\leq\mathbb E[ |A_{T_2}|^\kappa ]<\infty$ and so equations (3.5) and (3.6) hold.
Remark 3.1. In the case when ![]() $G^{\pm}$ are continuous, (3.2) is automatic. Indeed, by continuity, we can pick
$G^{\pm}$ are continuous, (3.2) is automatic. Indeed, by continuity, we can pick ![]() $\epsilon>0$ such that
$\epsilon>0$ such that ![]() $\psi^\pm(\kappa+\epsilon)-q^\pm<0$ and
$\psi^\pm(\kappa+\epsilon)-q^\pm<0$ and ![]() $G^\pm(\kappa+\epsilon)<\infty$. Then, from the proof of (3.4), we obtain
$G^\pm(\kappa+\epsilon)<\infty$. Then, from the proof of (3.4), we obtain
Since ![]() $\log(x)^+<x^\epsilon$ for all
$\log(x)^+<x^\epsilon$ for all ![]() $x\geq R$, for some sufficiently large
$x\geq R$, for some sufficiently large ![]() $R>0$ we have
$R>0$ we have
 \begin{align*} \mathbb E[|Y_{T_2}|^\kappa\log Y_{T_2}^+] &= \mathbb E[|Y_{T_2}|^\kappa\log Y_{T_2}^+ ;\, |Y_{T_2}|\leq R] + \mathbb E[|Y_{T_2}|^\kappa\log Y_{T_2}^+ ;\, |Y_{T_2}|> R]\\ &\leq R^{\kappa+\epsilon} + \mathbb E[|Y_{T_2}|^{\kappa+\epsilon}]\\ &<\infty.\end{align*}
\begin{align*} \mathbb E[|Y_{T_2}|^\kappa\log Y_{T_2}^+] &= \mathbb E[|Y_{T_2}|^\kappa\log Y_{T_2}^+ ;\, |Y_{T_2}|\leq R] + \mathbb E[|Y_{T_2}|^\kappa\log Y_{T_2}^+ ;\, |Y_{T_2}|> R]\\ &\leq R^{\kappa+\epsilon} + \mathbb E[|Y_{T_2}|^{\kappa+\epsilon}]\\ &<\infty.\end{align*}
Hence (3.2) holds.
4. Subexponential tails of  ${{A}}_{\boldsymbol\infty}$
${{A}}_{\boldsymbol\infty}$
When the conditions of Proposition 3.1 do not hold, a different approach to the investigation of the tails and moments of ![]() $A_\infty$ is required. In Proposition 3.1 it is assumed that
$A_\infty$ is required. In Proposition 3.1 it is assumed that ![]() $F(\kappa)$ exists, which requires that positive exponential moments of
$F(\kappa)$ exists, which requires that positive exponential moments of ![]() $\xi$ must exist. This is a condition that does not necessarily hold in general, and in particular, when
$\xi$ must exist. This is a condition that does not necessarily hold in general, and in particular, when ![]() $\xi_{T_2}$ is heavy-tailed.
$\xi_{T_2}$ is heavy-tailed.
In this section we will define Lamperti–Kiu processes of strong subexponential type and study the right tails of the exponential functional of such processes. The main result of this section is Theorem 4.1, which shows, under some conditions, that the exponential functional, ![]() $A_\infty$, is itself long-tailed and
$A_\infty$, is itself long-tailed and ![]() $\log(A_\infty)$ is subexponential.
$\log(A_\infty)$ is subexponential.
First we will prove two preliminary lemmas in Section 4.1. In Section 4.2 a framework is presented for bounding ![]() $\log(A_\infty)$ by considering a piecewise linear bound for
$\log(A_\infty)$ by considering a piecewise linear bound for ![]() $\{\xi_t\colon t\geq0\}$ with a.s. finitely many discontinuities. Finally, in Section 4.3, we define Lamperti–Kiu processes of strong subexponential type and use the framework from Section 4.2, in conjunction with the subexponential properties, to obtain the right tails of
$\{\xi_t\colon t\geq0\}$ with a.s. finitely many discontinuities. Finally, in Section 4.3, we define Lamperti–Kiu processes of strong subexponential type and use the framework from Section 4.2, in conjunction with the subexponential properties, to obtain the right tails of ![]() $A_\infty$. Interestingly, the resulting tails are of a very different nature to those considered under Cramér’s condition.
$A_\infty$. Interestingly, the resulting tails are of a very different nature to those considered under Cramér’s condition.
4.1. Preliminary results
We will need the following lemma, which bounds the probability distribution of the supremum of a Lévy process over an exponentially distributed interval of time in terms of the distribution of the Lévy process at the end of the interval. It is a variation of [Reference Willekens28, Lemma 1], where the time interval considered was fixed.
Lemma 4.1. Let X be a Lévy process, let ![]() $\tau$ be an independent exponentially distributed random variable, and suppose
$\tau$ be an independent exponentially distributed random variable, and suppose ![]() $0<u_0<u$. Then
$0<u_0<u$. Then
Proof. Let ![]() $S_u \,:\!=\, \inf\{t\geq0\colon X_t>u\}$. Then, since
$S_u \,:\!=\, \inf\{t\geq0\colon X_t>u\}$. Then, since ![]() $X_{S_u}\geq u$, by independence of increments of X and the memoryless property of
$X_{S_u}\geq u$, by independence of increments of X and the memoryless property of ![]() $\tau$, we have
$\tau$, we have
 \begin{align*} \mathbb P(S_u<\tau ;\, X_{\tau} < u-u_0 ) &\leq \mathbb P( S_u<\tau ;\, X_{\tau} - X_{S_u} < -u_0 )\\ & =\mathbb P( S_u<\tau ;\, \tilde{X}_{\tilde{\tau}} < -u_0 )\\ &= \mathbb P(S_u<\tau)\,\mathbb P(X_{\tau}<-u_0),\end{align*}
\begin{align*} \mathbb P(S_u<\tau ;\, X_{\tau} < u-u_0 ) &\leq \mathbb P( S_u<\tau ;\, X_{\tau} - X_{S_u} < -u_0 )\\ & =\mathbb P( S_u<\tau ;\, \tilde{X}_{\tilde{\tau}} < -u_0 )\\ &= \mathbb P(S_u<\tau)\,\mathbb P(X_{\tau}<-u_0),\end{align*}
where ![]() $\tilde{X}$ and
$\tilde{X}$ and ![]() $\tilde{\tau}$ are independent and identically distributed copies of X and
$\tilde{\tau}$ are independent and identically distributed copies of X and ![]() $\tau$, respectively. Then (4.1) can be obtained by rearranging the inequality
$\tau$, respectively. Then (4.1) can be obtained by rearranging the inequality
We now consider long-tailed distributions. Let ![]() $Q\colon \mathbb R^+\rightarrow[0,1]$ be a probability distribution and
$Q\colon \mathbb R^+\rightarrow[0,1]$ be a probability distribution and ![]() $\bar{Q}(x)\,:\!=\, 1-Q(x)$ for all
$\bar{Q}(x)\,:\!=\, 1-Q(x)$ for all ![]() $x\in\mathbb R^+$. Then Q is a long-tailed distribution if
$x\in\mathbb R^+$. Then Q is a long-tailed distribution if ![]() $Q(x+y)/Q(x)\rightarrow 1$ as
$Q(x+y)/Q(x)\rightarrow 1$ as ![]() $x\rightarrow\infty$, for any
$x\rightarrow\infty$, for any ![]() $y\in\mathbb R^+$. For any two functions
$y\in\mathbb R^+$. For any two functions ![]() $f,g\colon \mathbb R^+\rightarrow\mathbb R^+$, we will write
$f,g\colon \mathbb R^+\rightarrow\mathbb R^+$, we will write ![]() $f\sim g$ if
$f\sim g$ if ![]() $\lim_{x\rightarrow\infty}f(x)/g(x) = 1$ and say that f and g are asymptotically equivalent.
$\lim_{x\rightarrow\infty}f(x)/g(x) = 1$ and say that f and g are asymptotically equivalent.
For a random variable X, we define the functions
and refer to ![]() $H_X$ as the integrated tail of X.
$H_X$ as the integrated tail of X.
In the next lemma we show that the integrated tail of a long-tailed random variable is asymptotically equivalent to an infinite series. This will be used in Lemma 4.6 to show the asymptotic equivalence of the integrated tail ![]() $G_X$ and an infinite series that we will construct.
$G_X$ and an infinite series that we will construct.
Lemma 4.2. Suppose ![]() $K+\epsilon<0$ and that X is a long-tailed random variable, which is independent of
$K+\epsilon<0$ and that X is a long-tailed random variable, which is independent of ![]() $(T_{2n})_{n\in\mathbb N}$. Then the integrated tail of X has the asymptotics
$(T_{2n})_{n\in\mathbb N}$. Then the integrated tail of X has the asymptotics
Proof. By splitting the interval ![]() $(0,\infty)$ into a disjoint union, we can write
$(0,\infty)$ into a disjoint union, we can write
Then, by using the change of variables ![]() $u=-(K+\epsilon)^{-1}u_1$, we get
$u=-(K+\epsilon)^{-1}u_1$, we get
By independence of ![]() $\{T_{2n}\}_{n\in\mathbb N}$ and X, we can shift the domain of integration to obtain
$\{T_{2n}\}_{n\in\mathbb N}$ and X, we can shift the domain of integration to obtain
Taking expectations and noting that the left-hand side is not random, that ![]() $T_{2(n+1)}-T_{2n}\stackrel{\mathcal{L}}{=} T_2$, and that
$T_{2(n+1)}-T_{2n}\stackrel{\mathcal{L}}{=} T_2$, and that ![]() $T_{2(n+1)}-T_{2n}$ is independent of
$T_{2(n+1)}-T_{2n}$ is independent of ![]() $T_{2n}$ gives
$T_{2n}$ gives
 \begin{align*} G_X(x) &=|K+\epsilon|\sum_{n=0}^\infty \mathbb E\biggl[ \int_0^{\tilde{T}_2} \mathbb P( X > x-(K+\epsilon)(u + T_{2n}) \mid T_{2n} ) \,{\mathrm{d}} u \biggr],\end{align*}
\begin{align*} G_X(x) &=|K+\epsilon|\sum_{n=0}^\infty \mathbb E\biggl[ \int_0^{\tilde{T}_2} \mathbb P( X > x-(K+\epsilon)(u + T_{2n}) \mid T_{2n} ) \,{\mathrm{d}} u \biggr],\end{align*}
where ![]() $\tilde{T}_{2}$ is an independent and identically distributed copy of
$\tilde{T}_{2}$ is an independent and identically distributed copy of ![]() $T_2$. This can be written in the integral form
$T_2$. This can be written in the integral form
Let ![]() $\delta>0$; then, since X is long-tailed, for all
$\delta>0$; then, since X is long-tailed, for all ![]() $s>0$ there exists
$s>0$ there exists ![]() $R(s)>0$ such that, whenever
$R(s)>0$ such that, whenever ![]() $z>R(s)$ and
$z>R(s)$ and ![]() $y\in[0,-s(K+\epsilon)]$,
$y\in[0,-s(K+\epsilon)]$,
and since ![]() $-v(K+\epsilon)\geq 0$ for
$-v(K+\epsilon)\geq 0$ for ![]() $v\geq0$, we have for all
$v\geq0$, we have for all ![]() $x>R(s)$ and
$x>R(s)$ and ![]() $u\in[0,s]$
$u\in[0,s]$
To show the lower bound we use this inequality within the last two integrals of (4.3) to obtain, for ![]() $x>R(s)$,
$x>R(s)$,
 \begin{align*}& \int_0^s \int_0^\infty \mathbb P(T_{2n}\in {\mathrm{d}} v) \,\mathbb P (X> x - (K+\epsilon)(u + v) ) \,{\mathrm{d}} u\\[5pt]
&\quad \geq \int_0^s \int_0^\infty \mathbb P(T_{2n}\in {\mathrm{d}} v)(1-\delta)\,\mathbb P(X > x-(K+\epsilon)v) \,{\mathrm{d}} u.\end{align*}
\begin{align*}& \int_0^s \int_0^\infty \mathbb P(T_{2n}\in {\mathrm{d}} v) \,\mathbb P (X> x - (K+\epsilon)(u + v) ) \,{\mathrm{d}} u\\[5pt]
&\quad \geq \int_0^s \int_0^\infty \mathbb P(T_{2n}\in {\mathrm{d}} v)(1-\delta)\,\mathbb P(X > x-(K+\epsilon)v) \,{\mathrm{d}} u.\end{align*}
Then, evaluating the integrals and noticing that the integrand is constant with respect to u gives, for ![]() $x>R(s)$,
$x>R(s)$,
Now consider some ![]() $l>0$ and suppose
$l>0$ and suppose ![]() $x>R(l)$, so that
$x>R(l)$, so that ![]() $x>R(s)$ for any
$x>R(s)$ for any ![]() $s\in[0,l]$. Then
$s\in[0,l]$. Then
 \begin{align*} &\int_0^\infty \mathbb P(T_2 \in {\mathrm{d}} s)\int_0^s \int_0^\infty \mathbb P(T_{2n}\in {\mathrm{d}} v)\,\mathbb P(X>x-(K+\epsilon)(u+v)) \,{\mathrm{d}} u\\ &\quad \geq \int_0^l \mathbb P(T_2 \in {\mathrm{d}} s) s(1-\delta)\,\mathbb P(X>x-(K+\epsilon)T_{2n})\\ &\quad =(1-\delta)\,\mathbb P(X>x-(K+\epsilon)T_{2n})\,\mathbb E[T_2 ;\, T_2<l].\end{align*}
\begin{align*} &\int_0^\infty \mathbb P(T_2 \in {\mathrm{d}} s)\int_0^s \int_0^\infty \mathbb P(T_{2n}\in {\mathrm{d}} v)\,\mathbb P(X>x-(K+\epsilon)(u+v)) \,{\mathrm{d}} u\\ &\quad \geq \int_0^l \mathbb P(T_2 \in {\mathrm{d}} s) s(1-\delta)\,\mathbb P(X>x-(K+\epsilon)T_{2n})\\ &\quad =(1-\delta)\,\mathbb P(X>x-(K+\epsilon)T_{2n})\,\mathbb E[T_2 ;\, T_2<l].\end{align*}
Since ![]() $l>0$ and
$l>0$ and ![]() $\delta>0$ are arbitrary and
$\delta>0$ are arbitrary and ![]() $T_2$ is integrable, we can take l sufficiently large to obtain
$T_2$ is integrable, we can take l sufficiently large to obtain ![]() $\mathbb E[T_2 ;\, T_2<l]\geq(1-\delta)\,\mathbb E[T_2]$ and thus
$\mathbb E[T_2 ;\, T_2<l]\geq(1-\delta)\,\mathbb E[T_2]$ and thus
 \begin{align*}& \int_0^\infty \mathbb P(T_2 \in {\mathrm{d}} s)\int_0^s \int_0^\infty \mathbb P(T_{2n}\in {\mathrm{d}} v)\,\mathbb P(X>x-(K+\epsilon)(u+v)) \,{\mathrm{d}} u\\ &\quad \geq (1-\delta)^2\,\mathbb P(X>x-(K+\epsilon)T_{2n})\,\mathbb E[T_2].\end{align*}
\begin{align*}& \int_0^\infty \mathbb P(T_2 \in {\mathrm{d}} s)\int_0^s \int_0^\infty \mathbb P(T_{2n}\in {\mathrm{d}} v)\,\mathbb P(X>x-(K+\epsilon)(u+v)) \,{\mathrm{d}} u\\ &\quad \geq (1-\delta)^2\,\mathbb P(X>x-(K+\epsilon)T_{2n})\,\mathbb E[T_2].\end{align*}
If this is substituted into the expression for ![]() $G_X$ for
$G_X$ for ![]() $x>R(l)$, we have
$x>R(l)$, we have
For the upper bound, since ![]() $-(K+\epsilon)u>0$ for
$-(K+\epsilon)u>0$ for ![]() $u>0$,
$u>0$,
which, substituted into the expression for ![]() $G_X$, gives, for all
$G_X$, gives, for all ![]() $x>0$,
$x>0$,
Combining the upper and lower bounds gives (4.2).
4.2. Framework for an upper bound of  $\log({{A}}_{\boldsymbol\infty})$
$\log({{A}}_{\boldsymbol\infty})$
We now develop a framework for bounding ![]() $\log(A_\infty)$ whenever
$\log(A_\infty)$ whenever ![]() $\mathbb E[\xi_{T_2}]\in(-\infty,0)$. This will be used in the strong subexponential setting of Section 4.3 to obtain the right tails of
$\mathbb E[\xi_{T_2}]\in(-\infty,0)$. This will be used in the strong subexponential setting of Section 4.3 to obtain the right tails of ![]() $A_\infty$. This framework consists of constructing a series of stopping times between which
$A_\infty$. This framework consists of constructing a series of stopping times between which ![]() $\xi$ is bounded from above. By studying the properties of these stopping times and the behaviour of
$\xi$ is bounded from above. By studying the properties of these stopping times and the behaviour of ![]() $\xi$ at those times, we can begin to understand
$\xi$ at those times, we can begin to understand ![]() $\log(A_\infty)$.
$\log(A_\infty)$.
For ![]() $\epsilon\in(0,-K)$ and sufficiently large
$\epsilon\in(0,-K)$ and sufficiently large ![]() $A\in\mathbb R$, define a sequence of stopping times by
$A\in\mathbb R$, define a sequence of stopping times by ![]() $\sigma_0\,:\!=\, 0$ and
$\sigma_0\,:\!=\, 0$ and
for each ![]() $n\in\mathbb N$, with the convention
$n\in\mathbb N$, with the convention ![]() $\inf(\varnothing)=\infty$, and setting
$\inf(\varnothing)=\infty$, and setting ![]() $\sigma_n=\infty$ if
$\sigma_n=\infty$ if ![]() $\sigma_{n-1}=\infty$. Then also define
$\sigma_{n-1}=\infty$. Then also define
The next lemma concerns the finiteness of N.
Lemma 4.3. If ![]() $\mathbb E[\xi_{T_2}]<0$, then there exists an
$\mathbb E[\xi_{T_2}]<0$, then there exists an ![]() $A^*>0$ such that, for all
$A^*>0$ such that, for all ![]() $A>A^*$, N is a.s. finite.
$A>A^*$, N is a.s. finite.
Proof. Define a new MAP ![]() $\{(J_t,\tilde{\xi_t})\colon t\geq0\}$ by setting
$\{(J_t,\tilde{\xi_t})\colon t\geq0\}$ by setting ![]() $\tilde{\xi}_t \,:\!=\, \xi_t - (K+\epsilon) t$. For each
$\tilde{\xi}_t \,:\!=\, \xi_t - (K+\epsilon) t$. For each ![]() $n\in\mathbb N$,
$n\in\mathbb N$,
then, since ![]() $\sigma_{n-1}$ is a stopping time, using the Markov additive property and summing over the events
$\sigma_{n-1}$ is a stopping time, using the Markov additive property and summing over the events ![]() $\{J_{\sigma_{n-1}}=j\}$ for
$\{J_{\sigma_{n-1}}=j\}$ for ![]() $j\in\{+,-\}$,
$j\in\{+,-\}$,
By the strong law of large numbers,
and hence there a.s. exists ![]() $T>0$ such that if
$T>0$ such that if ![]() $t>T$ then
$t>T$ then ![]() $\tilde{\xi}_t<0$. From this we can conclude that
$\tilde{\xi}_t<0$. From this we can conclude that ![]() $\sup_{t\geq0}\tilde{\xi}_t = \max (0 , \sup_{t\in[0,T]}\tilde{\xi}_t )<\infty$, since the supremum of a càdlàg process over a compact interval is bounded.
$\sup_{t\geq0}\tilde{\xi}_t = \max (0 , \sup_{t\in[0,T]}\tilde{\xi}_t )<\infty$, since the supremum of a càdlàg process over a compact interval is bounded.
This implies that there exists an ![]() $A^*>0$ such that for all
$A^*>0$ such that for all ![]() $A>A^*$ we have
$A>A^*$ we have ![]() $\mathbb P (\sup_{t\geq0}\tilde{\xi}_t > A )<1$. From this, we conclude
$\mathbb P (\sup_{t\geq0}\tilde{\xi}_t > A )<1$. From this, we conclude ![]() $N<\infty$ a.s., since
$N<\infty$ a.s., since
Since there are conditions for N to be finite, we can bound ![]() $\log(A_\infty)$ by using the stopping times
$\log(A_\infty)$ by using the stopping times ![]() $\{\sigma_n\}_{n\in\mathbb N}$ to split the process
$\{\sigma_n\}_{n\in\mathbb N}$ to split the process ![]() $\{\xi_t\colon t\geq0\}$ into a finite number of bounded sections.
$\{\xi_t\colon t\geq0\}$ into a finite number of bounded sections.
Define the constant
and by taking ![]() $A>A^*$ sufficiently large we can ensure
$A>A^*$ sufficiently large we can ensure ![]() ${\mathrm{e}}^C>2$. Then we have the following upper bound for
${\mathrm{e}}^C>2$. Then we have the following upper bound for ![]() $\log(A_\infty)$.
$\log(A_\infty)$.
Lemma 4.4. If ![]() $\mathbb E[\xi_{T_2}]<0$, then
$\mathbb E[\xi_{T_2}]<0$, then
 \begin{equation*} \log{A_\infty} \leq (N+1)C + \sum_{n=1}^N(\xi_{\sigma_n} - \xi_{\sigma_{n-1}})^+{,}\end{equation*}
\begin{equation*} \log{A_\infty} \leq (N+1)C + \sum_{n=1}^N(\xi_{\sigma_n} - \xi_{\sigma_{n-1}})^+{,}\end{equation*}
where ![]() $(\cdot)^+$ denotes the positive part.
$(\cdot)^+$ denotes the positive part.
Proof. Following the approach of [Reference Maulik and Zwart21, Lemma 4.1], ![]() $A_\infty$ may be expanded as
$A_\infty$ may be expanded as
 \begin{align*} A_\infty &= \int_0^{\sigma_1} \,{\mathrm{e}}^{\xi_t} \,{\mathrm{d}} t + {\mathrm{e}}^{\xi_{\sigma_1}}\biggl( \int_{\sigma_1}^{\sigma_2}\,{\mathrm{e}}^{\xi_t - \xi_{\sigma_1}} \,{\mathrm{d}} t + {\mathrm{e}}^{\xi_{\sigma_2}-\xi_{\sigma_1}}\biggl( \int_{\sigma_2}^{\sigma_3}\,{\mathrm{e}}^{\xi_t - \xi_{\sigma_2}} \,{\mathrm{d}} t + \cdots \\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdots + {\mathrm{e}}^{\xi_{\sigma_N}-\xi_{\sigma_{N-1}}}\biggl( \int_{\sigma_N}^{\sigma_{N+1}}\,{\mathrm{e}}^{\xi_t - \xi_{\sigma_N}} \,{\mathrm{d}} t \biggr) \biggr)\biggr),\end{align*}
\begin{align*} A_\infty &= \int_0^{\sigma_1} \,{\mathrm{e}}^{\xi_t} \,{\mathrm{d}} t + {\mathrm{e}}^{\xi_{\sigma_1}}\biggl( \int_{\sigma_1}^{\sigma_2}\,{\mathrm{e}}^{\xi_t - \xi_{\sigma_1}} \,{\mathrm{d}} t + {\mathrm{e}}^{\xi_{\sigma_2}-\xi_{\sigma_1}}\biggl( \int_{\sigma_2}^{\sigma_3}\,{\mathrm{e}}^{\xi_t - \xi_{\sigma_2}} \,{\mathrm{d}} t + \cdots \\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdots + {\mathrm{e}}^{\xi_{\sigma_N}-\xi_{\sigma_{N-1}}}\biggl( \int_{\sigma_N}^{\sigma_{N+1}}\,{\mathrm{e}}^{\xi_t - \xi_{\sigma_N}} \,{\mathrm{d}} t \biggr) \biggr)\biggr),\end{align*}
noting that ![]() $\sigma_{N+1}=\infty$. By the definition of
$\sigma_{N+1}=\infty$. By the definition of ![]() $\sigma_n$, we have
$\sigma_n$, we have
which, when substituted into the expression for ![]() $A_\infty$, gives
$A_\infty$, gives
Then, by considering the logarithms of both sides of (4.5) and repeatedly using the property ![]() $\log(A+B)\leq\log(A)+\log(B)$ whenever
$\log(A+B)\leq\log(A)+\log(B)$ whenever ![]() $A,B>2$,
$A,B>2$,
 \begin{align*} \log(A_\infty) \leq(N+1)C + \sum_{n=1}^N(\xi_{\sigma_n} - \xi_{\sigma_{n-1}})^+{,}\end{align*}
\begin{align*} \log(A_\infty) \leq(N+1)C + \sum_{n=1}^N(\xi_{\sigma_n} - \xi_{\sigma_{n-1}})^+{,}\end{align*}
where we have made use of the fact that ![]() ${\mathrm{e}}^{(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})^+}\geq1$ and
${\mathrm{e}}^{(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})^+}\geq1$ and ![]() ${\mathrm{e}}^C>2$ in order to use the log inequality.
${\mathrm{e}}^C>2$ in order to use the log inequality.
As a consequence of this lemma, the right tails of ![]() $\log(A_\infty)$ can be studied by considering the evolution of the MAP between the stopping times
$\log(A_\infty)$ can be studied by considering the evolution of the MAP between the stopping times ![]() $\{\sigma_n\}_{n\in\mathbb N}.$ First we consider the J component.
$\{\sigma_n\}_{n\in\mathbb N}.$ First we consider the J component.
Let ![]() $(K_n)_{n\in\mathbb N_0}$ be the sequence of random variables, taking values in
$(K_n)_{n\in\mathbb N_0}$ be the sequence of random variables, taking values in ![]() $\{+,-,\infty\}$, such that for each
$\{+,-,\infty\}$, such that for each ![]() $n\in\mathbb N$, if
$n\in\mathbb N$, if ![]() $\sigma_n<\infty$ then
$\sigma_n<\infty$ then ![]() $K_n=J_{\sigma_n}$, otherwise
$K_n=J_{\sigma_n}$, otherwise ![]() $K_n=\infty$. For each
$K_n=\infty$. For each ![]() $\alpha,\beta\in\{+,-\}$ we will be interested in the number of times that
$\alpha,\beta\in\{+,-\}$ we will be interested in the number of times that ![]() $\{K_n\}_{n\in\mathbb N}$ transitions from
$\{K_n\}_{n\in\mathbb N}$ transitions from ![]() $\alpha$ to
$\alpha$ to ![]() $\beta$. For this purpose, define the random variable
$\beta$. For this purpose, define the random variable ![]() $N(\alpha,\beta)\,:\!=\, \sum_{k=1}^\infty\mathbb{1}_{\{K_{k-1}=\alpha,K_k=\beta\}}$. We also make use of the notation
$N(\alpha,\beta)\,:\!=\, \sum_{k=1}^\infty\mathbb{1}_{\{K_{k-1}=\alpha,K_k=\beta\}}$. We also make use of the notation ![]() $f={\mathrm{o}}(g)$ for any two functions
$f={\mathrm{o}}(g)$ for any two functions ![]() $f,g\colon \mathbb R^+\rightarrow\mathbb R^+$ such that
$f,g\colon \mathbb R^+\rightarrow\mathbb R^+$ such that ![]() $\lim_{x\rightarrow\infty}f(x)/g(x) = 0$.
$\lim_{x\rightarrow\infty}f(x)/g(x) = 0$.
Proposition 4.1. Suppose ![]() $\mathbb E[\xi_{T_2}]\in(-\infty,0)$. Then the sequence
$\mathbb E[\xi_{T_2}]\in(-\infty,0)$. Then the sequence ![]() $(K_n)_{n\in\mathbb N_0}$ is a discrete-time homogeneous Markov chain, with
$(K_n)_{n\in\mathbb N_0}$ is a discrete-time homogeneous Markov chain, with ![]() $\infty$ as an absorbing state. Moreover, if
$\infty$ as an absorbing state. Moreover, if ![]() $\eta$ is the stochastic matrix of
$\eta$ is the stochastic matrix of ![]() $\{K_n\}_{n\in\mathbb N}$ and
$\{K_n\}_{n\in\mathbb N}$ and ![]() $\alpha,\beta,\gamma\in\{+,-\}$ with
$\alpha,\beta,\gamma\in\{+,-\}$ with ![]() $\alpha\neq\beta$, then
$\alpha\neq\beta$, then
as ![]() $A\rightarrow\infty$.
$A\rightarrow\infty$.
Proof. First we show that ![]() $\{K_n\}_{n\in\mathbb N}$ is a Markov chain. If
$\{K_n\}_{n\in\mathbb N}$ is a Markov chain. If ![]() $K_{n-1}\neq\infty$, then by the Markov additive property, since
$K_{n-1}\neq\infty$, then by the Markov additive property, since ![]() $\sigma_{n-1}$ is a stopping time,
$\sigma_{n-1}$ is a stopping time, ![]() $\{\xi_{\sigma_{n-1}+t}-\xi_{\sigma_{n-1}}\mid t\geq0\}$ is independent of
$\{\xi_{\sigma_{n-1}+t}-\xi_{\sigma_{n-1}}\mid t\geq0\}$ is independent of ![]() $\mathcal{F}_{\sigma_{n-1}}$ given
$\mathcal{F}_{\sigma_{n-1}}$ given ![]() $K_{n-1}$. Moreover, the random variable
$K_{n-1}$. Moreover, the random variable
is a function of ![]() $\{\xi_{t+\sigma_{n-1}}-\xi_{\sigma_{n-1}}\colon t\geq0\}$. Thus the event
$\{\xi_{t+\sigma_{n-1}}-\xi_{\sigma_{n-1}}\colon t\geq0\}$. Thus the event ![]() $\{K_n=\infty\}=\{\Delta\sigma_n=\infty\}$ is independent of
$\{K_n=\infty\}=\{\Delta\sigma_n=\infty\}$ is independent of ![]() $\mathcal{F}_{\sigma_{n-1}}$ given
$\mathcal{F}_{\sigma_{n-1}}$ given ![]() $K_{n-1}$, and has the same law as the event
$K_{n-1}$, and has the same law as the event ![]() $\{K_1=\infty\}$ given
$\{K_1=\infty\}$ given ![]() $K_0$.
$K_0$.
Moreover, if ![]() $\Delta\sigma_n<\infty$ then
$\Delta\sigma_n<\infty$ then ![]() $K_n=J_{\sigma_n}=J_{\sigma_{n-1}+\Delta\sigma_n}$, hence
$K_n=J_{\sigma_n}=J_{\sigma_{n-1}+\Delta\sigma_n}$, hence ![]() $K_n$ is a function of
$K_n$ is a function of
and so by the Markov additive property is independent of ![]() $\mathcal{F}_{\sigma_{n-1}}$ given
$\mathcal{F}_{\sigma_{n-1}}$ given ![]() $K_{n-1}$ and has the same distribution as
$K_{n-1}$ and has the same distribution as ![]() $K_1$ given
$K_1$ given ![]() $K_0$. Hence the sequence
$K_0$. Hence the sequence ![]() $(K_n)_{n\in\mathbb N}$ is a time homogeneous Markov chain. By definition of
$(K_n)_{n\in\mathbb N}$ is a time homogeneous Markov chain. By definition of ![]() $\sigma_n$,
$\sigma_n$, ![]() $\infty$ is clearly an absorbing state for
$\infty$ is clearly an absorbing state for ![]() $(K_n)_{n\in\mathbb N}$.
$(K_n)_{n\in\mathbb N}$.
Now we consider the limiting behaviour of ![]() $\eta$ as
$\eta$ as ![]() $A\rightarrow\infty$. Let
$A\rightarrow\infty$. Let ![]() $\alpha,\gamma\in\{+,-\}$. From the proof of Lemma 4.3 we know that
$\alpha,\gamma\in\{+,-\}$. From the proof of Lemma 4.3 we know that ![]() $\sup_{t\geq0}\tilde{\xi}_t<\infty$ a.s., where
$\sup_{t\geq0}\tilde{\xi}_t<\infty$ a.s., where ![]() $\tilde{\xi_t}\,:\!=\, \xi_t-(K+\epsilon)t$. Thus
$\tilde{\xi_t}\,:\!=\, \xi_t-(K+\epsilon)t$. Thus
However,
and, since ![]() $\eta_{\alpha,\gamma}$ is non-negative, this implies
$\eta_{\alpha,\gamma}$ is non-negative, this implies ![]() $\lim_{A\rightarrow\infty}\eta_{\alpha,\gamma} = 0$.
$\lim_{A\rightarrow\infty}\eta_{\alpha,\gamma} = 0$.
Further assume that ![]() $\gamma\in\{+,-\}$ and
$\gamma\in\{+,-\}$ and ![]() $\alpha\neq\beta$. Then it is easily seen that
$\alpha\neq\beta$. Then it is easily seen that
where ![]() $\phi_\theta(\alpha) \,:\!=\, \sum_{n=1}^\infty \mathbb P_\theta(K_n=\alpha)$. Since
$\phi_\theta(\alpha) \,:\!=\, \sum_{n=1}^\infty \mathbb P_\theta(K_n=\alpha)$. Since ![]() $\infty$ is an absorbing state of the Markov chain
$\infty$ is an absorbing state of the Markov chain ![]() $(K_n)_{n\in\mathbb N}$ and
$(K_n)_{n\in\mathbb N}$ and ![]() $\alpha\neq\beta$, for each
$\alpha\neq\beta$, for each ![]() $n\in\mathbb N$,
$n\in\mathbb N$,
 \begin{align*} \mathbb P_\theta(K_n=\alpha) &= \mathbb P_\theta( K_n=\alpha\mid K_{n-1}=\alpha)\,\mathbb P_\theta(K_{n-1}=\alpha) \\ &\quad \, + \mathbb P_\theta( K_n=\alpha\mid K_{n-1}=\beta )\,\mathbb P_\theta(K_{n-1}=\beta)\\ &= \eta_{\alpha,\alpha}\mathbb P_\theta(K_{n-1}=\alpha) + \eta_{\beta,\alpha}\mathbb P_\theta(K_{n-1}=\beta),\end{align*}
\begin{align*} \mathbb P_\theta(K_n=\alpha) &= \mathbb P_\theta( K_n=\alpha\mid K_{n-1}=\alpha)\,\mathbb P_\theta(K_{n-1}=\alpha) \\ &\quad \, + \mathbb P_\theta( K_n=\alpha\mid K_{n-1}=\beta )\,\mathbb P_\theta(K_{n-1}=\beta)\\ &= \eta_{\alpha,\alpha}\mathbb P_\theta(K_{n-1}=\alpha) + \eta_{\beta,\alpha}\mathbb P_\theta(K_{n-1}=\beta),\end{align*}
then summing up over ![]() $n\in\mathbb N$ we have
$n\in\mathbb N$ we have
and by symmetry
Solving this system gives
and thus
from which the two asymptotic results for ![]() $\mathbb E_\theta[N(\alpha,\gamma)]$ are a consequence of the limiting behaviour of
$\mathbb E_\theta[N(\alpha,\gamma)]$ are a consequence of the limiting behaviour of ![]() $\eta$.
$\eta$.
In the next lemma we consider the evolution of ![]() $\xi$ between the stopping times
$\xi$ between the stopping times ![]() $\{\sigma_n\}_{n\in\mathbb N}$, conditioned on the values of
$\{\sigma_n\}_{n\in\mathbb N}$, conditioned on the values of ![]() $\{K_n\}_{n\in\mathbb N}$.
$\{K_n\}_{n\in\mathbb N}$.
Lemma 4.5. Suppose that ![]() $\mathbb E[\xi_{T_2}]\in(-\infty,0)$ and
$\mathbb E[\xi_{T_2}]\in(-\infty,0)$ and ![]() $m,n\in\mathbb N$ with
$m,n\in\mathbb N$ with ![]() $m<n$. Then, conditionally on
$m<n$. Then, conditionally on ![]() $K_{m-1}$,
$K_{m-1}$, ![]() $K_m$,
$K_m$, ![]() $K_{n-1}$, and
$K_{n-1}$, and ![]() $K_n$, the increments
$K_n$, the increments ![]() $\xi_{\sigma_m}-\xi_{\sigma_{m-1}}$ and
$\xi_{\sigma_m}-\xi_{\sigma_{m-1}}$ and ![]() $\xi_{\sigma_n} - \xi_{\sigma_{n-1}}$ are independent. If
$\xi_{\sigma_n} - \xi_{\sigma_{n-1}}$ are independent. If ![]() $\alpha,\beta\in\{+,-\}$, then conditional on the event
$\alpha,\beta\in\{+,-\}$, then conditional on the event ![]() $\{K_{n-1}=K_{m-1}=\alpha ;\, K_n=K_m=\beta\}$, the increments
$\{K_{n-1}=K_{m-1}=\alpha ;\, K_n=K_m=\beta\}$, the increments ![]() $\xi_{\sigma_m}-\xi_{\sigma_{m-1}}$ and
$\xi_{\sigma_m}-\xi_{\sigma_{m-1}}$ and ![]() $\xi_{\sigma_n} - \xi_{\sigma_{n-1}}$ are equal in distribution and independent. Furthermore, for any
$\xi_{\sigma_n} - \xi_{\sigma_{n-1}}$ are equal in distribution and independent. Furthermore, for any ![]() $l\in\mathbb N$ such that
$l\in\mathbb N$ such that ![]() $m\neq l$ and any bounded continuous function
$m\neq l$ and any bounded continuous function ![]() $f\colon \mathbb R\rightarrow\mathbb R^+$, we have
$f\colon \mathbb R\rightarrow\mathbb R^+$, we have
Proof. First suppose that ![]() $m<l$. Then we have
$m<l$. Then we have
 \begin{align*} &\mathbb E[f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} )\mid \sigma(K_{m-1},K_m,K_{l-1},K_l)]\\ &\quad =\sum_{\gamma,\delta\in\{+,-\}} \mathbb{1}_{\{K_{l-1}=\gamma,K_{l}=\delta\}}\dfrac{\mathbb E[f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) ;\, K_{l-1}=\gamma,K_l=\delta \mid \sigma(K_{m-1},K_m)]}{\mathbb P(K_{l-1}=\gamma,K_l=\delta \mid \sigma(K_{m-1},K_m))}.\end{align*}
\begin{align*} &\mathbb E[f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} )\mid \sigma(K_{m-1},K_m,K_{l-1},K_l)]\\ &\quad =\sum_{\gamma,\delta\in\{+,-\}} \mathbb{1}_{\{K_{l-1}=\gamma,K_{l}=\delta\}}\dfrac{\mathbb E[f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) ;\, K_{l-1}=\gamma,K_l=\delta \mid \sigma(K_{m-1},K_m)]}{\mathbb P(K_{l-1}=\gamma,K_l=\delta \mid \sigma(K_{m-1},K_m))}.\end{align*}
It follows that, by using the tower property and the fact that ![]() $(K_k)_{k\in\mathbb N}$ is a Markov chain, we have
$(K_k)_{k\in\mathbb N}$ is a Markov chain, we have
 \begin{align*} &\mathbb E[f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) ;\, K_{l-1}=\gamma,K_l=\delta \mid \sigma(K_{m-1},K_m)]\\ &\quad =\mathbb E [ f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \,\mathbb E [ \mathbb{1}_{\{K_{l-1}=\gamma,K_l=\delta\}} \mid \mathcal{F}_{\sigma_m} ] \mid \sigma(K_{m-1},K_m) ]\\ &\quad =\mathbb E [ f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \,\mathbb E [ \mathbb{1}_{\{K_{l-1}=\gamma,K_l=\delta\}} \mid \sigma(K_m) ] \mid \sigma(K_{m-1},K_m) ]\\ &\quad = \mathbb P (K_{l-1}=\gamma,K_l=\delta \mid \sigma(K_{m-1},K_m) ) \,\mathbb E [ f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \mid \sigma(K_{m-1},K_m) ],\end{align*}
\begin{align*} &\mathbb E[f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) ;\, K_{l-1}=\gamma,K_l=\delta \mid \sigma(K_{m-1},K_m)]\\ &\quad =\mathbb E [ f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \,\mathbb E [ \mathbb{1}_{\{K_{l-1}=\gamma,K_l=\delta\}} \mid \mathcal{F}_{\sigma_m} ] \mid \sigma(K_{m-1},K_m) ]\\ &\quad =\mathbb E [ f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \,\mathbb E [ \mathbb{1}_{\{K_{l-1}=\gamma,K_l=\delta\}} \mid \sigma(K_m) ] \mid \sigma(K_{m-1},K_m) ]\\ &\quad = \mathbb P (K_{l-1}=\gamma,K_l=\delta \mid \sigma(K_{m-1},K_m) ) \,\mathbb E [ f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \mid \sigma(K_{m-1},K_m) ],\end{align*}
which, when substituted into the previous equation, gives
 \begin{align*} &\mathbb E[f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \mid \sigma(K_{m-1},K_m,K_{l-1},K_l)]\\ &\quad = \sum_{\gamma,\delta\in\{+,-\}} \mathbb{1}_{\{K_{l-1}=\gamma,K_l=\delta\}}\,\mathbb E [ f ( \xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \mid \sigma(K_{m-1},K_m) ]\\ &\quad =\mathbb E [ f(\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \mid \sigma(K_{m-1},K_m) ].\end{align*}
\begin{align*} &\mathbb E[f (\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \mid \sigma(K_{m-1},K_m,K_{l-1},K_l)]\\ &\quad = \sum_{\gamma,\delta\in\{+,-\}} \mathbb{1}_{\{K_{l-1}=\gamma,K_l=\delta\}}\,\mathbb E [ f ( \xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \mid \sigma(K_{m-1},K_m) ]\\ &\quad =\mathbb E [ f(\xi_{\sigma_m}-\xi_{\sigma_{m-1}} ) \mid \sigma(K_{m-1},K_m) ].\end{align*}
Now suppose ![]() $m>l$, and through a direct application of the Markov additive property we have
$m>l$, and through a direct application of the Markov additive property we have
 \begin{align*} &\mathbb E [ f(\xi_{\sigma_{m}}-\xi_{\sigma_{m-1}}) \mid \sigma(K_{l-1},K_l,K_{m-1},K_m) ]\\ &\quad =\sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_m=\alpha\}}\dfrac{\mathbb E [ f(\xi_{\sigma_{m}}-\xi_{\sigma_{m-1}}) ;\, K_m=\alpha \mid \sigma(K_{l-1},K_l,K_{m-1}) ]}{\mathbb P(K_m=\alpha \mid \sigma(K_{l-1},K_l,K_{m-1}) ) }\\ &\quad =\sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_m=\alpha\}} \dfrac{\mathbb E [ f(\xi_{\sigma_{m}}-\xi_{\sigma_{m-1}}) ;\, K_m=\alpha \mid \sigma( K_{m-1} ) ]}{\mathbb P(K_m=\alpha \mid \sigma (K_{m-1}) )}\\ &\quad = \mathbb E [ f(\xi_{\sigma_{m}}-\xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m) ].\end{align*}
\begin{align*} &\mathbb E [ f(\xi_{\sigma_{m}}-\xi_{\sigma_{m-1}}) \mid \sigma(K_{l-1},K_l,K_{m-1},K_m) ]\\ &\quad =\sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_m=\alpha\}}\dfrac{\mathbb E [ f(\xi_{\sigma_{m}}-\xi_{\sigma_{m-1}}) ;\, K_m=\alpha \mid \sigma(K_{l-1},K_l,K_{m-1}) ]}{\mathbb P(K_m=\alpha \mid \sigma(K_{l-1},K_l,K_{m-1}) ) }\\ &\quad =\sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_m=\alpha\}} \dfrac{\mathbb E [ f(\xi_{\sigma_{m}}-\xi_{\sigma_{m-1}}) ;\, K_m=\alpha \mid \sigma( K_{m-1} ) ]}{\mathbb P(K_m=\alpha \mid \sigma (K_{m-1}) )}\\ &\quad = \mathbb E [ f(\xi_{\sigma_{m}}-\xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m) ].\end{align*}
To see the independence of increments, suppose that ![]() $f,g\colon \mathbb R\rightarrow\mathbb R^+$ are bounded continuous functions, and then
$f,g\colon \mathbb R\rightarrow\mathbb R^+$ are bounded continuous functions, and then
 \begin{align*} &\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m,K_{n-1},K_n) ]\\[4pt]
&\quad = \sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_n=\alpha\}}\dfrac{\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) ;\, K_n=\alpha \mid \sigma(K_{m-1},K_m,K_{n-1}) ]}{\mathbb P ( K_n=\alpha \mid \sigma(K_{m-1},K_m,K_{n-1}) )}.\end{align*}
\begin{align*} &\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m,K_{n-1},K_n) ]\\[4pt]
&\quad = \sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_n=\alpha\}}\dfrac{\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) ;\, K_n=\alpha \mid \sigma(K_{m-1},K_m,K_{n-1}) ]}{\mathbb P ( K_n=\alpha \mid \sigma(K_{m-1},K_m,K_{n-1}) )}.\end{align*}
Then, by the tower property, we get
 \begin{align*} &\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) ;\, K_n=\alpha \mid \sigma(K_{m-1},K_m,K_{n-1}) ]\\ &\quad =\mathbb E [ g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \,\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \mathcal{F}_{\sigma_{n-1}} ] \mid \sigma(K_{m-1},K_m,K_{n-1}) ]\\ &\quad =\mathbb E [ g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \,\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \sigma(K_{\sigma_{n-1}}) ] \mid \sigma(K_{m-1},K_m,K_{n-1}) ]\\ &\quad =\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \sigma(K_{\sigma_{n-1}}) ]\,\mathbb E [ g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m) ].\end{align*}
\begin{align*} &\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) ;\, K_n=\alpha \mid \sigma(K_{m-1},K_m,K_{n-1}) ]\\ &\quad =\mathbb E [ g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \,\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \mathcal{F}_{\sigma_{n-1}} ] \mid \sigma(K_{m-1},K_m,K_{n-1}) ]\\ &\quad =\mathbb E [ g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \,\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \sigma(K_{\sigma_{n-1}}) ] \mid \sigma(K_{m-1},K_m,K_{n-1}) ]\\ &\quad =\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \sigma(K_{\sigma_{n-1}}) ]\,\mathbb E [ g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m) ].\end{align*}
Plugging this into the previous equation yields
 \begin{align*} \qquad\qquad &\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m,K_{n-1},K_n) ]\\[4pt]
&\quad = \sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_n=\alpha\}}\dfrac{\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \sigma(K_{\sigma_{n-1}}) ]}{\mathbb P ( K_n=\alpha \mid \sigma(K_{m-1},K_m,K_{n-1}) )}\\[4pt]
&\quad \quad \, \times \mathbb E [ g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m) ] \\[4pt]
&\quad = \mathbb E [g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \times \sigma(K_{m-1},K_m) ]\\[4pt]
&\quad \quad \, \times \sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_n=\alpha\}}\dfrac{\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \sigma(K_{\sigma_{n-1}}) ] }{\mathbb P ( K_n=\alpha \mid \sigma(K_{n-1}) )}\\[4pt]
&\quad = \mathbb E [g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m) ]\,\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) \mid \sigma(K_{\sigma_{n-1}},K_{\sigma_n}) ].\end{align*}
\begin{align*} \qquad\qquad &\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}})g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m,K_{n-1},K_n) ]\\[4pt]
&\quad = \sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_n=\alpha\}}\dfrac{\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \sigma(K_{\sigma_{n-1}}) ]}{\mathbb P ( K_n=\alpha \mid \sigma(K_{m-1},K_m,K_{n-1}) )}\\[4pt]
&\quad \quad \, \times \mathbb E [ g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m) ] \\[4pt]
&\quad = \mathbb E [g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \times \sigma(K_{m-1},K_m) ]\\[4pt]
&\quad \quad \, \times \sum_{\alpha\in\{+,-\}}\mathbb{1}_{\{K_n=\alpha\}}\dfrac{\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) ;\, K_n=\alpha \mid \sigma(K_{\sigma_{n-1}}) ] }{\mathbb P ( K_n=\alpha \mid \sigma(K_{n-1}) )}\\[4pt]
&\quad = \mathbb E [g(\xi_{\sigma_m} - \xi_{\sigma_{m-1}}) \mid \sigma(K_{m-1},K_m) ]\,\mathbb E [ f(\xi_{\sigma_n}-\xi_{\sigma_{n-1}}) \mid \sigma(K_{\sigma_{n-1}},K_{\sigma_n}) ].\end{align*}
4.3. Lamperti–Kiu processes of strong subexponential type
Strong subexponential distributions are a widely studied class of heavy-tailed distributions, because of their mathematical tractability and their appearance in empirical data. We will use [Reference Foss, Korshunov and Zachary11] as a reference to the background theory of subexponential distributions, within which further discussion of the use of these distributions can be found.
For a probability distribution ![]() $Q\colon \mathbb R^+\rightarrow[0,1]$, define
$Q\colon \mathbb R^+\rightarrow[0,1]$, define ![]() $\bar{Q}(x)\,:\!=\,q 1-Q(x)$ for all
$\bar{Q}(x)\,:\!=\,q 1-Q(x)$ for all ![]() $x\in\mathbb R^+$. Then, if
$x\in\mathbb R^+$. Then, if ![]() $\overline{Q*Q}(x)/\overline{Q}(x)\rightarrow 2$ as
$\overline{Q*Q}(x)/\overline{Q}(x)\rightarrow 2$ as ![]() $x\rightarrow\infty$, we say that Q is a subexponential distribution. It can be shown (see e.g. [Reference Foss, Korshunov and Zachary11]) that all subexponential distributions are also long-tailed. The distribution Q is a strong subexponential distribution if it also satisfies the property that
$x\rightarrow\infty$, we say that Q is a subexponential distribution. It can be shown (see e.g. [Reference Foss, Korshunov and Zachary11]) that all subexponential distributions are also long-tailed. The distribution Q is a strong subexponential distribution if it also satisfies the property that
where ![]() $m=\mathbb E[X^+]$ and X is a random variable with distribution Q. We will refer to a random variable with a (strong) subexponential distribution as a (strong) subexponential random variable.
$m=\mathbb E[X^+]$ and X is a random variable with distribution Q. We will refer to a random variable with a (strong) subexponential distribution as a (strong) subexponential random variable.
Let ![]() $\mathcal{S}$ denote the set of real-valued subexponential random variables and let
$\mathcal{S}$ denote the set of real-valued subexponential random variables and let ![]() $\mathcal{S}^*$ denote the subset of
$\mathcal{S}^*$ denote the subset of ![]() $\mathcal{S}$ comprising strong subexponential random variables.
$\mathcal{S}$ comprising strong subexponential random variables.
For a random variable X, recall the definitions
If ![]() $H_X$ is a subexponential distribution then we write
$H_X$ is a subexponential distribution then we write ![]() $X\in\mathcal{S}_I$, and from [Reference Foss, Korshunov and Zachary11, Theorem 3.27] we have
$X\in\mathcal{S}_I$, and from [Reference Foss, Korshunov and Zachary11, Theorem 3.27] we have ![]() $\mathcal{S}^*\subset\mathcal{S}_I$.
$\mathcal{S}^*\subset\mathcal{S}_I$.
For ease of notation, we also define the integrated tails ![]() $H(x) \,:\!=\, H_{\xi_{T_2}}(x)$ and, for each
$H(x) \,:\!=\, H_{\xi_{T_2}}(x)$ and, for each ![]() $\alpha\in\{+,-\}$, define
$\alpha\in\{+,-\}$, define
Let us introduce a subset of components of the Lamperti–Kiu decomposition given by ![]() $L\,:\!=\, \{ \xi^{(+)}_{\zeta_+} , \xi^{(-)}_{\zeta_-} , U^+, U^- \}$.
$L\,:\!=\, \{ \xi^{(+)}_{\zeta_+} , \xi^{(-)}_{\zeta_-} , U^+, U^- \}$.
For any functions ![]() $f,g\colon \mathbb R^+\rightarrow\mathbb R^+$, we write
$f,g\colon \mathbb R^+\rightarrow\mathbb R^+$, we write ![]() $f={\mathrm{O}}(g)$ if
$f={\mathrm{O}}(g)$ if ![]() $\limsup_{x\rightarrow\infty}f(x)/g(x)\in\mathbb R$.
$\limsup_{x\rightarrow\infty}f(x)/g(x)\in\mathbb R$.
Definition 4.1. We will say that a Lamperti–Kiu process is of strong subexponential type if ![]() $\xi_{T_2}$ is long-tailed and there exists
$\xi_{T_2}$ is long-tailed and there exists ![]() $X\in L$ such that
$X\in L$ such that ![]() $X\in\mathcal{S}^*$ and for all
$X\in\mathcal{S}^*$ and for all ![]() $W\in L\setminus\{X\}$ we have
$W\in L\setminus\{X\}$ we have ![]() $\mathbb P(W>x)={\mathrm{O}}(\mathbb P(X>x))$.
$\mathbb P(W>x)={\mathrm{O}}(\mathbb P(X>x))$.
If a Lamperti–Kiu process is of this type, there is a heaviest-tailed component of the Lamperti–Kiu decomposition and it is strong subexponential. Denote this component by ![]() $X\in L$. Let
$X\in L$. Let ![]() $B\subseteq\{+,-\}$ be the set of all
$B\subseteq\{+,-\}$ be the set of all ![]() $\beta\in\{+,-\}$ such that
$\beta\in\{+,-\}$ such that
Then, for any ![]() $b\in B$ and
$b\in B$ and ![]() $\beta\in\{+,-\}\setminus B$, we have
$\beta\in\{+,-\}\setminus B$, we have ![]() $H^{(\beta)}(x) = {\mathrm{o}}( H^{(b)}(x) )$ as
$H^{(\beta)}(x) = {\mathrm{o}}( H^{(b)}(x) )$ as ![]() $x\rightarrow\infty$.
$x\rightarrow\infty$.
By the closure properties of ![]() $\mathcal{S}^*$ [Reference Foss, Korshunov and Zachary11, Corollary 3.16], it follows that
$\mathcal{S}^*$ [Reference Foss, Korshunov and Zachary11, Corollary 3.16], it follows that ![]() $\xi_{T_2}$ is also strong subexponential with tails and integrated tails, respectively, given, as
$\xi_{T_2}$ is also strong subexponential with tails and integrated tails, respectively, given, as ![]() $x\rightarrow\infty$, by
$x\rightarrow\infty$, by
and
Recall from Section 2 that ![]() $K\,:\!=\, \mathbb E[\xi_{T_2}]/\mathbb E[T_2]$, and hence, when
$K\,:\!=\, \mathbb E[\xi_{T_2}]/\mathbb E[T_2]$, and hence, when ![]() $\mathbb E[\xi_{T_2}]\neq0$, it follows that
$\mathbb E[\xi_{T_2}]\neq0$, it follows that ![]() $K\neq0$. The main result of this section, which extends [Reference Maulik and Zwart21, Section 4, p. 166] to Lamperti–Kiu processes, is the following result.
$K\neq0$. The main result of this section, which extends [Reference Maulik and Zwart21, Section 4, p. 166] to Lamperti–Kiu processes, is the following result.
Theorem 4.1. Suppose that Y is a Lamperti–Kiu process of strong subexponential type such that ![]() $\mathbb E[\xi_{T_2}]\in(-\infty,0)$. Then
$\mathbb E[\xi_{T_2}]\in(-\infty,0)$. Then
Furthermore, ![]() $A_\infty$ is long-tailed and
$A_\infty$ is long-tailed and ![]() $\log(A_\infty)$ is subexponential.
$\log(A_\infty)$ is subexponential.
The proof of Theorem 4.1 requires a number of intermediary lemmas. These lemmas are stated with proofs below, followed by the proof of Theorem 4.1 at the end of this section.
Set ![]() $Z_n \,:\!=\, \xi_{\sigma_n}-\xi_{\sigma_{n-1}}$ for each
$Z_n \,:\!=\, \xi_{\sigma_n}-\xi_{\sigma_{n-1}}$ for each ![]() $n\geq1$. We are now in a position to consider the asymptotic behaviour of the survival function of
$n\geq1$. We are now in a position to consider the asymptotic behaviour of the survival function of ![]() $Z_n$ conditioned on
$Z_n$ conditioned on ![]() $K_{n-1}$ and
$K_{n-1}$ and ![]() $K_n$, under the assumptions of Theorem 4.1. Recall that for
$K_n$, under the assumptions of Theorem 4.1. Recall that for ![]() $\alpha\in\{+,-\}$,
$\alpha\in\{+,-\}$, ![]() $H^{(\alpha)} = H_{\xi_\alpha}(x) + H_{U_{-\alpha}}(x)$.
$H^{(\alpha)} = H_{\xi_\alpha}(x) + H_{U_{-\alpha}}(x)$.
Lemma 4.6. Suppose that Y is a Lamperti–Kiu process of strong subexponential type such that ![]() $\mathbb E[\xi_{T_2}]\in(-\infty,0)$, and fix
$\mathbb E[\xi_{T_2}]\in(-\infty,0)$, and fix ![]() $\alpha,\beta\in\{+,-\}$. Then, if
$\alpha,\beta\in\{+,-\}$. Then, if ![]() $\beta\in B$, for each
$\beta\in B$, for each ![]() $n\in\mathbb N$,
$n\in\mathbb N$,
Furthermore, if ![]() $\beta\in\{+,-\}\setminus B$ and
$\beta\in\{+,-\}\setminus B$ and ![]() $b\in B$, then, for each
$b\in B$, then, for each ![]() $n\in\mathbb N$,
$n\in\mathbb N$,
Proof. Suppose that ![]() $x>A$, let
$x>A$, let ![]() $u_0\in(0,x-A)$, and fix
$u_0\in(0,x-A)$, and fix ![]() $\alpha,\beta\in\{+,-\}$. For ease of notation, let
$\alpha,\beta\in\{+,-\}$. For ease of notation, let ![]() $\sigma\,:\!=\, \sigma_1$. Then, since
$\sigma\,:\!=\, \sigma_1$. Then, since
we have
To bound the elements of the sum, first consider the strict inequality ![]() $T_{m}<\sigma<T_{m+1}$ for some
$T_{m}<\sigma<T_{m+1}$ for some ![]() $m\in\mathbb N$; then
$m\in\mathbb N$; then
and using the Lamperti–Kiu decomposition followed by Lemma 4.1, we have
 \begin{align*} \mathbb P_\alpha ( \xi_\sigma>x ;\, T_{m}<\sigma<T_{m+1} ;\, J_\sigma=\beta ) &\leq \mathbb P_\alpha\biggl( \sup_{0< u<\tilde{\zeta}_\beta} \tilde{\xi}^{(\beta)}_u > x - (K+\epsilon)T_m - A ;\, J_{T_m}=\beta \biggr)\\[3pt]
& \leq \dfrac{\mathbb P_\alpha\bigl( \tilde{\xi}^{(\beta)}_{\tilde{\zeta}_\beta} \geq x-(K+\epsilon)T_m-A-u_0 ;\, J_{T_m}=\beta \bigr)}{ \mathbb P\bigl( \xi^{(\beta)}_{\zeta_\beta} \geq -u_0 \bigr) }\end{align*}
\begin{align*} \mathbb P_\alpha ( \xi_\sigma>x ;\, T_{m}<\sigma<T_{m+1} ;\, J_\sigma=\beta ) &\leq \mathbb P_\alpha\biggl( \sup_{0< u<\tilde{\zeta}_\beta} \tilde{\xi}^{(\beta)}_u > x - (K+\epsilon)T_m - A ;\, J_{T_m}=\beta \biggr)\\[3pt]
& \leq \dfrac{\mathbb P_\alpha\bigl( \tilde{\xi}^{(\beta)}_{\tilde{\zeta}_\beta} \geq x-(K+\epsilon)T_m-A-u_0 ;\, J_{T_m}=\beta \bigr)}{ \mathbb P\bigl( \xi^{(\beta)}_{\zeta_\beta} \geq -u_0 \bigr) }\end{align*}
where ![]() $\tilde{\xi}^{(\beta)}$ and
$\tilde{\xi}^{(\beta)}$ and ![]() $\tilde{\zeta}_\beta$ are independent copies of the Lévy process
$\tilde{\zeta}_\beta$ are independent copies of the Lévy process ![]() $\xi^{(\beta)}$ and the exponential random variable
$\xi^{(\beta)}$ and the exponential random variable ![]() $\zeta_\beta$, respectively.
$\zeta_\beta$, respectively.
In the case when ![]() $\sigma=T_{m}$,
$\sigma=T_{m}$,
 \begin{align*} \mathbb P_\alpha (\xi_\sigma>x ;\, T_{m}=\sigma ;\, J_\sigma=\beta ) &\leq\mathbb P_\alpha ( \xi_{T_{m}}>x ;\, \xi_{T_m-} \leq (K+\epsilon)T_{m}+A ;\, J_{T_m}=\beta )\\ &\leq\mathbb P_\alpha ( \xi_{T_{m}} - \xi_{T_m-} > x - (K+\epsilon)T_{m}-A ;\, J_{T_m}=\beta ) \\&= \mathbb P_\alpha ( U^{(-\beta)}>x-(K+\epsilon)T_{m} - A ;\, J_{T_m}=\beta ).\end{align*}
\begin{align*} \mathbb P_\alpha (\xi_\sigma>x ;\, T_{m}=\sigma ;\, J_\sigma=\beta ) &\leq\mathbb P_\alpha ( \xi_{T_{m}}>x ;\, \xi_{T_m-} \leq (K+\epsilon)T_{m}+A ;\, J_{T_m}=\beta )\\ &\leq\mathbb P_\alpha ( \xi_{T_{m}} - \xi_{T_m-} > x - (K+\epsilon)T_{m}-A ;\, J_{T_m}=\beta ) \\&= \mathbb P_\alpha ( U^{(-\beta)}>x-(K+\epsilon)T_{m} - A ;\, J_{T_m}=\beta ).\end{align*}
If ![]() $\alpha=\beta$ then there must be an even number of changes of J before
$\alpha=\beta$ then there must be an even number of changes of J before ![]() $\sigma$, so there exists
$\sigma$, so there exists ![]() $m\in\mathbb N$ such that
$m\in\mathbb N$ such that ![]() $\sigma\in[T_{2m},T_{2m+1})$. Hence combining the two results above gives
$\sigma\in[T_{2m},T_{2m+1})$. Hence combining the two results above gives
 \begin{align*} \mathbb P ( Z_n >x \mid K_{n-1}=\alpha,K_n=\beta ) \leq& \dfrac{1}{\eta^{(\alpha,\beta)}} \biggl(\sum_{m=0}^\infty \dfrac{\mathbb P_\alpha\bigl(\tilde{\xi}_{\tilde{\zeta}_\beta}^{(\beta)} \geq x-(K+\epsilon)T_{2m}-A-u_0\bigr)}{\mathbb P\bigl(\xi^{(\beta)}_{\zeta_\beta}>-u_0\bigr)} \\* & + \sum_{m=0}^\infty\mathbb P_\alpha ( U^{(-\beta)} \geq x- (K+\epsilon)T_{2m} - A -u_0 ) \biggr).\end{align*}
\begin{align*} \mathbb P ( Z_n >x \mid K_{n-1}=\alpha,K_n=\beta ) \leq& \dfrac{1}{\eta^{(\alpha,\beta)}} \biggl(\sum_{m=0}^\infty \dfrac{\mathbb P_\alpha\bigl(\tilde{\xi}_{\tilde{\zeta}_\beta}^{(\beta)} \geq x-(K+\epsilon)T_{2m}-A-u_0\bigr)}{\mathbb P\bigl(\xi^{(\beta)}_{\zeta_\beta}>-u_0\bigr)} \\* & + \sum_{m=0}^\infty\mathbb P_\alpha ( U^{(-\beta)} \geq x- (K+\epsilon)T_{2m} - A -u_0 ) \biggr).\end{align*}
If ![]() $\alpha\neq\beta$ then there is an odd number of changes in J before time
$\alpha\neq\beta$ then there is an odd number of changes in J before time ![]() $\sigma$. However,
$\sigma$. However, ![]() $T_{2m+1}\geq T_{2m}$, so the inequalities can be weakened to give the same result as the
$T_{2m+1}\geq T_{2m}$, so the inequalities can be weakened to give the same result as the ![]() $\alpha=\beta$ case.
$\alpha=\beta$ case.
For ease of notation define
If ![]() $\xi^{(\beta)}_{\zeta_\beta}$ is long-tailed, we can use Lemma 4.2 to obtain the asymptotic approximation
$\xi^{(\beta)}_{\zeta_\beta}$ is long-tailed, we can use Lemma 4.2 to obtain the asymptotic approximation
as ![]() $x\rightarrow\infty$. Similarly, if
$x\rightarrow\infty$. Similarly, if ![]() $U^{(-\beta)}$ is long-tailed we have
$U^{(-\beta)}$ is long-tailed we have
as ![]() $x\rightarrow\infty$. We will consider separately the cases where both of the asymptotics hold, exactly one holds, or neither hold.
$x\rightarrow\infty$. We will consider separately the cases where both of the asymptotics hold, exactly one holds, or neither hold.
In the case when both ![]() $\xi^{(\beta)}_{\zeta_\beta}$ and
$\xi^{(\beta)}_{\zeta_\beta}$ and ![]() $U^{(-\beta)}$ are subexponential (and hence are long-tailed) for all
$U^{(-\beta)}$ are subexponential (and hence are long-tailed) for all ![]() $\delta>0$, there exists an
$\delta>0$, there exists an ![]() $R>0$ such that, for all
$R>0$ such that, for all ![]() $x>R$,
$x>R$,
 \begin{align*} \dfrac{\mathbb P (Z^{(\alpha,\beta)} > x )}{G_{\xi_\beta}(x) + G_{U^{(-\beta)}}(x)} &\leq \dfrac{1}{ (G_{\xi_\beta}(x)+G_{U^{(-\beta)}}(x) )\eta^{(\alpha,\beta)}} \\[3pt]
&\quad \, \times \biggl(\dfrac{(1+\delta)G_{\xi_\beta}(x)}{Q_\beta(u_0)|K+\epsilon|\,\mathbb E[T_2]} + \dfrac{(1+\delta)G_{U^{(-\beta)}}(x)}{|K+\epsilon|\,\mathbb E[T_2]} \biggr)\\[3pt]
&\leq \dfrac{(1+\delta)}{\eta^{(\alpha,\beta)}Q_\beta(u_0)|K+\epsilon|\,\mathbb E[T_2]}{,}\end{align*}
\begin{align*} \dfrac{\mathbb P (Z^{(\alpha,\beta)} > x )}{G_{\xi_\beta}(x) + G_{U^{(-\beta)}}(x)} &\leq \dfrac{1}{ (G_{\xi_\beta}(x)+G_{U^{(-\beta)}}(x) )\eta^{(\alpha,\beta)}} \\[3pt]
&\quad \, \times \biggl(\dfrac{(1+\delta)G_{\xi_\beta}(x)}{Q_\beta(u_0)|K+\epsilon|\,\mathbb E[T_2]} + \dfrac{(1+\delta)G_{U^{(-\beta)}}(x)}{|K+\epsilon|\,\mathbb E[T_2]} \biggr)\\[3pt]
&\leq \dfrac{(1+\delta)}{\eta^{(\alpha,\beta)}Q_\beta(u_0)|K+\epsilon|\,\mathbb E[T_2]}{,}\end{align*}
where the second inequality holds since ![]() $Q_\beta(u_0)<1$. Since
$Q_\beta(u_0)<1$. Since ![]() $\delta$ was arbitrary, taking the
$\delta$ was arbitrary, taking the ![]() $\limsup$ as
$\limsup$ as ![]() $x\rightarrow\infty$ yields
$x\rightarrow\infty$ yields
In the case when exactly one of ![]() $\xi^{(\beta)}_{\zeta_\beta}$ and
$\xi^{(\beta)}_{\zeta_\beta}$ and ![]() $U_{-\beta}$ is subexponential, it asymptotically dominates the other as
$U_{-\beta}$ is subexponential, it asymptotically dominates the other as ![]() $x\rightarrow\infty$, since Y is of strong subexponential type. Suppose that it is
$x\rightarrow\infty$, since Y is of strong subexponential type. Suppose that it is ![]() $\xi^{(\beta)}_{\zeta_\beta}$ that is subexponential and note that the following argument is symmetric in
$\xi^{(\beta)}_{\zeta_\beta}$ that is subexponential and note that the following argument is symmetric in ![]() $\xi^{(\beta)}_{\zeta_\beta}$ and
$\xi^{(\beta)}_{\zeta_\beta}$ and ![]() $U^{(-\beta)}$. For all
$U^{(-\beta)}$. For all ![]() $\delta>0$, there exists
$\delta>0$, there exists ![]() $\hat{\delta}>0$ such that
$\hat{\delta}>0$ such that ![]() $\hat{\delta}(1+\hat{\delta})<\delta/2$, and an
$\hat{\delta}(1+\hat{\delta})<\delta/2$, and an ![]() $R>0$ such that for all
$R>0$ such that for all ![]() $x>R$ and
$x>R$ and ![]() $n\in\mathbb N$,
$n\in\mathbb N$,
Thus, for all ![]() $x>R$, for suitably large R,
$x>R$, for suitably large R,
which gives for ![]() $x>R$
$x>R$
 \begin{align*} \dfrac{\mathbb P (Z_n >x \mid K_{n-1}=\alpha,K_n=\beta )}{G_{\xi_\beta}(x) + G_{U^{(-\beta)}}(x)} &\leq \dfrac{1}{\eta^{(\alpha,\beta)}G_{\xi_\beta}(x)} \biggl(\dfrac{(1+{\delta}/{2})G_{\xi_\beta}(x)}{|K+\epsilon|\,\mathbb E[T_2]Q_\beta(u_0)} + \dfrac{({\delta}/{2}) G_{\xi_\beta}}{|K+\epsilon|\,\mathbb E[T_2]} \biggr)\\[3pt]
&\leq \dfrac{1+\delta}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]Q_\beta(u_0)}.\end{align*}
\begin{align*} \dfrac{\mathbb P (Z_n >x \mid K_{n-1}=\alpha,K_n=\beta )}{G_{\xi_\beta}(x) + G_{U^{(-\beta)}}(x)} &\leq \dfrac{1}{\eta^{(\alpha,\beta)}G_{\xi_\beta}(x)} \biggl(\dfrac{(1+{\delta}/{2})G_{\xi_\beta}(x)}{|K+\epsilon|\,\mathbb E[T_2]Q_\beta(u_0)} + \dfrac{({\delta}/{2}) G_{\xi_\beta}}{|K+\epsilon|\,\mathbb E[T_2]} \biggr)\\[3pt]
&\leq \dfrac{1+\delta}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]Q_\beta(u_0)}.\end{align*}
Therefore, since ![]() $\delta>0$ was arbitrary, we may take the
$\delta>0$ was arbitrary, we may take the ![]() $\limsup$ first as
$\limsup$ first as ![]() $\delta\rightarrow0$ and then as
$\delta\rightarrow0$ and then as ![]() $x\rightarrow\infty$ to obtain
$x\rightarrow\infty$ to obtain
Finally, we consider the case when neither is subexponential. Since Y is of strong subexponential type, the tails of ![]() $\tilde{\xi}_{\tilde{\zeta}_\beta}^{(\beta)}$ and
$\tilde{\xi}_{\tilde{\zeta}_\beta}^{(\beta)}$ and ![]() $U^{(-\beta)}$ are dominated by the tails of at least one of either
$U^{(-\beta)}$ are dominated by the tails of at least one of either ![]() $\tilde{\xi}_{\tilde{\zeta}_{b}}^{(b)}$ or
$\tilde{\xi}_{\tilde{\zeta}_{b}}^{(b)}$ or ![]() $U^{(-b)}$. Denote the dominating random variable by X and let
$U^{(-b)}$. Denote the dominating random variable by X and let ![]() $W\in\bigl\{ \tilde{\xi}_{\tilde{\zeta}_\beta}^{(\beta)} , U^{(-\beta)} \bigr\}$. Following the above calculation, for all
$W\in\bigl\{ \tilde{\xi}_{\tilde{\zeta}_\beta}^{(\beta)} , U^{(-\beta)} \bigr\}$. Following the above calculation, for all ![]() $\delta>0$ there exists an
$\delta>0$ there exists an ![]() $R>0$ such that for any
$R>0$ such that for any ![]() $x>R$ and
$x>R$ and ![]() $n\in\mathbb N$,
$n\in\mathbb N$,
Then, by using the results of the previous two cases, for suitably large ![]() $R>0$ we have
$R>0$ we have
Hence, for ![]() $x>R$,
$x>R$,
so, as ![]() $x\rightarrow\infty$, since
$x\rightarrow\infty$, since ![]() $\delta>0$ was arbitrary,
$\delta>0$ was arbitrary,
Since all the components of the Lamperti–Kiu decomposition are finite, for sufficently large x we have ![]() $G_{(\cdot)}(x) = H_{(\cdot)}(x)$. Hence, in the first two cases, we obtain
$G_{(\cdot)}(x) = H_{(\cdot)}(x)$. Hence, in the first two cases, we obtain
As we are taking the limit ![]() $x\rightarrow\infty$, we may also take
$x\rightarrow\infty$, we may also take ![]() $u_0\rightarrow\infty$ and use the fact that
$u_0\rightarrow\infty$ and use the fact that ![]() $Q(u_0)\rightarrow1$ to obtain
$Q(u_0)\rightarrow1$ to obtain
whilst in the third case
This completes the proof.
The following lemma provides a way to use a bound on a random variables distribution function to produce an inequality between random variables.
Lemma 4.7. Suppose Z is a real-valued random variable with tail ![]() $\mathbb P(Z\geq x)$ that is bounded above by some function F(x) such that
$\mathbb P(Z\geq x)$ that is bounded above by some function F(x) such that ![]() $1-F(x)$ is a true distribution function. Then there exists a random variable X, which is a function of Z and an independent uniformly distributed random variable, such that
$1-F(x)$ is a true distribution function. Then there exists a random variable X, which is a function of Z and an independent uniformly distributed random variable, such that ![]() $Z\leq X$ and
$Z\leq X$ and ![]() $\mathbb P(X\geq x) = F(x)$.
$\mathbb P(X\geq x) = F(x)$.
Proof. Let ![]() $P(x) \,:\!=\, \mathbb P(Z\geq x)$ and
$P(x) \,:\!=\, \mathbb P(Z\geq x)$ and ![]() $V\sim \text{Unif}(0,1)$ be independent of Z. We will use the notation
$V\sim \text{Unif}(0,1)$ be independent of Z. We will use the notation ![]() $P(x^+)\,:\!=\, \lim_{y\downarrow x}P(y)$, which exists for all
$P(x^+)\,:\!=\, \lim_{y\downarrow x}P(y)$, which exists for all ![]() $x\geq0$ since P is non-increasing and bounded from below. Define the random function
$x\geq0$ since P is non-increasing and bounded from below. Define the random function ![]() $U\colon \mathbb R^+\rightarrow[0,1]$ by setting
$U\colon \mathbb R^+\rightarrow[0,1]$ by setting ![]() $ U(x) \,:\!=\, P(x) - V(P(x)-P(x^+)).$ Let
$ U(x) \,:\!=\, P(x) - V(P(x)-P(x^+)).$ Let ![]() $x_1<x_2$; then since P is non-increasing,
$x_1<x_2$; then since P is non-increasing, ![]() $P(x^{+})\leq U(x)\leq P(x)$ for all
$P(x^{+})\leq U(x)\leq P(x)$ for all ![]() $x\in\mathbb R$ and
$x\in\mathbb R$ and
hence U is also non-increasing.
Furthermore, suppose ![]() $U(x_1)=U(x_2)$ for some
$U(x_1)=U(x_2)$ for some ![]() $x_1<x_2$. Then
$x_1<x_2$. Then ![]() $ P(x_1^+) \leq U(x_1) = U(x_2) \leq P(x_2) \leq P(x_1^+) ,$ where the last inequality is because P is non-increasing and so
$ P(x_1^+) \leq U(x_1) = U(x_2) \leq P(x_2) \leq P(x_1^+) ,$ where the last inequality is because P is non-increasing and so ![]() $P(x_1^+)=P(x_2)$. If
$P(x_1^+)=P(x_2)$. If ![]() $P(x_1^+)=P(x_1)$, then we have
$P(x_1^+)=P(x_1)$, then we have ![]() $P(x_2)=P(x_1)$. Otherwise we have
$P(x_2)=P(x_1)$. Otherwise we have
This is a contradiction. Hence, if ![]() $x_1<x_2$ and
$x_1<x_2$ and ![]() $U(x_1)=U(x_2)$, then
$U(x_1)=U(x_2)$, then ![]() $P(x_1^+)=P(x_1)=P(x_2)$ a.s., so
$P(x_1^+)=P(x_1)=P(x_2)$ a.s., so ![]() $\mathbb P( x_1 \leq Z < x_2) = 0$.
$\mathbb P( x_1 \leq Z < x_2) = 0$.
From this we can now conclude that, for all ![]() $x\in\mathbb R$, we have
$x\in\mathbb R$, we have
However, by the above calculation, we get
and hence, for all ![]() $x\in\mathbb R$, we have
$x\in\mathbb R$, we have ![]() $ \mathbb P(U(z) \leq U(x) ) = P(x).$
$ \mathbb P(U(z) \leq U(x) ) = P(x).$
Now let ![]() $q\in[0,1]$ and suppose that there exists
$q\in[0,1]$ and suppose that there exists ![]() $x\in\mathbb R^+$ with
$x\in\mathbb R^+$ with ![]() $P(x^+)=P(x)=q$, so
$P(x^+)=P(x)=q$, so
If there is not such an x, then, since ![]() $\lim_{x\rightarrow-\infty}P(x)=1$ and
$\lim_{x\rightarrow-\infty}P(x)=1$ and ![]() $\lim_{x\rightarrow\infty}P(x)=0$, there exists
$\lim_{x\rightarrow\infty}P(x)=0$, there exists ![]() $x\in\mathbb R^+$ such that
$x\in\mathbb R^+$ such that ![]() $q\in[P(x^+),P(x))$. For any
$q\in[P(x^+),P(x))$. For any ![]() $y>x$, we have
$y>x$, we have ![]() $ U(y) \leq P(y) \leq P(x^+),$ so
$ U(y) \leq P(y) \leq P(x^+),$ so ![]() $U(y)\notin(P(x^+),P(x))$ and similarly, for any
$U(y)\notin(P(x^+),P(x))$ and similarly, for any ![]() $y<x$, we have
$y<x$, we have ![]() $ U(y) \geq U(y^+) \geq P(x) ,$ so
$ U(y) \geq U(y^+) \geq P(x) ,$ so ![]() $U(y)\notin(P(x^+),P(x))$. Hence
$U(y)\notin(P(x^+),P(x))$. Hence ![]() $U(Z)\in(q,P(x))\subset(P(x^+),P(x))$ implies
$U(Z)\in(q,P(x))\subset(P(x^+),P(x))$ implies ![]() $Z=x$.
$Z=x$.
Next we want to consider ![]() $\mathbb P( P(x)=U(Z) ;\, Z\neq x)$. Notice that if
$\mathbb P( P(x)=U(Z) ;\, Z\neq x)$. Notice that if ![]() $z>x$ then
$z>x$ then ![]() $U(z)\leq P(x^+)<P(x)$ and so
$U(z)\leq P(x^+)<P(x)$ and so ![]() $\mathbb P( P(x)=U(z) ;\, Z>x)=0$. If
$\mathbb P( P(x)=U(z) ;\, Z>x)=0$. If ![]() $z<x$ and
$z<x$ and ![]() $P(x)=U(z)$, then
$P(x)=U(z)$, then ![]() $P(x)=U(z)\geq P(z^+)\geq P(x)$ and so
$P(x)=U(z)\geq P(z^+)\geq P(x)$ and so ![]() $P(x)=P(z^+)$. However, if there is a discontinuity point
$P(x)=P(z^+)$. However, if there is a discontinuity point ![]() $y\in[z,x)$, then
$y\in[z,x)$, then ![]() $U(z)\geq P(z^+)\geq P(y)>P(y^+)\geq P(x)$ so
$U(z)\geq P(z^+)\geq P(y)>P(y^+)\geq P(x)$ so ![]() $\mathbb P(P(x)=U(z) ;\, Z<x)=0$, and we conclude that
$\mathbb P(P(x)=U(z) ;\, Z<x)=0$, and we conclude that ![]() $P(z)=P(z^+)=P(x)$ and hence
$P(z)=P(z^+)=P(x)$ and hence ![]() $ \mathbb P( P(x)=U(Z) ;\, Z\neq x ) = 0.$
$ \mathbb P( P(x)=U(Z) ;\, Z\neq x ) = 0.$
From this and since V is uniformly distributed on [0,1], we have
 \begin{align*} \mathbb P(U(Z)\in(q,P(x)]) &= \mathbb P(Z=x)\,\mathbb P(U(x)\in(q,P(x)]) + \mathbb P(Z\neq x ;\, U(Z)=P(x) )\\ &= \mathbb P(Z=x)\,\mathbb P\biggl( \dfrac{q-P(x^+)}{P(x)-P(x^+)}
< V \leq \dfrac{P(x)-P(x^+)}{P(x)-P(x^+)}\biggr) + 0\\ &= (P(x)-P(x^+) )\dfrac{q-P(x^+)}{P(x)-P(x^+)},\end{align*}
\begin{align*} \mathbb P(U(Z)\in(q,P(x)]) &= \mathbb P(Z=x)\,\mathbb P(U(x)\in(q,P(x)]) + \mathbb P(Z\neq x ;\, U(Z)=P(x) )\\ &= \mathbb P(Z=x)\,\mathbb P\biggl( \dfrac{q-P(x^+)}{P(x)-P(x^+)}
< V \leq \dfrac{P(x)-P(x^+)}{P(x)-P(x^+)}\biggr) + 0\\ &= (P(x)-P(x^+) )\dfrac{q-P(x^+)}{P(x)-P(x^+)},\end{align*}
and hence
 \begin{align*} \mathbb P( U(Z) \leq q ) &= \mathbb P( U(Z) \leq P(x) ) - \mathbb P( U(Z) \in (q,P(x)] )\\ &= P(x) - (P(x) - P(x^+))\dfrac{(P(x)-q)}{P(x) - P(x^+)} =q.\end{align*}
\begin{align*} \mathbb P( U(Z) \leq q ) &= \mathbb P( U(Z) \leq P(x) ) - \mathbb P( U(Z) \in (q,P(x)] )\\ &= P(x) - (P(x) - P(x^+))\dfrac{(P(x)-q)}{P(x) - P(x^+)} =q.\end{align*}
Hence U(Z) is uniformly distributed on [0,1]. Using [Reference Embrechts and Hofert9, Proposition 3.1], the random variable defined by ![]() $X\,:\!=\, U^{-}(Z)\,:\!=\, \inf \{ x\in\mathbb R^+ \mid F(x) < U(Z) \}$ has the distribution F. Moreover, since
$X\,:\!=\, U^{-}(Z)\,:\!=\, \inf \{ x\in\mathbb R^+ \mid F(x) < U(Z) \}$ has the distribution F. Moreover, since ![]() $F(x)\geq P(x)$ for all
$F(x)\geq P(x)$ for all ![]() $x\in\mathbb R^+$, we have
$x\in\mathbb R^+$, we have
and, since F is non-increasing, we have ![]() $ X = \inf \{ x\in\mathbb R^+ \mid F(x) < U(Z) \} \geq Z,$ as required.
$ X = \inf \{ x\in\mathbb R^+ \mid F(x) < U(Z) \} \geq Z,$ as required.
We are now able to derive the upper bound of Theorem 4.1.
Lemma 4.8. If Y is a Lamperti–Kiu process of strong subexponential type, then the right tail of ![]() $A_\infty$ satisfies
$A_\infty$ satisfies
where H is the integrated tail from Theorem 4.1.
Proof. Fix ![]() $\sigma\in\{+,-\}$ and let
$\sigma\in\{+,-\}$ and let ![]() $\delta_2>0$. For sufficiently large
$\delta_2>0$. For sufficiently large ![]() $A>0$, by Proposition 4.1, we know
$A>0$, by Proposition 4.1, we know ![]() $\mathbb E_\sigma[N(\alpha,\beta)]/\eta^{(\alpha,\beta)}\leq \mathbb{1}_{\{\sigma=\alpha\}} + \delta_2$. Now fix such an
$\mathbb E_\sigma[N(\alpha,\beta)]/\eta^{(\alpha,\beta)}\leq \mathbb{1}_{\{\sigma=\alpha\}} + \delta_2$. Now fix such an ![]() $A>0$ and let
$A>0$ and let ![]() $\delta_1>0$.
$\delta_1>0$.
From Lemma 4.4 we have ![]() $ \log(A_\infty) \leq (N+1)C + \sum_{i=1}^NZ_i^+.$
$ \log(A_\infty) \leq (N+1)C + \sum_{i=1}^NZ_i^+.$
For each ![]() $i\in\mathbb N$, we have a tail estimate for
$i\in\mathbb N$, we have a tail estimate for ![]() $Z_i^+$, given
$Z_i^+$, given ![]() $(K_n)_{n\in\mathbb N_0}$, from Lemma 4.6, which, used in conjunction with Lemma 4.7, gives the existence of random variables
$(K_n)_{n\in\mathbb N_0}$, from Lemma 4.6, which, used in conjunction with Lemma 4.7, gives the existence of random variables ![]() $X_i(k)$ for each
$X_i(k)$ for each ![]() $k\in\cup_{n\in\mathbb N}\{+,-\}^n$ with
$k\in\cup_{n\in\mathbb N}\{+,-\}^n$ with ![]() $k_0=\sigma$ such that:
$k_0=\sigma$ such that:
(1) each
 $X_i(k)$ is a function of
$X_i(k)$ is a function of  $Z_i$ and a random variable independent of the rest of the system,
$Z_i$ and a random variable independent of the rest of the system,-
(2)
 $X_i(k)\geq (Z_i^+ +C)\mathbb{1}_{\{N=n ;\, (K_0,\ldots,K_n)=k\}}$,
$X_i(k)\geq (Z_i^+ +C)\mathbb{1}_{\{N=n ;\, (K_0,\ldots,K_n)=k\}}$, -
(3)
 $X_i(k)$ has tails given by
$X_i(k)$ has tails given by  $\min (1,H^{(k_i)}(x)(\eta^{(k_{i-1},k_i)}|K+\epsilon|\,\mathbb E[T_2]|)^{-1} )$ if
$\min (1,H^{(k_i)}(x)(\eta^{(k_{i-1},k_i)}|K+\epsilon|\,\mathbb E[T_2]|)^{-1} )$ if  $k_i\in B$ and tails which are
$k_i\in B$ and tails which are  ${\mathrm{o}}(\min(1,H^{(b)}(x)))$ for
${\mathrm{o}}(\min(1,H^{(b)}(x)))$ for  $b\in B$ if
$b\in B$ if  $k_i\notin B$.
$k_i\notin B$.
Then, summing up over the sample paths of ![]() $(K_n)_{n\in\mathbb N_0}$, we have the upper bound
$(K_n)_{n\in\mathbb N_0}$, we have the upper bound
 \begin{align*} \mathbb P_\sigma\biggl( \sum_{i=1}^N Z_i^+ +C>x \biggr) &\leq\sum_{n\in\mathbb N}\sum_{\substack{ k\in\{+,-\}^{n+1} \\ k_0=\sigma } }\mathbb P_\sigma\biggl( \sum_{i=1}^n X_i(k)>x ;\, N=n ;\, (K_0,\ldots,K_n)=k \biggr).\end{align*}
\begin{align*} \mathbb P_\sigma\biggl( \sum_{i=1}^N Z_i^+ +C>x \biggr) &\leq\sum_{n\in\mathbb N}\sum_{\substack{ k\in\{+,-\}^{n+1} \\ k_0=\sigma } }\mathbb P_\sigma\biggl( \sum_{i=1}^n X_i(k)>x ;\, N=n ;\, (K_0,\ldots,K_n)=k \biggr).\end{align*}
For ease of notation, let ![]() $\bar{\eta}=\max_{\alpha,\beta\in\{+,-\}}\eta_{\alpha,\beta}$,
$\bar{\eta}=\max_{\alpha,\beta\in\{+,-\}}\eta_{\alpha,\beta}$, ![]() $\underline{\eta}=\min_{\alpha,\beta\in\{+,-\}}\eta_{\alpha,\beta}$, and
$\underline{\eta}=\min_{\alpha,\beta\in\{+,-\}}\eta_{\alpha,\beta}$, and ![]() $d\in(0,(1-2\bar{\eta})/2\bar{\eta})$.
$d\in(0,(1-2\bar{\eta})/2\bar{\eta})$.
For each ![]() $\alpha,\beta\in\{+,-\}$,
$\alpha,\beta\in\{+,-\}$, ![]() $n\in\mathbb N$ and
$n\in\mathbb N$ and ![]() $k\in\{+,-\}^{n+1}$ such that
$k\in\{+,-\}^{n+1}$ such that ![]() $k_0=\sigma$, let
$k_0=\sigma$, let
Then, by Lemma 4.5, given the event ![]() $\{N=n ;\, (K_0,\ldots,K_n)=k\}$, the sum
$\{N=n ;\, (K_0,\ldots,K_n)=k\}$, the sum
is a sum of ![]() $n_{\alpha,\beta}(k)$ i.i.d. random variables, and hence, in the case
$n_{\alpha,\beta}(k)$ i.i.d. random variables, and hence, in the case ![]() $\beta\in B$, from Kesten’s bound [Reference Foss, Korshunov and Zachary11, Theorem 3.34],
$\beta\in B$, from Kesten’s bound [Reference Foss, Korshunov and Zachary11, Theorem 3.34],
 \begin{align*} & \mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k)\mathbb{1}_{\{k_{i-1}=\alpha,k_i=\beta\}} >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\ &\quad \leq c(d)(1+d)^{n_{\alpha,\beta}(k)}\mathbb P_\sigma(X_1((\alpha,\beta))>x)\\ &\quad \leq \dfrac{c(d)(1+d)^nF(x)}{\underline{\eta}|K+\epsilon|\,\mathbb E[T_2]}.\end{align*}
\begin{align*} & \mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k)\mathbb{1}_{\{k_{i-1}=\alpha,k_i=\beta\}} >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\ &\quad \leq c(d)(1+d)^{n_{\alpha,\beta}(k)}\mathbb P_\sigma(X_1((\alpha,\beta))>x)\\ &\quad \leq \dfrac{c(d)(1+d)^nF(x)}{\underline{\eta}|K+\epsilon|\,\mathbb E[T_2]}.\end{align*}
In the case ![]() $\beta\notin B$, since Y is of strong subexponential type, for any
$\beta\notin B$, since Y is of strong subexponential type, for any ![]() $b\in B$,
$b\in B$,
 \begin{align*} & \mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k)\mathbb{1}_{\{k_{i-1}=\alpha,k_i=\beta\}} >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\ &\quad \leq \mathbb P_\sigma\biggl( \sum_{i=1}^nW_i\mathbb{1}_{\{k_{i-1}=\alpha,k_i=\beta\}} >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\&\quad \leq \dfrac{c(d)(1+d)^nH(x)}{\underline{\eta}|K+\epsilon|\,\mathbb E[T_2]},\end{align*}
\begin{align*} & \mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k)\mathbb{1}_{\{k_{i-1}=\alpha,k_i=\beta\}} >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\ &\quad \leq \mathbb P_\sigma\biggl( \sum_{i=1}^nW_i\mathbb{1}_{\{k_{i-1}=\alpha,k_i=\beta\}} >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\&\quad \leq \dfrac{c(d)(1+d)^nH(x)}{\underline{\eta}|K+\epsilon|\,\mathbb E[T_2]},\end{align*}
where for each ![]() $i\in\mathbb N$ the random variable
$i\in\mathbb N$ the random variable ![]() $W_i$ depends only on
$W_i$ depends only on ![]() $X_i(k)$ and has the distribution of
$X_i(k)$ and has the distribution of ![]() $X_1((\alpha,b))$. We can now use Corollaries 3.16 and 3.18 in [Reference Foss, Korshunov and Zachary11, Chapter 3, p. 52] to sum the
$X_1((\alpha,b))$. We can now use Corollaries 3.16 and 3.18 in [Reference Foss, Korshunov and Zachary11, Chapter 3, p. 52] to sum the ![]() $Y_{\alpha,\beta}$ and obtain the bound
$Y_{\alpha,\beta}$ and obtain the bound
 \begin{align*} &\mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k) >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\[4pt]
&\quad =\mathbb P_\sigma\biggl( \sum_{\alpha,\beta\in\{+,-\}}\sum_{i=1}^nX_i(k)\mathbb{1}_{\{k_{i-1}=\alpha,k_i=\beta\}} >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\[4pt]
&\quad \leq \dfrac{4c(d)(1+d)^nH(x)}{\underline{\eta}|K+\epsilon|\,\mathbb E[T_2]}.\end{align*}
\begin{align*} &\mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k) >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\[4pt]
&\quad =\mathbb P_\sigma\biggl( \sum_{\alpha,\beta\in\{+,-\}}\sum_{i=1}^nX_i(k)\mathbb{1}_{\{k_{i-1}=\alpha,k_i=\beta\}} >x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\[4pt]
&\quad \leq \dfrac{4c(d)(1+d)^nH(x)}{\underline{\eta}|K+\epsilon|\,\mathbb E[T_2]}.\end{align*}
Using the bound on the distribution of N from (4.4), we see that there is an ![]() $M\in\mathbb N$ such that
$M\in\mathbb N$ such that ![]() $\mathbb E[\underline{\eta}^{-1}4c(d)(1+d)^N ;\, N>M]\leq \delta_1$ for sufficiently small d. This then gives
$\mathbb E[\underline{\eta}^{-1}4c(d)(1+d)^N ;\, N>M]\leq \delta_1$ for sufficiently small d. This then gives
 \begin{align*} \mathbb P_\sigma\biggl( \sum_{i=1}^N X_i((K_n)_{n\in\mathbb N})>x ;\, N>M \biggr) \leq \dfrac{\delta_1 H(x)}{|K+\epsilon|\,\mathbb E[T_2]}.\end{align*}
\begin{align*} \mathbb P_\sigma\biggl( \sum_{i=1}^N X_i((K_n)_{n\in\mathbb N})>x ;\, N>M \biggr) \leq \dfrac{\delta_1 H(x)}{|K+\epsilon|\,\mathbb E[T_2]}.\end{align*}
Moreover, by [Reference Foss, Korshunov and Zachary11, Corollary 3.16], for all ![]() $n\leq M$ and
$n\leq M$ and ![]() $k\in\{+,-\}^{n+1}$ with
$k\in\{+,-\}^{n+1}$ with ![]() $k_0=\sigma$ there exists
$k_0=\sigma$ there exists ![]() $R_{n,k}>0$ such that, for all
$R_{n,k}>0$ such that, for all ![]() $x>R_{n,k}$,
$x>R_{n,k}$,
 \begin{align*} & \mathbb P_\sigma\biggl( \sum_{i=1}^n X_i(k)>x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr) \\ &\quad \leq \biggl( \biggl(1+\dfrac{\delta_1}{2}\biggr)\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B} n_{\alpha,\beta}(k)\dfrac{H^{\beta}(x)}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]}\biggr) \bar{*} \mathbb P_\sigma\biggl( \sum_{i=1}^n \mathbb{1}_{\{k_i \notin B\}} X_i(k) > x \biggr)(x),\end{align*}
\begin{align*} & \mathbb P_\sigma\biggl( \sum_{i=1}^n X_i(k)>x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr) \\ &\quad \leq \biggl( \biggl(1+\dfrac{\delta_1}{2}\biggr)\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B} n_{\alpha,\beta}(k)\dfrac{H^{\beta}(x)}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]}\biggr) \bar{*} \mathbb P_\sigma\biggl( \sum_{i=1}^n \mathbb{1}_{\{k_i \notin B\}} X_i(k) > x \biggr)(x),\end{align*}
where for two survival functions ![]() $\bar{F}$ and
$\bar{F}$ and ![]() $\bar{G}$ we write
$\bar{G}$ we write ![]() $\bar{F}\bar{*}\bar{G}$ for the survival function of the convolution of the distribution functions
$\bar{F}\bar{*}\bar{G}$ for the survival function of the convolution of the distribution functions ![]() $F \,:\!=\, 1-\bar{F}$ and
$F \,:\!=\, 1-\bar{F}$ and ![]() $G\,:\!=\, 1-\bar{G}$. Then, since
$G\,:\!=\, 1-\bar{G}$. Then, since
by [Reference Foss, Korshunov and Zachary11, Corollary 3.18] we have
 \begin{align*}& \mathbb P_\sigma\biggl( \sum_{i=1}^n X_i(k)>x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr) \\ &\quad \leq (1+\delta_1 )\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B} n_{\alpha,\beta}(k)\dfrac{H^{\beta}(x)}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]}.\end{align*}
\begin{align*}& \mathbb P_\sigma\biggl( \sum_{i=1}^n X_i(k)>x \mid N=n ;\, (K_0,\ldots,K_n)=k \biggr) \\ &\quad \leq (1+\delta_1 )\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B} n_{\alpha,\beta}(k)\dfrac{H^{\beta}(x)}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]}.\end{align*}
Since there are finitely many such pairs (n,k) with ![]() $n\leq M$, we can take
$n\leq M$, we can take ![]() $R\,:\!=\, \max_{n\leq M}R_{n,k}$ so that for all
$R\,:\!=\, \max_{n\leq M}R_{n,k}$ so that for all ![]() $x>R$ we get
$x>R$ we get
 \begin{align*} &\sum_{n=1}^{M}\sum_{ \substack{ k\in\{+,-\}^{n+1} \\ k_0=\sigma }} \mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k)>x ;\, N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\ &\quad \leq (1+\delta_1)\sum_{n=1}^{M}\sum_{\substack{ k\in\{+,-\}^{n+1} \\ k_0=\sigma }}\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B}n_{\alpha,\beta}(k)\dfrac{H^{(\beta)}(x)}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]}\\ &\quad \quad \, \times \mathbb P_\sigma(N=n ;\, (K_0,\ldots,K_n)=k) \\ &\quad = (1+\delta_1)\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B}\,\mathbb E_\sigma[n_{\alpha,\beta}(k) ;\, N\leq M]\dfrac{H^{(\beta)}(x)}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]}\\ &\quad \leq \dfrac{(1+\delta_1)}{|K+\epsilon|\,\mathbb E[T_2]}\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B}\dfrac{\mathbb E_\sigma[n_{\alpha,\beta}(k)]H^{(\beta)}(x)}{\eta^{(\alpha,\beta)}}.\end{align*}
\begin{align*} &\sum_{n=1}^{M}\sum_{ \substack{ k\in\{+,-\}^{n+1} \\ k_0=\sigma }} \mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k)>x ;\, N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\ &\quad \leq (1+\delta_1)\sum_{n=1}^{M}\sum_{\substack{ k\in\{+,-\}^{n+1} \\ k_0=\sigma }}\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B}n_{\alpha,\beta}(k)\dfrac{H^{(\beta)}(x)}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]}\\ &\quad \quad \, \times \mathbb P_\sigma(N=n ;\, (K_0,\ldots,K_n)=k) \\ &\quad = (1+\delta_1)\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B}\,\mathbb E_\sigma[n_{\alpha,\beta}(k) ;\, N\leq M]\dfrac{H^{(\beta)}(x)}{\eta^{(\alpha,\beta)}|K+\epsilon|\,\mathbb E[T_2]}\\ &\quad \leq \dfrac{(1+\delta_1)}{|K+\epsilon|\,\mathbb E[T_2]}\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B}\dfrac{\mathbb E_\sigma[n_{\alpha,\beta}(k)]H^{(\beta)}(x)}{\eta^{(\alpha,\beta)}}.\end{align*}
Next, by our choice of A we have ![]() $\mathbb E_\sigma[n(\alpha,\beta)]/\eta^{(\alpha,\beta)}\leq \mathbb{1}_{\sigma=\alpha} + \delta_2$ and thus
$\mathbb E_\sigma[n(\alpha,\beta)]/\eta^{(\alpha,\beta)}\leq \mathbb{1}_{\sigma=\alpha} + \delta_2$ and thus
 \begin{align*} &\sum_{n=1}^{M}\sum_{\substack{ k\in\{+,-\}^{n+1} \\ K_0=\sigma }} \mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k)>x ;\, N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\ &\quad \leq \dfrac{(1+\delta_1)}{|K+\epsilon|\,\mathbb E[T_2]}\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B} ( \mathbb{1}_{\{\sigma=\alpha\}} + \delta_2 )H^{(\beta)}(x)\\ &\quad = \dfrac{(1+\delta_1)}{|K+\epsilon|\,\mathbb E[T_2]}(1+2\delta_2)\sum_{\beta\in B}H^{(\beta)}(x)\\ &\quad \leq\dfrac{(1+\delta_1)^2}{|K+\epsilon|\,\mathbb E[T_2]}(1+2\delta_2)H(x),\end{align*}
\begin{align*} &\sum_{n=1}^{M}\sum_{\substack{ k\in\{+,-\}^{n+1} \\ K_0=\sigma }} \mathbb P_\sigma\biggl( \sum_{i=1}^nX_i(k)>x ;\, N=n ;\, (K_0,\ldots,K_n)=k \biggr)\\ &\quad \leq \dfrac{(1+\delta_1)}{|K+\epsilon|\,\mathbb E[T_2]}\sum_{\alpha\in\{+,-\}}\sum_{\beta\in B} ( \mathbb{1}_{\{\sigma=\alpha\}} + \delta_2 )H^{(\beta)}(x)\\ &\quad = \dfrac{(1+\delta_1)}{|K+\epsilon|\,\mathbb E[T_2]}(1+2\delta_2)\sum_{\beta\in B}H^{(\beta)}(x)\\ &\quad \leq\dfrac{(1+\delta_1)^2}{|K+\epsilon|\,\mathbb E[T_2]}(1+2\delta_2)H(x),\end{align*}
where the last inequality holds for sufficiently large x since Y is of strong subexponential type. Hence, for all ![]() $x>R$, we have
$x>R$, we have
 \begin{align*} \mathbb P_\sigma\biggl( \sum_{i=1}^N ( Z_i^+ +C ) >x \biggr) \leq \dfrac{(1+\delta_1)^2(1+2\delta_2)}{|K+\epsilon|\,\mathbb E[T_2]}F(x) +\dfrac{\delta_1 H(x)}{|K+\epsilon|\,\mathbb E[T_2]},\end{align*}
\begin{align*} \mathbb P_\sigma\biggl( \sum_{i=1}^N ( Z_i^+ +C ) >x \biggr) \leq \dfrac{(1+\delta_1)^2(1+2\delta_2)}{|K+\epsilon|\,\mathbb E[T_2]}F(x) +\dfrac{\delta_1 H(x)}{|K+\epsilon|\,\mathbb E[T_2]},\end{align*}
and so from the definition of ![]() $\limsup$,
$\limsup$,
However, because H is long-tailed, ![]() $\lim_{x\rightarrow\infty}H(x-C)/H(x) =1$ and therefore
$\lim_{x\rightarrow\infty}H(x-C)/H(x) =1$ and therefore
Then, by comparison,
and since both ![]() $\epsilon$ and
$\epsilon$ and ![]() $\delta_2$ were arbitrary, the result follows.
$\delta_2$ were arbitrary, the result follows.
It remains to show that the lower bound for ![]() $\liminf_{x\rightarrow\infty}\mathbb P(A_\infty>x)$ also holds. To this end, for each
$\liminf_{x\rightarrow\infty}\mathbb P(A_\infty>x)$ also holds. To this end, for each ![]() $x\in\mathbb R$, define the stopping time
$x\in\mathbb R$, define the stopping time
and notice that ![]() $\tau_d(x)<\infty$ if and only if
$\tau_d(x)<\infty$ if and only if ![]() $\sup_{n\in\mathbb N}\xi_{T_{2n}}\geq x$. Furthermore,
$\sup_{n\in\mathbb N}\xi_{T_{2n}}\geq x$. Furthermore, ![]() $J_{\tau_d(x)}=J_0$ whenever
$J_{\tau_d(x)}=J_0$ whenever ![]() $\tau_d(x)<\infty$. Since
$\tau_d(x)<\infty$. Since ![]() $\xi_{T_2}$ is strong subexponential, its integrated tail, H, is subexponential and thus, by [Reference Zachary29, Theorem 1(ii)],
$\xi_{T_2}$ is strong subexponential, its integrated tail, H, is subexponential and thus, by [Reference Zachary29, Theorem 1(ii)], ![]() $\mathbb P(\tau_d(x)<\infty)$ is also subexponential. Then, by considering the random walk
$\mathbb P(\tau_d(x)<\infty)$ is also subexponential. Then, by considering the random walk ![]() $ (\xi_{T_{2n}} )_{n\in\mathbb N}$ in the place of
$ (\xi_{T_{2n}} )_{n\in\mathbb N}$ in the place of ![]() $ ( \xi_n )_{n\in\mathbb N}$ in the proof of [Reference Maulik and Zwart21, Lemma 4.3], we find that for every
$ ( \xi_n )_{n\in\mathbb N}$ in the proof of [Reference Maulik and Zwart21, Lemma 4.3], we find that for every ![]() $y>0$
$y>0$
We are now able to prove Theorem 4.1.
Proof of Theorem 4.1. Equation (4.6) of Theorem 4.1 follows from inequality (4.7) of Lemma 4.8 and the inequality
which we will now prove.
The following inequality is immediate:
Applying the Markov additive property and recalling ![]() $J_{\tau_d(x)}=J_0$ gives
$J_{\tau_d(x)}=J_0$ gives
where ![]() $\hat{A}_{\infty,j}$ is an independent and identically distributed copy of
$\hat{A}_{\infty,j}$ is an independent and identically distributed copy of ![]() $A_\infty$ with
$A_\infty$ with ![]() $\hat{J}_0=j$. Then, by applying (4.8), we have
$\hat{J}_0=j$. Then, by applying (4.8), we have
However, ![]() $\xi_{T_{2n}}$ is a sum of the random variables
$\xi_{T_{2n}}$ is a sum of the random variables ![]() $\xi_{T_{2m}}-\xi_{T_{2(m-1)}}$, which are i.i.d. copies of
$\xi_{T_{2m}}-\xi_{T_{2(m-1)}}$, which are i.i.d. copies of ![]() $\xi_{T_2}$. Since Y is of strong subexponential type, the integrated tail, H, of
$\xi_{T_2}$. Since Y is of strong subexponential type, the integrated tail, H, of ![]() $\xi_{T_2}$ is long-tailed, and we can apply Veraverbeke’s theorem [Reference Zachary29, Theorem 1(i)] to conclude that
$\xi_{T_2}$ is long-tailed, and we can apply Veraverbeke’s theorem [Reference Zachary29, Theorem 1(i)] to conclude that
Remark 4.1. The results of this paper are presented only for settings where ![]() $|E| = 2$. However, they can easily be extended to the case of any finite E provided the modulating Markov chain J is irreducible. In the proofs, extensive use is made of the fact that
$|E| = 2$. However, they can easily be extended to the case of any finite E provided the modulating Markov chain J is irreducible. In the proofs, extensive use is made of the fact that ![]() $J_{T_{2n}} = J_0$ for all
$J_{T_{2n}} = J_0$ for all ![]() $n\in N$. To extend this to the case
$n\in N$. To extend this to the case ![]() $|E| > 2$, we replace
$|E| > 2$, we replace ![]() $\{T_{2n}\}_{n\in N }$ with the sequence of return times to
$\{T_{2n}\}_{n\in N }$ with the sequence of return times to ![]() $J_0$ of J, which have finite expectation. In the case
$J_0$ of J, which have finite expectation. In the case ![]() $|E| =\infty$, two further difficulties arise, which may prevent an extension of the results. Firstly, even if J is a recurrent Markov chain, it may be the case that the expected return time of J is infinite. Secondly, arguments that rely on taking maxima or sums over the elements of E are no longer valid. The reader may also be interested by the work in [Reference Behme and Sideris3], where a necessary and sufficient condition for finiteness of
$|E| =\infty$, two further difficulties arise, which may prevent an extension of the results. Firstly, even if J is a recurrent Markov chain, it may be the case that the expected return time of J is infinite. Secondly, arguments that rely on taking maxima or sums over the elements of E are no longer valid. The reader may also be interested by the work in [Reference Behme and Sideris3], where a necessary and sufficient condition for finiteness of ![]() $\int_0^{\infty} \,{\mathrm{e}}^{\xi_s}\,{\mathrm{d}} \eta_s $ is given, where
$\int_0^{\infty} \,{\mathrm{e}}^{\xi_s}\,{\mathrm{d}} \eta_s $ is given, where ![]() $(\xi, \eta)$ is a bivariate Markov additive process with some modulating Markov chain J.
$(\xi, \eta)$ is a bivariate Markov additive process with some modulating Markov chain J.
Acknowledgements
We are grateful to the anonymous referees for their careful reading of our manuscript and their valuable comments which helped to improve the paper.