Introduction
Ion acceleration via laser–plasma interaction has attracted much attention due to its lower cost and convenience compared with the conventional ion accelerator. The utilization of an ultra-intense laser provides an extremely strong electromagnetic field and an ultra-high acceleration rate for ion acceleration. This has generated an alternative of the conventional particle acceleration and has been used widely in numerous applications of high-energy ions, such as ion sources (Daido et al., Reference Daido, Nishiuchi and Pirozhkov2012; Wagner et al., Reference Wagner, Deppert, Brabetz, Fiala, Kleinschmidt, Poth, Schanz, Tebartz, Zielbauer, Roth, Stohlker and Bagnoud2016), radiography (Edwards et al., Reference Edwards, Sinclair, Goldsack, Krushelnick, Beg, Clark, Dangor, Najmudin, Tatarakis, Walton, Zepf, Ledingham, Spencer, Norreys, Clarke, Kodama, Toyama and Tampo2002), hadron therapy of diseases (Bulanov and Khoroshkov Reference Bulanov and Khoroshkov2002), and fast ignition inertial confinement fusion (Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001). It has also given a strong motivation to research pertinent questions (Wang et al., Reference Wang, Yan, Chen, He, Ma, Bin, Schreiber, Tajima and Habs2013; Kim et al., Reference Kim, Pae, Choi, Lee, Kim, Singhal, Sung, Lee, Lee, Nickles, Jeong, Kim and Nam2016; Honrubia et al., Reference Honrubia, Morace and Murakami2017; Yogo et al., Reference Yogo, Mima, Iwata, Tosaki, Morace, Arikawa, Fujioka, Johzaki, Sentoku, Nishimura, Sagisaka, Matsuo, Kamitsukasa, Kojima, Nagatomo, Nakai, Shiraga, Murakami, Tokita, Kawanaka, Miyanaga, Yamanoi, Norimatsu, Sakagami, Bulanov, Kondo and Azechi2017).
The basic scheme of ion acceleration via laser–plasma interaction is the relativistic flying mirror concept in which the ponderomotive force of laser pushes electrons away from rear surface of target when an ultra- intense laser pulse ejects into a plasma or a foil. The slap of electrons accelerated by strong electromagnetic waves to nearly light speed forms a strong charge separation field to pull ions to co-propagate with the laser pulse. Based on this frame, the mechanisms of ion acceleration via laser–plasma interaction include mainly the following aspects: Target normal sheath acceleration (Hatchett et al., Reference Hatchett, Brown, Cowan, Henry, Johnson, Key, Koch, Langdon, Lasinski, Lee, Mackinnon, Pennington, Perry, Phillips, Roth, Sangster, Singh, Snavely, Stoyer, Wilks and Yasuike2000; Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, Mackinnon and Snavely2001; Mora, Reference Mora2003), radiation pressure acceleration (RPA) (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Klimo et al., Reference Klimo, Psikal, Limpouch and Tikhonchuk2008; Robinson et al., Reference Robinson, Zepf, Kar, Evans and Bellei2008; Yan et al., Reference Yan, Wu, Sheng, Chen and Meyer-ter-Vehn2009), Coulomb explosion (Kovalev and Bychenkov Reference Kovalev and Bychenkov2003; Bulanov et al., Reference Bulanov, Brantov, Bychenkov, Chvykov, Kalinchenko, Matsuoka, Rousseau, Reed, Yanovsky, Litzenberg, Krushelnick and Maksimchuk2008), and so on. In this paper, we will focus on the enhancement of ion acceleration via RPA by using an external longitudinal magnetic field. RPA is one of the most efficient mechanisms because nearly all the laser energy is transferred to ions. When the electric field inspired by a laser is nearly the same as the charge separation field, which is defined as E m = 2πen e l where e, n e, and l are charge of electron, electron density, and the thickness of foil, ions and electrons will move together with the laser pulse. According to the double Doppler effect, the laser reflected by the plasma mirror will get a downshift of frequency Δω = (1 − 1/4γ 2)ωL. This means that each photon energy transferred to ions is referred to 
${\rm \Delta} \varepsilon = \hbar {\rm \Delta} \omega $, where γ and ωL are the Lorentz factor of plasma mirror and frequency of laser, respectively. In the relativistic regime, the velocity of electron-ion layer is almost equal to light speed, making γ ≫ 1. This will lead to an almost complete laser energy transferred to ions, making RPA a promising approach to obtain high-energy ions. However, some limitations of ion-beam quality such as (i) transverse target expansion (Dollar et al., Reference Dollar, Zulick, Thomas, Chvykov, Davis, Kalinchenko, Matsuoka, McGuffey, Petrov, Willingale, Yanovsky, Maksimchuk and Krushelnick2012), (ii) slightly focused laser group velocity (Bulanov et al., Reference Bulanov, Esarey, Schroeder, Bulanov, Esirkepov, Kando, Pegoraro and Leemans2015), and (iii) target transparency (Macchi et al., Reference Macchi, Veghini and Pegoraro2009) greatly harm the quality of proton via RPA. In this paper, we will focus on the influence of the transverse target expansion which results in reduction of electron density. This tends to terminate the process of RPA ahead of time. It may excite some harmful transverse instabilities such as Rayleigh–Taylor like instability (Pegoraro and Bulanov, Reference Pegoraro and Bulanov2007; Palmer et al., Reference Palmer, Schreiber, Nagel, Dover, Bellei, Beg, Bott, Clarke, Dangor, Hassan, Hilz, Jung, Kneip, Mangles, Lancaster, Rehman, Robinson, Spindloe, Szerypo, Tatarakis, Yeung, Zepf and Najmudin2012) and Weibel-like instability (Yoon and Davidson Reference Yoon and Davidson1987). Furthermore, deconstruction of foil caused by the transverse expansion enlarges the proton divergence and reduces the quality of proton. Significant work has been devoted to decreasing the proton divergence and improving the quality of proton (Weng et al., Reference Weng, Murakami and Sheng2015; Zou et al., Reference Zou, Zhuo, Yu, Wu, Yang, Shao, Ma, Yin and Ge2015; Shen et al., Reference Shen, Qiao, Zhang, Kar, Zhou, Chang, Borghesi and He2017).
A magnetic field of over several kilotesla has been obtained with a capacitor-coil target driven by a high-power laser. The strength of magnetic field has increased from 60 T to 1.5 kT over the past 30 years (Daido et al., Reference Daido, Miki, Mima, Fujita, Sawai, Fujita, Kitagawa, Nakai and Yamanaka1986; Fujioka et al., Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi2013; Abe et al., Reference Abe, Law, Korneev, Fujioka, Kojima, Lee, Sakata, Matsuo, Oshima, Arikawa, Yogo, Nakai, Norimatsu, Humiers, Santos, Kondo, Sunahara, Gus'kov and Tikhonchuk2018; Nakamura et al., Reference Nakamura, Ikeda, Sawabe, Matsuda and Takeyama2018). Therefore, it is expectable to obtain a higher magnetic field with the rapid development of laser technology and innovative laser–plasma research in the future. The investigation in combination of plasma and strong magnetic field has also attracted much attention (Arefiev et al., Reference Arefiev, Toncian and Fiksel2016; Stark et al., Reference Stark, Toncian and Arefiev2016; Gong et al., Reference Gong, Cao, Pan, Xiao, Wu, Zheng, Liu and He2017).
In this paper, 2D particle-in-cell (PIC) simulations have been carried out to investigate ion acceleration in RPA regime with an external magnetic field. The divergence of proton has been improved greatly in the RPA regime by using an external longitudinal magnetic field. In the absence of magnetic field, the foil develops into a bubble-like shape from the simulations. The foil prefers to be in a cone-like shape by using the magnetic field. Furthermore, the dependence of proton divergence on the strength of magnetic field has been studied, and an optimal magnetic field of nearly 60 kT is achieved under the conditions considered in this paper.
Simulation and results
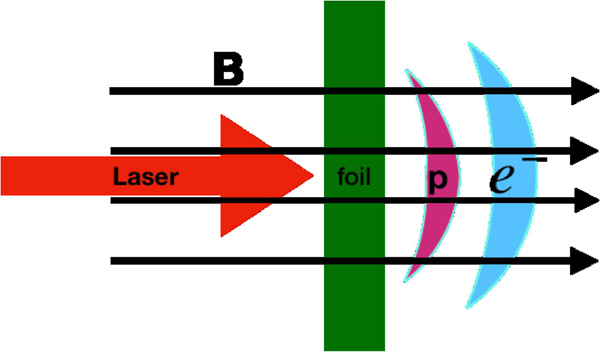
In order to investigate ion acceleration via RPA with a longitudinal strong magnetic field, some two-dimensional PIC simulations have been performed using the EPOCH code (Arber et al., Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and RIdgers2015). The simulation scheme is shown in Figure 1.
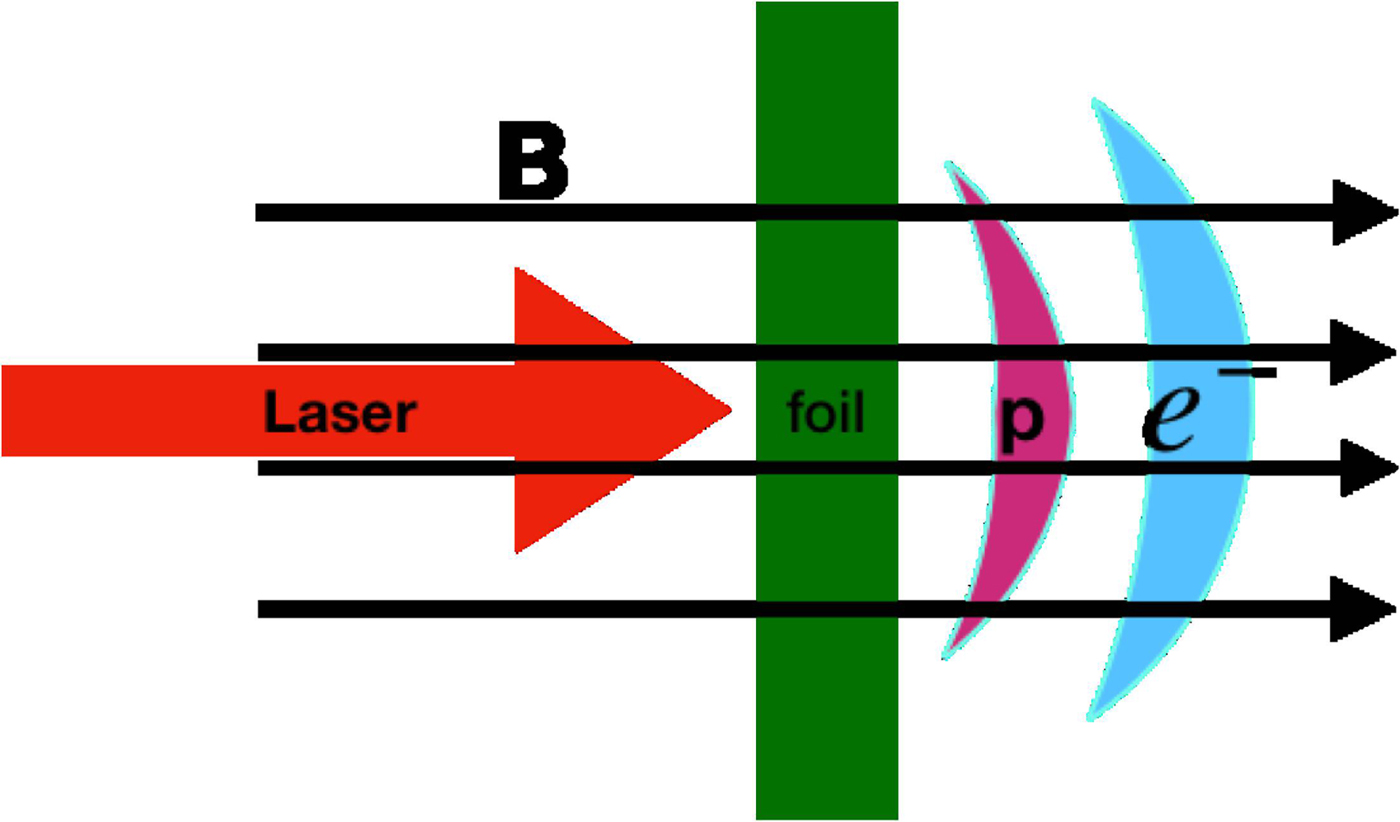
Fig. 1. A laser pulse with the normalized laser amplitude of a 0 = 70 ejects into a hydrogen foil with an external longitudinal magnetic field. The wavelength of laser is 1 µm and the density of hydrogen foil is 80n c, where n c is the critical density (1.1 × 1021/cm3).
A circularly polarized laser pulse irradiates the hydrogen foil, which is transversely Gaussian as E L(y) = E 0exp(−y 2/r 2), with a full width at half maximum (FWHM) of r = 10λ and a laser duration of 15 T L, where E 0 has been regarded as the electric field amplitude of the laser pulse, and λ is the wavelength of 1 µm, and T L is the normalized laser amplitude of a 0 = (eE 0)/(m ecω0) = 70, where m e, c, and ω0 are the mass of electron, the speed of light in vacuum, and the local frequency of light, respectively.
In our two-dimensional PIC simulations, the dimensions of the simulation box are 80 µm × 140 µm with 3200 × 5600 cells. There are 50 particles for each cell. The laser pulse ejects into the simulation box from the left boundary. The hydrogen foil locates at 2 µm < x < 2.5 µm, with a foil thickness of D = 0.5 µm, and the density of electron and proton is homogeneously 80n c, where n c = 1.1 × 1021 /cm3 is the critical density for the laser pulse. To study the effect of a strong magnetic field on ion acceleration via RPA, we compare two cases with or without magnetic field applied in the longitudinal direction. The comparison of electron and ion density is shown in Figure 2.
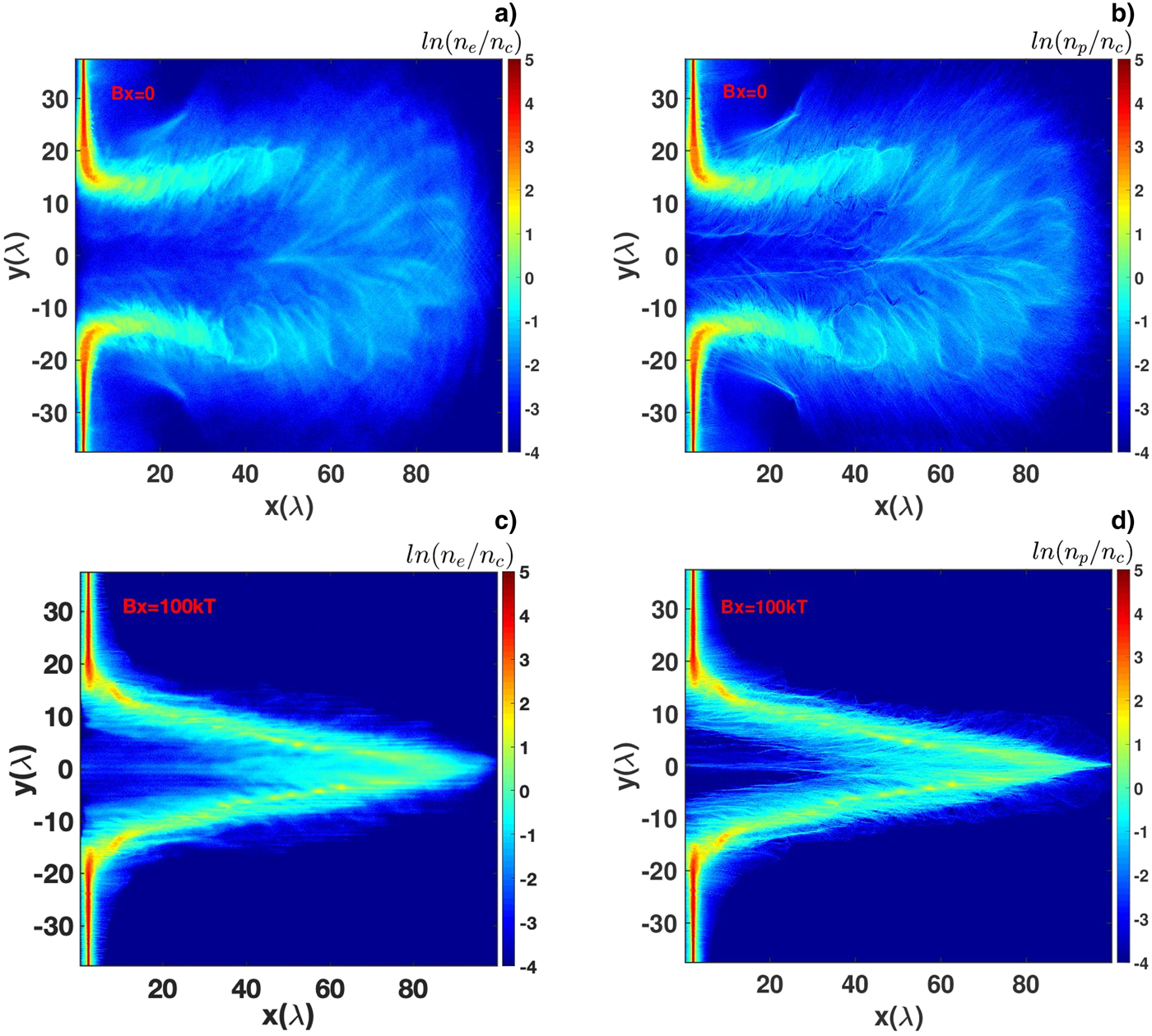
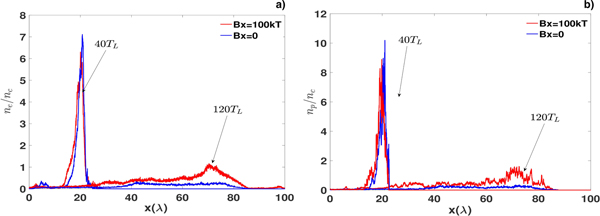
Fig. 2. The density of electrons (a and c) and protons (b and d) without magnetic field (a and b) and with magnetic field (c and d), B x = 100 kT. The density of electrons and protons are normalized to the critical density n c = 1.1 × 1021/cm3 at 140T L in the simulations.
As shown in Figure 2a and 2b, the foil is in bubble-like shape in the absence of a magnetic field. However, electrons expand comparatively more slowly with a longitudinal magnetic field of B x = 100 kT as shown in Figure 2c. In this case, the foil reveals a cone-like structure as shown in Figure 2c and 2d. The density of charged particles plays a key role in RPA. Reduction of electron areal density greatly harms the quality of proton. As shown in Figure 3a, the density of electrons decreases from 80n c to nearly 7n c along x-axis when y = 0 area in both cases. In the absence of a magnetic field, the electron density is nearly 0.2n c at 140T L. And the electron density with a magnetic field is near 1.1n c. It indicates a strong longitudinal field which greatly helps to restrict the transverse expansion and the structure of foil has also been changed into a cone-like shape. As shown in Figure 3b, the proton density with a magnetic field is almost seven times more than that without a magnetic field.
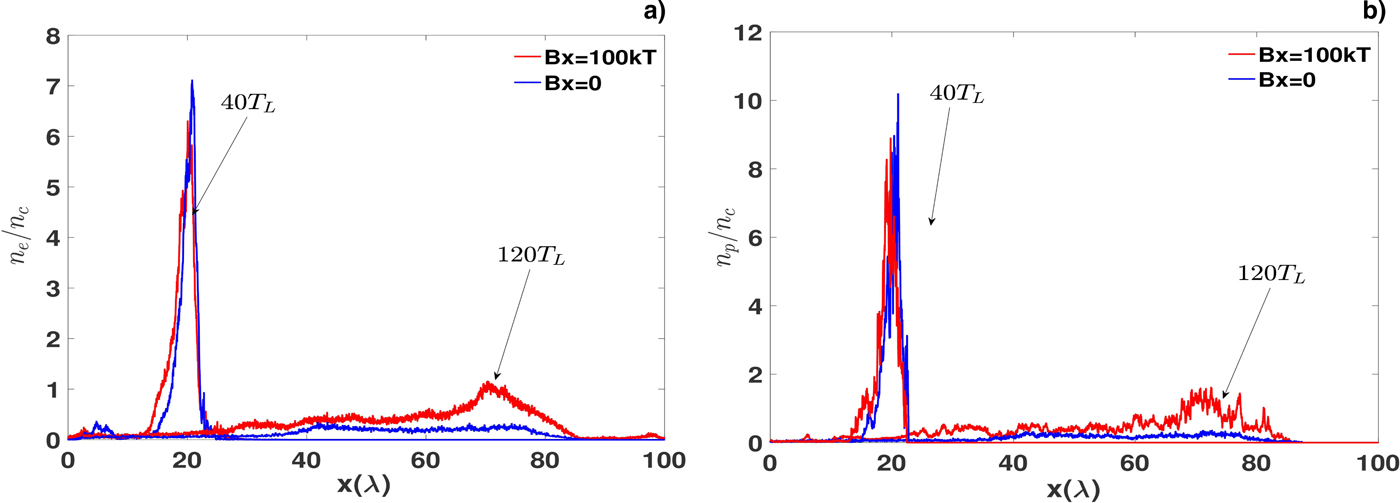
Fig. 3. Spatial evolution of density of electrons (a) and protons (b) along x-axis when y = 0 in the presence of magnetic field (red line) and in the absence of magnetic field (blue line) at 40T L and 140T L. The spatial variable is normalized by the wavelength of laser and the density of charged particles is normalized by the critical density.
Figure 4 presents the comparison of proton momentum distribution to study the effect of magnetic field on the divergence of proton. θ is the emission angle. As shown in Figure 4a and 4c, the configuration of electrons demonstrates that transverse expansion of electrons has been indeed suppressed by introducing of a longitudinal magnetic field. We define p x(e) and p y(e) as the longitudinal momentum and the transverse momentum of electrons, and p x(p) and p y(p) as the longitudinal momentum and the transverse momentum of proton. Although the maximum p y(e) in Figure 4a and 4c are almost the same, the maximum p x(e) in Figure 4c with a magnetic field has been promoted. And maxima p x(p) in Figure 4b and 4d are almost the same in both cases, but the maximum p y(p) in Figure 4d with magnetic field is 0.1m pc less than that in Figure 4b. This may contribute to the inhibition of the electron transverse motion. When electrons are driven by the longitudinal magnetic field, the transverse motion of electrons will be suppressed. And this restrains electrons to pull protons in the transverse direction and finally reduces the transverse momentum of protons. Meanwhile, the magnetic field has little impact on the longitudinal acceleration. However, p y(p) in Figure 4d is roughly 0.3m pc and 0.4m pc in Figure 4b. The maximum proton energy is 660 MeV with a magnetic field, and it is 700 MeV in the absence of a magnetic field. The notable improvement to divergence of proton beam and enhancement of the areal density are achieved, even if the maximum energy decreases slightly in the presence of magnetic field. As shown in Figure 4b and 4d, the proton distributions in the momentum are quite different in both cases. Therefore, the divergence of ion beams improved remarkably with an external magnetic field.
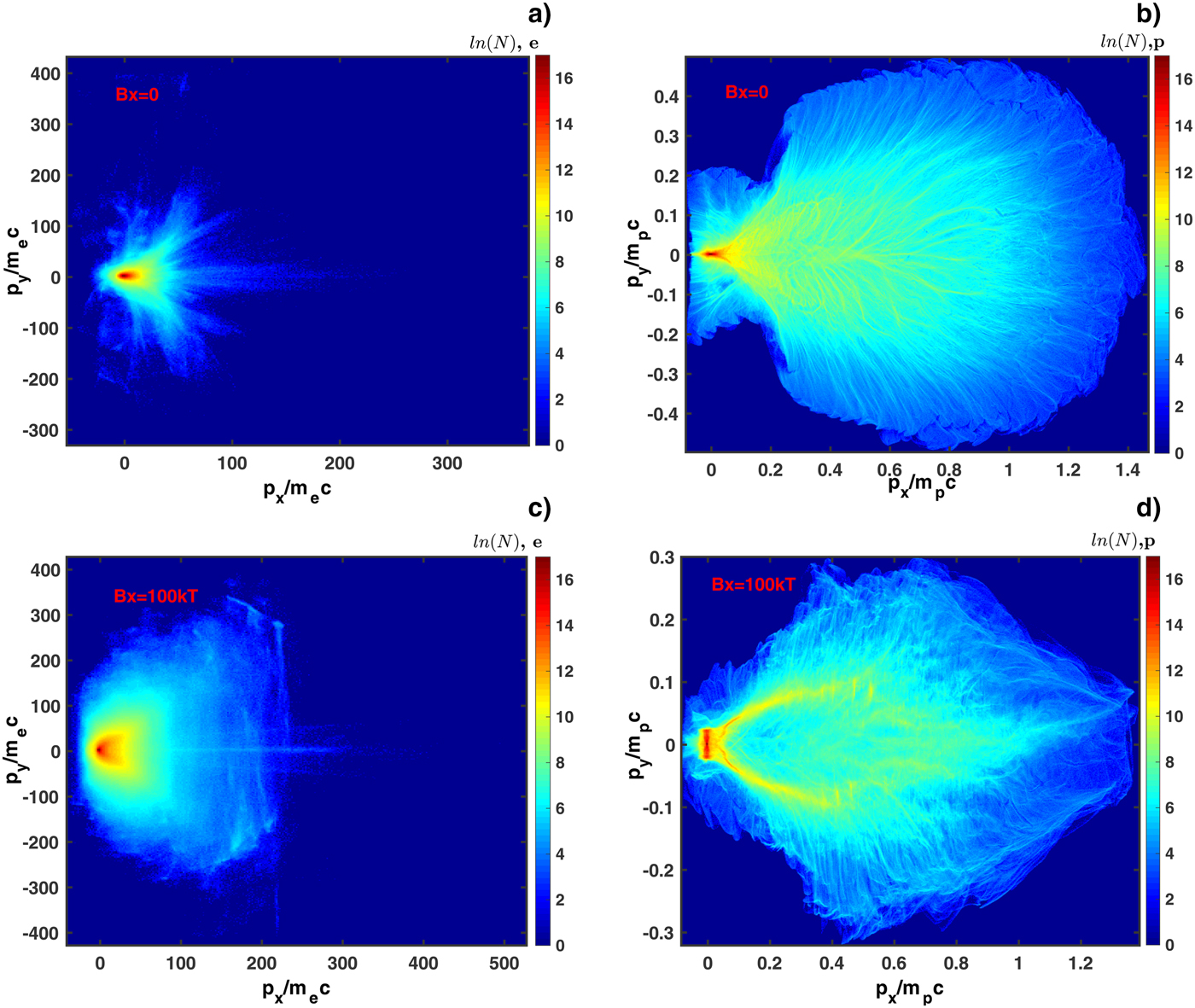
Fig. 4. The distribution in the momentum of electrons (a and c) and protons (b and d). (a) and (b) are the cases without magnetic field and (c) and (d) are the one with magnetic field (B x = 100 kT). The momentum of particles is normalized by the product of static mass and laser speed (m p(e)c), where m p and m e is the mass of electron and proton, respectively.
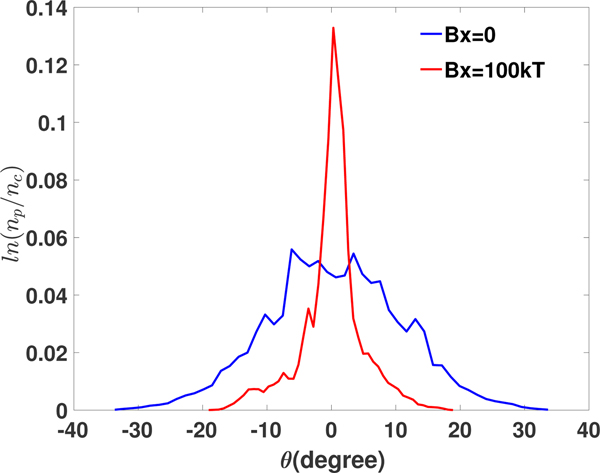
Now we focus on the proton divergence. The angular distribution of protons with energy larger than 300 MeV is shown in Figure 5. The FWHM of the proton angular distribution with a magnetic field is about 4° and it is 20° without a magnetic field. The distribution peaks at 0°. Restriction of electrons offered by the magnetic field impacts on directly the motion of protons and improves remarkably the proton divergence. Then we will study the dependence of proton divergence on strength of magnetic field. In the following simulations, the magnitudes of magnetic field are assumed to be 25, 40, and 100 kT. The proton distribution as a function of energy and emission angle at 140T L is given in Figure 6. As shown in Figure 6b–6d, the maximum energy of protons is almost 660 MeV and is slightly less than that in Figure 6a. It can be seen that the maximum proton energy is almost the same in different strengths of magnetic field.
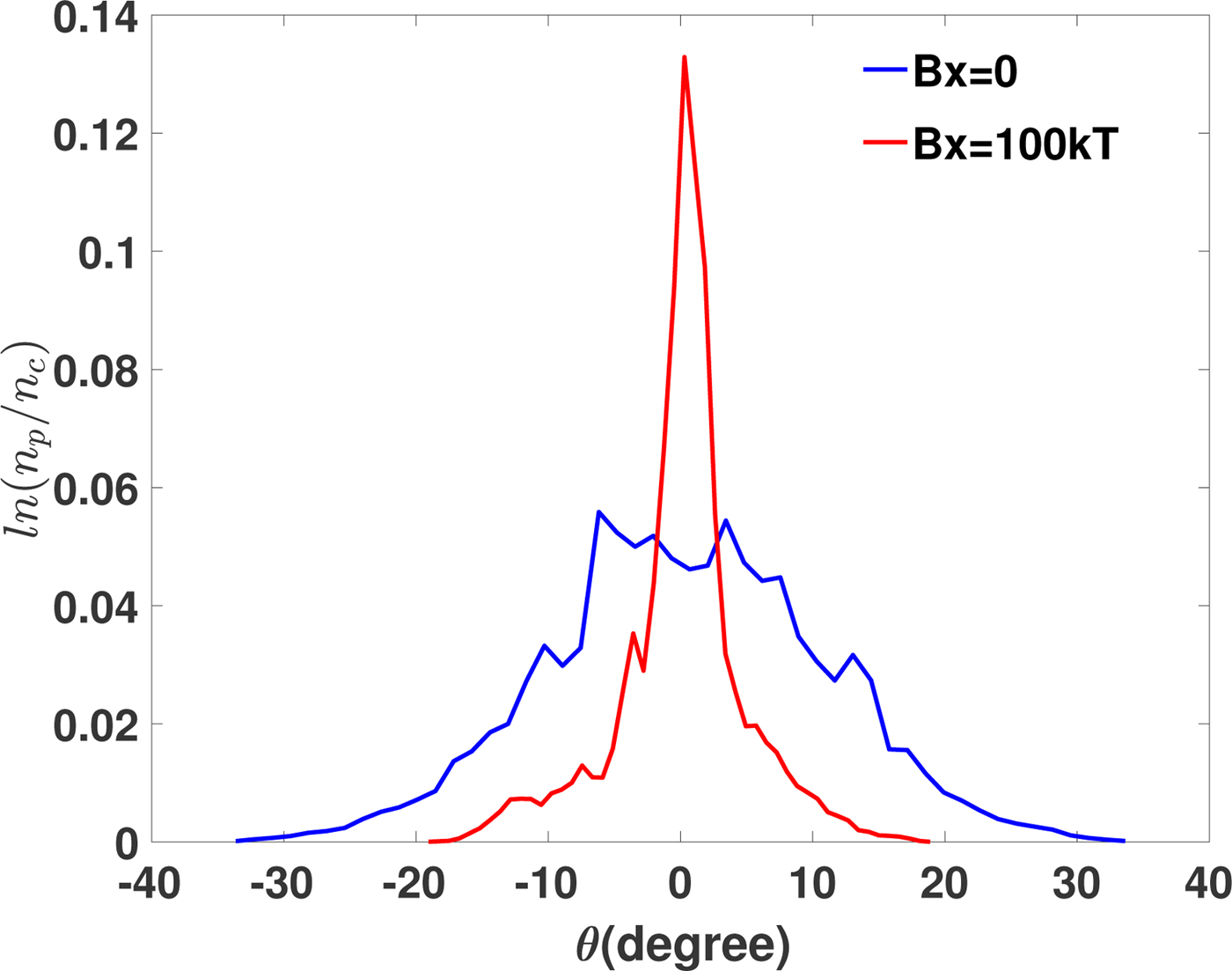
Fig. 5. The distribution of angle and density of protons whose energy is larger than 300 MeV with magnetic field (red line, B x = 100 kT) and without magnetic field (blue line). Here θ is the angle between the momentum of protons and the x-axis.
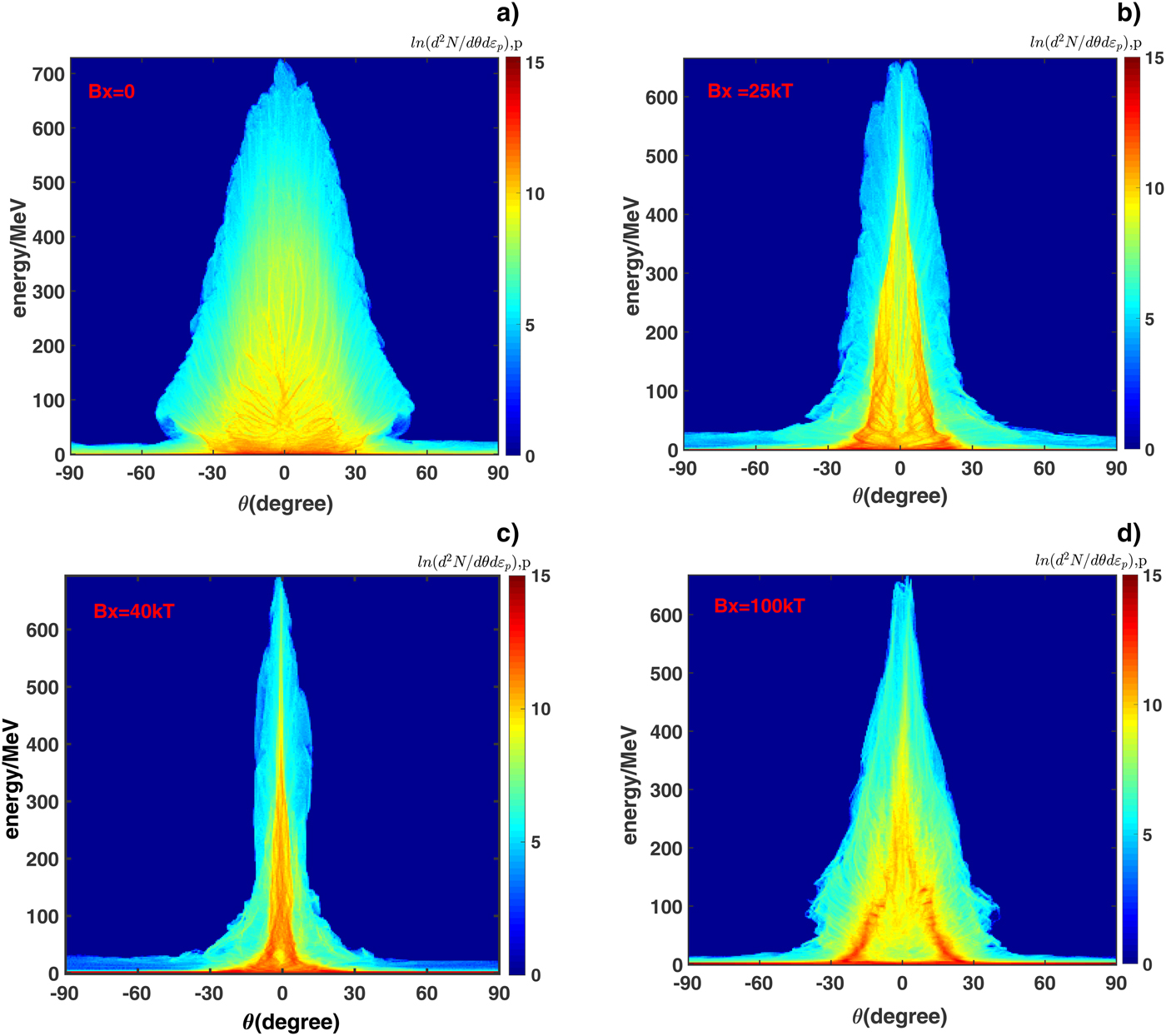
Fig. 6. The proton distribution as a function of energy and emission angle with different magnetic fields at 140T L. The magnetic field used is (a) 0 kT, (b) 25 kT, (c) 40 kT, and 100 kT. θ is the angle between the momentum of protons and the x-axis.
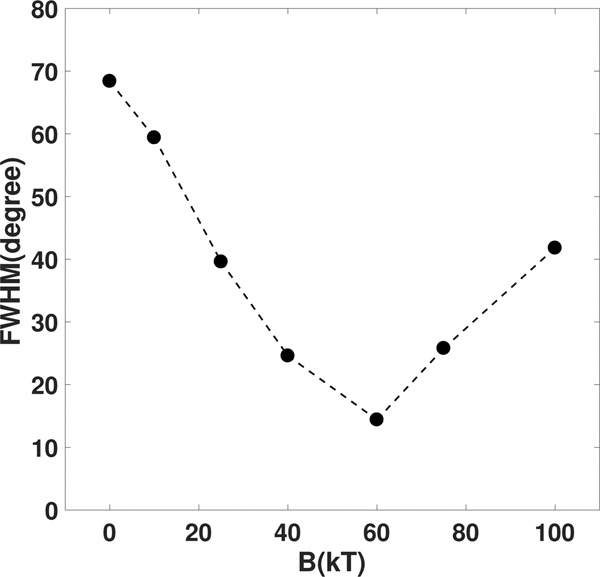
As shown in Figure 6, the emission angle of proton depends on the strength of magnetic field. The full width of the distribution envelop of Figure 6 at 300 MeV has been used to investigate the dependence of proton divergence on the strength of magnetic field. As shown in Figure 7, the range of proton emission angle whose energy is 300 MeV reduces to the minimum of 15° at 60 kT from 70° without magnetic field, then increases to 42° at 100 kT. From Figure 7, there exists an optimal magnetic field of 60 kT to achieve the minimum proton divergence. The intense magnetic field is required to overcome the transverse expansion. In fact, the foil is developing into a cone-like shape once the magnetic field exceeds the optimal magnetic field as shown in Figure 2c and 2d. In this case, the majority of protons move along the cone-like shape, which leads to increasing emission angle of proton.
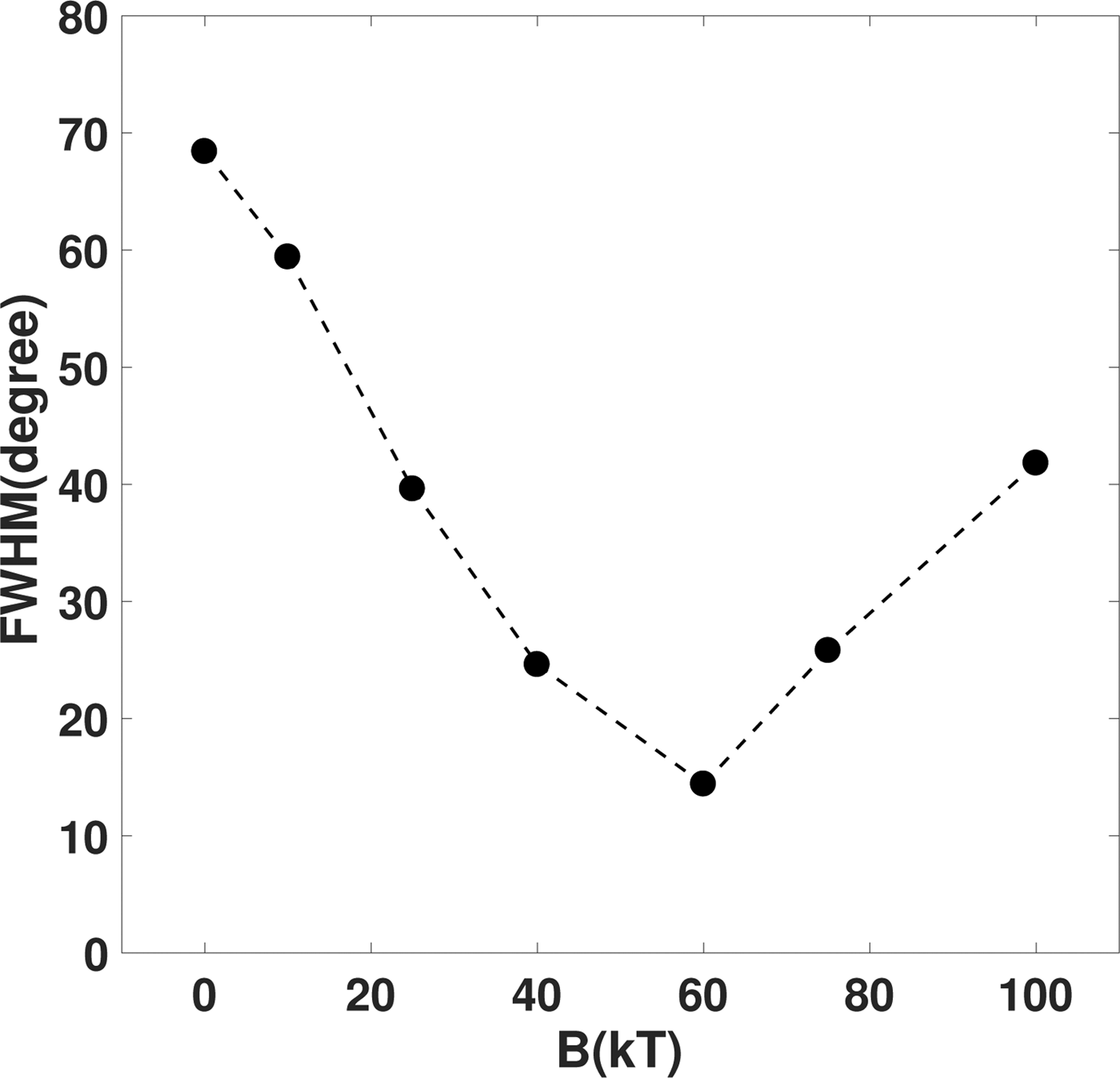
Fig. 7. The distribution of the range of proton emission angle whose energy is 300 MeV as a function of magnetic field. The magnitude if magnetic field varies from 0 to 100 kT.
Conclusion
We have implied several two-dimensional PIC simulations to investigate the effect of an external longitudinal magnetic field on RPA. Under the conditions of these simulations, with a strong magnetic field, the foil of n 0 = 80n c pushed by a laser of a 0 = 70 will become a cone-like shape instead of a bubble-like shape in the absence of a magnetic field. The density of the charged particle is almost seven times more than that without a magnetic field. It reveals that the transverse expansion of electrons has been suppressed by a strong longitudinal magnetic field. This greatly helps to improve the proton divergence. The dependence of proton divergence on the strength of a magnetic field has been studied, and an optimal magnetic field of nearly 60 kT is achieved in these simulations. It is expectable to obtain such a magnetic field in the future with the rapid development of new technology, although the required magnetic field of dozens of kilotesla is currently unachievable. Therefore, applying an external magnetic field via RPA is potentially promising to improve the quality of protons.
Author ORCIDs
H. Cheng, https://orcid.org/0000-0003-1511-6017.
Acknowledgment
The authors would like to thank the useful discussion of J. Q. Yu and X. Q. Yan. This work was supported by the National Natural Science Foundation of China (Grand Nos. 11875091 and 11475030) and the National Key Research and Development Program of China (Grant No. 2016YFA0401100).
