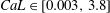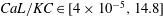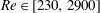1 Introduction
The understanding of the movement of and forces on submerged, flexible vegetation is of importance in several aspects of coastal engineering. These aspects are for instance the attenuation of waves through a patch of vegetation (Möller et al. Reference Möller, Kudella, Rupprecht, Spencer, Paul, Van Wesenbeeck, Wolters, Jensen, Bouma, Miranda-Lange and Schimmels2014), wave-induced mean currents (Luhar et al. Reference Luhar, Coutu, Infantes, Fox and Nepf2010) and the influence of the motion of the vegetation on nutrient uptake (Mullarney & Pilditch Reference Mullarney and Pilditch2017) and magnitude and direction of sediment transport (Ros et al. Reference Ros, Colomer, Serra, Pujol, Soler and Casamitjana2014; Tinoco & Coco Reference Tinoco and Coco2018).
The wave attenuation in vegetation fields has been studied extensively in medium scale laboratory experiments (Dubi & Tørum Reference Dubi and Tørum1994; Anderson & Smith Reference Anderson and Smith2014; Maza et al. Reference Maza, Lara, Losada, Ondiviela, Trinogga and Bouma2015; Losada, Maza & Lara Reference Losada, Maza and Lara2016), large scale laboratory experiments (Möller et al. Reference Möller, Kudella, Rupprecht, Spencer, Paul, Van Wesenbeeck, Wolters, Jensen, Bouma, Miranda-Lange and Schimmels2014) and field campaigns (Vo-Luong & Massel Reference Vo-Luong and Massel2008; Bradley & Houser Reference Bradley and Houser2009; Jadhav, Chen & Smith Reference Jadhav, Chen and Smith2013; Foster-Martinez et al. Reference Foster-Martinez, Lacy, Ferner and Variano2018). A quantification of the wave damping has a direct relevance for the ability to predict wave conditions at the toe of dikes or other coastal structures and, for instance, account for the influence of vegetation on overtopping over dikes (EurOtop 2018; Vuik et al. Reference Vuik, Van Vuren, Borsje, Van Wesenbeeck and Jonkmann2018). A common output from wave damping experiments is a bulk drag coefficient related to the amount of dissipation under the assumption of validity of linear wave theory within the canopy. The reported bulk drag coefficients are a function of the velocity attenuation within the canopy (Jadhav et al. Reference Jadhav, Chen and Smith2013; Jacobsen, McFall & van der A Reference Jacobsen, McFall and van der A2019), so they cannot be used to express the actual force observed by the individual stem.
A spectral dissipation model for vegetation (Suzuki et al. Reference Suzuki, Zijlema, Burger, Meijer and Narayan2012) is already included in the spectral wave model SWAN, where the user should define the length, density and bulk drag coefficient of the vegetation. The next improvement of practical engineering models for spectral wave transformation is to include the effect of stem flexibility on the wave damping under varying environmental conditions, e.g. changing length and – possibly – changing drag coefficients with wave climate. Here, the concept of effective length is a feasible approach (Luhar & Nepf Reference Luhar and Nepf2016; Lei & Nepf Reference Lei and Nepf2019). The derivation of the effective length relies on the assumption that the drag coefficient for a flexible stem is the same as the drag coefficient for a corresponding rigid stem under the same hydrodynamic conditions. The length of the rigid stem, which gives the same root force as measured for the flexible stem, is called the effective length. Validity of the assumption of identical drag coefficients has not been found documented in the literature, but a violation of the assumption could explain why some stems have an effective length in excess of unity (e.g. Luhar & Nepf Reference Luhar and Nepf2016; Lei & Nepf Reference Lei and Nepf2019). One of the goals in this work is to derive force coefficients for both flexible and rigid stems.
Ros et al. (Reference Ros, Colomer, Serra, Pujol, Soler and Casamitjana2014) and Tinoco & Coco (Reference Tinoco and Coco2018) observed experimentally that the presence of vegetation affects the suspended sediment concentration through a change in the turbulent kinetic energy. Furthermore, Zhang & Nepf (Reference Zhang and Nepf2019) saw that generation of wave orbital ripples was suppressed for high stem densities. Once in suspension, the net suspended sediment transport is driven by the mean current, but so far the mean current is mainly described with experiments (Luhar et al. Reference Luhar, Coutu, Infantes, Fox and Nepf2010; Pujol et al. Reference Pujol, Serra, Colomer and Casamitjana2013; Abdolahpour, Hambleton & Ghisalberti Reference Abdolahpour, Hambleton and Ghisalberti2017) and a single numerical study (Chen & Zou Reference Chen and Zou2019). A complete description of the mean current (forcing terms and velocity profile) is still missing in the literature, but it is expected that the gradient in the radiation stress tensor, the near-bed wave streaming stresses, the wave-induced set-up and the mean force on the vegetation all contribute. The listed properties, besides the mean vegetation force, are also relevant for the description of the undertow in the surf zone (Deigaard & Fredsøe Reference Deigaard and Fredsøe1989; Deigaard, Justesen & Fredsøe Reference Deigaard, Justesen and Fredsøe1991; Guannel & Özkan-Haller Reference Guannel and Özkan-Haller2014). Hence, the force on and the force coefficients for the individual stem are of importance for the gradient in the radiation stress tensor following wave damping and both the mean surface gradient and the mean force on the vegetation (Dean & Bender Reference Dean and Bender2006; Wu et al. Reference Wu, Ozeren, Chen, Holland, Ding, Kuiry, Zhang, Jadhav, Chatagnier, Chen and Gordji2011). Consequently, the mean sediment transport magnitudes will implicitly dependent on the stem motion and the force on the stems.
The discussion above shows that the wave dissipation, the sediment transport and mean flow within a canopy field all depend on the behaviour of the flexible stems and the force distribution along the stem. The lack of experimental evidence of the force coefficients on flexible stems was already discussed. With respect to the description of the stem motion, three different sets of non-dimensional parameters have been identified (Mullarney & Henderson Reference Mullarney and Henderson2010; Luhar & Nepf Reference Luhar and Nepf2016; Leclercq & De Langre Reference Leclercq and De Langre2018). Leclercq & De Langre (Reference Leclercq and De Langre2018) proposed a classification of stem motion in pure oscillatory flow and showed validation for a few cases, but the extension of their classification to real waves is not described. Maza, Lara & Losada (Reference Maza, Lara and Losada2013), Zeller et al. (Reference Zeller, Weitzman, Abbett, Zarama, Fringer and Koseff2014) and Luhar & Nepf (Reference Luhar and Nepf2016) made visual observations of the stem motion in waves, but only the intra-wave tip positions were extracted, so the data are not useful for classification. The three sets of non-dimensional parameters are revisited in this work, where novel experimental data are applied to determine the most suitable non-dimensional parameters.
The present work will address the motion of a single stem under regular waves in a controlled laboratory setting. The motion of the stems is recorded with a digital video camera and the displacement, velocity and acceleration are digitized. This gives a unique set of data to understand the interaction between the wave and stem: displacements, phase lags, relative velocities and the force coefficient as a function of non-dimensional parameters. Finally, the external loading along the stem and the internal shear force are estimated directly from the laboratory experiment. The data set is suitable for the validation of the numerical models for the motion of flexible stems (e.g. Dijkstra & Uittenbogaard Reference Dijkstra and Uittenbogaard2010; Luhar & Nepf Reference Luhar and Nepf2016; Leclercq & De Langre Reference Leclercq and De Langre2018). The experimental set-up and procedure are described in § 2. The relevant non-dimensional parameters are discussed in § 3.1, while the remainder of § 3 is devoted to the experimental analysis. A discussion is presented in § 4 and it is followed by conclusions in § 5.
2 Experimental campaign
The experimental investigation was performed in a wave flume at Delft University of Technology (Laboratory of Fluid Mechanics). The flume is 41.5 m long, 0.8 m wide and 0.9 m deep. The purpose of the investigation was to obtain a better understanding of the motion and forcing of a single flexible stem under regular waves. To this end, both point data (surface elevation, velocities and base forces) and video recordings were acquired.
2.1 Layout and experimental conditions
The layout of the flume and the placement of the point measurement devices are shown in figure 1. The false bottom in the middle of the flume was required to install the force transducer. A total of seven wave gauges, one force transducer and one EMF (electromagnetic flow meter) were used for point measurements. The EMF was placed at different vertical elevations between 0.025 m to 0.325 m above the bed to reconstruct the velocity profile over the height of the stem. Attention was paid to minimizing wave reflection at the end of the flume by installing a gently sloped porous absorber.
Figure 1. Layout of the wave flume with the location of the point instruments. The stem is the green patch in front of the camera. WG, wave gauge. EMF, electromagnetic flow meter.
Both the EMF and the wave gauges were developed by Delft Hydraulics. The EMF has a range of
$0.0{-}2.5~\text{m}~\text{s}^{-1}$
with an accuracy of
$0.025~\text{m}~\text{s}^{-1}$
and the wave gauge has an accuracy of 1 mm. The plastic mimics were mounted on a force transducer with two screws. The force transducer was from Utilcell (Model 104) and had a range of 1 to 3000 mN and an accuracy of 1 mN. All point measurements were sampled at 100 Hz.
A total of eight wave conditions were studied, see table 1, where
$H$
is the regular wave height and
$T$
is the wave period. The wave generation was performed with a Bosch Rexroth generator with active reflection compensation and the water depth in front of the paddle was 0.65 m. Each condition was repeated twice, there were four mimics (see below and table 2) and three lengths of the mimic so in total 192 tests were conducted. For each condition, a single stem was mounted on the force transducer and there were no neighbouring stems mimicking a canopy. The duration of the tests varied, but approximately 40 wave periods were generated before the stem motion was recorded. The quantities
$\overline{\unicode[STIX]{x1D702}}_{c}$
and
$\overline{\unicode[STIX]{x1D702}}_{t}$
(table 1) are the average crest and trough elevations, respectively. The average is taken over
$N_{w}$
wave periods (table 1).
Table 1. Summary of the target wave conditions (columns 1, 2) and the achieved conditions (columns 5, 6, 7). The water depth at the paddle was 0.65 m and 0.45 m at the measuring location. The remaining columns address reproducibility of the wave conditions (see text).
Four mimics with rectangular cross-section were used in the experimental campaign to cover a large range of Cauchy numbers (§ 3.1). The mechanical properties and dimensions of the mimics are provided in table 2:
$\unicode[STIX]{x1D6FF}_{y}$
is the width facing the waves,
$\unicode[STIX]{x1D6FF}_{x}$
is the thickness,
$E$
is Young’s modulus,
$l$
is the length and
$\unicode[STIX]{x1D70C}_{s}$
the stem density. The force on the mimic was recorded for two values of the length (0.15 m and 0.30 m) and reference tests with no mimic. The tests with no mimic were performed to evaluate whether there were any load recordings from the hydrodynamics on the force transducer itself. This was not the case. Results regarding motion and forces for mimic 2, 3 and 4 are presented in this work, while the motion of mimic 1 is not analysed, because it could not be extracted with the developed tracking software (see appendix B), due to heavy torsion of the stem. The velocities measured for mimic 1 and no mimics are still used in the reconstruction of the velocity profile. The numbering of mimics is retained to allow for consistency with the naming methodology in the underlying data sets.
Table 2. Mechanical properties of the plastic mimics (
$E$
and
$\unicode[STIX]{x1D70C}_{s}$
according to manufacturer). The motion of mimic 1 is not treated in this work. The plastic type is given in last column. The natural period,
$T_{n}$
, is described in § 3.1. ABS, acrylonitrile butadiene styrene.
The adopted coordinate system
$(x,y,z)$
has the origin at the base of the stem;
$x$
is positive in the wave propagation direction,
$z$
is positive upward and
$y$
is the horizontal coordinate normal to the wave propagation direction (figure 1).
2.2 Synchronization
Synchronization of the data between individual tests is required to reconstruct the velocity field from the
$N_{s}$
number of individual tests. (The value of
$N_{s}$
is reported in table 1 and it is less than 24 for all wave conditions. This comes from the fact some tests were too short to provide a velocity field overlapping the recording video material.) The reconstructed velocity field is needed for the evaluation of relative velocities and force coefficients. The synchronization ensures two aspects: (i) The wave signal is reproducible. (ii) The time axes for all recordings and the video footage are perfectly aligned; see details in appendix A.
The reproducibility is addressed through a zero-crossing analysis yielding individual wave heights
$H_{i}$
of which there are
$N_{w}$
(table 1). The simple average of
$H_{i}$
,
$\overline{H}_{i}$
, is reported in table 1 and it is larger than the target at the paddle; an overprediction which can be due to both shoaling over the false bottom and reflection. Similarly, the zero-crossing wave period,
$T_{i}$
, was evaluated and the deviation from target was of the order
$10^{-4}~\text{s}$
. The reproducibility of the individual wave conditions was evaluated with the error
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{H}(j,k)=\overline{\left(\frac{H_{i,j}-H_{i,k}}{H_{i,j}}\right)}^{i}\quad \text{for }\{j,k\}=1,\ldots ,N_{s}\end{eqnarray}$$
between two tests, with indices
$j$
and
$k$
for the
$i$
th zero-crossing wave. The average and standard deviation over all combinations of
$j$
and
$k$
are given in table 1 as
$\overline{\unicode[STIX]{x1D700}}_{H}$
and
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D700}_{H}}$
, respectively. The error is 1 % or less, so the reproducibility of the wave conditions is confirmed.
The correlation coefficient between the surface elevation signals for tests
$j$
and
$k$
was evaluated (
$R_{\unicode[STIX]{x1D702}}(j,k)$
) to verify synchronization between tests. The mean (
$\overline{R_{\unicode[STIX]{x1D702}}}$
) and standard deviation (
$\unicode[STIX]{x1D70E}_{R_{\unicode[STIX]{x1D702}}}$
) of
$R_{\unicode[STIX]{x1D702}}$
are provided in table 1. These two quantities are, respectively, close to unity and zero, consequently all experiments (for a given wave condition) are confirmed to be aligned in time.
The two velocity components were acquired at the same
$x$
-location as the force transducer. The velocity profile was constructed from point measurements of
$u$
and
$w$
from individual, synchronized tests.
The motion of the stems was captured with a digital video camera (Panasonic DC-HS200) with a sampling frequency of 25 Hz. The local coordinate system was obtained by capturing a gridded frame prior to execution of the tests. The coordinate system had a resolution of approximately
$2500~\text{pixel}~\text{m}^{-1}$
in both horizontal and vertical directions, which equals
$0.4~\text{mm}~\text{pixel}^{-1}$
. The synchronization between the video camera and the point measurements were achieved with a light-emitting diode (LED), see details in § A.3.
3 Results
First, a discussion on relevant non-dimensional parameters is presented. Secondly, the characteristic wave parameters are derived from the measurements. Thirdly, the motion of the stems is described together with the focus on the relative motion between stem and fluid. For instance, the relative velocity is defined as
$u_{r}=u-u_{s}$
and
$w_{r}=w-w_{s}$
, where the sub-indices
$r$
and
$s$
mean relative and stem velocities respectively;
$u$
and
$w$
are the measured flow velocities in the direction of wave propagation (
$x$
) and vertical (
$z$
) direction and
$y$
is the lateral direction.
Once the relative velocity and relative acceleration are evaluated, the average force coefficients for the swaying vegetation are estimated for mimics 2, 3 and 4 (§ 3.4). The average force coefficients are combined with the relative velocities to evaluate the temporal variation of the force along the stem and estimate the internal shear force (§ 3.5).
3.1 Non-dimensional considerations
The analysis of non-dimensional quantities is presented based on the Euler–Bernoulli beam theory (small deflections). The unsteady Euler–Bernoulli beam theory with constant
$EI$
reads
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FF}_{x}\unicode[STIX]{x1D6FF}_{y}\frac{\unicode[STIX]{x2202}^{2}x_{s}}{\unicode[STIX]{x2202}t^{2}}+EI\frac{\unicode[STIX]{x2202}^{4}x_{s}}{\unicode[STIX]{x2202}z^{4}} & = & \displaystyle \unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x1D6FF}_{y}^{2}}{4}\unicode[STIX]{x03C0}C_{M}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}-\frac{\unicode[STIX]{x2202}^{2}x_{s}}{\unicode[STIX]{x2202}t^{2}}\right)+\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}_{x}\unicode[STIX]{x1D6FF}_{y}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\unicode[STIX]{x1D70C}C_{D}\unicode[STIX]{x1D6FF}_{y}\left|u-\frac{\unicode[STIX]{x2202}x_{s}}{\unicode[STIX]{x2202}t}\right|\left(u-\frac{\unicode[STIX]{x2202}x_{s}}{\unicode[STIX]{x2202}t}\right).\end{eqnarray}$$
The left-hand side describes the acceleration of the stem and the internal elastic forces, where
$\unicode[STIX]{x1D70C}_{s}$
is the density of the stem,
$\unicode[STIX]{x1D6FF}_{x}$
and
$\unicode[STIX]{x1D6FF}_{y}$
are cross-sectional dimensions in the
$x$
and
$y$
directions,
$x_{s}$
is the stem deflection relative to
$x=0~\text{m}$
in the global coordinate system (figure 1) and
$t$
is time;
$E$
is Young’s modulus and
$I=1/12\unicode[STIX]{x1D6FF}_{x}^{3}\unicode[STIX]{x1D6FF}_{y}$
is the moment of inertia. The right-hand side describes the external forcing: the first term is the inertia force; the second term is the Froude–Krylov force and the third term is the drag force. Here,
$\unicode[STIX]{x1D70C}$
is the density of water,
$C_{M}$
is the inertia coefficient and
$C_{D}$
the drag coefficient.
Equation (3.1) is made non-dimensional with the following choice of non-dimensional parameters:
$t_{\ast }=t\unicode[STIX]{x1D714}$
,
$x_{\ast }=x/a_{w}$
,
$z_{\ast }=z/l$
and
$u_{\ast }=u/u_{w}$
, where
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}/T$
is the cyclic frequency,
$u_{w}$
a characteristic orbital velocity and
$a_{w}=u_{w}/\unicode[STIX]{x1D714}$
a characteristic wave orbital excursion. The experimental equivalents to
$u_{w}$
and
$a_{w}$
are defined below. Equation (3.1) becomes
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x03C0}^{2}}{2}C_{M}\frac{CaL}{KC}\left(\frac{\unicode[STIX]{x2202}u_{\ast }}{\unicode[STIX]{x2202}t_{\ast }}-\frac{\unicode[STIX]{x2202}^{2}x_{s,\ast }}{\unicode[STIX]{x2202}t_{\ast }^{2}}\right)+2\unicode[STIX]{x03C0}\frac{\unicode[STIX]{x1D6FF}_{x}}{\unicode[STIX]{x2202}_{y}}\frac{CaL}{KC}\left(\frac{\unicode[STIX]{x2202}u_{\ast }}{\unicode[STIX]{x2202}t_{\ast }}-\frac{\unicode[STIX]{x1D70C}_{s}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}^{2}x_{s,\ast }}{\unicode[STIX]{x2202}t_{\ast }^{2}}\right)/\frac{\unicode[STIX]{x2202}^{4}x_{s,\ast }}{\unicode[STIX]{x2202}z_{\ast }^{4}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{1}{2}C_{D}CaL\left|u_{\ast }-\frac{\unicode[STIX]{x2202}x_{s,\ast }}{\unicode[STIX]{x2202}t_{\ast }}\right|\left(u_{\ast }-\frac{\unicode[STIX]{x2202}x_{s,\ast }}{\unicode[STIX]{x2202}t_{\ast }}\right),\end{eqnarray}$$
where
$$\begin{eqnarray}Ca=\frac{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}_{y}u_{w}^{2}l^{3}}{EI},\quad KC=\frac{2\unicode[STIX]{x03C0}u_{w}}{\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}_{y}}\quad \text{and}\quad L=\frac{l}{a_{w}}=\frac{l\unicode[STIX]{x1D714}}{u_{w}}.\end{eqnarray}$$
Here,
$Ca$
is the Cauchy number and describes the ratio of external drag to internal stiffness of the stem,
$KC$
is the Keulegan–Carpenter number describing the ratio of drag-to-inertia and
$L$
describes the length of the stem to the wave orbital excursion. Mullarney & Henderson (Reference Mullarney and Henderson2010), their appendix A, arrived at a similar expression for a circular cross-section, but neglected inertia terms throughout the bulk of their work based on orders of magnitude considerations. Their stiffness parameter,
$S$
, is essentially
$(CaL)^{-1}$
for a stem with circular cross-section of radius
$r_{0}$
.
Luhar & Nepf (Reference Luhar and Nepf2016) applied
$x_{\ast }=x/l$
in their analysis of relevant non-dimensional quantities and it led to an involved discussion on dominating quantities, since – for instance – the drag term took the form
$$\begin{eqnarray}\frac{1}{2}C_{D}Ca\left|u_{\ast }-L\frac{\unicode[STIX]{x2202}x_{s,\ast }}{\unicode[STIX]{x2202}t_{\ast }}\right|\left(u_{\ast }-L\frac{\unicode[STIX]{x2202}x_{s,\ast }}{\unicode[STIX]{x2202}t_{\ast }}\right).\end{eqnarray}$$
They divided the discussion into the regimes
$L\ll 1$
and
$1\ll L$
and they stated
$Ca$
as the descriptive parameter for
$L\ll 1$
and
$CaL$
for
$1\ll L$
. The two
$L$
-regimes follow from their choice in
$x_{\ast }=x/l$
, meaning that the horizontal velocities
$u$
and
$\unicode[STIX]{x2202}x_{s}/\unicode[STIX]{x2202}t$
were made non-dimensional with two different length scales:
$l$
and
$a_{w}$
(
$u_{w}=\unicode[STIX]{x1D714}a_{w}$
). The scaling choices in the present work reduce the total number of combinations of non-dimensional parameters to
$CaL$
and
$CaL/KC$
. The geometrical ratios
$\unicode[STIX]{x1D6FF}_{x}/\unicode[STIX]{x1D6FF}_{y}$
and
$\unicode[STIX]{x1D70C}_{s}/\unicode[STIX]{x1D70C}$
are not considered further in this work.
Leclercq & De Langre (Reference Leclercq and De Langre2018) adopted another set of non-dimensional parameters:
$l$
as the length scale and
$T_{n}=l^{2}\sqrt{m_{a}/EI}$
as the time scale;
$T_{n}$
is the natural period of the submerged stem, where
$m_{a}=\unicode[STIX]{x1D70C}\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}_{y}^{2}/4$
is the added mass of the submerged stem for a unit added mass coefficient. Leclercq & De Langre (Reference Leclercq and De Langre2018) found that the product of the natural period and cyclic wave frequency
$T_{n}\unicode[STIX]{x1D714}=1$
describes the transition from ‘static’ regime to their ‘convective’ and ‘modal’ regimes for
$a_{w}/l<1$
. They also defined a fourth regime named the ‘large-amplitude regime, static reconfiguration with fast reversal’ for
$1<a_{w}/l$
. Their classification means that the shape of stem is independent of the magnitude of the oscillatory motion (
$a_{w}$
). In addition to
$T_{n}\unicode[STIX]{x1D714}$
, Leclercq & De Langre (Reference Leclercq and De Langre2018) found the non-dimensional parameters
$L^{-1}=a_{w}/l$
and
$2/\unicode[STIX]{x03C0}C_{D}l/\unicode[STIX]{x1D6FF}_{y}$
. It is easy to realize that
$L^{-1}=a_{w}/l=\unicode[STIX]{x1D6FF}_{y}KC/l$
. The values of
$T_{n}$
for the present experiment are listed in table 2.
Leclercq & De Langre (Reference Leclercq and De Langre2018) studied sinusoidal, oscillatory flow and found that the amplitude of the displacement increased with increasing
$a_{w}/l$
, while the overall shape of the displacement was the same for constant
$T_{n}\unicode[STIX]{x1D714}$
. For constant values of
$a_{w}/l$
, the deflection pattern changed from the static regime to more complicated patterns with multiple modes for increasing
$T_{n}\unicode[STIX]{x1D714}$
. They did not account for a mean deflection of the stem.
The similarity between the non-dimensional quantities in Leclercq & De Langre (Reference Leclercq and De Langre2018), Luhar & Nepf (Reference Luhar and Nepf2016) and the present work is established here. Inserting
$T_{n}$
in the expressions for
$CaL$
and
$CaL/KC$
gives
$$\begin{eqnarray}CaL=8(T_{n}\unicode[STIX]{x1D714})^{2}KC=8(T_{n}\unicode[STIX]{x1D714})^{2}\frac{a_{w}}{l}\frac{l}{\unicode[STIX]{x1D6FF}_{y}}\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{CaL}{KC}=\frac{2}{\unicode[STIX]{x03C0}^{2}}(T_{n}\unicode[STIX]{x1D714})^{2}.\end{eqnarray}$$
It is seen that
$CaL$
is a product of all three of the non-dimensional quantities suggested by Leclercq & De Langre (Reference Leclercq and De Langre2018), while
$CaL/KC$
is proportional to the square of
$T_{n}\unicode[STIX]{x1D714}$
. The classification by Leclercq & De Langre (Reference Leclercq and De Langre2018) is a function of
$T_{n}\unicode[STIX]{x1D714}$
and
$a_{w}/l$
, respectively, therefore it is unlikely that a product of these two parameters (as is the case for
$CaL$
) is a suitable non-dimensional parameter. This will be verified in the following.
The transition from the ‘static’ to ‘convective’ and ‘modal’ regimes for
$T_{n}\unicode[STIX]{x1D714}=1$
corresponds to
$CaL/KC=2/\unicode[STIX]{x03C0}^{2}=0.20$
. The value of 0.20 is for an added mass coefficient of 1.0.
3.2 Characteristic wave parameters
The characteristic orbital velocity,
$u_{w}$
, and the wave excursion,
$a_{w}$
, are used in the non-dimensional parameters. The following describes how they are calculated from the measured velocities. The characteristic velocity is defined as
$$\begin{eqnarray}u_{w}=\sqrt{2}\langle u_{rms}\rangle _{z},\end{eqnarray}$$
where
$u_{rms}$
is the root-mean-square velocity and
$\langle \,\rangle _{z}$
represents the depth-averaged value over the distance
$l$
from the bed. The depth-averaged value is adopted because it represents the dynamics over the full length of the stem better than the velocity at one height in the water column.
The measured velocity signal is decomposed into a mean and a wave part in the following manner:
$$\begin{eqnarray}u=\bar{u}+\tilde{u} ,\end{eqnarray}$$
where
$\bar{u}$
is the mean and
$\tilde{u}$
the wave component. Normally, a turbulent component is also included in the splitting, but due to the internal filtering of the EMF (7 Hz), the turbulence is assumed filtered out. The splitting in (3.8) is evaluated per vertical level and similarly for the vertical velocity
$w=\bar{w}+\tilde{w}$
, where
$\bar{w}=0~\text{m}~\text{s}^{-1}$
.
The orbital excursion is evaluated directly from the measured velocities in the following manner:
$$\begin{eqnarray}a_{w}=\frac{1}{4mT}\int _{t_{0}}^{t_{0}+mT}\langle |\tilde{u} (t)|\rangle _{z}\,\text{d}t.\end{eqnarray}$$
This expression reduces to
$a_{w}=u_{w}/\unicode[STIX]{x1D714}$
(linear wave theory), if
$\tilde{u}$
is purely sinusoidal;
$m$
is an integer.
The values of
$a_{w}$
,
$u_{w}$
,
$\langle \tilde{u} _{c}\rangle _{z}$
,
$\langle \tilde{u} _{t}\rangle _{z}$
,
$\langle \bar{u}\rangle _{z}$
are given in table 3 for all cases, and the quantities are evaluated for the part of the velocity signal that overlaps the video recordings;
$\langle \tilde{u} _{c}\rangle _{z}$
and
$\langle \tilde{u} _{t}\rangle _{z}$
are depth-averaged velocities evaluated under the crest and trough of the wave, respectively. It is seen that the two cases with
$H=0.04~\text{m}$
and the case with
$H=0.07~\text{s}$
and
$T=1.5~\text{s}$
are almost sinusoidal, since the crest and trough velocities are practically identical. Higher harmonics in the velocity field are present for all other wave conditions. The significance is that a sinusoidal flow would result in a vanishing mean force on a rigid stem, but it will be described below how this is not the case for flexible stems.
Furthermore, the non-dimensional numbers: Reynolds (
$Re=u_{w}\unicode[STIX]{x1D6FF}_{y}/\unicode[STIX]{x1D708}$
), Keulegan–Carpenter (
$KC$
), Cauchy (
$Ca$
),
$L$
,
$CaL$
and
$CaL/KC$
are tabulated;
$\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is the kinematic viscosity of water. The non-dimensional parameters covered in this work are depicted in figure 2.
Figure 2. The range of non-dimensional parameters tested. Markers and colours have the same meaning in all panels.
In summary, it is seen from table 3 and figure 2 that the ranges for
$Ca$
and
$CaL$
overlap each other for the three mimics;
$Ca$
is less than 0.01 for mimic 4, so it is effectively stiff, and no video recordings were made. The significance of
$CaL$
and
$CaL/KC$
for vegetation in waves was not identified upon design of the experiments, where
$Ca$
and
$KC$
were taken as the descriptive non-dimensional quantities. This is the reason that
$CaL$
has gaps over the full range, while
$Ca$
and
$KC$
do not.
3.3 The motion of flexible stems
3.3.1 Example of stem motion
Some examples of stem motion are depicted in figure 3. The depicted motion is based on ensemble averaging over multiple wave periods. The examples allow for a direct comparison of the effect of material and wave properties on the motion of a single stem. The sets of panels (a,c) and (b,d) each have the same
$L=l/a_{w}$
, so the difference of the motion is uniquely ascribed to the difference in material properties, which is captured by
$Ca$
and
$CaL/KC\propto (T_{n}\unicode[STIX]{x1D714})^{2}$
, and a small difference in
$KC$
, due to a difference in
$\unicode[STIX]{x1D6FF}_{y}$
between mimics. The stiffer the stem (the smaller
$Ca$
), the more upright it is.
Table 3. An overview of the characteristic wave parameters and the corresponding non-dimensional parameters relevant for the motion of the stem and force coefficients.
The motion in figure 3(a) is clearly asymmetric, while the velocity field is almost sinusoidal (table 3). Since the hydrodynamic forcing is symmetric, the asymmetry is mainly attributed to the Lagrangian motion of the stem in a spatially varying velocity field, as discussed in Gijón Mancheño (Reference Gijón Mancheño2016). She discussed that the mean forward bending is attributed to the co-following of the tip of the stem under the crest, i.e. vaguely similar to Stokes drift. This effectively results in a mean force on the stem and an associated mean deflection.
The stem motion in figure 3(c) is backward asymmetric. The mean deflection of the stem was negative in stagnant water, which is why it is hypothesized that the plastic material had anisotropic properties and was pre-tensioned into a slightly curving form. It is deemed to have limited practical influence on the results. A comparison between panels (c,d) (same mimic) shows that the latter is forward asymmetric, thus a certain threshold of forcing had to be exceeded to overcome the hypothesized non-uniformity in the mechanical properties of the material.
Figure 3. Four examples of single stem motion based on the ensemble-averaged displacement. All mimics have a length of
$l=0.30~\text{m}$
. (a) Mimic 2,
$H=0.04~\text{m}$
and
$T=2.0~\text{s}$
. (b) Mimic 2,
$H=0.11~\text{m}$
and
$T=3.0~\text{s}$
. (c) Mimic 3,
$H=0.04~\text{m}$
and
$T=2.0~\text{s}$
. (d) Mimic 3,
$H=0.11~\text{m}$
and
$T=3.0~\text{s}$
. The full lines depict forward motion
$(\unicode[STIX]{x2202}x_{s}/\unicode[STIX]{x2202}t>0)$
and dashed lines backward motion (
$\unicode[STIX]{x2202}x_{s}/\unicode[STIX]{x2202}t$
) of the tip. The time step between two lines is constant. The thick, dashed line is the mean position of the stem.
The mean position of the stems is also plotted in figure 3 and a forward mean displacement is seen in panels (a,b). This finite mean displacement must be associated with a mean force on the stems, so an equally large mean force is acting on the water column. The increase in hydrodynamic forcing gives a significant increase in tip displacement for mimic 3 (panels c,d), while a relatively smaller increase in tip displacement for mimic 2 under the same forcing. This is attributed to the larger mean displacement of the stem in panel (b), which limits the allowed oscillatory displacement from the mean. It is seen below that the mean displacement complicates a unified description of the stem motion.
Proper orthogonal decompositions (see appendix C) of the four examples are shown in figure 4. It is seen that the motion of mimic 3 is described by the mean and a single mode, while the displacement of mimic 2 also requires a second mode for an accurate description. This is in line with the prediction by Leclercq & De Langre (Reference Leclercq and De Langre2018), who give an upper limit of
$CaL/KC=0.20$
for the static regime. The static regime is defined as the quasi-static equilibrium between the internal elastic force and the hydrodynamic forcing, so only one mode shape is required.
Figure 4. Four examples of single stem motion decomposed into proper orthogonal decomposition (POD) modes. All mimics have a length of
$l=0.30~\text{m}$
. (a) Mimic 2,
$H=0.04~\text{m}$
and
$T=2.0~\text{s}$
. (b) Mimic 2,
$H=0.11~\text{m}$
and
$T=3.0~\text{s}$
. (c) Mimic 3,
$H=0.04~\text{m}$
and
$T=2.0~\text{s}$
. (d) Mimic 3,
$H=0.11~\text{m}$
and
$T=3.0~\text{s}$
. Red line, mean displacement. Full blue line, mode 1. Dashed blue line, mode 2. The percentage describes the importance of the mode for the time varying motion.
Four videos of the examples in figures 3 and 4 supplement this paper, see appendix D.
3.3.2 Motion characteristics
The results presented above show that there is a trend for the stem to be increasingly forward asymmetric when the value of
$Ca$
or
$CaL$
increases. The variation with
$CaL/KC$
is less intuitive for understanding the displacements (figure 3), but useful in understanding the relevance of a second mode shape (figure 4).
Some measures of the horizontal stem position,
$x_{s}$
, are investigated in this section:
$\max \langle \tilde{x}_{s}\rangle$
,
$\min \langle \tilde{x}_{s}\rangle$
,
$\unicode[STIX]{x1D6E5}\langle \tilde{x}_{s}\rangle$
and
$\overline{\langle x_{s}\rangle }$
. Here,
$\langle \rangle$
denotes ensemble averaging and
$\langle \tilde{x}_{s}\rangle =\langle x_{s}\rangle -\overline{\langle x_{s}\rangle }$
. The displacements are made non-dimensional with
$a_{w}$
in accordance with choice in § 3.1. The results are plotted as a function of
$CaL$
in figure 5 and
$CaL/KC$
in figure 6, where
$x_{s}$
is taken at the tip of the stem. A few of the data points are marked with a white dot to indicate that
$0.5<\overline{\langle x_{s}\rangle }/l$
, i.e. the mean tip displacement exceeds 50 % of the stem length. A large mean deflection will be seen to limit the magnitude of oscillatory displacements, because the tip displacement cannot exceed 100 % of the stem length.
Figure 5. Characteristic measures of the motion of the tip of the stem as a function of
$CaL$
. The data are for mimics 2 and 3. The red markers correspond to the cases depicted in figure 3. The white dots indicate cases with
$0.5<\overline{\langle x_{s}\rangle }/l$
.
The first observation is that
$CaL/KC$
describes the overall behaviour considerably better than
$CaL$
if the data points with large mean displacement are neglected; see the white dots. The difference is most noticeable in the range
$CaL\in [2,20]$
and
$CaL/KC\in [0.05,1]$
, where the data exhibit much less vertical scatter as a function of
$CaL/KC$
. Data points for both mimic 2 with
$l=0.15~\text{m}$
and mimic 3 with
$l=0.30~\text{m}$
overlap in these parameter intervals, but only
$CaL/KC$
leads to a collapse of the data. This means that the natural period (
$CaL/KC\propto (T_{n}\unicode[STIX]{x1D714})^{2}$
) is more important than the drag force exerted on the stem; the latter scaling with
$CaL$
in (3.2). The magnitude of the hydrodynamic forcing, incorporated by normalizing with
$a_{w}$
, is also justified. It is seen that
$\unicode[STIX]{x1D6E5}\langle \tilde{x}_{s}\rangle /a_{w}$
reaches values of 4.0, so the acceleration of the stem tip exceeds that of the water and the inertia force on the stem retards the tip displacement under these conditions (see also supplementary video material available at https://doi.org/10.1017/jfm.2019.739 and appendix D). Consequently, the investigated stems seem to have an upper allowed acceleration, because of the added mass effect. Leclercq & De Langre (Reference Leclercq and De Langre2018), in their figure 4, showed that the tip displacement converged to a asymptotic value of
$\max x_{s}/l\simeq 0.45$
for
$a_{w}/l=0.27$
for increasing
$\unicode[STIX]{x1D714}$
. The ratio
$\max x_{s}/a_{w}=0.45/0.27=1.67$
, a similar result as in the present study. Mimics 2 and 3 had a sufficiently large torsional stiffness to suppress torsional motion, while mimic 1 (otherwise not analysed here) showed a large degree of torsion during phases of large acceleration, thereby reducing the effect of added mass.
Figure 6. Characteristic measures of the motion of the tip of the stem as a function of
$CaL/KC\propto (T_{n}\unicode[STIX]{x1D714})^{2}$
. The data are for mimics 2 and 3. The red markers correspond to the cases depicted in figure 3. The white dots indicate cases with
$0.5<\overline{\langle x_{s}\rangle }/l$
.
The general picture is that there is no noticeable displacement of the stem up to approximately
$CaL=1.0$
, so at least the stem behaves as effectively rigid up to this value (see figure 5). This is in line with figure 5 in Luhar & Nepf (Reference Luhar and Nepf2011) and figure 11 in Luhar & Nepf (Reference Luhar and Nepf2016), who investigated the concept of effective length for pure current and waves, respectively.
For larger displacements, the displacements increase with increasing
$CaL/KC$
, yet still with close to vanishing mean displacements up to
$CaL/KC=0.8$
(figure 6). For
$CaL/KC>0.8$
,
$\max \langle x_{s}\rangle /a_{w}$
and
$|\min \langle x_{s}\rangle |/a_{w}$
show some scatter in the range
$0.5{-}2.0$
. The cases with values different from approximately 2 related to a large value of
$\overline{\langle x_{s}\rangle }/l$
, i.e. most of the deflection potential is already taken by the mean deflection (shown as white dots).
It was investigated whether a better representation of the data could be achieved by normalizing with
$l$
instead of
$a_{w}$
, e.g. in line with the choice by Luhar & Nepf (Reference Luhar and Nepf2016) and Leclercq & De Langre (Reference Leclercq and De Langre2018). The results conclusively showed that
$a_{w}$
is the better horizontal length scale of the two. The non-dimensional scaling adopted in the present work appears applicable to the description of flexible stems with small mean deflections.
3.3.3 Phase lags
The fluid and stem motions are not necessarily in phase, which was described theoretically and verified against field measurements for weakly flexible vegetation (Mullarney & Henderson Reference Mullarney and Henderson2010). The large flexibility in the present experiments (e.g. figure 3
b) and the presence of a second mode shape (figure 4
b) mean that the phase lag is not constant along the stem. This is easily seen in figure 3(b), where the tip of the stem reaches an extreme forward position later than any point below the inflection point at
$z\simeq 0.1~\text{m}$
. The tracking algorithm and the synchronization with the velocity field allow for an evaluation of this phase lag. All cases where the tip was displaced more than 3 mm (7.5 pixels) were included in the analysis. Cases with smaller tip displacements were too noisy for accurate estimates.
Figure 7. The variation of
$\unicode[STIX]{x1D711}_{s}$
(a) and
$\unicode[STIX]{x1D711}_{s}^{c}$
(b) over the length of the stem. The lines match panels (a–d) in figure 3.
$l=0.30~\text{m}$
.
Two phase lags were defined,
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{s}(s/l)=\frac{360^{\circ }}{T}(t_{u=max\,x_{w}}-t_{x_{s}=max\,x_{s}})\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{s}^{c}(s/l)=\unicode[STIX]{x1D711}_{s}(s/l)-\frac{360^{\circ }}{T}\frac{\max x_{s}}{c},\end{eqnarray}$$
where
$x_{w}$
is the water particle position,
$c$
is the wave celerity and
$s$
is a local coordinate along the length of the stem with
$s/l=0$
at the base of the stem and
$s/l=1$
at the tip. Equation (3.10) defines the phase lag between the instances at which
$x_{s}$
is maximum and the time at which the fluid particle position (
$x_{w}$
) is maximum (evaluated at
$x=0~\text{m}$
). Here,
$\unicode[STIX]{x1D711}_{s}^{c}$
accounts for the fact that the stem reaches its maximum position for
$x>0~\text{m}$
, so it experiences a different velocity field than at
$x=0$
. The fluid particle position is evaluated as
$$\begin{eqnarray}x_{w}(t)=\int _{0}^{t}\tilde{u} (\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
where
$\unicode[STIX]{x1D711}_{s}$
and
$\unicode[STIX]{x1D711}_{s}^{c}$
are plotted over the length of the stem (figure 7) for the four examples shown in figure 3. The results are plotted for
$s/l>0.1$
. Generally, the phase lag for mimic 2 has a gradually decreasing value of
$\unicode[STIX]{x1D711}_{s}$
over the length of the stem. For the stiffer mimic 3 with
$CaL/KC<0.2$
,
$\unicode[STIX]{x1D711}_{s}$
is practically constant over the length of the stem. It is seen that the behaviour is qualitatively identical for
$\unicode[STIX]{x1D711}_{s}$
and
$\unicode[STIX]{x1D711}_{s}^{c}$
, but differences of
$15^{\circ }$
are observed. The vertical variation in
$\unicode[STIX]{x1D711}_{s}^{c}$
for mimic 2 is attributed to the finite amount of energy on the second mode shape, while there is no energy on the second mode shape for mimic 3, so the phase lag is constant.
In figure 8,
$\unicode[STIX]{x1D711}_{s}^{c}$
is depicted for three points along the stem (
$s/l=\{0.2,0.6,1.0\}$
) as a function of
$CaL$
and
$CaL/KC$
, respectively. Values of
$\unicode[STIX]{x1D711}_{s}^{c}$
are found per wave period and the mean and the standard deviation are calculated. Neither of the two parameters
$CaL$
and
$CaL/KC$
gives a convincing relationship with the phase lag. Nonetheless, it is seen that all points along the stem have the same phase up to
$CaL<20$
and
$CaL/KC<0.5$
, so the stem shape must be described fully by a single mode shape. The limit of
$CaL/KC\simeq 0.5$
corresponds fairly well with the theoretical limit of transition away from the static regime proposed by Leclercq & De Langre (Reference Leclercq and De Langre2018) (see § 3.1).
Figure 8. The phase lag between the maximum fluid particle displacement and the maximum displacement of the stem,
$\unicode[STIX]{x1D711}_{s}^{c}$
. The error bars show the
$\pm \unicode[STIX]{x1D70E}$
range, where
$\unicode[STIX]{x1D70E}$
is the standard deviation. (a) The quantities are plotted as a function of
$CaL$
. (b) The quantities are plotted as a function of
$CaL/KC$
.
3.3.4 Relative velocities and accelerations
The relative velocities and accelerations between the orbital velocities and the stem motion are evaluated in order to describe the motion, but also to evaluate the force coefficients. The relative velocities and accelerations are defined as follows:
$$\begin{eqnarray}u_{r}^{c}|_{t}=u|_{t-\unicode[STIX]{x0394}t_{s}}-\left.\frac{\unicode[STIX]{x2202}x_{s}}{\unicode[STIX]{x2202}t}\right|_{t}\quad \text{and}\quad \left.\frac{\unicode[STIX]{x2202}u_{r}^{c}}{\unicode[STIX]{x2202}t}\right|_{t}=\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\right|_{t-\unicode[STIX]{x0394}t_{s}}-\left.\frac{\unicode[STIX]{x2202}^{2}x_{s}}{\unicode[STIX]{x2202}t^{2}}\right|_{t}.\end{eqnarray}$$
Here,
$\unicode[STIX]{x0394}t_{s}$
is
$x_{s}/c$
and superscript
$c$
is used to indicate the Lagrangian correction. The offset is introduced because the stem does not experience the velocity measured by the EMF at
$x=0~\text{m}$
. Therefore, when
$x_{s}>0~\text{m}$
, the stem is exposed to a velocity that has already been recorded at
$x=0~\text{m}$
. Similarly, the stem is exposed to velocities yet to be recorded, when
$x_{s}<0~\text{m}$
. Similar expressions hold for
$w_{r}$
and
$\unicode[STIX]{x2202}w_{r}/\unicode[STIX]{x2202}t$
. The velocity and acceleration of the stem segments are evaluated with proper orthogonal decomposition of the stem motion and algebraic differentiation (appendix C), while the temporal derivatives of
$u$
and
$w$
are based on a simple central finite difference scheme.
The orbital, stem and relative velocities are depicted in the following with Lissajous curves (see figures 9 and 10). Here,
$u$
is plotted along the horizontal axis and
$w$
along the vertical axis. Lissajous curves form an ellipse when
$u$
and
$w$
are
$90^{\circ }$
out of phase, while the curve forms a line when
$u$
and
$w$
are in phase;
$(u^{c},w^{c})$
can be seen as a closed curve, but the nonlinearity in the wave has shifted the curve towards the right and
$w^{c}\neq \max w^{c}$
when
$u^{c}=0$
.
The curves in figures 9 and 10 are depicted for four points along the length of the stem. The figures correspond to panels (b) (mimic 2) and (d) (mimic 3) in figure 3 and the only difference between the two sets of Lissajous curves is the stem properties (
$H=0.11~\text{m}$
,
$T=3/0~\text{s}$
and
$l=0.30~\text{m}$
). A comparison between the two figures shows that
$-\min u_{s}<\max u_{s}$
for mimic 2, while
$\max u_{s}<-\min u_{s}$
for mimic 3, i.e. either the forward or backward velocity is the largest. The more flexible stem (smaller
$EI$
) readily follows the flow, while the stiffer stem (larger
$EI$
) ‘shoots’ backward as soon as the hydrodynamic loading decreases. This is caused by the elastic energy stored in the stem during the forward motion (see also theoretical analysis in Mullarney & Henderson Reference Mullarney and Henderson2010).
Figure 9. Lissajous curves for
$(u^{c},w^{c})$
,
$(u_{s},w_{s})$
and
$(u_{r}^{c},w_{r}^{c})$
. Lines are ensemble averages. The small black/white dots on the curves mark time with a spacing of 0.2 s. The coloured markers indicate the direction of the temporal axis. Mimic 2,
$l=0.30~\text{m}$
,
$H=0.11~\text{m}$
and
$T=3.0~\text{s}$
. The aspect ratio is 1.0:0.8.
Figure 10. Lissajous curves for
$(u^{c},w^{c})$
,
$(u_{s},w_{s})$
and
$(u_{r}^{c},w_{r}^{c})$
. Lines are ensemble averages. The small black/white dots on the curves mark time with a spacing of 0.2 s. The coloured markers indicate the direction of the temporal axis. Mimic 3,
$l=0.30~\text{m}$
,
$H=0.11~\text{m}$
and
$T=3.0~\text{s}$
. The aspect ratio is 1.0:0.4.
The figures show that
$u_{r}^{c}$
is generally larger in the positive direction and the curve
$(u_{r}^{c},w_{r}^{c})$
follows a relatively simple closed curve for
$s/l<0.5$
. The pattern is more complex higher on the stem (
$0.5<s/l$
). The fluid velocity governs the hydrodynamic loading at the base of the stem, since
$u_{s}\ll u_{r}^{c}$
and
$u_{r}^{c}\simeq u$
. At the tip of the stem, the combined stem velocity and phase difference results in a lowering of
$u_{r}^{c}$
, so the hydrodynamic loading at the tip is expected to be smaller than at the bed (figure 9).
Finally, it is seen for both mimics that
$\max |u_{r}^{c}|<\max |u^{c}|$
, while
$\max |w^{c}|<\max |w_{r}^{c}|$
for mimic 2 and
$\max |w_{r}^{c}|<\max |w^{c}|$
for mimic 3. Consequently, the flexibility of the stem is expected to reduce the inline force. However, the vertical motion can cause vertical tip velocities of the same order of magnitude as the horizontal, so a flexible stem may still be subject to large forces in waves. How the vertical force transfers to the root cannot be evaluated in this work, since a one-dimensional force transducer was used. Nonetheless, given the large positive vertical velocity, an uprooting force is expected.
3.4 Average force coefficients
The average force coefficients
$C_{D}$
and
$C_{M}$
are derived for mimics 2, 3 and 4. The force coefficients are normally calculated based on a least-square method (e.g. Sumer & Fredsøe Reference Sumer and Fredsøe1999) with a representative velocity and acceleration. In the present case, the stem moves in the fluid and thereby changes its exposed area to the flow. This is illustrated in figure 11, where the maximum,
$F_{c}$
, and minimum,
$F_{t}$
, forces at the base are compared for stem lengths
$l=0.15~\text{m}$
and
$l=0.30~\text{m}$
and identical conditions.
$F_{c}$
and
$F_{t}$
were found with a zero-crossing analysis on the force time series. The forces for mimic 4 are approximately a factor of 2 larger for
$l=0.30~\text{m}$
than for
$l=0.15~\text{m}$
, while the forces do not scale linearly with
$l$
for mimics 2 and 3. The more the doubling from 0.15 m to 0.30 m for mimic 4 is due to the increase of orbital velocity with the distance from the bed;
$F_{t}$
shows a factor of 2 increase for both mimics 3 and 4, which is attributed to the fact that the stem is more upright under the wave trough than under the wave crest. The results for mimic 3 suggest that the exposed length of the stem varies over one wave period, so the instantaneous shape of the stem should be accounted for, when the force coefficients are evaluated.
Figure 11. The measured peak forces for mimics 2, 3 and 4. The minimum force,
$F_{t}$
, is shown with empty markers and the maximum force,
$F_{c}$
, with filled markers.
The force coefficients are found by integration of (3.1) along the instantaneous shape of the stem,
$$\begin{eqnarray}\displaystyle F_{x} & = & \displaystyle \int _{0}^{l}EI\frac{\unicode[STIX]{x2202}^{4}x_{s}}{\unicode[STIX]{x2202}z^{4}}\,\text{d}s=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}_{x}\unicode[STIX]{x1D6FF}_{y}\int _{0}^{l}\left(\frac{\unicode[STIX]{x2202}u^{c}}{\unicode[STIX]{x2202}t}-\frac{\unicode[STIX]{x1D70C}_{s}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}^{2}x_{s}}{\unicode[STIX]{x2202}t^{2}}\right)\,\text{d}s\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D70C}C_{M}\frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}_{y}^{2}}{4}\int _{0}^{l}\frac{\unicode[STIX]{x2202}u_{r}^{c}}{\unicode[STIX]{x2202}t}\cos \unicode[STIX]{x1D703}_{s}\,\text{d}s+\frac{1}{2}\unicode[STIX]{x1D70C}C_{D}\unicode[STIX]{x1D6FF}_{y}\int _{0}^{l}u_{r}^{c}\sqrt{u_{r}^{c,2}+w_{r}^{c,2}}\cos \unicode[STIX]{x1D703}_{s}\,\text{d}s,\qquad\end{eqnarray}$$
where
$F_{x}$
is the force at the base. Here,
$\cos \unicode[STIX]{x1D703}_{s}$
accounts for the effective length of a stem segment and
$\unicode[STIX]{x1D703}_{s}$
is the angle of the stem from the vertical;
$\unicode[STIX]{x1D703}_{s}$
varies along the length of the stem. Note that the Lagrangian correction to the relative velocities and accelerations is used, but it only matters for a few of the conditions with large
$CaL/KC$
. All properties in (3.14) are measured, so a least-squares approach can be used to calculate
$C_{M}$
and
$C_{D}$
. The Froude–Krylov and inertia terms are explicitly accounted for, but they only affect the value of
$C_{M}$
for mimic 4 with
$\unicode[STIX]{x1D6FF}_{y}=\unicode[STIX]{x1D6FF}_{x}$
.
Figure 12. The average force coefficients for mimics 2, 3 and 4. (a) The inertia coefficient
$C_{M}$
as a function of
$KC$
. (b) The drag coefficient
$C_{D}$
as a function of
$KC$
. (c)
$C_{D}$
as a function of
$KC_{r}$
. (d)
$C_{D}$
as a function of
$Re_{r}$
.
The values of
$C_{M}$
and
$C_{D}$
are plotted as a function of
$KC$
in figure 12(a,b), where
$C_{M}$
shows considerable scatter and there does not seem to be any organized trend when looking at individual mimics or individual values of
$l$
. This is attributed to the limited importance of the inertia force in the present experiments for
$KC>10$
and the fact that a part of the stem experiences large velocities at a given instance, while another part experiences large relative accelerations (for the more flexible stems). The value of
$C_{D}$
shows less scatter as a function of
$KC$
than
$C_{M}$
, but there are still clusters with separate trend curves: (i)
$KC<10$
; (ii)
$10<KC<30$
; (iii)
$30<KC$
.
The definition of
$KC$
(3.3) is based on the fluid velocity, while the stem experiences the relative velocity. Therefore, the relative Keulegan–Carpenter and Reynolds numbers were defined as
$$\begin{eqnarray}KC_{r}=\frac{2\unicode[STIX]{x03C0}u_{w,r}^{c}}{\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}_{y}}\quad \text{and}\quad Re_{r}=\frac{u_{w,r}^{c}\unicode[STIX]{x1D6FF}_{y}}{\unicode[STIX]{x1D708}},\end{eqnarray}$$
where
$$\begin{eqnarray}u_{w,r}^{c}=\sqrt{2}\left\langle \sqrt{\overline{(u_{r}^{c}-\bar{u}_{r}^{c})^{2}}}\right\rangle _{z}.\end{eqnarray}$$
The value of
$C_{D}$
is depicted as a function of
$KC_{r}$
and
$Re_{r}$
in figure 12(c,d). The change from
$KC$
to
$KC_{r}$
mostly affects
$KC$
for mimic 2, but it is enough to merge the two separate trends for
$10<KC$
;
$C_{D}$
shows less scatter as a function of
$Re_{r}$
than
$Re$
(the latter not depicted) and
$CD$
decreases with increasing
$Re_{r}$
.
There seem to be a separation of
$C_{D}$
for the three mimics for low values of
$KC_{r}$
and
$Re_{r}$
. The increase in
$C_{D}$
with decreasing
$Re_{r}$
and
$KC_{r}$
is commonly known and is due to the omission of viscous effects in the drag (e.g. Sumer & Fredsøe Reference Sumer and Fredsøe1999). Inclusion of a linear drag term was attempted, but due to the partial correlation between
$u_{r}^{c}|u_{r}^{c}|$
,
$u_{r}^{c}$
and
$\unicode[STIX]{x2202}u_{r}^{c}/\unicode[STIX]{x2202}t$
, the least-squares system provided poor results and a direct evaluation of linear and nonlinear drag coefficients was not achieved.
It was confirmed that the force coefficients (
$C_{D}$
and
$C_{M}$
) are not a function of either
$Ca$
,
$CaL$
or
$CaL/KC$
. This makes sense, because the force coefficients represent the interaction between stem and fluid, and they should not be a direct function of the mechanical properties of the stem.
The accuracy of the fitting is presented in figure 13, where the mean and standard deviation of
$F_{c}$
and
$F_{t}$
are presented for both measured and fitted values. It is seen that the fitted loads are captured accurately and generally within
$10\,\%{-}20\,\%$
of the measured force. The mean deviation over all data sets is 2 %.
Figure 13. Comparison between the measured and fitted forces for all mimics (2, 3 and 4). Markers show the mean value and the lines show the standard deviation. The standard deviation is shown for both measured and fitted values. (a) The maximum force,
$F_{c}$
. (b) The minimum force,
$F_{t}$
. Dashed line, 1:1 fit. Dash-dotted lines, 1:1.2 and 1.2:1 fits.
3.5 Distribution of the external and internal forces along the stem
The estimated average force coefficients allow for an evaluation of the force distribution,
$f_{x}$
, along the length of the stem. The force distribution subsequently allows for an approximate distribution of the internal shear force,
$V_{x}$
, within the stem as follows:
$$\begin{eqnarray}V_{x}(s)=\int _{s}^{l}f_{x}\,\text{d}s,\end{eqnarray}$$
where
$V_{x}(s)$
is only an approximation, because the force coefficients for vertical forces on the stem could not be derived.
An example is shown in figure 14 for mimic 3 with
$H=0.04~\text{m}$
,
$T=2.0~\text{s}$
and
$l=0.30~\text{m}$
(corresponding to figure 3
c). The stem only experiences small displacements and the total force and the inertia are seen to be out of phase (compare panels a,b). The inertia force contributes less than 10 % to the maximum distributed force. It can also be seen that the maximum loading on the stem takes place at the base of the stem and at the tip of the stem. The latter due to the large relative velocities at the tip of the stem and for the former because
$u_{r}^{c}=u^{c}$
at the base. Finally, panel (c) shows
$V_{x}$
, which changes in a monotonic fashion from the tip towards the base of the stem. Unless there are local weaknesses, the stem is most likely to break at the base or become uprooted.
Figure 14. (a) The distributed total force in
$\text{mN}~\text{m}^{-1}$
as a function of space and time. (b) The distributed inertia force in
$\text{mN}~\text{m}^{-1}$
(total subtracted drag). (c) An estimate of the internal shear force in mN. (d)
$x_{s}/l$
at four points along the stem. Mimic 3,
$l=0.30~\text{m}$
,
$H=0.04~\text{m}$
,
$T=2.0~\text{s}$
and the stem motion is that of figure 3(c).
Figure 15. (a) The distributed total force in
$\text{mN}~\text{m}^{-1}$
as a function of space and time. (b) The distributed inertia force in
$\text{mN}~\text{m}^{-1}$
(total subtracted drag). (c) An estimate of the internal shear force in mN. (d)
$x_{s}/l$
at four points along the stem. Mimic 2,
$l=0.30~\text{m}$
,
$H=0.04~\text{m}$
,
$T=2.0~\text{s}$
and the stem motion is that of figure 3(a).
Another example is shown in figure 15 for mimic 2 with
$H=0.04~\text{m}$
,
$T=2.0~\text{s}$
and
$l=0.30~\text{m}$
(corresponding to figure 3
a). This case differs from the above: (i) the displacements are larger. (ii) The phase lag over the length of the stem is not a constant (figure 7). It is clear to see that there are considerable temporal shifts in the maximum distributed force over the length of the stem, which is attributed to the fact that
$\unicode[STIX]{x1D711}_{s}^{c}$
varies from
$75^{\circ }$
at the base to
$0^{\circ }$
at the tip of the stem. The distributed force vanishes at
$s/l=0.70$
over the entire wave period. The inertia force shows a similar temporal shift; again attributed to
$\unicode[STIX]{x1D711}_{s}^{c}$
. The inertia force contributed 10 %–15 % of the maximum force.
Finally, figure 15(c) shows
$V_{x}$
, where oblique lines for
$V_{x}=0~\text{mN}$
are seen as a function of time. This is opposite to the example with mimic 3, where
$V_{x}=0~\text{mN}$
over the entire length of the stem at a given time instance. This effectively means that the force at the base only receives contributions from the lower part of the stem, which is approximately half the stem in the present case. Furthermore, while the maximum of
$|V_{x}|$
still takes place at the base, there are almost as large values of
$|V_{x}|$
along the upper half of the stem (approximately 70 % of the maximum base force). The maximum in
$V_{x}$
at
$z/l=0.75$
occurs almost simultaneously with the minimum in
$V_{x}$
at the base of the stem. Consequently, it is not unlikely that the stem will break away from the root, if the stem is already damaged.
The differences in internal shear stresses for the two examples are linked to the presence of a second mode shape for mimic 2 (see figure 4 a,c). Mimic 3 falls in the static regime (Leclercq & De Langre Reference Leclercq and De Langre2018) which explains the monotonic behaviour. The second mode shape for mimic 2 is seen to directly influence the shear distribution in the stem.
It was mentioned in conjunction with the Lissajous curves in figure 9 that the distributed force along the stem for mimic 2 with
$H=0.11~\text{m}$
,
$T=3.0~\text{s}$
and
$l=0.30~\text{m}$
would be maximum below the tip (the relative velocity is largest below the tip). Plots similar to figures 14 and 15 were made and it was indeed observed that the force ranges from
$-120$
to 500 mN at the base of the stem, while the force at the tip of the stem only ranges from
$-120$
to 200 mN. The force at the stem has a wide trough and a narrow and high peak and
$V_{x}$
shows a limited temporal shift, see figure 16.
Figure 16. An estimate of the internal shear force in mN. Mimic 2,
$l=0.30~\text{m}$
,
$H=0.11~\text{m}$
,
$T=2.0~\text{s}$
and the stem motion is that of figure 3(b).
The supplementary video material (appendix D) shows the distributed hydrodynamic force and the internal shear force.
3.6 Summary
The results have shown that the classification by Leclercq & De Langre (Reference Leclercq and De Langre2018) based on the ratio of the natural period to the wave period (
$T_{n}\unicode[STIX]{x1D714}$
) can be extended to flexible stems in real waves. It is also seen that the main non-dimensional parameters
$T_{n}\unicode[STIX]{x1D714}$
and
$CaL/KC$
(derived in this work) are equivalent. The motion of the stems can be subdivided into two aspects: (i) shape and (ii) magnitude. The results presented in § 3.3.2 suggest that the magnitude scales better with
$a_{w}$
than
$l$
; the former selected in the present work as the non-dimensional, horizontal length scale. The shape is described by
$CaL/KC$
, which effectively informs on the possibility that the motion of the stem will trigger higher mode shapes.
The existence of a second mode shape gives rise to a non-uniform phase lag along the length of the stem (§ 3.3.3). The second mode shape also gives rise to more complicated relative velocities and accelerations and a maximum in the internal shear force away from the stem (§ 3.5). Consequently, the existence of more than a single mode shape can be used to predict whether a stem will break at the base of the stem or higher up: the smaller the value of
$CaL/KC\propto (T_{n}\unicode[STIX]{x1D714})^{2}$
, the more likely it is that the stem will break at the base.
4 Discussion of canopy scale processes
Extrapolation of the motion characteristics of an individual stem to the characteristics of canopies is not necessarily possible. The presence of a canopy introduces a mean flow within and above the canopy (e.g. Luhar et al.
Reference Luhar, Coutu, Infantes, Fox and Nepf2010), where the most pronounced feature is a streaming-like mean current at the top of the canopy. The mean current will result in an increased mean deflection of the stems and thereby reduce the magnitude of the transient part of the motion. This is also seen experimentally in Lei & Nepf (Reference Lei and Nepf2019), who compared motion of a single stem with the motion in a canopy under identical conditions. As a first assessment, a stem is likely to be in the same motion regime (e.g. following Leclercq & De Langre Reference Leclercq and De Langre2018), when the wave period is the same, because
$CaL/KC\propto (T_{n}\unicode[STIX]{x1D714})^{2}$
is constant. On the one hand, the added mass increases from a single stem to multiple stems as known from offshore engineering for clusters of cylinders (Sarpkaya Reference Sarpkaya1979; Heideman & Sarpkaya Reference Heideman and Sarpkaya1985) and it leads to an increase in
$T_{n}$
and thus
$CaL/KC$
. On the other hand, a large (nonlinear) mean deflection can change the natural period of the stem as seen for oscillating cantilever beams (Conzalez-Cruz, Jauregui-Correa & Herrera-Ruiz Reference Conzalez-Cruz, Jauregui-Correa and Herrera-Ruiz2016). It is likely that buoyancy effects – otherwise neglected in this work – can have an influence on the natural period under large deflections. The nonlinear behaviour of the natural period, and thereby on the classification following
$CaL/KC$
, can be investigated with a validated nonlinear beam model.
The hydrodynamics within a canopy is influenced both by the intra-wave processes for vertical mixing and the period-averaged properties. The mean deflection of the stem, as discussed in § 3.3, is a clear proof that a mean force is acting on the stem, and there is thus an equal force acting on the water column. The mean force could potentially be important in a force equilibrium for the mean wave-induced set-up through and behind a canopy (Dean & Bender Reference Dean and Bender2006; Wu et al. Reference Wu, Ozeren, Chen, Holland, Ding, Kuiry, Zhang, Jadhav, Chatagnier, Chen and Gordji2011), because the force equilibrium would otherwise only include terms from the bottom shear stress, the gradient in the mean surface elevation and the gradient in the radiation stress. Inclusion of a mean force on the vegetation in the horizontal force equilibrium (Van Rooijen et al. Reference Van Rooijen, McCall, Van Thiel de Vries, Van Dongeren, Reniers and Roelvink2016; Zhu et al. Reference Zhu, Chen, Ding, Jafari and Rosati2019) thus balances part of the gradient in the radiation stress and reduces the equilibrium surface elevation gradient. The mean force will also contribute to the shear stress distribution responsible for the mean flow within canopies (see e.g. Luhar et al. Reference Luhar, Coutu, Infantes, Fox and Nepf2010; Abdolahpour et al. Reference Abdolahpour, Hambleton and Ghisalberti2017, for experimental data on mean flow in canopies).
At present, the mean force is estimated based on streamfunction wave theory (Dean & Bender Reference Dean and Bender2006), on the empirical wave shape by Ruessink, Ramaekers & Van Rijn (Reference Ruessink, Ramaekers and Van Rijn2012) as included in the XBeach model by Van Rooijen et al. (Reference Van Rooijen, McCall, Van Thiel de Vries, Van Dongeren, Reniers and Roelvink2016) or based on inclusion of second-order Stokes contributions in semi-analytical expressions of the mean force (Zhu et al.
Reference Zhu, Chen, Ding, Jafari and Rosati2019). These approaches are reasonable for stiff stems; however, in the case of flexible stems, it is still not understood whether the nonlinear wave kinematics or the Lagrangian motion is governing
$\bar{F}_{x}$
. This should be quantified for a correct parameterization for large scale engineering models. The main contribution (Lagrangian motion or nonlinear kinematics) was investigated with the present experimental data, but the investigation was inconclusive. Therefore, it is recommended that a nonlinear numerical beam model be applied to resolve this outstanding question.
5 Conclusion
A unique data set for the motion of a single flexible stem with rectangular cross-section in regular waves was presented in this work. The data set distinguishes itself from previous laboratory studies by describing the full intra-wave motion of the stem and not only the displacement of the tip. A total of 48 combinations of stem properties (material properties and dimensions) and wave conditions were reported.
It was established that the non-dimensional quantity
$CaL/KC$
represents the motion characteristics better than the quantity
$CaL$
. This was linked to the similarity between
$CaL/KC$
and
$(T_{n}\unicode[STIX]{x1D714})^{2}$
(the latter by Leclercq & De Langre Reference Leclercq and De Langre2018). Leclercq & De Langre (Reference Leclercq and De Langre2018) classified the response based on a ratio between the natural and wave periods. A small number of data points indicated that stems with a large mean deflection showed a different oscillatory behaviour from stems with a small mean deflection. This was explained by the fact that a large mean deflection restricts the oscillatory motion. This nonlinear effect cannot be described by existing theoretical models based on the linear Euler–Bernoulli beam theory and requires a nonlinear beam model such as those described in Dijkstra & Uittenbogaard (Reference Dijkstra and Uittenbogaard2010), Luhar & Nepf (Reference Luhar and Nepf2016) and Leclercq & De Langre (Reference Leclercq and De Langre2018).
The phase lag between hydrodynamics and stem motion was evaluated and stiffer stems were seen to have a uniform phase lag over the length of the stem, while more flexible stems showed along-stem variation in the phase lag. This is linked to the importance of a second mode shape for more flexible stems.
The relative velocities and accelerations were evaluated and subsequently inserted into the dynamic beam model to calculate the average force coefficients for a flexible stem. Only the drag coefficient,
$C_{D}$
, was accurately extracted given the large value of
$KC$
, indicating a limited inertia force. It was seen that
$C_{D}$
showed better overall coherence as a function of the Keulegan–Carpenter number based on the relative velocities: the velocities which are effectively seen by the stem. The value of
$C_{D}$
decreases with increasing
$KC$
, which was attributed to linear drag for low
$KC$
and
$Re$
numbers.
The processing of the data allowed for approximations of both the external hydrodynamic loading and the internal shear force. It was seen that some stems had a monotonic increase of the shear force towards the base of the stem, while others exhibited a local maximum in the shear force closer to the top of the stem. The local near-tip maximum was linked to the large variation of the phase lag over the length of the stem and thus also the motion regimes by Leclercq & De Langre (Reference Leclercq and De Langre2018). The local maxima in the internal shear force (away from or at the base of the stem) can explain breakage mechanisms and thus loss of biomass.
The presented data set is envisaged as a valuable data set for benchmarking of linear and nonlinear numerical models for the motion of a single flexible stem in waves.
Acknowledgements
The authors would like to thank B. McFall (US Army Corps of Engineers), the three anonymous referees, and editor Professor J. T. Kirby for valuable comments. The lead author would furthermore thank Deltares’ research programme ‘Nature based Flood Defences’ for financial support.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.739.
Appendix A. Matching measurements
There are several different signals that need to be synchronized to provide a reliable estimate of the force coefficients on the single stems. These signals are (i) synchronization of the velocity profile over the height of the water column, (ii) synchronization of the sampled velocity and force and (iii) synchronization of the video recording and the point measurements. These elements are described in the following sections.
A.1 Reconstructing the velocity profile
The two velocity components
$u$
and
$w$
were measured at a single location above the bed for each single test. Consequently, the velocity profile over the depth can only be reconstructed by a combination of several tests. The surface elevation,
$\unicode[STIX]{x1D702}$
, and velocity measurements both contained some low-frequency modulation, so an exact match of the time series was required to avoid temporal shifts in this modulation over the water column.
The synchronization of the velocity profile was based on the surface elevation at the same location as the mimic (WG5), see figure 1. The synchronization was done by evaluation of the correlation coefficient for
$\unicode[STIX]{x1D702}$
between two experiments, where one time series was given a temporal offset. The temporal offset leading to the largest correlation coefficient was adopted as the optimal synchronization. There were multiple velocity measurements for some vertical locations. In that case, the average velocity was used.
A.2 Synchronization of force and velocity measurements
There is an internal processing step in the EMF that leads to an offset between the sampling of the force transducer (no internal processing) and the EMF. The offset between the force transducer and the EMF was found to be approximately 0.11 s, i.e. 11 samples.
The offset was estimated by assuming that the maximum force for large velocities (large
$KC$
numbers) is drag dominated, i.e. correlated solely with
$u|u|$
(Sumer & Fredsøe Reference Sumer and Fredsøe1999). A correlation analysis for 12 cases for the rigid mimic (mimic 4) with
$KC>100$
was performed and the force was found to lead the velocity signal by 0.08–0.14 s with an average of 0.114 s. The sampling frequency was 100 Hz, so an offset of 11 samples is used throughout this work. Hence, there is a synchronization error between force transducer and velocity of up to
$\pm 0.03~\text{s}$
.
A.3 Synchronization of footage and point measurements
A LED was controlled by the acquisition system and the LED was captured by the digital video camera. The synchronization was automated by matching the control signal (point measurement) and the average of all pixel intensities in a frame (footage). The steering signal for the LED was set to activate the LED 1.12 s after the beginning of the control signal, so to avoid problems in the data treatment, the time signal for the LED was displaced manually by 1.12 s to a later time instance. The synchronization routine has a maximum uncertainty of 0.02 s, which equals half the time between each frame.
Appendix B. Outline of the stem tracking algorithm
The footage was acquired in colour (RGB), so the position of the stem could be identified on all three colour channels. This was used to actively decide on whether one of the colour channels resulted in an erroneous tracking. The criterion was that the position of the stem should be within 1 mm (2.5 pixels) of each other on the three colour channels to qualify as a valid tracking. If not, the position of the stem was regarded as unknown (see e.g. figure 17 b).
The basis of the stem tracking is as follows:
(i) Load all footage (except for frames with the LED on) into the matrices
$\boldsymbol{X}_{0}$
,
$\boldsymbol{X}_{1},\ldots ,\boldsymbol{X}_{N}$
of rank 3 (the third dimension contains each of the three colour channels).(ii) Evaluate the simple mean of the pixel intensity of these frames (
$\overline{\boldsymbol{X}}$
) and compute the perturbation from this mean
$\boldsymbol{X}_{n}^{\prime }=\boldsymbol{X}_{n}-\overline{\boldsymbol{X}}$
. This step effectively removed the EMF from the footage (which is otherwise present, see figure 17).(iii) Perform a Gaussian blur of the frames, where the size of the blurring kernel is 7-by-7 pixels. This step is used to reduce noise away from the stem, which would otherwise (erroneously) be considered part of the stem.
(iv) Perform edge detection with a compact kernel. (The compact kernel reads
$\boldsymbol{K}=[-2,0,2;-1,0,1;-2,0,2]$
for detection along one axis and
$\boldsymbol{K}^{T}$
for detection along the second axis.) The edge detection allows for evaluation of sharp gradients in
$\boldsymbol{X}^{\prime }$
.(v) Large values of the gradient in pixel intensity are tracked from the root of the stem and upward. The tracking for each frame is stopped, when either the tracked length of the stem equals the full length of the stem (figure 17 f) or the position of the stem is too blurred to provide a reliable tracking (figure 17 b).
The position of the root of the stem was identified manually prior to the execution of the automated tracking procedure. Examples of the raw footage and the result of the tracking algorithm are shown in figure 17.
Figure 17. Example of the tracking algorithm for six frames for a case with mimic 2 and
$l=0.30~\text{m}$
. The vertical lines at
$x=0~\text{m}$
are the EMF. The dashed orange line is the tracked position of the stem. Panel (b) shows an example where a part of the stem was not recognized.
It was not always possible to detect the end of the stem with the tracking algorithm, since the velocity of the stem occasionally exceeded
$0.3{-}0.4~\text{m}~\text{s}^{-1}$
(figure 17
b), which meant that the stem displaced more than 30 pixels within one frame. High speed cameras, optimal lighting and a short shutter time are all recommended for future works.
The blurring of the stem during the sweeping from one extreme position to another means that the location during this part of the motion is not always captured. However, the velocity of the stem vanishes in the extreme positions, which is why a reliable tracking of the extremities of the stem location was achieved for all tests with mimic 2 and 3.
The tracked position of the stem
$(x_{s}(s),z_{s}(s))$
was finally interpolated onto an equidistant coordinate system along the length of the stem,
$s$
. The resolution was set to
$\unicode[STIX]{x0394}s=2.5~\text{mm}$
, which is approximately 6 pixels.
Appendix C. Deriving the stem velocity and acceleration
At first, it was attempted to evaluate the velocities (
$\unicode[STIX]{x2202}x_{s}/\unicode[STIX]{x2202}t$
) and accelerations (
$\unicode[STIX]{x2202}^{2}x_{s}/\unicode[STIX]{x2202}t^{2}$
) of the stem segments with a simple 3-point finite difference stencil. This resulted in an accumulation of noise for each additional derivative (figure 18). The noise was expected to affect the fitting to the Morison equation, when deriving the force coefficients, why a different method was adopted.
Figure 18. Example of
$x_{s}$
,
${\dot{x}}_{s}$
and
$\ddot{x}_{s}$
at the tip of the stem for
$l=0.30$
,
$T=3.0~\text{s}$
and
$H=0.11~\text{m}$
(Mimic 2). The finite difference (discrete) and POD approach to evaluate
${\dot{x}}_{s}$
and
$\ddot{x}_{s}$
are shown.
Proper orthogonal decomposition was applied on the coordinate sets
$(x_{s},z_{s})$
. This method allows for the evaluation of case specific mode shapes
$\unicode[STIX]{x1D731}_{s}$
and the associated weights
$\unicode[STIX]{x1D6FC}_{s}(t)$
. The POD method is not detailed in this work, so reference is made to e.g. Birkemeier (Reference Birkemeier1984) and Jacobsen, van Velzen & Fredsøe (Reference Jacobsen, van Velzen and Fredsøe2014). Examples of mode shapes are shown in figures 4 and 19, and merely two mode shapes are enough to characterize 98.5 % of the motion for that particular example.
Figure 19. The two first mode shapes and the mean stem position. Same stem as in figure 18. The percentage is the importance of the mode in the description of the fluctuating motion.
The strength of the POD method is that the stem position can be reconstructed as follows:
$$\begin{eqnarray}[\boldsymbol{x}_{s};\boldsymbol{z}_{s}]=[\overline{\boldsymbol{x}}_{s};\overline{\boldsymbol{z}}_{s}]+\mathop{\sum }_{n}\unicode[STIX]{x1D6FC}_{s,n}(t)\unicode[STIX]{x1D731}_{s,n},\end{eqnarray}$$
where bold symbols are column vectors and
$n$
is the
$n$
th mode shape. Consequently, the stem velocities and accelerations read
$$\begin{eqnarray}[\dot{\boldsymbol{x}}_{s};\dot{\boldsymbol{z}}_{s}]=\mathop{\sum }_{n}\dot{\unicode[STIX]{x1D6FC}}_{s,n}\unicode[STIX]{x1D731}_{s,n}\quad \text{and}\quad [\ddot{\boldsymbol{x}}_{s};\ddot{\boldsymbol{z}}_{s}]=\mathop{\sum }_{n}\ddot{\unicode[STIX]{x1D6FC}}_{s,n}\unicode[STIX]{x1D731}_{s,n}.\end{eqnarray}$$
Evaluation of
$\dot{\unicode[STIX]{x1D6FC}}_{s}$
and
$\ddot{\unicode[STIX]{x1D6FC}}_{s}$
with a finite difference scheme would introduce noise as well. Consequently,
$\unicode[STIX]{x1D6FC}_{s}$
was first estimated with the following fit (filter):
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D6FC}}_{s}=a_{0}+\mathop{\sum }_{n=1}^{5}a_{n}\cos n\unicode[STIX]{x1D714}t+b_{n}\sin n\unicode[STIX]{x1D714}t,\end{eqnarray}$$
where
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}/T$
is the cyclic frequency and the fit is limited to the first five harmonics. This fitting is possible because regular waves were used. The temporal derivatives are then estimated through algebraic differentiation instead of a numerical equivalent
$$\begin{eqnarray}\dot{\tilde{\unicode[STIX]{x1D6FC}}}_{s}=\mathop{\sum }_{n=1}^{5}n\unicode[STIX]{x1D714}(-a_{n}\sin n\unicode[STIX]{x1D714}t+b_{n}\cos n\unicode[STIX]{x1D714}t)\end{eqnarray}$$
and
$$\begin{eqnarray}\ddot{\tilde{\unicode[STIX]{x1D6FC}}}_{s}=\mathop{\sum }_{n=1}^{5}n^{2}\unicode[STIX]{x1D714}^{2}(-a_{n}\cos n\unicode[STIX]{x1D714}t-b_{n}\sin n\unicode[STIX]{x1D714}t).\end{eqnarray}$$
The fitting approach in (C 3) was favoured over a Fourier decomposition of
$\unicode[STIX]{x1D6FC}_{s}$
for two reasons: (i) The time series for
$\unicode[STIX]{x1D6FC}_{s}$
are non-equidistant, which makes discrete Fourier transforms less straightforward. (ii) The match to the exact frequency
$\unicode[STIX]{x1D714}$
instead of a discrete frequency originating from a discrete Fourier transform was expected to result in more accurate approximations of
$\dot{\tilde{\unicode[STIX]{x1D6FC}}}_{s}$
and
$\ddot{\tilde{\unicode[STIX]{x1D6FC}}}_{s}$
.
The associated velocity and acceleration are shown in figure 18 and a noise reduction is seen. The drawback of the adopted approach is that slow variations in the stem motion are not included, so the POD-method results in a regularization of the signal. This will not have any consequence for the present analysis of the force coefficients, because the slow motion only affects the velocities and accelerations with small modifications, which are estimated to be
$O(1\,\%)$
.
Appendix D. Supplementary video material
Four videos are added as supplementary material. The videos have four panels showing (i) stem and relative velocities, (ii) the distributed, horizontal forces on the stem, (iii) the stem and relative accelerations and (iv) the distributed shear force in the stem. Metadata is provided in the footer of the video.
The four videos match the example cases used throughout this paper (e.g. figures 3 and 4). Movie 1 corresponds to figure 3(a), Movie 2 corresponds to figure 3(b), etc.
