Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T07:14:33.281Z Has data issue: false hasContentIssue false
  • English
  • Français

The Paul Trap Simulator Experiment

Published online by Cambridge University Press:  25 March 2004

ERIK P. GILSON ,
RONALD C. DAVIDSON ,
PHILIP C. EFTHIMION ,
RICHARD MAJESKI  and
HONG QIN
ERIK P. GILSON
Affiliation:
Plasma Physics Laboratory, Princeton University, Princeton, New Jersey
RONALD C. DAVIDSON
Affiliation:
Plasma Physics Laboratory, Princeton University, Princeton, New Jersey
PHILIP C. EFTHIMION
Affiliation:
Plasma Physics Laboratory, Princeton University, Princeton, New Jersey
RICHARD MAJESKI
Affiliation:
Plasma Physics Laboratory, Princeton University, Princeton, New Jersey
HONG QIN
Affiliation:
Plasma Physics Laboratory, Princeton University, Princeton, New Jersey
Rights & Permissions [Opens in a new window]

Abstract

The assembly of the Paul Trap Simulator Experiment (PTSX) is now complete and experimental operations have begun. The purpose of PTSX, a compact laboratory facility, is to simulate the nonlinear dynamics of intense charged particle beam propagation over a large distance through an alternating-gradient transport system. The simulation is possible because the quadrupole electric fields of the cylindrical Paul trap exert radial forces on the charged particles that are analogous to the radial forces that a periodic focusing quadrupole magnetic field exert on the beam particles in the beam frame. By controlling the waveform applied to the walls of the trap, PTSX will explore physics issues such as beam mismatch, envelope instabilities, halo particle production, compression techniques, collective wave excitations, and beam profile effects.

Keywords

Alternating-gradient transportCharged particle beamNonlinear dynamicsPaul trap
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 4 , October 2003 , pp. 549 - 552
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

Construction of the Paul Trap Simulator Experiment (PTSX) is now complete. PTSX is a cylindrical Paul trap (Paul & Steinwedel, 1953; Wineland et al., 1983) designed to simulate the dynamics of intense charged particle beams in alternating-gradient transport systems. The experiment is predicated on the similarity between the transverse Hamiltonians for the two systems (Davidson et al., 2000). The temporally varying forces that the Paul trap exerts on the plasma particles are equivalent to the periodic focusing forces that the alternating-gradient quadrupole lattice exerts on the beam particles in the beam frame. The advantage of the simulation is that PTSX is a compact laboratory experiment, whereas a magnetic quadrupole transport system used to study the same physics would be kilometers long.

Understanding the properties of intense charged beam propagation over large distances is important for a wide variety of accelerator applications (Chao, 1993; Reiser, 1994; Davidson, 2001) including high energy physics, heavy ion fusion, spallation neutron sources, tritium production, and nuclear waste transmutation. We are especially interested in studying the properties of high-intensity beams, where the self-field effects can significantly alter beam equilibrium, stability, and transport properties.

The PTSX trap consists of three cylindrical electrodes of radius rw that are sliced into four 90° sectors as shown in Figure 1. The trap confines particles radially by applying a voltage ±V0(t) to the four sectors. A dc bias voltage,

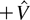
, applied to the end electrodes, confines the pure ion plasma axially. The oscillatory voltage V0(t) is such that

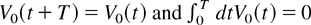
, where T is the period of the waveform. For r << rw, the transverse applied electric potential is

where κq(t) = 8qV0(t)/mπrw2 for a particle of mass m and charge q. The corrections to Eq. (1) are of the order of (1/3)(r/rw)4. As long as rp << L, the transverse force exerted on the particles by the electric potential in Eq. (1) is analogous to the transverse force acting on charged particles travelling with axial velocity v = βc through an alternating-gradient quadrupole magnetic field array that has a z-dependent, on-axis field gradient Bq′(z). The normalized transverse force in this case can be expressed as (Davidson et al., 2000)

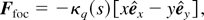
where s = βct is a normalized time variable, and the quadrupole focusing coefficient κq(s) = qBq′(s)/γmβc2 has dimensions of (length)−2. As discussed in detail in Davidson et al. (2000), the transverse particle dynamics in the Paul trap (Fig. 1) and the transverse particle dynamics for an intense beam propagating through a periodic focusing quadrupole magnetic field are similar provided that we make the appropriate identification of physical quantities.

A cylindrical Paul trap consists of a series of cylindrical electrodes, each sliced into four 90° sectors. An oscillating voltage, ±V0(t), applied to the electrodes, confines the plasma radially to a radius rp. Voltages, , applied to the end electrodes confine the pure ion plasma axially to a length 2L.

2. DESCRIPTION OF THE PTSX FACILITY

The PTSX facility consists of electrodes to confine the plasma, a cesium ion source, and a Faraday cup. The experiment sits within a stainless-steel vacuum chamber held at 5.25 × 10−10 Torr by a 1000 l/s turbomolecular pump after a 200°C bake. A laser-induced fluorescence (LIF) diagnostic and accompanying barium ion source are in development for future use.

The 2-m-long central electrodes and the 40-cm-long end electrodes are fabricated from 8-in. diameter gold-plated stainless steel tubes and Figure 2 shows a 40-cm set of electrodes protruding from the vacuum chamber. The aluminum rings with insulating spacers that support the electrodes are visible in Figure 2 as well. Adjustments on the aluminum rings allow alignment of the centers of the electrodes to within 1 mm.

The gold-plated stainless steel PTSX electrodes are supported by aluminum rings with teflon and vespel spacers.

The electrodes represent capacitive loads for the driving electronics and the capacitance of the long electrode sectors is measured to be 270 pF each with respect to ground. The short electrode sectors have a capacitance of 90 pF each with respect to ground.

To apply the oscillatory voltage V0(t), an arbitrary function generator is used with a 12-bit resolution, a 40-MS/s clock, and a 16-MB memory. The flexibility of this function generator that includes waveform linking and looping capabilities allows the formation of waveforms to simulate a wide variety of periodic focusing quadrupole lattices. The arbitrary function generator drives a dozen high-voltage operational amplifiers. The system can apply V0max = 400 V signals at 200 kHz.

The cesium source (Fig. 3) is located on the trap axis near the center of one of the sets of short electrodes and consists of an aluminosilicate cesium emitter, an acceleration grid, and a deceleration grid. The emitter produces a 0.6-in.-diameter beam of Cs+ ions when heated to 1100°C. The grids are fabricated from electroformed copper mesh that has 100 lines per inch and is 85% transparent. With an acceleration voltage of 200 V, the source produces [lsim ]30 μA of ion current, which is greater than the 200 nA estimated to be necessary for loading the trap to a density of 106 cm−3. The current-voltage characteristics of the cesium source are illustrated in Figure 4.

The ion source consists of an aluminosilicate cesium emitter, an acceleration grid, and a deceleration grid. Electroformed copper mesh that is 85% transparent forms the grids.

Current passing through the acceleration grid of the ion source in Figure 3 as a function of deceleration voltage for several acceleration voltages.

To study the complete (x,v) phase space, halo particles, and low-density as well as high-density plasmas, a LIF diagnostic will ultimately be employed. Because the atomic spectrum of cesium is not amenable to LIF, a barium source is under development.

Before the implementation of a LIF system, the main diagnostic is a Faraday cup shown in Figure 5. The assembly has a pair of coaxial 1-mm apertures in front of the cup to collimate the incoming ion beam. This permits measurement of the charge collected on any surface: the faceplate, the secondary electron suppression plate, and the cup itself. The Faraday cup is mounted on a linear motion feedthrough with a 6-in. stroke that allows the assembly to be moved from 1-in. beyond the center, to completely withdrawn from the trap. An electrometer with a 20-fC sensitivity measures the plasma charge.

Electrical connections to the Faraday cup, the faceplate, and the secondary electron suppression plate allow us to measure charge striking any surface. The copper shield prevents stray ions from impacting the wire leads.

3. EXPERIMENTAL RESEARCH PROGRAM

For a given plasma density and waveform V0(t), there are two primary constraints on the (V0 max,T) operating parameter space. The radial confining force increases with decreasing frequency, f = 1/T, which favors lower frequencies. On the other hand, for validity of Hamiltonian averaging techniques, and to avoid strong envelope instabilities (Reiser, 1994), higher frequencies are favored. Moreover, the capabilities of the present electronics limit V0max to values below 400 V.

These constraints are characterized by the frequency of the applied voltage, f, the plasma frequency, ωp, and the average transverse oscillation frequency in the confining potential, ωq, whose specific form depends on the waveform of V0(t). For radial confinement,

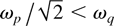
is required, where ωq is the transverse focusing frequency in the smooth-focusing approximation (Davidson & Qin, 2002). To ensure the validity of Hamiltonian averaging techniques (Davidson & Qin, 2002) and avoid the envelope instability (Reiser, 1994), ωq << 2πf/5 is assumed. This latter inequality is typically satisfied providing the vacuum phase advance σv is less than 72° (Davidson & Qin, 2002). These inequalities can be expressed for cesium ions as

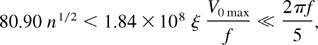
where the number density n is in cm−3. The factor

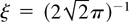
for a sinusoidal waveform for V0(t), and

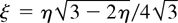
for a periodic step-function waveform with fill-factor η (Davidson & Qin, 2002). The parameter s = ωp2/2ωq2 determines whether the beam is emittance-dominated (s << 1) or space-charge dominated (s ∼ 1). Even with the constraints in Eq. (3), PTSX is capable of exploring the full range of s values.

Initial experiments consist of streaming ions from the ion source to the Faraday cup, without axial trapping. This will allow verification that a simple oscillating voltage applied to the trap walls exerts a sufficient radial force for transverse confinement of the ions. Next, the gross confinement properties of the trap will be explored by injecting a plasma and determining the maximum confinement time as a function of system parameters. Longer-term research goals include studies of many topics in beam physics.

Using different functional forms of V0(t) while keeping V0 max and f fixed will help to establish the conditions for quiescent beam propagation. Different radial density profiles, n(r), will be explored in conjunction with varying V0(t). Waveforms will include sine waves and periodic step functions with variable fill factor.

The envelope instability will be purposefully excited to study its detailed nonlinear evolution and saturation, and its dependence on s. Further, PTSX will be used to investigate the envelope instability's role in the creation of halo particles.

Taking advantage of the precise control of V0(t), individual cycles of V0(t) can be altered. Altering individual cycles of V0(t) will allow the simulation of faulty magnet sets that induce beam mismatch. This will help document the role of beam mismatch in the creation of halo particles.

Adiabatic variation of the amplitude of V0(t) will allow simulation of beam propagation through long transition regions. Such transition regions are used, for example, to compress the transverse dimension of the beam. PTSX will explore how gradual the transition must be to ensure matched-beam propagation.

The behavior of collective modes will be studied on PTSX. These are modes with frequencies that typically involve ωp, ωq, and (ωq2 − ωp2/2)1/2, modified by geometrical effects (rp /rw). As these modes depend on the details of the distribution function, they may serve as useful signatures of key beam properties.

The simplicity of the ion source allows the effects of various source configurations to be studied. By masking the present source, or by installing an array of sources, PTSX can be used to study the propagation of multiple beamlets.

4. CONCLUSION

The PTSX facility is now complete and experimental operation has begun. By controlling the wall voltage applied in a cylindrical Paul trap, PTSX can simulate a wide variety of beam physics phenomena. The advantage of these simulations over actual alternating-gradient transport systems is that they are performed in a compact laboratory setting.

ACKNOWLEDGMENT

This work was supported by the U.S. Department of Energy.

References

REFERENCES

Chao, A.W. (1993). Physics of Collective Beam Instabilities in High Energy Accelerators. New York: Wiley.
Davidson, R.C. (2001). Physics of Nonneutral Plasmas. Singapore: World Scientific.
Davidson, R.C. & Qin, H. (2002). Guiding-center Vlasov-Maxwell description of intense beam propagation through a periodic focusing field. Phys. Rev. Special Topics on Accelerators and Beams 4, 104401-1–104401-13.Google Scholar
Davidson, R.C., Qin, H. & Shvets, G. (2000). A Paul trap configuration to simulate intense non-neutral beam propagation over large distances through a periodic focusing quadrupole magnetic field. Phys. Plasmas 7, 1020–1025.Google Scholar
Paul, W. & Steinwedel, H. (1953). Ein neues massenspektrometer ohne magnetfeld. Z. Naturforsch. A 8, 448–450.Google Scholar
Reiser, M. (1994). Theory and Design of Charged Particle Beams. New York: Wiley.
Wineland, D.J., Itano, W.M. & Vandyck, R.S., Jr. (1983). High resolution spectroscopy of stored ions. Adv. At. Mol. Phys. 19, 135–186.Google Scholar
Figure 0

A cylindrical Paul trap consists of a series of cylindrical electrodes, each sliced into four 90° sectors. An oscillating voltage, ±V0(t), applied to the electrodes, confines the plasma radially to a radius rp. Voltages, , applied to the end electrodes confine the pure ion plasma axially to a length 2L.

Figure 1

The gold-plated stainless steel PTSX electrodes are supported by aluminum rings with teflon and vespel spacers.

Figure 2

The ion source consists of an aluminosilicate cesium emitter, an acceleration grid, and a deceleration grid. Electroformed copper mesh that is 85% transparent forms the grids.

Figure 3

Current passing through the acceleration grid of the ion source in Figure 3 as a function of deceleration voltage for several acceleration voltages.

Figure 4

Electrical connections to the Faraday cup, the faceplate, and the secondary electron suppression plate allow us to measure charge striking any surface. The copper shield prevents stray ions from impacting the wire leads.