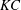1 Introduction
Oscillatory flow around a square cylinder has been the subject of a number of studies (Bearman et al.
Reference Bearman, Downie, Graham and Obasaju1985; Venugopal, Varyani & Barltrop Reference Venugopal, Varyani and Barltrop2006), although it is not as extensively explored as its circular cylinder counterpart. The sharp corners distinguish it from flow around smooth-edged bluff bodies, in that they constrain the locations of flow separation. One of the seminal studies on oscillatory sharp-edged bluff bodies was carried out by Keulegan & Carpenter (Reference Keulegan and Carpenter1958), who discovered the correlation between drag (
$C_{D}$
) and inertia (
$C_{M}$
) coefficients with the Keulegan–Carpenter number (
$KC$
), which is also called the period number and is defined as,
$$\begin{eqnarray}KC=\frac{U_{m}T}{D}=\frac{2\unicode[STIX]{x03C0}A}{D},\end{eqnarray}$$
where
$D$
is the characteristic length of the bluff body (i.e. edge length of a square);
$U_{m}$
and
$T$
are the amplitude and period of the velocity oscillation, respectively; and
$A$
is the amplitude of fluid particle excursions. An oscillatory Reynolds number (
$Re$
) can be defined as,
$$\begin{eqnarray}Re=\frac{U_{m}D}{\unicode[STIX]{x1D708}}=\frac{2\unicode[STIX]{x03C0}AD}{T\unicode[STIX]{x1D708}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of the fluid. The ratio of
$Re$
to
$KC$
is known as the frequency parameter or Stokes number (
$\unicode[STIX]{x1D6FD}$
), so that
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\frac{Re}{KC}=\frac{D^{2}}{\unicode[STIX]{x1D708}T}.\end{eqnarray}$$
Investigations on oscillatory flow around sharp-edged structures have been motivated largely by engineering applications, of which wave forces on structures provide a well-known example. Theoretical efforts were made by Graham (Reference Graham1980), who presented an analysis of the forces induced by oscillatory flow on sharp-edged cylinders at relatively low
$KC$
and high
$Re$
, with the drag coefficient being expressed as a function of
$KC$
and the internal angle (
$\unicode[STIX]{x1D6FC}$
) of the sharp corner. Bearman et al. (Reference Bearman, Downie, Graham and Obasaju1985) compared the in-line forces between theoretical and experimental results for a square-section cylinder with its face aligned normal (
$0^{\circ }$
) or
$45^{\circ }$
to the incoming flow. The inviscid theory was found to be valid for
$KC<3$
and the prediction on the inertia coefficient is more reasonable for the square cylinder than for the diamond cylinder. By assuming a laminar, non-separating flow condition Troesch & Kim (Reference Troesch and Kim1991) built a theoretical model based on experimental tests valid for a variety of shapes including squares, however the model is only adequate for
$KC$
close to zero. Bearman et al. (Reference Bearman, Graham, Obasaju and Drossopoulos1984) measured the effect of corner radius on the in-line forces in a parameter space of
$1\leqslant KC\leqslant 100$
and
$200\leqslant Re\leqslant 2\times 10^{4}$
. It was found that the variation of drag coefficient with
$KC$
behaves very differently from that of a circular cylinder and the drag coefficient is more sensitive to corner radius in oscillatory flow than in steady flow. It was suggested that flow separation around sharp-edged structures is responsible for the drag characteristics. Similarly, Venugopal et al. (Reference Venugopal, Varyani and Barltrop2006) observed that the sharp edges play a significant role in flow separation and vortex shedding around submerged rectangular cylinders under both regular and random free-surface waves. They concluded that sharp edges lead to the relatively large values of drag coefficients at low
$KC$
compared to that observed for a circular cylinder (at
$KC<5$
and
$Re\cong 10^{3}{-}10^{5}$
). Meanwhile, the inertia coefficient was observed to drop as much as 50 % with the increase of
$KC$
. Barrero-Gil (Reference Barrero-Gil2011) experimentally investigated in-line forces of a square cylinder at
$KC<15$
and
$\unicode[STIX]{x1D6FD}=29$
and 40 (
$Re<600$
). They found the drag coefficient evolves with
$KC$
in a similar way to that of a circular cylinder but at a higher value, while the inertia coefficient shows much less dependence on
$KC$
.
Numerical studies on the subject are less common, with the majority based on two-dimensional (2-D) models. Smith & Stansby (Reference Smith and Stansby1991) and Zheng & Dalton (Reference Zheng and Dalton1999), for example, carried out 2-D numerical studies of rectangular cylinders in oscillatory flow at low
$KC$
number (
${\leqslant}5$
). Both studies focused on the force coefficients with brief discussions on the flow features to interpret their results. Chern et al. (Reference Chern, Lu, Chang and Cheng2007) numerically studied the force coefficients and the flow field for a square cylinder in oscillatory flow at
$Re$
between
$200{-}500$
and
$KC\leqslant 15$
. They concluded, in agreement with Venugopal et al. (Reference Venugopal, Varyani and Barltrop2006), that
$Re$
only has very limited effect on the measured drag and inertia coefficients.
Summarised in table 1, the aforementioned studies were mainly concerned with hydrodynamic forces on the sharp-edged structure induced by the flow. However, little attention has been devoted to the flow regimes around this type of structure. On the contrary, oscillatory flow around a circular cylinder has been the subject of sustained research over the last few decades (Bearman et al. Reference Bearman, Downie, Graham and Obasaju1985; Williamson Reference Williamson1985; Tatsuno & Bearman Reference Tatsuno and Bearman1990; Sarpkaya Reference Sarpkaya2002; Elston, Blackburn & Sheridan Reference Elston, Blackburn and Sheridan2006). The aspects covered in those studies range from hydrodynamic forces to flow phenomena. Comprehensive flow regimes were firstly identified by Williamson (Reference Williamson1985) and then by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) in more detail. Unlike the flow field near the onset of instability around a circular cylinder in uniform flow (Williamson Reference Williamson1996), there is an intriguing set of 2-D and three-dimensional (3-D) instabilities when it is placed in sinusoidal oscillating flow.
Table 1. Selected studies on a square cylinder in oscillatory flow.
Williamson (Reference Williamson1985) investigated the cross-sectional flow regimes at
$\unicode[STIX]{x1D6FD}=255\;(Re<1.53\times 10^{4})$
for a circular cylinder and found that the vortices from a previous oscillation half-cycle interact with those formed in the present half-cycle, leading to several repeatable flow regimes. The vortex-shedding regimes were classified based on the number of vortex pairs generated per motion cycle. These include a pairing regime of attached vortices at
$KC<7$
; a transverse vortex street regime at
$7<KC<13$
; a single-pair regime of vortices at
$13<KC<15$
; a double-pair regime at
$15<KC<24$
; a three-pair regime at
$24<KC<32$
; and a four-pair regime for
$32<KC<40$
.
Shortly later, Tatsuno & Bearman (Reference Tatsuno and Bearman1990) identified eight regimes of remarkable flow patterns at a lower range of
$KC({<}15)$
and
$\unicode[STIX]{x1D6FD}$
(
${<}160$
, i.e.
$Re\lesssim 1200$
) through detailed flow visualisation in the cross-sectional plane and along the axis of the cylinder. Within these eight regimes, regimes A* and A represent flows that are 2-D and symmetric to the direction of motion, with vortex shedding occurring in regime A but not in A*. Regime B features the so-called ‘streaked flow’ along the axis of the circular cylinder, which is comprised of equally spaced streaks of mushroom-shape flow structure (Honji Reference Honji1981). An, Cheng & Zhao (Reference An, Cheng and Zhao2011) demonstrated through numerical simulations that the spacing between Honji vortices show strong correlations with
$KC$
over
$50\leqslant \unicode[STIX]{x1D6FD}\leqslant 500$
. A key observation in regime C is that the vortex shedding does not synchronise with the imposed oscillation; rather it is rearranged into larger vortices over a secondary period before emanating in the directions of motion. The transverse vortex streets are found in regimes D and E, where vortices are convected obliquely to one side of the axis of oscillation. Irregular switching of the convection direction is observed in regime E. Diagonal double-pair vortices feature in regime F. The last flow regime is regime G, which breaks the cross-sectional and spanwise symmetries and thus is chaotic and irregular. Flows in regimes B, D and F are all 3-D with a well-defined spatial periodicity in the spanwise direction, with the spanwise wavelength ranging from approximately one diameter (in regime B) to six diameters (in regime F). Regimes A, D, E and F are synchronous regimes, since the vortex shedding is synchronised with the oscillation. Except regime B, where the cross-sectional flow field at most locations resembles regime A*, subsequent 2-D numerical studies (Justesen Reference Justesen1991; Nehari, Armenio & Ballio Reference Nehari, Armenio and Ballio2004; Elston et al.
Reference Elston, Blackburn and Sheridan2006) have reproduced much of the cross-sectional flow feature in these eight regimes. This demonstrates that the three-dimensionality is weak and the cross-sectional vortex streets are induced by 2-D instabilities rather than 3-D instabilities.
Elston et al. (Reference Elston, Blackburn and Sheridan2006) studied the 2-D and 3-D symmetry-breaking instabilities of flows around a circular cylinder at
$KC\leqslant 10$
and
$\unicode[STIX]{x1D6FD}\leqslant 100\;(Re<1000)$
through Floquet analysis and direct numerical simulation. Flow regimes between A–C, A–D, A*–B and B–E were investigated in the
$KC$
and
$\unicode[STIX]{x1D6FD}$
parameter space. It was found from 2-D Floquet analysis that the instability is synchronous with the forcing at low
$\unicode[STIX]{x1D6FD}$
but becomes quasi-periodic with a well-defined secondary period at high
$\unicode[STIX]{x1D6FD}$
, resulting in distinct flow modes. In addition, at
$\unicode[STIX]{x1D6FD}<50$
, the flow is almost immediately unstable to 3-D secondary instabilities as soon as 2-D primary stability is broken, with the two marginal curves collapsing together. For
$\unicode[STIX]{x1D6FD}>50$
, however, a direct primary breakage was found, where with the increase of
$KC$
, the flow is unstable to 3-D instability before it breaks 2-D instability, and both of these two bifurcations are found to be supercritical.
These flow regimes are not necessarily restricted to circular cylinders, and recent research has revealed that they can appear around multiple bluff bodies (Zhao & Cheng Reference Zhao and Cheng2014; Tong et al.
Reference Tong, Cheng, Zhao and An2015), elliptical foils (Deng & Caulfield Reference Deng and Caulfield2016) as well as a circular cylinder undergoing combined oscillatory rotation and translation (Koehler et al.
Reference Koehler, Beran, Vanella and Balaras2015). Not surprisingly, the locations of these regimes in terms of
$KC$
and
$\unicode[STIX]{x1D6FD}$
are dependent on the parameters defining these scenarios.
It is worthwhile noting that in the majority of the previous studies on bluff bodies immersed in oscillatory flow,
$\unicode[STIX]{x1D6FD}$
, rather than
$Re$
, has been used as an independent parameter, along with
$KC$
. This is partially due to the classical analyses on inertia and drag forces by Stokes (Reference Stokes1851) and Wang (Reference Wang1968) at
$KC\ll 1$
, where the force can be expressed in the form of a power expansion of
$\unicode[STIX]{x1D6FD}^{-1/2}$
. On the other hand, at high
$Re$
and moderate
$KC$
, Sarpkaya (Reference Sarpkaya1976) found that
$\unicode[STIX]{x1D6FD}$
is important in describing the force behaviour as well as vortex-shedding frequencies for a circular cylinder. Despite this,
$Re$
is used as an independent parameter with
$KC$
here. The motivation is that both the oscillation amplitude and frequency, as represented by
$Re$
in (1.2), are key parameters that define the flow regime at low
$Re({\leqslant}200)$
and moderate
$KC({\leqslant}15)$
. It should be noted, however, that either
$\unicode[STIX]{x1D6FD}$
or
$Re$
can be easily reconstructed from each other.
The present work investigates oscillatory flow around a square cylinder via 2-D direct numerical simulations and Floquet analysis in a parameter space of
$KC\leqslant 15$
and
$Re\leqslant 200$
. The primary objective is to identify and explain various flow regimes. The 2-D numerical simulation is justified since the three-dimensionality is relatively weak in the selected parameter space. In addition, the transition between different flow regimes discovered by Tatsuno & Bearman (Reference Tatsuno and Bearman1990) is largely induced by 2-D instability (except regime B). It is acknowledged, however, that the map of flow regime obtained using 2-D simulations may differ from those produced by 3-D simulations, in a similar way to that observed for a circular cylinder (Elston et al.
Reference Elston, Blackburn and Sheridan2006). The remainder of the paper is organised in the following manner. In § 2, the governing equations, numerical models and model validations are introduced. Section 3 presents the classification of the flow regimes and proposes a correlation for the occurrence of the flow regimes with that in unidirectional flow. The major conclusions are drawn in § 4.
Figure 1. Schematic representation of the problem investigated in the present paper, (a); and mesh distribution around the square cylinder in the direct numerical simulation, (b). The coordinate system is defined in (a), where the spanwise direction,
$z$
-axis, is normal to the
$(x,y)$
-plane.
2 Methodology
2.1 Flow regime classification
As illustrated in figure 1(a), this paper investigates the flow regime formed around a stationary-square cross-section cylinder immersed in oscillatory flow under small
$KC$
and
$Re$
conditions. The flow regime classification is based on the nomenclature of Tatsuno & Bearman (Reference Tatsuno and Bearman1990) and the 2-D symmetry criteria used by Nehari et al. (Reference Nehari, Armenio and Ballio2004) and Elston et al. (Reference Elston, Blackburn and Sheridan2006). The symmetry breaking in the 2-D numerical simulations is visually identified by observing the non-dimensional vorticity field which is defined as,
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{z}=\unicode[STIX]{x1D735}\times \boldsymbol{U}(D/U_{m}),\end{eqnarray}$$
where
$\boldsymbol{U}$
is the velocity vector with velocity components
$u_{x}$
and
$u_{y}$
in the
$x$
- and
$y$
-directions, respectively. The symmetry states, defined by Elston et al. (Reference Elston, Blackburn and Sheridan2006), are listed below for convenience:
$$\begin{eqnarray}\displaystyle & \displaystyle y\text{-reflection},\quad K_{y}:\unicode[STIX]{x1D714}_{z}(x,y,t)=-\unicode[STIX]{x1D714}_{z}(x,-y,t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{spatio-temporal},\quad H_{1}:\unicode[STIX]{x1D714}_{z}(x,y,t)=-\unicode[STIX]{x1D714}_{z}(-x,y,t+T/2), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{spatio-temporal},\quad H_{2}:\unicode[STIX]{x1D714}_{z}(x,y,t)=\unicode[STIX]{x1D714}_{z}(-x,-y,t+T/2). & \displaystyle\end{eqnarray}$$
To consider the temporal behaviour, flow streaklines are generated by releasing massless fluid particles from the body. The particles are released after the simulations become fully established, generally after
$t=90T$
.
2.2 Direct numerical simulation model
The flow fields have been simulated using direct numerical simulation (DNS), which directly solves the Navier–Stokes (NS) equations without turbulence models. The vector form of incompressible NS equations are expressed as,
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{U}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{U}}{\unicode[STIX]{x2202}t}+(\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{U}=-\frac{1}{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{U}, & \displaystyle\end{eqnarray}$$
where
$t$
is time,
$\unicode[STIX]{x1D70C}$
is the density of the fluid and
$p$
is pressure. The above equations are solved in two dimensions using the open source field operation and manipulation (OpenFOAM®) C++ libraries. The finite volume method is used and pressure–velocity coupling is achieved following the pressure implicit with splitting of operators (PISO) method. The convection terms are discretised using the Gauss cubic scheme, while the Laplacian and pressure terms in the momentum equations are discretised using the Gauss linear scheme. The Euler implicit scheme is used for temporal discretisation.
A square computational domain is employed in the DNS study as shown in figure 1(a), with the cylinder being placed at the centre. Unless otherwise specified, the initial values of flow velocity and pressure are set to zero in the domain. Flow velocity and pressure boundary conditions on the left boundary are given as
$$\begin{eqnarray}\displaystyle & \displaystyle u_{x}(t)=U_{m}\sin (2\unicode[STIX]{x03C0}f_{o}t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}p(t)}{\unicode[STIX]{x2202}x}=U_{m}2\unicode[STIX]{x03C0}f_{o}\cos (2\unicode[STIX]{x03C0}f_{o}t), & \displaystyle\end{eqnarray}$$
where
$f_{o}$
is the oscillation frequency
$(=1/T)$
. At the right boundary, the velocity gradients in the
$x$
-direction and the pressure are set to zero. The free-slip flow condition is used at the two lateral boundaries that are parallel to the flow directions. A no-slip condition is applied on the body, where the velocity and normal pressure gradient are set to zero.
The computational domain size and mesh employed in the DNS study were chosen based on previous experience with modelling oscillatory flow around circular cylinders over a similar parameter space (Tong et al.
Reference Tong, Cheng, Zhao and An2015), following refinement based on a mesh dependence check. The length of the chosen square domain is
$100D$
, leading to a blockage ratio of 1 %. As shown in figure 1(b), a structured mesh that has a similar mesh density to Mesh 4 in Tong et al. (Reference Tong, Cheng, Zhao and An2015) is employed. The smallest mesh size in the face-normal direction of the cylinder is
$0.003D$
. The number of mesh elements on each face of the square cylinder is 120, resulting in 480 elements surrounding the body. This is three times that used for the circular cylinder due to a need to refine the mesh around the sharp corners. Since the present DNS model is well validated, only validation on drag (
$C_{D}$
) and inertia (
$C_{M}$
) coefficients of the square cylinder are presented in figure 2. The force coefficients are calculated from the Morison equation:
$$\begin{eqnarray}F_{x}=\frac{1}{2}\unicode[STIX]{x1D70C}DC_{D}|u_{x}(t)|u_{x}(t)+\unicode[STIX]{x1D70C}D^{2}C_{M}\frac{\text{d}u_{x}(t)}{\text{d}t},\end{eqnarray}$$
where
$F_{x}$
is the force on the cylinder in the in-line direction and is obtained by integrating the pressure and shear stress along the body. This validation is undertaken at
$\unicode[STIX]{x1D6FD}=40$
and the forces are compared to experimental data (Bearman et al.
Reference Bearman, Graham, Obasaju and Drossopoulos1984; Barrero-Gil Reference Barrero-Gil2011) and numerical results by Scolan & Faltinsen (Reference Scolan and Faltinsen1994). It can be seen that good agreement was generally achieved, even at larger
$KC$
values (
${>}5$
) where the flows in the experiments are believed to be weakly three-dimensional.
Figure 2. Comparison of the drag (
$C_{D}$
) and inertia (
$C_{M}$
) coefficients by the present DNS method at
$\unicode[STIX]{x1D6FD}=40$
(▫) with experimental data by Barrero-Gil (Reference Barrero-Gil2011) at
$\unicode[STIX]{x1D6FD}\approx 40$
(
$+$
) and Bearman et al. (Reference Bearman, Graham, Obasaju and Drossopoulos1984) at
$\unicode[STIX]{x1D6FD}=213$
(
$\times$
), and with numeric values computed by Scolan & Faltinsen (Reference Scolan and Faltinsen1994) at
$\unicode[STIX]{x1D6FD}=213$
(▵).
Figure 3. Comparison of (a) the vortex-shedding frequency (
$St$
) and (b) mean drag coefficient (
$C_{D}$
) of a square cylinder in steady flow at various Reynolds numbers (
$Re$
); experimental data of Norberg were taken from the numerical study by Sohankar, Norberg & Davidson (Reference Sohankar, Norberg and Davidson1997).
The model is also validated under the condition of steady current at low
$Re$
. The Strouhal number (
$St$
) in steady flow is defined as,
$$\begin{eqnarray}St=\frac{f_{vs}D}{U_{\infty }},\end{eqnarray}$$
where
$f_{vs}$
and
$U_{\infty }$
are the vortex-shedding frequency and the free-stream flow velocity, respectively. We compare
$St$
and the mean
$C_{D}$
over
$Re=40{-}200$
with an interval of 10 with published data in figure 3, anticipating that the results from steady flow will be utilised in interpreting the results for its oscillatory counterpart. Very good agreement is achieved. Vortex shedding is found at
$Re=50$
and onwards, and the
$St$
increases in line with
$Re$
for
$Re\leqslant 160$
. A decline is found in the mean
$C_{D}$
when the vortex shedding starts, and the drop trend continues gradually until approximately
$Re=160$
. The drag increases slightly with
$Re$
for
$Re>160$
.
2.3 Floquet stability analysis
Floquet linear stability analysis is also carried out in this study to determine the marginal curve of stability for the 2-D flow in breaking reflection symmetry about the axis of oscillation. An open source spectral element code, Nektar++ (Cantwell et al.
Reference Cantwell, Moxey, Comerford, Bolis, Rocco, Mengaldo, De Grazia, Yakovlev, Lombard and Ekelschot2015) is employed for this purpose. The linear stability analysis examines the evolution of an infinitesimal perturbation,
$\boldsymbol{u}^{\prime }(x,y,t)$
, over a
$T$
-periodic base flow,
$\boldsymbol{U}(x,y,t)$
, from cycle to cycle by computing the Navier–Stokes equations linearised to
$\boldsymbol{U}$
and
$\boldsymbol{u}^{\prime }$
(Barkley & Henderson Reference Barkley and Henderson1996). Solution of the perturbation can be decomposed into a sum of components
$\boldsymbol{u}^{\prime }(x,y,t)=\tilde{\boldsymbol{u}}(x,y,t)\exp (\unicode[STIX]{x1D70E}t)$
. Here, the Floquet eigenfunction
$\tilde{\boldsymbol{u}}(x,y,t)$
also holds
$T$
-periodicity; and the Floquet exponents
$\unicode[STIX]{x1D70E}$
are complex numbers. One usually looks at the Floquet multiplier to determine the stability state, which is expressed as
$\unicode[STIX]{x1D707}\equiv \exp (\unicode[STIX]{x1D70E}T)$
. When the Floquet multiplier leaves the unit circle,
$|\unicode[STIX]{x1D707}|>1$
(perturbation grows exponentially), the base flow
$\boldsymbol{U}$
is deemed to be unstable to the perturbation, thus instability occurs (Barkley & Henderson Reference Barkley and Henderson1996); while stability is signalled when the multiplier is inside the unit circle,
$|\unicode[STIX]{x1D707}|<1$
(perturbation decays exponentially). A convergence test for the code is provided in the Appendix.
3 Results discussion
Direct numerical simulations for oscillatory flow around a square cylinder were performed over a parameter space of
$KC\in [1,15]$
and
$Re\in [40,200]$
. Initially, the increments of
$KC$
and
$Re$
in DNS study were set to be 1 and 20, respectively, but these were then refined in regions where a better insight into the detailed characteristics of the flow was needed. The Floquet stability analysis was carried out where the refection symmetry in (2.2) is observed to be broken from DNS results, in order to capture the critical point of transition.
Figure 4. Flow fields represented by the streaklines at various
$Re$
and
$KC$
conditions. Streaklines were generated by releasing 100 massless particles evenly distributed on the body, at a frequency eight times the oscillatory frequency. The inlet oscillatory flow is in the horizontal direction.
Figure 5. Classification of flow regimes for a square cylinder in oscillatory flow based on 2-D DNS and Floquet analysis, (a), along with the map of the flow for a circular cylinder (Tatsuno & Bearman Reference Tatsuno and Bearman1990) for ease of comparison, (b). In (a), ○, regimes A
$/$
A*; ●, regime A
$^{\prime }$
; ▵, regime C;
$+$
, regime D; ♦, regime F
$^{\prime }$
; ♢, regime F;
$\times$
regimes E; ▿, regime G; solid lines with ▪, marginal stability curve from 2-D Floquet stability analysis of the square cylinder; dash-dotted lines, interpolated boundary lines for different flow regimes. In (b), symbols represent flow regimes.
3.1 Flow regimes
Flow fields corresponding to selected parameters are visualised through streaklines in figure 4. The streaklines have been generated by releasing 100 massless particles evenly distributed on the body surface, at a frequency of eight times the oscillation frequency. At low
$Re$
values the flow possesses a reflection symmetry to the axis of motion (
$K_{y}$
symmetry (2.2)). At large
$Re$
values, irregular streaklines are observed, especially in the far field away from the cylinder. Moreover, at intermediate
$Re$
values the flow shows a wide range of organised wake features, which lead to distinct spatio-temporal symmetries and quasi-periodic states.
These flow features, together with the vorticity field (spatial behaviour) and the force histories (temporal behaviour), are considered in mapping out the flow regimes shown in figure 5(a). The curve of marginal stability from 2-D Floquet stability analysis is also included, which will be detailed in § 3.2. The flow regimes in this figure share similarities to those observed for a circular cylinder in figure 5(b) reproduced from Tatsuno & Bearman (Reference Tatsuno and Bearman1990). Despite this, it should be noted that there are fundamental differences between the two maps of flow regimes. As pointed out by Elston et al. (Reference Elston, Blackburn and Sheridan2006), the former is the map of flow modes from 2-D simulations, which represent the cross-sectional subspace as opposed to the later where some are three-dimensional. The 2-D flow regimes are only accurate when the three-dimensionality is weak.
It is seen that the region occupied by regime C in the parameter space is considerably larger than that for the circular cylinder. In contrast, the area occupied by regime D for the square cylinder is relatively small. Due to the sharp corners, flow separation can be observed even at low
$KC$
and
$Re$
for the square cylinder, though the separated vortices are not able to travel far. Therefore, no attempt has been made to define the boundary between A and A*. For many cases, the streakline patterns associated with regime G are similar to regime F local to the cylinder, but intermittent switching of convection direction was observed for regime G, as seen in figure 4 at
$(Re,KC)=$
(200, 11 and 12). The two new flow regimes identified around the square cross-section cylinder, namely regime A
$^{\prime }$
and F
$^{\prime }$
, will now be mainly focused on.
Figure 6. Flow regime A
$^{\prime }$
at
$(Re,KC)=(200,2)$
as illustrated by vorticity contour between
$\unicode[STIX]{x1D714}_{z}=-0.5$
(light colours) and
$+0.5$
(dark ones) with cutoff level
$\pm 0.1$
. The inlet oscillatory flow is in the horizontal (
$x$
-axis) direction and the instantaneous time is shown as ● in the sinusoidal velocity signal.
3.1.1 Regime A
$^{\prime }$
At low
$KC$
but high
$Re$
number, a flow regime has been observed for the square cylinder which possesses
$K_{y}$
symmetry in (2.2). The massless particles released in the flow field are mainly convected in the direction perpendicular to the velocity oscillation direction (see figure 4). Figure 6 shows the vortices are mostly attached to the body during the oscillation period. The vortices aligned with the leading edges occupy much larger region than those extended in the oscillation direction. This flow pattern is classified as regime A
$^{\prime }$
to distinguish it from the regime A*, where massless particles are convected away from the cylinder in the direction of flow oscillation.
Okajima (Reference Okajima1982) demonstrated that at
$Re=150$
and 250 in steady flow, the flow detaches itself from the leading edge of a square cylinder and rolls up behind the cylinder. The separated flow can only reattach to the side surfaces when the aspect ratio extends to 2 (side length to height), where the flow moves along the surfaces, instead of rolling up into the wake. In regime A
$^{\prime }$
the shear layers generated from the leading edges are allowed neither to fully reattach to the body due to the short side ratio, nor to travel far from the body due to the short oscillation period. Therefore, when the flow reverses, the shear layer is pushed outwards, feeding a vortex aligned with the leading edge. This gives rise to the released particles moving away from the cylinder in a direction perpendicularly to the oscillation direction.
Regime A
$^{\prime }$
is only found at
$KC=1$
and 2, and at
$Re\gtrsim 160$
. This is because at larger
$KC$
, the shear layers can travel beyond the ends of the cylinder, while at smaller
$Re$
the shear layer is not strong enough to detach from the surface. DNS simulations were carried out in seeking regime A
$^{\prime }$
for a circular cylinder at
$(Re,KC)=$
(200
${-}$
240, 2) without success, where the attached vortices mainly extend in the oscillation direction. In fact experiments were carried out until
$Re\sim 300$
at
$KC=2$
by Tatsuno & Bearman (Reference Tatsuno and Bearman1990), and the released dye/aluminium dust were seen travelling in the oscillation direction.
3.1.2 Regime F
$^{\prime }$
Another new flow regime is observed at high values of
$KC$
and intermediate
$Re$
, just before regime F appears (for instance, at
$KC=11$
, between
$Re=126{-}160$
, and at
$Re=140$
, between
$KC=10.75{-}12$
). This flow is quasi-periodic (QP), which can be seen in figure 4 at
$(Re,KC)=$
(140, 11 and 12) and (120, 12). This regime is classified as F
$^{\prime }$
and is distinct from regime F because the shed vortices do not synchronise with the motion. Instead, they are rearranged into large vortex cores with a well-defined secondary period. Regime F
$^{\prime }$
differs from regime C in terms of the convection directions of the shed vortices.
Figure 7. Characteristics of typical regime F
$^{\prime }$
at
$(Re,KC)=(140,11)$
. (a) Time history of the lift coefficient; (b) fast Fourier transform (FFT) spectrum of the lift coefficient and (c) vorticity contour in 11 periods at the same phase instant of oscillation, when the inlet velocity is about to switch to upwards.
Detailed features typical to regime F
$^{\prime }$
are illustrated in figure 7 for
$(Re,KC)=(140,11)$
. It can be seen that a low secondary frequency (
$f_{s}$
) exists in the lift force, and this frequency modulates the main frequency at
$f/f_{o}=1$
(where frequency of lift force,
$f$
, is non-dimensionalised by flow oscillation frequency
$f_{o}=1/T$
), resulting in two peaks at 0.94 and 1.12. This suggests that the secondary period is approximately 11 times the flow oscillation period. This is consistent with figure 7(c), where vortices of the same sign merge with each other to form a larger vortex, whose sign switches approximately every
$5.5T$
. For instance, vortex I at
$t/T=86$
is replaced by vortex I
$^{\prime }$
at
$t/T=91$
. The shed vortices emanate in inclined diagonal directions, rather than in the flow direction as observed in regime C (figure 8
a). Regime F
$^{\prime }$
, along with the secondary period, are believed to be induced by the modulation between oscillation and vortex formation frequencies, which is explained in § 3.3.
Figure 8. Instantaneous vorticity contour of (a) regime C at
$(Re,KC)=(160,7)$
, (b) regime F
$^{\prime }$
at (140, 11.25) and (c) regime F at (100, 14).
Figure 9. Comparison of the force behaviours of regime C, regime F
$^{\prime }$
and regime F, from top to bottom from the cases in figure 8. From left to right, columns are the time history of lift coefficient
$C_{L}$
(a,d,g), Lissajous plots of lift coefficient against in-line force coefficient
$C_{I}$
(b,e,h), and FFT spectra of the lift coefficient (c,f,i).
Figures 8 and 9 compare regime F
$^{\prime }$
with F and another QP state regime C. This comparison is presented in terms of the flow field, the time history of lift coefficient
$C_{L}$
, the FFT spectrum of
$C_{L}$
and Lissajous plots of
$C_{L}$
against in-line force coefficient
$C_{I}$
. Here,
$C_{L}$
and
$C_{I}$
are defined as,
$$\begin{eqnarray}C_{L}=\frac{F_{y}}{0.5\unicode[STIX]{x1D70C}DU_{m}^{2}},\quad C_{I}=\frac{F_{x}}{0.5\unicode[STIX]{x1D70C}DU_{m}^{2}}.\end{eqnarray}$$
It is obvious that regime F
$^{\prime }$
is similar to regime C, in the sense of their quasi-periodicity. Unlike the Lissajous plots of regime F, which almost collapses into a single line,
$C_{L}$
of regime F
$^{\prime }$
and regime C show a periodicity over many periods of harmonic motion. This is further evidenced by the frequency spectra, where a modulation to the oscillation frequency is clear. A low non-dimensional frequency of 0.07 is detected at
$(Re,KC)=(160,7)$
for regime C, which modulates the main frequency, similar to that in regime F
$^{\prime }$
. It can also be seen that the generation processes of the Kármán vortex street at each side of the cylinder in regimes F
$^{\prime }$
and C are similar. The large vortex cores relatively far away from the body, as marked by I & II and III & IV in figure 8, are generated over multiple periods of oscillation and then shed alternately. Regime F
$^{\prime }$
and regime F are alike in the sense that the shed vortices are diagonally distributed.
It is believed due to the size of the secondary periods, regime F
$^{\prime }$
flows in figure 4 are visually distinct from one another. To examine the dependence of regime F
$^{\prime }$
flows on initial conditions, a DNS simulation was performed at (
$Re$
,
$KC$
)
$=$
(140, 11) with an initial condition of the fully developed flow field obtained at (200, 12) in figure 4. The result showed that the started regime G flow converted to regime F
$^{\prime }$
in less than 22 periods. This appears to suggest that regime F
$^{\prime }$
flows are not sensitive to initial conditions.
One further point worth mentioning in regime C and regime F
$^{\prime }$
is that although the combined vortex street at each side of the cylinder resembles a Kármán vortex street (Tatsuno & Bearman Reference Tatsuno and Bearman1990; Elston et al.
Reference Elston, Blackburn and Sheridan2006), the frequency at which the vortex cores are shed can be different, which is different from that of the Kármán vortex. Figure 10 illustrates this point at (
$Re$
,
$KC$
)
$=$
(140, 8). It is seen that
$C_{L}$
oscillates above the mean-zero value at approximately a period of
$24T$
, and this is the shedding frequency of the pair of vortices above the
$x$
-axis (similar to vortex I and III in figure 8
a). However below the mean-zero level,
$C_{L}$
oscillates at approximately a period of
$20T$
, leading to a slightly lower shedding frequency for the pair of vortices below the
$x$
-axis (similar to vortex II and IV). This feature happens at the boundary of regime C, where the flow is about to transition to regime E.
Figure 10. Frequency modulation as presented by the time history of the lift coefficient at
$(Re,KC)=(140,8)$
.
3.2 Outcome of stability analysis
In order to capture the curve of marginal stability where the flow breaks 2-D
$K_{y}$
symmetry in (2.2), Floquet stability analysis was performed on oscillatory flow around the square cylinder. The base flow was obtained by solving the full nonlinear incompressible NS equations with similar boundary conditions to those in the DNS study, but since only 2-D symmetry-breaking instabilities are considered here, a symmetry boundary condition along
$y=0$
is enforced by computing over a half-domain, following the method reported by Elston, Sheridan & Blackburn (Reference Elston, Sheridan and Blackburn2004). When the simulation reaches the saturated state, a total of 64 flow-field slices are sampled, equispaced in time over the oscillating period
$T$
. These flow slices were used to generate the base flow over the whole domain. Stability analysis with the base flow was then performed by computing the linearised NS equations and seeking the leading eigenvalues with the Floquet solver embedded in Nektar++. A random vector field was used as the initial perturbation, with
$\boldsymbol{u}^{\prime }(x,y,t)=\mathbf{0}$
on all boundaries and a high-order Neumann boundary condition for perturbation pressure (Karniadakis, Israeli & Orszag Reference Karniadakis, Israeli and Orszag1991). The marginal stability is estimated by extrapolating the Floquet multiplier to 1, from the two cases in which the magnitudes of
$\unicode[STIX]{x1D707}=\text{exp}(\unicode[STIX]{x1D70E}T)$
are just above 1 (Elston et al.
Reference Elston, Sheridan and Blackburn2004).
Figure 11. Outcomes of Floquet analysis for two-dimensional flows around a square and circular cylinder. (a) The curve of marginal stability for a square cylinder (▫). The marginal curve for the circular cylinder from Elston et al. (Reference Elston, Blackburn and Sheridan2006) is included (○) for comparison, along with data from the present simulations (
$\times$
). Filled symbols represent that real multipliers cross the unit circle at
$|\unicode[STIX]{x1D707}|=1$
, while void symbols indicate the critical multipliers occur in complex-conjugate pairs (again with
$|\unicode[STIX]{x1D707}|=1$
). A vertical dotted line shows the critical
$Re$
of the primary instability in unidirectional flow for both geometries (
${\sim}49$
). (b) The phase angles of the multipliers as a function of
$KC$
for the square cylinder. Approximate locations of the identified flow regimes for the square cylinder are given in both (a) and (b).
The resultant curve of marginal stability has been included in figure 5 and is reproduced in figure 11(a) for clarity. The overall agreement between DNS and stability analysis suggests that when the enforced symmetry condition is removed, the flow breaks the reflection symmetry (2.2) into four different types of periodic and quasi-periodic modes. In particular, the flow breaks
$H_{2}$
symmetry (2.4) in regime D at
$8.25<KC\leqslant 10$
and it breaks
$H_{1}$
symmetry (2.3) in regime F for
$KC\geqslant$
14. Staggered within these synchronous modes, the QP modes of regime C is observed at
$4<KC\leqslant 8.25$
and regime F
$^{\prime }$
at
$11\leqslant KC\leqslant 13$
. It is seen whenever the flow breaks into QP states (regime C and F
$^{\prime }$
) the critical multipliers are complex-conjugates,
$\unicode[STIX]{x1D707}_{c}=\text{exp}\pm \text{i}\unicode[STIX]{x1D703}$
; and whenever the flow breaks into synchronous states (regime D and F) the critical multiplier is real,
$\unicode[STIX]{x1D707}_{c}=+1$
. This demonstrates that the QP instability and the synchronous instability occur alternately for the square cylinder along the curve of marginal stability, extending on the findings of Elston et al. (Reference Elston, Blackburn and Sheridan2006).
Figure 12. Vorticity contours of the Floquet eigenfunction for the four identified reflection symmetry-breaking regimes. (a) Regime C at
$(Re,KC)=(150,6)$
with
$\unicode[STIX]{x1D707}=1.0007\text{exp}\pm \text{i}0.7945$
; (b) regime D at (116, 9) with
$\unicode[STIX]{x1D707}=+1.039$
; (c) regime F
$^{\prime }$
at (110, 12) with
$\unicode[STIX]{x1D707}=1.003\text{exp}\pm \text{i}0.2574$
; (d) regime F at (78, 14) with
$\unicode[STIX]{x1D707}=+1.043$
. Both imaginary (i) and real part (ii) of the eigenfunction are given for the two QP regimes.
For regime C and regime F
$^{\prime }$
a secondary period
$T_{s}$
appears along with a phase angle
$\unicode[STIX]{x1D703}$
in the critical multipliers. The relationship
$T_{s}/T=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D703}$
observed by Elston et al. (Reference Elston, Blackburn and Sheridan2006) for a circular cylinder in 2-D simulations also holds for the square cylinder. The ratios of
$2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D703}$
along the marginal curve of stability are plotted as a function of
$KC$
in figure 11(b), where it shows that the secondary period increases with
$KC$
before the flow switches to a synchronised mode. It should be noted that an effort was also made in seeking regime F
$^{\prime }$
around a circular cylinder along the curve of marginal stability, especially around
$KC=11$
, but no apparent characteristics of regime F
$^{\prime }$
flow were found.
It is interesting to see that the curve of marginal stability for the square cylinder stays to the right of the curve of the circular cylinder. Both marginal curves show strong inverse
$Re{-}KC$
relationships at low and high values of
$KC$
, except at intermediate
$KC$
. The shift is relatively small at either end of the
$KC$
range (
$KC<7$
and
$KC>13$
), but is more significant for intermediate values of
$KC$
. This appears to suggest that the influence of structural geometry is weak at either small or large
$KC$
, but relatively strong at intermediate
$KC$
. The observation is perhaps not coincidental. At low
$Re$
but high
$KC$
the difference in geometry is overshadowed by viscous effects. In unidirectional flow (to which the marginal curves in figure 11 are expected to limit towards for large
$KC$
), for example, the locations of primary instability of a square cylinder (zero incidence) and a circular cylinder are close: i.e.
$Re=47\pm 2$
(Sohankar, Norberg & Davidson Reference Sohankar, Norberg and Davidson1998) compared to
$Re=49$
(Williamson Reference Williamson1996). At low
$KC$
but high
$Re$
the whole shape of the geometry tends to be less significant due to the high frequency of oscillation. The shift in the curve for the square cylinder compared with the circular cylinder at intermediate
$KC$
and
$Re$
is discussed further in the next section.
The vorticity contours of the Floquet eigenfunction around criticality are shown in figure 12 for each of the identified flow regimes. It is seen that the leading eigenfunctions also occur in complex-conjugate pairs for the two QP modes, whereas they are real for the two synchronised modes. Depending on the phase angle of the critical multipliers, the size of the imaginary part can be almost equal to, or much smaller than, the real part (figure 12 a,c). The vorticity contour seems to extend further in the two synchronised modes than that in the QP modes. The vorticity contours within regime C and D are, respectively, visually similar to that reported around a circular cylinder (Elston et al. Reference Elston, Blackburn and Sheridan2006), which appears to suggest that the geometry difference brings limited influence to the contours of the critical eigenfunctions.
3.3 Modulation between oscillation and vortex formation frequencies
Since the vortex formation and shedding in oscillatory flow is heavily influenced by the oscillation period for the
$KC$
numbers considered, the intrinsic vortex-shedding feature in unidirectional flow is employed to explore the modulation between oscillation and vortex formation frequencies. For convenience we introduce
$KC_{St}$
to represent the non-dimensional vortex-shedding period due to steady flow, i.e. the reciprocal of
$St$
, to allow for comparison with
$KC$
in oscillatory flow. Thus,
$$\begin{eqnarray}KC_{St}=\frac{U_{\infty }}{f_{vs}D}=\frac{U_{\infty }T_{vs}}{D},\end{eqnarray}$$
where
$T_{vs}$
is the vortex-shedding period in unidirectional flow.
3.3.1 Flow evolution at a fixed
$Re$
Numerical simulations at various
$KC$
cutting through
$Re=140$
were performed to demonstrate how the flow evolves with
$KC/KC_{St}$
, the oscillation period number to the vortex formation period in otherwise steady flow. Figure 13 presents FFT spectra associated with the time series of the lift coefficient for
$6.25\leqslant KC\leqslant 14$
, along with instantaneous flow fields at selected
$KC$
numbers. The
$St$
at this selected
$Re$
is 0.153 (see figure 3), corresponding to
$KC_{St}=6.52$
and thus,
$KC/KC_{St}$
is in the range of
$0.96{-}2.15$
.
Figure 13. Characteristics of the flow regimes along
$Re=140$
and various
$KC$
(as labelled). Left, FFT spectra of the lift coefficient, where the frequency associated with the time series of the lift coefficient,
$f$
, is non-dimensionalised by oscillation frequency,
$f_{o}=1/T$
, for each case. To facilitate comparison, spectra of FFT are translated in the vertical axis, where the amplitudes between any two neighbouring cases is 0.25. Same line at
$KC=11$
is presented in figure 7 and at
$KC=11.25$
in figure 9. Right, the flow field as illustrated by vorticity contour (from top to bottom at
$KC=12.75$
, 11.75, 9, 7 and 6.25).
For
$KC\leqslant 6.25\;(KC/KC_{St}<0.96)\;C_{L}$
is zero for
$Re=140$
. The
$K_{y}$
symmetry (2.2) is maintained because during each half-cycle of movement, only a pair of vortices equal in size can generate, which are forced to detach from the cylinder by new vortices with opposite sign generated from near the body surface after the velocity reverses.
At
$KC=6.5\;(KC/KC_{St}\approxeq 1)$
the
$K_{y}$
symmetry (2.2) is broken in figure 13, where a low secondary frequency
$(f_{s}/f_{o}\sim 0.10)$
appears and modulates the major peaks so that a pair of peaks appear around
$f/f_{o}=2$
(and 4). This indicates the generation of the QP mode of regime C. The
$f_{s}/f_{o}$
then reduces as the
$KC$
increases beyond 6.5 so that the distance between the two peaks decreases. At about
$KC=9$
,
$f_{s}/f_{o}$
decreases to almost zero, thus the two peaks combine into one, leading to the start of regime D. In this sense, regime D is a special case of regime C in which
$f_{s}/f_{o}$
approaches zero.
When
$KC$
is within the range
$6.5{-}8.75\;(1<KC/KC_{St}<1.34)$
, as illustrated in figure 14, there is just enough time during each oscillation half-cycle to allow one pair of vortices (I and I
$^{\prime }$
at
$t/T=85$
) to develop into different sizes, but not enough time to allow either of them to completely shed in the present half-cycle. Instead in the second half-cycle of oscillation, the pair of vortices move backwards and experience a very complicated process of vortex splitting, merging and shedding. Following this, at
$t/T=86$
a new vortex pair II and II
$^{\prime }$
replace I and I
$^{\prime }$
, respectively. Because the majority of the vortices (which coincide with low pressure) are shed from the right-hand side of the cylinder over the time series shown in figure 14, the lift coefficient is mostly negative. Furthermore, because two major vortices are shed in one cycle, the period associated with the lift force is half of the oscillation period.
The consecutive development of vortex I
$^{\prime }$
and II
$^{\prime }$
after one cycle of oscillation is presented in figure 15. It is observed that the vortex slightly changes in size after each cycle and it is this difference which is believed to be responsible for modulating the shedding frequency. This difference is directly caused by the residual vortex I
$^{\prime }$
(or II
$^{\prime }$
) being forced to circulate around the cylinder during one cycle of movement. As
$KC$
increases within the range 6.5–9 an increased portion of vortex I
$^{\prime }$
is shed in the half-cycle following its generation, which means the residual vortex I
$^{\prime }$
, that modulates the flow field, decreases in strength and consequently the secondary period increases. When
$KC$
further increases from
$KC=9$
, regime D takes over. During each half-cycle, there is enough time for a pair of different size vortices to be completely shed in the next half-cycle, despite complicated vortex splitting and mergence. Thus the flow field is exactly the same after one cycle of oscillation.
Figure 14. Detailed instantaneous flow fields and the lift coefficient in regime C at
$(Re,KC)=(140,7)$
in one selected oscillatory period, corresponding to that when the lift reaches minimum in the secondary period, as seen in the dashed box in the top plot in figure 15.
Figure 15. The evolution of regime C flow at
$(Re,KC)=(140,7)$
. (a) Time history of lift coefficient; and (b) vorticity contour in 14 periods at selected time instants, corresponding to approximately a secondary period. The chosen instants are indicated by ○ in the graph of the lift coefficient.
At
$KC=11\;(KC/KC_{St}=1.69)$
a low frequency starts to modulate the major peaks again, leading to a pair of peaks at around
$f/f_{o}=1$
(and 3) in figure 13. This indicates the generation of another QP mode of regime F
$^{\prime }$
. Again,
$f_{s}/f_{o}$
reduces with a further increase in
$KC$
, so that the distance between the two peaks reduces. At approximately
$KC=12$
at
$Re=140$
(slightly lower than
$2KC_{St}=13.04$
),
$f_{s}/f_{o}$
decreases to a value close to zero and the two peaks combine into one. Physically, the reasons for the generation of regime F
$^{\prime }$
is similar to regime C. When
$KC$
is within the range
$11{-}12$
, the time between flow reversals is not long enough to allow a pair of vortices to be completely shed from the cylinder, as illustrated in figure 16. Consequently the vortex residual (i.e. the part of the vortex forced to move back with in the second half-cycle) modulates the flow field during its accumulation in multiple cycles of oscillation. This reasoning is consistent with figures 14 and 15, which indicates that the QP flow phenomenon appears to be induced by the mismatch between the oscillation period and the time required for vortex formation. For
$KC\geqslant 12$
, the flow transitions to regime F. This is because that for each half-cycle of oscillation there is enough time for a pair of vortices to shed from the cylinder.
Figure 16. Detailed instantaneous flow fields and lift coefficient in regime F
$^{\prime }$
at
$(Re,KC)=(140,11)$
in a selected oscillatory period, as seen in figure 7, where the amplitude of lift reaches maximum.
Figure 17. The dependence of the QP state on
$Re$
and
$KC$
as illustrated by the ratio of the secondary period (
$T_{s}$
) to the oscillation period (
$T$
) at (a)
$KC=6$
and (b)
$Re=140$
.
3.3.2 Regime locations relative to
$KC_{St}$
Figure 17 illustrates the ratio of the secondary period to oscillatory period,
$T_{s}/T$
, at fixed
$KC$
and
$Re$
, respectively, highlighting the required number of cycles over which the flow tends to repeat itself. Here,
$T_{s}$
is derived from
$f_{s}$
in the FFT spectrum. The magnitude of
$T_{s}/T$
is believed to be related to the time difference between
$KC$
and
$KC_{St}$
, which determines how much vortex can be shed in one cycle of oscillation. Because the actual vortex formation in oscillatory flow is dependent on the oscillation frequency, a precise relationship for
$T_{s}$
as a function of
$KC$
and
$KC_{St}$
is not readily available. Despite that,
$T_{s}$
appears to change in agreement with the change of
$KC_{St}$
. Here at a constant
$KC,T_{s}/T$
roughly follows the same trend of
$St$
by comparing figures 17(a) and 3(a) for
$Re=140{-}200$
. On the other hand at a constant
$Re,T_{s}/T$
becomes finite when
$KC$
is close to
$KC_{St}$
(or
$2KC_{St}$
).
Figure 18. The relative locations of oscillatory flow regimes around a cylinder and the non-dimensional vortex-shedding period (
$KC_{St}$
) of the cylinder in the unidirectional flow. (a) Square cylinder; the regime boundaries are from figure 5 and solid lines of
$KC_{St}$
and
$2KC_{St}$
are from figure 3. (b) Circular cylinder; the regime boundaries are from Tatsuno & Bearman (Reference Tatsuno and Bearman1990) and
$KC_{St}$
are from Williamson & Brown (Reference Williamson and Brown1998) with
$St=0.2731-1.1129/\sqrt{Re}+0.4821/Re$
.
Figure 18 presents a global view of all the flow regimes, and their relative locations in the parameter space compared to
$KC_{St}$
for both the square and circular cylinders, with the latter generated from published data. As discussed, the mechanism of the occurrence of two QP regimes C and F
$^{\prime }$
is thought to be related to the mismatch of oscillation period and the time required for vortex development and vortex shedding from the cylinder, which gives rise to the shedding of vortices in multiple cycles of oscillation. Although the vortex formation in oscillatory flow is highly influenced by
$KC$
, it is interesting that the two QP regimes locate close to the lines of
$KC_{St}$
or
$2KC_{St}$
, whereas regimes A, D and E fall mostly between the value of
$KC_{St}$
and
$2KC_{St}$
. The
$KC_{St}$
of the square cylinder is relatively larger than that of the circular cylinder for a given
$Re$
and it appears the flow regimes of the square cylinder shift upwards as a result. Furthermore, for intermediate values of
$KC$
number a lower
$Re$
is required for the flow around the circular cylinder to break
$K_{y}$
symmetry (2.2). Noting the shape of the
$KC_{St}$
curves in figure 18 this is consistent with the fact that for a given
$KC$
number,
$KC/KC_{St}\sim 1$
at a relatively smaller
$Re$
number for the circular cylinder, thus resulting in a leftwards shift in the flow regimes for the circular cylinder compared to the square cylinder.
3.3.3 Flow dependence on
$St$
The shift of flow regimes as observed between square and circular cylinders is further explored by considering rectangular cylinders with different aspect ratios (where the aspect ratio is defined as the ratio of the width of cylinder in the flow direction to its height). A rectangular cylinder is chosen because its
$St$
is dependent on the configuration. It is therefore anticipated that a similar shift in flow regimes will be evident for rectangles with different aspect ratios. It should be noted that in the following discussion,
$Re$
,
$St$
and
$KC$
are all defined based on
$D$
, the facing height of the rectangular cylinder.
Figure 19. The dependence of flow regimes on the length (in the streamwise direction) of a rectangular cylinder, increasing from left to right at
$(1/3)D$
,
$D$
and
$3D$
, while the heights of the cylinders are kept at
$D$
. Flow fields are obtained through 2-D DNS simulations at
$(Re,KC)=(160,9)$
.
Table 2. The non-dimensional vortex-shedding period (
$KC_{St}$
) of a rectangular cylinder with different aspect ratios placed in the uniform flow at
$Re=140$
.
In the laminar regime for unidirectional flow, a reduction in
$St$
with an increase in aspect ratio was observed in the study of Okajima (Reference Okajima1982) for a rectangular cylinder. This trend is consistent with the present DNS in table 2 at
$Re=140$
. Based on these results and the understanding gained for the square cylinder, one would expect that the curves of marginal stability along with the flow regimes for a rectangular cylinder will shift to the right as the aspect ratio increases. This is because a general reduction in
$St$
across all
$Re$
implies that for intermediate
$KC$
number
$KC/KC_{St}$
becomes close to unit at a lower
$Re$
. This is confirmed through both DNS and Floquet stability analysis. Figure 19 illustrates the flow fields from DNS for a rectangular cylinder with aspect ratio of
$1/3$
, 1 and 3 at
$(Re,KC)=(160,9)$
, corresponding to flow characteristics of regime F, D and A, respectively.
The curves of the marginal stability for rectangular cylinders with aspect ratio of
$2/3$
, 1 and
$3/2$
are shown in figure 20. It is observed that the marginal stability curve indeed moves towards the right as the aspect ratio increases. Similar dependence of flow regimes on aspect ratio was also observed in a recent work for elliptical foils in oscillatory flow, where the marginal stability curves move to a lower value of
$KC$
with the reduction of aspect ratio from 1 (circular cylinder) to 0.1 (see figure 5 in Deng & Caulfield Reference Deng and Caulfield2016).
Figure 20. The dependence of the curve of marginal stability on the aspect ratios of a rectangular cylinder, increasing from left to right at
$2/3$
, 1 and
$3/2$
. Results were obtained from Floquet analysis.
4 Conclusions
Flow regimes induced by oscillatory flow around a square cross-section cylinder at zero incidence angle were studied based on 2-D direct numerical simulations and Floquet stability analysis at intermediate Keulegan–Carpenter (
$1\leqslant KC\leqslant 15$
) and low Reynolds
$(Re\leqslant 200)$
number. The main findings from the present study are summarised as follows:
-
(i) Compared with the family of flow regimes around a circular cylinder in oscillatory flow, two new flow regimes have been discovered for the square cylinder. One is characterised by the transverse convection of fluid particles at
$KC\leqslant 2$
(regime A
$^{\prime }$
), where the shear layers are forced to align with the leading edges of the square, causing the released particles to move perpendicular to the direction of flow oscillation. The second new flow regime is characterised by quasi-periodic flows at approximately 10
${<}KC<13$
(regime F
$^{\prime }$
), where the flow holds a well-defined secondary period, which is much larger than the oscillation period. The secondary period increases with the increase of
$KC$
until the flow synchronises again with the oscillation. -
(ii) Moving along the curve of marginal stability, an alternate pattern in the modes of instability has been identified which break the reflection symmetry about the axis of motion. The instability is quasi-periodic at low
$KC$
, and becomes synchronous with the imposed oscillation between
$8.25<KC\leqslant 10$
. The instability reverts to quasi-periodic with further increase in
$KC$
and becomes synchronous again above
$KC=13$
. It is the second range of quasi-periodicity that leads to the newly observed flow regime F
$^{\prime }$
. -
(iii) The two quasi-periodic flow features appear to be induced by the mismatch between oscillation period and the time required for vortex formation and shedding. This has given rise to the incomplete shedding of a vortex core during one cycle of oscillation, whereas the residual vortex moves back with the reversed flow and accumulates in multiple cycles of motion. Compared to the non-dimensional vortex-shedding period in otherwise unidirectional flow (
$KC_{St}$
, the reciprocal of Strouhal number), the two quasi-periodic regimes locate close to the lines of
$KC_{St}$
or
$2KC_{St}$
. For oscillatory flow around a bluff body of different geometry from a circular cylinder, the marginal stability curve appears to shift in a way that is consistent with the shift of
$KC_{St}$
of the body from its circular counterpart, based on the results obtained with a limited number of rectangular geometries.
Figure 21. View of the domain and mesh used in the Floquet stability analysis. A domain size of
$80D\times 40D$
with a total of 528 quadrilateral elements was chosen, adapted from meshes (b) and (c) in Elston et al. (Reference Elston, Blackburn and Sheridan2006). Each element shown in the top half of the domain contains
$N_{p}^{2}$
mesh points, while in the bottom half,
$N_{p}=8$
.
Table 3.
$N_{p}$
-convergence results for the peak of in-line coefficients (
$C_{I}$
), drag and inertia coefficients (
$C_{D}$
and
$C_{M}$
) and the root-mean-square (r.m.s.) of the lift coefficients (
$C_{L}$
) of the square cylinder at (i)
$(Re,KC)=(100,8)$
and (ii) (200, 6). Only r.m.s.
$C_{L}$
at (ii) is given because the flow field of (i) is
$K_{y}$
symmetric.
Acknowledgements
The input from three anonymous referees is greatly appreciated. This work was supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia.
Appendix
A mesh check was carried out for the Nektar++ (Cantwell et al.
Reference Cantwell, Moxey, Comerford, Bolis, Rocco, Mengaldo, De Grazia, Yakovlev, Lombard and Ekelschot2015) code before carrying out the Floquet stability analysis. A domain size of
$80D\times 40D$
with 576 quadrilateral spectral elements was chosen based on the mesh checks from Elston et al. (Reference Elston, Blackburn and Sheridan2006). Figure 21 shows the computational domain and a typical mesh distribution, where the top half of the domain gives the distribution of the quadrilateral elements, while the bottom half illustrates the mesh points after eighth-order Lagrange polynomials expansion
$(N_{p}=8)$
. Here, the quadrilateral expansion was employed through the Gauss–Lobatto–Legendre quadrature points within each element. Table 3 provides a summary of the dependence study for a constant number of quadrilateral elements at two locations in the
$(Re,KC)$
-space.
$N_{p}$
from 4 to 10 were tested, resulting a global number of points ranging from 8448 to 52 800. The converged force coefficients in table 3 demonstrates that
$N_{p}$
effects are not significant for
$N_{p}\geqslant 6$
and
$N_{p}=8$
is deemed to be sufficient.
