1 Introduction
Let D be a bounded domain and
$\Omega $
a bounded homogeneous domain in
$\mathbb {C}^n$
and let
$z\in D$
. Denote by
$O(\Omega ,D)$
the set of holomorphic maps from
$\Omega $
into D. Denote by d either the Carathéodory pseudosdistance c or the Kobayashi pseudodistance k on D. Fridman [Reference Fridman6, Reference Fridman7] introduced a holomorphic invariant, now called the Fridman invariant:
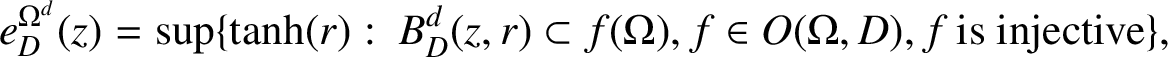$$ \begin{align*}e^{\Omega^{d}}_{D}(z)= \sup\{\tanh(r):\ B^{d}_{D}(z,r) \subset f(\Omega), f\in O(\Omega, D), f\:\textrm{is injective}\},\end{align*} $$
where
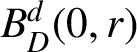$B^{d}_{D}(0, r)$
is the d-ball centred at z with radius r. (In [Reference Fridman6, Reference Fridman7],
$\inf {1}/{r}$
was used instead of
$\mathop {\mathrm {sup}} \tanh (r)$
.) We denote
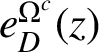$e^{\Omega ^c}_{D}(z)$
by
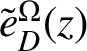$\tilde {e}^{\Omega }_{D}(z)$
and
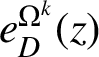$e^{\Omega ^k}_{D}(z)$
by
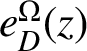$e^{\Omega }_{D}(z)$
in this paper. When
$\Omega $
is the unit ball
$B^n$
, we denote
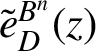$\tilde {e}^{B^n}_{D}(z)$
by
$\tilde {e}_{D}(z)$
and
$e^{B^n}_{D}(z)$
) by
$e_{D}(z)$
.
Let
$\mathbb D$
be the unit disk in
$\mathbb {C}$
. The Carathéodory pseudodistance on
$\Omega $
is defined as
$$ \begin{align*}c_\Omega (z,w)=\sup\{\operatorname{artanh}(|\lambda|): f\in O(\Omega,\mathbb D), f(z)=0, f(w)=\lambda \}.\end{align*} $$
Let
$$ \begin{align*}\ell_{\Omega}(z^{\prime}, z^{\prime \prime})=\inf \{\operatorname{artanh}(|\lambda|) : \varphi \in O(\mathbb{D}, \Omega), \varphi(0)=z^{\prime},\ \varphi(\lambda)=z^{\prime \prime}\}. \end{align*} $$
The Kobayashi pseudodistance for
$\Omega $
is
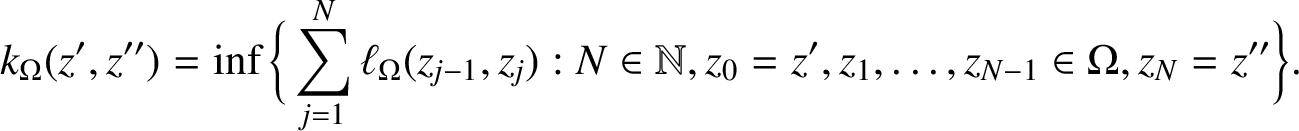$$ \begin{align*}k_{\Omega}(z^{\prime}, z^{\prime \prime})=\inf \bigg\{\sum\limits_{j=1}^{N} \ell_{\Omega}(z_{j-1}, z_{j}): N \in \mathbb{N}, z_{0}=z^{\prime}, z_{1}, \ldots, z_{N-1} \in \Omega, z_{N}=z^{\prime \prime}\bigg\}. \end{align*} $$
Another invariant, called the squeezing function, was introduced by Deng et al. [Reference Deng, Guan and Zhang2]:
$$ \begin{align*}s_{D}(z)=\sup\{r:\ rB^{n} \subset f(D),\ f\in O(D,B^{n}),\ f(z)=0,\ f\:\text{is injective}\}.\end{align*} $$
From the definitions, it is clear that
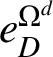$e^{\Omega ^{d}}_{D}$
and
$s_D$
are invariant under biholomorphisms. Many properties of
$\tilde {e}_{D}$
,
$e_{D}$
and
$s_D$
have been explored (see the survey paper [Reference Deng, Wang, Zhang and Zhou4] and the references therein). For results on the boundary behaviour of
$e_{D}$
, we refer to [Reference Fridman7, Reference Mahajan and Verma11, Reference Ng, Tang and Tsai12, Reference Nikolov and Verma14] and for the boundary behaviour of
$s_{D}(z)$
to [Reference Deng, Guan and Zhang3, Reference Fornaess and Wold5, Reference Kim and Zhang9, Reference Nikolov and Trybula13].
Recently, Nikolov and Verma [Reference Nikolov and Verma14, Proposition 4] proved that
$e_{D}$
goes to 1 near strongly pseudoconvex boundary points. Because
$\tilde {e}_{D}(z)\le e_{D}(z)$
, it is of interest to investigate whether the same result holds for
$\tilde {e}_{D}$
. Here we give a negative answer. In fact, for any
$c\in (0,1)$
, there exist a bounded nonpseudoconvex domain
$D_{c}$
and a strongly pseudoconvex boundary point a such that
$\lim _{z \rightarrow a} \tilde {e}_{D_c}(z)=c$
.
Theorem 1.1. Let
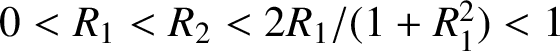$0<R_{1}<R_{2}<{2R_{1}}/{(1+R_{1}^2)}<1$
and let
$D=B^n\setminus K$
, where
$n\ge 2$
and
$K=\{z\in \mathbb {C}^n \mid R_{1}\leq \|z\|\leq R_{2}, {\textrm {Re}}\, z_{n}\ge 0 \}$
. Take
$p=(0,0,\ldots ,R_{1})$
and
$p_{k}=(0,0,\ldots ,(1-{1}/{k})R_{1})$
,
$k\in \mathbb {N}$
. Then,
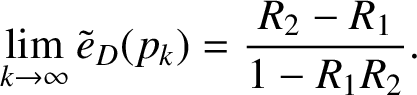$$ \begin{align*}\lim_{k \rightarrow \infty} \tilde{e}_{D}(p_{k})=\frac{R_{2}-R_{1}}{1-R_{1}R_{2}}.\end{align*} $$
Let
$\Omega $
be a bounded domain in
$\mathbb {C}^{n}$
,
$n\geq 2$
. Let K be a compact subset of
$\Omega $
such that
$D=\Omega \backslash K$
is connected. Bharali proved that
$s_{D}(z) \leq \tanh (k_{\Omega }(z; \partial D \cap K))$
[Reference Bharali1, Theorem 1.8]. From Theorem 1.1, it is clear that there is no such estimation for
$\tilde {e}_{D}$
under the same condition.
Let K be a compact subset of
$B^n$
,
$n\ge 2$
, such that
$D=B^n \backslash K$
is connected. In [Reference Rong and Yang17], we proved that
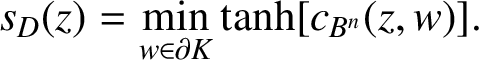$$ \begin{align*}s_{D}(z)=\min_{w\in \partial K}\tanh[c_{B^n}(z,w)].\end{align*} $$
Moreover, for some special K (for example, a pseudoconvex subdomain of
$B^n$
with dense strongly pseudoconvex points in
$\partial K$
), we have
$s_{D}(z)=\tilde {e}_{D}(z)$
. It follows from Theorem 1.1 that
$\tilde {e}_{D}=s_{D}$
does not hold for general compact subsets K. See [Reference Rong and Yang15–Reference Rong and Yang17] for more results on the comparison of the Fridman invariant and the squeezing function.
However, it is also natural to ask how
$\tilde {e}_{D}(z)$
behaves near nonpseudoconvex boundary points. We show that
$\tilde {e}_{D}(z)$
goes to 0 near such points.
Theorem 1.2. Let D be a bounded domain in
$\mathbb {C}^n$
,
$n\ge 2$
, and assume that
$\partial D$
is
$C^{2}$
smooth near
$p\in \partial D$
. If p is not pseudoconvex, then
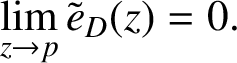$$ \begin{align*}\lim_{z \rightarrow p} \tilde{e}_{D}(z)=0.\end{align*} $$
Because
$s_{D}(z)\leq \tilde {e}_{D}(z)$
[Reference Nikolov and Verma14, Proposition 1], Theorem 1.2 immediately implies the following result.
Corollary 1.3. Let D be a bounded domain in
$\mathbb {C}^n$
,
$n\ge 2$
, and assume that
$\partial D$
is
$C^{2}$
smooth near
$p\in \partial D$
. If p is not pseudoconvex, then
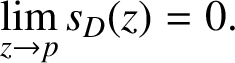$$ \begin{align*}\lim_{z \rightarrow p} s_{D}(z)=0.\end{align*} $$
Let
$D \subsetneq \mathbb {C}^{n}, n \geq 2$
, be a bounded domain and let
$\mathcal {S}$
be a subset of
$O(D)$
which contains all the bounded holomorphic functions. Define
$$ \begin{align*}\partial^{\mathcal{S}} D:=\left\{\xi \in \partial D: \begin{array}{@{}l@{}} \text{there exists } U, \mbox{ a connected open neighbourhood of } \xi, \\ \mbox{and } V, \mbox{ a connected component of } D \cap U, \mbox{ such that } \\ \text{for all } f \in \mathcal{S}, \text{ there exists } F_{f} \in O(U) \mbox{ satisfying } f|_{V}=F_{f}|_{V} \end{array} \right\}\end{align*} $$
Bharali [Reference Bharali1, Theorem 1.11] proved that
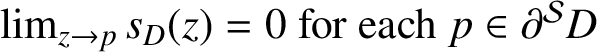$\lim _{z \rightarrow p} s_{D}(z)=0 \text { for each } p \in \partial ^{\mathcal {S}} D$
. If
$p\in \partial D$
is not pseudoconvex, then
$p\in \partial ^{\mathcal {S}} D$
. Thus, the above corollary can also be seen as a special case of [Reference Bharali1, Theorem 1.11].
Let
$\Omega $
be a bounded domain in
$\mathbb {C}^n$
,
$n\ge 2$
, and K a compact subset of
$\Omega $
such that
$D=\Omega \backslash K$
is connected. By Hartog’s extension theorem,
$\partial K \subset \partial ^{\mathcal {S}} D$
. Hence Theorem 1.1 shows that, for
$p\in \partial ^{\mathcal {S}} D$
, in general,
$\lim _{z \rightarrow p} \tilde {e}_{D}(z)\neq 0$
.
We have the following result.
Theorem 1.4. Let
$\Omega $
be a bounded domain in
$\mathbb {C}^n$
,
$n\ge 2$
, and let K be a compact subset of
$\Omega $
such that
$D=\Omega \backslash K$
is connected. Then
$\lim _{z \rightarrow p} \tilde {e}_{D}(z)$
exists for any
$p\in \partial K$
.
Let D and p be as in Theorem 1.1. Combining Theorem 1.1 with Theorem 1.4 shows that
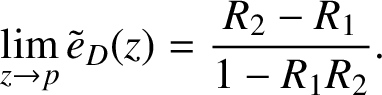$$ \begin{align*}\lim _{z \rightarrow p} \tilde{e}_{D}(z)=\frac{R_{2}-R_{1}}{1-R_{1}R_{2}}.\end{align*} $$
It is easy to see that for any
$c\in (0,1)$
, there exist
$R_1, R_2$
with
$0<R_{1}<R_{2}<1$
such that
${(R_{2}-R_{1})}/{(1-R_{1}R_{2})}=c$
.
It is then natural to ask whether the same result holds for
$e_{D}$
. The answer is negative as the following result shows.
Theorem 1.5. Let
$0<R_{1}<R_{2}<1$
,
$K_{1}=\{z \mid R_{1}\leq \|z\|\leq R_{2}, {\textrm {Re}}\, z_{n}\ge 0 \}$
and
$K_{2}=\{p_{j}\}_{j\in \mathbb {N}}$
, where
$p_{j}=((1-{1}/{j})R_{1},0,\ldots ,0)$
. Take
$K=K_{1}\cup K_{2}$
and
$D=B^n\setminus K$
,
$n\ge 2$
. Then
$e_{D}(z)$
cannot be extended continuously to
$\partial K$
.
2 Proof of the results
We will use Hartogs’s extension theorem (see, for example, [Reference Krantz10, Theorem 1.2.6]), which we state as the following lemma.
Lemma 2.1. Let
$\Omega $
be a domain in
$\mathbb C^{n}$
,
$n\ge 2$
, and let K be a compact subset of
$\Omega $
such that
$\Omega \backslash K$
is connected. If f is holomorphic on
$\Omega \backslash K$
, then there exists a holomorphic function F on
$\Omega $
such that
$F|_{\Omega \backslash K}=f$
.
Proof of Theorem 1.1
Because
$B^n$
is biholomorphic to
$B^n(0,R_{1})$
and they are both homogeneous, for
$p_{k}=(0,0,\ldots ,(1-{1}/{k})R_{1})$
, there exists a holomorphic embedding
$f_k:B^n \rightarrow B^n(0,R_{1})$
such that
$f_k(0)=p_{k}$
and
$f_k(B^n)=B^n(0,R_{1})$
. By Lemma 2.1,
$c_{D}(z_1,z_2)=c_{B^n}(z_1,z_2)$
, for all
$z_1, z_2 \in D$
. From [Reference Jarnicki and Pflug8, Corollary 2.3.5],
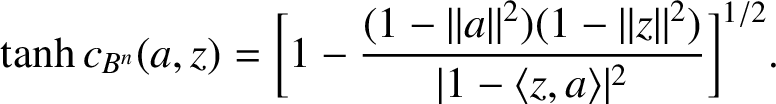$$ \begin{align*}\tanh c_{B^{n}}(a,z)=\bigg[1-\frac{(1-\|a\|^{2})(1-\|z\|^{2})}{|1-\langle z, a\rangle|^{2}}\bigg]^{{1}/{2}}.\end{align*} $$
Let
$w\in \{z\in B^n \mid {\textrm {Re}}\, z_{n}=0 \}$
. It is easy to see that
$$ \begin{align*}\tanh c_{B^{n}}(p,w)\ge \tanh c_{B^{n}}(p,0)=R_{1}.\end{align*} $$
Denote
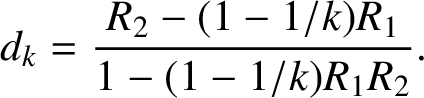$$ \begin{align*}d_{k}=\frac{R_{2}-(1-{1}/{k})R_{1}}{1-(1-{1}/{k})R_{1}R_{2}}.\end{align*} $$
Because
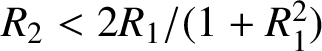$R_{2}<{2R_{1}}/{(1+R_{1}^2)}$
, there exists
$N>0$
such that for any
$k>N$
,
$$ \begin{align*}B^{c}_{D}(p_{k},\operatorname{artanh}(d_{k}))\subset B^n(0,R_{1})=f_k(B^n),\end{align*} $$
and hence
$\tilde {e}_{D}(p_{k})\ge d_{k}$
.
We claim that
$\tilde {e}_{D}(p_{k})\leq d_{k}$
. For w with
$\|w\|=R_{2}$
, it is obvious that
$$ \begin{align*}\tanh[c_{\Omega}(p_{k},w)]\leq \tanh[c_{\Omega}(p_{k},q)]=d_{k},\end{align*} $$
where
$q=(0,0,\ldots ,R_{2})$
. Suppose that
$\tilde {e}_{D}(p_{k})>d_{k}$
. Then, there exists
$r>\operatorname {artanh}(d_{k})$
and a holomorphic embedding
$g_k:B^n \rightarrow D$
such that
$g_k(0)=p_{k}$
and
$B^{c}_{D}(p_{k},r)\subset g_k(B^n)$
. Because the Carathéodory pseudodistance is continuous (see, for example, [Reference Jarnicki and Pflug8]), we know that
$B^{c}_{D}(p_{k},r)$
and
$B^{c}_{B^n}(p_{k},r)$
are open. It follows that there exists
$\delta>0$
such that
$B^{n}(q,\delta )\subset B^{c}_{B^n}(p_{k},r)$
. Because
$B^{c}_{D}(p_{k},r)\subset g_k(B^n)\subset D$
and
$c_{D}(z_1,z_2)=c_{B^n}(z_1,z_2)$
, we have
$B^{n}(q,\delta )\cap g_k(B^n) \neq \emptyset $
and
$B^{n}(q,\delta )\cap \partial B^n(0,R_{2})\subset \partial (g_k(B^n))$
.
However, it is clear that
$q\in \partial B^n(0,R_{2})$
is strongly pseudoconvex for
$B^n(0,R_{2})$
. Thus, there exists a local
$C^2$
defining function
$\rho $
such that
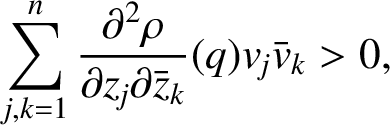$$ \begin{align*} \sum_{j, k=1}^{n} \frac{\partial^{2} \rho}{\partial z_{j} \partial \bar{z}_{k}}(q) v_{j} \bar{v}_{k}> 0, \end{align*} $$
for all
$v \in \mathbb {C}^{n}$
satisfying
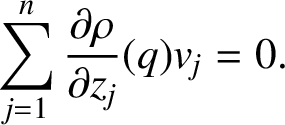$$ \begin{align*} \sum_{j=1}^{n} \frac{\partial \rho}{\partial z_{j}}(q) v_{j}=0. \end{align*} $$
However,
$g_k(B^n)$
is pseudoconvex and it is clear that
$-\rho (z)$
is a local defining function on some neighbourhood of q for
$g_k(B^n)$
. It follows that
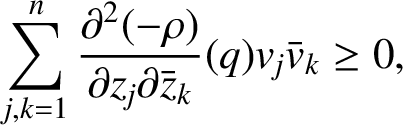$$ \begin{align*} \sum_{j, k=1}^{n} \frac{\partial^{2} (-\rho)}{\partial z_{j} \partial \bar{z}_{k}}(q) v_{j} \bar{v}_{k} \ge 0, \end{align*} $$
for all
$v \in \mathbb {C}^{n}$
satisfying
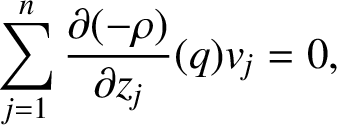$$ \begin{align*} \sum_{j=1}^{n} \frac{\partial (-\rho)}{\partial z_{j}}(q) v_{j}=0, \end{align*} $$
which is a contradiction. Hence
$\displaystyle \tilde {e}_{D}(p_{k})\leq d_{k}$
. So we have
$\tilde {e}_{D}(p_{k})= d_{k}$
, which implies
$$ \begin{align*}\lim _{k \rightarrow \infty} \tilde{e}_{D}(p_{k})=\frac{R_{2}-R_{1}}{1-R_{1}R_{2}}.\\[-42pt]\end{align*} $$
Proof of Theorem 1.2
Because p is not pseudoconvex, we can find a connected neighbourhood
$U_{p}$
of p such that for any holomorphic function f on D, there exists a holomorphic function F on
$U_{p}$
with
$F|_{U_{p}\cap D}=f|_{U_{p}\cap D}$
.
It is clear that
$D_1=U_{p}\cup D$
is a connected open set. We claim that
$c_{D}(z_1,z_2)=c_{D_{1}}(z_1,z_2)$
, for all
$z_1, z_2 \in D$
.
Let
$f\in O(D,\mathbb {D})$
. Then there exists a holomorphic function F on
$D_{1}$
such that
$F|_{D}=f$
. Moreover
$F(D_{1})=f(D)$
. Indeed, if there exists
$w\in D_{1}$
such that
$F(w)\notin f(D)$
, then
$h(z)={1}/{(f(z)-F(w))}$
is holomorphic on D, but with no holomorphic function
$H(z)$
on
$D_{1}$
such that
$H|_{D}=h$
, a contradiction. By the definition of Carathéodory pseudodistance, we have
$c_{D}(z_1,z_2)=c_{D_{1}}(z_1,z_2)$
, for all
$z_1, z_2 \in D$
.
Assume that
$\lim _{z \rightarrow p} \tilde {e}_{D}(z)=0$
does not hold. Then there exists
${p_{k}} \rightarrow p$
such that
$\lim _{k \rightarrow \infty } \tilde {e}_{D}(p_{k})=A>0$
. Because
$\lim _{k \rightarrow \infty }c_{D_{1}}(p_{k},p)=0$
, for
$0<\epsilon <{A}/{2}$
, we can find
$N>0$
such that for any
$k>N$
, there exist
$r_{k}>\operatorname {artanh}(A-\epsilon )$
and a holomorphic embedding
$f_{k}:B^n \rightarrow D$
such that
$f_{k}(0)=p_{k}$
,
$B^{c}_{D}(p_{k},r_k)\subset f_k(B^n)$
and
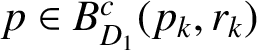$p\in B^{c}_{D_1}(p_{k},r_k)$
. Because the Carathéodory pseudodistance is continuous, there exists
$\delta _{k}>0$
such that
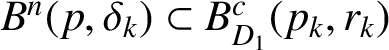$B^{n}(p,\delta _k)\subset B^{c}_{D_{1}}(p_{k},r_{k})$
. Because
$c_{D}(z_1,z_2)=c_{D_{1}}(z_1,z_2)$
, we have
$D_{1}(p,\delta _k)\cap f_k(B^n) \neq \emptyset $
and
$B^{n}(p,\delta _k)\cap \partial D\subset \partial (f_k(B^n))$
.
Because
$p\in \partial D$
is not pseudoconvex, there is a local
$C^2$
defining function
$\rho $
such that
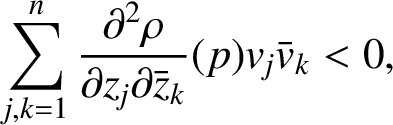$$ \begin{align*} \sum_{j, k=1}^{n} \frac{\partial^{2} \rho}{\partial z_{j} \partial \bar{z}_{k}}(p) v_{j} \bar{v}_{k} < 0, \end{align*} $$
for some
$v \in \mathbb {C}^{n}$
satisfying
$$ \begin{align*} \sum_{j=1}^{n} \frac{\partial \rho}{\partial z_{j}}(p) v_{j}=0. \end{align*} $$
However,
$f_k(B^n)$
is pseudoconvex and it is clear that
$\rho (z)$
is a local defining function on some neighbourhood of p for
$f_k(B^n)$
. It follows that
$$ \begin{align*} \sum_{j, k=1}^{n} \frac{\partial^{2} \rho}{\partial z_{j} \partial \bar{z}_{k}}(p) v_{j} \bar{v}_{k} \ge 0, \end{align*} $$
for all
$v \in \mathbb {C}^{n}$
satisfying
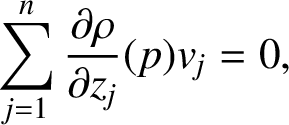$$ \begin{align*} \sum_{j=1}^{n} \frac{\partial \rho}{\partial z_{j}}(p) v_{j}=0, \end{align*} $$
which is a contradiction. This implies that
$\lim _{z \rightarrow p} \tilde {e}_{D}(z)=0$
.
To prove Theorem 1.4, the following lemma is needed.
Lemma 2.2. Let D be a bounded domain in
$\mathbb {C}^{n}$
. Then,
$$ \begin{align*}|\tilde{e}_{D}(z_{1})-\tilde{e}_{D}(z_{2})| \leq \tanh[c_{D}(z_{1},z_{2})],\quad \text{for all } z_{1},z_{2}\in D .\end{align*} $$
Proof. If
$\tilde {e}_{D}(z_{1})=\tilde {e}_{D}(z_{2})=0$
, then we have the conclusion. Thus, without loss of generality, assume that
$\tilde {e}_{D}(z_{1})>0$
.
Let
$0<\epsilon <\tilde {e}_{D}(z_{1})$
. By definition, there is a holomorphic embedding
$f: B^n \rightarrow D$
such that
$B^{c}_{D}(z_{1},\operatorname {artanh}[\tilde {e}_{D}(z_{1})-\epsilon ]) \subset f(B^n)$
.
If
$z_{2}\not \in B^{c}_{D}(z_{1},\operatorname {artanh}[\tilde {e}_{D}(z_{1})-\epsilon ])$
, then clearly
$$ \begin{align*}\tilde{e}_{D}(z_{2})\ge \tilde{e}_{D}(z_{1})-\epsilon-\tanh[c_{D}(z_{1},z_{2})].\end{align*} $$
Assume that
$z_{2}\in B^{c}_{D}(z_{1},\operatorname {artanh}[\tilde {e}_{D}(z_{1})-\epsilon ])$
. It is easy to check that
$\tanh (t_{3}) \leq \tanh (t_{1})+\tanh (t_{2})$
for all
$t_{i} \geq 0$
,
$i=1,2,3$
, with
$t_{3} \leq t_{1}+t_{2}$
. Then for all z with
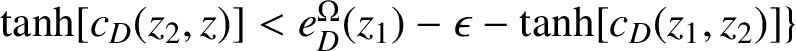$\tanh [c_{D}(z_{2},z)]< e^{\Omega }_{D}(z_{1})-\epsilon -\tanh [c_{D}(z_{1},z_{2})]\}$
,
$$ \begin{align*}\tanh[c_{D}(z_{1},z)]\leq \tanh[c_{D}(z_{2},z)]+\tanh[c_{D}(z_{1},z_{2})]<\tilde{e}_{D}(z_{1})-\epsilon.\end{align*} $$
This implies that
$$ \begin{align*}B^{c}_{D}(z_{2},\operatorname{artanh}[\tilde{e}_{D}(z_{1})-\epsilon-\tanh[c_{D}(z_{1},z_{2})]]) \subset B^{c}_{D}(z_{1},\operatorname{artanh}[\tilde{e}_{D}(z_{1})-\epsilon])\subset f(B^n).\end{align*} $$
Hence
$$ \begin{align*}\tilde{e}_{D}(z_{2})\ge \tilde{e}_{D}(z_{1})-\epsilon-\tanh[c_{D}(z_{2},z_{1})].\end{align*} $$
Because
$\epsilon $
is arbitrary,
$$ \begin{align*}\tilde{e}_{D}(z_{2})\ge \tilde{e}_{D}(z_{1})-\tanh[c_{D}(z_{1},z_{2})].\end{align*} $$
If
$\tilde {e}_{D}(z_{2})=0$
, then
$\tilde {e}_{D}(z_{1})\leq \tanh [c_{D}(z_{1},z_{2})]$
and hence
$$ \begin{align*}|\tilde{e}_{D}(z_{1})-\tilde{e}_{D}(z_{2})| \leq \tanh[c_{D}(z_{1},z_{2})].\end{align*} $$
If
$\tilde {e}_{D}(z_{2})>0$
, then following the same discussion as for
$\tilde {e}_{D}(z_{1})>0$
,
$$ \begin{align*}\tilde{e}_{D}(z_{1})\ge \tilde{e}_{D}(z_{2})-\tanh[c_{D}(z_{2},z_{1})].\end{align*} $$
This completes the proof.
Proof of Theorem 1.4
By Lemma 2.1,
$c_{D}(z_1,z_2)=c_{\Omega }(z_1,z_2)$
, for all
$z_1, z_2 \in D$
. Let
$p\in \partial K$
. For any
$\epsilon>0$
, there exists
$\delta>0$
such that
$\tanh c_{D}(z_1,z_2)\leq \epsilon $
for all
$z_1,z_2 \in B^n(p,\delta )\cap D$
. By Lemma 2.2,
$|\tilde {e}_{D}(z_{1})-\tilde {e}_{D}(z_{2})| \leq \tanh [c_{D}(z_{1},z_{2})]\leq \epsilon $
. Hence
$\lim _{z \rightarrow p} \tilde {e}_{D}(z)$
exists for any
$p\in \partial K$
.
For the proof of Theorem 1.5, we need the following two results.
Lemma 2.3 [Reference Jarnicki and Pflug8, Corollary 3.4.3]
Let D be a bounded domain and A an analytic subset of D of codimension at least two. Then,
$$ \begin{align*}k_{D \backslash A}=k_{D}|_{(D \backslash A) \times(D \backslash A).}\end{align*} $$
Lemma 2.4 [Reference Nikolov and Verma14, Proposition 4]
Let D be a bounded domain and
$p_{0}$
a strongly pseudoconvex boundary point. Then,
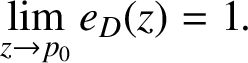$$ \begin{align*}\lim _{z \rightarrow p_{0}} e_{D}(z)=1.\end{align*} $$
Proof of Theorem 1.5
Let
$p=(R_{1},0,\ldots ,0)$
. It is clear that
$p\in \partial K$
and
$p_k \rightarrow p$
. Set
$D_j=D\cup \{p_j\}$
.
We will first prove that
$\lim _{z \rightarrow p_j} e_{D}(z)=0$
. Fix j and suppose that there exist
${z_{i}} \rightarrow p_j$
such that
$\lim _{i \rightarrow \infty } e_{D}(z_{i})=A>0$
. By Lemma 2.3,
$k_{D}(z_1,z_2)=k_{D_j}(z_1,z_2)$
, for all
$z_1, z_2 \in D$
. For
$0<\epsilon <{A}/{2}$
, we can find
$N>0$
such that for any
$i>N$
, there are
$r_{i}>\operatorname {artanh}{(A-\epsilon )}$
and a holomorphic embedding
$f_{i}:B^n \rightarrow D$
such that
${f_{i}(0)=z_{i}}$
,
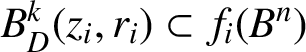$B^{k}_{D}(z_{i},r_i)\subset f_i(B^n)$
and
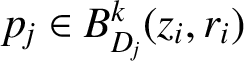$p_j\in B^{k}_{D_j}(z_{i},r_i)$
. Because the Kobayashi pseudodistance is continuous (see, for example, [Reference Jarnicki and Pflug8]), there exists
$\delta _{i}>0$
such that
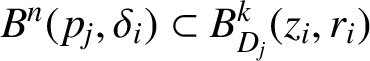$B^{n}(p_j,\delta _i)\subset B^{k}_{D_{j}}(z_{i},r_{i})$
. Because
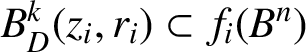$ B^{k}_{D}(z_{i},r_{i})\subset f_i(B^n)$
, we have
$\{z \mid 0<\|z-p_j\|<\delta _{i}\}\subset f_i(B^n)$
but
$p_j\notin f_i(B^n)$
, which contradicts the fact that
$f_i(B^n)$
is pseudoconvex.
Denote
$S=\{z \mid \|z\|=R_1, {\textrm {Re}}\, z_n>0\}$
. It is clear that S is a smooth subset of
$\partial D$
and each point of S is strongly pseudoconvex. Assume that
$e_{D}(z)$
can be extended continuously to
$\partial K$
. Because
$\lim _{z \rightarrow p_j} e_{D}(z)=0$
and
$p_j \rightarrow p$
, we have
$\lim _{z \rightarrow p} e_{D}(z)=0$
. However, there exist
$w_j\in S \rightarrow p$
. By Lemma 2.4,
$\lim _{z \rightarrow w_j} e_{D}(z)=1$
. Hence
$\lim _{z \rightarrow p} e_{D}(z)\,{=}\,1$
, which is a contradiction.
Acknowledgement
The author is grateful to the anonymous referee for many useful suggestions for improving this paper.
