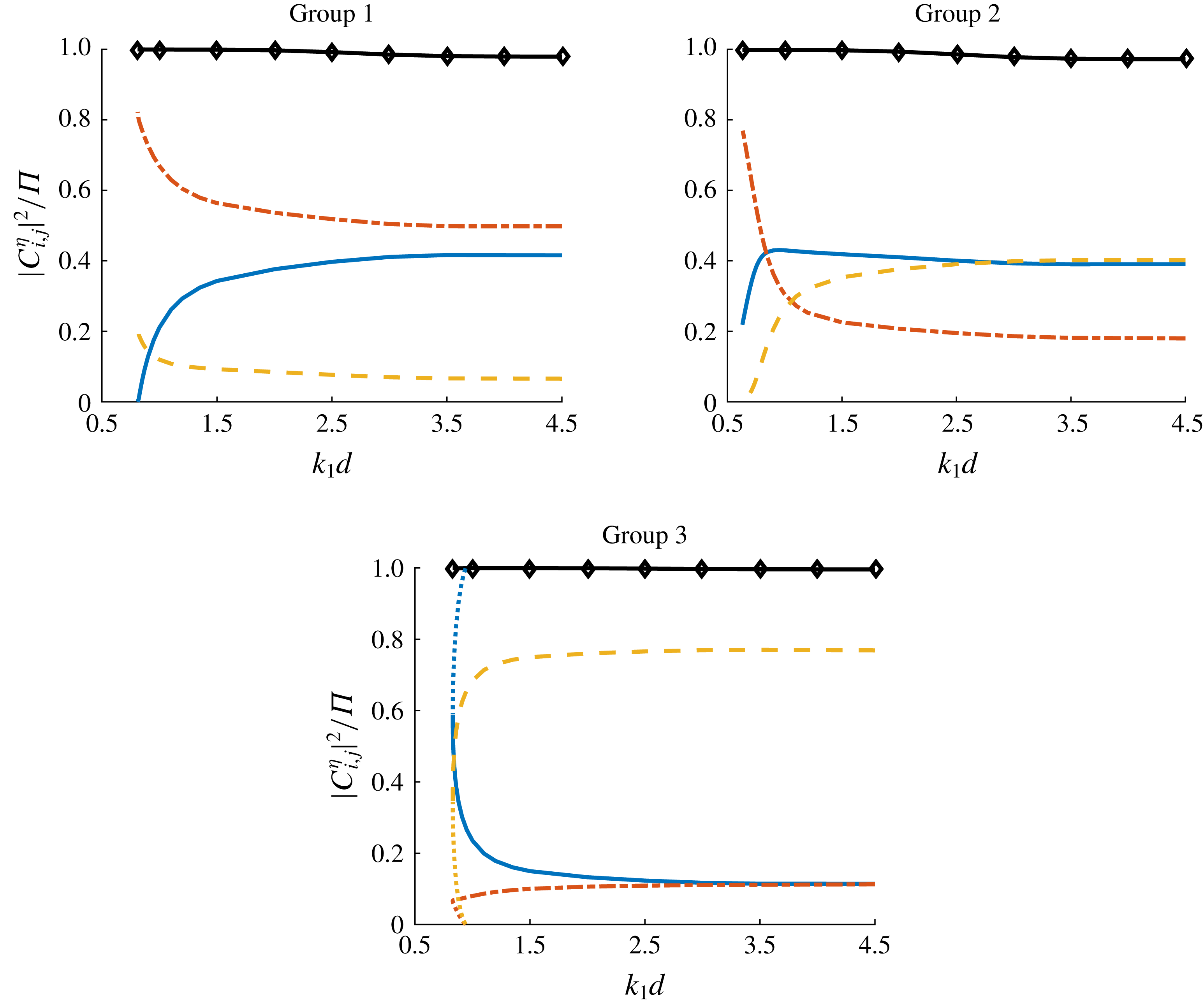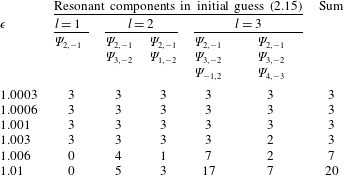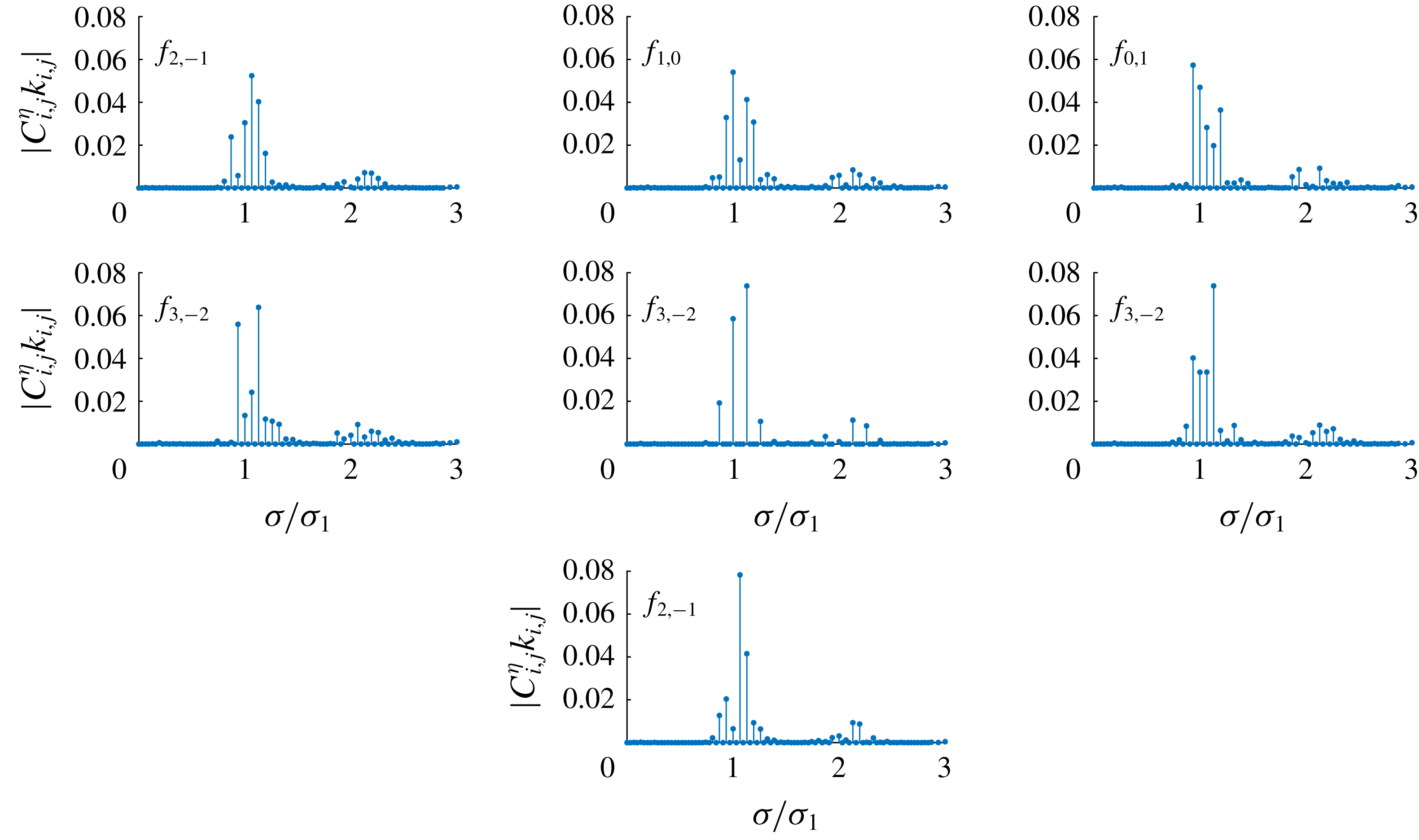1 Introduction
Inspired by the energy transfer due to nonlinear interactions between random components in a field of turbulence, Phillips (Reference Phillips1960) examined the interaction among two gravity wave trains by a perturbation method to see whether and under what conditions they would transfer energy to build up a third component (Phillips Reference Phillips1981). Phillips (Reference Phillips1960) found that if the condition
$$\begin{eqnarray}\displaystyle 2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}=\boldsymbol{k}_{0},\quad 2\unicode[STIX]{x1D714}_{1}-\unicode[STIX]{x1D714}_{2}=\unicode[STIX]{x1D714}_{0}, & & \displaystyle\end{eqnarray}$$
was satisfied by three components with
$\unicode[STIX]{x1D714}_{i}=\sqrt{gk_{i}}$
, then a steady-state solution did not exist. The amplitude of the third wave,
$a_{3}$
, if initially zero, would grow linearly in time. Hasselmann (Reference Hasselmann1962, Reference Hasselmann1963a
,Reference Hasselmann
b
) studied the transfer of energy among different wave components in a continuous spectrum at sea. Benney (Reference Benney1962) established the equations governing the time dependence of the resonant modes to demonstrate the energy-sharing mechanism more clearly. And experiments were conducted by Longuet-Higgins & Smith (Reference Longuet-Higgins and Smith1966) and McGoldrick et al. (Reference McGoldrick, Phillips, Huang and Hodgson1966) to confirm that resonant interactions indeed existed and the growth rates were correctly predicted. Nowadays, it is believed that four-wave resonant interactions play an important role in the evolution of the spectrum of surface gravity waves in deep water (Janssen Reference Janssen2003). As the waves travel into shallow areas, three-wave resonant interactions become the main nonlinear mechanism of energy transfer (Freilich, Guza & Elgar Reference Freilich, Guza and Elgar1990; Hammack & Henderson Reference Hammack and Henderson1993; Onorato et al.
Reference Onorato, Osborne, Janssen and Resio2009).
Compared with the huge literature concerning wave spectrum evolution due to resonant interactions in deep or shallow water, the investigation of wave evolution in finite depth is considerably less developed, owing to its complexity. Following Fenton (Reference Fenton1979) and Francius & Kharif (Reference Francius and Kharif2006), we define waves in finite water depth as
$\unicode[STIX]{x03C0}/4<kd<\unicode[STIX]{x03C0}$
. Taking the main existing model to study the evolution of sea states, the Zakharov equation (Zakharov Reference Zakharov1968; Zakharov & Kharitonov Reference Zakharov and Kharitonov1970; Lavrova Reference Lavrova1983), as our example, the kernel function
$T(\boldsymbol{k}_{a},\boldsymbol{k}_{b},\boldsymbol{k}_{c},\boldsymbol{k}_{d})$
contains singular terms and is non-unique in finite water depth when
$\boldsymbol{k}_{c}=\boldsymbol{k}_{a}$
and
$\boldsymbol{k}_{d}=\boldsymbol{k}_{b}$
(Stiassnie & Shemer Reference Stiassnie and Shemer1984; Zakharov Reference Zakharov1999). This non-unique limit has only been discussed recently by Janssen & Onorato (Reference Janssen and Onorato2007) for the special case of
$T(\boldsymbol{k}_{a},\boldsymbol{k}_{a},\boldsymbol{k}_{a},\boldsymbol{k}_{a})$
and by Stiassnie & Gramstad (Reference Stiassnie and Gramstad2009) for
$T(\boldsymbol{k}_{a},\boldsymbol{k}_{b},\boldsymbol{k}_{a},\boldsymbol{k}_{b})$
. Gramstad (Reference Gramstad2014) derived an alternative form of the Zakharov equation with a more simple kernel function in the Hamiltonian system.
Recently, Onorato et al. (Reference Onorato, Osborne, Janssen and Resio2009) found that the nonlinear transfer in shallow water is not so different from the deep-water one: in both cases it is ruled by a four-wave resonant interaction. Onorato et al. (Reference Onorato, Osborne, Janssen and Resio2009) suggested that the four-wave resonant interactions are naturally part of the shallow-water wave dynamics. These interactions are responsible for a constant flux of energy in the wave spectrum, i.e. an energy cascade towards high wavenumbers. Besides, Katsardi & Swan (Reference Katsardi and Swan2011) found that the nature of large unidirectional waves varies depending on the relative water depth. As the water depth reduces, both the bound and resonant interactions become more significant. However, the third-order resonant terms (four-wave resonant interactions) are able to alter both the amplitude and the phase of the freely propagating wave components and have the most profound influence. Meanwhile, Toffoli et al. (Reference Toffoli, Benoit, Onorato and Bitner-Gregersen2009) confirmed the strong deviation from Gaussian statistics of long-crested, deep-water waves caused by the third-order nonlinearity (four-wave resonant interactions). As the water depth decreases, however, the deviation from Gaussian statistics was gradually reduced. Up to now, the role that four-wave resonant interactions play in the nonlinear energy transfer of wave groups in finite water depth is not clear. Besides, to the best of our knowledge, little work has been done concerning the effect of three-wave resonant interactions on the spectrum evolution in finite water depth. The dominate resonant mechanism for the long-time evolution of the wave spectrum in finite water depths needs further investigation.
The dynamic spread of wave energy among multiple components is analytically intractable over time, so Alam, Liu & Yue (Reference Alam, Liu and Yue2010) concluded that such a scenario is suited to direct simulations such as the high-order spectrum method (Dommermuth & Yue Reference Dommermuth and Yue1987; Pan & Yue Reference Pan and Yue2014, Reference Pan and Yue2015; Miao & Liu Reference Miao and Liu2015; Qi et al. Reference Qi, Wu, Liu, Kim and Yue2018a ,Reference Qi, Wu, Liu and Yue b ). Steady-state waves provide the basic information about water waves and the simplest spectrum dates back to one-and-a-half centuries ago when Stokes (Reference Stokes1847) studied progressive periodic waves. When the resonance condition is satisfied, steady-state resonant waves with time-independent spectrum, i.e. all the amplitudes, frequencies and wavenumbers of the wave system are constant, have also been considered. Hui & Hamilton (Reference Hui and Hamilton1979) found that permanent wave groups of elliptic functions can be obtained from the Davey–Stewartson equation (Davey & Stewartson Reference Davey and Stewartson1974) in deep water. Besides, the shallow-water Davey–Stewartson equation is known to be integrable and, as a consequence, it does not admit a net flux of energy or wave action across the wave spectrum (Onorato et al. Reference Onorato, Osborne, Janssen and Resio2009).
Based on the homotopy analysis method (HAM) (Liao Reference Liao1992, Reference Liao2003, Reference Liao2012; Zhong & Liao Reference Zhong and Liao2018a ,Reference Zhong and Liao b ), Liao (Reference Liao2011) resolved the singularity caused by a single exact resonance and found that steady-state resonant waves in infinite depth can be obtained from the fully nonlinear water wave equations. Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) studied single exact resonance in finite water depth and Liu & Liao (Reference Liu and Liao2014) extended the work of Liao (Reference Liao2011) from a single quartet to coupled quartets and studied the coupled interactions among one exactly resonant set and six nearly resonant ones. The existence of such a kind of steady-state resonant waves was investigated experimentally in a basin at the State Key Laboratory of Ocean Engineering in Shanghai (Liu et al. Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015). For more general near-resonance, Liao, Xu & Stiassnie (Reference Liao, Xu and Stiassnie2016) proposed a solution procedure in HAM to resolve the single small divisor associated with the nearly resonant component. Liu, Xu & Liao (Reference Liu, Xu and Liao2018) further developed the solution procedure to resolve the small divisors associated with nearly resonant components, and finite-amplitude steady-state wave groups with multiple near-resonances have been obtained in deep water. As nonlinearity increases, Liu, Xu & Liao (Reference Liu, Xu and Liao2017) found that the bichromatic waves changed into steady-state resonant waves and the additional nearly resonant components influence the wave field distribution significantly. Yang, Dias & Liao (Reference Yang, Dias and Liao2018) considered the steady-state interaction of acoustic-gravity waves in an ocean of uniform depth.
It should be noted that Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) only obtained weakly nonlinear steady-state resonant waves with water depth
$kd$
decreasing from
$+\infty$
to
$1.88$
. Multiple solutions for steady-state waves were found, while the energy distribution within each group changed slightly with the water depth. No steady-state resonant waves have ever been reported as the water depth decreases further, even for weakly nonlinear waves. Besides, a system that admits one resonant set of waves often admits many resonant sets simultaneously (Hammack & Henderson Reference Hammack and Henderson1993). That is, waves often interact in coupled sets so that multiple resonances need to be considered. Up till now, finite-amplitude wave groups with multiple resonances have only been considered in infinite depth (Liu et al.
Reference Liu, Xu and Liao2018). The existence of steady-state resonant waves in finite water depth was confirmed (Xu et al.
Reference Xu, Lin, Liao and Stiassnie2012), while the effect of water depth on the spectrum of steady-state wave groups, especially for finite-amplitude ones, is still unknown.
The objective of this paper is to investigate the finite-amplitude steady-state wave groups with multiple near-resonances in finite water depth. It mainly extends the work of Liu et al. (Reference Liu, Xu and Liao2018) from steady-state wave groups in deep water to steady-state wave groups in finite water depth, and also extends the work of Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) from the weakly nonlinear quartet to finite-amplitude wave groups with multiple resonant sets. The extension from deep water to finite water depth is theoretically straightforward but practically difficult. The singularities or small divisors associated with exact or near-resonances are very challenging to resolve, as the perturbation theory breaks down due to singularities in the transfer functions when the resonance condition is satisfied (Madsen & Fuhrman Reference Madsen and Fuhrman2012). The HAM does not depend on small physical parameters and provides freedom to choose the initial guess and auxiliary linear operator so that the small divisors caused by multiple nearly resonant components can be removed successfully. However, the solution procedure that Liu et al. (Reference Liu, Xu and Liao2018) developed for finite-amplitude steady-state wave groups with multiple near-resonances in deep water does not work for finite-amplitude wave groups in finite water depth due to the following two difficulties. One difficulty is caused by the convergence rate of the series solution obtained from HAM being reduced with the shallower water depth. As the water depth decreases, convergent solutions are hard to obtain even for weakly nonlinear steady-state resonant waves. The other difficulty is associated with the additional nearly resonant components with non-small divisor (angular frequency mismatch) in finite water depth. These non-trivial components are hard to predict beforehand so that the solution procedure in HAM cannot change accordingly, which further reduces the convergence rate of the series solution in finite water depth. The slow convergence rate of series solutions obtained from HAM in finite water depth makes it impossible to consider steady-state resonant waves as the water depth further decreases beyond the domain that Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) considered.
Numerical methods, such as the collocation method (Okamura Reference Okamura1996; Ioualalen et al. Reference Ioualalen, Okamura, Cornier, Kharif and Roberts2006) and Galerkin method (Okamura Reference Okamura2003, Reference Okamura2010), could resolve the two above-mentioned difficulties. In the collocation method, the number of components in the truncated series is fixed equal to the number of discrete points on the free surface. While in the Galerkin method, the number of components required for a sufficient accuracy is less than the number of discrete points (Zhang & Melville Reference Zhang and Melville1987). The main advantage of the Galerkin method is the generality allowed in the spectral representation of the free surface (Ioualalen & Kharif Reference Ioualalen and Kharif1994). Thus, the Galerkin method is more efficient than the collocation method, especially for finite-amplitude wave groups with multiple resonant components. In this work, we use a combined solution procedure to search for finite-amplitude steady-state resonant wave groups in finite water depth. The HAM-based analytical approach is used to search for all possible steady-state solutions in finite water depth, and a Galerkin method-based numerical approach is used to obtain accurate steady-state solutions as the water depth decreases or nonlinearity increases.
The paper is organized as follows. In § 2.1, we describe the governing equation and the resonance criteria. Then the solution procedure of the analytical and numerical approach is introduced in §§ 2.2 and 2.3, respectively. The fully nonlinear water wave equations are solved when the resonance conditions are nearly satisfied and finite-amplitude steady-state wave groups with multiple and coupled resonances are obtained in different water depths. In § 3.1, we analyse the weakly nonlinear wave groups in finite water depth. Multiple solutions of the wave groups with increased nonlinearity are shown in § 3.2. Then § 3.3 shows the finite-amplitude wave groups together with the detailed spectrum and resonant sets configuration analysis to investigate the effect of water depth on the spectrum of steady-state wave groups, especially the main resonant mechanism in different water depths. Conclusions and discussion are given in § 4.
2 Mathematical formulas
2.1 Governing equation
We assume that the fluid is inviscid and incompressible, the flow is irrotational and the surface tension is neglected. Let
$(x,y,z)$
represent the usual Cartesian coordinate system, with
$(x,y)$
located at the mean water level and
$z$
measured vertically upwards. Consider a wave system that consists of two primary progressive waves with
$\boldsymbol{k}_{i}$
denoting the wavenumber and
$\unicode[STIX]{x1D70E}_{i}$
the actual angular frequency. After introducing the transformation
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}_{i}=\boldsymbol{k}_{i}\boldsymbol{\cdot }(x\,\boldsymbol{i}+y\,\boldsymbol{j})-\unicode[STIX]{x1D70E}_{i}t,\quad i=1,2, & & \displaystyle\end{eqnarray}$$
the governing equation for water waves in finite depth
$d$
reads
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{i}\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{j}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}z^{2}}=0,\quad -d<z<\unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}), & & \displaystyle\end{eqnarray}$$
subject to the two boundary conditions on the unknown free surface
$z=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})$
,
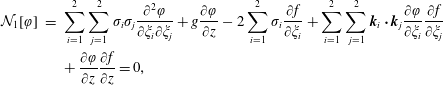$$\begin{eqnarray}\displaystyle {\mathcal{N}}_{1}[\unicode[STIX]{x1D711}] & = & \displaystyle \mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\unicode[STIX]{x1D70E}_{i}\unicode[STIX]{x1D70E}_{j}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{i}\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{j}}+g\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}z}-2\mathop{\sum }_{i=1}^{2}\unicode[STIX]{x1D70E}_{i}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{i}}+\mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{i}}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{j}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}z}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}z}=0,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{N}}_{2}[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]=\unicode[STIX]{x1D702}-\frac{1}{g}\left(\mathop{\sum }_{i=1}^{2}\unicode[STIX]{x1D70E}_{i}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{i}}-f\right)=0,\end{eqnarray}$$
and also the bottom condition,
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}z}=0,\quad \text{at }z=-d, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D711}$
denotes the velocity potential,
$\unicode[STIX]{x1D702}$
is the free-surface elevation,
${\mathcal{N}}_{1}$
and
${\mathcal{N}}_{2}$
are the nonlinear differential operators and
$$\begin{eqnarray}\displaystyle f=\frac{1}{2}\left[\mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{i}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{j}}+\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}z}\right)^{2}\right]. & & \displaystyle\end{eqnarray}$$
The wave elevation
$\unicode[STIX]{x1D702}$
and velocity potential
$\unicode[STIX]{x1D711}$
can be expressed in the form
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})=\mathop{\sum }_{i=-\infty }^{+\infty }\mathop{\sum }_{j=-\infty }^{+\infty }C_{i,j}^{\unicode[STIX]{x1D702}}\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)=\mathop{\sum }_{i=-\infty }^{+\infty }\mathop{\sum }_{j=-\infty }^{+\infty }C_{i,j}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D6F9}_{i,j}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z), & \displaystyle\end{eqnarray}$$
with the definition
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}_{i,j}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)=\sin (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})\frac{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|(z+d)]}{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|d]}, & & \displaystyle\end{eqnarray}$$
where
$C_{i,j}^{\unicode[STIX]{x1D702}}$
and
$C_{i,j}^{\unicode[STIX]{x1D711}}$
are constants to be determined. Consider a wave system with
$l$
nearly resonant components (
$\boldsymbol{k}_{0,1},\boldsymbol{k}_{0,2},\ldots ,\boldsymbol{k}_{0,l}$
) that are generated by the two primary ones (
$\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{2}$
). It satisfies the near-resonance criteria
$$\begin{eqnarray}\displaystyle m_{\unicode[STIX]{x1D704}}^{\ast }\boldsymbol{k}_{1}+n_{\unicode[STIX]{x1D704}}^{\ast }\boldsymbol{k}_{2}=\boldsymbol{k}_{0,\unicode[STIX]{x1D704}},\quad m_{\unicode[STIX]{x1D704}}^{\ast }\unicode[STIX]{x1D714}_{1}+n_{\unicode[STIX]{x1D704}}^{\ast }\unicode[STIX]{x1D714}_{2}=\unicode[STIX]{x1D714}_{0,\unicode[STIX]{x1D704}}+\text{d}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D704}},\quad \unicode[STIX]{x1D704}=1,2,\ldots ,l, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D714}_{0,\unicode[STIX]{x1D704}}$
denotes the linear angular frequency of the
$\unicode[STIX]{x1D704}$
th resonant component and
$\text{d}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D704}}$
is a small real number that represents the angular frequency mismatch.
2.2 Analytic solution approach
In the HAM-based approach, the solutions for wave elevation
$\unicode[STIX]{x1D702}$
and velocity potential
$\unicode[STIX]{x1D711}$
are approximated by the two series
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})=\mathop{\sum }_{m=1}^{+\infty }\unicode[STIX]{x1D702}_{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)=\unicode[STIX]{x1D711}_{0}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)+\mathop{\sum }_{m=1}^{+\infty }\unicode[STIX]{x1D711}_{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z), & \displaystyle\end{eqnarray}$$
which are governed by the high-order deformation equations
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})=c_{0}\unicode[STIX]{x1D6E5}_{m-1}^{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})+\unicode[STIX]{x1D712}_{m}\unicode[STIX]{x1D702}_{m-1}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{L}}[\unicode[STIX]{x1D711}_{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)]=c_{0}\unicode[STIX]{x1D6E5}_{m-1}^{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})-\bar{S}_{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})+\unicode[STIX]{x1D712}_{m}S_{m-1}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}), & \displaystyle\end{eqnarray}$$
with the definition
$\unicode[STIX]{x1D712}_{1}=0$
and
$\unicode[STIX]{x1D712}_{m}=1$
for
$m>1$
, where
${\mathcal{L}}$
is an auxiliary linear operator and
$c_{0}$
is a convergence control parameter. For detailed expressions of
${\mathcal{L}}$
,
$\unicode[STIX]{x1D6E5}_{m-1}^{\unicode[STIX]{x1D702}}$
,
$\unicode[STIX]{x1D6E5}_{m-1}^{\unicode[STIX]{x1D711}}$
,
$\bar{S}_{m}$
and
$S_{m-1}$
, please refer to Liao (Reference Liao2011) and Liu et al. (Reference Liu, Xu and Liao2018). The initial guess for the velocity potential
$\unicode[STIX]{x1D711}_{0}$
reads
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{0}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)=A_{0,1}\unicode[STIX]{x1D6F9}_{1,0}+A_{0,2}\unicode[STIX]{x1D6F9}_{0,1}+\mathop{\sum }_{\unicode[STIX]{x1D704}=1}^{l}A_{0,2+\unicode[STIX]{x1D704}}\unicode[STIX]{x1D6F9}_{m_{\unicode[STIX]{x1D704}}^{\ast },n_{\unicode[STIX]{x1D704}}^{\ast }}, & & \displaystyle\end{eqnarray}$$
where the coefficient
$A_{0,i}$
is determined by avoiding the secular terms or small divisors in the first-order approximation
$\unicode[STIX]{x1D711}_{1}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)$
. As shown in § 3.2, the number of components considered in the initial guess (2.15) increases with the nonlinearity.
2.3 Numerical solution approach
In the numerical solution approach, we express the wave elevation
$\unicode[STIX]{x1D702}$
and velocity potential
$\unicode[STIX]{x1D711}$
with truncated series as
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})=\mathop{\sum }_{i=1}^{+N}\mathop{\sum }_{j=-N}^{+N}C_{i,j}^{\unicode[STIX]{x1D702}}\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})+\mathop{\sum }_{j=0}^{+N}C_{0,j}^{\unicode[STIX]{x1D702}}\cos (j\unicode[STIX]{x1D709}_{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)=\mathop{\sum }_{i=1}^{+N}\mathop{\sum }_{j=-N}^{+N}C_{i,j}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D6F9}_{i,j}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)+\mathop{\sum }_{j=1}^{+N}C_{0,j}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D6F9}_{0,j}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z). & \displaystyle\end{eqnarray}$$
The total number of unknowns (
$C_{i,j}^{\unicode[STIX]{x1D702}}$
and
$C_{i,j}^{\unicode[STIX]{x1D711}}$
) is
$4N(N+1)+1$
. Following Okamura (Reference Okamura2010), we use Galerkin’s method to obtain the same number of independent relations as unknowns. Substituting (2.17) into (2.4), we numerically obtain the discrete free-surface profile
$$\begin{eqnarray}\displaystyle z=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})=\unicode[STIX]{x1D702}\left(\frac{2\unicode[STIX]{x03C0}(i-1)}{M},\frac{2\unicode[STIX]{x03C0}(j-1)}{M}\right),\quad i,j=1,2,\ldots ,M, & & \displaystyle\end{eqnarray}$$
by Newton’s method, where
$M$
is the number of discrete points. Substituting (2.18) into (2.3), we obtain the independent relations
$$\begin{eqnarray}P_{r,s}=\int _{0}^{2\unicode[STIX]{x03C0}}\!\int _{0}^{2\unicode[STIX]{x03C0}}{\mathcal{N}}_{1}[\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)]\sin (r\unicode[STIX]{x1D709}_{1}+s\unicode[STIX]{x1D709}_{2})\,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D709}_{2}=0,\quad z=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}),\end{eqnarray}$$
which are evaluated with an
$M$
-point Fourier transform. Set
$M>2N+1$
to evaluate the integral (2.19) accurately in obtaining finite-amplitude steady-state resonant waves. Therefore, we can obtain
$N(2N+2)$
independent relations from (2.19) for
$1\leqslant r\leqslant N$
,
$-N\leqslant s\leqslant N$
and
$1\leqslant s\leqslant N$
with
$r=0$
. The number of unknowns in the velocity potential,
$N(2N+2)$
, equals the number of independent relations in (2.19). So we obtain
$C_{i,j}^{\unicode[STIX]{x1D711}}$
by Newton’s method for various values of dimensionless frequency
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D70E}_{1}/\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D70E}_{2}/\unicode[STIX]{x1D714}_{2}$
and wavevectors
$\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{2}$
. Substituting again (2.17) into (2.4), we obtain the independent relations
$$\begin{eqnarray}\displaystyle Q_{r,s}=\int _{0}^{2\unicode[STIX]{x03C0}}\!\int _{0}^{2\unicode[STIX]{x03C0}}{\mathcal{N}}_{2}[\unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}),\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},z)]\cos (r\unicode[STIX]{x1D709}_{1}+s\unicode[STIX]{x1D709}_{2})\,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D709}_{2}=0,\quad z=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
which are evaluated with an
$M$
-point Fourier transform. Since
$M>2N+1$
, we can obtain
$N(2N+2)+1$
independent relations from (2.20) for
$1\leqslant r\leqslant N$
,
$-N\leqslant s\leqslant N$
and
$0\leqslant s\leqslant N$
with
$r=0$
. The number of unknowns in wave elevation,
$N(2N+2)+1$
, equals the number of independent relations in (2.20). So we obtain
$C_{i,j}^{\unicode[STIX]{x1D702}}$
by Newton’s method. The convergent series solution obtained by HAM is used as the initial solution of the iteration in the numerical approach. We stop the iteration if the maximum difference between the unknowns before an iteration and that after the iteration is smaller than
$10^{-7}$
. Detailed expressions of the Jacobian matrices, which are necessary for Newton’s method, are shown in appendix A.
Following Liu et al. (Reference Liu, Xu and Liao2018), we define the wave steepness
$$\begin{eqnarray}\displaystyle H_{s,j}=k_{j}\frac{\max [\unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})]-\min [\unicode[STIX]{x1D702}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})]}{2},\quad \unicode[STIX]{x1D709}_{i}\in [0,2\unicode[STIX]{x03C0}], & & \displaystyle\end{eqnarray}$$
for nonlinear wave groups. Table 1 shows the amplitude of component
$C_{1,0}^{\unicode[STIX]{x1D702}}$
and steepness
$H_{s,1}$
for various values of
$N$
and
$M$
in group 1 in the case of
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,0.726615)$
,
$d=0.9$
and
$\unicode[STIX]{x1D716}=1.035$
. For different truncation number
$N$
, the values of
$C_{1,0}^{\unicode[STIX]{x1D702}}$
and
$H_{s,1}$
remain unchanged after
$M\geqslant 171$
. Besides, the values of
$C_{1,0}^{\unicode[STIX]{x1D702}}$
and
$H_{s,1}$
converge as
$N$
increases from
$31$
to
$61$
. So,
$N=61$
and
$M=171$
are used for the maximum wave steepness case in this work. Four significant figures for the unknown
$C_{i,j}^{\unicode[STIX]{x1D702}}$
and
$C_{i,j}^{\unicode[STIX]{x1D711}}$
can be obtained.
Table 1. The amplitudes of component
$C_{1,0}^{\unicode[STIX]{x1D702}}$
and steepness
$H_{s,1}$
for various values of
$N$
and
$M$
in group 1. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,0.726615)$
, water depth
$d=0.9$
and dimensionless frequency
$\unicode[STIX]{x1D716}=1.035$
. A dash means no convergent solutions obtained.
3 Results and analysis
3.1 Weakly nonlinear wave groups
Consider the special resonant quartet
$$\begin{eqnarray}\displaystyle 2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}=\boldsymbol{k}_{0},\quad 2\unicode[STIX]{x1D714}_{1}-\unicode[STIX]{x1D714}_{2}=\unicode[STIX]{x1D714}_{0} & & \displaystyle\end{eqnarray}$$
in the weakly nonlinear case
$$\begin{eqnarray}\displaystyle \boldsymbol{k}_{1}=(1,0),\quad \boldsymbol{k}_{2}=(0.9,k_{2,y}),\quad \unicode[STIX]{x1D716}=\unicode[STIX]{x1D70E}_{i}/\unicode[STIX]{x1D714}_{i}=1.0003, & & \displaystyle\end{eqnarray}$$
where
$k_{2,y}$
is determined so that the resonance condition (3.1) is exactly satisfied as the water depth
$d$
changes. To overcome the slow convergence rate of the series solution obtained from HAM and search for weakly nonlinear steady-state resonant waves as the water depth further decreases, we use a combined solution procedure. The HAM is first used to find all possible steady-state solutions in deep water (
$k_{1}d=4.5$
). Two primary components and a resonant one are considered in the initial guess (2.15). Three groups of convergent high-order series solutions are obtained. Then, as the water depth decreases, we use Galerkin’s method to obtain convergent steady-state solutions in finite water depth.
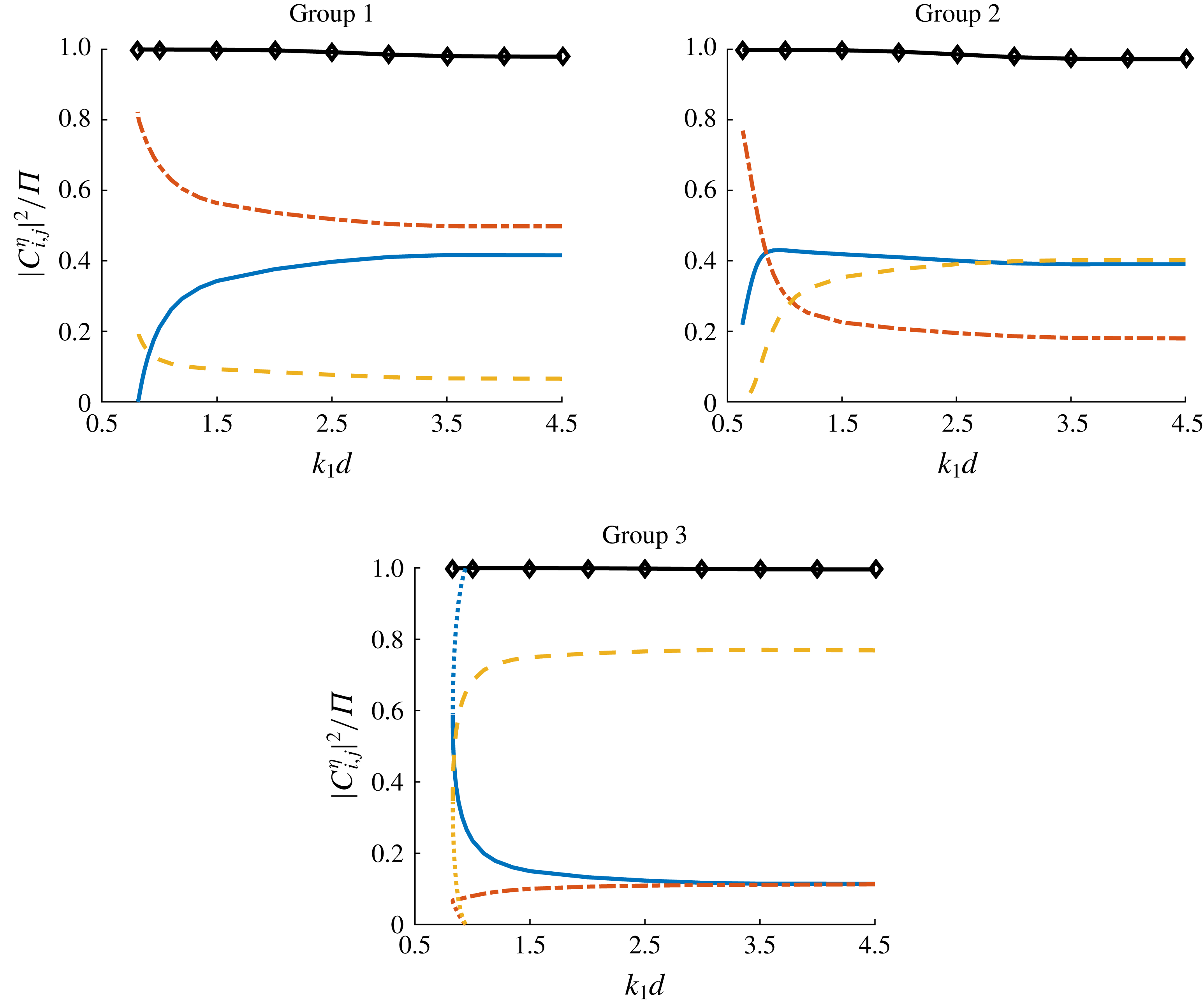
Figure 1. Wave energy distribution in weakly nonlinear quartet (3.1) and (3.2) with various water depths
$k_{1}d$
. Curves: solid blue line,
$|C_{1,0}^{\unicode[STIX]{x1D702}}|^{2}/\unicode[STIX]{x1D6F1}$
; dash-dotted red line,
$|C_{0,1}^{\unicode[STIX]{x1D702}}|^{2}/\unicode[STIX]{x1D6F1}$
; dashed orange line,
$|C_{2,-1}^{\unicode[STIX]{x1D702}}|^{2}/\unicode[STIX]{x1D6F1}$
. The black line with diamonds denotes the wave energy contained by three components in special quartet (3.1). The dotted lines denote another group of solutions that converges with group 3 near
$k_{1}d=0.83$
. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths.
Figure 1 shows the wave energy distribution in quartet (3.1) and (3.2) with various water depths
$k_{1}d$
. Compared with the steady-state resonant waves obtained by Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012), the solution domain obtained here is enlarged as the water depth decreases. The majority of the total wave energy
$\unicode[STIX]{x1D6F1}=\sum _{m=0}^{+\infty }\sum _{n=-\infty }^{+\infty }(C_{m,n}^{\unicode[STIX]{x1D702}})^{2}$
, more than
$97\,\%$
, is contained by three components in the quartet (3.1). For each component, the energy changes continuously with the water depth
$k_{1}d$
. The continuum of weakly nonlinear steady-state resonant waves from deep water to finite water depth is established. Besides, as the water depth
$k_{1}d$
decreases, the energy distribution changes slightly at first. After
$k_{1}d$
reaches
$1.0$
, the energy distribution begins to change rapidly as the water depth further decreases. Specifically, in groups 1 and 2 one component loses its energy and leaves the resonance with only two components, so we get bichromatic waves at
$k_{1}d=0.81$
and
$0.63$
, respectively. In group 3, a bifurcation is found as the solution converges with another group of solutions near
$k_{1}d=0.83$
. Water depth affects the energy distribution of weakly nonlinear waves significantly before the steady-state resonant waves disappear.
3.2 Wave groups with increased nonlinearity
The simulations conducted by Annenkov & Shrira (Reference Annenkov and Shrira2006) demonstrated the key importance of near-resonant interactions for the nonlinear evolution of statistical characteristics of wave fields. Taking
$k_{1}d=1.5$
,
$\boldsymbol{k}_{1}=(1,0)$
and
$\boldsymbol{k}_{2}=(0.9,0.893854)$
as example, we consider the steady-state resonant wave systems (2.10) with increased nonlinearity in finite water depth. The value
$k_{2,y}=0.893854$
is chosen so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one. Other non-trivial components, if they appear in the spectrum of steady-state resonant waves, are called nearly resonant ones.
For steady-state resonant waves in deep water, Liu et al. (Reference Liu, Xu and Liao2018) found that more components appear in wave spectra as the nonlinearity increases. Following Liu et al. (Reference Liu, Xu and Liao2018), we consider more nearly resonant components with small angular frequency mismatch
$\log _{10}(|\text{d}\unicode[STIX]{x1D714}_{i}|/\unicode[STIX]{x1D714}_{1})$
in the solution procedure of HAM to search for possible steady-state solutions. Different combinations of exactly resonant component
$\unicode[STIX]{x1D6F9}_{2,-1}$
and three nearly resonant ones
$\unicode[STIX]{x1D6F9}_{3,-2}$
,
$\unicode[STIX]{x1D6F9}_{4,-3}$
and
$\unicode[STIX]{x1D6F9}_{-1,2}$
are considered as non-trivial components in the initial guess (2.15) and the dimensionless frequency
$\unicode[STIX]{x1D716}$
increases from
$1.0003$
to
$1.01$
. As shown in table 2, the number of resonant components
$l$
increases step by step from one to three and the number of real solutions for initial guess coefficients
$A_{0,i}$
in (2.15) increases with
$\unicode[STIX]{x1D716}$
. At the same
$\unicode[STIX]{x1D716}$
, the number of real solutions increases when more components are considered in the initial guess (2.15). The increased number of algebraic solutions for larger value of
$\unicode[STIX]{x1D716}$
indicates that more steady-state resonant waves may exist when the nonlinearity increases.
Table 2. Number of real solutions for initial guess coefficients
$A_{0,i}$
in (2.15) when dimensionless frequency
$\unicode[STIX]{x1D716}$
increases from
$1.0003$
to
$1.01$
. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,0.893854)$
and water depth
$k_{1}d=1.5$
.
Table 3. Number of convergent solutions for resonant wave systems (2.10) when dimensionless frequency
$\unicode[STIX]{x1D716}$
increases from
$1.0003$
to
$1.01$
. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,0.893854)$
and water depth
$k_{1}d=1.5$
.
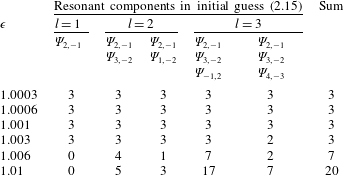
Table 3 shows the number of convergent solutions based on the initial guesses listed in table 2. For each choice of initial guess, the number of convergent solutions may increase or decrease with
$\unicode[STIX]{x1D716}$
, while in general it tends to increase when more components are considered in the initial guess (2.15). Note that, at
$\unicode[STIX]{x1D716}=1.01$
, no convergent solution has been obtained for
$l=1$
(corresponding to one resonant component) and the number of solutions increases for
$l=2,3$
(corresponding to two and three resonant ones). The last column in table 3 shows that the total number of convergent solutions increases from
$3$
at
$\unicode[STIX]{x1D716}=1.0003$
to
$20$
at
$\unicode[STIX]{x1D716}=1.01$
, i.e. the number of steady-state wave groups increases with respect to the nonlinearity. This indicates that the probability of existence of steady-state resonant waves in finite water depth increases with the nonlinearity. Steady-state waves with multiple near-resonances are obtained in finite water depth.
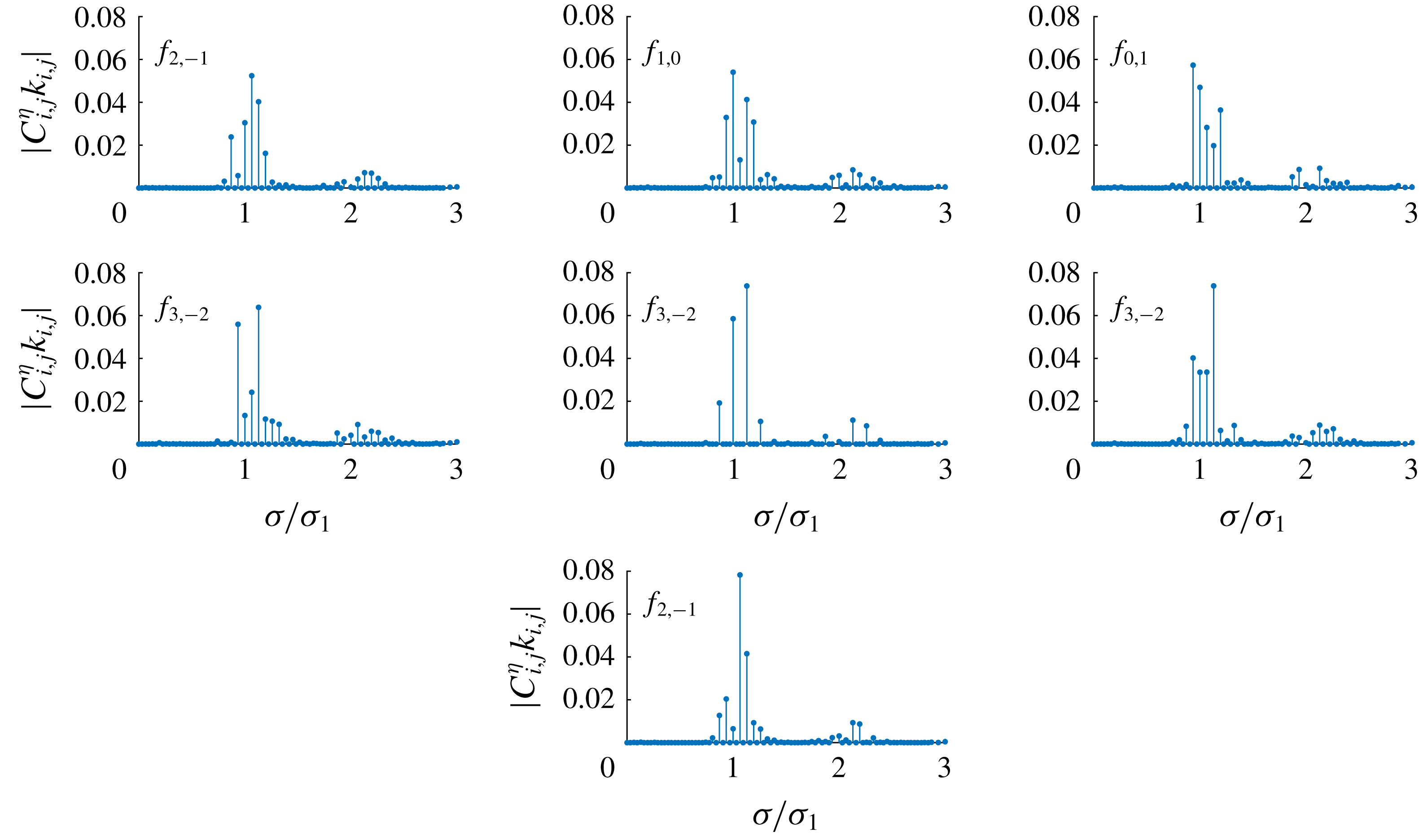
Figure 2. Amplitude spectrum
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of wave groups (2.10) in the case of dimensionless frequency
$\unicode[STIX]{x1D716}=1.006$
,
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,0.893854)$
and water depth
$k_{1}d=1.5$
;
$f_{i,j}$
denotes the dominant frequency.
Figure 3. Amplitude spectrum
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of wave groups (2.10) in the case of dimensionless frequency
$\unicode[STIX]{x1D716}=1.01$
,
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,0.893854)$
and water depth
$k_{1}d=1.5$
;
$f_{i,j}$
denotes the dominant frequency.
Figures 2 and 3 show the amplitude spectra of steady-state wave groups for dimensionless frequency
$\unicode[STIX]{x1D716}=1.006$
and
$1.01$
, respectively. The wave spectra are ordered based on the maximum dimensionless amplitude
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
, from smallest to largest. Within each spectrum, the dominant frequency
$f_{i,j}$
, i.e. the frequency of the largest component
$\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})$
that is surrounded by other smaller peaks, is indicated. The spectrum shape, especially frequency
$f_{i,j}$
and amplitude
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of the dominant component, changes among different groups. For most groups the energy is mainly contained by three or more components. The evidence of multiple resonances in steady-state waves is clearly shown. Compared with the spectra at
$\unicode[STIX]{x1D716}=1.006$
, two extra dominant frequencies
$f_{1,-2}$
and
$f_{4,-3}$
appear in the spectra at
$\unicode[STIX]{x1D716}=1.01$
. Besides, the maximum amplitude
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
increases and 13 more time-independent spectra are obtained at
$\unicode[STIX]{x1D716}=1.01$
. Spectral analysis confirms that both the number of components comprising the resonance and the number of steady-state waves in finite water depth increase with the nonlinearity.
3.3 Finite-amplitude wave groups
In this subsection, the nonlinearity of steady-state resonant waves in finite water depth is further increased to obtain finite-amplitude wave groups. Without loss of generality, we consider the case
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
with increased dimensionless frequency
$\unicode[STIX]{x1D716}$
. The value
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths. We use the Galerkin’s method to obtain the convergent steady-state solutions and three water depths
$k_{1}d=4.5$
,
$1.5$
and
$0.9$
are considered. For each wave group, the values of
$N$
and
$M$
increase with the dimensionless frequency
$\unicode[STIX]{x1D716}$
so that four significant figures can be obtained for the unknown constants
$C_{m,n}^{\unicode[STIX]{x1D702}}$
and
$C_{m,n}^{\unicode[STIX]{x1D711}}$
in (2.7) and (2.8).
Table 4. Maximum steepness of steady-state resonant wave groups (2.10) in three different water depths. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in water of different depths.
We define
$k_{d}$
as the wavenumber of the dominant component in the dimensionless amplitude spectrum. For two wavenumbers
$k_{1}$
and
$k_{d}$
, we get two steepness values
$H_{s,1}$
and
$H_{s,d}$
from (2.21). Table 4 shows the maximum steepness of steady-state resonant wave groups in three different water depths. For all cases considered,
$H_{s,1}\geqslant 0.20$
and
$H_{s,d}\geqslant 0.23$
. Therefore, it is reasonable to conclude that finite-amplitude steady-state resonant wave groups are obtained in finite water depth.
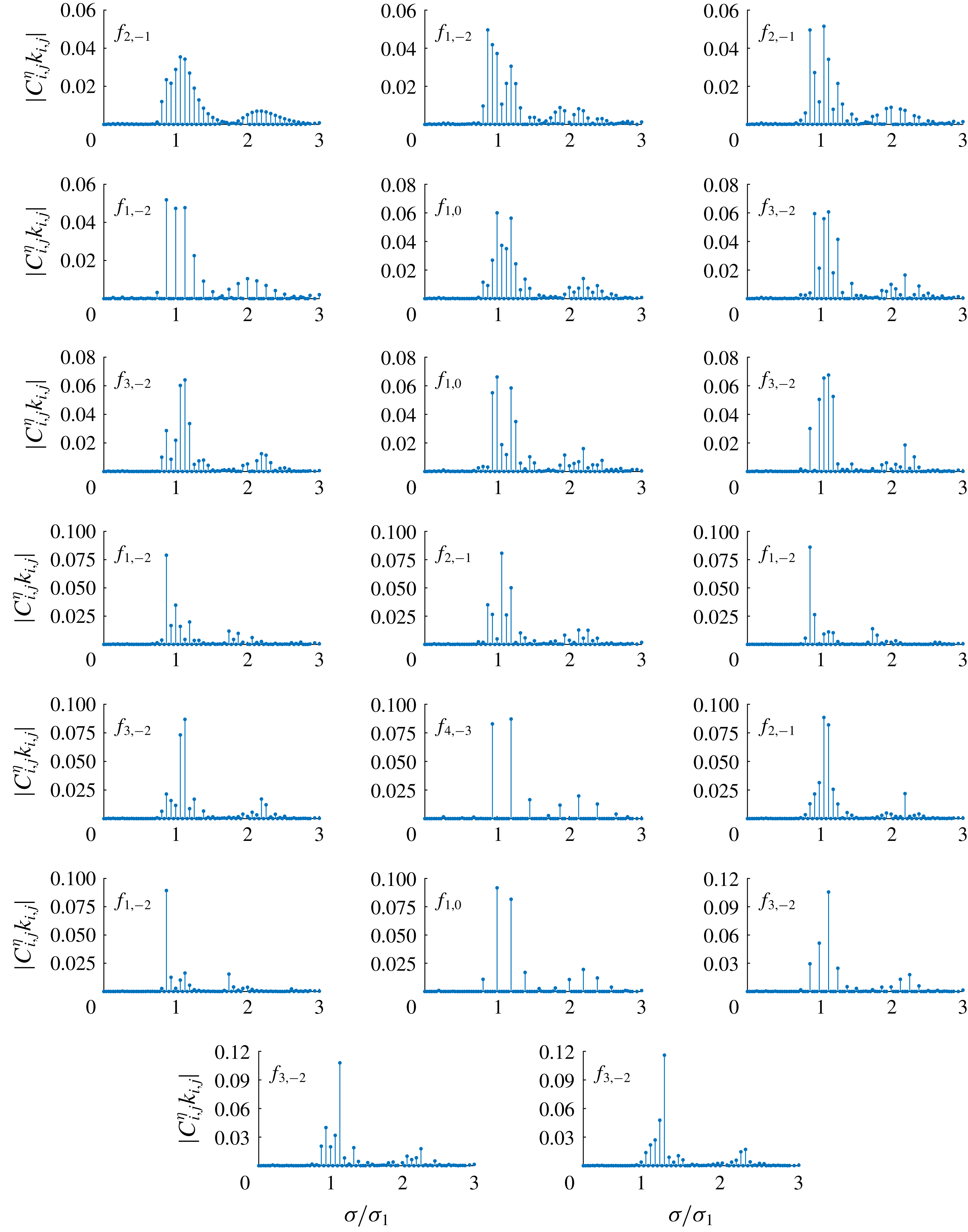
Figure 4. Dimensionless amplitude spectra
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of group 1 in the case of
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
with increased dimensionless frequency
$\unicode[STIX]{x1D716}$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
Figure 4 shows the amplitude spectra of group 1 with increased dimensionless frequency
$\unicode[STIX]{x1D716}$
. For all water depths, the frequency bands broaden with respect to increased
$\unicode[STIX]{x1D716}$
as more components appear in the spectra due to the resonant interactions among different wave components. Besides, the amplitude of some high-frequency components (
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}>1.9$
) increases as the water depth decreases. It should be noted that the angular frequency mismatches of these high-frequency nearly resonant components in finite water depth are not small. Since detailed high-frequency components cannot be predicted beforehand based on the magnitude of the angular frequency mismatch, convergent series solutions can hardly be obtained in HAM by the solution procedure that Liu et al. (Reference Liu, Xu and Liao2018) developed for multiple near-resonances in deep water. So, instead, a numerical approach based on the Galerkin method has been used as the nonlinearity increases further. For waves in deep water (
$k_{1}d=4.5$
), most non-trivial components appear around the primary ones (
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}\approx 1$
) in the spectra. The tail of the spectra decreases rapidly so that the high-frequency components can almost be neglected. As the water depth decreases, some non-trivial components start to appear in the high-frequency domain. Additional sub-peaks appear in the tail of the spectra in finite water depth (
$k_{1}d=1.5$
,
$0.9$
). These high-frequency components cannot be neglected and become increasingly important as the water depth decreases. Therefore, the spectra of steady-state resonant waves change as the water depth decreases and the significant role of high-frequency components in finite water depth is demonstrated.
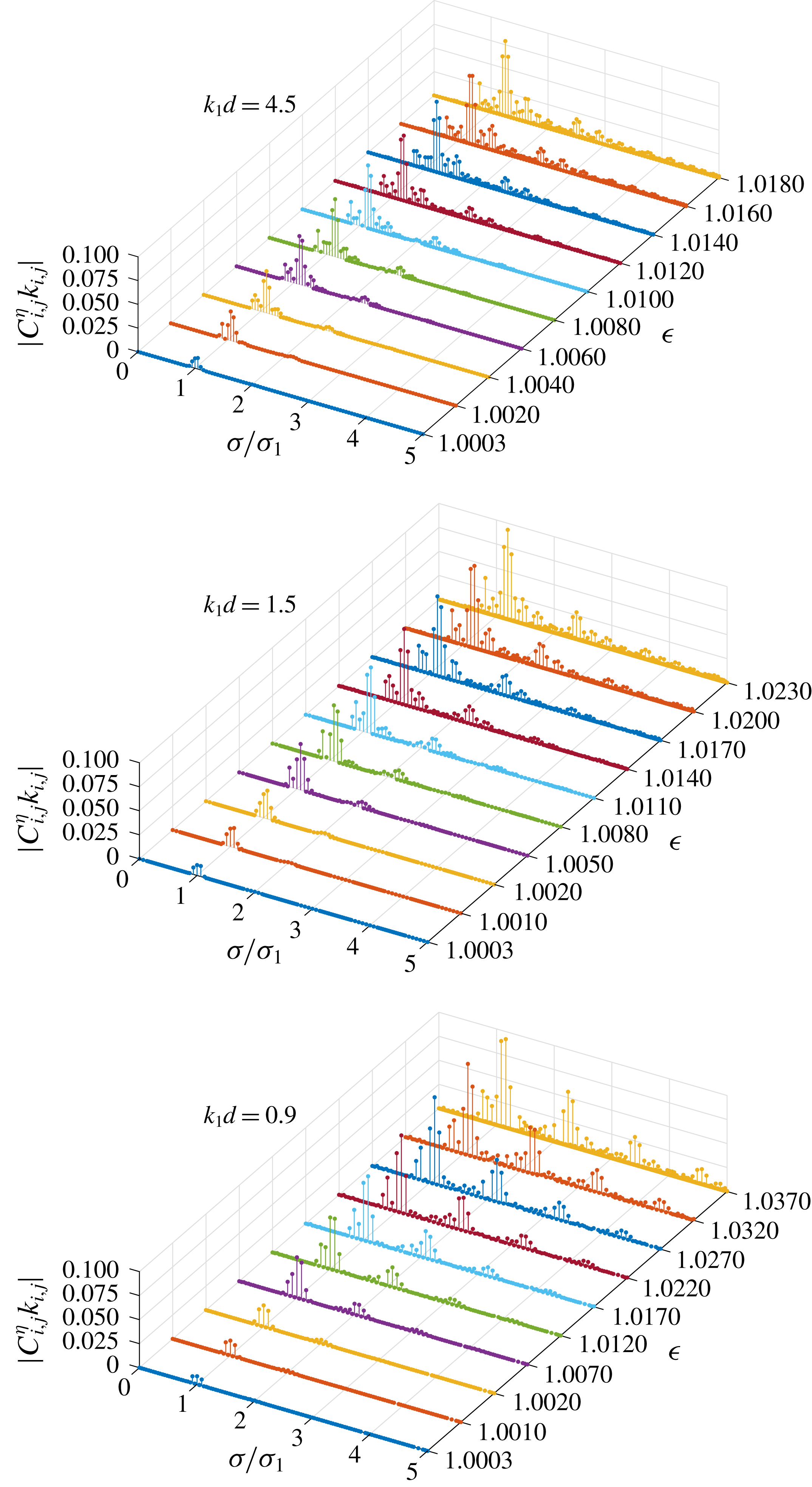
Figure 5. Dimensionless amplitude spectra
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of group 2 in the case of
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
with increased dimensionless frequency
$\unicode[STIX]{x1D716}$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
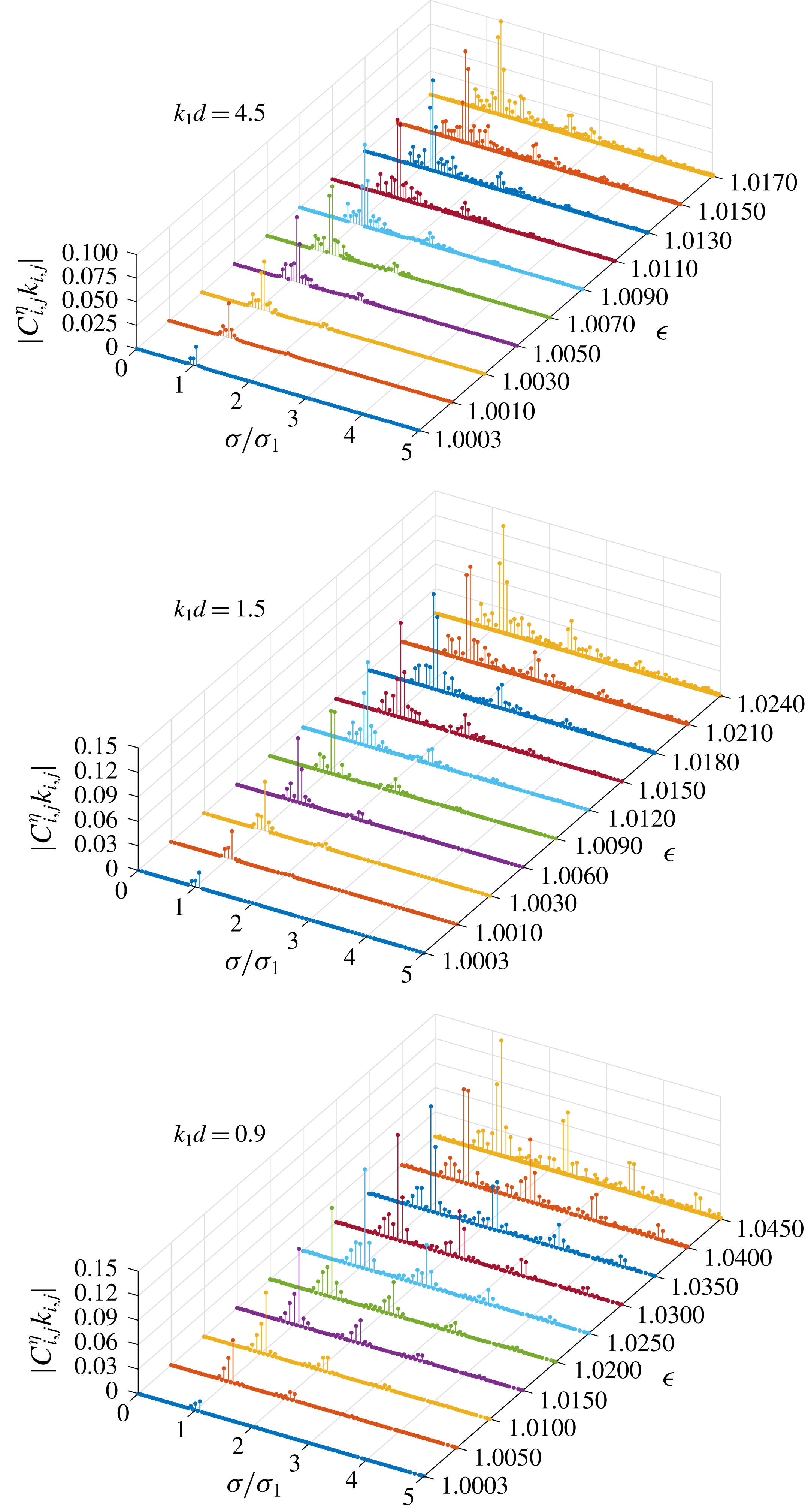
Figure 6. Dimensionless amplitude spectra
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of group 3 in the case of
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
with increased dimensionless frequency
$\unicode[STIX]{x1D716}$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
Figures 5 and 6 show the amplitude spectra of groups 2 and 3, respectively, with increased dimensionless frequency
$\unicode[STIX]{x1D716}$
. For all water depths, the frequency bands broaden with respect to the dimensionless frequency
$\unicode[STIX]{x1D716}$
. For waves in deep water (
$k_{1}d=4.5$
), all non-trivial components appear around the primary ones (
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}\approx 1$
) in the spectra. For waves in finite water depth (
$k_{1}d=1.5$
,
$0.9$
), high-frequency components start to appear in the spectra and the amplitude of these components increases further as the water depth decreases. The spectra of steady-state resonant waves indeed change with the water depth and the significant role of high-frequency components in finite water depth is confirmed.
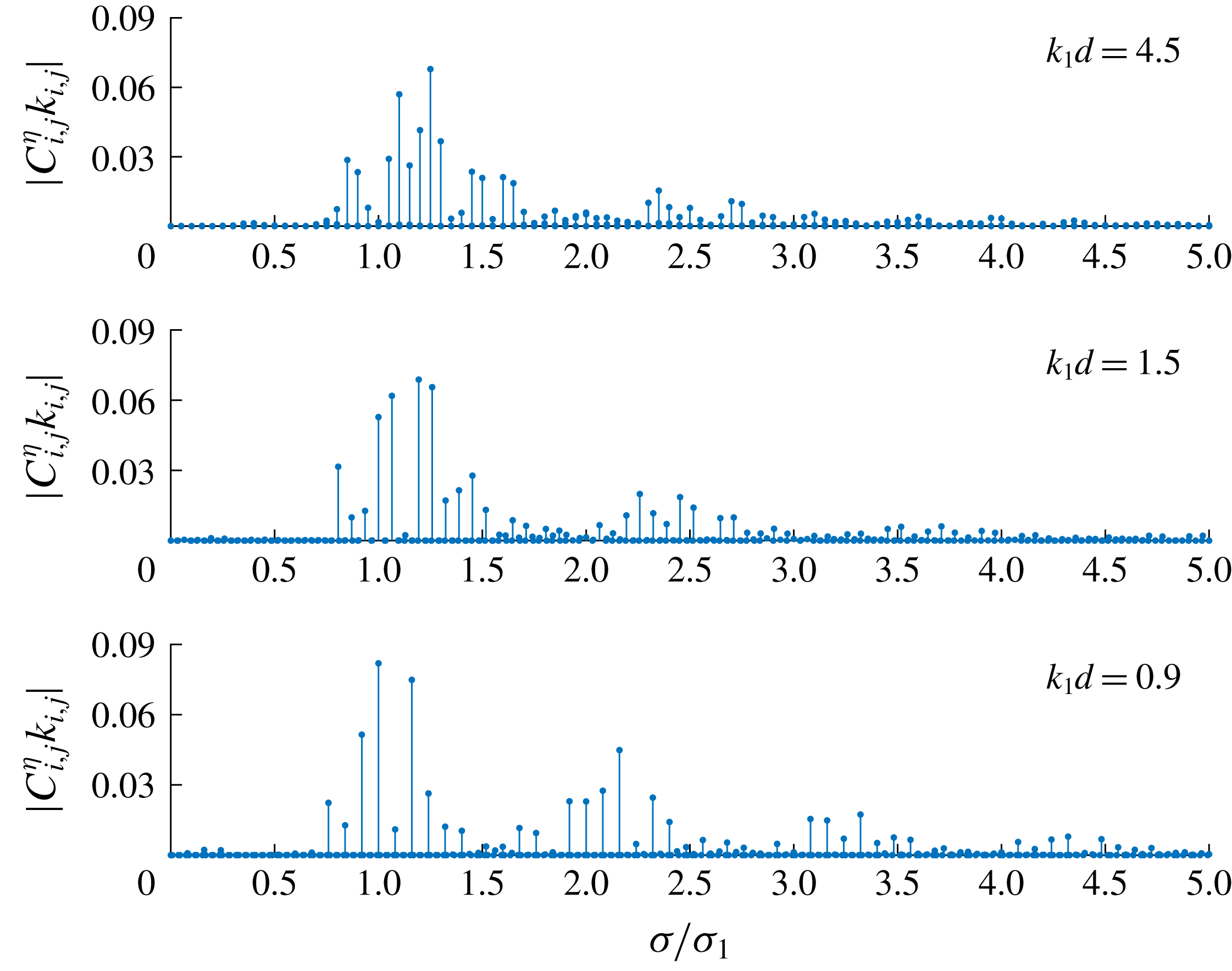
The spectra of steady-state wave groups with the same steepness are further analysed in different water depths. All three groups are considered and in each case the dimensionless frequency
$\unicode[STIX]{x1D716}$
is determined so that steepness
$H_{s,1}=0.20$
. Taking group 1 as an example, figure 7 shows the amplitude spectrum
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
with
$H_{s,1}=0.20$
. (Detailed frequency and amplitude values of the 15 largest components in the three groups are shown in tables 6–8 in appendix B.) As water depth decreases from
$4.5$
to
$0.9$
, it can be found that the dominant frequency
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}$
shifts towards the lower-frequency domain from
$1.25$
to
$1.00$
and the corresponding amplitude increases from
$0.068$
to
$0.083$
. Besides, the number of components around the dominant ones (
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}\in (0.5,1.9)$
) decreases from
$12$
to
$6$
while the number of high-frequency components (
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}>1.9$
) increases from
$3$
to
$9$
. Moreover, the amplitude of the largest high-frequency component also increases from
$0.015$
to
$0.045$
. The same effect can also be found for groups 2 and 3. For steady-state resonant waves of the same steepness, the total energy is decentralized towards the two sides of the spectrum as water depth decreases.
Figure 7. Amplitude spectrum
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of group 1 with steepness
$H_{s,1}=0.20$
. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
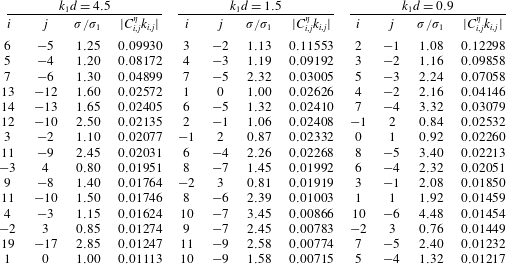
Table 5. Distribution of the 15 largest components in groups 1, 2 and 3 with
$H_{s,1}=0.20$
. Domains
$S1$
,
$S2$
,
$S3$
and
$S4$
represent the frequency intervals (
$0.5,1.9$
), (
$1.9,3.0$
), (
$3.0,4.0$
) and (
$4.0,5.0$
);
$c_{i,j}$
represents the component
$\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})$
. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
It should be noted that the non-trivial components in steady-state resonant waves actually join the resonant sets. Table 5 divides the 15 largest components in three groups with
$H_{s,1}=0.20$
into four domains according to their frequency distribution in the spectra. Components in the same domain would only join the resonant sets through the quartet, sextet, octet or decuplet
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D704}=1}^{l/2}k_{i_{\unicode[STIX]{x1D704}},j_{\unicode[STIX]{x1D704}}}^{Si}=\mathop{\sum }_{\unicode[STIX]{x1D704}=l/2+1}^{l}k_{i_{\unicode[STIX]{x1D704}},j_{\unicode[STIX]{x1D704}}}^{Si},\quad \mathop{\sum }_{\unicode[STIX]{x1D704}=1}^{l/2}\unicode[STIX]{x1D70E}_{i_{\unicode[STIX]{x1D704}},j_{\unicode[STIX]{x1D704}}}^{Si}=\mathop{\sum }_{\unicode[STIX]{x1D704}=l/2+1}^{l}\unicode[STIX]{x1D70E}_{i_{\unicode[STIX]{x1D704}},j_{\unicode[STIX]{x1D704}}}^{Si},\quad l=4,6,8,10. & & \displaystyle\end{eqnarray}$$
Here
$k_{i,j}^{Si}$
and
$\unicode[STIX]{x1D70E}_{i,j}^{Si}$
denote the wavenumber and actual angular frequency of component
$\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})$
in domain
$Si$
. In other words, only four-wave, six-wave, eight-wave or ten-wave resonant interactions would happen among different components within the same domain. Taking domain
$S1$
of group 1 in water depth
$k_{1}d=4.5$
as an example, the resonance conditions for quartet, sextet, octet and decuplet (3.3) could be satisfied by the following combinations of components:
$$\begin{eqnarray}\displaystyle & \displaystyle (c_{-2,3}^{S1},c_{-1,2}^{S1},c_{2,-1}^{S1},c_{3,-2}^{S1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (c_{2,-1}^{S1},c_{2,-1}^{S1},c_{3,-2}^{S1},c_{3,-2}^{S1},c_{3,-2}^{S1},c_{5,-4}^{S1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (c_{2,-1}^{S1},c_{3,-2}^{S1},c_{5,-4}^{S1},c_{6,-5}^{S1},c_{10,-9}^{S1},c_{11,-10}^{S1},c_{13,-12}^{S1},c_{14,-13}^{S1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (c_{2,-1}^{S1},c_{2,-1}^{S1},c_{2,-1}^{S1},c_{2,-1}^{S1},c_{3,-2}^{S1},c_{3,-2}^{S1},c_{3,-2}^{S1},c_{3,-2}^{S1},c_{3,-2}^{S1},c_{7,-6}^{S1}), & \displaystyle\end{eqnarray}$$
where
$c_{i,j}^{Si}$
denotes component
$\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})$
in domain
$Si$
. Besides, components in different domains would join the resonant sets through the trio, quartet, quintet or sextet:
$$\begin{eqnarray}k_{i_{1},j_{1}}^{Si}+k_{i_{2},j_{2}}^{Sj}=k_{i_{3},j_{3}}^{Si+j},\quad \unicode[STIX]{x1D70E}_{i_{1},j_{1}}^{Si}+\unicode[STIX]{x1D70E}_{i_{2},j_{2}}^{Sj}=\unicode[STIX]{x1D70E}_{i_{3},j_{3}}^{Si+j},\end{eqnarray}$$
$$\begin{eqnarray}k_{i_{1},j_{1}}^{Si}\pm k_{i_{2},j_{2}}^{Sj}\pm k_{i_{3},j_{3}}^{Sk}=k_{i_{4},j_{4}}^{Si\pm j\pm k},\quad \unicode[STIX]{x1D70E}_{i_{1},j_{1}}^{Si}\pm \unicode[STIX]{x1D70E}_{i_{2},j_{2}}^{Sj}\pm \unicode[STIX]{x1D70E}_{i_{3},j_{3}}^{Sk}=\unicode[STIX]{x1D70E}_{i_{4},j_{4}}^{Si\pm j\pm k},\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle k_{i_{1},j_{1}}^{Si}\pm k_{i_{2},j_{2}}^{Sj}\pm k_{i_{3},j_{3}}^{Sk}\pm k_{i_{4},j_{4}}^{Sl}=k_{i_{5},j_{5}}^{Si\pm j\pm k\pm l},\\ \displaystyle \unicode[STIX]{x1D70E}_{i_{1},j_{1}}^{Si}\pm \unicode[STIX]{x1D70E}_{i_{2},j_{2}}^{Sj}\pm \unicode[STIX]{x1D70E}_{i_{3},j_{3}}^{Sk}\pm \unicode[STIX]{x1D70E}_{i_{4},j_{4}}^{Sl}=\unicode[STIX]{x1D70E}_{i_{5},j_{5}}^{Si\pm j\pm k\pm l},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle k_{i_{1},j_{1}}^{Si}\pm k_{i_{2},j_{2}}^{Sj}\pm k_{i_{3},j_{3}}^{Sk}\pm k_{i_{4},j_{4}}^{Sl}\pm k_{i_{5},j_{5}}^{Sm}=k_{i_{6},j_{6}}^{Si\pm j\pm k\pm l\pm m},\\ \displaystyle \unicode[STIX]{x1D70E}_{i_{1},j_{1}}^{Si}\pm \unicode[STIX]{x1D70E}_{i_{2},j_{2}}^{Sj}\pm \unicode[STIX]{x1D70E}_{i_{3},j_{3}}^{Sk}\pm \unicode[STIX]{x1D70E}_{i_{4},j_{4}}^{Sl}\pm \unicode[STIX]{x1D70E}_{i_{5},j_{5}}^{Sm}=\unicode[STIX]{x1D70E}_{i_{6},j_{6}}^{Si\pm j\pm k\pm l\pm m}.\end{array}\right\}\end{eqnarray}$$
In other words, three-wave, four-wave, five-wave or six-wave resonant interactions would happen among components from different domains. Taking the four domains of group 3 in water depth
$k_{1}d=0.9$
as an example, the resonance condition for trio, quartet, quintet and sextet (3.8)–(3.11) could be satisfied by the following combinations of components:
$$\begin{eqnarray}\displaystyle & \displaystyle (c_{-1,2}^{S1},c_{2,-1}^{S1},c_{1,1}^{S2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (c_{3,-1}^{S2},c_{4,-2}^{S2},c_{7,-4}^{S3},c_{8,-5}^{S3}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (c_{0,1}^{S1},c_{2,-1}^{S1},c_{3,-2}^{S1},c_{5,-4}^{S1},c_{10,-6}^{S4}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (c_{-1,2}^{S1},c_{0,1}^{S1},c_{2,-1}^{S1},c_{3,-2}^{S1},c_{1,1}^{S2},c_{3,-1}^{S2}). & \displaystyle\end{eqnarray}$$
Distribution of the 15 largest components in groups 1, 2 and 3 with
$H_{s,1}=0.20$
is shown in table 5. It can be found that for waves in deep water (
$k_{1}d=4.5$
) the majority of non-trivial components appear around the primary ones in domain
$S1$
, with only a few in domain
$S2$
. Besides, the amplitude of the largest component in domain
$S2$
is much smaller compared with that in domain
$S1$
. So only the four-wave, six-wave, eight-wave or ten-wave resonant interactions among components within domain
$S1$
would affect the wave groups significantly in deep water. Note that components
$c_{5,-4}^{S1}$
,
$c_{6,-5}^{S1}$
and
$c_{7,-6}^{S1}$
are a few of the largest ones in all three groups and they join the resonant sets by a special quartet:
$$\begin{eqnarray}\displaystyle k_{5,-4}^{S1}+k_{7,-6}^{S1}=2k_{6,-5}^{S1},\quad \unicode[STIX]{x1D70E}_{5,-4}^{S1}+\unicode[STIX]{x1D70E}_{7,-6}^{S1}=2\unicode[STIX]{x1D70E}_{6,-5}^{S1}. & & \displaystyle\end{eqnarray}$$
Besides, other large components in group 1, i.e.
$c_{3,-2}^{S1}$
,
$c_{2,-1}^{S1}$
,
$c_{-2,3}^{S1}$
and
$c_{-1,2}^{S1}$
, could also join the resonant set by quartet
$$\begin{eqnarray}\displaystyle k_{3,-2}^{S1}+k_{-2,3}^{S1}=k_{2,-1}^{S1}+k_{-1,2}^{S1},\quad \unicode[STIX]{x1D70E}_{3,-2}^{S1}+\unicode[STIX]{x1D70E}_{-2,3}^{S1}=\unicode[STIX]{x1D70E}_{2,-1}^{S1}+\unicode[STIX]{x1D70E}_{-1,2}^{S1}. & & \displaystyle\end{eqnarray}$$
It is generally assumed that the lowest-order resonant interactions that occur will dominate wave field evolution (Hammack & Henderson Reference Hammack and Henderson1993), so we conclude that four-wave resonant interactions plays a dominant role in steady-state resonant wave groups in deep water.
As the water depth decreases, the number of non-trivial components in domain
$S1$
decreases while the number of non-trivial components in the other three high-frequency domains
$S2$
,
$S3$
and
$S4$
increases. Besides, the amplitude of these high-frequency components increases, too. So in finite water depths both the four-wave, six-wave, eight-wave or ten-wave resonant interactions among components within the same domains and the three-wave, four-wave, five-wave or six-wave resonant interactions among components from different domains would affect the wave groups significantly. Note that, at
$k_{1}d=0.9$
, the largest components in three groups with
$H_{s,1}=0.20$
join the resonant sets by two quartets
$$\begin{eqnarray}\displaystyle & k_{1,0}^{S1}+k_{0,1}^{S1}=k_{3,-2}^{S1}+k_{-2,3}^{S1},\quad \unicode[STIX]{x1D70E}_{1,0}^{S1}+\unicode[STIX]{x1D70E}_{0,1}^{S1}=\unicode[STIX]{x1D70E}_{3,-2}^{S1}+\unicode[STIX]{x1D70E}_{-2,3}^{S1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}k_{1,0}^{S1}+k_{3,-2}^{S1}=2k_{2,-1}^{S1},\quad \unicode[STIX]{x1D70E}_{1,0}^{S1}+\unicode[STIX]{x1D70E}_{3,-2}^{S1}=2\unicode[STIX]{x1D70E}_{2,-1}^{S1},\end{eqnarray}$$
and a trio
$$\begin{eqnarray}k_{2,-1}^{S1}+k_{3,-2}^{S1}=k_{5,-3}^{S2},\quad \unicode[STIX]{x1D70E}_{2,-1}^{S1}+\unicode[STIX]{x1D70E}_{3,-2}^{S1}=\unicode[STIX]{x1D70E}_{5,-3}^{S2}.\end{eqnarray}$$
Besides, component
$c_{4,-2}^{S2}$
, the fourth largest one in groups 1 and 2, could also join the resonant sets by a trio
$$\begin{eqnarray}\displaystyle k_{1,0}^{S1}+k_{3,-2}^{S1}=k_{4,-2}^{S2},\quad \unicode[STIX]{x1D70E}_{1,0}^{S1}+\unicode[STIX]{x1D70E}_{3,-2}^{S1}=\unicode[STIX]{x1D70E}_{4,-2}^{S2}, & & \displaystyle\end{eqnarray}$$
with two larger components
$c_{1,0}^{S1}$
and
$c_{3,-2}^{S1}$
. Therefore, in finite water depth, the resonant interactions in steady-state wave groups is more complex. Both components around the primary ones and components from the high-frequency domain join the resonance sets. As water depth decreases, resonant interactions among components from different domains, especially the three-wave resonant interactions, becomes increasingly important in steady-state resonant wave groups. The significant role of three-wave resonant interactions for steady-state resonant wave groups in finite water depth is demonstrated.
In this subsection, finite-amplitude steady-state wave groups with multiple resonances are obtained in finite water depth. Wave spectra are compared and resonant sets configuration are analysed for wave groups with the same steepness in different water depths.
For wave groups in deep water, the frequency bands broaden with respect to increased nonlinearity. More components join the resonant sets mainly due to the four-wave, six-wave, eight-wave or ten-wave resonant interactions among components around the primary ones. A few high-frequency components appear in the spectrum due to the three-wave resonant interactions. The amplitudes of these high-frequency components are small compared with the non-trivial components around the primary ones. In all three groups, a few of the largest components join the resonant sets by a quartet. Therefore, steady-state resonant wave groups in deep water are mainly controlled by four-wave resonant interactions.
For wave groups in finite water depth, the frequency bands broaden with respect to increased nonlinearity, too. More components join the resonant sets due to the four-wave, six-wave, eight-wave or ten-wave resonant interactions among components around the primary ones, and also due to the three-wave, four-wave, five-wave and six-wave resonant interactions among components around the primary ones and from the high-frequency domain. As the water depth decreases, the number of components around the primary ones decreases while the number of high-frequency components increases. The amplitudes of the largest components around the primary ones and from the high-frequency domain increase as the water depth decreases. Resonant interactions among components around the primary ones are suppressed while resonant interactions among components around the primary ones and from the high-frequency domain are enhanced. In each group, a few of the largest components join the resonance by a quartet or a trio. Therefore, steady-state resonant wave groups in finite water depths are controlled by resonant interactions among components both around the primary ones and from the high-frequency domain. More components join the resonant sets by a trio as the water depth decreases. The importance of three-wave resonant interactions for steady-state resonant wave groups in finite water depth is demonstrated.
4 Conclusion and discussion
Fully nonlinear water wave equations are solved by analytical and numerical approaches in finite water depth to obtain finite-amplitude wave groups with time-independent spectrum when the resonance conditions are nearly satisfied. The resonant sets configuration of the finite-amplitude wave groups is analysed to investigate the main resonant mechanism from deep water to finite water depth.
In finite water depth, the convergence rate of the series solution obtained by HAM for steady-state resonant wave groups decreases and additional high-frequency components that cannot be predicted join the resonant sets. A solution procedure that combines the HAM-based analytical approach and Galerkin method-based numerical approach has been proposed. It provides a robust and efficient way to obtain the finite-amplitude steady-state wave groups with multiple resonances in finite water depth.
For weakly nonlinear wave groups, the solution domain has been enlarged as the water depth decreases. The energy distribution of weakly nonlinear wave groups changes continuously with the water depth, so the continuum of steady-state resonant waves from deep water to finite water depth is established. As the water depth decreases, the energy distribution of weakly nonlinear wave groups changes rapidly before the resonant interactions disappear.
As the nonlinearity increases, steady-state waves with multiple near-resonances are obtained in finite water depth. More components join the resonances and more steady-state wave groups are obtained, so the probability of existence of steady-state resonant waves in finite water depth increases, too.
Finite-amplitude wave groups with steepness no less than
$0.20$
are obtained in finite water depth. The frequency bands broaden with respect to increased nonlinearity. For waves in deep water, the majority of the non-trivial components appear around the primary ones due to the four-wave, six-wave, eight-wave or even ten-wave resonant interactions. The dominant role of four-wave resonant interactions for steady-state wave groups in deep water is demonstrated. For waves in finite water depth, additional non-trivial high-frequency components appear in the spectra due to the three-wave, four-wave, five-wave or even six-wave resonant interactions with the components around the primary ones. The amplitudes of these high-frequency components increase further as the water depth decreases. Resonant interactions among components around the primary ones are suppressed while resonant interactions among components around the primary ones and from the high-frequency domain are enhanced. The spectra of steady-state resonant wave groups changes with the water depth and the significant role of three-wave resonant interactions in finite water depth is demonstrated.
The energy distribution in each resonant set may be measured to quantitatively analyse the effects of different interactions. However, in finite-amplitude wave groups, wave components often interact in coupled sets so that the same component may interact with other different components and join different resonant sets simultaneously. In this case, it is difficult to divide the total wave energy in different resonant sets to compare different wave interactions quantitatively. It would be interesting to search for some specific resonant set configuration so that different interactions could be quantitatively measured and compared. For non-steady-state resonant wave groups in finite water depth, the role that three-wave and four-wave resonant interactions play in the spectra would also be an interesting research topic. For real ocean waves, it is not only resonant interactions that determine the evolution of the wave spectrum. Wind input and dissipation due to breaking, which are also important for wave spectrum evolution in real oceanic conditions, are not considered here.
Acknowledgements
Z.L. thanks G. Ducrozet for offering the early references about steady-state resonant waves. Thanks also go to the anonymous reviewers for their valuable comments and suggestions, which greatly enhanced the quality of this article. This work was partly supported by the National Natural Science Foundation of China (approval no. 51609090) and Science Research Project of Huazhong University of Science and Technology (approval nos 0118140077 and 2006140115).
Appendix A. Detailed expressions of the Jacobian matrices
Here, we show the detailed expressions of the Jacobian matrices,
$\unicode[STIX]{x2202}\unicode[STIX]{x1D617}_{r,s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D60A}_{i,j}^{\unicode[STIX]{x1D711}}$
and
$\unicode[STIX]{x2202}\unicode[STIX]{x1D618}_{r,s}/\unicode[STIX]{x2202}\unicode[STIX]{x1D60A}_{i,j}^{\unicode[STIX]{x1D702}}$
. First,
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D617}_{r,s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D60A}_{i,j}^{\unicode[STIX]{x1D711}}}=\int _{0}^{2\unicode[STIX]{x03C0}}\!\int _{0}^{2\unicode[STIX]{x03C0}}\left(\frac{\unicode[STIX]{x2202}{\mathcal{N}}_{1}[\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}}+\frac{\unicode[STIX]{x2202}{\mathcal{N}}_{1}[\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}z}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}}\right)\sin (r\unicode[STIX]{x1D709}_{1}+s\unicode[STIX]{x1D709}_{2})\,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D709}_{2}. & & \displaystyle\end{eqnarray}$$
Since the expression for
$\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}$
is unknown in the present formulation, we get the relation
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}{\mathcal{N}}_{2}[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}}+\frac{\unicode[STIX]{x2202}{\mathcal{N}}_{2}[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}z}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}}=0, & & \displaystyle\end{eqnarray}$$
from (2.4) instead. After eliminating
$\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}$
from (A 1) and (A 2), we get
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D617}_{r,s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D60A}_{i,j}^{\unicode[STIX]{x1D711}}}=\int _{0}^{2\unicode[STIX]{x03C0}}\!\int _{0}^{2\unicode[STIX]{x03C0}}\left(\frac{\unicode[STIX]{x2202}{\mathcal{N}}_{1}[\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}}-\frac{\unicode[STIX]{x2202}{\mathcal{N}}_{1}[\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}z}\frac{\unicode[STIX]{x2202}{\mathcal{N}}_{2}[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]/\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}{\mathcal{N}}_{2}[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]/\unicode[STIX]{x2202}z}\right)\sin (r\unicode[STIX]{x1D709}_{1}+s\unicode[STIX]{x1D709}_{2})\,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D709}_{2}.\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D618}_{r,s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D60A}_{i,j}^{\unicode[STIX]{x1D702}}}=\frac{\unicode[STIX]{x2202}Q_{r,s}}{\unicode[STIX]{x2202}z}\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2}). & \displaystyle\end{eqnarray}$$
The terms within the Jacobian matrix can be expressed as
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}{\mathcal{N}}_{1}[\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}} & = & \displaystyle [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|^{2}\unicode[STIX]{x1D711}_{z}^{2}-(iTF+jTS)^{2}]\sin (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})\frac{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|(z+d)]}{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|d]}\nonumber\\ \displaystyle & & \displaystyle +\,(g+2TF\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}z}+2TS\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}z}+2\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{zz})|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|\sin (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\sinh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|(z+d)]}{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|d]}\nonumber\\ \displaystyle & & \displaystyle +\,2(iTF+jTS)\unicode[STIX]{x1D711}_{z}|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})\frac{\sinh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|(z+d)]}{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|d]}\nonumber\\ \displaystyle & & \displaystyle +\,[(2TF\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{1}}+2TS\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}}+2\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}z})(ik_{1}^{2}+j\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{k}_{2})\nonumber\\ \displaystyle & & \displaystyle +\,(2TS\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}\unicode[STIX]{x1D709}_{2}}+2TF\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}}+2\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}z})(jk_{2}^{2}+i\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{k}_{2})\!]\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|(z+d)]}{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|d]},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}{\mathcal{N}}_{2}[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}C_{i,j}^{\unicode[STIX]{x1D711}}} & = & \displaystyle (iTF+jTS)\cos (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})\frac{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|(z+d)]}{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|d]}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D711}_{z}|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|\sin (i\unicode[STIX]{x1D709}_{1}+j\unicode[STIX]{x1D709}_{2})\frac{\sinh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|(z+d)]}{\cosh [|i\boldsymbol{k}_{1}+j\boldsymbol{k}_{2}|d]},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}{\mathcal{N}}_{1}[\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}z} & = & \displaystyle TF^{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{1}z}+TS^{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}\unicode[STIX]{x1D709}_{2}z}+2TFTS\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}z}+2TF\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}zz}+2TS\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}zz}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D711}_{z}^{2}\unicode[STIX]{x1D711}_{zzz}+2(TF\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{1}}+TS\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}}+\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}z})TFz+2\!(\!TS\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}\unicode[STIX]{x1D709}_{2}}+TF\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}z}\! )\!TSz+(g+2TF\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}z}+2TS\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}z}+2\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{zz})\unicode[STIX]{x1D711}_{zz},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}{\mathcal{N}}_{2}[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]}{\unicode[STIX]{x2202}z}=g+TF\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}z}+TS\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}z}+\unicode[STIX]{x1D711}_{z}\unicode[STIX]{x1D711}_{zz},\end{eqnarray}$$
where
$$\begin{eqnarray}TF=k_{1}^{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}}+\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{k}_{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}}-\unicode[STIX]{x1D70E}_{1},\quad TS=k_{2}^{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}}+\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{k}_{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}}-\unicode[STIX]{x1D70E}_{2},\end{eqnarray}$$
$$\begin{eqnarray}TFz=k_{1}^{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}z}+\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{k}_{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}z},\quad TSz=k_{2}^{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{2}z}+\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{k}_{2}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D709}_{1}z}.\end{eqnarray}$$
Table 6. Frequency
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}$
and amplitude
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of the 15 largest components in group 1 with steepness
$H_{s,1}=0.20$
. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
Table 7. Frequency
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}$
and amplitude
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of the 15 largest components in group 2 with steepness
$H_{s,1}=0.20$
. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
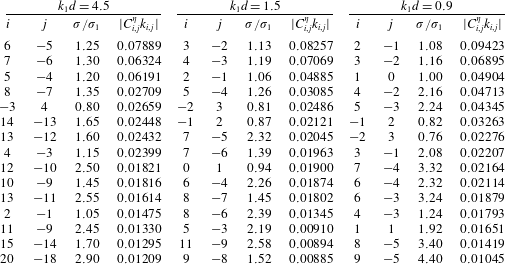
Appendix B. The 15 largest components in groups 1, 2 and 3 with steepness
$H_{s,1}=0.20$
Detailed frequency
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}$
and amplitude
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
values of the 15 largest components in groups 1, 2 and 3 with steepness
$H_{s,1}=0.20$
are shown in tables 6–8, respectively. Here
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
; and
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
Table 8. Frequency
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{1}$
and amplitude
$|C_{i,j}^{\unicode[STIX]{x1D702}}k_{i,j}|$
of the 15 largest components in group 3 with steepness
$H_{s,1}=0.20$
. Specification:
$\boldsymbol{k}_{1}=(1,0)$
,
$\boldsymbol{k}_{2}=(0.9,k_{2,y})$
;
$k_{2,y}$
is determined so that the component
$\unicode[STIX]{x1D6F9}_{2,-1}$
corresponds to an exactly resonant one in different water depths
$k_{1}d$
.
