2.1. Previous work on CBR in engineering

CADET (Navin-Chandra et al., 1991; Navin-Chandra, 1992a; Sycara et al., 1992; Sycara & Navin-Chandra, 1992; Miyashita & Sycara, 1993) and its descendent projects focus on conceptual design solving problems using relationships that capture function, structure, and behavior. CADET builds solutions to new design problems from pieces taken from previous design cases. CADET's representations are behavioral and functional, with input to the system consisting of symbolic descriptions of the desired device along with some physical constraints. The design knowledge base of CADET is a store of function, behavior, and the device's structural relationships. Indexing and retrieval are performed using linguistic descriptions of these properties as well as queries on the symbolic information and parameters. The retrieval and indexing methods are based on variations of graph matching and support retrieval at different degrees of abstraction.

Goel et al.'s KRITIK and its descendent systems (Chandrasekaran et al., 1993; Bhatta and Goel, 1994; Goel, Bhatta, et al., 1996; Goel, Gomez de Silva Garza, et al., 1996; Goel & Stroulia, 1996; Goel, 1997) operate on design problems using a case base of designs represented by symbolic component descriptions and their relationships and behaviors. A central contribution of KRITIK was the formalization of a structure–behavior–function model for designs, in which design cases can be indexed according to the functions they deliver. The functional representation is hierarchical, consisting of a component-substance model to capture the structure and performance of a given device.

KRITIK's design domain is not linked to specific CAD geometry and topology specifications (such as are captured in current engineering databases and product data management systems) and is limited to devices whose functions can be characterized as a flow of substances between components. The more recent work has extended many of the earlier KRITIK concepts; however, their powerful reasoning techniques are still primarily symbolic and have not been coupled with detailed engineering data.

Other systems include those for assembly (REV-ENG; Kim, 1997), architecture (Archie, Arichie II, Domeshek & Kolodner, 1997; CADRE, Hua & Faltings, 1993; Fabel, Voss, 1997), and civil engineering (Cadsyn, Casecad, Gencad; Maher & Zhang, 1993; Maher et al., 1995; Gomez de Silva Garza & Maher, 1996; Maher & Gomez de Silva Garza, 1996), among other engineering disciplines (Hennessy & Hinkle, 1992; Shi et al., 1997). Smithers (1989) describes the need to unite geometry with richer AI representations; Silverman and Mezher (1992) overview the work on design critics.

Work by Bose, Gini, and Riley (1997) applies CBR to the design of planar linkage assemblies. In this work, planar linkages are stored as parametrized 2-dimensional geometric information, along with functional information about the elements. The case storage structure is also multilevel, allowing for problem specification and retrieval at varying levels of abstraction. Case retrieval is executed using an algorithm that is a traversal of a variation of a KD tree, which hierarchically stores the cases.

Other case-based systems for problems in design and manufacturing include the case-based assembly planner of Pu and Reschberger (1991a, 1991b), Falting's Design-CADRE System (Hua & Faltings, 1993), and the Tsatsoulis application of the TOLTEC Planner (Tsatsoulis & Kashyap, 1993) to manufacturing problems. Lambright and Ume (1996) applied CBR/KBR to the design of flat panel displays. In addition, issues of IEEE Expert and Intelligent Systems have emphasized past accomplishments and current challenges in the extension of AI and CBR to complex engineering problems (Brown & Birmingham, 1997; Goldman & Boddy, 1997; Lee, 1997; Maher & Gomez de Silva Garza, 1997; Sauer & Bruns, 1997; Umeda & Tomiyama, 1997; Wielinga & Schreiber, 1997). Some of the observations in this series of articles include the following:

1. although there has been much research in knowledge-based engineering systems, the integration of this research into existing computer-aided design (CAD) tools has yet to really begin (Brown & Birmingham, 1997);
2. existing research systems still have great difficulty in scaling to complex design cases such as those posed by large CAD systems (Maher & Gomez de Silva Garza, 1997);
3. current CAD systems and their underlying representations are predominantly geometric and integrating knowledge about form and function is a major open research challenge (Umeda & Tomiyama, 1997); and
4. solving even the simplest design problems, such as the creation of a part configuration layout, requires advanced AI technology and novel extensions to the state of the art.

In a survey of work on variant and case-based design, Fowler (1996) makes several similar observations: better abstract models are needed for mechanical artifacts so that function information can be stored in the CAD knowledge base (in much the same way that functional indices are computed in KRITIK). Complex issues need to be considered to develop systems for automatically retrieving and applying existing designs to solve new design problems. Augmenting CAD systems with CBR/case-based design techniques can lead to great benefits to designers.

2.2. The CBR method

The CBR Cycle (Aamodt & Plaza, 1994) is a methodology to build a CBR system for a given domain. A CBR system can be viewed as a combination of case-base and knowledge reasoning process modules. These modules form a CBR (or reasoner), and they form the functions used to manipulate the knowledge in the case base. They act to process user inputs, recall similar cases, retrieve the most similar case, and evaluate and adapt the retrieved case and update the case memory.

Normally, the following problems must be addressed in the development of a CBR system: knowledge acquisition, knowledge representation, case retrieval, case adaptation, and learning mechanisms. We review the basic aspects of each step below:

1. Knowledge acquisition: How does one acquire useful knowledge from the application problem domain? This activity often consists of manual indexing of past design knowledge; sometimes automated or semiautomated indexing of design knowledge is possible.
2. Knowledge representation: How does one use a formal language, such as first order logic, to represent domain knowledge? The knowledge representation methodologies used in CBR systems are primarily concerned with how to structure knowledge stored in the case base to facilitate effective searching, matching, retrieving, adapting, and learning. One influential knowledge representation model is the dynamic memory model (Riesbeck & Schank, 1989), based on Memory Organization Packet (MOP) theory.
3. Case retrieval: Once we have determined how to represent knowledge and have populated a knowledge base with cases, how do we efficiently retrieve the case most similar to the current problem? There are two subprocesses involved in case retrieval: how to retrieve a set of similar cases from the case base and how to find the most similar case in this set. The first subprocess is accomplished by designing an appropriate index scheme for the domain problem. The second task is often done using techniques such as the Nearest Neighbor Matching Algorithm (NNM; Kolodner, 1993).
4. Case adaptation strategies: After a CBR system retrieves the most similar case from the case base, it normally needs to perform some modification on this retrieved case to adapt it to the new problem. There are several adaptation strategies that can be used in a CBR system. They include Simple Substitution, Parameter Adjustment, and Constraint Satisfaction (Kolodner, 1993).
5. Learning mechanisms: Learning is the last step in the CBR system. In a CBR system, after a new problem is solved, the case base is changed by adding the new case into it. In this way, the system can retain more knowledge along with problem-solving augmentation and achieve learning.

A CBR engine forms the control system that allows designers to use archived cases to solve new bearing design problems. Once domain knowledge has been used to build the case base, organize memory, build indices, and so forth, the reasoning engine can execute searches based on the index scheme. The engine also performs the other reasoning processes, including case retrieval, adaptation, and system learning.

2.3. Bearing design

Bearings are standard mechanical elements that play a very important role in product design and are used extensively in a wide array of mechanical artifacts. They usually support rotating shafts and make relative rotation possible among shafts and other parts (i.e., gears). Whenever a newly designed machine requires rotational function, it also requires bearings. A bearing designed for a certain machine must satisfy the requirements of the overall assembly structure and working environment. The basic way to solve this problem is to perform intensive calculations based on the working conditions and develop a bearing configuration which can satisfy these working requirements. Some computer programs have been developed to help deal with these intensive calculations (HEXAGON, 1999). Although these approaches release human engineers from manual mathematical calculation, they cannot perform higher level design actions.

Because of the complexity of the bearing design problem, the knowledge space in this domain is incomplete and dynamic. Therefore, knowledge acquisition has to be achieved by specifying only the important features relevant to solving the specific problem. Knowledge not directly related to solving the problem is discarded. In this work, we predefine a set of important features for the bearing design problem, and knowledge acquisition is done manually by a knowledge engineer.

3.1. Problem formulation

There are two basic types of bearings commonly used in industry: rolling bearings and sliding bearings. This paper consider only the former. Rolling bearings are further divided into subcategories according to the geometric shape of their rolling components. Some have rolling components that are cylinders and some are spheres, called ball bearings.

The basic components of a bearing are an inner ring, an outer ring, the rolling components and a supporting cage, which keeps the rolling components distributed uniformly. Figure 1 depicts the bearings, but the cages are not shown.

The bearings and where they are installed.

Normally, the bearings are installed on a rotating shaft. The inner ring of a bearing is fastened on a shaft, and the outer ring is installed in a housing. The fundamental purpose of a bearing is to transmit the load between a stationary part of a machine (commonly a housing) and the rotating part of the machine (commonly a shaft) with the minimum resistance.

3.1.2. Important design factors

The inputs include the working conditions, load to be applied on the bearings, shaft speed, lubrication (i.e., oil or grease), assembly space, ambient temperature, corrosive atmospheres and vibrations, and so forth. There are also other important factors that must be considered, such as misalignment, quiet running, and so forth. The primary design factors that are considered in this research are the following:

1. Load: The magnitude of the load is the factor that usually determines the size of the bearing to be used. The direction of loads applied on the bearings is also very important.
2. Speed: The speed at which rolling bearings can operate is limited by the permissible operating temperature.
3. Available space: When radial space is limited, it is necessary to choose bearings with a small cross section, particularly those with low cross section height (i.e., needle roller bearings; see Fig. 2).

The available space in the design configuration.

These design parameters, although not exhaustive, cover the major aspects of most bearing design problems.

3.1.3. Design calculations

The primary calculations are to predict the probability of bearing failure: “How long can a bearing be used in a certain working environment?” The first step in predicting bearing life expectancy is to calculate the equivalent load applied on the bearing. Figure 3 illustrates this calculation. Any load applied on a bearing can be decomposed into a radial load and an axial load. The radial load and axial load are the component forces of an equivalent compound force whose directions are radial and axial. Normally, a radial load and an axial load can be obtained from a special testing instrument and the equivalent compound load can be calculated from these measurements.

The calculations for the equivalent load applied on the bearing.

The variants of the formula given in Figure 3 can be expressed with two formulae. The first is the theoretical formula for computing equivalent load applied on a bearing (Wilcock & Booser, 1957):

The second is the heuristic formula for computing an equivalent load applied on a bearing (Wilcock & Booser, 1957):

where W is the bearing load (N), F_r is the radial load applied to bearing (N), F_t is the axial load applied to bearing (N), α is the operating contact angle (rad), and β is the initial contact angle (rad).

The formula for computing bearing life can be expressed as (Wilcock & Booser, 1957)

where L_n is the bearing life in millions of revolutions, L₁₀ is the bearing life (h), C is the load rating constant (N), N is the speed of the shaft (rpm), and W is the equivalent load imposed on the bearing (N).

Although other calculations do exist that are involved in bearing design problems, these calculations are omitted in order to simplify discussion of how we will represent domain knowledge for use in a case-based design system.

3.2. Case representation schema

The knowledge pertaining to bearing design problems can be represented in any kind of formal knowledge representation language. We have chosen to use CBR Language (CASL; Center for Intelligent Systems, 1999), a language specially designed for CBR. CASL can be used to define the contents of the case base (in a case file), and the reasoner uses this case file to create a case base to be accessed and adapted in order to solve design problems.

3.2.2. Examples for bearing design domain representation

The feature definitions for user input. When a bearing for a machine is designed, working conditions are specified and given to the CBR reasoner. The case definition is block in CASL is used to structure the input specifications. It structures the knowledge about case instances and input problems by defining the primary features of a problem. Following the case definition is keyword is the definition of problem features, which can have different weights according to their importance in the problem definition. The weight is keyword is used to specify the weight of a feature.

In the bearing design problem, the most important features are axial load and radial load. These features' weight values are set to be 5 (the reference weight). Load direction, shaft housing diameter, allowed radial limited space, and so forth are not that important, comparatively speaking. Therefore, their weight values are set to be 0 (the reference weight). A sample case definition using CASL can be given as:

case definition is

field shaft_housing_diameter type is

(d_12_24,d_12_28) weight is 5;

field load_direction type is

(radial,axial,combined) weight is 0;

field radial_limited_space_requirement type is

(Yes,No) weight is 0;

field radial_load type is number

weight is 5;

end;

Explanations of the case definition include the following:

1. The feature shaft_housing_diameter defines shaft and housing diameters. The purpose of this field is to define a series of possible shaft and housing diameters that may appear in the problems.
2. The load_direction field defines the load direction that is applied to the bearing. The purpose of defining this field is that some bearings can only carry axial direction loads, some can only carry radial direction loads, and some can carry loads in both directions.
3. The feature radial_limited_space_requirement defines the available radial space in the machine in which the designed bearing can be assembled. In some cases, the design has certain assembly space requirements for special purposes. That is, the available space for bearing design may be restricted in a certain dimension. These space requirements can help a designer predetermine his choice of bearing.
4. The field radial_load defines the magnitude of the load that is applied to the bearing in the radial direction. This is the most important factor in deciding the bearing design for a machine, and in this work the reference weight is specified as to be 5.

The index feature definition. This part defines the fields that are used as indices when searching for a matching case. The index scheme defines the methods by which the reasoner should access the case memory. Indices are intended to streamline the matching process. The index features are parts of the new problem specification. For example, we use the features shaft_housing_diameter and load_direction as main indices to search the knowledge base. The sample representation is given below:

index definition is

index on shaft_housing_diameter;

index on load_direction;

The definitions of adaptation rules. When the old bearing design whose “description of problem definition” part is the most “similar” to the current problem definition is retrieved from the case base, its solution part must be modified to fit the current problem definition. The reasoner performs adaptations to an old solution according to certain rules defined by domain experts. The repair rule definition is block of CASL can be used to define those rules. In the bearing design problem, the following strategies are defined:

1. Perform simple parameter substitution: substitute parameters of old problem definition into new user input.
2. Perform old solution adjustment to make it fit substituted user input (the current problem) according to domain formulae.
3. Check global constraints defined in the case base to guarantee that no conflicts result.

In the sample given in Algorithm 1, change_value_1 is an adaptation rule. It tests a certain condition (represented by a formula) first; when the condition is satisfied, the action is fired. The action here is the recalculation of bearing life (represented by a formula) according to the current user input.

The definition of a stored case. An experience (case) includes a problem statement part and a solution part. The case instance is block of CASL provides a kind of structure and function. This block defines the same structure of problem statement as the case definition is block defines.

In a bearing design for an application, some relationships between the problem statement and the solution are unique only for this design (case). For this reason, some features of a case are defined as “local,” meaning the attributes for these features are valid only for this design. For example, the features average_speed and expected_bearing_life are defined as local because every bearing designer specifies his or her own shaft speed and requires his or her own expected bearing life. In addition, every bearing has its own permissible speed limitation defined by the manufacturer and its own life expectancy according to the working environment.

If it is necessary to define some rules to adapt local features, then these rules must be specified as local. That is, the local rules are defined in a case instance is block. In the given sample below, the rule rule_1 is local because this rule checks the constraints for local features (i.e., expected_bearing_life). A sample representation of a case is Algorithm 2.

4.1. System overview

The CBR engine allows the designer to navigate and manipulate the case base through a graphical user interface. In this work, our CBR engine is implemented with C and the Microsoft Visual C++ programming environment. Our system uses CASL (Center for Intelligent Systems, 1999) to represent our design knowledge and the case base and MOP theory (Riesbeck & Schank, 1989) to develop a structure of the case base. The kernel of the CBR engine is based on the CASL environment from the University of Wales (Center for Intelligent Systems, 1999).

Once the user enters the problem specifications and provides a case base, the reasoner analyzes the problem and returns an answer to the user automatically. Our reasoning engine consists of four process modules, each performing certain functions to implement the complete CBR cycle. The first module, Retrieved Case, takes the current problem specifications as input and outputs a retrieved case. The second module, Solved Case, decides whether a retrieved case needs to be adapted. This module either returns the user a solution without further modification or passes a solution to the next module, which will perform adaptation on the case. The third module, Repaired Case, performs the adaptation and returns an adapted case to the next module. The fourth module, Learned Case, decides whether this new resolved case needs to be stored in the case base. The following sections will detail how these modules are implemented.

4.2. Reasoning engine

The flowchart in Figure 4 shows the main algorithm behind the implementation of a reasoning engine. The two hollow arrows in the figure illustrate that the reasoning engine must interact with the case base.

The primary functions of the CBR engine.

The flowchart shows that the requirements of a module can be broken into pieces or procedures called by the main function. It also shows that a CBR engine forms a reasoning loop. This reasoning loop begins with the procedure User Specification and ends with the procedure Add Case.

4.3. Building the case index

The performance of a CBR system is determined by the CBR reasoning engine whose efficiency in turn is determined by the design of the index scheme and case-base memory organization. The index scheme design includes how to specify index features and how to build them in computer memory. The index features are set by domain experts and are represented by the block index definition is of CASL. The procedure Build Indices takes the representations of index features as input and uses these to build the index scheme. A linked list data structure holds the index feature input. The procedure Build Indices places all the index features into the list and, at the same time, builds the case-base memory organization (shown in Fig. 5).

The index building and case-based memory organization.

In this CBR system, two features have been specified as index features: shaft diameter and load direction. Each index feature is a node in the list and the feature's attributes are associated with the nodes. Figure 5 shows this data structure for the index features and case-base memory. The procedure Build Index first links the index features shaft diameter and load direction. It then checks every attribute of the index features. For each attribute, Build Index searches for all the cases with the same attribute value in the case-base file and links all of these together.

4.4. Case matching, ranking, and retrieving

The purpose of building an index scheme is to speed up searching. Here, searching means to find a set of cases from the case base that are similar to the current input case. However, the goal here is to find the case which has the maximum similarity to the input case. Thus, a mechanism to rank the similarity of cases is needed. In section presents how to achieve these two goals: finding a similar case set and finding the most similar case in this set.

A mathematical model is first presented to show how to find a set of similar cases in the case base. What are similar cases? Given an input case with certain index features and their attributes, similar cases are those cases whose index features and attributes are exactly the same as the corresponding input case. Figure 6 shows these ideas.

The mathematical model and an example of searching similar cases.

The upper part of Figure 6 presents the mathematical model for finding similar cases. The left and right circles represent attributes F(A) and F(B) of index features A and B of an input case, respectively; and C(n) represents a case n. If the left circle includes C(b),C(d),C(h), and C(a), which are the cases with attribute F(A) of feature A, and the right circle includes C(i),C(j),C(a), and C(h), which are the cases with attribute F(B) of feature B, then their intersection contains cases C(a) and C(h), which have both attributes F(A) and F(B):

The lower part of Figure 6 gives a corresponding example that illustrates how this process occurs in the case base. After all similar cases are found, a mechanism to find the most similar case in this set is needed. We used the NNM algorithm (Kolodner, 1993). Figure 7 shows how this algorithm works in our CBR system for bearing design. To simplify discussion, we assume that all the component loads (axial load and radial load) applied on the bearing are in the same direction.

The nearest neighbor matching algorithm.

The basic idea of the NNM algorithm is to compare the attribute value of each feature of each case in the set of similar cases to every corresponding feature's attribute of the input case, calculate the comparison values, and then sum them for each case to get a total comparison value.

In the upper part of Figure 7 the circles represent cases, the dots represent attribute values of features, index i represents the input case, index j represents cases in the set of similar cases, and index k represents the features in a case. Case A and case B in the figure are the cases from the set of similar cases. The function d(k)(ij) represents the attribute's comparison value of one of the features (feature k) between the input case and case A, which is equal to the following formula (Kolodner, 1993):

where k is a feature of a case; W(ij) is the weight of a feature, defined in the case-base file; and sim(F(k)(R)i, F(k)(I)j) is the degree of similarity between one of the features in the input case and the corresponding feature in a case from the similar case set.

The total attributes' comparison value for a case is D(k)(IA), which is equal to the numeric function

The NNM algorithm ranks the case that has the highest value of D(k)(ij) as the most similar to the query case.

The key computation in the NNM algorithm determines the distance between the feature attributes for the input case and the cases in the case-base. A relevance matrix, shown in the lower part of Figure 7, is used to explain how to calculate every feature's attribute comparison value. In the matrix, F(k)(R)i represents “the feature k of a case from the similar case set that has possible attribute i, where the range of i can be from 1 to some finite number.” Except in reference to the input case, F(k)(I)j has a similar meaning. Thus, the first row of the matrix represents all the possible attributes of feature k of a similar case, and the first column represents all the possible attributes of feature k of the input case. The intersection of row and column is the comparison value of the feature k. Expression W(ij) is the weight of a feature in a similar case. The degree of similarity, sim(F(k)(R)i, F(k)(I)j), has three possible values. First, if two features match exactly, the degree of similarity equals 1. Second, if two abstract symbols are similar, its value is ¾. Third, if two numbers are similar (i.e., both fall within the range defined in the modification block), then a value is calculated that reflects how close they are in proportion to the range. Then, the sim(F(k)(R)i, F(k)(I)j) can be calculated by

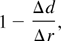
where Δd is the difference of the feature values between the input case and the retrieved case and Δr is the difference range value. For example, if the attribute value of feature radial load for the input case is 100 N and the corresponding value for a similar case is 120 N, then Δd = 120 − 100 = 20. If the definition for the range of similarity is from 90 to 140, then Δr = 140 − 90 = 50, where the similarity ratio is computed as 1 − (20/50) = 0.6.

Algorithm 3 defines the functions that implement the finding of similar cases and the most similar case, as mentioned above. The procedure Index_List_Searching() performs searching on the linked list of index features. Procedure Case_List_Searching() searches out cases whose attribute value for certain features is the same as the input case. Procedure Computing_Weight_Cases() performs calculation of the weight of a retrieved case. Procedure Evaluating_Similar_Cases() performs ranking for a case with a weight. Procedure Retrieving_Heaviest_Case() retrieves the case with the highest rank.

4.5. Adaptation of cases

Very rarely, a retrieved case is exactly the same as the newly defined problem. Most of the time, however, the retrieved case is only a similar situation and so problem definitions and corresponding solutions need to be modified so that the modified case fully fits the current situation and its solution fully satisfies the current problem requirements. This procedure as a whole is called the case adaptation (or repair) process. A series of rules are defined for adapting cases. These rules are provided by domain experts or domain axioms and are applied to each case whenever it is necessary.

Adaptation rules are divided into global rules and local rules The reasoner uses global rules to examine the problem fields and solution fields of the retrieved case. These rules are also used to adapt the parameters of the retrieved case and check constraints satisfaction conditions that are specified by the knowledge base. If there are any constraint conflicts, the repair rules provide a new problem-solving proposal. Otherwise, they adapt the solution of the retrieved case to the new problem. The sample adaptation rules for global repair are described in Algorithm 1.

After the reasoner finishes checking the global rules, it immediately checks the local rules defined in the retrieved case. It applies these local rules to the retrieved case to perform local adaptation (i.e., unique to this case). Some sample local adaptation rules are given in Algorithm 2.

Figure 8 shows that a linked list data structure is used to store these adaptation rules. In the figure, every node has two fields: one stores the condition of a rule, and the other stores the action. The procedure given in Algorithm 4 scans the rule list repeatedly as it performs adaptation on a retrieved case; if the condition part is true, it executes the corresponding actions on the case.

The data structure of global and local rules.

5.1. Building the case repository

Initially, the system allows designer to choose the search method. This function provides the designer with the flexibility to search the case base according to his or her own needs. If the designer chooses “Search for matching case,” the system will ask the designer to input problem definitions. If the designer selects “Search specifying indexes separately,” the system will ask the designer to specify the indexes and their desired values. Figure 9 illustrates how to select searching methods. In this window example, we select “Search for matching case.”

A system overview: the window for selecting searching methods.

5.2. Problem specifications

5.2.1. Global problem specifications

Knowledge is acquired through user interaction, as shown in Figure 10. The designer is prompted to input the problem specifications, like shaft (bearing bore) diameters, load direction, allowed bearing axial/radial space, and the amount of loads. Here, different inputs will bring up various other windows and message boxes to indicate different reasoning results.

A system overview: the window for problem specifications.

Shaft (bearing bore) and shaft diameter: The diameter is d_20_52, which means that the shaft diameter (bearing bore diameter) is 20 mm and housing diameter is 52 mm.

Load direction: Combined, which means that the loads applied on the bearing are combined (can be decomposed into an axial load and a radial load).

Required radial space: No, which means that bearing is designed without a radial space requirement, that is, it is rigidly mounted on the shaft.

Required axial space: No; see above explanation.

Radial load: 1000, which means the external radial load applied on the bearing is 1000 N.

Axial load: 500, which means the external axial load applied on the bearing is 500 N.

After the designer inputs all the above parameters, the system performs the following actions:

1. search the index list using the index features about the shaft (bearing bore) diameter and housing diameter (in this example, their values are 20mm and 52mm);
2. search the index list with the index feature load direction (in this example, its value is “combined”);
3. link all the cases satisfy above indices requirements;
4. compare other features to each case selected according to index features;
5. calculate the weight of each case; and
6. list the ranking of each case.

5.3. Local problem specification

After the designer finishes the global problem specifications, another message box will be brought up. It asks whether the designer wants to use the “Weight Algorithm.” If the designer's answer is “Yes,” the system will perform actions based on the NNM algorithm (Kolodner, 1993). If the designer's answer is “No,” the system will simple assign all the features' weight as 0 and find similar cases based on the numbers of matched features. Figure 11 shows a message box that asks the user whether to use the weight algorithm. In this window example, we select “Yes.”

A system overview: the window for the weight algorithm.

In our prototype, there are two local fields that define the specific features for each case. In this window, we input the rotation speed of the shaft and the bearing life that the designer expects. See Figure 12 to input local problem specifications.

A system overview: the window for the input of local problem specifications.

5.4. Case adaptation

Although the details of the adaptation procedures are hidden from the designer, the system presents a series of message boxes that indicate which case it is using to performing adaptation. In addition, the system keeps track of which cases that have failed during adaptation. This loop continues until the system finds a case that satisfies the problem specification or announces it failed to find any case that could fit the current problem (shown in Fig. 13).

A system overview: the message box shows the system is performing an adaptation on a retrieved case.

After the system has found a set of retrieved cases and performed successful adaptation on one of them, it automatically returns the adapted case. The system can also return a successful or failed case to the designer, allowing the designer to understand why the case is successful or why it failed. Hence, the designer can use these cases as a starting point for creating new designs. Figure 14 shows how the adaptation of successful cases is tracked. Figure 15 shows a case that failed adaptation.

A system overview: the window shows the successful case.

A system overview: the window shows the failed case.