2. ATTITUDE CONTROL MODE FOR THE NAVIGATION SATELLITES

The BDS navigation satellites have three attitude control modes, namely, YS mode, ON mode, and CYS mode. Attitude control of navigation satellites is dictated by two requirements or constraints: first, the transmitting antenna always points toward the Earth, and second, the solar panels are generally oriented perpendicular to the Sun-direction to ensure that the panels are facing the Sun. These requirements necessitate that the satellites constantly rotate (yaw) along the antenna axis, which points toward the Earth. The nominal yaw attitude control mode is the YS mode (Bar-Sever, Reference Bar-Sever1996).

The β angle is the acute angle between the Earth-Sun direction and the orbit plane. When the satellite is within the deep Earth eclipsing period, the lower the β angle, the higher the hardware yaw rate. The nominal yaw attitude has two singularities that decompose when the satellite–Earth and satellite–Sun vectors are collinear, which results in two 180° discontinuities. The collinear and nearly collinear vectors cause so-called “noon” and “midnight” rapid turn manoeuvres, which exceed the maximum hardware yaw rate. The noon turn is at the closest point to the Sun and the midnight turn is at the farthest point from the Sun, when a satellite is in Earth's shadow. The ON mode is employed not only to meet the power supply and thermal control requirements of the satellite, but also to avoid rapid yaw-slews near Sun–spacecraft–Earth collinearity for IGSO/MEOs in BDS-2 (Guo et al., Reference Guo, Chen, Zhao, Liu and Liu2017; Dai et al., Reference Dai, Ge, Lou, Shi, Wickert and Schuh2015). Melachroinos et al. (Reference Melachroinos, Tseng and Papanikolaou2017) have developed a model in which it makes more sense for the Attitude Determination and Control System (ADCS) system to follow a β°-fixed law for its yaw angle than a 0°-fixed law. In reality, the switch points from YS to ON for BDS-2 IGSO/MEOs are as follows: $\vert \beta\vert \lt 4^{\circ}$ and yaw angle $\vert \varphi\vert \leq 5^{\circ}$, the yaw angle is always zero in ON mode. So, the ADCS will perform sudden rump-up and rump-down “jumps” to 0° yaw angle at the switch points from YS to ON and ON to YS. Figure 1 shows the yaw angle from YS to ON and ON to YS by the telemetry data for C08, C11 and C12 satellites in the BDS-2 system. The ON mode begins and ends at φ = 5° and φ = −5°. The interruption of the yaw angle means that the satellite cannot be monitored by regional BDS monitoring stations. ON mode does not experience noon-turn and midnight-turn manoeuvres.

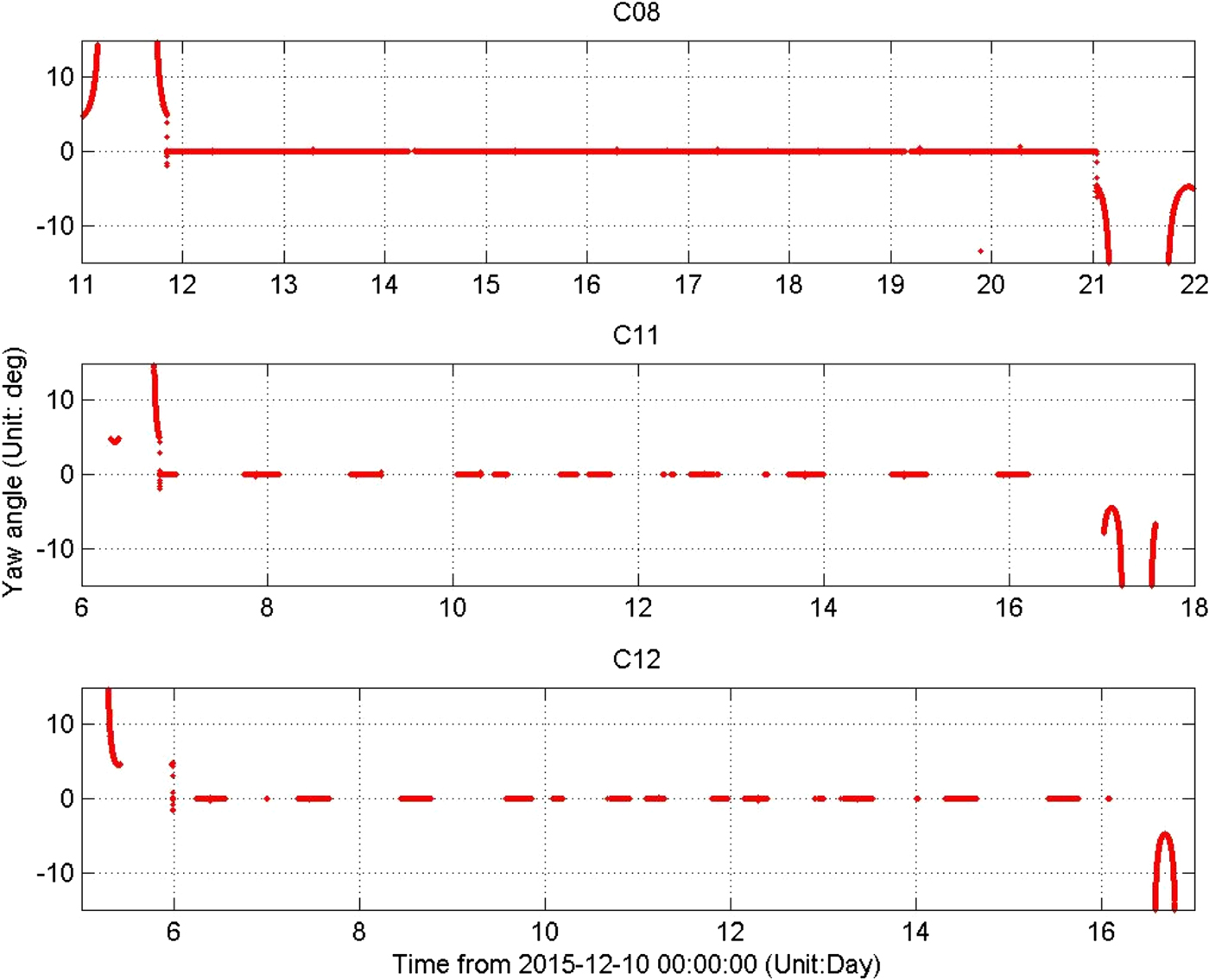
Figure 1. Yaw angle from YS to ON and ON to YS by the telemetry data in the BDS-2 system.

Figure 2 shows the declining orbit User Ranging Error (URE) accuracy for the C10 satellite during February 2013 in ON mode as operated by the Beidou ground control system. A straight line represents the beginning of ON mode, and the orbit accuracy declines to more than 70 m over 10 h.

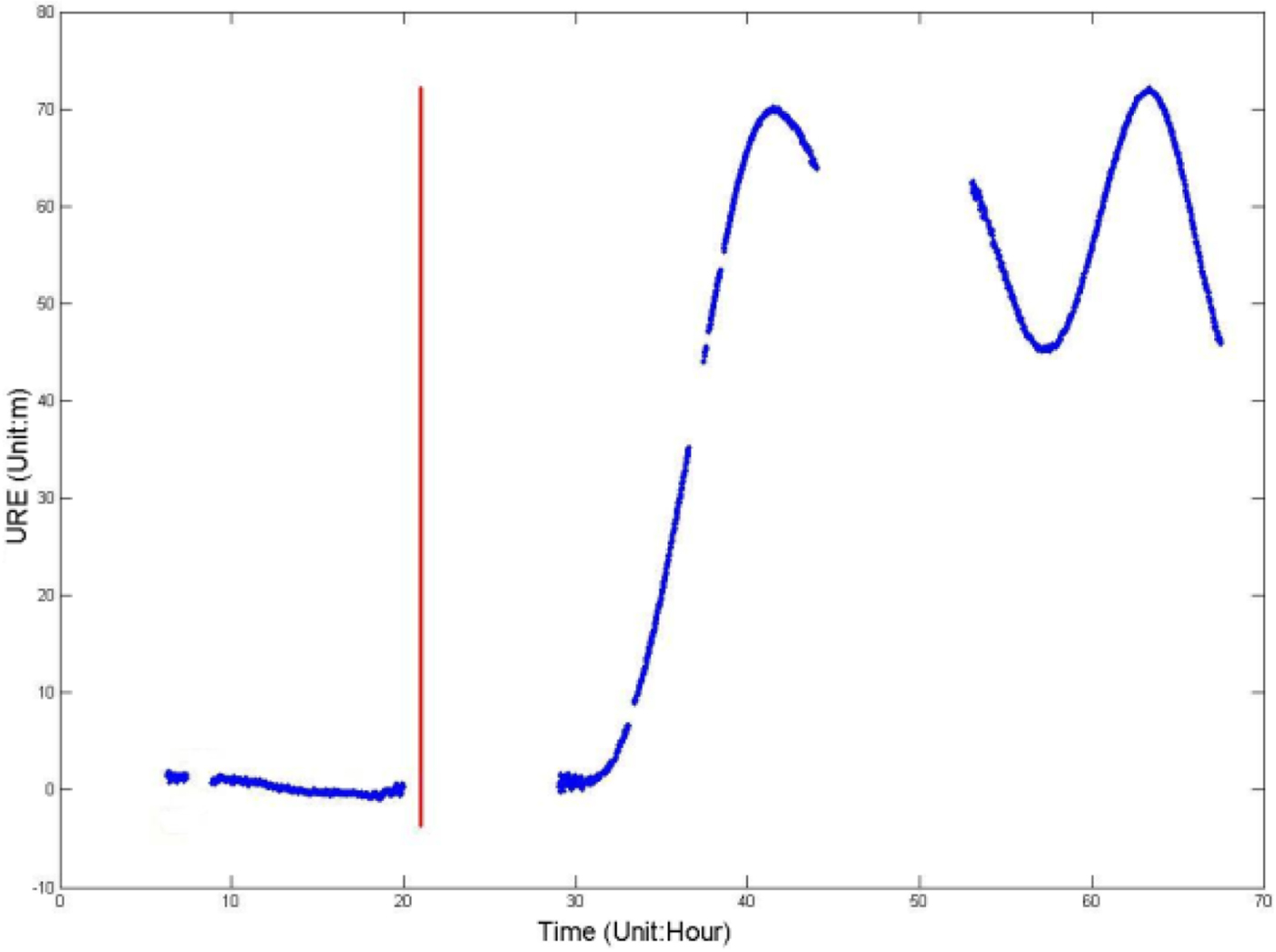
Figure 2. Orbit URE accuracy for the C10 satellite in ON mode.

The CYS mode is adopted not only to solve the problem of limited hardware yaw rate during the “noon” and “midnight” rapid turn manoeuvres, but also to meet the power supply and thermal control requirements of the IGSO/MEOs in BDS-3. Sun azimuth α is the angle between Earth-satellite vector and Earth-“noon” vector on the orbit plane. “Noon” turn and “midnight” turn start when $\vert \rbeta \vert < 3^{\circ}$, $\vert \alpha\vert \leq 10^{\circ}$ or $\vert \alpha \pm 180^{\circ}\vert \leq 10^{\circ}$ and the solar sensor can no longer control the yaw attitude. The satellites start to yaw with estimated (BDS and Galileo) or maximum (Global Positioning System (GPS) and GLONASS) hardware yaw rates to make the yaw angle transform 180°; at this time, the yaw attitude departs from the nominal values and it can take up to 30 min to 1 h to correct. Figure 3 shows the yaw angle in YS and CYS modes for BDS-3 satellites. The nominal yaw angle is followed in YS mode and the estimated yaw angle is followed in CYS mode.

Figure 3. Yaw angle in YS and CYS mode for BDS-3 satellites.

CYS mode is similar to the attitude control mode in “noon” and “midnight” rapid turn manoeuvres for GPS satellites. The noon and midnight turn problems for the GPS Block IIF satellites are due to insufficient hardware yaw rates, which cause the estimated yaw angle to temporarily lag behind the nominal yaw attitude (Dilssner et al., Reference Dilssner, Springer and Enderle2011a).

For the new generation BDS satellites, the estimated yaw angle φ is as follows:

(1)$$\varphi = \left\{ {\matrix{ {{\rm atan2}(\tan \beta ,\sin \mu )} \hfill & {\vert \beta \vert \ge \beta _0} \hfill \cr {{\rm atan2}(\tan \beta ^ * ,\sin \mu )} \hfill & {\vert \beta \vert < \beta _0,\;\vert \alpha \vert \le {10}^\circ \quad {\rm or}\quad \vert \alpha \pm {180}^\circ \vert \le {10}^\circ } \hfill \cr } } \right.$$

where β ₀ = 3. β* is a virtual function of α and μ is the satellite's angle on the orbit plane (that is, orbital angle). When α = 0° or α = ±180°, β*(α) = sign(β) · β ₀, when $\vert \alpha\vert \leq 10^{\circ}$ or $\vert \alpha\pm 180^{\circ}\vert \leq 10^{\circ}$, β* is expressed in the form of an exponential function of α.

In the BDS-3 system, IGSO/MEO satellites adopt the YS mode when β > 3° and the CYS mode when β < 3°. For the BDS GEO satellites, the ON mode is continuously maintained. The attitude mode and “noon” and “midnight” rapid turn manoeuvre modes for GNSS satellites are listed in Table 1.

Table 1. Attitude mode for GNSS satellites.

When β is large, the nominal yaw angle and YS mode are adopted, and attitude modes are different when β is small or during the deep eclipsing period. For “noon” and “midnight” turn modes, the eclipsing yaw attitude control consists of the following two distinct regimes: (1) ON mode, φ = 0 and (2) CYS mode, where the estimated yaw angle replaces the nominal yaw angle. BDS-2 and Quasi-Zenith Satellite System (QZSS) satellites adopt the ON mode within the deep Earth eclipsing period, whereas BDS-3, GPS, GLONASS, and GALILEO satellites adopt the CYS mode throughout this time, but there are small differences among the functions of the estimated yaw angle.

3. ANALYSIS OF THE CHARACTERISTICS OF THE SRP MODEL

The modelling accuracy of dynamic models affects the orbit accuracy, and SRP is the most difficult to model for Beidou satellites. In particular, an SRP model will depend on the satellite attitude, relative position between the satellite and Sun, area-mass ratio of the satellite, radiation intensity of the Sun, satellite geometry, surface material quality, and so on. Significant milestones in the history of SRP model development include the ROCK model, T10/T20/T30 model, Empirical CODE Orbit model (ECOM), GSPM.97/GSPM.04 model, and Adjustable Box-wing SRP model (Wu et al., Reference Wu, Song and Zhou2015).

At present, BDS does not have its own SRP model. The ECOM model is the most widely adopted empirical SRP model for GPS Block II, Block IIA, and Block IIR applications. The ECOM model expresses the SRP acceleration in the (B, Y, D) frame where the satellite-Sun vector is along the D-axis, the Y-axis lies along the solar panel rotation axis direction, and the B-axis completes the right-handed coordinate system. It uses an optimal parameterisation of SRP, which has been shown to be in the order of centimetres in magnitude for GPS satellites (Steigenberger and Montenbruck, Reference Steigenberger and Montenbruck2016). Thus, we conducted experiments on PODs for Beidou satellites in CYS mode based on the ECOM model. The formula is as follows:

(2)$$\matrix{{\mathop{a}\limits^{\rightharpoonup}}_{SPR} \hfill & { = {{\mathop{a}\limits^{\rightharpoonup}}_{ROCK}} + D(u) \times {{\mathop{e}\limits^{\rightharpoonup}}_{D}} + Y(u) \times {{\mathop{e}\limits^{\rightharpoonup}}_{Y}} + B(u) \times {{\mathop{e}\limits^{\rightharpoonup}}_{B}}} \hfill \cr {D(u)} \hfill & { = D_0 + D_c\cdot \cos u + D_s\cdot \sin u} \hfill \cr {Y(u)} \hfill & { = Y_0 + Y_c\cdot \cos u + Y_s\cdot \sin u} \hfill \cr {B(u)} \hfill & { = B_0 + B_C\cdot \cos u + B_s\cdot \sin u} \hfill \cr } $$

where $\mathop{a}\limits^{\rightharpoonup}{\!}_{SPR}$ is the acceleration of SRP; $\mathop{a}\limits^{\rightharpoonup}{\!}_{ROCK}$ is the acceleration of the ROCK model; u is the argument of the ascending node; and D ₀, D _c, D _s, Y ₀, Y _c, Y _s, B ₀, B _c and B _s are constant parameters, which are estimated in the orbit determination.

The accuracy of the ECOM 9 model is closely related to the quantity and quality of observation data. With low amounts of data, the accuracy of the ECOM 9 model results will be relatively low. The visibility arc for MEOs in Beidou is about 8 h every day because of the structure of the regional monitoring net, and the accuracy of the corresponding ECOM 9 model results is comparatively low. In regard to IGSO/MEOs in Beidou, there are not obvious periodic terms in the Y- and B-axis, and only a reduced set of five parameters (D ₀, D _c, D _s, Y ₀, B ₀) is usually estimated, namely, through the application of the ECOM 5 model; the correlation of these parameters is low, and hence, the orbit accuracy and stabilisation for IGSO/MEOs can be improved based on the ECOM 5 model. There are only D ₀, Y ₀, B ₀ in the ECOM 3 model. The relevant experiments follow.

4. EXPERIMENT AND DISCUSSION FOR GNSS SATELLITES IN THE EARTH ECLIPSING PERIOD

For navigation satellites, SLR represents a unique high precision measurement independent of radio carrier phase measurements, and it is an important endpoint to assess in the orbit validation approach (Montenbruck et al., Reference Montenbruck, Steigenberger and Kirchner2013; Urschl et al., Reference Urschl, Beutler, Gurtner, Hugentobler and Schaer2007).

GPS satellite PRN G06 is a Block IIA satellite. Orbit accuracy for GPS satellite PRN G06 during the Earth eclipsing period was analysed. In this paper, the POD experiment for 32 GPS satellites was completed by using 20 International GNSS Service (IGS) monitoring stations distributed evenly throughout the world and applying the five-parameter ECOM SRP model. The G06 satellite was in the deep Earth eclipsing period from 30 December 2012 to 11 January 2013, and the satellite attitude control mode was CYS. Nominal YS law is adopted to model the yaw attitude of G06. Data in the post-shadow yaw manoeuvre is not adopted in orbit determination according to the research of Bar-Sever (Reference Bar-Sever1996). The global SLR residuals are shown in Figure 4; the grey shaded areas indicate time in the deep Earth eclipsing period. The SLR residual RMS values in no eclipse seasons and eclipse seasons were 4·96 cm and 11·56 cm, respectively. Thus, the orbit accuracy in terms of the radial component for GPS G06 in the deep Earth eclipsing period was 6·6 cm lower than that in the no eclipse seasons. The experiment did not use all IGS stations, and while the orbit accuracy in this experiment was lower than that of IGS orbit products, it was enough to illustrate the difference of orbit accuracy between the deep Earth eclipsing period and no eclipsing period. This problem exists for IGS precise orbit products. Figure 5 shows global SLR residuals for GPS PRN G06 obtained by IGS precise orbit products from the years 2010–2014. Notably, the orbit accuracy decreases by about 0·3 m in the Earth eclipsing period.

Figure 4. SLR residual for the GPS PRN G06 satellite in the deep Earth eclipsing period.

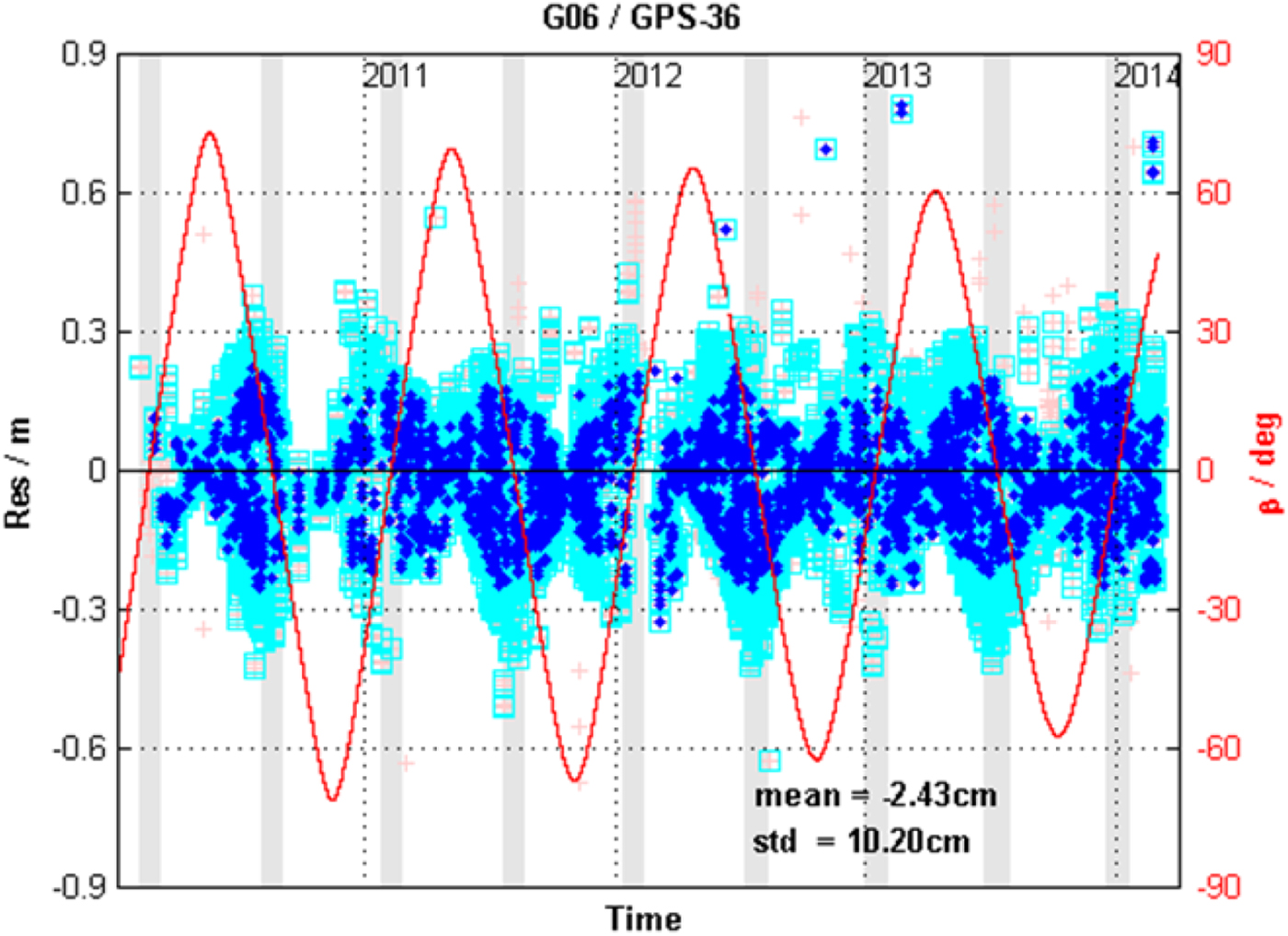
Figure 5. SLR residual for the GPS PRN G06 satellite from years 2010–2014 obtained from IGS precise orbit products.

5. EXPERIMENT AND DISCUSSION FOR BEIDOU SATELLITES IN THE EARTH ECLIPSING PERIOD

The MPOD method is an orbit determination strategy using L-band code and phase measurements for GEO/IGSO/MEOs collected at regional BDS monitoring stations (Zhou et al., Reference Zhou, Hu and Zhou2013) which was similar to the orbit determination strategy used by IGS for GPS. Seven monitoring stations including Beijing station, a station in Hainan, two stations in Xinjiang, a station in Sichuan, a station in Heilongjiang and a station in Guangdong were used and these are shown in Figure 6. Xinjiang1, Xinjiang2, Heilongj, Gudong in Figure 6 respectively present two stations in Xinjiang, a station in Heilongjiang and a station in Guangdong

Figure 6. Distribution of BDS regional monitoring stations.

Clock offset parameters of all satellites/receivers for each epoch and orbit parameter (initial orbital elements, SRP parameters, and empirical acceleration parameters), as well as site-dependent atmospheric zenith delay parameters and phase ambiguity, were estimated simultaneously. The perturbation modelled forces in the MPOD are shown in Table 2.

Table 2. Dynamic model information.

The POD for the new generation Beidou satellites in YS and CYS mode is based on the MPOD method. Specifically, the POD for BDS-2 satellites in ON mode builds on the new MPOD method supported by time synchronisation (Tang et al., Reference Tang, Hu, Zhou, Guo, He, Liu, Zhu, Li, Wu, Zhao, Yu and Cao2016), and in this method, high-precision satellite clock offsets were directly measured, instead of estimated, with a two-way time transfer between the satellites and the ground master station of the BDS. Those satellite clock offsets were then fixed to reduce the statistical correlations between other estimated parameters; consequently, the accuracy of the orbit determination was less susceptible to data quality issues than that from previous approaches. Additionally, one further constant acceleration in the along-track direction was added to the CODE SRP model to improve the POD accuracy for IGSO/MEOs in ON mode, according to the work of Guo (Reference Guo2014).

The evaluation method consisted of four steps, namely, analysis of the orbit internal consistency, calculation of the UERE, global SLR data fitting, RMS determinations and positioning performance analysis. The arc of the POD was 3 d. An orbit determination was made in a one-hour sliding window over a 72-hour session. Figure 7 shows the strategy of the orbit internal consistency with one-hour sliding windows; there are 24 POD solutions in each day, if the experiment lasts n days, there will be 24 × n POD solutions altogether. The internal consistency of satellite orbits can be evaluated by a two-day orbit fit through two consecutive one-day orbits. The red line represents the overlapping arc in Figure 7.

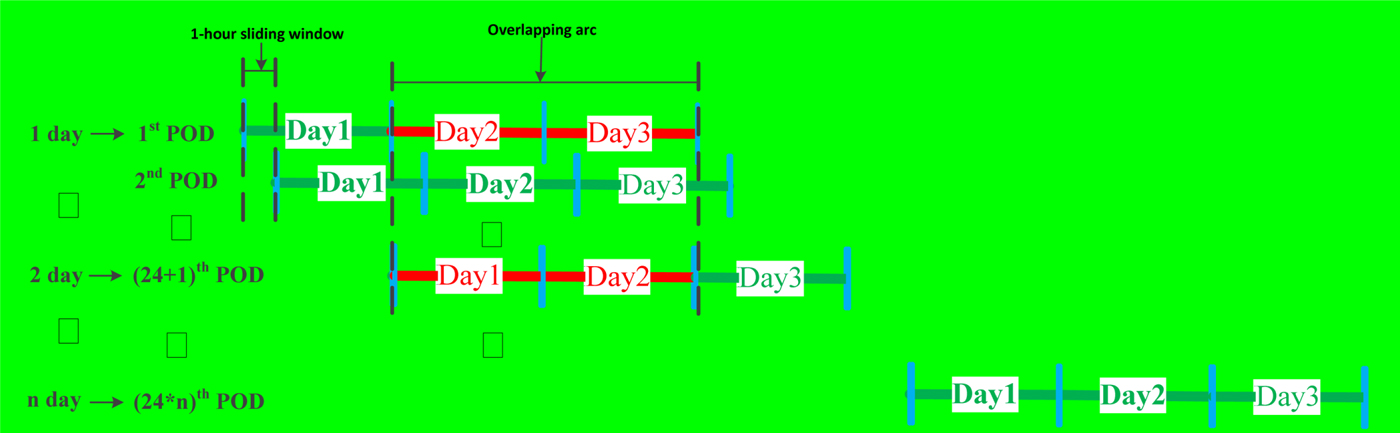
Figure 7. Strategy of POD with one-hour sliding window.

The orbit errors in the radial, along-track, and normal directions are obtained by the differences of overlapping orbits. The URE and Three-Dimensional (3D) position errors are then estimated, which serve as quality indicators (Steigenberger et al., Reference Steigenberger, Hugentobler, Loyer, Perosanz, Prange, Dach, Uhlemann, Gendt and Montenbruck2015). Equations (3) are URE _i for different Beidou satellites in an i-hour experiment and Equations (4) are the RMS of URE and 3D position errors in n-day experiments, which is the final result of orbit internal consistency.

(3)$$\left\{ {\matrix{ {GEO/IGSO:URE_i = \sqrt {1.0 \times \Delta R_i^2 + {(0.09 \times \Delta T_i)}^2 + {(0.09 \times \Delta N_i)}^2} } \cr {MEO:URE_i = \sqrt {{(0.99 \times \Delta R_i)}^2 + {(0.14 \times \Delta T_i)}^2 + {(0.14 \times \Delta N_i)}^2} } \cr } } \right.$$

(4)$$\matrix{ {URE_{RMS} = \sqrt {\sum\limits_{i = 1}^{{24}^ * n} U RE_i^2 /{24}^ * n} } \cr {POS_{RMS} = \sqrt {\sum\limits_{i = 1}^{{24}^ * n} P OS_i^2 /{24}^ * n} } \cr } $$

where Δ R _i, Δ T _i, Δ N _i, URE _i are respectively the orbit errors in the radial, along-track, normal directions and URE in an i-hour experiment.

The UERE is an important index parameter for evaluating the service capability of a navigation system, as it summarises the total errors of the space segment (satellite orbits and clock offsets), the propagation segment (ionospheric and tropospheric delay) and the user segment (multipath and random errors) (Li et al., Reference Li, Zhou, Hu, Liu, Guo and Zhou2015). When the precision of every error source except for that of the orbits is acceptable, UERE can be adopted to evaluate the precision of the orbits. For a receiver with known coordinates and a clock synchronous with BDT, the UERE is as follows:

(5)$$\matrix{ {UERE} \hfill & { = \rho - (R(t_k - \delta t_r - \tau ,t_k - \delta t_r) + C\delta t_r - C\delta t_s + \tau _r + \tau _s + \Delta D_{trop}} \hfill \cr {} \hfill & {\quad + \Delta D_{iono} + \Delta D_{rel} + \Delta D_{ant}^r + \Delta D_{ant}^s + \Delta D_{tide}} \hfill \cr } $$

where ρ is the pseudo-range measurement; R is the geometric range between the satellite and receiver; δt _r is the receiver clock offset (which is zero in this case); δt _s is the satellite clock offset in the navigation message; τ_r and τ_s are the equipment time delay of the receiver and satellite, respectively and ΔD _trop, ΔD _iono, Δ D _rel, $\Delta D^{r}_{ant}$, $\Delta D^{s}_{ant}$, and ΔD _tide respectively represent the tropospheric delay, ionospheric delay, relativistic effects delay, antenna phase centre delay of the satellite and receiver and tidal effects delay (Guo et al., Reference Guo, Zhou, Hu, Liu, Tang, Li and Wu2015).

The attitude control modes of the new generation Beidou satellite C31 in December 2015 and C33 and C34 in February 2016 were the CYS mode, and those of BDS-2 satellites C08, C11, and C12 in December 2015 were the ON mode. The POD experiments were conducted every hour so that 24 results were obtained every day. The experiment lasted for more than 60 d and included two CYS periods and one ON period. Table 3 shows the times of the different attitude control modes. In fact, β = 4° and φ = 5°, the orbit angle μ is about 90° (Guo et al., Reference Guo, Chen, Zhao, Liu and Liu2017; Dai et al., Reference Dai, Ge, Lou, Shi, Wickert and Schuh2015) at the moment of switch from YS to ON.

Table 3. Times of different attitude control modes for Beidou satellites.

5.1. Analysis of the orbit internal consistency

The orbit accuracies for GNSS satellites declined to different extents in the deepest shadow, which for certain types of satellites were different for different SRP models. Use of an appropriate SRP model could make the orbit accuracy in the deep Earth eclipsing period match that in the no eclipse seasons. Therefore the experiments for new generation Beidou satellites in CYS mode were based on the ECOM 9, ECOM 5 and ECOM 3 models. The experiments lasted 30 d, so there are 720 (24 × 30d) POD solutions altogether. The RMS of 720 POD solutions was the final result. Figure 8 shows the orbit internal consistency for C31, C32, C33 and C34, in which the radial directions based on the ECOM 9, ECOM 5 and ECOM 3 models were 0·62 m, 0·21 m and 0·21 m, respectively, the URE results were 0·65 m, 0·26 m and 0·29 m, respectively, and the 3D positions were 2·09 m, 1·78 m and 1·87 m, respectively. The orbit internal consistency based on the ECOM 5 model was the best, and improvements of 0·03 m and 0·39 m were achieved compared with the ECOM 3 and ECOM 9 model results. The URE of the orbit internal consistency was 0·26 m in CYS mode.

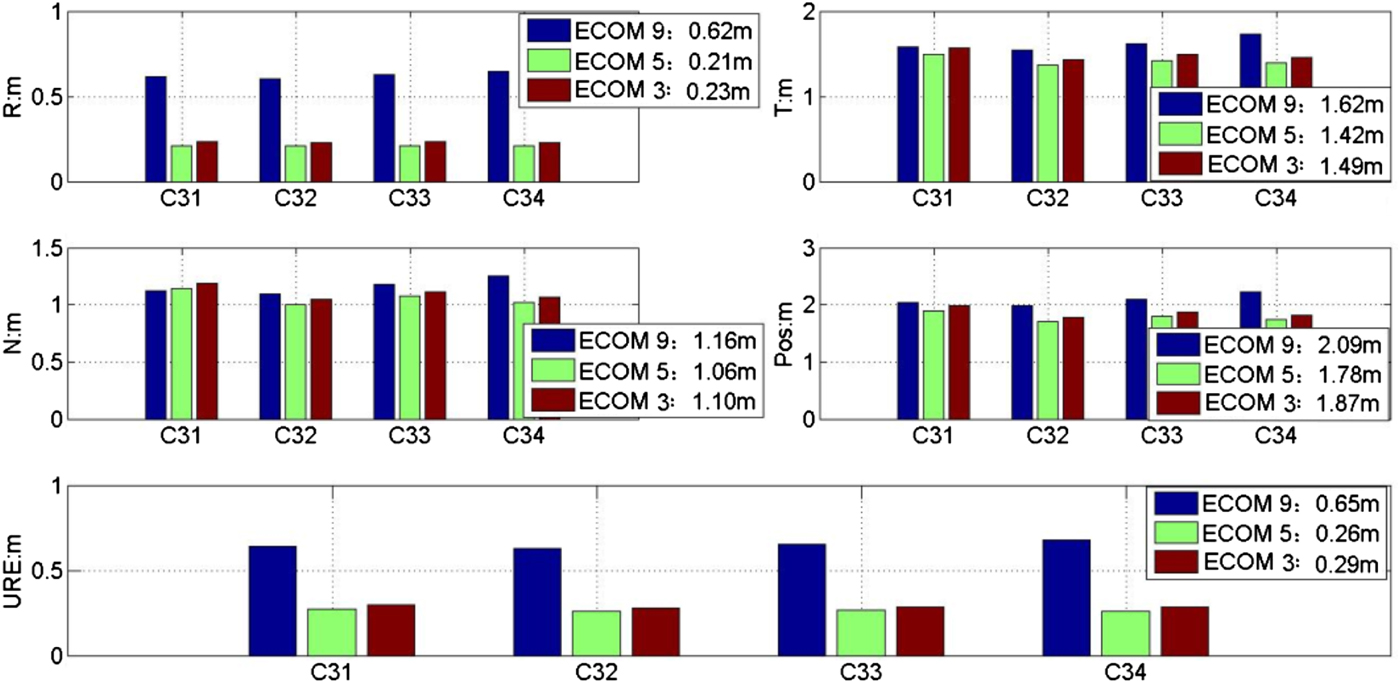
Figure 8. Overlapping arc accuracy based on three SRP models for new generation Beidou satellites.

5.2. Analysis of the UERE

The orbits and clock offsets were from broadcast messages of a receiver with known coordinates and clock times in Beijing. The SRP model results for ECOM 3 and UERE data for C31, C32, C33 and C34 in CYS and C08, C11 and C12 in ON mode are shown in Figure 9. The grey shaded areas indicate time periods with CYS or ON mode.

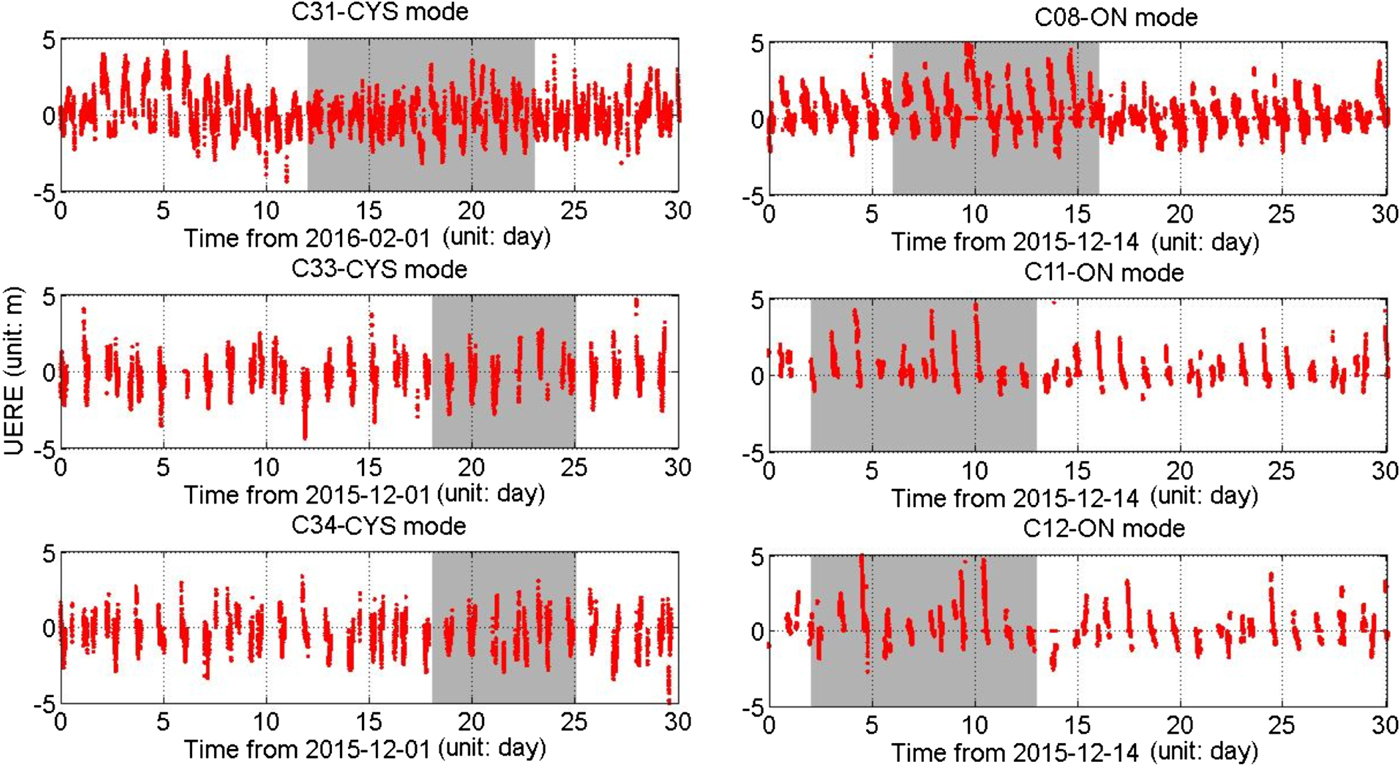
Figure 9. UERE for Beidou satellites based on different attitude control modes.

Figure 9 shows that (1) UERE values for C31, C33 and C34 in CYS mode matched those for the normal period of the YS mode and (2) UERE values for C08, C11 and C12 declined to about 4 m in the ON mode from about 2 m in the YS mode. Table 4 shows the UERE RMS results of the different attitude control modes.

Table 4. UERE RMS results of different attitude control modes for Beidou satellites (unit: m).

The data in Table 4 show that the average UERE RMS for C31, C33 and C34 in CYS mode was 1·31 m, which only declined by 2 cm in comparison with those for the same satellites in YS mode. The UERE RMS values for C08, C11 and C12 in ON mode declined by 0·6 m, 0·51 m and 0·46 m, respectively, and the average value was 1·78 m. However, the orbit accuracy did not decline to 70 m during the ON mode based on the new results from the MPOD method supported by time synchronisation.

The orbit accuracies based on different SRP models in CYS mode were estimated and the results are shown in Table 5.

Table 5. Orbit accuracies based on different SRP models in CYS mode (unit: m).

The data in Table 5 show that the average UERE RMS values for C31, C33 and C34 based on the ECOM 9, ECOM 5 and ECOM 3 models were 1·75 m, 1·22 m and 1·31 m, respectively. The orbit accuracy based on the ECOM 5 model was the best, and the results showed respective improvements of 0·09 m and 0·53 m compared to the results with the ECOM 3 and ECOM 9 models. The same conclusion was reached with the data based on overlapping arc accuracy.

The ECOM model expresses the SRP acceleration in the (B, Y, D) frame, which is suitable for describing the SRP for a satellite. The pressure from the direct light of the Sun is a major component of SRP, and the D-axis is right along the satellite-Sun vector. However, the orbit accuracy of the ECOM 9 model was low and the correlation of SRP parameters was high because of the limited data for IGSO/MEOs. Correlation of ECOM 3 parameters was lower and the orbit stability was higher than those of ECOM 9. However, ECOM 3 parameters only contained constant terms in the D/Y/B directions, not periodic terms; the orbit accuracy when applying ECOM 3 was lower than that when applying ECOM 5. The ECOM 5 model only contains five optimal parameters, and hence it is more suitable for IGSO/MEOs in CYS mode.

5.3. Orbit accuracy analysis based on global SLR data

Several satellites in the BDS have been employed in international SLR monitoring work. In particular, relatively large amounts of SLR tracking data have been collected for one Beidou GEO (C01), four Beidou IGSOs (C08, C10, C31 and C32), and four Beidou MEOs (C11, C33, C34 and C35) since 2012. The current global International Laser Ranging Service (ILRS) tracking network consists of around 40 ground stations. For BDS, the Australian Yarragadee and Chinese Changchun stations have been used to provide most of the observation data, and this data accounts for more than 90% of the global sum (Zhao et al., Reference Zhao, Zhou, Zhou and Wu2016).

In the process of SLR validation, the “theoretical” station-satellite distance is derived after the effects of solid tides, ocean tide loading, tectonic motion, station eccentricity, tropospheric delay, general relativity correction, and centre-of-mass correction have been eliminated from the SLR measurements. The corresponding L-band distance can be obtained from the L-band orbit by Chebyshev interpolation. The difference in the “theoretical” distance and L-band derived distance at the same time point is the SLR residual. Here, the cut-off elevation was set to 20° and the orbit accuracy according to the ECOM 5 model was evaluated by SLR measurements taken in December 2015 and February 2016. The SLR residuals for Beidou satellites are shown in Figure 10, and the corresponding statistics are shown in Table 6. The specific results for C33, C34 and C31 in CYS mode are shown in subgraphs 1 and 2 of Figure 10, and the specific results for C08 and C11 in YS mode and ON mode are shown in subgraphs 3 and 4 of Figure 10. The grey shaded areas indicate time periods with CYS or ON mode.

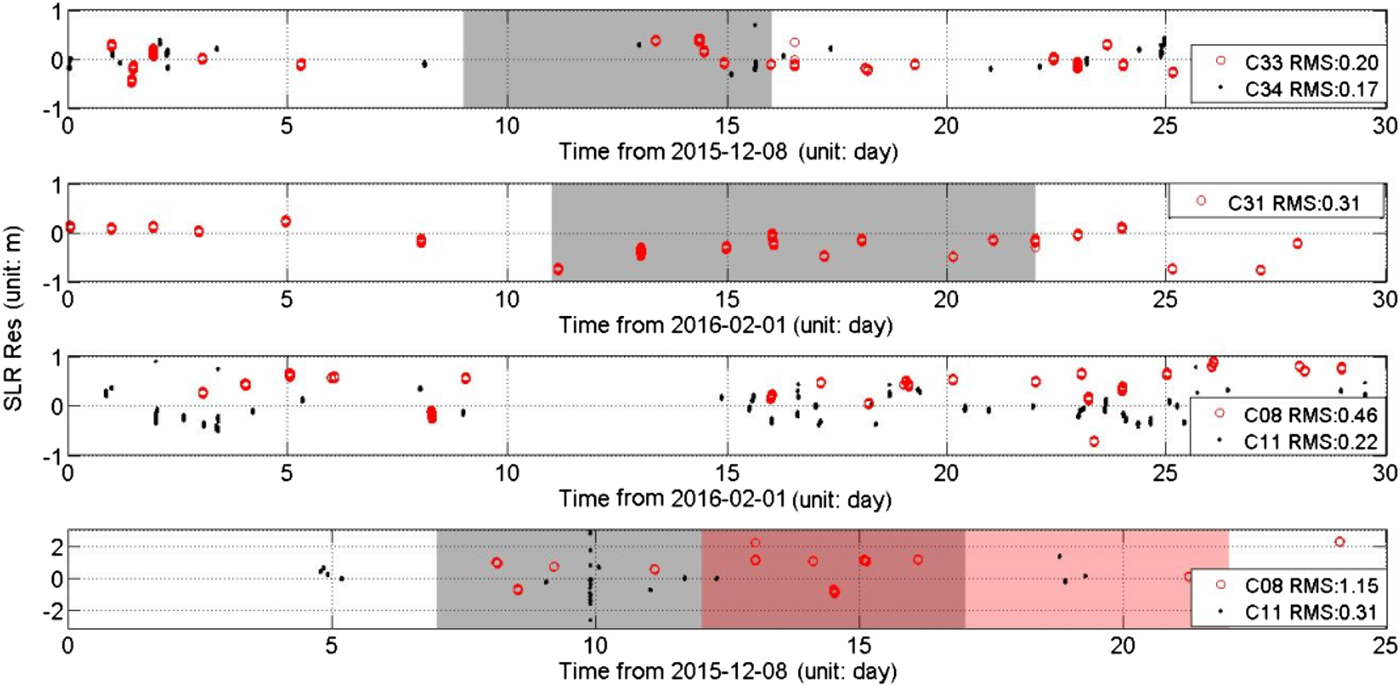
Figure 10. SLR residuals for different attitude control modes.

Table 6. SLR residual statistics for different attitude control modes.

The main findings of this analysis were as follows.

(1) As indicated in Figure 5 and Table 6, the quantities of SLR tracking data were limited and the data were distributed unevenly. As the echo amplitude of SLR is inversely proportional to the fourth power of distance, and additionally, the meteorological conditions will affect the SLR observations greatly, tracking Beidou satellites is relatively difficult.

(2) The SLR residuals for C31, C33 and C34 in CYS mode matched those in YS mode. The SLR residual RMS values for C31, C33 and C34 were 0·31 m, 0·20 m and 0·17 m, respectively, and the standard deviation was better than 0·3 m. Orbit accuracy in the radial component declined by 2 to 3 cm compared with that in YS mode.

(3) The SLR residual RMS for C08, C11, and C12 in ON mode was 1·15 m, which declined by 0·69 m compared with that in YS mode. The new MPOD method supported by time synchronisation and optimised SPR model were effective in avoiding an orbit accuracy decline of a few hundred metres over several hours in ON mode.

Although several publications (Guo et al., 2014; Guo et al., Reference Guo, Xu, Zhao and Liu2016; Mao et al., Reference Mao, Song, Wang, Jia and Wu2014; Mao et al., Reference Mao, Song, Wang, Jia and Wu2015; Melachroinos et al., Reference Melachroinos, Tseng and Papanikolaou2017; Montenbruck et al., Reference Montenbruck, Steigenberger and Darugna2017; Zhao et al., Reference Zhao, Wang, Guo, Wang and Liu2018) have discussed the question of why it is more difficult to model BDS satellites' dynamics in ON than in YS, the assumption is that it has a lot to do with the heat radiation panels at the −x side of the satellite bus. The solar panel axis is not perpendicular to the Sun direction with a small misalignment between 0° and 4°. The SRP model suitable for the YS mode does not do a good job of reflecting the characteristics of the SRP on the −X bus and coping with a small misalignment of the solar panels, thus the orbit accuracy declines in ON mode. Even if a priori analytical radiation models such as the ones from Tang et al. (Reference Tang, Hu, Zhou, Guo, He, Liu, Zhu, Li, Wu, Zhao, Yu and Cao2016) and Guo (Reference Guo2014) are employed, the orbit accuracy still declined to about 2 m. To avoid this problem, the new generation BDS satellites have all been upgraded with CYS capabilities. The –X bus is not illuminated by the Sun in CYS mode, similar to YS mode, and there are only about 40 minutes near “noon” and “midnight” where the CYS mode is required; at other times, a satellite will still adopt YS mode and the differences in SRP on the satellite will be small. Therefore, the differences in orbit accuracy will be small between YS mode and CYS mode.

5.4. Positioning performance analysis

To further validate the quality and consistency of orbit products in CYS mode, single point positioning accuracies with BDS pseudo-range data in YS, ON and CYS mode were analysed. The monitoring receiver was in Beijing, with data from 10 December 2015 to 28 January 2016 selected and processed, when the C08, C11 and C12 satellites were in ON mode and the C33 and C34 satellites are in CYS mode as shown in Table 3. In data processing, the ionosphere-free combination of B1I/B3I pseudo-range data recorded at 300 s intervals are used due to the 300 s clock products provided by BDS and orbit products in this paper. The static position coordinates and receiver clock offset are simultaneously estimated. The precise position coordinate is obtained by static Precise Point Positioning (PPP), which is used as the reference coordinate to evaluate the positioning accuracy. Two groups of satellites are used in the positioning analysis. The first group includes C01-C12 and C14, the difference between the second group and the first group is that C08,C11 and C12 in ON mode are substituted by the C31,C33 and C34 satellites in the second group. The positioning accuracies at the Beijing station from the two groups of satellites are shown in Figures 11 and 12 respectively. Table 7 lists the positioning accuracy in East, North and Up directions and overall position in YS, ON and CYS modes respectively.

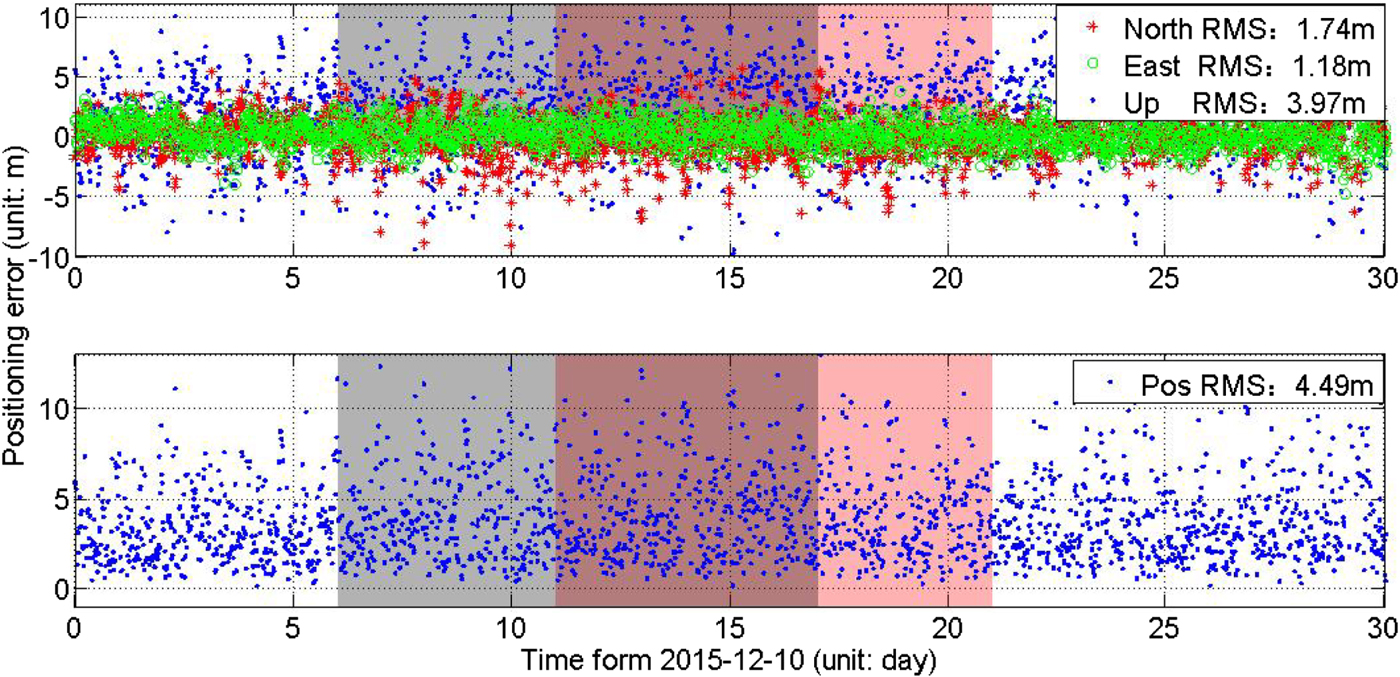
Figure 11. Positioning accuracy in Beijing by the first group of satellites. The grey shaded areas indicate time periods in ON mode of the C11 and C12 satellites, the light red shaded areas indicate time periods in ON mode for the C08 satellite.

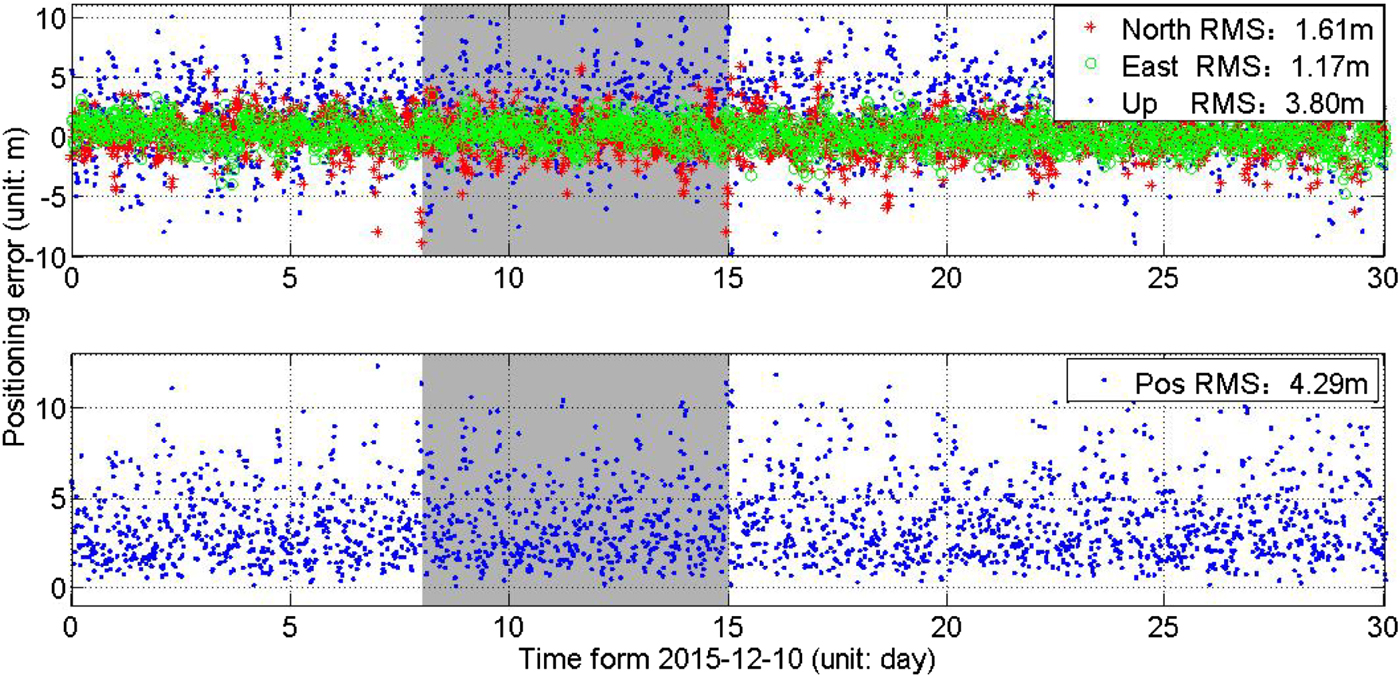
Figure 12. Positioning accuracy in Beijing by the second group of satellites. The grey shaded areas indicate time periods in CYS mode for the C33 and C34 satellites.

Table 7. Positioning accuracy in different attitude control modes (unit: m).

Figures 11 and 12 and Table 7 show that the positioning accuracy is 4.29 m, 4.49 m and 4.30 m respectively in YS, ON and CYS modes, which degrades by 0·2 m in ON mode over that in YS mode, and by only 1 cm in CYS mode over that in YS mode. GNSS positioning accuracy is generally the product of UERE and Position Dilution Of Precision (PDOP) (CSNO, 2013; DoD, 2018). The larger the orbit error, the larger the positioning error. So, the improvement of orbit accuracy will bring an improvement of the positioning accuracy in CYS mode compared with that in ON mode. Therefore, the design of CYS mode has been successful, and the positioning and navigation performance of BDS should be improved.