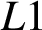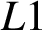1. Introduction
Apart from providing useful instruments for the study of important phenomena in different fields of engineering and science, fractional order derivatives have also been successfully applied in the financial field. The classical Black–Scholes [Reference Black and Scholes1] equation is one of the most powerful option pricing tools related to most of the models used for quantitative financial calculations. Generalizing the Black–Scholes equation to a fractional order can lead to the time-fractional and space-fractional Black–Scholes equations. Regarding option pricing under the modified Black–Scholes equation, different investigations have been sought, both in analytical and numerical settings.
Analytical solutions for the European options under the Black–Scholes fractional model have been derived previously [Reference Chen, Xu and Zhu7, Reference Jumarie19, Reference Wyss32]. The double barrier options were analytically priced by Chen et al. [Reference Chen, Xu and Zhu9]. However, these formulae are complicated and difficult to evaluate. As such, practical numerical approximate solutions for the Black–Scholes fractional order models were provided. An implicit finite-difference technique was considered for option pricing by Song and Wang [Reference Song and Wang31]. Chen et al. [Reference Chen, Xu and Zhu8] proposed a predictor–corrector approach to price the American options in the fractional framework. For the time-fractional Black–Scholes model, finite-difference approximations were also considered by Koleva and Vulkov [Reference Koleva and Vulkov20]. The effect of trend memory in financial option pricing was described by Farhadi et al. [Reference Farhadi, Salehi and Erjaee14] using the time-fractional Black–Scholes equation. Chen et al. [Reference Chen, Wang and Yang3] recently considered an operator splitting method for the evaluation of American options under the same model. Zhang et al. [Reference Zhang, Liu, Chen, Anh and Chen37] proposed a new fractional option pricing model employing both time- and space-fractional derivatives based on the finite moment log-stable (FMLS) model. The time-fractional Black–Scholes model was considered by Golbabai et al. [Reference Golbabai, Nikan and Nikazad16] using radial basis functions (RBFs) in the spatial sense and a finite-difference scheme for time. More recently, a two-dimensional fractional partial differential equation (FPDE) has been established, based on the two-dimensional FMLS model for option pricing [Reference Chen, Ding, Lei and Wang10]. Recently, several researchers [Reference Chen and Wang6, Reference Huang, Cen and Zhao17, Reference Mohammadi23, Reference Prathumwan and Trachoo25, Reference Roul27–Reference Roul and Goura29] have investigated the problem of option pricing under the Black–Scholes fractional framework or the generalized Black–Scholes equation. Such low-order convergence in both space and time implies that we need a lot of computational nodes in both dimensions to reach reasonable accuracies.
In this paper, we consider the time-fractional Black–Scholes model with a spectral element discretization in space. The approximation of the fractional time derivative is usually based on the finite-difference approach. The most common difference approximation of the time-fractional derivative is the
![]() $L1$
method, which is an implicit numerical scheme with accuracy proven to be of order
$L1$
method, which is an implicit numerical scheme with accuracy proven to be of order
![]() $2-\alpha $
for twice continuously differentiable functions [Reference Lin and Xu22]. Zhang et al. [Reference Zhang, Liu, Turner and Yang38] considered the
$2-\alpha $
for twice continuously differentiable functions [Reference Lin and Xu22]. Zhang et al. [Reference Zhang, Liu, Turner and Yang38] considered the
![]() $L1$
approximation [Reference Lin and Xu22] to approximate the Black–Scholes time-fractional derivative for the European options with a second-order finite-difference scheme for the spatial discretization. To improve their results [Reference Zhang, Liu, Turner and Yang38], De Staelen and Hendy [Reference De Staelen and Hendy12] later considered a fourth-order scheme in space with the same
$L1$
approximation [Reference Lin and Xu22] to approximate the Black–Scholes time-fractional derivative for the European options with a second-order finite-difference scheme for the spatial discretization. To improve their results [Reference Zhang, Liu, Turner and Yang38], De Staelen and Hendy [Reference De Staelen and Hendy12] later considered a fourth-order scheme in space with the same
![]() $2-\alpha $
scheme in time for the valuation of double barrier options under the time-fractional Black–Scholes model. However, the
$2-\alpha $
scheme in time for the valuation of double barrier options under the time-fractional Black–Scholes model. However, the
![]() $L1$
scheme exhibits only a first-order rate of convergence in time for FPDEs with nonsmooth initial data or without a source term, as proven in [Reference Jin, Lazarov and Zhou18, Reference Xing and Yan33, Reference Yan, Khan and Ford34]. This is also observed for option pricing problems for which the payoffs are all nonsmooth; there is no sourcing term and the solutions have low regularity near maturity. Moreover, Cen et al. [Reference Cen, Huang, Xu and Le2] obtained a first-order convergence in time under the time-fractional Black–Scholes model for the European call options. We further note that the main results obtained in the papers mentioned earlier [Reference De Staelen and Hendy12, Reference Golbabai, Nikan and Nikazad16, Reference Zhang, Liu, Turner and Yang38] are only valid for payoff functions that are smooth enough, which exclude the European or even the double barrier options.
$L1$
scheme exhibits only a first-order rate of convergence in time for FPDEs with nonsmooth initial data or without a source term, as proven in [Reference Jin, Lazarov and Zhou18, Reference Xing and Yan33, Reference Yan, Khan and Ford34]. This is also observed for option pricing problems for which the payoffs are all nonsmooth; there is no sourcing term and the solutions have low regularity near maturity. Moreover, Cen et al. [Reference Cen, Huang, Xu and Le2] obtained a first-order convergence in time under the time-fractional Black–Scholes model for the European call options. We further note that the main results obtained in the papers mentioned earlier [Reference De Staelen and Hendy12, Reference Golbabai, Nikan and Nikazad16, Reference Zhang, Liu, Turner and Yang38] are only valid for payoff functions that are smooth enough, which exclude the European or even the double barrier options.
To increase the temporal accuracy of the solution obtained using the
![]() $L1$
approximation [Reference Feng and Linetsky15], we propose to use the Richardson extrapolation approach. Since it is a well-known technique, this approach can be used to increase the speed and rate of convergence of any numerical scheme with a known order of convergence. As such, we employ the Richardson extrapolation approach with prior knowledge of the rate of convergence of the
$L1$
approximation [Reference Feng and Linetsky15], we propose to use the Richardson extrapolation approach. Since it is a well-known technique, this approach can be used to increase the speed and rate of convergence of any numerical scheme with a known order of convergence. As such, we employ the Richardson extrapolation approach with prior knowledge of the rate of convergence of the
![]() $L1$
discretization to obtain higher accuracy numerical solutions for the European and barrier options. We also consider a spectral approximation for the spatial discretization. More specifically, to approximate the spatial derivatives, we consider the spectral element method which retains exponential convergence. Splitting the computational domain into two parts, the Legendre basis functions are used in the finite sub-domain and the infinite sub-domain is expanded using the Laguerre functions [Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30], all with associated Gauss-quadrature rules [Reference Quarteroni26, Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30]. Spectral approximations for space discretizations of fractional diffusion equations is not new as it can be seen in several works [Reference Chen, Lü and Chen4, Reference Chen, Lü and Chen5, Reference Lin, Li and Xu21, Reference Lin and Xu22]. However, to the best our knowledge, the spectral element method has not been applied in option pricing under the time-fractional Black–Scholes model. Since the approximations over each element are almost separated, the spectral element method allows us to use a small number of grid nodes to attain spectral accuracy in space, such that linear systems of moderate sizes are solved at each time step. As shown later in our numerical experiments, highly accurate results are obtained using both the spectral approximation and the Richardson extrapolation methods. Exponential convergence is achieved with much fewer grid points compared with the finite-difference method. This considerably improves the computational time of the numerical schemes.
$L1$
discretization to obtain higher accuracy numerical solutions for the European and barrier options. We also consider a spectral approximation for the spatial discretization. More specifically, to approximate the spatial derivatives, we consider the spectral element method which retains exponential convergence. Splitting the computational domain into two parts, the Legendre basis functions are used in the finite sub-domain and the infinite sub-domain is expanded using the Laguerre functions [Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30], all with associated Gauss-quadrature rules [Reference Quarteroni26, Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30]. Spectral approximations for space discretizations of fractional diffusion equations is not new as it can be seen in several works [Reference Chen, Lü and Chen4, Reference Chen, Lü and Chen5, Reference Lin, Li and Xu21, Reference Lin and Xu22]. However, to the best our knowledge, the spectral element method has not been applied in option pricing under the time-fractional Black–Scholes model. Since the approximations over each element are almost separated, the spectral element method allows us to use a small number of grid nodes to attain spectral accuracy in space, such that linear systems of moderate sizes are solved at each time step. As shown later in our numerical experiments, highly accurate results are obtained using both the spectral approximation and the Richardson extrapolation methods. Exponential convergence is achieved with much fewer grid points compared with the finite-difference method. This considerably improves the computational time of the numerical schemes.
This paper is outlined as follows. In Section 2, we describe the pricing equation along with the initial and boundary conditions for pricing European and barrier options under the time-fractional Black–Scholes model. In Section 3, we review the finite-difference approximation of the time-fractional derivative, and the Legendre–Laguerre approximation is described in Section 4. In Section 5, we describe the Richardson extrapolation approach. The computational efficiency of the spectral element method and the Richardson extrapolation scheme is shown by our numerical results in Section 6, and concluding remarks are given in Section 7.
2. Time-fractional Black–Scholes model
We let
![]() $v(S,\tau )$
denote the value of a European put option price, with S being the underlying asset and
$v(S,\tau )$
denote the value of a European put option price, with S being the underlying asset and
![]() $\tau = T-t$
representing the time remaining for maturity T. Under the time-fractional Black–Scholes model,
$\tau = T-t$
representing the time remaining for maturity T. Under the time-fractional Black–Scholes model,
![]() $v(S,\tau )$
satisfies
$v(S,\tau )$
satisfies
where
 $$ \begin{align*} \mathcal{L} = \frac12 \sigma^2 S^2 \frac{\partial^2}{\partial S^2} + (r - \delta )S\frac{\partial}{\partial S} - r, \end{align*} $$
$$ \begin{align*} \mathcal{L} = \frac12 \sigma^2 S^2 \frac{\partial^2}{\partial S^2} + (r - \delta )S\frac{\partial}{\partial S} - r, \end{align*} $$
subject to the conditions
 $$ \begin{align*} &v_0 = v(S,0) = \max(K - S,0), \\ &v(0,\tau) = K e^{-r\tau} - S e^{-\delta \tau},\\ & \lim_{S \rightarrow +\infty} v(S,\tau) = 0, \end{align*} $$
$$ \begin{align*} &v_0 = v(S,0) = \max(K - S,0), \\ &v(0,\tau) = K e^{-r\tau} - S e^{-\delta \tau},\\ & \lim_{S \rightarrow +\infty} v(S,\tau) = 0, \end{align*} $$
where r,
![]() $\sigma $
and
$\sigma $
and
![]() $\delta $
are the risk-free interest rate, volatility and the continuous dividend yield, respectively. The fractional derivative in (2.1), also known as the Caputo derivative, is defined as
$\delta $
are the risk-free interest rate, volatility and the continuous dividend yield, respectively. The fractional derivative in (2.1), also known as the Caputo derivative, is defined as
 $$ \begin{align} \mathcal{D}_\tau^{\alpha} v(S,\tau) = \frac{1}{\Gamma(1-\alpha)} \int_{0}^\tau \frac{\partial v(S,\eta)}{\partial \eta} (\tau - \eta)^{-\alpha}~d\eta, \;\; 0 < \alpha < 1. \end{align} $$
$$ \begin{align} \mathcal{D}_\tau^{\alpha} v(S,\tau) = \frac{1}{\Gamma(1-\alpha)} \int_{0}^\tau \frac{\partial v(S,\eta)}{\partial \eta} (\tau - \eta)^{-\alpha}~d\eta, \;\; 0 < \alpha < 1. \end{align} $$
Among the most common exotic options traded in equity option markets are the barrier options. We consider a double knock-out call barrier option which consists of a “down-and-out” and an “up-and-out” barrier option with lower barrier level
![]() $B_l$
and upper barrier level
$B_l$
and upper barrier level
![]() $B_u$
, respectively. The valuation problem being similar to that of a European call option, the boundary and initial conditions are given by
$B_u$
, respectively. The valuation problem being similar to that of a European call option, the boundary and initial conditions are given by
 $$ \begin{align*} &v_0 = v(S,0) = \max(S - K,0), \quad B_l < S < B_u,\\ &v(B_l,\tau) = v(B_u,\tau) = 0. \end{align*} $$
$$ \begin{align*} &v_0 = v(S,0) = \max(S - K,0), \quad B_l < S < B_u,\\ &v(B_l,\tau) = v(B_u,\tau) = 0. \end{align*} $$
3.
 $L1$
approximation
$L1$
approximation
The
![]() $L1$
method is the most common difference approximation of the time-fractional derivative [Reference Lin and Xu22]. Let
$L1$
method is the most common difference approximation of the time-fractional derivative [Reference Lin and Xu22]. Let
![]() $\tau _m = m \Delta \tau $
,
$\tau _m = m \Delta \tau $
,
![]() $m = 0,1,\ldots ,M$
, denote the temporal mesh, where
$m = 0,1,\ldots ,M$
, denote the temporal mesh, where
![]() $\Delta \tau = T/M$
represents one time step. Then, (2.2) can be rewritten as
$\Delta \tau = T/M$
represents one time step. Then, (2.2) can be rewritten as
 $$ \begin{align*} \mathcal{D}^{\alpha}_\tau v(S,\tau_{m+1}) = \frac{1}{\Gamma(1-\alpha)}\sum_{j = 0}^m \int_{\tau_j}^{\tau_{j+1}} \frac{\partial v(S,\eta)}{\partial \eta} (\tau_{m+1} - \eta)^{-\alpha}~d\eta, \end{align*} $$
$$ \begin{align*} \mathcal{D}^{\alpha}_\tau v(S,\tau_{m+1}) = \frac{1}{\Gamma(1-\alpha)}\sum_{j = 0}^m \int_{\tau_j}^{\tau_{j+1}} \frac{\partial v(S,\eta)}{\partial \eta} (\tau_{m+1} - \eta)^{-\alpha}~d\eta, \end{align*} $$
such that further simplifications lead to the discrete fractional differential operator
![]() $\mathcal {F}^{\alpha }_\tau $
, defined by
$\mathcal {F}^{\alpha }_\tau $
, defined by
 $$ \begin{align*} \mathcal{F}^{\alpha}_{\tau}v(S,\tau_{m+1}) = \frac{1}{\Gamma(2-\alpha)} \sum_{j=0}^m b_j \frac{v(S,\tau_{m+1-j}) - v(S,\tau_{m-j})}{(\Delta \tau)^{\alpha}}, \end{align*} $$
$$ \begin{align*} \mathcal{F}^{\alpha}_{\tau}v(S,\tau_{m+1}) = \frac{1}{\Gamma(2-\alpha)} \sum_{j=0}^m b_j \frac{v(S,\tau_{m+1-j}) - v(S,\tau_{m-j})}{(\Delta \tau)^{\alpha}}, \end{align*} $$
where
 $b_j = (j+1)^{1-\alpha } - j^{1-\alpha }$
are the weights for
$b_j = (j+1)^{1-\alpha } - j^{1-\alpha }$
are the weights for
![]() $j = 0,1,\ldots ,m$
. This yields
$j = 0,1,\ldots ,m$
. This yields
 $$ \begin{align*} \mathcal{D}^{\alpha}_\tau v(S,\tau_{m+1}) = \mathcal{F}^{\alpha}_{\tau}v(S,\tau_{m+1}) + \varepsilon^{m+1}_{\Delta \tau}, \end{align*} $$
$$ \begin{align*} \mathcal{D}^{\alpha}_\tau v(S,\tau_{m+1}) = \mathcal{F}^{\alpha}_{\tau}v(S,\tau_{m+1}) + \varepsilon^{m+1}_{\Delta \tau}, \end{align*} $$
where
 $\varepsilon ^{m+1}_{\Delta \tau }$
is the truncation error. For smooth problems, the
$\varepsilon ^{m+1}_{\Delta \tau }$
is the truncation error. For smooth problems, the
![]() $L1$
-based scheme has time convergence
$L1$
-based scheme has time convergence
![]() $\mathcal {O}((\Delta \tau )^{2-\alpha })$
[Reference Lin and Xu22]. However, this scheme exhibits only first-order accuracy in time when solving FPDEs with nonsmooth initial data or without a source term [Reference Jin, Lazarov and Zhou18, Reference Xing and Yan33, Reference Yan, Khan and Ford34]. The same phenomena are observed when solving for the European and barrier option pricing problems in the time-fractional framework, for which the payoffs are all nonsmooth, there is no sourcing term and the solutions have low regularity near maturity [Reference Cen, Huang, Xu and Le2].
$\mathcal {O}((\Delta \tau )^{2-\alpha })$
[Reference Lin and Xu22]. However, this scheme exhibits only first-order accuracy in time when solving FPDEs with nonsmooth initial data or without a source term [Reference Jin, Lazarov and Zhou18, Reference Xing and Yan33, Reference Yan, Khan and Ford34]. The same phenomena are observed when solving for the European and barrier option pricing problems in the time-fractional framework, for which the payoffs are all nonsmooth, there is no sourcing term and the solutions have low regularity near maturity [Reference Cen, Huang, Xu and Le2].
Using
![]() $\mathcal {F}^{\alpha }_{\tau }v(S,\tau _{m+1})$
as an approximation of
$\mathcal {F}^{\alpha }_{\tau }v(S,\tau _{m+1})$
as an approximation of
![]() $\mathcal {D}^{\alpha }_\tau v(S,\tau _{m+1})$
, we have
$\mathcal {D}^{\alpha }_\tau v(S,\tau _{m+1})$
, we have
 $$ \begin{align} \mathcal{F}^{\alpha}_{\tau}v^{m+1} = \mathcal{L} v^{m+1}, \end{align} $$
$$ \begin{align} \mathcal{F}^{\alpha}_{\tau}v^{m+1} = \mathcal{L} v^{m+1}, \end{align} $$
for
![]() $ m = 0,1,\ldots ,M-1$
, where
$ m = 0,1,\ldots ,M-1$
, where
![]() $v^{m+1}$
is an approximation to
$v^{m+1}$
is an approximation to
![]() $V(S,\tau _{m+1})$
. Equation (3.1) can then be rewritten as
$V(S,\tau _{m+1})$
. Equation (3.1) can then be rewritten as
 $$ \begin{align} b_0 v^{m+1} - \Gamma(2-\alpha)\Delta \tau^{\alpha} \mathcal{L} v^{m+1} = b_0 v^m - \sum_{j = 1}^{m-1} b_{j+1} v^{m-j} + \sum_{j=1}^m b_j v^{m-j}. \end{align} $$
$$ \begin{align} b_0 v^{m+1} - \Gamma(2-\alpha)\Delta \tau^{\alpha} \mathcal{L} v^{m+1} = b_0 v^m - \sum_{j = 1}^{m-1} b_{j+1} v^{m-j} + \sum_{j=1}^m b_j v^{m-j}. \end{align} $$
With
![]() $b_0 = 1$
and letting
$b_0 = 1$
and letting
![]() $\alpha _0 = \Gamma (2 - \alpha )\Delta \tau ^{\alpha }$
, (3.2) can be rearranged such that
$\alpha _0 = \Gamma (2 - \alpha )\Delta \tau ^{\alpha }$
, (3.2) can be rearranged such that
 $$ \begin{align} v^{m+1} - \alpha_0 \mathcal{L}v^{m+1} = (1-b_1)v^m + \sum_{j=1}^{m-1}(b_j - b_{j+1})v^{m-j} + b_m v^0. \end{align} $$
$$ \begin{align} v^{m+1} - \alpha_0 \mathcal{L}v^{m+1} = (1-b_1)v^m + \sum_{j=1}^{m-1}(b_j - b_{j+1})v^{m-j} + b_m v^0. \end{align} $$
Let
![]() $\mathcal {B}(\mathcal {L}) = H^1(\Omega ) \cap H^2(\Omega )$
, where
$\mathcal {B}(\mathcal {L}) = H^1(\Omega ) \cap H^2(\Omega )$
, where
![]() $H^1(\Omega )$
and
$H^1(\Omega )$
and
![]() $H^2(\Omega )$
denote the usual Sobolev spaces with corresponding norms
$H^2(\Omega )$
denote the usual Sobolev spaces with corresponding norms
![]() $\|\cdot \|_{H^1(\Omega )}$
and
$\|\cdot \|_{H^1(\Omega )}$
and
![]() $\|\cdot \|_{H^2(\Omega )}$
, respectively.
$\|\cdot \|_{H^2(\Omega )}$
, respectively.
Theorem 3.1. [Reference Yan, Pal and Ford35, Theorem 3.2]
Let
![]() $v(\tau _m)$
and
$v(\tau _m)$
and
![]() $v^m$
be the solutions of (2.1) and (3.3), respectively, and let
$v^m$
be the solutions of (2.1) and (3.3), respectively, and let
![]() $v_0 \in \mathcal {B}(\mathcal {L})$
. Then, with
$v_0 \in \mathcal {B}(\mathcal {L})$
. Then, with
![]() $0 < \alpha < 1$
and the constant C positive,
$0 < \alpha < 1$
and the constant C positive,
 $$ \begin{align*} \|\bar{v}(\tau_m) - \bar{v}^m\|_{L_2(\Omega)} \leq C (\Delta \tau) \tau_m^{\alpha - 1} \|v_0\|_{L_2(\Omega)}. \end{align*} $$
$$ \begin{align*} \|\bar{v}(\tau_m) - \bar{v}^m\|_{L_2(\Omega)} \leq C (\Delta \tau) \tau_m^{\alpha - 1} \|v_0\|_{L_2(\Omega)}. \end{align*} $$
4. Legendre–Laguerre spectral method in space
We describe in this section the spectral element discretization in space of the time-fractional Black–Scholes equation (2.1). Before defining the weak formulation problem, we start with some basic notation. Consider the domain
![]() $\Omega $
with the Sobolev space,
$\Omega $
with the Sobolev space,
 $$ \begin{align*} H^m(\Omega) = \bigg\{u \in L^2(\Omega),~\frac{d^k u}{dx^k}\in L^2(\Omega),\ 0 \leq k \leq m \bigg\}, \end{align*} $$
$$ \begin{align*} H^m(\Omega) = \bigg\{u \in L^2(\Omega),~\frac{d^k u}{dx^k}\in L^2(\Omega),\ 0 \leq k \leq m \bigg\}, \end{align*} $$
where
![]() $L^2(\Omega )$
is the space of square integrable functions on
$L^2(\Omega )$
is the space of square integrable functions on
![]() $\Omega $
. The spaces
$\Omega $
. The spaces
![]() $L^2(\Omega )$
and
$L^2(\Omega )$
and
![]() $H^m(\Omega )$
are equipped with inner products defined by
$H^m(\Omega )$
are equipped with inner products defined by
 $$ \begin{align*} (u,\nu)_{\Omega} = \int_{\Omega} u(x) \nu(x)~dx, \quad (u,\nu)_{m,\Omega} = \sum_{k=0}^m \int_{\Omega} \frac{d^k u}{dx^k} \frac{d^k \nu}{dx^k}~dx, \end{align*} $$
$$ \begin{align*} (u,\nu)_{\Omega} = \int_{\Omega} u(x) \nu(x)~dx, \quad (u,\nu)_{m,\Omega} = \sum_{k=0}^m \int_{\Omega} \frac{d^k u}{dx^k} \frac{d^k \nu}{dx^k}~dx, \end{align*} $$
respectively; and for any two functions
![]() $u, \nu \in L^2(\Omega )$
, the corresponding norms are
$u, \nu \in L^2(\Omega )$
, the corresponding norms are
 $$ \begin{align*} \|\nu\|_{L^2(\Omega)} = (\nu,\nu)_{\Omega}^{1/2}, \quad \|\nu\|_{H^m(\Omega)} = (\nu,\nu)_{m,\Omega}^{1/2}. \end{align*} $$
$$ \begin{align*} \|\nu\|_{L^2(\Omega)} = (\nu,\nu)_{\Omega}^{1/2}, \quad \|\nu\|_{H^m(\Omega)} = (\nu,\nu)_{m,\Omega}^{1/2}. \end{align*} $$
In general, the entire domain is separated into several sub-domains depending on the smoothness of the solution in the different parts of the domain. Then different kinds of methods can be used accordingly in the different sub-domains. Generally, for the coupled Legendre–Laguerre spectral method, the interval
![]() $\Omega = [0,\infty )$
can be split, so that we let
$\Omega = [0,\infty )$
can be split, so that we let
![]() $\Omega _1 = [0,a]$
and
$\Omega _1 = [0,a]$
and
![]() $\Omega _2 = [a,\infty )$
for some
$\Omega _2 = [a,\infty )$
for some
![]() $a> 0$
. Then
$a> 0$
. Then
![]() $\Omega _1$
can be further partitioned into E nonoverlapping sub-domains,
$\Omega _1$
can be further partitioned into E nonoverlapping sub-domains,
![]() $\Omega ^e_1 = [a_{e-1},a_e]$
,
$\Omega ^e_1 = [a_{e-1},a_e]$
,
![]() $e = 1,2,\ldots ,E$
, where
$e = 1,2,\ldots ,E$
, where
![]() $a_e$
,
$a_e$
,
![]() $e = 0,1,\ldots ,E$
are the
$e = 0,1,\ldots ,E$
are the
![]() $E+1$
points such that
$E+1$
points such that
![]() $0 = a_0 < a_1 < \cdots <a_E = a$
. Within each sub-domain, the spectral representation will be established in a specific polynomial space. Over
$0 = a_0 < a_1 < \cdots <a_E = a$
. Within each sub-domain, the spectral representation will be established in a specific polynomial space. Over
![]() $\Omega _1$
, we use the Legendre polynomials
$\Omega _1$
, we use the Legendre polynomials
![]() $\{L_{n_1}, n_1 \geq 0\}$
which are orthogonal in the interval
$\{L_{n_1}, n_1 \geq 0\}$
which are orthogonal in the interval
![]() $[-1,1]$
with unitary weight. Let
$[-1,1]$
with unitary weight. Let
![]() $\mathbb {P}_{n_1}$
denote the space of all Legendre polynomials of degree at most
$\mathbb {P}_{n_1}$
denote the space of all Legendre polynomials of degree at most
![]() $n_1$
, then we can define the piecewise polynomial space
$n_1$
, then we can define the piecewise polynomial space
Let
 $\{x_k,w_k\}_{k=0}^{n_1}$
be the set of the Gauss–Lobatto–Legendre [Reference Quarteroni26] quadrature nodes and weights. Here,
$\{x_k,w_k\}_{k=0}^{n_1}$
be the set of the Gauss–Lobatto–Legendre [Reference Quarteroni26] quadrature nodes and weights. Here,
 $\{x_k\}_{k=0}^{n_1}$
are the roots of the polynomial
$\{x_k\}_{k=0}^{n_1}$
are the roots of the polynomial
![]() $L_{n_1 + 1}(x) - L_{n_1 - 1}(x)$
, and the corresponding weights associated with the grid points are
$L_{n_1 + 1}(x) - L_{n_1 - 1}(x)$
, and the corresponding weights associated with the grid points are
 $$ \begin{align*} w_k = \frac{2}{n_1(n_1 + 1)L^2_{n_1}(x_k)}, \quad k = 0,1,\ldots,n_1. \end{align*} $$
$$ \begin{align*} w_k = \frac{2}{n_1(n_1 + 1)L^2_{n_1}(x_k)}, \quad k = 0,1,\ldots,n_1. \end{align*} $$
Equivalent to the Lagrange interpolation polynomial, the Gauss–Lobatto–Legendre basis function,
![]() $\phi _k(x)$
, is defined as
$\phi _k(x)$
, is defined as
 $$ \begin{align*} \phi_k(x) = \frac{L_{n_1 + 1}(x) - L_{n_1 - 1}(x)}{(2n_1 + 1)(x - x_k)L_{n_1}(x_k)}, \quad k = 0,1,\ldots,n_1. \end{align*} $$
$$ \begin{align*} \phi_k(x) = \frac{L_{n_1 + 1}(x) - L_{n_1 - 1}(x)}{(2n_1 + 1)(x - x_k)L_{n_1}(x_k)}, \quad k = 0,1,\ldots,n_1. \end{align*} $$
In
![]() $\Omega _2$
, we consider the stable Gauss–Radau–Laguerre basis functions [Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30]. The Laguerre polynomials
$\Omega _2$
, we consider the stable Gauss–Radau–Laguerre basis functions [Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30]. The Laguerre polynomials
![]() $\{\mathcal {L}_{n_2}(x), n_2 \geq 0\}$
are orthogonal with respect to a weighting function
$\{\mathcal {L}_{n_2}(x), n_2 \geq 0\}$
are orthogonal with respect to a weighting function
![]() $\omega (x) = e^{-x}$
on
$\omega (x) = e^{-x}$
on
![]() $[0,\infty )$
. Since the weights decay very rapidly as
$[0,\infty )$
. Since the weights decay very rapidly as
![]() $n_2$
increases, for stability, we consider the modified Laguerre polynomial
$n_2$
increases, for stability, we consider the modified Laguerre polynomial
 $$ \begin{align*} \hat{\mathcal{L}}_{n_2}(x) = e^{-x/2} \mathcal{L}_{n_2}(x),\quad n_2 \geq 0. \end{align*} $$
$$ \begin{align*} \hat{\mathcal{L}}_{n_2}(x) = e^{-x/2} \mathcal{L}_{n_2}(x),\quad n_2 \geq 0. \end{align*} $$
We then let
 $\hat {\mathbb {P}}_{n_2}(\Omega _2)$
be the space of the modified Laguerre polynomials of degree less than or equal to
$\hat {\mathbb {P}}_{n_2}(\Omega _2)$
be the space of the modified Laguerre polynomials of degree less than or equal to
![]() $n_2$
. For the stable Gauss–Radau–Laguerre quadrature, with
$n_2$
. For the stable Gauss–Radau–Laguerre quadrature, with
![]() $\hat {x}_0=0$
,
$\hat {x}_0=0$
,
 $\{\hat {x}_k\}_{k=1}^{n_2}$
are the roots of
$\{\hat {x}_k\}_{k=1}^{n_2}$
are the roots of
 $\partial _x \hat {\mathcal {L}}_{n_2+1}(x)$
, and the associated weights are given as
$\partial _x \hat {\mathcal {L}}_{n_2+1}(x)$
, and the associated weights are given as
 $$ \begin{align*} \hat{w}_k = \frac{1}{(n_2+1)\hat{\mathcal{L}}_{n_2}^2(\hat{x}_k)}, \quad k = 0,1,\ldots,n_2. \end{align*} $$
$$ \begin{align*} \hat{w}_k = \frac{1}{(n_2+1)\hat{\mathcal{L}}_{n_2}^2(\hat{x}_k)}, \quad k = 0,1,\ldots,n_2. \end{align*} $$
We define the stable Gauss–Radau–Laguerre basis function as
 $$ \begin{align*} \hat{\phi}_k(x) = -\frac{\hat{\mathcal{L}}_{n_2+1}(x) - \hat{\mathcal{L}}_{n_2}(x)}{(x - \hat{x}_k)\hat{\mathcal{L}}_{n_2}(\hat{x}_k)}, \quad k = 0,1,\ldots,n_2. \end{align*} $$
$$ \begin{align*} \hat{\phi}_k(x) = -\frac{\hat{\mathcal{L}}_{n_2+1}(x) - \hat{\mathcal{L}}_{n_2}(x)}{(x - \hat{x}_k)\hat{\mathcal{L}}_{n_2}(\hat{x}_k)}, \quad k = 0,1,\ldots,n_2. \end{align*} $$
Note that the subscripts 1 and 2 are the parameters representing the first and second sub-domain, respectively. Furthermore, these polynomials must be continuous at the internal endpoints to enforce the continuity of the solution at the internal element boundaries.
For the European put option where the first derivative of the payoff function is discontinuous at the strike price, the interval is partitioned at K such that only two elements are sufficient to achieve high accuracy. Therefore, the infinite domain
![]() $\Omega $
will be decomposed into two sub-domains so that we let
$\Omega $
will be decomposed into two sub-domains so that we let
![]() $\Omega _1 = [0,K]$
and
$\Omega _1 = [0,K]$
and
![]() $\Omega _2 = [K,\infty )$
. For the first element, we approximate
$\Omega _2 = [K,\infty )$
. For the first element, we approximate
![]() $v_1(S,\tau )= v(S,\tau )_{|S \in \Omega _1}$
using the Gauss–Lobatto–Legendre quadrature and in the second element,
$v_1(S,\tau )= v(S,\tau )_{|S \in \Omega _1}$
using the Gauss–Lobatto–Legendre quadrature and in the second element,
![]() $v_2(S,\tau )=v(S,\tau )_{|S \in \Omega _2}$
will be expanded using the stable Gauss–Radau–Laguerre method. In the latter case, we have the following global approximation space:
$v_2(S,\tau )=v(S,\tau )_{|S \in \Omega _2}$
will be expanded using the stable Gauss–Radau–Laguerre method. In the latter case, we have the following global approximation space:
 $$ \begin{align*} \mathbb{X}_N = \{v \in C^0(\Omega); v_1 \in \mathbb{P}_{n_1,1}(\Omega_1),\, v_2 \in \hat{\mathbb{P}}_{n_2}(\Omega_2)\}, \quad \mathcal{X}_N = \mathbb{X}_N \cap H^1(\Omega), \end{align*} $$
$$ \begin{align*} \mathbb{X}_N = \{v \in C^0(\Omega); v_1 \in \mathbb{P}_{n_1,1}(\Omega_1),\, v_2 \in \hat{\mathbb{P}}_{n_2}(\Omega_2)\}, \quad \mathcal{X}_N = \mathbb{X}_N \cap H^1(\Omega), \end{align*} $$
where N is the dimension of
![]() $\mathbb {X}_N$
.
$\mathbb {X}_N$
.
4.1. Approximation results
In this section, we give some approximation results related to the spectral element method. Let
![]() $\omega _{\alpha }(x) = x^{\alpha } e^{-x}$
,
$\omega _{\alpha }(x) = x^{\alpha } e^{-x}$
,
![]() $\hat {\omega }_{\alpha }(x) = x^{\alpha }$
and
$\hat {\omega }_{\alpha }(x) = x^{\alpha }$
and
![]() $\hat {\partial }_x = \partial _x + 1/2$
. We define the space
$\hat {\partial }_x = \partial _x + 1/2$
. We define the space
 $$ \begin{align*} \hat{B}^m(\mathbb{R}^{+}) = \{u\mid \hat{\partial}^k_x u \in L^2_{\hat{\omega}_k}(\mathbb{R}^{+}), \, 0 \leq k \leq m\}, \end{align*} $$
$$ \begin{align*} \hat{B}^m(\mathbb{R}^{+}) = \{u\mid \hat{\partial}^k_x u \in L^2_{\hat{\omega}_k}(\mathbb{R}^{+}), \, 0 \leq k \leq m\}, \end{align*} $$
equipped with the norm
 $$ \begin{align*} \|u\|_{\hat{B}^m(\mathbb{R}^{+})} = \bigg(\sum_{k=0}^m \|\hat{\partial}^k_x u\|^2_{L^2_{\hat{\omega}_k}(\mathbb{R}^{+})}\bigg)^{1/2}, \end{align*} $$
$$ \begin{align*} \|u\|_{\hat{B}^m(\mathbb{R}^{+})} = \bigg(\sum_{k=0}^m \|\hat{\partial}^k_x u\|^2_{L^2_{\hat{\omega}_k}(\mathbb{R}^{+})}\bigg)^{1/2}, \end{align*} $$
where
![]() $\partial ^k_x u(x) = d^ku(x)/dx^k$
. Some projection operators are introduced next.
$\partial ^k_x u(x) = d^ku(x)/dx^k$
. Some projection operators are introduced next.
Let
 $\Pi ^{(1,e)}_{n_1}: L^2(\Omega _1^e)\rightarrow \mathbb {P}_{n_1}(\Omega _1^e)$
be the
$\Pi ^{(1,e)}_{n_1}: L^2(\Omega _1^e)\rightarrow \mathbb {P}_{n_1}(\Omega _1^e)$
be the
 $L^2(\Omega _1^e)$
-orthogonal projection operator defined by
$L^2(\Omega _1^e)$
-orthogonal projection operator defined by
 $$ \begin{align*} (u - \Pi^{(1,e)}_{n_1}u, \phi)_{\Omega_1^e} = 0 \quad \text{for all } \phi \in \mathbb{P}_{n_1}(\Omega_1^e), \end{align*} $$
$$ \begin{align*} (u - \Pi^{(1,e)}_{n_1}u, \phi)_{\Omega_1^e} = 0 \quad \text{for all } \phi \in \mathbb{P}_{n_1}(\Omega_1^e), \end{align*} $$
given
 $u \in L^2(\Omega _1^e)$
and let
$u \in L^2(\Omega _1^e)$
and let
 $\Pi ^{(2)}_{n_2}: L^2_{\omega }(\Omega _2)\rightarrow \mathbb {P}_{n_2}(\Omega _2)$
be the
$\Pi ^{(2)}_{n_2}: L^2_{\omega }(\Omega _2)\rightarrow \mathbb {P}_{n_2}(\Omega _2)$
be the
![]() $L^2_{\omega }$
-orthogonal projection operator defined by
$L^2_{\omega }$
-orthogonal projection operator defined by
 $$ \begin{align*} (u - \Pi^{(2)}_{n_2}u, \phi)_{\omega,\Omega_2}=0 \quad \text{for all } \phi \in \mathbb{P}_{n_2}(\Omega_2), \end{align*} $$
$$ \begin{align*} (u - \Pi^{(2)}_{n_2}u, \phi)_{\omega,\Omega_2}=0 \quad \text{for all } \phi \in \mathbb{P}_{n_2}(\Omega_2), \end{align*} $$
given
![]() $u \in L^2_{\omega }(\Omega _2)$
. We can then define the operator
$u \in L^2_{\omega }(\Omega _2)$
. We can then define the operator
 $\hat {\Pi }^2_{n_2}: L^2_{\hat {\omega }}(\Omega _2) \rightarrow \hat {\mathbb {P}}_{n_2}(\Omega _2)$
as
$\hat {\Pi }^2_{n_2}: L^2_{\hat {\omega }}(\Omega _2) \rightarrow \hat {\mathbb {P}}_{n_2}(\Omega _2)$
as
 $$ \begin{align*} \hat{\Pi}^{(2)}_{n_2} u(x) = e^{-x/2} \Pi^{(2)}_{n_2}(u(x) e^{x/2}) \quad \text{for all } u \in L^2_{\hat{\omega}}(\Omega_2). \end{align*} $$
$$ \begin{align*} \hat{\Pi}^{(2)}_{n_2} u(x) = e^{-x/2} \Pi^{(2)}_{n_2}(u(x) e^{x/2}) \quad \text{for all } u \in L^2_{\hat{\omega}}(\Omega_2). \end{align*} $$
Then for any
 $\hat {\phi } \in \hat {\mathbb {P}}_{n_2}(\Omega _2)$
,
$\hat {\phi } \in \hat {\mathbb {P}}_{n_2}(\Omega _2)$
,
 $$ \begin{align*} (u - \hat{\Pi}^{(2)}_{n_2}u, \hat{\phi})_{\hat{\omega},\Omega_2} = (u(x)e^{x/2} - \Pi_{n_2}^{(2)}(u(x)e^{x/2}), \hat{\phi}e^{x/2})_{\omega,\Omega_2} = 0. \end{align*} $$
$$ \begin{align*} (u - \hat{\Pi}^{(2)}_{n_2}u, \hat{\phi})_{\hat{\omega},\Omega_2} = (u(x)e^{x/2} - \Pi_{n_2}^{(2)}(u(x)e^{x/2}), \hat{\phi}e^{x/2})_{\omega,\Omega_2} = 0. \end{align*} $$
Hence,
 $\hat {\Pi }^{(2)}_{n_2}$
is the orthogonal projection operator from
$\hat {\Pi }^{(2)}_{n_2}$
is the orthogonal projection operator from
 $L^2_{\hat {\omega }}(\Omega _2)$
into
$L^2_{\hat {\omega }}(\Omega _2)$
into
 $\hat {\mathbb {P}}_{n_2}(\Omega _2)$
.
$\hat {\mathbb {P}}_{n_2}(\Omega _2)$
.
We now define the projectors with respect to the global domain
![]() $\Omega $
. Let
$\Omega $
. Let
![]() $\Pi _N: L^2(\Omega ) \rightarrow \mathbb {X}_N$
be the orthogonal projector, defined by
$\Pi _N: L^2(\Omega ) \rightarrow \mathbb {X}_N$
be the orthogonal projector, defined by
given
![]() $u \in L^2(\Omega )$
. Finally, let
$u \in L^2(\Omega )$
. Finally, let
 $\Pi ^1_N: H^1(\Omega ) \rightarrow \mathcal {X}_N$
be the
$\Pi ^1_N: H^1(\Omega ) \rightarrow \mathcal {X}_N$
be the
![]() $H^1(\Omega )$
-orthogonal projection operator, defined by,
$H^1(\Omega )$
-orthogonal projection operator, defined by,
 $$ \begin{align*} (\partial_x(u - \Pi^1_N u), \partial_x \phi_N)_{\Omega} = 0 \quad \text{for all } \phi_N \in \mathcal{X}_N, \end{align*} $$
$$ \begin{align*} (\partial_x(u - \Pi^1_N u), \partial_x \phi_N)_{\Omega} = 0 \quad \text{for all } \phi_N \in \mathcal{X}_N, \end{align*} $$
given
![]() $u \in H^1(\Omega )$
.
$u \in H^1(\Omega )$
.
Next, we present some approximation results for the multi-domain Legendre interpolation and the modified Laguerre interpolation [Reference Quarteroni26, Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30]. The following results hold from the work of Quarteroni [Reference Quarteroni26].
Lemma 4.1. Let
![]() $r \geq 1$
. Then there exists a positive constant
$r \geq 1$
. Then there exists a positive constant
![]() $c_1$
dependent only on r such that for all
$c_1$
dependent only on r such that for all
![]() $u \in H^r(\Omega _1^e)$
, we have
$u \in H^r(\Omega _1^e)$
, we have
 $$ \begin{align*} \|u - \Pi^{(1,e)}_{n_1}u\|_{H^1(\Omega^e_1)} \leq c_1 h_e^{\min(n_1,r-1)}n_1^{1-r} \|u\|_{H^{r}(\Omega_1^e)}. \end{align*} $$
$$ \begin{align*} \|u - \Pi^{(1,e)}_{n_1}u\|_{H^1(\Omega^e_1)} \leq c_1 h_e^{\min(n_1,r-1)}n_1^{1-r} \|u\|_{H^{r}(\Omega_1^e)}. \end{align*} $$
However, if u is continuous and composed of E pieces that are smooth in the closure of each interval
![]() $\Omega _1^e$
,
$\Omega _1^e$
,
![]() $e = 1,2,\ldots ,E$
, then the approximate solution will converge faster than any algebraic power, that is, the order of convergence becomes exponential. We then have an estimate of the form
$e = 1,2,\ldots ,E$
, then the approximate solution will converge faster than any algebraic power, that is, the order of convergence becomes exponential. We then have an estimate of the form
 $$ \begin{align} \|u - \Pi^{(1,e)}_{n_1}u\|_{H^1(\Omega^e_1)} \leq c_1 \exp(-\gamma_e n_1). \end{align} $$
$$ \begin{align} \|u - \Pi^{(1,e)}_{n_1}u\|_{H^1(\Omega^e_1)} \leq c_1 \exp(-\gamma_e n_1). \end{align} $$
Over the whole interval
![]() $\Omega _1$
, we can rewrite (4.1) such that
$\Omega _1$
, we can rewrite (4.1) such that
 $$ \begin{align*} \|u - \Pi^{(1)}_{n_1}u\|_{H^1(\Omega_1)} \leq C \sum_{e=1}^E \exp(-\gamma_e n_1), \end{align*} $$
$$ \begin{align*} \|u - \Pi^{(1)}_{n_1}u\|_{H^1(\Omega_1)} \leq C \sum_{e=1}^E \exp(-\gamma_e n_1), \end{align*} $$
where
![]() $\gamma _e$
depends on the regions
$\gamma _e$
depends on the regions
![]() $\Omega _e^1$
.
$\Omega _e^1$
.
The following lemma can be found in the work of Shen et al. [Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30].
Lemma 4.2. If
![]() $u \in H^1(\Omega _2)$
and
$u \in H^1(\Omega _2)$
and
![]() $\hat {\partial }_x u \in \hat {B}^{s-1}(\Omega _2)$
, then
$\hat {\partial }_x u \in \hat {B}^{s-1}(\Omega _2)$
, then
 $$ \begin{align*} \|u - \hat{\Pi}^{(2)}_{n_2}u\|_{H^1(\Omega_2)} \leq c_2 n_2^{(1-s)/2} \|u\|_{\hat{B}^s(\Omega_2)} \quad \text{for } 1 \leq s \leq n_2+1. \end{align*} $$
$$ \begin{align*} \|u - \hat{\Pi}^{(2)}_{n_2}u\|_{H^1(\Omega_2)} \leq c_2 n_2^{(1-s)/2} \|u\|_{\hat{B}^s(\Omega_2)} \quad \text{for } 1 \leq s \leq n_2+1. \end{align*} $$
In the same way, if u is smooth enough over
![]() $\Omega _2$
, then the error will decay exponentially fast such that
$\Omega _2$
, then the error will decay exponentially fast such that
 $$ \begin{align*} \|u - \hat{\Pi}^{(2)}_{n_2}u\|_{H^1(\Omega_2)} \leq c_2 \exp(-\beta n_2), \end{align*} $$
$$ \begin{align*} \|u - \hat{\Pi}^{(2)}_{n_2}u\|_{H^1(\Omega_2)} \leq c_2 \exp(-\beta n_2), \end{align*} $$
where
![]() $\beta $
depends on the region
$\beta $
depends on the region
![]() $\Omega _2$
.
$\Omega _2$
.
The conditions on the exponential convergence rates are determined case by case, as discussed in the work of Shen et al. [Reference Shen, Tang, Wang, Bank, Graham, Stoer, Varga and Yserentant30].
4.2. Weak formulation
A weak formulation of (2.1) is to find
![]() $v(\tau ) \in H^1(\Omega )$
such that
$v(\tau ) \in H^1(\Omega )$
such that
 $$ \begin{align} (\mathcal{D}^{\alpha}_\tau v(\tau),\varphi)_{\Omega} + \mathcal{A}_{\Omega} (v(\tau),\varphi) = b(\tau) \quad \text{for all } \varphi \in H^1(\Omega), \end{align} $$
$$ \begin{align} (\mathcal{D}^{\alpha}_\tau v(\tau),\varphi)_{\Omega} + \mathcal{A}_{\Omega} (v(\tau),\varphi) = b(\tau) \quad \text{for all } \varphi \in H^1(\Omega), \end{align} $$
where
 $(\mathcal {D}^{\alpha }_\tau v(\tau ),\varphi )_{\Omega } = \int _{\Omega } \mathcal {D}^\alpha _\tau v(S,\tau ) \varphi (S)~dS.$
Note that here,
$(\mathcal {D}^{\alpha }_\tau v(\tau ),\varphi )_{\Omega } = \int _{\Omega } \mathcal {D}^\alpha _\tau v(S,\tau ) \varphi (S)~dS.$
Note that here,
 $$ \begin{align*} A_{\Omega} (v(\tau),\varphi) &= \frac12 \sigma^2\int_{\Omega} S^2 \frac{\partial v(S,\tau)}{\partial S} \frac{\partial \varphi}{\partial S}~dS - (r - \delta - \sigma^2) \int_\Omega S \frac{\partial v(S,\tau)}{\partial S} \varphi(S)~dS \\ &\quad+ r \int_\Omega v(S,\tau) \varphi(S)~dS, \end{align*} $$
$$ \begin{align*} A_{\Omega} (v(\tau),\varphi) &= \frac12 \sigma^2\int_{\Omega} S^2 \frac{\partial v(S,\tau)}{\partial S} \frac{\partial \varphi}{\partial S}~dS - (r - \delta - \sigma^2) \int_\Omega S \frac{\partial v(S,\tau)}{\partial S} \varphi(S)~dS \\ &\quad+ r \int_\Omega v(S,\tau) \varphi(S)~dS, \end{align*} $$
where
![]() $\varphi \in H^1(\Omega )$
is a trial function that satisfies certain boundary conditions and
$\varphi \in H^1(\Omega )$
is a trial function that satisfies certain boundary conditions and
 $$\begin{align*}b(\tau) = \frac12 \sigma^2 \bigg[S^2 \frac{\partial v(S,\tau)}{\partial S} \varphi(S)\bigg]_0^\infty.\end{align*}$$
$$\begin{align*}b(\tau) = \frac12 \sigma^2 \bigg[S^2 \frac{\partial v(S,\tau)}{\partial S} \varphi(S)\bigg]_0^\infty.\end{align*}$$
The approximation of (4.2) by the spectral element method can be obtained by finding
![]() $\hat {v}(\tau ) \in \mathcal {X}_N$
such that
$\hat {v}(\tau ) \in \mathcal {X}_N$
such that
Equivalently, (4.3) can be rewritten as: find
![]() $\hat {v}(\tau )$
such that
$\hat {v}(\tau )$
such that
upon
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _2$
. Before applying the Gauss–Lobatto–Legendre and Gauss–Radau– Laguerre methods, we must first transform the sub-domains to corresponding reference domains as follows:
$\Omega _2$
. Before applying the Gauss–Lobatto–Legendre and Gauss–Radau– Laguerre methods, we must first transform the sub-domains to corresponding reference domains as follows:
 $$ \begin{align*} S = \text{J}^{(1)}(x + 1), \;\; \text{J}^{(1)} = \frac{K}{2}, \;\; x \in [-1,1], \;\; S \in \Omega_1,\\ S = \text{J}^{(2)} \hat{x} + K, \;\; \text{J}^{(2)} = \frac{S_{\max} - K}{\hat{x}_{n_2}}, \;\; \hat{x} \in [0,\infty), \;\; S \in \Omega_2, \end{align*} $$
$$ \begin{align*} S = \text{J}^{(1)}(x + 1), \;\; \text{J}^{(1)} = \frac{K}{2}, \;\; x \in [-1,1], \;\; S \in \Omega_1,\\ S = \text{J}^{(2)} \hat{x} + K, \;\; \text{J}^{(2)} = \frac{S_{\max} - K}{\hat{x}_{n_2}}, \;\; \hat{x} \in [0,\infty), \;\; S \in \Omega_2, \end{align*} $$
where
![]() $\text {J}^{(1)}$
and
$\text {J}^{(1)}$
and
![]() $\text {J}^{(2)}$
are the Jacobians of the transformations of
$\text {J}^{(2)}$
are the Jacobians of the transformations of
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _2$
, respectively, and
$\Omega _2$
, respectively, and
![]() $\hat {x}_{n_2}$
is the last grid point for the stable Gauss–Radau–Laguerre basis function.
$\hat {x}_{n_2}$
is the last grid point for the stable Gauss–Radau–Laguerre basis function.
For the option price to be continuous at the strike price, the last grid point of the first element and the first grid point of the second element will be taken as one single point, that is,
 $S^{(1)}_{n_1} = S^{(2)}_0$
such that we have
$S^{(1)}_{n_1} = S^{(2)}_0$
such that we have
![]() $N = n_1 + n_2 + 1$
distinct points. These approximations also require that
$N = n_1 + n_2 + 1$
distinct points. These approximations also require that
![]() $\phi _{n_1} = \hat {\phi }_0$
. The approximate solution over the whole domain can then be represented as
$\phi _{n_1} = \hat {\phi }_0$
. The approximate solution over the whole domain can then be represented as
 $$ \begin{align*} \hat{v}(S,\tau) = \sum_{l=0}^{n_1} \hat{v}_1(S_l,\tau)\phi_l(S)\bigg|_{S \in \Omega_1} + \sum_{l=1}^{n_2} \hat{v}_2(S_l,\tau)\hat{\phi}_l(S)\bigg|_{S \in \Omega_2}. \end{align*} $$
$$ \begin{align*} \hat{v}(S,\tau) = \sum_{l=0}^{n_1} \hat{v}_1(S_l,\tau)\phi_l(S)\bigg|_{S \in \Omega_1} + \sum_{l=1}^{n_2} \hat{v}_2(S_l,\tau)\hat{\phi}_l(S)\bigg|_{S \in \Omega_2}. \end{align*} $$
However, the weak formulation has to be considered separately for each element. The option price will then be obtained after the proper assemblage according to the structure of the global basis function. Taking
![]() $\varphi = \phi _m$
in the first element and
$\varphi = \phi _m$
in the first element and
![]() $\varphi = \hat {\phi }_m$
for the second element, we have, after the transformations in each element,
$\varphi = \hat {\phi }_m$
for the second element, we have, after the transformations in each element,
 $$ \begin{align} \nonumber (\mathcal{D}^{\alpha}_{\tau}\hat{v}(\tau),\varphi)_{\Omega_1} + \mathcal{A}_{\Omega_1}(\hat{v}(\tau),\varphi) &= \text{J}^{(1)}\sum_{l=0}^{n_1}\mathcal{D}_{\tau}^{\alpha}\hat{v}_1(S_l,\tau)\int_{-1}^1 \phi_l(x) \phi_m(x)~dx \\[5pt] \nonumber &\quad + \frac{1}{2 \text{J}^{(1)}} \sigma^2 \sum_{l=0}^{n_1} \hat{v}_1(S_l,\tau) \int_{-1}^1 {S}^2\frac{\partial \phi_l(x)}{\partial x} \frac{\partial \phi_m(x)}{\partial x}~dx\\[5pt] \nonumber &\quad - (r - \delta - \sigma^2) \sum_{l=0}^{n_1} \hat{v}_1(S_l,\tau) \int_{-1}^1 S \frac{\partial \phi_l(x)}{\partial x} \phi_m(x)~dx \\[5pt] & \quad+ r \text{J}^{(1)} \sum_{l=0}^{n_1} \hat{v}_1(S_l,\tau) \int_{-1}^1 \phi_l(x) \phi_m(x)~dx, \end{align} $$
$$ \begin{align} \nonumber (\mathcal{D}^{\alpha}_{\tau}\hat{v}(\tau),\varphi)_{\Omega_1} + \mathcal{A}_{\Omega_1}(\hat{v}(\tau),\varphi) &= \text{J}^{(1)}\sum_{l=0}^{n_1}\mathcal{D}_{\tau}^{\alpha}\hat{v}_1(S_l,\tau)\int_{-1}^1 \phi_l(x) \phi_m(x)~dx \\[5pt] \nonumber &\quad + \frac{1}{2 \text{J}^{(1)}} \sigma^2 \sum_{l=0}^{n_1} \hat{v}_1(S_l,\tau) \int_{-1}^1 {S}^2\frac{\partial \phi_l(x)}{\partial x} \frac{\partial \phi_m(x)}{\partial x}~dx\\[5pt] \nonumber &\quad - (r - \delta - \sigma^2) \sum_{l=0}^{n_1} \hat{v}_1(S_l,\tau) \int_{-1}^1 S \frac{\partial \phi_l(x)}{\partial x} \phi_m(x)~dx \\[5pt] & \quad+ r \text{J}^{(1)} \sum_{l=0}^{n_1} \hat{v}_1(S_l,\tau) \int_{-1}^1 \phi_l(x) \phi_m(x)~dx, \end{align} $$
over the first element for
![]() $m = 0,1,\ldots ,n_1$
and
$m = 0,1,\ldots ,n_1$
and
![]() $S \in \Omega _1$
, and
$S \in \Omega _1$
, and
 $$ \begin{align} \nonumber (\mathcal{D}^{\alpha}_{\tau}\hat{v}(\tau),\varphi)_{\Omega_2} + \mathcal{A}_{\Omega_2}(\hat{v}(\tau),\varphi) &= \text{J}^{(2)}\sum_{l=0}^{n_2}\mathcal{D}_{\tau}^{\alpha}\hat{v}_2(S_l,\tau)\int_{0}^\infty \hat{\phi}_l(x) \hat{\phi}_m(x)~dx \\[5pt] \nonumber &\quad+ \frac{1}{2 \text{J}^{(2)}} \sigma^2 \sum_{l=0}^{n_2} \hat{v}_2(S_l,\tau) \int_{0}^\infty {S}^2\frac{\partial \hat{\phi}_l(x)}{\partial x} \frac{\partial \hat{\phi}_m(x)}{\partial x}~dx\\[5pt] \nonumber &\quad - (r - \delta - \sigma^2) \sum_{l=0}^{n_2} \hat{v}_2(S_l,\tau) \int_{0}^\infty S \frac{\partial \hat{\phi}_l(x)}{\partial x} \hat{\phi}_m(x)~dx \\[5pt] &\quad+ r \text{J}^{(2)} \sum_{l=0}^{n_2} \hat{v}_2(S_l,\tau) \int_{0}^\infty \hat{\phi}_l(x) \hat{\phi}_m(x)~dx, \end{align} $$
$$ \begin{align} \nonumber (\mathcal{D}^{\alpha}_{\tau}\hat{v}(\tau),\varphi)_{\Omega_2} + \mathcal{A}_{\Omega_2}(\hat{v}(\tau),\varphi) &= \text{J}^{(2)}\sum_{l=0}^{n_2}\mathcal{D}_{\tau}^{\alpha}\hat{v}_2(S_l,\tau)\int_{0}^\infty \hat{\phi}_l(x) \hat{\phi}_m(x)~dx \\[5pt] \nonumber &\quad+ \frac{1}{2 \text{J}^{(2)}} \sigma^2 \sum_{l=0}^{n_2} \hat{v}_2(S_l,\tau) \int_{0}^\infty {S}^2\frac{\partial \hat{\phi}_l(x)}{\partial x} \frac{\partial \hat{\phi}_m(x)}{\partial x}~dx\\[5pt] \nonumber &\quad - (r - \delta - \sigma^2) \sum_{l=0}^{n_2} \hat{v}_2(S_l,\tau) \int_{0}^\infty S \frac{\partial \hat{\phi}_l(x)}{\partial x} \hat{\phi}_m(x)~dx \\[5pt] &\quad+ r \text{J}^{(2)} \sum_{l=0}^{n_2} \hat{v}_2(S_l,\tau) \int_{0}^\infty \hat{\phi}_l(x) \hat{\phi}_m(x)~dx, \end{align} $$
in the second element for
![]() $m = 0,1,\ldots ,n_2$
and
$m = 0,1,\ldots ,n_2$
and
![]() $S \in \Omega _2$
. Note that the boundary term
$S \in \Omega _2$
. Note that the boundary term
![]() $b(\tau )$
vanishes naturally when
$b(\tau )$
vanishes naturally when
![]() $S = 0$
and since
$S = 0$
and since
![]() $\varphi (S) = \hat {\phi }(x)$
in the second element decays exponentially with S,
$\varphi (S) = \hat {\phi }(x)$
in the second element decays exponentially with S,
![]() $b(\tau )$
also vanishes as
$b(\tau )$
also vanishes as
![]() $S \rightarrow \infty $
.
$S \rightarrow \infty $
.
In general, the integration terms, which we call the mass, advection and stiffness matrices, can be written as
 $$ \begin{align*} M_{lm}^{(e)} &= \text{J} \int \psi_l(\xi) \psi_m(\xi)~d\xi = \text{J}^{(e)} \sum_{k=0}^{n} \gamma_k \psi_l(\xi_k) \psi_m(\xi_k) = \text{J}^{(e)} \gamma_l \delta_{lm},\\[4pt] A_{lm}^{(e)} &= \int S(\xi)\frac{\partial \psi_l(\xi)}{\partial \xi} \psi_m(\xi)~d\xi = \sum_{k=0}^{n} \gamma_k S(\xi_k) D_{kl} \delta_{km} = \gamma_m S(\xi_m) D_{ml},\\[4pt] \mathcal{S}_{lm}^{(e)} &= \frac{1}{\text{J}^{(e)}} \int S(\xi)^2 \frac{\partial \psi_l(\xi)}{\partial \xi} \frac{\partial \psi_m(\xi)}{\partial \xi}~d\xi = \frac{1}{\text{J}^{(e)}} \sum_{k=0}^n \gamma_k S(\xi_k)^2 D_{kl} D_{km}, \end{align*} $$
$$ \begin{align*} M_{lm}^{(e)} &= \text{J} \int \psi_l(\xi) \psi_m(\xi)~d\xi = \text{J}^{(e)} \sum_{k=0}^{n} \gamma_k \psi_l(\xi_k) \psi_m(\xi_k) = \text{J}^{(e)} \gamma_l \delta_{lm},\\[4pt] A_{lm}^{(e)} &= \int S(\xi)\frac{\partial \psi_l(\xi)}{\partial \xi} \psi_m(\xi)~d\xi = \sum_{k=0}^{n} \gamma_k S(\xi_k) D_{kl} \delta_{km} = \gamma_m S(\xi_m) D_{ml},\\[4pt] \mathcal{S}_{lm}^{(e)} &= \frac{1}{\text{J}^{(e)}} \int S(\xi)^2 \frac{\partial \psi_l(\xi)}{\partial \xi} \frac{\partial \psi_m(\xi)}{\partial \xi}~d\xi = \frac{1}{\text{J}^{(e)}} \sum_{k=0}^n \gamma_k S(\xi_k)^2 D_{kl} D_{km}, \end{align*} $$
respectively, where
![]() $\psi $
,
$\psi $
,
![]() $\gamma $
and D represent the basis function, weights and first-derivative matrix of the basis function of the associated Gauss quadrature, respectively. In matrix form, we can then write
$\gamma $
and D represent the basis function, weights and first-derivative matrix of the basis function of the associated Gauss quadrature, respectively. In matrix form, we can then write
 $$ \begin{align*} \textbf{M}^{(e)} = \text{J}^{(e)} \textbf{W}^{(e)}, \;\; \textbf{A}^{(e)} = \textbf{S}^{(e)} \textbf{W}^{(e)} \textbf{D}^{(e)}\quad \text{and}\quad \boldsymbol{\mathcal{S}}^{(e)} = \frac{1}{\text{J}^{(e)}} \textbf{D}^{(e)^{\top}}(\textbf{S}^{(e)})^2\textbf{W}^{(e)} \textbf{D}^{(e)}, \end{align*} $$
$$ \begin{align*} \textbf{M}^{(e)} = \text{J}^{(e)} \textbf{W}^{(e)}, \;\; \textbf{A}^{(e)} = \textbf{S}^{(e)} \textbf{W}^{(e)} \textbf{D}^{(e)}\quad \text{and}\quad \boldsymbol{\mathcal{S}}^{(e)} = \frac{1}{\text{J}^{(e)}} \textbf{D}^{(e)^{\top}}(\textbf{S}^{(e)})^2\textbf{W}^{(e)} \textbf{D}^{(e)}, \end{align*} $$
where
![]() $\textbf {W}^{(e)}$
and
$\textbf {W}^{(e)}$
and
![]() $\textbf {S}^{(e)}$
are the diagonal matrices of the associated quadrature weights and element-wise asset price values, respectively. Each local matrix will then be assembled to form global matrices
$\textbf {S}^{(e)}$
are the diagonal matrices of the associated quadrature weights and element-wise asset price values, respectively. Each local matrix will then be assembled to form global matrices
![]() $\textbf {M}$
,
$\textbf {M}$
,
![]() $\textbf {A}$
and
$\textbf {A}$
and
![]() $\boldsymbol {\mathcal {S}}$
. This assembly procedure couples the contribution of each element together [Reference Yue36].
$\boldsymbol {\mathcal {S}}$
. This assembly procedure couples the contribution of each element together [Reference Yue36].
Let
![]() $\bar {v}(\tau ) = [\hat {v}_1(S_0,\tau ),\,\hat {v}_1(S_1,\tau ),\,\ldots ,\,\hat {v}_1(S_{n_1},\tau ),\,\hat {v}_2(S_1,\tau ),\,\hat {v}_2(S_2,\tau ),\,\ldots ,\,\hat {v}_2(S_{n_2},\tau )]^{\top }$
be the vector of the European put option prices, then the generated semi-discrete system is of the form
$\bar {v}(\tau ) = [\hat {v}_1(S_0,\tau ),\,\hat {v}_1(S_1,\tau ),\,\ldots ,\,\hat {v}_1(S_{n_1},\tau ),\,\hat {v}_2(S_1,\tau ),\,\hat {v}_2(S_2,\tau ),\,\ldots ,\,\hat {v}_2(S_{n_2},\tau )]^{\top }$
be the vector of the European put option prices, then the generated semi-discrete system is of the form
where
![]() $\textbf {L} = -(\sigma ^2/2) \boldsymbol {\mathcal {S}} + (r - \delta - \sigma ^2)\textbf {A} - r\textbf {M}$
is the matrix system obtained after the assembly of each local matrix from (4.4) and (4.5). Based on the
$\textbf {L} = -(\sigma ^2/2) \boldsymbol {\mathcal {S}} + (r - \delta - \sigma ^2)\textbf {A} - r\textbf {M}$
is the matrix system obtained after the assembly of each local matrix from (4.4) and (4.5). Based on the
![]() $L1$
approximation (3.3) of the time-fractional derivative, (4.6) then becomes
$L1$
approximation (3.3) of the time-fractional derivative, (4.6) then becomes
 $$\begin{align} (\textbf{M} - \alpha_0 \textbf{L})\bar{v}^{m+1} = \textbf{M} \sum_{j=0}^{m-1} (b_j - b_{j+1})\bar{v}^{m-j} + b_m\textbf{M} \bar{v}^0, \end{align} $$
$$\begin{align} (\textbf{M} - \alpha_0 \textbf{L})\bar{v}^{m+1} = \textbf{M} \sum_{j=0}^{m-1} (b_j - b_{j+1})\bar{v}^{m-j} + b_m\textbf{M} \bar{v}^0, \end{align} $$
for
![]() $m = 0,1,\ldots ,M-1$
.
$m = 0,1,\ldots ,M-1$
.
For the double knock-out call barrier option, we have Dirichlet boundary conditions and one more discontinuity exists at the upper barrier level in its payoff such that we use three elements:
![]() $\Omega _1 = [B_l,K]$
,
$\Omega _1 = [B_l,K]$
,
![]() $\Omega _2 = [K,B_u]$
and
$\Omega _2 = [K,B_u]$
and
![]() $\Omega _3 = [B_u,\infty )$
. In this case, we approximate
$\Omega _3 = [B_u,\infty )$
. In this case, we approximate
![]() $v_1(S,\tau ) = v(S,\tau )_{|S \in \Omega _1}$
and
$v_1(S,\tau ) = v(S,\tau )_{|S \in \Omega _1}$
and
![]() $v_2(S,\tau ) = v(S,\tau )_{|S \in \Omega _2}$
using the Gauss–Lobatto–Legendre quadrature and
$v_2(S,\tau ) = v(S,\tau )_{|S \in \Omega _2}$
using the Gauss–Lobatto–Legendre quadrature and
![]() $v_3(S,\tau ) = v(S,\tau )_{|S \in \Omega _3}$
is expanded using the stable Gauss–Radau–Laguerre method such that the approximate solution over
$v_3(S,\tau ) = v(S,\tau )_{|S \in \Omega _3}$
is expanded using the stable Gauss–Radau–Laguerre method such that the approximate solution over
![]() $\Omega $
can be represented as
$\Omega $
can be represented as
 $$ \begin{align*} \hat{v}(S,\tau) = \sum_{l=0}^{n_1}\hat{v}_1(S_l,\tau)\phi_l(S)\bigg|_{S \in \Omega_1} + \sum_{l=1}^{n_2}\hat{v}_2(S_l,\tau)\phi_l(S)\bigg|_{S \in \Omega_2} + \sum_{l=1}^{n_3} \hat{v}_3(S_l,\tau)\hat{\phi}_l(S) \bigg|_{S \in \Omega_3}, \end{align*} $$
$$ \begin{align*} \hat{v}(S,\tau) = \sum_{l=0}^{n_1}\hat{v}_1(S_l,\tau)\phi_l(S)\bigg|_{S \in \Omega_1} + \sum_{l=1}^{n_2}\hat{v}_2(S_l,\tau)\phi_l(S)\bigg|_{S \in \Omega_2} + \sum_{l=1}^{n_3} \hat{v}_3(S_l,\tau)\hat{\phi}_l(S) \bigg|_{S \in \Omega_3}, \end{align*} $$
where
![]() $n_3$
is, in this case, the degree of the modified Laguerre polynomials. To deal with the discontinuity at the upper barrier level, we adopt the discontinuous payoff spectral element method as in the work of Yue [Reference Yue36]. The left and right parts of the payoff function shall be considered separately at the initial time. With
$n_3$
is, in this case, the degree of the modified Laguerre polynomials. To deal with the discontinuity at the upper barrier level, we adopt the discontinuous payoff spectral element method as in the work of Yue [Reference Yue36]. The left and right parts of the payoff function shall be considered separately at the initial time. With
![]() $v_L(0)$
and
$v_L(0)$
and
![]() $v_R(0)$
being the barrier’s initial payoff at the immediate left and right to the barrier level,
$v_R(0)$
being the barrier’s initial payoff at the immediate left and right to the barrier level,
![]() $B_u$
, then
$B_u$
, then
![]() $\hat {v}(0)_{|\Omega _1,\Omega _2} = v_L(0) = S-K$
and
$\hat {v}(0)_{|\Omega _1,\Omega _2} = v_L(0) = S-K$
and
![]() $\hat {v}(0)_{|\Omega _3} = v_R(0) = 0$
. Over a tiny time step
$\hat {v}(0)_{|\Omega _3} = v_R(0) = 0$
. Over a tiny time step
![]() $\Delta \tau = 10^{-11}$
after the initial time, we use the Crank–Nicolson scheme [Reference Crank and Nicolson11] such that
$\Delta \tau = 10^{-11}$
after the initial time, we use the Crank–Nicolson scheme [Reference Crank and Nicolson11] such that
 $$ \begin{align*} \big[\textbf{M} - \tfrac12 \Delta \tau \textbf{L}\big]\bar{v}(\tau_m) = \big[\textbf{M}_L + \tfrac12 \Delta \tau \textbf{L}_L\big]\bar{v}_L(0) + \big[\textbf{M}_R + \tfrac12 \Delta \tau \textbf{L}_R\big]\bar{v}_R(0), \end{align*} $$
$$ \begin{align*} \big[\textbf{M} - \tfrac12 \Delta \tau \textbf{L}\big]\bar{v}(\tau_m) = \big[\textbf{M}_L + \tfrac12 \Delta \tau \textbf{L}_L\big]\bar{v}_L(0) + \big[\textbf{M}_R + \tfrac12 \Delta \tau \textbf{L}_R\big]\bar{v}_R(0), \end{align*} $$
where
![]() $\textbf {M}_L$
,
$\textbf {M}_L$
,
![]() $\textbf {L}_L$
,
$\textbf {L}_L$
,
![]() $\textbf {M}_R$
,
$\textbf {M}_R$
,
![]() $\textbf {L}_R$
are the left and right global matrices. More details about the structures of these matrices can be found in the work of Yue [Reference Yue36]. Then for the remaining time,
$\textbf {L}_R$
are the left and right global matrices. More details about the structures of these matrices can be found in the work of Yue [Reference Yue36]. Then for the remaining time,
![]() $T-\Delta \tau $
, the same procedure as for the European option can be implemented to obtain the option price.
$T-\Delta \tau $
, the same procedure as for the European option can be implemented to obtain the option price.
5. Richardson extrapolation
To improve the accuracy in time, we consider the Richardson extrapolation process with s stages [Reference Feng and Linetsky15] which is described next. As shown in several works [Reference Diethelm and Walz13, Reference Pal, Liu, Yan, Dimov, Faragó and Vulkov24, Reference Yan, Pal and Ford35], the approximated solutions of fractional order differential equations possess asymptotic expansions with respect to the step size. In the same way, to apply the Richardson extrapolation approach in time to guarantee higher order convergence, we assume the existence of asymptotic expansions for solutions obtained using the
![]() $L1$
scheme to approximate the Caputo time fractional derivative [Reference Lin and Xu22]. We emphasize that the
$L1$
scheme to approximate the Caputo time fractional derivative [Reference Lin and Xu22]. We emphasize that the
![]() $L1$
approximation scheme will only be
$L1$
approximation scheme will only be
![]() $\mathcal {O}((\Delta \tau )^{2-\alpha })$
provided the considered function is twice continuously differentiable. However, for the European and barrier options,
$\mathcal {O}((\Delta \tau )^{2-\alpha })$
provided the considered function is twice continuously differentiable. However, for the European and barrier options,
![]() $v(S,\tau )$
is only once continuously differentiable with respect to time such that only first-order accuracy can be attained [Reference Jin, Lazarov and Zhou18]. A sequence of approximations to
$v(S,\tau )$
is only once continuously differentiable with respect to time such that only first-order accuracy can be attained [Reference Jin, Lazarov and Zhou18]. A sequence of approximations to
![]() $v(\Delta \tau )$
can be constructed using the discretization method (4.7). Let
$v(\Delta \tau )$
can be constructed using the discretization method (4.7). Let
![]() $v_{k,l}$
denote the approximate solution obtained using the
$v_{k,l}$
denote the approximate solution obtained using the
![]() $L1$
scheme at time
$L1$
scheme at time
![]() $\Delta \tau $
with step size
$\Delta \tau $
with step size
![]() $\Delta \tau /2^{k-1}$
,
$\Delta \tau /2^{k-1}$
,
![]() $k = 1,2,\ldots ,s$
. As such, with prior knowledge of the rate of convergence of the
$k = 1,2,\ldots ,s$
. As such, with prior knowledge of the rate of convergence of the
![]() $L1$
discretization, we have the following s-stage extrapolation tableau given by
$L1$
discretization, we have the following s-stage extrapolation tableau given by
 $$\begin{align} \hat{v}_{k,l} = \frac{(2)^{k-1}\hat{v}_{k,l-1} - \hat{v}_{k-1,l-1}}{(2)^{k-1}-1}, \end{align} $$
$$\begin{align} \hat{v}_{k,l} = \frac{(2)^{k-1}\hat{v}_{k,l-1} - \hat{v}_{k-1,l-1}}{(2)^{k-1}-1}, \end{align} $$
for
![]() $k = 2,\ldots ,s$
and
$k = 2,\ldots ,s$
and
![]() $l=2,\ldots ,k$
. Starting with M initial time steps and doubling M at each extrapolation stage, the total number of time steps required after using the s-stage Richardson extrapolation is
$l=2,\ldots ,k$
. Starting with M initial time steps and doubling M at each extrapolation stage, the total number of time steps required after using the s-stage Richardson extrapolation is
![]() $M_s = (2^s-1)M$
.
$M_s = (2^s-1)M$
.
We next provide the algorithm for finding the European option value.

6. Numerical results
This section presents the numerical results to illustrate the efficiency of the Legendre–Laguerre spectral approximation and the Richardson extrapolation approach to price the European put and double barrier call options governed by the time-fractional Black–Scholes equation. All computations of our numerical experiments have been performed using MATLAB
![]() $^\circledR $
with a Core i5, 2.50 GHz processor and 8 GB RAM. With no analytical solutions available for option prices in the fractional framework, we consider reference solutions calculated over more refined grids with
$^\circledR $
with a Core i5, 2.50 GHz processor and 8 GB RAM. With no analytical solutions available for option prices in the fractional framework, we consider reference solutions calculated over more refined grids with
![]() $n_1 = n_2 = 40$
in the spatial direction and
$n_1 = n_2 = 40$
in the spatial direction and
![]() $s=6$
starting with an initial
$s=6$
starting with an initial
![]() $M = 20$
in the temporal direction. The errors are given in the
$M = 20$
in the temporal direction. The errors are given in the
![]() $L^2$
,
$L^2$
,
![]() $L^{\infty }$
and
$L^{\infty }$
and
![]() $H^1$
norms such that
$H^1$
norms such that
 $\text {Error} = v_{\text {ref}} - v_N^M$
, where
$\text {Error} = v_{\text {ref}} - v_N^M$
, where
![]() $v_{\text {ref}}$
is a vector of reference prices and
$v_{\text {ref}}$
is a vector of reference prices and
 $V_N^M$
represents the corresponding approximate computed solutions. The rates of convergence in the temporal direction can be computed by
$V_N^M$
represents the corresponding approximate computed solutions. The rates of convergence in the temporal direction can be computed by
 $$ \begin{align*} \text{Rate}_{\Delta \tau} = \log_2 \bigg(\frac{\|\text{Error}(\Delta \tau)\|}{\|\text{Error}(\Delta \tau/2)\|}\bigg). \end{align*} $$
$$ \begin{align*} \text{Rate}_{\Delta \tau} = \log_2 \bigg(\frac{\|\text{Error}(\Delta \tau)\|}{\|\text{Error}(\Delta \tau/2)\|}\bigg). \end{align*} $$
For the first numerical experiment, we consider the same first example as in the work of Zhang et al. [Reference Zhang, Liu, Turner and Yang38].
Example 6.1 Consider the following time-fractional equation with homogeneous boundary conditions:
 $$ \begin{align*} \mathcal{D}^{\alpha}_{\tau} u(x,\tau) = a \frac{\partial^2 u(x,\tau)}{\partial x^2} + b \frac{\partial u(x,\tau)}{\partial x} - c u(x,\tau) + g(x,\tau), \;\; x \in (0,1),~ \tau \in (0,T], \end{align*} $$
$$ \begin{align*} \mathcal{D}^{\alpha}_{\tau} u(x,\tau) = a \frac{\partial^2 u(x,\tau)}{\partial x^2} + b \frac{\partial u(x,\tau)}{\partial x} - c u(x,\tau) + g(x,\tau), \;\; x \in (0,1),~ \tau \in (0,T], \end{align*} $$
where
 $$ \begin{align*} g(x,\tau) = &\bigg[\frac{2\tau^{2-\alpha}}{\Gamma(3-\alpha)} + \frac{2\tau^{1-\alpha}}{\Gamma(2-\alpha)}\bigg]x^2(1-x) - (\tau+1)^2 [a(2-6x) + b(2x - 3x^2)\\ & - cx^2(1-x)]. \end{align*} $$
$$ \begin{align*} g(x,\tau) = &\bigg[\frac{2\tau^{2-\alpha}}{\Gamma(3-\alpha)} + \frac{2\tau^{1-\alpha}}{\Gamma(2-\alpha)}\bigg]x^2(1-x) - (\tau+1)^2 [a(2-6x) + b(2x - 3x^2)\\ & - cx^2(1-x)]. \end{align*} $$
The initial and boundary conditions are
 $$ \begin{align*} &u(x,0) = x^2(1 - x),\\ &u(0,\tau) = 0 \;\; \text{and} \;\; u(1,\tau) = 0. \end{align*} $$
$$ \begin{align*} &u(x,0) = x^2(1 - x),\\ &u(0,\tau) = 0 \;\; \text{and} \;\; u(1,\tau) = 0. \end{align*} $$
The exact analytical solution to this problem is
![]() $u(x,\tau ) = (\tau +1)^2 x^2(1-x)$
.
$u(x,\tau ) = (\tau +1)^2 x^2(1-x)$
.
Here the parameters are chosen as in the work of Zhang et al. [Reference Zhang, Liu, Turner and Yang38], that is,
 $$ \begin{align*} r = 0.05,\quad \sigma = 0.25,\quad T = 1,\quad a = \tfrac12 \sigma^2,\quad b = r - a,\quad c = r. \end{align*} $$
$$ \begin{align*} r = 0.05,\quad \sigma = 0.25,\quad T = 1,\quad a = \tfrac12 \sigma^2,\quad b = r - a,\quad c = r. \end{align*} $$
In Figure 1, we compare the second-order finite-difference scheme used in the work of Zhang et al. [Reference Zhang, Liu, Turner and Yang38] to the spectral approximation using only Legendre basis functions for Example 6.1 with the
![]() $L1$
approximation approach for the time discretization. Figure 1 also illustrates the performance of the extrapolation approach when used with both the finite-difference scheme and the spectral element discretization. We plot here the errors in the
$L1$
approximation approach for the time discretization. Figure 1 also illustrates the performance of the extrapolation approach when used with both the finite-difference scheme and the spectral element discretization. We plot here the errors in the
![]() $L^{\infty }$
norm against N, the total number of grid nodes for the finite-difference and spectral methods. To eliminate the temporal error, we fix
$L^{\infty }$
norm against N, the total number of grid nodes for the finite-difference and spectral methods. To eliminate the temporal error, we fix
![]() $M =$
10 000 for the
$M =$
10 000 for the
![]() $L1$
scheme and we use
$L1$
scheme and we use
![]() $s=6$
starting with an initial
$s=6$
starting with an initial
![]() $M = 20$
using the extrapolation approach. From Figure 1, we can observe the superior performance of the spectral method over the finite-difference approach, where the maximum errors for the spectral approximation decrease much faster than the finite-difference method which converges algebraically. Note that
$M = 20$
using the extrapolation approach. From Figure 1, we can observe the superior performance of the spectral method over the finite-difference approach, where the maximum errors for the spectral approximation decrease much faster than the finite-difference method which converges algebraically. Note that
![]() $N = 5$
is sufficient to achieve
$N = 5$
is sufficient to achieve
![]() $10^{-6}$
accuracy for the spectral method, while many more grid nodes will be required to reach the same level of accuracy using the finite-difference approach. Applying the extrapolation process, we can see the faster convergence of the spectral method while the extrapolated solution with the finite-difference scheme behaves in a similar way as the nonextrapolated scheme, since not enough grid nodes are used to achieve the required accuracy. We point out that similar graphs are obtained in the
$10^{-6}$
accuracy for the spectral method, while many more grid nodes will be required to reach the same level of accuracy using the finite-difference approach. Applying the extrapolation process, we can see the faster convergence of the spectral method while the extrapolated solution with the finite-difference scheme behaves in a similar way as the nonextrapolated scheme, since not enough grid nodes are used to achieve the required accuracy. We point out that similar graphs are obtained in the
![]() $L^2$
and
$L^2$
and
![]() $H^1$
norms.
$H^1$
norms.

Figure 1 Log plot of maximum errors against N for Example 6.1 for the finite-difference and spectral methods with
![]() $\alpha = 0.7$
.
$\alpha = 0.7$
.
In Table 1, we report the
![]() $L^2$
and
$L^2$
and
![]() $H^1$
errors for the time-fractional model in Example 6.1 using the
$H^1$
errors for the time-fractional model in Example 6.1 using the
![]() $L1$
approximation and the Richardson extrapolation approach for
$L1$
approximation and the Richardson extrapolation approach for
![]() $\alpha = 0.5,\,0.7$
and
$\alpha = 0.5,\,0.7$
and
![]() $0.9$
. It can be observed that the convergence rates for the
$0.9$
. It can be observed that the convergence rates for the
![]() $L1$
method are indeed
$L1$
method are indeed
![]() $\mathcal {O}((\Delta \tau )^{2-\alpha })$
for the different values of
$\mathcal {O}((\Delta \tau )^{2-\alpha })$
for the different values of
![]() $\alpha $
. Based on these rates of convergence, we can see the faster convergence of the Richardson extrapolation approach for all the values of
$\alpha $
. Based on these rates of convergence, we can see the faster convergence of the Richardson extrapolation approach for all the values of
![]() $\alpha $
considered. Note that many more time steps would be required to reach the same level of accuracy without extrapolation.
$\alpha $
considered. Note that many more time steps would be required to reach the same level of accuracy without extrapolation.
Table 1 The
![]() $L^2$
and
$L^2$
and
![]() $H^1$
errors for the
$H^1$
errors for the
![]() $L1$
approximation and the Richardson extrapolation approach for Example 6.1.
$L1$
approximation and the Richardson extrapolation approach for Example 6.1.

6.1. European options
We now consider the numerical comparison for the space discretization for the European put option under the time-fractional Black–Scholes model with parameters chosen as
In Figure 2, we compare the spectral element method with the finite element discretization under the time-fractional Black–Scholes framework, where the errors for the European put option are presented in the
![]() $L^2$
norms against the total number of grid nodes, N, to check the spatial accuracy for
$L^2$
norms against the total number of grid nodes, N, to check the spatial accuracy for
![]() $\alpha = 0.9$
. We can clearly see that the errors decay exponentially with far fewer mesh points which shows spectral accuracy compared with the linear finite element method achieving only second-order convergence. This validates that the theoretical results in Lemma 4.1 and Lemma 4.2 for the European option have adequate smooth solutions in the closure of each interval
$\alpha = 0.9$
. We can clearly see that the errors decay exponentially with far fewer mesh points which shows spectral accuracy compared with the linear finite element method achieving only second-order convergence. This validates that the theoretical results in Lemma 4.1 and Lemma 4.2 for the European option have adequate smooth solutions in the closure of each interval
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _2$
.
$\Omega _2$
.

Figure 2 Log plot of
![]() $L^2$
errors against N for a European put option with
$L^2$
errors against N for a European put option with
![]() $\alpha = 0.9$
with the finite element and spectral element methods.
$\alpha = 0.9$
with the finite element and spectral element methods.
Using the
![]() $L1$
scheme, we observe from Table 2 that only first-order convergence in time is achieved for
$L1$
scheme, we observe from Table 2 that only first-order convergence in time is achieved for
![]() $\alpha = 0.1, 0.3$
and 0.7. Higher accuracy is obtained using the Richardson extrapolation approach in much fewer time steps. Obviously, European option prices can be calculated more accurately than with the
$\alpha = 0.1, 0.3$
and 0.7. Higher accuracy is obtained using the Richardson extrapolation approach in much fewer time steps. Obviously, European option prices can be calculated more accurately than with the
![]() $L1$
scheme for different values of
$L1$
scheme for different values of
![]() $\alpha $
as done so far in the literature.
$\alpha $
as done so far in the literature.
Table 2 The
![]() $L^2$
and
$L^2$
and
![]() $L^{\infty }$
errors for the European option for the
$L^{\infty }$
errors for the European option for the
![]() $L1$
approximation and the Richardson extrapolation approach.
$L1$
approximation and the Richardson extrapolation approach.

We further illustrate the computational efficiency of the extrapolation approach in Figure 3. In particular, we plot the
![]() $L^2$
errors against M and computational times in seconds in log–log scale in Figures 3(a) and 3(b), respectively. We observe the faster convergence of the extrapolation scheme where a total of 620 time steps are needed to achieve an accuracy of
$L^2$
errors against M and computational times in seconds in log–log scale in Figures 3(a) and 3(b), respectively. We observe the faster convergence of the extrapolation scheme where a total of 620 time steps are needed to achieve an accuracy of
![]() $10^{-5}$
in contrast to
$10^{-5}$
in contrast to
![]() $M =$
327 680 for the
$M =$
327 680 for the
![]() $L1$
method to reach the same accuracy. We further observe that the computational times for the
$L1$
method to reach the same accuracy. We further observe that the computational times for the
![]() $L1$
scheme are much higher than for the extrapolation method where the accuracy of
$L1$
scheme are much higher than for the extrapolation method where the accuracy of
![]() $10^{-5}$
is achieved in 0.1052 seconds with the extrapolation approach compared with 43 090 seconds for the commonly used
$10^{-5}$
is achieved in 0.1052 seconds with the extrapolation approach compared with 43 090 seconds for the commonly used
![]() $L1$
scheme. It is obvious that a simple extrapolation approach is very efficient to achieve high accuracy with much fewer time steps. The practical importance of the present contribution therefore stems from the fact that the computational requirement for storing the numerical solution for all previous time steps is much less for an extrapolation scheme compared with a first-order scheme to reach similar levels of accuracy.
$L1$
scheme. It is obvious that a simple extrapolation approach is very efficient to achieve high accuracy with much fewer time steps. The practical importance of the present contribution therefore stems from the fact that the computational requirement for storing the numerical solution for all previous time steps is much less for an extrapolation scheme compared with a first-order scheme to reach similar levels of accuracy.

Figure 3 Log–log plots of
![]() $L^2$
errors and computational times in seconds for the
$L^2$
errors and computational times in seconds for the
![]() $L1$
scheme and the Richardson extrapolation method for a European put option under the time-fractional Black–Scholes model for
$L1$
scheme and the Richardson extrapolation method for a European put option under the time-fractional Black–Scholes model for
![]() $\alpha = 0.5$
.
$\alpha = 0.5$
.
6.2. Double barrier options
For the next test problem, we consider the double knock-out call barrier option with the following model parameters:
As previously mentioned, we use three elements, and only one node is sufficient for the third element to enforce the upper boundary. As such, for the error stemming from the spectral approximation to be negligible, we choose
![]() $n_1 = n_2 = 40$
and
$n_1 = n_2 = 40$
and
![]() $n_3 \,{=}\, 1$
. Table 3 reports the errors in the
$n_3 \,{=}\, 1$
. Table 3 reports the errors in the
![]() $L^2$
norm for
$L^2$
norm for
![]() $\alpha = 0.1,\,0.3,\,0.5,\,0.7$
for the
$\alpha = 0.1,\,0.3,\,0.5,\,0.7$
for the
![]() $L1$
approximation and the Richardson extrapolation approach for the double barrier call option. Again first-order accuracy is obtained using the
$L1$
approximation and the Richardson extrapolation approach for the double barrier call option. Again first-order accuracy is obtained using the
![]() $L1$
method while the Richardson extrapolation approach gives higher accuracy.
$L1$
method while the Richardson extrapolation approach gives higher accuracy.
Table 3 The
![]() $L^2$
errors for the
$L^2$
errors for the
![]() $L1$
approximation and the Richardson extrapolation approach for the double knock-out call barrier option.
$L1$
approximation and the Richardson extrapolation approach for the double knock-out call barrier option.

7. Conclusion
In this work, under the time-fractional Black–Scholes model, we considered a Legendre–Laguerre spectral approximation to price European and double barrier options. By breaking the domain into sub-domains, the option price within each element is approximated by the Legendre and Laguerre basis functions with the associated quadrature rules. A comparison with the second-order finite-difference approach indicates that the spectral approximation gives a viable alternative to the latter with far fewer grid points necessary to obtain highly accurate solutions in space. Consequently, at each time step, only linear systems of moderate dimensions are required to be solved, thus making the proposed scheme computationally faster and more efficient. To further improve the temporal convergence, a Richardson extrapolation scheme is applied based on the
![]() $L1$
approximation and, as demonstrated by the numerical results, this approach is very efficient to achieve higher accuracies in much fewer time steps.
$L1$
approximation and, as demonstrated by the numerical results, this approach is very efficient to achieve higher accuracies in much fewer time steps.
Acknowledgements
The authors gratefully acknowledge the funding support under the award number ID-2019-14 from the Tertiary Education Commission, Mauritius. The authors would also like to thank the anonymous reviewers for their valuable suggestions which have brought important enhancements to this work in a significant way.