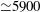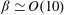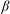1. Introduction
Pulsating flows are of interest in many engineering applications such as industrial, environmental and biological flows. This class of problems is characterized by a superposition of a steady flow onto a harmonic-like time-varying component typically generated by a rotating or popped valve in a mechanical engineering context. Alternatively, the oscillation may be induced by a variable displacement pump, or by a wave–current boundary layer interaction in a coastal environment. Another context where these problems might be relevant is that of blood circulation. Typical parameters are a peak Reynolds number of
${\approx}6500$
during the systole and a mean Reynolds number of
${\approx}1400$
averaged over the heart cycle. The ratio between the oscillating and the mean streamwise velocity is
${\approx}6$
although the waveform is not purely sinusoidal and it is determined by a complex interaction between the heart and the impedance of the circulatory system (Caro et al.
Reference Caro, Pedley, Schroter and Seed1978; de Tullio et al.
Reference de Tullio, Cristallo, Balaras and Verzicco2009). Finally, the ratio between the radius of the aorta and the Stokes layer thickness yields
${\it\Omega}\approx 12$
(see below for the definition), which classifies the flow as the ‘high-frequency regime’.
As a matter of fact, and despite their great environmental and biomedical relevance, little is known about the physics of pulsating turbulent flows even in simple geometries. One of the reasons lies in the enhanced complexities added by the oscillatory component of the motion which increases the relevant similarity parameters from one (in the case of steady flow) to three (Akhavan, Kamm & Shapiro Reference Akhavan, Kamm and Shapiro1991). While several choices are possible, a convenient triplet is (Yellin Reference Yellin1966)
$\mathit{Re}_{b}$
,
${\it\Omega}$
and
${\it\beta}$
with
$$\begin{eqnarray}\mathit{Re}_{b}=\frac{U_{b}D}{{\it\nu}},\quad {\it\Omega}=\frac{R}{{\it\delta}},\quad {\it\beta}=\frac{U_{o}}{U_{b}},\end{eqnarray}$$
where
$D$
,
$U_{b}$
and
${\it\nu}$
are the pipe diameter, the steady component of the bulk velocity and the fluid kinematic viscosity respectively. The pipe radius is
$R=D/2$
, while
${\it\delta}=\sqrt{2{\it\nu}/{\it\omega}}$
is the Stokes layer thickness,
${\it\omega}=2{\rm\pi}/T$
being the pulsation, with
$T$
the oscillation period. Finally,
$U_{o}$
is the amplitude of the oscillating component of the bulk velocity (with zero time average).
The available literature on pulsating pipe flows has been extensively reviewed in a previous paper (Manna, Vacca & Verzicco Reference Manna, Vacca and Verzicco2012), to which the reader is referred for further references.
While nearly the entire literature has dealt with pulsating pipe or channel flows with
${\it\beta}$
values less than one (the current-dominated (CD) regime) (Shemer & Kit Reference Shemer and Kit1984; Tardu & Binder Reference Tardu and Binder1993; Scotti & Piomelli Reference Scotti and Piomelli2001; He & Jackson Reference He and Jackson2009) (see table 1 in Manna et al.
Reference Manna, Vacca and Verzicco2012), very few studies have focused on values of
${\it\beta}$
beyond unity (the wave-dominated regime).
Lodahl, Sumer & Fredosoe (Reference Lodahl, Sumer and Fredosoe1998) experimentally analysed a large part of the parameter space. Introducing the oscillation Reynolds number
$\mathit{Re}_{{\it\omega}}=U_{m}^{2}/({\it\omega}{\it\nu})$
(it is easy to show that the relation
$\mathit{Re}_{{\it\omega}}{\it\Omega}^{2}=[({\it\beta}\,\mathit{Re}_{b})/(2\sqrt{2})(U_{m}/U_{o})]^{2}$
holds), with
$U_{m}$
the maximum value of the oscillatory flow at the centre of the pipe, the available data, in the high-frequency regime (
${\it\Omega}>10$
), have been represented in an (
$\mathit{Re}_{b},\mathit{Re}_{{\it\omega}}$
) plane (see figure 1). The laminar to turbulent transition was shown to depend on the (
$\mathit{Re}_{b},\mathit{Re}_{{\it\omega}}$
) pair. More specifically, for
$\mathit{Re}_{b}<\mathit{Re}_{b,tr}\simeq 2300$
, the flow remains laminar until
$\mathit{Re}_{{\it\omega}}$
reaches the transitional value in the absence of current (
$\mathit{Re}_{{\it\omega},tr}\sim 10^{5}$
). For
$\mathit{Re}_{b}>\mathit{Re}_{b,tr}$
, laminar conditions can only occur if
$\mathit{Re}_{{\it\omega}1}<\mathit{Re}_{{\it\omega}}<\mathit{Re}_{{\it\omega}2}$
; the difference between
$\mathit{Re}_{{\it\omega}2}$
and
$\mathit{Re}_{{\it\omega}1}$
reduces for increasing
$\mathit{Re}_{b}$
and it vanishes at
$\mathit{Re}_{b}/\mathit{Re}_{b,tr}\sim 3.5$
, with
$\mathit{Re}_{{\it\omega}}/\mathit{Re}_{{\it\omega},tr}\sim 0.7$
. In Manna et al. (Reference Manna, Vacca and Verzicco2012) (hereafter referred to as MVV), a few fully resolved direct numerical simulations were carried out for a fixed value of
${\it\Omega}\;(=53)$
and different oscillating velocity amplitudes. Four flow conditions characterized by different values of
${\it\beta}$
were considered and a turbulent to laminar reverse transition process was documented to occur for
${\it\beta}=5$
. For
${\it\beta}=10.6$
, turbulence was accompanied by a remarkable reduction of the cycle-averaged friction coefficient when compared with the steady value, and the first- and second-order moments showed appreciable deviations compared with the corresponding steady ones. In particular, the cycle-averaged vorticity and the velocity fluctuation budgets indicated an enhanced turbulence anisotropy in the near-wall region.
Figure 1. The laminar to turbulent transition boundary (dashed line) and available data for high-frequency regimes (
${\it\Omega}\geqslant 10$
): ○, Shemer & Kit (Reference Shemer and Kit1984); ▹, Tardu & Binder (Reference Tardu and Binder1993); ▫, Lodahl et al. (Reference Lodahl, Sumer and Fredosoe1998); ◃, Scotti & Piomelli (Reference Scotti and Piomelli2001); ▿, He & Jackson (Reference He and Jackson2009); ●, present calculations.
In this paper the dynamics of the relevant turbulent quantities is further analysed with respect to their time evolution within the pulsating period. To this end the phase-averaged decomposition was employed with the objective of unravelling the transient mechanisms and clarifying the cycle-averaged results. Particular attention has been paid to the phase dynamics of the wall layer structure described in terms of statistical parameters.
The paper is organized as follows. In § 2 the problem is described together with the numerical method. In § 3 the results are discussed; the phase dynamics of the mean velocity, Reynolds stresses and vorticity is given in § 3.1 while the Reynolds stress budget analysis is detailed in § 3.2. The conclusions are briefly outlined in § 4.
2. Problem and numerical method
The incompressible pulsating flow through a circular pipe with diameter
$D$
and axial length
$L_{z}$
is driven by a time-dependent harmonic body force of prescribed mean, amplitude and frequency. The resulting flow has a volume-averaged velocity with a steady component
$U_{b}$
and a harmonically time-varying one
$U_{o}$
with pulsation
${\it\omega}$
. The forcing term, later specified, is such that the desired values of the dimensionless parameters (1.1) are obtained.
We recall that the flow parameters, whose numerical values are given in table 1, have been chosen in such a way as to cross the hook-shaped laminar/turbulent transition boundary twice while keeping
$\mathit{Re}_{b}$
(approximately) constant.
Table 1. The run matrix.
The motivation for this study stems from the fact that, as shown in figure 1, there are no cases in the neighbourhood of the region inside which a reverse transition occurs (Lodahl et al.
Reference Lodahl, Sumer and Fredosoe1998). Accordingly, we have investigated via direct numerical simulation (DNS) the three flow conditions identified by the (
$\mathit{Re}_{b},\mathit{Re}_{{\it\omega}}$
) pairs detailed in table 1 and denoted with filled circles in figure 1.
A steady simulation at
$\mathit{Re}_{b}=5920$
(referred to as ST) has also been performed with the aim of comparing the pulsating dynamics with the steady one.
All pulsating cases are characterized by the same Stokes layer thickness (
${\it\Omega}=53$
) and an approximately constant bulk Reynolds number
$\mathit{Re}_{b}$
, while the oscillating Reynolds number
$\mathit{Re}_{{\it\omega}}$
is changed by three orders of magnitude, thus crossing both the lower and the upper branches of the hook-like transition boundary (see figure 1).
We solve the three-dimensional incompressible Navier–Stokes equations,
$$\begin{eqnarray}\frac{\partial \boldsymbol{u}}{\partial t}+\mathscr{N}(\boldsymbol{u})=-\boldsymbol{{\rm\nabla}}P+\mathscr{L}(\boldsymbol{u})+\mathscr{S},\quad \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0,\end{eqnarray}$$
where
$P=p/{\it\rho}$
, with
$p$
and
${\it\rho}$
the pressure and the fluid density respectively. The velocity components of
$\boldsymbol{u}$
in cylindrical coordinates are
$\boldsymbol{u}=(u_{z},u_{r},u_{{\it\theta}})^{\text{T}}=(u,v,w)^{\text{T}}$
, in the axial (streamwise), radial and azimuthal directions respectively. The differential operators
$\mathscr{N}(\boldsymbol{u})=(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u}$
and
$\mathscr{L}(\boldsymbol{u})={\it\nu}{\rm\Delta}\boldsymbol{u}$
represent the convective and diffusive terms. In the present flow the source term
$\mathscr{S}$
is given by
$\mathscr{S}=(S_{z},0,0)^{\text{T}}$
with
$$\begin{eqnarray}S_{z}=S_{0}\left[1+{\it\alpha}\cos ({\it\omega}t)\right].\end{eqnarray}$$
The triplet
$(S_{0},{\it\alpha},{\it\omega})$
has been prescribed so as to obtain the dimensionless parameters given in table 1. Due to the nonlinear dependence of the velocity field upon the body force
$\mathscr{S}$
, it is impossible to specify a priori a triplet yielding a precise value of the dimensionless parameters and therefore the constancy of
$\mathit{Re}_{b}$
, while changing
${\it\beta}$
, is only approximate.
The data were obtained with a spectral Chebyshev algorithm for the inhomogeneous (radial) direction and blended Fourier decomposition for the homogeneous (axial and azimuthal) ones, which has been successfully applied to both direct and large-eddy (Manna & Vacca Reference Manna and Vacca2005, Reference Manna and Vacca2007, Reference Manna and Vacca2009) simulation of turbulent flows. Efficiency was enhanced using a multidomain technique for the elliptic operators (Manna & Vacca Reference Manna and Vacca1999; Manna, Vacca & Deville Reference Manna, Vacca and Deville2004). Given the high resolution of the simulations, assessed a posteriori through the velocity spectra in the homogeneous directions, no dealiasing procedure was applied.
The dimensionless axial length
$l_{z}=L_{z}/R$
was set equal to 12 for the steady (ST) and CD simulations and to 28 for the wave-dominated ones (WD1 and WD2); this was necessary in order to account for the elongation of the near-wall coherent structures as
${\it\beta}$
is increased. The autocorrelation of the streamwise velocity, shown in MVV, has confirmed the adequacy of the computational domain length. Indeed, in the study of Chin et al. (Reference Chin, Ooi, Marusic and Blackburn2010) it has been shown that turbulent flows in pipes contain some very elongated structures that extend beyond the axial length of
${\approx}25R$
, although with limited energy content. The first- and second-order statistics, however, converge already for lengths of the order of
${\approx}10R$
, and these are the main focus of this study.
The computational domain was split radially into seven subdomains (
$N_{sub}=7$
), each one having
$N_{r}=12$
and
$N_{{\it\theta}}=192$
modes in the radial and azimuthal directions respectively. The number of Fourier modes in the axial direction was set to
$N_{z}=192$
in the steady and CD simulations. To preserve the resolution in the axial direction the number of modes in the wave-dominated regime was increased to
$N_{z}=450$
. In table 2 some details are given on the spatial discretization of the simulations scaled with the wall quantities computed from the friction velocity
$\overline{u}_{{\it\tau}}=\sqrt{S_{0}R/2}$
.
Table 2. Computational details.
The grid resolution, comparable to that of Eggels et al. (Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994), Orlandi & Fatica (Reference Orlandi and Fatica1997) and Quadrio & Sibilla (Reference Quadrio and Sibilla2000), satisfied the severe DNS requirements and ensured the reliability of the data. Further comparisons of our ST case with the results reported by Eggels et al. (Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994), Orlandi & Fatica (Reference Orlandi and Fatica1997) and Quadrio & Sibilla (Reference Quadrio and Sibilla2000) (see MVV) confirm the quantitative agreement of the present results with analogous cases from the literature. The CD simulation required slightly less than 1 GB of RAM and needed approximately 150 single-core equivalent hours per period.
In what follows we shall denote with the brackets (
$\langle \cdot \rangle$
) all quantities that have been phase averaged and with an overline (
$\overline{\;\cdot \;}$
) those that have been cycle averaged. Changes within the period, i.e. the modulation in the oscillating cycle, are computed as the difference between phase- and cycle-averaged quantities (
$\widetilde{\;\cdot \;}=\langle \cdot \rangle -\overline{\;\cdot \;}$
). The prime symbol (
$\cdot \prime$
) is used to indicate the deviation of the instantaneous values from the phase-averaged quantities. Denoting by
$N_{c}$
and
$N_{tot}$
the number of cycles and the number of samples used to describe the in-cycle variations respectively, the following definitions are adopted:
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \,f\left(r,t_{n}\right)\rangle =\frac{1}{N_{c}\hspace{2.22198pt}l_{z}2{\rm\pi}}\mathop{\sum }_{i=1}^{N_{c}}\int _{0}^{2{\rm\pi}}\int _{0}^{l_{z}}f(z,r,{\it\theta},t_{n}+\left(i-1\right)T)\text{d}z\text{d}{\it\theta}\quad n=1,\dots ,N_{tot}, & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{f}(r)=\frac{1}{N_{tot}}\mathop{\sum }_{n=1}^{N_{tot}}\langle \,f\left(r,t_{n}\right)\rangle . & \displaystyle\end{eqnarray}$$
We divide the oscillating period
$T$
into eight evenly spaced intervals, i.e.
$N_{tot}=8$
and
$t_{n}=(n-1)T/8$
, and denote by
${\it\phi}_{n}=(n-1){\rm\pi}/4$
the corresponding phases. Moreover, the data are shown as a function of the phase
${\it\phi}_{n}$
, with
${\it\phi}_{0}$
such that
$\widetilde{U}({\it\phi}_{3})=U_{o}$
. For the sake of brevity the subscript
$n$
is omitted in the following and the phases are directly specified with the corresponding angle.
The phase-averaged statistics have been evaluated by processing 50 flow cycles. In order to assess the convergence of the results, some statistics have been computed using only 30 periods and the results for the Reynolds stresses have shown a maximum deviation of 3 % with respect to the same quantities computed using the whole data set. The database, stored in single precision, consists of 400 files for a total size of 20 GB (
${\it\beta}=1$
case) and 46 GB (
${\it\beta}=10.6$
case).
3. Results
3.1. Velocity profiles and Reynolds stress analysis
In MVV it was shown that the time-averaged radial profiles of the streamwise velocity behaved very differently depending on the specific flow regime. In particular, the WD1 case was shown to be laminar with a parabolic Poiseuille-like profile, while the CD flow recovered the steady ST case. The WD2 case instead had an intermediate behaviour, still displaying a logarithmic region although with an upward shift that indicated some drag reduction. Moreover, it was shown that the oscillating flow obeys the Stokes solution in both current- and wave-dominated regimes. Therefore, the flow appears to be essentially uncoupled in the CD regime and one-way coupled in the wave-dominated one.
It is worth mentioning that the transitional aortic blood flow in an adult human, although the oscillating component is not purely harmonic, is in the wave-dominated regime since
${\it\beta}\simeq 6$
. Perhaps also this highly pulsatile flow under certain circumstances benefits from some drag reduction that decreases the load on the myocardial muscle.
This mean flow dynamics, summarized in figure 2, applies only to the cycle-averaged profiles, while the phase-averaged statistics show very different features.
Figure 2. Mean velocity profiles in inner coordinates: ——, ST case; — ⋅ —, CD case;
$\cdots \cdots$
, WD1 case; - - - -, WD2 case. The thin solid line is given for reference with
${\it\kappa}=0.41$
and
$B=5.5$
, the standard values for turbulent channel and pipe flows.
In the following we will analyse only the CD and WD2 cases since the WD1 flow, obtained for
${\it\beta}=5.0$
, completely relaminarized and yielded phase-averaged profiles that were just the decoupled superposition of a steady Poiseuille and a Stokes flow. In figure 3 the phase-averaged velocity profiles are shown in inner coordinates, for both the
${\it\beta}=1$
(CD) and
${\it\beta}=10.6$
(WD2) cases. Given the high value of
${\it\Omega}$
, the logarithmic region might be expected not to be altered by the pulsating flow and therefore its virtual origin to be displaced by a constant amount for each phase
${\it\phi}$
. This conjecture is based on the unproven assumption that current and oscillating flows decouple for large enough values of
$y/{\it\delta}$
, and the collected data corroborate the above idea for the profiles outside the wall layer (
$y^{+}>40$
). The magnitude of the shift is obviously phase- and
${\it\beta}$
-dependent, as clearly shown in figure 3. The reverse flow region in the range of the cycle
${\rm\pi}\leqslant {\it\phi}\leqslant (7/4){\rm\pi}$
is evident for both values of
${\it\beta}$
, and looking at the curvature of the velocity profiles therein it can be anticipated that large turbulent kinetic energy production will occur during the oscillating period due to the high local values of the shear (see also § 3.2).
Figure 3. Radial distributions of the phase-averaged streamwise velocity in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
; ——, mean value; - - - -, phase-averaged values. In this and the following figures, the profiles at different phases
${\it\Phi}$
are shifted upward by a suitable fixed amount in each panel.
In MVV it has been shown that, in the CD regime, the long time-averaged turbulence intensities did not appreciably differ from the corresponding ones in the ST case. Conversely, in the WD2 case, while the cross-stream components undergo substantial reductions, the streamwise one appears to be enhanced in magnitude for
$y^{+}<80$
and reduced elsewhere.
Figures 4(a) and 4(b) show the radial distributions of the phase-averaged modulation of the streamwise turbulence intensity normalized with the time-averaged wall friction velocity, for the
${\it\beta}=1$
and
${\it\beta}=10.6$
cases respectively. In both cases the perturbation can be viewed as a wave generated next to the wall at the beginning of the decelerating phase (
${\it\phi}\simeq {\rm\pi}/2$
) and propagating in the bulk with a penetration length of approximately 40 wall units. During this inward propagation the disturbance undergoes an amplification, and it reaches its maximum at
$y^{+}\simeq 8$
(respectively
$y^{+}\simeq 7$
) for the
${\it\beta}=1$
(respectively
${\it\beta}=10.6$
) case at the same phase
${\it\phi}\simeq 5{\rm\pi}/4$
, with a subsequent decay, independent of the
${\it\beta}$
value. The lifetime of the described phenomenon, that is, the time needed by the disturbance to span those 40 wall units from its birth until its death, is larger than the oscillating period but smaller than twice this value in both the wave- and current-dominated regimes. With obvious approximation associated with the identification of those beginning and ending phases, it can be stated that the above-described lifetime is approximately
$7{\rm\pi}/2$
, independent of the
${\it\beta}$
value. Therefore, during the cycle two peaks are observed, one from the newly generated amplifying wave and the other from the preceding decaying perturbation. Figure 4 also shows that the CD case is characterized by a perturbation of reduced intensity compared with the WD2 one.
Figure 4. Radial distributions of the phase-averaged streamwise turbulence intensity modulation in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
Figure 5. Radial distributions of the phase-averaged cross-stream turbulence intensity modulation in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
Using a single space–time constant value as the reference velocity scale (results not shown), the modulation of the streamwise turbulence intensity in the WD2 case remains larger than the corresponding CD one.
Figures 5 and 6 depict the phase-averaged modulation of the radial and azimuthal turbulence intensity across the pipe radius, using an identical scaling to that in figure 4. As for the streamwise component, the WD2 regime shows larger modulation of both stresses, which again behave as travelling waves, disappearing within 40 wall units. While the azimuthal component is characterized by the presence of the two peaks during the cycle for both
${\it\beta}$
values, such a peculiarity has not been detected for the radial component. In the wave-dominated regime, the largest positive modulation of the radial (respectively azimuthal) component occurs at
${\it\phi}={\rm\pi}$
(respectively
${\it\phi}=3{\rm\pi}/4$
), while the largest negative one is located at
${\it\phi}=0$
(respectively
${\it\phi}={\rm\pi}$
). In the CD regime, figures 4(a)–6(a), taken collectively, indicate that the in-cycle modulations are remarkably large while the long time-averaged diagonal components of the Reynolds stresses are not significantly affected by the time-varying forcing (see figure 8 of MVV). On comparing figures 4(b)–6(b) it turns out that, close to the wall, positive modulations of the streamwise component of the turbulent intensity are accompanied by negative modulations of the other two components, in the decelerating phase. Likewise, negative modulations of the
$\sqrt{u^{\prime }u^{\prime }}$
correspond to positive ones of both
$\sqrt{v^{\prime }v^{\prime }}$
and
$\sqrt{w^{\prime }w^{\prime }}$
, during the accelerating phase,
$0\leqslant {\it\phi}\leqslant {\rm\pi}/2$
. Therefore, it follows that while in the decelerating phase an enhanced turbulence anisotropy close to the wall is observed, in the accelerating phase a tendency to recover a more isotropic turbulence character occurs. The genesis of this return and departure from the anisotropy has to be investigated in terms of energy generation and distribution mechanisms. This entails the inspection of both the turbulent kinetic energy production and the pressure–strain role modulation, which will be addressed later on.
Figure 6. Radial distributions of the phase-averaged azimuthal turbulence intensity modulation in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
The use of a single space–time constant value as the reference velocity scale (results not shown) indicates that the modulation of both radial and azimuthal turbulence intensities in the wave-dominated case is smaller than the corresponding modulation in the CD one.
The radial profiles of the turbulent shear stress modulation, in inner coordinates, are characterized by a dynamics similar to the normal components of the Reynolds stress tensor, with the phase variations in the
${\it\beta}=1$
case significantly smaller than those at
${\it\beta}=10.6$
. A close inspection of the data of figure 7(a,b) reveals the presence of a time-varying disturbance propagating in the radial direction with a double peak, for both the CD and WD2 cases. The radial extent of the interaction region is slightly larger than those of the normal Reynolds stress components and roughly equal to 50 wall units. In the very first 10 wall units, the turbulent shear stress modulation appears to be positive for
${\rm\pi}/2\leqslant {\it\phi}\leqslant 5{\rm\pi}/4$
and negative in the remaining part of the cycle. This phenomenon is important for the comprehension of the temporal variation of the turbulent production term in the
$\langle u^{\prime }u^{\prime }\rangle$
budget, addressed later in § 3.2.
Figure 7. Radial distributions of the phase-averaged turbulent shear stress modulation in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
Figure 8. Radial distributions of the phase-averaged
$\langle Q_{4}/Q_{2}\rangle$
ratio in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
Considering a single space–time constant value as the reference velocity scale (results not shown), the modulation of the turbulent shear stress in the WD2 case remains slightly larger than the corresponding CD one.
Returning now to the modulation of the turbulent shear stress and recalling the relevance of the negative values of the
$\langle u^{\prime }v^{\prime }\rangle$
correlation with respect to the energy-producing events, we present in figure 8(a,b) the radial profiles of the phase-averaged ratio between the fourth (sweep) and second (ejection) quadrant events, for the current- and wave-dominated cases respectively. The sign of the radial component has been changed, in order to use the customary terminology to refer to ejections as events pertaining to the second quadrant, and sweeps to the fourth one.
Focusing on the
${\it\beta}=1$
data, figure 8(a) shows a persistent dominance of the ejection events (second quadrant) away from the wall and of the sweep events close to the wall (fourth quadrant,
$y^{+}\leqslant 15$
), in the whole period. Conversely, in the wave-dominated case (
${\it\beta}=10.6$
) the fourth and second quadrant events are always comparable, for
$y^{+}\leqslant 10$
, and the peak appearing in the buffer layer should be interpreted as the consequence of the near-wall reduction of the fourth quadrant events. Moreover, the temporal modulation of the
$\langle Q_{4}/Q_{2}\rangle$
ratio sheds light on the prevailing role of the ejections over the sweeps, in the near-wall region, just after the maximum acceleration instant (
$0\leqslant {\it\phi}\leqslant {\rm\pi}/4$
). This is possibly the effect of an alteration of the splatting mechanism associated with lumps of fluid converging rapidly towards the wall which are expected to enhance the turbulence components parallel to the wall. This enhancement is usually explained in terms of an energy transfer from the radial component to the axial and azimuthal ones (Moin & Kim Reference Moin and Kim1981).
Figure 9. Space–time diagrams of the streamwise turbulence intensities (a) and (c) and the turbulent shear stresses (b) and (d), in inner coordinates: (a) and (b)
${\it\beta}=1$
; (c) and (d)
${\it\beta}=10.6$
.
On the basis of this alteration, it is therefore reasonable to expect that the amount of turbulent energy transferred from the radial to the streamwise and azimuthal components, through pressure–strain interaction, will reduce for
$0\leqslant {\it\phi}\leqslant {\rm\pi}/4$
, in the wall region. The analysis of the modulation of the pressure–strain term in the turbulent kinetic energy budgets, postponed to the § 3.2, supports this hypothesis.
The characteristics of the above-mentioned travelling wave are better understood in a space–time diagram, like those given in figure 9, in which the streamwise turbulence intensities and the turbulent shear stresses, in inner coordinates, are represented, for the
${\it\beta}=1$
and
${\it\beta}=10.6$
cases. These figures report instantaneous realizations, lasting two periods, averaged in the homogeneous
$z{-}{\it\theta}$
directions, and therefore they are not exactly periodic over the selected time span. Concentrating on the contour level corresponding to the maximum value in figure 9(a,c), it is readily inferred that the perturbation is most intense in the region
$10\leqslant y^{+}\leqslant 20$
(respectively
$7\leqslant y^{+}\leqslant 14$
) in the
${\it\beta}=1$
(respectively
${\it\beta}=10.6$
) case. As far as the turbulent shear stress is concerned, figure 9(b,d) shows that the region of most intense activity is similar in extension although shifted further away from the wall (
$25\leqslant y^{+}\leqslant 50$
).
It is worth noting that both the streamwise turbulence intensity and the turbulent shear stress show fluctuations with frequencies larger than the fundamental, the energy content of which increases with
${\it\beta}$
. This is particularly evident in the wall region across the Stokes layer (
$3\leqslant y^{+}\leqslant 10$
). To investigate this matter quantitatively, in figure 10 we present the radial distributions of the amplitudes of the first three modes computed by Fourier transforming the signals of the streamwise turbulence intensity and turbulent shear stress. In the
${\it\beta}=1$
case the energy content of the first mode is substantially larger than the sum of the energies of the other two modes, especially for the turbulent shear stress. On the other hand, in the
${\it\beta}=10.6$
case the contribution to the total energy of the second and third harmonics is far from being negligible, especially for the streamwise turbulence intensity close to the wall. Therefore, any phase-locked analysis employing one single mode, whatever procedure is adopted to define it, has to be considered with caution in the wave-dominated regime.
Figure 10. Radial distributions, in inner coordinates of the amplitudes of the first three modes, of the streamwise turbulence intensities (a) and (c) and the turbulent shear stresses (b) and (d): (a) and (b)
${\it\beta}=1$
; (c) and (d)
${\it\beta}=10.6$
.
The results presented in figures 4–7, taken collectively, support the idea that in the very high frequency regime the amplitude of the pulsation has a definite effect on the Reynolds stresses. They are differently affected by the unsteady mean shear according to an energy redistribution mechanism among the several components, which will be analysed later on. In order to further elaborate on this energy distribution, in figure 11 the phase-averaged analysis of the anisotropy index
$AI$
, as introduced in MVV, is presented. Denoting by
$\langle II_{b}\rangle$
the second invariant of the phase-averaged Reynolds stress tensor,
$$\begin{eqnarray}\langle II_{b}\rangle =-\frac{1}{2}\left(\frac{\langle u_{i}^{\prime }u_{j}^{\prime }\rangle }{\langle {q^{\prime }}^{2}\rangle }-\frac{{\it\delta}_{ij}}{3}\right)\left(\frac{\langle u_{j}^{\prime }u_{i}^{\prime }\rangle }{\langle {q^{\prime }}^{2}\rangle }-\frac{{\it\delta}_{ji}}{3}\right),\end{eqnarray}$$
with
$(u_{1},u_{2},u_{3})=(u,v,w)$
and
$\langle {q^{\prime }}^{2}\rangle =\langle {u_{1}^{\prime }}^{2}+{u_{2}^{\prime }}^{2}+{u_{3}^{\prime }}^{2}\rangle$
, the anisotropy index is now defined as
$\langle AI\rangle =\langle II_{b}\rangle /\langle II_{1D}\rangle$
, with
$\langle II_{1D}\rangle =-(1/3)$
the value of the second invariant in one-component turbulence. It should be recalled that the closeness to unity of the
$AI$
is a measure of the one-dimensionality of the turbulence; likewise, an isotropic state corresponds to
$AI=0$
. The largest variations about the time mean occur in the
${\it\beta}=1$
case, and they are confined within the first 10 wall units. This is more clearly appreciated through the instantaneous
$AI$
contour maps presented in figure 12, from which the presence of large-
$AI$
space–time gradients close to the wall is observed. There is a marked tendency towards higher
$AI$
values during the decelerating phase (
${\rm\pi}/2\leqslant {\it\phi}\leqslant 3{\rm\pi}/2$
) close to the wall. This trend is also observed in the
${\it\beta}=10.6$
case, although the variations about the mean are generally smaller. It is worth noting that for
${\it\beta}=10.6$
the
$AI$
remains much larger than the corresponding values of the
${\it\beta}=1$
case. This behaviour is consistent with the modulation of the streamwise turbulence intensity associated with the previously discussed wave dynamics of the perturbation. The above results undoubtedly show that the net effect of the unsteady forcing is a clear tendency towards a more anisotropic behaviour of the turbulence in the wall layer, with a reduction of the cross-stream fluctuating components, during the decelerating phase. The cycle-averaged drag (respectively anisotropy) reduces (respectively increases) in the sense discussed in MVV. In Touber & Leschziner (Reference Touber and Leschziner2012) the net effect of their unsteadiness is an enhanced isotropy with an amplification of the spanwise fluctuations, which, through a streak modification mechanism, induces a drag reduction. There is no contradiction between the results of the two studies dealing with similar flows although forced along different directions.
Figure 11. Radial distributions of the anisotropy index
$AI$
in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
; ——, mean value; - - - -, phase-averaged values.
Figure 12. Space–time diagram of the anisotropy index
$\langle AI\rangle$
, in inner coordinates. (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
In order to characterize the structures of the wall layer and to identify those eddies that are most effective in draining energy from the mean flow, we show (figures 13
a–15
a) the phase- and plane-averaged (
$z{-}{\it\theta}$
) vorticity fluctuations for the
${\it\beta}=1$
case. The corresponding plane-averaged shaded contour plots, collected over two oscillating periods, are reported in figures 16(a)–18(a). The largest phase variations are visible in the buffer layer (
$y^{+}\sim 15$
) for all components. In this region all components show a tendency towards values exceeding the mean in the near-maximum decelerating instant (
$(3/4){\rm\pi}<{\it\Phi}<(5/4){\rm\pi}$
) and vice versa in the near-maximum accelerating instant (
$(7/4){\rm\pi}<{\it\Phi}<{\rm\pi}/4$
). Within a single oscillating cycle, these perturbations are seen to be generated twice, with a dynamics that is quite similar for all components. The analysis of the profiles of figures 16(a)–18(a) shows that the largest variations occur for the azimuthal component, while the streamwise component deviates least from the mean profiles. This is possibly a consequence of the effects of the gradient production term in the equation of the square vorticity fluctuations, which is only present in the azimuthal component (Tennekes & Lumley Reference Tennekes and Lumley1972). The perturbation originating at the wall with a frequency equal to the external driving force propagates in the wall-normal direction within the oscillating period. Figures 13(b)–15(b) and 16(b)–18(b) are the counterparts of the previous ones but in the wave-dominated regime (
${\it\beta}=10.6$
). Unlike the CD case (
${\it\beta}=1$
), here the phase–time dynamics of the vorticity fluctuations appears to be more involved. Not only is the amplitude of the variations with respect to the mean larger but also the footprint of the perturbation is different, in both size and shape, in the shaded contour plots. More interestingly, and differently from the CD case, higher modes appear in the wall region despite the identical applied forcing. Their frequency generation is seen to be twice the forcing value for all components. It is worth mentioning that, unlike the radial vorticity (
${\it\omega}_{r}$
) which is zero at the wall (figure 14), the axial and azimuthal components produce disturbances directly at the wall (figures 13 and 15), and the radial penetration of the disturbance is again approximately 40 wall units, just as for the normal Reynolds stresses. Figures 16(b) and 17(b) show that the streamwise and radial disturbance propagation patterns are approximately similar in the interaction region outside the Stokes layer (
$y^{+}>5$
). The azimuthal component (see figure 18
b) is characterized by a different temporal evolution within the Stokes layer and outside it. While in the former the disturbance propagation appears to be very large, in the latter it reduces appreciably.
Figure 13. Radial distributions of the streamwise vorticity fluctuation intensities in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
; ——, mean value; - - - -, phase-averaged values.
Figure 14. Radial distributions of the radial vorticity fluctuation intensities in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
; ——, mean value; - - - -, phase-averaged values.
Figure 15. Radial distributions of the azimuthal vorticity fluctuation intensities in inner coordinates: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
; ——, mean value; - - - -, phase-averaged values.
3.2. Budgets
In this section we present the phase-averaged transport equation for all normal stresses which, following the nomenclature of MVV, reads
$$\begin{eqnarray}\left\langle I\right\rangle =\left\langle P\right\rangle +\left\langle T\right\rangle +\left\langle {\it\Pi}\right\rangle +\left\langle D\right\rangle -\langle {\it\epsilon}\rangle .\end{eqnarray}$$
In (3.2) the terms
$\langle P\rangle$
,
$\langle T\rangle$
,
$\langle {\it\Pi}\rangle$
,
$\langle D\rangle$
,
$-\langle {\it\epsilon}\rangle$
and
$\langle I\rangle$
indicate the production, the turbulent transport, the velocity–pressure gradient, the viscous diffusion, the dissipation and the inertia terms respectively. Obviously
$\overline{\langle I\rangle }=0$
. They are as follows:
$$\begin{eqnarray}\displaystyle \underbrace{\left\langle \frac{\partial u^{\prime }u^{\prime }}{\partial t}\right\rangle }_{\langle I\rangle } & = & \displaystyle \underbrace{-2\langle u^{\prime }v^{\prime }\rangle \frac{\text{d}\langle u\rangle }{\text{d}r}}_{\langle P\rangle }\underbrace{-\frac{1}{r}\left\langle \frac{\partial \left(r{u^{\prime }}^{2}v^{\prime }\right)}{\partial r}\right\rangle }_{\langle T\rangle }\underbrace{+2\left\langle p^{\prime }\frac{\partial u^{\prime }}{\partial z}\right\rangle }_{\langle {\it\Pi}\rangle }\nonumber\\ \displaystyle & & \displaystyle \underbrace{+\frac{1}{\mathit{Re}}\frac{1}{r}\frac{\partial }{\partial r}\left(\!r\frac{\partial \langle {u^{\prime }}^{2}\rangle }{\partial r}\!\right)}_{\langle D\rangle }\underbrace{-\frac{2}{\mathit{Re}}\left[\left\langle \!\left(\frac{\partial u^{\prime }}{\partial z}\!\right)^{2}\right\rangle +\left\langle \!\left(\frac{\partial u^{\prime }}{\partial r}\!\right)^{2}\right\rangle +\left\langle \frac{1}{r^{2}}\left(\frac{\partial u^{\prime }}{\partial {\it\theta}}\right)^{2}\right\rangle \!\right]}_{\langle -{\it\epsilon}\rangle },\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \underbrace{\left\langle \frac{\partial v^{\prime }v^{\prime }}{\partial t}\right\rangle }_{\langle I\rangle } & = & \displaystyle \underbrace{-\frac{1}{r}\frac{\partial \left(r\langle {v^{\prime }}^{2}v^{\prime }\rangle \right)}{\partial r}+\frac{2}{r}\langle v^{\prime }{w^{\prime }}^{2}\rangle }_{\langle T\rangle }\underbrace{-2\left\langle v^{\prime }\frac{\partial p^{\prime }}{\partial r}\right\rangle }_{\langle {\it\Pi}\rangle }\nonumber\\ \displaystyle & & \displaystyle \underbrace{+\frac{1}{\mathit{Re}}\left[\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial \langle {v^{\prime }}^{2}\rangle }{\partial r}\right)+\frac{2}{r^{2}}\left(\langle {w^{\prime }}^{2}\rangle -\langle {v^{\prime }}^{2}\rangle \right)\right]}_{\langle D\rangle }\nonumber\\ \displaystyle & & \displaystyle \underbrace{-\frac{2}{\mathit{Re}}\left[\left\langle \left(\frac{\partial v^{\prime }}{\partial z}\right)^{2}\right\rangle +\left\langle \left(\frac{\partial v^{\prime }}{\partial r}\right)^{2}\right\rangle +\left\langle \frac{1}{r^{2}}\left(\frac{\partial v^{\prime }}{\partial {\it\theta}}-w^{\prime }\right)^{2}\right\rangle \right]}_{\langle -{\it\epsilon}\rangle },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \underbrace{\left\langle \frac{\partial w^{\prime }w^{\prime }}{\partial t}\right\rangle }_{\langle I\rangle } & = & \displaystyle \underbrace{-\frac{1}{r}\frac{\partial \left(r\langle v^{\prime }{w^{\prime }}^{2}\rangle \right)}{\partial r}-\frac{2}{r}\langle v^{\prime }{w^{\prime }}^{2}\rangle }_{\langle T\rangle }\underbrace{-\frac{2}{r}\left\langle p^{\prime }\frac{\partial w^{\prime }}{\partial {\it\theta}}\right\rangle }_{\langle {\it\Pi}\rangle }\nonumber\\ \displaystyle & & \displaystyle \underbrace{+\frac{1}{\mathit{Re}}\left[\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial \langle {w^{\prime }}^{2}\rangle }{\partial r}\right)-\frac{2}{r^{2}}\left(\langle {w^{\prime }}^{2}\rangle -\langle {v^{\prime }}^{2}\rangle \right)\right]}_{\langle D\rangle }\nonumber\\ \displaystyle & & \displaystyle \underbrace{-\frac{2}{\mathit{Re}}\left[\left\langle \left(\frac{\partial w^{\prime }}{\partial z}\right)^{2}\right\rangle +\left\langle \left(\frac{\partial w^{\prime }}{\partial r}\right)^{2}\right\rangle +\left\langle \frac{1}{r^{2}}\left(\frac{\partial w^{\prime }}{\partial {\it\theta}}+v^{\prime }\right)^{2}\right\rangle \right]}_{\langle -{\it\epsilon}\rangle }.\end{eqnarray}$$
We begin the analysis by focusing on the production term
$\langle P\rangle$
of the streamwise component of the CD case, which is seen to be strongly modulated by the unsteady forcing in both amplitude and peak position (figure 19). This is not surprising since the unsteady forcing changes the radial profile of
$\langle u\rangle$
, the
$r$
-derivative of which enters directly in the production term. It should be recalled, however, that the corresponding cycle-averaged production shows no significant differences compared with the steady flow distribution (see figure 14 of MVV). Thus, in this respect, the phase-dependent modulations of both
$u^{\prime }v^{\prime }$
and
$\text{d}u/\text{d}r$
do not appreciably alter the time-averaged production term. A small negative production corresponding to a sink of energy is observed in the phase range
${\rm\pi}<{\it\phi}<7{\rm\pi}/4$
and for
$y^{+}<7$
; this evidences the occurrence of kinetic energy transfer from the small scales to the larger ones (Tsinober Reference Tsinober2001). Although it is most marked for the production term, this in-cycle variation characterizes all the terms of the budget. Noticeably, the modulation of the time rate of change of the streamwise turbulent energy
$\langle I\rangle$
is in general agreement with the one of the production; the latter term attains its maximum at
${\it\phi}={\rm\pi}$
at
$y^{+}\sim 9$
with a value (
$\simeq 0.78$
) that is more than three times larger that the maximum of the time-averaged distribution (MVV). Likewise, the viscous diffusion shows a negative peak that closely follows that of the positive production.
Figure 16. Root mean square of the streamwise vorticity (
${\it\omega}_{z}$
) in the
${\it\Phi}{-}y^{+}$
plane: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
Figure 17. The same as figure 16 but for
${\it\omega}_{r}$
.
Figure 18. The same as figure 16 but for
${\it\omega}_{{\it\theta}}$
.
Figure 19. Phase-averaged streamwise velocity fluctuation energy budget:
${\it\beta}=1$
.
In the wave-dominated regime (WD2 case of figure 20) the phase modulation of all terms appears to be more pronounced. The general trend of all terms is similar to the one previously discussed for the
${\it\beta}=1$
case. Again, the maximum production occurs at
${\it\phi}={\rm\pi}$
at
$y^{+}\sim 7$
with a value of 2.8, which represents the triple of the maximum of the time-averaged distribution (MVV). Unlike the CD case, negative values of the production are seen to occur at all times for
$y^{+}<15$
in small pockets. Once more, the phase variations of the inertial term of the streamwise turbulent energy and the viscous diffusion are significant. Incidentally, let us recall that large values of inertia terms imply large temporal changes of the streamwise turbulent energy. The phase modulation of the dissipation appears to be more pronounced in comparison to the
${\it\beta}=1$
case and the maximum values occur in the region
$3<y^{+}<10$
. The peak negative value of
${\it\epsilon}$
occurs at
${\it\phi}=3{\rm\pi}/4$
and its value is 1.54 times larger than the time-averaged maximum (MVV).
Figure 20. Phase-averaged streamwise velocity fluctuation energy budget:
${\it\beta}=10.6$
.
Figure 21. Phase-averaged radial distribution of production terms:
${\it\beta}=1$
.
To investigate the interaction between the large-amplitude unsteady forcing and the shear stress modulation in the rapid oscillation regime, we decompose the phase-averaged production term as
$$\begin{eqnarray}\langle P\rangle =\underbrace{-2\overline{u^{\prime }v^{\prime }}\frac{\text{d}\overline{u}}{\text{d}r}}_{\langle P_{cc}\rangle }\;\;\underbrace{-2\overline{u^{\prime }v^{\prime }}\frac{\text{d}\widetilde{u}}{\text{d}r}}_{\langle P_{co}\rangle }\;\;\underbrace{-2\widetilde{u^{\prime }v^{\prime }}\frac{\text{d}\overline{u}}{\text{d}r}}_{\langle P_{oc}\rangle }\;\;\underbrace{-2\widetilde{u^{\prime }v^{\prime }}\frac{\text{d}\widetilde{u}}{\text{d}r}}_{\langle P_{oo}\rangle },\end{eqnarray}$$
which follows from the definition of
$\langle P\rangle$
after using the decomposition
$\langle \cdot \rangle =\overline{\cdot }+\widetilde{\cdot }$
. A similar splitting of the production term has been employed to study the drag reduction phenomenon resulting from the application an oscillatory spanwise wall motion to a fully developed channel (Touber & Leschziner Reference Touber and Leschziner2012) and to a space-developing boundary layer (Skote Reference Skote2013). In the above equation the direct term
$\langle P_{cc}\rangle$
(respectively
$\langle P_{oo}\rangle$
) represents the rate at which the mean (respectively modulating) Reynolds stress does deformation work against the mean (respectively modulating) shear. Likewise, the cross-term
$\langle P_{co}\rangle$
(respectively
$\langle P_{oc}\rangle$
) represents the rate at which the mean (respectively modulating) Reynolds stress does deformation work against the modulating (respectively mean) shear. The long-time average of
$\langle P_{cc}\rangle$
and
$\langle P_{oo}\rangle$
coincides with the terms
$P_{c}$
and
$P_{o}$
, introduced on p. 69 of MVV; that is, they also contribute to the cycle-averaged intensity, while the
$\langle P_{co}\rangle$
and
$\langle P_{oc}\rangle$
terms do not. Moreover, in the very-near-wall region, an order of magnitude analysis trivially suggests that both
$\langle P_{co}\rangle$
and
$\langle P_{oo}\rangle$
in the
${\it\beta}=10.6$
case are nearly one order of magnitude larger than the corresponding ones in the CD regime.
The above splitting of the phase-averaged production term is shown in figures 21 and 22 for both current- and wave-dominated cases. In the CD regime, figure 21 indicates that the positive (source)
$\langle P_{cc}\rangle$
term overwhelms the other ones, in the whole oscillating period. Moreover, the
$\langle P_{oo}\rangle$
contribution constantly acts as a source, although only in the region close to the wall (
$y^{+}\leqslant 20$
). In contrast,
$\langle P_{co}\rangle$
and
$\langle P_{oc}\rangle$
exhibit sign changes. In more detail, in the negative acceleration time interval they are positive, thus leading to the already mentioned large peak production values. Conversely, during the acceleration phase, i.e.
$7{\rm\pi}/4<{\it\phi}<{\rm\pi}/4$
, negative contributions of
$\langle P_{co}\rangle$
and
$\langle P_{oc}\rangle$
are encountered in the wall region. These negative contributions are accompanied by a similar variation of the
$\langle I\rangle$
term (see figure 19).
Figure 22. Phase-averaged radial distribution of production terms:
${\it\beta}=10.6$
.
In the
${\it\beta}=10.6$
case, figure 22 shows that
$\langle P_{oo}\rangle$
is always the leading term and, although it is generally positive, small regions with negative values are observed. The
$\langle P_{cc}\rangle$
term is always positive but, unlike the
${\it\beta}=1$
case, it is not the dominant contribution. The terms
$\langle P_{co}\rangle$
and
$\langle P_{oc}\rangle$
are characterized by a sign change during the oscillating period. Unlike the CD case, close to the wall the contribution of the
$\langle P_{co}\rangle$
term is similar in magnitude to the
$\langle P_{oo}\rangle$
term, although with an opposite sign for
$7{\rm\pi}/4<{\it\phi}<{\rm\pi}/2$
. In the decelerating phase,
$3{\rm\pi}/4<{\it\phi}<5{\rm\pi}/4$
, and for
$y^{+}<10$
all terms behave as energy sources, leading to the already mentioned peak value far exceeding the corresponding maximum value of the
${\it\beta}=1$
case. Because of the strong modulation of
$\widetilde{u^{\prime }v^{\prime }}$
and
$\text{d}\widetilde{u}/\text{d}r$
within the cycle, the comparison between the CD and WD2 cases in terms of the local
$\langle P_{oo}\rangle$
values is difficult to carry out. Such a comparison can be performed in an integral sense, evaluating the ratio of their volume averages and analysing its phase variation. This kind of analysis (results not shown herein) indicates that the volume average of
$\langle P_{oo}\rangle$
in the
${\it\beta}=10.6$
case exceeds the corresponding CD value by a factor ranging between 14 and 27.
In the wave-dominated regime, the above results, taken collectively, put into evidence the strong phase modulation of the turbulence intensity production term, characterized by regions of positive (source) and negative (sink) values.
This wavy shape of the production term has been documented to stem from the modulation of the shear
$\text{d}\widetilde{u}/\text{d}r$
and of the turbulent shear stress
$\widetilde{u^{\prime }v^{\prime }}$
. The penetration depth of the overall production, i.e.
$y^{+}<40$
, is therefore determined by the radial extent below which the above quantities are appreciable. They could be inferred either from the streamwise velocity profile amplitude reported in figure 12(a) of MVV (converting the
$y/{\it\delta}\sim 12$
value in wall units), for
$\text{d}\widetilde{u}/\text{d}r$
, or from figure 7, for
$\widetilde{u^{\prime }v^{\prime }}$
.
The effect of the modulation of the production term in the period is felt directly by the streamwise normal stress through a concordant inertia term and indirectly by the radial and the azimuthal ones via pressure–strain interaction, as will be documented later on. On account of the magnitude and complexity of this turbulence modulation within the cycle and the insensitivity of the oscillating component of the velocity profile, which has determined the modulation, it can be safely stated that the flow is one-way coupled, not only in a time-averaged but also in a phase-locked averaged sense. Therefore, the energy transfer from the streamwise to the other two components, regulated by the pressure–strain term, will be affected to a great extent by this time-varying phenomenon.
Figure 23, reporting the wall-normal turbulence budget, shows that the phase modulation of all terms is small and independent of
${\it\beta}$
. For both current- and wave-dominated regimes, the largest variations pertain to the inertia and velocity–pressure gradient terms.
Figure 23. Phase-averaged radial velocity fluctuation energy budget: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
The azimuthal turbulence budgets are shown in figure 24. Unlike the wall-normal component, all terms appearing in the budget present appreciable phase variations in the first 20 wall units. This is most evident for the velocity–pressure gradient (essentially a positive term), which is mainly balanced by the dissipation and inertia terms. Comparing the magnitudes of the modulations of the individual terms appearing in the budget of the three components, in the wave-dominated regime, it can be easily inferred that the energy transfer mechanism from the streamwise to the azimuthal and wall-normal components is not effective in both a cycle-averaged and an instantaneous sense.
Figure 24. Phase-averaged azimuthal velocity fluctuation energy budget: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
Incidentally, let us observe that the flow problem analysed in Touber & Leschziner (Reference Touber and Leschziner2012), although somewhat different from the present one, shows a similar alteration of the wall layer structure as a result of the application of a harmonically time-varying wall motion. The latter makes an additional production term appear in the Reynolds stress budget (
${\it\theta}$
component), which is responsible for a turbulence generation process in the spanwise direction (orthogonal to the mean flow) leading to a drag reduction. This phenomenon is attributed to a distortion and deflection of the near-wall streaks, a mechanism that ultimately leads to a complete destruction of the turbulence-generating events. In the present study the unsteady forcing causes additional production terms in the streamwise turbulent fluctuation budget. This term leads to an increased anisotropy in the present study and to an increased isotropy in Touber & Leschziner (Reference Touber and Leschziner2012). In order to investigate the temporal modulation of the energy transfer among the three components, we split the phase-averaged velocity–pressure gradient term into the pressure–strain
$\langle {\it\Phi}\rangle$
and pressure diffusion
$\langle {\it\Psi}\rangle$
terms,
$$\begin{eqnarray}\displaystyle & \displaystyle \langle {\it\Pi}_{u^{\prime }u^{\prime }}\rangle =\langle {\it\Phi}_{zz}\rangle +\langle {\it\Psi}_{zz}\rangle =2\left\langle p^{\prime }\frac{\partial u^{\prime }}{\partial z}\right\rangle +0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \langle {\it\Pi}_{v^{\prime }v^{\prime }}\rangle =\langle {\it\Phi}_{rr}\rangle +\langle {\it\Psi}_{rr}\rangle =2\left\langle p^{\prime }\frac{\partial v^{\prime }}{\partial r}\right\rangle -2\left\langle \frac{\partial \left(p^{\prime }v^{\prime }\right)}{\partial r}\right\rangle , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \langle {\it\Pi}_{w^{\prime }w^{\prime }}\rangle =\langle {\it\Phi}_{{\it\theta}{\it\theta}}\rangle +\langle {\it\Psi}_{{\it\theta}{\it\theta}}\rangle =\frac{2}{r}\left\langle p^{\prime }\left(\frac{\partial w^{\prime }}{\partial {\it\theta}}+v^{\prime }\right)\right\rangle -2\left\langle \frac{p^{\prime }v^{\prime }}{r}\right\rangle , & \displaystyle\end{eqnarray}$$
$\langle {u^{\prime }}^{2}\rangle$
,
$\langle {v^{\prime }}^{2}\rangle$
and
$\langle {w^{\prime }}^{2}\rangle$
budgets respectively.
The phase variation of the pressure–strain distribution is shown in figure 25 for the
${\it\beta}=1$
and
${\it\beta}=10.6$
cases. Following the notation of Hinze (Reference Hinze1975), a negative (positive) value of a term denotes a loss (gain) of energy; for example, a negative
$\langle {\it\Phi}_{zz}\rangle$
implies energy transfer from the streamwise to the other components.
Figure 25. Phase-averaged radial distribution of pressure–strain terms: (a)
${\it\beta}=1$
; (b)
${\it\beta}=10.6$
.
In the
${\it\beta}=1$
case, the harmonic forcing induces an appreciable temporal modulation of all pressure–strain terms, in the first 20 wall units, which however leaves the general shape of the curves unchanged. A noticeable exception is the
$\langle {\it\Phi}_{zz}\rangle$
term which, for
$3{\rm\pi}/4<{\it\phi}<0$
, is characterized by the presence of positive values close to the wall. While negative values of
$\langle {\it\Phi}_{zz}\rangle$
indicate transfer of energy from the streamwise to the other two components, positive values are usually associated with the well-known splatting phenomenon (Moin & Kim Reference Moin and Kim1981). However, inspection of figure 8(a) indicates that the above mentioned positive
$\langle {\it\Phi}_{zz}\rangle$
are poorly correlated with the corresponding
$\langle Q_{4}/Q_{2}\rangle$
ratio. This is in agreement with results presented in figure 18(a) of MVV, which shows that the time-averaged distributions of all
$\langle {\it\Phi}_{zz}\rangle$
,
$\langle {\it\Phi}_{rr}\rangle$
and
$\langle {\it\Phi}_{{\it\theta}{\it\theta}}\rangle$
do not differ appreciably from the corresponding steady ones. In the wave-dominated regime the situation is far more involved. The energy transfer from the radial to the other two components (splatting effect), represented by the negative
$\langle {\it\Phi}_{rr}\rangle$
contribution, appears to be less effective for
$0<{\it\phi}<{\rm\pi}/4$
. Such a behaviour agrees with the already documented reduction, in the near-wall region, of the sweeps over the ejections at the end of the accelerating phase (see figure 8
b). In the buffer layer and for
$3{\rm\pi}/4<{\it\phi}<3{\rm\pi}/2$
, the already documented higher production values are accompanied by positive (respectively negative) peaks of
$\langle {\it\Phi}_{zz}\rangle$
(respectively
$\langle {\it\Phi}_{rr}\rangle$
). Recalling that positive values of
$\langle {\it\Phi}_{zz}\rangle$
entail a lack of energy transfer to the other two components, this behaviour explains the modulation of the anisotropy reported in figure 12(b) in terms of the anisotropy index for the Reynolds stress.
4. Conclusions
This paper has presented the phase-averaged analysis of a data set coming from direct numerical simulations of pulsating pipe flow in the high-frequency regime (
${\it\Omega}=53$
). Among all the cases presented in MVV only the CD and WD2 cases (see figure 2) have been analysed in detail since the others are either statistically steady (ST) or turned out to be the superposition of laminar Poiseuille and Stokes flows (WD1). While the study of MVV has investigated the effects of the amplitude of the harmonic forcing on the cycle-averaged flow features, here the attention is focused on the changes within the cycle.
The phase-averaged streamwise velocity profiles showed that the logarithmic region was not altered by the magnitude of the pulsation, and preserved its shape within the period. Indeed, its virtual origin was simply displaced by a constant amount for each phase within the cycle despite the massive reverse flow region occurring at the beginning of the flow reversal phase.
The analysis of the phase-averaged modulation of the streamwise turbulence intensity revealed that, in both regimes, the temporal modulation of the radial profiles appears like a travelling wave originating underneath the Stokes layer and damped within 40 wall units from the wall. The lifetime of this wave phenomenon is seen to be larger than the oscillation period and smaller than twice this value. The amplitude of such a modulation in the wave-dominated regime has been shown to be larger than the one in the CD case, whatever the normalization adopted (inner or outer scaling). The phase-averaged modulation of the radial and azimuthal turbulence intensities, along with the turbulent shear stress, also behaves like a travelling wave with similar features to those of the streamwise component, with an amplitude that reduces on moving from the current- to the wave-dominated regime, in either inner or outer representation. The data analysis in the CD regime indicates that the phase-averaged Reynolds stress tensor is appreciably influenced by the pulsation, in the whole period, although the long time-averaged data reported in MVV were very similar to the steady values. This supports the conclusion that the CD flow is uncoupled in a long time-averaged sense, and one-way coupled in a phase-averaged sense. In the wave-dominated regime, positive modulations of the streamwise component are associated with negative modulation of the other two components in the decelerating phase, and vice versa in the accelerating phase. Thus, an enhanced (respectively reduced) turbulence anisotropy close to the wall is observed to occur in the decelerating (respectively accelerating) phase, as clearly evident from the anisotropy index based on the second invariant of the phase-averaged Reynolds stress tensor. A close inspection of the cycle modulation of the Reynolds stress tensor revealed that, especially in the wave-dominated regime, the energy content of the second and third harmonics of the Fourier transformed signal is far from being negligible. Therefore, phase-averaged analysis of the turbulence intensities employing one single mode, regardless its specific definition, has to be considered with caution. The phase-averaged data quadrant analysis of the fluctuating velocity components suggested that, in the wave-dominated regime, sweep and ejection events are nearly comparable for
$y^{+}<10$
at all times. Moreover, at the end of the accelerating phase, the data reveal the prevailing role of the ejections over the sweeps in the near-wall region.
In the wave-dominated regime, the analysis of the streamwise normal stress budget indicates that the highly modulated turbulence production term is characterized by regions of positive and negative values. This wavy shape of the production term has been documented to chiefly depend upon the rate at which the modulating Reynolds stress does deformation work against the modulating shear, resulting in a large inertia term. Furthermore, the remarkable modulation occurring during the oscillation is felt only indirectly by the radial and azimuthal normal stresses via pressure–strain interaction, which has been shown not to be effective during part of the cycle, causing an increased turbulence anisotropy. The analysis of the phase-averaged pressure–strain terms revealed that in the wave-dominated regime the large-amplitude forcing determines an alteration of the splatting mechanism close to the wall, at the end of the accelerating phase. This agrees well with the already mentioned prevailing role of the ejections over the sweeps.
Acknowledgements
This work has been developed within the F.A.R.O. project, funded by Polo delle Scienze e delle Tecnologie of Università degli Studi di Napoli ‘Federico II’. Mr R. Moreschi provided valuable technical support when processing the large-scale DNS database through optical storage devices on the quad-core workstation.
