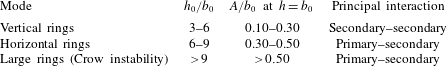1 Introduction
We study the approach of a vortex pair to a wall, in the case where the vortices are perturbed by a long-wavelength instability. The instability takes the form of a sinusoidal perturbation along the span of the vortices. This causes some regions of the vortex to encounter the wall before other regions, leading to dramatic changes in the vortex topology and the generation of many small-scale coherent structures. While we specifically examine vortices subject to the long-wave instability, the results we present are relevant to many flows in which vortices experience small perturbations close to a boundary, such as vortex rings approaching a boundary obliquely or initially two-dimensional vortices approaching a wavy wall, among other examples.
The study of vortex–wall interactions has relevance to many practical flows in both fundamental fluid mechanics and practical engineering applications. The presence of coherent vortical structures is vital to the energy cascade in turbulent flows, as is discussed extensively in the reviews of Cantwell (Reference Cantwell1981), Robinson (Reference Robinson1991) and Panton (Reference Panton2001). Furthermore, a vortex whose axis is parallel to a bounding wall generates a boundary layer at the surface. As fluid is pushed between the vortex and the wall, this boundary layer is subject to an adverse pressure gradient and can separate, rolling up into a secondary vortex, as shown by Harvey & Perry (Reference Harvey and Perry1971). The presence of the secondary vortex can lead to distinctly complex dynamics. In fact, experiments have demonstrated that structures resembling vortex rings can exist in the boundary layer and evolve into much more complex vortical structures (Chu & Falco Reference Chu and Falco1988).
The most well-known application of such a flow is the vortex wake generated by an aircraft, which is the subject of an extensive review by Spalart (Reference Spalart1998). All wings generating lift produce a sheet of streamwise vorticity in their wake which ultimately rolls up into a strong counter-rotating vortex pair, although the near-wake can comprise other vortex configurations. This trailing vortex phenomenon is particularly important in the context of airport operations, where many large aircraft operate in close proximity to each other and to the ground. Small aircraft following heavy transport-class aircraft for takeoff and final approach are subject to uncommanded rolling moments induced by the rotation of these trailing vortices, which can, in some cases, pose a significant hazard. The need to avoid such situations leads to constraints on runway and airport capacity.
In some cases, vortices near boundaries are used to modify aircraft performance rather than pose a hazard. Vortex generators are positioned on aircraft wings in order to adjust their stall behaviour by manipulating the turbulent boundary layer, thereby delaying separation. Beyond aviation, the interaction of vorticity with surfaces is relevant to any situation in which streamwise vorticity is generated near solid bodies. The flow around submersible vehicles and their appendages and control surfaces is one such application, and research into methods of accelerating the destruction of the vortex wake in order to enhance stealth has been conducted (Quackenbush, Bilanin & McKillip Reference Quackenbush, Bilanin, McKillip and Robert Crowe1996).
Counter-rotating and co-rotating vortex pairs are subject to several instabilities, which have recently been reviewed by Leweke, LeDizès & Williamson (Reference Leweke, LeDizès and Williamson2016). There have been a considerable number of studies of such flows due to their practical aerodynamic applications. The well-known Crow instability (Crow Reference Crow1970) is often observed behind real aircraft due to the presence of condensation trails at high altitudes. This phenomenon causes a pair of initially straight vortex tubes to become sinusoidally displaced in an axisymmetric fashion with a wavelength several times that of the vortex spacing (see figure 1 a) and eventually to undergo a reconnection process. Ultimately, a periodic series of vortex rings is formed. Reconnection has been studied computationally by a number of authors, including Melander (Reference Melander1988), Melander & Hussain (Reference Melander and Hussain1988) and Shelley, Meiron & Orszag (Reference Shelley, Meiron and Orszag1993), analysed by Saffman (Reference Saffman1989) and reviewed by Kida & Takaoka (Reference Kida and Takaoka1994). The Crow instability has also been observed in experiments performed in the laboratory (Leweke & Williamson Reference Leweke and Williamson2011), as shown in figure 1(a). Experimental studies show remarkable similarity to full-scale aircraft wakes observed in the atmosphere, despite several orders of magnitude difference in Reynolds number. In this work, we observe significant changes in vortex topology upon interaction of the Crow instability with a solid surface; however, the extent to which these changes exist at higher Reynolds numbers is presently unknown.
Figure 1. The principal instabilities associated with a counter-rotating vortex pair. (a) Long-wave Crow instability. (b) Short-wave elliptic instability (Leweke & Williamson Reference Leweke and Williamson2011). (It should be noted that the images are not to the same scale.)
Crow’s instability theory was later extended to unequal-strength vortex pairs, which were also shown to be unstable for any ratio of vortex circulations (Klein, Majda & Damodaran Reference Klein, Majda and Damodaran1995). This situation commonly arises when real aircraft deploy flaps during takeoff or landing and has been studied numerically by Crouch (Reference Crouch1997). Crouch models the vortex wake as a system of two vortex pairs: for each wing, one vortex is generated by the wingtip and one by the flap. This vortex system exhibits both long-wavelength and short-wavelength instabilities which are dependent on the vortex spacing and core size and the circulation ratio between the vortices in each pair. This scenario has also been examined experimentally by Ortega, Bristol & Savaş (Reference Ortega, Bristol and Savaş2003), where a wing equipped with adjustable flaps was towed in a towing tank. The flaps could be configured in a variety of ways to produce vortices of different strengths relative to vortices generated at the wingtip. Several scenarios emerge: in one case, the flap vortex deforms into a series of
$\unicode[STIX]{x1D6FA}$
-shaped loops. Ultimately, these loops can reconnect with part of the tip vortex, yielding a series of vortex rings.
In addition to the long-wavelength Crow instability, counter-rotating vortex pairs are also subject to an instability of shorter wavelength. Widnall, Bliss & Tsai (Reference Widnall, Bliss and Tsai1974) found that perturbations of a more complex structure can cause deformations within the vortex core to grow. This growth occurs when the rotation rate of the plane containing the perturbation caused by its self-induced motion and those effects induced by the presence of the other vortex becomes zero. Subsequently, the perturbation is amplified by the strain rate field of the other vortex. This instability is often referred to as an elliptic instability, since two-dimensional flows with elliptic streamlines become unstable in the presence of three-dimensional perturbations, as demonstrated by Bayly (Reference Bayly1986), Pierrehumbert (Reference Pierrehumbert1986) and Waleffe (Reference Waleffe1990). This instability was observed experimentally in the case of vortex pairs by Leweke & Williamson (Reference Leweke and Williamson1998), as shown in figure 1(b), who also discovered that the instability develops with a distinct anti-phase relationship between the two vortices.
In the present work, we consider the approach of a counter-rotating vortex pair to a wall. Line vortex pairs were investigated by Lamb (Reference Lamb1932), where he calculated that the vortices would move away from each other along hyperbolic trajectories as they approach a wall. Dee & Nicholas (Reference Dee and Nicholas1968) measured the actual trajectories of aircraft wake vortices and observed that they appeared to rebound away from the surface instead of continuing on an ideal hyperbolic trajectory. This effect was explained by Harvey & Perry (Reference Harvey and Perry1971) and further analysed by Peace & Riley (Reference Peace and Riley1983). The rebound of the primary vortices is a consequence of the generation of secondary vorticity at the wall. A vortex approaching a wall creates a boundary layer between itself and the wall that is subject to an adverse pressure gradient. The vorticity contained in the boundary layer then separates and rolls up into a discrete secondary vortex of the opposite sign, which then induces an upward velocity on the primary vortices, significantly changing their trajectories.
These secondary vortices are themselves subject to an instability of the Crow type in which the entire vortex tube is displaced. This instability was simulated by Luton & Ragab (Reference Luton and Ragab1997), where they observed the weaker secondary vortex to become wrapped around the stronger primary vortex and concluded that the instability was of the elliptic type. Other research groups including Moet (Reference Moet2003), Georges et al. (Reference Georges, Geuzaine, Duponcheel, Bricteux, Lonfils and Winckelmans2006) and Duponcheel et al. (Reference Duponcheel, Cottin, Daeninck, Leweke and Winckelmans2007) reached the same conclusion. Experimental evidence of the existence of this secondary vortex instability was provided by Harris & Williamson (Reference Harris and Williamson2012), where they observed bending of the entire secondary vortex tube. Comparison of the measured instability wavelength with that predicted from stability theory indicates that, at low Reynolds number, a displacement-type instability mode is principally responsible for the vortex dynamics rather than a higher-order elliptic instability, although it is possible that an elliptic instability might become dominant at early times at higher Reynolds number, as discussed in Williamson et al. (Reference Williamson, Leweke, Asselin and Harris2014) and Leweke et al. (Reference Leweke, LeDizès and Williamson2016).
The formation of secondary vorticity can have a significant influence on the later evolution of the primary vorticity. The rebound effect and the above instabilities are the most obvious initial phenomena to be found in this flow. In fact, this effect can occur more than once, as demonstrated through computations by Orlandi (Reference Orlandi1990), who showed that the secondary vorticity can be advected around the primary vortex for more than one revolution. Kramer, Clercx & van Heijst (Reference Kramer, Clercx and van Heijst2007) studied the interaction of a vortex dipole with a wall and demonstrated that multiple eruptions of secondary vorticity from the wall can occur, which strongly influence the trajectory of the primary vortex pair. A similar effect has also been observed for the collision of a vortex ring with a wall, in which multiple secondary rings are generated and then ejected from the wall (Walker et al. Reference Walker, Smith, Cerra and Doligalski1987), in some cases forming loop-like structures. The wavy instability of the secondary vortex ring was also observed numerically by Swearingen, Crouch & Handler (Reference Swearingen, Crouch and Handler1995). Further studies of vortex rings in wall effect were conducted by Lim (Reference Lim1989), in which the collision was oblique, meaning that the ring trajectory was not normal to the boundary. Rather than expanding in an axisymmetric fashion, as is the case for a normal (perpendicular) collision with the wall, the ring experienced significant axial flow away from the region of first contact with the wall (i.e. the location where secondary vorticity is first generated). Ultimately, one observes a secondary vortex loop lifting up away from the wall. This structure contains many features that bear a remarkable resemblance to the present experiments involving counter-rotating vortex pairs subject to the long-wave instability in wall effect.
The experiment conducted by Lim (Reference Lim1989), in which an oblique collision of a vortex ring with a wall was studied, was also simulated by Verzicco & Orlandi (Reference Verzicco and Orlandi1994). In their simulation, a similar ejection of a secondary vortex structure was observed, which they explained as a consequence of the interaction of vortex stretching and viscous annihilation. The part of the ring interacting with the wall first experiences a high rate of stretching, which leads to a local intensification of vorticity and the generation of secondary vorticity at small scales. The secondary vorticity annihilates the primary vortex through viscous vorticity cancellation. Ultimately, enough vorticity is cancelled in this region to produce a locally high pressure relative to the rest of the ring. Fluid is then advected by this pressure gradient to the part of the ring furthest from the wall, where it coalesces into a loop-like structure.
The manipulation of secondary vorticity might also serve as a practical method for accelerating the decay of the primary vortices. From our own experiments, we see that a rapid decrease in circulation occurs upon wall interaction. Stephan, Holzäpfel & Misaka (Reference Stephan, Holzäpfel and Misaka2013) have simulated the approach of a counter-rotating vortex pair to a wall containing a large rectangular obstacle. The obstacle is positioned such that it transects both descending vortices. Secondary vorticity is produced there first and then forms an
$\unicode[STIX]{x1D6FA}$
-shaped loop. Simultaneously, the circulation of the primary vortices decreases dramatically as a result of the primary–secondary interaction. Other researchers have sought to engineer the vortex wake to keep the trailing vortices in a region of high strain (Rennich & Lele Reference Rennich and Lele1999). For example, if the wake trailing an aircraft equipped with flaps is modelled with four vortices, two shed from the wingtips and two from the flaps, the inboard flap vortices could be kept in the strain field of the wingtip vortices by adjusting their relative strengths. If this is achieved, a Crow-type instability can grow very rapidly. The strain field of these perturbed vortices then induces a similar displacement-type perturbation on the stronger wingtip vortices, leading to accelerated destruction of the vortex wake. Analysis by Fabre & Jacquin (Reference Fabre and Jacquin2000) shows that the growth rate can be much larger than that of the Crow instability alone. Crouch (Reference Crouch2005) also describes several schemes involving purposeful oscillations in the lift distribution that can be used to accelerate vortex decay. The lift oscillations cause perturbations in the spatial position of the trailing vortices which cause them to approach each other. If the frequency of the lift oscillations is properly selected to excite a long-wave instability, then the vortices will pinch off into a series of vortex rings. Measurements indicate that this configuration poses much less risk to aircraft at closer following distances (Crouch Reference Crouch2005).
Figure 2. Schematic showing the approach of a vortex pair subject to the Crow instability to a wall. The Crow instability causes an initially straight vortex pair to develop a sinusoidal waviness with distinct ‘peak’ and ‘trough’ regions in a plane inclined at approximately
$45^{\circ }$
to the horizontal.
The present study specifically examines the interaction of a counter-rotating vortex pair subject to the Crow instability with a wall. The vortex pair is displaced from its initial position and develops distinct ‘peak’ and ‘trough’ regions (see figure 2) before it encounters a solid boundary. We present experimental methods in § 2, followed by § 3, which provides overviews of two fundamental flows, namely the Crow instability and the interaction of a two-dimensional vortex with a wall. These fundamental base flows are later compared with the behaviour of a counter-rotating vortex pair in the presence of a wall. In § 4, we present the topological changes produced when the vortices subject to the Crow instability encounter a solid boundary. These changes include the reorganization of the vorticity into a series of smaller rings which then rebound from the surface. The presence of these rings is observed from flow visualization experiments and confirmed by particle image velocimetry measurements. In § 5, we present quantitative measurements of parameters describing the evolution of the vortices as they interact with the wall. These measurements include the trajectories followed by the vortices, the amplitude and angular orientation of the instability, and the circulation as a function of time at several axial positions along the vortex. Axial flow along each vortex tube is an important feature of the phenomena we describe, and we discuss evidence for the presence of this flow and describe its driving mechanisms. Importantly, the phenomena we observe are not limited to the flow studied, and, in § 6, we discuss other flows involving perturbed vortices close to a wall which develop structures similar to those associated with the long-wave instability in wall effect. Conclusions follow in § 7.
2 Experimental details
Experiments were conducted at Cornell University’s Fluid Dynamics Research Laboratories using a vortex generator facility. This facility was originally constructed by Leweke, as described in Leweke & Williamson (Reference Leweke and Williamson1998), and has since been modified to improve the reliability and repeatability of the experiments. The facility consists of a rectangular glass water tank of dimensions
$180~\text{cm}\times 45~\text{cm}\times 60~\text{cm}$
. A schematic of the facility is shown in figure 3. A horizontal pair of aluminium flaps, which are hinged to a rectangular base and driven by a stepper motor, is lowered into the water using a separate system of lead screws and stepper motors. The flaps are 170 cm long, so that they extend to almost the entire length of the water tank. In order to ensure repeatability of the experiment, the Crow instability is triggered by including a very small (1 mm amplitude) sinusoidal perturbation on the lower edges of the flaps (see also Leweke & Williamson Reference Leweke and Williamson2011). The perturbation causes the peaks and troughs of the instability to develop in the same spanwise locations during each experiment, allowing the accurate placement of light sheets and cameras for investigation of flow features. In addition, the facility includes a horizontal transparent acrylic ground plane whose vertical position and angle can be adjusted using manual lead screws. The vortex pair encounters this horizontal wall during its descent in the tank. In each experiment, care was taken to ensure that the vortex generation process was unaffected by the presence of the wall. We determined the minimum height above the ground plane at which this is true, and all experiments were begun above this height.
Figure 3. Schematic of the vortex generator facility.
$S$
is the distance separating the bases of the flaps,
$B$
is the length of the flaps, and
$\unicode[STIX]{x1D703}$
is the angle of flap rotation, measured from the vertical.
Figure 4. (a) The motion profile used for closing the flaps, based on that developed by Leweke & Williamson (Reference Leweke and Williamson2011):
$\unicode[STIX]{x1D703}$
, the angle of flap rotation from the vertical, is shown as a function of time
$t$
. (b) A least-squares best fit of the superposition of two Gaussian vortices to the measured azimuthal velocity profile,
$v_{\unicode[STIX]{x1D703}}$
.
The counter-rotating vortex pair is formed by closing the flaps (shown in figure 3) underwater. Fluid is forced out through the gap between the flaps as they are closed, and the shear layers generated roll up into a vortex pair. The profile used to define the motion of the edges of the flaps was defined empirically by Leweke & Williamson (Reference Leweke and Williamson2011) in order to produce laminar vortex pairs and is shown in figure 4(a). Helpfully, the vortex pairs produced by this facility are well modelled by a superposition of two Lamb–Oseen (Gaussian) vortices, as shown in figure 4(b). The azimuthal velocity profile for a Lamb–Oseen vortex is given by
$$\begin{eqnarray}v_{\unicode[STIX]{x1D703}}(r)=\frac{\unicode[STIX]{x1D6E4}}{2\unicode[STIX]{x03C0}r}\left[1-\exp \left(-\frac{r^{2}}{a^{2}}\right)\right],\end{eqnarray}$$
where
$\unicode[STIX]{x1D6E4}$
is the vortex circulation,
$r$
is the distance measured from the vortex centre and
$a$
is a parameter characterizing the vortex core size.
This flow was investigated using several techniques, including both fluorescent dye visualization and particle image velocimetry (PIV). For flow visualization, a mixture of fluorescein dye and water is painted onto the flaps prior to running the experiment. This dye then marks the primary vorticity that is generated by the flaps. Illumination, which could be either of the entire flow or of a particular cross-section, is provided by a 5 W Coherent Innova 70 argon-ion laser. In addition, the secondary vorticity generated at the wall can also be visualized by first pooling a fluorescein dye mixture on the ground plane, as discussed in Harris & Williamson (Reference Harris and Williamson2012). A similar technique was used by Lim (Reference Lim1989) for his vortex ring studies. This technique is particularly powerful in that it allows selective visualization of either the primary or secondary vortices or both. Images of the flow visualization experiments are acquired by computer-controlled digital single lens reflex (DSLR) cameras at a rate of 1 Hz.
For PIV measurements, the tank was seeded with particles (Potters’ Industries Sphericel 110P8, mean diameter
$10~\unicode[STIX]{x03BC}\text{m}$
and density
$1.10~\text{g}~\text{cm}^{-3}$
) prior to running the experiment. Illumination of various cross-sections was again supplied by a 5 W argon-ion laser which was used with a cylindrical lens to create a 3 mm thick light sheet. Images were acquired by a Kodak MegaPlus 1 megapixel digital camera at a rate of 15 Hz. Pairs of images were then processed by PIVLab software (Thielicke Reference Thielicke2014; Thielicke & Stamhuis Reference Thielicke and Stamhuis2014a
,Reference Thielicke and Stamhuis
b
) in order to compute the velocity fields. A typical velocity field measures 800 by 500 pixels and contains approximately 100 by 60 velocity measurements, spaced approximately 1.5 mm apart. For orientation, figure 5 shows the various cross-sections used for PIV measurements and flow visualizations in this study. They will be referred to repeatedly in subsequent sections.
Figure 5. Schematic showing the various planes in which light sheets were positioned for PIV experiments.
Velocity fields obtained from PIV experiments were then further processed to obtain other parameters of interest. Vortex position was measured by tracking the point of maximum vorticity over time. Other parameters, such as the angular orientation of the plane containing the instability and the amplitude of the instability, could then be derived. Circulation was computed by taking the line integral of the velocity field around a contour representing 5 % of the maximum measured vorticity.
As the Crow instability produces a vortex pair with defined ‘peak’ and ‘trough’ locations (figure 2), PIV and flow visualization experiments were conducted at both of these cross-sections. Figure 6(a) shows the position of the light sheet relative to the vortex pair for each of these configurations. In addition, some experiments were conducted with light sheets positioned at the peak and the trough simultaneously, making use of a beam splitter. These dual-light-sheet experiments were previously used by Leweke & Williamson (Reference Leweke and Williamson2011), and greatly simplified the task of tracking the relative positions of the two cross-sections. In particular, these dual-light-sheet experiments are especially helpful for determining the amplitude of the instability, as both the peak and the trough cross-sections are made visible simultaneously. The amplitude can then be computed by simply noting their relative positions in the photographs. Figure 6(b) shows an example flow visualization image obtained in this way.
Figure 6. The measurement technique used to determine the instability amplitude and the angle of the plane containing the instability. (a) Position of dual light sheets at the peak and trough. (b) An example image acquired using the dual-light-sheet technique, showing both peak and trough cross-sections. (c) Schematic illustrating the relevant geometrical parameters, where
$A$
is the amplitude,
$b$
is the vortex separation and
$\unicode[STIX]{x1D703}$
is the angle of the plane containing the instability.
The time for each experiment is measured from the first motion of the flaps and is non-dimensionalized by the time required for the vortex pair to descend a distance equal to one initial vortex spacing. Therefore, the non-dimensional time
$t^{\ast }$
is given by
$$\begin{eqnarray}t^{\ast }=t\frac{\unicode[STIX]{x1D6E4}_{0}}{2\unicode[STIX]{x03C0}b_{0}^{2}},\end{eqnarray}$$
where
$t$
is the dimensional time,
$\unicode[STIX]{x1D6E4}_{0}$
is the initial vortex circulation and
$b_{0}$
is the initial vortex spacing.
Other parameters of interest in these experiments include the Reynolds number based on circulation,
$Re=\unicode[STIX]{x1D6E4}_{0}/\unicode[STIX]{x1D708}$
, where
$\unicode[STIX]{x1D6E4}_{0}$
is the initial circulation and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of water. The ratio of initial core size to initial vortex spacing,
$a_{0}/b_{0}$
, is also relevant. In all experiments presented in this study,
$Re\approx 1000$
and
$a_{0}/b_{0}\approx 0.4$
. The initial height
$h_{0}$
of the flap edges above the ground plane was the principal variable parameter, and experiments were conducted for values of
$h_{0}/b_{0}$
ranging from 3 to 12. In addition, the extent to which the Crow instability has developed was characterized by measuring the amplitude of the instability,
$A$
, at a height of
$b_{0}$
above the wall. Using this parameter, experiments were conducted for
$A/b_{0}$
between 0.10 and 0.60.
In order to characterize the uncertainty associated with measurements of circulation and other quantities, multiple experiments with the same initial conditions were conducted. The 95 % confidence interval for the value of
$\unicode[STIX]{x1D6E4}$
when the vortex pair is not in wall effect (
$t^{\ast }\approx 3$
) is
$\pm 2.8\,\%$
. In wall effect, at
$t^{\ast }\approx 8$
, the uncertainty for
$\unicode[STIX]{x1D6E4}$
is
$\pm 4.4\,\%$
. The variation in initial vortex spacing
$b_{0}$
is
$\pm 4.4\,\%$
, and the variation in vortex core size
$a_{0}$
is
$\pm 3.5\,\%$
. For the amplitude of the instability, the uncertainty out of wall effect (
$t^{\ast }\approx 3$
) is
$\pm 6.2\,\%$
, and it is
$\pm 6.6\,\%$
in wall effect (
$t^{\ast }\approx 8$
).
3 Two base studies in vortex dynamics
Before discussing the effects of wall interaction on the development of a long-wave instability, it is important to appreciate the key features of two fundamental scenarios. First, we study the free development of the Crow instability in the absence of a wall. Second, we examine the interaction of 2D straight vortices with a boundary.
We present a visual overview of the developing Crow instability in figure 7, in the manner of Leweke & Williamson (Reference Leweke and Williamson2011). The initially straight vortex tubes are displaced from their original positions. This displacement occurs when the rotation rate of the plane containing a perturbation is zero. This condition is met for perturbations located in a plane oriented at approximately
$48^{\circ }$
–
$50^{\circ }$
to the horizontal. As shown by Crow (Reference Crow1970), in order to achieve instability, three rotational effects are balanced in this plane: rotation of a vortex due to self-induction, rotation due to the mean strain field of the other vortex and rotation due to the perturbation strain field of the other vortex. In this ‘frozen’ plane orientation, the strain induced by the other vortex causes the perturbation amplitude to grow exponentially.
Figure 7. Development of the Crow instability, seen in plan view: (a)
$t^{\ast }=2.96$
; (b)
$t^{\ast }=6.52$
; (c)
$t^{\ast }=7.70$
; (d)
$t^{\ast }=11.0$
. The vortex pair is moving towards the observer.
As the wavy vortices approach each other at the trough cross-section, vorticity cancellation occurs, leading to a decrease in circulation and an increase in pressure at this location. The pressure gradient established by this process drives flow in the axial direction from the troughs to the peaks of the wavy vortex tube, as shown in figure 7. (Evidence for this pressure gradient in the case of wall interaction is shown in § 5.2.) Reconnection occurs between the two vortices at the troughs (Leweke & Williamson Reference Leweke and Williamson2011), leaving a periodic series of vortex rings linked by weak bridges, as shown in figure 7(c). These bridges of vorticity retain only approximately 10 % of their original circulation.
We show in figure 8 the circulation measured at the peak and trough cross-sections for the Crow instability using the technique described in § 2. The circulation at the peak remains relatively constant throughout the evolution of the instability, showing only minor and gradual decay due to diffusion. The circulation at the trough cross-section, however, decreases rapidly as the two vortices are forced into close proximity in this region. These data will be contrasted with measurements for the same experiment conducted with a ground plane installed in § 5.
Figure 8. Circulation of a vortex pair subject to the unbounded Crow instability, measured at the peak and trough cross-sections as a function of time.
As a second basic flow with which comparisons can be made, we consider the case of a two-dimensional counter-rotating vortex pair interacting with a solid boundary. For these experiments, we ensure that the vortex pair remains two-dimensional for a reasonable time by using flaps with straight edges. Combined with the low Reynolds number for the flow and a small
$h_{0}/b_{0}\approx 4$
, the vortices remain observably free of instabilities prior to reaching the wall. In this flow, the generation of secondary vorticity at the boundary is critically important to the evolution of the pair. According to Lamb (Reference Lamb1932), a point vortex pair approaching a free-slip wall should follow a hyperbolic trajectory, as discussed in § 1. When the no-slip condition is imposed at the wall, however, a boundary layer forms between the primary vortex and the wall, and begins to separate, rolling up into secondary vortices of the opposite sign, as shown in figure 9(a). Although weaker than the primary vortices, this secondary vorticity is able to modify the motion of the primary vortices significantly. This effect was first explained by Harvey & Perry (Reference Harvey and Perry1971) and further analysed by Peace & Riley (Reference Peace and Riley1983). The primary vortices rebound from the wall and often follow an epicyclic trajectory. Figure 9(b) shows the ideal hyperbolic vortex trajectories (solid lines) and the actual vortex trajectory measured from flow visualization images (symbols). Similar trajectories are shown in Kramer et al. (Reference Kramer, Clercx and van Heijst2007).
Figure 9. (a) Flow visualization from the transverse plane (see figure 5) of two-dimensional (straight) vortices interacting with the wall, showing the development of the secondary vorticity (Harris & Williamson Reference Harris and Williamson2012). (b) Comparison of the measured trajectories of the two primary vortices with the ideal hyperbolic trajectories predicted by Lamb (Reference Lamb1932).
Measurements of circulation for the two-dimensional vortex–wall interaction are presented in figure 10 and compared with numerical simulations for a two-dimensional vortex pair evolving without the presence of the wall (Gupta Reference Gupta2003). Without the wall interaction, the circulation decays slowly and gradually due to viscous diffusion. However, in the case with a wall present, the primary circulation decays rapidly as the secondary vortices begin to strengthen at
$t^{\ast }=4$
. Eventually, the circulations of both the primary and secondary vortices become comparable for
$t^{\ast }>16$
. This dramatic reduction of the primary vortex strength as the primary and secondary vortices are ‘pushed together’ is responsible for many of the changes in vortex topology we observe in cases involving a perturbed vortex in the presence of a wall.
Figure 10. Measured circulation of two-dimensional vortices in wall effect as a function of time, compared with a numerical simulation of the circulation for two-dimensional vortices out of ground effect (Gupta Reference Gupta2003). Also shown is the circulation of the secondary vorticity which develops as the primary pair encounters the wall. It should be noted that the sign of the secondary circulation has been inverted.
4 Modes of vortex pair dynamics interacting with a wall
In this section, we discuss the results of three-dimensional experiments in which a counter-rotating vortex pair, subject to a long-wave instability, encounters a solid boundary. It might be expected that a critical height would exist, above which the Crow instability would have sufficient time to cause reconnection of the primary vortices into vortex rings before interaction with the wall boundary. A series of vortex rings would then encounter the boundary. Below this critical height, we might suspect that the development of the Crow instability would be inhibited by the wall because the two vortices are pulled apart by the wall interaction. In this case, various final vortex configurations are produced, depending on the extent to which the instability has been allowed to develop before wall interaction. Specifically, we have identified three distinct modes, which may be delineated by the initial height
$h_{0}/b_{0}$
above the ground at which the vortices are generated, where
$h_{0}$
is the initial height and
$b_{0}$
is the initial vortex spacing. These modes may also be distinguished by the amplitude of the Crow instability measured at a distance
$b_{0}$
above the wall. This parameter serves as a gauge of the degree of progression of the Crow instability before wall interaction.
4.1 Vertical rings mode: secondary–secondary vortex interaction
For
$h_{0}/b_{0}$
between 3 and 6 (
$A/b_{0}$
between 0.1 and 0.3, measured at
$b_{0}$
above the wall), the vortices evolve as shown in figures 11 and 12, which present the primary and secondary vorticity respectively from both plan and side views. At these low initial heights, the Crow instability is inhibited as the vortex pair approaches the wall, and the vortices do not reconnect into rings. Instead, from examination of the primary vorticity, the principal feature is a strong axial flow, driven by a pressure gradient, which transfers fluid from the region of first contact, the trough, to the peak of the vortex tube, as shown in figure 11(a–h). This ‘collapsed vortex’, visible in figure 11(c), then rebounds away from the wall. ‘Vortex collapse’ is defined as the loss of spanwise uniformity as a result of axial pressure gradients and axial flows, which transport vorticity to concentrated regions along the vortex. The reason for the rebound of the collapsed region is the formation of small vertical vortex rings at the locations of the ‘collapsed vortices’, as discussed below. The final configuration of the primary vortices, seen in figure 11(d), comprises two regions of concentrated vorticity per instability wavelength and is markedly different from the rings associated with the Crow instability in unbounded fluid.
Figure 11. Visualization of the primary vorticity associated with the vertical rings mode (
$h_{0}/b_{0}=5$
). Panels (a–d) show a plan view, in which the vortices are moving towards the observer. Panels (e–h) show a side view, with images taken at the same time as those in (a–d). In (a,e), (b,f), (c,g) and (d,h), the images depict
$t^{\ast }=5.68$
, 7.78, 9.57 and 12.0 respectively.
The mechanism by which this configuration is produced can be discerned through examination of the evolution of the secondary vorticity. The small difference in height between the peak and the trough of the primary vortex means that the trough encounters the wall and generates secondary vorticity there first. The secondary vortex, shown in figure 12(a), then rolls up and separates from the wall, forming a ‘tongue’ that wraps around the primary vortex. The secondary vortex tongue (see figure 12 a) and other parts of the rolled up secondary vortex are transported to the peak, where distinct secondary vortex loops (marked T1 and T2) are formed (see figure 12 d,h). Simultaneously, the primary vortex circulation at the trough is weakened by viscous vorticity cancellation. This effect creates a region of higher pressure at the trough, as shown later, which drives fluid towards the peak, where the circulation is higher and the pressure is lower.
The tops T1 and T2 of the secondary vortex loops rotate by self-induction into a vertical orientation, as is apparent in figure 12(h). The loops from each side of the flow then move towards each other by self-induction and interact along the centreplane of the primary vortex system, as shown in figure 12(d,h). They then expand rapidly in a vertical plane, as shown in figure 13, in which side views of the primary vorticity (a) and secondary vorticity (b) are shown at a later time in their evolution. The vertical vortex loops are principally composed of the secondary vorticity in figure 13(b), although they are more faintly visible in the primary visualization in (a) due to diffusion of the dye into the secondary vorticity.
Figure 13. (a) Late-time development of the primary vorticity for the vertical rings mode (
$h_{0}/b_{0}=5$
), shown from the side. (b) Development of the secondary vorticity for the vertical rings mode, taken at the same time as (a).
We show in figure 14 a schematic depicting our interpretation of the principal vortex dynamics involved in this wall interaction. In (a), the secondary vortex is generated first at the trough location and then becomes wrapped around the primary vortex, forming a ‘tongue’ of vorticity. As the primary vortex is weakened by viscous vorticity cancellation, the pressure at the trough becomes higher, driving fluid towards the peaks of the primary vortex. Measurements of these effects are presented later. The result of this axial flow is the formation of a vortex loop from the secondary vorticity at the peak cross-section, as shown in (b). At this stage, the direction of rotation of the secondary vortex loops at T1 and T2 is such that they induce themselves to move upward away from the wall and then towards the centreline dividing the primary vortices, as depicted in (c). Reconnection of the secondary vorticity at the bottom of the loop to form a ring appears to occur and is visible in the flow visualization of figure 13(a). Further evidence suggesting reconnection from PIV measurements is discussed below.
Figure 14. Schematic showing the authors’ interpretation of the principal vortex dynamics in the vertical rings mode (
$h_{0}/b_{0}=5$
).
The sequence by which vertical vortex loops (in figures 13 and 14) rebound from the wall differs from the traditional two-dimensional rebound effect in several important ways. Figure 15 shows vorticity contours taken from PIV measurements made using the transverse cross-section plane (see figure 5) superposed with streamlines. Panels (a–d) show a two-dimensional vortex pair in ground effect, while panels (e–h) show a vortex pair subject to the Crow instability in ground effect. In the two-dimensional flow, the secondary vortices orbit the primaries and eventually return to the vicinity of the ground plane between the primary vortices, as shown in figure 15(a–d). The flow streamlines advect the secondary vortices down between the primaries. In contrast, when the flow has become three-dimensional by the action of the Crow instability, the secondary vorticity is induced upwards above the primary vortices, with no tendency to get pulled down between the primary vortex pair, as shown in (e–h). This is also indicated by the streamlines which, in contrast to the 2D case, are aligned upwards at the locations of the secondary vortices, taking the secondary vorticity away from the wall. The principal vortex interactions are between the secondary vortices. This ‘secondary–secondary’ interaction is indicated by the labelling in figure 15(h), which shows a vortex pair in cross-section, representing a cut into the top of the vertical vortex loops described earlier. Evidence suggesting that reconnection has occurred at the bottom of the loop to form a ring is visible in figure 15(h). There, two patches of vorticity, distinct from the primary vortices, are visible at the bottom of the PIV image. We suggest that these patches represent the bottom of each vortex ring.
Figure 15. Contours of vorticity and streamlines for a two-dimensional vortex pair interacting with a wall (a–d) and a vortex pair subject to the Crow instability interacting with a wall in the vertical rings mode (e–h). In (a,e), (b,f), (c,g) and (d,h), the images depict the vorticity at times
$t^{\ast }=2.74$
, 5.93, 8.31 and 11.1 respectively.
In order to confirm the presence of a vortex loop, additional experiments were conducted using a light sheet positioned in the horizontal plane (see figure 5). Figure 16 shows vorticity contours derived from PIV and flow visualization from the same cross-section. Two ‘vortex pairs’, representing the vertical arms of the vortex loops, are visible in this view. Furthermore, the circulation of the vortex pair measured in this plane is comparable to that measured for the secondary vortices in the transverse plane (approximately 20 % of the initial circulation of the primary vortex). As the cross-sections depicted in figures 15 and 16 are orthogonal and both depict vortex pairs, we have reasonable evidence that a vertical vortex ring has formed.
Figure 16. Contours of vorticity (a) and corresponding flow visualization (b) image taken in the horizontal plane (see figure 5), cutting through the legs of the vertical vortex loops. The position of the light sheet is shown in (c).
4.2 Horizontal rings mode: secondary–primary vortex interaction
For values of
$h_{0}/b_{0}$
between 6 and 9 (
$A/b_{0}$
between 0.3 and 0.5, measured at
$b_{0}$
above the wall), the behaviour of the vortex pair is distinctly different. Figure 17 shows the evolution of the primary vorticity in plan view. Immediately apparent here is the stronger axial flow from the trough to the peak. The trough cross-sections become almost entirely evacuated of dye, and later measurements of circulation show that they are weakened much more than for vortex pairs generated at lower values of
$h_{0}/b_{0}$
in § 4.1. The weakening of the trough cross-section is caused by two effects. First, the Crow instability has developed further and has consequently moved the vortices closer together at the trough, leading to more vorticity cancellation between the two primary vortices. This effect is visible in figure 17(b,c). Second, the primary vortices are further eroded by interaction with the secondary vorticity that is generated at the wall. The reduced circulation in the trough produces a higher pressure which drives the stronger axial flow from trough to peak. The Crow instability remains inhibited, and the wall interaction produces two ‘collapsed vortex’ structures per instability wavelength instead of forming a single vortex ring. These structures are labelled in (d).
Figure 17. Visualization of the primary vorticity associated with the horizontal rings mode (
$h_{0}/b_{0}=7.5$
) in plan view: (a)
$t^{\ast }=8.39$
; (b)
$t^{\ast }=10.1$
; (c)
$t^{\ast }=12.7$
; (d)
$t^{\ast }=15.6$
.
Figure 18. Contours of vorticity associated with the horizontal rings mode (
$h_{0}/b_{0}=7.5$
). Panels (a–c) show contours acquired using the transverse plane, and panels (d–f) show the longitudinal plane at the same time. Superimposed on the vorticity contours in (d–f) are flow visualization images acquired at the same non-dimensional time. In (a,d), (b,e) and (c,f), the images depict times
$t^{\ast }=12.1$
, 14.4 and 20.2 respectively.
Figure 19. Contours of vorticity (a) and corresponding flow visualization image (b) taken in the longitudinal plane (see figure 5), showing the rebounding horizontal vortex ring of the horizontal rings mode (
$h_{0}/b_{0}=7.5$
). The position of the light sheet is shown in (c).
Each of the ‘collapsed vortices’ contains a horizontally oriented vortex ring which then rebounds vertically upwards from the wall, although this is not clearly evident from the visualization alone. Figure 18 shows vorticity contours computed from PIV measurements taken in the transverse plane and the longitudinal plane (see figure 5). During the time that the secondary vorticity is generated at the wall, the primary vortex topology is altered by the axial flow moving towards the peak, and the structure begins to resemble a hollow vortex (see figure 18 b), in which the principal vorticity is situated around the perimeter of the vortex, similar to the hollow vortex described by Baker, Saffman & Sheffield (Reference Baker, Saffman and Sheffield1976) and Saffman (Reference Saffman1992). It seems that the vortex is entraining some irrotational fluid during the course of its evolution, probably as a result of the axial flow. The upper portion of the hollow vortex, labelled P1 in figure 18(c), interacts with and reconnects with the secondary vortex to form a vortex ring. Figure 18(d–f) shows the flow observed from the longitudinal plane (see figure 5). Here, vorticity contours and flow visualization images are overlaid and show the development of a vortex pair that rebounds rapidly from the wall. As this view is orthogonal to the transverse plane of (a–c), and both views contain ‘vortex pairs’ in the same location, we can confirm that a vortex ring has formed, although the actual process of reconnection is difficult to observe directly. Furthermore, the circulations of the ‘vortex pairs’ observed in each plane are comparable, approximately 25 % of the initial circulation of the primary vortex. In figure 19, we compare the vorticity contours acquired in the longitudinal plane with a flow visualization image acquired using the same cross-sectional light sheet. The sense of rotation of the ring is clearly marked by the dye.
Figure 20. Schematic showing the authors’ interpretation of the principal vortex dynamics leading to the development of horizontal vortex rings in the horizontal rings mode (
$h_{0}/b_{0}=7.5$
).
In figure 20, we present a schematic illustrating the principal vortex dynamics involved in the evolution of the horizontal rings mode. The secondary vortex is represented by the shaded regions shown in (a). During the evolution of the instability, the secondary vortex is deformed by the stronger primary in (b) and advected towards the peak cross-section by the axial flow described earlier. According to our PIV vorticity measurements, it seems that reconnection occurs between the secondary vortex and the primary vortex, leaving two horizontal vortex rings for each instability wavelength, as depicted in (c). These horizontal rings then propel themselves vertically away from the wall by self-induction (towards the observer in figure 20).
Reconnection is a critical process in the evolution of the vortex rings described above. This process has been extensively studied as it is a fundamental process by which vortical structures interact and change topology. It is well known as a key to the classical problem of the Crow instability without ground effect and to the evolution of vortex rings. The present flows are complex and would benefit from numerical simulations to interpret the vortex dynamics and topological changes in the vorticity distribution.
4.3 Large rings mode: vortex ring–surface interaction
As we shift to values of
$h_{0}/b_{0}$
greater than 9 (
$A/b_{0}$
greater than 0.5, measured at
$b_{0}$
above the wall), the long-wave instability develops to the point of reconnection and the formation of vortex rings prior to the vortices reaching the ground plane. Figure 21 shows the result of wall interaction for vortex rings formed in this manner. The final configuration of vorticity in this case is significantly different from both previously considered cases, with the rings rapidly expanding upon experiencing the effects of the wall. The primary ring can then generate secondary and tertiary vorticity at the wall. This effect has been observed in many other studies, and may itself result in the generation of other instabilities, such as those observed in the work of Walker et al. (Reference Walker, Smith, Cerra and Doligalski1987) and Swearingen et al. (Reference Swearingen, Crouch and Handler1995). Interestingly, this is not the only possible final vortex configuration for the ring–wall interaction. Because the Crow instability develops in a plane that is inclined to the horizontal, it produces rings that are non-planar. Furthermore, as described by Leweke & Williamson (Reference Leweke and Williamson2011), the rings can change their orientation due to the effects of self-induction. Consequently, depending on the precise moment at which the rings encounter the wall, phenomena, including the axial flow and vortex collapse described for the vertical and horizontal rings modes, can be triggered in addition to the behaviour shown in figure 21.
Figure 21. Interaction of vortex rings formed by the Crow instability with a wall in the large-rings mode (
$h_{0}/b_{0}=10$
): (a)
$t^{\ast }=8.00$
; (b)
$t^{\ast }=10.7$
.
5 Discussion
5.1 Vortex dynamics
In this section, we discuss how wall interaction alters other quantities describing the evolution of the vortex pair, such as the circulation of the vortices as a function of time, the amplitude of the instability, the angle of the plane containing the instability, and the vortex pair trajectories. Figure 22 shows the instability amplitude as a function of time for the vertical rings mode and the large-rings mode and the unbounded Crow instability. The amplitude was determined from dual-light-sheet visualization experiments conducted in the transverse plane (see figure 5), as described in § 2. Figure 22 presents the actual amplitude of the instability in the plane in which the instability exists.
Figure 22. The amplitudes of the unbounded Crow instability, the vertical rings mode and the large-rings mode as functions of time. The amplitudes presented here are measured in the plane of the instability and include both the horizontal and the vertical components.
The long-wave instability proceeds through several phases of development as the amplitude grows and the vortices reconnect to form vortex rings. The amplitude for the large-rings mode tracks that for the unbounded long-wave instability very closely until the wall effect is observed around
$t^{\ast }=11$
. After that point, the rings stop their downward motion and the amplitude reaches a plateau. In the unbounded case, the rings continue downward, leaving the trough regions behind and causing the amplitude to continue to grow. For the vertical rings mode, the Crow instability is inhibited long before it is able to form vortex rings. Consequently, the amplitude diverges from the other two cases early in its evolution, around
$t^{\ast }=5$
in our example. Interestingly, following wall interaction, the amplitude of the instability actually decreases due to rotation of the plane containing the instability, as explained below.
Figure 23. The angle of the plane containing the instability as a function of time for the vertical rings mode (
$h_{0}/b_{0}=5$
). Schematics depicting the relative positions of the peak and trough at the labelled points are also shown, in which the peak is represented by a filled circle and the trough by an open circle.
One characteristic of this flow becomes significantly modified when the ground plane is present, namely the orientation of the instability plane angle as a function of time. (The instability plane angle is the angle of the plane that contains the instability waviness, and it can be measured using the dual-light-sheet technique discussed earlier with figure 6.) Initially, with or without a wall, the instability angle is around
$48^{\circ }$
–
$50^{\circ }$
. Sketches of the peak locations (solid symbols) and trough locations (open symbols) are shown in figure 23 for different times A, B, C, D, where we also show a plot of the variation of instability angle. There is a significant difference when there is a ground plane present when compared with the variation of the angle for the unbounded Crow instability in Leweke & Williamson (Reference Leweke and Williamson2011). After the initial phase close to A, the instability plane angle decreases to point B, due to the rebound effect of secondary vorticity acting on the trough primary vorticity earlier than the peak primary vorticity. Thereafter, the plane angle increases as the ground effect pulls the troughs away from each other along the wall, and at C the plane angle is close to
$90^{\circ }$
(vertical). The angle further increases to point D. In essence, if one looks at the instability in plan view (vertically downwards in the diagrams of figure 23), for cases C and D, there is what could be called a ‘reverse waviness’. The trough is the location at which vortices initially make their closest approach in the long-wave instability; the effect of the ground causes the peaks to be the parts of the vortices that come closest together. In this sense, the waviness is reversed.
The circulation of the primary vortices experiences distinct changes upon wall interaction. Figure 24(a) shows the circulation measured at the peak and trough cross-sections for a vortex pair evolving according to the vertical rings mode. Here, the trough cross-section enters wall effect before the peak cross-section because the developing Crow instability has moved the troughs below the peaks, as shown in figure 23, schematic A. Because of this difference, the circulation of the trough decreases sooner and more rapidly than that of the peak cross-section. This spanwise difference in circulation creates a pressure gradient and drives axial flow along the vortex.
Figure 24(b) presents the circulation measured at the peak location for the unbounded Crow instability as well as circulation at the peak location for the large-rings mode, with
$h_{0}/b_{0}=10$
. In this mode, the Crow instability has sufficient time to cause vortex reconnection and the formation of vortex rings. The secondary vorticity near the wall weakens the primary vortices significantly. This is similar to the 2D vortex decay described in § 3. The trough circulation behaviour (not included in figure 24) is the same for both flows and also experiences a rapid decrease in vortex strength. In the case of the peak of the vortex, the circulation decay is due to a primary–secondary interaction at the wall. For the trough, the circulation decays as a result of primary–primary interaction as the Crow instability forces the vortices together during their descent.
Figure 24. (a) Circulation measured at the peak and trough cross-sections for a vortex pair subject to the Crow instability, evolving in wall effect in accordance with the vertical rings mode (
$h_{0}/b_{0}=5$
). (b) Circulation of a vortex pair subject to the Crow instability at the peak cross-section, both with and without the presence of a wall. Also shown is the development of the secondary vorticity at the wall. It should be noted that the sign of the secondary vorticity has been inverted.
5.2 Axial flow
Fundamental to all of the possible modes observed in this work is the presence of significant axial flow along the vortex tubes. This flow moves fluid away from the trough, the part of the vortex that contacts the wall first, and causes the vortex to ‘collapse’ towards the peak region.
Axial flow has been studied in the context of vortex bursting by Moet et al. (Reference Moet, Laporte, Chevalier and Poinsot2005). In their computations, a Gaussian vortex with a variable core radius was used to generate a pressure gradient along the length of the vortex. The region of larger cross-section had a correspondingly higher pressure than the part of the vortex with smaller cross-section. The consequent pressure gradient then pushed fluid from the larger diameter section towards the smaller cross-section.
In our experiment, the pressure gradient is generated not by a change in cross-sectional area along the vortex, but by the weakening of the circulation at specific spanwise locations. In our case, the thinning of the vortex core radius in the trough is associated with an increase in pressure, opposite to the flow illustrated in Moet et al. (Reference Moet, Laporte, Chevalier and Poinsot2005). This effect occurs at the trough cross-section first because that is the part of the vortex that encounters the wall first. Viscous vorticity cancellation caused by interaction with the secondary vorticity at the wall causes the primary circulation to decay, increasing the pressure locally.
In order to quantify the magnitude of the pressure gradient generating the axial flow, we have modelled the vortices as Gaussian. From the Navier–Stokes equations written in cylindrical coordinates, the pressure field in a Lamb–Oseen vortex can be defined by
$$\begin{eqnarray}\unicode[STIX]{x1D70C}\frac{v_{\unicode[STIX]{x1D703}}}{r^{2}}=\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}r},\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}$
is the fluid density,
$v_{\unicode[STIX]{x1D703}}$
is the azimuthal velocity,
$r$
is the radial coordinate and
$p$
is the pressure. The azimuthal velocity is given by (5.2) below and is a function of the circulation
$\unicode[STIX]{x1D6E4}$
and the vortex core size
$a$
,
$$\begin{eqnarray}v_{\unicode[STIX]{x1D703}}(r)=\frac{\unicode[STIX]{x1D6E4}}{2\unicode[STIX]{x03C0}r}\left[1-\exp \left(-\frac{r^{2}}{a^{2}}\right)\right].\end{eqnarray}$$
Using measured values of the circulation and vortex core size in (5.2) and integrating (5.1), figure 25(a) shows the computed pressure in both the peak and the trough as a function of time for the horizontal rings mode. As the troughs are weakened both by primary–primary interaction and then in wall effect by primary–secondary cancellation, the pressure in the trough becomes larger than the pressure at the peak. Consequently, a pressure gradient is established between the trough and the peak, which drives a relatively strong axial flow, ultimately leading to vortex collapse at the peak. The same weakening of circulation occurs at the peak, but it is delayed compared with the trough, allowing the establishment of the pressure gradient.
Figure 25. (a) Pressure computed at the vortex centre for the peak and trough cross-sections as a function of time in the horizontal rings mode. Here,
$P_{0}$
is the pressure far from the vortex centre and
$V$
is the initial self-induced descent velocity of the vortex pair. (b) Circulation and vortex core size for the trough cross-section of the horizontal rings mode (
$h_{0}/b_{0}=7.5$
).
From flow visualization images (see figure 17), the axial flow driven by this pressure gradient appears to be largely complete between
$t^{\ast }=12$
and
$t^{\ast }=15$
. This estimate correlates well with the computed pressure curves, which show the pressure gradient becoming very small for times greater than
$t^{\ast }=15$
.
To gain further insight into the parameters that govern the evolution of the pressure, we can consider the pressure coefficient of a Rankine vortex. The pressure at the centre of a Rankine vortex is well known and is given by
$$\begin{eqnarray}p-p_{0}=-2\frac{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6E4}}{8\unicode[STIX]{x03C0}a^{2}},\end{eqnarray}$$
where
$p$
is the pressure,
$p_{0}$
is the pressure far from the vortex,
$\unicode[STIX]{x1D6E4}$
is the circulation and
$a$
is the core size.
We define the pressure coefficient in the usual manner,
$$\begin{eqnarray}C_{p}=\frac{p-p_{0}}{{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}V^{2}},\end{eqnarray}$$
where
$V$
is the initial descent velocity of the vortex pair,
$\unicode[STIX]{x1D6E4}_{0}/2\unicode[STIX]{x03C0}b_{0}$
, and
$\unicode[STIX]{x1D6E4}_{0}$
and
$b_{0}$
are the initial vortex circulation and separation respectively.
By substituting (5.3) and the initial descent velocity into (5.4), we obtain
$$\begin{eqnarray}C_{p}=-2\left(\frac{b_{0}}{\unicode[STIX]{x1D6E4}_{0}}\right)^{2}\left(\frac{\unicode[STIX]{x1D6E4}}{a}\right)^{2}.\end{eqnarray}$$
Equation (5.5) shows that the pressure coefficient is simply a function of the ratio of the circulation
$\unicode[STIX]{x1D6E4}$
to the core size
$a$
. Figure 25(b) shows that the increase in pressure at the trough is due largely to the rapid weakening of the circulation at that location. The core size remains relatively constant during the wall interaction, whereas the circulation decreases markedly.
6 Discussion of other relevant studies of vortex–wall interactions
The present study is related to an entire class of flows in which a perturbed vortex approaches a parallel boundary. The general problem, in which viscous vorticity cancellation causes a pressure gradient and axial flow, is not solely tied to the existence of a vortex pair or the long-wave instability influenced by a wall. Similar phenomena occur for a single vortex close to a wall, and the perturbations need not be periodic. A single perturbation at some spanwise location along a vortex, under the influence of a boundary, can generate similar phenomena to what we have shown in the present work. In addition, remarkably similar phenomena and vortex structures are found resulting from an oblique collision of a vortex ring with a flat boundary, as studied by Lim (Reference Lim1989).
Figure 26. Comparison of the evolution of the primary vorticity of a vortex pair in wall effect and the collision of a vortex ring with an inclined wall from Lim (Reference Lim1989) (reproduced with permission of Springer). The vortex ring interaction is shown in (a–c), and a plan view of the vortex pair is shown in (d–f).
An axial flow phenomenon similar to that observed for the vortex pair appears to occur as the ring encounters the wall, as shown in figure 26. Just as for the vortex pair, the flow moves fluid away from the portion of the ring that encounters the wall first. This flow produces what we call a ‘collapsed vortex’. Both of these flows involve vorticity cancellation, the formation of a spanwise pressure gradient and a spanwise flow. Both flows also involve vortex rebound and the generation of smaller-scale vortex structures.
Examination of the secondary vorticity reveals more similarities. Figure 27 shows an example of our vortex pair evolving in the manner of the vertical rings mode and Lim’s vortex ring, both in plan view. The secondary vortex structure that gives rise to a vertical vortex ring in the case of the vortex pair is very similar to the loop observed in Lim’s vortex ring. It is possible, then, that a vortex ring colliding obliquely with a wall will change the vortex topology and evolve into a smaller-scale vortex ring or loop, which may then rebound away from the boundary, as we find in our flow. A principal difference between our flow and Lim’s, however, is that the secondary vortices produced by the vortex pair interact with each other along the centreline dividing the two vortices. In the vortex ring experiment, only one such loop is produced.
Figure 27. Comparison of the evolution of the secondary vorticity of a vortex pair in wall effect with the collision of a vortex ring with an inclined wall from Lim (Reference Lim1989) (reproduced with permission of Springer). (a) The secondary vorticity generated by the vortex ring. (b) The secondary vorticity generated by a vortex pair evolving according to the vertical rings mode.
In presenting his results, Lim (Reference Lim1989) described how the interaction of a vortex ring and an oblique wall causes the formation of ‘bi-helical’ vortex lines close to the location of first contact between the wall and the vortex ring. He suggests that these vortex lines are displaced along the circumferential axis, ultimately compressed around the portions of the ring furthest from the wall, by the induced velocity of the secondary vorticity. He deduces that the no-slip condition of the wall and the corresponding generation of secondary vorticity play a vital role in displacing these vortex lines. In the present work, clearly, the generation of secondary vorticity is at the heart of the 3D vortex dynamics, although there is no indication in our flow of the dynamics of helical vortex lines. Certainly, the vortex lines will assume roughly a helical orientation due to the combined axial flow with swirl in the vortex tubes, but we could not observe them directly.
Both Lim (Reference Lim1989) and the subsequent simulations of Verzicco & Orlandi (Reference Verzicco and Orlandi1994) discuss a sequence of events that leads to the significant changes in vortex topology for the oblique rings. As the oblique ring approaches the wall, vortex stretching occurs first where the ring first comes into contact with the wall. Essentially, in this region of the flow, the radius of the ring grows due to the image effect of the vortex ring in the wall. Due to this stretching, the rate of vorticity annihilation due to viscous diffusion is increased. As the vortex circulation decays, there is a local increase in pressure, which generates axial flow. The above authors then focus on the existence of a vortex loop that arises out of the secondary vorticity, convecting upwards due to its own self-induced motion.
In the case of our flow here, it should be emphasized that vigorous axial flows are found not only in the secondary vorticity but also in the primary vorticity, and both sources of vorticity can have a key role in the subsequent vortex dynamics.
It is suggested by Lim (Reference Lim1989) and Verzicco & Orlandi (Reference Verzicco and Orlandi1994) that ‘differential stretching’ causes the axial flow of the secondary vorticity and subsequent ejection of a vortex loop. In our case, the stretching in the manner of a ring spreading out with increasing radius does not occur. We believe that axial flow is not the result of vortex stretching; the stretching is the result of axial flow. However, they clearly occur together.
In the flows discussed here, the initial conditions consist of a vortex pair with a perturbation that approaches a wall. At the point where a vortex first comes into contact with the wall, the presence of the primary vortex causes a boundary layer to form and creates a pressure gradient, resulting in flow separation and the formation of secondary vorticity. Locally, the interaction between the primary and secondary vorticity has a ‘head start’ over other parts of the flow; the rapid growth of secondary vorticity leads to diffusion and rapid cancellation of primary vorticity. The local weakening of the primary vortex strength causes a local increase in pressure and induces axial flow in the vortex tube. The flow away from the point of first contact towards the parts of the vortex furthest from the wall leads to the collapse of the primary vortex. The net result of these vortex dynamics leads typically to the formation of vortex loops or vortex rings which rise up away from the horizontal wall. The formation of these three-dimensional structures ‘rebounding’ from the wall may represent a generic characteristic of such flows.
7 Conclusions
In this study, we examined the approach of a vortex pair to a solid boundary, in the case where the vortices are unstable to a long-wave instability. The effects of a wall lead to distinctly different vortex dynamics, almost unrecognizable compared with the unbounded Crow instability. The interaction of a vortex pair with a wall leads to inhibition of the long-wave instability. The vortices are then subject to localized vorticity cancellation, which causes the development of axial pressure gradients within each vortex, producing strong axial flows. Ultimately, quite distinct vortex topologies develop, involving small vortex rings. We believe that these characteristics are not limited to our flow, and are relevant to a broader class of fundamental flows in which a perturbed vortex (or vortex ring) becomes influenced by a wall. The most notable practical application is the vortex wake that forms behind aircraft near a runway and which imposes constraints on airport and runway capacity. However, the phenomena we discuss are also relevant to flows around submerged ship hull appendages as well as flows downstream of vortex generators.
If the vortex pair is generated below a critical initial height, the wall serves to inhibit the three-dimensional (Crow) instability. We observe two modes of vortex–wall interaction. For small heights, the primary vortices are close together, enabling the secondary vortices to interact with each other above the primary pair, forming vertically oriented vortex rings. This unexpected vortex structure represents the principal dynamics of vorticity in this ‘vertical rings mode’, and represents a three-dimensional version of vortex ‘rebound’.
In the ‘horizontal rings mode’, with a range of larger initial heights, the Crow instability develops to a greater extent before wall interaction. The perturbation amplitude grows larger, and this means that the peak locations are farther apart and the troughs closer together upon wall interaction. The proximity of the troughs also increases vorticity cancellation there, leading to a greater loss of circulation. Further reduction in circulation is caused by the generation of secondary vorticity in wall effect. This reduction of circulation at the troughs locally leads to a higher pressure compared with the peaks of the vortices, and triggers ‘vortex collapse’ as a result of strong axial flows moving fluid from the troughs towards the peaks. The secondary vortices generated at the peaks are also much farther apart, which inhibits any interaction between them. Instead, the secondary vortices interact with their individual primaries, leading to reconnection and the formation of a series of small horizontal vortex rings which ‘rebound’ from the wall. There are two small vortex rings in each instability wavelength, quite different from the large Crow vortex rings, one of which is formed per wavelength. As for the first mode, which generates vertical rings, these 3D ‘rebound effects’ of the horizontal rings mode are distinctly different from the 2D rebound observed for straight unperturbed vortex pairs in wall effect. The results of wall interaction arising from these modes are summarized in table 1.
Table 1. Summary of principal modes of wall interaction.
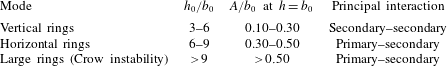
If the vortices are generated above the critical height, the long-wavelength instability causes reconnection to occur at the troughs and a series of vortex rings to be generated. However, because the instability occurs in a plane oriented at
$45^{\circ }$
to the horizontal, the rings are non-planar. The ‘large-rings mode’ then refers to the interaction of these deformed rings with a boundary. Because they are non-planar and also change their orientation continuously following reconnection, the behaviour of the rings in wall effect is dependent on the precise height at which they are generated. In many cases, the rings expand upon impinging with the ground plane, as would be expected for axisymmetric rings. In other cases, phenomena evolve that resemble the horizontal rings mode.
The physical mechanisms that are causing these vortex structures to evolve, breaking up spanwise coherence of the original vortex pairs, may be summarized as below.
$$\begin{eqnarray}\begin{array}{@{}c@{}}\text{Perturbed vortex tube approaches wall}\\ \downarrow \\ \text{Early generation of secondary vorticity where}\\ \text{vortex tube first contacts wall}\\ \downarrow \\ \text{Locally enhanced vorticity diffusion and cancellation}\\ \text{leads to locally higher pressure}\\ \downarrow \\ \text{Vortex collapse occurs as axial pressure gradient drives}\\ \text{axial flow away from point of first contact with wall}\\ \downarrow \\ \text{Formation of small}\text{-}\text{scale rebounding vortex ring structures}\end{array}\end{eqnarray}$$
We recognize that there is a significant difference in Reynolds number between this laboratory-scale flow and real flows that exist in the atmosphere. Despite this difference, other studies, such as that of Leweke & Williamson (Reference Leweke and Williamson2011), have shown striking similarities in the vortex structures produced across this span of Reynolds numbers. That said, it is unknown whether the structures observed in this study are also produced at higher Reynolds numbers. This does not detract, however, from the relevance of this flow to other situations where vortices exist approximately parallel to a surface.
Some studies of aircraft wake vortices, such as that of Stephan et al. (Reference Stephan, Holzäpfel and Misaka2013), show circulation decay (
$\unicode[STIX]{x1D6E4}(t)$
) within non-dimensional times (
$t^{\ast }\approx 8{-}10$
) that are shorter than some of those observed here. It appears that the time required for the circulation to decay (e.g. to 40 % of its initial value) is dependent not only on the configuration of the vortices but also on the Reynolds number. For example, with two-dimensional vortices (figure 10), the primary vorticity decays to 40 % of its starting value by
$t^{\ast }=20$
, while, for the Crow instability in wall effect (figure 24
b), this level of decay is reached by
$t^{\ast }=10$
. A further example is shown in figure 24(a), in which the peaks of the vortices decay to 40 % of their initial value by
$t^{\ast }=16$
, while the troughs have already decayed to this level at
$t^{\ast }=8$
.
The phenomena observed in these experiments are not limited to perturbed vortex pairs. Remarkably similar phenomena are found where vortex rings impinge obliquely with a wall, as discussed in Lim (Reference Lim1989) and Verzicco & Orlandi (Reference Verzicco and Orlandi1994). The changes in topology of the vorticity, the initiation of axial flow, and the creation of rebounding 3D vortex rings appear to be generic phenomena for flows where perturbed vortices are roughly parallel with a surface. Simulations on these and other flows would illuminate and clarify additional features of the vortex dynamics.
Acknowledgements
This work was supported by the Office of Naval Research Award no. N00014-12-421-0712, monitored by Dr R. Joslin. The authors would also like to acknowledge the support of the NASA Aeronautics Scholarship Program.
