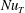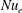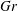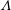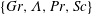1 Introduction
Mass, heat and momentum transfers in turbulent flows occur widely in nature, and very often they are coupled to each other. Examples include thermohaline convection in ocean circulation (Huppert & Turner Reference Huppert and Turner1981; Gent & Mcwilliams Reference Gent and Mcwilliams1990; Schmitt Reference Schmitt1994), pollutant dispersion in the atmosphere (Sini, Anquetin & Mestayer Reference Sini, Anquetin and Mestayer1996; Arya Reference Arya1999) and heat and moisture transfers in ocean evaporation (Liu Reference Liu1979; Fairall et al. Reference Fairall, Bradley, Rogers, Edson and Young1996, Reference Fairall, Bradley, Hare, Grachev and Edson2003). The last example has vital significances for both the global water cycle and climate change (Cane et al. Reference Cane, Clement, Kaplan, Kushnir, Pozdnyakov, Seager, Zebiak and Murtugudde1997; Levitus et al. Reference Levitus, Antonov, Boyer and Stephens2000; Durack, Wijffels & Matear Reference Durack, Wijffels and Matear2012), since evaporation is the major source of atmospheric water (Maidment Reference Maidment1993). In such a case, the transports of heat and mass are strongly coupled to each other, which makes the problem more difficult. Owing to the intrinsic complexity, measurements of transport properties of heat and mass in turbulent flows are, to our knowledge, scarce. In this paper we take evaporation above a fluid layer driven by natural convection (in the form of the classical Rayleigh–Bénard (RB) configuration) as an example and present an experimental method for indirectly measuring the mass transfer rates of water vapour. We then verify the measured results with direct numerical simulations (DNS). Owing to its well-defined boundary conditions and precisely tunable control parameters, RB convection has become a paradigmatic system in the studies of various convection phenomena occurring in nature (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012; Xia Reference Xia2013).
Classical turbulent RB convection concerns a fluid layer cooled from above and heated at the bottom. However, in atmospheric convection, the situation is more complicated (Emanuel Reference Emanuel1994). The key difference between atmospheric convection and RB convection is that the water in the atmosphere undergoes phase transition. Water evaporates from the Earth’s surface and will rise and condense at a certain height. Condensation of water vapour is accompanied by the release of latent heat, which results in a lower adiabatic lapse rate. Moreover, clouds formed by suspensions of the condensed water droplets will also affect the albedo and energy budget (Bodenschatz et al. Reference Bodenschatz, Malinowski, Shaw and Stratmann2010; Chandrakar et al. Reference Chandrakar, Cantrell, Chang, Ciochetto, Niedermeier, Ovchinnikov, Shaw and Yang2016). Developments of moist RB convection have been made to shed light on atmospheric convection. For example, Bretherton (Reference Bretherton1987, Reference Bretherton1988) developed an idealized model of non-precipitating moist convection. Schumacher & Pauluis (Reference Schumacher and Pauluis2010), Weidauer, Pauluis & Schumacher (Reference Weidauer, Pauluis and Schumacher2010) and Pauluis & Schumacher (Reference Pauluis and Schumacher2011) used a piecewise linear buoyancy equation to study moist convection in a conditionally unstable regime. Hernandez-Duenas et al. (Reference Hernandez-Duenas, Majda, Smith and Stechmann2013), on the other hand, proposed a minimal model that allows rain water to fall. More recently, Vallis, Parker & Tobias (Reference Vallis, Parker and Tobias2019) presented an idealized model of moist convection by adding a condensation term which obeys a simplified Clausius–Clapeyron relation.
In this paper, we focus on the mass transfer properties of water in a moist turbulent convection system. The remainder of the paper is organized as follows. We first describe our experimental method in § 2. In § 3 we introduce the governing equations. The correction for sidewall condensation is then described in § 4. We then verify our experimental results using DNS in § 5. The effect of density ratio is discussed in § 6. Based on the results in § 6, we deduce in § 7 the Schmidt number dependence of the transport efficiency when one of the scalars is passive. Our results are compared with a generalized Grossmann–Lohse theory in § 8. We then show the implications for evaporation in nature in § 9 and finally conclude our work in § 10.
Figure 1. Schematic of the experimental set-up. Arrows indicate the direction of heat flux. Open arrows denote the LHF and the filled arrows represent the SHF.
2 Method
In the experiment, a rectangular RB convection cell with dimensions 12.6 cm (height)
$\times$
12.6 cm (length)
$\times$
7.6 cm (width) is used. The system consists of a thin layer (1.6 cm in thickness) of distilled and deionized water at the bottom, with moist air above filling the rest of the cell. The system is kept at atmospheric pressure and the mixture of water vapour and dry air can be treated as an ideal gas. The top and bottom plates are made of copper. The top plate is cooled by a temperature-regulated refrigerator and the bottom plate is heated by a resistive heater. Three thermistors (0.7 cm away from the liquid–solid interface) are embedded in the plates to monitor the temperature therein, denoted by
$T_{p,bot}$
and
$T_{p,top}$
. An additional small thermistor (see figure 1) is placed in the centre of the liquid water layer in order to monitor the temperature in the centre of the liquid layer
$T_{l,c}$
. When the bottom plate is heated and the top plate is cooled, a temperature gradient will be built in the thin water layer. The temperature at the liquid–gas interface is then determined by
$T_{bot}=2T_{l,c}-T_{p,bot}$
. Water evaporates at the bottom liquid–gas interface and condenses on the top plate, forming a thin layer of liquid water thereon (Zhong, Funfschilling & Ahlers Reference Zhong, Funfschilling and Ahlers2009; Prabhakaran et al.
Reference Prabhakaran, Weiss, Krekhov, Pumir and Bodenschatz2017). In steady state, the upward mass flux of water vapour is balanced by the downward-dripping droplets. Since the top liquid–gas interface is a dynamic one and therefore difficult to measure directly, we approximate its temperature by
$T_{top}=T_{p,top}$
. During the experiment, the whole convection cell is placed in a home-made thermostat whose temperature is set to be the same as the bulk temperature of the mixture. The temperature stability of the thermostat is about
$\pm 0.02$
K. Data acquisition is made after all temperature signals reach statistical stationary states, and each heat transfer measurement lasts for more than two hours.
The total heat flux in this system can be divided into two parts, the sensible heat flux (SHF) and the latent heat flux (LHF) (Mangarella et al. Reference Mangarella, Chambers, Street and Hsu1973) (see figure 1). The former is what is typically measured in RB convection experiments (Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010) and the latter reflects the contribution of phase transition at both boundaries. It is with this LHF that we deduce the mass flux, or vapour transfer rate.
Since the system is free of condensation nuclei and far from the critical point, we expect that neither heterogeneous (Chandrakar et al.
Reference Chandrakar, Cantrell, Chang, Ciochetto, Niedermeier, Ovchinnikov, Shaw and Yang2016) nor homogeneous condensations (Prabhakaran et al.
Reference Prabhakaran, Weiss, Krekhov, Pumir and Bodenschatz2017) would occur in the bulk region of the convection cell. This fact was verified by a laser light scattering test, in which no visible droplets were observed. The total heat flux
$\unicode[STIX]{x1D6F7}_{q}$
can then be approximated as
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{q}=\unicode[STIX]{x1D6F7}_{S}+\unicode[STIX]{x1D6F7}_{L}=(Nu_{T}k\unicode[STIX]{x1D6E5}_{T}+Nu_{e}DL\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C},v})/H.\end{eqnarray}$$
Here,
$Nu_{T}=\unicode[STIX]{x1D6F7}_{S}H/(k\unicode[STIX]{x1D6E5}_{T})$
and
$Nu_{e}=\unicode[STIX]{x1D6F7}_{L}H/(DL\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C},v})$
are the Nusselt numbers for temperature and vapour pressure, respectively. They represent the non-dimensionalized heat and moisture transfer rates. In the above,
$\unicode[STIX]{x1D6F7}_{S}$
is the SHF and
$\unicode[STIX]{x1D6F7}_{L}$
is the LHF. Parameters
$k$
and
$D$
are the thermal conductivity and mass diffusivity of water vapour in dry air and
$L$
is the latent heat of water. The difference
$\unicode[STIX]{x1D6E5}_{T}=T_{bot}-T_{top}$
is the temperature difference across the layer of moist air, with
$T_{bot}$
the temperature at the lower liquid–gas interface and
$T_{top}$
the temperature at the upper liquid–gas interface. In the above,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C},v}$
denotes the water vapour density difference across the two liquid–gas interfaces, which can be further written as
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C},v}=(e_{s,bot}/T_{bot}-e_{s,top}/T_{top})M_{e}/R$
. Here
$e_{s,bot}$
and
$e_{s,top}$
are the saturation water vapour pressures at the bottom and top interfaces, with
$M_{e}$
the molar mass of water vapour and
$R$
the universal gas constant. We plot in figure 2(a) the experimentally measured total heat flux
$\unicode[STIX]{x1D6F7}_{q}$
as a function of the temperature difference across the two liquid–gas interfaces. It is seen that
$\unicode[STIX]{x1D6F7}_{q}$
shows an excellent power-law dependence on
$\unicode[STIX]{x1D6E5}_{T}$
. Meanwhile, for a fixed
$\unicode[STIX]{x1D6E5}_{T}$
, higher bulk temperature leads to a higher total heat flux. This can be understood by the fact that the difference of the saturation water vapour pressure between the two boundaries (
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C},v}$
) increases as bulk temperature is raised (Murray Reference Murray1967), so the corresponding LHF also increases. It is worth mentioning that since the latent heat of water is large, LHF accounts for over 90 % of the total heat flux in the parameter range explored in our experiment, as illustrated in figure 2(b). So LHF is the dominant factor in (2.1) for the present case.
Figure 2. (a) Total heat flux
$\unicode[STIX]{x1D6F7}_{q}$
as a function of the temperature difference
$\unicode[STIX]{x1D6E5}_{T}$
across the two liquid–gas interfaces, and for various values of the bulk temperature
$T_{bulk}$
which is measured at the cell centre. (b) The ratio of the LHF to the total heat flux
$\unicode[STIX]{x1D6F7}_{L}/\unicode[STIX]{x1D6F7}_{q}$
.
3 Governing equations
To obtain the moisture transfer rate
$Nu_{e}$
, we first consider the governing equations of the system. These equations can be derived (Landau & Lifshitz Reference Landau and Lifshitz2013) by choosing temperature
$T$
and water vapour pressure
$e$
as state variables and applying the Oberbeck–Boussinesq approximation,
$\unicode[STIX]{x1D70C}(T,e)=\unicode[STIX]{x1D70C}_{0}[1-\unicode[STIX]{x1D6FC}(T-T_{0})-\unicode[STIX]{x1D6FD}(e-e_{0})]=\unicode[STIX]{x1D70C}_{0}(1-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}T-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}e)$
, where
$T_{0}$
and
$e_{0}$
are the reference temperature and vapour pressure, which are usually taken to be their respective bulk values;
$\unicode[STIX]{x1D6FC}\equiv -\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}T$
and
$\unicode[STIX]{x1D6FD}\equiv -\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}e$
are the thermal expansion coefficient and the solutal expansion coefficient, respectively. These coefficients can be determined from the equation of state of the moist mixture:
$\unicode[STIX]{x1D70C}=[eM_{e}+(P_{0}-e)M_{d}]/(RT)$
(Andrews Reference Andrews2000). Here
$M_{d}$
is the molar mass of dry air and
$P_{0}$
is the atmospheric pressure. With this approximation, the buoyancy term in the usual Oberbeck–Boussinesq equations for classical RB convection becomes
$(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}e)\boldsymbol{g}$
. In addition, there is now also a diffusion–convection equation for
$e$
which is the same as that for
$T$
except
$\unicode[STIX]{x1D705}$
is replaced by
$D$
. Putting together, one has the following governing equations:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}=-\frac{1}{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}+(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}T+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}e)g\hat{k}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}T=\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}T, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}e}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}e=D\unicode[STIX]{x1D6FB}^{2}e, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0. & \displaystyle\end{eqnarray}$$
To non-dimensionalize these equations, one can follow the idea developed in double-diffusive convection and, more recently, two-scalar convection system (Radko Reference Radko2013; Yang, Verzicco & Lohse Reference Yang, Verzicco and Lohse2018), and get four control parameters, i.e. two Rayleigh numbers
$Ra_{T}=\unicode[STIX]{x1D6FC}g\unicode[STIX]{x1D6E5}_{T}H^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
and
$Ra_{e}=\unicode[STIX]{x1D6FD}g\unicode[STIX]{x1D6E5}_{e}H^{3}/(\unicode[STIX]{x1D708}D)$
, Prandtl number
$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
and Schmidt number
$Sc=\unicode[STIX]{x1D708}/D$
. Here
$Ra_{T}$
and
$Ra_{e}$
are Rayleigh numbers for the temperature and vapour pressure. They describe the relative driven strength induced by temperature difference and by vapour pressure drop, respectively.
Here, to better characterize this two-component convection system, we introduce a new type of non-dimensionlization for the governing equations by defining a generalized free-fall time
$t=\sqrt{H/(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}_{T}g+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}_{e}g)}$
as a typical time scale, and use cell height
$H$
, temperature difference
$\unicode[STIX]{x1D6E5}_{T}$
and vapour pressure difference
$\unicode[STIX]{x1D6E5}_{e}=e_{s,bot}-e_{s,top}$
as the other characteristic scales for the non-dimensionlization of related quantities. The non-dimensional governing equations read as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}^{\prime }}{\unicode[STIX]{x2202}t^{\prime }}+\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}^{\prime }=-\unicode[STIX]{x1D735}p^{\prime }+\sqrt{\frac{1}{Gr}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}^{\prime }+\left(\frac{\unicode[STIX]{x1D6EC}}{\unicode[STIX]{x1D6EC}+1}T^{\prime }+\frac{1}{\unicode[STIX]{x1D6EC}+1}e^{\prime }\right)\hat{k}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}T^{\prime }}{\unicode[STIX]{x2202}t^{\prime }}+\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}T^{\prime }=\sqrt{\frac{1}{Gr}}Pr^{-1}\unicode[STIX]{x1D6FB}^{2}T^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}e^{\prime }}{\unicode[STIX]{x2202}t^{\prime }}+\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}e^{\prime }=\sqrt{\frac{1}{Gr}}Sc^{-1}\unicode[STIX]{x1D6FB}^{2}e^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}^{\prime }=0, & \displaystyle\end{eqnarray}$$
where
$Gr=(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}_{T}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}_{e})gH^{3}/\unicode[STIX]{x1D708}^{2}$
is a generalized Grashof number (Sanders & Holman Reference Sanders and Holman1972; Bergman et al.
Reference Bergman, Incropera, DeWitt and Lavine2011), which represents the relative strength of the total buoyancy;
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}_{T}/(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}_{e})$
is the buoyancy ratio, or the ratio of buoyancy induced by temperature changes to that induced by changes in water vapour pressure; and
$Pr$
and
$Sc$
are the Prandtl number and Schmidt number, as usual. We note that, with the above normalization, the two scalars (
$T$
and
$e$
) are on equal footing, or symmetric, in the equations of motion. Parameters
$\{Gr,\unicode[STIX]{x1D6EC},Pr,Sc\}$
together with the aspect ratio
$\unicode[STIX]{x1D6E4}$
of the convection cell now form the full set of control parameters. The Grashof number and the buoyancy ratio can also be expressed in terms of the above Rayleigh numbers as
$Gr=(Ra_{T}/Pr+Ra_{e}/Sc)$
and
$\unicode[STIX]{x1D6EC}=(Ra_{T}/Pr)/(Ra_{e}/Sc)$
, respectively.
For the moist mixture in the experiment,
$Pr\simeq 0.7$
and
$Sc\simeq 0.6$
. Thus, the ratio between thermal diffusivity and mass diffusivity, namely the Lewis number
$Le\equiv \unicode[STIX]{x1D705}/D=Sc/Pr$
, is about 1. Therefore, we may expect that the water vapour field is similar to the temperature field, which led us to make the approximation
$Nu_{e}\simeq Nu_{T}$
. Physically this means that, with equal diffusivity, heat and moisture are carried by the turbulent flow with the same efficiency, which is also evident from the equations of motion. Under this approximation, we can obtain
$Nu_{e}$
from the experimentally measured total heat flux. The results are shown as square symbols in figure 3. A correction has been made to account for the additional LHF leakage from the sidewall, as described below.
Figure 3. Nusselt numbers
$Nu_{e}$
and
$Nu_{T}$
as functions of the Grashof number
$Gr$
. Filled squares: experimentally measured
$Nu_{e}$
; open squares:
$Nu_{e}$
from DNS; solid line:
$0.143Gr^{0.283}$
, which is a power-law fit to
$Nu_{e}$
from DNS; open triangles:
$Nu_{T}$
from DNS; dashed line:
$0.152Gr^{0.283}$
, which is a power-law fit to
$Nu_{T}$
from DNS. The colour bar shows the inverse buoyancy ratio. The upper inset shows a magnified view containing the experimental data. Lower inset: squares, correction coefficient (4.2) used for correcting the experimental data; circles, correction coefficient obtained from DNS.
4 Correction for sidewall condensation
In an ideal case, water evaporates at the lower interface, being transported to the opposite side by turbulent convection and condenses therein. The sidewall is assumed to be adiabatic and free of condensation. Despite the thermal insulations used to prevent sensible heat leakage, condensation on the sidewall is inevitable and a correction for the latent heat leakage from the sidewall must be made, which was done as follows. The saturation water vapour pressure depends only on temperature and is determined by the Tetens empirical formula (Murray Reference Murray1967):
$e_{s}(T)=6.1078\times \exp [17.2693882(T-273.16)/(T-35.86)]$
. The bulk temperature is simply the arithmetic mean of those at the interfaces:
$T_{bulk}=(T_{bot}+T_{top})/2$
. The bulk vapour pressure is approximated as
$$\begin{eqnarray}e_{bulk}=[(e_{s,bot}+e_{s,top})\times S_{plate}+e_{s,sidewall}\times S_{sidewall}]/(2S_{plate}+S_{sidewall}),\end{eqnarray}$$
where
$S_{plate}$
and
$S_{sidewall}$
are the areas of the conducting plate and the sidewall. For large aspect ratios, the above equation reduces to
$e_{bulk}=(e_{s,bot}+e_{s,top})/2$
. Since the saturation vapour pressure has an exponential dependence on temperature, the bulk vapour pressure is therefore higher than the corresponding saturation vapour pressure at bulk temperature
$e_{bulk}>e_{s,T_{bulk}}$
, which means there exists a vapour concentration boundary layer at the sidewall. By further assuming that the thickness of this boundary layer is the same as those over the two interfaces, the ratio of the LHF across the top liquid–gas interface to the total supply at the bottom plate can then be approximated as
$$\begin{eqnarray}\unicode[STIX]{x1D702}=\frac{\unicode[STIX]{x1D6F7}_{eff}}{\unicode[STIX]{x1D6F7}_{total}}=\frac{(e_{bulk}-e_{s,T_{top}})\times S_{plate}}{(e_{bulk}-e_{s,T_{top}})\times S_{plate}+(e_{bulk}-e_{s,T_{bulk}})\times S_{sidewall}}.\end{eqnarray}$$
We used the average value of this ratio as a correction coefficient for the sidewall latent heat leakage, and obtained the corrected Nusselt number for water vapour as
$$\begin{eqnarray}Nu_{e}=\frac{\unicode[STIX]{x1D6F7}_{q}}{k\unicode[STIX]{x1D6E5}_{T}/H+\unicode[STIX]{x1D702}^{-1}DL\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C},v}/H}.\end{eqnarray}$$
5 Verification by DNS
To verify this simplified two-component convection model, we use the CUPS code (Chong, Ding & Xia Reference Chong, Ding and Xia2018) to solve (3.5)–(3.8) by a fourth-order finite-volume method on staggered grids. In addition, the simulations cover a much wider range of both Grashof number
$Gr$
and buoyancy ratio
$\unicode[STIX]{x1D6EC}$
than our experiment. The Prandtl number and the Schmidt number are fixed at
$Pr=0.7$
and
$Sc=0.6$
. The DNS are conducted in a cubic domain. All boundaries are set to be impermeable and non-slip. Moreover, we apply constant-value boundary conditions at the top and bottom plates and zero-flux conditions at the sidewalls for both the temperature and the vapour fields. We also adopt a non-uniform mesh with denser grids at the boundaries (the grid spacing following a tanh function therein) in our simulations and use up to
$256^{3}$
grids for the highest Grashof number of
$3\times 10^{8}$
, to ensure that both the Kolmogorov and Batchelor scales are resolved (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010). The parameters as well as the time-averaged Nusselt number for both temperature and vapour can be found in table 1.
Table 1. Simulation parameters and time-averaged Nusselt numbers for the temperature
$Nu_{T}$
and water vapour
$Nu_{e}$
. The averaging time
$t_{avg}$
is given in the last column.
Table 2. Simulation parameters and time-averaged
$Nu_{T}$
and
$Nu_{e}$
at both plates when condensation on the sidewall is considered. The correction coefficient
$\unicode[STIX]{x1D702}_{DNS}$
is defined as
$Nu_{e,top}/Nu_{e,bot}$
.
The DNS results for the moisture transfer Nusselt number
$Nu_{e}$
are shown as open squares in figure 3. It is seen that, under the present resolution, all data points with different buoyancy ratios fall on a singe solid line,
$Nu_{e}=0.143Gr^{0.283}$
, which implies that the moisture transfer Nussult number
$Nu_{e}$
is mainly determined by the Grashof number
$Gr$
and is hardly affected by the buoyancy ratio
$\unicode[STIX]{x1D6EC}$
. In the same figure, we plot the sensible heat transfer Nussult number
$Nu_{T}$
as open triangles. It is seen that
$Nu_{T}$
exhibits the same scaling dependence on
$Gr$
as
$Nu_{e}$
, but with a slightly larger magnitude; a power-law fitting gives
$Nu_{T}=0.152Gr^{0.283}$
. The difference between
$Nu_{e}$
and
$Nu_{T}$
is about
$6\,\%$
. The fact that both
$Nu_{e}$
and
$Nu_{T}$
exhibit negligible dependence on the buoyancy ratio shows that the Grashof number is the primary control parameter in determining the transport properties of both scalars.
In the upper left-hand corner of figure 3, we show a magnified portion of the plot containing the experimental data (squares). It is seen that the experimentally determined moisture transfer rate
$Nu_{e}$
is in general higher than the corresponding DNS data. This difference may be attributed to the fact that, in our simulation, the upper boundary is treated as flat and non-slip. Whereas in the experiment, water condensed in the upper boundary forms a ‘rough’ liquid–gas interface and then drips down occasionally. Such effect is neglected for the moment and may introduce additional uncertainty. Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) studied the heat transport in RB convection with smooth bottom and rough top plate, which is close to the situation in our present experiment. They found that the heat transport efficiency in such a configuration is slightly higher than that in the smooth–smooth cell and much lower than that in the rough–rough cell. On the other hand, the dripping event will undoubtedly induce a perturbation in the flow field and thus might trigger a burst of the heat flux. We can make an estimation as follows. Taking the point of the top right-hand corner in figure 2 as an example and considering that the SHF cannot exceed the total heat flux, the mass flux of water vapour is about
$\text{d}m/\text{d}t=\unicode[STIX]{x1D6F7}_{L}\times S/L<\unicode[STIX]{x1D6F7}_{q}\times S/L\sim 6g/h$
. Therefore, we consider that the effects of dripping are relatively small compared to the sidewall condensation as we discussed in § 4.
It is worth mentioning that the boundary conditions associated with our experiment and DNS are quite different, which might also be responsible for the differences observed in figure 3. In our DNS, the flux of the water vapour is set to be zero; such a condition is more close to the ideal case or the situation in nature, where vapour transport takes place in an infinite or large lateral convection domain without condensation. However, for the present experimental set-up, a sidewall is present and kept at constant temperature, and so condensation is inevitable. Although a correction has been made in § 4, the validation of the method needs to be justified. As a test, we run several additional DNS by setting saturation vapour pressure at the sidewall,
$e=e_{s}(T)$
. As a result, there exits an outward vapour flux at the sidewall. The correction coefficient is then defined as
$\unicode[STIX]{x1D702}_{DNS}=\langle \unicode[STIX]{x2202}_{z}T\rangle _{top}/\langle \unicode[STIX]{x2202}_{z}T\rangle _{bot}$
. The tests are conducted at
$Gr=2.9\times 10^{6},\unicode[STIX]{x1D6EC}=1$
with four bulk temperatures (table 2). The temperature difference between the two interfaces is
$\unicode[STIX]{x1D6E5}_{T}=10$
K. We compare the correction coefficients acquired from DNS with those used for the experimental data (4.2) with similar parameters in the inset of figure 3. It is seen that both coefficients are insensitive to the changes in bulk temperature, and
$\unicode[STIX]{x1D702}_{DNS}$
is on average larger than
$\unicode[STIX]{x1D702}$
for the experiment by about 8 %. For the temperature, the adiabatic boundary condition we applied at the sidewall region may result in a slightly lower SHF than for the constant-temperature boundary condition (Stevens, Lohse & Verzicco Reference Stevens, Lohse and Verzicco2014). We nevertheless consider this as a minor effect since the SHF accounts for less than 10 % of the total flux (figure 2
b).
The fact that the two Nusselt numbers are almost the same can also be seen from figure 4, where simultaneous snapshots of the temperature and vapour pressure iso-surfaces are seen to be almost identical. For a close inspection, we show the contour plots of both temperature (dashed curve) and vapour field (solid curve) in figure 5, with the vertical cross-section in figure 5(a) and horizontal cross-section figure 5(b). It is seen that both fields indeed show similar features, especially near the top and bottom boundaries. The isolines of the temperature field nest in those of the vapour field, which is due to the fact that the thermal diffusivity is slightly smaller than the mass diffusivity of water vapour.
Figure 4. Snapshots of temperature (a) and water vapour content (b) isosurfaces taken simultaneously from DNS data at
$Gr=2.9\times 10^{7},\unicode[STIX]{x1D6EC}=1,Pr=0.7$
and
$Sc=0.6$
.
Figure 5. Contour plots of the temperature field (dashed curve) and vapour field (solid curve). (a) Snapshot of the vertical cross-section. (b) Snapshot of the horizontal cross-section. Colour map corresponding to the temperature fields.
Figure 6. (a) Parameter space of the study in the
$\{1/\unicode[STIX]{x1D6EC},Gr\}$
plane; squares: experimental data; circles: DNS data. (b) Experimentally measured
$Nu_{e}$
as a function of
$Ra_{T}$
and
$Ra_{e}$
; open squares: projection of the data to the parameter space in the
$Ra_{e},Ra_{T}$
plane. The colours in (a,b) correspond to different bulk temperatures and the colour code is the same as in figure 2(a). (c) Values of
$Nu_{e}$
from DNS.
In figure 6(a), we show the parameter ranges explored in both experimental and DNS studies in the
$1/\unicode[STIX]{x1D6EC}$
–
$Gr$
plane. It is seen that under the present parameterization, the experimental data for four different bulk temperatures correspond to four sets of measurement, each with a fixed value of buoyancy ratio but varying Grashof number
$Gr$
. In contrast, if the more conventional Rayleigh numbers
$Ra_{T}$
and
$Ra_{e}$
were to be used instead, the experimental data will correspond to measurements with the two control parameters both varying at the same time. This is shown in figures 6(b) (experiment) and 6(c) (DNS), where
$Nu_{e}$
are plotted against both
$Ra_{e}$
and
$Ra_{T}$
. The corresponding experimental parameter space is shown as open squares in the bottom plane. Different colours denote different bulk temperatures, corresponding to those in figure 2. It is seen that the moisture transfer rate
$Nu_{e}$
depends on
$Ra_{e}$
and
$Ra_{T}$
in a complicated way and a simple functional form such as a power law is not applicable. This further shows that the parameter set
$\{Gr,\unicode[STIX]{x1D6EC},Pr,Sc\}$
proposed here is a suitable choice for studying the two-component convection system in the present case.
6 The buoyancy ratio dependence
Although the two Nusselt numbers are mainly determined by the Grashof number, they may still have a weak dependence on the buoyancy ratio, which can be seen from figure 7. In this figure, the compensated
$Nu_{e}$
and
$Nu_{T}$
are plotted as functions of the inverse buoyancy ratio
$1/\unicode[STIX]{x1D6EC}$
using the DNS data. To determine the possible functional form of
$Nu(\unicode[STIX]{x1D6EC})$
, we use the two asymptotic limits of
$\unicode[STIX]{x1D6EC}$
as constraints. When
$\unicode[STIX]{x1D6EC}=\infty$
, the flow would be entirely temperature-driven and water vapour should act as a passive scalar (and vice versa when
$\unicode[STIX]{x1D6EC}=0$
); these two limiting behaviours can be realized by the asymptotic function
$(\unicode[STIX]{x1D6EC}Pr+Sc)/(\unicode[STIX]{x1D6EC}+1)$
. Fitting this to the data points in figure 7 and assuming a power-law dependence, we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle (Nu_{e}Gr^{-0.283})_{Pr=0.7,Sc=0.6}=0.138\left(\frac{Pr\unicode[STIX]{x1D6EC}+Sc}{\unicode[STIX]{x1D6EC}+1}\right)_{Pr=0.7,Sc=0.6}^{-0.089}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (Nu_{T}Gr^{-0.283})_{Pr=0.7,Sc=0.6}=0.147\left(\frac{Pr\unicode[STIX]{x1D6EC}+Sc}{\unicode[STIX]{x1D6EC}+1}\right)_{Pr=0.7,Sc=0.6}^{-0.087}. & \displaystyle\end{eqnarray}$$
Such a function incorporates the effect of buoyancy ratio
$\unicode[STIX]{x1D6EC}$
and would give the correct asymptotic limits.
7 The case when one of the scalars is passive
To demonstrate that the functional form used in (6.1) and (6.2) is justified, we consider the special case in which one of the scalars is active and the other is passive. Let temperature
$T$
be the active scalar and vapour pressure
$e$
be the passive one.
To deduce the
$Pr$
dependence of
$Nu_{T}$
, a minimum of two points are required. Here we choose
$Nu_{T}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.6)$
and
$Nu_{T}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.7)$
. While for the
$Sc$
dependence of
$Nu_{e}$
, the values at
$Nu_{e}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.7,Sc=0.7)$
and
$Nu_{e}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.7,Sc=0.6)$
are selected. However, equations (6.1)–(6.2) are only valid for
$Pr=0.7$
and
$Sc=0.6$
. We therefore consider two limiting cases as follows.
Taking advantage of the fact that the
$T$
and
$e$
fields are symmetric in the governing equations, we have
$Nu_{T}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.6)=Nu_{e}(\unicode[STIX]{x1D6EC}=0,Sc=0.6)$
(where the quantity on the right-hand side can be acquired by substituting
$\unicode[STIX]{x1D6EC}=0$
into (6.1)). The second point can be obtained by substituting
$\unicode[STIX]{x1D6EC}=\infty$
into (6.2), which gives
$Nu_{T}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.7)$
. Combining these two points, we obtain
$Nu_{T}\sim Gr^{0.28}Pr^{0.34}=Ra_{T}^{0.28}Pr^{0.06}$
, which is consistent with previously published results (Ahlers et al.
Reference Ahlers, Grossmann and Lohse2009). Although the
$Pr$
dependence of
$Nu_{T}$
is determined by only two points, the fact that it agrees with known results suggests that the functional form of (6.1) and (6.2), which is deduced based on asymptotic limits and symmetry of the governing equations, is reasonable.
We now consider the
$Sc$
dependence of
$Nu_{e}$
. Note that when
$Pr=Sc$
in (3.6) and (3.7), the two scalars are governed by the same equation, despite one being active and the other being passive. Therefore,
$Nu_{e}$
should be the same as
$Nu_{T}$
. Hence,
$Nu_{e}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.7,Sc=0.7)=Nu_{T}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.7,Sc=0.7)=Nu_{T}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.7,Sc=0.6)$
, where the last equality comes about because when
$\unicode[STIX]{x1D6EC}=\infty$
,
$Nu_{T}$
does not depend on
$Sc$
, because the vapour is now a passive scalar. We now need another point to determine the
$Sc$
dependence of
$Nu_{e}$
, which can be obtained by substituting
$\unicode[STIX]{x1D6EC}=\infty$
into (6.1), which yields
$Nu_{e}(\unicode[STIX]{x1D6EC}=\infty ,Pr=0.7,Sc=0.6)$
. Combining these two points, we obtain the Schmidt number dependence of the passive scalar, i.e.
$Nu_{e}\sim Gr^{0.28}Sc^{0.43}$
. This implies that the transport of a passive scalar with large Schmidt number (or low molecular diffusivity), which is usually the case for liquid solvent, is much more efficient than that of an active scalar. To our knowledge, this is the first time that the Schmidt number dependence of passive scalar transfer rate has been predicted, which of course would need verification by future experiments.
Figure 7. Compensated plot of
$Nu_{e}$
and
$Nu_{T}$
. Blue circles:
$Nu_{e}Gr^{-0.283}$
; red triangles:
$Nu_{T}Gr^{-0.283}$
; solid line:
$0.138Gr^{0.283}[(\unicode[STIX]{x1D6EC}Pr+Sc)/(\unicode[STIX]{x1D6EC}+1)]^{-0.089}$
; dashed line:
$0.147Gr^{0.283}[(\unicode[STIX]{x1D6EC}Pr+Sc)/(\unicode[STIX]{x1D6EC}+1)]^{-0.087}$
. The data scatter for the same
$\unicode[STIX]{x1D6EC}$
is about
$2\,\%$
and is the uncertainty of the DNS data.
8 A generalized Grossmann–Lohse theory
The Grossmann–Lohse (GL) theory (Grossmann & Lohse Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2002; Stevens et al.
Reference Stevens, van der Poel, Grossmann and Lohse2013), which has demonstrated great success in predicting both the
$Nu$
and
$Re$
behaviours in turbulent RB convection, has been recently extended to two-scaler convection system (Yang et al.
Reference Yang, Verzicco and Lohse2018). In this section, we extend the GL theory to a two-component system using the new parameter set
$\{Gr,\unicode[STIX]{x1D6EC},Pr,Sc\}$
. The basic idea of the GL theory is to divide the total energy and thermal dissipation rates into contributions from the boundary layer (BL) region and the bulk region:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}_{u}=\unicode[STIX]{x1D716}_{u,BL}+\unicode[STIX]{x1D716}_{u,bulk}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703},BL}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703},bulk}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}_{e}=\unicode[STIX]{x1D716}_{e,BL}+\unicode[STIX]{x1D716}_{e,bulk}. & \displaystyle\end{eqnarray}$$
Together with the exact relations for all three dissipation rates
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}_{u} & = & \displaystyle \frac{\unicode[STIX]{x1D708}^{3}}{H^{4}}Ra_{T}Pr^{-2}(Nu_{T}-1)+\frac{\unicode[STIX]{x1D708}^{3}}{H^{4}}Ra_{e}Sc^{-2}(Nu_{e}-1)\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D708}^{3}}{H^{4}}Gr\frac{\unicode[STIX]{x1D6EC}}{\unicode[STIX]{x1D6EC}+1}Pr^{-1}(Nu_{T}-1)+\frac{\unicode[STIX]{x1D708}^{3}}{H^{4}}Gr\frac{1}{\unicode[STIX]{x1D6EC}+1}Sc^{-1}(Nu_{e}-1),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D705}\frac{\unicode[STIX]{x1D6E5}_{T}^{2}}{H^{2}}Nu_{T}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}_{e}=D\frac{\unicode[STIX]{x1D6E5}_{e}^{2}}{H^{2}}Nu_{e}, & \displaystyle\end{eqnarray}$$
we can obtain
$$\begin{eqnarray}Gr\frac{\unicode[STIX]{x1D6EC}}{\unicode[STIX]{x1D6EC}+1}Pr^{-1}(Nu_{T}-1)+Gr\frac{1}{\unicode[STIX]{x1D6EC}+1}Sc^{-1}(Nu_{e}-1)=c_{1}\frac{Re^{2}}{g(\sqrt{Re_{c}/Re})}+c_{2}Re^{3},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Nu_{T}-1 & = & \displaystyle c_{3}Re^{1/2}Pr^{1/2}\left\{f\left[\frac{2aNu_{T}}{\sqrt{Re_{c}}}g\left(\sqrt{\frac{Re_{c}}{Re}}\right)\right]\right\}^{1/2}\nonumber\\ \displaystyle & & \displaystyle +\,c_{4}PrRef\left[\frac{2aNu_{T}}{\sqrt{Re_{c}}}g\left(\sqrt{\frac{Re_{c}}{Re}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Nu_{e}-1 & = & \displaystyle c_{3}Re^{1/2}Sc^{1/2}\left\{f\left[\frac{2aNu_{e}}{\sqrt{Re_{c}}}g\left(\sqrt{\frac{Re_{c}}{Re}}\right)\right]\right\}^{1/2}\nonumber\\ \displaystyle & & \displaystyle +\,c_{4}ScRef\left[\frac{2aNu_{e}}{\sqrt{Re_{c}}}g\left(\sqrt{\frac{Re_{c}}{Re}}\right)\right],\end{eqnarray}$$
where
$c_{1}=8.05$
,
$c_{2}=1.38$
,
$c_{3}=0.487$
,
$c_{4}=0.0252$
,
$a=0.922$
and
$Re_{c}=(2a)^{2}$
are constants determined by existing data (Stevens et al.
Reference Stevens, van der Poel, Grossmann and Lohse2013). Here we have used the fact that the temperature and water vapour are equivalent to each other in this system and thus the prefactors in both (8.8) and (8.9) are the same (Yang et al.
Reference Yang, Verzicco and Lohse2018). Now the three response parameters
$Re$
,
$Nu_{T}$
and
$Nu_{e}$
can be determined for given set of control parameters
$\{Gr,\unicode[STIX]{x1D6EC},Pr,Sc\}$
.
We compare our experimental and numerical results with the predictions of the generalized GL theory in figure 8. The Prandtl number and Schmidt number are fixed to be
$Pr=0.7$
and
$Sc=0.6$
, respectively. The dashed line (dark blue) corresponds to the prediction of the theory with density ratio equal to unity
$\unicode[STIX]{x1D6EC}=1$
, while the solid line (deep red) represents infinite density ratio (
$1/\unicode[STIX]{x1D6EC}=0$
). The generalized theory also predicts a negligible effect of density ratio on
$Nu_{e}$
. Furthermore, the
$Nu_{e}$
–
$Gr$
relation of the theory follows exactly the same trend as both our experimental and DNS results, despite some deviations at the lower end.
Figure 8. Nusselt number
$Nu_{e}$
as a function of
$Gr$
. Filled squares: experimentally measured
$Nu_{e}$
; open squares:
$Nu_{e}$
from DNS; solid line:
$0.143Gr^{0.283}$
; dashed line: GL prediction for
$1/\unicode[STIX]{x1D6EC}=1$
; dotted line: GL prediction for
$1/\unicode[STIX]{x1D6EC}=0$
; colour bar: inverse density ratio.
9 Implications for evaporation in nature
In hydrological cycles, the ocean is the ultimate source of all the water used in natural ecosystems and in human activity. Hence a comprehensive understanding of the worldwide ocean evaporation rate is necessary. However, the state-of-the-art bulk parameterization method (Liu Reference Liu1979; Fairall et al.
Reference Fairall, Bradley, Rogers, Edson and Young1996) may not be accurate when the mean wind is low and thus mechanical driving is weak. In such circumstances, the SHF and LHF generated entirely by natural convection, as in the present case, may serve as a robust lower bound. This lower bound may be estimated by using relevant parameters corresponding to sea surface and in the atmosphere. We can express the Grashof number with bulk parameters:
$Gr=16[\unicode[STIX]{x1D6FC}(SST-T_{bulk})+\unicode[STIX]{x1D6FD}(e_{s}(SST)-e_{bulk})]gH^{3}/\unicode[STIX]{x1D708}^{2}$
, where
$SST$
denotes the sea-surface temperature,
$T_{bulk}$
and
$e_{bulk}$
are the bulk temperature and bulk water vapour pressure,
$e_{s}(SST)$
is the saturation vapour pressure at the sea surface and
$H$
is the reference height. The LHF is then
$\unicode[STIX]{x1D6F7}_{L}=Nu_{e}DL\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C},v}/H=0.138Gr^{0.283}DL\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C},v}/H$
, and the SHF is
$\unicode[STIX]{x1D6F7}_{S}=Nu_{T}k\unicode[STIX]{x1D6E5}_{T}/H=0.147Gr^{0.283}k\unicode[STIX]{x1D6E5}_{T}/H$
. Here we have neglected the buoyancy ratio effect, which has been shown to be insignificant for moist air. It should also be pointed out that the choice of reference height
$H$
has only a minor influence on the above estimation since the Grashof number has a cubical dependence on
$H$
.
10 Conclusion
We have presented in this study an indirect experimental method for measuring moisture transfer rates using natural convection as an example. We choose temperature and water vapour pressure as state variables for this two-component system. The non-dimensional moisture transfer rate
$Nu_{e}$
is determined indirectly from the total heat flux, after a correction for the sidewall condensation. We also made a DNS study of the system, to verify the experimental results and expand the parameter space. We find reasonable agreement between the experimental and numerical results. Moreover, we propose to use the Grashof number
$Gr$
together with the buoyancy ratio
$\unicode[STIX]{x1D6EC}$
as control parameters, and find that the transfer rates for both heat (
$Nu_{T}$
) and water vapour (
$Nu_{e}$
) are mainly determined by the Grashof number
$Gr$
, and are only very weakly dependent on the buoyancy ratio
$\unicode[STIX]{x1D6EC}$
. We further find that
$\{Gr,\unicode[STIX]{x1D6EC},Pr,Sc\}$
form a full set of control parameters, and is more suitable than other choices for the present system. This set of parameters may also be applicable to describe other two-component systems. When one of the scalars is passive, its transport properties can also be inferred by considering the limiting cases. Moreover, the present results can be readily extended to the field of hydrology. An example is the no-wind evaporation limit of a water body, e.g. ocean, sea, lake or pond, which can be determined once the surface temperature, bulk temperature and bulk specific humidity are given. Therefore, the present results should complement existing bulk parameterization models for ocean evaporation.
Acknowledgements
We gratefully acknowledge support of this work by the Research Grants Council of HKSAR (nos CUHK14301115 and 14302317), a SUSTech Startup Fund and the support of the Center for Computational Science and Engineering of SUSTech.
