II. THE BACKGROUND: DECOMPOSING A TIME SERIES; DEALING WITH STRUCTURAL BREAKS

The concept of a trend is one that has intrigued economists for the last century or so, notwithstanding considerable improvements in econometric and statistical methods. But exactly what is a trend? Just prior to Carmichael’s Reference Carmichael1928 article, Karl Karsten wrote: “Trend-lines are intended to describe some imaginary state of ‘normalcy’ wherewith to compare the actual conditions depicted by the curve” (Karsten Reference Karsten1926, p. 31). Although still imprecise, perhaps deliberately so, this quotation serves to emphasize a trend as an underlying tendency (‘normalcy’) that is masked by periodic movements such as those due to cycles, seasonal effects, and random irregular events. Recently, Peter Phillips commented that a

Early concerns about the presence of a trend, which was often referred to as being ‘secular,’ were twofold, broadly arising from (a) modelling and (b) forecasting.^{Footnote 2} In the first case, there was a concern about whether trends should be removed from time series data and, in the second, about the implications of trends for projecting data series forward in time.

Following developments in correlation and regression analysis in the late nineteenth and early twentieth centuries (for example, Karl Pearson Reference Pearson1896, and G. Udny Yule Reference Yule1897), there was considerable interest in applying these new techniques of analysis to ‘uncover’ economic relationships.^{Footnote 3} However, there was also a widely expressed concern that short- and long-run movements would be confounded by regressing one possibly trended series on another;^{Footnote 4} see Reginald Hooker (Reference Hooker1901) and the later seminal contribution of Yule (Reference Yule1926). Thus, in what soon became a fairly standard procedure, the data were first linearly detrended and the resulting residuals (adjusted if necessary for seasonal movements) were termed ‘the cycle,’ and it was these cycles rather than the ‘raw’ series that were the subject of correlation analysis; see, for example, Persons (Reference Persons1916). Wesley Mitchell summarized this approach succinctly, if somewhat harshly: “Secular trends of time series have been computed mainly by men who were concerned to get rid of them” (Mitchell Reference Mitchell1927, p. 212).

Mitchell distinguishes the empirical method of determining trends from a more theoretical approach related to the interpretation and implications of particular forms of the trend. On the former, he provides a useful summary of empirical practice at the time as to how the trend may be modelled: fitting a mathematical curve to the series or its logarithm; fitting a moving average (mean or median); fitting a curve to the moving average; drawing a freehand curve; and using ratios between items paired in time where series are considered to have substantially the same secular trend. By contrast, motivating the form of a trend from possible underlying economic causes was relatively undeveloped.^{Footnote 5}

On this view the fitting of a trend is a rather practical matter, only very loosely, if at all, related to any theoretical considerations. This led to some rather ad hoc (but still used) ways of dealing with what we now recognize as nonstationarities in the underlying generating process. The influential work of Persons and his co-authors (‘the Harvard group’) illustrates the dominant line of thinking that had arisen at the time, especially in the construction of what were known as Business Barometers (for example, Persons Reference Persons1916).^{Footnote 6} The underlying methodology was to fit a linear trend and measure the cycle as the deviation of the original observation from the trend—a methodology that is not unfamiliar now. The barometer then aggregated a number of component cycles into a single indicator. A key consideration in the often prior graphical examination of the component time series was to establish ‘homogenous’ periods over which to fit the linear trend. A good example of the issues that were considered is provided by Persons (Reference Persons1919). In examining various time series, ranging from the price of pig iron and general wholesale prices through to immigration and the number of shares sold, Persons observed that the

Segmenting the trends implicitly assumes a discrete break, and hence a ‘jump,’ between adjacent points in time. For example, Persons (1919, Table H) reports the following estimates for two trends of the production of pig iron, here denoted ${y_t}$, and regarded as an important leading indicator of economic activity:

1879–1896: ${\hat y_t}\,\, = \,\,\,32.0\;\; + \,\,3.59t\,$

1897–1913: ${\hat y_t}\,\, = \,\,\,107.0\;\; + \,\,11.9t\,$

These trend lines indicate substantial, discrete jumps in the intercept and slope of trend production of pig iron, which occur between 1896 and 1897.

Even if this approach is somewhat ad hoc, it predates later and rather more sophisticated models of segmenting trends. For example, it can be considered as part of the general problem of (linear) regressions that may be subject to two regimes, as in Richard Quandt’s influential (1958) article, followed by Quandt (Reference Quandt1960), who proposed a now widely used approach to test for two regimes against the null hypothesis of a single regime. Subsequently, D. E. Robison (Reference Robison1964) and Derek Hudson (Reference Hudson1966) considered the problem of how to join the regression sub-models so as to minimize the discrete nature of the change in regimes.

It is perhaps too harsh to dismiss these early attempts to deal with nonstationarities, arising from structural breaks in the underlying process, as being purely ‘empirical.’ Modelling change in the form of a discrete jump between regimes is generally ‘shorthand’ for a more complex adjustment process. Apparently discrete changes, such as the start of the First World War, or more contemporaneously the ‘credit crisis,’ are often much more detailed than a simple ‘off/on switch.’ The interesting practical question is whether the data for such a period should be ignored or whether methods can be devised to either approximate a ‘local’ trend that adjusts to the changing economic circumstances or allows a non-instantaneous transition between regimes.

Some of the empirical approaches referred to by Mitchell can be viewed more positively in this light. Rather than assuming a linear trend subject to a discrete break, a method that adjusts the trend gradually, perhaps giving a greater weight to more recent observations, may be a better way of modelling what appears to be a break in a linear, or indeed a nonlinear, trend. Reginald Hooker (Reference Hooker1901) suggested using a (simple) moving average (MA) to represent the trend, from which a cycle would be measured. The moving average was centered on the period t, taking a window of p (usually an odd number) observations to compute a simple arithmetic average, referred to as the ‘instantaneous’ average. In effect, each observation receives an equal weight in the window, but the window moves through the sample and so a ‘local’ trend is constructed. The choice of window length was guided by what was thought to be the length of the cycle. The moving average offered some flexibility in modelling the trend, being responsive to the evolution of a time series, and is still a widely applied technique, but it has the disadvantage that, given a sample of length T, the MA trend cannot be computed for the first and last $T - {\raise0.5ex\hbox{$\scriptstyle 1$kern-0.1em/\kern-0.15elower0.25ex\hbox{$\scriptstyle 2$}}\left( {p - 1} \right)$ observations.

An alternative method that similarly constructed a local trend was due to Lincoln Hall (Reference Hall1925), who suggested a method that we now know as a form of recursive estimation, in which a moving (or rolling) window of observations of fixed length is used to estimate a local linear trend; as new observations become available, they replace the observations that were previously at the beginning of the sample. Hall’s method of recursive estimation was, however, another idea well ahead of its time and it was not taken up in force until much later in the development of econometric methods. It is likely that the computational demands of Hall’s method were too much for the pre-computer age in which his suggestion was made; to some extent he recognized this by offering a slightly simpler computational method in a later paper (see Hall Reference Hall1926).

The conceptual framework underlying these various methodologies was in effect an embryonic unobserved components (UC) model. This is the decomposition of a series into trend, seasonal, cycle, and irregular components; these components are not directly observed, but constructed from a (particular) modelling approach. Later developments in econometrics saw an increasing sophistication in the nature of the underlying models for each component, but within the same underlying paradigm; see, for example, the developments due to Stephen Beveridge and Charles Nelson (Reference Beveridge and Nelson1981), which are based on an underlying random walk framework, and the structural modelling approach due to Andrew Harvey (Reference Harvey1985).

In the methodology of the 1900s, the removal of the ‘secular’ trend was regarded as the first of two stages in analyzing a time series or relationships between time series, where the trend, in keeping with the absence of an accepted framework for a probabilistic interpretation, was generally regarded as deterministic. (This approach was sometimes labelled the “deviations from trend” or “individual trend” method.) Attention could then be focused on the ‘cycles’ that remained, as these were thought to be of greater interest than the trend itself; see Mary Morgan (1990, chs. 1–3).

However, there were two far-reaching contributions that showed that, in a linear framework, this two-stage procedure was not necessary. The first was due to Bradford Smith (Reference Smith1926), who showed that the time trend could be included in the regression of direct interest; that is, suppose there was interest in the relationship between two variables, say Y and X, each of which was trended; then Smith (1926, equation (8)) showed that the time trend, t, could be included directly in the regression of Y on X and that the resulting coefficients would be simply related to those in the deviation from trend approach. Smith’s approach was referred to by Ragnar Frisch and Frederick Waugh (Reference Frisch and Waugh1933) as the “partial trend regression,” and they went on to correct Smith in some respects, although they agreed with the fundamental approach: “The partial trend regression method can never, indeed, achieve anything which the individual trend method cannot, because the two methods lead by definition to identically the same results. They differ only in the technique of computation used in order to arrive at the results” (Frisch and Waugh Reference Frisch and Waugh1933, p. 388). Thus, the circle is ‘squared’: there is no need to regard trend removal as a prior and separate stage—nothing will be gained by such an approach.

III. CARMICHAELS’S ARCTAN TREND: MULTIPLE REGIMES AND SMOOTH TRANSITION

Neither a rolling window estimation of a linear trend nor a moving average trend would react instantaneously to a change in regime; both would have to ‘sense’ the change from new observations as they became available to their respective algorithms. Moreover, forecasting with Hall’s rolling window trend would not differ in principle from projecting a linear trend; in his case projecting the last local trend that had been estimated. Carmichael’s approach offered a change in method that would have implications for forecasting; indeed, one of the explicit rationalizations for his approach was expressed as follows: “While no attempt is made to summarize criteria for curve fitting, it is desired to emphasize the importance of reasonable projection into the future and the desirability of avoiding gaps in the analysis” (Carmichael Reference Carmichael1928, p. 253). Carmichael’s concerns find support in a recent assessment of modelling trending behavior: “if the trend mechanism is poorly captured in an empirical model, we can expect forecasts from the model to carry forward the poor approximation” (Phillips Reference Phillips2005, p. 402).

Rather than adopt a methodology that either smoothed the impact of a break, as in Hooker’s MA approach or Hall’s local trend method, or imposed a jump in the trend or foreshortened a sample, Carmichael suggested modelling the breaks by allowing a smooth transition between multiple regimes. Moreover, in his most general model, he allowed for the possibility of three regimes and so anticipated more recent developments that allow for multiple regime changes, on which there is now an extensive literature; see, for example, Jushan Bai (Reference Bai1997) and Bai and Pierre Perron (Reference Bai and Perron1998, Reference Bai and Perron2003). Carmichael thus not only suggested an alternative and inherently nonlinear trend, he also showed how to model multiple structural breaks in the fashion of smooth transition adjustment functions, which have become an important component in modern econometric methods.

Carmichael was not only aware that events, such as the First World War, could lead to structural breaks in the underlying economic processes, but also that to remove such data directly or to model the distinct regimes by means of a simple split trend were not the only, nor necessarily the most desirable, options. Using a split trend in effect involves a step change from one regime to another, whereas the adjustment could be modelled so as to allow a smooth transition between regimes and, moreover, there could be more than one adjustment process in any historical period. While accommodating the impact of the First World War was Carmichael’s impetus to nonlinear modelling, there is no shortage of recent events that have been considered as leading to structural breaks—hence the importance of Carmichael’s framework.

Against the background of the decomposition of a time series outlined in section II and the predominant practice of linear detrending, Carmichael observed that a number of time series did not exhibit uniformly smooth growth about which there was cyclical movement. This led him to consider a nonlinear trend that would be suitable in three circumstances: (i) inappropriate projection of a negative linear trend, leading, for example, to “negative or ridiculously small positive values when comparatively large positive values only are possible” (Carmichael Reference Carmichael1928, p. 253); (ii) approximately linear growth that is resumed after interruption by an abrupt change in level; (iii) as in (ii) but with a first interruption, for example a sharp drop, followed by another abrupt change in level, before resumption of the previous growth.

Carmichael’s suggested form, either to amend or supplement the linear trend, was the arctangent function. Three models were distinguished by Carmichael, corresponding to the cases discussed above, as follows:

(1)$$y = a\,\, + \,\,c\arctan (x)$$

(2)$$y = a\,\, + \,\,bx\,\, + \,\,c\arctan (x)$$

(3)$$y = a\,\, + \,\,bx\,\, + \,\,c\arctan (x)\,\, + \,\,d\arctan (\alpha x\,\, + \,\,\beta )$$

We would now conventionally add time subscripts to the variables y and x and include a random term, ${\varepsilon _t}$. Carmichael suggested that the variable y may either be the level or the logarithm of the original data, noting that the difference was between modelling constant absolute changes or constant rates of change (Carmichael Reference Carmichael1928, p. 255). The variable x is a ‘distance’ measure relative to an origin, for which $x = 0$; it is related, but is not necessarily equal, to the simple time trend t that increments by 1 (or some other constant) each time period. Carmichael worked in degrees rather than the now more usual radians. Consider an angle z that varies from –90° to 90°; its tangent then varies from –∞ to +∞. In general, $x = \tan (z)$, and conversely to obtain the angle from the tangent x, $z = {\tan ^{ - 1}}(x)$, where ${\tan ^{ - 1}}$ is the inverse function referred to as $\arctan (z)$; z is in degrees and the conversion to radians is $y = z({\pi \mathord{\left{\vphantom {\pi {180}}} \right\kern-\nulldelimiterspace} {180}})$. Thus, in radians, the limits of $\arctan (z)$ are $\pm (\pi /2) = \pm 1.5708$ and, by a suitable scaling constant, say c, the limits can be adjusted; for example, $c = {\pi ^{ - 1}}$ results in limits of $\pm {\raise0.5ex\hbox{$\scriptstyle 1$kern-0.1em/\kern-0.15elower0.25ex\hbox{$\scriptstyle 2$}}$.

While the estimated trend from the standard linear model is invariant to the scaling of x, this is not the case for the arctan function, so Carmichael also considered how to choose the origin for x and the increment $\Delta x$, which varied in his examples from $\Delta x = 0.25$ to $\Delta x = 1$. Carmichael commented that “it is necessary to make [an] arbitrary choice, based upon graphical considerations, of the point of origin and scale of the x axis” (Carmichael Reference Carmichael1928, p. 255), and continued in a footnote, “could it [the arbitrary choice] be obviated without loss of flexibility of the curve, the technique would be vastly improved.” As we illustrate below, these unknowns can be estimated although, at the time (the 1920s and 1930s), it seems likely that the skill required in making appropriate choices may well have hindered the practical dissemination of Carmichael’s ideas.

For our purposes, the arctan function can be reparameterized with $x = \delta (t\,\, - \,\,{t_0})$, where ${t_0}$ is the (fixed) origin in time and, therefore, $\Delta x = \delta \,\Delta t \Rightarrow {{\Delta x} \mathord{\left{\vphantom {{\Delta x} {\Delta t}}} \right\kern-\nulldelimiterspace} {\Delta t}} = {x \mathord{\left{\vphantom {x {\left( {t - {t_0}} \right)}}} \right\kern-\nulldelimiterspace} {\left( {t - {t_0}} \right)}}$ and $\delta = \Delta x$ for $\Delta t = 1$; thus the origin and the increment become explicit parameters, so that the arctan function, as a function of t, becomes $\arctan \left( {\delta \left( {t - {t_0}} \right)} \right)$. This reparameterization allows the interpretation that the coefficient $\delta$ governs the speed of transition, whereas the coefficient c governs the overall impact of the change in regime. Also, a simple generalization of Carmichael’s specification is to allow the arctan effect to operate on a function of x, $f(x)$, so that, for example, $y = a\,\, + \,\,cA[f(x)]$, where $A[f(x)] = \arctan \left( {f\left( x \right)} \right)$.

In a terminology that has now become almost universal, the function $A\left[ \cdot \right]$ is referred to as the “transition function,” so that it governs the path of adjustment, or transition, between regimes. Moreover, the transition between the regimes is, in Carmichael’s model, smooth rather being a discrete step change. Thus, although writers before Carmichael had suggested regime changes by fitting two linear trends, for example to take account of the First World War, their implicit transition function simply switched between 0 and 1, corresponding to regimes 1 and 2, respectively. The arctan function is able to capture this case because, as $\delta$ → ∞, the transition function becomes a switching function. On the other hand, for ‘small’ values of $\delta$ the transition is smooth and gradual, a feature that Carmichael was evidently aware of when determining empirical values of $\delta$.

Carmichael’s typology of models first allows for a single regime governed by a nonlinear trend; the second model then allows for a change in regime, where the change between regimes is smooth; and the third model allows for two changes in regime, and so three regimes overall, where each change between regimes is smooth. It seems reasonable to presume that Carmichael had in mind a model that would allow multiple regimes but that it was sufficient to illustrate the general pattern by his model (3). Carmichael’s ideas, therefore, clearly anticipated modern concerns about the existence of multiple regimes in economics, finance, and even (electrical) signal processing; to illustrate the breadth of applications, see, for example, Stephen Gray (Reference Gray1996), Suzanne Cooper (Reference Cooper1998), and Matthieu Sanquer et al. (Reference Sanquer, Chatelain, El-Guedri and Matin2013), respectively.

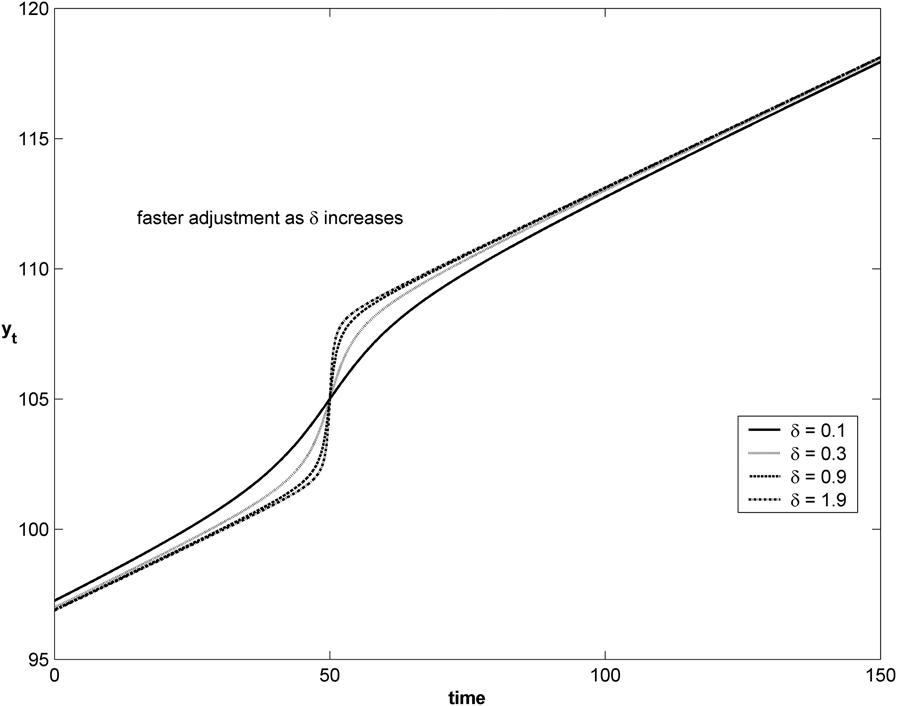
It may be helpful to stylize what Carmichael had in mind and, to that effect, we illustrate his model (2), the two-regime model, in figures 1a and 1b. In this case, the model taken to generate the data is (for clarity of illustration no random ‘errors’ are included):

$${y_t} = 100 + 0.1t + 2.0\left( {\arctan \left( {\delta \left( {t - 50} \right)} \right)} \right)\,t = 1,...,150.$$

Figure 1a. Stylised Arctan transition function.

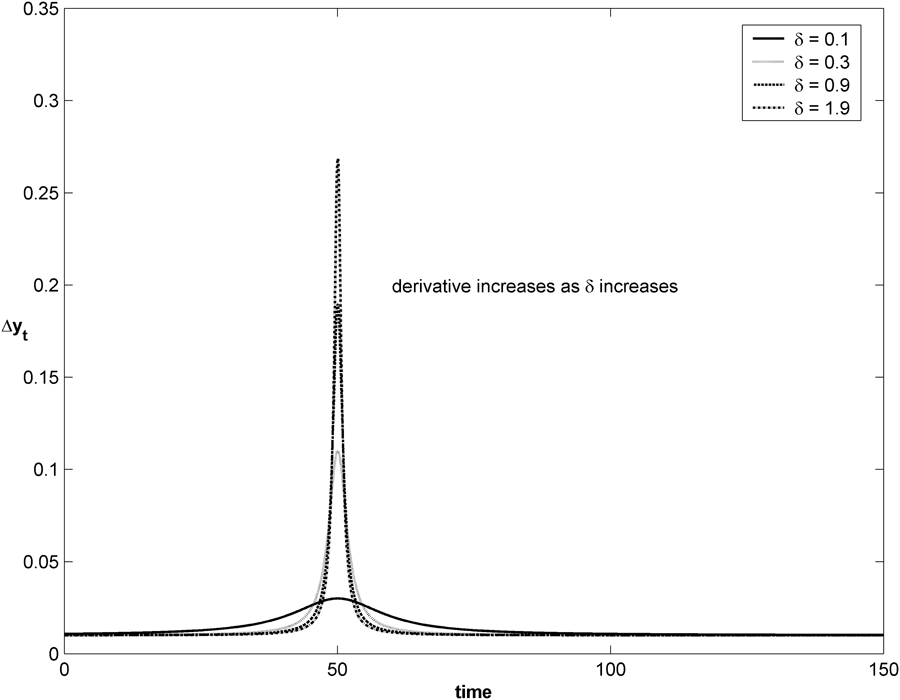
Figure 1b. Corresponding transition changes.

This is a linear trend modified by a nonlinear regime change, with the ‘origin’ at $t = 50$. The speed of adjustment coefficient $\delta$ is varied, starting from slow adjustment, $\delta = 0.1$, to increasingly fast adjustment, with the final $\delta = 1.9$. The successive values of ${y_t}$ are plotted in Figure 1a and the corresponding changes in ${y_t}$, $\Delta {y_t}$, are plotted in Figure 1b.

The variation in $\delta$ shows how adjustment can be relatively slow (the shallow adjustment path) or fast (the steep adjustment path). With the corresponding $\Delta {y_t}$ small and increasing with $\delta$ then in the limit $\delta \,\, \to \,\,\infty$, the adjustment becomes a step change.

IV. THE ARCTAN AND OTHER TRANSITION FUNCTIONS

Carmichael wanted a transition function that allowed for smooth nonlinear adjustment, with a parameter that would govern both very fast and very slow adjustment. He chose the arctan function for that purpose; the choice of a trigonometric function seems natural in the context of his likely exposure to such concepts (on the history of trigonometric education in the United States in the relevant period, see Jenna Van Sickle Reference Van Sickle2011). However, whatever the precise choice of function, it is important to realize that the idea precedes the choice of function, although one can only speculate as to what other functions Carmichael might have considered off the record; we are not given any clues in the text save for the general comment: “The inverse trigonometric function known as the arc tangent appears to be adapted to measuring the trend of series behaving as above described” (Carmichael Reference Carmichael1928, p. 253). In a footnote Carmichael commented: “Numerous examples are presented in subsequent paragraphs in which the arc tangent and logarithmic arc tangent curves appear to possess a decided advantage, so far as these requirements are concerned, over the equation types generally employed” (Carmichael Reference Carmichael1928, pp. 253–254).

By the nature of his choice, Carmichael is clearly aware of the sigmoid nature of the arctan function. In an influential article of a much later period, David Bacon and Donald Watts mentioned the arctan function as a possible transition function but noted: “There are many transition functions which could be used: for example, the cumulative distribution function of any symmetric probability density function or the hyperbolic tangent” (Bacon and Watts Reference Bacon and Watts1971, p. 527). Bacon and Watts used the hyperbolic tangent for purposes of illustrating the estimation of smooth transition models.^{Footnote 7}

Another possibility, although far less likely to be considered at the time that Carmichael was writing, is the logistic function, which (along with the exponential function) became the dominant choice in the (much) later work of Teräsvirta and his colleagues. Nevertheless, it is worth making a comparison between the arctan and logistic functions, given the present dominance of the latter as a transition function. The arctan function is close under some choice of parameters to the logistic function, $L\left( x \right) = \gamma /(1\,\, + \,\,\exp ( - \psi x))$, where $L\left( x \right) \to \gamma$ as $x \to \,\,\infty$, for $\psi > 0$. The logistic function was favored at the time in population studies: see, for example, Raymond Pearl and Lowell Reed (Reference Pearl and Reed1923). It was originally developed by Pierre-François Verhulst (Reference Verhulst1845) as an alternative to modelling the growth of a population as exponential, which was unsatisfactory because it was without a limit; in contrast the rate of growth of the logistic was not constant, but depended on how close the population was to its limiting value. Jan Cramer (Reference Cramer2002) notes that the logistic curve was discovered ‘anew’ by Pearl and Reed.

The derivatives of the arctan function are well known: for example, the first derivative with respect to x is

$${{\partial A\left[ . \right]} \over {\partial x}} = {{\partial f\left( x \right)/\partial x} \over {\left( {1 + f{{\left( x \right)}^2}} \right)}}\,{\rm{where}}\,y = a + cA\left[ {f\left( x \right)} \right]$$

$${{\partial A\left[ . \right]} \over {\partial x}} = {1 \over {\left( {1 + {x^2}} \right)}}\,for\,f\left( x \right) = x\,.$$

The derivative of $A\left[ \cdot \right]$ with respect to time (rather than the distance measure x) is

$${{\partial A\left[ . \right]} \over {\partial x}} = {{\left( {\partial f\left( x \right)/\partial x} \right)\left( {\partial x/\partial t} \right)} \over {\left( {1 + f{{\left( t \right)}^2}} \right)}}$$

$${{\partial A\left[ . \right]} \over {\partial t}} = {\delta \over {\left( {1 + f{{\left( t \right)}^2}} \right)}}\,{\rm{for}}\,f\left( t \right) = \delta \left( {t - {t_0}} \right)\,.$$

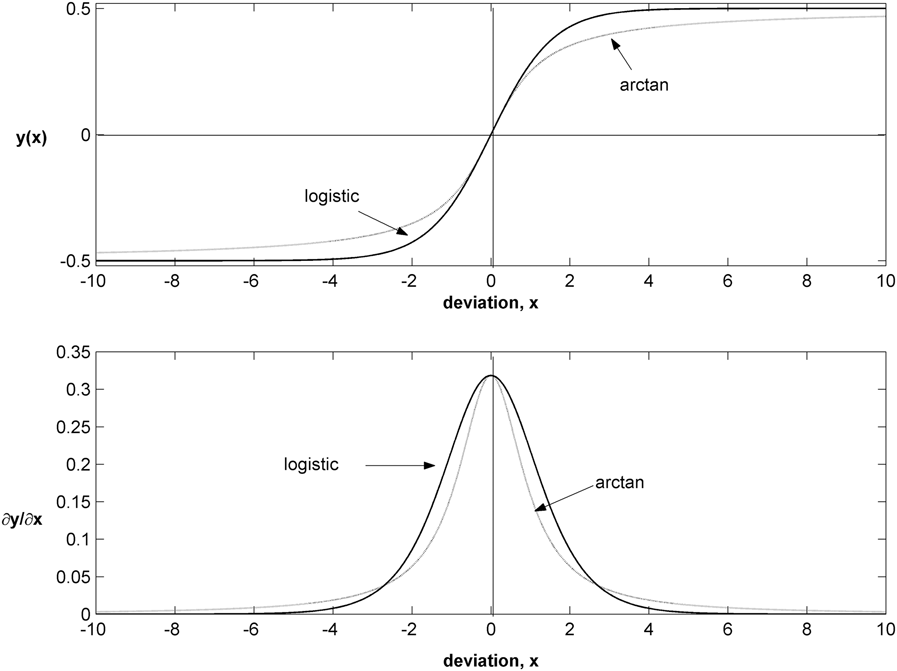
A simple arctan function is illustrated in Figure 2 with its derivative shown in the lower figure; in both cases these are compared with the centred logistic function $L\left( x \right) = {1 \mathord{\left{\vphantom {1 {[1\,\, + \,\,\exp ( - \psi x)]\,\, - \,\,0.5]}}} \right\kern-\nulldelimiterspace} {[1\,\, + \,\,\exp ( - \psi x)]\,\, - \,\,0.5]}}$, so that $L\left( x \right) \to \,\, \pm {\raise0.5ex\hbox{$\scriptstyle 1$kern-0.1em/\kern-0.15elower0.25ex\hbox{$\scriptstyle 2$}}$ for $x\,\, \to \,\, \pm \infty$ (for comparability, the arctan function is in units of radians and the calibration is $\psi = - 4c$, $c = {\pi ^{ - 1}}$). Although $x = 0$ is referred to as the “origin,” being the point at which ${t_0}$ is the origin on the time axis, it is perhaps better described as a switch point, or point of symmetry, where the sign of the first derivative with respect to x (and t) changes from positive to negative: see the lower panel in Figure 2.

Figure 2. Arctan and logistic trends/transition functions.

A relatively recent but important development in time series modelling is the TAR model of Tong (1977, Reference Tong and Hua Chen1978, Reference Tong1983). The basis of the TAR is the autoregressive (AR) model due to Yule (Reference Yule1927), in which the variable of interest, ${y_t}$, is regressed on, say, p lags of itself. A TAR model extends the AR model to allow for more than one regime or state. In the simplest extension the models are distinguished by state. For example, if, for some choice of the lag parameter d, ${y_{t - d}}\,\, < \,\,c$, then the model is generated in state 1; whereas if ${y_{t - d}}\,\, \ge \,\,c$, the model is generated in state 2. The models are distinguished by time if c is replaced by a time index, such that regimes 1 and 2 correspond to ${y_{t - d}}\,\, < \,\,{t_b}$ and ${y_{t - d}}\,\, \ge \,\,{t_b}$, respectively. The general idea is that there is a threshold, respectively c or ${t_b}$, the crossing of which triggers transition between the states/regimes.

The further development of the TAR to have smooth transition, as in Bacon and Watts (Reference Bacon and Watts1971), is due to Chan and Tong (Reference Chan and Tong1986), who introduced the acronym STAR, the S denoting ‘smooth’; their choice of transition function was the cumulative distribution function (cdf) of the normal, which, as the normal distribution is symmetric, gives the classic sigmoid shape.^{Footnote 8} Ritva Lukkonen et al. (Reference Lukkonen, Saikkonen and Teräsvirta1988) noted that using the logistic function, which has analytical derivatives, for the transition function was computationally easier than using the cdf of the normal and, moreover, that the logistic was a good approximation to the normal cdf. In subsequent applications of STAR models, the choice of the logistic function, leading to the acronym LSTAR (with the T sometimes now taken to refer to transition rather than threshold), has dominated the literature; for a review of the many variants of the TAR model, see Bruce Hansen (2007).

V. ESTIMATION

Carmichael’s examples were estimated using graphical inspection for the origin of the switch point and for two or three likely values of $\Delta x$; however, the model is linear given $\delta = \Delta x$ and conditionally on ${t_0}$, so we first define two sets each containing the respective true values, $\delta$ ∈ B and ${t_0} \in$T, and minimize the residual sum of squares $\sum\nolimits_{t = 1}^T {\hat \varepsilon _t^2}$ over B and T: that is ${\min _{{t_0}}}({\min _\delta }\sum\nolimits_{t = 1}^T {\hat \varepsilon _t^2} )$ over the two-dimensional grid formed by the Cartesian product B$\times$T. The resulting estimators are consistent under fairly standard conditions. (The procedure is an application of the principle in Dag Tjostheim [Reference Tjostheim1986], which has been used in various structural break papers that consider all possible break points in a particular sample; see, for example, Donald Andrews [Reference Andrews1993], and Hansen [Reference Hansen2000].) Note that ${t_0}$ is not constrained to lie between 1 and T, and in one of Carmichael’s examples the origin is taken to pre-date the beginning of the sample, in which case ${t_0}$ would be negative.

This method can be extended to a double break and, hence, to two transitions as in Carmichael’s model (3). In this extension it is convenient to define ${\delta _1}\,\, \equiv \,\,\Delta {x_1}$ and ${\delta _2}\,\, \equiv \,\,\Delta {x_2}$, and the corresponding sets ${\delta _1}$∈${B_1}$ and ${\delta _2}$∈${B_2}$; similarly define two origins and corresponding sets for the centred break points, ${t_{0,1}}$∈${T_1}$ and ${t_{0.2}}$∈${T_2}$. The least squares solution then minimizes over ${B_1} \times {B_2} \times {T_1} \times {T_2}$.

While this describes the modern approach, how did Carmichael solve the problem of obtaining estimates of the parameters? From his perspective he was faced with a problem without a practical solution unless it could be simplified. The simplifications came in the form of conditioning the least squares estimates on (a) the origin and (b) the speed of adjustment. In Carmichael’s own words:

Once these choices are made, and together with some consideration of whether the data is best modelled in terms of its original form or its logarithms, the estimation becomes simply that of a linear least squares model. What is evident from Carmichael’s careful prior analysis is the importance of understanding the nuances of movements in the data based on a careful graphical analysis.^{Footnote 9} This supports the views expressed in Jeff Biddle (Reference Biddle1999) and Mary Morgan (Reference Morgan1990) on the use and importance of graphs in the statistical analysis of the period. Moreover, while Carmichael does not report formal measures of the goodness of fit of his proposed trends, he is aware of the need to ‘fit the data well’ in making his choice of functional form and conditioning parameters.

VI. EXAMPLES

We consider two of Carmichael’s examples^{Footnote 10} to illustrate the application of the arctan function and how the selection of the choice parameters can be included in the process. In so doing we are able to see how well Carmichael did from a modern perspective.

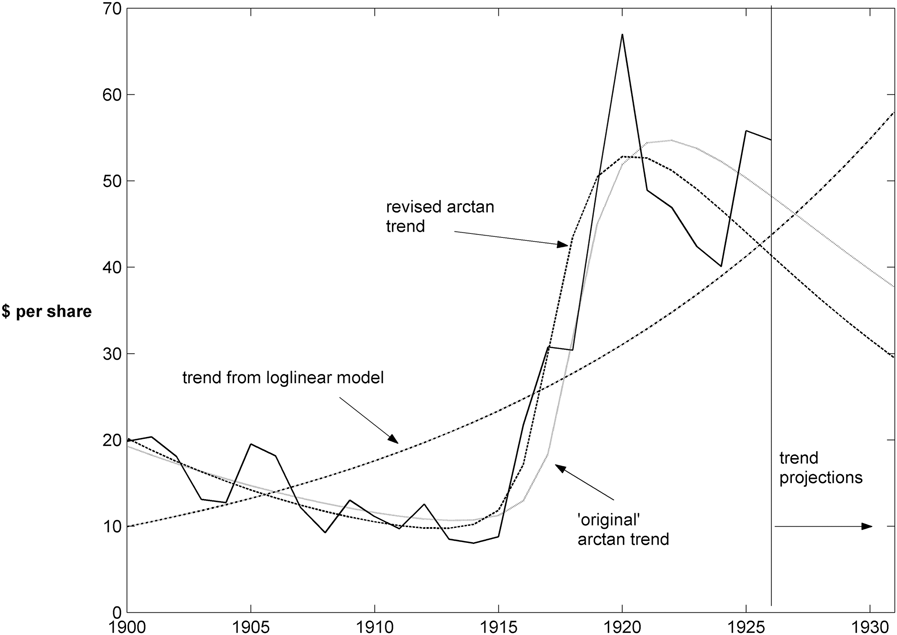
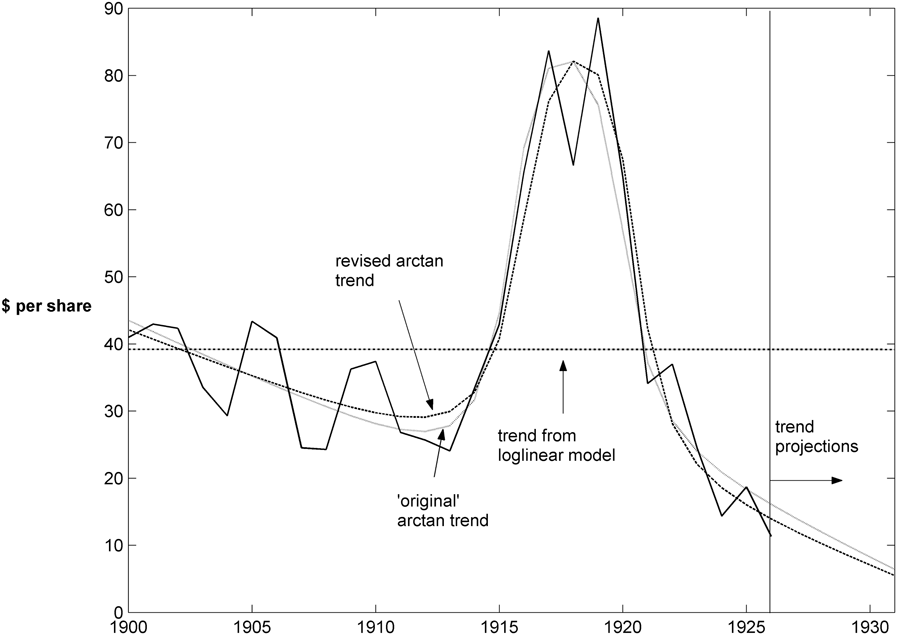
Carmichael’s first example concerns modelling the trend in the common stock price of International Paper, which poses a challenge because neither a linear nor an exponential trend would seem to capture the key trend features of the data, which embody a gradual, but sustained, increase about halfway through the sample period of 1900 to 1926. The data, which are annual and obtained as the yearly average of ‘tenth-of-month’ prices ($ per share), are plotted in Figure 3. Carmichael used logs of the data and obtained his results for choices of $\Delta x = 0.75$ and 0.6; he chose the origin of the switch point by a visual examination of a graph of the data and, by this method, chose the origin to be 25 December 1917 (with 25 June 1917 as a possible alternative). Estimation over the original sample period gives results very close to those reported by Carmichael; see Table 1, rows (1) and (2). The ‘original’ arctan trend is also plotted in Figure 3. To illustrate the difference with the then standard of the day, a linear (in logarithms) trend was also estimated and is also shown on Figure 3. Evidently the implied cycles (residuals) and even fairly short-term projections differ quite markedly, depending on the choice of trend.

Figure 3. Internationl Paper Stock Prices.

Table 1. International Paper common stock: single break, arctan estimation

Notes: logs are to the base 10; the number of decimal places reported follows Carmichael; RSS = residual sum of squares; n.a indicates not available.

Searching over $\delta = \Delta x$ and the origin ${t_0}$ locates the minimum at $\Delta x = 0.71$ and the switch point at ${t_0} =$ 25 December 1916, which is twelve months earlier than Carmichael’s choice; see row (3) of Table 1. This earlier choice is evident in Figure 3, which also shows the revised arctan trend, and picks up the increase in the series noticeably earlier than the ‘original’ arctan trend.

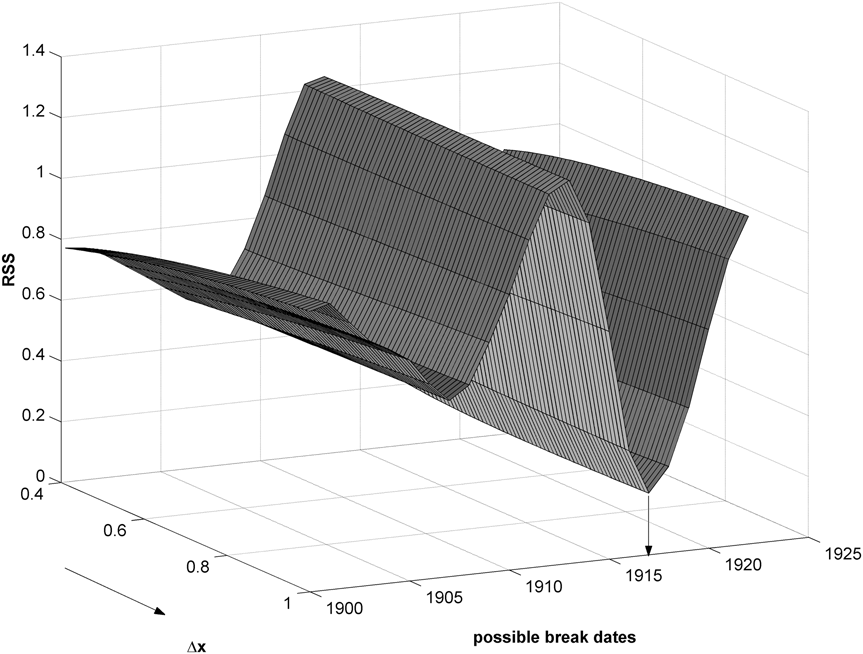
How well did Carmichael do in his original choices? In broad terms, Carmichael came fairly close to the best fitting trend by using his graphical methods. Figure 4 shows the residual sums of squares as a function of the break date and $\Delta x$. Note that the objective function has a distinct valley approaching 1916/1917 (the projection from left to right on the figure), although a choice of 1917/1918 is not far away, and there is also a local minimum much earlier in the sample around 1908, which Carmichael avoids. The objective function is much flatter for the choice of $\Delta x$ (see the projection from right to left), so selecting $\Delta x = 0.75$ is relatively close to the minimum that occurs at $\Delta x = 0.71$; nevertheless the residual sum of squares can be reduced by approximately 25% by moving to the minimum of the RSS function.

Figure 4. Minimising over the break and ∆X.

The second example illustrates Carmichael’s case (3), where a first ‘abrupt’ change is followed by a further change. The series is the price of Central Leather common stock; data are annual from 1900 to 1926, centred on 25 June of each year, and are shown as the unbroken line in Figure 5. In present terminology, the model embodies a double structural break, with smooth transition, the first captured by the arctan function $\arctan (x)$, with origin at $x = 0$, and the second by the arctan function $\arctan (\alpha x\,\, + \,\,\beta )$, with origin at $\alpha x\,\, + \,\,\beta = 0$. Carmichael again selected the break points by graphical methods, which are worth briefly recounting: the point of most rapid rise was identified as 25 December 1915, and that of most rapid decline as 25 June 1920, a difference in time of 4.5 years; the origin of x was, therefore, taken to be the first of these dates, and $\alpha$ and $\beta$ were then determined such that $\alpha x\,\, + \,\,\beta = 0$.

Figure 5. Central Leather Stock Prices.

The parameter $\alpha$ governs the ‘strength’ of the second adjustment function relative to the first, which Carmichael judged to be equal, and on setting $\alpha = 1$ this implies that $\beta = - 4.5$.

The double-switch model was estimated using Carmichael’s parameters and also by extending the search procedure over $\alpha$ and the second switch point (which implicitly determines $\beta$). The results are reported in Table 2. Row (1) constrains the choice parameters as in Carmichael (his reported results are confirmed; see footnote to table). The restrictions are then relaxed in stages: i) keep $\Delta x = 1$, but search for the best double switch points, which results in row (2); ii) constrain the $\Delta x$ to be equal but not equal to 1, which results in $\Delta x = 0.86$ and $\hat \beta = - 4.5$; the estimated switch dates are, however, each one year later than Carmichael’s estimates, although the difference between them is the same. Finally, iii) unrestricted estimation, that is, relax the restriction of equality of the $\Delta x$ in the two arctan functions: see row (3), where $\Delta {x_1}$ and $\Delta {x_2}$ are now distinguished.

Table 2. Central Leather common stock prices: double break, arctan estimation

Notes: Carmichael’s original estimates, $y = 24.47 - 1.7613\arctan (x) - 0.4193\arctan \left( {x - 4.5} \right)$

The results show that Carmichael was again ‘out’ by one year in his timing of the breaks, and relaxing the assumption that $\Delta x = 1$, and then distinguishing $\Delta {x_1}$ and $\Delta {x_2}$, shows that Carmichael overestimated $\Delta x$ for the first break point ($\Delta {x_1} = 0.81$), but was very close in his choice for the second break point ($\Delta {x_2} = 1.03$). However, given the four-dimensional search undertaken across two possible switch points and the values of $\Delta {x_1}$ and $\Delta {x_2}$, Carmichael clearly showed great skill in coming as close as he did to the global minimum in the RSS function. The original and revised trends, including the simple (log)linear trend, are also shown in Figure 5.

VII. CONCLUDING REMARKS

Carmichael’s opening sentence was prescient of present times: “During the past twelve years many economic series have undergone what appears to be a permanent change in level” (Carmichael Reference Carmichael1928, p. 253). As a result he recognized that fitting a simple linear trend to economic time series would often be inadequate and, instead, proposed a simple but effective method of modelling changes by means of smooth transition functions. While this is the language of the present, rather than of the 1920s, Carmichael was clear in his intentions and modelling strategy, of which there were three key principles: to allow continuity in the adjustment rather than a step jump from one regime to another; to use a sigmoid-type adjustment function in which the rate of adjustment varied depending on the stage in the path of adjustment; and to allow for multiple regimes, the number depending on the particular economic circumstances of the case at hand.

In proposing such a strategy Carmichael made a major, but previously unrecognized, contribution to time series analysis. The idea that economic processes may undergo shocks that result in permanent changes was taken up much later, especially in concerns about the implications for testing for unit roots; for example, Perron (Reference Perron1989, Reference Perron1992). The idea of smooth transition between regimes is now a standard part of the modelling ‘toolkit’; and the potential presence of multiple ‘structural breaks’ is a topic that has great relevance in a world of seemingly endless economic and political upheaval.

Moreover, although the technical means of solving the problems he had posed were many years away from Carmichael, his skillful reasoning and understanding of the issues involved in estimating the break date(s) and strength of adjustment of his arctan adjustment mechanism(s) were quite exceptional. A combination of graphical methods (which, as Biddle [Reference Biddle1999] notes, were an important part of the methodology of the era), and analysis of the changes in the data and economic circumstances, led him close to the solutions he would have obtained had he the benefit of modern methods. However, the inherently nonlinear nature of Carmichael’s models was probably a step too far at the time and for some time thereafter. The linear regression model was then, and for much later, the dominant paradigm for analysis. It was not until the 1970s, and even then somewhat hesitantly, that the seeds of nonlinear analysis began to come to fruition; see Tong’s (Reference Tong2010) interesting retrospective. The parallel of such developments with those in computing, especially ‘micro’ or personal computing, seems relevant and related, but is left for others to analyze.