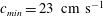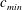1 Introduction
Wind makes gravity–capillary waves on the surface of deep water when both gravity and surface tension are equally important. Because of the large steepness of gravity–capillary waves, the area of the air–sea interface is significantly increased compared to gravity waves. Increase of the interfacial area facilitates mass, momentum and energy transfer between air and water. In addition, the resulting small-scale roughness on the water surface provides important data in the area of microwave remote sensing where the microwave wavelength (1 mm–1 m) is comparable to the scale of the gravity–capillary waves (Zhang Reference Zhang1995). Apart from wind-generated gravity–capillary waves, these waves can be found on the surface of gravity waves whose slopes are generally moderate. When gravity waves are about to break, the crest is steepened and the curvature effect becomes so pronounced that gravity–capillary waves appear on the forward face of breaking gravity waves, usually in the form of spilling-type waves (Duncan Reference Duncan2001). With the important role of gravity–capillary waves in air–sea interface transfer, ocean remote sensing and wave breaking in mind, in this paper, we report our experimental observations of gravity–capillary solitary waves generated by a moving air suction. When both gravity and surface tension are equally important, at a finite wavelength
![]() $\unicode[STIX]{x1D706}_{min}=2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g)^{1/2}=1.71$
cm, the phase speed of linear sinusoidal deep-water gravity–capillary waves is minimal,
$\unicode[STIX]{x1D706}_{min}=2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g)^{1/2}=1.71$
cm, the phase speed of linear sinusoidal deep-water gravity–capillary waves is minimal,
![]() $c_{min}=(4\unicode[STIX]{x1D70E}g/\unicode[STIX]{x1D70C})^{1/4}=23~\text{cm}~\text{s}^{-1}$
, where
$c_{min}=(4\unicode[STIX]{x1D70E}g/\unicode[STIX]{x1D70C})^{1/4}=23~\text{cm}~\text{s}^{-1}$
, where
![]() $g=9.81~\text{m}~\text{s}^{-2}$
is the gravitational acceleration,
$g=9.81~\text{m}~\text{s}^{-2}$
is the gravitational acceleration,
![]() $\unicode[STIX]{x1D70C}=1000~\text{kg}~\text{m}^{-3}$
the water density and
$\unicode[STIX]{x1D70C}=1000~\text{kg}~\text{m}^{-3}$
the water density and
![]() $\unicode[STIX]{x1D70E}=0.073~\text{N}~\text{m}^{-1}$
the surface tension of water. Therefore, if any waves exist with speeds below
$\unicode[STIX]{x1D70E}=0.073~\text{N}~\text{m}^{-1}$
the surface tension of water. Therefore, if any waves exist with speeds below
![]() $c_{min}$
, they will be locally confined nonlinear gravity–capillary solitary waves instead of linear waves. Both 2-D/3-D and depression/elevation-type solitary waves can theoretically exist under the influence of gravity and surface tension. However, most of these waves are unstable to longitudinal or transverse perturbations except finite-amplitude 3-D gravity–capillary waves of depression type. Although longitudinally stable, depression-type 2-D gravity–capillary solitary waves are unstable to transverse perturbation (Kim & Akylas Reference Kim and Akylas2006). Elevation-type 2-D gravity–capillary solitary waves are unstable to both transverse and longitudinal perturbations (Calvo, Yang & Akylas Reference Calvo, Yang and Akylas2000; Calvo & Akylas Reference Calvo and Akylas2002; Kim & Akylas Reference Kim and Akylas2006; Milewski, Vanden-broeck & Wang Reference Milewski, Vanden-broeck and Wang2010). Elevation-type 3-D gravity–capillary solitary waves are unstable to longitudinal perturbation (Akers & Milewski Reference Akers and Milewski2009). Small-amplitude 3-D gravity–capillary solitary waves of depression type are unstable to longitudinal perturbation (Akylas & Cho Reference Akylas and Cho2008; Akers & Milewski Reference Akers and Milewski2008, Reference Akers and Milewski2010). All these unstable solitary waves are predicted to finally evolve into finite-amplitude 3-D gravity–capillary solitary waves of depression type, the only stable ones. Longuet-Higgins and Zhang tried to generate 2-D gravity–capillary solitary waves of depression type by blowing compressed air through a stationary 2-D slit on the surface of deep water that moves with a speed below
$c_{min}$
, they will be locally confined nonlinear gravity–capillary solitary waves instead of linear waves. Both 2-D/3-D and depression/elevation-type solitary waves can theoretically exist under the influence of gravity and surface tension. However, most of these waves are unstable to longitudinal or transverse perturbations except finite-amplitude 3-D gravity–capillary waves of depression type. Although longitudinally stable, depression-type 2-D gravity–capillary solitary waves are unstable to transverse perturbation (Kim & Akylas Reference Kim and Akylas2006). Elevation-type 2-D gravity–capillary solitary waves are unstable to both transverse and longitudinal perturbations (Calvo, Yang & Akylas Reference Calvo, Yang and Akylas2000; Calvo & Akylas Reference Calvo and Akylas2002; Kim & Akylas Reference Kim and Akylas2006; Milewski, Vanden-broeck & Wang Reference Milewski, Vanden-broeck and Wang2010). Elevation-type 3-D gravity–capillary solitary waves are unstable to longitudinal perturbation (Akers & Milewski Reference Akers and Milewski2009). Small-amplitude 3-D gravity–capillary solitary waves of depression type are unstable to longitudinal perturbation (Akylas & Cho Reference Akylas and Cho2008; Akers & Milewski Reference Akers and Milewski2008, Reference Akers and Milewski2010). All these unstable solitary waves are predicted to finally evolve into finite-amplitude 3-D gravity–capillary solitary waves of depression type, the only stable ones. Longuet-Higgins and Zhang tried to generate 2-D gravity–capillary solitary waves of depression type by blowing compressed air through a stationary 2-D slit on the surface of deep water that moves with a speed below
![]() $c_{min}$
(Longuet-Higgins & Zhang Reference Longuet-Higgins and Zhang1997). They found that the lateral or transverse instability keeps the apparent 2-D gravity–capillary solitary waves from being sustainable. This observation has been verified by a few theoretical studies mainly using linear stability analysis with the assumption of small-amplitude transverse perturbations (Bridges Reference Bridges2001; Kim & Akylas Reference Kim and Akylas2007). Although not completely definitive, the first relevant experimental observation of stable 3-D gravity–capillary solitary waves was made by Zhang (Reference Zhang1995). Zhang carried out a closed-top wave tank experiment where compressed air was blown through a nozzle above the water at the upwind end of the tank and drawn by a suction fan at the downwind end of the tank (Zhang Reference Zhang1995). As a result, single or multiple 3-D gravity–capillary solitary waves of depression type are observed on the surface of deep water. In this experiment, wind-like widespread multiple pressure forcings may play a role of a combination of positive (air-blowing) and negative (air-suction) pressure sources in the generation of those solitary waves of depression type. Recently, the generation of these waves by a sole positive pressure forcing has been studied in combined experimental and theoretical works by blowing compressed air through a 3-D nozzle hole that moves horizontally on the surface of deep water with speeds close to
$c_{min}$
(Longuet-Higgins & Zhang Reference Longuet-Higgins and Zhang1997). They found that the lateral or transverse instability keeps the apparent 2-D gravity–capillary solitary waves from being sustainable. This observation has been verified by a few theoretical studies mainly using linear stability analysis with the assumption of small-amplitude transverse perturbations (Bridges Reference Bridges2001; Kim & Akylas Reference Kim and Akylas2007). Although not completely definitive, the first relevant experimental observation of stable 3-D gravity–capillary solitary waves was made by Zhang (Reference Zhang1995). Zhang carried out a closed-top wave tank experiment where compressed air was blown through a nozzle above the water at the upwind end of the tank and drawn by a suction fan at the downwind end of the tank (Zhang Reference Zhang1995). As a result, single or multiple 3-D gravity–capillary solitary waves of depression type are observed on the surface of deep water. In this experiment, wind-like widespread multiple pressure forcings may play a role of a combination of positive (air-blowing) and negative (air-suction) pressure sources in the generation of those solitary waves of depression type. Recently, the generation of these waves by a sole positive pressure forcing has been studied in combined experimental and theoretical works by blowing compressed air through a 3-D nozzle hole that moves horizontally on the surface of deep water with speeds close to
![]() $c_{min}$
(Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011; Cho et al.
Reference Cho, Diorio, Akylas and Duncan2011). Their experiment is the first definitive observation of 3-D stable gravity–capillary solitary waves. They identified three different states according to forcing speed below
$c_{min}$
(Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011; Cho et al.
Reference Cho, Diorio, Akylas and Duncan2011). Their experiment is the first definitive observation of 3-D stable gravity–capillary solitary waves. They identified three different states according to forcing speed below
![]() $c_{min}$
. At relatively low speeds below
$c_{min}$
. At relatively low speeds below
![]() $c_{min}$
, a simple dimple is observed below the moving air-blowing forcing. As the forcing speed increases close to
$c_{min}$
, a simple dimple is observed below the moving air-blowing forcing. As the forcing speed increases close to
![]() $c_{min}$
, however, nonlinear 3-D gravity–capillary solitary waves of depression type are observed, and they move steadily behind and along with the moving forcing. Finally, when the forcing speed is very close to
$c_{min}$
, however, nonlinear 3-D gravity–capillary solitary waves of depression type are observed, and they move steadily behind and along with the moving forcing. Finally, when the forcing speed is very close to
![]() $c_{min}$
, oblique shedding phenomena of 3-D gravity–capillary solitary waves are observed behind the moving forcing. In comparison, however, wave patterns by a sole negative pressure forcing have hardly been studied and this is the main theme of this paper. We carried out a twin experiment similar to Diorio et al.’s (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011); instead of blowing air, however, air is sucked through a 3-D nozzle that moves horizontally on the surface of deep water with speeds close to
$c_{min}$
, oblique shedding phenomena of 3-D gravity–capillary solitary waves are observed behind the moving forcing. In comparison, however, wave patterns by a sole negative pressure forcing have hardly been studied and this is the main theme of this paper. We carried out a twin experiment similar to Diorio et al.’s (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011); instead of blowing air, however, air is sucked through a 3-D nozzle that moves horizontally on the surface of deep water with speeds close to
![]() $c_{min}$
and we thereupon observed resultant wave patterns.
$c_{min}$
and we thereupon observed resultant wave patterns.

Figure 1. Schematic diagram of experimental set-up, (a) side view, (b) front view.
2 Experimental set-up
As mentioned earlier, the present suction experiment is very similar to earlier blowing experiments by Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011). The overall experimental set-up and observation techniques are very similar to each other. Therefore, we describe only the main features of the present experimental set-up. For more details about a relevant experimental set-up and observation techniques, one is recommended to consult with Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011). The present experiments were carried out in a water tank whose dimensions are 4 m in length, 0.9 m in width and 0.6 m in height (see figure 1). The tank wall is made of transparent glass through which side view observation is possible using a high-speed camera. During the whole test, the water depth is fixed to be 0.4 m such that any possible wavelength of linear gravity–capillary waves near 1.71 cm is less than the twice of the water depth (so-called deep-water condition). For the purification of water, we use a commercial water skimmer-filtration device (EHEIM skim 350). This device is easily attached to and detached from the inside walls of the water tank. After filling the tank with water, we attached ten of these devices on the four inside walls of the tank. The vertical positions of the devices are around the free surface. After turning on the devices for several hours, we removed them from the tank walls and performed approximately a one-hour main test. During the one-hour test, the surface tension remained at approximately
![]() $0.073~\text{N}~\text{m}^{-1}$
at
$0.073~\text{N}~\text{m}^{-1}$
at
![]() $25\,^{\circ }\text{C}$
and was measured by a Du Nöuy ring-type tensiometer. After the one-hour test, we repeated this purification process again before the next tests. A carriage is fixed to a belt–pulley system that is installed on top of the water tank. This belt–pulley system is servomotor controlled to move with a constant target speed
$25\,^{\circ }\text{C}$
and was measured by a Du Nöuy ring-type tensiometer. After the one-hour test, we repeated this purification process again before the next tests. A carriage is fixed to a belt–pulley system that is installed on top of the water tank. This belt–pulley system is servomotor controlled to move with a constant target speed
![]() $U$
near
$U$
near
![]() $c_{min}=23~\text{cm}~\text{s}^{-1}$
from right to left. In the preliminary test, to ensure that the computer-input target speed
$c_{min}=23~\text{cm}~\text{s}^{-1}$
from right to left. In the preliminary test, to ensure that the computer-input target speed
![]() $U$
is obtained during the real motion of the whole carriage system, we manually checked the position of the moving carriage from each snapshot at a certain instant extracted from the video-recording data. On average, the error between the computer-input target speed and the observed realized speed is approximately 0.02 %. Since the tank length is 4 m, the duration of each test is about 17 s. This time turns out to be sufficiently long enough to capture any steady state after some transient response from the start. A steel or transparent acrylic pipe (internal diameter
$U$
is obtained during the real motion of the whole carriage system, we manually checked the position of the moving carriage from each snapshot at a certain instant extracted from the video-recording data. On average, the error between the computer-input target speed and the observed realized speed is approximately 0.02 %. Since the tank length is 4 m, the duration of each test is about 17 s. This time turns out to be sufficiently long enough to capture any steady state after some transient response from the start. A steel or transparent acrylic pipe (internal diameter
![]() $D=1.95$
mm) through which air is sucked above the water surface is vertically attached to the moving carriage. Air suction is provided by a commercial vacuum cleaner but, unfortunately, there is no function for fine control of the suction power in this machine. Therefore, the degree of the air suction is varied by the distance (
$D=1.95$
mm) through which air is sucked above the water surface is vertically attached to the moving carriage. Air suction is provided by a commercial vacuum cleaner but, unfortunately, there is no function for fine control of the suction power in this machine. Therefore, the degree of the air suction is varied by the distance (
![]() $h$
) between the still water surface and the vertical positon of the pipe end when the carriage is stationary. Figure 2 shows steady-state profiles of the water surface due to the air suction according to
$h$
) between the still water surface and the vertical positon of the pipe end when the carriage is stationary. Figure 2 shows steady-state profiles of the water surface due to the air suction according to
![]() $h$
when the carriage is stationary. These profiles are observed using a transparent acrylic pipe. In each case, the water surface profile shows uprising steady motion of water. Between the still water surface and the vertical position of the pipe end, the shape of the surface resembles a hump with an increasing slope. The base diameter of a hump (
$h$
when the carriage is stationary. These profiles are observed using a transparent acrylic pipe. In each case, the water surface profile shows uprising steady motion of water. Between the still water surface and the vertical position of the pipe end, the shape of the surface resembles a hump with an increasing slope. The base diameter of a hump (
![]() $b$
) increases as
$b$
) increases as
![]() $h$
increases;
$h$
increases;
![]() $b=6$
mm for
$b=6$
mm for
![]() $h=1.5$
mm,
$h=1.5$
mm,
![]() $b=6.5$
mm for
$b=6.5$
mm for
![]() $h=2$
mm,
$h=2$
mm,
![]() $b=7.4$
mm for
$b=7.4$
mm for
![]() $h=3$
mm,
$h=3$
mm,
![]() $b=7.6$
mm for
$b=7.6$
mm for
![]() $h=3.2$
mm. For
$h=3.2$
mm. For
![]() $h>3.2$
mm, the water surface does not respond to the air suction and remains still. The slope of a hump becomes infinite around the position at the pipe end, and, from this point, a column of uprising water is developed. The diameter (
$h>3.2$
mm, the water surface does not respond to the air suction and remains still. The slope of a hump becomes infinite around the position at the pipe end, and, from this point, a column of uprising water is developed. The diameter (
![]() $d$
) of the water column on top of the water hump becomes smaller as
$d$
) of the water column on top of the water hump becomes smaller as
![]() $h$
increases;
$h$
increases;
![]() $d=0.8$
mm for
$d=0.8$
mm for
![]() $h=1.5$
mm,
$h=1.5$
mm,
![]() $d=0.5$
mm for
$d=0.5$
mm for
![]() $h=2$
mm,
$h=2$
mm,
![]() $d=0.3$
mm for
$d=0.3$
mm for
![]() $h=3$
mm,
$h=3$
mm,
![]() $d=0.2$
mm for
$d=0.2$
mm for
![]() $h=3.2$
mm. At the end of the fully developed water column, a flame-like turbulent pattern of water can be seen as shown in figures 2 and 3. This flame-like turbulent pattern of water at the end of the water column looks more vigorous as
$h=3.2$
mm. At the end of the fully developed water column, a flame-like turbulent pattern of water can be seen as shown in figures 2 and 3. This flame-like turbulent pattern of water at the end of the water column looks more vigorous as
![]() $h$
decreases. The overall height of the water column (including the flame-like end region) changes little and is comparable to each other for different
$h$
decreases. The overall height of the water column (including the flame-like end region) changes little and is comparable to each other for different
![]() $h$
. In addition, the turbulent motion of water inside a pipe does not disrupt the shape of a water hump below the pipe and any wave pattern around the hump, whether the pipe is stationary or not. In the experiment, for operational purposes, the distance
$h$
. In addition, the turbulent motion of water inside a pipe does not disrupt the shape of a water hump below the pipe and any wave pattern around the hump, whether the pipe is stationary or not. In the experiment, for operational purposes, the distance
![]() $h$
between the still water surface and the vertical position of the pipe end is varied to control the degree of air suction with a constant volume flow rate. However, to represent the degree of air suction physically rather than operationally, more appropriate dimensionless parameter can be introduced. Aforementioned observation shows that, as the degree of air suction changes due to the variation of
$h$
between the still water surface and the vertical position of the pipe end is varied to control the degree of air suction with a constant volume flow rate. However, to represent the degree of air suction physically rather than operationally, more appropriate dimensionless parameter can be introduced. Aforementioned observation shows that, as the degree of air suction changes due to the variation of
![]() $h$
, the base diameter
$h$
, the base diameter
![]() $b$
of a hump and the diameter
$b$
of a hump and the diameter
![]() $d$
of the water column on top of the hump changes significantly, but the overall height of the water column on top of the hump changes little. In more detail, as the degree of air suction increases (decreases), the base diameter of a hump
$d$
of the water column on top of the hump changes significantly, but the overall height of the water column on top of the hump changes little. In more detail, as the degree of air suction increases (decreases), the base diameter of a hump
![]() $b$
decreases (increases) and the diameter
$b$
decreases (increases) and the diameter
![]() $d$
of the water column increases (decreases), i.e.
$d$
of the water column increases (decreases), i.e.
![]() $d/b$
increases (decreases);
$d/b$
increases (decreases);
![]() $d/b=0.8/6=0.133$
for
$d/b=0.8/6=0.133$
for
![]() $h=1.5$
mm,
$h=1.5$
mm,
![]() $d/b=0.5/6.5=0.077$
for
$d/b=0.5/6.5=0.077$
for
![]() $h=2$
mm,
$h=2$
mm,
![]() $d/b=0.3/7.4=0.040$
for
$d/b=0.3/7.4=0.040$
for
![]() $h=3$
mm,
$h=3$
mm,
![]() $d/b=0.2/7.6=0.026$
for
$d/b=0.2/7.6=0.026$
for
![]() $h=3.2$
mm. Therefore, we decide to define
$h=3.2$
mm. Therefore, we decide to define
![]() $\unicode[STIX]{x1D6FE}=d/b$
as a forcing parameter such that a stronger/weaker air-suction forcing corresponds to a relatively higher/lower value of
$\unicode[STIX]{x1D6FE}=d/b$
as a forcing parameter such that a stronger/weaker air-suction forcing corresponds to a relatively higher/lower value of
![]() $\unicode[STIX]{x1D6FE}$
. For comparison, in case of air blowing, the resultant water surface shows a clean and gentle Gaussian-like depression as shown in figure 4. As the degree of air blowing increases (decreases), the depth of the depression (
$\unicode[STIX]{x1D6FE}$
. For comparison, in case of air blowing, the resultant water surface shows a clean and gentle Gaussian-like depression as shown in figure 4. As the degree of air blowing increases (decreases), the depth of the depression (
![]() $H$
) increases (decreases). However, not like the air-suction case, the base diameter of the depression changes little as the degree of air blowing changes, which is almost the same as the pipe diameter
$H$
) increases (decreases). However, not like the air-suction case, the base diameter of the depression changes little as the degree of air blowing changes, which is almost the same as the pipe diameter
![]() $D$
. Therefore, as in the earlier blowing experiment (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011), the dimensionless parameter
$D$
. Therefore, as in the earlier blowing experiment (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011), the dimensionless parameter
![]() $\unicode[STIX]{x1D716}=H/D$
has a physical meaning as the slope of a depression, which, in turn, represents the degree of air blowing. In the present experiment, as mentioned earlier, as the degree of air suction increases (decreases), the base diameter of a hump
$\unicode[STIX]{x1D716}=H/D$
has a physical meaning as the slope of a depression, which, in turn, represents the degree of air blowing. In the present experiment, as mentioned earlier, as the degree of air suction increases (decreases), the base diameter of a hump
![]() $b$
decreases (increases) and the diameter
$b$
decreases (increases) and the diameter
![]() $d$
of the water column increases (decreases). Geometrically, this means that the overall slope of a hump increases (decreases) as the degree of air suction increases (decreases). Therefore, the dimensionless parameter
$d$
of the water column increases (decreases). Geometrically, this means that the overall slope of a hump increases (decreases) as the degree of air suction increases (decreases). Therefore, the dimensionless parameter
![]() $\unicode[STIX]{x1D6FE}=d/b$
has a physical meaning with an implication of the slope of a hump, which, in turn, represents the degree of air suction.
$\unicode[STIX]{x1D6FE}=d/b$
has a physical meaning with an implication of the slope of a hump, which, in turn, represents the degree of air suction.

Figure 2. Steady-state profiles of water surface (long-distance and close-up plots) due to the air suction according to the distance (
![]() $h$
) between the still water surface and the vertical position of the pipe end (internal diameter
$h$
) between the still water surface and the vertical position of the pipe end (internal diameter
![]() $D=1.95$
mm) when the carriage is stationary. (a)
$D=1.95$
mm) when the carriage is stationary. (a)
![]() $h=1.5$
mm, (b)
$h=1.5$
mm, (b)
![]() $h=2.0$
mm, (c)
$h=2.0$
mm, (c)
![]() $h=3.0$
mm, (d)
$h=3.0$
mm, (d)
![]() $h=3.2$
mm.
$h=3.2$
mm.

Figure 3. Turbulent motion of water inside a pipe when the carriage is stationary according to the distance (
![]() $h$
) between the still water surface and the vertical position of the pipe end. (a)
$h$
) between the still water surface and the vertical position of the pipe end. (a)
![]() $h=1.5$
mm, (b)
$h=1.5$
mm, (b)
![]() $h=2$
mm, (c)
$h=2$
mm, (c)
![]() $h=3$
mm, (d)
$h=3$
mm, (d)
![]() $h=3.2$
mm. Time difference between each snapshot is 0.02 s.
$h=3.2$
mm. Time difference between each snapshot is 0.02 s.

Figure 4. Steady-state profiles of water surface due to the air blowing through a pipe (internal diameter
![]() $D=1.95$
mm) according to
$D=1.95$
mm) according to
![]() $\unicode[STIX]{x1D716}=H/D$
, where
$\unicode[STIX]{x1D716}=H/D$
, where
![]() $H$
is the depth of the depression when the carriage is stationary. In each figure, the upper image is the reflection of the lower one. (a)
$H$
is the depth of the depression when the carriage is stationary. In each figure, the upper image is the reflection of the lower one. (a)
![]() $\unicode[STIX]{x1D716}=0.31$
, (b)
$\unicode[STIX]{x1D716}=0.31$
, (b)
![]() $\unicode[STIX]{x1D716}=0.41$
, (c)
$\unicode[STIX]{x1D716}=0.41$
, (c)
![]() $\unicode[STIX]{x1D716}=0.51$
.
$\unicode[STIX]{x1D716}=0.51$
.
Surface wave patterns were observed by a high-speed digital camera (Phantom 9.1, Vision Research) equipped with a lens (AF-S VR Micro Nikkor ED 105 mm f/2.8F (IF)). The resolution of the camera is 1632 by 800 pixels, where one pixel size corresponds to the physical dimension of 0.06 mm by 0.06 mm. For the purpose of real-time observation of surface wave patterns, a custom-made aluminium profile structure was designed such that one end of the structure is attached to the moving carriage, and the other end of the structure is positioned outside and near the side tank wall (see figure 1
b). Then, using a commercial arm-type connecter (Manfrotto Variable Friction Arm), we connected the outside-wall end of the structure with the camera, thus positioning it outside and near the front tank wall. During the motion test with this configuration, there exists little apparent vibration and this is confirmed by checking recorded images. When necessary, the camera was positioned on the tripod which was fixed on the laboratory floor. For example, front-view or cross-track images of travelling waves toward the end of the wave tank were obtained by fixing the position of the camera at the end of the tank (see figure 9
b). The shadowgraph technique is adopted for the purpose of visualization of surface wave patterns and they are recorded on the carriage-attached high-speed camera which moves with the same speed as the air-suction forcing. With this experimental set-up, surface wave patterns are observed according to air-suction forcing speeds (
![]() $\unicode[STIX]{x1D6FC}=U/c_{min}$
) for several forcing magnitudes (
$\unicode[STIX]{x1D6FC}=U/c_{min}$
) for several forcing magnitudes (
![]() $\unicode[STIX]{x1D6FE}=d/b$
). The overall size of the resultant wave patterns is of the order of
$\unicode[STIX]{x1D6FE}=d/b$
). The overall size of the resultant wave patterns is of the order of
![]() $O(\unicode[STIX]{x1D706}_{min})\approx 1~\text{cm}$
, which is much smaller than the tank width 0.9 m, with no reflection being observed.
$O(\unicode[STIX]{x1D706}_{min})\approx 1~\text{cm}$
, which is much smaller than the tank width 0.9 m, with no reflection being observed.
3 Results and discussion
3.1 State I and state II

Figure 5. State-I surface wave patterns at zero and relatively low speeds below
![]() $c_{min}$
for the air-suction forcing magnitude
$c_{min}$
for the air-suction forcing magnitude
![]() $\unicode[STIX]{x1D6FE}=0.077$
(
$\unicode[STIX]{x1D6FE}=0.077$
(
![]() $h=2$
mm). Left figures (a–c) are the images from above the water surface for
$h=2$
mm). Left figures (a–c) are the images from above the water surface for
![]() $\unicode[STIX]{x1D6FC}=0$
, 0.91, 0.95, respectively. Right figures (d–f) are the images from below the water surface for
$\unicode[STIX]{x1D6FC}=0$
, 0.91, 0.95, respectively. Right figures (d–f) are the images from below the water surface for
![]() $\unicode[STIX]{x1D6FC}=0$
, 0.91, 0.95, respectively.
$\unicode[STIX]{x1D6FC}=0$
, 0.91, 0.95, respectively.
Figure 5 shows the surface wave patterns at zero and relatively low speeds below
![]() $c_{min}$
for the forcing magnitude
$c_{min}$
for the forcing magnitude
![]() $\unicode[STIX]{x1D6FE}=0.077$
(
$\unicode[STIX]{x1D6FE}=0.077$
(
![]() $h=2$
mm). Figures 5(a–c) and 5(d–f) are the images from above and below the water surface, respectively. In the (d–f), the camera is focused mainly on the depression of water surface. As a result, the elevation of water surface above the still water level is out of focus and thus cannot be seen in the figures. With this visualization limit in mind, the horizontal position of the forcing is marked by a black rectangle. When the forcing is stationary,
$h=2$
mm). Figures 5(a–c) and 5(d–f) are the images from above and below the water surface, respectively. In the (d–f), the camera is focused mainly on the depression of water surface. As a result, the elevation of water surface above the still water level is out of focus and thus cannot be seen in the figures. With this visualization limit in mind, the horizontal position of the forcing is marked by a black rectangle. When the forcing is stationary,
![]() $\unicode[STIX]{x1D6FC}=0$
, a symmetric water hump is seen just below the air-suction forcing (figure 5
a,d). For a non-stationary case, at forcing speed
$\unicode[STIX]{x1D6FC}=0$
, a symmetric water hump is seen just below the air-suction forcing (figure 5
a,d). For a non-stationary case, at forcing speed
![]() $\unicode[STIX]{x1D6FC}=0.91$
, just below the left-moving air-suction forcing is seen a steady weakly asymmetric water hump along with a small-amplitude circular depression (0.06 mm deep) ahead of it, which does not exist for a stationary forcing case (figure 5
b,e). At forcing speed
$\unicode[STIX]{x1D6FC}=0.91$
, just below the left-moving air-suction forcing is seen a steady weakly asymmetric water hump along with a small-amplitude circular depression (0.06 mm deep) ahead of it, which does not exist for a stationary forcing case (figure 5
b,e). At forcing speed
![]() $\unicode[STIX]{x1D6FC}=0.95$
, a similar wave pattern is observed with a deeper circular depression (1mm deep) ahead of the moving forcing (figure 5
c,f). The aforementioned are linear steady-state phenomena and we refer to this state as state I. Here, the word ‘linear’ is used for state I since this state can be theoretically predicted by a ‘linear’ wave (4.2) by setting nonlinear term zero as shown in figure 15(c). The state names I, II and III are used in the previous blowing experiments in Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011). There, state I is the state where there are no genuine waves and only isolated dimple exists below the moving blowing forcing. In terms of the overall surface pattern, there is no difference between the stationary and non-stationary cases of state I. For a fixed-magnitude blowing forcing, as the forcing speed increases from zero to a certain value near the minimum phase speed
$\unicode[STIX]{x1D6FC}=0.95$
, a similar wave pattern is observed with a deeper circular depression (1mm deep) ahead of the moving forcing (figure 5
c,f). The aforementioned are linear steady-state phenomena and we refer to this state as state I. Here, the word ‘linear’ is used for state I since this state can be theoretically predicted by a ‘linear’ wave (4.2) by setting nonlinear term zero as shown in figure 15(c). The state names I, II and III are used in the previous blowing experiments in Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011). There, state I is the state where there are no genuine waves and only isolated dimple exists below the moving blowing forcing. In terms of the overall surface pattern, there is no difference between the stationary and non-stationary cases of state I. For a fixed-magnitude blowing forcing, as the forcing speed increases from zero to a certain value near the minimum phase speed
![]() $c_{min}$
, the depth of the dimple linearly increases until the transition to a nonlinear state II occurs. Similarly, for a fixed-magnitude suction forcing, as the forcing speed increases from zero to a certain value near the minimum phase speed
$c_{min}$
, the depth of the dimple linearly increases until the transition to a nonlinear state II occurs. Similarly, for a fixed-magnitude suction forcing, as the forcing speed increases from zero to a certain value near the minimum phase speed
![]() $c_{min}$
, the depth of the dimple in front of the moving forcing linearly increases until the transition to a nonlinear state II occurs. Therefore, noting the lack of complete consistency in naming state I for the linear states between blowing and suction cases, we adopt the same naming state I in that the surface patterns are linear in both cases.
$c_{min}$
, the depth of the dimple in front of the moving forcing linearly increases until the transition to a nonlinear state II occurs. Therefore, noting the lack of complete consistency in naming state I for the linear states between blowing and suction cases, we adopt the same naming state I in that the surface patterns are linear in both cases.

Figure 6. State-II surface wave patterns at speeds close to
![]() $c_{min}$
for the air-suction forcing magnitude
$c_{min}$
for the air-suction forcing magnitude
![]() $\unicode[STIX]{x1D6FE}=0.077$
(
$\unicode[STIX]{x1D6FE}=0.077$
(
![]() $h=2.0$
mm). Left figures (a–c) are the images from above the water surface for
$h=2.0$
mm). Left figures (a–c) are the images from above the water surface for
![]() $\unicode[STIX]{x1D6FC}=0.96$
, 0.965, 0.97, respectively. Right figures (d–f) are the images from below the water surface for
$\unicode[STIX]{x1D6FC}=0.96$
, 0.965, 0.97, respectively. Right figures (d–f) are the images from below the water surface for
![]() $\unicode[STIX]{x1D6FC}=0.96$
, 0.965, 0.97, respectively.
$\unicode[STIX]{x1D6FC}=0.96$
, 0.965, 0.97, respectively.

Figure 7. Slanted top view of surface wave patterns at (a)
![]() $\unicode[STIX]{x1D6FC}=0.95$
and (b)
$\unicode[STIX]{x1D6FC}=0.95$
and (b)
![]() $\unicode[STIX]{x1D6FC}=0.96$
for the air-suction forcing
$\unicode[STIX]{x1D6FC}=0.96$
for the air-suction forcing
![]() $\unicode[STIX]{x1D6FE}=0.077$
. The upward arrows denote the positions of the air suctions.
$\unicode[STIX]{x1D6FE}=0.077$
. The upward arrows denote the positions of the air suctions.

Figure 8. Numerically computed 3-D gravity–capillary solitary wave solution to (3.1) for
![]() $\unicode[STIX]{x1D6FC}=0.96$
. (a) Slanted top view. The arrow denotes the direction of wave propagation. (b) Centreline profiles (solid line: centreline profile in the streamwise direction, dashed line: centreline profile in the transverse direction).
$\unicode[STIX]{x1D6FC}=0.96$
. (a) Slanted top view. The arrow denotes the direction of wave propagation. (b) Centreline profiles (solid line: centreline profile in the streamwise direction, dashed line: centreline profile in the transverse direction).

Figure 9. Side-view (along-track), front-view (cross-track) and slanted top-view wave profiles for the air-suction forcing
![]() $\unicode[STIX]{x1D6FE}=0.077$
, and
$\unicode[STIX]{x1D6FE}=0.077$
, and
![]() $\unicode[STIX]{x1D6FC}=0.96$
. (a) Along-track wave profiles (dashed line: figure 8
b). (b) Cross-track wave profiles (dashed line: figure 8
b). The upward arrows denote the positions of the air suctions. (c) Wave profiles obtained from the slanted top view of the air-suction experiment. (d) Wave profiles computed from the inviscid forcing-free model (3.1) (figure 8
a).
$\unicode[STIX]{x1D6FC}=0.96$
. (a) Along-track wave profiles (dashed line: figure 8
b). (b) Cross-track wave profiles (dashed line: figure 8
b). The upward arrows denote the positions of the air suctions. (c) Wave profiles obtained from the slanted top view of the air-suction experiment. (d) Wave profiles computed from the inviscid forcing-free model (3.1) (figure 8
a).
As the forcing speed is increased to
![]() $\unicode[STIX]{x1D6FC}=0.96$
and further to
$\unicode[STIX]{x1D6FC}=0.96$
and further to
![]() $\unicode[STIX]{x1D6FC}=0.97$
, completely different wave patterns are observed as shown in figure 6. At forcing speed
$\unicode[STIX]{x1D6FC}=0.97$
, completely different wave patterns are observed as shown in figure 6. At forcing speed
![]() $\unicode[STIX]{x1D6FC}=0.96$
, just below the left-moving air-suction forcing is seen a steady strongly asymmetric water hump along with a finite-amplitude or a relatively steeper transversely elongated non-circular depression (2 mm deep) ahead of it (figure 6
a,d). Figure 7 shows the slanted top-view wave patterns at
$\unicode[STIX]{x1D6FC}=0.96$
, just below the left-moving air-suction forcing is seen a steady strongly asymmetric water hump along with a finite-amplitude or a relatively steeper transversely elongated non-circular depression (2 mm deep) ahead of it (figure 6
a,d). Figure 7 shows the slanted top-view wave patterns at
![]() $\unicode[STIX]{x1D6FC}=0.95$
and
$\unicode[STIX]{x1D6FC}=0.95$
and
![]() $\unicode[STIX]{x1D6FC}=0.96$
and they are topologically different from each other. As the forcing speed increases, the depth of this nonlinear depression decreases (figure 6
b,e for
$\unicode[STIX]{x1D6FC}=0.96$
and they are topologically different from each other. As the forcing speed increases, the depth of this nonlinear depression decreases (figure 6
b,e for
![]() $\unicode[STIX]{x1D6FC}=0.965$
, figure 6
c,f for
$\unicode[STIX]{x1D6FC}=0.965$
, figure 6
c,f for
![]() $\unicode[STIX]{x1D6FC}=0.97$
). In addition, the position of this depression approaches the forcing position as the forcing speed increases. All these are nonlinear steady-state phenomena and we refer to this state as state II, the same denotation used in the previous blowing experiment in Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011). For comparison, for the air-blowing case, very similar 3-D nonlinear depression waves are observed ‘behind’ the moving forcing instead of ‘ahead of’ the moving forcing (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011). In particular, the shapes of the observed 3-D nonlinear depression waves in the blowing case are similar to the freely propagating 3-D gravity–capillary solitary waves obtained from the solution to the inviscid forcing-free full water-wave equations or Euler equations (Parau, Vanden-Broeck & Cooker Reference Parau, Vanden-Broeck and Cooker2005, figure 10 in Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2011). Based on the similitude of their appearances, we first infer that the 3-D nonlinear depression waves in the present suction case are also 3-D gravity–capillary solitary waves. To confirm that these steady steep depressions in state II are indeed 3-D gravity–capillary solitary waves, we compare measured wave profiles with the wave profiles of the following model equation whose solutions are depression-type inviscid forcing-free nonlinear 3-D gravity–capillary solitary waves (the detailed derivation is given in appendix A):
$\unicode[STIX]{x1D6FC}=0.97$
). In addition, the position of this depression approaches the forcing position as the forcing speed increases. All these are nonlinear steady-state phenomena and we refer to this state as state II, the same denotation used in the previous blowing experiment in Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011). For comparison, for the air-blowing case, very similar 3-D nonlinear depression waves are observed ‘behind’ the moving forcing instead of ‘ahead of’ the moving forcing (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011). In particular, the shapes of the observed 3-D nonlinear depression waves in the blowing case are similar to the freely propagating 3-D gravity–capillary solitary waves obtained from the solution to the inviscid forcing-free full water-wave equations or Euler equations (Parau, Vanden-Broeck & Cooker Reference Parau, Vanden-Broeck and Cooker2005, figure 10 in Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2011). Based on the similitude of their appearances, we first infer that the 3-D nonlinear depression waves in the present suction case are also 3-D gravity–capillary solitary waves. To confirm that these steady steep depressions in state II are indeed 3-D gravity–capillary solitary waves, we compare measured wave profiles with the wave profiles of the following model equation whose solutions are depression-type inviscid forcing-free nonlinear 3-D gravity–capillary solitary waves (the detailed derivation is given in appendix A):
Here,
![]() $\unicode[STIX]{x1D702}(x,y)$
is the dimensionless wave elevation,
$\unicode[STIX]{x1D702}(x,y)$
is the dimensionless wave elevation,
![]() $y$
is the dimensionless transverse coordinate to the dimensionless moving reference frame
$y$
is the dimensionless transverse coordinate to the dimensionless moving reference frame
![]() $x$
and
$x$
and
![]() ${\mathcal{H}}\{f\}={\mathcal{F}}^{-1}\{-\text{i}\text{sgn}(k){\mathcal{F}}(f)\}$
is the Hilbert transform, with
${\mathcal{H}}\{f\}={\mathcal{F}}^{-1}\{-\text{i}\text{sgn}(k){\mathcal{F}}(f)\}$
is the Hilbert transform, with
being the Fourier transform. The subscript denotes partial differentiation. For a dimensional result, the characteristic length
![]() $L=(\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g)^{1/2}=2.73$
mm needs to be multiplied. Figure 8 shows a 3-D gravity–capillary solitary wave solution to (3.1) for
$L=(\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g)^{1/2}=2.73$
mm needs to be multiplied. Figure 8 shows a 3-D gravity–capillary solitary wave solution to (3.1) for
![]() $\unicode[STIX]{x1D6FC}=0.96$
. Figure 8(a) is a slanted top view of the solitary wave and figure 8(b) shows the centreline profiles of the solitary wave, where solid and dashed lines represent the centreline profiles in the streamwise and transverse directions, respectively. The numerical method adopted is spectral method (Cho Reference Cho2015) and the dimensionless grid sizes are
$\unicode[STIX]{x1D6FC}=0.96$
. Figure 8(a) is a slanted top view of the solitary wave and figure 8(b) shows the centreline profiles of the solitary wave, where solid and dashed lines represent the centreline profiles in the streamwise and transverse directions, respectively. The numerical method adopted is spectral method (Cho Reference Cho2015) and the dimensionless grid sizes are
![]() $\unicode[STIX]{x0394}x=0.37$
,
$\unicode[STIX]{x0394}x=0.37$
,
![]() $\unicode[STIX]{x0394}y=0.49$
in the numerical computation. Similar results are obtained using the full water-wave equations or Euler equations as was done in Parau et al. (Reference Parau, Vanden-Broeck and Cooker2005). Figure 9(a,b) shows side-view (along-track) and front-view (cross-track) wave profiles measured from the experiment for the air-suction forcing
$\unicode[STIX]{x0394}y=0.49$
in the numerical computation. Similar results are obtained using the full water-wave equations or Euler equations as was done in Parau et al. (Reference Parau, Vanden-Broeck and Cooker2005). Figure 9(a,b) shows side-view (along-track) and front-view (cross-track) wave profiles measured from the experiment for the air-suction forcing
![]() $\unicode[STIX]{x1D6FE}=0.077$
and
$\unicode[STIX]{x1D6FE}=0.077$
and
![]() $\unicode[STIX]{x1D6FC}=0.96$
, which are compared with inviscid forcing-free solitary wave centreline profiles (figure 8
b). In the figures, the upward arrows denote the positions of the air suctions. As shown, the along-track and cross-track wave profiles show very good agreement between the measurement and the computation based on the (3.1). Figure 9(c) is a slanted top-view wave pattern observed in the experiment and figure 9(d) is a slanted top-view solitary wave pattern of inviscid forcing-free solitary waves (figure 8
a). The overall wave patterns and sizes are comparable to each other. Therefore, one can conclude that the steady steep depressions in state II are indeed 3-D gravity–capillary solitary waves.
$\unicode[STIX]{x1D6FC}=0.96$
, which are compared with inviscid forcing-free solitary wave centreline profiles (figure 8
b). In the figures, the upward arrows denote the positions of the air suctions. As shown, the along-track and cross-track wave profiles show very good agreement between the measurement and the computation based on the (3.1). Figure 9(c) is a slanted top-view wave pattern observed in the experiment and figure 9(d) is a slanted top-view solitary wave pattern of inviscid forcing-free solitary waves (figure 8
a). The overall wave patterns and sizes are comparable to each other. Therefore, one can conclude that the steady steep depressions in state II are indeed 3-D gravity–capillary solitary waves.

Figure 10. Depth of the depressions of states I and II according to forcing speeds
![]() $\unicode[STIX]{x1D6FC}$
for different magnitudes of the air-suction forcing (
$\unicode[STIX]{x1D6FC}$
for different magnitudes of the air-suction forcing (
![]() $\unicode[STIX]{x1D6FE}=0.026$
(
$\unicode[STIX]{x1D6FE}=0.026$
(
In figure 10(a), the maximum value of depths of the depressions in states I and II, denoted by
![]() $a_{max}$
, are plotted according to forcing speeds for different magnitudes of the air-suction forcing (
$a_{max}$
, are plotted according to forcing speeds for different magnitudes of the air-suction forcing (
![]() $\unicode[STIX]{x1D6FE}=0.026$
, 0.040, 0.077, 0.133). For a fixed magnitude of the suction forcing, as the forcing speed increases, the depth of the depression gradually increases (state I). However, at the critical speed (
$\unicode[STIX]{x1D6FE}=0.026$
, 0.040, 0.077, 0.133). For a fixed magnitude of the suction forcing, as the forcing speed increases, the depth of the depression gradually increases (state I). However, at the critical speed (
![]() $\unicode[STIX]{x1D6FC}_{crit}$
), there exists a jump in the increment of the depth of the depression. After this critical speed, the depth of the depression gradually decreases with increasing forcing speed (state II). The critical speed where the transition occurs from state I to state II increases as the magnitude of the suction forcing decreases or
$\unicode[STIX]{x1D6FC}_{crit}$
), there exists a jump in the increment of the depth of the depression. After this critical speed, the depth of the depression gradually decreases with increasing forcing speed (state II). The critical speed where the transition occurs from state I to state II increases as the magnitude of the suction forcing decreases or
![]() $\unicode[STIX]{x1D6FE}$
decreases;
$\unicode[STIX]{x1D6FE}$
decreases;
![]() $\unicode[STIX]{x1D6FC}_{crit}=0.94$
for
$\unicode[STIX]{x1D6FC}_{crit}=0.94$
for
![]() $\unicode[STIX]{x1D6FE}=0.133$
,
$\unicode[STIX]{x1D6FE}=0.133$
,
![]() $\unicode[STIX]{x1D6FC}_{crit}=0.956$
for
$\unicode[STIX]{x1D6FC}_{crit}=0.956$
for
![]() $\unicode[STIX]{x1D6FE}=0.077$
,
$\unicode[STIX]{x1D6FE}=0.077$
,
![]() $\unicode[STIX]{x1D6FC}_{crit}=0.96$
for
$\unicode[STIX]{x1D6FC}_{crit}=0.96$
for
![]() $\unicode[STIX]{x1D6FE}=0.040$
. For state I, the overall depth of the depression increases as the magnitude of the suction forcing increases. However, for state II, the depth of the depression does not depend on the forcing magnitude, and falls on or close to a single curve (solid). The single curve for the depth of the depression is predicted by the model (3.1). Near
$\unicode[STIX]{x1D6FE}=0.040$
. For state I, the overall depth of the depression increases as the magnitude of the suction forcing increases. However, for state II, the depth of the depression does not depend on the forcing magnitude, and falls on or close to a single curve (solid). The single curve for the depth of the depression is predicted by the model (3.1). Near
![]() $\unicode[STIX]{x1D6FC}=1$
, the solid curve is connected to the dashed curve which is predicted by the nonlinear Schrödinger (NLS) (A 12) which is reduced from both the model (3.1) and from the full water-wave or Euler equations. As shown, the depressions experimentally observed in state II are confirmed to be nonlinear 3-D gravity–capillary solitary waves of depression type predicted by the theory and the associated computation. Similar results have been reported for the case of air-blowing forcing (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011). When the air-blowing forcing speed is low, small-amplitude circular depressions are observed just below the moving forcing (state I). As the air-blowing forcing speed is further increased, finite-amplitude non-circular depressions or nonlinear 3-D gravity–capillary solitary waves are observed behind the moving forcing (state II). By carrying out an independent experiment using compressed air, we also obtained the same result as Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011), which are shown in the upper group in figure 10(a). Again, the depth of the depressions in states II obtained from the air blowing falls on or close to the single curve which is theoretically predicted by the above mentioned model (3.1). Therefore, 3-D gravity–capillary solitary waves of depression type can be generated not only behind a moving air-blowing forcing (see figure 10
b,c for
$\unicode[STIX]{x1D6FC}=1$
, the solid curve is connected to the dashed curve which is predicted by the nonlinear Schrödinger (NLS) (A 12) which is reduced from both the model (3.1) and from the full water-wave or Euler equations. As shown, the depressions experimentally observed in state II are confirmed to be nonlinear 3-D gravity–capillary solitary waves of depression type predicted by the theory and the associated computation. Similar results have been reported for the case of air-blowing forcing (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011). When the air-blowing forcing speed is low, small-amplitude circular depressions are observed just below the moving forcing (state I). As the air-blowing forcing speed is further increased, finite-amplitude non-circular depressions or nonlinear 3-D gravity–capillary solitary waves are observed behind the moving forcing (state II). By carrying out an independent experiment using compressed air, we also obtained the same result as Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011), which are shown in the upper group in figure 10(a). Again, the depth of the depressions in states II obtained from the air blowing falls on or close to the single curve which is theoretically predicted by the above mentioned model (3.1). Therefore, 3-D gravity–capillary solitary waves of depression type can be generated not only behind a moving air-blowing forcing (see figure 10
b,c for
![]() $\unicode[STIX]{x1D6FC}=0.93$
and
$\unicode[STIX]{x1D6FC}=0.93$
and
![]() $\unicode[STIX]{x1D716}=0.35$
), but also ahead of a moving air-suction forcing (see figure 10
d,e for
$\unicode[STIX]{x1D716}=0.35$
), but also ahead of a moving air-suction forcing (see figure 10
d,e for
![]() $\unicode[STIX]{x1D6FC}=0.965$
and
$\unicode[STIX]{x1D6FC}=0.965$
and
![]() $\unicode[STIX]{x1D6FE}=0.077$
).
$\unicode[STIX]{x1D6FE}=0.077$
).
3.2 State III
As the forcing speed approaches close to
![]() $c_{min}$
, another transition from state II occurs, which is characterized as a periodic shedding of 3-D gravity–capillary solitary waves in the oblique direction downstream ahead of the left-moving forcing. Figure 11 shows one shedding sequence of the depression solitary waves for the forcing speed
$c_{min}$
, another transition from state II occurs, which is characterized as a periodic shedding of 3-D gravity–capillary solitary waves in the oblique direction downstream ahead of the left-moving forcing. Figure 11 shows one shedding sequence of the depression solitary waves for the forcing speed
![]() $\unicode[STIX]{x1D6FC}=0.995$
and the forcing magnitude
$\unicode[STIX]{x1D6FC}=0.995$
and the forcing magnitude
![]() $\unicode[STIX]{x1D6FE}=0.077$
. Initially, a state-II-like depression is seen ahead of and very close to the moving forcing (figure 11
a). Then, this depression is transformed itself into two disturbances which start to move in the oblique direction (figure 11
b). Next, these disturbances are further stretched out making a ‘V’ pattern on the water surface (figure 11
c,d). Thereafter, two depression solitary waves are shed from the tips of the V-shape pattern (figure 11
e). Finally, these shed solitary waves gradually disappear due to viscous dissipation, and, at the same time, another depression is being prepared ahead of the moving forcing (figure 11
f). The process from figures 11(a) to 11(f) is a usual one shedding sequence of gravity–capillary solitary waves. However, sometimes, at the end of one shedding sequence, we observed that the thread of water column above the water hump suddenly ‘snaps’ and the water hump collapses instantaneously (figure 11
g). Then, after a short time, the water hump ‘sticks’ to the air-suction hole again (figure 11
h). Once it happens, the ‘snap-stick’ phenomena are repeated with a period of about 0.09 s and no shedding happens any longer. These snap-stick phenomena are not observed for the relatively strong air-suction forcing magnitude
$\unicode[STIX]{x1D6FE}=0.077$
. Initially, a state-II-like depression is seen ahead of and very close to the moving forcing (figure 11
a). Then, this depression is transformed itself into two disturbances which start to move in the oblique direction (figure 11
b). Next, these disturbances are further stretched out making a ‘V’ pattern on the water surface (figure 11
c,d). Thereafter, two depression solitary waves are shed from the tips of the V-shape pattern (figure 11
e). Finally, these shed solitary waves gradually disappear due to viscous dissipation, and, at the same time, another depression is being prepared ahead of the moving forcing (figure 11
f). The process from figures 11(a) to 11(f) is a usual one shedding sequence of gravity–capillary solitary waves. However, sometimes, at the end of one shedding sequence, we observed that the thread of water column above the water hump suddenly ‘snaps’ and the water hump collapses instantaneously (figure 11
g). Then, after a short time, the water hump ‘sticks’ to the air-suction hole again (figure 11
h). Once it happens, the ‘snap-stick’ phenomena are repeated with a period of about 0.09 s and no shedding happens any longer. These snap-stick phenomena are not observed for the relatively strong air-suction forcing magnitude
![]() $\unicode[STIX]{x1D6FE}=0.133$
. Apart from these snap-stick phenomena, the usual shedding phenomena (figure 11
a–f) are nonlinear unsteady phenomena and we refer to this state as state III, the same denotation used in the previous blowing experiments in Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011). For comparison, for the air-blowing case, similar shedding phenomena occur ‘behind’ the moving forcing instead of ‘ahead of’ the moving forcing (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011).
$\unicode[STIX]{x1D6FE}=0.133$
. Apart from these snap-stick phenomena, the usual shedding phenomena (figure 11
a–f) are nonlinear unsteady phenomena and we refer to this state as state III, the same denotation used in the previous blowing experiments in Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2009) and Diorio et al. (Reference Diorio, Cho, Duncan and Akylas2011). For comparison, for the air-blowing case, similar shedding phenomena occur ‘behind’ the moving forcing instead of ‘ahead of’ the moving forcing (Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011).

Figure 11. (a–f) One shedding sequence of the depression solitary waves in state III for the air-suction forcing (
![]() $\unicode[STIX]{x1D6FE}=0.077$
) with speed
$\unicode[STIX]{x1D6FE}=0.077$
) with speed
![]() $\unicode[STIX]{x1D6FC}=0.995$
. Each snapshot is separated by 0.26 s. (g,h) ‘Snap-stick’ phenomenon which sometimes occurs after the usual shedding sequence. Once it happens, the snap-stick phenomenon repeats itself with a period of 0.09 s and no shedding happens any longer.
$\unicode[STIX]{x1D6FC}=0.995$
. Each snapshot is separated by 0.26 s. (g,h) ‘Snap-stick’ phenomenon which sometimes occurs after the usual shedding sequence. Once it happens, the snap-stick phenomenon repeats itself with a period of 0.09 s and no shedding happens any longer.

Figure 12. State between II and III for the air-suction forcing (
![]() $\unicode[STIX]{x1D6FE}=0.077$
) with speed
$\unicode[STIX]{x1D6FE}=0.077$
) with speed
![]() $\unicode[STIX]{x1D6FC}=0.978$
. A repeated state II exists due to the repeated snap-stick phenomena of the water hump below the moving forcing. Each snapshot is separated by 0.143 s.
$\unicode[STIX]{x1D6FC}=0.978$
. A repeated state II exists due to the repeated snap-stick phenomena of the water hump below the moving forcing. Each snapshot is separated by 0.143 s.
3.3 State between II and III
In addition to states II and III, a careful observation reveals that there exists another state in the narrow speed range between these two. For example, for the air-suction forcing magnitude
![]() $\unicode[STIX]{x1D6FE}=0.077$
, state II occurs when
$\unicode[STIX]{x1D6FE}=0.077$
, state II occurs when
![]() $0.95<\unicode[STIX]{x1D6FC}<0.97$
and state III occurs when
$0.95<\unicode[STIX]{x1D6FC}<0.97$
and state III occurs when
![]() $0.98<\unicode[STIX]{x1D6FC}<1$
. Then, in the narrow speed range
$0.98<\unicode[STIX]{x1D6FC}<1$
. Then, in the narrow speed range
![]() $0.97<\unicode[STIX]{x1D6FC}<0.98$
, for example, for
$0.97<\unicode[STIX]{x1D6FC}<0.98$
, for example, for
![]() $\unicode[STIX]{x1D6FC}=0.978$
, we observed snap-stick phenomena similar to the aforementioned ones in state III. Figure 12 shows one sequence of this state. Initially, a steady state-II depression is seen ahead of and very close to the water hump below the moving forcing (figure 12
a). As shown in figure 2(b), a thread of water column exists on top of this water hump. After a short time, this thread of water column suddenly snaps (figure 12
b). The water hump and the solitary wave ahead of it then collapse together (figure 12
c). Next, after almost the same time interval during which the collapse occurs, they appear together and, in particular, the water hump instantaneously sticks to the air-suction hole again (figure 12
d,e). Finally, the surface pattern returns to the initial state (figure 12
f). In summary, a repeated state II exists due to the repeated snap-stick phenomena of the water hump below the moving forcing. These states are marked as a thin-lined symbol in figure 10(a). These phenomena are not observed for the relatively strong air-suction forcing magnitudes
$\unicode[STIX]{x1D6FC}=0.978$
, we observed snap-stick phenomena similar to the aforementioned ones in state III. Figure 12 shows one sequence of this state. Initially, a steady state-II depression is seen ahead of and very close to the water hump below the moving forcing (figure 12
a). As shown in figure 2(b), a thread of water column exists on top of this water hump. After a short time, this thread of water column suddenly snaps (figure 12
b). The water hump and the solitary wave ahead of it then collapse together (figure 12
c). Next, after almost the same time interval during which the collapse occurs, they appear together and, in particular, the water hump instantaneously sticks to the air-suction hole again (figure 12
d,e). Finally, the surface pattern returns to the initial state (figure 12
f). In summary, a repeated state II exists due to the repeated snap-stick phenomena of the water hump below the moving forcing. These states are marked as a thin-lined symbol in figure 10(a). These phenomena are not observed for the relatively strong air-suction forcing magnitudes
![]() $\unicode[STIX]{x1D6FE}=0.133$
. In the previous sections, we see that there exist three states (states I, II and III) for a relatively strong forcing (
$\unicode[STIX]{x1D6FE}=0.133$
. In the previous sections, we see that there exist three states (states I, II and III) for a relatively strong forcing (
![]() $\unicode[STIX]{x1D6FE}=0.133$
) and there exist four states (states I, II, III and repeated state II) for intermediate forcings (
$\unicode[STIX]{x1D6FE}=0.133$
) and there exist four states (states I, II, III and repeated state II) for intermediate forcings (
![]() $\unicode[STIX]{x1D6FE}=0.077$
, 0.040). Compared to these, when the forcing is relatively weak (
$\unicode[STIX]{x1D6FE}=0.077$
, 0.040). Compared to these, when the forcing is relatively weak (
![]() $\unicode[STIX]{x1D6FE}=0.026$
), we observed that there exist only two states; state I and repeated state II (state between II and III). There are no steady state IIs and unsteady state IIIs. Figure 13 shows state-I steady surface wave patterns according to forcing speeds for
$\unicode[STIX]{x1D6FE}=0.026$
), we observed that there exist only two states; state I and repeated state II (state between II and III). There are no steady state IIs and unsteady state IIIs. Figure 13 shows state-I steady surface wave patterns according to forcing speeds for
![]() $\unicode[STIX]{x1D6FC}=0.95$
, 0.96, and figure 14 shows unsteady snap-stick surface wave patterns according to time when the forcing speed
$\unicode[STIX]{x1D6FC}=0.95$
, 0.96, and figure 14 shows unsteady snap-stick surface wave patterns according to time when the forcing speed
![]() $\unicode[STIX]{x1D6FC}=0.99$
.
$\unicode[STIX]{x1D6FC}=0.99$
.

Figure 13. State-I surface wave patterns at relatively low speeds below
![]() $c_{min}$
for the air-suction forcing magnitude
$c_{min}$
for the air-suction forcing magnitude
![]() $\unicode[STIX]{x1D6FE}=0.026$
(
$\unicode[STIX]{x1D6FE}=0.026$
(
![]() $h=3.2$
mm). Left figures (a) and (b) are the images from above the water surface for
$h=3.2$
mm). Left figures (a) and (b) are the images from above the water surface for
![]() $\unicode[STIX]{x1D6FC}=0.95$
and 0.96, respectively. Right figures (c) and (d) are the images from below the water surface for
$\unicode[STIX]{x1D6FC}=0.95$
and 0.96, respectively. Right figures (c) and (d) are the images from below the water surface for
![]() $\unicode[STIX]{x1D6FC}=0.95$
and 0.96, respectively.
$\unicode[STIX]{x1D6FC}=0.95$
and 0.96, respectively.
4 Summary and discussion
We investigated gravity–capillary wave patterns generated by a moving air suction with speeds close to the minimum linear phase speed
![]() $c_{min}=23~\text{cm}~\text{s}^{-1}$
over the surface of deep water. For a relatively strong forcing, three different states are observed according to forcing speeds below
$c_{min}=23~\text{cm}~\text{s}^{-1}$
over the surface of deep water. For a relatively strong forcing, three different states are observed according to forcing speeds below
![]() $c_{min}$
; state I (small-amplitude steady linear circular depressions ahead of the moving forcing), state II (nonlinear steady 3-D gravity–capillary solitary waves ahead of the moving forcing) and state III (oblique shedding of 3-D gravity–capillary solitary waves ahead of the moving forcing). We found that all the linear and nonlinear wave patterns generated by the air-suction forcing correspond to those generated by the air-blowing forcing. The main difference is that 3-D gravity–capillary solitary waves are observed ‘ahead of’ the air-suction forcing and the same waves are observed ‘behind’ the air-blowing forcing. For an intermediate magnitude of forcing, in addition to states I, II and III, there exists another state in the narrow speed range between states II and III. In this speed range, a repeated state II exists due to the repeated snap-stick phenomena of the water hump below the moving forcing. Finally, for a relatively weak forcing, there exist only state I and repeated state II (state between II and III). There are no steady state II and unsteady state III. The present work may provide a clue regarding how 3-D gravity–capillary solitary waves of depression type observed in nature can be generated by random pressure fluctuations due to wind.
$c_{min}$
; state I (small-amplitude steady linear circular depressions ahead of the moving forcing), state II (nonlinear steady 3-D gravity–capillary solitary waves ahead of the moving forcing) and state III (oblique shedding of 3-D gravity–capillary solitary waves ahead of the moving forcing). We found that all the linear and nonlinear wave patterns generated by the air-suction forcing correspond to those generated by the air-blowing forcing. The main difference is that 3-D gravity–capillary solitary waves are observed ‘ahead of’ the air-suction forcing and the same waves are observed ‘behind’ the air-blowing forcing. For an intermediate magnitude of forcing, in addition to states I, II and III, there exists another state in the narrow speed range between states II and III. In this speed range, a repeated state II exists due to the repeated snap-stick phenomena of the water hump below the moving forcing. Finally, for a relatively weak forcing, there exist only state I and repeated state II (state between II and III). There are no steady state II and unsteady state III. The present work may provide a clue regarding how 3-D gravity–capillary solitary waves of depression type observed in nature can be generated by random pressure fluctuations due to wind.

Figure 14. Unsteady surface wave patterns according to time when the forcing speed
![]() $\unicode[STIX]{x1D6FC}=0.99$
for the air-suction forcing magnitude
$\unicode[STIX]{x1D6FC}=0.99$
for the air-suction forcing magnitude
![]() $\unicode[STIX]{x1D6FE}=0.026$
(
$\unicode[STIX]{x1D6FE}=0.026$
(
![]() $h=3.2$
mm). Each snapshot is separated by 0.1 s.
$h=3.2$
mm). Each snapshot is separated by 0.1 s.

Figure 15. Numerically computed surface wave patterns based on (4.2) with
![]() $A=-1.13$
,
$A=-1.13$
,
![]() $p(x,y)=\exp (-2x^{2}-2y^{2})$
,
$p(x,y)=\exp (-2x^{2}-2y^{2})$
,
![]() $C=10$
for
$C=10$
for
![]() $\unicode[STIX]{x1D6FC}=0.95$
and 0.96. (a) Slanted top view for
$\unicode[STIX]{x1D6FC}=0.95$
and 0.96. (a) Slanted top view for
![]() $\unicode[STIX]{x1D6FC}=0.95$
. (b) Slanted top view for
$\unicode[STIX]{x1D6FC}=0.95$
. (b) Slanted top view for
![]() $\unicode[STIX]{x1D6FC}=0.96$
. (c) Centreline profile in the streamwise direction for
$\unicode[STIX]{x1D6FC}=0.96$
. (c) Centreline profile in the streamwise direction for
![]() $\unicode[STIX]{x1D6FC}=0.95$
. (d) Centreline profile in the streamwise direction for
$\unicode[STIX]{x1D6FC}=0.95$
. (d) Centreline profile in the streamwise direction for
![]() $\unicode[STIX]{x1D6FC}=0.96$
. In figure 15(c), the dashed curve represents numerically computed surface wave patterns by setting the nonlinear coefficient
$\unicode[STIX]{x1D6FC}=0.96$
. In figure 15(c), the dashed curve represents numerically computed surface wave patterns by setting the nonlinear coefficient
![]() $\unicode[STIX]{x1D6FD}$
to be zero, i.e. linear waves.
$\unicode[STIX]{x1D6FD}$
to be zero, i.e. linear waves.
As a final remark, we compared measured wave profiles with solutions to the model equation which are the inviscid forcing-free nonlinear 3-D gravity–capillary solitary waves of depression. The focus of this comparison is only on the resultant wave profiles not the whole process of the generation of waves, i.e. to assess whether the measured waves are indeed 3-D gravity–capillary solitary waves. Admittedly, for a more straightforward comparison between the experiments and computations, it is necessary to consider not only the nonlinearity and the dispersion, which are reflected in (3.1), but also the air-suction forcing and the viscous effect. The viscous effect can be reflected in the inviscid dispersion relation as follows (Cho et al. Reference Cho, Diorio, Akylas and Duncan2011):
Here,
![]() $\widetilde{\unicode[STIX]{x1D708}}=C\unicode[STIX]{x1D708}(4g)^{1/4}(\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70E})^{3/4}$
is the dimensionless kinematic viscosity, where
$\widetilde{\unicode[STIX]{x1D708}}=C\unicode[STIX]{x1D708}(4g)^{1/4}(\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70E})^{3/4}$
is the dimensionless kinematic viscosity, where
![]() $\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is the kinematic viscosity of water,
$\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
is the kinematic viscosity of water,
![]() $C$
the control parameter (
$C$
the control parameter (
![]() $C=1$
for linear sinusoidal waves,
$C=1$
for linear sinusoidal waves,
![]() $C>1$
for nonlinear solitary waves). Based on (4.1), including the forcing, the following model equation can be derived:
$C>1$
for nonlinear solitary waves). Based on (4.1), including the forcing, the following model equation can be derived:
Here,
![]() $A$
is the forcing magnitude and
$A$
is the forcing magnitude and
![]() $p(x,y)$
is a forcing function. In the previous studies where the forcing is air-blowing type, the experimental results agree very well with the solutions to the above (4.2) for a Gaussian forcing and a certain positive value of
$p(x,y)$
is a forcing function. In the previous studies where the forcing is air-blowing type, the experimental results agree very well with the solutions to the above (4.2) for a Gaussian forcing and a certain positive value of
![]() $A$
for the whole range of forcing speeds
$A$
for the whole range of forcing speeds
![]() $\unicode[STIX]{x1D6FC}$
(Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011; Cho et al.
Reference Cho, Diorio, Akylas and Duncan2011). In the case of the present air-suction forcing, the same (4.2) is numerically computed for a Gaussian forcing, but with some negative values of
$\unicode[STIX]{x1D6FC}$
(Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009, Reference Diorio, Cho, Duncan and Akylas2011; Cho et al.
Reference Cho, Diorio, Akylas and Duncan2011). In the case of the present air-suction forcing, the same (4.2) is numerically computed for a Gaussian forcing, but with some negative values of
![]() $A$
. The simulation results, however, do not agree with the experimental ones for the whole range of forcing speeds
$A$
. The simulation results, however, do not agree with the experimental ones for the whole range of forcing speeds
![]() $\unicode[STIX]{x1D6FC}$
. Varying the values of controllable parameters
$\unicode[STIX]{x1D6FC}$
. Varying the values of controllable parameters
![]() $C$
,
$C$
,
![]() $A$
and the shape of a Gaussian forcing does not work satisfactorily. With one choice of a set of these parameters, the results show two states; state I and state-II-like steady wave patterns but with different magnitudes of depressions. With another choice of a set of these parameters, the results show yet another different two states; state I and state-III-like unsteady wave patterns but with different magnitudes of depressions and shedding rates. In other words, there always exists a transition between state I and another state, but that another state does not agree with states II or III which are observed in the experiments. However, regardless of any values of
$A$
and the shape of a Gaussian forcing does not work satisfactorily. With one choice of a set of these parameters, the results show two states; state I and state-II-like steady wave patterns but with different magnitudes of depressions. With another choice of a set of these parameters, the results show yet another different two states; state I and state-III-like unsteady wave patterns but with different magnitudes of depressions and shedding rates. In other words, there always exists a transition between state I and another state, but that another state does not agree with states II or III which are observed in the experiments. However, regardless of any values of
![]() $A$
and the forcing shapes, when the forcing speeds are relatively low, the numerically computed state-I wave patterns are very similar to those observed in the experiments. For example, figure 15 shows numerically computed surface wave patterns (solid curves) for
$A$
and the forcing shapes, when the forcing speeds are relatively low, the numerically computed state-I wave patterns are very similar to those observed in the experiments. For example, figure 15 shows numerically computed surface wave patterns (solid curves) for
![]() $\unicode[STIX]{x1D6FC}=0.95$
and 0.96 by solving (4.2) with
$\unicode[STIX]{x1D6FC}=0.95$
and 0.96 by solving (4.2) with
![]() $A=-1.13$
,
$A=-1.13$
,
![]() $p(x,y)=\exp (-2x^{2}-2y^{2})$
,
$p(x,y)=\exp (-2x^{2}-2y^{2})$
,
![]() $C=10$
. These parameters are chosen such that there exists a transition between states I and state II at the speed parameter
$C=10$
. These parameters are chosen such that there exists a transition between states I and state II at the speed parameter
![]() $\unicode[STIX]{x1D6FC}$
between 0.95 and 0.96 like the experimental cases in figures 5 and 6, where the forcing magnitude is
$\unicode[STIX]{x1D6FC}$
between 0.95 and 0.96 like the experimental cases in figures 5 and 6, where the forcing magnitude is
![]() $\unicode[STIX]{x1D6FE}=0.077$
. In the numerical computation, spectral method is used in space, and predictor–corrector method is used in time. Dimensionless grid sizes are
$\unicode[STIX]{x1D6FE}=0.077$
. In the numerical computation, spectral method is used in space, and predictor–corrector method is used in time. Dimensionless grid sizes are
![]() $\unicode[STIX]{x0394}x=0.18$
and
$\unicode[STIX]{x0394}x=0.18$
and
![]() $\unicode[STIX]{x0394}y=0.25$
and dimensionless time step is
$\unicode[STIX]{x0394}y=0.25$
and dimensionless time step is
![]() $\unicode[STIX]{x0394}t=10^{-3}$
. For dimensional results,
$\unicode[STIX]{x0394}t=10^{-3}$
. For dimensional results,
![]() $L=2.73$
mm and
$L=2.73$
mm and
![]() $T=L/c_{min}=0.0118$
s are to be multiplied to the dimensionless spatial and temporal results, respectively. The wave pattern at
$T=L/c_{min}=0.0118$
s are to be multiplied to the dimensionless spatial and temporal results, respectively. The wave pattern at
![]() $\unicode[STIX]{x1D6FC}=0.95$
is very similar to that in figure 5 in terms of their shapes and the magnitude of depression. The wave pattern at
$\unicode[STIX]{x1D6FC}=0.95$
is very similar to that in figure 5 in terms of their shapes and the magnitude of depression. The wave pattern at
![]() $\unicode[STIX]{x1D6FC}=0.96$
is very similar to that in figure 6 in terms of their shapes, but the magnitude of depression is quite different. Wave patterns for forcing speeds larger than
$\unicode[STIX]{x1D6FC}=0.96$
is very similar to that in figure 6 in terms of their shapes, but the magnitude of depression is quite different. Wave patterns for forcing speeds larger than
![]() $\unicode[STIX]{x1D6FC}=0.96$
do not show any differences compared to that for
$\unicode[STIX]{x1D6FC}=0.96$
do not show any differences compared to that for
![]() $\unicode[STIX]{x1D6FC}=0.96$
. In addition, there exists no state III. In figure 15(c), for
$\unicode[STIX]{x1D6FC}=0.96$
. In addition, there exists no state III. In figure 15(c), for
![]() $\unicode[STIX]{x1D6FC}=0.95$
, also is added the dashed curve which represents numerically computed surface wave patterns by setting the nonlinear coefficient
$\unicode[STIX]{x1D6FC}=0.95$
, also is added the dashed curve which represents numerically computed surface wave patterns by setting the nonlinear coefficient
![]() $\unicode[STIX]{x1D6FD}$
to be zero, i.e. linear waves. As shown, those two curves show little difference from each other. Therefore, state I is indeed a linear state as was already commented in § 3.1. One possible reason for the overall disagreement is the wrong choice of the forcing function
$\unicode[STIX]{x1D6FD}$
to be zero, i.e. linear waves. As shown, those two curves show little difference from each other. Therefore, state I is indeed a linear state as was already commented in § 3.1. One possible reason for the overall disagreement is the wrong choice of the forcing function
![]() $p(x,y)$
. As shown in figure 2, the overall shape of the water surface due to the air-suction forcing is not a simple Gaussian, although the lower water hump resembles a Gaussian, on top of which a water column exists. As the forcing magnitude changes, both the base diameter of the hump and the diameter of the water column on top of it changes simultaneously, but not the overall height of the water column. In addition, as one of the reviewers pointed out, the mechanism of the air-suction forcing not only applies a pressure distribution, but it also involves a significant air stream that generates shear stresses and, in turn, vorticity on the free surface. Significant air-stream motion was indeed observed in the experiment, as shown in figures 2 and 3. Derivation of a model equation including all of these considerations is under current investigation and is left as future work as a theoretical continuation of the present paper.
$p(x,y)$
. As shown in figure 2, the overall shape of the water surface due to the air-suction forcing is not a simple Gaussian, although the lower water hump resembles a Gaussian, on top of which a water column exists. As the forcing magnitude changes, both the base diameter of the hump and the diameter of the water column on top of it changes simultaneously, but not the overall height of the water column. In addition, as one of the reviewers pointed out, the mechanism of the air-suction forcing not only applies a pressure distribution, but it also involves a significant air stream that generates shear stresses and, in turn, vorticity on the free surface. Significant air-stream motion was indeed observed in the experiment, as shown in figures 2 and 3. Derivation of a model equation including all of these considerations is under current investigation and is left as future work as a theoretical continuation of the present paper.
Acknowledgements
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2014R1A1A1002441).
Appendix A. Derivation of (3.1)
The model (3.1) is derived from the inviscid dispersion relation of the potential-flow theory for linear sinusoidal gravity–capillary waves on deep water,
where
![]() $\unicode[STIX]{x1D714}$
is the angular frequency,
$\unicode[STIX]{x1D714}$
is the angular frequency,
![]() $g$
is the gravitational acceleration,
$g$
is the gravitational acceleration,
![]() $\unicode[STIX]{x1D705}$
is the magnitude of the wavenumber vector
$\unicode[STIX]{x1D705}$
is the magnitude of the wavenumber vector
![]() $\unicode[STIX]{x1D705}=\sqrt{k^{2}+l^{2}}$
,
$\unicode[STIX]{x1D705}=\sqrt{k^{2}+l^{2}}$
,
![]() $k$
is the wavenumber in the
$k$
is the wavenumber in the
![]() $x$
direction,
$x$
direction,
![]() $l$
is the wavenumber in the
$l$
is the wavenumber in the
![]() $y$
direction,
$y$
direction,
![]() $\unicode[STIX]{x1D70E}$
is the coefficient of surface tension and
$\unicode[STIX]{x1D70E}$
is the coefficient of surface tension and
![]() $\unicode[STIX]{x1D70C}$
is the fluid density. Assuming a linear wave propagating in positive or negative
$\unicode[STIX]{x1D70C}$
is the fluid density. Assuming a linear wave propagating in positive or negative
![]() $x$
direction, the phase speed
$x$
direction, the phase speed
![]() $c=\pm \text{sgn}(k)\unicode[STIX]{x1D714}/\unicode[STIX]{x1D705}$
features a minimum
$c=\pm \text{sgn}(k)\unicode[STIX]{x1D714}/\unicode[STIX]{x1D705}$
features a minimum
![]() $c_{min}$
at a non-zero finite wavenumber
$c_{min}$
at a non-zero finite wavenumber
![]() $(k,l)=(\pm \sqrt{\unicode[STIX]{x1D70C}g/\unicode[STIX]{x1D70E}},0)$
. Using the length scale
$(k,l)=(\pm \sqrt{\unicode[STIX]{x1D70C}g/\unicode[STIX]{x1D70E}},0)$
. Using the length scale
![]() $\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g}$
and the time scale
$\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g}$
and the time scale
![]() $\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g}/c_{min}$
, the dispersion relation (A 1) becomes dimensionless
$\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g}/c_{min}$
, the dispersion relation (A 1) becomes dimensionless
whose phase-speed minimum becomes
![]() $c_{min}=1$
at
$c_{min}=1$
at
![]() $(k,l)=(k_{m},l_{m})=(\pm 1,0)$
. To capture the essential wave phenomena near the minimum phase speed
$(k,l)=(k_{m},l_{m})=(\pm 1,0)$
. To capture the essential wave phenomena near the minimum phase speed
![]() $c_{min}$
, (A 2) is Taylor expanded around
$c_{min}$
, (A 2) is Taylor expanded around
![]() $(k,l)=(k_{m},l_{m})$
(Akers & Milewski Reference Akers and Milewski2009; Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009; Cho et al.
Reference Cho, Diorio, Akylas and Duncan2011; Cho Reference Cho2014):
$(k,l)=(k_{m},l_{m})$
(Akers & Milewski Reference Akers and Milewski2009; Diorio et al.
Reference Diorio, Cho, Duncan and Akylas2009; Cho et al.
Reference Cho, Diorio, Akylas and Duncan2011; Cho Reference Cho2014):
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}(k,l) & = & \displaystyle \pm \text{sgn}(k)\sqrt{\frac{1}{2}(\unicode[STIX]{x1D705}+\unicode[STIX]{x1D705}^{3})}=\pm \text{sgn}(k)\sqrt{\frac{1}{2}}\sqrt{(k^{2}+l^{2})^{1/2}+(k^{2}+l^{2})^{3/2}}\nonumber\\ \displaystyle & {\approx} & \displaystyle \pm \text{sgn}(k)\left\{\unicode[STIX]{x1D714}(k_{m},l_{m})+\left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k}\right|_{m}(k-k_{m})+\left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}l}\right|_{m}(l-l_{m})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left.\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}\right|_{m}(k-k_{m})^{2}+2\left.\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k\unicode[STIX]{x2202}l}\right|_{m}(k-k_{m})(l-l_{m})+\left.\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}l^{2}}\right|_{m}(l-l_{m})^{2}\right\}\nonumber\\ \displaystyle & = & \displaystyle \pm \frac{1}{4}\text{sgn}(k)(1+2|k|+k^{2}+2l^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}(k,l) & = & \displaystyle \pm \text{sgn}(k)\sqrt{\frac{1}{2}(\unicode[STIX]{x1D705}+\unicode[STIX]{x1D705}^{3})}=\pm \text{sgn}(k)\sqrt{\frac{1}{2}}\sqrt{(k^{2}+l^{2})^{1/2}+(k^{2}+l^{2})^{3/2}}\nonumber\\ \displaystyle & {\approx} & \displaystyle \pm \text{sgn}(k)\left\{\unicode[STIX]{x1D714}(k_{m},l_{m})+\left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k}\right|_{m}(k-k_{m})+\left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}l}\right|_{m}(l-l_{m})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\left.\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}\right|_{m}(k-k_{m})^{2}+2\left.\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k\unicode[STIX]{x2202}l}\right|_{m}(k-k_{m})(l-l_{m})+\left.\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}l^{2}}\right|_{m}(l-l_{m})^{2}\right\}\nonumber\\ \displaystyle & = & \displaystyle \pm \frac{1}{4}\text{sgn}(k)(1+2|k|+k^{2}+2l^{2}).\end{eqnarray}$$
Assuming a left-going wave, the linear dispersion relation is
Now, from (A 4), one can replace variables (
![]() $\unicode[STIX]{x1D714},k,l$
) in the temporal and spatial frequency domains with those (
$\unicode[STIX]{x1D714},k,l$
) in the temporal and spatial frequency domains with those (
![]() $t,x,y$
) in the physical domain:
$t,x,y$
) in the physical domain:
where
![]() ${\mathcal{H}}\{f\}={\mathcal{F}}^{-1}\{-\text{i}\text{sgn}(k){\mathcal{F}}\{f\}\}$
stands for the Hilbert transform, with
${\mathcal{H}}\{f\}={\mathcal{F}}^{-1}\{-\text{i}\text{sgn}(k){\mathcal{F}}\{f\}\}$
stands for the Hilbert transform, with
being the Fourier transform. Consequently, one obtains the following model equation for linear gravity–capillary waves on deep water:
where
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(x,y,t)$
is the wave elevation, and the subscript denotes the partial differentiation. To account for the nonlinearity, one can add a quadratic nonlinearity term
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(x,y,t)$
is the wave elevation, and the subscript denotes the partial differentiation. To account for the nonlinearity, one can add a quadratic nonlinearity term
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D702}^{2})_{x}$
in the equation:
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D702}^{2})_{x}$
in the equation:
By replacing
![]() $x$
with
$x$
with
![]() $x+\unicode[STIX]{x1D6FC}t$
in the (A 8), the wave equation which is expressed in the left-moving frame of reference with a dimensionless speed
$x+\unicode[STIX]{x1D6FC}t$
in the (A 8), the wave equation which is expressed in the left-moving frame of reference with a dimensionless speed
![]() $\unicode[STIX]{x1D6FC}=c/c_{min}$
is obtained as follows:
$\unicode[STIX]{x1D6FC}=c/c_{min}$
is obtained as follows:
In the weakly nonlinear small-amplitude limit near
![]() $\unicode[STIX]{x1D6FC}=1$
, the solution to (A 9) can be expressed as
$\unicode[STIX]{x1D6FC}=1$
, the solution to (A 9) can be expressed as
where
![]() $\unicode[STIX]{x1D6FC}=1-\unicode[STIX]{x1D716}^{2}(0<\unicode[STIX]{x1D716}\ll 1)$
and
$\unicode[STIX]{x1D6FC}=1-\unicode[STIX]{x1D716}^{2}(0<\unicode[STIX]{x1D716}\ll 1)$
and
![]() $(X,Y)=\unicode[STIX]{x1D716}(x,y)$
. Substituting (A 10) into (A 9), one obtains the following NLS equation:
$(X,Y)=\unicode[STIX]{x1D716}(x,y)$
. Substituting (A 10) into (A 9), one obtains the following NLS equation:
On the other hand, from the full water-wave or Euler equations on deep water, the NLS equation is derived as Hogan (Reference Hogan1985).
Finally, by equating (A 11) and (A 12), the nonlinear coefficient is determined as
![]() $\unicode[STIX]{x1D6FD}=\sqrt{11/2}/8$
.
$\unicode[STIX]{x1D6FD}=\sqrt{11/2}/8$
.