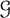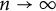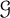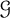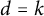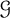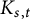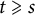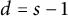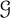1 Introduction
Many classical theorems in extremal graph theory concern the maximum number of copies of a fixed graph H in an n-vertex graphFootnote
1
in some class
$\mathcal {G}$
. Here, a copy means a subgraph isomorphic to H. For example, Turán’s Theorem determines the maximum number of copies of
$K_{2}$
(that is, edges) in an n-vertex
$K_{t}$
-free graph [Reference Turán94]. More generally, Zykov’s Theorem determines the maximum number of copies of a given complete graph
$K_{s}$
in an n-vertex
$K_{t}$
-free graph [Reference Zykov99]. The excluded graph need not be complete. The Erdős–Stone Theorem [Reference Erdős and Stone35] determines, for every nonbipartite graph X, the asymptotic maximum number of copies of
$K_{2}$
in an n-vertex graph with no X-subgraph. Analogues of the Erdős–Stone Theorem for the number of (induced) copies of a given graph within a graph class defined by an excluded (induced) subgraph have recently been widely studied [Reference Alon, Kostochka and Shikhelman4–Reference Alon and Shikhelman6, Reference Ergemlidze, Methuku, Salia and Győri36, Reference Gerbner, Győri, Methuku and Vizer48–Reference Gerbner and Palmer50, Reference Győri, Salia, Tompkins and Zamora55, Reference Letzter67, Reference Ma and Qiu72, Reference Nešetřil and de Mendez76].
For graphs H and G, let
$C(H,G)$
be the number of copies of H in G. For a graph class
$\mathcal {G}$
, let
$$ \begin{align*}C(H,\mathcal{G},n) := \max_{G\in\mathcal{G},\,|V(G)|=n} C(H,G).\end{align*} $$
This paper determines the asymptotic behavior of
$C(T,\mathcal {G},n)$
as
$n\to \infty $
for various sparse graph classes
$\mathcal {G}$
and for an arbitrary fixed forest T. In particular, we show that
$C(T,\mathcal {G},n) \in \Theta (n^{k})$
for some k depending on T and
$\mathcal {G}$
.
It turns out that k depends on the size of particular stable sets in T. A set S of vertices in a graph G is stable if no two vertices in S are adjacent. Let
$\alpha (G)$
be the size of a largest stable set in G. For a graph G and
$s\in \mathbb {N}_{0}$
, let
$$ \begin{align*}\alpha_{s}(G):= \alpha( G[\{ v\in V(G): \deg_{G}(v)\leqslant s\}]).\end{align*} $$
Note that for a forest T (indeed any bipartite graph),
$\alpha _{s}(T)$
can be computed in polynomial time. See [Reference Biedl and Wilkinson10, Reference Bose, Dujmović and Wood12, Reference Bose, Smid and Wood13] for bounds on the size of bounded degree stable sets in forests, planar graphs, and other classes.
The first sparse class we consider are the graphs of given degeneracy.Footnote 2
Theorem 1.1 Fix
$k\in \mathbb {N}$
and let
$\mathcal {D}_{k}$
be the class of k-degenerate graphs. Then for every fixed forest T,
$$ \begin{align*}C(T,\mathcal{D}_{k},n) \in \Theta(n^{\alpha_{k}(T)}).\end{align*} $$
Our second main theorem determines
$C(T,\mathcal {G},n)$
for many minor-closed classes.Footnote
3
,
Footnote
4
Several examples of this result are given in Section 4.
Theorem 1.2 Fix
$s,t\in \mathbb {N}$
and let
$\mathcal {G}$
be a minor-closed class such that every graph with treewidth at most s is in
$\mathcal {G}$
and
$K_{s+1,t}\not \in \mathcal {G}$
. Then for every fixed forest T,
$$ \begin{align*}C(T,\mathcal{G},n) \in \Theta(n^{\alpha_{s}(T)}).\end{align*} $$
The lower bounds in Theorems 1.1 and 1.2 are proved via the same construction given in Section 2. The upper bounds in Theorems 1.1 and 1.2 are proved in Section 3. We in fact prove a stronger result (Lemma 3.3) that shows that for any fixed forest T and
$s\in \mathbb {N}$
there is a particular finite set
$\mathcal {F}$
such that
$C(T,G) \in O(n^{\alpha _{s}(T)})$
for every n-vertex graph G with
$O(n)$
edges and containing no subgraph in
$\mathcal {F}$
. This result is applied in Section 5 to determine
$C(T,\mathcal {G},n)$
for various non-minor-closed classes
$\mathcal {G}$
. For example, we show a
$\Theta (n^{\alpha _{2}(T)})$
bound for graphs that can be drawn in a fixed surface with a bounded average number of crossings per edge, which matches the known bound with no crossings.
1.1 Related results
Before continuing we mention related results from the literature. For a fixed complete graph
$K_{s}$
,
$C(K_{s},\mathcal {G},n)$
has been extensively studied for various graph classes
$\mathcal {G}$
including: graphs of given maximum degree [Reference Alexander, Cutler and Mink2, Reference Chase14, Reference Cutler and Radcliffe20, Reference Cutler and Radcliffe21, Reference Engbers and Galvin31, Reference Galvin46, Reference Gan, Loh and Sudakov47, Reference Kahn60, Reference Wood97]; graphs with a given number of edges, or more generally, a given number of smaller complete graphs [Reference Cutler and Radcliffe19, Reference Eckhoff29, Reference Eckhoff30, Reference Fisher and Ryan38, Reference Fisher and Ryan39, Reference Frohmader45, Reference Hedman58, Reference Khadzhiivanov and Nenov61, Reference Kirsch and Radcliffe62, Reference Petingi and Rodriguez82]; graphs without long cycles [Reference Luo71]; planar graphs [Reference Hakimi and Schmeichel69, Reference Papadimitriou and Yannakakis81, Reference Wood97]; graphs with given Euler genus [Reference Dujmović, Fijavž, Joret, Sulanke and Wood27, Reference Huynh, Joret and Wood59]; and graphs excluding a fixed minor or subdivision [Reference Fomin, Oum and Thilikos42–Reference Fox and Wei44, Reference Lee and Oum66, Reference Norine, Seymour, Thomas and Wollan79, Reference Reed and Wood84].
When
$\mathcal {J}$
is the class of planar graphs,
$C(H,\mathcal {J},n)$
has been determined for various graphs H including: complete bipartite graphs [Reference Alon and Caro3], planar triangulations without nonfacial triangles [Reference Alon and Caro3], triangles [Reference Harant, Horňák and Skupień56, Reference Hakimi and Schmeichel69, Reference Hakimi and Schmeichel70, Reference Wood97], four-cycles [Reference Alameddine1, Reference Hakimi and Schmeichel69], five-cycles [Reference Győri, Paulos, Salia, Tompkins and Zamora53], four-vertex paths [Reference Győri, Paulos, Salia, Tompkins and Zamora54], and four-vertex complete graphs [Reference Alon and Caro3, Reference Wood97].
$C(H,\mathcal {J},n)$
has also been studied for more general planar graphs H. Perles (see [Reference Alon and Caro3]) conjectured that if H is a fixed three-connected planar graph, then
$C(H,\mathbb {S}_{0},n) \in \Theta (n)$
. Perles noted the converse: If H is planar, not three-connected and
$|V(H)|\geqslant 4$
, then
$C(H,\mathbb {S}_{0},n) \in \Omega (n^{2})$
. Perles’ conjecture was proved by Wormald [Reference Wormald98] and independently by Eppstein [Reference Eppstein32], Recently, Huynh et al. [Reference Huynh, Joret and Wood59] extended these results to all surfaces and all graphs H (see Section 4).
Finally, we mention a result of Nešetřil and Ossona de Mendez [Reference Nešetřil and de Mendez76], who proved that for every infinite nowhere dense hereditary graph class
$\mathcal {G}$
and for every fixed graph F, the maximum, taken over all n-vertex graphs
$G\in \mathcal {G}$
, of the number of induced subgraphs of G isomorphic to F is
$\Omega ( n^{\beta })$
and
$O( n^{\beta +o(1)})$
for some integer
$\beta \leqslant \alpha (F)$
. Our results (when F is a forest and
$\mathcal {G}$
is one of the classes that we consider) imply this upper bound (since the number of induced copies of T in G is at most
$C(T,G)$
). Moreover, our bounds are often more precise since
$\alpha _{s}(T)$
can be significantly less than
$\alpha (T)$
.
2 Lower bound
Lemma 2.1 Fix
$s\in \mathbb {N}$
and let T be a fixed forest with
$\alpha _{s}(T)=k$
. Then there exists a constant
$c_{2.1}(k):= (2k)^{-k}$
such that for all sufficiently large
$n\in \mathbb {N}$
, there exists a graph G with
$|V(G)|\leqslant n$
and
$\operatorname {\mathrm {\mathsf {tw}}}(G)\leqslant s$
and
$C(T,G)\geqslant c_{2.1}(k) n^{k}$
.
Proof Let S be a maximum stable set in
$T[\{ v\in V(T): \deg _{T}(v)\leqslant s\}]$
with
$|S|=k$
. Let
$m:=\lfloor \frac {n-|V(T)|}{k} \rfloor $
. Let G be the graph obtained from T as follows: for each vertex v in S add to G a set
$C_{v}$
of m vertices, such that
$N_{G}(x):= N_{T}(v)$
for each vertex
$x\in C_{v}$
. Observe that G has at most n vertices. Each choice of one vertex
$x\in C_{v}$
(for each
$v\in S$
), along with the vertices in
$V(T)\setminus S$
, induces a copy of T. Thus
$C(T,G)\geqslant m^{k}$
, which is at least
$c_{2.1}(k) n^{k}$
for
$n\geqslant 2|V(T)| + 2k$
.
We now show
$\operatorname {\mathrm {\mathsf {tw}}}(G) \leqslant s$
. Let
$T_{1}$
be a connected component of T and
$G_{1}$
be the corresponding connected component of G. Since the treewidth of a graph equals the maximum treewidth of its components, it suffices to show
$\operatorname {\mathrm {\mathsf {tw}}}(G_{1}) \leqslant s$
. We may assume
$|V(T_{1})| \geqslant 2$
, as otherwise
$\operatorname {\mathrm {\mathsf {tw}}}(G_{1})=0$
. Let
$T_{1}^{\prime }$
be the tree obtained from
$T_{1}$
as follows: for each vertex
$v\in S \cap V(T_{1})$
and each vertex
$x\in C_{v}$
, add one new vertex x and one new edge
$xv$
to
$T_{1}^{\prime }$
. Choose
$r \in V(T_{1}) \setminus S$
and consider
$T_{1}^{\prime }$
to be rooted at r. We use
$T_{1}^{\prime }$
to define a tree-decomposition of
$G_{1}$
, where the bags are defined as follows. Let
$B_{r}:=\{r\}$
. For each vertex
$w\in V(T_{1})\setminus (S\cup \{r\})$
, if p is the parent of w in
$T_{1}^{\prime }$
, let
$B_{w}:=\{w,p\}$
. For each vertex
$v\in S \cap V(T_{1})$
and each vertex x in
$C_{v}$
, let
$B_{v}:=N_{T_{1}}(v) \cup \{v\}$
and
$B_{x} := N_{T_{1}}(v) \cup \{x\}$
.
We now show that
$(B_{x}:x\in V(T_{1}^{\prime }))$
is a tree-decomposition of
$G_{1}$
. The bags containing r are indexed by
$N_{T_{1}}(r)\cup \{r\}$
, which induces a (connected) subtree of
$T_{1}^{\prime }$
. For each vertex
$w\in V(T_{1})\setminus (S\cup \{r\})$
with parent p, the bags containing w are those indexed by
$\cup \{ C_{v}\cup \{v\} : v \in N_{T_{1}}(w) \cap S \}\cup \{w\}\cup (N_{T_{1}}(w)\setminus \{p\})$
, which induces a subtree of
$T_{1}^{\prime }$
(since
$vx\in E(T_{1}^{\prime })$
for each
$x\in C_{v}$
where
$v\in N_{T_{1}}(w)\cap S$
). For each vertex
$v\in S$
with parent p, the bags containing v are those indexed by
$N_{T_{1}}(v) \cup \{v\} \setminus \{p\}$
, which induces a subtree of
$T_{1}^{\prime }$
. For each vertex
$v\in S$
and
$x\in C_{v}$
,
$B_{x}$
is the only bag that contains x. Hence propery (T1) in the definition of tree-decomposition holds. For each edge
$pv$
of
$T_{1}$
where p is the parent of v, the bag
$B_{v}$
contains both p and v. Every other edge of
$G_{1}$
joins x and w for some
$v\in S$
and
$x\in C_{v}$
and
$w\in N_{T_{1}}(v)$
, in which case
$B_{x}$
contains both x and w. Hence (T2) holds. Therefore
$(B_{x}:x\in V(T_{1}^{\prime }))$
is a tree-decomposition of
$G_{1}$
. Since each bag has size at most
$s+1$
, we have
$\operatorname {\mathrm {\mathsf {tw}}}(G_{1})\leqslant s$
.▪
3 Upper bound
To prove upper bounds on
$C(T,\mathcal {G},n)$
, it is convenient to work in the following setting. For graphs G and H, an image of H in G is an injection
$\phi : V(H) \to V(G)$
such that
$\phi (u)\phi (v) \in E(G)$
for all
$uv \in E(H)$
. Let
$I(H,G)$
be the number of images of H in G. For a graph class
$\mathcal {G}$
, let
$I(H,\mathcal {G},n)$
be the maximum of
$I(H,G)$
taken over all n-vertex graphs
$G\in \mathcal {G}$
. If H is fixed then
$C(H,G)$
and
$I(H,G)$
differ by a constant factor. In particular, if
$|V(H)|=h$
then
$$ \begin{align} C(H,G)& \leqslant I(H,G) \leqslant h!\, C(H,G), \nonumber \\ C(H,\mathcal{G},n)& \leqslant I(H,\mathcal{G},n) \leqslant h!\, C(H,\mathcal{G},n). \end{align} $$
So to bound
$C(T,\mathcal {G},n)$
it suffices to work with images rather than copies.
Our proof needs two tools from the literature. The first is due to Eppstein [Reference Eppstein32]. A collection
$\mathcal {H}$
of images of a graph H in a graph G is coherent if for all distinct images
$\phi _{1}, \phi _{2} \in \mathcal {H}$
and for all distinct vertices
$x,y\in V(H)$
, we have
$\phi _{1}(x) \neq \phi _{2}(y)$
.
Lemma 3.1 [Reference Eppstein32]
Let H be a graph with h vertices and let G be a graph. Every collection of at least
$c_{3.1}(h,t):=h!^{2} t^{h}$
images of H in G contains a coherent subcollection of size at least t.
We also use the following result of Erdős and Rado [Reference Erdős and Rado34]; see [Reference Alweiss, Lovett, Wu and Zhang7, Reference Bell, Chueluecha and Warnke9] for recent quantitative improvements. A t-sunflower is a collection
$\mathcal {S}$
of t sets for which there exists a set R such that
$X\cap Y=R$
for all distinct
$X,Y\in \mathcal {S}$
. The set R is called the kernel of
$\mathcal {S}$
.
Lemma 3.2 (Sunflower Lemma [Reference Erdős and Rado34])
Every collection of at least
$c_{3.2}(h,t):=h!(t-1)^{h} +1$
many h-subsets of a set contains a t-sunflower.
Consider graphs H and G. An H-model in a graph G is a collection
$(X_{v}:v\in V(H))$
of pairwise disjoint connected subgraphs of G indexed by the vertices of H, such that for each edge
$vw\in E(H)$
there is an edge of G joining
$X_{v}$
and
$X_{w}$
. Each subgraph
$X_{v}$
is called a branch set. A graph G contains an H-model if and only if H is a minor of G. An H-model
$(X_{v}:v\in V(H))$
in G is c-shallow if
$X_{v}$
has radius at most c for each
$v\in V(H)$
. An H-model
$(X_{v}:v\in V(H))$
in G is c-small if
$|V(X_{v})|\leqslant c$
for each
$v\in V(H)$
. Shallow models are key components in the sparsity theory of Nešetřil and de Mendez [Reference Nešetřil and de Mendez77]. Small models have also been studied [Reference Fiorini, Joret, Theis and Wood37, Reference Montgomery75, Reference Shapira and Sudakov91, Reference van Batenburg, Huynh, Joret and Raymond95].
The next lemma is the heart of the paper. To describe the result we need the following construction, illustrated in Figure 1. For a graph H, and
$s,t\in \mathbb {N}$
, and
$v\in V(H)$
let
$$ \begin{align*}\overline{\deg}_{H,s}(v) := \max\{s+1-\deg_{H}(v),0\}.\end{align*} $$
Then define
${H}^{\langle {s,t}\rangle }$
to be the graph with vertex set
$$ \begin{align*} V( {H}^{\langle{s,t}\rangle}) := \, & \{(v,i):v\in V(H),i\in[t]\} \; \cup\\ & \{(v,j)^{\star}:v\in V(H),j\in[\overline{\deg}_{H,s}(v)]\} \end{align*} $$
and edge set
$$ \begin{align*} E( {H}^{\langle{s,t}\rangle}) := \, & \{(v,i)(w,i):vw\in E(H),i\in[t]\}\; \cup\\ & \{(v,i)(v,j)^{\star}:v\in V(H),i\in[t],j\in[\overline{\deg}_{H,s}(v)]\}. \end{align*} $$
Figure 1:
${H}^{\langle {3,4}\rangle }$
where
$V(H)=\{a,b,c,d,e\}$
.
Several notes about
${H}^{\langle {s,t}\rangle }$
are in order:
-
(A) For each
$i\in [t]$
, let
$X_{i}$
be the subgraph of
${H}^{\langle {s,t}\rangle }$
induced by
$\{(v,i):v\in V(H)\}$
. Then
$X_{i}\cong H$
. Contracting each
$X_{i}$
to a single vertex produces
$K_{s^{\prime },t}$
where If H is a nonempty tree then
$$ \begin{align*}s^{\prime}:=\!\! \sum_{v\in V(H)} \!\! \overline{\deg}_{H,s}(v) \geqslant \!\! \sum_{v\in V(H)} \!\! ( s+1-\deg_{H}(v) ) = (s+1)\,|V(H)| -2|E(H)|.\end{align*} $$
$s^{\prime }\geqslant |V(H)|(s-1)+2\geqslant s+1$
, implying
$K_{s+1,t}$
is a minor of
${H}^{\langle {s,t}\rangle }$
.
-
(B) Each vertex
$(v,j)^{\star }$
has degree t and each vertex
$(v,i)$
has degree
$\deg _{H}(v)+\overline {\deg }_{H,s}(v)\geqslant s+1$
. In particular, if
$t\geqslant s+1$
then
${H}^{\langle {s,t}\rangle }$
has minimum degree at least
$s+1$
. -
(C) If H is connected then
$\text {diameter}({H}^{\langle {s,t}\rangle })\leqslant \text {diameter}(H)+2$
.
Define the density of a graph G to be
$\rho (G):=\frac {|E(G)|}{|V(G)|}$
. For a graph class
$\mathcal {G}$
, let
$\rho (\mathcal {G}):=\sup \{ \rho (G): G\in \mathcal {G}\}$
Lemma 3.3 For all
$s,t, h \in \mathbb {N}$
and
$\rho \in \mathbb {R}_{\geqslant 0}$
, there exists a constant
$c:=c_{3.3}(s,t,h,\rho ) := c_{3.1}( h, c_{3.2}(h,t))\, (\rho +1)^{h}$
such that for every forest T with h vertices, if G is a graph with
$\rho (G)\leqslant \rho $
and
$I(T,G) \geqslant c\,|V(G)|^{\alpha _{s}(T)}$
, then G contains
${U}^{\langle {s,t}\rangle }$
as a subgraph for some (non-empty) subtree U of T.
Proof Let
$S:=\{ v \in V(T): \deg _{T}(v)\leqslant s\}$
. Let X be a stable set in
$F:=T[S]$
of size
$k:=\alpha _{s}(T)$
. Since F is bipartite, by Konig’s Edge Cover Theorem [Reference König64], there is a set
$Y\subseteq V(F)\cup E(F)$
with
$|Y|=|X|$
such that each vertex of F is either in Y or is incident to an edge in Y. In fact,
$Y\cap V(F)$
is the set of isolated vertices of F, although we will not need this property.
Let G be an n-vertex graph with
$\rho (G)\leqslant \rho $
and
$I(T,G) \geqslant c\,n^{k}$
. Let
$\mathcal {I}$
be the set of images of T in G. So
$|\mathcal {I}|\geqslant c\,n^{k}$
. Let
$\mathcal {X} := \binom { V(G) \cup E(G)}{k}$
. Note that
$|\mathcal {X}| \leqslant \binom {(\rho +1)n}{k} \leqslant (\rho +1)^{k} n^{k}$
. For each
$\phi \in \mathcal {I}$
, let
$$ \begin{align*}Y_{\phi} := \{ \phi(x):x\in Y\cap V(F)\} \cup \{ \phi(x)\phi(y) : xy \in Y \cap E(F)\},\end{align*} $$
which is an element of
$\mathcal {X}$
since
$|Y|=k$
. For each
$Z\in \mathcal {X}$
, let
$\mathcal {I}_{Z}:= \{\phi \in \mathcal {I}: Y_{\phi }=Z\}$
. By the pigeonhole principle, there exists
$Z\in \mathcal {X}$
such that
$$ \begin{align*}|\mathcal{I}_{Z}|\geqslant |\mathcal{I}| / |\mathcal{X}| \geqslant c /(\rho+1)^{k} \geqslant c /(\rho+1)^{h} = c_{3.1}( h, c_{3.2}(h,t)).\end{align*} $$
By Lemma 3.1 applied to
$\mathcal {I}_{Z}$
, there is a coherent family
$\mathcal {I}_{1}\subseteq \mathcal {I}_{Z}$
with
$|\mathcal {I}_{1}|=c_{3.2}(h,t)$
.
We claim that the vertex sets in G corresponding to the images of T in
$\mathcal {I}_{1}$
are all distinct. Suppose that
$V(\phi _{1}(V(T)))=V(\phi _{2}(V(T)))$
for
$\phi _{1},\phi _{2}\in \mathcal {I}_{1}$
. Let x be any vertex in T. If
$\phi _{1}(x)\neq \phi _{2}(x)$
, then
$\phi _{2}(y)=\phi _{1}(x)$
for some vertex y of T with
$y\neq x$
(since
$V(\phi _{1}(V(T)))=V(\phi _{2}(V(T)))$
), which contradicts the definition of coherence. Thus
$\phi _{1}(x)=\phi _{2}(x)$
for each vertex x of T. Thus
$\phi _{1}=\phi _{2}$
. This proves our claim.
Therefore, by Lemma 3.2 applied to
$\{ \phi (V(T)) : \phi \in \mathcal {I}_{1}\}$
, there is a set R of vertices in G and a subfamily
$\mathcal {I}_{2} \subseteq \mathcal {I}_{1}$
such that
$\phi _{1}(V(T))\cap \phi _{2}(V(T))=R$
for all distinct
$\phi _{1}, \phi _{2} \in \mathcal {I}_{2}$
, and
$|\mathcal {I}_{2}|=t$
.
Fix
$\phi _{0} \in \mathcal {I}_{2}$
and let
$K:=\phi _{0}^{-1}(R)$
. Note that K does not depend on the choice of
$\phi _{0}$
. Moreover,
$S \subseteq K$
because
$Y_{\phi }=Z$
for every
$\phi \in \mathcal {I}_{2}$
, and each vertex in S is either in Y or is incident to an edge in Y. Let U be some connected component of
$T - K$
. Note that
$V(U) \cap S=\emptyset $
, since
$S \subseteq K$
. Thus, each vertex
$v\in V(U)$
has
$\deg _{T}(v)\geqslant s+1$
and thus there is a set
$N_{v}$
of at least
$\overline {\deg }_{U,s}(v)$
neighbors of v in K. Again by coherence,
$\phi _{1}(N_{v})=\phi _{2}(N_{v})$
for all
$\phi _{1},\phi _{2}\in \mathcal {I}_{2}$
and
$v\in V(U)$
. Observe that
$N_{v_{1}}\cap N_{v_{2}}=\emptyset $
for distinct
$v_{1}, v_{2} \in U$
, as otherwise T would contain a cycle. Thus
$(\phi (U):\phi \in \mathcal {I}_{2})$
and
$(\phi _{0}(N_{v}):v\in V(U))$
define a subgraph of G isomorphic to
${U}^{\langle {s,t}\rangle }$
.▪
We now prove our first main result.
Proof of Theorem 1.1 Since every graph with treewidth k is in
$\mathcal {D}_{k}$
, Lemma 2.1 implies
$C(T,\mathcal {D}_{k},n)\in \Omega (n^{\alpha _{k}(T)})$
. For the upper bound, let G be a k-degenerate graph. So
$\rho (G)\leqslant k$
. By Lemma 3.3 with
$s=k$
and
$t=k+1$
, if
$I(T,G) \geqslant c\,|V(G)|^{k}$
then G contains
${U}^{\langle {k,k+1}\rangle }$
as a subgraph for some subtree U of T. However,
${U}^{\langle {k,k+1}\rangle }$
has minimum degree
$k+1$
, contradicting the k-degeneracy of G. Hence
$I(T,G) \leqslant c\,|V(G)|^{k}$
and
$C(T,\mathcal {D}_{k},n)\in O(n^{\alpha _{k}(T)})$
by Equation (3.1).▪
The following special case of Lemma 3.3 will be useful. Say
$\{X_{1},\dots ,X_{s};Y_{1},\dots ,Y_{t}\}$
is a
$(p,q)$
-model of
$K_{s,t}$
in a graph G if:
-
•
$X_{1},\dots ,X_{s},Y_{1},\dots ,Y_{t}$
are pairwise disjoint connected subgraphs of G, -
• for each
$i\in [s]$
and
$j\in [t]$
there is an edge in G between
$X_{i}$
and
$Y_{j}$
, -
•
$|V(X_{i})|\leqslant p$
for each
$i\in [s]$
and
$|V(Y_{j})|\leqslant q$
for each
$j\in [t]$
.
Corollary 3.4 For all
$s,t, h \in \mathbb {N}$
and
$\rho \in \mathbb {R}_{\geqslant 0}$
, for every forest T with h vertices, if G is a graph with
$\rho (G)\leqslant \rho $
and
$I(T,G) \geqslant c_{3.3}(s,t,h,\rho ) \,|V(G)|^{\alpha _{s}(T)}$
, then for some
$h^{\prime } \in [h]$
, G contains a subgraph of diameter at most
$h^{\prime }+1$
that contains a
$(1,h^{\prime })$
-model of
$K_{h^{\prime }(s-1)+2,t}$
. In particular, G contains a
$(1,h)$
-model of
$K_{s+1,t}$
.
Proof By Lemma 3.3, G contains
${U}^{\langle {s,t}\rangle }$
as a subgraph for some subtree U of T. The main claim follows from (A) and (C) where
$h^{\prime }:=|V(U)|$
. The final claim follows since
$h^{\prime }\in [h]$
, implying
$h^{\prime }(s-1)+2 \geqslant s+1$
.▪
4 Minor-closed classes
Theorem 1.2 is implied by Lemma 2.1 and Corollary 3.4 and since every minor-closed class has bounded density [Reference Kostochka65, Reference Thomason93]. We now give several examples of Theorem 1.2.
Treewidth:
Let
$\mathcal {T}_{k}$
be the class of graphs with treewidth at most k. Then
$\mathcal {T}_{k}$
is a minor-closed class, and every graph in
$\mathcal {T}_{k}$
has minimum degree at most k, implying
$\rho (\mathcal {T}_{k})\leqslant k$
and
$K_{k+1,k+1}\not \in \mathcal {T}_{k}$
. Thus Theorem 1.2 with
$s=k$
implies that for every fixed forest T,
$$ \begin{align*}C(T,\mathcal{T}_{k},n) \in \Theta(n^{\alpha_{k}(T)}). \end{align*} $$
Surfaces:
Let
$\mathcal {S}_{\Sigma }$
be the class of graphs that embedFootnote
5
in a surface
$\Sigma $
. Then
$\mathcal {S}_{\Sigma }$
is a minor-closed class. Huynh et al. [Reference Huynh, Joret and Wood59] proved that for every
$H\in \mathcal {S}_{\Sigma }$
,
$$ \begin{align*}C(H, \mathcal{S}_{\Sigma}, n)\in \Theta(n^{f(H)}),\end{align*} $$
where
$f(H)$
is a graph invariant called the flap-number of H, which is independent of
$\Sigma $
. Huynh et al. [Reference Huynh, Joret and Wood59] noted that
$f(T)=\alpha _{2}(T)$
for a forest T. So, in particular,
$$ \begin{align*}C(T, \mathcal{S}_{\Sigma}, n) \in \Theta(n^{\alpha_{2}(T)}).\end{align*} $$
This result is also implied by Theorem 1.2 since for every surface
$\Sigma $
of Euler genus g, Euler’s formula implies that
$K_{3,2g+3}$
is not in
$\mathcal {S}_{\Sigma }$
(first observed by Ringel [Reference Ringel86]), and
$$ \begin{align*}\rho(\mathcal{S}_{\Sigma})\leqslant \rho_{g}:= \max\{3,\tfrac14 (5 + \sqrt{24g+1} \};\end{align*} $$
see [Reference de Mendez, Oum and Wood22] for a proof.
Excluding a complete bipartite minor:
Let
$\mathcal {B}_{s,t}$
be the class of graphs containing no complete bipartite graph
$K_{s,t}$
minor, where
$t\geqslant s$
. Since
$K_{s,t}$
has treewidth s, every graph with treewidth at most
$s-1$
is in
$\mathcal {B}_{s,t}$
. By Theorem 1.2, for every fixed forest T,
$$ \begin{align} C(T,\mathcal{B}_{s,t},n)\in \Theta(n^{\alpha_{s-1}(T)}). \end{align} $$
This answers affirmatively a question raised by Huynh et al. [Reference Huynh, Joret and Wood59].
Excluding a complete minor:
Let
$\mathcal {C}_{k}$
be the class of graphs containing no complete graph
$K_{k}$
minor. Then
$K_{k-1,k-1}\not \in \mathcal {C}_{k}$
(since contracting a
$(k-2)$
-edge matching in
$K_{k-1,k-1}$
gives
$K_{k}$
). Every graph with treewidth at most
$k-2$
is in
$\mathcal {C}_{k}$
. Thus Theorem 1.2 with
$s=k-2$
implies that for every fixed forest T,
$$ \begin{align*}C(T,\mathcal{C}_{k},n) \in \Theta(n^{\alpha_{k-2}(T)}).\end{align*} $$
Colin de Verdiére number:
The Colin de Verdière parameter
$\mu (G)$
is an important graph invariant introduced by de Verdière [Reference de Verdière23, Reference de Verdière24]; see [Reference Schrijver90, Reference van der Holst, Lovász and Schrijver96] for surveys. It is known that
$\mu (G)\leqslant 1$
if and only if G is a disjoint union of paths,
$\mu (G)\leqslant 2$
if and only if G is outerplanar,
$\mu (G)\leqslant 3$
if and only if G is planar, and
$\mu (G)\leqslant 4$
if and only if G is linklessly embeddable. Let
$\mathcal {V}_{k}:=\{G:\mu (G)\leqslant k\}$
. Then
$\mathcal {V}_{k}$
is a minor-closed class [Reference de Verdière23, Reference de Verdière24]. Goldberg and Berman [Reference Goldberg and Berman51] proved that
$\mu (G) \leqslant \operatorname {\mathrm {\mathsf {tw}}}(G)+1$
. So every graph with treewidth at most
$k-1$
is in
$\mathcal {V}_{k}$
. van der Holst et al. [Reference van der Holst, Lovász and Schrijver96] proved that
$\mu (K_{s,t}) = s+1$
for
$t\geqslant \max \{s,3\}$
, so
$K_{k,\max \{k,3\}} \not \in \mathcal {V}_{k}$
. Thus Theorem 1.2 with
$s=k-1$
and
$t=\max \{k,3\}$
implies that for every fixed forest T,
$$ \begin{align} C(T,\mathcal{V}_{k},n) \in \Theta(n^{\alpha_{k-1}(T)}). \end{align} $$
Linkless graphs:
A graph is linklessly embeddable if it has an embedding in
$\mathbb {R}^{3}$
with no two linked cycles [Reference Robertson, Seymour, Thomas, Robertson and Seymour87, Reference Sachs, Borowiecki, Kennedy and Syslo89]. Let
$\mathcal {L}$
be the class of linklessly embeddable graphs. Then
$\mathcal {L}$
is a minor-closed class whose minimal excluded minors are the so-called Petersen family [Reference Robertson, Seymour and Thomas88], which includes
$K_{6}$
,
$K_{4,4}$
minus an edge, and the Petersen graph. As mentioned above,
$\mathcal {L}=\mathcal {V}_{4}$
. Thus Equation (4.2) with
$k=4$
implies for every fixed forest T,
$$ \begin{align*}C(T,\mathcal{L},n) \in \Theta(n^{\alpha_{3}(T)}).\end{align*} $$
Knotless graphs:
A graph is knotlessly embeddable if it has an embedding in
$\mathbb {R}^{3}$
in which every cycle forms a trivial knot; see [Reference Ramírez Alfonsín83] for a survey. Let
$\mathcal {K}$
be the class of knotlessly embeddable graphs. Then
$\mathcal {K}$
is a minor-closed class whose minimal excluded minors include
$K_{7}$
and
$K_{3,3,1,1}$
(see [Reference Conway and Gordon18, Reference Foisy40]). More than 260 minimal excluded minors are known [Reference Goldberg, Mattman and Naimi52], but the full list of minimal excluded minors is unknown. Since
$K_{7}\not \in \mathcal {K}$
, we have
$\rho (\mathcal {K})\leqslant \rho (\mathcal {C}_{7})<5$
by a theorem of Mader [Reference Mader73]. Shimabara [Reference Shimabara92] proved that
$K_{5,5}\not \in \mathcal {K}$
. By Theorem 1.2,
$$ \begin{align*}C(T,\mathcal{K},n)\in O(n^{\alpha_{4}(T)}).\end{align*} $$
This bound would be tight if every treewidth 4 graph is knotlessly embeddable, which is an open problem of independent interest.
The above results all depend on excluded complete bipartite minors. We now show that excluded complete bipartite minors determine
$C(T,\mathcal {G},n)$
for a broad family of minor-closed classes.
Theorem 4.1 Let
$\mathcal {G}$
be a minor-closed class such that every minimal forbidden minor of
$\mathcal {G}$
is two-connected. Let s be the maximum integer such that
$K_{s,t} \in \mathcal {G}$
for every
$t\in \mathbb {N}$
. Then for every forest T,
$$ \begin{align*}C(T,\mathcal{G},n) = \Theta( n^{\alpha_{s}(T)} ).\end{align*} $$
Proof Note that the condition that every minimal forbidden minor of
$\mathcal {G}$
is two-connected is equivalent to saying that
$\mathcal {G}$
is closed under the one-sum operation (that is, if
$G_{1},G_{2}\in \mathcal {G}$
, and
$|V(G_{1}\cap G_{2})|\leqslant 1$
, then
$G_{1}\cup G_{2}\in \mathcal {G}$
).
The proof of Lemma 2.1 shows that for all sufficiently large
$n\in \mathbb {N}$
there exists an n-vertex graph G with
$C(T,G)\geqslant c n^{\alpha _{s}(T)}$
, where G is obtained from one-sums of complete bipartite graphs
$K_{s^{\prime },t}$
with
$s^{\prime }\leqslant s$
. By the definition of s and since
$\mathcal {G}$
is closed under one-sums,
$G\in \mathcal {G}$
. Thus
$C(T,\mathcal {G},n) \in \Omega ( n^{\alpha _{s}(T)} )$
.
Now we prove the upper bound. Since
$\mathcal {G}$
is minor-closed,
$\mathcal {G}$
has bounded density [Reference Kostochka65, Reference Thomason93]. By the definition of s, there exists
$t\in \mathbb {N}$
such that
$K_{s+1,t}\not \in \mathcal {G}$
. By (A), we have
${U}^{\langle {s,t}\rangle }\not \in \mathcal {G}$
for every nonempty subtree U of T. Thus
$I(T,\mathcal {G},n) \in O( n^{\alpha _{s}(T)})$
by Lemma 3.3.▪
Note that minor-closed classes with bounded pathwidth (that is, those excluding a fixed forest as a minor [Reference Bienstock, Robertson, Seymour and Thomas11]) are examples not covered by Theorem 4.1. Determining
$C(T,\mathcal {G}_{k},n)$
, where
$\mathcal {G}_{k}$
is the class of pathwidth k graphs, is an interesting open problem.
5 Beyond minor-closed classes
This section asymptotically determines
$C(T,\mathcal {G},n)$
for several nonminor-closed graph classes
$\mathcal {G}$
.
5.1 Shortcut systems
Dujmović et al. [Reference Dujmović, Morin and Wood28] introduced the following definition which generalizes the notion of shallow immersion [Reference Nešetřil and de Mendez78] and provides a way to describe a graph class in terms of a simpler graph class. Then properties of the original class are (in some sense) transferred to the new class. Let
$\mathcal {P}$
be a set of nontrivial paths in a graph G. Each path
$P\in \mathcal {P}$
is called a shortcut; if P has endpoints v and w then it is a
$vw$
-shortcut. Given a graph G and a shortcut system
$\mathcal {P}$
for G, let
$G^{\mathcal {P}}$
be the simple supergraph of G obtained by adding the edge
$vw$
for each
$vw$
-shortcut in
$\mathcal {P}$
. Dujmović et al. [Reference Dujmović, Morin and Wood28] defined
$\mathcal {P}$
to be a
$(k,d)$
-shortcut system (for G) if:
-
• every path in
$\mathcal {P}$
has length at most k and -
• for every
$v\in V(G)$
, the number of paths in
$\mathcal {P}$
that use v as an internal vertex is at most d.
We use the following variation. Say
$\mathcal {P}$
is a
$(k,d)^{\star }$
-shortcut system (for G) if:
-
• every path in
$\mathcal {P}$
has length at most k and -
• for every
$v\in V(G)$
, if
$M_{v}$
is the set of vertices
$u\in V(G)$
such that there exists a
$uw$
-shortcut in
$\mathcal {P}$
in which v is an internal vertex, then
$|M_{v}| \leqslant d$
.
Clearly, every
$(k,d)^{\star }$
-shortcut system is a
$(k,\binom {d}{2})$
-shortcut system (since
$G^{\mathcal {P}}$
is simple), and every
$(k,d)$
-shortcut system is a
$(k,2d)^{\star }$
-shortcut system.
The next lemma shows that if
$G^{\mathcal {P}}$
contains a “small” model of a “large” complete bipartite graph, then so does G.
Lemma 5.1 For all
$s,t,d,k,p,q\in \mathbb {N}$
, let
$s^{\prime }:= (d(k-1)(p-1) + 1)(s-1)+1$
and
$t^{\prime }:= ( 2d(k-1)(s+q-1) + 1 )(t-1) + 1 + sd ( p+(k-1)(p-1) )$
. Let
$\mathcal {P}$
be a
$(k,d)^{\star }$
-shortcut system for a graph G. If
$G^{\mathcal {P}}$
contains a
$(p,q)$
-model of
$K_{s^{\prime },t^{\prime }}$
, then G contains a
$( p+(k-1)(p-1),q+(k-1)(s+q-1))$
-model of
$K_{s,t}$
.
Proof Let
$(X_{1},\dots ,X_{s^{\prime }};Y_{1},\dots ,Y_{t^{\prime }})$
be a
$(p,q)$
-model of
$K_{s^{\prime },t^{\prime }}$
in
$G^{\mathcal {P}}$
. We may assume that each edge of G is (a path of length 1) in
$\mathcal {P}$
. Let
$I:=[s^{\prime }]$
and
$J:=[t^{\prime }]$
. We may assume that
$X_{i}$
and
$Y_{j}$
are subtrees of
$G^{\mathcal {P}}$
for
$i\in I$
and
$j\in J$
.
Consider each
$i\in I$
. Let
$C_{i}$
be the set of all vertices internal to some
$uw$
-shortcut with
$uw\in E(X_{i})$
. Since
$|E(X_{i})| \leqslant p-1$
, we have
$|C_{i}|\leqslant (k-1)(p-1)$
. For each
$i\in I$
, let
$\hat {X}_{i}$
be the subgraph of G induced by
$V(X_{i})\cup C_{i}$
. By construction,
$\hat {X}_{i}$
is connected and
$|V(\hat {X}_{i})| \leqslant p+(k-1)(p-1)$
.
Consider the graph A with
$V(A):=I$
where two vertices
$i,i^{\prime }\in V(A)$
are adjacent if
$V(\hat {X_{i}}) \cap V(\hat {X_{i^{\prime }}}) \neq \emptyset $
. For each
$ii^{\prime } \in E(A)$
, fix a vertex
$v_{i,i^{\prime }}$
in
$V(\hat {X}_{i})\cap V(\hat {X}_{i^{\prime }})$
, which is in
$C_{i} \cup C_{i^{\prime }}$
since
$V(X_{i}) \cap V(X_{i^{\prime }}) = \emptyset $
. For
$i\in I$
and
$v \in C_{i}$
, define
$E_{v,i}$
to be the set of all edges
$ii^{\prime }\in E(A)$
with
$v_{i,i^{\prime }} = v$
. If
$ii^{\prime }$
is in
$E_{v,i}$
and
$v\not \in X_{i^{\prime }}$
, then
$|M_{v}\cap X_{i^{\prime }}|\geqslant 2$
. Also
$|M_{v}\cap X_{i}|\geqslant 2$
. Since v is in at most one
$X_{i^{\prime }}$
, in total,
$|M_{v}|\geqslant 2|E_{v,i}|$
, implying
$|E_{v,i}|\leqslant \frac {d}{2}$
. Since
$|I|=|V(A)|$
and
$|C_{i}|\leqslant (k-1)(p-1)$
,
$$ \begin{align*}|E(A)| \leqslant \sum_{i\in I} \sum_{v\in C_{i}} |E_{v,i}| \leqslant \tfrac{d}{2}(k-1)(p-1)\, |V(A)|.\end{align*} $$
Thus, A has average degree at most
$d(k-1)(p-1)$
. By Turán’s Theorem, A contains a stable set
$I^{\prime }$
of size
$\lceil |I|/ ( d(k-1)(p-1) + 1 ) \rceil =s$
. For distinct
$i,i^{\prime }\in I^{\prime }$
, the subgraphs
$\hat {X}_{i}$
and
$\hat {X}_{i^{\prime }}$
are disjoint. Let
$\mathcal {X}:=\bigcup _{i \in I^{\prime }} V(\hat {X}_{i})$
. Note that
$|\mathcal {X}| \leqslant s ( p+(k-1)(p-1) )$
.
Let
$Z:=\bigcup _{x\in \mathcal {X}}M_{x}$
. Then
$|Z|\leqslant sd ( p+(k-1)(p-1) )$
. Thus,
$Y_{j}$
intersects Z for at most
$sd ( p+(k-1)(p-1) )$
elements
$j\in J$
. Hence, J contains a subset K of size
$( 2d(k-1)(s+q-1) + 1 )(t-1) +1$
such that
$V(Y_{j}) \cap Z=\emptyset $
for each
$j\in K$
.
Consider each
$j\in K$
. Initialize
$D_{j}:=\emptyset $
. For each
$i\in I^{\prime }$
, choose
$x\in V(X_{i})$
and
$w\in V(Y_{j})$
such that
$xw \in E(G^{\mathcal P})$
, and add all the internal vertices of the
$xw$
-shortcut
$P \in \mathcal P$
to
$D_{j}$
. For each edge
$uw$
of
$Y_{j}$
, add all the internal vertices of the
$uw$
-shortcut
$P\in \mathcal {P}$
to
$D_{j}$
. Note that
$$ \begin{align*}|D_{j}| \leqslant (k-1)|I^{\prime}| + (k-1)|E(Y_{j})| \leqslant (k-1)(s+q-1),\end{align*} $$
since
$Y_{j}$
has at most
$q-1$
edges. Moreover,
$D_{j} \cap \mathcal {X} = \emptyset $
since
$V(Y_{j})\cap Z=\emptyset $
.
For each
$j\in K$
, let
$\hat {Y}_{j}$
be the subgraph of G induced by
$V(Y_{j})\cup D_{j}$
. By construction,
$\hat {Y}_{j}$
is connected with at most
$q+(k-1)(s+q-1)$
vertices and is disjoint from
$\mathcal {X}$
.
Consider the graph B with
$V(B):=K$
where two vertices
$j,j^{\prime }\in V(B)$
are adjacent if
$V(\hat {Y_{j}}) \cap V(\hat {Y_{j^{\prime }}}) \neq \emptyset $
. For each
$jj^{\prime } \in E(B)$
, fix a vertex
$v_{j,j^{\prime }}$
in
$V(\hat {Y}_{j})\cap V(\hat {Y}_{j^{\prime }})$
, which is in
$D_{j} \cup D_{j^{\prime }}$
since
$V(Y_{j}) \cap V(Y_{j^{\prime }}) = \emptyset $
. For
$j\in K$
and
$v \in D_{j}$
, define
$E_{v,j}$
to be the set of all edges
$jj^{\prime }\in E(B)$
with
$v_{j,j^{\prime }} = v$
.
We now bound
$|E(B)|$
. If
$jj^{\prime }$
is in
$E_{v,j}$
and
$v\not \in Y_{j^{\prime }}$
, then
$|M_{v}\cap Y_{j^{\prime }}|\geqslant 1$
. Also
$|M_{v}\cap Y_{j}|\geqslant 1$
. Since v is in at most one
$Y_{j^{\prime }}$
, in total,
$|M_{v}| \geqslant |E_{v,j}|$
, implying
$|E_{v,j}| \leqslant d$
. Since
$|K|=|V(B)|$
and
$|D_{j}|\leqslant (k-1)(s+q-1)$
,
$$ \begin{align*}|E(B)| \leqslant \sum_{j\in K} \sum_{v\in D_{j}} |E_{v,j}| \leqslant d(k-1)(s+q-1)\, |V(B)|,\end{align*} $$
implying B has average degree at most
$2d(k-1)(s+q-1)$
. By Turán’s Theorem, B contains a stable set L of size
$\lceil |K|/ ( 2d(k-1)(s+q-1) + 1 ) \rceil =t$
.
For distinct
$j,{j^{\prime }}\in L$
, since L is a stable set in B,
$\hat {Y}_{j}$
and
$\hat {Y}_{j^{\prime }}$
are disjoint. For each
$j\in L$
,
$Y_{j}$
and
$\mathcal {X}$
are disjoint by assumption, and
$D_{j}$
and
$\mathcal {X}$
are disjoint by construction. Also, for each
$i\in I^{\prime }$
and
$j\in L$
, there is an edge between
$\hat {X}_{i}$
and
$\hat {Y}_{j}$
by construction. Thus
$\{\hat {X}_{i}:i\in I^{\prime }\}$
and
$\{\hat {Y}_{j}:j \in L\}$
form a
$( p+(k-1)(p-1),q+k(s+q-1))$
-model of
$K_{s,t}$
in G.▪
Lemma 5.1 with
$p=1$
implies the following result. We emphasize that the value of s does not change in the two models.
Corollary 5.2 Fix
$s,t,k,d,q\in \mathbb {N}$
. Let
$t^{\prime }:= ( 2d(k-1)(s+q-1) + 1 )(t-1) + 1 + sd$
. Let
$\mathcal {P}$
be a
$(k,d)^{\star }$
-shortcut system for a graph G. If
$G^{\mathcal {P}}$
contains a
$(1,q)$
-model of
$K_{s,t^{\prime }}$
, then G contains a
$(1,q+(k-1)(s+q-1))$
-model of
$K_{s,t}$
.
5.2 Low-degree squares of graphs
The above result on shortcut systems leads to the following extension of our results for minor-closed classes. For a graph G and
$d\in \mathbb {N}$
, let
$G^{(d)}$
be the graph obtained from G by adding a clique on
$N_{G}(v)$
for each vertex
$v\in V(G)$
with
$\deg _{G}(v)\leqslant d$
. (This definition incorporates and generalizes the square of a graph with maximum degree d.) Note that
$G^{(d)}=G^{\mathcal {P}}$
, where
$\mathcal {P}$
is the
$(2,d)^{\star }$
-shortcut system
$\{uvw: v\in V(G);\deg _{G}(v)\leqslant d; u,w\in N_{G}(v); u\neq w\}$
. For a graph class
$\mathcal {G}$
, let
$\mathcal {G}^{(d)}:=\{G^{(d)}:G\in \mathcal {G}\}$
. Note that
$\rho (G^{(d)}) \leqslant \rho (G)+\binom {d}{2}$
. Corollary 3.4 and Corollary 5.2 with
$k=2$
and
$q=h$
imply:
Corollary 5.3 Fix
$s,t,d,h\in \mathbb {N}$
and
$\rho \in \mathbb {R}_{\geqslant 0}$
. Let T be fixed forest with h vertices. Let
$t^{\prime }:= ( 2d(s+h-1) + 1 )(t-1) + 1 + sd$
. Let G be a graph with
$\rho (G)\leqslant \rho $
and containing no
$(1,2h+s-1)$
-model of
$K_{s,t}$
. Then
$G^{(d)}$
contains no
$(1,h)$
-model of
$K_{s,t^{\prime }}$
, and
$$ \begin{align*}C(T,G^{(d)}) \leqslant I(T,G^{(d)}) \leqslant c_{3.3}(s-1,t^{\prime},h,\rho+\tbinom{d}{2}) \,|V(G)|^{\alpha_{s-1}(T)}.\end{align*} $$
With Lemma 2.1 we have:
Theorem 5.4 Fix
$s,t,d,h\in \mathbb {N}$
and
$\rho \in \mathbb {R}_{\geqslant 0}$
. Let T be fixed forest with h vertices. Let
$t^{\prime }:= ( 2d(s+h-1) + 1 )(t-1) + 1 + sd$
. Let
$\mathcal {G}$
be a graph class such that
$\rho (\mathcal {G})\leqslant \rho $
, every graph with treewidth at most
$s-1$
is in
$\mathcal {G}$
, and no graph in
$\mathcal {G}$
contains a
$(1,2h+s-1)$
-model of
$K_{s,t}$
. Then no graph in
$\mathcal {G}^{(d)}$
contains a
$(1,h)$
-model of
$K_{s,t^{\prime }}$
, and
$$ \begin{align*}C(T,\mathcal{G}^{(d)},n) = \Theta( n^{\alpha_{s-1}(T)} ).\end{align*} $$
Theorem 5.4 is applicable to all the minor-closed classes discussed in Section 4. For example, we have the following extension of Equation (4.1). Recall that
$\mathcal {B}_{s,t}^{(d)}$
is the class of graphs
$G^{(d)}$
where G contains no
$K_{s,t}$
-minor. Then for every fixed forest T,
$$ \begin{align*}C(T,\mathcal{B}_{s,t}^{(d)},n) = \Theta( n^{\alpha_{s-1}(T)}).\end{align*} $$
5.3 Map graphs
Map graphs are defined as follows. Start with a graph
$G_{0}$
embedded in a surface
$\Sigma $
, with each face labelled a “nation” or a “lake,” where each vertex of
$G_{0}$
is incident with at most d nations. Let G be the graph whose vertices are the nations of
$G_{0}$
, where two vertices are adjacent in G if the corresponding faces in
$G_{0}$
share a vertex. Then G is called a
$(\Sigma ,d)$
-map graph. A
$(\mathbb {S}_{0},d)$
-map graph is called a (plane) d-map graph; such graphs have been extensively studied [Reference Chen15–Reference Chen, Grigni and Papadimitriou17, Reference Demaine, Fomin, Hajiaghayi and Thilikos25, Reference Fomin, Lokshtanov and Saurabh41]. Let
$\mathcal {M}_{\Sigma ,d}$
be the set of all
$(\Sigma ,d)$
-map graphs. Since
$\mathcal {M}_{\Sigma ,3}=\mathcal {S}_{\Sigma }$
(see [Reference Chen, Grigni and Papadimitriou17, Reference Dujmović, Eppstein and Wood26]), map graphs provide a natural generalization of graphs embeddable in a surface.
Let
$G\in \mathcal {M}_{\Sigma ,d}$
where
$\Sigma $
has Euler genus g. Let T be a fixed forest with h vertices. Dujmović et al. [Reference Dujmović, Morin and Wood28] proved that G is a subgraph of
$G_{0}^{\mathcal {P}}$
for some graph
$G_{0}\in \mathcal {S}_{\Sigma }$
and some
$(2,\frac 12 d(d-3))$
-shortcut system
$\mathcal {P}$
of
$G_{0}$
. Inspecting the proof in [Reference Dujmović, Morin and Wood28] one observes that
$\mathcal {P}$
is a
$(2,d)^{\star }$
-shortcut system. In the plane case, Chen [Reference Chen15] proved that
$\rho (\mathcal {M}_{\mathbb {S}_{0},d})< d$
. An analogous argument shows that
$\rho (\mathcal {M}_{\Sigma ,d})\in O(d \sqrt {g+1})$
. The same bound can also be concluded from Equation (5.2). Since
$G_{0}$
contains no
$K_{3,2g+3}$
minor, by Corollary 5.2, for each
$q\in \mathbb {N}$
,
$G_{0}^{\mathcal {P}}$
and thus G contains no
$(1,q)$
-model of
$K_{3,t^{\prime }}$
where
$t^{\prime }:= ( 2d(q+2) + 1 )(2g+2) +1 + 3d$
. With
$q=h$
, Corollary 3.4 then implies that
$C(T,G) \leqslant I(T,G) \leqslant c_{3.3}(2,t^{\prime },h,\rho ) \,|V(G)|^{\alpha _{2}(T)}$
. Hence
$$ \begin{align*}C(T,\mathcal{M}_{\Sigma,d},n) \in \Theta( n^{\alpha_{2}(T)} ),\end{align*} $$
where the lower bound follows from Lemma 2.1 since every graph with treewidth 2 is planar and is thus a
$(\Sigma ,d)$
-map graph. Also note the
$q=1$
case above shows that
$$ \begin{align*}K_{3,( 6d + 1 )(2g+2)+1 + 3d} \not\in \mathcal{M}_{\Sigma,d}.\end{align*} $$
5.4 Bounded number of crossings
Here, we consider drawings of graphs with a bounded number of crossings per edge. Throughout the paper, we assume that no three edges cross at a single point in a drawing of a graph. For a surface
$\Sigma $
and
$k\in \mathbb {N}$
, let
$\mathcal {S}_{\Sigma ,k}$
be the class of graphs G that have a drawing in
$\Sigma $
such that each edge is in at most k crossings. Since
$\mathcal {S}_{\Sigma ,0}=\mathcal {S}_{\Sigma }$
, this class provides a natural generalization of graphs embeddable in surfaces and is widely studied [Reference de Mendez, Oum and Wood22, Reference Dujmović, Morin and Wood28, Reference Pach and Tóth80]. Graphs in
$\mathcal {S}_{\mathbb {S}_{0},k}$
are called k-planar. The case
$k=1$
is particularly important in the graph drawing literature; see [Reference Kobourov, Liotta and Montecchiani63] for a bibliography with over 100 references.
Let T be a fixed forest with h vertices. Let
$G\in \mathcal {S}_{\Sigma ,k}$
where
$\Sigma $
has Euler genus g. Dujmović et al. [Reference Dujmović, Morin and Wood28] noted that by replacing each crossing point by a dummy vertex, we obtain a graph
$G_{0}\in \mathcal {S}_{\Sigma }$
such that G is a subgraph of
$G_{0}^{\mathcal {P}}$
for some
$(k+1,2)$
-shortcut system
$\mathcal {P}$
, which is a
$(k+1,4)^{\star }$
-shortcut system. Results of Ossona de Mendez et al. [Reference de Mendez, Oum and Wood22] show that
$\rho (\mathcal {S}_{\Sigma ,k}) \leqslant 2\sqrt {k+1}\rho _{g}$
(see Equation (5.2) below). Since
$G_{0}$
contains no
$K_{3,2g+3}$
minor, by Corollary 5.2, for all
$q\in \mathbb {N}$
,
$G_{0}^{\mathcal {P}}$
and thus G contains no
$(1,q)$
-model of
$K_{3,t^{\prime }}$
where
$t^{\prime }:= ( 8k(q+2) + 1 )(2g+2) + 13$
. Applying this result with
$q=h$
, Corollary 3.4 then implies
$C(T,G) \leqslant I(T,G) \leqslant c_{3.3}(2,t^{\prime },h,2\sqrt {k+1}\rho _{g}) \,|V(G)|^{\alpha _{2}(T)}$
. Hence,
$$ \begin{align} C(T,\mathcal{S}_{\Sigma,k},n) \in \Theta(n^{\alpha_{2}(T)}), \end{align} $$
where the lower bound follows from Lemma 2.1 since every treewidth 2 graph is planar and is thus in
$\mathcal {S}_{\Sigma ,k}$
. Also note the
$q=1$
case above shows that
$$ \begin{align*}K_{3,( 24k + 1 )(2g+2) + 13} \not\in \mathcal{S}_{\Sigma,k}.\end{align*} $$
5.5 Bounded average number of crossings
Here, we generalize the results from the previous section for graphs that can be drawn with a bounded average number of crossings per edge. Ossona de Mendez et al. [Reference de Mendez, Oum and Wood22] defined a graph G to be k-close to Euler genus g if every subgraph
$G^{\prime }$
of G has a drawing in a surface of Euler genus at most g with at most
$k\,|E(G^{\prime })|$
crossings.Footnote
6
Let
$\mathcal {E}_{g,k}$
be the class of graphs k-close to Euler genus g. This is a broader class than
$\mathcal {S}_{\Sigma ,k}$
since it allows an average of k crossings per edge, whereas
$\mathcal {S}_{\Sigma ,k}$
requires a maximum of k crossings per edge. In particular, if
$\Sigma $
has Euler genus g, then
$\mathcal {S}_{\Sigma ,k} \subseteq \mathcal {E}_{g,k/2}$
.
The next lemma is of independent interest.
Lemma 5.5 Fix
$g,r\in \mathbb {N}_{0}$
and
$d\in \mathbb {N}$
and
$k\in \mathbb {R}_{\geqslant 0}$
. Assume that graph
$G\in \mathcal {E}_{g,k}$
contains an r-shallow H-model
$(X_{v}:v\in V(H))$
such that for every vertex
$v\in V(H)$
we have
$\deg _{H}(v)\leqslant d$
or
$|V(X_{v})|=1$
. Then H is in
$\mathcal {E}_{g,2kd^{2}(2r+1)}$
.
Proof For each
$v\in V(H)$
, let
$a_{v}$
be the central vertex of
$X_{v}$
. We may assume that
$X_{v}$
is a Breadth-first search (BFS) spanning tree of
$G[V(X_{v})]$
rooted at
$a_{v}$
and with radius at most r. Orient the edges of
$X_{v}$
away from
$a_{v}$
.
Let
$H^{\prime }$
be an arbitrary subgraph of H. For each
$v\in V(H^{\prime })$
, let
$X^{\prime }_{v}$
be a minimal subtree of
$X_{v}$
rooted at
$a_{v}$
, such that
$(X^{\prime }_{v}:v\in V(H^{\prime }))$
is an r-shallow
$H^{\prime }$
-model. By minimality,
$X^{\prime }_{v}$
has at most
$\deg _{H^{\prime }}(v)$
leaves. Each edge of
$X^{\prime }_{v}$
is on a path from a leaf to
$a_{v}$
, implying
$|E(X^{\prime }_{v})| \leqslant r\deg _{H^{\prime }}(v)$
.
Let
$G^{\prime }$
be the subgraph of G consisting of
$\bigcup _{v\in V(H^{\prime })}X^{\prime }_{v}$
along with one undirected edge
$y_{vw}y_{wv}$
for each edge
$vw\in E(H^{\prime })$
, where
$y_{vw}\in V(X^{\prime }_{v})$
and
$y_{wv}\in V(X^{\prime }_{w})$
. Let
$P_{vw}$
be the directed
$a_{v}y_{vw}$
-path in
$X^{\prime }_{v}$
. Note that
$$ \begin{align*}|E(G^{\prime})| \,=\, |E(H^{\prime})| + \!\! \sum_{v\in V(H^{\prime})} \!\!\! |E(X^{\prime}_{v})| \,\leqslant\, |E(H^{\prime})| + r \!\! \sum_{v\in V(H^{\prime})} \!\!\! \deg_{H^{\prime}}(v) \,=\, (2r+1) |E(H^{\prime})| .\end{align*} $$
Since G is k-close to Euler genus g,
$G^{\prime }$
has a drawing in a surface of Euler genus at most g with at most
$k\,|E(G^{\prime })|$
crossings. For each
$e\in E(G^{\prime })$
, let
$\ell (e)$
be the number of crossings on e in this drawing of
$G^{\prime }$
. Since each crossing contributes towards
$\ell $
for exactly two edges,
$$ \begin{align*}\sum_{e\in E(G^{\prime})}\!\!\ell(e) \leqslant 2k\,|E(G^{\prime})| \leqslant 2k(2r+1)|E(H^{\prime})| .\end{align*} $$
Let
$G^{\prime \prime }$
be the multigraph obtained from
$G^{\prime }$
as follows: for each vertex
$v\in V(H^{\prime })$
and edge e in
$X^{\prime }_{v}$
, let the multiplicity of e in
$G^{\prime \prime }$
equal the number of edges
$vw\in E(H^{\prime })$
for which the path
$P_{vw}$
uses e. Edges of
$G^{\prime \prime }$
inherit their orientation from
$G^{\prime }$
. Note that
$G^{\prime \prime }$
has multiplicity at most d. By replicating edges in the drawing of
$G^{\prime }$
we obtain a drawing of
$G^{\prime \prime }$
such that every edge of
$G^{\prime \prime }$
corresponding to
$e\in E(G^{\prime })$
is in at most
$d\, \ell (e)$
crossings. Since each edge
$e\in E(G^{\prime })$
has multiplicity at most d in
$G^{\prime \prime }$
, the number of crossings in the drawing of
$G^{\prime \prime }$
is at most
$\sum _{e\in E(G^{\prime })} d^{2}\ell (e) \leqslant 2kd^{2}(2r+1)\,|E(H^{\prime })|$
.
Note that at each vertex y in
$G^{\prime \prime }$
, in the circular ordering of edges in
$G^{\prime \prime }$
incident to y determined by the drawing of
$G^{\prime \prime }$
, all the incoming edges form an interval. We now use the drawing of
$G^{\prime }$
to produce a drawing of a graph
$G^{\prime \prime \prime }$
, which is a subdivision of
$H^{\prime }$
, where each vertex
$v\in V(H^{\prime })$
is drawn at the location of
$a_{v}$
. Here is the idea (see Figure 2): First “assign” each edge
$y_{vw}y_{wv}$
of
$G^{\prime }$
to the edge
$vw$
of
$H^{\prime }$
. Next “assign” each edge of
$G^{\prime }$
arising from some
$X^{\prime }_{v}$
to exactly one edge incident to v, such that for each edge
$vw$
of
$H^{\prime }$
incident to v there is a path in
$G^{\prime }$
from
$a_{v}$
to
$y_{vw}$
consisting of edges assigned to
$vw$
. Then each edge
$vw$
in
$H^{\prime }$
is drawn by following this path.
Figure 2: Construction of the drawing of H.
We now provide the details of this idea. Initialize
$V(G^{\prime \prime \prime }):= V(G^{\prime })$
and
$E(G^{\prime \prime \prime }):=\{ y_{vw}y_{wv}: vw\in E(H)\}$
. Consider each vertex
$v\in V(H^{\prime })$
. Consider the vertices
$y\in V(X^{\prime }_{v})\setminus \{a_{v}\}$
in nonincreasing order of
$\text {dist}_{X^{\prime }_{v}}(a_{v},y)$
(that is, we consider the vertices of
$X^{\prime }_{v}$
furthest from
$a_{v}$
first, and then move towards the root). Let x be the parent of y in
$X^{\prime }_{v}$
. The incoming edges at y are copies of
$xy$
. Each outgoing/undirected edge
$yz$
at y is already assigned to one edge
$vw$
incident to v. Say
$yz_{1},\dots ,yz_{q}$
are the outgoing/undirected edges of
$G^{\prime \prime }$
incident to y in clockwise order in the drawing of
$G^{\prime \prime }$
, where
$yz_{i}$
is assigned to edge
$vw_{i}$
. If
$e_{1},\dots ,e_{q}$
are the incoming edges at y in clockwise order, then assign
$e_{q-i+1}$
to
$vw_{i}$
for each
$i\in [q]$
. Now in
$G^{\prime \prime \prime }$
replace vertex y by vertices
$y_{1},\dots ,y_{q}$
drawn in a sufficiently small disc around y, where
$y_{i}$
is incident to
$e_{q-i+1}$
and
$y_{i}z_{i}$
in
$G^{\prime \prime \prime }$
. Thus the edges in
$G^{\prime \prime \prime }$
assigned to
$vw$
form a path from
$a_{v}$
to
$y_{vw}$
and a path from
$a_{w}$
to
$y_{wv}$
. Hence
$G^{\prime \prime \prime }$
is a subdivision of
$H^{\prime }$
(since
$y_{vw}y_{wv}$
is an edge of
$G^{\prime \prime \prime }$
). Each edge of
$G^{\prime \prime \prime }$
has the same number of crossings as the corresponding edge of
$G^{\prime \prime }$
. Thus, the total number of crossings in the drawing of
$G^{\prime \prime \prime }$
is at most
$2kd^{2}(2r+1)|E(H^{\prime })|$
. Since
$G^{\prime \prime \prime }$
is a subdivision of
$H^{\prime }$
, the drawing of
$G^{\prime \prime \prime }$
determines a drawing of
$H^{\prime }$
with the same number of crossings. Therefore H is
$2kd^{2}(2r+1)$
-close to Euler genus g.▪
We need the following results of Ossona de Mendez et al. [Reference de Mendez, Oum and Wood22]:
$$ \begin{align} \rho( \mathcal{E}_{k,g} ) & \leqslant 2\sqrt{2k+1}\,\rho_{g} \end{align} $$
$$ \begin{align} K_{3,3k(2g+3)(2g+2)+2} & \not\in \mathcal{E}_{g,k}. \end{align} $$
We now reach the main result of this section.
Theorem 5.6 For fixed
$k,g\in \mathbb {N}_{0}$
and every fixed forest T,
$$ \begin{align*}C(T,\mathcal{E}_{g,k},n) \in \Theta(n^{\alpha_{2}(T)}).\end{align*} $$
Proof First, we prove the lower bound. By Lemma 2.1 with
$s=2$
, for all sufficiently large
$n\in \mathbb {N}$
, there exists a graph G with
$|V(G)|\leqslant n$
and
$\operatorname {\mathrm {\mathsf {tw}}}(G)\leqslant 2$
and
$C(T,G)\geqslant c_{2.1}(\alpha _{2}(T))\, n^{\alpha _{2}(T)}$
. Since
$\operatorname {\mathrm {\mathsf {tw}}}(G)\leqslant 2$
, G is planar and is thus in
$\mathcal {E}_{g,k}$
. Hence,
$C(T,\mathcal {E}_{g,k},n)\in \Omega (n^{\alpha _{2}(T)})$
.
Now, we prove the upper bound. Let
$s:=2$
and
$r:=|V(T)|$
and
$t:= 54k(2r+1)(2g+3)(2g+2)+2$
. Let G be an n-vertex graph in
$\mathcal {E}_{g,k}$
. By Equation (5.2),
$\rho (G) \leqslant 2\sqrt {2k+1}\,\rho _{g} $
. Suppose on the contrary that
$I(T,G)\geqslant cn^{\alpha _{2}(T)}$
, where
$c:=c_{3.3}(s,t,r,2\sqrt {2k+1}\,\rho _{g} )$
.
Let
$H:=K_{3,t}$
. Corollary 3.4 implies that G contains a
$(1,r)$
-model
$(X_{v}:v\in V(H))$
of H. This model is r-shallow and for every vertex
$v\in V(H)$
we have
$\deg _{H}(v)\leqslant 3$
or
$|V(X_{v})|=1$
. Thus, Lemma 5.5 is applicable with
$d=3$
, implying that
$K_{3,t} \in \mathcal {E}_{g,18k(2r+1)}$
, which contradicts Equation (5.3).▪
An almost identical proof to that of Lemma 5.5 shows the following analogous result for
$\mathcal {S}_{\Sigma ,k}$
. This can be used to prove Equation (5.1) without using shortcut systems.
Lemma 5.7 Fix a surface
$\Sigma $
and
$k,r\in \mathbb {N}_{0}$
and
$d\in \mathbb {N}$
. Let G be a graph in
$\mathcal {S}_{\Sigma ,k}$
that contains an r-shallow H-model
$(X_{v}:v\in V(H))$
such that for every vertex
$v\in V(H)$
we have
$\deg _{H}(v)\leqslant d$
or
$|V(X_{v})|=1$
. Then H is in
$\mathcal {S}_{\Sigma ,kd^{2}(2r+1)}$
.
6 Open problems
In this paper, we determined the asymptotic behavior of
$C(T,\mathcal {G},n)$
as
$n\to \infty $
for various sparse graph classes
$\mathcal {G}$
and for an arbitrary fixed forest T. One obvious question is what happens when T is not a forest?
For arbitrary graphs H, the answer is no longer given by
$\alpha _{s}(H)$
. Huynh et al. [Reference Huynh, Joret and Wood59] define a more general graph parameter, which they conjecture governs the behavior of
$C(H,\mathcal {G},n)$
. An s-separation of H is a pair
$(A,B)$
of edge-disjoint subgraphs of H such that
$A \cup B=H$
,
$V(A) \setminus V(B) \neq \emptyset $
,
$V(B) \setminus V(A) \neq \emptyset $
, and
$|V(A) \cap V(B)|=s$
. A
$(\leqslant s)$
-separation is an
$s^{\prime }$
-separation for some
$s^{\prime } \leqslant s$
. Separations
$(A,B)$
and
$(C,D)$
of H are independent if
$E(A) \cap E(C) = \emptyset $
and
$(V(A) \setminus V(B)) \cap (V(C) \setminus V(D))=\emptyset $
. If H has no
$(\leqslant s)$
-separation, then let
$f_{s}(H):=1$
; otherwise, let
$f_{s}(H)$
be the maximum number of pairwise independent
$(\leqslant s)$
-separations in H.
Conjecture 6.1 [Reference Huynh, Joret and Wood59]
Let
$\mathcal {B}_{s,t}$
be the class of graphs containing no
$K_{s,t}$
minor, where
$t\geqslant s \geqslant 1$
. Then for every fixed graph H with no
$K_{s,t}$
minor,
$$ \begin{align*}C(H,\mathcal{B}_{s,t},n) \in \Theta(n^{f_{s-1}(H)}).\end{align*} $$
As evidence for Conjecture 6.1, Eppstein [Reference Eppstein32] proved it when
$f_{s-1}(H)=1$
and Huynh et al. [Reference Huynh, Joret and Wood59] proved it when
$s \leqslant 3$
(and that the lower bound holds for all
$s \geqslant 1$
). It is easy to show that
$f_{s}(T)=\alpha _{s}(T)$
for all
$s \geqslant 1$
and every forest T. Thus, if true, Conjecture 6.1 would simultaneously generalize Theorem 1.2 and results from [Reference Huynh, Joret and Wood59].
In light of Theorem 1.1, we also conjecture the following generalization.
Conjecture 6.2 Let
$\mathcal {D}_{k}$
be the class of k-degenerate graphs. Then for every fixed k-degenerate graph H,
$$ \begin{align*}C(H,\mathcal{D}_{k},n) \in \Theta(n^{f_{k}(H)}).\end{align*} $$
Acknowledgement
Many thanks to both referees for several helpful comments.
