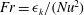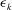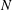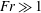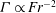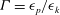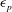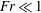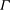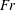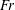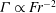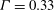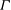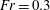1 Introduction
The manifestation of mixing in the atmosphere and oceans takes different forms from phytoplankton blooms in the oceans to the creation of well-mixed fronts in the atmosphere. Mixing in the atmosphere and oceans is a key factor to consider when estimating global energetics. Central to the attempt to quantify mixing in the oceans is the concept of eddy diffusivity, defined as
$K_{{\it\rho}}=B/N^{2}$
(Osborn & Cox Reference Osborn and Cox1972) where
$B=-\langle bu_{z}\rangle$
is the buoyancy flux,
$b=-{\it\rho}^{\prime }g/{\it\rho}_{0}$
being the buoyancy acceleration related to the density perturbation
${\it\rho}^{\prime }$
from the background stratification and
$u_{z}$
being the vertical velocity perturbation. The idea is that the buoyancy flux can be modelled as
$B=-\langle bu_{z}\rangle =K_{{\it\rho}}\,\text{d}\bar{b}/\text{d}z$
, where the mean buoyancy gradient is
$\text{d}\bar{b}/\text{d}z=N^{2}$
. Osborn (Reference Osborn1980) inspected the turbulent kinetic energy equation in the presence of buoyancy and, assuming steady-state conditions, introduced the flux Richardson number
$Ri_{f}=B/(B+{\it\epsilon}_{k})$
, which is the ratio of buoyancy flux to turbulence production by the mean flow and can be thought of as a mixing efficiency. A related quantity is the mixing coefficient
${\it\Gamma}=B/{\it\epsilon}_{k}$
, so that
$K_{{\it\rho}}={\it\Gamma}{\it\epsilon}_{k}/N^{2}$
. A constant mixing efficiency
${\it\eta}=Ri_{f}=0.17$
was assumed by Osborn (Reference Osborn1980), leading to a mixing coefficient
${\it\Gamma}=Ri_{f}/(1-Ri_{f})=0.2$
, a value that has been widely used in oceanographic applications ever since. Salehipour & Peltier (Reference Salehipour and Peltier2015) suggested the use of
${\it\epsilon}_{p}$
instead of the buoyancy flux
$B$
when calculating the mixing coefficient, because the buoyancy flux contains both reversible and irreversible exchanges of kinetic and available potential energy, while we are interested in the irreversible conversion of available potential energy into background potential energy, quantified by
${\it\epsilon}_{p}$
. Throughout the paper we therefore use the definitions
${\it\Gamma}={\it\epsilon}_{p}/{\it\epsilon}_{k}$
for the mixing coefficient and
${\it\eta}={\it\epsilon}_{p}/({\it\epsilon}_{k}+{\it\epsilon}_{p})$
for the mixing efficiency. Direct support for an eddy diffusivity of the form
$K_{{\it\rho}}={\it\epsilon}_{p}/N^{2}={\it\Gamma}{\it\epsilon}_{k}/N^{2}$
was provided by the work of Lindborg & Brethouwer (Reference Lindborg and Brethouwer2008), who derive an analytical expression for the mean square particle displacement
$(1/2)\langle {\it\delta}z^{2}\rangle$
, which increases linearly in time, the constant of proportionality being
$K_{{\it\rho}}$
.
The parameters that could conceivably affect mixing in stratified turbulence are the buoyancy Reynolds number
$Re_{b}$
, the turbulent Froude number
$Fr$
and the Reynolds number
$Re$
. Taking advantage of the estimate
${\it\epsilon}_{k}\sim u^{3}/\ell$
, we define these as
$$\begin{eqnarray}Re_{b}=\frac{{\it\epsilon}_{k}}{{\it\nu}N^{2}},\quad Fr=\frac{{\it\epsilon}_{k}}{Nu^{2}},\quad Re=\frac{u^{4}}{{\it\nu}{\it\epsilon}_{k}}.\end{eqnarray}$$
These definitions differentiate themselves from the more classical definitions using a turbulent length scale
$\ell$
. Throughout the paper
$u$
and
$\ell$
are considered to be horizontal scales so that the results generalize to the case of strongly stratified turbulence and its anisotropic conditions. In this case then
$Fr$
represents a horizontal Froude number, as opposed to the vertical Froude number
$Fr_{v}=u/(N\ell _{v})$
based on a vertical length scale
$\ell _{v}$
. As shown by Billant & Chomaz (Reference Billant and Chomaz2001),
$Fr_{v}=O(1)$
in the limit of low
$Fr$
and therefore
$Fr_{v}$
does not further influence the dynamics. As pointed out for example by Ivey, Winters & Koseff (Reference Ivey, Winters and Koseff2008) the three parameters listed in (1.1) are not independent since
$Re_{b}=Re\,Fr^{2}$
. In problems of mixing through a density discontinuity a relevant parameter is the bulk Richardson number
$Ri_{b}=g{\rm\Delta}{\it\rho}\ell /({\it\rho}_{0}u^{2})$
where
${\rm\Delta}{\it\rho}$
is the density jump across the interface and
${\it\rho}_{0}$
is a reference density. If we substitute
${\rm\Delta}{\it\rho}/\ell$
with the continuous stratification density gradient
$|\text{d}\bar{{\it\rho}}/\text{d}z|$
it is clear that
$Ri_{b}\sim N^{2}\ell ^{2}/u^{2}\sim Fr^{-2}$
using the definition of
$N=\sqrt{-(g/{\it\rho}_{0})\text{d}\bar{{\it\rho}}/\text{d}z}$
. Hence problems with a density interface can also effectively be characterized by the parameters given in (1.1).
Since the seminal work of Osborn & Cox (Reference Osborn and Cox1972) and Osborn (Reference Osborn1980) it has been found that mixing efficiency and mixing coefficient are not constants but vary in a certain parameter range. Barry et al. (Reference Barry, Ivey, Winters and Imberger2001) found a variation of the mixing coefficient in their grid stirring experiments for buoyancy Reynolds numbers
$Re_{b}={\it\epsilon}_{k}/({\it\nu}N^{2})>300$
that was well described by
${\it\Gamma}\propto Re_{b}^{-2/3}$
. In their direct numerical simulations (DNS) of stratified shear flow, Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005) found a constant mixing coefficient
${\it\Gamma}\approx 0.2$
for
$7<Re_{b}<100$
but a mixing coefficient that varied as
${\it\Gamma}\propto Re_{b}^{-1/2}$
for
$Re_{b}>100$
. Ocean field measurements by Davis & Moninsmith (Reference Davis and Moninsmith2011) and Walter et al. (Reference Walter, Squibb, Woodson, Koseff and Monismith2014) have found similar variations of
${\it\Gamma}\propto Re_{b}^{-1/2}$
at high
$Re_{b}>100$
. Atmospheric boundary layer measurements within the vertical transport and mixing experiment (VTMX) also have a similar variation of
${\it\Gamma}$
with
$Re_{b}$
but now at
$Re_{b}>10^{4}$
, suggesting a completely different bound on the buoyancy Reynolds number (see Lozovatsky & Fernando Reference Lozovatsky and Fernando2013). Recently, Mater & Venayagamoorthy (Reference Mater and Venayagamoorthy2014) have suggested that a multi-parameter approach is more suitable to describe mixing processes in stratified turbulence.
Classical parametrizations of mixing have focused on the bulk Richardson number
$Ri_{b}$
, which is closely related to the turbulent Froude number since
$Ri_{b}\sim Fr^{-2}$
. In experiments on mixing across a density interface by Turner (Reference Turner1968) and Kato & Philipps (Reference Kato and Philipps1969) the focus was on the entrainment velocity
$u_{e}$
across the interface. This is closely related to the mixing efficiency and it can be shown that
${\it\eta}=Ri_{b}(u_{e}/u)\sim Fr^{-2}(u_{e}/u)$
(see Turner Reference Turner1973). In the limit of weak stratification, corresponding to high values of
$Fr$
, Turner (Reference Turner1968) found that the normalized entrainment velocity
$u_{e}/u$
reaches a constant, implying the result
${\it\eta}\propto Fr^{-2}$
for weakly stratified turbulence. This result has also been suggested by Holford & Linden (Reference Holford and Linden1999), who state that the buoyancy field behaves as a passive scalar in the limit of high
$Fr$
. At the other end of the spectrum, strong stratification and low
$Fr$
lead to an entrainment velocity
$u_{e}/u\propto Ri_{b}^{-1}\sim Fr^{2}$
in the experiments by Kato & Philipps (Reference Kato and Philipps1969). This means a constant mixing efficiency
${\it\eta}$
in the limit of strongly stratified turbulence, which has been confirmed by several more recent experiments (Park, Whitehead & Gnanadeskian Reference Park, Whitehead and Gnanadeskian1994; Oglethorpe, Caulfield & Woods Reference Oglethorpe, Caulfield and Woods2013; Olsthoorn & Dalziel Reference Olsthoorn and Dalziel2015).
Hence two parametrizations of mixing exist: a more classical one based on
$Ri_{b}$
and therefore essentially on the turbulent Froude number
$Fr$
and a more recent one based on
$Re_{b}$
. We now turn to the evidence from scaling of the equations of motion to try to shed light on this debate.
The Boussinesq set of equations for a linearly stratified fluid is given by
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}=-\frac{1}{{\it\rho}_{0}}\boldsymbol{{\rm\nabla}}p+b\,\boldsymbol{e}_{z}+{\it\nu}{\rm\nabla}^{2}\boldsymbol{u}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial b}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}b=-N^{2}u_{z}+\mathscr{D}{\rm\nabla}^{2}b. & \displaystyle\end{eqnarray}$$
We consider first the limit of weak stratification and high
$Fr$
where horizontal and vertical length scales can be assumed to be approximately equal, as can horizontal and vertical velocity scales. From the buoyancy equation (1.3) a simple balance between advection
$\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}b$
and the background stratification term
$N^{2}u_{z}$
leads to a scaling for the buoyancy as
$b\sim N^{2}\ell$
. Comparing this to the advection term in the Boussinesq momentum equation (1.2),
$\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}\sim u^{2}/\ell$
, it is clear that their ratio is
$N^{2}\ell /(u^{2}/\ell )=N^{2}\ell ^{2}/u^{2}\sim Fr^{-2}$
. Hence in the limit of
$Fr\gg 1$
, the buoyancy term can be neglected to leading order in the momentum equation and buoyancy effectively behaves as a passive scalar in the presence of a mean scalar gradient
$N^{2}$
, as pointed out by Holford & Linden (Reference Holford and Linden1999). It is possible from (1.2)–(1.3) to form equations for the turbulent kinetic energy and potential energy. At high Reynolds number and high Péclet number, the dissipation rates of kinetic and potential energy reach a finite and positive limit that is of the same order as the advection term in these energy equations:
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\epsilon}_{k}\sim \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\left(\frac{|\boldsymbol{u}|^{2}}{2}\right)\sim \frac{u^{3}}{\ell }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\epsilon}_{p}\sim \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\left(\frac{b^{2}}{2N^{2}}\right)\sim \frac{b^{2}u}{N^{2}\ell }\sim N^{2}u\ell . & \displaystyle\end{eqnarray}$$
From these scalings it follows that the mixing coefficient
${\it\Gamma}={\it\epsilon}_{p}/{\it\epsilon}_{k}\sim N^{2}u\ell /(u^{3}/\ell )=N^{2}\ell ^{2}/u^{2}\sim Fr^{-2}$
in the limit of high
$Fr$
. This result is analogous to that obtained when considering Turner’s experiment. The Prandtl number
$Pr={\it\nu}/\mathscr{D}$
does not affect the analysis, because we assume that the Reynolds number
$Re$
and Péclet number
$Pe=Re\,Pr$
are both sufficiently high that the kinetic and potential energy dissipation rates become independent of viscosity
${\it\nu}$
and diffusivity
$\mathscr{D}$
, respectively.
The strongly stratified turbulence theory was developed by several researchers in this field; its two main conditions are
$Fr\ll 1$
and
$Re_{b}\gg 1$
, and these conditions both have to be met within the theoretical framework (developed by Billant & Chomaz (Reference Billant and Chomaz2001) and Lindborg (Reference Lindborg2006)). The scaling analyses behind this work have proven to be able to describe the layered large-scale appearance of strongly stratified turbulence, observed previously by many authors and reviewed extensively by Riley & Lelong (Reference Riley and Lelong2000). A consensus has emerged recently that for values
$Re_{b}>10$
stratified turbulence has the expected form of the horizontal energy spectrum
$E_{h}(k_{h})\sim {\it\epsilon}_{k}^{2/3}\,k_{h}^{-5/3}$
and that the vertical length scale is approximately equal to
$\ell _{v}=u/N$
. This has been shown in many numerical works in the last ten years (Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007; Waite Reference Waite2011; Bartello & Tobias Reference Bartello and Tobias2013; Augier, Billant & Chomaz Reference Augier, Billant and Chomaz2015; Maffioli & Davidson Reference Maffioli and Davidson2015). Brethouwer et al. (Reference Brethouwer, Billant, Lindborg and Chomaz2007) tested many of the predicted results of the strongly stratified turbulence theory and plotted, for example, the anisotropy of the dissipation
$S_{\mathit{diss}}$
against
$Re_{b}$
in their forced stratified DNS simulations. This quantity is defined as
$S_{\mathit{diss}}={\it\nu}\langle (\partial u_{x}/\partial z)^{2}+(\partial u_{y}/\partial z)^{2}\rangle /{\it\epsilon}_{k}$
and represents the ratio of dissipation due to vertical gradients to the overall dissipation. The authors of this work found that
$S_{\mathit{diss}}$
rapidly tends towards the isotropic value of
$4/15\approx 0.267$
(Taylor Reference Taylor1935) as the buoyancy Reynolds number is increased. Similar results were obtained in decaying stratified turbulence by Riley & de Bruyn Kops (Reference Riley and de Bruyn Kops2003) and Maffioli & Davidson (Reference Maffioli and Davidson2015), who both found values close to
$S_{\mathit{diss}}\approx 0.41$
at times when the stratified turbulence in their DNS was most vigorous and
$Re_{b}=5$
–9. Furthermore, as discussed extensively in Smyth & Moum (Reference Smyth and Moum2000) and Smyth, Nash & Moum (Reference Smyth, Nash and Moum2005), in the case of stratified mixing layers a good condition for determining whether there is active three-dimensional turbulence at the small scales is that
$Re_{b}>20$
. The issue of whether the isotropic limit of the dissipation terms will be reached in strongly stratified turbulence is still being studied and constitutes an active area of research. Note, however, that the isotropic limit is not necessary for our main scaling analysis to be applicable because the scaling is based on the classical assumption that the dissipation rates reach a finite and positive limit at high Reynolds number, irrespective of the values of viscosity and diffusivity.
We now proceed to the main part of this paper, which is concerned with estimating the dependence of
${\it\Gamma}$
on the important physical parameters of the problem. Considering our novel scaling analysis at high
$Fr$
and the above arguments, it is our contention that in stratified turbulence the mixing efficiency is described by the Froude number only. The buoyancy Reynolds number
$Re_{b}$
should not play any role. To test this theoretical reasoning, we have performed DNS of stratified turbulence across a large range of Froude numbers and Reynolds numbers.
2 Numerical methodology
We perform direct numerical simulations (DNS) of turbulence in a linearly stratified fluid, with constant Brunt–Väisälä frequency
$N$
. The equations that are solved directly are the Boussinesq set of equations (1.2)–(1.3) together with the continuity equation
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0$
. We have included a body force
$\boldsymbol{f}$
in the Boussinesq momentum equation (1.2) to ensure that the turbulence reaches statistical stationarity. These equations are solved using a pseudospectral method based on Rogallo’s algorithm (Rogallo Reference Rogallo1981). Time advancement is carried out using a second-order Runge–Kutta predictor–corrector integration scheme, while the viscous and diffusive terms are integrated exactly by using suitable integrating factors. De-aliasing of the nonlinear terms is performed using a combination of truncation and phase shifting (for more details see Rogallo (Reference Rogallo1981)).
The turbulence is kept in a steady state through the use of forcing. We use random forcing that is uncorrelated in time, in such a way that the physical location of the body force keeps changing in time. Most of the simulations are at high
$Fr$
, for which we use isotropic forcing in spherical shells of radius
$k_{f}^{\mathit{max}}=5$
. The forcing is mostly concentrated at smaller wavenumbers with a forcing power spectrum
$P(k)={\it\alpha}^{2}\exp [-(k-k_{f}^{\mathit{peak}})^{2}]$
with
$k_{f}^{\mathit{peak}}=3$
. The value of
${\it\alpha}$
is determined at every time step to ensure that the forcing power
$P_{f}=\sum _{\mathit{all}\;\boldsymbol{k}}[\hat{\boldsymbol{u}}^{\ast }\boldsymbol{\cdot }\hat{\boldsymbol{f}}+(1/2)|\hat{\boldsymbol{f}}|^{2}{\rm\Delta}t]$
is kept to a constant value. Since
$\hat{\boldsymbol{f}}\propto {\it\alpha}$
this results in a quadratic equation for
${\it\alpha}$
, which we solve at every time step. Of the two roots for
${\it\alpha}$
we choose the one with minimum absolute value, which therefore minimizes the magnitude of the force; we find that this technique reduces the oscillations in time for most quantities of interest, such as
${\it\epsilon}_{k}$
,
${\it\epsilon}_{p}$
and RMS values of the velocity components. At low Froude numbers
$Fr<0.2$
, we found that isotropic forcing leads to non-stationary solutions, with growth of energy in the shear modes (modes with
$k_{x}=k_{y}=0$
) that quickly dominate the overall kinetic energy. We therefore utilize vortical forcing concentrated in the vertically rotational modes with
$k_{z}=0$
. This type of forcing in modes with
$k_{z}=0$
and finite and small
$k_{h}$
takes a long time to leak energy to the shear modes, with finite and small
$k_{z}$
and
$k_{h}=0$
, and hence a quasistationary state can be reached at intermediate times. Vortical forcing has been used by numerous authors when studying stratified turbulence at low
$Fr$
(see Waite & Bartello Reference Waite and Bartello2004; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007; Augier et al.
Reference Augier, Billant and Chomaz2015).
Most simulations are run on cubic domains except for the three simulations with strongest stratification, for which we take advantage of the anisotropy of the length scales and use rectangular domains with
$L_{z}<L_{h}$
. In all cases, since we expect isotropic dissipation at high
$Re$
, the grid spacing is constant in all directions and it is chosen to ensure
$k_{\mathit{max}}{\it\eta}=1.5$
. The Prandtl number in all cases is
$Pr=1$
. The list of all simulations that have been performed for this study is given in table 1 together with the important physical parameters for each run. The strongly stratified runs are performed on increasingly large grids in order to meet the condition
$Re_{b}>10$
as
$Fr$
is decreased. As a result, our most strongly stratified run with
$Fr=0.02$
and
$Re_{b}=17$
requires a grid of
$4096^{2}\times 1024$
collocation points. The values quoted are time averages over the stationary period of each simulation, as are all the values plotted in the next section, in which we discuss the results of the various stratified DNS performed.
Table 1. List of DNS runs performed: relevant non-dimensional parameters and type of forcing.
3 Results of DNS runs
3.1 Variation of mixing coefficient at constant
$Re_{b}$
We have performed simulations at constant buoyancy Reynolds number and at different Froude numbers. This was achieved by using a different number of grid points for each simulation and hence varying also the Reynolds number while keeping
$Re_{b}\approx 1000$
. This value of
$Re_{b}$
is well within the energetic regime of Barry et al. (Reference Barry, Ivey, Winters and Imberger2001) and Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005) so that the mixing coefficient is expected to not be constant. As shown in figure 1, we indeed find a variation of
${\it\Gamma}$
across the five runs but this can now not be due to variations in
$Re_{b}$
, which is kept constant, but rather is due to a changing
$Fr$
. The values of
${\it\Gamma}$
span an order of magnitude, as do the values of
$Fr$
in the simulations. At
$Fr=0.29$
we have
${\it\Gamma}=0.51$
, a high value compared to the often quoted value
${\it\Gamma}=0.2$
(Osborn Reference Osborn1980). At the other end of the
$Fr$
-range,
$Fr=2.9$
(but at the same
$Re_{b}$
), we have
${\it\Gamma}=0.05$
. Such a low value of the mixing coefficient is a result of the weak stratification, meaning that there is not much of a density difference for the turbulent flow to mix.
3.2 Mixing coefficient at varying Reynolds numbers
The dissipation rates of kinetic and potential energy reach the finite and positive limits given in (1.4)–(1.5) at high
$Re_{{\it\lambda}}$
, the Reynolds number based on the Taylor microscale, defined as
$Re_{{\it\lambda}}=u{\it\lambda}/{\it\nu}$
with
${\it\lambda}=[u^{2}/\langle (\partial u_{x}/\partial x)^{2}\rangle ]^{1/2}$
. This was shown by Donzis, Sreenivasan & Yeung (Reference Donzis, Sreenivasan and Yeung2005) for turbulence with a passive scalar and is expected to be true also for stratified turbulence. If
$Re_{{\it\lambda}}$
is not high enough both the non-dimensional dissipations become a function of the Reynolds number, that is
${\it\epsilon}_{k}\ell /u^{3}=f(Re_{{\it\lambda}})$
and
${\it\epsilon}_{p}\ell /(ub^{2}/N^{2})=g(Re_{{\it\lambda}})$
, and these functions are given in Donzis et al. (Reference Donzis, Sreenivasan and Yeung2005) in the case of passive scalar advection. Because the result
${\it\Gamma}\propto Fr^{-2}$
follows from the dissipation scalings in (1.4)–(1.5), at finite Reynolds number we expect instead
${\it\Gamma}=h(Fr,Re_{{\it\lambda}})$
and the mixing efficiency now depends not only on the Froude number but also on the Taylor scale Reynolds number.
Figure 1. Mixing coefficient as a function of Froude number at a constant
$Re_{b}\approx 1000$
. Each point corresponds to one of the five simulations labelled R1kF2.9 through to R1kF0.3.
To confirm these ideas we consider first the non-dimensionalized dissipation rates given in figure 2 for four runs at constant
$Fr\approx 3$
but performed on successively larger grids so as to increase
$Re_{{\it\lambda}}$
from low values to
$Re_{{\it\lambda}}\approx 240$
. This latter value is considered to be a good high value above which both dissipations reach a constant limit when non-dimensionalized (see Donzis et al.
Reference Donzis, Sreenivasan and Yeung2005; de Bruyn Kops Reference de Bruyn Kops2015). In making the dissipations non-dimensional we use the standard isotropic definition of the turbulent length scale,
$\ell =({\rm\pi}/u^{2})\int (E(k)/k)\,\text{d}k$
based on the 3-D energy spectrum
$E(k)$
, expected to be valid at this high
$Fr$
. We find a non-dimensionalized kinetic energy dissipation that is remarkably close to the form found by Donzis et al. (Reference Donzis, Sreenivasan and Yeung2005) in their collection of DNS (the exact same constants as in their paper are used in the curve shown in figure 2
a). Also the non-dimensionalized potential energy dissipation is similar to the prediction of Donzis et al. (Reference Donzis, Sreenivasan and Yeung2005) for the non-dimensionalized dissipation of passive scalar variance, confirming that buoyancy behaves as a passive scalar at high Froude numbers.
Figure 2. (a) Kinetic energy dissipation and (b) potential energy dissipation, both non-dimensionalized, for four runs with
$Fr\approx 3$
. The relevant DNS runs are R1kF2.9, 256F2.9, 512F3 and 1024F3.1. The curves represent the fit proposed by Donzis et al. (Reference Donzis, Sreenivasan and Yeung2005) with the same constants in the case of
${\it\epsilon}_{k}\ell /u^{3}$
, and the same value for
$D$
but a slightly different value for
$C$
in the case of
${\it\epsilon}_{p}\ell /(ub^{2}/N^{2})$
(we use
$C=0.31$
).
The next step is to check that, for these four simulations at small to moderate
$Re_{{\it\lambda}}$
, the mixing coefficient
${\it\Gamma}$
also changes, approaching a constant at the highest
$Re_{{\it\lambda}}$
. The steady-state value of
${\it\Gamma}$
obtained for the four runs is given in figure 3, and there is clearly a significant variation, with
${\it\Gamma}$
decreasing for increasing values of
$Re_{{\it\lambda}}$
and, possibly, the approach of a constant value
${\it\Gamma}\approx 0.033$
at the highest
$Re_{{\it\lambda}}=242$
.
Figure 3. Mixing coefficient
${\it\Gamma}$
as a function of
$Re_{{\it\lambda}}$
at a constant
$Fr\approx 3$
.
3.3 Mixing coefficient at high
$Re_{{\it\lambda}}$
We now consider only the runs with
$Re_{{\it\lambda}}>200$
, for which the dissipation rates
${\it\epsilon}_{k}$
and
${\it\epsilon}_{p}$
have approximately reached their respective finite and positive limits.
Figure 4. Mixing coefficient as a function of Froude number (log–log plot shown in the inset).
In figure 4 we show
${\it\Gamma}$
as a function of
$Fr$
for these runs. If we focus on the high-
$Fr$
behaviour we see that indeed
${\it\Gamma}\propto Fr^{-2}$
for
$Fr>1$
, which confirms the scaling arguments delineated in § 1. These scaling arguments have as a first result
$E_{P}/E_{K}\sim E_{P}/u^{2}\propto Fr^{-2}$
and this is also confirmed by the simulations for
$Fr>1$
as shown in figure 5. Of course our simulations are in a stationary state, which makes them easier to analyse, while time-evolving simulations such as those of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005) and Salehipour & Peltier (Reference Salehipour and Peltier2015) have an extra degree of freedom. It may be that some definition of the Reynolds number may be important to describe the decay of the turbulence, or the ‘age of a mixing event’ as described by Smyth & Moum (Reference Smyth and Moum2000), in this case. However, at
$Fr>1$
the relevant Reynolds number should not be the buoyancy Reynolds number. This follows from a simple argument, the Ozmidov scale
$\ell _{\mathit{oz}}\sim Fr^{3/2}\ell >\ell \approx L_{\mathit{box}}$
for
$Fr>1$
. The buoyancy Reynolds number is a measure of the dynamic range from the Kolmogorov scale through to
$\ell _{\mathit{oz}}$
since it can be written as
$Re_{b}=(\ell _{\mathit{oz}}/{\it\eta})^{4/3}$
. However, the Ozmidov scale is now larger than
$\ell$
, the largest physical scale in the problem, and for this reason
$Re_{b}$
does not have a physical influence on the stratified turbulence being simulated.
Figure 5. Ratio of potential energy to horizontal kinetic energy as a function of Froude number (log–log plot shown in the inset).
In the limit of low
$Fr$
and strong stratification, we expect the mixing coefficient to reach a constant value as in the experiments by Park et al. (Reference Park, Whitehead and Gnanadeskian1994), Oglethorpe et al. (Reference Oglethorpe, Caulfield and Woods2013) and Olsthoorn & Dalziel (Reference Olsthoorn and Dalziel2015) as long as
$Re_{b}>10$
. We have chosen this criterion because there is evidence that for
$Re_{b}=O(10)$
the turbulence starts showing the characteristics of strongly stratified turbulence as discussed in § 1. In figure 4 we see that
${\it\Gamma}$
has a maximum around
$Fr=0.3$
and then drops as the stratification is increased. Our results confirm that
${\it\Gamma}$
indeed approaches a constant value
${\it\Gamma}\approx 0.33$
as
$Fr\rightarrow 0$
. The ratio
$E_{P}/u^{2}$
is also predicted to be a constant of order unity by the strongly stratified turbulence theory (see Billant & Chomaz Reference Billant and Chomaz2001). From figure 5 this ratio appears to tend slowly to a constant value
$E_{P}/u^{2}\approx 0.15$
for
$Fr<0.3$
.
4 Discussion and conclusions
There is a revealing relationship linking
$Fr$
and
$Re_{b}$
in the limit of high Reynolds number when the dissipative scales are isotropic and
${\it\epsilon}_{k}=15{\it\nu}\langle (\partial u_{x}/\partial x)^{2}\rangle$
:
$$\begin{eqnarray}Fr=\frac{\sqrt{15Re_{b}}}{Re_{{\it\lambda}}}.\end{eqnarray}$$
In the case of the DNS of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005)
$Re_{{\it\lambda}}\approx 90$
for most of their simulations. Considering their value of
$Re_{b}=100$
at which
${\it\Gamma}$
starts to decrease, we can use (4.1) to find that the corresponding turbulent Froude number is
$Fr=0.45$
, which is close to the value of
$Fr=0.3$
at which we observed the drop in
${\it\Gamma}$
(see figure 4).
We can take this a step further and try to estimate the value of
$Fr$
at which
${\it\Gamma}$
starts varying in ocean and atmosphere field data. Davis & Moninsmith (Reference Davis and Moninsmith2011) report turbulence Reynolds numbers greater than
$Re_{\ell }=1500$
in their ocean measurements. Using
$Re_{\ell }=u\ell /{\it\nu}\sim u^{4}/({\it\nu}{\it\epsilon}_{k})=15Re_{{\it\lambda}}^{2}$
we can make the estimate
$Re_{{\it\lambda}}\approx \sqrt{15Re}=150$
, not much larger than the value from the DNS of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005). The variation in
${\it\Gamma}$
was observed for
$Re_{b}>100$
or for
$Fr>\sqrt{15Re_{b}}/Re_{{\it\lambda}}=0.26$
, again close to our transition Froude number.
We finally consider the atmospheric data of Lozovatsky & Fernando (Reference Lozovatsky and Fernando2013). From the data of the VTMX experiment in Monti et al. (Reference Monti, Fernando, Princevac, Chan, Kowalewski and Pardyjak2002), night-time values for the horizontal turbulent velocity were
$u\approx 0.3~\text{m}~\text{s}^{-1}$
, while a value for the dissipation can be inferred from the compensated spectra in figure 4(b) of Lozovatsky & Fernando (Reference Lozovatsky and Fernando2013) as
${\it\epsilon}_{k}\approx 1.8\times 10^{-3}~\text{m}^{2}~\text{s}^{-3}$
. Using
${\it\nu}=1.4\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
for air at
$10\,^{\circ }\text{C}$
one obtains a value for the Taylor microscale as
${\it\lambda}=0.1~\text{m}$
and
$Re_{{\it\lambda}}\approx 2000$
. This finally gives a transition Froude number as
$Fr=0.39$
, corresponding to
$Re_{b}=40\,000$
. So for completely different transition values based on buoyancy Reynolds number (to which we can add
$Re_{b}=1000$
from the present DNS) we have similar values of turbulent Froude number close to
$Fr\approx 0.3$
at which the mixing coefficient starts dropping considerably. The variation in
${\it\Gamma}$
does therefore appear to be an effect of the Froude number. It remains to clearly show
${\it\Gamma}\propto Fr^{-2}$
in field data, which is essential in our eyes to finish resolving this open issue in stratified turbulent mixing. The first evidence in this direction comes from the work of Wells, Cenedese & Caulfield (Reference Wells, Cenedese and Caulfield2010), who find
${\it\Gamma}\sim Fr^{-2}$
at high
$Fr$
in the case of oceanic gravity currents.
In conclusion, we have presented results from direct numerical simulations of constant-
$N$
forced stratified turbulence covering almost three orders of magnitude in
$Fr$
and a vast range of
$Re_{b}$
. The simulations at high
$Re_{{\it\lambda}}$
show a clear behaviour of the mixing coefficient as
${\it\Gamma}\propto Fr^{-2}$
for
$Fr>1$
, confirming the scaling analysis for weakly stratified turbulence. In the opposite limit,
$Fr<1$
, a peak in
${\it\Gamma}$
is found at
$Fr\approx 0.3$
with a high value of mixing coefficient
${\it\Gamma}=0.51$
, significantly larger than the value
${\it\Gamma}=0.2$
that is commonly used in oceanographic applications. The mixing coefficient then drops to values around
${\it\Gamma}=0.33$
; these are still high values and are due to the presence of a strong stratification, which high-
$Re_{b}$
turbulence is able to mix efficiently. To what extent our results can be generalized to all types of flows is an open question. We find it very likely that the general dependence of
${\it\Gamma}$
on
$Fr$
in the two limits
$Fr\ll 1$
and
$Fr\gg 1$
will show some degree of universality.
Acknowledgements
We would like to thank P. K. Yeung for providing us with the DNS code used for this study. We thank P. Augier for helpful discussions on mixing efficiency. We are indebted to the Leverhulme Trust network on Waves & Turbulence headed by P. Davidson for the many discussions it generated between its participants. We acknowledge PRACE for awarding us via the StratForce project access to the Fermi cluster at CINECA in Italy. Computational resources at PDC in Sweden were made available by SNIC. G.B. acknowledges financial support by the Swedish Research Council (grant number 621-2013-5784).
