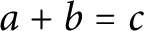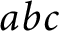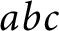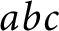1 Introduction
1.1 A map satisfying the Leibniz rule
There is great interest in constructing derivatives on
$\mathbb {Z}$
behaving like derivatives on function fields, as they are expected to have remarkable applications. For instance, the arithmetic analogue of the Mason–Stothers theorem is the
$abc$
Conjecture, but the proof for polynomials heavily uses derivatives, and it is unclear how to adapt it to
$\mathbb {Z}$
.
Let us discuss a first attempt by focusing only on the Leibniz rule. For each prime p, let
$v_p$
denote the p-adic valuation on
$\mathbb {Q}$
, and let
$\xi _p$
be a variable. Let
$\Omega $
be the free
$\mathbb {Z}$
-module generated by the variables
$\xi _p$
. Let
$\mathrm {d} : \mathbb {Z}\to \Omega $
be the map defined by
$\mathrm {d} 0=0$
and by
$$ \begin{align*}\mathrm{d} n =n\sum_{p|n} \frac{v_p(n)}{p}\cdot \xi_p, \end{align*} $$
for
$n\ne 0$
, where p varies over the different prime divisors of n. (A version of
$\mathrm {d}: \mathbb {Z}\to \Omega $
and generalizations can be found in [Reference Kurokawa, Ochiai and Wakayama7].) Note that
$n\cdot v_p(n)/p\in \mathbb {Z}$
when
$p|n$
, so
$\mathrm {d} n\in \Omega $
for all
$n\in \mathbb {Z}$
. In particular, when p is prime, we get
$\mathrm {d} p=\xi _p$
. One immediately checks the following lemma.
Lemma 1.1 (Leibniz rule for
$\mathrm {d}$
)
For all
$a,b\in \mathbb {Z}$
, we have
$\mathrm {d}(ab)=a\mathrm {d} b + b\mathrm {d} a$
.
In fact, there is a sense in which
$\mathrm {d}:\mathbb {Z}\to \Omega $
is the universal map on
$\mathbb {Z}$
satisfying the Leibniz rule (see Section 5). Unfortunately, this map
$\mathrm {d}$
is not a good analogue of a derivative, because it is not additive: For instance,
$\mathrm {d}(1)=0$
,
$\mathrm {d}(2)=\xi _2$
, and
$\mathrm {d}(3)=\xi _3$
, but we certainly have
$0+\xi _2\ne \xi _3$
.
1.2 Arithmetic derivatives
The starting point of our work is the following suggestion due to Thanases Pheidas: When derivatives are applied in function field arithmetic, it is often the case that additivity is only needed finitely many times. Thus, one might still assign values to the variables
$\xi _p$
in order to make
$\mathrm {d}$
additive in the finitely many needed cases. For instance, in our previous example, we may replace
$\xi _2$
and
$\xi _3$
by
$1$
to get
$0+1=1$
from the equation
$1+2=3$
.
Our aim is to investigate this construction in the simplest nontrivial case: when exactly one additive condition is imposed. For this, it is convenient to give an algebraic formulation of Pheidas’s suggestion.
Consider a group morphism
$\psi :\Omega \to \mathbb {Z}$
. The arithmetic derivative
$\mathrm {d}^\psi $
attached to
$\psi $
is simply defined as
$d^\psi =\psi \circ \mathrm {d}:\mathbb {Z}\to \mathbb {Z}$
. Note that
$\mathrm {d}^\psi :\mathbb {Z}\to \mathbb {Z}$
still respects the Leibniz rule.
Given coprime positive integers
$a,b,c$
with
$a+b=c$
, the condition
$\mathrm {d}^\psi (a)+\mathrm {d}^\psi (b) = \mathrm {d}^\psi (c)$
imposes a linear equation on the values
$\psi (\xi _p)$
. When
$c>2$
, the set of all such maps
$\psi $
satisfying
$\psi (\xi _p)=0$
whenever
$p\nmid abc$
turns out to be a nontrivial free abelian group (cf. Lemma 2.4). We denote this group by
$\mathscr {T}(a,b)$
. With this notation, one can ask to what extent an arithmetic derivative
$\mathrm {d}^\psi $
for
$\psi \in \mathscr {T}(a,b)$
can be used to mimic arguments from function field arithmetic.
1.3 The Small Derivatives Conjecture
Let us focus our attention on a particular kind of morphism
$\psi :\Omega \to \mathbb {Z}$
. For us, a derivation is a group morphism
$\psi :\Omega \to \mathbb {Z}$
satisfying that its norm
$\|\psi \|:=\sup _p |\psi (\xi _p)|$
is finite. The set of all such maps is a
$\mathbb {Z}$
-module denoted by
$\mathscr {T}$
, which comes equipped with the norm
$\|-\|$
. The previously defined groups
$\mathscr {T}(a,b)$
are contained in
$\mathscr {T}$
.
In addition to these definitions, we also introduce the notion of
$\psi $
-independence for a pair of integers
$(a,b)$
and a derivation
$\psi $
, by requiring that the arithmetic Wronskian
$W^\psi (a,b)=a\mathrm {d}^\psi b-b\mathrm {d}^\psi a$
is nonzero. Our study focuses on the question of existence of small (in the sense of
$\|-\|$
) derivations
$\psi \in \mathscr {T}(a,b)$
satisfying that
$a,b$
are
$\psi $
-independent. We propose the following conjecture.
Conjecture 1.2 (Small Derivatives Conjecture; cf. Conjecture 3.9)
There is an absolute constant
$0<\eta <1$
such that for all but finitely many triples of coprime positive integers
$(a,b,c)$
satisfying
$a+b=c$
and not of the form
$(1,N, q)$
with q prime (up to order), the following holds: There is
$\psi \in \mathscr {T}(a,b)$
such that
$a,b$
are
$\psi $
-independent and
$\|\psi \| < c^{\eta }$
.
This conjecture seems to capture the usefulness of derivatives in function field arithmetic in the sense that it allows one to translate arguments from function fields to
$\mathbb {Z}$
, provided that additivity of derivatives is used just once. In order to clarify how to use our arithmetic derivatives together with the Small Derivatives Conjecture to perform such a translation, in Section 3.4, we give a short proof of the analogue of Fermat’s Last Theorem (FLT) for
$\mathbb {C}[x]$
based on derivatives without using the Mason–Stothers theorem or radicals, and then we translate the argument to
$\mathbb {Z}$
. We conclude that the Small Derivatives Conjecture implies the asymptotic form of FLT.
The connection with FLT is of course just an example to clarify the analogy between our arithmetic derivatives and the usual function field derivatives. Actually, our main goal is to show that the Small Derivatives Conjecture is equivalent to the
$abc$
Conjecture (with a suitable choice of exponents). Let us give a brief outline of the main results.
1.4 Main results
In Theorem 2.6, we will use Geometry of Numbers to show that
$\mathscr {T}(a,b)$
admits a full set of linearly independent derivations with controlled norm. In Theorem 3.3, we prove an unconditional
$abc$
-type bound which explicitly includes a contribution coming from the norm of arithmetic derivatives. This motivates the problem of producing
$\psi \in \mathscr {T}(a,b)$
for a given pair of coprime positive integers
$(a,b)$
such that
$\|\psi \|$
is small and
$a,b$
are
$\psi $
-independent. We prove such a result in Lemma 3.5, but unfortunately, it is insufficient to prove the
$abc$
Conjecture. Nevertheless, this analysis motivates a heuristic (cf. Section 3.3) leading to the formulation of the Small Derivatives Conjecture discussed above. As for evidence, in addition to Lemma 3.5 and the heuristic in Section 3.3, we prove a version of the Small Derivatives Conjecture with exponent
$\eta =1/2 +\epsilon $
, provided that the
$\psi $
-independence condition is replaced by a somewhat weaker nondegeneracy condition (see Theorem 2.8).
Our main results concerning the arithmetic relevance of these notions are Lemma 4.1 and Theorem 4.5 (see also Corollary 4.6). These results show that the Small Derivatives Conjecture is equivalent to the
$abc$
Conjecture, with a precise dependence of exponents.
1.5 Some algebraic context
In Section 5, we include a discussion on a generalization of the constructions
$\Omega $
and
$\mathscr {T}$
from an algebraic point of view. Consider a commutative monoid R, a commutative unitary ring A, and a morphism of monoids
$\alpha :R\to A$
, where A is taken as a multiplicative monoid. For an A-module U, we say that a map
$D:R\to U$
is an
$\alpha $
-derivation (with values in U) if
$D(\alpha (r))=0$
for every
$r\in R$
and
$D(ab)=aD(b)+bD(a)$
for all
$a,b\in A$
.
We will construct a universal
$\alpha $
-derivation
$\mathrm {d}_{(A,\alpha )}: A\to \Omega _{(A,\alpha )}$
and compute it in some examples. One of these examples shows that our map
$\mathrm {d}:\mathbb {Z}\to \Omega $
is precisely the universal
$\alpha $
-derivation on
$\mathbb {Z}$
for the inclusion map
$\alpha :\{-1,1\}\to \mathbb {Z}$
. So, in this sense, the map
$\mathrm {d}:\mathbb {Z}\to \Omega $
is not artificial.
Our notion of
$\alpha $
-derivations is very similar to the theory of absolute derivations from [Reference Kurokawa, Ochiai and Wakayama7], except that we keep track of the additional data of a morphism of monoids
$\alpha :R\to A$
—in fact, when
$R=\{1\}$
, we recover the absolute derivations from [Reference Kurokawa, Ochiai and Wakayama7].
The additional data of a morphism of monoids are natural from various points of view. First, in our arithmetic applications, it corresponds to restricting the support of the derivations
$\psi \in \mathscr {T}$
, which was necessary in the definition of
$\mathscr {T}(a,b)$
. Second, one can check compatibility with localization of our
$\alpha $
-derivations, leading to sheaves of
$\alpha $
-derivations on pre-log schemes (although we do not pursue this direction in this work). From this point of view, our modules
$\mathscr {T}(a,b)$
give normed sheaves on
$\mathrm {Spec}(\mathbb {Z})$
endowed with a suitable pre-log structure. Finally, monoids are often considered as the most basic “ground field” in the general
$\mathbb {F}_1$
philosophy, which motivates the construction of derivatives on
$\mathbb {Z}$
by requiring compatibility with monoids rather than requiring linearity.
1.6 Remarks on arithmetic derivatives
In summary, this work formalizes the widespread intuition that some sort of arithmetic derivative on
$\mathbb {Z}$
should be closely related to the
$abc$
Conjecture. Our results are in line with Vojta’s proposed analogy comparing Geometry of Numbers in arithmetic to derivatives in the setting of function fields and Nevanlinna theory (see Chapter 6 in [Reference Vojta12]). We stress the fact that—despite the close relation with more sophisticated concepts such as “geometry over
$\mathbb {F}_1$
”—our constructions only involve classical tools.
It is worth pointing out that Vojta has a different proposal for arithmetic derivatives in terms of the existence of small rational points in the total space of certain projective bundles (the Tautological Conjecture; cf. Section 30 in [Reference Vojta, Corvaja and Gasbarri13]). Furthermore, Faltings [Reference Faltings, Pragacz, Szurek and Wiśniewski6] investigated yet another possible notion of arithmetic derivative in terms of certain axiomatically defined arithmetic analogue of the Kodaira–Spencer class for fibrations, showing that such an object cannot exist.
Finally, we mention that Buium (see [Reference Buium3] and the references therein) developed a theory of p-derivations, which affords some analogies between differential calculus and the arithmetic of local fields. Buium’s p-derivations, however, are purely local, and they do not seem to be related to the global notion of arithmetic derivative in the present work.
2 Derivations and arithmetic derivatives
2.1 The module
$\mathscr {T}$
and arithmetic derivatives
Recall (from the Introduction) that
$\Omega $
is the free
$\mathbb {Z}$
-module generated by the variables
$\xi _p$
for p varying over prime numbers. For a
$\mathbb {Z}$
-linear map
$\psi :\Omega \to \mathbb {Z}$
, we define
$\|\psi \| = \sup _p |\psi (\xi _p)|$
. We will often use the observation that if
$\psi \ne 0$
, then
$\|\psi \|\ge 1$
. Let
$$ \begin{align*}\mathscr{T} = \{\psi\in \mathrm{Hom}_{\mathbb{Z}}(\Omega,\mathbb{Z}) : \|\psi\| \mbox{ is finite}\}. \end{align*} $$
Elements of
$\mathscr {T}$
will be called derivations, and
$\|-\| $
is a norm on the
$\mathbb {Z}$
-module
$\mathscr {T}$
.
Given a derivation
$\psi \in \mathscr {T}$
, we define the arithmetic derivative attached to
$\psi $
as the map
$$ \begin{align*}\mathrm{d}^\psi:\mathbb{Z}\to \mathbb{Z} \quad\mbox{defined by } \quad \mathrm{d}^\psi:=\psi\circ \mathrm{d}. \end{align*} $$
For example, the classical “arithmetic derivative” that one encounters in elementary number theory [Reference Barbeau1, Reference Mingot Shelly10] is precisely
$\mathrm {d}^{\sigma }$
where
$\sigma (\sum _p a_p\xi _p)=\sum _p a_p$
—note that
$\|\sigma \| =1$
, so
$\sigma \in \mathscr {T}$
.
Returning to the general case, observe that upon composing with
$\psi \in \mathscr {T}$
, Lemma 1.1 gives the following result.
Lemma 2.1 (Leibniz rule for arithmetic derivatives)
Let
$\psi \in \mathscr {T}$
. For every
$a,b\in \mathbb {Z}$
, we have
$\mathrm {d}^\psi (ab)=a\mathrm {d}^\psi b +b\mathrm {d}^\psi a$
. Thus, for all integers
$n\ge 1$
and all
$a\in \mathbb {Z}$
, we have
$\mathrm {d}^\psi (a^n)=na^{n-1}\mathrm {d}^\psi a$
.
Concerning norms, the following estimates are useful.
Lemma 2.2 For every positive integer n, we have
$\sum _{p|n}v_p(n)/p\le (2\log 2)^{-1} \log n$
. In particular, if
$n\ge 2$
and
$\psi \in \mathscr {T}$
, then
$|\mathrm {d}^\psi (n)| < \|\psi \|\cdot n\log n$
.
Proof. We can assume
$n\ge 2$
. Then, we get
$$ \begin{align*}\sum_{p|n}\frac{v_p(n)}{p}=\sum_{p|n}v_p(n)\log p\cdot \frac{1}{p\log p}\le \left(\max_{p|n}\frac{1}{p\log p}\right)\log n\le \frac{\log n}{2\log 2}. \end{align*} $$
The last claim is immediate from
$\mathrm {d}^\psi (n)=n\sum _{p|n} v_p(n)p^{-1} \psi (\xi _p)$
.▪
2.2 The modules
$\mathscr {T}(a,b)$
The support of
$\psi \in \mathscr {T}$
is the set of primes
$\mathrm {supp}(\psi )=\{p : \psi (\xi _p)\ne 0\}$
. The support of a nonzero integer n is
$\mathrm {supp}(n)=\{p : p|n\}$
, and the number of different prime factors is
$\omega (n)=\# \mathrm {supp}(n)$
. We recall the following elementary fact.
Lemma 2.3 We have
$\omega (n)=O(\log (n)/\log \log n)$
. In particular, for each
$\epsilon>0$
, we have the bound
$\omega (n)<\epsilon \log n$
for all but finitely many positive integers n.
For a pair of positive integers
$a,b$
, we define
$$ \begin{align*}\mathscr{T}(a,b)=\{\psi\in \mathscr{T} : \mathrm{supp}(\psi)\subseteq \mathrm{supp} (ab(a+b))\mbox{ and }\mathrm{d}^\psi(a+b)=\mathrm{d}^\psi a+\mathrm{d}^\psi b\} \end{align*} $$
(because a and b are positive,
$\mathrm {supp} (ab(a+b))$
is a finite set). Thus, for
$\psi \in \mathscr {T}(a,b)$
, we have that the arithmetic derivative
$\mathrm {d}^\psi $
not only satisfies the Leibniz rule, but also satisfies
$\mathrm {d}^\psi (a+b)=\mathrm {d}^\psi a+\mathrm {d}^\psi b$
for the chosen integers a and b. Explicitly, the condition
$\mathrm {d}^\psi (a+b)=\mathrm {d}^\psi a+\mathrm {d}^\psi b$
is
$$ \begin{align} a\sum_{p|a}\frac{v_p(a)}{p}\cdot \psi(\xi_p)+b\sum_{p|b}\frac{v_p(b)}{p}\cdot \psi(\xi_p) = (a+b)\sum_{p|a+b}\frac{v_p(a+b)}{p}\cdot \psi(\xi_p), \end{align} $$
which is a homogeneous linear equation on the unknowns
$ \psi (\xi _p)$
for
$p\in \mathrm {supp}(ab(a+b))$
. Hence:
Lemma 2.4 (Basic existence lemma)
Let a and b be positive integers. Then,
$\mathscr {T}(a,b)$
is a saturated
$\mathbb {Z}$
-submodule of
$\mathscr {T}$
of rank
$\omega (ab(a+b))-1$
.
2.3 Bounding the norm
We aim for a more precise version of Lemma 2.4. First, we note that for all
$m,n,k\in \mathbb {Z}$
, we have
$$ \begin{align*}\mathrm{d} (km+kn)-\mathrm{d}(km) - \mathrm{d}(kn)=k\cdot \left(\mathrm{d}(m+n)-\mathrm{d} m -\mathrm{d} n\right) \end{align*} $$
and similarly for
$\mathrm {d}^\psi $
for any
$\psi \in \mathscr {T}$
. Hence, the question of existence of arithmetic derivatives respecting additivity for a chosen pair of numbers can be reduced to the coprime case.
We will need the following version of Siegel’s lemma which builds on Minkowski’s second theorem in Geometry of Numbers (see Theorem 2 in [Reference Bombieri and Vaaler2]).
Theorem 2.5 (Siegel’s lemma)
Let
$a_1,\ldots ,a_N\in \mathbb {Z}$
. The equation
$a_1X_1+\cdots +a_NX_N=0$
has linearly independent solutions
${\textbf {x}}_i = (x_{i1},\ldots ,x_{iN})\in \mathbb {Z}^N$
for
$1\le i\le N-1$
satisfying
$$ \begin{align*}\prod_{i=1}^{N-1} \max_{1\le j\le N} |x_{ij}|\le N\cdot \max_{1\le j\le N}|a_j|. \end{align*} $$
With this at hand, we can prove a more precise version of Lemma 2.4, which we state in the case of positive integers for the sake of simplicity.
Theorem 2.6 (Existence of arithmetic derivatives of controlled size)
Suppose that
$a,b$
are coprime positive integers with
$c:=a+b>2$
, i.e.,
$(a,b)\ne (1,1)$
. Then,
$\mathscr {T}(a,b)$
has rank
$r:=\omega (abc)-1\ge 1$
, and there are
$\mathbb {Z}$
-linearly independent derivations
$\psi _1,\ldots ,\psi _r\in \mathscr {T}(a,b)$
satisfying
$$ \begin{align*}\prod_{i=1}^r \|\psi_i\| \le \frac{\omega(abc)}{2\log 2}\cdot c\log c. \end{align*} $$
Proof. As in (2.1), the condition
$\mathrm {d}^{\psi } a+ \mathrm {d}^{\psi } b = \mathrm {d}^{\psi } c$
defining
$\mathscr {T}(a,b)$
becomes
$$ \begin{align*}a\sum_{p|a}\frac{v_p(a)}{p}\cdot \psi(\xi_p)+b\sum_{p|b}\frac{v_p(b)}{p}\cdot \psi(\xi_p) = c\sum_{p|c}\frac{v_p(c)}{p}\cdot \psi(\xi_p). \end{align*} $$
Because
$(a,b)\ne (1,1)$
, we have
$r\ge 1$
. Treating
$\psi (\xi _p)$
as unknowns and using the fact that a, b, and c are pairwise coprime, the coefficients of the previous equation are positive integers bounded by
$c\log _2(c)/2$
, where
$\log _2$
is the base
$2$
logarithm. The result follows by Theorem 2.5.▪
Choosing the smallest derivation provided by the previous theorem, one deduces the following corollary.
Corollary 2.7 (Existence of a small derivative)
Let
$\epsilon>0$
. For all but finitely many triples of coprime integers
$a,b,c$
with
$c>2$
and satisfying
$a+b=c$
, there is a nonzero
$\psi \in \mathscr {T}(a,b)$
with
$\|\psi \|< c^{\frac {1}{r} +\epsilon }$
, where
$r=\omega (abc)-1$
.
However, Corollary 2.7 does not ensure any sort of nondegeneracy for the arithmetic derivative it provides. For instance, although
$\psi $
is not zero, it can occur that
$\mathrm {d}^\psi (a)=\mathrm {d}^\psi (b)=\mathrm {d}^\psi (c)=0$
. The following result remedies this situation.
Theorem 2.8 (Small nontrivial derivatives)
Let
$\epsilon>0$
. For all but finitely many triples of coprime integers
$a,b,c$
larger than
$1$
that satisfy
$a+b=c$
, there is
$\psi \in \mathscr {T}(a,b)$
with
$\|\psi \|< c^{\frac {1}{2} +\epsilon }$
such that not all the integers
$\mathrm {d}^\psi (a)$
,
$\mathrm {d}^\psi (b)$
,
$\mathrm {d}^\psi (c)$
are zero.
Proof. Because
$a,b,c$
are larger than
$1$
, each one of them has prime divisors. Thus, the conditions (2.1),
$\mathrm {d}^\psi (a)=0$
, and
$\mathrm {d}^\psi (b)=0$
are linearly independent when we consider the terms
$\psi (\xi _p)$
as unknowns. Let
$\mathscr {K}(a,b)\subseteq \mathscr {T}(a,b)$
be the subgroup defined by these conditions, and note that
$\mathrm {rk} \mathscr {K}(a,b)=r-2$
, where
$r=\mathrm {rk} \mathscr {T}(a,b)=\omega (abc)-1$
(see Lemma 2.4).
Let
$\psi _1,\ldots ,\psi _r\in \mathscr {T}(a,b)$
be as provided by Theorem 2.6, and assume that they are labeled in such a way that
$\|\psi _1\|\le \|\psi _2\|\le \cdots \le \|\psi _r\|$
. Because the
$\psi _i$
are linearly independent, there are indices
$i_1<i_2$
such that
$\psi _{i_1}$
and
$\psi _{i_2}$
are not in
$\mathscr {K}(a,b)$
. Then, we have
$$ \begin{align*}\|\psi_{i_1}\|^2\le \|\psi_{i_1}\|\cdot \|\psi_{i_2}\|\le \prod_{i=1}^r \|\psi_i\|\le \frac{\omega(abc)}{2\log 2}\cdot c\log c, \end{align*} $$
and we conclude by Lemma 2.3.▪
We will be interested in a more delicate notion of nondegeneracy for a derivation
$\psi \in \mathscr {T}(a,b)$
, for which we need to introduce certain arithmetic Wronskians.
2.4 Independence
One might be tempted to explore analogues of various notions from differential calculus using the functions
$\mathrm {d}^\psi :\mathbb {Z}\to \mathbb {Z}$
instead of an actual derivative. Rather than giving a lengthy list of such definitions, let us simply mention here a notion that will be useful for us. Given
$\psi \in \mathscr {T}$
, the
$\psi $
-Wronskian of two integers
$a,b$
is defined by
$$ \begin{align*}W^\psi(a,b)=\det\left[ \begin{array}{cc} a&b\\ \mathrm{d}^\psi a& \mathrm{d}^\psi b \end{array} \right]=a\mathrm{d}^\psi b-b\mathrm{d}^\psi a \in\mathbb{Z}. \end{align*} $$
Let us also note the formula
$$ \begin{align} W^\psi(a,b)=ab\cdot \left(\sum_{p|b}\frac{v_p(b)}{p}\psi(\xi_p) - \sum_{p|a}\frac{v_p(a)}{p}\psi(\xi_p)\right). \end{align} $$
We say that
$a,b$
are
$\psi $
-dependent if
$W^\psi (a,b)= 0$
. Otherwise, they are
$\psi $
-independent. From (2.2), we deduce that
$a,b$
are
$\psi $
-dependent if and only if
$$ \begin{align} \sum_{p|a}\frac{v_p(a)}{p}\psi(\xi_p) = \sum_{p|b}\frac{v_p(b)}{p}\psi(\xi_p). \end{align} $$
Given positive integers a and b, we define
$$ \begin{align*}\mathscr{T}^\circ(a,b)=\{\psi\in \mathscr{T}(a,b) : a,b \mbox{ are}\ \psi\mbox{-dependent}\}. \end{align*} $$
Lemma 2.9 Let
$a,b$
be coprime positive integers with
$(a,b)\ne (1,1)$
. The set
$\mathscr {T}^\circ (a,b)$
is a saturated
$\mathbb {Z}$
-submodule of
$\mathscr {T}(a,b)$
with
$\mathrm {rk} \mathscr {T}^{\circ }(a,b)= \mathrm {rk} \mathscr {T}(a,b)-1=\omega (ab(a+b))-2$
. In particular,
$\mathscr {T}^\circ (a,b)$
is properly contained in
$\mathscr {T}(a,b)$
.
Proof. Because
$(a,b)\ne (1,1)$
, there is some prime
$q|ab$
. Hence, equation (2.3) defining
$\mathscr {T}^\circ (a,b)$
is nontrivial. Furthermore, no term corresponding to primes
$p|c$
contributes to (2.3), while they appear in equation (2.1) defining
$\mathscr {T}(a,b)$
. This proves that, considering the values
$\psi (\xi _p)$
as variables, equations (2.1) and (2.3) are linearly independent. We conclude by Lemma 2.4.▪
3 An
$abc$
bound and the problem of small arithmetic derivatives
3.1 The
$abc$
Conjecture
The radical of a positive integer n, denoted by
$\mathrm {rad}(n)$
, is the product without repetitions of the different primes dividing n. The celebrated
$abc$
Conjecture is the following.
Conjecture 3.1 (The Masser–Oesterlé
$abc$
Conjecture)
Given
$\epsilon>0$
, there is a constant
$\kappa _\epsilon>0$
such that for all coprime positive integers
$a,b,c$
with
$a+b=c$
, we have
$c<\kappa _\epsilon \cdot \mathrm {rad}(abc)^{1+\epsilon }$
.
For many applications, even the following weaker version would suffice the following conjecture.
Conjecture 3.2 (Oesterlé’s
$abc$
Conjecture)
There is an absolute constant M such that for all coprime positive integers
$a,b,c$
with
$c=a+b$
, we have
$c< \mathrm {rad}(abc)^{M}$
.
Oesterlé’s version of the
$abc$
Conjecture was proposed first in 1985, and it was later refined into the Masser–Oesterlé
$abc$
Conjecture by Masser. See [Reference Masser8] for a historical account of how these conjectures were formulated. To the best of the author’s knowledge, they remain open.
3.2 An
$abc$
bound using arithmetic derivatives
The notion of derivation considered in the previous section is enough to get an estimate in the spirit of the
$abc$
Conjecture, with a proof analogous to Snyder’s proof of Mason’s theorem in the function field setting (see [Reference Snyder11]) or to the proof of the Second Main Theorem in Nevanlinna theory using Wronskians or logarithmic derivatives.
Theorem 3.3 (An
$abc$
estimate)
Let
$a,b$
be coprime positive integers with
$(a,b)\ne (1,1)$
, and let
$\psi \in \mathscr {T}(a,b)$
. Suppose that a and b are
$\psi $
-independent. Writing
$c=a+b$
, we have
$$ \begin{align*}\frac{c}{\log c}\le \mathrm{rad}(abc)\cdot \frac{\|\psi\| }{\log 2}. \end{align*} $$
For the proof, we need a simple observation.
Lemma 3.4 For any positive integer n and any
$\psi \in \mathscr {T}$
, we have that n divides
$\gcd (n, \mathrm {d}^\psi n)\cdot \mathrm {rad}(n)$
.
Proof.
n divides
$n\cdot \mathrm {rad}(n)$
. From the definition of
$\mathrm {d}^\psi $
, we see that n divides
$(\mathrm {d}^\psi n )\cdot \mathrm {rad}(n)$
.▪
Proof of Theorem 3.3
The equation
$\mathrm {d}^\psi a+\mathrm {d}^\psi b=\mathrm {d}^\psi c$
gives
$$ \begin{align*}W:=W^\psi(a,b)=W^\psi(a,c)=W^\psi(c,b), \end{align*} $$
which is nonzero, because
$a,b$
are
$\psi $
-independent. By Lemma 3.4, we see that
$a/\mathrm {rad}(a)$
divides
$W=W^\psi (a,b)$
, and similarly for b and c. By coprimality of a, b, and c, we get that
$abc$
divides
$W\cdot \mathrm {rad}(abc)$
. Because
$W\ne 0$
, we conclude
$abc\le |W|\cdot \mathrm {rad}(abc)$
. From (2.2), we deduce
$$ \begin{align*}\begin{aligned} \frac{abc}{\mathrm{rad}(abc)}&\le |W|=ab \left|\sum_p\frac{v_p(a)}{p}\psi(\xi_p)-\sum_p\frac{v_p(b)}{p}\psi(\xi_p)\right|\\ &\le ab\|\psi\| \sum_{p|ab}\frac{v_p(ab)}{p}\le ab\|\psi\| \cdot \frac{\log (ab)}{2\log 2}\,, \end{aligned}\end{align*} $$
where the last bound is by Lemma 2.2. The result follows from
$\log (ab)\le 2\log c$
.▪
3.3 Small arithmetic derivatives
In view of Theorem 3.3, we cannot avoid the question of existence of small derivations
$\psi \in \mathscr {T}(a,b)$
subject to the condition that
$a,b$
be
$\psi $
-independent. A first result is directly deduced from Lemma 2.9 and Theorem 2.6.
Lemma 3.5 (Small arithmetic derivatives satisfying independence)
Let
$a,b$
be coprime positive integers with
$(a,b)\ne (1,1)$
, and let
$c=a+b$
. Let
$r=\omega (abc)-1$
, and note that
$r\ge 1$
. For any list of linearly independent derivations
$\psi _1,\ldots ,\psi _r\in \mathscr {T}(a,b)$
, there is at least one index
$1\le i_0\le r$
such that
$a,b$
are
$\psi _{i_0}$
-independent. Furthermore, choosing
$\psi _1,\ldots ,\psi _r$
as in Theorem
2.6
, we get
$$ \begin{align*}\|\psi_{i_0}\| \le \frac{\omega(abc)}{2\log 2} \cdot c\log c. \end{align*} $$
Example 3.6 Let
$q=2^n-1$
be a Mersenne prime, and take
$a=1$
,
$b=q$
, and
$c=2^n$
. Then,
$\mathscr {T}(1,q)=\mathbb {Z}\cdot \psi _1$
, where the
$\psi _1(\xi _2)=1$
,
$\psi _1(\xi _q)=n\cdot 2^{n-1}$
, and
$\psi _1(p)=0$
, for all
$p\ne 2,q$
. Thus, in this example, the bound given by Lemma 3.5 is sharp up to a factor of
$2$
, because we actually have:
$$ \begin{align*}\|\psi_1\| = n\cdot 2^{n-1} = \frac{\omega(abc)}{4\log 2}\cdot c\log c. \end{align*} $$
Unfortunately, Lemma 3.5 combined with Theorem 3.3 falls short of proving the
$abc$
Conjecture. Nevertheless, it clarifies the fact that in order to prove the
$abc$
Conjecture, one must get a power-saving improvement over the bound in Lemma 3.5.
Optimistically, we may expect that in Theorem 2.6, one can choose the
$\psi _i$
such that all the
$\log \|\psi _i\| $
have roughly the same size. Proceeding as in Lemma 3.5, if
$\omega (abc)\ge 3$
(i.e.,
$r\ge 2$
), this would give the desired power-saving improvement. Regarding the condition
$\omega (abc)\ge 3$
, we have the following lemma.
Lemma 3.7 Up to order, the only triples of coprime positive integers
$a,b,c$
with
$a+b=c$
having
$\omega (abc)\le 2$
are the following:
$(1,1,2)$
,
$(1,8,9)$
, and
$(1,2^n,q)$
with q prime and
$n\ge 1$
.
This follows from Mihailescu’s theorem [Reference Mihailescu9]. Of course, it is not known whether there are infinitely many primes of the form
$q=2^n+1$
(Fermat primes) or
$q=2^n-1$
(Mersenne primes).
There is, however, an additional caveat in the previous heuristic. If
$a,b,c$
are, up to order,
$1,q,N$
for some prime q, then from the defining equations (2.1) and (2.3), we see that every
$\psi \in \mathscr {T}^\circ (a,b)$
satisfies the unexpected condition
$\psi (\xi _q)=0$
. If in addition N is the product of powers of small primes, then it can happen that
$\mathscr {T}^\circ (a,b)$
is generated by unusually small derivations, in which case our heuristic justification on how to get a power-saving improvement over Lemma 3.5 fails.
Example 3.8 Consider
$a=1$
,
$b=108=2^2\cdot 3^3$
, and
$c=q=109$
. Then,
$r=2$
, and the group
$\mathscr {T}^0(1,108)\simeq \mathbb {Z}$
is generated by the derivation
$\psi _1$
determined by
$(\psi _1(2),\psi _2(3),\psi _3(109)) = (1,-1,0)$
. On the other hand, any derivation
$\psi _2\in \mathscr {T}(1,108)$
which is linearly independent from
$\psi _1$
satisfies
$\|\psi _2\|\ge 108$
, with equality achieved (for instance) at
$(\psi _2(2),\psi _2(3),\psi _2(109)) = (2,-1,108)$
.
The previous considerations motivate our main conjecture.
Conjecture 3.9 (Small Derivatives Conjecture)
There is an absolute constant
$0<\eta <1$
such that for all but finitely many triples of coprime positive integers
$(a,b,c)$
satisfying
$a+b=c$
and not of the form
$(1,N, q)$
with q prime (up to order), the following holds: There is
$\psi \in \mathscr {T}(a,b)$
such that
$a,b$
are
$\psi $
-independent and
$\|\psi \| < c^{\eta }$
.
The crucial aspects of Conjecture 3.9 are that the exponent
$\eta $
is strictly less than
$1$
, and that
$a,b$
must be
$\psi $
-independent. Some of our results provide unconditional evidence:
-
• Corollary 2.7 shows that if we completely drop the
$\psi $
-independence condition, then the desired bound holds for any
$\eta>0$
, for those triples
$a,b,c$
satisfying
$\omega (abc)>1+1/\eta $
. -
• Theorem 2.8 shows that if we replace the
$\psi $
-independence condition by the weaker requirement that
$\mathrm {d}^\psi (a)$
or
$\mathrm {d}^\psi (b)$
be nonzero, then one can indeed achieve a bound with exponent
$\eta <1$
—in fact, any
$\eta>1/2$
works. (Note that if
$\psi \in \mathscr {T}(a,b)$
and
$a,b$
are
$\psi $
-independent, then necessarily
$\mathrm {d}^\psi (a)$
or
$\mathrm {d}^\psi (b)$
is nonzero.) -
• Lemma 3.5 shows that if we keep the
$\psi $
-independence condition, then a version of the Small Derivatives Conjecture holds with exponent
$\eta =1+\epsilon $
rather than the sought
$\eta <1$
.
3.4 Proof of concept: Fermat’s Last Theorem
As it is well known, the analogue of FLT over polynomials can be deduced from the Mason–Stothers theorem, and the same argument over
$\mathbb {Z}$
shows that the
$abc$
Conjecture implies the “asymptotic” FLT, meaning FLT up to finitely many exponents (of course, FLT was proved by Wiles [Reference Wiles14], while the
$abc$
Conjecture remains open.) Let us give a direct proofFootnote
1
of FLT for the polynomial ring
$\mathbb {C}[x]$
without using the Mason–Stothers theorem or radicals. Recall that the Wronskian of
$f,g\in \mathbb {C}[x]$
is
$W(f,g)=fg'-f'g$
.
Proposition 3.10 (FLT for polynomials)
Let
$n \ge 3$
. Let
$f,g,h\in \mathbb {C}[x]$
be coprime nonzero polynomials with at least one of them nonconstant. Then,
$f^n+g^n\ne h^n$
.
Proof. For the sake of contradiction, suppose that
$f^n+g^n=h^n$
. Without loss of generality, assume that h has the largest degree among
$f,g,h$
. Note that
$W(f,h)\ne 0$
, for otherwise we would have
$f=\lambda h$
and
$g=(1-\lambda )h$
for some
$\lambda \in \mathbb {C}$
, which is not possible.
Taking derivatives and multiplying by f, we find
$f^{n}f'+fg^{n-1}g' = fh^{n-1}h'$
. Using
$f^nf'=(h^n-g^n)f'$
, we get
$g^{n-1}W(f,g)=h^{n-1}W(f,h)$
. Because
$W(f,h)\ne 0$
and
$g,h$
are coprime, we find
$$ \begin{align*}(n-1)\deg(h)\le \deg W(f,g) \le \deg(fg)-1< 2\deg(h), \end{align*} $$
which implies
$n<3$
, a contradiction.▪
Our theory of arithmetic derivatives affords a smooth translation of the previous proof into the setting of integers, conditional on the Small Derivatives Conjecture 3.9.
Proposition 3.11 (Asymptotic FLT conditional on the Small Derivatives Conjecture)
Assume Conjecture
3.9
. There is a positive integer
$n_0$
such that for all
$n\ge n_0$
, the following holds: If
$a,b,c$
are coprime positive integers, then
$a^n+b^n\ne c^n$
.
Proof. Assume Conjecture 3.9 with some exponent
$\eta <1$
, and let
$n\ge 2$
be a positive integer. Thus, for all but finitely many triples of coprime integers
$a,b,c$
with
$a^n+b^n=c^n$
, there is
$\psi \in \mathscr {T}(a^n,b^n)$
such that
$\|\psi \| < c^{n\cdot \eta }$
and
$W^\psi (a^n,b^n)\ne 0$
(
$a^n,b^n,c^n$
are not prime). Note that
$\mathrm {d}^\psi (a^n)=na^{n-1}\mathrm {d}^\psi a$
by Lemma 2.1 and similarly for b, so
$W^\psi (a^n,b^n)=n(ab)^{n-1}W^\psi (a,b)$
, concluding
$W^\psi (a,b)\ne 0$
.
Starting from
$a^n+b^n=c^n$
, we repeat the computation from the polynomial case using Lemma 2.1 and the fact that
$\psi \in \mathscr {T}(a^n,b^n)$
. We get
$b^{n-1}W^\psi (a,b)=c^{n-1}W^\psi (a,c)$
. Because
$W^\psi (a,b)\ne 0$
and
$b,c$
are coprime, Lemma 2.2 yields
$$ \begin{align*}c^{n-1}\le |W^\psi(a,b)| = |a\mathrm{d}^\psi b - b\mathrm{d}^\psi a|< \|\psi\| \cdot 2c^2\log c<2c^{2+n\cdot \eta}\log c. \end{align*} $$
Up to finitely many triples
$(a,b,c)$
, this shows
$n\le 3/(1-\eta )$
, which suffices to prove the result.▪
In Section 4, we will show that the Small Derivatives Conjecture is equivalent to the
$abc$
Conjecture, and in this way, one can prove Proposition 3.11 by using the
$abc$
Conjecture as an intermediate step. Nevertheless, the previous proof gives an example of how to use our arithmetic derivatives to directly translate arguments from function field arithmetic to the integers.
4 Small arithmetic derivatives are equivalent to the
$abc$
Conjecture
4.1 The Small Derivatives Conjecture implies the
$abc$
Conjecture
Lemma 4.1 If the Small Derivative Conjecture
3.9
holds for some value of
$\eta $
, then Oesterlé’s
$abc$
Conjecture
3.2
holds for every
$M>1/(1-\eta )$
.
Proof. Assume Conjecture 3.9 for some exponent
$0<\eta <1$
. If up to order we have
$(a,b,c)=(1,N,q)$
with q prime and
$N\ge 2$
, then
$\mathrm {rad}(abc)\ge 2q> q+1\ge c$
; hence, the
$abc$
Conjecture holds in such cases. So, we may assume we are not in the previous case. For all but finitely many triples of coprime positive integers
$a,b,c$
with
$a+b=c$
, we have
$$ \begin{align*}\frac{c}{\log c} < \mathrm{rad}(abc)\cdot \frac{c^\eta}{\log 2}\,, \end{align*} $$
where we applied Theorem 3.3 and Conjecture 3.9. The result follows.▪
It turns out that the converse is also true (cf. Theorem 4.5), but the proof is more delicate.
4.2 Preliminary lemmas
Lemma 4.2 Let K be a field, and let
$m<n$
be positive integers. Let
${\textbf {v}}_i=(v_{i,1},\ldots ,v_{i,n})\in K^n$
for
$1\le i\le m$
be linearly independent over K. Let
$j_0$
be such that
$v_{i,j_0}\ne 0$
for some i. There is an injective function
$\tau :\{1,\ldots ,m\}\to \{1,\ldots ,n\}$
such that
$j_0$
is in the image of
$\tau $
, and for each
$1\le i\le m$
, we have
$v_{i,\tau (i)}\ne 0$
.
Proof. Let
$I=\{1,\ldots ,m\}$
and
$J=\{1,\ldots ,n\}$
. Let
$A=[v_{i,j}]_{i\in I, j\in J}$
, and note that this matrix has rank m by linear independence of its rows. The
$j_0$
-th column is not the zero vector, so we may choose
$J'\subseteq J$
with
$\# J'=m$
such that the square matrix
$A'=[v_{i,j}]_{i\in I, j\in J'}$
still has rank m. In particular,
$\det (A')\ne 0$
. Writing
$\det (A')=\sum _\sigma \pm \prod _{i} v_{i,\sigma (i)}$
where
$\sigma $
varies over bijective functions
$I\to J'$
(with suitable choice of signs), we see that for some bijective
$\tau :I\to J'$
, we have
$\prod _{i} v_{i,\tau (i)}\ne 0$
.▪
Lemma 4.3 Let
$\epsilon>0$
. For all but finitely many positive integers n, we have
$\prod _{p|n}v_p(n) < n^\epsilon $
.
Proof. Note that
$\prod _{p|n}v_p(n)\le \sigma _0(n)$
where
$\sigma _0(n)$
is the number of positive divisors of n. Thus, the result follows from standard bounds on
$\sigma _0(n)$
.▪
We remark that a much more precise version of Lemma 4.3 is due to de Weger [Reference de Weger4].
The following result limits how small
$\|\psi \|$
can be when
$a,b$
are
$\psi $
-dependent. Note that the condition that
$a,b,c$
are not of the form
$1,N,q$
with q prime (up to order) from our heuristic in Section 3.3 naturally appears here again.
Lemma 4.4 Let
$a,b,c$
be coprime positive integers with
$a+b=c$
, not of the form
$(1,8,9)$
or
$(1,N,q)$
with q prime (up to order). Define
$r=\omega (abc)-1$
. Let
$\psi _1,\ldots ,\psi _{r-1} \in \mathscr {T}^\circ (a,b)$
be linearly independent derivations; in particular, a and b are
$\psi _i$
-dependent for each i. Suppose that there is some number M satisfying
$1<M<2$
and
$c<\mathrm {rad}(abc)^M$
, and let
$\mu = (2-M)/(4M)$
. Then,
$$ \begin{align*}\prod_{i=1}^{r-1} \|\psi_i\| \ge \frac{c^{\mu}}{\prod_{p|abc} v_p(abc)}. \end{align*} $$
Proof. Recall that
$\mathscr {T}^\circ (a,b)$
is defined by the conditions (2.1) and (2.3). Together they give
$$ \begin{align} \sum_{p|a} \frac{v_p(a)}{p}\psi(\xi_p) =\sum_{p|b} \frac{v_p(b)}{p} \psi(\xi_p) = \sum_{p|c} \frac{v_p(c)}{p} \psi(\xi_p), \end{align} $$
which holds for every
$\psi \in \mathscr {T}^\circ (a,b)$
, in particular for each
$\psi _i$
. In fact, (2.1) and (2.3) together are equivalent to (4.1), so
$$ \begin{align*}\mathscr{T}^\circ(a,b)=\{\psi\in \mathscr{T} : \mathrm{supp}(\psi)\subseteq \mathrm{supp}(abc)\mbox{ and (4.1) holds}\}. \end{align*} $$
We distinguish three cases (Lemma 3.7 and our assumptions imply that there is no other case):
-
(i) Up to order, both
$ab$
and c have at least two different prime factors each. -
(ii) Up to order, we have
$(a,b,c)=(1,q^s,N)$
for a prime q and some integer
$s\ge 2$
and N with at least two prime factors. -
(iii)
$(a,b,c)=(q_1^{s_1}, q_2^{s_2}, q_3^{s_3})$
where
$q_1, q_2, q_3$
are different primes and
$s_i\ge 1$
for each i.
Let us first deal with cases (i) and (ii).
In case (i), suppose that there is some prime
$q|abc$
such that
$\psi _i(\xi _q)=0$
for each i. Then, every
$\psi \in \mathscr {T}^\circ (a,b)$
would satisfy
$\psi (\xi _q)=0$
, because the derivations
$\psi _1,\ldots ,\psi _{r-1}$
generate a finite index subgroup of
$\mathscr {T}^{\circ }(a,b)$
(cf. Lemma 2.9). This is not possible, because the condition
$\psi (\xi _q)=0$
is linearly independent from the two equations in (4.1) that define
$\mathscr {T}^\circ (a,b)$
. This proves that in case (i), for each prime
$p|abc$
, we have
$(\psi _i(\xi _p))_i\ne (0,\ldots ,0)$
.
In case (ii), we note that one of the equations in (4.1) is
$0=s\psi (\xi _q)/q$
, which is equivalent to
$\psi (\xi _q)=0$
. Therefore,
$\mathscr {T}^0(a,b)$
is defined by
$\psi (\xi _q)=0$
and
$\sum _{p|N} v_p(N)\psi (\xi _p)/p=0$
. This last equation is linearly independent from any condition of the form
$\psi (\xi _p)=0$
with
$p\ne q$
, because N has at least two prime factors. This proves that in case (ii), for each
$p|abc$
with
$p\ne q$
, we have
$(\psi _i(\xi _p))_i\ne (0,\ldots ,0)$
.
Let
$q'$
be the largest prime factor of
$abc$
in case (i), and let it be the largest prime factor of
$abc$
subject to the condition
$q'\ne q$
in case (ii). In either case,
$(\psi _i(\xi _{q'}))_i\ne (0,\ldots ,0)$
.
Let
$I=\{1,\ldots ,r-1\}$
and
$J=\{ p : p|abc\}$
, so that
$\#I=r-1 < \#J=r+1$
. Choosing the vectors
${\textbf {v}}_i = (\psi _i(\xi _p))_{p\in J}$
for
$i\in I$
, Lemma 4.2 gives an injective function
$\tau :I\to J$
having
$q'$
in its image such that for every
$i\in I$
, we have
$\psi _i(\xi _{p_i})\ne 0$
, where
$p_i:=\tau (i)$
.
By coprimality of
$a,b,c$
and considering the denominators in (4.1), we see that for each
$p|abc$
and each i, we have that p divides
$v_p(abc)\psi _i(\xi _p)$
. Together with the previous nonvanishing, for each
$i=1,\ldots ,r-1$
, we find
$v_{p_i}(abc)\|\psi _i\| \ge p_i$
. This gives
$$ \begin{align*}\prod_{p|abc} v_p(abc)\cdot \prod_{i=1}^{r-1}\|\psi_i\|\ge\prod_{i=1}^{r-1}(v_{p_i}(abc)\|\psi_i\| )\ge \prod_{i=1}^{r-1} p_i =Pq', \end{align*} $$
where P is the product of the primes
$p_i\ne q'$
. Let
$\ell _1,\ell _2\in J$
be the two primes not in the image of
$\tau $
. Then,
$\mathrm {rad}(abc)=P\ell _1\ell _2q'$
.
In case (i), we have
$\ell _1,\ell _2<q'$
, so
$\mathrm {rad}(abc)=P\ell _1\ell _2q'< P\cdot (q')^3\le (Pq')^3$
. This proves
$\prod _{i=1}^{r-1} p_i \ge \mathrm {rad}(abc)^{1/3}\ge c^{1/(3M)}$
, which concludes the proof in case (i).
In case (ii), notice that
$q=\ell _j$
, for
$j=1$
or
$j=2$
. Let us assume
$q=\ell _1$
, in particular,
$\ell _2<q'$
. Observe that
$\ell _1^2=q^2\le q^s\le c$
, so
$\ell _1\le c^{1/2}$
. Then, we get
$$ \begin{align*}c^{1/M}\le \mathrm{rad}(abc)=P\ell_1\ell_2 q' \le P(q')^2c^{1/2} \le (Pq')^2c^{1/2}. \end{align*} $$
This proves
$\prod _{i=1}^{r-1} p_i \ge c^{(2-M)/(4M)}$
, which concludes the proof in case (ii).
Finally, let us consider case (iii). Naturally, one of the primes
$q_i$
is
$2$
, but this will not be relevant. Note that
$r=2$
, so we need a lower bound for
$\|\psi _1\|$
. By (4.1), we find
$s_1\psi _1(\xi _{q_1})/q_1=s_2\psi _1(\xi _{q_2})/q_2=s_3\psi _1(\xi _{q_3})/q_3$
, and it follows that
$\mathrm {rad}(abc)=q_1q_2q_3$
divides
$s_1s_2s_3\psi _1(\xi _{q_1})\psi _1(\xi _{q_2})\psi _1(\xi _{q_3})$
. In particular,
$$ \begin{align*}\|\psi_1\|^3\cdot\prod_{p|abc} v_p(abc)^3\ge \|\psi_1\|^3\cdot \prod_{p|abc} v_p(abc)\ge \mathrm{rad}(abc)>c^{1/M}, \end{align*} $$
which gives the result in case (iii).▪
4.3 The
$abc$
Conjecture implies the Small Derivatives Conjecture
Theorem 4.5 If Oesterlé’s
$abc$
Conjecture
3.2
holds with some exponent
$1<M<2$
, then the Small Derivatives Conjecture
3.9
holds for each exponent
$\eta> 1-(2-M)/(4M)$
.
Let us remark that for
$1<M<2$
, the quantity
$\mu =(2-M)/(4M)$
satisfies
$3/4<1-\mu < 1$
. We see that any exponent
$\eta>1-\mu $
sufficiently close to
$1-\mu $
satisfies
$\eta <1$
; hence, it is admissible for the Small Derivatives Conjecture 3.9.
Proof of Theorem 4.5
We assume that Oesterlé’s
$abc$
Conjecture 3.2 holds for some exponent M with
$1<M<2$
. Let us fix
$\epsilon>0$
. In the argument below, we may need to implicitly discard finitely many triples
$(a,b,c)$
for some inequalities to hold, which we indicate by writing “
$\le _*$
” instead of “
$\le $
.” The finitely many discarded triples will only depend on M and
$\epsilon $
.
Let
$a,b$
be coprime positive integers, set
$c=a+b$
, and assume that
$(a,b,c)$
is not of the form
$(1,N,q)$
with q prime, up to order.
Let
$\psi _1,\ldots ,\psi _r\in \mathscr {T}(a,b)$
be as provided by Theorem 2.6, and label these derivations in such a way that
$\|\psi _1\|\le \|\psi _2\|\le \cdots \le \|\psi _r\|$
. Let
$i_0\in \{1,2,\ldots ,r\}$
be the least index such that
$\psi _{i_0}\notin \mathscr {T}^\circ (a,b)$
, which exists by Lemma 2.9. We distinguish two cases:
-
(a)
$i_0<r$
. In this case, using Lemma 2.3, we get
$\|\psi _{i_0}\|\le _* c^{(1+\epsilon )/2}$
, because
$$ \begin{align*}\|\psi_{i_0}\|^{2}\le \prod_{i=i_0}^r\|\psi_{i}\|\le \frac{\omega(abc)}{2\log 2} c\log c\le_* c^{1+\epsilon}. \end{align*} $$
-
(b)
$i_0=r$
. In this case, we have
$\psi _1,\ldots ,\psi _{r-1}\in \mathscr {T}^\circ (a,b)$
, and we can apply Lemma 4.4, because we are assuming Conjecture 3.2 for some exponent
$1<M<2$
. Let us define
$\mu = (2-M)/(4M)$
. Lemmas 2.3 and 4.3 give
$\|\psi _r\| \le _* c^{1-\mu + \epsilon }$
, because
$$ \begin{align*}c^{\mu-\epsilon/2} \cdot \|\psi_r\| \le_* \frac{c^\mu}{\prod_{p|abc} v_p(abc)} \cdot \|\psi_r\| \le \prod_{i=1}^r \|\psi_i\|\le \frac{\omega(abc)}{2\log 2} c\log c\le_* c^{1+\epsilon/2}. \end{align*} $$
The second case is the one giving the worst bound, hence the result.▪
In particular, Lemma 4.1 and Theorem 4.5 give the following result.
5 Differentials of rings over monoids
5.1 Definitions
Let A be a commutative unitary ring, let R be a commutative monoid, and let
$\alpha :R\to A$
be a morphism of monoids with A taken as a multiplicative monoid. Given an A-module U, a U-valued
$\alpha $
-derivation on A is a function
$D:A\to U$
satisfying
-
(Diff1) R-triviality:
$D(\alpha (r))=0$
for all
$r\in R$
; -
(Diff2) Leibniz rule:
$D(ab)=aD(b)+bD(a)$
for all
$a,b\in A$
.
A differential
$(A,\alpha )$
-module is a pair
$(U,D)$
, where U is an A-module and D is a U-valued
$\alpha $
-derivation on A.
Naturally, these definitions can also be formulated when A is just assumed to be a commutative monoid, which is perhaps better suited for the theory of monoid schemes (“geometry over
$\mathbb {F}_1$
”; cf. [Reference Deitmar, van der Geer, Moonen and Schoof5]). However, we keep the assumption that A be a ring to simplify the exposition and because this is the case of interest for us. Another observation is that when
$R=\{1\}$
, we recover the notion of absolute derivation from [Reference Kurokawa, Ochiai and Wakayama7], and in fact, most of that theory can be generalized to our setting.
One directly checks the following result.
Lemma 5.1 Let
$(U,D)$
be a differential
$(A,\alpha )$
-module. We have:
-
(i)
$D(0)=D(1)=0$
. -
(ii) For all
$r\in R$
and
$b\in A$
, we have
$D(\alpha (r)b)=\alpha (r)D(b)$
. -
(iii) Given
$a\in A$
and a positive integer n, we have
$D(a^n)=na^{n-1}D(a)$
. -
(iv) Given
$u\in A^\times $
and a positive integer n, we have
$D(u^{-n})=-nu^{-(n+1)}D(u)$
.
Given differential
$(A,\alpha )$
-modules
$(U,D)$
and
$(V,E)$
, a morphism of differential
$(A,\alpha )$
-modules is a morphism of A-modules
$f:U\to V$
that satisfies
$E=f\circ D$
. We obtain a category of differential
$(A,\alpha )$
-modules which we denote by
$\Phi _{(A,\alpha )}$
.
For an A-module U, let
$\mathrm {Der}_{(A,\alpha )}(U)=\{D:A\to U \, : (U,D)\in Ob(\Phi _{(A,\alpha )})\}$
. This is an A-module with the structure induced by U. Given A-modules U and V and a morphism
$f\in \mathrm {Hom}_A(U,V)$
, we define
$\mathrm {Der}_{(A,\alpha )}(f):\mathrm {Der}_{(A,\alpha )}(U)\to \mathrm {Der}_{(A,\alpha )}(V)$
by
$\mathrm {Der}_{(A,\alpha )}(f)(D)=f\circ D$
.
Lemma 5.2 The rule
$\mathrm {Der}_{(A,\alpha )}$
defines a functor
$A\mbox {-}\mathbf{Mod}\to A\mbox {-}\mathbf{Mod}$
.
5.2 Universal object
Consider
$\alpha :R\to A$
as before. Let
$X_A$
be the free A-module on the generators
$e_a$
for
$a\in A$
. Let
$M_{(A,\alpha )}\subseteq X_A$
be the sub A-module generated by the elements
$e_{\alpha (r)}$
for
$r\in R$
and
$e_{ab}-ae_b-be_a$
for
$a,b\in A$
. We consider the quotient A-module
$\Omega _{(A,\alpha )}=X_A/M_{(A,\alpha )}$
and define
$\mathrm {d}_{(A,\alpha )}:A\to \Omega _{(A,\alpha )}$
by
$\mathrm {d}_{(A,\alpha )} (a)= e_a\bmod M_{(A,\alpha )}$
. By construction,
$(\Omega _{(A,\alpha )},\mathrm {d}_{(A,\alpha )})$
is a differential
$(A,\alpha )$
-module. If there is no risk of confusion, we will simply write
$\mathrm {d}$
instead of
$\mathrm {d}_{(A,\alpha )}$
.
Lemma 5.3 (Universal property of
$\Omega _{(A,\alpha )}$
)
For each A-module U, the rule
$\psi \mapsto \psi \circ \mathrm {d}$
defines a functorial isomorphism of A-modules
$\eta _{U}:\mathrm {Hom}_A(\Omega _{(A,\alpha )}, U)\to \mathrm {Der}_{(A,\alpha )}(U)$
. Thus,
$\Omega _{(A,\alpha )}$
represents the functor
$\mathrm {Der}_{(A,\alpha )}$
. In particular,
$(\Omega _{(A,\alpha )},\mathrm {d})$
is an initial object in the category
$\Phi _{(A,\alpha )}$
.
Proof. Functoriality on U and A-linearity are immediate. Let us check that
$\eta _U$
is an isomorphism.
Let
$\psi \in \mathrm {Hom}_A(\Omega _{(A,\alpha )},U)$
with
$\eta _U(\psi )=0$
. This means that
$\psi \circ \mathrm {d} : A\to U$
is the zero map. The set
$\mathrm {d}(A)$
generates
$\Omega _{(A,\alpha )}$
as an A-module, so
$\psi =0$
, because it vanishes on a generating set of
$\Omega _{(A,\alpha )}$
. Thus,
$\eta _U$
is injective.
Let
$D\in \mathrm {Der}_{(A,\alpha )}(U)$
. Let
$\theta :X_A\to U$
be the A-module map determined by
$\theta (e_a)=D(a)$
on the standard basis
$\{e_a\}_{a\in A}$
of the free A-module
$X_A$
. Let
$\tilde {\mathrm {d}}:A\to X_A$
be the function
$\tilde {\mathrm {d}}(a)=e_a$
, and let
$\pi :X_A\to X_A/M_{(A,\alpha )}=\Omega _{(A,\alpha )}$
be the quotient map. Note that
$\theta \circ \tilde {\mathrm {d}}=D$
and
$\mathrm {d}=\pi \circ \tilde {\mathrm {d}}$
. Because D satisfies (Diff1) and (Diff2), we have that a generating set for
$M_{(A,\alpha )}$
is contained in
$\ker (\theta )$
, and because
$\theta $
is A-linear, we get
$M_{(A,\alpha )}\subseteq \ker (\theta )$
. Thus, there is an A-module map
$\psi :\Omega _{(A,\alpha )}\to U$
with
$\theta =\psi \circ \pi $
. Therefore,
$D=\theta \circ \tilde {\mathrm {d}} = \psi \circ \pi \circ \tilde {\mathrm {d}} = \psi \circ \mathrm {d} =\eta _U(\psi )$
, proving that
$\eta _U$
is surjective.▪
We call
$(\Omega _{(A,\alpha )},\mathrm {d})$
the universal differential
$(A,\alpha )$
-module.
5.3 Examples
We conclude by discussing some concrete examples.
Example 5.4 Let
$A=\mathbb {F}_q$
be a finite field with q elements and
$\alpha :R\to \mathbb {F}_q$
be arbitrary. The elements
$\mathrm {d}(x)$
for
$x\in \mathbb {F}_q$
generate
$\Omega _{(\mathbb {F}_q,\alpha )}$
, and
$\mathrm {d}(x)=\mathrm {d}(x^q)=qx^{q-1}\mathrm {d}(x)=0$
. Therefore,
$\Omega _{(\mathbb {F}_p,\alpha )}=(0)$
.
Example 5.5 Let
$A=\mathbb {Z}/4\mathbb {Z}$
, and let
$\alpha :\{1\}\to \mathbb {Z}/4\mathbb {Z}$
be the inclusion. In this case, it is not so lengthy to directly compute
$M_{(A,\alpha )}\subseteq X_A=(\mathbb {Z}/4\mathbb {Z})^4$
. One finds that the universal
$\alpha $
-derivation is
$\mathrm {d}:\mathbb {Z}/4\mathbb {Z}\to \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
defined by
$\mathrm {d}(0)=\mathrm {d}(1)=(0,0)$
,
$\mathrm {d}(2)=(1,0)$
, and
$\mathrm {d}(3)=(0,1)$
. Note that
$ \mathrm {d}(1)+\mathrm {d}(2) = (1,0)\ne (0,1) =\mathrm {d}(3)$
, so
$\mathrm {d}$
is not additive. Nevertheless, let
$\sigma :(\mathbb {Z}/2\mathbb {Z})^2\to \mathbb {Z}/2$
be
$\sigma (x,y)=x+y$
. Then, the
$\alpha $
-derivation
$\sigma \circ \mathrm {d}:\mathbb {Z}/4\mathbb {Z}\to \mathbb {Z}/2\mathbb {Z}$
respects the equation
$1+2=3$
.
Example 5.6 Let A be a UFD, and let T be a set of pairwise nonassociated irreducible elements. Let
$R=A - \cup _{t\in T} (t)$
, let
$\alpha :R\to A$
be the inclusion, and let
$U=\bigoplus _{t\in T} A$
. Define
$D:A\to U$
by
$D(a)=(v_t(a)\cdot at^{-1})_{t\in T}$
, where
$v_t$
is the t-adic valuation. Then,
$D:A\to U$
is an
$\alpha $
-derivation, and we claim it is the universal one. Indeed, given
$a=rt_1^{n_1}\cdots t_k^{n_k}\in A$
with
$r\in R$
,
$n_j\ge 1$
, and
$t_j\in T$
different, the map
$\mathrm {d}=\mathrm {d}_{(A, \alpha )}$
satisfies
$\mathrm {d}(a)=\sum _{j=1}^k n_j at_j^{-1}\mathrm {d}(t_j)$
. Because U is free, there is an A-module map
$\phi : U\to \Omega _{(A,\alpha )}$
satisfying
$\mathrm {d}=\phi \circ D$
. We conclude by universality of
$\Omega _{(A,\alpha )}$
.
Example 5.7 In the previous example, consider the special case
$A=\mathbb {Z}$
and T the set of all prime numbers, so that
$R=\{-1,1\}$
. Then,
$D:A\to U$
turns out to be our map
$\mathrm {d}:\mathbb {Z}\to \Omega $
. So, the latter is the universal
$\alpha $
-derivation when
$\alpha :\{-1,1\}\to \mathbb {Z}$
is the inclusion. Thus,
$\mathrm {Hom}_{\mathbb {Z}}(\Omega ,\mathbb {Z})\simeq \mathrm {Der}_{(\mathbb {Z},\alpha )}(\mathbb {Z})$
is the module of all
$\alpha $
-derivations
$D:\mathbb {Z}\to \mathbb {Z}$
. Our
$\mathbb {Z}$
-module
$\mathscr {T}$
is a metrized version of this.
Acknowledgment
The initial motivation for this project was a conversation with Thanases Pheidas that took place at the 2016 Oberwolfach workshop Definability and Decidability Problems in Number Theory. I heartily thank the MFO for their support and hospitality, as well as T. Pheidas for bringing the topic of arithmetic derivatives to my attention. Comments by Jerson Caro and Natalia Garcia-Fritz on the first version of this manuscript are gratefully acknowledged. I also thank the referee for carefully reading this article and for valuable suggestions and corrections.
