Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T12:01:34.112Z Has data issue: false hasContentIssue false
  • English
  • Français

Radiative reaction effect on electron dynamics in an ultra intense laser field

Published online by Cambridge University Press:  21 January 2010

Q.Q. Mao ,
Q. Kong ,
Y.K. Ho ,
H.O. Che ,
H.Y. Ban ,
Y.J. Gu  and
S. Kawata
Q.Q. Mao
Affiliation:
Applied Ion Beam Physics Laboratory, Key Laboratory of the Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai, China
Q. Kong*
Affiliation:
Applied Ion Beam Physics Laboratory, Key Laboratory of the Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai, China
Y.K. Ho
Affiliation:
Applied Ion Beam Physics Laboratory, Key Laboratory of the Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai, China
H.O. Che
Affiliation:
Applied Ion Beam Physics Laboratory, Key Laboratory of the Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai, China
H.Y. Ban
Affiliation:
Applied Ion Beam Physics Laboratory, Key Laboratory of the Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai, China
Y.J. Gu
Affiliation:
Applied Ion Beam Physics Laboratory, Key Laboratory of the Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai, China
S. Kawata
Affiliation:
Department of Electrical and Electronic Engineering, Utsunomiya University, Utsunomiya, Japan
*
Address correspondence and reprint requests to: Q. Kong, Applied Ion Beam Physics Laboratory, Key Laboratory of the Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai 200433, China. E-mail: qkong@fudan.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

The radiative reaction effect of an electron is usually very small and can be neglected in most cases. But for an ultra intensity laser-electron interaction region, the radiation can become large. The influence of the radiative reaction effect of an electron interacting with an ultra intense laser pulses in vacuum on electron dynamics is investigated within the classical relativistic Lorentz-Dirac approach. A predictor-corrector method is proposed to numerically solve the equation of motion with the electron radiative reaction included. We study the counter-propagating case (for Thomson scattering scheme) and the same direction propagating cases (for laser acceleration). Our simulation results show that radiation can have great effect in the counter-propagating case. But in the vacuum laser electron acceleration regime, both the ponderomotive acceleration scenario case and the capture and acceleration scenario, radiative reaction effect can totally be ignored for laser intensity available presently or in the near-future.

Keywords

Electron dynamicsLaser accelerationRadiative reaction
Type
Research Article
Information
Laser and Particle Beams , Volume 28 , Issue 1 , March 2010 , pp. 83 - 90
Copyright
Copyright © Cambridge University Press 2010

INTRODUCTION

Due to the development of the ultra intense lasers with chirped pulse amplification (CPA) technique, currently laser intensity close to 1022 W/cm2 has been achieved (Mourou et al., Reference Mourou, Tajima and Bulanov2006). Many new research fields have appeared in both applied and fundamental physics, such as laser acceleration of particles (Chen et al., Reference Chen, Unick, Vafaei-Najafabadi, Tsui, Fedosejevs, Naseri, Masson-Laborde and Rozmus2008; Dombi et al., Reference Dombi, Racz and Bodi2009; Gupta & Suk, Reference Gupta and Suk2007; Karmakar & Pukhov, Reference Karmakar and Pukhov2007; Kulagin et al., Reference Kulagin, Cherepenin, Hur, Lee and Suk2008; Limpouch et al., Reference Limpouch, Psikal, Andreev, Platonov and Kawata2008; Lin et al., Reference Lin, Ho, Kong, Chen, Wang, Xu and Kawata2007; Liu et al., Reference Liu, Xie, Huang, Liu and Yu2009; Nickles et al., Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Sandner, Schreiber, Hilscher, Jahnke, Andreev and Tikhonchuk2007; Sadighi-Bonabi et al., Reference Sadighi-Bonabi, Navid and Zobdeh2009; Shi, Reference Shi2007; Singh & Malik, Reference Singh and Malik2008; Torrisi et al., Reference Torrisi, Margarone, Gammino and Ando2007; Xie et al., Reference Xie, Aimidula, Niu, Liu and Yu2009; Zhou et al., Reference Zhou, Yu and He2007), high-order harmonic generations (Dromey et al., Reference Dromey, Bellei, Carroll, Clarke, Green, Kar, Kneip, Markey, Nagel, Willingale, Mckenna, Neely, Najmudin, Krushelnick, Norreys and Zepf2009; Ozaki et al., Reference Ozaki, Bom, Ganeev, Kieffer, Suzuki and Kuroda2007, Reference Ozaki, Bom and Ganeev2008), X-ray lasers (Hu et al., Reference Hu, Zhang, Zheng, Shen, Liu, Yang, Ding, Hu, Huang, Du, Yi, Lei and Xu2008; Kolacek et al., Reference Kolacek, Schmidt, Prukner, Frolov and Straus2008; Priebe et al., Reference Priebe, Laundy, Macdonald, Diakun, Jamison, Jones, Holder, Smith, Phillips, Fell, Sheehy, Naumova, Sokolov, Ter-Avetisyan, Spohr, Krafft, Rosenzweig, Schramm, Gruner, Hirst, Collier, Chattopadhyay and Seddon2008; Yu et al., Reference Yu, Cao, Yu, Cai, Xu, Yang, Lei, Tanaka and Kodama2009), ICF fast ignition (Deutsch et al., Reference Deutsch, Bret, Firpo, Gremillet, Lefebvre and Lifschitz2008; Eliezer et al., Reference Eliezer, Murakaml and Val2007; Hora, Reference Hora2007; Zvorykin et al., Reference Zvorykin, Didenko, Ionin, Kholin, Konyashchenko, Krokhin, Levchenko, Mavritskii, Mesyats, Molchanov, Rogulev, Seleznev, Sinitsyn, Tenyakov, Ustinovskii and Zayarnyi2007), nonlinear Compton scattering (Chouffani et al., Reference Chouffani, Harmon, Wells, Jones and Lancaster2006; Priebe et al., Reference Priebe, Laundy, Macdonald, Diakun, Jamison, Jones, Holder, Smith, Phillips, Fell, Sheehy, Naumova, Sokolov, Ter-Avetisyan, Spohr, Krafft, Rosenzweig, Schramm, Gruner, Hirst, Collier, Chattopadhyay and Seddon2008), etc. Among these, the interaction between the particle and the lasers, including the laser acceleration of particle, especially electrons, and the laser-electron scattering, have received wide attentions because the electric field can be as high as 107 MV/m for such lasers with 1 µm wavelength, much larger than that of conventional accelerators, which are about 20 MV/m. Many acceleration schemes have been proposed (Badziak et al., Reference Badziak, Glowacz, Jablonski, Parys, Wolowski and Hora2005; Glinec et al., Reference Glinec, Faure, Pukhov, Kiselev, Gordienko, Mercier and Malka2005; Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Ferná Ndez2006; Hora et al., Reference Hora, Hoelss, Scheid, Wang, Ho, Osman and Castillo2000; Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakajima, Masuda, Ho, Miyanaga, Limpouch and Andreev2005; Lifschitz et al., 2006; Malka et al., Reference Malka, Lefebvre and Miquel1997; Mangles et al., Reference Mangles, Walton, Najmudin, Dangor, Krushelnick, Malka, Manclossi, Lopes, Carias, Mendes and Dorchies2006; Roth et al., Reference Roth, Brambrink, Audebert, Blazevic, Clarke, Cobble, Cowan, Fernandez, Fuchs, Geissel, Habs, Hegelich, Karsch, Ledingham, Neely, Ruhl, Schlegel and Schreiber2005; Shorokhov & Pukhov, Reference Shorokhov and Pukhov2004; Toncian et al., Reference Toncian, Borghesi, Fuchs, D'humiè Res, Antici, Audebert, Brambrink, Cecchetti, Pipahl, Romagnani and Willi2006; Yin et al., Reference Yin, Albright, Hegelich and Fernandez2006), such as laser-induced beat-wave or wakefield electron accelerations in plasmas and inverse Cherenkov accelerations, etc. Our principal research interest is in the far-field acceleration, i.e., free electrons interacting with electromagnetic wave propagating in free space. Among the many vacuum acceleration schemes, the ponderomotive acceleration scenario (PAS) (Stupakov & Zolotorev, Reference Stupakov and Zolotorev2001; Lin et al., Reference Lin, Ho, Kong, Chen, Wang, Xu and Kawata2007) normally refers to an interaction process where an intense laser pulse catches non-relativistic free electrons in the focal region, then interacts with and accelerates them. On the other hand, the capture acceleration scenario (CAS) (Xu et al., Reference Xu, Ho, Kong, Chen, Wang, Wang and Lin2005; Wang et al., Reference Wang, Ho, Yuan, Kong, Cao and Shao2002) deals with vacuum laser acceleration of relativistic electrons making use of the low wave phase velocity region of a laser beam.

Radiation is emitted when the electron is accelerating or decelerating by the external field. The radiative reaction effects are usually very weak and can often be neglected. However, when the electrons interact with ultra intense laser pulse, the emitted radiation could be relatively intense. In laser acceleration, radiative reaction may limit the energy, which the electrons can gain from the laser field. Then the questions arise such as how the presence of this radiative reaction affects the motion of the electrons in the ultra intense laser field, and whether the accelerated electrons will lose most of their energy through the radiation in laser acceleration. For the laser-electron scattering in vacuum, the radiation effect may influence the electron dynamic very much.

To understand fully the electron dynamics in ultra intense field, in this paper, we will put our emphasis on the influence of the electron radiative reaction to the electron dynamic characteristics in an ultra intense laser pulse, especially to the laser electron acceleration. We will first address the simulation model to obtain the electron dynamics with radiative reaction included. Then, we will discuss three schemes: high-energy electron counter-propagating with the laser pulse (Thomson scattering scheme), low-energy hot electron interacting with the laser pulse (PAS scheme), high-energy electron injecting into the laser pulse with a little incident angle (CAS scheme). All the calculation results with and without the radiation effect are presented and analyzed. Finally, there is a summary of this paper.

SIMULATION MODEL

For the motion of charged particles in external force fields, radiations are emitted whenever the charges are accelerated. The emitted radiation causes the charged particles to lose energy, momentum, and angular momentum, and will influence the subsequent motion of the charged particles. Since the motion of the sources of radiation is influenced by the emission of radiation, a correct treatment should include the radiative reaction, or radiative damping on the motion of sources. A number of derivations of the radiative damping force have been given in the past. The non-relativistic equation of motion for a point charge including radiative reaction was given by Lorentz. Its relativistic generalization was first derived by Abraham, and later the covariant form was derived by Dirac (Reference Dirac1938):

(1)
mc {du^i \over ds} = {e \over c} F^{ik} u_k + g^{i}\comma \;
(2)
g^i = {2e^2 \over 3c} \left[{d^2 u^i \over ds^2} - u^i u^k {d^2 u_k \over ds^2} \right]\comma \;

where F ik is the electromagnetic field tensor, u i is the four velocity, and g i is the radiative reaction term.

This Lorentz-Dirac equation can well describe the damping of a relativistic point charge interacting with an external electromagnetic field. However, a certain number of problems, conceptual and practical, are known to be associated with the Lorentz-Dirac equation. These difficulties may be traced to the fact that there are second order derivatives in the velocity, which implies an extra condition is necessary, in order to solve the equation, besides the usual initial conditions on position and velocity of classical mechanics. Even without an external field, there exist solutions of exponentially increasing velocity (run-away solutions). Another problem is the solution violates causality in Compton time scale τ 0 (Jackson, Reference Jackson1975). These problems are related to some underlying inconsistencies of the classical electrodynamics (Landau & Lifschitz, Reference Landau and Lifschitz1994). To avoid the run-away solutions, as suggested by Rohrlich (Reference Rohrlich1995), asymptotic constraint is used that the acceleration should vanish at infinity. Here, we use another expression of the radiative reaction in terms of fields. We assume the radiative reaction term g i is a small perturbation, and then g i can be expressed in the terms of the field tensor of the external field acting on the particle (Landau & Lifschitz, Reference Landau and Lifschitz1994):

(3)
\eqalign{g^i & = \left[{2e^3 \over 3mc^3}{\partial F^{ik} \over \partial x^l} u^l u_k + {2e^{4} \over 3m^2 c^{5}} F^{ik} F_{kl} u^l \right. \cr & \left. \quad - {2e^4 \over 3m^2 c^5} \left(F_{km} u^k\right)\left(F^{ml} u_l\right)u^i \right]. \cr}

In addition, the spatial part of the equation can be expressed as

(4)
{d{\bf p} \over dt} = e \left({\bf E} + {\bf \beta \times B}\right)+ {\bf g}\comma \;
(5)
\eqalign{{\bf g} & = {2e^3 \over 3mc^2} \gamma \left({\partial \over c\partial t} + {\bf \beta} \cdot \nabla\right)\lpar {\bf E} + {\bf \beta} \times {\bf B}\rpar \cr & \quad + {2e^{4} \over 3m^2 c^4} \left[\left({\bf \beta} \cdot {\bf E}\right){\bf E} + \left({\bf E} + {\bf \beta} \times {\bf B}\right)\times {\bf B}\right]\cr & \quad - {2e^4 \over 3m^2 c^4} \gamma^2 {\bf \beta} \left[\left({\bf E} + {\bf \beta} \times {\bf B}\right)^2 - \left({\bf \beta} \cdot {\bf E}\right)^2 \right]\comma \; \cr}

where β = v/c, and p is the momentum of the particle. This so-called Landau-Lifschitz equation has been proposed as the exact equation of motion for a point charge (Rohrlich, Reference Rohrlich2001). It avoids the run-away problem. The first term in this equation includes derivatives of fields. In order to simulate numerically the laser electron acceleration including radiative reaction, a predictor-corrector numerical method (Hildebrand, Reference Hildebrand1974) is used to find the self-consistent solution. Concretely, in each simulation step, first with the absence of the radiation reaction, we integrate the equation of motion by using the fourth-order Runge-Kutta method together with Richardson's first-order extrapolation procedure, and obtain the new status of the electron. Then, we can calculate the derivatives of the fields, and include the radiation reaction in the above step to get result that is more precise. Now, the difficulty related to the Lorentz-Dirac equation mentioned above does not appear, and the numerical method we used is able to obtain a convergent solution.

The lowest order Hermite-Gaussian (0,0) mode is used for describing the electromagnetic field of the laser. When we consider a laser pulse with x polarized and propagating along the z-axis, the expression for the transverse electric component can be written as:

(6)
\eqalign{E_x & = E_0 {w_0 \over w\lpar z\rpar } \exp \left(-{x^2+y^2 \over w^2 \lpar z\rpar }\right)\exp \left[i\left(kz - \omega t - \varphi \lpar z\rpar \right.\right. \cr & \quad \left.\left.- \varphi_0 + {k\lpar x^2+y^2\rpar \over 2R\lpar z\rpar }\right)\right]f\lpar \eta\rpar \comma \; \cr}

where E 0 is the reference electric-field strength, w 0 is the beam width at the focus center, k is the laser wave number, φ0 is the initial phase, and

(7)
w\lpar z\rpar =w_0 \left[1 + \left(\displaystyle{{2z \over kw_0 ^2}}\right)^2 \right]^{1/2}\comma \; \eqno \lpar 7\rpar
(8)
R\lpar z\rpar = z \left[1 + \left(\displaystyle{{kw_0^2 \over 2z}}\right)^2\right]\comma \;
(9)
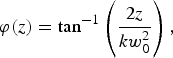
\varphi \lpar z\rpar = \tan^{-1} \left(\displaystyle{{2z \over kw_0^2}}\right)\comma \;
(10)
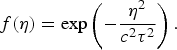
\,f\lpar \eta\rpar = \exp \left(-\displaystyle{{\eta ^2 \over c^2 \tau^2}}\right).

A Gaussian profile is adopted for the laser pulse. Here τ is the pulse duration and η = z−ct. The other electric and magnetic components can be obtained by using

(11)
E_z = \lpar i/k\rpar \lpar \partial E_x/\partial x\rpar \comma \;
(12)
{\bf B} = -\lpar i/\omega\rpar \nabla \times {\bf E}.

We can now investigate the interaction of the free electron and the Gaussian beam in vacuum by solving the equation of motion with the radiative reaction included. For simplicity, throughout this paper, length and time are normalized by 1/k and 1/ω, energy and momentum by m ec 2 and m ec, respectively.

RESULTING AND DISCUSSION

First, we investigate the case that the laser pulse counter-propagates with a high-energy electron. This so-called counter-streaming configuration is for the study of nonlinear Thomson scattering, which can be used to produce short-pulse X-ray (Lee & Cha, Reference Lee and Cha2003). The intensity of the laser pulse is a 0 = 100, here a 0 = eE 0/m eω0c is a dimensionless parameter measuring of the field intensity, where, e and m e are the electron's charge and rest mass, respectively, ω0 is the laser circular frequency, and c is the speed of light in vacuum, and the laser width w 0 = 60, pulse duration τ0 = 60, and wavelength of λ 0 = 1 µm. The laser pulse is propagating from the left to the right, while the electron is propagating from the right to the left with the initial energy of γ = 200. The laser pulse and the electron meet at the zero point of the propagating axis. Figure 1a shows the electron's trajectory and energy without and with damping. We can see that the oscillation of the electron with radiative reaction is larger than without radiative reaction due to losing energy by radiation. Figure 1b is the electron's energy γ versus x. It shows that the electron can lose about 65% energy with radiative reaction effect include. The radiative reaction force is related to the energy of the electron and the derivatives of the field. In this counter-propagating case, the initial energy of the electron is very high, and the field that the electron experienced is changing rapidly, therefore the radiation is very strong. Hereby, in the case of intense laser counter-propagating with high-energy electron, the radiation does have great effect on the electron dynamics. The radiative reaction cannot be neglected in such a case.

Fig. 1. (Color online) The electron's trajectory (a) and energy (b) when counter-propagating to the laser pulse. The laser is propagating from left to right with a 0 = 100, w 0 = 60, τ0 = 60. The electron is moving from right to left with initial energy γ = 200. Dash line is the result with radiation effect included, while solid line is the result without radiation effect.

Then, let us study the case of laser hot electron interaction. An intense laser pulse can catch non-relativistic free electrons in the focal region, then interacts with and accelerates them. This so-called ponderomotive acceleration senario (PAS) has been experimentally demonstrated by Malka et al. (Reference Malka, Lefebvre and Miquel1997). They found that electrons with KeV incident energy can get MeV final energy from a laser with a 0 = 3. The basic physics underlying the PAS is the asymmetry between the acceleration and deceleration stages experienced by the accelerated electrons. When a laser pulse catches an electron in the focal region, the intensity experienced by the electron in the acceleration stage is greater than that in the deceleration stage owing to the diffraction effect of the focused laser beam. As a result, the electron can finally gain net energy in the interaction process.

Here, we use a typical setting of PAS, with the laser intensity a 0 = 3, the beam width w 0 = 60, and the pulse duration τ0 = 60. The initial velocity of the electron is 0.1c. When the electron radiation effect is included, we found that the influence by considering this effect is extremely small. Figure 2 shows a comparison between the two models of with and without the radiation effect. One can see that, either to the electron trajectory in space (Fig. 2a, 2b) or the variation of the electron energy γ with time (Fig. 2c, 2d), the discrepancy is extremely small that the curves of the two models are entirely overlapped in the figure. From the calculation results, we get the same conclusion too. The deviation of electron final energy γf between two models is about 10−6. It can be supported by the following viewpoint. We can see that the radiative reaction force is related to the velocity of the electron. In this case, the velocity of the electron is relatively too small, so that the radiative reaction force is too small to take effect. On the other hand, the electron is quickly scattered by the intense laser field, and the interaction time is so short that the effect of radiative reaction is very limited. Thus, the electron radiation reaction makes very little influence on the electron dynamic characteristics in PAS.

Fig. 2. (Color online) A typical PAS case with (dash line) and without (solid line) radiation reaction. The laser parameters are a 0 = 3, w 0 = 60, τ0 = 60. The initial velocity of the electron is 0.1c. (a) Electron trajectories in x-z coordinate plane. (c) Electron energy γ vs. time t (b), and (d) are enlargements of (a) and (c).

Now we turn to the CAS scheme. In our previous works by studying of electron dynamics in intense vacuum laser fields with three-dimensional numerical simulation program, we proposed a vacuum laser acceleration scheme, i.e., the CAS. In this scheme, electrons injected with some energy and small crossing angle relative to the laser propagation direction may not be reflected from the beam as predicted by the conventional ponderomotive potential model. Instead, they can enter the strong-field region and keep moving along for a long time as if captured by the laser field. Through this CAS scheme, the electron can gain substantial net energy, over GeV, from the laser field with the intensity large enough, for example, a 0 < 70. We found that in a focused laser beam propagating in vacuum, there are regions characterized by low wave phase velocity, i.e., the phase velocity of the laser is smaller than c, the speed of light in vacuum. In conjunction with the strong longitudinal electric field component of the laser field, this region forms a natural acceleration channel. The relativistic electrons injected into this channel can be trapped in the acceleration phase and remain in this acceleration phase with the laser field for sufficient long time, thereby gaining considerable energy from the field.

In Figure 3, we present the comparison between two models of neglecting and including the radiation effect for a typical case of CAS phenomenon. The laser intensity is a 0 = 100, the width is w 0 = 60, and the pulse duration is τ 0 = 60, while the electron's incident momentum p zi = 20 and incident angle θ = arctan(0.1). We can find that the discrepancy between the curves, which are calculated by the two models, are too small to distinguish from the electron trajectory (Fig. 3a) and the electron energies (Fig. 3b). The deviation of the electron final energy γf is less than 0.01%. It fully illuminates that the electron radiation reaction made very little influence on the CAS electron too. In Figure 4, we keep other parameters and only change a 0. We find that the deviation is always very small even when a 0 is more than 400. We can conclude that our previous results on the CAS phenomenon are still valid when the electron radiation reaction is included.

Fig. 3. (Color online) A typical CAS case with laser a 0 = 100, w 0 = 60, τ0 = 60, and incident electron p zi = 20, θ = tan−1(0.1). The results with (dash line) and without (solid line) radiative reaction are represented. (a) Electron trajectories in x-z coordinate plane. The dash-dot line represent the beam width w(z). (b) Electron energy γ vs. time t. The inset in (b) is enlargement of (b).

Fig. 4. (Color online) The difference between the electron's final energy with and without radiative reaction vs. a 0. Other parameters used are the same as in Figure 3. Even when a 0 is very big, the energy deviation is still less than 0.01%.

Why does the radiation effect make so little influence on the CAS scheme, even if the laser intensity is very high? It can be explained from two points of views. First, relative to the electromagnetic force of the laser field, the radiative reaction force is very small. The radiative reaction force is less than the electromagnetic force of the laser field for more than five orders of magnitudes. Thus, the effects of damping force on the electron dynamic trajectories are very small. On the other hand, after entering the acceleration region and in most of the electron acceleration regions, the CAS electrons move nearly straightway. As is already known, the power of the electron radiation is (Jackson, Reference Jackson1975):

(13)
\eqalign{P & =-{2e^2 \over 3m_e^2 c^3} \left({dp_\mu \over d\tau}{dp^\mu \over d\tau}\right)\cr & = {2e^2 \over 3m_e^2 c^3} \left[\left({dp \over d\tau}\right)^{2} - \beta^{2} \left({dp \over d\tau}\right)^{2}\right]\cr & = -{2e^2 \over 3m_e^2 c^3} \left({dp \over dt}\right)^2 \lpar \hbox{In Linear Accelerator}\rpar \cr & = -{2e^2 \over 3m_e^2 c^3} \left({dE \over dx}\right)^2 \cr}.

Thus, the rate of the power of the electron energy loss through the electron radiation effect and the energy increasing is

(14)
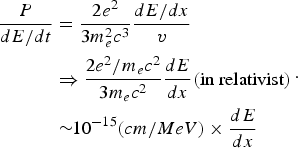
\eqalign{{P \over dE/dt} & = {2e^2 \over 3m_e ^2 c^3}{dE/dx \over v} \cr & \Rightarrow {2e^2/m_e c^2 \over 3m_e c^2}{dE \over dx} \lpar \hbox{in relativist}\rpar \cr & \sim\!\! 10^{-15} \lpar cm/MeV\rpar \times {dE \over dx} \cr}.

In the CAS scheme, the rate of CAS electron's energy increasing dE/dx is far less than 1015 MeV/cm so that the electron energy loss through the radiation effect in the CAS phenomenon is extremely small. From the discussion above, we can draw a conclusion that the electron radiation reaction makes little influence on the CAS electrons. This result supports strongly our previous work on the interaction between the electron and the intense laser, especially the CAS scheme.

At last, we analyze the components of the radiative reaction force. From Eq. (5), we can find that the radiative reaction is the sum of three components:

(15)
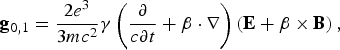
{\bf g}_{0\comma 1} = {2e^3 \over 3mc^2} \gamma \left({\partial \over c\partial t} + {\bf \beta} \cdot {\bf \nabla}\right)\left({\bf E} + {\bf \beta} \times {\bf B}\right)\comma \;
(16)
{\bf g}_{0\comma 2} = {2e^{\rm 4} \over 3m^{2} c^{4}} \left[\left({\bf \beta} \cdot {\bf E}\right){\bf E} + \left({\bf E} + {\bf \beta} \times {\bf B}\right)\times {\bf B}\right]\comma \;
(17)
{\bf g}_{0\comma 3} = -{2e^{4} \over 3m^{2} c^{4}} \gamma^2 {\bf \beta} \left[\left({\bf E} + {\bf \beta} \times {\bf B}\right)^2 - \;\left({\bf \beta} \cdot {\bf E}\right)^2\right].

The first term includes derivatives of fields, while the second and the third are only related to the current motion status of the electron. We use the same parameters as in Figure 3 to see how the three components of the radiative reaction force at z direction change in the whole laser-electron interaction progress. At the beginning, the first term is dominating, as shown in Figure 5a. However, at that time all three components are very small, at least 10 orders smaller than the Lorentz force, because the electron's energy is relatively low and the field is not very strong. When the electron enters the strong field region and is captured and accelerated, the third component becomes large (Fig. 5b), and finally dominating (Fig. 5c). The second term is always very small. This can be explained that the third term is related to γ2 and it increases rapidly while the electron is strongly accelerated by the laser pulse. While the electron's is staying in acceleration phase, the external field that the electron is experiencing is relatively not changing so rapidly, so the first term will not be very strong in this CAS progress even if the electron's energy is very high. Since the third term is the most important in the acceleration progress, we can use Eq. (17) to calculate the radiative reaction force even for high energy region. This can avoid the calculation of derivatives of the field, and make the numerical simulation much easier.

Fig. 5. (Color online) Analysis of the three components of the radiative reaction force at z direction. Parameters used are the same as in Figure 3. Dash line, dash-dot line and solid line represent the first, the second and the third component respectively. (a, b, c) refer to different stages of the whole progress of laser electron interaction.

CONCLUSIONS

In summary, we have investigated the electron radiation effect on electron dynamic characteristic in an ultra intense laser field. Energy loss of the electron can be great when high-energy electron counter-propagates with a strong laser pulse. However, we found that the electron radiative reaction make extremely little influence on laser electron acceleration in vacuum, both PAS and CAS. The main features of the CAS scheme, the electron keeping running in the laser beam and violent accelerated by the laser field, have still kept. This work supports our previous work on the laser electron acceleration in vacuum.

ACKNOWLEDGMENTS

This work was partly supported by the National Natural Science Foundation of China under Contract No. 10605010 and Shanghai Leading Academic Discipline Project with Project No. B107, and partly by the JSPS-CAS Core-University Program on Plasma and Nuclear Fusion.

References

REFERENCES

Badziak, J., Glowacz, S., Jablonski, S., Parys, P., Wolowski, J. & Hora, H. (2005). Laser-driven generation of high-current ion beams using skin-layer ponderomotive acceleration. Laser Part. Beams 23, 401–409.CrossRefGoogle Scholar
Chen, Z.L., Unick, C., Vafaei-Najafabadi, N., Tsui, Y.Y., Fedosejevs, R., Naseri, N., Masson-Laborde, P.E. & Rozmus, W. (2008). Quasi-monoenergetic electron beams generated from 7 TW laser pulses in N-2 and He gas targets. Laser Part. Beams 26, 147–155.CrossRefGoogle Scholar
Chouffani, K., Harmon, F., Wells, D., Jones, J. & Lancaster, G. (2006). Laser-compton scattering as a tool for electron beam diagnostics. Laser Part. Beams 24, 411–419.CrossRefGoogle Scholar
Deutsch, C., Bret, A., Firpo, M.C., Gremillet, L., Lefebvre, E. & Lifschitz, A. (2008). Onset of coherent electromagnetic structures in the relativistic electron beam deuterium-tritium fuel interaction of fast ignition concern. Laser Part. Beams 26, 157–165.CrossRefGoogle Scholar
Dirac, P.A.M. (1938). Classical theory of radiating electrons. Proc. Roy. Soc. London Ser. A 167, 148–169.Google Scholar
Dombi, P., Racz, P. & Bodi, B. (2009). Surface plasmon enhanced electron acceleration with few-cycle laser pulses. Laser Part. Beam 27, 291–296.CrossRefGoogle Scholar
Dromey, B., Bellei, C., Carroll, D.C., Clarke, R.J., Green, J.S., Kar, S., Kneip, S., Markey, K., Nagel, S.R., Willingale, L., Mckenna, P., Neely, D., Najmudin, Z., Krushelnick, K., Norreys, P.A. & Zepf, M. (2009). Third harmonic order imaging as a focal spot diagnostic for high intensity laser-solid interactions. Laser Part. Beams 27, 243–248.CrossRefGoogle Scholar
Eliezer, S., Murakaml, M. & Val, J.M.M. (2007). Equation of state and optimum compression in inertial fusion energy. Laser Part. Beams 25, 585–592.CrossRefGoogle Scholar
Glinec, Y., Faure, J., Pukhov, A., Kiselev, S., Gordienko, S., Mercier, B. & Malka, V. (2005). Generation of quasimonoenergetic electron beams using ultrashort and ultraintense laser pulses. Laser Part. Beams 23, 161–166.CrossRefGoogle Scholar
Gupta, D.N. & Suk, H. (2007). Electron acceleration to high energy by using two chirped lasers. Laser Part. Beams 25, 31–36.CrossRefGoogle Scholar
Hegelich, B.M., Albright, B.J., Cobble, J., Flippo, K., Letzring, S., Paffett, M., Ruhl, H., Schreiber, J., Schulze, R.K. & Ferná Ndez, J.C. (2006). Laser acceleration of quasi-monoenergetic MeV ion beams. Nat. 439, 441–444.CrossRefGoogle ScholarPubMed
Hildebrand, F.B. (1974). Introduction to Numerical Analysis. New York: McGraw-Hill.Google Scholar
Hora, H. (2007). New aspects for fusion energy using inertial confinement. Laser Part. Beams 25, 37–45.CrossRefGoogle Scholar
Hora, H., Hoelss, M., Scheid, W., Wang, J.W., Ho, Y.K., Osman, F. & Castillo, R. (2000). Principle of high accuracy for the nonlinear theory of the acceleration of electrons in a vacuum by lasers at relativistic intensities. Laser Part. Beams 18, 135–144.CrossRefGoogle Scholar
Hu, G.Y., Zhang, J.Y., Zheng, J., Shen, B.F., Liu, S.Y., Yang, J.M., Ding, Y.K., Hu, X., Huang, Y.X., Du, H.B., Yi, R.Q., Lei, A.L. & Xu, Z.Z. (2008). Angular distribution and conversion of multi-KeV L-shell X-ray sources produced from nanosecond laser irradiated thick-foil targets. Laser Part. Beams 26, 661–670.CrossRefGoogle Scholar
Jackson, J.D. (1975). Classical Electrodynamics. New York: John Wiley & Sons.Google Scholar
Karmakar, A. & Pukhov, A. (2007). Collimated attosecond GeV electron bunches from ionization of high-Z material by radially polarized ultra-relativistic laser pulses. Laser Part. Beams 25, 371–377.CrossRefGoogle Scholar
Kawata, S., Kong, Q., Miyazaki, S., Miyauchi, K., Sonobe, R., Sakai, K., Nakajima, K., Masuda, S., Ho, Y.K., Miyanaga, N., Limpouch, J. & Andreev, A.A. (2005). Electron bunch acceleration and trapping by ponderomotive force of an intense shortpulse laser. Laser Part. Beams 23, 61–67.CrossRefGoogle Scholar
Kolacek, K., Schmidt, J., Prukner, V., Frolov, O. & Straus, J. (2008). Ways to discharge-based soft X-ray lasers with the wavelength lambda < 15 nm. Laser Part. Beams 26, 167–178.CrossRefGoogle Scholar
Kulagin, V.V., Cherepenin, V.A., Hur, M.S., Lee, J. & Suk, H. (2008). Evolution of a high-density electron beam in the field of a super-intense laser pulse. Laser Part. Beams 26, 397–409.CrossRefGoogle Scholar
Landau, L.D. & Lifschitz, E.M. (1994). The Classical Theory of Fields. New York: Pergamon.Google Scholar
Lee, K. & Cha, Y.H. (2003). Relativistic nonlinear Thomson scattering as attosecond x-ray source. Phys. Rev. E 67, 026502.CrossRefGoogle ScholarPubMed
Lifschitz, A.F., Faure, J., Glinec, Y., Malka, V. & Mora, P. (2006). Proposed scheme for compact GeV laser plasma accelerator. Laser Part. Beams 24, 255–259.CrossRefGoogle Scholar
Limpouch, J., Psikal, J., Andreev, A.A., Platonov, K.Y. & Kawata, S. (2008). Enhanced laser ion acceleration from mass-limited targets. Laser Part. Beams 26, 225–234.CrossRefGoogle Scholar
Lin, D., Ho, Y.K., Kong, Q., Chen, Z., Wang, P.X., Xu, J.J. & Kawata, S. (2007). Bifurcating energy-angular spectrum of electrons accelerated by intense laser pulse. Laser Part. Beams 25, 365–370.CrossRefGoogle Scholar
Liu, M.P., Xie, B.S., Huang, Y.S., Liu, J. & Yu, M.Y. (2009). Enhanced ion acceleration by collisionless electrostatic shock in thin foils irradiated by ultraintense laser pulse. Laser Part. Beams 27, 327–333.CrossRefGoogle Scholar
Malka, G., Lefebvre, E. & Miquel, J.L. (1997). Experimental observation of electrons accelerated in vacuum to relativistic energies by a high-intensity laser. Phys. Rev. Lett. 78, 3314.CrossRefGoogle Scholar
Mangles, S.P.D., Walton, B.R., Najmudin, Z., Dangor, A.E., Krushelnick, K., Malka, V., Manclossi, M., Lopes, N., Carias, C., Mendes, G. & Dorchies, F. (2006). Table-top laser-plasma acceleration as an electron radiography source. Laser Part. Beams 24, 185–190.CrossRefGoogle Scholar
Mourou, G.A., Tajima, T. & Bulanov, S.V. (2006). Optics in the relativistic regime. Rev. Mod. Phys. 78, 309–371.CrossRefGoogle Scholar
Nickles, P.V., Ter-Avetisyan, S., Schnuerer, M., Sokollik, T., Sandner, W., Schreiber, J., Hilscher, D., Jahnke, U., Andreev, A. & Tikhonchuk, V. (2007). Review of ultrafast ion acceleration experiments in laser plasma at Max Born Institute. Laser Part. Beams 25, 347–363.CrossRefGoogle Scholar
Ozaki, T., Bom, L.B.E., Ganeev, R., Kieffer, J.C., Suzuki, M. & Kuroda, H. (2007). Intense harmonic generation from silver ablation. Laser Part. Beams 25, 321–325.CrossRefGoogle Scholar
Ozaki, T., Bom, L.E. & Ganeev, R.A. (2008). Extending the capabilities of ablation harmonies to shorter wavelengths and higher intensity. Laser Part. Beams 26, 235–240.CrossRefGoogle Scholar
Priebe, G., Laundy, D., Macdonald, M.A., Diakun, G.P., Jamison, S.P., Jones, L.B., Holder, D.J., Smith, S.L., Phillips, P.J., Fell, B.D., Sheehy, B., Naumova, N., Sokolov, I.V., Ter-Avetisyan, S., Spohr, K., Krafft, G.A., Rosenzweig, J.B., Schramm, U., Gruner, F., Hirst, G.J., Collier, J., Chattopadhyay, S. & Seddon, E.A. (2008). Inverse Compton backscattering source driven by the multi-10 TW laser installed at Daresbury. Laser Part. Beams 26, 649–660.CrossRefGoogle Scholar
Rohrlich, F. (1995). Classical Charged Particles. Reading, MA: Addison-Wesley.Google Scholar
Rohrlich, F. (2001). The correct equation of motion of a classical point charge. Phys. Lett. A 283, 276–278.Google Scholar
Roth, M., Brambrink, E., Audebert, P., Blazevic, A., Clarke, R., Cobble, J., Cowan, T.E., Fernandez, J., Fuchs, J., Geissel, M., Habs, D., Hegelich, M., Karsch, S., Ledingham, K., Neely, D., Ruhl, H., Schlegel, T. & Schreiber, J. (2005). Laser accelerated ions and electron transport in ultra-intense laser matter interaction. Laser Part. Beams 23, 95–100.CrossRefGoogle Scholar
Sadighi-Bonabi, R., Navid, H.A. & Zobdeh, P. (2009). Observation of quasi mono-energetic electron bunches in the new ellipsoid cavity model. Laser Part. Beams 27, 223–231.CrossRefGoogle Scholar
Shi, Y.J. (2007). Laser electron accelerator in plasma with adiabatically attenuating density. Laser Part. Beams 25, 259–265.CrossRefGoogle Scholar
Shorokhov, O. & Pukhov, A. (2004). Ion acceleration in overdense plasma by short laser pulse. Laser Part. Beams 22, 175–181.CrossRefGoogle Scholar
Singh, K.P. & Malik, H.K. (2008). Resonant enhancement of electron energy by frequency chirp during, laser acceleration in an azimuthal magnetic field in a plasma. Laser Part. Beams 26, 363–369.CrossRefGoogle Scholar
Stupakov, G.V. & Zolotorev, M.S. (2001). Ponderomotive Laser Acceleration and Focusing in Vacuum for Generation of Attosecond Electron Bunches. Phys. Rev. Lett. 86, 5274–5277.CrossRefGoogle ScholarPubMed
Toncian, T., Borghesi, M., Fuchs, J., D'humiè Res, E., Antici, P., Audebert, P., Brambrink, E., Cecchetti, C.A., Pipahl, A., Romagnani, L. & Willi, O. (2006). Ultrafast laser-driven microlens to focus and energy-select mega-electron volt protons. Sci. 312, 410–413.CrossRefGoogle ScholarPubMed
Torrisi, L., Margarone, D., Gammino, S. & Ando, L. (2007). Ion energy increase in laser-generated plasma expanding through axial magnetic field trap. Laser Part. Beams 25, 453–464.CrossRefGoogle Scholar
Wang, P.X., Ho, Y.K., Yuan, X.Q., Kong, Q., Cao, N. & Shao, L. (2002). Characteristics of laser-driven electron acceleration in vacuum. J. Appl. Phys. 91, 856–866.CrossRefGoogle Scholar
Xie, B.S., Aimidula, A., Niu, J.S., Liu, J. & Yu, M.Y. (2009). Electron acceleration in the wakefield of asymmetric laser pulses. Laser Part. Beams 27, 27–32.CrossRefGoogle Scholar
Xu, J.J., Ho, Y.K., Kong, Q., Chen, Z., Wang, P.X., Wang, W. & Lin, D. (2005). Properties of electron acceleration by a circularly polarized laser in vacuum. J. Appl. Phys. 98, 056105.CrossRefGoogle Scholar
Yin, L., Albright, B.J., Hegelich, B.M. & Fernandez, J.C. (2006). GeV laser ion acceleration from ultrathin targets: The laser break-out afterburner. Laser Part. Beams 24, 291–298.CrossRefGoogle Scholar
Yu, W., Cao, L., Yu, M.Y., Cai, H., Xu, H., Yang, X., Lei, A., Tanaka, K.A. & Kodama, R. (2009). Plasma channeling by multiple short-pulse lasers. Laser Part. Beams 27, 109–114.CrossRefGoogle Scholar
Zhou, C.T., Yu, M.Y. & He, X.T. (2007). Electron acceleration by high current-density relativistic electron bunch in plasmas. Laser Part. Beams 25, 313–319.CrossRefGoogle Scholar
Zvorykin, V.D., Didenko, N.V., Ionin, A.A., Kholin, I.V., Konyashchenko, A.V., Krokhin, O.N., Levchenko, A.O., Mavritskii, A.O., Mesyats, G.A., Molchanov, A.G., Rogulev, M.A., Seleznev, L.V., Sinitsyn, D.V., Tenyakov, S.Y., Ustinovskii, N.N. & Zayarnyi, D.A. (2007). GARPUN-MTW: A hybrid Ti : Sapphire/KrF laser facility for simultaneous amplification of subpicosecond/nanosecond pulses relevant to fast-ignition ICF concept. Laser Part. Beams 25, 435–451.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) The electron's trajectory (a) and energy (b) when counter-propagating to the laser pulse. The laser is propagating from left to right with a0 = 100, w0 = 60, τ0 = 60. The electron is moving from right to left with initial energy γ = 200. Dash line is the result with radiation effect included, while solid line is the result without radiation effect.

Figure 1

Fig. 2. (Color online) A typical PAS case with (dash line) and without (solid line) radiation reaction. The laser parameters are a0 = 3, w0 = 60, τ0 = 60. The initial velocity of the electron is 0.1c. (a) Electron trajectories in x-z coordinate plane. (c) Electron energy γ vs. time t (b), and (d) are enlargements of (a) and (c).

Figure 2

Fig. 3. (Color online) A typical CAS case with laser a0 = 100, w0 = 60, τ0 = 60, and incident electron pzi = 20, θ = tan−1(0.1). The results with (dash line) and without (solid line) radiative reaction are represented. (a) Electron trajectories in x-z coordinate plane. The dash-dot line represent the beam width w(z). (b) Electron energy γ vs. time t. The inset in (b) is enlargement of (b).

Figure 3

Fig. 4. (Color online) The difference between the electron's final energy with and without radiative reaction vs. a0. Other parameters used are the same as in Figure 3. Even when a0 is very big, the energy deviation is still less than 0.01%.

Figure 4

Fig. 5. (Color online) Analysis of the three components of the radiative reaction force at z direction. Parameters used are the same as in Figure 3. Dash line, dash-dot line and solid line represent the first, the second and the third component respectively. (a, b, c) refer to different stages of the whole progress of laser electron interaction.