1. INTRODUCTION
The variance ratio (VR) statistic is one of the popular tests
that has been employed in the literature to test the random walk
hypothesis for financial and economic data. The statistic is obtained as
the sample variance of k-period differences,
xt −
xt−k, of the time series
xt, divided by k times the sample
variance of the first difference, xt −
xt−1, for some integer k. The
VR statistic has been found by several authors (see, e.g., Faust, 1992) to be particularly powerful when testing
against mean reverting alternatives to the random walk model, particularly
when k is large. However, the practical use of the statistic has
been impeded by the fact that the asymptotic theory provides a poor
approximation to the small-sample distribution of the VR
statistic. More specifically, rather than being normally distributed as
the theory states, the statistics are severely biased and right skewed for
large k (see Lo and MacKinlay, 1989),
which makes application of the statistic problematic. To circumvent this
problem, Richardson and Stock (1989) derived the
asymptotic distribution of the VR statistic under the random walk
null, assuming that both k and n increase to infinity
but in such a way that k/n converges to a positive
constant δ that is strictly less than 1. They showed that the
VR statistic, without any normalization, converges to a
functional of Brownian motion. Through Monte Carlo simulations, they
demonstrated that this new distribution provides a far more robust
approximation to the small-sample distribution of the VR
statistic. However, Deo and Richardson (2003)
have recently shown that the VR statistic is inconsistent against
an important class of mean reverting alternatives under this framework.
Thus, though the VR statistic would have vastly improved size
properties under the null hypothesis of a random walk if k were
chosen to be a fraction of the sample size n, it would fail to
detect such alternatives with probability approaching 1 as the sample size
increased. Currently there is no proposal in the literature that provides
a way of using the VR statistic without compromising either its
finite-sample size properties or its large-sample power properties.
With this backdrop, we provide several contributions to the
literature. First, it is intuitively appealing to maintain the assumption
that the multiperiod horizon k is large, not least because longer
horizons have a better chance of capturing mean reversion in the series.
Thus, under general conditions that allow for conditional
heteroskedasticity in the innovations, we study the limiting behavior of
the VR statistic for large k but now under the
restriction that k/n → 0. Specifically, we show
that when k → ∞, n → ∞, but
k/n → 0, then under the null of a random walk,
the VR statistic is asymptotically normal with a mean of 1. The
requirement that k is large is important because as stated
before, previous authors have shown that large values of k are to
be preferred when testing for mean reversion. Furthermore, we prove that
under this alternative distribution theory, the test is consistent, in
that the probability of it detecting a wide variety of mean reversion
alternatives approaches 1 as the sample size n increases.
Unfortunately, this new distribution does not solve the
well-documented skewness problem of the VR statistic's
sampling distribution. The second contribution of this paper is to propose
a method that is shown to improve the asymptotic normal approximation to
the distribution of the statistic by an order of magnitude in finite
samples, via a simple power transformation of the VR statistic.
Monte Carlo simulations confirm the theoretical assertion of the vast
improvement of the normal approximation afforded by the power
transformation. Our Monte Carlo simulations also show that this
improvement in the normal approximation leads to significant gains in
power against mean reverting alternatives. Our simulations also show that
the performance of the test based on using the Richardson and Stock
asymptotics is sensitive to both sample size and conditional
heteroskedasticity. Furthermore, using the Richardson and Stock
asymptotics also results in uniformly lower power when compared to the new
asymptotic approach that we present. Thus, our new approach uniformly
dominates the Richardson and Stock asymptotic approach.
The third contribution of this paper is to implement a new joint test
that uses VR statistics computed at different differencing
periods to test the random walk null hypothesis. The joint test statistic
that has been studied so far in the literature is the Wald type chi-square
test statistic that jointly tests whether a sequence of population
variance ratios at several differencing periods all equal 1. However, this
test is blind to the inherent one-sided nature of a mean reverting
alternative hypothesis, because under such an alternative all the
population variance ratios should be less than 1. See Lo and MacKinlay
(1989). In this paper, we adapt a test procedure
proposed by Follmann (1996) for testing against
one-sided alternatives for the mean vector of a multivariate normal
distribution. Our Monte Carlo simulations show that this adapted test in
combination with the power transformation results in significant power
gains over the usual chi-square test when testing for mean reverting
alternatives, while retaining the appropriate size.
The paper is organized as follows. In Section 2, we define the
VR statistic and provide its asymptotic distribution under
conditional heteroskedasticity for large k such that
k−1 + k/n → 0. We
also demonstrate in that section that in this framework the VR
statistic is consistent against a wide range of alternatives. In Section
3, we provide an alternative equivalent representation of the VR
statistic that motivates the power transformation that provides a better
approximation to the normal distribution. A new joint test that combines
information from several differencing periods and is useful against
one-sided alternatives is also introduced. Section 4 presents Monte Carlo
results for the various statistics that we have proposed under two
different null hypotheses and three alternative hypotheses. All technical
proofs are relegated to the Appendix.
2. ASYMPTOTIC THEORY FOR THE VARIANCE RATIO
STATISTIC
Given n + 1 observations
x0,x1,…,xn
of a time series, the VR statistic with a positive integer
k(< n) as differencing period is defined as
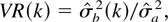
where
In the usual fixed k asymptotic treatment, under the null
hypothesis that the {xt} follow a random walk
with possible drift, given by
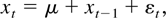
where μ is a real number and {εt} is a
sequence of zero mean independent random variables, it is possible to show
(see, e.g., Lo and MacKinlay, 1988) that
where σk2 is some simple function
of k. This result extends to the case where the
{εt} are a martingale difference series with
conditional heteroskedasticity (see, e.g., Campbell,
Lo, and MacKinlay, 1997), though the variance
σk2 has to be adjusted to account for
the conditional heteroskedasticity. However, the asymptotic behavior of
the VR statistic for large values of k, such that
k−1 + k/n → 0, is not
known when the innovations εt are conditionally
heteroskedastic. In this section, we provide precisely this asymptotic
distribution, in obtaining which the following assumptions on the series
of innovations {εt} are made.
(A1) {εt} is ergodic and
for all t, where
is a sigma field, εt is
measurable, and
for all t.
(A2) E(εt2) =
σ2 < ∞.
(A3) For any integer q, 2 ≤ q ≤ 8, and for
q nonnegative integers si,
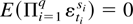
when at least one si is exactly one and
.
(A4) For any integer r, 2 ≤ r ≤ 4, and for
r nonnegative integers si,
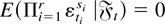
when at least one si is exactly one and
,
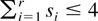
for all t < ti, i =
1,2,3,4.
(A5)
uniformly in j for every j > 0.
(A6)
.
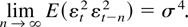
Conditions (A1)–(A6) allow the innovations
εt to be a martingale difference sequence with
conditional heteroskedasticity. As a matter of fact, Lemmas 1 and 2, which
follow, show that the stochastic volatility model (see Shephard, 1996) and the GARCH model (Bollerslev, 1986), which are two of the most popular
models in the literature for conditional heteroskedastic martingale
differences, satisfy conditions (A1)–(A6). Conditions
(A3)–(A4) state that the series {εt} shows
product moment behavior similar to that of an independent white noise
process. Conditions (A5)–(A6) state that
εt and
εt−n are roughly independent for
large lags n.
The following two lemmas assert that two major models of conditionally
heteroskedastic martingale differences, namely, the stochastic volatility
model and the generalized autoregressive conditionally heteroskedastic
(GARCH) model, satisfy the assumptions (A1)–(A6). The proofs of the
lemmas are in the Appendix.
LEMMA 1. Let the series {εt} be
generated by the stochastic volatility model
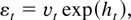
where {vt} is an
independent (0,σv2) stationary
series, {ht} is a stationary zero
mean Gaussian series, and {vt}
and {ht} are independent. Assume
that E(vt8) < ∞.
Then {εt} satisfies the assumptions
(A1)–(A6).
See Shephard (1996) for a discussion of
model (3) and its applications.
Our next lemma asserts that under some conditions the GARCH(1,1)
family of models also satisfies conditions (A1)–(A6). We have
restricted attention to the GARCH(1,1) case for simplicity of exposition.
We conjecture that conditions (A1)–(A6) will continue to hold for a
general GARCH(p,q) model, the proof following along
similar lines by referring to the work of Bougerol and Picard (1992).
LEMMA 2. Let the series {εt} be
a GARCH(1,1) process given by
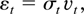
where σt2 = ω +
βσt−12 +
αεt−12 and
{vt} is a sequence of independent
standard normal variables. Let ω > 0, β ≥ 0,
and α > 0. Furthermore, let α and
β be such that E {loge(β +
αvt2)} < 0 and E
{(β + αvt2)4}
< 1. Then {εt} satisfies the
assumptions (A1)–(A6).
The condition E {loge(β +
αvt2)} < 0 in Lemma 2 is
satisfied by any pair (α,β) in the set S = {(α,β)
: α + β < 1} (see Nelson, 1990),
whereas the condition E {(β +
αvt2)4} < 1 will
be satisfied by a nonempty subset of S (see Bollerslev, 1986).
We now state our result on the limiting distribution of the
VR statistic in the following theorem.
THEOREM 3. Let the series {xt}
satisfy equation (2) and assume that conditions
(A1)–(A6) hold. For a fixed positive integer
s, let k1 < k2 <
··· < ks < n
be positive integers such that k1 → ∞,
ksn−1 → 0, and
ki
kj−1 →
aij for 1 ≤ i ≤
j ≤ s. Let Dn be an
s × s diagonal matrix with diagonal elements
. Then
where Vn =
(VR(k1),VR(k2),…,VR(ks))′,
1 is an s × 1 vector of ones and
Σ = (σij) is an s ×
s matrix such that σij =
4aij1/2(3 −
aij)/6.
Note that the limiting distribution of the VR statistic is
free of nuisance parameters and is identical to that obtained when the
εt are assumed to be independent. See Theorem
9.4.1 of Anderson (1994). Furthermore, the
VR statistics computed at different differencing periods
ki are asymptotically independent when
ki
kj−1 → 0 for i
< j. Both of these results are in contrast to those obtained
when the differencing periods are fixed and not allowed to increase to
infinity with the sample size. See Lo and MacKinlay (1989). It is interesting to note that the limiting
distribution of the VR statistic is free of nuisance parameters
depending on higher moments that might arise as a result of conditional
heteroskedasticity. This is quite different from the behavior of other
tests of the random walk hypothesis in the presence of conditional
heteroskedasticity. See Deo (2000).
We have established the asymptotic distribution of the VR
statistic under the null hypothesis of a random walk with conditional
heteroskedasticity when k → ∞, n →
∞, and k/n → 0. The next theorem states
that under this framework, the VR statistic also provides a
consistent test against a large class of mean reverting alternatives.
THEOREM 4. Let {et} and
{ut} be two series of zero mean
independent processes with finite fourth moments and which are independent
of each other. Define the processes {yt}
and {zt} by
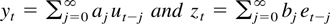
, where
|aj| ≤
Cλj and
|bj| ≤
Cλj for some constant C and 0
< λ < 1. Let rt = μ +
rt−1 + zt
and xt = rt +
yt. If k → ∞, n
→ ∞, and k/n → 0, then
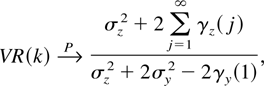
where σz2 and
σy2 are the variances of
zt and yt,
respectively, whereas γz(j)
and γy(j) are the respective
autocovariances at lag j.
Theorem 4 shows that the power properties of the VR statistic
under the k/n → 0 framework are markedly
different from those when k/n → δ > 0,
in which case Deo and Richardson (2003) have
shown the VR statistic to be inconsistent against the
alternatives considered in Theorem 4.
Though the VR statistic has an asymptotic normal distribution
when k/n → 0, it is obvious that in finite
samples the normal distribution may not provide a good approximation
because the statistic is a quadratic form and hence must be right skewed.
A common method that has a long history in statistics to reduce skewness
and induce normality in such random variables is to consider power
transformations. The obvious question, naturally, is which power one
should use, and we address this question for the VR statistic in
the next section.
3. POWER TRANSFORMATIONS OF THE VARIANCE
RATIO STATISTIC
In attempting to address the skewness of the finite-sample
distribution of the VR statistic, it helps to express the
VR statistic in an alternative form, which lends more insight
into how the normal distribution approximation can be improved. Inspection
of the proof of Theorem 3 in the Appendix shows that
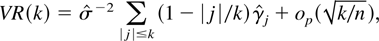
where
and
Now, using the fact that
where
is the periodogram, we get from (5)
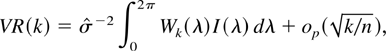
where
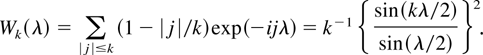
As shown in part (i) of Lemma 7 in the Appendix, the integral in (6)
can be approximated by a discrete sum over the Fourier frequencies
λj = 2πj/n with error
,
and hence we get
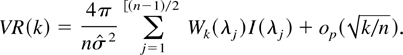
The behavior of VR(k) is thus dictated by the
behavior of the periodogram values I(λj)
at the Fourier frequencies. If the εt series is
Gaussian, then it is well known (Brockwell and Davis,
1996) that the variables
2πI(λj)/σ2 are
exactly independent and identically distributed (i.i.d.) standard
exponential random variables for all sample sizes. This behavior of the
variables
2πI(λj)/σ2 can be
shown to continue to hold asymptotically if the
εt are a martingale difference sequence with
finite fourth moment, by applying the central limit theorem for martingale
differences to
.
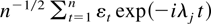
These observations in conjunction with (7) and the fact that
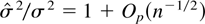
imply that, in general, we may think of the VR statistic as
being of the form
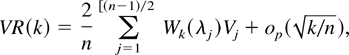
where the Vj are independent standard
exponential random variables. As we next show, this approximate expression
for the VR statistic as a weighted linear combination of
independent standard exponential random variables helps us both to
understand why the normal distribution provides a bad approximation for
large k and also to obtain an appropriate power transformation
that improves the normal approximation.
It is known (see, e.g., Anderson, 1994, p.
509) that Wk(λ) has a peak at the origin
and then damps down to zero for values of λ further from the origin.
Furthermore, the larger k is, the more quickly
Wk(λ) damps down to zero, which can be
seen in Figure 1, where we plot
Wk(λ) for n = 128 and k
= 8 and 16. Thus, for large values of k, we see from (8) that
VR(k) will essentially be a sum of too few independent
standard exponential random variables for the central limit theorem to
properly take effect, resulting in right skewed distributions. However,
Chen and Deo (2004) have recently shown that
power transformations may be gainfully applied to random variables that
have approximate linear representations of the form in (8), yielding much
better normal approximations. Using their results (see Chen and Deo, 2004, eqn. (9)), it follows that if one sets
then the Gaussian distribution provides a better approximation to the
distribution of VRβ(k) than to that of
VR(k). Indeed, from the results of Chen and Deo (2004), the Gaussian distribution approximation to the
distribution of VRβ(k) is an entire order
of magnitude better than the Gaussian approximation to the distribution of
VR(k). A dramatic visual display of this improvement is
shown in Figure 2. The plot on the left is a QQ
plot of 20,000 replications of the VR(k) statistic,
based on a sample size of n = 128 and k = 16 where the
εt are i.i.d. standard normal. The extreme
curvature is indicative of the right skewness of the distribution of
VR(k). The plot on the right is a QQ plot of
VRβ(k), where β was computed using
(9). The plot now shows a straight line as would be expected for
observations from a normal distribution. The power transformation thus
provides a very simple method of getting almost near perfect normality for
the finite-sample distribution of the VR statistic. A standard
Taylor series argument applied to the result of Theorem 3 yields the
asymptotic distribution of VRβ(k), which
can then be used for inference. However, we feel that because the power
transformation is motivated by the representation (7), it might be
preferable to redefine the VR statistic and also its power
transformation directly in terms of the leading term of that expression,
thus avoiding any effects of the remainder term on its finite-sample
distribution. Toward that end, we now define the VR statistic
based on the periodogram, for differencing period k, as
where
.
Because the periodogram is shift invariant at nonzero Fourier
frequencies, we have
I[utri ]X(λj) =
I(λj), and hence the
VRp(k) statistic as defined in (10)
based on the observed data
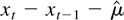
is identical to the first term in (7), which is based on the unobserved
εt. It should be noted that this expression for
the VR statistic, apart from the normalization of (1 −
k/n)−1, which is just a
finite-sample correction ensuring a unit mean, is precisely the normalized
discrete periodogram average estimate of the spectral density of a
stationary process at the origin and has a long tradition in time series
analysis. See Brockwell and Davis (1996). From
(7) it follows that VRp(k) will have
the same asymptotic distribution as that of VR(k) given
in Theorem 3 and hence, by the usual Taylor series argument, the
asymptotic distribution of
VRpβ(k) may be
obtained. It is however preferable to have an expression for the variance
of VRp(k), and thus for that of
VRpβ(k), that is
accurate in finite samples and accounts for the finite-sample effects of
conditional heteroskedasticity. Toward this end, we first define the
quantities Cn,k =
n(n − k)−1 and
where
is an estimator of
σ−4E(εt2εt−j2).
In part (ii) of Lemma 7, we show that the finite-sample variance
covariance matrix of Vp =
(VRp(k1),VRp(k2),…,
VRp(ks))′
with remainder terms of order
o(ks2/n2)
is consistently estimated by
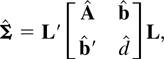
where L =
(lk1,…,lks),
is a ks × 1 vector such that its
jth element is given by
.
We are now in a position to state the following theorem.
Wk(λ) for n = 128 and
k = 8 and 16.
QQ plots of VR(k) and
VRβ(k) on 20,000 replications with
n = 128, k = 16 and εt ∼
N(0,1).
THEOREM 5. Let the series {xt}
satisfy equation (2) and assume that conditions (A1)–(A6) hold.
For a fixed positive integer s, let k1 <
k2 < ··· <
ks < n be positive integers such that
k1 → ∞, ks
n−1 → 0, and
ki
kj−1 →
aij for 1 ≤ i ≤
j ≤ s. For each ki, let
βi be given by (9) and define
Vp,β =
(VRpβ1(k1),VRpβ2(k2),…,VRpβs(ks))′.
Then
where the (i,j)th element of
Σβ is
and the ith element of μβ
is
where
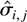
is the (i,j)th entry of
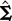
given in (11).
It is trivially seen that both
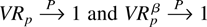
under conditions (A1)–(A6). Our next theorem shows that both
VRp and
VRpβ also retain the
consistency of the VR statistic with regard to detecting the
alternative hypotheses assumed in Theorem 4.
THEOREM 6. Let the assumptions of Theorem 4 hold. Then
where σz2 and
σy2 are the variances of
zt and yt,
respectively, whereas γz(j)
and γy(j) are the respective
autocovariances at lag j.
We have, so far, obtained the joint distribution of the
VRp statistic computed at various
differencing periods. These VR statistics can be combined into a
single statistic by computing the quadratic form
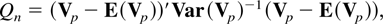
where Vp =
(VRp(k1),…,VRp(ks))′.
Because of the asymptotic normality of Vp,
this quadratic form will have an asymptotic chi-squared distribution with
s degrees of freedom under the null hypothesis of a random walk.
The test statistic Qn can then be used to
test whether the sequence of population variance ratios all equal one for
i = 1,2,…,s. Because the quadratic form
Qn is always positive, rejection of the null
hypothesis of a random walk occurs only in the upper tail of the
distribution of Qn. However, under the
important alternative of mean reverting processes of the kind imposed in
finance applications, the population variance ratios, given by
,
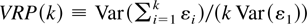
are generally expected to be less than 1 for large k. For
example, it can be easily shown that for the alternative models that are
the sum of permanent and transitory components (see Poterba and Summers, 1988; Fama and
French, 1988), VRP(k) is less than 1 for all
values of k. Hence, under such mean reverting processes, the
alternative hypothesis actually has the one-sided form
Ha : VRP(k) < 1 for
i = 1,…,s. In such circumstances, ignoring the
one-sided nature of the alternative can lead to a loss of power of the
test. However, Follmann (1996) has proposed a
test for the null hypothesis that the mean vector of a multivariate normal
random variable is zero, which has good power for alternatives where all
the elements of the mean vector are negative. Thus, Follmann's
procedure would be directly applicable in the setting where the
alternative of interest is a mean reverting process. We now adapt
Follmann's procedure to test for mean reverting alternatives using
VRp statistics as follows. In testing the
null hypothesis of a random walk
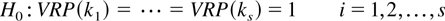
versus the one-sided alternative
at the α level of significance, reject the null hypothesis if
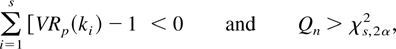
where χs,2α2 is the upper
2α critical value of a chi-square distribution with s degrees
of freedom. From the asymptotic normality of
VRp and Theorem 2.1 of Follmann (1996), it follows that the procedure given previously
has an asymptotic level of significance equal to α. An analogous
procedure can be developed using the power transformation as follows.
Reject the null hypothesis if
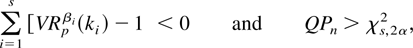
where
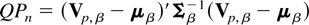
and μβ, Σβ are
as in Theorem 5. The test procedure based on the power transformation
would be expected to have better size and power properties compared to the
one based on the original VRp statistics
because the quadratic form QPn should be
expected to have a distribution closer to the expected chi-square
distribution. In the next section, we report the results from a Monte
Carlo study, which evaluates the effectiveness of the new proposals we
have made.
4. SIMULATION RESULTS
We carried out Monte Carlo simulations to evaluate the finite-sample
performance of tests based on our modified VR statistic. The size
properties under the null hypothesis were evaluated using the following
two models: (i) xt =
xt−1 + εt,
where εt ∼ i.i.d.
N(0,1), (ii) xt =
xt−1 + εt,
where εt = σt
vt, vt ∼
i.i.d. N(0,1), and
σt2 = 0.0001 +
0.8575σt−12 +
0.1171εt−12. The parameter
values for the GARCH(1,1) model in (ii) were chosen to reflect values
obtained when fitting such models to real data. The sample sizes we
considered were n = 128 and 512, and the number of replications
was 20,000. For n = 128, we used k1 = 8 and
k2 = 16, whereas for n = 512 we used
k1 = 16 and k2 = 32. The first
part of Table 1 reports the Monte Carlo sizes of
the test statistics under the Gaussian white noise case, whereas the
second part of the table is for the GARCH(1,1) model. In both parts the
nominal level of significance is 5% and the test is two tailed. The sizes
are reported for the statistics VRp and
VRpβ for each combination of
sample size and k, where β was computed for each case using
(9). The sizes are reported for both the left and right tail to
demonstrate the skewness and the effect of the power transformation on it.
We also report the sizes of the quadratic tests (13), denoted in the table
by Qn, based upon both the untransformed and
transformed VR statistics. Sizes for the modified intersection
tests given in (14) and (15), denoted in the table by
IQn, are also shown.
Sizes in percentage of the null of random walk:
xt = μ +
xt−1 +
εt
It is also of interest to study the finite-sample performance of the
VR statistic under the k/n → δ
> 0 asymptotics as proposed by Richardson and Stock (1989). We therefore also present empirical sizes and
power of the VR statistics for our configuration of
(k,n) values based on asymptotic critical values of the
Richardson–Stock distribution that were computed as follows. For
each combination of (k,n), we generated 20,000
replications of the VR statistic based on Gaussian noise with
n∞ = 12,000 and k∞ =
(k/n)n∞ =
(k/n)12,000 and the percentiles of these 20,000
values were used to obtain the asymptotic critical values. The empirical
sizes and powers based on these critical values are presented in Tables
1, 2, and 3 in the row labeled RS.
Power in percentage against the alternative of random walk +
AR(1)
Power in percentage against the alternative of AR(1)
It is immediately apparent from Table 1 that
whereas the distribution of VRp is very right
skewed, as is well known, the power transformation is able to correct it
and provide near perfect normality with sizes in each tail that are very
close to nominal. One can also see that the power transformed statistic
VRpβ is able to retain the
size close to the nominal even in the presence of GARCH innovations. On
the other hand, it is seen from these tables that the finite-sample
performance of the VR statistic when compared to the critical
values of the Richardson–Stock distribution is not as good. In the
case of Gaussian noise, the test is undersized, particularly for
n = 128, whereas in the case of GARCH innovations, the test is
oversized for n = 512. Note that for our configuration of
(k,n) values, the ratio k/n takes
values 0.03125, 0.0625, and 0.125. This clearly indicates that the
k/n → δ > 0 asymptotic distribution
cannot approximate the finite-sample distribution of the VR
statistic when k/n is small and is sensitive to the
presence of conditional heteroskedasticity.
Table 1 also demonstrates that the quadratic
and the modified intersection tests based on the transformed VR
statistics have much better size properties than those using their
untransformed counterparts.
To evaluate the power properties of our tests, we generated data from
the mean reverting process given by xt =
rt + yt, where
rt = rt−1
+ wt, yt =
0.9yt−1 +
ut, and ut ∼
i.i.d. N(0,1) and also independent of
{wt}. The errors
wt were assumed to be
i.i.d.
N(0,σw2) where
σw2 = 0.1, 0.25, and 0.5. This model
with similar parameter configurations was considered in Lo and MacKinlay
(1989) and Richardson and Smith (1991). Table 2 reports the
Monte Carlo power values at 5% level of significance for this alternative
model for the three different values of
σw2. As the value of
σw2 increases, the permanent component
dominates the process and the power of all tests decreases, as is to be
expected. However, similar behavior of the tests is seen across the table.
It is clear that the individual tests based on the transformed VR
statistics provide power that is significantly superior to that of the
untransformed ones, in some cases increasing the power by as much as 10%.
Furthermore, the test based on the transformed VR statistic
provides power that is uniformly higher than the power of the VR
statistics under the Richardson–Stock asymptotic distribution.
The quadratic test based on the transformed statistics also provides
significant power gain over that based on the untransformed statistics.
Furthermore, it is seen that the modified intersection test, which is
specially geared to take into account the unidirectional nature of mean
reverting alternatives, is able to provide a significant advantage over
the quadratic test, when based on the transformed VR
statistics.
We also generated data from the alternative mean reverting process
given by xt =
0.92xt−1 +
ut where ut
∼ i.i.d. N(0,1). This process is
also considered in Lo and MacKinlay (1989). The
simulation results are presented in Table 3. It
is seen that the test based on the transformed VR statistics once
again provides significantly higher power than that based on the
untransformed statistics as well as that based on the
Richardson–Stock distribution.
The simulations we present here are for the modified variance ratio
statistic, VRp, which is defined in the
frequency domain as given in equation (10). It is of interest to see how
good an approximation this statistic is to the variance ratio statistic,
VR, defined in the time domain in equation (1). In Table 4, we present the empirical size and power of
the transformed statistics VRβ and
VRpβ. It is seen that the size
and power are very similar, indicating that the approximation is good,
though as the theory suggests, this approximation will worsen as
k gets larger relative to n.
Comparison of size and power of
VRpβ and
VRβ
It should also be noted that according to our theory the normal
approximation to the transformed statistics will be good only when
k is not too large relative to n. In the simulations we
present here, the largest value of the ratio k/n we
consider is 0.125, and the normal approximation works well in this case.
We also did a simulation study, not presented here, in which
k/n was set to be 0.25. In this case, the normal
approximation to even the transformed ratio statistic was poor. This is
not surprising because k is now very large relative to n
and thus violates the assumption. Furthermore, in practice, one should not
be using such large values of k because, as Deo and Richardson
(2003) have shown, the test would then be
inconsistent against a wide class of alternatives.
5. CONCLUSION
From Deo and Richardson (2003), it is clear
that large values of k should not be used when testing for the
mean revision using the VR statistic. From our theoretical
results and Monte Carlo study, we conclude that when k is not too
large, the transformed VR statistic proposed in the paper is able
to solve the problem of skewness and is thus well approximated by the
normal distribution in finite samples. This provides good size properties
in addition to significant power gains. Furthermore, the distribution of
the transformed VR statistic is shown, both theoretically and
through simulations, to be robust to conditional heteroskedasticity.
Our simulation study also shows that the k/n
→ δ > 0 asymptotic distribution cannot approximate the
finite-sample distribution of the VR statistic when
k/n is small and is sensitive to conditional
heteroskedasticity. Furthermore, our transformed VR statistic
provides power that is uniformly higher than that of the VR
statistic based on the k/n → δ > 0
asymptotic distribution.
Finally, the modified intersection test is also able to incorporate
information from various differencing periods and yet maintain good
power.
APPENDIX
Proof of Lemma 1. Because {ht}
is a Gaussian stationary series with zero mean, it can be expressed as
,
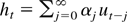
where
and {ut} is a sequence of independent
standard normal variables. Furthermore, {ut}
and {vt} will also be independent. Let
.
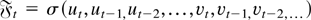
By Lemma 3.5.8 and Theorem 3.5.8 of Stout (1974), {εt} is an ergodic
sequence. Furthermore, Lemma 1 in Deo (2000)
shows that εt satisfies (A1)–(A3). Because
{vt} is an independent zero mean sequence,
(A4) is trivially true. Also,
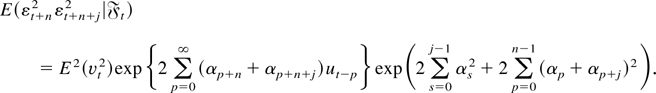
Because
,
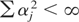
to prove (A5) it suffices to show that
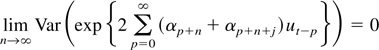
uniformly in j. But
Because
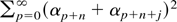
converges to 0 uniformly in j, (A.1) is established. The proof
of (A6) follows along similar lines. █
Proof of Lemma 2. Lemma 2 in Deo (2000) proves (A1)–(A3). An argument similar to
the one provided on page 309 in the proof of Lemma 2 of Deo (2000) also establishes (A4). We now turn to proving
(A5). Iterating the expression for εt, we
have
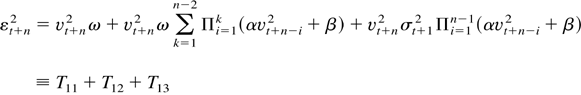
and
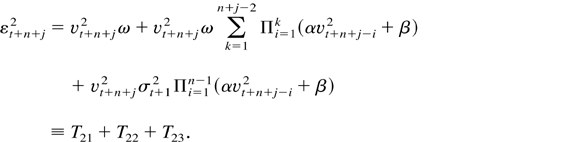
Thus,
Consider the term T12T23. Then
we can easily see that we can express
T12T23 as the product
T12T23 = AB, where
Letting θ1 =
E(αvt2 + β) and
θ2 =
E(αvt2 +
β)2 and noting that
Evt+n4 = 3, we get
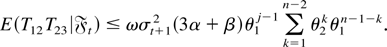
Because γ = max(θ1,θ2) < 1, it
follows that for all j ≥ 1 there exists some finite constant
C such that
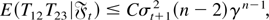
and hence
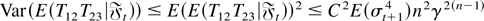
uniformly in j. Thus,
uniformly in j. Similar arguments yield
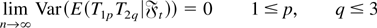
uniformly in j. Thus, (A5) follows from (A.3), (A.4), and the
Cauchy–Schwarz inequality. To prove (A6), we first note that using
(A.2),
Thus,
,
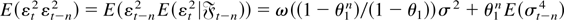
and so
Proof of Theorem 3. By simple but tedious algebraic
manipulation, it can be shown that
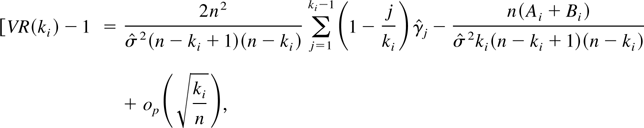
where
Because E(Bi) =
O(ki2) trivially, it
follows that [ki(n −
ki + 1)(n −
ki)]−1nBi
=
op([n−1ki]1/2).
By condition (A1), we have E(Ai) =
0. Furthermore, by using condition (A3), it can be easily seen that
E(Ai12) =
E(Ai22) =
O(ki4). By the
Cauchy–Schwarz inequality, it follows that
Var(Ai) =
O(ki4) and hence
[ki(n −
ki + 1)(n −
ki)]−1nAi
=
op([n−1ki]1/2).
Because
,
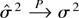
we have
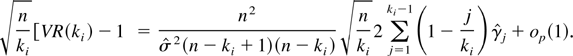
Now consider
By conditions (A1) and (A3), respectively, it follows that
E(Ri2) = 0 and
E(Ri22) = o(1),
and hence
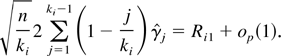
Now define
.
Then, M → ∞, N → ∞,
n−1N → 0, and
N−1ki → 0 for
i = 1,2,…,s. Also, define
Then we can decompose Ri1 as
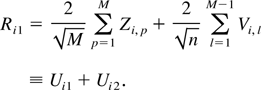
By condition (A3), it follows that
E(Wi,aWi,b)
= 0 for a < b and hence
E(Vi,aVi,b)
= 0 for a < b. Thus,
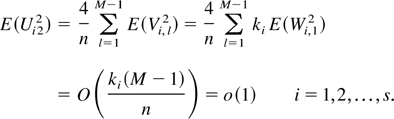
From equations (A.6)–(A.8) it follows that
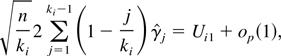
and hence, from equation (A.5),
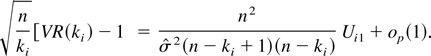
Because
,
the theorem will be proved if we show that the vector
(U11,U21,…,Us1)′
converges in distribution to a multivariate normal distribution with mean
zero and variance covariance matrix σ4Σ. To do
this, it is sufficient to show that for any set of s real numbers
ci,
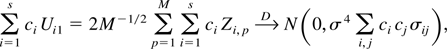
which we now proceed to demonstrate.
Let
be the sigma algebra generated by
{εpN,εpN−1,
εpN−2,…}. Then, for any set of
s real numbers ci, the sequence
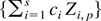
forms a martingale difference with respect to
.
To show (A.9), we first need to establish that
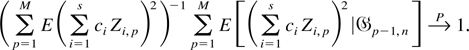
Now, by condition (A3)
By conditions (A3) and (A6),
for i < u. Hence, we have
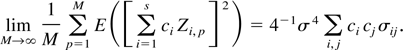
We now show that
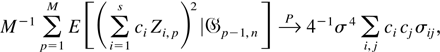
which along with (A.11) will prove (A.10). We have
Letting
and using condition (A4), we get for i ≤ u,
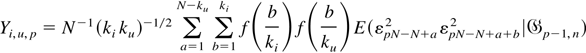
By condition (A6), there exists C < ∞ such that
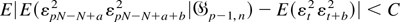
for all p, a, and b. Furthermore, given any
δ > 0, by condition (A5) and Jensen's inequality there exists
an integer N0 such that
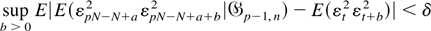
for all a > N0. Hence, letting
,
we have for any ε > 0
where the last inequality follows from equations (A.13) and (A.14).
Because δ can be chosen to be arbitrarily small and N large
enough that N−1N0 → 0,
it follows from equation (A.15) that
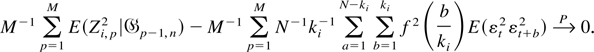
Because, by condition (A6) we also have
we obtain
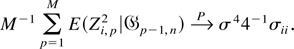
A similar argument as before in conjunction with the fact that
ku−1ki
→ aiu for i < u
yields
Thus, (A.12) is established giving equation (A.10).
By using condition (A3), one can employ the same argument given on
page 539 of Anderson (1994) to show that
E(Zi,p4) is
uniformly bounded in n for i = 1,2,…,s.
This implies that
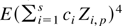
is also uniformly bounded in n, from whence we get
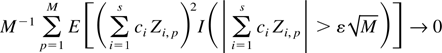
for every ε > 0. By Chebyshev's inequality, equation
(A.16) implies that
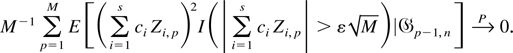
Hence, equation (A.9) follows from equations (A.10) and (A.17) and
Theorem 5.3.4 of Fuller (1996). █
Proof of Theorem 4. We first note that by the weak law of
large numbers,
.
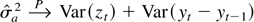
Now, letting
,
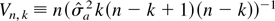
we get
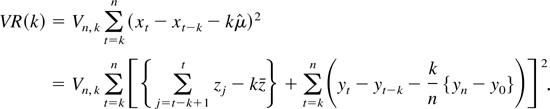
It is trivial to show that
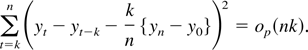
Now
From (A.20), we get
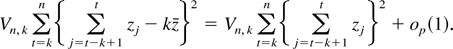
Letting
,
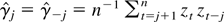
some tedious algebra yields
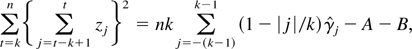
where
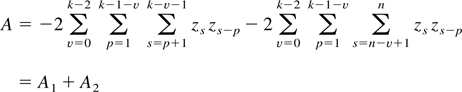
and
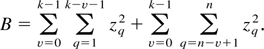
Now
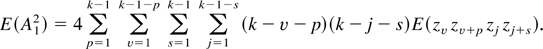
From equation (6.2.5) on page 315 of Fuller (1996), we have
|E(zv
zv+p zj
zj+s)| =
O(λ|v|+|p|+|
j|+|s|), and hence
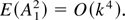
A similar argument shows that
E(A22) =
O(k4), and hence, by the Cauchy–Schwarz
and Chebyshev inequalities, we get
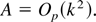
Because E(B) = O(k2)
trivially, it follows from (A.23), (A.22), and (A.21) that
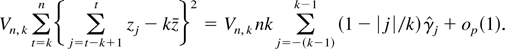
From Theorem 9.3.3 and Theorem 9.4.1 of Anderson (1994), it follows that
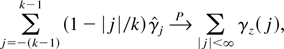
and hence
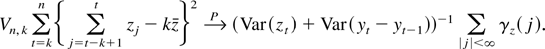
From (A.18), (A.19), (A.24), and the Cauchy–Schwarz inequality,
we get
LEMMA 7.
Proof of (i). Using the fact that
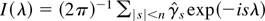
and that
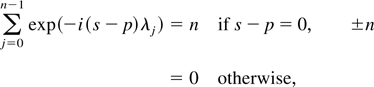
we get
where the last step follows from the identity
.
We now note that because
,
it follows that
.
Furthermore,
,
whereas
,
which implies that
.
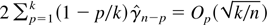
Part (i) of the lemma now follows by noting that
where δ is the indicator function due to the periodicity of the
sine and cosine functions on [0,2π]. █
Proof of (ii). Using a Taylor series expansion and equation
(A.25) in the proof of part (i), we get
Now define the random vector
.
Because
,
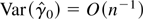
it is seen that
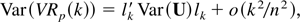
where lk is as defined in (12). Letting
τj =
σ−4E(εt2εt−j2),
tedious but elementary calculation shows that
where A0 = diag(((n −
j)/n2)τj +
(j/n2)τn−j)
for j = 1,…,ks,
b0 is a ks × 1
vector such that its jth element is given by
.
Using the fact that by assumption (A6) τj →
1 as j → ∞, it is easily seen that
and using these facts in conjunction with substituting (A.27) in (A.26),
we get
where A = diag(((n −
j)/n2)τj +
(j/n2)) for j =
1,…,ks, b is a
ks × 1 vector such that its
jth element is given by (2(n −
j)n−3τj +
2jn−3), and d =
2n−2. The estimated variance covariance matrix
is now obtained by replacing τj in the entries of
A and b by
,
and standard arguments from smoothing theory establish consistency of the
resulting estimated covariance matrix. █
Proof of Theorem 6. In the proof of Lemma 7, we noted
that
It is trivially true that under the assumptions of Theorem 6,
.
The results for VRp(k) now follows
by noting that
,
that
,
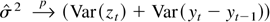
and that by Theorem 9.3.3 and Theorem 9.4.1 of Anderson (1994),
The result for
VRpβ(k) follows by
continuity. █
