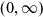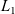1 Introduction
The well-posedness of the fragmentation equation with size diffusion
 \begin{align} \partial_t \phi(t,x) & = D \partial_x^2 \phi(t,x) - a(x) \phi(t,x) \nonumber\\[3pt] & \qquad + \int_x^\infty a(y) b(x,y) \phi(t,y)\ \mathrm{d}y\,, \qquad (t,x)\in (0,\infty)^2\,, \end{align}
\begin{align} \partial_t \phi(t,x) & = D \partial_x^2 \phi(t,x) - a(x) \phi(t,x) \nonumber\\[3pt] & \qquad + \int_x^\infty a(y) b(x,y) \phi(t,y)\ \mathrm{d}y\,, \qquad (t,x)\in (0,\infty)^2\,, \end{align}
along with the long-term behaviour of its solutions is investigated by a semigroup approach. In (1.1),
![]() $\phi=\phi(t,x)\ge 0$
denotes the size distribution function of particles of size
$\phi=\phi(t,x)\ge 0$
denotes the size distribution function of particles of size
![]() $x\in (0,\infty)$
at time
$x\in (0,\infty)$
at time
![]() $t>0$
, while
$t>0$
, while
![]() $a(x)\ge 0$
is the overall fragmentation rate of particles of size x, and b(x, y) is the daughter distribution function that describes the distribution of fragments resulting from the breakup of a particle of size y. Besides undergoing fragmentation events, particles are also assumed to modify their size by diffusion at a constant diffusion rate
$a(x)\ge 0$
is the overall fragmentation rate of particles of size x, and b(x, y) is the daughter distribution function that describes the distribution of fragments resulting from the breakup of a particle of size y. Besides undergoing fragmentation events, particles are also assumed to modify their size by diffusion at a constant diffusion rate
![]() $D>0$
. Finally, nucleation is not taken into account in this model that leads to the homogeneous boundary condition (1.1b) at
$D>0$
. Finally, nucleation is not taken into account in this model that leads to the homogeneous boundary condition (1.1b) at
![]() $x=0$
.
$x=0$
.
An interplay between diffusion and fragmentation as depicted by (1.1) is met in the growth of ice crystals, see [Reference Ferkinghoff-Borg, Jensen, Mathiesen, Olesen and Sneppen16, Reference Mathiesen, Ferkinghoff-Borg, Jensen, Levinsen, Olesen, Dahl-Jensen and Svenson27]. Indeed, on the one hand, ice crystals grow or shrink in a way which looks like diffusion and break apart due to internal stresses, the latter process being referred to as polygonization or rotation recrystallization in ice physics. The fragmentation equation with size diffusion (1.1) is also derived in [Reference Flyvbjerg, Holy and Leibler18] to describe the growth of microtubules. In the absence of diffusion (i.e.
![]() $D=0$
), equation (1.1) is the spontaneous fragmentation equation which has a long and rich history and has been extensively studied in the mathematical and physical literature since the pioneering works [Reference Filippov17, Reference McGrady and Ziff28, Reference Ziff and McGrady32], see [Reference Banasiak5, Reference Banasiak and Arlotti7–Reference Bertoin10], and the references therein.
$D=0$
), equation (1.1) is the spontaneous fragmentation equation which has a long and rich history and has been extensively studied in the mathematical and physical literature since the pioneering works [Reference Filippov17, Reference McGrady and Ziff28, Reference Ziff and McGrady32], see [Reference Banasiak5, Reference Banasiak and Arlotti7–Reference Bertoin10], and the references therein.
An important role is played in the dynamics by the total mass of the particles’ distribution
which is expected to be conserved throughout time evolution when there is no loss of matter during fragmentation events; that is, when b satisfies
Thus,
![]() $X_1 := L_1((0,\infty),x\mathrm{d}x)$
is a natural functional framework for the study of the fragmentation operator. We further observe that the homogeneous Dirichlet boundary condition (1.1b) corresponds actually to a no-flux boundary condition for the Laplace operator in
$X_1 := L_1((0,\infty),x\mathrm{d}x)$
is a natural functional framework for the study of the fragmentation operator. We further observe that the homogeneous Dirichlet boundary condition (1.1b) corresponds actually to a no-flux boundary condition for the Laplace operator in
![]() $X_1$
, so that this space turns out to be also well suited for diffusion. However, the analysis already performed on the fragmentation equation without diffusion reveals that a complete scale of weighted
$X_1$
, so that this space turns out to be also well suited for diffusion. However, the analysis already performed on the fragmentation equation without diffusion reveals that a complete scale of weighted
![]() $L_1$
-spaces is needed besides
$L_1$
-spaces is needed besides
![]() $X_1$
. In this regard, we introduce the spaces
$X_1$
. In this regard, we introduce the spaces
for
![]() $m\in\mathbb{R}$
. We denote the positive cone of
$m\in\mathbb{R}$
. We denote the positive cone of
![]() $X_{1,m}$
by
$X_{1,m}$
by
![]() $X_{1,m}^+$
. For
$X_{1,m}^+$
. For
![]() $f\in X_m$
and
$f\in X_m$
and
![]() $m\in\mathbb{R}$
, we also define the moment
$m\in\mathbb{R}$
, we also define the moment
![]() $M_m(f)$
of order m of f by
$M_m(f)$
of order m of f by
so that
![]() $\|f\|_{X_m}=M_m(|f|)$
. For definiteness, we equip
$\|f\|_{X_m}=M_m(|f|)$
. For definiteness, we equip
![]() $X_{1,m}$
with the norm
$X_{1,m}$
with the norm
and note that
![]() $X_1 \doteq X_{1,1}$
. Finally, we set
$X_1 \doteq X_{1,1}$
. Finally, we set
![]() $BC([0,\infty)) := C([0,\infty)) \cap L_\infty(0,\infty)$
and recall that
$BC([0,\infty)) := C([0,\infty)) \cap L_\infty(0,\infty)$
and recall that
![]() $C_c^\infty((0,\infty))$
stands for the space of
$C_c^\infty((0,\infty))$
stands for the space of
![]() $C^\infty$
-smooth functions on
$C^\infty$
-smooth functions on
![]() $(0,\infty)$
with compact support in
$(0,\infty)$
with compact support in
![]() $(0,\infty)$
.
$(0,\infty)$
.
Our strategy to study the well posedness and the long-term behaviour of (1.1) is to write it as an abstract Cauchy problem in
![]() $X_{1,m}$
for
$X_{1,m}$
for
![]() $m\ge 1$
and show that the corresponding operator generates a semigroup with properties depending on m, a, and b. To this end, we assume throughout the paper that
$m\ge 1$
and show that the corresponding operator generates a semigroup with properties depending on m, a, and b. To this end, we assume throughout the paper that
and that the daughter distribution function b is a nonnegative measurable function on
![]() $(0,\infty)^2$
satisfying
$(0,\infty)^2$
satisfying
Moreover, the diffusion rate D is normalized to
![]() $D=1$
.
$D=1$
.
For
![]() $m\ge 1$
we then define the (Schrödinger) operator
$m\ge 1$
we then define the (Schrödinger) operator
![]() $A_{a,m}$
on
$A_{a,m}$
on
![]() $X_{1,m}$
by
$X_{1,m}$
by
as well as the nonlocal operator
![]() $B_{m}$
on
$B_{m}$
on
![]() $X_{1,m}$
by
$X_{1,m}$
by
 \begin{align} \mathrm{dom}(B_m) & := \{ f\in X_{1,m}\ : \ af \in X_{1,m}\}\subset \mathrm{dom}(A_{a,m})\,, \nonumber\\ B_mf(x) & := \int_x^\infty a(y) b(x,y) f(y)\ \mathrm{d}y\,, \quad x\in (0,\infty)\,, \qquad f\in \mathrm{dom}(B_m)\,. \end{align}
\begin{align} \mathrm{dom}(B_m) & := \{ f\in X_{1,m}\ : \ af \in X_{1,m}\}\subset \mathrm{dom}(A_{a,m})\,, \nonumber\\ B_mf(x) & := \int_x^\infty a(y) b(x,y) f(y)\ \mathrm{d}y\,, \quad x\in (0,\infty)\,, \qquad f\in \mathrm{dom}(B_m)\,. \end{align}
Owing to (1.3) the operator
![]() $B_m$
turns out to be well defined, see Lemma 5.1. Setting
$B_m$
turns out to be well defined, see Lemma 5.1. Setting
equation (1.1) can be equivalently formulated as the Cauchy problem
in
![]() $X_{1,m}$
, and we shall investigate generation properties of the operator
$X_{1,m}$
, and we shall investigate generation properties of the operator
![]() $\mathbb{A}_m$
.
$\mathbb{A}_m$
.
For concise statements we introduce the following notation: Given
![]() $\kappa\ge 1$
and
$\kappa\ge 1$
and
![]() $\omega\in\mathbb{R}$
, we write
$\omega\in\mathbb{R}$
, we write
![]() $A\in \mathcal{G}(X_{1,m},\kappa,\omega)$
if the (unbounded) linear operator A on
$A\in \mathcal{G}(X_{1,m},\kappa,\omega)$
if the (unbounded) linear operator A on
![]() $X_{1,m}$
is the generator of a strongly continuous semigroup
$X_{1,m}$
is the generator of a strongly continuous semigroup
![]() $(e^{tA})_{t\ge 0}$
on
$(e^{tA})_{t\ge 0}$
on
![]() $X_{1,m}$
and
$X_{1,m}$
and
We set
Moreover, we write
![]() $A\in \mathcal{G}_+(X_{1,m})$
if the semigroup
$A\in \mathcal{G}_+(X_{1,m})$
if the semigroup
![]() $(e^{tA})_{t\ge 0}$
is positive on the Banach lattice
$(e^{tA})_{t\ge 0}$
is positive on the Banach lattice
![]() $X_{1,m}$
. We denote the domain of the (unbounded) operator A in
$X_{1,m}$
. We denote the domain of the (unbounded) operator A in
![]() $X_{1,m}$
by
$X_{1,m}$
by
![]() $\mathrm{dom} (A)$
and set
$\mathrm{dom} (A)$
and set
where
![]() $\|f\|_A:=\|f\|_{X_{1,m}} + \|Af\|_{X_{1,m}}$
for
$\|f\|_A:=\|f\|_{X_{1,m}} + \|Af\|_{X_{1,m}}$
for
![]() $f\in \mathrm{dom}(A)$
is the graph norm. Finally, we write
$f\in \mathrm{dom}(A)$
is the graph norm. Finally, we write
![]() $A\in \mathcal{H}(X_{1,m})$
if
$A\in \mathcal{H}(X_{1,m})$
if
![]() $A\in \mathcal{G}(X_{1,m})$
and the semigroup
$A\in \mathcal{G}(X_{1,m})$
and the semigroup
![]() $(e^{tA})_{t\ge 0}$
is analytic.
$(e^{tA})_{t\ge 0}$
is analytic.
With this notation we may formulate the generation result in
![]() $X_{1,m}$
for
$X_{1,m}$
for
![]() $m\ge 1$
:
$m\ge 1$
:
Theorem 1.1 Assume that a and b satisfy (1.2) and (1.3).
-
(a) There is an extension
 $\tilde{\mathbb{A}}_1\in \mathcal{G}_+(X_1,1,0)$
of
$\tilde{\mathbb{A}}_1\in \mathcal{G}_+(X_1,1,0)$
of
 $\mathbb{A}_1$
.
$\mathbb{A}_1$
. -
(b) Assume further that there is
 $\delta_2\in (0,1)$
such that (1.8)If
$\delta_2\in (0,1)$
such that (1.8)If \begin{equation} (1-\delta_2) y^2 \ge \int_0^y x^2 b(x,y)\ \mathrm{d}x\,, \qquad y\in (0,\infty)\,. \end{equation}
\begin{equation} (1-\delta_2) y^2 \ge \int_0^y x^2 b(x,y)\ \mathrm{d}x\,, \qquad y\in (0,\infty)\,. \end{equation}
 $m>1$
, then
$m>1$
, then
 $\mathbb{A}_m\in \mathcal{G}_+(X_{1,m})\cap \mathcal{H}(X_{1,m})$
. In addition, for all
$\mathbb{A}_m\in \mathcal{G}_+(X_{1,m})\cap \mathcal{H}(X_{1,m})$
. In addition, for all
 $f\in X_{1,m}$
, (1.9)
$f\in X_{1,m}$
, (1.9) \begin{equation} M_1\left(e^{t\mathbb{A}_m}f \right) = M_1(f)\,, \qquad t\ge 0\,. \end{equation}
\begin{equation} M_1\left(e^{t\mathbb{A}_m}f \right) = M_1(f)\,, \qquad t\ge 0\,. \end{equation}
-
(c) Assume that a satisfies
(1.10)and that b satisfies (1.8). Then, \begin{equation} \lim_{x\to\infty} a(x) = \infty \end{equation}
\begin{equation} \lim_{x\to\infty} a(x) = \infty \end{equation}
 $(e^{t\mathbb{A}_m})_{t\ge 0}$
is immediately compact on
$(e^{t\mathbb{A}_m})_{t\ge 0}$
is immediately compact on
 $X_{1,m}$
for
$X_{1,m}$
for
 $m>1$
.
$m>1$
.
Assumption (1.8) is commonly encountered in the investigation of the fragmentation equation and somehow excludes the concentration of b along the diagonal. Recall that the exponent 2 in (1.8) plays no particular role and may be replaced by any exponent
![]() $p>1$
, since (1.8) is equivalent to the existence of
$p>1$
, since (1.8) is equivalent to the existence of
![]() $p>1$
and
$p>1$
and
![]() $\delta_p\in (0,1)$
such that
$\delta_p\in (0,1)$
such that
see [Reference Banasiak, Lamb and Laurençot8, Theorem 5.1.47 (c)].
At this stage, the extension
![]() $\tilde{\mathbb{A}}_1$
of
$\tilde{\mathbb{A}}_1$
of
![]() $\mathbb{A}_1$
is not completely identified. In particular, we do not know whether or not
$\mathbb{A}_1$
is not completely identified. In particular, we do not know whether or not
![]() $\tilde{\mathbb{A}}_1$
coincides with
$\tilde{\mathbb{A}}_1$
coincides with
![]() $\mathbb{A}_1$
. Still, it is a question worth of investigation and we refer to [Reference Banasiak, Lamb and Laurençot8] for a thorough discussion of this issue for the fragmentation equation without diffusion. Anyway, a positive answer is straightforward when
$\mathbb{A}_1$
. Still, it is a question worth of investigation and we refer to [Reference Banasiak, Lamb and Laurençot8] for a thorough discussion of this issue for the fragmentation equation without diffusion. Anyway, a positive answer is straightforward when
![]() $a\in L_\infty(0,\infty)$
and reported in the next result.
$a\in L_\infty(0,\infty)$
and reported in the next result.
Proposition 1.2 Assume that
![]() $a\in L_\infty(0,\infty)$
is nonnegative and that b satisfies (1.3).
$a\in L_\infty(0,\infty)$
is nonnegative and that b satisfies (1.3).
-
(a) For
 $m\ge 1$
,
$m\ge 1$
,
 $\mathbb{A}_m\in \mathcal{G}_+(X_{1,m})\cap \mathcal{H}(X_{1,m})$
and (1.9) is satisfied. In addition,
$\mathbb{A}_m\in \mathcal{G}_+(X_{1,m})\cap \mathcal{H}(X_{1,m})$
and (1.9) is satisfied. In addition,
 $\mathbb{A}_1\in \mathcal{G}_+(X_1,1,0)$
.
$\mathbb{A}_1\in \mathcal{G}_+(X_1,1,0)$
. -
(b) The semigroup
 $(e^{t\mathbb{A}_m})_{t\ge 0}$
is not compact on
$(e^{t\mathbb{A}_m})_{t\ge 0}$
is not compact on
 $X_{1,m}$
.
$X_{1,m}$
.
We immediately obtain the well posedness of the Cauchy problem (1.7) in
![]() $X_{1,m}$
and, equivalently, of (1.1) in a classical sense. Since we shall see that
$X_{1,m}$
and, equivalently, of (1.1) in a classical sense. Since we shall see that
![]() $D(\mathbb{A}_m)\doteq D(A_{a,m})$
, we can formulate the result as follows:
$D(\mathbb{A}_m)\doteq D(A_{a,m})$
, we can formulate the result as follows:
Corollary 1.3 Assume that a and b satisfy (1.2) and (1.3). Assume further that, either
![]() $m=1$
and
$m=1$
and
![]() $a\in L_\infty(0,\infty)$
, or
$a\in L_\infty(0,\infty)$
, or
![]() $m>1$
and b satisfies (1.8). Then, for any
$m>1$
and b satisfies (1.8). Then, for any
![]() $f\in X_{1,m}$
, there is a unique classical solution
$f\in X_{1,m}$
, there is a unique classical solution
to (1.1) which is given by
![]() $\phi(t) = e^{t\mathbb{A}_m}f$
for
$\phi(t) = e^{t\mathbb{A}_m}f$
for
![]() $t\ge 0$
and satisfies
$t\ge 0$
and satisfies
Moreover, if
![]() $f\ge 0$
a.e. in
$f\ge 0$
a.e. in
![]() $(0,\infty)$
, then
$(0,\infty)$
, then
![]() $\phi(t)\ge 0$
for all
$\phi(t)\ge 0$
for all
![]() $t>0$
.
$t>0$
.
Remark 1.4 Given
![]() $f\in X_{1,m}^+$
, the corresponding solution
$f\in X_{1,m}^+$
, the corresponding solution
![]() $\phi$
to (1.1) provided by Corollary 1.3 satisfies the mass conservation (1.11), a feature which is in particular due to the assumed boundedness (1.2) of a on (0,1). Indeed, even when b satisfies (1.3), infringement of mass conservation is known to occur when the overall fragmentation a is unbounded for small sizes. In that case, the total mass is a decreasing function of time, a phenomenon usually referred to as shattering which is closely related to the honesty property of the associated semigroup, see [Reference Banasiak4, Reference Banasiak, Lamb and Laurençot8, Reference Cheng and Redner11, Reference Filippov17, Reference Haas21, Reference Jeon22, Reference McGrady and Ziff28]. In fact, shattering takes place as soon as
$\phi$
to (1.1) provided by Corollary 1.3 satisfies the mass conservation (1.11), a feature which is in particular due to the assumed boundedness (1.2) of a on (0,1). Indeed, even when b satisfies (1.3), infringement of mass conservation is known to occur when the overall fragmentation a is unbounded for small sizes. In that case, the total mass is a decreasing function of time, a phenomenon usually referred to as shattering which is closely related to the honesty property of the associated semigroup, see [Reference Banasiak4, Reference Banasiak, Lamb and Laurençot8, Reference Cheng and Redner11, Reference Filippov17, Reference Haas21, Reference Jeon22, Reference McGrady and Ziff28]. In fact, shattering takes place as soon as
![]() $x\mapsto 1/(xa(x))$
fails to be integrable at
$x\mapsto 1/(xa(x))$
fails to be integrable at
![]() $x=0$
.
$x=0$
.
Having settled the well posedness of (1.1), we next turn to qualitative properties of its dynamics. As a guideline, it was pointed out in [Reference Ferkinghoff-Borg, Jensen, Mathiesen, Olesen and Sneppen16] that the interplay between diffusion and fragmentation results in the stabilization of solutions to (1.1) to a stationary solution. This is in sharp contrast to the fragmentation equation without diffusion, since fragmentation is an irreversible process driving the particle distribution to zero. When diffusion is turned on, a closed-form stationary solution to (1.1) can be computed for the particular choice
![]() $a(x)=x$
and
$a(x)=x$
and
![]() $b(x,y) = 2 y^{-1} \textbf{1}_{(0,y)}(x)$
, see [Reference Ferkinghoff-Borg, Jensen, Mathiesen, Olesen and Sneppen16]. The existence of stationary solutions is also established in [Reference Laurençot25] for an overall fragmentation rate a obeying a power law (
$b(x,y) = 2 y^{-1} \textbf{1}_{(0,y)}(x)$
, see [Reference Ferkinghoff-Borg, Jensen, Mathiesen, Olesen and Sneppen16]. The existence of stationary solutions is also established in [Reference Laurençot25] for an overall fragmentation rate a obeying a power law (
![]() $a(x)=x^\gamma$
,
$a(x)=x^\gamma$
,
![]() $\gamma\ge 0$
) and for a specific class of daughter distribution functions b. Here we extend this existence result to a broader class of fragmentation coefficients a and b, see Proposition 1.6. In addition, when a diverges to infinity as
$\gamma\ge 0$
) and for a specific class of daughter distribution functions b. Here we extend this existence result to a broader class of fragmentation coefficients a and b, see Proposition 1.6. In addition, when a diverges to infinity as
![]() $x\to\infty$
, we provide the exponential decay of the solution to (1.1) to the steady state with the total mass of the initial value.
$x\to\infty$
, we provide the exponential decay of the solution to (1.1) to the steady state with the total mass of the initial value.
Theorem 1.5 Assume that a and b satisfy (1.2), (1.3), (1.8), and (1.10), and that
![]() $a>0$
and
$a>0$
and
![]() $b>0$
. There is a unique nonnegative
$b>0$
. There is a unique nonnegative
such that
![]() $M_1(\psi_1)=1$
and
$M_1(\psi_1)=1$
and
![]() $\mathrm{ker}(\mathbb{A}_m) = \mathbb{R}\psi_1 := \{ r\psi_1\ :\ r\in\mathbb{R}\}$
for every
$\mathrm{ker}(\mathbb{A}_m) = \mathbb{R}\psi_1 := \{ r\psi_1\ :\ r\in\mathbb{R}\}$
for every
![]() $m>1$
. In particular, for
$m>1$
. In particular, for
![]() $m>1$
, the spectral bound
$m>1$
, the spectral bound
![]() $s(\mathbb{A}_m)=0$
is a dominant eigenvalue of
$s(\mathbb{A}_m)=0$
is a dominant eigenvalue of
![]() $\mathbb{A}_m$
and there are
$\mathbb{A}_m$
and there are
![]() $N_m\ge 1$
and
$N_m\ge 1$
and
![]() $\nu_m>0$
such that, for all
$\nu_m>0$
such that, for all
![]() $f\in X_{1,m}$
,
$f\in X_{1,m}$
,
It is worth pointing out that the stationary solution
![]() $\psi_1$
decays faster than algebraically at infinity, a property which is perfectly consistent with the exponentially decaying tail experimentally observed in [Reference Mathiesen, Ferkinghoff-Borg, Jensen, Levinsen, Olesen, Dahl-Jensen and Svenson27]. Also, combining Theorem 1.5 with Lemma 2.1 below implies that
$\psi_1$
decays faster than algebraically at infinity, a property which is perfectly consistent with the exponentially decaying tail experimentally observed in [Reference Mathiesen, Ferkinghoff-Borg, Jensen, Levinsen, Olesen, Dahl-Jensen and Svenson27]. Also, combining Theorem 1.5 with Lemma 2.1 below implies that
![]() $\psi_1\in X_{r}$
for all
$\psi_1\in X_{r}$
for all
![]() $r>-1$
.
$r>-1$
.
Theorem 1.5 provides a complete description of the long-term behaviour of solutions to (1.1) when a diverges to infinity as
![]() $x\to \infty$
. However, the unboundedness of a at infinity is not a necessary condition for the existence of stationary solutions. In fact, when
$x\to \infty$
. However, the unboundedness of a at infinity is not a necessary condition for the existence of stationary solutions. In fact, when
we notice that equation (1.1) has an explicit stationary solution
![]() $\psi_1(x) = x e^{-x}$
,
$\psi_1(x) = x e^{-x}$
,
![]() $x>0$
.Footnote
1
This particular example is not peculiar, and we actually obtain the existence of stationary solutions to (1.1) as soon as there is a positive lower bound for a as
$x>0$
.Footnote
1
This particular example is not peculiar, and we actually obtain the existence of stationary solutions to (1.1) as soon as there is a positive lower bound for a as
![]() $x\to \infty$
.
$x\to \infty$
.
Proposition 1.6 Assume that a and b satisfy (1.2), (1.3), and (1.8) and that
![]() $a>0$
and
$a>0$
and
![]() $b>0$
. Assume further that
$b>0$
. Assume further that
There is a unique nonnegative
such that
![]() $M_1(\psi_1)=1$
and
$M_1(\psi_1)=1$
and
![]() $\mathrm{ker}(\mathbb{A}_m) = \mathbb{R}\psi_1$
for every
$\mathrm{ker}(\mathbb{A}_m) = \mathbb{R}\psi_1$
for every
![]() $m>1$
.
$m>1$
.
Let us mention here that there is no loss of generality in assuming the finiteness of
![]() $\liminf_{x\to\infty} a(x)$
in (1.12). Indeed, if
$\liminf_{x\to\infty} a(x)$
in (1.12). Indeed, if
![]() $\liminf_{x\to\infty} a(x)=\infty$
, then a satisfies (1.10), a situation which is dealt with in Theorem 1.5.
$\liminf_{x\to\infty} a(x)=\infty$
, then a satisfies (1.10), a situation which is dealt with in Theorem 1.5.
When a only satisfies (1.12), the associated semigroup
![]() $\left( e^{t \mathbb{A}_m} \right)_{t\ge 0}$
need not be compact, see Proposition 1.2. We thus take a different route to prove Proposition 1.6 by an approximation procedure. This approach does not allow us to retrieve information on the long-term behaviour and it is likely that, either a more precise study of the operator
$\left( e^{t \mathbb{A}_m} \right)_{t\ge 0}$
need not be compact, see Proposition 1.2. We thus take a different route to prove Proposition 1.6 by an approximation procedure. This approach does not allow us to retrieve information on the long-term behaviour and it is likely that, either a more precise study of the operator
![]() $\mathbb{A}_1$
or a different approach (such as the one developed in [Reference Michel, Mischler and Perthame29]) is required to fully identify the long-term behaviour when a only satisfies (1.12).
$\mathbb{A}_1$
or a different approach (such as the one developed in [Reference Michel, Mischler and Perthame29]) is required to fully identify the long-term behaviour when a only satisfies (1.12).
Let us end this introduction with a brief outline of the paper. Auxiliary results are gathered in the next section, which includes integrability properties of elements of
![]() $\mathrm{dom}(A_{0,1})$
on the one hand and a weighted version of Kato’s inequality on the other hand. In Section 3, we recall some properties of the heat semigroup in the weighted
$\mathrm{dom}(A_{0,1})$
on the one hand and a weighted version of Kato’s inequality on the other hand. In Section 3, we recall some properties of the heat semigroup in the weighted
![]() $L_1$
-space
$L_1$
-space
![]() $X_{1,m}$
with
$X_{1,m}$
with
![]() $m\ge 1$
, relying on the explicit representation formula which is available in that case. Section 4 is devoted to the Schrödinger operator
$m\ge 1$
, relying on the explicit representation formula which is available in that case. Section 4 is devoted to the Schrödinger operator
![]() $A_{a,m}$
and the associated absorption semigroup and is mostly a consequence of the thorough study performed in [Reference Arendt and Batty3]. We then use a perturbation argument in Section 5 to study the full fragmentation-diffusion operator
$A_{a,m}$
and the associated absorption semigroup and is mostly a consequence of the thorough study performed in [Reference Arendt and Batty3]. We then use a perturbation argument in Section 5 to study the full fragmentation-diffusion operator
![]() $\mathbb{A}_m=A_{a,m}+B_m$
. On the one hand, for
$\mathbb{A}_m=A_{a,m}+B_m$
. On the one hand, for
![]() $m=1$
, the existence of an extension
$m=1$
, the existence of an extension
![]() $\tilde{\mathbb{A}}_1\in \mathcal{G}_+(X_1,1,0)$
of
$\tilde{\mathbb{A}}_1\in \mathcal{G}_+(X_1,1,0)$
of
![]() $\mathbb{A}_1$
is a consequence of [Reference Voigt31]. On the other hand, if
$\mathbb{A}_1$
is a consequence of [Reference Voigt31]. On the other hand, if
![]() $m>1$
, then we can use a Miyadera perturbation technique to prove that
$m>1$
, then we can use a Miyadera perturbation technique to prove that
![]() $\mathbb{A}_m\in \mathcal{H}(X_{1,m})$
. We recall that this approach has already proved successful for the fragmentation equation without size diffusion, see [Reference Banasiak6]. The remainder of the paper is then devoted to the long-term dynamics. As a preliminary step, we first establish in Section 6 the immediate compactness of the semigroup in
$\mathbb{A}_m\in \mathcal{H}(X_{1,m})$
. We recall that this approach has already proved successful for the fragmentation equation without size diffusion, see [Reference Banasiak6]. The remainder of the paper is then devoted to the long-term dynamics. As a preliminary step, we first establish in Section 6 the immediate compactness of the semigroup in
![]() $X_{1,m}$
for
$X_{1,m}$
for
![]() $m>1$
when a diverges to infinity as
$m>1$
when a diverges to infinity as
![]() $x\to\infty$
. We then construct in Section 7 a bounded convex subset of
$x\to\infty$
. We then construct in Section 7 a bounded convex subset of
![]() $X_{1,m}$
which is invariant with respect to the semigroup. This feature, along with the immediate compactness of the semigroup, implies the existence of at least one stationary solution for any given mass. After showing that the latter is unique, we perform a detailed study of the spectrum of
$X_{1,m}$
which is invariant with respect to the semigroup. This feature, along with the immediate compactness of the semigroup, implies the existence of at least one stationary solution for any given mass. After showing that the latter is unique, we perform a detailed study of the spectrum of
![]() $\mathbb{A}_m$
and end up with the announced convergence at a (yet non-explicit) exponential rate. Building upon the analysis performed in Section 7, we turn to the proof of Proposition 1.6 in Section 8 which relies on an approximation procedure. Specifically, introducing
$\mathbb{A}_m$
and end up with the announced convergence at a (yet non-explicit) exponential rate. Building upon the analysis performed in Section 7, we turn to the proof of Proposition 1.6 in Section 8 which relies on an approximation procedure. Specifically, introducing
![]() $a_n(x) := a(x) + x/n$
for
$a_n(x) := a(x) + x/n$
for
![]() $x>0$
and
$x>0$
and
![]() $n\ge 1$
, we deduce from Theorem 1.5 that there is a unique nonnegative stationary solution
$n\ge 1$
, we deduce from Theorem 1.5 that there is a unique nonnegative stationary solution
![]() $\psi_{1,n}$
to (1.1) with
$\psi_{1,n}$
to (1.1) with
![]() $a_n$
instead of a. We then show that cluster points as
$a_n$
instead of a. We then show that cluster points as
![]() $n\to\infty$
of this sequence are stationary solutions to (1.1).
$n\to\infty$
of this sequence are stationary solutions to (1.1).
2 Auxiliary results
According to the definition of
![]() $\mathrm{dom}(A_{0,1})$
, an important role is played in the forthcoming analysis by functions
$\mathrm{dom}(A_{0,1})$
, an important role is played in the forthcoming analysis by functions
![]() $f\in X_1$
such that
$f\in X_1$
such that
![]() $f''\in X_1$
. We collect useful properties of this class of functions in the next lemma and show, in particular, that the boundary condition (1.1c) is well defined for such functions.
$f''\in X_1$
. We collect useful properties of this class of functions in the next lemma and show, in particular, that the boundary condition (1.1c) is well defined for such functions.
Lemma 2.1 Consider
![]() $f\in X_1$
such that
$f\in X_1$
such that
![]() $f''\in X_1$
. Then
$f''\in X_1$
. Then
![]() $f\in BC([0,\infty))\cap C^1((0,\infty))$
,
$f\in BC([0,\infty))\cap C^1((0,\infty))$
,
![]() $f'\in L_1(0,\infty)$
, and, for
$f'\in L_1(0,\infty)$
, and, for
![]() $x> 0$
,
$x> 0$
,
Moreover,
In fact, f and
![]() $^f{\prime}$
are given by
$^f{\prime}$
are given by
Also,
![]() $f\in X_m$
for any
$f\in X_m$
for any
![]() $m\in (-1,1)$
and, for all
$m\in (-1,1)$
and, for all
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
Equivalently,
Proof. Introducing
it follows from the integrability of f
![]() $^{\prime\prime}$
that
$^{\prime\prime}$
that
so that F(x) is well defined for
![]() $x\ge 0$
. Moreover,
$x\ge 0$
. Moreover,
and satisfies
and
In particular, we infer from (2.4) that there is
![]() $(\alpha,\beta)\in\mathbb{R}^2$
such that
$(\alpha,\beta)\in\mathbb{R}^2$
such that
![]() $(f-F)(x) = \alpha + \beta x$
for
$(f-F)(x) = \alpha + \beta x$
for
![]() $x>0$
. Moreover, since
$x>0$
. Moreover, since
![]() $f\in X_1$
, it follows from (2.5) that
$f\in X_1$
, it follows from (2.5) that
which readily gives
![]() $\alpha=\beta=0$
and
$\alpha=\beta=0$
and
![]() $F=f$
, thereby establishing (2.1), except for the limiting behavior of f at infinity. To this end, we observe that, since
$F=f$
, thereby establishing (2.1), except for the limiting behavior of f at infinity. To this end, we observe that, since
![]() $f\in L_\infty(0,\infty)$
and
$f\in L_\infty(0,\infty)$
and
![]() $f'\in L_1(0,\infty)$
, a formula for
$f'\in L_1(0,\infty)$
, a formula for
![]() $f(x)^2$
reads
$f(x)^2$
reads
We then deduce from (2.1a) that
which implies that
![]() $x f(x)\to 0$
as
$x f(x)\to 0$
as
![]() $x\to\infty$
due to
$x\to\infty$
due to
![]() $f\in X_1$
.
$f\in X_1$
.
Next, let
![]() $\varepsilon>\delta>0$
. It follows from (2.1c) that
$\varepsilon>\delta>0$
. It follows from (2.1c) that
 \begin{align*} \int_\delta^\infty x^m |f(x)|\ \mathrm{d}x & \le \int_\delta^\varepsilon x^m |f(x)|\ \mathrm{d}x + \varepsilon^{m-1} \int_\varepsilon^\infty x\ |f(x)|\ \mathrm{d}x \\[3pt] & \le \int_\delta^\varepsilon x^m \int_x^\infty |f'(y)|\ \mathrm{d}y \mathrm{d}x + \varepsilon^{m-1} \|f\|_{X_1} \\[3pt] & \le \int_\delta^\varepsilon x^m \int_x^\varepsilon |f'(y)|\ \mathrm{d}y \mathrm{d}x + \frac{\varepsilon^{m+1}}{m+1} \int_\varepsilon^\infty |f'(y)|\ \mathrm{d}y + \varepsilon^{m-1} \|f\|_{X_1} \,. \end{align*}
\begin{align*} \int_\delta^\infty x^m |f(x)|\ \mathrm{d}x & \le \int_\delta^\varepsilon x^m |f(x)|\ \mathrm{d}x + \varepsilon^{m-1} \int_\varepsilon^\infty x\ |f(x)|\ \mathrm{d}x \\[3pt] & \le \int_\delta^\varepsilon x^m \int_x^\infty |f'(y)|\ \mathrm{d}y \mathrm{d}x + \varepsilon^{m-1} \|f\|_{X_1} \\[3pt] & \le \int_\delta^\varepsilon x^m \int_x^\varepsilon |f'(y)|\ \mathrm{d}y \mathrm{d}x + \frac{\varepsilon^{m+1}}{m+1} \int_\varepsilon^\infty |f'(y)|\ \mathrm{d}y + \varepsilon^{m-1} \|f\|_{X_1} \,. \end{align*}
By Fubini’s theorem,
Combining the above inequalities with (2.1a) gives
Letting
![]() $\delta\to 0$
completes the proof of (2.2). We next optimize (2.2) with respect to
$\delta\to 0$
completes the proof of (2.2). We next optimize (2.2) with respect to
![]() $\varepsilon\in (0,\infty)$
to derive (2.3).
$\varepsilon\in (0,\infty)$
to derive (2.3).
We next state for the sake of completeness the density in
![]() $X_{1,m}$
of smooth functions with compact support in
$X_{1,m}$
of smooth functions with compact support in
![]() $(0,\infty)$
, which is actually a straightforward consequence of the density of
$(0,\infty)$
, which is actually a straightforward consequence of the density of
![]() $C_c^\infty((0,\infty))$
in
$C_c^\infty((0,\infty))$
in
![]() $L_1(0,\infty)$
.
$L_1(0,\infty)$
.
Lemma 2.2 The space
![]() $C_c^\infty((0,\infty))$
is dense in
$C_c^\infty((0,\infty))$
is dense in
![]() $X_{1,m}$
for
$X_{1,m}$
for
![]() $m\ge 1$
.
$m\ge 1$
.
We finally recall a variant of the celebrated inequality of Kato [Reference Kato23, Lemma A].
Lemma 2.3 Let
![]() $\ell$
be a nonnegative function in
$\ell$
be a nonnegative function in
![]() $W_{\infty,loc}^1([0,\infty))$
with
$W_{\infty,loc}^1([0,\infty))$
with
![]() $\ell(0)=0$
and consider
$\ell(0)=0$
and consider
![]() $f\in W_{1,loc}^2(0,\infty) \cap X_1$
such that
$f\in W_{1,loc}^2(0,\infty) \cap X_1$
such that
![]() $f'\ell'\in L_1((0,\infty))$
and
$f'\ell'\in L_1((0,\infty))$
and
![]() $f''\in L_1((0,\infty),\ell(x)\mathrm{d}x)$
. Then
$f''\in L_1((0,\infty),\ell(x)\mathrm{d}x)$
. Then
Proof. For
![]() $\varepsilon\in (0,1)$
, we define
$\varepsilon\in (0,1)$
, we define
![]() $\beta_\varepsilon\in W_{\infty,loc}^2(\mathbb{R})$
by
$\beta_\varepsilon\in W_{\infty,loc}^2(\mathbb{R})$
by
![]() $\beta_\varepsilon(0)=0$
and
$\beta_\varepsilon(0)=0$
and
Since
![]() $f\in X_1$
, we note that
$f\in X_1$
, we note that
while the integrability assumptions on f and
![]() $\ell$
imply that
$\ell$
imply that
 \begin{align*} |(\ell f')(x)| & \le |(\ell f')(1)| + \int_1^x |(\ell' f' + \ell f'')(y)|\ \mathrm{d}y \\[3pt] & \le |(\ell f')(1)| + \|\ell' f'\|_{L_1(0,\infty)} + \|\ell f''\|_{L_1(0,\infty)}\,, \qquad x\ge 1\,. \end{align*}
\begin{align*} |(\ell f')(x)| & \le |(\ell f')(1)| + \int_1^x |(\ell' f' + \ell f'')(y)|\ \mathrm{d}y \\[3pt] & \le |(\ell f')(1)| + \|\ell' f'\|_{L_1(0,\infty)} + \|\ell f''\|_{L_1(0,\infty)}\,, \qquad x\ge 1\,. \end{align*}
Next, integration by parts gives
observing that the boundary terms vanish due to
![]() $\ell(0)=0$
,
$\ell(0)=0$
,
![]() $\ell f'\in L_\infty(1,\infty)$
, and
$\ell f'\in L_\infty(1,\infty)$
, and
![]() $\beta_\varepsilon^{\prime}(f)\in L_1(1,\infty)$
. We then deduce from the nonnegativity of
$\beta_\varepsilon^{\prime}(f)\in L_1(1,\infty)$
. We then deduce from the nonnegativity of
![]() $\beta_\varepsilon^{\prime\prime}$
on
$\beta_\varepsilon^{\prime\prime}$
on
![]() $\mathbb{R}$
that
$\mathbb{R}$
that
Since
![]() $|\beta_\varepsilon(r)-|r||\le \varepsilon$
for
$|\beta_\varepsilon(r)-|r||\le \varepsilon$
for
![]() $r\in\mathbb{R}$
and since
$r\in\mathbb{R}$
and since
![]() $\beta_\varepsilon^{\prime}$
converges pointwise to the sign function in
$\beta_\varepsilon^{\prime}$
converges pointwise to the sign function in
![]() $\mathbb{R}$
as
$\mathbb{R}$
as
![]() $\varepsilon \to 0$
with
$\varepsilon \to 0$
with
![]() $|\beta_\varepsilon^{\prime}|\le 1$
, we may pass to the limit as
$|\beta_\varepsilon^{\prime}|\le 1$
, we may pass to the limit as
![]() $\varepsilon \to 0$
in the previous inequality with the help of Lebesgue’s dominated convergence theorem and the integrability properties of f
$\varepsilon \to 0$
in the previous inequality with the help of Lebesgue’s dominated convergence theorem and the integrability properties of f
![]() $^{\prime}$
and f
$^{\prime}$
and f
![]() $^{\prime\prime}$
and find
$^{\prime\prime}$
and find
We finally use the classical property
![]() $|f|'=\mathrm{sign}(f) f'$
a.e. in
$|f|'=\mathrm{sign}(f) f'$
a.e. in
![]() $(0,\infty)$
, see [Reference Kinderlehrer and Stampacchia24, Chapter II, Theorem A.2], to complete the proof.
$(0,\infty)$
, see [Reference Kinderlehrer and Stampacchia24, Chapter II, Theorem A.2], to complete the proof.
3 The heat semigroup
It is well known, see [Reference Craig13, Section 3.4] for instance, that the solution to the heat equation with homogeneous Dirichlet boundary conditions at
![]() $x=0$
,
$x=0$
,
 \begin{align*} \partial_t w - \partial_x^2 w & = 0\,, \qquad (t,x)\in (0,\infty)\times (0,\infty)\,, \\[3pt] w(t,0) & = 0\,, \qquad t\in (0,\infty)\,, \\[3pt] w(0,x) & = f(x)\,, \qquad x\in (0,\infty)\,,\end{align*}
\begin{align*} \partial_t w - \partial_x^2 w & = 0\,, \qquad (t,x)\in (0,\infty)\times (0,\infty)\,, \\[3pt] w(t,0) & = 0\,, \qquad t\in (0,\infty)\,, \\[3pt] w(0,x) & = f(x)\,, \qquad x\in (0,\infty)\,,\end{align*}
is given by the representation formula
where
Moreover,
![]() $(W(t))_{t\ge 0}$
(with
$(W(t))_{t\ge 0}$
(with
![]() $W(0):=\mathrm{id}_{L_1(0,\infty)}$
) is a positive analytic semigroup of contractions on
$W(0):=\mathrm{id}_{L_1(0,\infty)}$
) is a positive analytic semigroup of contractions on
![]() $L_1(0,\infty)$
with generator G given by
$L_1(0,\infty)$
with generator G given by
That is,
![]() $G\in\mathcal{G}_+(L_1(0,\infty),1,0)\cap \mathcal{H}(L_1(0,\infty))$
and
$G\in\mathcal{G}_+(L_1(0,\infty),1,0)\cap \mathcal{H}(L_1(0,\infty))$
and
![]() $e^{tG}=W(t)$
for
$e^{tG}=W(t)$
for
![]() $t\ge 0$
. We now consider this semigroup in the weighted space
$t\ge 0$
. We now consider this semigroup in the weighted space
![]() $X_{1,m}$
. More precisely, for
$X_{1,m}$
. More precisely, for
![]() $m\ge 1$
, we recall the definition (1.4) (with
$m\ge 1$
, we recall the definition (1.4) (with
![]() $a=0$
) of the unbounded operator
$a=0$
) of the unbounded operator
![]() $A_{0,m}$
on
$A_{0,m}$
on
![]() $X_{1,m}$
, given by
$X_{1,m}$
, given by
and show that it is the generator of the heat semigroup in
![]() $X_{1,m}$
.
$X_{1,m}$
.
Proposition 3.1 Let
![]() $m\ge 1$
. There is
$m\ge 1$
. There is
![]() $\omega_m\ge 0$
such
$\omega_m\ge 0$
such
![]() $A_{0,m}\in \mathcal{G}_+(X_{1,m},1,\omega_m)\cap \mathcal{H}(X_{1,m})$
with
$A_{0,m}\in \mathcal{G}_+(X_{1,m},1,\omega_m)\cap \mathcal{H}(X_{1,m})$
with
![]() $(0,\infty)\subset \rho(A_{0,m})$
. The semigroup
$(0,\infty)\subset \rho(A_{0,m})$
. The semigroup
![]() $\left( e^{tA_{0,m}} \right)_{t\ge 0}$
is given by
$\left( e^{tA_{0,m}} \right)_{t\ge 0}$
is given by
for
![]() $f\in X_{1,m}$
, where k is defined in (3.2). Moreover,
$f\in X_{1,m}$
, where k is defined in (3.2). Moreover,
![]() $e^{tA_{0,m}} = e^{tA_{0,1}}|_{X_{1,m}}$
for
$e^{tA_{0,m}} = e^{tA_{0,1}}|_{X_{1,m}}$
for
![]() $t\ge 0$
and
$t\ge 0$
and
Two steps are needed to show Proposition 3.1. We first establish Proposition 3.1 for
![]() $m=1$
and
$m=1$
and
![]() $m\ge 3$
, see Lemma 3.2 below. An interpolation argument then completes the proof for
$m\ge 3$
, see Lemma 3.2 below. An interpolation argument then completes the proof for
![]() $m\in (1,3)$
.
$m\in (1,3)$
.
Lemma 3.2 Let
![]() $m\in \{1\} \cup (3,\infty)$
. Then
$m\in \{1\} \cup (3,\infty)$
. Then
![]() $A_{0,m}\in \mathcal{G}_+(X_{1,m},1,\omega_m)\cap \mathcal{H}(X_{1,m})$
with
$A_{0,m}\in \mathcal{G}_+(X_{1,m},1,\omega_m)\cap \mathcal{H}(X_{1,m})$
with
Moreover,
![]() $e^{tA_{0,m}} = e^{tA_{0,1}}|_{X_{1,m}}$
for
$e^{tA_{0,m}} = e^{tA_{0,1}}|_{X_{1,m}}$
for
![]() $t\ge 0$
,
$t\ge 0$
,
![]() $(0,\infty)\subset \rho(A_{0,m})$
, and
$(0,\infty)\subset \rho(A_{0,m})$
, and
Proof. We first note that
![]() $A_{0,m}$
is a closed operator on
$A_{0,m}$
is a closed operator on
![]() $X_{1,m}$
and that its domain is dense in
$X_{1,m}$
and that its domain is dense in
![]() $X_{1,m}$
due to Lemmas 2.1 and 2.2. We divide the remainder of the proof into several steps.
$X_{1,m}$
due to Lemmas 2.1 and 2.2. We divide the remainder of the proof into several steps.
Step 1. We first show the dissipativity of
![]() $A_{0,m}-\omega_m$
on
$A_{0,m}-\omega_m$
on
![]() $X_{1,m}$
. To this end, let
$X_{1,m}$
. To this end, let
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $f\in \mathrm{dom}(A_{0,m})$
. Using the inequality
$f\in \mathrm{dom}(A_{0,m})$
. Using the inequality
along with the nonnegativity of
![]() $\lambda$
and
$\lambda$
and
![]() $\omega_m$
, gives
$\omega_m$
, gives
 \begin{align*} \|\lambda f - (A_{0,m}-\omega_m)f\|_{X_m} & = \|(\lambda+\omega_m) f - A_{0,m} f\|_{X_m}\\ & \ge \int_0^\infty x^m\ \mathrm{sign}(f(x)) [(\lambda+\omega_m) f(x)-f''(x)]\ \mathrm{d}x\,. \end{align*}
\begin{align*} \|\lambda f - (A_{0,m}-\omega_m)f\|_{X_m} & = \|(\lambda+\omega_m) f - A_{0,m} f\|_{X_m}\\ & \ge \int_0^\infty x^m\ \mathrm{sign}(f(x)) [(\lambda+\omega_m) f(x)-f''(x)]\ \mathrm{d}x\,. \end{align*}
By Kato’s inequality (2.6) (with
![]() $\ell(x) = x^m$
), Lemma 2.1, and the boundary condition
$\ell(x) = x^m$
), Lemma 2.1, and the boundary condition
![]() $f(0)=0$
, we further obtain
$f(0)=0$
, we further obtain
 \begin{align*} \|\lambda f - (A_{0,m}-\omega_m)f\|_{X_m} & \ge (\lambda+\omega_m) \|f\|_{X_m} + m \int_0^\infty x^{m-1}\ |f|'(x)\ \mathrm{d}x \\ & = (\lambda+\omega_m) \|f\|_{X_m} - m(m-1) \|f\|_{X_{m-2}}\,. \end{align*}
\begin{align*} \|\lambda f - (A_{0,m}-\omega_m)f\|_{X_m} & \ge (\lambda+\omega_m) \|f\|_{X_m} + m \int_0^\infty x^{m-1}\ |f|'(x)\ \mathrm{d}x \\ & = (\lambda+\omega_m) \|f\|_{X_m} - m(m-1) \|f\|_{X_{m-2}}\,. \end{align*}
In particular, when
![]() $m=1$
,
$m=1$
,
so that
![]() $A_{0,1}$
is dissipative on
$A_{0,1}$
is dissipative on
![]() $X_1$
. We next handle the case
$X_1$
. We next handle the case
![]() $m\ge 3$
. Then
$m\ge 3$
. Then
![]() $m-2\in [1,m)$
and we infer from Young’s inequality that, for
$m-2\in [1,m)$
and we infer from Young’s inequality that, for
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
Hence,
Combining (3.5) with this inequality gives
We now choose
![]() $\varepsilon = \varepsilon_m := (2/(m-3))^{2/(m-1)}$
. Since
$\varepsilon = \varepsilon_m := (2/(m-3))^{2/(m-1)}$
. Since
we readily conclude that
so that
![]() $A_{0,m}-\omega_m I$
is a dissipative operator on
$A_{0,m}-\omega_m I$
is a dissipative operator on
![]() $X_{1,m}$
.
$X_{1,m}$
.
Step 2. We next show that
![]() $\mathrm{rg}(\lambda - A_{0,m})=X_{1,m}$
for
$\mathrm{rg}(\lambda - A_{0,m})=X_{1,m}$
for
![]() $\lambda>0$
. Consider
$\lambda>0$
. Consider
![]() $g\in X_{1,m}$
. According to Lemma 2.2, there is a sequence
$g\in X_{1,m}$
. According to Lemma 2.2, there is a sequence
![]() $(g_n)_{n\ge 1}$
in
$(g_n)_{n\ge 1}$
in
![]() $C_c^\infty((0,\infty))$
such that
$C_c^\infty((0,\infty))$
such that
Since
![]() $g_n\in L_1(0,\infty)$
and
$g_n\in L_1(0,\infty)$
and
![]() $(0,\infty)\subset \rho(G)$
, there is a unique
$(0,\infty)\subset \rho(G)$
, there is a unique
![]() $f_n\in \mathrm{dom}(G)$
such that
$f_n\in \mathrm{dom}(G)$
such that
![]() $\lambda f_n - G f_n = g_n$
; that is,
$\lambda f_n - G f_n = g_n$
; that is,
Now, let
![]() $R>1$
. We multiply (3.7) by
$R>1$
. We multiply (3.7) by
![]() $(x\wedge R)^m\ \mathrm{sign}(f_n(x))$
and integrate over
$(x\wedge R)^m\ \mathrm{sign}(f_n(x))$
and integrate over
![]() $(0,\infty)$
. Using Kato’s inequality (2.6) (with
$(0,\infty)$
. Using Kato’s inequality (2.6) (with
![]() $\ell(x)= (x\wedge R)^m$
), we obtain
$\ell(x)= (x\wedge R)^m$
), we obtain
 \begin{align*} \|g_n\|_{X_m} & \ge \int_0^\infty (x\wedge R)^m\ \mathrm{sign}(f_n(x)) [\lambda f_n(x)-f_n^{\prime\prime}(x)]\ \mathrm{d}x \\[3pt] & \ge \lambda \int_0^\infty (x\wedge R)^m\ |f_n(x)|\ \mathrm{d}x + m \int_0^R x^{m-1} |f_n|'(x)\ \mathrm{d}x \\[3pt] & = \lambda \int_0^\infty (x\wedge R)^m\ |f_n(x)|\ \mathrm{d}x - m(m-1) \int_0^R x^{m-2}\ f_n(x)\ \mathrm{d}x \,. \end{align*}
\begin{align*} \|g_n\|_{X_m} & \ge \int_0^\infty (x\wedge R)^m\ \mathrm{sign}(f_n(x)) [\lambda f_n(x)-f_n^{\prime\prime}(x)]\ \mathrm{d}x \\[3pt] & \ge \lambda \int_0^\infty (x\wedge R)^m\ |f_n(x)|\ \mathrm{d}x + m \int_0^R x^{m-1} |f_n|'(x)\ \mathrm{d}x \\[3pt] & = \lambda \int_0^\infty (x\wedge R)^m\ |f_n(x)|\ \mathrm{d}x - m(m-1) \int_0^R x^{m-2}\ f_n(x)\ \mathrm{d}x \,. \end{align*}
In particular, for
![]() $m=1$
we get
$m=1$
we get
so that, letting
![]() $R\to \infty$
and using Fatou’s lemma,
$R\to \infty$
and using Fatou’s lemma,
The same argument entails that
If
![]() $m\ge 3$
, then
$m\ge 3$
, then
![]() $m-2\in [1,m)$
, and we use Young’s inequality to deduce that, for
$m-2\in [1,m)$
, and we use Young’s inequality to deduce that, for
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 \begin{align*} \lambda \int_0^\infty (x\wedge R)^m\ |f_n(x)|\ \mathrm{d}x & \le \|g_n\|_{X_m} + m(m-3)\varepsilon \int_0^R x^m\ |f_n(x)|\ \mathrm{d}x\\ & \qquad + 2m \varepsilon^{(3-m)/2} \int_0^R x\ |f_n(x)|\ \mathrm{d}x \\ & \le \|g_n\|_{X_m} + m(m-3)\varepsilon \int_0^\infty (x\wedge R)^m\ |f_n(x)|\ \mathrm{d}x\\ & \qquad + 2m \varepsilon^{(3-m)/2} \|f_n\|_{X_1}\,. \end{align*}
\begin{align*} \lambda \int_0^\infty (x\wedge R)^m\ |f_n(x)|\ \mathrm{d}x & \le \|g_n\|_{X_m} + m(m-3)\varepsilon \int_0^R x^m\ |f_n(x)|\ \mathrm{d}x\\ & \qquad + 2m \varepsilon^{(3-m)/2} \int_0^R x\ |f_n(x)|\ \mathrm{d}x \\ & \le \|g_n\|_{X_m} + m(m-3)\varepsilon \int_0^\infty (x\wedge R)^m\ |f_n(x)|\ \mathrm{d}x\\ & \qquad + 2m \varepsilon^{(3-m)/2} \|f_n\|_{X_1}\,. \end{align*}
Choosing
![]() $\varepsilon = \lambda/(2m(m-3))$
, we combine (3.8) and the above inequality to conclude that
$\varepsilon = \lambda/(2m(m-3))$
, we combine (3.8) and the above inequality to conclude that
We now let
![]() $R\to\infty$
in this inequality and deduce from Fatou’s lemma that
$R\to\infty$
in this inequality and deduce from Fatou’s lemma that
![]() $f_n\in X_m$
with
$f_n\in X_m$
with
The same argument entails that
for
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $l\ge 1$
. Therefore, for
$l\ge 1$
. Therefore, for
![]() $m\in \{1\}\cup [3,\infty)$
, the estimates (3.9) and (3.11) along with (3.6) guarantee that
$m\in \{1\}\cup [3,\infty)$
, the estimates (3.9) and (3.11) along with (3.6) guarantee that
![]() $(f_n)_{n\ge 1}$
is a Cauchy sequence in
$(f_n)_{n\ge 1}$
is a Cauchy sequence in
![]() $X_{1,m}$
and that there is
$X_{1,m}$
and that there is
![]() $f\in X_{1,m}$
such that
$f\in X_{1,m}$
such that
Since
![]() $f_n^{\prime\prime}=\lambda f_n-g_n$
for all
$f_n^{\prime\prime}=\lambda f_n-g_n$
for all
![]() $n\ge 1$
by (3.7), it readily follows from (3.6) and (3.12) that
$n\ge 1$
by (3.7), it readily follows from (3.6) and (3.12) that
![]() $(f_n^{\prime\prime})_{n\ge 1}$
converges to
$(f_n^{\prime\prime})_{n\ge 1}$
converges to
![]() $\lambda f-g$
in
$\lambda f-g$
in
![]() $X_{1,m}$
and to f
$X_{1,m}$
and to f
![]() $^{\prime\prime}$
in the sense of distributions. Therefore,
$^{\prime\prime}$
in the sense of distributions. Therefore,
![]() $f''\in X_{1,m}$
,
$f''\in X_{1,m}$
,
![]() $f''=\lambda f-g$
, and
$f''=\lambda f-g$
, and
![]() $\|f_n^{\prime\prime}-f''\|_{X_{1,m}}\to 0$
as
$\|f_n^{\prime\prime}-f''\|_{X_{1,m}}\to 0$
as
![]() $n\to\infty$
. Finally, by (2.1c),
$n\to\infty$
. Finally, by (2.1c),
 \begin{align*} |f(0)| & = |f(0)-f_n(0)| \le \int_0^\infty |(f'-f_n^{\prime})(x)|\ \mathrm{d}x \\ & \le \int_0^\infty \int_x^\infty |(f''-f_n^{\prime\prime})(y)|\ \mathrm{d}y\mathrm{d}x = \int_0^\infty y\ |(f''-f_n^{\prime\prime})(y)|\ \mathrm{d}y = \|f''-f_n^{\prime\prime}\|_{X_1}\,, \end{align*}
\begin{align*} |f(0)| & = |f(0)-f_n(0)| \le \int_0^\infty |(f'-f_n^{\prime})(x)|\ \mathrm{d}x \\ & \le \int_0^\infty \int_x^\infty |(f''-f_n^{\prime\prime})(y)|\ \mathrm{d}y\mathrm{d}x = \int_0^\infty y\ |(f''-f_n^{\prime\prime})(y)|\ \mathrm{d}y = \|f''-f_n^{\prime\prime}\|_{X_1}\,, \end{align*}
from which we deduce that
![]() $f(0)=0$
. Consequently,
$f(0)=0$
. Consequently,
![]() $f\in \mathrm{dom}(A_{0,m})$
and
$f\in \mathrm{dom}(A_{0,m})$
and
![]() $\lambda f - A_{0,m}\, f = g$
. Since
$\lambda f - A_{0,m}\, f = g$
. Since
![]() $\lambda - A_{0,m}$
is one-to-one by (3.5), we have thus shown for any
$\lambda - A_{0,m}$
is one-to-one by (3.5), we have thus shown for any
![]() $\lambda>0$
that
$\lambda>0$
that
Step 3. For
![]() $m\in \{1\}\cup [3,\infty)$
, we infer from Step 1 to Step 2 and the Lumer-Phillips theorem [Reference Pazy30, Theorem 1.4.3] that
$m\in \{1\}\cup [3,\infty)$
, we infer from Step 1 to Step 2 and the Lumer-Phillips theorem [Reference Pazy30, Theorem 1.4.3] that
![]() $A_{0,m}-\omega_m$
belongs to
$A_{0,m}-\omega_m$
belongs to
![]() $\mathcal{G}(X_{1,m},1,0)$
. Hence,
$\mathcal{G}(X_{1,m},1,0)$
. Hence,
![]() $A_{0,m}\in \mathcal{G}(X_{1,m},1,\omega_m)$
. Also, it readily follows from (3.13) that
$A_{0,m}\in \mathcal{G}(X_{1,m},1,\omega_m)$
. Also, it readily follows from (3.13) that
![]() $(0,\infty)\subset \rho(A_{0,m})$
and
$(0,\infty)\subset \rho(A_{0,m})$
and
In particular, the latter, along with the exponential formula [Reference Pazy30, Theorem 1.8.3], entails that
![]() $e^{tA_{0,m}} = e^{tA_{0,1}}|_{X_{1,m}}$
for all
$e^{tA_{0,m}} = e^{tA_{0,1}}|_{X_{1,m}}$
for all
![]() $t\ge 0$
.
$t\ge 0$
.
Step 4. We next derive the representation formulation for
![]() $(e^{tA_{0,1}})_{t\ge 0}$
. To this end, we first note that, for
$(e^{tA_{0,1}})_{t\ge 0}$
. To this end, we first note that, for
![]() $t>0$
, the operator W(t) defined in (1.3) is a bounded operator on
$t>0$
, the operator W(t) defined in (1.3) is a bounded operator on
![]() $X_1$
. Indeed, since
$X_1$
. Indeed, since
![]() $|x-y|\le |x+y|=x+y$
for
$|x-y|\le |x+y|=x+y$
for
![]() $(x,y)\in (0,\infty)^2$
,
$(x,y)\in (0,\infty)^2$
,
for
![]() $ (x,y)\in (0,\infty)^2$
. By Fubini–Tonelli’s theorem and (3.14),
$ (x,y)\in (0,\infty)^2$
. By Fubini–Tonelli’s theorem and (3.14),
 \begin{align*} \|W(t)f\|_{X_1} & \le \int_0^\infty x \int_0^\infty [k(t,x-y) - k(t,x+y)] |f(y)|\ \mathrm{d}y\mathrm{d}x \\[3pt] & = \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-y/2\sqrt{t}}^\infty (y+2z\sqrt{t}) e^{-z^2}\ \mathrm{d}z \mathrm{d}y \\[3pt] & \qquad - \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-\infty}^{-y/2\sqrt{t}} (-y-2z\sqrt{t}) e^{-z^2}\ \mathrm{d}z \mathrm{d}y \\[3pt] & = \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \left( \int_{-\infty}^\infty (y+2z\sqrt{t}) e^{-z^2}\ \mathrm{d}z \right)\ \mathrm{d}y = \|f\|_{X_1}\,. \end{align*}
\begin{align*} \|W(t)f\|_{X_1} & \le \int_0^\infty x \int_0^\infty [k(t,x-y) - k(t,x+y)] |f(y)|\ \mathrm{d}y\mathrm{d}x \\[3pt] & = \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-y/2\sqrt{t}}^\infty (y+2z\sqrt{t}) e^{-z^2}\ \mathrm{d}z \mathrm{d}y \\[3pt] & \qquad - \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-\infty}^{-y/2\sqrt{t}} (-y-2z\sqrt{t}) e^{-z^2}\ \mathrm{d}z \mathrm{d}y \\[3pt] & = \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \left( \int_{-\infty}^\infty (y+2z\sqrt{t}) e^{-z^2}\ \mathrm{d}z \right)\ \mathrm{d}y = \|f\|_{X_1}\,. \end{align*}
Thus, W(t) is a contraction on
![]() $X_1$
. Since
$X_1$
. Since
![]() $(\lambda - G)^{-1} = (\lambda - A_{0,1})^{-1}$
on
$(\lambda - G)^{-1} = (\lambda - A_{0,1})^{-1}$
on
![]() $L_1(0,\infty)\cap X_1$
for all
$L_1(0,\infty)\cap X_1$
for all
![]() $\lambda>0$
, it follows from the exponential formula, see [Reference Pazy30, Theorem 1.8.3], that
$\lambda>0$
, it follows from the exponential formula, see [Reference Pazy30, Theorem 1.8.3], that
![]() $e^{tG}=e^{tA_{0,1}}$
on
$e^{tG}=e^{tA_{0,1}}$
on
![]() $L_1(0,\infty)\cap X_1$
for all
$L_1(0,\infty)\cap X_1$
for all
![]() $t\ge 0$
. Therefore,
$t\ge 0$
. Therefore,
![]() $W(t)=e^{tA_{0,1}}$
on
$W(t)=e^{tA_{0,1}}$
on
![]() $L_1(0,\infty)\cap X_1$
for all
$L_1(0,\infty)\cap X_1$
for all
![]() $t\ge 0$
. Since
$t\ge 0$
. Since
![]() $L_1(0,\infty)\cap X_1$
is dense in
$L_1(0,\infty)\cap X_1$
is dense in
![]() $X_1$
by Lemma 2.2 and
$X_1$
by Lemma 2.2 and
![]() $e^{tA_{0,1}}$
and W(t) are both bounded operators on
$e^{tA_{0,1}}$
and W(t) are both bounded operators on
![]() $X_1$
, we conclude that
$X_1$
, we conclude that
![]() $e^{tA_{0,1}}=W(t)$
on
$e^{tA_{0,1}}=W(t)$
on
![]() $X_1$
for all
$X_1$
for all
![]() $t\ge 0$
. Together with the outcome of Step 3, this identity proves (3.4). In particular,
$t\ge 0$
. Together with the outcome of Step 3, this identity proves (3.4). In particular,
![]() $(e^{tA_{0,m}})_{t\ge 0}$
is a positive semigroup according to (3.14).
$(e^{tA_{0,m}})_{t\ge 0}$
is a positive semigroup according to (3.14).
Step 5. We are left with showing the analyticity of
![]() $(e^{tA_{0,m}})_{t\ge 0}$
on
$(e^{tA_{0,m}})_{t\ge 0}$
on
![]() $X_{1,m}$
. To this end, let
$X_{1,m}$
. To this end, let
![]() $f\in X_{1,m}$
. Clearly,
$f\in X_{1,m}$
. Clearly,
is differentiable on
![]() $(0,\infty)$
and, since
$(0,\infty)$
and, since
we derive for
![]() $(t,x)\in (0,\infty)^2$
that
$(t,x)\in (0,\infty)^2$
that
 \begin{align*} 2t\frac{\mathrm{d}}{\mathrm{d}t} e^{tA_{0,m}}f(x) & = - e^{tA_{0,m}}f(x) \\[3pt] & \qquad + 2 \int_0^\infty \left( \frac{|x-y|^2}{4t} k(t,x-y) - \frac{|x+y|^2}{4t} k(t,x+y) \right) f(y)\ \mathrm{d}y \\[3pt] & = - 3 e^{tA_{0,m}}f(x) \\[3pt] & \qquad + 2 \int_0^\infty \left( 1 + \frac{|x-y|^2}{4t} \right) k(t,x-y) f(y)\ \mathrm{d}y \\[3pt] & \qquad - 2 \int_0^\infty \left( 1+ \frac{|x+y|^2}{4t} \right) k(t,x+y) f(y)\ \mathrm{d}y\,. \end{align*}
\begin{align*} 2t\frac{\mathrm{d}}{\mathrm{d}t} e^{tA_{0,m}}f(x) & = - e^{tA_{0,m}}f(x) \\[3pt] & \qquad + 2 \int_0^\infty \left( \frac{|x-y|^2}{4t} k(t,x-y) - \frac{|x+y|^2}{4t} k(t,x+y) \right) f(y)\ \mathrm{d}y \\[3pt] & = - 3 e^{tA_{0,m}}f(x) \\[3pt] & \qquad + 2 \int_0^\infty \left( 1 + \frac{|x-y|^2}{4t} \right) k(t,x-y) f(y)\ \mathrm{d}y \\[3pt] & \qquad - 2 \int_0^\infty \left( 1+ \frac{|x+y|^2}{4t} \right) k(t,x+y) f(y)\ \mathrm{d}y\,. \end{align*}
Let
![]() $t>0$
. Since
$t>0$
. Since
![]() $z\mapsto (1+z) e^{-z}$
is non-increasing on
$z\mapsto (1+z) e^{-z}$
is non-increasing on
![]() $(0,\infty)$
and
$(0,\infty)$
and
![]() $|x-y|\le x+y$
for
$|x-y|\le x+y$
for
![]() $(x,y)\in (0,\infty)^2$
, we see that
$(x,y)\in (0,\infty)^2$
, we see that
for
![]() $(x,y)\in (0,\infty)^2$
and infer from Fubini–Tonelli’s theorem that
$(x,y)\in (0,\infty)^2$
and infer from Fubini–Tonelli’s theorem that
 \begin{align*} & \int_0^\infty x^m \left| \int_0^\infty \left[ \left( 1 + \frac{|x-y|^2}{4t} \right) k(t,x-y) - \left( 1+ \frac{|x+y|^2}{4t} \right) k(t,x+y) \right] f(y)\ \mathrm{d}y \right|\ \mathrm{d}x \\[6pt] & \le \int_0^\infty x^m \int_0^\infty \left[ \left( 1 + \frac{|x-y|^2}{4t} \right) k(t,x-y) - \left( 1+ \frac{|x+y|^2}{4t} \right) k(t,x+y) \right] |f(y)|\ \mathrm{d}y\mathrm{d}x \\[6pt] & = \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \left[ \int_{-y/2\sqrt{t}}^\infty \left( y+2z\sqrt{t} \right)^m (1+z^2) e^{-z^2}\ \mathrm{d}z \right. \\[6pt] &\qquad\qquad\qquad\quad\qquad\qquad\quad \left. - \int_{-\infty}^{-y/2\sqrt{t}} \left( -y-2z\sqrt{t} \right)^m (1+z^2) e^{-z^2}\ \mathrm{d}z \right]\ \mathrm{d}y \\[6pt] & = \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-\infty}^\infty \left| y+2z\sqrt{t} \right|^{m-1} \left( y+2z\sqrt{t} \right) (1+z^2) e^{-z^2}\ \mathrm{d}z\mathrm{d}y \,. \end{align*}
\begin{align*} & \int_0^\infty x^m \left| \int_0^\infty \left[ \left( 1 + \frac{|x-y|^2}{4t} \right) k(t,x-y) - \left( 1+ \frac{|x+y|^2}{4t} \right) k(t,x+y) \right] f(y)\ \mathrm{d}y \right|\ \mathrm{d}x \\[6pt] & \le \int_0^\infty x^m \int_0^\infty \left[ \left( 1 + \frac{|x-y|^2}{4t} \right) k(t,x-y) - \left( 1+ \frac{|x+y|^2}{4t} \right) k(t,x+y) \right] |f(y)|\ \mathrm{d}y\mathrm{d}x \\[6pt] & = \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \left[ \int_{-y/2\sqrt{t}}^\infty \left( y+2z\sqrt{t} \right)^m (1+z^2) e^{-z^2}\ \mathrm{d}z \right. \\[6pt] &\qquad\qquad\qquad\quad\qquad\qquad\quad \left. - \int_{-\infty}^{-y/2\sqrt{t}} \left( -y-2z\sqrt{t} \right)^m (1+z^2) e^{-z^2}\ \mathrm{d}z \right]\ \mathrm{d}y \\[6pt] & = \frac{1}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-\infty}^\infty \left| y+2z\sqrt{t} \right|^{m-1} \left( y+2z\sqrt{t} \right) (1+z^2) e^{-z^2}\ \mathrm{d}z\mathrm{d}y \,. \end{align*}
Consequently,
 \begin{align*} & 2t \left\| \frac{\mathrm{d}}{\mathrm{d}t} e^{tA_{0,m}}f \right\|_{X_{1,m}} \\[3pt] & \qquad \le 3 \left\| e^{tA_{0,m}}f \right\|_{X_{1,m}} + \frac{2}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-\infty}^\infty \left( y+2z\sqrt{t} \right) (1+z^2) e^{-z^2}\ \mathrm{d}z\mathrm{d}y \\ & \qquad\qquad + \frac{2}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-\infty}^\infty \left| y+2z\sqrt{t} \right|^{m-1} \left( y+2z\sqrt{t} \right) (1+z^2) e^{-z^2}\ \mathrm{d}z \, \mathrm{d}y\,, \end{align*}
\begin{align*} & 2t \left\| \frac{\mathrm{d}}{\mathrm{d}t} e^{tA_{0,m}}f \right\|_{X_{1,m}} \\[3pt] & \qquad \le 3 \left\| e^{tA_{0,m}}f \right\|_{X_{1,m}} + \frac{2}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-\infty}^\infty \left( y+2z\sqrt{t} \right) (1+z^2) e^{-z^2}\ \mathrm{d}z\mathrm{d}y \\ & \qquad\qquad + \frac{2}{\sqrt{\pi}} \int_0^\infty |f(y)| \int_{-\infty}^\infty \left| y+2z\sqrt{t} \right|^{m-1} \left( y+2z\sqrt{t} \right) (1+z^2) e^{-z^2}\ \mathrm{d}z \, \mathrm{d}y\,, \end{align*}
so that
by Lebesgue’s convergence theorem. It then follows from [Reference Engel and Nagel14, Theorem II.4.6 (c)] that this property implies the analyticity of
![]() $(e^{tA_{0,m}})_{t\ge 0}$
on
$(e^{tA_{0,m}})_{t\ge 0}$
on
![]() $X_{1,m}$
. Thus, the proof is complete.
$X_{1,m}$
. Thus, the proof is complete.
The proof of Proposition 3.1 is now a consequence of the previous lemma and an interpolation argument as shown next.
Proof of Proposition 3.1. We only have to consider the case
![]() $m\in (1,3)$
. Since
$m\in (1,3)$
. Since
![]() $A_{0,1}\in\mathcal{H}( X_{1,1})$
and
$A_{0,1}\in\mathcal{H}( X_{1,1})$
and
![]() $A_{0,3}\in\mathcal{H}(X_{1,3})$
according to Lemma 3.2, Hille’s characterization implies that there are
$A_{0,3}\in\mathcal{H}(X_{1,3})$
according to Lemma 3.2, Hille’s characterization implies that there are
![]() $\lambda_0>0$
and
$\lambda_0>0$
and
![]() $\kappa\ge 1$
such that
$\kappa\ge 1$
such that
see [Reference Engel and Nagel14, Theorem II.4.6 (d)] for instance. Since
![]() $(\lambda-A_{0,3})^{-1}=(\lambda-A_{0,1})^{-1}|_{X_{1,3}}$
, it readily follows by interpolation that
$(\lambda-A_{0,3})^{-1}=(\lambda-A_{0,1})^{-1}|_{X_{1,3}}$
, it readily follows by interpolation that
Obviously,
![]() $A_{0,m}$
is closed and densely defined in
$A_{0,m}$
is closed and densely defined in
![]() $X_{1,m}$
. Let
$X_{1,m}$
. Let
![]() $g\in X_{1,m}$
be arbitrary and
$g\in X_{1,m}$
be arbitrary and
![]() $\textsf{Re}\, \lambda> \lambda_0$
. There is a unique
$\textsf{Re}\, \lambda> \lambda_0$
. There is a unique
![]() $f\in \mathrm{dom}(A_{0,1})$
such that
$f\in \mathrm{dom}(A_{0,1})$
such that
![]() $(\lambda-A_{0,1})f=g$
. By (3.16),
$(\lambda-A_{0,1})f=g$
. By (3.16),
![]() $f=(\lambda-A_{0,1})^{-1}|_{X_{1,m}}g\in X_{1,m}$
and
$f=(\lambda-A_{0,1})^{-1}|_{X_{1,m}}g\in X_{1,m}$
and
![]() $f''=A_{0,m}f=\lambda f-g\in X_{1,m}$
. From this identity, we deduce
$f''=A_{0,m}f=\lambda f-g\in X_{1,m}$
. From this identity, we deduce
![]() $f\in \mathrm{dom}(A_{0,m})$
with
$f\in \mathrm{dom}(A_{0,m})$
with
![]() $A_{0,m} f=A_{0,1}f$
and
$A_{0,m} f=A_{0,1}f$
and
![]() $(\lambda-A_{0,m})f=g$
. Since f is unique, we conclude that
$(\lambda-A_{0,m})f=g$
. Since f is unique, we conclude that
![]() $\lambda\in\rho(A_{0,m})$
and
$\lambda\in\rho(A_{0,m})$
and
that is,
![]() $(\lambda-A_{0,m})^{-1}=(\lambda-A_{0,1})^{-1}|_{X_{1,m}}$
. Invoking (3.16) we derive that
$(\lambda-A_{0,m})^{-1}=(\lambda-A_{0,1})^{-1}|_{X_{1,m}}$
. Invoking (3.16) we derive that
and thus conclude that
![]() $A_{0,m}\in\mathcal{H}(X_{1,m})$
with
$A_{0,m}\in\mathcal{H}(X_{1,m})$
with
![]() $e^{tA_{0,m}} = e^{tA_{0,1}}|_{X_{1,m}}$
for
$e^{tA_{0,m}} = e^{tA_{0,1}}|_{X_{1,m}}$
for
![]() $t\ge 0$
. The fact that
$t\ge 0$
. The fact that
![]() $A_{0,m} \in \mathcal{G}(X_{1,m},1,\omega_m)$
follows again by interpolation using Lemma 3.2.
$A_{0,m} \in \mathcal{G}(X_{1,m},1,\omega_m)$
follows again by interpolation using Lemma 3.2.
4 The absorption semigroup
Let
![]() $a\in L_{\infty,loc}([0,\infty))$
be a nonnegative function and
$a\in L_{\infty,loc}([0,\infty))$
be a nonnegative function and
![]() $m\ge 1$
. We recall the definition (1.4) of the Schrödinger operator
$m\ge 1$
. We recall the definition (1.4) of the Schrödinger operator
![]() $A_{a,m}$
on
$A_{a,m}$
on
![]() $X_{1,m}$
given by
$X_{1,m}$
given by
The main result of this section is that
![]() $A_{a,m}\in \mathcal{G}_+(X_{1,m},1,\omega_m)\cap \mathcal{H}(X_{1,m})$
, the parameter
$A_{a,m}\in \mathcal{G}_+(X_{1,m},1,\omega_m)\cap \mathcal{H}(X_{1,m})$
, the parameter
![]() $\omega_m$
being defined in Proposition 3.1. The proof relies on [Reference Arendt and Batty3].
$\omega_m$
being defined in Proposition 3.1. The proof relies on [Reference Arendt and Batty3].
Proposition 4.1 Assume that a satisfies (1.2) and let
![]() $m\ge 1$
. Then
$m\ge 1$
. Then
Moreover,
![]() $e^{tA_{a,m}} = e^{tA_{a,1}}|_{X_{1,m}}$
for
$e^{tA_{a,m}} = e^{tA_{a,1}}|_{X_{1,m}}$
for
![]() $t\ge 0$
.
$t\ge 0$
.
Proof. Let us recall that
![]() $X_{1,m}$
is a Banach lattice with order-continuous norm, see [Reference Aliprantis and Burkinshaw1, Chapter 4] for a precise definition and a complete list of properties, and introduce
$X_{1,m}$
is a Banach lattice with order-continuous norm, see [Reference Aliprantis and Burkinshaw1, Chapter 4] for a precise definition and a complete list of properties, and introduce
We first observe that
![]() $\left( \mathrm{dom}(A_{0,m})\cap Y \right)^\perp = \{0\}$
, where the disjoint complement
$\left( \mathrm{dom}(A_{0,m})\cap Y \right)^\perp = \{0\}$
, where the disjoint complement
![]() $F^\perp$
of a subset F of the vector lattice
$F^\perp$
of a subset F of the vector lattice
![]() $X_{1,m}$
is given by
$X_{1,m}$
is given by
Indeed, since
![]() $C_c^\infty((0,\infty))$
is a subset of
$C_c^\infty((0,\infty))$
is a subset of
![]() $\mathrm{dom}(A_{0,m})\cap Y$
, we readily deduce that
$\mathrm{dom}(A_{0,m})\cap Y$
, we readily deduce that
![]() $g\equiv 0$
for
$g\equiv 0$
for
![]() $g\in \left( \mathrm{dom}(A_{0,m})\cap Y \right)^\perp$
. Consequently, we are in a position to apply [Reference Arendt and Batty3, Proposition 4.3] and conclude that there is an extension
$g\in \left( \mathrm{dom}(A_{0,m})\cap Y \right)^\perp$
. Consequently, we are in a position to apply [Reference Arendt and Batty3, Proposition 4.3] and conclude that there is an extension
![]() $\hat{A}_{a,m}\in \mathcal{G}_+(X_{1,m})$
of
$\hat{A}_{a,m}\in \mathcal{G}_+(X_{1,m})$
of
![]() $A_{a,m}$
with domain
$A_{a,m}$
with domain
![]() $\mathrm{dom}(\hat{A}_{a,m})$
defined as follows:
$\mathrm{dom}(\hat{A}_{a,m})$
defined as follows:
![]() $f\in \mathrm{dom}(\hat{A}_{a,m})$
if and only if
$f\in \mathrm{dom}(\hat{A}_{a,m})$
if and only if
![]() $f\in X_{1,m}$
and there exist
$f\in X_{1,m}$
and there exist
![]() $(f_n)_{n\ge 1}$
in
$(f_n)_{n\ge 1}$
in
![]() $\mathrm{dom}(A_{0,m})$
and
$\mathrm{dom}(A_{0,m})$
and
![]() $g\in X_{1,m}$
such that
$g\in X_{1,m}$
such that
It first follows from Lemma 4.2 below that
![]() $\mathrm{dom}(\hat{A}_{a,m})=\mathrm{dom}(A_{a,m})$
and therefore
$\mathrm{dom}(\hat{A}_{a,m})=\mathrm{dom}(A_{a,m})$
and therefore
![]() $\hat{A}_{a,m}=A_{a,m}$
. Moreover,
$\hat{A}_{a,m}=A_{a,m}$
. Moreover,
![]() $0\le e^{t A_{a,m}}=e^{t \hat{A}_{a,m}}\le e^{t A_{0,m}}$
for
$0\le e^{t A_{a,m}}=e^{t \hat{A}_{a,m}}\le e^{t A_{0,m}}$
for
![]() $t\ge 0$
by [Reference Arendt and Batty3, p. 432]. Since
$t\ge 0$
by [Reference Arendt and Batty3, p. 432]. Since
![]() $A_{0,m}\in\mathcal{G}_+(X_{1,m},1,\omega_m)$
due to Proposition 3.1, this ordering property, along with [Reference Banasiak and Arlotti7, Remark 2.68], implies
$A_{0,m}\in\mathcal{G}_+(X_{1,m},1,\omega_m)$
due to Proposition 3.1, this ordering property, along with [Reference Banasiak and Arlotti7, Remark 2.68], implies
Hence
![]() $\hat{A}_{a,m}\in \mathcal{G}_+(X_{1,m},1,\omega_m)$
. Finally, recalling that
$\hat{A}_{a,m}\in \mathcal{G}_+(X_{1,m},1,\omega_m)$
. Finally, recalling that
by Proposition 3.1, we infer from [Reference Arendt and Batty3, Theorem 6.1] that
![]() $A_{a,m}\in \mathcal{H}(X_{1,m})$
.
$A_{a,m}\in \mathcal{H}(X_{1,m})$
.
It remains to check that
![]() $\mathrm{dom}(\hat{A}_{a,m})=\mathrm{dom}(A_{a,m})$
. This property actually follows from the monotonicity of the Laplace operator
$\mathrm{dom}(\hat{A}_{a,m})=\mathrm{dom}(A_{a,m})$
. This property actually follows from the monotonicity of the Laplace operator
![]() $A_{0,m}$
and the multiplication
$A_{0,m}$
and the multiplication
![]() $f\mapsto af$
.
$f\mapsto af$
.
Lemma 4.2 Assume that a satisfies (1.2) and let
![]() $m\ge 1$
. Then
$m\ge 1$
. Then
![]() $\mathrm{dom}(\hat{A}_{a,m})=\mathrm{dom}(A_{a,m})$
.
$\mathrm{dom}(\hat{A}_{a,m})=\mathrm{dom}(A_{a,m})$
.
Proof. Pick
![]() $f\in \mathrm{dom}(\hat{A}_{a,m})$
. Then there are a sequence
$f\in \mathrm{dom}(\hat{A}_{a,m})$
. Then there are a sequence
![]() $(f_n)_{n\ge 1}$
in
$(f_n)_{n\ge 1}$
in
![]() $\mathrm{dom}(A_{0,m})$
and
$\mathrm{dom}(A_{0,m})$
and
![]() $g\in X_{1,m}$
such that
$g\in X_{1,m}$
such that
with
![]() $g_n := - A_{0,m}f_n + (a\wedge n) f_n$
for
$g_n := - A_{0,m}f_n + (a\wedge n) f_n$
for
![]() $n\ge 1$
. In particular,
$n\ge 1$
. In particular,
Step 1. Let us first prove that
![]() $af\in X_{1,m}$
. We infer from Lemma 2.3 that, for
$af\in X_{1,m}$
. We infer from Lemma 2.3 that, for
![]() $n\ge 1$
,
$n\ge 1$
,
 \begin{align*} \|g_n\|_{X_m} & \ge \int_0^\infty x^m\, \mathrm{sign}(f_n(x))\, g_n(x)\ \mathrm{d}x \\[3pt] & \ge m \int_0^\infty x^{m-1}\ |f_n|'(x)\ \mathrm{d}x + \int_0^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x \\[3pt] & = - m(m-1) \|f_n\|_{X_{m-2}} + \int_0^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x\,. \end{align*}
\begin{align*} \|g_n\|_{X_m} & \ge \int_0^\infty x^m\, \mathrm{sign}(f_n(x))\, g_n(x)\ \mathrm{d}x \\[3pt] & \ge m \int_0^\infty x^{m-1}\ |f_n|'(x)\ \mathrm{d}x + \int_0^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x \\[3pt] & = - m(m-1) \|f_n\|_{X_{m-2}} + \int_0^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x\,. \end{align*}
In particular, we derive
Next, if
![]() $m\ge 3$
, then it follows from Young’s inequality that
$m\ge 3$
, then it follows from Young’s inequality that
 \begin{align*} \int_0^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x & \le m(m-1) \left[ \frac{m-3}{m-1} \|f_n\|_{X_m} + \frac{2}{m-1} \|f_n\|_{X_1} \right] + \|g_n\|_{X_m} \\[3pt] & \le [m(m-1)+1] \kappa\,. \end{align*}
\begin{align*} \int_0^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x & \le m(m-1) \left[ \frac{m-3}{m-1} \|f_n\|_{X_m} + \frac{2}{m-1} \|f_n\|_{X_1} \right] + \|g_n\|_{X_m} \\[3pt] & \le [m(m-1)+1] \kappa\,. \end{align*}
Likewise, if
![]() $m\in (1,3)$
, then Lemma 2.1 implies that
$m\in (1,3)$
, then Lemma 2.1 implies that
 \begin{align*} \int_0^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x & \le m(m-1) \left[ \frac{1}{m-1} \|f_n^{\prime\prime}\|_{X_1} + \|f_n\|_{X_1} \right] + \|g_n\|_{X_m} \\[3pt] & \le m \|(a\wedge n) f_n -g_n\|_{X_1} + [m(m-1)+1]\kappa \\[3pt] & \le m \sup_{l\ge 1} \{\|(a\wedge l) f_l\|_{X_1}\} + (m^2+1) \kappa\\[3pt] & \le(m^2+m+1) \kappa \,, \end{align*}
\begin{align*} \int_0^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x & \le m(m-1) \left[ \frac{1}{m-1} \|f_n^{\prime\prime}\|_{X_1} + \|f_n\|_{X_1} \right] + \|g_n\|_{X_m} \\[3pt] & \le m \|(a\wedge n) f_n -g_n\|_{X_1} + [m(m-1)+1]\kappa \\[3pt] & \le m \sup_{l\ge 1} \{\|(a\wedge l) f_l\|_{X_1}\} + (m^2+1) \kappa\\[3pt] & \le(m^2+m+1) \kappa \,, \end{align*}
where the last inequality is due to (4.2). Thus, in all cases for
![]() $m\ge 1$
, we have shown that
$m\ge 1$
, we have shown that
Fixing
![]() $N\ge 1$
, we deduce from the previous estimate that, for all
$N\ge 1$
, we deduce from the previous estimate that, for all
![]() $n\ge N$
,
$n\ge N$
,
We then let
![]() $n\to\infty$
and infer from (4.1) that
$n\to\infty$
and infer from (4.1) that
Using Fatou’s lemma to let
![]() $N\to\infty$
, we conclude that
$N\to\infty$
, we conclude that
![]() $af\in X_{1,m}$
with
$af\in X_{1,m}$
with
Step 2. We next show that
![]() $((a\wedge n) f_n)_{n\ge 1}$
converges to af in
$((a\wedge n) f_n)_{n\ge 1}$
converges to af in
![]() $X_{1,m}$
. Let
$X_{1,m}$
. Let
![]() $\chi\in C^\infty((0,\infty))$
be such that
$\chi\in C^\infty((0,\infty))$
be such that
![]() $\chi(x)=1$
for
$\chi(x)=1$
for
![]() $x> 2$
,
$x> 2$
,
![]() $\chi(x)=0$
for
$\chi(x)=0$
for
![]() $x\in (0,1)$
, and
$x\in (0,1)$
, and
![]() $\chi(x)\in [0,1]$
for
$\chi(x)\in [0,1]$
for
![]() $x\in [1,2]$
. Introducing
$x\in [1,2]$
. Introducing
![]() $\chi_R(x) := \chi(x/R)$
for
$\chi_R(x) := \chi(x/R)$
for
![]() $x\in (0,\infty)$
and
$x\in (0,\infty)$
and
![]() $R>1$
, we deduce from Lemma 2.3 (with
$R>1$
, we deduce from Lemma 2.3 (with
![]() $\ell(x) = x^m \chi_R(x)$
) that
$\ell(x) = x^m \chi_R(x)$
) that
 \begin{align*} \int_0^\infty x^m\ (a(x)\wedge n) \chi_R(x) |f_n(x)|\ \mathrm{d}x & + \int_0^\infty [x^m \chi_R^{\prime}(x) + m x^{m-1} \chi_R(x)] |f_n|'(x)\ \mathrm{d}x \\[3pt] & \le \int_0^\infty x\chi_R(x) \mathrm{sign}(f_n(x)) g_n(x)\ \mathrm{d}x \\[3pt] & \le \int_R^\infty x\ |g_n(x)|\ \mathrm{d}x\,. \end{align*}
\begin{align*} \int_0^\infty x^m\ (a(x)\wedge n) \chi_R(x) |f_n(x)|\ \mathrm{d}x & + \int_0^\infty [x^m \chi_R^{\prime}(x) + m x^{m-1} \chi_R(x)] |f_n|'(x)\ \mathrm{d}x \\[3pt] & \le \int_0^\infty x\chi_R(x) \mathrm{sign}(f_n(x)) g_n(x)\ \mathrm{d}x \\[3pt] & \le \int_R^\infty x\ |g_n(x)|\ \mathrm{d}x\,. \end{align*}
Since
 \begin{align*} & \int_0^\infty [x^m \chi_R^{\prime}(x) + m x^{m-1} \chi_R(x)] |f_n|'(x)\ \mathrm{d}x \\[3pt] & = - \int_0^\infty [x^m \chi_R^{\prime\prime}(x) + 2m x^{m-1} \chi_R^{\prime}(x) + m(m-1) x^{m-2} \chi_R(x)] |f_n(x)|\ \mathrm{d}x \\[3pt] & = - \int_0^\infty x^m\ |f_n(x)| \left[ \frac{1}{R^2} \chi''\left( \frac{x}{R} \right) + \frac{2m}{Rx} \chi'\left( \frac{x}{R} \right) + \frac{m(m-1)}{x^2} \chi\left( \frac{x}{R} \right) \right]\ \mathrm{d}x \end{align*}
\begin{align*} & \int_0^\infty [x^m \chi_R^{\prime}(x) + m x^{m-1} \chi_R(x)] |f_n|'(x)\ \mathrm{d}x \\[3pt] & = - \int_0^\infty [x^m \chi_R^{\prime\prime}(x) + 2m x^{m-1} \chi_R^{\prime}(x) + m(m-1) x^{m-2} \chi_R(x)] |f_n(x)|\ \mathrm{d}x \\[3pt] & = - \int_0^\infty x^m\ |f_n(x)| \left[ \frac{1}{R^2} \chi''\left( \frac{x}{R} \right) + \frac{2m}{Rx} \chi'\left( \frac{x}{R} \right) + \frac{m(m-1)}{x^2} \chi\left( \frac{x}{R} \right) \right]\ \mathrm{d}x \end{align*}
and
we further obtain
 \begin{align*} \int_{2R}^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x & \le \int_0^\infty x^m\ (a(x)\wedge n) \chi_R(x) |f_n(x)|\ \mathrm{d}x \\[3pt] & \le \sup_{l\ge 1} \left\{ \int_R^\infty x^m\ |g_l(x)|\ \mathrm{d}x \right\} + \frac{3m^2}{R^2} \|\chi''\|_{L_\infty(0,\infty)} \|f_n\|_{X_m} \\[3pt] & \le \sup_{l\ge 1} \left\{ \int_R^\infty x^m\ |g_l(x)|\ \mathrm{d}x \right\} + \frac{3m^2\kappa}{R^2} \|\chi''\|_{L_\infty(0,\infty)} \end{align*}
\begin{align*} \int_{2R}^\infty x^m\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x & \le \int_0^\infty x^m\ (a(x)\wedge n) \chi_R(x) |f_n(x)|\ \mathrm{d}x \\[3pt] & \le \sup_{l\ge 1} \left\{ \int_R^\infty x^m\ |g_l(x)|\ \mathrm{d}x \right\} + \frac{3m^2}{R^2} \|\chi''\|_{L_\infty(0,\infty)} \|f_n\|_{X_m} \\[3pt] & \le \sup_{l\ge 1} \left\{ \int_R^\infty x^m\ |g_l(x)|\ \mathrm{d}x \right\} + \frac{3m^2\kappa}{R^2} \|\chi''\|_{L_\infty(0,\infty)} \end{align*}
for
![]() $n\ge 1$
. Since
$n\ge 1$
. Since
by (4.1), we conclude
Now, let
![]() $R>1$
. Since
$R>1$
. Since
![]() $a\in L_\infty(0,2R)$
by (1.2), there is
$a\in L_\infty(0,2R)$
by (1.2), there is
![]() $n_R\ge 1$
such that
$n_R\ge 1$
such that
![]() $a(x)\wedge n=a(x)$
for
$a(x)\wedge n=a(x)$
for
![]() $x\in (0,2R)$
and
$x\in (0,2R)$
and
![]() $n\ge n_R$
. Consequently, for
$n\ge n_R$
. Consequently, for
![]() $n\ge n_R$
,
$n\ge n_R$
,
 \begin{align*} \|(a\wedge n) f_n - af\|_{X_{1,m}} & \le \int_0^{2R} (x+x^m)\ a(x) |(f_n-f)(x)|\ \mathrm{d}x \\[3pt] & + \int_{2R}^\infty (x+x^m)\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x \\[3pt] & + \int_{2R}^\infty (x+x^m)\ a(x) |f(x)|\ \mathrm{d}x \\[3pt] & \le \|a\|_{L_\infty(0,2R)} \|f_n-f\|_{X_{1,m}} \\[3pt] & + \sup_{l\ge 1} \left\{ \int_{2R}^\infty (x+x^m)\ (a(x)\wedge l) |f_l(x)|\ \mathrm{d}x \right\} \\ & + \int_{2R}^\infty (x+x^m)\ a(x) |f(x)|\ \mathrm{d}x \,. \end{align*}
\begin{align*} \|(a\wedge n) f_n - af\|_{X_{1,m}} & \le \int_0^{2R} (x+x^m)\ a(x) |(f_n-f)(x)|\ \mathrm{d}x \\[3pt] & + \int_{2R}^\infty (x+x^m)\ (a(x)\wedge n) |f_n(x)|\ \mathrm{d}x \\[3pt] & + \int_{2R}^\infty (x+x^m)\ a(x) |f(x)|\ \mathrm{d}x \\[3pt] & \le \|a\|_{L_\infty(0,2R)} \|f_n-f\|_{X_{1,m}} \\[3pt] & + \sup_{l\ge 1} \left\{ \int_{2R}^\infty (x+x^m)\ (a(x)\wedge l) |f_l(x)|\ \mathrm{d}x \right\} \\ & + \int_{2R}^\infty (x+x^m)\ a(x) |f(x)|\ \mathrm{d}x \,. \end{align*}
We then pass to the limit as
![]() $n\to\infty$
and infer from (4.1) that
$n\to\infty$
and infer from (4.1) that
 \begin{align*} \limsup_{n\to\infty} \|(a\wedge n) f_n - af\|_{X_{1,m}} &\le \sup_{l\ge 1} \left\{ \int_{2R}^\infty (x+x^m)\ (a(x)\wedge l) |f_l(x)|\ \mathrm{d}x \right\}\\[3pt] &\qquad + \int_{2R}^\infty (x+x^m)\ a(x) |f(x)|\ \mathrm{d}x\,. \end{align*}
\begin{align*} \limsup_{n\to\infty} \|(a\wedge n) f_n - af\|_{X_{1,m}} &\le \sup_{l\ge 1} \left\{ \int_{2R}^\infty (x+x^m)\ (a(x)\wedge l) |f_l(x)|\ \mathrm{d}x \right\}\\[3pt] &\qquad + \int_{2R}^\infty (x+x^m)\ a(x) |f(x)|\ \mathrm{d}x\,. \end{align*}
We finally let
![]() $R\to\infty$
with the help of (4.3) and (4.4) and end up with
$R\to\infty$
with the help of (4.3) and (4.4) and end up with
Step 3. We finally show that
![]() $f\in \mathrm{dom}( A_{0,m})$
. Indeed, it readily follows from (4.1) that
$f\in \mathrm{dom}( A_{0,m})$
. Indeed, it readily follows from (4.1) that
![]() $(f_n^{\prime\prime})_{n\ge 1}$
converges to f
$(f_n^{\prime\prime})_{n\ge 1}$
converges to f
![]() $^{\prime\prime}$
in the sense of distributions, while (4.1), (4.3), and (4.5) guarantee that
$^{\prime\prime}$
in the sense of distributions, while (4.1), (4.3), and (4.5) guarantee that
![]() $(f_n^{\prime\prime})_{n\ge 1}=((a\wedge n) f_n - g_n)_{n\ge 1}$
converges to
$(f_n^{\prime\prime})_{n\ge 1}=((a\wedge n) f_n - g_n)_{n\ge 1}$
converges to
![]() $af -g$
in
$af -g$
in
![]() $X_{1,m}$
. Therefore, f
$X_{1,m}$
. Therefore, f
![]() $^{\prime\prime}$
belongs to
$^{\prime\prime}$
belongs to
![]() $X_{1,m}$
with
$X_{1,m}$
with
![]() $f''=af-g$
and
$f''=af-g$
and
![]() $(f_n^{\prime\prime})_{n\ge 1}$
converges to f
$(f_n^{\prime\prime})_{n\ge 1}$
converges to f
![]() $^{\prime\prime}$
in
$^{\prime\prime}$
in
![]() $X_{1,m}$
. Since
$X_{1,m}$
. Since
![]() $f_n(0)=0$
for
$f_n(0)=0$
for
![]() $n\ge 1$
, this convergence along with Lemma 2.1 ensures that
$n\ge 1$
, this convergence along with Lemma 2.1 ensures that
![]() $f(0)=0$
and we have proved that
$f(0)=0$
and we have proved that
![]() $f\in \mathrm{dom}(A_{0,m})$
.
$f\in \mathrm{dom}(A_{0,m})$
.
For further use, we show that the graph norm of
![]() $A_{a,m}$
in
$A_{a,m}$
in
![]() $X_{1,m}$
controls independently the diffusive and absorption terms in
$X_{1,m}$
controls independently the diffusive and absorption terms in
![]() $X_{1,m}$
.
$X_{1,m}$
.
Lemma 4.3 Assume (1.2). For
![]() $f\in \mathrm{dom}(A_{a,1})$
,
$f\in \mathrm{dom}(A_{a,1})$
,
Let
![]() $m>1$
. For
$m>1$
. For
![]() $f\in \mathrm{dom}(A_{a,m})$
,
$f\in \mathrm{dom}(A_{a,m})$
,
Proof. Let
![]() $f\in \mathrm{dom}(A_{a,1})$
and set
$f\in \mathrm{dom}(A_{a,1})$
and set
![]() $g:= -A_{a,1}f = -f''+af$
. It follows from Lemma 2.3 (with
$g:= -A_{a,1}f = -f''+af$
. It follows from Lemma 2.3 (with
![]() $\ell(x)=x$
) that
$\ell(x)=x$
) that
Consequently,
from which we deduce (4.6).
Next, let
![]() $m>1$
and consider
$m>1$
and consider
![]() $f\in \mathrm{dom}(A_{a,m})$
. We set
$f\in \mathrm{dom}(A_{a,m})$
. We set
![]() $g:= -A_{a,m}f = -f''+af$
and infer from Lemma 2.3 (with
$g:= -A_{a,m}f = -f''+af$
and infer from Lemma 2.3 (with
![]() $\ell(x)=x^m$
) that
$\ell(x)=x^m$
) that
 \begin{align*} \|g\|_{X_m} & \ge \int_0^\infty x^m\ \mathrm{sign}(f(x)) g(x)\ \mathrm{d}x \ge m \int_0^\infty x^{m-1} |f|'(x)\ \mathrm{d}x + \|a f\|_{X_m} \\[3pt] & = \|a f\|_{X_m} - m(m-1) \|f\|_{X_{m-2}}\,. \end{align*}
\begin{align*} \|g\|_{X_m} & \ge \int_0^\infty x^m\ \mathrm{sign}(f(x)) g(x)\ \mathrm{d}x \ge m \int_0^\infty x^{m-1} |f|'(x)\ \mathrm{d}x + \|a f\|_{X_m} \\[3pt] & = \|a f\|_{X_m} - m(m-1) \|f\|_{X_{m-2}}\,. \end{align*}
Either
![]() $m\ge 3$
and it follows from Young’s inequality and the above inequality that
$m\ge 3$
and it follows from Young’s inequality and the above inequality that
 \begin{align} \|a f\|_{X_m} & \le \|g\|_{X_m} + m(m-1) \left( \frac{m-3}{m-1} \|f\|_{X_m} + \frac{2}{m-1} \|f\|_{X_1} \right) \nonumber \\[3pt] & \le \|g\|_{X_m} + m(m-3) \|f\|_{X_m} + 2m \|f\|_{X_1} \nonumber \\[3pt] & \le \|g\|_{X_m} + m^2 \|f\|_{X_{1,m}} \,. \end{align}
\begin{align} \|a f\|_{X_m} & \le \|g\|_{X_m} + m(m-1) \left( \frac{m-3}{m-1} \|f\|_{X_m} + \frac{2}{m-1} \|f\|_{X_1} \right) \nonumber \\[3pt] & \le \|g\|_{X_m} + m(m-3) \|f\|_{X_m} + 2m \|f\|_{X_1} \nonumber \\[3pt] & \le \|g\|_{X_m} + m^2 \|f\|_{X_{1,m}} \,. \end{align}
Or
![]() $m\in (1,3)$
and we infer from (2.2) and (4.8) that
$m\in (1,3)$
and we infer from (2.2) and (4.8) that
 \begin{align} \|a f\|_{X_m} & \le \|g\|_{X_m} + m(m-1) \left( \frac{1}{m-1} \|f''\|_{X_1} + \|f\|_{X_1} \right) \nonumber \\[3pt] & \le \|g\|_{X_m} + m \|A_{0,1}f\|_{X_1} + m(m-1) \|f\|_{X_1} \nonumber \\[3pt] & \le \|g\|_{X_m} + 2m \|A_{a,1}f\|_{X_1} + m^2 \|f\|_{X_1} \,. \end{align}
\begin{align} \|a f\|_{X_m} & \le \|g\|_{X_m} + m(m-1) \left( \frac{1}{m-1} \|f''\|_{X_1} + \|f\|_{X_1} \right) \nonumber \\[3pt] & \le \|g\|_{X_m} + m \|A_{0,1}f\|_{X_1} + m(m-1) \|f\|_{X_1} \nonumber \\[3pt] & \le \|g\|_{X_m} + 2m \|A_{a,1}f\|_{X_1} + m^2 \|f\|_{X_1} \,. \end{align}
Collecting (4.8) and (4.9) leads us to
which in turn gives
Consequently,
from which (4.7) follows.
5 The fragmentation-diffusion semigroup
We now consider the operator
![]() $\mathbb{A}_m=A_{a,m}+B_m$
, where we recall that the nonlocal operator
$\mathbb{A}_m=A_{a,m}+B_m$
, where we recall that the nonlocal operator
![]() $B_{m}$
on
$B_{m}$
on
![]() $X_{1,m}$
is defined by
$X_{1,m}$
is defined by
 \begin{align*} \mathrm{dom}(B_m) & = \{ f\in X_{1,m}\ : \ af \in X_{1,m}\}\,, \\ B_mf(x) & = \int_x^\infty a(y) b(x,y) f(y)\ \mathrm{d}y\,, \quad x\in (0,\infty)\,, \qquad f\in \mathrm{dom}(B_m)\,. \end{align*}
\begin{align*} \mathrm{dom}(B_m) & = \{ f\in X_{1,m}\ : \ af \in X_{1,m}\}\,, \\ B_mf(x) & = \int_x^\infty a(y) b(x,y) f(y)\ \mathrm{d}y\,, \quad x\in (0,\infty)\,, \qquad f\in \mathrm{dom}(B_m)\,. \end{align*}
We first show that
![]() $B_m$
is
$B_m$
is
![]() $A_{a,m}$
-bounded in
$A_{a,m}$
-bounded in
![]() $X_{1,m}$
.
$X_{1,m}$
.
Lemma 5.1 Assume (1.2) and (1.3). Let
![]() $m\ge 1$
and consider a measurable function f on
$m\ge 1$
and consider a measurable function f on
![]() $(0,\infty)$
such that
$(0,\infty)$
such that
![]() $af\in X_m$
. Then
$af\in X_m$
. Then
In addition,
and
![]() $B_m$
is
$B_m$
is
![]() $A_{a,m}$
-bounded in
$A_{a,m}$
-bounded in
![]() $X_{1,m}$
.
$X_{1,m}$
.
Proof. We infer from (1.3) and Fubini–Tonelli’s theorem that
 \begin{align*} \int_0^\infty x^m \int_x^\infty a(y) b(x,y) |f(y)|\ \mathrm{d}y\mathrm{d}x & = \int_0^\infty a(y) |f(y)| \int_0^y x^m b(x,y)\ \mathrm{d}x\mathrm{d}y \\[3pt] & \le \int_0^\infty y^{m-1} a(y) |f(y)| \int_0^y x b(x,y)\ \mathrm{d}x\mathrm{d}y = \|af\|_{X_m}\,, \end{align*}
\begin{align*} \int_0^\infty x^m \int_x^\infty a(y) b(x,y) |f(y)|\ \mathrm{d}y\mathrm{d}x & = \int_0^\infty a(y) |f(y)| \int_0^y x^m b(x,y)\ \mathrm{d}x\mathrm{d}y \\[3pt] & \le \int_0^\infty y^{m-1} a(y) |f(y)| \int_0^y x b(x,y)\ \mathrm{d}x\mathrm{d}y = \|af\|_{X_m}\,, \end{align*}
from which (5.1) readily follows. Next, (5.2) is a straightforward consequence of (1.3) and Fubini’s theorem.
Finally, let
![]() $f\in \mathrm{dom}(A_{a,m}) \subset \mathrm{dom}(B_m)$
. By (4.7) and (5.1),
$f\in \mathrm{dom}(A_{a,m}) \subset \mathrm{dom}(B_m)$
. By (4.7) and (5.1),
 \begin{align*} \|B_mf \|_{X_{1,m}} & \le \int_0^\infty (x+x^m) \left| \int_x^\infty a(y) b(x,y) f(y)\ \mathrm{d}y \right|\ \mathrm{d}x \le \|a f\|_{X_{1,m}} \\[3pt] & \le 4 (m+1) \|A_{a,m}f\|_{X_{1,m}} + 4m(m+1) \|f\|_{X_{1,m}}\,, \end{align*}
\begin{align*} \|B_mf \|_{X_{1,m}} & \le \int_0^\infty (x+x^m) \left| \int_x^\infty a(y) b(x,y) f(y)\ \mathrm{d}y \right|\ \mathrm{d}x \le \|a f\|_{X_{1,m}} \\[3pt] & \le 4 (m+1) \|A_{a,m}f\|_{X_{1,m}} + 4m(m+1) \|f\|_{X_{1,m}}\,, \end{align*}
so that
![]() $B_m$
is
$B_m$
is
![]() $A_{a,m}$
-bounded.
$A_{a,m}$
-bounded.
As already observed in the literature, see, e.g., [Reference Banasiak, Lamb and Laurençot8, Theorem 5.1.47 (c)], the inequality (1.8) implies that, for each
![]() $m>1$
, there is
$m>1$
, there is
![]() $\delta_m\in (0,1)$
such that
$\delta_m\in (0,1)$
such that
An immediate consequence of (5.3) is a strict domination of a f over
![]() $B_m f$
in
$B_m f$
in
![]() $X_m$
.
$X_m$
.
Lemma 5.2 Assume (1.2), (1.3), and (1.8). Let
![]() $m>1$
and consider
$m>1$
and consider
![]() $f\in \mathrm{dom}(B_m)$
. Then
$f\in \mathrm{dom}(B_m)$
. Then
Proof. It readily follows from (5.3) and Fubini’s theorem that
 \begin{align*} \|B_m f\|_{X_m} & \le \int_0^\infty x^m \int_x^\infty a(y) b(x,y) |f(y)|\ \mathrm{d}y\mathrm{d}x = \int_0^\infty a(y) |f(y)| \int_0^y x^m b(x,y)\ \mathrm{d}x\mathrm{d}y \\[3pt] & \le (1-\delta_m) \int_0^\infty y^m a(y) |f(y)| \mathrm{d}y =(1-\delta_m) \|af\|_{X_m}\,. \end{align*}
\begin{align*} \|B_m f\|_{X_m} & \le \int_0^\infty x^m \int_x^\infty a(y) b(x,y) |f(y)|\ \mathrm{d}y\mathrm{d}x = \int_0^\infty a(y) |f(y)| \int_0^y x^m b(x,y)\ \mathrm{d}x\mathrm{d}y \\[3pt] & \le (1-\delta_m) \int_0^\infty y^m a(y) |f(y)| \mathrm{d}y =(1-\delta_m) \|af\|_{X_m}\,. \end{align*}
We shall see next that the property (5.3) ensures that
![]() $B_m$
is a Miyadera perturbation of
$B_m$
is a Miyadera perturbation of
![]() $A_{a,m}$
. Recall that a similar result is available for the fragmentation equation without diffusion [Reference Banasiak6].
$A_{a,m}$
. Recall that a similar result is available for the fragmentation equation without diffusion [Reference Banasiak6].
Proposition 5.3 Let
![]() $m>1$
and assume (1.2), (1.3), and (1.8). Then there are
$m>1$
and assume (1.2), (1.3), and (1.8). Then there are
![]() $q_m\in (0,1)$
and
$q_m\in (0,1)$
and
![]() $t_m>0$
such that
$t_m>0$
such that
In particular,
![]() $B_m$
is a Miyadera perturbation of
$B_m$
is a Miyadera perturbation of
![]() $A_{a,m}$
.
$A_{a,m}$
.
Proof. Consider
![]() $f\in \mathrm{dom}(A_{a,m})$
and set
$f\in \mathrm{dom}(A_{a,m})$
and set
![]() $F(t) := e^{tA_{a,m}}f$
for
$F(t) := e^{tA_{a,m}}f$
for
![]() $t\ge 0$
. Owing to Proposition 4.1, we have
$t\ge 0$
. Owing to Proposition 4.1, we have
In addition, F is a classical solution to
and we deduce from Lemma 2.3 (with
![]() $\ell(x)=x^m$
) that
$\ell(x)=x^m$
) that
Hence, after integration with respect to time,
Now, let
![]() $t>0$
. It follows from (1.3), (5.1) (with
$t>0$
. It follows from (1.3), (5.1) (with
![]() $m=1$
), and Lemma 5.2 that
$m=1$
), and Lemma 5.2 that
For
![]() $R>1$
, we infer from (1.2) and (5.4) that
$R>1$
, we infer from (1.2) and (5.4) that
 \begin{align*} \int_0^t \|a F(s)\|_{X_1}\ \mathrm{d}s & \le \|a\|_{L_\infty(0,R)} \int_0^t \int_0^R x |F(s,x)|\ \mathrm{d}x\mathrm{d}s \\[3pt] & \qquad + R^{1-m} \int_0^t \int_R^\infty x^m a(x) |F(s,x)|\ \mathrm{d}x\mathrm{d}s \\[3pt] & \le \|a\|_{L_\infty(0,R)} \int_0^t \|F(s)\|_{X_1}\ \mathrm{d}s + R^{1-m} \int_0^t \int_0^\infty x^m a(x) |F(s,x)|\ \mathrm{d}x\mathrm{d}s \\[3pt] & \le \|a\|_{L_\infty(0,R)} \|f\|_{X_1} t + R^{1-m} \int_0^t \| a F(s)\|_{X_m}\ \mathrm{d}s\,. \end{align*}
\begin{align*} \int_0^t \|a F(s)\|_{X_1}\ \mathrm{d}s & \le \|a\|_{L_\infty(0,R)} \int_0^t \int_0^R x |F(s,x)|\ \mathrm{d}x\mathrm{d}s \\[3pt] & \qquad + R^{1-m} \int_0^t \int_R^\infty x^m a(x) |F(s,x)|\ \mathrm{d}x\mathrm{d}s \\[3pt] & \le \|a\|_{L_\infty(0,R)} \int_0^t \|F(s)\|_{X_1}\ \mathrm{d}s + R^{1-m} \int_0^t \int_0^\infty x^m a(x) |F(s,x)|\ \mathrm{d}x\mathrm{d}s \\[3pt] & \le \|a\|_{L_\infty(0,R)} \|f\|_{X_1} t + R^{1-m} \int_0^t \| a F(s)\|_{X_m}\ \mathrm{d}s\,. \end{align*}
Combining (5.5), (5.6), and the above estimate with
![]() $R=R_m:=(\delta_m/2)^{1/(1-m)}$
gives
$R=R_m:=(\delta_m/2)^{1/(1-m)}$
gives
 \begin{align} \int_0^t \| B_mF(s)\|_{X_{1,m}}\ \mathrm{d}s & \le \|a\|_{L_\infty(0,R_m)} \|f\|_{X_1} t + \left( 1 - \frac{\delta_m}{2} \right) \int_0^t \| a F(s)\|_{X_m}\ \mathrm{d}s \nonumber \\[3pt] & \le \|a\|_{L_\infty(0,R_m)} \|f\|_{X_1} t + \left( 1 - \frac{\delta_m}{2} \right) \|f\|_{X_m} \nonumber \\[3pt] & \qquad + m(m-1)\left( 1 - \frac{\delta_m}{2} \right) \int_0^t \|F(s)\|_{X_{m-2}}\ \mathrm{d}s \nonumber \\[3pt] & \le \|a\|_{L_\infty(0,R_m)} \|f\|_{X_1} t + \left( 1 - \frac{\delta_m}{2} \right) \|f\|_{X_m} \nonumber \\[3pt] & \qquad + m(m-1) \int_0^t \|F(s)\|_{X_{m-2}}\ \mathrm{d}s\,. \end{align}
\begin{align} \int_0^t \| B_mF(s)\|_{X_{1,m}}\ \mathrm{d}s & \le \|a\|_{L_\infty(0,R_m)} \|f\|_{X_1} t + \left( 1 - \frac{\delta_m}{2} \right) \int_0^t \| a F(s)\|_{X_m}\ \mathrm{d}s \nonumber \\[3pt] & \le \|a\|_{L_\infty(0,R_m)} \|f\|_{X_1} t + \left( 1 - \frac{\delta_m}{2} \right) \|f\|_{X_m} \nonumber \\[3pt] & \qquad + m(m-1)\left( 1 - \frac{\delta_m}{2} \right) \int_0^t \|F(s)\|_{X_{m-2}}\ \mathrm{d}s \nonumber \\[3pt] & \le \|a\|_{L_\infty(0,R_m)} \|f\|_{X_1} t + \left( 1 - \frac{\delta_m}{2} \right) \|f\|_{X_m} \nonumber \\[3pt] & \qquad + m(m-1) \int_0^t \|F(s)\|_{X_{m-2}}\ \mathrm{d}s\,. \end{align}
At this point, we handle the cases
![]() $m\ge 3$
and
$m\ge 3$
and
![]() $m\in (1,3)$
in a different way. We first consider
$m\in (1,3)$
in a different way. We first consider
![]() $m\ge 3$
. We use Young’s inequality, along with (5.4), to obtain
$m\ge 3$
. We use Young’s inequality, along with (5.4), to obtain
 \begin{align} m(m-1) \int_0^t \|F(s)\|_{X_{m-2}}\ \mathrm{d}s & \le m(m-1) \int_0^t \left[ \frac{m-3}{m-1} \|F(s)\|_{X_m} + \frac{2}{m-1} \|F(s)\|_{X_1} \right]\ \mathrm{d}s \nonumber \\[3pt] & \le \frac{m(m-3)}{1+\omega_m} \|f\|_{X_{1,m}} \left( e^{(1+\omega_m)t} - 1 \right) + 2m \|f\|_{X_1} t\,. \end{align}
\begin{align} m(m-1) \int_0^t \|F(s)\|_{X_{m-2}}\ \mathrm{d}s & \le m(m-1) \int_0^t \left[ \frac{m-3}{m-1} \|F(s)\|_{X_m} + \frac{2}{m-1} \|F(s)\|_{X_1} \right]\ \mathrm{d}s \nonumber \\[3pt] & \le \frac{m(m-3)}{1+\omega_m} \|f\|_{X_{1,m}} \left( e^{(1+\omega_m)t} - 1 \right) + 2m \|f\|_{X_1} t\,. \end{align}
Collecting (5.7) and (5.8) leads us to
 \begin{align*} \int_0^t \| B_mF(s)\|_{X_{1,m}}\ \mathrm{d}s & \le \left[ \|a\|_{L_\infty(0,R_m)} t + \frac{m(m-3)}{1+\omega_m} \left( e^{(1+\omega_m)t} - 1 \right) + 2m t \right] \|f\|_{X_1} \\[3pt] & \qquad + \left[ 1 - \frac{\delta_m}{2} + \frac{m(m-3)}{1+\omega_m} \left( e^{(1+\omega_m)t} - 1 \right) \right] \|f\|_{X_m}\,. \end{align*}
\begin{align*} \int_0^t \| B_mF(s)\|_{X_{1,m}}\ \mathrm{d}s & \le \left[ \|a\|_{L_\infty(0,R_m)} t + \frac{m(m-3)}{1+\omega_m} \left( e^{(1+\omega_m)t} - 1 \right) + 2m t \right] \|f\|_{X_1} \\[3pt] & \qquad + \left[ 1 - \frac{\delta_m}{2} + \frac{m(m-3)}{1+\omega_m} \left( e^{(1+\omega_m)t} - 1 \right) \right] \|f\|_{X_m}\,. \end{align*}
We now pick
![]() $t_m>0$
such that
$t_m>0$
such that
and infer from the previous estimate (with
![]() $t=t_m$
) that
$t=t_m$
) that
Recalling that
![]() $B_m$
is
$B_m$
is
![]() $A_{a,m}$
-bounded by Lemma 5.1, we have thus established that
$A_{a,m}$
-bounded by Lemma 5.1, we have thus established that
![]() $B_m$
is a Miyadera perturbation of
$B_m$
is a Miyadera perturbation of
![]() $A_{a,m}$
for
$A_{a,m}$
for
![]() $m\ge 3$
.
$m\ge 3$
.
Let us now consider
![]() $m\in (1,3)$
. In that case,
$m\in (1,3)$
. In that case,
![]() $m-2\in (-1,1)$
and it follows from Lemmas 2.1, 4.3, and (5.4) that, for
$m-2\in (-1,1)$
and it follows from Lemmas 2.1, 4.3, and (5.4) that, for
![]() $s\in (0,t)$
,
$s\in (0,t)$
,
 \begin{align*} \|F(s)\|_{X_{m-2}} & \le \frac{2(3-m)^{(m-3)/2}}{m-1} \|F''(s)\|_{X_1}^{(3-m)/2} \|F(s)\|_{X_1}^{(m-1)/2} \\[3pt] & \le \frac{6(3-m)^{(m-3)/2}}{m-1} \|A_{a,1}F(s)\|_{X_1}^{(3-m)/2} \|f\|_{X_1}^{(m-1)/2}\,. \end{align*}
\begin{align*} \|F(s)\|_{X_{m-2}} & \le \frac{2(3-m)^{(m-3)/2}}{m-1} \|F''(s)\|_{X_1}^{(3-m)/2} \|F(s)\|_{X_1}^{(m-1)/2} \\[3pt] & \le \frac{6(3-m)^{(m-3)/2}}{m-1} \|A_{a,1}F(s)\|_{X_1}^{(3-m)/2} \|f\|_{X_1}^{(m-1)/2}\,. \end{align*}
Owing to the analyticity of
![]() $\left( e^{tA_{a,m}} \right)_{t\ge 0}$
, see Proposition 4.1, we further infer from [Reference Pazy30, Theorem 2.5.2] that there is
$\left( e^{tA_{a,m}} \right)_{t\ge 0}$
, see Proposition 4.1, we further infer from [Reference Pazy30, Theorem 2.5.2] that there is
![]() $C>0$
such that
$C>0$
such that
Combining the above two estimates gives
Hence, recalling (5.7),
 \begin{align*} \int_0^t \| B_m F(s)\|_{X_{1,m}}\ \mathrm{d}s & \le \left[ \|a\|_{L_\infty(0,R_m)} t + C(m) e^{(3-m)t/2} t^{(m-1)/2} \right] \|f\|_{X_1} \\[3pt] & \qquad + \left( 1 - \frac{\delta_m}{2} \right) \|f\|_{X_m} \,. \end{align*}
\begin{align*} \int_0^t \| B_m F(s)\|_{X_{1,m}}\ \mathrm{d}s & \le \left[ \|a\|_{L_\infty(0,R_m)} t + C(m) e^{(3-m)t/2} t^{(m-1)/2} \right] \|f\|_{X_1} \\[3pt] & \qquad + \left( 1 - \frac{\delta_m}{2} \right) \|f\|_{X_m} \,. \end{align*}
We now choose
![]() $t_m>0$
such that
$t_m>0$
such that
and deduce from the previous inequality (with
![]() $t=t_m$
) that
$t=t_m$
) that
Consequently, using again Lemma 5.1,
![]() $B_m$
is also a Miyadera perturbation of
$B_m$
is also a Miyadera perturbation of
![]() $A_{a,m}$
when
$A_{a,m}$
when
![]() $m\in (1,3)$
.
$m\in (1,3)$
.
We are now in a position to prove the first two statements in Theorem 1.1 for the operator
![]() $\mathbb{A}_m=A_{a,m}+B_m$
:
$\mathbb{A}_m=A_{a,m}+B_m$
:
Proof of Theorem 1.1(a)-(b). We handle the cases
![]() $m=1$
and
$m=1$
and
![]() $m>1$
separately.
$m>1$
separately.
-
(a) If
 $m=1$
, then
$m=1$
, then
 $A_{a,1}\in \mathcal{G}_+(X_1,1,0)$
by Proposition 4.1, so that it generates a substochastic semigroup in
$A_{a,1}\in \mathcal{G}_+(X_1,1,0)$
by Proposition 4.1, so that it generates a substochastic semigroup in
 $X_1$
. Moreover,
$X_1$
. Moreover,
 $\mathrm{dom}(A_{a,1})\subset \mathrm{dom}(B_1)$
and
$\mathrm{dom}(A_{a,1})\subset \mathrm{dom}(B_1)$
and
 $B_1$
is obviously positive due to the nonnegativity of a and b. Also, for
$B_1$
is obviously positive due to the nonnegativity of a and b. Also, for
 $f\in \mathrm{dom}(A_{a,1})$
, by Lemma 2.1, (5.2), and the Dirichlet boundary condition. Consequently, we infer from [Reference Voigt31] and [Reference Banasiak, Lamb and Laurençot8, Theorem 4.9.16] that there is an extension
$f\in \mathrm{dom}(A_{a,1})$
, by Lemma 2.1, (5.2), and the Dirichlet boundary condition. Consequently, we infer from [Reference Voigt31] and [Reference Banasiak, Lamb and Laurençot8, Theorem 4.9.16] that there is an extension \begin{equation*} M_1(A_{a,1}f+B_1f) = - \int_0^\infty f'(x)\ \mathrm{d}x - M_1(af) + M_1(B_1f) = 0 \end{equation*}
\begin{equation*} M_1(A_{a,1}f+B_1f) = - \int_0^\infty f'(x)\ \mathrm{d}x - M_1(af) + M_1(B_1f) = 0 \end{equation*}
 $\tilde{\mathbb{A}}_1\in \mathcal{G}_+(X_1,1,0)$
of
$\tilde{\mathbb{A}}_1\in \mathcal{G}_+(X_1,1,0)$
of
 $\mathbb{A}_1$
.
$\mathbb{A}_1$
.
-
(b) Let
 $m>1$
. Since
$m>1$
. Since
 $A_{a,m}\in\mathcal{H}(X_{1,m})$
by Proposition 4.1 and
$A_{a,m}\in\mathcal{H}(X_{1,m})$
by Proposition 4.1 and
 $B_m$
is a Miyadera perturbation of
$B_m$
is a Miyadera perturbation of
 $A_{a,m}$
by Proposition 5.3, it follows from [Reference Engel and Nagel14, Corollary III.3.16 & Exercise III.3.17] that
$A_{a,m}$
by Proposition 5.3, it follows from [Reference Engel and Nagel14, Corollary III.3.16 & Exercise III.3.17] that
 $\mathbb{A}_m=A_{a,m}+B_m\in \mathcal{H}(X_{1,m})$
with
$\mathbb{A}_m=A_{a,m}+B_m\in \mathcal{H}(X_{1,m})$
with
 $\mathrm{dom}(\mathbb{A}_m) = \mathrm{dom}(A_{a,m})$
. Note that
$\mathrm{dom}(\mathbb{A}_m) = \mathrm{dom}(A_{a,m})$
. Note that
 $D(A_{a,m})$
and
$D(A_{a,m})$
and
 $D(\mathbb{A}_m)$
are both Banach spaces and that
$D(\mathbb{A}_m)$
are both Banach spaces and that
 $D(A_{a,m})$
is continuously embedded in
$D(A_{a,m})$
is continuously embedded in
 $D(\mathbb{A}_m)$
, since
$D(\mathbb{A}_m)$
, since
 $B_m$
is
$B_m$
is
 $A_{a,m}$
-bounded in
$A_{a,m}$
-bounded in
 $X_{1,m}$
according to Lemma 5.1. Consequently,
$X_{1,m}$
according to Lemma 5.1. Consequently,
 $D(\mathbb{A}_m)\doteq D(A_{a,m})$
by the open mapping theorem.
$D(\mathbb{A}_m)\doteq D(A_{a,m})$
by the open mapping theorem.
We now check the positivity of
![]() $\left( e^{t\mathbb{A}_m} \right)_{t\ge 0}$
, bearing in mind that we already know from Proposition 4.1 that
$\left( e^{t\mathbb{A}_m} \right)_{t\ge 0}$
, bearing in mind that we already know from Proposition 4.1 that
![]() $A_{a,m}$
is resolvent positive. Pick
$A_{a,m}$
is resolvent positive. Pick
![]() $\lambda>0$
sufficiently large. Then
$\lambda>0$
sufficiently large. Then
![]() $\lambda - \mathbb{A}_m$
is invertible with inverse given by
$\lambda - \mathbb{A}_m$
is invertible with inverse given by
 \begin{align*} (\lambda-\mathbb{A}_m)^{-1}&=(\lambda-A_{a,m}-B_m)^{-1} = (\lambda-A_{a,m})^{-1} \left( 1 - B_m (\lambda - A_{a,m})^{-1} \right)^{-1} \\[3pt] & = (\lambda-A_{a,m})^{-1} \sum_{j=0}^\infty \left[ B_m (\lambda - A_{a,m})^{-1} \right]^j\,, \end{align*}
\begin{align*} (\lambda-\mathbb{A}_m)^{-1}&=(\lambda-A_{a,m}-B_m)^{-1} = (\lambda-A_{a,m})^{-1} \left( 1 - B_m (\lambda - A_{a,m})^{-1} \right)^{-1} \\[3pt] & = (\lambda-A_{a,m})^{-1} \sum_{j=0}^\infty \left[ B_m (\lambda - A_{a,m})^{-1} \right]^j\,, \end{align*}
where the Neumann series converges since
![]() $B_m$
is a Miyadera perturbation of
$B_m$
is a Miyadera perturbation of
![]() $A_{a,m}$
, see the proof of [Reference Engel and Nagel14, Theorem III.3.14]. Now,
$A_{a,m}$
, see the proof of [Reference Engel and Nagel14, Theorem III.3.14]. Now,
![]() $B_m$
is obviously a positive operator on
$B_m$
is obviously a positive operator on
![]() $X_{1,m}$
due to the nonnegativity of a and b, and the positivity of
$X_{1,m}$
due to the nonnegativity of a and b, and the positivity of
![]() $(\lambda-\mathbb{A}_m)^{-1}$
directly follows from the above identity.
$(\lambda-\mathbb{A}_m)^{-1}$
directly follows from the above identity.
Finally, as in the proof of (a), we have
![]() $M_1(\mathbb{A}_m f) = 0$
for any
$M_1(\mathbb{A}_m f) = 0$
for any
![]() $f\in \mathrm{dom}(A_{a,m})$
by Lemma 2.1, (5.2), and the Dirichlet boundary condition, so that (1.9) immediately follows.
$f\in \mathrm{dom}(A_{a,m})$
by Lemma 2.1, (5.2), and the Dirichlet boundary condition, so that (1.9) immediately follows.
Proof of Proposition 1.2(a). Let
![]() $m\ge 1$
. The operator
$m\ge 1$
. The operator
![]() $A_{a,m}$
belongs to
$A_{a,m}$
belongs to
![]() $\mathcal{G}_+(X_{1,m})\cap \mathcal{H}(X_{1,m})$
by Proposition 4.1. Since
$\mathcal{G}_+(X_{1,m})\cap \mathcal{H}(X_{1,m})$
by Proposition 4.1. Since
![]() $a\in L_\infty(0,\infty)$
and b satisfies (1.3), the operator
$a\in L_\infty(0,\infty)$
and b satisfies (1.3), the operator
![]() $B_m$
is a positive bounded operator on
$B_m$
is a positive bounded operator on
![]() $X_{1,m}$
. On the one hand, it now follows from well-known perturbation results that
$X_{1,m}$
. On the one hand, it now follows from well-known perturbation results that
![]() $\mathbb{A}_m=A_{a,m}+B_m$
belongs to
$\mathbb{A}_m=A_{a,m}+B_m$
belongs to
![]() $\mathcal{H}(X_{1,m})$
, see [Reference Pazy30, Theorem 3.2.1]. On the other hand, the same argument as in the proof of Theorem 1.1(b) ensures the positivity of
$\mathcal{H}(X_{1,m})$
, see [Reference Pazy30, Theorem 3.2.1]. On the other hand, the same argument as in the proof of Theorem 1.1(b) ensures the positivity of
![]() $\left( e^{t\mathbb{A}_m} \right)_{t\ge 0}$
. Finally, for
$\left( e^{t\mathbb{A}_m} \right)_{t\ge 0}$
. Finally, for
![]() $m=1$
, it readily follows from [Reference Banasiak, Lamb and Laurençot8, Proposition 4.9.16] that
$m=1$
, it readily follows from [Reference Banasiak, Lamb and Laurençot8, Proposition 4.9.16] that
![]() $\mathbb{A}_1=\tilde{\mathbb{A}}_1\in \mathcal{G}_+(X_1,1,0)$
, thereby completing the proof.
$\mathbb{A}_1=\tilde{\mathbb{A}}_1\in \mathcal{G}_+(X_1,1,0)$
, thereby completing the proof.
6 Immediate compactness of the semigroup
We now turn to compactness properties of the semigroup
![]() $(e^{t\mathbb{A}_m})_{t\ge 0}$
for
$(e^{t\mathbb{A}_m})_{t\ge 0}$
for
![]() $m>1$
as stated in Theorem 1.1 (c). To avoid loss of compactness for large sizes, we further require a to diverge to infinity for large sizes, thus excluding bounded overall fragmentation rates.
$m>1$
as stated in Theorem 1.1 (c). To avoid loss of compactness for large sizes, we further require a to diverge to infinity for large sizes, thus excluding bounded overall fragmentation rates.
Lemma 6.1 Let
![]() $m\ge 1$
and assume that a satisfies (1.2) and (1.10). Then
$m\ge 1$
and assume that a satisfies (1.2) and (1.10). Then
![]() $D(A_{a,m})\doteq D(\mathbb{A}_m)$
is compactly embedded in
$D(A_{a,m})\doteq D(\mathbb{A}_m)$
is compactly embedded in
![]() $X_{1,m}$
.
$X_{1,m}$
.
Proof. Recall that the relation
![]() $D(A_{a,m})\doteq D(\mathbb{A}_m)$
is established in the proof of Theorem 1.1 (b). Let
$D(A_{a,m})\doteq D(\mathbb{A}_m)$
is established in the proof of Theorem 1.1 (b). Let
![]() $(f_n)_{n\ge 1}$
be a bounded sequence in
$(f_n)_{n\ge 1}$
be a bounded sequence in
![]() $D (A_{a,m})$
. According to Lemma 2.1 and Lemma 4.3, there is
$D (A_{a,m})$
. According to Lemma 2.1 and Lemma 4.3, there is
![]() $C>0$
such that
$C>0$
such that
On the one hand, we infer from (6.1a) and Arzelà–Ascoli’s theorem that
![]() $(f_n)_{n\ge 1}$
is relatively compact in
$(f_n)_{n\ge 1}$
is relatively compact in
![]() $C([1/R,R])$
for each
$C([1/R,R])$
for each
![]() $R>1$
. There are thus a subsequence
$R>1$
. There are thus a subsequence
![]() $(f_{n_j})_{j\ge 1}$
and
$(f_{n_j})_{j\ge 1}$
and
![]() $f\in C((0,\infty))$
such that
$f\in C((0,\infty))$
such that
On the other hand, it follows from (6.1) that, if
![]() $R>1$
and E is a measurable subset of
$R>1$
and E is a measurable subset of
![]() $(0,\infty)$
, then, for
$(0,\infty)$
, then, for
![]() $n\ge 1$
,
$n\ge 1$
,
 \begin{align} \int_E (x+x^m) |f_n(x)|\ \mathrm{d}x & \le \int_{E\cap (0,R)} (x+x^m) |f_n(x)|\ \mathrm{d}x + \int_R^\infty (x+x^m) |f_n(x)|\ \mathrm{d}x \nonumber \\[3pt] & \le (R+R^m) \|f_n\|_{L_\infty(0,\infty)} |E\cap (0,R)| \nonumber \\[3pt] & \qquad + \dfrac{2}{\inf_{x\ge R} \{a(x)\}} \int_R^\infty x^m\ a(x) |f_n(x)|\ \mathrm{d}x \nonumber \\[3pt] & \le 2 C R^m |E\cap (0,R)| + \dfrac{2C}{\inf_{x\ge R} \{a(x)\}}\,. \end{align}
\begin{align} \int_E (x+x^m) |f_n(x)|\ \mathrm{d}x & \le \int_{E\cap (0,R)} (x+x^m) |f_n(x)|\ \mathrm{d}x + \int_R^\infty (x+x^m) |f_n(x)|\ \mathrm{d}x \nonumber \\[3pt] & \le (R+R^m) \|f_n\|_{L_\infty(0,\infty)} |E\cap (0,R)| \nonumber \\[3pt] & \qquad + \dfrac{2}{\inf_{x\ge R} \{a(x)\}} \int_R^\infty x^m\ a(x) |f_n(x)|\ \mathrm{d}x \nonumber \\[3pt] & \le 2 C R^m |E\cap (0,R)| + \dfrac{2C}{\inf_{x\ge R} \{a(x)\}}\,. \end{align}
A first consequence of (6.3) with
![]() $E=(R,\infty)$
is that
$E=(R,\infty)$
is that
from which we deduce by (1.10) that
We next infer from (6.3) that, for
![]() $\delta>0$
,
$\delta>0$
,
satisfies
for all
![]() $R>1$
. Therefore,
$R>1$
. Therefore,
for all
![]() $R>1$
and we use once more (1.10) to conclude that
$R>1$
and we use once more (1.10) to conclude that
Gathering (6.4) and (6.5) implies that the sequence
![]() $(f_n)_{n\ge 1}$
is uniformly integrable in
$(f_n)_{n\ge 1}$
is uniformly integrable in
![]() $X_{1,m}$
and thus weakly compact in
$X_{1,m}$
and thus weakly compact in
![]() $X_{1,m}$
by Dunford–Pettis’ theorem. This just established weak compactness in
$X_{1,m}$
by Dunford–Pettis’ theorem. This just established weak compactness in
![]() $X_{1,m}$
, along with the pointwise convergence (6.2) and Vitali’s theorem, see [Reference Fonseca and Leoni19, Theorem 2.24] for instance, entails that
$X_{1,m}$
, along with the pointwise convergence (6.2) and Vitali’s theorem, see [Reference Fonseca and Leoni19, Theorem 2.24] for instance, entails that
![]() $(f_{n_j})_{j\ge 1}$
converges to f in
$(f_{n_j})_{j\ge 1}$
converges to f in
![]() $X_{1,m}$
, thereby completing the proof.
$X_{1,m}$
, thereby completing the proof.
We are now in a position to finish off the proof of Theorem 1.1.
Proof of Theorem 1.1(c). Let
![]() $m>1$
. By Lemma 6.1,
$m>1$
. By Lemma 6.1,
![]() $(\lambda - \mathbb{A}_m)^{-1}$
is compact for
$(\lambda - \mathbb{A}_m)^{-1}$
is compact for
![]() $\lambda>0$
large enough and, since
$\lambda>0$
large enough and, since
![]() $m>1$
, the analyticity of
$m>1$
, the analyticity of
![]() $\left( e^{t\mathbb{A}_m} \right)_{t\ge 0}$
implies that it is continuous with respect to the operator norm for positive times [Reference Pazy30, Lemma 2.4.2]. We now may apply [Reference Pazy30, Theorem 2.3.3] to conclude that
$\left( e^{t\mathbb{A}_m} \right)_{t\ge 0}$
implies that it is continuous with respect to the operator norm for positive times [Reference Pazy30, Lemma 2.4.2]. We now may apply [Reference Pazy30, Theorem 2.3.3] to conclude that
![]() $\left( e^{t\mathbb{A}_m} \right)_{t\ge 0}$
is immediately compact.
$\left( e^{t\mathbb{A}_m} \right)_{t\ge 0}$
is immediately compact.
The compactness result of Lemma 6.1 is not valid under the sole assumption (1.2) on a. In particular, we show that it fails when a is bounded.
Lemma 6.2 Let
![]() $m\ge 1$
and
$m\ge 1$
and
![]() $a\in L_\infty(0,\infty)$
. Then the embedding of
$a\in L_\infty(0,\infty)$
. Then the embedding of
![]() $D(A_{a,m})\doteq D(\mathbb{A}_m)$
in
$D(A_{a,m})\doteq D(\mathbb{A}_m)$
in
![]() $X_{1,m}$
is not compact.
$X_{1,m}$
is not compact.
Proof. Let
![]() $\varphi\in C_c^\infty(\mathbb{R})$
be such that
$\varphi\in C_c^\infty(\mathbb{R})$
be such that
![]() $0\le \varphi\le 1$
,
$0\le \varphi\le 1$
,
![]() $\mathrm{supp}\ \varphi\subset [-1,1]$
, and
$\mathrm{supp}\ \varphi\subset [-1,1]$
, and
![]() $\|\varphi\|_{L_1(\mathbb{R})}=1$
. We fix
$\|\varphi\|_{L_1(\mathbb{R})}=1$
. We fix
![]() $m\ge 1$
and set
$m\ge 1$
and set
Straightforward computations show that
 \begin{align*} \|\varphi_n\|_{X_{1,m}} + \|a \varphi_n\|_{X_{1,m}} & \le \left( 1 + \|a\|_{L_\infty(0,\infty)} \right) \|\varphi_n\|_{X_{1,m}} \\[3pt] & \le \left( 1 + \|a\|_{L_\infty(0,\infty)} \right) \left( 1 + \int_{-1}^1 \frac{1+m2^m n^{m-1}}{n+n^m} \varphi(y)\ \mathrm{d}y \right) \\ & \le (2 + m 2^m) \left( 1 + \|a\|_{L_\infty(0,\infty)} \right) \end{align*}
\begin{align*} \|\varphi_n\|_{X_{1,m}} + \|a \varphi_n\|_{X_{1,m}} & \le \left( 1 + \|a\|_{L_\infty(0,\infty)} \right) \|\varphi_n\|_{X_{1,m}} \\[3pt] & \le \left( 1 + \|a\|_{L_\infty(0,\infty)} \right) \left( 1 + \int_{-1}^1 \frac{1+m2^m n^{m-1}}{n+n^m} \varphi(y)\ \mathrm{d}y \right) \\ & \le (2 + m 2^m) \left( 1 + \|a\|_{L_\infty(0,\infty)} \right) \end{align*}
and
as well as
Therefore, the sequence
![]() $(\varphi_n)_{n\ge 1}$
is bounded in
$(\varphi_n)_{n\ge 1}$
is bounded in
![]() $D(A_{a,m})$
but cannot converge in
$D(A_{a,m})$
but cannot converge in
![]() $X_{1,m}$
due to (6.6).
$X_{1,m}$
due to (6.6).
Proof of Proposition 1.2(b). Let
![]() $m\ge 1$
and
$m\ge 1$
and
![]() $a\in L_\infty(0,\infty)$
. Since
$a\in L_\infty(0,\infty)$
. Since
![]() $D(\mathbb{A}_m)$
is not compactly embedded in
$D(\mathbb{A}_m)$
is not compactly embedded in
![]() $X_{1,m}$
by Lemma 6.2, the resolvent
$X_{1,m}$
by Lemma 6.2, the resolvent
![]() $(\lambda-\mathbb{A}_m)^{-1}$
is not compact. Hence, [Reference Pazy30, Theorem 2.3.3] implies that the semigroup
$(\lambda-\mathbb{A}_m)^{-1}$
is not compact. Hence, [Reference Pazy30, Theorem 2.3.3] implies that the semigroup
![]() $(e^{t\mathbb{A}_m})_{t\ge 0}$
is not compact.
$(e^{t\mathbb{A}_m})_{t\ge 0}$
is not compact.
7 Steady states and convergence
Throughout this section, we assume that a and b satisfy (1.2), (1.3), (1.8), and (1.10) and that
![]() $a>0$
and
$a>0$
and
![]() $b>0$
.
$b>0$
.
We begin with the construction of stationary solutions with the help of Schauder’s fixed point theorem.
Lemma 7.1 There is a unique nonnegative
such that
![]() $M_1(\psi_1)=1$
and
$M_1(\psi_1)=1$
and
![]() $\mathrm{ker}(\mathbb{A}_m) = \mathrm{ker}(\mathbb{A}_m^2) = \mathbb{R}\psi_1 = \{ r\psi_1\ :\ r\in\mathbb{R}\}$
for all
$\mathrm{ker}(\mathbb{A}_m) = \mathrm{ker}(\mathbb{A}_m^2) = \mathbb{R}\psi_1 = \{ r\psi_1\ :\ r\in\mathbb{R}\}$
for all
![]() $m\ge 1$
.
$m\ge 1$
.
Proof. We split the proof into three steps.
Step 1. The uniqueness of a solution
![]() $\psi\in \mathrm{dom}(\mathbb{A}_1)$
to
$\psi\in \mathrm{dom}(\mathbb{A}_1)$
to
![]() $\mathbb{A}_1\psi=0$
satisfying
$\mathbb{A}_1\psi=0$
satisfying
![]() $M_1(\psi)=1$
relies on the dissipativity properties of
$M_1(\psi)=1$
relies on the dissipativity properties of
![]() $\mathbb{A}_1$
in
$\mathbb{A}_1$
in
![]() $X_1$
and can be shown exactly as in the proofs of [Reference Escobedo, Mischler and Rodriguez Ricard15, Lemma 3.5] and [Reference Laurençot25, Proposition 3], to which we refer.
$X_1$
and can be shown exactly as in the proofs of [Reference Escobedo, Mischler and Rodriguez Ricard15, Lemma 3.5] and [Reference Laurençot25, Proposition 3], to which we refer.
Step 2. We now turn to the existence part. Let
![]() $m\ge 3$
and consider
$m\ge 3$
and consider
![]() $f\in X_{1,m}^+$
satisfying
$f\in X_{1,m}^+$
satisfying
![]() $M_1(f)=1$
. Setting
$M_1(f)=1$
. Setting
![]() $F(t) := e^{t\mathbb{A}_m}f$
for
$F(t) := e^{t\mathbb{A}_m}f$
for
![]() $t\ge 0$
, it readily follows from Theorem 1.1 (b) that
$t\ge 0$
, it readily follows from Theorem 1.1 (b) that
Next, by (5.3) and Fubini’s theorem,
 \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) & = - m \int_0^\infty x^{m-1} \partial_x F(t,x)\ \mathrm{d}x - \int_0^\infty x^m a(x) F(t,x)\ \mathrm{d}x \\[3pt] & \qquad + \int_0^\infty a(y) F(t,y) \int_0^y x^m b(x,y)\ \mathrm{d}x\mathrm{d}y \\[3pt] & \le m(m-1) M_{m-2}(F(t)) - \delta_m M_m(aF(t))\,. \end{align*}
\begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) & = - m \int_0^\infty x^{m-1} \partial_x F(t,x)\ \mathrm{d}x - \int_0^\infty x^m a(x) F(t,x)\ \mathrm{d}x \\[3pt] & \qquad + \int_0^\infty a(y) F(t,y) \int_0^y x^m b(x,y)\ \mathrm{d}x\mathrm{d}y \\[3pt] & \le m(m-1) M_{m-2}(F(t)) - \delta_m M_m(aF(t))\,. \end{align*}
Owing to (1.10), there is
![]() $x_*>0$
such that
$x_*>0$
such that
![]() $a(x)\ge 1$
for
$a(x)\ge 1$
for
![]() $x\ge x_*$
. Consequently, using (7.1),
$x\ge x_*$
. Consequently, using (7.1),
 \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) & + \delta_m M_m(F(t)) \\[3pt] & \le \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) + \delta_m \int_{x_*}^\infty x^m F(t,x)\ \mathrm{d}x + \delta_m \int_0^{x_*} x^m F(t,x)\ \mathrm{d}x \\[3pt] & \le \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) + \delta_m M_m(aF(t)) + \delta_m x_*^{m-1} \int_0^{x_*} x F(t,x)\ \mathrm{d}x \\[3pt] & \le m(m-1) M_{m-2}(F(t)) + \delta_m x_*^{m-1} \,. \end{align*}
\begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) & + \delta_m M_m(F(t)) \\[3pt] & \le \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) + \delta_m \int_{x_*}^\infty x^m F(t,x)\ \mathrm{d}x + \delta_m \int_0^{x_*} x^m F(t,x)\ \mathrm{d}x \\[3pt] & \le \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) + \delta_m M_m(aF(t)) + \delta_m x_*^{m-1} \int_0^{x_*} x F(t,x)\ \mathrm{d}x \\[3pt] & \le m(m-1) M_{m-2}(F(t)) + \delta_m x_*^{m-1} \,. \end{align*}
Since
![]() $m\ge 3$
, we now deduce from Young’s inequality that
$m\ge 3$
, we now deduce from Young’s inequality that
 \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) + \delta_m M_m(F(t)) & \le \frac{\delta_m}{2} M_m(F(t)) + 2m \left( \frac{2m(m-3)}{\delta_m} \right)^{(m-3)/2} M_1(F(t)) \\[3pt] & \qquad + \delta_m x_*^{m-1} \,. \end{align*}
\begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} M_m(F(t)) + \delta_m M_m(F(t)) & \le \frac{\delta_m}{2} M_m(F(t)) + 2m \left( \frac{2m(m-3)}{\delta_m} \right)^{(m-3)/2} M_1(F(t)) \\[3pt] & \qquad + \delta_m x_*^{m-1} \,. \end{align*}
Hence, by (7.1),
for
![]() $t\ge 0$
. After integration with respect to time, we conclude that
$t\ge 0$
. After integration with respect to time, we conclude that
Now, introducing
which is a closed convex subset of
![]() $X_{1,m}$
, an immediate consequence of (7.1) and (7.2) is that
$X_{1,m}$
, an immediate consequence of (7.1) and (7.2) is that
Owing to the compactness of
![]() $e^{t\mathbb{A}_m}$
in
$e^{t\mathbb{A}_m}$
in
![]() $X_{1,m}$
for all
$X_{1,m}$
for all
![]() $t>0$
, see Theorem 1.1(c), we argue as in the proofs of [Reference Amann2, Theorem 22.13] and [Reference Gamba, Panferov and Villani20, Theorem 5.2] to deduce from Schauder’s fixed point theorem that there is
$t>0$
, see Theorem 1.1(c), we argue as in the proofs of [Reference Amann2, Theorem 22.13] and [Reference Gamba, Panferov and Villani20, Theorem 5.2] to deduce from Schauder’s fixed point theorem that there is
![]() $\psi_m\in \mathcal{C}_m$
such that
$\psi_m\in \mathcal{C}_m$
such that
Equivalently,
![]() $\mathbb{A}_m\psi_m=0$
and we have thus shown the existence of a stationary solution to (1.1a) for
$\mathbb{A}_m\psi_m=0$
and we have thus shown the existence of a stationary solution to (1.1a) for
![]() $m\ge 3$
. Obviously,
$m\ge 3$
. Obviously,
![]() $\psi_3$
also belongs to
$\psi_3$
also belongs to
![]() $\mathrm{dom}(\mathbb{A}_m)$
and satisfies
$\mathrm{dom}(\mathbb{A}_m)$
and satisfies
![]() $\mathbb{A}_m\psi_3=0$
for any
$\mathbb{A}_m\psi_3=0$
for any
![]() $m\in [1,3)$
. Thus, there is at least one stationary solution
$m\in [1,3)$
. Thus, there is at least one stationary solution
![]() $\psi_m$
to (1.1) for any
$\psi_m$
to (1.1) for any
![]() $m\ge 1$
. Obviously,
$m\ge 1$
. Obviously,
![]() $\psi_m\in \mathrm{dom}(\mathbb{A}_1)$
solves
$\psi_m\in \mathrm{dom}(\mathbb{A}_1)$
solves
![]() $\mathbb{A}_1\psi_m=0$
for every
$\mathbb{A}_1\psi_m=0$
for every
![]() $m\ge 1$
, and we infer from Step 1 that
$m\ge 1$
, and we infer from Step 1 that
![]() $\psi_m=\psi_1$
for every
$\psi_m=\psi_1$
for every
![]() $m\ge 1$
.
$m\ge 1$
.
Step 3. We finally identify
![]() $\mathrm{ker}(\mathbb{A}_m^2)$
. To this end, let
$\mathrm{ker}(\mathbb{A}_m^2)$
. To this end, let
![]() $f\in \mathrm{ker}(\mathbb{A}_m^2)$
. Then
$f\in \mathrm{ker}(\mathbb{A}_m^2)$
. Then
![]() $\mathbb{A}_m f$
belongs to
$\mathbb{A}_m f$
belongs to
![]() $\mathrm{ker}(\mathbb{A}_m)$
, so that Step 2 implies that there is
$\mathrm{ker}(\mathbb{A}_m)$
, so that Step 2 implies that there is
![]() $\mu\in\mathbb{C}$
such that
$\mu\in\mathbb{C}$
such that
![]() $\mathbb{A}_m f = \mu \psi_1$
. Therefore,
$\mathbb{A}_m f = \mu \psi_1$
. Therefore,
Hence,
![]() $f\in \mathrm{ker}(\mathbb{A}_m)$
.
$f\in \mathrm{ker}(\mathbb{A}_m)$
.
We now supply refined information on the spectrum of
![]() $\mathbb{A}_m$
for
$\mathbb{A}_m$
for
![]() $m>1$
.
$m>1$
.
Lemma 7.2 Let
![]() $m>1$
. The spectrum
$m>1$
. The spectrum
![]() $\sigma(\mathbb{A}_m)$
of
$\sigma(\mathbb{A}_m)$
of
![]() $\mathbb{A}_m$
only consists of isolated eigenvalues and satisfies
$\mathbb{A}_m$
only consists of isolated eigenvalues and satisfies
for some
![]() $\varepsilon_m>0$
. Moreover, the spectral bound
$\varepsilon_m>0$
. Moreover, the spectral bound
![]() $s(\mathbb{A}_m)=0$
is a simple eigenvalue of
$s(\mathbb{A}_m)=0$
is a simple eigenvalue of
![]() $\mathbb{A}_m$
.
$\mathbb{A}_m$
.
Proof. Owing to the immediate compactness of
![]() $(e^{t\mathbb{A}_m})_{t\ge 0}$
, see Theorem 1.1 (c), and [Reference Engel and Nagel14, Corollary V.3.2], the spectrum
$(e^{t\mathbb{A}_m})_{t\ge 0}$
, see Theorem 1.1 (c), and [Reference Engel and Nagel14, Corollary V.3.2], the spectrum
![]() $\sigma(\mathbb{A}_m)$
only consists of isolated eigenvalues which are poles of the resolvent with finite algebraic multiplicity. Moreover, for any
$\sigma(\mathbb{A}_m)$
only consists of isolated eigenvalues which are poles of the resolvent with finite algebraic multiplicity. Moreover, for any
![]() $r\in\mathbb{R}$
,
$r\in\mathbb{R}$
,
We next claim that
![]() $s(\mathbb{A}_m)=0$
. Indeed, since
$s(\mathbb{A}_m)=0$
. Indeed, since
![]() $\mathbb{A}_m \subset \mathbb{A}_1 \subset \tilde{\mathbb{A}}_1$
and
$\mathbb{A}_m \subset \mathbb{A}_1 \subset \tilde{\mathbb{A}}_1$
and
![]() $\tilde{\mathbb{A}}_1\in \mathcal{G}(X_1,1,0)$
by Theorem 1.1, any eigenvalue of
$\tilde{\mathbb{A}}_1\in \mathcal{G}(X_1,1,0)$
by Theorem 1.1, any eigenvalue of
![]() $\mathbb{A}_m$
is also an eigenvalue of
$\mathbb{A}_m$
is also an eigenvalue of
![]() $\tilde{\mathbb{A}}_1$
and it follows from [Reference Pazy30, Corollary 1.3.6] that
$\tilde{\mathbb{A}}_1$
and it follows from [Reference Pazy30, Corollary 1.3.6] that
Consequently, any eigenvalue of
![]() $\mathbb{A}_m$
has a non-positive real part. Thus,
$\mathbb{A}_m$
has a non-positive real part. Thus,
Since zero belongs to the spectrum of
![]() $\mathbb{A}_m$
by Lemma 7.1, we deduce from (7.5) that
$\mathbb{A}_m$
by Lemma 7.1, we deduce from (7.5) that
![]() $s(\mathbb{A}_m)=0$
is a pole of the resolvent of
$s(\mathbb{A}_m)=0$
is a pole of the resolvent of
![]() $\mathbb{A}_m$
. Recalling that
$\mathbb{A}_m$
. Recalling that
![]() $(e^{t\mathbb{A}_m})_{t\ge 0}$
is a positive semigroup on the Banach lattice
$(e^{t\mathbb{A}_m})_{t\ge 0}$
is a positive semigroup on the Banach lattice
![]() $X_{1,m}$
, it follows from [Reference Clément, Heijmans, Angenent, van Duijn and de Pagter12, Theorem 8.14] that
$X_{1,m}$
, it follows from [Reference Clément, Heijmans, Angenent, van Duijn and de Pagter12, Theorem 8.14] that
![]() $\sigma(\mathbb{A}_m)\cap i\mathbb{R}$
is either reduced to
$\sigma(\mathbb{A}_m)\cap i\mathbb{R}$
is either reduced to
![]() $\{0\}$
or contains infinitely many elements. The latter being ruled out by (7.4), we conclude that
$\{0\}$
or contains infinitely many elements. The latter being ruled out by (7.4), we conclude that
![]() $\sigma(\mathbb{A}_m)\cap i\mathbb{R} = \{0\}$
. Since all eigenvalues are isolated, this last property ensures that there is
$\sigma(\mathbb{A}_m)\cap i\mathbb{R} = \{0\}$
. Since all eigenvalues are isolated, this last property ensures that there is
![]() $\varepsilon_m>0$
such that (7.3) holds true.
$\varepsilon_m>0$
such that (7.3) holds true.
Finally, since
![]() $\mathrm{ker}(\mathbb{A}_m) = \mathrm{ker}(\mathbb{A}_m^2) = \mathbb{R}\psi_1$
by Lemma 7.1, zero is a simple eigenvalue of
$\mathrm{ker}(\mathbb{A}_m) = \mathrm{ker}(\mathbb{A}_m^2) = \mathbb{R}\psi_1$
by Lemma 7.1, zero is a simple eigenvalue of
![]() $\mathbb{A}_m$
according to [Reference Engel and Nagel14, Section IV.1.17].
$\mathbb{A}_m$
according to [Reference Engel and Nagel14, Section IV.1.17].
Proof of Theorem 1.5. Let
![]() $m>1$
. From Lemma 7.1 we obtain the existence of a unique nonnegative
$m>1$
. From Lemma 7.1 we obtain the existence of a unique nonnegative
such that
![]() $M_1(\psi_1)=1$
and
$M_1(\psi_1)=1$
and
![]() $\mathrm{ker}(\mathbb{A}_m) = \mathbb{R}\psi_1$
. We next infer from Lemma 7.2 that zero is a dominant eigenvalue of
$\mathrm{ker}(\mathbb{A}_m) = \mathbb{R}\psi_1$
. We next infer from Lemma 7.2 that zero is a dominant eigenvalue of
![]() $\mathbb{A}_m$
and a first-order pole of its resolvent with residue P, where
$\mathbb{A}_m$
and a first-order pole of its resolvent with residue P, where
![]() $P\in\mathcal{L}(X_{1,m})$
denotes the spectral projection onto
$P\in\mathcal{L}(X_{1,m})$
denotes the spectral projection onto
![]() $\mathrm{ker}(\mathbb{A}_m)$
and is given by
$\mathrm{ker}(\mathbb{A}_m)$
and is given by
see, e.g., [Reference Engel and Nagel14, Section IV.1.17]. It then follows from [Reference Engel and Nagel14, Corollary V.3.3] that there are
![]() $N_m\ge 1$
and
$N_m\ge 1$
and
![]() $\nu_m>0$
such that
$\nu_m>0$
such that
It only remains to identify the spectral projection P. Introducing
![]() $g_\lambda := \lambda (\lambda - \mathbb{A}_m)^{-1}f$
for
$g_\lambda := \lambda (\lambda - \mathbb{A}_m)^{-1}f$
for
![]() $f\in X_{1,m}$
, we have
$f\in X_{1,m}$
, we have
from which we readily deduce that
![]() $M_1(f) = M_1(g_\lambda)$
. Therefore, (7.6) implies
$M_1(f) = M_1(g_\lambda)$
. Therefore, (7.6) implies
![]() $M_1(Pf) = M_1(f)$
. Since
$M_1(Pf) = M_1(f)$
. Since
![]() $Pf\in \mathbb{R}\psi_1$
and
$Pf\in \mathbb{R}\psi_1$
and
![]() $M_1(\psi_1)=1$
, we conclude that
$M_1(\psi_1)=1$
, we conclude that
Recalling (7.7), the above identity completes the proof of Theorem 1.5.
Remark 7.3 Since
![]() $\mathbb{A}_m\in \mathcal{H}(X_{1,m})$
and since
$\mathbb{A}_m\in \mathcal{H}(X_{1,m})$
and since
![]() $s(\mathbb{A}_m)=0$
, we infer from [Reference Engel and Nagel14, Corollary IV.3.12] that there exists
$s(\mathbb{A}_m)=0$
, we infer from [Reference Engel and Nagel14, Corollary IV.3.12] that there exists
![]() $\kappa\ge 1$
such that
$\kappa\ge 1$
such that
![]() $\mathbb{A}_m\in \mathcal{G}(X_{1,m},\kappa,0)$
.
$\mathbb{A}_m\in \mathcal{G}(X_{1,m},\kappa,0)$
.
8 Stationary solutions revisited
We now prove the existence of a stationary solution to (1.1) when the overall fragmentation rate a may be bounded for large sizes but does not decay to zero. Specifically, we assume that a satisfies (1.12); that is,
Proof of Proposition 1.6. As in Lemma 7.1, the proof of the uniqueness assertion in Proposition 1.6 relies on the dissipativity properties of
![]() $\mathbb{A}_1$
in
$\mathbb{A}_1$
in
![]() $X_1$
and can be shown exactly as in the proofs of [Reference Escobedo, Mischler and Rodriguez Ricard15, Lemma 3.5] and [Reference Laurençot25, Proposition 3], to which we refer.
$X_1$
and can be shown exactly as in the proofs of [Reference Escobedo, Mischler and Rodriguez Ricard15, Lemma 3.5] and [Reference Laurençot25, Proposition 3], to which we refer.
As for the existence assertion, we employ a compactness method. Let
![]() $n\ge 1$
. We set
$n\ge 1$
. We set
![]() $a_n(x) := a(x) +x/n$
for
$a_n(x) := a(x) +x/n$
for
![]() $x>0$
and, for
$x>0$
and, for
![]() $m\ge 1$
, we denote the operators
$m\ge 1$
, we denote the operators
![]() $B_m$
and
$B_m$
and
![]() $\mathbb{A}_m$
with
$\mathbb{A}_m$
with
![]() $a_n$
instead of a by
$a_n$
instead of a by
![]() $B_{m,n}$
and
$B_{m,n}$
and
![]() $\mathbb{A}_{m,n}$
, respectively. Since
$\mathbb{A}_{m,n}$
, respectively. Since
![]() $a_n(x)\to \infty$
as
$a_n(x)\to \infty$
as
![]() $x\to\infty$
, we infer from Lemma 7.1 that there is a unique nonnegative
$x\to\infty$
, we infer from Lemma 7.1 that there is a unique nonnegative
such that
![]() $M_1(\psi_{1,n})=1$
and
$M_1(\psi_{1,n})=1$
and
![]() $\mathrm{ker}(\mathbb{A}_{m,n}) = \mathbb{R}\psi_{1,n}$
for all
$\mathrm{ker}(\mathbb{A}_{m,n}) = \mathbb{R}\psi_{1,n}$
for all
![]() $m\ge 1$
. In particular, given
$m\ge 1$
. In particular, given
![]() $m>3$
, the function
$m>3$
, the function
![]() $\psi_{1,n}$
belongs to
$\psi_{1,n}$
belongs to
![]() $\mathrm{dom}(A_{0,m})$
with
$\mathrm{dom}(A_{0,m})$
with
![]() $a_n \psi_{1,n}\in X_{1,m}$
and solves
$a_n \psi_{1,n}\in X_{1,m}$
and solves
It follows from (8.1), Lemma 5.2, and Young’s inequality that, for
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 \begin{align*} M_m(a_n \psi_{1,n}) & = M_m(B_{m,n}\psi_{1,n}) - m \int_0^\infty x^{m-1} \psi_{1,n}^{\prime}(x)\ \mathrm{d}x \\[3pt] & \le (1-\delta_m) M_m(a_n \psi_{1,n}) + m(m-1) M_{m-2}(\psi_{1,n}) \\[3pt] & \le (1-\delta_m) M_m(a_n \psi_{1,n}) + m(m-3) \varepsilon M_{m}(\psi_{1,n}) + 2m \varepsilon^{(3-m)/2} M_1(\psi_{1,n})\,. \end{align*}
\begin{align*} M_m(a_n \psi_{1,n}) & = M_m(B_{m,n}\psi_{1,n}) - m \int_0^\infty x^{m-1} \psi_{1,n}^{\prime}(x)\ \mathrm{d}x \\[3pt] & \le (1-\delta_m) M_m(a_n \psi_{1,n}) + m(m-1) M_{m-2}(\psi_{1,n}) \\[3pt] & \le (1-\delta_m) M_m(a_n \psi_{1,n}) + m(m-3) \varepsilon M_{m}(\psi_{1,n}) + 2m \varepsilon^{(3-m)/2} M_1(\psi_{1,n})\,. \end{align*}
Hence,
Owing to (1.12), there is
![]() $x_*>0$
such that
$x_*>0$
such that
In view of (8.2) and (8.3), we obtain
 \begin{align*} \alpha \delta_m M_m(\psi_{1,n}) & \le \alpha\delta_m x_*^{m-1} \int_0^{x_*} x \psi_{1,n}(x)\ \mathrm{d}x + \delta_m \int_{x_*}^\infty x^m a_n(x) \psi_{1,n}(x)\ \mathrm{d}x \\[3pt] & \le \alpha\delta_m x_*^{m-1} M_1(\psi_{1,n}) + m(m-3) \varepsilon M_{m}(\psi_{1,n}) + 2m \varepsilon^{(3-m)/2}\,. \end{align*}
\begin{align*} \alpha \delta_m M_m(\psi_{1,n}) & \le \alpha\delta_m x_*^{m-1} \int_0^{x_*} x \psi_{1,n}(x)\ \mathrm{d}x + \delta_m \int_{x_*}^\infty x^m a_n(x) \psi_{1,n}(x)\ \mathrm{d}x \\[3pt] & \le \alpha\delta_m x_*^{m-1} M_1(\psi_{1,n}) + m(m-3) \varepsilon M_{m}(\psi_{1,n}) + 2m \varepsilon^{(3-m)/2}\,. \end{align*}
Choosing
![]() $\varepsilon=\alpha\delta_m/2m(m-3)$
in the above inequality gives
$\varepsilon=\alpha\delta_m/2m(m-3)$
in the above inequality gives
Therefore, there is a positive constant
![]() $c_1(m)$
depending only on a and m such that
$c_1(m)$
depending only on a and m such that
Several additional estimates can now be derived from (8.4). Indeed, it readily follows from (8.1), (8.2) (with
![]() $\varepsilon=1$
), and Lemma 5.2 that, for
$\varepsilon=1$
), and Lemma 5.2 that, for
![]() $n\ge 1$
,
$n\ge 1$
,
 \begin{align} \|\psi_{1,n}^{\prime\prime}\|_{X_m} + \|a_n \psi_{1,n}\|_{X_m} + \| B_{m,n}\psi_{1,n}\|_{X_m} & \le 2 \left( \|a_n \psi_{1,n}\|_{X_m} + \| B_{m,n}\psi_{1,n}\|_{X_m} \right) \nonumber \\[3pt] & \le 2(2-\delta_m) \|a_n \psi_{1,n}\|_{X_m} \le 4 M_m(a_n \psi_{1,n}) \nonumber \\[3pt] & \le \frac{4m(m-3)c_1(m)+8m}{\delta_m} =:c_2(m)\,. \end{align}
\begin{align} \|\psi_{1,n}^{\prime\prime}\|_{X_m} + \|a_n \psi_{1,n}\|_{X_m} + \| B_{m,n}\psi_{1,n}\|_{X_m} & \le 2 \left( \|a_n \psi_{1,n}\|_{X_m} + \| B_{m,n}\psi_{1,n}\|_{X_m} \right) \nonumber \\[3pt] & \le 2(2-\delta_m) \|a_n \psi_{1,n}\|_{X_m} \le 4 M_m(a_n \psi_{1,n}) \nonumber \\[3pt] & \le \frac{4m(m-3)c_1(m)+8m}{\delta_m} =:c_2(m)\,. \end{align}
Similarly, by (1.2), (8.1), (8.4) (with
![]() $m=4$
), and Lemma 5.1,
$m=4$
), and Lemma 5.1,
 \begin{align} & \|\psi_{1,n}^{\prime\prime}\|_{X_1} + \|a_n \psi_{1,n}\|_{X_1} + \| B_{m,n}\psi_{1,n}\|_{X_1} \nonumber\\[3pt] & \qquad\qquad \le 2 \left( \|a_n \psi_{1,n}\|_{X_1} + \| B_{m,n}\psi_{1,n}\|_{X_1} \right) \le 4 \|a_n \psi_{1,n}\|_{X_m} \nonumber \\[3pt] & \qquad\qquad \le 4 \left( 1 + \|a\|_{L_\infty(0,1)} \right) \int_0^1 x \psi_{1,n}(x)\ \mathrm{d}x + 4 \int_1^\infty x^4 a_n(x) \psi_{1,n}(x)\ \mathrm{d}x \nonumber \\[3pt] & \qquad\qquad \le 4 \left( 1 + \|a\|_{L_\infty(0,1)} \right) + 4 c_2(4)=:c_3 \end{align}
\begin{align} & \|\psi_{1,n}^{\prime\prime}\|_{X_1} + \|a_n \psi_{1,n}\|_{X_1} + \| B_{m,n}\psi_{1,n}\|_{X_1} \nonumber\\[3pt] & \qquad\qquad \le 2 \left( \|a_n \psi_{1,n}\|_{X_1} + \| B_{m,n}\psi_{1,n}\|_{X_1} \right) \le 4 \|a_n \psi_{1,n}\|_{X_m} \nonumber \\[3pt] & \qquad\qquad \le 4 \left( 1 + \|a\|_{L_\infty(0,1)} \right) \int_0^1 x \psi_{1,n}(x)\ \mathrm{d}x + 4 \int_1^\infty x^4 a_n(x) \psi_{1,n}(x)\ \mathrm{d}x \nonumber \\[3pt] & \qquad\qquad \le 4 \left( 1 + \|a\|_{L_\infty(0,1)} \right) + 4 c_2(4)=:c_3 \end{align}
for
![]() $n\ge 1$
. Moreover, a straightforward consequence of (8.5), (8.6), and Hölder’s inequality is that (8.5) is also true for
$n\ge 1$
. Moreover, a straightforward consequence of (8.5), (8.6), and Hölder’s inequality is that (8.5) is also true for
![]() $m\in (1,3]$
with a suitable constant
$m\in (1,3]$
with a suitable constant
![]() $c_2(m)$
.
$c_2(m)$
.
We next claim that
![]() $(\psi_{1,n})_{n\ge 1}$
is relatively compact in
$(\psi_{1,n})_{n\ge 1}$
is relatively compact in
![]() $X_{1,m}$
for any
$X_{1,m}$
for any
![]() $m\ge 1$
. To this end, we note that, thanks to (8.5), (8.6), Lemma 2.1, and Fubini’s theorem,
$m\ge 1$
. To this end, we note that, thanks to (8.5), (8.6), Lemma 2.1, and Fubini’s theorem,
and
for
![]() $n\ge 1$
. Now, let
$n\ge 1$
. Now, let
![]() $m\ge 2$
. In view of (8.5) and the above estimates,
$m\ge 2$
. In view of (8.5) and the above estimates,
![]() $(\psi_{1,n})_{n\ge 1}$
is a bounded sequence in
$(\psi_{1,n})_{n\ge 1}$
is a bounded sequence in
![]() $X_0\cap X_m\cap W_1^1((0,\infty),x\mathrm{d}x)$
and it follows from [Reference Banasiak, Lamb and Laurençot9, Proposition 7.2.2] that
$X_0\cap X_m\cap W_1^1((0,\infty),x\mathrm{d}x)$
and it follows from [Reference Banasiak, Lamb and Laurençot9, Proposition 7.2.2] that
![]() $(\psi_{1,n})_{n\ge 1}$
is relatively compact in
$(\psi_{1,n})_{n\ge 1}$
is relatively compact in
![]() $X_r$
for any
$X_r$
for any
![]() $r\in (0,m)$
. As
$r\in (0,m)$
. As
![]() $m\ge 2$
is arbitrary, we conclude that there are
$m\ge 2$
is arbitrary, we conclude that there are
![]() $\psi_1\in \bigcap_{r>0} X_r$
and a subsequence
$\psi_1\in \bigcap_{r>0} X_r$
and a subsequence
![]() $(\psi_{1,n_j})_{j\ge 1}$
of
$(\psi_{1,n_j})_{j\ge 1}$
of
![]() $(\psi_{1,n})_{n\ge 1}$
such that
$(\psi_{1,n})_{n\ge 1}$
such that
An immediate consequence of (8.7) and the properties of
![]() $(\psi_{1,n})_{n\ge 1}$
is that
$(\psi_{1,n})_{n\ge 1}$
is that
Finally, let
![]() $m\ge 1$
. We observe that
$m\ge 1$
. We observe that
![]() $\mathrm{dom}(\mathbb{A}_{m,n})\subset \mathrm{dom}(\mathbb{A}_m)$
for
$\mathrm{dom}(\mathbb{A}_{m,n})\subset \mathrm{dom}(\mathbb{A}_m)$
for
![]() $n\ge 1$
(as
$n\ge 1$
(as
![]() $a_n\ge a$
) and that (8.1) also reads
$a_n\ge a$
) and that (8.1) also reads
where
It readily follows from (8.5) that
so that
In view of (8.8) and (8.9), the sequence
![]() $(\mathbb{A}_m \psi_{1,n_j})_{j\ge 1}$
converges to zero in
$(\mathbb{A}_m \psi_{1,n_j})_{j\ge 1}$
converges to zero in
![]() $X_{1,m}$
as
$X_{1,m}$
as
![]() $j\to\infty$
and, since
$j\to\infty$
and, since
![]() $\mathbb{A}_m$
is closed on
$\mathbb{A}_m$
is closed on
![]() $X_{1,m}$
, we readily deduce from (8.7) that
$X_{1,m}$
, we readily deduce from (8.7) that
![]() $\psi_1\in \mathrm{dom}(\mathbb{A}_m)$
and
$\psi_1\in \mathrm{dom}(\mathbb{A}_m)$
and
![]() $\mathbb{A}_m\psi_1=0$
.
$\mathbb{A}_m\psi_1=0$
.
Acknowledgments
PhL gratefully acknowledges the support of the Deutscher Akademischer Austauschdienst funding programme Research Stays for University Academics and Scientists, 2021 (57552334). This work was done while PhL enjoyed the kind hospitality of the Institut für Angewandte Mathematik, Leibniz Universität Hannover. We gratefully thank the referees for their careful reading of the manuscript and helpful suggestions.
Conflicts of interest
There is no conflicts of interest.