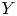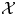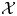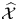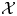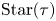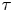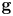1. Introduction
1.1 Overview
In [Reference Gross, Hacking and KeelGHK15], Gross, Hacking and Keel began a systematic study of cluster varieties from the perspective of mirror symmetry and the minimal model program. Together with Kontsevich, they used this geometric approach in [Reference Gross, Hacking, Keel and KontsevichGHKK18] to settle various important and long-standing conjectures in cluster theory. The insights of [Reference Gross, Hacking and KeelGHK15, Reference Gross, Hacking, Keel and KontsevichGHKK18] reveal a strong link between cluster theory and toric geometry. One of the main purposes of this paper is to explore the connections between these theories. In particular, we pursue the idea that compactifications of 
$\mathcal {A}$-cluster varieties are a generalization of toric varieties associated to polytopes, while partial compactifications of 
$\mathcal {X}$-cluster varieties generalize toric varieties associated to fans. Recall that toric degenerations of compactified 
$\mathcal {A}$-cluster varieties were studied in great detail in [Reference Gross, Hacking, Keel and KontsevichGHKK18]. They arise from positive polytopes, which define a family of graded rings, and hence projective varieties. Here we develop a theory of toric degenerations for partially compactified 
$\mathcal {X}$-cluster varieties. Both the partial compactifications and the toric degenerations arise from a fan construction rather than a polytope construction. More precisely, given a special completion 
$\widehat {\mathcal {X} }$ of 
$\mathcal {X}$ (in the sense of [Reference Fock and GoncharovFG16]) of complex dimension 
$n$, we construct for each seed 
$s$ a flat family
defining a degeneration of 
$\widehat {\mathcal {X} }$ with the following properties:
– the fiber over
$(1,\ldots ,1)$ is $\widehat {\mathcal {X} }$;– if
$\widehat {\mathcal {X} }$ has no frozen directions then the fiber over $(0,\ldots ,0)$ (also called the central fiber) is the toric variety associated to the cluster complex $\Delta ^{+}_s$;– if
$\widehat {\mathcal {X} }$ has frozen directions then the fiber over $(0,\ldots ,0)$ is the toric variety associated to a fan contained in a superpotential cone. The fan structure comes from the cluster structure;– in both cases the cluster variety
$\mathcal {X}$ degenerates to the dense torus inside the toric central fiber.
One of the key ideas is to make a distinction between coefficients and frozen variables, concepts that are usually identified. We think of coefficients as parameters deforming the mutation formulas: deformation parameters for the families. Frozen variables are 
$\mathcal {A}$-cluster variables associated to frozen directions; they relate to the geometry of individual fibers rather than the deformations of these fibers. This approach allows us to consider the toric varieties in the central fibers as a very degenerate class of cluster varieties.
To construct the family 
$\widehat {\mathscr {X} }_{s}$ we develop the notion of a 
$Y$-pattern with coefficients and its geometric counterpart: 
$\mathcal {X}$-cluster varieties with coefficients. Moreover, we develop cluster duality for cluster varieties with coefficients and prove that our degeneration is cluster dual in this generalized sense to the Gross–Hacking–Keel–Kontsevich 
$\mathcal {A}_{\mathrm {prin}}$-degeneration of 
$\mathcal {A}$-cluster varieties. By doing so, we solve simultaneously two problems in cluster theory. On the one hand, we find a way to include coefficients in the 
$Y$-mutation formula. This was an aim of Fomin and Zelevinsky (private communication) when they developed the foundations of cluster algebras. On the other hand, we define spaces that are cluster dual to 
$\mathcal {A}$-cluster varieties with coefficients, a problem posed in [Reference Gross, Hacking, Keel and KontsevichGHKK18, § 7] which we are about to describe. Let 
$\mathcal {A} _{s}$ be an 
$\mathcal {A}$-cluster variety with initial seed 
$s$. In [Reference Gross, Hacking and KeelGHK15] the authors introduced a family 
$\mathcal {A}_{\mathrm {prin},{s}} \to \mathbb {A}^{n}_{\mathbb {C} }$ of deformations of 
$\mathcal {A} _s$. The space 
$\mathcal {A}_{\mathrm {prin},{s}}$ and the fibers 
$\mathcal {A} _{\mathbf {t}}$ over closed points 
$\mathbf {t}\in \mathbb {A}^{n}_{\mathbb {C} }$ are themselves cluster varieties with coefficients. In [Reference Gross, Hacking, Keel and KontsevichGHKK18, § 7] the authors predicted the existence of a cluster dual 
$\mathcal {A} _{\mathbf {t}}^{\vee }$ to the fibers but stated it was unclear how the coefficients should be handled under dualization. Consider the Langlands dual seed 
$s^{\vee }$. Inside 
$\widehat {\mathscr {X} }_{s^{\vee }}$ there is an 
$\mathcal {X}$-cluster variety with coefficients 
$\mathscr {X} _{s^{\vee }}$. The restriction of 
$\pi$ to 
$\mathscr {X} _{s^{\vee }}$ gives a map 
$\mathscr {X} _{s^{\vee }}\to \mathbb {A} ^{n}_{\mathbb {C} }$ with fiber 
$\mathcal {X} _\textbf {t}$ over 
$\textbf {t}$. We show that the varieties 
$\mathscr {X} _{s^{\vee }}$ and 
${\mathcal {A}_{\mathrm {prin},{s}} }$ are cluster dual as cluster varieties with coefficients. Moreover, we show that the fibers 
$\mathcal {X} _{\mathbf {t}}$ are exactly the wanted cluster duals 
$\mathcal {A} _{\mathbf {t}}^{\vee }$. For more details the reader is referred to § 3, in particular Remark 3.27.
This is the first of a series of papers. In a sequel, along with M.-W. Cheung, we will explore how the notion of cluster duality with coefficients is related to Batyrev–Borisov duality in the context of mirror symmetry. Further, we will show that the toric degeneration of the Grassmannian given by [Reference Rietsch and WilliamsRW19] coincides with the toric degeneration given by the 
$\mathcal {A}_{\mathrm {prin}}$-construction for all 
$\operatorname {Gr}_k\left ({\mathbb {C} ^{n}}\right )$.
1.2 Toric degenerations
For the past 25 years, constructions of toric degenerations have been of increasing interest in algebraic geometry, with particular development in representation theory (we refer to the overview [Reference Fang, Fourier and LittelmannFFL16] and references therein). The core idea is to glean information about varieties of interest by passing through the world of toric geometry, where otherwise difficult questions become readily approachable. If we construct a flat family whose generic fiber is isomorphic to the variety of interest while a special fiber is a toric variety, this allows us to deduce properties of the generic fiber from the special fiber (e.g. degree, Hilbert-polynomial or smoothness). Typically for polarized projective varieties 
$\left ({Y,\mathcal {L} }\right )$ this is realized using Newton–Okounkov bodies, where a valuation on the section ring of 
$\mathcal {L}$ determines a convex body generalizing the toric notion of a Newton polytope (see e.g. [Reference OkounkovOko98, Reference Lazarsfeld and MustaţăLM09, Reference Kaveh and KhovanskiiKK12, Reference AndersonAnd13]).
Cluster varieties (and their compactifications) entered the stage of toric degenerations in [Reference Gross, Hacking, Keel and KontsevichGHKK18, Reference Rietsch and WilliamsRW19]. In both aforementioned papers the authors construct toric degenerations using polytopes (in a broad sense) related to section rings of ample line bundles over compactified cluster varieties. While [Reference Rietsch and WilliamsRW19] use Newton–Okounkov bodies for Grassmannians directly, the construction given in [Reference Gross, Hacking, Keel and KontsevichGHKK18] is more general and is expected to recover toric degenerations of many representation theoretic objects. For example, the case of flag varieties is addressed in [Reference MageeMag20, Reference Bossinger and FourierBF19, Reference Genz, Koshevoy and SchumannGKS16, Reference Genz, Koshevoy and SchumannGKS20].
We take a slightly different approach in this paper and construct toric degenerations associated to fans naturally occurring in cluster theory. The theory developed in this paper can be used to understand the relation between the approach taken in [Reference Gross, Hacking, Keel and KontsevichGHKK18] and that of [Reference Rietsch and WilliamsRW19]. We illustrate this in the example of 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$ (see § 7.1), and in a sequel we will treat the general case.
1.3 The geometric setting
In the world of toric geometry, there are two main combinatorial devices encoding toric varieties: fans and polytopes. A fan gives a recipe for gluing affine schemes together to construct the toric variety. A polytope gives a graded ring in terms of a basis of homogeneous elements and relations. So, it gives a projective toric variety equipped with an ample line bundle and a vector space basis for each homogeneous component of the section ring of this line bundle. A philosophical take-away of this paper is that 
$\mathcal {X}$-varieties compactify with a fan construction, while 
$\mathcal {A}$-varieties compactify with a polytope construction.
Take as a starting point the scattering diagram description of 
$\mathcal {A}$- and 
$\mathcal {X}$-varieties introduced in [Reference Gross, Hacking, Keel and KontsevichGHKK18]. The same scattering diagram (living in 
$\mathcal {X} ^{\mathrm {trop} }\left ({\mathbb {R} }\right )$) encodes both 
$\mathcal {A}$ and 
$\mathcal {X}$, but in different ways. We outline both below.
The scattering diagram tells us how to write down a basis of global regular functions on 
$\mathcal {A}$, whose elements are called 
$\vartheta$-functions, as well as the structure constants for multiplying these 
$\vartheta$-functions. That is, the scattering diagram encodes 
$\mathcal {O} (\mathcal {A} )$, together with a distinguished vector space basis. This generalizes the toric notion that the cocharacter lattice 
$M$ of 
$T^{\vee }$ is a distinguished vector space basis for 
$\mathcal {O} (T)$, where 
$T\cong \left ({\mathbb {C} ^{*}}\right )^{n}$ is an algebraic torus and 
$T^{\vee }$ is the dual torus. To address projective varieties compactifying 
$\mathcal {A}$, Gross, Hacking, Keel and Kontsevich introduce positive polytopes 
$\Xi$ in 
$\mathcal {X}^{\mathrm{trop}} \left ({\mathbb {R} }\right )$ (see [Reference Gross, Hacking, Keel and KontsevichGHKK18, Definition 8.6]). Positivity is precisely what is needed for the integer points (
$\vartheta$-functions) of 
$\Xi$ to define a graded ring. The result is a polarized projective variety 
$\left ({Y,\mathcal {L} }\right )$ together with a basis of 
$\vartheta$-functions for the section ring of 
$\mathcal {L}$. In the 
$\mathcal {A}_{\text {prin}}$-construction, they then give a flat family of deformations of 
$\mathcal {A}$ over 
$\mathbb {A} ^{n}$, with central fiber simply the torus 
$T_{N,s} \subset \mathcal {A}$ associated to the seed 
$s$. The 
$\vartheta$-functions extend canonically to 
$\mathcal {A}_{\mathrm {prin},{s}}$, yielding a toric degeneration of 
$\left ({Y,\mathcal {L} }\right )$.
On the other side of the picture, a subset of the scattering diagram (known as the 
$\mathbf {g}$-fan) has a simplicial fan structure. The key idea here is to exploit this fan structure. In the atlas for the 
$\mathcal {X}$-variety itself, there is a torus for every maximal cone of the 
$\mathbf {g}$-fan. Specifically, given a maximal cone 
$\mathcal {G}$ (a 
$\mathbf {g}$-cone) with dual cone 
$\mathcal {C}$ (a 
$\mathbf {c}$-cone), we have the torus
\[ {T_{M,\mathcal{G}}:= \operatorname{Spec}\left({ \mathbb{C} \left[{ \mathcal{C}(\mathbb{Z} )^{\mathrm{gp}} }\right]}\right),} \]
where 
$\mathcal {C}(\mathbb {Z} )$ is the monoid of integral points in 
$\mathcal {C}$ and 
$\mathcal {C}(\mathbb {Z} )^{\mathrm{gp}}$ is its group completion. These tori are glued by the 
$\mathcal {X}$-mutation formula, with the (non-zero) monoid generators of 
$\mathcal {C}(\mathbb {Z} )$ giving rise to an 
$\mathcal {X}$-cluster. From the perspective of toric geometry, it is far more natural to glue the affine spaces
\[ {\mathbb{A} _{M,\mathcal{G}}^{n}:= \operatorname{Spec}\left({ \mathbb{C} \left[{ \mathcal{C}(\mathbb{Z} )}\right]}\right)} \]
by 
$\mathcal {X}$-mutation. The resulting space is a partial compactification of 
$\mathcal {X}$: the special completion 
$\widehat {\mathcal {X} }$ of [Reference Fock and GoncharovFG16]. Refinements 
$\Sigma$ of the 
$\mathbf {g}$-fan similarly yield partial compactifications.
Rather than deforming global sections of line bundles as for the compactification of 
$\mathcal {A}$, we can deform the gluing of patches 
$\mathbb {A} _{M,\mathcal {G}}^{n}$. To define these deformations, we introduce the notion of 
$\mathcal {X}$-cluster varieties with coefficients, see § 3.2. As an important case of this notion, we describe how to deform the gluing in a manner dual to the deformation of 
$\vartheta$-functions in 
$\mathcal {A}_{\mathrm {prin}}$.
Definition 1.1 Fix an initial seed 
$s_0$, with associated 
$\mathbf {g}$-cone 
$\mathcal {G}_0$, and take principal coefficients 
$t_1, \ldots , t_n$ at 
$s_0$. Let 
$R= \mathbb {C} \left [{t_1,\ldots , t_n}\right ]$. The 
$\mathcal {X}$-cluster variety with coefficients in 
$R$ and its special completion are the 
$R$-schemes
\[ \mathscr{X} _{\mathcal{G}_0}:=\bigcup_{\mathcal{G}} T_{M,\mathcal{G}}(R)\quad \text{and}\quad \widehat{\mathscr{X} }_{\mathcal{G}_0} :=\bigcup_{\mathcal{G}} \mathbb{A} ^{n}_{M,\mathcal{G}}(R) \]with patches glued birationally via the mutation formula with coefficients (5.1).
Below we summarize some of our main results.
Theorem 1.2 (Proposition 5.7, Theorem 5.8, Proposition 5.11, Corollary 5.13) The family 
${\widehat {\mathscr {X} }_{\mathcal {G}_0} \to \operatorname {Spec}(R)}$ is a flat toric degeneration of 
$\widehat {\mathcal {X} }$ to the toric variety defined by the 
$\mathbf {g}$-fan, realized here with 
$\mathcal {G}_0$ as the positive orthant. Generic fibers of this family are isomorphic and smooth.
Theorem 1.3 (Propositions 5.3, 5.4) The 
$\mathcal {X}$-variables 
$X_{i;\mathcal {G}}$ extend canonically to homogeneous rational functions on 
$\widehat {\mathscr {X} }_{\mathcal {G}_0}$. The degree of the extension of 
$X_{i;\mathcal {G}}$ is its 
$\mathbf {c}$-vector 
$\mathbf {c} _{i;\mathcal {G}}$, and in the central fiber the extension restricts to the monomial whose exponent vector is this 
$\mathbf {c}$-vector.
Theorem 1.4 (Theorems 6.2, 6.3) The fibers of 
$\widehat {\mathscr {X} }_{\mathcal {G}_0} \to \operatorname {Spec}\left ({R}\right )$ are stratified, with each stratum encoded by 
$\operatorname {Star}(\tau )$ for some cone 
$\tau$ of the 
$\mathbf {g}$-fan. These strata 
$V(\tau )_{\mathbf {t}}$ are again specially completed 
$\mathcal {X}$-varieties with coefficients, and the stratum 
$V(\tau )_{\mathbf {t}}$ degenerates to the toric stratum 
$V(\tau )$ defined by 
$\operatorname {Star}(\tau )$ in the central fiber.
We can replace the 
$\mathbf {g}$-fan with any refinement 
$\Sigma$ and obtain results analogous to each of the theorems above (see Remark 5.9).
In the toric setting, fans and polytopes are both used to compactify tori. Here, we find fans compactifying 
$\mathcal {X}$-varieties and polytopes compactifying 
$\mathcal {A}$-varieties. This is completely natural in the scattering diagram description of cluster varieties, as discussed above. But there are other reasons to expect different types of compactifications for the two flavors of cluster varieties. First, 
$\mathcal {A}$-variables are 
$\vartheta$-functions, globally regular on 
$\mathcal {A}$, while 
$\mathcal {X}$-variables are only locally defined. In fact, as observed in [Reference Gross, Hacking and KeelGHK15], 
$\mathcal {X}$-varieties may not have many global functions at all. From this perspective, 
$\mathcal {A}$-varieties are primed for a polytope-
$\operatorname {Proj}$ construction, while it is more natural to think of an 
$\mathcal {X}$-variety in terms of an atlas of affine schemes. Moreover, it is usually hopeless to attempt to compactify an 
$\mathcal {X}$-variety with a 
$\operatorname {Proj}$ construction as 
$\mathcal {X}$-varieties are generally not separated [Reference Gross, Hacking and KeelGHK15, Remark 2.6], while 
$\operatorname {Proj}$ of a graded ring is always separated.
Remark 1.5 That said, there are many interesting cases where the 
$\mathcal {A}$- and 
$\mathcal {X}$-varieties are isomorphic. Namely, if there is a unimodular 
$p^{*}$-map [Reference Gross, Hacking and KeelGHK15, Equation (2.1)], then we have isomorphic 
$\mathcal {A}$- and 
$\mathcal {X}$-varieties. However, the different ways of viewing this space lead to very different compactifications. In this case, our family 
$\mathscr {X}_{s_0}$ of Definition 5.6 is just 
$\mathcal {A}_{\mathrm {prin},{s_0}}$, with 
$p$ giving fiberwise identifications of 
$\mathcal {A} _{\mathbf {t}}$ and 
$\mathcal {X} _{\mathbf {t}}$. But 
$\widehat {\mathscr {X} }_{s_0}$ and the partial compactifications of 
$\mathcal {A}_{\mathrm {prin},{s_0}}$ considered in [Reference Gross, Hacking, Keel and KontsevichGHKK18] differ.
We would like to emphasize here that 
$\mathcal {X}$-varieties, although generally non-separated, are indeed spaces of interest. They are nice in many other ways: they are, for instance, smooth log Calabi–Yau varieties equipped with a positive structure. They entered center stage through the work of Fock and Goncharov, particularly [Reference Fock and GoncharovFG06]. Here, a stacky version of the 
$\mathcal {X}$-variety serves as the moduli stack of framed 
$G$-local systems on a marked surface with boundary, where 
$G$ is a split semisimple algebraic group with trivial center. Furthermore, Fock and Goncharov describe how the positive real points of the 
$\mathcal {X}$-variety define higher Teichmüller spaces, while tropical points define lamination spaces. They study Teichmüller and lamination spaces further in [Reference Fock and GoncharovFG07], where they exhibit a canonical pairing between 
$\mathcal {X}$ (respectively 
$\mathcal {A}$) Teichmüller spaces and 
$\mathcal {A}$ (respectively 
$\mathcal {X}$) lamination spaces. Moreover, in [Reference Fock and GoncharovFG16] they introduce completions of Teichmüller spaces for decorated surfaces with marked points in the boundary. They prove that the set of positive points of a specially completed 
$\mathcal {X}$-cluster variety gives a completion of the corresponding Teichmüller space with boundary components corresponding to simple laminations. In this context, 
$\mathcal {X}$-cluster varieties provide a formalism for quantizing such Teichmüller spaces following the approach of Chekhov and Fock [Reference Fock and ChekhovFC99]. Le studies higher Teichmüller and lamination spaces à la Thurston in [Reference LeLe16] and similarly gives a compactification of higher Teichmüller space with projective laminations. Allegretti and Bridgeland relate the moduli stacks mentioned above for 
$G=\operatorname {PGL}_2(\mathbb {C} )$ to projective structures on the corresponding surfaces in [Reference Allegretti and BridgelandAB20]. On the algebraic side of the picture, cluster variables associated to finite type 
$\mathcal {X}$-cluster varieties have been studied in great detail in [Reference Sherman-BennettShe19].
1.4 The algebraic foundations
At the heart of cluster theory there are two central notions: cluster patterns and 
$Y$-patterns. These are certain recurrences extensively studied by Fomin and Zelevinsky in [Reference Fomin and ZelevinskyFZ02, Reference Fomin and ZelevinskyFZ03a, Reference Fomin and ZelevinskyFZ03b, Reference Fomin and ZelevinskyFZ07]. The geometric incarnation of a cluster pattern (respectively 
$Y$-pattern) is an 
$\mathcal {A}$-cluster variety (respectively 
$\mathcal {X}$-cluster variety). To define a cluster algebra with coefficients one considers a cluster pattern with coefficients in a 
$Y$-pattern. Such a cluster algebra lives in an ambient field 
$\mathcal {F}=K(x_1,\ldots ,x_n)$ of rational functions. By construction, 
$Y$-patterns are clusters of elements of the coefficient field 
$K$ and cluster patterns are clusters of functions in 
$\mathcal {F}$ generating the cluster algebra. The geometric considerations discussed above suggest that there should exist a notion of a 
$Y$-pattern with coefficients, which we define as follows.
Every seed of such a pattern is given by a triple 
$(\mathbf {y},\mathbf {p}, B)$, where 
$(\mathbf {p},B)$ is a 
$Y$-seed in some semifield 
$\mathbb {P}$ and 
$(\mathbf {y},B)$ is a 
$Y$-seed in a universal semifield with coefficients in 
$\mathbb {Q} \mathbb {P}$ (see (2.1)). Then 
$(\mathbf {y}',\mathbf {p}',B')$ is the mutation in direction 
$k$ of 
$(\mathbf {y},\mathbf {p},B)$, if 
$(\mathbf {p}',B')$ is the usual 
$Y$-mutation in direction 
$k$ of 
$(\mathbf {p},B)$ and 
$\mathbf {y}'=(y'_1,\ldots ,y'_n)$ is given by
\[ y'_j := \left\{\begin{array}{@{}ll@{}} y_j^{-1} & \text{ if } j=k, \\ y_j \left({ p_k^{[\kern-1pt[ b_{kj}]\kern-1pt]} + p_k^{[\kern-1pt[ -b_{kj}]\kern-1pt]} y_k^{-\operatorname*{sgn}(b_{kj})} }\right) ^{-b_{kj}} & \text{ if } j\not =k, \end{array}\right. \]
where 
$p_k^{[\kern-1pt[ \pm b_{kj}]\kern-1pt] }$ are certain expressions in 
$\mathbb {P}$ (see Definition 2.8 below, respectively § 2.4 for more details). As expected such a pattern lives in an ambient field of rational functions. Indeed, 
$x$-cluster variables are functions on an 
$\mathcal {A}$-cluster variety, while the 
$y$-variables are local functions on an 
$\mathcal {X}$-cluster variety.Footnote 1
We prove similar to the case of cluster patterns with coefficients, that 
$Y$-patterns with coefficients satisfy separation formulas in Theorem 2.33. Further, in Theorem 2.34 we show that the periodicities of 
$Y$-patterns with coefficients agree with those of the coefficient-free case.
1.5 An example
We illustrate our theory in the smallest non-trivial example. Let 
$\Sigma$ be the complete fan in 
$\mathbb {R} ^{2}$ depicted in Figure 1. It is defined by the rays spanned by 
$(1,0), (0,1), (-1,1), (-1,0)$ and 
$(0,-1)$. This fan is the 
$\textbf {g}$-fan of an 
$\mathcal {X}$-cluster variety of type 
$A_2$. There are two geometric objects naturally associated to the fan 
$\Sigma$:
(i) the toric variety
$\text {TV}(\Sigma )$;(ii) the special completion of the corresponding
$\mathcal {X}$-cluster variety.Footnote 2
Figure 1. Visualization of 
$\hat {\mathscr {X} }_s$ defined by a 
$Y$-pattern with principal coefficients in type 
$A_2$. For more details see Table 2.
Both these varieties are obtained by gluing affine spaces isomorphic to 
$\mathbb {A} ^{2}_{\mathbb {C} }$ via birational transformations. The cluster gluing can be deformed to obtain the toric gluing. To see this, we describe the family 
$\pi :\hat {\mathscr {X} }_s\to \mathbb {A} ^{2}_{\mathbb {C} }$ (see Definition 5.6) explicitly and show how it simultaneously embodies both of the aforementioned geometric objects. The family 
$\hat {\mathscr {X} }_s$ is an 
$R$-scheme for 
$R=\mathbb {C} [t_1,t_2]$ glued from five affine spaces 
$U_{\sigma _0}, \ldots , U_{\sigma _4}$ each one isomorphic to 
$\mathbb {A} ^{2}_R$. These affine spaces are in one-to-one correspondence with maximal cones (or 
$\mathbf {g}$-cones) 
$\sigma \in \Sigma$. Figure 1 captures the local coordinates of the affine pieces defining 
$\widehat {\mathscr {X} _s}$ (in the algebraic language we will refer to this data as the 
$Y$-seeds of the 
$Y$-pattern with principal coefficients). They are depicted in their associated 
$\mathbf {g}$-cones. Explicitly, each affine piece 
$U_{\sigma _i}$ is the spectrum of the polynomial ring generated by the 
$Y$-cluster variables of the underlying 
$Y$-seed. We have,
\[ U_{\sigma_i}:=\operatorname{Spec}\left({ R[X_1^{i},X_2^{i}]}\right), \]
where we set 
$X_j:=X_j^{0}$. The dashed arrows in Figure 1 indicate the expressions of the variables 
$X_j^{i}$ in terms of the initial variables 
$X_1,X_2$. The pull-backs of the gluing morphisms are obtained from these. For example, 
$U_{\sigma _0}\dashrightarrow U_{\sigma _1}$ is given by
\[ R[X_1^{1},X_2^{1}] \to R[X_1,X_2],\quad \text{where }\ X_2^{1} \mapsto X_2^{-1}\quad \text{and} \quad X_1^{1} \mapsto X_1(t_2X_2+1). \]
From this family we can recover the toric and the cluster gluing associated with the fan 
$\Sigma$ from above as fibers by specifying values for the coefficients 
$(t_1,t_2)$.
(i) The special completion
$\widehat {\mathcal {X} } _s$ is the $(1,1)$-fiber of the family. In particular, it is a $\mathbb {C}$-scheme glued from affine pieces $U_{\sigma _j}|_{t_i=1}$. It can be read from Figure 1 by specifying $t_1=t_2=1$. For example, the affine piece corresponding to $\sigma _1$ is $U_{\sigma _1}|_{t_i=1}=\operatorname {Spec} \left ({\mathbb {C} [X_1^{1},X_2^{1}]}\right )$ with gluing $U_{\sigma _0}|_{t_i=1}\dashrightarrow U_{\sigma _1}|_{t_i=1}$ given by
It can be verified that we obtain the usual cluster transformations for the\[ \mathbb{C} [X_1^{1},X_2^{1}] \to \mathbb{C} [X_1,X_2], \quad \text{where} \ X_2^{1} \mapsto X_2^{-1} \quad \text{and}\quad X_1^{1} \mapsto X_1(X_2+1). \]$\mathcal {X}$-cluster variety this way.(ii) The toric variety
$\text {TV}(\Sigma )$ is the $(0,0)$-fiber of the family. Hence, it is the $\mathbb {C}$-scheme glued from affine pieces $U_{\sigma _j}|_{t_i=0}$ and is encoded in Figure 1 by specifying $t_1=t_2=0$. The affine piece $U_{\sigma _1}|_{t_i=0}$ for example, is $\operatorname {Spec}\left ({ \mathbb {C} [X_1^{1},X_2^{1}]}\right )$ with gluing $U_{\sigma _0}|_{t_i=0}\dashrightarrow U_{\sigma _1}|_{t_i=0}$ given by
Note that all variables degenerate to monomials. Further, the gluing morphisms indicated by the dashed arrows in Figure 1 degenerate to the classical toric gluing as described, e.g. in [Reference Cox, Little and SchenckCLS11, § 3.1]. In this case the toric variety\[ \mathbb{C} [X_1^{1},X_2^{1}] \to \mathbb{C} [X_1,X_2], \quad \text{where} \ X_2^{1} \mapsto X_2^{-1} \quad\text{and} \quad X_1^{1} \mapsto X_1. \]$\text {TV}(\Sigma )$ is the blow-up of $\mathbb {P} ^{1}\times \mathbb {P} ^{1}$ in a point.
The toric variety associated to the polytope 
$P$ (see Figure 9) whose face-fan is 
$\Sigma$ is the central fiber of the corresponding 
$\mathcal {A} _{\text {prin}}$-family. Both 
$\text {TV}(\Sigma )$ and 
$\text {TV}(P)$ are toric Fano varieties and they are in fact Batyrev-dual. We elaborate on this example in § 7.2, and we will explore the connection between cluster duality and Batyrev duality in general in a sequel with M.-W. Cheung.
A natural question to ask is: which kind of fans can arise in cluster theory? This problem is closely related to the representation theory of quivers. For instance, in [Reference Derksen, Weyman and ZelevinskyDWZ10, Reference Fu and KellerFK10] the reader can find a representation-theoretic approach to g-vectors (which are the primitive integer vectors spanning the g-cones). For a representation theoretic approach to c-vectors (the primitive integer vectors spanning the cones dual to the g-cones) the reader can consult [Reference FuFu17, Reference Nájera ChávezNaj15, Reference Nájera ChávezNaj13, Reference Nakanishi and StellaNS14]. It is therefore desirable to understand the relationship between toric varieties and quiver representations. Another combinatorial approach to study these fans along with their richer structure of a scattering diagrams is given in [Reference ReadingRea17, Reference ReadingRea20]. Moreover, the reader might also want to consult [Reference BridgelandBri17] for an approach to scattering diagrams closer to representation theory.
We would like to stress that 
$\mathcal {X}$-mutation formulas with principal coefficients can be obtained using the approach of [Reference Li and RupelLR20] where the authors construct symplectic groupoids integrating log-canonical Poisson structures on 
$\mathcal {X}$-cluster varieties and their special completions. In their setting the deformation of the toric gluing is obtained using Hamiltonian flows of the groupoid charts. It is a very interesting problem to explore the relation of our approach and that of [Reference Li and RupelLR20].
1.6 Structure of the paper
We try to make this paper as self contained as possible and seek to overcome the discrepancy between the algebraic and the geometric notation in cluster theory by writing this paper in a bilingual fashion. Therefore, we survey some of the algebraic and geometric foundations of the theory we will use.
In § 2 we develop the algebraic foundations of the paper. Namely, we introduce the notion of a 
$Y$-pattern with coefficients in complete generality. We study the periodicities of these patterns and obtain their separation formulas. For convenience of the reader we also recall some basic facts of cluster theory as developed by Fomin and Zelevinsky in [Reference Fomin and ZelevinskyFZ02, Reference Fomin and ZelevinskyFZ07].
Sections 3 to 7 have a geometric focus. We start § 3 by recalling some basic facts of cluster varieties as presented in [Reference Gross, Hacking and KeelGHK15] (see § 3.1). In § 3.2 we introduce a new notion of cluster varieties with coefficients, and we study cluster duality in this setting in § 3.3. This is followed by a detailed discussion of the case of principal coefficients in § 3.4. All throughout § 3 we translate some of the results in § 2 from an algebraic language to a geometric one. Readers with more interest in the geometry might consider reading this paper from § 3 in a first read. However, the general algebraic features of 
$Y$-patterns with coefficients analyzed in §§ 2.4 to 2.7 are of great importance and might also be interesting to geometers.
The succeeding § 4 is dedicated to the tropical geometry of cluster varieties and the special completion 
$\widehat {\mathcal {X} }$. We recall necessary notions from [Reference Fock and GoncharovFG09a] in § 4.1 and from [Reference Nakanishi and ZelevinskyNZ12] in § 4.2.
In § 5 we construct toric degenerations of 
$\widehat {\mathcal {X} }$. We review the construction of toric varieties via fans in § 5.1. In § 5.2 we introduce the degeneration, and show that it is indeed a flat family over 
$\mathbb {A}^{n}_{\mathbb {C} }$ with generic fibers being isomorphic.
Moreover, in § 6 we study the stratification of 
$\widehat {\mathcal {X} }$ and show that the cluster strata of 
$\widehat {\mathcal {X} }$ degenerate to the toric strata of the central fiber.
In § 7 we present detailed examples and applications of the theory developed in this paper. In particular, we treat the example of the Grassmannian 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$ and of the del Pezzo surface of degree five.
2. $Y$-patterns with coefficients
In this section we define 
$Y$-patterns with coefficients and study their basic properties. This concept will be used throughout the paper.
The section is structured as follows: in § 2.1 we summarize preliminaries on semifields and in § 2.2 we recall coefficient-free cluster patterns and 
$Y$-patterns as introduced by Fomin and Zelevinsky. In § 2.3 we remind the reader about cluster patterns with coefficients (as in [Reference Fomin and ZelevinskyFZ07]). In particular, we recall the definition of g-vectors and 
$F$-polynomials. In § 2.4 we define 
$Y$-patterns with coefficients. Finally in § 2.5 we treat periodicities and separation formulas of the latter.
2.1 Semifields
We summarize below the necessary background on semifields and introduce relevant notions that are being used throughout the rest of the paper. For a natural number 
$n$ let
\[ [1,n]:=\lbrace 1, \ldots, n \rbrace. \]
For 
$x$ any real number, set
\[ \operatorname*{sgn}(x):= \left\{\begin{matrix}-1 & \text{if } x<0,\\ 0 & \text{if } x=0,\\ 1 & \text{if } x>0.\end{matrix}\right. \]
Further, let 
$[x]_+:=\max (x,0)$, and extend to 
$[\left ({x_1,\ldots ,x_n}\right )]_+:=\left ({\left [{x_1}\right ]_+,\ldots ,\left [{x_n}\right ]_+}\right )$.
Definition 2.1 A semifield is a quadruple 
$(\mathbb {P} ,\oplus ,\cdot ,1)$ that satisfies the axioms of a field, with the exception that there might not exist a neutral element nor inverses for the operation 
$\oplus$, called the auxiliary addition.
Example 2.2 (Tropical semifields) Let 
$I$ be a set. The free abelian group (written multiplicatively) with generating set 
$\lbrace p_i:i\in I\rbrace$ can be endowed with the structure of a semifield by setting
\[ \biggl( \prod_{i\in I}p_i^{a_i}\biggr)\oplus \biggl(\prod_{i\in I}p_i^{b_i}\biggr):=\prod_{i\in I}p_i^{\min(a_i,b_i)}. \]
We denote the resulting semifield by 
$\text {Trop}(p_i:i\in I)$ and call it the tropical semifield generated by 
$\lbrace p_i:i\in I\rbrace$.
Example 2.3 (Universal semifields) Let 
$S$ be a set and 
$\mathbb {Q} (S)$ be the field of rational functions on commuting variables 
$s\in S$ with coefficients in 
$\mathbb {Q}$. The universal semifield 
$\mathbb {Q} _{\text {sf}}(S)$ is the subset of 
$\mathbb {Q} (S)$ formed by the elements that can be expressed as a ratio of two subtraction-free polynomials, i.e. polynomials in 
$\mathbb {Z} _{>0}[S]$. Hence, 
$\mathbb {Q} _{\text {sf}}(S)$ is a semifield with respect to the usual operations of multiplication and addition.
Universal semifields satisfy the following universal property that will be used frequently. When 
$S$ is finite this property is precisely [Reference Berenstein, Fomin and ZelevinskyBFZ96, Lemma 2.1.6]. The proof of the infinite case is a straightforward generalization of [Reference Berenstein, Fomin and ZelevinskyBFZ96, Lemma 2.1.6].
Lemma 2.4 (Universal property of universal semifields) Let 
$\mathbb {P}$ be a semifield, 
$S$ a set and 
$\varphi : S\to \mathbb {P}$ a function of sets. Then there exists a unique morphism of semifields 
$\mathbb {Q} _{{\rm sf}}(S)\to \mathbb {P}$, such that 
$s \mapsto \varphi (s)$ for all 
$s\in S$.
Example 2.5 The expression 
$x^{2}-x+1\in \mathbb {Q} _{\text {sf}}(x)$. Indeed, 
$x^{2}-x+1$ can be expressed as the ratio 
${(x^{3}+1)}/{(x+1)}$. Notice that by the universal property in Lemma 2.4 this expression as a rational function is unique.
It was shown in [Reference Fomin and ZelevinskyFZ07, p. 5] that the group ring 
$\mathbb {Z} \mathbb {P}$ associated to any semifield 
$\mathbb {P}$ is a domain. We let 
$\mathbb {Q} \mathbb {P}$ be the field of fractions of 
$\mathbb {Z} \mathbb {P}$. Notice that any field of rational functions of the form 
$\mathbb {Q} \mathbb {P} (u_1,\ldots , u_\ell )$ contains a semifield 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots , u_\ell )$ of subtraction-free rational functions. Explicitly, an element 
$h\in \mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots ,u_\ell )$ is a rational function 
${f}/{g}$ where 
$f$ and 
$g$ are polynomials in 
$u_1,\ldots ,u_\ell$ with coefficients in 
$\mathbb {Z} _{>0}[\mathbb {P} ]\subset \mathbb {Z} \mathbb {P}$. In particular,
\begin{equation} \mathbb{Q} \mathbb{P} _{\text{sf}}(u_1,\ldots,u_\ell)=\mathbb{Q} _{>0}[\mathbb{P} ](u_1,\ldots,u_\ell)\subset \mathbb{Q} _{\text{sf}}(\mathbb{P} \cup\{u_1,\ldots,u_\ell\}). \end{equation}
Therefore, 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots ,u_\ell )$ satisfies the following universal property.
Corollary 2.6 (Universal property of 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots ,u_\ell )$)
Let 
$\mathbb {P} '$ and 
$\mathbb {P}$ be semifields, 
$p_1,\ldots , p_\ell \in \mathbb {P} '$ and 
$\mathbb {P} \to \mathbb {P} '$ a function of the underlying sets. Then there exists a unique morphism of semifields 
$\mathbb {Q} \mathbb {P} _{\rm sf}(u_1,\ldots ,u_\ell )\to \mathbb {P} '$ such that 
$u_i \mapsto p_i$ for all 
$i\in [1,\ell ]$.
Proof. Let 
$\mathbb {P} \cup \{u_1,\ldots ,u_\ell \}\to \mathbb {P} '$ be the extension of 
$\mathbb {P} \to \mathbb {P} '$ given by sending 
$u_i$ to 
$p_i$ for 
$i\in [1,\ell ]$. The claim then follows by restricting the unique morphism of semifields
\[ \mathbb{Q} _{\text{sf}}(\mathbb{P} \cup\{u_1,\ldots,u_\ell\})\to \mathbb{P} ' \]
of Lemma 2.4 to 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots ,u_\ell )$ exploiting (2.1).
Notation 2.7 Given elements 
$p_1,\ldots , p_\ell$ of a semifield 
$\mathbb {P} '$, a function of the underlying sets 
$\mathbb {P} \to \mathbb {P} '$ and 
$f\in \mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots ,u_\ell )$ we denote by
\[ f^{\mathbb{P} }(p_1,\ldots,p_\ell) \]
the image of 
$f$ under the morphism 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots ,u_\ell )\to \mathbb {P} '$ given by the universal property of 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots ,u_\ell )$.
Definition 2.8 Let 
$p$ be an element of 
$\mathbb {P}$. We define 
$p^{+}$ and 
$p^{-}$ as
\begin{equation} p^{+}:=\frac{p}{p\oplus 1} \quad\text{and}\quad p^{-}:=\frac{1}{p\oplus 1}. \end{equation} Notice that the expression 
$p^{+}$ (respectively 
$p^{-}$) is in general very different from the expression 
$p^{+1}$ (respectively 
$p^{-1}$). We will introduce a mutation formula that involves both kinds of expressions. Therefore, to avoid confusion we use the notation for 
$p\in \mathbb {P}$ and 
$x\in \mathbb {R}$:
\[ p^{[\kern-1pt[ x ]\kern-1pt] }:= \begin{cases} p^{-} & \text{if } x<0,\\ 1 & \text{if } x=0,\\ p^{+} & \text{if } x>0. \end{cases}\]Example 2.9 The notation introduced in Definition 2.8 is particularly transparent for tropical semifields. For example, let 
$p=p_1^{2}p_2^{-1}\in \text {Trop}(p_1,p_2)$. Then we have 
$p^{{[\kern-1pt[ x ]\kern-1pt] }}=p^{+}=p_1^{2}$ for 
$x\in \mathbb {R}_{>0}$, 
$p^{{[\kern-1pt[ 0 ]\kern-1pt] }}=1$, and 
$p^{{[\kern-1pt[ x ]\kern-1pt] }}=p^{-}=p_2$ for 
$x\in \mathbb {R}_{<0}$.
2.2 Reminder on cluster and $Y$-patterns
In this section we recall the notion of (coefficient-free) cluster patterns, originally called exchange patterns in [Reference Fomin and ZelevinskyFZ02]. At the same time we recall the notion of (coefficient-free) 
$Y$-patterns as introduced in [Reference Fomin and ZelevinskyFZ07].
Throughout §§ 2.2 and 2.3 we fix a semifield 
$(\mathbb {P} ,\oplus , \cdot , 1)$ and a positive integer 
$n$. Further, for § 2.2 we fix the ambient field 
$\mathcal {F}$, which is isomorphic to rational functions in 
$n$ independent variables with coefficients in 
$\mathbb {Q}$. In § 2.3 we generalize 
$\mathcal {F}$ to have coefficients in 
$\mathbb {Q} \mathbb {P}$.
Definition 2.10 A (skew-symmetrizable) labeled seed (respectively labeled 
$Y$-seed) is a pair 
$(\mathbf {x}, B )$ (respectively 
$(\mathbf {y}, B )$), where
–
$B=(b_{ij})$ is a skew-symmetrizable $(n\times n)$-matrix, called an exchange matrix,–
$\mathbf {x}=(x_1,\ldots ,x_n)$ is an $n$-tuple of elements in the ambient field $\mathcal {F}$ forming a free generating set, i.e. $\mathcal {F}\cong \mathbb {Q} (x_1,\ldots ,x_n)$,– respectively
$\mathbf {y}=(y_1,\ldots ,y_n)$ is a $n$-tuple of elements of $\mathbb {P}$.
The tuple 
$\mathbf {x}$ is called a cluster and its components 
$x_1,\ldots ,x_n$ cluster variables. The components 
$y_1,\ldots ,y_n$ of 
$\mathbf {y}$ are referred to as 
$Y$-variables.
Notice that a skew-symmetric (respectively skew-symmetrizable) matrix determines a quiver (respectively valued quiver). Therefore, we will often talk about quivers instead of matrices.
Definition 2.11 Let 
$(\mathbf {x},B)$ be a labeled seed (respectively 
$(\mathbf {y},B)$ a labeled 
$Y$-seed) and 
$k\in [1,n]$. The mutation in direction 
$k$ of 
$(\mathbf {x},B)$ (respectively 
$(\mathbf {y},B)$) is the labeled seed 
$(\mathbf {x}',B')$ (respectively labeled 
$Y$-seed 
$(\mathbf {y}',B')$), where the following hold:
–
$B'=(b'_{ij})$ is the usual mutation of $B$ in direction $k$, that is
(2.3)\begin{align} b'_{ij}:= \begin{cases} -b_{ij} & \text{if } i=k\ \text{or}\ j=k,\\ b_{ij} +\operatorname*{sgn}\left({b_{ik}}\right)\left[{b_{ik}b_{kj}}\right]_+ & \text{else;}\end{cases}; \end{align}–
$\mathbf {x}'=(x_1',\ldots ,x_n')$, where $x'_j:=x_j$ for $j\not =k$ and
(2.4)\begin{equation} x_k' := \frac{\prod x_i^{[b_{ik}]_+} + \prod x_i^{[-b_{ik}]_+}}{x_k}\in \mathcal{F}; \end{equation}– respectively
$\mathbf {y}'=(y'_1,\ldots , y'_n)$, where
(2.5)\begin{align} y'_j := \begin{cases} y_j^{-1} & \text{if } j=k,\\ y_j(1 \oplus y_k^{-\operatorname*{sgn}(b_{kj})})^{-b_{kj}} & \text{if } j\not =k.\end{cases}\end{align}
Lemma 2.12 Mutation of labeled seeds (respectively 
$Y$-seeds) is involutive. That is, 
$(\mathbf {x}', B')$ is the mutation in direction 
$k$ of 
$(\mathbf {x}, B)$ if and only if 
$(\mathbf {x}, B)$ is the mutation in direction 
$k$ of 
$(\mathbf {x}', B')$ (and equivalently for 
$Y$-seeds).
To construct cluster patterns and 
$Y$-patterns of rank 
$n$ one has to consider the 
$n$-regular tree 
$\mathbb {T}^{n}$. The edges of 
$\mathbb {T}^{n}$ are labeled by the numbers 
$1,\ldots ,n$ in such a way that the 
$n$ edges incident to the same vertex receive different labels. We write 
$v\in \mathbb {T}^{n}$ to express that 
$v$ is a vertex of 
$\mathbb {T}^{n}$. Moreover, we assume that 
$\mathbb {T}^{n}$ is endowed with a distinguished vertex 
$v_0$ called the initial vertex.
Definition 2.13 A cluster pattern (respectively 
$Y$-pattern) of rank 
$n$ is an assignment 
$v\mapsto (\mathbf {x}_v, B_v)$ (respectively 
$v\mapsto (\mathbf {y}_v,B_v)$) of a labeled seed (respectively labeled 
$Y$-seed) to each 
$v \in \mathbb {T}^{n}$ such that 
$(\mathbf {x}_{v'},B_{v'})$ (respectively 
$(\mathbf {y}_{v'},B_{v'})$) is the mutation in direction 
$k$ of 
$(\mathbf {x}_v,B_v)$ (respectively 
$(\mathbf {y}_v,B_v)$) whenever 
$v, v'\in \mathbb {T}^{n}$ are vertices joined by an edge labeled by 
$k$. The elements of a cluster pattern (respectively 
$Y$-pattern) are written as follows:
\[ B_v=(b_{ij}^{v}),\quad \mathbf{x}_v=(x_{1;v},\ldots,x_{n;v}),\quad \text{respectively}\ \mathbf{y}_v=(y_{1;v} ,\ldots,y_{n;v}). \]Remark 2.14 Notice that a cluster (and similarly a 
$Y$-pattern) is completely determined by its value at a single vertex. In particular, considering an initial assignment 
$v_0 \mapsto ((y_1,\ldots , y_n), B_{v_0})$ of a 
$Y$-seed to the initial vertex 
$v_0$, the rest of the 
$Y$-pattern is obtained by iterating the mutation formula (2.5). We will later make use of this observation.
2.3 Reminders on cluster patterns with coefficients
In this section we recall Fomin and Zelevinsky's extension of the notion of cluster pattern to cluster pattern with coefficients as introduced in [Reference Fomin and ZelevinskyFZ07]. We want to treat cluster patterns and 
$Y$-patterns on an equal footing in the sense that both kinds of patterns can be endowed with coefficients. Therefore, we will make very small changes to the original nomenclature used by Fomin and Zelevinsky.
Definition 2.15 A (skew-symmetrizable) labeled seed with coefficients Footnote 3 is a tuple 
$(\mathbf {x}, \mathbf {p},B)$:
–
$(\mathbf {p},B)$ is a labeled $Y$-seed in $\mathbb {P}$;–
$\mathbf {x}=(x_1,\ldots ,x_n)$ is an $n$-tuple of elements in the ambient field $\mathcal {F}$ forming a free generating set, i.e. ${\mathcal {F}\cong \mathbb {Q} \mathbb {P} (x_1,\ldots ,x_n)}$.
Remark 2.16 In § 2.4 we will combine two 
$Y$-patterns 
$v\mapsto (\mathbf {y}_v,B_v)$ and 
$v\mapsto (\mathbf {p}_v,B_v)$ to obtain the notion of a 
$Y$-pattern with coefficients. The two 
$Y$-patterns play different (non-symmetric) roles in Definition 2.27: one is the coefficient 
$Y$-pattern, for which we reserve the notation 
$(\mathbf {p}, B)$, while the other one is the 
$Y$-pattern that will be endowed with coefficients, denoted by 
$(\mathbf {y},B)$. This explains the use of 
$(\mathbf {p},B)$ in Definition 2.15 opposed to 
$(\textbf {y},B)$.
Definition 2.17 Let 
$(\mathbf {x},\mathbf {p},B)$ be a labeled seed with coefficients and take 
$k\in [1,n]$ with 
${\mathbf {p}=(p_1,\ldots , p_n)}$. The mutation in direction 
$k$ of 
$(\mathbf {x},\mathbf {p},B)$ is the labeled seed with coefficients 
$(\mathbf {x}',\mathbf {p}',B')$, where 
$(\mathbf {p}',B')$ is the mutation in direction 
$k$ of the 
$Y$-seed 
$(\mathbf {p},B)$ and 
$\mathbf {x}'=(x_1',\ldots ,x_n')$ with 
$x'_j:=x_j$ for 
$j\not =k$ and
\begin{equation} x_k':=\frac{\displaystyle p_k^{-} \prod_{i:b_{ik}<0} x^{ -b_{ik} }_{i} +p_k^{+} \prod_{i:b_{ik}>0} x^{ b_{ik} }_{i}}{x_k}\in \mathcal{F}. \end{equation}Definition 2.18 A cluster pattern with coefficients of rank 
$n$ is an assignment 
$v\mapsto (\mathbf {x}_v,\mathbf {p}_v, B_v)$ of a labeled seed with coefficients to each 
$v \in \mathbb {T}^{n}$ such that 
$(\mathbf {x}_{v'},\mathbf {p}_{v'},B_{v'})$ is the mutation in direction 
$k$ of 
$(\mathbf {x}_v,\mathbf {p}_v,B_v)$ whenever 
$v, v'\in \mathbb {T}^{n}$ are vertices joined by an edge labeled by 
$k$. The elements of a cluster pattern with coefficients are written as
\[ \mathbf{x}_v=(x_{1;v},\ldots,x_{n;v}),\quad \mathbf{p}_v=(p_{1;v},\ldots,p_{n;v})\quad \text{and}\quad B_v=(b_{ij}^{v}). \]The following theorem is [Reference Fomin and ZelevinskyFZ02, Theorem 3.1].
Theorem 2.19 (Laurent phenomenon) Let 
$v\mapsto ( \boldsymbol {x}_v,\mathbf {p}_v, B_v)$ be a cluster pattern with coefficients and 
$\mathbf {x}_{v_0}=(x_1,\ldots , x_n)$ the initial cluster. Then for 
$j\in [1,n]$ and 
$v\in \mathbb {T}^{n}$:
\[ x_{j;v}\in \mathbb{Z} \mathbb{P} [x_1^{\pm 1},\ldots, x_n^{\pm 1}]. \]Definition 2.20 A cluster pattern with principal coefficients at vertex 
$v_0$ refers to a cluster pattern with coefficients 
$v\mapsto (\mathbf {x}_v,\mathbf {p}_v,B_v)$ with 
$\mathbb {P} =\text {Trop}(p_{1},\ldots ,p_{n})$ as underlying semifield, where 
$\mathbf {p}_{v_0}= (p_{1},\ldots ,p_n)$.
Definition 2.21 The Laurent polynomials
\[ X^{\text{FZ}}_{j;v}\in\mathbb{Z} [x_1^{\pm 1},\ldots,x_n^{\pm 1};p_1,\ldots,p_n] \]
are the cluster variables of a cluster pattern with principal coefficients (by [Reference Fomin and ZelevinskyFZ07, Proposition 3.6]). Further, we have the 
$F$-polynomials 
$F_{j;v}$ defined as
\begin{equation} F_{j;v}(p_1,\ldots,p_n) := X^{\text{FZ}}_{j;v}(1,\ldots,1;p_1,\ldots,p_n) \in \mathbb{Z} [p_1,\ldots,p_n]. \end{equation}Remark 2.22 The superscript FZ is used to avoid confusion: in the next sections we adopt the standard geometric notation in which cluster variables are denoted by 
$A$ and 
$y$-variables by 
$X$. In § 3 we provide an explicit dictionary between the algebraic and geometric framework. See Remark 3.8, Notation 3.13, Remark 3.23 and Notation 3.38.
Definition 2.23 [FZ07, Proposition 6.1] Every Laurent polynomial 
$X_{j;v}^{\text {FZ}}$ is homogeneous with respect to the 
$\mathbb {Z} ^{n}$-grading in 
$\mathbb {Z} [x_1^{\pm 1}, \ldots , x_n^{\pm 1};p_1,\ldots , p_n]$ given by 
$\deg (x_i)=\textbf {e}_i$ and 
$\deg (p_j)=-\textbf {b}_j$, where 
$\textbf {e}_1,\ldots , \textbf {e}_n$ is the standard basis of 
$\mathbb {Z} ^{n}$ and 
$\textbf {b}_j$ is the 
$j$th column of 
$B_{v_0}$. The degree of 
$X^{\text {FZ}}_{j;v}$ is called the 
$\textbf {g}$-vector associated to 
$j$ and 
$v$ denoted
\[ \textbf{g}_{j;v}\in \mathbb{Z} ^{n}. \]2.4 $Y$-patterns with coefficients
In analogy with the previous section we introduce a generalization of 
$Y$-pattern to 
$Y$-pattern with coefficients. We study their periodicities in § 2.5 and obtain separation formulas for 
$Y$-patterns with coefficients, which turn out to be very similar to the separation formulas for cluster patterns with coefficients presented in [Reference Fomin and ZelevinskyFZ07, § 3].
To have labeled 
$Y$-seeds on an equal footing with labeled seeds we endow them similarly with coefficients as follows.
Definition 2.24 A (skew-symmetrizable) labeled 
$Y$-seed with coefficients (in 
$\mathbb {P}$) is a triple 
$(\mathbf {y},\mathbf {p},B)$, where the following hold:
–
$(\mathbf {p},B)$ is a $Y$-seed in $\mathbb {P}$;–
$(\mathbf {y}, B)$ is a $Y$-seed in some universal semifield $\mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots , u_\ell )$.
We define analogously the mutation of labeled 
$Y$-seeds with coefficients below.
Definition 2.25 Let 
$(\mathbf {y},\mathbf {p},B)$ be a labeled 
$Y$-seed with coefficients, where 
$\mathbf {y}=(y_1,\ldots ,y_n)$, 
$\mathbf {p}= (p_1,\ldots ,p_n)$ and 
$B=(b_{ij})$. For 
$k\in [1,n]$, the mutation in direction 
$k$ of 
$(\boldsymbol {y},\boldsymbol {p},B)$ is the labeled 
$Y$-seed with coefficients 
$(\mathbf {y}',\mathbf {p}',B')$, where the following hold:
–
$(\mathbf {p}',B')$ is the mutation in direction $k$ of $(\mathbf {p},B)$; and–
$\mathbf {y}'=(y_1',\ldots ,y_n')$, where
(2.8)\begin{equation} y'_j := \begin{cases} y_j^{-1} & \text{if } j=k, \\ y_j \left({ p_k^{[\kern-1pt[ b_{kj}]\kern-1pt]} + p_k^{[\kern-1pt[ -b_{kj}]\kern-1pt]} y_k^{-\operatorname*{sgn}(b_{kj})} }\right) ^{-b_{kj}} & \text{if } j\not =k. \end{cases}\end{equation}
See Definition 2.8 for the 
$p^{[\kern-1pt[ x ]\kern-1pt] }$ notation.
Remark 2.26 Unlabeled 
$Y$-seeds with coefficients are obtained by identifying labeled 
$Y$-seeds with coefficients that differ from each other by simultaneous permutations of the components in 
$\mathbf {p}$, in 
$\mathbf {y}$, and of the rows and columns of 
$B$. In a similar fashion, one obtains unlabeled seeds, unlabeled 
$Y$-seeds and unlabeled seeds with coefficients as in [Reference Fomin and ZelevinskyFZ07, Definition 4.1].
It is straightforward to prove that mutation of 
$Y$-seeds with coefficients is involutive. This implies that the following notion of 
$Y$-pattern with coefficients is well defined. The underlying semifield for such a pattern is 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(u_1,\ldots ,u_\ell )$.
Definition 2.27 A 
$Y$-pattern with coefficients is an assignment 
$v \mapsto (\mathbf {y}_v, \mathbf {p}_v, B_v)$ of a labeled 
$Y$-seed with coefficients to each 
$v \in \mathbb {T}^{n}$ such that 
$(\mathbf {y}_{v'},\mathbf {p}_{v'},B_{v'})$ is the mutation in direction 
$k$ of 
$(\mathbf {y}_v, \mathbf {p}_v,B_v)$ whenever 
$v, v'\in \mathbb {T}^{n}$ are vertices joined by an edge labeled by 
$k$. The components 
$\mathbf {y}_v$ are written as 
$(y_{1;v},\ldots ,y_{n;v})$.
A particular choice of coefficients for cluster patterns is introduced in [Reference Fomin and ZelevinskyFZ07]. We extend it to 
$Y$-patterns as follows.
Definition 2.28 A 
$Y$-pattern with principal coefficients at vertex 
$v_0$ refers to a 
$Y$-pattern with coefficients 
$v\mapsto (\mathbf {y}_v,\mathbf {p}_v,B_v)$ with 
$\mathbb {P} =\text {Trop}(p_{1},\ldots ,p_{n})$ as underlying semifield for coefficients, where 
$\mathbf {p}_{v_0}= (p_{1},\ldots ,p_n)$.
Recall from [Reference Fomin and ZelevinskyFZ07, Definition 3.10] the rational functions for 
$Y$-patterns
\begin{equation} Y_{j;v}\in \mathbb{Q} _{\text{sf}}(y_1,\ldots,y_n). \end{equation}
They are the components of the (coefficient-free) 
$Y$-pattern 
$v\mapsto ((Y_{1;v},\ldots , Y_{n;v}),B_v)$ with values in 
$\mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$ and 
$((y_1,\ldots , y_n),B^{0})$ as initial labeled 
$Y$-seed at 
$v_0$. In analogy, we have the following definition for the case with coefficients. We fix for the rest of the section an initial exchange matrix 
$B^{0}$.
Definition 2.29 Fix an initial 
$Y$-seed of coefficients 
$((p_1,\ldots ,p_n),B^{0})$. We define the rational functions
\begin{equation} \tilde{Y}_{j;v}\in \mathbb{Q} \mathbb{P} _{\text{sf}}(y_1,\ldots,y_n) \end{equation}
as the components of the 
$Y$-pattern with coefficients 
$v\mapsto ((\tilde {Y}_{1;v},\ldots , \tilde {Y}_{n;v}),\mathbf {p}_v,B_v)$ whose initial labeled 
$Y$-seed with coefficients is 
$((y_1,\ldots , y_n),(p_1,\ldots , p_n),B^{0})$ at 
$v_0$. Notice that 
$\tilde {Y}_{j;v}$ depends on 
$((p_1,\ldots ,p_n),B^{0})$. Nevertheless, we will omit this in the notation since we think of 
$((p_1,\ldots ,p_n),B^{0})$ as fixed once and for all. We illustrate this definition in Example 2.31.
In later sections we will specify this definition to the case of 
$Y$-patterns with principal coefficients. To make notation lighter we denote 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(y_1,\ldots , y_n)$ by 
$\mathcal {S}$ from now on. The following result provides a way to compute 
$\tilde {Y}_{j;v}$ from 
$Y_{j;v}^{\mathcal {S}}$ and 
$p_{j;v}$ (see Notation 2.7).
Lemma 2.30 Fix an initial vertex 
$v_0$ and let 
$p_j:=p_{j;v_0}$ for all 
$1\leq j \leq n$. Then for every vertex 
$v\in \mathbb {T}^{n}$ and every 
$j\in [1,n]$ we have
\begin{equation} \tilde{Y}_{j;v}=\frac{Y_{j;v}^{\mathcal{S}}(p_1y_1,\ldots,p_ny_n)}{p_{j;v}}. \end{equation}Proof. The statement is clear for the initial vertex 
$v_0$ and all 
$i\in [1,n]$. Let 
$v,v'\in \mathbb {T}^{n}$ be connected by an edge with label 
$k$ and assume that (2.11) holds for 
$v$ and for all 
$j$. We have to prove that (2.11) also holds for 
$v'$ and all 
$j$. The case 
$j=k$ follows from 
$p_{j;v'}=p_{j;v}^{-1}$, 
$Y_{j;v'}=Y_{j;v}^{-1}$ and 
$\tilde {Y}_{j;v'}= \tilde {Y}_{j;v}^{-1}$. So we assume that 
$j\neq k$. Since (2.11) holds for 
$v$ we have the following:
\begin{align*} Y^{\mathcal{S}}_{j;v'}(p_1y_1,\ldots,p_ny_n)&=Y^{\mathcal{S}}_{j;v}(p_1y_1,\ldots,p_ny_n) (1+Y^{\mathcal{S}}_{k;v}(p_1y_1,\ldots,p_ny_n)^{-\operatorname*{sgn}(b_{kj})})^{-b_{kj}}\\ &= p_{j;v}\tilde{Y}_{j;v}(1+(p_{k;v}\tilde{Y}_{k;v})^{-\operatorname*{sgn}(b_{kj})})^{-b_{kj}}. \end{align*}We distinguish two cases as follows.
Case 1. If
$b_{kj}\le 0$ we apply the $Y$-pattern mutation formula (2.5) and obtain
which is exactly what we wanted to prove.\[ \frac{Y^{\mathcal{S}}_{j;v'}(p_1y_1,\ldots,p_ny_n)}{p_{j,v'}}= \frac{\tilde{Y}_{j;v}(1+p_{k;v}\tilde{Y}_{k;v})^{-b_{kj}}}{(1\oplus p_{k;v})^{-b_{kj}}}= \tilde{Y}_{j;v}(p^{-}_{k;v}+p^{+}_{k;v}\tilde{Y}_{k;v})^{-b_{kj}}, \]Case 2. If
$b_{jk}>0$ we proceed in an analogous way.
Example 2.31 We identify the vertices of the two-regular tree 
$\mathbb {T}^{2}$ with the integers by fixing 
$v_0=0$. In Table 1 we illustrate both, a 
$Y$-pattern and a 
$Y$-pattern with coefficients in type 
$A_2$ (i.e. 
$B^{0}$ corresponds to an orientations of a Dynkin diagram of type 
$A_2$). Computing only five mutations of the initial 
$Y$-seed with coefficients, we observe that for all 
$i\in \mathbb {Z}$ the labeled Y-seeds (with and without coefficients) at a vertex 
$i$ and 
$i+5$ are equal as unlabeled 
$Y$-seeds.
Table 1. A 
$Y$-pattern 
$v\mapsto ((p_{1;v},p_{2;v}),B_v)$ and the corresponding 
$Y$-pattern with coefficients 
$v\mapsto ((\tilde {Y}_{1;v},\tilde {Y}_{2;v}),(p_{1;v},p_{2;v}),B_v)$ in type 
$A_2$ introduced in Definition 2.29 (see also Remark 2.16). Observe that the first four columns coincide with the first three columns of [Reference Fomin and ZelevinskyFZ07, Table 1] upon change of notation.
2.5 Separation formulas and periodicities
In this section we analyze properties of 
$Y$-patterns with coefficients in complete generality (unless specified otherwise).
We apply the universal property of 
$\mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$ to the tropical semifield with 
$y_1,\ldots ,y_n \in \text {Trop}(y_1,\ldots ,y_n)$. As elements of 
$\text {Trop}(y_1,\ldots , y_n)$ are Laurent monomials in 
$y_1,\ldots ,y_n$, the rational function 
$Y_{j;v}$ in (2.9) yield Laurent monomials:
\begin{equation} Y_{j;v}^{\text{Trop}(y_1,\ldots, y_n)} (y_1,\ldots, y_n )= \prod_{i=1}^{n} y_i^{c_{ij;v}} =:{\mathbf{y}}^{\mathbf{c}_{j;v}}. \end{equation}Definition 2.32 The vector 
${\mathbf {c}_{j;v}}=(c_{1j;v},\ldots ,c_{nj;v})\in \mathbb {Z}^{n}$ in (2.12) is called the c-vector associated to 
$j$ and 
$v$.
As a consequence of Lemma 2.30 we obtain for 
$Y$-patterns the analog of Fomin and Zelevinsky's separation formulas for cluster patterns. To state this result we consider the 
$F$-polynomials in (2.7) associated to the initial matrix 
$B$.
Theorem 2.33 (Separation formulas) For every 
$j$ and 
$v$ we have the following:
\begin{equation} \tilde{Y}_{j;v}= \biggl( \prod^n_{i=1}(F_{i;v}^{-b^v_{ij}})^{\mathbb{P}}(p_1,\ldots, p_n)\biggr) \biggl( \prod^n_{i=1}(F_{i;v}^{b^v_{ij}})^{\mathcal{S}}(p_1y_1,\ldots,p_ny_n)\biggr) \boldsymbol{y}^{{\mathbf c_{j;v}}}. \end{equation}Proof. We denote the exchange matrix 
$B_v=(b_{ij})$ and by 
$F_{i;v}$ the 
$F$-polynomial associated to 
$i$ and 
$v$. Recall that by [Reference Fomin and ZelevinskyFZ07, Proposition 3.13]
\[ Y_{j;v}= \prod_{i=1}^{n} y_i^{c_{ij;v}} \prod^{n}_{i=1}F_{i;v}^{b_{ij}}. \]
Hence, the universal property of 
$\mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$ applied to 
$\mathcal {S}\ni p_1y_1,\ldots ,p_ny_n$ gives
\begin{equation} Y^{\mathcal{S}}_{j;v}(p_1y_1,\ldots,p_ny_n)=\prod^{n}_{i=1}(p_iy_i)^{c_{ij;v}} \prod^{n}_{i=1}(F_{i;v}^{b_{ij}})^{\mathcal{S}}(p_1y_1,\ldots,p_ny_n). \end{equation}
By the universal property of 
$\mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$ applied to 
$\mathbb {P} \ni p_1,\ldots ,p_n$ we have
\begin{equation} p_{j;v}=\prod^{n}_{i=1}p_i^{c_{ij;v}}\prod^{n}_{i=1}(F_{i;v}^{b_{ij}})^{\mathbb{P} }(p_1,\ldots, p_n). \end{equation}We obtain the desired formula dividing (2.14) by (2.15) and then using (2.11).
Note that only the first factor on the right hand side of (2.13) involves the auxiliary addition in 
$\mathbb {P}$.
Theorem 2.34 The 
$Y$-pattern 
$v\mapsto ((Y_{1;v},\ldots , Y_{n;v}),B_v)$ and the 
$Y$-pattern with coefficients 
$v \mapsto ((\tilde {Y}_{1;v},\ldots , \tilde {Y}_{n;v}),\mathbf {p}_v,B_v)$ share the same periodicities. That is,
\[ Y_{i;v}=Y_{j;v'} \quad \text{if and only if } \tilde{Y}_{i;v}=\tilde{Y}_{j;v'}. \]Proof. Using the universal property of 
$\mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$ the coefficient 
$Y$-pattern 
$v\mapsto (\mathbf {p}_v,B_v)$ can be obtained from the 
$Y$-pattern 
$v \mapsto ((Y_{1;v},\ldots , Y_{n;v}),B_v)$ by specifying 
$y_i\mapsto p_i$. In particular, 
$Y_{i;v}=Y_{j;v'}$ implies 
$p_{i;v}=p_{j;v'}$. Now we can use Lemma 2.30 to conclude that 
$Y_{i;v}=Y_{j;v'}$ implies 
$\tilde {Y}_{i;v}=\tilde {Y}_{j;v'}$.
For the reverse implication we use the universal property of 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(y_1,\ldots ,y_n)$ applied to 
$\mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$. We fix 
$y_1,\ldots ,y_n\in \mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$ and the map 
$\mathbb {P} \to \mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$ sending every 
$p\in \mathbb {P}$ to 
$1$. The induced morphism of semifields 
$\mathbb {Q} \mathbb {P} _{\text {sf}}(y_1,\ldots ,y_n)\to \mathbb {Q} _{\text {sf}}(y_1,\ldots ,y_n)$ sends 
$\tilde {Y}_{i;v}$ to 
$Y_{i;v}$ for all 
$i$ and 
$v$.
2.6 Geometric coefficients and frozen directions
So far we have considered patterns in which all 
$n$ directions are mutable. However, it is very useful to consider patterns in which there are frozen (or non-mutable) directions. Indeed, this formalism can be used to describe in a simplified way cluster patterns with coefficients in a tropical semifield (see Lemma 2.39 below). Further, frozen directions can be used to construct partial compactifications of cluster varieties as discussed in [Reference Gross, Hacking, Keel and KontsevichGHKK18, § 9]. In this subsection we let 
$m\in \mathbb {N}$ be an arbitrary positive integer.
Definition 2.35 A cluster pattern with coefficients of rank 
$n$ with 
$m$ frozen directions is an assignment 
$v \mapsto ({\mathbf {x}}_v, \mathbf {p}_v, B_v)$, where the following hold:
–
$v\in \mathbb {T}^{n}$;–
${\mathbf {x}}_v$ is a cluster of size $n+m$;–
${\mathbf {p}}_v$ is a $Y$-seed of size $n+m$;–
$B_v$ is a skew-symmetrizable $(n+m)\times (n+m)$-matrix;– for every pair of vertices
$v,v'\in \mathbb {T}^{n}$ joined by an edge labeled by $k\in [1,n]$, we have that $({\mathbf {x}}_{v'}, B_{v'})= \mu _k ({\mathbf {x}}_v, B_v)$.
We can define in an analogous way 
$Y$-patterns with coefficients of rank 
$n$ and 
$m$ frozen directions, and the coefficient-free version of these concepts.
Observe that given a cluster pattern (or a 
$Y$-pattern) of rank 
$n$ without frozen directions one can declare some of these directions to be frozen to obtain a cluster pattern of lower rank with frozen directions. Similarly, given a cluster pattern (or a 
$Y$-pattern) with coefficients of rank 
$n$ and 
$m$ frozen directions we can decide to unfreeze some directions to obtain a pattern of rank 
$>n$ and with fewer frozen directions.
Definition 2.36 A cluster pattern has geometric coefficients if the underlying semifield 
$\mathbb {P}$ is a tropical semifield.
Notation 2.37 Let 
$B=(b_{ij})$ be a 
$(n + m)\times (n+m)$-square matrix. We introduce the following notation to denote four distinguished submatrices of 
$B$:
– the upper-left matrix
$B_{\text {ul}}:=(b_{i,j})_{1\leq i,j \leq n}$, an $n\times n$ submatrix;– the lower-left matrix
$B_{\text {ll}}:=(b_{n+i,j})_{1\leq i \leq m,\ 1 \leq j \leq n}$, an $m\times n$ submatrix;– the upper-right matrix
$B_{\text {ur}}:=(b_{i,n+j})_{1\leq i \leq n,\ 1 \leq j \leq m}$, an $n\times m$ submatrix;– the lower-right matrix
$B_{\text {lr}}:=(b_{n+i,n+j})_{1\leq i,j \leq m}$, an $m\times m$ submatrix.
Definition 2.38 Let 
$v\mapsto (\textbf {x}_v,\mathbf {p}_v,B_v)$ be a rank 
$n$ cluster pattern with geometric coefficients in 
$\mathbb {P} =\text {Trop}(p_1,\ldots , p_m)$. For every 
$v\in \mathbb {T}^{n}$ we define
\[ \textbf{x}^{\text{ext}}_v:=(x_{1;v},\ldots , x_{n;v},p_1,\ldots , p_m), \]
and refer to it as the extended cluster. Further, let 
$B^{\text {ext}}_v$ be the 
$(n+m)\times (n+m)$-matrix defined as follows:
–
$(B^{\text {ext}}_v)_{\text {ul}}=B_v$;–
$(B^{\text {ext}}_v)_{\text {ll}}=(a_{ij}^{v})$, where $p_{j;v}= \prod _{i=1}^{m} p_i^{a_{ij}^{v}}$ for every $j \in [1,n]$;–
$(B^{\text {ext}}_v)_{\text {ur}}=-(B^{\text {ext}}_v)_{\text {ll}}^{T}$, where $A^{T}$ denotes the transpose of a matrix $A$;–
$(B^{\text {ext}}_v)_{\text {lr}}$ is the zero $(m\times m)$-matrix.
Lemma 2.39 The assignment 
$v\mapsto (\textbf {x}^{\rm ext}_v,B^{\rm ext}_v)$ defines a (coefficient-free!) cluster pattern of rank 
$n$ with 
$m$ frozen directions.
Proof. This follows from the discussion at the end of [Reference Fomin and ZelevinskyFZ07, § 2].
Warning: We use Lemma 2.39 frequently to interpret cluster patterns with geometric coefficients as coefficient-free cluster patterns with frozen directions. As an important special case, a cluster pattern with principal coefficients of rank 
$n$ can be treated as a coefficient-free cluster pattern of rank 
$n$ with 
$n$ frozen direction. However, the meaning in geometry of coefficients is very different from the meaning in geometry of frozen directions. We systematically think of coefficients as parameters deforming the mutation formulas. Frozen directions are just directions in which we do not perform mutations and they can be used to partially compactify cluster varieties. We discuss these ideas extensively in § 3.
Example 2.40 Let 
$v\mapsto (\mathbf {x}_v,\mathbf {p}_v,B_v)$ be the cluster pattern with principal coefficients at 
$v_0$ of type 
$A_2$. We follow the recipe of Definition 2.38 using the ingredients from Table 1: the matrices 
$B_v$ are in the second column and the monomials 
$p_{i;v}\in \text {Trop}(p_1,p_2)$ can be read from columns three and four specifying 
$\oplus$ as in Example 2.2.
The matrices 
$B_{v_i}^{\text {ext}}$ for 
$i\in [0,4]$ are incidence matrices of the quivers shown in Figure 2. We enclose in a box 
${\color {black}{\boxed {\phantom {:}}}}$ the vertices corresponding to the rows of the matrices 
$(B^{\text {ext}}_v)_{\text {ll}}$. Observe that they change according to the matrix mutation in (2.3), as Lemma 2.39 predicts.
Figure 2. Quivers associated to a type 
$A_2$ cluster pattern with principal coefficients at 
$v_0$. The boxes refer to frozen vertices.
Example 2.41 This example corresponds to the cluster structure on the coordinate ring of the affine cone of the Grassmannian 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$ (for more details see § 7.1). Consider the cluster pattern 
$v\mapsto (\mathbf {x}_v,\mathbf {p}_v,B_v)$ of type 
$A_2$ with geometric coefficients in 
$\text {Trop}(p_{12},p_{23},p_{34},p_{45},p_{15})$. Let
\[ \boldsymbol{x}_{v_0}=(x_1,x_2),\quad \boldsymbol{p}_{v_0}=(p_{12}^{-1}p_{23}p_{34}^{-1},p_{34}p_{45}^{-1}p_{15}) \quad\text{and}\quad B_{v_0}=\left(\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\right). \]
The associated 
$(7\times 7)$-matrix 
$B_{v_0}^{\text {ext}}$ is the incidence matrix of the quiver shown in Figure 6, identifying 
$x_1=p_{13}$ and 
$x_2=p_{14}$. The corresponding extended cluster is
\[ \mathbf{x}_{v_0}^{\text{ext}}=(p_{13},p_{14},p_{12},p_{23},p_{34},p_{45},p_{15}). \]2.7 Comparison of cluster and $Y$-patterns with coefficients
We explain how every cluster pattern with coefficients 
$v \mapsto (\boldsymbol {x}_v,\mathbf {p}_v, B_v)$ gives rise to a 
$Y$-pattern with coefficients in a natural way. For each 
$v\in \mathbb {T}^{n}$ let 
$B_v=(b_{ij}^{v})$. We define
\begin{equation} \tilde{y}_{j;v}:=\prod_{i=1}^{n} x_{i;v}^{b^{v}_{ij}} \end{equation}
for each 
$v\in \mathbb {T}^{n}$ and 
$j\in [1,n]$. Moreover, let 
$\tilde {\mathbf {y}}_v=(\tilde {y}_{1;v},\ldots ,\tilde {y}_{n;v})$.
Remark 2.42 Notice that (2.16) still makes sense when we have trivial coefficients, i.e. 
$p_{i;v}=1$ for all 
$i \in [1,n]$ and all 
$v\in \mathbb {T}^{n}$. Moreover, we can extend the definition of the 
$\tilde {y}$ for cluster patterns with coefficients and frozen directions.
Lemma 2.43 The assignment 
$v \mapsto (\tilde {\mathbf {y}}_v,\mathbf {p}_v ,B_v)$ is a 
$Y$-pattern with coefficients.
Proof. For pairs of vertices 
$v,v' \in \mathbb {T}^{n}$ joined by an edge labeled by 
$k$ we have to show
\[ \tilde{y}_{j;v}\left({ p_{k;v}^{[\kern-1pt[ b^{v}_{kj}]\kern-1pt]} + p_{k;v}^{[\kern-1pt[ -b^{v}_{kj}]\kern-1pt]} \tilde{y}_{k;v} }\right) ^{-b^{v}_{kj}}=\tilde{y}_{j;v'}. \]
To make notation lighter let 
$b_{ij}^{v}=b_{ij}$ and 
$b_{ij}^{v'}=b'_{ij}$ for all 
$i,j \in [1,n]$. Since 
$b'_{ik}=-b_{ik}$ for all 
$i\in [1,n]$ the result follows for 
$j=k$. So we assume 
$j\neq k$. Notice that if 
$b_{kj}=0$ then 
$b'_{ij}=b_{ij}$ for all 
$i\in [1,n]$. In particular, 
$\tilde {y}_{j,v'}=\tilde {y}_{j,v}$, which is what we need to prove. Therefore, we assume 
$b_{jk}\neq 0$ and distinguish two cases.
Case 1. If
$b_{kj}<0$, we have the following:
\begin{align*} & \tilde{y}_{j;v} \left( p_{k;v}^{[\kern-1pt[ b_{kj}]\kern-1pt]} + p_{k;v}^{[\kern-1pt[ -b_{kj}]\kern-1pt]}\tilde{y}_{k;v}\right)^{-b_{kj}} =\prod_{i=1}^n x^{ b_{ij} }_{i;v}\biggl(p_{k;v}^- + p_{k;v}^+\prod_{i=1}^{n} x_{i;v}^{b_{ik}}\biggr)^{-b_{kj}}\\ &\quad =\prod_{i=1}^n x^{ b_{ij} }_{i;v}\biggl(\biggl(p_{k;v}^- \prod_{i:b_{ik}<0} x^{ -b_{ik} }_{i;v} +p_{k;v}^+ \prod_{i:b_{ik}>0} x^{ b_{ik} }_{i;v}\biggr) \prod_{i:b_{ik}<0} x^{ b_{ik} }_{i;v}\biggr)^{-b_{kj}}\\ &\quad =x^{ -b_{kj}}_{k;v'}\prod_{i\neq k} x^{b_{ij} }_{i;v} \prod_{i:b_{ik}<0} x^{-b_{ik}b_{kj}}_{i:v}= \prod_{i=1}^n x^{b'_{ij}}_{i;v'}=\tilde{y}_{j;v'}. \end{align*}Case 2. If
$b_{kj}>0$, the proof is done in exactly the same way.
Remark 2.44 Given a cluster pattern with coefficients 
$v\mapsto (\mathbf {x}_v,\mathbf {p}_v,B_v)$ in [Reference Fomin and ZelevinskyFZ07, Equation (3.7)] the authors define 
$\hat {\mathbf {y}}_v=(\hat {y}_{1;v},\ldots , \hat {y}_{n;v})$, where
\begin{equation} \hat{y}_{j;v}:=p_{j;v}\prod_{i=1}^{n} x_{i;v}^{\ b^{v}_{ij} }. \end{equation}
They prove in [Reference Fomin and ZelevinskyFZ07, Proposition 3.9] that 
$v\mapsto (\hat {\mathbf {y}}_v,B_v)$ is a 
$Y$-pattern. If the cluster pattern with coefficients 
$v\mapsto (\mathbf {x}_v,\mathbf {p}_v,B_v)$ has frozen directions then the 
$Y$-pattern 
$v\mapsto (\hat {\mathbf {y}}_v,B_v)$ has the same frozen directions. Moreover, observe that (2.17) is also well defined for cluster patterns with trivial coefficients.
If the cluster pattern 
$v\mapsto (\mathbf {x}_v,\mathbf {p}_v,B_v)$ has geometric coefficients we can consider the cluster pattern with frozen directions 
$v\mapsto (\textbf {x}^{\text {ext}}_v,B^{\text {ext}}_v)$ afforded by Lemma 2.39. Let 
$v\mapsto (\hat {\mathbf {y}}^{\text {ext}}_v,B^{\text {ext}}_v)$ be the 
$Y$-pattern with frozen directions given by [Reference Fomin and ZelevinskyFZ07, Proposition 3.9] applied to the cluster pattern with frozen directions 
${v\mapsto (\textbf {x}^{\text {ext}}_v,B^{\text {ext}}_v)}$. Similarly, let 
$v\mapsto (\tilde {\mathbf {y}}^{\text {ext}}_v,B^{\text {ext}}_v)$ be the 
$Y$-pattern with frozen directions (and trivial coefficients) given by Lemma 2.43 applied to 
$v\mapsto (\textbf {x}^{\text {ext}}_v,B^{\text {ext}}_v)$. Then 
$\hat {\mathbf {y}}^{\text {ext}}_v=\tilde {\mathbf {y}}^{\text {ext}}_v$ for all 
$v$.
Remark 2.45 In the context of cluster varieties the patterns defined by the 
$\hat {y}$ and 
$\tilde {y}$ are both very useful. The former will define a map 
$p:\mathcal {A} \to \mathcal {X}$ between cluster varieties with frozen directions (see Definition 3.16); the latter a map 
$p:\mathcal {A} _{\mathbf {p}} \to \mathcal {X} _{\mathbf {p}}$ of cluster varieties with coefficients and frozen directions.
3. Cluster duality for cluster varieties with coefficients
In this section we give a geometric perspective of cluster and 
$Y$-patterns with coefficients. One of the most important ideas we want to communicate is the following:
we make a distinction between frozen variables and coefficients.
A cluster variety with 
$n$ mutable directions and 
$m$ frozen directions is a scheme over 
$\mathbb {C}$ built by gluing complex tori isomorphic to 
$(\mathbb {C} ^{\ast })^{n+m}$ via the usual mutation formulas. The coefficients we introduce live in a ring 
$R$ of form 
$\mathbb {C} [p_1^{\pm 1},\ldots , p_r^{\pm 1}]$ in case they are invertible, respectively of form 
$\mathbb {C} [p_1,\ldots , p_r]$ if they are not invertible. A cluster variety with (geometric) coefficients, with 
$n$ mutable directions and 
$m$ frozen directions is a scheme over 
$R$ obtained by gluing schemes of the form 
$\operatorname {Spec} (R[z^{\pm 1}_1,\ldots , z^{\pm 1}_{n+m}])$. To glue these schemes we consider mutations with coefficients, which we think of as deformations of the usual mutation formulas. On the 
$\mathcal {A}$-side, the notions of frozen variables and coefficients interact with each other as explained in § 2.6: on the one hand, the coefficients are organized in a 
$Y$-pattern; on the other, 
$\mathcal {A}$-cluster variables associated to frozen directions give rise in a natural way to a 
$Y$-pattern in a tropical semifield. In this case the mutation formulas of the cluster pattern with frozen directions will be exactly the same as the mutation formulas of the cluster pattern with coefficients in the 
$Y$-pattern associated to the frozen 
$\mathcal {A}$-variables. However, the disparity between coefficients and frozen variables becomes more evident when we consider 
$\mathcal {X}$-cluster varieties since 
$\mathcal {X}$-cluster variables associated to frozen directions usually change after applying a mutation in a mutable direction. Moreover, it is crucial to make this distinction to discover the correct notion of duality for cluster varieties with coefficients. This notion of duality was predicted in [Reference Gross, Hacking, Keel and KontsevichGHKK18, § 7, Definition 7.15] and here we develop it in full detail.
In [Reference Gross, Hacking and KeelGHK15, Reference Gross, Hacking, Keel and KontsevichGHKK18] 
$\mathcal {A}$-cluster varieties with (geometric) coefficients are considered as 
$\mathcal {A}$-cluster varieties with frozen directions. Therefore, they are treated as schemes over 
$\mathbb {C}$. In § 3.2 we develop a new perspective and treat them as schemes over 
$\operatorname {Spec}(R)$. Further, we introduce the concept of 
$\mathcal {X}$-cluster varieties with coefficients and cluster varieties with specified coefficients. The former are schemes over 
$\operatorname {Spec}(R)$ while the latter are schemes over 
$\mathbb {C}$. Moreover, in § 3.3 we show how the results of the previous section lead to the notion of cluster duality for cluster varieties with coefficients and with specified coefficients.
3.1 Reminders on cluster varieties
Cluster patterns and 
$Y$-patterns define schemes over 
$\mathbb {C}$ by interpreting the mutation formulas as birational maps between algebraic tori (see [Reference Gross, Hacking and KeelGHK15, p. 149]). For this geometric perspective, it is convenient to fragment the notion of a seed (respectively 
$Y$-seed) into two parts, one changes under mutation while the other remains unchanged.
We introduce some new nomenclature. We believe this makes it easier to work with the algebraic and geometric settings simultaneously.
Definition 3.1 The (skew-symmetrizable) fixed data 
$\Gamma$ consists of the following:
– a finite set
$I$ of directions with a subset of unfrozen directions ${I_{\text {uf}}}$;– a lattice
$N$ of rank $|I|$;– a saturated sublattice
${N_{\text {uf}}} \subseteq N$ of rank $|I_{\text {uf}}|$;– a skew-symmetric bilinear form
$\lbrace \cdot , \cdot \rbrace : N\times N \to \mathbb {Q}$;– a sublattice
$N^{\circ }\subseteq N$ of finite index satisfying
\[ \lbrace N_{\text{uf}}, N^{\circ}\rbrace \subset \mathbb{Z} \ \text{and}\ \lbrace N,N_{\text{uf}}\cap N^{\circ}\rbrace \subset \mathbb{Z} ; \]– a tuple of positive integers
$(d_i:i\in I)$ with greatest common divisor 1;–
$M=\operatorname {Hom}(N,\mathbb {Z} )$ and $M^{\circ }=\operatorname {Hom}(N^{\circ },\mathbb {Z} )$.
We say that 
$\Gamma$ is skew-symmetric if 
$d_i=1$ for all 
$i\in I$.
Definition 3.2 An 
$N$-seed for 
$\Gamma$ is a tuple 
$s=(e_i\in N :i\in I)$ such that 
$\{e_i:i\in I\}$ is a basis of 
$N$ and further the following hold:
–
$\{ e_i : i\in I_{\text {uf}}\}$ is a $\mathbb {Z}$-basis of $N_{\text {uf}}$;–
$\{d_i e_i : i\in I\}$ is a $\mathbb {Z}$-basis of $N^{\circ }$;– the elements
$v_i:=\{ e_i, \cdot \}\in M^{\circ }$ are non-zero for every $i\in {I_{\text {uf}}}$.
Consider the dual basis 
$\{e^{*}_i\in M:i\in I\}$ of 
$M$. The associated 
$M^{\circ }$-seed is the tuple 
$(f_i: i\in I)$, where 
$\{f_i:i\in I\}$ is a basis of 
$M^{\circ }$ given by
\[ f_i:=d_i^{-1}e_i^{*}\in M^{\circ}. \] For a fixed 
$N$-seed 
$s$ we define the matrix 
$\boldsymbol {\varepsilon }_s:=(\epsilon _{ij})_{i,j\in I}$ by 
$\epsilon _{ij}:=\{ e_i,e_j\}d_j$. For the pairing given by evaluation we use the notation
\[ \langle \cdot,\cdot \rangle:N\times M^{\circ}\to \mathbb{Q} . \]Definition 3.3 Given an 
$N$-seed 
$s$ and 
$k \in {I_{\text {uf}}}$, the mutation in direction 
$k$ of 
$s$ is the 
$N$-seed 
$\mu _k(s)=({e'}_i:i\in I)$ given by
\begin{equation} e_i':=\begin{cases} e_i+[\epsilon_{ik}]_+e_k & i\neq k,\\ -e_k & i=k. \end{cases} \end{equation}
The mutation in direction 
$k$ of the associated 
$M^{\circ }$-seed is 
$(f'_i:i\in I)$, where
\begin{equation} f_i':=\begin{cases} -f_k+\displaystyle \sum_j [-\epsilon_{kj}]_+f_j & i=k,\\ f_i & i\not=k. \end{cases} \end{equation} Unlike the mutations introduced in the preceding section, notice that mutation of 
$N$-seeds is not an involution, i.e. 
$\mu _k(\mu _k(s))\neq s$. This motivates the following definition.
Definition 3.4 The oriented tree 
$\overset {\longrightarrow }{\mathbb {T}^{n}}$ is the canonical orientation of 
$\mathbb {T}^{n}$ determined by the following conditions:
– the
$n$ edges incident to $v_0$ are oriented in outgoing direction from $v_0$;– every vertex
$v\neq v_0$ has one incoming edge and $n-1$ outgoing edges.
We write 
$v\overset {k}{\longrightarrow }v'\in \overset {\longrightarrow }{\mathbb {T}^{n}}$ to indicate that the edge in between the vertices 
$v,v'$ of 
$\overset {\longrightarrow }{\mathbb {T}^{n}}$ is oriented from 
$v$ to 
$v'$ and labeled by 
$k$.
Definition 3.5 Let 
$n= |{I_{\text {uf}}}|$. An N-pattern is the assignment 
$v \mapsto s_v$ of an 
$N$-seed 
$s_v$ to every 
$v\in \overset {\longrightarrow }{\mathbb {T}^{n}}$, such that 
$s_{v'}=\mu _k(s_v)$ whenever 
$v\overset {k}{\longrightarrow }v'\in \overset {\longrightarrow }{\mathbb {T}^{n}}$. We let 
$s_0:=s_{v_0}$ be the initial 
$N$-seed.
In what follows we identify a vertex 
$v\in \overset {\longrightarrow }{\mathbb {T}^{n}}$ with the 
$N$-seed 
$s_v$ and write 
$s_v\in \overset {\longrightarrow }{\mathbb {T}^{n}}$.
Definition 3.6 Let 
$\Gamma$ be fixed data, 
$s$ an 
$N$-seed and 
$k\in I_{\text {uf}}$. The 
$\mathcal {A}$-cluster mutation is the birational map on the torus 
$T_{N^{\circ }}:=\operatorname {Spec}\mathbb {C} [M^{\circ }]$
\[ \mu_{k;s}: T_{N^{\circ}} \dashrightarrow T_{N^{\circ}} \]
specified by the pull-back formula at the level of characters of 
$T_{N^{\circ }}$ by
\begin{equation} \mu_{k;s}^{*}(z^{m}):=z^{m} (1 + z^{v_k})^{-\langle d_ke_k,m\rangle}, \end{equation}
for every 
$z^{m}\in \mathbb {C} [M^{\circ }]=\mathbb {C} [T_{N^{\circ }}]$. Similarly, the 
$\mathcal {X}$-cluster mutation is the birational map on the torus 
$T_M:=\operatorname {Spec}\mathbb {C} [N]$
\[ \mu_{k;s}: T_M \dashrightarrow T_M \]specified by the pull-back formula
\begin{equation} \mu_{k;s}^{*}(z^{n}):=z^{n} (1 + z^{e_k})^{- [n,e_k]_s}, \end{equation}
for every 
$z^{n} \in \mathbb {C} [N]=\mathbb {C} [T_M]$, and 
$[\cdot ,\cdot ]_s:N\times N\to \mathbb {Q}$ the bilinear form given by
\[ [e_i,e_j]_s=\epsilon_{ij}. \]Remark 3.7 To make notation lighter we denote the 
$\mathcal {A}$- and 
$\mathcal {X}$-mutation by the same symbol. The kind of tori that we are considering tells us which kind of mutation we have to consider. These mutation formulas are also called cluster transformations.
Remark 3.8 We can pass from the geometric framework of this section to the algebraic framework of the last section as follows:
– set
$I=[1,n+m]$ and $I_{\text {uf}}=[1,n]$;– the set of frozen directions is
${I_{\text {fr}}}:=I\setminus {I_{\text {uf}}}$ (see § 2.6);– the skew-symmetrizable matrix
$B=(b_{ij})_{(i,j)\in {I_{\text {uf}}} \times {I_{\text {uf}}}}$ is the transpose of the (sub-)matrix associated to $[\cdot ,\cdot ]_s$, i.e. for all $i,j \in {I_{\text {uf}}}$:
\[ b_{ij}=\epsilon_{ji}; \]– to construct a coefficient-free
$Y$-pattern with frozen directions we take as ambient semifield $\mathbb {P} =\mathbb {Q} _{\text {sf}}(z^{e_1},\ldots , z^{e_{n+m}})$. The initial $Y$-seed is $((z^{e_1},\ldots ,z^{e_{n+m}}),B)$;– to construct a coefficient-free cluster pattern with frozen directions we take as ambient field
$\mathcal {F}=\mathbb {Q} (z^{f_1},\ldots ,z^{f_{n+m}})$. The initial seed is $((z^{f_1},\ldots , z^{f_{n+m}}),B)$.
Definition 3.9 Fix an 
$N$-pattern 
$v \mapsto s_v$. For every seed 
$s \in \overset {\longrightarrow }{\mathbb {T}^{n}}$ let 
$T_{N^{\circ },s}$ be a torus isomorphic to 
$T_{N^{\circ }}$ endowed with the basis of characters 
$\{ z^{f_i}\in \mathbb {C} [M^{\circ }]:s=(e_i:i\in I) \}$. We define the birational map 
$\mu ^{\phantom {-1}}_{s_0,s}:T_{N^{\circ },s_0}\dashrightarrow T_{N^{\circ },s}$ as
\[ \mu^{\phantom{-1}}_{s_0,s}:=\begin{cases} \text{Id} & \text{if } s=s_0, \\ \mu_{k_l;s_{l}}\circ \cdots \circ \mu_{k_0;s_0} & \text{if } s\neq s_0, \end{cases} \]
where 
$s_0 \overset {k_0}{\longrightarrow } s_1 \overset {k_1}{\longrightarrow } \cdots \overset {k_l}{\longrightarrow } s_{l+1}=s$ is the unique oriented path from 
$s_0$ to 
$s$. For two seeds 
$s,s'\in \overset {\longrightarrow }{\mathbb {T}^{n}}$ we define
\begin{equation} \mu^{\phantom{-1}}_{s,s'}:=\mu^{\phantom{-1}}_{s_0,s'}\circ \mu_{s_0,s}^{-1}: T_{N^{\circ},s} \dashrightarrow T_{N^{\circ},s'}. \end{equation}
By construction 
$\mu ^{\phantom {-1}}_{s',s''}\circ \mu ^{\phantom {-1}}_{s,s'}= \mu ^{\phantom {-1}}_{s,s''}$. We define the analogous transformations for the tori 
$T_{M,s}$.
Lemma 3.10 [GHK15, Proposition 2.4] Let 
$\mathcal {I}$ be a set and 
$\{ S_i :i \in \mathcal {I} \}$ be a collection of integral separated schemes of finite type over a locally Noetherian ring 
$R$, with birational maps 
$f_{ij}:S_i \dashrightarrow S_j$ for all 
$i,j$, verifying the cocycle condition 
$f_{jk}\circ f_{ij}=f_{ik}$ as rational maps and such that 
$f_{ii}={\rm Id}$. Let 
$U_{ij}\subset S_i$ be the largest open subscheme such that 
$f_{ij}:U_{ij}\to f_{ij}(U_{ij})$ is an isomorphism. Then there is a scheme
\[ S=\bigcup_{i \in \mathcal{I}}S_{i} \]
obtained by gluing the 
$S_i$ along the open sets 
$U_{ij}$ via the maps 
$f_{ij}$.
Remark 3.11 In [Reference Gross, Hacking and KeelGHK15, Proposition 2.4] the authors prove Lemma 3.10 when 
$R$ is a field because this is the generality they need. In the next section we will take 
$R$ to be a (Laurent) polynomial ring, which is Noetherian. The proof of [Reference Gross, Hacking and KeelGHK15, Proposition 2.4] is based on [Reference Grothendieck and DieudonnéGD60, Proposition 6.5.4] and [Reference Grothendieck and DieudonnéGD60, Proposition 8.2.8]. Both results hold in the more general case in which 
$R$ is a locally Noetherian ring. Therefore, the same proof can be used to prove Lemma 3.10.
Definition 3.12 Fix an 
$N$-pattern. We apply Lemma 3.10 to the collection of tori 
${\{ T_{N^{\circ },s}: s\in \overset {\longrightarrow }{\mathbb {T}^{n}} \}}$ and the birational maps 
$\mu _{s,s'}$ to define the scheme
\[ \mathcal{A} _{\Gamma,s_0}:=\bigcup_{s\in \overset{\longrightarrow}{\mathbb{T}^{n}}}T_{N^{\circ},s}. \]
This is the 
$\mathcal {A}$-cluster variety associated to 
$\Gamma$ and 
$s_0$. In a completely analogous way we define the 
$\mathcal {X}$-cluster variety associated to 
$\Gamma$ and 
$s_0$
\[ \mathcal{X} _{\Gamma,s_0}:=\bigcup_{s\in \overset{\longrightarrow}{\mathbb{T}^{n}}}T_{M,s}. \]
We say that a cluster variety (of any kind) has frozen directions if 
$I\backslash {I_{\text {uf}}}\neq \varnothing$.
Notation 3.13 The characters of the torus 
$T_M$ (respectively 
$T_{N^{\circ }}$) are of the form 
$z^{n}$ (respectively 
$z^{m}$) for 
$n\in N$ (respectively 
$m\in M^{\circ }$). Fix an 
$N$-pattern, from now on we use the following identifications relating the notation of §§ 2 and 3:
\[ Y_{i;v}=X_{i;s_v}=z^{e_{i;s_v}} \quad \textrm{and}\quad x_{i;v}=A_{i;s_v}=z^{f_{i;s_v}}. \]
However, notice that the identification 
$X_{i;s}=z^{e_{i;s}}$ (respectively 
$A_{i;s}=z^{f_{i;s}}$) is only valid on the torus 
$T_{M,s}$ (respectively 
$T_{N^{\circ },s}$). We refer to the symbols 
$X_{i;s}$ (respectively 
$A_{i;s}$) as 
$\mathcal {X}$-cluster variables (respectively 
$\mathcal {A}$-cluster variables).
Remark 3.14 In this paper (coefficient-free) cluster varieties are schemes over the complex numbers. It is possible to work over more general rings of definition such as 
$\mathbb {Z}$. This is the approach taken for example in [Reference Fock and GoncharovFG09b]. The varieties considered in this paper are simply the 
$\mathbb {C}$-points of such 
$\mathbb {Z}$-schemes.
Remark 3.15 We will write 
$\mu _k$ instead of 
$\mu _{k;s}$ since the tori we glue already tell us which 
$s$ we are considering.
There is a fundamental map relating 
$\mathcal {A}$- and 
$\mathcal {X}$-cluster varieties. It is induced by the skew-symmetric bilinear form 
$\{\cdot ,\cdot \}$ as follows. There are two natural maps
for 
$n_1\in N^{\circ }$, respectively 
$n_2\in N_{\text {uf}}\cap N^{\circ }$.
Definition 3.16 A 
$p^{*}$-map is a map 
$N\to M^{\circ }$, such that the following diagram commutes.
Different choices of such a map differ by different choices of maps 
$N/N_{\text {uf}}\to N_{\text {uf}}^{\perp }$. A map 
${p^{*}:N\to M^{\circ }}$ gives a map 
$p:T_{N^{\circ },s}\to T_{M,s}$ for every seed 
$s$. We can see from Lemma 2.43 and Remark 2.44 that 
$p$ commutes with the cluster transformations. Therefore, it further extends to a globally defined map 
$p:\mathcal {A} _{\Gamma ,s_0}\to \mathcal {X} _{\Gamma ,s_0}$.
Remark 3.17 For simplicity assume we are in the skew-symmetric case and fix an 
$N$-seed 
$s=(e_i:i\in I)$ in an 
$N$-pattern with 
$s=s_v$. We can choose 
$p^{*}(e_i)=\{e_i,\cdot \}=e_i B_v^{T}=b_i$, the 
$i$th column of the matrix 
$\boldsymbol {\varepsilon }_s^{T}=B_v$ (see Remark 3.8). Comparing to Remark 2.45 and the 
$\hat {y}_{i;v}$ defined in (2.17) this corresponds to
\[ p^{*}(X_{i;s})=p^{*}(z^{e_i})=z^{b_i}=\prod_{j\in I} (z^{f_j})^{b_{ji}}=\prod_{j\in I} A_{j;s}^{b_{ji}}=\hat{y}_{i;v}. \]3.2 Cluster varieties with coefficients
In what follows we give a new perspective on 
$\mathcal {A}$-cluster varieties with coefficients treating them as schemes over (Laurent) polynomial rings. Further, we introduce the concept of 
$\mathcal {X}$-cluster varieties with coefficients and cluster varieties with specified coefficients.
We fix the tropical semifield 
$\mathbb {P} =\text {Trop}(p_1,\ldots , p_r)$. In particular, recall that 
$\mathbb {P}$ is a free abelian group generated by 
$p_1, \ldots , p_r$ written multiplicatively.
Definition 3.18 Let 
$\Gamma$ be fixed data and 
$s_{v_0}=(e_i:i\in I)$ an initial 
$N$-seed (in this situation we will usually call the pair 
$(\Gamma ,s_{v_0})$ initial data). A 
$Y$-pattern 
$v \mapsto (\mathbf {p}_v, B_v)$ of rank 
$|I_{\text {uf}}|$ is compatible with 
$\Gamma$ and 
$s_{v_0}$ if the initial matrix 
$B_{v_0}=(b_{ij})$ is the transpose of the matrix associated to 
$[ \cdot , \cdot ]_{s_{v_0}}$ (see Remark 3.8).
Let 
$R$ be either 
$\mathbb {C} [p_1,\ldots , p_r]$ or 
$\mathbb {C} [p^{\pm 1}_1,\ldots , p^{\pm 1}_r]$.Footnote 4 In particular, 
$\operatorname {Spec} (R)$ is either an algebraic torus or an affine space. For a lattice 
$L$ we denote
\[ T_{L}(R) :=\operatorname{Spec}(\mathbb{C} [L^{*}] \otimes_{\mathbb{C} } R) = T_{L} \times_{\mathbb{C} } \operatorname{Spec}(R). \]
In particular, the coordinate ring of 
$T_{L}(R)$ is isomorphic to 
$R[L^{\ast }]$, where 
$L^{*}=\operatorname {Hom}(L,\mathbb {Z} )$.
Recall that for every 
$p\in \mathbb {P}$, we have 
$p^{+}$ and 
$p^{-}$, which are monomials in 
$p_1,\ldots , p_r$, from Definition 2.8.
Definition 3.19 Let 
$\Gamma$ be fixed data, 
$s$ an 
$N$-seed, 
$p\in \mathbb {P}$ and 
$k\in I_{\text {uf}}$. The associated 
$\mathcal {A}$-cluster mutation with coefficients is the birational map
\[ \mu_{k;s;p}: T_{N^{\circ}}(R) \dashrightarrow T_{N^{\circ}}(R) \]specified by the pull-back formula
\begin{equation} \mu_{k;s;p}^{*}(z^{m}):=z^{m} (p^{-} + p^{+}z^{v_k})^{-\langle d_ke_k,m\rangle}, \end{equation}
for every 
$z^{m} \in R[M^{\circ }]$. Similarly, the associated 
$\mathcal {X}$-cluster mutation with coefficients is the birational map
\[ \mu_{k;s;p}: T_M (R) \dashrightarrow T_M (R) \]
specified by the pull-back formula for every 
$z^{n} \in R[N]$:
\begin{equation} \mu_{k;s;p}^{*}(z^{n}):=z^{n} (p^{-} + p^{+}z^{e_k})^{- [n,e_k]_s}. \end{equation} Using the above mutations with coefficients we construct cluster varieties with coefficients. Before defining them, first note that given fixed data 
$\Gamma$, an initial 
$N$-seed 
$s_0=(e_i : i \in I)$ and a compatible 
$Y$-pattern 
$v \mapsto (\mathbf {p}_v, B_v)$, then for every seed 
$s\in \overset {\longrightarrow }{\mathbb {T}^{n}}$ we obtain a birational map 
$\mu _{s_0,s}: T_{N^{\circ }, s_0}(R) \dashrightarrow T_{N^{\circ }, s}(R)$ analogously to Definition 3.9:
\[ \mu^{\phantom{-1}}_{s_0,s}:=\begin{cases} \text{Id} & \text{if } s=s_0, \\ \mu_{k_l;s_l;p_{k_l;v_l},}\circ \cdots \circ \mu_{k_0;s_0;p_{k_0;v_0}} & \text{if } s\neq s_0, \end{cases} \]
taking the unique oriented path from 
$s_0$ to 
$s$, 
$s_0 \overset {k_0}{\longrightarrow } s_1 \overset {k_1}{\longrightarrow } \cdots \overset {k_l}{\longrightarrow } s_{l+1}=s$. For 
$s,s'\in \overset {\longrightarrow }{\mathbb {T}^{n}}$ we define
\begin{equation} \mu^{\phantom{-1}}_{s,s'}:=\mu^{\phantom{-1}}_{s_0,s'}\circ \mu_{s_0,s}^{-1}: T_{N^{\circ},s}(R) \dashrightarrow T_{N^{\circ},s'}(R). \end{equation} We define the birational transformation 
$\mu _{s,s'}: T_{M,s}(R) \dashrightarrow T_{M,s'}(R)$ for 
$s,s'\in \overset {\longrightarrow }{\mathbb {T}^{n}}$ in a completely analogous way. For both kinds of tori the cocycle condition 
$\mu _{s',s''} \circ \mu _{s,s'} =\mu _{s,s''}$ follows by definition.
Definition 3.20 Consider fixed data 
$\Gamma$, an initial 
$N$-seed 
$s_0=(e_i : i \in I)$ and a compatible 
$Y$-pattern 
$v \mapsto (\mathbf {p}_v, B_v)$. We apply Lemma 3.10 and Remark 3.11 to the tori 
$\{ T_{N^{\circ },s}(R):s \in \overset {\longrightarrow }{\mathbb {T}^{n}} \}$ and the 
$\mathcal {A}$-cluster mutation with coefficients 
$\mu _{s,s'}$ to define the 
$\mathcal {A}$-cluster variety with coefficients as the scheme
\[ \mathcal{A} _{\Gamma,s_0,\mathbf{p}_{v_0}}:=\bigcup_{s\in \overset{\longrightarrow}{\mathbb{T}^{n}}}T_{N^{\circ},s}(R). \]
In a completely analogous way using the tori 
$\{ T_{M,s}(R): s \in \overset {\longrightarrow }{\mathbb {T}^{n}} \}$ and the 
$\mathcal {X}$-cluster mutation with coefficients we define the 
$\mathcal {X}$-cluster variety with coefficients
\[ \mathcal{X} _{\Gamma,s_0,\mathbf{p}_{v_0}}:=\bigcup_{s\in \overset{\longrightarrow}{\mathbb{T}^{n}}}T_{M,s}(R). \]
We say that a cluster variety with coefficients has frozen directions if 
$I\setminus I_{\text {uf}}\not = \varnothing$.
Remark 3.21 Similarly to the coefficient-free case, we write 
$\mu _{k;p}$ instead of 
$\mu _{k;s;p}$.
Remark 3.22 Note that the notion of initial data for cluster varieties with coefficients coincides with the notion of initial data in the coefficient-free case. Moreover, the map 
$p^{*}:N\to M^{\circ }$ defined in Definition 3.16 relies only on the notion of initial data. Hence, we obtain as above for every seed 
$s$ a map 
$p:T_{N^{\circ },s}(R)\to T_{M,s}(R)$ via the pull-back on characters 
$z^{m}\in R[M^{\circ }]$ given by 
$p^{*}$. In view of Lemma 2.43 this extends to a map
\[ p:\mathcal{A} _{\Gamma,s_0,\mathbf{p}_{v_0}}\to \mathcal{X} _{\Gamma,s_0,\mathbf{p}_{v_0}}. \]Remark 3.23 Remark 3.8 extends to cluster and 
$Y$-patterns with coefficients in 
$\mathbb {P}$:
– the associated
$Y$-pattern with coefficients and frozen directions lives in
\[ \mathbb{Q} \mathbb{P} _{\text{sf}}(z^{e_1},\ldots,z^{e_{n+m}})=\mathbb{Q} (p_1,\ldots,p_r)_{\text{sf}}(z^{e_1},\ldots,z^{e_{n+m}}); \]– the associated cluster pattern with coefficients and frozen directions lives in
\[ \mathbb{Q} \mathbb{P} (z^{f_1},\ldots,z^{f_{n+m}})=\mathbb{Q} (p_1,\ldots,p_r,z^{f_1},\ldots,z^{f_{n+m}}). \]
Considering Remark 3.8, Notation 3.13 and Remark 3.23 we obtain the following.
Lemma 3.24 The 
$\mathcal {A}$-cluster mutation with coefficients corresponds to cluster mutation with geometric coefficients, and the 
$\mathcal {X}$-cluster mutation with coefficients corresponds to 
$Y$-mutation with geometric coefficients.
Proof. We only prove the statement on the 
$\mathcal {X}$-side, the proof on the 
$\mathcal {A}$-side is analogous. We have to check that formula (3.7) is equivalent to formula (2.8) for 
$\mathbb {P} =\text {Trop}(p_1,\ldots ,p_r)$. This follows at once from the following computation:
\[ \mu_{k;p}^{*}(z^{e'_k})= z^{e'_k}(p^{-}+p^{+}z^{e_k})^{-\epsilon_{ik}}=\begin{cases} z^{e_k}(p^{-}z^{-e_k}+p^{+})^{-\epsilon_{ik}} & \text{if } \epsilon_{ik}>0, \\ z^{e_k}(p^{-}+p^{+}z^{e_k})^{-\epsilon_{ik}} & \text{if } \epsilon_{ik}\leq 0.\end{cases}\]Remark 3.25 We can view cluster varieties with coefficients as schemes over 
$\mathbb {C}$ via the canonical inclusion 
$\mathbb {C} \hookrightarrow R$. On the 
$\mathcal {A}$-side frozen variables can be thought of as coefficients as explained in § 2.6. Therefore, an 
$\mathcal {A}$-cluster variety with coefficients considered as a scheme over 
$\mathbb {C}$ has the structure of a coefficient-free 
$\mathcal {A}$-cluster variety with frozen directions. We just have to construct an appropriate 
$\Gamma$ following Definition 2.38. However, this is not the case on the 
$\mathcal {X}$-side because 
$\mathcal {X}$-variables associated to frozen directions may change after mutation in a non-frozen direction.
Let 
$\Gamma$ be fixed data, 
$s_0$ an initial 
$N$-seed and 
$v \mapsto (\mathbf {p}_v, B_v)$ a compatible 
$Y$-pattern. Let 
$L$ be either the lattice 
$N^{\circ }$ or 
$M$. The canonical inclusion
\[ T_{L}\hookrightarrow T_{L}(R)=T_{L}\times_{\mathbb{C} }\operatorname{Spec}(R) \]
induces a left action of the group scheme 
$T_{L}$ on 
$T_L(R)$. Explicitly, this action is given by the canonical projection 
$T_{L}\times _{\mathbb {C} } \operatorname {Spec}(R)\to \operatorname {Spec} (R)$. Moreover, if 
$s, s'\in \overset {\longrightarrow }{\mathbb {T}^{n}}$ we have the following commutative diagram.
This implies that we can glue these morphisms to obtain morphisms of schemes as follows.
Notice that these morphism are flat. Indeed, as flatness is a local property to verify it we can restrict to 
$T_{L,s}(R)$. The induced map of rings 
$R \to R[L^{*}]$ is flat, so both 
$\pi _{\mathcal {A} }$ and 
$\pi _{\mathcal {X} }$ are flat morphisms of schemes.
Definition 3.26 Let 
$\lambda \in \operatorname {Spec}(R)$ be a fixed parameter. The 
$\mathcal {A}$-cluster variety with specified coefficients 
$\mathcal {A} _{\Gamma ,s_0,\mathbf {p}_{v_0},\lambda }$ is the fiber 
$\pi ^{-1}_{\mathcal {A} }(\lambda )$. We define the 
$\mathcal {X}$-cluster variety with specified coefficients 
$\mathcal {X} _{\Gamma , s_0,\mathbf {p}_{v_0}, \lambda }$ as the fiber 
$\pi _{\mathcal {X} }^{-1}(\lambda )$.
Notice that if 
$\lambda \in \operatorname {Spec}(R)$ is a closed point then 
$\mathcal {A} _{\Gamma ,s_0,\mathbf {p}_{v_0},\lambda }$ is a scheme over 
$\mathbb {C}$ in a canonical way. In particular, if 
$\mathbf {1}=(1,\ldots ,1)$, then
\[ \mathcal{A} _{\Gamma,s_0,\mathbf{p}_{v_0},\mathbf{1}}=\mathcal{A} _{\Gamma,s_0}\quad \text{and}\quad \mathcal{X} _{\Gamma,s_0,\mathbf{p}_{v_0},\mathbf{1}}=\mathcal{X} _{\Gamma,s_0}. \]
More generally, let 
$\mathcal {M} =\{\prod _{i=1}^{r} p_i^{a_i}\in \mathbb {P} :a_i\geq 0 \}$ and 
$p\in \mathbb {P}$. Fix a morphism of monoids 
$\phi : \mathcal {M} \to \mathbb {C}$. The mutation with specified coefficients associated to 
$\mu _{k;p}$ and 
$\phi$ is the birational map
\[ \mu_{k;\phi(p)}:T_{N^{\circ}}\dashrightarrow T_{N^{\circ}} \]given by the pull-back formula
\[ \mu_{k;\phi(p)}^{*}(z^{m}):= z^{m}(\phi(p^{-})+\phi(p^{+})z^{v_k})^{-\langle d_ke_k,m\rangle}, \]
for every 
$z^{m}\in R[M^{\circ }]$. We define in an analogous way the 
$\mathcal {X}$-mutation with specified coefficients. If 
$\lambda =(\lambda _1,\ldots ,\lambda _r)$ is a closed point of 
$\operatorname {Spec}(R)$ and 
$\phi :\mathcal {M}\to \mathbb {C}$ is defined by 
$\phi (p_i)=\lambda _i$ then
\[ \mathcal{A} _{\Gamma, \mathbf{p}, \lambda}= \bigcup_{s\in \overset{\longrightarrow}{\mathbb{T}^{n}}} T_{N^{\circ},s}, \]
where the tori 
$T_{N^{\circ },s}$ are glued by 
$\mu _{k;\phi (p)}$. Similarly, we have
\[ \mathcal{X} _{\Gamma, \mathbf{p}, \lambda}= \bigcup_{s\in \overset{\longrightarrow}{\mathbb{T}^{n}}} T_{M,s}, \]
where the tori 
$T_{M,s}$ are glued with the mutations with specified coefficients.
Remark 3.27 In [Reference Gross, Hacking and KeelGHK15] the authors introduce the cluster varieties 
$\mathcal {A} _{\mathbf {t}}$ for 
$\mathbf {t}\in \mathbb {C} ^{r}$ and call them cluster varieties with general coefficients. These varieties are obtained specifying Definition 3.26 to the case of principal coefficients and identifying the parameters 
$p_1,\ldots , p_r$ with the complex values 
$\phi (p_1)=t_1,\ldots ,\phi (p_r)=t_r$. In [Reference Gross, Hacking, Keel and KontsevichGHKK18, § 7, p. 555], Gross, Hacking, Keel and Kontsevich mention that it is not clear how to dualize the birational gluing maps for 
$\mathcal {A}$-varieties with specified coefficients as it is not obvious how the parameters should be treated. The formalism developed in this section is meant to solve this problem. We would like to mention that 
$\mathcal {A} _{\mathbf {t}}$ and 
$\mathcal {A} _{\mathbf {t}'}$ are isomorphic if 
$\mathbf {t},\mathbf {t}'\in \operatorname {Spec}(R)$ are generic closed points. We prove the analogous result for the 
$\mathcal {X}$-side in Proposition 5.11 below.
3.3 Cluster duality with coefficients
As explained in [Reference Gross, Hacking and KeelGHK15], the 
$\mathcal {A}$- and 
$\mathcal {X}$-mutation formulas are canonically dual to each other. In this subsection we recall this duality and extend it to the context of cluster varieties with coefficients and specified coefficients.
Definition 3.28 The Langlands dual of 
$\Gamma$ is the fixed data 
$\Gamma ^{\vee }$ given by the following.
–
$I^{\vee }=I$ and ${I_{\text {uf}}}^{\vee }={I_{\text {uf}}}$;–
$N^{\vee }=N^{\circ }$;–
$({N_{\text {uf}}})^{\vee } ={N_{\text {uf}}} \cap N^{\circ }$;–
$\lbrace \cdot , \cdot \rbrace ^{\vee }=d^{-1}\lbrace \cdot , \cdot \rbrace$, where $d:=\text {lcm}(d_i:i\in I)$;–
$(N^{\vee })^{\circ }=dN$;–
$d^{\vee }_i=dd_i^{-1}$ for all $i\in I$;–
$M^{\vee }=M^{\circ }$ and $(M^{\vee })^{\circ }=d^{-1}M$.
The Langlands dual of 
$s$ is 
$s^{\vee }:=(d_ie_i:i\in I)$. The Fock–Goncharov dual cluster varieties of 
$\mathcal {A} _{\Gamma ,s}$ and 
$\mathcal {X} _{\Gamma ,s}$ are
\[ \mathcal{A} ^{\vee}_{\Gamma,s}:=\mathcal{X} _{\Gamma^{\vee},s^{\vee}}\quad \text{and} \quad \mathcal{X} ^{\vee}_{\Gamma,s}:=\mathcal{A} _{\Gamma^{\vee},s^{\vee}}. \]Remark 3.29 Notice that if 
$B$ is the initial matrix associated to 
$\Gamma$ and 
$s$ then 
$-B^{T}$ is the initial matrix associated to 
$\Gamma ^{\vee }$ and 
$s^{\vee }$. In particular, in the skew-symmetric case we have 
$\Gamma ^{\vee }=\Gamma$ and 
$s^{\vee }=s$. Moreover, 
$\Gamma$ (respectively 
$s$) is equal to 
$(\Gamma ^{\vee })^{\vee }$ (respectively 
$(s^{\vee })^{\vee }$) up to the morphism of lattices 
$dN \to N$ given by 
$n\mapsto d^{-1}n$.
Definition 3.30 Every pair 
$(n,m)\in N^{\circ } \times M^{\circ }$ with 
$\langle n,m \rangle =0$ defines a mutationFootnote 5
\[ \mu^{\phantom{x}}_{(n,m)}:T_{N^{\circ}} \dashrightarrow T_{N^{\circ}} \]specified by the formula
\[ \mu_{(n,m)}^{*}(z^{m'}):=z^{m'} (1+z^{m})^{\langle m',n\rangle}, \]
for every 
$z^{m'}\in \mathbb {C} [M^{\circ }]$. The dual mutation is defined as the birational map
\[ \mu^{\phantom{x}}_{(m,-n)}:T_{M^{\vee}} \dashrightarrow T_{M^{\vee}} \]
associated to the pair 
$(m,-n)\in \operatorname {Hom}(N^{\circ }\times M^{\circ }, \mathbb {Z} )=M^{\circ } \times N^{\circ } =M^{\vee }\times N^{\vee }$.
The 
$\mathcal {A}$-cluster mutation (3.3) associated to 
$\Gamma$ and 
$s$ is 
$\mu _{(-d_ke_k,v_k)}$, and the 
$\mathcal {X}$-cluster mutation (3.4) associated to 
$\Gamma ^{\vee }$ and 
$s^{\vee }$ is 
$\mu _{(v_k,d_ke_k)}$. This explains the duality between 
$\mathcal {A}$- and 
$\mathcal {X}$-cluster varieties.
Definition 3.31 Let 
$p\in \text {Trop}(p_1,\ldots , p_r)$ and 
$(n,m)\in N^{\circ } \times M^{\circ }$. The mutation associated to 
$(n,m)$ with deformation parameter 
$p$ is the birational map
\[ \mu^{\phantom{x}}_{(n,m);p}:T_{N^{\circ}}(R) \dashrightarrow T_{N^{\circ}}(R) \]
defined at the level of characters for every 
$z^{m'}\in R[M^{\circ }]$ by
\begin{equation} \mu_{(n,m);p}^{*}(z^{m'}):=z^{m'} (p^{-} + p^{+}z^{m})^{\langle m',n\rangle}. \end{equation}
Let 
$\phi :\mathcal {M}\to \mathbb {C}$ be a map + of monoids. The mutation associated to 
$(n,m)$, 
$\phi$ and 
$p$ is
\begin{equation} \mu_{(n,m);\phi(p)}^{*}(z^{m'}):=z^{m'} (\phi(p^{-}) + \phi(p^{+})z^{m})^{\langle m',n\rangle}. \end{equation} We define a notion of duality for (3.10) and (3.11) that generalizes Definition 3.30. Moreover, this notion of duality specializes to the duality between 
$\mathcal {A} _{\varGamma ,s}$ and 
$\mathcal {X} _{\varGamma ^{\vee },s^{\vee }}$ when we take trivial coefficients, i.e. 
$R=\mathbb {C}$.
Definition 3.32 Let 
$v\mapsto (\mathbf {p}_v,B_v)$ be an initial 
$Y$-pattern. The 
$Y$-pattern 
$v \mapsto (\mathbf {p}_v^{\vee },B_v^{\vee })$ is defined by setting
\[ \mathbf{p}_{v_0}^{\vee}=\mathbf{p}_{v_0} \quad \text{and}\quad B^{\vee}_{v_0}=-B_{v_0}^{T}. \]
Let 
$\mathbf {p}_{v}=(p_{1;v},\ldots , p_{n;v})$ be a 
$Y$-seed of the initial 
$Y$-pattern. The mutation dual to 
$\mu _{(n,m);p_{k;v}}$ is
\[ \mu_{(m,-n);p^{\vee}_{k;v}}: T_{M^{\vee}}(R)\dashrightarrow T_{M^{\vee}}(R). \]
Explicitly, at the level of characters 
$\mu _{(m,-n);p^{\vee }_{k;v}}$ is given by
\[ z^{n'}\mapsto z^{n'} ((p^{\vee}_{k;v})^{-} + (p^{\vee}_{k;v})^{+}z^{-n})^{\langle n',m\rangle} \]
for every 
$z^{n'}\in R[N^{\vee }]$. Similarly, the mutation dual to 
$\mu _{(n,m);\phi (p_{k;v})}$ is
\[ \mu_{(m,-n);\phi(p^{\vee}_{k;v})}: T_{M^{\vee}}\dashrightarrow T_{M^{\vee}}. \] Observe that if the 
$Y$-pattern 
$v\mapsto (\mathbf {p}_v,B_v)$ is compatible with 
$\varGamma$ and 
$s$ then the 
$Y$-pattern 
$v \mapsto (\mathbf {p}_v^{\vee },B_v^{\vee })$ is compatible with 
$\varGamma ^{\vee }$ and 
$s^{\vee }$.
Definition 3.33 The duals of 
$\mathcal {A} _{\varGamma ,s_0,\mathbf {p}_{v_0}}$ and 
$\mathcal {X} _{\varGamma ,s_0,\mathbf {p}_{v_0}}$ are
\[ \mathcal{A} ^{\vee}_{\varGamma,s_0,\mathbf{p}_{v_0}}:=\mathcal{X} _{\varGamma^{\vee},s_0^{\vee},\mathbf{p}_{v_0}^{\vee}}\quad \text{and}\quad \mathcal{X} ^{\vee}_{\varGamma,s_0,\mathbf{p}_{v_0}}:=\mathcal{A} _{\varGamma^{\vee},s^{\vee}_0,\mathbf{p}^{\vee}_{v_0}}. \]3.4 Cluster varieties with principal coefficients
We specify the constructions given in §§ 3.2 and 3.3 to the case of principal coefficients.
Definition 3.34 The fixed data with principal coefficients 
$\varGamma _{\text {prin}}$ associated to given fixed data 
$\varGamma$ is specified by the following:
– the indexing set
$\tilde {I}$ is a disjoint union of two copies of $I$;– the set of unfrozen indices
$\tilde {I}_{\text {uf}}$ is the subset ${I_{\text {uf}}}$ of the first copy of $I$;–
$\tilde {N}:=N\oplus M^{\circ }$;–
$\tilde {N}_{\text {uf}}:={N_{\text {uf}}}\oplus 0$;– the skew-symmetric bilinear form
$\lbrace \cdot , \cdot \rbrace :\tilde {N}\times \tilde {N}\to \mathbb {Q}$ is given by
\[ \{(n_1,m_1),(n_2,m_2) \}:= \{ n_1,n_2\}+\langle n_1,m_2\rangle - \langle n_2,m_1\rangle; \]–
$\tilde {N}^{\circ }:=N^{\circ }\times M$;– the same
$d_i$ as for $\varGamma$.
Moreover, the 
$N$-seed 
$s$ defines the 
$\tilde {N}$-seed 
$\tilde {s}=((e_1,0), \ldots , (e_n,0),(0,f_1),\ldots (0,f_n))$.
Definition 3.35 The 
$\mathcal {A}$-cluster variety with principal coefficients associated to 
$\varGamma$ and 
$s$ is the 
$\mathcal {A}$-cluster variety with coefficients
\[ \mathcal{A}_{\mathrm{prin}} :=\mathcal{A} _{\varGamma_{\text{prin}},\tilde{s}}. \]Remark 3.36 In light of Remark 3.25, 
$\mathcal {A}_{\mathrm {prin}}$ can be viewed as a coefficient-free 
$\mathcal {A}$-cluster variety with frozen directions. In [Reference Gross, Hacking, Keel and KontsevichGHKK18] the authors define the cluster variety 
$\mathcal {X} _{\text {prin}}$ as the (coefficient-free) 
$\mathcal {X}$-cluster variety associated to 
$(\varGamma ^{\vee })_{\text {prin}}$ and 
$\widetilde {(s^{\vee })}$. From the framework developed above we can see that
\begin{gather*} \mathcal{X}_{\mathrm{prin}} \textit{ is cluster dual to } \mathcal{A}_{\mathrm{prin}} \textit{ as a scheme over } \mathbb{C}, \textit{i.e.}\\ \textit{as a coefficient-free cluster variety with frozen directions.} \end{gather*} The dual of 
$\mathcal {A}_{\mathrm {prin}}$ as a cluster variety with coefficients, denoted by 
$\mathscr {X}$, is a very interesting object and the main object of study throughout the rest of the paper.
We conclude this section with definitions and notation that will be useful in the remainder of the paper. So far our notation for cluster varieties includes the subscript 
$\varGamma$. From now on we drop this subscript and denote 
$\mathcal {A} _{\varGamma ,s_0}$ simply by 
$\mathcal {A}$, respectively 
$\mathcal {A} _{\varGamma ,s_0,\mathbf {p}_{v_0}}$ by 
$\mathcal {A} _{\mathbf {p}_{v_0}}$. We use analogous notation for 
$\mathcal {X}$-cluster varieties.
Definition 3.37 A rational function on a cluster variety (of whichever type) is called a cluster monomial if it is a Laurent monomial in the variables of some seed.
Notation 3.38 Let 
$A_{i;s}$ be a cluster variable of 
$\mathcal {A}$. By the Laurent phenomenon (Theorem 2.19) the 
$A_{i;s}$ are global regular functions on 
$\mathcal {A}$. We denote by 
$\tilde {A}_{i;s}$ the extension of 
$A_{i;s}$ to 
$\mathcal {A}_{\mathrm {prin},{s_0}}$. These extensions are again globally regular. Explicitly, in the language of the preceding section we have
\[ X^{\text{FZ}}_{i;v}=\tilde{A}_{i;s_v}. \]
We extend this notation to cluster monomials. Similarly, if 
$X_{i;s}$ is an 
$\mathcal {X}$-cluster variable associated to 
$\mathcal {X}$, we let 
$\tilde {X}_{i;s}$ denote the extension of 
$X_{i;s}$ to 
$\mathscr {X} _{s_0}$. Like the 
$\mathcal {X}$-variables themselves, these extensions are only locally defined.
We often want to express functions in terms of the variables of the initial seed 
$s_0$. We introduce the following notation for this purpose.
Notation 3.39 Let 
$\mathcal {V}$ be a cluster variety of whichever type, with or without frozen directions and coefficients. Let 
$f$ be a function on any torus in the atlas of 
$\mathcal {V}$. We denote by 
$\mu _{s_0}^{*}\left ({f}\right )$ the pull-back of 
$f$ to the initial torus associated to 
$s_0$, given by iterated mutations.
4. Tropical duality, the $\mathbf {g}$-fan and the special completion of $\mathcal {X}$
In this section we recall some basic facts about the tropical geometry of cluster varieties. We explain how two important results in this area (tropical duality of [Reference Nakanishi and ZelevinskyNZ12] and the fan structure of the cluster complex, see [Reference Gross, Hacking, Keel and KontsevichGHKK18, Theorem 2.13]) lead very naturally to the special completion 
$\widehat {\mathcal {X} }$ of the 
$\mathcal {X}$-variety (see [Reference Fock and GoncharovFG16]).
4.1 Tropicalization
Cluster varieties have a particularly rich theory of tropicalization. As described in [Reference Gross, Hacking and KeelGHK15], cluster varieties are a very special class of log Calabi–Yau varieties. As such, we can describe the tropicalization of a cluster variety in terms of divisorial discrete valuations and view the tropical space as encoding the cluster variety's log geometry. Meanwhile, in [Reference Fock and GoncharovFG09a] Fock and Goncharov described cluster varieties as positive schemes. From this perspective, we can apply a functor of points and ask for the 
$\mathbb {P}$-points of a cluster variety, for any semifield 
$\mathbb {P}$. In particular, we can take 
$\mathbb {P}$ to be a tropical semifield (see [Reference Fock and GoncharovFG09a, § 1.1]). These perspectives are discussed and related in [Reference Gross, Hacking, Keel and KontsevichGHKK18, § 2]. For us it will be enough to recall the following facts.
– For every lattice
$L$, the $\mathbb {P}$-points of $T_L$ are given by
where\[ T_L^{\mathrm{trop} }(\mathbb{P} )\cong L\otimes_{\mathbb{Z} } \mathbb{P} , \]$\otimes$ is the tensor product of abelian groups.– Mutation
$\mu _k : T_{L,s}\dashrightarrow T_{L,s'}$ induces a piecewise linear isomorphism
In particular, the inclusions of cluster charts\[ \mu_k^{\mathrm{trop} }: T_{L,s}^{\mathrm{trop} }(\mathbb{P} ) \to T_{L,s'}^{\mathrm{trop} }(\mathbb{P} ). \]$T_{N^{\circ }}\hookrightarrow \mathcal {A}$ and $T_{M}\hookrightarrow \mathcal {X}$ induce bijections of $\mathbb {P}$-points:
\[ T_{N^{\circ}}^{\mathrm{trop} }(\mathbb{P} )\cong \mathcal{A} ^{\mathrm{trop} }(\mathbb{P} ) \quad \text{and} \quad T_{M}^{\mathrm{trop} }(\mathbb{P} )\cong \mathcal{X} ^{\mathrm{trop} }(\mathbb{P} ). \]
We often consider 
$\mathbb {Z}$ and 
$\mathbb {R}$ endowed with the auxiliary addition given by 
$x\oplus y:= \min (x,y)$ for 
$x,y\in \mathbb {Z}$ or 
$\mathbb {R}$. Whenever we write 
$\mathcal {X} ^{\mathrm{trop}} (\mathbb {Z} )$ (respectively 
$\mathcal {X} ^{\mathrm{trop}} (\mathbb {R} )$), we implicitly mean taking the tropical points with respect to 
$\mathbb {Z}$ (respectively 
$\mathbb {R}$) with the aforementioned semifield structure. In particular, tropicalizing a mutation is given by the usual tropicalization of a rational function (replace 
$+$ by 
$\min$, and 
$\cdot$ by 
$+$).
Remark 4.1 Let 
$\mathcal {V}$ be a cluster variety. Even if 
$\mathcal {V}^{\mathrm{trop}} (\mathbb {Z} )$ and 
$\mathcal {V}^{\mathrm{trop}} (\mathbb {R} )$ can be identified as sets with 
$\mathbb {Z}$ and 
$\mathbb {R}$, respectively, these tropical spaces do not have a natural notion of addition. However, they possess in a natural way the structure of an 
$\mathbb {N}$-torsor (we can multiply tropical points by elements of 
$\mathbb {N}$) and a piecewise linear structure.
4.2 Tropical duality
Fix an initial exchange matrix 
$B$ corresponding to an initial 
$N$-seed 
$s$ (see Remark 3.8). Recall the definitions of g- and c-vectors (Definitions 2.23 and 2.32, respectively). Let us recall a list of fundamental results concerning these vectors.
Definition 4.2 Let 
$v\in \mathbb {T}^{n}$. The c-matrix 
$C_{v}^{B}$ is the square matrix whose 
$j$th column is the c-vector 
$\textbf {c}_{j;v}$. Similarly, the g-matrix 
$G_{v}^{B}$ is the square matrix whose 
$j$th column is the g-vector 
$\textbf {g}_{j;v}$.
Theorem 4.3 (Sign-coherence of c-vectors [GHKK18, Corollary 5.5)] For each 
$i\in [1,n]$ and 
$v\in \mathbb {T}^{n}$ the c-vector c 
$_{i;v}$ is non-zero and has either all entries non-negative or all entries non-positive.
Theorem 4.4 (Tropical duality [NZ12]) For any skew-symmetrizable initial exchange matrix 
$B$ and any 
$v\in \mathbb {T}^{n}$, we have
\begin{equation} (G^{B}_v)^{T}=(C^{-B^{T}}_v)^{-1}. \end{equation}Remark 4.5 Nakanishi and Zelevinsky proved Theorem 4.4 provided sign coherence of c-vectors holds. Special cases of Theorem 4.3 were known before the most general case was tackled in [Reference Gross, Hacking, Keel and KontsevichGHKK18].
Corollary 4.6 Let 
$v\in \mathbb {T}^{n}$. The g-vectors g 
$^{B}_{1;v},\dots,\,$g 
$^{B}_{n;v}$ span a rational strongly convex polyhedral cone 
$\mathcal {G}^{B}_v$ of dimension 
$n$ in 
$\mathbb {R} ^{n}$. The dual cone 
$\left ({\mathcal {G}^{B}_v}\right )^{\vee }=\mathcal {C}^{-B^{T}}_v$ is the rational polyhedral cone spanned by the c-vectors c 
$^{-B^{T}}_{1;v},\ldots,\,$c 
$^{-B^{T}}_{n;v}$.
Theorem 4.7 [GHKK18, Theorem 2.13] For any initial data the cones 
$\mathcal {G}_{v}^{B}$ are the maximal cones of a possibly infinite simplicial fan.
This was originally conjectured by Fock and Goncharov in [Reference Fock and GoncharovFG16, Conjecture 1.3], and lead to the notion of the special completion of an 
$\mathcal {X}$-variety as we will see below. In their proof of Theorem 4.7, Gross, Hacking, Keel and Kontsevich build scattering diagrams for cluster varieties (see [Reference Gross, Hacking, Keel and KontsevichGHKK18, § 1], [Reference Gross and SiebertGS11, Reference Kontsevich and SoibelmanKS14] where the authors use the term wall crossing structures). They show that a subset of the scattering diagram (called the cluster complex) has a generalized fan structure, with chambers full-dimensional simplicial cones when there are no frozen directions. They then identify these chambers with the cones 
$\mathcal {G}_{v}^{B}$. When there are frozen directions, the chambers in the scattering diagram are no longer strongly convex.Footnote 6 This lack of strong convexity corresponds to invertibility of frozen 
$\mathcal {A}$-variables. Allowing these frozen variables to vanish partially compactifies 
$\mathcal {A}$, and correspondingly cuts a convex subset 
$\varXi$ out of the scattering diagram.Footnote 7 This subset 
$\varXi$ inherits a fan structure from the scattering diagram, and the maximal cones of this fan are precisely the cones 
$\mathcal {G}_{v}^{B}$. More precisely, we have the following definition.
Definition 4.8 Let 
$\Delta ^{+}$ be the (Fock–Goncharov) cluster complex associated to the initial data 
$\left ({\varGamma ,v_0}\right )$ without frozen directions (see [Reference Gross, Hacking, Keel and KontsevichGHKK18, Definition 2.9]). Let 
$F\subset I$ be a subset of the index set. We denote by 
$\Delta ^{+}_F$ the subfan of 
$\Delta ^{+}$ consisting of cones that can be linked to the initial cone by iterated mutations at vertices in 
$I\setminus F$. We call 
$\Delta ^{+}_F$ the 
$\mathbf {g}$-fan associated to the initial data 
$\left ({\varGamma ',v_0}\right )$ obtained from 
$\left ({\varGamma ,v_0}\right )$ by freezing 
$F \subset I$.
See Figure 3 for an example in type 
$A_3$.
Remark 4.9 We do not lose any generality in the above definition by starting in the case without frozen directions, since we can reduce to this case by simply unfreezing all directions.
Remark 4.10 Until this point we have been working with labeled clusters and labeled 
$Y$-seeds. Notice that the cones 
$\mathcal {G}^{B}_v$ and 
$\mathcal {G}^{B}_{v'}$ are equal whenever the unlabeled cluster associated to 
$v$ is equal to the unlabeled cluster associated to 
$v'$ (see Remark 2.26). Algebraically this corresponds to the periodicity of the cluster pattern associated to 
$B$ and geometrically to the redundancies in the atlas of 
$\mathcal {A}$. By [Reference NakanishiNak19, Theroem 5.9] the periodicity of the cluster pattern associated to 
$B$ is the same as the periodicity of the 
$Y$-pattern associated to 
$B$. Further, by Theorem 2.34 and [Reference Cao and LiCL20, Proposition 6.1] we know that any cluster or 
$Y$-pattern with coefficients with initial matrix 
$B$ has the same periodicity as its coefficient-free counterpart. Therefore, to avoid redundancies, we can index the tori in the atlas of a cluster variety (of either type 
$\mathcal {A}$ or 
$\mathcal {X}$, with or without coefficients) by the maximal cones of the corresponding 
$\mathbf {g}$-fan rather than vertices of 
$\mathbb {T}^{n}$, e.g. we can replace ‘
$T_{N^{\circ },s}$ for 
$s\in \overset {\longrightarrow }{\mathbb {T}^{n}}$’ by ‘
$T_{N^{\circ },\mathcal {G}}$ for 
$\mathcal {G}\in \Delta ^{+}_F(\mathrm {max})$’, where 
$\Delta ^{+}_F(\mathrm {max})$ denotes the set of maximal cones of 
$\Delta ^{+}_F$.
Figure 3. Comparison of 
$\mathbf {g}$-fan 
$\Delta ^{+}_F$ and cluster complex 
${{\Delta ^{+}} }$ for 
$A_3$ quiver with one frozen direction. Here 
$Q = {1}\leftarrow 2 \leftarrow 3$ and 
$F= \left \{{1}\right \}$. A schematic of the 
$\mathbf {g}$-fan appears on the left and corresponds to the case in which 
$A_1$ is non-invertible. The cluster complex is on the right, corresponding to an invertible 
$A_1$ variable.
We are now prepared to describe the special completion of an 
$\mathcal {X}$-variety. By the above discussion, we have a fan whose maximal cones are 
$\mathcal {G} \in \Delta ^{+}_F(\textrm {max})$, and along with it we have the dual cones 
$\mathcal {C}$. This brings to mind the construction of toric varieties via fans, a construction which we review in § 5.1.
Let 
$S_{\mathcal {G}}$ be the monoid of 
$M^{\circ }$-points of 
$\mathcal {C}$. The monoid algebra 
$\mathbb {C} \left [{S_{\mathcal {G}}}\right ]$ is a polynomial algebra in 
$n$ algebraically independent variables. We write
\[ \mathbb{A} ^{n}_{M^{\circ},\mathcal{G}}:= \operatorname{Spec}\left({\mathbb{C} \left[{ S_{\mathcal{G}}}\right]}\right) \quad \text{and}\quad T_{M^{\circ},\mathcal{G}}:= \operatorname{Spec}\left({\mathbb{C} \left[{ S_{\mathcal{G}}^{\mathrm{gp} }}\right]}\right), \]
where 
$S_{\mathcal {G}}^{\mathrm {gp} }$ is the group completion of the monoid 
$S_{\mathcal {G}}$.
Definition 4.11 The special completion of the 
$\mathcal {X}$-cluster variety 
$\mathcal {X} _{\varGamma ^{\vee }} = \mathcal {A} ^{\vee }$ is
\[ \widehat{\mathcal{X} } _{\varGamma^{\vee}} := \bigcup_{\mathcal{G} \in \Delta^{+}_F(\mathrm{max})}\mathbb{A} ^{n}_{M^{\circ},\mathcal{G}}, \]
the scheme with the patches 
$\mathbb {A} ^{n}_{M^{\circ },\mathcal {G}}$ glued by the usual 
$\mathcal {X}$-mutation formula (3.4).
Remark 4.12 Observe that this definition treats cluster varieties with and without frozen directions together. Additionally, by starting with the Langlands dual data 
$\varGamma ^{\vee }$, we obtain the special completion 
$\widehat {\mathcal {X} } _{\varGamma }$ of 
$\mathcal {X} _{\varGamma }$.
We elaborate on this definition. We take advantage of Remark 4.12 to treat the special completion 
$\widehat {\mathcal {X} } _{\varGamma }$, which allows us to drop the superscript 
${}^{\circ }$. Explicitly, the birational map 
$\mu _k: \mathbb {A} ^{n}_{M,\mathcal {G}} \dashrightarrow \mathbb {A} ^{n}_{M,\mathcal {G}'}$ restricts to an isomorphism
\[ \mathbb{A} ^{n}_{M,\mathcal{G}} \setminus \left({ \left\{{X_k=0}\right\} \cup \left\{{X_k=-1}\right\} }\right) \stackrel{\cong}{\longrightarrow} \mathbb{A} ^{n}_{M,\mathcal{G}'} \setminus \left({ \left\{{X'_k=0}\right\} \cup \left\{{X'_k=-1}\right\} }\right), \]
and we glue 
$\mathbb {A} ^{n}_{M,\mathcal {G}}$ to 
$\mathbb {A} ^{n}_{M,\mathcal {G}'}$ along these subsets. To see that this restriction is indeed an isomorphism, we show that 
$\mu _k^{*}$ identifies the rings
\[ A_{\mathcal{G}}:= \mathbb{C} \left[{X_k^{\pm 1},X_{i\neq k}, \left({X_k+1}\right)^{-1}}\right] \quad \text{and}\quad A_{\mathcal{G}'}:=\mathbb{C} \left[{{X'_k}^{\pm 1},X'_{i\neq k}, \left({X'_k+1}\right)^{-1}}\right]. \]
Note that it does not matter whether we adjoin 
$(X_k +1)^{-1}$ or 
$(X_k^{-1} +1)^{-1}$ as a generator of 
$A_{\mathcal {G}}$ since 
$(X_k^{-1} +1)^{-1} = X_k (X_k+1)^{-1}$ and 
$X_k^{\pm 1}$ is in 
$A_{\mathcal {G}}$.
Applying 
$\mu _k^{*}$ to generators of 
$A_{\mathcal {G}'}$ gives the polynomial ring
\[ \mathbb{C} \left[{X_k^{\pm 1},X_{i\neq k}\left({1+X_k^{- \operatorname*{sgn} \epsilon_{ik}}}\right)^{-\epsilon_{ik}},\left({X_k^{-1} +1}\right)^{-1}}\right], \]
and since this ring contains the elements 
$(1+X_k)^{\pm 1}$ and 
$(1+X_k^{-1})^{\pm 1}$, we can always cancel the factor 
$( 1+X_k^{- \operatorname *{sgn} \epsilon _{ik}} )^{-\epsilon _{ik}}$, leaving 
$X_{i\neq k}$. So
\[ \mathbb{C} \left[{X_k^{\pm 1},X_{i\neq k}\left({1+X_k^{- \operatorname*{sgn} \epsilon_{ik}}}\right)^{-\epsilon_{ik}},\left({X_k^{-1} +1}\right)^{-1}}\right] = A_{\mathcal{G}}, \]
and 
$\mu _k$ restricts to an isomorphism of the open subschemes described above.
Remark 4.13 It is well known that 
$\mathcal {X}$-cluster varieties are generally not separated (see e.g. [Reference Gross, Hacking and KeelGHK15, Remark 4.2]). However, with only one exception, special completions of 
$\mathcal {X}$-cluster varieties are never separated. The one exception is type 
$A_1$, where we simply obtain 
$\mathbb {P} ^{1}$. In all other cases, let 
$p$ be the point in 
$\mathbb {A} _{M,{\mathcal {G}}}^{n}$ given by 
$X_k = -1$, 
$X_{i\neq k} =0$, and 
$q$ the point in 
$\mathbb {A} _{M,{\mathcal {G}'}}^{n}$ given by 
$X_k' = -1$, 
$X_{i\neq k}' =0$. Note that 
$p$ and 
$q$ are not identified since they lie in the complement of the gluing locus. But, any (complex analytic) neighborhood of one must contain the other.
5. Toric degenerations of the special completion of $\mathcal {X}$
In this section we build toric degenerations of specially completed 
$\mathcal {X}$-varieties (with and without frozen directions). We then discuss properties of both the fibers and the total space. The toric degenerations we construct here are flat families over 
$\mathbb {A} ^{n}= \operatorname {Spec}\left ({\mathbb {C} \left [{t_1,\ldots ,t_n}\right ]}\right )$ whose central fibers are toric varieties. The idea is to take the 
$\mathbb {A} ^{n}$-patches in the atlas for 
$\widehat {\mathcal {X} }$ and alter the way they glue together. So each fiber of the family will have the same collection of 
$\mathbb {A} ^{n}$-patches, but we introduce coefficients to the mutation formula (3.4), i.e. to the transition functions. This modified mutation formula is the specialization of (2.8) to the case of principal coefficients.
Remark 5.1 For expository purposes, we restrict to the skew-symmetric case. All of our results hold in the skew-symmetrizable case too.
Before getting into this discussion, we briefly recall the construction of toric varieties via fans. The discussion here closely follows portions of [Reference FultonFul93, Reference Cox, Little and SchenckCLS11, Reference OdaOda88].
5.1 Fans for toric varieties
A fan is a combinatorial object that gives an explicit recipe for building a toric variety as a scheme. It is in essence a pictorial representation of an atlas, where the building blocks (affine schemes) are drawn as cones and gluing is given by intersection of cones.
We start with a lattice 
$N\cong \mathbb {Z} ^{n}$, the cocharacter lattice of the defining torus 
$T$. The fan will live in 
$N_\mathbb {R} := N\otimes \mathbb {R}$. We call the fan 
$\varSigma$, and the associated toric variety 
${\operatorname {TV}({\varSigma })}$. By definition, 
$\varSigma$ is a collection of strongly convex rational polyhedral cones in 
$N_\mathbb {R}$ satisfying certain properties, which we detail after explaining the italicized terms. A rational polyhedral cone in 
$N_\mathbb {R}$ is the 
$\mathbb {R} _{\geq 0}$-span of a finite number of integral vectors. It is strongly convex if does not contain a non-zero linear subspace. Observe that every face of a polyhedral cone is again a polyhedral cone, no matter the codimension of the face. Now for 
$\varSigma$ to be a fan, it must satisfy the following:
– if
$\sigma \in \varSigma$, and $\tau$ is a face of $\sigma$, then $\tau \in \varSigma$ as well;– if
$\sigma , \sigma ' \in \varSigma$, then their intersection $\sigma \cap \sigma '$ is a face $\tau$ of each.
Remark 5.2 In much of the literature, e.g. [Reference FultonFul93, Reference Cox, Little and SchenckCLS11], fans are assumed to consist of a finite collection of cones. The resulting toric varieties are then schemes of finite type over 
$\mathbb {C}$. Most cluster varieties are only locally of finite type, so unsurprisingly, we do not require our fans to have finitely many cones. Toric varieties with infinite fans are treated in [Reference OdaOda88]. Both, toric varieties and cluster varieties are schemes of finite type precisely when the fan (
$\mathbf {g}$-fan in the cluster case) is finite. Observe that a cluster variety is of cluster finite type (meaning there are only finitely many seeds) precisely when it is a finite type scheme over 
$\mathbb {C}$.
Given a fan 
$\varSigma$ in 
$N_{\mathbb {R} }$, every cone 
$\sigma \in \varSigma$ defines an affine scheme in the atlas for 
${\operatorname {TV}({\varSigma })}$ as follows. Let 
$M= \operatorname {Hom}\left ({N,\mathbb {Z} }\right )$ and consider the dual cone 
$\sigma ^{\vee }\subset M_{\mathbb {R} }$. Its integral points live in 
$M$, so are characters of 
$T$. These integral points 
$\sigma ^{\vee } \cap M$ form a submonoid of 
$M$, denoted 
$S_\sigma$. The affine patches in the atlas for 
${\operatorname {TV}({\varSigma })}$ are spectra of the monoid rings 
$\mathbb {C} \left [{S_\sigma }\right ]$. We write 
$U_\sigma := \operatorname {Spec}\left ({\mathbb {C} \left [{\sigma ^{\vee } \cap M}\right ]}\right )$.
Every face of 
$\sigma$ is the intersection of 
$\sigma$ with some hyperplane 
$m^{\perp }$, where 
$m\in \sigma ^{\vee } \cap M$. If 
$\tau$ is a face of 
$\sigma$, then 
$\sigma ^{\vee } \subset \tau ^{\vee }$ and 
$S_\tau = S_\sigma + \mathbb {Z} _{\geq 0}\left ({-m}\right )$ (see Figure 4). Then 
$\mathbb {C} \left [{S_\tau }\right ]$ is the localization of 
$\mathbb {C} \left [{S_\sigma }\right ]$ by the character 
$z^{m}$. This gives an embedding 
$U_\tau \hookrightarrow U_\sigma$.
Figure 4. Two adjacent cones 
$\sigma ,\sigma '\subset N_{\mathbb {R}}$ with 
$\sigma \cap \sigma '=\tau$ on the left and their dual cones 
$\sigma ^{\vee },\sigma '^{\vee }\subset \tau ^{\vee }\subset M_{\mathbb {R}}$ on the right.
If 
$\tau$ is a common face of 
$\sigma$ and 
$\sigma '$, then the inclusions of 
$U_\tau \hookrightarrow U_\sigma$ and 
$U_\tau \hookrightarrow U_{\sigma '}$ glue the affine patches 
$U_\sigma$ and 
$U_{\sigma '}$ along 
$U_\tau$, just as the inclusion of 
$\tau$ into 
$\sigma$ and 
$\sigma '$ glues the cones 
$\sigma$ and 
$\sigma '$ together. More precisely, if 
$\tau = \sigma \cap \sigma '$ then 
$\sigma \cap m^{\perp } = \tau = \sigma ' \cap m^{\perp }$ for some 
$m \in \sigma ^{\vee } \cap -\sigma '^{\vee } \cap M$, and we have
\[ U_\sigma \hookleftarrow \left({U_\sigma}\right)_{z^{m}} = U_\tau = \left({U_{\sigma'}}\right)_{z^{-m}} \hookrightarrow U_{\sigma'}. \]5.2 Toric degenerations of $\widehat {\mathcal {X} }$
Consider fixed data 
$\varGamma _{\text {prin}}$ as in Definition 3.34 and fix an initial 
$\mathbf {g}$-cone 
$\mathcal {G}_0$. Let 
$F\subset I$ be the set of frozen directions. In view of Remarks 3.23 and 4.10 set 
$t_i := p_i = p_{i;\mathcal {G}_0}$ and 
$X_i= X_{i;\mathcal {G}_0} :=y_i$ for all 
$1 \leq i \leq n$. Then the mutation formula (3.7) specializes for 
$\mathcal {X}$-variables with principal coefficients to
\begin{equation} \mu_k^{*}\left({\widetilde{X} _{i;\mathcal{G}'}}\right) = \begin{cases} \widetilde{X} _{i;\mathcal{G}}^{-1} & \text{if } i=k,\\ \widetilde{X} _{i;\mathcal{G}}\left({\mathbf{t}^{[\operatorname*{sgn}(\epsilon_{ik})\mathbf{c}_{k;\mathcal{G}}]_+} + \mathbf{t}^{[-\operatorname*{sgn}(\epsilon_{ik})\mathbf{c}_{k;\mathcal{G}}]_+}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}(\epsilon_{ik})}}\right)^{-\epsilon_{ik}} & \text{if } i\not =k. \end{cases}\end{equation}
We can use sign coherence of 
$\mathbf {c}$-vectors (Theorem 4.3) to rewrite the 
$i\neq k$ case. If the sign of 
$\mathbf {c}_{k;\mathcal {G}}$ coincides with 
$\operatorname *{sgn}(\epsilon _{ik})$, then for 
$i\not =k$ (5.1) simplifies to
\begin{equation} \mu_k^{*}\left({\widetilde{X} _{i;\mathcal{G}'}}\right)=\widetilde{X} _{i;\mathcal{G}}\left({\mathbf{t}^{|\mathbf{c}_{k;\mathcal{G}}|}+\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}(\epsilon_{ik})}}\right)^{-\epsilon_{ik}}. \end{equation}
If 
$\mathbf {c}_k$ and 
$\epsilon _{ik}$ have opposite signs we instead obtain
\begin{equation} \mu_k^{*}\left({\widetilde{X} _{i;\mathcal{G}'}}\right)=\widetilde{X} _{i;\mathcal{G}}\left({1+\mathbf{t}^{|\mathbf{c}_{k;\mathcal{G}}|}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}(\epsilon_{ik})}}\right)^{-\epsilon_{ik}}. \end{equation}
Here 
$|\mathbf {c}_{k;\mathcal {G}}|$ denotes the positive 
$\mathbf {c}$-vector, i.e. 
$|\mathbf {c}_{k;\mathcal {G}}|=\left ({|c_{k1;\mathcal {G}}|,\ldots , |c_{kn;\mathcal {G}}|}\right )\in \mathbb {Z} _{\ge 0}^{n}$. An example in type 
$A_2$ is given in Table 2.
Table 2. Example in type 
$A_2$. Our convention agrees with [Reference Fomin and ZelevinskyFZ07, Tables 1–4], note only that we are considering geometric notation and hence the matrices 
$\boldsymbol {\varepsilon }_s=B_s^{T}$.
In order to talk about degrees of 
$\mathcal {X}$-variables with principal coefficients we consider the usual 
$\mathbb {Z} ^{n}_{\ge 0}$-grading on the polynomial ring in 
$n$ variables 
$X_{1},\ldots ,X_{n}$. We extend this notion to a 
$\mathbb {Z} ^{n}$-grading on the ring of rational functions 
$\mathbb {C} (X_{1},\ldots ,X_{n})$. For 
$h={f}/{g}$ with 
$f$ and 
$g$ non-zero homogeneous polynomials let 
$\deg (h):=\deg (f)-\deg (g)$. We call this the standard grading. In the case of 
$\mathcal {A}_{\mathrm {prin}}$ by Definition 2.23, Remark 3.17 and Notation 3.38 we see that 
$-\deg (t_i)=b_i=\deg (\widetilde {p^{*}\left ({X_{i}}\right )})$. Motivated by the desire to construct a family fiber-wise dual to 
$\mathcal {A}_{\mathrm {prin}}$, we therefore set
\[ \deg\left({t_i}\right) := -\deg(\widetilde{X} _{i}). \]
Note that for 
$R=\mathbb {C} [t_1,\ldots ,t_n]$ this gives us the notion of the standard 
$\mathbb {Z} ^{n}$-grading also on 
$R(\widetilde {X} _{1},\ldots ,\widetilde {X} _{n})$.
Proposition 5.3 The pull-back to 
$s_0$ of an 
$\mathcal {X}$-variable with principal coefficients
\[ \mu_{s_0}^{*}\left({\widetilde{X} _{i;\mathcal{G}}}\right)\in R(\widetilde{X} _{1},\ldots,\widetilde{X} _{n}) \]
is homogeneous with respect to the standard 
$\mathbb {Z} ^{n}$-grading. Its degree is the 
$\mathbf {c}$-vector of 
$X_{i;\mathcal {G}}$ with respect to 
$s_0$:
\[ \deg\left({\mu_{s_0}^{*}({\widetilde{X} _{i;\mathcal{G}}})}\right)= \mathbf{c}_{i;\mathcal{G}}. \]Proof. This follows from Lemma 2.30 by specializing to principal coefficients. We have
\[ p_{i;\mathcal{G}}=\prod_{j=1}^{n} p_j^{c_{ji;\mathcal{G}}} = \mathbf{t}^{\mathbf{c}_{i;\mathcal{G}}}. \]
Consider the expression 
$Y_{i;\mathcal {G}}\left ({p_1 y_1,\ldots ,p_n y_n}\right )$ in the numerator of (2.11), with 
$y_i =X_i$ and 
$p_i=t_i$. Since by definition we have 
$\deg (t_i X_{i})=0$ for all 
$i$, we deduce 
${\deg (Y_{i;\mathcal {G}}\left ({t_1X_1,\ldots ,t_nX_n}\right ))=0}$. Then as by (2.11)
\[ \mu_{s_0}^{*}\left({\widetilde{X} _{i;\mathcal{G}}}\right)=\frac{Y_{i;\mathcal{G}}(t_1 X_1,\ldots,t_n X_n)}{\mathbf{t}^{\mathbf{c}_{i;\mathcal{G}}}}, \]
it follows that 
$\deg (\mu _{s_0}^{*}(\widetilde {X} _{i;\mathcal {G}}))= -\deg \left ({\mathbf {t}^{\mathbf {c}_{i;\mathcal {G}}}}\right ) = \mathbf {c}_{i;\mathcal {G}}$.
On account of Proposition 5.3, it is natural to ask whether there is any special relationship between 
$\mu _{s_0}^{*}(\widetilde {X} _{i;\mathcal {G}})$ and 
$\widetilde{\mathbf{X}}^{\mathbf {c} _{i;\mathcal {G}}} := {\widetilde {X} _{1}}^{c_{i_1;\mathcal {G}}}\cdots {\widetilde {X} _{n}}^{c_{i_n;\mathcal {G}}}$. The answer is yes, and the following proposition makes this relationship precise.
Proposition 5.4 The pull-back 
$\mu _{s_0}^{*}(\widetilde {X} _{i;\mathcal {G}})$ of an 
$\mathcal {X}$-variable with principal coefficients satisfies
\begin{equation} \lim_{\mathbf{t}\to 0}\mu_{s_0}^{*}\left({\widetilde{X} _{i;\mathcal{G}}}\right) =\widetilde{\mathbf{X}}^{\mathbf{c} _{i;\mathcal{G}}}. \end{equation}
Moreover, 
$\mu _{s_0}^{*}(\widetilde {X} _{i;\mathcal {G}})$ is the unique homogenization of the coefficient-free expression 
$\mu _{s_0}^{*}(\widetilde {X} _{i;\mathcal {G}})|_{\mathbf {t} = \mathbf {1} }$ of degree 
$\mathbf {c} _{i;\mathcal {G}}$ satisfying (5.4).
Proof. For 
$\mathcal {G}=\mathcal {G}_0$, (5.4) is clear. Suppose now that it holds for some arbitrary 
$\mathbf {g}$-cone 
$\mathcal {G}$. We show that it must hold for all 
$\mathbf {g}$-cones 
$\mathcal {G}'$ sharing a facet with 
$\mathcal {G}$ as well. Take 
$\mathcal {G}'$ to be related to 
$\mathcal {G}$ by mutation in direction 
$k$. Using (5.1), we can express 
$\widetilde {X} _{i;\mathcal {G}'}$ in terms of 
$\widetilde {X} _{1;\mathcal {G}},\ldots , \widetilde {X} _{n;\mathcal {G}}$, and then take the 
$\mathbf {t}\to 0$ limit. First note that (2.5) gives us the following mutation formula for 
$\mathbf {c}$-vectors:
\begin{equation} \mathbf{c} _i'= \begin{cases} -\mathbf{c} _i & \text{if } i=k\\ \mathbf{c} _i + \operatorname*{sgn}\left({\epsilon_{ik}}\right) \left[{\epsilon_{ik} \mathbf{c} _k}\right]_+ & \text{if } i\neq k. \end{cases} \end{equation}
For 
$i=k$ we have
\[ \lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({\widetilde{X} _{k;\mathcal{G}'}}\right) =\lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({\mu_k^{*}({\widetilde{X} _{k;\mathcal{G}'}})}\right) =\lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({\widetilde{X} _{k;\mathcal{G}}^{-1}}\right) =\widetilde{\mathbf{X}}^{-\mathbf{c} _{k;\mathcal{G}}} =\widetilde{\mathbf{X}}^{\mathbf{c} _{k;\mathcal{G}'}}. \]
Now take 
$i\neq k$. First suppose 
$\epsilon _{ik}$ and 
$\mathbf {c} _{k;\mathcal {G}}$ have the same sign. Then
\begin{align*} \lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({\widetilde{X} _{i;\mathcal{G}'}}\right) &=\lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({\mu_k^{*}({\widetilde{X} _{i;\mathcal{G}'}})}\right)\\ &=\lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({ \widetilde{X} _{i;\mathcal{G}}({\mathbf{t}^{\left|{\mathbf{c} _{k;\mathcal{G}}}\right|}+\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}(\epsilon_{ik})}})^{-\epsilon_{ik}}}\right) = \widetilde{\mathbf{X}}^{\mathbf{c} _{i;\mathcal{G}} + \left|{\epsilon_{ik}}\right| \mathbf{c} _{k;\mathcal{G}} } = \widetilde{\mathbf{X}}^{\mathbf{c} _{i;\mathcal{G}'}}. \end{align*}
If 
$\epsilon _{ik}$ and 
$\mathbf {c} _{k;\mathcal {G}}$ have opposite signs, we have
\begin{align*} \lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({\widetilde{X} _{i;\mathcal{G}'}}\right) &=\lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({\mu_k^{*}({\widetilde{X} _{i;\mathcal{G}'}})}\right)\\ &=\lim_{\mathbf{t}\to 0} \mu_{s_0}^{*}\left({\widetilde{X} _{i;\mathcal{G}} ({1+\mathbf{t}^{\left|{\mathbf{c} _{k;\mathcal{G}}}\right|}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}(\epsilon_{ik})}})^{-\epsilon_{ik}}}\right) = \widetilde{\mathbf{X}}^{\mathbf{c} _{i;\mathcal{G}} } = \widetilde{\mathbf{X}}^{\mathbf{c} _{i;\mathcal{G}'}}. \end{align*}This establishes (5.4).
We move on to uniqueness. The coefficient-free expression 
$\mu _{s_0}^{*}(\widetilde {X} _{i;\mathcal {G}})|_{\mathbf {t} = \mathbf {1} }$ is a rational function in 
$\mathbb {C} (\widetilde {X} _1, \ldots ,\widetilde {X} _n)$. Write
\[
\left.\mu_{s_0}^{*}\left({\widetilde{X} _{i;\mathcal{G}}}\right)\right|_{\mathbf{t} = \mathbf{1} } = \frac{f(\widetilde{X} _1, \ldots,\widetilde{X} _n)}{g(\widetilde{X} _1, \ldots,\widetilde{X} _n)}=:\frac{f(\widetilde{\mathbf{X}})}{g(\widetilde{\mathbf{X}})}.
\]
Assume there are two homogenizations of 
$\mu _{s_0}^{*}(\widetilde {X} _{i;\mathcal {G}})|_{\mathbf {t} = \mathbf {1} }$ such that (5.4) holds. The key observation is that if (5.4) holds for some homogenization, then for this homogenization there must be exactly one monomial in each 
$f$ and 
$g$ that does not pick up a (non-trivial) 
$\mathbf {t}^{\mathbf {n}}$ coefficient.Footnote 8 The result follows immediately from here.
For the observation, first suppose 
$({f(\widetilde{\mathbf{X}},\mathbf {t})}/{g(\widetilde{\mathbf{X}},\mathbf {t})})\in R(\widetilde {X} _1,\ldots ,\widetilde {X} _n)$ is some arbitrary rational function in 
$\widetilde {X} _i$ and 
$t_i$. Given a path 
$\gamma : \left [{0,1}\right ] \to \mathbb {C} ^{n}$ with 
$\gamma (1) = 0$, the limit
\[ \lim_{\mathbf{t} \stackrel{\gamma}{\to} 0} {{\frac{f(\widetilde{\mathbf{X}},\mathbf{t})}{g(\widetilde{\mathbf{X}},\mathbf{t})}}} \]
picks out the summands of 
$f$ and 
$g$ that vanish most slowly along 
$\gamma$. The result, if it exists, is a new rational function whose numerator is a partial sum coming from 
$f$ and denominator is a partial sum coming from 
$g$. If this limit is a non-zero Laurent monomial, then the partial sums contain exactly one term. We are interested in the case where this limit is the monomial 
${\widetilde{\mathbf{X}}}^{\mathbf {c}_{i;\mathcal {G}}}$ for every such 
$\gamma$. Take 
$\gamma$ and 
$\gamma '$ with
\[ \lim_{\mathbf{t} \stackrel{\gamma, \gamma'}{\to} 0} {{\frac{f(\widetilde{\mathbf{X}},\mathbf{t})}{g(\widetilde{\mathbf{X}},\mathbf{t})}}} = \widetilde{\mathbf{X}}^{\mathbf{c}_{i;\mathcal{G}}}. \]
Associated to 
$\gamma$ we have the summands 
${\widetilde{\mathbf{X}}}^{{\mathbf {n}_f}}$ of 
$f$ and 
${\widetilde{\mathbf{X}}}^{{\mathbf {n}_g}}$ of 
$g$, with 
${\mathbf {n}_f}$, 
${\mathbf {n}_g}$ 
$\in \mathbb {Z} _{\geq 0}^{n}$ and
\[ {{\frac{{\widetilde{\mathbf{X}}}^{{\mathbf{n}_f}}}{{\widetilde{\mathbf{X}}}^{{\mathbf{n}_g}}}}} = {\widetilde{\mathbf{X}}}^{\mathbf{c}_{i;\mathcal{G}}}. \]
We similarly associate 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f'}$ and 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_g'}$ to 
$\gamma '$. There are two cases to consider: either 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f}$ divides 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f'}$, respectively vice versa, or neither divides the other. Suppose 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f}$ divides 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f'}$. Then to homogenize 
$f$, we have to multiply 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f'}$ by the coefficient 
$\mathbf {t}^{\mathbf {n}_f'-\mathbf {n}_f}$. In this case, assuming 
${\mathbf {n}_f'-\mathbf {n}_f \neq 0}$, there cannot exist a path along which the summand 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f}$ vanishes more quickly than the summand 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f'}$. So we must have 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f}={\widetilde{\mathbf{X}}}^{\mathbf {n}_f'}$, and hence 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_g}={\widetilde{\mathbf{X}}}^{\mathbf {n}_g'}$ as well.
On the other hand, suppose neither 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f}$ nor 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f'}$ divides the other. Let 
$\mathbf {n}_f = \left ({n_{f;1}, \ldots , n_{f;n}}\right )$ and 
$\mathbf {n}_f' = (n_{f;1}', \ldots , n_{f;n}')$. Set 
$\mathbf {d} = \sum _i [n_{f;i} - n_{f;i}']_+ e_i$ and 
$\mathbf {d}' = \sum _i [n_{f;i}' - n_{f;i}]_+ e_i$. Both are non-zero. In homogenizing 
$f$, 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f}$ must obtain a coefficient of (at least) 
$\mathbf {t}^{\mathbf {d}}$ and 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_f'}$ a coefficient of 
$\mathbf {t}^{\mathbf {d}'}$. Any additional factors of 
$\mathbf {t}$ the two summands obtain must match. Therefore, 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_g}$ and 
${\widetilde{\mathbf{X}}}^{\mathbf {n}_g'}$ must obtain these coefficients as well. Along any path 
$\gamma ''$ contained in the hyperplane 
$\mathbf {t}^{\mathbf {d}} = \mathbf {t}^{\mathbf {d}'}$, we will have
\[ \lim_{\mathbf{t} \stackrel{\gamma''}{\to} 0} {{\frac{\mathbf{t}^{\mathbf{d}} {\widetilde{\mathbf{X}}}^{\mathbf{n}_f} + \mathbf{t}^{\mathbf{d}'} {\widetilde{\mathbf{X}}}^{\mathbf{n}_f'}}{\mathbf{t}^{\mathbf{d}} {\widetilde{\mathbf{X}}}^{\mathbf{n}_g} + \mathbf{t}^{\mathbf{d}'} {\widetilde{\mathbf{X}}}^{\mathbf{n}_g'}} = \frac{ {\widetilde{\mathbf{X}}}^{\mathbf{n}_f} + {\widetilde{\mathbf{X}}}^{\mathbf{n}_f'}}{{\widetilde{\mathbf{X}}}^{\mathbf{n}_g} + {\widetilde{\mathbf{X}}}^{\mathbf{n}_g'}}.}} \]
Perhaps after considering additional summands (in the case that some other summand vanishes more quickly along 
$\gamma ''$), we find that the limit along some path is not a Laurent monomial. This contradicts our assumption and proves the claim.
Remark 5.5 The above proposition tells us we have a canonical homogenization of cluster variables. Note that this in turn gives a homogenization of all cluster monomials.
We are now prepared to describe toric degenerations of 
$\widehat {\mathcal {X} }$.
Definition 5.6 We define 
$\widehat {\mathscr {X} }_{\mathcal {G}_0}$ to be the scheme over 
$R$ with affine patches
\[ U_\mathcal{G}:=\operatorname{Spec}\left({R \left[{\widetilde{X} _{1;\mathcal{G}},\ldots,\widetilde{X} _{n;\mathcal{G}}}\right]}\right) \]
and gluing given by (5.1). By analogy, we denote by 
$\mathscr {X}_{\mathcal {G}_0}$ the scheme obtained by instead gluing 
$U_\mathcal {G}^{\pm }:=\operatorname {Spec}( R [\widetilde {X} _{1;\mathcal {G}}{}^{\pm 1},\ldots ,\widetilde {X} _{n;\mathcal {G}}{}^{\pm 1}])$. Recall from Remark 4.10 that the schemes 
$\mathscr {X}_{\mathcal {G}_0}$ and 
$\mathscr {X} _{s_0}$ are isomorphic.
The open subschemes along which 
$U_\mathcal {G}$ and 
$U_{\mathcal {G}'}$ are glued have a very similar description to those discussed below Definition 4.11. To simplify notation, let 
$\mathbf {c}_k=\mathbf {c}_{k;\mathcal {G}}$ and 
$\mathbf {c}_{k}'=\mathbf {c}_{k;\mathcal {G}'}$ for two adjacent 
$\mathbf {g}$-cones 
$\mathcal {G}$ and 
$\mathcal {G}'$ sharing a facet contained in 
$\mathbf {c} _k^{\perp }$. On the level of rings we set
\[ A_\mathcal{G} = R\left[{\widetilde{X} _{k;\mathcal{G}}^{\pm 1}, \widetilde{X} _{i;\mathcal{G}}, \left({ \mathbf{t}^{[{\operatorname*{sgn}({\epsilon_{ik}}) \mathbf{c} _k}]_+} + \mathbf{t}^{[{\operatorname*{sgn}({\epsilon_{ik}}) \mathbf{c} _k}]_+ }\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}({\epsilon_{ik}})}}\right)^{-1} }\right]_{i\neq k}. \]
Note that 
$\operatorname *{sgn}(\epsilon _{ik}) \mathbf {c} _k = \operatorname *{sgn}(\epsilon '_{ik}) \mathbf {c} _k'$ and 
$\mu _k^{*}( \widetilde {X} _{k;\mathcal {G}'}^{ -\operatorname *{sgn} (\epsilon '_{ik}) } )= \widetilde {X} _{k;\mathcal {G}}^{ -\operatorname *{sgn} \left ({\epsilon _{ik}}\right ) } .$ Then applying 
$\mu _k^{*}$ to generators of 
$A_{\mathcal {G}'}$ yields
\begin{gather} \mu_k^{*}\left({ \widetilde{X} _{k;\mathcal{G}'}^{\mp 1} }\right)= \widetilde{X} _{k;\mathcal{G}}^{\pm 1}, \end{gather}
\begin{gather} \mu_k^{*}\left({\widetilde{X} _{i;\mathcal{G}'}}\right) = \widetilde{X} _{i;\mathcal{G}} \left({ \mathbf{t}^{\left[{\operatorname*{sgn}({\epsilon_{ik}}) \mathbf{c} _k}\right]_+} + \mathbf{t}^{\left[{-\operatorname*{sgn}({\epsilon_{ik}}) \mathbf{c} _k}\right]_+ }\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}({\epsilon_{ik}})}}\right)^{-\epsilon_{ik}}, \end{gather}
\begin{gather} \mu_k^{*}\left({ \mathbf{t}^{[\operatorname*{sgn}(\epsilon'_{ik}) \mathbf{c} _k']_+} + \mathbf{t}^{[-\operatorname*{sgn}(\epsilon'_{ik}) \mathbf{c} _k']_+ } \widetilde{X} _{k;\mathcal{G}'}^{-\operatorname*{sgn}(\epsilon'_{ik}) }}\right)^{-1} = \left({ \mathbf{t}^{\left[{\operatorname*{sgn}({\epsilon_{ik}}) \mathbf{c} _k}\right]_+} + \mathbf{t}^{\left[{-\operatorname*{sgn}({\epsilon_{ik}}) \mathbf{c} _k}\right]_+ } \widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}({\epsilon_{ik}})}}\right)^{-1}. \end{gather}
Only (5.7) needs further consideration. If 
$-\epsilon _{ik} > 0$, we can use (5.8) to recover 
$\widetilde {X} _{i;\mathcal {G}}$ from (5.7). Meanwhile, if 
$-\epsilon _{ik} < 0$, the term within parenthesis is in 
$R[X_{k;\mathcal {G}}^{\pm 1}]$, so we can use (5.6) to recover (5.7). On the other hand, the expressions on the right hand side of (5.6), (5.7) and (5.8) are all in 
$A_\mathcal {G}$, so 
$\mu _k^{*}$ defines an isomorphism of 
$A_\mathcal {G}$ and 
$A_{\mathcal {G}'}$. Geometrically, we are gluing the subschemes
\begin{align} & U_\mathcal{G} \setminus \left({ \left\{{\widetilde{X} _{k;\mathcal{G}} = 0 }\right\} \bigcup \left\{{ \mathbf{t}^{\left[{\operatorname*{sgn}({\epsilon_{ik}}) \mathbf{c} _k}\right]_+} + \mathbf{t}^{\left[{-\operatorname*{sgn}({\epsilon_{ik}}) \mathbf{c} _k}\right]_+}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}({\epsilon_{ik}})} = 0 }\right\}_{i\neq k}}\right), \end{align}
\begin{align} & U_{\mathcal{G}'} \setminus \left({ \left\{{\widetilde{X} _{k;\mathcal{G}'} =0 }\right\} \bigcup \left\{{ \mathbf{t}^{[\operatorname*{sgn}(\epsilon'_{ik}) \mathbf{c} '_k]_+} + \mathbf{t}^{[-\operatorname*{sgn}(\epsilon'_{ik}) \mathbf{c} '_k]_+}\widetilde{X} _{k;\mathcal{G}'}^{-\operatorname*{sgn}(\epsilon'_{ik}) } = 0 }\right\}_{i\neq k}}\right). \end{align}
To see that Definition 5.6 makes sense, we also need to verify that the cocycle condition holds. But this follows immediately from Theorem 2.34. Now observe that the fiber over 1 is precisely 
$\widehat {\mathcal {X} }$, and the restriction of 
$\widetilde {X} _{i;\mathcal {G}}$ to this fiber is 
$X_{i;\mathcal {G}}$.
Proposition 5.7 The family 
$\pi :\widehat {\mathscr {X} }_{\mathcal {G}_0} \to \operatorname {Spec}\left ({R}\right )$ is a flat family.
Proof. This follows from the definition of 
$\widehat {\mathscr {X} }_{\mathcal {G}_0}$. Flatness is a local property, so we are free to restrict to affine patches. The induced map of rings 
$R \to R[\widetilde {X} _{1;\mathcal {G}}, \ldots , \widetilde {X} _{n;\mathcal {G}}]$ is flat for every 
$\mathcal {G}$, so 
$\widehat {\mathscr {X} }_{\mathcal {G}_0} \to \operatorname {Spec}\left ({R}\right )$ is a flat morphism of schemes.
Theorem 5.8 The flat family 
$\widehat {\mathscr {X} }_{\mathcal {G}_0} \to \operatorname {Spec}\left ({R}\right )$ is a toric degeneration of 
$\widehat {\mathcal {X} }$ to 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$.
Proof. We have already noted that the fiber over 
$1$ is 
$\widehat {\mathcal {X} }$ and shown flatness. We only need to check that the central fiber 
$\widehat {\mathcal {X} } _0$ is indeed 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$. Clearly, we can identify the affine patches of 
$\widehat {\mathcal {X} } _0$ associated to maximal cones of 
${{\Delta ^{+}_F} }$ with those of 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$; in both cases we have a copy of 
$\mathbb {A} ^{n}$ for every maximal cone of 
${{\Delta ^{+}_F} }$. We just need to demonstrate that the gluing of these patches in 
$\widehat {\mathcal {X} } _0$ coincides with the gluing in 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$. This amounts to verifying the following two things:
(i) the overlap of neighboring affine patches in
$\widehat {\mathcal {X} } _0$ and ${\operatorname {TV}({{{\Delta ^{+}_F} }})}$ agree;(ii) the transition functions on these overlaps agree.
For 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$, 
$S_{\mathcal {G}}$ is the monoid of integral points in the dual cone 
$\mathcal {C}$. The non-identity generators of this monoid are precisely 
$\mathbf {c}_{1;\mathcal {G}},\ldots ,\mathbf {c}_{n;\mathcal {G}}$, with 
$\mathbf {c} _{k;\mathcal {G}}$ normal to the facet of 
$\mathcal {G}$ spanned by 
$\left \{{\mathbf {g} _{i;\mathcal {G}}}\right \}_{i\neq k}$. If 
$\mathcal {G}'$ shares this facet with 
$\mathcal {G}$, then in 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$ the subscheme of 
$\mathbb {A} ^{n}_{\mathcal {G}}$ overlapping 
$\mathbb {A} ^{n}_{\mathcal {G}'}$ is the localization 
$\left ({\mathbb {A} ^{n}_{\mathcal {G}}}\right )_{\widetilde {X} _{k;\mathcal {G}}} = \mathbb {A} ^{n}_\mathcal {G} \setminus \{\widetilde {X} _{k;\mathcal {G}} = 0 \}$.
To establish (i), we need to see that specializing 
$\mathbf {t}=0$ in (5.9) results in precisely the same subset of 
$\mathbb {A} ^{n}_\mathcal {G}$ being removed. The first piece removed in (5.9) is exactly 
$\{ \widetilde {X} _{k;\mathcal {G}} = 0 \}$, so we have to show that nothing else is removed when 
$\mathbf {t} = 0$. When 
$\epsilon _{ik}$ and 
$\mathbf {c} _k$ have the same sign,
\[ \mathbf{t}^{\left[{\operatorname*{sgn}\left({\epsilon_{ik}}\right)\mathbf{c}_k}\right]_+} + \mathbf{t}^{\left[{-\operatorname*{sgn}\left({\epsilon_{ik}}\right)\mathbf{c}_k}\right]_+}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}\left({\epsilon_{ik}}\right)} = \mathbf{t}^{\left|{\mathbf{c}_k}\right|}+\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}\left({\epsilon_{ik}}\right)}. \]
For 
$\mathbf {t}=0$ we eliminate the locus 
$\{\widetilde {X} _{k;\mathcal {G}}^{-\operatorname *{sgn}(\epsilon _{ik})} = 0 \}$. If the exponent is positive, we have already removed this. If it is negative, the locus is empty. On the other hand, when 
$\epsilon _{ik}$ and 
$\mathbf {c} _k$ have opposite signs,
\[ \mathbf{t}^{\left[{\operatorname*{sgn}\left({\epsilon_{ik}}\right)\mathbf{c}_k}\right]_+} + \mathbf{t}^{\left[{-\operatorname*{sgn}\left({\epsilon_{ik}}\right)\mathbf{c}_k}\right]_+}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}\left({\epsilon_{ik}}\right)} = 1+ \mathbf{t}^{\left|{\mathbf{c}_k}\right|}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}\left({\epsilon_{ik}}\right)}. \]
When 
$\mathbf {t} = 0$ in this case, we eliminate the locus 
$\left \{{1=0}\right \}$, which is obviously empty. This establishes (i).
For (ii), note that elements of 
$S_{\mathcal {G}}$ correspond to functions on 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$ that restrict to characters on the defining torus of 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$. Specifically, they are the characters whose exponent vectors are integral points of 
$\mathcal {C}$. On intersections, the relations between elements of 
$S_{\mathcal {G}}$ and 
$S_{\mathcal {G}'}$ are precisely the relations between their exponent vectors, living in 
$\mathcal {C}$ and 
$\mathcal {C}'$, respectively. The first part of Proposition 5.4 and Remark 5.5 show that the 
$\mathcal {X}$-monomials on the patches 
$\mathbb {A} ^{n}_\mathcal {G}$ and 
$\mathbb {A} ^{n}_{\mathcal {G}'}$ of 
$\widehat {\mathcal {X} } _0$ are related in the same way.
Remark 5.9 The key idea here is that by restricting to a domain of linearity in 
$\mathcal {X} ^{\mathrm{trop}} \left ({\mathbb {R} }\right )$ we find ourselves in the cozy world of toric varieties, where relations between generators are as straightforward as vector addition. When we cross a wall of the scattering diagram, we relate generators by mutation instead. As we approach the central fiber, mutation relations revert back to the toric version where we simply add exponent vectors. It is not necessary to insist that the patches we glue by mutation be copies of 
$\mathbb {A} ^{n}$. We can repeat the construction with different compactifications of the cluster tori. If we consider a refinement 
$\varSigma$ of the 
$\mathbf {g}$-fan, we can take our ‘patches’ to be the toric varieties associated to subfans whose support is a domain of linearity. This gives a different partial minimal model 
$\widehat {\mathcal {X} } _\varSigma$ of 
$\mathcal {X}$. Mutation gives the gluing of these patches as before, and the family is a toric degeneration of 
$\widehat {\mathcal {X} } _\varSigma$ to 
${\operatorname {TV}({\varSigma })}$. We will see examples of this in a sequel with M.-W. Cheung, with such compactifications and their toric degenerations arising as duals to compactified 
$\mathcal {A}$-varieties and the 
$\mathcal {A}_{\mathrm {prin}}$-family.
We can use the family 
$\widehat {\mathscr {X} }_{\mathcal {G}_0}$ to give a new notion of 
$\mathbf {c}$-vector analogously to the definition of 
$\mathbf {g}$-vectors given in [Reference Gross, Hacking, Keel and KontsevichGHKK18, Definition 5.6].
Definition 5.10 Let 
$f\in R(X_1,\ldots ,X_n)$ be a homogeneous rational function on 
$\widehat {\mathscr {X} }_{\mathcal {G}_0}$. We define the 
$\mathbf {c}$-vector of 
$f$ at 
$\mathcal {G}_0$ (or at 
$s_0$) by 
$\mathbf {c} _{\mathcal {G}_0}(f)=\mathbf {c} _{s_0}(f) := \deg (f)$ and the 
$\mathbf {c}$-vector at 
$\mathcal {G}_0$ of a cluster monomial on 
$\mathcal {X}$ as the 
$\mathbf {c}$-vector at 
$\mathcal {G}_0$ of its extension to 
$\widehat {\mathscr {X} }_{\mathcal {G}_0}$.
We now turn our attention to the fibers of the family.
Proposition 5.11 For 
${\rm \mathbf{u}},{\rm \mathbf{u}}'\in (\mathbb {C}^{*})^{n}$ the two fibers 
$\widehat {\mathcal {X} } _{\mathbf {u}}$ and 
$\widehat {\mathcal {X} } _{\mathbf {u}'}$ of the family 
${\widehat {\mathscr {X} }_{\mathcal {G}_0} \to \operatorname {Spec}\left ({R}\right )}$ are isomorphic.
Proof. For a given 
$\mathbf {g}$-cone 
$\mathcal {G}$ let 
$U_\mathcal {G}|_{\mathbf {t}=\mathbf {u}}$ denote by a little abuse of notation the affine patch 
$\operatorname {Spec}(\mathbb {C}[\widetilde {X} _{1;\mathcal {G}},\ldots ,\widetilde {X} _{n;\mathcal {G}}])$ of 
$\widehat {\mathcal {X} } _{\mathbf {u}}$. Similarly, let 
$U_{\mathcal {G}}|_{\mathbf {t}=\mathbf {u}'}$ be 
$\operatorname {Spec}(\mathbb {C}[\widetilde {X} '_{1;\mathcal {G}},\ldots ,\widetilde {X} '_{n;\mathcal {G}}])$ of 
$\widehat {\mathcal {X} } _{\mathbf {u}'}$. We define an isomorphism 
$\psi _\mathcal {G}:U_{\mathcal {G}}\vert _{\mathbf {t}=\mathbf {u}'}\to U_{\mathcal {G}}\vert _{\mathbf {t}=\mathbf {u}}$ by the pull-back on functions:
\[ \psi^{*}_\mathcal{G}: \mathbb{C}[\widetilde{X} _{1;\mathcal{G}},\ldots,\widetilde{X} _{n;\mathcal{G}}] \to \mathbb{C}[\widetilde{X} '_{1;\mathcal{G}},\ldots,\widetilde{X} '_{n;\mathcal{G}}],\quad \text{where}\ \widetilde{X} _{i;\mathcal{G}} \mapsto \frac{\mathbf{u}'^{\mathbf{c} _{i;\mathcal{G}}}}{\mathbf{u}^{\mathbf{c} _{i;\mathcal{G}}}}\widetilde{X} '_{i;\mathcal{G}} \ \forall i. \]
Let 
$\mathcal {G}'$ be the 
$\mathbf {g}$-cone related to 
$\mathcal {G}$ by mutation in direction 
$k$, i.e. sharing the facet in 
$\mathbf {c} _k^{\perp }$. We have to show that this isomorphism commutes with the gluing given by 
$\mu _k$. The transition functions on intersections of the affine patches in 
$\widehat {\mathcal {X} } _{\mathbf {u}}$ are obtained by specializing 
$\mathbf {t}=\mathbf {u}$ in (5.1) and similarly for 
$\widehat {\mathcal {X} } _{\mathbf {u}'}$. We show commutativity on the level of rings, i.e. 
$\psi _{\mathcal {G}}^{*}\circ \mu _k^{*}(\widetilde {X} _{i;\mathcal {G}'})=\mu _k^{*}\circ \psi ^{*}_{\mathcal {G}'}(\widetilde {X} _{i;\mathcal {G}'})$ for every 
$i\in [1,n]$. For 
$i=k$ by (5.1) and (5.5) we have
\begin{align*} {\psi_\mathcal{G}^{*}}\circ \mu_k^{*}\left({{\widetilde{X} }_{k;\mathcal{G}'}}\right) &= \psi_\mathcal{G}^{*}\left({{\widetilde{X} }{}^{-1}_{k;\mathcal{G}}}\right) = \frac{\mathbf{u}^{\mathbf{c}_{k;\mathcal{G}}}}{{\mathbf{u}'}{}^{\mathbf{c}_{k;\mathcal{G}}}}{{\widetilde{X} }'{}^{-1}_{k;\mathcal{G}}}\\ &= {\frac{{\mathbf{u}'}^{\mathbf{c}_{k;\mathcal{G}'}}}{\mathbf{u}^{\mathbf{c}_{k;\mathcal{G}'}}}}{{\widetilde{X} }'{}^{-1}_{k;\mathcal{G}}} = \mu_k^{*}\left({ \frac{{\mathbf{u}'}^{\mathbf{c}_{k;\mathcal{G}'}}}{\mathbf{u}^{\mathbf{c}_{k;\mathcal{G}'}}}{\widetilde{X} }'_{k;\mathcal{G}'}}\right)= {\mu_k^{*}}\circ \psi^{*}_{\mathcal{G}'}\left({\widetilde{X} _{k;\mathcal{G}'}}\right). \end{align*}
For 
$i\not =k$ we distinguish two cases as follows.
Case 1. If
$\operatorname *{sgn}(\epsilon _{ik})\not =\operatorname *{sgn}(\mathbf {c}_{k;\mathcal {G}})$, note that $\mathbf {c} _{i;\mathcal {G}'}=\mathbf {c} _{i;\mathcal {G}}+\operatorname *{sgn}(\epsilon _{ik})[\epsilon _{ik}\mathbf {c} _{k;\mathcal {G}}]_+=\mathbf {c} _{i;\mathcal {G}}$, then
\begin{align*} \psi_\mathcal{G}^{*} \circ \mu_k^{*} \left({ \widetilde{X} _{i;\mathcal{G}'} }\right) &= \psi_\mathcal{G}^{*} \left({ \widetilde{X} _{i;\mathcal{G}} ({1+\mathbf{u}^{|\mathbf{c} _{k;\mathcal{G}}|}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}(\epsilon_{ik})}})^{-\epsilon_{ik} } }\right) \\ &= \frac{ {\mathbf{u}'}^{\mathbf{c} _{i;\mathcal{G}}} }{ \mathbf{u}^{\mathbf{c} _{i;\mathcal{G}}} }\widetilde{X} '_{i;\mathcal{G}} \left({ 1+\mathbf{u}^{| \mathbf{c} _{k;\mathcal{G}} |} \left({ \frac{ {\mathbf{u}'}^{\mathbf{c} _{k;\mathcal{G}}} }{ \mathbf{u}^{\mathbf{c} _{k;\mathcal{G}}} } \widetilde{X} '_{k;\mathcal{G}}}\right)^{-\operatorname*{sgn}(\epsilon_{ik})} }\right)^{-\epsilon_{ik}} \\ &\hspace{-3pc}\stackrel{ |\mathbf{c} _{k;\mathcal{G}}|=-\operatorname*{sgn}(\epsilon_{ik})\mathbf{c} _{k;\mathcal{G}} }{=} \frac{ {\mathbf{u}'}^{\mathbf{c}_{i;\mathcal{G}}}}{ \mathbf{u}^{\mathbf{c} _{i;\mathcal{G}}} }\widetilde{X} '_{i;\mathcal{G}} \left({ 1+{\mathbf{u}'}^{| \mathbf{c} _{k;\mathcal{G}}|}{{\widetilde{X} }'_{k;\mathcal{G}}}{}^{-\operatorname*{sgn}(\epsilon_{ik})} }\right)^{-\epsilon_{ik}} \\ &\hspace{-1.2pc}\stackrel{ \mathbf{c} _{i;\mathcal{G}'}=\mathbf{c} _{i;\mathcal{G}} }{=} \frac{ {\mathbf{u}'}^{\mathbf{c} _{i;\mathcal{G}'}} }{ \mathbf{u}^{\mathbf{c} _{i;\mathcal{G}'}} }\widetilde{X} '_{i;\mathcal{G}} \left({ 1+{\mathbf{u}'}^{ |\mathbf{c} _{k;\mathcal{G}}| } {\widetilde{X} '_{k;\mathcal{G}}}{}^{ -\operatorname*{sgn}(\epsilon_{ik}) } }\right)^{-\epsilon_{ik}} \\ &= \mu_k^{*} \left({ \frac{{\mathbf{u}'}^{\mathbf{c} _{i;\mathcal{G}'}}}{\mathbf{u}^{\mathbf{c} _{i;\mathcal{G}'}}}\widetilde{X} '_{i;\mathcal{G}'} }\right) = \mu_k^{*} \circ \psi_{\mathcal{G}'}^{*} \left({ \widetilde{X} _{i;\mathcal{G}'} }\right). \end{align*}Case 2. If
$\operatorname *{sgn}(\epsilon _{ik})=\operatorname *{sgn}(\mathbf {c}_{k;\mathcal {G}})$ note that $\mathbf {c} _{i;\mathcal {G}'}=\mathbf {c} _{i;\mathcal {G}}+\operatorname *{sgn}(\epsilon _{ik})[\epsilon _{ik}\mathbf {c} _{k;\mathcal {G}}]_+=\mathbf {c} _{i;\mathcal {G}}+\operatorname *{sgn}(\epsilon _{ik})\epsilon _{ik}\mathbf {c} _{k;\mathcal {G}}$. This is used in the step labeled by $\bigstar$ below. We compute the following:
\begin{align*} \psi_\mathcal{G}^{*}\circ \mu_k^{*}\left({\widetilde{X} _{i;\mathcal{G}'}}\right) &= \psi_\mathcal{G}^{*}\left({ \widetilde{X} _{i;\mathcal{G}}({\mathbf{u}^{| \mathbf{c} _{k;\mathcal{G}}|}+ \widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}(\epsilon_{ik})}})^{-\epsilon_{ik}} }\right)\\ &= \frac{\mathbf{u}'^{\mathbf{c} _{i;\mathcal{G}}}}{\mathbf{u}^{\mathbf{c} _{i;\mathcal{G}}}}\widetilde{X} _{i;\mathcal{G}}'\left({\mathbf{u}^{| \mathbf{c} _{k;\mathcal{G}} |}+ \left({\frac{\mathbf{u}'^{\mathbf{c} _{k;\mathcal{G}}}}{\mathbf{u}^{\mathbf{c} _{k;\mathcal{G}}}}\widetilde{X} '_{k;\mathcal{G}}}\right)^{-\operatorname*{sgn}(\epsilon_{ik})}}\right)^{-\epsilon_{ik}}\\ &\hspace{-2.7pc}\stackrel{| \mathbf{c} _{k;\mathcal{G}}|=\operatorname*{sgn}(\epsilon_{ik})\mathbf{c} _{k;\mathcal{G}}}{=} \frac{\mathbf{u}'^{\mathbf{c} _{i;\mathcal{G}}}}{\mathbf{u}^{\mathbf{c} _{i;\mathcal{G}}}}\widetilde{X} _{i;\mathcal{G}}' \left({ \frac{1}{\mathbf{u}^{-\operatorname*{sgn}(\epsilon_{ik})\mathbf{c} _{k;\mathcal{G}}}}+ \frac{\mathbf{u}'^{-\operatorname*{sgn}(\epsilon_{ik})\mathbf{c} _{k;\mathcal{G}}}}{\mathbf{u}^{-\operatorname*{sgn}(\epsilon_{ik})\mathbf{c} _{k;\mathcal{G}}}} \widetilde{X} _{k;\mathcal{G}}'^{-\operatorname*{sgn}(\epsilon_{ik})} }\right)^{-\epsilon_{ik}}\\ &= \frac{\mathbf{u}'^{\mathbf{c} _{i;\mathcal{G}}}}{\mathbf{u}^{\mathbf{c} _{i;\mathcal{G}}}}\widetilde{X} _{i;\mathcal{G}}' \left({ \frac{\mathbf{u}'^{-\operatorname*{sgn}(\epsilon_{ik})\mathbf{c} _{k;\mathcal{G}}}}{\mathbf{u}^{-\operatorname*{sgn}(\epsilon_{ik})\mathbf{c} _{k;\mathcal{G}}}} \left({\frac{1}{\mathbf{u}'^{-\operatorname*{sgn}(\epsilon_{ik})\mathbf{c} _{k;\mathcal{G}}}} + \widetilde{X} _{k;\mathcal{G}}'^{-\operatorname*{sgn}(\epsilon_{ik})} }\right)}\right)^{-\epsilon_{ik}}\\ &=\frac{\mathbf{u}'^{\mathbf{c} _{i;\mathcal{G}}+\operatorname*{sgn}(\epsilon_{ik})\epsilon_{ik}\mathbf{c} _{k;\mathcal{G}}}}{\mathbf{u}^{\mathbf{c} _{i;\mathcal{G}}+ \operatorname*{sgn}(\epsilon_{ik})\epsilon_{ik}\mathbf{c} _{k;\mathcal{G}}}}\widetilde{X} _{i;\mathcal{G}}' \left({ \mathbf{u}'^{| \mathbf{c} _{k;\mathcal{G}}|} + \widetilde{X} _{k;\mathcal{G}}'^{-\operatorname*{sgn}(\epsilon_{ik})} }\right)^{-\epsilon_{ik}}\\ &\stackrel{\bigstar}{=} \mu_{k}^{*}\left({\frac{\mathbf{u}'^{\mathbf{c} _{i;\mathcal{G}'}}}{\mathbf{u}^{\mathbf{c} _{i;\mathcal{G}'}}} \widetilde{X} _{i;\mathcal{G}'}' }\right) = \mu_k^{*}\circ \psi_\mathcal{G}'^{*}\left({\widetilde{X} _{i;\mathcal{G}'}}\right).\end{align*}
Proposition 5.12 
$\widehat {\mathscr {X} }_{\mathcal {G}_0} \to \operatorname {Spec}\left ({R}\right )$ is an open morphism.
Proof. Openness is a local property of morphisms so we are free to restrict to affine patches. We just need to see that 
$\operatorname {Spec}(R[\widetilde {X} _{1;\mathcal {G}}, \ldots , \widetilde {X} _{n;\mathcal {G}}]) \to \operatorname {Spec}\left ({R}\right )$ is open. But this is clear, see e.g. [Sta18, Lemma 037G].
Corollary 5.13 For 
$\mathbf {u} \in \left ({\mathbb {C} ^{*}}\right )^{n}$ the fiber 
$\widehat {\mathcal {X} } _{\mathbf {u}}$ is smooth. In particular, 
$\widehat {\mathcal {X} }$ is smooth.
Proof. First, we observe that 
$\widehat {\mathcal {X} } _0$ is smooth. The 
$\mathbf {g}$-fan is simplicial, with the generators of each maximal cone forming a 
$\mathbb {Z}$-basis of 
$M$. This implies smoothness for the toric central fiber [Reference OdaOda88, Theorem 1.10]. By [Reference Grothendieck and DieudonnéGD66, Theorem 12.1.6(iii)], the set of 
$x\in \widehat {\mathscr {X} }_{\mathcal {G}_0}$ such that 
$\widehat {\mathcal {X} } _{\pi (x)}$ is smooth is open in 
$\widehat {\mathscr {X} }_{\mathcal {G}_0}$. So, by Proposition 5.12, the set of 
$\mathbf {u} \in \operatorname {Spec}\left ({R}\right )$ such that 
$\widehat {\mathcal {X} } _{\mathbf {u}}$ is smooth is open in 
$\operatorname {Spec}\left ({R}\right )$. Then there is an open neighborhood of 
$0$ having smooth fibers. The claim follows from Proposition 5.11.
6. Strata and their degenerations
The results of the last section show that 
$\widehat {\mathcal {X} } _{\mathbf {t} }$ (for a given 
$\mathbf {t}\in \mathbb {C}^{n}$) is constructed from a fan much the same way as a toric variety. Unsurprisingly then, 
$\widehat {\mathcal {X} } _{\mathbf {t} }$ is naturally stratified in a manner reminiscent of the usual stratification of a toric variety by lower dimensional toric subvarieties. In fact, the affine patches 
$\mathbb {A}^{n}_\mathcal {G}$ defining 
$\widehat {\mathcal {X} } _{\mathbf {t} }$ are toric varieties, and the restriction of 
$\widehat {\mathcal {X} } _{\mathbf {t} }$ strata to 
$\mathbb {A}^{n}_\mathcal {G}$ gives exactly the toric strata of 
$\mathbb {A}^{n}_\mathcal {G}$. To get the full strata for 
$\widehat {\mathcal {X} } _{\mathbf {t} }$, we simply glue together toric strata from different affine patches via the extended 
$\widehat {\mathscr {X} }_{\mathcal {G}_0}$ mutation formula. The main results of this section are that this does indeed yield a stratification of 
$\widehat {\mathcal {X} } _{\mathbf {t}}$, the resulting strata are lower dimensional 
$\widehat {\mathcal {X} }$-cluster varieties with specified coefficients, and these strata degenerate precisely to the toric strata of the central fiber 
$\widehat {\mathcal {X} } _0 = {\operatorname {TV}({{{\Delta ^{+}_F} }})}$.
Let us start by fixing terminology and briefly reviewing the toric description, following [Reference FultonFul93, § 3.1]. We say a scheme 
$Y$ is stratified by subschemes of type 
$P$ if there is a collection 
$\mathcal {S}$ of subschemes 
$Y_i$ of type 
$P$ (called strata) such that
\[ Y= \bigcup_{\mathcal{S}} Y_i \]
and for every pair 
$\left ({Y_i,Y_j}\right )$ of elements of 
$\mathcal {S}$, 
$Y_i \cap Y_j$ is also in 
$\mathcal {S}$. For example, we discuss below how every toric variety is stratified by toric varieties: the torus orbit closures. Alternatively, though this is not the approach we adopt, we can stratify toric varieties by tori (torus orbits) viewing 
$\varnothing$ as a torus of dimension 
$-1$.Footnote 9
Let 
${\operatorname {TV}({\varSigma })}$ be the toric variety associated to a fan 
$\varSigma$. Let 
$N$ be the cocharacter lattice of the defining torus and 
$M$ its character lattice. For every cone 
$\tau$ in 
$\varSigma$, we have a torus orbit 
$O(\tau )$, which itself is a torus. We denote the closure of 
$O(\tau )$ by 
$V(\tau )$. Then 
$V(\tau )$ is a toric variety, and it is what we refer to as a toric stratum. The torus 
$O(\tau )$ is 
$\operatorname {Spec}(\mathbb {C} [\tau ^{\perp } \cap M ])$, so the fan for 
$V(\tau )$ lives in 
$(\tau ^{\perp } \cap M)^{*} \otimes \mathbb {R}$. Let 
$N(\tau ):= (\tau ^{\perp } \cap M)^{*}$ be the quotient of 
$N$ by the group completion of 
$\tau \cap N$. The fan for 
$V(\tau )$, denoted 
$\operatorname {Star}(\tau )$, is built from the cones of 
$\varSigma$ containing 
$\tau$ as a face. If 
$\sigma$ is such a cone, we take its image 
$\bar {\sigma }$ in 
$N(\tau ) \otimes \mathbb {R}$. The collection of these 
$\sigma$ form a subfan of 
$\varSigma$, and their images 
$\bar {\sigma }$ form the fan 
$\operatorname {Star}(\tau )$ in 
$N(\tau )\otimes \mathbb {R}$.
To realize 
$V(\tau )$ as a closed subscheme of 
${\operatorname {TV}({\varSigma })}$, we work with the defining affine patches. In 
$V(\tau )$, these have the form 
$\operatorname {Spec}(\mathbb {C} [\bar {\sigma }^{\vee } \cap \tau ^{\perp } \cap M])$. Note that 
$\bar {\sigma }^{\vee } \cap \tau ^{\perp } \cap M$ is the same as 
$\sigma ^{\vee } \cap \tau ^{\perp } \cap M$, and 
$\operatorname {Spec}\left ({\mathbb {C} \left [{\sigma ^{\vee } \cap M}\right ]}\right )$ is a defining affine patch of 
${\operatorname {TV}({\varSigma })}$. We have 
$\operatorname {Spec}(\mathbb {C} [\sigma ^{\vee } \cap \tau ^{\perp } \cap M]) \hookrightarrow \operatorname {Spec}(\mathbb {C} [\sigma ^{\vee } \cap M])$ via the projection of rings:
\[ \mathbb{C} [\sigma^{\vee} \cap M] \to \mathbb{C} [\sigma^{\vee} \cap \tau^{\perp} \cap M],\quad z^{m} \mapsto \begin{cases} z^{m} & \mathrm{if }\ m \in \sigma^{\vee} \cap \tau^{\perp} \cap M, \\ 0 & \mathrm{otherwise}. \end{cases} \] Since the defining affine patches of 
$\widehat {\mathcal {X} } _{\mathbf {t} }$ are precisely the maximal affine toric varieties making up 
${\operatorname {TV}({{{\Delta ^{+}_F} }})}$, these affine patches are stratified as described above. But how do the strata of different patches relate? Extending the toric analogy, if we fix a cone 
$\tau$ in 
${{\Delta ^{+}_F} }$, do the associated strata in distinct affine patches glue together to form a closed subscheme of 
$\widehat {\mathcal {X} } _{\mathbf {t}}$? And if so, does this subscheme inherit any structure from 
$\widehat {\mathcal {X} } _{\mathbf {t}}$, particularly structure encoded by a tropical version of 
$\operatorname {Star}(\tau )$?
In [Reference Fock and GoncharovFG16] Fock and Goncharov give results in this direction for 
$\widehat {\mathcal {X} } = \widehat {\mathcal {X} } _{\mathbf {1}}$. Specifically, they show that if we take an 
$M$-seed 
$s$, freeze some directions and set the corresponding 
$\mathcal {X}$-variables to 
$0$, we obtain an 
$\mathcal {X}$-cluster variety as an immersed subscheme at the boundary of 
$\widehat {\mathcal {X} }$. This line of reasoning extends directly to the case of coefficients and is a central argument in Theorem 6.2. The other key ingredient is Cao and Li's result [Reference Cao and LiCL20, Theorem 6.2]. Stated in the terminology of this paper it is as follows.
Theorem 6.1 {[CL20]} Let 
$\left ({\varGamma ,v_0}\right )$ be arbitrary skew-symmetrizable initial data with frozen directions. Then any two clusters containing the same subset 
$\lbrace A_1,\ldots ,A_a\rbrace$ of 
$\mathcal {A}$-cluster variables can be connected to each other by iterated mutation without exchanging any of the cluster variables in 
$\lbrace A_1,\ldots ,A_a\rbrace$.
This result leads to the stratification of 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ by specially completed 
$\mathcal {X}$-varieties with specified coefficients, an upgrade on 
$\widehat {\mathcal {X} } _{\mathbf {t}} \setminus \mathcal {X} _{\mathbf {t}}$ having immersed specially completed 
$\mathcal {X}$-varieties with specified coefficients.
Theorem 6.2 Let 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ be a specially completed 
$\mathcal {X}$-variety with specified coefficients, and let 
$\tau$ be a 
$k$-dimensional cone in 
${{\Delta ^{+}_F} }$. Then 
$\tau$ defines a codimension 
$k$ closed subscheme 
$V(\tau )_{\mathbf {t}}$ of 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ for each 
$\mathbf {t}$. Moreover, 
$V(\tau )_{\mathbf {t}}$ is again a specially completed 
$\mathcal {X}$-variety with specified coefficients 
$\mathbf {t}$.
Proof. On the affine patches defining 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ we still have the inclusion
\[ \operatorname{Spec}\left({\mathbb{C} \left[{ \sigma^{\vee} \cap \tau^{\perp} \cap M}\right]}\right) \hookrightarrow \operatorname{Spec}\left({\mathbb{C} \left[{ \sigma^{\vee} \cap M}\right]}\right) \]
for all cones 
$\sigma$ of 
${{\Delta ^{+}_F} }$ containing 
$\tau$. Note that 
$\tau$ is the 
$\mathbb {R} _{\geq 0}$-span of 
$k$-many 
$\mathbf {g}$-vectors. Then for any 
$\mathbf {g}$-cone 
$\mathcal {G}$ containing 
$\tau$, 
$\tau ^{\perp }$ is the 
$\mathbb {R}$-span of the 
$(n-k)$-many 
$\mathbf {c}$-vector generators of 
$\mathcal {C} = \mathcal {G}^{\vee }$ that are orthogonal to 
$\tau$.
Take 
$\sigma$ to be an 
$m$-dimensional cone of 
${{\Delta ^{+}_F} }$ with 
$\tau \subset \sigma \subset \mathcal {G}$. Then 
${\mathbb {C} [\sigma ^{\vee } \cap \tau ^{\perp } \cap M]}$ is just 
$\mathbb {C} [ X_{i_1},\ldots , X_{i_{m-k}},X_{i_{m-k+1}}^{\pm 1},\ldots ,X_{i_{n-k}}^{\pm 1} ]$. Here the first 
$m-k$ terms are the 
$\mathcal {X}$-variables associated to generators of 
$\mathcal {C}$ that are orthogonal to 
$\tau$ but not 
$\sigma$, while the remaining terms correspond to generators orthogonal to both 
$\tau$ and 
$\sigma$. There are two extreme cases. When 
$\sigma = \tau$, we have 
$\sigma ^{\vee } \cap \tau ^{\perp } = \tau ^{\perp }$. Then
\[ \operatorname{Spec}\left({\mathbb{C} \left[{ \sigma^{\vee} \cap \tau^{\perp} \cap M}\right]}\right) = \operatorname{Spec}\left({ \mathbb{C} \left[{X_{i_1}^{\pm 1},\ldots,X_{i_{n-k}}^{\pm 1}}\right]}\right), \]
which will be a torus in the atlas of the 
$\mathcal {X}$-variety associated to 
$\tau$. We call it 
$T_{M,\mathcal {G}}(\tau )$. On the other side of the spectrum, when 
$\sigma = \mathcal {G}$ we have
\[ \operatorname{Spec}\left({\mathbb{C} \left[{ \sigma^{\vee} \cap \tau^{\perp} \cap M}\right]}\right) = \operatorname{Spec}\left({ \mathbb{C} \left[{X_{i_1},\ldots,X_{i_{n-k}}}\right]}\right). \]
This will be the corresponding copy of 
$\mathbb {A} ^{n-k}$ in the atlas of this 
$\mathcal {X}$-variety's special completion with specified coefficients. Call it 
$\mathbb {A} ^{n-k}_{M,\mathcal {G}}\left ({\tau }\right )$.
Mutation is given by crossing walls of 
${{\Delta ^{+}_F} }$. The relevant mutations here correspond to walls containing 
$\tau$, and mutation directions correspond to indices of 
$\tau ^{\perp }$. Specifically, if we set 
${I(\tau ) :=\left \{{i_1,\ldots ,i_{n-k}}\right \}}$, the relevant mutation directions are 
${I_{\text {uf}}}(\tau ):= I(\tau )\setminus F$. Observe the following.
(i) Since we will never mutate at
$j \notin I(\tau )$, by the mutation formula (5.1) we have
for all\[ \mu_k^{*}\left({\widetilde{X} _{j;\mathcal{G}'}}\right) = \widetilde{X} _{j;\mathcal{G}}\left({\mathbf{t}^{[\operatorname*{sgn}(\epsilon_{jk})\mathbf{c}_{k;\mathcal{G}}]_+} + \mathbf{t}^{[-\operatorname*{sgn}(\epsilon_{jk})\mathbf{c}_{k;\mathcal{G}}]_+}\widetilde{X} _{k;\mathcal{G}}^{-\operatorname*{sgn}(\epsilon_{jk})}}\right)^{-\epsilon_{jk}} \]$j \notin I(\tau )$.(ii) For
$i \in I(\tau )$, the mutation formula (5.1) is independent of $\widetilde {X} _{j;\mathcal {G}}$ for all $j \notin I(\tau )$.
On account of (i), we can consistently set 
$\widetilde {X} _{j;\mathcal {G}}=0$ for all 
$j \notin I(\tau )$ and all 
$\mathbf {g}$-cones 
$\mathcal {G}$ containing 
$\tau$. By (ii), doing so will not alter the relations among the variables we have not set to 0: those indexed by 
$I(\tau )$. Now fix some 
$\mathcal {G}_0 \supset \tau$. By the preceding discussion, if we set 
$\widetilde {X} _{j;\mathcal {G}}=0$ for 
$j \notin {I_{\text {uf}}}(\tau )$, 
$\mathcal {G} \supset \tau$, and restrict the indices of our exchange matrix 
$\boldsymbol {\varepsilon }$ at 
$\mathcal {G}_0$ to 
$I(\tau )$, what we obtain will be an immersed 
$(n-k)$-dimensional 
$\mathcal {X}$-variety with specified coefficients 
$\mathcal {X} _{\mathbf {t}}(\tau )_{\mathcal {G}_0}$ glued from the tori 
$T_{M,\mathcal {G}}(\tau )$ mutation equivalent to 
$T_{M,\mathcal {G}_0}(\tau )$. Replacing 
$T_{M,\mathcal {G}}(\tau )$ with 
$\mathbb {A} ^{n-k}_{M,\mathcal {G}}(\tau )$ gives its special completion 
$\widehat {\mathcal {X} } _{\mathbf {t}}(\tau )_{\mathcal {G}_0}$.
Now let 
$\mathcal {G}_0'$ be another 
$\mathbf {g}$-cone containing 
$\tau$. If 
$\mathcal {G}_0$ and 
$\mathcal {G}_0'$ are connected by mutation in 
${I_{\text {uf}}}(\tau )$, then 
$\mathcal {X} _{\mathbf {t}}(\tau )_{\mathcal {G}_0} = \mathcal {X} _{\mathbf {t}}(\tau )_{\mathcal {G}_0'}$ and 
$\widehat {\mathcal {X} } _{\mathbf {t}}(\tau )_{\mathcal {G}_0} = \widehat {\mathcal {X} } _{\mathbf {t}}(\tau )_{\mathcal {G}_0'}$. If, on the other hand, 
$\mathcal {G}_0$ and 
$\mathcal {G}_0'$ were only connected by mutation in 
${I_{\text {uf}}}$ (rather than 
${I_{\text {uf}}}(\tau )$) then mutation in 
${I_{\text {uf}}}$ would glue 
$\mathcal {X} _{\mathbf {t}}(\tau )_{\mathcal {G}_0}$ with 
$\mathcal {X} _{\mathbf {t}}(\tau )_{\mathcal {G}_0'}$ and 
$\widehat {\mathcal {X} } _{\mathbf {t}}(\tau )_{\mathcal {G}_0}$ with 
$\widehat {\mathcal {X} } _{\mathbf {t}}(\tau )_{\mathcal {G}_0'}$ in the ambient space 
$\widehat {\mathcal {X} } _{\mathbf {t}}$. But 
$\mathcal {X} _{\mathbf {t}}(\tau )_{\mathcal {G}_0}$ and 
$\mathcal {X} _{\mathbf {t}}(\tau )_{\mathcal {G}_0'}$ would be distinct immersed 
$\mathcal {X}$-cluster varieties with specified coefficients (and their special completions would likewise be distinct), and we would not have the claimed stratification. However, the content of [Reference Cao and LiCL20, Theorem 6.2] is precisely that 
$\mathcal {G}_0$ and 
$\mathcal {G}_0'$ are connected by mutation in 
${I_{\text {uf}}}(\tau )$. That is, 
$\widehat {\mathcal {X} } _{\mathbf {t}}(\tau )_{\mathcal {G}}$ is independent of 
$\mathcal {G}$, and is exactly the immersed subscheme given by 
$\operatorname {Star}\left ({\tau }\right )$. We call it 
$V\left ({\tau }\right )_{\mathbf {t}}$.
From this perspective, we have a family of specially completed 
$\mathcal {X}$-varieties with specified coefficients, which are in turn stratified by specially completed 
$\mathcal {X}$-varieties with specified coefficients. The 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ degenerate to toric varieties, which themselves are stratified by toric varieties. It would be very satisfying then if the 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ strata degenerate to the toric strata. In fact, from the description of the 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ strata given above, it is almost immediate that this occurs. Taking 
$\mathbf {t}$ to 
$0$ in (5.1) yields the following result.
Theorem 6.3 Let 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ and 
$V(\tau )_{\mathbf {t}}$ be as in Theorem 6.2. Then 
$V(\tau )_{\mathbf {t}}$ degenerates to the toric stratum 
$V(\tau )$ of the toric central fiber.
7. Examples and applications
In this section we give examples of toric degenerations of compactified cluster varieties, and we relate the 
$\mathcal {A}$ and 
$\mathcal {X}$ degenerations in these examples.
7.1 Rietsch–Williams degeneration of Grassmannians
In [Reference Rietsch and WilliamsRW19], Rietsch and Williams study Newton–Okounkov bodies for the anticanonical divisor of the Grassmannian. For a given seed in the underlying cluster algebra they construct a valuation using flow polynomials and Postnikov's plabic graphs Footnote 10 (see [Reference PostnikovPos06]). By [Reference AndersonAnd13, Reference KavehKav15] the Newton–Okounkov bodies (rational polytopes in this case) induce toric degenerations of the Grassmannian. Further, they show that the Newton–Okounkov polytopes are in fact equal to polytopes arising from a Landau–Ginzburg potential introduced by Marsh and Rietsch in [Reference Marsh and RietschMR20].
Below we relate the Rietsch–Williams construction to the 
$\mathscr {X}$- and 
$\mathcal {A}_{\mathrm {prin}}$-families for 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$. Passing though 
$\mathscr {X}$, we show that the Rietsch–Williams toric degeneration is precisely the 
$\mathcal {A}_{\mathrm {prin}}$-family of [Reference Gross, Hacking, Keel and KontsevichGHKK18]. We identify both the Newton–Okounkov body 
$\Delta _{\mathrm {RW}}$ and the superpotential polytope 
$\varGamma _{\mathrm {RW}}$ of [Reference Rietsch and WilliamsRW19] with the superpotential polytope 
$\varXi _{\mathrm {GHKK}}$ of [Reference Gross, Hacking, Keel and KontsevichGHKK18], giving a new proof of the equality of the Rietsch–Williams polytopes. We will treat the general case of 
$\operatorname {Gr}_k\left ({\mathbb {C} ^{n}}\right )$ in a forthcoming paper by Bossinger, Cheung, Magee and Nájera Chávez. We use the notation introduced in [Reference Rietsch and WilliamsRW19]. The strategy is as follows.
(i) Identify the Marsh–Rietsch potential on
$\check {\mathbb {X}}^{\circ } \subset \operatorname {Gr}_2(\mathbb {C} ^{5})$ with the Gross–Hacking–Keel–Kontsevich potential on its mirror $\mathbb {X}^{\circ }$ via an isomorphism of $\check {\mathbb {X}}^{\circ } \stackrel {\sim }{\to } \mathbb {X}^{\circ }$. This identifies $\varGamma _{\mathrm {RW}}$ with $\varXi _{\mathrm {GHKK}}$ and it identifies as well the uncompactified families $\mathscr {X}$ and $\mathcal {A}_{\mathrm {prin}}$.(ii) Use this isomorphism to reinterpret the Rietsch–Williams flow polynomials for Plücker coordinates on
$\check {\mathbb {X}}^{\circ }$ as polynomials in the $\mathcal {X}$-variables of $\mathbb {X}^{\circ }$.(iii) Extend the flow polynomials to
$\mathscr {X}$ and identify the Rietsch–Williams valuation $\operatorname {val}_G\left ({p_{ij}}\right )$ of each Plücker coordinate $p_{ij}$ with $\mathbf {c} \left ({p_{ij}}\right )$. This identifies $\Delta _{\mathrm {RW}}$ with $\varXi _{\mathrm {GHKK}}$, and establishes that the toric degeneration of the compactification $\operatorname {Gr}_2(\mathbb {C} ^{5})$ in [Reference Rietsch and WilliamsRW19] matches the [Reference Gross, Hacking, Keel and KontsevichGHKK18] toric degeneration $\overline {\mathcal {A}_{\mathrm {prin}} }$.
In the affine cone 
$C(\operatorname {Gr}_2(\mathbb {C} ^{5}))$ of 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$ take the divisors 
$D_{i,i+1}:=\left \{{p_{i,i+1}=0}\right \}$ for 
$i\in \mathbb {Z} / 5 \mathbb {Z}$ and let 
$D$ be their union. The 
$\mathcal {A}$-cluster variety we are considering is the complement of 
$D$ in 
$C(\operatorname {Gr}_2(\mathbb {C} ^{5}))$. We discussed this cluster variety briefly in Example 2.41 to illustrate how to pass from a cluster pattern with geometric coefficients to a higher rank coefficient-free cluster pattern with frozen directions. Let 
$\check {\mathbb {X}}^{\circ }$ denote the image of 
$\mathcal {A}$ in 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$. It inherits a cluster structure from 
$\mathcal {A}$. Consider the plabic graph 
$G^{\mathrm {rec}}_{3,5}$ with perfect orientation as shown in Figure 5.
Figure 5. 
$G^{\mathrm {rec}}_{3,5}$ with perfect orientation, as in [Reference Rietsch and WilliamsRW19, Figure 7].
Faces of the plabic graph, labeled by Young diagrams 
$\mu$, are associated with variables 
$x_{\mu }$. The flow model assigns to every Plücker coordinate 
$p_{ij}\in \mathbb {C} [C(\operatorname {Gr}_2(\mathbb {C} ^{5}))]$ a polynomial in the variables 
$x_{\mu }$. This yields the flow polynomials (see [Reference Rietsch and WilliamsRW19, Example 6.11]):
We interpret 
$\operatorname {Flow}(p_{12}) = 1$ as a normalization. Dividing every Plücker coordinate by 
$p_{12}$ allows us to think of them as functions on 
$\check {\mathbb {X}}^{\circ }$ rather than 
$\mathcal {A}$. In light of this, we view the arguments of 
$\operatorname {Flow}$ as functions on 
$\check {\mathbb {X}}^{\circ }$. We will reinterpret the flow polynomials in terms of 
$\mathcal {X}$-variables, and then extend the resulting functions to 
$\mathscr {X}$. Observe that the flow polynomials in (7.1) which are actually monomials determine the cluster depicted in Figure 6.
Figure 6. Cluster determined by the monomials of (7.1).
We take this to be the initial cluster and write 
$s_0$ for the initial seed. Throughout this example, cluster variables written without a subscript specifying the seed will come from this seed. So when we write, for instance, 
$X_{i}$, we will mean 
$X_{i;s_0}$.
The Plücker coordinates are 
$\mathcal {A}$-variables, and we want to express them in terms of 
$\mathcal {X}$-variables. To do this, we make use of a map 
$p:\mathcal {A} \to \mathcal {X}$ (see Definition 3.16). Recall that this map 
$p$ is defined in terms of pull-backs of functions. On character lattices of cluster tori, it is given by a map 
$p^{*}:N {\to } M$ that agrees with 
$n\mapsto \left \{{ {n} , {\ \cdot \ } }\right \}$ up to a choice of map 
$N/{N_{\text {uf}}} \to N_{\text {uf}}^{\perp }$.Footnote 11
Recall that 
$A_i= z^{f_i}$ and 
$X_i = z^{e_i}$. For 
$e_{13}$ and 
$e_{14}$, we compute
The remaining pull-backs depend on the choice of map 
$N/{N_{\text {uf}}} \to {N_{\text {uf}}}^{\perp }$, and we will compare the Marsh–Rietsch and Gross–Hacking–Keel–Kontsevich potentials in order to make this choice. From the [Reference Gross, Hacking, Keel and KontsevichGHKK18] perspective, each component 
$D_{i,i+1}$ of 
$D$ defines a 
$\vartheta$-function 
$\vartheta _{i,i+1}$ on the mirror 
$\mathcal {X}$ of 
$\mathcal {A}$. If 
$s$ is a seed optimizedFootnote 12 for the frozen index 
${}_{i,i+1}$ (see [Reference Gross, Hacking, Keel and KontsevichGHKK18, Definition 9.1, Lemma 9.3]), the 
$\vartheta$-function 
$\vartheta _{i,i+1}$ is given by 
$\vartheta _{i,i+1} = z^{-e_{i,i+1;s}} = X_{i,i+1;s}^{-1}$. We can mutate from 
$s$ to 
$s_0$ to express 
$\vartheta _{i,i+1}$ in terms of the variables of the initial seed. The potential 
$W_{\text {GHKK}}:\mathcal {X} \to \mathbb {C}$ is the sum of the 
$\vartheta$-functions associated to each component 
$D_{i,i+1}$ of 
$D$. It is straightforward to compute these 
$\vartheta$-functions in terms of the 
$\mathcal {X}$-variables of 
$s_0$:
\begin{equation} \begin{aligned} \vartheta _{12} & = X_{12}^{-1}, \\ \vartheta _{23} & = X_{23}^{-1} + X_{23}^{-1} X_{13}^{-1}, \\ \vartheta _{34} & = X_{34}^{-1} + X_{34}^{-1} X_{14}^{-1}, \\ \vartheta _{45} & = X_{45}^{-1}, \\ \vartheta _{15} & = X_{15}^{-1} + X_{15}^{-1} X_{14}^{-1} + X_{15}^{-1} X_{14}^{-1} X_{13}^{-1}. \end{aligned} \end{equation}
Next, the Marsh–Rietsch potential 
$W_{\text {MR}}$ on 
$\check {\mathbb {X}}^{\circ } \times \mathbb {C} ^{*}$ also has a summand 
$W_i$ associated to each component of 
$D$, and the potential 
$W_{\text {MR}}|_{q=1}:\check {\mathbb {X}}^{\circ } \to \mathbb {C}$ is the sum of the 
$W_i$. See [Reference Rietsch and WilliamsRW19, Equations 10.1 and 10.2]. We can choose the map 
$N/{N_{\text {uf}}} \to N_{\text {uf}}^{\perp }$ such that 
$p^{*}\left ({\vartheta _{i+1,i+2}}\right )$ is the summand 
$W_i= {p_{i+1,i+3}}/{p_{i+1,i+2}}$ of [Reference Rietsch and WilliamsRW19, Equation 10.2]. For each 
$i$ we compute 
$\operatorname {Flow}(W_i)={\operatorname {Flow}(p_{i+1,i+3})}/{\operatorname {Flow}(p_{i+1,i+2})}$ and obtain
Note that functions on 
$\check {\mathbb {X}}^{\circ }$ are functions on 
$\mathcal {A}$ fixed by the 
$\mathbb {C} ^{*}$-action of simultaneous scaling. We have a 
$\vartheta$-basis for 
$\mathcal {O} (\mathcal {A} )$ from 
$\mathcal {X} ^{\mathrm{trop}} (\mathbb {Z} )$. The slice 
$\left ({\mathbb {X}^{\circ } }\right )^{\mathrm{trop}} (\mathbb {Z} )$ corresponding to functions fixed by this action gives a 
$\vartheta$-basis for 
$\mathcal {O} (\check {\mathbb {X}}^{\circ } )$. Explicitly, let
\[ a = a_{12} f_{12} + a_{13} f_{13} + a_{14} f_{14} + a_{15} f_{15}+ a_{23} f_{23} + a_{34} f_{34} + a_{45} f_{45} \]
be an arbitrary element of 
$M \cong \mathcal {X} ^{\mathrm{trop}} (\mathbb {Z} )$. Then 
$a\in \left ({\mathbb {X}^{\circ } }\right )^{\mathrm{trop}} (\mathbb {Z} )$ if and only if
\[ a_{12} + a_{13} + a_{14} + a_{15} + a_{23} + a_{34} + a_{45} = 0. \]
Dually, we identify 
$(\check {\mathbb {X}}^{\circ } )^{\mathrm{trop}} \left ({\mathbb {Z} }\right )$ with the quotient of 
$N$ by
\[ \mathbf{1}=e_{12}+ e_{13} + e_{14} + e_{15} + e_{23} + e_{34} + e_{45}. \]
Observe that 
$p^{*}\left ({N}\right )= \mathbf {1}^{\perp }\subset M$ and 
$\mathbb {Z} \cdot \mathbf {1} = \ker \left ({p^{*}}\right )$, so 
$p^{*}$ induces an isomorphism
\begin{equation} \bar{p}^{*}: (\check{\mathbb{X}}^{\circ} )^{\mathrm{trop}} \left({\mathbb{Z} }\right) \stackrel{\sim}{\to}\left({\mathbb{X}^{\circ} }\right)^{\mathrm{trop}} \left({\mathbb{Z} }\right), \end{equation}
i.e. an isomorphism 
$\bar {p}:\check {\mathbb {X}}^{\circ } \stackrel {\sim }{\to } \mathbb {X}^{\circ }$. We have the following commutative diagrams.
Below, we identify the 
$x_\mu$ with functions on 
$\mathbb {X}^{\circ }$, and conclude that 
$\operatorname {Flow}$ is precisely 
$\left ({\bar {p}^{-1}}\right )^{*}$. Given a function 
$F$ on 
$\mathcal {X}$ (denoted with a capital letter), denote by 
$f$ (in lowercase) the associated function 
$\left ({\bar {p}^{-1}}\right )^{*}(p^{*}\left ({F}\right ))$ on 
$\mathbb {X}^{\circ }$. For example, for every 
$\mathcal {X}$-variable 
$X_{ij}$ we obtain a function on 
$\mathbb {X}^{\circ }$ denoted 
$x_{ij}=(\bar {p}^{-1})^{*}\circ (p^{*}(X_{ij}))$.
In light of (7.2), we make the identifications
Next, comparing (7.3) and (7.4), we set
Finally, observe
\[ \mathbf{c} \left({X_{13}}\right)+\mathbf{c} \left({X_{14}}\right)+\mathbf{c} \left({\vartheta _{12}}\right)+\mathbf{c} \left({\vartheta _{23}}\right)+\mathbf{c} \left({\vartheta _{34}}\right)+\mathbf{c} \left({\vartheta _{45}}\right)+\mathbf{c} \left({\vartheta _{15}}\right) = -\mathbf{1} \in \ker(p^{*}). \]With this in mind, we set
With these identifications, it is immediate that 
$\operatorname {Flow}=\left ({\bar {p}^{-1}}\right )^{*}$. We can now extend all flow polynomials to the family 
$\mathscr {X}_{s_0}$ deforming 
$\mathbb {X}^{\circ }$ (as opposed to the family deforming 
$\mathcal {X}$). The coefficients satisfy the same relations as the 
$x$ variables. The monomials in (7.1) extend directly, e.g.
The extensions of the three remaining flow polynomials are
Remark 7.1 Note that the homogeneous degree of the extension, i.e. its 
$\mathbf {c}$-vector, is precisely Rietsch–Williams’ valuation 
$\operatorname {val}_G$ of [Reference Rietsch and WilliamsRW19, Definition 8.1].
On account of (7.5), the family 
$\mathscr {X}_{s_0}$ deforming 
$\mathbb {X}^{\circ }$ is the 
$\mathcal {A}_{\mathrm {prin},{s_0}}$-family for 
$\check {\mathbb {X}}^{\circ }$, with 
$\bar {p}$ identifying the fibers of the two families. As mentioned in Remark 1.5, the partial compactifications of these families on the other hand are different. Since the uncompactified families agree, we have a choice to make here. Rietsch and Williams describe the Grassmannian in terms of a Newton–Okounkov body for the anticanonical divisor: the integral points of the Newton–Okounkov body give a basis of global sections for the anticanonical bundle. This is how we view the 
$\mathcal {A}$-side of the picture, so the relevant partial compactification and toric degeneration here is [Reference Gross, Hacking, Keel and KontsevichGHKK18]'s 
$\overline {\mathcal {A}_{\mathrm {prin},{s_0}} }$. Indeed, as the Grassmannian is separated, this toric degeneration can not be 
$\widehat {\mathscr {X} }_{s_0}$. The functions and valuations however come from 
$\mathscr {X}_{s_0}$, with 
$\bar {p}$ allowing us to identify the uncompactified families.
We complete the identification of the two pictures as follows. Fixing 
$q=1$ in [Reference Rietsch and WilliamsRW19, Equation (10.1)] gives the potential 
$W_{\text {MR}}|_{q=1}:\check {\mathbb {X}}^{\circ } \to \mathbb {C}$ on 
$\check {\mathbb {X}}^{\circ }$ rather than 
$\check {\mathbb {X}}^{\circ } \times \mathbb {C} ^{*}$. From the Gross–Hacking–Keel–Kontsevich potential 
$W_{\text {GHKK}}:\mathcal {X} \to \mathbb {C}$ (see [Reference Gross, Hacking, Keel and KontsevichGHKK18, p.506]) we obtain 
$w_{\text {GHKK}}:\mathbb {X}^{\circ } \to \mathbb {C}$ given as a sum of 
$\vartheta$-functions on 
$\mathbb {X}^{\circ }$. It pulls back to the Marsh–Rietsch potential on 
$\check {\mathbb {X}}^{\circ }$:
\[ \bar{p}^{*}\left({w_{\mathrm{GHKK}}}\right) = W_{\mathrm{MR}}|_{q=1}. \]Identifying potentials identifies the polytopes defined by these potentials:
\[ \bar{p}^{*}\left({\varGamma_{\mathrm{RW}}}\right)=\varXi_{\mathrm{GHKK}}. \]
Compare [Reference Rietsch and WilliamsRW19, Definition 10.10] and [Reference Gross, Hacking, Keel and KontsevichGHKK18, Equation 8.7]. Finally, on account of Remark 7.1, 
$\operatorname {Flow}=\left ({\bar {p}^{-1}}\right )^{*}$ identifies the 
$\mathbf {g}$-vector of a 
$\vartheta$-function on 
$\check {\mathbb {X}}^{\circ }$ with the valuation of the function: the 
$\mathbf {c}$-vector of 
$\left ({\bar {p}^{-1}}\right )^{*}\left ({\vartheta }\right )$ on 
$\mathbb {X}^{\circ }$. So, taking 
$\bar {p}: \check {\mathbb {X}}^{\circ } \to \mathbb {X}^{\circ }$ rather than 
$\bar {p}^{-1}: \mathbb {X}^{\circ } \to \check {\mathbb {X}}^{\circ }$, we also have
\[ \bar{p}^{*}\left({\Delta_{\mathrm{RW}}}\right) = \varXi_{\mathrm{GHKK}}. \]
See [Reference Rietsch and WilliamsRW19, Definition 8.2]. This explains from the [Reference Gross, Hacking, Keel and KontsevichGHKK18] point of view the equality of the polytopes 
$\varGamma$ and 
$\Delta$ in [Reference Rietsch and WilliamsRW19].
7.2 Del Pezzo surface of degree five
The point of this example is to indicate a potential connection between cluster duality for cluster varieties with coefficients and Batyrev duality for Gorenstein toric Fano varieties. Recall that Batyrev introduced a method for constructing mirror families of Calabi–Yau varieties in [Reference BatyrevBat94], taking families of anticanonical hypersurfaces in a pair of Gorenstein toric Fano varieties. The pair of Fanos are the toric varieties associated to a pair of (polar) dual reflexive polytopes, or equivalently to a reflexive polytope and its face-fan. As described in the introduction, outside of the toric world these two descriptions are inequivalent, and the one relevant here is the latter.
There is a natural bounded polytope 
$P\subset \mathcal {X} _{\varGamma ^{\vee }}^{\mathrm {trop}} \left ({\mathbb {R} }\right )$ we can associate to a finite type 
$\mathcal {A}$-cluster variety without frozen directions. First, we build a simplex in each chamber by taking the convex hull of the origin and the 
$\mathbf {g}$-vectors generating the chamber. Then we take 
$P$ to be the union of these simplices. After identifying 
$\mathcal {X} _{\varGamma ^{\vee }}^{\mathrm{trop}} \left ({\mathbb {R} }\right )$ with 
$M_{\mathbb {R} }^{\circ }$ by a choice of seed, if 
$P$ is convex, then it is a reflexive polytope whose unique integral interior point is the origin.Footnote 13 The 
$\mathbf {g}$-fan is the face-fan of 
$P$. Suppose we compactify the 
$\mathcal {A}$-cluster variety using 
$P$ and produce a toric degeneration using [Reference Gross, Hacking, Keel and KontsevichGHKK18]'s 
$\mathcal {A}_{\mathrm {prin},{s}}$ construction, having central fiber 
${\operatorname {TV}({P})}$. Then 
${\operatorname {TV}({P})}$ is a Gorenstein toric Fano variety, and the central fiber 
${\operatorname {TV}({{{\Delta ^{+}} }})}$ of 
$\widehat {\mathscr {X} }_{s}$ is the Batyrev dual Gorenstein toric Fano. While the general fibers of 
$\widehat {\mathscr {X} }_{s}$ are non-separated, and a fortiori not Fano, we are really interested in a family of hypersurfaces in these fibers. These hypersurfaces may remain well-behaved away from the central fiber. This observation will be explored and generalized in the sequel with M.-W. Cheung. Below we study the case of the del Pezzo surface of degree five. This surface can be realized as a compactification of the 
$\mathcal {A}$-cluster variety associated to the 
$A_2$ quiver (see [Reference Gross, Hacking, Keel and KontsevichGHKK18, Example 8.31]). We review this construction. For more details on the degree five del Pezzo surface we refer the reader to [Reference DolgachevDol12, § 8.5].
The del Pezzo surface of degree five 
$S$ is isomorphic to a surface obtained by blow-up of the projective plane 
$\mathbb {P}^{2}$ at four points 
$q_1, q_2, q_3,q_4$ in general position. It is well-known that 
$S$ contains ten 
$(-1)$-curves, four corresponding to the exceptional divisors and six corresponding to the strict transforms of lines joining pairs of points, and the incidence graph of these curves is given by the Petersen graph.
Once we choose an anticanonical divisor consisting of curves forming a cycle, one can contract two non-consecutive curves to obtain a toric model of 
$S$. Without loss of generality, we can assume that the anticanonical cycle is the inner cycle in the Petersen graph. Considering Figure 7, we obtain the five toric models contracting the curves 
$\{ E_4, E_2\}$, 
$\{ E_2, \ell _{14} \}$, 
$\{ \ell _{14}, \ell _{24} \}$, 
$\{ \ell _{24}, \ell _{23} \}$ and 
$\{ \ell _{23}, E_4\}$. Here, 
$E_i$ stands for the exceptional divisor associated to the point 
$q_i$ and 
$\ell _{ij}$ stands for the strict transform of the line in 
$\mathbb {P}^{2}$ joining 
$q_i$ and 
$q_j$. These models are isomorphic to the blow-up of 
$\mathbb {P}^{1}\times \mathbb {P}^{1}$ at one point and are related by performing an elementary transformation at one point lying on a curve of self-intersection zero in the cycle. For example, Figure 8 shows how the toric model associated to 
$\{ E_2, \ell _{14} \}$ can be obtained from the model associated to 
$\{ E_2, E_4\}$ by performing an elementary transformation at a point lying on 
$\ell _{34}$.
Figure 7. Petersen graph associated to the surface 
$S$.
Figure 8. Elementary transformation between two toric models of 
$S$.
Another important feature about the del Pezzo surface of degree five is that it is isomorphic to a linear section of the Grassmannian variety 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$ (see [Reference DolgachevDol12, Proposition 8.5.1]). We use this property to prove that the del Pezzo surface of degree five is a compactification of the 
$\mathcal {A}$-cluster variety constructed from a type 
$A_2$ quiver. Note that we can recover the defining equations of 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$ with respect to the Plücker embedding considering triangulations of the five-cycle, with Plücker coordinates associated to lines in the triangulations (see [Reference Fomin and ZelevinskyFZ02, p. 8]). Considering all possible mutations we obtain the equations:
\begin{align*} p_{13}p_{24}&=p_{23}p_{14}+p_{12}p_{34},\\ p_{14}p_{25}&=p_{15}p_{24}+p_{12}p_{45}, \\ p_{24}p_{35}&=p_{34}p_{25}+p_{23}p_{45}, \\ p_{13}p_{25}&=p_{12}p_{35}+p_{15}p_{23}, \\ p_{14}p_{35}&=p_{45}p_{13}+p_{15}p_{34}. \end{align*}
Now consider the variety 
$Y\subset \mathbb {P}^{9}$ defined by 
$V(p_{12}-p_{23}, p_{23}-p_{34}, p_{34}-p_{45}, p_{45}-p_{15})$ and take the intersection of 
$\operatorname {Gr}_2(\mathbb {C} ^{5}) \subset \mathbb {P} ^{9}$ with 
$Y$. The intersection, denoted by 
$T$, is defined by the following equations in 
$Y\cong \mathbb {P}^{5}$:
\begin{equation} \begin{aligned} p_{13}p_{24} & =p_{12}p_{14}+p_{12}^{2},\\ p_{14}p_{25} & =p_{12}p_{24}+p_{12}^{2},\\ p_{24}p_{35} & =p_{12}p_{25}+p_{12}^{2},\\ p_{13}p_{25} & =p_{12}p_{35}+p_{12}^{2},\\ p_{14}p_{35} & =p_{12}p_{13}+p_{12}^{2}. \end{aligned} \end{equation}
One verifies computationally that 
$T$ is a smooth irreducible surface. To construct the canonical divisor of 
$T$ we do the following. We consider 
$D_1=V(p_{12}-p_{23})$, 
$D_2=V(p_{23}-p_{34})$, 
$D_3=V(p_{34}-p_{45})$, and 
$D_4=V(p_{45}-p_{15})$ as divisors in 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$. Notice that all of them are linearly equivalent. In this way we have 
$T=\cap _{i=1}^{4}D_i$. Let 
$D=D_1+D_2+D_3+D_4$. We write the anticanonical divisor of 
$\operatorname {Gr}_2(\mathbb {C} ^{5})$ as 
$\sum _{ i\in \mathbb {Z}/5 \mathbb {Z}} D_{i,i+1}$, where 
$D_{i,j}=V(p_{ij})$. Note that the components here are also linearly equivalent to the 
$D_i$ above. Then by the adjunction formula
\begin{equation} K_T =(K_{\operatorname{Gr}_2(\mathbb{C} ^{5})}+D)|_{T} = \mathcal{O} _{\operatorname{Gr}_2(\mathbb{C} ^{5})}(-D_{i,j})|_T. \end{equation}
Therefore, 
$\omega _T\cong \mathcal {O} _T(-1)$ and then 
$-K_T$ is an ample divisor. Since all del Pezzo surfaces of degree five are isomorphic, we conclude that 
$T$ is isomorphic to 
$S$. So, without loss of generality we may assume that the equations of (7.6) define 
$S$.
Now, identifying Plücker coordinates with 
$\mathcal {A}$-cluster variables as follows
\begin{equation} A_1:=p_{13},\quad A_2:=p_{14},\quad A_3:=p_{24},\quad A_4:=p_{25},\quad A_5:=p_{35}, \end{equation}
and taking the divisor 
$H=V(p_{12})$, it follows from (7.7) that 
$H$ is an anticanonical divisor on 
$S$. Then 
$U=S\backslash H$ is a log Calabi–Yau surface defined by the equations 
$A_{i-1}A_{i+1}=A_i+1$ for 
$i\in \mathbb {Z}/5\mathbb {Z}$. Note that such equations are the exchange relations for the 
$\mathcal {A}$-cluster variety obtained from a type 
$A_2$ quiver.
We can describe the above, and deformations of it, using the notion of a positive polytope, see [Reference Gross, Hacking, Keel and KontsevichGHKK18, Definiton 8.6].
Warning: To be in harmony with [Reference Gross, Hacking, Keel and KontsevichGHKK18, Example 8.31], we flip the orientation of the 
$A_2$ quiver relative to previous examples, where orientation was chosen for ease of comparison with [Reference Fomin and ZelevinskyFZ07, Tables 1–4]. This change is the source of the difference in wall placement between Figures 1 and 9.
Figure 9. The 
$A_2$ scattering diagram and the polytope 
$P$. The integral points of 
$P$, shown as filled circles, correspond to 
$\vartheta$-function generators of a graded algebra. The scattering functions shown include principal coefficients. To recover the 
$\mathbf {g}$-fan, simply forget the scattering functions and wall directions.
The cones of the 
$\mathbf {g}$-fan are domains of linearity of 
$\mathcal {X} ^{\mathrm{trop}} \left ({\mathbb {R} }\right )$. So, we can take the convex hull of the 
$\mathbf {g}$-vectors that generate each cone together with the origin. We define the polytope 
$P$ as the union of these convex hulls, see Figure 9.
To describe the family of projective varieties, we view the integral points of 
$P$ and its dilations as giving a 
$\vartheta$-function basis for a graded 
$R$-algebra, where 
$R= \mathbb {C} [t_1,t_2]$. Following [Reference Gross, Hacking, Keel and KontsevichGHKK18, Example 8.31], we call the 
$\vartheta$-function associated to the interior point 
$\vartheta _0$, and the remainder 
$\vartheta _1, \ldots , \vartheta _5$ starting with the point at 
$\left ({1,0}\right )$ and proceeding counter-clockwise. Observe that for 
$i\neq 0$, 
$\vartheta _i$ is the extension of 
$A_i$ (from (7.8)) to 
$\mathcal {A}_{\mathrm {prin}}$. We take 
$\vartheta _0$ to be a homogenization variable, much like 
$p_{12}$ in (7.6). The graded 
$R$-algebra is generated in degree one by these six 
$\vartheta$-functions. The relations between degree one generators are given by homogenizing the wall-crossing relations (i.e. the mutation relations in 
$\mathcal {A}_{\mathrm {prin}}$), giving the following:
\begin{align*} \vartheta _1 \vartheta _3 &= t_1 \vartheta _0 \vartheta _2 + \vartheta _0^{2},\\ \vartheta _2 \vartheta _4 &= t_2 \vartheta _0 \vartheta _3 + \vartheta _0^{2},\\ \vartheta _3 \vartheta _5 &= \vartheta _0 \vartheta _4 + t_1 \vartheta _0^{2},\\ \vartheta _4 \vartheta _1 &= \vartheta _0 \vartheta _5 + t_1 t_2 \vartheta _0^{2},\\ \vartheta _5 \vartheta _2 &= \vartheta _0 \vartheta _1 + t_2 \vartheta _0^{2}. \end{align*}
(Again, see [Reference Gross, Hacking, Keel and KontsevichGHKK18, Example 8.31].) The central fiber in this family, i.e. when 
$t_1=t_2=0$, is simply the toric variety 
${\operatorname {TV}({P})}$ associated to 
$P$. Observe that 
$P$ is the polytope 5a in [Reference Cox, Little and SchenckCLS11, § 8, Table 2], and 
${\operatorname {TV}({P})}$ the associated Gorenstein toric Fano.
Meanwhile, the 
$\mathbf {g}$-fan also gives us a compactification and toric degeneration of the 
$\mathcal {X}$-variety associated to the 
$A_2$ quiver. This is described in § 1.5, albeit for the opposite orientation of this quiver.Footnote 14 In this case the central fiber is the toric variety 
${\operatorname {TV}({{{\Delta ^{+}} }})}$ associated to the underlying fan 
${{\Delta ^{+}} }$ of Figure 9. Note that 
${\operatorname {TV}({{{\Delta ^{+}} }})}$ is the del Pezzo surface of degree seven. It is straightforward to verify that 
${{\Delta ^{+}} }$ is the normal fan of the polytope 7a of [Reference Cox, Little and SchenckCLS11, § 8, Table 2]. The polytopes 5a and 7a are polar dual, and the central fibers 
${\operatorname {TV}({P})}$ and 
${\operatorname {TV}({{{\Delta ^{+}} }})}$ of the two families are Batyrev dual toric Fanos. Our hope, which we will explore in further work with M.-W. Cheung, is that general fibers of the two families have the right to be called Batyrev dual as well. We formalize this hope with the following question.
Question 7.2 Does there exist a family 
$\mathcal {F}_{\mathbf {t}}$ of Calabi–Yau hypersurfaces in 
$\widehat {\mathcal {X} } _{\mathbf {t}}$ satisfying the following:
(i)
$\mathcal {F}_{\mathbf {t}}$ degenerates in $\widehat {\mathscr {X} }_{s}$ to a family of anticanonical hypersurfaces in ${\operatorname {TV}({{{\Delta ^{+}} }})}$; and(ii) the Calabi–Yau hypersurfaces of
$\mathcal {F}_{\mathbf {t}}$ are mirror to generic anticanonical hypersurfaces in the minimal model for $\mathcal {A} _{\mathbf {t}}$ determined by $P$?
Acknowledgements
We are deeply grateful to Bernhard Keller for pointing us to the new result [Reference Cao and LiCL20, Theorem 6.2] of Peigen Cao and Fang Li, which is essential for our Theorem 6.2. We would further like to thank Man-Wai Cheung, Chris Fraser, Sean Keel, Konstanze Rietsch, Harold Williams, Lauren Williams and Tony Yue Yu for enlightening discussions during the preparation of this paper. We are grateful to Melissa Sherman-Bennett for pointing out misprints in an earlier version of this paper. The third and fourth authors additionally extend their gratitude to Reyna Sánchez for hospitality and support during the preparation of this article.
