What is the element extraction method?

Mesh generation is considered a design problem and can be resolved recursively into the atomic design and a sub-design problem (Zeng and Cheng, Reference Zeng and Cheng1991; Zeng and Yao, Reference Zeng and Yao2009). The quad mesh design should satisfy the following conditions: (1) each element is a quadrilateral; (2) the inner corner of each element should be between 45° and 135°; (3) the aspect ratio (the ratio of opposite edges) and taper ratio (the ratio of neighboring edges) of each quadrilateral should be within a predefined range; (4) the transition from a dense mesh to a coarse mesh should be smooth (Zeng and Cheng, Reference Zeng and Cheng1991; Zeng and Yao, Reference Zeng and Yao2009). Zeng and Cheng (Reference Zeng and Cheng1993) proposed a knowledge-based method, FREEMESH, to recursively extract quadrilateral elements following a domain boundary until the remaining boundary becomes a quadrilateral element, based on the recursive logic of design (Zeng and Cheng, Reference Zeng and Cheng1991). In FREEMESH, the atomic design is to generate an element in a specified boundary region, while the corresponding sub-design problem is to generate a good quality mesh over the domain by cutting the generated element from the original domain (see Fig. 1).

Fig. 1. Quad mesh generation process (Yao et al., Reference Yao, Yan, Chen and Zeng2005).

In extracting elements one by one, three types of element extraction rules (i.e., adding one, two, and three edges) are defined to construct a good quality element (see Fig. 2). The challenge is for these rules to generate a good quality element around the current domain boundary while guaranteeing that these design rules are still applicable to the remaining domain for the subsequent construction of good elements.

Fig. 2. Three primitive generation rules (Zeng and Cheng, Reference Zeng and Cheng1993).

How is the element extraction method smart?

A smart system can make adaptive decisions corresponding to various environmental situations. For an element extraction method, the environment is domain boundaries, which keep changing throughout the entire mesh generation process. Even with a simple domain, the initial boundary can evolve into many complex intermediate boundary shapes. Following the process specified in Figures 1 and 3 shows an example element extraction process, where the initial boundary is shown in Figure 3 (1) and the final mesh is shown in Figure 3 (10). The intermediate boundaries could include various situations, which are not predictable.

Fig. 3. Changes of intermediate boundary shapes: all boundaries are represented in red lines from (2) to (9).

The smartness of element extraction systems lies in how various complex boundary shapes are processed by the three element-extraction rules shown in Figure 2. First, each edge in any boundary shape can be processed by one of those three extraction rules. The three rules define three kinds of patterns for a selected boundary edge V ₁V ₂ in a domain, as specified in solid lines in Figure 2a–c. The three rules are sufficient to process any environmental situation (boundary shapes). Secondly, among all the boundary edges, the system would be able to smartly pick up one edge and a corresponding rule to generate an element. In Figure 4, V ₁, V ₂, V ₃ and V ₄ are all the same for different environment situations while different rules are preferred if more conditions are considered from the environment. For instance, the boundary edge V ₁V ₂ is selected as the target edge in Figure 4a–f; the extraction rule in Figure 2c is applied in situations in Figure 4a,c,d; the extraction rule in Figure 2b is applied in situations in Figure 4b,e; and the last extraction rule in Figure 2a is applied in the situation in Figure 4f. This example demonstrates that it is challenging to select a proper rule even considering two more connected boundary points.

Fig. 4. Challenges in selecting a proper rule to extract an element for an edge V ₁V ₂.

Thirdly, when rules in Figure 2a or Figure 2b are selected for a boundary edge, the positioning of the newly added point(s) will be smartly determined according to its local surrounding environment situations so that a good element can be generated while the remaining boundary does not create an impossible situation for the three rules to process. For instance, Figure 5 shows the challenges in positioning the new point in extracting a new element for two base situations in Figure 4b,f. The red lines represent different remaining boundary shapes to form a complete domain boundary. Although Points B, B1, and B2 can form a better element in each situation, Points A, A1, and A2 are the optimal options due to the trade-off of quality of the element quality and the remaining boundary. The coordinates of newly added point(s) are adapted to various remaining boundary shapes.

Fig. 5. Trade-off between qualities of an extracted element and the remaining boundary. (a–c) correspond to the situation in Figure 4b; (d) and (e) correspond to the situation in Figure 4f. Points A, A1, and A2 form better elements than B, B1, and B2.

In summary, the smart element extraction process is enabled by a knowledge-based reasoning process, where the three basic rules shown in Figure 2 can process complex 2D domain boundaries recursively. The method smartly extracts elements one by one adaptive to the situations implied in the current domain boundary.

Architecture similarity between element extraction and reinforcement learning

The element extraction process in Figure 1 can be generalized into architecture, as shown in Figure 6. The mesh generator applies the extraction rules to a domain boundary and generates an element; the domain boundary will be updated by removing the extracted element, which is scored for its quality. This recursive process continues until mesh elements fill the domain. However, one must specify the mesh generator's extraction rules in advance. By formulating this process into an RL problem, the machine itself can automatically learn these extraction rules (i.e., the mesh generator).

Fig. 6. Element extraction architecture.

Reinforcement learning (RL) is a technique that enables an agent to learn from the interactions with its environment by trial-and-error via reward feedback from its actions and experiences (Kaelbling et al., Reference Kaelbling, Littman and Moore1996; Sutton and Barto, Reference Sutton and Barto2018). The hypothesis behind RL is that all the goals can be represented by the maximization of the expected cumulative reward. As is shown in Figure 7, the agent, at each time step t, observes a state S _t from the environment, and conducts an action A _t applied to the environment. The environment responds to the action and transits into a new state S _t+1. It then reveals the new state and provides reward R_t to the agent. This process forms an iteration and repeats until a given condition is satisfied (i.e., the RL problem is solved).

Fig. 7. Architecture of reinforcement learning (Sutton and Barto, Reference Sutton and Barto2018).

It can be seen from Figures 6 and 7 that element extraction and reinforcement learning bear a similar framework of problem-solving. As illustrated in Figure 8, the mesh generation process shown in Figure 6 has the same architecture as the RL process does, and the mesh generation process can be seen as an instance of an RL process. In the context of element extraction, the agent is a mesh generator; the environment is a domain boundary to mesh; the state of the environment consists of a set of focused vertices and edges in the boundary; an action to take by the agent is to extract an element from an edge in the state; the reward is the combination of qualities of both the current extracted element and the remaining boundary; a policy of the agent guides the selection of a specific action; the agent's goal is to maximize the aggregated rewards – the total quality of all extracted elements and their corresponding boundaries.

Fig. 8. Element extraction process as reinforcement learning.

Formulation of the element extraction problem in the reinforcement learning framework

In RL, how the learning agent behaves (to select an action at each state) is described as the agent's policy. Mathematically, a policy is represented as a probability distribution over all possible actions at each state, denoted as π(a|s). A state's value is the expected future rewards starting at that state, which determines how beneficial for the agent to enter that state. A value function is designed to estimate the value for each state. The value function $V^\pi ( s )$ of a state S _t under a policy π is formally denoted as, $V^\pi ( s ) = E[ {G_t{\rm \vert }S_t = s, \;\;\pi }] , \;$ for any s ∈ S , where S is a set of environment states; and G _t is a discounted sum of the sequence of rewards achieved over time, which is calculated by,

(1)$$G_t = \mathop \sum \limits_{k = t + 1}^T \gamma ^{k-t-1}R_k, \;$$

where 0 ≤ γ  ≤ 1 is a discount rate, and T is a final time step. The value function of an action at a state under a policy can be expressed as $Q^\pi ( {s, \;\;a} ) = E[ {G_t{\rm \vert }S_t = s, \;A_t = a, \;\;\pi }].$ These value functions can be estimated from experience with different methods. Policy and value functions are essential for almost every RL algorithms.

Mathematically, the RL is a sequential decision-making process, which can be formalized as a Markov Decision Process (MDP) consisting of a set of environment states S, a set of possible actions A(s) for a given state s, a set of rewards R, and a transition probability P(S _t+1 = s', R _t+1 = r|S _t = s, A _t = a) where s', s  ∈ S, a ∈ A(s), r ∈ R, s' is the new state at t + 1 and r is the reward after action a at state s. The transition probability indicates that the current state is only dependent on the preceding state and action, the so-called Markov property, thereby defining the MDP dynamics. This requires that the state contain information about the past interactions that could distinguish the future and the present. The MDP and agent then produce a sequence [S ₀, A ₀, R ₀, S ₁, A ₁, R ₁, S ₂, A ₂, R ₂, … ]. In general, the MDP framework can be applied to various problems in many ways because of its flexibility. Once a goal is represented as agents’ choices, the basis for choice from the environment, and a reward measurement of the goal, it can be formalized as an RL problem. Existing reinforcement learning algorithms can be categorized into three types: policy-based, value-based, and model-based methods (Kaelbling et al., Reference Kaelbling, Littman and Moore1996; Sutton and Barto, Reference Sutton and Barto2018), which learn policies, value functions, and models (Grondman et al., Reference Grondman, Busoniu, Lopes and Babuska2012). Deep reinforcement learning (DRL) intends to make behavioral decisions through learning from the experience of interacting with the environment and from the evaluative feedback (Littman, Reference Littman2015).

Mathematically, as RL does, the element extraction process can also be represented as an MDP, which consists of a set of boundary environment states S, a set of possible actions A(s) in state s to form an element for each boundary state, a set of rewards R, and a state transition probability P(s', r|s, a). The extraction process will produce a sequence [S ₀, A ₀, R ₀, S ₁, A ₁, R ₁, S ₂, A ₂, R ₂, … ], where the notations are explained as follows:

• t: denotes the index associated with the time step of element extraction;

• S _t: the partial boundary of the domain (at time t) from which the tth element will be extracted;

• A _t: the action to produce the tth extracted element, which consists of four vertices of the extracted element.

This process shows the natural alignment of the element extraction method with reinforcement learning.

Correspondingly, the three rules, which are used to extract elements in Figure 2, can be viewed as three actions: (a) to add two new vertices and three edges; (b) to add one new vertex and two edges; (c) to add just one edge. The determination of which rule to apply and especially where to position a candidate vertex to form a high-quality element is highly challenging because the position of a new vertex has substantial impacts on the quality of meshing in the future steps. These actions address the two questions raised in Section “How can the element extraction system be smartly evolving and designed?”.

In this work, we focus on using RL to select the optimal position of a candidate vertex, and the action is defined as locating a vertex position. In this way, the action space could be a two-dimensional continuous domain. The policy that needs to be learned with RL is the element extraction rule, which maps a state to an action (positioning the new vertex). The full state of the environment at time t would consist of all boundary vertices at the time. However, not all vertices are equally useful for extracting a new element. Zeng and Cheng (Reference Zeng and Cheng1993) identified a small set of vertices on the current boundary, which are highly relevant to constructing a new element. We select this partial boundary to represent the state, making computing much more efficient. This selected partial boundary denoted as S _t, is composed of four parts (1) a reference point, P ₀, which is a vertex selected from the current boundary and will be used as the relative origin for the new element to be constructed and extracted; (2) n neighboring vertices in the right side, where n = 2 in this paper; (3) n neighbor vertices in the left side, where n = 2; (4) three neighboring points $P_{\theta _1}$, $P_{\theta _2}$, and $P_{\theta _3}$ in the fan-shaped area θ ₁, θ ₂, and θ ₃ with radius d, as shown in Figure 9. This partial boundary is denoted as:

(2)$$S_t = \{ P_{l2}, \;\;P_{l1}, \;\;P_0, \;{\rm \;}P_{r1}, \;\;P_{r2}, \;\;P_{\theta _1}, \;P_{\theta _2}, \;P_{\theta _3}\} , \;$$

which is still a high dimensional continuous domain, but its dimension is significantly reduced from the full boundary. We treat this partial boundary as the state partially observed by the agent (Kaelbling et al., Reference Kaelbling, Littman and Moore1996).

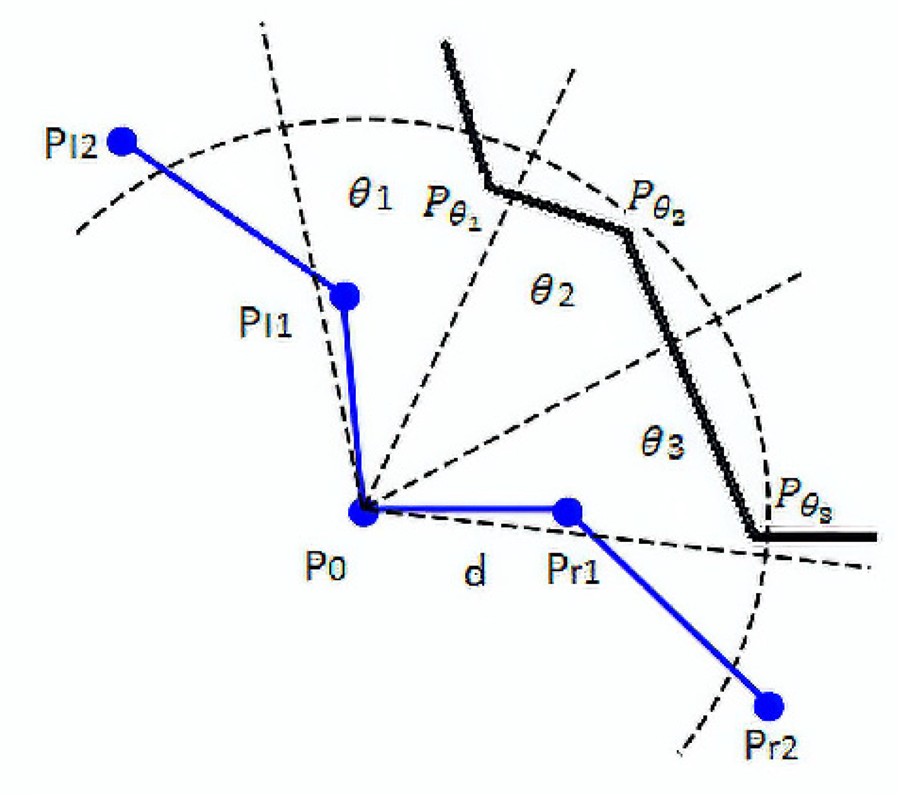
Fig. 9. Partial boundary.

Regarding reward, we define it as the combination of qualities of both the extracted element and the remaining boundary because their trade-off is essential to the overall quality of the final mesh. The reward details will be defined in Section “Reward function”.

Regarding the agent's policy and the value function of a state (or action under a state), as discussed earlier, the position of a new vertex for a new element has substantial impacts on the quality of meshing in the future steps; it is highly challenging to find an optimized policy to locate the vertex position and to find a reasonable estimation of that position. Both an optimal policy and the value function are unknown to the agent but can be approximated with a parameterized function by learning from experience. For this reason, the advantage actor-critic method is used in this paper.

A2C

The RL problem is to learn how to select an action at each state over time to maximize the accumulated reward G _t, which is a discounted sum of the sequence of rewards achieved over time, as shown in Eq. (1). Actor-critic is a subclass of policy-gradient methods, which learns approximations to both policy and value functions (Grondman et al., Reference Grondman, Busoniu, Lopes and Babuska2012; Sutton and Barto, Reference Sutton and Barto2018). Policy-gradient methods directly optimize an agent's actions without consulting a value function. Policy-gradient methods are via learning a parameterized policy $\pi _\theta$, where θ is the policy's parameter vector. The probability that an action a has been taken in state s at time t with policy parameter θ is represented as π(a|s, θ) = Pr{A _t = a|S _t = s, θ _t = θ}. The general idea is to increase the probability of actions being taken in each state when they have high optimality. The performance of the policy can be denoted as ${\cal J}( \theta ) = V^{\pi _\theta }( s )$, which is calculated by

(3)$$V^{\pi _\theta }( s ) = \mathop \sum \limits_{a\in A} \pi _\theta ( a\vert s) \mathop \sum \limits_{{s}^{\prime}\in {\boldsymbol S}} \Pr ( {{s}^{\prime}\vert s, \;\;a} ) \{ {r + {\rm \;}\gamma V^{\pi_\theta }( {{s}^{\prime}} ) }\} , \;$$

when every episode starts in state s. r is the reward after action a at state s. According to the policy gradient theorem, the gradient of this performance is denoted as,

(4)$$\nabla _\theta {\cal J}( \theta ) \propto \mathop \sum \limits_s d( s ) \mathop \sum \limits_a Q^\pi ( {s, \;\;a} ) \nabla _\theta \pi ( {a{\rm \vert }s, \;\theta } ) , \;$$

where d(s) is a state distribution under policy $\pi , \;\;Q^\pi ( {s, \;\;a} )$ is state-action value function under policy π. The gradient-ascent algorithm improves the policy as

(5)$$\theta _{t + 1} = \theta _t + \alpha \nabla _\theta {\cal J}( \theta ) , \;$$

where α is a step size.

We can estimate the performance gradient using Monte Carlo sampling, which is proportional to the actual gradient. The gradient can then be represented as,

(6)$$\nabla _\theta {\cal J}( \theta ) \;\propto E\left[{\mathop \sum \limits_a Q^\pi ( {S_t, \;\;a} ) \nabla_\theta \pi ( {a{\rm \vert }S_t, \;\theta } ) } \right] = E[ {G_t\nabla_\theta {\rm ln}\pi ( {A_t{\rm \vert }S_t, \;\theta } ) }] , \;$$

where S _t and A _t are sampled state and action at time t, G _t is the return after t, and; E[.] is the expected value of the expression with random variables S _t and A _t in the Monte Carlo sampling. The gradient-ascent algorithm could be,

(7)$$\theta _{t + 1} = \theta _t + \alpha G_t\nabla _\theta {\rm ln}\pi ( {A_t{\rm \vert }S_t, \;\theta } ).\;$$

Because the variance of return is high in Monte Carlo policy gradient, the learned value function can reduce the gradient variance and provide an informative direction for policy optimization. The actor represents the learned policy, whereas the critic is the learned value function. The critic estimates the state-action value function as an approximator with parameters w, that is $\hat{Q}^{\pi _\theta }( {s, \;\;a; \;w} ) \;\approx Q^{\pi _\theta }( {s, \;\;a} )$, where $Q^{\pi _\theta }( {s, \;a} )$ is the state-action value function using policy $\pi _\theta$. Correspondingly, $V^{\pi _\theta }( s )$ can be estimated as $\hat{V}^{\pi _\theta }( {s; \;w} ) = E_{a\sim \pi }[ {{\hat{Q}}^{\pi_\theta }( {s, \;\;a; \;w} ) }]$. By introducing an advantage function to the critic,

(8)$${\rm \;}A^{\pi _\theta }( {s, \;{\rm \;}a} ) = Q^{\pi _\theta }( {s, \;a} ) -V^{\pi _\theta }( s ) , \;$$

In this way, the policy optimization will be more directional. It leads to the advantage actor-critic (A2C) method. The gradient is changed to the following:

(9)$$\nabla _\theta {\cal J}( \theta ) \propto E\left[{\mathop \sum \limits_a {\rm }A^{\pi_\theta }( {s, {\rm \;}a} ) \nabla_\theta {\rm ln}\pi ( {a{\rm \vert }S_t, \;\theta } ) } \right].$$

The actor updates the policy parameters by

(10)$$\theta _{t + 1} = {\rm \;}\theta _t + \alpha A^{\pi _\theta }( {S_t, \;\;A_t} ) \nabla _\theta {\rm ln\;}\pi ( {A_t{\rm \vert }S_t, \;\theta } ).$$

The critic updates its weights by

(11)$$w_{t + 1} = {\rm \;}w_t + \beta A^{\pi _\theta }( {S_t, \;\;A_t} ) \nabla _w\hat{V}^{\pi _\theta }( {s; \;w} ).$$

By the definition of the value function $V^{\pi _\theta }( s ) , \;$ advantage function $A^{\pi _\theta }( {S_t, \;\;A_t} )$ can be estimated as

(12)$$\delta _t = R_{t + 1} + \gamma \hat{V}^{\pi _\theta }( {S_{t + 1}; \;w} ) -\hat{V}^{\pi _\theta }( {S_t; \;w} ) , \;$$

which is also called temporal difference (TD) error for state value at time t. For a more detailed description of the A2C model please refer to (Sutton and Barto, Reference Sutton and Barto2018). For the specific description of our A2C RL model for mesh, please refer to the next subsection. Advantage Actor-Critic (A2C) network is a class of A2C model, in which an artificial neural network is used as an approximator for the policy or the value function. We use this approach for mesh generation.

A2C RL network for element extraction

In the proposed self-learning element extraction system, the A2C network is responsible for the preliminary sampling of the element extraction rules (a set of three rules in Figure 2). Its network structure is shown in Figure 11. The actor and critic are the two heads of the network and share the same input and hidden layer. The input is the partial boundary S _t. The value head of the critic is the estimation of the state-value function. The policy head of the actor will output two variables (i.e., two means) to form two normal distributions in which both the variances are set to 1, to sample the coordinates, x and y, of the candidate point, respectively. The training process of the A2C network is illustrated in Algorithm 1. For a given 2D domain environment, the A2C network updates the parameters of the actor and the critic during each episode using the temporal difference (TD) method [i.e., Eq. (12)]. Each episode terminates when the domain is full of quadrilateral elements or exceeds the maximum step. The episode number M indicates the maximum iteration. The maximum step in each episode is defined by T. Symbol λ is the discount factor during reward accumulation.

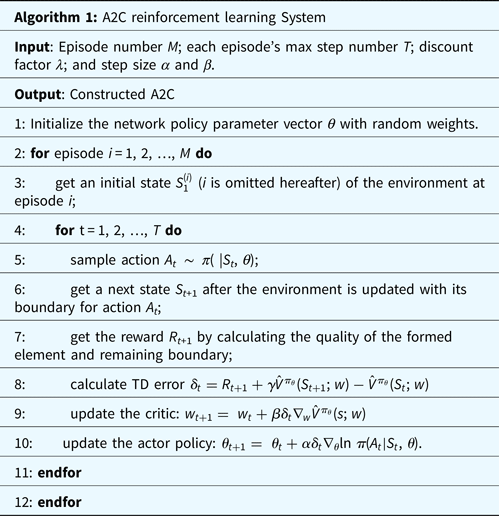
Fig. 11. A2C network structure. In general, the actor will simulate three primitive rules, as shown in Figure 2a–c. In the current implementation, the extraction rule in Figure 2a is not considered, and it will be implemented in the next version of the system.

State representation

The state is the actor's observation of the environment, which is defined as a partial boundary S _t, expressed as Eq. (2). Two fundamental steps are needed to determine which part of the boundary is considered the state: (1) to identify the reference point P ₀ from the existing boundary; and (2) to find the remaining points according to Eq. (2). A new element will be extracted around this formed partial boundary. First, the reference point is calculated by iterating all the points on the boundary, computing the angle of each point formed by its left and right connected points, and selecting the point having the least angle as the P ₀. Then, the other points in S _t will be determined by Eq. (2). The absolute coordinates of all points selected for representing a state will be transformed into a new coordinate system that assumes the reference point P ₀ as the origin, and the vector from the reference point to the first neighboring point along the counter-clock direction as the unit vector, along the positive direction of the x-axis (Yao et al., Reference Yao, Yan, Chen and Zeng2005). The transformation (i.e., rotation, scaling, and transit) from the original coordinate system Oxy to the new one O'x'y' is shown in Figure 12, and can be represented as:

$$\eqalign{\left({\matrix{ {{x}^{\prime}} \cr {\matrix{ {{y}^{\prime}} \cr 1 \cr } } \cr } } \right) &= \left[{\matrix{ {{\rm cos}\;\theta } & {{\rm sin}\;\theta } & 0 \cr {-{\rm sin}\;\theta } & {{\rm cos}\;\theta } & 0 \cr 0 & 0 & 1 \cr } } \right]\;\;\left[{\matrix{ {\displaystyle{1 \over d}} & 0 & 0 \cr 0 & {\displaystyle{1 \over d}} & 0 \cr 0 & 0 & 1 \cr } } \right]\;\;\left[{\matrix{ 1 & 0 & {-x_0} \cr 0 & 1 & {-y_0} \cr 0 & 0 & 1 \cr } } \right] \cr &\quad \times \left({\matrix{ x \cr {\matrix{ y \cr 1 \cr } } \cr } } \right),} \;$$

(13)$$d = \sqrt {{( {x_0-x_{r1}} ) }^2 + {( {y_0-y_{r1}} ) }^2}.$$

Fig. 12. Coordinate transformation.

Reward function

The actor will receive reward feedback from the environment to indicate how good the performed action is at the current state S _t, which the environment in RL refers to as the mesh domain boundary. The reward function is defined as follows:

1. 1) if the point (action) is outside the domain, the reward is set to be −0.1;

2. 2) if the generated element has straddled segments with itself or other elements, as shown in Figure 13, the reward is set to be −0.1;

3. 3) if the element has no situation with (1) and (2), the reward is the combination of current ith element quality $\eta _i^e$ and the quality of the remaining boundary $\eta _i^b$, which is calculated by $\sqrt {\eta _i^e \ast \eta _i^b }$. The element quality $\eta _i^e$ is measured by both its edge quality and angle quality, and calculated as follows, which are adapted from (Zeng and Yao, 2009),

   (14)$$\eta _i^e = \sqrt {q^e\ast q^a} , \;$$
   (15)$$q^e = \root 4 \of {\mathop \prod \limits_{\,j = 1}^4 {\left({\displaystyle{{l_j} \over {\sqrt {A_i} }}} \right)}^{{\rm sign}\left({\sqrt {A_i} -l_j} \right)}} , \;$$
   (16)$$q^a = \root 4 \of {\mathop \prod \limits_{\,j = 1}^4 \left({1-\displaystyle{{\vert {a_j-90} \vert } \over {90}}} \right)} , \;$$

where q ^e refers to the quality of edges of this element; l _j is the length of the jth edge of the element; A _i is the area of the ith element; q ^a refers to the quality of the angles of the element; and a _j is the degree of jth inner angle of the element. The quality $\eta _i^e$ will range from 0 to 1, which is better if greater. Examples of various element qualities are shown in Figure 14.

Fig. 13. Invalid situations of the element. P ₀ is the reference point, and P is the newly generated point.

Fig. 14. Different quality of elements.

The quality of remaining boundary, $\eta _i^b$, is calculated as follows,

(17)$$\eta _i^b = \sqrt {\mathop \prod \limits_{k = 1}^2 \left({\displaystyle{{{\rm Min}( {\theta_k, \;60} ) } \over {60}}} \right)} , \;$$

where θ _k refers to the degree of the kth generated angle, as shown in Figure 15. The quality $\eta _i^b$ also ranges from 0 to 1, which the higher value is, the better.

Fig. 15. New boundary angles.

Finally, we have the reward function as

(18)$$R_t = \left\{{\matrix{ {-0.1, \;\;{\rm if\;the\;generated\;point\;is\;outside\;the\;domain\;or}} \hfill \cr {\;{\rm the\;formed\;elements\;has\;straddled\;segments}; \;} \hfill \cr {\sqrt {\eta_i^e \ast \eta_i^b } , \;\;{\rm otherwise}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \hfill \cr } } \right.$$

To have a negative reward prevents the actor from performing inappropriate actions and generating invalid elements. Once the actor generates a valid element, it will immediately receive a reward value to tell how good that action is. This is a stepwise reward signal, which smoothly guides the actor to achieve the final goal. The reason to consider both the quality of the current element and the remaining boundary is that the actor needs to learn the trade-off between them to achieve an overall good mesh quality and complete the meshing task.

Actor representation

In a fully observable MDP, the agent observes the true state of the environment at each time t and acts according to a parameterized policy $\pi _\theta$. The actor constantly chooses actions and produces the best one for a given environmental state S _t overtime. Typically for type (b) action shown in Figure 2, the selected action A _t (line 5 of Algorithm 1) is to sample a point P _t within a specified area with the reference point P ₀ as the center. The selection is sampled from the parameterized policy, $A_t = P_t\sim \;\pi _\theta ( {s_t} )$. Finally, a new element is formed by four points, P _t, P _l1, P ₀, and P _r1, after the environment receives the point P _i.

The actor will also update (line 10 of Algorithm 1) the policy distribution at each time step concerning the parameter vector θ by using the sampled policy gradient:

(19)$$\nabla _\theta {\cal J}( {\pi_\theta } ) = {\rm \;}\mathop \sum \limits_{s, {\rm \;}a} [ {\nabla_\theta {\rm ln}\pi_\theta ( {a{\rm \vert }s} ) A^{\pi_\theta }( {s, {\rm \;}a} ) }] , \;$$

in which the direction $A^{\pi _\theta }( {s, \;{\rm \;}a} )$ is suggested by the critic (Section “Critic representation”).

FNN learning

The FNN module can learn from the acquired data from the experience extraction module to (1) decide which extraction rule should be applied and (2) determine the position of the newly generated point for a new element when necessary. Its network structure is shown in Figure 17 and mathematically described as follows (Yao et al., Reference Yao, Yan, Chen and Zeng2005):

(20)$$[ {{\rm typ}{\rm e}_i, \;\;P_i}] = f( [ P_{( {l, \;N} ) }, \;\;\ldots , \;P_{l2}, \;\;P_{l1}, \;\;P_0, \;\;P_{r1}, \;\ldots , \;\;P_{( {r, \;N} ) }, \;P_{\theta _1}, \;P_{\theta _2}, \;P_{\theta _3}]), \;$$

where type_i is the output type, as shown in Figure 18, which equals to one of the three values (i.e., 0, 1, and 2); P _i is the output point, consisting of (x _i, y _i); the input points are the state; and N equals 2 in this paper. The objective function used in FNN is denoted in the following formula:

(21)$${\rm MSE} = \displaystyle{1 \over n}\;\mathop \sum \limits_i^n [ {{( {x_i-\widetilde{{x_i}}} ) }^2 + {( {y_i-\widetilde{{y_i}}} ) }^2 + {( {{\rm typ}{\rm e}_i-\widetilde{{{\rm typ}{\rm e}_{\rm i}}}} ) }^2}] , \;$$

where $\widetilde{{x_i}}, \;\;\widetilde{{y_i}}, \;\;\widetilde{{{\rm typ}{\rm e}_{\rm i}}}$ are the FNN model output for ith input and MSE is the sum of the mean squared errors of these three variables.

Fig. 17. FNN module structure.

Fig. 18. Three types of outputs.

Through supervised learning, these element extraction rules are quickly acquired. The trained model can easily distinguish which rule should be applied under a specific environment state (input) and can generate a point (output) to form a high-quality element correspondingly. In this way, the experience is transferred from the slow trial-and-error A2C process to the fast one-step FNN. This process also simulates the human decision process as specified by Kahneman (Reference Kahneman2011).

Experience extraction

The experience extraction (EE) module intends to extract samples from existing elements derived from the A2C model for the FNN model training. A sample here is an instance of extraction rules, which is represented by the mappings from a state (input) to the output type and point, as shown in Figure 17. For the meshing result generated in each episode by the A2C, EE will check if they are qualified to be extracted as samples. Two criteria are hence used to determine the quality of samples: (1) element quality $\eta _i^e$ is used to filter out unqualified elements, and; (2) the number of total qualified elements in a meshing result of A2C should exceed a threshold η.

An example of the sample extraction process is shown in Figure 19. A trajectory stops when no valid elements are generated within the maximum step T. A trajectory from the A2C module is illustrated in Figure 19a, which meets the second criterion (e.g., η = 20) as previously mentioned. Each element has a property defined by a tuple <element id; element quality>, where Element id is defined as the order of the element extracted. Many mesh elements can be used for EE based on the first criterion (i.e., $\eta _i^e > 0.7$), such as elements 0, 1, 3, 7, 14, 15, 19 and 23 while some other elements will be excluded, such as 5, 12, 13, and 17. For example, element 15 with element quality 0.91 in Figure 19a is used to show the experience extraction process. Three types of extracted samples are shown in Figure 19b–d. Eight points are selected as the input for each rule type, where points P _l2, P _l1, P ₀, P _r1, and P _r2 (in red), are points in the boundary from left to right with P ₀ as the reference point, and points $P_{\theta _1}$, $P_{\theta _2}$, and $P_{\theta _3}$ (in blue) are collected from the fan-shaped area θ ₁, θ ₂ and θ ₃ with radius d=3 with the unit length being P ₀P _r1, as shown in Figure 9; and the output point is chosen as P _i (in black). It should be noted that the point P _r2 is P _i in Figure 19c and the point P _l2 is P _i in Figure 19d.

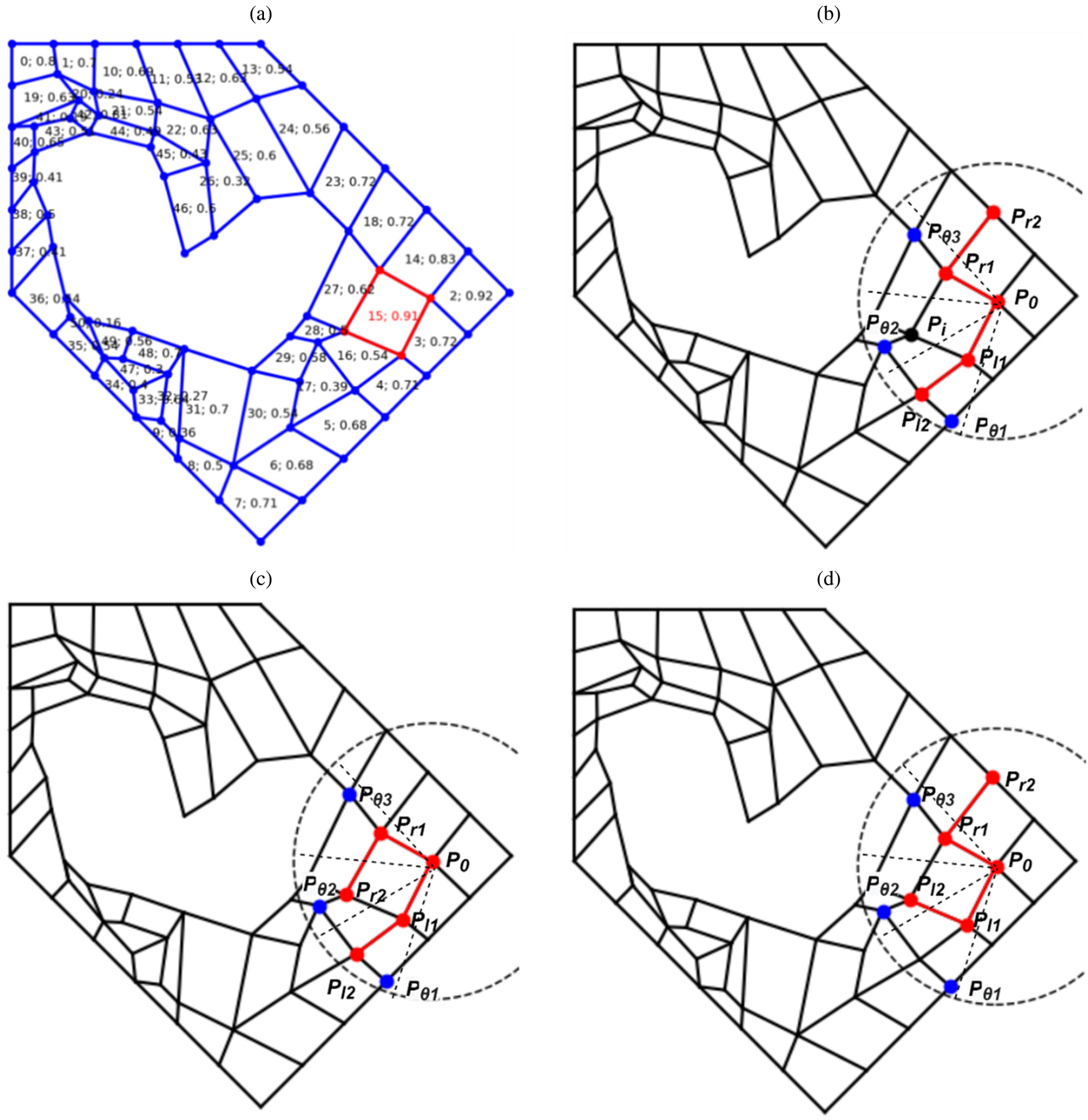
Fig. 19. Example of experience extraction of one element. In (a), each element has a tuple < element id; element quality > inside, where element id refers to the generation order of the element; and element quality is calculated by $\eta _i^e$; (b)–(d) show three types of patterns collected for training samples: (b) type 0; (c) type 1; (d) type 2.

The input-output pair for each training sample will be arranged according to Eq. (20). Ten training samples with the same reference point and output point are shown in Table 1. Those input-output pairs will be normalized and transformed from the original coordinate system Oxy to the new one O'x'y' (see Fig. 12). The transformation results are shown in Table 2. Consequently, all the sampling points’ coordinates are constructed into the same scale, and their relationships remain unchanged.

Table 1. Examples of extracted samples for element 15: the reference point P ₀(x ₀, y ₀) and output point P _i(x _i, y _i) are the same across these samples, respectively

Table 2. Examples of extracted samples in Table 1 after coordinate transformation following Eq. (13)

The extraction process will be repeated for all the qualified elements in an existing mesh to gather training samples. In this way, a large number of training data can be easily extracted with a single mesh. Furthermore, the training data contains sufficiently diversified situations in meshing any complex geometric domain.

Experimental domain boundaries

To provide comprehensive and various challenging situations for meshing, testing domain boundaries are chosen based on whether a boundary includes sharp angles, bottleneck regions, unevenly distributed segments, and holes. Hence, ten domain boundaries are selected to test the proposed system's performance (see Fig. 21 and Table 3).

Fig. 21. 10 experimental domains.

Table 3. Description of 10 testing domains

Mesh performance evaluation metrics

The meshing performance is measured by seven mesh quality metrics, including six geometric metrics and one topological metric, as shown in Table 4.

Table 4. Mesh quality metrics

Seven quality metrics are:

• • Singularity: the number of irregular nodes in the interior of a mesh. A node is considered irregular if it does not have four incident edges (Verma and Suresh, Reference Verma and Suresh2017);

• • Element quality η ^e: an index defined by Eq. (14);

• • |MinAngle-90|: the absolute differences between the smallest internal angle of an element and 90°; The smaller differences imply a better element;

• • |MaxAngle-90|: the absolute differences between the largest internal angle of an element and 90°; The smaller differences imply a better element;

• • Scaled Jacobian: the minimum Jacobian (Knupp, Reference Knupp2000) at each corner of an element divided by the lengths of the two edge vectors, which varies from minus one to plus one, where a higher value implies a better element; the negative value, typically, means the element is inverted;

• • Stretch: an index referring to the ratio between the shortest element edge length and the longest diagonal length;

• • Taper: the maximum absolute difference between the value one and the ratio of two triangles’ areas are separated by a diagonal within a quadrilateral element. The smaller value represents that the element becomes closer to a triangular shape.

All the metrics are averaged for all elements in the mesh, respectively. Some indices (e.g., scaled Jacobian, stretch, and taper) are calculated using Verdict software (Pébay et al., Reference Pébay, Thompson, Shepherd and Grosland2008).

Self-sampling and evolving of A2C and FNN training

There are two steps to complete the FNN network's training, as is shown in Figure 22. In Step 1, the A2C module will generate a mesh, covering only a partial domain to mesh. The generated mesh is then used to produce initial training samples for FNN. In Step 2, the FNN will be trained, applied, and further evolved.

Fig. 22. Model training process.

In this presented research, an empty domain, such as shown in Figure 23a, is used to generate elements without any prior knowledge about the parameters in the extraction rules in Figure 2. The A2C network can generate high-quality elements in the domain after some rounds of trial and error. Those high-quality elements in each episode of training can be extracted as training samples for the FNN network, which can be reused for the boundary of different shapes. Figure 23d–f are episodes that include sufficient good samples to train the FNN. An episode can be selected as a source for element sampling if two criteria are met: $\eta _i^e$ > 0.7 and η > 20, as introduced in Section “Experience extraction”.

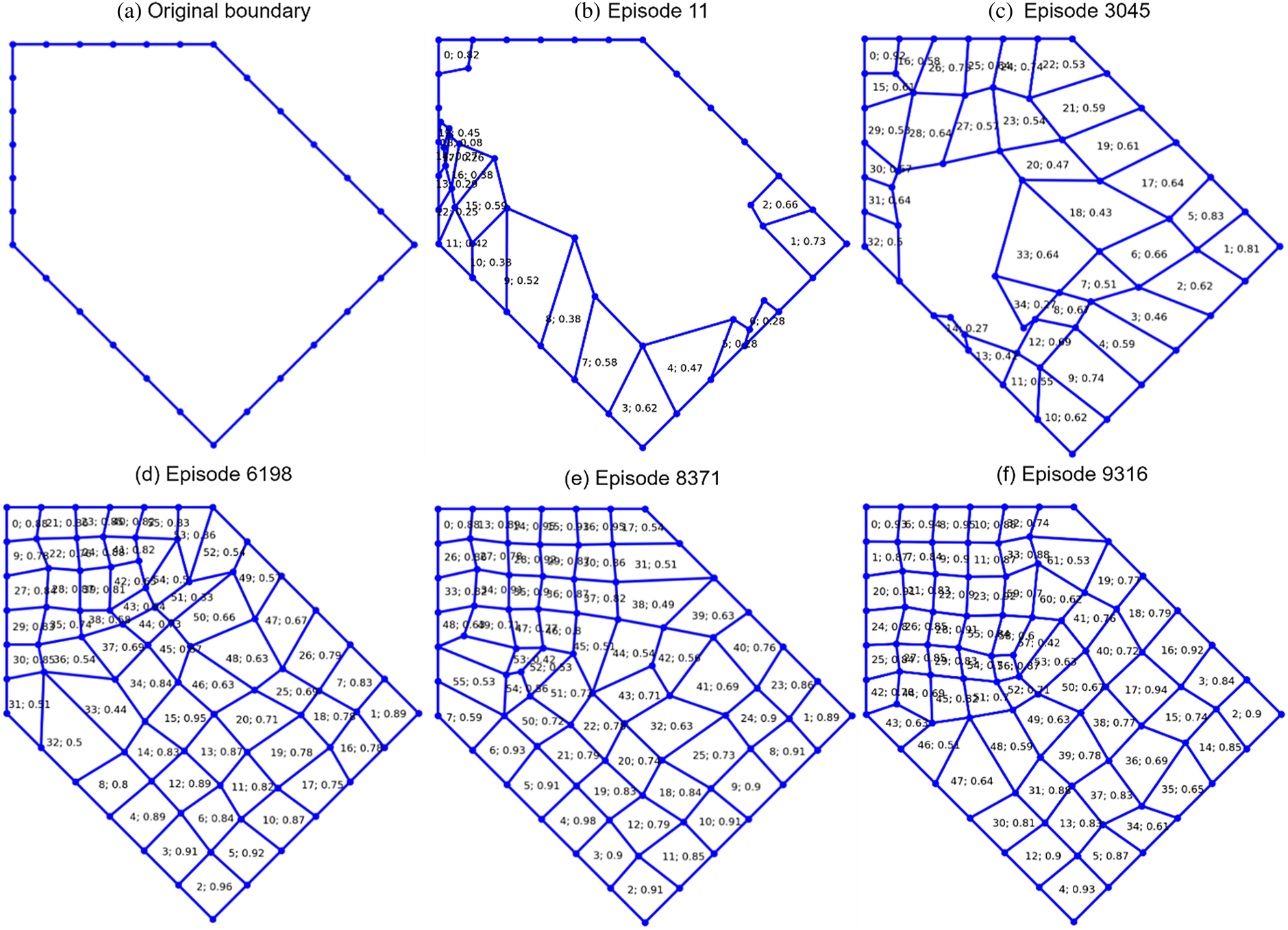
Fig. 23. Partial results of sampling.

Table 5 shows the total number of elements (#tE), number of valid elements (#vE), number of extracted samples (#eS), and the number of samples per valid element (#S2E) for each episode. The samples are extracted using the experience extraction (EE) module introduced in Section “FNN learning”. It can be seen from Table 5 that the episode in Figure 23d has 37 valid elements, which allows the extraction of 10,369 different samples (see the extraction process in Figure 19 ), where the number of samples per valid element has reached 280. Similar information can be observed in Figure 23e, f. This significant number of leverage over an element brings the EE module's tremendous efficiency and effectiveness in collecting samples. This effectiveness and efficiency in data collection ensure that the FNN model can be sufficiently trained.

Table 5. Extracted sample records from valid elements

#tE – total number of elements;

#vE – number of valid elements with quality η ^e > 0.7;

#eS – number of extracted samples;

#S2E – the number of samples per valid element

Then trained FNN model can be applied to another domain, such as domain D2, to do the meshing even though the extracted samples are from a different domain (see Fig. 23a). The meshing result of this FNN model is shown in Figure 24.

Fig. 24. The first meshing result of the FNN model.

The meshing, however, is not complete in this domain. In step 2 of the training process, as illustrated in Figure 22; therefore, there is a self-evolving process of the FNN model by learning from the meshing results generated by itself. While repeating step 2, the element extraction rules simulated by the model are gradually evolved and adapted to the characteristics of the boundary shape. For example, the training process of the subsequent four rounds of step 2 is shown in Table 6. In each round, the same FNN model will be trained using the extracted samples from the previous meshing result (i.e., sample source), and then the trained model is applied to generate a new mesh. Obviously, the meshing performance is getting improved and adapted to the boundary shape continuously while a significantly high number of valid samples can be extracted.

Table 6. Self-evolving process of FNN model

The hidden layer of this FNN model is [256, 256];

#tE: total number of elements;

#vE: number of valid elements with quality η ^e > 0.7;

#eS: number of extracted samples.

Efficiency of A2C training

The time cost for training the A2C network on the domain (see Fig. 23a) is shown in Figure 25. It shows the temporal changes in the average number of elements per continuous 100 episodes during the training process. The red line accounts for the total number of elements whose quality meets η ^e> 0. The black, green, and blue lines refer to η ^e > 0.3, η ^e > 0.5, and η ^e > 0.7, respectively. All the lines show an increasing trend over time, which means that the learning process is successful. The black and red lines are very close, which indicates that almost every element has a quality bigger than 0.3. The number of elements with quality η ^e > 0.7 accounts for around 30% of total number of elements when the training is converged. At the end of the training period, the domain has an average element number of about 75, and the average number of elements with η ^e > 0.7 is around 22.

Fig. 25. Temporal training cost of A2C network.

Impact of training parameters on mesh metrics

Element quality thresholds comparison

In the module of experience extraction, the quality threshold is used to control the selection of elements and determines whose experience is valuable for subsequent learning. To compare the different performances of the trained FNN model against the quality of selected samples, three different element selection thresholds (η ^e> 0.5, η ^e> 0.7, and η ^e> 0.8) are tested on the three experimental domains (D1, D2, and D3). The seven quality metrics measure the performance.

The comparison results are shown in Table 7. Taking the quality threshold η ^e> 0.7 achieves best performance in 4 metrics (i.e., Singularity, |MaxAngle - 90|, Scaled Jacobian, and Taper); taking the threshold η ^e> 0.8 has best results in Element quality, |MinAngle – 90|, and Scaled Jacobian; and the last threshold has the best performance only in Stretch. Understandably, the FNN model has better performance in most metrics when the experience of elements with higher quality is sampled. However, the FNN model with a higher element quality threshold may not produce sufficient training data because the number of extracted samples will decrease when the threshold is raised. The other metrics, such as Stretch, are not sensitive to whether the higher quality elements are chosen. Therefore, this paper chooses quality η ^e> 0.7 as the ideal and balanced threshold for experience extraction, which trains FNN models.

Table 7. Different element quality threshold comparison: L, H indicates if the lower value or higher value is preferred, respectively.

The hidden layer of this FNN model is [32, 64, 128, 64, 32, 16]. Each metric value is the average value of the three domains (D1, D2, and D3).

FNN structures comparison

To compare different performances of FNN models against the network structures, 4 different hidden layer structures ([64, 64], [256, 256], [64, 128, 64, 32, 16], and [32, 64, 128, 64, 32, 16]) are tested on three experimental domains. Four FNN models are trained using the four different structures according to the process introduced at the beginning of this section. The seven quality metrics measure the model performance. The comparison results are shown in Table 8, where each metric value is the average of values for three respective domains. The models have better performance in slender structures than the structures of [64, 64] and [256, 256]; and especially, the model having the structure of [64, 128, 64, 32, 16] achieves the best performance in the six metrics. This paper, therefore, chooses this structure as the optimal FNN network structure and uses this trained FNN model to compare the meshing performance with other meshing approaches.

Table 8. Comparison of FNN network structures: L, H indicate if the lower value or higher value is preferred, respectively.

Each metric value is the average value over the three domains (D1, D2, and D3).

Comparison of meshing speed for A2C and FNN

The mesh generation speed is essential to finite element analysis applications. In this paper, an extra indicator, elements per second, is adopted to measure the performance differences between the A2C and FNN models, both of which were developed by the same team under similar resources. Other methods are not compared since they are developed by different teams of various software development capabilities and with different programming languages, which will significantly impact the system's performance. These two models are tested on the ten domains given in Figure 21. The comparison result is shown in Table 9. The average speed for A2C over ten domains is 19.71 elements per second, while FNN equals 28.73. The FNN model excels A2C by almost nine elements per second. The performance difference is that FNN can directly predict the coordinate of the candidate point to form an element and the A2C model still needs two sampling operations from two normal distributions to get the x and y coordinates. Besides, the A2C model may not be adaptable to all domains and could require some trial-and-error to generate a valid element, which causes a significant drop in the speed. For example, the meshing speed of A2C is only 3.82 elements per second in domain D7. The standard deviations of A2C and FNN are high, and both the meshing speeds increase when the domain has fewer vertex numbers. This trend's probable reason is that the proposed method will update the boundary and find the following reference point every time after an element was extracted. Hence, the iteration number will be correspondingly greater for more boundary vertices.

Table 9. Meshing speed (elements per second) of A2C and FNN for all ten domains.

Avg. Indicates the average speed; STD indicates the standard deviation.

Experimental comparison approaches

The meshing performance of the self-learning system will be compared with three popular quad meshing approaches, Blossom-Quad (Remacle et al., Reference Remacle, Lambrechts, Seny, Marchandise, Johnen and Geuzainet2012), Delquad (Remacle et al., Reference Remacle, Henrotte, Carrier-Baudouin and Mouton2013), and Paving algorithm (Blacker and Stephenson, Reference Blacker and Stephenson1991; White and Kinney, Reference White and Kinney1997). Blossom-Quad and DelQuad are two indirect algorithms to generate quad meshes in 2D domains. The former takes advantage of the blossom algorithm to find the perfect matching of a pair of triangles generated by the Delaunay triangulation algorithm and then combine matched pairs into quadrilateral elements. The latter improves the triangulation process of Blossom-Quad by building triangular elements that are more suitable to recombine into quadrilaterals. Paving and its redesigned version are direct methods to generate quadrilaterals from domain boundaries. They generate layered quadrilateral elements from the boundary toward the interior until only six boundary nodes are left, tackled following predefined patterns.

In the following, two widely used software systems, Gmsh (Geuzaine and Remacle, Reference Geuzaine and Remacle2009) (implements the Blossom-Quad and Delquad algorithms) and CUBIT (Blacker et al., Reference Blacker, Owen, Staten and Morris2016) (implements the Paving approach), are used as quad element generator to compare meshing performance with the proposed self-learning system FreeMesh-S. Gmsh and CUBIT are both prevalent meshing software and have been developed by researchers for many years since 1991. CUBIT is developed at Sandia National Laboratories and even has a commercial product (Csimsoft). The comparisons will be made only on the quality indices, while the computational time will not be considered since it depends on how the systems are designed and implemented and which programming language is used. The computational complexity of FreeMesh-S and Paving is O(n ²), which is calculated using their respective procedures, whereas that of Blossom-Quad and DelQuad is reported to be O(n ²) (Johnen Reference Johnen2016).

Model applicability validation

The ten experimental domains are tested to validate if the trained FNN model can be applied to arbitrary domain boundaries without any additional training. The meshing results of FreeMesh-S are shown in Figure 26. All the domains are discretized into high-quality quadrilateral elements successfully, and the transition of elements is smooth, which demonstrates the excellent applicability to various boundary shapes without additional A2C and FNN training.

Fig. 26. All the meshing results of freeMesh-S.

Comparing results and analysis

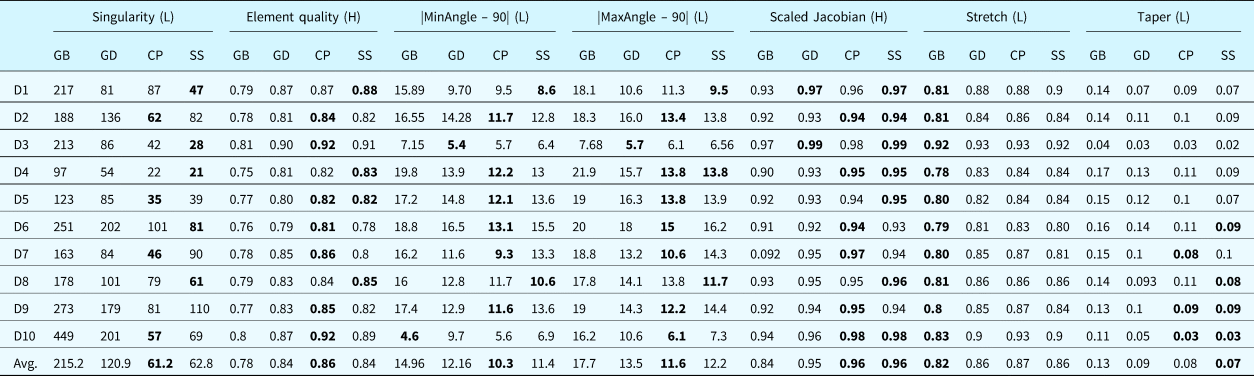
All the meshing results of four methods, Gmsh-Blossom (GB), Gmsh-DelQuad (GD), and CUBIT-Pave (CP), and the proposed self-learning system FreeMesh-S (SS), on the ten experimental domains, are shown in Figures 27–29, and 21, respectively. All the domains have been successfully discretized into mesh elements, in which the methods CP and SS have more regular quadrilateral elements than GB and GD; and GD performs better than GB. The increase of meshes’ regularity can reduce computational consumption and improve the analysis results’ accuracy. GD and CP methods, however, cannot mesh all the domains into quadrilaterals. There are triangles in certain experimental domains, which require extra cleanup operations to eliminate them.

Fig. 27. Meshing results of GB method.

Fig. 28. Meshing results of GD method.

Fig. 29. Meshing results of CP method.

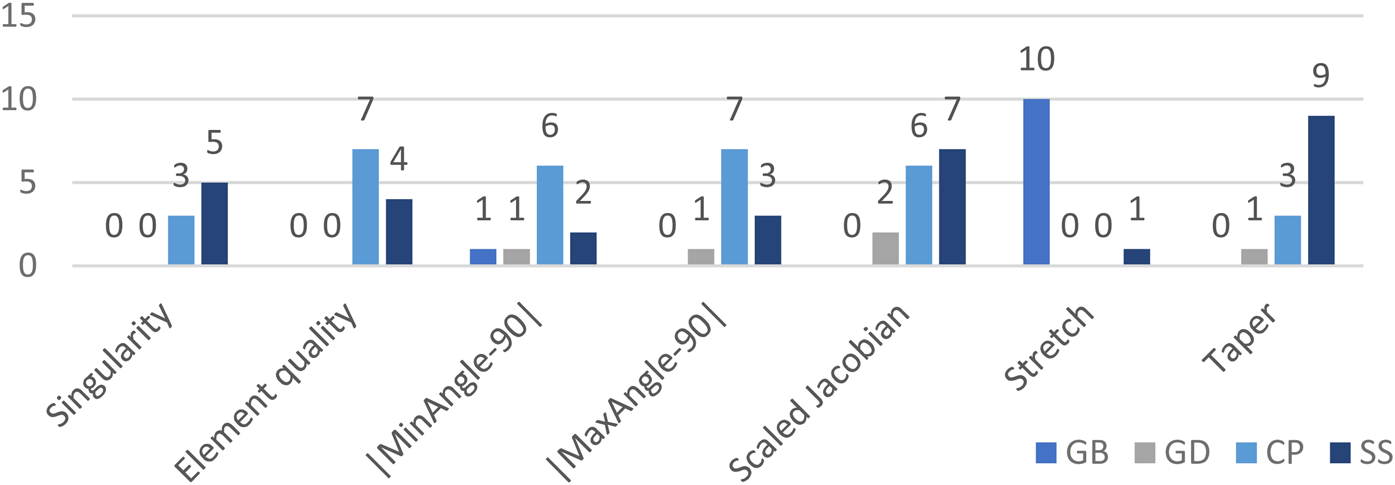
The statistics of the seven metrics are illustrated in Table 12 to measure the different performances of the four methods quantitatively. Each value in the table is the average over 10 domains (see detailed statistics in Table 10). The proposed SS method achieves the best performance in 2 quality metrics (Scaled Jacobian and Taper); CP method achieves the best performance in 5 quality metrics (Singularity, Element quality, Min angle, Max angle, and Scaled Jacobian); and GB is the best method from the aspect of Stretch. Moreover, the number of domains that each method achieves the best in each metric is shown in Figure 30. For each metric there are the following results.

• • Singularity: Even though the CP method obtains the best-averaged performance against other methods, the self-learning system FreeMesh-S (SS) has very close results and excels in 2 domains when counting domains with best performances. GB and GD methods are less likely to handle the irregular vertices during meshing because of their dependence on triangulation. They cannot achieve good performance in all the domains. GD method, however, is better than GB because it conducts a pre-processing on the triangulation to make the triangular elements more suitable to be merged into quadrilaterals. Singularity impacts the numerical stability in CFD applications, wrinkles in subdivision surfaces, and breakdown of structured patterns on manifolds (Suresh and Verma, Reference Suresh and Verma2019).

• • Element quality: FreeMesh-S (SS) resembles GD method and outperforms GB in this metric, while the CP method is the best one and excels in 7 domains. Nevertheless, SS is still comparable with other methods in the four domains. This measure is to identify how good a single element is, which can be calculated by Eq. (14).

• • |Min/Max Angle - 90|: CP is better than the other three methods. FreeMesh-S (SS) has a similar performance with the GD method and outperforms GB. These two metrics show the difference between the minimal or maximum internal corners of an element and the degree of 90 because a square is considered the perfect element in quad meshing, that is, both of them are 90°.

• • Scaled Jacobian: CP and SS have better results than the other two methods, while SS is slightly better than CP by excelling in 1 domain with the best performance. GB is the worst one. Scaled Jacobian relates to the interpolation error of finite element solution, for which the value of the best shape is 1.

• • Stretch: GB is the best among the four methods and defeats all the methods in 10 domains. FreeMesh-S (SS) has a very similar performance with GD, while CP is slightly worse than the two methods by 0.01. Stretch is calculated by the ratio between the shortest edge and longest diagonal length, which indicates the degree of deformation.

• • Taper: SS outperforms all the other methods and excels in 9 domains. Taper represents the ratio of the two triangles’ areas separated by a diagonal within a quadrilateral element, which indicates the balanced shape of an element.

Table 10. Mesh quality metrics of four methods on ten domains：L, H indicate if the lower value or higher value is preferred, respectively. The value in bold means the best among other approaches in a domain. GB refers to Gmsh-Blossom; GD indicates Gmsh-DelQuad; CP is CUBIT-Pave; and SS means the proposed self-learning system, FreeMesh-S

Fig. 30. Number of domains that each method achieves the best performance in each metrics.

In general, the proposed system, FreeMesh-S (SS), achieves high performance in all the metrics. All the values are within acceptable ranges as specified by the Verdict (Pébay et al., Reference Pébay, Thompson, Shepherd and Grosland2008) and outperform the other three approaches in Scaled Jacobian and Taper metrics. The CP approach has the best performance in Singularity, Element quality, |MinAngle - 90|, |MaxAngle - 90|, and Scaled Jacobian metrics. Even though almost losing all the competitions with other methods, the GB method has the best performance in the aspect of Stretch. The GD method exceeds the GB method in all the other metrics except the Stretch but is still poorer than SS and CP. GD is a quad-dominant method, which cannot discretize the whole domain into quadrilateral elements. Without extra cleanup operations (i.e., element deleting and insertion), CP and GD methods are challenging to generate a full-quad mesh. The proposed FreeMesh-S (SS) directly generates full-quadrilateral elements by the simulated extraction rules from A2C and FNN modules, which does not require any heuristic operations to handle exceptional triangle elements and inverted or flat quadrilateral elements.