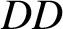1. Introduction
A bundle gerbe [Reference Murray13] is a geometric object that sits over a given space or manifold X classified by elements of
$H^3(X,\mathbb {Z})$
, in the same way that (complex) line bundles on X are classified by elements of
$H^2(X,\mathbb {Z})$
. Just as line bundles on manifolds have connections giving rise to curvature, a 2-form giving a class in
$H^2_{dR}(X)$
, bundle gerbes have a notion of geometric ‘connection’ data, with curvature a 3-form and hence a class in
$H^3_{dR}(X)$
. Since de Rham cohomology sees only the nontorsion part of integral cohomology, bundle gerbes that are classified by torsion classes in
$H^3$
are trickier in one sense to ‘see’ geometrically. The problem is compounded by the fact that bundle gerbes with the same 3-class may look wildly different, as the correct notion of equivalence is much coarser than isomorphism. Thus, different constructions that lead to the same class are still of interest, due to the flexibility this introduces.
One wide class of bundle gerbes, so-called lifting bundle gerbes, arises from the following data. Given a Lie group G, a principal G-bundle
$P\to X$
and a central extension
$$ \begin{align} \textrm{U}(1)\to \widehat{G} \to G \end{align} $$
of Lie groups, there is a bundle gerbe on X that is precisely the obstruction to the extension of a
$\widehat {G}$
-bundle lifting P. One can see the cohomology class corresponding to the bundle gerbe as analogous to the class
$w_2\in H^2(M,\mathbb {Z}/2)$
obstructing the lifting of the frame bundle
$F(M)$
to a spin bundle.
For a nontrivial example, consider the central extension
$\textrm{U}(1) \to \textrm{U}(n) \to \textrm{PU}(n)$
and P a principal
$\textrm{PU}(n)$
-bundle. The lifting bundle gerbe associated to such a
$\textrm{PU}(n)$
-bundle has torsion class in
$H^3(X,\mathbb {Z})$
. Conversely, by a result of Serre published by Grothendieck [Reference Grothendieck, Giraud, Grothendieck, Kleiman, Raynaud and Tate9, Théorème 1.6], every torsion class in
$H^3(X,\mathbb {Z})$
is associated to at least one lifting bundle gerbe of this form. Given a torsion element, it is nontrivial to find ranks n where this is possible.
In the other direction, one can consider the extension
$\textrm{U}(1) \to \textrm{U}(\mathcal {H}) \to \textrm{PU}(\mathcal {H})$
of infinite-dimensional groups, where
$\mathcal {H}\simeq L^2[0,1]$
, and lifting bundle gerbes of principal
$\textrm{PU}(\mathcal {H})$
-bundles. These bundle gerbes are infinite-dimensional and every class in
$H^3(X,\mathbb {Z})$
can be realised by some lifting bundle gerbe of this form. There are also constructions of bundle gerbes on compact, simply-connected, simple Lie groups G that use lifting bundle gerbes for the infinite-dimensional Kac–Moody central extensions
$\textrm{U}(1) \to \widehat {\Omega _kG} \to \Omega G$
and these are also nontorsion gerbes.
Between these examples, then, one might wonder when an a priori given finite-dimensional lifting bundle gerbe on X has a torsion class in
$H^3(X,\mathbb {Z})$
. That is, given a finite-dimensional central extension (1.1) and a principal G-bundle
$P\to X$
, is the lifting bundle gerbe classified by a torsion class? There are explicit and easy examples where it is nontorsion, for instance over
$X=S^2\times S^1$
(see Example 4.4 below). However, under a mild condition on X, it is true.
Murray’s original paper [Reference Murray13] claimed a sufficient condition for a finite-dimensional bundle gerbe to be torsion, though the proof had a subtle error. Murray and Stevenson later [Reference Murray and Stevenson15] gave a correct proof of a slightly stronger result, demanding (i) simple-connectivity of the base manifold X and (ii) that the fibres of a certain submersion
$Y\to X$
(part of the bundle gerbe data) are connected. This result was not specifically about lifting bundle gerbes, but it suffices to prove that lifting gerbes for G-bundles on simply-connected spaces X, where G is a connected Lie group, are torsion. The proof in [Reference Murray and Stevenson15] is more general and does not use anything specific about lifting bundle gerbes, which are somewhat more rigid than the general case.
In this note I shall prove the following result.
Theorem 1.1. Given any connected manifold X with finite fundamental group, any central extension (1.1) of finite-dimensional Lie groups and any principal G-bundle
$P\to X$
, the corresponding lifting bundle gerbe is torsion.
In fact, the proof suffices to give a slightly stronger result for topological spaces, assuming a group-theoretical fact about homomorphisms
$\pi _1(X)\to \pi _0(G)$
. We shall give this result below as Theorem 3.7 and some applications in the final section.
2. Preliminaries
We first recall the definition of a bundle gerbe.
Definition 2.1 [Reference Murray13]
A bundle gerbe on a manifold M consists of the following data.
-
• A surjective submersion
$Y\to M$
. -
• A principal
$\textrm{U}(1)$
-bundle
$E\to Y^{[2]}:=Y\times _M Y $
. -
• An isomorphism
$\mu \colon \operatorname {\mathrm {pr}}_{12}^*E\otimes _{\textrm{U}(1)} \operatorname {\mathrm {pr}}_{23}^*E \to \operatorname {\mathrm {pr}}_{13}^*E$
of
$\textrm{U}(1)$
-bundles, called the bundle gerbe multiplication. The tensor product is defined, for arbitrary
$\textrm{U}(1)$
-bundles
$E,F$
on X, to be
$(E\times _X F)/\textrm{U}(1)$
, where
$\textrm{U}(1)$
acts via the anti-diagonal action on
$Y^{[3]}:=Y\times _MY\times _MY$
. -
• This isomorphism satisfies an associativity condition, namely that the diagram
of isomorphisms of
$\textrm{U}(1)$
-bundles on
$Y^{[4]}$
commutes. Here
$E_{ij} = \operatorname {\mathrm {pr}}_{ij}^*E$
, with
$\operatorname {\mathrm {pr}}_{ij}\colon Y^{[4]}\to Y^{[2]}$
, and I have suppressed some canonical isomorphisms for clarity.
A bundle gerbe will be denoted by
$(E,Y)$
with the other data implicit. A bundle gerbe on a topological space is defined in the same way, except that we require instead that
$Y\to M$
admits local sections.
Here is the only type of example we will need. Fix a locally trivial central extension
$\textrm{U}(1)\to \widehat {G} \to G$
of Lie groups (so that, ignoring group structures, it is a principal bundle). Recall that the multiplication map of
$\widehat {G}$
induces an isomorphism
$\operatorname {\mathrm {pr}}_1^*\widehat {G}\otimes _{\textrm{U}(1)}\operatorname {\mathrm {pr}}_2^*\widehat {G} \simeq m^*\widehat {G}$
over
$G\times G$
, where
$m\colon G\times G\to G$
is the multiplication map.
Example 2.2 [Reference Murray13]
Let
$P\to X$
be a principal G-bundle. The lifting bundle gerbe associated to this bundle (and the fixed central extension) is given by the following data.
-
• The submersion is
$P\to X$
. Recall that the action map induces an isomorphism
${P\times G\simeq P\times _X P}$
over X; we will use this silently from now on. -
• The
$\textrm{U}(1)$
-bundle is
$P\times \widehat {G} \to P\times G$
. -
• Using the isomorphism
$P\times G\times G\to P^{[3]}$
,
$(p,g,h)\mapsto (p,pg,pgh)$
, the multiplication is given by the composite
$$ \begin{align*} \operatorname{\mathrm{pr}}_{12}^*(P\times \widehat{G})\otimes_{\textrm{U}(1)} \operatorname{\mathrm{pr}}_{23}^*(P\times \widehat{G}) \simeq P \times \operatorname{\mathrm{pr}}_1^*\widehat{G}\otimes_{\textrm{U}(1)}\operatorname{\mathrm{pr}}_2^*\widehat{G} \simeq P\times m^*\widehat{G}\simeq \operatorname{\mathrm{pr}}_{13}^*(P\times \widehat{G}). \end{align*} $$
-
• The associativity condition follows from associativity in the group
$\widehat {G}$
.
Given a bundle gerbe on a space X and a map
$f\colon X'\to X$
, there is a bundle gerbe on
$X'$
given by the data
$f^*Y\to X'$
and
$(p^{[2]})^*E$
, where
$p\colon f^*Y\to Y$
is the projection. Moreover, the maps
$$ \begin{align*} (p^{[2]})^*E \to E,\quad (f^*Y)^{[2]} \to Y^{[2]},\quad p\colon f^*Y\to Y \end{align*} $$
are compatible with all the bundle gerbe structure. This is the pullback of
$(E,Y)$
by f, denoted
$f^*(E,Y)$
. If
$(P\times \widehat {G},P)$
is a lifting bundle gerbe, then
$f^*(P\times \widehat {G},P) \simeq (f^*P\times \widehat {G},f^*P)$
.
More generally, given bundle gerbes
$(F,Z)$
and
$(E,Y)$
on X, one can take a map
$g\colon Z\to Y$
commuting with the projections to X and a map
$k\colon F\to E$
of
$\textrm{U}(1)$
-bundles covering
$g^{[2]}$
as in the diagram
such that the bundle gerbe multiplications are respected. The data of g and k is then a morphism of bundle gerbes, denoted
$(k,g)\colon (F,Z)\to (E,Y)$
. In this case,
$F\simeq (g^{[2]})^*E$
, as k is a map of principal bundles. An isomorphism
$(E,Y)\simeq (F,Z)$
of bundle gerbes on X will be meant in the strictest possible sense, namely where g and k are isomorphisms.
Definition 2.3. Given a bundle gerbe
$(E,Y)$
, a stable trivialisation consists of a principal
$\textrm{U}(1)$
-bundle
$T\to Y$
and an isomorphism
$\operatorname {\mathrm {pr}}_1^*T^*\times \operatorname {\mathrm {pr}}_2T \simeq E$
of bundles on
$Y^{[2]}$
, making an isomorphism of bundle gerbes along with
$\operatorname {\mathrm {id}}_Y$
.
Example 2.4. Given a lifting bundle gerbe associated to
$P\to X$
and
$\textrm{U}(1) \to \widehat {G}\to G$
, a stable trivialisation is equivalent data to a principal
$\widehat {G}$
-bundle
$\widehat {P}\to X$
lifting P. The quotient map
$\widehat {P}\to P$
is the required principal
$\textrm{U}(1)$
-bundle and vice versa.
There is a general notion of tensor product of a pair of bundle gerbes, analogous to the tensor product of
$\textrm{U}(1)$
-bundles, but we will not need it here. However, the notion of a power of a single given bundle gerbe is easier to describe. Namely, if
$(E,Y)$
is a bundle gerbe, then
$(E,Y)^{\otimes n} := (E^{\otimes n},Y)$
is also a bundle gerbe, using the tensor powers of the
$\textrm{U}(1)$
-bundle E.
Example 2.5. Let
$P\to X$
and
$\textrm{U}(1)\to \widehat {G}\to G$
be the data necessary to build a lifting bundle gerbe. Then
$(P\times \widehat {G},P)^{\otimes n} \simeq (P\times \widehat {G}^{\otimes n},P)$
, where
$\textrm{U}(1)\to \widehat {G}^{\otimes n} \to G$
is the n-fold central product of
$\widehat {G}$
with itself, which is the same as the n-fold tensor power of the underlying
$\textrm{U}(1)$
-bundle over G.
Associated to each bundle gerbe
$(E,Y)$
on X there is a class
$DD(E,Y) \in H^3(X,\mathbb {Z})$
, the Dixmier–Douady or
$DD$
-class, with the following properties (see [Reference Murray13], and [Reference Murray and Stevenson14] for the last item).
Lemma 2.6.
-
(1) Given
$f\colon X'\to X$
, then
$f^*DD(E,Y) = DD(f^*(E,Y))$
. -
(2) Given a morphism
$(k,g)\colon (F,Z)\to (E,Y)$
of bundle gerbes on X, then
$DD(F,Z)=DD(E,Y)$
. -
(3) For all integers n,
$DD((E,Y)^{\otimes n})=n\cdot DD(E,Y)$
, where a negative tensor power involves the dual
$\text{U}(1)$
-bundle. -
(4)
$DD(E,Y)=0$
if and only if the bundle gerbe
$(E,Y)$
has a stable trivialisation. -
(5) Given a central extension
$\text{U}(1)\to \widehat {G}\to G$
classified by
$\alpha \in H^3(BG,\mathbb {Z})\simeq H^2(BG,\underline {\mathrm{U}(1)})$
and a principal G-bundle classified by some map
$\chi \colon X\to BG$
, the lifting bundle gerbe has class in
$H^3(X,\mathbb {Z})$
corresponding to
$\chi ^*\alpha $
.
We shall say that a bundle gerbe
$(E,Y)$
is torsion if
$DD(E,Y)$
is a torsion element. Bundle gerbes of this form are the main focus of this note. The reader can rephrase all the results of this paper without mentioning gerbes, if desired, using the following easy result.
Corollary 2.7. Given a principal G-bundle
$P\to X$
and a central extension
$\text{U}(1)\to \widehat {G}\to G$
, the associated lifting bundle gerbe
$(P\times \widehat {G},P)$
is torsion if and only if there is some
$n>0$
such that the G-bundle P lifts to a principal
$\widehat {G}^{\otimes n}$
-bundle.
3. Main results
The relatively short proof of Theorem 1.1 serves to illustrate the idea of the more complex proof of Theorem 3.7.
Proof Proof of Theorem 1.1
Let us fix a lifting bundle gerbe
$(E,P)$
associated to a principal G-bundle
$P\to X$
and an extension
$\textrm{U}(1)\to \widehat {G}\to G$
. Let
$G_0$
denote the connected component of the identity. We can induce a principal
$\pi _0(G)$
-bundle on X by defining
$Q := P/G_0$
, where we use the fact that
$\pi _0(G) = G/G_0$
. Let
$\pi \colon \tilde {X}\to X$
denote the universal covering space of X and recall that for any covering space on X, the pullback to
$\tilde {X}$
is trivialisable. Hence, if we form the covering space
$\pi ^*Q \to \tilde {X}$
, it is trivialisable. From this it follows that the structure group of the G-bundle
$\tilde{P}$
defined by
$\tilde {P}:=\pi ^*P\to \tilde {X}$
reduces to
$G_0$
. Thus, we can find a subbundle
$P' \subset \tilde {P}$
that on fibres looks like the inclusion
$G_0 \hookrightarrow G$
.
If we denote by
$\widehat {G}_0\subset \widehat {G}$
the preimage of
$G_0$
, then we can form the lifting bundle gerbe on
$\tilde {X}$
associated to
$P'\to \tilde {X}$
and the central extension
$\textrm{U}(1) \to \widehat {G}_0\to G_0$
. By the construction of a lifting bundle gerbe, there is a morphism of bundle gerbes on
$\tilde {X}$
:
Thus, the
$DD$
-class
$DD(P')$
of the lifting gerbe of
$P'$
is equal to
$DD(\tilde {P})$
.
Following [Reference Schommer-Pries18, Section 4.1], the central extension of
$G_0$
is classified by an element of Segal–Mitchison cohomology
$H^2_{{SM}}(G_0;\textrm{U}(1))$
and the lifting bundle gerbe on
$BG_0$
is classified by its image
$\alpha $
under
$H^2_{{SM}}(G_0;\textrm{U}(1))\to H^3_{{SM}}(G_0;\mathbb {Z})\simeq H^3(BG_0,\mathbb {Z})$
. This latter cohomology group is pure torsion [Reference Borel2, Lemme 26.1], where we use the fact that the (singular) cohomology of the classifying space of a connected Lie group is isomorphic to the cohomology of the classifying space of the maximal compact subgroup. More precisely, the torsion subgroup of
$H^*(BG_0,\mathbb {Z})$
is exactly the kernel of the restriction map
$H^*(BG_0,\mathbb {Z})\to H^*(BT,\mathbb {Z})$
[Reference Feshbach6], where
$T\subseteq G_0$
is a maximal torus of
$G_0$
(and
$H^*(BT,\mathbb {Z})$
is torsion-free). Now
$DD(P')$
is the image of
$\alpha $
under
$\chi ^*\colon H^3(BG_0,\mathbb {Z})\to H^3(\tilde {X},\mathbb {Z})$
, where
$\chi \colon \tilde {X}\to BG_0$
is a classifying map. Thus, the lifting gerbe associated to
$P'$
is torsion and so is the lifting gerbe (on
$\tilde {X}$
) associated to
$\tilde {P}$
. Now we can apply the following lemma, as
$\pi _1(X)$
is finite, and conclude that the lifting gerbe associated to P is also torsion, since
$DD(\tilde {P}) = \pi ^*DD(P)$
.
Lemma 3.1. Given a k-sheeted covering space
$\pi \colon Y\to X$
and a class
$c\in H^n(X,\mathbb {Z})$
, if
$\pi ^*c\in H^n(Y,\mathbb {Z})$
is torsion, then c is torsion.
Proof. The composite
$H^n(X,\mathbb {Z})\otimes \mathbb {Q} \xrightarrow {\pi ^*} H^n(Y,\mathbb {Z})\otimes \mathbb {Q} \xrightarrow {\pi _*} H^n(X,\mathbb {Z})\otimes \mathbb {Q}$
is multiplication by k, which is invertible, so the pushforward map
$\pi _*$
is a retraction of
$\pi ^*$
and hence the latter is injective. Now, given a class
$c\in H^n(X,\mathbb {Z})$
, if
$\pi ^*c$
is torsion, then
$\pi ^*c\otimes \mathbb {Q}$
is zero; hence,
$c\otimes \mathbb {Q}$
is zero and hence c is a torsion class.
Remark 3.2. The proof of Theorem 3.6 of [Reference Murray and Stevenson15] actually tells us a tiny bit more than is claimed. What it shows is that instead of demanding the base space M is simply-connected, it is sufficient to ask that the composite
$\pi _3(M)\to H_3(M)\to H_3(M)/\mathrm {tors}$
is surjective; this is because
$\operatorname {\mathrm {Hom}}(H_3(M)/\mathrm {tors},\mathbb {Z}) \simeq \operatorname {\mathrm {Hom}}(H_3(M),\mathbb {Z})$
and it is the latter group that is used in the proof.
In applying Lemma 3.1, we need only ask that there is a finite-sheeted covering space
$\tilde {M}\to M$
with
$\pi _3(\tilde {M})\to H_3(\tilde {M})/\mathrm {tors}$
a surjective map.
Returning to the case of lifting gerbes, we can make a sharper claim, leaving the smooth category altogether. We first need a preparatory technical lemma.
Lemma 3.3. Let K be a discrete group such that
$H_3(K,\mathbb {Z})$
,
$\operatorname {\mathrm {Ext}}(H_2(K,\mathbb {Z}),\mathbb {Z})$
and
$H_1(K,A)$
are torsion, where A is any K-module with underlying abelian group
$A\simeq \mathbb {Z}^n$
. If G is a finite-dimensional Lie group with
$\pi _0(G)\simeq K$
, then
$H^3(BG,\mathbb {Z})$
is torsion.
Proof. For the rest of the proof, unspecified coefficients for cohomology should be taken as
$\mathbb {Z}$
. Given a Lie group as in the statement, there is a short exact sequence of Lie groups
$G_0\to G\xrightarrow {\pi } K$
, where
$G_0$
is the connected component of the identity. This gives a fibration
$BG_0\to BG\xrightarrow {B\pi } BK$
, where the fibre
$BG_0$
is connected. There is a (first-quadrant) Serre spectral sequence for this fibration given by
$$ \begin{align*} E_2^{s,t} = H^s(K,\mathcal{H}^t(BG_0)) \Longrightarrow H^{s+t}(BG), \end{align*} $$
where
$\mathcal {H}^t(BG_0)$
is the K-module arising from the local system on
$BK$
with fibre over
$x\in BK$
given by
$H^t(B\pi ^{-1}(x))\simeq H^t(BG_0)$
. Note in particular that
$\mathcal {H}^0(BG_0)\simeq \mathbb {Z}$
carries the trivial K-action, since it can be identified with the constant
$\mathbb {Z}$
-valued functions on
$BG_0$
. Recall that
$H^k(BG_0)$
is finitely generated and is torsion for odd k [Reference Borel2].
Figure 1 shows part of the
$E_2$
page, making the substitutions that
$H^0(K,A) = A^K$
, the invariants of the K-action on the module A and that
$H^1(BG_0)=H_1(BG_0)=0$
, as
$G_0$
is connected, giving the zeros in the 1-row. The asterisk entries are not needed.
Figure 1 The
$E_2$
page of the Serre spectral sequence associated to the fibre sequence
$BG_0 \to BG\to BK$
. Boxed entries lie on the line
$s+t=3$
.
By the universal coefficient theorem (UCT), there is a short exact sequence
$$ \begin{align*} 0\to \operatorname{\mathrm{Ext}}(H_2(K),\mathbb{Z})\to H^3(K)\to \operatorname{\mathrm{Hom}}(H_3(K),\mathbb{Z})\to 0 \end{align*} $$
and, hence, if
$H_3(K)$
is torsion, the right-hand term vanishes and so
$H^3(K)$
is torsion, by the assumption on the Ext group.
The short exact sequence
$H^2(BG_0)_{\mathrm {tors}} \hookrightarrow H^2(BG_0)\to H^2(BG_0)/\mathrm {tors}$
of groups is also a short exact sequence of K-modules, so there is a long exact sequence which reads in part
$$ \begin{align*} \cdots \to H^1(K,\mathcal{H}^2(BG_0)_{\mathrm{tors}}) \to H^1(K,\mathcal{H}^2(BG_0))\to H^1(K,\mathcal{H}^2(BG_0)/\mathrm{tors})\to\cdots. \end{align*} $$
As
$\mathcal {H}^2(BG_0)_{\mathrm {tors}}$
is finite, the left-hand term is torsion and so it suffices to know that
$H^1(K,\mathcal {H}^2(BG_0)/\mathrm {tors})$
is torsion to conclude that
$H^1(K,\mathcal {H}^2(BG_0))$
a torsion group.
There is a version of the UCT for cohomology with local coefficients that generally only holds under slightly special extra assumptions. Notice that while everything here is in terms of group cohomology of K, this is the same as the singular cohomology of
$BK$
. Finding this UCT was set as an exercise by Spanier [Reference Spanier19, Ch. 5, Exercise J.4] and can be completed by using [Reference Cartan and Eilenberg5, Ch. VI, Theorem 3.3a] under the special assumption (3a’) there. The formulation I use here was given in [Reference Randal-Williams17]; a detailed conceptual derivation is given in [Reference Ramzi16]. The special assumptions are satisfied by the setup here, as we are working over the integers and the local coefficient system
$\mathcal {H}^2(BG_0)/\mathrm {tors}$
has fibres that are finitely generated free abelian groups. The latter fact means that we can also rely on the local system being reflexive, in that it is naturally isomorphic to its double dual.
The upshot is that there is a short exact sequence
$$ \begin{align*} 0\to \operatorname{\mathrm{Ext}}(H_0(K,A^*),\mathbb{Z})\to H^1(K,A)\to \operatorname{\mathrm{Hom}}(H_1(K,A^*),\mathbb{Z})\to 0, \end{align*} $$
where
$A^*=\operatorname {\mathrm {Hom}}_{\mathbb {Z}}(A,\mathbb {Z})$
is the dual module, also with underlying abelian group isomorphic to
$\mathbb {Z}^n$
. Then
$H_0(K,A^*)$
is a quotient of
$A^*$
; hence, it is finitely generated and so
$\operatorname {\mathrm {Ext}}(H_0(K,A^*),\mathbb {Z})$
is torsion (as it only sees the torsion subgroup of
$H_0(K,A^*)$
, which is finite). Thus, if
$H_1(K,A^*)$
is torsion, the right-hand term vanishes and so
$H^1(K,A)$
is torsion, as needed, where we take
$A=\mathcal {H}^2(BG_0)/\mathrm {tors}$
.
We thus know that all the boxed groups are torsion groups and so the groups
$E_\infty ^{s,t}$
for
$s+t=3$
, being subquotients of them, are also torsion. Further, this implies that
$H^3(BG,\mathbb {Z})$
, being an iterated extension of torsion groups, is torsion, as needed.
Note that nontrivial coefficients for
$H_1$
are essential in this result, since the action of K on
$\mathcal {H}^2(BG_0)$
is nontrivial in general.
Example 3.4. For the group
$G=\textrm{U}(1)\rtimes \operatorname {\mathrm {Aut}}((\textrm{U}(1))$
, the
$\operatorname {\mathrm {Aut}}(\textrm{U}(1))\simeq \{\pm 1\}$
-action on
$\mathcal {H}^2(B\text{U}(1))\simeq \mathbb {Z}$
is nontrivial, as the inversion map on
$\textrm{U}(1)$
induces a map on
$B\text{U}(1)$
that pulls back the Chern class of the universal line bundle to its negative. More generally, given a group K with a surjection
$K\to \{\pm 1\}$
, we get a nontrivial semidirect product
$\textrm{U}(1)\rtimes K$
whereby
$\mathcal {H}^2(B\text{U}(1))$
is a nontrivial K-module.
It is not immediately obvious what the action can be for our class of examples appearing in Example 4.3, so this is not a redundant assumption.
Remark 3.5. Given more specific information about the torsion in
$H^*(BG_0,\mathbb {Z})$
, for instance if it vanishes, or is all P-torsion for some class P of primes, and K is a P-torsion group, then more information about what sort of torsion appears in
$H^3(BG,\mathbb {Z})$
is available.
Recall that a locally finite group is a discrete group that is the filtered colimit of finite groups or, equivalently, the direct limit of its finite subgroups. For instance, an infinite direct sum of finite groups is locally finite.
Corollary 3.6. Let K be a locally finite group such that
$\operatorname {\mathrm {Ext}}(H_2(K),\mathbb {Z})$
is torsion. If G is a finite-dimensional Lie group with
$\pi _0(G)\simeq K$
, then
$H^3(BG,\mathbb {Z})$
is torsion.
Proof. The key fact we need is that homology of groups commutes with taking filtered colimits, and this is true even with nontrivial coefficients, assuming that the coefficients are also expressed as a direct limit. For a locally finite group K acting on an abelian group A, we can restrict the action on A to finite subgroups
$K_\alpha \subset K$
and so then A as a K-module is the colimit of
$K_\alpha $
-modules.
Now, since the group homology of a finite group is torsion, the homology groups
$H_n(K,\mathbb {Z})$
,
$n=2,3$
, of a locally finite group are also torsion. By the observation about homology with nontrivial module coefficients, we can even conclude that
$H_1(K,A)$
is torsion for A a K-module.
Thus, if we also know that
$\operatorname {\mathrm {Ext}}(H_2(K),\mathbb {Z})$
is torsion, then we have all the hypotheses for Lemma 3.3 and so we can conclude that
$H^3(BG,\mathbb {Z})$
, as required.
With Lemma 3.3 in hand, we can prove the sharper version of the main result.
Theorem 3.7. Fix a finite-dimensional Lie group G and a connected topological space X such that there is a finite-sheeted covering space
$Y\to X$
such that every homomorphism
$\pi _1(Y)\to \pi _0(G)$
factors through a group K satisfying the algebraic properties in Lemma 3.3. Then, for any central extension
$\text{U}(1)\to \widehat {G}\to G$
and principal G-bundle
$P\to X$
, the associated lifting gerbe is torsion.
Proof. The proof is similar to that for Theorem 1.1, except that instead of reducing the structure group to
$G_0$
, we proceed as follows.
Fix a central extension
$\textrm{U}(1)\to \widehat {G}\to G$
. First note that the lifting bundle gerbe for the universal G-bundle
$EG\to BG$
has
$DD$
-class given by the the class in
$H^3(BG,\mathbb {Z})$
classifying the central extension, by Lemma 2.6(5) applied to the identity map of
$BG$
.
Then, given a group K satisfying the hypothesis of Lemma 3.3 and a homomorphism
$K\to \pi _0(G)$
, the pullback group
$G_K := K\times _{\pi _0(G)} G$
has a central extension
$\textrm{U}(1)\to K\times _{\pi _0}\widehat {G}\to G_K$
. Since
$H^3(G_K,\mathbb {Z})$
is torsion (as
$\pi _0(G_K) \simeq K$
), all lifting gerbes associated to
$G_K$
-bundles are torsion. Further, the lifting gerbe of the pulled-back G-bundle
$BG_K\times _{BG} EG \to BG_K$
is also torsion. Hence, if the classifying map of a G-bundle factors through
$BG_K$
, even up to homotopy, then the G-bundle has a torsion lifting gerbe.
Now fix a G-bundle
$P\to X$
and take the covering space
$Y\to X$
as in the statement of the theorem and the classifying map
$Y\to X \to BG$
. The diagram
commutes (up to homotopy), where K is as in the theorem statement. Since
$BG_K$
is the (homotopy) pullback
$BK\times _{B\pi _0(G)}BG$
, the classifying map
$Y\to BG$
factors through
$BG_K$
, up to homotopy. Thus, the lifting gerbe for
$Y\times _X P\to Y$
is the pullback of the torsion lifting gerbe on
$BG_K$
and hence is torsion.
The rest of the proof of Theorem 1.1 applies, to arrive at the conclusion that
$DD(P)$
is torsion.
Remark 3.8. The hypothesis on homomorphisms
$\pi _1(Y) \to \pi _0(G)$
is stated so that one recovers both the cases
$K=\pi _1(Y)$
and
$K\subseteq \pi _0(G)$
, which are what will presumably occur most often in practice.
4. Examples and applications
4.1. Examples
Theorem 3.7 applies fairly trivially when G is a finite-dimensional Lie group with
$\pi _0(G)$
finite, so the interesting cases are when
$\pi _0(G)$
is infinite.
Corollary 4.1. If X is a topological space with a locally finite fundamental group
$\pi =\pi _1(X)$
and with
$\operatorname {\mathrm {Ext}}(H_2(\pi ),\mathbb {Z})$
torsion and G is a finite-dimensional Lie group, then every lifting gerbe arising from a G-bundle on X is torsion.
Similarly, if G is a finite-dimensional Lie group with
$\pi =\pi _0(G)$
locally finite with
$\operatorname {\mathrm {Ext}}(H_2(\pi ),\mathbb {Z})$
torsion, then for any topological space X, every lifting gerbe associated to a G-bundle on X and central extension of G is torsion.
The main difficulty thus lies in arranging that the
$\operatorname {\mathrm {Ext}}$
group is torsion. But there are certainly infinite groups where this is so.
Lemma 4.2. Let K be a locally finite group given by a countable direct limit of finite abelian groups
$K_\alpha $
, the exponents of which are bounded, but whose orders can be unbounded. Then K is an infinite group satisfying the hypotheses of Lemma 3.3.
Proof. The hypotheses imply that K has finite exponent, namely the least common multiple of the exponents of the groups
$K_\alpha $
, and also that
$H_2(K,\mathbb {Z}) \simeq \operatorname {\mathrm {colim}}_\alpha H_2(K_\alpha ,\mathbb {Z})$
is torsion, since each
$H_2(K_\alpha ,\mathbb {Z})$
is finitely generated and torsion, hence finite, and the torsion in
$H_2(K_\alpha ,\mathbb {Z})$
is bounded in terms of the exponent of
$K_\alpha $
, so there is a uniform bound on the torsion as
$\alpha $
varies.
Using the fact that a countable directed diagram has a cofinal subsequence
$(A_n)_{n\in \mathbb {N}}$
, the colimit defining K can be assumed without loss of generality to be sequential. We can then consider the exact sequence (all homology with integer coefficients)
$$ \begin{align*} 0\to \mathop{\lim\nolimits^1}\operatorname{\mathrm{Hom}}(H_2(K_n),\mathbb{Z})\to \operatorname{\mathrm{Ext}}(H_2(K),\mathbb{Z}) \to \lim_{\mathbb{N}}\operatorname{\mathrm{Ext}}(H_2(K_n),\mathbb{Z})\to 0. \end{align*} $$
Now
$\operatorname {\mathrm {Hom}}(H_2(K_n),\mathbb {Z})=0$
for all n, as
$H_2(K_n,\mathbb {Z})$
is finite, and hence the
$\mathop {\lim \nolimits ^1}$
term is trivial. Now we use the fact that the sequence
$H_2(K_n,\mathbb {Z})$
has bounded exponent, and hence
$\operatorname {\mathrm {Ext}}(H_2(K_n),\mathbb {Z})$
has bounded torsion, so that
$\lim _{\mathbb {N}}\operatorname {\mathrm {Ext}}(H_2(K_n),\mathbb {Z})$
is still torsion. This, finally, shows that
$\operatorname {\mathrm {Ext}}(H_2(K,\mathbb {Z}),\mathbb {Z})$
is torsion and hence we can apply Corollary 3.6.
Example 4.3. Consider the infinite direct sum
$\bigoplus _{n\in \mathbb {N}} A$
for any finite abelian group A. This is locally finite, as it is the colimit of the subgroups given by finite direct sums, and its exponent is the same as that of A. More generally, if
$K_0 \subset K_1 \subset K_2\subset \cdots $
is a countable increasing sequence of finite abelian groups with eventually constant exponent e, then
$\bigcup _n K_n$
is locally finite with exponent e.
In the other direction, here is a counterexample to Theorem 3.7 that was used in [Reference Murray and Stevenson15]. The specific hypothesis of [Reference Murray and Stevenson15, Theorem 3.6] that is violated – connectivity of G – is not one required for the version of the theorem here, but it still breaks our hypotheses in other ways.
Example 4.4 [Reference Brylinski3, Section 4.1] and [Reference Johnson11, Section 3.5]
Take a principal
$\textrm{U}(1)$
-bundle
$Q\to X$
and a function
$X\to \textrm{U}(1)$
with classes
$\alpha \in H^2(X,\mathbb {Z})$
and
$\beta \in H^1(X,\mathbb {Z})$
. The bundle gerbe classified by the cup product
$\alpha \cup \beta $
is given by the lifting bundle gerbe corresponding to the principal
$(\textrm{U}(1)\times \mathbb {Z})$
-bundle
$Q\times _X f^*\mathbb {R}\to X$
and central extension
$$ \begin{align*} \textrm{U}(1) \to (\textrm{U}(1)\times \mathbb{Z}) \tilde\times \textrm{U}(1) \to \textrm{U}(1)\times \mathbb{Z} \end{align*} $$
with product
$(n_1,z_1;w_1)\cdot (n_2,z_2;w_2) = (n_1+n_2,z_1z_2;w_1w_2z_1^{n_2})$
(see [Reference Brylinski3, Equation (4.10)]; there is a typo in the definition of the product in [Reference Murray and Stevenson15]).
If
$X=M\times S^1$
, then every finite-index subgroup
$H < \pi _1(M\times S^1)\simeq \pi _1(M)\times \mathbb {Z}$
admits a surjection onto a finite-index subgroup of
$\mathbb {Z}$
(for example, the one induced by the composite
$Y\to M\times S^1\xrightarrow {\operatorname {\mathrm {pr}}_2} S^1$
). Thus, for every finite-sheeted covering space
$Y\to M\times S^1$
, every nontrivial homomorphism
$\phi \colon \pi _1(Y)\to \pi _0(\textrm{U}(1)\times \mathbb {Z})=\mathbb {Z}$
fails to factor through a subgroup satisfying Lemma 3.3, as
$\operatorname {\mathrm {im}}(\phi )\simeq \mathbb {Z}$
and
$H_1(\mathbb {Z},\mathbb {Z})=\mathbb {Z}$
.
If
$H^2(M,\mathbb {Z})$
contains nontorsion classes, then, by Künneth,
$H^3(M\times S^1,\mathbb {Z}) \simeq H^2(M,\mathbb {Z})\otimes H^1(S^1,\mathbb {Z})\oplus H^3(M,\mathbb {Z})\otimes H^0(S^1,\mathbb {Z})$
, which means that there are cup product classes that are nontorsion and correspond to finite-dimensional lifting gerbes by the above construction.
What happens if we are in the situation where we know that K is locally finite and so Corollary 3.6 has a chance of applying?
Example 4.5. Even if K is locally finite, if there is a nontorsion class in
$H^3(K,\mathbb {Z})$
, this gives rise to a nontrivial central extension
$\textrm{U}(1) \to \widehat {K}\to K$
. Given any semidirect product
$G = G_0\rtimes K$
, we can form the pullback
$G\times _K \widehat {K}$
, which is then a nontrivial central extension of G. In fact, it is classified by a nontorsion class in
$H^3(BG,\mathbb {Z})$
, since
$H^3(K,\mathbb {Z})\to H^3(BG,\mathbb {Z})$
has a retraction induced by the section of
$G\to K$
.
How might one get nontrivial classes in
$H^3(K,\mathbb {Z})$
for a locally finite group K? If there is some nontrivial
$c\in \operatorname {\mathrm {Ext}}(H_2(K),\mathbb {Z})$
, then, using the exact sequence
$$ \begin{align*} 0=\operatorname{\mathrm{Hom}}(H_2(K),\mathbb{R}) \to \operatorname{\mathrm{Hom}}(H_2(K),\mathbb{R}/\mathbb{Z}) \xrightarrow{\simeq} \operatorname{\mathrm{Ext}}(H_2(K),\mathbb{Z}) \to \operatorname{\mathrm{Ext}}(H_2(K),\mathbb{R}) = 0, \end{align*} $$
we get a nontrivial homomorphism
$\phi _c\colon H_2(K)\to \mathbb {R}/\mathbb {Z}\simeq \textrm{U}(1)$
(here using the fact that
$\mathbb {R}$
is divisible and hence an injective group, and
$H_2(K)$
is torsion). Further, since
$H^2(K,H_2(K)) \to \operatorname {\mathrm {Hom}}(H_2(K),H_2(K))$
has a section, by the universal coefficient theorem for group homology, the identity map on
$H_2(K)$
corresponds to a nontrivial central extension
$H_2(K) \to \widehat {K} \to K$
classified by class in
$H^2(K,H_2(K))$
. We can then induce a central extension of K by
$\textrm{U}(1)$
using the homomorphism
$\phi _c$
and central extensions by
$\textrm{U}(1)$
are classified by
$H^3(K,\mathbb {Z})$
. All of these constructions are induced by homomorphisms, so all up we have an injective homomorphism
$$ \begin{align*} \operatorname{\mathrm{Ext}}(H_2(K),\mathbb{Z})\simeq \operatorname{\mathrm{Hom}}(H_2(K),\textrm{U}(1)) \hookrightarrow H^2(K,\textrm{U}(1)) \xrightarrow{\simeq} H^3(K,\mathbb{Z}) \to H^3(BG,\mathbb{Z}) \end{align*} $$
and so nontorsion elements in
$\operatorname {\mathrm {Ext}}(H_2(K),\mathbb {Z})$
are a source of nontorsion elements in
$H^3(BG,\mathbb {Z})$
.
Now the
$E_3$
page of the spectral sequence in Figure 1 has a potentially nontrivial differential
$d_3^{0,2}\colon \mathcal {H}^2(BG_0)^K\to H^3(K,\mathbb {Z})$
. Moreover,
$\operatorname {\mathrm {im}}(d_3^{0,2})$
is the kernel of the edge homomorphism
$H^3(K,\mathbb {Z}) \to H^3(BG,\mathbb {Z})$
, since
$H^3(K,\mathbb {Z})/\operatorname {\mathrm {im}}(d_3^{0,2}) \simeq E_\infty ^{3,0} \subset H^3(BG,\mathbb {Z})$
. Without more specific analysis of the differential
$d_3^{0,2}$
, it is not immediately obvious that a nontorsion element remains nontorsion in
$H^3(BG,\mathbb {Z})$
, in general.
Some simple examples can be calculated directly.
Example 4.6. Take K some locally finite group with a surjection
$\alpha \colon K\to \{\pm 1\}$
and define
$G = \textrm{U}(1)\rtimes K$
as in Example 3.4, so that
$\mathcal {H}^2(B\text{U}(1))^K=\{0\}$
and so that
$\operatorname {\mathrm {Ext}}(H_2(K),\mathbb {Z})$
injects into
$H^3(BG)$
.
We can even give a concrete example of a locally finite group K where
$\operatorname {\mathrm {Ext}}(H_2(K),\mathbb {Z})$
has many nontorsion elements, giving nontorsion elements in
$H^3(\textrm{U}(1)\rtimes K)$
. This is despite
$\pi _0(\textrm{U}(1)\rtimes K)$
being purely torsion, in contrast to
$\textrm{U}(1)\times \mathbb {Z}$
in Example 4.4.
Example 4.7. Consider the locally finite group
$$ \begin{align*} K := \mathbb{Z}/2 \oplus \bigoplus_{p\text{ prime}} (\mathbb{Z}/p)^2, \end{align*} $$
which is the colimit of the groups
$K_p:=\mathbb {Z}/2\oplus (\mathbb {Z}/2)^2\oplus (\mathbb {Z}/3)^2\oplus \cdots \oplus (\mathbb {Z}/p)^2$
. It is a classical result that
$H_2((\mathbb {Z}/p)^2,\mathbb {Z})\simeq \mathbb {Z}/p$
and
$H_2(\mathbb {Z}/2,\mathbb {Z})=0$
, so that
$$ \begin{align*} H_2(K,\mathbb{Z}) \simeq \mathbb{Z}/2 \oplus\bigoplus_{p\text{ prime}} \mathbb{Z}/p. \end{align*} $$
These follow from the formula
$H_2(G\times H,\mathbb {Z})\simeq H_2(G,\mathbb {Z})\oplus H_2(H,\mathbb {Z})\oplus (G^{ab}\otimes H^{ab})$
. Since
$\operatorname {\mathrm {Ext}}$
sends direct sums to direct products,
$$ \begin{align*} \operatorname{\mathrm{Ext}}(H_2(K,\mathbb{Z}),\mathbb{Z}) \simeq \mathbb{Z}/2 \times \prod_{p\text{ prime}}\mathbb{Z}/p \end{align*} $$
and so
$H^3(K,\mathbb {Z})$
and hence
$H^3(\textrm{U}(1)\rtimes K,\mathbb {Z})$
have plenty of nontorsion elements.
For the sake of concreteness, take the element
$(1;1,1,1,\ldots )\in \operatorname {\mathrm {Ext}}(H_2(K,\mathbb {Z}),\mathbb {Z})$
and from this induce a central extension
$$ \begin{align*} \textrm{U}(1) \to \mathcal{T} \to \textrm{U}(1)\rtimes K \end{align*} $$
with nontorsion characteristic class in
$H^3(B(\textrm{U}(1)\rtimes K),\mathbb {Z})$
. This class is the
$DD$
-class of a lifting bundle gerbe following Lemma 2.6(5).
As a result of this example, we can see that the assumption of torsion
$\operatorname {\mathrm {Ext}}(H_2(K),\mathbb {Z})$
in Corollary 3.6 is necessary if one wants to make a statement about all possible finite-dimensional Lie groups with group of connected components K.
4.2. Applications
These results give strong obstructions to finding finite- dimensional lifting bundle gerbes. Namely, take a manifold or space X satisfying the hypotheses of Theorem 3.7 with
$H^3(X,\mathbb {Z})$
torsion-free. Then all finite-dimensional lifting gerbes on X have a stable trivialisation.
An example of particular focus in the literature considers a generic connected, compact simple Lie group, not necessarily simply-connected, which always has nontrivial third integral cohomology.
Proposition 4.8. The only connected, compact simple Lie groups G that admit a nontrivial lifting bundle gerbe are the groups
${\text{PSO}}(4n)$
for
$n>1$
and in this case there is precisely one, up to stable isomorphism. (It is enough to know that stable isomorphism in this context is equivalent to having the same
$DD$
-class.)
Proof. First recall that for a Lie group as in the proposition, the fundamental group is finite, so we can apply Theorem 1.1. Then, for all
$G\neq {\textrm {PSO}}(4n)$
,
$H^3(G,\mathbb {Z})\simeq \mathbb {Z}$
and hence any lifting gerbe must be trivial and, for
${\textrm {PSO}}(4)\simeq {\textrm {SO}}(3)\times {\textrm {SO}}(3)$
,
$H^3\simeq \mathbb {Z}\oplus \mathbb {Z}$
, with the same conclusion.
For
$G={\textrm {PSO}}(4n)$
with
$n>1$
, as
$H^3({\textrm {PSO}}(4n),\mathbb {Z})\simeq \mathbb {Z}\oplus \mathbb {Z}/2$
, there is only one nontrivial torsion class and this can be realised by a lifting gerbe, following [Reference Krepski12, Remark 5.1]. Namely, there is a nontrivial central extension
$$ \begin{align*} \textrm{U}(1) \to \widehat{Z}\to \mathbb{Z}/2\times \mathbb{Z}/2 =: Z, \end{align*} $$
where the underlying manifold of
$\widehat {Z}$
is
$\textrm{U}(1)\times \mathbb {Z}/2\times \mathbb {Z}/2$
with multiplication arising from the nontrivial 2-cocycle
$\beta \colon Z\times Z\to \textrm{U}(1)$
with
$\beta ((n_1,n_2),(m_1,m_2)) = (-1)^{n_1+m_2}$
[Reference Gawȩdzki and Waldorf8]. Then there is a nontrivial lifting bundle gerbe arising from the
$(\mathbb {Z}/2\times \mathbb {Z}/2)$
-bundle
$\operatorname {\mathrm {Spin}}(4n)\to {\textrm {PSO}}(4n)$
and this has torsion
$DD$
-class in
$H^3({\textrm {PSO}}(4n),\mathbb {Z})$
.
The following corollary is immediate, as a basic gerbe on a Lie group is, by definition, a nontorsion generator of
$H^3(G,\mathbb {Z})$
[Reference Gawȩdzki and Reis7].
Corollary 4.9. No basic gerbe on a connected, compact simple Lie group G, not necessarily simply-connected, can be constructed as a lifting bundle gerbe.
Remark 4.10. Note, however, that the pullback of a basic gerbe can be a finite-dimensional lifting bundle gerbe. For example, the basic gerbe on
${\textrm {SU}}(2)$
can be constructed via a carefully constructed submersion and is not a lifting gerbe. Its pullback along the Weyl map
$\textrm{U}(1)\times {\textrm {SU}}(2)/\textrm{U}(1) \to {\textrm {SU}}(2)$
(where
$\textrm{U}(1)\subset {\textrm {SU}}(2)$
are the diagonal matrices), however, is stably isomorphic to the Weyl bundle gerbe [Reference Becker, Murray and Stevenson1], which is a lifting bundle gerbe.
This theorem has algebraic consequences, as well. Recall that a crossed module of Lie groups consists of a homomorphism
$t\colon \hat {K} \to L$
of Lie groups such that
$\ker (t) \to \hat {K} \to t(\hat {K}) =: K$
is a central extension, K is a normal closed subgroup of L, and a lift of the adjoint action of L on K to
$\hat {K}$
, such that
$\hat {K}\to L\to \operatorname {\mathrm {Aut}}(\hat {K})$
agrees with the adjoint action of
$\hat {K}$
on itself. Moreover,
$L\to \operatorname {\mathrm {coker}}(t)$
is a principal K-bundle and we can consider the corresponding lifting bundle gerbe.
Corollary 4.11. Let G be a finite-dimensional connected, compact simple Lie group. Then there is no finite-dimensional crossed module
$t\colon \hat {K}\to L$
of Lie groups with
$\ker (t)\simeq \text{U}(1)$
and
$\operatorname {\mathrm {coker}}(t)\simeq G$
whose associated lifting bundle gerbe is nontrivial. More generally, no multiplicative bundle gerbe on G can be stably isomorphic to a finite-dimensional lifting bundle gerbe with nontorsion
$DD$
-class.
Proof. By Proposition 4.8, if
$\hat {K}\to L$
is a crossed module with
$\operatorname {\mathrm {coker}}(t)=G$
, then the corresponding lifting bundle gerbe must be torsion and hence we can consider just the case of
$G={\textrm {PSO}}(4n)$
,
$n>1$
.
The lifting bundle gerbe arising from a crossed module
$\hat {K}\to L$
is multiplicative [Reference Carey, Johnson, Murray, Stevenson and Wang4], as it fits into a strict 2-group extension corresponding to the extension of crossed modules
of
$\operatorname {\mathrm {coker}}(t)$
by
$\mathbf {B}\textrm{U}(1)$
(as strict Lie 2-groups). By [Reference Carey, Johnson, Murray, Stevenson and Wang4, Proposition 5.2], the
$DD$
-class of a multiplicative bundle gerbe on G is in the image of the transgression map
$H^4(BG,\mathbb {Z})\to H^3(G,\mathbb {Z})$
. But, by [Reference Henriques, Barron, Jurisich, Milas and Misra10, Theorem 6], for any connected compact Lie group G, the restriction map
$H^4(BG,\mathbb {Z}) \to H^4(BT,\mathbb {Z})$
induced by a maximal torus
$T\subset G$
is injective and hence
$H^4(BG,\mathbb {Z})$
is torsion-free, including for
$G={\textrm {PSO}}(4n)$
. Thus, the only class in
$H^3({\textrm {PSO}}(4n),\mathbb {Z})$
represented by some lifting gerbe is not the
$DD$
-class of the lifting gerbe arising from a crossed module.
The more general statement follows, as multiplicative bundle gerbes on G are classified by
$H^4(BG,\mathbb {Z})$
[Reference Carey, Johnson, Murray, Stevenson and Wang4, Proposition 5.2] (see also [Reference Gawȩdzki and Waldorf8], where the image of the injective map
$H^4(BG,\mathbb {Z})\to H^4(B\tilde {G},\mathbb {Z})$
is characterised for all possible compact connected simple Lie groups).
This tells us that for any finite-dimensional crossed module
$t\colon \hat {K}\to L$
as in Corollary 4.11, there is a principal
$\textrm{U}(1)$
-bundle
$T\to L$
whose restriction to
$K \subset L$
is
$\hat {K}\to K$
and there is a
$\hat {K}$
-action of T covering the action on L by multiplication via t. This corollary places a constraint on the structure of a crossed module analogous to that for group extensions that are topologically trivial but still algebraically nontrivial. There may still be algebraically nontrivial crossed modules with cokernel G.
As Corollary 4.11 constrains the structure of finite-dimensional crossed modules, it means that the higher geometry of principal 2-bundles with strict structure 2-group (that is, a crossed module), as in [Reference Waldorf20], for example, really must use infinite-dimensional constructions. A connection for such a bundle takes its values in the truncated
$L_\infty $
-algebra that is the crossed module of Lie algebras associated to the given crossed module of Lie groups [Reference Waldorf20, Definition 5.1.1]. As a result of the preceding corollary, finite-dimensional crossed modules
$\tau \colon \hat {\mathfrak {k}} \to \mathfrak {l}$
of Lie algebras where
$\operatorname {\mathrm {coker}}(\tau )$
is simple are insufficient to capture all examples of interest.
Finally, recall that twisted K-theory is a particular cohomology theory generalising topological K-theory, where a twist is an extra piece of data. Homotopy-theoretically a twist is a map to the classifying space for bundles of spectra with fibre the K-theory spectrum. The most well-studied twists arise from a factor of
$K(\mathbb {Z},3)$
of this classifying space and, hence, when constructing K-theory using geometric objects, geometric objects classified by maps to
$K(\mathbb {Z},3)$
are used. As such, bundle gerbes are one model for twists, as are principal
$\textrm{PU}(\mathcal {H})$
-bundles. The latter give rise to lifting bundle gerbes and, as noted in the introduction, every bundle gerbe is (noncanonically) the lifting gerbe of some
$\textrm{PU}(\mathcal {H})$
-bundle. But finite-dimensional bundle gerbes coming from
$\textrm{PU}(n)$
-bundles can be used as well and, more generally, the lifting bundle gerbes of principal G-bundles for other groups G.
Corollary 4.12. Given a space X as in Theorem 3.7, a finite-dimensional G-bundle P and central extension
$\widehat {G}$
, the twist
$\tau =\tau (P,\widehat {G})$
of the K-theory of X coming from this data is a torsion twist. In particular, if
$H^3(X,\mathbb {Z})$
is torsion-free, the resulting twisted K-theory
$K^{\ast ,\tau }(X)$
is just ordinary K-theory.
We can view this result as putting strong constraints on the maps
$$ \begin{align*} H^1(X,G)\times H^3(BG,\mathbb{Z}) \to \{\text{twists of}\ K\text{-theory on}\ X\}. \end{align*} $$
For instance, in the case that
$\pi _1(X)$
is locally finite and
$\operatorname {\mathrm {Ext}}(H^2(\pi _1(X)),\mathbb {Z})$
is torsion, arbitrary finite-dimensional Lie groups give only torsion twists.
Acknowledgements
I thank Konrad Waldorf for asking me whether all finite-dimensional lifting bundle gerbes are torsion, inspiring this note, and Maxime Ramzi for patient, extensive discussions. David Baraglia and MathOverflow users at https://mathoverflow.net/q/ 389703 also provided helpful information.
