3.1 Geometry and simulation parameters

The set-up of the three-dimensional simulations is sketched in figure 1. A droplet of radius $R_{0}$ is placed above the surface in equilibrium with the vapour. A uniform downward velocity is imposed on the drop while surrounding vapour is initialized with zero velocity. Initially the drop is sufficiently elevated to allow the liquid–vapour interface to equilibrate before the impact. No gravity is considered in the simulations due to the small time scales involved. All simulations, unless otherwise stated, were run on computational domain of $6R_{0}\times 6R_{0}\times 6R_{0}$ . Parameters of the simulated fluid are the same as the ones employed for investigation of droplets collisions (Mazloomi Moqaddam et al. Reference Mazloomi Moqaddam, Chikatamarla and Karlin2016) and the droplet–surface interactions (Mazloomi Moqaddam et al. Reference Mazloomi Moqaddam, Chikatamarla and Karlin2015c ): $\unicode[STIX]{x1D70C}_{l}=7.82$ (liquid density), $\unicode[STIX]{x1D70C}_{v}=0.071$ (vapour density), $\unicode[STIX]{x1D70E}=0.353$ (surface tension, corresponding to $\unicode[STIX]{x1D705}=0.00468$ in (2.2)) and $\unicode[STIX]{x1D707}_{v}=0.01$ (vapour dynamic viscosity); all are in lattice units (see below the match to physical units). The impact velocity was computed in accord with the Weber number $We=\unicode[STIX]{x1D70C}_{l}R_{0}U_{0}^{2}/\unicode[STIX]{x1D70E}$ , and the range $6\leqslant We\leqslant 150$ was studied. The dynamic viscosity of the droplet was fixed at $\unicode[STIX]{x1D707}_{l}=0.415$ corresponding to Ohnesorge number $Oh=0.025$ ( $Oh=\unicode[STIX]{x1D707}_{l}/\sqrt{\unicode[STIX]{x1D70C}_{l}\unicode[STIX]{x1D70E}R_{0}}$ ). This corresponds to a range of Reynolds number $Re=\sqrt{We}/Oh$ as $98\leqslant Re\leqslant 490$ .

A comment on the parameters of the simulated liquid and those used by the experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) (water) is in order. The density contrast $\unicode[STIX]{x1D70C}_{l}/\unicode[STIX]{x1D70C}_{v}\approx 100$ and the Ohnesorge number $Oh=0.025$ used in the ELBM simulations were shown before to be sufficient to recover the pertinent flow dynamics of colliding droplets and impacts on flat surfaces (Mazloomi Moqaddam et al. Reference Mazloomi Moqaddam, Chikatamarla and Karlin2015c , Reference Mazloomi Moqaddam, Chikatamarla and Karlin2016). The density contrast for water is an order of magnitude higher, whereas the Ohnesorge number is an order of magnitude lower than those of the simulation ( $Oh\approx 0.003$ for water). Nevertheless, similar to previously studied cases, we expect the essential dynamics to be captured correctly also in the present simulations with complex textures since the vapour state is too light to influence the liquid (Mazloomi Moqaddam et al. Reference Mazloomi Moqaddam, Chikatamarla and Karlin2015c , Reference Mazloomi Moqaddam, Chikatamarla and Karlin2016). Further evidence is provided below by comparing ELBM simulations with experiments.

The structure of the substrate is a square lattice of tapered posts placed uniformly with the centre-to-centre spacing $w$ on a flat plate. Each post is modelled as a right conical frustum of the height $h$ , with the smaller and larger base diameters $b$ and $B$ , respectively. The droplet radius $R_{0}$ is the input of the simulations while the rest of the geometry matches the experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014): $R_{0}/h=1.8$ (droplet radius to post height), $b/B\approx 0.28$ and $b=B-2h\tan \unicode[STIX]{x1D711}$ ( $\unicode[STIX]{x1D711}=2.6^{\circ }$ is the apex angle (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014)). We introduce the density of the texture (DoT) $\unicode[STIX]{x1D6EC}=R_{0}/w$ (parameter $\unicode[STIX]{x1D6EC}$ reflects the relative number of posts ‘seen’ by the droplet at impact). The spacing between the posts was chosen to reproduce $\unicode[STIX]{x1D6EC}_{exp}\approx 7.25$ (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) in the simulations of § 3.2 below. Both the surface of the conical frustum and the supporting flat plate are considered SHS with a contact angle $\unicode[STIX]{x1D703}=165^{\circ }$ .

Finally, in order to convert lattice time $t_{LB}$ into seconds, we first compute the inertia–capillary time $\unicode[STIX]{x1D70F}_{LB}=\sqrt{\unicode[STIX]{x1D70C}_{l}R_{0}^{3}/\unicode[STIX]{x1D70E}}$ using the density, droplet radius and surface tension in lattice units. Next, $\unicode[STIX]{x1D70F}$ is extracted from the experimental data and the reduced time for both the experiment and the simulation are matched, $t_{LB}/\unicode[STIX]{x1D70F}_{LB}=t/\unicode[STIX]{x1D70F}$ . Thus, given $t_{LB}$ (the number of time steps), we uniquely obtain the corresponding physical time $t=(\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{LB})t_{LB}$ . A droplet radius of $R_{0}=100$ grid units was used unless stated otherwise. All simulations were checked for grid convergence using $R_{0}=100$ and lower; only the highest resolution results are reported here.

3.2 Validation with experimental data

In this section we validate the simulations with published data from experiments (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014; Gauthier et al. Reference Gauthier, Symon, Clanet and Quéré2015). For a flat SHS, it was shown in Richard et al. (Reference Richard, Clanet and Quéré2002) that the contact time $t_{contact}$ is independent of Weber number in a wide range and can be scaled with the inertial–capillary time scale: $t_{contact}/\unicode[STIX]{x1D70F}\approx 2.5$ . Figure 2 reports the variation of contact time on the flat SHS for a range of Weber numbers; simulation results agree well with the experiment (Gauthier et al. Reference Gauthier, Symon, Clanet and Quéré2015). In figure 3, the history of the drop spread on a flat SHS at $We=26.6$ is reported. Excellent agreement between results obtained by numerical simulations and experimental observations reported in Bird et al. (Reference Bird, Dhiman, Kwon and Varanasi2013) is evident from figure 3.

Figure 2. Contact time on a flat superhydrophobic surface with the contact angle $\unicode[STIX]{x1D703}=161^{\circ }$ as a function of Weber number. Open symbols: ELBM simulations; solid symbols: experiment (Gauthier et al. Reference Gauthier, Symon, Clanet and Quéré2015). Dashed line: $t_{contact}/\unicode[STIX]{x1D70F}=2.5$ .

Figure 3. Lateral expansion of a water drop impacting on a flat superhydrophobic surface at $We=26.6$ (supplementary movie 1 available at https://doi.org/10.1017/ jfm.2017.306). Line: simulation; symbols: experiment (Bird et al. Reference Bird, Dhiman, Kwon and Varanasi2013).

We note that the flat SHS test validates the use of the Ohnesorge number of $Oh=0.025$ for the ELBM fluid in the present context. Indeed, as it has been shown by many authors, e.g. Antonini et al. (Reference Antonini, Bernagozzi, Jung, Poulikakos and Marengo2013a ), Maitra et al. (Reference Maitra, Antonini, Tiwari, Mularczyk, Imeri, Schoch and Poulikakos2014), that the Ohnesorge number takes effect on the contact time at much higher values, $Oh\approx 1$ (i.e. for highly viscous liquids such as glycerol ( $Oh\approx 3$ ) or silicon oil). For $Oh<0.1$ , there is no effect of viscosity during impact on flat surfaces, and thus it is not surprising that the present simulation agrees well with the experiments which use water. We refer to Mazloomi Moqaddam et al. (Reference Mazloomi Moqaddam, Chikatamarla and Karlin2015c ) for other comparisons of ELBM with experiments on a flat SHS.

Now we proceed with the textured SHS. Following Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014), we introduce characteristic time instances ( $t=0$ corresponds to the time of first contact): $t_{\uparrow }$ is the time at which the texture is fully emptied (emptying time); at $t_{max}$ the drop reaches its maximal lateral extension; $t_{contact}$ is the time at which the drop loses contact with the surface (contact time). Snapshots of a drop impinging on a texture of tapered posts at $We=14.1$ are shown in figure 4(a) along with the images from the experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014). Pancake formation and rebound is clearly seen in the simulation. Simulation results for both the shape of the drop and the characteristic times are in excellent agreement with experimental observations.

Along with the tapered posts texture of figure 1, we simulated a simpler case of rectangular prism posts which was also considered in the experiment of Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014). The droplet radius for this simulation was $R_{0}=34$ lattice units. The height of posts $h$ , the posts centre-to-centre spacing, $w$ and the side of the square cross-section $b$ were computed according to the aspect ratios $R_{0}/h$ , $R_{0}/w$ and $b/h$ of the experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) and the results are presented in figure 4(b) for $We=7.9$ . Also in this case excellent agreement between simulation and experiment is observed.

Figure 4. Comparison of simulation (bottom) and experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) (top) for the pancake bouncing of a drop impinging on (a) the tapered posts at $We=14.1$ and (b) the straight square posts at $We=7.9$ .

Figure 5. Drop rebound from macro-texture at various Weber numbers. Symbol: simulation; line: experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014). Characteristic times: $t_{\uparrow }$ (emptying time, blue), $t_{max}$ (maximum lateral extension time, red), $t_{contact}$ (contact time, magenta); pancake quality $Q=d_{jump}/d_{max}$ (green) where $d_{jump}$ and $d_{max}$ are the diameters of the drop at $t_{contact}$ and $t_{max}$ , respectively. (a) Tapered posts. Geometry of the posts used in the simulations matches the experiment: $R_{0}/h=1.8$ (droplet radius to post height), density of texture $R_{0}/w\approx 7.25$ (droplet radius to centre-to-centre spacing), $b/B\approx 0.28$ (smaller to larger diameter of the bases) and $b=B-2h\tan \unicode[STIX]{x1D711}$ ( $\unicode[STIX]{x1D711}=2.6^{\circ }$ is the apex angle) (supplementary movies 2 and 3). (b) Square posts.

For validation, simulations were performed within the experimentally accessed range of Weber numbers $6<We<25$ . Dependence of characteristic times $t_{\uparrow }$ , $t_{max}$ , and $t_{contact}$ on Weber number is compared with the experiment in figure 5(a) (tapered posts) and figure 5(b) (square posts). Also the so-called pancake quality $Q=d_{jump}/d_{max}$ is compared to the experiment, where $d_{jump}$ and $d_{max}$ are the diameters of the drop at $t_{contact}$ and $t_{max}$ , respectively.

Simulations in figure 5(a) show that for $We<12$ the contact time is $t_{contact}\simeq 16~(\text{ms})$ which is in good agreement with the conventional complete rebound from a flat surface (Richard et al. Reference Richard, Clanet and Quéré2002). The onset of the pancake bouncing regime at critical Weber number $We^{\ast }\approx 12$ agrees well with experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014). Reduction in contact time by a factor four is observed. We repeated the measurements of the characteristic times scales for the drop impinging on the straight square posts. Simulation results compare well with the experiment in figure 5(b).

Summarizing, ELBM simulation demonstrates excellent agreement with the existing experimental data. In the remainder of this paper, we shall address regimes which were so far not studied experimentally in order to gain a more comprehensive picture of bouncing off macro-textured surfaces.

3.3 Textures with perfect coating

Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) reported experiments in a narrow range of Weber numbers ( $We<25$ ). When the Weber number is increased, penetration depth into the texture increases and the deforming drop will eventually reach the base of the substrate. It is difficult to study the liquid inside the texture in the experiments. Here we extend the ELBM simulations to higher Weber numbers, $6<We<150$ . We first consider the same geometry as in the previous section, and assume perfect coating, that is, both the posts and the base are SHS with contact angle $\unicode[STIX]{x1D703}=165^{\circ }$ .

Figure 6. Snapshots of the rebound from tapered posts at (a) $We=40$ , (b) $We=50$ , (c) $We=80$ , (d) $We=120$ . Density of the texture $\unicode[STIX]{x1D6EC}_{exp}=7.25$ . Invading liquid hits the base of the texture at $We\geqslant 50$ . Perfect coating is assumed for both the posts and the base plate (contact angle is set to $\unicode[STIX]{x1D703}=165^{\circ }$ ). After hitting the base, penetrated liquid experiences a quick lateral extension, detaches from the base, returns to the top of the posts and demonstrates pancake rebound (supplementary movies 4 and 5). Geometry of the macro-texture is same as in figure 5(a).

Figure 7. Contact time $t_{contact}$ (squares) and pancake quality $Q$ (circles) of a drop impinging on perfectly coated tapered posts with the density of texture $\unicode[STIX]{x1D6EC}_{exp}=7.25$ , for a range $6\leqslant We\leqslant 150$ . Geometry of the macro-texture is same as in figure 5(a).

Figure 8. Square: dependence of the critical Weber number $We^{\ast }$ on the density of texture $\unicode[STIX]{x1D6EC}=R_{0}/w$ ; Line: quadratic fit of the critical Weber number for the realizations between $\unicode[STIX]{x1D6EC}=4$ and $\unicode[STIX]{x1D6EC}=12.5$ . Circle: contact time at $We^{\ast }$ for the corresponding density of texture. Open symbols indicate that the critical Weber number was not observed for the corresponding density of texture. Various $\unicode[STIX]{x1D6EC}$ were realized by changing the post’s centre-to-centre spacing $w$ under fixed drop radius $R_{0}$ . At $\unicode[STIX]{x1D6EC}=12.5$ , the bases of the conical posts touch each other. Dimensions of the posts are same as in the experiment.

Figure 6 shows snapshots of the impact on the perfectly coated texture at various Weber numbers. For $We>40$ , the penetrated liquid interacts with the base plate at the time $t_{mpl}$ (maximal penetration of the drop). Simulations show that pancake bouncing is still observed for a much wider range of Weber numbers, $12<We<150$ . Figure 7 shows that both the reduction of the contact time (squares) and the pancake quality (circles) remain unaffected until at least $We\approx 150$ . This can be attributed to the fact that the base plate of the texture is also considered an SHS with a uniform contact angle (see § 3.5).

Summarizing, under the assumption of perfect SHS coating, we found that the pancake bouncing extends to much higher Weber numbers, with the critical Weber number clearly identified and in agreement with experimental observations.

3.4 Critical Weber number and density of texture

In the above simulations, the density of the texture, $\unicode[STIX]{x1D6EC}=R_{0}/w\approx 7.25$ , matched the experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) and the critical Weber number $We^{\ast }\approx 12$ at the onset of the contact time reduction was found in both simulation and experiment (see figures 5 a, 7). Next we study the effect of density of the texture (DoT) $\unicode[STIX]{x1D6EC}=R_{0}/w$ on the contact time reduction by varying the centre-to-centre spacing $w$ . Intuitively, one expects the limit of contact time of the flat SHS to be reached for both sparse ( $\unicode[STIX]{x1D6EC}\approx 1$ ) and dense textures ( $\unicode[STIX]{x1D6EC}\gg 1$ ; in the present simulation, the maximal texture density is reached at $\unicode[STIX]{x1D6EC}\approx 12.5$ when the bases of the posts start to overlap). In the intermediate range, the critical Weber number $We^{\ast }$ can be observed, at which the reduction of the rebound time occurs.

Figure 8 shows the dependence of the critical Weber number on the density of texture $We^{\ast }(\unicode[STIX]{x1D6EC})$ , and the corresponding contact time, $t^{\ast }(\unicode[STIX]{x1D6EC})=t_{contact}(We^{\ast }(\unicode[STIX]{x1D6EC}))$ . From figure 8, one can see that the critical Weber number and the associated contact time reduction is first found at $\unicode[STIX]{x1D6EC}=4$ and extends to higher DoT. Note that, while $We^{\ast }$ was found at DoT as high as $\unicode[STIX]{x1D6EC}\approx 12.5$ in the simulation, the corresponding value $We^{\ast }(12.5)\approx 42.5$ is far off the range of Weber numbers probed in the experiment ( $We<30$ ). In other words, if a limited range of Weber numbers is concerned, the case of very dense textures ( $\unicode[STIX]{x1D6EC}=12.5$ was the most dense texture in the simulation since the bases of the cones start to overlap) shows the limit of the flat SHS as the drop resists to penetrate into the texture.

A qualitative estimate of the dependence $We^{\ast }(\unicode[STIX]{x1D6EC})$ can be based on the following arguments. First, we recall the explanation of contact time reduction on the macro-wedges in Gauthier et al. (Reference Gauthier, Symon, Clanet and Quéré2015). If the drop is deformed by the macro-structure in such a way that it can be represented by a partition into $N$ smaller blobs, the inertia–capillary time $\unicode[STIX]{x1D70F}\sim \sqrt{\unicode[STIX]{x1D70C}R_{0}^{3}/\unicode[STIX]{x1D70E}}$ transforms to $\unicode[STIX]{x1D70F}\sim \sqrt{\unicode[STIX]{x1D70C}R_{0}^{3}/N\unicode[STIX]{x1D70E}}$ , which explains the experimentally observed scaling of contact time reduction, $t_{contact}\sim N^{-1/2}$ (see Gauthier et al. Reference Gauthier, Symon, Clanet and Quéré2015). In the present case, the ‘blobs picture’ pertains to the penetrated liquid. The number of blobs (liquid filaments invading the spacing between the posts) can be estimated as $N\sim \unicode[STIX]{x1D6EC}^{2}$ , and thus the emptying time $t_{\uparrow }$ scales as $t_{\uparrow }\sim \sqrt{\unicode[STIX]{x1D70C}R_{0}^{3}/\unicode[STIX]{x1D6EC}^{2}\unicode[STIX]{x1D70E}}\sim (R_{0}/U)\sqrt{We/\unicode[STIX]{x1D6EC}^{2}}$ . Second, the spreading time of the part of the drop over the top of the texture $t_{\rightarrow }$ can be estimated by the crashing time (Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004), $t_{\rightarrow }\sim R_{0}/U$ , that is, it does not depend on DoT $\unicode[STIX]{x1D6EC}$ . Finally, following the argument of Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014), at the critical Weber number, the spreading and the emptying times should match (see figure 5 a), $t_{\rightarrow }\approx t_{\uparrow }$ . Using the above estimates, we obtain $We^{\ast }\sim \unicode[STIX]{x1D6EC}^{2}$ . Thus, the present simple arguments, although not universal, imply a quadratic dependence of the critical Weber number on the density of texture, which is consistent with the simulation results in figure 8.

The blue circles in figure 8 shows the contact time as a function of DoT, measured at the critical Weber number for each $\unicode[STIX]{x1D6EC}$ . The onset of contact time reduction is clearly visible at $\unicode[STIX]{x1D6EC}=4$ . Note that the critical $t^{\ast }(\unicode[STIX]{x1D6EC})$ is confined to a band between a two to four times reduction with respect to the contact time of the flat SHS. In other words, while the contact time reduction may be not as significant for lower DoT as compared to the spectacular four times reduction at the close to optimal DoT $\unicode[STIX]{x1D6EC}\approx 7$ of the experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014), it is still clearly lower than the flat SHS values. In that respect, the blue circles in figure 8 are reminiscent of the ‘quantization’ of the contact time plots on the SHS wedge macro-structures (see figure 3a of Gauthier et al. Reference Gauthier, Symon, Clanet and Quéré2015), with relatively narrow band of reduced contact times for a range of DoTs.

Summarizing, under the assumption of perfect SHS coating, we find that the density of the texture strongly affects the critical Weber number, with the transition to reduced contact time growing nonlinearly (quadratically) with DoT. Hence, during a design process, one needs to consider the trade-off between the amount of reduction in the contact time and the critical Weber number at which the contact time reduction sets in. Also, the observation of significant time reduction in a wide range of DoTs makes it possible to avoid the perfect arrangements of pillars. In the next section we shall investigate the effect of imperfect coating on the contact time reduction.

3.5 Imperfect coating

So far we have assumed that the SHS quality is maintained uniformly throughout the texture and the base plate. However, this is unlikely to hold when, for example, the SHS coating is produced by spraying a polymer solution on the texture. According to Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014), controlling the quality and uniformity of coating throughout the posts, and especially in the valleys between them, is a difficult task. Hence it is reasonable to assume that the contact angle at the base plate is lower than that on the upper part of the posts. Since the drop interacts with the base plate at $We\geqslant 50$ (see figure 6), we probe the effect of imperfect coating by assigning a smaller contact angle for the base plate and the bottom part of the posts ( $10\,\%$ of the height). Since SHS are usually manufactured by coating hydrophobic surfaces with nano-scale structures, we choose three different contact angles at the base plate and the bottom part of the posts, $\unicode[STIX]{x1D703}_{bottom}=132^{\circ }$ ( $\unicode[STIX]{x1D705}_{w}=-0.09625$ ) (2.3), $140^{\circ }$ ( $\unicode[STIX]{x1D705}_{w}=-0.105$ ) and $145^{\circ }$ ( $\unicode[STIX]{x1D705}_{w}=-0.115$ ). These values are reasonable for conventional hydrophobic surfaces. The upper part the posts is maintained at the SHS contact angle $\unicode[STIX]{x1D703}=165^{\circ }$ as before, and the density of texture is fixed at $\unicode[STIX]{x1D6EC}_{exp}=7.25$ .

Figure 9. Contact time $t_{contact}~(\text{ms})$ for imperfectly coated textures at three different contact angles at the substrate base, $\unicode[STIX]{x1D703}_{bottom}=145^{\circ }$ , $\unicode[STIX]{x1D703}_{bottom}=140^{\circ }$ and $\unicode[STIX]{x1D703}_{bottom}=132^{\circ }$ , as a function of Weber number. Reference data for perfectly coated texture $\unicode[STIX]{x1D703}_{bottom}=165^{\circ }$ are also shown. Geometry of the texture is same as in figure 5(a).

Contact time for imperfectly coated textures is shown in figure 9. For $We\leqslant 40$ , the contact time is the same for all coatings considered; since liquid penetrates the texture without touching the base, the quality of coating has no effect on the contact time. However, for $We>40$ , the liquid reaches the substrate base, and degraded coating alters significantly the contact time droplet dynamics and the pancake quality. As seen from figure 9, deterioration of the contact time becomes progressively more severe with lowering of the contact angle at the bottom, as expected. For the smallest contact angle $\unicode[STIX]{x1D703}_{bottom}=132^{\circ }$ , for $We>40$ , the impacting drop sticks to the substrate base. Consequently, the drop rebounds in a conventional fashion, with approximately the same contact time as for the flat SHS, in the entire range of Weber numbers $We=65-150$ . However, for a less severe degradation, $\unicode[STIX]{x1D703}_{bottom}=140^{\circ }$ and $145^{\circ }$ , we observe a nonlinear dependence of the contact time on the Weber number $We>40$ .

In order to elucidate this nonlinearity, in figure 10 we present snapshots of the impact for $\unicode[STIX]{x1D703}_{bottom}=140^{\circ }$ , for different Weber numbers. For $We=50$ , $80$ and $120$ , the drop contacts with the substrate base at $t_{mpl}$ . Due to lack of superhydrophobicity at the bottom, the penetrated liquid tends to stick to the texture base before it is pulled out by the rest of drop moving upward. In figure 10(b) ( $We=50$ ), although the penetrated liquid sticks to the substrate base, it returns to the top of the texture quickly thus enabling pancake bouncing but with an almost double contact time, $t_{contact}\approx 7~(\text{ms})$ . At a higher Weber number $We=80$ , figure 10(c), due to a larger contact area between the liquid and the texture base, the penetrated liquid returns to the top of the posts with a delay. Consequently, the drop has enough time to retract and the overall picture resembles the conventional bouncing rather than a pancake rebound. The contact time $t_{contact}\approx 14~(\text{ms})$ becomes closer to the conventional bouncing value (see Supplementary Movie 6). However, as the Weber number is further increased, figure 10(d), $We=120$ , the contact time reduces back to the value $t_{contact}\approx 7~(\text{ms})$ . In this case, since the contact area between the drop and the base becomes even larger, also the number of invaded valleys increases. The force due to surface tension is thus able to overcome the pinning effect of the imperfectly coated base and the texture is emptied faster. This explains the return of a pancake-like bouncing at $We=120$ , and the contact time becomes smaller than at $We=80$ .

Figure 10. Snapshots of impact on imperfectly coated texture at (a) $We=40$ , (b) $We=50$ , (c) $We=80$ , (d) $We=120$ . Contact angle at the base plate and $10\,\%$ above it set to $\unicode[STIX]{x1D703}_{bottom}=140^{\circ }$ , and for the rest of the texture the contact angle is $\unicode[STIX]{x1D703}=165^{\circ }$ . For $We\geqslant 50$ , the penetrated liquid reaches the base at $t_{mpl}$ . Geometry of the macro-texture is same as in figure 5(a). (Supplementary Movies 6 and 7.)

Summarizing, a moderately degraded coating at the bottom of the texture features a nonlinear dependence of the contact time on the Weber number and significantly affects the rebound pattern.

3.6 Energy budget

Energy considerations were invoked in Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) to quantify the mechanism of pancake bouncing. The assumption behind this analysis was that the kinetic energy of the drop is fully converted into the surface energy at the maximal penetration into the texture. However, neglecting energy dissipation is less obvious for an impact on textured surfaces. Indeed, since the shape of the droplet is considerably more distorted as compared to the flat SHS (the flow ‘sees more walls’), stresses in the boundary layers contribute more to the dissipation. On the other hand, ELBM was shown to quantitatively capture the energy budget in binary droplet collisions (Mazloomi Moqaddam et al. Reference Mazloomi Moqaddam, Chikatamarla and Karlin2016). In this section we report and discuss the energy budget of the pancake bouncing regime from the ELBM simulations. For a drop with volume $V$ and surface area $A$ , let us introduce the kinetic energy, $K=\int _{V}(\unicode[STIX]{x1D70C}u^{2}\,\text{d}V)/2$ , the surface energy $S=\unicode[STIX]{x1D70E}A$ and the energy loss due to viscous dissipation $\unicode[STIX]{x1D6EF}$ ,

Further introducing normalized energies, $\tilde{K}=K/E_{0}$ , $\tilde{S}=S/E_{0}$ and $\tilde{\unicode[STIX]{x1D6EF}}=\unicode[STIX]{x1D6EF}/E_{0}$ , where $E_{0}=K_{0}+S_{0}$ is the energy of the drop at $t=0$ , the energy balance is written as,

All three components of the energy balance equation (3.2) were evaluated individually for the impact on a perfectly coated texture with the texture density $\unicode[STIX]{x1D6EC}_{exp}=7.25$ (§§ 3.2 and 3.3). In figure 11 we present the time evolution of $\tilde{K}$ , $\tilde{S}$ and $\tilde{\unicode[STIX]{x1D6EF}}$ . We also show the normalized centre-of-mass kinetic energy $\tilde{K}_{cm}=K_{cm}/E_{0}$ where $K_{cm}=(mU_{cm}^{2})/2$ is the kinetic energy of centre-of-mass, with $m$ the mass of the liquid and $U_{cm}$ the centre-of-mass velocity. Results for three representative Weber numbers are shown: $We=15$ (shortly after the onset of pancake bouncing at $We^{\ast }\approx 12$ ); $We=30$ (at the limit of the experimentally accessed Weber numbers; significant intrusion of liquid into the texture) and $We=80$ (large intrusion).

Before discussing the results, a brief comment on the validation of the numerics is in order. First, the numerical result at $t=0$ (spherical unperturbed drop moving with the velocity $U_{0}$ ) satisfies well the exact relations, $\tilde{K}_{0}=We/(We+6)$ , $\tilde{S}_{0}=6/(We+6)$ ; see table 1. Also, the energy balance (3.2) is satisfied within $2\,\%$ for all times and Weber numbers which is consistent within the accuracy of evaluation of velocity gradients in the computation of energy dissipation.

The first observation concerns the kinetic energy $\tilde{K}$ and the centre-of-mass kinetic energy $\tilde{K}_{cm}$ . While the latter vanishes at the maximal penetration of the drop into the texture, the kinetic energy itself is different from $\tilde{K}_{cm}$ . This difference is attributed to the flow inside the rim of the upper part of the drop remaining on top of posts as well as the opposing flow directions observed inside the droplet. Flow inside the deformed droplet is visualized by snapshots of velocity field in figure 12. The non-negligible amount of kinetic energy carried by the flow of this type was indicated in Clanet et al. (Reference Clanet, Béguin, Richard and Quéré2004) for drop impact on a flat surface. With the increase of Weber number, a greater part of the droplet penetrates the texture, hence the amount of energy carried by this flow decreases. This is consistent with the result of simulation which shows that the relative difference between $\tilde{K}$ and $\tilde{K}_{cm}$ decreases with the Weber number.

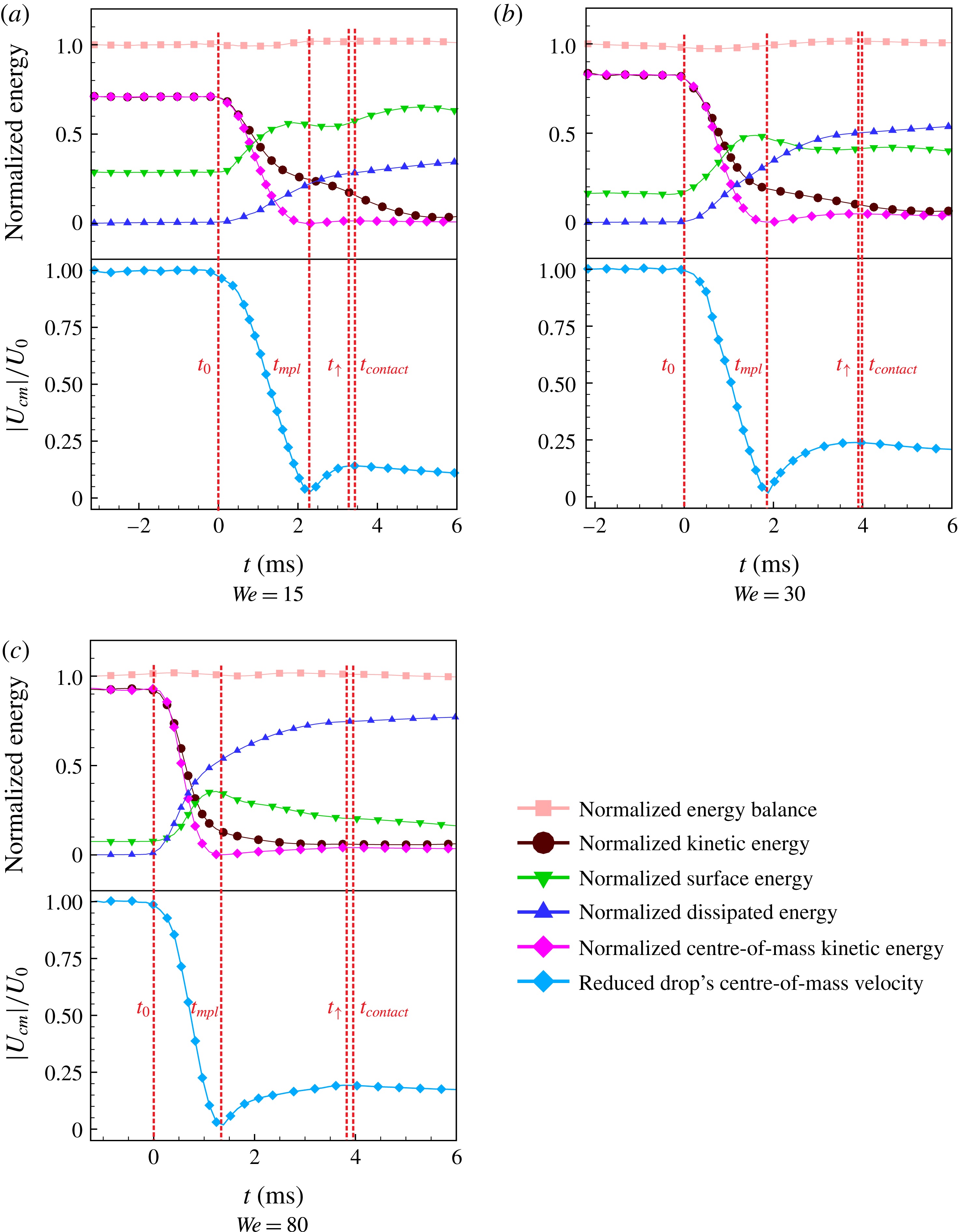
Figure 11. (a,b) History of various components of the energy balance. Circles: normalized kinetic energy $\tilde{K}$ ; downward triangles: normalized surface energy $\tilde{S}$ ; upward triangles: normalized dissipated energy $\tilde{\unicode[STIX]{x1D6EF}}$ . Squares: normalized energy balance $\tilde{K}+\tilde{S}+\tilde{\unicode[STIX]{x1D6EF}}$ . Diamonds: normalized centre-of-mass kinetic energy $\tilde{K}_{cm}$ . (c) Reduced centre-of-mass velocity of the drop $U_{cm}/U_{0}$ . Impact on a perfectly coated SHS $\unicode[STIX]{x1D703}=165^{\circ }$ for low and high Weber numbers (supplementary movie 8).

Figure 12. Visualization of the velocity vectors inside the middle plane of the drop impacting on the tapered posts for different times, $We=30$ .

Second, the surface energy $\tilde{S}$ rapidly increases after the impact, as expected. For $We=15$ we see two maxima of $\tilde{S}$ , a local maximum close to the zero of the centre-of-mass velocity (the drop has stopped penetrating into the texture) and then the global maximum at the time of maximum lateral extension. Note that in this case, maximal extension comes after the droplet bounces off the texture. However, with the increase of the Weber number, the second maximum tends to disappear and is not present at $We=80$ . This situation can be termed a pseudo-pancake rebound in order to distinguish it from the true rebound at $We=15$ : the maximal stretching synchronizes with the maximum penetration time and does not affect the contact time, as was shown above.

Finally, it is clear from the energy balance at all Weber numbers that the dissipation is not negligible in any of the cases for the simulated Ohnesorge number $Oh=0.025$ . While for the lower $We=15$ , the surface energy becomes dominant soon after the impact, dissipation is not small even in that case with levels around $25\,\%$ at the rebound. It is seen from figure 11 the fraction of energy loss at higher Weber numbers is even larger and dominates others at $We=80$ .

Liu et al. (Reference Liu, Whyman, Bormashenko, Hao and Wang2015b ) discussed a possibility that macroscopic air pockets get trapped between the droplet and the substrate. Such trapped pockets of air or vapour can undergo compression which could serve as an additional storage of energy to be released into the kinetic energy during the capillary emptying. However, the energy balance evaluation above suggests that such a scenario need not be present.

Summarizing, for the macroscopically flat superhydrophobic surface, the scaling of the contact time holds whenever the Ohnesorge number is not too large ( $Oh<1$ ) (Antonini et al. Reference Antonini, Jung, Wetzel, Heer, Schoch, Mazloomi Moqaddam, Chikatamarla, Karlin, Marengo and Poulikakos2016). Similar universality holds also in the case of tapered macro-texture: while the dissipation is not necessarily negligible for $Oh=0.025$ , the contact time of the pancake bouncing scales the same way as in the experiment with water droplets. The only important requirement for that mechanism to be realized is the clear dominance of the surface energy over the kinetic energy at the instance of maximal penetration into the texture. Thus, such energy balance analysis could be very handy in estimating the role played by kinetic, surface and viscous forces for a droplet–wall interaction. Such analysis is of greater use when the underlying mechanisms of droplet bouncing are not well understood, for example complex macro-textured surfaces. Moreover, imbalance in energy analysis could lead to a better understanding of the role played by external factors such as trapped air pockets, thus enabling the design and optimization of novel surface textures. However, the study of the compressibility effects due to presences of the air pockets is not within the scope of this paper. Indeed, full access to compressibility effects requires a viable compressible flow lattice Boltzmann (LB) model and thus further advancements are required to extend the present quasi-incompressible LB model to capture these effects. A reliable compressible LB model for single-phase flows was recently introduced in (Frapolli, Chikatamarla & Karlin Reference Frapolli, Chikatamarla and Karlin2015, Reference Frapolli, Chikatamarla and Karlin2016) and incorporation of this model into the multiphase/multicomponent setting should be the subject of future work.

3.7 Impact on a tilted macro-texture

Finally, we apply our model to capture the impact of a drop on tilted macro-textured surface. Figure 13 demonstrates that pancake bouncing takes place also for the surface tilted at $\unicode[STIX]{x1D719}=30^{\circ }$ . Both the snapshots and the contact time $t_{contact}=3.6~(\text{ms})$ for the situation shown in figure 13 are in good agreement with those observed in the experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014). Figure 14 reports the contact time for an inclined surface for different tilt angles in a range of Weber numbers from $We=6$ to $We=150$ . From figure 14, at a tilt angle of $\unicode[STIX]{x1D719}=30^{\circ }$ , the pancake bouncing sets in at $We\geqslant 25$ , that is, at an almost twice as high Weber number as compared to the normal impact ( $\unicode[STIX]{x1D719}=0^{\circ }$ ). This happens since the motion along the slope delays the penetration of the liquid into the texture. It is also noted that by increasing the inclination angle, the transition to the pancake bouncing is more gradual than a sharp transition observed for the horizontally aligned substrate.

Figure 13. Snapshots of an impact on tapered posts tilted at $\unicode[STIX]{x1D719}=30^{\circ }$ ; $We=31.2$ . The drop rebounds at $t_{contact}=3.6~(\text{ms})$ which is in excellent agreement with the experiment (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014). Snapshots correspond to figure 1(d) of Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) (supplementary movie 9).

Figure 14. Contact time of a liquid drop impinging on tapered surface for two tilt angles, $\unicode[STIX]{x1D719}=30^{\circ }$ and $\unicode[STIX]{x1D719}=45^{\circ }$ in a range of Weber numbers, $6\leqslant We\leqslant 150$ . Reference data for the normal impact, $\unicode[STIX]{x1D719}=0^{\circ }$ are also shown. Significant reduction in the contact time occurs at larger Weber numbers by increasing the tilt angle.