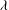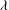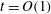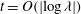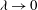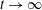1. Introduction
The moving contact line problem is explained as follows. The theory of traditional macroscopic fluid mechanics imposes the requirement that the velocity of a fluid in contact with a solid substrate must be equal to the velocity of the substrate (the ‘no-slip condition’). However, this condition is obviously violated at a moving contact line, such as what occurs for a spreading droplet. In order to resolve this difficulty, the no-slip condition can be changed to an alternative condition that allows for slip. The challenges in resolving the moving contact line problem are to (i) better understand the current slip models, their advantages and disadvantages, and (ii) propose alternative slip models that better represent the physics. In this paper, we shall focus on the former problem, and, in particular, we discuss the distinguished nature of the zero-slip limit.
Here, we shall deal exclusively with the case that the contact line dynamics is modelled using the classical Navier slip condition. In two dimensions, where
$u$
is the velocity parallel to the plane surface and
$z$
is measured normally away from it, this condition imposes
$$\begin{eqnarray}u={\it\lambda}\frac{\partial u}{\partial z}\end{eqnarray}$$
for a fluid in contact with a solid boundary at rest, and
${\it\lambda}$
is the slip coefficient, which is a measure of the length over which slip is significant. There are a multitude of papers in the literature on the asymptotics of the contact line problem as the slip parameter tends to zero (see, e.g., Voinov Reference Voinov1976, Hocking & Rivers Reference Hocking and Rivers1982 and Lacey Reference Lacey1982), and our paper seeks to highlight the idea of the non-uniformity of the perturbation methods as slip tends to zero and for different choices of time scales. This is most similar to the study of King & Bowen (Reference King and Bowen2001) and Flitton & King (Reference Flitton and King2004). We provide a more comprehensive listing of the vast literature on the topic of the moving contact line in § 1.1.
More specifically, in this work, we wish to demonstrate that when time is held at
$O(1)$
, the dynamics of contact line spreading converges to a slipless equation as
${\it\lambda}\rightarrow 0$
. However, in the limit
$t\rightarrow \infty$
, a rescaling of time is necessary. Thus, convergence can be achieved in the zero-slip limit by using a slip-free equation, but only at finite time. Our analysis seeks to explore this idea of non-uniformity using a combination of asymptotic techniques, and also accurate numerical results which clearly show the expected limiting behaviours in the singular regime.
We present an asymptotic analysis of the lubrication equations for a droplet spreading under the effect of surface tension. In particular, there are two regimes:
$$\begin{eqnarray}\displaystyle (\text{i}) & & \displaystyle {\it\lambda}\rightarrow 0\quad \text{and}\quad t=t^{\ast }~\text{fixed}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\text{ii}) & & \displaystyle {\it\lambda}\rightarrow 0\quad \text{and}\quad t\gg 1.\end{eqnarray}$$
${\it\lambda}\rightarrow 0$
, the macroscopic motion of the droplet converges to the slipless equation (
${\it\lambda}=0$
), and the apparent contact angle,
${\it\theta}_{app}$
converges to a value that can be determined solely by solving this particular equation. The apparent contact angle is not influenced by the microscopic conditions. In this regime, the contact line displacement tends to zero as slip tends to zero, and any contact line slippage is a higher-order effect within the macroscopic region. It should be noted that slippage remains a leading-order contribution within the inner region near the contact line.
However, in the distinguished limit which involves the dual limit
${\it\lambda}\rightarrow 0$
and
$t\rightarrow \infty$
, the solutions in regime (i) are no longer valid, and the asymptotic approximations in this regime become disordered. A rescaling of time is necessary; once time is rescaled, we recover the equivalent analyses of others (cf. Hocking Reference Hocking1981, Hocking Reference Hocking1983 and Cox Reference Cox1986), and contact line displacement becomes a significant effect. In particular,
${\it\theta}_{app}$
is now a function of the unknown contact line location and depends on the microscopic properties of the substrate. As is well known through these previous works, the contact line speed is logarithmically small in the slip length, and involves the key quantity
$$\begin{eqnarray}{\it\epsilon}=1/|\!\log {\it\lambda}|.\end{eqnarray}$$
The principal result of this paper is shown in figure 1, which plots a rescaled contact line velocity,
${\dot{a}}(t)/{\it\epsilon}$
, as a function of time for a spreading droplet. The graph demonstrates that the contact line moves rapidly initially, then slows as time increases. The two time scales determining the dynamics are clearly visible, and the asymptotic approximations developed in this paper are shown as determining the contact line movement in each respective region.
Figure 1. Solid line: rescaled velocity,
${\dot{a}}(t)/{\it\epsilon}={\dot{a}}(t)|\!\log {\it\lambda}|$
, as a function of time for a spreading droplet released far from its quasi-static state. Dashed line: the classical quasi-static prediction of contact line speed via (7.5) and (8.1b
) is only valid for large times (as the slip
${\it\lambda}\rightarrow 0$
). Dashed markers: for
$t=O(1)$
, the slip-free formulation using (6.7a
) and (8.1a
) provides a better fit. Numerical computations are for the initial profile (3.4) and
${\it\lambda}=9\times 10^{-7}$
. The details of this figure are discussed in § 7.
This notion of multiple scalings of time influencing the resultant contact line asymptotics allows us to better understand the nature of the zero-slip limit. For example, we seek to better understand the early work by Moriarty & Schwartz (Reference Moriarty and Schwartz1992), who studied the quasi-static state (Greenspan Reference Greenspan1978) of the moving contact line, and sought to understand the relationship between the slip coefficient and the finite difference grid spacing necessary to achieve convergent results. They explained that
…converged finite results, if slip is ignored, can never be obtained. This is the numerical manifestation of the non-integrable force singularity at a moving contact-line when slip is not permitted.
One of the goals of our paper is to demonstrate that if time is held at
$O(1)$
, then converged numerical results can in fact be obtained; a zero-slip condition can be applied to the macroscopic model.
We shall begin in § 1.1 by briefly reviewing the literature behind theories on the moving contact line, with particular emphasis on the classical macroscopic models, molecular models and mesoscopic models. The discussion in this paper will focus on the simplest case of a thin spreading droplet, and the mathematical formulation is presented in § 2. We analyse the
$t=O(1)$
problem in §§ 3–6, and relate this to the classical analyses of, for example, workers such as Hocking (Reference Hocking1983) in § 7. We conclude with a discussion in § 8, focusing on the topic of the role of distinguished limits in more complicated systems involving contact lines.
1.1. A variety of contact line models
It would be misleading for us to proceed without fully acknowledging the great body of literature that already exists on the moving contact line problem. Theoretical models of moving contact lines can be roughly divided into three categories: (i) molecular kinetic models, (ii) molecular dynamic models and (iii) hydrodynamic models. A sampling of reference works, separated by these three classifications, is given in table 1.
Table 1. A sample of works using the kinetic, molecular dynamic or hydrodynamic theories of contact line motion.
The molecular kinetics model of contact lines was first proposed by Blake & Haynes (Reference Blake and Haynes1969), and later extended by Blake (Reference Blake1993) and Blake & De Coninck (Reference Blake and De Coninck2002). In this model, the dynamics of the contact line is described by an absorption and desorption process of the fluid molecules on the solid surface. The theory provides a quantitative description for the contact line friction at the microscopic scale, and gives a link between microscopic quantities, such as the frequency and length of molecular displacements, and the macroscopic behaviour of the dynamic contact angle.
The search to better understand microscopic details of contact lines leads naturally to the idea of using molecular dynamics, and studies in this vein include the works by Koplik et al. (Reference Koplik, Banavar and Willemsen1988, Reference Koplik, Banavar and Willemsen1989), Thompson & Robbins (Reference Thompson and Robbins1989), Blake et al. (Reference Blake, Clarke, De Coninck and de Ruijter1997, Reference Blake, Bracke and Shikhmurzaev1999), Ren & E (Reference Ren and E2007) and De Coninck & Blake (Reference De Coninck and Blake2008). The approach has been very successful and computations have revealed much in regards to the physical processes near the contact line. The disadvantage, however, is that such simulations are limited to systems of small scale and within small temporal intervals. As such, it remains difficult to relate molecular dynamics to the macroscopic scale.
Lastly, moving contact lines can be studied using hydrodynamic models, and these include the classical works of, for example, Huh & Scriven (Reference Huh and Scriven1971), Dussan V & Davis (Reference Dussan V and Davis1974), Voinov (Reference Voinov1976), Hocking & Rivers (Reference Hocking and Rivers1982) and Cox (Reference Cox1986), and the recent work of Ren et al. (Reference Ren, Hu and E2010). Such models impose slip through a boundary condition on the macroscopic variables, and thus assume the specification of an effective condition for the underlying microscopic mechanisms (e.g. the Navier slip condition of (1.1)). The primary advantage of such approaches is that the usual governing equations (e.g. Navier–Stokes) are used with little modification, except for a replacement of the no-slip condition.
As a middle ground between the molecular and classical macroscopic approaches, it is also possible to incorporate intermolecular forces and more detailed physics of the finite-width fluid interface into the hydrodynamics. Such mesoscopic continuum models include the diffuse interface models studied in Jacqmin (Reference Jacqmin2000), Pismen (Reference Pismen2002), Qian et al. (Reference Qian, Wang and Sheng2003) and Yue et al. (Reference Yue, Zhou and Feng2010), as well as the work by Shikhmurzaev (Reference Shikhmurzaev1997, Reference Shikhmurzaev2007) and Billingham (Reference Billingham2008), where interface creation and destruction processes are modelled.
Our work in this paper is primarily inspired by the body of work following from Lacey (Reference Lacey1982) and Hocking (Reference Hocking1983), and thus we shall focus on the standard classical hydrodynamic model with Navier slip. However, it is important that we mention that all three models of contact line motion are appreciated, and it is still an active area of research to establish the advantages and disadvantages of each of the models. For more details, see the reviews by Dussan V & Davis (Reference Dussan V and Davis1974), Kistler (Reference Kistler1993), Pomeau (Reference Pomeau2002), Blake (Reference Blake2006) and Lauga, Brenner & Stone (Reference Lauga, Brenner, Stone, Tropea, Yarin and Foss2007), as well as the collected volume edited by Velarde (Reference Velarde2011).
2. Mathematical formulation
We shall consider the symmetrical spreading of a thin viscous droplet of height
$z=h(x,t)$
, over a flat surface, where the slip on the surface is governed by the Navier slip law (1.1). The governing equation (see, e.g., Lacey Reference Lacey1982) is given by
$$\begin{eqnarray}\frac{\partial h}{\partial t}+\frac{\partial }{\partial x}\left(h^{2}\left(\frac{h}{3}+{\it\lambda}\right)\frac{\partial ^{3}h}{\partial x^{3}}\right)=0,\end{eqnarray}$$
on the domain
$0\leqslant x\leqslant a(t)$
. The droplet begins from an initial state
$h(x,0)=g(x)$
, and is subject to symmetry boundary conditions at the origin,
$$\begin{eqnarray}\partial h/\partial x=0=\partial ^{3}h/\partial x^{3}\quad \text{at }x=0,\end{eqnarray}$$
and the height of the droplet vanishes at the moving edge,
$$\begin{eqnarray}h=0,\quad \text{at }x=a(t).\end{eqnarray}$$
We assume that the equilibrium angle is
${\it\theta}_{y}\neq 0$
(partial wetting) and that the contact line
$a(t)$
is advected according to the constitutive relation
$$\begin{eqnarray}{\it\beta}{\dot{a}}={\textstyle \frac{1}{2}}[(\partial h/\partial x)^{2}-{\it\theta}_{y}^{2}]\quad \text{at }x=a(t),\end{eqnarray}$$
where
${\dot{a}}=\text{d}a/\text{d}t$
is the velocity of the contact line. This constitutive law can be viewed as a force balance at the moving contact line, where the friction force on the left-hand side is balanced by the unbalanced Young stress on the right-hand side (Ren et al.
Reference Ren, Hu and E2010). Other constitutive laws for the advective behaviour are possible (see discussions in, for example, Haley & Miksis Reference Haley and Miksis1991), but the details of our analysis will be largely independent of this choice. The case of complete wetting is addressed in appendix B.
For convenience, we rescale the variables as follows:
$\widehat{h}=3h$
,
$\widehat{x}=3x$
,
$\widehat{a}=3a$
and
$\widehat{t}=t$
. Writing
$\widehat{{\it\lambda}}=9{\it\lambda}$
and
$\widehat{{\it\beta}}={\it\beta}/3$
, this has the effect of changing the equation to (dropping hats)
$$\begin{eqnarray}\frac{\partial h}{\partial t}+\frac{\partial }{\partial x}\left(h^{2}(h+{\it\lambda})\frac{\partial ^{3}h}{\partial x^{3}}\right)=0,\end{eqnarray}$$
with boundary conditions (2.2) and (2.3a
), and the condition for the contact line (2.3b
). Finally, we introduce local coordinates relative to the contact line. Letting
$x=a(t)-X$
and
$h(x,t)=H(X,t)$
, the governing equation yields
$$\begin{eqnarray}\frac{\partial H}{\partial t}+{\dot{a}}\frac{\partial H}{\partial X}+\frac{\partial }{\partial X}\left(H^{2}(H+{\it\lambda})\frac{\partial ^{3}H}{\partial X^{3}}\right)=0.\end{eqnarray}$$
3. Asymptotic analysis of the outer region at
$t=O(1)$
We are interested in the solution in the
${\it\lambda}\rightarrow 0$
limit; in this limit, the contact line speed tends to zero, so we make the expansion
$$\begin{eqnarray}a(t)=a_{0}+{\it\epsilon}a_{1}(t)+{\it\epsilon}^{2}a_{2}(t)+\cdots ,\end{eqnarray}$$
where
$a_{0}$
is the initial contact line location. We claim, and this can be verified a posteriori, that
${\it\epsilon}\gg {\it\lambda}$
. Thus, we expand
$H=H_{0}+{\it\epsilon}H_{1}+O({\it\epsilon}^{2},{\it\lambda})$
, where the first correction term is indeed
$O({\it\epsilon})$
with the assumption
${\it\epsilon}\gg {\it\lambda}$
. Temporarily keeping the
${\it\lambda}$
term, we have at leading order
$$\begin{eqnarray}\frac{\partial H_{0}}{\partial t}+\frac{\partial }{\partial X}\left(H_{0}^{2}(H_{0}+{\it\lambda})\frac{\partial ^{3}H_{0}}{\partial X^{3}}\right)=0.\end{eqnarray}$$
3.1. Leading-order outer equation
Away from
$X=0$
, we may ignore the
${\it\lambda}$
slip term, and this gives for the outer approximation
$$\begin{eqnarray}\frac{\partial H_{0}}{\partial t}+\frac{\partial }{\partial X}\left(H_{0}^{3}\frac{\partial ^{3}H_{0}}{\partial X^{3}}\right)=0.\end{eqnarray}$$
One may solve (3.3) using only the single contact line condition
$H_{0}(0,t)=0$
. This would be consistent with the idea that the microscopic contact angle cannot be applied within this outer region.
Figure 2. (a) The solution to the leading-order outer equation (3.3) at
$t=0.005$
(solid line),
$t=0.01$
(dashed line) and
$t=0.03$
(dotted line). The contact line is at
$X=0$
for equilibrium contact angle
${\it\theta}_{Y}=1$
. (b) The first derivative of the solution versus
$X$
. (c) The second derivative of the solution versus
$\log X$
. The initial condition used is (3.4).
In this paper, we use a semi-implicit finite difference scheme to numerically solve the partial differential equation (2.4) and its slip-free reduction (3.3). Within this scheme, the spatial derivatives are treated implicitly and the nonlinear terms explicitly. The numerical verification of the results in this paper presents a challenging problem (cf. further discussion of the issues in Moriarty & Schwartz Reference Moriarty and Schwartz1992), and we use a refined mesh near the contact line to ensure convergent results. The scheme is detailed in appendix A. The initial condition is mostly unimportant (so long as it begins away from the quasi-static state), and throughout this work, we shall use an equilibrium contact angle,
${\it\theta}_{y}=1$
, and initial condition
$$\begin{eqnarray}h(x,0)=3\cos ({\rm\pi}x^{2}/18).\end{eqnarray}$$
The numerical solution to (3.3), and its first and second spatial derivatives are shown in figure 2. It should be noted that the slope remains well behaved as
$X\rightarrow 0$
, so
$H_{0}$
provides a well-defined apparent contact angle (figure 2
b), given by
$$\begin{eqnarray}{\it\theta}_{app}(t)\sim \left.\frac{\partial H_{0}}{\partial X}\right|_{X=0}.\end{eqnarray}$$
Moreover, the second derivative of the solution, i.e. the curvature of the interface, diverges as
$\log X$
as
$X\rightarrow 0$
, and this can be seen in figure 2(c).
Based on the observation from the numerics, we make the series expansion in the limit that
$X\rightarrow 0$
,
$$\begin{eqnarray}H_{0}(X,t)=B_{10}(t)X+\mathop{\sum }_{i=2}^{\infty }(B_{i0}(t)+B_{i1}(t)\log X)X^{i}.\end{eqnarray}$$
From (3.3), this gives for the first two orders
$$\begin{eqnarray}\displaystyle & O(X)\!:4B_{10}^{3}B_{21}+{\dot{B}}_{10}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & O(X^{2}\log X)\!:18B_{10}^{2}B_{21}^{2}+18B_{10}^{3}B_{31}+{\dot{B}}_{21}=0, & \displaystyle\end{eqnarray}$$
$2{\it\theta}_{app}^{3}(\partial ^{2}H/\partial X^{2})/\log X+\text{d}{\it\theta}_{app}/\text{d}t=0$
, between the divergent curvature with the apparent contact angle and its time evolution.
We now seek to verify the relation between the divergent curvature and the apparent angle in (3.7a
). The slip-free equation (3.3) is solved with the single contact line condition,
$H_{0}(0,t)=0$
, and the profiles of
$H_{0}$
and its derivatives are shown in figure 2. At the origin,
$X=0$
, by comparing
$\partial H_{0}/\partial X$
with
$X$
, the value of
$B_{10}$
is extracted, and by comparing
$\partial ^{2}H_{0}/\partial X^{2}$
with
$\log X$
, the value of
$B_{21}$
is extracted (figure 2
c). Once the time-dependent
$B_{10}$
and
$B_{21}$
have been computed, we can verify the relation (3.7a
). It is seen in figure 3 that the numerical solution obeys the relation (3.7a
) very well.
Figure 3. Numerical verification of the relation (3.7a
) between the contact angle and the rate of divergence of the curvature. The solid curve is
${\dot{B}}_{10}$
and the circles are
$-4B_{10}^{3}B_{21}$
, where
$B_{10}$
and
$B_{21}$
are computed from the numerical solution
$H_{0}$
for
${\it\theta}_{y}=1$
and the initial condition (3.4).
3.2. First-order outer equation
Turning to the next order, if we ignore the terms with
${\it\lambda}$
, then we have
$$\begin{eqnarray}\frac{\partial H_{1}}{\partial t}+{\dot{a}}_{1}\frac{\partial H_{0}}{\partial X}+\frac{\partial }{\partial X}\left(H_{0}^{3}\frac{\partial ^{3}H_{1}}{\partial X^{3}}+3H_{0}^{2}H_{1}\frac{\partial ^{3}H_{0}}{\partial X^{3}}\right)=0.\end{eqnarray}$$
We shall assume that
${\dot{a}}_{1}(t)=O(1)$
, and the boundary condition also requires that
$H_{1}(0,t)=0$
. The only consistent leading-order balance of the four groups of terms in (3.8) occurs between the second and fourth terms. In this case, we may verify that as
$X\rightarrow 0$
, the expansion for
$H_{1}$
follows
$H_{1}=O(X\log X)$
. The correct expansion for
$H_{1}$
as
$X\rightarrow 0$
is
$$\begin{eqnarray}H_{1}(X,t)=C_{10}(t)X+C_{11}(t)X\log X+\mathop{\sum }_{i=2}^{\infty }(C_{i0}(t)+C_{i1}(t)\log X)X^{i},\end{eqnarray}$$
where the functions
$C_{ij}(t)$
are to be determined. This gives the two leading-order equations:
$$\begin{eqnarray}\displaystyle & O(1)\!:{\dot{a}}_{1}B_{10}-B_{10}^{3}C_{11}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & O(X\log X)\!:2{\dot{a}}_{1}B_{21}+6B_{10}^{2}B_{21}C_{11}+{\dot{C}}_{11}=0. & \displaystyle\end{eqnarray}$$
$C_{11}$
, while the second one allows us to solve for
$B_{21}$
. In summary, combining (3.6)–(3.7b
) and (3.9)–(3.10b
), we have as
$X\rightarrow 0$
the inner limit of the outer approximation: 
$$\begin{eqnarray}H_{\mathit{out}\rightarrow \mathit{in}}=\{B_{10}X+B_{21}X^{2}\log X+\cdots \}+{\it\epsilon}\left\{\!\left(\frac{{\dot{a}}_{1}}{B_{10}^{2}}\right)X\log X+C_{10}X+\cdots \right\}.\end{eqnarray}$$
4. Asymptotic analysis of the inner region at
$t=O(1)$
For the outer approximation of the previous section, we did not apply the exact wall condition given by (2.3b
). Moreover, it should be clear that the expression (3.11) breaks down when
${\it\epsilon}\log X=O(1)$
or when
$X=O(\text{e}^{-1/{\it\epsilon}})$
; in this smaller region, the terms in the outer approximation begin to rearrange. However, when
$H$
and
$X$
are small, then there is an inner region whose size is determined by the slip parameter,
${\it\lambda}$
. Thus, the correct scaling for the contact line speed,
${\it\epsilon}$
, is given by precisely balancing the size of the slip region with the predicted breakdown of the outer approximation, and we require
${\it\lambda}=O(\text{e}^{-1/{\it\epsilon}})$
. We thus set
$$\begin{eqnarray}{\it\epsilon}=1/|\!\log {\it\lambda}|.\end{eqnarray}$$
For the inner region, we rescale
$H={\it\lambda}\overline{H}$
and
$X={\it\lambda}s$
, then (2.5) gives
$$\begin{eqnarray}{\it\lambda}\frac{\partial \overline{H}}{\partial t}+{\dot{a}}\frac{\partial \overline{H}}{\partial s}+\frac{\partial }{\partial s}\left[\overline{H}^{2}(\overline{H}+1)\frac{\partial ^{3}\overline{H}}{\partial s^{3}}\right]=0.\end{eqnarray}$$
We expand
$\overline{H}=\overline{H}_{0}+{\it\epsilon}\overline{H}_{1}+O({\it\epsilon}^{2},{\it\lambda})$
, and this gives the first two orders as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial s}\left[\overline{H}_{0}^{2}(\overline{H}_{0}+1)\frac{\partial ^{3}\overline{H}_{0}}{\partial s^{3}}\right]=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\dot{a}}_{1}\frac{\partial \overline{H}_{0}}{\partial s}+\frac{\partial }{\partial s}\left[\overline{H}_{0}^{2}(\overline{H}_{0}+1)\frac{\partial ^{3}\overline{H}_{1}}{\partial s^{3}}+(3\overline{H}_{0}^{2}\overline{H}_{1}+2\overline{H}_{0}\overline{H}_{1})\frac{\partial ^{3}\overline{H}_{0}}{\partial s^{3}}\right]=0. & \displaystyle\end{eqnarray}$$
$s=0$
are given by (2.3a
) and (2.3b
): 
$$\begin{eqnarray}\overline{H}=0\quad \text{and}\quad \partial \overline{H}/\partial s={\it\theta}_{y}+{\it\epsilon}({\it\beta}{\dot{a}}_{1}/{\it\theta}_{y})+O({\it\epsilon}^{2}).\end{eqnarray}$$
The leading-order problem is solved, giving
$$\begin{eqnarray}\overline{H}_{0}(s,t)={\it\theta}_{y}s.\end{eqnarray}$$
The first-order problem can be integrated once and gives
$$\begin{eqnarray}{\dot{a}}_{1}\overline{H}_{0}+(\overline{H}_{0}^{3}+\overline{H}_{0}^{2})\frac{\partial ^{3}\overline{H}_{1}}{\partial s^{3}}=C(t).\end{eqnarray}$$
With
$\overline{H}_{0}$
given by (4.5), it can be verified a posteriori that the third derivative of
$\overline{H}_{1}$
is
$O(s^{-1})$
as
$s\rightarrow 0$
, so
$C(t)\equiv 0$
. The resultant equation is integrated for
$\overline{H}_{1}$
, and application of the boundary conditions (4.4) gives
$$\begin{eqnarray}\displaystyle \overline{H}_{1}(s,t) & = & \displaystyle C_{1}(t)s^{2}+{\dot{a}}_{1}\left(-\frac{s}{2{\it\theta}_{y}^{2}}+\frac{{\it\beta}s}{{\it\theta}_{y}}-\frac{s^{2}\log s}{2{\it\theta}_{y}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\log (1+{\it\theta}_{y}s)}{2{\it\theta}_{y}^{3}}+\frac{s\log (1+{\it\theta}_{y}s)}{{\it\theta}_{y}^{2}}+\frac{s^{2}\log (1+{\it\theta}_{y}s)}{2{\it\theta}_{y}}\right).\end{eqnarray}$$
We shall assume that
$\overline{H}_{1}(s,t)$
does not diverge faster than
$s\log s$
as
$s\rightarrow \infty$
, so we set
$C_{1}(t)=-{\dot{a}}_{1}\log {\it\theta}_{y}/(2{\it\theta}_{y})$
, leaving us with the final first-order solution
$$\begin{eqnarray}\displaystyle \overline{H}_{1}(s,t) & = & \displaystyle {\dot{a}}_{1}\left(-\frac{s}{2{\it\theta}_{y}^{2}}+\frac{{\it\beta}s}{{\it\theta}_{y}}-\frac{s^{2}\log {\it\theta}_{y}}{2{\it\theta}_{y}}-\frac{s^{2}\log s}{2{\it\theta}_{y}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\log (1+{\it\theta}_{y}s)}{2{\it\theta}_{y}^{3}}+\frac{s\log (1+{\it\theta}_{y}s)}{{\it\theta}_{y}^{2}}+\frac{s^{2}\log (1+{\it\theta}_{y}s)}{2{\it\theta}_{y}}\right).\end{eqnarray}$$
It can be noticed that as
$s\rightarrow 0$
, the third derivative of
$\overline{H}_{1}$
is
$O(s^{-1})$
, so the assumption made after (4.6) is verified. All together, as
$s\rightarrow \infty$
, we have the outer limit of the inner solution:
$$\begin{eqnarray}\overline{H}_{in\rightarrow out}\sim {\it\theta}_{y}s+{\it\epsilon}{\dot{a}}_{1}\left[\left(\frac{1}{{\it\theta}_{y}^{2}}\right)s\log s+\left(\frac{{\it\beta}}{{\it\theta}_{y}}+\frac{\log {\it\theta}_{y}}{{\it\theta}_{y}^{2}}\right)s+\cdots \right].\end{eqnarray}$$
5. Asymptotic analysis of the intermediate region at
$t=O(1)$
In general, we cannot expect
$H$
to match directly with
$\overline{H}$
(since the out-to-in limit is a time-dependent angle, and the in-to-out limit is a specified constant angle). We need an intermediate region to perform the matching, and this is given by the larger
${\it\epsilon}$
parameter. In this region, we write
$$\begin{eqnarray}s=\text{e}^{z/{\it\epsilon}},\quad \overline{H}=Q(z,t)\text{e}^{z/{\it\epsilon}},\end{eqnarray}$$
where
$0<z<1$
provides the intermediate scaling between the inner and outer regions. We must now change (4.2) to make use of differentiation in
$z$
. Before doing this, however, let us examine the first time-dependent term in (4.2). This term becomes
${\it\lambda}\partial \overline{H}/\partial t=\text{e}^{(z-1)/{\it\epsilon}}\partial Q/\partial t$
. Within the intermediate region, this term is exponentially small, and should be ignored. Thus, within the intermediate region, we have
$$\begin{eqnarray}{\dot{a}}\frac{\partial \overline{H}}{\partial s}+\frac{\partial }{\partial s}\left(\overline{H}^{2}(\overline{H}+1)\frac{\partial ^{3}\overline{H}}{\partial s^{3}}\right)=0.\end{eqnarray}$$
Integrating the equation once and setting the constant of integration to zero, then rewriting in intermediate variables gives
$$\begin{eqnarray}{\dot{a}}+Q(Q+\text{e}^{-z/{\it\epsilon}})\left(-{\it\epsilon}\frac{\partial Q}{\partial z}+{\it\epsilon}^{3}\frac{\partial ^{3}Q}{\partial z^{3}}\right)=0.\end{eqnarray}$$
We ignore the exponentially small term and expand the velocity. This gives
$$\begin{eqnarray}({\it\epsilon}{\dot{a}}_{1}+{\it\epsilon}^{2}{\dot{a}}_{2}+O({\it\epsilon}^{3}))+Q^{2}\left(-{\it\epsilon}\frac{\partial Q}{\partial z}+{\it\epsilon}^{3}\frac{\partial ^{3}Q}{\partial z^{3}}\right)=0.\end{eqnarray}$$
It can be noticed that up to order
${\it\epsilon}^{3}$
in the above equation, we can derive a portion of the solution as
$Q^{3}=(c_{0}+{\it\epsilon}c_{1})+3({\dot{a}}_{1}+{\it\epsilon}{\dot{a}}_{2})z+O({\it\epsilon}^{2})$
, which gives
$$\begin{eqnarray}Q(z,t)=(c_{0}+3{\dot{a}}_{1}z)^{1/3}+{\it\epsilon}\left(\frac{c_{1}+3{\dot{a}}_{2}z}{3(c_{0}+3{\dot{a}}_{1}z)^{2/3}}\right)+O({\it\epsilon}^{2}).\end{eqnarray}$$
We can thus write the asymptotic expansion of the intermediate solution as
$$\begin{eqnarray}\overline{H}_{interm}=(c_{0}+3{\dot{a}}_{1}z)^{1/3}s+{\it\epsilon}\left(\frac{c_{1}+3{\dot{a}}_{2}z}{3(c_{0}+3{\dot{a}}_{1}z)^{2/3}}\right)s+O({\it\epsilon}^{2}).\end{eqnarray}$$
6. Matching of inner, intermediate and outer solutions
In order to perform the matching between the solution in the intermediate region (5.6) and the solution in the inner region (4.9), we apply van Dyke’s matching rule (Van Dyke Reference Van Dyke1975): the two-term expansion of the intermediate solution (2:int), rewritten in inner coordinates and re-expanded to two terms (2:inner), is equal to the two-term inner expansion, rewritten in intermediate coordinates, and re-expanded to two terms. Or, simply,
$\text{(2:inner)(2:int)}=\text{(2:int)(2:inner)}$
. We thus have
$$\begin{eqnarray}\displaystyle \text{(2:inner)(2:int)} & = & \displaystyle [c_{0}+{\it\epsilon}(3{\dot{a}}_{1}\log s)]^{1/3}s+{\it\epsilon}\left[\frac{c_{1}+3{\dot{a}}_{2}{\it\epsilon}\log s}{3(c_{0}+3{\dot{a}}_{1}{\it\epsilon}\log s)^{2/3}}\right]s\nonumber\\ \displaystyle & = & \displaystyle c_{0}^{1/3}s+{\it\epsilon}\left[\left(\frac{{\dot{a}}_{1}}{c_{0}^{2/3}}\right)s\log s+\left(\frac{c_{1}}{3c_{0}^{2/3}}\right)s+\cdots \right],\end{eqnarray}$$
which is matched to
$$\begin{eqnarray}\text{(2:int)(2:inner)}={\it\theta}_{y}s+{\it\epsilon}{\dot{a}}_{1}\left[\left(\frac{1}{{\it\theta}_{y}^{2}}\right)s\log s+\left(\frac{{\it\beta}}{{\it\theta}_{y}}+\frac{\log {\it\theta}_{y}}{{\it\theta}_{y}^{2}}\right)s+\cdots \right]\end{eqnarray}$$
and yields
$$\begin{eqnarray}c_{0}={\it\theta}_{y}^{3}\quad \text{and}\quad c_{1}=3{\dot{a}}_{1}\left({\it\beta}{\it\theta}_{y}+\log {\it\theta}_{y}\right).\end{eqnarray}$$
This leaves the matching of intermediate and outer solutions. Substituting the outer variables
$H={\it\lambda}\overline{H}$
and
$X={\it\lambda}s$
into the intermediate solution (5.6), we have
$$\begin{eqnarray}H_{interm}=[c_{0}+3{\dot{a}}_{1}\left(1+{\it\epsilon}\log X\right)]^{1/3}X+{\it\epsilon}\left[\frac{c_{1}+3{\dot{a}}_{2}\left(1+{\it\epsilon}\log X\right)}{3\left(c_{0}+3{\dot{a}}_{1}\left(1+{\it\epsilon}\log X\right)\right)^{2/3}}\right]X+\cdots .\end{eqnarray}$$
The two-term intermediate limit (2:int) of (5.6), expressed in outer variables and re-expanded to two terms (2:out), gives
$$\begin{eqnarray}\displaystyle \text{(2:out)(2:int)}=\left(c_{0}+3{\dot{a}}_{1}\right)^{1/3}X+{\it\epsilon}\left[\left(\frac{{\dot{a}}_{1}}{(c_{0}+3{\dot{a}}_{1})^{2/3}}\right)X\log X+\left(\frac{c_{1}+3{\dot{a}}_{2}}{3(c_{0}+3{\dot{a}}_{1})^{2/3}}\right)X\right], & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
whereas from (3.11), we have
$$\begin{eqnarray}\text{(2:int)(2:out)}=(B_{10}X+\cdots )+{\it\epsilon}\left[\left(\frac{{\dot{a}}_{1}}{B_{10}^{2}(t)}\right)X\log X+C_{10}X+\cdots \right].\end{eqnarray}$$
Thus, we have the two equations
$$\begin{eqnarray}\displaystyle & \displaystyle B_{10}^{3}(t)-{\it\theta}_{y}^{3}=3\frac{\text{d}a_{1}}{\text{d}t}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & B_{10}^{2}(t)\cdot C_{10}(t)={\dot{a}}_{1}({\it\beta}{\it\theta}_{y}+\log {\it\theta}_{y})+{\dot{a}}_{2}. & \displaystyle\end{eqnarray}$$
The relation between the contact angle and the contact line speed, (6.7a
), is verified by numerics. The left-hand side of the relation follows from the computation of the leading-order slip-free outer solution
$H_{0}$
in § 3. The right-hand side requires an accurate extraction of the limiting contact line velocity as
${\it\lambda}\rightarrow 0$
. In order to obtain this value, we plot in figure 4(b) the velocity at fixed values of time and in decreasing values of the slip length. It should be noted that the plot of the velocity versus
${\it\epsilon}=1/|\!\log {\it\lambda}|$
appears to tend to a straight line passing through the origin. The right-hand side of (6.7a
),
${\dot{a}}_{1}$
, is estimated as the slope of the line joining the origin and the last data point (
${\it\lambda}=9\times 10^{-7}$
) at the different times.
Figure 4. (a) The velocity of the contact line versus time for the spreading droplet with
${\it\theta}_{y}=1$
. From top to bottom, the four curves are the velocities for
${\it\lambda}=9\times 10^{-4},9\times 10^{-5},9\times 10^{-6}$
and
$9\times 10^{-7}$
. (b) The velocity of the contact line versus
${\it\epsilon}=1/|\!\log {\it\lambda}|$
, at the time
$t=0.005$
(left triangles), 0.01 (diamonds), 0.02 (squares), 0.03 (circles), 0.04 (down triangles) and 0.05 (up triangles).
Finally, a check of the angle–speed relation (6.7a
) is given in figure 5. The solid curve is the plot of
$(B_{10}^{3}(t)-{\it\theta}_{y}^{3})/3$
, whereas the circles are the extracted values of
${\dot{a}}_{1}$
at the different times. These two sets of data agree well except for small time,
$t$
. We would expect that for a fixed value of
$t$
, the relation would only hold in the limit
${\it\lambda}\rightarrow 0$
. The error in the relation (6.7a
) is due to our inability to resolve the contact line problem for sufficiently small values of slip.
Figure 5. Verification of the relation (6.7a
) between the contact angle and the contact line velocity. The solid curve is
$(B_{10}^{3}-{\it\theta}_{y}^{3})/3$
versus time, where
$B_{10}(t)$
is computed from the numerical solution of the leading-order outer equation (3.3). The circles are the plot of
${\dot{a}}_{1}$
at different times, where the data for
${\dot{a}}_{1}$
are computed from the slope of the line joining the origin and the last data point
$({\it\lambda}=9\times 10^{-7})$
in figure 4(b).
7. Breakdown as
$t\rightarrow \infty$
and recovery of the quasi-static limit
We notice that as
$t\rightarrow \infty$
, the above asymptotic analysis fails, since the expansion (3.1) becomes disordered once the correction to the contact line position
$a_{1}(t)=O(1/{\it\epsilon})$
. In the double limit of
$t\rightarrow \infty$
and
${\it\lambda}\rightarrow 0$
, we have a distinguished limit which requires a rescaling of time using
${\it\tau}={\it\epsilon}t$
. From (2.5), this gives
$$\begin{eqnarray}{\it\epsilon}\frac{\partial H}{\partial {\it\tau}}+{\it\epsilon}\frac{\text{d}a}{\text{d}{\it\tau}}\frac{\partial H}{\partial X}+\frac{\partial }{\partial X}\left(H^{2}(H+{\it\lambda})\frac{\partial ^{3}H}{\partial X^{3}}\right)=0.\end{eqnarray}$$
If we expand
$H=H_{0}+{\it\epsilon}H_{1}+\cdots ,$
and the velocities
$\text{d}a/\text{d}{\it\tau}=\text{d}a_{1}/\text{d}{\it\tau}+{\it\epsilon}\text{d}a_{2}/\text{d}{\it\tau}+\cdots \!,$
then at leading order, we obtain a quasi-static solution, with
$H_{0}=((3{\it\kappa})/(2a^{3}({\it\tau})))$
$X[2a({\it\tau})-X]$
, where
${\it\kappa}$
can be solved by applying conservation of mass and using the initial profile of the droplet,
${\it\kappa}=\int _{0}^{a}h(x,0)\text{d}x$
.
It can be noticed that time dependence only enters into
$H_{0}$
via the
$a({\it\tau})$
term, and since all the subsequent orders depend solely on derivatives of the previous orders (with one term multiplying
$\text{d}a/\text{d}{\it\tau}$
), then the profile shape only depends on time as a function of the droplet location. The classical quasi-static analysis then follows (cf. Hocking (Reference Hocking1981) and other references in § 1.1). In this case, the full outer solution is given by
$$\begin{eqnarray}\displaystyle H(X,a) & = & \displaystyle \frac{3{\it\kappa}}{2a^{3}}X[2a-X]+{\it\epsilon}\frac{\text{d}a_{1}}{\text{d}{\it\tau}}\left[\frac{a^{4}}{9{\it\kappa}^{2}}\right]\left[(2a-X)\log (2a-X)\vphantom{\frac{3}{2a}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,X\log X-2a\log (2a)+\frac{3}{2a}X(2a-X)\right]+\cdots .\end{eqnarray}$$
Since the time-dependent term
$\partial H/\partial t$
only affects the outer analysis of the previous sections, then the inner and intermediate solutions, given by (4.5), (4.8) and (5.6), continue to be valid, and we have for the outer-to-inner and inner-to-outer limits
$$\begin{eqnarray}\displaystyle & \displaystyle H_{out\rightarrow in}=\left[\frac{3{\it\kappa}}{a^{2}}X+\cdots \right]+{\it\epsilon}\frac{\text{d}a_{1}}{\text{d}{\it\tau}}\frac{a^{4}}{9{\it\kappa}^{2}}[X\log X+\{2-\log (2a)\}X+\cdots ]+\cdots \!,\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{H}_{in\rightarrow out}={\it\theta}_{y}s+{\it\epsilon}\frac{\text{d}a_{1}}{\text{d}{\it\tau}}\left[\left(\frac{1}{{\it\theta}_{y}^{2}}\right)s\log s+\left(\frac{1}{{\it\theta}_{y}}+\frac{\log {\it\theta}_{y}}{{\it\theta}_{y}^{2}}\right)s\right]+\cdots . & \displaystyle\end{eqnarray}$$
${\it\theta}_{app}$
as the leading-order outer contact angle (the apparent contact angle), then we have from (7.3a
)
${\it\theta}_{app}=3{\it\kappa}/a^{2}$
, which confirms that the apparent contact angle can be predicted once the contact line location is known. Use of (6.3)–(6.5), (7.3a
) and (7.3b
) allows the matching between inner and outer solutions through the intermediate layer, giving 
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\theta}_{app}^{3}-{\it\theta}_{y}^{3}=3\frac{\text{d}a_{1}}{\text{d}{\it\tau}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}a_{2}}{\text{d}{\it\tau}}=\frac{\text{d}a_{1}}{\text{d}{\it\tau}}\left[-{\it\beta}{\it\theta}_{y}+\log \left(\frac{\text{e}^{2}}{2a{\it\theta}_{y}}\right)\right], & \displaystyle\end{eqnarray}$$
$t=O(1)$
problem. Using (7.4a
) and (7.4b
), we then have a differential equation for the droplet location, accurate to two orders: 
$$\begin{eqnarray}\displaystyle \frac{\text{d}a}{\text{d}{\it\tau}} & {\sim} & \displaystyle \frac{\text{d}a_{1}}{\text{d}{\it\tau}}\left[1+{\it\epsilon}\left\{-{\it\beta}{\it\theta}_{y}+\log \left(\frac{\text{e}^{2}}{2a{\it\theta}_{y}}\right)\right\}\right]\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{3}[(3{\it\kappa}/a^{2})^{3}-{\it\theta}_{y}^{3}]\left[1+{\it\epsilon}\left\{-{\it\beta}{\it\theta}_{y}+\log \left(\frac{\text{e}^{2}}{2a{\it\theta}_{y}}\right)\right\}\right].\end{eqnarray}$$
This is analogous to the results of Hocking (Reference Hocking1983) using the alternative constitutive relationship (2.3b ).
The principal result of this paper is shown in figure 1. Here, the rescaled velocity
${\dot{a}}(t)/{\it\epsilon}$
is plotted as a function of time for the case of a spreading droplet with slip coefficient
${\it\lambda}=9\times 10^{-7}$
. The two time scales determining the dynamics are clearly visible (note that the shaded region is only illustrative); we indeed confirm that the classical quasi-static approximation of (7.5) is an excellent fit once time is appreciable. However, for
$t=O(1)$
, the slip-free approximation of (6.7a
) will capture the correct dynamics. We note that because the second time scaling is only logarithmically large in the slip,
${\it\lambda}$
, then for most practical values of the slip, the transition to the quasi-static regime occurs quite rapidly. However, as
${\it\lambda}\rightarrow 0$
, we would indeed expect the transition point (e.g. in figure 1) to move to infinity.
8. Discussion
The difference between the two distinguished limits is well encapsulated in the two angle–speed relations (6.7a ) and (7.4a ) which, although very similar in appearance, have completely different interpretations:
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle (\text{i})~{\it\lambda}\rightarrow 0,\quad t=t^{\ast },\quad {\it\theta}_{app}^{3}(t^{\ast })-{\it\theta}_{y}^{3}=3\frac{\text{d}a_{1}}{\text{d}t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle (\text{ii})~{\it\lambda}\rightarrow 0,\quad t=|\!\log {\it\lambda}|{\it\tau},\quad {\it\theta}_{app}^{3}[a({\it\tau})]-{\it\theta}_{y}^{3}=3\frac{\text{d}a_{1}}{\text{d}{\it\tau}}.\end{eqnarray}$$
In the case of (i), where
$t=O(1)$
, the apparent contact angle is a known function given by the solution of the leading-order zero-slip equation (3.3); thus, the leading-order slip velocity is also known, and in the limit
${\it\lambda}\rightarrow 0$
, contact line slippage is a ‘regular’ perturbative effect. By ‘regular’, we mean that the contact line position tends to a constant,
$a(t^{\ast })\rightarrow a_{0}$
as
${\it\lambda}\rightarrow 0$
. To leading order, one would say that the contact line is fixed. Thus, (8.1a
) provides a closed relation between the apparent angle and the first-order contact line speed once the
${\it\lambda}=0$
equation has been solved. No microscopic properties are necessary in determining the contact line dynamics at this order.
However, in the limit that
$t\rightarrow \infty$
, significant contact line movement occurs, and the asymptotic relations used to derive (i) are invalid. Contact line movement can be brought in by rescaling time. Thus, in the case of (ii), where time is logarithmically large in the slip number, the apparent angle is no longer a directly known value. It can only be computed once the droplet location,
$a({\it\tau})$
, is known, and this value must be found by solving an ordinary differential equation for the position, given by (7.5). Although the methodology we have used to study the
$t=O(1)$
problem is very similar to the methodology used in the classical quasi-static work of, for example, Hocking (Reference Hocking1983), the principal motivation of our work is to highlight this idea of the non-uniformity within the time variable.
While the principal setting of our work was the lubrication equations of thin-film flow, the same ideas hold for slow viscous Stokes flow. The difficulty, however, is that even the simplest free-surface problems in Stokes flow are too unwieldy to solve, and so classical works on contact line dynamics in slow flow (e.g. in Cox Reference Cox1986) have relied upon very general descriptions of how the inner, intermediate and outer asymptotics are performed. Moreover, we believe that other contact line models (e.g. in table 1) will exhibit the same subtleties in their asymptotic analysis; the notion of a distinguished limit in time is a generic aspect that arises due to the separation of macroscopic and microscopic time scales.
In a general problem, there may be multiple choices for the velocity scale and the resultant capillary number. Consider a system that begins at
$t=0$
with an imposed (macroscopic) velocity scale of
$U_{macro}$
(for example, this may correspond to forced flow through a channel with speed
$U_{macro}$
). In this case, this initial macroscopic velocity sets the capillary number,
$$\begin{eqnarray}\mathit{Ca}_{macro}=\frac{{\it\mu}U_{macro}}{{\it\sigma}}.\end{eqnarray}$$
The leading-order contact line condition to impose on the outer flow is that the contact line is fixed. To an observer positioned away from the contact line, the contact line seems stationary, with surrounding bulk fluid moving at an
$O(1)$
velocity. This is emphasized by the analysis of the
$t=O(1)$
scaling of § 3 for the case of lubrication theory, and where
$U_{macro}$
corresponds to the initial relaxation speed of a droplet deposited far from its quasi-static state.
However, at large times, the bulk fluid slows down from its initial relaxation velocity and is now moving at the same rate as the contact line. The macroscopic flow is now governed by a smaller capillary number:
$$\begin{eqnarray}\mathit{Ca}_{cl}={\it\epsilon}\mathit{Ca}_{macro},\end{eqnarray}$$
where
${\it\epsilon}$
is the contact line velocity. Relative to this velocity scale, the inner limit of the outer velocity field must now take into account contact line movement. It can be seen by examining the slow-flow equations and free-surface conditions that in the limit
$\mathit{Ca}_{cl}\rightarrow 0$
, the fluid interface is flat to leading order. In essence, this justifies the assumptions found in the slow-flow contact line analysis of Cox (Reference Cox1986), where the leading-order outer solution consisted of flow in a fixed wedge for small-capillary-number flow.
8.1. Problems with patching between time-dependent and quasi-static regions
The above discussion highlights the difficulties of studying contact line dynamics in situations where, in the large-time limit, the quasi-static flow near the contact line is not the entirety of the flow. Consider the situation of a plate pulled from a bath. Such a scenario is described by the non-dimensional thin-film equation
$$\begin{eqnarray}\frac{\partial h}{\partial t}+\frac{\partial }{\partial x}\left[h^{2}\left(\frac{h}{3}+{\it\lambda}\right)\left(\frac{\partial {\it\kappa}}{\partial x}-1\right)+\mathit{Ca}_{macro}h\right]=0,\end{eqnarray}$$
on the domain
$x\in [0,R(t)]$
, where we use the full nonlinear curvature
${\it\kappa}=h_{xx}/[1+(h_{x})^{2}]^{3/2}$
. This classical dewetting problem has been studied by, for example, Eggers (Reference Eggers2004a
, Reference Eggers2005), Eggers & Stone (Reference Eggers and Stone2004) and Snoeijer et al. (Reference Snoeijer, Delon, Fermigier and Andreotti2006). The point
$x=0$
corresponds to the matching region to the bath, and we use the illustrative boundary conditions
$h=1$
and
$h_{x}=-1$
. On the right, at
$x=R(t)$
, we apply the contact line conditions (2.3). In figure 6, we plot solutions at different times, corresponding to the capillary number
$\mathit{Ca}_{macro}=0.017$
and slip
${\it\lambda}=1.3\times 10^{-5}$
. These values have been chosen specifically to demonstrate the fascinating structure of the solution, and they have been used in Snoeijer et al. (Reference Snoeijer, Delon, Fermigier and Andreotti2006).
Figure 6. Thin-film profiles for a plate pulled from a bath, modelled by (8.4) using
$\mathit{Ca}_{macro}=0.017$
and
${\it\lambda}=1.3\times 10^{-5}$
. The dashed line is the initial profile.
In the limit that
$t\rightarrow \infty$
, it is seen that the bulk fluid near the bath tends to the ‘Landau–Levich solution’ (cf. Wilson Reference Wilson1982), where the plate is covered by a uniform film governed by the macroscopic capillary number
$\mathit{Ca}_{macro}$
. However, in a localized region near the contact line, the flow is increasingly quasi-static as
$t\rightarrow \infty$
, and the governing capillary number
$\mathit{Ca}_{cl}$
tends to zero as the slip is taken to zero. The size of this quasi-static region grows as time increases, and a contact line analysis would require matching of the solution near the bath with the solution near the contact line, through an intermediate time-dependent region whose length is a priori unknown. Compare and contrast this with the situation of a spreading droplet, where in the limit
$t\rightarrow \infty$
, the leading-order solution is globally solved by the quasi-static solution with constant curvature.
The time-dependent drag-out problem has been studied by, for example, Snoeijer et al. (Reference Snoeijer, Delon, Fermigier and Andreotti2006, Reference Snoeijer, Ziegler, Andreotti, Fermigier and Eggers2008), and there it was shown that the analysis is complicated further by the possibility of multiple solutions at large times. A similar system was studied in the work of Benilov et al. (Reference Benilov, Chapman, McLeod, Ockendon and Zubkov2010), where it was demonstrated that for such problems, there exist an infinite number of zones, logarithmically spaced apart, where the fluid height oscillates between maxima and minima. The key aspect of such problems is that, because the solution is only quasi-static near the very tip, an asymptotic analysis of the sort we have performed here for
$t=O(1)$
is made difficult due to the required patching of multiple regions changing in time. Indeed, problems such as the case of gravity-driven draining down a vertical wall may not possess a well-defined limit as
${\it\lambda}\rightarrow 0$
and
$t=O(1)$
, which is evident in the overturning profiles of Moriarty, Schwartz & Tuck (Reference Moriarty, Schwartz and Tuck1991). For such problems, not only is one required to contend with distinguished limits in time, as we have done in this paper, but also distinguished limits between the two (or more) capillary numbers. Such problems with more complicated global structure are the subject of ongoing investigation.
Acknowledgements
We gratefully thank the referees for their insightful comments and suggestions. We also thank Professors J. Eggers (Bristol), H. A. Stone (Princeton), J. M. Oliver (Oxford) and A. Münch (Oxford) for many helpful discussions during the course of this work. The work of W.R. was partially supported by Singapore A*STAR SERC PSF grant (project no. 1321202071).
Appendix A. Numerical methods
To solve the thin-film equation (2.4) (and its reductions, such as (3.3)) on the time-dependent domain
$[0,a(t)]$
, where
$a(t)$
is the moving contact line, we introduce the coordinate transformation
$$\begin{eqnarray}x({\it\xi},t)=a(t)f({\it\xi}),\end{eqnarray}$$
where the map
$f({\it\xi}):[0,1]\rightarrow [0,1]$
is monotonic and
$f(0)=0$
,
$f(1)=1$
. The purpose of the map
$f$
is to concentrate most of the grid points near the contact line. In this work, we use
$f({\it\xi})=\tanh ({\it\xi}/{\it\varepsilon})/\tanh (1/{\it\varepsilon})$
, where
${\it\varepsilon}=0.2$
.
In terms of the new variable, the thin-film equation becomes
$$\begin{eqnarray}\frac{\partial h}{\partial t}-\frac{x_{t}}{x_{{\it\xi}}}\frac{\partial h}{\partial {\it\xi}}+\frac{1}{x_{{\it\xi}}}\frac{\partial }{\partial {\it\xi}}\left(h^{2}(h+{\it\lambda})\left({\it\alpha}\frac{\partial h}{\partial {\it\xi}}+{\it\beta}\frac{\partial ^{2}h}{\partial {\it\xi}^{2}}+{\it\gamma}\frac{\partial ^{3}h}{\partial {\it\xi}^{3}}\right)\right)=0,\end{eqnarray}$$
where we have introduced
$$\begin{eqnarray}{\it\alpha}=-\frac{x_{{\it\xi}{\it\xi}{\it\xi}}}{x_{{\it\xi}}^{4}}+\frac{3x_{{\it\xi}{\it\xi}}^{2}}{x_{{\it\xi}}^{5}},\quad {\it\beta}=-\frac{3x_{{\it\xi}{\it\xi}}}{x_{{\it\xi}}^{4}},\quad {\it\gamma}=\frac{1}{x_{{\it\xi}}^{3}},\end{eqnarray}$$
and subscripts are used for partial derivatives.
Equation (A 2) is solved on a uniform mesh covering the fixed domain
${\it\xi}\in [0,1]$
and
$t\in [0,T]$
. The solution is computed on the mid-grid points
$({\it\xi}_{i+1/2},t_{n})=((i+1/2){\rm\Delta}{\it\xi},n{\rm\Delta}t)$
, where
${\rm\Delta}{\it\xi}=1/N$
and
$t_{n}=1/M$
are the mesh steps in space and time respectively. The numerical solution is denoted by
$h_{i+1/2}^{n}$
.
We use a semi-implicit scheme to evolve
$h$
in time:
$$\begin{eqnarray}\frac{h_{i+1/2}^{n+1}-h_{i+1/2}^{n}}{{\rm\Delta}t}-\left(\frac{x_{t}}{x_{{\it\xi}}}\right)_{i+1/2}^{n}\left(\frac{\partial h}{\partial {\it\xi}}\right)_{i+1/2}^{n+1}+\left(\frac{1}{x_{{\it\xi}}}\right)_{i+1/2}^{n}\frac{R_{i+1}^{n+1}-R_{i}^{n+1}}{{\rm\Delta}{\it\xi}}=0,\end{eqnarray}$$
for
$i=0,1,\dots ,N-1$
. In the above equation,
$R_{i}^{n}$
is the flux at the grid point
$({\it\xi}_{i},t_{n})$
, which is given by
$$\begin{eqnarray}R_{i}^{n+1}=(h^{2}(h+{\it\lambda}))_{i}^{n}\left({\it\alpha}_{i}^{n}\left(\frac{\partial h}{\partial {\it\xi}}\right)_{i}^{n+1}+{\it\beta}_{i}^{n}\left(\frac{\partial ^{2}h}{\partial {\it\xi}^{2}}\right)_{i}^{n+1}+{\it\gamma}_{i}^{n}\left(\frac{\partial ^{3}h}{\partial {\it\xi}^{3}}\right)_{i}^{n+1}\right)\!,\end{eqnarray}$$
for
$i=1,2,\dots ,N-1$
and
$R_{0}^{n+1}=R_{N}^{n+1}=0$
.
The spatial derivatives are discretized using the standard finite differences:
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\partial h}{\partial {\it\xi}}\right)_{i+1/2}^{n+1}\approx \frac{1}{2{\rm\Delta}{\it\xi}}\left(h_{i+3/2}^{n+1}-h_{i-1/2}^{n+1}\right)\!, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\partial h}{\partial {\it\xi}}\right)_{i}^{n+1}\approx \frac{1}{{\rm\Delta}{\it\xi}}\left(h_{i+1/2}^{n+1}-h_{i-1/2}^{n+1}\right)\!, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\partial ^{2}h}{\partial {\it\xi}^{2}}\right)_{i}^{n+1}\approx \frac{1}{2{\rm\Delta}{\it\xi}^{2}}\left(h_{i+3/2}^{n+1}-h_{i-1/2}^{n+1}-h_{i+1/2}^{n+1}+h_{i-3/2}^{n+1}\right)\!, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\partial ^{3}h}{\partial {\it\xi}^{3}}\right)_{i}^{n+1}\approx \frac{1}{{\rm\Delta}{\it\xi}^{3}}\left(h_{i+3/2}^{n+1}-3h_{i+1/2}^{n+1}+3h_{i-1/2}^{n+1}-h_{i-3/2}^{n+1}\right). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}h_{-1/2}^{n+1}=h_{1/2}^{n+1},\quad h_{N+1/2}^{n+1}=-h_{N-1/2}^{n+1}.\end{eqnarray}$$
In matrix form, the linear system in (A 4) has a banded structure, and it is easily solved using the LU (lower–upper) factorization to produce
$h_{i+1/2}^{n+1}$
for
$i=0,1,\dots ,N-1$
, the interface at the new time step. After the new interface is obtained, the contact line
$a(t)$
is updated using the condition (2.3b
).
Appendix B. Complete wetting
The case of complete wetting, that is,
${\it\theta}_{y}=0$
in (2.3b
), requires a modification to the asymptotic analysis of § 3. If we assume again that the velocity is expanded into powers of
${\it\epsilon}$
, then the degenerate boundary condition becomes
$\partial H/\partial X=O({\it\epsilon})$
, and thus, at first glance, the inner scaling of § 4 would be such that the inner variables,
$\overline{H}$
and
$s$
, satisfy
$\partial \overline{H}/\partial s={\it\epsilon}$
; this would allow the wall-angle condition to be applied to the leading-order inner solution. However, this is not the case, and one finds that such a scaling makes it impossible to perform the necessary matching between inner and outer solutions.
In fact, the correct scaling for the inner region is such that the advective, capillary and slip terms of (2.5) are all balanced at leading order. This requires
$H={\it\lambda}\overline{H}$
and
$X={\it\lambda}{\it\epsilon}^{-1/3}s$
. Thus, for the case of complete wetting, the inner length scale is algebraically larger than that in the case of partial wetting. The inner solution is then expanded into the series
$\overline{H}=\overline{H}_{0}+{\it\epsilon}\overline{H}_{1}+O({\it\epsilon}^{2})$
, and the leading-order problem satisfies
$$\begin{eqnarray}{\dot{a}}_{1}+\overline{H}_{0}(\overline{H}_{0}+1)\frac{\partial ^{3}\overline{H}_{0}}{\partial s^{3}}=0,\end{eqnarray}$$
with boundary conditions
$\overline{H}_{0}(0)=\overline{H}_{0}^{\prime }(0)=0$
. The third boundary condition is a matching condition. As was shown by Hocking (Reference Hocking1992), the outer limit of the leading-order inner solution satisfies
$\overline{H}\sim s[3{\dot{a}}_{1}\log s+C]^{1/3}$
, where the value of
$C$
is chosen to match the inner and outer solutions (through the intermediate layer). Because this involves the numerical solution of (B 1), we have chosen to only present the details for the case of partial wetting; however, it should be clear that the main point of this paper (that of understanding the importance of time rescaling) continues to hold true, even for the case of complete wetting.
