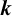1 Introduction
Let n be an arbitrary positive integer and let R be a commutative ring. For every
![]() $n\times n$
matrix
$n\times n$
matrix
![]() $M=[a_{ij}]_{1\le i,j\le n}$
with
$M=[a_{ij}]_{1\le i,j\le n}$
with
![]() $a_{ij}\in R$
, we use the symbol
$a_{ij}\in R$
, we use the symbol
![]() $\det M$
or
$\det M$
or
![]() $|M|$
to denote the determinant of M. Given any elements
$|M|$
to denote the determinant of M. Given any elements
![]() $b_0,b_1,\ldots ,b_{n-1}\in R$
, the circulant matrix of the n-tuple
$b_0,b_1,\ldots ,b_{n-1}\in R$
, the circulant matrix of the n-tuple
![]() $(b_0,\ldots ,b_{n-1})$
is the
$(b_0,\ldots ,b_{n-1})$
is the
![]() $n\times n$
matrix over R whose
$n\times n$
matrix over R whose
![]() $(i,j)$
-entry is
$(i,j)$
-entry is
![]() $b_{i-j}$
, where the indices are cyclic modulo n. We also denote this matrix by
$b_{i-j}$
, where the indices are cyclic modulo n. We also denote this matrix by
![]() $C(b_0,b_1,\ldots ,b_{n-1})$
. Circulant matrices have many applications in both number theory and combinatorics. We refer to the survey paper [Reference Kra and Simanca5] for results on circulant matrices.
$C(b_0,b_1,\ldots ,b_{n-1})$
. Circulant matrices have many applications in both number theory and combinatorics. We refer to the survey paper [Reference Kra and Simanca5] for results on circulant matrices.
1.1 Circulant matrices involving Legendre symbols
Let p be an odd prime and let
![]() $\, \chi (\cdot )$
be a multiplicative character modulo p. Carlitz [Reference Carlitz2] investigated the circulant matrix
$\, \chi (\cdot )$
be a multiplicative character modulo p. Carlitz [Reference Carlitz2] investigated the circulant matrix
where
![]() $c_i=\mu +\, \chi (i)$
for
$c_i=\mu +\, \chi (i)$
for
![]() $0\le i\le p-1$
. Carlitz [Reference Carlitz2, Theorem 4] determined the characteristic polynomial of this circulant matrix. In particular, when
$0\le i\le p-1$
. Carlitz [Reference Carlitz2, Theorem 4] determined the characteristic polynomial of this circulant matrix. In particular, when
![]() $\, \chi (\cdot )=\big(\frac{\cdot}{p}\big)$
is the Legendre symbol, the characteristic polynomial of the matrix
$\, \chi (\cdot )=\big(\frac{\cdot}{p}\big)$
is the Legendre symbol, the characteristic polynomial of the matrix
![]() $[\mu +({(i-j)}/{p})]_{1\le i,j\le p-1}$
is
$[\mu +({(i-j)}/{p})]_{1\le i,j\le p-1}$
is
Later, Chapman [Reference Chapman3, Reference Chapman4] and Vsemirnov [Reference Vsemirnov10, Reference Vsemirnov11] studied variants of Carlitz’s results.
Let
![]() $p=2n+1$
be an odd prime. Recently, Sun [Reference Sun9] studied the determinant
$p=2n+1$
be an odd prime. Recently, Sun [Reference Sun9] studied the determinant
 $$ \begin{align*} S(d,p):=\det\bigg[\bigg(\frac{i^2+dj^2}{p}\bigg)\bigg]_{1\le i,j\le n}, \end{align*} $$
$$ \begin{align*} S(d,p):=\det\bigg[\bigg(\frac{i^2+dj^2}{p}\bigg)\bigg]_{1\le i,j\le n}, \end{align*} $$
where
![]() $\big(\frac{\cdot}{p}\big)$
is the Legendre symbol and
$\big(\frac{\cdot}{p}\big)$
is the Legendre symbol and
![]() $d\in \mathbb {Z}$
with
$d\in \mathbb {Z}$
with
![]() $p\nmid d$
. Sun [Reference Sun9, Theorems 1.2(iii) and 1.3(i)] proved that
$p\nmid d$
. Sun [Reference Sun9, Theorems 1.2(iii) and 1.3(i)] proved that
![]() $-S(d,p)$
is a quadratic residue modulo p whenever
$-S(d,p)$
is a quadratic residue modulo p whenever
![]() $\big(\frac{d}{p}\big)=1$
. (See [Reference Krachun, Petrov, Sun and Vsemirnov6, Reference Wu13] for recent progress on this topic.) Sun also investigated some global properties of this determinant and conjectured that
$\big(\frac{d}{p}\big)=1$
. (See [Reference Krachun, Petrov, Sun and Vsemirnov6, Reference Wu13] for recent progress on this topic.) Sun also investigated some global properties of this determinant and conjectured that
![]() $-S(1,p)$
is an integral square if
$-S(1,p)$
is an integral square if
![]() $p\equiv 3\ ({\textrm {mod}}\ 4)$
. Later, by using a sophisticated matrix decomposition, Alekseyev and Krachun proved this conjecture. In the case
$p\equiv 3\ ({\textrm {mod}}\ 4)$
. Later, by using a sophisticated matrix decomposition, Alekseyev and Krachun proved this conjecture. In the case
![]() $p\equiv 1\ ({\textrm {mod}}\ 4)$
, writing
$p\equiv 1\ ({\textrm {mod}}\ 4)$
, writing
![]() $p=a^2+4b^2$
with
$p=a^2+4b^2$
with
![]() $a,b\in \Bbb Z$
and
$a,b\in \Bbb Z$
and
![]() $a\equiv 1\ ({\textrm {mod}}\ 4)$
, Cohen, Sun and Vsemirnov conjectured that
$a\equiv 1\ ({\textrm {mod}}\ 4)$
, Cohen, Sun and Vsemirnov conjectured that
![]() $S(1,p)/a$
is an integral square (see [Reference Sun9, Remark 4.2]). This conjecture was later proved by the first author [Reference Wu12, Theorem 3].
$S(1,p)/a$
is an integral square (see [Reference Sun9, Remark 4.2]). This conjecture was later proved by the first author [Reference Wu12, Theorem 3].
Note that
![]() $S(d,p)$
is indeed a determinant of a certain circulant matrix. In fact, fix a primitive root g modulo p. Then it is clear that
$S(d,p)$
is indeed a determinant of a certain circulant matrix. In fact, fix a primitive root g modulo p. Then it is clear that
![]() $S(d,p)$
is equal to
$S(d,p)$
is equal to
 $$ \begin{align*} \det\bigg[\bigg(\frac{g^{2i}+dg^{2j}}{p}\bigg)\bigg]_{0\le i,j\le n-1} =\det\bigg[\bigg(\frac{g^{2(i-j)}+d}{p}\bigg)\bigg]_{0\le i,j\le n-1} =\det C(s_0,s_1,\ldots,s_{n-1}), \end{align*} $$
$$ \begin{align*} \det\bigg[\bigg(\frac{g^{2i}+dg^{2j}}{p}\bigg)\bigg]_{0\le i,j\le n-1} =\det\bigg[\bigg(\frac{g^{2(i-j)}+d}{p}\bigg)\bigg]_{0\le i,j\le n-1} =\det C(s_0,s_1,\ldots,s_{n-1}), \end{align*} $$
where
![]() $s_i=({(g^{2i}+d)}/{p})$
for
$s_i=({(g^{2i}+d)}/{p})$
for
![]() $0\le i\le n-1$
.
$0\le i\le n-1$
.
Motivated by Sun’s determinant
![]() $S(d,p)$
, we study some determinants containing kth power residues. Let p be an odd prime and let
$S(d,p)$
, we study some determinants containing kth power residues. Let p be an odd prime and let
![]() $k\ge 2$
be an integer dividing
$k\ge 2$
be an integer dividing
![]() $p-1$
. Write
$p-1$
. Write
![]() $p=km+1$
and let
$p=km+1$
and let
be all the kth power residues modulo p in the interval
![]() $(0,p)$
. We consider the matrix
$(0,p)$
. We consider the matrix
To state our results, we first introduce some notation. Let
![]() $\mathbb {F}_p$
denote the finite field of p elements. Let
$\mathbb {F}_p$
denote the finite field of p elements. Let
![]() $\mathcal {C}_{p,k,\psi }$
and
$\mathcal {C}_{p,k,\psi }$
and
![]() $\mathcal {C}_{p,k,\phi }$
be the curves over
$\mathcal {C}_{p,k,\phi }$
be the curves over
![]() $\mathbb {F}_p$
defined by the equations
$\mathbb {F}_p$
defined by the equations
![]() $y^2=x^k+1$
and
$y^2=x^k+1$
and
![]() $y^2=x(x^k+1)$
, respectively. Define
$y^2=x(x^k+1)$
, respectively. Define
![]() $a_p(k)$
and
$a_p(k)$
and
![]() $b_p(k)$
by
$b_p(k)$
by
and
where
![]() $\infty $
denotes the point at infinity and
$\infty $
denotes the point at infinity and
![]() $\#S$
denotes the cardinality of a set S.
$\#S$
denotes the cardinality of a set S.
When k is even, the following result generalises Sun’s determinant
![]() $S(1,p)$
.
$S(1,p)$
.
Theorem 1.1. Let p be an odd prime and let
![]() $k\ge 2$
be an even integer dividing
$k\ge 2$
be an even integer dividing
![]() $p-1$
. Let
$p-1$
. Let
![]() $m=(p-1)/k$
.
$m=(p-1)/k$
.
-
(i) If m is odd, then
 $\det W_p(k)=-(a_p(k)+1)u_p(k)^2/k$
for some
$\det W_p(k)=-(a_p(k)+1)u_p(k)^2/k$
for some
 $u_p(k)\in \mathbb {Z}$
.
$u_p(k)\in \mathbb {Z}$
. -
(ii) If m is even, then
 $ \det W_p(k)=(a_p(k)+1)b_p(k)v_p(k)^2/k^2 $
for some
$ \det W_p(k)=(a_p(k)+1)b_p(k)v_p(k)^2/k^2 $
for some
 $v_p(k)\in \mathbb {Z}$
.
$v_p(k)\in \mathbb {Z}$
.
Remark 1.2. (1) When
![]() $k=2$
and
$k=2$
and
![]() $p\equiv 3\ ({\textrm {mod}}\ 4)$
, it is easy to see that
$p\equiv 3\ ({\textrm {mod}}\ 4)$
, it is easy to see that
![]() $a_p(2)=1$
. This implies that
$a_p(2)=1$
. This implies that
![]() $-\det W_p(2)=-S(1,p)$
is an integral square, which also confirms the conjecture of Sun.
$-\det W_p(2)=-S(1,p)$
is an integral square, which also confirms the conjecture of Sun.
(2) When
![]() $k=2$
and
$k=2$
and
![]() $p\equiv 1\ ({\textrm {mod}}\ 4)$
with
$p\equiv 1\ ({\textrm {mod}}\ 4)$
with
![]() $p=a^2+4b^2$
, where
$p=a^2+4b^2$
, where
![]() $a\equiv 1\ ({\textrm {mod}}\ 4)$
, it is known that
$a\equiv 1\ ({\textrm {mod}}\ 4)$
, it is known that
![]() $a_p(2)=1$
and
$a_p(2)=1$
and
![]() $b_p(2)=2a$
[Reference Berndt, Evans and Williams1, Theorem 6.2.9]. Thus,
$b_p(2)=2a$
[Reference Berndt, Evans and Williams1, Theorem 6.2.9]. Thus,
![]() $\det W_p(2)/a=S(1,p)/a$
is an integral square, which coincides with the result in [Reference Wu12, Theorem 3].
$\det W_p(2)/a=S(1,p)/a$
is an integral square, which coincides with the result in [Reference Wu12, Theorem 3].
Now we consider the case when k is odd. Fix a primitive root g modulo p. Let
![]() $E_{p,k,1}$
and
$E_{p,k,1}$
and
![]() $E_{p,k,g}$
be the hyperelliptic curves over
$E_{p,k,g}$
be the hyperelliptic curves over
![]() $\mathbb {F}_p$
defined by the equations
$\mathbb {F}_p$
defined by the equations
![]() $y^2=x(x^{2k}+1)$
and
$y^2=x(x^{2k}+1)$
and
![]() $y^2=x(x^{2k}+g^k)$
, respectively. Define
$y^2=x(x^{2k}+g^k)$
, respectively. Define
![]() $c_p(k)$
and
$c_p(k)$
and
![]() $d_p(k)$
by
$d_p(k)$
by
and
Theorem 1.3.
-
(i) Let
 $p\equiv 1\ ({\mathrm {mod}}\ 4)$
be a prime and let
$p\equiv 1\ ({\mathrm {mod}}\ 4)$
be a prime and let
 $k\ge 3$
be an odd integer dividing
$k\ge 3$
be an odd integer dividing
 $p-1$
. Then, for some
$p-1$
. Then, for some $$ \begin{align*}\det W_p(k)=\frac{z_p(k)^2}{4k^2}(c_p(k)^2+d_p(k)^2) \end{align*} $$
$$ \begin{align*}\det W_p(k)=\frac{z_p(k)^2}{4k^2}(c_p(k)^2+d_p(k)^2) \end{align*} $$
 $z_p(k)\in \mathbb {Z}$
.
$z_p(k)\in \mathbb {Z}$
.
-
(ii) Let
 $p\equiv 3\ ({\mathrm {mod}}\ 4)$
be a prime and let
$p\equiv 3\ ({\mathrm {mod}}\ 4)$
be a prime and let
 $k\ge 2$
be an odd integer dividing
$k\ge 2$
be an odd integer dividing
 $p-1$
. Then,
$p-1$
. Then,
 $-\det W_p(k)$
is an integral square.
$-\det W_p(k)$
is an integral square.
When
![]() $k=3$
, we deduce the following consequence.
$k=3$
, we deduce the following consequence.
Corollary 1.4. Suppose that
![]() $p\equiv 1\ ({\mathrm {mod}}\ 12)$
is a prime and write
$p\equiv 1\ ({\mathrm {mod}}\ 12)$
is a prime and write
![]() $p=c^2+9d^2$
with
$p=c^2+9d^2$
with
![]() $c,d\in \mathbb {Z}$
. Then
$c,d\in \mathbb {Z}$
. Then
-
(i)
 $\det W_p(3)/(c^2+d^2)$
is an integral square.
$\det W_p(3)/(c^2+d^2)$
is an integral square. -
(ii) Moreover, if
 $p\nmid \det W_p(3)$
, then
$p\nmid \det W_p(3)$
, then
 $$ \begin{align*}\bigg(\frac{\det W_p(3)}{p}\bigg)=\bigg(\frac{2}{p}\bigg). \end{align*} $$
$$ \begin{align*}\bigg(\frac{\det W_p(3)}{p}\bigg)=\bigg(\frac{2}{p}\bigg). \end{align*} $$
Remark 1.5. There are primes
![]() $p\equiv 1\ ({\textrm {mod}}\ 12)$
such that
$p\equiv 1\ ({\textrm {mod}}\ 12)$
such that
![]() $p\mid \det W_p(3)$
. In fact,
$p\mid \det W_p(3)$
. In fact,
![]() $1117,1129,1381,1597,1861,2557,2749$
are all the primes
$1117,1129,1381,1597,1861,2557,2749$
are all the primes
![]() $p\equiv 1\ ({\textrm {mod}}\ 12)$
less than
$p\equiv 1\ ({\textrm {mod}}\ 12)$
less than
![]() $3000$
such that
$3000$
such that
![]() $p\mid W_p(3)$
.
$p\mid W_p(3)$
.
Corollary 1.6.
-
(i) Let
 $p\equiv 1\ ({\mathrm {mod}}\ 4)$
be a prime and let
$p\equiv 1\ ({\mathrm {mod}}\ 4)$
be a prime and let
 $k\ge 2$
be an odd integer dividing
$k\ge 2$
be an odd integer dividing
 $p-1$
. Then,
$p-1$
. Then,
 $\det W_p(k)\ge 0$
.
$\det W_p(k)\ge 0$
. -
(ii) Let
 $p\equiv 3\ ({\mathrm {mod}}\ 4)$
be a prime and let
$p\equiv 3\ ({\mathrm {mod}}\ 4)$
be a prime and let
 $k\ge 2$
be an odd integer dividing
$k\ge 2$
be an odd integer dividing
 $p-1$
. Then,
$p-1$
. Then,
 $\det W_p(k)\le 0$
.
$\det W_p(k)\le 0$
.
1.2 Determinants of the form
 $\textbf {det}[{1}/{(\alpha _i+\alpha _j)}]_{1\le i,j\le m}$
$\textbf {det}[{1}/{(\alpha _i+\alpha _j)}]_{1\le i,j\le m}$
Let p be an odd prime. For any integer t with
![]() $p\nmid t$
, the element
$p\nmid t$
, the element
![]() $1/t$
mod p denotes the multiplicative inverse of t mod p. In 2019, Sun [Reference Sun9] also studied the determinant
$1/t$
mod p denotes the multiplicative inverse of t mod p. In 2019, Sun [Reference Sun9] also studied the determinant
 $$ \begin{align*}A_p:=\det\bigg[\frac{1}{i^2+j^2}\bigg]_{1\le i,j\le (p-1)/2}. \end{align*} $$
$$ \begin{align*}A_p:=\det\bigg[\frac{1}{i^2+j^2}\bigg]_{1\le i,j\le (p-1)/2}. \end{align*} $$
When
![]() $p\equiv 3\ ({\textrm {mod}}\ 4)$
, Sun [Reference Sun9, Theorem 1.4(ii)] showed that
$p\equiv 3\ ({\textrm {mod}}\ 4)$
, Sun [Reference Sun9, Theorem 1.4(ii)] showed that
 $$ \begin{align*}A_p\equiv \bigg(\frac{2}{p}\bigg)\ ({\textrm{mod}}\ p). \end{align*} $$
$$ \begin{align*}A_p\equiv \bigg(\frac{2}{p}\bigg)\ ({\textrm{mod}}\ p). \end{align*} $$
In [Reference Sun9, Remark 1.3], Sun also conjectured that if
![]() $p\equiv 2\ ({\textrm {mod}}\ 3)$
is odd, then
$p\equiv 2\ ({\textrm {mod}}\ 3)$
is odd, then
![]() $2B_p$
is a quadratic residue modulo p, where
$2B_p$
is a quadratic residue modulo p, where
 $$ \begin{align*}B_p:=\det\bigg[\frac{1}{i^2-ij+j^2}\bigg]_{1\le i,j\le p-1}. \end{align*} $$
$$ \begin{align*}B_p:=\det\bigg[\frac{1}{i^2-ij+j^2}\bigg]_{1\le i,j\le p-1}. \end{align*} $$
This conjecture was later confirmed in [Reference Wu, She and Ni14]. With the notation established in the previous subsection, we consider the matrix
 $$ \begin{align*} I_p(k):=\bigg[\frac{1}{\alpha_i+\alpha_j}\bigg]_{1\le i,j\le m}. \end{align*} $$
$$ \begin{align*} I_p(k):=\bigg[\frac{1}{\alpha_i+\alpha_j}\bigg]_{1\le i,j\le m}. \end{align*} $$
As a generalisation of Sun’s determinant
![]() $\det A_p$
, we obtain the following result.
$\det A_p$
, we obtain the following result.
Theorem 1.7. Let p be an odd prime and let
![]() $k\ge 2$
be an even integer dividing
$k\ge 2$
be an even integer dividing
![]() $p-1$
. Write
$p-1$
. Write
![]() $p=km+1$
. Suppose that
$p=km+1$
. Suppose that
![]() $-1$
is not a kth power residue modulo p. Then
$-1$
is not a kth power residue modulo p. Then
 $$ \begin{align*}\det I_p(k)\equiv \frac{(-1)^{{m+1}/{2}}}{(2k)^m}\ ({\mathrm{mod}}\ p). \end{align*} $$
$$ \begin{align*}\det I_p(k)\equiv \frac{(-1)^{{m+1}/{2}}}{(2k)^m}\ ({\mathrm{mod}}\ p). \end{align*} $$
Remark 1.8. When
![]() $p\equiv 3\ ({\textrm {mod}}\ 4)$
and
$p\equiv 3\ ({\textrm {mod}}\ 4)$
and
![]() $k=2$
, the theorem gives
$k=2$
, the theorem gives
 $$ \begin{align*}\det I_p(2)\equiv (-1)^{{p+1}/{4}}=\bigg(\frac{2}{p}\bigg)\ ({\textrm{mod}}\ p). \end{align*} $$
$$ \begin{align*}\det I_p(2)\equiv (-1)^{{p+1}/{4}}=\bigg(\frac{2}{p}\bigg)\ ({\textrm{mod}}\ p). \end{align*} $$
This coincides with Sun’s result [Reference Sun9, Theorem 1.4(ii)].
The outline of the paper is as follows. We will prove Theorems 1.1–1.3 and their corollaries in Section 2. The proof of Theorem 1.7 will be given in Section 3.
2 Proofs of Theorems 1.1–1.3
Recall that
![]() $C(a_0,\ldots ,a_{n-1})$
denotes the circulant matrix of the n-tuple
$C(a_0,\ldots ,a_{n-1})$
denotes the circulant matrix of the n-tuple
![]() $(a_0,\ldots ,a_{n-1})$
. The following lemma is Lemma 3.4 of [Reference Wu13] and is the key element of our proofs.
$(a_0,\ldots ,a_{n-1})$
. The following lemma is Lemma 3.4 of [Reference Wu13] and is the key element of our proofs.
Lemma 2.1. Let R be a commutative ring, n a positive integer and
![]() $a_0,a_1,\ldots ,a_{n-1}\in R$
such that
$a_0,a_1,\ldots ,a_{n-1}\in R$
such that
If n is even, then there exists an element
![]() $u\in R$
such that
$u\in R$
such that
 $$ \begin{align*} \det C(a_0,a_1,\ldots,a_{n-1})=\bigg(\sum_{i=0}^{n-1}a_i\bigg) \bigg(\sum_{i=0}^{n-1}(-1)^ia_i\bigg) u^2. \end{align*} $$
$$ \begin{align*} \det C(a_0,a_1,\ldots,a_{n-1})=\bigg(\sum_{i=0}^{n-1}a_i\bigg) \bigg(\sum_{i=0}^{n-1}(-1)^ia_i\bigg) u^2. \end{align*} $$
If n is odd, then there exists an element
![]() $v\in R$
such that
$v\in R$
such that
 $$ \begin{align*} \det C(a_0,a_1,\ldots,a_{n-1})=\bigg(\sum_{i=0}^{n-1}a_i\bigg) v^2. \end{align*} $$
$$ \begin{align*} \det C(a_0,a_1,\ldots,a_{n-1})=\bigg(\sum_{i=0}^{n-1}a_i\bigg) v^2. \end{align*} $$
Proof of Theorem 1.1.
Fix a primitive root g modulo p. As k is even,
 $$ \begin{align*} \det W_p(k) & =\det\bigg[\bigg(\frac{1+\alpha_i/\alpha_j}{p}\bigg)\bigg]_{1\le i,j\le m} =\det\bigg[\bigg(\frac{1+g^{k(i-j)}}{p}\bigg)\bigg]_{0\le i,j\le m-1}\\ &=\det C(e_0,e_1,\ldots,e_{m-1}), \quad\mbox{where } e_i=\bigg(\frac{1+g^{ki}}{p}\bigg)\ \mbox{for } 0\le i\le m-1. \end{align*} $$
$$ \begin{align*} \det W_p(k) & =\det\bigg[\bigg(\frac{1+\alpha_i/\alpha_j}{p}\bigg)\bigg]_{1\le i,j\le m} =\det\bigg[\bigg(\frac{1+g^{k(i-j)}}{p}\bigg)\bigg]_{0\le i,j\le m-1}\\ &=\det C(e_0,e_1,\ldots,e_{m-1}), \quad\mbox{where } e_i=\bigg(\frac{1+g^{ki}}{p}\bigg)\ \mbox{for } 0\le i\le m-1. \end{align*} $$
Clearly
![]() $e_0,\ldots ,e_{m-1}$
satisfy the condition (2.1). Moreover,
$e_0,\ldots ,e_{m-1}$
satisfy the condition (2.1). Moreover,
 $$ \begin{align} \sum_{i=0}^{m-1}e_i =\frac{1}{k}\sum_{x=1}^{p-1}\bigg(\frac{1+x^k}{p}\bigg) =\frac{1}{k}\bigg(-1+\sum_{x=0}^{p-1}\bigg(\frac{1+x^k}{p}\bigg)\bigg) =-\frac{1+a_p(k)}{k}, \end{align} $$
$$ \begin{align} \sum_{i=0}^{m-1}e_i =\frac{1}{k}\sum_{x=1}^{p-1}\bigg(\frac{1+x^k}{p}\bigg) =\frac{1}{k}\bigg(-1+\sum_{x=0}^{p-1}\bigg(\frac{1+x^k}{p}\bigg)\bigg) =-\frac{1+a_p(k)}{k}, \end{align} $$
where
![]() $a_p(k)$
is defined by (1.1). Also,
$a_p(k)$
is defined by (1.1). Also,
 $$ \begin{align} \sum_{i=0}^{m-2}(-1)^ie_i=\frac{1}{k}\sum_{x=1}^{p-1}\bigg(\frac{x^k+1}{p}\bigg)\bigg(\frac{x}{p}\bigg) =-\frac{b_p(k)}{k}, \end{align} $$
$$ \begin{align} \sum_{i=0}^{m-2}(-1)^ie_i=\frac{1}{k}\sum_{x=1}^{p-1}\bigg(\frac{x^k+1}{p}\bigg)\bigg(\frac{x}{p}\bigg) =-\frac{b_p(k)}{k}, \end{align} $$
where
![]() $b_p(k)$
is defined by (1.2). Combining Lemma 2.1 with (2.2) and (2.3) yields the desired result.
$b_p(k)$
is defined by (1.2). Combining Lemma 2.1 with (2.2) and (2.3) yields the desired result.
Now we turn to the proof of Theorem 1.3. We first need the following well-known result in linear algebra.
Lemma 2.2. Let M be an
![]() $n\times n$
complex matrix. Let
$n\times n$
complex matrix. Let
![]() $\lambda _1,\ldots ,\lambda _n$
be complex numbers and let
$\lambda _1,\ldots ,\lambda _n$
be complex numbers and let
![]() $\mathbf {u}_1,\ldots , \mathbf {u}_n$
be m-dimensional column vectors. Suppose that
$\mathbf {u}_1,\ldots , \mathbf {u}_n$
be m-dimensional column vectors. Suppose that
![]() $M\mathbf {u}_i=\lambda _i\mathbf {u}_i$
for
$M\mathbf {u}_i=\lambda _i\mathbf {u}_i$
for
![]() $1\le i\le n$
and that
$1\le i\le n$
and that
![]() $\mathbf {u}_1,\ldots , \mathbf {u}_n$
are linearly independent. Then
$\mathbf {u}_1,\ldots , \mathbf {u}_n$
are linearly independent. Then
![]() $\lambda _1,\ldots ,\lambda _n$
are exactly all the eigenvalues of M (counting multiplicities).
$\lambda _1,\ldots ,\lambda _n$
are exactly all the eigenvalues of M (counting multiplicities).
Let
![]() $\widehat {\mathbb {F}_p^{\times }}$
denote the cyclic group of all multiplicative characters of
$\widehat {\mathbb {F}_p^{\times }}$
denote the cyclic group of all multiplicative characters of
![]() $\mathbb {F}_p$
and let
$\mathbb {F}_p$
and let
![]() $\, \chi _p(\cdot )$
be a generator of
$\, \chi _p(\cdot )$
be a generator of
![]() $\widehat {\mathbb {F}_p^{\times }}$
. For any matrix M, we use the symbol
$\widehat {\mathbb {F}_p^{\times }}$
. For any matrix M, we use the symbol
![]() $M^T$
to denote the transpose of M.
$M^T$
to denote the transpose of M.
Proof of Theorem 1.3.
Recall that
![]() $k\ge 2$
is an odd integer dividing
$k\ge 2$
is an odd integer dividing
![]() $p-1$
and
$p-1$
and
![]() $p=km+1$
.
$p=km+1$
.
(i) We first consider the case
![]() $p\equiv 1\ ({\textrm {mod}}\ 4)$
. Clearly, the elements
$p\equiv 1\ ({\textrm {mod}}\ 4)$
. Clearly, the elements
![]() $\alpha _1\ \textrm {mod}\ p ,\ldots , \alpha _m \textrm { mod}\ p$
are exactly m distinct roots of the polynomial
$\alpha _1\ \textrm {mod}\ p ,\ldots , \alpha _m \textrm { mod}\ p$
are exactly m distinct roots of the polynomial
![]() $X^m-1$
over
$X^m-1$
over
![]() $\mathbb {F}_p=\mathbb {Z}/p\mathbb {Z}$
. Therefore,
$\mathbb {F}_p=\mathbb {Z}/p\mathbb {Z}$
. Therefore,
 $$ \begin{align} X^m-1\equiv \prod_{i=1}^{m}(X-\alpha_i)\ ({\textrm{mod}}\ p). \end{align} $$
$$ \begin{align} X^m-1\equiv \prod_{i=1}^{m}(X-\alpha_i)\ ({\textrm{mod}}\ p). \end{align} $$
By (2.4),
 $$ \begin{align} \prod_{j=1}^m\alpha_j\equiv -1^{m+1}=-1\ ({\textrm{mod}}\ p). \end{align} $$
$$ \begin{align} \prod_{j=1}^m\alpha_j\equiv -1^{m+1}=-1\ ({\textrm{mod}}\ p). \end{align} $$
By (2.5), it is easy to see that
![]() $\det W_p(k)$
is equal to
$\det W_p(k)$
is equal to
 $$ \begin{align*} \bigg(\frac{-1}{p}\bigg) \det\bigg[\bigg(\frac{\alpha_i+\alpha_j}{p}\bigg)\bigg]_{1\le i,j\le m} =\det\bigg[\bigg(\frac{\alpha_i+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg)\bigg]_{1\le i,j\le m}. \end{align*} $$
$$ \begin{align*} \bigg(\frac{-1}{p}\bigg) \det\bigg[\bigg(\frac{\alpha_i+\alpha_j}{p}\bigg)\bigg]_{1\le i,j\le m} =\det\bigg[\bigg(\frac{\alpha_i+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg)\bigg]_{1\le i,j\le m}. \end{align*} $$
Next, we determine all the eigenvalues of the matrix
For each r with
![]() $1\le r\le m$
,
$1\le r\le m$
,
 $$ \begin{align*} \sum_{j=1}^{m}\bigg(\frac{\alpha_i+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg)\,\, \chi_p^r(\alpha_j) &=\sum_{j=1}^{m}\bigg(\frac{1+\alpha_j/\alpha_i}{p}\bigg)\bigg(\frac{\alpha_j/\alpha_i}{p}\bigg)\, \, \chi_p(\alpha_j/\alpha_i)\,\, \chi_p^r(\alpha_i)\\ &=\sum_{j=1}^{m}\bigg(\frac{1+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg) \,\, \chi_p^r(\alpha_j)\,\, \chi_p^r(\alpha_i). \end{align*} $$
$$ \begin{align*} \sum_{j=1}^{m}\bigg(\frac{\alpha_i+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg)\,\, \chi_p^r(\alpha_j) &=\sum_{j=1}^{m}\bigg(\frac{1+\alpha_j/\alpha_i}{p}\bigg)\bigg(\frac{\alpha_j/\alpha_i}{p}\bigg)\, \, \chi_p(\alpha_j/\alpha_i)\,\, \chi_p^r(\alpha_i)\\ &=\sum_{j=1}^{m}\bigg(\frac{1+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg) \,\, \chi_p^r(\alpha_j)\,\, \chi_p^r(\alpha_i). \end{align*} $$
This implies that for
![]() $1\le r\le m$
,
$1\le r\le m$
,
where
 $$ \begin{align*}\lambda_r=\sum_{j=1}^{m}\bigg(\frac{1+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg) \, \chi_p^r(\alpha_j) \quad\mbox{and}\quad \mathbf{v}_r=(\, \chi_p^r(\alpha_1),\ldots,\, \chi_p^r(\alpha_m))^T. \end{align*} $$
$$ \begin{align*}\lambda_r=\sum_{j=1}^{m}\bigg(\frac{1+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg) \, \chi_p^r(\alpha_j) \quad\mbox{and}\quad \mathbf{v}_r=(\, \chi_p^r(\alpha_1),\ldots,\, \chi_p^r(\alpha_m))^T. \end{align*} $$
Note that
 $$ \begin{align*}\left| \begin{array}{cccccccc} \, \chi_p^1(\alpha_1) & \, \chi_p^2(\alpha_1) & \ldots & \, \chi_p^m(\alpha_1) \\ \, \chi_p^1(\alpha_2) & \, \chi_p^2(\alpha_2) & \ldots & \, \chi_p^n(\alpha_2)\\ \vdots & \vdots & \ddots & \vdots \\ \, \chi_p^1(\alpha_n)& \, \chi_p^2(\alpha_n) & \ldots & \, \chi_p^m(\alpha_m)\\ \end{array} \right| = \pm\prod_{1\le i<j\le m} (\, \chi_p(\alpha_j)-\, \chi_p(\alpha_i) )\ne0. \end{align*} $$
$$ \begin{align*}\left| \begin{array}{cccccccc} \, \chi_p^1(\alpha_1) & \, \chi_p^2(\alpha_1) & \ldots & \, \chi_p^m(\alpha_1) \\ \, \chi_p^1(\alpha_2) & \, \chi_p^2(\alpha_2) & \ldots & \, \chi_p^n(\alpha_2)\\ \vdots & \vdots & \ddots & \vdots \\ \, \chi_p^1(\alpha_n)& \, \chi_p^2(\alpha_n) & \ldots & \, \chi_p^m(\alpha_m)\\ \end{array} \right| = \pm\prod_{1\le i<j\le m} (\, \chi_p(\alpha_j)-\, \chi_p(\alpha_i) )\ne0. \end{align*} $$
Hence, the vectors
![]() $\mathbf {v}_1,\ldots , \mathbf {v}_m$
are linearly independent. Now by Lemma 2.2, the numbers
$\mathbf {v}_1,\ldots , \mathbf {v}_m$
are linearly independent. Now by Lemma 2.2, the numbers
![]() $\lambda _1,\ldots ,\lambda _m$
are exactly all the eigenvalues of
$\lambda _1,\ldots ,\lambda _m$
are exactly all the eigenvalues of
![]() $W^*_p(k)$
(counting multiplicities).
$W^*_p(k)$
(counting multiplicities).
When
![]() $r=m$
,
$r=m$
,
 $$ \begin{align*} \lambda_m=\sum_{j=1}^m\bigg(\frac{1+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg) =\frac{1}{k}\sum_{x=1}^{p-1}\bigg(\frac{1+x^k}{p}\bigg)\bigg(\frac{x}{p}\bigg). \end{align*} $$
$$ \begin{align*} \lambda_m=\sum_{j=1}^m\bigg(\frac{1+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg) =\frac{1}{k}\sum_{x=1}^{p-1}\bigg(\frac{1+x^k}{p}\bigg)\bigg(\frac{x}{p}\bigg). \end{align*} $$
When
![]() $r=m/2$
,
$r=m/2$
,
 $$ \begin{align*} \lambda_{m/2}=\sum_{j=1}^m\bigg(\frac{1+\alpha_j}{p}\bigg) =\frac{1}{k}\sum_{x=1}^{p-1}\bigg(\frac{1+x^k}{p}\bigg). \end{align*} $$
$$ \begin{align*} \lambda_{m/2}=\sum_{j=1}^m\bigg(\frac{1+\alpha_j}{p}\bigg) =\frac{1}{k}\sum_{x=1}^{p-1}\bigg(\frac{1+x^k}{p}\bigg). \end{align*} $$
By [Reference Berndt, Evans and Williams1, Proposition 6.1.7],
In addition, when
![]() $1\le r\le m/2-1$
, it is clear that
$1\le r\le m/2-1$
, it is clear that
![]() $\overline {\lambda _r}=\lambda _{m-r}$
, where
$\overline {\lambda _r}=\lambda _{m-r}$
, where
![]() $\bar {z}$
denotes the complex conjugate of a complex number z. Combining this with (2.6),
$\bar {z}$
denotes the complex conjugate of a complex number z. Combining this with (2.6),
 $$ \begin{align} \det W_p(k)=\det W^*_p(k)=\prod_{r=1}^m\lambda_r =\lambda_m^2\prod_{1\le r\le m/2-1}\lambda_r\overline{\lambda_r}\ge0. \end{align} $$
$$ \begin{align} \det W_p(k)=\det W^*_p(k)=\prod_{r=1}^m\lambda_r =\lambda_m^2\prod_{1\le r\le m/2-1}\lambda_r\overline{\lambda_r}\ge0. \end{align} $$
Let
![]() $\mathbf {i}\in \mathbb {C}$
be a primitive fourth root of unity. Fix a primitive root g modulo p. Then
$\mathbf {i}\in \mathbb {C}$
be a primitive fourth root of unity. Fix a primitive root g modulo p. Then
 $$ \begin{align*} \det W^*_p(k) &=\det\bigg[\bigg(\frac{\alpha_i+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg)\,\mathbf{i}^{i-j}\bigg]_{1\le i,j\le m}\\ &=\det\bigg[\bigg(\frac{1+g^{k(i-j)}}{p}\bigg)\,\mathbf{i}^{i-j}\bigg]_{0\le i,j\le m-1}\\ &=\det C(\omega_0,\ldots,\omega_{m-1}) \quad\mbox{where } \omega_r=\bigg(\frac{1+g^{kr}}{p}\bigg)\,\mathbf{i}^r \ \mbox{for } 0\le r\le m-1. \end{align*} $$
$$ \begin{align*} \det W^*_p(k) &=\det\bigg[\bigg(\frac{\alpha_i+\alpha_j}{p}\bigg)\bigg(\frac{\alpha_j}{p}\bigg)\,\mathbf{i}^{i-j}\bigg]_{1\le i,j\le m}\\ &=\det\bigg[\bigg(\frac{1+g^{k(i-j)}}{p}\bigg)\,\mathbf{i}^{i-j}\bigg]_{0\le i,j\le m-1}\\ &=\det C(\omega_0,\ldots,\omega_{m-1}) \quad\mbox{where } \omega_r=\bigg(\frac{1+g^{kr}}{p}\bigg)\,\mathbf{i}^r \ \mbox{for } 0\le r\le m-1. \end{align*} $$
One can verify that
![]() $\omega _0,\ldots ,\omega _{m-1}$
satisfy the condition (2.1). Fix a multiplicative character
$\omega _0,\ldots ,\omega _{m-1}$
satisfy the condition (2.1). Fix a multiplicative character
![]() $\psi \in \widehat {\mathbb {F}_p^{\times }}$
of order
$\psi \in \widehat {\mathbb {F}_p^{\times }}$
of order
![]() $4$
with
$4$
with
![]() $\psi (g)=\mathbf {i}$
. Then
$\psi (g)=\mathbf {i}$
. Then
 $$ \begin{align*} \sum_{r=0}^{m-1}\omega_r =\sum_{r=0}^{m-1}\bigg(\frac{1+g^{kr}}{p}\bigg)\psi(g^r) =\frac{1}{k}\sum_{r=0}^{p-2}\bigg(\frac{1+g^{kr}}{p}\bigg)\psi(g^r). \end{align*} $$
$$ \begin{align*} \sum_{r=0}^{m-1}\omega_r =\sum_{r=0}^{m-1}\bigg(\frac{1+g^{kr}}{p}\bigg)\psi(g^r) =\frac{1}{k}\sum_{r=0}^{p-2}\bigg(\frac{1+g^{kr}}{p}\bigg)\psi(g^r). \end{align*} $$
One can also verify the following equalities:
 $$ \begin{align*} \sum_{r=0}^{p-2}\bigg(\frac{1+g^{kr}}{p}\bigg)\psi(g^r) &=\sum_{r=0}^{{(p-3)}/{2}}\bigg(\frac{1+g^{2kr}}{p}\bigg)\bigg(\frac{g^r}{p}\bigg) +\mathbf{i}\sum_{r=0}^{({p-3})/{2}}\bigg(\frac{1+g^{2kr}g^k}{p}\bigg)\bigg(\frac{g^r}{p}\bigg)\\ &=\frac{1}{2}\sum_{x=1}^{p-1}\bigg(\frac{1+x^{2k}}{p}\bigg)\bigg(\frac{x}{p}\bigg) +\frac{1}{2}\mathbf{i}\sum_{x=1}^{p-1}\bigg(\frac{1+x^{2k}g^k}{p}\bigg)\bigg(\frac{x}{p}\bigg)\\ &=\frac{1}{2}\sum_{x=1}^{p-1}\bigg(\frac{1+x^{2k}}{p}\bigg)\bigg(\frac{x}{p}\bigg) +\frac{1}{2}\mathbf{i}\sum_{x=1}^{p-1}\bigg(\frac{g^k+x^{2k}}{p}\bigg)\bigg(\frac{x}{p}\bigg)\\ &=-\frac{c_p(k)+\mathbf{i}d_p(k)}{2}, \end{align*} $$
$$ \begin{align*} \sum_{r=0}^{p-2}\bigg(\frac{1+g^{kr}}{p}\bigg)\psi(g^r) &=\sum_{r=0}^{{(p-3)}/{2}}\bigg(\frac{1+g^{2kr}}{p}\bigg)\bigg(\frac{g^r}{p}\bigg) +\mathbf{i}\sum_{r=0}^{({p-3})/{2}}\bigg(\frac{1+g^{2kr}g^k}{p}\bigg)\bigg(\frac{g^r}{p}\bigg)\\ &=\frac{1}{2}\sum_{x=1}^{p-1}\bigg(\frac{1+x^{2k}}{p}\bigg)\bigg(\frac{x}{p}\bigg) +\frac{1}{2}\mathbf{i}\sum_{x=1}^{p-1}\bigg(\frac{1+x^{2k}g^k}{p}\bigg)\bigg(\frac{x}{p}\bigg)\\ &=\frac{1}{2}\sum_{x=1}^{p-1}\bigg(\frac{1+x^{2k}}{p}\bigg)\bigg(\frac{x}{p}\bigg) +\frac{1}{2}\mathbf{i}\sum_{x=1}^{p-1}\bigg(\frac{g^k+x^{2k}}{p}\bigg)\bigg(\frac{x}{p}\bigg)\\ &=-\frac{c_p(k)+\mathbf{i}d_p(k)}{2}, \end{align*} $$
where
![]() $c_p(k)$
and
$c_p(k)$
and
![]() $d_p(k)$
are defined by (1.3) and (1.4), respectively. Hence,
$d_p(k)$
are defined by (1.3) and (1.4), respectively. Hence,
 $$ \begin{align} \sum_{r=0}^{m-1}\omega_r= - \frac{c_p(k)+\mathbf{i}d_p(k)}{2k}. \end{align} $$
$$ \begin{align} \sum_{r=0}^{m-1}\omega_r= - \frac{c_p(k)+\mathbf{i}d_p(k)}{2k}. \end{align} $$
With essentially the same method, one can also verify that
 $$ \begin{align} \sum_{r=0}^{m-1}(-1)^r\omega_r= - \frac{c_p(k)-\mathbf{i}d_p(k)}{2k}. \end{align} $$
$$ \begin{align} \sum_{r=0}^{m-1}(-1)^r\omega_r= - \frac{c_p(k)-\mathbf{i}d_p(k)}{2k}. \end{align} $$
If
![]() $\det W_p(k)=0$
, then one can get the desired result directly. Suppose now that
$\det W_p(k)=0$
, then one can get the desired result directly. Suppose now that
![]() $\det W_p(k)\ne 0$
. By (2.7), we have
$\det W_p(k)\ne 0$
. By (2.7), we have
![]() $\det W_p(k)>0$
under this assumption. Combining Lemma 2.1 with (2.8) and (2.9), there exists an element
$\det W_p(k)>0$
under this assumption. Combining Lemma 2.1 with (2.8) and (2.9), there exists an element
![]() $z_p(k)\in \mathbb {Z}[\mathbf {i}]$
such that
$z_p(k)\in \mathbb {Z}[\mathbf {i}]$
such that
 $$ \begin{align*}\det W_p(k)=\det W_p^*(k)=\frac{z_p(k)^2}{4k^2}(c_p(k)^2+d_p(k)^2). \end{align*} $$
$$ \begin{align*}\det W_p(k)=\det W_p^*(k)=\frac{z_p(k)^2}{4k^2}(c_p(k)^2+d_p(k)^2). \end{align*} $$
As
![]() $\det W_p(k)\in \mathbb {Z}$
and
$\det W_p(k)\in \mathbb {Z}$
and
![]() $\det W_p(k)>0$
, the number
$\det W_p(k)>0$
, the number
![]() $z_p(k)$
must be an integer. This completes the proof of (i).
$z_p(k)$
must be an integer. This completes the proof of (i).
(ii) We now consider the case
![]() $p\equiv 3\ ({\textrm {mod}}\ 4)$
. As k is odd, it is clear that
$p\equiv 3\ ({\textrm {mod}}\ 4)$
. As k is odd, it is clear that
is a permutation
![]() $\pi $
of the sequence
$\pi $
of the sequence
and clearly
 $$ \begin{align*}\textrm{sgn}(\pi)\equiv\prod_{1\le i<j\le m}\frac{-\alpha_j-(-\alpha_i)}{\alpha_j-\alpha_i}=(-1)^{m(m-1)/2}\ ({\textrm{mod}}\ p), \end{align*} $$
$$ \begin{align*}\textrm{sgn}(\pi)\equiv\prod_{1\le i<j\le m}\frac{-\alpha_j-(-\alpha_i)}{\alpha_j-\alpha_i}=(-1)^{m(m-1)/2}\ ({\textrm{mod}}\ p), \end{align*} $$
where
![]() $\textrm {sgn}(\pi )$
is the sign of
$\textrm {sgn}(\pi )$
is the sign of
![]() $\pi $
. When
$\pi $
. When
![]() $p\equiv 3\ ({\textrm {mod}}\ 4)$
and k is odd, since
$p\equiv 3\ ({\textrm {mod}}\ 4)$
and k is odd, since
![]() $m\equiv 2\ ({\textrm {mod}}\ 4)$
, the number
$m\equiv 2\ ({\textrm {mod}}\ 4)$
, the number
![]() $\det W_p(k)$
is equal to
$\det W_p(k)$
is equal to
Clearly, the matrix
![]() $M_p:=[({(\alpha _i-\alpha _j)}/{p})]_{1\le i,j\le m}$
is skew-symmetric, that is,
$M_p:=[({(\alpha _i-\alpha _j)}/{p})]_{1\le i,j\le m}$
is skew-symmetric, that is,
![]() $M_p^{T}=-M_p$
. The determinant of a skew-symmetric matrix of even order with integer entries is always an integral square (see [Reference Stembridge8, Proposition 2.2]). This implies that
$M_p^{T}=-M_p$
. The determinant of a skew-symmetric matrix of even order with integer entries is always an integral square (see [Reference Stembridge8, Proposition 2.2]). This implies that
![]() $-\det W_p(k)$
is an integral square.
$-\det W_p(k)$
is an integral square.
This completes the proof.
Proof of Corollary 1.4.
(i) Let
![]() $k=3$
and
$k=3$
and
![]() $p\equiv 1\ ({\textrm {mod}}\ 12)$
. Write
$p\equiv 1\ ({\textrm {mod}}\ 12)$
. Write
![]() $p=\alpha ^2+\beta ^2$
with
$p=\alpha ^2+\beta ^2$
with
![]() $\alpha ,\beta \in \mathbb {Z}$
and
$\alpha ,\beta \in \mathbb {Z}$
and
![]() $\alpha \equiv -({2}/{p})\ ({\textrm {mod}}\ 4)$
. From [Reference Berndt, Evans and Williams1, Theorem 6.2.5],
$\alpha \equiv -({2}/{p})\ ({\textrm {mod}}\ 4)$
. From [Reference Berndt, Evans and Williams1, Theorem 6.2.5],
 $$ \begin{align*}c_p(3)^2=\begin{cases}36\alpha^2&\mbox{if}\ 3\nmid \alpha,\\ 4\alpha^2&\mbox{if}\ 3\mid\alpha,\end{cases},\quad d_p(3)^2=\begin{cases}4\beta^2&\mbox{if}\ 3\nmid \alpha,\\ 36\beta^2&\mbox{if}\ 3\mid\alpha.\end{cases} \end{align*} $$
$$ \begin{align*}c_p(3)^2=\begin{cases}36\alpha^2&\mbox{if}\ 3\nmid \alpha,\\ 4\alpha^2&\mbox{if}\ 3\mid\alpha,\end{cases},\quad d_p(3)^2=\begin{cases}4\beta^2&\mbox{if}\ 3\nmid \alpha,\\ 36\beta^2&\mbox{if}\ 3\mid\alpha.\end{cases} \end{align*} $$
Hence, if we write
![]() $p=c^2+9d^2$
with
$p=c^2+9d^2$
with
![]() $c,d\in \Bbb Z$
, then one can easily verify that
$c,d\in \Bbb Z$
, then one can easily verify that
 $$ \begin{align*}\frac{c_p(3)^2+d_p(3)^2}{36}=c^2+d^2. \end{align*} $$
$$ \begin{align*}\frac{c_p(3)^2+d_p(3)^2}{36}=c^2+d^2. \end{align*} $$
By Theorem 1.3,
![]() $\det W_p(3)/(c^2+d^2)$
is an integral square if
$\det W_p(3)/(c^2+d^2)$
is an integral square if
![]() $p\equiv 1\ ({\textrm {mod}}\ 12)$
.
$p\equiv 1\ ({\textrm {mod}}\ 12)$
.
(ii) If
![]() $p\nmid \det W_p(3)$
, then
$p\nmid \det W_p(3)$
, then
 $$ \begin{align*}\bigg(\frac{\det W_p(3)}{p}\bigg)=\bigg(\frac{c^2+d^2}{p}\bigg) =\bigg(\frac{8c^2+p}{p}\bigg)=\bigg(\frac{2}{p}\bigg). \end{align*} $$
$$ \begin{align*}\bigg(\frac{\det W_p(3)}{p}\bigg)=\bigg(\frac{c^2+d^2}{p}\bigg) =\bigg(\frac{8c^2+p}{p}\bigg)=\bigg(\frac{2}{p}\bigg). \end{align*} $$
This completes the proof.
3 Proof of Theorem 1.7
Recall that
 $$ \begin{align*}I_p(k)=\bigg[\frac{1}{\alpha_i+\alpha_j}\bigg]_{1\le i,j\le m}. \end{align*} $$
$$ \begin{align*}I_p(k)=\bigg[\frac{1}{\alpha_i+\alpha_j}\bigg]_{1\le i,j\le m}. \end{align*} $$
As
![]() $-1$
is not a kth power residue modulo p, clearly we have
$-1$
is not a kth power residue modulo p, clearly we have
![]() $2\nmid m$
.
$2\nmid m$
.
Proof of Theorem 1.7.
By [Reference Krattenthaler7, Theorem 12(5.5)],
 $$ \begin{align*} \det I_p(k)=\frac{\prod_{1\le i<j\le m}(\alpha_i-\alpha_j)^2} {\prod_{1\le i\le m}\prod_{1\le j\le m}(\alpha_i+\alpha_j)}. \end{align*} $$
$$ \begin{align*} \det I_p(k)=\frac{\prod_{1\le i<j\le m}(\alpha_i-\alpha_j)^2} {\prod_{1\le i\le m}\prod_{1\le j\le m}(\alpha_i+\alpha_j)}. \end{align*} $$
We first consider the numerator. One can verify the equalities
 $$ \begin{align*} N_p:=\prod_{1\le i<j\le m}(\alpha_i-\alpha_j)^2 &=(-1)^{{m(m-1)}/{2}}\prod_{1\le i\ne j\le m}(\alpha_i-\alpha_j)\\[4pt] &=(-1)^{{(m-1)}/{2}}\prod_{1\le j\le m}\prod_{i\ne j}(\alpha_j-\alpha_i)\\[4pt] &=(-1)^{{(m-1)}/{2}}\prod_{1\le j\le m}G'(\alpha_j), \end{align*} $$
$$ \begin{align*} N_p:=\prod_{1\le i<j\le m}(\alpha_i-\alpha_j)^2 &=(-1)^{{m(m-1)}/{2}}\prod_{1\le i\ne j\le m}(\alpha_i-\alpha_j)\\[4pt] &=(-1)^{{(m-1)}/{2}}\prod_{1\le j\le m}\prod_{i\ne j}(\alpha_j-\alpha_i)\\[4pt] &=(-1)^{{(m-1)}/{2}}\prod_{1\le j\le m}G'(\alpha_j), \end{align*} $$
where
![]() $G'(X)$
is the derivative of
$G'(X)$
is the derivative of
![]() $G(X)=\prod _{1\le i\le m}(X-\alpha _i)$
. Observe that
$G(X)=\prod _{1\le i\le m}(X-\alpha _i)$
. Observe that
Hence,
![]() $G'(X)\equiv mX^{m-1}\ ({\textrm {mod}}\ p)$
and
$G'(X)\equiv mX^{m-1}\ ({\textrm {mod}}\ p)$
and
![]() $\prod _{1\le i\le m}\alpha _i\equiv (-1)^{m+1}=1\ ({\textrm {mod}}\ p)$
. This gives
$\prod _{1\le i\le m}\alpha _i\equiv (-1)^{m+1}=1\ ({\textrm {mod}}\ p)$
. This gives
 $$ \begin{align} N_p = \prod_{1\le i<j\le m}(\alpha_i-\alpha_j)^2 &=(-1)^{{(m-1)}/{2}}\prod_{1\le j\le m}G'(\alpha_j) \nonumber\\[4pt] &\equiv (-1)^{{(m-1)}/{2}}m^m\prod_{1\le j\le m}\alpha_j^{m-1}\equiv (-1)^{{(m-1)}/{2}}m^m\ ({\textrm{mod}}\ p). \end{align} $$
$$ \begin{align} N_p = \prod_{1\le i<j\le m}(\alpha_i-\alpha_j)^2 &=(-1)^{{(m-1)}/{2}}\prod_{1\le j\le m}G'(\alpha_j) \nonumber\\[4pt] &\equiv (-1)^{{(m-1)}/{2}}m^m\prod_{1\le j\le m}\alpha_j^{m-1}\equiv (-1)^{{(m-1)}/{2}}m^m\ ({\textrm{mod}}\ p). \end{align} $$
Now we turn to the denominator. One can verify the equalities
 $$ \begin{align*} D_p:=\prod_{i=1}^m\prod_{j=1}^m(\alpha_i+\alpha_j) & =\prod_{i=1}^m\alpha_i^m\prod_{j=1}^m(1+\alpha_j/\alpha_i) \\ & \equiv \prod_{i=1}^m\prod_{j=1}^m(1+\alpha_j) =\prod_{j=1}^m(1+\alpha_j)^m\ ({\textrm{mod}}\ p). \end{align*} $$
$$ \begin{align*} D_p:=\prod_{i=1}^m\prod_{j=1}^m(\alpha_i+\alpha_j) & =\prod_{i=1}^m\alpha_i^m\prod_{j=1}^m(1+\alpha_j/\alpha_i) \\ & \equiv \prod_{i=1}^m\prod_{j=1}^m(1+\alpha_j) =\prod_{j=1}^m(1+\alpha_j)^m\ ({\textrm{mod}}\ p). \end{align*} $$
Hence, by (3.1),
Combining (3.2) with (3.3), we finally obtain
 $$ \begin{align*}\det I_p(k)\equiv \frac{(-1)^{(m-1)/{2}}m^m}{2^m}\equiv\frac{(-1)^{(m+1)/2}}{(2k)^m}\ ({\textrm{mod}}\ p). \end{align*} $$
$$ \begin{align*}\det I_p(k)\equiv \frac{(-1)^{(m-1)/{2}}m^m}{2^m}\equiv\frac{(-1)^{(m+1)/2}}{(2k)^m}\ ({\textrm{mod}}\ p). \end{align*} $$
This completes the proof.
Acknowledgement
We would like to thank the referee for helpful comments.