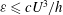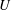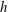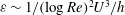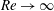1 Introduction
In every turbulent flow, there is some key quantity of interest which is either enhanced or suppressed compared to its laminar value and it is of fundamental interest to understand this effect as a function of the parameters of the problem. Well-known examples include the mass flux along a channel driven by an applied pressure gradient, the heat flux across a differentially heated fluid layer or the wall shear stress exerted by a fluid sheared between two parallel plates. One approach is to derive strict inequality information on these key global flow quantities as a function of the system parameters in the hope that this captures the correct scaling relationship. This ‘bounding’ approach is attractive because it seeks to extract just enough of the physics from the governing equations to make the correct prediction while eschewing other secondary flow details which arise from directly solving the governing equations and just may not be attainable in the asymptotic regime of interest (e.g. vanishing viscosity). The downside of the bounding approach is that the bound derived can be too conservative. Well-known examples are the energy dissipation rate
$\unicode[STIX]{x1D700}$
in a smooth pipe where the best (lowest) bound known predicts that
$\unicode[STIX]{x1D700}$
approaches a finite constant (in units of
$U^{3}/h$
) as the Reynolds number
$Re$
becomes large – the so-called Kolmogorov scaling (Frisch Reference Frisch1995) – whereas data suggest a
${\sim}1/(\log Re)^{2}$
drop off, and the scaling of the Nusselt number
$Nu$
(normalised heat flux) in Boussinesq convection with Rayleigh number
$Ra$
: the bound has
$Nu\lesssim Ra^{\unicode[STIX]{x1D6FC}}$
with
$\unicode[STIX]{x1D6FC}=1/2$
for
$Ra\rightarrow \infty$
whereas current data suggest
$\unicode[STIX]{x1D6FC}\approx 0.31$
(e.g. see the discussion in Waleffe, Boonkasame & Smith (Reference Waleffe, Boonkasame and Smith2015)) with probable dependence on the Prandtl number too (Grossmann & Lohse Reference Grossmann and Lohse2000).
The bounding approach owes its roots to a suggestion by Malkus (Reference Malkus1954) that turbulent flows want to maximise their transport and was first applied in convection by Howard (Reference Howard1963) and in shear flows by Busse (Reference Busse1969, Reference Busse1970) (see Howard (Reference Howard1972) and Busse (Reference Busse1978) for early reviews). The original approach was based on using certain simple projections of the governing equations as constraints in an optimisation problem. After initial successes, it quickly became hard to pose more constrained yet still tractable problems and the field languished in the late 70s and 80s. In the early 90s, a new ‘background’ method introduced by Doering & Constantin (Reference Doering and Constantin1992, Reference Doering and Constantin1994, Reference Doering and Constantin1996), Constantin & Doering (Reference Constantin and Doering1995) revitalised the field by providing an alternative way to systematically derive rigorous bounding results (Marchioro Reference Marchioro1994; Kerswell Reference Kerswell1996, Reference Kerswell2002; Nicodemus, Grossmann & Holthaus Reference Nicodemus, Grossmann and Holthaus1997; Wang Reference Wang1997; Hoffmann & Vitanov Reference Hoffmann and Vitanov1999; Doering & Constantin Reference Doering and Constantin2001; Doering & Foias Reference Doering and Foias2002; Otero et al.
Reference Otero, Wittenberg, Worthing and Doering2002; Plasting & Kerswell Reference Plasting and Kerswell2003, Reference Plasting and Kerswell2005; Plasting & Ierley Reference Plasting and Ierley2005; Wittenberg Reference Wittenberg2010; Whitehead & Doering Reference Whitehead and Doering2011; Wen et al.
Reference Wen, Chini, Dianati and Doering2013; Whitehead & Wittenberg Reference Whitehead and Wittenberg2014). The key idea (traceable back to Hopf) is to decompose the flow variables into a steady incompressible ‘background’ field which carries the inhomogeneities of the problem and a fluctuating incompressible part which is unforced and hence of arbitrary amplitude. The method then proceeds by designing the background field (typically with a boundary layer of thickness
$\unicode[STIX]{x1D6FF}$
) so that the influence of the unknown fluctuating field on the key functional of interest can be bounded (by taking
$\unicode[STIX]{x1D6FF}$
small enough). While very successful (e.g. see Wang (Reference Wang1997) for a proof of an upper bound on
$\unicode[STIX]{x1D700}$
for a general domain where the boundary moves tangentially to itself everywhere), the method does have its limitations, most notably illustrated by the problem of pressure-driven flow across a rough wall (see also Nobili & Otto (Reference Nobili and Otto2016) for work in the convection problem). In flow driven across a rough wall, the background flow must bring an
$O(1)$
(relative to
$\unicode[STIX]{x1D6FF}\rightarrow 0$
) normal component of the exterior flow to zero at the rough wall surface over a boundary layer distance of
$O(\unicode[STIX]{x1D6FF})$
. Incompressibility then forces the background flow to have an
$O(1/\unicode[STIX]{x1D6FF})$
component locally tangent to the rough wall and control of the unknown fluctuating part is lost (technically the required spectral constraint cannot be satisfied). Incompressibility of the background field is the key obstacle here: relaxing the constraint on the background field causes problems elsewhere (the fluid pressure cannot be eliminated from the analysis) or when it is not relevant – in the case of convection where only a background temperature field is needed – there is no problem (Goluskin & Doering Reference Goluskin and Doering2016).
In the last 5 years, a second new bounding method has been developed by Otto & Seis (Reference Otto and Seis2011), Seis (Reference Seis2015) – hereafter referred to as the ‘boundary layer’ method – which potentially offers a new line of attack on the roughness problem. In this paper we discuss how this method can indeed be extended to deliver a first rigorous upper bound on the energy dissipation rate for pressure-driven flow through a rough channel. Interestingly, the same scaling law emerges for the bound on
$\unicode[STIX]{x1D700}$
in terms of the applied pressure gradient as for the smooth channel situation (albeit with an enlarged numerical prefactor dependent on the exact form of the roughness). This is exactly what has also been found very recently for rough wall convection (using the background technique) in Goluskin & Doering (Reference Goluskin and Doering2016). Assuming the bound carries over to rough pipe flow, this then matches the observed scaling law for turbulent data (Moody Reference Moody1944). There are two immediate implications: (i) a smooth wall is a singular limit of rough wall flows at high
$Re$
flows yet a regular limit for current upper bounding techniques; and (ii) current upper bounding techniques are actually better at capturing scaling laws than has been immediately apparent by focussing on the singular case of smooth wall problems (see Goluskin & Doering (Reference Goluskin and Doering2016) for references which suggest that their rough wall bound may be consistent with convection data). To illustrate how the new energy dissipation rate bound can be utilized, we extend the result to oscillatory free-surface flow over one rough boundary which is a simple model of tidal flow over topography. Understanding how topography such as isolated ridges enhance dissipation and especially mixing processes is an important yet poorly understood ingredient for ocean circulation modelling (e.g. see Melet, Legg & Hallberg (Reference Melet, Legg and Hallberg2016) and references therein).
2 Three-dimensional rough channel flow
Imagine a channel of average height
$h$
, periodic extent
$hL_{x}$
in the (streamwise) direction of an applied pressure gradient and periodic spanwise extent
$hL_{y}$
. If
$\unicode[STIX]{x1D708}$
is the kinematic viscosity, then introduce
$\unicode[STIX]{x1D708}/h$
as the unit of speed,
$h$
as the unit of length and
$h^{2}/\unicode[STIX]{x1D708}$
as the unit of time. The governing Navier–Stokes equations become
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}p-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}=Gr\hat{\boldsymbol{x}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$
where
$Gr:=h^{3}{\mathcal{G}}/\unicode[STIX]{x1D708}^{2}$
, the Grashof number, is the non-dimensionalised applied pressure gradient
${\mathcal{G}}$
driving the flow. For convenience, we refer to the cross-channel
$z$
-direction as the ‘vertical’ direction and the
$x$
and
$y$
directions as ‘horizontal’ and imagine rough channel boundaries at
$z=f(x,y)$
(the lower boundary) and
$z=g(x,y)$
(the upper boundary). The roughness functions
$f$
and
$g$
will be assumed at least
$C^{3}$
(3 times differentiable), periodic over
${\mathcal{A}}:=[0,L_{x}]\times [0,L_{y}]$
such that
$$\begin{eqnarray}\iint _{{\mathcal{A}}}f\,\text{d}x\,\text{d}y=0\quad \text{ and }\quad \frac{1}{A}\iint _{{\mathcal{A}}}g\,\text{d}x\,\text{d}y=1\end{eqnarray}$$
(to preserve the average channel height as 1 in non-dimensional units and non-dimensional volume as
$A:=L_{x}L_{y}$
) and to be such that the channel is never blocked at any point (i.e.
$f<g$
for any
$(x,y)\in {\mathcal{A}}$
). In the following we work with a one-dimensional (1-D) family of interior surfaces
$$\begin{eqnarray}{\mathcal{S}}(\unicode[STIX]{x1D706}):=\{(x,y,z)|z=F(x,y,\unicode[STIX]{x1D706}):=(1-\unicode[STIX]{x1D706})f(x,y)+\unicode[STIX]{x1D706}g(x,y)\text{ for }(x,y)\in {\mathcal{A}}\}\end{eqnarray}$$
with
$\unicode[STIX]{x1D706}\in [0,1]$
which smoothly interpolate between the two rough boundaries:
$\unicode[STIX]{x1D706}=0$
giving the lower boundary and
$\unicode[STIX]{x1D706}=1$
the upper boundary: see figure 1. Let
${\mathcal{C}}(\unicode[STIX]{x1D706},y^{\ast })$
be the line formed from the intersection of
${\mathcal{S}}(\unicode[STIX]{x1D706})$
with the
$y=y^{\ast }$
plane. Let
${\mathcal{V}}(\unicode[STIX]{x1D706})$
be the volume enclosed by
${\mathcal{S}}(\unicode[STIX]{x1D706})$
,
${\mathcal{S}}(0)$
(the lower boundary) and the planes
$x=0$
,
$x=L_{x}$
,
$y=0$
and
$y=L_{y}$
, and let
$\unicode[STIX]{x2202}{\mathcal{V}}(\unicode[STIX]{x1D706})$
be the boundary of
${\mathcal{V}}(\unicode[STIX]{x1D706})$
. The flow conditions at the edges of each surface are periodic so that the flow is invariant under the transformations
$x\rightarrow x+L_{x}$
and
$y\rightarrow y+L_{y}$
. A long-time average is defined as
$$\begin{eqnarray}\langle (\cdot )\rangle :=\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}(\cdot )\,\text{d}t.\end{eqnarray}$$
Figure 1. The flow geometry. The top boundary is given by
$z=g(x,y)$
and the bottom by
$z=f(x,y)$
. The intermediate surface shown in outline is parametrised by
$\unicode[STIX]{x1D706}$
and defined by
$z=F(x,y,\unicode[STIX]{x1D706}):=(1-\unicode[STIX]{x1D706})f(x,y)+\unicode[STIX]{x1D706}g(x,y)$
.
We start the ‘boundary layer’ bounding analysis (Otto & Seis Reference Otto and Seis2011; Seis Reference Seis2015) by taking the line integral of (2.1) along
${\mathcal{C}}(\unicode[STIX]{x1D706},y)$
(in the direction of increasing
$x$
) followed by an integration over
$y$
,
$$\begin{eqnarray}\int _{0}^{L_{y}}\int _{{\mathcal{C}}(\unicode[STIX]{x1D706},y)}\hat{\boldsymbol{s}}\boldsymbol{\cdot }\biggl[\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}p-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}\biggr]\,\text{d}s\,\text{d}y=Gr\int _{0}^{L_{y}}\int _{{\mathcal{C}}(\unicode[STIX]{x1D706},y)}\hat{\boldsymbol{s}}\boldsymbol{\cdot }\hat{\boldsymbol{x}}\,\text{d}s\,\text{d}y,\end{eqnarray}$$
where
$s$
is the arc-length along
${\mathcal{C}}(\unicode[STIX]{x1D706},y)$
and
$\hat{\boldsymbol{s}}:=(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})/\sqrt{1+F_{x}^{2}}$
is the unit tangent vector (subscripts indicate partial derivatives so that
$F_{x}=\unicode[STIX]{x2202}F/\unicode[STIX]{x2202}x$
with
$y$
and
$\unicode[STIX]{x1D706}$
held fixed). Crucially, this procedure kills the pressure term as
$$\begin{eqnarray}\int _{{\mathcal{C}}(\unicode[STIX]{x1D706},y)}\hat{\boldsymbol{s}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p\,\text{d}s=p(L_{x},y,F(L_{x},y,\unicode[STIX]{x1D706}),t)-p(0,y,F(0,y,\unicode[STIX]{x1D706}),t)=0\end{eqnarray}$$
by periodicity in
$x$
. With this, and converting the line integral to an integration over
$x$
, we get
$$\begin{eqnarray}A\,Gr=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\iint _{{\mathcal{A}}}(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})\,\boldsymbol{\cdot }\,\boldsymbol{u}\,\text{d}x\,\text{d}y+\iint _{{\mathcal{A}}}(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})\boldsymbol{\cdot }[\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}]\,\text{d}x\,\text{d}y.\end{eqnarray}$$
The first term on the right-hand side can be dropped after long-time averages, assuming that the kinetic energy remains bounded in time, to leave
$$\begin{eqnarray}Gr=\left\langle \frac{1}{A}\iint _{{\mathcal{A}}}(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})\boldsymbol{\cdot }[\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}]\,\text{d}x\,\text{d}y\,\right\rangle ,\end{eqnarray}$$
which is an identity for any
$\unicode[STIX]{x1D706}\in [0,1]$
. We now generate volume integrals from this expression which can be related to the long-time-averaged energy dissipation rate per unit mass (in units of
$\unicode[STIX]{x1D708}^{3}/h^{4}$
)
$$\begin{eqnarray}\unicode[STIX]{x1D700}:=\left\langle \frac{1}{A}\int \!\!\!\int \!\!\!\int \!\!|\unicode[STIX]{x1D735}\boldsymbol{u}|^{2}\,\text{d}V\right\rangle :=\left\langle \frac{1}{A}\int _{0}^{L_{x}}\int _{0}^{L_{y}}\int _{z=f(x,y)}^{z=g(x,y)}|\unicode[STIX]{x1D735}\boldsymbol{u}|^{2}\,\text{d}z\,\text{d}y\,\text{d}x\right\rangle .\end{eqnarray}$$
To do this, (2.9) is integrated over
$\unicode[STIX]{x1D706}\in [0,\unicode[STIX]{x1D6EC}]$
to give
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}Gr=\left\langle \frac{1}{A}\int _{0}^{\unicode[STIX]{x1D6EC}}\iint _{{\mathcal{A}}}(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})\boldsymbol{\cdot }[\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}]\,\text{d}x\,\text{d}y\,\text{d}\unicode[STIX]{x1D706}\right\rangle .\end{eqnarray}$$
This can be converted into a volume integral by converting the integral over
$\unicode[STIX]{x1D706}$
to one over
$z$
with the addition of a (Jacobian) scaling factor
$\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D706}|_{x,y}=\,F_{\unicode[STIX]{x1D706}}(x,y,\unicode[STIX]{x1D706})$
:
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}Gr=\left\langle \frac{1}{A}\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}\boldsymbol{a}\boldsymbol{\cdot }[\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}]\,\text{d}x\,\text{d}y\,\text{d}z\right\rangle \quad \forall \unicode[STIX]{x1D6EC}\in [0,1],\end{eqnarray}$$
where
$$\begin{eqnarray}\boldsymbol{a}:=\frac{\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}}}{F_{\unicode[STIX]{x1D706}}}=\frac{\hat{\boldsymbol{x}}+[f_{x}+(z-f)[\ln (g-f)]_{x}]\hat{\boldsymbol{z}}}{(g-f)}\end{eqnarray}$$
eliminating
$\unicode[STIX]{x1D706}$
in favour of
$z$
(recall
$g=g(x,y)$
and
$f=f(x,y)$
). The key now is to lift spatial derivatives off
$\boldsymbol{u}$
and onto
$\boldsymbol{a}$
by judicious use of the divergence theorem. This leads to
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}Gr & = & \displaystyle \frac{1}{A}\left\langle \oint _{\unicode[STIX]{x2202}{\mathcal{V}}(\unicode[STIX]{x1D6EC})}(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{u})\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}+\boldsymbol{u}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}-\boldsymbol{a}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}\,\text{d}S\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}\boldsymbol{u}\boldsymbol{\cdot }(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}\,\text{d}V\,\right\rangle \quad \forall \unicode[STIX]{x1D6EC}\in [0,1]\end{eqnarray}$$
(note the last term requires the roughness functions
$f$
and
$g$
to be at least
$C^{3}$
). Due to periodicity over
$(x,y)\in [0,L_{x}]\times [0,L_{y}]$
, the only parts of
$\unicode[STIX]{x2202}{\mathcal{V}}(\unicode[STIX]{x1D6EC})$
which need to be considered are the lower boundary
${\mathcal{S}}(0)$
where
$\boldsymbol{u}=\mathbf{0}$
and the interior surface
${\mathcal{S}}(\unicode[STIX]{x1D6EC})$
. Hence, in fact
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}Gr & = & \displaystyle \frac{1}{A}\left\langle \int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{u})\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}+\boldsymbol{u}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}-\boldsymbol{a}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}\,\text{d}S\right.\nonumber\\ \displaystyle & & \displaystyle -\,\int _{{\mathcal{S}}(0)}\boldsymbol{a}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}\,\text{d}S\nonumber\\ \displaystyle & & \displaystyle -\left.\,\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}\boldsymbol{u}\boldsymbol{\cdot }(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}\,\text{d}V\,\right\rangle \quad \forall \unicode[STIX]{x1D6EC}\in [0,1].\end{eqnarray}$$
Now the strategy is to separately average (2.15) over
$\unicode[STIX]{x1D6EC}\in [0,\ell ]$
and over
$\unicode[STIX]{x1D6EC}\in [1-\ell ,1]$
and then compute the difference in order to eliminate the
$\unicode[STIX]{x1D6EC}$
-independent
${\mathcal{S}}(0)$
boundary term. Subtracting
$1/\ell \int _{0}^{\ell }$
(2.15)
$\text{d}\unicode[STIX]{x1D6EC}$
from
$1/\ell \int _{1-\ell }^{1}$
(2.15)
$\text{d}\unicode[STIX]{x1D6EC}$
gives
$$\begin{eqnarray}\displaystyle (1-\ell )Gr & = & \displaystyle \frac{1}{A}\left\langle \frac{1}{\ell }\int _{1-\ell }^{1}\int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{u})\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}+\boldsymbol{u}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}-\boldsymbol{a}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}\,\text{d}S\,\text{d}\unicode[STIX]{x1D6EC}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{\ell }\int _{0}^{\ell }\int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{u})\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}+\boldsymbol{u}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}-\boldsymbol{a}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}\,\text{d}S\,\text{d}\unicode[STIX]{x1D6EC}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{\ell }\int _{1-\ell }^{1}\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}\boldsymbol{u}\boldsymbol{\cdot }(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}\,\text{d}V\,\text{d}\unicode[STIX]{x1D6EC}\,\,\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{1}{\ell }\int _{0}^{\ell }\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}\boldsymbol{u}\boldsymbol{\cdot }(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}\,\text{d}V\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle .\end{eqnarray}$$
This is the generalisation of Seis’s (Reference Seis2015) expression (4.10) which can be recovered by setting
$\boldsymbol{a}=\hat{\boldsymbol{x}}$
, taking
${\mathcal{S}}(\unicode[STIX]{x1D6EC})$
as the horizontal plane
$z=\unicode[STIX]{x1D6EC}$
over
$[0,L_{x}]\times [0,L_{y}]$
and
$\hat{\boldsymbol{n}}=\hat{\boldsymbol{z}}$
. Notably, there are new integrated volume terms because the linear momentum directed along
${\mathcal{C}}(\unicode[STIX]{x1D706},y)$
is not conserved but these turn out to be subdominant in what follows. From here, the exercise is to bound the right-hand side of (2.16) in terms of the energy dissipation rate
$\unicode[STIX]{x1D700}$
and then to optimise over
$\ell \in [0,1/2]$
to produce the best bound on
$Gr$
as in Seis (Reference Seis2015). Since our focus is on establishing the scaling exponent of how
$Gr$
scales with
$\unicode[STIX]{x1D700}$
rather than the secondary issue of producing the best estimate for the numerical prefactor, we proceed by employing straightforward conservative estimates. This has the advantage of securing our key result quickly and relatively clearly but more careful estimates could lower the (numerical) bound on
$Gr$
but not, we contend, the scaling exponent. Firstly,
$$\begin{eqnarray}\displaystyle Gr & {\leqslant} & \displaystyle \frac{1}{A\ell (1-\ell )}\left\{\!\left\langle \int _{1-\ell }^{1}\int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{u}||\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}|\,\text{d}S\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle +\left\langle \int _{1-\ell }^{1}\int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}\!|\boldsymbol{u}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}|\,\text{d}S\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle \right.\nonumber\\ \displaystyle & & \displaystyle +\left\langle \int _{1-\ell }^{1}\int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{a}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}|\,\text{d}S\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle +\left\langle \int _{0}^{\ell }\int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{u}||\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}|\,\text{d}S\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle ^{(1)}\nonumber\\ \displaystyle & & \displaystyle +\left\langle \int _{0}^{\ell }\int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{u}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}|\,\text{d}S\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle ^{(2)}+\left\langle \int _{0}^{\ell }\int _{{\mathcal{S}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{a}\boldsymbol{\cdot }(\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}|\,\text{d}S\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle ^{(3)}\nonumber\\ \displaystyle & & \displaystyle +\left\langle \int _{1-\ell }^{1}\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{u}\boldsymbol{\cdot }(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}|\,\text{d}V\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle +\left\langle \int _{1-\ell }^{1}\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}|\,\text{d}V\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle \nonumber\\ \displaystyle & & \displaystyle +\left.\left\langle \int _{0}^{\ell }\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{u}\boldsymbol{\cdot }(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{a}|\,\text{d}V\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle ^{(4)}+\left\langle \int _{0}^{\ell }\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}|\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}|\,\text{d}V\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle ^{(5)}\right\}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
(the superscripts in parentheses are just labels). Each of the integrals in (2.17) need to be bounded by a function of
$\unicode[STIX]{x1D700}$
. We focus on integrals concentrated at the lower boundary and treat first the integral,
$I_{1}$
, labelled
$^{(1)}$
in (2.17). Firstly converting the surface integral into one over
${\mathcal{A}}$
$$\begin{eqnarray}I_{1}\leqslant \left\langle \int _{0}^{\ell }\iint _{{\mathcal{A}}}|\boldsymbol{a}|\sqrt{1+F_{x}^{2}+F_{y}^{2}}|\boldsymbol{u}|^{2}\,\text{d}x\,\text{d}y\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle .\end{eqnarray}$$
Then using the fundamental theorem of calculus since
$\boldsymbol{u}(x,y,f(x,y))=\mathbf{0}$
(i.e. on
${\mathcal{S}}(0)$
) and Cauchy–Schwarz gives
$$\begin{eqnarray}\displaystyle I_{1} & {\leqslant} & \displaystyle \left\langle \int _{0}^{\ell }\iint _{{\mathcal{A}}}|\boldsymbol{a}|\sqrt{1+F_{x}^{2}+F_{y}^{2}}\,\biggl|\int _{f(x,y)}^{z}\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}\overline{z}}\,\text{d}\overline{z}\biggr|^{2}\,\text{d}x\,\text{d}y\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle \nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left\langle \int _{0}^{\ell }\iint _{{\mathcal{A}}}|\boldsymbol{a}|\sqrt{1+F_{x}^{2}+F_{y}^{2}}\biggl(\int _{f(x,y)}^{z}1^{2}\,\text{d}\overline{z}\int _{f(x,y)}^{z}\biggl|\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}\overline{z}}\biggr|^{2}\,\text{d}\overline{z}\,\biggr)\,\text{d}x\,\text{d}y,\text{d}\unicode[STIX]{x1D6EC}\right\rangle \nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left\langle \int _{0}^{\ell }\iint _{{\mathcal{A}}}\,|\boldsymbol{a}|\sqrt{1+F_{x}^{2}+F_{y}^{2}}\,\unicode[STIX]{x1D6EC}F_{\unicode[STIX]{x1D706}}\int _{f(x,y)}^{z}\biggl|\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}\overline{z}}\biggr|^{2}\,\text{d}\overline{z}\,\text{d}x\,\text{d}y\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle \nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max _{x,y,\unicode[STIX]{x1D706}\in {\mathcal{V}}(\ell )}\biggl\{|\boldsymbol{a}|F_{\unicode[STIX]{x1D706}}\sqrt{1+F_{x}^{2}+F_{y}^{2}}\biggr\}\int _{0}^{\ell }\unicode[STIX]{x1D6EC}d\unicode[STIX]{x1D6EC}\left\langle \int \!\!\!\int \!\!\!\int \!\!|\unicode[STIX]{x1D735}\boldsymbol{u}|^{2}\,\text{d}V\,\right\rangle \nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max _{x,y,\unicode[STIX]{x1D706}\in {\mathcal{V}}(\ell )}\biggl\{\sqrt{1+F_{x}^{2}}\sqrt{1+F_{x}^{2}+F_{y}^{2}}\biggr\}\times \frac{1}{2}\ell ^{2}A\unicode[STIX]{x1D700}.\end{eqnarray}$$
Integral
$I_{4}$
(labelled
$^{(4)}$
in (2.17) ) is treated similarly albeit with an extra integration in
$\unicode[STIX]{x1D6EC}$
giving rise to
$\ell ^{3}$
in the estimate:
$$\begin{eqnarray}\displaystyle I_{4} & {\leqslant} & \displaystyle \left\langle \int _{0}^{\ell }\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}|\unicode[STIX]{x1D735}\boldsymbol{a}||\boldsymbol{u}|^{2}\,\text{d}V\,\text{d}\unicode[STIX]{x1D6EC}\,\right\rangle \leqslant \left\langle \int _{0}^{\ell }\int _{0}^{\unicode[STIX]{x1D6EC}}\iint _{{\mathcal{A}}}F_{\unicode[STIX]{x1D706}}|\unicode[STIX]{x1D735}\boldsymbol{a}||\boldsymbol{u}|^{2}\,\text{d}x\,\text{d}y\,\text{d}\unicode[STIX]{x1D706}\,\text{d}\unicode[STIX]{x1D6EC}\right\rangle \nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max _{x,y,\unicode[STIX]{x1D706}\in {\mathcal{V}}(\ell )}\{F_{\unicode[STIX]{x1D706}}^{2}|\unicode[STIX]{x1D735}\boldsymbol{a}|\}\int _{0}^{\ell }\int _{0}^{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D706}\,\text{d}\unicode[STIX]{x1D706}\,\text{d}\unicode[STIX]{x1D6EC}\left\langle \int \!\!\!\int \!\!\!\int \!\!|\unicode[STIX]{x1D735}\boldsymbol{u}|^{2}\,\text{d}V\,\right\rangle \nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max _{x,y,\unicode[STIX]{x1D706}\in {\mathcal{V}}(\ell )}\{F_{\unicode[STIX]{x1D706}}^{2}|\unicode[STIX]{x1D735}\boldsymbol{a}|\}\times \frac{1}{6}\ell ^{3}A\unicode[STIX]{x1D700}.\end{eqnarray}$$
The remaining integrals,
$I_{2}$
,
$I_{3}$
and
$I_{5}$
, are treated as follows:
$$\begin{eqnarray}\displaystyle I_{2} & {\leqslant} & \displaystyle \left\langle \iint _{{\mathcal{A}}}\int _{f(x,y)}^{F(x,y,\ell )}\frac{|\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{a}|\sqrt{1+F_{x}^{2}+F_{y}^{2}}}{F_{\unicode[STIX]{x1D706}}}|\boldsymbol{u}|\,\text{d}z\,\text{d}x\,\text{d}y\right\rangle \nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl[\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\ell )}\frac{|\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{a}|^{2}(1+F_{x}^{2}+F_{y}^{2})}{F_{\unicode[STIX]{x1D706}}^{2}}\,\text{d}V\biggr]^{1/2}\biggl[\left\langle \int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\ell )}|\boldsymbol{u}|^{2}\,\,\text{d}V\right\rangle \biggr]^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl[\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\ell )}\frac{|\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{a}|^{2}(1+F_{x}^{2}+F_{y}^{2})}{F_{\unicode[STIX]{x1D706}}^{2}}\,\text{d}V\biggr]^{1/2}\times \Bigl[\max _{(x,y)\in {\mathcal{A}}}F_{\unicode[STIX]{x1D706}}^{2}\Bigr]^{1/2}\times \sqrt{\frac{1}{2}\ell ^{2}A\unicode[STIX]{x1D700}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl[\frac{1}{A}\iint _{{\mathcal{A}}}\max _{\unicode[STIX]{x1D6EC}\in [0,\ell ]}\{|\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{a}|^{2}(1+F_{x}^{2}+F_{y}^{2})\}\frac{\text{d}x\,\text{d}y}{F_{\unicode[STIX]{x1D706}}}\biggr]^{1/2}\times \Bigl[\max _{(x,y)\in {\mathcal{A}}}F_{\unicode[STIX]{x1D706}}^{2}\Bigr]^{1/2}\times A\sqrt{\frac{1}{2}\ell ^{3}\unicode[STIX]{x1D700}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$\hat{\boldsymbol{n}}=(-F_{x}\hat{\boldsymbol{x}}-F_{y}\hat{\boldsymbol{y}}+\hat{\boldsymbol{z}})/\sqrt{1+F_{x}^{2}+F_{y}^{2}}$
and the last two lines follow using the same type of estimates as in (2.19) and noting that
$F_{\unicode[STIX]{x1D706}}=g(x,y)-f(x,y)$
is independent of
$\unicode[STIX]{x1D706}$
and strictly positive. Respectively
$$\begin{eqnarray}\displaystyle I_{3} & {\leqslant} & \displaystyle \left\langle \iint _{{\mathcal{A}}}\int _{f(x,y)}^{F(x,y,\ell )}\frac{|\boldsymbol{a}|\sqrt{1+F_{x}^{2}+F_{y}^{2}}}{F_{\unicode[STIX]{x1D706}}}|\unicode[STIX]{x1D735}\boldsymbol{u}|\,\text{d}z\,\text{d}x\,\text{d}y\,\right\rangle \nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl[\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\ell )}\frac{|\boldsymbol{a}|^{2}(1+F_{x}^{2}+F_{y}^{2})}{F_{\unicode[STIX]{x1D706}}^{2}}\,\text{d}V\biggr]^{1/2}\times \sqrt{A\unicode[STIX]{x1D700}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl[\iint _{{\mathcal{A}}}\int _{0}^{\ell }\frac{(1+F_{x}^{2})(1+F_{x}^{2}+F_{y}^{2})}{F_{\unicode[STIX]{x1D706}}^{3}}\,\text{d}\unicode[STIX]{x1D6EC}\,\text{d}x\,\text{d}y\biggr]^{1/2}\times \sqrt{A\unicode[STIX]{x1D700}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl[\frac{1}{A}\iint _{{\mathcal{A}}}\max _{\unicode[STIX]{x1D6EC}\in [0,\ell ]}\{(1+F_{x}^{2})(1+F_{x}^{2}+F_{y}^{2})\}\,\,\frac{\text{d}x\,\text{d}y}{F_{\unicode[STIX]{x1D706}}^{3}}\biggr]^{1/2}\times A\sqrt{\ell \unicode[STIX]{x1D700}}\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle I_{5} & {\leqslant} & \displaystyle \int _{0}^{\ell }\biggl[\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\ell )}|\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}|^{2}\,\text{d}V\biggr]^{1/2}\biggl[\left\langle \int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\ell )}|\boldsymbol{u}|^{2}\,\text{d}V\right\rangle \biggr]^{1/2}\,\text{d}\unicode[STIX]{x1D6EC}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl[\frac{1}{A}\int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\ell )}|\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}|^{2}\,\text{d}V\biggr]^{1/2}\times \Bigl[\max _{(x,y)\in {\mathcal{A}}}F_{\unicode[STIX]{x1D706}}^{2}\Bigr]^{1/2}\times \ell ^{2}A\sqrt{\frac{1}{2}\unicode[STIX]{x1D700}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl[\frac{1}{A}\iint _{{\mathcal{A}}}F_{\unicode[STIX]{x1D706}}\max _{\unicode[STIX]{x1D6EC}\in [0,\ell ]}~|\unicode[STIX]{x1D6FB}^{2}\boldsymbol{a}|^{2}\,\text{d}x\,\text{d}y\biggr]^{1/2}\times \Bigl[\max _{(x,y)\in {\mathcal{A}}}F_{\unicode[STIX]{x1D706}}^{2}\Bigr]^{1/2}\times A\sqrt{\frac{1}{2}\ell ^{5}\unicode[STIX]{x1D700}}.\end{eqnarray}$$
The estimates for the corresponding integrals centred at the top boundary are exactly analogous, and grouping the contributions together for each term, we get a simplified ‘inequality’ version of (2.16)
$$\begin{eqnarray}Gr\leqslant \frac{1}{\ell (1-\ell )}\{(B_{1}\ell ^{2}+B_{4}\ell ^{3})\unicode[STIX]{x1D700}+(B_{2}\ell +B_{3}+B_{5}\ell ^{2})\sqrt{\ell \unicode[STIX]{x1D700}}\}.\end{eqnarray}$$
where the coefficients
$B_{i}$
represent the O(1) numerical factors (in the sense of
$Gr\rightarrow \infty$
) of the
$i$
th integral bound (summed for both boundaries) when a factor of
$A$
is factored out and the dominant
$\ell$
and
$\unicode[STIX]{x1D700}$
behaviour (which both are not
$O(1)$
) is separated off. The idea now is to minimise the right-hand side over the choice of
$\ell \in (0,1/2)$
in the turbulent limit
$Gr\rightarrow \infty$
. Here,
$\unicode[STIX]{x1D700}\rightarrow \infty$
(naive scalings suggest
$Gr\lesssim \unicode[STIX]{x1D700}\lesssim Gr^{2}$
) and the optimal
$\ell \rightarrow 0$
so, working to leading order,
$$\begin{eqnarray}Gr\leqslant B_{1}\ell \unicode[STIX]{x1D700}+B_{3}\sqrt{\unicode[STIX]{x1D700}/\ell }+\text{h.o.t.}\end{eqnarray}$$
and now it is clear that all the new integral contributions due to the roughness are subdominant. Instead the roughness manifests itself as adjusted numerical coefficients for the integrals which arise in the smooth situation (Seis Reference Seis2015). The minimising
$\ell$
is
$(B_{3}/2B_{1})^{2/3}\unicode[STIX]{x1D700}^{-1/3}$
and
$$\begin{eqnarray}Gr\leqslant \frac{3}{2}(2B_{1}B_{3}^{2})^{1/3}\times \unicode[STIX]{x1D700}^{2/3}\quad \text{or}\quad \frac{2\sqrt{3}}{9B_{3}\sqrt{B_{1}}}\times Gr^{3/2}\leqslant \unicode[STIX]{x1D700},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle B_{1}=\mathop{\sum }_{\unicode[STIX]{x1D706}=0}^{1}\max _{(x,y)\in {\mathcal{A}}}\biggl\{\frac{1}{2}\sqrt{1+F_{x}^{2}}\sqrt{1+F_{x}^{2}+F_{y}^{2}}\biggr\}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{3}=\mathop{\sum }_{\unicode[STIX]{x1D706}=0}^{1}\biggl[\frac{1}{A}\iint _{{\mathcal{A}}}\frac{(1+F_{x}^{2})(1+F_{x}^{2}+F_{y}^{2})}{[g(x,y)-f(x,y)]^{3}}\,\text{d}x\,\text{d}y\biggr]^{1/2} & \displaystyle\end{eqnarray}$$
(since
$\ell \ll 1$
, it is sufficient to leading order to replace
$\max _{\unicode[STIX]{x1D6EC}\in [0,\ell ]}$
by the value at
$\unicode[STIX]{x1D6EC}=0$
and similarly for the upper boundary). The lower bound in (2.26) indicates that turbulence decreases dissipation for a given applied pressure gradient as per the smooth wall case (Constantin & Doering Reference Constantin and Doering1995; Seis Reference Seis2015). However, as there, rewriting the result in terms of the a priori unknown mean flow recovers the familiar upper bound situation. Taking
$\langle \int \!\int \!\int \boldsymbol{u}\boldsymbol{\cdot }(2.1)\,\text{d}V\rangle$
connects the mean flow
$U$
with the applied pressure gradient and ensuing dissipation rate,
$$\begin{eqnarray}U:=\left\langle \frac{1}{A}\int \!\!\!\int \!\!\!\int \!\!\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{x}}\,\text{d}V\right\rangle =\unicode[STIX]{x1D700}/Gr.\end{eqnarray}$$
This can be used to eliminate the pressure gradient (
$Gr$
) to get
$$\begin{eqnarray}\unicode[STIX]{x1D700}\leqslant {\textstyle \frac{27}{4}}B_{1}B_{3}^{2}U^{3}\quad \text{or}\quad \unicode[STIX]{x1D700}\leqslant {\textstyle \frac{27}{4}}B_{1}B_{3}^{2}\quad (\text{in units of }U^{3}/h)\end{eqnarray}$$
so that the bound predicts that the energy dissipation rate becomes independent of the viscosity as the viscosity goes to zero – Kolmogorov scaling – just as in the smooth wall calculation (Constantin & Doering Reference Constantin and Doering1995; Seis Reference Seis2015, and Plasting & Kerswell Reference Plasting and Kerswell2005 for pipe flow).
3 Oscillatory flow across topography: the tidal problem
As a simple application of the above result, we now consider the ocean tidal problem of oscillatory flow across bottom topography (and a free top surface). This situation is modelled by assuming an oscillatory pressure gradient driving the flow directly i.e.
${\mathcal{G}}\sim \unicode[STIX]{x1D714}^{\ast }U^{\ast }$
where the tidal frequency
$\unicode[STIX]{x1D714}^{\ast }=2\unicode[STIX]{x03C0}/12~\text{hours}=1.4\times 10^{-4}~\text{s}^{-1}$
and
$U^{\ast }\approx 0.1~\text{m}~\text{s}^{-1}$
. We consider a symmetrised problem where the top boundary is defined by
$g(x,y)=1-f(x,y)$
so that the real free surface position on average is the (symmetric) midplane of the extended domain and
$h/2$
is then the mean ocean depth. By symmetry, the maximum dissipation in the extended domain is exactly double the maximum dissipation in the ‘ocean’ domain. Further restricting the flow in the extended domain to have zero vertical motion and zero stress across
$z=1/2$
(the horizontal free-surface approximation) can only reduce the maximum dissipation possible (by restricting the competitor space) so halving the dissipation bound from the unrestricted, extended domain should be an upper bound on the dissipation in a flat surface ocean (
$z\leqslant 1/2$
).
Taking a typical ocean depth
$h/2=1000~\text{m}$
, the Grashof number
$Gr=1.12\times 10^{17}\gg 1$
and the non-dimensionalised tidal frequency
$$\begin{eqnarray}1\,\ll \unicode[STIX]{x1D714}:=\frac{h^{2}\unicode[STIX]{x1D714}^{\ast }}{\unicode[STIX]{x1D708}}=\sqrt{\frac{h{\mathcal{G}}}{U^{2}}}\sqrt{Gr}\,\ll Gr,\end{eqnarray}$$
where
$\unicode[STIX]{x1D6F6}:=h{\mathcal{G}}/U^{2}$
is a second non-dimensional number independent of
$\unicode[STIX]{x1D708}$
which is here
$O(1)$
. This makes it clear that in the limit
$\unicode[STIX]{x1D708}\rightarrow 0$
(with everything else kept fixed),
$Gr\rightarrow \infty$
with
$\unicode[STIX]{x1D714}\sim \sqrt{Gr}$
. The governing equation for the problem is then
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+2\unicode[STIX]{x1D734}\times \boldsymbol{u}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}p-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}=Gr\,\unicode[STIX]{x1D6E4}(t)\hat{\boldsymbol{x}},\end{eqnarray}$$
the flow is assumed incompressible and a planetary rotation
$\unicode[STIX]{x1D734}$
is also included for completeness (
$|\unicode[STIX]{x1D734}|=\unicode[STIX]{x1D714}/2$
). The oscillatory function
$\unicode[STIX]{x1D6E4}(t)$
is defined such that
$$\begin{eqnarray}\max _{t\in [0,2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}]}|\unicode[STIX]{x1D6E4}(t)|=1\end{eqnarray}$$
but is otherwise left unspecified for clarity. As before, the analysis starts by taking the line integral of (3.2) along
${\mathcal{C}}(\unicode[STIX]{x1D706},y)$
and integrating over
$y$
as above in § 2 but now also multiplying by
$\unicode[STIX]{x1D6E4}(t)$
to rectify the forcing pressure gradient. This leads to an extended version of (2.8)
$$\begin{eqnarray}\displaystyle AGr\unicode[STIX]{x1D6E4}(t)^{2} & = & \displaystyle \unicode[STIX]{x1D6E4}(t)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\iint _{{\mathcal{A}}}(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}x\,\text{d}y\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6E4}(t)\iint _{{\mathcal{A}}}(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})\boldsymbol{\cdot }[2\unicode[STIX]{x1D734}\times \boldsymbol{u}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}]\,\text{d}x\,\text{d}y.\end{eqnarray}$$
Now long-time averaging leads to
$$\begin{eqnarray}\displaystyle AGr\langle \unicode[STIX]{x1D6E4}(t)^{2}\rangle & = & \displaystyle -\left\langle \unicode[STIX]{x1D6E4}_{t}\iint _{{\mathcal{A}}}(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}x\,\text{d}y\right\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\left\langle \unicode[STIX]{x1D6E4}(t)\iint _{{\mathcal{A}}}(\hat{\boldsymbol{x}}+F_{x}\hat{\boldsymbol{z}})\boldsymbol{\cdot }[2\unicode[STIX]{x1D734}\times \boldsymbol{u}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}]\,\text{d}x\,\text{d}y\right\rangle ,\end{eqnarray}$$
where integration by parts in time has been used to transfer the time derivative onto
$\unicode[STIX]{x1D6E4}$
. Integrating over
$\unicode[STIX]{x1D706}\in [0,\unicode[STIX]{x1D6EC}]$
and converting to a volume integral over
${\mathcal{V}}(\unicode[STIX]{x1D6EC})$
, gives
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}Gr\langle \unicode[STIX]{x1D6E4}(t)^{2}\rangle =\frac{1}{A}\left\langle \int \!\!\!\int \!\!\!\int _{{\mathcal{V}}(\unicode[STIX]{x1D6EC})}\unicode[STIX]{x1D6E4}(t)\boldsymbol{a}\boldsymbol{\cdot }[\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}]+[\unicode[STIX]{x1D6E4}\boldsymbol{a}\times 2\unicode[STIX]{x1D734}-\unicode[STIX]{x1D6E4}_{t}\boldsymbol{a}]\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}x\,\text{d}y\,\text{d}z\right\rangle\end{eqnarray}$$
for all
$\unicode[STIX]{x1D6EC}\in [0,1]$
. The first term on the right-hand side is as before, albeit with an extra factor of
$\unicode[STIX]{x1D6E4}(t)$
. Since this is bounded in modulus by 1, the subsequent estimates are unchanged. The new second term on the right-hand side is of the form of
$I_{5}$
and can be similarly estimated as adding a new term
$$\begin{eqnarray}\biggl[\frac{1}{A}\iint _{{\mathcal{A}}}F_{\unicode[STIX]{x1D706}}\max _{\unicode[STIX]{x1D6EC}\in [0,\ell ]}|\unicode[STIX]{x1D6E4}\boldsymbol{a}\times 2\unicode[STIX]{x1D734}-\unicode[STIX]{x1D6E4}_{t}\boldsymbol{a}|^{2}\,\text{d}x\,\text{d}y\biggr]^{1/2}\times \Bigl[\max _{(x,y)\in {\mathcal{A}}}F_{\unicode[STIX]{x1D706}}^{2}\Bigr]^{1/2}\times A\sqrt{\frac{1}{2}\ell ^{5}\unicode[STIX]{x1D700}}\end{eqnarray}$$
to (2.24). Since both
$\unicode[STIX]{x1D734}$
and
$\unicode[STIX]{x1D6E4}_{t}=O(\unicode[STIX]{x1D714}\unicode[STIX]{x1D6E4})$
are
$O(\sqrt{Gr})$
, the leading-order version of (2.24) is potentially modified to
$$\begin{eqnarray}Gr\leqslant B_{1}\ell \unicode[STIX]{x1D700}+(B_{3}+B_{5}\ell ^{2}\sqrt{Gr})\sqrt{\unicode[STIX]{x1D700}/\ell }+\text{h.o.t.}\end{eqnarray}$$
The minimiser, however, remains
$\ell \sim \unicode[STIX]{x1D700}^{-1/3}$
with the new term
$O(Gr^{-1/2})$
smaller than the other two terms. Hence the rotation and oscillation are not important at leading order in the bound on the energy dissipation rate for tidal flow over topography.
Figure 2. (a) The 2-D ridge tidal problem with the ocean represented by the region
$z\leqslant 1/2$
. (b) A cartoon of the Moody diagram for pipe flow (Moody Reference Moody1944):
$C_{f}:=\unicode[STIX]{x1D700}/(U^{3}/h)$
, laminar flow has
$C_{f}\sim 1/Re$
, turbulent smooth pipe data suggest
$C_{f}\sim 1/(\log Re)^{2}$
at least to
$Re=O(10^{8})$
and turbulent rough pipe data have
$C_{f}\sim O(1)$
as
$Re\rightarrow \infty$
. Three lines are shown for rough pipe flow with the data increasing to higher
$C_{f}$
as the representative height of the roughness increases.
3.1 A simple example
Here we consider a 2-D ridge of height
$a<1/2$
and horizontal extent
$a\unicode[STIX]{x1D6FF}$
$$\begin{eqnarray}f(x):=a\text{sech}^{2}\biggl(\frac{x-{\textstyle \frac{1}{2}}L}{a\unicode[STIX]{x1D6FF}}\biggr)-\frac{2a^{2}\unicode[STIX]{x1D6FF}}{L}\text{tanh}\biggl(\frac{L}{2a\unicode[STIX]{x1D6FF}}\biggr)\end{eqnarray}$$
over
$x\in [0,L]$
(the second term on the right-hand side ensures the roughness has zero mean over
$x$
): see figure 2. This roughness function is not periodic over
$[0,L]$
but in the steep (
$\unicode[STIX]{x1D6FF}\ll 1$
) isolated (
$a\unicode[STIX]{x1D6FF}\ll L$
) ridge limit this can be ignored. In this limit, it is straightforward to approximate
$B_{1}$
and
$B_{3}$
as follows
$$\begin{eqnarray}B_{1}=\max _{x\in [0,L]}(1+f_{x}^{2})\approx \frac{16}{27\unicode[STIX]{x1D6FF}^{2}},\quad B_{3}=2\biggl[\frac{1}{L}\int \,\frac{(1+f_{x}^{2})^{2}}{(1-2f)^{3}}\,\text{d}x\biggr]^{1/2}\lesssim \biggl[\frac{2a}{L(1-2a)^{3}\unicode[STIX]{x1D6FF}^{3}}\biggr]^{1/2},\end{eqnarray}$$
(using the fact that
$2048/1155<2$
) so the dissipation rate per unit mass is
$$\begin{eqnarray}\unicode[STIX]{x1D700}\leqslant \frac{4aU^{3}}{L(1-2a)^{3}\unicode[STIX]{x1D6FF}^{5}}\quad (\text{in units of }\unicode[STIX]{x1D708}^{3}/h^{4})\end{eqnarray}$$
(including the
$1/2$
to reflect the fact that the ocean is strictly in
$z\leqslant 1/2$
). This can be re-expressed using inertial units to give the familiar bound independent of the viscosity
$$\begin{eqnarray}\unicode[STIX]{x1D700}\leqslant \frac{4a}{L(1-2a)^{3}\unicode[STIX]{x1D6FF}^{5}}\quad (\text{in units of }U^{3}/h).\end{eqnarray}$$
Since this is the leading term due to the ridge (the dissipation bound for zero topography is
$O(\unicode[STIX]{x1D6FF}^{5})$
smaller), this expression can be viewed as giving the enhanced dissipation caused by the ridge per unit length of the domain
$[0,L]$
.
4 Discussion
Using a new bounding technique (Otto & Seis Reference Otto and Seis2011; Seis Reference Seis2015), this paper has derived an upper bound on the energy dissipation rate (per unit mass)
$\unicode[STIX]{x1D700}$
for pressure-driven flow through a rough channel with bottom
$z=f(x,y)$
and top
$z=g(x,y)$
(
$f$
and
$g$
at least
$C^{3}$
) such that the average height is
$h$
in the limit of vanishing viscosity of the form
$$\begin{eqnarray}\unicode[STIX]{x1D700}\leqslant cU^{3}/h,\end{eqnarray}$$
where
$U$
is the mean flow through the channel and
$$\begin{eqnarray}\displaystyle c & := & \displaystyle \frac{27}{8}\mathop{\sum }_{\unicode[STIX]{x1D706}=0}^{1}\max _{(x,y)\in {\mathcal{A}}}\biggl\{\sqrt{1+F_{x}^{2}}\sqrt{1+F_{x}^{2}+F_{y}^{2}}\biggr\}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\sum }_{\unicode[STIX]{x1D706}=0}^{1}\biggl[\frac{1}{A}\iint _{{\mathcal{A}}}\frac{(1+F_{x}^{2})(1+F_{x}^{2}+F_{y}^{2})}{[g(x,y)-f(x,y)]^{3}}\,\text{d}x\,\text{d}y\biggr]^{1/2}\biggr)^{2},\end{eqnarray}$$
with
$F(x,y,\unicode[STIX]{x1D706}):=(1-\unicode[STIX]{x1D706})f(x,y)+\unicode[STIX]{x1D706}g(x,y)$
and
${\mathcal{A}}:=[0,L_{x}]\times [0,L_{y}]$
. The fact that bound predicts that the dissipation rate approaches a finite limit (in inertial units) as the viscosity vanishes – so-called Kolmogorov scaling – then captures the observed scaling of turbulent data in rough pipes – see figure 2 for a cartoon of the classic Moody diagram (Moody Reference Moody1944) – and indicates that the well-known discrepancy between the bound and data scalings in the smooth wall case (Constantin & Doering (Reference Constantin and Doering1995), Plasting & Kerswell (Reference Plasting and Kerswell2005), Seis (Reference Seis2015) and figure 2) is an exception rather than the rule. Interestingly, boundary cross-flow produced by suction instead of roughness also seems to achieve the same effect in plane Couette flow: bounds and data have the same Kolmogorov scaling for non-zero suction but disagree for zero suction (Doering, Spiegel & Worthing Reference Doering, Spiegel and Worthing2000). These observations, which may also extend to convection although the available data are so far only suggestive (see Goluskin & Doering Reference Goluskin and Doering2016), substantially enhance the credentials of the bounding approach as a viable way to extract key scaling laws in real turbulent flows where smooth walls are not generic.
There is, of course, room for improvement. The bound derived here requires
$C^{3}$
differentiability of the roughness whereas it would be better (and more realistic) to only require continuity and piecewise differentiability. This would allow sharp corners, such as those present in roughness created by sand granules, to be treated. It is possible that better functional analytic estimates may achieve this as well as reducing the numerical prefactor
$c$
(e.g. by replacing the infinity norm present by a less extreme norm). However, it seems difficult to see how the exponent in the scaling law (i.e.
$\unicode[STIX]{x1D700}\sim Re^{0}U^{3}/h$
as
$Re\rightarrow \infty$
) could be changed. From a mathematical perspective, formulating the full variational equations underlying the Otto–Seis ‘boundary layer’ method presents an enticing challenge with the potential for revealing valuable insights into this new method. It was, after all, only after the full variational equations were identified for the Doering–Constantin background method that an intimate connection was made to the Malkus–Howard–Busse bounding approach (Kerswell Reference Kerswell1997, Reference Kerswell1998).
A significant challenge for the bounding approach remains, however, deriving a dissipation bound on shearing systems with rough boundaries (e.g. rough plane Couette flow). Here, unlike pressure-driven flow through a stationary rough channel, one rough boundary moving relative to another means that there has to be motion locally perpendicular to one boundary and therefore work done by the pressure enters the calculation. So far all bounding approaches eliminate the pressure as soon as possible so a totally different approach will be needed. Nevertheless it is reasonable to suppose that a dissipation bound will be derived with Kolmogorov scaling which is what is observed in rough-walled Taylor–Couette flow. If one or both of the walls are smooth, however, the observed dissipation rate then drops off like
${\sim}1/(\log Re)^{2}$
mimicking the situation in pipe flow (Cadot et al.
Reference Cadot, Couder, Daerr, Douady and Tsinober1997; van den Berg et al.
Reference van den Berg, Doering, Lohse and Lathrop2003).
Finally, an application of the new bound has been made to a problem of interest in ocean modelling. This warrants further development to include stable stratification and a refocus on the turbulent mixing that can be caused by isolated topography (typically by internal wave breaking) as this is an important yet poorly known input in ocean models (e.g. see Melet et al. (Reference Melet, Legg and Hallberg2016) and references therein).
Acknowledgement
Many thanks to the referees who helped eliminate some typos in the submitted manuscript.
