1. Introduction
Not only several developed countries such as Japan, Germany, and Italy, but also newly industrialized economies in East Asia such as Singapore, Hong Kong, Taiwan and South Korea are faced with low fertility and (future) population decline.Footnote 1 On the other hand, although the environmental concern is relatively high in these countries, some of them do not control polluting emissions appropriately, and are suffering from excessive emissions. Even in terms of the local environment, there still exist various types of problems such as water pollution in rivers, lakes and sea areas, along with air pollution.Footnote 2 This may imply that, while excessive population growth is considered to be a major environmental threat, environmental degradation can be ongoing even without population growth. The N-shaped correlation between pollution and income per capita, which is proposed by empirical studies such as de Bruyn et al. (Reference de Bruyn, van den Bergh and Opschoor1998), Friedl and Getzner (Reference Friedl and Getzner2003), and Martínez-Zarzoso and Bengochea-Morancho (Reference Martínez-Zarzoso and Bengochea-Morancho2004), and provided with a rationale by Varvarigos and Zakaria (Reference Varvarigos and Zakaria2017), is in line with this observation. According to the N-shaped curve, where pollution correlates positively with income per capita in a later stage of development, even under a low fertility rate, pollution may increase as long as income per capita grows in a high-income country. In this paper, we attempt to provide an explanation of how lower fertility and higher pollution simultaneously arise in the competitive economy rather than in the social optimum.
The relation between fertility and environmental quality may depend on the types of utility parents can obtain from having children, which may change with the stage of economic development. As Leibenstein (Reference Leibenstein1974) argues, ‘work or income utility’ and ‘old age security utility’ are important factors in fertility decisions in the early stage of development.Footnote 3 On the other hand, as economic development proceeds and income per capita increases, the use of child labor decreases and old age security systems outside the family develop, implying that work and old age security utility declines. Hence, in a later stage of economic development, parental altruism could explain a larger part of utility obtained from having children and could be a more significant factor for fertility decisions.
Jouvet et al. (Reference Jouvet, Michel and Vidal2000b) and Jouvet et al. (Reference Jouvet, Michel and Pestieau2000a) investigate environmental issues introducing altruistic bequests (Barro, Reference Barro1974; Becker and Barro, Reference Becker and Barro1988).Footnote 4 Assuming that individuals voluntarily contribute to pollution abatement, these studies show that a market economy results in under-contribution to pollution abatement and thus an under-provision of environmental quality due to the free rider problem. In these models, bequests also create environmental externalities via the production process, which lead to an over-accumulation of capital. To attain the social optimum, therefore, the government requires subsidies on contributions to pollution abatement and taxes on capital. These studies, however, assume exogenous fertility and the relation between fertility and environmental qualities is outside their scope.
In this paper, we assume that production causes pollution, and bequests embodied in productive capital create environmental externalities as in Jouvet et al. (Reference Jouvet, Michel and Vidal2000b) and Jouvet et al. (Reference Jouvet, Michel and Pestieau2000a). Since aggregate production is increasing in the population, pollution externalities of childbearing also prevail in our model. The co-existence of these two externalities leads to a result different from that obtained in the previous studies on environmental externalities incorporating endogenous fertility (presented in section 2), namely, that the fertility rate determined in a market economy may be lower than the social optimum, although childbearing has a negative external effect on the environment. Parents choose the number of children so that the marginal benefit equals the marginal cost of having a child, and bequests toward each child constitute the marginal cost of a child. Thus, an increase in bequests raises the marginal cost of a child, and has a negative effect on the number of children. Therefore, if the level of bequests in the competitive equilibrium is higher than the socially optimal level, this over-provision of bequests raises the private marginal cost of a child possibly to a level above its social marginal cost. In such a case, the number of children in the competitive equilibrium instead falls below the social optimum. According to our numerical examples, many combinations of plausible parameter values support an equilibrium in which the number of children is insufficient. On the other hand, we show that the level of pollution is unambiguously higher than the social optimum, whether the fertility rate is too high or too low.
Moreover, we consider the parents' perceived rate of the effect of their behavior on pollution, and show that, as this rate rises, the number of children in the competitive equilibrium approaches that in the social optimum. In our model, the insufficiency in the number of children arises when the negative externality effect of fertility is dominated by the effect of the interaction of inheritance, which also creates a negative externality, and fertility. In this case, a rise in the parents' perceived rate lessens both of these externalities and increases fertility.Footnote 5 This implies that environmental concern is closely related to fertility decisions, and the difference in environmental concern can be a factor in explaining the difference in fertility rates among countries.
We also examine what kind of policy is required to achieve social optimality. It is shown that, if the social discount factor for a child equals the private degree of altruism, the government needs to tax both childbearing and inheritance so as to restore efficiency, even if the fertility rate is lower than its socially optimal level. This is because an over-accumulation of capital is a necessary condition for under-production of children. Once capital is adjusted to its optimal level by inheritance taxes, the factor in the under-production of children disappears, and the fertility rate exceeds its socially optimal level due to its environmental externalities. On the other hand, if the social discount factor for a child is higher than the private degree of altruism, child allowances and/or subsidies on inheritance may be required to attain the social optimum. However, the optimal policy never involves a combination of taxes on childbearing and subsidies on inheritance. Furthermore, our numerical examples suggest that a combination of child allowances and inheritance taxes is consistent with social optimality, as long as the weight to private utility in the social welfare function does not differ greatly among generations.
While the above result suggests that child allowances and inheritance taxes can constitute the optimal policy, these policies have been adopted in most high-income countries including those with low fertility. One reason why the fertility rates remain low even under these policies may be that the amount of child allowances is not large enough. In fact, public expenditure on family in percentage of GDP differs substantially between high-fertility and low-fertility countries: cash benefits are 0.8 per cent in Japan and 0.176 per cent in South Korea, while 1.565 per cent in France, whose TFR is 2.01, and 1.448 per cent in Sweden, whose TFR is 1.88; benefits in kind are 0.461 per cent in Japan and 0.949 per cent in South Korea, while 1.349 per cent in France and 2.19 per cent in Sweden, in 2013 (OECD, 2016).
The rest of the paper is organized as follows. Section 2 reviews previous studies closely relating to this paper to make our contribution clear. Section 3 presents a model, and characterizes the competitive equilibrium. Section 4 characterizes the social optimum, and compares it to competitive equilibrium in the benchmark case where the social discount factor is equal to the private degree of altruism. Section 5 examines what kind of policy is required to decentralize the social optimum. Section 6, assuming that the social discount factor differs from the private degree of altruism, reexamines the result obtained in the previous sections. Section 7 provides the conclusions.
2. Related studies
There are a few studies that address the issues of fertility choices and environmental externalities in the presence of altruism, which include Harford (Reference Harford1997, Reference Harford1998), Schou (Reference Schou2002), Jöst and Quaas (Reference Jöst and Quaas2010), and Marsiglio (Reference Marsiglio2017). Harford (Reference Harford1998) considers a consumable capital good and a non-capital good, and consumption of the latter is assumed to create a pollution externality. While an increase in the number of children implies an increase in aggregate consumption of the polluting good, parents do not recognize such an impact of an extra child on pollution, and hence childbearing has an external effect, which results in excessive fertility. Harford shows that Pareto efficiency requires taxes on childbearing as well as Pigovian pollution taxes. Taxes on capital are not called for in his model, since bequests of capital do not entail externalities.
Schou (Reference Schou2002) introduces human capital accumulation as the engine of economic growth into a model with endogenous fertility decisions, which create negative pollution externality via production, and examines consequences for optimal policy of endogenizing fertility. He shows that a pollution tax is sufficient to attain optimality, when the revenue from it is redistributed to dynasties; but fertility is still excessive, when the revenue is redistributed to individuals. In the latter case, while a pollution tax must be supplemented with a fertility tax as in Harford (Reference Harford1997, Reference Harford1998), the fertility tax can be replaced by an appropriate debt policy, which has negative effects on fertility (Lapan and Enders, Reference Lapan and Enders1990).
Jöst and Quaas (Reference Jöst and Quaas2010) extend Harford (Reference Harford1997, Reference Harford1998) to an optimal control model with a production system that emits pollutants. They consider two types of households: dynastic households (Barro and Becker, Reference Barro and Becker1989) and ‘micro households’ in which children leave their parents' household to form a new decision-making unit immediately after birth. In their model, two kinds of external effects, which arise from the individual decisions on polluting emissions and fertility, cause excessive total emissions and excessive population relative to the socially optimal. While the pollution externality may be internalized by a Pigovian tax on emissions, the optimal population policy is different according to the type of household. Taxes on the household size are required in the case of dynastic households, while taxes on the number of children are required in the case of micro households.
These studies and ours are along the same lines in that the social optimum is defined, and the role of economic policy in restoring the social optimum in the decentralized economy is examined. However, differently from these studies, where negative externality causes excessive fertility, and thus a fertility tax or another child-control policy is required to create optimality, we will show that insufficient fertility may arise simultaneously with excessive pollution, and a child-support policy in the form of child allowances may be consistent with optimality.
Marsiglio (Reference Marsiglio2017) analyzes the interactions among population, economic growth and environment in a model where not only production but also population directly affects the environmental quality. He shows that, for low fertility rate, population growth increases both economic and environmental growth, while for high fertility rate, it decreases both of them. Then he demonstrates that a child-support policy is an effective tool to improve both economic and environmental outcomes in economies with low fertility, in contrast to the findings of Harford (Reference Harford1997, Reference Harford1998), Schou (Reference Schou2002), and Jöst and Quaas (Reference Jöst and Quaas2010), where a child-control policy is required to restore the social optimum. On the other hand, he does not discuss whether the equilibrium fertility rate is too high or too low, or whether demographic policy can achieve social optimality or not. This is a difference from our study (as well as the four studies mentioned above).
Among studies on the effect of environmental factors on fertility without altruism, Varvarigos and Zakaria (Reference Varvarigos and Zakaria2017) incorporate endogenous fertility decisions into Varvarigos (Reference Varvarigos2014), which derives multiple equilibria characterized by higher (lower) income with higher (lower) environmental quality and higher (lower) longevity, and show the positive relation between pollution and fertility rates.Footnote 6 Moreover, they show that, in the presence of an emission tax, the economy experiences a reduction in the fertility rate at some point in the process of development, due to the entrepreneurial choice of less polluting production method. The N-shaped correlation between pollution and income per capita is also explained theoretically in their study.Footnote 7 While fertility decline emerges in their model, they do not discuss whether the resulting fertility rate is insufficient or not as they do not deal with the social optimum.
3. The basic model
Suppose that there are two periods and two generations. The parents' generation (generation 0) lives for period 0 and the children's generation (generation 1) lives for period 1, with no overlapping of the periods. Each member of the same generation is identical. The population of generation 0 is N, and each member of generation 0 produces n children.
As in Becker and Barro (Reference Becker and Barro1988), the parents decide to have n children because they are altruistic toward their children in that each child's welfare directly enters their utility functions. It is assumed that each child costs β (>0), so that n β is the total cost of raising children. The parents allocate the remaining income after they have paid the cost of raising children between their own consumption and bequests toward their children. We also assume that the inheritance from the former generation determines the income of each generation.
The parents derive disutility from the level of pollution while deriving utility from consumption and their children's welfare. Their utility function is thus defined by
$$U_0 ( c_0\comma \; \pi _0\comma \; n\comma \; U_1 ) =u_0 [( 1+r) b_0 -n( b_1 +\beta ) ] -V_0 ( \pi _0 ) +n\delta ( n) U_1\comma \; $$
where c 0 ( = (1 + r) b 0 − n(b 1 + β)) is their consumption, b 0 is the inheritance they receive, b 1 is the bequests to each child, r is the interest rate, π 0 is the level of pollution in period 0, U 1 is the utility of each child, and δ (n) is the weight attached to each child's utility. We assume that u′0 > 0, 
$u^{\prime\prime}_{0} < 0\comma \; V^{\prime}_{0}> 0$, V″0 > 0, 0 < δ(n) < 1, δ ′(n) < 0, δ(n) + δ ′(n) n > 0 and 2δ ′(n) + δ ′′(n) n < 0.Footnote 8
The children consume the inheritance from their parents, and their utility function is defined by
$$U_1 ( c_1\comma \; \pi _1 ) =u_1 [( 1+r) b_1 ] -V_1 ( \pi _1) \comma \;$$
where π 1 is the level of pollution in period 1. We assume that u′1 > 0, 
$u^{\prime\prime}_{1} < 0\comma \; V^{\prime}_{1}> 0$, and V″1 > 0.
We assume the level of pollution in each period to be a linear function of current production Y i:
$$\pi _i =\alpha Y_i \semicolon \; \quad \alpha >0\comma \; \qquad i=0\comma \; 1. $$As in Harford (Reference Harford1998) and Schou (Reference Schou2002), we model pollution as a flow variable and do not address stock pollution. In this model, however, it may be reasonable to assume that no pollutants survive the period, because one period corresponds to a lifetime of an individual, implying that the depreciation rate is likely to be sufficiently high. Assuming a linear technology, we define the production function as
$$Y_i =AK_i\semicolon \; \quad A>0\comma \; \qquad i=0\comma \; 1\comma \; $$where K i is the stock of capital in period i.
Equilibrium on the capital market implies
$$b_i =k_i \semicolon \; \quad i=0\comma \; 1\comma \; $$where k 0 ≡ K 0/N and k 1 ≡ K 1/nN. At equilibrium the rate of interest is equal to the marginal productivity of the capital net of depreciation:Footnote 9
$$1+r=A. $$We hereafter denote k 1 as k for notational simplicity.
The parents are assumed not to recognize that producing children and bequeathing their wealth to their children should degrade the future environment via the production process. Given π 1 as well as (1 + r)b 0, β and π 0, therefore, the parents choose the number of children and the level of bequests so as to maximize (1). Substituting (2), (3), (4) and (5) into the first-order conditions yields
$$F( k\comma \; n) \equiv -n{u}^{\prime}_0 [Ak_0 -n( k+\beta ) ] +n \delta ( n) A{u}^{\prime}_1 ( Ak) =0\comma \; $$
$$\eqalign{G( k\comma \; n) & \equiv -( k+\beta ) {u}^{\prime}_0 [Ak_0 -n( k+\beta ) ] \cr & \quad +[\delta ( n) +n{\delta }^{\prime}( n) ] \lcub {u_1 ( Ak) -V_1 ( \alpha ANnk) } \rcub =0.}$$The competitive equilibrium (k*, n*) is characterized by (6) and (7).
We define G(k, n) in (7) as the private marginal net benefit (PMNB) of a child. Similarly, F(k, n) in (6) as the PMNB of bequests. The first term in (7) is the marginal disutility from the decrease in parental consumption by having an additional child, and represents the private marginal cost of a child. The second term in the RHS of (7) is the increase in parental utility derived from altruism when adding an additional child, and represents the private marginal benefit of a child.
4. Social optimum
In this section, we characterize the social optimum, and compare it to the competitive equilibrium obtained in the previous section. In particular, we show that the number of children chosen may be lower in the competitive equilibrium than in the social optimal allocation, albeit children create negative environmental externalities.
4.1. Characterizing the social optimum
We assume that the government adopts a utilitarian social welfare function consisting of the discounted sum of individuals' utilities. According to Blumkin and Sadka (Reference Blumkin and Sadka2004), the social welfare function is defined by
$$W=N[U_0 ( c_0\comma \; \pi _0\comma \; n\comma \; U_1 ) +\rho nU_1 ( c_1\comma \; \pi _1 )].$$Although the welfare of the children's generation is already incorporated into the social welfare function through the parent's utility, the government may also assign a positive weight to the children's welfare in itself. If this is the case, then ρ > 0. On the other hand, if the government counts the children's welfare only through the parent's utility, then ρ = 0. As a benchmark, we first assume that ρ = 0, under which the social discount factor equals the parent's degree of altruism, and examine the case of ρ > 0 in section 6.
Given k 0, A, β and α, the government chooses n and k so as to maximize (8). The first-order conditions are
$$\eqalign{F^S( k\comma \; n) & \equiv -n{u}'_0 [Ak_0 -n( k+\beta ) ] \cr & \quad{}+ n[\delta ( n) +\rho] [A{u}'_1 ( Ak) -\alpha ANn{V}'_1 ( \alpha ANnk) ] =0\comma \; } $$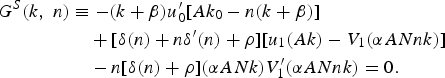
$$\eqalign{G^S( k\comma \; n) & \equiv -( k+\beta ) {u}'_0 [Ak_0 -n( k+\beta ) ] \cr & \quad +[\delta ( n) +n{\delta}'( n) +\rho ] [u_1 ( Ak) -V_1 ( \alpha ANnk) ] \cr & \quad -n[\delta ( n) +\rho ] ( \alpha ANk) {V}'_1 ( \alpha ANnk) =0.}$$We obtain the social optimum (k S, n S) from (9) and (10). G S(k, n) can be defined as the social marginal net benefit (SMNB) of a child. Similarly, F S(k, n) in (9) can be defined as the SMNB of bequests.
4.2. Comparing the competitive equilibrium to the social optimum
In our model, the parents do not take into account the effects of k and n on pollution via the production process. This implies that both childbearing and bequeathing to children have pollution externalities. Comparing (7) to (10) with ρ = 0, it follows that the PMNB of n is greater than its SMNB by n δ(n) (α ANk)V′1 given k. Similarly, a comparison between (6) and (9) with ρ = 0 indicates that the PMNB of k is greater than its SMNB by n δ(n) (α ANn)V′1 given n. This does not imply, however, that k and n are determined higher in the competitive equilibrium than in the social optimum, because there exists an interaction between k and n. That is, an increase in bequests raises the marginal cost of having a child, and thus has a negative effect on the number of children. Therefore, if the level of capital accumulation in the competitive equilibrium is higher than the socially optimal level, and this over-accumulation of capital lowers the PMNB of a child to a level below its SMNB, then the number of children in the competitive equilibrium instead falls below that in the social optimum.Footnote 10
Paying attention to the interaction of k and n, we now derive a condition for n* < n S. For this purpose, we consider the following equations:
$${\hat {F}}( k\comma \; n\semicolon \; \mu ) \equiv F( k\comma \; n) -\mu \lcub {n\delta ( n) \alpha ANn{V}'_1 ( \alpha ANnk) } \rcub =0\comma \; $$
$${\hat {G}}( k\comma \; n\semicolon \; \mu ) \equiv G( k\comma \; n) -\mu [n\delta ( n) \alpha ANk{V}'_1 ( \alpha ANnk) ] =0. $$Note that the competitive equilibrium (k*, n*) satisfies (11) and (12) when μ = 0, whereas the social optimum (k S, n S) satisfies them when μ = 1. Furthermore, μ ∈ [0, 1] can be thought of as the parents' perceived rate of the effect of their behavior on pollution. Using this terminology, our model supposes the case where the parents' perceived rate is 0. On the other hand, if it were 1, the competitive equilibrium would coincide with the social optimum.
Differentiating (11) and (12) yieldsFootnote 11
$$\displaystyle{{dk} \over {d\mu }} = \displaystyle{{{\hat{F}}_\mu } \over {D( \mu ) }}\left[{\displaystyle{k \over n}F_n-G_n} \right]\comma \; $$
$$\displaystyle{{dn} \over {d\mu }} = \displaystyle{{{\hat{F}}_\mu } \over {D( \mu ) }}\left[{-\displaystyle{k \over n}F_k + G_k} \right]\comma \; $$
where F k ≡ ∂F/∂k( < 0), F n ≡ ∂F/∂n( < 0), G k ≡ ∂G/∂k( < 0), G n ≡ ∂G/∂n( < 0), 
$\hat{F}_{\mu}\equiv \partial\hat{F}/\partial \mu( <0) $ and D(μ)(>0) is the determinant of the Jacobian.Footnote 12
As shown in the appendix, the sign of (14) is positive if
$$-n^\ast \delta ( n^\ast ) ( \alpha ANk^\ast ) {V}'_1 ( \alpha ANn^\ast k^\ast) +G_k ( k^\ast\comma \; n^\ast ) \left. {\displaystyle{{\partial k}\over{\partial \mu }}}\right\vert _{\mu =0} >0\comma \; $$
where 
$( \partial k/\partial \mu ) _{\mu =0} =-( \hat{F}_{\mu}/F_{k}) <0$. Since dn/d μ > 0 is a sufficient condition for n* < n S, we obtain the following proposition.
Proposition 1.
If (15) is satisfied, then the number of children in the competitive equilibrium is smaller than that in the social optimum.
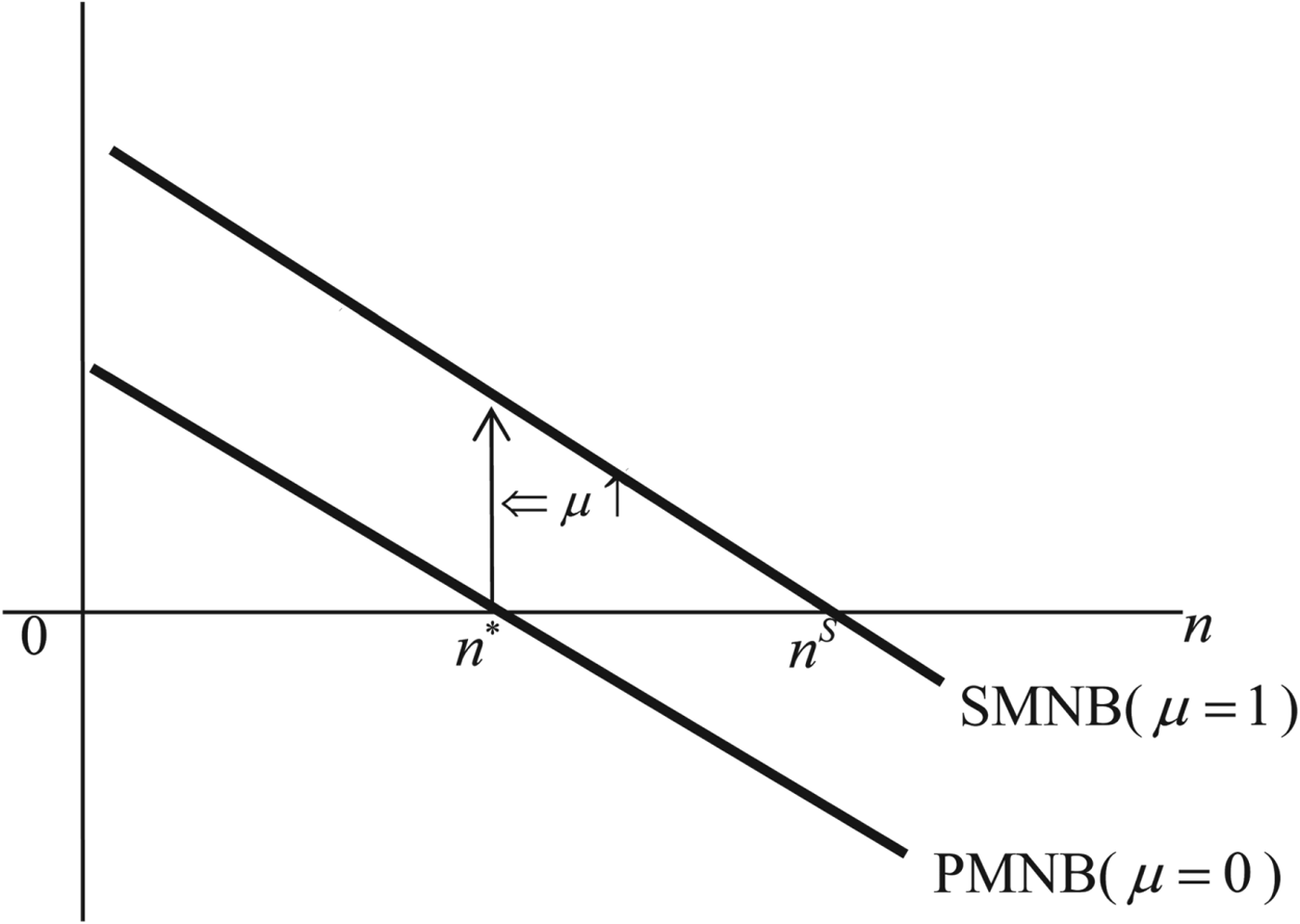
The intuition behind proposition 1 is straightforward. The LHS of (15) represents the change in the marginal net benefit of a child when the parents' perceived rate rises from 0. The first term is the environmental effects of n which the parents do not take into account in calculating the PMNB of a child. If they take these effects into account, the marginal net benefit of a child decreases. The second term is the effects through the change in capital (i.e., bequest). If the parents realize the environmental effects of k, they choose smaller amounts of bequests per child ((∂k/∂μ) μ=0 < 0). The decrease in bequests implies the decrease in the marginal cost of a child and the increase in the marginal net benefit of the child. Therefore, if the second term dominates the first term, the marginal net benefit of a child and thus the number of children increase. Figure 1 shows the SMNB of n and the PMNB of n when (15) is satisfied. Equation (15) implies that the PMNB is shifted upward by an increase in μ, and equivalently that the SMNB exceeds the PMNB, given n = n*. Hence, the number of children determined in the competitive equilibrium is lower than the social optimum (n* < n s).Footnote 13
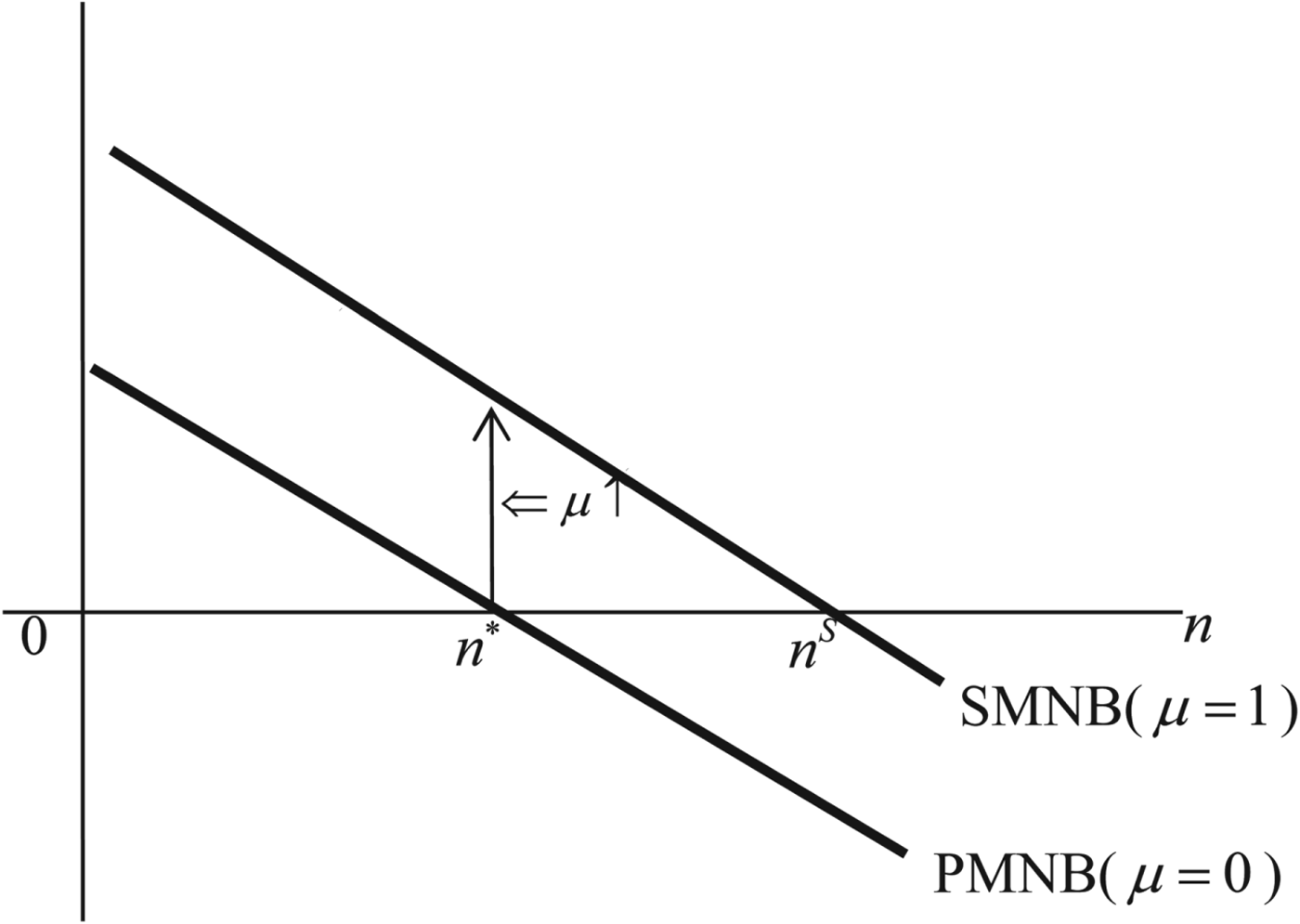
Figure 1. Number of children: competitive equilibrium and social optimum
As to the comparison of the level of capital in the competitive equilibrium to its socially optimal level, we obtain the following proposition.
Proposition 2.
In the competitive equilibrium, if the number of children is insufficient, then capital is over-accumulated, relative to the social optimum.
Proof: See appendix. □
Together with proposition 1, proposition 2 implies that, if (15) is satisfied, n* < n s and k* > k s simultaneously holds.
The above result is in marked contrast with Jöst and Quaas (Reference Jöst and Quaas2010), in which the fertility rate in the competitive equilibrium is higher than that in the social optimum for two types of households: dynastic households and micro-households. The family (or household) considered here is basically the same as the dynastic household in Jöst and Quaas in that the parents decide their children's consumption, while our family consists only of two generations. In the case of dynastic households in Jöst and Quaas, while the cost of raising children depends on per-capita capital, there is no external effect from the firm's decision on capital and the equilibrium level of capital is socially optimal. On the other hand, in our model, the household's decision on bequests creates an externality, which may lead to the higher cost of raising children and thus the lower fertility rate in comparison to the social optimum.
We next examine the relative magnitude of pollution between the competitive equilibrium and the social optimum. The result is summarized in the following proposition.
Proposition 3.
The level of pollution is higher in the competitive equilibrium than in the social optimum.
Proof: See appendix. □
It should be noted that we have π* > π s irrespective of the relative magnitude between n* and n S and between k* and k S. This is due to the external effects of childbearing and bequests on the environment. Furthermore, propositions 1 and 3 imply that society may suffer from insufficient fertility and excess pollution at the same time. This result seems to be in line with a phenomenon prevailing in several countries.
4.3. Numerical examples
In this section, we quantitatively assess the results obtained in section 4.2. in a numerical example. For this purpose, we specify the utility and disutility functions as u 0 (c) = u 1 (c) = c 0.6 and V 0 (π) = V 1 (π) = π 2/2, respectively. Following Becker and Barro (Reference Becker and Barro1988), the degree of altruism toward children is assumed to take a form of constant elasticity with respect to the number of children, i.e., δ(n) = ξ n −0.2, where ξ > 0. We set ξ = 0.65 as the baseline value, with which we can see that the degree of altruism toward each child is about 0.6 in the competitive equilibrium. We assume the population of the parent's generation and the initial endowment of each parent as N 0 = 1 and b 0 = 1, respectively. The total capital stock in the first period (K 0) is then equal to 1. The productivity parameter (A) is set equal to 2.666, which corresponds to the annual interest rate 0.04 when one period is taken as 25 years (i.e., 2.666 ≈ (1 + 0.04) 25). The other parameters are set as α = 0.15 and β = 0.25. The value of β implies that the share of child rearing cost in income ( = n β/y 0) is 12 per cent in the competitive equilibrium.
With each parameter set equal to its baseline value, the competitive equilibrium is given by k* = 1.156 and n* = 1.271, while the social optimum is calculated as k S = 0.794 and n S = 1.424. Notice that, in the baseline case, the number of children in the competitive equilibrium is lower than that in the social optimum.
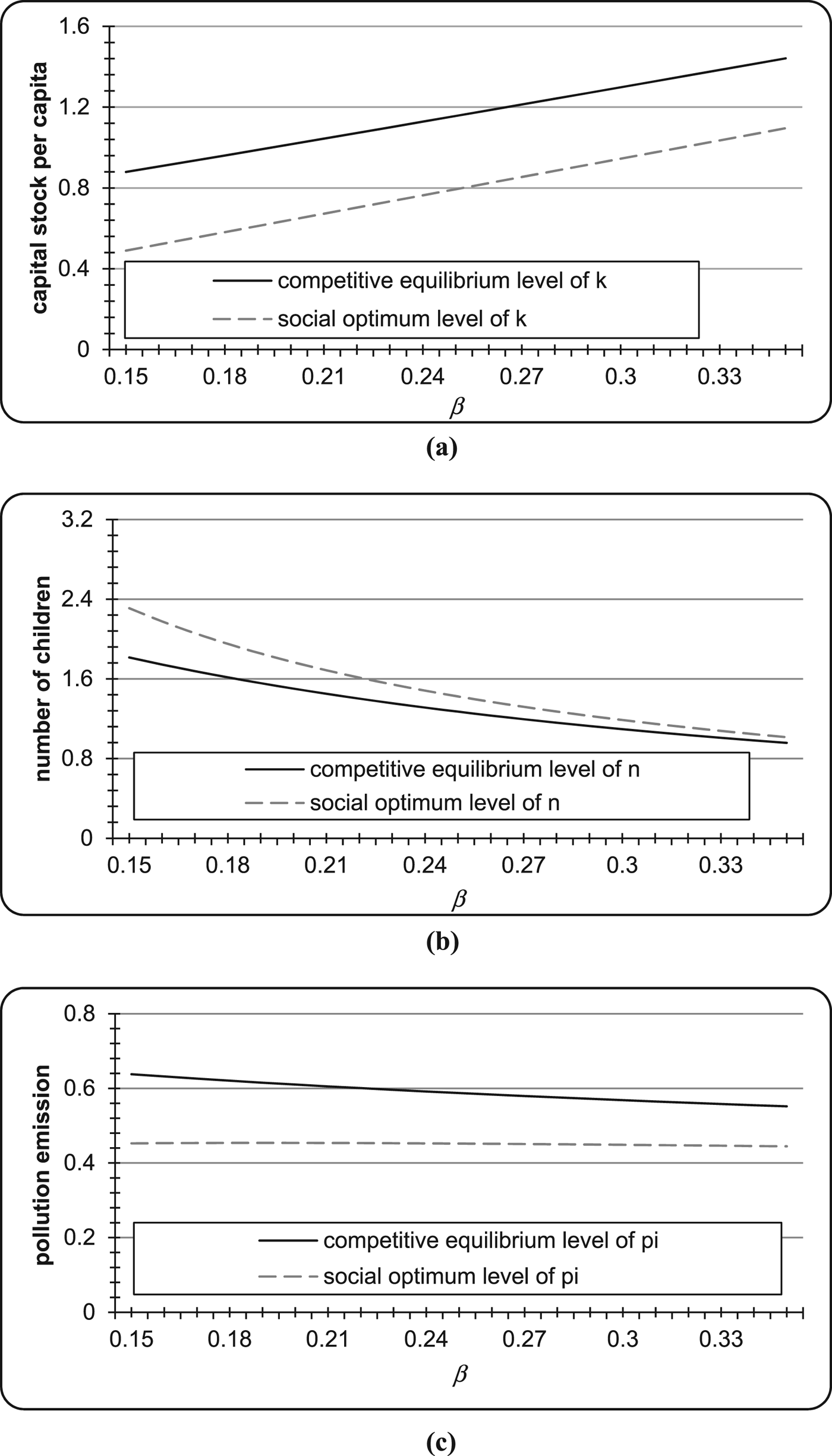
In the following, we examine how the variables k, n and π depend on key parameters: the level parameter of the altruism toward children ξ and rearing cost per child β. The former result is depicted in figure 2 and the latter in figure 3.
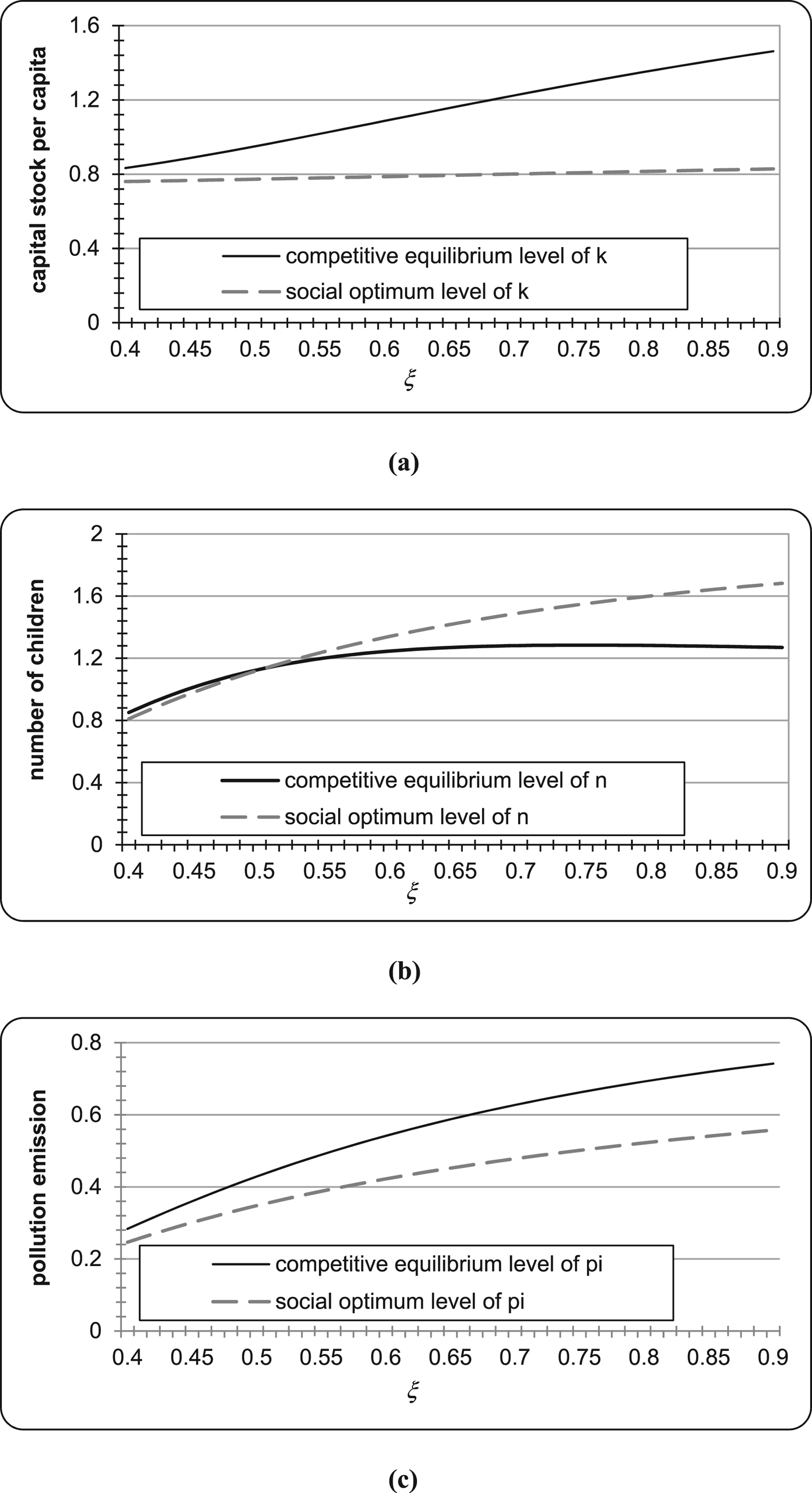
Figure 2. (a) Sensitivity of capital stock per capita to ξ. (b) Sensitivity of number of children to ξ. (c) Sensitivity of pollution emission to ξ
Figure 3. (a) Sensitivity of capital stock per capita to β. (b) Sensitivity of number of children to β. (c) Sensitivity of pollution emission to β
Figures 2(a)–(c) show the competitive equilibrium and the social optimum values of k, n and π for ξ ranging from 0.4 to 0.9 respectively. The results can be summarized as follows:
• both k* and k S are increasing in ξ, while k* increases more sharply than k S;
• n S is monotonically increasing in ξ, while n* shows the inverted U-shaped relation with ξ;
• when ξ is relatively large (i.e., ξ ≥ 0.5), the number of children in a competitive equilibrium is smaller than that in the corresponding social optimum, while it is larger when ξ is relatively small (i.e., ξ < 0.5);
• the gap between the number of children in a competitive equilibrium and that in the social optimum becomes greater as ξ increases. From figures 2(a) and (b), we can see that, when the altruism parameter ξ is relatively large, the number of children is insufficient in the competitive equilibrium and then the capital is overly accumulated, which illustrates proposition 2, although, in our numerical example, the capital is overly accumulated even when the number of children is higher in the competitive equilibrium;
• the level of pollution in the social optimum π S is increasing in ξ since both k S and n S monotonically increase, while π* is also increasing in ξ, although n* decreases when ξ is relatively large. In our example, the positive effect (i.e., increases in k*) dominates the negative effect (i.e., decreases in n*), and hence π* increases with ξ;
• over the whole range of ξ, the pollution emission is larger in the competitive equilibrium than in the socially optimum, which demonstrates proposition 3. We can also see from figure 2(c) that the over-emission becomes greater as ξ increases, that is, the competitive equilibrium becomes more inefficient as the parents become more altruistic toward children.
The values of k, n and π for β ranging from 0.15 to 0.35 are shown in figure 3(a)–(c). These results are summarized as follows:
• an increase in β raises k and reduces n both in the competitive equilibrium and in the social optimum;
• over the whole range of β, k* is higher than k S, and n* is lower than n S;
• as β increases, the gap between the number of children in the competitive equilibrium and the social optimum becomes smaller;
• a change in β affects the pollution levels through two channels: (i) the positive effect on k, and (ii) the negative effect on n. In our numerical example, the latter effect dominates the former in the competitive equilibrium and hence an increase in β reduces π*, while these effects are almost canceled out in the social optimum and hence a change in β does not have significant impact on π S, as shown in figure 3(c).
It should be noticed that, according to our numerical examples, the number of children in the competitive equilibrium becomes insufficient for a wide range of parameter values, including the baseline case which is considered to be plausible.
5. Optimal policy
This section examines whether the social optimum can be decentralized. In our model, since the parents fail to take into account the effects of production on pollution in choosing the number of children and the amount of bequests to each child, laissez faire leads both the fertility rate and per capita capital to become suboptimal. To control two variables, decentralization requires two policy instruments. Among the many instruments the government can use, we consider taxes (or subsidies) on inheritance and taxes on childbearing (or child allowances), which would directly affect the decisions on fertility and bequests in the family.
5.1. Decentralizing the social optimum
The government budget is balanced by lump-sum transfers to private individuals in each period. We thus have
$$nT =\theta\comma \; $$
$$( 1+r) b_1 \tau =\eta\comma \; $$where T is a tax per child imposed on the parents, τ is the tax rate on bequests to each child, θ is a lump-sum transfer to each parent, and η is a lump-sum transfer to each child.
The parent's utility function (1) is rewritten as
$$\eqalign{U_0 &=u_0 [( 1+r) b_0 -n( b_1 +\beta +T) +\theta ] -V_0 ( \pi _0 ) \cr & \quad +n\delta ( n) \lcub {u_1 [( 1-\tau ) ( 1+r) b_1 +\eta ] -V_1 ( \pi_1 ) } \rcub .}$$The competitive equilibrium in this case, k = k* (τ, T) and n = n* (τ, T), satisfies the following conditions:
$$\eqalign{\tilde {F}( k\comma \; n\semicolon \; \tau\comma \; T) & \equiv -n{u}'_0 [Ak_0 -n( k+\beta +T) +\theta ] \cr & \quad +n\delta ( n) ( 1-\tau ) A{u}'_1 [( 1-\tau ) Ak+\eta ] =0,}$$
$$\eqalign{\tilde {G}( k\comma \; n\semicolon \; \tau\comma \; T) & \equiv -( k+\beta +T) {u}'_0 [Ak_0 -n( k+\beta +T) +\theta ] \cr & \quad +( \delta ( n) +n\delta'( n) ) \lcub {u_1 [( 1-\tau ) Ak+\eta ] -V_1 ( \alpha ANnk) } \rcub =0.}$$If the government realizes the social optimum in a decentralized economy with τ = τ* and T = T*, we have
$$k^{\ast} ( \tau^{\ast}\comma \; T^{\ast}) =k^S,$$
$$n^{\ast} ( \tau^{\ast}\comma \; T^{\ast}) =n^S.$$Substituting (16), (17), (20) and (21) into (18) and (19) yields
$$\eqalign{&-n^S{u}'_0 [Ak_0 -n^S( k^S+\beta ) ] +n^S\delta ( n^S) ( 1-\tau ^\ast ) A{u}'_1 ( Ak^S) =0\comma \; \cr & -( k^S+\beta +T^\ast ) {u}'_0 [Ak_0 -n^S( k^S+\beta )].}$$
$$+( \delta ( n^S) +n^S{\delta}'( n^S) ) [u_1 ( Ak^S) -V_1 ( \alpha ANn^{S}k^{S}) ] =0. $$Since (k S, n S) also satisfies (9) and (10) with ρ = 0, (22) and (9) with k = k S and n = n S imply
$$\tau ^* = \displaystyle{{\alpha Nn^S{{V}^{\prime}}_1( \alpha ANn^Sk^S) } \over {{{u}^{\prime}}_1( Ak^S) }} > 0. $$Also, (23) and (10) with k = k S and n = n S imply
$$T^* = \displaystyle{{n^S\delta ( n^S) \alpha ANk^S{{V}^{\prime}}_1( \alpha ANn^Sk^S) } \over {{{u}^{\prime}}_0[Ak_0-n^S( k^S + \beta ) ] }} > 0.$$Hence we have the following proposition:
5.2. Implications of the optimal policy
Equation (25) implies that T* is positive independent of the relative magnitude between n* and n S. We now discuss why childbearing should be taxed to achieve social optimality, even when the number of children is insufficient relative to the social optimum.Footnote 14
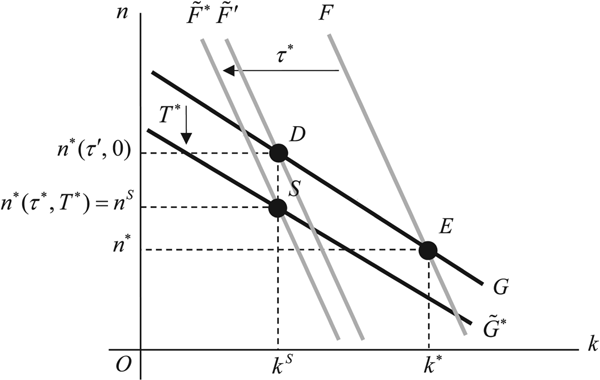
In figure 4, lines F and G respectively represent (18) and (19) with τ = T = 0 in the (k, n) plane.Footnote 15 In this case, the number of children is too low and the level of bequests is too high at the equilibrium point E. Since an increase in τ shifts F to the left, and an increase in T shifts G downward,Footnote 16 these lines move to 
$\tilde{F}^{\ast}( =\tilde{F}( k\comma \; n\semicolon \; \tau^{\ast}\comma \; T^{\ast}) ) $ and 
$\tilde{G}^{\ast} ( =\tilde{G}( k\comma \; n\semicolon \; \tau^{\ast}\comma \; T^{\ast}) ) $ if the government adopts τ = τ* ( > 0) and T = T* ( > 0). As a result, the social optimum S is achieved in the decentralized economy.
Figure 4. Optimal policies when ρ = 0
To explain why the government should tax childbearing although the number of children is insufficient in the initial equilibrium, we first suppose that the government uses only an inheritance tax τ as a policy tool. We see that an inheritance tax suffices to attain the optimal level of capital k S as shown in figure 4, in which a bequest tax of τ = τ′ alters the equilibrium to point D by shifting F to 
$\tilde{F}^{\prime}$. However, the new equilibrium D is suboptimal because the number of children is too high relative to the social optimum (n* (τ′, 0) > n S). Once k is adjusted to its optimal level, the factor in the insufficiency of n disappears, and n exceeds its optimal level. In this stage, the government needs to tax childbearing to internalize a pollution externality children will create.
6. Alternative social discount rate
Throughout the previous sections, we have maintained the assumption that the government counts the children's welfare only through the parents' welfare, namely, ρ = 0. In this section, we consider the case where the social discount factor differs from the parents' degree of altruism, namely, ρ > 0 in (8). The social optimum is characterized by (9) and (10) with ρ > 0.
In this case, the parents value the children's welfare less than the government, and the parents' behavior in terms of fertility and inheritance creates other types of externalities. As a result, while proposition 1 would be maintained by slight modification of the sufficient condition, proposition 2 is no longer valid. Whether k* is higher or lower than k S, the number of children can be too low due to the positive externality of childbearing that stems from the difference between the private and social welfare weights. Thus, k* > k S is not a necessary condition for n* < n S.
Furthermore, we have policy implications different from those in the previous section. That is, proposition 4 is not fully maintained in the sense that the social optimum can be still decentralized, but the optimal policy does not necessarily imply taxing both on childbearing and inheritance.
Equations (24) and (25) are reduced to
$$\tau ^{**} = \displaystyle{{[\delta ( n^S) + \rho ] \alpha Nn^S{{V}^{\prime}}_1( \alpha ANn^Sk^S) -\rho {{u}^{\prime}}_1( Ak^S) } \over {\delta ( n^S) {{u}^{\prime}}_1( Ak^S) }}\comma \; $$
$$T^{**} = \displaystyle{{n^S[\delta ( n^S) + \rho ] \alpha ANk^S{{V}^{\prime}}_1( \alpha ANn^Sk^S) -\rho [u_1( Ak^S) -V_1( \alpha ANn^Sk^S) ] } \over {{{u}^{\prime}}_0[Ak_0-n^S( k^S + \beta ) ] }}. $$The sign of τ** and T** may be positive or negative, depending on whether the pollution externalities, whose effects are captured by the first term in the numerator of (26) and (27), dominate or are dominated by the externalities arising from the parents' underestimation of the children's welfare, whose effects are captured by the second term in the numerator of (26) and (27). In contrast to the result under ρ = 0 (proposition 4), therefore, child allowances and/or subsidies on bequests may be required to achieve optimality. It should be noted, however, that the sign of τ** and T** is not to be determined independent of the sign of the other. More specifically, we have that, if τ** ≤ 0, then T** < 0, as shown in the appendix. This implies the following proposition.
Proposition 5.
If the social welfare function is given by (8) with ρ > 0, a combination of taxes on childbearing and subsidies on inheritance cannot achieve the social optimum in a market economy.
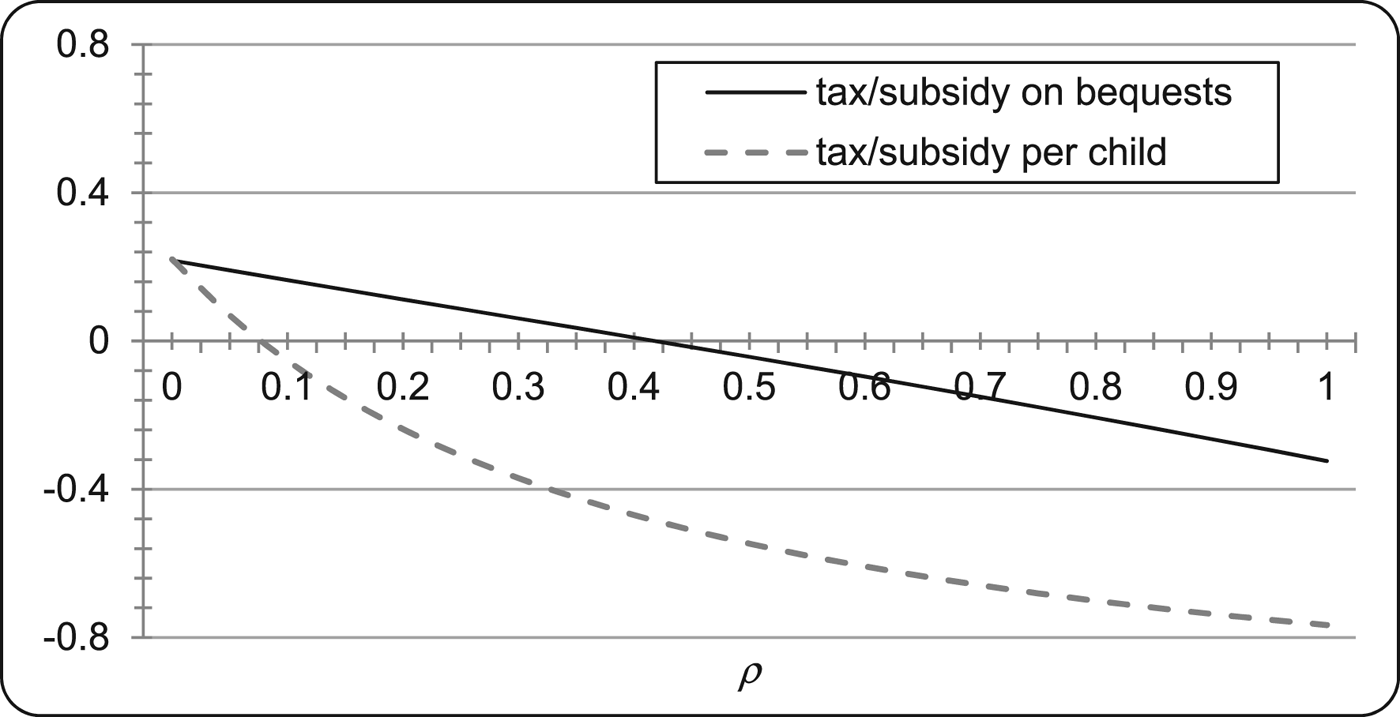
We now examine the relations between the value of ρ and the optimal policy choices (i.e., τ** and T**) numerically. Specification of functional forms and the baseline parameter values are the same as in section 4.3. The optimal policies are then calculated by substituting the parameter values into (26) and (27) with the functional specification. Figure 5 shows the values of τ** and T** for ρ ranging from 0 to 0.8. We can see from the figure that three cases appear, depending on the values of ρ. If the weight ρ is moderate (i.e., 0.05 < ρ < 0.45), then τ** is positive (i.e., inheritance tax) and T** is negative (i.e., child subsidy). In contrast, when ρ is sufficiently small (i.e., ρ ≤ 0.05), both τ** and T** are positive (i.e., tax on both inheritance and child rearing), whereas, when ρ is sufficiently large (i.e., 0.45 ≤ ρ), both τ** and T** are negative (i.e., subsidy for both inheritance and child rearing).
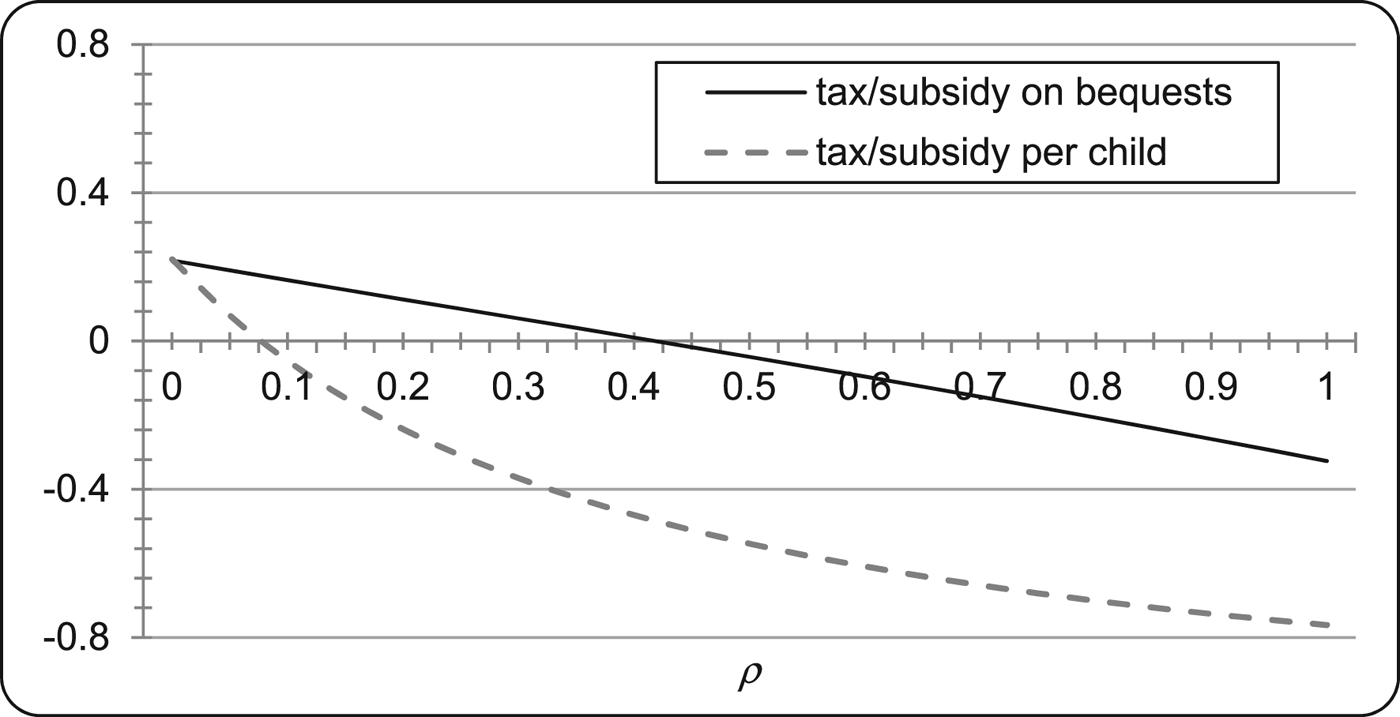
Figure 5. Optimal policies for various values of ρ
In our numerical example, we can see that, if the value of ρ is in the range of the first case above, the weight on the utilities of children in the social welfare function is smaller than one, i.e., δ(n S) + ρ < 1. This seems to be admissible since, in the economics literature, it is common practice to discount utilities of future generations, and then, τ** > 0 and T** < 0 hold as stated above. This result suggests that child allowances constitute the optimal policy under a plausible assumption on the social welfare function, in contrast to previous studies such as Harford (Reference Harford1998) and Jöst and Quaas (Reference Jöst and Quaas2010), in which taxes on the number of children or the household size are required to achieve optimality.
7. Conclusion
Using an altruistic bequest model with endogenous fertility, in which both childbearing and bequests entail pollution externalities, we showed that the fertility rate may be too low in the competitive equilibrium despite the negative externality created by childbearing. On the other hand, the level of pollution is unambiguously higher than the social optimum, whether the fertility rate (or per capita capital) is too high or too low.
Furthermore, we investigated what kind of policy is required to achieve social optimality. If the social discount factor for a child equals the private degree of altruism, the government needs to tax both childbearing and inheritance so as to restore efficiency, even if fertility or capital accumulation falls short of the respective optimal level. On the other hand, if the social discount factor for a child is greater than the private degree of altruism, child allowances and/or subsidies to inheritance may be required to achieve optimality. It should be noted, however, that the optimal policy never involves a combination of taxes on childbearing and subsidies on inheritance. Our numerical examples suggest that, under a plausible assumption on the social welfare function, inheritance taxes and child allowances can attain the social optimum.
In this paper, we do not consider several important aspects of economy and environment including economic growth, longevity, abatement activities and stock pollution to maintain the model tractable. However, in order to capture problems of the real world more comprehensively, these limitations should motivate further research. In particular, we could have incorporated economic growth, for example, by extending the model to an overlapping generations model, so that we could analyze the case of low-income countries with excessive population growth, and/or N-shaped correlation between pollution and income per capita. Furthermore, endogenous longevity could provide another channel enriching the linkages between population and environment, because pollution should have a direct effect on health and longevity (Varvarigos, Reference Varvarigos2010; Varvarigos and Zakaria, Reference Varvarigos and Zakaria2017), and also longevity should affect fertility decisions (Hirazawa and Yakita, Reference Hirazawa and Yakita2017).
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S1355770X19000068
Acknowledgements
We thank Kurt Brekke, Toshihiro Ihori, Jun-ichi Itaya, Yasushi Iwamoto, Dirk Schindler, Emilson Caputo Delfino Silva and the seminar/conference participants at University of Tokyo, Norwegian School of Economics, and the 2015 congress of the International Institute of Public Finance in Dublin, for their useful comments. We are indebted to two anonymous referees for suggestions, which were helpful in improving the paper. We also acknowledge financial support from the Institute of Economics, Chukyo University and Japan Society for the Promotion of Science (Grant-in-Aid for Scientific Research Grant Number JP16530215).
Appendix
A.1 Derivation of dk/d μ and dn/d μ:
Differentiating (11) and (12) with respect to k, n and μ yields
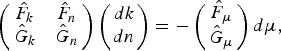$$\left({\matrix{{\hat {F}_k } & {\hat {F}_n } \cr {\hat {G}_k } & {\hat {G}_n } \cr }}\right)\left({\matrix{{dk} \cr {dn} \cr }}\right)=-\left({\matrix{ {\hat {F}_\mu } \cr {\hat {G}_\mu } \cr }} \right)d\mu\comma \;$$where
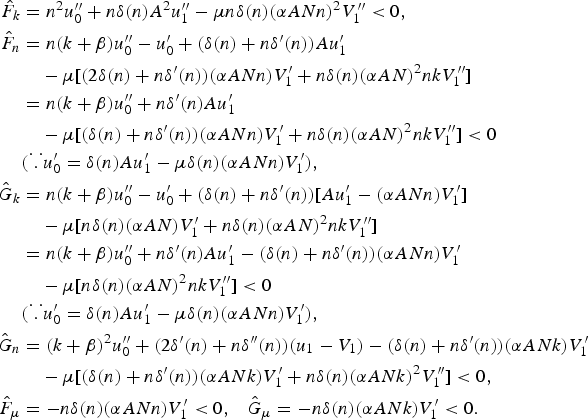$$\eqalign{\hat {F}_k &=n^2{u}''_0 +n\delta ( n) A^2{u}''_1 -\mu n\delta ( n) ( \alpha ANn) ^2{V}''_1 < 0\comma \; \cr \hat {F}_n &=n( k+\beta ) {u}''_0 -{u}'_0 +( {\delta ( n) +n{\delta }'( n) } ) A{u}'_1 \cr & \quad -\mu [( {2\delta ( n) +n{\delta }'( n) } ) ( \alpha ANn) {V}'_1 +n\delta ( n) ( \alpha AN) ^2nk{V}''_1 ] \cr & =n( k+\beta ) {u}''_0 +n{\delta }'( n) A{u}'_1 \cr & \quad -\mu [( {\delta ( n) +n{\delta }'( n) } ) ( \alpha ANn) {V}'_1 +n\delta ( n) ( \alpha AN) ^2nk{V}''_1 ] < 0 \cr &( \because{u}'_0 =\delta ( n) A{u}'_1 -\mu \delta ( n) ( \alpha ANn) {V}'_1 ) \comma \; \cr \hat {G}_k &=n( k+\beta ) {u}''_0 -{u}'_0 +( \delta ( n) +n{\delta }'( n) ) [A{u}'_1 -( \alpha ANn) {V}'_1 ] \cr & \quad -\mu [{n\delta ( n) ( \alpha AN) {V}'_1 +n\delta ( n) ( \alpha AN)^2nk{V}''_1 } ] \cr & =n( k+\beta ) {u}''_0 +n{\delta }'( n) A{u}'_1 -( \delta ( n) +n{\delta }'( n) ) ( \alpha ANn) {V}'_1 \cr & \quad -\mu [{n\delta ( n) ( \alpha AN)^2nk{V}''_1 } ] < 0 \cr &( \because{u}'_0 =\delta ( n) A{u}'_1 -\mu \delta ( n) ( \alpha ANn) {V}'_1 ) \comma \; \cr \hat {G}_n &=( k+\beta ) ^2{u}''_0 +( 2{\delta }'( n) +n{\delta }''( n) ) ( u_1 -V_1 ) -( \delta ( n) +n{\delta }'( n) ) ( \alpha ANk) {V}'_1 \cr & \quad -\mu [{( \delta ( n) +n{\delta }'( n) ) ( \alpha ANk) {V}'_1 +n\delta ( n) ( \alpha ANk)^2{V}''_1 } ] < 0\comma \; \cr \hat {F}_\mu &=-n\delta ( n) ( \alpha ANn) {V}'_1 < 0\comma \; \, \, \, \hat {G}_\mu =-n\delta ( n) ( \alpha ANk) {V}'_1 < 0.}$$ Noting that 
$\hat {G}_{\mu} =\hat {F}_{\mu} k/n$, we have
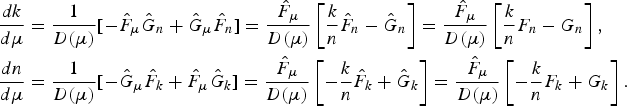$$\eqalign{& \displaystyle{{dk} \over {d\mu }} = \displaystyle{1 \over {D( \mu ) }}[{-{\hat{F}}_\mu {\hat{G}}_n + {\hat{G}}_\mu {\hat{F}}_n} ] = \displaystyle{{{\hat{F}}_\mu } \over {D( \mu ) }}\left[{\displaystyle{k \over n}{\hat{F}}_n-{\hat{G}}_n} \right]= \displaystyle{{{\hat{F}}_\mu } \over {D( \mu ) }}\left[{\displaystyle{k \over n}F_n-G_n} \right]\comma \; \cr & \displaystyle{{dn} \over {d\mu }} = \displaystyle{1 \over {D( \mu ) }}[{-{\hat{G}}_\mu {\hat{F}}_k + {\hat{F}}_\mu {\hat{G}}_k} ] = \displaystyle{{{\hat{F}}_\mu } \over {D( \mu ) }}\left[{-\displaystyle{k \over n}{\hat{F}}_k + {\hat{G}}_k} \right]= \displaystyle{{{\hat{F}}_\mu } \over {D( \mu ) }}\left[{-\displaystyle{k \over n}F_k + G_k} \right].}$$A.2 Proof of D(μ) > 0
We have D(μ) = D(0) + μφ(0 ≤ μ ≤ 1), where 
$\varphi =F_{k} \hat {G}_{n\mu } +G_{n} \hat {F}_{k\mu } -F_{n} \hat {G}_{k\mu } -G_{k} \hat {F}_{n\mu } $,
$$\eqalign{\hat {G}_{n\mu } & \equiv \partial \hat {G}_n /\partial \mu =-[( \delta ( n) +n{\delta }'( n) ) ( \alpha ANk) {V}'_1 +n\delta ( n) ( \alpha ANk) ^2{V}''_1 ] \comma \; \cr \hat {F}_{k\mu } & \equiv \partial \hat {F}_k /\partial \mu =-n\delta ( n) ( \alpha ANn) ^2{V}''_1\comma \; \, \, \hat {G}_{k\mu } \equiv \partial \hat {G}_k /\partial \mu =-n\delta ( n) ( \alpha AN) ^2nk{V}''_1}$$and
$$\hat {F}_{n\mu } \equiv \partial \hat {F}_n /\partial \mu =-[( {\delta ( n) +n{\delta }'( n) } ) ( \alpha ANn) {V}'_1 +n\delta ( n) ( \alpha AN) ^2nk{V}''_1 ] .$$ The second-order condition for parental utility maximization and the condition for stability of the competitive equilibrium imply D(0) > 0, and the second-order condition for social welfare maximization implies D(1) > 0. Since φ does not depend on μ, we have 
$D( \mu) >0 \forall \mu $.
A.3 Proof of proposition 1
Noting that 
$\hat {G}_{\mu} =( k/n) \hat {F}_{\mu} $, we rewrite (14) as
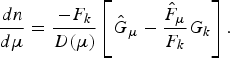$$\displaystyle{{dn} \over {d\mu }} = \displaystyle{{-F_k} \over {D( \mu ) }}\left[{{\hat{G}}_\mu -\displaystyle{{{\hat{F}}_\mu } \over {F_k}}G_k} \right]. $$Differentiating (11) with respect to k and μ and substituting μ = 0 into the resulting equation yields
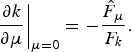$$\left. {\displaystyle{{\partial k} \over {\partial \mu }}} \right\vert _{\mu = 0} = -\displaystyle{{{\hat{F}}_\mu } \over {F_k}}.$$ From (A1), (A2) and 
$\hat {G}_{\mu} =-n\delta ( n) ( \alpha ANk) {V}'$, we have
$$\left. {\displaystyle{{dn} \over {d\mu }}} \right\vert _{\mu = 0} = -\displaystyle{{F_k( k^*\comma \; n^*) } \over {D( \mu ) }}\left[{-n^*\delta ( n^*) ( \alpha ANk^*) {{V}^{\prime}}_1( \alpha ANn^*k^*) + G_k( k^*\comma \; n^*) {\left. {\displaystyle{{\partial k} \over {\partial \mu }}} \right\vert }_{\mu = 0}} \right].$$ Noting that the sign of dn/d μ does not depend on μ, (A3) implies that, if (15) is satisfied, then 
$dn/d\mu >0\forall \mu $.
A.4 Proof of proposition 2
Defining k* (n S) as k that satisfies F(k, n S) = 0, (6) and (9) imply that k* (n S) > k S. Differentiating (6) with respect to k and n yields ∂k/∂n = −F n/F k < 0. Hence, if n* ≤ n S, then k* ≥ k* (n S) > k S.
A.5 Proof of proposition 3
Differentiating π 1 = α ANnk with respect to μ and substituting (13) and (14) yields
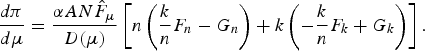$$\displaystyle{{d\pi } \over {d\mu }} = \displaystyle{{\alpha AN{\hat{F}}_\mu } \over {D( \mu ) }}\left[{n\left({\displaystyle{k \over n}F_n-G_n} \right)+ k\left({-\displaystyle{k \over n}F_k + G_k} \right)} \right]. $$Furthermore, substituting G k = F n − (δ(n) + n δ′(n))α ANnV′1 and G n = U nn − (δ(n) + n δ′(n))α ANkV′1 (where U nn ≡ ∂2U 0/∂n 2) into (A4) yields
$$\eqalign{& \displaystyle{{d\pi } \over {d\mu }} = \displaystyle{{-\alpha ANn{\hat{F}}_\mu } \over {D( \mu ) }}\left[{{\left({\displaystyle{k \over n}} \right)}^2F_k-2\displaystyle{k \over n}F_n + U_{nn}} \right]\cr & \quad \quad = \displaystyle{{-\alpha ANn{\hat{F}}_\mu } \over {D( \mu ) F_k}}\left[{{( \displaystyle{k \over n}F_k-F_n) }^2 + F_kU_{nn}-{( F_n) }^2} \right].}$$We have F k U nn − (F n) 2 > 0 from the second-order conditions for the parents' utility maximization, and hence dπ/dμ < 0.
A.6 Proof of proposition 5
Using (9) and (10), we rewrite (26) and (27), respectively, as follows:
$$\hat{\tau }^* = \displaystyle{{[\delta ( n^S) + \rho ] \delta ( n^S) \alpha ANn^Sk^S{{V}^{\prime}}_1-\rho k^S{{u}^{\prime}}_0} \over {Ak^S[\delta ( n^S) + \rho ] \delta ( n^S) {{u}^{\prime}}_1}}\comma \; $$
$$\hat{T}^* = \displaystyle{{[\delta ( n^S) + \rho ] [\delta ( n^S) + n^S{\delta }^{\prime}( n^S) ] \alpha ANn^Sk^S{{V}^{\prime}}_1-\rho ( k^S + \beta ) {{u}^{\prime}}_0} \over {[\delta ( n^S) + \rho + n^S{\delta }^{\prime}( n^S) ] {{u}^{\prime}}_0}}. $$Subtracting the numerator of (A6) from that of (A5) yields
$$-n^S{\delta }'( n^S) [\delta ( n^S) +\rho ] \alpha ANn^Sk^S{V}'_1 +\rho \beta {u}'_0 >0.$$ Since the denominators of (A6) and (A5) are both positive, we have that, if 
$\hat {\tau }^{\ast} \le 0$, then 
$\hat {T}^{\ast} <0$.
