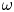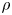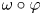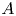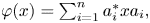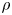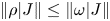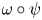1. Introduction
For two states $\omega$![]() and $\rho$
and $\rho$![]() on a C$^{*}$
on a C$^{*}$![]() -algebra $\mathcal {R}$
-algebra $\mathcal {R}$![]() , $\rho$
, $\rho$![]() is regarded to be unitarily more mixed than $\omega$
is regarded to be unitarily more mixed than $\omega$![]() if $\rho$
if $\rho$![]() is contained in the weak* closure of the convex hull of the unitary orbit of $\omega$
is contained in the weak* closure of the convex hull of the unitary orbit of $\omega$![]() . In [Reference Alberti1, Reference Alberti and Uhlmann2, Reference Wehrl29], Alberti, Uhlmann and Wehrl studied the notion of maximally unitarily mixed states on von Neumann algebras and such states were characterized by Alberti in [Reference Alberti1]. Recently, this topic has been revitalized in the broader context of C$^{*}$
. In [Reference Alberti1, Reference Alberti and Uhlmann2, Reference Wehrl29], Alberti, Uhlmann and Wehrl studied the notion of maximally unitarily mixed states on von Neumann algebras and such states were characterized by Alberti in [Reference Alberti1]. Recently, this topic has been revitalized in the broader context of C$^{*}$![]() -algebras by Archbold et al. [Reference Archbold, Robert and Tikuisis4], who proved among other things that the weak*closure of the set of maximally unitarily mixed states on a C$^{*}$
-algebras by Archbold et al. [Reference Archbold, Robert and Tikuisis4], who proved among other things that the weak*closure of the set of maximally unitarily mixed states on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() is equal to the weak* closure of the convex hull of tracial states and states that factor through simple traceless quotients of $A$
is equal to the weak* closure of the convex hull of tracial states and states that factor through simple traceless quotients of $A$![]() . However, the evolution of open quantum systems is not always unitary, but is described by more general completely positive (trace preserving) maps of the form $\omega \mapsto \sum \nolimits a_i\omega a_i^{*}$
. However, the evolution of open quantum systems is not always unitary, but is described by more general completely positive (trace preserving) maps of the form $\omega \mapsto \sum \nolimits a_i\omega a_i^{*}$![]() , say on the predual of ${{\rm B}(\mathcal {H})}$
, say on the predual of ${{\rm B}(\mathcal {H})}$![]() , so it seems worthwhile to study also a less restrictive notion of when one state is more mixed than the other. The dual of such a map is a unital completely positive map of the form
, so it seems worthwhile to study also a less restrictive notion of when one state is more mixed than the other. The dual of such a map is a unital completely positive map of the form
on $\mathcal {R}={{\rm B}(\mathcal {H})}$![]() . Let ${{\rm E}(A)}$
. Let ${{\rm E}(A)}$![]() be the set of all unital completely positive maps on $A$
be the set of all unital completely positive maps on $A$![]() of the form (1.1), where $a_i\in A$
of the form (1.1), where $a_i\in A$![]() and the sums have only finitely many terms. A natural question in this context is, when a state $\rho$
and the sums have only finitely many terms. A natural question in this context is, when a state $\rho$![]() on a C$^{*}$
on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() (or a normal state on a von Neumann algebra $\mathcal {R}$
(or a normal state on a von Neumann algebra $\mathcal {R}$![]() ) is in the weak* closure (or the norm closure) of the set $\omega \circ {{\rm E}(A)}$
) is in the weak* closure (or the norm closure) of the set $\omega \circ {{\rm E}(A)}$![]() of all states of the form $\omega \circ \psi$
of all states of the form $\omega \circ \psi$![]() , where $\omega$
, where $\omega$![]() is a fixed state (perhaps normal in the case of von Neumann algebras) and $\psi$
is a fixed state (perhaps normal in the case of von Neumann algebras) and $\psi$![]() runs over the set ${{\rm E}(A)}$
runs over the set ${{\rm E}(A)}$![]() . In § 2, we show for normal states on a von Neumann algebra $\mathcal {R}$
. In § 2, we show for normal states on a von Neumann algebra $\mathcal {R}$![]() that $\rho$
that $\rho$![]() is in the norm closure of $\omega \circ {{\rm E}(\mathcal {R})}$
is in the norm closure of $\omega \circ {{\rm E}(\mathcal {R})}$![]() if and only if $\rho$
if and only if $\rho$![]() and $\omega$
and $\omega$![]() agree on the centre of $\mathcal {R}$
agree on the centre of $\mathcal {R}$![]() . We also study the same topic for hermitian normal functionals on $\mathcal {R}$
. We also study the same topic for hermitian normal functionals on $\mathcal {R}$![]() and provide an explicit normal mapping $\psi$
and provide an explicit normal mapping $\psi$![]() in the point-weak* closure of ${{\rm E}(\mathcal {R})}$
in the point-weak* closure of ${{\rm E}(\mathcal {R})}$![]() such that $\rho =\omega \circ \psi$
such that $\rho =\omega \circ \psi$![]() . In the special case of $\mathcal {R}={{\rm B}(\mathcal {H})}$
. In the special case of $\mathcal {R}={{\rm B}(\mathcal {H})}$![]() , hermitian normal functionals are just hermitian trace class operators and maps mapping one such operator to another have been constructed by Hsu et al. in [Reference Hsu, Li-Wei Kuo and Tsai19] and by Li and Du in [Reference Li and Du21], but they do not study the question if such maps are in the closure of ${\rm E}({{\rm B}(\mathcal {H})})$
, hermitian normal functionals are just hermitian trace class operators and maps mapping one such operator to another have been constructed by Hsu et al. in [Reference Hsu, Li-Wei Kuo and Tsai19] and by Li and Du in [Reference Li and Du21], but they do not study the question if such maps are in the closure of ${\rm E}({{\rm B}(\mathcal {H})})$![]() .
.
For a normal state $\omega$![]() on a von Neumann algebra $\mathcal {R}\subseteq {{\rm B}(\mathcal {H})}$
on a von Neumann algebra $\mathcal {R}\subseteq {{\rm B}(\mathcal {H})}$![]() and a map $\phi$
and a map $\phi$![]() of the form (1.1), where $a_i\in \mathcal {R}$
of the form (1.1), where $a_i\in \mathcal {R}$![]() and the sums may have infinitely many terms (that is, $\phi$
and the sums may have infinitely many terms (that is, $\phi$![]() is a quantum channel) any state of the form $\rho =\omega \circ \phi$
is a quantum channel) any state of the form $\rho =\omega \circ \phi$![]() has the following property: if $\tilde {\omega }$
has the following property: if $\tilde {\omega }$![]() is a normal state on ${{\rm B}(\mathcal {H})}$
is a normal state on ${{\rm B}(\mathcal {H})}$![]() that extends $\omega$
that extends $\omega$![]() , then there is a normal state $\tilde {\rho }$
, then there is a normal state $\tilde {\rho }$![]() on ${{\rm B}(\mathcal {H})}$
on ${{\rm B}(\mathcal {H})}$![]() that extends $\rho$
that extends $\rho$![]() such that $\tilde {\rho }$
such that $\tilde {\rho }$![]() and $\tilde {\omega }$
and $\tilde {\omega }$![]() coincide on the commutant $\mathcal {R}^{\prime }$
coincide on the commutant $\mathcal {R}^{\prime }$![]() of $\mathcal {R}$
of $\mathcal {R}$![]() (namely, $\tilde {\rho }=\tilde {\omega }\circ \tilde {\phi }$
(namely, $\tilde {\rho }=\tilde {\omega }\circ \tilde {\phi }$![]() , where $\tilde {\phi }$
, where $\tilde {\phi }$![]() is the map on ${{\rm B}(\mathcal {H})}$
is the map on ${{\rm B}(\mathcal {H})}$![]() given by the same formula as $\phi$
given by the same formula as $\phi$![]() on $\mathcal {R}$
on $\mathcal {R}$![]() ). This property holds in any faithful normal representation of $\mathcal {R}$
). This property holds in any faithful normal representation of $\mathcal {R}$![]() on a Hilbert space $\mathcal {H}$
on a Hilbert space $\mathcal {H}$![]() . In § 2, we will see that this property characterizes states of the form $\omega \circ \phi$
. In § 2, we will see that this property characterizes states of the form $\omega \circ \phi$![]() , where $\phi$
, where $\phi$![]() runs over quantum channels on $\mathcal {R}$
runs over quantum channels on $\mathcal {R}$![]() .
.
Then, in § 3, we study the analogous topic for hermitian functionals $\rho,\, \omega$![]() on a unital C$^{*}$
on a unital C$^{*}$![]() -algebra $A$
-algebra $A$![]() . If $A$
. If $A$![]() has Hausdorff primitive spectrum, Theorem 3.1 shows that $\rho$
has Hausdorff primitive spectrum, Theorem 3.1 shows that $\rho$![]() is in the weak* closure of $\omega \circ {{\rm E}(A)}$
is in the weak* closure of $\omega \circ {{\rm E}(A)}$![]() if and only if $\omega$
if and only if $\omega$![]() and $\rho$
and $\rho$![]() agree on the centre of $A$
agree on the centre of $A$![]() and $\|c\rho \|\leq \|c\omega \|$
and $\|c\rho \|\leq \|c\omega \|$![]() for each positive element $c$
for each positive element $c$![]() in the centre of $A$
in the centre of $A$![]() . If the primitive spectrum of $A$
. If the primitive spectrum of $A$![]() is not Hausdorff, this characterization is not true any more, but an alternative one is given in Theorem 3.7.
is not Hausdorff, this characterization is not true any more, but an alternative one is given in Theorem 3.7.
For two states $\omega$![]() and $\rho$
and $\rho$![]() on a C$^{*}$
on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() , $\rho$
, $\rho$![]() is regarded here to be more mixed than $\omega$
is regarded here to be more mixed than $\omega$![]() . if $\rho$
. if $\rho$![]() is contained in the weak* closure $\overline {\omega \circ {{\rm E}(A)}}$
is contained in the weak* closure $\overline {\omega \circ {{\rm E}(A)}}$![]() of the set $\omega \circ {{\rm E}(A)}:=\{\omega \circ \psi :\, \psi \in {{\rm E}(A)}\}$
of the set $\omega \circ {{\rm E}(A)}:=\{\omega \circ \psi :\, \psi \in {{\rm E}(A)}\}$![]() . Then, $\omega$
. Then, $\omega$![]() is called maximally mixed if for each state $\rho$
is called maximally mixed if for each state $\rho$![]() on $A$
on $A$![]() the condition that $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
the condition that $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() implies that $\omega \in \overline {\rho \circ {{\rm E}(A)}}$
implies that $\omega \in \overline {\rho \circ {{\rm E}(A)}}$![]() ; in other words, $\overline {\omega \circ {{\rm E}(A)}}$
; in other words, $\overline {\omega \circ {{\rm E}(A)}}$![]() is minimal among weak* closed ${{\rm E}(A)}$
is minimal among weak* closed ${{\rm E}(A)}$![]() -invariant subsets of the set $S(A)$
-invariant subsets of the set $S(A)$![]() of all states on $A$
of all states on $A$![]() . This is a coarser relation than the one considered in the references mentioned above, where instead of ${{\rm E}(A)}$
. This is a coarser relation than the one considered in the references mentioned above, where instead of ${{\rm E}(A)}$![]() , only convex combinations of unitary similarities are considered. In § 4, we show that each maximally mixed state on a unital C$^{*}$
, only convex combinations of unitary similarities are considered. In § 4, we show that each maximally mixed state on a unital C$^{*}$![]() -algebra $A$
-algebra $A$![]() must annihilate the strong radical $J_A$
must annihilate the strong radical $J_A$![]() of $A$
of $A$![]() (= the intersection of all two-sided maximal ideals of $A$
(= the intersection of all two-sided maximal ideals of $A$![]() ) and, if $A$
) and, if $A$![]() is a properly infinite von Neumann algebra, the converse is also true. Furthermore, the set $S_m(A)$
is a properly infinite von Neumann algebra, the converse is also true. Furthermore, the set $S_m(A)$![]() of all maximally mixed states contains all states that annihilate some intersection of finitely many maximal ideals of $A$
of all maximally mixed states contains all states that annihilate some intersection of finitely many maximal ideals of $A$![]() and is therefore weak* dense in $S(A/J_A)$
and is therefore weak* dense in $S(A/J_A)$![]() . These results are analogous to those of [Reference Archbold, Robert and Tikuisis4] and [Reference Alberti1] for unitarily maximally mixed states. For C$^{*}$
. These results are analogous to those of [Reference Archbold, Robert and Tikuisis4] and [Reference Alberti1] for unitarily maximally mixed states. For C$^{*}$![]() -algebras with the Dixmier property, the authors of [Reference Archbold, Robert and Tikuisis4] provided a more precise determination of maximally unitarily mixed states than for general C$^{*}$
-algebras with the Dixmier property, the authors of [Reference Archbold, Robert and Tikuisis4] provided a more precise determination of maximally unitarily mixed states than for general C$^{*}$![]() -algebras. In our present context, the role of C$^{*}$
-algebras. In our present context, the role of C$^{*}$![]() -algebras with the Dixmier property can be played by weakly central C$^{*}$
-algebras with the Dixmier property can be played by weakly central C$^{*}$![]() -algebras. For a weakly central C$^{*}$
-algebras. For a weakly central C$^{*}$![]() -algebra $A$
-algebra $A$![]() , we show that the set $S_m(A)$
, we show that the set $S_m(A)$![]() is weak* closed (and hence equal to the set of all states that annihilate $J_A$
is weak* closed (and hence equal to the set of all states that annihilate $J_A$![]() ) if and only if each primitive ideal of $A$
) if and only if each primitive ideal of $A$![]() which contains $J_A$
which contains $J_A$![]() is maximal. States in $S_m(\mathcal {R})$
is maximal. States in $S_m(\mathcal {R})$![]() for a general von Neumann algebra $\mathcal {R}$
for a general von Neumann algebra $\mathcal {R}$![]() are also characterized.
are also characterized.
Throughout the paper, an ideal means a norm closed two-sided ideal and all C $^{*}$![]() -algebras are assumed to be unital unless explicitly stated otherwise.
-algebras are assumed to be unital unless explicitly stated otherwise.
2. The case of normal states on a von Neumann algebra
We denote by $A^{\sharp }$![]() the dual of a Banach case $A$
the dual of a Banach case $A$![]() . In what follows $A$
. In what follows $A$![]() will usually be a C$^{*}$
will usually be a C$^{*}$![]() -algebra. Throughout this article, $\mathcal {R}$
-algebra. Throughout this article, $\mathcal {R}$![]() is a von Neumann algebra, $\mathcal {R}_{\sharp }$
is a von Neumann algebra, $\mathcal {R}_{\sharp }$![]() its predual (that is, the space of all weak* continuous linear functionals on $\mathcal {R}$
its predual (that is, the space of all weak* continuous linear functionals on $\mathcal {R}$![]() ) and $\mathcal {Z}$
) and $\mathcal {Z}$![]() the centre of $R$
the centre of $R$![]() . Basic facts concerning von Neumann algebras, that will be used here without explicitly mentioning a reference, can be found in [Reference Kadison and Ringrose20, Reference Takesaki28].
. Basic facts concerning von Neumann algebras, that will be used here without explicitly mentioning a reference, can be found in [Reference Kadison and Ringrose20, Reference Takesaki28].
We will need a preliminary result of independent interest, which in the special case (when, in the notation of Theorem 2.1, $\mathcal {A}=\mathcal {R}$![]() and $\mathcal {R}$
and $\mathcal {R}$![]() is a factor or has a separable predual, and positivity was not considered), has been proved by Chatterjee and Smith [Reference Chatterjee and Smith9]. We would like to avoid the separability assumption. In its proof, we will use the notion of the minimal C$^{*}$
is a factor or has a separable predual, and positivity was not considered), has been proved by Chatterjee and Smith [Reference Chatterjee and Smith9]. We would like to avoid the separability assumption. In its proof, we will use the notion of the minimal C$^{*}$![]() -tensor product over $\mathcal {Z}$
-tensor product over $\mathcal {Z}$![]() of two C$^{*}$
of two C$^{*}$![]() -algebras $A$
-algebras $A$![]() and $B$
and $B$![]() both containing an abelian W$^{*}$
both containing an abelian W$^{*}$![]() -algebra $\mathcal {Z}$
-algebra $\mathcal {Z}$![]() in their centres. This product $A\otimes _{\mathcal {Z}}B$
in their centres. This product $A\otimes _{\mathcal {Z}}B$![]() [Reference Blanchard6, Reference Giordano and Mingo13, Reference Magajna22], can be defined as the closure of the image of the algebraic tensor product $A\odot _{\mathcal {Z}}B$
[Reference Blanchard6, Reference Giordano and Mingo13, Reference Magajna22], can be defined as the closure of the image of the algebraic tensor product $A\odot _{\mathcal {Z}}B$![]() in $\oplus _{t\in \Delta }A(t)\otimes B(t)$
in $\oplus _{t\in \Delta }A(t)\otimes B(t)$![]() , where $\Delta$
, where $\Delta$![]() is the maximal ideal space of $\mathcal {Z}$
is the maximal ideal space of $\mathcal {Z}$![]() and, for each $t\in \Delta$
and, for each $t\in \Delta$![]() , $A(t)$
, $A(t)$![]() denotes the quotient C$^{*}$
denotes the quotient C$^{*}$![]() -algebra $A/(tA)$
-algebra $A/(tA)$![]() , where $tA$
, where $tA$![]() is the closed ideal in $A$
is the closed ideal in $A$![]() generated by $t$
generated by $t$![]() (and similarly for $B(t)$
(and similarly for $B(t)$![]() ). (If at least one of the algebras $A$
). (If at least one of the algebras $A$![]() , $B$
, $B$![]() is exact, which will be the case in our application in the proof of Theorem 2.3, $A\otimes _{\mathcal {Z}}B$
is exact, which will be the case in our application in the proof of Theorem 2.3, $A\otimes _{\mathcal {Z}}B$![]() coincides with the quotient of $A\otimes B$
coincides with the quotient of $A\otimes B$![]() by the closed ideal generated by all elements of the form $az\otimes b-a\otimes zb$
by the closed ideal generated by all elements of the form $az\otimes b-a\otimes zb$![]() ($a\in A$
($a\in A$![]() , $b\in B$
, $b\in B$![]() , $z\in \mathcal {Z}$
, $z\in \mathcal {Z}$![]() ) [Reference Magajna22, 3.12].)
) [Reference Magajna22, 3.12].)
Theorem 2.1 Let $\mathcal {A}$![]() be an injective von Neumann subalgebra of a von Neumann algebra $\mathcal {R}$
be an injective von Neumann subalgebra of a von Neumann algebra $\mathcal {R}$![]() containing the centre $\mathcal {Z}$
containing the centre $\mathcal {Z}$![]() of $\mathcal {R}$
of $\mathcal {R}$![]() . Then, each completely contractive $\mathcal {Z}$
. Then, each completely contractive $\mathcal {Z}$![]() -module map $\psi :\mathcal {R}\to \mathcal {A}$
-module map $\psi :\mathcal {R}\to \mathcal {A}$![]() is (as a map into $\mathcal {R}$
is (as a map into $\mathcal {R}$![]() ) in the point-weak* closure of the set consisting of all maps of the form $x\mapsto \sum \nolimits _{i=1}^{n}a_i^{*}xb_i$
) in the point-weak* closure of the set consisting of all maps of the form $x\mapsto \sum \nolimits _{i=1}^{n}a_i^{*}xb_i$![]() ($x\in \mathcal {R}$
($x\in \mathcal {R}$![]() ), where $n\in \mathbb {N}$
), where $n\in \mathbb {N}$![]() and $a_i,\, b_i\in \mathcal {R}$
and $a_i,\, b_i\in \mathcal {R}$![]() satisfy $\sum \nolimits _{i=1}^{n}a_i^{*}a_i\leq 1$
satisfy $\sum \nolimits _{i=1}^{n}a_i^{*}a_i\leq 1$![]() and $\sum \nolimits _{i=1}^{n}b_i^{*}b_i\leq 1$
and $\sum \nolimits _{i=1}^{n}b_i^{*}b_i\leq 1$![]() . If in addition $\psi$
. If in addition $\psi$![]() is unital, then $\psi$
is unital, then $\psi$![]() is in the point-weak* closure of ${{\rm E}(\mathcal {R})}$
is in the point-weak* closure of ${{\rm E}(\mathcal {R})}$![]() .
.
Proof. Let $\mathcal {H}$![]() be a Hilbert space such that $\mathcal {R}\subseteq {{\rm B}(\mathcal {H})}$
be a Hilbert space such that $\mathcal {R}\subseteq {{\rm B}(\mathcal {H})}$![]() . It follows from [Reference Kadison and Ringrose20, 5.5.4] that there is a natural $*$
. It follows from [Reference Kadison and Ringrose20, 5.5.4] that there is a natural $*$![]() -isomorphism $\iota$
-isomorphism $\iota$![]() from $\mathcal {R}\mathcal {R}^{\prime }$
from $\mathcal {R}\mathcal {R}^{\prime }$![]() (the subalgebra of ${{\rm B}(\mathcal {H})}$
(the subalgebra of ${{\rm B}(\mathcal {H})}$![]() generated by $\mathcal {R}\cup \mathcal {R}^{\prime }$
generated by $\mathcal {R}\cup \mathcal {R}^{\prime }$![]() ) onto the algebraic tensor product $\mathcal {R}\odot _{\mathcal {Z}}\mathcal {R}^{\prime }$
) onto the algebraic tensor product $\mathcal {R}\odot _{\mathcal {Z}}\mathcal {R}^{\prime }$![]() , given by $rr^{\prime }\mapsto r\otimes _{\mathcal {Z}} r^{\prime }$
, given by $rr^{\prime }\mapsto r\otimes _{\mathcal {Z}} r^{\prime }$![]() . By [Reference Blanchard6, 2.9], the tensor norm on $\mathcal {R}{\otimes }_{\mathcal {Z}}\mathcal {R}^{\prime }$
. By [Reference Blanchard6, 2.9], the tensor norm on $\mathcal {R}{\otimes }_{\mathcal {Z}}\mathcal {R}^{\prime }$![]() restricted to $\mathcal {R}\odot _{\mathcal {Z}}\mathcal {R}^{\prime }$
restricted to $\mathcal {R}\odot _{\mathcal {Z}}\mathcal {R}^{\prime }$![]() is minimal among all C$^{*}$
is minimal among all C$^{*}$![]() -tensor norms on $\mathcal {R}\odot _{\mathcal {Z}}\mathcal {R}^{\prime }$
-tensor norms on $\mathcal {R}\odot _{\mathcal {Z}}\mathcal {R}^{\prime }$![]() , hence the $*$
, hence the $*$![]() -homomorphism $\iota$
-homomorphism $\iota$![]() extends uniquely to the norm closure $\overline {\overline {\mathcal {R}\mathcal {R}^{\prime }}}$
extends uniquely to the norm closure $\overline {\overline {\mathcal {R}\mathcal {R}^{\prime }}}$![]() . Since $\mathcal {A}$
. Since $\mathcal {A}$![]() is injective and commutes with $\mathcal {R}^{\prime }$
is injective and commutes with $\mathcal {R}^{\prime }$![]() the multiplication $\mu _0:\mathcal {A}\otimes \mathcal {R}^{\prime }\to \overline {\overline {\mathcal {A}\mathcal {R}^{\prime }}}\subseteq {{\rm B}(\mathcal {H})}$
the multiplication $\mu _0:\mathcal {A}\otimes \mathcal {R}^{\prime }\to \overline {\overline {\mathcal {A}\mathcal {R}^{\prime }}}\subseteq {{\rm B}(\mathcal {H})}$![]() is a completely contractive $*$
is a completely contractive $*$![]() -homomorphism [Reference Brown and Ozawa8, 9.3.3, 3.8.5]. But more is true: by [Reference Giordano and Mingo13, 4.2], the natural map $\mathcal {A}\odot _{\mathcal {Z}}\mathcal {R}^{\prime }\to \mathcal {A}\mathcal {R}^{\prime }$
-homomorphism [Reference Brown and Ozawa8, 9.3.3, 3.8.5]. But more is true: by [Reference Giordano and Mingo13, 4.2], the natural map $\mathcal {A}\odot _{\mathcal {Z}}\mathcal {R}^{\prime }\to \mathcal {A}\mathcal {R}^{\prime }$![]() extends (uniquely) to a $*$
extends (uniquely) to a $*$![]() -isomorphism $\mathcal {A}\otimes _{\mathcal {Z}}\mathcal {R}^{\prime }\to \overline {\overline {\mathcal {A}\mathcal {R}^{\prime }}}$
-isomorphism $\mathcal {A}\otimes _{\mathcal {Z}}\mathcal {R}^{\prime }\to \overline {\overline {\mathcal {A}\mathcal {R}^{\prime }}}$![]() . It follows that the composition
. It follows that the composition
is completely contractive and clearly, it is an $\mathcal {R}^{\prime }$![]() -bimodule map, hence extending to such a map $\phi$
-bimodule map, hence extending to such a map $\phi$![]() on ${{\rm B}(\mathcal {H})}$
on ${{\rm B}(\mathcal {H})}$![]() by the Wittstock extension theorem (see [Reference Wittstock30] or [Reference Blecher and Le Merdy7, 3.6.2]). By [Reference Effros and Kishimoto11], $\phi$
by the Wittstock extension theorem (see [Reference Wittstock30] or [Reference Blecher and Le Merdy7, 3.6.2]). By [Reference Effros and Kishimoto11], $\phi$![]() can be approximated in the point-weak* topology by a net of elementary complete contractions of the form
can be approximated in the point-weak* topology by a net of elementary complete contractions of the form
where $a(k)=(a_1(k),\,\ldots,\,a_n(k))^{T}$![]() and $b(k)=(b_1(k),\,\ldots,\,b_n(k))^{T}$
and $b(k)=(b_1(k),\,\ldots,\,b_n(k))^{T}$![]() are columns with the entries $a_i(k),\,b_i(k)\in \mathcal {R}$
are columns with the entries $a_i(k),\,b_i(k)\in \mathcal {R}$![]() and
and
Thus, $\psi$![]() (=$\phi |\mathcal {R}$
(=$\phi |\mathcal {R}$![]() ) can also be approximated by such maps.
) can also be approximated by such maps.
Assume now in addition that $\psi$![]() is unital and consider a point-weak* approximation of $\psi$
is unital and consider a point-weak* approximation of $\psi$![]() of the form (2.1), (2.2). Since
of the form (2.1), (2.2). Since
it follows that $b(k)-a(k)$![]() tends to $0$
tends to $0$![]() in the strong operator topology. Hence, $\psi$
in the strong operator topology. Hence, $\psi$![]() can be approximated by maps of the form $x\mapsto a(k)^{*}xa(k)$
can be approximated by maps of the form $x\mapsto a(k)^{*}xa(k)$![]() in the point-weak* operator topology. To see this, write
in the point-weak* operator topology. To see this, write
and note that $\|a(k)^{*}x(b(k)-a(k))\xi \|\leq \|x\|\|(b(k)-a(k))\xi \|$![]() for each vector $\xi \in \mathcal {H}$
for each vector $\xi \in \mathcal {H}$![]() . Finally, as $a(k)^{*}a(k)$
. Finally, as $a(k)^{*}a(k)$![]() tends to $\psi (1)=1$
tends to $\psi (1)=1$![]() in the strong operator topology, $\psi$
in the strong operator topology, $\psi$![]() can be approximated by maps of the form
can be approximated by maps of the form
that is, by unital completely positive elementary maps.
Lemma 2.2 Let $\omega$![]() and $\rho$
and $\rho$![]() be hermitian functionals on a C$^{*}$
be hermitian functionals on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() such that $\rho |Z=\omega |Z$
such that $\rho |Z=\omega |Z$![]() and $\|c\rho \|\leq \|c\omega \|$
and $\|c\rho \|\leq \|c\omega \|$![]() for all $c\in Z_+$
for all $c\in Z_+$![]() , where $Z$
, where $Z$![]() is the centre of $A$
is the centre of $A$![]() . Then, $\rho _+|Z\leq \omega _+|Z$
. Then, $\rho _+|Z\leq \omega _+|Z$![]() and $\rho _-|Z\leq \omega _-|Z$
and $\rho _-|Z\leq \omega _-|Z$![]() .
.
Thus, if $Z$![]() is a von Neumann algebra, $\omega$
is a von Neumann algebra, $\omega$![]() and $\rho$
and $\rho$![]() are normal and $p^{+}$
are normal and $p^{+}$![]() and $p^{-}$
and $p^{-}$![]() are the support projections of $\omega _+|Z$
are the support projections of $\omega _+|Z$![]() and $\omega _-|Z,$
and $\omega _-|Z,$![]() then there exist elements $c_+$
then there exist elements $c_+$![]() and $c_-$
and $c_-$![]() in $Z$
in $Z$![]() such that $0\leq c_+\leq p^{+}$
such that $0\leq c_+\leq p^{+}$![]() , $0\leq c_-\leq p^{-},$
, $0\leq c_-\leq p^{-},$![]()
Proof. For each $c\in Z_+$![]() and $\theta \in (A^{\sharp })_+$
and $\theta \in (A^{\sharp })_+$![]() , we have that $\|c\theta \|=(c\theta )(1)=\theta (c)$
, we have that $\|c\theta \|=(c\theta )(1)=\theta (c)$![]() and it is also well-known that for each hermitian functional $\sigma$
and it is also well-known that for each hermitian functional $\sigma$![]() the equality $\|\sigma \|=\sigma _+(1)+\sigma _-(1)=\|\sigma _+\|+\|\sigma _-\|$
the equality $\|\sigma \|=\sigma _+(1)+\sigma _-(1)=\|\sigma _+\|+\|\sigma _-\|$![]() holds, hence
holds, hence
Adding and subtracting these two relations, we find that $\rho _+(c)\leq \omega _+(c)$![]() and $\rho _-(c)\leq \omega _-(c)$
and $\rho _-(c)\leq \omega _-(c)$![]() for all $c\in Z_+$
for all $c\in Z_+$![]() . If $Z$
. If $Z$![]() , $\omega$
, $\omega$![]() , $\rho$
, $\rho$![]() , $p^{+}$
, $p^{+}$![]() and $p^{-}$
and $p^{-}$![]() are as in the second part of the lemma, we may regard $Z$
are as in the second part of the lemma, we may regard $Z$![]() as $L^{\infty }(\mu )$
as $L^{\infty }(\mu )$![]() for some positive measure $\mu$
for some positive measure $\mu$![]() and then the existence of elements $c_+$
and then the existence of elements $c_+$![]() and $c_-$
and $c_-$![]() in $Z$
in $Z$![]() satisfying $0\leq c_+\leq p_+$
satisfying $0\leq c_+\leq p_+$![]() , $0\leq c_-\leq p^{-}$
, $0\leq c_-\leq p^{-}$![]() and $\rho _+|Z=c_+\omega _+|Z$
and $\rho _+|Z=c_+\omega _+|Z$![]() , $\rho _-|Z=c_-\omega _-|Z$
, $\rho _-|Z=c_-\omega _-|Z$![]() follows easily, so we will verify here only the last equality in the lemma. The condition $\rho |Z=\omega |Z$
follows easily, so we will verify here only the last equality in the lemma. The condition $\rho |Z=\omega |Z$![]() can be written as $(c_+\omega _+-c_-\omega _-)|Z=(\omega _+-\omega _-)|Z$
can be written as $(c_+\omega _+-c_-\omega _-)|Z=(\omega _+-\omega _-)|Z$![]() , hence $(1-c_+)\omega _+|Z=(1-c_-)\omega _-|Z$
, hence $(1-c_+)\omega _+|Z=(1-c_-)\omega _-|Z$![]() . But $\omega _+=p^{+}\omega _+$
. But $\omega _+=p^{+}\omega _+$![]() and $\omega _-=p^{-}\omega _-$
and $\omega _-=p^{-}\omega _-$![]() , since $p^{+}$
, since $p^{+}$![]() and $p^{-}$
and $p^{-}$![]() are the support projections of $\omega _+|Z$
are the support projections of $\omega _+|Z$![]() and $\omega _-|Z$
and $\omega _-|Z$![]() , hence the required equality follows.
, hence the required equality follows.
By [Reference Halpern17] or [Reference Strătilă and Zsidó27], each positive functional $\omega$![]() on $\mathcal {R}$
on $\mathcal {R}$![]() , such that $\omega |\mathcal {Z}$
, such that $\omega |\mathcal {Z}$![]() is weak* continuous, can be uniquely expressed as
is weak* continuous, can be uniquely expressed as
where $\omega _{\mathcal {Z}}$![]() is a (completely) positive $\mathcal {Z}$
is a (completely) positive $\mathcal {Z}$![]() -module map from $\mathcal {R}$
-module map from $\mathcal {R}$![]() to $\mathcal {Z}$
to $\mathcal {Z}$![]() such that $\omega _{\mathcal {Z}}(1)$
such that $\omega _{\mathcal {Z}}(1)$![]() is the support projection $q\in \mathcal {Z}$
is the support projection $q\in \mathcal {Z}$![]() of $\omega |{\mathcal {Z}}$
of $\omega |{\mathcal {Z}}$![]() . If $\omega$
. If $\omega$![]() is weak* continuous, then so is also $\omega _{\mathcal {Z}}$
is weak* continuous, then so is also $\omega _{\mathcal {Z}}$![]() . Observe that the support projections of $\omega$
. Observe that the support projections of $\omega$![]() and $\omega _{\mathcal {Z}}$
and $\omega _{\mathcal {Z}}$![]() coincide, if $\omega$
coincide, if $\omega$![]() is normal. (Indeed, for each projection $e\in \mathcal {R}$
is normal. (Indeed, for each projection $e\in \mathcal {R}$![]() , we have $0\leq \omega _{\mathcal {Z}}(e)\leq \omega _{\mathcal {Z}}(1)=q$
, we have $0\leq \omega _{\mathcal {Z}}(e)\leq \omega _{\mathcal {Z}}(1)=q$![]() , hence $\omega (e)=(\omega |\mathcal {Z})(\omega _{\mathcal {Z}}(e))=0$
, hence $\omega (e)=(\omega |\mathcal {Z})(\omega _{\mathcal {Z}}(e))=0$![]() if and only if $\omega _{\mathcal {Z}}(e)=0$
if and only if $\omega _{\mathcal {Z}}(e)=0$![]() since $q$
since $q$![]() is the support projection of $\omega |\mathcal {Z}$
is the support projection of $\omega |\mathcal {Z}$![]() .)
.)
Theorem 2.3 Let $\omega,\,\rho$![]() be normal hermitian functionals on $\mathcal {R}$
be normal hermitian functionals on $\mathcal {R}$![]() . There exists a normal unital completely positive map $\psi :\mathcal {R}\to \mathcal {R}$
. There exists a normal unital completely positive map $\psi :\mathcal {R}\to \mathcal {R}$![]() in the point-weak* closure of ${{\rm E}(\mathcal {R})}$
in the point-weak* closure of ${{\rm E}(\mathcal {R})}$![]() satisfying $\psi (1)=1$
satisfying $\psi (1)=1$![]() and $\psi _{\sharp }(\omega )=\rho$
and $\psi _{\sharp }(\omega )=\rho$![]() if and only if
if and only if
Under this condition, $\rho$![]() is in the norm closure of $\omega \circ {{\rm E}(\mathcal {R})}$
is in the norm closure of $\omega \circ {{\rm E}(\mathcal {R})}$![]() .
.
Proof. Since maps in ${{\rm E}(\mathcal {R})}$![]() are unital and completely positive, they are also completely contractive. Each map in ${{\rm E}(\mathcal {R})}$
are unital and completely positive, they are also completely contractive. Each map in ${{\rm E}(\mathcal {R})}$![]() is of the form $\psi (x)=\sum \nolimits _{i=1}^{n}a_i^{*}xa_i$
is of the form $\psi (x)=\sum \nolimits _{i=1}^{n}a_i^{*}xa_i$![]() , where $a_i\in \mathcal {R}$
, where $a_i\in \mathcal {R}$![]() and $\sum \nolimits _{i=1}^{n}a_i^{*}a_i=1$
and $\sum \nolimits _{i=1}^{n}a_i^{*}a_i=1$![]() , hence weak* continuous and the corresponding map $\psi _{\sharp }$
, hence weak* continuous and the corresponding map $\psi _{\sharp }$![]() on the predual $\mathcal {R}_{\sharp }$
on the predual $\mathcal {R}_{\sharp }$![]() of $\mathcal {R}$
of $\mathcal {R}$![]() is given by $\psi _{\sharp }(\omega )=\sum \nolimits _{i=1}^{n}a_i\omega a_i^{*}$
is given by $\psi _{\sharp }(\omega )=\sum \nolimits _{i=1}^{n}a_i\omega a_i^{*}$![]() and is a $\mathcal {Z}$
and is a $\mathcal {Z}$![]() -module map with $\|\psi _{\sharp }\|=\|\psi \|=1$
-module map with $\|\psi _{\sharp }\|=\|\psi \|=1$![]() . Hence $\|c\psi _{\sharp }(\omega )\|=\|\psi _{\sharp }(c\omega )\|\leq \|c\omega \|$
. Hence $\|c\psi _{\sharp }(\omega )\|=\|\psi _{\sharp }(c\omega )\|\leq \|c\omega \|$![]() for each $c\in \mathcal {Z}$
for each $c\in \mathcal {Z}$![]() . This means that the inequality $\|(c \omega )\circ \psi \|\leq \|c\omega \|$
. This means that the inequality $\|(c \omega )\circ \psi \|\leq \|c\omega \|$![]() holds for all $\psi \in {{\rm E}(\mathcal {R})}$
holds for all $\psi \in {{\rm E}(\mathcal {R})}$![]() , hence also for all $\psi$
, hence also for all $\psi$![]() in the point-weak* closure of ${{\rm E}(\mathcal {R})}$
in the point-weak* closure of ${{\rm E}(\mathcal {R})}$![]() since $c\omega$
since $c\omega$![]() is weak* continuous. If $\psi$
is weak* continuous. If $\psi$![]() is a weak* continuous such map and $\rho =\psi _{\sharp }(\omega )$
is a weak* continuous such map and $\rho =\psi _{\sharp }(\omega )$![]() , then $\|c\rho \|=\|(c\omega )\circ \psi \|\leq \|c\omega \|$
, then $\|c\rho \|=\|(c\omega )\circ \psi \|\leq \|c\omega \|$![]() . Furthermore, since $\psi |\mathcal {Z}={{\rm id}}$
. Furthermore, since $\psi |\mathcal {Z}={{\rm id}}$![]() for each such map $\psi$
for each such map $\psi$![]() , it follows that $\rho |\mathcal {Z}=\omega |\mathcal {Z}$
, it follows that $\rho |\mathcal {Z}=\omega |\mathcal {Z}$![]() for each $\rho \in \overline {\omega \circ {{\rm E}(\mathcal {R})}}$
for each $\rho \in \overline {\omega \circ {{\rm E}(\mathcal {R})}}$![]() .
.
Assume now that the condition (2.4) holds. Decompose each of the functionals $\omega _+,\,\omega _-,\,\rho _+,\,\rho _-$![]() as described in (2.3), so that
as described in (2.3), so that
where $\rho _{\mathcal {Z}}^{+},\,\rho _{\mathcal {Z}}^{-},\,\omega _{\mathcal {Z}}^{+},\,\omega _{\mathcal {Z}}^{-}$![]() are $\mathcal {Z}$
are $\mathcal {Z}$![]() -module homomorphisms from $\mathcal {R}$
-module homomorphisms from $\mathcal {R}$![]() to $\mathcal {Z}$
to $\mathcal {Z}$![]() such that $p^{+}:=\omega _{\mathcal {Z}}^{+}(1)$
such that $p^{+}:=\omega _{\mathcal {Z}}^{+}(1)$![]() and $p^{-}:=\omega _{\mathcal {Z}}^{-}(1)$
and $p^{-}:=\omega _{\mathcal {Z}}^{-}(1)$![]() are the support projections of $\omega _+|\mathcal {Z}$
are the support projections of $\omega _+|\mathcal {Z}$![]() and $\omega _-|\mathcal {Z}$
and $\omega _-|\mathcal {Z}$![]() . Let $p_+$
. Let $p_+$![]() and $p_-$
and $p_-$![]() be the support projections of $\omega _+$
be the support projections of $\omega _+$![]() and $\omega _-$
and $\omega _-$![]() . Observe that $p_+\leq p^{+}$
. Observe that $p_+\leq p^{+}$![]() and $p_-\leq p^{-}$
and $p_-\leq p^{-}$![]() . (Namely, $\omega _+ (1-p^{+})=(\omega _+|\mathcal {Z})(1-p^{+})=0$
. (Namely, $\omega _+ (1-p^{+})=(\omega _+|\mathcal {Z})(1-p^{+})=0$![]() implies that $1-p^{+}\leq 1-p_+$
implies that $1-p^{+}\leq 1-p_+$![]() , hence $p_+\leq p^{+}$
, hence $p_+\leq p^{+}$![]() .) By Lemma 2.2, there exists $c_+,\, c_-\in \mathcal {Z}$
.) By Lemma 2.2, there exists $c_+,\, c_-\in \mathcal {Z}$![]() such that $0\leq c_+\leq p^{+}$
such that $0\leq c_+\leq p^{+}$![]() , $0\leq c_-\leq p^{-}$
, $0\leq c_-\leq p^{-}$![]() ,
,
When we first tried to find a map $\psi$![]() satisfying the requirements of the theorem to be of the form $\psi =a\rho _{\mathcal {Z}}^{+}+b\rho _{\mathcal {Z}}^{-}$
satisfying the requirements of the theorem to be of the form $\psi =a\rho _{\mathcal {Z}}^{+}+b\rho _{\mathcal {Z}}^{-}$![]() , where $a,\,b\in \mathcal {R}_+$
, where $a,\,b\in \mathcal {R}_+$![]() , we found that it is not always possible to simultaneously satisfy the conditions $\psi (1)=1$
, we found that it is not always possible to simultaneously satisfy the conditions $\psi (1)=1$![]() and $\omega \circ \psi =\rho$
and $\omega \circ \psi =\rho$![]() by maps of such a form. But after several attempts we arrived to the following map:
by maps of such a form. But after several attempts we arrived to the following map:
Here, $\theta$![]() is any fixed normal positive unital $\mathcal {Z}$
is any fixed normal positive unital $\mathcal {Z}$![]() -module map from $\mathcal {R}$
-module map from $\mathcal {R}$![]() to $\mathcal {Z}$
to $\mathcal {Z}$![]() . (Such a map exists even on $\mathcal {Z}^{\prime }\supseteq \mathcal {R}$
. (Such a map exists even on $\mathcal {Z}^{\prime }\supseteq \mathcal {R}$![]() since $\mathcal {Z}^{\prime }$
since $\mathcal {Z}^{\prime }$![]() is of type $I$
is of type $I$![]() , hence isomorphic to a direct sum of matrix algebras of the form ${{\rm M}}_n(\mathcal {Z})$
, hence isomorphic to a direct sum of matrix algebras of the form ${{\rm M}}_n(\mathcal {Z})$![]() , where $n$
, where $n$![]() can be infinite.) This map $\psi$
can be infinite.) This map $\psi$![]() is positive, weak* continuous, $\mathcal {Z}$
is positive, weak* continuous, $\mathcal {Z}$![]() -module map, with the range contained in the commutative C$^{*}$
-module map, with the range contained in the commutative C$^{*}$![]() -algebra generated by $\mathcal {Z}\cup \{p_+\}$
-algebra generated by $\mathcal {Z}\cup \{p_+\}$![]() , hence completely positive. We can immediately verify that $\psi$
, hence completely positive. We can immediately verify that $\psi$![]() is also unital:
is also unital:
Now, we are going to compute
For this, first observe that if $f,\,g:\mathcal {R}\to \mathcal {Z}$![]() are $\mathcal {Z}$
are $\mathcal {Z}$![]() -module maps and $a\in \mathcal {R}$
-module maps and $a\in \mathcal {R}$![]() , then $(f\circ (ag))(x)=f(ag(x))=f(a)g(x)=(f(a)g)(x)$
, then $(f\circ (ag))(x)=f(ag(x))=f(a)g(x)=(f(a)g)(x)$![]() , that is, $f\circ (ag)=f(a)g$
, that is, $f\circ (ag)=f(a)g$![]() . Note also that $p^{+}\rho _{\mathcal {Z}}^{+}=\rho _{\mathcal {Z}}^{+}$
. Note also that $p^{+}\rho _{\mathcal {Z}}^{+}=\rho _{\mathcal {Z}}^{+}$![]() and $p^{-}\rho _{\mathcal {Z}}^{-}=\rho_{\mathcal{Z}}^{-}$
and $p^{-}\rho _{\mathcal {Z}}^{-}=\rho_{\mathcal{Z}}^{-}$![]() since Lemma 2.2 implies that the support projection of $\rho _+|\mathcal {Z}$
since Lemma 2.2 implies that the support projection of $\rho _+|\mathcal {Z}$![]() is dominated by the support projection of $\omega _+|\mathcal {Z}$
is dominated by the support projection of $\omega _+|\mathcal {Z}$![]() and similarly for $\rho _-|\mathcal {Z}$
and similarly for $\rho _-|\mathcal {Z}$![]() and $\omega _-|\mathcal {Z}$
and $\omega _-|\mathcal {Z}$![]() . From the definition (2.6) of $\psi$
. From the definition (2.6) of $\psi$![]() and using that $\omega _{\mathcal {Z}}^{+}$
and using that $\omega _{\mathcal {Z}}^{+}$![]() and $\omega _{\mathcal {Z}}^{-}$
and $\omega _{\mathcal {Z}}^{-}$![]() are $\mathcal {Z}$
are $\mathcal {Z}$![]() -module maps with ranges contained in $\mathcal {Z}$
-module maps with ranges contained in $\mathcal {Z}$![]() and mutually orthogonal support projections $p_+$
and mutually orthogonal support projections $p_+$![]() and $p_-$
and $p_-$![]() (which are just the support projections of $\omega _+$
(which are just the support projections of $\omega _+$![]() and $\omega _-$
and $\omega _-$![]() , respectively), we now compute
, respectively), we now compute

and similarly
From (2.7), (2.8) and (2.9) we have, using also (2.5) and (2.6),

It follows from Theorem 2.1 that $\psi$![]() is in the point-weak* closure of ${{\rm E}(\mathcal {R})}$
is in the point-weak* closure of ${{\rm E}(\mathcal {R})}$![]() . Thus, $\rho =\omega \circ \psi$
. Thus, $\rho =\omega \circ \psi$![]() is in the weak closure of the convex set $\omega \circ {{\rm E}(\mathcal {R})}$
is in the weak closure of the convex set $\omega \circ {{\rm E}(\mathcal {R})}$![]() , which is the same as the norm closure by the Hahn–Banach theorem and the fact that $\mathcal {R}$
, which is the same as the norm closure by the Hahn–Banach theorem and the fact that $\mathcal {R}$![]() is the dual of $\mathcal {R}_{\sharp }$
is the dual of $\mathcal {R}_{\sharp }$![]() .
.
When $\omega$![]() and $\rho$
and $\rho$![]() are states, Theorem 2.3 simplifies to the following corollary:
are states, Theorem 2.3 simplifies to the following corollary:
Corollary 2.4 Let $\omega$![]() and $\rho$
and $\rho$![]() be normal states on $\mathcal {R}$
be normal states on $\mathcal {R}$![]() . There exists a normal unital completely positive map $\psi$
. There exists a normal unital completely positive map $\psi$![]() in the point-weak* closure of ${{\rm E}(\mathcal {R})}$
in the point-weak* closure of ${{\rm E}(\mathcal {R})}$![]() satisfying $\psi _{\sharp }(\omega )=\rho$
satisfying $\psi _{\sharp }(\omega )=\rho$![]() if and only if $\rho |\mathcal {Z}=\omega |\mathcal {Z}$
if and only if $\rho |\mathcal {Z}=\omega |\mathcal {Z}$![]() . This condition is satisfied if and only if $\|c\rho \|\leq \|c\omega \|$
. This condition is satisfied if and only if $\|c\rho \|\leq \|c\omega \|$![]() for all $c\in \mathcal {Z}_+$
for all $c\in \mathcal {Z}_+$![]() .
.
Proof. By Theorem 2.3, we only need to verify that the condition $\rho |\mathcal {Z}=\omega |\mathcal {Z}$![]() implies that $\|c\rho \|\leq \|c\omega \|$
implies that $\|c\rho \|\leq \|c\omega \|$![]() for all $c\in \mathcal {Z}_+$
for all $c\in \mathcal {Z}_+$![]() and conversely. Since $\omega$
and conversely. Since $\omega$![]() and $\rho$
and $\rho$![]() are positive, we have $\|c\rho \|=(c\rho )(1)=\rho (c)$
are positive, we have $\|c\rho \|=(c\rho )(1)=\rho (c)$![]() and $\omega (c)=\|c\omega \|$
and $\omega (c)=\|c\omega \|$![]() for all $c\in \mathcal {Z}_+$
for all $c\in \mathcal {Z}_+$![]() . If $\|c\rho \|\leq \|c\omega \|$
. If $\|c\rho \|\leq \|c\omega \|$![]() for all $c\in \mathcal {Z}_+$
for all $c\in \mathcal {Z}_+$![]() , then $\rho (c)\leq \omega (c)$
, then $\rho (c)\leq \omega (c)$![]() . Applying this to $1-c$
. Applying this to $1-c$![]() instead of $c$
instead of $c$![]() , where $0\leq c\leq 1$
, where $0\leq c\leq 1$![]() , it follows that $\rho (c)=\omega (c)$
, it follows that $\rho (c)=\omega (c)$![]() for all such $c$
for all such $c$![]() . But such elements span $\mathcal {Z}$
. But such elements span $\mathcal {Z}$![]() , hence it follows that $\rho |\mathcal {Z}=\omega |\mathcal {Z}$
, hence it follows that $\rho |\mathcal {Z}=\omega |\mathcal {Z}$![]() if and only if $\|c\rho \|\leq \|c\omega \|$
if and only if $\|c\rho \|\leq \|c\omega \|$![]() for all $c\in \mathcal {Z}_+$
for all $c\in \mathcal {Z}_+$![]() .
.
It is well known that on $\mathcal {R}={{\rm B}(\mathcal {H})}$![]() , all normal completely positive unital maps are of the form
, all normal completely positive unital maps are of the form
where $\mathbb {J}$![]() is some set of indexes and $a_j\in \mathcal {R}$
is some set of indexes and $a_j\in \mathcal {R}$![]() are such that $\sum \nolimits _{j\in \mathbb {J}}a_j^{*}a_j=1$
are such that $\sum \nolimits _{j\in \mathbb {J}}a_j^{*}a_j=1$![]() with the convergence in the strong operator topology. Maps on ${{\rm B}(\mathcal {H})}$
with the convergence in the strong operator topology. Maps on ${{\rm B}(\mathcal {H})}$![]() of the form (2.10) are called quantum channels and we will use the same name for maps of such a form on a general von Neumann algebra $\mathcal {R}$
of the form (2.10) are called quantum channels and we will use the same name for maps of such a form on a general von Neumann algebra $\mathcal {R}$![]() . It is well known that on a general von Neumann algebra, not all unital normal completely positive maps are of the form (2.10), so we still have to answer the following question: If $\omega$
. It is well known that on a general von Neumann algebra, not all unital normal completely positive maps are of the form (2.10), so we still have to answer the following question: If $\omega$![]() and $\rho$
and $\rho$![]() are normal states on a von Neumann algebra $\mathcal {R}$
are normal states on a von Neumann algebra $\mathcal {R}$![]() , when does there exist a quantum channel $\phi$
, when does there exist a quantum channel $\phi$![]() on $\mathcal {R}$
on $\mathcal {R}$![]() such that $\omega \circ \phi =\rho ?$
such that $\omega \circ \phi =\rho ?$![]()
Theorem 2.5 For normal states $\omega$![]() and $\rho$
and $\rho$![]() on $\mathcal {R}$
on $\mathcal {R}$![]() , the following statements are equivalent:
, the following statements are equivalent:
(i) There exists a quantum channel $\phi$
 on $\mathcal {R}$
on $\mathcal {R}$ such that $\omega \circ \phi =\rho$
such that $\omega \circ \phi =\rho$ .
.(ii) For every faithful normal representation $\pi$
 of $\mathcal {R}$
of $\mathcal {R}$ on a Hilbert space $\mathcal {H}_{\pi }$
on a Hilbert space $\mathcal {H}_{\pi }$ and any normal state $\tilde {\omega }$
and any normal state $\tilde {\omega }$ on ${{\rm B}(\mathcal {H}_{\pi })}$
on ${{\rm B}(\mathcal {H}_{\pi })}$ that extends $\omega \circ \pi ^{-1}$
that extends $\omega \circ \pi ^{-1}$ , there exists a normal state $\tilde {\rho }$
, there exists a normal state $\tilde {\rho }$ on ${{\rm B}(\mathcal {H}_{\pi })}$
on ${{\rm B}(\mathcal {H}_{\pi })}$ that extends $\rho \circ \pi ^{-1}$
that extends $\rho \circ \pi ^{-1}$ such that $\tilde {\omega }|\pi (\mathcal {R})^{\prime }=\tilde {\rho }|\pi (\mathcal {R})^{\prime }$
such that $\tilde {\omega }|\pi (\mathcal {R})^{\prime }=\tilde {\rho }|\pi (\mathcal {R})^{\prime }$ .
.(iii) For some faithful normal representation of $\mathcal {R}$
 on a Hilbert space $\mathcal {H}$
on a Hilbert space $\mathcal {H}$ , such that $\omega$
, such that $\omega$ is the restriction to $\mathcal {R}$
is the restriction to $\mathcal {R}$ of a vector state $\tilde {\omega }$
of a vector state $\tilde {\omega }$ on ${{\rm B}(\mathcal {H})}$
on ${{\rm B}(\mathcal {H})}$ , there exists a normal state $\tilde {\rho }$
, there exists a normal state $\tilde {\rho }$ on ${{\rm B}(\mathcal {H})}$
on ${{\rm B}(\mathcal {H})}$ such that $\tilde {\rho }|\mathcal {R}=\rho$
such that $\tilde {\rho }|\mathcal {R}=\rho$ and $\tilde {\rho }|\mathcal {R}^{\prime }=\tilde {\omega }|\mathcal {R}^{\prime }$
and $\tilde {\rho }|\mathcal {R}^{\prime }=\tilde {\omega }|\mathcal {R}^{\prime }$ .
.(iv) Let $\pi _{\omega }$
 be the GNS representation of $\mathcal {R}$
be the GNS representation of $\mathcal {R}$ engendered by $\omega$
engendered by $\omega$ on a Hilbert space $\mathcal {H}_{\omega }$
on a Hilbert space $\mathcal {H}_{\omega }$ and let $\xi _{\omega }$
and let $\xi _{\omega }$ be the corresponding cyclic vector. The state $\rho$
be the corresponding cyclic vector. The state $\rho$ annihilates the kernel of $\pi _{\omega }$
annihilates the kernel of $\pi _{\omega }$ and there exists a normal state $\tilde {\rho }$
and there exists a normal state $\tilde {\rho }$ on ${{\rm B}}(\mathcal {H}_{\omega })$
on ${{\rm B}}(\mathcal {H}_{\omega })$ such that $\tilde {\rho }|\pi _{\omega }(\mathcal {R})$
such that $\tilde {\rho }|\pi _{\omega }(\mathcal {R})$ is the state induced by $\rho$
is the state induced by $\rho$ on $\pi _{\omega }(\mathcal {R})\cong \mathcal {R}/\ker \pi _{\omega }$
on $\pi _{\omega }(\mathcal {R})\cong \mathcal {R}/\ker \pi _{\omega }$ and $\tilde {\rho }|\pi _{\omega }(\mathcal {R})^{\prime }=\tilde {\omega }|\pi _{\omega }(\mathcal {R})^{\prime }$
and $\tilde {\rho }|\pi _{\omega }(\mathcal {R})^{\prime }=\tilde {\omega }|\pi _{\omega }(\mathcal {R})^{\prime }$ , where $\tilde {\omega }$
, where $\tilde {\omega }$ is the vector state $x\mapsto \langle x\xi _{\omega },\,\xi _{\omega }\rangle$
is the vector state $x\mapsto \langle x\xi _{\omega },\,\xi _{\omega }\rangle$ on ${{\rm B}}(\mathcal {H}_{\omega })$
on ${{\rm B}}(\mathcal {H}_{\omega })$ .
.
Proof. (i)$\Rightarrow$![]() (ii) If $\rho =\omega \circ \phi$
(ii) If $\rho =\omega \circ \phi$![]() , where $\phi$
, where $\phi$![]() is of the form (2.10), then let $\tilde {\omega }$
is of the form (2.10), then let $\tilde {\omega }$![]() be any state on ${{\rm B}(\mathcal {H}_{\pi })}$
be any state on ${{\rm B}(\mathcal {H}_{\pi })}$![]() extending $\omega \circ \pi ^{-1}$
extending $\omega \circ \pi ^{-1}$![]() , let $\tilde {\phi }$
, let $\tilde {\phi }$![]() be the map on ${{\rm B}(\mathcal {H}_{\pi })}$
be the map on ${{\rm B}(\mathcal {H}_{\pi })}$![]() defined by $\tilde {\phi }(x)=\sum \nolimits _{j\in \mathbb {J}}\pi (a_j^{*})x\pi (a_j)$
defined by $\tilde {\phi }(x)=\sum \nolimits _{j\in \mathbb {J}}\pi (a_j^{*})x\pi (a_j)$![]() and set $\tilde {\rho }=\tilde {\omega }\circ \tilde \phi$
and set $\tilde {\rho }=\tilde {\omega }\circ \tilde \phi$![]() . Then, $\tilde {\phi }(x)=x$
. Then, $\tilde {\phi }(x)=x$![]() for each $x\in \pi (\mathcal {R})^{\prime }$
for each $x\in \pi (\mathcal {R})^{\prime }$![]() , hence $\tilde {\rho }|\pi (\mathcal {R})^{\prime }=\tilde {\omega }|\pi (\mathcal {R})^{\prime }$
, hence $\tilde {\rho }|\pi (\mathcal {R})^{\prime }=\tilde {\omega }|\pi (\mathcal {R})^{\prime }$![]() . Moreover, $\tilde {\rho }$
. Moreover, $\tilde {\rho }$![]() extends $\rho \circ \pi ^{-1}$
extends $\rho \circ \pi ^{-1}$![]() .
.
(ii)$\Rightarrow$![]() (iii) Take for $\pi$
(iii) Take for $\pi$![]() a faithful normal representation on a Hilbert space $\mathcal {H}$
a faithful normal representation on a Hilbert space $\mathcal {H}$![]() such that $\omega$
such that $\omega$![]() is the restriction of a vector state $\tilde {\omega }$
is the restriction of a vector state $\tilde {\omega }$![]() on ${{\rm B}(\mathcal {H})}$
on ${{\rm B}(\mathcal {H})}$![]() . (For example, $\mathcal {R}$
. (For example, $\mathcal {R}$![]() may be in the standard form [Reference Takesaki28, Chapter IX] so that all normal states on $\mathcal {R}$
may be in the standard form [Reference Takesaki28, Chapter IX] so that all normal states on $\mathcal {R}$![]() and $\mathcal {R}^{\prime }$
and $\mathcal {R}^{\prime }$![]() are vector states.) For simplicity of notation, we may assume that $\mathcal {R}\subseteq {{\rm B}(\mathcal {H})}$
are vector states.) For simplicity of notation, we may assume that $\mathcal {R}\subseteq {{\rm B}(\mathcal {H})}$![]() , that is, $\pi ={{\rm id}}$
, that is, $\pi ={{\rm id}}$![]() . Then, with $\tilde {\rho }$
. Then, with $\tilde {\rho }$![]() as in (ii), we have $\tilde {\rho }|\mathcal {R}=\rho$
as in (ii), we have $\tilde {\rho }|\mathcal {R}=\rho$![]() and $\tilde {\rho }|\mathcal {R}^{\prime }=\tilde {\omega }|\mathcal {R}^{\prime }$
and $\tilde {\rho }|\mathcal {R}^{\prime }=\tilde {\omega }|\mathcal {R}^{\prime }$![]() .
.
(iii)$\Rightarrow$![]() (i) Assume that $\mathcal {R}$
(i) Assume that $\mathcal {R}$![]() is represented faithfully on a Hilbert space $\mathcal {H}$
is represented faithfully on a Hilbert space $\mathcal {H}$![]() such that $\omega$
such that $\omega$![]() is the restriction of a vector state $\tilde {\omega }$
is the restriction of a vector state $\tilde {\omega }$![]() on ${{\rm B}(\mathcal {H})}$
on ${{\rm B}(\mathcal {H})}$![]() and that $\tilde {\rho }$
and that $\tilde {\rho }$![]() is a normal state on ${{\rm B}(\mathcal {H})}$
is a normal state on ${{\rm B}(\mathcal {H})}$![]() such that $\tilde {\rho }|\mathcal {R}=\rho$
such that $\tilde {\rho }|\mathcal {R}=\rho$![]() and $\tilde {\rho }|\mathcal {R}^{\prime }=\tilde {\omega }|\mathcal {R}^{\prime }$
and $\tilde {\rho }|\mathcal {R}^{\prime }=\tilde {\omega }|\mathcal {R}^{\prime }$![]() . Let $\xi \in \mathcal {H}$
. Let $\xi \in \mathcal {H}$![]() be such that $\tilde {\omega }(x)=\langle x\xi,\,\xi \rangle$
be such that $\tilde {\omega }(x)=\langle x\xi,\,\xi \rangle$![]() ($x\in {{\rm B}(\mathcal {H})}$
($x\in {{\rm B}(\mathcal {H})}$![]() ). As a normal state, $\tilde {\rho }$
). As a normal state, $\tilde {\rho }$![]() is of the form
is of the form
where $x^{(\infty )}$![]() denotes the direct sum of countably many copies of $x$
denotes the direct sum of countably many copies of $x$![]() acting on the direct sum $\mathcal {H}^{\infty }$
acting on the direct sum $\mathcal {H}^{\infty }$![]() of countably many copies of $\mathcal {H}$
of countably many copies of $\mathcal {H}$![]() and $\eta \in \mathcal {H}^{\infty }$
and $\eta \in \mathcal {H}^{\infty }$![]() . Now, from $\tilde {\omega }(x)=\tilde {\rho }(x)$
. Now, from $\tilde {\omega }(x)=\tilde {\rho }(x)$![]() for all $x\in \mathcal {R}^{\prime }$
for all $x\in \mathcal {R}^{\prime }$![]() , we have
, we have
Replacing $x$![]() by $x^{*}x$
by $x^{*}x$![]() , it follows that there exists an isometry $u:[\mathcal {R}^{\prime }\xi ]\to [(\mathcal {R}^{\prime })^{(\infty )}\eta ]$
, it follows that there exists an isometry $u:[\mathcal {R}^{\prime }\xi ]\to [(\mathcal {R}^{\prime })^{(\infty )}\eta ]$![]() such that $u\xi =\eta$
such that $u\xi =\eta$![]() and $uy=y^{(\infty )}u$
and $uy=y^{(\infty )}u$![]() for all $y\in \mathcal {R}^{\prime }$
for all $y\in \mathcal {R}^{\prime }$![]() . This $u$
. This $u$![]() can be extended to a partial isometry from $\mathcal {H}$
can be extended to a partial isometry from $\mathcal {H}$![]() into $\mathcal {H}^{\infty }$
into $\mathcal {H}^{\infty }$![]() , denoted again by $u$
, denoted again by $u$![]() , by declaring it to be $0$
, by declaring it to be $0$![]() on the orthogonal complement of $[\mathcal {R}^{\prime }\xi ]$
on the orthogonal complement of $[\mathcal {R}^{\prime }\xi ]$![]() in $\mathcal {H}$
in $\mathcal {H}$![]() . Then, $u$
. Then, $u$![]() intertwines the identity representation ${{\rm id}}$
intertwines the identity representation ${{\rm id}}$![]() of $\mathcal {R}^{\prime }$
of $\mathcal {R}^{\prime }$![]() and the representation ${{\rm id}}^{\infty }$
and the representation ${{\rm id}}^{\infty }$![]() and, is therefore, a column $(u_j)$
and, is therefore, a column $(u_j)$![]() , where $u_j\in \mathcal {R}$
, where $u_j\in \mathcal {R}$![]() . For $r\in \mathcal {R}$
. For $r\in \mathcal {R}$![]() , we have
, we have
Thus, $\rho =\omega \circ \psi$![]() , where $\psi$
, where $\psi$![]() is a map on $\mathcal {R}$
is a map on $\mathcal {R}$![]() , defined by $\psi (r)=u^{*}r^{(\infty )}u=\sum \nolimits _ju_j^{*}ru_j$
, defined by $\psi (r)=u^{*}r^{(\infty )}u=\sum \nolimits _ju_j^{*}ru_j$![]() . This map $\psi$
. This map $\psi$![]() is not necessarily unital, but from
is not necessarily unital, but from

we infer that $1-u^{*}u\leq 1-p$![]() , where $p$
, where $p$![]() is the support projection of $\omega$
is the support projection of $\omega$![]() . Hence, $p\leq u^{*}u$
. Hence, $p\leq u^{*}u$![]() and we may replace $\psi$
and we may replace $\psi$![]() by the unital map $\phi$
by the unital map $\phi$![]() defined by $\phi (r)=p\psi (r)p+(1-p)r(1-p)$
defined by $\phi (r)=p\psi (r)p+(1-p)r(1-p)$![]() , which satisfies $\omega \circ \phi =\omega \circ \psi =\rho$
, which satisfies $\omega \circ \phi =\omega \circ \psi =\rho$![]() and has the required form:
and has the required form:
The equivalence (i)$\Leftrightarrow$![]() (iv) is proved by similar arguments and we will omit the details, just note that $\mathcal {R}\cong \pi _{\omega }(\mathcal {R})\oplus \ker \pi _{\omega }$
(iv) is proved by similar arguments and we will omit the details, just note that $\mathcal {R}\cong \pi _{\omega }(\mathcal {R})\oplus \ker \pi _{\omega }$![]() .
.
3. The case of C$^{*}$ -algebras
-algebras
In a general C$^{*}$![]() -algebra $A$
-algebra $A$![]() , there are usually not enough module homomorphisms of $A$
, there are usually not enough module homomorphisms of $A$![]() into its centre $Z$
into its centre $Z$![]() and even if $Z=\mathbb {C} 1$
and even if $Z=\mathbb {C} 1$![]() , there can be many ideals in $A$
, there can be many ideals in $A$![]() . Functionals on $A$
. Functionals on $A$![]() usually do not preserve ideals, hence can not be approximated by elementary operators. Therefore, we will use for general C$^{*}$
usually do not preserve ideals, hence can not be approximated by elementary operators. Therefore, we will use for general C$^{*}$![]() -algebras a different approach from that in the previous section, not trying to construct an explicit map sending one state to another. For C$^{*}$
-algebras a different approach from that in the previous section, not trying to construct an explicit map sending one state to another. For C$^{*}$![]() -algebras with Hausdorff primitive spectrum, the situation nevertheless resembles the one for von Neumann algebras.
-algebras with Hausdorff primitive spectrum, the situation nevertheless resembles the one for von Neumann algebras.
Theorem 3.1 Let $\omega,\,\rho$![]() be hermitian linear functionals on a C$^{*}$
be hermitian linear functionals on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() with Hausdorff primitive spectrum $\check {A}$
with Hausdorff primitive spectrum $\check {A}$![]() and centre $Z$
and centre $Z$![]() . Then, $\rho$
. Then, $\rho$![]() is in the weak* closure $\overline {\omega \circ {{\rm E}(A)}}$
is in the weak* closure $\overline {\omega \circ {{\rm E}(A)}}$![]() of the set $\omega \circ {{\rm E}(A)}$
of the set $\omega \circ {{\rm E}(A)}$![]() if and only if the following condition is satisfied: (A) $\rho |Z=\omega |Z$
if and only if the following condition is satisfied: (A) $\rho |Z=\omega |Z$![]() and $\|c\rho \|\leq \|c\omega \|$
and $\|c\rho \|\leq \|c\omega \|$![]() for each $c\in Z_+$
for each $c\in Z_+$![]() .
.
Proof. To prove the non-trivial direction of the theorem, suppose that the condition (A) is satisfied, but that $\rho \notin \overline {\omega \circ {{\rm E}(A)}}$![]() . Then, by the Hahn–Banach theorem, there exist $h\in A_h$
. Then, by the Hahn–Banach theorem, there exist $h\in A_h$![]() and $\alpha,\,\delta \in \mathbb {R}$
and $\alpha,\,\delta \in \mathbb {R}$![]() , $\delta >0$
, $\delta >0$![]() , such that
, such that
Since $\rho |Z=\omega |Z$![]() , in particular $\rho (1)=\omega (1)$
, in particular $\rho (1)=\omega (1)$![]() , we may replace $h$
, we may replace $h$![]() by $h+\gamma 1$
by $h+\gamma 1$![]() (and $\alpha$
(and $\alpha$![]() with $\alpha +\gamma \omega (1)$
with $\alpha +\gamma \omega (1)$![]() ) for a sufficiently large $\gamma \in \mathbb {R}$
) for a sufficiently large $\gamma \in \mathbb {R}$![]() and thus assume that $h$
and thus assume that $h$![]() is positive in invertible. Given $\varepsilon >0$
is positive in invertible. Given $\varepsilon >0$![]() , let $a\in A_h$
, let $a\in A_h$![]() be such that
be such that
By a well-known argument, which we now recall, this implies the relations (3.2). Namely, from the above, we have $\omega _+(1-a)<-\omega _-(1+a)+\varepsilon$![]() and (since $1-a\geq 0$
and (since $1-a\geq 0$![]() and $1+a\geq 0$
and $1+a\geq 0$![]() ) this implies that $\omega _+(1-a)<\varepsilon$
) this implies that $\omega _+(1-a)<\varepsilon$![]() and $\omega _-(1+a)\leq \varepsilon$
and $\omega _-(1+a)\leq \varepsilon$![]() . Thus $\omega _+(a_+)\geq \omega _+(a)>\omega _+(1)-\varepsilon$
. Thus $\omega _+(a_+)\geq \omega _+(a)>\omega _+(1)-\varepsilon$![]() and $\omega _-(a_+)=\omega _-(1+a)-\omega _-(1-a_-)\leq \omega _-(1+a)\leq \varepsilon$
and $\omega _-(a_+)=\omega _-(1+a)-\omega _-(1-a_-)\leq \omega _-(1+a)\leq \varepsilon$![]() . In conclusion,
. In conclusion,
For each $t\in \check {A}$![]() let $m(t)$
let $m(t)$![]() and $M(t)$
and $M(t)$![]() be the smallest and the largest point in the spectrum $\sigma (h(t))$
be the smallest and the largest point in the spectrum $\sigma (h(t))$![]() of $h(t)\in A/t$
of $h(t)\in A/t$![]() . Since $\check {A}$
. Since $\check {A}$![]() is Hausdorff by assumption, the two functions $M$
is Hausdorff by assumption, the two functions $M$![]() and $m$
and $m$![]() (given by $M(t)=\|h(t)\|$
(given by $M(t)=\|h(t)\|$![]() and $m(t)=\|h(t)^{-1}\|^{-1}$
and $m(t)=\|h(t)^{-1}\|^{-1}$![]() ) are continuous [Reference Pedersen26, 4.4.5] and therefore define elements of the centre $Z$
) are continuous [Reference Pedersen26, 4.4.5] and therefore define elements of the centre $Z$![]() of $A$
of $A$![]() by the Dauns–Hoffman theorem. Set
by the Dauns–Hoffman theorem. Set
For each $t\in \check {A}$![]() , the spectrum of $b(t)$
, the spectrum of $b(t)$![]() is $\sigma (m(t)1+(M(t)-m(t))a_+(t))$
is $\sigma (m(t)1+(M(t)-m(t))a_+(t))$![]() and is contained in $m(t)+(M(t)-m(t))[0,\,1]\subseteq [m(t),\,M(t)]$
and is contained in $m(t)+(M(t)-m(t))[0,\,1]\subseteq [m(t),\,M(t)]$![]() since $\sigma (a_+(t))\subseteq \sigma (a_+)\subseteq [0,\,1]$
since $\sigma (a_+(t))\subseteq \sigma (a_+)\subseteq [0,\,1]$![]() . Thus, the numerical range $W(b(t))$
. Thus, the numerical range $W(b(t))$![]() of $b(t)$
of $b(t)$![]() (which for normal elements coincides with the convex hull of the spectrum) is contained in $W(h(t))=[m(t),\,M(t)]$
(which for normal elements coincides with the convex hull of the spectrum) is contained in $W(h(t))=[m(t),\,M(t)]$![]() . Therefore, by [Reference Magajna23, 4.1], $b$
. Therefore, by [Reference Magajna23, 4.1], $b$![]() is in the norm closure of the set $\{\psi (h):\, \psi \in {{\rm E}(A)}\}$
is in the norm closure of the set $\{\psi (h):\, \psi \in {{\rm E}(A)}\}$![]() , hence
, hence
by the first relation in (3.1). On the other hand, we can estimate $\omega (b)$![]() as
as

(since $0\leq (M-m)(1-a_+)\leq \|M-m\|(1-a_+)$![]() and $0\leq (M-m)a_+\leq \|M-m\|a_+$
and $0\leq (M-m)a_+\leq \|M-m\|a_+$![]() )
)
Thus, by (3.1), (3.3) and since $m\leq h\leq M$![]() implies that $\rho _+(h)\leq \rho _+(M)$
implies that $\rho _+(h)\leq \rho _+(M)$![]() and $\rho _-(h)\geq \rho _-(m)$
and $\rho _-(h)\geq \rho _-(m)$![]() , we have now
, we have now
This can be rewritten as
or (since $\omega |Z=\rho |Z$![]() implies that $(\omega _--\rho _-)|Z=(\omega _+-\rho _+)|Z$
implies that $(\omega _--\rho _-)|Z=(\omega _+-\rho _+)|Z$![]() and since $M,\,m\in Z$
and since $M,\,m\in Z$![]() )
)
Since this holds for all $\varepsilon >0$![]() , by choosing small enough $\varepsilon$
, by choosing small enough $\varepsilon$![]() , it follows that $(\omega _+-\rho _+) (M-m)<0$
, it follows that $(\omega _+-\rho _+) (M-m)<0$![]() . But, $Z\ni M-m\geq 0$
. But, $Z\ni M-m\geq 0$![]() and $\omega _+|Z\geq \rho _+|Z$
and $\omega _+|Z\geq \rho _+|Z$![]() by Lemma 2.2, hence $(\omega _+-\rho _+) (M-m)\geq 0$
by Lemma 2.2, hence $(\omega _+-\rho _+) (M-m)\geq 0$![]() , which is a contradiction.
, which is a contradiction.
The following corollary can be proved in the same way as Corollary 2.4, so we will omit the proof.
Corollary 3.2 If $\omega$![]() and $\rho$
and $\rho$![]() are states on a C$^{*}$
are states on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() with Hausdorff primitive spectrum, then $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
with Hausdorff primitive spectrum, then $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() if and only if $\rho |Z=\omega |Z$
if and only if $\rho |Z=\omega |Z$![]() .
.
Before stating our main result in this section, we need a lemma. Recall that a projection $p$![]() in the centre of the universal von Neumann envelope $\mathcal {R}$
in the centre of the universal von Neumann envelope $\mathcal {R}$![]() of a C$^{*}$
of a C$^{*}$![]() -algebra $A$
-algebra $A$![]() is called open if there is an ideal $J$
is called open if there is an ideal $J$![]() in $A$
in $A$![]() such that $\overline {J}=p\mathcal {R}$
such that $\overline {J}=p\mathcal {R}$![]() , where $\overline {J}$
, where $\overline {J}$![]() is the weak* closure of $J$
is the weak* closure of $J$![]() in $\mathcal {R}$
in $\mathcal {R}$![]() .
.
Lemma 3.3 Let $\mathcal {R}$![]() be the universal von Neumann envelope of a C$^{*}$
be the universal von Neumann envelope of a C$^{*}$![]() -algebra $A$
-algebra $A$![]() and $\mathcal {Z}$
and $\mathcal {Z}$![]() the centre of $\mathcal {R}$
the centre of $\mathcal {R}$![]() . For each $h\in A_+$
. For each $h\in A_+$![]() , the central carrier $C_h$
, the central carrier $C_h$![]() of $h$
of $h$![]() in $\mathcal {R}$
in $\mathcal {R}$![]() can be approximated in norm by linear combinations of open central projections in $\mathcal {R}$
can be approximated in norm by linear combinations of open central projections in $\mathcal {R}$![]() , where the coefficients in each combination are positive.
, where the coefficients in each combination are positive.
Proof. By definition, the central carrier $z$![]() of $h$
of $h$![]() is the infimum of all $c$
is the infimum of all $c$![]() in $\mathcal {Z}$
in $\mathcal {Z}$![]() such that $h\leq c$
such that $h\leq c$![]() . If $\Delta$
. If $\Delta$![]() is the maximal ideal space of $\mathcal {Z}$
is the maximal ideal space of $\mathcal {Z}$![]() , then $z$
, then $z$![]() corresponds (via the Gelfand isomorphism) to the function $\Delta \ni t\mapsto \|h(t)\|$
corresponds (via the Gelfand isomorphism) to the function $\Delta \ni t\mapsto \|h(t)\|$![]() , where $h(t)$
, where $h(t)$![]() is the coset of $h$
is the coset of $h$![]() in $\mathcal {R}/t\mathcal {R}$
in $\mathcal {R}/t\mathcal {R}$![]() . (This function is continuous by [Reference Glimm14].) Thus, we will regard $z$
. (This function is continuous by [Reference Glimm14].) Thus, we will regard $z$![]() as a function on $\Delta$
as a function on $\Delta$![]() . Let $[m,\,M]$
. Let $[m,\,M]$![]() be an interval containing the range of $z$
be an interval containing the range of $z$![]() , where $m\geq 0$
, where $m\geq 0$![]() and $M=\|h\|=\|z\|$
and $M=\|h\|=\|z\|$![]() . Given $a\in A_+$
. Given $a\in A_+$![]() , the set $U=\{t\in \delta :\ a(t)\ne 0\}$
, the set $U=\{t\in \delta :\ a(t)\ne 0\}$![]() is open since the function $\Delta \ni t\mapsto \|a(t)\|\in \mathbb {R}$
is open since the function $\Delta \ni t\mapsto \|a(t)\|\in \mathbb {R}$![]() is continuous. The weak* closure of the ideal generated by $a$
is continuous. The weak* closure of the ideal generated by $a$![]() in $\mathcal {R}$
in $\mathcal {R}$![]() is of the form $p\mathcal {R}$
is of the form $p\mathcal {R}$![]() for a unique projection $p\in \mathcal {Z}$
for a unique projection $p\in \mathcal {Z}$![]() and $p$
and $p$![]() is open by definition. Since the quotient algebras $\mathcal {R}/t\mathcal {R}$
is open by definition. Since the quotient algebras $\mathcal {R}/t\mathcal {R}$![]() have only scalars in their centres, $p(t)=1$
have only scalars in their centres, $p(t)=1$![]() for each $t\in U$
for each $t\in U$![]() , hence also for each $t\in \overline {U}$
, hence also for each $t\in \overline {U}$![]() by continuity, so $p\geq q$
by continuity, so $p\geq q$![]() , where $q\in \mathcal {Z}$
, where $q\in \mathcal {Z}$![]() is the projection that corresponds to the characteristic function of $\overline {U}$
is the projection that corresponds to the characteristic function of $\overline {U}$![]() . But from the definition of $U$
. But from the definition of $U$![]() , we see that $qa=a$
, we see that $qa=a$![]() and this implies that $qb=b$
and this implies that $qb=b$![]() for each $b$
for each $b$![]() in the ideal generated by $a$
in the ideal generated by $a$![]() . Hence, $qp=p$
. Hence, $qp=p$![]() and it follows that $q=p$
and it follows that $q=p$![]() . In particular, for each $r\in \mathbb {R}_+$
. In particular, for each $r\in \mathbb {R}_+$![]() the projection that corresponds to the closure of the set $U_r=\{t\in \Delta :\, z(t)>r\}$
the projection that corresponds to the closure of the set $U_r=\{t\in \Delta :\, z(t)>r\}$![]() is open since $U_r$
is open since $U_r$![]() is just the set $\{t\in \Delta :\, a(t)\ne 0\}$
is just the set $\{t\in \Delta :\, a(t)\ne 0\}$![]() , where $a=(h-r)_+$
, where $a=(h-r)_+$![]() . (This has been observed already by Halpern in [Reference Halpern18, proof of Lemma 6].) Given $\varepsilon >0$
. (This has been observed already by Halpern in [Reference Halpern18, proof of Lemma 6].) Given $\varepsilon >0$![]() , for each $k\in \mathbb {N}$
, for each $k\in \mathbb {N}$![]() let $p_k$
let $p_k$![]() be the projection corresponding to the closure of the set $U_k=\{t\in \Delta :\, z(t)>M-k\varepsilon \}$
be the projection corresponding to the closure of the set $U_k=\{t\in \Delta :\, z(t)>M-k\varepsilon \}$![]() . Then, $0=p_0\leq p_1\leq p_2\leq \ldots \leq p_n=1$
. Then, $0=p_0\leq p_1\leq p_2\leq \ldots \leq p_n=1$![]() , where $n\in \mathbb {N}$
, where $n\in \mathbb {N}$![]() is such that $M-n\varepsilon < m$
is such that $M-n\varepsilon < m$![]() and $M-(n-1)\varepsilon \geq m$
and $M-(n-1)\varepsilon \geq m$![]() . Now, from $1=(p_1-p_0)+(p_2-p_1)+\ldots +(p_n-p_{n-1})$
. Now, from $1=(p_1-p_0)+(p_2-p_1)+\ldots +(p_n-p_{n-1})$![]() , we have that $F_k:=\overline {U}_{k}\setminus \overline {U}_{k-1}$
, we have that $F_k:=\overline {U}_{k}\setminus \overline {U}_{k-1}$![]() are disjoint closed and open sets that cover $\Delta$
are disjoint closed and open sets that cover $\Delta$![]() and for $t\in F_k$
and for $t\in F_k$![]() , we have that $M-k\varepsilon \leq z(t)\leq M-(k-1)\varepsilon$
, we have that $M-k\varepsilon \leq z(t)\leq M-(k-1)\varepsilon$![]() . Thus, if we choose in each interval $[M-k\varepsilon,\,M-(k-1)\varepsilon ]$
. Thus, if we choose in each interval $[M-k\varepsilon,\,M-(k-1)\varepsilon ]$![]() a point $\lambda _k\geq 0$
a point $\lambda _k\geq 0$![]() and set $c:=\sum \nolimits _{k=1}^{n}\lambda _k(p_k-p_{k-1})$
and set $c:=\sum \nolimits _{k=1}^{n}\lambda _k(p_k-p_{k-1})$![]() , it follows that $\|z-c\|\leq \varepsilon$
, it follows that $\|z-c\|\leq \varepsilon$![]() . Finally, observe that
. Finally, observe that
is a linear combination with positive coefficients of open projections.
The following theorem is a special case of Theorem 3.7, but it is used in the proof of that theorem.
Theorem 3.4 Let $\omega$![]() and $\rho$
and $\rho$![]() be states on a C$^{*}$
be states on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() . Then, $\rho$
. Then, $\rho$![]() is in the weak* closure $\overline {\omega \circ {{\rm E}(A)}}$
is in the weak* closure $\overline {\omega \circ {{\rm E}(A)}}$![]() of the set $\omega \circ {{\rm E}(A)}=\{\omega \circ \psi :\, \psi \in {{\rm E}(A)}\},$
of the set $\omega \circ {{\rm E}(A)}=\{\omega \circ \psi :\, \psi \in {{\rm E}(A)}\},$![]() where ${{\rm E}(A)}$
where ${{\rm E}(A)}$![]() is the set of all unital completely positive elementary complete contractions on $A,$
is the set of all unital completely positive elementary complete contractions on $A,$![]() if and only if $\|\rho |J\|\leq \|\omega |J\|$
if and only if $\|\rho |J\|\leq \|\omega |J\|$![]() for each ideal $J$
for each ideal $J$![]() of $A$
of $A$![]() .
.
Proof. Evidently, $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() implies that $\|\rho |J\|\leq \|\omega |J\|$
implies that $\|\rho |J\|\leq \|\omega |J\|$![]() for each ideal $J$
for each ideal $J$![]() in $A$
in $A$![]() since maps in ${{\rm E}(A)}$
since maps in ${{\rm E}(A)}$![]() are contractive and preserve ideals. For the converse, suppose that $\rho \notin \overline {\omega \circ {{\rm E}(A)}}$
are contractive and preserve ideals. For the converse, suppose that $\rho \notin \overline {\omega \circ {{\rm E}(A)}}$![]() . Then, by the Hahn–Banach theorem there exist $h\in A_h$
. Then, by the Hahn–Banach theorem there exist $h\in A_h$![]() and $\alpha \in \mathbb {R}$
and $\alpha \in \mathbb {R}$![]() such that (3.1) holds, that is $\omega (\psi (h))\leq \alpha$
such that (3.1) holds, that is $\omega (\psi (h))\leq \alpha$![]() for all $\psi \in {{\rm E}(A)}$
for all $\psi \in {{\rm E}(A)}$![]() , while $\rho (h)>\alpha.$
, while $\rho (h)>\alpha.$![]() Replacing $h$
Replacing $h$![]() by $h+\beta 1$
by $h+\beta 1$![]() for a sufficiently large $\beta \in \mathbb {R}$
for a sufficiently large $\beta \in \mathbb {R}$![]() (and consequently $\alpha$
(and consequently $\alpha$![]() by $\alpha +\beta$
by $\alpha +\beta$![]() ), we may assume that $h$
), we may assume that $h$![]() is positive.
is positive.
Let $\mathcal {R}$![]() be the universal von Neumann envelope of $A$
be the universal von Neumann envelope of $A$![]() and denote the unique weak* continuous extensions of $\omega$
and denote the unique weak* continuous extensions of $\omega$![]() and $\rho$
and $\rho$![]() to $\mathcal {R}$
to $\mathcal {R}$![]() by the same two letters. We will use the same notation as in the proof of Lemma 3.3. Thus, $z$
by the same two letters. We will use the same notation as in the proof of Lemma 3.3. Thus, $z$![]() is the infimum of all $c$
is the infimum of all $c$![]() in $\mathcal {Z}$
in $\mathcal {Z}$![]() such that $h\leq c$
such that $h\leq c$![]() . Since $W(z(t)1)=\{z(t)\}\subseteq W(h(t))$
. Since $W(z(t)1)=\{z(t)\}\subseteq W(h(t))$![]() for each $t\in \Delta$
for each $t\in \Delta$![]() , it follows by [Reference Magajna23, 3.3] that $z\in \overline {{{\rm co}}_{\mathcal {R}}}(h)$
, it follows by [Reference Magajna23, 3.3] that $z\in \overline {{{\rm co}}_{\mathcal {R}}}(h)$![]() (= the weak* closure of the $\mathcal {R}$
(= the weak* closure of the $\mathcal {R}$![]() -convex hull of $h$
-convex hull of $h$![]() ), hence by the first relation in (3.1)
), hence by the first relation in (3.1)
since each map $\psi$![]() of the form $x\mapsto \sum \nolimits _ib_i^{*}xb_i$
of the form $x\mapsto \sum \nolimits _ib_i^{*}xb_i$![]() ($b_i\in \mathcal {R}$
($b_i\in \mathcal {R}$![]() , $\sum \nolimits _ib_i^{*}b_i=1$
, $\sum \nolimits _ib_i^{*}b_i=1$![]() ) can be approximated by maps of the form $x\mapsto \sum \nolimits _ia_i^{*}xa_i$
) can be approximated by maps of the form $x\mapsto \sum \nolimits _ia_i^{*}xa_i$![]() ($a_i\in A$
($a_i\in A$![]() , $\sum \nolimits _ia_i^{*}a_i=1$
, $\sum \nolimits _ia_i^{*}a_i=1$![]() ). (This follows by using the Kaplansky density theorem in ${{\rm M}}_n(\mathcal {R})$
). (This follows by using the Kaplansky density theorem in ${{\rm M}}_n(\mathcal {R})$![]() to approximate the column $b=(b_1,\,\ldots,\,b_n)^{T}$
to approximate the column $b=(b_1,\,\ldots,\,b_n)^{T}$![]() by $(a_1,\,\ldots,\,a_n)^{T}$
by $(a_1,\,\ldots,\,a_n)^{T}$![]() .) Since $\omega$
.) Since $\omega$![]() and $\rho$
and $\rho$![]() are states, the hypothesis $\|\rho |J\|\leq \|\omega |J\|$
are states, the hypothesis $\|\rho |J\|\leq \|\omega |J\|$![]() for each ideal $J$
for each ideal $J$![]() in $A$
in $A$![]() means that $\rho (p)\leq \omega (p)$
means that $\rho (p)\leq \omega (p)$![]() for each open projection $p\in \mathcal {Z}$
for each open projection $p\in \mathcal {Z}$![]() . Then, it follows by Lemma 3.3 that $\rho (z)\leq \omega (z)$
. Then, it follows by Lemma 3.3 that $\rho (z)\leq \omega (z)$![]() . But from $h\leq z$
. But from $h\leq z$![]() and using (3.5), we have now that $\rho (h)\leq \rho (z)\leq \omega (z)\leq \alpha$
and using (3.5), we have now that $\rho (h)\leq \rho (z)\leq \omega (z)\leq \alpha$![]() , which is in contradiction with the previously established relation $\rho (h)>\alpha$
, which is in contradiction with the previously established relation $\rho (h)>\alpha$![]() .
.
The naive attempt to generalize Theorem 3.4 to hermitian functionals fails, as shown by the following example. The example also shows that the assumption in Theorem 3.1, that $A$![]() has Hausdorff primitive spectrum, is not redundant and that in Theorem 2.3 the normality of $\omega$
has Hausdorff primitive spectrum, is not redundant and that in Theorem 2.3 the normality of $\omega$![]() and $\rho$
and $\rho$![]() is not redundant.
is not redundant.
Example 3.5 For a separable Hilbert space $\mathcal {H}$![]() , let $\omega _1$
, let $\omega _1$![]() be a normal and $\omega _2$
be a normal and $\omega _2$![]() a singular state on ${{\rm B}(\mathcal {H})}$
a singular state on ${{\rm B}(\mathcal {H})}$![]() , $\rho _1$
, $\rho _1$![]() and $\rho _2$
and $\rho _2$![]() positive normal functionals on ${{\rm B}(\mathcal {H})}$
positive normal functionals on ${{\rm B}(\mathcal {H})}$![]() with orthogonal supports such that $\rho _1(1)=\frac {1}{2}=\rho _2(1)$
with orthogonal supports such that $\rho _1(1)=\frac {1}{2}=\rho _2(1)$![]() . Set $\omega =\omega _1-\omega _2$
. Set $\omega =\omega _1-\omega _2$![]() and $\rho =\rho _1-\rho _2$
and $\rho =\rho _1-\rho _2$![]() . Then, $\rho (1)=0=\omega (1)$
. Then, $\rho (1)=0=\omega (1)$![]() , $\|\rho \|=\rho _1(1)+\rho _2(1)=1=\omega _1(1)\leq \|\omega \|$
, $\|\rho \|=\rho _1(1)+\rho _2(1)=1=\omega _1(1)\leq \|\omega \|$![]() . Since $\rho _1$
. Since $\rho _1$![]() , $\rho _2$
, $\rho _2$![]() and $\omega _1$
and $\omega _1$![]() are normal, while $\omega _2$
are normal, while $\omega _2$![]() is singular (which means that $\omega _2$
is singular (which means that $\omega _2$![]() annihilates the ideal ${{\rm K}(\mathcal {H})}$
annihilates the ideal ${{\rm K}(\mathcal {H})}$![]() of all compact operators on $\mathcal {H}$
of all compact operators on $\mathcal {H}$![]() ), we have $\|\rho |{{\rm K}(\mathcal {H})}\|=\|\rho \|=\rho _1(1)+\rho _2(1)=\omega _1(1)=\|\omega _1|{{\rm K}(\mathcal {H})}\|=\|\omega |{{\rm K}(\mathcal {H})}\|\leq \|\omega \|$
), we have $\|\rho |{{\rm K}(\mathcal {H})}\|=\|\rho \|=\rho _1(1)+\rho _2(1)=\omega _1(1)=\|\omega _1|{{\rm K}(\mathcal {H})}\|=\|\omega |{{\rm K}(\mathcal {H})}\|\leq \|\omega \|$![]() . Thus, $\|\rho |J\|\leq \|\omega |J\|$
. Thus, $\|\rho |J\|\leq \|\omega |J\|$![]() for each ideal $J$
for each ideal $J$![]() of ${{\rm B}(\mathcal {H})}$
of ${{\rm B}(\mathcal {H})}$![]() and $\omega$
and $\omega$![]() and $\rho$
and $\rho$![]() agree on the centre $\mathbb {C} 1$
agree on the centre $\mathbb {C} 1$![]() of ${{\rm B}(\mathcal {H})}$
of ${{\rm B}(\mathcal {H})}$![]() . But nevertheless, $\rho \notin \overline {\omega \circ {\rm E}({{\rm B}(\mathcal {H})})}$
. But nevertheless, $\rho \notin \overline {\omega \circ {\rm E}({{\rm B}(\mathcal {H})})}$![]() since on ${{\rm K}(\mathcal {H})}$
since on ${{\rm K}(\mathcal {H})}$![]() all elements of $\overline {\omega \circ {\rm E}({{\rm B}(\mathcal {H})})}$
all elements of $\overline {\omega \circ {\rm E}({{\rm B}(\mathcal {H})})}$![]() act as elements of $\overline {\omega _1\circ {\rm E}({{\rm B}(\mathcal {H})})}|{{\rm K}(\mathcal {H})}$
act as elements of $\overline {\omega _1\circ {\rm E}({{\rm B}(\mathcal {H})})}|{{\rm K}(\mathcal {H})}$![]() and are therefore positive, while $\rho |{{\rm K}(\mathcal {H})}=(\rho _1-\rho _2)|{{\rm K}(\mathcal {H})}$
and are therefore positive, while $\rho |{{\rm K}(\mathcal {H})}=(\rho _1-\rho _2)|{{\rm K}(\mathcal {H})}$![]() is not positive.
is not positive.
To generalize Theorem 3.4 to hermitian functionals, we need a lemma.
Lemma 3.6 For each hermitian functional $\omega$![]() on a C$^{*}$
on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() , we have
, we have
Proof. Suppose that $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() and let $(\psi _k)$
and let $(\psi _k)$![]() be a net in ${{\rm E}(A)}$
be a net in ${{\rm E}(A)}$![]() such that $\rho (a)=\lim _k\omega (\psi _k(a))$
such that $\rho (a)=\lim _k\omega (\psi _k(a))$![]() for all $a\in A$
for all $a\in A$![]() . Extend $\omega$
. Extend $\omega$![]() , $\rho$
, $\rho$![]() and each $\psi _k$
and each $\psi _k$![]() weak* continuously to the universal von Neumann envelope $\mathcal {R}$
weak* continuously to the universal von Neumann envelope $\mathcal {R}$![]() of $A$
of $A$![]() and denote the extensions by the same symbols. Let $\psi$
and denote the extensions by the same symbols. Let $\psi$![]() be a weak* limit point of the net $(\psi _k)$
be a weak* limit point of the net $(\psi _k)$![]() and note that $\psi$
and note that $\psi$![]() is a unital completely positive (hence contractive) module map over the centre $\mathcal {Z}$
is a unital completely positive (hence contractive) module map over the centre $\mathcal {Z}$![]() of $\mathcal {R}$
of $\mathcal {R}$![]() . Set $\rho _1=\omega _+\circ \psi |A$
. Set $\rho _1=\omega _+\circ \psi |A$![]() and $\rho _2=\omega _-\circ \psi |A$
and $\rho _2=\omega _-\circ \psi |A$![]() . Then $\rho _1\in \overline {\omega _+\circ {{\rm E}(A)}}$
. Then $\rho _1\in \overline {\omega _+\circ {{\rm E}(A)}}$![]() , $\rho _2\in \overline {\omega _-\circ {{\rm E}(A)}}$
, $\rho _2\in \overline {\omega _-\circ {{\rm E}(A)}}$![]() and $\rho =\omega \circ \psi |A=\rho _1-\rho _2$
and $\rho =\omega \circ \psi |A=\rho _1-\rho _2$![]() . This proves the inclusion $\overline {\omega \circ {{\rm E}(A)}}\subseteq \overline {\omega _+\circ {{\rm E}(A)}}-\overline {\omega _-\circ {{\rm E}(A)}}$
. This proves the inclusion $\overline {\omega \circ {{\rm E}(A)}}\subseteq \overline {\omega _+\circ {{\rm E}(A)}}-\overline {\omega _-\circ {{\rm E}(A)}}$![]() .
.
To prove the reverse inclusion, suppose that $\rho _1\in \overline {\omega _+\circ {{\rm E}(A)}}$![]() and $\rho _2\in \overline {\omega _-\circ {{\rm E}(A)}}$
and $\rho _2\in \overline {\omega _-\circ {{\rm E}(A)}}$![]() . Then, there exist nets of maps $\phi _k$
. Then, there exist nets of maps $\phi _k$![]() and $\psi _k$
and $\psi _k$![]() in ${{\rm E}(A)}$
in ${{\rm E}(A)}$![]() such that $\rho _1=\lim _k\omega _+\circ \phi _k$
such that $\rho _1=\lim _k\omega _+\circ \phi _k$![]() and $\rho _2=\lim _k\omega _-\circ \psi _k$
and $\rho _2=\lim _k\omega _-\circ \psi _k$![]() . Let $p$
. Let $p$![]() and $q$
and $q$![]() be the support projections in $\mathcal {R}$
be the support projections in $\mathcal {R}$![]() of $\omega _+$
of $\omega _+$![]() and $\omega _-$
and $\omega _-$![]() (where $\omega _+$
(where $\omega _+$![]() and $\omega _-$
and $\omega _-$![]() have been weak* continuously extended to $\mathcal {R}$
have been weak* continuously extended to $\mathcal {R}$![]() ). Let $(a_n)$
). Let $(a_n)$![]() be a net of positive contractions in $A$
be a net of positive contractions in $A$![]() strongly converging to $p$
strongly converging to $p$![]() in $\mathcal {R}$
in $\mathcal {R}$![]() , set $b_n=\sqrt {1-a_n^{2}}$
, set $b_n=\sqrt {1-a_n^{2}}$![]() and define maps $\phi _{k,n}$
and define maps $\phi _{k,n}$![]() and $\psi _{k,n}$
and $\psi _{k,n}$![]() on $A$
on $A$![]() by
by
The nets $(\omega _+(b_n^{2}))=(\omega _+(1-a_n^{2}))$![]() and $(\omega _-(a_n^{2}))= (\omega _-(1-b_n^{2}))$
and $(\omega _-(a_n^{2}))= (\omega _-(1-b_n^{2}))$![]() all converge to $0$
all converge to $0$![]() . From this, we will verify in the following by using the Cauchy–Schwarz inequality for positive functionals that $\lim _{k,n}\omega _+\circ \phi _{k,n}=\rho _1$
. From this, we will verify in the following by using the Cauchy–Schwarz inequality for positive functionals that $\lim _{k,n}\omega _+\circ \phi _{k,n}=\rho _1$![]() , $\lim _{k,n}\omega _-\circ \psi _{k,n}=\rho _2$
, $\lim _{k,n}\omega _-\circ \psi _{k,n}=\rho _2$![]() , $\lim _{k,n}\omega _+\circ \psi _{k,n}=0$
, $\lim _{k,n}\omega _+\circ \psi _{k,n}=0$![]() and $\lim _{k,n}\omega _-\circ \phi _{k,n}=0$
and $\lim _{k,n}\omega _-\circ \phi _{k,n}=0$![]() pointwise on $A$
pointwise on $A$![]() , hence
, hence
where $\theta _{k,n}:=\phi _{k,n}+\psi _{k,n}$![]() . Evidently each $\theta _{k,n}$
. Evidently each $\theta _{k,n}$![]() is elementary completely positive map and also unital since $\theta _{k,n}(1)=a_n\phi _k(1)a_n+b_n\psi _k(1)b_n=a_n^{2}+b_n^{2}=1$
is elementary completely positive map and also unital since $\theta _{k,n}(1)=a_n\phi _k(1)a_n+b_n\psi _k(1)b_n=a_n^{2}+b_n^{2}=1$![]() . Thus, $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
. Thus, $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() , verifying the inclusion $\overline {\omega \circ {{\rm E}(A)}}\supseteq \overline {\omega _+\circ {{\rm E}(A)}}-\overline {\omega _-\circ {{\rm E}(A)}}$
, verifying the inclusion $\overline {\omega \circ {{\rm E}(A)}}\supseteq \overline {\omega _+\circ {{\rm E}(A)}}-\overline {\omega _-\circ {{\rm E}(A)}}$![]() . Now, we will verify that $\lim _{k,n}\omega _+\phi _{k,n}=\rho _1$
. Now, we will verify that $\lim _{k,n}\omega _+\phi _{k,n}=\rho _1$![]() , the verification of the other three limits that we have used is similar. For each $x\in A$
, the verification of the other three limits that we have used is similar. For each $x\in A$![]() , we estimate
, we estimate

Both terms in the last line of the above expression converge to $0$![]() .
.
Theorem 3.7 Let $\omega$![]() and $\rho$
and $\rho$![]() be hermitian functionals on a C$^{*}$
be hermitian functionals on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() . Then $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
. Then $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() if and only if there exist positive functionals $\rho _1$
if and only if there exist positive functionals $\rho _1$![]() and $\rho _2$
and $\rho _2$![]() on $A$
on $A$![]() satisfying the following condition:
satisfying the following condition:
(B) $\rho =\rho _1-\rho _2$![]() , $\rho _1(1)=\omega _+(1)$
, $\rho _1(1)=\omega _+(1)$![]() , $\rho _2(1)=\omega _-(1)$
, $\rho _2(1)=\omega _-(1)$![]() , $\|\rho _1|J\|\leq \|\omega _+|J\|$
, $\|\rho _1|J\|\leq \|\omega _+|J\|$![]() and $\|\rho _2|J\|\leq \|\omega _-|J\|$
and $\|\rho _2|J\|\leq \|\omega _-|J\|$![]() for all ideals $J$
for all ideals $J$![]() in $A$
in $A$![]() .
.
(In particular $\|\rho |J\|\leq \|\omega |J\|$![]() .) If $\omega$
.) If $\omega$![]() is positive, then the condition (B) simplifies to $\rho (1)=\omega (1)$
is positive, then the condition (B) simplifies to $\rho (1)=\omega (1)$![]() and $\|\rho |J\|\leq \|\omega |J\|$
and $\|\rho |J\|\leq \|\omega |J\|$![]() for all ideals $J$
for all ideals $J$![]() .
.
Proof. Suppose that $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() . Using the notation introduced in the first part of the proof of Lemma 3.6, we have observed that the map $\psi$
. Using the notation introduced in the first part of the proof of Lemma 3.6, we have observed that the map $\psi$![]() on $\mathcal {R}$
on $\mathcal {R}$![]() introduced in that proof is a contractive unital $\mathcal {Z}$
introduced in that proof is a contractive unital $\mathcal {Z}$![]() -bimodule map. Thus, for any ideal $J$
-bimodule map. Thus, for any ideal $J$![]() in $A$
in $A$![]() , if $p\in \mathcal {Z}$
, if $p\in \mathcal {Z}$![]() is the projection satisfying $\overline {J}=p\mathcal {R}$
is the projection satisfying $\overline {J}=p\mathcal {R}$![]() , then $\psi (\overline {J})=\psi (p\mathcal {R})=p\psi (\mathcal {R})\subseteq \overline {J}$
, then $\psi (\overline {J})=\psi (p\mathcal {R})=p\psi (\mathcal {R})\subseteq \overline {J}$![]() . Since $\omega$
. Since $\omega$![]() (and hence also $\omega _+$
(and hence also $\omega _+$![]() and $\omega _-$
and $\omega _-$![]() ) are weak* continuous on $\mathcal {R}$
) are weak* continuous on $\mathcal {R}$![]() , we have $\|\omega _+|\overline {J}\|=\|\omega _+|J\|$
, we have $\|\omega _+|\overline {J}\|=\|\omega _+|J\|$![]() and $\|\omega _-|\overline {J}\|=\|\omega _-|J\|$
and $\|\omega _-|\overline {J}\|=\|\omega _-|J\|$![]() . With $\rho _1=\omega _+\circ \psi |A$
. With $\rho _1=\omega _+\circ \psi |A$![]() and $\rho _2=\omega _-\circ \psi |A$
and $\rho _2=\omega _-\circ \psi |A$![]() (as in the proof of Lemma 3.6), we have $\rho =\rho _1-\rho _2$
(as in the proof of Lemma 3.6), we have $\rho =\rho _1-\rho _2$![]() , $\rho _1(1)=\omega _+(1)$
, $\rho _1(1)=\omega _+(1)$![]() , $\rho _2(1)=\omega _-(1)$
, $\rho _2(1)=\omega _-(1)$![]() ,
,
and similarly $\|\rho _2|J\|\leq \|\omega _-|J\|$![]() . Therefore, also
. Therefore, also
Conversely, assume the existence of positive functionals $\rho _1$![]() and $\rho _2$
and $\rho _2$![]() on $A$
on $A$![]() satisfying the norm inequalities in condition (B). Then, by Theorem 3.4 $\rho _1\in \overline {\omega _+\circ {{\rm E}(A)}}$
satisfying the norm inequalities in condition (B). Then, by Theorem 3.4 $\rho _1\in \overline {\omega _+\circ {{\rm E}(A)}}$![]() and $\rho _2\in \overline {\omega _-\circ {{\rm E}(A)}}$
and $\rho _2\in \overline {\omega _-\circ {{\rm E}(A)}}$![]() , hence by Lemma 3.6 $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
, hence by Lemma 3.6 $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() .
.
4. Maximally mixed states
For functionals $\omega$![]() and $\rho$
and $\rho$![]() on a C$^{*}$
on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() let us say that $\rho$
let us say that $\rho$![]() is more mixed than $\omega$
is more mixed than $\omega$![]() if $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
if $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() (where the bar denotes weak* closure). Applying Zorn's lemma to the family of all weak* closed ${{\rm E}(A)}$
(where the bar denotes weak* closure). Applying Zorn's lemma to the family of all weak* closed ${{\rm E}(A)}$![]() -invariant subsets of $\overline {\omega \circ {{\rm E}(A)}}$
-invariant subsets of $\overline {\omega \circ {{\rm E}(A)}}$![]() we see that in $\overline {\omega \circ {{\rm E}(A)}}$
we see that in $\overline {\omega \circ {{\rm E}(A)}}$![]() , there exist minimal ${{\rm E}(A)}$
, there exist minimal ${{\rm E}(A)}$![]() -invariant compact non-empty subsets, which are evidently of the form $\overline {\rho \circ {{\rm E}(A)}}$
-invariant compact non-empty subsets, which are evidently of the form $\overline {\rho \circ {{\rm E}(A)}}$![]() for some $\rho$
for some $\rho$![]() and such $\rho$
and such $\rho$![]() are called maximally mixed. Thus, a functional $\omega$
are called maximally mixed. Thus, a functional $\omega$![]() is maximally mixed if $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
is maximally mixed if $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() implies that $\omega \in \overline {\rho \circ {{\rm E}(A)}}$
implies that $\omega \in \overline {\rho \circ {{\rm E}(A)}}$![]() . If $A$
. If $A$![]() has Hausdorff primitive spectrum, Corollary 3.2 implies that all states on $A$
has Hausdorff primitive spectrum, Corollary 3.2 implies that all states on $A$![]() are maximally mixed. The same conclusion holds for liminal C$^{*}$
are maximally mixed. The same conclusion holds for liminal C$^{*}$![]() -algebras.
-algebras.
Corollary 4.1 On a liminal C$^{*}$![]() -algebra $A$
-algebra $A$![]() every state $\omega$
every state $\omega$![]() is maximally mixed.
is maximally mixed.
Proof. If $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() , then by Theorem 3.4 $\|\rho |J\|\leq \|\omega |J\|$
, then by Theorem 3.4 $\|\rho |J\|\leq \|\omega |J\|$![]() for each ideal $J$
for each ideal $J$![]() in $A$
in $A$![]() . Denoting by $p$
. Denoting by $p$![]() the projection in $\mathcal {R}:=A^{\sharp \sharp }$
the projection in $\mathcal {R}:=A^{\sharp \sharp }$![]() such that $\overline {J}=p\mathcal {R}$
such that $\overline {J}=p\mathcal {R}$![]() , this means that $\rho (p)\leq \omega (p)$
, this means that $\rho (p)\leq \omega (p)$![]() for each open central projection $p$
for each open central projection $p$![]() , where $\omega$
, where $\omega$![]() and $\rho$
and $\rho$![]() have been weak* continuously extended to $\mathcal {R}$
have been weak* continuously extended to $\mathcal {R}$![]() . Since $A$
. Since $A$![]() is liminal, such projections are strongly dense in the set of all central projections by [Reference Digernes and Halpern10], hence it follows that $\rho (p^{\perp })\leq \omega (p^{\perp })$
is liminal, such projections are strongly dense in the set of all central projections by [Reference Digernes and Halpern10], hence it follows that $\rho (p^{\perp })\leq \omega (p^{\perp })$![]() . Since $\rho (p)+\rho (p^{\perp }=\rho (1)=1=\omega (1)=\omega (p)+\omega (p^{\perp })$
. Since $\rho (p)+\rho (p^{\perp }=\rho (1)=1=\omega (1)=\omega (p)+\omega (p^{\perp })$![]() , we conclude that $\rho (p)=\omega (p)$
, we conclude that $\rho (p)=\omega (p)$![]() , that is $\|\rho |J\|=\|\omega |J\|$
, that is $\|\rho |J\|=\|\omega |J\|$![]() . By Theorem 3.4, this implies that $\omega \in \overline {\rho \circ {{\rm E}(A)}}$
. By Theorem 3.4, this implies that $\omega \in \overline {\rho \circ {{\rm E}(A)}}$![]() .
.
Perhaps, the simplest C$^{*}$![]() -algebras on which not all states are maximally mixed are C$^{*}$
-algebras on which not all states are maximally mixed are C$^{*}$![]() -algebras that have only one maximal ideal and this ideal is not $0$
-algebras that have only one maximal ideal and this ideal is not $0$![]() .
.
Example 4.2 Suppose that a unital C$^{*}$![]() -algebra $A$
-algebra $A$![]() has only one maximal ideal $M$
has only one maximal ideal $M$![]() (for example, $A$
(for example, $A$![]() may be simple or a factor). Then, a state $\omega$
may be simple or a factor). Then, a state $\omega$![]() on $A$
on $A$![]() is maximally mixed if and only if $\omega |M=0$
is maximally mixed if and only if $\omega |M=0$![]() .
.
Proof. Suppose that $\omega |M=0$![]() and let $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
and let $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() . Then, $\rho |M\!=\!0$
. Then, $\rho |M\!=\!0$![]() , hence also $\rho (J)\!=\!0$
, hence also $\rho (J)\!=\!0$![]() for each proper ideal $J$
for each proper ideal $J$![]() of $A$
of $A$![]() since $J\subseteq M$
since $J\subseteq M$![]() . Thus, $\|\omega |J\|=\|\rho |J\|$
. Thus, $\|\omega |J\|=\|\rho |J\|$![]() for each ideal $J$
for each ideal $J$![]() of $A$
of $A$![]() , so $\omega \in \overline {\rho \circ {{\rm E}(A)}}$
, so $\omega \in \overline {\rho \circ {{\rm E}(A)}}$![]() by Theorem 3.4.
by Theorem 3.4.
Suppose now that $\omega |M\ne 0$![]() . Let $\rho$
. Let $\rho$![]() be any state on $A$
be any state on $A$![]() such that $\rho |M=0$
such that $\rho |M=0$![]() . Then $\|\rho |J\|\leq \|\omega |J\|$
. Then $\|\rho |J\|\leq \|\omega |J\|$![]() for all ideals $J$
for all ideals $J$![]() , hence $\rho \in \overline {\omega \circ {{\rm E}(A)}}$
, hence $\rho \in \overline {\omega \circ {{\rm E}(A)}}$![]() by Theorem 3.4. But $\omega \notin \overline {\rho \circ {{\rm E}(A)}}$
by Theorem 3.4. But $\omega \notin \overline {\rho \circ {{\rm E}(A)}}$![]() since $\rho |M=0$
since $\rho |M=0$![]() and $\omega |M\ne 0$
and $\omega |M\ne 0$![]() , thus $\omega$
, thus $\omega$![]() is not maximally mixed.
is not maximally mixed.
Remark 4.3 If $K$![]() is an ideal of $A$
is an ideal of $A$![]() , each state $\omega$
, each state $\omega$![]() on $A$
on $A$![]() satisfying $\omega (K)=0$
satisfying $\omega (K)=0$![]() may be regarded as a state on $A/K$
may be regarded as a state on $A/K$![]() , say $\dot \omega$
, say $\dot \omega$![]() . Note that $\dot \omega$
. Note that $\dot \omega$![]() is maximally mixed on $A/K$
is maximally mixed on $A/K$![]() if and only if $\omega$
if and only if $\omega$![]() is maximally mixed on $A$
is maximally mixed on $A$![]() . Indeed, denoting by $q:A\to A/K$
. Indeed, denoting by $q:A\to A/K$![]() the natural map, $q(J)$
the natural map, $q(J)$![]() is an ideal in $A/K$
is an ideal in $A/K$![]() for each ideal $J$
for each ideal $J$![]() in $A$
in $A$![]() and all ideals in $A/K$
and all ideals in $A/K$![]() are of such a form. Moreover, $\|\omega |J\|=\|\dot \omega |q(J)\|$
are of such a form. Moreover, $\|\omega |J\|=\|\dot \omega |q(J)\|$![]() , hence the claim follows from Theorem 3.4.
, hence the claim follows from Theorem 3.4.
Example 4.2 is generalized in Theorem 4.4. The proof of Theorem 4.4 is inspired by an idea from [Reference Archbold, Robert and Tikuisis4, 3.10], but we will avoid using a background result from [Reference Archbold, Robert and Tikuisis5], that is used in [Reference Archbold, Robert and Tikuisis4, 3.10], and present a short self-contained proof. Recall that the strong radical $J_A$![]() of $A$
of $A$![]() is the intersection of all maximal ideals in $A$
is the intersection of all maximal ideals in $A$![]() .
.
Theorem 4.4
(i) $\omega (J_A)=0$
 for each maximally mixed state $\omega$
for each maximally mixed state $\omega$ on $A$
on $A$ .
.(ii) If a state $\omega$
 on $A$
on $A$ annihilates some intersection $M_1\cap M_2\cap \ldots \cap M_n$
annihilates some intersection $M_1\cap M_2\cap \ldots \cap M_n$ of finitely many maximal ideals in $A,$
of finitely many maximal ideals in $A,$ then $\omega$
then $\omega$ is maximally mixed.
is maximally mixed.
Thus, the set $S_m(A)$![]() of maximally mixed states on $A$
of maximally mixed states on $A$![]() is a weak* dense subset of $S(A/J_A)$
is a weak* dense subset of $S(A/J_A)$![]() (= the set of states on $A$
(= the set of states on $A$![]() that annihilate $J_A$
that annihilate $J_A$![]() ).
).
Proof.
(i) Let $D=S(A/J_A)$
 and $\omega$
and $\omega$ a maximally mixed state on $A$
a maximally mixed state on $A$ . Suppose that $\omega \notin D$
. Suppose that $\omega \notin D$ . Then, $\overline {\omega \circ {{\rm E}(A)}}\cap D=\emptyset$
. Then, $\overline {\omega \circ {{\rm E}(A)}}\cap D=\emptyset$ , otherwise this intersection would be a weak* closed proper ${{\rm E}(A)}$
, otherwise this intersection would be a weak* closed proper ${{\rm E}(A)}$ -invariant subset of $\overline {\omega \circ {{\rm E}(A)}}$
-invariant subset of $\overline {\omega \circ {{\rm E}(A)}}$ , which would contradict the fact that $\omega$
, which would contradict the fact that $\omega$ is maximally mixed. Thus, by the Hahn–Banach theorem, there exist $\alpha,\,\beta \in \mathbb {R}$
is maximally mixed. Thus, by the Hahn–Banach theorem, there exist $\alpha,\,\beta \in \mathbb {R}$ and $h\in A_h$
and $h\in A_h$ such that
(4.1)\begin{equation} \rho(h)\leq\alpha\ \forall\rho\in D\text{ and } \omega(\psi(h))\geq\beta>\alpha\ \forall\psi\in{{\rm E}(A)}. \end{equation}Replacing $h$
such that
(4.1)\begin{equation} \rho(h)\leq\alpha\ \forall\rho\in D\text{ and } \omega(\psi(h))\geq\beta>\alpha\ \forall\psi\in{{\rm E}(A)}. \end{equation}Replacing $h$
 by $h+\gamma 1$
by $h+\gamma 1$ for a sufficiently large $\gamma \in \mathbb {R}_+$
for a sufficiently large $\gamma \in \mathbb {R}_+$ (and modifying $\alpha,\, \beta$
(and modifying $\alpha,\, \beta$ ), we may assume that $h$
), we may assume that $h$ is positive. Then, the first relation in (4.1) means that $\|\dot {h}\|\leq \alpha$
is positive. Then, the first relation in (4.1) means that $\|\dot {h}\|\leq \alpha$ , where $\dot {h}$
, where $\dot {h}$ denotes the coset of $h$
denotes the coset of $h$ in $A/J_A$
in $A/J_A$ . The (algebraic) numerical range $W_{A/J_A}(h)$
. The (algebraic) numerical range $W_{A/J_A}(h)$ of $\dot {h}$
of $\dot {h}$ is an interval, say $[c,\,d]$
is an interval, say $[c,\,d]$ , contained in the numerical range $W_A(h)$
, contained in the numerical range $W_A(h)$ of $h$
of $h$ , which is an interval, say $[a,\,b]$
, which is an interval, say $[a,\,b]$ ; note that $a\leq c\leq d=\|\dot {h}\|\leq b=\|h\|$
; note that $a\leq c\leq d=\|\dot {h}\|\leq b=\|h\|$ . Let $f:[a,\,b]\to [c,\,d]$
. Let $f:[a,\,b]\to [c,\,d]$ be the function, which act as the identity on $[c,\,d]$
be the function, which act as the identity on $[c,\,d]$ , and maps $[a,\,c]$
, and maps $[a,\,c]$ into $\{c\}$
into $\{c\}$ and $[d,\,b]$
and $[d,\,b]$ into $\{d\}$
into $\{d\}$ . For every proper ideal $K$
. For every proper ideal $K$ in $A$
in $A$ the quotient $A/(K+J_A)$
the quotient $A/(K+J_A)$ is non-zero, for $K$
is non-zero, for $K$ is contained in a maximal ideal $M$
is contained in a maximal ideal $M$ and hence $K+J_A\subseteq M+J_A=M\ne A$
and hence $K+J_A\subseteq M+J_A=M\ne A$ . Since $W_{A/(K+J_A)}(h)\subseteq W_{A/K}(h)\cap W_{A/J_A}(h)$
. Since $W_{A/(K+J_A)}(h)\subseteq W_{A/K}(h)\cap W_{A/J_A}(h)$ , this intersection is not empty, hence the interval $W_{A/K}(h)$
, this intersection is not empty, hence the interval $W_{A/K}(h)$ intersects $[c,\,d]$
intersects $[c,\,d]$ and is therefore mapped by $f$
and is therefore mapped by $f$ into itself. The numerical range $W_{A/K}(f(h))$
into itself. The numerical range $W_{A/K}(f(h))$ of the coset of $f(h)$
of the coset of $f(h)$ in $A/K$
in $A/K$ is just the convex hull of the spectrum $\sigma _{A/K}(f(h))=f(\sigma _{A/K}(h)$
is just the convex hull of the spectrum $\sigma _{A/K}(f(h))=f(\sigma _{A/K}(h)$ , hence $W_{A/K}(f(h))\subseteq f(W_{A/K}(h))\subseteq W_{A/K}(h)$
, hence $W_{A/K}(f(h))\subseteq f(W_{A/K}(h))\subseteq W_{A/K}(h)$ . This inclusion implies that $f(h)\in \overline {{{\rm E}(A)}(h)}$
. This inclusion implies that $f(h)\in \overline {{{\rm E}(A)}(h)}$ by [Reference Magajna23], hence $\omega (f(h))>\alpha$
by [Reference Magajna23], hence $\omega (f(h))>\alpha$ by the second relation in (4.1). Since $\omega$
by the second relation in (4.1). Since $\omega$ is a state, it follows that $W_A(f(h))$
is a state, it follows that $W_A(f(h))$ intersects $(\alpha,\,\infty )$
intersects $(\alpha,\,\infty )$ . But this is a contradiction since $W_A(f(h))$
. But this is a contradiction since $W_A(f(h))$ is the convex hull of the spectrum $\sigma _A(f(h))=f(\sigma _A(h))\subseteq [c,\,d]=[c,\,\|\dot {h}\|]\subseteq [c,\,\alpha ]$
is the convex hull of the spectrum $\sigma _A(f(h))=f(\sigma _A(h))\subseteq [c,\,d]=[c,\,\|\dot {h}\|]\subseteq [c,\,\alpha ]$ . Thus, $\omega \in D$
. Thus, $\omega \in D$ .
.(ii) By the Chinese remainder theorem [Reference Grove15, 6.3], there is a natural isomorphism $A/\cap _{j=1}^{n}M_j\cong \oplus _{j=1}^{n}A/M_j$
 , thus we may regard $\omega$
, thus we may regard $\omega$ as a state on $\oplus _{j=1}^{n}A/M_j$
as a state on $\oplus _{j=1}^{n}A/M_j$ . Since the algebras $A/M_j$
. Since the algebras $A/M_j$ are simple, all states on them are maximally mixed by Example 4.2. The same then holds for their direct sum, so all states on $A/\cap _{j=1}^{n}M_j$
are simple, all states on them are maximally mixed by Example 4.2. The same then holds for their direct sum, so all states on $A/\cap _{j=1}^{n}M_j$ are maximally mixed and (ii) follows by Remark 4.3.
are maximally mixed and (ii) follows by Remark 4.3.
The set of all states that annihilate some finite intersection of maximal ideals of $A$![]() is convex and norming for $A/J_A$
is convex and norming for $A/J_A$![]() (since the natural map $A/J_A\to \oplus _MA/M$
(since the natural map $A/J_A\to \oplus _MA/M$![]() , where the sum is over all maximal ideals in $A$
, where the sum is over all maximal ideals in $A$![]() , is a monomorphism, thus isometric), hence weak* dense in $S(A/J_A)$
, is a monomorphism, thus isometric), hence weak* dense in $S(A/J_A)$![]() [Reference Kadison and Ringrose20, 4.3.9].
[Reference Kadison and Ringrose20, 4.3.9].
Remark 4.5 A similar argument as in [Reference Archbold, Robert and Tikuisis4, 3.2] shows that the set $S_m(A)$![]() of all maximally mixed states on a C$^{*}$
of all maximally mixed states on a C$^{*}$![]() -algebra $A$
-algebra $A$![]() is always norm closed.
is always norm closed.
Recall that a C$^{*}$![]() -algebra $A$
-algebra $A$![]() is weakly central if different maximal ideals of $A$
is weakly central if different maximal ideals of $A$![]() have different intersections with the centre $Z$
have different intersections with the centre $Z$![]() of $A$
of $A$![]() .
.
Theorem 4.6 If the set $S_m(A)$![]() of all maximally mixed states is weak* closed (which by Theorem 4.4 just means that $S_m(A)=S(A/J_A)$
of all maximally mixed states is weak* closed (which by Theorem 4.4 just means that $S_m(A)=S(A/J_A)$![]() ), then each primitive ideal of $A$
), then each primitive ideal of $A$![]() containing $J_A$
containing $J_A$![]() is maximal. If $A$
is maximal. If $A$![]() is weakly central, then the converse also holds: if each primitive ideal containing $J_A$
is weakly central, then the converse also holds: if each primitive ideal containing $J_A$![]() is maximal, then $S_m(A)=S(A/J_A)$
is maximal, then $S_m(A)=S(A/J_A)$![]() .
.
Proof. By Remark 4.3 a state $\omega$![]() on $A/J_A$
on $A/J_A$![]() is maximally mixed if and only if it is maximally mixed on $A$
is maximally mixed if and only if it is maximally mixed on $A$![]() . By [Reference Archbold and Gogić3, 3.10], the quotients of weakly central C$^{*}$
. By [Reference Archbold and Gogić3, 3.10], the quotients of weakly central C$^{*}$![]() -algebras are weakly central, so in particular $A/J_A$
-algebras are weakly central, so in particular $A/J_A$![]() is weakly central. In this way, we reduce the proof to the algebra $A/J_A$
is weakly central. In this way, we reduce the proof to the algebra $A/J_A$![]() (instead of $A$
(instead of $A$![]() ), which has strong radical $0$
), which has strong radical $0$![]() . Thus, we may assume that $J_A=0$
. Thus, we may assume that $J_A=0$![]() .
.
Suppose now that $S_m(A)=S(A)$![]() . Then, $S_m(A/P)=S(A/P)$
. Then, $S_m(A/P)=S(A/P)$![]() for each primitive ideal $P$
for each primitive ideal $P$![]() of $A$
of $A$![]() by Remark 4.3. If $M$
by Remark 4.3. If $M$![]() is a maximal ideal of $A$
is a maximal ideal of $A$![]() containing $P$
containing $P$![]() , then $A/M$
, then $A/M$![]() is a quotient of $A/P$
is a quotient of $A/P$![]() , hence each state $\rho \in S(A/M)$
, hence each state $\rho \in S(A/M)$![]() can be regarded as a state on $A/P$
can be regarded as a state on $A/P$![]() and therefore can be weak* approximated by convex combinations of vector states on $A/P$
and therefore can be weak* approximated by convex combinations of vector states on $A/P$![]() , where $A/P$
, where $A/P$![]() has been faithfully represented on a Hilbert space. Since $A/P$
has been faithfully represented on a Hilbert space. Since $A/P$![]() is primitive, as a consequence of the Kadison transitivity theorem, each vector state is of the form $x\mapsto \theta (u^{*}xu)$
is primitive, as a consequence of the Kadison transitivity theorem, each vector state is of the form $x\mapsto \theta (u^{*}xu)$![]() for a fixed state $\theta$
for a fixed state $\theta$![]() on $A/P$
on $A/P$![]() with $\theta (M/P)\ne 0$
with $\theta (M/P)\ne 0$![]() , where $u\in A/P$
, where $u\in A/P$![]() is unitary [Reference Kadison and Ringrose20, 5.4.5]. Thus, $\rho \in \overline {\theta \circ {{\rm E}}(A/P)}$
is unitary [Reference Kadison and Ringrose20, 5.4.5]. Thus, $\rho \in \overline {\theta \circ {{\rm E}}(A/P)}$![]() . But $\rho (M/P)=0$
. But $\rho (M/P)=0$![]() , while $\theta (M/P)\ne 0$
, while $\theta (M/P)\ne 0$![]() if $M\ne P$
if $M\ne P$![]() , hence $\theta \notin \overline {\rho \circ {{\rm E}}(A/P)}$
, hence $\theta \notin \overline {\rho \circ {{\rm E}}(A/P)}$![]() if $M\ne P$
if $M\ne P$![]() . Thus, $\rho$
. Thus, $\rho$![]() can not be maximally mixed (on $A/P$
can not be maximally mixed (on $A/P$![]() and hence also on $A$
and hence also on $A$![]() ) if $P$
) if $P$![]() is not maximal. This argument, which we have found in [Reference Archbold, Robert and Tikuisis4, proof of 3.15], shows that in general the equality $S_m(A)=S(A)$
is not maximal. This argument, which we have found in [Reference Archbold, Robert and Tikuisis4, proof of 3.15], shows that in general the equality $S_m(A)=S(A)$![]() can hold only if all primitive ideals containing $J_A$
can hold only if all primitive ideals containing $J_A$![]() are maximal. If $A$
are maximal. If $A$![]() is weakly central and by our reduction above $J_A=0$
is weakly central and by our reduction above $J_A=0$![]() , then the assumption that all primitive ideals are maximal implies that the primitive spectrum $\check {A}$
, then the assumption that all primitive ideals are maximal implies that the primitive spectrum $\check {A}$![]() of $A$
of $A$![]() is homeomorphic to the maximal ideal space $\Delta$
is homeomorphic to the maximal ideal space $\Delta$![]() of $Z$
of $Z$![]() (via the map $\check {A}\ni M\mapsto M\cap Z\in \Delta$
(via the map $\check {A}\ni M\mapsto M\cap Z\in \Delta$![]() ). Thus, $\check {A}$
). Thus, $\check {A}$![]() is Hausdorff and in this case, Corollary 3.2 shows that all states on $A$
is Hausdorff and in this case, Corollary 3.2 shows that all states on $A$![]() are maximally mixed.
are maximally mixed.
It is well known that each W$^{*}$![]() -algebra $\mathcal {R}$
-algebra $\mathcal {R}$![]() is weakly central. If $\mathcal {R}$
is weakly central. If $\mathcal {R}$![]() is properly infinite, each primitive ideal $P$
is properly infinite, each primitive ideal $P$![]() containing $J_{\mathcal {R}}$
containing $J_{\mathcal {R}}$![]() is maximal. (Namely, by [Reference Halpern16, 2.3] or [Reference Kadison and Ringrose20, 8.7.21], the ideal $M:=P+J_{\mathcal {R}}\supseteq \mathcal {R}(P\cap \mathcal {Z})+J_{\mathcal {R}}$
is maximal. (Namely, by [Reference Halpern16, 2.3] or [Reference Kadison and Ringrose20, 8.7.21], the ideal $M:=P+J_{\mathcal {R}}\supseteq \mathcal {R}(P\cap \mathcal {Z})+J_{\mathcal {R}}$![]() is maximal, and $M=P$
is maximal, and $M=P$![]() if $P\supseteq J_{\mathcal {R}}$
if $P\supseteq J_{\mathcal {R}}$![]() .) So, we can state the following corollary.
.) So, we can state the following corollary.
Corollary 4.7 In a properly infinite von Neumann algebra $\mathcal {R}$![]() maximally mixed states are just the states that annihilate the strong radical $J_{\mathcal {R}}$
maximally mixed states are just the states that annihilate the strong radical $J_{\mathcal {R}}$![]() .
.
If $\mathcal {R}$![]() is finite, primitive ideals are not necessarily maximal. (By [Reference Halpern17, 4.7], any ideal $\mathcal {R} t$
is finite, primitive ideals are not necessarily maximal. (By [Reference Halpern17, 4.7], any ideal $\mathcal {R} t$![]() , where $t$
, where $t$![]() is a maximal ideal of the centre of $\mathcal {R}$
is a maximal ideal of the centre of $\mathcal {R}$![]() , is primitive, while using the central trace, one can show that not all such ideals are maximal in $\mathcal {R}=\oplus _{n}{\rm M}_n(\mathbb {C})$
, is primitive, while using the central trace, one can show that not all such ideals are maximal in $\mathcal {R}=\oplus _{n}{\rm M}_n(\mathbb {C})$![]() , for example.) Thus, the set of maximally mixed states on $\mathcal {R}$
, for example.) Thus, the set of maximally mixed states on $\mathcal {R}$![]() is not weak* closed.
is not weak* closed.
Throughout the rest of the paper $\mathcal {R}$![]() is a W $^{*}$
is a W $^{*}$![]() -algebra, $\mathcal {Z}$
-algebra, $\mathcal {Z}$![]() its centre and $\Delta$
its centre and $\Delta$![]() the maximal ideal space of $\mathcal {Z}$
the maximal ideal space of $\mathcal {Z}$![]() . For each $t\in \Delta$
. For each $t\in \Delta$![]() let $M_t$
let $M_t$![]() be the unique maximal ideal of $\mathcal {R}$
be the unique maximal ideal of $\mathcal {R}$![]() that contains $t$
that contains $t$![]() [Reference Kadison and Ringrose20, 8.7.15]). Note that $\phi (\mathcal {R} t)=\phi (\mathcal {R})t\subseteq t$
[Reference Kadison and Ringrose20, 8.7.15]). Note that $\phi (\mathcal {R} t)=\phi (\mathcal {R})t\subseteq t$![]() for each $\mathcal {Z}$
for each $\mathcal {Z}$![]() -module map $\phi :\mathcal {R}\to \mathcal {Z}$
-module map $\phi :\mathcal {R}\to \mathcal {Z}$![]() .
.
To prove that tracial states are maximally mixed, we need a lemma.
Lemma 4.8 A bounded $\mathcal {Z}$![]() -module map $\phi :\mathcal {R}\to \mathcal {Z}\subseteq \mathcal {R}$
-module map $\phi :\mathcal {R}\to \mathcal {Z}\subseteq \mathcal {R}$![]() preserves all ideals of $\mathcal {R}$
preserves all ideals of $\mathcal {R}$![]() if and only if $\phi (M_t)\subseteq t$
if and only if $\phi (M_t)\subseteq t$![]() for each $t\in \Delta$
for each $t\in \Delta$![]() . If $\mathcal {R}$
. If $\mathcal {R}$![]() is properly infinite, this is equivalent to $\phi (J_{\mathcal {R}})=0$
is properly infinite, this is equivalent to $\phi (J_{\mathcal {R}})=0$![]() .
.
Proof. Let $J$![]() be an ideal in $\mathcal {R}$
be an ideal in $\mathcal {R}$![]() and $K=J\cap \mathcal {Z}$
and $K=J\cap \mathcal {Z}$![]() . As an ideal in $\mathcal {Z}$
. As an ideal in $\mathcal {Z}$![]() , $K$
, $K$![]() can be identified with the set of all continuous functions on $\Delta$
can be identified with the set of all continuous functions on $\Delta$![]() than vanish on some closed subset $\Delta _K$
than vanish on some closed subset $\Delta _K$![]() of $\Delta$
of $\Delta$![]() , hence $K$
, hence $K$![]() is the intersection of a family $\{t: t\in \Delta _K\}$
is the intersection of a family $\{t: t\in \Delta _K\}$![]() of maximal ideals of $\mathcal {Z}$
of maximal ideals of $\mathcal {Z}$![]() . By [Reference Kadison and Ringrose20, 8.7.15], there exists the largest ideal $J(K)$
. By [Reference Kadison and Ringrose20, 8.7.15], there exists the largest ideal $J(K)$![]() in $\mathcal {R}$
in $\mathcal {R}$![]() such that $J(K)\cap \mathcal {Z}=K$
such that $J(K)\cap \mathcal {Z}=K$![]() , and it follows from [Reference Kadison and Ringrose20, 8.7.16] that $J(K)=\cap _{t\in \Delta _K}M_t$
, and it follows from [Reference Kadison and Ringrose20, 8.7.16] that $J(K)=\cap _{t\in \Delta _K}M_t$![]() . Now $J\cap \mathcal {Z}=K$
. Now $J\cap \mathcal {Z}=K$![]() implies that $J\subseteq J(K)$
implies that $J\subseteq J(K)$![]() . Thus, if $\phi$
. Thus, if $\phi$![]() has the property that $\phi (M_t)\subseteq t$
has the property that $\phi (M_t)\subseteq t$![]() for all $t\in \Delta$
for all $t\in \Delta$![]() , then $\phi (J)\subseteq \phi (J(K))\subseteq \cap _{t\in \Delta _K}\phi (M_t)\subseteq \cap _{t\in \Delta _K}t=K\subseteq J$
, then $\phi (J)\subseteq \phi (J(K))\subseteq \cap _{t\in \Delta _K}\phi (M_t)\subseteq \cap _{t\in \Delta _K}t=K\subseteq J$![]() .
.
If $\mathcal {R}$![]() is properly infinite, then $M_t=\mathcal {R} t+J_{\mathcal {R}}$
is properly infinite, then $M_t=\mathcal {R} t+J_{\mathcal {R}}$![]() for each $t\in \Delta$
for each $t\in \Delta$![]() by [Reference Kadison and Ringrose20, 8.7.21 (1)]. Thus, if $\phi (J_{\mathcal {R}})=0$
by [Reference Kadison and Ringrose20, 8.7.21 (1)]. Thus, if $\phi (J_{\mathcal {R}})=0$![]() , then we have $\phi (M_t)=\phi (\mathcal {R})t\subseteq t$
, then we have $\phi (M_t)=\phi (\mathcal {R})t\subseteq t$![]() for all $t\in \Delta$
for all $t\in \Delta$![]() . Conversely, if $\phi (M_t)\subseteq t$
. Conversely, if $\phi (M_t)\subseteq t$![]() for all $t$
for all $t$![]() , then $\phi (J_{\mathcal {R}})=\phi (\cap _{t\in \Delta }M_t)\subseteq \cap _{t\in \Delta }t=0$
, then $\phi (J_{\mathcal {R}})=\phi (\cap _{t\in \Delta }M_t)\subseteq \cap _{t\in \Delta }t=0$![]() .
.
Corollary 4.9 A unital positive $\mathcal {Z}$![]() -module map $\phi :\mathcal {R}\to \mathcal {Z}\subseteq \mathcal {R}$
-module map $\phi :\mathcal {R}\to \mathcal {Z}\subseteq \mathcal {R}$![]() is in the point-norm closure of elementary such maps (that is, $\phi \in \overline {{{\rm E}(\mathcal {R})}}^{\rm {p.n.}}$
is in the point-norm closure of elementary such maps (that is, $\phi \in \overline {{{\rm E}(\mathcal {R})}}^{\rm {p.n.}}$![]() ) if and only if $\phi (M_t)\subseteq t$
) if and only if $\phi (M_t)\subseteq t$![]() for each $t\in \Delta$
for each $t\in \Delta$![]() .
.
Proof. By [Reference Magajna24, 2.2] and [Reference Magajna25, 2.1] each completely contractive map $\phi :\mathcal {R}\to \mathcal {Z}\subseteq \mathcal {R}$![]() which preserves all ideals of $\mathcal {R}$
which preserves all ideals of $\mathcal {R}$![]() is in the point-norm closure of maps of the form $x\mapsto a^{*}xb=\sum \nolimits _{j=1}^{n}a_j^{*}xb_j$
is in the point-norm closure of maps of the form $x\mapsto a^{*}xb=\sum \nolimits _{j=1}^{n}a_j^{*}xb_j$![]() , where $n\in \mathbb {N}$
, where $n\in \mathbb {N}$![]() , $a_j,\,b_j\in \mathcal {R}$
, $a_j,\,b_j\in \mathcal {R}$![]() , $a:=(a_1,\,\ldots,\,a_n)^{T}$
, $a:=(a_1,\,\ldots,\,a_n)^{T}$![]() , $b:=(b_1,\,\ldots,\,b_n)$
, $b:=(b_1,\,\ldots,\,b_n)$![]() , $\|a\|\leq 1$
, $\|a\|\leq 1$![]() and $\|b\|\leq 1$
and $\|b\|\leq 1$![]() . If $\phi$
. If $\phi$![]() is unital, then we can modify such maps to unital maps in the same way as in the proof of Theorem 2.1, which shows that $\phi \in \overline {{{\rm E}(\mathcal {R})}}^{{\rm p.n.}}$
is unital, then we can modify such maps to unital maps in the same way as in the proof of Theorem 2.1, which shows that $\phi \in \overline {{{\rm E}(\mathcal {R})}}^{{\rm p.n.}}$![]() .
.
Corollary 4.10 Let $\omega$![]() be a state of the form $\omega =\mu \circ \phi,$
be a state of the form $\omega =\mu \circ \phi,$![]() where $\mu =\omega |\mathcal {Z}$
where $\mu =\omega |\mathcal {Z}$![]() and $\phi :\mathcal {R}\to \mathcal {Z}$
and $\phi :\mathcal {R}\to \mathcal {Z}$![]() is a unital positive $\mathcal {Z}$
is a unital positive $\mathcal {Z}$![]() -module map. If $\phi (M_t)\subseteq t$
-module map. If $\phi (M_t)\subseteq t$![]() for each $t\in \Delta,$
for each $t\in \Delta,$![]() then $\omega$
then $\omega$![]() is maximally mixed. In particular, tracial states are maximally mixed.
is maximally mixed. In particular, tracial states are maximally mixed.
Proof. Suppose that $\rho \in \overline {\omega \circ {{\rm E}(\mathcal {R})}}$![]() . Then, $\rho |\mathcal {Z}=\omega |\mathcal {Z}=\mu$
. Then, $\rho |\mathcal {Z}=\omega |\mathcal {Z}=\mu$![]() , hence
, hence
By Corollary 4.9 $\phi$![]() can be approximated in the point-norm topology by a net of maps $\phi _k\in \overline {{{\rm E}(\mathcal {R})}}^{{\rm p.n.}}$
can be approximated in the point-norm topology by a net of maps $\phi _k\in \overline {{{\rm E}(\mathcal {R})}}^{{\rm p.n.}}$![]() . Then, $\omega (x)=\lim _k(\rho (\phi _k(x)))$
. Then, $\omega (x)=\lim _k(\rho (\phi _k(x)))$![]() for all $x\in \mathcal {R}$
for all $x\in \mathcal {R}$![]() . This shows that $\overline {\omega \in \rho \circ {{\rm E}(\mathcal {R})}}$
. This shows that $\overline {\omega \in \rho \circ {{\rm E}(\mathcal {R})}}$![]() , so $\omega$
, so $\omega$![]() is maximally mixed.
is maximally mixed.
Any tracial state $\omega$![]() annihilates the properly infinite part of $\mathcal {R}$
annihilates the properly infinite part of $\mathcal {R}$![]() , hence we assume that $\mathcal {R}$
, hence we assume that $\mathcal {R}$![]() is finite. Then, $\omega =(\omega |\mathcal {Z})\circ \tau$
is finite. Then, $\omega =(\omega |\mathcal {Z})\circ \tau$![]() , where $\tau$
, where $\tau$![]() is the central trace on $\mathcal {R}$
is the central trace on $\mathcal {R}$![]() [Reference Kadison and Ringrose20, 8.3.10]. Since $M_t$
[Reference Kadison and Ringrose20, 8.3.10]. Since $M_t$![]() is of the form $M_t=\{a\in \mathcal {R}:\, \tau (a^{*}a)\in t\}$
is of the form $M_t=\{a\in \mathcal {R}:\, \tau (a^{*}a)\in t\}$![]() by [Reference Kadison and Ringrose20, 8.7.17], for $a\in M_t$
by [Reference Kadison and Ringrose20, 8.7.17], for $a\in M_t$![]() , we have by the Schwarz inequality $\tau (a)^{*}\tau (a)\leq \tau (a^{*}a)\in t$
, we have by the Schwarz inequality $\tau (a)^{*}\tau (a)\leq \tau (a^{*}a)\in t$![]() . This implies that $\tau (a)\in t$
. This implies that $\tau (a)\in t$![]() . Thus, $\tau (M_t)\subseteq t$
. Thus, $\tau (M_t)\subseteq t$![]() , hence $\omega$
, hence $\omega$![]() is maximally mixed by the first part of the corollary.
is maximally mixed by the first part of the corollary.
Are all maximally mixed states on W$^{*}$![]() -algebras of the form specified in Corollary 4.10? Not quite. To investigate this, we still need some preparation.
-algebras of the form specified in Corollary 4.10? Not quite. To investigate this, we still need some preparation.
Lemma 4.11 For each state $\omega$![]() on $\mathcal {R}$
on $\mathcal {R}$![]() there exists a positive $\mathcal {Z}$
there exists a positive $\mathcal {Z}$![]() -module map $\phi :\mathcal {R}\to \mathcal {Z}$
-module map $\phi :\mathcal {R}\to \mathcal {Z}$![]() such that $\omega =(\omega |\mathcal {Z})\circ \phi$
such that $\omega =(\omega |\mathcal {Z})\circ \phi$![]() and $p:=\phi (1)$
and $p:=\phi (1)$![]() is a projection with $\omega (p)=1$
is a projection with $\omega (p)=1$![]() .
.
Proof. Let $\Phi$![]() be the universal representation of $\mathcal {R}$
be the universal representation of $\mathcal {R}$![]() , so that $\mathcal {R}^{\sharp \sharp }$
, so that $\mathcal {R}^{\sharp \sharp }$![]() is the weak* closure of $\Phi (\mathcal {R})$
is the weak* closure of $\Phi (\mathcal {R})$![]() . Then, the $*$
. Then, the $*$![]() -homomorphism $\Phi ^{-1}:\Phi (\mathcal {R})\to \mathcal {R}$
-homomorphism $\Phi ^{-1}:\Phi (\mathcal {R})\to \mathcal {R}$![]() can be weak* continuously extended to a $*$
can be weak* continuously extended to a $*$![]() -homomorphism $\Psi :\mathcal {R}^{\sharp \sharp }\to \mathcal {R}$
-homomorphism $\Psi :\mathcal {R}^{\sharp \sharp }\to \mathcal {R}$![]() ; set $\tilde {\omega }=\omega \circ \Psi$
; set $\tilde {\omega }=\omega \circ \Psi$![]() [Reference Kadison and Ringrose20, 10.1.1, 10.1.12]. Let $\tilde {\mathcal {Z}}$
[Reference Kadison and Ringrose20, 10.1.1, 10.1.12]. Let $\tilde {\mathcal {Z}}$![]() be the centre of $\mathcal {R}^{\sharp \sharp }$
be the centre of $\mathcal {R}^{\sharp \sharp }$![]() . Since $\tilde {\omega }$
. Since $\tilde {\omega }$![]() is weak* continuous, by [Reference Halpern17] or [Reference Strătilă and Zsidó27, 1.4], there exists a unique $\tilde {\mathcal {Z}}$
is weak* continuous, by [Reference Halpern17] or [Reference Strătilă and Zsidó27, 1.4], there exists a unique $\tilde {\mathcal {Z}}$![]() -module homomorphism $\psi :\mathcal {R}^{\sharp \sharp }\to \tilde {\mathcal {Z}}$
-module homomorphism $\psi :\mathcal {R}^{\sharp \sharp }\to \tilde {\mathcal {Z}}$![]() such that $\tilde {\omega }=(\tilde {\omega }|\tilde {\mathcal {Z}})\circ \psi$
such that $\tilde {\omega }=(\tilde {\omega }|\tilde {\mathcal {Z}})\circ \psi$![]() and $\psi (1)$
and $\psi (1)$![]() is the support projection $q$
is the support projection $q$![]() of $\tilde {\omega }|\tilde {\mathcal {Z}}$
of $\tilde {\omega }|\tilde {\mathcal {Z}}$![]() . It is not hard to verify that $\phi :=(\Psi |\tilde {\mathcal {Z}})\circ \psi \circ \Phi$
. It is not hard to verify that $\phi :=(\Psi |\tilde {\mathcal {Z}})\circ \psi \circ \Phi$![]() has the properties stated in the lemma.
has the properties stated in the lemma.
Let $\omega$![]() be a state on $\mathcal {R}$
be a state on $\mathcal {R}$![]() , $\mu =\omega |\mathcal {Z}$
, $\mu =\omega |\mathcal {Z}$![]() and let $\phi$
and let $\phi$![]() , $p$
, $p$![]() be as in Lemma 4.11, so that $\omega =\mu \circ \phi$
be as in Lemma 4.11, so that $\omega =\mu \circ \phi$![]() . Let $J$
. Let $J$![]() be an ideal of $\mathcal {R}$
be an ideal of $\mathcal {R}$![]() and $K=J\cap \mathcal {Z}$
and $K=J\cap \mathcal {Z}$![]() . Let $(e_k)$
. Let $(e_k)$![]() and $(f_l)$
and $(f_l)$![]() be approximate units in $J$
be approximate units in $J$![]() and $K$
and $K$![]() (respectively). Then
(respectively). Then
We may regard $(f_l)$![]() and $(\phi (e_k))$
and $(\phi (e_k))$![]() as two bounded increasing nets in the positive part of the unit ball of $C(\Delta )$
as two bounded increasing nets in the positive part of the unit ball of $C(\Delta )$![]() ($\cong \mathcal {Z}$
($\cong \mathcal {Z}$![]() ), hence they converge pointwise to some lower semi-continuous functions $f$
), hence they converge pointwise to some lower semi-continuous functions $f$![]() and $g$
and $g$![]() (respectively) on $\Delta$
(respectively) on $\Delta$![]() . The ideal $K$
. The ideal $K$![]() of $C(\Delta )$
of $C(\Delta )$![]() is of the form $K=\{a\in C(\Delta ):\, a|\Delta _K^{c}=0\}$
is of the form $K=\{a\in C(\Delta ):\, a|\Delta _K^{c}=0\}$![]() for some open subset $\Delta _K$
for some open subset $\Delta _K$![]() of $\Delta$
of $\Delta$![]() and since $(f_l)$
and since $(f_l)$![]() is an approximate unit for $K$
is an approximate unit for $K$![]() , it follows that $f$
, it follows that $f$![]() is just the indicator function $\chi _{\Delta _K}$
is just the indicator function $\chi _{\Delta _K}$![]() of $\Delta _K$
of $\Delta _K$![]() . Let $\Delta _p$
. Let $\Delta _p$![]() be the clopen subset of $\Delta$
be the clopen subset of $\Delta$![]() that correspond to the projection $p=\phi (1)$
that correspond to the projection $p=\phi (1)$![]() (that is, $p=\chi _{\Delta _p}$
(that is, $p=\chi _{\Delta _p}$![]() , the indicator function of $\Delta _p$
, the indicator function of $\Delta _p$![]() ). Since $f_l\in J$
). Since $f_l\in J$![]() and $(e_k)$
and $(e_k)$![]() is an approximate unit for $J$
is an approximate unit for $J$![]() , $\lim _ke_kf_l=f_l$
, $\lim _ke_kf_l=f_l$![]() , hence $gf_l=\lim _k\phi (e_k)f_l=\lim _k\phi (e_kf_l)=\phi (f_l)=f_l\phi (1)=f_lp$
, hence $gf_l=\lim _k\phi (e_k)f_l=\lim _k\phi (e_kf_l)=\phi (f_l)=f_l\phi (1)=f_lp$![]() and $gf=\lim _lgf_l=\lim _lf_lp=fp$
and $gf=\lim _lgf_l=\lim _lf_lp=fp$![]() , that is $(g-\chi _{\Delta _p})\chi _{\Delta _K}=0$
, that is $(g-\chi _{\Delta _p})\chi _{\Delta _K}=0$![]() . This means that
. This means that
Since $(e_k)$![]() is an approximate unit, for any $k_1$
is an approximate unit, for any $k_1$![]() and $k_2$
and $k_2$![]() , there exists $k_3\geq k_1,\,k_2$
, there exists $k_3\geq k_1,\,k_2$![]() so that $e_{k_3}\geq e_{k_1}$
so that $e_{k_3}\geq e_{k_1}$![]() and $e_{k_3}\geq e_{k_2}$
and $e_{k_3}\geq e_{k_2}$![]() , and $(f_l)$
, and $(f_l)$![]() have the analogous property. Thus, $f=\sup _lf_l$
have the analogous property. Thus, $f=\sup _lf_l$![]() , $g=\sup _k\phi (e_k)$
, $g=\sup _k\phi (e_k)$![]() and we may apply the version of the monotone convergence theorem for nets [Reference Folland12, 7.12]. Thus, denoting by $\hat {\mu }$
and we may apply the version of the monotone convergence theorem for nets [Reference Folland12, 7.12]. Thus, denoting by $\hat {\mu }$![]() , the Radon measure on $\Delta$
, the Radon measure on $\Delta$![]() that corresponds to $\mu$
that corresponds to $\mu$![]() , we have $\lim _l\mu (f_l)=\sup _l\mu (f_l)=\sup _l\int _{\Delta }f_l\,d\hat {\mu }=\int _{\Delta }\sup _l f_l\,d\hat \mu =\int _{\Delta }f\, d\hat {\mu }=\hat {\mu }(f)$
, we have $\lim _l\mu (f_l)=\sup _l\mu (f_l)=\sup _l\int _{\Delta }f_l\,d\hat {\mu }=\int _{\Delta }\sup _l f_l\,d\hat \mu =\int _{\Delta }f\, d\hat {\mu }=\hat {\mu }(f)$![]() and similarly $\lim _k\mu (\phi (e_k))=\hat {\mu }(g)$
and similarly $\lim _k\mu (\phi (e_k))=\hat {\mu }(g)$![]() . Therefore, by (4.2), the equality $\|\omega |J\|=\|\omega |K\|$
. Therefore, by (4.2), the equality $\|\omega |J\|=\|\omega |K\|$![]() is equivalent to $\hat \mu (g)=\hat \mu (f)=\hat \mu (\Delta _K)$
is equivalent to $\hat \mu (g)=\hat \mu (f)=\hat \mu (\Delta _K)$![]() . By (4.3), this condition $\hat \mu (g)=\hat \mu (f))$
. By (4.3), this condition $\hat \mu (g)=\hat \mu (f))$![]() means that $0=\hat \mu (g-f)=\int _{\Delta _K^{c}\cup \Delta _p^{c}}(g-f)\,d\hat \mu =\int _{\Delta _K^{c}}(g-\chi _{\Delta _K})\,d\hat \mu =\int _{\Delta _K^{c}}g\, d\hat \mu$
means that $0=\hat \mu (g-f)=\int _{\Delta _K^{c}\cup \Delta _p^{c}}(g-f)\,d\hat \mu =\int _{\Delta _K^{c}}(g-\chi _{\Delta _K})\,d\hat \mu =\int _{\Delta _K^{c}}g\, d\hat \mu$![]() , since $\hat \mu (\Delta _p^{c})=0$
, since $\hat \mu (\Delta _p^{c})=0$![]() (because $\mu (p)=1$
(because $\mu (p)=1$![]() ). As $g\geq 0$
). As $g\geq 0$![]() , we conclude that $\|\omega |J\|=\|\omega |K\|$
, we conclude that $\|\omega |J\|=\|\omega |K\|$![]() if and only if $g(t)=0$
if and only if $g(t)=0$![]() for $\hat \mu$
for $\hat \mu$![]() -almost all $t\in \Delta _K^{c}$
-almost all $t\in \Delta _K^{c}$![]() . Since $(e_k)$
. Since $(e_k)$![]() is an approximate unit of $J$
is an approximate unit of $J$![]() , $\phi (e_k)(t)>0$
, $\phi (e_k)(t)>0$![]() for some $k$
for some $k$![]() if and only if $\phi (a)(t)\ne 0$
if and only if $\phi (a)(t)\ne 0$![]() for some $a\in J$
for some $a\in J$![]() . Hence, since $g=\sup _k\phi (e_k)$
. Hence, since $g=\sup _k\phi (e_k)$![]() ,
,
This proves the following lemma. (Note that $g$![]() is lower semi-continuous, hence the set $\Delta _{\phi (J)|\Delta _K^{c}\ne 0}$
is lower semi-continuous, hence the set $\Delta _{\phi (J)|\Delta _K^{c}\ne 0}$![]() in the lemma is $\hat \mu$
in the lemma is $\hat \mu$![]() -measurable.)
-measurable.)
Lemma 4.12 $\|\omega |J\|=\|\omega |(J\cap \mathcal {Z})\|$![]() if and only if $\hat \mu (\Delta _{\phi (J)|\Delta _K^{c}\ne 0})=0,$
if and only if $\hat \mu (\Delta _{\phi (J)|\Delta _K^{c}\ne 0})=0,$![]() where
where
Here, $K=J\cap \mathcal {Z}$![]() and $\Delta _K^{c}$
and $\Delta _K^{c}$![]() is the set of all common zeros of elements of $K$
is the set of all common zeros of elements of $K$![]() .
.
The following theorem says that maximally mixed states are those for which the corresponding $\phi$![]() almost (with respect to $\hat \mu$
almost (with respect to $\hat \mu$![]() ) preserve ideals.
) preserve ideals.
Theorem 4.13 Let $\omega$![]() be any state on $\mathcal {R}$
be any state on $\mathcal {R}$![]() . Let $\omega =\mu \circ \phi,$
. Let $\omega =\mu \circ \phi,$![]() where $\mu =\omega |\mathcal {Z}$
where $\mu =\omega |\mathcal {Z}$![]() and $\phi :\mathcal {R}\to \mathcal {Z}$
and $\phi :\mathcal {R}\to \mathcal {Z}$![]() is a positive $\mathcal {Z}$
is a positive $\mathcal {Z}$![]() -module map with $\phi (1)$
-module map with $\phi (1)$![]() a projection. Denote by $\hat \mu$
a projection. Denote by $\hat \mu$![]() the Radon measure on $\Delta$
the Radon measure on $\Delta$![]() that corresponds to $\mu$
that corresponds to $\mu$![]() . Then, $\omega$
. Then, $\omega$![]() is maximally mixed if and only if $\hat \mu (\Delta _{\phi (J)|\Delta _K^{c}\ne 0})=0$
is maximally mixed if and only if $\hat \mu (\Delta _{\phi (J)|\Delta _K^{c}\ne 0})=0$![]() for each ideal $J$
for each ideal $J$![]() in $\mathcal {R}$
in $\mathcal {R}$![]() , where $K=J\cap \mathcal {Z}$
, where $K=J\cap \mathcal {Z}$![]() , $\Delta _K^{c}=\{t\in \Delta :\, K\subseteq t\}$
, $\Delta _K^{c}=\{t\in \Delta :\, K\subseteq t\}$![]() and $\Delta _{\phi (J)|\Delta _K^{c}\ne 0}$
and $\Delta _{\phi (J)|\Delta _K^{c}\ne 0}$![]() is the set defined in (4.4).
is the set defined in (4.4).
Proof. Suppose that $\rho \in \overline {\omega \circ {{\rm E}(\mathcal {R})}}$![]() . Then, $\rho |\mathcal {Z}=\omega |\mathcal {Z}$
. Then, $\rho |\mathcal {Z}=\omega |\mathcal {Z}$![]() and by Theorem 3.4 $\|\rho |J\|\leq \|\omega |J\|$
and by Theorem 3.4 $\|\rho |J\|\leq \|\omega |J\|$![]() for each ideal $J$
for each ideal $J$![]() of $\mathcal {R}$
of $\mathcal {R}$![]() . If $\hat \mu (\Delta _{\phi (J)|\Delta _K^{c}\ne 0})=0$
. If $\hat \mu (\Delta _{\phi (J)|\Delta _K^{c}\ne 0})=0$![]() for each $J$
for each $J$![]() , then by Lemma 4.12 $\|\omega |J\|=\|\omega |(J\cap \mathcal {Z})\|$
, then by Lemma 4.12 $\|\omega |J\|=\|\omega |(J\cap \mathcal {Z})\|$![]() for each $J$
for each $J$![]() , hence $\|\omega |J\|=\|\omega |(J\cap \mathcal {Z})\|=\|\rho |(J\cap \mathcal {Z})\|\leq \|\rho |J\|.$
, hence $\|\omega |J\|=\|\omega |(J\cap \mathcal {Z})\|=\|\rho |(J\cap \mathcal {Z})\|\leq \|\rho |J\|.$![]() Therefore, by Theorem 3.4 $\omega \in \overline {\rho \circ {{\rm E}(\mathcal {R})}}$
Therefore, by Theorem 3.4 $\omega \in \overline {\rho \circ {{\rm E}(\mathcal {R})}}$![]() , which proves that $\omega$
, which proves that $\omega$![]() is maximally mixed.
is maximally mixed.
Conversely, if $\hat \mu (\Delta _{\phi (J_0)|\Delta _K^{c}\ne 0})>0$![]() for some ideal $J_0$
for some ideal $J_0$![]() , then by Lemma 4.12 $\|\omega |(J_0\cap \mathcal {Z})\|<\|\omega |J_0\|$
, then by Lemma 4.12 $\|\omega |(J_0\cap \mathcal {Z})\|<\|\omega |J_0\|$![]() . Let $\psi :\mathcal {R}\to \mathcal {Z}$
. Let $\psi :\mathcal {R}\to \mathcal {Z}$![]() be any positive unital $\mathcal {Z}$
be any positive unital $\mathcal {Z}$![]() -module map that preserves ideals. (For example, the central trace, if $\mathcal {R}$
-module map that preserves ideals. (For example, the central trace, if $\mathcal {R}$![]() is finite, as we have seen in the proof of Corollary 4.10. If $\mathcal {R}$
is finite, as we have seen in the proof of Corollary 4.10. If $\mathcal {R}$![]() is properly infinite, preservation of ideals is equivalent to $\psi (J_{\mathcal {R}})=0$
is properly infinite, preservation of ideals is equivalent to $\psi (J_{\mathcal {R}})=0$![]() by Lemma 4.8, so we can take for $\psi$
by Lemma 4.8, so we can take for $\psi$![]() the composition $\mathcal {R}\stackrel {\eta }{\to }\mathcal {R}/J_{\mathcal {R}}\stackrel {\iota }{\to }\mathcal {Z}$
the composition $\mathcal {R}\stackrel {\eta }{\to }\mathcal {R}/J_{\mathcal {R}}\stackrel {\iota }{\to }\mathcal {Z}$![]() , where $\eta$
, where $\eta$![]() is the natural map and $\iota$
is the natural map and $\iota$![]() is an extension of the inclusion $\mathcal {Z}\to \mathcal {R}/J_{\mathcal {R}}$
is an extension of the inclusion $\mathcal {Z}\to \mathcal {R}/J_{\mathcal {R}}$![]() . Here $\mathcal {Z}$
. Here $\mathcal {Z}$![]() is regarded as contained in $\mathcal {R}/J_{\mathcal {R}}$
is regarded as contained in $\mathcal {R}/J_{\mathcal {R}}$![]() since $\mathcal {Z}\cap J_{\mathcal {R}}=0$
since $\mathcal {Z}\cap J_{\mathcal {R}}=0$![]() , and $\iota$
, and $\iota$![]() exists by the C$^{*}$
exists by the C$^{*}$![]() -injectivity of $\mathcal {Z}$
-injectivity of $\mathcal {Z}$![]() .) Let $\rho =\mu \circ \psi$
.) Let $\rho =\mu \circ \psi$![]() . Since $\psi (J)\subseteq J\cap \mathcal {Z}$
. Since $\psi (J)\subseteq J\cap \mathcal {Z}$![]() for each $J$
for each $J$![]() , the set $\Delta _{\psi (J)|\Delta _{J\cap \mathcal {Z}}^{c}\ne 0}$
, the set $\Delta _{\psi (J)|\Delta _{J\cap \mathcal {Z}}^{c}\ne 0}$![]() is empty, hence by Lemma 4.12 $\|\rho |J\|=\|\rho |(J\cap \mathcal {Z})\|$
is empty, hence by Lemma 4.12 $\|\rho |J\|=\|\rho |(J\cap \mathcal {Z})\|$![]() . Since $\rho |\mathcal {Z}=\mu =\omega |\mathcal {Z}$
. Since $\rho |\mathcal {Z}=\mu =\omega |\mathcal {Z}$![]() , we have $\|\rho |J\|=\|\rho |(J\cap \mathcal {Z})\|=\|\omega |(J\cap \mathcal {Z})\|\leq \|\omega |J\|$
, we have $\|\rho |J\|=\|\rho |(J\cap \mathcal {Z})\|=\|\omega |(J\cap \mathcal {Z})\|\leq \|\omega |J\|$![]() for all $J$
for all $J$![]() , hence $\rho \in \overline {\omega \circ {{\rm E}(\mathcal {R})}}$
, hence $\rho \in \overline {\omega \circ {{\rm E}(\mathcal {R})}}$![]() by Theorem 3.4. But $\|\omega |J_0\|>\|\omega |(J_0\cap \mathcal {Z})\|=\|\rho |(J_0\cap \mathcal {Z})\|=\|\rho |J_0\|$
by Theorem 3.4. But $\|\omega |J_0\|>\|\omega |(J_0\cap \mathcal {Z})\|=\|\rho |(J_0\cap \mathcal {Z})\|=\|\rho |J_0\|$![]() implies that $\omega \notin \overline {\rho \circ {{\rm E}(\mathcal {R})}}$
implies that $\omega \notin \overline {\rho \circ {{\rm E}(\mathcal {R})}}$![]() . Hence, $\omega$
. Hence, $\omega$![]() is not maximally mixed.
is not maximally mixed.
Acknowledgements
The author acknowledges the financial support from the Slovenian Research Agency (research core funding no. P1-0288).