Hostname: page-component-6dbcb7884d-t8hx9 Total loading time: 0 Render date: 2025-02-13T17:11:32.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Anisotropic weighted isoperimetric inequalities for star-shaped and F-mean convex hypersurface

Part of: Global differential geometry

Published online by Cambridge University Press:  10 February 2025

Rong Zhou Open the ORCID record for Rong Zhou [Opens in a new window]  and
Tailong Zhou Open the ORCID record for Tailong Zhou [Opens in a new window]
Rong Zhou
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, 230026 Hefei, P.R. China (zhourong@mail.ustc.edu.cn)
Tailong Zhou*
Affiliation:
School of Mathematics, Sichuan University, Chengdu, 610065 Sichuan, P.R. China (zhoutailong@scu.edu.cn) (corresponding author)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove two sharp anisotropic weighted geometric inequalities that hold for star-shaped and F-mean convex hypersurfaces in 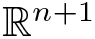$\mathbb{R}^{n+1}$, which involve the anisotropic p-momentum, the anisotropic perimeter, and the volume of the region enclosed by the hypersurface. We also consider their quantitative versions characterized by asymmetry index and the Hausdorff distance between the hypersurface and a rescaled Wulff shape. As a corollary, we obtain the stability of the Weinstock inequality for the first non-zero Steklov eigenvalue for star-shaped and strictly mean convex domains.

Keywords

anisotropic isoperimetric inequalityF-mean convexinverse anisotropic mean curvature flowquantitative Weinstock inequalitySteklov eigenvalue

MSC classification

Primary: 53C44: Geometric evolution equations (mean curvature flow, Ricci flow, etc.)
Secondary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 17
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, B.. Evolving convex curves. Calc. Var. 7 (1998), 315–371.CrossRefGoogle Scholar
Andrews, B.. Volume-preserving anisotropic mean curvature flow. Indiana Univ. Math. J. 50 (2001), 783–827.CrossRefGoogle Scholar
Brasco, L. and Franzina, G.. An anisotropic eigenvalue problem of Stekloff type and weighted Wulff inequalities. Nonlinear Differ. Equ. Appl. 20 (2013), 1795–1830.CrossRefGoogle Scholar
Brothers, J. E. and Morgan, F.. The isoperimetric theorem for general integrands. Michigan Math. J. 41 (1994), 419–431.CrossRefGoogle Scholar
Bucur, D., Ferone, V., Nitsch, C. and Trombetti, C.. Weinstock inequality in higher dimensions. J. Differ. Geom. 118 (2021), 1–21.CrossRefGoogle Scholar
De Rosa, A., KolasiŃski, S. and Santilli, M.. Uniqueness of critical points of the anisotropic isoperimetric problem for finite perimeter sets. Arch. Ration. Mech. Anal. 238 (2020) 1157–1198.CrossRefGoogle Scholar
Figalli, A., Maggi, F. and Pratelli, A.. A mass transport approach to quantitative isoperimetric inequalities. Invent. Math. 182 (2010), 167–211.CrossRefGoogle Scholar
Fonseca, I. and Müller, S.. A uniqueness proof for the Wulff theorem. Proc. Roy. Soc. Edinburgh Sect. A 119 (1991), 125–136.CrossRefGoogle Scholar
Gavitone, N., Angelo La Manna, D., Paoli, G. and Trani, L.. A quantitative Weinstock inequality for convex sets. Calc. Var. Partial Differ. Equ. 59 (2020).CrossRefGoogle Scholar
Girão, F. and Rodrigues, D.. Weighted geometric inequalities for hypersurfaces in sub-static manifolds. Bull. London Math. Soc. 52 (2020), 121–136.CrossRefGoogle Scholar
Guan, P. and Li, J.. The quermassintegral inequalities for k-convex starshaped domains. Adv. Math. 221 (2009), 1725–1732.CrossRefGoogle Scholar
He, Y., Li, H., Ma, H. and Ge, J.. Compact embedded hypersurfaces with constant higher order anisotropic mean curvature. Indiana Univ. Math. J. 58 (2009), 853–868.CrossRefGoogle Scholar
Kwong, K. -K. and Wei, Y.. Geometric inequalities involving three quantities in warped product manifolds. Adv. Math. 430 (2023), .CrossRefGoogle Scholar
Maggi, F.. Sets of finite perimeter and geometric variational problems: An introduction to geometric measure theory, Cambridge Studies in Advanced Mathematics, Vol. 135 (Cambridge University Press, Cambridge, 2012).Google Scholar
Neumayer, R.. A strong form of the quantitative Wulff inequality. SIAM J. Math. Anal. 48 (2016), 1727–1772.CrossRefGoogle Scholar
Paoli, G. and Trani, L.. Anisotropic isoperimetric inequalities involving boundary momentum, perimeter and volume. Nonlinear Anal. 187 (2020), 229–246.CrossRefGoogle Scholar
Sahjwani, P. and Scheuer, J.. Stability of the quermassintegral inequalities in hyperbolic space. J. Geom. Anal. 34 (2023).Google Scholar
Scheuer, J.. Stability from rigidity via umbilicity. Adv. Calc. Var. (2024), doi:10.1515/acv-2023-0119.CrossRefGoogle Scholar
Scheuer, J. and Zhang, X.. Stability of the Wulff shape with respect to anisotropic curvature functions. J. Func. Anal. 288 (3) (2023), . doi:10.1016/j.jfa.2024.110715.Google Scholar
Taylor, J.. Unique structure of solutions to a class of nonelliptic variational problems. Proc. Sympos. Pure Math. 27 (1975), 419–427.CrossRefGoogle Scholar
Taylor, J.. Crystalline variational problems. Bull. Amer. Math. Soc. 84 (1978), 568–588.CrossRefGoogle Scholar
Wulff, G.. Zur Frage der Geschwindigkeit des Wachsturms und der auflösungder Kristall-Flächen. Z. Kristallogr. 34 (1901), 449–530.CrossRefGoogle Scholar
Xia, C.. On an anisotropic Minkowski problem. Indiana Univ. Math. J. 62 (2013), 1399–1430.CrossRefGoogle Scholar
Xia, C.. Inverse anisotropic curvature flow from convex hypersurfaces. J. Geom. Anal.27 (2017), 2131–2154.CrossRefGoogle Scholar
Xia, C.. Inverse anisotropic mean curvature flow and a Minkowski type inequality. Adv. Math. 315 (2017), 102–129.CrossRefGoogle Scholar