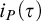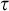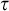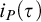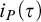1 Introduction
The central notion of proof complexity is that of a propositional proof system as defined by Cook and Reckhow [Reference Cook and Reckhow7]: a p-time function
whose range is exactly the set of propositional tautologies TAUT; for the definiteness we take all tautologies in the DeMorgan language. Any
![]() $w \in {\{0,1\}^*}$
such that
$w \in {\{0,1\}^*}$
such that
![]() $P(w) = \tau $
is called a P-proof of
$P(w) = \tau $
is called a P-proof of
![]() $\tau $
.
$\tau $
.
The primary concern is the size of proofs (i.e., their bit-length) and, in particular, the existence of short proofs. The efficiency of a proof system P is measured by the growth rate of the length-of-proof function:
(We are interested in values of these functions on TAUT only and may, for the definiteness, define it to be equal to
![]() $\infty $
outside TAUT.)
$\infty $
outside TAUT.)
The fundamental problem of proof complexity theory asks if this function is, for some P, bounded by
![]() $|\tau |^{O(1)}$
, for all
$|\tau |^{O(1)}$
, for all
![]() $\tau \in \text {TAUT}$
. This is equivalent to the question whether the computational complexity class NP is closed under complementation: NP
$\tau \in \text {TAUT}$
. This is equivalent to the question whether the computational complexity class NP is closed under complementation: NP
![]() $=_?$
coNP, cf. Cook and Reckhow [Reference Cook and Reckhow7].
$=_?$
coNP, cf. Cook and Reckhow [Reference Cook and Reckhow7].
The second principal open problem of proof complexity is the optimality problem: Is there a proof system P such that
![]() $s_P$
has at most polynomial slow-down over any
$s_P$
has at most polynomial slow-down over any
![]() $s_Q$
? If we define a quasi-ordering
$s_Q$
? If we define a quasi-ordering
![]() $P \geq Q$
on the set of all proof systems by
$P \geq Q$
on the set of all proof systems by
then the problem asks if there is a
![]() $\geq $
-maximal proof system. Such a maximal proof system P would be lengths-of-proofs optimal. The quasi-ordering
$\geq $
-maximal proof system. Such a maximal proof system P would be lengths-of-proofs optimal. The quasi-ordering
![]() $\geq $
has a finer version
$\geq $
has a finer version
![]() $\geq _p$
:
$\geq _p$
:
![]() $P \geq _p Q$
iff there is a p-time function f (called p-simulation) such that for all
$P \geq _p Q$
iff there is a p-time function f (called p-simulation) such that for all
![]() $w$
:
$w$
:
In words: f translates Q-proofs into P-proofs of the same formulas. The reader can find this basic background in [Reference Krajíček17, Chapter 1].
While the existence of short proofs of tautologies is the primary concern of proof complexity, the theory also relates quite closely to the complexity of proof search and SAT algorithms. For proof search algorithms this is obvious: the time complexity of an algorithm searching for P-proofs is lower-bounded by function
![]() $s_P$
.
$s_P$
.
For SAT algorithms (i.e., algorithms finding a satisfying assignment for a propositional formula, if it exists) the relation is indirect. In particular, we can interpret the run of a SAT algorithm S that fails to find a satisfying assignment for
![]() $\neg \tau $
as a proof that
$\neg \tau $
as a proof that
![]() $\tau \in \text {TAUT}$
. Hence S can be studied also as a proof system
$\tau \in \text {TAUT}$
. Hence S can be studied also as a proof system
![]() $P_S$
:
$P_S$
:
and the time complexity of S on unsatisfiable formulas is essentially the same as the length-of-proof function for proof systemFootnote
1
![]() $P_S$
. Hence lower bounds to the latter function imply lower bounds for the time complexity of S. In fact, proof complexity lower bounds apply more generally: a lower bound for
$P_S$
. Hence lower bounds to the latter function imply lower bounds for the time complexity of S. In fact, proof complexity lower bounds apply more generally: a lower bound for
![]() $s_Q$
implies time lower bounds for all SAT algorithms whose soundness is efficiently provableFootnote
2
in Q, cf. [Reference Krajíček16].
$s_Q$
implies time lower bounds for all SAT algorithms whose soundness is efficiently provableFootnote
2
in Q, cf. [Reference Krajíček16].
While
![]() $P_S$
is defined more abstractly than usual logical calculi, the proof system is actually often equal (or close)—in the sense of p-simulation—to some standard logical calculi as is, for example, resolution R. This then allows to interpret various technical proof complexity results as results about the original algorithm S. In this sense proof complexity contributes to the analysis of some classes of SAT algorithms. This facet of proof complexity is surveyed by Buss and Nordström [Reference Buss and Nordström3].
$P_S$
is defined more abstractly than usual logical calculi, the proof system is actually often equal (or close)—in the sense of p-simulation—to some standard logical calculi as is, for example, resolution R. This then allows to interpret various technical proof complexity results as results about the original algorithm S. In this sense proof complexity contributes to the analysis of some classes of SAT algorithms. This facet of proof complexity is surveyed by Buss and Nordström [Reference Buss and Nordström3].
In this paper we are interested in efficiency of proof search algorithms. However, rather than analyzing particular algorithms we consider an outstanding informal problemFootnote 3 :
-
• Is there an optimal way to search for propositional proofs?
Surely this problem must have occurred to everybody interested in proof search, and there are other natural informal questions one can ask (cf. [Reference Krajíček18] for example).
In this paper we investigate what can proof complexity say about the problem in precise mathematical terms. We start with a definition of a proof search algorithm that seems natural (cf. [Reference Krajíček17, Section 21.5]).
Definition 1.1. A proof search algorithm is a pair
![]() $(A,P)$
, where P is a proof system and A is a deterministic algorithm that stops on every inputFootnote
4
and such that
$(A,P)$
, where P is a proof system and A is a deterministic algorithm that stops on every inputFootnote
4
and such that
![]() $A(\tau )$
is a P-proof of
$A(\tau )$
is a P-proof of
![]() $\tau $
, for all tautologies
$\tau $
, for all tautologies
![]() $\tau \in \text {TAUT}$
.
$\tau \in \text {TAUT}$
.
A key to a formalization of the proof search problem is to define a suitable quasi-ordering on the class of all proof search algorithms. In Section 2 we consider a quasi-ordering by the time complexity and in Section 3 we resort to algorithmic information theory and replace time with information, introducing a new notion of information-efficiency of proof systems. This notion offers a precise characterization of the time any algorithm searching for a proof of a particular formula must use.
In both quasi-orderings (by time or information efficiency) there are optimal proof search algorithms when the proof system is fixed, and these two algorithms are essentially the same. Hence the question whether there is an overall optimal proof search algorithm
![]() $(A,P)$
(a maximal element in the respective quasi-ordering) depends only on proof systems P and not on algorithms A. We show that in both quasi-orderings the existence of such an optimal system is equivalent to the existence of a p-optimal proof system, and thus the proof search problem reduces to the optimality problem.
$(A,P)$
(a maximal element in the respective quasi-ordering) depends only on proof systems P and not on algorithms A. We show that in both quasi-orderings the existence of such an optimal system is equivalent to the existence of a p-optimal proof system, and thus the proof search problem reduces to the optimality problem.
Time a proof search algorithm needs to use is traditionally lower bounded by the minimum size of any proof of the formula in question. In Section 4 we compare size (measure) with information (measure) and we note that for non-automatizable proof systems the information measure is more precise for proving time lower bounds than proof size is: there are formulas having short proofs but having large information measure (i.e., while the proofs are short to find them requires long time). Note that it is known that essentially all complete proof systems are non-automatizable under various plausible computational complexity hypotheses. In Section 5 we motivate and isolate the problem to establish unconditional lower bounds for
![]() $i_P(\tau )$
where no lower bounds are known for
$i_P(\tau )$
where no lower bounds are known for
![]() $s_P(\tau )$
. We conclude the paper with remarks on several connections of the information measure to proof complexity in Section 6 and with some further comments in Section 7.
$s_P(\tau )$
. We conclude the paper with remarks on several connections of the information measure to proof complexity in Section 6 and with some further comments in Section 7.
The reader can find basic proof complexity background in [Reference Krajíček17, Chapter 1]. We use only classic facts and we always point to a place in [Reference Krajíček17] where they can be found. From algorithmic information theory we use only the original ideas and notions from Kolmogorov [Reference Kolmogorov10, Reference Kolmogorov11] modified to a time-bounded version of Levin [Reference Levin23]. Standard notions from computational complexity (as are classes P, NP, one-way permutations or pseudo-random generators) can be found in any textbook.
2 Time optimality
The first thing that comes to mind is perhaps to compare two proof search algorithms by the time they use. This is analogous to the fact that in the optimality problem we compare two proof systems by the growth rate of their lengths-of-proofs functions, i.e., by the non-deterministic time. For a deterministic algorithm A that stops on all inputs we denote by
![]() $time_A(w)$
the time A needs to stop on input
$time_A(w)$
the time A needs to stop on input
![]() $w$
.
$w$
.
We shall assume that proof search algorithms stop on every input, not just on inputs from TAUT. Namely, if A is an algorithm that stops on TAUT but maybe not everywhere outside TAUT, define new algorithm
![]() $A'$
that in even steps computes as A, and stops if A does, and in odd steps performs an exhaustive search for a falsifying assignment and stops if it finds one before A stopped. The time complexity of A and
$A'$
that in even steps computes as A, and stops if A does, and in odd steps performs an exhaustive search for a falsifying assignment and stops if it finds one before A stopped. The time complexity of A and
![]() $A'$
on inputs from TAUT are proportional and
$A'$
on inputs from TAUT are proportional and
![]() $A'$
stops everywhere.
$A'$
stops everywhere.
Note that in the following definition the two proof search algorithms do not necessarily use the same proof system.
Definition 2.1. For two proof search algorithms
![]() $(A,P)$
and
$(A,P)$
and
![]() $(B,Q)$
define
$(B,Q)$
define
iff
![]() $(A,P)$
has at most polynomial slow-down over
$(A,P)$
has at most polynomial slow-down over
![]() $(B,Q){:}$
$(B,Q){:}$
for all
![]() $\tau \in \text {TAUT}$
(the constant implicit in
$\tau \in \text {TAUT}$
(the constant implicit in
![]() $O(1)$
depends on the pair of the algorithms).
$O(1)$
depends on the pair of the algorithms).
Lemma 2.2. For any fixed proof system P there is algorithm A such that
![]() $(A,P)$
is
$(A,P)$
is
![]() $\geq _t$
-maximal among all
$\geq _t$
-maximal among all
![]() $(B,P)$
, i.e., it is time-optimal among all
$(B,P)$
, i.e., it is time-optimal among all
![]() $(B,P)$
.
$(B,P)$
.
Proof. This is proved analogously as the existence of a universal NP search algorithm (cf. Levin [Reference Levin22]): given input
![]() $\tau $
, A tries for
$\tau $
, A tries for
![]() $i = 1, 2, \dots $
lexicographically first i algorithms for i steps until it finds a P-proof of
$i = 1, 2, \dots $
lexicographically first i algorithms for i steps until it finds a P-proof of
![]() $\tau $
.
$\tau $
.
We may assume w.l.o.g. that the size of the i-th algorithm is
![]() $O(\log i)$
and that A simulates its t steps in time polynomial in
$O(\log i)$
and that A simulates its t steps in time polynomial in
![]() $t + \log i$
. Hence for a fixed B that is j-th in the ordering then
$t + \log i$
. Hence for a fixed B that is j-th in the ordering then
⊣
Notation.
Let
![]() $(A_P,P)$
denote the proof search algorithm described in the above proof. Hence
$(A_P,P)$
denote the proof search algorithm described in the above proof. Hence
![]() $(A_P,P)$
is time-optimal among all
$(A_P,P)$
is time-optimal among all
![]() $(B,P)$
.
$(B,P)$
.
The optimality problem (both its versions for
![]() $\geq $
and
$\geq $
and
![]() $\geq _p$
) relates to a number of questions in a surprisingly varied areas and there are quite a few relevant statements known (cf. [Reference Krajíček17, Chapter 21]). We shall recall just one statement that we will use in the second proof of Theorem 2.4.
$\geq _p$
) relates to a number of questions in a surprisingly varied areas and there are quite a few relevant statements known (cf. [Reference Krajíček17, Chapter 21]). We shall recall just one statement that we will use in the second proof of Theorem 2.4.
Theorem 2.3. (Krajíček and Pudlák [Reference Krajíček and Pudlák19, Theorem 2.1])
A p-optimal proof system exists iff there is a deterministic algorithm M computing the characteristic function
![]() $\chi _{TAUT}$
of TAUT such that for any other deterministic algorithm
$\chi _{TAUT}$
of TAUT such that for any other deterministic algorithm
![]() $M'$
computing
$M'$
computing
![]() $\chi _{TAUT}$
it holds that:
$\chi _{TAUT}$
it holds that:
Now we shall relate the existence of p-optimal proof systems and time-optimal proof search algorithms. We give two proofs as they illustrate different facets of the statement.
Theorem 2.4. Let P be any proof system containing resolution R and having the property that for some
![]() $c \geq 1$
, for every
$c \geq 1$
, for every
![]() $\tau $
and every
$\tau $
and every
![]() $\tau '$
obtained from
$\tau '$
obtained from
![]() $\tau $
by substituting constants for some atoms it holds
$\tau $
by substituting constants for some atoms it holds
![]() $s_P(\tau ') \le s_P(\tau )^c$
.
$s_P(\tau ') \le s_P(\tau )^c$
.
Then P is p-optimal iff
![]() $(A_P,P)$
is time-optimal among all proof search algorithms
$(A_P,P)$
is time-optimal among all proof search algorithms
![]() $(B,Q)$
.
$(B,Q)$
.
In particular, a p-optimal proof system exists iff a time-optimal proof search algorithm (i.e.,
![]() $\geq _t$
-maximal) exists.
$\geq _t$
-maximal) exists.
First proof. The only-if-direction is obvious, using Lemma 2.2. For the non-trivial if-direction of the theorem we use the fact that for any Q there is a p-time construable sequence of tautologies
such that
![]() $n \le |\langle \textit{Ref}_Q\rangle _n|$
and if P-proofs of these formulas are p-time computable then P p-simulates Q. These formulas formalize the soundnessFootnote
5
of Q and their exact definition is not important here. Their relation to (p-)simulations is a classic fact of proof complexity going back to Cook [Reference Cook5]; see [Reference Krajíček17, Section 19.2 or 21.1] for this background.
$n \le |\langle \textit{Ref}_Q\rangle _n|$
and if P-proofs of these formulas are p-time computable then P p-simulates Q. These formulas formalize the soundnessFootnote
5
of Q and their exact definition is not important here. Their relation to (p-)simulations is a classic fact of proof complexity going back to Cook [Reference Cook5]; see [Reference Krajíček17, Section 19.2 or 21.1] for this background.
Define a proof system
![]() $Q'$
in which
$Q'$
in which
![]() $1^{(n)}$
is a proof of
$1^{(n)}$
is a proof of
![]() $\langle \textit{Ref}_Q\rangle _n$
and any other
$\langle \textit{Ref}_Q\rangle _n$
and any other
![]() $w$
is interpreted as a resolution proof. Further take algorithm B which upon receiving
$w$
is interpreted as a resolution proof. Further take algorithm B which upon receiving
![]() $\tau $
first looks whether
$\tau $
first looks whether
![]() $\tau = \langle \textit{Ref}_Q\rangle _n$
for some n (a priori
$\tau = \langle \textit{Ref}_Q\rangle _n$
for some n (a priori
![]() $\le |\tau |$
) in which case it produces
$\le |\tau |$
) in which case it produces
![]() $1^{(n)}$
, and otherwise it uses some fixed resolution searching algorithm to find a proof.
$1^{(n)}$
, and otherwise it uses some fixed resolution searching algorithm to find a proof.
Because
![]() $(A_P,P)$
is supposed to be time optimal,
$(A_P,P)$
is supposed to be time optimal,
![]() $A_P(\langle \textit{Ref}_Q\rangle _n)$
has to compute in p-time a P-proof of
$A_P(\langle \textit{Ref}_Q\rangle _n)$
has to compute in p-time a P-proof of
![]() $\langle \textit{Ref}_Q\rangle _n$
. But by the stated properties of these formulas
$\langle \textit{Ref}_Q\rangle _n$
. But by the stated properties of these formulas
![]() $P \geq _p Q$
follows.
$P \geq _p Q$
follows.
Second proof. We now give a second, alternative proof for the last statement of the theorem, using Theorem 2.3. For a proof search algorithm
![]() $(A,P)$
define algorithm
$(A,P)$
define algorithm
![]() $M_{(A,P)}$
computing
$M_{(A,P)}$
computing
![]() $\chi _{TAUT}$
as follows: On input
$\chi _{TAUT}$
as follows: On input
![]() $\tau $
it computes
$\tau $
it computes
![]() $A(\tau )$
and checks that
$A(\tau )$
and checks that
![]() $P(A(\tau )) = \tau $
. If so, it outputs
$P(A(\tau )) = \tau $
. If so, it outputs
![]() $1$
, otherwise it outputs
$1$
, otherwise it outputs
![]() $0$
.
$0$
.
On the other hand, if M computes
![]() $\chi _{TAUT}$
define proof system
$\chi _{TAUT}$
define proof system
![]() $P_M$
by
$P_M$
by
and algorithm
![]() $A_M$
: On input
$A_M$
: On input
![]() $\tau $
output the computation of M and
$\tau $
output the computation of M and
![]() $\tau $
.
$\tau $
.
It is easy to verify that:
-
• if
 $(A,P)$
is a time-optimal proof search algorithm then
$(A,P)$
is a time-optimal proof search algorithm then
 $M_{(A,P)}$
is a deterministic algorithm computing
$M_{(A,P)}$
is a deterministic algorithm computing
 $\chi _{TAUT}$
having the time-optimality property from Theorem 2.3, and
$\chi _{TAUT}$
having the time-optimality property from Theorem 2.3, and -
• if M is a deterministic algorithm computing
 $\chi _{TAUT}$
having the time-optimality property from Theorem 2.3 then
$\chi _{TAUT}$
having the time-optimality property from Theorem 2.3 then
 $(A_M, P_M)$
is time-optimal proof search algorithm.
$(A_M, P_M)$
is time-optimal proof search algorithm.
Theorem 2.3 then implies the statement.⊣
If
![]() $P \geq _p Q$
then in any reasonable quasi-ordering of proof search algorithms
$P \geq _p Q$
then in any reasonable quasi-ordering of proof search algorithms
![]() $(A_p,P)$
will be at least as strong as
$(A_p,P)$
will be at least as strong as
![]() $(A_Q,Q)$
. For the opposite direction (the if-direction) of the theorem we utilized the fact that
$(A_Q,Q)$
. For the opposite direction (the if-direction) of the theorem we utilized the fact that
![]() $(A_P,P)$
is required to find in p-time proofs of simple sequences of formulas as are
$(A_P,P)$
is required to find in p-time proofs of simple sequences of formulas as are
![]() $\langle \textit{Ref}_Q\rangle _n$
. A simple sequence of formulas appears also in the following situation. Take any proof search algorithm
$\langle \textit{Ref}_Q\rangle _n$
. A simple sequence of formulas appears also in the following situation. Take any proof search algorithm
![]() $(A,\text {R})$
searching for resolution proofs. Take a sequence of tautologies that are computed by a p-time function from
$(A,\text {R})$
searching for resolution proofs. Take a sequence of tautologies that are computed by a p-time function from
![]() $1^{(n)}$
and that are hard for R but easy for Extended resolution ER and, moreover, their ER-proofs can be computed from
$1^{(n)}$
and that are hard for R but easy for Extended resolution ER and, moreover, their ER-proofs can be computed from
![]() $1^{(n)}$
in p-time by some function f. Examples of such formulas are formulas
$1^{(n)}$
in p-time by some function f. Examples of such formulas are formulas
![]() $PHP_n$
formalizing the pigeonhole principle, cf. Haken [Reference Haken9] and Cook and Reckhow [Reference Cook and Reckhow7] (or see [Reference Krajíček17]). Now define a proof search algorithm
$PHP_n$
formalizing the pigeonhole principle, cf. Haken [Reference Haken9] and Cook and Reckhow [Reference Cook and Reckhow7] (or see [Reference Krajíček17]). Now define a proof search algorithm
![]() $(B,\text {ER})$
that on input
$(B,\text {ER})$
that on input
![]() $\tau $
computes as follows:
$\tau $
computes as follows:
-
1. B checks if
 $\tau = PHP_n$
for some
$\tau = PHP_n$
for some
 $n \geq 1$
(this is p-time because it needs to consider only
$n \geq 1$
(this is p-time because it needs to consider only
 $n \le |\tau |$
).
$n \le |\tau |$
). -
2. If yes, i.e.,
 $\tau = PHP_n$
, then B outputs
$\tau = PHP_n$
, then B outputs
 $f(1^{(n)})$
.
$f(1^{(n)})$
. -
3. Otherwise B outputs
 $A(\tau )$
.
$A(\tau )$
.
Then
![]() $(B,ER)>_t (A,R)$
but intuitively it does not seem quite right to claim that
$(B,ER)>_t (A,R)$
but intuitively it does not seem quite right to claim that
![]() $(B,ER)$
is a better algorithm than
$(B,ER)$
is a better algorithm than
![]() $(A,R)$
; B does not do anything extra except that it remembers one type of simple formulas. One would like to
$(A,R)$
; B does not do anything extra except that it remembers one type of simple formulas. One would like to
-
(*) compare A and B on inputs
 $\tau $
where they actually do something non-trivial.
$\tau $
where they actually do something non-trivial.
In [Reference Krajíček17, Section 21.5] we proposed a definition of a quasi-ordering of proof search algorithms by time as is
![]() $\geq _t$
but measured only on TAUT from which we are allowed to take out a simple (in particular, a p-time construable) sequence of tautologies. Subsequently in [Reference Krajíček18] a stronger variant of that (avoiding all such sequences) was proposed. This could, in principle, allow for the situation that there is an optimal proof search algorithm without having a p-optimal proof system, and thus separate the two questions. However, the resulting quasi-orderings are unintuitive and it is not clear whether they actually help to avoid the if-direction of Theorem 2.4.
$\geq _t$
but measured only on TAUT from which we are allowed to take out a simple (in particular, a p-time construable) sequence of tautologies. Subsequently in [Reference Krajíček18] a stronger variant of that (avoiding all such sequences) was proposed. This could, in principle, allow for the situation that there is an optimal proof search algorithm without having a p-optimal proof system, and thus separate the two questions. However, the resulting quasi-orderings are unintuitive and it is not clear whether they actually help to avoid the if-direction of Theorem 2.4.
A more fundamental issue, related to (*) above, is that the decision not to count (or not count)
![]() $\tau = PHP_n$
when comparing two proof search algorithms is not based only on the individual tautology
$\tau = PHP_n$
when comparing two proof search algorithms is not based only on the individual tautology
![]() $\tau $
but depends on the fact that it is one of an infinite series of tautologies defined in a particular uniform way.
$\tau $
but depends on the fact that it is one of an infinite series of tautologies defined in a particular uniform way.
These considerations are, of course, quite informal but lead us to formal notions discussed in the next section.
3 Information optimality
We shall assume that every
![]() $e \in {\{0,1\}^*}$
is also a code of a unique Turing machine and we shall consider a universal Turing machine U with three inputs
$e \in {\{0,1\}^*}$
is also a code of a unique Turing machine and we shall consider a universal Turing machine U with three inputs
![]() $e,u,1^{(t)}$
that simulates machine e on input u for at most t steps, stops with the same output if e stops in
$e,u,1^{(t)}$
that simulates machine e on input u for at most t steps, stops with the same output if e stops in
![]() $\le t$
steps, and otherwise outputs
$\le t$
steps, and otherwise outputs
![]() $0$
. We shall assume that U runs in polynomial time.
$0$
. We shall assume that U runs in polynomial time.
Using this setup recall the time-bounded Kolmogorov complexity of a string
![]() $w \in {\{0,1\}^*}$
as defined by Levin [Reference Levin22]:
$w \in {\{0,1\}^*}$
as defined by Levin [Reference Levin22]:
(we use
![]() $\lceil \log t\rceil $
instead of
$\lceil \log t\rceil $
instead of
![]() $\log t$
as we want integer values) and
$\log t$
as we want integer values) and
Intuitively, smaller
![]() $Kt(w)$
is simpler
$Kt(w)$
is simpler
![]() $w$
is, in the sense that it can be compressed to a shorter string without loosing information.
$w$
is, in the sense that it can be compressed to a shorter string without loosing information.
Note that we have trivial estimates to
![]() $Kt(w|u)$
and
$Kt(w|u)$
and
![]() $Kt(w)$
in terms of the size
$Kt(w)$
in terms of the size
![]() $|w|$
:
$|w|$
:
The left inequality holds as need time
![]() $|w|$
to write
$|w|$
to write
![]() $w$
, the middle one is trivial and the right inequality follows from considering a machine that has
$w$
, the middle one is trivial and the right inequality follows from considering a machine that has
![]() $w$
hardwired into its program.
$w$
hardwired into its program.
We would like to have inequality
![]() $Kt(w) \le Kt(w|u) + Kt(u)$
that is intuitively justified by composing machine
$Kt(w) \le Kt(w|u) + Kt(u)$
that is intuitively justified by composing machine
![]() $e_1$
computing u with machine
$e_1$
computing u with machine
![]() $e_2$
computing
$e_2$
computing
![]() $w$
from u. However, as pointed out in Kolmogorov [Reference Kolmogorov11], the code of the composed machine (and, in general, of the pair
$w$
from u. However, as pointed out in Kolmogorov [Reference Kolmogorov11], the code of the composed machine (and, in general, of the pair
![]() $(e_1,e_2)$
) does not have length
$(e_1,e_2)$
) does not have length
![]() $|e_1| + |e_2|$
but rather can be defined of length
$|e_1| + |e_2|$
but rather can be defined of length
![]() $|e_1| + |e_2| + O(\log (|e_1|) + \log (|e_2|))$
. Hence we get a slightly worse inequality:
$|e_1| + |e_2| + O(\log (|e_1|) + \log (|e_2|))$
. Hence we get a slightly worse inequality:
and similarly
We use
![]() $Kt$
to define a new measure of complexity of proofs.
$Kt$
to define a new measure of complexity of proofs.
Definition 3.1. Let P be a proof system. For any
![]() $\tau \in TAUT$
define
$\tau \in TAUT$
define
We shall call
![]() $i_P$
the information efficiency function.
$i_P$
the information efficiency function.
The function measures the minimal amount of information any P-proof of
![]() $\tau $
has to contain, knowing what
$\tau $
has to contain, knowing what
![]() $\tau $
is. The next statement shows that stronger proof systems do not require much more information.
$\tau $
is. The next statement shows that stronger proof systems do not require much more information.
Lemma 3.2. For any
![]() $P, Q$
,
$P, Q$
,
![]() $P \geq _p Q$
implies
$P \geq _p Q$
implies
![]() $i_P(\tau ) \le O(i_Q(\tau ))$
.
$i_P(\tau ) \le O(i_Q(\tau ))$
.
Proof. Let f be a p-simulation of Q by P. Take
![]() $w$
that is a Q-proof of
$w$
that is a Q-proof of
![]() $\tau $
with
$\tau $
with
![]() $Kt(w|\tau ) = i_Q(\tau )$
.
$Kt(w|\tau ) = i_Q(\tau )$
.
Using (3) we can estimate
![]() $i_P(\tau ) \le Kt(f(w)|\tau )$
from above by the sum
$i_P(\tau ) \le Kt(f(w)|\tau )$
from above by the sum
![]() $Kt(f(w)|w) + Kt(w|\tau ) = Kt(f(w)|w) + i_Q(\tau )$
plus some log-small terms. But
$Kt(f(w)|w) + Kt(w|\tau ) = Kt(f(w)|w) + i_Q(\tau )$
plus some log-small terms. But
![]() $Kt(f(w)|w) \le O(\log |w|) + O(1)$
(the
$Kt(f(w)|w) \le O(\log |w|) + O(1)$
(the
![]() $O(1)$
is for the machine computing f and the computation runs in time polynomial in
$O(1)$
is for the machine computing f and the computation runs in time polynomial in
![]() $|w|$
) which is also bounded by
$|w|$
) which is also bounded by
![]() $O(i_Q(\tau ))$
by (1).⊣
$O(i_Q(\tau ))$
by (1).⊣
The next two statements relate the information measure fairly precisely to time in proof search.
Lemma 3.3. Let
![]() $(A,P)$
be any proof search algorithm. Then for all
$(A,P)$
be any proof search algorithm. Then for all
![]() $\tau \in TAUT{:}$
$\tau \in TAUT{:}$
In particular,
![]() $time_A(\tau ) \geq \Omega (2^{i_P(\tau )})$
.
$time_A(\tau ) \geq \Omega (2^{i_P(\tau )})$
.
Proof. The first inequality is obvious, and the second follows from the definition as
![]() $A(\tau ) = U(A, \tau , 1^{(t)})$
, where
$A(\tau ) = U(A, \tau , 1^{(t)})$
, where
![]() $t = time_A(\tau )$
.⊣
$t = time_A(\tau )$
.⊣
This statement is complemented by the next one essentially saying that easy proofs are easy to find. Footnote 6
Lemma 3.4. (i-automatizability)
For every proof system P there is an algorithm B such that for all
![]() $\tau \in TAUT{:}$
$\tau \in TAUT{:}$
and
Proof. For
![]() $i = 1,2, \dots $
algorithm B (using the universal machine U) does the following:
$i = 1,2, \dots $
algorithm B (using the universal machine U) does the following:
-
• In the lexico-graphic order tries all pairs
 $(e,t)$
such that
$(e,t)$
such that
 $|e| + \lceil \log t \rceil = i$
and checks whether
$|e| + \lceil \log t \rceil = i$
and checks whether
 $U(e, \tau , 1^{(t)})$
is a P-proof of
$U(e, \tau , 1^{(t)})$
is a P-proof of
 $\tau $
. If so, it outputs the proof and stops.
$\tau $
. If so, it outputs the proof and stops.
There are
![]() $\le 2^{2i}$
such pairs
$\le 2^{2i}$
such pairs
![]() $(e,t)$
to consider, computing
$(e,t)$
to consider, computing
![]() $U(e, \tau , 1^{(t)})$
takes time
$U(e, \tau , 1^{(t)})$
takes time
![]() $poly(|e|, t) \le 2^{O(i)}$
and checking whether
$poly(|e|, t) \le 2^{O(i)}$
and checking whether
![]() $P(U(e, \tau , 1^{(t)})) = \tau $
takes time
$P(U(e, \tau , 1^{(t)})) = \tau $
takes time
![]() $poly(|U(e, \tau , 1^{(t)})|) \le 2^{O(i)}$
. The procedure takes for one i overall time
$poly(|U(e, \tau , 1^{(t)})|) \le 2^{O(i)}$
. The procedure takes for one i overall time
![]() $2^{O(i)}$
and because B succeeds in the round for
$2^{O(i)}$
and because B succeeds in the round for
![]() $i = i_P(\tau )$
, the overall time B takes is
$i = i_P(\tau )$
, the overall time B takes is
![]() $\le 2^{O(i_P(\tau ))}$
.⊣
$\le 2^{O(i_P(\tau ))}$
.⊣
Notation.
Let us denote the algorithm described in the proof by
![]() $B_P$
.
$B_P$
.
In fact, the argument in the proof of Lemma 3.4 is another version of the universal search as the next statement shows.
Corollary 3.5. Let P be any proof system and let
![]() $A_P$
and
$A_P$
and
![]() $B_P$
be the two algorithms defined earlier. Then
$B_P$
be the two algorithms defined earlier. Then
Because the algorithm
![]() $B_P$
achieves the optimal information efficiency it seems natural to define a quasi-ordering of proof systems based on comparing their information-efficiency functions.
$B_P$
achieves the optimal information efficiency it seems natural to define a quasi-ordering of proof systems based on comparing their information-efficiency functions.
Definition 3.6. For two proof systems P and Q define:
for all
![]() $\tau \in TAUT$
.
$\tau \in TAUT$
.
This is a quasi-ordering of proof systems that is, by Lemma 3.2, coarser that
![]() $\geq _p$
but, presumably, different than both
$\geq _p$
but, presumably, different than both
![]() $\geq _p$
and
$\geq _p$
and
![]() $\geq $
. But as far as optimality goes it does not allow for a new notion.
$\geq $
. But as far as optimality goes it does not allow for a new notion.
Theorem 3.7. Let P be any proof system containing resolution R and having the property that for some
![]() $c \geq 1$
, for every
$c \geq 1$
, for every
![]() $\tau $
and every
$\tau $
and every
![]() $\tau '$
obtained from
$\tau '$
obtained from
![]() $\tau $
by substituting constants for some atoms it holds
$\tau $
by substituting constants for some atoms it holds
![]() $s_P(\tau ') \le s_P(\tau )^c$
.
$s_P(\tau ') \le s_P(\tau )^c$
.
Then P is information-optimal (i.e.,
![]() $\geq _i$
-maximal) iff it is p-optimal.
$\geq _i$
-maximal) iff it is p-optimal.
Proof. Let P be a p-optimal proof system and let Q be any proof system. Assume f is a p-simulation of Q by P.
Let
![]() $\tau \in TAUT$
and assume
$\tau \in TAUT$
and assume
![]() $Kt(w|\tau ) = i_Q(\tau )$
for some Q-proof
$Kt(w|\tau ) = i_Q(\tau )$
for some Q-proof
![]() $w$
of
$w$
of
![]() $\tau $
. Then
$\tau $
. Then
![]() $f(w)$
is a P-proof of
$f(w)$
is a P-proof of
![]() $\tau $
and
$\tau $
and
![]() $Kt(f(w)|w) \le O(1) + O(\log |w|)$
. But
$Kt(f(w)|w) \le O(1) + O(\log |w|)$
. But
![]() $|w| \le 2^{i_Q(\tau )}$
, so
$|w| \le 2^{i_Q(\tau )}$
, so
![]() $Kt(f(w)|w) \le O(i_Q(\tau ))$
and
$Kt(f(w)|w) \le O(i_Q(\tau ))$
and
![]() $Kt(f(w)|\tau ) \le O(i_Q(\tau ))$
follows by (3). Hence
$Kt(f(w)|\tau ) \le O(i_Q(\tau ))$
follows by (3). Hence
For the only-if-direction assume that P is an information-optimal proof system and Q is an arbitrary proof system. Take the sequence
![]() $\langle \textit{Ref}_Q\rangle _n$
,
$\langle \textit{Ref}_Q\rangle _n$
,
![]() $n \geq 1$
, as in the first proof of Theorem 2.4, and interpret strings
$n \geq 1$
, as in the first proof of Theorem 2.4, and interpret strings
![]() $1^{(n)}$
as proofs of these formulas in some proof system
$1^{(n)}$
as proofs of these formulas in some proof system
![]() $Q'$
. We see that
$Q'$
. We see that
By the information optimality of P also
which, by Lemma 3.4, means that the algorithm
![]() $B_P$
finds P-proofs of formulas
$B_P$
finds P-proofs of formulas
![]() $\langle \textit{Ref}_Q\rangle _n$
in time
$\langle \textit{Ref}_Q\rangle _n$
in time
![]() $n^{O(1)}$
. This implies, as in the first proof of Theorem 2.4, that
$n^{O(1)}$
. This implies, as in the first proof of Theorem 2.4, that
![]() $P \geq _p Q$
.⊣
$P \geq _p Q$
.⊣
Theorem 3.7 implies that the information measure approach does not lead to a separation of the proof search problem from the optimality problem either.
4 Information vs. size
A natural question is whether the information-efficiency function may give, at least in principle, better time lower bounds for proof search algorithms than the length-of-proof function. By Lemma 3.3 information gives super-polynomially better time lower bound than size if
![]() $i_P(\tau )$
cannot be in general bounded above by
$i_P(\tau )$
cannot be in general bounded above by
![]() $O(\log s_P(\tau ))$
.
$O(\log s_P(\tau ))$
.
Recall a notion introduced by Bonet, Pitassi and Raz [Reference Bonet, Pitassi and Raz2]: a proof system P is automatizable iff there is a proof search algorithm
![]() $(A,P)$
such that for all
$(A,P)$
such that for all
![]() $\tau \in \text {TAUT}$
:
$\tau \in \text {TAUT}$
:
Considering that there are no known non-trivial complete automatizable proof systems this author saw as the only use of the notion that it gives a nice meaning to the failure of feasible interpolation, cf. [Reference Krajíček17, Section 17.3]. But now it is exactly what we need to characterize the separation of size from information; using Lemma 3.3 the following statement is obvious.
Theorem 4.1. A proof system P is non-automatizable iff there is an infinite set X of tautologies
![]() $\tau $
of unbounded size such that
$\tau $
of unbounded size such that
on X.
To illustrate what type of formulas witness the separation of size from information we shall paraphrase the construction from [Reference Krajíček and Pudlák20]; there it was done for
![]() $P = \text {ER}$
and
$P = \text {ER}$
and
![]() $h := \text {RSA}$
.
$h := \text {RSA}$
.
Let
![]() $h : {\{0,1\}^*} \rightarrow {\{0,1\}^*}$
be a p-time permutation of each
$h : {\{0,1\}^*} \rightarrow {\{0,1\}^*}$
be a p-time permutation of each
![]() ${\{0,1\}^n}$
, i.e., it is a length-preserving and injective function, and let
${\{0,1\}^n}$
, i.e., it is a length-preserving and injective function, and let
![]() $h_n$
be the restriction of h to
$h_n$
be the restriction of h to
![]() ${\{0,1\}^n}$
. For any
${\{0,1\}^n}$
. For any
![]() $b \in {\{0,1\}^n}$
define formula
$b \in {\{0,1\}^n}$
define formula
where
![]() $B(x)$
is a hard-bit of permutation h; the statement
$B(x)$
is a hard-bit of permutation h; the statement
![]() $h_n(x) = b$
is expressed by a p-size circuit (if P allows them), or using auxiliary variables whose values are uniquely determined by values of
$h_n(x) = b$
is expressed by a p-size circuit (if P allows them), or using auxiliary variables whose values are uniquely determined by values of
![]() $x_1, \dots , x_n$
. Note that
$x_1, \dots , x_n$
. Note that
![]() $|\mu _b| \le n^{O(1)}$
.
$|\mu _b| \le n^{O(1)}$
.
Lemma 4.2. Let P be any proof system containing resolution R and having the property that for some
![]() $c \geq 1$
, for every
$c \geq 1$
, for every
![]() $\tau $
and every
$\tau $
and every
![]() $\tau '$
obtained from
$\tau '$
obtained from
![]() $\tau $
by substituting constants for some atoms it holds
$\tau $
by substituting constants for some atoms it holds
![]() $s_P(\tau ') \le s_P(\tau )^c$
.
$s_P(\tau ') \le s_P(\tau )^c$
.
Assume that P proves by p-size proofs tautologies expressing that
![]() $h_n$
are injective:
$h_n$
are injective:
Assume that h is a one-way permutation and B is its hard bit predicate.Footnote 7
Then there are P-proofs
![]() $\pi _b$
of formulas
$\pi _b$
of formulas
![]() $\mu _b$
such that:
$\mu _b$
such that:
-
1.
 $|\pi _b| \le n^{O(1)}$
, i.e.,
$|\pi _b| \le n^{O(1)}$
, i.e.,
 $s_P(\mu _b)\ \le \ n^{O(1)}$
,
$s_P(\mu _b)\ \le \ n^{O(1)}$
, -
2. for a random
 $b \in {\{0,1\}^n}$
, with a probability going to
$b \in {\{0,1\}^n}$
, with a probability going to
 $1$
as
$1$
as
 $n \rightarrow \infty $
, it holds that (5)If h is secure even against algorithms running in time
$n \rightarrow \infty $
, it holds that (5)If h is secure even against algorithms running in time $$ \begin{align} i_P(\mu_b) \geq \omega(\log\, n). \end{align} $$
$$ \begin{align} i_P(\mu_b) \geq \omega(\log\, n). \end{align} $$
 $2^{n^\epsilon }$
, for some
$2^{n^\epsilon }$
, for some
 $\epsilon> 0$
, then the right-hand term in (5) can be improved to
$\epsilon> 0$
, then the right-hand term in (5) can be improved to
 $n^{\Omega (1)}$
.
$n^{\Omega (1)}$
.
Proof. Define the wanted P-proof
![]() $\pi _b$
as follows. Pick
$\pi _b$
as follows. Pick
![]() $a \in {\{0,1\}^n}$
such that
$a \in {\{0,1\}^n}$
such that
![]() $h(a) = b$
and prove in P in p-size, using the injectivity of
$h(a) = b$
and prove in P in p-size, using the injectivity of
![]() $h_n$
, that
$h_n$
, that
From this implication we can derive
![]() $\mu _b$
using implication
$\mu _b$
using implication
that has p-size resolution proofs. This proves the first statement.
The second statement follows from the hypothesis that h is one-way: we can try the algorithm
![]() $B_P$
from Section 3 on formulas
$B_P$
from Section 3 on formulas
for
![]() $c = 0, 1$
and compute in this way the hard bit in p-time. But that is impossible if B is indeed a hard bit of h.⊣
$c = 0, 1$
and compute in this way the hard bit in p-time. But that is impossible if B is indeed a hard bit of h.⊣
Related formulas can be defined as follows. Let
![]() $\varphi _n(x)$
,
$\varphi _n(x)$
,
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $x = (x_1, \dots , x_n)$
, be a sequence of formulas that have p-size
$x = (x_1, \dots , x_n)$
, be a sequence of formulas that have p-size
![]() $|\varphi _n| \le n^{O(1)}$
but that do not have p-size P-proofs:
$|\varphi _n| \le n^{O(1)}$
but that do not have p-size P-proofs:
For some proof systems we have such formulas unconditionally, for those which are not p-optimal we can take formulas
![]() $\langle \textit{Ref}_Q\rangle _n$
used earlier, for some
$\langle \textit{Ref}_Q\rangle _n$
used earlier, for some
![]() $Q>_p P$
.
$Q>_p P$
.
For any
![]() $b \in {\{0,1\}^n}$
define formula
$b \in {\{0,1\}^n}$
define formula
Note that
![]() $|\eta _n| \le n^{O(1)}$
. Analogously with the proof of the lemma, the formulas have p-size P-proofs
$|\eta _n| \le n^{O(1)}$
. Analogously with the proof of the lemma, the formulas have p-size P-proofs
![]() $\pi _b$
and these particular proofs satisfy
$\pi _b$
and these particular proofs satisfy
![]() $Kt(\pi _b | \eta _b) \geq \omega (\log\, n)$
. It would be interesting if for some P it would hold that any short proof of
$Kt(\pi _b | \eta _b) \geq \omega (\log\, n)$
. It would be interesting if for some P it would hold that any short proof of
![]() $\eta _b$
must contain some non-trivial information about
$\eta _b$
must contain some non-trivial information about
![]() $h^{(-1)}(b)$
.
$h^{(-1)}(b)$
.
5 Information alone
A separation of size from information in the sense of (4) implies that no p-time algorithm finds, given
![]() $\tau $
and
$\tau $
and
![]() $s_P(\tau )$
in unary, a p-time recognizable (by P) object (a P-proof), and hence it implies that
$s_P(\tau )$
in unary, a p-time recognizable (by P) object (a P-proof), and hence it implies that
![]() $\text {P} \neq \text {NP}$
. In fact, a number of proof systems are known to be non-automatizable assuming various conjectures from complexity theory (cf. [Reference Krajíček17, Section 17.3]). We mention just resolution R and its non-automatizability proved under the weakest possible hypothesis that
$\text {P} \neq \text {NP}$
. In fact, a number of proof systems are known to be non-automatizable assuming various conjectures from complexity theory (cf. [Reference Krajíček17, Section 17.3]). We mention just resolution R and its non-automatizability proved under the weakest possible hypothesis that
![]() $\text {P} \neq \text {NP}$
by Atserias and Müller [Reference Atserias and Müller1]; references for earlier work and other examples can be found there or in [Reference Krajíček17, Section 17.3].
$\text {P} \neq \text {NP}$
by Atserias and Müller [Reference Atserias and Müller1]; references for earlier work and other examples can be found there or in [Reference Krajíček17, Section 17.3].
Proofs of non-automatizability depend on a p-time reduction of some hard set Y (NP-complete in [Reference Atserias and Müller1] or hard bit of RSA in [Reference Krajíček and Pudlák20] or similar, cf. [Reference Krajíček17, Section 17.3]) to a set of formulas with p-size proofs that maps the complement
![]() ${\{0,1\}^*} \setminus Y$
to formulas with only long (or none) proofs. These arguments do not yield lower bounds for
${\{0,1\}^*} \setminus Y$
to formulas with only long (or none) proofs. These arguments do not yield lower bounds for
![]() $i_P(\tau )$
for individual formulas but only speak about the asymptotic behavior of an automatizing algorithm.
$i_P(\tau )$
for individual formulas but only speak about the asymptotic behavior of an automatizing algorithm.
We are interested in the question whether one can establish a lower bound for
![]() $i_P(\tau )$
by considering formulas individually, not as members of an infinite set or sequence. This would be in a way analogous to lengths-of-proofs lower bounds (e.g., for
$i_P(\tau )$
by considering formulas individually, not as members of an infinite set or sequence. This would be in a way analogous to lengths-of-proofs lower bounds (e.g., for
![]() $PHP_n$
in R in [Reference Haken9]) which work with individual formulas.
$PHP_n$
in R in [Reference Haken9]) which work with individual formulas.
A super-polynomial lower bound for
![]() $s_P(\tau )$
is used primarily for three purposes:
$s_P(\tau )$
is used primarily for three purposes:
-
1. It implies that no
 $Q \le P$
is p-bounded, an instance of
$Q \le P$
is p-bounded, an instance of
 $\text {NP} \neq \text {coNP}$
, and if true for all P then indeed
$\text {NP} \neq \text {coNP}$
, and if true for all P then indeed
 $\text {NP} \neq \text {coNP}$
follows.
$\text {NP} \neq \text {coNP}$
follows. -
2. It implies super-polynomial time lower bounds for a class of SAT algorithms S that are simulated by
 $P: P \geq P_S (P_S$
defined in the Introduction). Currently known lengths-of-proofs lower bounds imply time lower bounds for large classes of SAT algorithms.
$P: P \geq P_S (P_S$
defined in the Introduction). Currently known lengths-of-proofs lower bounds imply time lower bounds for large classes of SAT algorithms. -
3. It implies independence results from a first-order theory attached to P and, in particular, that
 $\text {P} \neq \text {NP}$
is consistent with the theory (see [Reference Krajíček17, Section 86]).
$\text {P} \neq \text {NP}$
is consistent with the theory (see [Reference Krajíček17, Section 86]).
But having a super-logarithmic lower bound for
![]() $i_P(\tau )$
is just as good. Items 2 and 3 hold literally: in the former this is by Lemma 3.3 and for the latter this holds because propositional translations of first-order proofs are performed by p-time algorithms (cf. [Reference Krajíček17, Part 2]). In item 1 one has to compromise on weakening
$i_P(\tau )$
is just as good. Items 2 and 3 hold literally: in the former this is by Lemma 3.3 and for the latter this holds because propositional translations of first-order proofs are performed by p-time algorithms (cf. [Reference Krajíček17, Part 2]). In item 1 one has to compromise on weakening
![]() $\text {NP} \neq \text {coNP}$
to
$\text {NP} \neq \text {coNP}$
to
![]() $\text {P} \neq \text {NP}$
.
$\text {P} \neq \text {NP}$
.
This motivates the following problem that seems to us to be quite fundamental.
Problem 5.1. Establish unconditional super-logarithmic lower bound
for
![]() $\tau $
from a set
$\tau $
from a set
![]() $X \subseteq \text {TAUT}$
of tautologies of unbounded size, for a proof system P for which no super-polynomial lowers bounds for the length-of-proof function
$X \subseteq \text {TAUT}$
of tautologies of unbounded size, for a proof system P for which no super-polynomial lowers bounds for the length-of-proof function
![]() $s_P$
are known.
$s_P$
are known.
As a step towards solving the problem it would be interesting to have such unconditional lower bounds at least for P for which super-polynomial lower bounds for
![]() $s_P$
are known, but not for formulas from X.
$s_P$
are known, but not for formulas from X.
Note the emphasis on the requirement that the lower bound is unconditional. Allowing some unproven computational complexity hypotheses the problem becomes easy. For example, if it were that
![]() $i_P(\tau ) \le O(\log |\tau |)$
for all
$i_P(\tau ) \le O(\log |\tau |)$
for all
![]() $\tau $
then the algorithm
$\tau $
then the algorithm
![]() $B_P$
form Section 3 runs in p-time and hence
$B_P$
form Section 3 runs in p-time and hence
![]() $\text {P} = \text {NP}$
. Or you may take any pseudo-random number generator
$\text {P} = \text {NP}$
. Or you may take any pseudo-random number generator
![]() $g : {\{0,1\}^n} \rightarrow \{0,1\}^{n+1}$
and for
$g : {\{0,1\}^n} \rightarrow \{0,1\}^{n+1}$
and for
![]() $b \in \{0,1\}^{n+1}$
take a formulaFootnote
8
$b \in \{0,1\}^{n+1}$
take a formulaFootnote
8
![]() $\tau _b$
expressing that
$\tau _b$
expressing that
![]() $b \notin Rng(g)$
. Then
$b \notin Rng(g)$
. Then
![]() $i_P(\tau _b)$
cannot be bounded by
$i_P(\tau _b)$
cannot be bounded by
![]() $O(\log |\tau _b|)$
as otherwise
$O(\log |\tau _b|)$
as otherwise
![]() $B_P$
would break the generator in p-time.
$B_P$
would break the generator in p-time.
In what follows we shall discuss the existence of formulas
![]() $\tau $
whose length we shall denote m. The formulas will not be a priori members of some infinite series but are considered individually. This means that questions and statements about them do depend just on them and not on asymptotic properties of some ambient sequence. But we still wish to use the handy O-,
$\tau $
whose length we shall denote m. The formulas will not be a priori members of some infinite series but are considered individually. This means that questions and statements about them do depend just on them and not on asymptotic properties of some ambient sequence. But we still wish to use the handy O-,
![]() $\Omega $
- and
$\Omega $
- and
![]() $\omega $
- notations and in doing so we imagine what happens in each particular construction or statement as
$\omega $
- notations and in doing so we imagine what happens in each particular construction or statement as
![]() $m \rightarrow \infty $
.
$m \rightarrow \infty $
.
For the sake of the following discussion let us call a size m formula simple if
![]() $Kt(\tau ) = O(\log\, m)$
and complex otherwise, and we apply similar qualifications to its proofs
$Kt(\tau ) = O(\log\, m)$
and complex otherwise, and we apply similar qualifications to its proofs
![]() $\pi $
but still relative to parameter m (i.e., not relative to
$\pi $
but still relative to parameter m (i.e., not relative to
![]() $|\pi |$
).
$|\pi |$
).
For example, for the truth-table proof system TT, any tautology
![]() $\tau $
in
$\tau $
in
![]() $m^{\Omega (1)}$
variables, simple or complex, will have only a complex truth-table proof
$m^{\Omega (1)}$
variables, simple or complex, will have only a complex truth-table proof
![]() $\pi $
: its size is exponential in
$\pi $
: its size is exponential in
![]() $m^{\Omega (1)}$
and (1) implies that
$m^{\Omega (1)}$
and (1) implies that
![]() $Kt(\pi ) \geq i_{TT}(\tau ) \geq m^{\Omega (1)}$
as well.
$Kt(\pi ) \geq i_{TT}(\tau ) \geq m^{\Omega (1)}$
as well.
To solve Problem 5.1 we want a class
![]() $X \subseteq \text {TAUT}$
of formulas
$X \subseteq \text {TAUT}$
of formulas
![]() $\tau $
,
$\tau $
,
![]() $|\tau | = m \rightarrow \infty $
, such that
$|\tau | = m \rightarrow \infty $
, such that
The following lemma formulates two simple conditions on X, one necessary and one sufficient.
Lemma 5.2. Let
![]() $X \subseteq \text {TAUT}$
be a set of formulas of unbounded size.
$X \subseteq \text {TAUT}$
be a set of formulas of unbounded size.
-
1. (a necessary condition)
For X to solve Problem 5.1 it is necessary that all P-proofs
 $\pi $
of all
$\pi $
of all
 $\tau \in X$
are complex:
$\tau \in X$
are complex: $$ \begin{align*}Kt(\pi) \geq \omega(\log\, m). \end{align*} $$
$$ \begin{align*}Kt(\pi) \geq \omega(\log\, m). \end{align*} $$
-
2. (a sufficient condition)
If X satisfies item 1 then a sufficient condition for it to solve the problem is that all
 $\tau \in X$
are simple:
$\tau \in X$
are simple: $$ \begin{align*}Kt(\tau) \le O(\log\, m). \end{align*} $$
$$ \begin{align*}Kt(\tau) \le O(\log\, m). \end{align*} $$
Proof. For item 1 note that by (1) we have
![]() $i_P(\tau ) \le Kt(\pi |\tau ) \le Kt(\pi )$
. For item 2 we have by (2):
$i_P(\tau ) \le Kt(\pi |\tau ) \le Kt(\pi )$
. For item 2 we have by (2):
By (1) we may estimate the last term by
![]() $O(\log\, m)$
for any
$O(\log\, m)$
for any
![]() $\tau $
, and by the hypothesis
$\tau $
, and by the hypothesis
![]() $Kt(\tau ) \le O(\log\, m)$
as well. Hence we can rewrite the inequality as
$Kt(\tau ) \le O(\log\, m)$
as well. Hence we can rewrite the inequality as
Now distinguish two cases. Either
![]() $\pi \le m^{O(1)}$
or
$\pi \le m^{O(1)}$
or
![]() $\pi \geq m^{\omega (1)}$
. In the latter case we are done as
$\pi \geq m^{\omega (1)}$
. In the latter case we are done as
![]() $i_P(\tau )$
is lower bounded by
$i_P(\tau )$
is lower bounded by
![]() $\log s_P(\tau )$
. In the former case we can estimate the last term in (6) by
$\log s_P(\tau )$
. In the former case we can estimate the last term in (6) by
![]() $O(\log\, m)$
and hence get
$O(\log\, m)$
and hence get
This implies what we need because, by item 1,
![]() $Kt(\pi ) \geq \omega (\log\, m)$
.⊣
$Kt(\pi ) \geq \omega (\log\, m)$
.⊣
Note that condition 1 in the lemma is not sufficient. To see this take
![]() $\tau $
of the form
$\tau $
of the form
![]() $\rho \vee \neg \rho $
, where
$\rho \vee \neg \rho $
, where
![]() $\rho $
is random a hence of high
$\rho $
is random a hence of high
![]() $Kt$
-complexity. But
$Kt$
-complexity. But
![]() $\tau $
is a proof of itself in a suitable Frege system (or even in R if
$\tau $
is a proof of itself in a suitable Frege system (or even in R if
![]() $\rho $
is just a clause and
$\rho $
is just a clause and
![]() $\neg \rho $
is the set of singleton clauses consisting of negations of literals in
$\neg \rho $
is the set of singleton clauses consisting of negations of literals in
![]() $\rho $
) and
$\rho $
) and
![]() $Kt(\tau |\tau ) = \log (|\tau |) + O(1)$
is small.
$Kt(\tau |\tau ) = \log (|\tau |) + O(1)$
is small.
When
![]() $\tau $
are complex then the necessary condition holds automatically: given a P-proof
$\tau $
are complex then the necessary condition holds automatically: given a P-proof
![]() $\pi $
of
$\pi $
of
![]() $\tau $
, either
$\tau $
, either
![]() $|\pi | \geq m^{\omega (1)}$
and hence
$|\pi | \geq m^{\omega (1)}$
and hence
![]() $\omega (\log\, m)$
lower bounds
$\omega (\log\, m)$
lower bounds
![]() $Kt(\pi |\tau )$
by (1), or
$Kt(\pi |\tau )$
by (1), or
![]() $|\pi | \le m^{O(1)}$
. In the latter case, because
$|\pi | \le m^{O(1)}$
. In the latter case, because
![]() $P(\pi ) = \tau $
and using (2):
$P(\pi ) = \tau $
and using (2):
which yields
Estimating
![]() $\log |\pi | \le O(\log\, m)$
we derive:
$\log |\pi | \le O(\log\, m)$
we derive:
On the other hand, the computation in the proof of item 2 does not yield anything for complex formulas. But the quantity being estimated from above in (7) still makes sense and if (7) holds for an X (satisfying item 1) then X solves the problem.
In fact, this quantity has been isolated already by Kolmogorov [Reference Kolmogorov10, Reference Kolmogorov11]; following him define (the
![]() $Kt$
-version of) information that u conveys about w as
$Kt$
-version of) information that u conveys about w as
Hence what we want is
![]() $\tau $
, simple or complex, having only complex proofs such that for any proof
$\tau $
, simple or complex, having only complex proofs such that for any proof
![]() $\pi $
it holds that:
$\pi $
it holds that:
In words:
![]() $\tau $
knows very little about its proofs.
$\tau $
knows very little about its proofs.
Many formulas that appear in various contexts of proof complexity (as formulas
![]() $PHP_n$
or
$PHP_n$
or
![]() $\langle \textit{Ref}_Q\rangle _n$
we encountered earlier) occur as members in a uniformly constructed sequence
$\langle \textit{Ref}_Q\rangle _n$
we encountered earlier) occur as members in a uniformly constructed sequence
![]() $\{\tau _n\}_n$
. The sequence is often p-time construable from
$\{\tau _n\}_n$
. The sequence is often p-time construable from
![]() $1^{(n)}$
or, in fact, has even stricter levels of uniformity (cf. [Reference Krajíček17, Section 19.1]). When such formulas have short proofs
$1^{(n)}$
or, in fact, has even stricter levels of uniformity (cf. [Reference Krajíček17, Section 19.1]). When such formulas have short proofs
![]() $\pi _n$
in some proof system P it is often the case that the proofs are also uniformly constructed from
$\pi _n$
in some proof system P it is often the case that the proofs are also uniformly constructed from
![]() $1^{(n)}$
. But that forces
$1^{(n)}$
. But that forces
![]() $Kt(\pi _n)$
to be
$Kt(\pi _n)$
to be
![]() $O(\log\, n)$
.
$O(\log\, n)$
.
Hence if we wanted to use for X some uniform formulas they ought to be expected to have only long P-proofs (but we may not be able to prove that). Leaving the reflection principles aside, two examples that come to mind are
-
•
 $AC^0[p]$
-Frege systems and the
$AC^0[p]$
-Frege systems and the
 $PHP_n$
formulas, cf. [Reference Krajíček17, Section 10.1 and Problem 15.6.1].
$PHP_n$
formulas, cf. [Reference Krajíček17, Section 10.1 and Problem 15.6.1].(No super-polynomial size lower bounds are known for this proof system, cf. [Reference Krajíček17, Problem 15.6.1].)
-
•
 $AC^0$
-Frege systems and the
$AC^0$
-Frege systems and the
 $WPHP_n$
formulas (expressing weak PHP).
$WPHP_n$
formulas (expressing weak PHP).(Lower bounds for
 $AC^0$
-Frege systems are known but not for formulas
$AC^0$
-Frege systems are known but not for formulas
 $WPHP_n$
expressing a form of the weak PHP, cf. [Reference Krajíček17, Problem 15.3.2].)
$WPHP_n$
expressing a form of the weak PHP, cf. [Reference Krajíček17, Problem 15.3.2].)
For stronger systems the only candidates for hard formulasFootnote
9
which are supported by some theory are
![]() $\tau $
-formulas, called also proof complexity generators. These formulas are described in Section 6.1. For some generators, as those defined in [Reference Krajíček15, Sections 29.4 and 29.5] these formulas are expected to be all complex in the sense of
$\tau $
-formulas, called also proof complexity generators. These formulas are described in Section 6.1. For some generators, as those defined in [Reference Krajíček15, Sections 29.4 and 29.5] these formulas are expected to be all complex in the sense of
![]() $Kt$
complexity.
$Kt$
complexity.
But for the
![]() $\tau $
-formulas based on the truth-table function
$\tau $
-formulas based on the truth-table function
![]() ${\textbf {tt}}_{s,k}$
there are uniform examples possibly hard for ER (Extended resolution). The formulas express that a size
${\textbf {tt}}_{s,k}$
there are uniform examples possibly hard for ER (Extended resolution). The formulas express that a size
![]() $2^k$
string is not the truth-table of a Boolean function computed by a size
$2^k$
string is not the truth-table of a Boolean function computed by a size
![]() $\le s$
circuit. Truth tables of SAT (in fact, of any language in the class E) are constructible in p-time (i.e., in time polynomial in
$\le s$
circuit. Truth tables of SAT (in fact, of any language in the class E) are constructible in p-time (i.e., in time polynomial in
![]() $2^k$
) and there is a theory (cf. [Reference Krajíček12, Section 5]) supporting the conjecture that the corresponding
$2^k$
) and there is a theory (cf. [Reference Krajíček12, Section 5]) supporting the conjecture that the corresponding
![]() $\tau $
-formulas are hard for ER.
$\tau $
-formulas are hard for ER.
The theory of proof complexity generators is now fairly extensive and it is not feasible to repeat its key points here. More information is in Section 6.1 and in the references given there.
6 Proof complexity remarks
In this section we remark on several topics in proof complexity that seem to be related to the information measure. It may be worthwhile to explore if there are some deeper connections. The section aims primarily at proof complexity readers but we give references to relevant places in [Reference Krajíček17] to aid non-specialists.
6.1 Proof complexity generators
A fairly succinct exposition of the theory of proof complexity generators can be found in [Reference Krajíček17, Sections 19.4 and 19.6] or in older [Reference Krajíček15, Chapters 29 and 30]. The theory investigates, in particular, functions g extending n bit strings to m-bit strings,
![]() $m = m(n)> n$
, computable in p-time, and such that formulas
$m = m(n)> n$
, computable in p-time, and such that formulas
![]() $\tau (g)_b$
, expressing for
$\tau (g)_b$
, expressing for
![]() $b \in \{0,1\}^m$
that
$b \in \{0,1\}^m$
that
![]() $b \notin Rng(g)$
, ought to be hard to prove in a given proof system. In particular, function g is defined to be hard for P iff for any
$b \notin Rng(g)$
, ought to be hard to prove in a given proof system. In particular, function g is defined to be hard for P iff for any
![]() $c\geq 1$
only finitely many formulas
$c\geq 1$
only finitely many formulas
![]() $\tau (g)_b$
have a P-proof of size
$\tau (g)_b$
have a P-proof of size
![]() $\le |\tau (g)_b|^c$
.
$\le |\tau (g)_b|^c$
.
Function g can be thought of as a decompression algorithm and for
![]() $w \in Rng(g)$
we have
$w \in Rng(g)$
we have
![]() $Kt(w) \le n + O(\log\, n) + O(1)$
which is
$Kt(w) \le n + O(\log\, n) + O(1)$
which is
![]() $<< m$
if, for example,
$<< m$
if, for example,
![]() $3n \le m$
. Note that for
$3n \le m$
. Note that for
![]() $w \in {\{0,1\}^m}$
,
$w \in {\{0,1\}^m}$
,
![]() $3n \le m$
, the condition
$3n \le m$
, the condition
![]() $Kt(w) \geq m/2$
implies that
$Kt(w) \geq m/2$
implies that
![]() $Kt(w)> n + O(\log\, n) + O(1)$
and hence also
$Kt(w)> n + O(\log\, n) + O(1)$
and hence also
![]() $w \notin Rng(g)$
. The property
$w \notin Rng(g)$
. The property
![]() $Kt(w) \geq m/2$
cannot be expressed by a p-size tautology as the time involved in the computation of the universal machine may be exponential in m. But for a fixed p-time
$Kt(w) \geq m/2$
cannot be expressed by a p-size tautology as the time involved in the computation of the universal machine may be exponential in m. But for a fixed p-time
![]() $t(n)$
we can consider complexity
$t(n)$
we can consider complexity
![]() $K^t$
by restricting the decompression to a universal Turing machine
$K^t$
by restricting the decompression to a universal Turing machine
![]() $U^t$
on inputs
$U^t$
on inputs
![]() $e,u$
(i.e., no time input) simulating e on u for time t. By padding (or restricting) all outputs in some canonical way to size
$e,u$
(i.e., no time input) simulating e on u for time t. By padding (or restricting) all outputs in some canonical way to size
![]() $m = m(n)$
exactly, and taking for the domain
$m = m(n)$
exactly, and taking for the domain
![]() $n'$
-bit strings with, say,
$n'$
-bit strings with, say,
![]() $n':= n + \log\, n$
(the term
$n':= n + \log\, n$
(the term
![]() $\log\, n$
swallowing the description of a machine), we can think of
$\log\, n$
swallowing the description of a machine), we can think of
![]() $U^t$
as of a generator as well.
$U^t$
as of a generator as well.
By the virtue of constructions of universal
![]() $U^t$
(for time t machines) it is straightforward to show in theory PV that
$U^t$
(for time t machines) it is straightforward to show in theory PV that
![]() $Rng(g) \subseteq Rng(U^t)$
for any generator g as above running in time
$Rng(g) \subseteq Rng(U^t)$
for any generator g as above running in time
![]() $\le t(n)$
. Hence (the propositional translations of) this fact are shortly provable in ER, cf. [Reference Krajíček17, Chapter 12]). It follows that for any
$\le t(n)$
. Hence (the propositional translations of) this fact are shortly provable in ER, cf. [Reference Krajíček17, Chapter 12]). It follows that for any
![]() $P \geq ER$
, if some
$P \geq ER$
, if some
![]() $\tau $
-formulas resulting from
$\tau $
-formulas resulting from
![]() $U^t$
have short proofs so do some formulas resulting from g. That is, if there is any g computable in time t and hard for P then
$U^t$
have short proofs so do some formulas resulting from g. That is, if there is any g computable in time t and hard for P then
![]() $U^t$
must be hard as well. Putting it differently, proving tautologiesFootnote
10
expressing
$U^t$
must be hard as well. Putting it differently, proving tautologiesFootnote
10
expressing
![]() $K^t(w)> m/2$
must be hard for P.Footnote
11
$K^t(w)> m/2$
must be hard for P.Footnote
11
6.2 Implicit proof systems
Implicit proof systems, introduced in [Reference Krajíček13], operate with proofs
![]() $\pi $
computed bit-by-bit by a circuit (but that is not all). Proof
$\pi $
computed bit-by-bit by a circuit (but that is not all). Proof
![]() $\pi $
may have size exponential in comparison with the size of the defining circuit. Hence its
$\pi $
may have size exponential in comparison with the size of the defining circuit. Hence its
![]() $Kt$
-complexity may be close to the lower bound
$Kt$
-complexity may be close to the lower bound
![]() $\log |\pi |$
from (1).
$\log |\pi |$
from (1).
For two proof systems
![]() $P, Q$
the implicit proof system
$P, Q$
the implicit proof system
![]() $[P,Q]$
considers a proof of a tautology
$[P,Q]$
considers a proof of a tautology
![]() $\tau $
to be a pair
$\tau $
to be a pair
![]() $(\alpha ,\beta )$
, where
$(\alpha ,\beta )$
, where
![]() $\beta $
is a circuit whose truth-table is a Q-proof of
$\beta $
is a circuit whose truth-table is a Q-proof of
![]() $\tau $
and
$\tau $
and
![]() $\alpha $
is a P-proof (of the propositional statement formalizing) that
$\alpha $
is a P-proof (of the propositional statement formalizing) that
![]() $\beta $
indeed computes a Q-proof. Note that using circuits
$\beta $
indeed computes a Q-proof. Note that using circuits
![]() $\beta $
alone would not constitute a Cook–Reckhow proof system. For the formal definition see [Reference Krajíček13] or [Reference Krajíček17, Section 7.3].
$\beta $
alone would not constitute a Cook–Reckhow proof system. For the formal definition see [Reference Krajíček13] or [Reference Krajíček17, Section 7.3].
Implicit proof systems get incredibly strong very fast. For example, implicit resolution
![]() $iR := [R,R]$
p-simulates ER and iER p-simulates quantified propositional system G, cf. [Reference Krajíček17, Section 7.3].
$iR := [R,R]$
p-simulates ER and iER p-simulates quantified propositional system G, cf. [Reference Krajíček17, Section 7.3].
6.3 Proof systems with advice
Recall from Cook and Krajíček [Reference Cook and Krajíček6] that a functional
Footnote
12
proof system with
![]() $k(n)$
bits of advice is a
$k(n)$
bits of advice is a
![]() $P : {\{0,1\}^*} \rightarrow {\{0,1\}^*}$
whose range is exactly
$P : {\{0,1\}^*} \rightarrow {\{0,1\}^*}$
whose range is exactly
![]() $\text {TAUT}$
and such that P is computable in polynomial time using
$\text {TAUT}$
and such that P is computable in polynomial time using
![]() $k(n)$
bits of advice on inputs (i.e., proofs) of length n. Cook and Krajíček [Reference Cook and Krajíček6, Theorem 6.6] proved that there exists a proof system with
$k(n)$
bits of advice on inputs (i.e., proofs) of length n. Cook and Krajíček [Reference Cook and Krajíček6, Theorem 6.6] proved that there exists a proof system with
![]() $1$
bit of advice that p-simulates all classical Cook–Reckhow’s proof systems. This suggestsFootnote
13
to use the only-if direction of Theorem 2.4 and to conclude that there is a proof search algorithm with advice
$1$
bit of advice that p-simulates all classical Cook–Reckhow’s proof systems. This suggestsFootnote
13
to use the only-if direction of Theorem 2.4 and to conclude that there is a proof search algorithm with advice
![]() $(A,P)$
which is
$(A,P)$
which is
![]() $\geq _t$
-better than all ordinary proof search algorithms of Definition 1.1. Here P is the proof system with
$\geq _t$
-better than all ordinary proof search algorithms of Definition 1.1. Here P is the proof system with
![]() $1$
bit of advice from [Reference Cook and Krajíček6, Theorem 6.6] and A is a non-uniform p-time algorithm, i.e., it uses p-size advice.
$1$
bit of advice from [Reference Cook and Krajíček6, Theorem 6.6] and A is a non-uniform p-time algorithm, i.e., it uses p-size advice.
To see this note that the proof of the only-if direction in Theorem 2.4 appeals to Lemma 2.2 that there is a time-optimal algorithm for any fixed proof system: in the universal search construction we need to check many—but only polynomially many—potential proofs of different lengths and each length requires its own bit of advice. Algorithm A will use the advice that collects together all these individual bits.
6.4 Diagonalization
Diagonalization in proof complexity was used in [Reference Krajíček14] (or see [Reference Krajíček17, Section 21.4]) to prove that at least one of the following three statements is true:
-
1. There is a function
 $f : {\{0,1\}^*} \rightarrow \{0,1\}$
computable in time
$f : {\{0,1\}^*} \rightarrow \{0,1\}$
computable in time
 $2^{O(n)}$
that has circuit complexity
$2^{O(n)}$
that has circuit complexity
 $2^{\Omega (n)}$
.
$2^{\Omega (n)}$
. -
2.
 $\text {NP} \neq \text {coNP}$
.
$\text {NP} \neq \text {coNP}$
. -
3. There is no p-optimal propositional proof system.
A key part of that is a way, assuming that item 1 fails, how to compress possibly very long proofs and to represent them by small circuits. Using instead the
![]() $Kt$
measure may possibly allow for a stronger result.
$Kt$
measure may possibly allow for a stronger result.
6.5 Random formulas
Müller and Tzameret [Reference Müller and Tzameret24] proved that random 3CNFs with
![]() $\Omega (n^{1.4})$
clauses do have (with the probability going to
$\Omega (n^{1.4})$
clauses do have (with the probability going to
![]() $1$
) polynomial size refutations in a
$1$
) polynomial size refutations in a
![]() $TC^0$
-Frege system. Their argument is based on formalizing in the proof system (via bounded arithmetic) the soundness of the unsatisfiability witnesses proved to exists with a high probability by Feige, Kim and Ofek [Reference Feige, Kim and Ofek8].
$TC^0$
-Frege system. Their argument is based on formalizing in the proof system (via bounded arithmetic) the soundness of the unsatisfiability witnesses proved to exists with a high probability by Feige, Kim and Ofek [Reference Feige, Kim and Ofek8].
Such a formula
![]() $\tau $
has bit size
$\tau $
has bit size
![]() $m = O(n^{1.4} \log\, n)$
(and, by virtue of being random, it has Kt-complexity
$m = O(n^{1.4} \log\, n)$
(and, by virtue of being random, it has Kt-complexity
![]() $\Omega (m)$
). Feige, Kim and Ofek [Reference Feige, Kim and Ofek8] proved that their witness (i.e., also the p-size
$\Omega (m)$
). Feige, Kim and Ofek [Reference Feige, Kim and Ofek8] proved that their witness (i.e., also the p-size
![]() $TC^0$
-Frege proof
$TC^0$
-Frege proof
![]() $\pi $
from [Reference Müller and Tzameret24]) can be found in time
$\pi $
from [Reference Müller and Tzameret24]) can be found in time
![]() $2^{O(n^{0.2}\log\, n)}$
which is exponential in
$2^{O(n^{0.2}\log\, n)}$
which is exponential in
![]() $m^{\Omega (1)}$
. That is, we know that
$m^{\Omega (1)}$
. That is, we know that
This leaves open the possibility that this inequality cannot be significantly improved. In that case the formulas would be witness for Theorem 4.1 for
![]() $TC^0$
-Frege systems demonstrating even exponential gap.
$TC^0$
-Frege systems demonstrating even exponential gap.
7 Concluding remarks
Results in Sections 2 and 3 show that the optimality of proof search algorithms reduces to p-optimality of proof systems in both quasi-orderings based on time or information, respectively. This leaves some room for a totally different definition of a quasi-ordering of proof search algorithms that is coarser than those studied here and in which there could be an optimal algorithm without implying also the existence of a p-optimal proof system. On the other hand, the ordering by time of Section 2 is perhaps so rudimentary that it is the finest one among all sensible quasi-orderings; hence the opposite implication ought to hold always. However, it is our view that—from the point of view of proof complexity—the situation is clarified and the proof search problem as formulated in [Reference Krajíček17, Section 21.5] is simply the p-optimality problem.
This does not quite dispel the doubts about the
![]() $\geq _t$
ordering discussed at the end of Section 2. The quasi-orderings considered here are theoretical models of a comparison of proof search algorithms and have shortcomings in modeling actual comparison of practical algorithms that are, we think, quite analogous to shortcomings of p-time algorithms as a theoretical model of practical feasible algorithms. The comparison of real-life algorithms is also more purpose specific and classifying all purposes that arise in practice may not be theoretically possible or useful.
$\geq _t$
ordering discussed at the end of Section 2. The quasi-orderings considered here are theoretical models of a comparison of proof search algorithms and have shortcomings in modeling actual comparison of practical algorithms that are, we think, quite analogous to shortcomings of p-time algorithms as a theoretical model of practical feasible algorithms. The comparison of real-life algorithms is also more purpose specific and classifying all purposes that arise in practice may not be theoretically possible or useful.
However, measure
![]() $i_P(\tau )$
may still have some uses for comparing two proof systems from the practical proof search point of view. For example, it can be used to kill all uniform formulas when testing algorithms (cf. the discussion at the end of Section 2) by accepting as test formulas only those satisfying, say,
$i_P(\tau )$
may still have some uses for comparing two proof systems from the practical proof search point of view. For example, it can be used to kill all uniform formulas when testing algorithms (cf. the discussion at the end of Section 2) by accepting as test formulas only those satisfying, say,
![]() $Kt(\tau ) \geq (\log |\tau |)^2$
. Also, the information-efficiency functions for P, Q such that
$Kt(\tau ) \geq (\log |\tau |)^2$
. Also, the information-efficiency functions for P, Q such that
![]() $P>_p Q$
could lead to a suitable distance function measuring how much better P than Q is, by counting how much more information Q-proofs require than P-proofs do.
$P>_p Q$
could lead to a suitable distance function measuring how much better P than Q is, by counting how much more information Q-proofs require than P-proofs do.
Acknowledgment
I thank Igor C. Oliveira (Warwick U.) for a discussion about an early draft of the paper.