1. Introduction
Simple shear in ductile shear zones is a deformation where the boundaries of the zone move parallel to themselves relative to each other (e.g. Twiss & Moores, Reference Twiss and Moores2007, pp. 330–1). Since geological deformations take place at exceedingly slow rates, usually ranging from a fraction of a millimetre per year (e.g. Wobus, Heimsath & Whipple, Reference Wobus, Heimsath and Whipple2005 and references therein) up to a few centimetres per year (as referred to in Annen, Scaillet & Sparks, Reference Annen, Scaillet and Sparks2005), simple shearing of plastically deforming rocks inevitably leads to creep. Thus, simple shear in geology leads to very slow laminar motion of material points, with a Reynolds Number of the order of ≤ 10−15 (Mukherjee & Koyi, Reference Mukherjee and Koyi2010a ,Reference Mukherjee and Koyi b ).
Ductile deformation of rocks is conventionally modelled by flowing fluids (Ramsay & Lisle, Reference Ramsay and Lisle2000). Here simple shear is equated with Couette flow (in the sense of Schlichting & Gersten, Reference Schlichting and Gersten1999) and Poiseuille flow to describe fluid flow through static infinitely long parallel boundaries (Pai, Reference Pai1956). The boundaries of Poiseuille flow could have any spatial orientation, cross-section geometry and dip (in the sense used by Pai, Reference Pai1956; Schlichting & Gersten, Reference Schlichting and Gersten1999).
Better understanding of ductile shear zones, and hence their shear sense, is of fundamental importance in plate tectonics since such zones define plate boundaries (including collisional mountains) (Regenauer-Lieb & Yuen, Reference Regenauer-Lieb and Yuen2003). In the last 30 years or so, previous workers (such as England & Holland, Reference England and Holland1979; Moores & Twiss, Reference Moores and Twiss1995) envisaged simple shear as one of the possible mechanisms of subduction and underplating of sediments through inclined zones with parallel boundaries. For example, in his figure 6.39, Stüwe (Reference Stüwe2007) described parabolic patterns in a subduction zone of parabolic profiles. The component of flow that tends to extrude rocks along the channel was mentioned as ‘hydraulic potential’, and any shear that tends to produce a linear profile if the zone is horizontal as ‘drag’. Another reason why understanding the theory of ductile shearing through field studies and/or modelling is crucial is that shear can also modify pre-existing ore deposits (e.g. Evans, Reference Evans1980).
This work investigates the kinematics of simple shear and the development of shear senses in ductile simple shear zones and their significance in extrusion. Shear fabrics (see Passchier & Trouw, Reference Passchier and Trouw2005 for review; Mukherjee, Reference Mukherjee2011) allow deducing only the relative sense of movement of the shear zone boundaries. Notwithstanding, this study considers absolute movement of the boundaries. The way folds and microstructures evolve are not addressed.
2. The model
A kilometre-scale shear zone with parallel, dipping, very long and rigid boundaries is here considered to have the rheology of an incompressible Newtonian viscous fluid, in which applied stress and the resultant strain rate are proportional (Schlichting & Gersten, Reference Schlichting and Gersten1999). The bottom end of the shear zone is assumed to have a pressure higher than the top end. This gives rise to a pressure gradient that tends to drive rock up the shear zone. The boundaries of the shear zone are considered to undergo reverse-sense simple shear (Figs 1–3). The ‘Poisson equation’ of flow (Eqn 1 in the Appendix) is chosen to deduce the velocity profile. This flow equation is equated with deformation in ductile shear zones as it has been adopted by previous workers (e.g. Grujic et al. Reference Grujic, Casey, Davidson, Hollister, Kündig, Pavlis and Schmid1996; Ramsay & Lisle, Reference Ramsay and Lisle2000; Grujic, Hollister & Parrish, Reference Grujic, Hollister and Parrish2002; Stüwe, Reference Stüwe2007; Mancktelow, Reference Mancktelow2008). The co-ordinate axes are chosen such that the positive direction of the z-axis is in the updip direction (Figs 1–3). A component of gravity, given by the product of density, acceleration due to gravity and the sine of the dip of the shear zone, tends to drive the rock downward between its parallel dipping boundaries (Eqns 1 and 2 in the Appendix). The gravity component counteracts the pressure gradient and tends to extrude the rock.
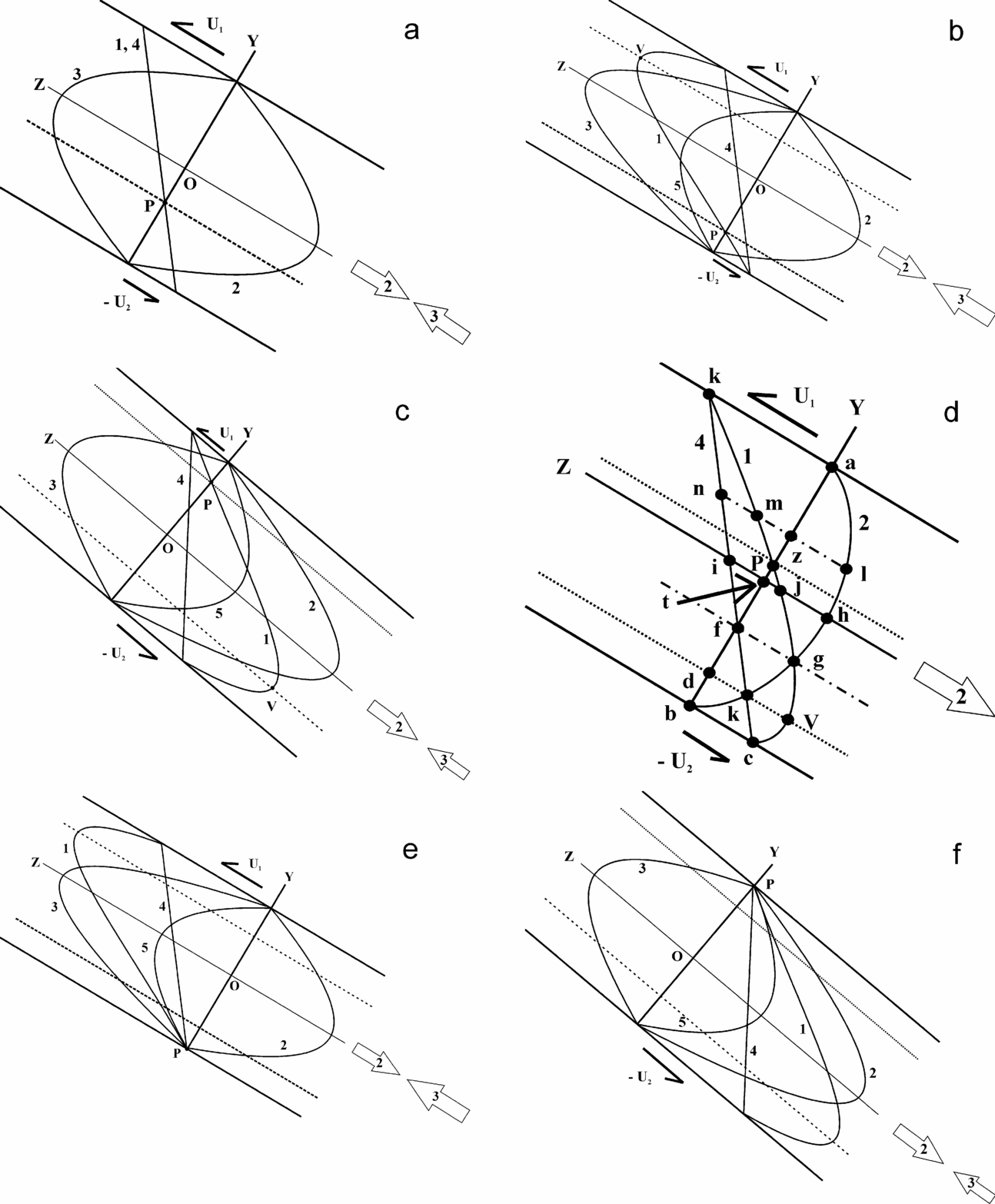
Figure 1. Simple shear of a shear zone of incompressible Newtonian fluid with parallel boundaries. The profile ‘3’ represents the flow due to pressure gradient, ‘2’ indicates the flow due to gravity and ‘1’ is the resultant flow profile. The full arrows ‘2’ and ‘3’ represent intensities of the respective flows (similar to fig. 11 of Zhao et al. Reference Zhao, Niu, Christensen, Zhou, Hou, Zhang, Xie, Zhang and Liu2011). Profiles ‘4’ and ‘5’ represent the profile due to shear of the boundaries, and the resultant of profiles ‘2’ and ‘3’, respectively. V – vertex; P – pivot. Dashed lines passing through them mark sub-zones of opposite shear senses and sub-zones of opposite bulk movements (extrusion and subduction), respectively. (a) An inclined shear zone where the component of gravity equals the pressure gradient. The resultant is a linear velocity profile arising from shear of the boundaries. (b) An inclined shear zone where the component of gravity is lower than the pressure gradient. The resultant of these two flows has its vertex pointing updip. (c) An inclined shear zone where the component of gravity exceeds the pressure gradient. The resultant parabola has its vertex pointing downdip. (d) Combination of shear of the boundaries and the flow component of gravity in an inclined shear zone with no pressure gradient. The resultant profile ‘1’ is deduced point by point using vector addition as follows: (nz – zl) = mz; 2 * dk = dv; (th – ti) = tj. (e) The situation is as in (b) except that U2 = 0. The entire shear zone extrudes. (f) The situation is as in (c) except that U1 = 0. The entire shear zone subducts.
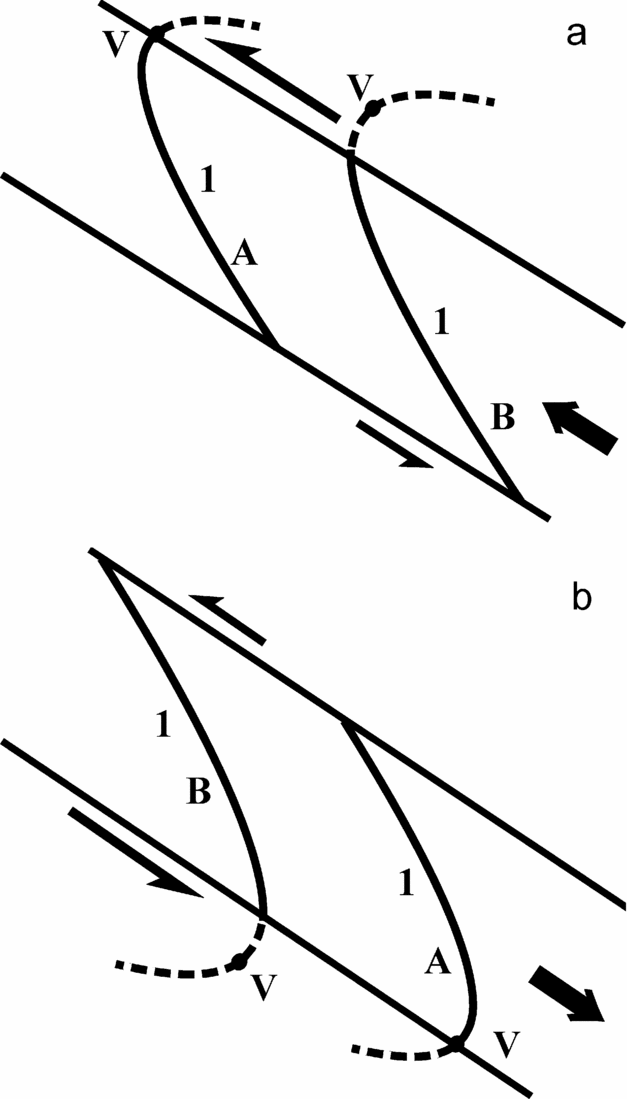
Figure 2. Two special cases of resultant velocity profiles in an inclined shear zone. In profile ‘A’, the vertex (‘V’) is coincident with the upper boundary of the shear zone, whereas in the profile ‘B’, it lies outside the shear zone.
Figure 3. In an inclined shear zone, both boundaries’ shear move updip, but the upper boundary moves with a greater velocity. See caption of Figure 1 for explanation of numbers for different profiles and those within the full arrows. The pressure gradient and the component of gravity are equal. Extrapolation of the resultant velocity profile meets the y-axis at ‘P’ that defines the pivot.
The presence of these components can be understood from field studies and mechanical considerations. For example, (i) the relative movement of the shear zone boundaries is exemplified by a number of shear sense indicators, most ubiquitously by S–C fabrics and mineral fish (Berthé, Choukroune & Jegouzo, Reference Berthé, Choukroune and Jegouzo1979; Passchier & Trouw, Reference Passchier and Trouw2005; Mukherjee, Reference Mukherjee2011). (ii) The presence of leucosomes in sheared migmatites, boudins, pressure shadows and solutions, veins and reaction textures indicate the activity of a pressure gradient along the shear zone (Mancktelow, Reference Mancktelow2008; also Hollister, Reference Hollister1993; Li, Gerya & Burg, Reference Li, Gerya and Burg2010). Schulmann et al. (Reference Schulmann, Lexa, Štípská, Racek, Tajčmanová, Konopásek, Edel, Peschler and Lehmann2008) categorized tectonic models of extrusion (of the ultrahigh pressure rocks) into (a) corner flow in an accretionary wedge with buoyancy-driven extrusion; (b) gravity-driven exhumation guided either by removal of the mountain roots; and (c) focused erosion or topographic load driven the flow of partially molten rocks along sub-horizontal channels driven by either focused erosion or topographic load. Apart from these, a fourth method involving (b) and (c), i.e. buoyancy-driven extrusion augmented by erosion, has also recently been modelled by many (e.g. Weinberger et al. Reference Weinberger, Lyakhovsky, Baer and Begin2006; Warren, Beaumont & Jamieson, Reference Warren, Beaumont and Jamieson2008a –Reference Warren, Beaumont and Jamieson c ; Whipple, Reference Whipple2009). In all these cases, pressure gradient is implicit in fluid mechanical derivations. Deviatoric stress that leads to ductile deformation of rocks in tectonic contexts (Li, Gerya & Burg, Reference Li, Gerya and Burg2010) can also create a pressure gradient, which could ultimately be correlated with lithostatic pressure gradient (Grujic et al. Reference Grujic, Casey, Davidson, Hollister, Kündig, Pavlis and Schmid1996; Vannay & Grasemann, Reference Vannay and Grasemann2001; Godin et al. Reference Godin, Grujic, Law, Searle, Law, Searle and Godin2006). Alternately, even a small percentage of melt would favour buoyant extrusion along the shear zone and develop a pressure gradient (Beaumont et al. Reference Beaumont, Jamieson, Nguyen and Lee2001). (iii) In tectonic scenarios, an inclined shear zone will always have its component of weight acting in the downdip direction.
Under these conditions, the velocity profile within the shear zone is usually a parabola, and not a straight line. A line passing through the vertex of the profile that parallels the shear zone boundaries divides the whole zone into two unequal sub-zones of opposite ductile shear senses (Fig. 1b–f). As in a purely Poiseuille flow, the vertex is also the point of fastest velocity and least shear strain in the shear zone. The velocity profile depends on the following parameters: (i) the absolute velocities of the two boundaries; (ii) thickness and (iii) dip of the shear zone; (iv) acceleration due to gravity; (v) pressure gradient along the shear zone; and (vi) density and (vii) viscosity of the rock (Eqn 3 in the Appendix). Several specific cases and the corresponding velocity profiles are presented as follows.
I. A case in which the sense of shear throughout the zone is identical, and, independent of density and acceleration due to gravity, is for any dip of the shear zone where the effect of gravity and the pressure gradient nullify each other (the case of Eqn 11 in the Appendix). This is the case that matches the homogeneous simple shear of a pack of cards depicted in many textbooks.
II. When the boundaries are sheared and the pressure gradient overpowers the component of gravity, the convex side of the parabolic profile points updip along the shear zone (Fig. 1b, e). While the sub-zone in contact with the lower boundary acquires the same shear sense as that of the shear on the boundaries, the smaller sub-zone at the top undergoes a reverse shear. In other words, while a narrower zone of ductile normal shearing forms in contact with the upper boundary, a wider zone of reverse shear develops in contact with the lower boundary.
III. When the component of gravity exceeds the pressure gradient, and the boundaries are sheared, the parabolic profile is convex downdip. The vertex of the flow profile in this case is closer to the lower boundary of the shear zone (Fig. 1c, d, f). In this case, while a narrower sub-zone in contact with the lower boundary develops a normal shear sense, opposite to the reverse shear sense between the two boundaries, the other wider sub-zone at the top acts as a ductile thrust with the same shear as that on the boundaries.
In the two latter cases (II and III), the imaginary lines that parallel the shear zone boundaries and pass through the vertices demarcate a thinner sub-zone in which the shear sense reverses. Under certain algebraic relations among the seven flow parameters, the vertices of the parabolic velocity profiles touch one of the boundaries (curve A in Fig. 2a and 2b for cases II and III, respectively), or can even plot outside the shear zone (curve B in Fig. 2a and 2b for cases II and III, respectively). In such situations, a uniform shear sense develops across the complete width of the shear zone.
IV. The point at which the velocity profile (or its extrapolation outside the shear zone) intersects the co-ordinate axis that is perpendicular to the linear boundaries of the zone (i.e. the ‘y-axis’ in the figures), is denoted as a ‘pivot’ (Fig. 1a–e). The shear sense does not alter across the pivot as it does across the vertex. The pivot lies inside the shear zone only if the two boundaries shear in opposite directions (i.e. one downdip and the other updip). In such a case, while a part of the non-horizontal (inclined or even vertical) shear zone extrudes across the pivot, the remainder subducts simultaneously. A line that parallels the shear zone boundary and passes through the pivot demarcates those two sub-zones. Along this line, all points remain static throughout the shearing process. On the other hand, (i) if both the boundaries move in the same direction (either updip or downdip), the pivot locates outside the shear zone (Fig. 3); (ii) if either of the boundaries remains stationary but the other moves, the pivot locates on the stationary boundary (Fig. 1e, f). In the last two cases, the shear zones either entirely extrude or subduct. In the cases of a dipping shear zone where the effect of gravity nullifies the pressure gradient (Fig. 1a), the position of the pivot is the same and is defined only by: (i) the thickness of the shear zone; and (ii) the absolute velocities of the shear zone boundaries (Eqn 11 in the Appendix).
V. In addition to fluid mechanical derivations, various combinations of flow mechanisms can also be understood graphically. After drawing velocity profiles for different types of simple shear, vector addition of velocities is necessary to construct the resultant velocity profile (Fig. 1d and its caption). This is in conformity with fluid mechanical deductions (Eqn 15 in the Appendix).
VI. The kinematics of simple shear zones that are not a part of any large hot orogen and are devoid of the pressure gradient along them can also be worked out from the presented model by putting ∂P/∂x = 0 in Eqn 1 in the Appendix. For reverse ductile shearing of the boundaries, a thicker sub-zone of reverse shear develops within the top zone and a thinner sub-zone of normal shear sense develops within the bottom boundary (Fig. 1d). As in the case in Figure 2b, if the vertex plots on the bottom boundary or even outside the shear zone, a single shear sense will develop.
3. Discussion
Any slip at the boundaries and the pressure gradient are considered two independent parameters although they could act simultaneously. An example of this is the ascent of partially molten rocks within the upper portion of the Higher Himalayan Shear Zone along with coeval ductile shear of its boundaries (reviews by Godin et al. Reference Godin, Grujic, Law, Searle, Law, Searle and Godin2006; Yin, Reference Yin2006). The present model is set in the way that shear along the boundaries is deciphered from geochronology (e.g. Harrison et al. Reference Harrison, Ryerson, LeFort, Yin, Lovera and Catlos1997; Catlos, et al. Reference Catlos, Harrison, Kohn, Grove, Ryerson, Manning and Upreti2001), and the pressure gradient from geothermobarometry (e.g. E. J. Catlos, unpub. Ph.D. thesis, Univ. California, 2000) of natural shear zones could be used to predict sub-zones of reverse shear. Since the fluid mechanics (Eqn 1 in the Appendix) on which this paper is based considers infinitely long shear zones, it should not be applied to any metre-scale or smaller ‘sporadic’ shear zones.
Shear zones of conflicting (or ‘opposite’) shear senses have commonly been attributed to a retro-shear of the whole zone, e.g. from an initial top-to-SW into a late top-to-NE in the South Tibetan Detachment System in the Himalaya (Patel et al. Reference Patel, Singh, Asokan, Jain, Treloar and Searle1993; Jain & Patel, Reference Jain, Patel, Jain and Manickavasagam1999; review by Godin et al. Reference Godin, Grujic, Law, Searle, Law, Searle and Godin2006; Yin, Reference Yin2006). Such thinking also led to postulation of specific extrusion models for the major shear zones. The present model indicates that two shear senses can form simultaneously well within any shear zone subject to a uniform simple shear of its boundaries (Fig. 1b–f).
Secondly, merely changing the magnitudes of a few of the flow parameters (shear rate, dip of the boundaries, density and viscosity of the rock types and the pressure gradient) over time can invert an early pro-shear into a late retro-shear. One such possibility could be where an initially uniform shear persisted and the pressure gradient was balanced by the component of gravity (Fig. 1a). Later the density of the rock, dip of the shear zone and the pressure gradient might change to the extent that the component of gravity becomes weaker than the pressure gradient. This would then produce an opposed shear sense near the upper boundary of the shear zone (Fig. 1b). (i) The pressure gradient along an orogen-parallel shear zone can vary by about an order of magnitude in different locations (E. J. Catlos, unpub. Ph.D. thesis, Univ. California, 2000; Fraser, Worley & Sandiford, Reference Fraser, Worley and Sandiford2000; Hollister & Grujic, Reference Hollister, Grujic, Law, Searle and Godin2006). The extrusion rate of an intra-continental shear zone can change significantly with time (Ganguli et al. Reference Ganguli, Dasgupta, Cheng and Neogi2000). (ii) The rate of slip of a shear zone boundary can vary in both space and time (Harrison et al. Reference Harrison, Ryerson, LeFort, Yin, Lovera and Catlos1997; Valdiya, Reference Valdiya2001; Catlos et al. Reference Catlos, Harrison, Kohn, Grove, Ryerson, Manning and Upreti2001). (iii) The viscosity of the partially molten mid-crustal rocks could vary by 14 orders of magnitude (Scaillet, Holtz & Pichavant, Reference Scaillet, Holtz and Pichavant1996; Beaumont et al. Reference Beaumont, Jamieson, Nguyen and Lee2001). (iv) In compressional regimes, shear zones may rotate and change their dip (Leech et al. Reference Leech, Singh, Jain, Klemperer and Manickavasagam2005).
The present analytical models of simple shear investigate a reverse shear (top-to-updip). The starting equation of fluid mechanics (Eqn 1 in Appendix) also has potential for constraining shear senses for a normal shear sense (top-to-downdip) by reversing shear senses at the shear zone boundaries. Assuming similar vector addition (as in Fig. 1d) allows deduction of different flow profiles, co-ordinates of pivots and vertices, and anticipation of the development of two opposed shear senses in the general case, and in the special cases of a uniform sense (similar to Fig. 1a). In general, normal sense shear will also lead to subduction simultaneous with extrusion (similar to Fig. 1a–d).
The models presented here should be compared with natural shear zones with utmost caution because of the following possibilities. Shear zones may develop non-Newtonian behaviour (as interpreted from Dasgupta, Chakraborty & Neogi's, Reference Dasgupta, Chakraborty and Neogi2009 findings by Mukherjee & Koyi, Reference Mukherjee and Koyi2010a ) or involve molten rocks (Webb & Dingwell, Reference Webb and Dingwell1990). The boundaries of the shear zone act rigidly only if the ratio of viscosity between the shear zone and its surroundings is ≤ 10−7 (Mancktelow, Reference Mancktelow2008). Melting during ductile shearing (Marchildon & Brown, Reference Marchildon and Brown2003) means that the shear zone is no longer incompressible. Fluid channelling during ductile shearing can lead to up to 60% volume loss from the middle of the shear zone (Selverstone, Morteani & Staude, Reference Selverstone, Morteani and Staude1991). Thickness of orogenic shear zones can vary by an order of magnitude (Lombardo, Pertusati & Borghi, Reference Lombardo, Pertusati, Borghi, Treloar and Searle1993; Jain & Anand, Reference Jain and Anand1988). In natural shear zones, a component of pure shear might apply either uniformly (Vannay & Grasemann, Reference Vannay and Grasemann2001), or non-uniformly (Exner, Grasemann & Mancktelow, Reference Exner, Grasemann, Mancktelow, Butler and Shreurs2006). Natural shear zones can contain more than one lithology. Assigning single values for the density and viscosity while modelling may obscure some of their kinematic details. The kinematics for a ‘single lithology’ may also be non-uniform because of local variations in composition or grain size.
In their advanced thermal mechanical model of extrusion induced by ductile shear, the Dalhousie group of modellers (e.g. Beaumont et al. Reference Beaumont, Jamieson, Nguyen and Medvedev2004; also Kellett et al. Reference Kellett, Grujic, Warren, Cottle, Jamieson and Tenzin2010 as the latest example) considered a number of additional parameters such as geothermal gradient, radioactive heat production, thermal expansion coefficients and power law behaviour, together with density changes due to phase transition during metamorphism and extrusion augmented by focused erosion. However, this work takes a minimalist approach and considers only the most significant parameters as followed by Ramsay (Reference Ramsay1980), Ramsay & Lisle (Reference Ramsay and Lisle2000) and Grasemann, Edwards & Wiesmayr (Reference Grasemann, Edwards, Wiesmayr, Law, Searle and Godin2006). In addition, the following factors were also ignored: gravitational spreading or erosion of materials extruded from the top end of the shear zone; kinematic dilatancy (Grasemann, Edwards & Wiesmayr, Reference Grasemann, Edwards, Wiesmayr, Law, Searle and Godin2006); strain partitioning (Mancktelow, Reference Mancktelow2006); and changes in rock rheologies (von Huene, Ranero, & Scholl, Reference von Huene, Ranero, Scholl, Lallemand and Funiciello2009).
4. Conclusions
The shear senses of inclined simple shear zones with parallel long boundaries are investigated by considering them as having incompressible Newtonian viscous rheologies. A parabolic velocity profile develops with a vertex that moves fastest, denotes the point of least shear strain and lies on a line that demarcates two sub-zones of opposite shear senses. The flow profile is dependent on the size and the orientation of the shear zones, pressure gradient, density and viscosity of the rocks, and gravity. A pressure gradient stronger than the gravity component makes the parabolic profile convex upward, and a weaker one downdip. Reverse shear on this profile leads to a thinner sub-zone of normal shear developing near the top of the shear zone. The intersection between the velocity profile and a line perpendicular to the flow direction/shear zone defines the ‘pivot’ that remains static throughout the deformation history as long as the flow parameters remain unchanged. The pivot falls inside the shear zone if the boundaries shear in opposite directions; otherwise it falls outside. For an internal pivot, a part of a non-horizontal shear zone across the pivot extrudes while the other part subducts. The whole shear zone either extrudes or subducts (i) if only a single boundary of the shear zone moves and when the pivot falls on the stationary boundary; and (ii) if both the boundaries move in the same direction and the pivot falls outside the shear zone. Changes in magnitude of flow parameters can develop a sub-zone of retro-shear in contact with one of the boundaries of the shear zone where initially a pro-shear was persistent.
Acknowledgements
Supported by IIT Bombay's Seed Grant: Spons/GS/SM-1/2009; and Department of Science and Technology's (New Delhi) SERC Fast Track Scheme: SR/FTP/ES-117/2009. Chris Talbot made three rounds of in depth informal review that significantly improved the scientific content and the English. A very detailed review by Haakon Fossen, and those by Paul Bons and an anonymous reviewer of a previous version greatly improved and significantly shortened the manuscript. Interaction with Kirti Chandra Sahu helped to clarify several points. Katarzyna Piper is thanked for her thorough copyediting and Sally Thomas for technical editing.
Appendix. Equations
The ‘Poisson equation’ of rectilinear flow of an incompressible Newtonian viscous fluid in the z-direction through a very long parallel rigid boundary inclined shear zone is given by eqn 6.190 of Papanastasiou, Georgiou & Alexandrou (Reference Papanastasiou, Georgiou and Alexandrou2000):
![\begin{equation}
{\rm (}\partial ^{\rm 2} {\rm U}_{\rm z} {\rm /}\partial {\rm x}^{\rm 2} {\rm) + (}\partial ^{\rm 2} {\rm U}_{\rm z} {\rm /}\partial {\rm y}^{\rm 2} {\rm) = \mu}^{{- 1}} {\rm \, [}\partial {\rm P/}\partial {\rm z - d\, g \,Sin\theta]}\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn1.gif?pub-status=live){kind=small}
Here ‘x’ and ‘y’ are perpendicular directions and lie on the cross-section of the shear zone; Uz is the velocity of the fluid along the z-direction; ‘μ’ is the dynamic viscosity of the fluid; (∂P/∂z) is the pressure gradient along the shear zone that forces the fluid to extrude; ‘d’ is the density of the fluid, ‘g’ is the acceleration due to gravity, and ‘θ’ is the dip of the shear zone.
If only the y–z cross-section of the flow is considered, then (∂2Uz/∂x2) = 0. Thus,
![\begin{equation}
{\rm (}\partial ^{\rm 2} {\rm U_{z}/}\partial {\rm y}^{\rm 2} {\rm) = \mu}^{{- 1}} {\rm \, [}\partial {\rm P/}\partial {\rm z - d\, g\, Sin\theta]}\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn2.gif?pub-status=live){kind=small}
Integrating twice, taking the thickness of the shear zone to be 2y0 units, and considering the boundary conditions of simple shear on both the boundaries, i.e. at y = y0, Uz = U1, and at y = −y0, Uz = −U2 leads to the following flow profile:
![\begin{eqnarray}
{\rm U}_{\rm z} & =& 0.5 \,\mu^{{-1}}\, [\partial {\rm P}/\partial {\rm z - d\, g\, Sin}\theta ]\, \big({\rm y}^{2}-{\rm y}_{0}^{2}\big) \nonumber\\
&& +\,0.5 \,\{{\rm y\, y}_{0}^{{-1}}\,({\rm U}_{1} + {\rm U}_{2}) + ({\rm U}_{1}-{\rm U}_{2})\}\end{eqnarray}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn3.gif?pub-status=live){kind=small}
The vertex of the parabolic profile (3) is given by
For the absolute value of ∂P/∂z > than that of ‘d g Sinθ’, and U1, U2 ≠ 0, both the ‘z-’ and the y-ordinates of the vertex are > 0 (Fig. 1b). For the absolute value of ∂P/∂z < than that of ‘d g Sinθ’, and U1, U2 ≠ 0, both the ‘z-’ and the y-ordinates of the vertex are < 0 (Fig. 1c, d).
∂P/∂z being < 0 (this is because, as ‘z’ increases, ‘P’ falls), ‘y1’ is always > 0. Thus, using (5), the thickness of the sub-zone with a shear sense opposed to the remainder of the master zone is:
The thickness of the studied master shear zone is ‘2y0’ units. The remaining sub-zone where the shear sense is the same as that given by shearing of the boundaries is given by:
Clearly, y1′ < y2′.
For y1 > y0 (profile ‘B’ in Fig. 2a, b), the vertex of the profile is outside the shear zone.
For y1 = y0 (profile ‘A’ in Fig. 2a, b), the vertex lies on the upper boundary of the shear zone.
To find the co-ordinate of the point of intersection between the y-axis and the velocity profile given by (3), Uz = 0 is inserted in (3):
![\begin{eqnarray}
0 &=& 0.5\, \mu ^{{- 1}} \, [\partial {\rm P}/\partial {\rm z - d\, g\, Sin\theta ]\, (y}^{2} {\rm - y}_{\rm 0} ^{2}) \nonumber\\
&&+ \, 0.5 \,\{{\rm y\, y}_{\rm 0} ^{{- 1}}\, {\rm (U}_{1} {\rm + U}_{2} {\rm) + (U}_{1} {\rm - U}_{2} {\rm)\}}\end{eqnarray}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn8.gif?pub-status=live){kind=small}
Now if U2 = 0 (Fig. 1e), (8) simplifies to:
![\begin{eqnarray}
0 &=& 0.5\, \mu ^{{- 1}}\, [\partial {\rm P}/\partial {\rm z - d\, g\, Sin\theta ]\, (y}^{2} {\rm - y}_{\rm 0} ^{2} {\rm)} \nonumber\\
&& +\, {\rm 0}{\rm .5\, U}_{1}\, {\rm (y\, y}_{\rm 0} ^{{- 1}} {\rm + 1)}\end{eqnarray}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn9.gif?pub-status=live){kind=small}
The point (0, −y0) is satisfied in (9). Thus (0, −y0) is the pivot.
Similarly, if U1 = 0 (Fig. 1f), (8) simplifies to:
![\begin{eqnarray}
0 &=& 0.5\, \mu ^{{- 1}}\, [\partial {\rm P}/\partial {\rm z - d\, g\, Sin\theta ]\, (y}^{2} {\rm - y}_{\rm 0} ^{2} {\rm)} \nonumber\\
&& +\, {\rm 0}{\rm .5\, U}_{2} {\rm \{y\, y}_{\rm 0} ^{{- 1}} {\rm - 1\}}\end{eqnarray}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn10.gif?pub-status=live){kind=small}
The point (0, y0) is satisfactory with respect to (10). Thus (0, y0) is the pivot.
For ∂P/∂z = d g Sinθ (Fig. 1a), the co-ordinate of the pivot is derived from (8) as:
![\begin{equation}
{\rm [0, y}_{\rm 0}\, {\rm (U}_{2} {\rm - U}_{1} {\rm)\, (U}_{2} {\rm \, +\, U}_{1} {\rm)^{- 1}]}\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn11.gif?pub-status=live){kind=small}
When θ ≠ 0, and U1 = U2 = ∂P/∂z = 0, the velocity profile in (3) simplifies to:
![\begin{equation}
{\rm U}_{\rm z} ^\prime {\rm = - 0}{\rm .5 \,\mu}^{{- 1}}\, {\rm [d\, g\, Sin\theta ]\, (y}^{2} {\rm - y}_{\rm 0} ^{2} {\rm)}\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn12.gif?pub-status=live){kind=small}
And, for θ = 0, and U1 = U2 ≠ 0,
When θ, U1, U2, ∂P/∂z ≠ 0,
![\begin{eqnarray}
{\rm U}_{\rm z} ^{\prime \prime \prime} &=& 0{\rm .5\, \mu}^{{- 1}}\, [\partial {\rm P}/\partial {\rm z - d\, g\, Sin\theta ]\, (y}^{2} {\rm - y}_{\rm 0} ^{2}) \nonumber \\
&&+\, 0.5 \,\{{\rm y\, y}_{\rm 0} ^{{- 1}} {\rm (U}_{1} {\rm + U}_{2} {\rm) + (U}_{1} {\rm - U}_{2} {\rm)\}}\end{eqnarray}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20180417041455671-0753:S0016756811001075:S0016756811001075_eqn14.gif?pub-status=live){kind=small}
