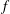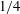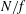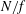1 Introduction
The interaction between vortices and waves is a long-standing problem in fluid turbulence. It can lead to a self-sustaining process that is dominant, for example in pipe flows, due to the strong wall-induced shear. A quasi-linear analysis around a mean but unsteady flow allows for a prediction of large-scale coherent structures in such flows (McKeon & Sharma Reference Mckeon and Sharma2010; Farrell & Ioannou Reference Farrell and Ioannou2012; Sharma & McKeon Reference Sharma and Mckeon2013), to the prediction of jets in baroclinic turbulence in the atmosphere of planets (Farrell & Ioannou Reference Farrell and Ioannou2009), and it can also be used as a tool to control the onset of turbulence using travelling waves (Moarref & Jovanović Reference Moarref and Jovanović2010). The dynamics of geophysical flows involves complex interactions between nonlinear eddies and waves due to the combination of planetary rotation and density stratification as well as the formation of shear layers. Typical parameters for the atmosphere and the ocean at large scales (larger than approximately 1000 km) are such that the dynamics of the fast waves is slaved to that of the eddies, and this leads to a quasi-geostrophic quasi-linear regime characterized by a balance between the pressure gradient and the Coriolis and gravity forces (Charney Reference Charney1971). Then, the eddy turnover time is much larger than typical wave frequencies: the Brunt–Väisälä frequency
![]() $N$
or the inertial frequency
$N$
or the inertial frequency
![]() $f=2\unicode[STIX]{x1D6FA}$
(with
$f=2\unicode[STIX]{x1D6FA}$
(with
![]() $\unicode[STIX]{x1D6FA}$
the rotation rate). For instance, frequency spectra obtained from in situ measurements in the ocean show distinct power laws for internal waves in the
$\unicode[STIX]{x1D6FA}$
the rotation rate). For instance, frequency spectra obtained from in situ measurements in the ocean show distinct power laws for internal waves in the
![]() $[f,N]$
band and geostrophic eddies at lower frequencies (Ferrari & Wunsch Reference Ferrari and Wunsch2009). The quasi-geostrophic regime is well understood theoretically and provides a good description of the large scales of the atmosphere and the ocean (Vallis Reference Vallis2006, e.g.). However, the range of scales in these geophysical flows before dissipation prevails at small scales is such that other scale-dependent regimes can arise in which turbulence comes into play, with the eddy turnover time becoming comparable to the Brunt–Väisälä frequency, the inertial frequency, or their combinations which arise in the dispersion relation of internal waves. Lilly (Reference Lilly1983), in particular, has underlined the emergence of a regime, coined stratified turbulence, between quasi-geostrophic turbulence and homogeneous isotropic turbulence (see also the scale analysis by Riley, Metcalfe & Weissman (Reference Riley, Metcalfe and Weissman1981)), and its importance for the mesoscales (with horizontal scales between 1 and 100 km, approximately) in the atmosphere. Indeed, the measured horizontal spectra of kinetic and potential energy in the upper troposphere and lower stratosphere (Nastrom, Gage & Jasperson Reference Nastrom, Gage and Jasperson1984) has a long history of opposite interpretations: some have claimed that this unambiguous
$[f,N]$
band and geostrophic eddies at lower frequencies (Ferrari & Wunsch Reference Ferrari and Wunsch2009). The quasi-geostrophic regime is well understood theoretically and provides a good description of the large scales of the atmosphere and the ocean (Vallis Reference Vallis2006, e.g.). However, the range of scales in these geophysical flows before dissipation prevails at small scales is such that other scale-dependent regimes can arise in which turbulence comes into play, with the eddy turnover time becoming comparable to the Brunt–Väisälä frequency, the inertial frequency, or their combinations which arise in the dispersion relation of internal waves. Lilly (Reference Lilly1983), in particular, has underlined the emergence of a regime, coined stratified turbulence, between quasi-geostrophic turbulence and homogeneous isotropic turbulence (see also the scale analysis by Riley, Metcalfe & Weissman (Reference Riley, Metcalfe and Weissman1981)), and its importance for the mesoscales (with horizontal scales between 1 and 100 km, approximately) in the atmosphere. Indeed, the measured horizontal spectra of kinetic and potential energy in the upper troposphere and lower stratosphere (Nastrom, Gage & Jasperson Reference Nastrom, Gage and Jasperson1984) has a long history of opposite interpretations: some have claimed that this unambiguous
![]() $k^{-5/3}$
range corresponds to an inverse cascade of quasi-two-dimensional eddies (Gage Reference Gage1979; Lilly Reference Lilly1983; Métais et al.
Reference Métais, Bartello, Garnier, Riley and Lesieur1996), while others have argued that it was in fact a direct energy cascade dominated by internal waves (Dewan Reference Dewan1979), or yet another type of turbulence corresponding to a different scaling of the equations of motions (Lindborg Reference Lindborg2006). This example emphasizes the importance of analysing data – be it observational, experimental or numerical – in terms of eddies or vortices on the one hand, and waves on the other hand. In this paper, we shall try to disentangle these two types of motion in the idealized context of direct numerical simulations of stratified flows with and without rotation in a periodic box, focusing on the classical quantities characterizing the statistical behaviour of nonlinear interactions in turbulent flows, in particular energy spectra and transfer functions. Our main goal is to better understand the fluid mechanics of rotating-stratified flows, motivated by geophysical flows. However, due to the computational difficulties in reaching geophysical flow parameter regimes (small Froude number and very large Reynolds number), we shall also discuss viscous effects which do not arise in geophysical flows, but are relevant for laboratory experiments such as those of Praud, Fincham & Sommeria (Reference Praud, Fincham and Sommeria2005).
$k^{-5/3}$
range corresponds to an inverse cascade of quasi-two-dimensional eddies (Gage Reference Gage1979; Lilly Reference Lilly1983; Métais et al.
Reference Métais, Bartello, Garnier, Riley and Lesieur1996), while others have argued that it was in fact a direct energy cascade dominated by internal waves (Dewan Reference Dewan1979), or yet another type of turbulence corresponding to a different scaling of the equations of motions (Lindborg Reference Lindborg2006). This example emphasizes the importance of analysing data – be it observational, experimental or numerical – in terms of eddies or vortices on the one hand, and waves on the other hand. In this paper, we shall try to disentangle these two types of motion in the idealized context of direct numerical simulations of stratified flows with and without rotation in a periodic box, focusing on the classical quantities characterizing the statistical behaviour of nonlinear interactions in turbulent flows, in particular energy spectra and transfer functions. Our main goal is to better understand the fluid mechanics of rotating-stratified flows, motivated by geophysical flows. However, due to the computational difficulties in reaching geophysical flow parameter regimes (small Froude number and very large Reynolds number), we shall also discuss viscous effects which do not arise in geophysical flows, but are relevant for laboratory experiments such as those of Praud, Fincham & Sommeria (Reference Praud, Fincham and Sommeria2005).
One way to distinguish between waves and eddies is through a decomposition of the flow onto the normal modes of the linearized system (Bartello Reference Bartello1995, see also below, § 3). Normal mode decomposition is a standard technique which has been used in a variety of theoretical (Errico Reference Errico1984; Warn Reference Warn1986; Lien & Müller Reference Lien and Müller1992; Bartello Reference Bartello1995; Waite & Bartello Reference Waite and Bartello2004; Herbert, Pouquet & Marino Reference Herbert, Pouquet and Marino2014) and numerical studies (Bartello Reference Bartello1995; Smith & Waleffe Reference Smith and Waleffe2002; Waite & Bartello Reference Waite and Bartello2006a ,Reference Waite and Bartello b ; Sukhatme & Smith Reference Sukhatme and Smith2008; Kitamura & Matsuda Reference Kitamura and Matsuda2010; Kurien & Smith Reference Kurien and Smith2012; Brunner-Suzuki, Sundermeyer & Lelong Reference Brunner-Suzuki, Sundermeyer and Lelong2014; Kurien & Smith Reference Kurien and Smith2014), for the Boussinesq equations, which we shall investigate here, as well as for other dynamical equations. Recently, another approach has been proposed (Bühler, Callies & Ferrari Reference Bühler, Callies and Ferrari2014), which relies on a few additional assumptions in order to be able to achieve a similar decomposition without a complete knowledge of the dynamical fields. This is particularly useful when working with observational data, such as ship track data or aeroplane measurements. Callies, Ferrari & Bühler (Reference Callies, Ferrari and Bühler2014) have used this method to claim that observational data supported the internal wave interpretation of the forward cascade of the atmospheric mesoscales, although Lindborg (Reference Lindborg2015) argues using a similar technique that the forward cascade of energy could in fact be of another type, corresponding to the scaling regime of stratified turbulence identified in Billant & Chomaz (Reference Billant and Chomaz2001) (see also Lindborg Reference Lindborg2006). Another interesting approach consists of computing a full frequency-wavenumber energy spectrum in the four-dimensional Fourier space (Clark di Leoni & Mininni (Reference Clark di Leoni and Mininni2015); see also Campagne et al. (Reference Campagne, Gallet, Moisy and Cortet2015) for an analogous analysis in a laboratory experiment of rotating flow). This allows one to directly assess how the energy is partitioned between modes which exhibit phase coherence, like waves, and other modes. However, this is a computationally expensive technique which requires a good time resolution in addition to a good space resolution (and hence, a lot of disk space).
In this context, a pioneering analytical and numerical study of strongly rotating-stratified turbulence in terms of normal modes was done by Bartello (Reference Bartello1995). The link between geostrophic adjustment at large scale and the inverse cascade of energy due to the conservation of (linearized) potential vorticity is clearly established through a decoupling of the (fast) wave modes and vortical (slow) modes. By truncating the nonlinear interactions to some specific subsets of modes, as for example between three slow modes that lead to the inverse cascade of energy (Charney Reference Charney1971), dominant effects can thus be identified. It is shown in particular that there are nonlinear interactions using a slow mode as a catalyst to push the wave energy to small scales (whereas triads involving three fast modes are negligible); furthermore, as the rotation is increased, the energetic exchanges between the slow vortical modes and the fast wave modes are weakened and such modes can be seen as actually being progressively decoupled. It was noticed by Smith & Waleffe (Reference Smith and Waleffe2002) that, for long times, the growth of large-scale energy is associated with geostrophic modes for
![]() $1/2\leqslant N/f\leqslant 2$
(in which domain three-wave resonances vanish completely), whereas for large
$1/2\leqslant N/f\leqslant 2$
(in which domain three-wave resonances vanish completely), whereas for large
![]() $N/f$
, the vertically sheared horizontal flows (VSHF), with no variation in the horizontal and no vertical velocity, are dominant. One should note that if the forcing wavenumber is not well separated from the box overall dimension, finite-size effects can develop that quench the possible (discrete) resonances, as already noted in the context of water-wave turbulence (see e.g. Kartashova, Nazarenko & Rudenko (Reference Kartashova, Nazarenko and Rudenko2008) and references therein).
$N/f$
, the vertically sheared horizontal flows (VSHF), with no variation in the horizontal and no vertical velocity, are dominant. One should note that if the forcing wavenumber is not well separated from the box overall dimension, finite-size effects can develop that quench the possible (discrete) resonances, as already noted in the context of water-wave turbulence (see e.g. Kartashova, Nazarenko & Rudenko (Reference Kartashova, Nazarenko and Rudenko2008) and references therein).
In the purely stratified case, it was found by Waite & Bartello (Reference Waite and Bartello2004, Reference Waite and Bartello2006b
) that the vertical spectrum of the waves moves to larger vertical wavenumber as stratification increases, in agreement with the argument found by Billant & Chomaz (Reference Billant and Chomaz2001) that the characteristic scale in the vertical is proportional to
![]() $U/N$
, with
$U/N$
, with
![]() $U$
a typical large-scale velocity; at smaller scales the structures break down in a nonlinear fashion, although isotropy may not be restored, depending on the buoyancy Reynolds number and whether the Ozmidov scale is resolved (see § 2.2 below for definitions): the buoyancy scale
$U$
a typical large-scale velocity; at smaller scales the structures break down in a nonlinear fashion, although isotropy may not be restored, depending on the buoyancy Reynolds number and whether the Ozmidov scale is resolved (see § 2.2 below for definitions): the buoyancy scale
![]() $L_{B}=U/N$
must be sufficiently resolved for overturning to take place. The case of comparable (but not identical) strengths for rotation and stratification was analysed by Sukhatme & Smith (Reference Sukhatme and Smith2008), where it is shown that there is a transition in behaviour for
$L_{B}=U/N$
must be sufficiently resolved for overturning to take place. The case of comparable (but not identical) strengths for rotation and stratification was analysed by Sukhatme & Smith (Reference Sukhatme and Smith2008), where it is shown that there is a transition in behaviour for
![]() $N/f\approx 1$
: for smaller values, large scales are dominated by the vortical mode and small scales by wave modes, whereas for larger values of
$N/f\approx 1$
: for smaller values, large scales are dominated by the vortical mode and small scales by wave modes, whereas for larger values of
![]() $N/f$
, the wave modes dominate at all scales smaller than the forcing.
$N/f$
, the wave modes dominate at all scales smaller than the forcing.
The scaling behaviour of slow and fast modes for rotating-stratified flows is analysed in Kurien & Smith (Reference Kurien and Smith2012, Reference Kurien and Smith2014) for regimes where potential vorticity is linear, for small aspect ratio of the domain size in the vertical (
![]() $\unicode[STIX]{x1D6FF}=L_{\Vert }/L_{\bot }=1/4$
), but with a unit Burger number
$\unicode[STIX]{x1D6FF}=L_{\Vert }/L_{\bot }=1/4$
), but with a unit Burger number
![]() $Bu=\unicode[STIX]{x1D6FF}N/f$
, using high-resolution direct numerical simulations and hyper-viscosity. When compared to similar flows with
$Bu=\unicode[STIX]{x1D6FF}N/f$
, using high-resolution direct numerical simulations and hyper-viscosity. When compared to similar flows with
![]() $\unicode[STIX]{x1D6FF}=1$
, differences arise, as for example when examining the steepness of the wave component of the energy spectrum, viewed as a signature of the layered structure of the flow. The case
$\unicode[STIX]{x1D6FF}=1$
, differences arise, as for example when examining the steepness of the wave component of the energy spectrum, viewed as a signature of the layered structure of the flow. The case
![]() $\unicode[STIX]{x1D6FF}\not =1$
was also examined for either purely rotating (Deusebio et al.
Reference Deusebio, Boffetta, Lindborg and Musacchio2014) or purely stratified flows (Sozza et al.
Reference Sozza, Boffetta, Muratore-Ginanneschi and Musacchio2015), where it is shown that the aspect ratio can affect the strength of the inverse cascade of energy to large scales. The combined effect of varying
$\unicode[STIX]{x1D6FF}\not =1$
was also examined for either purely rotating (Deusebio et al.
Reference Deusebio, Boffetta, Lindborg and Musacchio2014) or purely stratified flows (Sozza et al.
Reference Sozza, Boffetta, Muratore-Ginanneschi and Musacchio2015), where it is shown that the aspect ratio can affect the strength of the inverse cascade of energy to large scales. The combined effect of varying
![]() $N/f$
and
$N/f$
and
![]() $\unicode[STIX]{x1D6FF}$
on the formation of characteristic structures was further studied in Kurien & Smith (Reference Kurien and Smith2014) for low Froude number (
$\unicode[STIX]{x1D6FF}$
on the formation of characteristic structures was further studied in Kurien & Smith (Reference Kurien and Smith2014) for low Froude number (
![]() $Fr=0.002$
, ensuring that potential vorticity is again linear, i.e. for low effective turbulence) and varying either the Rossby number at fixed
$Fr=0.002$
, ensuring that potential vorticity is again linear, i.e. for low effective turbulence) and varying either the Rossby number at fixed
![]() $\unicode[STIX]{x1D6FF}$
or vice versa (in which case, the choice was made of
$\unicode[STIX]{x1D6FF}$
or vice versa (in which case, the choice was made of
![]() $N=f$
). The layering of the flow is clearly dependent on the strength of the rotation (
$N=f$
). The layering of the flow is clearly dependent on the strength of the rotation (
![]() $Fr$
being fixed), and the wave and slow mode spectra are quite different (when the total spectra are more difficult to distinguish). The inverse cascade of energy is clearly associated with the vortical (slow) mode, as shown as well in Brunner-Suzuki et al. (Reference Brunner-Suzuki, Sundermeyer and Lelong2014) for a variety of forcing functions in the context of sub-mesoscale oceanic mixing. It is also shown in Brunner-Suzuki et al. (Reference Brunner-Suzuki, Sundermeyer and Lelong2014) that small-scale (shear) layers do not directly modify the inverse cascade, although it could strengthen it when bringing together nearby vortices through nonlinear advection when they are sufficiently numerous. Recently, Whitehead & Wingate (Reference Whitehead and Wingate2014) have studied the energy transfers between slow and fast modes in the Boussinesq equations, in the three asymptotic regimes of strong stratification/weak rotation, strong rotation/weak stratification and the quasi-geostrophic regime. Their findings also point out the role of the slow modes in the linear growth of kinetic energy.
$Fr$
being fixed), and the wave and slow mode spectra are quite different (when the total spectra are more difficult to distinguish). The inverse cascade of energy is clearly associated with the vortical (slow) mode, as shown as well in Brunner-Suzuki et al. (Reference Brunner-Suzuki, Sundermeyer and Lelong2014) for a variety of forcing functions in the context of sub-mesoscale oceanic mixing. It is also shown in Brunner-Suzuki et al. (Reference Brunner-Suzuki, Sundermeyer and Lelong2014) that small-scale (shear) layers do not directly modify the inverse cascade, although it could strengthen it when bringing together nearby vortices through nonlinear advection when they are sufficiently numerous. Recently, Whitehead & Wingate (Reference Whitehead and Wingate2014) have studied the energy transfers between slow and fast modes in the Boussinesq equations, in the three asymptotic regimes of strong stratification/weak rotation, strong rotation/weak stratification and the quasi-geostrophic regime. Their findings also point out the role of the slow modes in the linear growth of kinetic energy.
Our study uses similar methods as the above-mentioned authors, but pursues a slightly different goal: here, we focus on the possibility of an inverse cascade and its relation with the inviscid invariants of the system. We are interested in understanding the difference between the rotating-stratified case, for which an inverse cascade is possible (Bartello Reference Bartello1995; Lindborg Reference Lindborg2005; Aluie & Kurien Reference Aluie and Kurien2011; Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2013), and the purely stratified case, where there is no such thing (Waite & Bartello Reference Waite and Bartello2004, Reference Waite and Bartello2006b
), although there is some transfer of energy towards the large scale. This difference has already been considered from the point of view of anisotropic energy transfers (Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2014); here we adopt a different point of view and we investigate the role of vortices and waves in the inverse cascade (or lack thereof). We also aim at characterizing the transition between these two regimes. Indeed, although previous studies have established that, when an inverse cascade is present, it is due to the slow vortices, it is not clear how this phenomenology breaks up. We shall see that in the regime of parameters considered, we can identify three coexisting inertial mechanisms. To do so, we examine data stemming from direct numerical simulations of rotating-stratified turbulence, forced at small scales, for a variety of
![]() $N/f$
ratios (and Froude and Rossby numbers) in cubic boxes at a Reynolds number of 1000. Since geophysically relevant buoyancy Reynolds numbers are currently out of reach for inverse cascade studies, the vertical shear associated with moderate buoyancy Reynolds numbers leads to potentially important viscous effects which we shall discuss in comparison to the inertial mechanisms. After describing the relevant equations, the theoretical framework and the numerical simulations in § 2, we review the normal mode decomposition in § 3, and analyse the numerical data in terms of the normal modes in § 4. Viscous effects and the role of the buoyancy Reynolds number are considered in § 5. In § 6, we discuss the results and present our conclusions.
$N/f$
ratios (and Froude and Rossby numbers) in cubic boxes at a Reynolds number of 1000. Since geophysically relevant buoyancy Reynolds numbers are currently out of reach for inverse cascade studies, the vertical shear associated with moderate buoyancy Reynolds numbers leads to potentially important viscous effects which we shall discuss in comparison to the inertial mechanisms. After describing the relevant equations, the theoretical framework and the numerical simulations in § 2, we review the normal mode decomposition in § 3, and analyse the numerical data in terms of the normal modes in § 4. Viscous effects and the role of the buoyancy Reynolds number are considered in § 5. In § 6, we discuss the results and present our conclusions.
2 Theoretical framework and numerical data
2.1 Equations of motion and direct numerical simulations
We consider incompressible flows in a reference frame rotating with angular velocity
![]() $\unicode[STIX]{x1D6FA}$
around axis
$\unicode[STIX]{x1D6FA}$
around axis
![]() $\boldsymbol{e}_{z}$
(we note
$\boldsymbol{e}_{z}$
(we note
![]() $\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}\boldsymbol{e}_{z}$
and
$\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}\boldsymbol{e}_{z}$
and
![]() $f=2\unicode[STIX]{x1D6FA}$
the Coriolis parameter). The gravity field is anti-aligned with the direction of rotation:
$f=2\unicode[STIX]{x1D6FA}$
the Coriolis parameter). The gravity field is anti-aligned with the direction of rotation:
![]() $\boldsymbol{g}=-g\boldsymbol{e}_{z}$
. We work in the Boussinesq approximation: the density is assumed constant, equal to
$\boldsymbol{g}=-g\boldsymbol{e}_{z}$
. We work in the Boussinesq approximation: the density is assumed constant, equal to
![]() $\unicode[STIX]{x1D70C}_{0}>0$
, except in the buoyancy force term, and we assume a linear background stratification: the density field is given by
$\unicode[STIX]{x1D70C}_{0}>0$
, except in the buoyancy force term, and we assume a linear background stratification: the density field is given by
![]() $\unicode[STIX]{x1D70C}(\boldsymbol{x})=\unicode[STIX]{x1D70C}_{0}(1-(N^{2}/g)z)+\unicode[STIX]{x1D70C}^{\prime }(\boldsymbol{x})$
, with
$\unicode[STIX]{x1D70C}(\boldsymbol{x})=\unicode[STIX]{x1D70C}_{0}(1-(N^{2}/g)z)+\unicode[STIX]{x1D70C}^{\prime }(\boldsymbol{x})$
, with
![]() $N$
the Brunt–Väisälä frequency. Note that we are only considering the case of stably stratified flows. We introduce the temperature field (with the dimension of a velocity)
$N$
the Brunt–Väisälä frequency. Note that we are only considering the case of stably stratified flows. We introduce the temperature field (with the dimension of a velocity)
![]() $\unicode[STIX]{x1D703}(\boldsymbol{x})=(g/N\unicode[STIX]{x1D70C}_{0})\unicode[STIX]{x1D70C}^{\prime }(\boldsymbol{x})$
. The velocity field is denoted by
$\unicode[STIX]{x1D703}(\boldsymbol{x})=(g/N\unicode[STIX]{x1D70C}_{0})\unicode[STIX]{x1D70C}^{\prime }(\boldsymbol{x})$
. The velocity field is denoted by
![]() $\boldsymbol{u}$
. Given the assumptions mentioned above, the equations governing the dynamics of the fields
$\boldsymbol{u}$
. Given the assumptions mentioned above, the equations governing the dynamics of the fields
![]() $\boldsymbol{u},\unicode[STIX]{x1D703}$
are as follows:
$\boldsymbol{u},\unicode[STIX]{x1D703}$
are as follows:
where
![]() $P$
denotes the (rescaled) pressure field, fixed by the incompressibility condition,
$P$
denotes the (rescaled) pressure field, fixed by the incompressibility condition,
![]() $\unicode[STIX]{x1D708}$
the viscosity and
$\unicode[STIX]{x1D708}$
the viscosity and
![]() $\unicode[STIX]{x1D705}$
the thermal diffusivity; we work with Prandtl number equal to unity:
$\unicode[STIX]{x1D705}$
the thermal diffusivity; we work with Prandtl number equal to unity:
![]() $\mathit{Pr}=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$
. Finally,
$\mathit{Pr}=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$
. Finally,
![]() $\boldsymbol{F}$
is an isotropic forcing introduced only in the momentum equation; it has a fixed amplitude in a prescribed narrow shell centred on wavenumber
$\boldsymbol{F}$
is an isotropic forcing introduced only in the momentum equation; it has a fixed amplitude in a prescribed narrow shell centred on wavenumber
![]() $k_{F}$
, and random but constant in time phases. Note that, contrary to other studies (Kurien & Smith Reference Kurien and Smith2012, Reference Kurien and Smith2014, for instance), there is no forcing in the buoyancy equation, but the forcing has a vertical component (unlike, e.g. Waite & Bartello (Reference Waite and Bartello2004) or Sozza et al. (Reference Sozza, Boffetta, Muratore-Ginanneschi and Musacchio2015)) and does not satisfy balance relations, even at the lowest order (unlike e.g. Waite & Bartello (Reference Waite and Bartello2006b
), where the forcing is only in the slow modes). The projection of the forcing on the waves and slow modes (see § 3) has the same magnitude; hence we are not favouring any of these modes a priori.
$k_{F}$
, and random but constant in time phases. Note that, contrary to other studies (Kurien & Smith Reference Kurien and Smith2012, Reference Kurien and Smith2014, for instance), there is no forcing in the buoyancy equation, but the forcing has a vertical component (unlike, e.g. Waite & Bartello (Reference Waite and Bartello2004) or Sozza et al. (Reference Sozza, Boffetta, Muratore-Ginanneschi and Musacchio2015)) and does not satisfy balance relations, even at the lowest order (unlike e.g. Waite & Bartello (Reference Waite and Bartello2006b
), where the forcing is only in the slow modes). The projection of the forcing on the waves and slow modes (see § 3) has the same magnitude; hence we are not favouring any of these modes a priori.
We integrate (2.1)–(2.3) numerically with a pseudo-spectral code, the geophysical high-order suite for turbulence (GHOST) in a tri-periodic cubic domain of length
![]() $L=2\unicode[STIX]{x03C0}$
. GHOST is parallelized using an hybrid MPI/OpenMP method and scales linearly up to
$L=2\unicode[STIX]{x03C0}$
. GHOST is parallelized using an hybrid MPI/OpenMP method and scales linearly up to
![]() $10^{5}$
compute cores on grids of up to
$10^{5}$
compute cores on grids of up to
![]() $6144^{3}$
points (Mininni et al.
Reference Mininni, Rosenberg, Reddy and Pouquet2011). No model is used for subgrid scales, and dissipation occurs through standard Laplacian terms. The runs considered here all have a resolution of
$6144^{3}$
points (Mininni et al.
Reference Mininni, Rosenberg, Reddy and Pouquet2011). No model is used for subgrid scales, and dissipation occurs through standard Laplacian terms. The runs considered here all have a resolution of
![]() $512^{3}$
, with forcing at wavenumber
$512^{3}$
, with forcing at wavenumber
![]() $k_{F}\in [22,23]$
, and therefore Reynolds numbers
$k_{F}\in [22,23]$
, and therefore Reynolds numbers
![]() $\mathit{Re}\approx 10^{3}$
. The Rossby and Froude numbers vary as indicated in table 1; the runs can be grouped in two series, one with constant Froude number (
$\mathit{Re}\approx 10^{3}$
. The Rossby and Froude numbers vary as indicated in table 1; the runs can be grouped in two series, one with constant Froude number (
![]() $\mathit{Fr}=0.04$
) and varying
$\mathit{Fr}=0.04$
) and varying
![]() $N/f$
(and therefore
$N/f$
(and therefore
![]() $\mathit{Ro}$
) and one with constant Rossby number (
$\mathit{Ro}$
) and one with constant Rossby number (
![]() $\mathit{Ro}=0.08$
) and varying
$\mathit{Ro}=0.08$
) and varying
![]() $N/f$
(and therefore
$N/f$
(and therefore
![]() $\mathit{Fr}$
). The isotropic energy spectra and fluxes of the above runs have already been analysed in Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2013), providing evidence for the existence of an inverse cascade of energy in the presence of rotation and stratification, but not in the purely stratified case (see also Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2014).
$\mathit{Fr}$
). The isotropic energy spectra and fluxes of the above runs have already been analysed in Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2013), providing evidence for the existence of an inverse cascade of energy in the presence of rotation and stratification, but not in the purely stratified case (see also Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2014).
Table 1. Model run parameters; names of runs at fixed Rossby number (respectively fixed Froude number) begin with a R (respectively F), followed by its
![]() $N/f$
value.
$N/f$
value.
![]() $n_{p}$
is the number of grid points,
$n_{p}$
is the number of grid points,
![]() $N$
and
$N$
and
![]() $f$
are the Brunt–Väisälä and the inertial frequency (with
$f$
are the Brunt–Väisälä and the inertial frequency (with
![]() $f=2\unicode[STIX]{x1D6FA}$
,
$f=2\unicode[STIX]{x1D6FA}$
,
![]() $\unicode[STIX]{x1D6FA}$
being the imposed rotation),
$\unicode[STIX]{x1D6FA}$
being the imposed rotation),
![]() $Fr=U/[LN]$
and
$Fr=U/[LN]$
and
![]() $Ro=U/[Lf]$
are the Froude and Rossby numbers based on large-scale data, and the Burger number is defined as
$Ro=U/[Lf]$
are the Froude and Rossby numbers based on large-scale data, and the Burger number is defined as
![]() $Bu=N/f$
for a cubic box as used here;
$Bu=N/f$
for a cubic box as used here;
![]() ${\mathcal{R}}_{B}=\mathit{Re}\mathit{Fr}^{2}$
and
${\mathcal{R}}_{B}=\mathit{Re}\mathit{Fr}^{2}$
and
![]() $R_{\unicode[STIX]{x1D714}}=\mathit{Re}^{1/2}\mathit{Ro}=\unicode[STIX]{x1D714}_{rms}/f$
are, respectively, the buoyancy Reynolds number and the micro-Rossby number, and
$R_{\unicode[STIX]{x1D714}}=\mathit{Re}^{1/2}\mathit{Ro}=\unicode[STIX]{x1D714}_{rms}/f$
are, respectively, the buoyancy Reynolds number and the micro-Rossby number, and
![]() $k_{F}$
is the forcing wavenumber. The runs belonging to the no-resonance zone have a shaded background. The primed and starred runs in the last four lines are sensitivity tests with respect to the buoyancy Reynolds number, described in § 5.2.
$k_{F}$
is the forcing wavenumber. The runs belonging to the no-resonance zone have a shaded background. The primed and starred runs in the last four lines are sensitivity tests with respect to the buoyancy Reynolds number, described in § 5.2.

2.2 Characteristic scales
Rotating-stratified turbulence covers a wide range of physical regimes, which can be characterized by three non-dimensional numbers, besides
![]() $Pr$
. Given a characteristic length scale
$Pr$
. Given a characteristic length scale
![]() $L$
and a characteristic velocity
$L$
and a characteristic velocity
![]() $U$
at that scale, we introduce as usual the Reynolds number
$U$
at that scale, we introduce as usual the Reynolds number
![]() $\mathit{Re}=UL/\unicode[STIX]{x1D708}$
, the Rossby number
$\mathit{Re}=UL/\unicode[STIX]{x1D708}$
, the Rossby number
![]() $\mathit{Ro}=U/(fL)$
and the Froude number
$\mathit{Ro}=U/(fL)$
and the Froude number
![]() $\mathit{Fr}=U/(NL)$
. The Rossby and Froude numbers quantify the strength of the Coriolis and buoyancy forces, respectively. They correspond to the ratio between a wave period (
$\mathit{Fr}=U/(NL)$
. The Rossby and Froude numbers quantify the strength of the Coriolis and buoyancy forces, respectively. They correspond to the ratio between a wave period (
![]() $f^{-1}$
and
$f^{-1}$
and
![]() $N^{-1}$
, respectively) and the eddy turnover time
$N^{-1}$
, respectively) and the eddy turnover time
![]() $L/U$
.
$L/U$
.
A difficulty in rotating-stratified flows arises from the variety of characteristic scales one can construct. To start with, the Froude number can be based on a characteristic horizontal length scale or a vertical length scale. It is known that stratified turbulence develops strong gradients in the vertical (leading to the ubiquitous layered structure of the flow, see e.g. Herring & Métais (Reference Herring and Métais1989)), in such a way that the vertical Froude number remains of order unity (Billant & Chomaz Reference Billant and Chomaz2001; Lindborg Reference Lindborg2006), even when the horizontal Froude number is small. The corresponding vertical length scale is the buoyancy scale,
![]() $L_{B}=U/N$
and can be identified readily in such flows (see e.g. Rorai, Mininni & Pouquet Reference Rorai, Mininni and Pouquet2014). In the presence of rotation, the layers are expected to be slanted (with respect to the horizontal). In that case, it was conjectured that the characteristic length scale in the vertical also involves both
$L_{B}=U/N$
and can be identified readily in such flows (see e.g. Rorai, Mininni & Pouquet Reference Rorai, Mininni and Pouquet2014). In the presence of rotation, the layers are expected to be slanted (with respect to the horizontal). In that case, it was conjectured that the characteristic length scale in the vertical also involves both
![]() $N$
and
$N$
and
![]() $f$
, like a deformation radius, for which the effects of rotation and stratification balance each other, with
$f$
, like a deformation radius, for which the effects of rotation and stratification balance each other, with
![]() $Nk_{\bot }\sim fk_{\Vert }$
(Charney Reference Charney1971). It was shown by Rosenberg et al. (Reference Rosenberg, Pouquet, Marino and Mininni2015) that a Froude number based on a vertical Taylor scale involving vertical velocity gradients,
$Nk_{\bot }\sim fk_{\Vert }$
(Charney Reference Charney1971). It was shown by Rosenberg et al. (Reference Rosenberg, Pouquet, Marino and Mininni2015) that a Froude number based on a vertical Taylor scale involving vertical velocity gradients,
![]() $\ell _{z}=\sqrt{\langle u_{\bot }^{2}\rangle /\langle (\unicode[STIX]{x2202}_{z}u_{\bot })^{2}\rangle }$
(where the angular brackets denote spatial averaging) is also very close to unity. Here, we define the Froude and Rossby numbers (as well as the Reynolds number) based on the scale of the forcing,
$\ell _{z}=\sqrt{\langle u_{\bot }^{2}\rangle /\langle (\unicode[STIX]{x2202}_{z}u_{\bot })^{2}\rangle }$
(where the angular brackets denote spatial averaging) is also very close to unity. Here, we define the Froude and Rossby numbers (as well as the Reynolds number) based on the scale of the forcing,
![]() $L_{F}=2\unicode[STIX]{x03C0}/k_{F}$
. Since the forcing is isotropic, there is no reason to distinguish between vertical and horizontal Froude number with this definition, although anisotropies and different characteristic scales in the horizontal and the vertical will of course develop spontaneously in the flow. It follows that for the purpose of our study, at unit aspect ratio, the ratio of the Rossby and Froude numbers
$L_{F}=2\unicode[STIX]{x03C0}/k_{F}$
. Since the forcing is isotropic, there is no reason to distinguish between vertical and horizontal Froude number with this definition, although anisotropies and different characteristic scales in the horizontal and the vertical will of course develop spontaneously in the flow. It follows that for the purpose of our study, at unit aspect ratio, the ratio of the Rossby and Froude numbers
![]() $\mathit{Bu}=\mathit{Ro}/\mathit{Fr}$
, referred to as the Burger number, reduces to the ratio of the Brunt–Väisälä frequency and the Coriolis parameter:
$\mathit{Bu}=\mathit{Ro}/\mathit{Fr}$
, referred to as the Burger number, reduces to the ratio of the Brunt–Väisälä frequency and the Coriolis parameter:
![]() $\mathit{Bu}=N/f$
. The characteristic velocity
$\mathit{Bu}=N/f$
. The characteristic velocity
![]() $U$
used to evaluate the non-dimensional numbers is the rms velocity of the initial condition.
$U$
used to evaluate the non-dimensional numbers is the rms velocity of the initial condition.
The recovery of isotropy should occur at a scale for which the eddy turnover time and the wave period become comparable. This allows one to define an Ozmidov and a Zeman scale (Zeman Reference Zeman1994; Mininni, Rosenberg & Pouquet Reference Mininni, Rosenberg and Pouquet2012) written, respectively, for purely stratified or purely rotating flows, assuming an isotropic Kolmogorov range,
![]() $E_{V}(k)\sim \unicode[STIX]{x1D716}_{V}^{2/3}k^{-5/3}$
at small scale, as:
$E_{V}(k)\sim \unicode[STIX]{x1D716}_{V}^{2/3}k^{-5/3}$
at small scale, as:
with
![]() $\unicode[STIX]{x1D716}_{V}=\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D74E}^{2}\rangle$
the kinetic energy dissipation rate. The Froude and Rossby numbers measure the ratio of these scales to the characteristic scale:
$\unicode[STIX]{x1D716}_{V}=\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D74E}^{2}\rangle$
the kinetic energy dissipation rate. The Froude and Rossby numbers measure the ratio of these scales to the characteristic scale:
![]() $\mathit{Fr}=(\ell _{Oz}/L)^{2/3}$
,
$\mathit{Fr}=(\ell _{Oz}/L)^{2/3}$
,
![]() $\mathit{Ro}=(\ell _{Ze}/L)^{2/3}$
. Finally, if one wants to construct a measure of the actual development of small scales in the flow, a buoyancy Reynolds number
$\mathit{Ro}=(\ell _{Ze}/L)^{2/3}$
. Finally, if one wants to construct a measure of the actual development of small scales in the flow, a buoyancy Reynolds number
![]() ${\mathcal{R}}_{B}$
and a micro-Rossby number
${\mathcal{R}}_{B}$
and a micro-Rossby number
![]() $R_{\unicode[STIX]{x1D714}}$
can be defined in the following way:
$R_{\unicode[STIX]{x1D714}}$
can be defined in the following way:
so that
![]() $R_{\unicode[STIX]{x1D714}}^{2}$
is the equivalent, for rotation, of the buoyancy Reynolds number. The buoyancy Reynolds number
$R_{\unicode[STIX]{x1D714}}^{2}$
is the equivalent, for rotation, of the buoyancy Reynolds number. The buoyancy Reynolds number
![]() ${\mathcal{R}}_{B}$
corresponds to the ratio of vertical advection to vertical diffusion (Riley & de Bruyn Kops Reference Riley and de Bruyn Kops2003; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007), in the scaling regime of Riley et al. (Reference Riley, Metcalfe and Weissman1981) and Billant & Chomaz (Reference Billant and Chomaz2001).
${\mathcal{R}}_{B}$
corresponds to the ratio of vertical advection to vertical diffusion (Riley & de Bruyn Kops Reference Riley and de Bruyn Kops2003; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007), in the scaling regime of Riley et al. (Reference Riley, Metcalfe and Weissman1981) and Billant & Chomaz (Reference Billant and Chomaz2001).
With these definitions, and recalling the Kolmogorov dissipation scale
![]() $\ell _{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716}_{V})^{1/4}$
, one can show that
$\ell _{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716}_{V})^{1/4}$
, one can show that
![]() ${\mathcal{R}}_{B}=(\ell _{Oz}/\ell _{\unicode[STIX]{x1D702}})^{4/3}$
. In other words, when one wants to measure the intensity of stratified turbulence, the Ozmidov scale plays the role of the integral scale and
${\mathcal{R}}_{B}=(\ell _{Oz}/\ell _{\unicode[STIX]{x1D702}})^{4/3}$
. In other words, when one wants to measure the intensity of stratified turbulence, the Ozmidov scale plays the role of the integral scale and
![]() ${\mathcal{R}}_{B}$
that of the Reynolds number. In particular, when
${\mathcal{R}}_{B}$
that of the Reynolds number. In particular, when
![]() ${\mathcal{R}}_{B}$
is of order one, like in most of the runs shown here (see table 1), the Ozmidov scale coincides with the dissipation scale. Also note that, when
${\mathcal{R}}_{B}$
is of order one, like in most of the runs shown here (see table 1), the Ozmidov scale coincides with the dissipation scale. Also note that, when
![]() $R_{\unicode[STIX]{x1D714}}\approx 1$
, the small-scale turbulence is at least as vigorous as the imposed rotation frequency (see, e.g. Sagaut & Cambon Reference Sagaut and Cambon2008). These non-dimensional numbers are computed in table 1. Some references (e.g. Smyth & Moum Reference Smyth and Moum2000a
,Reference Smyth and Moum
b
) define the buoyancy Reynolds number as
$R_{\unicode[STIX]{x1D714}}\approx 1$
, the small-scale turbulence is at least as vigorous as the imposed rotation frequency (see, e.g. Sagaut & Cambon Reference Sagaut and Cambon2008). These non-dimensional numbers are computed in table 1. Some references (e.g. Smyth & Moum Reference Smyth and Moum2000a
,Reference Smyth and Moum
b
) define the buoyancy Reynolds number as
![]() $\unicode[STIX]{x1D716}_{V}/(\unicode[STIX]{x1D708}N^{2})$
. The two definitions should coincide when the characteristic scales satisfy the Taylor relationship
$\unicode[STIX]{x1D716}_{V}/(\unicode[STIX]{x1D708}N^{2})$
. The two definitions should coincide when the characteristic scales satisfy the Taylor relationship
![]() $\unicode[STIX]{x1D716}_{V}=U^{3}/L$
. For the runs under study here, this dimensional estimate of the energy dissipation rate does not hold, and using the small-scale kinetic energy dissipation rate, the buoyancy Reynolds number computed with this alternative definition differs from the one given in table 1 (for instance it is of the order of
$\unicode[STIX]{x1D716}_{V}=U^{3}/L$
. For the runs under study here, this dimensional estimate of the energy dissipation rate does not hold, and using the small-scale kinetic energy dissipation rate, the buoyancy Reynolds number computed with this alternative definition differs from the one given in table 1 (for instance it is of the order of
![]() $10^{-2}$
for the strongly stratified runs with
$10^{-2}$
for the strongly stratified runs with
![]() ${\mathcal{R}}_{B}=1.6$
). This is consistent with the idea that, for strong stratification, the effective dissipation is related to the dimensional estimate by a
${\mathcal{R}}_{B}=1.6$
). This is consistent with the idea that, for strong stratification, the effective dissipation is related to the dimensional estimate by a
![]() $\mathit{Fr}$
factor.
$\mathit{Fr}$
factor.
One of the goals of this paper is to study how the respective role of waves and vortices (see below) depends on the ratio
![]() $N/f$
. Note that there is a range that can be expected to have a special behaviour: when
$N/f$
. Note that there is a range that can be expected to have a special behaviour: when
![]() $1/2\leqslant N/f\leqslant 2$
, there are no three-wave resonances (the simple proof relies on the fact that the inertia–gravity wave frequency
$1/2\leqslant N/f\leqslant 2$
, there are no three-wave resonances (the simple proof relies on the fact that the inertia–gravity wave frequency
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{k})$
, defined by (3.4), is bounded by
$\unicode[STIX]{x1D70E}(\boldsymbol{k})$
, defined by (3.4), is bounded by
![]() $f$
and
$f$
and
![]() $N$
; see for instance Smith & Waleffe (Reference Smith and Waleffe2002), § 6.1). Hence the no-resonance zone separates two regimes:
$N$
; see for instance Smith & Waleffe (Reference Smith and Waleffe2002), § 6.1). Hence the no-resonance zone separates two regimes:
![]() $N/f<1/2$
and
$N/f<1/2$
and
![]() $N/f>2$
. Here we shall focus on the latter range. Note that these two regimes also correspond to cases where the deformation length is respectively smaller and larger than the forcing scale.
$N/f>2$
. Here we shall focus on the latter range. Note that these two regimes also correspond to cases where the deformation length is respectively smaller and larger than the forcing scale.
2.3 Potential vorticity
We define potential vorticity as usual:
where
![]() $\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
is the standard vorticity. Potential vorticity is a Lagrangian invariant of ideal Boussinesq flows: in the absence of forcing and dissipation, it is conserved along the trajectory of a fluid parcel, as expressed by the equation
$\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
is the standard vorticity. Potential vorticity is a Lagrangian invariant of ideal Boussinesq flows: in the absence of forcing and dissipation, it is conserved along the trajectory of a fluid parcel, as expressed by the equation
![]() $\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6F1}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F1}=0$
. Hence, it is analogous to vertical vorticity in two-dimensional (2D) turbulence, a fundamental difference being that potential vorticity is not a linear functional of the dynamical fields, because of the quadratic term
$\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6F1}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F1}=0$
. Hence, it is analogous to vertical vorticity in two-dimensional (2D) turbulence, a fundamental difference being that potential vorticity is not a linear functional of the dynamical fields, because of the quadratic term
![]() $\unicode[STIX]{x1D6F1}_{2}=\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$
, in addition to the linear term
$\unicode[STIX]{x1D6F1}_{2}=\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$
, in addition to the linear term
![]() $\unicode[STIX]{x1D6F1}_{1}=f\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}-N\unicode[STIX]{x1D714}_{z}$
. It follows that, unlike the 2D case, the
$\unicode[STIX]{x1D6F1}_{1}=f\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}-N\unicode[STIX]{x1D714}_{z}$
. It follows that, unlike the 2D case, the
![]() $L_{2}$
norm of potential vorticity, referred to as potential enstrophy and denoted by
$L_{2}$
norm of potential vorticity, referred to as potential enstrophy and denoted by
![]() $\unicode[STIX]{x1D6E4}$
, is quartic and is not necessarily conserved by the Fourier truncation (see, e.g. Aluie & Kurien Reference Aluie and Kurien2011). We show in figure 1 the time evolution of potential enstrophy in the two series of runs presented here. In the series of runs at constant Froude number, potential enstrophy decays to approximately 25 % of its initial value, then seems to remain constant in time. The decay is faster for higher
$\unicode[STIX]{x1D6E4}$
, is quartic and is not necessarily conserved by the Fourier truncation (see, e.g. Aluie & Kurien Reference Aluie and Kurien2011). We show in figure 1 the time evolution of potential enstrophy in the two series of runs presented here. In the series of runs at constant Froude number, potential enstrophy decays to approximately 25 % of its initial value, then seems to remain constant in time. The decay is faster for higher
![]() $N/f$
ratios, but the final potential enstrophy level is approximately the same for all the runs. In contrast, the series of runs at constant Rossby number exhibits very different levels of potential enstrophy, across approximately three orders of magnitude, and it increases with increasing
$N/f$
ratios, but the final potential enstrophy level is approximately the same for all the runs. In contrast, the series of runs at constant Rossby number exhibits very different levels of potential enstrophy, across approximately three orders of magnitude, and it increases with increasing
![]() $N/f$
, i.e. decreasing Froude number. We conclude from these two graphs that, in the inverse cascade regime studied here, the value of potential enstrophy at late times is a function of the Froude number only. Also, potential enstrophy conservation is better satisfied when stratification is strong. We now introduce the quadratic, cubic and quartic components of potential enstrophy, defined respectively as
$N/f$
, i.e. decreasing Froude number. We conclude from these two graphs that, in the inverse cascade regime studied here, the value of potential enstrophy at late times is a function of the Froude number only. Also, potential enstrophy conservation is better satisfied when stratification is strong. We now introduce the quadratic, cubic and quartic components of potential enstrophy, defined respectively as
such that
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{2}+\unicode[STIX]{x1D6E4}_{3}+\unicode[STIX]{x1D6E4}_{4}$
.
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{2}+\unicode[STIX]{x1D6E4}_{3}+\unicode[STIX]{x1D6E4}_{4}$
.
![]() $\unicode[STIX]{x1D6E4}_{2},\unicode[STIX]{x1D6E4}_{3}$
and
$\unicode[STIX]{x1D6E4}_{2},\unicode[STIX]{x1D6E4}_{3}$
and
![]() $\unicode[STIX]{x1D6E4}_{4}$
are respectively quadratic, cubic and quartic in the field variables, but they all have the same physical dimension, that of frequency square or square vorticity. The ratio
$\unicode[STIX]{x1D6E4}_{4}$
are respectively quadratic, cubic and quartic in the field variables, but they all have the same physical dimension, that of frequency square or square vorticity. The ratio
![]() $\unicode[STIX]{x1D6E4}_{2}/\unicode[STIX]{x1D6E4}$
is shown in figure 2. Note that this ratio can exceed unity, since the cubic component of total potential enstrophy is not positive definite (it measures correlations between the linear part of potential vorticity and the nonlinear part). This figure shows that, in all the runs, total potential enstrophy is well approximated by its quadratic part, in agreement with the findings of Kurien & Smith (Reference Kurien and Smith2014), although it is less and less the case as rotation decreases (constant Froude series of runs) or in the
$\unicode[STIX]{x1D6E4}_{2}/\unicode[STIX]{x1D6E4}$
is shown in figure 2. Note that this ratio can exceed unity, since the cubic component of total potential enstrophy is not positive definite (it measures correlations between the linear part of potential vorticity and the nonlinear part). This figure shows that, in all the runs, total potential enstrophy is well approximated by its quadratic part, in agreement with the findings of Kurien & Smith (Reference Kurien and Smith2014), although it is less and less the case as rotation decreases (constant Froude series of runs) or in the
![]() $N/f=1/4$
(weak stratification) case, which also has the highest buoyancy Reynolds number of approximately 100 and the smaller deformation length (see table 1). Waite (Reference Waite2013) has argued that in the large-
$N/f=1/4$
(weak stratification) case, which also has the highest buoyancy Reynolds number of approximately 100 and the smaller deformation length (see table 1). Waite (Reference Waite2013) has argued that in the large-
![]() $N/f$
case, total potential enstrophy is dominated by its quadratic part due to viscous effects in the small buoyancy Reynolds number regime. We further discuss the role of viscosity and buoyancy Reynolds number in § 5.
$N/f$
case, total potential enstrophy is dominated by its quadratic part due to viscous effects in the small buoyancy Reynolds number regime. We further discuss the role of viscosity and buoyancy Reynolds number in § 5.

Figure 1. Time evolution of the potential enstrophy for the series of runs at constant Froude number (a) and at constant Rossby number (b) with various
![]() $N/f$
. The vertical scale is in logarithmic coordinates for the constant Rossby number series.
$N/f$
. The vertical scale is in logarithmic coordinates for the constant Rossby number series.

Figure 2. Time evolution of the ratio of quadratic potential enstrophy to total potential enstrophy, for the series of runs at constant Froude number (a) and at constant Rossby number (b) with various
![]() $N/f$
.
$N/f$
.
In 2D turbulence, enstrophy conservation has very important consequences: it is ultimately responsible for the inverse cascade. It is a legitimate question to ask whether potential enstrophy conservation places such a strong constraint on rotating-stratified flows. Another important aim of this paper is to show that this constraint is strongly dependent on whether there is rotation or not.
2.4 Inviscid invariants and the direction of the energy cascade
A framework which is quite robust for understanding direct and inverse cascades, introduced by Lee (Reference Lee1952) and Kraichnan (Reference Kraichnan1967), is that of the inviscid invariants of the system. More precisely, the existence of a second definite positive invariant, often quadratic, in addition to energy, may prevent the downscale cascade of energy and lead to an inverse cascade. This is what happens in 2D turbulence (Kraichnan & Montgomery Reference Kraichnan and Montgomery1980). In stratified turbulence, with or without rotation, there is such a second inviscid invariant, though not quadratic in principle: potential enstrophy
![]() $\unicode[STIX]{x1D6E4}$
(see § 2.3). Although this invariant exists regardless of whether there is rotation or not, the phenomenology is not the same: numerical evidence has accumulated over the years (Métais, Riley & Lesieur Reference Métais, Riley, Lesieur, Castro and Rockliff1994; Bartello Reference Bartello1995; Métais et al.
Reference Métais, Bartello, Garnier, Riley and Lesieur1996; Lilly et al.
Reference Lilly, Bassett, Droegemeier and Bartello1998; Smith & Waleffe Reference Smith and Waleffe2002; Lindborg Reference Lindborg2005; Waite & Bartello Reference Waite and Bartello2006b
; Aluie & Kurien Reference Aluie and Kurien2011; Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2013) to show that an inverse cascade in stably stratified flows is only possible when there is sufficient rotation, even though the parameter controlling the transition remains unclear. A subtlety here is that the second invariant has constant sign (it is always positive), but is not definite: some combinations of the fields make potential vorticity vanish. Such combinations correspond to the wave modes (see § 3). Hence, a natural way of thinking is to say that if waves and slow modes did not exchange energy, the wave and slow mode energy would be separately conserved, and slow modes would have invariants similar to 2D turbulence, while waves would have invariants similar to 3D homogeneous isotropic turbulence. Therefore, in that case one should expect an inverse cascade of slow mode energy and a direct cascade of wave energy. This idea was formulated in pioneering studies such as those of Warn (Reference Warn1986), Bartello (Reference Bartello1995) and Waite & Bartello (Reference Waite and Bartello2004).
$\unicode[STIX]{x1D6E4}$
(see § 2.3). Although this invariant exists regardless of whether there is rotation or not, the phenomenology is not the same: numerical evidence has accumulated over the years (Métais, Riley & Lesieur Reference Métais, Riley, Lesieur, Castro and Rockliff1994; Bartello Reference Bartello1995; Métais et al.
Reference Métais, Bartello, Garnier, Riley and Lesieur1996; Lilly et al.
Reference Lilly, Bassett, Droegemeier and Bartello1998; Smith & Waleffe Reference Smith and Waleffe2002; Lindborg Reference Lindborg2005; Waite & Bartello Reference Waite and Bartello2006b
; Aluie & Kurien Reference Aluie and Kurien2011; Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2013) to show that an inverse cascade in stably stratified flows is only possible when there is sufficient rotation, even though the parameter controlling the transition remains unclear. A subtlety here is that the second invariant has constant sign (it is always positive), but is not definite: some combinations of the fields make potential vorticity vanish. Such combinations correspond to the wave modes (see § 3). Hence, a natural way of thinking is to say that if waves and slow modes did not exchange energy, the wave and slow mode energy would be separately conserved, and slow modes would have invariants similar to 2D turbulence, while waves would have invariants similar to 3D homogeneous isotropic turbulence. Therefore, in that case one should expect an inverse cascade of slow mode energy and a direct cascade of wave energy. This idea was formulated in pioneering studies such as those of Warn (Reference Warn1986), Bartello (Reference Bartello1995) and Waite & Bartello (Reference Waite and Bartello2004).
However, in the purely stratified case, this reasoning does not hold since then, potential enstrophy is still degenerate even when we restrict it to the slow modes. Indeed, in the non-rotating case, only slow modes with
![]() $k_{\bot }\neq 0$
contribute to potential enstrophy (see § 3.3). This peculiarity was used in a statistical mechanics argument (Herbert et al.
Reference Herbert, Pouquet and Marino2014) in order to explain why the two cases have opposite cascade directions in spite of having the same inviscid invariants. From this point of view, it could also be because of the presence of the vertically sheared horizontal flow modes that stratified turbulence does not have an inverse cascade.
$k_{\bot }\neq 0$
contribute to potential enstrophy (see § 3.3). This peculiarity was used in a statistical mechanics argument (Herbert et al.
Reference Herbert, Pouquet and Marino2014) in order to explain why the two cases have opposite cascade directions in spite of having the same inviscid invariants. From this point of view, it could also be because of the presence of the vertically sheared horizontal flow modes that stratified turbulence does not have an inverse cascade.
A major goal of this work is to study how the roles played by slow modes and waves in the inverse cascade, inferred from the above reasoning on the inviscid invariants, evolve when non-dimensional parameters vary, and how the mechanisms described in this section come into play to break the inverse cascade when stratification dominates.
3 Waves and vortices: normal mode decomposition
3.1 The linear dynamics
Inertia–gravity wave dynamics has been studied for a long time (see for example Hasselmann Reference Hasselmann1966; Garrett & Munk Reference Garrett and Munk1979; Müller et al. Reference Müller, Holloway, Henyey and Pomphrey1986; Bartello Reference Bartello1995; Staquet & Sommeria Reference Staquet and Sommeria2002) and is summarized very briefly here in order to recall essential concepts and to define notations. Indeed, the linear terms introduced by the Coriolis force and the buoyancy force in (2.1)–(2.3) allow for the propagation of dispersive waves. The linearized inviscid and unforced dynamics reads:
This set of equations corresponds to the low-Froude-number limit (
![]() $\mathit{Fr}\rightarrow 0$
) of the Boussinesq equations, if we assume that the time scale is the buoyancy time scale
$\mathit{Fr}\rightarrow 0$
) of the Boussinesq equations, if we assume that the time scale is the buoyancy time scale
![]() $N^{-1}$
(Lilly Reference Lilly1983). The above equations admit travelling wave solutions of the form
$N^{-1}$
(Lilly Reference Lilly1983). The above equations admit travelling wave solutions of the form
![]() $u_{j}(\boldsymbol{x},t)=U_{j}\text{e}^{\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}-\unicode[STIX]{x1D70E}(\boldsymbol{k})t)}$
,
$u_{j}(\boldsymbol{x},t)=U_{j}\text{e}^{\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}-\unicode[STIX]{x1D70E}(\boldsymbol{k})t)}$
,
![]() $\unicode[STIX]{x1D703}(\boldsymbol{x},t)=\unicode[STIX]{x1D6E9}\text{e}^{\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}-\unicode[STIX]{x1D70E}(\boldsymbol{k})t)}$
,
$\unicode[STIX]{x1D703}(\boldsymbol{x},t)=\unicode[STIX]{x1D6E9}\text{e}^{\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}-\unicode[STIX]{x1D70E}(\boldsymbol{k})t)}$
,
![]() $P=P_{0}\text{e}^{\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}-\unicode[STIX]{x1D70E}(\boldsymbol{k})t)}$
, for arbitrary wave vector
$P=P_{0}\text{e}^{\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}-\unicode[STIX]{x1D70E}(\boldsymbol{k})t)}$
, for arbitrary wave vector
![]() $\boldsymbol{k}$
, with relations between the complex amplitudes
$\boldsymbol{k}$
, with relations between the complex amplitudes
![]() $U_{j},\unicode[STIX]{x1D6E9},P_{0}$
fixed by the above equations, and with the dispersion relation
$U_{j},\unicode[STIX]{x1D6E9},P_{0}$
fixed by the above equations, and with the dispersion relation
Such waves are called inertia–gravity waves (and include, of course, waves travelling in the
![]() $-\boldsymbol{k}$
direction). Note that although the Coriolis parameter only appears in the evolution equation for the horizontal velocity, and the Brunt–Väisälä frequency only for the vertical velocity and temperature, inertia–gravity waves couple the four dynamical fields because of the incompressibility condition. Without pressure, we would simply have inertial oscillations, at frequency
$-\boldsymbol{k}$
direction). Note that although the Coriolis parameter only appears in the evolution equation for the horizontal velocity, and the Brunt–Väisälä frequency only for the vertical velocity and temperature, inertia–gravity waves couple the four dynamical fields because of the incompressibility condition. Without pressure, we would simply have inertial oscillations, at frequency
![]() $f$
, for the horizontal velocity, decoupled from gravity waves of frequency
$f$
, for the horizontal velocity, decoupled from gravity waves of frequency
![]() $N$
acting on the vertical velocity and the temperature.
$N$
acting on the vertical velocity and the temperature.
The nonlinear term introduces a coupling between waves with different wave vectors. A possible approach is to treat the dynamical fields as a wave field with slow nonlinear evolution of the magnitude of each wave mode, using a perturbative approach. Resonant interactions (Longuet-Higgins, Gill & Kenyon Reference Longuet-Higgins, Gill and Kenyon1967; Newell Reference Newell1969) offer a natural way to close the hierarchy of moments. This is a first kind of turbulence, referred to as wave turbulence (Zakharov, Lvov & Falkovich Reference Zakharov, Lvov and Falkovich1992; Nazarenko Reference Nazarenko2010; Newell & Rumpf Reference Newell and Rumpf2011).
Now, the set of linearized equations also admits stationary solutions, where the right-hand side of (3.1)–(3.2) vanishes. These solutions have no vertical velocity (
![]() $u_{z}=0$
), and the pressure gradient balances at the same time the Coriolis force (geostrophic balance,
$u_{z}=0$
), and the pressure gradient balances at the same time the Coriolis force (geostrophic balance,
![]() $\unicode[STIX]{x1D735}_{\bot }P=-f\boldsymbol{e}_{z}\times \boldsymbol{u}$
) and the buoyancy force (hydrostatic balance,
$\unicode[STIX]{x1D735}_{\bot }P=-f\boldsymbol{e}_{z}\times \boldsymbol{u}$
) and the buoyancy force (hydrostatic balance,
![]() $\unicode[STIX]{x2202}_{z}P=-N\unicode[STIX]{x1D703}\boldsymbol{e}_{z}$
). In other words, rotation and stratification act to maintain horizontal motion. This kind of balanced motion can also be seen as a low-Froude-number limit (
$\unicode[STIX]{x2202}_{z}P=-N\unicode[STIX]{x1D703}\boldsymbol{e}_{z}$
). In other words, rotation and stratification act to maintain horizontal motion. This kind of balanced motion can also be seen as a low-Froude-number limit (
![]() $\mathit{Fr}\rightarrow 0$
) solution of the Boussinesq equations, assuming that
$\mathit{Fr}\rightarrow 0$
) solution of the Boussinesq equations, assuming that
![]() $\mathit{Bu}=1$
and that the time scale is the eddy turnover time (Lilly Reference Lilly1983). It corresponds to eddies of typical aspect ratio
$\mathit{Bu}=1$
and that the time scale is the eddy turnover time (Lilly Reference Lilly1983). It corresponds to eddies of typical aspect ratio
![]() $f/N$
, which are advected by the horizontal velocity field, much like vortices in 2D turbulence. Hence, another kind of turbulence, referred to as geostrophic turbulence, is encapsulated in the Boussinesq equations.
$f/N$
, which are advected by the horizontal velocity field, much like vortices in 2D turbulence. Hence, another kind of turbulence, referred to as geostrophic turbulence, is encapsulated in the Boussinesq equations.
3.2 The normal mode decomposition in Fourier space
The two kinds of motion, waves and vortices, described above, correspond to normal modes of the linearized Boussinesq equations. Although they are coupled in the nonlinear dynamics, they provide a useful framework for analysing the full system. Here, we shall try to disentangle the behaviour of these two contributions in the simulated fields. To separate the two contributions, it is convenient to express them in Fourier space (Bartello Reference Bartello1995, see also Herbert et al.
Reference Herbert, Pouquet and Marino2014): we introduce
![]() ${\mathcal{B}}=\mathbb{Z}^{3}$
the set of wave vectors, and for each wave vector
${\mathcal{B}}=\mathbb{Z}^{3}$
the set of wave vectors, and for each wave vector
![]() $\boldsymbol{k}\in {\mathcal{B}}$
, the vectors
$\boldsymbol{k}\in {\mathcal{B}}$
, the vectors
 $$\begin{eqnarray}\boldsymbol{Z}_{0}(\boldsymbol{k})=\unicode[STIX]{x1D648}(\boldsymbol{k})\left(\begin{array}{@{}c@{}}0\\ 1\\ 0\end{array}\right),\quad \boldsymbol{Z}_{-}(\boldsymbol{k})=\unicode[STIX]{x1D648}(\boldsymbol{k})\left(\begin{array}{@{}c@{}}1\\ 0\\ 0\end{array}\right),\quad \text{and}\quad \boldsymbol{Z}_{+}(\boldsymbol{k})=\unicode[STIX]{x1D648}(\boldsymbol{k})\left(\begin{array}{@{}c@{}}0\\ 0\\ 1\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}_{0}(\boldsymbol{k})=\unicode[STIX]{x1D648}(\boldsymbol{k})\left(\begin{array}{@{}c@{}}0\\ 1\\ 0\end{array}\right),\quad \boldsymbol{Z}_{-}(\boldsymbol{k})=\unicode[STIX]{x1D648}(\boldsymbol{k})\left(\begin{array}{@{}c@{}}1\\ 0\\ 0\end{array}\right),\quad \text{and}\quad \boldsymbol{Z}_{+}(\boldsymbol{k})=\unicode[STIX]{x1D648}(\boldsymbol{k})\left(\begin{array}{@{}c@{}}0\\ 0\\ 1\end{array}\right),\end{eqnarray}$$
where the expression of the matrix
![]() $\unicode[STIX]{x1D648}(\boldsymbol{k})$
is given by:
$\unicode[STIX]{x1D648}(\boldsymbol{k})$
is given by:
 $$\begin{eqnarray}\unicode[STIX]{x1D648}(\boldsymbol{k})=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{1}{\sqrt{2}kk_{\bot }\unicode[STIX]{x1D70E}(\boldsymbol{k})}}\left(\begin{array}{@{}ccc@{}}fk_{2}k_{\Vert }-\text{i}k_{1}k_{\Vert }\unicode[STIX]{x1D70E}(\boldsymbol{k}) & -\sqrt{2}Nk_{2}k_{\bot } & fk_{2}k_{\Vert }+\text{i}k_{1}k_{\Vert }\unicode[STIX]{x1D70E}(\boldsymbol{k})\\ -fk_{1}k_{\Vert }-\text{i}k_{2}k_{\Vert }\unicode[STIX]{x1D70E}(\boldsymbol{k}) & \sqrt{2}Nk_{1}k_{\bot } & -fk_{1}k_{\Vert }+\text{i}k_{2}k_{\Vert }\unicode[STIX]{x1D70E}(\boldsymbol{k})\\ \text{i}k_{\bot }^{2}\unicode[STIX]{x1D70E}(\boldsymbol{k}) & 0 & -\text{i}k_{\bot }^{2}\unicode[STIX]{x1D70E}(\boldsymbol{k})\\ -Nk_{\bot }^{2} & -\sqrt{2}fk_{\Vert }k_{\bot } & -Nk_{\bot }^{2}\end{array}\right)\quad & \text{if}~k_{\bot }\neq 0,\\ {\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{@{}ccc@{}}\text{i} & 0 & -\text{i}\\ 1 & 0 & 1\\ 0 & 0 & 0\\ 0 & -\sqrt{2} & 0\end{array}\right)\quad & \text{if}~k_{\bot }=0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D648}(\boldsymbol{k})=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{1}{\sqrt{2}kk_{\bot }\unicode[STIX]{x1D70E}(\boldsymbol{k})}}\left(\begin{array}{@{}ccc@{}}fk_{2}k_{\Vert }-\text{i}k_{1}k_{\Vert }\unicode[STIX]{x1D70E}(\boldsymbol{k}) & -\sqrt{2}Nk_{2}k_{\bot } & fk_{2}k_{\Vert }+\text{i}k_{1}k_{\Vert }\unicode[STIX]{x1D70E}(\boldsymbol{k})\\ -fk_{1}k_{\Vert }-\text{i}k_{2}k_{\Vert }\unicode[STIX]{x1D70E}(\boldsymbol{k}) & \sqrt{2}Nk_{1}k_{\bot } & -fk_{1}k_{\Vert }+\text{i}k_{2}k_{\Vert }\unicode[STIX]{x1D70E}(\boldsymbol{k})\\ \text{i}k_{\bot }^{2}\unicode[STIX]{x1D70E}(\boldsymbol{k}) & 0 & -\text{i}k_{\bot }^{2}\unicode[STIX]{x1D70E}(\boldsymbol{k})\\ -Nk_{\bot }^{2} & -\sqrt{2}fk_{\Vert }k_{\bot } & -Nk_{\bot }^{2}\end{array}\right)\quad & \text{if}~k_{\bot }\neq 0,\\ {\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{@{}ccc@{}}\text{i} & 0 & -\text{i}\\ 1 & 0 & 1\\ 0 & 0 & 0\\ 0 & -\sqrt{2} & 0\end{array}\right)\quad & \text{if}~k_{\bot }=0.\end{array}\right.\end{eqnarray}$$
The vectors
![]() $\boldsymbol{Z}_{0}(\boldsymbol{k}),\boldsymbol{Z}_{-}(\boldsymbol{k})$
and
$\boldsymbol{Z}_{0}(\boldsymbol{k}),\boldsymbol{Z}_{-}(\boldsymbol{k})$
and
![]() $\boldsymbol{Z}_{+}(\boldsymbol{k})$
are mutually orthogonal, and normalized to unity:
$\boldsymbol{Z}_{+}(\boldsymbol{k})$
are mutually orthogonal, and normalized to unity:
where
![]() $\dagger$
denotes the transpose and complex conjugation. Although the matrix
$\dagger$
denotes the transpose and complex conjugation. Although the matrix
![]() $\unicode[STIX]{x1D648}(\boldsymbol{k})$
is rectangular, it satisfies the hermitian identity
$\unicode[STIX]{x1D648}(\boldsymbol{k})$
is rectangular, it satisfies the hermitian identity
![]() $\unicode[STIX]{x1D648}(\boldsymbol{k})^{\dagger }\unicode[STIX]{x1D648}(\boldsymbol{k})=I_{3}$
. They are the normal modes of the linearized dynamics: their evolution in the linearized dynamics is given by
$\unicode[STIX]{x1D648}(\boldsymbol{k})^{\dagger }\unicode[STIX]{x1D648}(\boldsymbol{k})=I_{3}$
. They are the normal modes of the linearized dynamics: their evolution in the linearized dynamics is given by
where
![]() $\unicode[STIX]{x1D647}(\boldsymbol{k})$
is the linear operator in Fourier space associated to the linearized dynamics give by (3.1)–(3.3). We see that the mode
$\unicode[STIX]{x1D647}(\boldsymbol{k})$
is the linear operator in Fourier space associated to the linearized dynamics give by (3.1)–(3.3). We see that the mode
![]() $\boldsymbol{Z}_{0}(\boldsymbol{k})$
is conserved by the linear dynamics, while the modes
$\boldsymbol{Z}_{0}(\boldsymbol{k})$
is conserved by the linear dynamics, while the modes
![]() $\boldsymbol{Z}_{\pm }(\boldsymbol{k})$
, corresponding to the inertia–gravity waves, propagate with frequency
$\boldsymbol{Z}_{\pm }(\boldsymbol{k})$
, corresponding to the inertia–gravity waves, propagate with frequency
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{k})$
. Therefore,
$\unicode[STIX]{x1D70E}(\boldsymbol{k})$
. Therefore,
![]() $\boldsymbol{Z}_{0}$
, whose characteristic evolution time is the eddy turnover time, is referred to as the slow mode. The normal modes can be used as a basis for the Fourier modes of the dynamical fields. Introducing the Fourier decomposition of the velocity and temperature fields
$\boldsymbol{Z}_{0}$
, whose characteristic evolution time is the eddy turnover time, is referred to as the slow mode. The normal modes can be used as a basis for the Fourier modes of the dynamical fields. Introducing the Fourier decomposition of the velocity and temperature fields
and denoting
![]() $\boldsymbol{X}(\boldsymbol{k})=^{t}(\hat{u} _{1}(\boldsymbol{k}),\hat{u} _{2}(\boldsymbol{k}),\hat{u} _{3}(\boldsymbol{k}),\hat{\unicode[STIX]{x1D703}}(\boldsymbol{k}))$
the Fourier coefficients for wave vector
$\boldsymbol{X}(\boldsymbol{k})=^{t}(\hat{u} _{1}(\boldsymbol{k}),\hat{u} _{2}(\boldsymbol{k}),\hat{u} _{3}(\boldsymbol{k}),\hat{\unicode[STIX]{x1D703}}(\boldsymbol{k}))$
the Fourier coefficients for wave vector
![]() $\boldsymbol{k}$
, they can be expressed as a linear combination of the normal modes:
$\boldsymbol{k}$
, they can be expressed as a linear combination of the normal modes:
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \unicode[STIX]{x1D648}(\boldsymbol{k})\underbrace{\left(\begin{array}{@{}c@{}}A_{-}(\boldsymbol{k})\\ A_{0}(\boldsymbol{k})\\ A_{+}(\boldsymbol{k})\end{array}\right)}_{\boldsymbol{A}(\boldsymbol{k})}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \unicode[STIX]{x1D648}(\boldsymbol{k})\underbrace{\left(\begin{array}{@{}c@{}}A_{-}(\boldsymbol{k})\\ A_{0}(\boldsymbol{k})\\ A_{+}(\boldsymbol{k})\end{array}\right)}_{\boldsymbol{A}(\boldsymbol{k})}.\end{eqnarray}$$
Introducing the projectors
![]() $\unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})=\boldsymbol{Z}_{0}(\boldsymbol{k})\boldsymbol{Z}_{0}(\boldsymbol{k})^{\dagger }$
and
$\unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})=\boldsymbol{Z}_{0}(\boldsymbol{k})\boldsymbol{Z}_{0}(\boldsymbol{k})^{\dagger }$
and
![]() $\unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})=\boldsymbol{Z}_{-}(\boldsymbol{k})\boldsymbol{Z}_{-}(\boldsymbol{k})^{\dagger }+\boldsymbol{Z}_{+}(\boldsymbol{k})\boldsymbol{Z}_{+}(\boldsymbol{k})^{\dagger }$
, we have of course
$\unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})=\boldsymbol{Z}_{-}(\boldsymbol{k})\boldsymbol{Z}_{-}(\boldsymbol{k})^{\dagger }+\boldsymbol{Z}_{+}(\boldsymbol{k})\boldsymbol{Z}_{+}(\boldsymbol{k})^{\dagger }$
, we have of course
![]() $\unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k})=A_{0}(\boldsymbol{k})\boldsymbol{Z}_{0}(\boldsymbol{k})$
and
$\unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k})=A_{0}(\boldsymbol{k})\boldsymbol{Z}_{0}(\boldsymbol{k})$
and
![]() $\unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k})=A_{-}(\boldsymbol{k})\boldsymbol{Z}_{-}(\boldsymbol{k})+A_{+}(\boldsymbol{k})\boldsymbol{Z}_{+}(\boldsymbol{k})$
, and the two projectors are mutually orthogonal, so that
$\unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k})=A_{-}(\boldsymbol{k})\boldsymbol{Z}_{-}(\boldsymbol{k})+A_{+}(\boldsymbol{k})\boldsymbol{Z}_{+}(\boldsymbol{k})$
, and the two projectors are mutually orthogonal, so that
![]() $\unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})\oplus \unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})=I_{4}$
. Denoting
$\unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})\oplus \unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})=I_{4}$
. Denoting
![]() $\mathscr{F}:(u_{1},u_{2},u_{3},\unicode[STIX]{x1D703})\mapsto (\hat{u} _{1},\hat{u} _{2},\hat{u} _{3},\hat{\unicode[STIX]{x1D703}})$
, with
$\mathscr{F}:(u_{1},u_{2},u_{3},\unicode[STIX]{x1D703})\mapsto (\hat{u} _{1},\hat{u} _{2},\hat{u} _{3},\hat{\unicode[STIX]{x1D703}})$
, with
![]() $\hat{x}:\boldsymbol{k}\in {\mathcal{B}}\mapsto \hat{x}(\boldsymbol{k})\in \mathbb{C}$
, the Fourier transform, and
$\hat{x}:\boldsymbol{k}\in {\mathcal{B}}\mapsto \hat{x}(\boldsymbol{k})\in \mathbb{C}$
, the Fourier transform, and
![]() $\hat{\mathscr{P}}_{0}:(\hat{u} _{1},\hat{u} _{2},\hat{u} _{3},\hat{\unicode[STIX]{x1D703}})\mapsto (\boldsymbol{k}\mapsto \unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k}))$
,
$\hat{\mathscr{P}}_{0}:(\hat{u} _{1},\hat{u} _{2},\hat{u} _{3},\hat{\unicode[STIX]{x1D703}})\mapsto (\boldsymbol{k}\mapsto \unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k}))$
,
![]() $\hat{\mathscr{P}}_{W}:(\hat{u} _{1},\hat{u} _{2},\hat{u} _{3},\hat{\unicode[STIX]{x1D703}})\mapsto (\boldsymbol{k}\mapsto \unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k}))$
, the operators
$\hat{\mathscr{P}}_{W}:(\hat{u} _{1},\hat{u} _{2},\hat{u} _{3},\hat{\unicode[STIX]{x1D703}})\mapsto (\boldsymbol{k}\mapsto \unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k}))$
, the operators
![]() $\mathscr{P}_{0}=\mathscr{F}^{-1}\circ \hat{\mathscr{P}}_{0}\circ \mathscr{F}$
and
$\mathscr{P}_{0}=\mathscr{F}^{-1}\circ \hat{\mathscr{P}}_{0}\circ \mathscr{F}$
and
![]() $\mathscr{P}_{W}=\mathscr{F}^{-1}\circ \hat{\mathscr{P}}_{W}\circ \mathscr{F}$
are mutually orthogonal projectors acting on the set of dynamical fields:
$\mathscr{P}_{W}=\mathscr{F}^{-1}\circ \hat{\mathscr{P}}_{W}\circ \mathscr{F}$
are mutually orthogonal projectors acting on the set of dynamical fields:
Hence, we may write
![]() $\boldsymbol{u}=\boldsymbol{u}_{0}+\boldsymbol{u}_{W}$
and
$\boldsymbol{u}=\boldsymbol{u}_{0}+\boldsymbol{u}_{W}$
and
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}+\unicode[STIX]{x1D703}_{W}$
, with
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{0}+\unicode[STIX]{x1D703}_{W}$
, with
![]() $(u_{0}^{1},u_{0}^{2},u_{0}^{3},\unicode[STIX]{x1D703}_{0})=\mathscr{P}_{0}(u^{1},u^{2},u^{3},\unicode[STIX]{x1D703})$
, and
$(u_{0}^{1},u_{0}^{2},u_{0}^{3},\unicode[STIX]{x1D703}_{0})=\mathscr{P}_{0}(u^{1},u^{2},u^{3},\unicode[STIX]{x1D703})$
, and
![]() $(u_{W}^{1},u_{W}^{2},u_{W}^{3},\unicode[STIX]{x1D703}_{W})=\mathscr{P}_{W}(u^{1},u^{2},u^{3},\unicode[STIX]{x1D703})$
. It is easily checked that the projection on the slow modes defined above has vanishing vertical velocity:
$(u_{W}^{1},u_{W}^{2},u_{W}^{3},\unicode[STIX]{x1D703}_{W})=\mathscr{P}_{W}(u^{1},u^{2},u^{3},\unicode[STIX]{x1D703})$
. It is easily checked that the projection on the slow modes defined above has vanishing vertical velocity:
![]() $u_{0}^{3}=0$
, and is divergence free:
$u_{0}^{3}=0$
, and is divergence free:
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{0}=\unicode[STIX]{x1D735}_{\bot }\boldsymbol{\cdot }\boldsymbol{u}_{0}=0$
. The explicit expression in real space of the projection operators introduced above is given by Whitehead & Wingate (Reference Whitehead and Wingate2014). They also describe the projection operators on the slow manifolds obtained in the limit of rapid rotation and weak stratification on the one hand, and strong stratification and weak rotation on the other hand.
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{0}=\unicode[STIX]{x1D735}_{\bot }\boldsymbol{\cdot }\boldsymbol{u}_{0}=0$
. The explicit expression in real space of the projection operators introduced above is given by Whitehead & Wingate (Reference Whitehead and Wingate2014). They also describe the projection operators on the slow manifolds obtained in the limit of rapid rotation and weak stratification on the one hand, and strong stratification and weak rotation on the other hand.
It follows from the above that the total energy
breaks up in two pieces:
![]() $E_{T}=E_{0}+E_{W}$
, where
$E_{T}=E_{0}+E_{W}$
, where
![]() $E_{0}$
is the energy in the slow modes:
$E_{0}$
is the energy in the slow modes:
and
![]() $E_{W}$
the energy in the wave modes:
$E_{W}$
the energy in the wave modes:
Note that, due to the orthogonality property of the projections, the cross-terms in physical space cancel out:
![]() $\int \boldsymbol{u}_{0}\boldsymbol{\cdot }\boldsymbol{u}_{W}+\int \unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D703}_{W}=0$
. However, these terms do not vanish individually. In other words, the vector
$\int \boldsymbol{u}_{0}\boldsymbol{\cdot }\boldsymbol{u}_{W}+\int \unicode[STIX]{x1D703}_{0}\unicode[STIX]{x1D703}_{W}=0$
. However, these terms do not vanish individually. In other words, the vector
![]() $(\boldsymbol{u}_{0},\unicode[STIX]{x1D703}_{0})$
is indeed orthogonal to the vector
$(\boldsymbol{u}_{0},\unicode[STIX]{x1D703}_{0})$
is indeed orthogonal to the vector
![]() $(\boldsymbol{u}_{w},\unicode[STIX]{x1D703}_{w})$
, but this does not imply that the vector
$(\boldsymbol{u}_{w},\unicode[STIX]{x1D703}_{w})$
, but this does not imply that the vector
![]() $\boldsymbol{u}_{0}$
is orthogonal to
$\boldsymbol{u}_{0}$
is orthogonal to
![]() $\boldsymbol{u}_{w}$
, where orthogonality refers to the canonical scalar product in each of these two Hilbert spaces. A consequence is that care should be taken when trying to mix decomposition of the energy in terms of kinetic/potential energy and in terms of vortical/wave modes. Here, we shall avoid altogether distinguishing between kinetic and potential energy.
$\boldsymbol{u}_{w}$
, where orthogonality refers to the canonical scalar product in each of these two Hilbert spaces. A consequence is that care should be taken when trying to mix decomposition of the energy in terms of kinetic/potential energy and in terms of vortical/wave modes. Here, we shall avoid altogether distinguishing between kinetic and potential energy.
3.3 Normal mode decomposition, balance and potential vorticity
As can be checked explicitly (Herbert et al.
Reference Herbert, Pouquet and Marino2014, e.g.), in the linear framework, the slow modes satisfy balance relations: in the presence of rotation, they are in both geostrophic and hydrostatic balance. By contrast, for purely stratified flows, the slow modes are not in hydrostatic balance, except for purely vertical wave vectors, i.e. for horizontally homogeneous modes (the VSHF modes, see § 4.3). Of course, nonlinear effects break these relations, and a flow initialized in the image of the projector
![]() $\mathscr{P}_{0}$
(i.e. containing no wave modes initially) will eventually lose balance and radiate inertia–gravity waves. If one is interested in maintaining the balance relations, as much as possible, without generating such oscillations, the initial state should contain a wave component designed to compensate the nonlinear effects; such nonlinear initialization procedures have been designed in numerical weather prediction (Baer & Tribbia Reference Baer and Tribbia1977; Leith Reference Leith1980). Alternatively, balanced models, where the dynamics of the waves is slaved to that of the slow modes, can be written to remain on a slow manifold in phase space (Warn et al.
Reference Warn, Bokhove, Shepherd and Vallis1995; Vanneste Reference Vanneste2013). For the sake of simplicity, we shall be content here with projecting the data on the vector space spanned by the slow modes (which can be seen geometrically as a tangent subspace for the slow manifold, or as a zeroth-order approximation to the slow manifold) and its orthogonal subspace, spanned by the wave modes, as defined above. This means that although the normal modes introduced above are always well defined, care should be taken when interpreting the projections in terms of balance relations.
$\mathscr{P}_{0}$
(i.e. containing no wave modes initially) will eventually lose balance and radiate inertia–gravity waves. If one is interested in maintaining the balance relations, as much as possible, without generating such oscillations, the initial state should contain a wave component designed to compensate the nonlinear effects; such nonlinear initialization procedures have been designed in numerical weather prediction (Baer & Tribbia Reference Baer and Tribbia1977; Leith Reference Leith1980). Alternatively, balanced models, where the dynamics of the waves is slaved to that of the slow modes, can be written to remain on a slow manifold in phase space (Warn et al.
Reference Warn, Bokhove, Shepherd and Vallis1995; Vanneste Reference Vanneste2013). For the sake of simplicity, we shall be content here with projecting the data on the vector space spanned by the slow modes (which can be seen geometrically as a tangent subspace for the slow manifold, or as a zeroth-order approximation to the slow manifold) and its orthogonal subspace, spanned by the wave modes, as defined above. This means that although the normal modes introduced above are always well defined, care should be taken when interpreting the projections in terms of balance relations.
The normal modes are also related to potential vorticity. An argument due in particular to Smith & Waleffe (Reference Smith and Waleffe2002) relies on the fact that in the linear dynamics,
![]() $\unicode[STIX]{x1D6F1}_{1}$
is a point-wise invariant:
$\unicode[STIX]{x1D6F1}_{1}$
is a point-wise invariant:
![]() $\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6F1}_{1}=0$
. It follows, by applying the Fourier transform in both space and time, that
$\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6F1}_{1}=0$
. It follows, by applying the Fourier transform in both space and time, that
![]() $\unicode[STIX]{x1D70E}\hat{\unicode[STIX]{x1D6F1}}_{1}(\boldsymbol{k},\unicode[STIX]{x1D70E})=0$
, where
$\unicode[STIX]{x1D70E}\hat{\unicode[STIX]{x1D6F1}}_{1}(\boldsymbol{k},\unicode[STIX]{x1D70E})=0$
, where
![]() $\unicode[STIX]{x1D70E}$
is the time frequency. Hence, wave modes, for which
$\unicode[STIX]{x1D70E}$
is the time frequency. Hence, wave modes, for which
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{k})\neq 0$
must have
$\unicode[STIX]{x1D70E}(\boldsymbol{k})\neq 0$
must have
![]() $\hat{\unicode[STIX]{x1D6F1}}_{1}(\boldsymbol{k},\unicode[STIX]{x1D70E})=0$
, while vortical modes (i.e. by definition, those for which
$\hat{\unicode[STIX]{x1D6F1}}_{1}(\boldsymbol{k},\unicode[STIX]{x1D70E})=0$
, while vortical modes (i.e. by definition, those for which
![]() $\hat{\unicode[STIX]{x1D6F1}}_{1}(\boldsymbol{k},\unicode[STIX]{x1D70E})\neq 0$
) must have zero frequency. In fact, it is easily shown that, in general, the identity
$\hat{\unicode[STIX]{x1D6F1}}_{1}(\boldsymbol{k},\unicode[STIX]{x1D70E})\neq 0$
) must have zero frequency. In fact, it is easily shown that, in general, the identity
![]() $\hat{\unicode[STIX]{x1D6F1}}_{1}(\boldsymbol{k},t)=-\text{i}k\unicode[STIX]{x1D70E}(\boldsymbol{k})A_{0}(\boldsymbol{k},t)$
holds, and therefore (Bartello Reference Bartello1995; Herbert et al.
Reference Herbert, Pouquet and Marino2014):
$\hat{\unicode[STIX]{x1D6F1}}_{1}(\boldsymbol{k},t)=-\text{i}k\unicode[STIX]{x1D70E}(\boldsymbol{k})A_{0}(\boldsymbol{k},t)$
holds, and therefore (Bartello Reference Bartello1995; Herbert et al.
Reference Herbert, Pouquet and Marino2014):
It follows that, even when considering the full nonlinear dynamics, waves do not carry any linear potential vorticity. Similarly, we know that in the presence of rotation, all the slow modes contribute to linear potential vorticity. In the purely stratified case, however, the slow component of the VSHF modes (
![]() $k_{\bot }=0$
) contributes neither to linear potential vorticity, nor, therefore, to quadratic potential enstrophy
$k_{\bot }=0$
) contributes neither to linear potential vorticity, nor, therefore, to quadratic potential enstrophy
![]() $\unicode[STIX]{x1D6E4}_{2}$
. All the other slow modes still carry linear potential vorticity.
$\unicode[STIX]{x1D6E4}_{2}$
. All the other slow modes still carry linear potential vorticity.
The fact that the connection between slow modes and vortical modes (i.e. modes which contribute to linear potential vorticity) does not depend on whether we are considering the linear or the full nonlinear dynamics, while the connection between slow modes and balanced modes does, is due to the kinematic nature of the connection between linear potential vorticity and the dynamical fields. By contrast, the notion of balance is dynamical in the sense that it involves pressure, which is determined by the equations of motion. When including the nonlinear term in the dynamics, another component of pressure appears, which breaks the balance relations.

Figure 3. Time evolution of the wave (dashed lines) and vortical (solid lines) parts of the total energy for the series of runs at constant Froude number (a) and at constant Rossby number (b) with various
![]() $N/f$
. Runs within the no-resonance zone have been excluded for clarity. Note that the curves corresponding to the decay of the wave energy almost collapse onto a single curve: see figure 5 for a figure in logarithmic coordinates where they can be distinguished.
$N/f$
. Runs within the no-resonance zone have been excluded for clarity. Note that the curves corresponding to the decay of the wave energy almost collapse onto a single curve: see figure 5 for a figure in logarithmic coordinates where they can be distinguished.
4 Partition of energy between slow and wave modes
4.1 Time evolution of global quantities
The time evolution of the two energy components, wave and vortical, is shown in figure 3 (see also figure 5) for the series of runs at constant Froude number (a) and at constant Rossby number (b), excluding the runs for which the three-wave resonances are suppressed. Although the initial conditions all have approximately the same energy in each component, we see that, in all the runs, the wave energy decays very fast and the slow modes dominate, even for the runs that do not undergo a strong inverse cascade (in the purely stratified case, there is no inverse cascade at all). This is also true for the runs in the series at constant Rossby number (figure 3
b) and in the no-resonance zone (not shown). After an initial phase, we observe in the runs for which
![]() $N/f$
is small enough (
$N/f$
is small enough (
![]() $N/f\leqslant 10$
) a linear growth of the energy in the slow modes, characteristic of an inverse cascade. For
$N/f\leqslant 10$
) a linear growth of the energy in the slow modes, characteristic of an inverse cascade. For
![]() $N/f\geqslant 2$
, the growth rate appears to be a decreasing function of
$N/f\geqslant 2$
, the growth rate appears to be a decreasing function of
![]() $N/f$
, and this is confirmed by plotting the time average of the time derivative of the energy in the slow modes (figure 4
a). This figure also confirms that the growth rate vanishes at
$N/f$
, and this is confirmed by plotting the time average of the time derivative of the energy in the slow modes (figure 4
a). This figure also confirms that the growth rate vanishes at
![]() $N/f=20$
or in the purely stratified case (see also Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2014)). There is also a linear growth of the energy in the slow modes for the runs in the no-resonance zone in the series at constant Froude and for all the runs in the series at constant Rossby. For both series of runs, the growth rate appears to reach a maximum located inside the no-resonance zone (figure 4
a). In addition, the growth rate seems to depend primarily on
$N/f=20$
or in the purely stratified case (see also Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2014)). There is also a linear growth of the energy in the slow modes for the runs in the no-resonance zone in the series at constant Froude and for all the runs in the series at constant Rossby. For both series of runs, the growth rate appears to reach a maximum located inside the no-resonance zone (figure 4
a). In addition, the growth rate seems to depend primarily on
![]() $N/f$
rather than the Froude and Rossby numbers. These conclusions are consistent with the analysis of the time evolution of the kinetic energy obtained earlier (Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2013). Figure 4(b) summarizes how the fraction of energy in the slow modes, averaged in time (over all the snapshots following the peak of enstrophy), evolves as a function of
$N/f$
rather than the Froude and Rossby numbers. These conclusions are consistent with the analysis of the time evolution of the kinetic energy obtained earlier (Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2013). Figure 4(b) summarizes how the fraction of energy in the slow modes, averaged in time (over all the snapshots following the peak of enstrophy), evolves as a function of
![]() $N/f$
. Surprisingly, the case where this fraction attains its minimum value, although it is still approximately 0.9, is not the purely stratified case, but the rotation-dominated case
$N/f$
. Surprisingly, the case where this fraction attains its minimum value, although it is still approximately 0.9, is not the purely stratified case, but the rotation-dominated case
![]() $N/f=1/4$
, which also has the highest
$N/f=1/4$
, which also has the highest
![]() ${\mathcal{R}}_{B}$
and the smallest deformation length. One should keep in mind, however, that the ratio will keep increasing towards unit value for all the runs which exhibit a growth of
${\mathcal{R}}_{B}$
and the smallest deformation length. One should keep in mind, however, that the ratio will keep increasing towards unit value for all the runs which exhibit a growth of
![]() $E_{0}$
. Many of the runs are already very close to this limit value, and for the runs which do not exhibit such a growth of
$E_{0}$
. Many of the runs are already very close to this limit value, and for the runs which do not exhibit such a growth of
![]() $E_{0}$
, the ratio would not change with longer integration times. Since figure 3 does not allow one to distinguish the different curves for the wave energy at various
$E_{0}$
, the ratio would not change with longer integration times. Since figure 3 does not allow one to distinguish the different curves for the wave energy at various
![]() $N/f$
ratios, we show this quantity in logarithmic scale in figure 5. For values of
$N/f$
ratios, we show this quantity in logarithmic scale in figure 5. For values of
![]() $N/f$
above 7 (this is also true for the case
$N/f$
above 7 (this is also true for the case
![]() $N/f=1/4$
), we see a decay phase followed by a regime where the level of energy in the waves stays constant. For the other
$N/f=1/4$
), we see a decay phase followed by a regime where the level of energy in the waves stays constant. For the other
![]() $N/f$
values, the wave energy drops suddenly at the end of the decay phase, then increases back to more or less its value before the drop, and seems to stay constant afterwards. Although the time resolution is not sufficient for precise measurements, the decay seems to follow roughly a power law, and it is steeper for smaller
$N/f$
values, the wave energy drops suddenly at the end of the decay phase, then increases back to more or less its value before the drop, and seems to stay constant afterwards. Although the time resolution is not sufficient for precise measurements, the decay seems to follow roughly a power law, and it is steeper for smaller
![]() $N/f$
ratios (except for the
$N/f$
ratios (except for the
![]() $N/f=1/4$
and
$N/f=1/4$
and
![]() $N/f=1/2$
cases, at substantially higher
$N/f=1/2$
cases, at substantially higher
![]() ${\mathcal{R}}_{B}$
).
${\mathcal{R}}_{B}$
).

Figure 4. (a) Time-averaged growth rate of the energy in the slow modes as a function of
![]() $N/f$
, for the two series of runs, at constant Froude number (circles) and at constant Rossby number (squares), respectively. (b) Time-averaged fraction of energy in the slow modes as a function of
$N/f$
, for the two series of runs, at constant Froude number (circles) and at constant Rossby number (squares), respectively. (b) Time-averaged fraction of energy in the slow modes as a function of
![]() $N/f$
, for the two series of runs, at constant Froude number (circles) and at constant Rossby number (squares), respectively. The no-resonance zone is the shaded area.
$N/f$
, for the two series of runs, at constant Froude number (circles) and at constant Rossby number (squares), respectively. The no-resonance zone is the shaded area.

Figure 5. Time evolution of the wave component of the total energy in logarithmic coordinates, for the series of runs at constant Froude number (a) and at constant Rossby number (b) with various
![]() $N/f$
.
$N/f$
.
4.2 Spectral analysis
We show in figure 6 the isotropic spectra of energy in the wave and slow modes, denoted respectively
![]() $E_{W}(k)$
and
$E_{W}(k)$
and
![]() $E_{0}(k)$
, for the series of runs at constant Froude number. The isotropic spectra are defined, as usual, as integrals over spherical shells in Fourier space:
$E_{0}(k)$
, for the series of runs at constant Froude number. The isotropic spectra are defined, as usual, as integrals over spherical shells in Fourier space:
For all the runs, at early times (
![]() $t=1.5$
, before the peak of enstrophy), the slow mode component dominates at large scales while the wave component dominates at small scales. Note that the wavenumber at which the two spectra cross increases with
$t=1.5$
, before the peak of enstrophy), the slow mode component dominates at large scales while the wave component dominates at small scales. Note that the wavenumber at which the two spectra cross increases with
![]() $N/f$
. When the turbulence develops, the wave energy spectrum decays rapidly, including at small scales, and the slow mode spectrum dominates at all scales. However, the wave energy at small scales increases when
$N/f$
. When the turbulence develops, the wave energy spectrum decays rapidly, including at small scales, and the slow mode spectrum dominates at all scales. However, the wave energy at small scales increases when
![]() $N/f$
increases. The other salient feature of the isotropic energy spectra is the growth of the slow mode energy at scales larger than the forcing scale. In most of the runs, up to approximately
$N/f$
increases. The other salient feature of the isotropic energy spectra is the growth of the slow mode energy at scales larger than the forcing scale. In most of the runs, up to approximately
![]() $N/f=7$
, this growth takes the form of an inverse cascade, with a spectral slope that is consistent with
$N/f=7$
, this growth takes the form of an inverse cascade, with a spectral slope that is consistent with
![]() $k^{-5/3}$
. However, the inverse cascade of the slow modes weakens as
$k^{-5/3}$
. However, the inverse cascade of the slow modes weakens as
![]() $N/f$
increases, as already found from the analysis of global quantities. Already, at
$N/f$
increases, as already found from the analysis of global quantities. Already, at
![]() $N/f=7$
, the spectrum at the final time of the simulation has a narrow
$N/f=7$
, the spectrum at the final time of the simulation has a narrow
![]() $k^{-5/3}$
range, and at
$k^{-5/3}$
range, and at
![]() $N/f=10$
, the energy in the slow modes seems to saturate at large scale with a flat spectrum
$N/f=10$
, the energy in the slow modes seems to saturate at large scale with a flat spectrum
![]() $k^{0}$
. Note that we cannot rule out completely the possibility that the
$k^{0}$
. Note that we cannot rule out completely the possibility that the
![]() $-5/3$
range would extend further towards large scales with a larger integration time. However, it should be noted that the growth rate of the energy in the slow modes for these values of
$-5/3$
range would extend further towards large scales with a larger integration time. However, it should be noted that the growth rate of the energy in the slow modes for these values of
![]() $N/f$
is very small (see figure 4) and that the slow mode energy spectrum has not evolved much between
$N/f$
is very small (see figure 4) and that the slow mode energy spectrum has not evolved much between
![]() $t=22.5$
and
$t=22.5$
and
![]() $t=30$
. This indicates that even if the
$t=30$
. This indicates that even if the
![]() $-5/3$
range was to extend towards larger scales, it would require a very long integration time. Besides, the growth does not seem to be self-similar, since the spectral slope at scales larger than the
$-5/3$
range was to extend towards larger scales, it would require a very long integration time. Besides, the growth does not seem to be self-similar, since the spectral slope at scales larger than the
![]() $-5/3$
range becomes shallower (almost flat), unlike traditional inverse cascade phenomena. The flat spectrum for slow mode energy at large scales is the only notable feature of the
$-5/3$
range becomes shallower (almost flat), unlike traditional inverse cascade phenomena. The flat spectrum for slow mode energy at large scales is the only notable feature of the
![]() $N/f=20$
run, and it is also present in the purely stratified run, although in that case there is an accumulation of energy in the
$N/f=20$
run, and it is also present in the purely stratified run, although in that case there is an accumulation of energy in the
![]() $k=1$
modes. Such a flat spectrum has already been observed for kinetic energy in Smith & Waleffe (Reference Smith and Waleffe2002) for
$k=1$
modes. Such a flat spectrum has already been observed for kinetic energy in Smith & Waleffe (Reference Smith and Waleffe2002) for
![]() $N/f=10$
(see also Kimura & Herring (Reference Kimura and Herring2012) and Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2013, Reference Marino, Mininni, Rosenberg and Pouquet2014)).
$N/f=10$
(see also Kimura & Herring (Reference Kimura and Herring2012) and Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2013, Reference Marino, Mininni, Rosenberg and Pouquet2014)).

Figure 6. Isotropic energy spectra of the wave (solid lines) and slow mode (dashed lines) for the series of runs with constant Froude number (
![]() $\mathit{Fr}=0.04$
) and varying
$\mathit{Fr}=0.04$
) and varying
![]() $N/f$
. The times shown are indicated in the legend at the bottom, going from purple to blue, green, yellow and red in increasing order. Two different spectral laws are indicated as well for comparison.
$N/f$
. The times shown are indicated in the legend at the bottom, going from purple to blue, green, yellow and red in increasing order. Two different spectral laws are indicated as well for comparison.
The transition between these two scenarios is further described in figure 10, which shows the spectral slope
![]() $\unicode[STIX]{x1D6FC}$
of the isotropic energy spectrum of the slow modes at large scale, defined by
$\unicode[STIX]{x1D6FC}$
of the isotropic energy spectrum of the slow modes at large scale, defined by
![]() $E_{0}(k)\sim k^{\unicode[STIX]{x1D6FC}}$
for
$E_{0}(k)\sim k^{\unicode[STIX]{x1D6FC}}$
for
![]() $k\leqslant k_{F}$
, and computed numerically by a least-squares fit, as a function of
$k\leqslant k_{F}$
, and computed numerically by a least-squares fit, as a function of
![]() $N/f$
. This figure shows that the transition appears to be continuous, although the specific values of the spectral slopes lack in accuracy since the inertial range is rather short (remember that
$N/f$
. This figure shows that the transition appears to be continuous, although the specific values of the spectral slopes lack in accuracy since the inertial range is rather short (remember that
![]() $k_{F}\in [22,23]$
), and since they may depend on the details of the least-squares fitting procedure: choice of snapshot, excluding the
$k_{F}\in [22,23]$
), and since they may depend on the details of the least-squares fitting procedure: choice of snapshot, excluding the
![]() $k=1$
modes to get rid of the formation of a possible condensate at the largest scale, … . In particular, no time averaging has been performed here. Higher resolutions would also provide improvements in accuracy. Another caveat is that, as noted above, the intermediate values (e.g.
$k=1$
modes to get rid of the formation of a possible condensate at the largest scale, … . In particular, no time averaging has been performed here. Higher resolutions would also provide improvements in accuracy. Another caveat is that, as noted above, the intermediate values (e.g.
![]() $N/f=7$
or 10) may move closer to
$N/f=7$
or 10) may move closer to
![]() $-5/3$
with a larger integration time.
$-5/3$
with a larger integration time.

Figure 7. Isotropic spectra of the wave and slow mode components of energy for the series of runs with constant Rossby number (
![]() $\mathit{Ro}=0.08$
) and varying
$\mathit{Ro}=0.08$
) and varying
![]() $N/f$
. The symbols are the same as in figure 6.
$N/f$
. The symbols are the same as in figure 6.
The inverse cascade of the slow mode energy spectrum is also seen in the series of runs at constant Rossby number (figure 7). Interestingly, for the runs with small
![]() $N/f$
ratios (
$N/f$
ratios (
![]() $N/f=1/4$
or
$N/f=1/4$
or
![]() $1/2$
), i.e. the runs with the highest Froude numbers, the waves dominate at small scales even at late times, when these scales seem to have attained stationarity. This is probably a consequence of the higher buoyancy Reynolds number, rather than the Burger number or the deformation length (see the discussion in § 5.2).
$1/2$
), i.e. the runs with the highest Froude numbers, the waves dominate at small scales even at late times, when these scales seem to have attained stationarity. This is probably a consequence of the higher buoyancy Reynolds number, rather than the Burger number or the deformation length (see the discussion in § 5.2).

Figure 8. Perpendicular spectra of the wave and slow mode components of energy for selected values of the parameters. Scaling laws are represented only for reference. Line encoding and colours are similar to the two preceding figures.
In addition to the isotropic spectrum, obtained by summing over spherical shells in Fourier space, it is always relevant for anisotropic flows to compute the so-called reduced spectra, where the summation is done either on cylinders (fixed
![]() $k_{\bot }$
) or planes (fixed
$k_{\bot }$
) or planes (fixed
![]() $k_{\Vert }$
) in Fourier space (see e.g. Godeferd & Staquet Reference Godeferd and Staquet2003; Sagaut & Cambon Reference Sagaut and Cambon2008; Mininni Reference Mininni2011; Mininni et al.
Reference Mininni, Rosenberg and Pouquet2012; Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2014). Introducing the axisymmetric spectra
$k_{\Vert }$
) in Fourier space (see e.g. Godeferd & Staquet Reference Godeferd and Staquet2003; Sagaut & Cambon Reference Sagaut and Cambon2008; Mininni Reference Mininni2011; Mininni et al.
Reference Mininni, Rosenberg and Pouquet2012; Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2014). Introducing the axisymmetric spectra
![]() $e_{0}(k_{\bot },k_{\Vert }),e_{W}(k_{\bot },k_{\Vert })$
defined by
$e_{0}(k_{\bot },k_{\Vert }),e_{W}(k_{\bot },k_{\Vert })$
defined by
 $$\begin{eqnarray}\displaystyle e_{W}(k_{\bot },k_{\Vert }) & = & \displaystyle \int _{0}^{2\unicode[STIX]{x03C0}} [|A_{+}(k_{\bot }\cos \unicode[STIX]{x1D719}\boldsymbol{e}_{x}+k_{\bot }\sin \unicode[STIX]{x1D719}\boldsymbol{e}_{y}+k_{\Vert }\boldsymbol{e}_{z})|^{2}\nonumber\\ \displaystyle & & \displaystyle +|A_{-}(k_{\bot }\cos \unicode[STIX]{x1D719}\boldsymbol{e}_{x}+k_{\bot }\sin \unicode[STIX]{x1D719}\boldsymbol{e}_{y}+k_{\Vert }\boldsymbol{e}_{z})|^{2} ]k_{\bot }\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{W}(k_{\bot },k_{\Vert }) & = & \displaystyle \int _{0}^{2\unicode[STIX]{x03C0}} [|A_{+}(k_{\bot }\cos \unicode[STIX]{x1D719}\boldsymbol{e}_{x}+k_{\bot }\sin \unicode[STIX]{x1D719}\boldsymbol{e}_{y}+k_{\Vert }\boldsymbol{e}_{z})|^{2}\nonumber\\ \displaystyle & & \displaystyle +|A_{-}(k_{\bot }\cos \unicode[STIX]{x1D719}\boldsymbol{e}_{x}+k_{\bot }\sin \unicode[STIX]{x1D719}\boldsymbol{e}_{y}+k_{\Vert }\boldsymbol{e}_{z})|^{2} ]k_{\bot }\,\text{d}\unicode[STIX]{x1D719},\end{eqnarray}$$
the perpendicular and parallel spectra are defined as follows for each type of mode,
![]() $s=0,W$
:
$s=0,W$
:
Figure 8 shows the perpendicular spectrum of energy in the wave (
![]() $E_{W}(k_{\bot })$
) and slow modes (
$E_{W}(k_{\bot })$
) and slow modes (
![]() $E_{0}(k_{\bot })$
); again, except for the runs with the highest Froude number (
$E_{0}(k_{\bot })$
); again, except for the runs with the highest Froude number (
![]() $Fr=0.32$
and
$Fr=0.32$
and
![]() $Fr=0.16$
, not shown) and, therefore, buoyancy Reynolds number, the slow modes dominate at all horizontal scales after the peak of enstrophy. In all cases, the perpendicular spectrum of the slow modes undergoes a growth of energy in horizontal scales larger than the forcing scale (note, however, that since the forcing acts on a spherical shell in Fourier space, there is some injection of energy at all the horizontal scales such that
$Fr=0.16$
, not shown) and, therefore, buoyancy Reynolds number, the slow modes dominate at all horizontal scales after the peak of enstrophy. In all cases, the perpendicular spectrum of the slow modes undergoes a growth of energy in horizontal scales larger than the forcing scale (note, however, that since the forcing acts on a spherical shell in Fourier space, there is some injection of energy at all the horizontal scales such that
![]() $0\leqslant k_{\bot }\leqslant k_{F}$
). As for the isotropic spectrum, this growth appears to be self-similar for
$0\leqslant k_{\bot }\leqslant k_{F}$
). As for the isotropic spectrum, this growth appears to be self-similar for
![]() $N/f$
ratios smaller than 10. As
$N/f$
ratios smaller than 10. As
![]() $N/f$
increases, the perpendicular spectrum saturates at large horizontal scales; see for instance the purely stratified case in figure 8. The spectral slope in this range varies depending on the non-dimensional parameters, and it is difficult to provide precise values here. Nevertheless, it appears that the perpendicular spectrum becomes shallower as
$N/f$
increases, the perpendicular spectrum saturates at large horizontal scales; see for instance the purely stratified case in figure 8. The spectral slope in this range varies depending on the non-dimensional parameters, and it is difficult to provide precise values here. Nevertheless, it appears that the perpendicular spectrum becomes shallower as
![]() $N/f$
increases. The spectral index
$N/f$
increases. The spectral index
![]() $\unicode[STIX]{x1D6FC}_{\bot }$
, defined by
$\unicode[STIX]{x1D6FC}_{\bot }$
, defined by
![]() $E_{0}(k_{\bot })\sim k_{\bot }^{\unicode[STIX]{x1D6FC}_{\bot }}$
for
$E_{0}(k_{\bot })\sim k_{\bot }^{\unicode[STIX]{x1D6FC}_{\bot }}$
for
![]() $k_{\bot }\leqslant k_{F}$
, and computed numerically by a least-squares fit, is represented as a function of
$k_{\bot }\leqslant k_{F}$
, and computed numerically by a least-squares fit, is represented as a function of
![]() $N/f$
in figure 10. The caveats mentioned above regarding accuracy of this spectral index still apply here. For instance, a slightly steeper spectral slope might have been obtained in the purely stratified case if we had chosen a range of wavenumbers closer to the forcing wavenumber: Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2014) find that the kinetic energy (here we are showing the slow mode energy) has a
$N/f$
in figure 10. The caveats mentioned above regarding accuracy of this spectral index still apply here. For instance, a slightly steeper spectral slope might have been obtained in the purely stratified case if we had chosen a range of wavenumbers closer to the forcing wavenumber: Marino et al. (Reference Marino, Mininni, Rosenberg and Pouquet2014) find that the kinetic energy (here we are showing the slow mode energy) has a
![]() $-5/3$
slope in this range. The perpendicular wave spectrum differs markedly in the rotation-dominated, weakly stratified case and in the strongly stratified cases. In the former case, more energy remains at small horizontal scales, while in the latter case it falls off sharply at scales smaller than the forcing scales, and it is shallow or flat at scales larger than the forcing scales. Note that steep horizontal spectra such as those we observe at scales smaller than the forcing scale have been reported before and related to viscous effects (Laval, McWilliams & Dubrulle Reference Laval, Mcwilliams and Dubrulle2003; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007).
$-5/3$
slope in this range. The perpendicular wave spectrum differs markedly in the rotation-dominated, weakly stratified case and in the strongly stratified cases. In the former case, more energy remains at small horizontal scales, while in the latter case it falls off sharply at scales smaller than the forcing scales, and it is shallow or flat at scales larger than the forcing scales. Note that steep horizontal spectra such as those we observe at scales smaller than the forcing scale have been reported before and related to viscous effects (Laval, McWilliams & Dubrulle Reference Laval, Mcwilliams and Dubrulle2003; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007).

Figure 9. Parallel spectra of the wave and slow mode components of energy for selected values of the parameters. Scaling laws are represented only for reference. Line encoding and colours are similar to the three preceding figures.
Similarly, the parallel spectra
![]() $E_{W}(k_{\Vert }),E_{0}(k_{\Vert })$
of energy in the wave and slow modes, respectively, are shown in figure 9. Again, once the turbulence sets in, the slow modes dominate at all vertical scales, except in the two cases with high buoyancy Reynolds numbers, where the waves dominate at small scales (for the case
$E_{W}(k_{\Vert }),E_{0}(k_{\Vert })$
of energy in the wave and slow modes, respectively, are shown in figure 9. Again, once the turbulence sets in, the slow modes dominate at all vertical scales, except in the two cases with high buoyancy Reynolds numbers, where the waves dominate at small scales (for the case
![]() $N/f=1/4$
, the waves dominate roughly at all the vertical scales smaller than the forcing scale
$N/f=1/4$
, the waves dominate roughly at all the vertical scales smaller than the forcing scale
![]() $k_{F}$
, although the energy in these scales decay extremely fast). Overall, the energy in the small scales increases as we move from the rotation-dominated case (where the spectrum is very steep) to the purely stratified case (note the different vertical scales on the panels of figure 9). This statement also holds for the wave component of the energy: while the waves have most of their energy at large scales for rotation-dominated cases or cases where rotation and stratification are comparable (i.e. relatively low
$k_{F}$
, although the energy in these scales decay extremely fast). Overall, the energy in the small scales increases as we move from the rotation-dominated case (where the spectrum is very steep) to the purely stratified case (note the different vertical scales on the panels of figure 9). This statement also holds for the wave component of the energy: while the waves have most of their energy at large scales for rotation-dominated cases or cases where rotation and stratification are comparable (i.e. relatively low
![]() $N/f$
ratios), they become mostly small scale when stratification prevails. The build-up of slow mode energy at large vertical scales occurs differently from the perpendicular spectra: already at very early times, the parallel spectrum of the slow modes is more or less flat at scales larger than the forcing scale. Besides, for the lowest
$N/f$
ratios), they become mostly small scale when stratification prevails. The build-up of slow mode energy at large vertical scales occurs differently from the perpendicular spectra: already at very early times, the parallel spectrum of the slow modes is more or less flat at scales larger than the forcing scale. Besides, for the lowest
![]() $N/f$
ratio (
$N/f$
ratio (
![]() $1/4$
), there is relatively little change in the slow mode parallel spectrum at large scales. As for the perpendicular spectra, there does not seem to be a universal scaling law in this range: the spectral slope
$1/4$
), there is relatively little change in the slow mode parallel spectrum at large scales. As for the perpendicular spectra, there does not seem to be a universal scaling law in this range: the spectral slope
![]() $\unicode[STIX]{x1D6FC}_{\Vert }$
(defined by
$\unicode[STIX]{x1D6FC}_{\Vert }$
(defined by
![]() $E_{0}(k_{\Vert })\sim k_{\Vert }^{\unicode[STIX]{x1D6FC}_{\Vert }}$
for
$E_{0}(k_{\Vert })\sim k_{\Vert }^{\unicode[STIX]{x1D6FC}_{\Vert }}$
for
![]() $k_{\Vert }\leqslant k_{F}$
) varies between approximately
$k_{\Vert }\leqslant k_{F}$
) varies between approximately
![]() $-2$
and
$-2$
and
![]() $-5/3$
until
$-5/3$
until
![]() $N/f=4$
(see figure 10), then the spectrum becomes much shallower at large scales, and it is almost flat for the purely stratified case and for the case with
$N/f=4$
(see figure 10), then the spectrum becomes much shallower at large scales, and it is almost flat for the purely stratified case and for the case with
![]() $N/f=20$
. Note that shallow or flat vertical spectra (and steep horizontal spectra) have been observed in previous studies (e.g. Waite & Bartello Reference Waite and Bartello2004), and is associated with rapid decay of vertical velocity correlation functions due to the decoupling of horizontal layers in the limit of strong stratification. Unlike previous studies, this behaviour occurs here for scales larger than the forcing scale. Hence a possible interpretation of the non-universal large-scale vertical spectrum is that it results from a competition between the scrambling effect of the forcing and the build-up of large-scale vertical correlations by inertial effects when rotation is strong enough.
$N/f=20$
. Note that shallow or flat vertical spectra (and steep horizontal spectra) have been observed in previous studies (e.g. Waite & Bartello Reference Waite and Bartello2004), and is associated with rapid decay of vertical velocity correlation functions due to the decoupling of horizontal layers in the limit of strong stratification. Unlike previous studies, this behaviour occurs here for scales larger than the forcing scale. Hence a possible interpretation of the non-universal large-scale vertical spectrum is that it results from a competition between the scrambling effect of the forcing and the build-up of large-scale vertical correlations by inertial effects when rotation is strong enough.

Figure 10. Spectral indices for the isotropic (solid lines), perpendicular (dashed lines) and parallel (dash-dotted lines) vortical energy spectra at scales larger than the forcing, as a function of
![]() $N/f$
, for the two series of runs: constant Froude number (star,
$N/f$
, for the two series of runs: constant Froude number (star,
![]() $\times$
and
$\times$
and
![]() $+$
symbols), and constant Rossby number (circle, square and diamond symbols). The no-resonance zone is the shaded area.
$+$
symbols), and constant Rossby number (circle, square and diamond symbols). The no-resonance zone is the shaded area.
4.3 Role of the VSHF modes
Several studies of stratified flows have underlined the role of horizontally homogeneous modes: Herring & Métais (Reference Herring and Métais1989) and Staquet & Godeferd (Reference Staquet and Godeferd1998) have reported a tendency towards layering, while Smith & Waleffe (Reference Smith and Waleffe2002, see also Godeferd & Cambon (Reference Godeferd and Cambon1994) for an EDQNM perspective) have shown that at very long time, energy accumulates in the horizontally homogeneous modes (defined by
![]() $k_{\bot }=0$
), with a peak at some value of
$k_{\bot }=0$
), with a peak at some value of
![]() $k_{\Vert }$
which defines the number of horizontal layers in the vertical, hence the name vertically sheared horizontal flows (VSHF). Our numerical simulations are stopped earlier in order to avoid the accumulation of energy in the gravest mode of the system that is inherent to all inverse cascade phenomena (see e.g. Boffetta & Ecke (Reference Boffetta and Ecke2012) for a recent review in 2D). Asymptotic analysis has also established that the VSHF modes contribute to the slow component of the limiting dynamics in the low-Froude-number, finite-Rossby-number limit (Babin et al.
Reference Babin, Mahalov, Nicolaenko and Zhou1997; Embid & Majda Reference Embid and Majda1998). This provides an incentive for looking at these modes in the direct numerical simulations carried out here.
$k_{\Vert }$
which defines the number of horizontal layers in the vertical, hence the name vertically sheared horizontal flows (VSHF). Our numerical simulations are stopped earlier in order to avoid the accumulation of energy in the gravest mode of the system that is inherent to all inverse cascade phenomena (see e.g. Boffetta & Ecke (Reference Boffetta and Ecke2012) for a recent review in 2D). Asymptotic analysis has also established that the VSHF modes contribute to the slow component of the limiting dynamics in the low-Froude-number, finite-Rossby-number limit (Babin et al.
Reference Babin, Mahalov, Nicolaenko and Zhou1997; Embid & Majda Reference Embid and Majda1998). This provides an incentive for looking at these modes in the direct numerical simulations carried out here.
By definition, the VSHF modes are horizontally homogeneous, but may depend on the vertical coordinate. In general, they have an inertial wave component (whose frequency is the Coriolis frequency
![]() $f$
) corresponding to an oscillation of the horizontal components of velocity, with vanishing vertical velocity, and a slow mode component that is proportional to temperature fluctuations. Hence, their wave component is purely kinetic and their slow mode component is purely potential. When rotation vanishes, the dispersion relation also vanishes and there is no longer an oscillatory component.
$f$
) corresponding to an oscillation of the horizontal components of velocity, with vanishing vertical velocity, and a slow mode component that is proportional to temperature fluctuations. Hence, their wave component is purely kinetic and their slow mode component is purely potential. When rotation vanishes, the dispersion relation also vanishes and there is no longer an oscillatory component.
The ratio of energy in these VSHF modes is shown in figure 11, as a function of
![]() $N/f$
for the two series of runs. It is striking that it remains of the same order of magnitude (and relatively small; it is in fact negligible compared to the waves for instance, see figure 5) for all finite values of
$N/f$
for the two series of runs. It is striking that it remains of the same order of magnitude (and relatively small; it is in fact negligible compared to the waves for instance, see figure 5) for all finite values of
![]() $N/f$
; it is only when we move to the strictly non-rotating case that the energy in the VSHF modes jumps by approximately two orders of magnitude. Then, the energy in the
$N/f$
; it is only when we move to the strictly non-rotating case that the energy in the VSHF modes jumps by approximately two orders of magnitude. Then, the energy in the
![]() $k_{\bot }=0$
modes becomes comparable to the energy in waves with any other wave vector. Smith & Waleffe (Reference Smith and Waleffe2002) and Waite & Bartello (Reference Waite and Bartello2006b
) also observed an increase of the energy transfer to the VSHF modes when rotation decreases, but here the transition seems to be more abrupt, and the energy fraction in the VSHF modes is also at least an order of magnitude smaller here. However, energy transfers to the VSHF modes is known to occur on very long time scales, and this may simply be a matter of integration time.
$k_{\bot }=0$
modes becomes comparable to the energy in waves with any other wave vector. Smith & Waleffe (Reference Smith and Waleffe2002) and Waite & Bartello (Reference Waite and Bartello2006b
) also observed an increase of the energy transfer to the VSHF modes when rotation decreases, but here the transition seems to be more abrupt, and the energy fraction in the VSHF modes is also at least an order of magnitude smaller here. However, energy transfers to the VSHF modes is known to occur on very long time scales, and this may simply be a matter of integration time.
Note that, although we do not have enough runs at high buoyancy Reynolds number for a systematic study, it does not seem to be a relevant parameter as far as this issue is concerned, since the two runs with higher buoyancy Reynolds have a similar level of energy in the VSHF modes as the other runs.

Figure 11. Fraction of energy in the vertically sheared horizontal modes (
![]() $k_{\bot }=0$
modes) as a function of
$k_{\bot }=0$
modes) as a function of
![]() $N/f$
, for the two series of runs. The no-resonance zone is the shaded area.
$N/f$
, for the two series of runs. The no-resonance zone is the shaded area.
4.4 Energy fluxes
Let us now turn to the fluxes of energy in the different modes. We first define the transfer functions
![]() $T_{0}(\boldsymbol{k})$
and
$T_{0}(\boldsymbol{k})$
and
![]() $T_{W}(\boldsymbol{k})$
:
$T_{W}(\boldsymbol{k})$
:
where we have introduced the projections
![]() $\boldsymbol{X}_{0}(\boldsymbol{k})=\unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k})$
and
$\boldsymbol{X}_{0}(\boldsymbol{k})=\unicode[STIX]{x1D64B}_{0}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k})$
and
![]() $\boldsymbol{X}_{W}(\boldsymbol{k})=\unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k})$
. The evolution of the energy in the slow and wave modes at wave vector
$\boldsymbol{X}_{W}(\boldsymbol{k})=\unicode[STIX]{x1D64B}_{W}(\boldsymbol{k})\boldsymbol{X}(\boldsymbol{k})$
. The evolution of the energy in the slow and wave modes at wave vector
![]() $\boldsymbol{k}$
is simply governed by
$\boldsymbol{k}$
is simply governed by
As usual, we can define the isotropic, perpendicular and parallel transfer functions
![]() $T_{s}(k)$
,
$T_{s}(k)$
,
![]() $T_{s}(k_{\bot })$
and
$T_{s}(k_{\bot })$
and
![]() $T_{s}(k_{\Vert })$
(with
$T_{s}(k_{\Vert })$
(with
![]() $s=0,W$
) by integrating over a spherical shell, a plane or a cylinder in Fourier space. Then we introduce the fluxes:
$s=0,W$
) by integrating over a spherical shell, a plane or a cylinder in Fourier space. Then we introduce the fluxes:
and similarly for the perpendicular and parallel fluxes
![]() $\unicode[STIX]{x1D6F1}_{s}(k_{\bot })$
and
$\unicode[STIX]{x1D6F1}_{s}(k_{\bot })$
and
![]() $\unicode[STIX]{x1D6F1}_{s}(k_{\Vert })$
.
$\unicode[STIX]{x1D6F1}_{s}(k_{\Vert })$
.

Figure 12. Isotropic fluxes of energy for the slow modes (a,b) and for the wave modes (c,d) for the series of runs at constant Froude number (a,c) and at constant Rossby number (b,d) with various
![]() $N/f$
. Note the different scale (they differ by a factor of 10) for
$N/f$
. Note the different scale (they differ by a factor of 10) for
![]() $\unicode[STIX]{x1D6F1}_{0}$
and
$\unicode[STIX]{x1D6F1}_{0}$
and
![]() $\unicode[STIX]{x1D6F1}_{W}$
.
$\unicode[STIX]{x1D6F1}_{W}$
.

Figure 13. Total energy flux from the slow modes to the wave modes as a function of
![]() $N/f$
.
$N/f$
.
The isotropic energy fluxes for the slow modes and for the waves are shown in figure 12 for the latest time (
![]() $t=30$
). We see that for all
$t=30$
). We see that for all
![]() $N/f$
ratios, the energy fluxes for the slow modes are negative, and more or less independent of
$N/f$
ratios, the energy fluxes for the slow modes are negative, and more or less independent of
![]() $k$
, at scales larger than the forcing. Furthermore, the magnitude of this negative flux seems to be larger for relatively small values of
$k$
, at scales larger than the forcing. Furthermore, the magnitude of this negative flux seems to be larger for relatively small values of
![]() $N/f$
(the runs with
$N/f$
(the runs with
![]() $N/f=2,3,4$
have approximately the same magnitude), while it is reduced when stratification prevails. In contrast, the fluxes are positive at scales smaller than the forcing. In this range, the positive flux is an increasing function of
$N/f=2,3,4$
have approximately the same magnitude), while it is reduced when stratification prevails. In contrast, the fluxes are positive at scales smaller than the forcing. In this range, the positive flux is an increasing function of
![]() $N/f$
. On the other hand, the energy fluxes for the wave modes do not change sign at the forcing scale: they are always positive. The absence of a range with constant small-scale fluxes can be attributed to the small size of the
$N/f$
. On the other hand, the energy fluxes for the wave modes do not change sign at the forcing scale: they are always positive. The absence of a range with constant small-scale fluxes can be attributed to the small size of the
![]() $k>k_{F}$
wavenumber range, a problem remedied when using higher resolutions and/or lower forcing wavenumber (Pouquet & Marino Reference Pouquet and Marino2013; Marino, Pouquet & Rosenberg Reference Marino, Pouquet and Rosenberg2015), or a parametrization scheme (Pouquet et al.
Reference Pouquet, Sen, Rosenberg, Mininni and Baerenzung2013). Note that, unlike the traditional (total) energy fluxes, we need not have
$k>k_{F}$
wavenumber range, a problem remedied when using higher resolutions and/or lower forcing wavenumber (Pouquet & Marino Reference Pouquet and Marino2013; Marino, Pouquet & Rosenberg Reference Marino, Pouquet and Rosenberg2015), or a parametrization scheme (Pouquet et al.
Reference Pouquet, Sen, Rosenberg, Mininni and Baerenzung2013). Note that, unlike the traditional (total) energy fluxes, we need not have
![]() $\unicode[STIX]{x1D6F1}_{s}(0)=0$
, because
$\unicode[STIX]{x1D6F1}_{s}(0)=0$
, because
![]() $E_{0}$
and
$E_{0}$
and
![]() $E_{W}$
are not independently conserved (only their sum is). This means that care should be taken when interpreting fluxes, since the value of the flux for one given mode (slow or wave) at
$E_{W}$
are not independently conserved (only their sum is). This means that care should be taken when interpreting fluxes, since the value of the flux for one given mode (slow or wave) at
![]() $k$
is not only the amount of energy transferred from wavenumbers smaller than
$k$
is not only the amount of energy transferred from wavenumbers smaller than
![]() $k$
to wavenumbers larger than
$k$
to wavenumbers larger than
![]() $k$
, but also includes the contributions from the other mode. The total flux of energy from the slow modes to the waves
$k$
, but also includes the contributions from the other mode. The total flux of energy from the slow modes to the waves
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, which coincides with
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, which coincides with
![]() $\unicode[STIX]{x1D6F1}_{W}(0)$
, or equivalently
$\unicode[STIX]{x1D6F1}_{W}(0)$
, or equivalently
![]() $-\unicode[STIX]{x1D6F1}_{0}(0)$
(up to numerical errors), is shown as a function of
$-\unicode[STIX]{x1D6F1}_{0}(0)$
(up to numerical errors), is shown as a function of
![]() $N/f$
in figure 13. Such global energy exchanges between slow and fast modes have been considered in more details (including the partition of energy into kinetic and potential components) by Whitehead & Wingate (Reference Whitehead and Wingate2014); here we use the global flux to interpret the spectral distribution of the energy fluxes.
$N/f$
in figure 13. Such global energy exchanges between slow and fast modes have been considered in more details (including the partition of energy into kinetic and potential components) by Whitehead & Wingate (Reference Whitehead and Wingate2014); here we use the global flux to interpret the spectral distribution of the energy fluxes.
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
is small when
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
is small when
![]() $N/f$
is small (up to
$N/f$
is small (up to
![]() $N/f=4$
) and then increases almost linearly with
$N/f=4$
) and then increases almost linearly with
![]() $N/f$
. For all values of
$N/f$
. For all values of
![]() $N/f$
larger than unity, the energy flux for the wave modes (figure 12) is never significantly larger than
$N/f$
larger than unity, the energy flux for the wave modes (figure 12) is never significantly larger than
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, which means that the transfer of wave energy is dominated by the leakage from slow modes. However, note that for the two cases
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, which means that the transfer of wave energy is dominated by the leakage from slow modes. However, note that for the two cases
![]() $N/f=1/4$
and
$N/f=1/4$
and
![]() $N/f=1/2$
, the flux at scales smaller than the forcing scale is much larger than
$N/f=1/2$
, the flux at scales smaller than the forcing scale is much larger than
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, meaning that, in those cases, there is a significant transfer of energy towards the small scales from the waves themselves. This interpretation is consistent with the fact that in the
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, meaning that, in those cases, there is a significant transfer of energy towards the small scales from the waves themselves. This interpretation is consistent with the fact that in the
![]() $N/f=1/4$
case the energy in the wave modes is significantly larger than in any other case, and these two cases are those for which the waves dominate at small scales (see figure 7), and for which the buoyancy Reynolds number is significantly larger. Similarly, the negative flux at scales larger than the forcing scales for the slow modes is of the order of
$N/f=1/4$
case the energy in the wave modes is significantly larger than in any other case, and these two cases are those for which the waves dominate at small scales (see figure 7), and for which the buoyancy Reynolds number is significantly larger. Similarly, the negative flux at scales larger than the forcing scales for the slow modes is of the order of
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
when
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
when
![]() $N/f\geqslant 7$
. This means that the negative flux alone does not allow one to claim with certainty that we have an inverse cascade of slow modes. For instance, slow energy in the stratified case has a negative flux, while we have seen above that it lacks some characteristics of the inverse cascade. What is more meaningful is the fact that, in the range of scales between the forcing scale and the plateau of the flux at the largest scales, the flux decreases with
$N/f\geqslant 7$
. This means that the negative flux alone does not allow one to claim with certainty that we have an inverse cascade of slow modes. For instance, slow energy in the stratified case has a negative flux, while we have seen above that it lacks some characteristics of the inverse cascade. What is more meaningful is the fact that, in the range of scales between the forcing scale and the plateau of the flux at the largest scales, the flux decreases with
![]() $k$
and goes below the level of
$k$
and goes below the level of
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, all the more so that
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, all the more so that
![]() $N/f$
is small, consistently with the above analysis. For the runs with
$N/f$
is small, consistently with the above analysis. For the runs with
![]() $N/f\leqslant 4$
, the interpretation of the negative flux of slow energy is much easier: the magnitude of the more or less constant flux over scales larger than the forcing scales is much larger than
$N/f\leqslant 4$
, the interpretation of the negative flux of slow energy is much easier: the magnitude of the more or less constant flux over scales larger than the forcing scales is much larger than
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, which means that it can safely be attributed to an inverse cascade of slow mode energy.
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
, which means that it can safely be attributed to an inverse cascade of slow mode energy.

Figure 14. Perpendicular fluxes of energy for the slow modes (a,b) and for the wave modes (c,d) for the series of runs at constant Froude number (a,c) and at constant Rossby number (b,d) with various
![]() $N/f$
.
$N/f$
.
In figure 14, we show the perpendicular fluxes of energy in the slow modes and in the waves,
![]() $\unicode[STIX]{x1D6F1}_{0}(k_{\bot })$
and
$\unicode[STIX]{x1D6F1}_{0}(k_{\bot })$
and
![]() $\unicode[STIX]{x1D6F1}_{W}(k_{\bot })$
. For the slow modes, the fluxes are similar to the isotropic fluxes, with a notable difference: the negative fluxes at scales larger than the forcing scale are enhanced. In particular, now all the runs have a wide range of scales (larger than the forcing scale) for which the flux has larger magnitude than
$\unicode[STIX]{x1D6F1}_{W}(k_{\bot })$
. For the slow modes, the fluxes are similar to the isotropic fluxes, with a notable difference: the negative fluxes at scales larger than the forcing scale are enhanced. In particular, now all the runs have a wide range of scales (larger than the forcing scale) for which the flux has larger magnitude than
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
. That means that, regardless of
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
. That means that, regardless of
![]() $N/f$
, slow mode energy tends to be transferred towards large horizontal scales. This is known to be true even for purely stratified flows or flows strongly dominated by rotation, which tend to form uniform layers (Riley & Lelong Reference Riley and Lelong2000). As a matter of fact, runs dominated by stratification have a (negative) peak in the slow mode energy flux whose magnitude increases with
$N/f$
, slow mode energy tends to be transferred towards large horizontal scales. This is known to be true even for purely stratified flows or flows strongly dominated by rotation, which tend to form uniform layers (Riley & Lelong Reference Riley and Lelong2000). As a matter of fact, runs dominated by stratification have a (negative) peak in the slow mode energy flux whose magnitude increases with
![]() $N/f$
. The fluxes indicate, however, that for stratification-dominated runs (e.g.
$N/f$
. The fluxes indicate, however, that for stratification-dominated runs (e.g.
![]() $N/f=20$
or
$N/f=20$
or
![]() $\infty$
), this transfer of slow energy is arrested at some horizontal scales (like kinetic energy; see Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2014), while it continues all the way to the largest scales when stratification is weaker (e.g.
$\infty$
), this transfer of slow energy is arrested at some horizontal scales (like kinetic energy; see Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2014), while it continues all the way to the largest scales when stratification is weaker (e.g.
![]() $N/f=2,3,4$
or even 7 and 10). In contrast, the energy fluxes in the wave modes are always smaller than
$N/f=2,3,4$
or even 7 and 10). In contrast, the energy fluxes in the wave modes are always smaller than
![]() $\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
and, contrary to the isotropic fluxes, they do not have any range of constant value. This indicates that the transfer of energy from the slow modes to the waves probably occurs at large horizontal scales (we cannot in principle draw definitive conclusions since there might be cancellations between energy transfer from slow to wave modes and transfer across scales of wave modes, but it does not seem very plausible that they are of different signs). Note that the forcing scale is difficult to identify from this figure alone. It should be emphasized that, since we are forcing in a spherical shell in Fourier space, energy is actually injected in the full range
$\unicode[STIX]{x1D6F1}_{0\rightarrow W}$
and, contrary to the isotropic fluxes, they do not have any range of constant value. This indicates that the transfer of energy from the slow modes to the waves probably occurs at large horizontal scales (we cannot in principle draw definitive conclusions since there might be cancellations between energy transfer from slow to wave modes and transfer across scales of wave modes, but it does not seem very plausible that they are of different signs). Note that the forcing scale is difficult to identify from this figure alone. It should be emphasized that, since we are forcing in a spherical shell in Fourier space, energy is actually injected in the full range
![]() $k_{\bot }\in [0,k_{F}]$
(the same goes for
$k_{\bot }\in [0,k_{F}]$
(the same goes for
![]() $k_{\Vert }$
of course). Hence a caveat in the interpretation of anisotropic fluxes is that the forcing scale is not so well defined. However, in almost all cases, except the above-mentioned, the forcing scale can still be identified unambiguously in
$k_{\Vert }$
of course). Hence a caveat in the interpretation of anisotropic fluxes is that the forcing scale is not so well defined. However, in almost all cases, except the above-mentioned, the forcing scale can still be identified unambiguously in
![]() $\unicode[STIX]{x1D6F1}_{s}(k_{\bot })$
and
$\unicode[STIX]{x1D6F1}_{s}(k_{\bot })$
and
![]() $\unicode[STIX]{x1D6F1}_{s}(k_{\Vert })$
, which gives us confidence that the forcing is not contaminating the results too much. Finally, the perpendicular fluxes of wave energy for the two cases
$\unicode[STIX]{x1D6F1}_{s}(k_{\Vert })$
, which gives us confidence that the forcing is not contaminating the results too much. Finally, the perpendicular fluxes of wave energy for the two cases
![]() $N/f=1/4$
and
$N/f=1/4$
and
![]() $N/f=1/2$
are very similar to the isotropic fluxes, which means that, in those cases, the near-inertial waves tend to transfer their energy towards small horizontal scales.
$N/f=1/2$
are very similar to the isotropic fluxes, which means that, in those cases, the near-inertial waves tend to transfer their energy towards small horizontal scales.

Figure 15. Parallel fluxes of energy for the slow modes (a,b) and for the wave modes (c,d) for the series of runs at constant Froude number (a,c) and at constant Rossby number (b,d) with various
![]() $N/f$
.
$N/f$
.
Now, we turn to the examination of the parallel flux of energy in the slow modes and in the wave modes (figure 15). The most notable results are that runs with
![]() $N/f\geqslant 7$
have positive fluxes of slow energy across the whole range of vertical scales, corresponding to the maintenance of horizontal layers, whose thickness decreases with
$N/f\geqslant 7$
have positive fluxes of slow energy across the whole range of vertical scales, corresponding to the maintenance of horizontal layers, whose thickness decreases with
![]() $N/f$
. This process is less clear when stratification is weaker, since the parallel flux then remains negative at the very large scales. For all the runs with
$N/f$
. This process is less clear when stratification is weaker, since the parallel flux then remains negative at the very large scales. For all the runs with
![]() $N/f\geqslant 2$
, the parallel flux of wave energy is identical to the isotropic flux, indicating that vertical transfers dominate, although interpretation is still polluted by the exchange with slow modes. When
$N/f\geqslant 2$
, the parallel flux of wave energy is identical to the isotropic flux, indicating that vertical transfers dominate, although interpretation is still polluted by the exchange with slow modes. When
![]() $N/f=1/4$
or
$N/f=1/4$
or
![]() $N/f=1/2$
, it is interesting to note that there is a peak at vertical scales larger than the forcing scale (this is another case where the isotropic forcing scale does not appear clearly), although its magnitude is relatively small. This peak does not correspond to any identifiable feature in the isotropic fluxes.
$N/f=1/2$
, it is interesting to note that there is a peak at vertical scales larger than the forcing scale (this is another case where the isotropic forcing scale does not appear clearly), although its magnitude is relatively small. This peak does not correspond to any identifiable feature in the isotropic fluxes.
5 Viscous dissipation due to vertical shearing and the role of the buoyancy Reynolds number
5.1 Impact of viscous effects on spectral energy budgets
As mentioned in § 2.2, the non-dimensional parameters characterizing the numerical simulations being studied here correspond to a regime where vertical diffusion terms are of the order of vertical advection (Billant & Chomaz Reference Billant and Chomaz2001; Godoy-Diana, Chomaz & Billant Reference Godoy-Diana, Chomaz and Billant2004; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007). In this regime, viscous dissipation can affect the large horizontal scales through vertical shearing of the layers (the so-called ‘pancakes’) formed by the dynamics. Following the work of Brethouwer et al. (Reference Brethouwer, Billant, Lindborg and Chomaz2007) – see their (4.1) and figure 10 – for purely stratified flows, we check this effect explicitly by considering the ratio of the dissipation due to vertical shear
![]() $\unicode[STIX]{x1D716}_{S}$
to the total dissipation
$\unicode[STIX]{x1D716}_{S}$
to the total dissipation
![]() $\unicode[STIX]{x1D716}$
. These two quantities are given by:
$\unicode[STIX]{x1D716}$
. These two quantities are given by:
The ratio
![]() $\unicode[STIX]{x1D716}_{S}/\unicode[STIX]{x1D716}$
is represented as a function of
$\unicode[STIX]{x1D716}_{S}/\unicode[STIX]{x1D716}$
is represented as a function of
![]() $N/f$
in figure 16, for both series of runs. For low
$N/f$
in figure 16, for both series of runs. For low
![]() $N/f$
, this ratio is very small and, as expected, it increases when thinner horizontal layers form which allow vertical dissipation to act, until reaching values for
$N/f$
, this ratio is very small and, as expected, it increases when thinner horizontal layers form which allow vertical dissipation to act, until reaching values for
![]() $N/f=20$
or
$N/f=20$
or
![]() $N/f=\infty$
similar to the stratified runs of Brethouwer et al. (Reference Brethouwer, Billant, Lindborg and Chomaz2007) at similar
$N/f=\infty$
similar to the stratified runs of Brethouwer et al. (Reference Brethouwer, Billant, Lindborg and Chomaz2007) at similar
![]() ${\mathcal{R}}_{B}$
, for which the major part of dissipation is due to these large-scale viscous effects.
${\mathcal{R}}_{B}$
, for which the major part of dissipation is due to these large-scale viscous effects.

Figure 16. Fraction of the kinetic energy dissipation rate due to vertical shearing of the horizontal velocity field.
Now, we would like to know what part this large-scale dissipation mechanism potentially plays in preventing the energy transfers towards the large scales when
![]() $N/f$
varies. To do so, we would like to compare the dissipation rate in a given range of scales to the flux of energy transferred by the nonlinear term in the same range. Hence, we introduce the following integrals of the viscous term:
$N/f$
varies. To do so, we would like to compare the dissipation rate in a given range of scales to the flux of energy transferred by the nonlinear term in the same range. Hence, we introduce the following integrals of the viscous term:
and we similarly define the fluxes
![]() $\unicode[STIX]{x1D6F1}_{{<}},\unicode[STIX]{x1D6F1}_{{>}}$
by integrating the transfer functions. Note that
$\unicode[STIX]{x1D6F1}_{{<}},\unicode[STIX]{x1D6F1}_{{>}}$
by integrating the transfer functions. Note that
![]() $\unicode[STIX]{x1D6F1}_{{<}}=-\unicode[STIX]{x1D6F1}_{{>}}$
(because the integral of the transfer functions over all wave vectors vanishes), but of course there is no analogous property for the dissipation term, which is positive definite. Now we can write integrated energy budgets for large and small scales:
$\unicode[STIX]{x1D6F1}_{{<}}=-\unicode[STIX]{x1D6F1}_{{>}}$
(because the integral of the transfer functions over all wave vectors vanishes), but of course there is no analogous property for the dissipation term, which is positive definite. Now we can write integrated energy budgets for large and small scales:
We can proceed analogously for the perpendicular and the parallel directions, with the caveat that, for the type of forcing considered here, there is an additional energy injection term in the large-scale budget, due to the projection of the forcing term in the spherical shell of radius
![]() $k_{f}$
on horizontal and vertical wavenumbers in the interval
$k_{f}$
on horizontal and vertical wavenumbers in the interval
![]() $[0,k_{f}]$
. In figure 17, we show the two terms on the right-hand side of the large-scale energy budget, for isotropic and horizontal scales, for the four highest values of
$[0,k_{f}]$
. In figure 17, we show the two terms on the right-hand side of the large-scale energy budget, for isotropic and horizontal scales, for the four highest values of
![]() $N/f$
. For isotropic scales larger than the forcing scale, the small flux of energy towards large scale which exists near
$N/f$
. For isotropic scales larger than the forcing scale, the small flux of energy towards large scale which exists near
![]() $k_{f}$
in the purely stratified case is annihilated by dissipation. As
$k_{f}$
in the purely stratified case is annihilated by dissipation. As
![]() $N/f$
decreases, both the value of the flux of energy towards large scales and the range where it is positive grow, as has already been reported (Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2013, Reference Marino, Mininni, Rosenberg and Pouquet2014). In addition, the difference between the energy flux and dissipation also grows at all scales
$N/f$
decreases, both the value of the flux of energy towards large scales and the range where it is positive grow, as has already been reported (Marino et al.
Reference Marino, Mininni, Rosenberg and Pouquet2013, Reference Marino, Mininni, Rosenberg and Pouquet2014). In addition, the difference between the energy flux and dissipation also grows at all scales
![]() $k<k_{f}$
, although the large-scale energy dissipation itself increases when
$k<k_{f}$
, although the large-scale energy dissipation itself increases when
![]() $N/f$
decreases. This shows that, in the parameter regime considered here (
$N/f$
decreases. This shows that, in the parameter regime considered here (
![]() ${\mathcal{R}}_{B}\sim 1$
), the disappearance of the inverse cascade when
${\mathcal{R}}_{B}\sim 1$
), the disappearance of the inverse cascade when
![]() $N/f$
increases is due to the combination of two effects. First of all, the nonlinear term does not transfer energy to the large scale as efficiently. Besides, the small amount of energy which is still transferred to large isotropic scales is damped by viscous dissipation due to vertical shearing. The situation is slightly different when considering perpendicular scales. While the behaviour of the energy flux when
$N/f$
increases is due to the combination of two effects. First of all, the nonlinear term does not transfer energy to the large scale as efficiently. Besides, the small amount of energy which is still transferred to large isotropic scales is damped by viscous dissipation due to vertical shearing. The situation is slightly different when considering perpendicular scales. While the behaviour of the energy flux when
![]() $N/f$
varies as been described above, the energy dissipation at large horizontal scales increases with
$N/f$
varies as been described above, the energy dissipation at large horizontal scales increases with
![]() $N/f$
, for all
$N/f$
, for all
![]() $k_{\bot }<k_{f}$
and more markedly for
$k_{\bot }<k_{f}$
and more markedly for
![]() $k_{\bot }$
closer to
$k_{\bot }$
closer to
![]() $k_{f}$
. It should be noted that for stratification-dominated flows (here the runs with
$k_{f}$
. It should be noted that for stratification-dominated flows (here the runs with
![]() $N/f=20$
or
$N/f=20$
or
![]() $\infty$
for instance), dissipation is larger than energy flux at all horizontal scales larger than the forcing scale. As
$\infty$
for instance), dissipation is larger than energy flux at all horizontal scales larger than the forcing scale. As
![]() $N/f$
decreases, the energy flux starts prevailing at the largest scales, and the crossing scale decreases with
$N/f$
decreases, the energy flux starts prevailing at the largest scales, and the crossing scale decreases with
![]() $N/f$
. This explains how the blob in the energy flux towards large horizontal scales in the stratified case does not lead to accumulation of energy at large scales.
$N/f$
. This explains how the blob in the energy flux towards large horizontal scales in the stratified case does not lead to accumulation of energy at large scales.

Figure 17. Isotropic (a) and perpendicular (b) fluxes of kinetic energy into the large scales (solid lines),
![]() $-\unicode[STIX]{x1D6F1}_{{<}}(k)$
and
$-\unicode[STIX]{x1D6F1}_{{<}}(k)$
and
![]() $-\unicode[STIX]{x1D6F1}_{{<}}(k_{\bot })$
, respectively, and rate of kinetic energy dissipation by viscosity at large scales (dashed lines),
$-\unicode[STIX]{x1D6F1}_{{<}}(k_{\bot })$
, respectively, and rate of kinetic energy dissipation by viscosity at large scales (dashed lines),
![]() $D_{{<}}(k)$
and
$D_{{<}}(k)$
and
![]() $D_{{<}}(k_{\bot })$
, respectively. Only the scales larger than the forcing scale are shown. Note the different vertical scale for the two plots.
$D_{{<}}(k_{\bot })$
, respectively. Only the scales larger than the forcing scale are shown. Note the different vertical scale for the two plots.
The integrated budget for large parallel scales (not shown) exhibits yet another scenario: there, nonlinear transfer and viscous dissipation act together to remove energy from large parallel scales. The source of energy at
![]() $k_{\Vert }<k_{f}$
is the projection of the forcing, and the major part of this input is transferred towards small vertical scales by the nonlinear term, the remaining energy being damped by viscosity. The ratio of the energy flux towards small vertical scales and the viscous dissipation increases as
$k_{\Vert }<k_{f}$
is the projection of the forcing, and the major part of this input is transferred towards small vertical scales by the nonlinear term, the remaining energy being damped by viscosity. The ratio of the energy flux towards small vertical scales and the viscous dissipation increases as
![]() $N/f$
increases, indicating the trend for stratification-dominated flows to form thinner layers.
$N/f$
increases, indicating the trend for stratification-dominated flows to form thinner layers.
In all the runs considered here, the small-scale integrated energy budget exhibits an exact balance between nonlinear energy transfers and dissipation (not shown), in agreement with the fact that those scales are in a steady state. This holds for isotropic, perpendicular and parallel scales alike.
5.2 Impact of the buoyancy Reynolds number
As pointed out by several authors (Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007; Ivey, Winters & Koseff Reference Ivey, Winters and Koseff2008; Bartello & Tobias Reference Bartello and Tobias2013; Waite Reference Waite2013), the buoyancy Reynolds number
![]() ${\mathcal{R}}_{B}$
plays an important role in stratified turbulence, and it is likely doing so as well when rotation is included. In particular, the regime of low buoyancy Reynolds number corresponds to a case where horizontal layers are viscously coupled. It is characterized by a vertical scale set by the viscous scale
${\mathcal{R}}_{B}$
plays an important role in stratified turbulence, and it is likely doing so as well when rotation is included. In particular, the regime of low buoyancy Reynolds number corresponds to a case where horizontal layers are viscously coupled. It is characterized by a vertical scale set by the viscous scale
![]() $\sqrt{\unicode[STIX]{x1D708}L_{h}/U}$
rather than the buoyancy scale
$\sqrt{\unicode[STIX]{x1D708}L_{h}/U}$
rather than the buoyancy scale
![]() $U/N$
(Riley & de Bruyn Kops Reference Riley and de Bruyn Kops2003; Godoy-Diana et al.
Reference Godoy-Diana, Chomaz and Billant2004; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007; Rorai et al.
Reference Rorai, Mininni and Pouquet2014), a small vertical Froude number (in contrast, at high buoyancy Reynolds number, the vertical Froude number remains of order unity (Billant & Chomaz Reference Billant and Chomaz2001)) and a potential enstrophy which is dominated by its quadratic component (Waite Reference Waite2013). The runs commented upon so far fall within this parameter regime and, as explained in the previous section, viscous dissipation due to vertical shearing has to be taken into account to understand the energy budget, even at large (horizontal) scales. Nevertheless, the results presented here tend to show that in this regime, the system relaxes to a balanced state where the velocity field is almost horizontal (the slow modes have vanishing vertical velocity), and slow mode energy is cascaded upscale provided rotation is strong enough.
$U/N$
(Riley & de Bruyn Kops Reference Riley and de Bruyn Kops2003; Godoy-Diana et al.
Reference Godoy-Diana, Chomaz and Billant2004; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007; Rorai et al.
Reference Rorai, Mininni and Pouquet2014), a small vertical Froude number (in contrast, at high buoyancy Reynolds number, the vertical Froude number remains of order unity (Billant & Chomaz Reference Billant and Chomaz2001)) and a potential enstrophy which is dominated by its quadratic component (Waite Reference Waite2013). The runs commented upon so far fall within this parameter regime and, as explained in the previous section, viscous dissipation due to vertical shearing has to be taken into account to understand the energy budget, even at large (horizontal) scales. Nevertheless, the results presented here tend to show that in this regime, the system relaxes to a balanced state where the velocity field is almost horizontal (the slow modes have vanishing vertical velocity), and slow mode energy is cascaded upscale provided rotation is strong enough.
It is a natural question to ask how both the inertial and viscous mechanisms outlined above, which account for the collapse of the inverse cascade when
![]() $N/f$
increases, are affected when the buoyancy Reynolds number moves closer to a regime relevant for geophysical flows. One expects that when
$N/f$
increases, are affected when the buoyancy Reynolds number moves closer to a regime relevant for geophysical flows. One expects that when
![]() ${\mathcal{R}}_{B}$
becomes large, the viscous effects should disappear, the non-quadratic components of potential enstrophy will grow and the transfer of energy to the waves will also be larger. However, it remains unclear whether these transitions all occur at the same time or if some of those effects vanish before the others. A systematic study of the effect of the buoyancy Reynolds number across a wide range of
${\mathcal{R}}_{B}$
becomes large, the viscous effects should disappear, the non-quadratic components of potential enstrophy will grow and the transfer of energy to the waves will also be larger. However, it remains unclear whether these transitions all occur at the same time or if some of those effects vanish before the others. A systematic study of the effect of the buoyancy Reynolds number across a wide range of
![]() $N/f$
such as the one studied here would be extremely expensive computationally speaking. Indeed, two incompatible conditions are required: on the one hand a reasonable scale separation between the forcing scale and the box scale is needed to discuss the inverse cascade regime, which reduces the Reynolds number, but on the other hand a very large Reynolds number is needed to reach a high
$N/f$
such as the one studied here would be extremely expensive computationally speaking. Indeed, two incompatible conditions are required: on the one hand a reasonable scale separation between the forcing scale and the box scale is needed to discuss the inverse cascade regime, which reduces the Reynolds number, but on the other hand a very large Reynolds number is needed to reach a high
![]() ${\mathcal{R}}_{B}$
. In addition, the option of decreasing the forcing wavenumber suffers from another limit: in the purely stratified case, when
${\mathcal{R}}_{B}$
. In addition, the option of decreasing the forcing wavenumber suffers from another limit: in the purely stratified case, when
![]() $k_{F}$
is too low, we observe an accumulation of energy at the forcing scale. A possible explanation for this behaviour is that the number of modes excited does not suffice to spread the energy across the whole spectrum of scales.
$k_{F}$
is too low, we observe an accumulation of energy at the forcing scale. A possible explanation for this behaviour is that the number of modes excited does not suffice to spread the energy across the whole spectrum of scales.
To get a rough idea of how the results obtained above in the low
![]() ${\mathcal{R}}_{B}$
regime change when
${\mathcal{R}}_{B}$
regime change when
![]() ${\mathcal{R}}_{B}$
increases, we have carried out four additional simulations (see table 1). One purely stratified run and one with
${\mathcal{R}}_{B}$
increases, we have carried out four additional simulations (see table 1). One purely stratified run and one with
![]() $N/f=20$
were carried out at
$N/f=20$
were carried out at
![]() $512^{3}$
resolution and
$512^{3}$
resolution and
![]() $k_{F}=11$
. The last two have a
$k_{F}=11$
. The last two have a
![]() $1024^{3}$
resolution and
$1024^{3}$
resolution and
![]() $k_{F}=22$
, again with
$k_{F}=22$
, again with
![]() $N/f=20$
or
$N/f=20$
or
![]() $\infty$
. In all these cases, the buoyancy Reynolds number is twice the value of the original runs.
$\infty$
. In all these cases, the buoyancy Reynolds number is twice the value of the original runs.
Many features of these runs are similar to the ones already analysed. In particular, the isotropic and parallel spectra are all more or less flat at scales larger than the forcing scale. However, there are also notable differences. First of all, run F
![]() $^{\prime }$
20 undergoes a linear growth of slow energy, unlike run F20. However, this growth of energy does not correspond to a self-similar growth of the spectrum, which remains relatively shallow. The purely stratified runs
$^{\prime }$
20 undergoes a linear growth of slow energy, unlike run F20. However, this growth of energy does not correspond to a self-similar growth of the spectrum, which remains relatively shallow. The purely stratified runs
![]() $\text{F}^{\star }20$
and
$\text{F}^{\star }20$
and
![]() $\text{F}^{\star }\infty$
both exhibit a slow decay of slow energy and a corresponding growth of wave energy, which ultimately dominates at the latest stages of run
$\text{F}^{\star }\infty$
both exhibit a slow decay of slow energy and a corresponding growth of wave energy, which ultimately dominates at the latest stages of run
![]() $\text{F}^{\star }20$
, indicating that the transfer of energy towards waves is much larger at larger
$\text{F}^{\star }20$
, indicating that the transfer of energy towards waves is much larger at larger
![]() ${\mathcal{R}}_{B}$
. Besides, in all the runs and as anticipated above, waves dominate at small scales, especially at small horizontal scales. Regarding potential vorticity,
${\mathcal{R}}_{B}$
. Besides, in all the runs and as anticipated above, waves dominate at small scales, especially at small horizontal scales. Regarding potential vorticity,
![]() $\unicode[STIX]{x1D6E4}_{2}/\unicode[STIX]{x1D6E4}$
is approximately 0.975 in the
$\unicode[STIX]{x1D6E4}_{2}/\unicode[STIX]{x1D6E4}$
is approximately 0.975 in the
![]() $N/f=20$
case, a value which is close to that observed in figure 2. In the purely stratified case, this ratio is around 0.92 and keeps increasing slowly in time until the end of the run. The run with
$N/f=20$
case, a value which is close to that observed in figure 2. In the purely stratified case, this ratio is around 0.92 and keeps increasing slowly in time until the end of the run. The run with
![]() $k_{F}=11$
and the
$k_{F}=11$
and the
![]() $1024^{3}$
run agree reasonably well on this value, which is slightly lower than in the low-
$1024^{3}$
run agree reasonably well on this value, which is slightly lower than in the low-
![]() ${\mathcal{R}}_{B}$
case (see figure 2). Perhaps the most interesting thing to compare with the low-
${\mathcal{R}}_{B}$
case (see figure 2). Perhaps the most interesting thing to compare with the low-
![]() ${\mathcal{R}}_{B}$
runs is the large-scale energy budget as described in § 5.2. It is represented in figure 18. While the effect of large-scale dissipation is as expected slightly lower than in the lower-
${\mathcal{R}}_{B}$
runs is the large-scale energy budget as described in § 5.2. It is represented in figure 18. While the effect of large-scale dissipation is as expected slightly lower than in the lower-
![]() ${\mathcal{R}}_{B}$
case, the most notable difference is in the nonlinear energy transfer. Indeed, in the purely stratified case, the contribution of the nonlinear term to the energy budget of the (isotropic) scales larger than the forcing scale is negative, at variance with the lower-
${\mathcal{R}}_{B}$
case, the most notable difference is in the nonlinear energy transfer. Indeed, in the purely stratified case, the contribution of the nonlinear term to the energy budget of the (isotropic) scales larger than the forcing scale is negative, at variance with the lower-
![]() ${\mathcal{R}}_{B}$
case. It is slightly smaller (though still positive when
${\mathcal{R}}_{B}$
case. It is slightly smaller (though still positive when
![]() $N/f=\infty$
) when looking at the horizontal scales, and becomes negative for
$N/f=\infty$
) when looking at the horizontal scales, and becomes negative for
![]() $k_{\bot }$
closer to
$k_{\bot }$
closer to
![]() $k_{F}$
when
$k_{F}$
when
![]() $N/f=20$
. In the case
$N/f=20$
. In the case
![]() $N/f=20$
, the nonlinear energy transfers overcome viscous dissipation in the isotropic large-scale budget. This explains the linear growth of energy mentioned above.
$N/f=20$
, the nonlinear energy transfers overcome viscous dissipation in the isotropic large-scale budget. This explains the linear growth of energy mentioned above.

Figure 18. Impact of the buoyancy Reynolds number on the large-scale energy budgets. The curves are similar to figure 17.
6 Conclusion
We have studied the partition of energy in terms of waves and vortices, defined through the normal modes of the linearized equations, in stratified flows with or without rotation. We have focused on the inverse cascade regime, which appears when rotation is sufficiently strong but not when stratification dominates. Using numerical simulations covering a wide range of
![]() $N/f$
ratios, we have characterized this transition in terms of the waves and vortices. To sum up, §§ 4.1–4.4 have established that in all the runs shown here:
$N/f$
ratios, we have characterized this transition in terms of the waves and vortices. To sum up, §§ 4.1–4.4 have established that in all the runs shown here:
-
(i) The total energy is dominated by the slow mode component, even when stratification is strong, although the fraction of energy in the waves increases when
 $N/f\geqslant 2$
increases. This happens in spite of the fact that the forcing has roughly equal projections on the slow and wave modes. The increase in wave energy with
$N/f\geqslant 2$
increases. This happens in spite of the fact that the forcing has roughly equal projections on the slow and wave modes. The increase in wave energy with
 $N/f$
is consistent with the observed total flux of energy from the slow modes to the wave modes, which also increases with
$N/f$
is consistent with the observed total flux of energy from the slow modes to the wave modes, which also increases with
 $N/f$
.
$N/f$
. -
(ii) The slow mode component dominates at all scales, except in the two runs with higher buoyancy Reynolds number (those with
 $N/f=1/4$
and
$N/f=1/4$
and
 $1/2$
), where they only dominate at large scale, similarly to the large-scale forcing case (Sukhatme & Smith Reference Sukhatme and Smith2008; Kurien & Smith Reference Kurien and Smith2012, Reference Kurien and Smith2014). This also holds when distinguishing horizontal and vertical scales.
$1/2$
), where they only dominate at large scale, similarly to the large-scale forcing case (Sukhatme & Smith Reference Sukhatme and Smith2008; Kurien & Smith Reference Kurien and Smith2012, Reference Kurien and Smith2014). This also holds when distinguishing horizontal and vertical scales. -
(iii) When
 $N/f$
is small enough (roughly
$N/f$
is small enough (roughly
 $N/f\leqslant 7$
, although the specific value may depend on the details of the set-up, and, in particular, the buoyancy Reynolds number and the strength of the waves due to rotation and/or stratification), the slow mode component has all the characteristics of an inverse cascade of energy: linear growth of their global energy, self-similar growth of their energy at scales larger than the forcing scales, and negative and constant fluxes at scales larger than the forcing scale. This is consistent with the results obtained in different set-ups in previous studies (Brunner-Suzuki et al.
Reference Brunner-Suzuki, Sundermeyer and Lelong2014; Kurien & Smith Reference Kurien and Smith2014; Whitehead & Wingate Reference Whitehead and Wingate2014).
$N/f\leqslant 7$
, although the specific value may depend on the details of the set-up, and, in particular, the buoyancy Reynolds number and the strength of the waves due to rotation and/or stratification), the slow mode component has all the characteristics of an inverse cascade of energy: linear growth of their global energy, self-similar growth of their energy at scales larger than the forcing scales, and negative and constant fluxes at scales larger than the forcing scale. This is consistent with the results obtained in different set-ups in previous studies (Brunner-Suzuki et al.
Reference Brunner-Suzuki, Sundermeyer and Lelong2014; Kurien & Smith Reference Kurien and Smith2014; Whitehead & Wingate Reference Whitehead and Wingate2014). -
(iv) When
 $N/f$
is higher (here because rotation is decreased), this inverse cascade of slow energy is arrested. When stratification prevails, slow modes still dominate the total energy, and there is some transfer of these modes towards the large scales, but it does not take the form of an inverse cascade: it saturates with a flat spectrum at large isotropic and vertical scales (like the full spectrum (Smith & Waleffe Reference Smith and Waleffe2002; Waite & Bartello Reference Waite and Bartello2004; Kimura & Herring Reference Kimura and Herring2012)), and there is no significant negative flux of energy for those scales. The spectrum is not flat at large horizontal scales, consistent with the presence of significant negative flux of slow mode energy, but it is still much shallower than in the presence of rotation. Note that the inverse cascade starts vanishing at a value of
$N/f$
is higher (here because rotation is decreased), this inverse cascade of slow energy is arrested. When stratification prevails, slow modes still dominate the total energy, and there is some transfer of these modes towards the large scales, but it does not take the form of an inverse cascade: it saturates with a flat spectrum at large isotropic and vertical scales (like the full spectrum (Smith & Waleffe Reference Smith and Waleffe2002; Waite & Bartello Reference Waite and Bartello2004; Kimura & Herring Reference Kimura and Herring2012)), and there is no significant negative flux of energy for those scales. The spectrum is not flat at large horizontal scales, consistent with the presence of significant negative flux of slow mode energy, but it is still much shallower than in the presence of rotation. Note that the inverse cascade starts vanishing at a value of
 $N/f$
for which the deformation scale becomes comparable to the box size. This can be interpreted intuitively as the fact that rotation is not directly felt at any of the resolved scales.
$N/f$
for which the deformation scale becomes comparable to the box size. This can be interpreted intuitively as the fact that rotation is not directly felt at any of the resolved scales. -
(v) As long as rotation is present, the fraction of energy in horizontally homogeneous modes (VSHF modes, satisfying
 $k_{\bot }=0$
) does not vary much with
$k_{\bot }=0$
) does not vary much with
 $N/f$
, and this fraction is always much lower than the energy in the waves, which is itself much lower than the energy in the slow modes. In contrast, in the purely stratified case, the VSHF modes reach a level of energy comparable with the waves. Interestingly, this transition appears to be pretty sharp, in contrast to all the other properties of the flows we have studied here (e.g. global partition of energy between waves and slow modes, growth rate of the slow mode energy and spectral indices), which seem to have a smoother transition as
$N/f$
, and this fraction is always much lower than the energy in the waves, which is itself much lower than the energy in the slow modes. In contrast, in the purely stratified case, the VSHF modes reach a level of energy comparable with the waves. Interestingly, this transition appears to be pretty sharp, in contrast to all the other properties of the flows we have studied here (e.g. global partition of energy between waves and slow modes, growth rate of the slow mode energy and spectral indices), which seem to have a smoother transition as
 $N/f$
increases.
$N/f$
increases.
The above results add up to those of Smith & Waleffe (Reference Smith and Waleffe2002) in an effort to better understand the role of vortices and waves in the inverse cascade of rotating-stratified flows, and more generally, to the above-mentioned studies in the wider context of geophysical flows. They also shed light on a paradox regarding the fundamental fluid mechanics of such flows. Indeed, the idea that the inverse cascade observed in the presence of rotation collapses when
![]() $N/f$
increases has been in the literature for a while (Métais et al.
Reference Métais, Riley, Lesieur, Castro and Rockliff1994; Bartello Reference Bartello1995; Lilly et al.
Reference Lilly, Bassett, Droegemeier and Bartello1998; Smith & Waleffe Reference Smith and Waleffe2002; Lindborg Reference Lindborg2005; Waite & Bartello Reference Waite and Bartello2006b
; Aluie & Kurien Reference Aluie and Kurien2011). However, from a theoretical point of view, this may come as a surprise because the inviscid invariants, which are traditionally reliable indicators of the direction of the energy cascade, are the same regardless of the
$N/f$
increases has been in the literature for a while (Métais et al.
Reference Métais, Riley, Lesieur, Castro and Rockliff1994; Bartello Reference Bartello1995; Lilly et al.
Reference Lilly, Bassett, Droegemeier and Bartello1998; Smith & Waleffe Reference Smith and Waleffe2002; Lindborg Reference Lindborg2005; Waite & Bartello Reference Waite and Bartello2006b
; Aluie & Kurien Reference Aluie and Kurien2011). However, from a theoretical point of view, this may come as a surprise because the inviscid invariants, which are traditionally reliable indicators of the direction of the energy cascade, are the same regardless of the
![]() $N/f$
ratio (including in the purely stratified case). Here, we have attempted to reconcile these two facts. A major ingredient is that the second invariant (in addition to energy), potential enstrophy, is degenerate. A similar situation occurs in homogeneous isotropic turbulence, where helicity is not sign-definite in general (in our case the sign of potential enstrophy is constant; it vanishes for wave modes and, in the non-rotating case, for VSHF modes). When one decimates the system by keeping only helical modes of a given sign, helicity becomes sign-definite and an inverse cascade results, as observed numerically (Biferale, Musacchio & Toschi Reference Biferale, Musacchio and Toschi2012) and in agreement with statistical mechanics arguments (Herbert Reference Herbert2014; Zhu, Yang & Zhu Reference Zhu, Yang and Zhu2014). But when one starts reintroducing in the dynamics a fraction of the modes which destroy sign-definiteness of the invariant, the inverse cascade collapses very soon (Sahoo, Bonaccorso & Biferale Reference Sahoo, Bonaccorso and Biferale2015), which again seems in agreement with the statistical mechanics prediction (Herbert Reference Herbert2014) and the behaviour of purely stratified flows described above. An alternative constraint which leads to the reversal of the energy flux is confinement: when the aspect ratio of the domain is small, enstrophy production is inhibited at scales larger than the layer thickness, even in the presence of stratification (Smith, Chasnov & Waleffe Reference Smith, Chasnov and Waleffe1996; Celani, Musacchio & Vincenzi Reference Celani, Musacchio and Vincenzi2010; Sozza et al.
Reference Sozza, Boffetta, Muratore-Ginanneschi and Musacchio2015).
$N/f$
ratio (including in the purely stratified case). Here, we have attempted to reconcile these two facts. A major ingredient is that the second invariant (in addition to energy), potential enstrophy, is degenerate. A similar situation occurs in homogeneous isotropic turbulence, where helicity is not sign-definite in general (in our case the sign of potential enstrophy is constant; it vanishes for wave modes and, in the non-rotating case, for VSHF modes). When one decimates the system by keeping only helical modes of a given sign, helicity becomes sign-definite and an inverse cascade results, as observed numerically (Biferale, Musacchio & Toschi Reference Biferale, Musacchio and Toschi2012) and in agreement with statistical mechanics arguments (Herbert Reference Herbert2014; Zhu, Yang & Zhu Reference Zhu, Yang and Zhu2014). But when one starts reintroducing in the dynamics a fraction of the modes which destroy sign-definiteness of the invariant, the inverse cascade collapses very soon (Sahoo, Bonaccorso & Biferale Reference Sahoo, Bonaccorso and Biferale2015), which again seems in agreement with the statistical mechanics prediction (Herbert Reference Herbert2014) and the behaviour of purely stratified flows described above. An alternative constraint which leads to the reversal of the energy flux is confinement: when the aspect ratio of the domain is small, enstrophy production is inhibited at scales larger than the layer thickness, even in the presence of stratification (Smith, Chasnov & Waleffe Reference Smith, Chasnov and Waleffe1996; Celani, Musacchio & Vincenzi Reference Celani, Musacchio and Vincenzi2010; Sozza et al.
Reference Sozza, Boffetta, Muratore-Ginanneschi and Musacchio2015).
Based on the inviscid invariants (Herbert et al.
Reference Herbert, Pouquet and Marino2014), we have identified three inertial mechanisms which can account for the collapse of the inverse cascade of slow modes, and which the numerical simulations proved to be simultaneously at play: first of all, although vortices dominate in all cases, the total flux of energy from slow modes to waves increases as
![]() $N/f$
increases (see figure 13), and consequently the fraction of energy in the waves also increases (see figure 5). Besides, in the purely stratified case, there is an accumulation of energy in the VSHF modes, which do not contribute to quadratic potential enstrophy (see figure 11). Finally, as
$N/f$
increases (see figure 13), and consequently the fraction of energy in the waves also increases (see figure 5). Besides, in the purely stratified case, there is an accumulation of energy in the VSHF modes, which do not contribute to quadratic potential enstrophy (see figure 11). Finally, as
![]() $N/f$
increases, the approximation of potential enstrophy by its quadratic part, on which the inviscid invariants argument is based, becomes less and less accurate (see figure 2). In addition to these inertial mechanisms, viscous effects also play a part at low buoyancy Reynolds number: in the purely stratified case, the energy transfer by the nonlinear term towards large scales (in particular horizontal scales) is sufficiently small to be completely dissipated by viscous effects at large horizontal scales due to vertical shearing.
$N/f$
increases, the approximation of potential enstrophy by its quadratic part, on which the inviscid invariants argument is based, becomes less and less accurate (see figure 2). In addition to these inertial mechanisms, viscous effects also play a part at low buoyancy Reynolds number: in the purely stratified case, the energy transfer by the nonlinear term towards large scales (in particular horizontal scales) is sufficiently small to be completely dissipated by viscous effects at large horizontal scales due to vertical shearing.
When the buoyancy Reynolds number increases, it is expected that such viscous effects should vanish, but the other mechanisms described above should be affected as well. Our preliminary sensitivity tests give a first indication that, while viscous effects are indeed reduced, the larger transfer of energy towards wave modes (which dominate at small scales) will probably play a major part. This is bound to happen when the Ozmidov scale is resolved, since then isotropy is recovered and there is no longer any reason for the velocity field to be mostly horizontal: since the vertical velocity in the normal mode decomposition framework is entirely accounted for by the wave modes, their contribution has to be larger at these scales. In this regime, the nonlinear components of potential vorticity are also stronger. To add further complication, numerical simulations have shown that in this high-
![]() ${\mathcal{R}}_{B}$
regime, both an inverse and a direct cascade of energy could exist simultaneously (Pouquet & Marino Reference Pouquet and Marino2013; Marino et al.
Reference Marino, Pouquet and Rosenberg2015). From the point of view of the inviscid invariants of the system, this is a puzzling result since inverse cascades usually arise when a second invariant prevents the direct cascade (see § 2.4). The key to this phenomenon presumably also lies in the fact that the energy breaks up into a wave component (not constrained by potential enstrophy conservation) and a vortical component (constrained by potential enstrophy conservation), even though, in this regime, more energy is transferred from the slow modes to the waves. Given that geophysical flows, which are a major motivation for better understanding the role of internal waves and vortices in rotating-stratified flows, fall within this high-
${\mathcal{R}}_{B}$
regime, both an inverse and a direct cascade of energy could exist simultaneously (Pouquet & Marino Reference Pouquet and Marino2013; Marino et al.
Reference Marino, Pouquet and Rosenberg2015). From the point of view of the inviscid invariants of the system, this is a puzzling result since inverse cascades usually arise when a second invariant prevents the direct cascade (see § 2.4). The key to this phenomenon presumably also lies in the fact that the energy breaks up into a wave component (not constrained by potential enstrophy conservation) and a vortical component (constrained by potential enstrophy conservation), even though, in this regime, more energy is transferred from the slow modes to the waves. Given that geophysical flows, which are a major motivation for better understanding the role of internal waves and vortices in rotating-stratified flows, fall within this high-
![]() ${\mathcal{R}}_{B}$
regime, more efforts should be devoted to studying such questions in future research.
${\mathcal{R}}_{B}$
regime, more efforts should be devoted to studying such questions in future research.
Acknowledgements
The work of C.H. on this research was partially supported by the Advanced Study Program and the Geophysical Turbulence Program at NCAR. The National Center for Atmospheric Research is sponsored by the National Science Foundation. R.M. was supported by the Regional Operative Program, Calabria ESF 2007/2013 and the European Community’s Seventh Framework Programme FP7-PEOPLE-2010-IRSES under grant agreement no. 269297 – TURBOPLASMAS. A.P. acknowledges support from the Laboratory for Atmospheric and Space Physics, University of Colorado. D.R. acknowledges support from the Oak Ridge Leadership Computing Facility at ORNL via the Office of Science under DOE Contract no. DE-AC05-00OR22725. Computer time was provided by ASD/ASP (NCAR) and the WEXAC cluster (Weizmann Institute). The authors would like to thank the referees for valuable comments and interesting suggestions which helped in improving the manuscript.