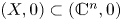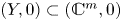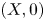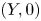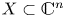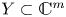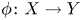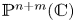1. Introduction
Zariski's famous multiplicity conjecture, stated by Zariski in 1971 (see [Reference ZariskiZar71]), is formulated as follows.
Conjecture 1 (Zariski's multiplicity conjecture)
Let 
$f,g \colon (\mathbb {C}^{n},0)\to (\mathbb {C},0)$ be two reduced complex analytic functions. If there is a homeomorphism 
$\varphi \colon (\mathbb {C}^{n},V(f),0)\to (\mathbb {C}^{n},V(g),0)$, then 
$m(V(f),0)=m(V(g),0)$.
This is still an open problem; see [Reference EyralEyr07] for a survey on this conjecture. In the real case, of course, Zariski's multiplicity conjecture does not hold in the same form as in the complex case. However, we have the following conjecture, stated by Fukui et al. [Reference Fukui, Kurdyka and PaunescuFKP04, Conjecture 3.3].
Conjecture 2 (Fukui–Kurdyka–Paunescu conjecture)
Let 
$X,Y\subset \mathbb {R}^{n}$ be two germs at the origin of irreducible real analytic subsets. If 
$h\colon (\mathbb {R}^{n},0)\to (\mathbb {R}^{n},0)$ is the germ of a sub-analytic, arc-analytic and bi-Lipschitz homeomorphism such that 
$h(X)=Y$, then 
$m(X,0)\equiv m(Y,0) \ {\rm mod}~2$.
Several authors approached this conjecture: For example, Risler [Reference RislerRis01] proved that multiplicity 
${\rm mod}~2$ of a real analytic curve is invariant under bi-Lipschitz homeomorphisms; Fukui et al. [Reference Fukui, Kurdyka and PaunescuFKP04] confirmed the conjecture in the case that 
$X$ and 
$Y$ are real analytic curves; and Valette [Reference ValetteVal10] showed that multiplicity 
${\rm mod}~2$ of real analytic hypersurfaces is invariant under arc-analytic bi-Lipschitz homeomorphisms. The third named author of this paper proved in [Reference SampaioSam22a] the real version of the Gau–Lipman theorem: i.e. multiplicity 
${\rm mod}~2$ of real analytic sets is invariant under homeomorphisms 
$\varphi \colon (\mathbb {R}^{n},0)\to (\mathbb {R}^{n},0)$ such that 
$\varphi$ and 
$\varphi ^{-1}$ have a derivative at the origin. A generalization of this result was presented in [Reference SampaioSam22b].
In this paper, we give a complete, positive answer to the Fukui–Kurdyka–Paunescu conjecture (see Theorem 7.14). A global version of this conjecture is also proved (see Corollary 4.8).
Coming back to the complex case, let us list some contributions to Zariski's multiplicity conjecture from the Lipschitz point of view. For instance, Neumann and Pichon [Reference Neumann and PichonNP14], with previous contributions of Pham and Teissier [Reference Pham and TeissierPT69] and Fernandes [Reference FernandesFer03], proved that the bi-Lipschitz geometry of plane curves determines the Puiseux pairs, and as a consequence if two germs of complex analytic curves with any codimension are bi-Lipschitz homeomorphic (with respect to the outer metric), then they have the same multiplicity. Comte [Reference ComteCom98] proved that multiplicity of complex analytic germs (not necessarily codimension-one sets) is invariant under bi-Lipschitz homeomorphisms with the severe assumption that the Lipschitz constants are close enough to one. This motivated the following conjecture in [Reference de Bobadilla, Fernandes and SampaiodBFS18].
Conjecture 3 Let 
$X\subset \mathbb {C}^{n}$ and 
$Y\subset \mathbb {C}^{m}$ be two complex analytic sets with 
$\dim X= \dim Y=d$. If their germs at zero are bi-Lipschitz homeomorphic, then their multiplicities 
$m(X,0)$ and 
$m(Y,0)$ are equal.
In [Reference de Bobadilla, Fernandes and SampaiodBFS18] the following conjecture was also posed.
Conjecture 4 Let 
$X\subset \mathbb {C}^{n}$ and 
$Y\subset \mathbb {C}^{m}$ be two complex algebraic sets with 
$\dim X= \dim Y=d$. If 
$X$ and 
$Y$ are bi-Lipschitz homeomorphic at infinity, then 
${\rm deg}(X)={\rm deg}(Y)$.
Still in [Reference de Bobadilla, Fernandes and SampaiodBFS18] the authors proved that Conjectures 3 and 4 are equivalent and, moreover, have positive answers for 
$d=1$ and 
$d=2$. However, Birbrair et al. [Reference Birbrair, Fernandes, Sampaio and VerbitskyBFSV20] disproved these conjectures when 
$d\geqslant 3$, by showing explicit counter-examples. More precisely, it was shown that we have two different embeddings of 
$\mathbb {P}^{1}(\mathbb {C})\times \mathbb {P}^{1}(\mathbb {C})$ into 
$\mathbb {P}^{5}(\mathbb {C})$, say 
$X$ and 
$Y$, such that their affine cones 
$ {\rm Cone}(X), {\rm Cone}(Y)\subset \mathbb {C}^{6}$ are bi-Lipschitz equivalent, but they have different degrees. Hence, the problem of invariance of degree under bi-Lipschitz homeomorphisms is still open in the important case of affine hypersurfaces in 
$\mathbb {C}^{n}$ with 
$n>3$. Moreover, there are several cases where Conjectures 3 and 4 hold true, for instance, the Lipschitz regularity theorem [Reference SampaioSam16, Theorem 4.2] (see also [Reference Birbrair, Fernandes, Lê and SampaioBFLS16, Reference Fernandes and SampaioFS22]) shows that if a germ of an analytic set is bi-Lipschitz equivalent to a smooth germ, then it is smooth itself, which implies that multiplicity 
$1$ of a complex analytic germ is a bi-Lipschitz invariant. Fernandes and Sampaio [Reference Fernandes and SampaioFS20] proved that degree one of a complex algebraic set is invariant under bi-Lipschitz homeomorphism at infinity and Sampaio in [Reference SampaioSam19] proved the version of Comte's result for the degree: the degree of complex algebraic sets is invariant under bi-Lipschitz homeomorphism at infinity with Lipschitz constant close enough to one. Recently, Jelonek [Reference JelonekJel21] proved that the multiplicity of complex analytic sets is invariant under bi-Lipschitz homeomorphisms which have analytic graphs, and the degree of complex algebraic sets is invariant under bi-Lipschitz homeomorphisms (at infinity) which have algebraic graph.
In this paper, we prove some generalizations of the results proved by Jelonek [Reference JelonekJel21]. For instance, we show that the multiplicity of complex analytic sets is invariant under semi-bi-Lipschitz homeomorphisms which have analytic graph (see Theorem 6.1) and the degree of complex algebraic sets is invariant under semi-bi-Lipschitz homeomorphisms at infinity which have algebraic graph (see Theorem 5.1). We also prove that degree of a complex algebraic set is invariant under semi-algebraic semi-bi-Lipschitz homeomorphisms at infinity such that the closure of their graphs are orientable homological cycles (see Theorem 3.1).
2. Preliminaries
2.1 Lipschitz and semi-bi-Lipschitz mappings
Definition 2.1 Let 
$X\subset \mathbb {R}^{n}$ and 
$Y\subset \mathbb {R}^{m}$ be two sets and let 
$h\colon X\to Y$.
(i) We say that
$h$ is Lipschitz if there exists a positive constant $C$ such that
\[ \|h(x)-h(y)\|\leqslant C\|x-y\|, \quad \forall x, y\in X. \](ii) We say that
$h$ is bi-Lipschitz if $h$ is a homeomorphism, it is Lipschitz and its inverse is also Lipschitz.(iii) We say that
$h$ is bi-Lipschitz at infinity (respectively, a homeomorphism at infinity) if there exist compact subsets $K\subset \mathbb {R}^{n}$ and $K'\subset \mathbb {R}^{m}$ such that $h|_{X\setminus K}\colon X\setminus K\to Y\setminus K'$ is bi-Lipschitz (respectively, a homeomorphism).(iv) We say that
$h$ is semi-Lipschitz at $x_0\in X$ if there exist a positive constant $C$ such that
\[ \|h(x)-h(x_0)\|\leqslant C\|x-x_0\|, \quad \forall x\in X. \](v) We say that
$h$ is semi-bi-Lipschitz at $x_0\in X$ if $h$ is a homeomorphism, it is semi-Lipschitz at $x_0$ and its inverse is also semi-Lipschitz at $h(x_0)$. We say that $h$ is semi-bi-Lipschitz if $h$ is semi-bi-Lipschitz at some $x_0\in X$.(vi) We say that
$h$ is semi-bi-Lipschitz at infinity if there exist compact subsets $K\subset \mathbb {R}^{n}$ and $K'\subset \mathbb {R}^{m}$ such that $h|_{X\setminus K}\colon X\setminus K\to Y\setminus K'$ is semi-bi-Lipschitz at some point $x_0\in X\setminus K$.
Now we give a geometric characterization of semi-bi-Lipschitz mappings. For a similar characterization of bi-Lipschitz mappings see [Reference JelonekJel21].
Definition 2.2 Let 
$L^{s}, H^{n-s-1}$ be two disjoint linear subspaces of 
$\mathbb {P}^{n}(\mathbb {C})$. Let 
$\pi _\infty$ be a hyperplane (a hyperplane at infinity) and assume that 
$L^{s} \subset \pi _\infty$. The projection 
$\pi _L$ with center 
$L^{s}$ is the mapping
\[ \pi_L \colon \mathbb{C}^{n}=\mathbb{P}^{n}(\mathbb{C})\setminus \pi_\infty\ni x \mapsto \langle L^{s},x \rangle \cap H^{n-s-1}\in H^{n-s-1}\setminus \pi_\infty=\mathbb{C}^{n-s-1}. \]
Here 
$\langle L,x\rangle$ we mean the linear projective subspace spanned by 
$L$ and 
$\{x\}$.
Lemma 2.3 Let 
$X$ be a closed subset of 
$\mathbb {C}^{n}$. Denote by 
$\Lambda _0\subset \pi _\infty$ the set of directions of all secants of 
$X$ which contain 
$x_0$ and let 
$\Sigma _0= \overline {\Lambda _0}$, where 
$\pi _\infty$ is the hyperplane at infinity and we consider the euclidean closure. Let 
$\pi _L:\mathbb {C}^{n}\to \mathbb {C}^{l}$ be the projection with center 
$L$. Then 
$\pi _L|_X$ is semi-bi-Lipschitz at 
$x_0$ if and only if 
$L\cap \Sigma _0=\emptyset$.
Proof. (a) Assume that 
$L\cap \Sigma _0=\emptyset$. We proceed by induction. As a linear affine isomorphism is a bi-Lipschitz homeomorphism, we can assume that 
$\pi _L$ coincides with the projection 
$\pi \colon \mathbb {C}^{n}\ni (x_1,\ldots,x_n) \mapsto (x_1,\ldots,x_k,0,\ldots,0)\in \mathbb {C}^{k}\times \{0,\ldots,0\}$. We can decompose 
$\pi$ into two projections: 
$\pi =\pi _{2}\circ \pi _{1}$, where 
$\pi _1\colon \mathbb {C}^{n} \ni (x_1,\ldots,x_n)\mapsto (x_1,\ldots,x_{n-1},0)=\mathbb {C}^{n-1}\times 0$ is the projection with center 
$P_1=(0:0:\cdots :1)$ and 
$\pi _2 \colon \mathbb {C}^{n-1}\ni (x_1,\ldots,x_{n-1},0)\mapsto (x_1,\ldots,x_{k},0,\ldots,0)\in \mathbb {C}^{k}\times \{(0,\ldots,0)\}$ is the projection with center 
$L':=\{ x_0=0,\ldots,x_{k}=0\}$. Since 
$P_1\in L$ and consequently 
$P_1\not \in \Sigma$, we prove that 
$\pi _1$ is a semi-bi-Lipschitz homeomorphism. Indeed, 
$P_1\in \mathbb {P}^{n-1}(\mathbb {C})\setminus \Sigma _0$. We show that the projection 
$p=\pi _1|_X\colon X\to \mathbb {C}^{n-1}\times 0$ is semi-bi-Lipschitz. Of course 
$\|p(x)-p(x_0)\|\leqslant \|x-x_0\|$. Assume that 
$p$ is not semi-bi-Lipschitz, i.e. there is a sequence of points 
$x_j\in X$ such that
\[ \frac{\|p(x_j)-p(x_0)\|}{\|x_j-x_0\|}\to 0 \]
as 
$j\to \infty$. Let 
$x_j-x_0=(a_1(j),\ldots,a_{n-1}(j),b(j))$ and denote by 
$P_j$ the corresponding point 
$(a_1(j):\cdots :a_{n-1}(j):b(j))$ in 
$\mathbb {P}^{n-1}(\mathbb {C})$. Hence,
\[ P_j=\frac{(a_1(j):\cdots:a_{n-1}(j):b(j))}{\|x_j-x_0\|}. \]As
\[ \frac{(a_1(j),\ldots,a_{n-1}(j))}{\|x_j-x_0\|}= \frac{p(x_j)-p(x_0)}{\|x_j-x_0\|}\to 0, \]
we see that 
$P_j\to P$. It is a contradiction. Note that if 
$\pi _1(X)=X'$, then 
$\Sigma _0'=\pi _1(\Sigma _0), x_0'=p(x_0)$. Moreover 
$L'=L\cap \{ x_n=0\}$ and 
$\langle L', P_1\rangle =L$. This means that 
$\Sigma _0'\cap L'=\emptyset$. Now by induction the projection 
$\pi _2|_{p(X)}$ is semi-bi-Lipschitz at 
$p(x_0)$, hence also 
$\pi =\pi _1\circ \pi _2$ is semi-bi-Lipschitz.
(b) Assume that 
$\pi _L|_X$ is a semi-bi-Lipschitz mapping and 
$\Sigma _0 \cap L\not =\emptyset$. As before we can change the system of coordinates in such a way that 
$\pi \colon \mathbb {C}^{n}\ni (x_1,\ldots,x_n) \mapsto (x_1,\ldots,x_k,0,\ldots,0)\in \mathbb {C}^{k}\times \{0,\ldots,0\}$. Moreover, we can assume that 
$P_1=(0:0:\cdots :1)\in \Sigma _0$. Actually 
$\pi _1$ is not semi-bi-Lipschitz. Indeed there is a sequence of secants 
$l_n=\langle x_n,x_0\rangle$ of 
$X$ whose directions tend to 
$P_1$. Let 
$x_j-x_0=(a_1(j),\ldots,a_{n-1}(j),b(j))$ and denote by 
$P_j$ the corresponding point 
$(a_1(j):\cdots :a_{n-1}(j):b(j))$ in 
$\mathbb {P}^{n-1}(\mathbb {C})$. Hence,
\[ P_j=\frac{(a_1(j):\cdots:a_{n-1}(j):b(j))}{\|x_j-x_0\|}. \]
As 
$P_j\to P$ we have
\[\frac{(a_1(j),\ldots,a_{n-1}(j))}{\|x_j-x_0\|}= \frac{p(x_j)-p(x_0)}{\|x_j-x_0\|}\to 0. \]
Hence, the mapping 
$\pi _1$ is not semi-bi-Lipschitz at 
$x_0$.
Let 
$x_0'=\pi _1(x_0)$. Now it is enough to note that 
$\|\pi _2(x)-\pi _2(x_0')\|\leqslant \|x-x_0'\|$, hence 
$\|\pi (x_n)-\pi (x_0)\|=\|\pi _2(\pi _1(x_n))-\pi _2(\pi _1(x_0))\|\leqslant \|\pi _1(x_n)-\pi _1(x_0)\|$. Thus,
\[ \frac{\|x_n-x_0\|}{\|\pi(x_n)-\pi(x_0)\|}\geqslant \frac{\|x_n-x_0\|}{\|\pi_1(x_n)-\pi_1(x_0)\|}\to \infty. \]This contradiction finishes the proof.
Lemma 2.4 Let 
$X\subset \mathbb {C}^{n}$ be a closed set and let 
$f\colon X\to \mathbb {C}^{m}$ be semi-Lipschitz at 
$x_0$. Let 
$Y:= {\rm graph}(f)\subset \mathbb {C}^{n}\times \mathbb {C}^{m}$. Then the mapping 
$\phi \colon X\ni x \mapsto (x,f(x)) \in Y$ is semi-bi-Lipschitz at 
$x_0$.
Proof. As 
$f$ is semi-Lipschitz at 
$x_0$, there is a constant 
$C$ such that
\[ \|f(x)-f(x_0)\|\leqslant C\|x-x_0\|. \]We have
\begin{align*} \|\phi(x)-\phi(x_0)\|&=\|(x-x_0,f(x)-f(x_0))\|\\ &\leqslant \|x-x_0\|+\|f(x)-f(x_0)\|\leqslant \|x-x_0\|+C\|x-x_0\|\\ &\leqslant (1+C)\|x-x_0\|. \end{align*}Moreover
\[ \|x-x_0\| \leqslant \|\phi(x)-\phi(x_0)\|. \]Hence,
\[ \|x-x_0\|\leqslant \|\phi(x)-\phi(x_0)\|\leqslant (1+C)\|x-x_0\|. \]Definition 2.6 Let 
$A\subset \mathbb {R}^{n}$ be a subset. We say that 
$v\in \mathbb {R}^{n}$ is a tangent vector to 
$A$ at 
$p\in \overline {A}$ (respectively, at infinity) if there is a sequence of points 
$\{x_i\}_{i\in \mathbb {N}}\subset A$ such that 
$\lim _{i\to \infty } \|x_i-p\|=0$ (respectively, 
$\lim _{i\to \infty } \|x_i\|=+\infty$) and there is a sequence of positive numbers 
$\{t_i\}_{i\in \mathbb {N}}\subset \mathbb {R}^{+}$ such that
\[ \lim_{i\to \infty} \frac{1}{t_i}(x_i-p)= v\quad \bigg(\mbox{respectively, } \lim_{i\to \infty} \frac{1}{t_i}x_i= v\bigg). \]
Let 
$C(A,p)$ (respectively, 
$C_{\infty }(A)$) denote the set of all tangent vectors to 
$A$ at 
$p$ (respectively, at infinity). The subset 
$C(A,p)$ (respectively, 
$C_{\infty }(A)$) is called the tangent cone of 
$A$ at 
$p$ (respectively, at infinity).
Definition 2.7 Let 
$X\subset \mathbb {R}^{n}$ and 
$Y\subset \mathbb {R}^{m}$ be sub-analytic sets with 
$0\in X$ and 
$0\in Y$ and let 
$h\colon (X,0)\to (Y,0)$ be a sub-analytic Lipschitz mapping. We define the pseudo-derivative of 
$h$ at 
$0$, 
$d_{0}h\colon C(X,0)\to C(Y,0)$, by 
$d_{0}h(v)=\lim _{t\to 0^{+}} {h(\gamma (t))}/{t}$, where 
$\gamma \colon [0,+\varepsilon )\to X$ satisfies 
$\lim _{t\to 0^{+}} {\gamma (t)}/{t}=v$.
Definition 2.8 Let 
$X\subset \mathbb {R}^{n}$ and 
$Y\subset \mathbb {R}^{m}$ be semi-algebraic sets and let 
$h\colon X\to Y$ be a semi-algebraic Lipschitz mapping. We define the pseudo-derivative of 
$h$ at infinity 
$d_{\infty }h\colon C(X,\infty )\to C(Y,\infty )$ by 
$d_{\infty }h(v)=\lim _{t\to +\infty } {h(\gamma (t))}/{t}$, where 
$\gamma \colon (r,+\infty )\to X$ satisfies 
$\lim _{t\to +\infty } {\gamma (t)}/{t}=v$.
2.2 Multiplicity and degree of real sets
Let 
$X\subset \mathbb {R}^{n}$ be a 
$d$-dimensional real analytic set with 
$0\in X$ and
\[ X_{\mathbb{C}}= V(\mathcal{I}_{\mathbb{R}}(X,0)), \]
where 
$\mathcal {I}_{\mathbb {R}}(X,0)$ is the ideal in 
$\mathbb {C}\{z_1,\ldots,z_n\}$ generated by the complexifications of all germs of real analytic functions that vanish on the germ 
$(X,0)$. We know that 
$X_{\mathbb {C}}$ is a germ of a complex analytic set and 
$\dim _{\mathbb {C}}X_{\mathbb {C}}=\dim _{\mathbb {R}}X$ (see [Reference NarasimhanNar66, Propositions 1 and 3, pp. 91–93]). Then, for a linear projection 
$\pi :\mathbb {C}^{n}\to \mathbb {C}^{d}$ such that 
$\pi ^{-1}(0)\cap C(X_{\mathbb {C}},0) =\{0\}$, there exists an open neighborhood 
$U\subset \mathbb {C}^{n}$ of 
$0$ such that 
$\# (\pi ^{-1}(x)\cap (X_{\mathbb {C}}\cap U))$ is constant for a generic point 
$x\in \pi (U)\subset \mathbb {C}^{d}$. This number is the multiplicity of 
$X_{\mathbb {C}}$ at the origin and it is denoted by 
$m(X_{\mathbb {C}},0)$.
Please note that 
$m(X_{\mathbb {C}},0)$ is well posed even if 
$X_{\mathbb {C}}$ is not of pure dimension. However, if 
$X_{\mathbb {C}}$ is of pure dimension, then our definition of multiplicity coincides with the classical one.
Definition 2.9 With the above notation, we define the multiplicity of 
$X$ at the origin by 
$m(X,0):=m(X_{\mathbb {C}},0)$.
In the same way, we define the degree of a real algebraic set 
$A\subset \mathbb {R}^{n}$ by 
${\rm deg}(A):={\rm deg}(A_{\mathbb {C}})$, where 
$A_{\mathbb {C}}=V(\mathcal {I}_{\mathbb {R}}(A))$ and 
$\mathcal {I}_{\mathbb {R}}(A)$ is the ideal in 
$\mathbb {C}[z_1,\ldots,z_n]$ generated by the complexifications of all real polynomials that vanish on 
$A$.
Definition 2.10 We shall not distinguish between a 
$2(n-d)$-dimensional real linear subspace in 
$\mathbb {C}^{n}$ and its canonical image in the Grassmannian 
$G^{2n}_{2(n-d)}(\mathbb {R})$. Thus, we regard the Grassmannian 
$G^{n}_{n-d}(\mathbb {C})$ as a subset of 
$G^{2n}_{2(n-d)}(\mathbb {R})$. Let 
$\mathcal {E}(X_{\mathbb {C}})$ denote the subset of 
$G^{2n}_{2(n-d)}(\mathbb {R})$ consisting of all 
$L\in G^{2n}_{2(n-d)}(\mathbb {R})$ such that 
$L\cap C(X_{\mathbb {C}},0)=\{0\}$.
Remark 2.11 [Reference SampaioSam22a]
We have the following comments on the set 
$\mathcal {E}(X_{\mathbb {C}})$.
(i) We have that 
$\mathcal {E}(X_{\mathbb {C}})$ is an open dense set in 
$G^{2n}_{2(n-d)}(\mathbb {R})\cong G^{2n}_{2d}(\mathbb {R})$.
(ii) For each 
$L \in \mathcal {E}(X_{\mathbb {C}})\cap G^{n}_{n-d}(\mathbb {C})$, let 
$\pi _L\colon \mathbb {C}^{n}\to L^{\perp }$ be the orthogonal projection along 
$L$. Then there exist a polydisc 
$U\subset \mathbb {C}^{n}$ and a complex analytic set 
$\sigma \subset U':=\pi _L(U)$ such that 
$\dim \sigma <\dim X_{\mathbb {C}}$ and 
$\pi _L\colon (U\cap X_{\mathbb {C}})\setminus \pi _L^{-1}(\sigma )\to U'\setminus \sigma$ is a 
$k$-sheeted cover with 
$k=m(X_{\mathbb {C}},0)$.
(iii) As 
$\pi :=\pi _L$ is an 
$\mathbb {R}$-linear mapping, we identify the 
$d$-dimensional real linear subspace 
$\pi (\mathbb {R}^{n})$ with 
$\mathbb {R}^{d}$ and, with this identification, we find that 
$\mathbb {R}^{d}\cap \sigma$ is a closed nowhere dense subset of 
$\mathbb {R}^{d}\cap U'$. Indeed, it is clear that 
$\mathbb {R}^{d}\cap \sigma$ is a closed subset of 
$\mathbb {R}^{d}\cap U'$ and, thus, if 
$\sigma$ is somewhere dense in 
$\mathbb {R}^{d}\cap U'$, then 
$\sigma$ contains an open ball 
$B_r(p)\subset \mathbb {R}^{d}\cap U'$, which implies that 
$\sigma$ must contain a non-empty open subset of 
$U'$ a contradiction. Therefore, 
$\sigma$ is nowhere dense in 
$\mathbb {R}^{d}\cap U'$ and so 
$\mathbb {R}^{d}\cap U'\setminus \sigma$ is an open dense subset of 
$\mathbb {R}^{d}\cap U'$.
(iv) For a generic point 
$x\in \mathbb {R}^{d}$ near the origin (i.e. for 
$x\in (\mathbb {R}^{d}\cap U')\setminus \sigma$), we have
\begin{align*} m(X_{\mathbb{C}},0)&=\# (\pi^{-1}(x)\cap (X_{\mathbb{C}}\cap U))\\ &=\# (\mathbb{R}^{n}\cap \pi^{-1}(x)\cap (X_{\mathbb{C}}\cap U))+\# ((\mathbb{C}^{n}\setminus \mathbb{R}^{n})\cap \pi^{-1}(x)\cap (X_{\mathbb{C}}\cap U))\\ &=\# (\pi^{-1}(x)\cap (X\cap U))+\# (\pi^{-1}(x)\cap ((X_{\mathbb{C}}\setminus \mathbb{R}^{n})\cap U)). \end{align*}
As for each 
$f\in \mathcal {I}_{\mathbb {R}}(X,0)$, we may write 
$f(z)=\sum _{|I|=k}^{\infty }a_Iz^{I}$ with 
$a_I\in \mathbb {R}$ for all 
$I$, it follows that 
$f(z_1,\ldots,z_n)=0$ if and only if 
$f(\bar z_1,\ldots,\bar z_n)=0$, where each 
$\bar z_i$ denotes the complex conjugate of 
$z_i$. In particular, 
$\# (\pi ^{-1}(x)\cap ((X_{\mathbb {C}}\setminus \mathbb {R}^{n})\cap U))$ is an even number. Therefore, 
$m(X,0)\equiv \# (\pi ^{-1}(x)\cap (X\cap U)) \ {\rm mod}~2$ for a generic point 
$x\in \mathbb {R}^{d}$ near the origin.
3. Homological cycles
Let 
$M$ be a smooth compact manifold of (real) dimension 
$n$. Given homology classes 
$\alpha \in H_k(M)$ and 
$\beta \in H_{n-k}(M)$, we choose representative cycles 
$\tilde \alpha$ and 
$\tilde \beta$, respectively. We can assume that every singular simplex appearing in each of these cycles is a smooth mapping and also that any two simplices meet transversally. This means that the only points of intersection are where the interior of a 
$k$-simplex in 
$\tilde \alpha$ meets the interior of an 
$(n-k)$-simplex in 
$\tilde \beta$. At every such point 
$x$ of intersection both 
$\tilde \alpha$ and 
$\tilde \beta$ are local embeddings and their tangent spaces are complementary in 
$T_xM$. We assign a sign to each point of intersection by comparing the direct sum of the orientations of the tangent spaces of 
$\tilde \alpha$ and of 
$\tilde \beta$ with the ambient orientation of the tangent space of 
$M$. The sum of the signs over the (finitely many) points of intersection gives the intersection pairing applied to 
$(\alpha,\beta )$.
If 
$M=\mathbb {P}^{n}(\mathbb {C})$, then 
$H_{2i}(M,\mathbb {Z})=\mathbb {Z}$ for 
$i=0,1,\ldots,n$ and 
$H_{2i-1}(M,\mathbb {Z})=0$. The space 
$H_{2i}(M,\mathbb {Z})$ is generated by the class 
$L^{i}$ where 
$L^{i}$ is a complex linear subspace of dimension 
$i$ (see, e.g., [Reference GreenbergGre66, 19.21]). Hence, every 
$2i$-dimensional homological cycle 
$\alpha$ can be described as 
$dL^{i}$. We say that the number 
$|d|$ is the topological degree of 
$\alpha$. Note that if 
$X\subset M$ is an 
$i$-dimensional projective subvariety, then the algebraic degree of 
$X$ coincides with the topological degree.
Similarly, if 
$M=\mathbb {P}^{n}(\mathbb {R})$, then 
$H_{i}(M,\mathbb {Z}/(2))=\mathbb {Z}/(2)$ for 
$i=0,1,\ldots,n$. The space 
$H_{i}(M,\mathbb {Z}/(2))$ is generated by the class 
$L^{i}$ where 
$L^{i}$ is a linear subspace of dimension 
$i$ (see, e.g., [Reference GreenbergGre66, 19.25]). Hence, every 
$i$-dimensional homological cycle 
$\alpha$ can be described as 
$dL^{i}$. We say that the number 
$d$ is the topological degree mod 2 of 
$\alpha$. Note that if 
$X\subset M$ is an 
$i$-dimensional projective subvariety, then the algebraic degree mod 2 coincides with the topological degree. More generally, if 
$X\subset \mathbb {R}^{n}$ is a closed subset, such that its projective closure is a homological cycle, then we define the topological degree of 
$X$ as the topological degree of 
$\overline {X}$.
Let 
$R=\mathbb {Z}$ or 
$R=\mathbb {Z}/(2)$. Let 
$X$ be a compact semi-algebraic set of dimension 
$d$. We say that 
$X$ is a homological cycle over 
$R$, if there exists a stratification 
$\mathcal {S}$ of 
$X$ such that it gives on 
$X$ a structure of a 
$R$-homological 
$d$-cycle 
$\alpha$. We say that this cycle is orientable if 
$R=\mathbb {Z}$ and 
$[\alpha ]\not =0$ in 
$H_d(X,\mathbb {Z})$. It is well known that if 
$X\subset \mathbb {P}^{n}(\mathbb {C})$ is an irreducible algebraic variety, then it is an orientable homological cycle.
The next result generalizes Theorem 3.4 in [Reference JelonekJel21].
Theorem 3.1 Let 
$X\subset \mathbb {C}^{n},Y\subset \mathbb {C}^{m}$ be complex algebraic varieties of dimension 
$d$ and let 
$h\colon X\to Y$ be a semi-algebraic and semi-bi-Lipschitz homeomorphism. Assume that the closure of 
$Graph(h)$ in 
$\mathbb {P}^{n+m}(\mathbb {C})$ is an orientable homological cycle. Then 
${\rm deg} (X)= {\rm deg}(Y)$.
Proof. Let 
$G$ be the closure of 
$ {\rm graph}(h)$ in 
$\mathbb {P}^{n+m}(\mathbb {C})$ and 
$\overline X$ be the closure of 
$X$ in 
$\mathbb {P}^{n}(\mathbb {C})$. Let 
$\alpha$ be a homological cycle of 
$G$. First we show that 
$p_*(\alpha )$ is a fundamental class of 
$\overline {X}$, where 
$p:G\to \overline {X}$ is a projection. We use the notation 
$A=\overline {X}\setminus X$ and 
$B=G\setminus graph(h)$. As 
$\overline {X}\setminus A$ is homeomorphic to 
$G\setminus B$ we have isomorphism 
$p_*:H(\overline {X},A)\cong H(G,B)$ (see [Reference LamotkeLam81]). Let us consider the following diagram.
As 
$\overline {X}$ is a projective variety we have 
$H_{2d}(\overline {X},\mathbb {Z})=\mathbb {Z}$ and 
$H_{2d-1}(A,\mathbb {Z})=0$. In particular, 
$H_{2d}(\overline {X},A,\mathbb {Z})=\mathbb {Z}$. As 
$[\alpha ]\not =0$, the diagram above shows that 
$[p_*([\alpha ])=m\beta \not =0$. Here 
$\beta$ denotes the fundamental class of 
$\overline {X}$. Changing the orientation of 
$\alpha$ if necessary, we can assume that 
$m>0$. Let 
$L^{n-d}$ be a linear space which cuts 
$X$ transversally such that 
$\#L\cap X={\rm deg}\, X$. It is easy to see that 
$|p_*([\alpha ])\cdot L|\leqslant {\rm deg}\, X$. This implies that 
$m=1$ and, consequently, 
$p_*([\alpha ])=\beta$.
Hence, we can take the orientations of 
$2d$-dimensional simplices in 
$G$ to be the same as in 
$\overline X$ (using a projection 
$p\colon G\to \overline {X})$. Now if a linear space meets 
$X$ transversally with 
$\#L\cap X={\rm deg}\, X$ then also 
$p^{-1}(L)$ meets 
$G$ transversally and it is easy to see that the intersection number is 
$+1$. Indeed, let 
$M= {\rm Ker} (\pi )$ where 
$\pi : \mathbb {C}^{n}\times \mathbb {C}^{m}\to \mathbb {C}^{n}$ is the projection. Hence, 
$\pi ^{-1}(L)=L\times M$. Fix a canonical orientation on 
$M$ given by vectors 
$v_1,\ldots,v_{2m}$, on 
$L$ given by 
$w_1,\ldots, w_{2n-2d}$ and on a 
$2d$-dimensional simplex 
$\sigma$ in 
$X$ - 
$u_1,\ldots,u_{2d}$. Let 
$\sigma '$ be a simplex in 
$G$ such that 
$\pi (\sigma ')=\sigma$ and let 
$u_1',\ldots,u_{2d}'$ be its orientation at a generic point such that 
$\pi (u_i')=u_i$. In particular, 
$u_i'=u_i+\sum _{j=1}^{2m} a_{ij} v_j$. Hence, the cycles 
$L$ and 
$X$ at a point of intersection have orientation given by 
$w_1,\ldots,w_{2n-2d}$, 
$u_1,\ldots,u_{2d}$. The cycles 
$\pi ^{-1}(L)$ and 
$G$ have orientation given by 
$v_1,\ldots,v_{2m}$, 
$w_1,\ldots, w_{2n-2d}$ , 
$u_1',\ldots,u_{2d}'$ (note that 
$\pi ^{-1}(L)=L\times M$). Now it is easy to see that the determinant of the vectors 
$v_1,\ldots,v_{2m};w_1,\ldots, w_{2n-2d};u_1',\ldots,u_{2d}'$ is equal to the product of the determinant of 
$v_1,\ldots,v_d$ and the determinant of the 
$w_1,\ldots,w_{2n-2d}; u_1,\ldots,u_{2d}$. Consequently, the sign of these two determinant is the same. This means that the orientation of the vectors 
$w_1,\ldots,w_{2n-2d}$, 
$u_1,\ldots,u_{2d}$ is the same as the orientation of 
$v_1,\ldots,v_{2m}$, 
$w_1,\ldots, w_{2n-2d}$, 
$u_1',\ldots,u_{2d}'$.
Moreover, by Lemma 2.3, the set 
$\overline {\pi ^{-1}(L)}\cap G$ has no points at infinity, because otherwise 
$\overline {L}\cap \overline {X}$ would have points at infinity (the center of the projection is disjoint from 
$G$).
This means that the topological degree of 
$G$ coincides with the algebraic degree of 
$X$. The same holds for 
$Y$. Hence, 
${\rm deg} (X)= {\rm deg} (Y)$.
In the same way (in fact, the proof is simpler, because we do not have to control the orientation) we have the following result.
Theorem 3.2 Let 
$X\subset \mathbb {R}^{n},Y\subset \mathbb {R}^{m}$ be real algebraic sets and let 
$h\colon X\to Y$ be a semi-algebraic and semi-bi-Lipschitz homeomorphism. Assume that the projective closure of the graph of 
$h$ is a 
$\mathbb {Z}/(2)$ homological cycle. Then 
$ {\rm deg} (X)= {\rm deg} (Y) \ {\rm mod}~2$.
In the sequel we need the following definition.
Definition 3.3 (See [Reference ValetteVal10])
Let 
$C$ be an 
$n$-dimensional sub-analytic subset. We say that 
$C$ is an Euler cycle, if it is locally compact and if, for a stratification of 
$C$ (and, hence, for any that refines it), the number of 
$n$-dimensional strata containing a given 
$(n-1)$-dimensional stratum in their closure is even.
In particular, if 
$C$ is compact and it is an Euler cycle, then it is 
$\mathbb {Z}/2$ homological cycle.
Remark 3.4 This definition is slightly weaker than that introduced in [Reference ParusińskiPar04].
Remark 3.5 In fact, more general statements are true. It is easy to see that our proof works if 
$h$ is semi-bi-Lipschitz at infinity. Indeed, under this assumption, we still have 
$\overline {\Gamma }\setminus \Gamma \subset \Sigma _0$, where 
$\Gamma = {\rm graph}(h)$. Moreover, there are sufficiently general linear subspaces 
$L$ which omit 
$K$ (or 
$K'$). Theorem 3.2 holds if the mapping is sub-analytic and 
$X,Y$ are sub-analytic sets with sub-analytic projective closures, which are homological cycles, e.g. for full sub-analytic cones with Euler links (at 
$0$).
4. On the global version of the Fukui–Kurdyka–Paunescu conjecture
Here we need the concept of arc-symmetric sets and arc-analytic mapping, which was developed by Kurdyka and later by Parusiński (see, e.g., [Reference KurdykaKur88, Reference ParusińskiPar04, Reference Kurdyka and ParusinskiKP08]).
Definition 4.1 [Reference ParusińskiPar04, Definition 4.2] and [Reference Kurdyka and ParusinskiKP08, Proposition 3.2]
We say that a semi-algebraic subset 
$E\subset \mathbb {P}^{N}(\mathbb {R})$ is an 
$\mathcal {AS}$ set, if for any analytic arc 
$\gamma \colon (-1,1)\to \mathbb {P}^{N}(\mathbb {R})$ such that 
$\gamma ((-1,0))\subset E$, we have 
$\gamma ((0,\epsilon ))\subset E$, for some 
$\epsilon >0$.
Remark 4.2 The arc-symmetric sets were first introduced and studied by Kurdyka [Reference KurdykaKur88]. His definition is slightly different to ours (taken from the Parusiński paper [Reference ParusińskiPar04]). In [Reference KurdykaKur88] Kurdyka considers only closed semi-algebraic subsets of 
$\mathbb {R}^{n}$ such that for every real analytic arc 
$\gamma : (-\epsilon,\epsilon )\to \mathbb {R}^{n}$ if 
$\gamma ((-\epsilon,0))\subset X$, then 
$\gamma (-\epsilon,\epsilon )\subset X$. Parusiński's 
$\mathcal {AS}$ sets are Euler cycles and they form a constructible category. Kurdyka's arc-symmetric sets are also Euler, however they do not form a constructible category.
Definition 4.3 [Reference KurdykaKur88]
Let 
$M$ and 
$N$ be analytic manifolds. Let 
$X\subset M$ and 
$Y\subset N$ be analytic subsets. We say that a mapping 
$f\colon X\to Y$ is arc-analytic if for any analytic arc 
$\gamma \colon (-1,1)\to X$, the mapping 
$f\circ \gamma$ is an analytic arc as well.
Theorem 4.4 Let 
$A\subset \mathbb {R}^{n}, B\subset \mathbb {R}^{m}$ be real algebraic 
$d$-dimensional sets and let 
$h\colon A\to B$ be a semi-algebraic and semi-bi-Lipschitz homeomorphism. If the graph of 
$h$ is an 
$\mathcal {AS}$ set, then 
${\rm deg}(A)\equiv {\rm deg}(B)\ {\rm mod}~2$.
Proof. Let 
$\Gamma ={\rm graph}(h)$. Let 
$\overline {\Gamma }$ be the closure of 
$\Gamma$ in 
$\mathbb {P}^{n+m}(\mathbb {R})$. Let 
$Z$ be the Zariski closure of 
$\overline {\Gamma }\setminus \Gamma$ in 
$\mathbb {P}^{n+m}(\mathbb {R})$. As the 
$\mathcal {AS}$ sets form a constructible category [Reference ParusińskiPar04], we find that 
$\Gamma ':=\Gamma \cup Z$ is an 
$\mathcal {AS}$ set.
Take a semi-algebraic triangulation 
$\mathcal {S}$ of 
$\Gamma '$ such that the set 
$Z$ is a union of strata. Hence, all 
$d$-dimensional cells of this stratification are contained in 
$\mathbb {R}^{n+m}$. On 
$\overline {\Gamma }$ we have the induced stratification 
$\mathcal {S}'$. Now every 
$(d-1)$-dimensional cell 
$C$ in 
$\mathcal {S}'$ comes from 
$\mathcal {S}$. As the set 
$\Gamma '$ is an 
$\mathcal {AS}$ set it is an Euler cycle, see [Reference ParusińskiPar04]. This means that 
$C$ meets an even number of 
$d$-dimensional cells. But every 
$d$-dimensional cell is contained in 
$\Gamma$. Finally 
$C$ meets an even number of 
$d$-dimensional cells in 
$\mathcal {S}'$. This means that 
$\overline {\Gamma }$ is a 
${\mathbb {Z}}/{(2)}$ homological cycle. By Theorem 3.2, 
${\rm deg}(A)\equiv {\rm deg}(B)\ {\rm mod}~2$.
Corollary 4.5 Let 
$A\subset \mathbb {R}^{n}, B\subset \mathbb {R}^{m}$ be real algebraic 
$d$-dimensional sets and let 
$h\colon A\to B$ be a polynomial (or even regular) and semi-bi-Lipschitz homeomorphism. Then 
${\rm deg}(A)\equiv {\rm deg}(B)\ {\rm mod}~2$.
Definition 4.6 Let 
$X\subset \mathbb {R}^{n}$ and 
$Y\subset \mathbb {R}^{m}$ be semi-algebraic subsets and let 
$\overline {X}$ be the closure of 
$X$ in 
$\mathbb {P}^{n}(\mathbb {R})$. We say that a mapping 
$f\colon X\to Y$ is arc-analytic at 
$\overline {X}$ if for any analytic arc 
$\gamma \colon (-1,1)\to \mathbb {P}^{n}(\mathbb {R})$ such that 
$\gamma ((-1,0)\cup (0,1))\subset X$, we have 
$f\circ \gamma |_{(-1,0)\cup (0,1)}$ extends to an analytic arc 
$\tilde \gamma \colon (-1,1)\to \mathbb {P}^{m}(\mathbb {R})$.
Remark 4.7 It is worth noting that a similar concept of arc-analyticity at infinity appeared in [Reference Kurdyka and RusekKR88].
Corollary 4.8 Let 
$A\subset \mathbb {R}^{n}, B\subset \mathbb {R}^{m}$ be real algebraic 
$d-$dimensional sets, let 
$\overline {A}$ be the closure of 
$A$ in 
$\mathbb {P}^{n}(\mathbb {R})$ and let 
$h\colon A\to B$ be a semi-algebraic and semi-bi-Lipschitz homeomorphism. Assume that 
$h$ is arc-analytic at 
$\overline {A}$. Then 
${\rm deg}(A)\equiv {\rm deg}(B)\ {\rm mod}~2$.
Remark 4.9 In fact, Corollary 4.8 holds true for a more general class of homeomorphisms, i.e. for semi-algebraic and semi-bi-Lipschitz homeomorphisms 
$h\colon A\to B$ such that the following holds: for an analytic arc 
$\gamma \colon (-1,1)\to \mathbb {P}^{n}(\mathbb {R})$ with 
$\gamma ((-1,0))\subset A$, if 
$h\circ \gamma |_{(-1,0)}$ is an analytic arc and there is an analytic arc 
$\tilde \gamma \colon (-1,1)\to \mathbb {P}^{m}(\mathbb {R})$, such that 
$\tilde \gamma |_{(-1,0)}=h\circ \gamma |_{(-1,0)}$, then 
$h\circ \gamma |_{(0,\epsilon )}=\tilde \gamma |_{(0,\epsilon )}$ for some 
$\epsilon >0$.
5. Invariance of the degree
Theorem 5.1 Let 
$X\subset \mathbb {C}^{n},Y\subset \mathbb {C}^{m}$ be complex algebraic sets and let 
$h\colon X\to Y$ be a mapping. Assume that 
$h$ is semi-bi-Lipschitz at infinity and its graph is a complex algebraic set. Then 
${\rm deg} (X)= {\rm deg\ }(Y)$.
Proof. This follows directly from Theorem 3.1.
Remark 5.2 In Theorem 5.1, if 
$h$ is bi-Lipschitz at infinity, we only have to ask that its graph is a complex analytic set (see [Reference SampaioSam21b, Theorem 3.1]).
Theorem 5.3 Let 
$X\subset \mathbb {C}^{n}$, 
$Y\subset \mathbb {C}^{m}$ be complex algebraic sets and let 
$h\colon X\to Y$ be a semi-algebraic and bi-Lipschitz homeomorphism. Assume that 
$d_{\infty }h$ is 
$\mathbb {C}$-homogeneous. Then 
${\rm deg} (X)= {\rm deg\ } (Y)$.
Proof. We can extend the mapping 
$h$ to the infinity: we simply take a path 
$a(t)=wt+o_{\infty }(t)$ which tends to the point 
$[0:w]\in \mathbb {P}^{n}(\mathbb {C})$ and by semi-linearity the limit 
$\lim _{t\to \infty } f(a(t))$ does not depend on 
$w$ but only on 
$[0:w]$. Hence, we can take 
$\overline {h}([0:w])= [0:d_{\infty }h(w)]$.
In the same way we have an induced homeomorphism 
$\bar \iota \colon \overline {X}\to G$, where 
$\overline X$ is the closure of 
$X$ in 
$\mathbb {P}^{n}(\mathbb {C})$ and 
$G$ is the closure of 
${\rm graph}(h)$ in 
$\mathbb {P}^{n+m}(\mathbb {C})$. Indeed if we take a path 
$a(t)=wt+o_{\infty }(t)$ which tends to the point 
$[0:w]\in \mathbb {P}^{n}(\mathbb {C})$, then the limit 
$\lim _{t\to \infty } (a(t), f(a(t))=[0:w:d_{\infty }h(w)]$ does not depend on 
$w$ but only on 
$[0:w]$. Hence we can take 
$\bar \iota ([0:w])=\lim _{t\to \infty } (a(t), f(a(t))=[0:w:d_{\infty }h(w)]$.
Hence, 
$G$ is an orientable homological cycle. Then the conclusion follows from Theorem 3.1.
In the same way as in Theorem 5.3 we have the following result.
Theorem 5.4 Let 
$X\subset \mathbb {R}^{n},Y\subset \mathbb {R}^{m}$ be real algebraic sets and let 
$h\colon X\to Y$ be a semi-algebraic and bi-Lipschitz homeomorphism. Assume that 
$d_{\infty }h$ is 
$\mathbb {R}$-homogeneous, i.e. if 
$v, -v\in C_{\infty }(X)$, then 
$d_{\infty }h(-v)=-d_{\infty }h(v)$. Then 
${\rm deg} (X)= {\rm deg\ } (Y) \ {\rm mod}~2$.
Definition 5.5 We say that a set 
$C \subset \mathbb {R}^{n}$ is 
$a$-invariant if it is preserved by the antipodal mapping (i.e. 
$a(C) = C$, with 
$a(x) = -x$). If 
$V$ is an 
$a$-invariant cone, then we say that 
$V$ is a full cone.
Remark 5.6 Let 
$V\subset \mathbb {R}^{n}$ be a full sub-analytic cone. Assume that a link of this cone is an Euler cycle. The closure of 
$V$ in 
$\mathbb {P}^{n}(\mathbb {R})$ is also an Euler cycle.
Now we can state Theorem 5.4 in the form which will be useful later (here we use the topological degree):
Corollary 5.7 Let 
$X\subset \mathbb {R}^{n},Y\subset \mathbb {R}^{m}$ be full sub-analytic cones with Euler links and let 
$h\colon X\to Y$ be a sub-analytic and bi-Lipschitz homeomorphism. Assume that 
$d_{\infty }h$ is 
$\mathbb {R}$-homogeneous. Then 
${\rm deg} (X)= {\rm deg\ } (Y) \ {\rm mod}~2$.
6. Invariance of the multiplicity
The next result generalizes Theorem 4.1 in [Reference JelonekJel21].
Theorem 6.1 Let 
$(X,0)\subset (\mathbb {C}^{n},0), (Y,0)\subset (\mathbb {C}^{m},0)$ be germs of complex analytic sets and let 
$h\colon (X,0)\to (Y,0)$ be a germ of homeomorphism which is also semi-bi-Lipschitz at 
$0$. Assume that the graph of 
$h$ is a complex analytic set. Then 
$m(X,0)= m(Y,0)$.
Proof. Let 
$U,V$ be small neighborhoods of 
$0$ in 
$\mathbb {C}^{n}$ and 
$\mathbb {C}^{m}$ such that the mapping 
$h:U\cap X=X'\to V\cap Y=Y'$ is defined and it is semi-bi-Lipschitz. Denote by 
$\Gamma \subset U\times V$ the graph of 
$h$. By Lemma 2.4 the projections 
$\pi _{X'}:\Gamma \to X'$ and 
$\pi _{Y'}:\Gamma \to Y'$ are semi-bi-Lipschitz homeomorphism. Let 
$\pi _1\colon \mathbb {C}^{n}\times \mathbb {C}^{m}\to \mathbb {C}^{n}$ and 
$\pi _2\colon \mathbb {C}^{n}\times \mathbb {C}^{m}\to \mathbb {C}^{m}$ be projections and denote by 
$S_1,S_2\subset \pi _\infty =\mathbb {P}^{n+m-1}(\mathbb {C})$ the centers of these projections. Denote by 
$\Lambda _0\subset \pi _\infty$ the set of directions of all secants of 
$\Gamma$ which contain 
$0$ and let 
$\Sigma _0= cl(\Lambda _0)$. As 
$\pi _1|_\Gamma =\pi _X$ and 
$\pi _2|_\Gamma =\pi _Y$ we see by Lemma 2.3 that 
$\Sigma _0 \cap S_1=\Sigma \cap S_2=\emptyset$. Let 
$C(\Gamma,0)$ denote the tangent cone of 
$\Gamma$ at 
$0$. We have 
$\overline {C(\Gamma,0)}\setminus C(\Gamma,0)\subset \Sigma _0$ and consequently 
$\overline {C(\Gamma,0)}\cap S_i=\emptyset$ for 
$i=1,2$. Now let 
$L\subset \mathbb {C}^{n}$ be a generic linear subspace of dimension 
$k={\rm codim}\, X$. Then 
$\#(L\cap X')={\rm mult}_0\, X$ and 
$L$ has no common points with 
$C(X,0)$ at infinity (we can shrink 
$U,V$ if necessary). This implies that also 
$(\overline {C(\Gamma,0)}\setminus C(\Gamma,0))\cap \langle S_1,L\rangle =\emptyset$ and, consequently, 
$\#(\langle S_1,L\rangle \cap \ \Gamma )={\rm mult}_0\, \Gamma$, where 
$\langle S_1,L\rangle$ is the linear (projective) subspace spanned by 
$L$ and 
$S_1$. However, the mapping 
$\pi _{X'}$ is a bijection, hence 
$\#(\langle S_1,L\rangle \cap \Gamma )={\rm mult}_0\, X$. In particular, 
${\rm mult}_0\, \Gamma ={\rm mult}_0\, X$. In the same way 
${\rm mult}_0\, \Gamma ={\rm mult}_0\, Y$. Hence 
${\rm mult}_0\, X={\rm mult}_0 \, Y$.
7. Proof of the Fukui–Kurdyka–Paunescu conjecture
Definition 7.1 The mapping 
$\beta _n:\mathbb {S}^{n-1}\times \mathbb {R}^{+}\to \mathbb {R}^{n}$ given by 
$\beta _n(x,r)=rx$ is called the spherical blowing-up (at the origin) of 
$\mathbb {R}^{n}$.
Note that 
$\beta _n:\mathbb {S}^{n-1}\times (0,+\infty )\to \mathbb {R}^{n}\setminus \{0\}$ is a homeomorphism with inverse 
$\beta _n^{-1}:\mathbb {R}^{n}\setminus \{0\}\to \mathbb {S}^{n-1}\times (0,+\infty )$ given by 
$\beta _n^{-1}(x)=( {x}/{\|x\|},\|x\|)$.
Definition 7.2 The strict transform of the subset 
$X$ under the spherical blowing-up 
$\beta _n$ is 
$X':=\overline {\beta _n^{-1}(X\setminus \{0\})}$ and the boundary 
$\partial X'$ of the strict transform is 
$\partial X':=X'\cap (\mathbb {S}^{n-1}\times \{0\})$.
Note that 
$\partial X'=C_X\times \{0\}$, where 
$C_X=C(X,0)\cap \mathbb {S}^{n-1}$.
Definition 7.3 Let 
$X\subset \mathbb {R}^{n}$ be a sub-analytic set such that 
$0\in \overline {X}$ is a non-isolated point. We say that 
$x\in \partial X'$ is a simple point of 
$\partial X'$ if there is an open 
$U\subset \mathbb {R}^{n+1}$ with 
$x\in U$ such that:
(a) the connected components of
$(X'\cap U)\setminus \partial X'$, say $X_1,\ldots, X_r$, are $C^{1}$ manifolds with $\dim X_i=\dim X$, $i=1,\ldots,r$;(b)
$(X_i\cup \partial X')\cap U$ are $C^{1}$ manifolds with boundary.
Let 
$ {\rm Smp}(\partial X')$ be the set of simple points of 
$\partial X'$.
Definition 7.4 Let 
$X\subset \mathbb {R}^{n}$ be a sub-analytic set such that 
$0\in X$. We define 
$k_X: {\rm Smp}(\partial X')\to \mathbb {N}$, by letting 
$k_X(x)$ be the number of connected components of the germ 
$(\beta _n^{-1}(X\setminus \{0\}),x)$.
Remark 7.5 It is clear that the function 
$k_X$ is locally constant. In fact, 
$k_X$ is constant in each connected component 
$C_j$ of 
$ {\rm Smp}(\partial X')$. Then, we define 
$k_X(C_j):=k_X(x)$ with 
$x\in C_j$.
Remark 7.6 By Theorems 2.1 and 2.2 in [Reference Pawłucki and ŁawrynowiczPaw85], 
$ {\rm Smp}(\partial X')$ is an open dense subset of the 
$(d-1)$-dimensional part of 
$\partial X'$ whenever 
$\partial X'$ is a 
$(d-1)$-dimensional subset, where 
$d=\dim X$.
Remark 7.7 The numbers 
$k_X(C_j)$ are equal to the numbers 
$n_j$ defined by Kurdyka and Raby [Reference Kurdyka and RabyKR89, p. 762].
Definition 7.8 Let 
$X\subset \mathbb {R}^{n}$ be a real analytic set. We denote by 
$C_X'$ the closure of the union of all connected components 
$C_j$ of 
$ {\rm Smp}(\partial X')$ such that 
$k_X(C_j)$ is an odd number. We call 
$C_X'$ the odd part of 
$C_X\subset \mathbb {S}^{n}$. We denote by 
$C'(X,0)$ the cone over 
$C_X'$ (respectively, 
$ {\rm Smp}(\partial X')$), i.e. 
$C'(X,0)=\{tx;t > 0$ and 
$(x,0)\in C_X'\}$.
The next proposition follows directly from the more general fact from [Reference SampaioSam21a, Theorem 4.2], however for the sake of completeness we give here a simple proof, which works in our situation.
Proposition 7.9 Let 
$(X,0)$ and 
$(Y,0)$ be germs of sub-analytic subsets of 
$\mathbb {R}^{n}$ and 
$\mathbb {R}^{m}$, respectively. If 
$h\colon (X,0)\rightarrow (Y,0)$ is bi-Lipschitz and sub-analytic, then its pseudo-derivative 
$d_0h$ transforms 
$C'(X,0)$ onto 
$C'(Y,0)$.
Proof. Let us denote by 
$\{C_j\}$ the components of 
$\mathrm {Smp}(\partial X')$ and by 
$\{\widetilde {C}_i\}$ the components of 
$\mathrm {Smp}(\partial Y')$. Let 
$\phi = \beta _m^{-1}\circ h\circ \beta _n\colon \beta _n^{-1}(X\setminus 0)\rightarrow \beta _m^{-1}(Y\setminus 0)$. We see that 
$\phi$ is a sub-analytic homeomorphism (with inverse mapping given by 
$\beta _n^{-1}\circ h^{-1}\circ \beta _m$). As 
$h$ is bi-Lipschitz and sub-analytic, 
$\phi$ extends to a sub-analytic homeomorphism from the strict transform 
$X'$ of 
$(X,0)$ onto the strict transform 
$Y'$ of 
$(Y,0)$. Let us denote that extension by 
$\Phi$. We have the restriction of 
$\Phi$ to the boundary 
$\partial X'= C_{X}\times \{0\}$ gives a homeomorphism from 
$\partial X'= C_{X}\times \{0\}$ onto 
$\partial Y'= C_{Y}\times \{0\}$ where 
$C_X=C(X,0)\cap \mathbb {S}^{n-1}$ and 
$C_Y=C(Y,0)\cap \mathbb {S}^{m-1}$, given by
\[ \Phi (v,0)= \bigg(\frac{d_0h(v)}{\|d_0h(v)\|},0\bigg). \]
In particular, 
$\Phi (\mathrm {Smp}(\partial X'))=\mathrm {Smp}(\partial Y')$.
Finally, because (up to a re-ordering of the components, if necessary), 
$\Phi (C_j) =\widetilde {C}_j$ 
$\forall j$, and 
$\Phi$ defines a homeomorphism from 
$\beta _n^{-1}(X\setminus \{0\},x)$ onto 
$\beta _m^{-1}(Y\setminus \{0\},\Phi (x))$ 
$\forall x\in \mathrm {Smp}(\partial X')$, we obtain 
$k_X(C_j)=k_Y(\widetilde {C}_j)$ 
$\forall j$, hence 
$\Phi (C'_X)=C'_Y$ and, therefore, 
$d_0h$ sends 
$C'(X,0)$ onto 
$C'(Y,0)$ as we had claimed.
Definition 7.10 Let 
$A\subset \mathbb {R}^{n}$, 
$B\subset \mathbb {R}^{d}$ and 
$C\subset A$ be sub-analytic sets and 
$\pi \colon A\to B$ be a continuous mapping. If 
$\#(\pi ^{-1}(x)\cap C)$ is constant 
${\rm mod}~2$ for a generic 
$x\in B$, we define the degree of 
$C$ with respect to 
$\pi$ to be 
${\rm deg}_{\pi }(C):=\#(\pi ^{-1}(x)\cap C)\ {\rm mod}~2$, for a generic 
$x\in B$.
Let 
$X\subset \mathbb {R}^{n}$ be a sub-analytic set. If 
${\rm deg}_{\pi }(X)$ is defined and does not depend on a generic projection 
$\pi \colon \mathbb {R}^{n}\to \mathbb {R}^{d}$, then we denote 
${\rm deg}_{\pi }(X)$ just by 
${\rm deg}_2(X)$.
Remark 7.11 If 
$X\subset \mathbb {R}^{n}$ is an algebraic set, then 
${\rm deg}_2(X)$ is defined and 
${\rm deg}_2(X)\equiv {\rm deg}(X)\ {\rm mod}~2$. Moreover, it coincides with the topological degree of 
$\overline {X}$. Similarly, if 
$X$ is sub-analytic with sub-analytic projective closure, which is a homological cycle, then 
${\rm deg}_2(X)$ coincides with the topological degree of 
$\overline {X}$.
Proposition 2.14 in [Reference SampaioSam22b] (see also [Reference ValetteVal10]) implies the following result.
Proposition 7.12 Let 
$X\subset \mathbb {R}^{n}$ be a 
$d$-dimensional real analytic set with 
$0\in X$ and 
$\pi \colon \mathbb {C}^{n}\to \mathbb {C}^{d}$ be a projection such that 
$\pi ^{-1}(0)\cap C(X_{\mathbb {C}},0)=\{0\}$. Let 
$\pi '\colon \mathbb {S}^{n}\setminus \pi ^{-1}(0)\to \mathbb {S}^{d-1}$ be the mapping given by 
$\pi '(u)= {\pi (u)}/{\|\pi (u)\|}$. Then 
${\rm deg}_{\pi '}(C_X')$ is defined and satisfies 
${\rm deg}_{\pi '}(C_X')\equiv m(X,0) \ {\rm mod}~2$.
Definition 7.13 Let 
$M$ and 
$N$ be analytic manifolds. Let 
$X\subset M$ and 
$Y\subset N$ be analytic subsets. We say that a mapping 
$f\colon X\to Y$ is arc-analytic if for any analytic arc 
$\gamma \colon (-1,1)\to X$, the mapping 
$f\circ \gamma$ is an analytic arc as well.
The next result gives the following strong version of the Fukui–Kurdyka–Paunescu (we do not require here that the germs 
$(X,0)$ and 
$(Y,0)$ have to be irreducible or that 
$h$ has to be defined on a neighborhood of 
$0\in \mathbb {R}^{n}$).
Theorem 7.14 Let 
$(X,0)\subset (\mathbb {R}^{n},0), (Y,0)\subset (\mathbb {R}^{m},0)$ be germs of real analytic sets and let 
$h\colon (X,0)\to (Y,0)$ be a sub-analytic arc-analytic bi-Lipschitz homeomorphism. Then 
$m(X,0)\equiv m(Y,0) \ {\rm mod}~2$.
Proof. By Proposition 7.12, for any projection 
$p\colon \mathbb {C}^{n}\to \mathbb {C}^{d}$ such that 
$p^{-1}(0)\cap C(X_{\mathbb {C}},0)=\{0\}$, the degree of 
$C_X'$ with respect to 
$\pi '$, 
${\rm deg}_{\pi '}(C_X')$, is well defined and 
${\rm deg}_{\pi '}(C_X')\equiv m(X,0) \ {\rm mod}~2$, where 
$\pi =p|_{\mathbb {R}^{n}}\colon \mathbb {R}^{n}\to \mathbb {R}^{d}$ and 
$\pi '\colon \mathbb {S}^{n-1}\setminus \pi ^{-1}(0)\to \mathbb {S}^{d-1}$ is given by 
$\pi '(u)= {\pi (u)}/{\|\pi (u)\|}$. In particular, 
$m(X,0)\equiv 0 \ {\rm mod}~2$ whenever 
$C_X'=\emptyset$. However, by Proposition 7.9 (or Theorem 4.2 in [Reference SampaioSam21a]), we know that 
$C_X'=\emptyset$ if and only if 
$C_{Y}'=\emptyset$. Thus, we can assume that 
$C_X'\not =\emptyset$ and, thus, 
$C_{Y}'\not =\emptyset$.
As 
$C'(X,0)$ is the cone over 
$C_X'$, the degree of 
$C'(X,0)$ with respect to 
$\pi |_{\mathbb {R}^{n}}\colon \mathbb {R}^{n} \to \mathbb {R}^{d}$, 
${\rm deg}_{\pi }(C'(X,0))$, is well defined and
\[ {\rm deg}_{\pi}(C'(X,0)) \equiv {\rm deg}_{\pi'}(C_X')\equiv m(X,0) \ {\rm mod}~2. \] It follows from Proposition 2.2 in [Reference ValetteVal10] that 
$C_X'$ is an Euler cycle.
Claim 7.14.1 We claim that 
$C_X'$ is 
$a$-invariant.
Proof of Claim 7.14.1. Let 
$v\in C_X'\cap {\rm Smp}(\partial X')$. Take an orthogonal projection 
$\pi \colon \mathbb {C}^{n}\to \pi (\mathbb {C}^{n})\cong \mathbb {C}^{d}$ such that 
$\pi (v)=v$ and 
$\pi ^{-1}(0)\cap C(X_{\mathbb {C}},0)=\{0\}$. Changing 
$\pi$ by its composition with a small rotation around the direction 
$v$, we can assume that 
$\pi$ is transversal to 
$C'(X,0)$ at 
$v$. Thus, 
$C=\pi ^{-1}((-\delta v,\delta v))\cap X$ is an analytic curve. Then, by Lemma 3.3 in [Reference MilnorMil68], there are an open neighborhood 
$U\subset \mathbb {R}^{n}$ of 
$0$ and 
$\Gamma _1,\ldots,\Gamma _r\subset \mathbb {R}^{n+1}$ such that 
$\Gamma _i\cap \Gamma _j=\{0\}$ if 
$i\not =j$ and
\[ C\cap U=\bigcup _{i=1}^{r}\Gamma_i. \]
Moreover, for each 
$i\in \{1,\ldots,r\}$, there is an analytic homeomorphism 
$\gamma _i\colon (-\varepsilon,\varepsilon )\to \Gamma _i$.
We consider the following subsets of 
$\{1,\ldots,r\}$:
\[ I=\bigg\{i;\lim_{t\to 0^{-}}\frac{\gamma_i(t)}{\|\gamma_i(t)\|}=-\lim_{t\to 0^{+}}\frac{\gamma_i(t)}{\|\gamma_i(t)\|}=\pm v\bigg\}, \]
\[ J_+=\bigg\{j;\lim_{t\to 0^{-}}\frac{\gamma_j(t)}{\|\gamma_j(t)\|}=\lim_{t\to 0^{+}}\frac{\gamma_j(t)}{\|\gamma_j(t)\|}=v\bigg\} \]and
\[ J_-=\bigg\{j;\lim_{t\to 0^{-}}\frac{\gamma_j(t)}{\|\gamma_j(t)\|}=\lim_{t\to 0^{+}}\frac{\gamma_j(t)}{\|\gamma_j(t)\|}=-v\bigg\}. \]
As 
$k_X(v)=\#I+2\#J_+$ is an odd number, then 
$I$ is not the empty set and, thus, 
$-v\in C(X,0)$. By the density of 
${\rm Smp}(\partial X')$ in 
$C(X,0)\cap \mathbb {S}^{n-1}$, we can assume that 
$-v\in {\rm Smp}(\partial X')$. Since 
$k_X(-v)=\#I+2\#J_-$, we find that 
$-v\in C_X'$. Therefore, 
$C_X'$ is 
$a$-invariant.
As 
$h$ is a bi-Lipschitz sub-analytic homeomorphism, it follows that 
$d_0h\colon C(X,0)\to C(Y,0)$ is also a sub-analytic bi-Lipschitz homeomorphism (see, e.g., [Reference Bernig and LytchakBL07] or [Reference SampaioSam16]). By Proposition 7.9, 
$\psi =d_0h|_{C'(X,0)}\colon C'(X,0)\to C'(Y,0)$ is a bi-Lipschitz homeomorphism and by the proof of Claim 7.14.1 and using the fact that 
$h$ is arc-analytic, 
$\psi$ satisfies 
$\psi (-v)=-\psi (v)$ whenever 
$v\in C'(X,0)$. Thus, 
$d_\infty \psi =\psi$ is 
$\mathbb {R}$-homogeneous and we conclude the proof by Corollary 5.7.
Finally we have to remark that we cannot expect in the Fukui–Kurdyka–Paunescu conjecture invariance of multiplicity without mod 2, as we can see in the next example.
Example 7.15 Consider 
$X=\{(x,y,z)\in \mathbb {R}^{3}; z(x^{2}+y^{2})=y^{3}\}$ and 
$Y=\{(x,y,z)\in \mathbb {R}^{3}; z(x^{4}+y^{4})=y^{5}\}$. Let 
$h\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{3},0)$ be the mapping given by
\[ h(x,y,z)=\begin{cases} \left(x,y,z-\dfrac{y^{3}}{x^{2}+y^{2}}+\dfrac{y^{5}}{x^{4}+y^{4}}\right) & \mbox{if }x^{2}+y^{2}\not =0,\\ (0,0,z) & \mbox{if }x^{2}+y^{2}=0. \end{cases} \]
Then 
$X$ and 
$Y$ are irreducible real analytic sets such that 
$m(X,0)=3$ and 
$m(Y,0)=5$. Moreover, 
$h$ is a semi-algebraic arc-analytic bi-Lipschitz homeomorphism such that 
$h(X)=Y$.
8. Fukui–Kurdyka–Paunescu conjecture in the complex case
The next result is a direct consequence of Theorem 7.14, but we present a proof which is a little easier.
Theorem 8.1 Let 
$X\subset \mathbb {C}^{n},Y\subset \mathbb {C}^{m}$ be complex analytic sets and let 
$h\colon (X,0)\to (Y,0)$ be a sub-analytic arc-analytic bi-Lipschitz homeomorphism. Then 
$m(X,0)\equiv m(Y,0)\ {\rm mod}~2$.
Proof. Let 
$\psi =d_0h\colon C(X,0)\to C(Y,0)$ be the pseudo-derivative of 
$h$ at 
$0$. Let 
$A_1,\ldots,A_r$ be the irreducible components of 
$C(X,0)$. Thus, 
$B_1=\psi (A_1),\ldots,B_r=\psi (A_r)$ are the irreducible components of 
$C(Y,0)$.
As 
$h$ is arc-analytic, 
$\Gamma _i={\rm graph}(\psi _i)$ is an 
$a$-invariant Euler cycle, where 
$\psi _i=\psi |_{A_i}$. Therefore, the closure 
$\overline {\Gamma }_i$ of 
$\Gamma _i$ in 
$\mathbb {P}^{2(n+m)}(\mathbb {R})$ is a 
$\mathbb {Z}/(2)$ homological cycle. By Theorem 3.2, 
${\rm deg} (A_i)= {\rm deg\ } (B_i) \ {\rm mod}~2$. As 
${\rm deg} (A_i)=m(A_i,0)$ and 
${\rm deg} (B_i)=m(B_i,0)$, we obtain 
$m(A_i,0)\equiv m(B_i,0)\ {\rm mod}~2$, for each 
$i\in \{1,\ldots,r\}$. Moreover, 
$m(X,0)=\sum _{i=1}^{r}k_X(A_i)m(A_i,0)$ and 
$m(Y,0)=\sum _{i=1}^{r}k_Y(B_i)m(B_i,0)$. By Proposition 1.6 in [Reference Fernandes and SampaioFS16], 
$k_X(A_i)=k_Y(B_i)$ for each 
$i\in \{1,\ldots,r\}$. Therefore, 
$m(X,0)\equiv m(Y,0)\ {\rm mod}~2$.
We have also the following version of the Fukui–Kurdyka–Paunescu conjecture in the complex case.
Theorem 8.2 Let 
$(X,0)\subset (\mathbb {C}^{n},0), (Y,0)\subset (\mathbb {C}^{m},0)$ be germs of analytic sets and let 
$h\colon (X,0)\to (Y,0)$ be a sub-analytic bi-Lipschitz homeomorphism. If 
$d_0 h$ is a 
$\mathbb {C}-$homogenous mapping, then 
$m(X,0) = m(Y,0)$.
Proof. Let 
$\psi =d_0h\colon C(X,0)\to C(Y,0)$ be the pseudo-derivative of 
$h$ at 
$0$. Let 
$A_1,\ldots,A_r$ be the irreducible components of 
$C(X,0)$. Thus, 
$B_1=\psi (A_1),\ldots,B_r=\psi (A_r)$ are the irreducible components of 
$C(Y,0)$. As the mapping 
$\psi$ is 
$\mathbb {C}$-homogenous, so is the mapping 
$d_\infty \psi =\psi$. Hence, by Theorem 5.3 we have 
${\rm deg}\, A_i={\rm deg}\, B_i$ for 
$i=1,\ldots,r$, and we obtain 
$m(A_i,0) = m(B_i,0)$, for each 
$i\in \{1,\ldots,r\}$. Moreover, 
$m(X,0)=\sum _{i=1}^{r}k_X(A_i)m(A_i,0)$ and 
$m(Y,0)=\sum _{i=1}^{r}k_Y(B_i)m(B_i,0)$. We finish as before.
Acknowledgements
We are grateful to Professor Wojciech Kucharz from Jagiellonian University at Kraków for helpful conversations. We are also grateful to the anonymous referee for his useful suggestions.
