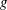1. Introduction
The transition from steady laminar to unsteady turbulent flow in ducts is one of the main research areas in fluid mechanics. For open-shear flows, the mechanisms of this transition (or routes to turbulence) are not yet perfectly known – particularly for subcritical instability – despite the major efforts made. Most shear-flow studies consider flat walls in the context of parallel or quasi-parallel flows, i.e. with slight velocity variation in the main stream flow direction (Monkewitz, Huerre & Chomaz Reference Monkewitz, Huerre and Chomaz1993). The stability of open spatially periodic shear flows has not been studied much in terms of the large main stream variation of the velocity module. There are two primary ways to study the shear-flow transition: first, the classical linear stability analysis in which we look at the minimum Reynolds number for which an infinitesimal perturbation will be exponentially amplified at an asymptotically long time (Drazin & Reid Reference Drazin and Reid2004); and second, the more recent non-modal stability approach which addresses transient growth analysis of an initial perturbation (Schmid & Henningson Reference Schmid and Henningson2001) for which the non-normal nature of the linear operator is highlighted (Chomaz Reference Chomaz2005). In this study, we consider the global 2D linear stability analysis. Then, from this modal study, weak nonlinear stability is used to determine the sub- or supercritical nature of the transition and quantify the amplitude of the most unstable modes. This paper contributes to the knowledge of the transition in the particular case of 2D symmetric wavy channel flow using the methods described above. We consider a 2D
$(x,y)$
symmetric wavy channel with a minimum height
$2H_{0}$
defined by two periodic walls:
$Hu(x)$
,
$Hl(x)$
with the same period
$L$
, and amplitude
$E$
as shown in figure 1. This geometry is found, in particular, in heat and/or mass transfer applications, in the transition regime where unsteadiness is supposed to promote heat and/or mass transfer. The determination of the critical conditions for the appearance of instability and the spatio-temporal structure of the most unstable mode is of great importance for these applications. Many similar geometries have been studied, such as wavy channel (Sobey Reference Sobey1980; Nishimura, Ohori & Kawamura Reference Nishimura, Ohori and Kawamura1983; Wang & Vanka Reference Wang and Vanka1995), grooved channel (Ghaddar et al.
Reference Ghaddar, Korczak, Mikic and Patera1986) and saw-tooth (Greiner, Chen & Wirtz Reference Greiner, Chen and Wirtz1990). All the geometries considered in these studies are 2D channels for which the laminar flow presents a core flow with quasi-parallel streamlines (for example, see figure 2 for Reynolds number
$\mathit{Re}=100$
). This quasi-parallel core flow has a main direction. Geometries for which the flow exhibits a strong change in its main direction – as in a sinuous channel – are not covered in this paper. In most cases, the transitional flow regime (often called self-sustained oscillatory flow) is characterised by a relatively low critical Reynolds number
$\mathit{Re}=O(100)$
, large spatial structure (of the order of the characteristic length of the geometry) and low temporal frequency. Most studies exclusively consider the ‘spatially periodic fully developed’ regime, and generally the spatial period of the fluctuations is supposed to be equal to the geometric period. Thus, very few studies address the verification of the validity of this hypothesis. The main questions we wish to address are as follows. Near criticality, does the ‘spatially periodic’ unsteady fully developed regime exist for this 2D hypothesis, even for a large wall amplitude? What is its spatio-temporal structure, i.e. the geometric structure of the instabilities, and are they correlated with the spatial periodicity of the channel? Otherwise, what is the nature of the first bifurcation (sub- or supercritical)?
Figure 1. Example of the geometry of a symmetric wavy channel with a straight main core flow.
Figure 2. Streamlines of the steady base flow for Nishimura geometry and different Reynolds numbers
$\mathit{Re}$
from 1 to 100 (
$M=2$
).
2. Bibliography
2.1. Experiments and visualisations
It is well established that in a 2D periodic section channel, for very low Reynolds numbers (creeping flows,
$\mathit{Re}=O(1)$
), after a few waves, the flow is 2D, steady and spatially periodic with the same period and symmetries as the geometry. These features are highlighted by visualisations made by Stephanoff, Sobey & Bellhouse (Reference Stephanoff, Sobey and Bellhouse1980), Nishimura et al. (Reference Nishimura, Ohori and Kawamura1983) and Kim (Reference Kim2001) for a wavy channel and Herman & Mayinger (Reference Herman and Mayinger1990) for a grooved channel. In particular cases, asymmetric steady flow has been shown in symmetric geometries such as that studied by Takaoka et al. (Reference Takaoka, Sano, Yamamoto and Mizushima2009). All these experiments show, beyond a first critical Reynolds number, the birth of vortices in the furrows, and these vortices grow in size with the Reynolds number. Adachi & Hasegawa (Reference Adachi and Hasegawa2006) showed that the flow is unsteady for Reynolds numbers beyond 220 and that the spatial period seems to be equal to one geometric period for some flow conditions and equal to two for other conditions. Unfortunately, they did not clarify these conditions. Gschwind & Kottke (Reference Gschwind, Kottke and Laneville2000) showed 3D structures in symmetric and asymmetric periodic channel flows, but their visualisations were made for Reynolds numbers much greater than the critical Reynolds number. Nishimura et al. (Reference Nishimura, Murakami, Arakawa and Kawamura1990) made snapshots of steady and unsteady flow regimes for large wall amplitude modulation and large aspect ratios of a wavy symmetric channel. The flow seems to be globally spatially periodic for a low Reynolds number, but beyond a critical Reynolds number of approximately 200 the flow becomes unsteady, and the visualisations made show no particular spatial structure for the sixth to eighth wave sections. The flow seems to have lost its spatial periodicity, particularly visible in the vortex zone. The visualisations made from the ninth to the eleventh modules show a period equal to two geometric periods. For an asymmetric channel flow, the visualisations made by Nishimura et al. (Reference Nishimura, Kajimoto, Tarumoto and Kawamura1986) show the interaction between adjacent waves (the sixth and seventh) at
$\mathit{Re}=350$
, and then no spatial periodicity is found. For this Reynolds number, intermittency and 3D spanwise structures are observed. In the same way, Nishimura et al. (Reference Nishimura, Bian, Matsumoto and Kunitsugu2003) have shown by visualisations that the transition occurs at a low Reynolds number (
$\mathit{Re}_{c}=170$
) in a wavy-walled tube with a large amplitude. As for a symmetric wavy plane channel, no spatial periodicity was observed at supercritical Reynolds number but an intermittent flow behaviour in the transitional regime (
$170<\mathit{Re}<200$
). Rush, Newell & Jacobi (Reference Rush, Newell and Jacobi1999) visualised the unsteady developing flow in wavy geometries. For symmetric wavy geometry, they showed that beyond a critical Reynolds number equal to 300 and a critical entry length (from the eighth wave for
$\mathit{Re}=300$
and until the third for
$\mathit{Re}=900$
), the flow presents macroscopic unsteadiness leading to high mixing. They write the following: ‘The onset of mixing is accompanied by small oscillations in the core flow, and once roller vortices form and are advected downstream, this shear layer-driven exchange of fluid results in macroscopic mixing.’ The visualisation performed does not show spatial periodic structure but rather a more complex flow in the main flow direction. The same kinds of results have been obtained by Stephanoff (Reference Stephanoff1986), but no structure analysis of the unsteady flow was performed. Kim (Reference Kim2001) present nice PIV instantaneous velocity measurements in a wavy channel. For
$\mathit{Re}=500$
, the velocity fields in the fifth and sixth modules are completely different. The symmetry appears to be clearly broken at the sixth module. No information is given about the eventual 3D structure.
In conclusion, it appears that visualisations of the unsteady laminar flow in periodic section passages do not allows us to suppose that ‘periodic fully developed laminar unsteady flow’ exists and is spatially periodic. This assumption, commonly used in linear stability analysis or numerical simulation of unsteady laminar flow (self-sustained), seems to be completely unfounded.
2.2. Numerical studies
There are many numerical studies on laminar flow in this kind of geometry, essentially for heat and mass transfer applications. Many of them consider the steady fully developed problem, as in the first model by Sobey (Reference Sobey1980). For all these studies, the fully developed steady flow is supposed to be 2D and spatially periodic with the same period as the geometry. Among the unsteady simulations, we note those of Guzman & Amon (Reference Guzman and Amon1994, Reference Guzman and Amon1996) and Amon, Guzmán & Morel (Reference Amon, Guzmán and Morel1996), who made a 2D direct numerical simulation of the laminar flow for a Nishimura symmetric wavy channel (period
$L=9.33H_{0}$
; amplitude
$E=2.33H_{0}$
). Assuming a spatially periodic developed flow with a period equal to the geometric period, they show that a chaotic flow regime is reached after a sequence of supercritical Hopf bifurcations from periodic to quasi-periodic and finally chaotic self-sustained flow regimes. With these conditions, they obtained a first critical Reynolds number of 130, at which the flow becomes unsteady and periodic in time. They noted that the perturbations look like a Tollmien–Schlichting (TS) wave. For Reynolds numbers beyond 200, the flow exhibits temporal quasi-periodic behaviour with two main frequencies and their harmonics. For
$\mathit{Re}=400$
, a frequency-locking phenomenon is obtained, and when the Reynolds number is further increased, a third frequency appears and chaos is obtained. They concluded that this scenario is similar to the Ruelle–Takens–Newhouse scenario, but all these results were made assuming a perturbation with the same period as the geometry. They completed this study with a 3D simulation, in order to determine whether the spanwise flow disturbance could affect their 2D conclusions. They used a 3D channel with a spanwise aspect ratio equal to 5.7 geometrical periods. For
$\mathit{Re}=226$
(quasi-periodic flow), they observed a spanwise standing wave resulting in an inflectional streamwise velocity profile. They noted that the frequency of the streamwise and transverse velocity is not affected by the 3D effect. They concluded the following: ‘The effects of the spanwise standing waves are localised near the sidewalls, not affecting the quasi-periodic flow regime and the transition route to chaos for the three-dimensional flows.’ Now, the question is whether these results are affected by the strong hypothesis of simple spatial periodicity.
Many other authors have made direct numerical unsteady simulations following the same hypothesis but without real validation. Wang & Vanka (Reference Wang and Vanka1995), for the same Nishimura experimental geometry, tried to validate this hypothesis by solving 2D laminar unsteady flow with three spatial periods. They concluded that ‘no differences were observed between the instantaneous flow patterns in individual furrows, thus demonstrating the adequacy of using only one wave as the computational domain’. Numerous authors referred to this paper to justify this main hypothesis (Ničeno & Nobile Reference Ničeno and Nobile2001 for example). Unfortunately, the visualisation of the velocity vectors cannot really show the perturbation, and, as we will show, the velocity amplitude of the supercritical perturbation is
$O(10^{-2})$
, so they are very difficult to observe experimentally. Cho, Kim & Shin (Reference Cho, Kim and Shin1998) studied the linear stability of two-dimensional steady flow in wavy-wall channels. They simulated the behaviour of an infinitesimal disturbance of the steady 2D solution with the use of an unsteady 3D code. They considered a periodic wall such as
$L=3H_{m}$
(where
$H_{m}$
is the half mean height of the channel) and a variable modulation amplitude
$E$
. They showed that for
$E/H_{m}$
greater than 0.26 (
$E>0.7H_{0}$
), the 2D critical Reynolds number is greater than that obtained by a 3D study. This condition was verified for the geometry studied by Nishimura and Amon. Unsteady two-dimensional studies were then numerically validated for this geometry. Again, it must be noted that all these results supposed that the spatial structure of the disturbances have the same period as the geometry.
A few authors have chosen another way, namely working on rough channels. Cabal, Szumbarski & Floryan (Reference Cabal, Szumbarski and Floryan2002) studied the linear stability of the steady flow in a wavy channel with a small wall amplitude (
$E<0.1H_{m}$
). They used Floquet theory, considering a spatial perturbation whose wavelength is totally independent of the geometric period. They showed that the first instability mode has the form of steady streamwise vortices that do not propagate (are time independent). For a fixed Reynolds number equal to 3000 and with a wall amplitude of
$E=0.02H_{m}$
, the most unstable situation corresponds to a geometric spatial period with a wavenumber of
${\it\alpha}=3$
(wavelength
$L=2.1H_{m}$
) and a spanwise wavelength corresponding to
$2.15H_{m}$
. The second mode gives rise to travelling wave instability that can be viewed as a TS wave. These results are in keeping with those of Kim (Reference Kim2001) and the visualisations of Nishimura et al. (Reference Nishimura, Murakami, Arakawa and Kawamura1990) and Gschwind & Kottke (Reference Gschwind, Kottke and Laneville2000). Floryan (Reference Floryan2003) examined the question of stability in a diverging–converging channel with very small amplitude, such as steady base flow, and found that it does not present vortices. In Cabal et al. (Reference Cabal, Szumbarski and Floryan2002), the authors considered a 3D small periodic disturbance whose wavelength is not equal to the geometric period. They found that the first instability corresponds to standing streamwise vortices and the second instability to a travelling wave. These streamwise vortex disturbances were considered to be a centrifugal instability effect. For the limiting case corresponding to a plane Poiseuille flow (zero amplitude wall modulation), they showed that the first linear instability corresponded to 2D TS travelling waves (Orszag Reference Orszag1971), while the second corresponded to streamwise steady vortices (Orszag & Patera Reference Orszag and Patera1983). The spatial structure of the TS wave was not investigated. In the following paper, Floryan (Reference Floryan2005) considered a 2D linear stability analysis for small wall amplitude by Floquet theory. They supposed a perturbation with a wavenumber of
$k={\it\delta}+n{\it\alpha}$
(where
${\it\alpha}$
is the geometric wavenumber) and noted that all the disturbances can be separated into two groups, i.e. those whose structure is related to the structure of distributed roughness (
${\it\alpha}/{\it\delta}$
rational) and those independent of the roughness (
${\it\alpha}/{\it\delta}$
irrational). They determined neutral curves for a roughness amplitude of
$E/H_{m}=8\times 10^{-3}$
and wall wavenumber varying from 0.01 to 10. They showed, for
$\mathit{Re}=6000$
and for wavenumbers
${\it\alpha}$
in the range from 0.01 to 10, that the unstable disturbance Floquet exponent
${\it\delta}$
verifies the condition
$0.97<{\it\delta}<1.05$
; they obtained the same behaviour for different Reynolds numbers. Then, they defined a ‘global’ critical Reynolds number
$\mathit{Re}_{t}$
associated with a critical roughness wavenumber
$E_{c}/H_{m}$
and a critical disturbance wavenumber
${\it\delta}_{c}$
. Comparing their results with the stability of plane Poiseuille flow, they concluded that the instability is governed by a non-normal operator, as for Poiseuille flow, and thus that the instability remains subcritical in the case of rough walls.
We will discuss these results in the following sections. We note that the most unstable disturbance wavenumber is in the range shown previously, even for grooves with rectangular or triangular shapes. Finally, these results have been validated by an experimental study (Asai & Floryan Reference Asai and Floryan2006) focused on the two-dimensional travelling wave instability excited by a loudspeaker. The critical Reynolds number and spatial growth rate were analysed, but the wavelength chosen (equal to the critical wavelength of plane Poiseuille flow) does not gives us any information on the interaction between the spatial geometric wave and the spatial structure of the unsteady flow. The same kind of analyses have been made by Selvarajan, Tulapurkara & Ram (Reference Selvarajan, Tulapurkara and Ram1999) for a channel with a large geometric period (
${\it\alpha}=2{\rm\pi}H_{m}/L=0.1$
) and a weak amplitude.
All the previous studies consider fully developed spatially periodic flows. There are very few numerical studies concerning the developing flow problem. We have analysed (Blancher, Creff & Le Quéré Reference Blancher, Creff and Le Quéré2004) the flow development in a channel such as Nishimura’s. We have shown that, beyond a critical Reynolds number (which is the critical Reynolds number obtained by linear stability analysis for the fully developed flow:
$\mathit{Re}=76$
), the entry perturbations are spatially exponentially amplified with a spatial growth rate proportional to the temporal amplification rate of the linear stability analysis as well as the symmetric or antisymmetric perturbations. The factor of proportionality is related to the group velocity of the wavepacket observed. For Reynolds numbers beyond this critical value, the convective nature of the flow instability is demonstrated. The growing wavepacket is centred on a dominant wavenumber
$k_{c}$
, which does not correspond to the geometrical period, as linear stability analysis has shown. We previously studied the temporal linear stability analysis of the fully developed 2D steady laminar flow (Blancher Reference Blancher1991; Blancher et al.
Reference Blancher, Creff, Batina and André1994) using a spectral method for the same geometry as Nishimura with a 2D perturbation hypothesis. In all cases studied, the most unstable mode corresponds to a sinuous TS wave with broken symmetry. This symmetry breaking is the sign of a supercritical Hopf bifurcation, as observed by Guzman & Amon (Reference Guzman and Amon1994). We have shown that the most unstable mode does not have the same period as the geometry. The critical Reynolds number obtained for two geometric periods (
$M=2$
, where
$M$
is the number of geometric periods of the perturbation in the linear stability analysis) is lower than the critical Reynolds number obtained for only one period. This result has been used in heat transfer simulation (Blancher, Creff & Le Quéré Reference Blancher, Creff and Le Quéré1998), showing the importance of the ‘fully developed periodicity’ hypothesis in heat transfer computations. Finally, we have shown (Blancher et al.
Reference Blancher, Creff and Le Quéré2004) that increasing the number of periods used for the linear stability analysis up to
$M=3$
and
$M=4$
gives a maximum temporal amplification rate for a disturbance characterised by
$N=7$
waves on
$M=4$
periods for
$\mathit{Re}=150$
. This most unstable mode is a sinuous mode, like a TS wave with a wavelength of
${\it\lambda}=4L/7H_{0}$
, corresponding to a wavenumber
$k=2{\rm\pi}NH_{0}/(ML)=1.17$
. Now, the question we have to ask is what happens with
$M=8,10$
or more periods? We will try to answer this question in the present study.
The paper is organised as follows. First, we present the numerical method used for the linear stability analysis, and we validate the method against some results for a straight channel (
$e=0$
). Then, we complete the previous 2D linear stability analysis considering up to
$M=10$
geometric periods for Nishimura geometry. We obtain the critical Reynolds number, the neutral curves and the dispersion relations. The spatial structure of the different modes will be discussed. The linear stability analysis is then performed for other wavy symmetric geometries. The limits of this parametric study range from a small spatial period (
$L=0.6H_{0},{\it\alpha}=10$
) – related to a rough surface – to a large one (
$L=18H_{0},{\it\alpha}=0.33$
) associated with a relative amplitude
$e=E/L$
varying from the limiting plane Poiseuille flow case (
$e=0$
) to
$e=0.5$
. Second, by a weakly nonlinear analysis using the dispersion relation, we compute the Landau coefficient
$g$
, whose real part allows us to determines the sub- or supercritical nature of the transition versus the geometrical parameters. Finally, the conclusion gives the main results obtained in this parametric linear and weakly nonlinear stability analysis of symmetric wavy channels.
3. Geometry and governing equations
As shown in figure 1, we consider a 2D
$(X,Y)$
channel with the main direction
$X$
defined by two periodic walls of shapes
$H_{U}(X)$
and
$H_{L}(X)$
with the same spatial period
$L$
(wavenumber
${\it\alpha}=2{\rm\pi}H_{0}/L$
). They are such that
$H_{U}>H_{L}$
for all
$X$
, and we suppose that there exists a straight main core flow between
$\min (H_{U})$
and
$\max (H_{L})$
. We denote
$H_{0}$
as half of the minimum height of the channel chosen as the reference length (
$(X,Y)=H_{0}(x,y)$
) as follows:
$$\begin{eqnarray}2H_{0}=\min (H_{U})-\max (H_{L}).\end{eqnarray}$$
The amplitudes of the walls are respectively
$E_{U}$
and
$E_{L}$
, defined as
$$\begin{eqnarray}E_{U}=\max (H_{U})-\min (H_{U})\quad \text{and}\quad E_{L}=\max (H_{L})-\min (H_{L}).\end{eqnarray}$$
To reduce the computational domain, we use a transformation of coordinates as follows:
$$\begin{eqnarray}{\it\xi}=\frac{2{\rm\pi}xH_{0}}{L}={\it\alpha}x=\frac{x}{{\it\lambda}}\quad \text{and}\quad {\it\eta}=\frac{y-g(x)}{h(x)},\end{eqnarray}$$
where
$g(x)=(h_{U}+h_{L})/2$
and
$h(x)=(h_{U}-h_{L})/2$
. The computational domain is then
$0\leqslant {\it\xi}\leqslant 2{\rm\pi}$
and
$-1\leqslant {\it\eta}\leqslant +1$
.
For a symmetric channel considered here,
$g(x)=0$
,
$h(x)=h_{U}(x)$
and the amplitude of the wavy walls is
$E=E_{U}=E_{L}$
. The 2D unsteady Navier–Stokes equations written in the vorticity–streamfunction formulation with the mapping coordinates (3.3) can be written as follows after some transformations:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \tilde{{\it\omega}}={\rm\Delta}^{\prime }{\it\psi},\\ \displaystyle \frac{1}{{\it\alpha}}h^{2}\tilde{{\it\omega}}_{t}+h({\it\psi}_{{\it\eta}}\tilde{{\it\omega}}_{{\it\xi}}-\displaystyle {\it\psi}_{{\it\xi}}\tilde{{\it\omega}}_{{\it\eta}})-2h^{\prime }{\it\psi}_{{\it\eta}}\tilde{{\it\omega}}=\frac{{\it\alpha}}{\mathit{Re}}{\rm\Delta}^{\prime \prime }\tilde{{\it\omega}}.\end{array}\right\}\end{eqnarray}$$
The Reynolds number is defined as
$\mathit{Re}=U_{0}H_{0}/{\it\nu}$
, with
$U_{0}$
the mean flow rate velocity at the minimum section (
$2H_{0}$
). The operators
${\rm\Delta}^{\prime }$
and
${\rm\Delta}^{\prime \prime }$
are defined in appendix A,
$\tilde{{\it\omega}}$
and
${\it\psi}$
are the modified vorticity and streamfunction as defined in Blancher et al. (Reference Blancher, Creff and Le Quéré1998, (3a)).
4. Steady base flow
All the experiments, visualisations and numerical simulations discussed in the introduction show that for a small enough Reynolds number the fully developed flow is laminar and steady. In this steady regime, the fully developed flow has all the symmetries of the geometry, in particular spatial periodicity with the same period as the geometry. For very low Reynolds numbers, we observe ‘creeping’ flows that follow the shapes of the walls. Beyond the critical Reynolds number, we observe (Nishimura et al.
Reference Nishimura, Murakami, Arakawa and Kawamura1990; Blancher Reference Blancher1991) the birth of a streamline detachment in the diverging part of the channel (
$\mathit{Re}=8$
for the Nishimura geometry). On increasing the Reynolds number, we note a growth of the vortex size, which fills the quasi-totality of the furrows and leads to the creation of a steady quasi-parallel main core flow. Further increase of the Reynolds number will lead to destabilisation of the flow. The steady streamfunction
${\it\psi}^{S}({\it\xi},{\it\eta})$
is then supposed to be
$2{\rm\pi}$
periodic, and, by use of the Galerkin method, the streamfunction is as follows:
$$\begin{eqnarray}{\it\psi}^{S}({\it\xi},{\it\eta})={\it\eta}+1/2{\it\eta}(1-{\it\eta}^{2})+\mathop{\sum }_{n=0}^{Nx}\mathop{\sum }_{j=4}^{\mathit{Ny}}[{\it\psi}_{n,j}^{S}\cos (n{\it\xi})+{\it\phi}_{n,j}^{S}\sin (n{\it\xi})]P_{j}({\it\eta}),\end{eqnarray}$$
where
$P_{j}({\it\eta})$
is a polynomial basis made with Chebyshev polynomials that verifies the homogeneous boundary conditions. To obtain better precision and avoid spurious modes, the vorticity is developed on a larger number of harmonics,
$Kx$
, depending on the shape of the geometry (
$Kx=Nx+2$
for a pure sinusoidal shape). The unknown streamfunction is expanded on the truncated basis of
$N=(2Nx+1)(\mathit{Ny}-3)$
functions, defining a basis (
$\boldsymbol{B}$
). The dimension of the basis (
$\boldsymbol{B}$
) is
$N$
and is not orthogonally related to the scalar product (Blancher Reference Blancher1991). Writing the unknown coefficients
${\it\psi}_{n,j}^{S},{\it\phi}_{n,j}^{S}$
as vector
$\boldsymbol{X}^{\boldsymbol{S}}$
on the basis
$\boldsymbol{B}$
, (3.4) can be written as follows:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{Y}^{\boldsymbol{S}}=\unicode[STIX]{x1D63F}^{\prime }\boldsymbol{X}^{\boldsymbol{S}},\\ \displaystyle \boldsymbol{N}(\boldsymbol{X}^{\boldsymbol{S}},\boldsymbol{Y}^{\boldsymbol{S}})=\frac{{\it\alpha}}{\mathit{Re}}\unicode[STIX]{x1D63F}^{\prime \prime }\boldsymbol{Y}^{\boldsymbol{S}},\end{array}\right\}\end{eqnarray}$$
where
$\boldsymbol{N}(\boldsymbol{X},\boldsymbol{Y})$
is a nonlinear quadratic operator, and
$\unicode[STIX]{x1D63F}^{\prime }$
and
$\unicode[STIX]{x1D63F}^{\prime \prime }$
are linear ones,
$\boldsymbol{Y}^{\boldsymbol{S}}$
represents the vector of the vorticity coefficients. The expressions of the operators
$\unicode[STIX]{x1D63F}^{\prime }$
and
$\unicode[STIX]{x1D63F}^{\prime \prime }$
are given in appendix A. These equations are solved by a Newton algorithm, giving the steady solution
$\boldsymbol{X}^{\boldsymbol{S}}$
. These results are illustrated in figure 2, which presents steady streamlines, and can also be found in Blancher (Reference Blancher1991).
5. Linear stability analysis
To determine the critical Reynolds number for the fully developed laminar flow and the spatio-temporal structure of the instabilities, we perform a linear temporal normal mode instability analysis. Because the velocity profiles are strongly streamwise-dependent, this stability analysis is a 2D global analysis as defined by Theofilis (Reference Theofilis2003). We consider an unsteady streamfunction
${\it\psi}^{T}({\it\xi},{\it\eta},t)$
such as
$$\begin{eqnarray}{\it\psi}^{T}({\it\xi},{\it\eta},t)={\it\psi}^{S}({\it\xi},{\it\eta})+{\it\psi}({\it\xi},{\it\eta},t),\end{eqnarray}$$
where
${\it\psi}({\it\xi},{\it\eta},t)$
is considered to be a perturbation of the steady solution
${\it\psi}^{S}({\it\xi},{\it\eta})$
. Assuming
${\it\omega}^{T}({\it\xi},{\it\eta},t)={\it\omega}^{S}({\it\xi},{\it\eta})+{\it\omega}({\it\xi},{\it\eta},t)$
and infinitesimal perturbations, after linearisation, we obtain the following linear stability equations:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \tilde{{\it\omega}}={\rm\Delta}^{\prime }{\it\psi},\\ \displaystyle \frac{1}{{\it\alpha}}h^{2}\tilde{{\it\omega}}_{t}+h({\it\psi}_{{\it\eta}}^{S}\tilde{{\it\omega}}_{{\it\xi}}-{\it\psi}_{{\it\xi}}^{S}\tilde{{\it\omega}}_{{\it\eta}})-2h^{\prime }{\it\psi}_{{\it\eta}}^{S}\tilde{{\it\omega}}+h({\it\psi}_{{\it\eta}}\tilde{{\it\omega}}_{{\it\xi}}^{S}-{\it\psi}_{{\it\xi}}\tilde{{\it\omega}}_{{\it\eta}}^{S})-2h^{\prime }{\it\psi}_{{\it\eta}}\tilde{{\it\omega}}^{S}=\frac{{\it\alpha}}{\mathit{Re}}{\rm\Delta}^{\prime \prime }\tilde{{\it\omega}}.\end{array}\right\}\end{eqnarray}$$
Looking at (5.2), we note that these linear partial differential equations have spatial periodic coefficients, and following an analysis based on spatial Floquet theory, such as that by Floryan (Reference Floryan2005), we consider an infinitesimal unsteady 2D perturbation as follows:
$$\begin{eqnarray}{\it\psi}({\it\xi},{\it\eta},t)=\text{Re}\left[\exp (\text{i}{\it\delta}{\it\xi}+{\it\zeta}t)\mathop{\sum }_{n=-\infty }^{\infty }\mathop{\sum }_{j=4}^{\infty }\;[{\it\psi}_{n,j}\exp (\text{i}n{\it\xi})+{\it\phi}_{n,j}\exp (\text{i}n{\it\xi})]P_{j}({\it\eta})\right]\!,\end{eqnarray}$$
where
${\it\delta}$
is the Floquet exponent, assumed to be real, and
${\it\zeta}={\it\sigma}+\text{i}{\it\gamma}$
is the complex pulsation; both are to be determined. The first question to answer is the domain for which we should perform this analysis. We note that the spatial structure of the perturbation is directly linked to the Floquet exponent and that the perturbation will be spatially periodic only if
${\it\delta}$
is rational. However, we do not know anything about it, so we have chosen to approach its value by a rational. Along with the assumption that the flow is two-dimensional, this is the main assumption that we have made. To determine the Floquet exponent
${\it\delta}$
, we consider the approximate rational value
${\it\delta}=P/M$
; i.e. we will search for a spatially periodic perturbation for which the period is a multiple
$M$
of the geometric period (
$ML$
) as follows:
$$\begin{eqnarray}{\it\psi}({\it\xi},{\it\eta},t)=\text{Re}\left[\exp ({\it\zeta}t)\mathop{\sum }_{m=0}^{\infty }\mathop{\sum }_{j=4}^{\infty }\;[{\it\psi}_{m,j}\cos (m{\it\xi}/M)+{\it\phi}_{m,j}\sin (m{\it\xi}/M)]P_{j}({\it\eta})\right].\end{eqnarray}$$
With truncation at orders
$Nx$
and
$\mathit{Ny}$
, with use of the vector formulation – we use the perturbation vector
$\boldsymbol{X}$
– and introducing this streamfunction hypothesis into the linearised perturbation Navier–Stokes equations (5.2), we obtain a linear eigenvalue problem as follows:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{Y}=\unicode[STIX]{x1D63F}^{\prime }\boldsymbol{X},\\ \displaystyle \frac{1}{{\it\alpha}}{\it\zeta}\unicode[STIX]{x1D643}\boldsymbol{Y}=\frac{{\it\alpha}}{\mathit{Re}}\unicode[STIX]{x1D63F}^{\prime \prime }\boldsymbol{Y}-\unicode[STIX]{x1D647}^{\boldsymbol{S}}\boldsymbol{Y}-\unicode[STIX]{x1D647}^{\ast \boldsymbol{S}}\boldsymbol{X},\end{array}\right\}\end{eqnarray}$$
where
$\unicode[STIX]{x1D643},\unicode[STIX]{x1D63F}^{\prime },\unicode[STIX]{x1D63F}^{\prime \prime },\unicode[STIX]{x1D647}^{\boldsymbol{S}},\unicode[STIX]{x1D647}^{\ast \boldsymbol{S}}$
are real linear operators (see appendix A). This is a generalised eigenvalue problem that can be formally written as follows:
$$\begin{eqnarray}{\it\zeta}\unicode[STIX]{x1D64C}\boldsymbol{X}=\unicode[STIX]{x1D647}\boldsymbol{X}\quad \text{with}~\unicode[STIX]{x1D647}=\left[\frac{{\it\alpha}}{\mathit{Re}}\unicode[STIX]{x1D63F}^{\prime \prime }\unicode[STIX]{x1D63F}^{\prime }-\unicode[STIX]{x1D647}^{\boldsymbol{S}}\unicode[STIX]{x1D63F}^{\prime }-\unicode[STIX]{x1D647}^{\ast \boldsymbol{S}}\right]\quad \text{and}\quad \unicode[STIX]{x1D64C}=\frac{1}{{\it\alpha}}\unicode[STIX]{x1D643}\unicode[STIX]{x1D63F}^{\prime }.\end{eqnarray}$$
The main question we wish to answer is thus how many geometrical periods
$M$
we should use for the linear stability analysis in order to approach the most unstable mode, i.e. is the first instability that appears in the steady periodic fully developed flow spatially periodic? Then, if yes, what is its wavelength?
First, in order to validate the model, we consider the particular case of a straight plane channel (amplitude
$E=0$
). Thus, the stability problem is that of plane Poiseuille fully developed flow. For this particular case, the stability analysis is reduced to the classical Orr–Sommerfeld problem; no Floquet exponent has to be determined, and a simple monochromatic wave (wavenumber
${\it\alpha}$
with
$M=1$
) can describe the most unstable mode. With an order development order
$\mathit{Ny}=128$
we retrieved perfectly the classical results of Orszag (Reference Orszag1971): critical Reynolds number
$\mathit{Re}_{c}=3848$
(based on the mean flow rate velocity), most unstable critical wavenumber
$k_{c}=1.0205$
associated with a symmetric streamfunction perturbation (sinuous mode) as the dispersion and marginal stability curves.
5.1. Results: linear stability, Nishimura geometry
The first geometry we have considered is that of Nishimura’s experiments,
$L=9.333H_{0}$
and
$E=2.333H_{0}$
. The spatial modulation of the main stream velocity
$u^{S}$
in the flow direction associated with the presence of a quasi-parallel core flow is the main characteristic of the base flow whose stability we want to study. As an example, figure 2 presents the steady streamlines for different Reynolds numbers. The vortex in the furrow appears from a detachment Reynolds number
$\mathit{Re}_{d}$
equal to 8. It grows with the Reynolds number and leads to a quasi-parallel main core flow for
$\mathit{Re}=100$
. It is clear that the velocity profiles present a large inflexion due to the vortex in the furrow. These results confirm the large variation of the velocity along
$x$
and the necessity of a global linear stability approach.
Figure 3. Part of the eigenvalue spectrum:
${\it\zeta}={\it\sigma}+\text{i}{\it\gamma}$
with
${\it\gamma}\geqslant 0$
for different periodicity hypotheses
$M$
for Nishimura geometry and
$\mathit{Re}=100$
.
Figure 4. The first most unstable sinuous modes (S1) for Nishimura geometry (
$M=5$
) and
$\mathit{Re}=100$
. Here,
$N$
is the number of waves observed for a particular mode.
5.1.1. Spectrum
Figure 3 shows part of the eigenvalue spectrum
${\it\zeta}={\it\sigma}+\text{i}{\it\gamma}$
with
${\it\gamma}\geqslant 0$
(the spectrum is, of course, symmetric) for
$\mathit{Re}=100$
and for different periodicity hypotheses
$M$
. The spectrum for
$M=5,7,8$
is presented. We observe the remarkable arrangement of the eigenvalues on particular branches such as those obtained for the plane channel. These curves are independent of the hypothesis
$M$
, so they are intrinsic to the geometry. We also note the existence of eigenvalues on the real axis associated with non-oscillating modes (
${\it\gamma}=0$
). It has recently been shown (Rivera-Alvarez & Ordonez Reference Rivera-Alvarez and Ordonez2014) that these modes become the most unstable modes when the geometric period increases beyond a critical value (
$L>24H_{0}$
, i.e.
${\it\alpha}<0.25$
). The results presented here are outside this range (
$0.3<{\it\alpha}<5$
). All these results were obtained with the polynomial development orders
$Nx=8M$
and
$\mathit{Ny}=32$
. This choice results from different order trials and gives a good approximation (
${<}0.1\,\%$
) of the first eigenvalue spectrum. These orders must be adjusted for other geometries or Reynolds numbers.
On increasing the number of geometric periods in hypothesis
$M$
, we expect to obtain a series of continuous or quasi-continuous curves because the flow is supposed to be open (infinite) in the
$x$
direction. The discontinuities observed on the curves associated with high frequencies are in fact due to the order of truncation of
$Nx$
. We have observed that increasing the order of
$Nx$
makes these discontinuities disappear. The first curve on the right (with some positive real eigenvalue part that indicates that these modes can be amplified) corresponds to sinuous modes (symmetric streamfunction or even polynomials, named S1 modes, as for the straight channel), as shown by the first snapshot of the perturbation streamfunction (the associated eigenmode) presented in figure 4. Similarly, the second curve (on the left) is related to varicose modes (antisymmetric streamfunction or odd polynomials, the V1 mode shown in figure 5). They are all associated with a negative eigenvalue real part (for this Reynolds number, no amplification is expected in the linear regime for these modes). The other branches on the left are alternatively associated with sinuous and varicose ‘degenerated’ modes as the modes of the plane channel. Indeed, as shown in figure 4 (obtained for
$\mathit{Re}=100$
and
$M=5$
), the first modes are symmetric with respect to the
$x$
axis; they correspond to sinuous modes. In contrast, the 12th, 14th and 15th modes are antisymmetric (varicose modes, figure 5). We note that, on one hand, the first mode is sinuous and looks like a TS wave like those observed in plane Poiseuille flow instability (Orszag Reference Orszag1971). On the other hand, this mode does not adopt the spatial period of the geometry but instead exhibits
$N=8$
wavelength for
$M=5$
periods. Table 1 gives the first 20 eigenvalues (
${\it\sigma},{\it\gamma}$
), the type S or V, the number
$N$
of waves for the modes presented in figures 4 and 5 and their reduced wavenumber
$k$
as follows:
$$\begin{eqnarray}k=(2{\rm\pi}NH_{0})/ML.\end{eqnarray}$$
Figure 5. The first most unstable varicose modes (V1) for Nishimura geometry (
$M=5$
) and
$\mathit{Re}=100$
. Here,
$N$
is the number of waves observed.
Table 1. The first 20 eigenvalues
${\it\zeta}$
classified by decreasing real part
${\it\sigma}$
for
$\mathit{Re}=100$
and
$M=5$
for Nishimura geometry.
We also observe that the spectrum presents eigenvalues on the real axis (corresponding to steady perturbation modes, the zero-frequency mode), while the plane channel spectrum does not contain these modes. This result is due to the non-monochromatic form of the perturbation streamfunction searched for. Another difference from the plane channel spectrum is the fact that – as observed in the sinuous modes – the most unstable varicose modes curve presents a maximum that grows with the Reynolds number. There is a critical Reynolds number for which the most unstable varicose mode can be amplified. However, for this Reynolds number the hypothesis of infinitesimal perturbation may no longer be valid. This question will be discussed later.
5.1.2. Dispersion relation
In figure 6(a), we have plotted the temporal amplification factor
${\it\sigma}$
(real part of the eigenvalues) of the most unstable modes versus their wavenumber
$k$
for
$\mathit{Re}=100$
for different spatial periodicities up to
$M=10$
. This figure shows that the ‘potentially’ amplified modes are all sinuous and correspond to a spectral band between
$k_{min}=0.519$
and
$k_{max}=1.642$
, and that the most unstable mode corresponding to the extremum wavenumber
$k_{ext}=1.134$
is associated with a maximum temporal amplification rate
$({\it\sigma}_{ext}=0.085)$
. All these results were obtained using a polynomial interpolation (up to degree 6) of the spectrum results for spatial periodicities from
$M=2$
to
$M=10$
. We note that for this Reynolds number, the most unstable varicose mode is not ‘potentially’ amplified. Together with these results, we have plotted (figure 6
b) the dispersion relation
${\it\gamma}=f(k)$
, i.e. the curve of the dependence of the temporal pulsation of the perturbation
${\it\gamma}$
on the spatial wavenumber
$k$
for the sinuous and varicose modes. We note that the points characterising the sinuous modes are almost aligned for the potentially amplified band
$[k_{min},k_{max}]$
. We recall that the slope of this line gives the group velocity
$v_{g}$
of the wavepacket. Therefore, for the amplified bandwidth, the dispersion relation can be written as follows:
$$\begin{eqnarray}{\it\gamma}(k)=v_{g}k-{\it\gamma}_{0};\end{eqnarray}$$
$v_{g}=0.787$
and
${\it\gamma}_{0}=0.291$
for these particular conditions. Here,
${\it\gamma}_{0}$
is positive and the phase velocity
$c(k)=v_{g}-{\it\gamma}_{0}/k$
is always smaller than the group velocity. The varicose modes present the same kind of behaviour with a smaller group velocity. We also have to note that increasing the spatial periodicity hypothesis
$M$
towards infinity results in more and more points on the dispersion curve
${\it\sigma}(k)$
. We can then ask the question of whether or not this curve is ‘continuous’. The question of the ‘continuity’ of the dispersion curves is open; we cannot be sure that on increasing the index periodicity
$M$
we will obtain the entire spectrum. It seems more likely that we will obtain an infinite (countable) number of points on this curve as the rational
$N/M$
on the real axis. This question is directly linked to the spatially periodic open flow considered, i.e. the weak confinement in the main direction
$x$
. We have repeated this calculus for different Reynolds numbers ranging from
$\mathit{Re}=50$
to
$\mathit{Re}=500$
. Looking at figure 6(a,b) we observe the superimposition of points at particular values:
$k={\it\alpha},(3/2){\it\alpha},2{\it\alpha}$
. These wavenumbers are proportional to the geometric wavenumber
${\it\alpha}$
. Therefore, the geometry characteristics are present in the spectrum through these particular values of
$k$
. Otherwise, for this geometry we note that the
$k=(3/2){\it\alpha}$
point is very close the extremum
$k_{ext}$
.
Figure 6. (a) Temporal amplification factor
${\it\sigma}$
and (b) temporal frequency
${\it\gamma}$
as a function of the wavenumber
$k$
,
$\mathit{Re}=100$
.
In figure 7(a), we have plotted the amplified wavenumber band
$[k_{min},k_{max}]$
versus the Reynolds number for the sinuous and varicose modes. We obtain curves, called neutral curves (or marginal stability curves), of the instability such as those for the plane Poiseuille flow instability (Drazin & Reid Reference Drazin and Reid2004). The sinuous mode curve clearly shows that the critical Reynolds number is approximately
$\mathit{Re}_{c}=76$
, and the most unstable mode corresponds to a sinuous travelling wave with a critical wavenumber of
$k_{c}=0.94$
. We note that the extremum wavenumber (most amplified mode) varies from
$k=0.9$
to
$k=1.3$
. These values are in agreement with the results presented by Floryan (Reference Floryan2005), who found a perturbation wavenumber between 1.02 and 1.06 for very small wall amplitude of a wavy wall using Floquet’s theory. It seems that this is a general result, and we confirm this result by computing the neutral curve for different geometries. The neutral curve for the varicose modes is similar to that for the sinuous modes with a critical Reynolds number equal to 185 and associated with a critical wavenumber equal to 0.92. Figure 7(b) shows that the dispersion relation is practically independent of the Reynolds number for values of the wavenumber in the ‘potentially’ amplified range, and the group and phase velocity are quasi-independent of the Reynolds number in the linear amplified range. We can then suppose that the wavepacket characteristics are relatively close to those of the main core flow (quasi-parallel streamlines) for all Reynolds numbers slightly larger than the critical Reynolds number. We note that the results we have obtained for a geometry with a large wall amplitude
$(E=2.333H_{0})$
are very close to those Floryan obtained for a very small amplitude (Floryan Reference Floryan2005). We now consider whether this result is always valid for other geometric parameters.
Figure 7. (a) Marginal stability curves
$k_{min},k_{max}$
and
$k_{ext}$
versus the Reynolds number and (b) dispersion curves for ‘sinuous’ (S1) and ‘varicose’ (V1) modes for the Nishimura geometry.
5.2. Results: other symmetric geometries
5.2.1. Constant geometric period
$L$
, variable amplitude
$E$
First, we have kept the same geometric period
$L=9.3333H_{0}~({\it\alpha}=0.673)$
and varied the wall amplitude
$E$
. With the same method as that previously used, for geometric amplitudes ranging from
$e=0$
to
$e=0.5$
we computed the critical Reynolds number
$\mathit{Re}_{c}$
, the critical wavenumber
$k_{c}$
and the detachment Reynolds number
$\mathit{Re}_{d}$
(beyond which detachment appears, leading to the formation of a vortex in the furrows). For all these cases, we computed the dispersion relations with
$Nx=8M$
,
$\mathit{Ny}=32$
and for
$M=5,6,7$
and 8.
Figure 8(a) presents the critical Reynolds number
$\mathit{Re}_{c}$
and the ‘detachment’ Reynolds number
$\mathit{Re}_{d}$
versus the wall amplitude ratio
$e$
.
Figure 8. (a) Critical Reynolds numbers
$\mathit{Re}_{c}$
and
$\mathit{Re}_{d}$
and (b) critical wavenumber
$k_{c}$
versus wall amplitude
$e$
for a geometric wavenumber
${\it\alpha}=0.673~(L=9.333)$
.
We observe that the two curves cross for a particular value of the wall amplitude ratio,
$e^{\ast }=0.04$
. For a small wall amplitude (
$e<e^{\ast }$
), the critical Reynolds number is smaller than the ‘detachment’ Reynolds number, and transition occurs without reverse flow. Reciprocally, for a large wall amplitude the critical Reynolds number is lower than the detachment one, and the transition occurs with reverse flow in the furrows. We expect the origin or nature of the transition to be different in each of these two cases, as supposed by Zhou et al. (Reference Zhou, Martinuzzi, Khayat, Straatman and Abu-Ramadan2003) in their analysis. This result highlights the fundamental importance of the wall amplitude
$e$
in the transition phenomenon for periodic section channels. This first conclusion has to be confirmed by the weakly nonlinear analysis we have undertaken later in this work. We note that for sufficiently large wall amplitude
$e>0.07$
, the critical Reynolds number
$\mathit{Re}_{c}$
exhibits exponential decreasing behaviour versus
$e$
,
$\mathit{Re}_{c}=17.26\,\exp (-0.99e)$
, with a correlation coefficient equal to 0.995. It is clear that the critical Reynolds number is practically inversely proportional to the wall amplitude ratio
$e$
if the ratio is not too small. We have plotted the critical wavenumber
$k_{c}$
versus the wall amplitude
$e$
in figure 8(b). It appears that the critical wavenumber depends slightly on the wall amplitude and that the curve presents two distinct regions. For
$e<0.03$
, the critical wavenumber
$k_{c}$
increases slightly with the wall amplitude (from 1 to 1.2) and obviously tends towards the value 1.0206 when
$e$
approaches zero (plane Poiseuille flow). However, for
$e>0.03$
, the critical wavenumber decreases with increase of the geometrical amplitude until values lower than one are reached (large perturbation wavelengths). We observe that the particular wall amplitude
$e^{\ast }$
coincides with the maximum perturbation wavenumber
$k_{c}$
. This particularity is not always verified, as we will show later.
Figure 9. (a) Reduced marginal curves
$k{-}k_{c}$
versus
${\it\epsilon}=(\mathit{Re}-\mathit{Re}_{c})/\mathit{Re}_{c}$
with wall amplitude
$0.03<e<0.25$
, (b) with
$0<e<0.015$
for
${\it\alpha}=0.673~(L=9.333)$
.
Figure 9(a) gives the reduced neutral (or marginal) curves
$k_{min}{-}k_{c}$
and
$k_{max}{-}k_{c}$
versus the relative Reynolds number gap
${\it\epsilon}=(\mathit{Re}-\mathit{Re}_{c})/\mathit{Re}_{c}$
for large wall amplitudes
$0.06<e<0.5$
. The curves present the same shape, particularly for very small
${\it\epsilon}$
, i.e. in the linear range. We note that the critical band wavenumber
$[k_{min},k_{max}]$
increases with the geometric amplitude for the same relative Reynolds number gap
${\it\epsilon}$
. However, we have to note that the ‘extremum’ curves
$k_{ext}{-}k_{c}$
(corresponding to the maxima of the eigenvalue real part) increase slightly with
${\it\epsilon}$
but more and more weakly. These results can easily be justified by the quasi-uniform main core flow associated with the presence of vortices in the steady flow (the critical Reynolds number is greater than the detachment Reynolds number for these amplitudes (figure 8
a)). For smaller amplitudes
$(e<0.03)$
, figure 9(b) shows the same results. In this case, we observe that the amplified wavenumber bands are different, and the ‘extremum’ curves are almost the same, but they present different behaviour in that the ‘extremum’ wavenumber decreases with
$e$
(from 1.2 to 1). The dispersion relations of pulsation
${\it\gamma}$
versus wavenumber
$k$
such as those presented in figure 9(b) have been plotted in figure 10(a) for large amplitude (
$0.03<e<0.5$
) and in figure 10(b) for small amplitude (
$e\leqslant 0.03$
) for a slightly supercritical Reynolds number. As expected, the dispersion relation has a weak dependence on the wall amplitude for this particular geometric period. These results, i.e. the slight dependence of the critical wavenumber and dispersion relation on the wall amplitude, are explained by the quasi-parallel steady base core flow due to the vortices in the furrow when they are present. From these figures, it appears that the group velocity is quasi-constant and equal to 0.78 for large wall amplitudes and decreases slightly with the wall amplitude for
$e<0.03$
. All the previous results have been obtained for a constant and relatively large wall period
$L=9.333H_{0}$
. We now consider what happens for other geometric periods.
Figure 10. (a) Dispersion relation: pulsation
${\it\gamma}$
versus wavenumber
$k$
for wall amplitude
$0.03<e<0.25$
, (b) for
$0<e<0.015$
for a geometric wavenumber
${\it\alpha}=0.673~(L=9.333)$
.
5.2.2. Effect of the period of the geometry
For these computations, we have chosen different values for the number of periods (
$M$
hypothesis) depending on
${\it\alpha}$
:
$M=3,4,5$
for
${\it\alpha}=5.385$
up to
$M=13,14,15,16$
for
${\it\alpha}=0.3366$
. As described previously, the truncation orders are equal to
$Nx=8M$
and
$\mathit{Ny}=32$
. Figure 11 presents the critical Reynolds number (
$\mathit{Re}_{c}$
) and the critical detachment Reynolds number (
$\mathit{Re}_{d}$
) versus the geometric wall amplitude
$e$
for different geometric wavenumbers
${\it\alpha}$
. We note that keeping
$e$
constant and varying
${\it\alpha}$
corresponds to varying the height
$H$
between the two walls defining the 2D channel. Bringing the walls closer increases the reduced period
$L$
(i.e. decreases the geometric wavenumber). This figure shows for each wavenumber considered the critical amplitude
$e^{\ast }$
beyond which the instability is associated with detachment for the steady flow (intersection of the curves
$\mathit{Re}_{c}$
and
$\mathit{Re}_{d}$
).
Figure 11. Critical Reynolds numbers
$\mathit{Re}_{c}$
and
$\mathit{Re}_{d}$
versus the geometric wall amplitude
$e$
with the wall wavenumber
${\it\alpha}$
as a parameter.
Figure 12. Critical wavenumber
$k_{c}$
versus geometric wavenumber
${\it\alpha}$
for different wall amplitudes
$e$
. The straight lines 1:1 and 1:2 allow the determination of the geometric wavenumber
${\it\alpha}$
for particular geometries.
Figure 12 presents the critical wavenumber
$k_{c}$
versus the geometry wavenumber
${\it\alpha}$
for different wall amplitudes
$e$
. All the curves have the same behaviour, increasing from a small wavenumber
${\it\alpha}$
(large geometric period
$L$
) to a maximum and then decreasing with increase of the geometric wavenumber (small period
$L$
) towards the straight channel critical wavenumber. From these curves, we can define particular geometries for each wall amplitude parameter
$e$
such that their wavenumber
${\it\alpha}$
is proportional to the spatial structure of the most unstable mode instability. Plotting straight lines as
$pk_{c}=q{\it\alpha}$
, we define a geometry corresponding to the
$q$
wavelength instability mode wave for
$p$
geometric periods. We name these particular types of wavy geometries
$p:q$
geometries. For example, the 1:1 geometry corresponds to a geometry for which the most unstable mode has (for the critical Reynolds number) the same wavenumber as the geometry. We must also notice that the Nishimura geometry is very close to the 3:2 particular geometry for
$e=0.25$
.
For all these particular geometries, the most unstable mode does not depend on the geometric hypothesis
$M$
. Then, we can affirm that near the onset of instability, the spatial structure of the instability will have
$p$
wavelengths corresponding to
$q$
geometric periods. Taking
$M=q$
, we can precisely determine the spatio-temporal structure of the instabilities for the critical Reynolds number, but only if the bifurcation is supercritical. Then, a weakly nonlinear stability analysis giving the Landau constant is necessary to know whether the bifurcation is sub- or supercritical. These geometries, particularly the 1:2 geometries, for which the critical wavelength instability is equal to two geometric periods, seem to be an interesting way to enhance heat and/or mass transfer in a transitional regime and will be studied further in the future.
6. Weakly nonlinear stability analysis
6.1. Introduction
The 2D global modal linear stability considering infinitesimal perturbation allows us to obtain the patterns (modes) that could be amplified. The amplitude of these modes is unknown, so in order to know the spatio-temporal structure of the flow we have to compute this amplitude taking into account the nonlinear terms in the Navier–Stokes equations. For this reason we have developed a weakly nonlinear analysis, i.e. an analysis of the amplitude of the first most unstable mode slightly beyond the critical Reynolds number. An envelope equation is then obtained by a Taylor approximation of the dispersion relations. This allows us to write a Ginzburg–Landau equation with complex coefficients depending on the geometric parameters: wall wavenumber
${\it\alpha}$
and amplitude
$e$
. In particular, the sign of the Landau constant
$g$
will give us the sub/supercritical nature of the instability.
6.2. Amplitude equations
We look at an unsteady streamfunction defined as in (5.1), solution of the full nonlinear equation (3.4). The unsteady part of the streamfunction
${\it\psi}({\it\xi},{\it\eta},t)$
, written in the eigenvector basis
${\it\psi}_{k}$
for a particular periodicity hypothesis
$M$
, is
$$\begin{eqnarray}{\it\psi}({\it\xi},{\it\eta},t)=\text{Re}\left[\mathop{\sum }_{k=1}^{K}A_{k}(t){\it\psi}_{k}({\it\xi},{\it\eta})\right],\end{eqnarray}$$
where
$A_{k}$
is the amplitude of the
$k$
th mode:
${\it\psi}_{k}({\it\xi},{\it\eta})$
(the modes are sorted by decreasing real part of the eigenvalues). These eigenvectors are denoted
$\boldsymbol{V}_{k}$
in the (
$\boldsymbol{B}$
) basis defined previously. Introducing this definition in the unsteady equation (3.4) leads to the amplitude equation:
$$\begin{eqnarray}\mathop{\sum }_{k=1}^{K}\frac{\text{d}A_{k}}{\text{d}t}\boldsymbol{V}_{k}=\mathop{\sum }_{k=1}^{K}{\it\zeta}_{k}A_{k}\boldsymbol{V}_{k}-\unicode[STIX]{x1D64C}^{-1}\boldsymbol{N}\left(\mathop{\sum }_{l=1}^{K}A_{l}\boldsymbol{V}_{l},\mathop{\sum }_{m=1}^{K}A_{m}\unicode[STIX]{x1D63F}^{\prime }\boldsymbol{V}_{m}\right).\end{eqnarray}$$
In order to obtain a system of ordinary differential equations (ODEs) we have to determine the adjoint operator
$\unicode[STIX]{x1D647}^{\ast }$
of the tangent operator
$\unicode[STIX]{x1D647}$
. For this we first define a inner product such as
$$\begin{eqnarray}\langle \boldsymbol{U};\boldsymbol{V}\rangle =\mathop{\sum }_{i}\mathop{\sum }_{j}s_{i,j}\overline{\boldsymbol{U}}_{i}\boldsymbol{V}_{j}=\overline{\boldsymbol{U}}^{t}\unicode[STIX]{x1D64E}\boldsymbol{V}.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D64E}$
is a definite and positive symmetric matrix, defined from the basis (
$\boldsymbol{B}$
) such that
$$\begin{eqnarray}s_{i,j}=\frac{1}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}\!\int _{-1}^{1}b_{l}b_{m}{\it\mu}({\it\eta})\text{d}{\it\eta}\text{d}{\it\xi}.\end{eqnarray}$$
Here,
${\it\mu}({\it\eta})$
is a weight function associated with the Chebyshev polynomials. We would like to mention that the basis (
$\boldsymbol{B}$
) is not orthogonal and, with the choice we made,
$\unicode[STIX]{x1D64E}$
is a symmetric band matrix around the diagonal with seven bands. The adjoint operator must verify
$$\begin{eqnarray}\langle \unicode[STIX]{x1D647}^{\ast }\boldsymbol{V}_{k};\boldsymbol{V}_{n}\rangle =\langle \boldsymbol{V}_{k};\unicode[STIX]{x1D647}\boldsymbol{V}_{n}\rangle ;\end{eqnarray}$$
then
$$\begin{eqnarray}(\overline{\boldsymbol{V}_{k}})^{t}\unicode[STIX]{x1D64E}\unicode[STIX]{x1D647}\boldsymbol{V}_{n}=(\overline{\unicode[STIX]{x1D647}^{\ast }\boldsymbol{V}_{k}})^{t}\unicode[STIX]{x1D64E}\boldsymbol{V}_{n}=(\overline{\boldsymbol{V}_{k}})^{t}\overline{\unicode[STIX]{x1D647}^{\ast }}^{t}\unicode[STIX]{x1D64E}\boldsymbol{V}_{n}.\end{eqnarray}$$
This relation has to be verified for all the eigenvectors, leading to
$(\overline{\unicode[STIX]{x1D647}^{\ast }})^{t}\unicode[STIX]{x1D64E}=\unicode[STIX]{x1D64E}\unicode[STIX]{x1D647}$
, and finally the adjoint matrix is
$$\begin{eqnarray}\unicode[STIX]{x1D647}^{\ast }=\unicode[STIX]{x1D64E}^{-1}\unicode[STIX]{x1D647}^{t}\unicode[STIX]{x1D64E},\end{eqnarray}$$
since the matrix
$\unicode[STIX]{x1D64E}$
is real and symmetric and
$\unicode[STIX]{x1D647}$
and
$\unicode[STIX]{x1D647}^{\ast }$
are real.
We have noted that the adjoint eigenmode associated with the most unstable sinuous (S1) mode has the same symmetry and spatial periodicity as the (S1) mode but with a negative phase velocity, i.e. a wave travelling upstream.
Let us denote by
$\boldsymbol{V}_{k}^{\ast }$
the eigenvector of
$\unicode[STIX]{x1D647}^{\ast }$
associated with the eigenvalue
${\it\zeta}_{k}$
. The initial nonlinear problem (3.4) can then be written as
$$\begin{eqnarray}{\it\zeta}\unicode[STIX]{x1D64C}\boldsymbol{X}=\unicode[STIX]{x1D647}\boldsymbol{X}-\boldsymbol{N}(\boldsymbol{X},\unicode[STIX]{x1D63F}^{\prime }\boldsymbol{X}).\end{eqnarray}$$
Projecting (6.2) on
$\boldsymbol{V}_{k}^{\ast }$
, and using the properties of the adjoint operator, we obtain a system of
$K$
ODEs:
$$\begin{eqnarray}\frac{\text{d}A_{k}}{\text{d}t}={\it\zeta}_{k}A_{k}-\mathop{\sum }_{i=1}^{K}\mathop{\sum }_{j=1}^{K}G_{k;i,j}A_{i}A_{j}\quad (k=1,K),\end{eqnarray}$$
with
$$\begin{eqnarray}G_{k;i,j}=\langle \unicode[STIX]{x1D64C}^{-1}\boldsymbol{N}(\boldsymbol{V}_{i},\unicode[STIX]{x1D63F}^{\prime }\boldsymbol{V}_{j});\boldsymbol{V}_{k}^{\ast }\rangle /\langle \boldsymbol{V}_{k};\boldsymbol{V}_{k}^{\ast }\rangle .\end{eqnarray}$$
If we look at the coefficient
$G_{k;i,j}$
we observe that it represents the nonlinearity of the Navier–Stokes equations, i.e. the effect of resonance between modes. The modes (i.e. the eigenvectors) are characterised by their geometrical properties: their symmetry versus the
$x$
axis (sinuous or varicose modes) and the wavenumber
$N$
on
$M$
geometric periods. The symmetries of the most unstable modes give interesting results for the nonlinear effect on mode amplitudes; for example, if
$\boldsymbol{V}^{k}$
is a sinuous mode (a symmetric streamfunction, i.e. an even function of
${\it\eta}$
), then the coefficient
$G_{k;i,j}$
will be different from zero if and only if the nonlinear term
$\boldsymbol{N}(\boldsymbol{V}^{i},\unicode[STIX]{x1D63F}^{\prime }\boldsymbol{V}^{j})$
is symmetric. Looking at the operator
$\unicode[STIX]{x1D63F}^{\prime }$
in the case of a symmetric channel, we note that it will be symmetric only when
$\boldsymbol{V}^{i}$
and
$\boldsymbol{V}^{j}$
have opposed symmetries. Then, a symmetric mode cannot be resonant with itself for symmetric geometries; only symmetric (sinuous) and antisymmetric (varicose) modes can be resonant. In particular, the most unstable mode (always sinuous) will be resonant only with an antisymmetric (varicose) mode. If
$\boldsymbol{V}^{k}$
is a varicose mode (an antisymmetric mode, i.e. an odd function of
${\it\eta}$
), then the coefficient
$G_{k;i,j}$
will be different from zero if and only if
$\boldsymbol{N}(\boldsymbol{V}^{i},\unicode[STIX]{x1D63F}^{\prime }\boldsymbol{V}^{j})$
is antisymmetric. Therefore, if the geometry is symmetric, it is necessary that
$\boldsymbol{V}^{i}$
and
$\boldsymbol{V}^{j}$
have the same symmetry. Then, a varicose mode can be resonant with itself, and its amplitude will depend on the amplitude of the coupling between varicose/varicose modes or sinuous/sinuous ones.
In the same way, looking at the symmetry of the shape of the geometry
$h(x)$
, we observe two kinds of modes: the ‘even modes’, such that the number of waves
$N$
is even, and the ‘odd modes’, such that the number
$N$
is odd. We named this property the ‘parity’ of the modes, so by a simple symmetry analysis, we can conclude the following.
-
(i) If
$h(x)$
is a simple cosine (as in the Nishimura geometry), we note that if the mode
$\boldsymbol{V}^{k}$
corresponds to an ‘odd mode’, the resonant modes
$\boldsymbol{V}^{i}$
and
$\boldsymbol{V}^{j}$
will be of opposite ‘parity’. -
(ii) On the contrary, if the mode
$\boldsymbol{V}^{k}$
is an ‘even mode’, then the resonance will be between modes with the same ‘parity’.
A complete study and resolution of these ODEs will be made in another study.
6.3. Weakly nonlinear analysis: the Ginzburg–Landau equation
6.3.1. Landau equation
In this weakly nonlinear study, following Manneville (Reference Manneville1990) and Newell, Passot & Lega (Reference Newell, Passot and Lega1993), the first
$K$
modes in (6.9) are separated into two groups: active modes (a) (the most unstable ones) and passive modes
$(p)$
. Using classical vocabulary, passive modes are ‘slaved’ by active ones and then, using the formalism developed by Plaut (Reference Plaut2008), we are looking for a weakly nonlinear solution such as
$$\begin{eqnarray}\boldsymbol{V}^{(\text{a})}=\mathop{\sum }_{k}A_{k}(t)\boldsymbol{V}_{k}^{(\text{a})}\quad \text{and}\quad \boldsymbol{V}^{(p)}=\mathop{\sum }_{k}A_{k}(t)\boldsymbol{V}_{k}^{(p)}.\end{eqnarray}$$
Using the symmetries of active modes (Plaut Reference Plaut2008, see chapter 2.2), the passive modes are obtained by
$$\begin{eqnarray}\boldsymbol{V}^{(p)}=\unicode[STIX]{x1D647}^{-1}\boldsymbol{N}(\boldsymbol{V}^{(\text{a})},\unicode[STIX]{x1D63F}^{\prime }\boldsymbol{V}^{(\text{a})}).\end{eqnarray}$$
If the most unstable mode is sufficiently isolated, the amplitude equation of the most active unstable mode
$A_{1}$
is then the classical Landau equation:
$$\begin{eqnarray}\frac{\text{d}A_{1}}{\text{d}t}={\it\zeta}_{1}A_{1}-g|A_{1}|^{2}A_{1},\end{eqnarray}$$
with
$g$
the Landau constant as computed by Plaut (Reference Plaut2008),
$$\begin{eqnarray}g=\langle \boldsymbol{N}(\overline{\boldsymbol{V}_{1}}|\boldsymbol{U}_{1})+\boldsymbol{N}(\boldsymbol{V}_{1}|\boldsymbol{U}_{0});\boldsymbol{V}_{1}^{\ast }\rangle ,\end{eqnarray}$$
where
$$\begin{eqnarray}\boldsymbol{U}_{1}=-(\unicode[STIX]{x1D647}+2{\rm\pi}{\it\gamma}_{c}\unicode[STIX]{x1D64C})^{-1}\boldsymbol{N}(\boldsymbol{V}_{1},\boldsymbol{V}_{1})\end{eqnarray}$$
and
$$\begin{eqnarray}\boldsymbol{U}_{0}=-(\unicode[STIX]{x1D647}+2{\rm\pi}{\it\gamma}_{c}\unicode[STIX]{x1D64C})^{-1}\boldsymbol{N}(\boldsymbol{V}_{1}|\overline{\boldsymbol{V}_{1}}).\end{eqnarray}$$
The sign of the real part of the Landau constant
$g$
will give us the nature of the bifurcation (subcritical if
$\text{Re}(g)<0$
or supercritical if
$\text{Re}(g)>0$
). Obviously, all these parameters depend on the periodicity hypothesis
$M$
chosen.
6.3.2. Envelope equation, the complex Ginzburg–Landau equation
We have shown that in most cases the spectrum presents different branches associated with particular modes (sinuous, varicose). For ordinary symmetric geometry, the most unstable critical mode needs a large enough geometric periodicity hypothesis
$M$
to obtain a good approximation for the determination of the critical wavenumber
$k_{c}$
and critical Reynolds number
$\mathit{Re}_{c}$
. In the hypothesis of a continuous branch of the dispersion relation we have made implicitly, we can use the analysis developed by Manneville (Reference Manneville1990) and Plaut (Reference Plaut2008) on dynamical dissipative systems with a view to obtaining an envelope equation as the complex amplitude Ginzburg–Landau equation:
$$\begin{eqnarray}{\it\tau}\left(\frac{\partial A_{1}}{\partial t}+v_{g}\frac{\partial A_{1}}{\partial x}\right)={\it\epsilon}(1+\text{i}s)A_{1}+{\it\chi}^{2}(1+\text{i}b)\frac{\partial ^{2}A_{1}}{\partial x^{2}}-{\it\Gamma}(1+\text{i}c)|A_{1}^{2}|A_{1},\end{eqnarray}$$
where
$A_{1}(x,t)$
is the complex amplitude of the most unstable mode
$\boldsymbol{V}_{1}$
at criticality:
$(\mathit{Re}_{c},{\it\gamma}_{c},k_{c})$
.
Here,
${\it\epsilon}=(\mathit{Re}-\mathit{Re}_{c})/(\mathit{Re}_{c})$
represents the deviation from the criticality,
${\it\tau}=1/(\mathit{Re}_{c}\partial {\it\sigma}/\partial \mathit{Re}|_{c})$
is the characteristic time,
${\it\chi}^{2}=-{\it\tau}(\partial ^{2}{\it\sigma})/(\partial k^{2})|_{c}/2$
is the characteristic length,
$v_{g}=\partial {\it\gamma}/\partial k|_{c}$
is the group velocity,
$s=\mathit{Re}_{c}\partial {\it\gamma}/\partial \mathit{Re}|_{c}$
and
$b=(\partial ^{2}{\it\gamma})/\partial k^{2}|_{c}$
are two constants, and
${\it\Gamma}(1+\text{i}c)={\it\tau}g$
is the Landau constant, supposed to be identical to the previous discrete problem. The values of these parameters are given in the next section for the Nishimura geometry.
6.4. Results
All the results presented hereafter concern the Nishimura geometry (see § 5.1).
Figure 13 presents the adjoint eigenmodes associated with the most unstable mode for the
$M=2$
hypothesis. We observe that the adjoint eigenmodes associated with the most unstable mode have the same spatio-temporal structure (same symmetries and spatial periodicity) as the direct modes, but it is highly stretched, which characterises a travelling wave going upstream, as is well known.
Figure 13. Instantaneous streamlines of the adjoint streamfunction associated with the most unstable mode for the Nishimura geometry.
Table 2 gives the Landau coefficients we have obtained for different periodicity hypotheses (
$\mathit{Re}=\mathit{Re}_{c}$
). From these results we can determine the Landau constant by linear approximation for the critical wavenumber
$k_{c}=0.946$
, giving
$g=36.6+29.4\text{i}$
. The real part of the Landau coefficient
$g$
is clearly positive, then the first transition must be supercritical for the Nishimura geometry, which is an argument in favour of the 2D perturbation hypothesis.
Table 2. The real part of the ‘Landau coefficient’
$g$
versus the periodicity hypothesis
$M$
.Here,
$N$
is the number of waves for
$M$
geometric periods and
$k$
is the associated critical wavenumber. The Reynolds number is the critical Reynolds number
$\mathit{Re}_{c}=76$
.
We have repeated the same calculus for the different geometries considered, and figure 14 shows the real part of the Landau coefficient versus the geometrical parameters. It appears that there is a critical amplitude
$e_{c}$
for which the bifurcation would undergo a transition from subcritical (
$\text{Re}(g)<0$
) to supercritical (
$\text{Re}(g)>0$
). We have to note that at first order, looking at the Landau amplitude equation, the module of the asymptotic amplitude
$|A_{1}|$
of the most unstable mode will be such that
$$\begin{eqnarray}\frac{\text{d}|A_{1}|}{\text{d}t}=0,\quad \text{then}~|A_{1}|=\sqrt{\frac{{\it\epsilon}}{{\it\tau}\text{Re}(g)}}.\end{eqnarray}$$
Figure 14. Real part of the Landau coefficient
$g$
versus the geometric amplitude
$e$
and wavenumber
${\it\alpha}$
, for the critical Reynolds number.
It appears clearly that the module of the amplitude is inversely proportional to the real part of the Landau constant. Then, we can suppose that we will have a large amplitude
$|A_{1}|$
for a geometric amplitude
$e$
slightly larger than the critical one
$e_{c}$
.
Figure 15 gives this critical amplitude
$e_{c}$
versus the geometry’s wavenumber
${\it\alpha}$
. On the same figure we have also plotted the critical detachment amplitude for steady base flow (amplitude for which there exists a reverse flow for the critical Reynolds number). We note that the two curves intersect at
${\it\alpha}=0.8$
and
$e=0.03$
, and then four zones are highlighted: zone I, supercritical 2D transition with reverse flow; zone II, supercritical transition without reverse flow; zone III, subcritical transition with reverse flow; and zone IV, subcritical transition without reverse flow, as Poiseuille flow (
$e=0$
). Although these results are valid only in the 2D hypothesis, we would expect that they must have some impact on the ongoing 3D analysis. We expect also to show that for the supercritical zones, we would observe a first 2D Hopf bifurcation associated with a sinuous TS wave perturbation. However, for the subcritical zones, we expect a 3D subcritical first bifurcation as for Poiseuille flow (viscous instability?), linked to a large temporal growth in the transient regime as developed by Schmid & Henningson (Reference Schmid and Henningson2001); this non-modal analysis will be undertaken elsewhere. In the case of steady reverse flow and subcritical bifurcation or steady quasi-parallel flow without reverse flow but with a supercritical bifurcation, the nature of the transition is currently unknown. A 3D stability analysis is then essential with a view to understanding the transition.
Figure 15. Critical geometric amplitudes
$e_{c}$
(onset of detachment and the sub- to supercritical transition) versus the wavenumber of the geometry
${\it\alpha}$
. The different zones correspond to zone I, steady reverse flow and supercritical bifurcation; zone II, no reverse steady flow and supercritical bifurcation; zone III, reverse steady flow with a subcritical bifurcation; zone IV, no reverse steady flow with a subcritical bifurcation.
As an example, table 3 presents the coefficients of the Ginzburg–Landau equation (6.17) we have obtained for the Nishimura geometry. A complete study of this equation versus the geometrical parameters is ongoing.
Table 3. Parameters of the Ginzburg–Landau equation (6.17) for the Nishimura geometry.
7. Conclusions
In conclusion, under the 2D hypothesis and for a ‘periodic fully developed’ steady base flow, for an ordinary symmetric wavy geometry, it does not seem that the 2D transition has a spatially periodic structure. In all studied cases, the first stage of the transition is characterised by a breaking of the symmetry along with a breaking of the periodical invariance in the main stream direction. The most unstable mode is always a sinuous mode (symmetric streamfunction) associated with a Hopf bifurcation. In all the cases studied, the spatial structure of the 2D most unstable mode is not ‘tuned’ with the geometry. Thus, within the limit of this 2D linear stability analysis and slightly beyond the critical Reynolds number, we expect the spatial structure of the unsteady flow – after a developing length – to exhibit a quasi-periodic spatio-temporal structure. It appears that the amplitude of the geometry defined by
$e=E/L$
plays a leading role in the transition, with the critical Reynolds number varying as
$\mathit{Re}^{-1}$
for sufficiently large amplitudes. Otherwise, the critical wavenumber
$k_{c}$
varies between 0.8 and 1.5 for geometrical wavenumbers
${\it\alpha}$
ranging from 0.3 to 10. This result shows that the most unstable perturbation wave is affected by the amplitude of the geometry. For a fixed spatial periodicity, small geometric amplitudes are associated with smaller perturbation wavenumbers than for the reference straight channel with a TS wave. Reciprocally higher geometric amplitudes are associated with larger wavelength perturbations. We also observed that the most unstable varicose mode has a wavelength that is always equal to a multiple of the geometric period. Thus, the varicose modes are naturally ‘tuned’ to the geometry characteristics, and in most cases the associated eigenvector is a steady mode (
${\it\gamma}=0$
).
For particular geometries, we expect to have near criticality a 2D spatio-temporal periodic instability that is spatially proportional to the geometric period. These particular geometries will be studied in a subsequent work. The method described here can be applied to other symmetric geometries such as grooved channels, triangular tooth channels, etc. as well as non-symmetric geometries. The only condition is that a channel with a main straight stream flow modulated by periodic walls must be considered, and of course the existence of a supercritical Hopf bifurcation.
Subsequently, a weakly nonlinear analysis based on these modal results allows us to determine the super- or subcritical nature of the transition and the associated complex Ginzburg–Landau equation. It is shown that for each geometric period, there is a critical geometrical amplitude beyond which the transition is supercritical (possibly 2D), and reciprocally below this value, the transition could be subcritical (then possibly 3D). The existence of a reverse steady flow is not related to the super- or subcritical nature of the transition. A discussion around the main assumption considered in this paper, i.e. the existence of a 2D and fully developed base flow, is undertaken. These 2D conclusions have to be verified by a 3D modal and non-modal stability analysis, which is ongoing.
Acknowledgements
We would like to express our sincere gratitude to Patrick L. Quéré and E. Plaut for their valuable advice and interesting discussions. The authors would also like to thank the anonymous reviewers for their relevant comments and suggestions to improve the quality of the paper.
Appendix A
The operators that appear in the linear eigenvalue problem (5.5) are given in this appendix.
Operator
$\unicode[STIX]{x1D63F}^{\prime }$
:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\prime }(\,)=h^{2}(\,)_{{\it\xi}{\it\xi}}+a({\it\xi},{\it\eta})(\,)_{{\it\xi},{\it\eta}}+b({\it\xi},{\it\eta})(\,)_{{\it\eta},{\it\eta}}+c({\it\xi},{\it\eta})(\,)_{{\it\eta}},\end{eqnarray}$$
with
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}a({\it\xi},{\it\eta})=-2hg^{\prime }-(h^{2})^{\prime }{\it\eta}\\ b({\it\xi},{\it\eta})=1/{\it\alpha}^{2}+g^{\prime 2}+2h^{\prime }g^{\prime }{\it\eta}+h^{\prime 2}{\it\eta}^{2}\\ c({\it\xi},{\it\eta})=2h^{\prime }g^{\prime }-hg^{\prime \prime }-((h^{2})^{\prime \prime }/2-3h^{\prime 2}){\it\eta}\end{array}\right\}.\end{eqnarray}$$
Operator
$\unicode[STIX]{x1D63F}^{\prime \prime }$
:
$$\begin{eqnarray}\unicode[STIX]{x1D63F}^{\prime \prime }(\,)=h^{2}(\,)_{{\it\xi}{\it\xi}}+a({\it\xi},{\it\eta})(\,)_{{\it\xi},{\it\eta}}+b({\it\xi},{\it\eta})(\,)_{{\it\eta},{\it\eta}}+c^{\ast }({\it\xi},{\it\eta})(\,)_{{\it\eta}}+d({\it\xi},{\it\eta})(\,)_{{\it\xi}}+e({\it\xi},{\it\eta})f,\end{eqnarray}$$
with
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}c^{\ast }({\it\xi},{\it\eta})=c({\it\xi},{\it\eta})+4h^{\prime }g^{\prime }+4h^{\prime 2}{\it\eta}\\ d({\it\xi},{\it\eta})=-2(h^{2})^{\prime }\\ e({\it\xi},{\it\eta})=-2(hh^{\prime \prime }-3h^{\prime 2})\end{array}\right\}.\end{eqnarray}$$
The other operators
$\unicode[STIX]{x1D647}^{\boldsymbol{S}},\unicode[STIX]{x1D647}^{\ast \boldsymbol{S}}$
and
$\unicode[STIX]{x1D643}$
are
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D647}^{\boldsymbol{S}}(\,)=h({\it\psi}_{{\it\eta}}^{S}(\,)_{{\it\xi}}-{\it\psi}_{{\it\xi}}^{S}(\,)_{{\it\eta}})-2h^{\prime }{\it\psi}_{{\it\eta}}^{S}(\,)\\ \unicode[STIX]{x1D647}^{\ast \boldsymbol{S}}(\,)=h(\tilde{{\it\omega}}_{{\it\xi}}^{S}(\,)_{{\it\eta}}-\tilde{{\it\omega}}_{{\it\eta}}^{S}(\,)_{{\it\xi}})-2h^{\prime }\tilde{{\it\omega}}^{S}(\,)_{{\it\eta}}\\ \unicode[STIX]{x1D643}(\,)=h^{2}(\,)\end{array}\right\}.\end{eqnarray}$$
