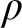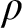2 The variety of proof systems

Mathematical logicians and proof-theorists have invented a wide array of proof systems, deploying a variety of different formats for the presentation of proofs.

Let us at the outset name two proof-formats that ought to be avoided. First there are the original Frege–Hilbert systems, which generate conclusions from premises in highly artificial ways, employing many complex axiom-schemes and highly restricted rules of inference. They have featured prominently in the literature of metalogic, going back to Gödel’s proof of the completeness of first-order logic (see Gödel [Reference Gödel13]). Proofs in these systems, however, simply fail to do justice to the actual patterns of (correct) deductive reasoning undertaken by expert mathematicians. This remains true even if the Frege–Hilbert formal proofs, which are finite sequences of formula occurrences, are re-arranged into the tree-like arrays that make vivid the partial ordering of rule-applications involved in them.Footnote ¹² The second kind of proof-format that ought to be avoided is Jeffrey’s ‘tree method’ of Jeffrey [Reference Jeffrey18]. While this is an accessible format enabling proof-search with simple deductive examples for the beginner (in Classical Logic), Jeffrey’s ‘tree proofs’ bear little structural affinity with the lines of reasoning typically involved in mathematical proofs. It is also impossible, with the rules for tree proofs, to distinguish important subsystems of Classical Logic, such as Intuitionistic Logic. It would take one too far afield to make this objection dispositively stick; the reader is advised simply to take this dismissal on trust. As an exercise in order to be persuaded, the reader could sympathetically inquire whether the task of proving $\psi $ from premises $\varphi _1,\ldots ,\varphi _n$ always takes the form of chasing contradictions along all branches of a tree that results from unraveling the new set of assumptions $\varphi _1,\ldots ,\varphi _n, \neg \psi $ (the tree’s ‘trunk’), in (ultimately fruitless but thorough) search for a way of satisfying them on some branch progressing from that trunk. The constructivist would dismiss such a suggestion out of hand. The classicist will dismiss it after being discombobulated in the task of, say, formalizing as such a tree proof Cantor’s simple argument establishing that every set has strictly more subsets than members. The resulting Jeffrey tree bears no structural resemblance at all to the real underlying tree of sentence occurrences that is involved in Cantor’s deductive reasoning. The latter tree really needs to be regimented, instead, as a Gentzen-style natural deduction (for general discussion of which, see below). This remark applies quite generally, to all informal mathematical proofs. Cantor’s informal proof is here taken as just one tractable example by means of which one can convince oneself of the general point here being made. In so far as mathematical proofs are ‘tree-like’, they are to be regimented as Gentzenian trees, not Jeffrey trees.

Gentzen’s work (Gentzen [Reference Gentzen10, Reference Gentzen11]) on systems of natural deduction, and their associated sequent calculi, was the great advance in this regard. At long last expert mathematical reasoning could be regimented, or formalized, as natural deductions. These would merely fill in suppressed details within informal but rigorous proofs, while preserving the essential ‘lines of argument’ within them. Natural deductions, or proofs, are tree-like arrays of sentence occurrences, whose branchings arise from applications of primitive rules of inference. Premises of the proof occupy leaf-nodes; the conclusion is at the root.

That the contrast between Gentzen’s system of natural deduction and the earlier, much more artificial Frege–Hilbert systems reflects favorably on the former appears to be tacitly conceded at p. 25 in Hilbert and Ackermann [Reference Hilbert and Ackermann15]—the second, ‘improved’ (verbesserte) edition of Grundzüge der theoretischen Logik (whose first edition had appeared in 1928, before Gentzen’s breakthrough work). In their second edition Hilbert and Ackermann—the former, in context and to his great credit, magnanimously—wroteFootnote ¹³

Note how in the final clause of this quote Hilbert and Ackermann are commending Gentzen’s regimentation of the deductive method of making assumptions ‘for the sake of argument’ and subsequently discharging them when applying a particular rule. Examples of such rules would be the now familiar $\neg $ -I (Constructive Reductio), $\rightarrow $ -I (Conditional Proof), $\vee $ -E (Proof by Cases), $\exists $ -E (Existential Elimination), and CR (Classical Reductio). That they involve potential discharge of assumptions is ‘built into’ their very nature as rules of inference. Moreover, if one replaces the usual serial elimination rules for $\wedge $ , $\rightarrow $ , and $\forall $ :

$$ \begin{align*} {\begin{array}{c} \underline{\varphi\wedge\psi}\\ \varphi \end{array}} {\begin{array}{c} \underline{\varphi\wedge\psi}\\ \psi \end{array}} \kern3em {\begin{array}{c} \underline{\varphi\rightarrow\psi\kern1.5em\varphi}\\ \psi \end{array}} \kern3em {\begin{array}{c} \underline{\forall x\psi}\\ \psi^x_t \end{array}} \end{align*} $$

with their parallelized forms, then one has a new deductive environment calling for the use of dischargeable assumptions:

(2) $$ \begin{equation*}\kern-2em{\begin{array}{l}\kern.49in_{(i)}\underline{\kern.15in}_{_\Box}\!\underline{\kern.15in}_{(i)}\\\;\kern.6in\underbrace{ \varphi \; ,\; \psi }\\\kern.78in\vdots\\\kern1em\underline{ \varphi \wedge \psi \kern2em \theta \;}_{(i)}\\\kern4em \theta\end{array}};\kern-.8em{\begin{array}{c}\kern1em\underline{{\begin{array}{c}\varphi\rightarrow\psi\\\end{array}}\kern1em{\begin{array}{c}\vdots\\\varphi\\\end{array}}{\begin{array}{c}\;_{{_\Box}\!}\underline{\kern1em}_{(i)}\\\psi\\\vdots\\\theta\end{array}}\kern-1.2em}_{(i)}\\\kern1em\theta\end{array}};\kern-.8em{\begin{array}{c}\kern1em\underline{\kern-.3em{\begin{array}{c}\forall x\psi\\\end{array}}\kern-.5em{\begin{array}{c}\underbrace{\kern-1.5em{\begin{array}{c}_{(i)}\underline{\kern1.5em}\kern1em\\\psi^x_{t_1}\end{array}}\kern-2em{\begin{array}{c}_{\;\;\;\;\;\;\;\ldots_{\;{\Box}}\ldots\;\;}\\\;,\;\;\ldots\;\;,\;\,\end{array}}\kern-1.8em{\begin{array}{c}\kern.5em\underline{\kern1.5em}_{(i)}\\\psi^x_{t_n}\end{array}}\kern-1.2em}\\\vdots\\\theta\end{array}}\kern-2.5em}_{(i)}\\\kern1em\theta\end{array}}.\end{equation*} $$

(See §3.5 for an explanation of our use here of the box notation □ on the inference strokes.)

The winning format for the regimentation of mathematical proofs, in our carefully considered opinion, is that of natural deduction. The reader should be cautioned, however, that proof-theorists since Gentzen have introduced variations of ‘formatting’ that can distract from a focused discussion of fundamentals.

Closely related to the system of natural deduction is Gentzen’s sequent calculus.Footnote ¹⁴ In the case of the sequent calculus, some, like Gentzen himself, take sequents $\Delta :\Gamma $ to involve sequences $\Delta $ and $\Gamma $ of formal sentences. Yet others treat $\Delta $ and $\Gamma $ as multisets of formal sentences. Sequences present their member-sentences in a particular linear order, allowing repetitions. Multisets are ‘in between’ sequences and sets. Like sets, they are unordered; but, like sequences, multisets register how many occurrences each member-sentence enjoys. It was this initial reluctance to treat only of sets $\Delta $ and $\Gamma $ of sentences that occasioned the need for the rather unusual ‘structural’ rules (in sequent calculi) of interchange and contraction. This was by way of contrast with the systems of natural deduction, all of whose rules were focused strictly on the logical operators. There are no ‘structural rules’ in systems of natural deduction. In intuitionistic (hence also classical) natural deduction, however, there is the Absurdity Rule, or Ex Falso Quodlibet:

$$ \begin{align*} {\begin{array}{c} \underline{\, \bot \,}\\ \varphi \end{array}}\!\!. \end{align*} $$

This rule in natural deduction has the same (disastrous, because irrelevantizing) effect as the sequent-calculus structural rule of Thinning on the Right, in permitting proof of the First Lewis Paradox

$$ \begin{align*} {\begin{array}{c} \underline{ A \kern1em \neg A }\\ B \end{array}}\!\!. \end{align*} $$

Gentzen’s resort to non-singleton succedents was a device to achieve classicism in his sequent calculus. The sequent calculus for Intuitionistic Logic needs only single-conclusion sequents. These points are well known. There is, however, a general lack of appreciation of the fact that Gentzen’s resort to multiple succedents $\Gamma $ —in sequents of the form $\Delta :\Gamma $ for his sequent calculus for Classical Logic—is not actually required in order to get Classical Logic. One can provide a perfectly adequate sequent calculus for Classical Logic by, for example, employing the strictly classical rules of Classical Reductio or Dilemma in a single-conclusion sequent setting (where $\Gamma $ is at most a singleton). For details, see Tennant [Reference Tennant45]. The single-conclusion sequent setting also reveals how all proofs in Core Logic, but not the strictly classical proofs to be had in Classical Core Logic, satisfy the ‘subformula property’: all sentences occurring in proofs occur as subsentences of a premise or of the conclusion. In the case of strictly classical proofs, there will be negations that do not occur as subsentences of a premise or of the conclusion. These negations would be the assumptions discharged by applications of Classical Reductio, or the negative-horn assumptions that are discharged by applications of Dilemma. Their easier identification makes for a more precise determination of the degree of nonconstructivity of a proof. See especially, in this connection, Tennant [Reference Tennant43], §9.Footnote ¹⁵

In this paper we shall follow the terminological tradition begun by Gentzen, and speak of sequents (rather than, say, arguments) being established by proofs. But our sequents are not to be confused with those of Gentzen.

This definition accommodates the outcomes of all mathematical proofs. Such a proof establishes a mathematical theorem $\varphi $ from a set $\Delta $ of mathematical axioms. Alternatively, the proof might establish the inconsistency of those axioms (by having $\bot $ as its conclusion). The raison d’être of mathematical logic, ever since Frege, has been the absolutely rigorous regimentation of mathematical proofs. Rules, and proofs constructed using them, need only have single conclusions. It is important, at the very outset, to be explicit about this (well-motivated) ‘limitation’ of focus.Footnote ¹⁶

We now shelve this discussion of sequent calculus, and re-focus our attention on systems of natural deduction. For this is the setting, or way of formatting regimented proofs, that most readers with a grounding in logic would find most familiar.

3 A variety of considerations concerning rules of inference

In this section we inquire after every feature that might be relevant for the exact statement or formulation of a logical rule of inference.

3.1 Rules involve subproofs, not just immediate premises

Exponents of natural-deduction systems typically present their logical rules of inference in an intuitively appealing, graphic form. For example, the rule of $\wedge $ -Introduction is usually stated as follows:

$$ \begin{align*} {\begin{array}{c} \underline{ \varphi \kern2em \psi }\\ \varphi\wedge\psi \end{array}}\!\!. \end{align*} $$

Now the beginner might form the mistaken impression that such a rule (or, at least, the intended rule, thus presented) may be applied only at the very outset of a proof, to two of the available premises, $\varphi $ and $\psi $ , of the argument to be proved. If so, one can correct that impression by adding another visual clue:

$$ \begin{align*} {\begin{array}{c} \underline{\kern-.5em {\begin{array}{c} \vdots\\ \varphi \end{array}} \kern1em {\begin{array}{c} \vdots\\ \psi \end{array}} \kern-.5em}\\ \varphi\wedge\psi \end{array}}\!\!. \end{align*} $$

This reassures the learner that the rule can be applied not just at the outset (‘to two given premises’), but also ‘anywhere in the middle’ of the proof; indeed, even ‘right at the end’. But a better way to put the matter is to observe that rules of inference, fundamentally, serve to produce new, more complex, proofs from immediate subproofs that have already been constructed. The rule of $\wedge $ -Introduction, despite its deceptively simple graphic statement, does exactly this.

3.2 Distinguishing the sets of assumptions of subproofs

But now another misunderstanding might arise. Must the two immediate subproofs, gestured at here by the descending dots, each use the same set of undischarged assumptions, or premises? In general, we want to say ‘No’. To make that answer clear in advance, and thereby prevent such a misunderstanding from arising, we can embellish the graphic form of the rule further:

$$ \begin{align*} {\begin{array}{c} \underline{\kern-.5em {\begin{array}{c} \Delta\\ \vdots\\ \varphi \end{array}} \kern.5em {\begin{array}{c} \Gamma\\ \vdots\\ \psi \end{array}} \kern-.5em}\\ \varphi\wedge\psi \end{array}}\!\!. \end{align*} $$

The different symbols $\Delta $ and $\Gamma $ , standing for the respective premise sets of the immediate subproofs, now make it clear that those sets can be distinct. It is left to the discerning beginner now to realize that the overall set of premises on which the newly drawn conclusion $\varphi \wedge \psi $ rests is $\Delta \cup \Gamma $ . Indeed, we have to allow in general for $\Delta $ to be not only distinct from $\Gamma $ , but even, on occasion, disjoint. For, how else could

$$ \begin{align*} {\begin{array}{c} \underline{ A \kern1.5em B }\\ A\wedge B \end{array}} \end{align*} $$

count as a proof (which it is!) of $A\wedge B$ from the set $\{A,B\}$ of premises?

And of course the two subproofs themselves will in general be distinct. This much is already obvious from the fact that their respective conclusions, $\varphi $ and $\psi $ , can in general be distinct. So, we might as well make that consideration explicit too, by eliminating the equiform lines of dots, and supplying explicit, distinct, symbols for the immediate subproofs themselves:

$$ \begin{align*} {\begin{array}{c} \underline{\kern-.5em {\begin{array}{c} \Delta\\ \Pi\\ \varphi \end{array}} \kern.5em {\begin{array}{c} \Gamma\\ \Sigma\\ \psi \end{array}} \kern-.5em}\\ \varphi\wedge\psi \end{array}}\!\!. \end{align*} $$

When one sets about finding a proof whose terminal step will be an application of the rule of $\wedge $ -Introduction, one makes no ‘assumptions for the sake of argument’ (that is, assumptions to be used in at least one of the subproofs, but to be discharged upon application of the rule). This is clear from the graphic notation. The two sets $\Delta $ and $\Gamma $ sit up at the top, with no subtractions (i.e., with no discharges taking place), and one is given to understand that it will be their union $\Delta \cup \Gamma $ upon which the newly drawn conclusion $\varphi \wedge \psi $ finally depends.

With this more expansive mode of stating a rule such as $\wedge $ -I, we are now incorporating explicit mention of the sets $\Delta $ and $\Gamma $ of premises of the respective immediate subproofs, and making clear what the overall set of premises of the newly constructed proof will be (namely, their union $\Delta \cup \Gamma $ ). This contrasts with what happens in Martin-Löf’s type theory, where the corresponding rule would be

$$ \begin{align*} {\begin{array}{c} \underline{ {\begin{array}{c} t_1:\varphi \end{array}} \kern1em {\begin{array}{c} t_2:\psi \end{array}} }\\ \langle t_1,t_2\rangle: \varphi\wedge\psi \end{array}}\!\!. \end{align*} $$

Here, the t-terms to the left of the colons code proofs, which are taken to be of the conclusion-propositions to the right of the colons respectively. One would still need some way of determining (effectively) what the (three) respective premise-sets are. So, this way of framing $\wedge $ -I in type theory is about as cryptic and not-fully-explicit as the highly condensed graphic rule

$$ \begin{align*} {\begin{array}{c} \underline{ A \kern1.5em B }\\ A\wedge B \end{array}} \end{align*} $$

that it has been our concern to make fully explicit. To the extent that a similar making-explicit can occur with Martin-Löf’s rules, by interpreting them in due course as inductive clauses in an inductive definition of the notion ‘t is a proof of A from …’ (with ‘…’ eventually filled in), what emerges from this process will be roughly equivalent, or homologous, to what we shall have to say about the ordinary rules of natural deduction. The ordinary rules deal, conveniently, with what is prima facie, without adopting any high-level theoretical re-construal, an untyped object-language;Footnote ¹⁷ and it is in this simple setting that our motivating question ‘What exactly is a primitive rule of inference?’ can both reveal its challenging complexity and be worthy of a full and clarifying investigation. So we shall opt to set Martin-Löf’s type theory to one side, in order to pursue our investigations to a satisfying conclusion, while being mindful that their outcome ought to be able to furnish a methodology for answering the same question posed with specific reference to the primitive rules of Martin-Löf’s type theory.Footnote ¹⁸

3.3 Rules involving assumptions for the sake of argument

With another very familiar introduction rule, however, matters are different. The reader will no doubt be in mind here of the Rule of Conditional Proof, as it is usually known. In the more uniform rule-terminology of the natural-deduction theorist, it is called the rule of $\rightarrow $ -Introduction. Its usual graphic statement takes either one of the following two (equivalent) forms:

$$ \begin{align*} {\begin{array}{c} \kern1.2em\underline{\kern1.2em}_{(i)}\\ \varphi\\ \vdots\\ \kern1.2em\underline{\kern1.3em\psi\kern1.3em}_{(i)}\\ \varphi\rightarrow\psi \end{array}}, \kern2em {\begin{array}{c} [\varphi]\\ \vdots\\ \underline{\kern1.3em\psi\kern1.3em}\\ \varphi\rightarrow\psi \end{array}}\!\!. \end{align*} $$

Here, we shall prefer the first of these two forms. It offers at least two advantages. First, it makes the useful suggestion that one can and should, in the construction of a natural deduction, avail oneself of the various numerals 1, 2, 3, … in place of i in order to show which assumption-occurrences are discharged at which steps. For, any given occurrence of an assumption ‘for the sake of argument’, when it is finally discharged, is discharged by a particular application, lower down in the proof-tree, of a rule of inference such as $\rightarrow $ -Introduction. Second, placing a discharge stroke over any assumption-occurrences being discharged provides an effective visual reminder that the assumption in question no longer qualifies for inclusion among the assumptions on which the newly drawn conditional conclusion depends.

The standard understanding, to which we shall adhere, is that when any assumption such as $\varphi $ for $\rightarrow $ -Introduction above gets discharged, it is discharged at its every eligible occurrence as a leaf-node of the proof-tree. So the sentence $\varphi $ is in effect subtracted from the set of sentences on which the subordinate conclusion $\psi $ , according to the subordinate proof, depends. This is what discharging $\varphi $ consists in.

The usual graphic form for $\rightarrow $ -Introduction of course falls short of being fully explicit, in much the same ways as did the rule for $\wedge $ -Introduction. Indeed, matters are now subtly more complicated by the fact that discharge of assumptions may take place. When we supply the extra symbols for maximal explicitness, we need to stress that the set $\Delta $ of undischarged assumptions (after the rule has been applied) does not contain the assumption $\varphi $ , since it is being dischargedFootnote ¹⁹ :

$$ \begin{align*} {\begin{array}{c} \underbrace{ \kern-.4em {\begin{array}{c} \;\\ \Delta \end{array}} {\begin{array}{c} \;\\ \kern-1.8em, \kern1.8em\end{array}} {\begin{array}{c} \kern1.2em\underline{\kern1.2em}_{(1)}\\ \varphi \end{array}} \kern-1.6em }\\ \Pi\\ \kern1em\underline{\kern1.3em\psi\kern1.3em}_{(i)}\\ \varphi\rightarrow\psi \end{array}}\!\!. \end{align*} $$

But it is clear also that the set of undischarged assumptions of the immediate subproof $\Pi $ (of the conclusion $\psi $ ) is $\Delta \cup \{\varphi \}$ (if indeed $\varphi $ has been used as an assumption—see below).

Of course, $\Delta $ itself may be empty. But it is important to realize that in general $\Delta $ may be nonempty. That is why it is advisable to make $\Delta $ explicit. For one wants no misunderstanding on this score.

3.4 The possibility of vacuous discharge of assumptions

What beginners often fail to realize for themselves is that an application of $\rightarrow $ -Introduction may be licit even when there is no use made of the assumption $\varphi $ . Thus, for example, the following one-step proof involves an application of $\rightarrow $ -Introduction:

$$ \begin{align*} {\begin{array}{c} \underline{\kern1.2em \psi \kern1.2em}\\ \varphi\rightarrow\psi \end{array}}\!\!. \end{align*} $$

There is no assumption of the form $\varphi $ within the degenerate proof $\psi $ (of conclusion $\psi $ from premise set $\{\psi \}$ ) that serves as the immediate subproof $\Pi $ for this application of $\rightarrow $ -Introduction. The step is said to involve vacuous discharge of assumptions; that is to say, it does not discharge any assumptions at all.

This vacuous-discharge step can be followed by another application of $\rightarrow $ -Introduction, this time discharging the assumption $\psi $ (which has been used), in order to obtain a proof of the logical theorem $\psi \rightarrow (\varphi \rightarrow \psi )$ . It is called a logical theorem because the proof produces it as a conclusion ‘from’ the empty set of assumptions (i.e., from no assumptions at all):

$$ \begin{align*} {\begin{array}{c} \kern1.2em\underline{\kern1.2em}_{(1)}\\ \underline{\kern1.2em \psi \kern1.2em}\\ \kern1.2em\underline{\kern1.5em\varphi\rightarrow\psi\kern1.5em}_{(1)}\\ \psi\rightarrow(\varphi\rightarrow\psi) \end{array}}\!\!. \end{align*} $$

So: the rule of $\rightarrow $ -Introduction (in Gentzen’s original formulation) is to be construed as permitted in application without any assumption-occurrence of $\varphi $ having been used (in order to derive $\psi $ in the subordinate proof) and therefore being available for discharge. This permission (for rule-application) ought to be marked explicitly in our graphic notation for stating the rule. We shall opt for a use of the diamond symbol as follows:

$$ \begin{align*} {\begin{array}{c} \underbrace{ \kern-.4em {\begin{array}{c} \;\\ \Delta \end{array}} {\begin{array}{c} \;\\ \kern1.2pt,\kern-1.5em \end{array}} {\begin{array}{c} _{\;\;\diamondsuit}\underline{\kern1.2em}_{(i)}\\ \varphi \end{array}} \kern-1.6em }\\ \Pi\\ \kern1em\underline{\kern1.3em\psi\kern1.3em}_{(i)}\\ \varphi\rightarrow\psi \end{array}}. \end{align*} $$

We choose the symbol $\diamondsuit $ because of its connotation, from deontic logic, of permission. The rule of $\rightarrow $ -Introduction is permitted to be applied even without the antecedent $\varphi $ of the conditional having been used as an assumption in the subproof $\Pi $ .

3.5 On rules with nonvacuous discharge of assumptions

In deontic logic, there is another symbol, □, which represents obligatoriness; and this makes it a suitable choice as a marker on the discharge stroke when it is required that the assumption in question should actually have been used, and be available for discharge, when the rule in question is applied. Put another way: the rule-applier is obliged to have made use of the (thus far, undischarged) assumption in question in the immediate subproof concerned. Thus the standard graphic formulation of Proof by Cases, or $\vee $ -Elimination:

$$ \begin{align*} {\begin{array}{c} \kern1.2em\underline{ \kern-.4em {\begin{array}{c} \vdots\\ \varphi\vee\psi\\ \end{array}} \kern-.8em {\begin{array}{c} \kern1.2em\underline{\kern1.2em}_{(i)}\\ \varphi\\ \vdots\\ \theta \end{array}} \kern-1em {\begin{array}{c} \kern1.2em\underline{\kern1.2em}_{(i)}\\ \psi\\ \vdots\\ \theta \end{array}} \kern-1em }_{(i)}\\ \theta \end{array}} \end{align*} $$

could be made fully explicit, and have its case-assumptions annotated, as followsFootnote ²⁰ :

$$ \begin{align*} {\begin{array}{c} \kern1.2em\underline{ \kern-.4em {\begin{array}{c} \Xi\\ \Omega\\ \varphi\vee\psi\\ \end{array}} \kern.8em {\begin{array}{c} \underbrace{ \kern-.6em {\begin{array}{c} \;\\ \Delta \end{array}} \kern-.4em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} _{\;\;\Box{}}\underline{\kern1.2em}_{(i)}\\ \varphi \end{array}} \kern-1.6em }\\ \Pi\\ \theta \end{array}} \kern1em {\begin{array}{c} \underbrace{ \kern-.6em {\begin{array}{c} \;\\ \Gamma \end{array}} \kern-.4em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} _{\;\;\Box{}}\underline{\kern1.2em}_{(i)}\\ \psi \end{array}} \kern-1.6em }\\ \Sigma\\ \theta \end{array}} \kern-1em }_{(i)}\\ \;\theta \end{array}}. \end{align*} $$

The reason for imposing this requirement on the case-assumptions is that it would be pointlessly unproductive to violate it. If, for example, the subproof $\Pi $ did not involve $\varphi $ among its undischarged assumptions, then $\Pi $ would establish the sequent $\Delta :\theta $ —a potentially stronger result than the sequent $\Xi ,\Delta ,\Gamma :\theta $ that would be established by applying the rule.Footnote ²¹

Prawitz [Reference Prawitz23] took over from Gentzen [Reference Gentzen10, Reference Gentzen11] the formulations of both $\vee $ -E and $\exists $ -E as permitting vacuous discharge of assumptions (the formulation that in the graphic notation proposed here would involve annotating the discharge strokes with $\diamondsuit $ ). Prawitz was aware, however, that a requirement of non-vacuous discharge (which we indicate instead with □) could be imposed on these rules without loss of completeness. At pp. 49–50 he wrote:

By a normal deduction, I shall … mean a deduction that contains no maximum segment and no redundant applications of $\vee $ E or $\exists $ E. An application of $\vee $ E or $\exists $ E in a deduction is said to be redundant if it has a minor premiss at which no assumption is discharged; obviously, such applications are superfluous … We now have:

Theorem 1. If $\Gamma \vdash A$ holds in the system for intuitionistic or minimal logic, then there is a normal deduction in this system of A from $\Gamma $ .

Indeed, there is no loss of completeness in the case of classical logic either, if one insists on nonvacuous discharge with $\vee $ -E or $\exists $ -E.

We turn finally to another kind of rule-restriction that could be imposed in the classical case without any loss of completeness. An anonymous referee raised the following interesting question. Consider this restricted form of the $\vee $ -E rule:

$$ \begin{align*} {\begin{array}{c} \kern1.2em\underline{ \kern-.4em {\begin{array}{c} \Xi\\ \Omega\\ \varphi\vee\psi\\ \end{array}} \kern.8em {\begin{array}{c} \underbrace{ \kern-.6em {\begin{array}{c} \;\\ \Delta \end{array}} \kern-.4em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} _{\;\;\Box{}}\underline{\kern1.2em}_{(i)}\\ \varphi \end{array}} \kern-1.6em }\\ \Pi\\ \bot \end{array}} \kern1em {\begin{array}{c} \underbrace{ \kern-.6em {\begin{array}{c} \;\\ \Gamma \end{array}} \kern-.4em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} _{\;\;\Box{}}\underline{\kern1.2em}_{(i)}\\ \psi \end{array}} \kern-1.6em }\\ \Sigma\\ \bot \end{array}} \kern-1em }_{(i)}\\ \;\bot \end{array}}. \end{align*} $$

In Classical Core Logic $\mathbb {C}^+$ one can prove Disjunctive Syllogism as follows:

$$ \begin{align*} {\begin{array}{c} \kern1em\underline{\kern-.5em {\begin{array}{c} A\vee B\\ \end{array}} \kern1em {\begin{array}{c} \underline{\kern-.5em {\begin{array}{c} \;\\ \neg A \end{array}} \kern-.5em {\begin{array}{c} \kern1em\underline{\kern1em}_{(1)}\\ A \end{array}} \kern-1.5em }\\ \bot \end{array}} \kern1em {\begin{array}{c} \underline{\kern-1.5em {\begin{array}{c} \kern1em\underline{\kern-1.7em}_{(2)}\\ \neg B \end{array}} \kern-1.5em {\begin{array}{c} \kern1em\underline{\kern1em}_{(1)}\\ B \end{array}} \kern-1.5em }\\ \bot \end{array}} \kern-1.5em }_{(1)}\\ _{\text{(CR)}}\underline{\kern.5em\bot\kern.5em}_{(2)}\;\;\\ B \end{array}}. \end{align*} $$

The question is: Can one make do, in $\mathbb {C}^+$ , with $\vee $ -Eliminations only in this restricted form? The answer is affirmative. This is a feature of classical reasoning akin to being able to obtain all desired classical results using only terminal applications of Classical Reductio (i.e., using CR only at the final step of the proof)—see §5.2; or using only atomic applications of Dilemma (in the propositional case)—again, see §5.2.

3.6 Empty sets of assumptions

We noted above that the set $\Delta $ of assumptions for conditional proof may be empty. Now there are some rules where one wishes to insist, by contrast, that there be no assumptions at all, i.e. that $\Delta $ be empty. Perhaps the best known example of such a rule is the Rule of Necessitation in modal logic: when one has deduced $\varphi $ from no assumptions, then one may infer $\Box{} \varphi $ . Many an author has observed that it would be very unwise to formulate this rule graphically as

$$ \begin{align*} {\begin{array}{c} \underline{\;\,\varphi\;\,}\\ \Box{}\varphi \end{array}}\!\!. \end{align*} $$

This is because such a cryptic formulation does not advert in any way to the requirement that $\varphi $ should have been deduced from no assumptions at all. In order to remedy this, a fully explicit graphic formulation of the Rule of Necessitation would be

$$ \begin{align*} {\begin{array}{c} \emptyset\\ \Pi\\ \underline{\;\,\varphi\;\,}\\ \Box{}\varphi \end{array}}\!\!. \end{align*} $$

Here, $\emptyset $ is the empty set.

3.7 Major premises of eliminations can stand proud

In connection with Proof by Cases ( $\vee $ -Elimination) we spoke of sequents being established by proofs. A sequent, in this sense, as explained in Definition 1, is of the form $\Delta :\varphi $ or $\Delta :\bot $ , where $\Delta $ is a finite set of sentences (the premises, or undischarged assumptions) and $\varphi $ (or $\bot $ ) is a single conclusion.

The introduction and elimination rules of natural deduction have analogs in the sequent calculus. These latter rules are known as Right logical rules and Left logical rules respectively. It would be instructive at this juncture to inspect just the Left logical rule for $\vee $ , which is what corresponds to the rule of $\vee $ -Elimination in natural deduction:

$$ \begin{align*} {\begin{array}{c} \underline{ \varphi,\Delta:\theta \kern2em \psi,\Gamma:\theta }\\ \varphi\vee\psi,\Delta,\Gamma:\theta \end{array}}\!\!. \end{align*} $$

With the left logical rule for $\vee $ stated in this form, it is to be understood that $\varphi $ is not a member of $\Delta $ , and $\psi $ is not a member of $\Gamma $ . Note that the formulation of $\vee $ -Elimination that would really correspond directly to this sequent rule is

$$ \begin{align*}\kern-1.7pc {\begin{array}{c} \kern1.2em\underline{ \kern-.4em {\begin{array}{c} \varphi\vee\psi\\ \end{array}} \kern-.1em {\begin{array}{c} \underbrace{ \kern-.4em {\begin{array}{c} \;\\ \Delta \end{array}} \kern-.2em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} _{\;\;\Box{}}\underline{\kern1.2em}_{(i)}\\ \varphi \end{array}} \kern-1.6em }\\ \Pi\\ \theta \end{array}} \kern1em {\begin{array}{c} \underbrace{ \kern-.4em {\begin{array}{c} \;\\ \Gamma \end{array}} \kern-.2em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} _{\;\;\Box{}}\underline{\kern1.2em}_{(i)}\\ \psi \end{array}} \kern-1.6em }\\ \Sigma\\ \theta \end{array}} \kern-1em }_{(i)}\\ \theta\;\;\; \end{array}}, \end{align*} $$

where the absence of any symbol for a proof above the major premise $\varphi \vee \psi $ is taken to indicate that there is no proof-work at all above $\varphi \vee \psi $ . That is, the major premise $\varphi \vee \psi $ stands proud, as a leaf-node of the proof-tree that is created by applying the rule. To be sure, it is a very ‘low down’ leaf node, on a shortest possible twig leading up from the bottommost indicated occurrence of $\theta $ ; but it is a leaf node nonetheless.

4 Are constraints in rule-applications partly constitutive of the rules themselves?

It is an important fact, not widely registered, that the elimination rules of a system of natural deduction can always be stated in parallelized form (see the examples on p. 28) and indeed also in the more austere form just mentioned, in which major premises stand proud, with no proof-work above them. This constraint ensures that all the resulting proofs will be in normal form.

In the three orthodox systems M of Minimal Logic, I of Intuitionistic Logic, and C of Classical Logic (for which, most conveniently, see Prawitz [Reference Prawitz23]), the rules $\wedge $ -E, $\rightarrow $ -E and $\forall $ -E are stated in their serial forms; and the rules $\neg $ -I, $\rightarrow $ -I, and Classical Reductio (for C) permit vacuous discharge. Moreover, in these three orthodox systems, all major premises for eliminations—be they serial eliminations, or parallelized ones, such as $\vee $ -E or $\exists $ -E—are allowed to stand as conclusions of nontrivial proof-work.

It is nevertheless the case that every proof in these orthodox systems (in which major premises for eliminations are permitted to stand as conclusions of nontrivial proofs) can be effectively transformed into a proof in normal form. And these normal-form proofs can be re-written in such a way that all eliminations are parallelized, with their major premises standing proud. Thus normal proofs in this more exigent form still furnish a complete proof system.

The systems of Core Logic and Classical Core Logic differ from the three aforementioned orthodox systems in certain crucial ways. First, all eliminations are parallelized. Second, all major premises for eliminations must stand proud. Third, there is no rule of Ex Falso Quodlibet. This is in order to ensure relevance of premises to conclusions. Fourth, certain rules are subtly but importantly tweaked.

The tweaks that the Core systems impose, of which there are three, are as follows. First, $\neg $ -I does not allow vacuous discharge. This holds for both the Core systems. Likewise, in Classical Core Logic, Classical Reductio does not allow vacuous discharge.

Second, the rule of $\rightarrow $ -I is liberalized, by being furnished with a new part:

$$ \begin{equation*}{\begin{array}{c}\underbrace{\kern-.4em{\begin{array}{c}\;\\\Delta\end{array}}{\begin{array}{c}\;\\,\kern-2.5em\end{array}}{\begin{array}{c}\;\;_\Box\underline{\kern1.2em}_{(i)}\\\varphi\end{array}}\kern-1.6em}\\\Pi\\\kern1em\underline{\kern1.3em\bot\kern1.3em}_{(i)}\\\varphi\rightarrow\psi\end{array}}.\\\end{equation*} $$

This new part of $\rightarrow $ -I allows one to prove, without forced recourse to EFQ, that if a conditional’s antecedent is false then the conditional is true (which is what we are told by the third and fourth lines of the truth table for $\rightarrow $ ):

$$ \begin{align*} \neg A:A\rightarrow B. \end{align*} $$

Lest the reader think that this reference to truth tables renders the point being made provincial to Classical Logic, the author hastens to point out that we are using here only the ‘left-to-right’ readings of the lines of the truth tables, and these are intuitionistically valid.Footnote ²²

Third, the rule $\vee $ -E (Proof by Cases) is also liberalized, so as to allow the following: if one of the case-proofs has $\bot $ as its conclusion, then one can bring down, as the main conclusion, the conclusion of the other case-proof. This liberalized form of $\vee $ -E can be represented graphically as follows:

$$ \begin{equation*}{\begin{array}{c}\kern1.2em\underline{\kern-.4em{\begin{array}{c}\varphi\vee\psi\\[-5pt]\end{array}}\kern-.1em{\begin{array}{c}\underbrace{\kern-.4em{\begin{array}{c}\;\\\Delta\end{array}}{\begin{array}{c}\;\\\kern2.5em,\kern-2.5em\end{array}}\kern-1.4em{\begin{array}{c}\;\;_\Box\underline{\kern1.2em}_{(i)}\\\varphi\end{array}}\kern-1.6em}\\\Pi\\\theta/\bot\end{array}}\kern1em{\begin{array}{c}\underbrace{\kern-.4em{\begin{array}{c}\;\\\Gamma\end{array}}\kern-.2em{\begin{array}{c}\;\\\,,\,\end{array}}\kern-1.4em{\begin{array}{c}\;\;_\Box\underline{\kern1.2em}_{(i)}\\\psi\end{array}}\kern-1.6em}\\\Sigma\\\theta/\bot\end{array}}\kern-1em}_{(i)}\\\theta/\bot\;\;\;\end{array}}.\end{equation*} $$

This liberalized form of $\vee $ -E allows one to prove Disjunctive Syllogism

$$ \begin{align*} A\vee B,\neg A:B \end{align*} $$

without forced recourse to EFQ. Here is the proof:

$$ \begin{align*} {\begin{array}{c} \kern1em\underline{ {\begin{array}{c} A\vee B\\[-5pt] \end{array}} \kern-.1em {\begin{array}{c} \underline{\kern-.3em {\begin{array}{c} \;\\ \neg A \end{array}} \kern-.1em {\begin{array}{c} \kern1em\underline{\kern1em}_{(1)}\\ A \end{array}} \kern-1em }\\ \bot \end{array}} \kern-.5em {\begin{array}{c} \;\\ \kern1em\underline{\kern1em}_{(1)}\\ B\\[-5pt] \end{array}} \kern-1em }_{(1)}\\ \kern-1em B \end{array}}\!\!. \end{align*} $$

The foregoing tweaks for the rules of the core systems $\mathbb {C}$ and $\mathbb {C}^+$ are made in order to ensure relevance of premises to conclusions, without sacrificing completeness. Importantly, the two core systems do not contain the rule Ex Falso Quodlibet.Footnote ²³

Now for the conceptual question that cries out for an answer here: are we justified in thinking that we are ‘merely tweaking’ a pre-existing rule, which somehow maintains its identity as the rule that it ‘is’, rather than formulating a completely distinct rule, masquerading, one might say, under the former respective label ( $\neg $ -I; CR; $\rightarrow $ -I; or $\vee $ -E)? When are ‘slightly’ altered conditions of applicability serious enough not to count as mere strategic constraints on the application of prior, stably identifiable rules, but rather as such important constitutive ingredients in the formulation of ‘the’ rule that it has become a different rule altogether from its prior namesake?

This worry about rule-identifications can arise, in principle, for any of the variable aspects canvassed above: serial v. parallelized form of elimination; requiring major premises of eliminations to stand proud; requiring non-vacuous discharge; and allowing a more ‘liberalized’ range of application. It would seem, at first glance, as though the ‘stable rule but with tweaks’ conception can be sustained only by concentrating on one particular (but ‘double-barreled’) central aspect, as solely constitutive of the ‘identity’ of the rule in question, which is: Does the rule concern just one occurrence of ‘its’ logical operator? And does that operator occur immediately below the inference stroke (in the conclusion)?; or immediately above it (in the major premise)?; or—so as to accommodate the classicist—only in assumptions that applications of the rule discharge?

At this point we should address a question raised by an anonymous referee, which bears on the identification problem that we are raising here. The referee invites one to consider two different conditional operators $\rightarrow $ and $\Rightarrow $ . They both enjoy Modus Ponens as their elimination rule. But they differ in their introduction rules. The conditional $\rightarrow $ is governed by the usual rule of Conditional Proof, permitting vacuous discharge of the antecedent as an assumption. The otherwise similar-looking introduction rule for the conditional $\Rightarrow $ , however, prohibits vacuous discharge. It is an easy exercise to deduce $A\rightarrow B$ from $A\Rightarrow B$ , and vice versa. Thus the two conditionals satisfy Belnap’s ‘uniqueness condition’ (Belnap [Reference Belnap2], p. 133). The referee asks ‘Should one then conclude that $\rightarrow $ and $\Rightarrow $ are the the same connective and that their rules are thus fundamentally the same?’. The referee answers in the negative, giving as reason that ‘Belnap’s uniqueness condition is a condition concerning the provability (or derivability) level—since it concerns the inter-derivability of $A\rightarrow B$ and $A\Rightarrow B$ —and not the proof level.’ We agree with this assessment; and would point out also that one should invoke here the criterion of synonymy (in this case, of the two conditionals under discussion) that Smiley formulated quite generally for connectives in Smiley [Reference Smiley36]. For synonymy, the two conditionals would need to be interreplaceable, salva veritate, in all (metalinguistic) statements of deducibility. And in general, their mere interdeducibility is not a sufficient condition for this to hold. This can be seen in the present instance from the simple facts that

$$ \begin{align*} B\vdash A\rightarrow B \kern1em\text{but}\kern1em B\not\vdash A\Rightarrow B, \end{align*} $$

which together show that by Smiley’s criterion the two conditionals are not synonymous.

4.1 Rules can have parts

In every logical system dealing with disjunction, the rule of $\vee $ -Introduction is stated in two parts:

$$ \begin{align*} {\begin{array}{c} \underline{\kern1em \varphi \kern1em}\\ \varphi\vee\psi \end{array}}; \kern2em {\begin{array}{c} \underline{\kern1em \psi \kern1em}\\ \varphi\vee\psi \end{array}}\!\!. \end{align*} $$

It is difficult to say exactly what the criteria are for identifying the parts of a rule. Would one have succeeded, for example, in stating the rule of $\vee $ -Introduction in ‘just one part’ if one were to write

$$ \begin{align*} {\begin{array}{c} \underline{\kern1em \theta \kern1em}\\ \varphi\vee\psi \end{array}}\text{ where }\theta=\varphi\text{ or }\theta=\psi \kern2em\ldots? \end{align*} $$

In the other direction—of fission of a single whole into parts, rather than fusion of parts into a single whole—one might suggest that the earlier rule of $\rightarrow $ -Introduction:

$$ \begin{align*} {\begin{array}{c} \underbrace{ \kern-.4em {\begin{array}{c} \;\\ \Delta \end{array}} \kern-.2em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} _{\;\;\diamondsuit}\underline{\kern1.2em}_{(i)}\\ \varphi \end{array}} \kern-1.6em }\\ \Pi\\ \kern1em\underline{\kern1.3em\psi\kern1.3em}_{(i)}\\ \varphi\rightarrow\psi \end{array}} \end{align*} $$

could (and should) be re-written in two parts, thus:

$$ \begin{align*} (\rightarrow\text{-I})_1{\begin{array}{c} \underbrace{ \kern-.4em {\begin{array}{c} \;\\ \Delta \end{array}} \kern-.2em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} \kern1.2em\underline{\kern1.2em}_{(i)}\\ \varphi \end{array}} \kern-1.6em }\\ \Pi\\ \kern1em\underline{\kern1.3em\psi\kern1.3em}_{(i)}\\ \varphi\rightarrow\psi \end{array}}; \kern3em \text{and} \kern3em (\rightarrow\text{-I})_2{\begin{array}{c} \Delta\\ \Pi\\ \kern-.2em\underline{\kern1.3em\psi\kern1.3em}\\ \varphi\rightarrow\psi \end{array}},\ \text{ where }\varphi\not\in\Delta. \end{align*} $$

Our earlier two-step proof could have each of its steps annotated as follows, in order to make clear which part of the rule is being applied:

$$ \begin{align*} {\begin{array}{c} \kern-2.3em\underline{\kern.8em}_{(1)}\\ \kern-2.4em{\begin{array}{c} _{}\scriptsize {(\rightarrow\!\text{-I})_2}\\[-5pt] \end{array}}\kern-.4em \underline{\kern1.2em \psi \kern1.2em}\\ \kern-1.6em{\begin{array}{c} _{}\scriptsize {(\rightarrow\!\text{-I})_1}\\[-5pt] \end{array}}\kern-.4em\underline{\kern-1.7em\varphi\rightarrow\psi\kern-1.6em}_{(1)}\\ \kern-1.1em\psi\rightarrow(\varphi\rightarrow\psi) \end{array}}\!\!. \end{align*} $$

4.2 Generalized or parallelized forms of the elimination rules

The apartness of the two usual parts of $\vee $ -Introduction is much more entrenched than the apparent apartness of the two usual parts of the serial form of the rule of $\wedge $ -Elimination, which is usually the favored form:

$$ \begin{align*} {\begin{array}{c} \underline{\varphi\wedge\psi}\\ \varphi \end{array}}\;; \kern2em {\begin{array}{c} \underline{\varphi\wedge\psi}\\ \psi \end{array}}\!\!. \end{align*} $$

But, as we pointed out earlier, the rule of $\wedge $ -Elimination can also be stated in the single generalized or parallelized form

$$ \begin{equation*}\kern-2.1pc{\begin{array}{l}\kern.55in_{(i)}\underline{\kern.15in}_{{_\Box}\!}\underline{\kern.15in}_{(i)}\\\kern.7in\underbrace{ \varphi \; \,,\; \psi }\\\kern.85in\vdots\\\kern-1.7em\underline{ \varphi \wedge \psi \kern2em \theta \;}_{(i)}\\\kern4em \theta\end{array}}\end{equation*} $$

where the box indicates that at least one of $\varphi $ , $\psi $ must have been used as an assumption and thereby be available for discharge. Of course, the rule applies when both $\varphi $ and $\psi $ have been used. In such a circumstance, both of them are available for discharge, and get discharged.

The rule of $\vee $ -Elimination (Proof by Cases), as we have seen, is already in generalized or parallelized form, as is the rule of $\neg $ -Elimination:

$$ \begin{align*} {\begin{array}{c} \underline{ \kern-.05in {\begin{array}{c} \;\\ \neg\varphi \end{array}} \kern.1in {\begin{array}{c} \vdots\\ \varphi \end{array}} \kern-.05in }\\ \bot \end{array}}\!\!. \end{align*} $$

The remaining standard connective to discuss in this regard is $\rightarrow $ . As already mentioned, the time-honored rule of Modus Ponens is the usual (but serial) form of $\rightarrow $ -Elimination (which we now state with its major premise leftmost, for uniformity):

$$ \begin{align*} {\begin{array}{c} \underline{ \varphi\rightarrow\psi \kern-1.7em \varphi }\\ \psi \end{array}}\!\!. \end{align*} $$

And as we saw on p. 10, this rule too can be parallelized; but in this case, unlike the case involving $\wedge $ , the re-formulation does not involve fusion of erstwhile separate parts of the rule:

$$ \begin{equation*}{\begin{array}{c}\underline{{\begin{array}{c}\;\\\;\\\;\\\;\\\varphi\!\rightarrow\! \psi\end{array}}\kern.1in{\begin{array}{c}\;\\\;\\\vdots\\\varphi\end{array}}{\begin{array}{c}\kern.1in_{_\Box\!}\underline{\kern.15in}_{(i)}\\\psi\\\vdots\\\theta\end{array}}\kern-.15in}_{(i)}\\\;\theta\end{array}}.\end{equation*} $$

The reader can check that in natural deduction it is the parallelized forms rather than the serial forms of elimination rules that make for homology with the corresponding ‘Left logical rules’ in the sequent calculus. Consider, for example, the fully explicit form of parallelized $\rightarrow $ -Elimination:

$$ \begin{align*} {\begin{array}{c} \kern1.2em\underline{ \kern-.4em {\begin{array}{c} \varphi\rightarrow\psi\\ \end{array}} \kern1em {\begin{array}{c} \Delta\\ \Pi\\ \varphi\\ \end{array}} \kern1em {\begin{array}{c} \underbrace{ \kern-.4em {\begin{array}{c} \;\\ \Gamma \end{array}} \kern-.2em {\begin{array}{c} \;\\ , \end{array}} \kern-1.4em {\begin{array}{c} _{\;\;\Box{}}\underline{\kern1.2em}_{(i)}\\ \psi \end{array}} \kern-1.6em }\\ \Sigma\\ \theta \end{array}} \kern-1em }_{(i)}\\ \;\;\theta \end{array}}. \end{align*} $$

The Left logical rule of the sequent calculus that corresponds to this is

$$ \begin{align*} \kern4em{\begin{array}{c} \underline{ \Delta:\varphi \kern1.4em \Gamma,\psi:\theta }\\ \varphi\rightarrow\psi,\Delta,\Gamma:\theta \end{array}},\text{ where }\psi\not\in\Gamma. \end{align*} $$

(One can even go so far as to insist, in both the natural-deduction rule and the corresponding sequent-rule, that the conditional $\varphi \rightarrow \psi $ also not be a member of $\Gamma $ . One cannot, however, exclude $\varphi \rightarrow \psi $ from $\Delta $ , on pain of incompleteness for intuitionistic consequence.)

Only one natural-deduction rule (for a connective) has thus far escaped mention, and that is the rule of constructive Reductio ad Absurdum, or $\neg $ -Introduction. Its usual graphic statement is as follows:

$$ \begin{align*} {\begin{array}{c} \kern1.2em\underline{\kern1.2em}_{(i)}\\ \varphi\\ \vdots\\ \kern1em\underline{\kern.6em\bot\kern.6em}_{(i)}\\ \neg\varphi \end{array}}\!\!. \end{align*} $$

The reader will by now be aware of the potential shortcomings in such a cryptic (i.e., graphically under-specific) statement of the rule. The most important question to be settled is this: Does it permit vacuous discharge of assumptions? If the answer is affirmative—that is to say, if the graphic statement of the rule, when made fully explicit, is

$$ \begin{equation*}{\begin{array}{c}\underbrace{\kern-.4em{\begin{array}{c}\;\\\Delta\end{array}}\kern-.2em{\begin{array}{c}\;\\,\end{array}}\kern-1.4em{\begin{array}{c}_{\;\;\Diamond}\underline{\kern1.2em}_{(i)}\\\varphi\end{array}}\kern-1.6em}\\\Pi\\\kern1em\underline{\kern.6em\bot\kern.6em}_{(i)}\\\neg\varphi\end{array}}\end{equation*} $$

—then any proof system that contains this rule will allow one to prove the negative form of Lewis’s First Paradox:

$$ \begin{equation*}{\begin{array}{c}\underline{\neg\psi\kern2em\psi}\\\neg\varphi\end{array}}\!.\end{equation*} $$

The proof is this simple:

$$ \begin{equation*}{\begin{array}{c}\underline{\neg\psi\kern2em\psi}\\\underline{\;\,\bot\;\,}\\\neg\varphi\end{array}}\!.\end{equation*} $$

An application of $\neg $ -Elimination is followed here by an application of $\neg $ -Introduction with vacuous discharge.

This provides the relevantist—who seeks to avoid both the positive and the negative forms of the first Lewis Paradox—strong motivation to make the rule of $\neg $ -Introduction a ‘no vacuous discharge’ rule:

$$ \begin{equation*}{\begin{array}{c}\underbrace{\kern-.4em{\begin{array}{c}\;\\\Delta\end{array}}\kern-.2em{\begin{array}{c}\;\\,\end{array}}\kern-1.4em{\begin{array}{c}_{\;\;\Box}\underline{\kern1.2em}_{(i)}\\\varphi\end{array}}\kern-1.6em}\\\Pi\\\kern1em\underline{\kern.6em\bot\kern.6em}_{(i)}\\\neg\varphi\end{array}}.\end{equation*} $$

5 What is a rule of inference, really?

Our concern here is not so much to argue for the choice of any particular logical system (i.e., any particular collection of primitive rules of inference), as it is to get clear about what kind of thing, exactly, a primitive rule of inference is, from a metalogical or proof-theoretic point of view. The problematic here presents itself quite generally, to anyone thinking about rules of inference. But it is especially pressing for inferentialists, since they are the theorists of meaning who are taking the notion of a rule of inference as central and basic for their theorizing.Footnote ²⁴

Tennant [Reference Tennant37] characterized primitive rules of inference in natural deduction as inductive clauses in an inductive definition of the notion of proof-in-a-system- $\mathcal {S}$ . These inductive clauses collectively define the ternary notionFootnote ²⁵

$$ \begin{align*} \mathcal{P}_{\mathcal{S}}(\Pi,\varphi,\Delta) \end{align*} $$

—‘the finitary tree-like construction $\Pi $ is a proof, in the system $\mathcal {S}$ , of the conclusion $\varphi $ from the set $\Delta $ of undischarged assumptions’—for which the basis clause is the obvious

$$ \begin{align*} \mathcal{P}_{\mathcal{S}}(\varphi,\varphi,\{\varphi\}). \end{align*} $$

In Gentzen [Reference Gentzen10, Reference Gentzen11], the definition of a ‘Herleitung’ (in accordance with his stated rules) is not an explicitly inductive one, although it would invite being recast as an inductive definition were it to be regimented more rigorously. Such regimentation was undertaken by Prawitz [Reference Prawitz23]. He contented himself, however, with stating only what we are here calling the graphic forms of rules. He did not make the explicit point that these graphic forms are really only convenient ways of picturing to oneself the metalinguistic effect of the respective inductive-clause forms of the rules in question. This understanding of proof-constructional matters is arrived at (op. cit., p. 24) rather circuitously in Prawitz’s presentation, by way of a distinction (pp. 22–23) between what he calls ‘proper’ inference rules (ones not involving any potential discharge of assumptions) and ‘deduction’ rules (ones that do involve potential discharge of assumptions). This distinction, though, works against seeing immediately that they are all inference rules, tout court; and that foundational questions about the nature of inference rules would affect them all equally.

Here we re-visit the more unifying explanatory conception of rules of inference as inductive clauses in a metalinguistic definition of what counts as a proof, in a system, of a conclusion from a set of undischarged assumptions. We do so in order to explain the conception thoroughly, and in order to explore further subtleties of which the inferentialist must nevertheless be mindful. Even if our implied conclusions end up being pessimistic about the prospects for complete clarification of the notion of a logical rule of inference, we nevertheless remain convinced that it is the inductive clause conception that holds any prospect of serving the inferentialist’s conceptual and foundational needs when it comes to the problem of characterizing exactly what kind of thing a primitive rule of inference is.

The sought clarity about primitive rules will be attained by exploring the implications of our having described any rule $\rho $ , in general, as saying what can be done when constructing proofs in a given system (containing $\rho $ ).

This pushes our considerations in a possibly holist direction. Proofs in which particular system?, one might ask. Consider the straightforward answer ‘Whichever system $\mathcal {S}$ one happens to be using, of which the rule $\rho $ in question is a rule’.

5.1 Rules of inference as inductive-definitional clauses in an inductive definition of proof

Suppose the system one happens to be using is intuitionistic logic, for a language whose only logical operators are $\neg $ and $\wedge $ . The proof system $\textbf{I}_{\{\neg ,\wedge \}}$ of intuitionistic logic for these two connectives consists of just those proofs $\Pi $ generated by the following inductive definition of the ternary relation $\mathcal {P}_{\scriptsize \mathbf {I}_{\{\neg ,\wedge \}}}(\Pi ,\varphi ,\Delta )$ —‘ $\Pi $ is a proof of $\varphi $ , in the system $\textbf{I}_{\{\neg ,\wedge \}}$ , from the set $\Delta $ of undischarged assumptions’. We shall use here the parallelized form of $\wedge $ -E, not the serial form. We shall also suppress any overly complex system subscript when it can be understood from the context.

Definition 2 of $\mathcal {P}(\Pi ,\varphi ,\Delta )$ for I $_{\{\neg ,\wedge \}}$

Basis clause: $\mathcal {P}(\varphi ,\varphi ,\{\varphi \})$ .

Inductive clauses (in the form of metalinguistic inference rules, and with convenient labels):

$$ \begin{equation*}\begin{array}{c}(\neg\text{-I})\end{array}\begin{array}{c}\underline{\kern2.5em{\cal P}(\Pi,\bot,\Delta)\kern2.5em}\\{\cal P}\Big(\begin{array}{c}\underline{\;\,\Pi\;\,}\\\neg\varphi\end{array}\!\!,\,\neg\varphi,\Delta\setminus\{\varphi\}\Big)\end{array}\end{equation*} $$

$$ \begin{equation*}\begin{array}{c}(\neg\text{-E})\end{array}\begin{array}{c}\underline{\kern3.7em\mathcal{P}(\Pi,\varphi,\Delta)\kern3.7em}\\\mathcal{P}\Big(\begin{array}{c}\underline{\neg\varphi\kern1em\Pi}\\\bot\end{array}\!\!,\bot,\Delta\cup\{\neg\varphi\}\Big)\end{array}\end{equation*} $$

$$ \begin{equation*}\begin{array}{c}(\wedge\text{-I})\end{array}\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1)\kern2em\mathcal{P}(\Pi_2,\varphi_2,\Delta_2)}\\\mathcal{P}\Big(\begin{array}{c}\underline{\Pi_1\kern1em\Pi_2}\\\varphi_1\wedge\varphi_2\end{array}\!\!,\varphi_1\wedge\varphi_2,\Delta_1\cup\Delta_2\Big)\end{array}\end{equation*} $$

$$ \begin{equation*}\begin{array}{c}(\wedge\text{-E})\end{array}\begin{array}{c}\underline{\mathcal{P}(\Pi,\theta,\Delta)\kern2.6em\Delta\cap\{\varphi_1,\varphi_2\}\neq\emptyset}\\\mathcal{P}\Big(\begin{array}{c}\underline{\varphi_1\wedge\varphi_2\kern1em\Pi}\\\theta\end{array}\!\!,\theta,\Delta\setminus\{\varphi_1,\varphi_2\}\Big)\end{array}\end{equation*} $$

$$ \begin{equation*}\begin{array}{c}(\text{EFQ})\end{array}\begin{array}{c}\underline{\kern.8em\mathcal{P}(\Pi,\bot,\Delta)\kern.8em}\\\mathcal{P}\Big(\begin{array}{c}\underline{\,\Pi\,}\\\\\varphi\end{array}\!\!,\varphi,\Delta\Big)\end{array}\end{equation*} $$

Closure clause: If $\mathcal {P}(\Pi ,\varphi ,\Delta )$ , then this can be shown from the preceding clauses.

The attentive reader will have noticed that we are doing something new here, by bringing into the conclusions of these metalinguistic rules a way of referring to newly constructed proofs—such as

$$ \begin{equation*}\begin{array}{c}\underline{\;\,\Pi\;\,}\\\neg\varphi\end{array}\!\!;\kern1em\begin{array}{c}\underline{\neg\varphi\kern1em\Pi}\\\bot\end{array}\!\!;\kern1em\begin{array}{c}\underline{\Pi_1\kern1em\Pi_2}\\\varphi_1\wedge\varphi_2\end{array}\!\!;\kern1em\begin{array}{c}\underline{\varphi_1\wedge\varphi_2\kern1em\Pi}\\\theta\end{array}\!\!;\kern1em\text{and}\kern1em\begin{array}{c}\underline{\,\Pi\,}\\\\\varphi\end{array}\end{equation*} $$

—that calls for an explanation of the proof-term notation being employed. This is very simple, and is given by the following inductive definition.

Definition 3 Basis clause: Any sentence is a proof-term.

Inductive clause: If $\Pi _1,\ldots ,\Pi _n$ are proof-terms, then so too is $\begin {array}{c}\underline {\Pi _1,\ldots ,\Pi _n}\\ \theta \end{array}$ , where $\theta $ is either a sentence or the absurdity symbol $\bot $ .

Closure clause: Any proof-term can be shown to be such by means of the Basis and Inductive clauses.

It is obvious that fully expanded proof-terms are tree-like arrays of (i) occurrences of sentences or of $\bot $ , and (ii) horizontal inference-strokes. Which of these proof-terms $\Pi $ succeed in denoting proofs will be determined, for any proof-system $\mathcal {S}$ , by the definition of the ternary notion $\mathcal {P}(\Pi ,\varphi ,\Delta )$ .Footnote ²⁶

Now the thing about Definition 2 is that it defines the notion of proof in a very particular system. We have called that system $\textbf{I}_{\{\neg ,\wedge \}}$ .Footnote ²⁷ The ternary relation $\mathcal {P}(\Pi ,\varphi ,\Delta )$ that Definition 2 defines is not one that captures the notion of a proof $\Pi $ in general—that is, in any system whatsoever; rather, we should regard it as capturing only the provincial relation $\mathcal {P}_{\scriptsize \mathbf {I}_{\{\neg ,\wedge \}}}(\Pi ,\varphi ,\Delta )$ Alternatively, the ‘system-specificity subscript’ could be elevated so as to occupy an explicit, fourth argument place in the inductively defined proof-relation:

$$ \begin{align*} \mathcal{P}(\Pi,\varphi,\Delta,\mathbf{I}_{\{\neg,\wedge\}}). \end{align*} $$

This now puts any particular clause in Definition 2, construed as a rule of inference, in an interesting new light. Let us focus on ( $\wedge $ -I). In the context of this particular proof-system, it needs to be understood as the newly illuminated inductive-definitional clause

$$ \begin{equation*}{\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge\}}}\end{array}}{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathbf{I}_{\{\neg,\wedge\}})\kern2em\mathcal{P}(\Pi_2,\varphi_2,\Delta_2,\mathbf{I}_{\{\neg,\wedge\}})}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1\kern1em\Pi_2}\\\varphi_1\wedge\varphi_2\end{array}}\!\!,\varphi_1\wedge\varphi_2,\Delta_1\cup\Delta_2,\mathbf{I}_{\{\neg,\wedge\}}\Big)\end{array}}\!.\end{equation*} $$

Yet we want to be able to say that a rule such as $\wedge $ -Introduction is somehow the very same rule within any proof-system in which it is included, regardless of what other rules (for other logical operators) might be included with it. Surely, the intuition goes, we are dealing with the very same rule of $\wedge $ -Introduction, whichever system of proof is having its proofs defined. Otherwise we shall be beset by an inferentialist Babel of captious characterizations of the rule in question as, respectively,

$$ \begin{equation*}{\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}{\{\neg,\wedge\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\vee\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\rightarrow\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\vee,\rightarrow\}}}\end{array}},\ \end{equation*} $$

$$ \begin{equation*}{\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\exists\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\vee,\exists\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\rightarrow,\exists\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\vee,\rightarrow,\exists\}}}\end{array}},\ \end{equation*} $$

$$ \begin{equation*}{\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\forall\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\vee,\forall\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\rightarrow,\forall\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\vee,\rightarrow,\forall\}}}\end{array}},\ \end{equation*} $$

$$ \begin{equation*}{\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\exists,\forall\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\vee,\exists,\forall\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\rightarrow,\exists,\forall\}}}\end{array}},\ {\begin{array}{c}(\wedge\text{-I})_{\scriptsize\mathbf{I}_{\{\neg,\wedge,\vee,\rightarrow,\exists,\forall\}}}\end{array}},\ \ldots\end{equation*} $$

Enough of this unruly menagerie! one wishes to say. Shouldn’t we be permitted to simply construe $\wedge $ -Introduction as

$$ \begin{equation*}{\begin{array}{c}(\wedge\text{-I})_{\mathcal{S}},\text{ for any proof-system }\mathcal{S}\text{ that }\ldots?\end{array}}\end{equation*} $$

For any proof-system $\mathcal {S}$ that what, exactly? That contains it (‘the’ rule)? But then what exactly is the ‘it’ in question here? What exactly is the rule? Are we dealing here with a surprising but essential case of impredicativity in our frustrated attempt to say, clearly, what a rule of inference is?

It would appear that it is impossible to identify a rule such as $\wedge $ -Introduction except as an inductive-definitional clause of the form

$$ \begin{equation*}{\begin{array}{c}(\wedge\text{-I})_{\mathcal{S}}\end{array}}{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathcal{S})\kern2em\mathcal{P}(\Pi_2,\varphi_2,\Delta_2,\mathcal{S})}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1\kern1em\Pi_2}\\\varphi_1\wedge\varphi_2\end{array}},\varphi_1\wedge\varphi_2,\Delta_1\cup\Delta_2,\mathcal{S}\Big)\end{array}}\end{equation*} $$

that is eligible for inclusion in the definition of any proof-system $\mathcal {S}$ .

This last suggestion, however, won’t quite do. The rule displays a degree of uniformity in its formulation that is not generally attainable. Note how the system $\mathcal {S}$ is mentioned (at the fourth argument place) both in the premises, and in the conclusion, of this definitional rule. It is the mention in the conclusion that determines what proof-system it is that contains the proofs that result from applying the rule. But the mention in the premise(s) might well be of some proper subsystem of $\mathcal {S}$ , rather than $\mathcal {S}$ itself. Examples to be offered in §5.3 and §5.4 will make this point clear. But first, in §5.2, we shall emphasize how rules are to be identified by how they contribute to the variety of proofs, rather than by the field of the deducibility relation that those proofs generate.

5.2 Extension of Intuitionistic Logic by atomic applications of Dilemma

At the propositional level, if one adds to Intuitionistic Logic I the strictly classical rule of Dilemma:

$$ \begin{equation*}(\textit{Dil}){\begin{array}{c}\kern1.2em\underline{\kern-1.2em{\begin{array}{c}\kern1.2em\underline{\kern1.2em}_{(i)}\\\varphi\\\vdots\\\psi\end{array}}\kern-.1em{\begin{array}{c}\kern1em\underline{\kern1.5em}_{(i)}\\\neg\varphi\\\vdots\\\psi\end{array}}\kern-1.2em}_{(i)}\\\psi\end{array}}\end{equation*} $$

one obtains full Classical Logic C. Here, $\varphi $ may be any sentence. So let us call this ‘version’ of the rule General Dilemma.

One also obtains C even if one restricts $\varphi $ (the ‘positive-horn’ assumption) to be atomic. Let us call this ‘version’ of the rule Atomic Dilemma. In the following statement of this rule, A is taken to be an atom:Footnote ²⁸

$$ \begin{equation*}(\textit{Atomic Dil}){\begin{array}{c}\kern1.2em\underline{\kern-1.2em{\begin{array}{c}\kern1.2em\underline{\kern1.2em}_{(i)}\\A\\\vdots\\\psi\end{array}}\kern-.1em{\begin{array}{c}\kern1em\underline{\kern1.5em}_{(i)}\\\neg A\\\vdots\\\psi\end{array}}\kern-1.2em}_{(i)}\\\psi\end{array}}.\end{equation*} $$

If rules are to be identified only by their net effects on the deducibility relation, then General Dilemma and Atomic Dilemma would have to count as the same rule. Each of them extends Intuitionistic Logic I to Classical Logic C. But intuitively they are rather different rules. The former is applicable in situations in which the latter is not. The conclusion that forces itself upon one is that rules are to be identified at least by considering the variety of proofs that they enable us to construct, and not just by the grosser measure of the variety of arguments $\Delta :\varphi $ for which they enable us to supply some proof or other. Otherwise, not only would General Dilemma and Atomic Dilemma count as one and the same rule; so too, either form of Dilemma would be identifiable with the Law of Excluded Middle:

$$ \begin{equation*}(\textit{LEM})\kern2em{\begin{array}{c}\underline{\kern3.4em}\\\varphi\vee\neg\varphi\end{array}};\end{equation*} $$

with Cldassical Reductio:

$$ \begin{equation*}(\textit{CR})\kern1em{\begin{array}{c}\\{\begin{array}{c}\kern-2.5em\\\underbrace{\kern-.4em{\begin{array}{c}\;\\\Delta\end{array}}\kern-.2em{\begin{array}{c}\;\\,\end{array}}\kern-1.4em{\begin{array}{c}_{\;\;\Diamond}\underline{\kern1.8em}_{(i)}\\\neg\varphi\end{array}}\kern-1.6em}\\\Pi\\\kern1em\underline{\kern.3em\bot\kern.3em}_{(i)}\end{array}}\\\varphi\end{array}};\end{equation*} $$

and with Double Negation Elimination:

$$ \begin{equation*}(\textit{DNE})\kern1em{\begin{array}{c}\underline{\neg\neg\varphi}\\\varphi\end{array}}.\end{equation*} $$

This is because any one of the latter ‘classical negation’ rules, appended to I, yields C.Footnote ²⁹ Yet these classical negation rules are all very distinct from one another, given their individually idiosyncratic ‘local conditions’ for application. That they respectively produce the same overall systemic effect appears to be neither here nor there, as far as the problem of rule-identification is concerned.

5.3 Extension of Intuitionistic Logic by terminal applications of Classical Reductio

We turn now to the first of our examples promised above, of how the systems mentioned in the premises of an inductive clause in the definition of proof can be (proper) subsystems of the system of proof in question.

Consider the proof-system for classical propositional logic $\textbf{C}_{\{\neg ,\wedge ,\vee ,\rightarrow \}}$ that has, as its only classical negation rule, the following:

$$ \begin{equation*}(\textit{CR})_{{\mathbf C}_{\{\neg,\wedge,\vee,\rightarrow\}}}\frac{{\mathcal{P}}\Big(\Pi,\bot,\Delta,{\mathbf{I}}_{\{\neg,\wedge,\vee,\rightarrow\}}\Big)}{{\mathcal{P}}\Big(\begin{array}{c}\underline{\Pi}\\\varphi\end{array}\!\!,\varphi,\Delta\!\setminus\!\{\neg\varphi\},{\mathbf{C}}_{\{\neg,\wedge,\vee,\rightarrow\}}\Big)}.\end{equation*} $$

This is the rule of Classical Reductio ad Absurdum, confined to subordinate reductio proofs of $\neg \varphi $ that are intuitionistic:

$$ \begin{equation*}{\begin{array}{c}\\{\left.\begin{array}{c}\kern-2.5em\\\underbrace{\kern-.4em{\begin{array}{c}\;\\\Delta'\end{array}}\kern-.2em{\begin{array}{c}\;\\,\end{array}}\kern-1.4em{\begin{array}{c}_{\;\;\Diamond}\underline{\kern1.8em}_{(i)}\\\neg\varphi\end{array}}\kern-1.6em}\\\Pi\\\kern1em\underline{\kern.3em\bot\kern.3em}_{(i)}\end{array}\;\;\;\right\}}\\\varphi\hphantom{\varphi\,}\kern1.5em\end{array}}{\begin{array}{c}\text{ intuitionistic.}\\\end{array}}\end{equation*} $$

It is well known that every classically inconsistent set of sentences in a first-order language based on $\{\neg ,\wedge ,\vee \rightarrow ,\exists \}$ is intuitionistically inconsistent.Footnote ³⁰ It follows that, despite its restriction to intuitionistic subproofs, the foregoing rule of Classical Reductio yields the full classical system (of propositional logic, and indeed of first-order logic with $\exists $ as its only quantifier) as an extension of the intuitionistic one. The formulation of this rule (and of the intuitionistic I- and E-rules) ensures that in any strictly classical proof, Classical Reductio need only be applied once, and—if all other rules require their subordinate proofs to be intuitionistic—only as its terminal step.

5.4 The Rule of Necessitation in S0.5

A second example of the same kind of trouble will be useful here. In modal (propositional) logic the Rule of Necessitation mentioned in §3.6 is standardly thought of as applying to subproofs in the system to produce new proofs in the very same system. Graphically:

$$ \begin{equation*}{\left.\begin{array}{c}{\begin{array}{c}{\left.\begin{array}{c}\emptyset\\\Pi\\\underline{\;\,\varphi\;\,}\end{array}\right\}}\\\Box\varphi\hphantom{\varphi}\kern.8em\end{array}}{\begin{array}{c}\text{in system }\mathcal{S}\\\end{array}}\end{array}\right\}}{\begin{array}{c}\text{in system }\mathcal{S}\\\end{array}}\!\!\!\!.\end{equation*} $$

The Rule of Necessitation in this form gives one a so-called normal modal logic. (This modal-logical notion of normality, by the way, has nothing at all to do with the proof-theorist’s notion of a proof being in normal form.)

Now, the Lemmon system S0.5 is not a normal modal logic. But it does have a Rule of Necessitation of sorts. The rule in question says that any classical propositional tautology (or theorem) may be necessitated. Graphically:

$$ \begin{equation*}{\left.\begin{array}{c}{\begin{array}{c}{\left.\begin{array}{c}\emptyset\\\Pi\\\underline{\;\,\varphi\;\,}\end{array}\right\}}\\\Box\varphi\hphantom{\varphi}\kern.8em\end{array}}{\begin{array}{c}\text{in nonmodal propositional logic}\\\end{array}}\end{array}\right\}}{\begin{array}{c}\text{in modal system S0.5}\\\end{array}}\!\!.\end{equation*} $$

Formulated alternatively as an inductive-definitional rule, the Rule of Necessitation in S0.5 would be

$$ \begin{equation*}{\begin{array}{c}(\mathbf{N})_{\scriptsize\mathbf{S0.5}_{\{\neg,\wedge,\vee,\rightarrow,\Box\}}}\end{array}}{\begin{array}{c}\underline{\kern-2.3em\mathcal{P}\Big(\Pi,\varphi,\emptyset,\mathbf{C}_{\{\neg,\wedge,\vee,\rightarrow\}}\Big)\kern-2.3em}\\\mathcal{P}\Big({\begin{array}{c}\underline{\;\,\Pi\;\,}\\\Box\varphi\end{array}}\!\!,\Box\varphi,\emptyset,\mathbf{S0.5}_{\{\neg,\wedge,\vee,\rightarrow,\Box\}}\Big)\end{array}}\!\!.\end{equation*} $$

Once again we have a rule in a system that is restricted in its applications to subproofs from a properly contained subsystem.

5.5 Towards a satisfactory ‘most general’ form of any particular rule

In general, we can expect there to be rules $\rho $ whose formulation as metalinguistic inductive-definitional clauses will be of the following overall form, for various subsystems $\mathcal {S}_1,\ldots ,\mathcal {S}_n$ of $\mathcal {S}$ :

$$ \begin{equation*}(\rho)_{\mathcal{S}}\kern-1.6em{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathcal{S}_1)\kern1em\ldots\kern1em\mathcal{P}(\Pi_n,\varphi_n,\Delta_n,\mathcal{S}_n)\kern1em\mathcal{C}(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n)}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1,\ldots ,\Pi_n}\\\varphi\end{array}}\!\!,\varphi,\Delta,\mathcal{S}\Big)\end{array}}\end{equation*} $$

where $\mathcal {C}(\Delta _1,\varphi _1,\ldots ,\Delta _n,\varphi _n)$ is an effectively decidable relational property on the indicated arguments; and where the overall premise set $\Delta $ will be of some effectively computable form

$$ \begin{align*} \delta(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n). \end{align*} $$

Presumably one would also be allowed to ‘minimize’ $\mathcal {S}$ by setting

$$ \begin{align*} \mathcal{S} = \bigcup_{i=1}^n S_i \cup\{(\rho)\}. \end{align*} $$

We are avoiding here the yet further complexities that would be involved in indicating how the set $\Delta $ of undischarged assumptions in the newly formed proof would indeed be effectively determinable from the various $\Delta _i$ ; and how the overall conclusion $\varphi $ relates both to the various $\varphi _i$ and to the various assumptions among the $\Delta _i$ that might be discharged. But, as we have indicated, there might also be an effectively decidable condition $\mathcal {C}$ on the premises and conclusions of the subordinate proofs, which needs to be stated separately, and for whose presence one would have to check before applying the rule $\rho $ to construct the more complex proof—we can call it $\rho (\Pi _1,\ldots ,\Pi _n)|\varphi $ —of the conclusion $\varphi $ by applying the rule $\rho $ to the immediate subproofs $\Pi _1,\ldots ,\Pi _n$ .

6 A tentative proposal about how to identify rules of inference

Our discussion thus far has sought to shake the confidence that the reader might have had at the outset in our ability to say precisely what a logical rule of inference is. We have encountered at least the following aspects of the identification-problem.

First, there appears to be an ineliminable system-relativity, hence a kind of ‘holism’, involved in characterizing any rule of inference as a means of constructing new proofs from given proofs. The ‘input’ proofs can be from various systems; and the ‘output’ proof might be in yet another system. And even if the systems in question are ‘all the same’—so that the same system-parameter $\mathcal {S}$ occurs throughout the inductive clause for proof-formation in question—this immediately makes one worry about the possibility of some kind of impredicativity in our conception of such a rule. The rule is supposed to belong to the system $\mathcal {S}$ , indeed is crucially constitutive of the system $\mathcal {S}$ ; yet one seems to require reference to the system $\mathcal {S}$ in order to so much as give expression to the rule (as in the minimization suggestion towards the end of §5.5).

It would be instructive to compare the situation here concerning proof systems and their rules of inference with a familiar and more standard example of impredicativity in mathematics.Footnote ³¹ One says that a real number y is an upper bound to the set $\{x|\Phi (x)\}$ of real numbers just in case

$$ \begin{align*} \forall z(\Phi(z)\rightarrow z\leq y). \end{align*} $$

The least upper bound $\lambda x\Phi (x)$ of this set is that upper bound whose every lesser is no such upper bound. That is:

$$ \begin{align*} \lambda x\Phi(x)={{\textit{df}}}\;\;\iota w(\forall z(\Phi(z)\rightarrow z\leq w)\wedge\forall v(v<w\rightarrow \neg \forall z(\Phi(z)\rightarrow z\leq v))). \end{align*} $$

An unproblematic instance is where for $\Phi (x)$ we take $x<0$ . For then we have

$$ \begin{align*} \lambda x\,x<0={{\textit{df}}}\;\;\iota w(\forall z(z<0\rightarrow z\leq w)\wedge\forall v(v<w\rightarrow \neg \forall z(z<0\rightarrow z\leq v))). \end{align*} $$

Note that $\lambda x(x<0)=0$ ; whence $\lambda x(x<0)\;\not <\;0$ .

The problem of impredicativity arises, however, when one considers the possibility that $\Phi (\lambda x\Phi (x))$ . For then the definition involves quantifying over numbers among which is the very number that is to be denoted by the defined expression.

This possibility is realized if for $\Phi (x)$ we take $x\leq 0$ . For then we have $\lambda x(x\leq 0)=0$ ; whence $\lambda x(x\leq 0)\leq 0$ :

$$ \begin{align*} \lambda x\,x\leq 0={\!{\textit{df}}}\;\;\iota w(\forall z(z\leq 0\rightarrow z\leq w)\wedge\forall v(v<w\rightarrow \neg \forall z(z\leq 0\rightarrow z\leq v))). \end{align*} $$

Platonists about numbers are unruffled by such impredicativity. The least upper bound is ‘out there’, and just happens to be picked out by an expression involving quantification over a range that contains it. But what, in the context of our discussion of systems of proof and rules of inference, would be the reassuring analogue of Platonism about numbers, which could ensure that the rule-theorist could be similarly unruffled?Footnote ³²

Returning to the way a rule $\rho $ and a system $\mathcal {S}$ invoke each other: one really has to ask oneself whether one has here a vicious or a virtuous circle of conceptual constitution. We confine ourselves to simply raising this question here. At present, we see no clear answer as to whether whatever circle is involved is vicious or virtuous. All we wish to bring to the reader’s awareness is that there is such a circle; and it has not, to the best of the present author’s knowledge, been brought clearly into focus before.Footnote ³³ Inferentialists about meaning, especially, will now owe their audience an argument for the conclusion that the circle is virtuous, after all; whereas their opponents might see here an opportunity to discredit inferentialism by arguing, to the contrary, that the circle is somehow vicious.

Secondly, it would appear that ‘one and the same rule’ can be framed in different ‘versions’, to the same overall systemic effect (as far as deducibility is concerned), but with different effects at the level of proof-structures. If we take the latter differences seriously, we should be inclined to regard these different versions of (putatively) the ‘same’ rule as nothing of the sort; rather, they are simply distinct rules.

Thirdly, thinking of a rule of inference as licensing a certain kind of truth-preserving passage from premises (immediately above the inference stroke) to a conclusion (immediately below the inference stroke) is much too simplistic. Even if we confine our attention here to the introduction and elimination rules for the standard logical operators, the over-simplification involved in the ‘ $P_1,\ldots ,P_n$ ; so Q’ conception is readily apparent. Among those rules, the only ones that simple are $\neg $ -E, $\wedge $ -I, $\wedge $ -E (serial form only), $\vee $ -I, $\rightarrow $ -E (serial form only, i.e., Modus Ponens), $\exists $ -I and $\forall $ -E. The other rules for these operators are more complicated. Some involve conditions on expressions other than their immediate premises and their conclusions. Such is the case with discharge of assumptions—as with $\neg $ -I, $\wedge $ -E (parallelized form), $\vee $ -E (i.e., Proof by Cases), $\rightarrow $ -I (i.e., Conditional Proof), $\exists $ -E and $\forall $ -I. And some involve conditions on parameters—as with $\exists $ -E and $\forall $ -I.

The appropriate general conception of what an application of any rule of inference vouchsafes is not truth-preservation from the immediate premises involved to the conclusion involved; rather, what is vouchsafed is validity-preservation from the immediate subproofs involved in any application of the rule, to the overall proof that results from that application!Footnote ³⁴ This is particularly evident when we consider the Right and Left rules of the sequent calculus. These can be understood as reprising the effect of the introduction and elimination rules.

Moving on to Intuitionistic Logic, even the rule EFQ:

$$ \begin{equation*}{\begin{array}{c}\underline{\,\bot\,}\\\varphi\end{array}}\end{equation*} $$

is hard to reckon to the ‘ $P_1,\ldots ,P_n$ ; so Q’ mold. To be sure, we can take n to be 1; but can we really take $\bot $ as a premise P? This author thinks of $\bot $ only as a punctuation marker in proofs, not eligible to be regarded as a sentence in its own right, and a fortiori not able to feature as a subsentence of any sentence.Footnote ³⁵ (Hence it is ill-advised to define $\neg \varphi $ as $\varphi \!\rightarrow \!\bot $ .)

Finally, moving on to Classical Logic: LEM has to be construed as a zero-premise rule; and DNE is a genuine single-premise rule. But both Dil and CR involve discharge of assumptions, and therefore they too fail to conform to the ‘ $P_1,\ldots ,P_n$ ; so Q’ mold.

As we survey these problems, a certain line of resolution has considerable appeal. As our discussion of the third problem reveals, the ‘ $P_1,\ldots ,P_n$ ; so Q’ conception is way too impoverished. Far better is the conception, already advanced above, of rules as particular means of building up new proofs from given proofs; that is, the conception of rules as given by, or corresponding to, inductive clauses in an inductive definition of the ternary notion ‘ $\Pi $ is a proof of the conclusion $\varphi $ from the set $\Delta $ of premises (i.e., undischarged assumptions)’. The latter notion smoothly subsumes the likes of $\wedge $ -I with those of $\exists $ -E (to choose but two rules with striking enough points of contrast to make the matter clear). Moreover, the semantic property to be preserved is not truth-of-sentences, but rather the Prawitzian one of validity-of-argument. (When a proof is of the conclusion Q from (exactly) the premises $P_1,\dots ,P_n$ , then the argument it proves is the sequent $P_1,\dots ,P_n:Q$ .)

Note that one can endorse this Prawitzian conception of preservation-of-argument-validity with the catholicity of intent already remarked on in §1.3—that is, without advancing any particular conception of validity that might lead to a preference for one logical system over another (such as for Intuitionistic Logic over Classical Logic). Now of course Prawitz’s own recursive definition of validity of argument, given the conceptual materials that he brought to bear, did lead to a preference for Intuitionistic Logic over Classical Logic.Footnote ³⁶ The professed ‘catholicity of intent’, however, can be exhibited by offering an alternative conception of validity of argument, formed and applied in a manner analogous to that of Prawitz, but employing, rather than the epistemic notion of a canonical warrant for assertion, the notion of a model-relative truthmaker; and proceeding, thus equipped, to a demonstration that one’s rules of inference preserve argument validity, rather than truth-of-sentences. A first foray in this direction can be found in Chapter 9 of Tennant [Reference Tennant45] (with an important correction in Brauer and Tennant [Reference Brauer and Tennant4]). For the logical theory of truthmakers and falsitymakers there deployed, see Tennant [Reference Tennant, Lear and Oliver41 and Reference Tennant and Glanzberg46].

One can also ‘uniformize’ in search of a solution to the holism or impredicativity problem—indeed, perhaps even turn it to one’s advantage. Let us set aside those challenging pathologies of ‘rules’ we pointed out above, such as terminal CR, Atomic Dilemma, and Necessitation. Let us assume instead that the system-parameter $\mathcal {S}$ will be held constant throughout. When characterizing a rule $\rho $ the only assumption one needs to make is that $\rho $ will belong to $\mathcal {S}$ , whatever that system $\mathcal {S}$ might turn out to be. The rule $\rho $ must be formulated, or identified, in such a way as to carry within it its own seeds of extendability to ever-enlarged systems $\mathcal {S}$ to which it might subsequently be taken to belong. In this way we come to see rules of inference as open-textured. Whether one confines one’s attention to the fragment of intuitionistic propositional logic based on $\neg $ and $\wedge $ (say), or the full system of classical first-order logic with all the usual operators primitive, we can focus on the rule of $\wedge $ -I (just to pick an easy illustration of the main idea) and say that it would be essentially the same rule in each of those two systems, because it is to be understood as the following virtuously self-referential claim:

$$ \begin{align*} (\wedge\text{-I}) \;\text{For any system }\mathcal{S}\text{ containing }(\wedge\text{-I}): \end{align*} $$

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathcal{S})\kern2em\mathcal{P}(\Pi_2,\varphi_2,\Delta_2,\mathcal{S})}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1\kern1em\Pi_2}\\\varphi_1\wedge\varphi_2\end{array}}\!\!,\varphi_1\wedge\varphi_2,\Delta_1\cup\Delta_2,\mathcal{S}\Big)\end{array}}.\end{equation*} $$

Note how—rather ironically—we have ascended to the metalevel (in formulating our definition of the ternary relation $\mathcal {P}$ ) and have used there the two-premise, atomic inference rule

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathcal{S})\kern2em\mathcal{P}(\Pi_2,\varphi_2,\Delta_2,\mathcal{S})}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1\kern1em\Pi_2}\\\varphi_1\wedge\varphi_2\end{array}}\!\!,\varphi_1\wedge\varphi_2,\Delta_1\cup\Delta_2,\mathcal{S}\Big)\end{array}}\end{equation*} $$

And we can make do with this kind of format even when the rule in question is not, like $\wedge $ -I, a rule that invites simplistic representation as a two-premise rule not involving discharge of assumptions, and not involving any more ‘global’ pre-conditions on applicability. Consider, for example, the following re-formulation in the new format of the inductive clause for $\exists $ -E, where the premises of the metalinguistic inference are now arranged vertically, in order to avoid sideways spread:

$(\exists \text {-E})$ For any system $\mathcal {S}$ containing ( $\exists $ -E):

$$ \begin {array}{l} \mathcal {P}(\Pi ,\exists x\varphi ,\Delta ,\mathcal {S})\\ \mathcal {P}(\Sigma ,\psi ,\Gamma ,\mathcal {S})\\ \underline {\varphi ^x_a\in \Gamma \text { and }a\text { does not occur in }\exists x\varphi,\;\psi ,\text {or }\Gamma \setminus \{\varphi ^x_a\}}.\\ \mathcal {P}\Big ({\begin {array}{c} \underline { \Pi _1 \kern1em \Pi _2 }\\ \psi \end {array}}\!\!,\psi ,\Delta \cup (\Gamma \setminus \{\varphi ^x_a\}),\mathcal {S}\Big )\end {array} $$

Note that the third premise for the metalinguistic inference rule is of the form $\mathcal {C}(\Delta ,\exists x\varphi ,\Gamma ,\psi )$ , and is effectively decidable, since all the sets involved are finite.

It is clear from these two examples (namely, the rules $\wedge $ -I and $\exists $ -E) that the suggested general form of a rule in the new format is the following:

$(\rho )\kern1em\text {For any system }\mathcal {S}\text { containing }(\rho ) \text { [one may reason thus about proofs]}\!:$

$$ \begin{equation*}\kern1em{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathcal{S})\kern1em\ldots\kern1em\mathcal{P}(\Pi_n,\varphi_n,\Delta_n,\mathcal{S})\kern1em\mathcal{C}(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n)}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1,\ldots ,\Pi_n}\\\varphi\end{array}}\!\!,\varphi,\delta(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n),\mathcal{S}\Big)\end{array}}.\end{equation*} $$

The ascent to the metalevel here appears to be essential for our purposes. A rational agent fully apprised of what rule is being applied in any given inferential step would need to have this kind of metalinguistic awareness of what is guiding the inferential transition. We attain the (not over-)simplifying case of transitions of the form ‘ $P_1,\ldots ,P_n$ ; so, Q’ only by this metalinguistic ascent. This is what allows us to take in our stride all the complications of discharge of assumptions, checking for correct parametric behavior with quantifier moves, etc. But the price is that the rule becomes self-referring (as indicated by the two occurrences of ‘ $\rho$ ’), in order for its statement to carry within it the seeds of its own future applicability within whatever further extension of the proof system it continues to play ‘its’ part. That is what we meant by rules being ‘open-textured’.

To repeat: our framing of the general form $(\rho )$ here would have to be virtuously self-referential in order to serve our purposes. And the big question that then arises is simply: Is it?

7 Identifying rules via metalinguistic inductive-definitional clauses using only literals

Recall our earlier suggested general form of an inference rule in any system $\mathcal {S}$ containing it:

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathcal{S})\kern1em\ldots\kern1em\mathcal{P}(\Pi_n,\varphi_n,\Delta_n,\mathcal{S})\kern1em\mathcal{C}(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n)}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1,\ldots ,\Pi_n}\\\varphi\end{array}}\!\!,\varphi,\delta(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n),\mathcal{S}\Big)\end{array}}.\end{equation*} $$

It now needs to be stressed not only that the $\mathcal {P}$ -predications are atomic (in the metalanguage); but also that the condition(s) $\mathcal {C}$ need to be spelled out by means of (metalinguistic) literals—that is, atomic statements or negations thereof. In particular, one wishes to avoid using explicitly disjunctive conditions at all costs. The maxim guiding rule-formulations is to keep matters as simple as possible; and, in order to do so, we must state these rules in what turn out to be, inferentially, the most basic way possible.

Let us illustrate by considering the rule $\vee $ -I. As already pointed out in §4.1, it is always stated in two parts, which we shall render here in our usual graphic way with all the earlier suppressed details filled in:

$$ \begin{equation*}{\begin{array}{c}\Delta\\\Pi\\\underline{\kern1em\varphi\kern1em}\\\varphi\vee\psi\end{array}}\!\!;\kern2em{\begin{array}{c}\Delta\\\Pi\\\underline{\kern1em\psi\kern1em}\\\varphi\vee\psi\end{array}}\!\!.\end{equation*} $$

The corresponding metalinguistic inductive-definitional clauses (for the notion $\mathcal {P}$ of proof) are the following. Note how they instantiate the general form just reiterated. The condition $\mathcal {C}$ in each part is the null condition, by virtue of the separation of this rule into its two parts:

$$ \begin{equation*}{\begin{array}{c}\underline{\kern2.5em\mathcal{P}(\Pi,\varphi,\Delta,\mathcal{S})\kern2.5em}\\\mathcal{P}\Big(\!\!{\begin{array}{c}\underline{\kern1em\Pi\kern1em}\\\varphi\vee\psi\end{array}}\!\!,\varphi\vee\psi,\Delta,\mathcal{S}\Big)\end{array}};\kern2em{\begin{array}{c}\underline{\kern2.5em\mathcal{P}(\Pi,\psi,\Delta,\mathcal{S})\kern2.5em}\\\mathcal{P}\Big(\!\!{\begin{array}{c}\underline{\kern1em\Pi\kern1em}\\\varphi\vee\psi\end{array}}\!\!,\varphi\vee\psi,\Delta,\mathcal{S}\Big)\end{array}}.\end{equation*} $$

If we had attempted to frame this rule by means of only one definitional clause, then we would have been forced to use a disjunctive condition $\mathcal {C}$ , as follows:

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi,\chi,\Delta,\mathcal{S})\kern2em\chi\!=\!\varphi\ { \textit{ or} }\ \chi\!=\!\psi}\\\mathcal{P}\Big(\!\!{\begin{array}{c}\underline{\kern1em\Pi\kern1em}\\\varphi\vee\psi\end{array}}\!\!,\varphi\vee\psi,\Delta,\mathcal{S}\Big)\end{array}}.\end{equation*} $$

This disjunctive condition is obviously not a literal; so the preceding null-condition clauses are to be preferred. Basically, what we are saying, methodologically, is this: our inductive-definitional clauses for the proof-predicate $\mathcal {P}$ are to be metalinguistic Horn clauses. An inference of the form

$$ \begin{equation*}{\begin{array}{c}\underline{P_1,\ldots,P_n,Q\vee R}\\S\end{array}}\end{equation*} $$

is not in Horn form; whereas each of the inferences

$$ \begin{equation*}{\begin{array}{c}\underline{P_1,\ldots,P_n,Q}\\S\end{array}}\kern2em{\begin{array}{c}\underline{P_1,\ldots,P_n,R}\\S\end{array}}\end{equation*} $$

is in Horn form. And the latter two inferences are jointly equivalent to the former one.

So much for $\vee $ -I. Let us turn now to $\vee $ -E—in particular, the liberalized form of $\vee $ -E, mentioned above, that is to be found in Core Logic (and its classicized extension). There are three distinct parts to this liberalized rule. They differ from one another solely in whether their subordinate proofs have the same conclusion, or whether one of them (but not the other) has $\bot $ as its conclusion.

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi,\theta,\Delta,\mathcal{S})\kern2em\mathcal{P}(\Sigma,\theta,\Gamma,\mathcal{S})\kern2em\varphi\in\Delta\kern2em\psi\in\Gamma}\\\mathcal{P}\Big({\begin{array}{c}\underline{\varphi\!\vee\!\psi\kern.5em\Pi\kern.5em\Sigma}\\\theta\end{array}}\!\!,\theta,\{\varphi\!\vee\!\psi\}\!\cup\!(\Delta\!\setminus\!\{\varphi\})\!\cup\!(\Gamma\!\setminus\!\{\psi\}),\mathcal{S}\Big)\end{array}};\end{equation*} $$

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi,\theta,\Delta,\mathcal{S})\kern2em\mathcal{P}(\Sigma,\bot,\Gamma,\mathcal{S})\kern2em\varphi\in\Delta\kern2em\psi\in\Gamma}\\\mathcal{P}\Big({\begin{array}{c}\underline{\varphi\!\vee\!\psi\kern.5em\Pi\kern.5em\Sigma}\\\theta\end{array}}\!\!,\theta,\{\varphi\!\vee\!\psi\}\!\cup\!(\Delta\!\setminus\!\{\varphi\})\!\cup\!(\Gamma\!\setminus\!\{\psi\}),\mathcal{S}\Big)\end{array}};\end{equation*} $$

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi,\bot,\Delta,\mathcal{S})\kern2em\mathcal{P}(\Sigma,\theta,\Gamma,\mathcal{S})\kern2em\varphi\in\Delta\kern2em\psi\in\Gamma}\\\mathcal{P}\Big({\begin{array}{c}\underline{\varphi\!\vee\!\psi\kern.5em\Pi\kern.5em\Sigma}\\\theta\end{array}}\!\!,\theta,\{\varphi\!\vee\!\psi\}\!\cup\!(\Delta\!\setminus\!\{\varphi\})\!\cup\!(\Gamma\!\setminus\!\{\psi\}),\mathcal{S}\Big)\end{array}}.\end{equation*} $$

Separating out these three distinct parts of the liberalized rule of $\vee $ -E enables us to keep them in Horn form. This would not be the case if we were to attempt to combine them into ‘just one’ inductive-definitional clause, even though the following ‘single’ clause is inferentially equivalent to the three foregoing clauses taken together:

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi,\chi,\Delta,\mathcal{S})\kern1em\mathcal{P}(\Sigma,\eta,\Gamma,\mathcal{S})\kern1em(\chi=\theta\wedge\eta=\theta)\textit{{or} }(\chi=\theta\wedge\eta=\bot)\textit{{or} }(\chi=\bot\wedge\eta=\theta)}\\\mathcal{P}\Big({\begin{array}{c}\underline{\varphi\!\vee\!\psi\kern.5em\Pi\kern.5em\Sigma}\\\theta\end{array}}\!\!,\theta,\{\varphi\!\vee\!\psi\}\!\cup\!(\Delta\!\setminus\!\{\varphi\})\!\cup\!(\Gamma\!\setminus\!\{\psi\}),\mathcal{S}\Big)\end{array}}.\end{equation*} $$

We note another feature of the preferred ‘canonical’ form taken by inferential Horn clauses: they minimize the number of distinct variables involved in their formulation of the permitted inference(s). Note how the extra variables $\color {black}\chi $ and $\color {black}\eta $ above are involved only in the noncanonical clauses, not in the canonical, because Horn, clauses.

We have finally arrived at a tentative answer to our original question. As far as the rule of Classical Reductio is concerned, it is unitary—it has only one part, and it can be expressed in canonical Horn form:

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi,\bot,\Delta,\mathcal{S})\kern2em\neg\varphi\in\Delta}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi}\\\theta\end{array}}\!\!,\theta,(\Delta\!\setminus\!\{\neg\varphi\}),\mathcal{S}\Big)\end{array}}.\end{equation*} $$

As far as the rule of Dilemma is concerned, its form for Classical Core Logic $\mathbb {C}^+$ is in two parts, each expressible in canonical Horn form:

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi,\theta,\Delta,\mathcal{S})\kern2em\mathcal{P}(\Sigma,\theta,\Gamma,\mathcal{S})\kern2em\varphi\in\Delta\kern2em\neg\varphi\in\Gamma}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi\kern.5em\Sigma}\\\theta\end{array}}\!\!,\theta,(\Delta\!\setminus\!\{\varphi\})\!\cup\!(\Gamma\!\setminus\!\{\neg\varphi\}),\mathcal{S}\Big)\end{array}};\end{equation*} $$

$$ \begin{equation*}{\begin{array}{c}\underline{\mathcal{P}(\Pi,\theta,\Delta,\mathcal{S})\kern2em\mathcal{P}(\Sigma,\bot,\Gamma,\mathcal{S})\kern2em\varphi\in\Delta\kern2em\neg\varphi\in\Gamma}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi\kern.5em\Sigma}\\\theta\end{array}}\!\!,\theta,(\Delta\!\setminus\!\{\varphi\})\!\cup\!(\Gamma\!\setminus\!\{\neg\varphi\}),\mathcal{S}\Big)\end{array}}.\end{equation*} $$

As far as the introduction and elimination rules are concerned, we take each logical operator in turn, and gather together the ‘rule-parts’ of each kind. These rule-parts must be in canonical Horn form, when formulated as metalinguistic inductive-definitional clauses in the definition of the ternary proof-predicate $\mathcal {P}$ . The various parts of a given introduction or elimination rule ( $\rho $ ) can then be gathered together according to our earlier rubric for a self-referential rule, but making clear that it can consist in k distinct parts:

$(\rho )$ For any system $\mathcal {S}$ containing ( $\rho $ ) [one may reason about proofs in any of the following $\color {black}k$ ways]:

$$ \begin{equation*}\kern1em{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathcal{S})\kern1em\ldots\kern1em\mathcal{P}(\Pi_n,\varphi_n,\Delta_n,\mathcal{S})\kern1em\mathcal{C}_1(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n)}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1,\ldots ,\Pi_n}\\\varphi\end{array}}\!\!,\varphi,\delta_1(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n),\mathcal{S}\Big)\end{array}};\end{equation*} $$

$$ \begin{align*}\vdots \end{align*} $$

$$ \begin{equation*}\kern1em{\begin{array}{c}\underline{\mathcal{P}(\Pi_1,\varphi_1,\Delta_1,\mathcal{S})\kern1em\ldots\kern1em\mathcal{P}(\Pi_n,\varphi_n,\Delta_n,\mathcal{S})\kern1em\mathcal{C}_k(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n)}\\\mathcal{P}\Big({\begin{array}{c}\underline{\Pi_1,\ldots ,\Pi_n}\\\varphi\end{array}}\!\!,\varphi,\delta_k(\Delta_1,\varphi_1,\ldots ,\Delta_n,\varphi_n),\mathcal{S}\Big)\end{array}}.\end{equation*} $$

This explication of rule-identity seems to cohere well with pre-theoretic intuitions, even after informing oneself of all the potentially complicating, often unfamiliar, considerations that have been broached in our investigations. We are now in a position to appreciate how and why two proponents of different logical systems can engage in a productive dispute about the right form that a particular rule should take. It should not be the case that two disputants advocating different forms for a rule (for, say, $\vee $ -E) should be regarded as ‘talking past one another’ by allegedly talking about altogether different rules.