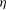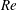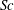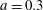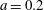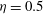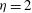1. Introduction
For many years, electrohydrodynamics has attracted extensive research due to its wide applications in microfluidic devices, such as in ink jetting, drug delivery and chemical analysis. One favourable application of the use of an electric field is to pump liquids in micro-channels as it will not induce mechanical noise. Another potential use of an electric field is to enhance the mixing in microfluidic devices (Lin Reference Lin2009). When an external electric field is applied across a liquid layer, the Maxwell stress can initiate flow instability in the liquid layer with spatial changes in the electrical properties. In previous studies, the instability of flow systems could be triggered by an electric field due to abrupt changes (Melcher & Schwartz Reference Melcher and Schwartz1968; Melcher & Smith Reference Melcher and Smith1969) or spatial gradients in electrical properties (Melcher & Firebaugh Reference Melcher and Firebaugh1967).
In the former case, the liquids are usually assumed to be immiscible and the interfacial instability is of particular interest (Saville Reference Saville1997; Ozen et al. Reference Ozen, Aubry, Papageorgiou and Petropoulos2006). It is assumed that there is no electrical charge within the bulk region, while electrical charges accumulate on the interface. One such model proposed was the leaky-dielectric model by Taylor (Reference Taylor1966). Recently, Wang (Reference Wang2012) discussed the influence of surface charge transportation on the breakup of a poorly conducting liquid thread surrounded by an insulating liquid layer in a radial electric field. Ding, Wong & Li (Reference Ding, Wong and Li2013) investigated the instability of two leaky-dielectric co-flows in an annulus duct in a radial electric field. There was an abrupt change in the electrical conductivity as well as the electrical permittivity, such that the Maxwell stress could either enhance or impede the interfacial deformation. Their results demonstrated that the electric field may inhibit the capillary instability caused by surface tension and interfacial wave instability due to viscosity stratification (Ding et al. Reference Ding, Wong and Li2013).
The latter study of liquids with spatial electrical property gradients focused on the influence of electrical body force on the stability of electro-convection. The gradients may be caused by non-isothermal heating (Yoshikawa, Crumeyrolle & Mutabazi Reference Yoshikawa, Crumeyrolle and Mutabazi2013) or due to the non-uniform distribution of ionic concentration (Lin Reference Lin2009). To the best of our knowledge, previous studies of electro-convection in a liquid layer with electrical conductivity gradients in an isothermal environment have been focused on flows in a square duct in past decades.
Pioneering work on electro-convection in a planar liquid layer with an electrical conductivity gradient was carried out by Baygents & Baldessari (Reference Baygents and Baldessari1998). A wall-normal electric field was imposed between two parallel plates. They proposed that the occurrence of instability was triggered by the dielectrophoretic effect (Baygents & Baldessari Reference Baygents and Baldessari1998). They found that the lower conductivity boundary had a strong stabilizing effect when the conductivity gradient was large. It should be noted that the assumption of exchange of stability made by them was incorrect because the critical unstable mode may be oscillatory (Baygents & Baldessari Reference Baygents and Baldessari1998). Chang, Ruo & Chen (Reference Chang, Ruo and Chen2009) dropped the assumption of exchange of stability and considered the influence of an imposed shear flow wherein the oscillatory and stationary unstable modes were discovered. It was found that the instability could be enhanced by a very weak shear flow, and the transverse mode (zero spanwise wavenumber) became critical rather than the longitudinal model (zero streamwise wavenumber). However, as the shear flow became stronger, they found that the longitudinal mode became critical and the critical mode was independent of the shear flow (Chang et al. Reference Chang, Ruo and Chen2009). Ruo, Chang & Chen (Reference Ruo, Chang and Chen2010) extended the study of Chang et al. (Reference Chang, Ruo and Chen2009) and considered the rotating effect. Their results showed that rotation played a stabilizing role in the system while the electric field was the major cause of instability (Ruo et al. Reference Ruo, Chang and Chen2010). Recently, Ding & Wong (Reference Ding and Wong2014) investigated the instability of an annular liquid layer with electrical conductivity gradients. Their results showed that the critical unstable mode depended on the geometry of the duct and the critical unstable mode may be either stationary or oscillatory (Ding & Wong Reference Ding and Wong2014).
Unlike the studies of Baygents & Baldessari (Reference Baygents and Baldessari1998), Chang et al. (Reference Chang, Ruo and Chen2009), Ruo et al. (Reference Ruo, Chang and Chen2010) and Ding & Wong (Reference Ding and Wong2014), in which the electro-convection was triggered due to a spatial gradient in the electrical conductivity, Lin et al. (Reference Lin, Storey, Oddy, Chen and Santiago2004) considered two miscible flows with an electrical conductivity stratification. To achieve such a conductivity stratification flow in experiments, Lin et al. (Reference Lin, Storey, Oddy, Chen and Santiago2004) used two electrolytes with different ionic concentrations. The liquids were pumped into the channel using a syringe pump. A Couette flow arose from a tangential electric field due to the electro-osmosis phenomenon after removing the pressure gradient. The electro-osmosis phenomenon was treated as a slippery boundary condition and the slip velocity was related to the zeta potential in the electrical double layer. However, it should be noted that the electro-osmosis flow was rather weak. They investigated the linear stability by assuming a quasi-steady base flow and verified their results via a direct numerical simulation. A depth-averaged model was proposed by Storey, Lin & Santiago (Reference Storey, Lin and Santiago2005) to investigate the electrohydrodynamical instability in a square pipe. The depth-averaged model simplified the problem to a two-dimensional flow, but showed good agreement with the three-dimensional results (Storey et al. Reference Storey, Lin and Santiago2005). The convective and absolute electrokinetic instability with a conductivity stratification was extended by Chen et al. (Reference Chen, Lin, Lele and Santiago2005). Chen et al. (Reference Chen, Lin, Lele and Santiago2005) used aqueous electrolytes of 10:1 conductivity ratio and applied a streamwise electric field. The two-dimensional instability was studied via a thin-layer assumption that the channel width was much larger than the channel depth. Santos & Storey (Reference Santos and Storey2008) extended the studies to a flow with streamwise conductivity gradients and investigated the linear instability as well as the nonlinear evolution. Notably, in these studies (Baygents & Baldessari Reference Baygents and Baldessari1998; Chang et al. Reference Chang, Ruo and Chen2009; Ruo et al. Reference Ruo, Chang and Chen2010) non-slippery conditions were adopted, while in other studies (Lin et al. Reference Lin, Storey, Oddy, Chen and Santiago2004; Chen et al. Reference Chen, Lin, Lele and Santiago2005; Storey et al. Reference Storey, Lin and Santiago2005; Santos & Storey Reference Santos and Storey2008) a slippery boundary condition was considered. The latter focused on the stability of electro-osmosis flow.
Previously, investigations of the electrohydrodynamical instability of multi-immiscible electrolyte flows in a circular pipe have mainly focused on the interfacial instability. Georgiou et al. (Reference Georgiou, Papageorriou, Maldarelli and Rumschitzki1991) investigated the influence of an electro-double-layer on the long-wave instability of a core–annular electrolyte film. They found that double layer repulsion can impede the capillary instability, while double layer attraction enhances the capillary instability. Extension of such a flow was performed by Conroy et al. (Reference Conroy, Craster, Matar and Papageorgiou2010, Reference Conroy, Matar, Craster and Papageorgiou2011, Reference Conroy, Matar, Craster and Papageorgiou2012). They considered a two-electrolyte flow in a pipe. The interfacial instability and dynamics were studied in the framework of long-wave theory in which the system was reduced asymptotically (Conroy et al. Reference Conroy, Craster, Matar and Papageorgiou2010, Reference Conroy, Matar, Craster and Papageorgiou2011, Reference Conroy, Matar, Craster and Papageorgiou2012). When an axial electric field is applied, most previous studies have been focused on the stability of a liquid jet. Theoretical and experimental studies have shown that the electric field has a stabilizing (Melstel Reference Melstel1996) or destabilizing (Hohman et al. Reference Hohman, Shin, Rutledge and Brenner2001) effect in electrified jets. For miscible flows in a circular pipe, we note that previous studies focused on the problem of viscosity stratification flows (Selvam et al. Reference Selvam, Merk, Govindarajan and Meiburg2007; d’Olce et al. Reference d’Olce, Rakotomalala, Salin and Talon2008, Reference d’Olce, Rakotomalala, Salin and Talon2009). The core–annular flows were driven by two coaxial pumps (Selvam et al. Reference Selvam, Merk, Govindarajan and Meiburg2007; d’Olce et al. Reference d’Olce, Rakotomalala, Salin and Talon2008, Reference d’Olce, Rakotomalala, Salin and Talon2009). Water–natrosol mixtures were used in experiments which could provide a large viscosity contrast but small variations in densities (Selvam et al. Reference Selvam, Merk, Govindarajan and Meiburg2007; d’Olce et al. Reference d’Olce, Rakotomalala, Salin and Talon2008, Reference d’Olce, Rakotomalala, Salin and Talon2009). Experiments by d’Olce et al. (Reference d’Olce, Rakotomalala, Salin and Talon2008, Reference d’Olce, Rakotomalala, Salin and Talon2009) demonstrated that perfect core–annular flows can be observed in such flow systems. For a single fluid flow in a circular micro-pipe, experimental study showed that the fluid was laminar and the electro-osmotic moving speed was very small (Sinton & Li Reference Sinton and Li2003). A careful look at the literature indicates that studies on electrohydrodynamic instability of miscible liquid flows in a pipe are very limited. In this paper, our aim is to extend the electrohydrodynamical instability of immiscible flows in a circular pipe to miscible flows. In addition, in micro-channel flows, the Reynolds number is usually very small, therefore mixing due to turbulence will not occur (Sinton & Li Reference Sinton and Li2003). This paper provides a potential method that can facilitate the mixing in a micro-pipe through electrohydrodynamic instability.
The rest of this paper is organized as follows. In § 2, the mathematical formulation is constructed. Section 3 presents the base state and non-dimensional governing system. In § 4, the linear stability analysis is implemented and the normal mode analysis is considered. In § 5, the energy analysis is carried out to interpret the instability mechanism. Section 6 presents the parametric studies of the dimensionless parameters. In the last section, our conclusion is given.
2. Mathematical formulation
We consider a pipe flow system as shown in figure 1. The radius of the pipe is
$b$
. The two liquids are miscible dilute electrolyte solutions. The liquids are Newtonian and the values of the density
${\it\rho}$
, kinematic viscosity
${\it\nu}$
and dynamic viscosity
${\it\mu}={\it\rho}{\it\nu}$
of the two liquids are assumed to be the same (Lin et al.
Reference Lin, Storey, Oddy, Chen and Santiago2004). There is a sharp change in the ionic concentration where the two liquids meet at
$r=a$
. Therefore, a sharp change in the electrical conductivity occurs at
$r=a$
. A constant electric field is imposed in the axial direction. A constant pressure gradient is imposed along the axis.
Figure 1. The geometry of the system.
${\it\sigma}_{1}$
and
${\it\sigma}_{2}$
represent the electrical conductivity in the inner and outer layers respectively.
In this paper, the three-dimensional hydrodynamical problem is considered. Cylindrical coordinates
$(r,{\it\theta},z)$
are chosen; gravity is neglected. The motion of the liquids is governed by the continuity equation and the momentum equation,
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}\frac{\text{D}\boldsymbol{v}}{\text{D}t}=-\boldsymbol{{\rm\nabla}}p+{\it\mu}{\rm\nabla}^{2}\boldsymbol{v}+\boldsymbol{f}, & \displaystyle\end{eqnarray}$$
$\boldsymbol{v}=u\boldsymbol{e}_{r}+v\boldsymbol{e}_{{\it\theta}}+w\boldsymbol{e}_{z}$
is the velocity and
$\text{D}/\text{D}t=\partial /\partial t+u(\partial /\partial r)+(v/r)(\partial /\partial {\it\theta})+w(\partial /\partial z)$
is the material derivative operator. Here,
$\boldsymbol{f}$
is the electrical force which can be related to the Maxwell stress tensor
$\unicode[STIX]{x1D64F}^{M}$
by 
$$\begin{eqnarray}\boldsymbol{f}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}^{M}.\end{eqnarray}$$
Usually, analysis of (2.2) is difficult because the electric field is coupled to the free charge density
${\it\rho}_{e}$
according to Maxwell’s equations. Moreover, the free charge density is coupled to the flow field. In this paper, we assume that the electrical current density
$\boldsymbol{J}_{e}$
and the induced current density
$(\partial {\it\epsilon}\boldsymbol{E}/\partial t)$
are modest, such that the induced magnetic field is negligible. Therefore, the electrostatic problem is considered in this paper,
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\times \boldsymbol{E}=0.\end{eqnarray}$$
Hence, the Maxwell stress
$\unicode[STIX]{x1D64F}^{M}={\it\epsilon}\boldsymbol{EE}-(1/2){\it\epsilon}\Vert \boldsymbol{E}\Vert ^{2}\unicode[STIX]{x1D644}$
. The parameter
${\it\epsilon}$
is the dielectric permittivity and
$\boldsymbol{E}$
is the electric field. Here,
$\Vert \boldsymbol{E}\Vert ^{2}=\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{E}$
and
$\unicode[STIX]{x1D644}$
is the identity tensor. The charge density is given by Gauss’s law,
$$\begin{eqnarray}{\it\rho}_{e}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\epsilon}\boldsymbol{E}).\end{eqnarray}$$
Hence, the momentum equation (2.2) is now written as
$$\begin{eqnarray}{\it\rho}\frac{\text{D}\boldsymbol{v}}{\text{D}t}=-\boldsymbol{{\rm\nabla}}p+{\it\mu}{\rm\nabla}^{2}\boldsymbol{v}+{\it\rho}_{e}\boldsymbol{E}-\frac{1}{2}\Vert \boldsymbol{E}\Vert ^{2}\boldsymbol{{\rm\nabla}}{\it\epsilon}.\end{eqnarray}$$
In isothermal and dilute electrolyte solution conditions, the electrical permittivity
${\it\epsilon}$
is approximately that of the solvent (Lin et al.
Reference Lin, Storey, Oddy, Chen and Santiago2004). In some non-isothermal conditions, this term
$(\Vert \boldsymbol{E}\Vert ^{2}\boldsymbol{{\rm\nabla}}{\it\epsilon})/2$
is crucial since there is a gradient of permittivity due to the non-isothermal condition which causes a circulation flow in the system (Yoshikawa et al.
Reference Yoshikawa, Crumeyrolle and Mutabazi2013). In this paper, we consider isothermal conditions and the electrical permittivity is assumed to be constant for dilute electrolyte solutions. Therefore, the term
$(\Vert \boldsymbol{E}\Vert ^{2}\boldsymbol{{\rm\nabla}}{\it\epsilon})/2$
is ignored. In previous studies by Chang et al. (Reference Chang, Ruo and Chen2009) and Ding et al. (Reference Ding, Wong and Li2013), this term
$(\Vert \boldsymbol{E}\Vert ^{2}\boldsymbol{{\rm\nabla}}{\it\epsilon})/2$
was also neglected under the assumptions of dilute electrolyte solution and an isothermal environment. The term
${\it\rho}_{e}\boldsymbol{E}$
is called the electrical body force.
Because the electrostatics is considered, the electric field
$\boldsymbol{E}$
can be related to the electrical potential by
$$\begin{eqnarray}\boldsymbol{E}=-\boldsymbol{{\rm\nabla}}{\it\phi}.\end{eqnarray}$$
Hence, Gauss’s law (2.5) is expressed by the following Poisson equation:
$$\begin{eqnarray}{\rm\nabla}^{2}{\it\phi}=-\frac{{\it\rho}_{e}}{{\it\epsilon}}.\end{eqnarray}$$
Conservation of electrical charge gives
$$\begin{eqnarray}\frac{\partial {\it\rho}_{e}}{\partial t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{J}_{e}=0.\end{eqnarray}$$
In this paper, the electrolyte solution is considered as an ohmic conductor, which means that diffusion of the charge can be neglected. Then, the current density
$\boldsymbol{J}_{e}$
is given by
$$\begin{eqnarray}\boldsymbol{J}_{e}={\it\sigma}\boldsymbol{E}+{\it\rho}_{e}\boldsymbol{v},\end{eqnarray}$$
where
${\it\sigma}$
is the electrical conductivity. Substituting (2.10) into the current conservative law, we obtain
$$\begin{eqnarray}\frac{\text{D}{\it\rho}_{e}}{\text{D}t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\sigma}\boldsymbol{E})=0.\end{eqnarray}$$
Because the electrolyte solution is considered to be an ionic conductor, the conductivity depends on the local ion concentration. Accordingly, the conductivity can be described by the following diffusion equation (Melcher Reference Melcher1981; Baygents & Baldessari Reference Baygents and Baldessari1998; Chang et al. Reference Chang, Ruo and Chen2009):
$$\begin{eqnarray}\frac{\text{D}{\it\sigma}}{\text{D}t}=K_{eff}{\rm\nabla}^{2}{\it\sigma},\end{eqnarray}$$
where
$K_{eff}$
is an effective diffusivity due to the Brownian motion of the ions. Equation (2.12) is valid if the local electrical time is much shorter than the fluid time and the time for ion electromigration,
$$\begin{eqnarray}\frac{{\it\epsilon}}{{\it\sigma}}\ll \frac{b^{2}}{{\it\nu}}\ll \frac{b}{{\it\omega}E}\quad \text{and}\quad \frac{b^{2}}{{\it\omega}k_{B}T},\end{eqnarray}$$
in which
$k_{B}T$
is the Boltzmann temperature and
${\it\omega}$
is the characteristic mobility of the charge-carrying solutes. The conditions imply that the ions are carried by a fluid parcel. Typical values of these parameters can be found in Melcher’s book (Melcher Reference Melcher1981) and Lin et al.’s work (Lin et al.
Reference Lin, Storey, Oddy, Chen and Santiago2004):
${\it\epsilon}\approx 10^{-10}~\text{C}~\text{V}^{-1},{\it\omega}\approx 10^{-8}~\text{m}^{2}~\text{V}^{-1}~\text{s}^{-1}$
, kinematic viscosity
${\it\nu}\approx 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
, conductivity
${\it\sigma}\approx 10^{-4}~\text{S}~\text{m}^{-1}$
, strength of a typical electric field
$E=O(10^{3})~\text{V}~\text{m}^{-1}$
and pipe radius
$b=10^{-3}~\text{m}$
. A similar form to (2.12) was also derived by Lin et al. (Reference Lin, Storey, Oddy, Chen and Santiago2004) from the species conservation law if the electromigration was neglected. Baygents & Baldessari (Reference Baygents and Baldessari1998) indicated that the diffusion term
$K_{eff}{\rm\nabla}^{2}{\it\sigma}$
is responsible for the existence of a threshold electric field and cannot be neglected. This was also mentioned in the following works of Lin et al. (Reference Lin, Storey, Oddy, Chen and Santiago2004), Chang et al. (Reference Chang, Ruo and Chen2009) and Ding & Wong (Reference Ding and Wong2014).
At the initial time, the electrical conductivity in each layer is
${\it\sigma}={\it\sigma}_{1}|_{r<a}$
,
${\it\sigma}_{2}|_{a<r<b}$
(
${\it\sigma}_{1}\neq {\it\sigma}_{2}$
). The subscript
$i=1,2$
denotes the inner layer and outer layer respectively. This can be achieved by using two aqueous electrolytes with different ionic concentrations (Lin et al.
Reference Lin, Storey, Oddy, Chen and Santiago2004; Chen et al.
Reference Chen, Lin, Lele and Santiago2005).
In this paper, we apply the non-slip and non-penetration boundary conditions at
$r=b$
:
$$\begin{eqnarray}u=v=w=0.\end{eqnarray}$$
Here, the basic flow is driven by pressure, and the maximum speed occurring at the centreline is approximately
$10^{-4}{-}10^{-2}~\text{m}~\text{s}^{-1}$
. Usually, the electro-osmosis flow is very weak and the flow velocity can be estimated by the Helmholtz–Smoluchowski formula
$U_{E}=-{\it\epsilon}E{\it\zeta}/{\it\mu}$
, where
${\it\zeta}$
is the zeta potential which is responsible for the electro-osmosis flow. This velocity usually has an order of
$O(10^{-6})~\text{m}~\text{s}^{-1}$
provided
${\it\zeta}=-10^{-2}~\text{V}$
,
${\it\epsilon}=10^{-10}~\text{C}~\text{V}^{-1}~\text{m}^{-1}$
,
${\it\mu}=10^{-3}~\text{kg}~\text{m}^{-1}~\text{s}^{-1}$
and
$E=10^{3}~\text{V}~\text{m}^{-1}$
. Clearly, the electro-osmotic velocity is much weaker than the pressure driven flow in this paper. Hence, in what follows, the non-slip and non-penetration boundary conditions in (2.14) are applied so that the electro-osmosis phenomenon is neglected.
There is no flux of the ions at
$r=b$
; therefore,
$$\begin{eqnarray}\frac{\partial {\it\sigma}}{\partial r}=0.\end{eqnarray}$$
The circular pipe is non-conducting,
$$\begin{eqnarray}\frac{\partial {\it\phi}}{\partial r}=0.\end{eqnarray}$$
3. Base state and scalings
At the base state, the flow field and the electric field are decoupled because the electrolyte solution is initially neutral, i.e. the net charge density is zero. The flow is driven by a constant pressure gradient
$\partial _{z}\bar{p}$
. Therefore, the base velocity profile is
$$\begin{eqnarray}\bar{w}=\frac{\partial _{z}\bar{p}}{4{\it\mu}}(r^{2}-b^{2}).\end{eqnarray}$$
We assume that the interface between the two liquids has grown diffusively to a finite thickness
${\it\delta}$
. Moreover, we assume that the diffusion is sufficiently slow to allow us to employ a quasi-steady base state for the linear stability analysis. Provided
${\it\delta}\ll 1$
, the profile of the conductivity can be approximated by the error function:
$$\begin{eqnarray}\bar{{\it\sigma}}=\frac{{\it\sigma}_{1}+{\it\sigma}_{2}}{2}+\frac{{\it\sigma}_{2}-{\it\sigma}_{1}}{2}\text{erf}\left(\frac{r-a}{{\it\delta}}\right).\end{eqnarray}$$
Equation (3.2) was used by Selvam et al. (Reference Selvam, Merk, Govindarajan and Meiburg2007) in their study to describe the profile of the viscosity of a viscosity stratified flow in a circular pipe.
The base electrical conductivity profile can also be obtained via solution of the following equation (Lin et al. Reference Lin, Storey, Oddy, Chen and Santiago2004):
$$\begin{eqnarray}\frac{\partial {\it\sigma}}{\partial t}=K_{eff}\left(\frac{\partial ^{2}{\it\sigma}}{\partial r^{2}}+\frac{1}{r}\frac{\partial {\it\sigma}}{\partial r}\right).\end{eqnarray}$$
In experiments,
$K_{eff}$
ranges from
$10^{-9}$
to
$10^{-12}~\text{m}^{2}~\text{s}^{-1}$
.
The charge density
${\it\rho}_{e}$
is zero, and the electric field exists only in the axial direction. This gives the base state of the electrical potential:
$$\begin{eqnarray}\bar{{\it\phi}}={\it\phi}_{0}-Ez,\end{eqnarray}$$
where
$E$
is the strength of the imposed electric field and
${\it\phi}_{0}$
is the reference electrical potential.
Taking the velocity scale
$W=-(\partial _{z}\bar{p}b^{2})/4{\it\mu}$
, the length scale
$b$
, the time scale
$b/W$
, the pressure scale
${\it\rho}W^{2}$
, the electrical potential scale
$Eb$
and the conductivity scale
${\it\sigma}_{2}-{\it\sigma}_{1}$
, we non-dimensionalize the system (2.1)–(2.16):
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}\boldsymbol{v}}{\text{D}t}=-\boldsymbol{{\rm\nabla}}p+\frac{1}{\mathit{Re}}{\rm\nabla}^{2}\boldsymbol{v}+\frac{Q}{\mathit{Re}^{2}\mathit{Sc}}{\rm\nabla}^{2}{\it\phi}\boldsymbol{{\rm\nabla}}{\it\phi}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{R_{t}}\frac{\text{D}({\rm\nabla}^{2}{\it\phi})}{\text{D}t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\{[({\it\eta}-1){\it\sigma}+1]\boldsymbol{{\rm\nabla}}{\it\phi}\}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}{\it\sigma}}{\text{D}t}=\frac{1}{\mathit{Re}\mathit{Sc}}{\rm\nabla}^{2}{\it\sigma}, & \displaystyle\end{eqnarray}$$
$\mathit{Re}={\it\rho}Wb/{\it\mu}$
is the Reynolds number,
$Q=({\it\epsilon}E^{2}b^{2}/{\it\mu}K_{eff})$
is the scaled electrical energy and is defined as the electrical number in this paper,
${\it\eta}={\it\sigma}_{2}/{\it\sigma}_{1}$
denotes the conductivity ratio and
$\mathit{Sc}={\it\nu}/K_{eff}$
is the electrical Schmidt number. Baygents & Baldessari (Reference Baygents and Baldessari1998) proposed that
$\mathit{Sc}\in [10^{3},10^{6}]$
. In the study of Chang et al. (Reference Chang, Ruo and Chen2009),
$\mathit{Sc}$
was assumed to vary in
$[10^{2},10^{5}]$
. The parameter
$R_{t}=(d/W)/({\it\epsilon}/{\it\sigma}_{1})$
measures the ratio of fluid time to electrical time. We assume that
$R_{t}$
is very large so that the electric time is significantly smaller than the fluid time. Therefore, (3.7) can be simplified to 
$$\begin{eqnarray}[({\it\eta}-1){\it\sigma}+1]{\rm\nabla}^{2}{\it\phi}+({\it\eta}-1)\boldsymbol{{\rm\nabla}}{\it\sigma}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\phi}=0.\end{eqnarray}$$
The dimensionless boundary conditions at
$r=1$
are
$$\begin{eqnarray}u=v=w=\frac{\partial {\it\sigma}}{\partial r}=\frac{\partial {\it\phi}}{\partial r}=0.\end{eqnarray}$$
The dimensionless base state is defined as follows:
$$\begin{eqnarray}\displaystyle & \bar{w}=1-r^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\sigma}}=\frac{1}{2}+\frac{1}{2}\text{erf}\left(\frac{r-a}{{\it\delta}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \bar{{\it\phi}}=-z, & \displaystyle\end{eqnarray}$$
$a$
is scaled on the length scale
$b$
which falls in the range of
$(0,1)$
. It should be noted that
${\rm\nabla}^{2}\bar{{\it\phi}}=0$
and
$\partial \bar{{\it\sigma}}/\partial r=1/{\it\delta}\sqrt{{\rm\pi}}\exp (-(r-a)^{2}/{\it\delta}^{2})$
. In this paper, the range of
${\it\delta}$
is fixed,
${\it\delta}\in [0.05,0.15]$
. To verify (3.12), we assume that the concentration has a Heaviside profile initially, the conductivity profile at time instant
$t$
is solved numerically by the dimensionless form of (3.3) and a regular condition is imposed at the centreline
$\text{d}{\it\sigma}/\text{d}r=0$
.
The base conductivity profile is shown in figure 2. It is obvious that the electrical conductivity profile can be approximated by the error function in (3.12) by adjusting the value of
${\it\delta}$
at an instant
$t$
. In the following study, we use (3.12) as the profile of the electrical conductivity at the base state for convenience in the study of linear stability.
4. Linear stability analysis
The linear stability analysis of the flow system is implemented by perturbing the base state with infinitesimal disturbances:
$$\begin{eqnarray}[u,v,w,p,{\it\sigma},{\it\phi}]=[0,0,\bar{w},\bar{p},\bar{{\it\sigma}},\bar{{\it\phi}}]+[u^{\prime },v^{\prime },w^{\prime },p^{\prime },{\it\sigma}^{\prime },{\it\phi}^{\prime }],\end{eqnarray}$$
where the primed variables are the infinitesimal disturbances. In a standard way, we consider the normal mode analysis:
$$\begin{eqnarray}[u^{\prime },v^{\prime },w^{\prime },p^{\prime },{\it\sigma}^{\prime },{\it\phi}^{\prime }]=[\hat{u} ,\hat{v},{\hat{w}},\hat{p},\hat{{\it\sigma}},\hat{{\it\phi}}]\exp (\text{i}(m{\it\theta}+{\it\alpha}z)+{\it\lambda}t),\end{eqnarray}$$
in which
$[\hat{u} ,\hat{v},{\hat{w}},\hat{p},\hat{{\it\sigma}},\hat{{\it\phi}}]$
is the Fourier amplitude,
$m$
is the azimuthal wavenumber,
${\it\alpha}$
is the streamwise wavenumber and
${\it\lambda}$
is the complex temporal growth rate.
On substituting (4.1) with the normal mode analysis into (3.5), (3.6), (3.8) and (3.9) and after linearizing, we obtain the governing equations of the eigenvalue problem:
$$\begin{eqnarray}\displaystyle & \displaystyle \mathtt{D}\hat{u} +\frac{\hat{u} +\text{i}m\hat{v}}{r}+\text{i}{\it\alpha}{\hat{w}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}\hat{u} =-\mathtt{D}\hat{p}-\text{i}{\it\alpha}\bar{w}\hat{u} +\frac{1}{\mathit{Re}}\left(\mathscr{L}\hat{u} -\frac{\hat{u} +2\text{i}m\hat{v}}{r^{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}\hat{v}=-\frac{\text{i}m\hat{p}}{r}-\text{i}{\it\alpha}\bar{w}\hat{v}+\frac{1}{\mathit{Re}}\left(\mathscr{L}\hat{v}-\frac{\hat{v}-2\text{i}m\hat{u} }{r^{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\lambda}{\hat{w}}=-\text{i}{\it\alpha}\hat{p}-\text{i}{\it\alpha}\bar{w}{\hat{w}}-\mathtt{D}\bar{w}\hat{u} +\frac{1}{\mathit{Re}}\mathscr{L}{\hat{w}}-\frac{Q}{\mathit{Pe}\mathit{Re}}\mathscr{L}\hat{{\it\phi}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \mathit{Pe}{\it\lambda}\hat{{\it\sigma}}=-\mathit{Pe}\mathtt{D}\bar{{\it\sigma}}\hat{u} -\text{i}\mathit{Pe}{\it\alpha}\bar{w}\hat{{\it\sigma}}+\mathscr{L}\hat{{\it\sigma}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & [({\it\eta}-1)\bar{{\it\sigma}}+1]\mathscr{L}\hat{{\it\phi}}+({\it\eta}-1)\mathtt{D}\bar{{\it\sigma}}\mathtt{D}\hat{{\it\phi}}-\text{i}{\it\alpha}({\it\eta}-1)\hat{{\it\sigma}}=0, & \displaystyle\end{eqnarray}$$
$\mathscr{L}=\mathtt{D}^{2}+(1/r)\mathtt{D}-(m^{2}/r^{2})-{\it\alpha}^{2}$
,
$\mathtt{D}=\text{d}/\text{d}r$
. The Péclet number
$\mathit{Pe}=\mathit{Re}\mathit{Sc}$
. It should be noted that the value of
$\mathit{Pe}$
cannot be small because diffusion of conductivity is slow.
The boundary conditions at
$r=1$
are
$$\begin{eqnarray}\hat{u} =\hat{v}={\hat{w}}=\mathtt{D}\hat{{\it\sigma}}=\mathtt{D}\hat{{\it\phi}}=0.\end{eqnarray}$$
At the centreline
$r=0$
, the singular nature of the cylindrical coordinate system requires special treatment. To deal with the singular point of the system (4.3)–(4.8), we use the fact that the velocity vector and the other scalar variables have a vanishing azimuthal dependence as they approach the centreline, i.e.
$$\begin{eqnarray}\lim _{r=0}\frac{\partial \boldsymbol{v}^{\prime }}{\partial {\it\theta}}=\lim _{r=0}\frac{\partial p^{\prime }}{\partial {\it\theta}}=\lim _{r=0}\frac{\partial {\it\sigma}^{\prime }}{\partial {\it\theta}}=\lim _{r=0}\frac{\partial {\it\phi}^{\prime }}{\partial {\it\theta}}=0,\end{eqnarray}$$
where
$\boldsymbol{v}^{\prime }=u^{\prime }\boldsymbol{e}_{r}+v^{\prime }\boldsymbol{e}_{{\it\theta}}+w^{\prime }\boldsymbol{e}_{z}$
is the velocity disturbance.
In the form of Fourier modes, the regular boundary conditions are
$$\begin{eqnarray}\text{i}m\hat{u} -\hat{v}=\hat{u} +\text{i}m\hat{v}=m{\hat{w}}=m\hat{p}=m\hat{{\it\sigma}}=m\hat{{\it\phi}}=0.\end{eqnarray}$$
If
$m=0$
, the boundary conditions are
$$\begin{eqnarray}\hat{u} =\hat{v}=\mathtt{D}{\hat{w}}=\mathtt{D}\hat{p}=\mathtt{D}\hat{{\it\sigma}}=\mathtt{D}\hat{{\it\phi}}=0.\end{eqnarray}$$
If
$m=1$
, the boundary conditions are
$$\begin{eqnarray}\mathtt{D}\hat{u} =\mathtt{D}\hat{v}={\hat{w}}=\hat{p}=\hat{{\it\sigma}}=\hat{{\it\phi}}=0.\end{eqnarray}$$
The velocity conditions of
$m=1$
agree with the boundary conditions given by Khorrami (Reference Khorrami1991) for a single fluid flow in a circular pipe.
When
$m\geqslant 2$
, the boundary conditions are
$$\begin{eqnarray}\hat{u} =\hat{v}={\hat{w}}=\hat{p}=\hat{{\it\sigma}}=\hat{{\it\phi}}=0.\end{eqnarray}$$
A Chebyshev collocation method is implemented to solve the eigenvalue problem, and the physical domain is transformed into the Chebyshev domain,
$$\begin{eqnarray}{\it\zeta}=2r-1.\end{eqnarray}$$
The variables
$\hat{u}$
,
$\hat{v}$
,
${\hat{w}}$
,
$\hat{p}$
,
$\hat{{\it\sigma}}$
,
$\hat{{\it\phi}}$
are expanded as
$$\begin{eqnarray}\hat{u} =\mathop{\sum }_{0}^{N}a_{n}T_{n}({\it\zeta}),\quad \hat{v}=\mathop{\sum }_{0}^{N}b_{n}T_{n}({\it\zeta}),\quad {\hat{w}}=\mathop{\sum }_{0}^{N}c_{n}T_{n}({\it\zeta}),\end{eqnarray}$$
$$\begin{eqnarray}\hat{p}=\mathop{\sum }_{0}^{N}d_{n}T_{n}({\it\zeta}),\quad \hat{{\it\sigma}}=\mathop{\sum }_{0}^{N}f_{n}T_{n}({\it\zeta}),\quad \hat{{\it\phi}}=\mathop{\sum }_{0}^{N}e_{n}T_{n}({\it\zeta}),\end{eqnarray}$$
where
$T_{n}({\it\zeta})$
denotes the
$n$
th Chebyshev polynomial.
In order to modify the computation near the interface
$r=a$
, the Chebyshev collocation points are clustered in the mixing region at
$r=a$
using the following stretching function (Govindarajan Reference Govindarajan2004):
$$\begin{eqnarray}{\it\xi}=\frac{a}{\sinh (\,f_{b}r_{0})}[\sinh [(r-r_{0})]+\sinh (\,f_{b}a)],\end{eqnarray}$$
where
$r_{0}=1/2f_{b}\ln [(1+(\exp (\,f_{b}-1)a)/1+(\exp (-f_{b})-1)a)]$
. The coefficient
$f_{b}$
determines the degree of clustering, and
$f_{b}=6$
in this paper. The parameter
$a$
represents the location of the interface around which clustering is desired.
After clustering the Chebyshev collocation points into the diffusion region, we need to calculate the eigenvalue problem via the clustered grid. Therefore, a transformation on the derivatives between the clustered grid and the Chebyshev grid should be made,
$$\begin{eqnarray}\frac{\text{d}f}{\text{d}{\it\xi}}=\frac{\text{d}f}{\text{d}r}\frac{\text{d}r}{\text{d}{\it\xi}}=\frac{1}{G^{\prime }(r)}\frac{\text{d}f}{\text{d}r},\end{eqnarray}$$
where
$G(r)={\it\xi}$
and
$f$
stands for the variable
$\hat{u}$
,
$\hat{v}$
,
${\hat{w}}$
,
$\hat{p}$
,
$\hat{{\it\sigma}}$
or
$\hat{{\it\phi}}$
. It should be noted that the derivative
$\text{d}f/\text{d}r=2(\text{d}f/\text{d}{\it\zeta})$
.
For the second derivative of
$f$
, using the chain rule, the transformation is written
$$\begin{eqnarray}\frac{\text{d}^{2}f}{\text{d}{\it\xi}^{2}}=\frac{1}{(G^{\prime })^{2}}\frac{\text{d}^{2}f}{\text{d}r^{2}}-\frac{G^{\prime \prime }}{(G^{\prime })^{3}}\frac{\text{d}f}{\text{d}r}.\end{eqnarray}$$
The derivative
$\text{d}^{2}f/\text{d}r^{2}=4(\text{d}^{2}f/\text{d}{\it\zeta}^{2})$
. Numerical validation of our method will be made in the following discussion.
5. Energy analysis
In order to understand the physical mechanism, we apply the energy analysis (Govindarajan, L’vov & Procaccia Reference Govindarajan, L’vov and Procaccia2001). We multiply the conjugates of the variables
$\hat{u} ^{\ast }$
,
$\hat{v}^{\ast }$
${\hat{w}}^{\ast }$
on both sides of (4.4)–(4.6). The real part of the equation obtained by summing these equations and integrating over the cross-sectional area gives the energy balance:
$$\begin{eqnarray}{\dot{E}}_{k}=I+V+E_{e}.\end{eqnarray}$$
Here, the kinetic energy growth rate is
$$\begin{eqnarray}{\dot{E}}_{k}={\it\lambda}_{r}\int _{0}^{1}r(|\hat{u} |^{2}+|\hat{v}|^{2}+|{\hat{w}}|^{2})\text{d}r,\end{eqnarray}$$
the work done by the Reynolds stress is
$$\begin{eqnarray}I=-\int _{0}^{1}r\text{Re}(\mathtt{D}\bar{w}{\hat{w}}^{\ast }\hat{u} )\text{d}r\end{eqnarray}$$
and the viscous dissipation is
$$\begin{eqnarray}\displaystyle V & = & \displaystyle -\frac{1}{\mathit{Re}}\int _{0}^{1}r\left\{(|\mathtt{D}\hat{u} |^{2}+|\mathtt{D}\hat{v}|^{2}+|\mathtt{D}{\hat{w}}|^{2})+\left(\frac{m^{2}}{r^{2}}+{\it\alpha}^{2}\right)(|\hat{u} |^{2}+|\hat{v}|^{2}+|{\hat{w}}|^{2})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{|\hat{u} |^{2}+|\hat{v}|^{2}}{r^{2}}-4m\frac{\text{Im}(\hat{u} ^{\ast }\hat{v})}{r^{2}}\right\}\text{d}r.\end{eqnarray}$$
The work done by the electrical force is
$$\begin{eqnarray}E_{e}=\frac{Q}{\mathit{Pe}\mathit{Re}}\int _{0}^{1}r\text{Re}\left(\mathtt{D}{\hat{w}}^{\ast }\mathtt{D}\hat{{\it\phi}}+\frac{m^{2}{\hat{w}}^{\ast }{\it\phi}}{r^{2}}+{\it\alpha}^{2}{\hat{w}}^{\ast }{\it\phi}\right)\text{d}r.\end{eqnarray}$$
Since the magnitude of the eigenfunction is arbitrary, we normalize the eigenfunction by its maximum absolute value. The terms in the energy analysis are rescaled with respect to the total kinetic energy
$\int _{0}^{1}r(|\hat{u} |^{2}+|\hat{v}|^{2}+|{\hat{w}}|^{2})\text{d}r$
. For an unstable flow,
${\dot{E}}$
should be positive. The energy analysis will be applied to interpret the instability mechanism in the following discussion.
6. Results and discussion
6.1. Validation of numerical methods
We examine the validation of our numerical method by setting
$Q=\mathit{Pe}=0$
; therefore, the electric field is turned off and ionic advection is absent. Since we are setting
$Q=0$
and (4.8) does not produce any eigenvalues, the conductivity profile has no influence on the spectrum of the problem and the eigenvalue problem should be identical to a single fluid flowing in a circular pipe. We compare our numerical results with those of Schmid & Henningson (Reference Schmid and Henningson2001) (hereafter referred to as SH) for
$\mathit{Re}=2000$
. The leading eigenvalue is listed in table 1. Excellent agreement between our numerical results and those of SH demonstrates the validity of our numerical method.
Table 1. The first leading eigenvalues of the system for
$\mathit{Re}=2000$
,
$\mathit{Pe}=Q=0$
. We have utilized 51 points for the eigenvalue problem and related the eigenvalues to those of SH by defining
${\it\lambda}^{\prime }=\text{i}{\it\lambda}$
and
$c={\it\lambda}^{\prime }/{\it\alpha}$
.
It should be noted that, when
$\mathit{Re}\rightarrow 0$
, i.e. the inertia of the fluid is negligible, the growth rate is determined by the ionic diffusion equation (4.7). In a viscosity stratified plane-Poiseuille flow (Talon & Meiburg Reference Talon and Meiburg2011), the eigenspectrum of the diffusion equation presents a similar structure to the Orr–Sommerfeld problem. Hence, the diffusion equation will produce more eigenvalues in the stratified flow than a single fluid flow (Talon & Meiburg Reference Talon and Meiburg2011). Similarly, in pipe flow with conductivity stratification, the eigenspectrum structure will be different from the result of SH, as demonstrated in figure 3. In the following discussion, we consider that the base flow in the pipe is weak and focus on the instability caused by the electrical force in microfluidic channels.
Figure 3. Eigenspectra for
$\mathit{Re}=2000$
,
$m=0$
,
${\it\alpha}=1$
. (a) The eigenspectrum for Hagen–Poiseuille flow which is identical to that of SH. (b) A comparison of conductivity stratified pipe flow (triangular points) and Hagen–Poiseuille flow (circles). The conductivity ratio
${\it\eta}=2$
and the parameters are
$Q=0$
,
$a=0.5$
,
${\it\delta}=0.05$
. It is obvious that when
$\mathit{Pe}>0$
, there are some extra eigenvalues compared with Hagen–Poiseuille flow. The parameter
$c=\text{i}{\it\lambda}/{\it\alpha}$
.
6.2. Parametric study
6.2.1. Effect of the conductivity ratio
The influence of the conductivity ratio on the linear stability analysis is of particular interest and will be investigated in this section. Before presenting the numerical study, let us consider the case of two liquids with the same electrical conductivity, i.e.
${\it\eta}=1$
. The linearized electrical current conservation (4.8) reduces to
$$\begin{eqnarray}\mathscr{L}\hat{{\it\phi}}=0.\end{eqnarray}$$
Hence, in the linearized momentum equation (4.6), the electrical force that can trigger instability is absent. Therefore, the system will be linearly stable. Numerical study also indicates that the eigenvalue
${\it\lambda}$
is not influenced by the electrical number
$Q$
for
${\it\eta}=1$
and
${\it\lambda}_{r}<0$
(see table 3 in appendix A). We can obtain a useful result here: the system becomes more stable as
${\it\eta}$
increases when
${\it\eta}<1$
, while the system becomes more unstable as
${\it\eta}$
increases when
${\it\eta}>1$
. To study the influence of the conductivity ratio on the linear stability, the other parameters are fixed:
$\mathit{Re}=1$
,
$\mathit{Sc}=1000$
,
$a=0.5$
and
${\it\delta}=0.1$
. To study the linear stability problem, 51 collocation points are sufficient to provide satisfying accuracy.
Figure 4. The real temporal growth rate
${\it\lambda}_{r}$
versus the wavenumber
${\it\alpha}$
: (a)
$Q=5\times 10^{4}$
,
${\it\eta}=0.5$
; (b)
$Q=10^{4}$
,
${\it\eta}=2$
.
Figure 5. The marginal stability curves: (a)
${\it\eta}=0.5$
; (b)
${\it\eta}=2$
.
First, we consider two typical cases:
${\it\eta}=0.5$
,
${\it\eta}=2$
. The electrical number
$Q$
is fixed so as to study the growth rate of the disturbance. The results in figure 4(a) demonstrate that the azimuthal disturbances make the system more unstable. They also imply that the azimuthal wavenumber
$m$
of the critical mode is
$m=1$
. The results are different in figure 4(b). They show that the azimuthal wavenumber of the most unstable mode is
$m=0$
for
${\it\eta}=2$
. These results imply that the critical unstable mode of the system varies with the conductivity ratio
${\it\eta}$
. To elucidate the critical unstable mode in the system, we investigate the marginal curves in the
$Q{-}{\it\alpha}$
plane. Figure 5 demonstrates that the wavenumber
$m$
of the critical unstable mode for
${\it\eta}=0.5,2$
is
$m=1,0$
respectively. The azimuthal wavenumber of the critical unstable mode is defined as the critical azimuthal wavenumber
$m_{c}$
. Here, we define
$Q_{c}$
as the critical electrical number and
${\it\alpha}_{c}$
as the critical streamwise wavenumber. We have examined the eigenvalue
${\it\lambda}$
of the critical unstable modes in figure 5 whose imaginary part is non-zero. It indicates that the critical unstable modes are oscillatory. The perturbed fields of the charge density and the conductivity in the
$r{-}{\it\theta}$
plane are shown in figure 6 to illustrate the two different unstable modes. In figure 6(a,b), the unstable mode is defined as the corkscrew mode, while the unstable mode in 6(c,d) is defined as the axisymmetric mode. We numerically evaluate the energy contribution of
$E_{e}$
which is always positive. It demonstrates that the electrical force is the main factor that destabilizes the system. The instability is referred to as the dielectrophoretic instability (Baygents & Baldessari Reference Baygents and Baldessari1998; Chang et al.
Reference Chang, Ruo and Chen2009; Ding & Wong Reference Ding and Wong2014).
Figure 6. (a,b) The perturbed field of the electrical charge
${\it\rho}_{e}$
and the perturbed field of the conductivity
${\it\sigma}$
for
${\it\eta}=0.5$
,
$Q_{c}=4505.8$
,
$m_{c}=1$
,
${\it\alpha}_{c}=1.75$
in the
$r{-}{\it\theta}$
plane. (c,d) The perturbed field of the electrical charge
${\it\rho}_{e}$
and the perturbed field of the conductivity
${\it\sigma}$
for
${\it\eta}=2$
,
$Q_{c}=6197.0$
,
$m_{c}=0$
,
${\it\alpha}_{c}=2.75$
in the
$r{-}{\it\theta}$
plane.
In order to reveal the influence of the conductivity ratio on the critical unstable mode, i.e. in what range of
${\it\eta}$
the critical unstable mode is the corkscrew mode or the axisymmetric mode, we investigate the behaviour of
$(Q_{c},m_{c},c)$
versus the value of
${\it\eta}$
. The wave speed
$c$
of the critical mode is defined as
$$\begin{eqnarray}c=-{\it\lambda}_{i}/{\it\alpha}_{c}.\end{eqnarray}$$
The results in figure 7(a) indicate that the system becomes more unstable for a larger contrast in the electrical conductivity between the two layers. A similar phenomenon has been observed by Lin et al. (Reference Lin, Storey, Oddy, Chen and Santiago2004) in a liquid layer with conductivity stratification in a square channel. Experimental observation and stability analysis suggested that the flow became more unstable for a larger conductivity contrast (Lin et al.
Reference Lin, Storey, Oddy, Chen and Santiago2004). However, they focused on the two-dimensional instability, and the way in which the conductivity ratio influenced the three-dimensional stability was not investigated (Lin et al.
Reference Lin, Storey, Oddy, Chen and Santiago2004). In this paper, we investigate the three-dimensional instability and our results in figure 7(c) show that the critical wavenumber
$m_{c}$
jumps from 1 to 0 as the conductivity ratio increases to
${\it\eta}=1$
. This figure indicates that, for the selected input values of other dimensionless parameters, the critical unstable mode is dominated by the corkscrew mode when the inner conductivity is larger, while the axisymmetric mode dominates the instability when the outer conductivity is larger. Moreover, in a square-duct flow system, Lin et al. (Reference Lin, Storey, Oddy, Chen and Santiago2004) gave the physical properties of the flow system for a conductivity ratio
${\it\eta}=10$
, which are applied to estimate the critical strength of the applied electric field in our present system. Our results show that, for
${\it\eta}=10$
, the critical value electrical number
$Q_{c}\approx 10^{3}$
. This gives the critical electrical strength
$E\approx 2\times 10^{3}~\text{V}~\text{m}^{-1}$
provided that the electrical permittivity
${\it\epsilon}=6.9\times 10^{-10}~\text{C}~\text{V}^{-1}~\text{m}^{-1}$
, the dynamic viscosity
${\it\mu}=10^{-3}~\text{kg}~\text{m}^{-1}~\text{s}^{-1}$
, the effective diffusivity
$K_{eff}=2\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
and the pipe radius
$b=10^{-3}~\text{m}$
. Hence, it is possible to achieve electromixing in a circular pipe at small Reynolds flow by an electric field in experiments. Figure 7(b) shows that
${\it\lambda}_{i}\neq 0$
, which demonstrates that the unstable mode is oscillatory. Figure 7(d) shows that the critical wave speed
$c$
increases with increasing
${\it\eta}$
. Figure 7(d) also shows that, when
${\it\eta}<1$
, the wave speed is smaller for a larger conductivity contrast; when
${\it\eta}>1$
, the wave speed is larger for a larger conductivity contrast. Additionally, the wave speed
$c>0$
indicates that the linear wave propagates downstream.
Figure 7. (a) The critical electrical strength number
$Q_{c}$
versus
${\it\eta}$
; (b) the critical frequency
$|{\it\lambda}_{i}|$
versus
${\it\eta}$
; (c) the critical wavenumber
$m_{c}$
versus
${\it\eta}$
; (d) the wave speed of the critical mode
$c$
versus
${\it\eta}$
.
6.2.2. Effect of interface location
This section discusses the influence of the interface location on the linear stability of the system. The other parameters are fixed at
$\mathit{Re}=1$
,
$\mathit{Sc}=1000$
,
${\it\delta}=0.05$
so as to investigate the dielectrophoretic instability. Here,
${\it\delta}=0.05$
is chosen under the consideration of a sharper interface. Two conductivity ratios
${\it\eta}=0.5,2$
will be considered in the following discussion. We examined the convergence of our numerical method and found that
$N=60$
is sufficient to provide adequate resolution at reasonable computational cost.
Selvam et al. (Reference Selvam, Merk, Govindarajan and Meiburg2007) found that the interface location had a significant influence on the critical instability of a viscosity stratified pipe flow and the least unstable mode occurred at approximately 0.6 times the pipe radius. In our problem of a liquid with conductivity stratification, a similar phenomenon is observed. However, the instability of our problem is triggered by the electric field, while in the problem studied by Selvam et al. (Reference Selvam, Merk, Govindarajan and Meiburg2007), the instability is due to the Reynolds stress. If the interfacial location is very near the centreline or the pipe wall, the diffusion of ions will rapidly remove the conductivity difference. Furthermore, we consider a very sharp interface, when
$a\rightarrow 0$
or
$a\rightarrow 1$
, so no matter how large an electric field is imposed, the system should be stable due to the homogenous conductivity profile. Hence, it can be concluded that, as the interface is slightly moved away from the centreline, the system becomes more unstable. As the interface approaches the outer boundary, the system should become more stable. Therefore, there should be an optimal location of the interface where the flow is least stable. Two typical cases of
${\it\eta}=0.5,2$
have been investigated numerically and the range of the interface location
$a$
is considered to be in
$[0.1,0.9]$
. The variation of the critical wavenumber
$m_{c}$
and the critical electrical number
$Q_{c}$
with the location
$a$
is shown in figure 8. Figure 8(a) demonstrates that, for
${\it\eta}=0.5,2$
, the system becomes more unstable as
$a$
increases from 0.1 until
$a\approx 0.3$
,
$a\approx 0.2$
respectively, while it becomes more stable as
$a$
increases further. Additionally, for
${\it\eta}=0.5$
, we observe that the critical unstable mode shifts from the corkscrew mode
$m_{c}=1$
to the axisymmetric mode
$m_{c}=0$
as
$a$
increases to a critical value
$a\approx 0.83$
. For
${\it\eta}=2$
, the axisymmetric mode dominates the instability.
Figure 8. (a) The critical electrical strength number
$Q_{c}$
versus
$a$
; (b) the critical wavenumber
$m_{c}$
versus
$a$
.
Figure 9. The maximum growth rate
${\it\lambda}_{m}$
versus
$a$
: (a)
$Q=5\times 10^{4}$
,
${\it\eta}=0.5$
; (b)
$Q=5\times 10^{4}$
,
${\it\eta}=2$
.
We are interested in the maximum growth rate of the system since the rapid mixing is of particular interest (Lin et al.
Reference Lin, Storey, Oddy, Chen and Santiago2004). To investigate the maximum growth rate, the electrical number is fixed. We examine the behaviour of the maximum growth rate
${\it\lambda}_{m}=\max (\text{Re}({\it\lambda}))$
versus the interface location
$a$
. The maximum growth rate
${\it\lambda}_{m}$
describes the growth rate of the most unstable mode. The corkscrew mode and the axisymmetric mode are investigated, as shown in figure 9. Figure 9(a) shows that the maximum growth rate occurs at
$a\approx 0.6$
. We examined the maximum growth rate
${\it\lambda}_{m}$
versus
$a$
by reducing the value of
$Q$
and found that the peak point in the
${\it\lambda}_{m}{-}a$
plane moved leftwards, as shown in figure 10(a). This implies that, for a strong electric field, the most unstable mode prefers an intermediate
$a$
for
${\it\eta}=0.5$
although the critical unstable mode prefers
$a\approx 0.3$
. The mechanism is very complex because the electrical force destabilizes the flow while the viscous dissipation and the ionic diffusion tend to stabilize the system. In order to explain the results, we apply the energy analysis. As the interface location
$a$
increases, the viscous dissipation effect becomes weaker until
$a\approx 0.6$
, after which it becomes stronger as
$a$
increases further, as shown in figure 10(b). This is the reason why for an unstable flow,
$Q=5\times 10^{4}$
, the maximum growth rate occurs at
$a\approx 0.6$
. In addition, we observe that, for
${\it\eta}=0.5$
, the maximum growth rate of the axisymmetric mode dominates the corkscrew mode when
$a\gtrapprox 0.83$
for
$Q=5\times 10^{4}$
. This indicates that the axisymmetric mode becomes critical when the interface approaches the pipe wall. Figure 9(b) demonstrates that the maximum growth rate occurs at
$a\approx 0.2$
, which indicates that the most unstable mode and the critical unstable mode prefer
$a\approx 0.2$
. Additionally, it is observed that, for
${\it\eta}=2$
, the axisymmetric mode always dominates the corkscrew mode.
Figure 10. (a) The maximum growth rate
${\it\lambda}_{m}$
of the corkscrew mode
$m=1$
versus
$a$
for different values of the input electrical number
$Q$
. (b) The log ratio between the energy
$E_{e}$
and
$V$
, in which the electrical number
$Q=5\times 10^{4}$
and the wavenumber
${\it\alpha}$
corresponds to the most unstable mode.
Figure 11. The marginal stability curves: (a)
${\it\eta}=0.5$
; (b)
${\it\eta}=2$
.
6.2.3. Effect of interface thickness
This section investigates of the influence of the interface thickness on the critical instability. The other parameters are fixed:
$\mathit{Re}=1$
,
$\mathit{Sc}=1000$
,
$a=0.5$
. In the above discussion, we have considered two values of
${\it\delta}$
. It is observed that the system becomes more stable for a larger value of
${\it\delta}$
. The marginal stable curves for three typical values of
${\it\delta}$
are shown in figure 11. For a liquid with viscosity stratification, Selvam et al. (Reference Selvam, Merk, Govindarajan and Meiburg2007) reported that, for a thicker interface, the flow became more stable. Selvam et al. (Reference Selvam, Merk, Govindarajan and Meiburg2007) explained that the stabilizing effect was due to the diffusion effect becoming more significant for a thicker interface, which dissipated the kinetic energy and inhibited the instability. Two studies by Chang et al. (Reference Chang, Ruo and Chen2009) and Ding & Wong (Reference Ding and Wong2014) show that the system becomes more stable with reduction of the conductivity gradient when the conductivity gradient is small, while the flow becomes more stable as the conductivity gradient increases when the conductivity gradient is large. In our present study, if we fix the conductivity ratio, the conductivity gradient within the interface becomes smaller as the interface becomes thicker. Our study shows that the flow becomes more stable as the conductivity gradient decreases, which is different from the previous two studies by Chang et al. (Reference Chang, Ruo and Chen2009) and Ding & Wong (Reference Ding and Wong2014). In fact, in our current study, a thicker interface implies that the system undergoes a longer diffusion time. Assuming that the conductivity is uniform in the system due to diffusion for quite a long time, we would expect a completely stable flow. Therefore, the system may become more stable as the interface becomes thicker. Numerical studies demonstrate that, with increasing interface thickness
${\it\delta}$
, the marginal curve rises up in the
$Q{-}{\it\alpha}$
plane, which indicates that the flow becomes more stable as the interface becomes thicker, supporting our analysis. Our result is similar to the phenomenon in a viscosity stratified flow (Selvam et al.
Reference Selvam, Merk, Govindarajan and Meiburg2007), but different from the studies by Chang et al. (Reference Chang, Ruo and Chen2009) and Ding & Wong (Reference Ding and Wong2014). The difference is due to the fact that the flow studied by Chang et al. (Reference Chang, Ruo and Chen2009) and Ding & Wong (Reference Ding and Wong2014) is bounded by two solid walls. However, in our problem, the flow is only bounded by the outer pipe wall. We observe that, for the axisymmetric mode,
${\it\eta}=2$
, the critical wavenumber
${\it\alpha}_{c}$
becomes smaller as
${\it\delta}$
increases, as seen in figure 11(b). This indicates that the wavelength of the disturbance becomes longer as
${\it\delta}$
increases. In order to show the effect of
${\it\delta}$
on the critical stability, the critical electrical number
$Q_{c}$
is plotted against
${\it\delta}$
in figure 12. Figure 12 also demonstrates that the system becomes more stable as
${\it\delta}$
increases. Additionally, the corkscrew mode dominates the instability for
${\it\eta}=0.5$
, and the axisymmetric mode dominates the instability for
${\it\eta}=2$
.
Figure 12. The critical electrical strength number
$Q_{c}$
versus
${\it\delta}$
: (a)
${\it\eta}=0.5$
; (b)
${\it\eta}=2$
.
6.2.4. Effect of shear flow
In this section, we aim to reveal the influence of the shear flow on the dielectrophoretic instability. The other parameters are fixed at
$a=0.5$
,
${\it\delta}=0.1$
. Before presenting the numerical study, let us consider the electrical force term in the linearized axial momentum equation (4.6):
$$\begin{eqnarray}-\frac{Q}{\mathit{Re}\mathit{Pe}}\mathscr{L}\hat{{\it\phi}}=\frac{Q}{\mathit{Re}^{2}\mathit{Sc}}\hat{{\it\rho}}_{e}.\end{eqnarray}$$
The value of
$\mathit{Sc}$
is fixed at
$\mathit{Sc}=1000$
. Equating
$Q/(\mathit{Re}^{2}\mathit{Sc})$
at two different values of
$\mathit{Re}$
gives
$$\begin{eqnarray}Q_{2}=\frac{\mathit{Re}_{2}^{2}}{\mathit{Re}_{1}^{2}}Q_{1}.\end{eqnarray}$$
This relation reflects the fact that, when the value of
$Q/(\mathit{Re}^{2}\mathit{Sc})$
is fixed, a smaller
$\mathit{Re}$
describes a smaller
$Q$
. This implies that, when the Reynolds number is small, the system may be more unstable. In this paper, we consider a weak shear flow under the consideration of flow in a microfluidic channel and propose that
$\mathit{Re}$
has a range of
$[0.1,10]$
provided that the pipe radius is
$10^{-3}~\text{m}$
and the kinematic viscosity
${\it\nu}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
. The maximum velocity occurring at the centreline
$r=0$
can be varied from
$10^{-4}$
to
$10^{-2}~\text{m}~\text{s}^{-1}$
.
Figure 13. The critical electrical strength number
$Q_{c}$
versus
$\mathit{Re}$
: (a)
${\it\eta}=0.5$
; (b)
${\it\eta}=2$
.
It is observed that, for
${\it\eta}=0.5$
, the corkscrew mode dominates the instability, and for
${\it\eta}=2$
, the axisymmetric mode dominates the instability. Figure 13 illustrates that the critical electrical number
$Q_{c}$
increases as
$\mathit{Re}$
increases, indicating that the shear flow impedes the electro-convection in the system. Interestingly, the corkscrew mode for
${\it\eta}=2$
can be enhanced by the shear flow, as seen in figure 13(b), although it never becomes critical for the selected input values of
$\mathit{Re}$
,
${\it\eta}$
and
$\mathit{Sc}$
. It is different from the previous studies by Chang et al. (Reference Chang, Ruo and Chen2009) and Ding & Wong (Reference Ding and Wong2014), which show that the critical instability can be either enhanced or impeded by the shear flow. In the present study, we observe that the shear flow always impedes the critical instability. In order to understand the physical mechanism, we fix the value of
$Q$
and the wavenumber
${\it\alpha}$
to investigate the energy contributions of the electrical force, Reynolds stress and viscous stress. For some
$\mathit{Re}$
, the flow is stable, e.g.
$\mathit{Re}>2.5$
for
${\it\eta}=0.5$
and
$\mathit{Re}>2$
for
${\it\eta}=2$
. The electrical energy becomes smaller, as demonstrated in figure 14(a). We have found that
${\dot{E}}_{k}$
becomes smaller as
$\mathit{Re}$
increases and becomes negative as
$\mathit{Re}$
exceeds some critical value, which indicates that the system becomes stable as
$\mathit{Re}$
increases. However, the underlying factor that stabilizes the system is not the reduction in the electrical energy. Figure 14(b) shows that, as the Reynolds number increases,
$\ln (|E_{e}/V|)$
decreases for
${\it\eta}=0.5$
, while
$\ln (|E_{e}/V|)$
increases for
${\it\eta}=2$
. This indicates that the stabilizing mechanisms in the two cases
${\it\eta}=0.5,2$
are different. We have examined the case of
$\mathit{Re}=10$
and found that, for
${\it\eta}=0.5$
,
$\ln (|E_{e}/V|)<0$
, while for
${\it\eta}=2$
,
$\ln (|E_{e}/V|)>0$
. This indicates that, for
${\it\eta}=0.5$
, the increase of the viscous dissipation is the major factor that stabilizes the flow, although the Reynolds stress also plays a stabilizing role, as shown in figure 14(c). For
${\it\eta}=2$
, because the electrical energy always dominates the viscous dissipation, i.e.
$E_{e}>|V|$
, the stabilizing factor in the system is due to the Reynolds stress, which dissipates the kinetic energy of the perturbation. The results indicate that the imposed shear flow can impede the dielectrophoretic instability via the dissipation mechanisms of the viscous stress and the Reynolds stress.
Figure 14. (a) Electrical energy
$E_{e}$
versus
$\mathit{Re}$
; (b) the log ratio between the electrical energy and the viscous dissipation versus
$\mathit{Re}$
; (c) the work of the Reynolds stress versus
$\mathit{Re}$
. The electrical number
$Q=10^{4}$
.
Furthermore, we investigated the influence of
$\mathit{Re}$
on the wave speed
$c$
. Results are shown in figure 15. It is observed that, for
${\it\eta}=0.5$
, the critical wave speed
$c$
increases slightly as
$\mathit{Re}$
increases initially, then it has a negligible influence on the wave speed. However, the wave speed decreases slightly as
$\mathit{Re}$
increases from
$\mathit{Re}=1$
for
${\it\eta}=2$
, and then the wave speed seems to be independent of
$\mathit{Re}$
. The results by Chang et al. (Reference Chang, Ruo and Chen2009) indicated that the critical frequency of the critical transverse unstable mode
$-{\it\lambda}_{i}$
was independent of the Reynolds number when
$\mathit{Re}>1$
. This implies that the critical wave speed is independent of
$\mathit{Re}$
. In our system, we observe that the wave speed
$c$
is independent of
$\mathit{Re}$
for both the two critical unstable modes, the corkscrew mode and the axisymmetric mode, when
$\mathit{Re}>2$
.
Figure 15. The wave speed of the critical unstable mode versus the Reynolds number.
6.2.5. Effect of ionic diffusion
This section presents a study of the influence of the ionic diffusion on the dielectrophoretic instability. The other parameters are fixed:
$\mathit{Re}=1$
,
$a=0.5$
,
${\it\delta}=0.1$
. In the governing equations (4.3)–(4.8), replacing
$\mathit{Re}$
by
$\mathit{Pe}$
does not change the governing equations, which indicates that the effect of ionic diffusion on the flow instability should be similar to that of
$\mathit{Re}$
. However, the results should not be the same as shown in § 6.2.4 above, in which
$\mathit{Re}$
is varied while
$\mathit{Sc}$
is fixed. Therefore, it is necessary to investigate the influence of
$\mathit{Sc}$
on the stability by fixing the value of
$\mathit{Re}$
.
The critical electrical number
$Q_{c}$
versus the Schmidt number is shown in figure 16. The corkscrew mode dominates the instability for
${\it\eta}=0.5$
and the axisymmetric mode dominates the instability for
${\it\eta}=2$
, as shown in figure 16. The system becomes more stable as
$\mathit{Sc}$
increases. The results in figure 16 are quite similar to those in figure 13, which demonstrates that the influence of
$\mathit{Sc}$
on the flow stability is similar to that of
$\mathit{Re}$
.
Figure 16. The critical electrical strength number
$Q_{c}$
versus
$\mathit{Sc}$
: (a)
${\it\eta}=0.5$
; (b)
${\it\eta}=2$
.
The instability mechanism is then interpreted by the energy analysis. We consider the critical instability of the system when
${\dot{E}}_{k}=0$
. The viscous dissipation term
$V$
is always negative and plays a stabilizing role. The electrical force work
$E_{e}>0$
, which triggers the electro-convection in the system. We calculated
$\ln (|E_{e}/V|)$
and found that its value increased with
$\mathit{Sc}$
initially, then it decreased as
$\mathit{Sc}$
increased further, as shown in figure 17(a). This indicates that the viscous dissipation effect becomes weaker as
$\mathit{Sc}$
increases from
$\mathit{Sc}=100$
, while it becomes stronger when
$\mathit{Sc}$
is very large. When
$\mathit{Sc}$
is not too large,
$\mathit{Sc}=O(10^{2})$
, the Reynolds stress plays a key role in stabilizing the system since its dissipation effect becomes stronger as
$\mathit{Sc}$
increases, as shown in figure 17(b). As
$\mathit{Sc}$
increases further, for
${\it\eta}=0.5$
, the dissipation effect by the Reynolds stress becomes weaker, while for
${\it\eta}=2$
, the work of the Reynolds stress reaches a plateau, as seen in 17(b). Such a phenomenon indicates that, although the Reynolds stress dissipates the kinetic energy, it is not the major factor that causes the system to be more stable when we increase
$\mathit{Sc}$
. As shown in figure 17(a),
$\ln (|E_{e}/V|)$
starts to decrease when
$\mathit{Sc}$
exceeds a certain value. This indicates that the viscous dissipation increases with
$\mathit{Sc}$
and becomes the major stabilizing factor. Moreover, we recall the definition of
$\mathit{Sc}={\it\nu}/K_{eff}$
. This indicates that the viscous effect becomes stronger as the parameter
$\mathit{Sc}$
increases. Since viscous dissipation plays a stabilizing role, the system becomes more stable as
$\mathit{Sc}$
increases. The effect of
$\mathit{Sc}$
on the critical stability in this system is different from that in the previous studies by Chang et al. (Reference Chang, Ruo and Chen2009) and Ding & Wong (Reference Ding and Wong2014). In these studies (Chang et al.
Reference Chang, Ruo and Chen2009; Ding & Wong Reference Ding and Wong2014),
$\mathit{Sc}$
was found to have a dual effect: increasing
$\mathit{Sc}$
can either enhance or inhibit the critical instability. Our study shows that, for
${\it\eta}=2$
, the corkscrew mode can be either enhanced or impeded as
$\mathit{Sc}$
increases, as seen in 16(b). However, the critical unstable mode always becomes stable. For an unstable flow, we observed that
$\mathit{Sc}$
can play a dual role in the system, in that the growth rate of disturbances can become either larger or smaller as
$\mathit{Sc}$
increases; this is not shown here since we are only interested in the critical stability of this system.
Figure 17. (a) The log ratio between the electrical energy and the viscous dissipation versus
$\mathit{Sc}$
; (b) the work of the Reynolds stress versus
$\mathit{Sc}$
.
Table 2. The first leading eigenvalues of the system for
$\mathit{Re}=1$
,
$Q=10^{4}$
,
$\mathit{Sc}=10^{3}$
,
${\it\eta}=0.5$
,
$a=0.5$
,
${\it\delta}=0.05$
,
${\it\alpha}=2$
,
$m=1$
. This shows that our numerical method converges quickly by clustering the Chebyshev collocation points into the interfacial region.
7. Conclusion
This paper investigated the electrodynamical instability of two miscible flows in a micro-pipe with electrical conductivity stratification. An axial electric field was imposed, which can trigger electro-convection in the system. A weak shear flow arose from an axial pressure gradient. A three-dimensional linear stability analysis was implemented to discuss the influences of conductivity ratio, interface location, interface thickness, shear flow and ionic diffusion on the critical stability of the flow. An energy analysis was carried out to interpret the instability mechanism.
It was found that the system was more unstable for a larger electrical conductivity contrast. When the electrical conductivity was larger within the inner layer, the critical unstable mode could be either the corkscrew mode or the axisymmetric mode, depending on the interface location. A detailed study showed that the critical unstable mode shifted from the corkscrew mode to the axisymmetric mode as the interface approached the pipe wall. When the electrical conductivity was larger in the outer layer, the critical unstable mode was dominated by the axisymmetric mode. The interface location had a significant influence on the critical unstable mode. The system was more stable when the interface was close to the centreline or the pipe wall. The flow became more stable as the interface became thicker, and the shear flow and ionic diffusion were found to have a stabilizing effect via the dissipation mechanisms of the Reynolds stress and viscous stress.
Table 3. The first leading eigenvalues of the system for
$\mathit{Re}=2000$
,
$\mathit{Pe}=0$
,
${\it\alpha}=0.5$
,
$m=1$
,
${\it\eta}=1$
. We have also considered some other values of
$\mathit{Re}$
and the result shows that the eigenvalue is only dependent on
$\mathit{Re}$
. Changing the value of
$Q^{\prime }=({\it\epsilon}E^{2}/{\it\rho}W^{2})$
does not affect the eigenvalue for
${\it\eta}=1$
. The parameter
$Q^{\prime }$
measures the ratio of electrical force to the fluid inertia.
Acknowledgements
The authors acknowledge support from Singapore Ministry of Education, Academic Research Fund Tier 2 research grant MOE2011-T2-1-036. They also acknowledge the referees for their many helpful suggestions and comments.
Appendix A
The general eigenvalue problem is denoted as
$$\begin{eqnarray}\mathscr{A}\boldsymbol{q}={\it\lambda}\mathscr{B}\boldsymbol{q},\end{eqnarray}$$
where
$\boldsymbol{q}=(\hat{u} ,\hat{v},{\hat{w}},\hat{p},\hat{{\it\phi}},\hat{{\it\sigma}})^{\text{T}}$
and
$$\begin{eqnarray}\displaystyle & \mathscr{A}=\left(\begin{array}{@{}cccccc@{}}\displaystyle \mathtt{D}+\frac{1}{r} & \displaystyle \frac{\text{i}m}{r} & \text{i}{\it\alpha} & 0 & 0 & 0\\ L_{1} & \displaystyle -\frac{2\text{i}m}{\mathit{Re}r^{2}} & 0 & -\mathtt{D} & 0 & 0\\ \displaystyle \frac{2\text{i}m}{\mathit{Re}r^{2}} & L_{2} & 0 & \displaystyle -\frac{\text{i}m}{r} & 0 & 0\\ -\mathtt{D}\bar{w} & 0 & L_{3} & -\text{i}{\it\alpha} & L_{4} & 0\\ -\mathit{Pe}\mathtt{D}\bar{{\it\sigma}} & 0 & 0 & 0 & 0 & L_{5}\\ 0 & 0 & 0 & 0 & L_{6} & -\text{i}{\it\alpha}({\it\eta}-1)\end{array}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \mathscr{B}=\left(\begin{array}{@{}cccccc@{}}0 & 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & \mathit{Pe}\\ 0 & 0 & 0 & 0 & 0 & 0\end{array}\right), & \displaystyle\end{eqnarray}$$
$L_{1}=L_{2}=1/\mathit{Re}(\mathscr{L}-1/r^{2})-\text{i}{\it\alpha}\bar{w}$
,
$L_{3}=(1/\mathit{Re})\mathscr{L}-\text{i}{\it\alpha}\bar{w}$
,
$L_{4}=-Q/(\mathit{Re}\mathit{Pe})\mathscr{L}$
,
$L_{5}=\mathscr{L}-\text{i}{\it\alpha}\mathit{Pe}\bar{w}$
and
$L_{6}=[({\it\eta}-1)\bar{{\it\sigma}}+1]\mathscr{L}+({\it\eta}-1)(\mathtt{D}\bar{{\it\sigma}})\mathtt{D}$
. The operator
$\mathtt{D}=\text{d}/\text{d}r$
and
$\mathscr{L}=\mathtt{D}^{2}+\mathtt{D}/r-m^{2}/r^{2}-{\it\alpha}^{2}$
. After imposing the boundary conditions at the centreline
$r=0$
and the wall
$r=1$
, the general eigenvalue problem is solved by the standard MATLAB subroutine EIG (Schmid & Henningson Reference Schmid and Henningson2001).
The convergence of our numerical method is tested here, see table 2. In the work of Selvam et al. (Reference Selvam, Merk, Govindarajan and Meiburg2007), 251 Chebyshev collocation points were used to achieve high numerical accuracy without using the technique of clustering the points into the interfacial region, which is quite time consuming. They modified their numerical method by clustering the collocation points into the interfacial region in their further study (Selvam et al.
Reference Selvam, Talon, Lesshafft and Meiburg2009). Another test is made by considering a special case:
${\it\eta}=1$
, see table 3. The results in table 3 also agree with the results of SH since this special case corresponds to a single fluid flow. They also demonstrate that our numerical method is valid.
