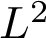1 Introduction
1.1 Background
The Ohsawa–Takegoshi
![]() $L^{2}$
extension theorem concerning the extension problem with
$L^{2}$
extension theorem concerning the extension problem with
![]() $L^{2}$
estimates of holomorphic sections of a Hermitian holomorphic bundle over complex manifolds under certain geometric conditions is one of the most important results in several complex variables and complex geometry. After it was established in [Reference Ohsawa15], many versions of the Ohsawa–Takegoshi type extension theorems have been obtained such as the generalizations given in a series of papers on the extension of
$L^{2}$
estimates of holomorphic sections of a Hermitian holomorphic bundle over complex manifolds under certain geometric conditions is one of the most important results in several complex variables and complex geometry. After it was established in [Reference Ohsawa15], many versions of the Ohsawa–Takegoshi type extension theorems have been obtained such as the generalizations given in a series of papers on the extension of
![]() $L^{2}$
holomorphic functions by Ohsawa himself [Reference Ohsawa15–Reference Ohsawa17], Manivel–Demailly
$L^{2}$
holomorphic functions by Ohsawa himself [Reference Ohsawa15–Reference Ohsawa17], Manivel–Demailly
![]() $L^{2}$
extension theorem [Reference Demailly, Dolbeault, Iordan, Henkin, Skoda and Trépreau3, Reference Manivel13], the
$L^{2}$
extension theorem [Reference Demailly, Dolbeault, Iordan, Henkin, Skoda and Trépreau3, Reference Manivel13], the
![]() $L^{2}$
extension theorems by Siu [Reference Siu, Noguchi, Fujimoto, Kajiwara and Ohsawa21] and Berndtsson [Reference Berndtsson1], the
$L^{2}$
extension theorems by Siu [Reference Siu, Noguchi, Fujimoto, Kajiwara and Ohsawa21] and Berndtsson [Reference Berndtsson1], the
![]() $L^{2}$
extension theorem with gain by McNeal and Varolin [Reference McNeal and Varolin14] and an
$L^{2}$
extension theorem with gain by McNeal and Varolin [Reference McNeal and Varolin14] and an
![]() $L^{2}$
extension theorem of Demailly et al. [Reference Demailly, Hacon and Păun4], and so on. We remark here that recently Guan and Zhou have established in a unified way an optimal version of
$L^{2}$
extension theorem of Demailly et al. [Reference Demailly, Hacon and Păun4], and so on. We remark here that recently Guan and Zhou have established in a unified way an optimal version of
![]() $L^{2}$
extension theorem [Reference Guan and Zhou6, Reference Guan and Zhou7, Reference Guan and Zhou8] which gives all optimal estimates of the above theorems.
$L^{2}$
extension theorem [Reference Guan and Zhou6, Reference Guan and Zhou7, Reference Guan and Zhou8] which gives all optimal estimates of the above theorems.
Also various results have been established by using the Ohsawa–Takegoshi extension theorem as well as its optimal version, such as the invariance of plurigenera on projective manifolds [Reference Siu22, Reference Siu23], Demailly’s strong openness conjecture [Reference Guan and Zhou9], the Suita conjecture, L-conjecture, Berndtsson’s theorem [Reference Berndtsson2] on the log-plurisubharmonicity of the relative Bergman kernel (see [Reference Guan and Zhou8]), and so on. We remark here that the last one can be directly derived by the optimal version of
![]() $L^{2}$
extension theorem. Also as an application of the above mentioned Guan-Zhou’s unified result about the Ohsawa–Takegoshi extension theorem with optimal estimates, a complete solution of the Suita conjecture [Reference Guan and Zhou8] has been obtained by Guan-Zhou.
$L^{2}$
extension theorem. Also as an application of the above mentioned Guan-Zhou’s unified result about the Ohsawa–Takegoshi extension theorem with optimal estimates, a complete solution of the Suita conjecture [Reference Guan and Zhou8] has been obtained by Guan-Zhou.
In [Reference Ohsawa17], Ohsawa posed the following question about
![]() $L^{2}$
extension.
$L^{2}$
extension.
Question. Given a subharmonic function
![]() $\psi $
on
$\psi $
on
![]() $\mathbb {C}$
such that
$\mathbb {C}$
such that
 $$ \begin{align*} \int_{\mathbb{C}}e^{-\psi}\bigg(=\int_{\mathbb{C}}e^{-\psi}dxdy\bigg)<\infty, \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}}e^{-\psi}\bigg(=\int_{\mathbb{C}}e^{-\psi}dxdy\bigg)<\infty, \end{align*} $$
and any subharmonic function
![]() $\varphi $
on
$\varphi $
on
![]() $\mathbb {C}$
, does there exist a holomorphic function f on
$\mathbb {C}$
, does there exist a holomorphic function f on
![]() $\mathbb {C}$
such that
$\mathbb {C}$
such that
and
 $$ \begin{align*} \int_{\mathbb{C}}|f(z)|^{2}e^{-\varphi(z)-\psi(z)}\leq e^{-\varphi(0)}\int_{\mathbb{C}}e^{-\psi} \ ? \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}}|f(z)|^{2}e^{-\varphi(z)-\psi(z)}\leq e^{-\varphi(0)}\int_{\mathbb{C}}e^{-\psi} \ ? \end{align*} $$
In the present paper, we give an answer to this question by using Guan-Zhou’s optimal
![]() $L^{2}$
extension theorem.
$L^{2}$
extension theorem.
1.2 Notions and notations
In order to state the optimal
![]() $L^{2}$
extension theorem which we’ll use, we recall some symbols and notions in [Reference Ohsawa15] and [Reference Ohsawa16]. For the fundamentals on
$L^{2}$
extension theorem which we’ll use, we recall some symbols and notions in [Reference Ohsawa15] and [Reference Ohsawa16]. For the fundamentals on
![]() $L^{2}$
method, the reader is referred to [Reference Hörmander11, Reference Hörmander12].
$L^{2}$
method, the reader is referred to [Reference Hörmander11, Reference Hörmander12].
Let M be a complex n-dimensional manifold, and S be a closed complex subvariety of M. Let
![]() $dV_{M}$
be a continuous volume form on M. We consider a class of upper-semi-continuous function
$dV_{M}$
be a continuous volume form on M. We consider a class of upper-semi-continuous function
![]() $\Psi $
from M to the interval
$\Psi $
from M to the interval
![]() $[-\infty ,A)$
, where
$[-\infty ,A)$
, where
![]() $A\in (-\infty ,+\infty ]$
, such that
$A\in (-\infty ,+\infty ]$
, such that
![]() $(1)$
$(1)$
 $\Psi ^{-1}(-\infty )\supset S$
, and
$\Psi ^{-1}(-\infty )\supset S$
, and
 $\Psi ^{-1}(-\infty )$
is a closed subset of M;
$\Psi ^{-1}(-\infty )$
is a closed subset of M;
![]() $(2)$
If S is l-dimensional around a point
$(2)$
If S is l-dimensional around a point
![]() $x\in S_{reg}$
(
$x\in S_{reg}$
(
![]() $S_{reg}$
is the regular part of S), there exists a local coordinate
$S_{reg}$
is the regular part of S), there exists a local coordinate
![]() $(z_{1},\ldots ,z_{n})$
on a neighborhood U of x such that
$(z_{1},\ldots ,z_{n})$
on a neighborhood U of x such that
![]() $z_{l+1}=\cdots =z_{n}=0$
on
$z_{l+1}=\cdots =z_{n}=0$
on
![]() $S\cap U$
and
$S\cap U$
and
 $$ \begin{align*} \mathrm{sup}_{U\setminus S}|\Psi(z)-(n-l)\log\sum_{l+1}^{n}|z_{j}|^{2}|<\infty. \end{align*} $$
$$ \begin{align*} \mathrm{sup}_{U\setminus S}|\Psi(z)-(n-l)\log\sum_{l+1}^{n}|z_{j}|^{2}|<\infty. \end{align*} $$
The set of such polar functions
![]() $\Psi $
will be denoted by
$\Psi $
will be denoted by
![]() $\#_{A}(S)$
and the subset of plurisubharmonic functions
$\#_{A}(S)$
and the subset of plurisubharmonic functions
![]() $\Psi $
in
$\Psi $
in
![]() $\#_{A}(S)$
will be denoted by
$\#_{A}(S)$
will be denoted by
![]() $\Delta _{A}(S)$
.
$\Delta _{A}(S)$
.
For each
![]() $\Psi \in \#_{A}(S)$
, one can associate a positive measure
$\Psi \in \#_{A}(S)$
, one can associate a positive measure
![]() $dV_{M}[\Psi ]$
on
$dV_{M}[\Psi ]$
on
![]() $S_{reg}$
as the minimum element of the partially ordered set of positive measures
$S_{reg}$
as the minimum element of the partially ordered set of positive measures
![]() $d\mu $
satisfying
$d\mu $
satisfying
 $$ \begin{align*} \int_{S_{l}}fd\mu\geq\limsup_{t\to\infty}\frac{2(n-l)} {\sigma_{2n-2l-1}}\int_{M}fe^{-\Psi}\mathbb{I}_{\{-1-t<\Psi<-t\}}dV_{M} \end{align*} $$
$$ \begin{align*} \int_{S_{l}}fd\mu\geq\limsup_{t\to\infty}\frac{2(n-l)} {\sigma_{2n-2l-1}}\int_{M}fe^{-\Psi}\mathbb{I}_{\{-1-t<\Psi<-t\}}dV_{M} \end{align*} $$
for any nonnegative continuous function f with supp
![]() $ f\Subset M$
, where
$ f\Subset M$
, where
![]() $\mathbb {I}_{\{-1-t<\Psi <-t\}}$
is the characteristic function of the set
$\mathbb {I}_{\{-1-t<\Psi <-t\}}$
is the characteristic function of the set
![]() $\{-1-t<\Psi <-t\}$
. Here we denote by
$\{-1-t<\Psi <-t\}$
. Here we denote by
![]() $S_{l}$
the l-dimensional component of
$S_{l}$
the l-dimensional component of
![]() $S_{reg}$
, denote by
$S_{reg}$
, denote by
![]() $\sigma _{m}$
the volume of the unit sphere in
$\sigma _{m}$
the volume of the unit sphere in
![]() $\mathbb {R}^{m+1}$
.
$\mathbb {R}^{m+1}$
.
Let
![]() $\omega $
be a Kähler metric on
$\omega $
be a Kähler metric on
![]() $M\setminus (X\cup S)$
, where X is a closed subset of M such that
$M\setminus (X\cup S)$
, where X is a closed subset of M such that
![]() $S_{sing}\subset X$
(
$S_{sing}\subset X$
(
![]() $S_{sing}$
is the singular part of S). We can also define a measure
$S_{sing}$
is the singular part of S). We can also define a measure
![]() $dV_{\omega }[\Psi ]$
on
$dV_{\omega }[\Psi ]$
on
![]() $S\setminus X$
as the minimum element of the partially ordered set of positive measures
$S\setminus X$
as the minimum element of the partially ordered set of positive measures
![]() $d{\mu '}$
satisfying
$d{\mu '}$
satisfying
 $$ \begin{align*} \int_{S_{l}}fd{\mu'}\geq\limsup_{t\to\infty}\frac{2(n-l)} {\sigma_{2n-2l-1}}\int_{M\setminus (X\cup S)}fe^{-\Psi}\mathbb{I}_{\{-1-t<\Psi<-t\}}dV_{\omega} \end{align*} $$
$$ \begin{align*} \int_{S_{l}}fd{\mu'}\geq\limsup_{t\to\infty}\frac{2(n-l)} {\sigma_{2n-2l-1}}\int_{M\setminus (X\cup S)}fe^{-\Psi}\mathbb{I}_{\{-1-t<\Psi<-t\}}dV_{\omega} \end{align*} $$
for any nonnegative continuous function f with supp
![]() $(f)\Subset M\setminus X$
. As
$(f)\Subset M\setminus X$
. As
the right-hand side of the above inequality is well-defined.
Let u be a continuous section of
![]() $K_{M}\otimes E$
, where E is a holomorphic vector bundle equipped with a continuous metric h on M. We define
$K_{M}\otimes E$
, where E is a holomorphic vector bundle equipped with a continuous metric h on M. We define
 $$ \begin{align*} |u|^{2}_{h}|_{V}:=\frac{c_{n}h(e,e)v\wedge\bar{v}}{dV_{M}}, \end{align*} $$
$$ \begin{align*} |u|^{2}_{h}|_{V}:=\frac{c_{n}h(e,e)v\wedge\bar{v}}{dV_{M}}, \end{align*} $$
and
 $$ \begin{align*} |u|^{2}_{h,\omega}|_{V}:=\frac{c_{n}h(e,e)v\wedge\bar{v}}{dV_{\omega}}, \end{align*} $$
$$ \begin{align*} |u|^{2}_{h,\omega}|_{V}:=\frac{c_{n}h(e,e)v\wedge\bar{v}}{dV_{\omega}}, \end{align*} $$
where
![]() $u|_{V}=v\otimes e$
for an open set
$u|_{V}=v\otimes e$
for an open set
![]() $V\subset M\setminus (X\cup S)$
, v is a continuous section of
$V\subset M\setminus (X\cup S)$
, v is a continuous section of
![]() $K_{M}|_{V}$
, e is a continuous section of
$K_{M}|_{V}$
, e is a continuous section of
![]() $E|_{V}$
and
$E|_{V}$
and
 $c_{n}=i^{n^{2}}$
such that
$c_{n}=i^{n^{2}}$
such that
![]() $c_{n} v\wedge \bar {v}$
is positive (especially, we define
$c_{n} v\wedge \bar {v}$
is positive (especially, we define
 $$ \begin{align*} |u|^{2}|_{V}:=\frac{c_{n}u\wedge\bar{u}}{dV_{M}}, \end{align*} $$
$$ \begin{align*} |u|^{2}|_{V}:=\frac{c_{n}u\wedge\bar{u}}{dV_{M}}, \end{align*} $$
when u is a continuous section of
![]() $K_{M}$
). It is clear that
$K_{M}$
). It is clear that
 $|u|^{2}_{h}$
is independent of the choices of V. In fact, one may see the relationship between
$|u|^{2}_{h}$
is independent of the choices of V. In fact, one may see the relationship between
![]() $dV_{\omega }[\Psi ]$
and
$dV_{\omega }[\Psi ]$
and
![]() $dV_{M}[\Psi ]$
(respectively,
$dV_{M}[\Psi ]$
(respectively,
![]() $dV_{\omega }$
and
$dV_{\omega }$
and
![]() $dV_{M}$
). It is clear that
$dV_{M}$
). It is clear that
 $$ \begin{align*}\int_{M\setminus(X\cup S)}f|u|^{2}_{h,\omega}dV_{\omega}[\Psi]& =\int_{M\setminus(X\cup S)}f|u|^{2}_{h}dV_{M}[\Psi],\\\Bigg(\text{resp.} \int_{M\setminus(X\cup S)}f|u|^{2}_{h,\omega}dV_{\omega} &=\int_{M\setminus(X\cup S)}f|u|^{2}_{h}dV_{M},\Bigg),\end{align*} $$
$$ \begin{align*}\int_{M\setminus(X\cup S)}f|u|^{2}_{h,\omega}dV_{\omega}[\Psi]& =\int_{M\setminus(X\cup S)}f|u|^{2}_{h}dV_{M}[\Psi],\\\Bigg(\text{resp.} \int_{M\setminus(X\cup S)}f|u|^{2}_{h,\omega}dV_{\omega} &=\int_{M\setminus(X\cup S)}f|u|^{2}_{h}dV_{M},\Bigg),\end{align*} $$
where f is a continuous function with compact support on
![]() $M\setminus X$
.
$M\setminus X$
.
It is clear that
 $|u|^{2}_{h}$
is independent of the choices of U, while
$|u|^{2}_{h}$
is independent of the choices of U, while
 $|u|^{2}_{h}dV_{M}$
is independent of the choices of
$|u|^{2}_{h}dV_{M}$
is independent of the choices of
![]() $dV_{M}$
(respectively,
$dV_{M}$
(respectively,
 $|u|^{2}_{h}dV_{M}[\Psi ]$
is independent of the choices of
$|u|^{2}_{h}dV_{M}[\Psi ]$
is independent of the choices of
![]() $dV_{M}$
).
$dV_{M}$
).
Definition 1.1. Let M be an n-dimensional complex manifold with a continuous volume form
![]() $dV_{M}$
, and let S be a closed complex subvariety of M. We call a pair
$dV_{M}$
, and let S be a closed complex subvariety of M. We call a pair
![]() $(M,S)$
an almost Stein pair if M and S satisfy the following conditions:
$(M,S)$
an almost Stein pair if M and S satisfy the following conditions:
There exists a closed subset
![]() $X\subset M$
such that:
$X\subset M$
such that:
-
(a) X is locally negligible with respect to
 $L^{2}$
holomorphic functions, that is, for any local coordinate neighborhood
$L^{2}$
holomorphic functions, that is, for any local coordinate neighborhood
 $U\subset M$
and for any
$U\subset M$
and for any
 $L^{2}$
holomorphic function f on
$L^{2}$
holomorphic function f on
 $U\setminus X$
, there exists an
$U\setminus X$
, there exists an
 $L^{2}$
holomorphic function
$L^{2}$
holomorphic function
 $\tilde {f}$
on U such that
$\tilde {f}$
on U such that
 $\tilde {f}|_{U\setminus X}=f$
with the same
$\tilde {f}|_{U\setminus X}=f$
with the same
 $L^{2}$
norm.
$L^{2}$
norm. -
(b)
 $M\setminus X$
is a Stein manifold which intersects every component of S, such that
$M\setminus X$
is a Stein manifold which intersects every component of S, such that
 $S_{sing}\subset X$
.
$S_{sing}\subset X$
.
Remark 1.2. In fact, when S is smooth, the conditions of an almost Stein pair are the same as in [Reference Ohsawa15] and [Reference Ohsawa16]. The almost Stein pair
![]() $(M,S)$
includes all the following well-known examples:
$(M,S)$
includes all the following well-known examples:
-
(1) M is a Stein manifold (including any open Riemann surface), and S is any closed complex submanifold of M;
-
(2) M is a complex projective algebraic manifold (including any compact Riemann surface), and S is any closed complex submanifold of M;
-
(3) M is a projective family (see [Reference Siu23]), and S is any closed complex submanifold of M.
Remark 1.3. Actually, all
![]() $L^{2}$
holomorphic sections of the holomorphic vector bundles can be extended holomorphically from
$L^{2}$
holomorphic sections of the holomorphic vector bundles can be extended holomorphically from
![]() $M\setminus X$
to M. In fact, let
$M\setminus X$
to M. In fact, let
![]() $(M,S)$
be an almost Stein pair, h be a singular metric on holomorphic line bundle L on M (respectively, continuous metric on holomorphic vector bundle E on M with rank r), where h has a locally positive lower bound.
$(M,S)$
be an almost Stein pair, h be a singular metric on holomorphic line bundle L on M (respectively, continuous metric on holomorphic vector bundle E on M with rank r), where h has a locally positive lower bound.
Let F be a holomorphic section of
 $K_{M\setminus X}\otimes L|_{M\setminus X}$
(respectively,
$K_{M\setminus X}\otimes L|_{M\setminus X}$
(respectively,
 $K_{M\setminus X}\otimes E|_{M\setminus X}$
), which satisfies
$K_{M\setminus X}\otimes E|_{M\setminus X}$
), which satisfies
 $\int _{M\setminus X}|F|^{2}_{h}<\infty $
. As h has a locally positive lower bound and M satisfies (a) of the above condition (ab), there is a holomorphic section
$\int _{M\setminus X}|F|^{2}_{h}<\infty $
. As h has a locally positive lower bound and M satisfies (a) of the above condition (ab), there is a holomorphic section
![]() $\tilde {F}$
of
$\tilde {F}$
of
![]() $K_{M}\otimes L$
on M (resp.
$K_{M}\otimes L$
on M (resp.
![]() $K_{M}\otimes E$
), such that
$K_{M}\otimes E$
), such that
 $\tilde {F}|_{M\setminus X}=F$
.
$\tilde {F}|_{M\setminus X}=F$
.
1.3 The optimal
 $L^{2}$
extension theorem
$L^{2}$
extension theorem
In [Reference Guan and Zhou8], Guan and Zhou found an Ohsawa–Takegoshi type
![]() $L^{2}$
extension theorem with an optimal
$L^{2}$
extension theorem with an optimal
![]() $L^{2}$
estimate, which is stated as follows.
$L^{2}$
estimate, which is stated as follows.
Let
![]() $c_{A}(t)$
be a positive function in
$c_{A}(t)$
be a positive function in
![]() $C^{\infty }((-A,+\infty ))$
$C^{\infty }((-A,+\infty ))$
![]() $(A\in (-\infty ,+\infty ])$
, satisfying
$(A\in (-\infty ,+\infty ])$
, satisfying
 $$ \begin{align*} \int_{-A}^{\infty}c_{A}(t)e^{-t}dt<\infty \end{align*} $$
$$ \begin{align*} \int_{-A}^{\infty}c_{A}(t)e^{-t}dt<\infty \end{align*} $$
and
 $$ \begin{align} (\int_{-A}^{t}c_{A}(t_{1})e^{-t_{1}}dt_{1})^{2}>c_{A}(t)e^{-t} \int_{-A}^{t}\int_{-A}^{t_{2}}c_{A}(t_{1})e^{-t_{1}}dt_{1}dt_{2}, \end{align} $$
$$ \begin{align} (\int_{-A}^{t}c_{A}(t_{1})e^{-t_{1}}dt_{1})^{2}>c_{A}(t)e^{-t} \int_{-A}^{t}\int_{-A}^{t_{2}}c_{A}(t_{1})e^{-t_{1}}dt_{1}dt_{2}, \end{align} $$
for any
![]() $t\in (-A,+\infty )$
, that is,
$t\in (-A,+\infty )$
, that is,
 $$ \begin{align*} F(t)=\log\bigg(\int_{-A}^{t}\int_{-A}^{t_{2}}c_{A}(t_{1})e^{-t_{1}}dt_{1}dt_{2}\bigg) \end{align*} $$
$$ \begin{align*} F(t)=\log\bigg(\int_{-A}^{t}\int_{-A}^{t_{2}}c_{A}(t_{1})e^{-t_{1}}dt_{1}dt_{2}\bigg) \end{align*} $$
is strictly concave for any
![]() $t\in (-A,+\infty )$
.
$t\in (-A,+\infty )$
.
An easy example of such functions
![]() $c_{A}(t)$
is when
$c_{A}(t)$
is when
![]() $c_{A}(t)e^{-t}$
is decreasing with respect to t.
$c_{A}(t)e^{-t}$
is decreasing with respect to t.
Remark 1.4 (See [Reference Guan and Zhou8]). Another important class of functions
![]() $c_{A}(t)$
satisfying (1.1) contains the functions satisfying the following,
$c_{A}(t)$
satisfying (1.1) contains the functions satisfying the following,
-
(1)
 $\frac {d}{dt}c_{A}(t)e^{-t}>0$
, for
$\frac {d}{dt}c_{A}(t)e^{-t}>0$
, for
 $t\in (-A, a)$
;
$t\in (-A, a)$
; -
(2)
 $\frac {d}{dt}c_{A}(t)e^{-t}\leq 0$
, for
$\frac {d}{dt}c_{A}(t)e^{-t}\leq 0$
, for
 $t\in [a,\infty )$
;
$t\in [a,\infty )$
; -
(3)
 $\frac {d^{2}}{dt^{2}}\log (c_{A}(t)e^{-t})< 0$
, for
$\frac {d^{2}}{dt^{2}}\log (c_{A}(t)e^{-t})< 0$
, for
 $t\in (-A, a),$
$t\in (-A, a),$
where
![]() $a\geq -A$
is a constant.
$a\geq -A$
is a constant.
Theorem 1.5. Let
![]() $(M,S)$
be an almost Stein pair, and
$(M,S)$
be an almost Stein pair, and
![]() $\Psi $
be a plurisubharmonic function in
$\Psi $
be a plurisubharmonic function in
![]() $\Delta _{A}(S)\cap C^{\infty }(M\setminus (S\cup X))$
(X is as in the definition of almost Stein pair). Let h be a smooth metric on a holomorphic vector bundle E on M with rank r, such that
$\Delta _{A}(S)\cap C^{\infty }(M\setminus (S\cup X))$
(X is as in the definition of almost Stein pair). Let h be a smooth metric on a holomorphic vector bundle E on M with rank r, such that
![]() $he^{-\Psi }$
is semi-positive in the sense of Nakano on
$he^{-\Psi }$
is semi-positive in the sense of Nakano on
![]() $M\setminus (S\cup X)$
(when E is a line bundle, h can be chosen as a semipositive singular metric). Then there exists a uniform constant
$M\setminus (S\cup X)$
(when E is a line bundle, h can be chosen as a semipositive singular metric). Then there exists a uniform constant
![]() $\mathbf {C}=1$
, which is optimal, such that, for any holomorphic section f of
$\mathbf {C}=1$
, which is optimal, such that, for any holomorphic section f of
![]() $K_{M}\otimes E|_{S}$
on S satisfying condition that
$K_{M}\otimes E|_{S}$
on S satisfying condition that
 $$ \begin{align*} \sum_{k=1}^{n}\frac{\pi^{k}}{k!}\int_{S_{n-k}}|f|^{2}_{h}dV_{M}[\Psi]<\infty, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{n}\frac{\pi^{k}}{k!}\int_{S_{n-k}}|f|^{2}_{h}dV_{M}[\Psi]<\infty, \end{align*} $$
there exists a holomorphic section F of
![]() $K_{M}\otimes E$
on M satisfying
$K_{M}\otimes E$
on M satisfying
![]() $F = f$
on
$F = f$
on
![]() $ S$
and
$ S$
and
 $$ \begin{align*} \int_{M}c_{A}(-\Psi)|F|^{2}_{h}dV_{M} \leq\mathbf{C}\int_{-A}^{\infty}c_{A}(t)e^{-t}dt\sum_{k=1}^{n}\frac{\pi^{k}}{k!}\int_{S_{n-k}}|f|^{2}_{h}dV_{M}[\Psi]. \end{align*} $$
$$ \begin{align*} \int_{M}c_{A}(-\Psi)|F|^{2}_{h}dV_{M} \leq\mathbf{C}\int_{-A}^{\infty}c_{A}(t)e^{-t}dt\sum_{k=1}^{n}\frac{\pi^{k}}{k!}\int_{S_{n-k}}|f|^{2}_{h}dV_{M}[\Psi]. \end{align*} $$
As we have mentioned, various results have been derived from the above theorem. A survey about the optimal
![]() $L^{2}$
extension and its applications is given in [Reference Zhou24].
$L^{2}$
extension and its applications is given in [Reference Zhou24].
Especially, when we take M to be a pseudoconvex domain D in
![]() $\mathbb {C}^{n}$
with coordinates
$\mathbb {C}^{n}$
with coordinates
![]() $(z_{1},z_{2},\ldots ,z_{n})$
, H be the intersection of the set
$(z_{1},z_{2},\ldots ,z_{n})$
, H be the intersection of the set
![]() $\{z_{n-l+1}=\cdots =z_{n}=0\}$
with D, let
$\{z_{n-l+1}=\cdots =z_{n}=0\}$
with D, let
![]() $dV_{D}$
and
$dV_{D}$
and
![]() $dV_{H}$
be the Lebesgue measures on D and
$dV_{H}$
be the Lebesgue measures on D and
![]() $H,$
respectively,
$H,$
respectively,
 $\Psi (z)=l\log (|z_{n-l+1}|^{2}+\cdots +|z_{n}|^{2})$
, then
$\Psi (z)=l\log (|z_{n-l+1}|^{2}+\cdots +|z_{n}|^{2})$
, then
 $dV_{D}[l\log (|z_{n-l+1}|^{2}+\cdots +|z_{n}|^{2})] = dV_{H}$
. For any positive function
$dV_{D}[l\log (|z_{n-l+1}|^{2}+\cdots +|z_{n}|^{2})] = dV_{H}$
. For any positive function
![]() $c_{A}(t)$
that satisfies (1.1), Theorem 1.5 degenerates to the following.
$c_{A}(t)$
that satisfies (1.1), Theorem 1.5 degenerates to the following.
Theorem 1.6. Let
![]() $D\subset \mathbb {C}^{n}$
be a pseudoconvex domain, let l be an integer between
$D\subset \mathbb {C}^{n}$
be a pseudoconvex domain, let l be an integer between
![]() $1$
and n, let
$1$
and n, let
![]() $\varphi $
be a plurisubharmonic function on
$\varphi $
be a plurisubharmonic function on
![]() $D,$
and let
$D,$
and let
![]() $H=D\cap \{z_{n}=\cdots =z_{n-l+1}=0\}$
. Then for any holomorphic function f on H satisfying
$H=D\cap \{z_{n}=\cdots =z_{n-l+1}=0\}$
. Then for any holomorphic function f on H satisfying
 $$ \begin{align*} \int_{H}|f|^{2}e^{-\varphi}dV_{H}<\infty, \end{align*} $$
$$ \begin{align*} \int_{H}|f|^{2}e^{-\varphi}dV_{H}<\infty, \end{align*} $$
there exists a holomorphic function F on D satisfying
![]() $F=f$
on H and
$F=f$
on H and
 $$ \begin{align*} \int_{D}c_{A}(-l\log(|z_{n}|^{2}+\cdots+|z_{n-l+1}|^{2}))|F|^{2}e^{-\varphi}dV_{D} \leq\frac{\pi^{l}}{l!}\int_{-A}^{\infty}c_{A}(t)e^{-t}dt\int_{H}|f|^{2}e^{-\varphi}dV_{H}. \end{align*} $$
$$ \begin{align*} \int_{D}c_{A}(-l\log(|z_{n}|^{2}+\cdots+|z_{n-l+1}|^{2}))|F|^{2}e^{-\varphi}dV_{D} \leq\frac{\pi^{l}}{l!}\int_{-A}^{\infty}c_{A}(t)e^{-t}dt\int_{H}|f|^{2}e^{-\varphi}dV_{H}. \end{align*} $$
By using Theorem 1.6, we obtain the following
Theorem 1.7. If
![]() $D\subset \mathbb {C}^{n}$
be a pseudoconvex domain, l be an integer between
$D\subset \mathbb {C}^{n}$
be a pseudoconvex domain, l be an integer between
![]() $1$
and n,
$1$
and n,
![]() $H=D\cap \{z_{n-l+1}=\cdots =z_{n}=0\}$
,
$H=D\cap \{z_{n-l+1}=\cdots =z_{n}=0\}$
,
 $\psi (z)=\rho ((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})$
where
$\psi (z)=\rho ((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})$
where
![]() $\rho $
is a radial subharmonic function on
$\rho $
is a radial subharmonic function on
![]() $\mathbb {C}$
. Then for every plurisubharmonic function
$\mathbb {C}$
. Then for every plurisubharmonic function
![]() $\varphi $
on D and every holomorphic function f on H such that
$\varphi $
on D and every holomorphic function f on H such that
 $$ \begin{align*} \int_{H}|f|^{2} e^{-\varphi}dV_{H}<\infty, \end{align*} $$
$$ \begin{align*} \int_{H}|f|^{2} e^{-\varphi}dV_{H}<\infty, \end{align*} $$
there exists a holomorphic function F on D such that
on H and
 $$ \begin{align} \int_{D}|F|^{2} e^{-\varphi-\psi}dV_{D}\leqslant 2{\sigma_{l}}\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(t)}tdt \int_{H}|f|^{2} e^{-\varphi}dV_{H}, \end{align} $$
$$ \begin{align} \int_{D}|F|^{2} e^{-\varphi-\psi}dV_{D}\leqslant 2{\sigma_{l}}\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(t)}tdt \int_{H}|f|^{2} e^{-\varphi}dV_{H}, \end{align} $$
where
 $A=\mathrm {sup}_{z\in D} l\log (\sum _{j=n-l+1}^{n}|z_{j}|^{2})$
.
$A=\mathrm {sup}_{z\in D} l\log (\sum _{j=n-l+1}^{n}|z_{j}|^{2})$
.
Remark 1.8. Since
![]() $\rho $
is radial, we may regard
$\rho $
is radial, we may regard
![]() $\rho $
as a function defined on
$\rho $
as a function defined on
![]() $\mathbb {R}_{\geq 0}$
and thus
$\mathbb {R}_{\geq 0}$
and thus
 $\rho ((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})$
and
$\rho ((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})$
and
![]() $\rho (t)$
in the right-hand side of (1.2) make sense.
$\rho (t)$
in the right-hand side of (1.2) make sense.
When
![]() $n=1$
, as a corollary of Theorem 1.7, we conclude that the question of Ohsawa holds under a natural condition.
$n=1$
, as a corollary of Theorem 1.7, we conclude that the question of Ohsawa holds under a natural condition.
Corollary 1.9. If
![]() $\psi $
is a subharmonic function on
$\psi $
is a subharmonic function on
![]() $\mathbb {C}$
such that
$\mathbb {C}$
such that
![]() $i\partial \bar \partial \psi $
is rotational invariant and satisfies
$i\partial \bar \partial \psi $
is rotational invariant and satisfies
 $$ \begin{align*} \int_{\mathbb{C}}e^{-\psi}<\infty, \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}}e^{-\psi}<\infty, \end{align*} $$
then for every subharmonic function
![]() $\varphi $
on
$\varphi $
on
![]() $\mathbb {C}$
, there exists a holomorphic function f on
$\mathbb {C}$
, there exists a holomorphic function f on
![]() $\mathbb {C}$
such that
$\mathbb {C}$
such that
and
 $$ \begin{align*} \int_{\mathbb{C}}|f|^{2} e^{-\varphi-\psi}\leqslant e^{-\varphi(0)}\int_{\mathbb{C}} e^{-\psi}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}}|f|^{2} e^{-\varphi-\psi}\leqslant e^{-\varphi(0)}\int_{\mathbb{C}} e^{-\psi}. \end{align*} $$
However, without the condition that
![]() $i\partial \bar \partial \psi $
is rotational invariant, the above question of Ohsawa fails in general. Recently, Guan gave a counterexample in [Reference Guan5] by showing that there exist subharmonic functions
$i\partial \bar \partial \psi $
is rotational invariant, the above question of Ohsawa fails in general. Recently, Guan gave a counterexample in [Reference Guan5] by showing that there exist subharmonic functions
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
on
$\varphi $
on
![]() $\mathbb {C}$
such that the Bergman space
$\mathbb {C}$
such that the Bergman space
 $A^{2}(\mathbb {C},e^{-\varphi -\psi })$
with respect to
$A^{2}(\mathbb {C},e^{-\varphi -\psi })$
with respect to
![]() $\varphi +\psi $
contains only zero. In the last section, we will give another counterexample with nontrivial
$\varphi +\psi $
contains only zero. In the last section, we will give another counterexample with nontrivial
 $A^{2}(\mathbb {C},e^{-\varphi -\psi })$
.
$A^{2}(\mathbb {C},e^{-\varphi -\psi })$
.
2 Proof of main results
In order to prove our main theorem and corollaries, we recall some well-known results.
Proposition 2.1. Let
![]() $D\subset \mathbb {C}^{n}$
be a domain and set
$D\subset \mathbb {C}^{n}$
be a domain and set
 $D_{j}=\{z\in D: |z|<j \ and\ \delta _{D}(z)>\frac {1}{j}\}\,(\delta _{D}(z)$
denotes the distance between z and
$D_{j}=\{z\in D: |z|<j \ and\ \delta _{D}(z)>\frac {1}{j}\}\,(\delta _{D}(z)$
denotes the distance between z and
![]() $\partial D)$
,
$\partial D)$
,
![]() $j=1,2, \ldots $
. Suppose
$j=1,2, \ldots $
. Suppose
![]() $u\not \equiv -\infty $
is plurisubharmonic on D. Assume that
$u\not \equiv -\infty $
is plurisubharmonic on D. Assume that
![]() $u(z)$
is radial. Then there is a sequence
$u(z)$
is radial. Then there is a sequence
 $\{u_{j}\}_{j=1}^{\infty }\subset C^{\infty }(D)$
with the following properties:
$\{u_{j}\}_{j=1}^{\infty }\subset C^{\infty }(D)$
with the following properties:
-
(1)
 $u_{j}$
is radial and strictly plurisubharmonic on
$u_{j}$
is radial and strictly plurisubharmonic on
 $D_{j}$
.
$D_{j}$
. -
(2)
 $u_{j}\geq u_{j+1}$
on
$u_{j}\geq u_{j+1}$
on
 $D_{j}$
and
$D_{j}$
and
 $\lim _{j\rightarrow \infty } u_{j}(z) = u(z)$
for any
$\lim _{j\rightarrow \infty } u_{j}(z) = u(z)$
for any
 $z\in D$
.
$z\in D$
.
Proof. This is the classical regularization theorem of plurisubharmonic functions on domains in
![]() $\mathbb {C}^{n}$
which can be done by taking convolution (see [Reference Range19]). Note that if we choose the mollifier in the convolution to be radial, that is, depends only on
$\mathbb {C}^{n}$
which can be done by taking convolution (see [Reference Range19]). Note that if we choose the mollifier in the convolution to be radial, that is, depends only on
![]() $|z|$
, it is easy to verify the convolution leads to a plurisubharmonic function satisfying the requirements.
$|z|$
, it is easy to verify the convolution leads to a plurisubharmonic function satisfying the requirements.
Proposition 2.2 (See [Reference Guan and Zhou8]). Let D be a domain in
![]() $\mathbb {C}^{n}$
and
$\mathbb {C}^{n}$
and
 $\{F_{j}\}_{j=1}^{\infty }$
be a sequence of holomorphic functions on D. Assume that for any compact subset K of D, there exists a constant
$\{F_{j}\}_{j=1}^{\infty }$
be a sequence of holomorphic functions on D. Assume that for any compact subset K of D, there exists a constant
![]() $C_{K}>0$
, such that
$C_{K}>0$
, such that
 $$ \begin{align*} \int_{K}|F_{j}|^{2}dV\leq C_{K} \end{align*} $$
$$ \begin{align*} \int_{K}|F_{j}|^{2}dV\leq C_{K} \end{align*} $$
holds for any
![]() $j=1,2,\ldots $
. Then we have a subsequence of
$j=1,2,\ldots $
. Then we have a subsequence of
 $\{F_{j}\}_{j=1}^{\infty }$
, which is convergent to a holomorphic function uniformly on any compact subset of D.
$\{F_{j}\}_{j=1}^{\infty }$
, which is convergent to a holomorphic function uniformly on any compact subset of D.
Proposition 2.3 (Riesz’s decomposition, see [Reference Ransford20]). Let
![]() $\psi \not \equiv -\infty $
be a subharmonic function on a domain D in
$\psi \not \equiv -\infty $
be a subharmonic function on a domain D in
![]() $\mathbb {C}$
. Then for any given relatively compact open subset U of D, we can write
$\mathbb {C}$
. Then for any given relatively compact open subset U of D, we can write
![]() $\psi $
as
$\psi $
as
 $$ \begin{align*} \psi(z)=\frac{1}{2\pi}\int_{U}\log|z-\zeta|i\partial\bar\partial\psi(\zeta)+h(z) \end{align*} $$
$$ \begin{align*} \psi(z)=\frac{1}{2\pi}\int_{U}\log|z-\zeta|i\partial\bar\partial\psi(\zeta)+h(z) \end{align*} $$
on U, where h is a harmonic function on U.
Now we turn to prove Theorem 1.7.
Proof. First, we prove the result with the assumption that
![]() $\rho $
is smooth and strictly subharmonic.
$\rho $
is smooth and strictly subharmonic.
Let
 $\Psi (z)=l\log \sum _{j=n-l+1}^{n}|z_{j}|^{2}$
and let
$\Psi (z)=l\log \sum _{j=n-l+1}^{n}|z_{j}|^{2}$
and let
 $c_{A}(t)=e^{-\rho (e^{-t/2})}$
. As we have mentioned in Remark 1.8, we regard
$c_{A}(t)=e^{-\rho (e^{-t/2})}$
. As we have mentioned in Remark 1.8, we regard
![]() $\rho $
as a function defined on
$\rho $
as a function defined on
![]() $\mathbb {R}_{\geq 0}$
. It is clear that
$\mathbb {R}_{\geq 0}$
. It is clear that
 $c_{A}(-\Psi (z))=e^{-\rho ((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})}=e^{-\psi (z)}$
.
$c_{A}(-\Psi (z))=e^{-\rho ((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})}=e^{-\psi (z)}$
.
Let
![]() $T=e^{-\frac {t}{2}}$
, then we have
$T=e^{-\frac {t}{2}}$
, then we have
 $$ \begin{align*} \int_{-A}^{\infty}c_{A}(t)e^{-t}dt=-2\int_{-A}^{\infty}e^{-\rho({e^{-\frac{t}{2}}})}e^{-\frac{t}{2}}de^{-\frac{t}{2}} =2\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(T)}TdT. \end{align*} $$
$$ \begin{align*} \int_{-A}^{\infty}c_{A}(t)e^{-t}dt=-2\int_{-A}^{\infty}e^{-\rho({e^{-\frac{t}{2}}})}e^{-\frac{t}{2}}de^{-\frac{t}{2}} =2\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(T)}TdT. \end{align*} $$
On the other hand, our choice of
 $c_{A}(t)=e^{-\rho (e^{-t/2})}$
belongs to the class mentioned in Remark 1.4. Indeed, we have
$c_{A}(t)=e^{-\rho (e^{-t/2})}$
belongs to the class mentioned in Remark 1.4. Indeed, we have
 $$ \begin{align*} \begin{aligned} \frac{d}{dt}c_{A}(t)e^{-t}=&\frac{d}{dT}(e^{-\rho(T)}T^{2})\frac{dT}{dt}\\=&(2Te^{-\rho(T)}-T^{2}{\rho'}(T)e^{-\rho(T)})(-\frac{1}{2}T), \\=&-\frac{1}{2}T^{2}(2-T{\rho'}(T))e^{-\rho(T)} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{d}{dt}c_{A}(t)e^{-t}=&\frac{d}{dT}(e^{-\rho(T)}T^{2})\frac{dT}{dt}\\=&(2Te^{-\rho(T)}-T^{2}{\rho'}(T)e^{-\rho(T)})(-\frac{1}{2}T), \\=&-\frac{1}{2}T^{2}(2-T{\rho'}(T))e^{-\rho(T)} \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \log (c_{A}(t)e^{-t})=\log(e^{-\rho(T)}T^{2})=\log T^{2}-\rho(T). \end{align*} $$
$$ \begin{align*} \log (c_{A}(t)e^{-t})=\log(e^{-\rho(T)}T^{2})=\log T^{2}-\rho(T). \end{align*} $$
Then we have
 $$ \begin{align*} \begin{aligned} \frac{d}{dT}\log (c_{A}(t)e^{-t})=\frac{2}{T}-{\rho'}(T), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{d}{dT}\log (c_{A}(t)e^{-t})=\frac{2}{T}-{\rho'}(T), \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} \frac{d^{2}}{dT^{2}}\log (c_{A}(t)e^{-t})=&\frac{d}{dT}(\frac{2}{T}-{\rho'}(T))=-\frac{2}{T^{2}}-{\rho''}(T). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{d^{2}}{dT^{2}}\log (c_{A}(t)e^{-t})=&\frac{d}{dT}(\frac{2}{T}-{\rho'}(T))=-\frac{2}{T^{2}}-{\rho''}(T). \end{aligned} \end{align*} $$
Therefore,
 $$ \begin{align*} \begin{aligned} \frac{d^{2}}{dt^{2}}\log (c_{A}(t)e^{-t})=&\frac{d}{dt}(\frac{d}{dT}\log (e^{-\rho(T)}T^{2})\frac{dT}{dt}) \\=&\frac{d}{dT}\frac{d}{dT}\log (e^{-\rho(T)}T^{2})(\frac{dT}{dt})^{2}+\frac{d}{dT}\log (e^{-\rho(T)}T^{2})\frac{d^{2}T}{dt^{2}} \\=&(-\frac{2}{T^{2}}-{\rho''}(T))\frac{1}{4}T^{2}+(\frac{2}{T}-{\rho'}(T))\frac{1}{4}T \\=&-\frac{1}{4}T({\rho'}(T)+{\rho''}(T)T). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{d^{2}}{dt^{2}}\log (c_{A}(t)e^{-t})=&\frac{d}{dt}(\frac{d}{dT}\log (e^{-\rho(T)}T^{2})\frac{dT}{dt}) \\=&\frac{d}{dT}\frac{d}{dT}\log (e^{-\rho(T)}T^{2})(\frac{dT}{dt})^{2}+\frac{d}{dT}\log (e^{-\rho(T)}T^{2})\frac{d^{2}T}{dt^{2}} \\=&(-\frac{2}{T^{2}}-{\rho''}(T))\frac{1}{4}T^{2}+(\frac{2}{T}-{\rho'}(T))\frac{1}{4}T \\=&-\frac{1}{4}T({\rho'}(T)+{\rho''}(T)T). \end{aligned} \end{align*} $$
Note that
is exactly the condition of a radial smooth function on
![]() $\mathbb {C}$
being a strictly subharmonic function. It is then obvious that
$\mathbb {C}$
being a strictly subharmonic function. It is then obvious that
 $\frac {d^{2}}{dt^{2}}\log (c_{A}(t)e^{-t})<0$
and thus
$\frac {d^{2}}{dt^{2}}\log (c_{A}(t)e^{-t})<0$
and thus
![]() $c_{A}(t)$
satisfies the condition (3) in Remark 1.4.
$c_{A}(t)$
satisfies the condition (3) in Remark 1.4.
Now we denote
and we get a nonhomogeneous linear ordinary differential equation. Solving this differential equation, we get
 $$ \begin{align*} \rho(T)=(\int_{0}^{T}g(x)dx)\log T-\int_{0}^{T}g(x)\log xdx. \end{align*} $$
$$ \begin{align*} \rho(T)=(\int_{0}^{T}g(x)dx)\log T-\int_{0}^{T}g(x)\log xdx. \end{align*} $$
Notice that
 $$ \begin{align*} T{\rho '}(T)=\int_{0}^{T}g(x){d}x \end{align*} $$
$$ \begin{align*} T{\rho '}(T)=\int_{0}^{T}g(x){d}x \end{align*} $$
is an increasing function. Thus, the set such that
 $\frac {d}{dt}c_{A}(t)e^{-t}>0$
or
$\frac {d}{dt}c_{A}(t)e^{-t}>0$
or
 $\frac {d}{dt}c_{A}(t)e^{-t}\leq 0$
is indeed an interval. Therefore by Theorem 1.6, we have proved the theorem with the assumption that
$\frac {d}{dt}c_{A}(t)e^{-t}\leq 0$
is indeed an interval. Therefore by Theorem 1.6, we have proved the theorem with the assumption that
![]() $\rho $
is smooth and strictly subharmonic.
$\rho $
is smooth and strictly subharmonic.
For the general case, let
 $\{D_{j}\}_{j=1}^{\infty }$
be a sequence of pseudoconvex domains satisfying
$\{D_{j}\}_{j=1}^{\infty }$
be a sequence of pseudoconvex domains satisfying
![]() $D_{j}\Subset D_{j+1}$
for all j and
$D_{j}\Subset D_{j+1}$
for all j and
 $\bigcup _{j=1}^{\infty }D_{j}=D$
. By Proposition 2.1, we can find a sequence of smooth radial strictly subharmonic functions
$\bigcup _{j=1}^{\infty }D_{j}=D$
. By Proposition 2.1, we can find a sequence of smooth radial strictly subharmonic functions
 $\{{\rho }_{j}\}_{j=1}^{\infty }$
such that for any
$\{{\rho }_{j}\}_{j=1}^{\infty }$
such that for any
![]() $k\geq j$
,
$k\geq j$
,
 $\rho _{k}((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})$
decreases to
$\rho _{k}((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})$
decreases to
 $\rho ((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})$
on
$\rho ((\sum _{j=n-l+1}^{n}|z_{j}|^{2})^{l/2})$
on
![]() $D_{j}$
.
$D_{j}$
.
Let
 $$ \begin{align*} \psi_{k}(z)=\rho_{k}((\sum_{j=n-l+1}^{n}|z_{j}|^{2})^{l/2}), \end{align*} $$
$$ \begin{align*} \psi_{k}(z)=\rho_{k}((\sum_{j=n-l+1}^{n}|z_{j}|^{2})^{l/2}), \end{align*} $$
then on
![]() $D_{j}$
, for every
$D_{j}$
, for every
![]() $k\geq j$
we have a holomorphic function
$k\geq j$
we have a holomorphic function
![]() $F_{j,k}$
on
$F_{j,k}$
on
![]() $D_{j}$
such that
$D_{j}$
such that
 $$ \begin{align*} \begin{aligned} \int_{D_{j}}|F_{j,k}(z)|^{2}e^{-\varphi}e^{-{\psi_{k}}}&\leq 2\frac{\pi^{l}}{l!}\int_{0}^{e^{\frac{A_{j}}{2}}}e^{-\rho(t)}tdt\int_{H_{j}}|f|^{2}e^{-\varphi}dV_{H_{j}} \\&\leq 2\frac{\pi^{l}}{l!}\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(t)}tdt\int_{H}|f|^{2}e^{-\varphi}dV_{H}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \int_{D_{j}}|F_{j,k}(z)|^{2}e^{-\varphi}e^{-{\psi_{k}}}&\leq 2\frac{\pi^{l}}{l!}\int_{0}^{e^{\frac{A_{j}}{2}}}e^{-\rho(t)}tdt\int_{H_{j}}|f|^{2}e^{-\varphi}dV_{H_{j}} \\&\leq 2\frac{\pi^{l}}{l!}\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(t)}tdt\int_{H}|f|^{2}e^{-\varphi}dV_{H}. \end{aligned} \end{align*} $$
where
![]() $H_{j}=H\cap D_{j}$
and
$H_{j}=H\cap D_{j}$
and
 $A_{j}=\mathrm {sup}_{z\in D_{j}}l\log (\sum _{m=n-l+1}^{n}|z_{m}|^{2})$
. Note that for any
$A_{j}=\mathrm {sup}_{z\in D_{j}}l\log (\sum _{m=n-l+1}^{n}|z_{m}|^{2})$
. Note that for any
![]() $k\geq j$
,
$k\geq j$
,
![]() $\varphi +\psi _{k}$
is bounded from above on
$\varphi +\psi _{k}$
is bounded from above on
![]() $D_{j}$
, by Proposition 2.2, we may find a subsequence of
$D_{j}$
, by Proposition 2.2, we may find a subsequence of
![]() $\{F_{j,k}\}_{k}$
, still denoted by
$\{F_{j,k}\}_{k}$
, still denoted by
![]() $\{F_{j,k}\}_{k}$
, which is convergent to a holomorphic function
$\{F_{j,k}\}_{k}$
, which is convergent to a holomorphic function
![]() $F_{j}$
uniformly on any compact subset of
$F_{j}$
uniformly on any compact subset of
![]() $D_{j}$
.
$D_{j}$
.
By Fatou’s lemma, we have
 $$ \begin{align*} \int_{D_{j}}|F_{j}|^{2}e^{-\varphi-\psi}\leq \liminf_{k\rightarrow\infty}\int_{D_{j}}|F_{j,k}(z)|^{2}e^{-\varphi}e^{-{\psi_{k}}} \leq2\frac{\pi^{l}}{l!}\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(t)}tdt\int_{H}|f|^{2}e^{-\varphi}dV_{H}. \end{align*} $$
$$ \begin{align*} \int_{D_{j}}|F_{j}|^{2}e^{-\varphi-\psi}\leq \liminf_{k\rightarrow\infty}\int_{D_{j}}|F_{j,k}(z)|^{2}e^{-\varphi}e^{-{\psi_{k}}} \leq2\frac{\pi^{l}}{l!}\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(t)}tdt\int_{H}|f|^{2}e^{-\varphi}dV_{H}. \end{align*} $$
Again, since
![]() $\varphi +\psi $
is bounded from above on any compact subset of D, by the same reason, we may find a subsequence of
$\varphi +\psi $
is bounded from above on any compact subset of D, by the same reason, we may find a subsequence of
![]() $\{F_{j}\}_{j}$
, still denoted by
$\{F_{j}\}_{j}$
, still denoted by
![]() $\{F_{j}\}_{j}$
, which is convergent to a holomorphic function F uniformly on any compact subset of D and
$\{F_{j}\}_{j}$
, which is convergent to a holomorphic function F uniformly on any compact subset of D and
 $$ \begin{align*} \int_{D}|F|^{2}e^{-\varphi-\psi}\leq & \liminf_{k\rightarrow\infty}\int_{D}\mathbb{I}_{\overline{D_{j}}}|F_{j}(z)|^{2}e^{-\varphi}e^{-{\psi}} \\& \leq2\frac{\pi^{l}}{l!}\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(t)}tdt\int_{H}|f|^{2}e^{-\varphi}dV_{H}.\\[-40pt] \end{align*} $$
$$ \begin{align*} \int_{D}|F|^{2}e^{-\varphi-\psi}\leq & \liminf_{k\rightarrow\infty}\int_{D}\mathbb{I}_{\overline{D_{j}}}|F_{j}(z)|^{2}e^{-\varphi}e^{-{\psi}} \\& \leq2\frac{\pi^{l}}{l!}\int_{0}^{e^{\frac{A}{2}}}e^{-\rho(t)}tdt\int_{H}|f|^{2}e^{-\varphi}dV_{H}.\\[-40pt] \end{align*} $$
If we take
 $\psi (z)=\alpha |z_{n}|^{2}$
for
$\psi (z)=\alpha |z_{n}|^{2}$
for
![]() $\alpha>0$
, then we have Theorem 1.7 in [Reference Guan and Zhou10] and Theorem 4.1 in [Reference Ohsawa17].
$\alpha>0$
, then we have Theorem 1.7 in [Reference Guan and Zhou10] and Theorem 4.1 in [Reference Ohsawa17].
Corollary 2.4. Let
![]() $\alpha>0$
be a constant, D be a pseudoconvex domain in
$\alpha>0$
be a constant, D be a pseudoconvex domain in
![]() $\mathbb {C}^{n}$
,
$\mathbb {C}^{n}$
,
![]() $\varphi $
be a plurisubharmonic function on D and
$\varphi $
be a plurisubharmonic function on D and
![]() $H=D\cap \{z_{n}=0\}$
. Then for any holomorphic function f on H satisfying
$H=D\cap \{z_{n}=0\}$
. Then for any holomorphic function f on H satisfying
 $$ \begin{align*} \int_{H}|f|^{2}e^{-\varphi}dV_{H}<\infty, \end{align*} $$
$$ \begin{align*} \int_{H}|f|^{2}e^{-\varphi}dV_{H}<\infty, \end{align*} $$
there exists a holomorphic function F on D satisfying
![]() $F=f$
on H and
$F=f$
on H and
 $$ \begin{align*} \int_{D}|F|^{2}e^{-\varphi-\alpha|z_{n}|^{2}}dV_{D}\leq \frac{\pi}{\alpha}\int_{H}|f|^{2}e^{-\varphi}dV_{H}. \end{align*} $$
$$ \begin{align*} \int_{D}|F|^{2}e^{-\varphi-\alpha|z_{n}|^{2}}dV_{D}\leq \frac{\pi}{\alpha}\int_{H}|f|^{2}e^{-\varphi}dV_{H}. \end{align*} $$
Let
![]() $\epsilon>0$
be an arbitrary constant, if we take
$\epsilon>0$
be an arbitrary constant, if we take
 $\psi =(1+\epsilon )\log (1+|z_{n}|^{2})$
, we have Corollary 3.14 in [Reference Guan and Zhou8] (see also Theorem 0.1 in [Reference Ohsawa17]).
$\psi =(1+\epsilon )\log (1+|z_{n}|^{2})$
, we have Corollary 3.14 in [Reference Guan and Zhou8] (see also Theorem 0.1 in [Reference Ohsawa17]).
Corollary 2.5. Let D be a pseudoconvex domain in
![]() $\mathbb {C}^{n}$
,
$\mathbb {C}^{n}$
,
![]() $\varphi $
be a plurisubharmonic function. For any plurisubharmonic function
$\varphi $
be a plurisubharmonic function. For any plurisubharmonic function
![]() $\varphi $
on D, for any
$\varphi $
on D, for any
![]() $\varepsilon>0$
and for any holomorphic function f on
$\varepsilon>0$
and for any holomorphic function f on
![]() $H=D\cap \{z_{n}=0\}$
, there exists a holomorphic function F on D such that
$H=D\cap \{z_{n}=0\}$
, there exists a holomorphic function F on D such that
![]() $F=f$
on H and
$F=f$
on H and
 $$ \begin{align*} \int_{D}\frac{|F|^{2}}{(1+|z_{n}|^{2})^{1+\varepsilon}}e^{-\varphi}\leq\frac{\pi}{\varepsilon}\int_{H}|f|^{2}e^{-\varphi}. \end{align*} $$
$$ \begin{align*} \int_{D}\frac{|F|^{2}}{(1+|z_{n}|^{2})^{1+\varepsilon}}e^{-\varphi}\leq\frac{\pi}{\varepsilon}\int_{H}|f|^{2}e^{-\varphi}. \end{align*} $$
Now we prove Corollary 1.9.
Proof. For every
![]() $R>0$
, denote by
$R>0$
, denote by
![]() $D(0,R)$
the disc centered at
$D(0,R)$
the disc centered at
![]() $0$
of radius R. By Proposition 2.3, we can write
$0$
of radius R. By Proposition 2.3, we can write
![]() $\psi $
on
$\psi $
on
![]() $D(0,R)$
as
$D(0,R)$
as
 $$ \begin{align*} \psi(z)=\frac{1}{2\pi}\int_{D(0,R)}\log |z-\zeta|i\partial\bar\partial\psi(\zeta)+h(z), \end{align*} $$
$$ \begin{align*} \psi(z)=\frac{1}{2\pi}\int_{D(0,R)}\log |z-\zeta|i\partial\bar\partial\psi(\zeta)+h(z), \end{align*} $$
where h is a harmonic function on
![]() $D(0,R)$
.
$D(0,R)$
.
Let
 $\psi _{1}(z)=\frac {1}{2\pi }\int _{D(0,R)}\log |z-\zeta |i\partial \bar \partial \psi (\zeta )$
, then
$\psi _{1}(z)=\frac {1}{2\pi }\int _{D(0,R)}\log |z-\zeta |i\partial \bar \partial \psi (\zeta )$
, then
![]() $\psi _{1}$
is a radial subharmonic function. By Theorem 1.7, we have a holomorphic function f such that
$\psi _{1}$
is a radial subharmonic function. By Theorem 1.7, we have a holomorphic function f such that
![]() $f(0)=1$
and
$f(0)=1$
and
 $$ \begin{align*} \int_{D(0,R)}|f|^{2} e^{-\varphi-\psi_{1}-h}\leqslant\bigg( 2\pi\int_{0}^{R} e^{-\psi_{1}(r)}r\mathrm{d}r \bigg)e^{-\varphi(0)-h(0)}=\Bigg( \int_{D(0,R)} e^{-\psi_{1}} \Bigg)e^{-\varphi(0)-h(0)}. \end{align*} $$
$$ \begin{align*} \int_{D(0,R)}|f|^{2} e^{-\varphi-\psi_{1}-h}\leqslant\bigg( 2\pi\int_{0}^{R} e^{-\psi_{1}(r)}r\mathrm{d}r \bigg)e^{-\varphi(0)-h(0)}=\Bigg( \int_{D(0,R)} e^{-\psi_{1}} \Bigg)e^{-\varphi(0)-h(0)}. \end{align*} $$
Because h is a harmonic function and
![]() $e^{x}$
is an increasing convex function,
$e^{x}$
is an increasing convex function,
![]() $e^{-h}$
is a subharmonic function, thus
$e^{-h}$
is a subharmonic function, thus
 $$ \begin{align*} e^{-h(0)}\int_{D(0,R)}e^{-\psi_{1}}\leqslant\int_{D(0,R)}e^{-\psi_{1}-h} \end{align*} $$
$$ \begin{align*} e^{-h(0)}\int_{D(0,R)}e^{-\psi_{1}}\leqslant\int_{D(0,R)}e^{-\psi_{1}-h} \end{align*} $$
and therefore we have
 $$ \begin{align} \int_{D(0,R)}|f|^{2} e^{-\varphi-\psi}\leqslant e^{-\varphi(0)}\int_{D(0,R)} e^{-\psi}\leqslant e^{-\varphi(0)}\int_{\mathbb{C}} e^{-\psi}. \end{align} $$
$$ \begin{align} \int_{D(0,R)}|f|^{2} e^{-\varphi-\psi}\leqslant e^{-\varphi(0)}\int_{D(0,R)} e^{-\psi}\leqslant e^{-\varphi(0)}\int_{\mathbb{C}} e^{-\psi}. \end{align} $$
Now for every
![]() $R>0$
, we have a holomorphic function
$R>0$
, we have a holomorphic function
![]() $F_{R}$
satisfying
$F_{R}$
satisfying
![]() $F_{R}(0)=1$
and (2.1). By Proposition 2.2 and a diagonal argument, we have a subsequence of
$F_{R}(0)=1$
and (2.1). By Proposition 2.2 and a diagonal argument, we have a subsequence of
![]() $\{F_{R}\}$
, still denoted by
$\{F_{R}\}$
, still denoted by
![]() $\{F_{R}\}$
, which is convergent to a holomorphic function F uniformly on any compact subset of
$\{F_{R}\}$
, which is convergent to a holomorphic function F uniformly on any compact subset of
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
By Fatou’s lemma, we have
 $$ \begin{align*}\int_{\mathbb{C}}|F|^{2} e^{-\varphi-\psi} &\leq \liminf_{R\rightarrow\infty}\int_{\mathbb{C}}\mathbb{I}_{\overline{D(0,R)}}|F_{R}|e^{-\varphi-\psi} \\ & \leq e^{-\varphi(0)}\int_{\mathbb{C}} e^{-\psi}.\\[-40pt] \end{align*} $$
$$ \begin{align*}\int_{\mathbb{C}}|F|^{2} e^{-\varphi-\psi} &\leq \liminf_{R\rightarrow\infty}\int_{\mathbb{C}}\mathbb{I}_{\overline{D(0,R)}}|F_{R}|e^{-\varphi-\psi} \\ & \leq e^{-\varphi(0)}\int_{\mathbb{C}} e^{-\psi}.\\[-40pt] \end{align*} $$
3 A counterexample of Ohsawa’s question
The following example shows that the above-mentioned question posed by Ohsawa does not hold if
![]() $i\partial \bar \partial \psi $
is not rotationally invariant.
$i\partial \bar \partial \psi $
is not rotationally invariant.
On
![]() $\mathbb {C}$
, take
$\mathbb {C}$
, take
![]() $\varphi =2(1-\alpha )\log |z+1|$
,
$\varphi =2(1-\alpha )\log |z+1|$
,
 $\psi =2\alpha \log |z+1|+h(|z+1|^{2})$
where
$\psi =2\alpha \log |z+1|+h(|z+1|^{2})$
where
![]() $0<\alpha <1 $
is a constant and
$0<\alpha <1 $
is a constant and
 $$ \begin{align*} h(x)= \Bigg\{ \begin{array}{ll} R_{1}+\frac{1}{4}, & x<R_{1} \\ (x-R_{1})^{2}+R_{1}+\frac{1}{4}, & R_{1}\leqslant x\leqslant R_{1}+\frac{1}{2} \\ x, & x>R_{1}+\frac{1}{2} \\ \end{array} \end{align*} $$
$$ \begin{align*} h(x)= \Bigg\{ \begin{array}{ll} R_{1}+\frac{1}{4}, & x<R_{1} \\ (x-R_{1})^{2}+R_{1}+\frac{1}{4}, & R_{1}\leqslant x\leqslant R_{1}+\frac{1}{2} \\ x, & x>R_{1}+\frac{1}{2} \\ \end{array} \end{align*} $$
where
![]() $R_{1}$
is a positive number that will be determined later.
$R_{1}$
is a positive number that will be determined later.
Note that h is an increasing convex function, so
 $h(|z+1|^{2})$
is subharmonic.
$h(|z+1|^{2})$
is subharmonic.
We see that
 $$ \begin{align*} \begin{aligned} \int_{\mathbb{C}}e^{-\psi}&= \int_{\{|z+1|^{2}<R_{1}+\frac{1}{2}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})}+\int_{\{|z+1|^{2}>R_{1}+\frac{1}{2}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})} \\ &=\int_{\{|z+1|^{2}<R_{1}+\frac{1}{2}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})}+\int_{\{|z+1|^{2}>R_{1}+\frac{1}{2}\}}\frac{1}{|z+1|^{2\alpha}}e^{-|z+1|^{2}} <\infty. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \int_{\mathbb{C}}e^{-\psi}&= \int_{\{|z+1|^{2}<R_{1}+\frac{1}{2}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})}+\int_{\{|z+1|^{2}>R_{1}+\frac{1}{2}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})} \\ &=\int_{\{|z+1|^{2}<R_{1}+\frac{1}{2}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})}+\int_{\{|z+1|^{2}>R_{1}+\frac{1}{2}\}}\frac{1}{|z+1|^{2\alpha}}e^{-|z+1|^{2}} <\infty. \end{aligned} \end{align*} $$
The square integrable holomorphic functions with respect to
 $\varphi +\psi =2\log |z+1|+h(|z+1|^{2})$
have an orthogonal basis
$\varphi +\psi =2\log |z+1|+h(|z+1|^{2})$
have an orthogonal basis
 $\{(z+1)^{k}\}$
,
$\{(z+1)^{k}\}$
,
![]() $k\geqslant 1$
. So the minimal
$k\geqslant 1$
. So the minimal
![]() $L^{2}$
-norm element such that
$L^{2}$
-norm element such that
![]() $f(0)=1$
is just
$f(0)=1$
is just
![]() $f(z)=z+1$
. We see
$f(z)=z+1$
. We see
 $$ \begin{align*}I:=\int_{\mathbb{C}} |z+1|^{2}\frac{1}{|z+1|^{2}}e^{-h(|z+1|^{2})} &= \int_{\mathbb{C} } e^{-h(|z+1|^{2})} \\ & = \int_{\{|z+1|^{2}<R_{1}\}}e^{-R_{1}-\frac{1}{4}} +\int_{\{|z+1|^{2}>R_{1}\}} e^{-h(|z+1|^{2})}\\ & = e^{-R_{1}-\frac{1}{4}} \pi R_{1}+\int_{\{|z+1|^{2}>R_{1}\}} e^{-h(|z+1|^{2})},\\ II:=e^{-\varphi(0)}\int_{\mathbb{C}}e^{-\psi} & =\int_{\mathbb{C}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})} \\ & =\int_{\{|z+1|^{2}<R_{1}\}}\frac{1}{|z+1|^{2\alpha}}e^{-R_{1}-\frac{1}{4}}\\ &\quad +\int_{\{|z+1|^{2}>R_{1}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})} \\ & =e^{-R_{1}-\frac{1}{4}}\frac{\pi}{1-\alpha}R_{1}^{1-\alpha}+\int_{\{|z+1|^{2}>R_{1}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})}. \end{align*} $$
$$ \begin{align*}I:=\int_{\mathbb{C}} |z+1|^{2}\frac{1}{|z+1|^{2}}e^{-h(|z+1|^{2})} &= \int_{\mathbb{C} } e^{-h(|z+1|^{2})} \\ & = \int_{\{|z+1|^{2}<R_{1}\}}e^{-R_{1}-\frac{1}{4}} +\int_{\{|z+1|^{2}>R_{1}\}} e^{-h(|z+1|^{2})}\\ & = e^{-R_{1}-\frac{1}{4}} \pi R_{1}+\int_{\{|z+1|^{2}>R_{1}\}} e^{-h(|z+1|^{2})},\\ II:=e^{-\varphi(0)}\int_{\mathbb{C}}e^{-\psi} & =\int_{\mathbb{C}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})} \\ & =\int_{\{|z+1|^{2}<R_{1}\}}\frac{1}{|z+1|^{2\alpha}}e^{-R_{1}-\frac{1}{4}}\\ &\quad +\int_{\{|z+1|^{2}>R_{1}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})} \\ & =e^{-R_{1}-\frac{1}{4}}\frac{\pi}{1-\alpha}R_{1}^{1-\alpha}+\int_{\{|z+1|^{2}>R_{1}\}}\frac{1}{|z+1|^{2\alpha}}e^{-h(|z+1|^{2})}. \end{align*} $$
We can choose
![]() $R_{1}$
large enough such that
$R_{1}$
large enough such that
 $$ \begin{align*} I-II=e^{-R_{1}-\frac{1}{4}}\pi\bigg(R_{1}-\frac{1}{1-\alpha}R_{1}^{1-\alpha}\bigg)+\int_{\{|z+1|^{2}>R_{1}\}}\left(1-\frac{1}{|z+1|^{2\alpha}}\right)e^{-h(|z+1|^{2})}>0. \end{align*} $$
$$ \begin{align*} I-II=e^{-R_{1}-\frac{1}{4}}\pi\bigg(R_{1}-\frac{1}{1-\alpha}R_{1}^{1-\alpha}\bigg)+\int_{\{|z+1|^{2}>R_{1}\}}\left(1-\frac{1}{|z+1|^{2\alpha}}\right)e^{-h(|z+1|^{2})}>0. \end{align*} $$
Thus the minimal
![]() $L^{2}$
extension with respect to
$L^{2}$
extension with respect to
![]() $\psi +\varphi $
satisfying
$\psi +\varphi $
satisfying
![]() $f(0)=1$
exceeds
$f(0)=1$
exceeds
 $e^{-\varphi (0)}\cdot \int _{\mathbb {C}}e^{-\psi }$
.
$e^{-\varphi (0)}\cdot \int _{\mathbb {C}}e^{-\psi }$
.
This example also shows that Theorem 1.7 fails in general without the assumptions posed in the theorem.