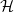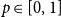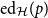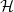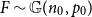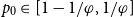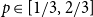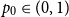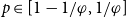1. Introduction
All graphs are finite and simple, i.e., without loops and multi-edges. A graph is non-empty if it has at least one edge. Denote
![]() $P_n$
to be the path graph on n vertices.
$P_n$
to be the path graph on n vertices.
For any
![]() $p\in [0,1]$
and any positive integer n, write
$p\in [0,1]$
and any positive integer n, write
![]() ${\mathbb{G}}(n,p)$
to be the distribution of graphs according to the Erdős–Rényi random graph model with edge probability p. That is,
${\mathbb{G}}(n,p)$
to be the distribution of graphs according to the Erdős–Rényi random graph model with edge probability p. That is,
![]() $G\sim{\mathbb{G}}(n,p)$
means that the event that
$G\sim{\mathbb{G}}(n,p)$
means that the event that
![]() $uv\in E(G)$
for
$uv\in E(G)$
for
![]() $uv\in \binom{\{1,\dots,n\}}{2}$
are independent and identically distributed (i.i.d.) with common probability p. We write a.a.s. to mean that a sequence of events holds with probability approaching 1 under some implied limit. The limit will be clear by the context. All logarithms are natural unless explicitly stated otherwise.
$uv\in \binom{\{1,\dots,n\}}{2}$
are independent and identically distributed (i.i.d.) with common probability p. We write a.a.s. to mean that a sequence of events holds with probability approaching 1 under some implied limit. The limit will be clear by the context. All logarithms are natural unless explicitly stated otherwise.
1.1. Edit distance results and forbidding a random graph
The edit distance measures the minimum number of ‘edits’ (that is, edge additions plus edge deletions) sufficient to turn one graph into another. This metric has been studied in contexts such as property testing and evolutionary biology (see [Reference Alon and Stav3,Reference Martin11]). Formally, for any two n-vertex graphs G,H on the same vertex set,
where
![]() $\triangle$
is the symmetric difference operation for sets.
$\triangle$
is the symmetric difference operation for sets.
A graph property
![]() ${\mathcal{H}}$
is hereditary if
${\mathcal{H}}$
is hereditary if
![]() ${\mathcal{H}}$
is closed under isomorphism and vertex deletion. For any family
${\mathcal{H}}$
is closed under isomorphism and vertex deletion. For any family
![]() ${\mathcal{F}}$
of graphs, we may write
${\mathcal{F}}$
of graphs, we may write
![]() ${\textrm{Forb}}({\mathcal{F}})$
for the hereditary property of graphs which do not contain an induced copy of F for any
${\textrm{Forb}}({\mathcal{F}})$
for the hereditary property of graphs which do not contain an induced copy of F for any
![]() $F\in{\mathcal{F}}$
. Any hereditary property is of the form
$F\in{\mathcal{F}}$
. Any hereditary property is of the form
![]() ${\textrm{Forb}}({\mathcal{F}})$
for some
${\textrm{Forb}}({\mathcal{F}})$
for some
![]() ${\mathcal{F}}$
. A hereditary property of the form
${\mathcal{F}}$
. A hereditary property of the form
![]() ${\textrm{Forb}}(\{F\})$
for a single graph F is called a principal hereditary property and we will write
${\textrm{Forb}}(\{F\})$
for a single graph F is called a principal hereditary property and we will write
![]() ${\textrm{Forb}}(F)$
for simplicity.
${\textrm{Forb}}(F)$
for simplicity.
A hereditary property
![]() ${\mathcal{H}}$
is non-trivial if, for every positive integer n, there exists a graph in
${\mathcal{H}}$
is non-trivial if, for every positive integer n, there exists a graph in
![]() ${\mathcal{H}}$
of order n. All hereditary properties in this paper are non-trivial. If
${\mathcal{H}}$
of order n. All hereditary properties in this paper are non-trivial. If
![]() ${\mathcal{H}}$
is a non-trivial hereditary property, then for all graphs G, we define
${\mathcal{H}}$
is a non-trivial hereditary property, then for all graphs G, we define
An early result that has motivated subsequent research is as follows:
Theorem 1
(Alon-Stav [Reference Alon and Stav2]). For a non-trivial hereditary property
![]() ${\mathcal{H}}$
, there exists a
${\mathcal{H}}$
, there exists a
![]() $p^* = p_{\mathcal{H}}^* \in [0,1]$
so that with
$p^* = p_{\mathcal{H}}^* \in [0,1]$
so that with
![]() $G\sim{\mathbb{G}}(n,p^*)$
,
$G\sim{\mathbb{G}}(n,p^*)$
,
In other words, random graphs of density
![]() $p^*$
asymptotically achieve the maximum distance to
$p^*$
asymptotically achieve the maximum distance to
![]() ${\mathcal{H}}$
. For any
${\mathcal{H}}$
. For any
![]() $p\in [0,1]$
and any property
$p\in [0,1]$
and any property
![]() ${\mathcal{H}}$
non-trivial and hereditary, let
${\mathcal{H}}$
non-trivial and hereditary, let
 \begin{align} {\textrm{ed}}_{\mathcal{H}}(p) \,:\!=\, \limsup_{n\to\infty} \max_{\substack{ |V(G)| = n, \\ e(G) = \lfloor p\binom{n}{2}\rfloor }} {\textrm{dist}}(G,{\mathcal{H}}) .\end{align}
\begin{align} {\textrm{ed}}_{\mathcal{H}}(p) \,:\!=\, \limsup_{n\to\infty} \max_{\substack{ |V(G)| = n, \\ e(G) = \lfloor p\binom{n}{2}\rfloor }} {\textrm{dist}}(G,{\mathcal{H}}) .\end{align}
We call
![]() ${\textrm{ed}}_{\mathcal{H}}$
the edit distance function of
${\textrm{ed}}_{\mathcal{H}}$
the edit distance function of
![]() ${\mathcal{H}}$
. Theorem 2 below demonstrates that the maximum distance
${\mathcal{H}}$
. Theorem 2 below demonstrates that the maximum distance
![]() ${\mathcal{H}}$
among all density-p graphs is achieved asymptotically by Erdős–Rényi random graphs of expected density p.
${\mathcal{H}}$
among all density-p graphs is achieved asymptotically by Erdős–Rényi random graphs of expected density p.
Theorem 2
(Balogh-Martin [Reference Balogh and Martin4]). Let
![]() ${\mathcal{H}}$
be a non-trivial hereditary property. For all
${\mathcal{H}}$
be a non-trivial hereditary property. For all
![]() $p\in [0,1]$
, if
$p\in [0,1]$
, if
![]() $G\sim{\mathbb{G}}(n,p)$
, then
$G\sim{\mathbb{G}}(n,p)$
, then
Moreover the function
![]() ${\textrm{ed}}_{\mathcal{H}}$
is continuous and concave down.
${\textrm{ed}}_{\mathcal{H}}$
is continuous and concave down.
Proposition 3 below has several short proofs and follows from Bollobás’ asymptotic result on the chromatic number of a random graph (see [Reference Bollobás5]), together with established techniques for computing edit distance functions (see [Reference Martin11]).
Proposition 3
(Alon-Stav [Reference Alon and Stav2]). Let
![]() $F\sim{\mathbb{G}}(n_0,1/2)$
and define
$F\sim{\mathbb{G}}(n_0,1/2)$
and define
![]() ${\mathcal{H}}\,:\!=\,{\textrm{Forb}}(F)$
. Then a.a.s. with
${\mathcal{H}}\,:\!=\,{\textrm{Forb}}(F)$
. Then a.a.s. with
![]() $n_0\to\infty$
,
$n_0\to\infty$
,
Our main result extends Proposition 3 so that we are able to determine the edit distance function asymptotically for all
![]() $p_0$
in a relatively large open interval around
$p_0$
in a relatively large open interval around
![]() $1/2$
. Let
$1/2$
. Let
![]() $\varphi = (1+\sqrt{5})/2$
be the golden ratio. Note that
$\varphi = (1+\sqrt{5})/2$
be the golden ratio. Note that
![]() $1-\varphi^{-1}\approx 0.381966$
and
$1-\varphi^{-1}\approx 0.381966$
and
![]() $\varphi^{-1}\approx 0.618034$
.
$\varphi^{-1}\approx 0.618034$
.
Theorem 4. Fix
![]() $p_0 \in (0,1)$
, let
$p_0 \in (0,1)$
, let
![]() $F\sim{\mathbb{G}}(n_0,p_0)$
, and define
$F\sim{\mathbb{G}}(n_0,p_0)$
, and define
![]() ${\mathcal{H}}\,:\!=\,{\textrm{Forb}}(F)$
. If
${\mathcal{H}}\,:\!=\,{\textrm{Forb}}(F)$
. If
![]() $p_0\in [1-\varphi^{-1},\varphi^{-1}]$
then a.a.s. with
$p_0\in [1-\varphi^{-1},\varphi^{-1}]$
then a.a.s. with
![]() $n_0\rightarrow\infty$
,
$n_0\rightarrow\infty$
,
 \begin{align} {\textrm{ed}}_{\mathcal{H}}(p) = (1+o(1))\,\dfrac{2\log n_0}{n_0}\cdot\min\left\{ \dfrac{p}{-\log(1-p_0)}, \dfrac{1-p}{-\log p_0} \right\}, \end{align}
\begin{align} {\textrm{ed}}_{\mathcal{H}}(p) = (1+o(1))\,\dfrac{2\log n_0}{n_0}\cdot\min\left\{ \dfrac{p}{-\log(1-p_0)}, \dfrac{1-p}{-\log p_0} \right\}, \end{align}
holds for all
![]() $p\in [0,1]$
. If
$p\in [0,1]$
. If
![]() $p_0\in [0,1-\varphi^{-1})$
, then a.a.s. (2) holds for all
$p_0\in [0,1-\varphi^{-1})$
, then a.a.s. (2) holds for all
![]() $p\in [1/3,1]$
. If
$p\in [1/3,1]$
. If
![]() $p_0\in (\varphi^{-1},1]$
, then a.a.s. (2) holds for all
$p_0\in (\varphi^{-1},1]$
, then a.a.s. (2) holds for all
![]() $p\in [0,2/3]$
.
$p\in [0,2/3]$
.
In fact, the o(1) error term depends only on
![]() $p_0$
and
$p_0$
and
![]() $n_0$
, and holds uniformly for all p in each of the respective intervals.
$n_0$
, and holds uniformly for all p in each of the respective intervals.
The first author conjectured (see [Reference Martin11]) that for all
![]() $p_0\in [0,1]$
, (2) holds a.a.s. for all
$p_0\in [0,1]$
, (2) holds a.a.s. for all
![]() $p\in [0,1]$
. Theorem 4 proves this for a range of
$p\in [0,1]$
. Theorem 4 proves this for a range of
![]() $p_0$
of size
$p_0$
of size
![]() $\approx 0.236068$
.
$\approx 0.236068$
.
1.2. Equivalent parameters
The edit distance function is also interesting because of its connection to other parameters involving random graphs. For
![]() ${\mathcal{H}}$
any non-trivial hereditary property and any
${\mathcal{H}}$
any non-trivial hereditary property and any
![]() $p\in (0,1)$
, the speed of
$p\in (0,1)$
, the speed of
![]() ${\mathcal{H}}$
is
${\mathcal{H}}$
is
Indeed, this limit does exist and a proof of that fact appears in [Reference Alekseev1] and in [Reference Bollobás and Thomason6]. See also the survey [Reference Martin11].
The following observation was made by Thomason but it can be shown to follow from a prior result due to Bollobás and Thomason [Reference Bollobás and Thomason6].
Theorem 5
(Thomason [13]). Let
![]() ${\mathcal{H}}$
be a non-trivial hereditary property. Then for all
${\mathcal{H}}$
be a non-trivial hereditary property. Then for all
![]() $p\in (0,1)$
,
$p\in (0,1)$
,
Note that the function
![]() $f\,:\,(0,1)\to(0,1)$
defined by
$f\,:\,(0,1)\to(0,1)$
defined by
on
![]() $x\in (0,1)$
is invertible. Since
$x\in (0,1)$
is invertible. Since
![]() ${\textrm{ed}}_{\mathcal{H}}$
is continuous,
${\textrm{ed}}_{\mathcal{H}}$
is continuous,
![]() $c_{\mathcal{H}}$
can be computed from
$c_{\mathcal{H}}$
can be computed from
![]() ${\textrm{ed}}_{\mathcal{H}}$
and vice versa. As a result, combining Theorem 5 with Theorem 4 yields a result on the speed function of hereditary properties defined by random graphs.
${\textrm{ed}}_{\mathcal{H}}$
and vice versa. As a result, combining Theorem 5 with Theorem 4 yields a result on the speed function of hereditary properties defined by random graphs.
Corollary 6. Fix
![]() $p_0 \in (0,1)$
, let
$p_0 \in (0,1)$
, let
![]() $F\sim{\mathbb{G}}(n_0,p_0)$
, and define
$F\sim{\mathbb{G}}(n_0,p_0)$
, and define
![]() ${\mathcal{H}}\,:\!=\,{\textrm{Forb}}(F)$
. If
${\mathcal{H}}\,:\!=\,{\textrm{Forb}}(F)$
. If
![]() $p_0\in [1-\varphi^{-1},\varphi^{-1}]$
then a.a.s. with
$p_0\in [1-\varphi^{-1},\varphi^{-1}]$
then a.a.s. with
![]() $n_0\to\infty$
,
$n_0\to\infty$
,
 \begin{align} c_{\mathcal{H}}(p) = (1+o(1))\,\dfrac{2\log_2 n_0}{n_0}\cdot\min\left\{ \dfrac{\log (1-p)}{\log(1-p_0)}, \dfrac{\log p}{\log p_0}, \right\} \end{align}
\begin{align} c_{\mathcal{H}}(p) = (1+o(1))\,\dfrac{2\log_2 n_0}{n_0}\cdot\min\left\{ \dfrac{\log (1-p)}{\log(1-p_0)}, \dfrac{\log p}{\log p_0}, \right\} \end{align}
holds for all
![]() $p\in [0,1]$
. If
$p\in [0,1]$
. If
![]() $p_0\in [0,1-\varphi^{-1})$
, then a.a.s. (3) holds for all
$p_0\in [0,1-\varphi^{-1})$
, then a.a.s. (3) holds for all
![]() $p\in [1-\varphi^{-1},1]$
. If
$p\in [1-\varphi^{-1},1]$
. If
![]() $p_0\in (\varphi^{-1},1]$
, then a.a.s. (3) holds for all
$p_0\in (\varphi^{-1},1]$
, then a.a.s. (3) holds for all
![]() $p\in [0,\varphi^{-1}]$
.
$p\in [0,\varphi^{-1}]$
.
For any hereditary property
![]() ${\mathcal{H}}$
and any graph G, let
${\mathcal{H}}$
and any graph G, let
![]() $\chi_{\mathcal{H}}(G)$
be the
$\chi_{\mathcal{H}}(G)$
be the
![]() ${\mathcal{H}}$
-chromatic number of G. This is the minimum non-negative integer k for which there exists a partition
${\mathcal{H}}$
-chromatic number of G. This is the minimum non-negative integer k for which there exists a partition ![]() such that
such that
![]() $G[V_i]$
satisfies
$G[V_i]$
satisfies
![]() ${\mathcal{H}}$
for all
${\mathcal{H}}$
for all
![]() $i\in\{1,\ldots,k\}$
. If
$i\in\{1,\ldots,k\}$
. If
![]() ${\mathcal{H}}$
is the property of being an empty graph, then
${\mathcal{H}}$
is the property of being an empty graph, then
![]() $\chi_{\mathcal{H}}(G)$
is the chromatic number of G.
$\chi_{\mathcal{H}}(G)$
is the chromatic number of G.
Bollobás and Thomason established Theorem 7 for the
![]() ${\mathcal{H}}$
-chromatic number of a random graph. (In their paper, they had a different definition of ‘trivial’. Rather than a hereditary property being trivial if it is finite, they say that a hereditary property is trivial if it is not the set of all graphs.) For convenience, we state this result in our language.
${\mathcal{H}}$
-chromatic number of a random graph. (In their paper, they had a different definition of ‘trivial’. Rather than a hereditary property being trivial if it is finite, they say that a hereditary property is trivial if it is not the set of all graphs.) For convenience, we state this result in our language.
Theorem 7
(Bollobás-Thomason [Reference Bollobás and Thomason6]). Let
![]() $p\in (0,1)$
and let
$p\in (0,1)$
and let
![]() ${\mathcal{H}}$
be a non-trivial hereditary property where
${\mathcal{H}}$
be a non-trivial hereditary property where
![]() ${\mathcal{H}}$
is not the property satisfied by all graphs. Then a.a.s. with
${\mathcal{H}}$
is not the property satisfied by all graphs. Then a.a.s. with
![]() $G\sim{\mathbb{G}}(n,p)$
,
$G\sim{\mathbb{G}}(n,p)$
,
 \begin{align} \chi_{{\mathcal{H}}}(G) = (1+o(1))\, c_{\mathcal{H}}(p)\, \dfrac{n}{2\log_2n}. \end{align}
\begin{align} \chi_{{\mathcal{H}}}(G) = (1+o(1))\, c_{\mathcal{H}}(p)\, \dfrac{n}{2\log_2n}. \end{align}
Bollobás’ classic asymptotic result [Reference Bollobás5] on the chromatic number of the random graph can be derived from Theorem 7 by observing that if
![]() ${\mathcal{H}}_{{\textrm{em}}}$
is the property of being an empty graph, then
${\mathcal{H}}_{{\textrm{em}}}$
is the property of being an empty graph, then
![]() $c_{{\mathcal{H}}_{{\textrm{em}}}}(p) = -\log_2 (1-p)$
and so
$c_{{\mathcal{H}}_{{\textrm{em}}}}(p) = -\log_2 (1-p)$
and so
![]() $\chi_{{\mathcal{H}}_{{\textrm{em}}}}(G)=(1+o(1))\, \frac{n}{2 \log_{1/(1-p)} n}$
a.a.s.
$\chi_{{\mathcal{H}}_{{\textrm{em}}}}(G)=(1+o(1))\, \frac{n}{2 \log_{1/(1-p)} n}$
a.a.s.
However, the fact that
![]() $c_{{\mathcal{H}}_{{\textrm{em}}}}(p)=-\log_2 (1-p)$
can itself be derived from Theorem 5 and the entirely trivial observation that
$c_{{\mathcal{H}}_{{\textrm{em}}}}(p)=-\log_2 (1-p)$
can itself be derived from Theorem 5 and the entirely trivial observation that
![]() ${\textrm{ed}}_{{\mathcal{H}}_{{\textrm{em}}}}(p)=p$
. In general,
${\textrm{ed}}_{{\mathcal{H}}_{{\textrm{em}}}}(p)=p$
. In general,
![]() $\chi_{{\mathcal{H}}}$
has a close relationship with both
$\chi_{{\mathcal{H}}}$
has a close relationship with both
![]() $c_{{\mathcal{H}}}$
and
$c_{{\mathcal{H}}}$
and
![]() ${\textrm{ed}}_{{\mathcal{H}}}$
.
${\textrm{ed}}_{{\mathcal{H}}}$
.
The rest of the paper is organized as follows: In Section 2, we discuss coloured regularity graphs (CRGs) and prove some basic results that have the potential to apply to a wide variety of edit distance results beyond the scope of this paper. In Section 3, we give the proof of Theorem 4. Section 4 includes a proof of the fact that for all
![]() $p\in[1-\varphi^{-1},\varphi^{-1}]$
,
$p\in[1-\varphi^{-1},\varphi^{-1}]$
,
![]() ${\textrm{ed}}_{{\mathcal{H}}}(p)$
can be computed by a set CRGs whose order is bounded by a constant depending only on
${\textrm{ed}}_{{\mathcal{H}}}(p)$
can be computed by a set CRGs whose order is bounded by a constant depending only on
![]() ${\mathcal{H}}$
. Section 4 also includes a discussion of the role paths play in CRGs. In Section 5, we discuss open questions and potential future work.
${\mathcal{H}}$
. Section 4 also includes a discussion of the role paths play in CRGs. In Section 5, we discuss open questions and potential future work.
Of special note is Theorem 23 in Section 2, in which it is established that the set of p-core CRGs is restricted for
![]() $p\in[1-\varphi^{-1},\varphi^{-1}]$
. In particular, the non-grey edges of such CRGs must form vertex-disjoint cliques.
$p\in[1-\varphi^{-1},\varphi^{-1}]$
. In particular, the non-grey edges of such CRGs must form vertex-disjoint cliques.
2. Coloured regularity graphs
In this section, we address coloured regularity graphs. In Section 2.1, we address background and basic facts about coloured regularity graphs. Section 2.2 discusses the new notion of p-prohibited CRGs. Lemma 20 and Theorem 23 are important new results on p-prohibited CRGs. They are proven in Sections 2.3 and 2.4, respectively.
2.1. Background on CRGs
The key element to studying the edit distance problem is the coloured regularity graph, which was defined by Alon and Stav [Reference Alon and Stav2] but appeared as types in the prior literature by Bollobás and Thomason (see [Reference Bollobás and Thomason6]).
Definition 8. A coloured regularity graph K is a complete graph, together with a partition ![]() of the vertex set into white and black vertices, and a partition
of the vertex set into white and black vertices, and a partition ![]() of the edge set into white, black, and grey edges.
of the edge set into white, black, and grey edges.
A CRG K
′ is called a sub-CRG of CRG K (denoted
![]() $K'\subseteq K$
) if K
′ is obtained by deleting some vertices from K and all incident edges.
$K'\subseteq K$
) if K
′ is obtained by deleting some vertices from K and all incident edges.
CRGs approximate large graphs and we want to know whether a forbidden graph F is in a graph approximated by a given CRG. We express this in terms of embeddings of graphs into CRGs.
Definition 9. A graph F embeds into CRG K (written
![]() $F\mapsto K$
) if there exists a function
$F\mapsto K$
) if there exists a function
![]() $\phi\,:\,V(F)\to V(K)$
such that:
$\phi\,:\,V(F)\to V(K)$
such that:
-
If
 $uv\in E(F)$
, then either
$uv\in E(F)$
, then either
 $\phi(u)=\phi(v)\in{\textrm{VB}}(K)$
, or
$\phi(u)=\phi(v)\in{\textrm{VB}}(K)$
, or
 $\phi(u)\phi(v)\in{{\textrm{EB}}}(K)\cup {{\textrm{EG}}}(K)$
.
$\phi(u)\phi(v)\in{{\textrm{EB}}}(K)\cup {{\textrm{EG}}}(K)$
. -
If
 $uv\in E(F^c)$
, then either
$uv\in E(F^c)$
, then either
 $\phi(u)=\phi(v)\in{\textrm{VW}}(K)$
, or
$\phi(u)=\phi(v)\in{\textrm{VW}}(K)$
, or
 $\phi(u)\phi(v)\in{\textrm{EW}}(K)\cup {{\textrm{EG}}}(K)$
.
$\phi(u)\phi(v)\in{\textrm{EW}}(K)\cup {{\textrm{EG}}}(K)$
.
For any CRG K, we will treat the elements of
![]() ${\mathbb{R}}^{V(K)}$
both as functions on V(K) and as vectors indexed by the vertices of K. For any two such
${\mathbb{R}}^{V(K)}$
both as functions on V(K) and as vectors indexed by the vertices of K. For any two such
![]() ${\bf x},{\bf y}\in {\mathbb{R}}^{V(K)}$
, we define
${\bf x},{\bf y}\in {\mathbb{R}}^{V(K)}$
, we define
![]() $\langle {\bf x},{\bf y}\rangle \,:\!=\, \sum_{u\in V(K)}{\bf x}(u){\bf y}(u)$
. We also let
$\langle {\bf x},{\bf y}\rangle \,:\!=\, \sum_{u\in V(K)}{\bf x}(u){\bf y}(u)$
. We also let
![]() $M_K(p)\in{\mathbb{R}}^{V(K)\times V(K)}$
be the matrix whose uv-th entry is
$M_K(p)\in{\mathbb{R}}^{V(K)\times V(K)}$
be the matrix whose uv-th entry is
 \begin{equation} m_{uv} \,:\!=\, \left\{\begin{array}{rl} p, &\mbox{$u\neq v$ and $uv\in {\textrm{EW}}(K)$, or $u=v$ and $u\in {\textrm{VW}}(K)$;} \\ 1-p, &\mbox{$u\neq v$ and $uv\in {{\textrm{EB}}}(K)$, or $u=v$ and $u\in {\textrm{VB}}(K)$;} \\ 0, &\mbox{$u\neq v$ and $uv\in{{\textrm{EG}}}(K)$.} \end{array} \right.\end{equation}
\begin{equation} m_{uv} \,:\!=\, \left\{\begin{array}{rl} p, &\mbox{$u\neq v$ and $uv\in {\textrm{EW}}(K)$, or $u=v$ and $u\in {\textrm{VW}}(K)$;} \\ 1-p, &\mbox{$u\neq v$ and $uv\in {{\textrm{EB}}}(K)$, or $u=v$ and $u\in {\textrm{VB}}(K)$;} \\ 0, &\mbox{$u\neq v$ and $uv\in{{\textrm{EG}}}(K)$.} \end{array} \right.\end{equation}
The all-ones vector
![]() ${\bf 1}\in{\mathbb{R}}^{V(K)}$
is defined by
${\bf 1}\in{\mathbb{R}}^{V(K)}$
is defined by
![]() ${\bf 1}(u) = 1$
for all
${\bf 1}(u) = 1$
for all
![]() $u\in V(K)$
and the all-zeroes vector is just
$u\in V(K)$
and the all-zeroes vector is just
![]() ${\bf 0} = 0\cdot {\bf 1}$
. Furthermore, we let
${\bf 0} = 0\cdot {\bf 1}$
. Furthermore, we let
![]() $\Delta_K$
be the standard simplex associated to K which consists of all
$\Delta_K$
be the standard simplex associated to K which consists of all
![]() ${\bf x}\in{\mathbb{R}}^{V(K)}$
so that
${\bf x}\in{\mathbb{R}}^{V(K)}$
so that
![]() ${\bf x}\geq{\bf 0}$
in the component-wise sense and
${\bf x}\geq{\bf 0}$
in the component-wise sense and
![]() $\langle {\bf x}, {\bf 1}\rangle = 1$
. The elements of
$\langle {\bf x}, {\bf 1}\rangle = 1$
. The elements of
![]() $\Delta_K$
will be called weight vectors.
$\Delta_K$
will be called weight vectors.
Now define
A weight vector
![]() ${\bf x}\in\Delta_K$
is said to be optimal for K if
${\bf x}\in\Delta_K$
is said to be optimal for K if
![]() $g_K(p,{\bf x}) = g_K(p)$
. For any
$g_K(p,{\bf x}) = g_K(p)$
. For any
![]() $p\in [0,1]$
, a CRG K is said to be p-core if for any optimal weight vector x,
$p\in [0,1]$
, a CRG K is said to be p-core if for any optimal weight vector x,
![]() ${\bf x}(u) > 0$
for all
${\bf x}(u) > 0$
for all
![]() $u\in V(K)$
. It follows that for K a p-core CRG, there exists a unique optimal weight vector.
$u\in V(K)$
. It follows that for K a p-core CRG, there exists a unique optimal weight vector.
For any hereditary property
![]() ${\mathcal{H}} = {\textrm{Forb}}({\mathcal{F}})$
we define the following family of CRGs:
${\mathcal{H}} = {\textrm{Forb}}({\mathcal{F}})$
we define the following family of CRGs:
Theorem 10 is the main technique for computing
![]() ${\textrm{ed}}_{\mathcal{H}}(p)$
, hence understanding the set
${\textrm{ed}}_{\mathcal{H}}(p)$
, hence understanding the set
![]() ${\mathcal{K}}_{\mathcal{H}}$
is crucial to understanding
${\mathcal{K}}_{\mathcal{H}}$
is crucial to understanding
![]() ${\textrm{ed}}_{\mathcal{H}}(p)$
. The first equality was given by Balogh and Martin [Reference Balogh and Martin4] and the second by Marchant and Thomason [Reference Marchant and Thomason10].
${\textrm{ed}}_{\mathcal{H}}(p)$
. The first equality was given by Balogh and Martin [Reference Balogh and Martin4] and the second by Marchant and Thomason [Reference Marchant and Thomason10].
Theorem 10. Let
![]() ${\mathcal{H}}$
be a non-trivial hereditary property. Then for all
${\mathcal{H}}$
be a non-trivial hereditary property. Then for all
![]() $p\in [0,1]$
,
$p\in [0,1]$
,
It follows by definition that the minimum in Theorem 10 is obtained by a p-core CRG and as Theorem 11 shows, p-core CRGs have a well-defined structure.
Theorem 11
(Marchant-Thomason [Reference Marchant and Thomason10]). Let
![]() $p\in [0,1]$
and suppose K is a p-core CRG.
$p\in [0,1]$
and suppose K is a p-core CRG.
-
(a) If
 $p\in [0,1/2]$
, then
$p\in [0,1/2]$
, then
 ${{\textrm{EB}}}(K) = \emptyset$
and for all
${{\textrm{EB}}}(K) = \emptyset$
and for all
 $uv\in {\textrm{EW}}(K)$
,
$uv\in {\textrm{EW}}(K)$
,
 $u,v\in{\textrm{VB}}(K)$
.
$u,v\in{\textrm{VB}}(K)$
. -
(b) If
 $p\in [1/2,1]$
, then
$p\in [1/2,1]$
, then
 ${\textrm{EW}}(K) = \emptyset$
and for all
${\textrm{EW}}(K) = \emptyset$
and for all
 $uv\in {{\textrm{EB}}}(K)$
,
$uv\in {{\textrm{EB}}}(K)$
,
 $u,v\in {\textrm{VW}}(K)$
.
$u,v\in {\textrm{VW}}(K)$
.
To summarize, if
![]() $p\leq 1/2$
, then a p-core CRG has no black edges and all white edges must be between black vertices. If
$p\leq 1/2$
, then a p-core CRG has no black edges and all white edges must be between black vertices. If
![]() $p\geq 1/2$
, then a p-core CRG has no white edges and all black edges must be between white vertices. As a result, if
$p\geq 1/2$
, then a p-core CRG has no white edges and all black edges must be between white vertices. As a result, if
![]() $p=1/2$
, p-core CRGs have neither black nor white edges.
$p=1/2$
, p-core CRGs have neither black nor white edges.
Remark 12. A CRG K is
![]() $1/2$
-core if and only if all edges of K are grey.
$1/2$
-core if and only if all edges of K are grey.
2.2. p-prohibited CRGs
In this paper, we introduce the notion of a prohibited CRG.
Definition 13. For any
![]() $p\in [0,1]$
and any CRG J, we say that J is p-prohibited if for any p-core CRG K, J is not a sub-CRG of K.
$p\in [0,1]$
and any CRG J, we say that J is p-prohibited if for any p-core CRG K, J is not a sub-CRG of K.
For example, Theorem 11 shows that if
![]() $p\in [0,1/2)$
, then the only 2-vertex CRGs that are not p-prohibited are those with a grey edge or the CRG with two black vertices and a white edge. See Figure 1.
$p\in [0,1/2)$
, then the only 2-vertex CRGs that are not p-prohibited are those with a grey edge or the CRG with two black vertices and a white edge. See Figure 1.

Figure 1. All two-vertex CRGs. The five on the left are p-prohibited for all
![]() $p\in [0,1/2]$
. The four on the right are p-core for all
$p\in [0,1/2]$
. The four on the right are p-core for all
![]() $p\in [0,1/2)$
.
$p\in [0,1/2)$
.
Remark 14. There is an abundance of CRGs which are neither p-core nor p-prohibited. For example, consider the CRGs K and K
′ defined as follows. Let K consist of three black vertices with two white edges and one grey edge. For all
![]() $p\in [0,1]$
, K is not p-core. Now let K
′ be the CRG on 4 black vertices whose white edges induce a
$p\in [0,1]$
, K is not p-core. Now let K
′ be the CRG on 4 black vertices whose white edges induce a
![]() $P_4$
and all other edges are grey. Clearly K
′ contains K. It is an exercise to see that K
′ is p-core for all
$P_4$
and all other edges are grey. Clearly K
′ contains K. It is an exercise to see that K
′ is p-core for all
![]() $p\in [0,1-\varphi^{-1})$
, so K is not p-prohibited on this interval.
$p\in [0,1-\varphi^{-1})$
, so K is not p-prohibited on this interval.
We also want to introduce the notion of the complement of a CRG.
Definition 15. If K is a CRG, then the complement of K is the unique CRG
![]() $\overline{K}$
, such that
$\overline{K}$
, such that
-
 ${\textrm{VW}}(\overline{K})={\textrm{VB}}(K)$
,
${\textrm{VW}}(\overline{K})={\textrm{VB}}(K)$
,
 ${\textrm{VB}}(\overline{K})={\textrm{VW}}(K)$
,
${\textrm{VB}}(\overline{K})={\textrm{VW}}(K)$
, -
 ${\textrm{EW}}(\overline{K})={{\textrm{EB}}}(K)$
,
${\textrm{EW}}(\overline{K})={{\textrm{EB}}}(K)$
,
 ${{\textrm{EB}}}(\overline{K})={\textrm{EW}}(K)$
, and
${{\textrm{EB}}}(\overline{K})={\textrm{EW}}(K)$
, and
 ${{\textrm{EG}}}(\overline{K})={{\textrm{EG}}}(K)$
.
${{\textrm{EG}}}(\overline{K})={{\textrm{EG}}}(K)$
.
For a graph G, the notation is
![]() $G^c$
is used to denote the graph complement, so as to avoid confusion. There is symmetry in the edit distance function about
$G^c$
is used to denote the graph complement, so as to avoid confusion. There is symmetry in the edit distance function about
![]() $p=1/2$
with respect to complements.
$p=1/2$
with respect to complements.
Proposition 16. If
![]() $p\in[0,1]$
and K is a CRG, then
$p\in[0,1]$
and K is a CRG, then
![]() $g_K(p)=g_{\overline{K}}(1-p)$
.
$g_K(p)=g_{\overline{K}}(1-p)$
.
Proof. This follows from the equality of the matrices
![]() $M_K(p)=M_{\overline{K}}(1-p)$
:
$M_K(p)=M_{\overline{K}}(1-p)$
:
There is also symmetry in the edit distance function about
![]() $p=1/2$
when it comes to p-prohibition.
$p=1/2$
when it comes to p-prohibition.
Proposition 17. For all
![]() $p\in[0,1]$
, a CRG J is p-prohibited if and only if
$p\in[0,1]$
, a CRG J is p-prohibited if and only if
![]() $\overline{J}$
is
$\overline{J}$
is
![]() $(1-p)$
-prohibited.
$(1-p)$
-prohibited.
Proof. Suppose J is p-prohibited but
![]() $\overline{J}$
is not
$\overline{J}$
is not
![]() $(1-p)$
-prohibited. Then, there is a
$(1-p)$
-prohibited. Then, there is a
![]() $(1-p)$
-core CRG
$(1-p)$
-core CRG
![]() $\overline{K}$
that contains
$\overline{K}$
that contains
![]() $\overline{J}$
as a sub-CRG. If K is not p-core, then there is a
$\overline{J}$
as a sub-CRG. If K is not p-core, then there is a
![]() $K'\subseteq K$
such that
$K'\subseteq K$
such that
![]() $g_{K'}(p)=g_K(p)$
, but Proposition 16 gives that
$g_{K'}(p)=g_K(p)$
, but Proposition 16 gives that
![]() $g_{\overline{K'}}(1-p)=g_{\overline{K}}(1-p)$
, a contradiction to
$g_{\overline{K'}}(1-p)=g_{\overline{K}}(1-p)$
, a contradiction to
![]() $\overline{K}$
being
$\overline{K}$
being
![]() $(1-p)$
-core.
$(1-p)$
-core.
Next, we introduce terminology which is useful in describing the structure of p-core and p-prohibited CRGs.
Definition 18. Let K be a CRG.
-
The underlying graph of K is the graph
 $G = (V(K), {{\textrm{EB}}}(K) \cup {\textrm{EW}}(K))$
.
$G = (V(K), {{\textrm{EB}}}(K) \cup {\textrm{EW}}(K))$
. -
A component of K is a component of the underlying graph of K.
-
A disjoint union of vertex-disjoint CRGs J,K, denoted
 $J\oplus K$
, is a CRG with vertex set
$J\oplus K$
, is a CRG with vertex set
 $V_J\oplus V_K$
, where the sub-CRG induced on
$V_J\oplus V_K$
, where the sub-CRG induced on
 $V_J$
is isomorphic to J, the sub-CRG induced on
$V_J$
is isomorphic to J, the sub-CRG induced on
 $V_K$
is isomorphic to K, and every edge incident to a vertex in each of
$V_K$
is isomorphic to K, and every edge incident to a vertex in each of
 $V_J$
and in
$V_J$
and in
 $V_K$
has colour grey. The disjoint union of k copies of K is
$V_K$
has colour grey. The disjoint union of k copies of K is
 $k\cdot K$
.
$k\cdot K$
. -
Let G be a non-empty graph. The CRG, K, associated to G is defined as follows: If
 $p\in [0,1/2]$
, then
$p\in [0,1/2]$
, then
 ${\textrm{VW}}(K)={{\textrm{EB}}}(K)=\emptyset$
,
${\textrm{VW}}(K)={{\textrm{EB}}}(K)=\emptyset$
,
 ${\textrm{VB}}(K)=V(G)$
,
${\textrm{VB}}(K)=V(G)$
,
 ${\textrm{EW}}(K)=E(G)$
, and
${\textrm{EW}}(K)=E(G)$
, and
 ${{\textrm{EG}}}(K)=E(\overline{G})$
. If
${{\textrm{EG}}}(K)=E(\overline{G})$
. If
 $p\in (1/2,1]$
, then
$p\in (1/2,1]$
, then
 ${\textrm{VB}}(K)={\textrm{EW}}(K)=\emptyset$
,
${\textrm{VB}}(K)={\textrm{EW}}(K)=\emptyset$
,
 ${\textrm{VW}}(K)=V(G)$
,
${\textrm{VW}}(K)=V(G)$
,
 ${{\textrm{EB}}}(K)=E(G)$
, and
${{\textrm{EB}}}(K)=E(G)$
, and
 ${{\textrm{EG}}}(K)=E(\overline{G})$
.
${{\textrm{EG}}}(K)=E(\overline{G})$
.
We associate CRGs to graphs for the purposes of discussing p-core CRGs. See Figure 2 for an example. Since
![]() $1/2$
-core CRGs are precisely those which have only grey edges, the definition of the CRG associated to a graph for
$1/2$
-core CRGs are precisely those which have only grey edges, the definition of the CRG associated to a graph for
![]() $p=1/2$
is made purely out of convenience.
$p=1/2$
is made purely out of convenience.

Figure 2. A CRG with five components. One component is the CRG associated to the cycle
![]() $C_4$
for
$C_4$
for
![]() $p\in [0,1/2)$
. The edges satisfy the necessary conditions from Theorem 11 for a p-core CRG with
$p\in [0,1/2)$
. The edges satisfy the necessary conditions from Theorem 11 for a p-core CRG with
![]() $p\in [0,1/2)$
.
$p\in [0,1/2)$
.
In order to apply Lemma 20 below, we need the minimum adjacency eigenvalue to be at most
![]() $-1$
. This occurs for all non-empty graphs. See [Reference Brouwer and Haemers7] for a more detailed discussion about eigenvalues associated to graphs.
$-1$
. This occurs for all non-empty graphs. See [Reference Brouwer and Haemers7] for a more detailed discussion about eigenvalues associated to graphs.
Proposition 19. Every non-empty graph that is not disjoint cliques has minimum adjacency eigenvalue at most
![]() $-\sqrt{2}$
. If a non-empty graph consists of disjoint cliques, its minimum adjacency eigenvalue is
$-\sqrt{2}$
. If a non-empty graph consists of disjoint cliques, its minimum adjacency eigenvalue is
![]() $-1$
. An empty graph has all adjacency eigenvalues zero.
$-1$
. An empty graph has all adjacency eigenvalues zero.
Lemma 20. Let G be a non-empty graph and let
![]() $\lambda\leq-1$
be the minimum eigenvalue of the adjacency matrix of G. The CRG associated to G is p-prohibited for all
$\lambda\leq-1$
be the minimum eigenvalue of the adjacency matrix of G. The CRG associated to G is p-prohibited for all
In Section 2.3, we prove Lemma 20. First, we need some essential terms.
Definition 21. For any positive integer t, the t-dalmatian CRG is the CRG, denoted
![]() $D_t$
, consisting of t black vertices and all edges white. The
$D_t$
, consisting of t black vertices and all edges white. The
![]() $\infty$
-dalmatian CRG is the CRG, denoted
$\infty$
-dalmatian CRG is the CRG, denoted
![]() $D_\infty$
, which is a single white vertex. The set of CRGs denoted by
$D_\infty$
, which is a single white vertex. The set of CRGs denoted by
![]() ${\mathcal{D}}_p$
is as follows:
${\mathcal{D}}_p$
is as follows:
-
If
 $p\in [0,1/2)$
, then
$p\in [0,1/2)$
, then
 ${\mathcal{D}}_p$
is the set of all CRGs whose components are dalmatian CRGs.
${\mathcal{D}}_p$
is the set of all CRGs whose components are dalmatian CRGs. -
If
 $p\in (1/2,1]$
, then
$p\in (1/2,1]$
, then
 ${\mathcal{D}}_p$
is the set of all CRGs whose components are complements of dalmatian CRGs.
${\mathcal{D}}_p$
is the set of all CRGs whose components are complements of dalmatian CRGs. -
If
 $p=1/2$
, then
$p=1/2$
, then
 ${\mathcal{D}}_{1/2}$
is the set of all CRGs whose components are single vertices.
${\mathcal{D}}_{1/2}$
is the set of all CRGs whose components are single vertices.
See Figure 3 for dalmatian CRGs of small order.

Figure 3. The dalmatian CRGs
![]() $D_\infty=\overline{D_1},\, D_1=\overline{D_{\infty}},D_2, D_3,$
and
$D_\infty=\overline{D_1},\, D_1=\overline{D_{\infty}},D_2, D_3,$
and
![]() $D_4$
.
$D_4$
.
Remark 22. For all
![]() $p\in [0,1]$
and each
$p\in [0,1]$
and each
![]() $K\in {\mathcal{D}}_p$
, K is a p-core CRG. Moreover, if
$K\in {\mathcal{D}}_p$
, K is a p-core CRG. Moreover, if
![]() $p\in [0,1/2]$
, then
$p\in [0,1/2]$
, then
![]() $g_{D_\infty}(p)=p$
and for each positive integer t,
$g_{D_\infty}(p)=p$
and for each positive integer t,
If
![]() $p\in [1/2,1]$
, then
$p\in [1/2,1]$
, then
![]() $g_{\overline{D_\infty}}(p)=1-p$
and for each positive integer t,
$g_{\overline{D_\infty}}(p)=1-p$
and for each positive integer t,
![]() $g_{\overline{D_t}}(p) = 1-p + \frac{2p-1}{t}$
.
$g_{\overline{D_t}}(p) = 1-p + \frac{2p-1}{t}$
.
In Theorem 23, we show that for all
![]() $p\in [1-\varphi^{-1},\varphi^{-1}]$
, the only p-core CRGs are those that belong to
$p\in [1-\varphi^{-1},\varphi^{-1}]$
, the only p-core CRGs are those that belong to
![]() ${\mathcal{D}}_p$
.
${\mathcal{D}}_p$
.
Theorem 23. For
![]() $p\in [0,1]$
, the CRG associated to
$p\in [0,1]$
, the CRG associated to
![]() $P_3$
is p-prohibited if and only if
$P_3$
is p-prohibited if and only if
![]() $p\in [1-\varphi^{-1},\varphi^{-1}]$
. In particular for all
$p\in [1-\varphi^{-1},\varphi^{-1}]$
. In particular for all
![]() $p\in [1-\varphi^{-1},\varphi^{-1}]$
, a CRG K is p-core if and only if
$p\in [1-\varphi^{-1},\varphi^{-1}]$
, a CRG K is p-core if and only if
![]() $K\in{\mathcal{D}}_p$
.
$K\in{\mathcal{D}}_p$
.
Remark 24. Since the minimum eigenvalue of the adjacency matrix of
![]() $P_3$
is
$P_3$
is
![]() $-\sqrt{2}$
, Lemma 20 gives that
$-\sqrt{2}$
, Lemma 20 gives that
![]() $P_3$
is prohibited for p in the interval
$P_3$
is prohibited for p in the interval
![]() $[\sqrt{2}-1,2-\sqrt{2}]\approx [0.414,0.586]$
. Theorem 23, however, gives that
$[\sqrt{2}-1,2-\sqrt{2}]\approx [0.414,0.586]$
. Theorem 23, however, gives that
![]() $P_3$
is prohibited on the larger interval
$P_3$
is prohibited on the larger interval
![]() $[1-\varphi^{-1},\varphi^{-1}]\approx [0.382,0.618]$
.
$[1-\varphi^{-1},\varphi^{-1}]\approx [0.382,0.618]$
.
2.3. Proof of Lemma 20
The result from Theorem 25 below was originally shown by Sidorenko [Reference Sidorenko12] using different language and has appeared in several other forms throughout the study of hereditary properties. See [Reference Martin11] for a more detailed history. For convenience, we state it in the language of CRGs.
Theorem 25. Let K be a p-core CRG with optimal weight vector
![]() ${\bf x}\in\Delta_K$
. Then
${\bf x}\in\Delta_K$
. Then
So, Theorem 25 establishes that the optimal weight vector produces a weighting that is balanced.
Lemma 26. Let
![]() $0\leq p\leq 1$
and J be a CRG. If there exists a non-zero vector
$0\leq p\leq 1$
and J be a CRG. If there exists a non-zero vector
![]() ${\boldsymbol{\delta}}\in{\mathbb{R}}^{V(J)}$
so that
${\boldsymbol{\delta}}\in{\mathbb{R}}^{V(J)}$
so that
![]() $\langle{\boldsymbol{\delta}},{\bf 1}\rangle=0$
and
$\langle{\boldsymbol{\delta}},{\bf 1}\rangle=0$
and
then J is p-prohibited.
Proof. We proceed by contradiction. Suppose J is not p-prohibited and that there exists
![]() ${\boldsymbol{\delta}}$
as above. Then there exists a p-core CRG K containing J and we may let x denote the optimal weight vector for K. We extend
${\boldsymbol{\delta}}$
as above. Then there exists a p-core CRG K containing J and we may let x denote the optimal weight vector for K. We extend
![]() ${\boldsymbol{\delta}}$
to a vector
${\boldsymbol{\delta}}$
to a vector
![]() ${\boldsymbol{\delta}}'\in{\mathbb{R}}^{V(K)}$
by letting
${\boldsymbol{\delta}}'\in{\mathbb{R}}^{V(K)}$
by letting
![]() ${\boldsymbol{\delta}}'(u)\,:\!=\,0$
if
${\boldsymbol{\delta}}'(u)\,:\!=\,0$
if
![]() $u\in V(K)\setminus V(J)$
and
$u\in V(K)\setminus V(J)$
and
![]() ${\boldsymbol{\delta}}'(u)\,:\!=\,{\boldsymbol{\delta}}(u)$
if
${\boldsymbol{\delta}}'(u)\,:\!=\,{\boldsymbol{\delta}}(u)$
if
![]() $u\in V(J)$
. Note that
$u\in V(J)$
. Note that
![]() $\langle{\boldsymbol{\delta}}',{\bf 1}\rangle=0$
.
$\langle{\boldsymbol{\delta}}',{\bf 1}\rangle=0$
.
Since x is the optimal weight vector for the p-core CRG K,
![]() ${\bf x}(u) > 0$
for all
${\bf x}(u) > 0$
for all
![]() $u\in V(K)$
and it follows that there exists some
$u\in V(K)$
and it follows that there exists some
![]() $\varepsilon > 0$
so that
$\varepsilon > 0$
so that
![]() ${\bf x}'\,:\!=\,{\bf x} + \varepsilon{\boldsymbol{\delta}}'$
lies in
${\bf x}'\,:\!=\,{\bf x} + \varepsilon{\boldsymbol{\delta}}'$
lies in
![]() $\Delta_K$
and
$\Delta_K$
and
![]() ${\bf x}'(u) = 0$
for some
${\bf x}'(u) = 0$
for some
![]() $u\in V(K)$
. By the definition of
$u\in V(K)$
. By the definition of
![]() $g_K(p)$
, the fact that x is optimal, and Theorem 25,
$g_K(p)$
, the fact that x is optimal, and Theorem 25,
 \begin{align*} 0 &< g_K(p,{\bf x}') - g_K(p,{\bf x})\\ &= \langle {\bf x}+\varepsilon{\boldsymbol{\delta}}', M_K(p)({\bf x}+\varepsilon{\boldsymbol{\delta}}')\rangle - \langle {\bf x}, M_K(p){\bf x}\rangle\\ &= 2\varepsilon\langle {\boldsymbol{\delta}}, M_K(p){\bf x}\rangle + \varepsilon^2\langle {\boldsymbol{\delta}}', M_K(p){\boldsymbol{\delta}}'\rangle\\ &= 2\varepsilon\langle {\boldsymbol{\delta}}', g_K(p){\bf 1}\rangle + \varepsilon^2\langle {\boldsymbol{\delta}}, M_J(p){\boldsymbol{\delta}}\rangle\\ &= \varepsilon^2\langle {\boldsymbol{\delta}}, M_J(p){\boldsymbol{\delta}}\rangle \leq 0, \end{align*}
\begin{align*} 0 &< g_K(p,{\bf x}') - g_K(p,{\bf x})\\ &= \langle {\bf x}+\varepsilon{\boldsymbol{\delta}}', M_K(p)({\bf x}+\varepsilon{\boldsymbol{\delta}}')\rangle - \langle {\bf x}, M_K(p){\bf x}\rangle\\ &= 2\varepsilon\langle {\boldsymbol{\delta}}, M_K(p){\bf x}\rangle + \varepsilon^2\langle {\boldsymbol{\delta}}', M_K(p){\boldsymbol{\delta}}'\rangle\\ &= 2\varepsilon\langle {\boldsymbol{\delta}}', g_K(p){\bf 1}\rangle + \varepsilon^2\langle {\boldsymbol{\delta}}, M_J(p){\boldsymbol{\delta}}\rangle\\ &= \varepsilon^2\langle {\boldsymbol{\delta}}, M_J(p){\boldsymbol{\delta}}\rangle \leq 0, \end{align*}
a contradiction to the assumption that J is not p-prohibited.
We include one more well-known fact about p-core CRGs.
Proposition 27
(See [Reference Martin11]). Let
![]() $K_1,\ldots,K_{\ell}$
be CRGs and let
$K_1,\ldots,K_{\ell}$
be CRGs and let
![]() $K=K_1\oplus\cdots\oplus K_{\ell}$
. Then for all
$K=K_1\oplus\cdots\oplus K_{\ell}$
. Then for all
![]() $p\in [0,1]$
,
$p\in [0,1]$
,
 \begin{equation} g_{K}(p)^{-1} = \sum_{i=1}^{\ell} g_{K_i}(p)^{-1} . \end{equation}
\begin{equation} g_{K}(p)^{-1} = \sum_{i=1}^{\ell} g_{K_i}(p)^{-1} . \end{equation}
In particular, K is p-core if and only if each of
![]() $K_1,\ldots,K_{\ell}$
are p-core.
$K_1,\ldots,K_{\ell}$
are p-core.
Lemma 28. Let
![]() $p\in [0,1]$
. A CRG J is p-prohibited if and only if for all p-core CRGs K and all positive integers k, the CRG
$p\in [0,1]$
. A CRG J is p-prohibited if and only if for all p-core CRGs K and all positive integers k, the CRG
![]() $(k\cdot J)\oplus K$
is p-prohibited.
$(k\cdot J)\oplus K$
is p-prohibited.
Proof. To prove the forward implication, if J is p-prohibited, then no p-core CRG can contain
![]() $k\cdot J$
because it would contain J. To prove the reverse implication, if J is not p-prohibited then there exists a p-core CRG, L, containing J. Then
$k\cdot J$
because it would contain J. To prove the reverse implication, if J is not p-prohibited then there exists a p-core CRG, L, containing J. Then
![]() $J\oplus K$
is contained in
$J\oplus K$
is contained in
![]() $L\oplus K$
, which is p-core by Proposition 27, as desired.
$L\oplus K$
, which is p-core by Proposition 27, as desired.
With the primary tools of Lemmas 26 and 28 established, we now proceed to prove Lemma 20 itself.
Let J be the CRG associated to a non-empty graph G. If
![]() $p=1/2$
, then by Theorem 11, J is
$p=1/2$
, then by Theorem 11, J is
![]() $1/2$
-prohibited if and only if J has an edge that is not grey. Thus, any non-empty G gives that J is
$1/2$
-prohibited if and only if J has an edge that is not grey. Thus, any non-empty G gives that J is
![]() $1/2$
-prohibited, settling the case where
$1/2$
-prohibited, settling the case where
![]() $p=1/2$
.
$p=1/2$
.
Now suppose
![]() $p\in (0,1/2)$
. Write A for the adjacency matrix of G and suppose
$p\in (0,1/2)$
. Write A for the adjacency matrix of G and suppose
![]() $A{\bf x} = \lambda {\bf x}$
for some unit vector x where
$A{\bf x} = \lambda {\bf x}$
for some unit vector x where
![]() $\lambda$
is the minimum eigenvalue of A. Then J is the the CRG on V(G) with all vertices black, and where edge uv is white if
$\lambda$
is the minimum eigenvalue of A. Then J is the the CRG on V(G) with all vertices black, and where edge uv is white if
![]() $uv\in E(G)$
, and uv is grey if
$uv\in E(G)$
, and uv is grey if
![]() $uv\in E(G^c)$
. So
$uv\in E(G^c)$
. So
![]() $M_J(p) = (1-p)I + pA$
.
$M_J(p) = (1-p)I + pA$
.
For convenience, we write
![]() $V_1$
and
$V_1$
and
![]() $V_2$
for the vertex sets in
$V_2$
for the vertex sets in
![]() $2\cdot J$
corresponding to each copy of J. Let
$2\cdot J$
corresponding to each copy of J. Let
![]() ${\boldsymbol{\delta}}\in{\mathbb{R}}^{V(2\cdot J)}$
be defined by
${\boldsymbol{\delta}}\in{\mathbb{R}}^{V(2\cdot J)}$
be defined by
 \begin{align*} {\boldsymbol{\delta}}(u) \,:\!=\, \left\{ \begin{array}{rl} {\bf x}(u), & u\in V_1; \\ -{\bf x}(u), & u\in V_2 . \end{array}\right.\end{align*}
\begin{align*} {\boldsymbol{\delta}}(u) \,:\!=\, \left\{ \begin{array}{rl} {\bf x}(u), & u\in V_1; \\ -{\bf x}(u), & u\in V_2 . \end{array}\right.\end{align*}
By definition,
![]() $\langle {\bf 1}, {\boldsymbol{\delta}}\rangle = 0$
. Moreover note that
$\langle {\bf 1}, {\boldsymbol{\delta}}\rangle = 0$
. Moreover note that
 \begin{align*} \langle{\boldsymbol{\delta}}, M_{2\cdot J}(p){\boldsymbol{\delta}}\rangle &= \langle {\bf x}, M_J(p){\bf x} \rangle + \langle -{\bf x}, M_J(p)(-{\bf x}) \rangle \\ &= 2 \langle {\bf x}, M_J(p){\bf x} \rangle \\ &= 2 \langle {\bf x}, ((1-p)I+pA){\bf x} \rangle \\ &= 2(1-p) \langle {\bf x}, I{\bf x} \rangle + 2p \langle {\bf x}, A{\bf x} \rangle \\ &= 2(1-p) \langle {\bf x}, {\bf x} \rangle + 2p \lambda \langle {\bf x}, {\bf x} \rangle \\ &= 2\cdot(1-(1-\lambda)p) \cdot \langle {\bf x}, {\bf x} \rangle.\end{align*}
\begin{align*} \langle{\boldsymbol{\delta}}, M_{2\cdot J}(p){\boldsymbol{\delta}}\rangle &= \langle {\bf x}, M_J(p){\bf x} \rangle + \langle -{\bf x}, M_J(p)(-{\bf x}) \rangle \\ &= 2 \langle {\bf x}, M_J(p){\bf x} \rangle \\ &= 2 \langle {\bf x}, ((1-p)I+pA){\bf x} \rangle \\ &= 2(1-p) \langle {\bf x}, I{\bf x} \rangle + 2p \langle {\bf x}, A{\bf x} \rangle \\ &= 2(1-p) \langle {\bf x}, {\bf x} \rangle + 2p \lambda \langle {\bf x}, {\bf x} \rangle \\ &= 2\cdot(1-(1-\lambda)p) \cdot \langle {\bf x}, {\bf x} \rangle.\end{align*}
If
![]() $p\geq 1/(1-\lambda)$
, then
$p\geq 1/(1-\lambda)$
, then
![]() $\langle{\boldsymbol{\delta}}, M_{2\cdot J}(p){\boldsymbol{\delta}}\rangle\leq 0$
. By Lemma 26, the CRG
$\langle{\boldsymbol{\delta}}, M_{2\cdot J}(p){\boldsymbol{\delta}}\rangle\leq 0$
. By Lemma 26, the CRG
![]() $2\cdot J$
is p-prohibited and by Lemma 28, J itself is p-prohibited. This settles the case where
$2\cdot J$
is p-prohibited and by Lemma 28, J itself is p-prohibited. This settles the case where
![]() $p\in (0,1/2)$
.
$p\in (0,1/2)$
.
Finally, for the case of
![]() $p\in (1/2,1)$
, Proposition 17 gives that J is p-prohibited if and only if J is
$p\in (1/2,1)$
, Proposition 17 gives that J is p-prohibited if and only if J is
![]() $(1-p)$
-prohibited. This concludes the proof of Lemma 20.
$(1-p)$
-prohibited. This concludes the proof of Lemma 20.
2.4. Proof of Theorem 23
Lemma 29 below is a result in pure graph theory that is reminiscent of the theorem that categorizes
![]() $\{P_4,C_4,C_4^c\}$
-free graphs as threshold graphs. A dominant vertex in a graph is one for which every other vertex is its neighbour.
$\{P_4,C_4,C_4^c\}$
-free graphs as threshold graphs. A dominant vertex in a graph is one for which every other vertex is its neighbour.
Lemma 29. If G is a connected
![]() $\{P_4,C_4\}$
-free graph, then G has a dominant vertex.
$\{P_4,C_4\}$
-free graph, then G has a dominant vertex.
Proof. Let u be a vertex of G which attains the maximum degree
![]() $\Delta=\Delta(G)$
and let
$\Delta=\Delta(G)$
and let
![]() $A\,:\!=\,N_G(u)$
and
$A\,:\!=\,N_G(u)$
and
![]() $B\,:\!=\,V(G)\setminus(A\cup\{u\})$
. If
$B\,:\!=\,V(G)\setminus(A\cup\{u\})$
. If
![]() $B = \emptyset$
, then u is the desired vertex, so we assume otherwise. Let
$B = \emptyset$
, then u is the desired vertex, so we assume otherwise. Let
![]() $w\in B$
. Since G avoids induced
$w\in B$
. Since G avoids induced
![]() $P_4$
-s, connectivity implies G has diameter at most 2.
$P_4$
-s, connectivity implies G has diameter at most 2.
In particular,
![]() ${\textrm{dist}}_G(u,w) = 2$
, so there exists some vertex
${\textrm{dist}}_G(u,w) = 2$
, so there exists some vertex
![]() $v\in A$
so that uvw is an induced path on 3 vertices. Let
$v\in A$
so that uvw is an induced path on 3 vertices. Let
![]() $v'\in A\setminus\{v\}$
. Note that v
′
uvw is a path on 4 vertices but since it cannot be induced and cannot form an induced
$v'\in A\setminus\{v\}$
. Note that v
′
uvw is a path on 4 vertices but since it cannot be induced and cannot form an induced
![]() $C_4$
, either
$C_4$
, either
![]() $uw\in E(G)$
or
$uw\in E(G)$
or
![]() $vv'\in E(G)$
. However,
$vv'\in E(G)$
. However,
![]() $uw\notin E(G)$
because
$uw\notin E(G)$
because
![]() ${\textrm{dist}}_G(u,w)=2$
. Thus, it follows that
${\textrm{dist}}_G(u,w)=2$
. Thus, it follows that
![]() $vv'\in E(G)$
. So v is adjacent to
$vv'\in E(G)$
. So v is adjacent to
![]() $\{u,w\}\cup (A\setminus\{v\})$
and has degree at least
$\{u,w\}\cup (A\setminus\{v\})$
and has degree at least
![]() $\Delta+1$
, a contradiction.
$\Delta+1$
, a contradiction.
Lemma 29 yields a very strong structural theorem on CRGs, Lemma 30. Recall the definition of the underlying graph of CRG, K, in Definition 18: the graph whose vertices are the vertices of K and whose edges are the non-grey edges of K.
Lemma 30. Let
![]() $p\in [1/3,2/3]$
. If a p-core CRG has an underlying graph which is
$p\in [1/3,2/3]$
. If a p-core CRG has an underlying graph which is
![]() $\{P_4,C_4\}$
-free, then every component of the underlying graph is a clique. That is, every component of such a CRG must be a member of
$\{P_4,C_4\}$
-free, then every component of the underlying graph is a clique. That is, every component of such a CRG must be a member of
![]() ${\mathcal{D}}_p$
.
${\mathcal{D}}_p$
.
Proof. If
![]() $p=1/2$
, then as we saw in Remark 12, a p-core CRG has only grey edges and so the underlying graph is empty.
$p=1/2$
, then as we saw in Remark 12, a p-core CRG has only grey edges and so the underlying graph is empty.
Let
![]() $p\in [1/3,1/2)$
. Every trivial component of the underlying graph is simply a vertex in the CRG. Let K be a non-trivial component of the CRG. By Theorem 11, the vertices of K must be black and by Lemma 29, the underlying graph of K has a dominant vertex u.
$p\in [1/3,1/2)$
. Every trivial component of the underlying graph is simply a vertex in the CRG. Let K be a non-trivial component of the CRG. By Theorem 11, the vertices of K must be black and by Lemma 29, the underlying graph of K has a dominant vertex u.
Let
![]() ${\bf x}\in\Delta_K$
be the optimal weight vector for K and define
${\bf x}\in\Delta_K$
be the optimal weight vector for K and define
![]() $g \,:\!=\, g_K(p)$
. By Theorem 25,
$g \,:\!=\, g_K(p)$
. By Theorem 25,
![]() $M_K(p){\bf x} = g{\bf 1}$
and by inspecting the entry indexed by u,
$M_K(p){\bf x} = g{\bf 1}$
and by inspecting the entry indexed by u,
For a contradiction, we now suppose K is not a dalmatian CRG. Hence, there exists some grey edge vw, and the sub-CRG K ′ on v and w is the disjoint union of two black vertices. Since K is p-core,
Altogether,
![]() $p<g<(1-p)/2$
which implies that
$p<g<(1-p)/2$
which implies that
![]() $p < 1/3$
, a contradiction.
$p < 1/3$
, a contradiction.
The case where
![]() $p\in (1/2,2/3]$
follows by symmetry.
$p\in (1/2,2/3]$
follows by symmetry.
We now prove Theorem 23 itself with the primary tool being Lemma 30. As mentioned in Remark 14, we leave it as an exercise to verify that the CRG associated with
![]() $P_4$
is p-core for
$P_4$
is p-core for
![]() $p\in (0,1-\varphi^{-1})\cup (\varphi^{-1},1)$
. Hence,
$p\in (0,1-\varphi^{-1})\cup (\varphi^{-1},1)$
. Hence,
![]() $P_3$
is not p-prohibited in this range, proving the forward implication.
$P_3$
is not p-prohibited in this range, proving the forward implication.
For the reverse implication, let
![]() $p\in [1-\varphi^{-1},\varphi^{-1}]$
. Since the minimum eigenvalues of the adjacency matrices of
$p\in [1-\varphi^{-1},\varphi^{-1}]$
. Since the minimum eigenvalues of the adjacency matrices of
![]() $C_4$
and
$C_4$
and
![]() $P_4$
are
$P_4$
are
![]() $-2$
and
$-2$
and
![]() $-\varphi^{-1}$
respectively, Lemma 20 implies that the CRGs associated with
$-\varphi^{-1}$
respectively, Lemma 20 implies that the CRGs associated with
![]() $C_4$
and
$C_4$
and
![]() $P_4$
are p-prohibited for
$P_4$
are p-prohibited for
![]() $p\in [1-\varphi^{-1},\varphi^{-1}]$
.
$p\in [1-\varphi^{-1},\varphi^{-1}]$
.
Suppose K is a p-core CRG. Since
![]() $p\in [1/3,2/3]$
, it follows from Lemma 30 that the components of the underlying graph of K are cliques. No such graph contains an induced
$p\in [1/3,2/3]$
, it follows from Lemma 30 that the components of the underlying graph of K are cliques. No such graph contains an induced
![]() $P_3$
and so
$P_3$
and so
![]() $P_3$
is p-prohibited for all
$P_3$
is p-prohibited for all
![]() $p\in [1-\varphi^{-1},\varphi^{-1}]$
, as desired.
$p\in [1-\varphi^{-1},\varphi^{-1}]$
, as desired.
For the second statement of the theorem, since
![]() $P_3$
is p-prohibited, the only underlying graphs of a p-core CRG can be disjoint cliques, which is exactly the condition of being in
$P_3$
is p-prohibited, the only underlying graphs of a p-core CRG can be disjoint cliques, which is exactly the condition of being in
![]() ${\mathcal{D}}_p$
. As observed in Remark 22, all CRGs in
${\mathcal{D}}_p$
. As observed in Remark 22, all CRGs in
![]() ${\mathcal{D}}_p$
are p-core. This concludes the proof of Theorem 23.
${\mathcal{D}}_p$
are p-core. This concludes the proof of Theorem 23.
3. Proof of the main result
To proceed with the proof of Theorem 4, we need some preparation. In Section 3.1, Lemma 31 shows that for all
![]() $p\in (1/3,2/3)$
and for any CRG K, there exists a sub-CRG K
′ of K so that
$p\in (1/3,2/3)$
and for any CRG K, there exists a sub-CRG K
′ of K so that
![]() $g_{K'}(p)$
is close to
$g_{K'}(p)$
is close to
![]() $g_K(p)$
and K
′ has components whose order is bounded by a function of p and a tolerance term
$g_K(p)$
and K
′ has components whose order is bounded by a function of p and a tolerance term
![]() $\varepsilon$
.
$\varepsilon$
.
For the remaining discussion, let
![]() $p_0\in (0,1)$
and define
$p_0\in (0,1)$
and define
 \begin{align} p^* \,:\!=\, \dfrac{\log(1-p_0)}{\log(p_0(1-p_0))} . \end{align}
\begin{align} p^* \,:\!=\, \dfrac{\log(1-p_0)}{\log(p_0(1-p_0))} . \end{align}
In Section 3.2, we investigate when a random graph
![]() $F\sim{\mathbb{G}}(n_0,p_0)$
embeds into a CRG (i.e., when
$F\sim{\mathbb{G}}(n_0,p_0)$
embeds into a CRG (i.e., when
![]() $F\mapsto K$
). There we show that a.a.s., if a CRG, K, has bounded components in the above sense and the random graph does not map into K, then
$F\mapsto K$
). There we show that a.a.s., if a CRG, K, has bounded components in the above sense and the random graph does not map into K, then
![]() $g_K(p^*)$
has to be at least the desired value to within a small tolerance. Applying Lemma 31, this is true even if the components of K are not bounded.
$g_K(p^*)$
has to be at least the desired value to within a small tolerance. Applying Lemma 31, this is true even if the components of K are not bounded.
Finally in Section 3.3, we put together these ideas to prove our main result.
3.1. Trimming p-core CRGs
The main result in this subsection is Lemma 31, which establishes that, for
![]() $p\in(1/3,2/3)$
, a CRG has a sub-CRG with bounded component sizes and a negligible change in the value of the g-function.
$p\in(1/3,2/3)$
, a CRG has a sub-CRG with bounded component sizes and a negligible change in the value of the g-function.
Lemma 31. Fix
![]() $p\in (1/3,2/3)$
and
$p\in (1/3,2/3)$
and
![]() $\varepsilon\in(0,1)$
. There exists a positive integer
$\varepsilon\in(0,1)$
. There exists a positive integer
![]() $B = B(p,\varepsilon)$
such that the following holds: For all CRGs K, there exists a p-core sub-CRG K′ whose components have order at most B, and
$B = B(p,\varepsilon)$
such that the following holds: For all CRGs K, there exists a p-core sub-CRG K′ whose components have order at most B, and
![]() $g_{K'}(p) \leq (1+\varepsilon)g_K(p)$
.
$g_{K'}(p) \leq (1+\varepsilon)g_K(p)$
.
The first part of the proof is to remove vertices from a CRG K one-by-one in a way which does not affect
![]() $g_K(p)$
too much. Once enough vertices are removed, we show that each remaining vertex is incident to a bounded number of non-grey edges. Finally, we use Lemma 20 to bound the diameter of p-core CRGs on the interval
$g_K(p)$
too much. Once enough vertices are removed, we show that each remaining vertex is incident to a bounded number of non-grey edges. Finally, we use Lemma 20 to bound the diameter of p-core CRGs on the interval
![]() $p\in (1/3,2/3)$
. The underlying graph has bounded degree and diameter, thus its connected components have bounded order.
$p\in (1/3,2/3)$
. The underlying graph has bounded degree and diameter, thus its connected components have bounded order.
The proof consists of a sequence of propositions:
Proposition 32. Fix
![]() $p\in [0,1]$
and suppose K is a p-core CRG with least two vertices. If
$p\in [0,1]$
and suppose K is a p-core CRG with least two vertices. If
![]() ${\bf x}\in\Delta_K$
is the optimal weight vector for K, i.e.,
${\bf x}\in\Delta_K$
is the optimal weight vector for K, i.e.,
![]() $g = g_K(p) = g_K(p,{\bf x})$
, then for all
$g = g_K(p) = g_K(p,{\bf x})$
, then for all
![]() $u\in V(K)$
,
$u\in V(K)$
,
Proof. Let
![]() $K'\,:\!=\,K\setminus\{u\}$
. Since K is p-core with at least two vertices,
$K'\,:\!=\,K\setminus\{u\}$
. Since K is p-core with at least two vertices,
![]() ${\bf x}(u)<1$
and we may define
${\bf x}(u)<1$
and we may define
![]() ${\bf x}'\in\Delta_K$
by
${\bf x}'\in\Delta_K$
by
 \begin{align*} {\bf x}'(v)\,:\!=\,\left\{\begin{array}{ll} 0, &v=u\\[4pt] \dfrac{{\bf x}(v)}{1-{\bf x}(u)}, &\text{otherwise} \end{array}\right. . \end{align*}
\begin{align*} {\bf x}'(v)\,:\!=\,\left\{\begin{array}{ll} 0, &v=u\\[4pt] \dfrac{{\bf x}(v)}{1-{\bf x}(u)}, &\text{otherwise} \end{array}\right. . \end{align*}
In other words, if
![]() ${\bf e}_u\in{\mathbb{R}}^{V(K)}$
is the indicator vector for the vertex u, then
${\bf e}_u\in{\mathbb{R}}^{V(K)}$
is the indicator vector for the vertex u, then
![]() $(1-{\bf x}(u)){\bf x}' = {\bf x} - {\bf x}(u){\bf e}_u$
. Recall that
$(1-{\bf x}(u)){\bf x}' = {\bf x} - {\bf x}(u){\bf e}_u$
. Recall that
![]() $M_K(p)$
denotes the weighted adjacency matrix of K. By Theorem 25,
$M_K(p)$
denotes the weighted adjacency matrix of K. By Theorem 25,
![]() $M_K(p){\bf x} = g{\bf 1}$
and so
$M_K(p){\bf x} = g{\bf 1}$
and so
 \begin{align*} (1-{\bf x}(u))^2\langle {\bf x}', M_K(p){\bf x}'\rangle &= \langle {\bf x}-{\bf x}(u){\bf e}_u, M_K(p)( {\bf x}-{\bf x}(u){\bf e}_u )\rangle \\ &= \langle {\bf x},g{\bf 1}\rangle - 2{\bf x}(u)\langle {\bf e}_u, g{\bf 1}\rangle + {\bf x}(u)^2\langle {\bf e}_u, M_K(p){\bf e}_u\rangle\\ &\leq g - 2g\,{\bf x}(u) + {\bf x}(u)^2. \end{align*}
\begin{align*} (1-{\bf x}(u))^2\langle {\bf x}', M_K(p){\bf x}'\rangle &= \langle {\bf x}-{\bf x}(u){\bf e}_u, M_K(p)( {\bf x}-{\bf x}(u){\bf e}_u )\rangle \\ &= \langle {\bf x},g{\bf 1}\rangle - 2{\bf x}(u)\langle {\bf e}_u, g{\bf 1}\rangle + {\bf x}(u)^2\langle {\bf e}_u, M_K(p){\bf e}_u\rangle\\ &\leq g - 2g\,{\bf x}(u) + {\bf x}(u)^2. \end{align*}
By definition of
![]() $g_{K'}(p)$
and since
$g_{K'}(p)$
and since
![]() ${\bf x}'(u) = 0$
,
${\bf x}'(u) = 0$
,
 \begin{align*} g_{K'}(p) &\leq g_K(p,{\bf x}') \\ &= \dfrac{\langle {\bf x}', M_K(p){\bf x}'\rangle}{(1-{\bf x}(u))^2} \\ &= \dfrac{g - 2g\,{\bf x}(u)+{\bf x}(u)^2}{(1-{\bf x}(u))^2} \\ &= g + \dfrac{(1 - g){\bf x}(u)^2}{(1-{\bf x}(u))^2}\\ &\leq g+\dfrac{{\bf x}(u)^2}{(1-{\bf x}(u))^2}, \end{align*}
\begin{align*} g_{K'}(p) &\leq g_K(p,{\bf x}') \\ &= \dfrac{\langle {\bf x}', M_K(p){\bf x}'\rangle}{(1-{\bf x}(u))^2} \\ &= \dfrac{g - 2g\,{\bf x}(u)+{\bf x}(u)^2}{(1-{\bf x}(u))^2} \\ &= g + \dfrac{(1 - g){\bf x}(u)^2}{(1-{\bf x}(u))^2}\\ &\leq g+\dfrac{{\bf x}(u)^2}{(1-{\bf x}(u))^2}, \end{align*}
which completes the proof.
Proposition 33. Fix
![]() $p\in [0,1]$
and
$p\in [0,1]$
and
![]() $\varepsilon\in (0,1)$
. If K is a p-core CRG with
$\varepsilon\in (0,1)$
. If K is a p-core CRG with
![]() $g = g_K(p)$
, then there exists a p-core sub-CRG K′ of K such that the following holds:
$g = g_K(p)$
, then there exists a p-core sub-CRG K′ of K such that the following holds:
-
(1).
 $|V(K')|\leq 4/(\varepsilon g)$
,
$|V(K')|\leq 4/(\varepsilon g)$
, -
(2).
 $g_{K'}(p) \leq (1+17\varepsilon) g$
, and
$g_{K'}(p) \leq (1+17\varepsilon) g$
, and -
(3). if
 ${\bf x}'\in\Delta_{K'}$
is the optimal weight vector for K
′, then
${\bf x}'\in\Delta_{K'}$
is the optimal weight vector for K
′, then  \begin{align*} \min_{u\in V(K')}{\bf x}'(u)\geq \varepsilon g. \end{align*}
\begin{align*} \min_{u\in V(K')}{\bf x}'(u)\geq \varepsilon g. \end{align*}
Proof. Define a finite sequence of sub-CRGs
as follows: First let
![]() $K\,:\!=\,K_0$
and
$K\,:\!=\,K_0$
and
![]() $g_0 \,:\!=\, g_K(p)$
. For any
$g_0 \,:\!=\, g_K(p)$
. For any
![]() $k\geq 0$
so that
$k\geq 0$
so that
![]() $|V(K_k)| \geq 2$
, do the following:
$|V(K_k)| \geq 2$
, do the following:
-
(i) Let
 ${\bf x}_k\in\Delta_{K_k}$
be the optimal weight vector for
${\bf x}_k\in\Delta_{K_k}$
be the optimal weight vector for
 $K_k$
, i.e.,
$K_k$
, i.e.,
 $g_{K_k}(p,{\bf x}_k) = g_{K_k}(p)$
.
$g_{K_k}(p,{\bf x}_k) = g_{K_k}(p)$
. -
(ii) Let
 $u_k\in V(K_k)$
so that
$u_k\in V(K_k)$
so that
 ${\bf x}_k(u_k) = \min\left\{{\bf x}_k(v) \,:\, v\in V(K_k)\right\}$
.
${\bf x}_k(u_k) = \min\left\{{\bf x}_k(v) \,:\, v\in V(K_k)\right\}$
. -
(iii) Let
 $K_{k+1}$
be any p-core sub-CRG of
$K_{k+1}$
be any p-core sub-CRG of
 $K_k\setminus\{u_k\}$
.
$K_k\setminus\{u_k\}$
.
Since each step removes at least one vertex,
![]() $\ell\leq|V(K)|$
. For each
$\ell\leq|V(K)|$
. For each
![]() $k\in\{0,\ldots,\ell\}$
, denote
$k\in\{0,\ldots,\ell\}$
, denote
![]() $g_k\,:\!=\,g_{K_k}(p)$
.
$g_k\,:\!=\,g_{K_k}(p)$
.
Let
![]() $a\in\{0,\ldots,\ell\}$
be the minimum index a so that
$a\in\{0,\ldots,\ell\}$
be the minimum index a so that
![]() $|V(K_a)| \leq 4/(\varepsilon g)$
. By the definition of a and by the fact that
$|V(K_a)| \leq 4/(\varepsilon g)$
. By the definition of a and by the fact that
![]() $\varepsilon,g < 1$
,
$\varepsilon,g < 1$
,
for all
![]() $k\in\{0,\ldots,a-1\}$
. By Proposition 32,
$k\in\{0,\ldots,a-1\}$
. By Proposition 32,
Because
![]() $|V(K_k)| \geq |V(K_{a-1})| + (a-1-k)$
for all
$|V(K_k)| \geq |V(K_{a-1})| + (a-1-k)$
for all
![]() $k\in\{0,\ldots,a-1\}$
,
$k\in\{0,\ldots,a-1\}$
,
 \begin{align*} g_a &< g + \sum_{ k=0 }^{ a-1 }\dfrac{2}{|V(K_k)|^2} \\[3pt] &\leq g + \sum_{ k=0 }^{ a-1 }\dfrac{2}{\left(|V(K_{a-1})| + (a-1-k)\right)^2} \\[3pt] &< g + \sum_{i = |V(K_{a-1})|}^\infty\dfrac{2}{i^2} \\[3pt] &< g + \int_{i = |V(K_{a-1})|-1}^\infty \dfrac{2}{x^2} \, dx \\[3pt] &= g + \frac{2}{|V(K_{a-1})|-1} \\[3pt] &\leq g + \frac{2}{\lfloor 4/(\varepsilon g)\rfloor} . \end{align*}
\begin{align*} g_a &< g + \sum_{ k=0 }^{ a-1 }\dfrac{2}{|V(K_k)|^2} \\[3pt] &\leq g + \sum_{ k=0 }^{ a-1 }\dfrac{2}{\left(|V(K_{a-1})| + (a-1-k)\right)^2} \\[3pt] &< g + \sum_{i = |V(K_{a-1})|}^\infty\dfrac{2}{i^2} \\[3pt] &< g + \int_{i = |V(K_{a-1})|-1}^\infty \dfrac{2}{x^2} \, dx \\[3pt] &= g + \frac{2}{|V(K_{a-1})|-1} \\[3pt] &\leq g + \frac{2}{\lfloor 4/(\varepsilon g)\rfloor} . \end{align*}
Since
![]() $\varepsilon g < 1$
, it is the case that
$\varepsilon g < 1$
, it is the case that
![]() $\lfloor 4/(\varepsilon g)\rfloor > 2/(\varepsilon g)$
. Consequently,
$\lfloor 4/(\varepsilon g)\rfloor > 2/(\varepsilon g)$
. Consequently,
Let b be the least index
![]() $a\leq b\leq \ell$
so that
$a\leq b\leq \ell$
so that
![]() ${\bf x}_b(u)\geq \varepsilon g$
for all
${\bf x}_b(u)\geq \varepsilon g$
for all
![]() $u\in V(K_b)$
. Note that b is well defined since
$u\in V(K_b)$
. Note that b is well defined since
![]() ${\bf x}_{\ell}(u) = 1 > \varepsilon g$
where
${\bf x}_{\ell}(u) = 1 > \varepsilon g$
where
![]() ${\bf x}_{\ell}$
is the optimal weighting for
${\bf x}_{\ell}$
is the optimal weighting for
![]() $K_\ell$
, a CRG with a single vertex. For any
$K_\ell$
, a CRG with a single vertex. For any
![]() $k\in\{a,\ldots,b-1\}$
, it is the case that
$k\in\{a,\ldots,b-1\}$
, it is the case that
![]() ${\bf x}_k(u_k) < \varepsilon g$
and that
${\bf x}_k(u_k) < \varepsilon g$
and that
![]() ${\bf x}_k(u_k) \leq 1/|V(K_k)|\leq 1/2$
and again by Proposition 32,
${\bf x}_k(u_k) \leq 1/|V(K_k)|\leq 1/2$
and again by Proposition 32,
Finally by (10) and since
![]() $b-a\leq |V(K_a)|\leq 4/(\varepsilon g)$
,
$b-a\leq |V(K_a)|\leq 4/(\varepsilon g)$
,
 \begin{align*} g_b \leq g_a + \sum_{ k=a }^{b-1}4\varepsilon^2g^2 \leq (1+\varepsilon)g + |V(K_a)|\cdot 4\varepsilon^2g^2 \leq (1+17\varepsilon)g. \end{align*}
\begin{align*} g_b \leq g_a + \sum_{ k=a }^{b-1}4\varepsilon^2g^2 \leq (1+\varepsilon)g + |V(K_a)|\cdot 4\varepsilon^2g^2 \leq (1+17\varepsilon)g. \end{align*}
Letting
![]() $K'\,:\!=\,K_b$
, we have the desired sub-CRG.
$K'\,:\!=\,K_b$
, we have the desired sub-CRG.
Proposition 34 below implies that we can decrease the degree of the underlying graph of a CRG K without changing
![]() $g_K(p)$
too much.
$g_K(p)$
too much.
Proposition 34. Fix
![]() $p\in (0,1)$
and
$p\in (0,1)$
and
![]() $\varepsilon\in (0,1)$
. If K is a p-core CRG, then there exists a p-core sub-CRG K′ of K so that
$\varepsilon\in (0,1)$
. If K is a p-core CRG, then there exists a p-core sub-CRG K′ of K so that
-
(1)
 $g_{K'}(p) \leq (1+\varepsilon)g_K(p)$
, and
$g_{K'}(p) \leq (1+\varepsilon)g_K(p)$
, and -
(2) for each
 $u\in V(K')$
, u is incident in K
′ to at most black or white edges.
$u\in V(K')$
, u is incident in K
′ to at most black or white edges. \begin{align*} 34\varepsilon^{-1}\cdot\max\left\{\dfrac1{p}, \dfrac1{1-p}\right\}, \end{align*}
\begin{align*} 34\varepsilon^{-1}\cdot\max\left\{\dfrac1{p}, \dfrac1{1-p}\right\}, \end{align*}
Proof. We prove the claim for a fixed
![]() $p\in (0,1/2]$
. By duality (that is, by replacing K with
$p\in (0,1/2]$
. By duality (that is, by replacing K with
![]() $\overline{K}$
and p with
$\overline{K}$
and p with
![]() $1-p$
) the claim holds also for all
$1-p$
) the claim holds also for all
![]() $p\in [1/2,1)$
. For ease of notation, let
$p\in [1/2,1)$
. For ease of notation, let
![]() $g=g_K(p)$
.
$g=g_K(p)$
.
By Proposition 33 applied to K and
![]() $\varepsilon/17$
, there exists a sub-CRG K
′ of K so that
$\varepsilon/17$
, there exists a sub-CRG K
′ of K so that
![]() $g_{K'}(p)\leq (1+\varepsilon)g$
and whose optimal weight vector
$g_{K'}(p)\leq (1+\varepsilon)g$
and whose optimal weight vector
![]() ${\bf x}\in\Delta_{K'}$
has
${\bf x}\in\Delta_{K'}$
has
![]() ${\bf x}(u)\geq \varepsilon g/17$
for all
${\bf x}(u)\geq \varepsilon g/17$
for all
![]() $u\in V(K')$
. Let
$u\in V(K')$
. Let
![]() $g'=g_{K'}(p)$
.
$g'=g_{K'}(p)$
.
By Theorem 11, the white vertices of K
′ are incident to no white or black edges. So it suffices to prove the desired inequality for black vertices. Suppose
![]() $u\in {\textrm{VB}}(K')$
. By Theorem 25,
$u\in {\textrm{VB}}(K')$
. By Theorem 25,
![]() $M_{K'}(p){\bf x} = g'{\bf 1}$
and it follows that
$M_{K'}(p){\bf x} = g'{\bf 1}$
and it follows that
 \begin{align*} \dfrac{(1+\varepsilon)g}{p} > \dfrac{g'}{p} - \dfrac{1-p}p\,{\bf x}(u) = \sum_{uv\in{\textrm{EW}}(K')}{\bf x}(v) \geq \dfrac{\varepsilon g}{17}\cdot \left|\{v \,:\, uv\in{\textrm{EW}}(K')\}\right| . \end{align*}
\begin{align*} \dfrac{(1+\varepsilon)g}{p} > \dfrac{g'}{p} - \dfrac{1-p}p\,{\bf x}(u) = \sum_{uv\in{\textrm{EW}}(K')}{\bf x}(v) \geq \dfrac{\varepsilon g}{17}\cdot \left|\{v \,:\, uv\in{\textrm{EW}}(K')\}\right| . \end{align*}
So the number of vertices adjacent to a vertex via a non-grey edge is at most
![]() $17(1+\varepsilon)/(\varepsilon p)\leq 34/(\varepsilon p)$
, as desired.
$17(1+\varepsilon)/(\varepsilon p)\leq 34/(\varepsilon p)$
, as desired.
Next, we uniformly bound the diameter of all p-core CRGs, for each
![]() $p\in (1/3,2/3)$
.
$p\in (1/3,2/3)$
.
Proposition 35. For all positive integers d, the CRG associated to the path
![]() $P_d$
on d vertices is p-prohibited for all
$P_d$
on d vertices is p-prohibited for all
 \begin{align} p\in \left[\dfrac{1}{1+2\cos(\pi/(d+1))}, 1-\dfrac{1}{1+2\cos(\pi/(d+1))}\right]. \end{align}
\begin{align} p\in \left[\dfrac{1}{1+2\cos(\pi/(d+1))}, 1-\dfrac{1}{1+2\cos(\pi/(d+1))}\right]. \end{align}
Proof. It is a well-known fact from spectral graph theory that the spectrum of the adjacency matrix of
![]() $P_d$
, the path on d vertices is the multiset
$P_d$
, the path on d vertices is the multiset
![]() $\left\{2\cos\left(\frac{\pi k}{d+1}\right) \,:\, k\in\left\{1,\ldots,d\right\}\right\}$
. See, for example, [Reference Cvetković, Rowlinson and Simić8]. In particular, the minimum such eigenvalue is
$\left\{2\cos\left(\frac{\pi k}{d+1}\right) \,:\, k\in\left\{1,\ldots,d\right\}\right\}$
. See, for example, [Reference Cvetković, Rowlinson and Simić8]. In particular, the minimum such eigenvalue is
![]() $-2\cos(\pi/(d+1))$
. Lemma 20 gives that
$-2\cos(\pi/(d+1))$
. Lemma 20 gives that
![]() $P_d$
is p-prohibited for p in the stated range.
$P_d$
is p-prohibited for p in the stated range.
Finally, we prove Lemma 31.
Proof of Lemma 31. Since the sequence
![]() $\left\{\frac{1}{1+2\cos(\pi/(d+1))}\right\}$
is monotone decreasing and converges to
$\left\{\frac{1}{1+2\cos(\pi/(d+1))}\right\}$
is monotone decreasing and converges to
![]() $1/3$
, there exists a positive integer
$1/3$
, there exists a positive integer
![]() $d = d_p$
so that
$d = d_p$
so that
![]() $P_d$
is p-prohibited. Let K
′ be the sub-CRG from Proposition 34 and write G for its underlying graph. Then by construction, G has degree at most
$P_d$
is p-prohibited. Let K
′ be the sub-CRG from Proposition 34 and write G for its underlying graph. Then by construction, G has degree at most
Let C be any component of G. Since
![]() $P_d$
is p-prohibited, C has diameter at most
$P_d$
is p-prohibited, C has diameter at most
![]() $d-1$
. It follows that
$d-1$
. It follows that
as desired.
3.2. Forbidding a random graph
Now we proceed to prove our main result, Theorem 4. First, recall that Theorem 7 says that if
![]() $F'\sim{\mathbb{G}}(n^{\prime}_0,p_0)$
then a.a.s.,
$F'\sim{\mathbb{G}}(n^{\prime}_0,p_0)$
then a.a.s.,
This is useful because in the proof of Lemma 37, we repeatedly decompose induced subgraphs of a random graph of order
![]() $n_0\gg n^{\prime}_0$
. An essential tool is the following, which is a restatement of Theorem 4.4 from [13]. Recall from (9) that
$n_0\gg n^{\prime}_0$
. An essential tool is the following, which is a restatement of Theorem 4.4 from [13]. Recall from (9) that
![]() $p^*=\frac{\log (1-p_0)}{\log(p_0(1-p_0))}$
.
$p^*=\frac{\log (1-p_0)}{\log(p_0(1-p_0))}$
.
Lemma 36
(Thomason [13]). Let K be a CRG and define
![]() ${\mathcal{H}}$
to be the hereditary property of graphs, G, such that
${\mathcal{H}}$
to be the hereditary property of graphs, G, such that
![]() $G\mapsto K$
. For all
$G\mapsto K$
. For all
![]() $p_0\in (0,1)$
,
$p_0\in (0,1)$
,
Lemma 37. Let
![]() $p_0$
and
$p_0$
and
![]() $\varepsilon$
be fixed such that
$\varepsilon$
be fixed such that
![]() $p_0\in (0,1)$
and
$p_0\in (0,1)$
and
![]() $\varepsilon\in (0,1)$
. Moreover, fix
$\varepsilon\in (0,1)$
. Moreover, fix
![]() ${\mathcal{B}}$
to be a finite set of CRGs. If
${\mathcal{B}}$
to be a finite set of CRGs. If
![]() $F\sim{\mathbb{G}}(n_0,p_0)$
, the following holds a.a.s. as
$F\sim{\mathbb{G}}(n_0,p_0)$
, the following holds a.a.s. as
![]() $n_0\to\infty$
: For all CRGs K such that all components of K lie in
$n_0\to\infty$
: For all CRGs K such that all components of K lie in
![]() ${\mathcal{B}}$
and
${\mathcal{B}}$
and
![]() $F\not\mapsto K$
, then
$F\not\mapsto K$
, then
 \begin{align} (1+\varepsilon)\, g_{K}\left(p^*\right) \geq\dfrac{2\log n_0}{-\log(p_0(1-p_0))\cdot n_0} . \end{align}
\begin{align} (1+\varepsilon)\, g_{K}\left(p^*\right) \geq\dfrac{2\log n_0}{-\log(p_0(1-p_0))\cdot n_0} . \end{align}
Proof. For any function
![]() $\mu\,:\,{\mathcal{B}}\to\{0,1,\dots\}$
, define the CRG,
$\mu\,:\,{\mathcal{B}}\to\{0,1,\dots\}$
, define the CRG,
![]() $K_{\mu}$
as follows:
$K_{\mu}$
as follows:
That is,
![]() $K_{\mu}$
consists of a disjoint union of
$K_{\mu}$
consists of a disjoint union of
![]() $\mu(B)$
copies of B, for all
$\mu(B)$
copies of B, for all
![]() $B\in{\mathcal{B}}$
. For any induced subgraph G of the random graph
$B\in{\mathcal{B}}$
. For any induced subgraph G of the random graph
![]() $F\sim{\mathbb{G}}(n_0,p_0)$
and any CRG K, we will denote the event that G embeds into K by
$F\sim{\mathbb{G}}(n_0,p_0)$
and any CRG K, we will denote the event that G embeds into K by
![]() $[G\mapsto K]$
. Additionally, let
$[G\mapsto K]$
. Additionally, let
Let
To prove the desired claim, it is equivalent to show that the probability that
![]() $F\not\mapsto K_{\mu}$
for all
$F\not\mapsto K_{\mu}$
for all
![]() $\mu\in{\mathcal{B}}_0$
goes to zero. That is,
$\mu\in{\mathcal{B}}_0$
goes to zero. That is,
 \begin{align} \lim_{n_0\to\infty} {\mathbb{P}}\left[ \bigcup_{\mu\in{\mathcal{B}}_0} \overline{E_{\mu}} \right] = 0. \end{align}
\begin{align} \lim_{n_0\to\infty} {\mathbb{P}}\left[ \bigcup_{\mu\in{\mathcal{B}}_0} \overline{E_{\mu}} \right] = 0. \end{align}
Recall
![]() $F\sim{\mathbb{G}}(n_0,p_0)$
. We will partition V(F) by setting
$F\sim{\mathbb{G}}(n_0,p_0)$
. We will partition V(F) by setting
and let
![]() $I_1,\ldots,I_C$
be an equipartition of V(F), i.e.,
$I_1,\ldots,I_C$
be an equipartition of V(F), i.e.,
![]() $|I_k|\in\{\lfloor n_0/C\rfloor,\lceil n_0/C\rceil\}$
for
$|I_k|\in\{\lfloor n_0/C\rfloor,\lceil n_0/C\rceil\}$
for
![]() $k\in \{1,\ldots,C\}$
. Let
$k\in \{1,\ldots,C\}$
. Let
![]() $n^{\prime}_0=\lceil n_0/C\rceil$
.
$n^{\prime}_0=\lceil n_0/C\rceil$
.
For any
![]() $B\in{\mathcal{B}}$
, set
$B\in{\mathcal{B}}$
, set
 \begin{align*} m_B \,:\!=\, \left\lfloor \dfrac{(1+\varepsilon/2)\cdot (n_0/C) \cdot \left(-\log(p_0(1-p_0))\right) \cdot g_B(p^*)}{2\log (n_0/C)} \right\rfloor . \end{align*}
\begin{align*} m_B \,:\!=\, \left\lfloor \dfrac{(1+\varepsilon/2)\cdot (n_0/C) \cdot \left(-\log(p_0(1-p_0))\right) \cdot g_B(p^*)}{2\log (n_0/C)} \right\rfloor . \end{align*}
We expect to be able to
![]() $(m_B\cdot B)$
-colour a
$(m_B\cdot B)$
-colour a
![]() ${\mathbb{G}}(n^{\prime}_0, p_0)$
graph (hence a
${\mathbb{G}}(n^{\prime}_0, p_0)$
graph (hence a
![]() ${\mathbb{G}}(n^{\prime}_0-1, p_0)$
graph as well). Now for any
${\mathbb{G}}(n^{\prime}_0-1, p_0)$
graph as well). Now for any
![]() $k\in\{1,\ldots,C\}$
and any
$k\in\{1,\ldots,C\}$
and any
![]() $B\in{\mathcal{B}}$
, we define the event
$B\in{\mathcal{B}}$
, we define the event
In other words,
![]() $E_{k,B}$
is the event that the subgraph of F that is induced by vertices in
$E_{k,B}$
is the event that the subgraph of F that is induced by vertices in
![]() $I_k$
is colourable by
$I_k$
is colourable by
![]() $m_B$
copies of the CRG B.
$m_B$
copies of the CRG B.
The induced subgraphs
![]() $F[I_1],\dots,F[I_C]$
are each independently sampled according to the Erdős–Rényi random graph model
$F[I_1],\dots,F[I_C]$
are each independently sampled according to the Erdős–Rényi random graph model
![]() ${\mathbb{G}}(n^{\prime}_0,p_0)$
. Moreover, the number of events of the form
${\mathbb{G}}(n^{\prime}_0,p_0)$
. Moreover, the number of events of the form
![]() $E_{k,B}$
is equal to
$E_{k,B}$
is equal to
![]() $C\cdot |{\mathcal{B}}|$
, which is bounded as a function of the constants
$C\cdot |{\mathcal{B}}|$
, which is bounded as a function of the constants
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $|\mathcal{B}|$
.
$|\mathcal{B}|$
.
For any
![]() $K\in{\mathcal{B}}$
, the property of all graphs G such that
$K\in{\mathcal{B}}$
, the property of all graphs G such that
![]() $G\mapsto K$
is not satisfied by all graphs. Then by Theorem 7 and Lemma 36, since the number of vertices in each
$G\mapsto K$
is not satisfied by all graphs. Then by Theorem 7 and Lemma 36, since the number of vertices in each
![]() $I_k$
uniformly tends to
$I_k$
uniformly tends to
![]() $\infty$
,
$\infty$
,
 \begin{align} \lim_{n_0\to\infty} {\mathbb{P}}\left[\bigcup_{k\in\{1,\ldots,C\}} \bigcup_{B\in{\mathcal{B}}} \overline{E_{k,B}}\right] = 0. \end{align}
\begin{align} \lim_{n_0\to\infty} {\mathbb{P}}\left[\bigcup_{k\in\{1,\ldots,C\}} \bigcup_{B\in{\mathcal{B}}} \overline{E_{k,B}}\right] = 0. \end{align}
It suffices to show that
because then (14) will imply (13) and complete the proof.
Indeed, suppose
![]() $\mu\in {\mathcal{B}}_0$
and suppose
$\mu\in {\mathcal{B}}_0$
and suppose
![]() $\varphi_{k,B}$
are embeddings defined by the events
$\varphi_{k,B}$
are embeddings defined by the events
![]() $E_{k,B}$
, for all
$E_{k,B}$
, for all
![]() $k\in \{1,\ldots,C\}$
and all
$k\in \{1,\ldots,C\}$
and all
![]() $B\in{\mathcal{B}}$
. Further, for any
$B\in{\mathcal{B}}$
. Further, for any
![]() $B\in{\mathcal{B}}$
, let
$B\in{\mathcal{B}}$
, let
We will show that if
![]() $\sum_{B\in{\mathcal{B}}} M_B\geq C$
, then F can be coloured by
$\sum_{B\in{\mathcal{B}}} M_B\geq C$
, then F can be coloured by
![]() $M_B$
copies of
$M_B$
copies of
![]() $m_B\cdot B$
, over all
$m_B\cdot B$
, over all
![]() $B\in{\mathcal{B}}$
, and so
$B\in{\mathcal{B}}$
, and so
![]() $F\mapsto K_{\mu}$
. We begin by summing the
$F\mapsto K_{\mu}$
. We begin by summing the
![]() $M_B$
’s.
$M_B$
’s.
 \begin{align*} \sum_{B\in{\mathcal{B}}} M_B &= \sum_{B\in{\mathcal{B}}} \left\lfloor\dfrac{\mu(B)}{m_B}\right\rfloor\\ &\geq \sum_{B\in{\mathcal{B}}} \left(\dfrac{\mu(B)}{m_B}-1\right) \\ &= -|{\mathcal{B}}| + \sum_{B\in{\mathcal{B}}} \dfrac{\mu(B)\cdot 2\log(n_0/C)}{(1+\varepsilon/2)\cdot (n_0/C) \cdot \left(-\log(p_0(1-p_0))\right)\cdot g_B(p^*)} \\ &= -|{\mathcal{B}}| + \dfrac{2C\log(n_0/C)}{(1+\varepsilon/2)n_0} \cdot \sum_{B\in{\mathcal{B}}} \dfrac{\mu(B)}{-\log(p_0(1-p_0))\cdot g_B(p^*)} . \end{align*}
\begin{align*} \sum_{B\in{\mathcal{B}}} M_B &= \sum_{B\in{\mathcal{B}}} \left\lfloor\dfrac{\mu(B)}{m_B}\right\rfloor\\ &\geq \sum_{B\in{\mathcal{B}}} \left(\dfrac{\mu(B)}{m_B}-1\right) \\ &= -|{\mathcal{B}}| + \sum_{B\in{\mathcal{B}}} \dfrac{\mu(B)\cdot 2\log(n_0/C)}{(1+\varepsilon/2)\cdot (n_0/C) \cdot \left(-\log(p_0(1-p_0))\right)\cdot g_B(p^*)} \\ &= -|{\mathcal{B}}| + \dfrac{2C\log(n_0/C)}{(1+\varepsilon/2)n_0} \cdot \sum_{B\in{\mathcal{B}}} \dfrac{\mu(B)}{-\log(p_0(1-p_0))\cdot g_B(p^*)} . \end{align*}
By Proposition 27,
By the definition of
![]() ${\mathcal{B}}_0$
,
${\mathcal{B}}_0$
,
 \begin{align*} \sum_{B\in{\mathcal{B}}} M_B &\geq -|{\mathcal{B}}| + \dfrac{2C\log(n_0/C)}{(1+\varepsilon/2)n_0} \cdot \dfrac{(1+\varepsilon)n_0}{2\log n_0} \\ &= -|{\mathcal{B}}| + C \left(1 - \frac{\log C}{\log n_0}\right) \left(1 + \frac{\varepsilon}{2+\varepsilon}\right) \\ &= C + C \left(\frac{\varepsilon}{2+\varepsilon} - \frac{2+2\varepsilon}{2+\varepsilon}\cdot\frac{\log C}{\log n_0}\right) - |{\mathcal{B}}|. \end{align*}
\begin{align*} \sum_{B\in{\mathcal{B}}} M_B &\geq -|{\mathcal{B}}| + \dfrac{2C\log(n_0/C)}{(1+\varepsilon/2)n_0} \cdot \dfrac{(1+\varepsilon)n_0}{2\log n_0} \\ &= -|{\mathcal{B}}| + C \left(1 - \frac{\log C}{\log n_0}\right) \left(1 + \frac{\varepsilon}{2+\varepsilon}\right) \\ &= C + C \left(\frac{\varepsilon}{2+\varepsilon} - \frac{2+2\varepsilon}{2+\varepsilon}\cdot\frac{\log C}{\log n_0}\right) - |{\mathcal{B}}|. \end{align*}
With
![]() $\varepsilon$
fixed and
$\varepsilon$
fixed and
![]() $n_0 \gg C \gg |{\mathcal{B}}|$
, we have
$n_0 \gg C \gg |{\mathcal{B}}|$
, we have
![]() $\sum_{B\in{\mathcal{B}}} M_B \geq C$
, as desired. Thus, the index set
$\sum_{B\in{\mathcal{B}}} M_B \geq C$
, as desired. Thus, the index set
![]() $\{1,\ldots,C\}$
may be partitioned as
$\{1,\ldots,C\}$
may be partitioned as
so that
![]() $|S_B|\leq M_B$
, for each
$|S_B|\leq M_B$
, for each
![]() $B\in{\mathcal{B}}$
. Also, for each
$B\in{\mathcal{B}}$
. Also, for each
![]() $B\in{\mathcal{B}}$
, we combine the embeddings
$B\in{\mathcal{B}}$
, we combine the embeddings
![]() $\varphi_{B,k}$
for all
$\varphi_{B,k}$
for all
![]() $k\in S_B$
to form an embedding
$k\in S_B$
to form an embedding
![]()
Combining all such embeddings,
![]() $F\mapsto K_\mu$
, as desired. So
$F\mapsto K_\mu$
, as desired. So
This completes the proof of the desired claim.
Finally, we are ready to prove Theorem 4.
3.3. Proof of Theorem 4
Formally, our goal is to show that for each
![]() $\varepsilon\in(0,1)$
, the following occurs a.a.s. as
$\varepsilon\in(0,1)$
, the following occurs a.a.s. as
![]() $n_0\rightarrow\infty$
:
$n_0\rightarrow\infty$
:
 \begin{align} \sup_{p\in I}\left|{\textrm{ed}}_{{\mathcal{H}}}(p) \left(\dfrac{2\log n_0}{n_0} \cdot \min\left\{\dfrac{p}{-\log(1-p_0)}, \dfrac{1-p}{-\log p_0}\right\}\right)^{-1} - 1\right|<\varepsilon , \end{align}
\begin{align} \sup_{p\in I}\left|{\textrm{ed}}_{{\mathcal{H}}}(p) \left(\dfrac{2\log n_0}{n_0} \cdot \min\left\{\dfrac{p}{-\log(1-p_0)}, \dfrac{1-p}{-\log p_0}\right\}\right)^{-1} - 1\right|<\varepsilon , \end{align}
where
 \begin{align*} I = \left\{ \begin{array}{rl} \left[0,1\right] , & \mbox{if $p^*\in [1-\varphi^{-1},\varphi^{-1}]$;} \\ \left[1/3,1\right] , & \mbox{if $p^*\in [0,1-\varphi^{-1})$;} \\ \left[0,2/3\right] , & \mbox{if $p^*\in (\varphi^{-1},1]$.} \end{array}\right. \end{align*}
\begin{align*} I = \left\{ \begin{array}{rl} \left[0,1\right] , & \mbox{if $p^*\in [1-\varphi^{-1},\varphi^{-1}]$;} \\ \left[1/3,1\right] , & \mbox{if $p^*\in [0,1-\varphi^{-1})$;} \\ \left[0,2/3\right] , & \mbox{if $p^*\in (\varphi^{-1},1]$.} \end{array}\right. \end{align*}
We first establish an upper bound for
![]() ${\textrm{ed}}_{{\mathcal{H}}}(p)$
for all
${\textrm{ed}}_{{\mathcal{H}}}(p)$
for all
![]() $p\in [0,1]$
. By the main result in [Reference Bollobás5], if
$p\in [0,1]$
. By the main result in [Reference Bollobás5], if
![]() $F\sim{\mathbb{G}}(n_0,p_0)$
, then a.a.s. as
$F\sim{\mathbb{G}}(n_0,p_0)$
, then a.a.s. as
![]() $n_0\rightarrow\infty$
,
$n_0\rightarrow\infty$
,
 \begin{align*} \chi(F)-1 &\geq (1-\varepsilon/2)\; \dfrac{n_0}{2 \log_{1/(1-p_0)} n_0} , \\ \chi(F^c)-1 &\geq (1-\varepsilon/2)\; \dfrac{n_0}{2 \log_{1/p_0} n_0} . \end{align*}
\begin{align*} \chi(F)-1 &\geq (1-\varepsilon/2)\; \dfrac{n_0}{2 \log_{1/(1-p_0)} n_0} , \\ \chi(F^c)-1 &\geq (1-\varepsilon/2)\; \dfrac{n_0}{2 \log_{1/p_0} n_0} . \end{align*}
Clearly F does not map into
![]() $\chi(F)-1$
white vertices or
$\chi(F)-1$
white vertices or
![]() $\chi(F^c)-1$
black vertices. By, for example, Theorem 10, and the fact that
$\chi(F^c)-1$
black vertices. By, for example, Theorem 10, and the fact that
![]() $1/(1-\varepsilon/2) < 1+\varepsilon$
, then the following occurs a.a.s.:
$1/(1-\varepsilon/2) < 1+\varepsilon$
, then the following occurs a.a.s.:
 \begin{align} {\textrm{ed}}_{{\mathcal{H}}}(p) & \leq (1+\varepsilon)\; \min\left\{\dfrac{p}{n_0/(2 \log_{1/(1-p_0)} n_0)}, \dfrac{1-p}{n_0/(2 \log_{1/p_0} n_0)}\right\} \nonumber \\[5pt] & = (1+\varepsilon)\; \dfrac{2\log n_0}{n_0} \cdot \min\left\{\dfrac{p}{-\log(1-p_0)}, \dfrac{1-p}{-\log p_0}\right\} . \end{align}
\begin{align} {\textrm{ed}}_{{\mathcal{H}}}(p) & \leq (1+\varepsilon)\; \min\left\{\dfrac{p}{n_0/(2 \log_{1/(1-p_0)} n_0)}, \dfrac{1-p}{n_0/(2 \log_{1/p_0} n_0)}\right\} \nonumber \\[5pt] & = (1+\varepsilon)\; \dfrac{2\log n_0}{n_0} \cdot \min\left\{\dfrac{p}{-\log(1-p_0)}, \dfrac{1-p}{-\log p_0}\right\} . \end{align}
We now find a lower bound to match Inequality (16) over the interval I as stated above. We will do this by finding the lower bound for
![]() $p\in (1/3,2/3)$
and then use concavity show how this extends to I in the various cases.
$p\in (1/3,2/3)$
and then use concavity show how this extends to I in the various cases.
We will choose a
![]() $\tilde{p}\in (1/3,2/3)$
depending on the case:
$\tilde{p}\in (1/3,2/3)$
depending on the case:
 \begin{align*} \tilde{p} &\,:\!=\, \left\{ \begin{array}{rl} p^*, & \mbox{if $p^*\in (1/3,2/3)$;} \\ 1/3+\varepsilon/9, & \mbox{if $p^*\in (0,1/3]$;} \\ 2/3-\varepsilon/9, & \mbox{if $p^*\in [2/3,1)$.} \end{array} \right. \end{align*}
\begin{align*} \tilde{p} &\,:\!=\, \left\{ \begin{array}{rl} p^*, & \mbox{if $p^*\in (1/3,2/3)$;} \\ 1/3+\varepsilon/9, & \mbox{if $p^*\in (0,1/3]$;} \\ 2/3-\varepsilon/9, & \mbox{if $p^*\in [2/3,1)$.} \end{array} \right. \end{align*}
Let
![]() $K = K(\tilde{p})\in{\mathcal{K}}_{\mathcal{H}}$
be a
$K = K(\tilde{p})\in{\mathcal{K}}_{\mathcal{H}}$
be a
![]() $\tilde{p}$
-core CRG that satisfies
$\tilde{p}$
-core CRG that satisfies
![]() ${\textrm{ed}}_{{\mathcal{H}}}(\tilde{p}) = g_K(\tilde{p})$
, as guaranteed by Theorem 10.
${\textrm{ed}}_{{\mathcal{H}}}(\tilde{p}) = g_K(\tilde{p})$
, as guaranteed by Theorem 10.
Since
![]() $\tilde{p}\in (1/3,2/3)$
, Lemma 31 gives that there exists a sub-CRG
$\tilde{p}\in (1/3,2/3)$
, Lemma 31 gives that there exists a sub-CRG
![]() $K' = K'(\tilde{p},\varepsilon/4)$
of K so that
$K' = K'(\tilde{p},\varepsilon/4)$
of K so that
and whose components lie in some finite set
![]() ${\mathcal{B}} = {\mathcal{B}}(\tilde{p},\varepsilon/4)$
of CRGs.
${\mathcal{B}} = {\mathcal{B}}(\tilde{p},\varepsilon/4)$
of CRGs.
The function
![]() $g_{K'} \,:\, [0,1]\to [0,1]$
is concave down. To see this, let
$g_{K'} \,:\, [0,1]\to [0,1]$
is concave down. To see this, let
![]() $M_{K'}(p)$
be the matrix defined by the CRG K
′. Let
$M_{K'}(p)$
be the matrix defined by the CRG K
′. Let
![]() $p_1,p_2\in [0,1]$
,
$p_1,p_2\in [0,1]$
,
![]() $t\in [0,1]$
, and let
$t\in [0,1]$
, and let
![]() ${\bf x}\in\Delta_{K'}$
be the vector that witnesses the value of
${\bf x}\in\Delta_{K'}$
be the vector that witnesses the value of
![]() $g_{K'}$
at
$g_{K'}$
at
![]() $t p_1 + (1-t) p_2$
,
$t p_1 + (1-t) p_2$
,
 \begin{align*} g_{K'}\left(t p_1 + (1-t) p_2\right) &= \langle {\bf x}, M_{K'}\left(t p_1 + (1-t) p_2\right) {\bf x}\rangle \\ &= t\cdot\langle{\bf x}, M_{K'}(p_1){\bf x}\rangle + (1-t)\cdot\langle {\bf x}, M_{K'}(p_2) {\bf x}\rangle \\ &\geq t\cdot g_{K'}(p_1) + (1-t)\cdot g_{K'}(p_2) , \end{align*}
\begin{align*} g_{K'}\left(t p_1 + (1-t) p_2\right) &= \langle {\bf x}, M_{K'}\left(t p_1 + (1-t) p_2\right) {\bf x}\rangle \\ &= t\cdot\langle{\bf x}, M_{K'}(p_1){\bf x}\rangle + (1-t)\cdot\langle {\bf x}, M_{K'}(p_2) {\bf x}\rangle \\ &\geq t\cdot g_{K'}(p_1) + (1-t)\cdot g_{K'}(p_2) , \end{align*}
establishing the concavity of
![]() $g_{K'}$
. Since
$g_{K'}$
. Since
![]() $g_{K'}(0),g_{K'}(1)\geq 0$
, the graph of
$g_{K'}(0),g_{K'}(1)\geq 0$
, the graph of
![]() $g_{K'}$
lies above the line segment from (0,0) to
$g_{K'}$
lies above the line segment from (0,0) to
![]() $(p^*,g_{K'}(p^*))$
and above the line segment from
$(p^*,g_{K'}(p^*))$
and above the line segment from
![]() $(p^*,g_{K'}(p^*))$
to (1,0). So, for every
$(p^*,g_{K'}(p^*))$
to (1,0). So, for every
![]() $p\in [0,1]$
,
$p\in [0,1]$
,
 \begin{align} g_{K'}(p) \geq g_{K'}(p^*)\cdot \min\left\{\dfrac{p}{p^*}, \dfrac{1-p}{1-p^*}\right\} . \end{align}
\begin{align} g_{K'}(p) \geq g_{K'}(p^*)\cdot \min\left\{\dfrac{p}{p^*}, \dfrac{1-p}{1-p^*}\right\} . \end{align}
Also by Lemma 37 (recall that
![]() $p^*=\frac{\log (1-p_0)}{\log(p_0(1-p_0))}$
from (9)), the following is true a.a.s.:
$p^*=\frac{\log (1-p_0)}{\log(p_0(1-p_0))}$
from (9)), the following is true a.a.s.:
 \begin{align} g_{K'}(p^*) \geq (1-\varepsilon/4)\cdot\dfrac{2\log n_0}{-\log(p_0(1-p_0)) \cdot n_0}. \end{align}
\begin{align} g_{K'}(p^*) \geq (1-\varepsilon/4)\cdot\dfrac{2\log n_0}{-\log(p_0(1-p_0)) \cdot n_0}. \end{align}
Combining (17), (18), and (19),
 \begin{align} {\textrm{ed}}_{\mathcal{H}}(\tilde{p}) &= g_K(\tilde{p}) \nonumber \\[5pt] &\geq \frac{1}{1+\varepsilon/4}\, g_{K'}(\tilde{p}) \nonumber \\[5pt] &\geq \frac{1}{1+\varepsilon/4}\, g_{K'}(p^*)\cdot \min\left\{\dfrac{\tilde{p}}{p^*}, \dfrac{1-\tilde{p}}{1-p^*}\right\} \nonumber \\[5pt] &\geq \frac{1-\varepsilon/4}{1+\varepsilon/4}\cdot \frac{2\log n_0}{-\log (p_0(1-p_0))\cdot n_0}\cdot \min\left\{\dfrac{\tilde{p}}{p^*}, \dfrac{1-\tilde{p}}{1-p^*}\right\} \nonumber \\[5pt] &\geq (1-\varepsilon/2)\, \frac{2\log n_0}{-\log (p_0(1-p_0))\cdot n_0}\cdot \min\left\{\dfrac{\tilde{p}}{p^*}, \dfrac{1-\tilde{p}}{1-p^*}\right\} . \end{align}
\begin{align} {\textrm{ed}}_{\mathcal{H}}(\tilde{p}) &= g_K(\tilde{p}) \nonumber \\[5pt] &\geq \frac{1}{1+\varepsilon/4}\, g_{K'}(\tilde{p}) \nonumber \\[5pt] &\geq \frac{1}{1+\varepsilon/4}\, g_{K'}(p^*)\cdot \min\left\{\dfrac{\tilde{p}}{p^*}, \dfrac{1-\tilde{p}}{1-p^*}\right\} \nonumber \\[5pt] &\geq \frac{1-\varepsilon/4}{1+\varepsilon/4}\cdot \frac{2\log n_0}{-\log (p_0(1-p_0))\cdot n_0}\cdot \min\left\{\dfrac{\tilde{p}}{p^*}, \dfrac{1-\tilde{p}}{1-p^*}\right\} \nonumber \\[5pt] &\geq (1-\varepsilon/2)\, \frac{2\log n_0}{-\log (p_0(1-p_0))\cdot n_0}\cdot \min\left\{\dfrac{\tilde{p}}{p^*}, \dfrac{1-\tilde{p}}{1-p^*}\right\} . \end{align}
Case 1.
![]() $p_0\in (1-\varphi^{-1},\varphi^{-1})$
$p_0\in (1-\varphi^{-1},\varphi^{-1})$
![]() $\Longleftrightarrow$
$\Longleftrightarrow$
![]() $p^*\in (1/3,2/3)$
.
$p^*\in (1/3,2/3)$
.
In this case,
![]() $\tilde{p} = p^*$
. By (20),
$\tilde{p} = p^*$
. By (20),
By the concavity of
![]() ${\textrm{ed}}_{{\mathcal{H}}}(p)$
and the fact that
${\textrm{ed}}_{{\mathcal{H}}}(p)$
and the fact that
![]() ${\textrm{ed}}_{{\mathcal{H}}}(0)={\textrm{ed}}_{{\mathcal{H}}}(1)=0$
, if
${\textrm{ed}}_{{\mathcal{H}}}(0)={\textrm{ed}}_{{\mathcal{H}}}(1)=0$
, if
![]() $p\in[0,1]$
then
$p\in[0,1]$
then
 \begin{align*} {\textrm{ed}}_{{\mathcal{H}}}(p) &\geq (1-\varepsilon/2)\, \frac{2\log n_0}{-\log (p_0(1-p_0))\cdot n_0}\cdot \min\left\{\dfrac{p}{p^*}, \dfrac{1-p}{1-p^*}\right\} \\[5pt] &= (1-\varepsilon/2)\, \frac{2\log n_0}{n_0}\cdot \min\left\{\dfrac{p}{-\log (1-p_0)}, \dfrac{1-p}{-\log p_0}\right\} . \end{align*}
\begin{align*} {\textrm{ed}}_{{\mathcal{H}}}(p) &\geq (1-\varepsilon/2)\, \frac{2\log n_0}{-\log (p_0(1-p_0))\cdot n_0}\cdot \min\left\{\dfrac{p}{p^*}, \dfrac{1-p}{1-p^*}\right\} \\[5pt] &= (1-\varepsilon/2)\, \frac{2\log n_0}{n_0}\cdot \min\left\{\dfrac{p}{-\log (1-p_0)}, \dfrac{1-p}{-\log p_0}\right\} . \end{align*}
This satisfies (15) for all
![]() $p\in [0,1]$
, completing the proof in this case.
$p\in [0,1]$
, completing the proof in this case.
Case 2.
![]() $p_0\in (0,1-\varphi^{-1}]$
$p_0\in (0,1-\varphi^{-1}]$
![]() $\Longleftrightarrow$
$\Longleftrightarrow$
![]() $p^*\in (0,1/3]$
.
$p^*\in (0,1/3]$
.
In this case,
![]() $\tilde{p} = 1/3 + \varepsilon/9 > p^*$
. By (20),
$\tilde{p} = 1/3 + \varepsilon/9 > p^*$
. By (20),
By the concavity of
![]() ${\textrm{ed}}_{{\mathcal{H}}}(p)$
and the fact that
${\textrm{ed}}_{{\mathcal{H}}}(p)$
and the fact that
![]() ${\textrm{ed}}_{{\mathcal{H}}}(0)={\textrm{ed}}_{{\mathcal{H}}}(1)=0$
, if
${\textrm{ed}}_{{\mathcal{H}}}(0)={\textrm{ed}}_{{\mathcal{H}}}(1)=0$
, if
![]() $p\in[0,1]$
then
$p\in[0,1]$
then
Observe that
![]() $-\log (p_0(1-p_0)) (1-p^*) = -\log p_0$
. Substituting
$-\log (p_0(1-p_0)) (1-p^*) = -\log p_0$
. Substituting
![]() $\tilde{p}=1/3+\varepsilon/9$
and
$\tilde{p}=1/3+\varepsilon/9$
and
![]() $p=1/3$
,
$p=1/3$
,
 \begin{align*} {\textrm{ed}}_{{\mathcal{H}}}(1/3) &\geq (1-\varepsilon/2)\, \frac{2\log n_0}{-\log (p_0(1-p_0))\cdot n_0}\cdot \dfrac{2/3-\varepsilon/9}{1-p^*}\cdot \dfrac{1/3}{1/3+\varepsilon/9} \\[5pt] &= \dfrac{(1-\varepsilon/2)(1/3-\varepsilon/18)}{1/3+\varepsilon/9}\cdot \frac{2\log n_0}{n_0}\cdot \dfrac{2/3}{-\log p_0} \\[5pt] &\geq (1-\varepsilon)\, \frac{2\log n_0}{n_0}\cdot \dfrac{2/3}{-\log p_0} . \end{align*}
\begin{align*} {\textrm{ed}}_{{\mathcal{H}}}(1/3) &\geq (1-\varepsilon/2)\, \frac{2\log n_0}{-\log (p_0(1-p_0))\cdot n_0}\cdot \dfrac{2/3-\varepsilon/9}{1-p^*}\cdot \dfrac{1/3}{1/3+\varepsilon/9} \\[5pt] &= \dfrac{(1-\varepsilon/2)(1/3-\varepsilon/18)}{1/3+\varepsilon/9}\cdot \frac{2\log n_0}{n_0}\cdot \dfrac{2/3}{-\log p_0} \\[5pt] &\geq (1-\varepsilon)\, \frac{2\log n_0}{n_0}\cdot \dfrac{2/3}{-\log p_0} . \end{align*}
Again by concavity,
This matches the upper bound (16) for all
![]() $p\in [1/3,1]$
and, in fact, if
$p\in [1/3,1]$
and, in fact, if
![]() $p^*=1/3$
, then it matches the upper bound for all
$p^*=1/3$
, then it matches the upper bound for all
![]() $p\in [0,1]$
. This completes the proof in this case.
$p\in [0,1]$
. This completes the proof in this case.
Case 3.
![]() $p_0\in [\varphi^{-1},1)$
$p_0\in [\varphi^{-1},1)$
![]() $\Longleftrightarrow$
$\Longleftrightarrow$
![]() $p^*\in [2/3,1)$
.
$p^*\in [2/3,1)$
.
This case may be shown with a similar argument as Case 2. In this case,
![]() $\tilde{p} = 2/3-\varepsilon/9 < p^*$
. By (20), the concavity of
$\tilde{p} = 2/3-\varepsilon/9 < p^*$
. By (20), the concavity of
![]() ${\textrm{ed}}_{\mathcal{H}}(p)$
, and substituting
${\textrm{ed}}_{\mathcal{H}}(p)$
, and substituting
![]() $\tilde{p}=2/3-\varepsilon/9$
and
$\tilde{p}=2/3-\varepsilon/9$
and
![]() $p=2/3$
,
$p=2/3$
,
This matches the upper bound (16) for all
![]() $p\in [0,2/3]$
and if
$p\in [0,2/3]$
and if
![]() $p^*=2/3$
, then it matches the upper bound for all
$p^*=2/3$
, then it matches the upper bound for all
![]() $p\in[0,1]$
. This completes the proof in this case and the proof of Theorem 4.
$p\in[0,1]$
. This completes the proof in this case and the proof of Theorem 4.
4. Discussion
In the process of proving the main result, Theorem 4, we have developed a number of observations that apply generally to computing edit distance functions. Lemma 20 gives a general condition for which a CRG is p-prohibited and Theorem 23 shows that for
![]() $p\in [1-\varphi^{-1},\varphi^{-1}]$
, the only CRGs that need to be considered are dalmatian sets and their complements.
$p\in [1-\varphi^{-1},\varphi^{-1}]$
, the only CRGs that need to be considered are dalmatian sets and their complements.
In this section, we discuss some other general results.
4.1. Defining the edit distance function with a finite set of CRGs
The following was conjectured by the first author:
Conjecture 38
([Reference Martin11]). Let
![]() ${\mathcal{H}}$
be a non-trivial hereditary property. For every
${\mathcal{H}}$
be a non-trivial hereditary property. For every
![]() $\varepsilon>0$
there exists a finite set of CRGs
$\varepsilon>0$
there exists a finite set of CRGs
![]() ${\mathcal{K}}'={\mathcal{K}}'(\varepsilon,{\mathcal{H}})$
such that
${\mathcal{K}}'={\mathcal{K}}'(\varepsilon,{\mathcal{H}})$
such that
Note that this is stronger than the Marchant-Thomason result in Theorem 10 which says that, for every p there is a finite set of CRGs that define
![]() ${\textrm{ed}}_{{\mathcal{H}}}(p)$
. Conjecture 38 asserts that a single finite set will define
${\textrm{ed}}_{{\mathcal{H}}}(p)$
. Conjecture 38 asserts that a single finite set will define
![]() ${\textrm{ed}}_{{\mathcal{H}}}(p)$
for all p an arbitrary open interval in (0,1). In Theorem 39, we provide a partial answer by showing that the conjecture is true for
${\textrm{ed}}_{{\mathcal{H}}}(p)$
for all p an arbitrary open interval in (0,1). In Theorem 39, we provide a partial answer by showing that the conjecture is true for
![]() $\varepsilon\geq 1-\varphi^{-1}$
.
$\varepsilon\geq 1-\varphi^{-1}$
.
Theorem 39. Let
![]() ${\mathcal{H}}$
be a non-trivial hereditary property. There exists a finite set of CRGs,
${\mathcal{H}}$
be a non-trivial hereditary property. There exists a finite set of CRGs,
![]() ${\mathcal{K}}'={\mathcal{K}}'({\mathcal{H}})$
, such that
${\mathcal{K}}'={\mathcal{K}}'({\mathcal{H}})$
, such that
Proof. By Theorem 23, the only p-core CRGs are denoted
![]() ${\mathcal{D}}_p$
and consist of components which are dalmatian CRGs if
${\mathcal{D}}_p$
and consist of components which are dalmatian CRGs if
![]() $p\in [1-\varphi^{-1},1/2)$
, complements of dalmatian CRGs if
$p\in [1-\varphi^{-1},1/2)$
, complements of dalmatian CRGs if
![]() $p\in (1/2,\varphi^{-1}]$
, and CRGs with only grey edges if
$p\in (1/2,\varphi^{-1}]$
, and CRGs with only grey edges if
![]() $p=1/2$
.
$p=1/2$
.
It is easy to see that if
![]() $p=1/2$
and
$p=1/2$
and
![]() ${\mathcal{H}}={\textrm{Forb}}({\mathcal{F}})$
, then for any
${\mathcal{H}}={\textrm{Forb}}({\mathcal{F}})$
, then for any
![]() $F\in{\mathcal{F}}$
such that
$F\in{\mathcal{F}}$
such that
![]() $F\not\mapsto K$
, the number of vertices of K is bounded by
$F\not\mapsto K$
, the number of vertices of K is bounded by
![]() $\chi(F) + \chi(F^c)$
, so the number of such CRGs is finite. We will now show that a finite set of CRGs suffice for
$\chi(F) + \chi(F^c)$
, so the number of such CRGs is finite. We will now show that a finite set of CRGs suffice for
![]() $p\in[1-\varphi^{-1},1/2)$
. The case
$p\in[1-\varphi^{-1},1/2)$
. The case
![]() $p\in(1/2,\varphi^{-1}]$
follows by symmetry. Note that
$p\in(1/2,\varphi^{-1}]$
follows by symmetry. Note that
![]() ${\mathcal{D}}_p$
is the same for all
${\mathcal{D}}_p$
is the same for all
![]() $p\in[0,1/2)$
(that is, CRGs whose components are all dalmatian CRGs) so we denote
$p\in[0,1/2)$
(that is, CRGs whose components are all dalmatian CRGs) so we denote
![]() ${\mathcal{D}}_{0,{\mathcal{H}}} \,:\!=\, {\mathcal{D}}_p\cap{\mathcal{K}}_{{\mathcal{H}}}$
.
${\mathcal{D}}_{0,{\mathcal{H}}} \,:\!=\, {\mathcal{D}}_p\cap{\mathcal{K}}_{{\mathcal{H}}}$
.
Write
![]() ${\mathcal{H}} = {\textrm{Forb}}({\mathcal{F}})$
and, for a contradiction, let
${\mathcal{H}} = {\textrm{Forb}}({\mathcal{F}})$
and, for a contradiction, let
![]() $\{p_k\}_{k=1}^{\infty}\subset[1-\varphi^{-1},1/2)$
be an infinite set and let
$\{p_k\}_{k=1}^{\infty}\subset[1-\varphi^{-1},1/2)$
be an infinite set and let
![]() ${\mathcal{K}}' \,:\!=\, \{K_k\}_{k=1}^{\infty}\subset{\mathcal{D}}_{0,{\mathcal{H}}}$
an infinite set of CRGs such that
${\mathcal{K}}' \,:\!=\, \{K_k\}_{k=1}^{\infty}\subset{\mathcal{D}}_{0,{\mathcal{H}}}$
an infinite set of CRGs such that
![]() $K_k$
is
$K_k$
is
![]() $p_k$
-core and
$p_k$
-core and
![]() $g_{K_k}(p_k)={\textrm{ed}}_{{\mathcal{H}}}(p_k)$
.
$g_{K_k}(p_k)={\textrm{ed}}_{{\mathcal{H}}}(p_k)$
.
For all
![]() $k\geq 1$
, with
$k\geq 1$
, with
![]() $D_i$
denoting a dalmatian CRG of order i, we may write
$D_i$
denoting a dalmatian CRG of order i, we may write
where
![]() $w_k,\ell_k, c_k^{(1)},\ldots,c_k^{(\ell_k)}$
are non-negative integers and
$w_k,\ell_k, c_k^{(1)},\ldots,c_k^{(\ell_k)}$
are non-negative integers and
![]() $c_k^{(1)}\geq \cdots \geq c_k^{(\ell_k)}$
.
$c_k^{(1)}\geq \cdots \geq c_k^{(\ell_k)}$
.
For all
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $w_k+\ell_k\leq |V(F)|$
for any
$w_k+\ell_k\leq |V(F)|$
for any
![]() $F\in{\mathcal{F}}$
because otherwise
$F\in{\mathcal{F}}$
because otherwise
![]() $F\mapsto K_k$
by embedding each vertex of F into a different component of
$F\mapsto K_k$
by embedding each vertex of F into a different component of
![]() $K_k$
. Thus,
$K_k$
. Thus,
![]() $\ell_k$
is bounded by an absolute constant
$\ell_k$
is bounded by an absolute constant
![]() $\ell=\ell({\mathcal{H}})$
. So we associate each
$\ell=\ell({\mathcal{H}})$
. So we associate each
![]() $K_k$
in (21) with the
$K_k$
in (21) with the
![]() $(\ell+1)$
-tuple
$(\ell+1)$
-tuple
where
![]() $c_k^{(\ell_k+1)}=\cdots=c_k^{(\ell)}=0$
if
$c_k^{(\ell_k+1)}=\cdots=c_k^{(\ell)}=0$
if
![]() $\ell>\ell_k$
.
$\ell>\ell_k$
.
Because
![]() ${\mathcal{K}}'$
is infinite, there exists a maximum
${\mathcal{K}}'$
is infinite, there exists a maximum
![]() $m\in\{1,\ldots,\ell\}$
such that
$m\in\{1,\ldots,\ell\}$
such that
![]() $\sup_k \{c_k^{(1)}\}=\cdots=\sup_k \{c_k^{(m)}\}=\infty$
. That is, if
$\sup_k \{c_k^{(1)}\}=\cdots=\sup_k \{c_k^{(m)}\}=\infty$
. That is, if
![]() $m<\ell$
, then
$m<\ell$
, then
![]() $\sup_k \{c_k^{(m+1)}\}<\infty$
. Thus, there is a fixed (possibly empty) tuple
$\sup_k \{c_k^{(m+1)}\}<\infty$
. Thus, there is a fixed (possibly empty) tuple
![]() $\left(c_*^{(m+1)},\ldots,c_*^{(\ell)};w_*\right)$
and an infinite subsequence
$\left(c_*^{(m+1)},\ldots,c_*^{(\ell)};w_*\right)$
and an infinite subsequence
![]() $k_1,k_2,\ldots$
such that
$k_1,k_2,\ldots$
such that
![]() $K_{k_i}$
is associated with
$K_{k_i}$
is associated with
![]() $(\ell+1)$
-tuple
$(\ell+1)$
-tuple
![]() $\left(c_{k_i}^{(1)},\ldots,c_{k_i}^{(m)},c_*^{(m+1)},\ldots,c_*^{(\ell)};w_*\right)$
.
$\left(c_{k_i}^{(1)},\ldots,c_{k_i}^{(m)},c_*^{(m+1)},\ldots,c_*^{(\ell)};w_*\right)$
.
With this choice of
![]() $\left(c_*^{(m+1)},\ldots,c_*^{(\ell)};w_*\right)$
, if
$\left(c_*^{(m+1)},\ldots,c_*^{(\ell)};w_*\right)$
, if
![]() $\ell'$
is the largest entry such that
$\ell'$
is the largest entry such that
![]() $c_*^{(\ell')}\geq 1$
, then define
$c_*^{(\ell')}\geq 1$
, then define
We claim that
![]() $K_*\in{\mathcal{D}}_{0,{\mathcal{H}}}\subseteq{\mathcal{K}}_{\mathcal{H}}$
.
$K_*\in{\mathcal{D}}_{0,{\mathcal{H}}}\subseteq{\mathcal{K}}_{\mathcal{H}}$
.
If not, then there exists some
![]() $F\in{\mathcal{F}}$
and some embedding
$F\in{\mathcal{F}}$
and some embedding
![]() $\phi\,:\,V(F)\to V(K_*)$
. Let
$\phi\,:\,V(F)\to V(K_*)$
. Let
![]() $A_1,\dots,A_m$
be the preimages of the first m copies of
$A_1,\dots,A_m$
be the preimages of the first m copies of
![]() $D_\infty$
under
$D_\infty$
under
![]() $\varphi$
, respectively. Then
$\varphi$
, respectively. Then
![]() $A_1,\dots,A_m$
are independent sets in F.
$A_1,\dots,A_m$
are independent sets in F.
Let k be sufficiently large so that
![]() $c_1^k,\dots,c_m^k\geq |V(F)|$
. Then we define
$c_1^k,\dots,c_m^k\geq |V(F)|$
. Then we define
![]() $\phi'\,:\,V(F)\to V(K_k)$
by instead sending the vertices of
$\phi'\,:\,V(F)\to V(K_k)$
by instead sending the vertices of
![]() $A_i$
to distinct vertices of the dalmatian set
$A_i$
to distinct vertices of the dalmatian set
![]() $D_{c_i^k}$
, for each
$D_{c_i^k}$
, for each
![]() $i\in\{1,\ldots,m\}$
. As a result,
$i\in\{1,\ldots,m\}$
. As a result,
![]() $\phi'$
is an embedding of F into
$\phi'$
is an embedding of F into
![]() $K_k$
, a contradiction.
$K_k$
, a contradiction.
Finally by Proposition 27 and Remark 22, for all
![]() $p\in (0,1/2)$
and k chosen as above,
$p\in (0,1/2)$
and k chosen as above,
 \begin{align*} g_{K_k}(p)^{-1} &= \dfrac{w}{p} + \sum_{i=1}^m\dfrac{1}{p+(1-2p)/c_i^k} + \sum_{i=1}^{\ell-m}\dfrac{1}{p+(1-2p)/c_i} \\ &< \dfrac{w+m}{p} + \sum_{i=1}^{\ell-m}\dfrac{1}{p+(1-2p)/c_i} \\ &= g_{K_*}(p)^{-1}. \end{align*}
\begin{align*} g_{K_k}(p)^{-1} &= \dfrac{w}{p} + \sum_{i=1}^m\dfrac{1}{p+(1-2p)/c_i^k} + \sum_{i=1}^{\ell-m}\dfrac{1}{p+(1-2p)/c_i} \\ &< \dfrac{w+m}{p} + \sum_{i=1}^{\ell-m}\dfrac{1}{p+(1-2p)/c_i} \\ &= g_{K_*}(p)^{-1}. \end{align*}
The fact that
![]() $g_{K_*}(p_k) < g_{K_k}(p_k) = {\textrm{ed}}_{{\mathcal{H}}}(p_k)$
contradicts
$g_{K_*}(p_k) < g_{K_k}(p_k) = {\textrm{ed}}_{{\mathcal{H}}}(p_k)$
contradicts
![]() $K_*\in{\mathcal{K}}_{{\mathcal{H}}}$
, hence the original assumption that
$K_*\in{\mathcal{K}}_{{\mathcal{H}}}$
, hence the original assumption that
![]() ${\mathcal{K}}'$
is infinite.
${\mathcal{K}}'$
is infinite.
4.2. Paths
In Proposition 35, it is established that
![]() $P_d$
is p-prohibited for
$P_d$
is p-prohibited for
![]() $p\in\left[\frac{1}{1+2\cos(\pi/(d+1))}, 1-\frac{1}{1+2\cos(\pi/(d+1))}\right]$
. In the case of
$p\in\left[\frac{1}{1+2\cos(\pi/(d+1))}, 1-\frac{1}{1+2\cos(\pi/(d+1))}\right]$
. In the case of
![]() $d=3$
,
$d=3$
,
![]() $P_3$
is p-prohibited for p in the interval
$P_3$
is p-prohibited for p in the interval
However, Theorem 23 establishes that
![]() $P_3$
is p-prohibited if and only if p is in the interval
$P_3$
is p-prohibited if and only if p is in the interval
 \begin{align*} [1-\varphi^{-1},\varphi^{-1}] = \left[\frac{3-\sqrt{5}}{2}, \frac{\sqrt{5}-1}{2}\right] \approx [0.381966,0.618034] .\end{align*}
\begin{align*} [1-\varphi^{-1},\varphi^{-1}] = \left[\frac{3-\sqrt{5}}{2}, \frac{\sqrt{5}-1}{2}\right] \approx [0.381966,0.618034] .\end{align*}
We ask whether
![]() $P_d$
is p-prohibited over a larger interval than given in (11). See Table 1 for small values.
$P_d$
is p-prohibited over a larger interval than given in (11). See Table 1 for small values.
Table 1. Table for endpoints of an interval where
![]() $P_d$
is prohibited
$P_d$
is prohibited

Question 40. For
![]() $d\geq 4$
, what is the largest interval over which
$d\geq 4$
, what is the largest interval over which
![]() $P_d$
is p-prohibited?
$P_d$
is p-prohibited?
5. Questions and future work
5.1. p-core CRGs
Theorem 23 classifies all p-core CRGs on the interval
![]() $[1-\varphi^{-1},\varphi^{-1}]$
.
$[1-\varphi^{-1},\varphi^{-1}]$
.
Question 41. For which
![]() $a\in (0,1-\varphi^{-1})$
does there exist an elementary classification of all p-core CRGs for all
$a\in (0,1-\varphi^{-1})$
does there exist an elementary classification of all p-core CRGs for all
![]() $p\in [a,1-a]$
? Additionally, are all sufficiently large connected p-core CRGs either dalmatian CRGs (if
$p\in [a,1-a]$
? Additionally, are all sufficiently large connected p-core CRGs either dalmatian CRGs (if
![]() $p\leq 1/2$
) or the complement of a dalmatian CRG (if
$p\leq 1/2$
) or the complement of a dalmatian CRG (if
![]() $p\geq 1/2$
)?
$p\geq 1/2$
)?
A crucial part of the proof of Theorem 4 is Lemma 31, which establishes that, for
![]() $p\in (1/3,2/3)$
, a p-core CRG can be approximated so that the g function does not increase by much, but the components are bounded.
$p\in (1/3,2/3)$
, a p-core CRG can be approximated so that the g function does not increase by much, but the components are bounded.
Question 42. Does Lemma 31 hold if the interval
![]() $(1/3,2/3)$
is widened to
$(1/3,2/3)$
is widened to
![]() $(a,1-a)$
for some
$(a,1-a)$
for some
![]() $a \in (0,1/3)$
?
$a \in (0,1/3)$
?
5.2. Inhomogeneous random graphs
Since the development of graph limits, inhomogeneous generalizations
![]() ${\mathbb{G}}(n,W)$
of the Erdős–Rényi random graph models have emerged as a topic of research interest (see [Reference Lovász9]). Here,
${\mathbb{G}}(n,W)$
of the Erdős–Rényi random graph models have emerged as a topic of research interest (see [Reference Lovász9]). Here,
![]() $W\,:\,\Omega^2\to[0,1]$
is a graphon, which is a symmetric measurable function where
$W\,:\,\Omega^2\to[0,1]$
is a graphon, which is a symmetric measurable function where
![]() $\Omega$
is a probability space, frequently [0,1] equipped with the Lebesgue measure. To form a W-random graph
$\Omega$
is a probability space, frequently [0,1] equipped with the Lebesgue measure. To form a W-random graph
![]() $G\sim{\mathbb{G}}(n,W)$
, sample n elements
$G\sim{\mathbb{G}}(n,W)$
, sample n elements
![]() $x_1,\dots,x_n\sim \Omega$
independently and form a graph on
$x_1,\dots,x_n\sim \Omega$
independently and form a graph on
![]() $\{1,\ldots,n\}$
by adding edge ij independently with probability
$\{1,\ldots,n\}$
by adding edge ij independently with probability
![]() $W(x_i,x_j)$
. We may also generate a sequence of W-random graphs
$W(x_i,x_j)$
. We may also generate a sequence of W-random graphs
![]() $(G_n)_{n=1}^\infty\sim{\mathbb{G}}(\mathbb{N},W)$
adding the vertices corresponding to
$(G_n)_{n=1}^\infty\sim{\mathbb{G}}(\mathbb{N},W)$
adding the vertices corresponding to
![]() $x_1,x_2,\ldots$
, one at a time.
$x_1,x_2,\ldots$
, one at a time.
There are several questions we may ask related to the edit distance problem and inhomogeneous random graphs.
First, note that Theorem 4 implies that with
![]() $p_0\in [1-\varphi^{-1},\varphi^{-1}]$
and
$p_0\in [1-\varphi^{-1},\varphi^{-1}]$
and
![]() $(F_n)\sim {\mathbb{G}}(\mathbb{N},p_0)$
, then a.a.s. as
$(F_n)\sim {\mathbb{G}}(\mathbb{N},p_0)$
, then a.a.s. as
![]() $n_0\to\infty$
,
$n_0\to\infty$
,
where
![]() $r\,:\,\mathbb{N}\to[0,1]$
and
$r\,:\,\mathbb{N}\to[0,1]$
and
![]() $s\,:\,[0,1]\to[0,1]$
are some functions.
$s\,:\,[0,1]\to[0,1]$
are some functions.
Question 43. If W is a graphon, does equation (22) a.a.s. hold for
![]() $(F_n)\sim{\mathbb{G}}(\mathbb{N},W)$
with some suitable functions
$(F_n)\sim{\mathbb{G}}(\mathbb{N},W)$
with some suitable functions
![]() $r = r_W$
and
$r = r_W$
and
![]() $s = s_W$
?
$s = s_W$
?
For the next question, we note the following expression for the distance from a homogeneous random graph to a hereditary property. Combining Theorems 2 and 10, we see that if
![]() ${\mathcal{H}}$
is a (fixed) non-trivial hereditary property and
${\mathcal{H}}$
is a (fixed) non-trivial hereditary property and
![]() $p\in [0,1]$
, then with
$p\in [0,1]$
, then with
![]() $G_n\sim{\mathbb{G}}(n,p)$
,
$G_n\sim{\mathbb{G}}(n,p)$
,
Question 44. If instead
![]() $G_n\sim{\mathbb{G}}(n,W)$
, is there a similar expression for
$G_n\sim{\mathbb{G}}(n,W)$
, is there a similar expression for
![]() $\limsup_{n\to\infty} {\mathbb E}$
$\limsup_{n\to\infty} {\mathbb E}$
![]() $[{\textrm{dist}}(G_n,{\mathcal{H}})]$
? In particular, can we extend the functions
$[{\textrm{dist}}(G_n,{\mathcal{H}})]$
? In particular, can we extend the functions
![]() $g_K(\cdot)$
from [0,1] to the set of all graphons so that equation (23) holds?
$g_K(\cdot)$
from [0,1] to the set of all graphons so that equation (23) holds?
Acknowledgements
The authors would like to thank Jan Hladký and Josh Cooper for helpful comments.