1. INTRODUCTION
The Richtmyer–Meshkov (RM) instability occurs at the
perturbed interface between two fluids of different densities
after its interaction with a shock wave. The perturbation first grows
linearly and then goes into an intermediate nonlinear regime. When
harmonics appear, the interface can even cease being single valued as
it evolves into mushroomlike structures. To study the weakly nonlinear
regime of interfacial instability, perturbation methods are commonly
used (Holyer, 1979). It has been applied to
the RM instabilities by Zhang and Sohn (1997)
and Vandenboomgaerde et al. (2002).
As Cartesian (x, z) coordinates are used to describe
the interface z = η(x, t), only a
single-valued shape can be computed. The perturbation expansions have a
finite range of validity in time tv;
numerical simulations show that it can be estimated by
a0 kσtv =
1, where a0 k is the initial wave
steepness and σ the initial growth rate.
In Section 2, we present the principle of analytic continuation of
the perturbation expansion for single mode RM instability. In Setion 3,
some hypothesis are made to build an analytic function for the
amplitude of the perturbation. In Setion 4, this function is compared
with numerical results and experimental data. We conclude with some
remarks.
2. PERTURBATION EXPANSION FOR THE GROWTH
RATE OF A SINGLE MODE RM INSTABILITY
The full perturbation method derived by Zhang and Sohn (1997) has been drastically simplified by
Vandenboomgaerde et al. (2002).
Keeping at each order only the terms with the highest power in time
transforms the solution from an n2 to an n
algorithm at the nth order. Approximate perturbation
expansions are obtained. The validity of such approximations has been
checked by comparisons with simulations for single mode and multimode
configurations. For single-mode ones, the shape of the interface can be
written as
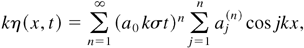
where aj(n) are real
functions that are functions of the Atwood number. This number is
defined as A = (ρ′ − ρ)/(ρ′
+ ρ), where ρ is the density of the first shocked fluid. From
expression (1) the half crest-to-crest amplitude,
a(t), of the interface can be derived:
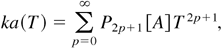
where T = a0 kσt,
and P2p+1 are polynomials of the
2pth degree. Numerical studies have shown that the truncated
series (2) diverge at T ≈ 1. On the other hand, the full
series (2) can be considered as the Taylor expansion of an unknown
analytic function F(A,T). This function
allows analytic continuation of the series (2) beyond T =
1.
3. HYPOTHESIS FOR THE ANALYTIC CONTINUATION
The P2p+1 polynomials have peculiar
shapes. By inspection among the orthogonal polynomial classes, we have
found that they fit quite well modified Jacobi's polynomials (the
Jacobi's polynomials will be hereafter noted JP). In Figure 1 are plotted the first six odd
P2p+1 polynomials and the corresponding
modified Jacobi's polynomials (noted
Q2p+1) defined as
P and Q polynomials as defined by Eqs. (2) and (3),
respectively. First ones are in full lines and the others are in dashed
lines.
As can be seen, the Q2p+1 polynomial
seems to be a good approximation of the
P2p+1 polynomial. They have the same
parity, same number of roots, and very close values for all Atwood
numbers. The main hypothesis of this study is to assume that the
discrepancies between P2p+1 and
Q2p+1 are negligible in the computation of
series (2). We shall now write
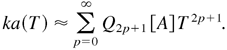
The generating function G for the Jacobi's polynomials
Q is
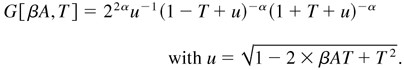
Combining Eqs. (3) and (4), an approximation for the nonlinear growth
rate of a single-mode RM instability can be built:
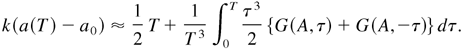
Eq. (5) has no singularity and is valid beyond T = 1. In
Figure 2, the 9th- and 11th-order Taylor
expansions (2) are plotted for three different values of the Atwood
number (full line). These curves are compared with the approximate
analytic continuation (5; dashed lines). For T < 1,
analytic function and Taylor series cannot be distinguished. After that
time, whereas expansions diverge, Eq. (5) still describes a nonlinear
growth.
Growth rates obtained by the perturbation series and the analytic
continuation for three values of the Atwood number, in full and dashed
lines, respectively.
4. COMPARISONS WITH EXPERIMENTS
The code CADMÉE (Mügler et
al., 1996; Mügler & Gauthier,
2000) has been used to estimate the growth of a perturbed
He/air interface subjected to a 1.09 Mach number shock wave. The
wave number and the amplitude are k = 224.855
m−1 and a0 = 0.35 ×
10−3 m, respectively. The low value of the Mach number
was chosen to keep the flow in a quasi-incompressible and irrotational
regime. The values of k and a0 were chosen
to start the instability in the linear regime (a0
k = 0.08) and reach easily the weakly nonlinear regime. The
choice of such parameters has been motivated by the framework of the
theoretical model. In Figure 3a, the results
of the simulations, the 9th and 11th Taylor expansions and the analytic
continuation are plotted in full, dashed, and dash-dotted lines,
respectively.
a: Growth rates obtained by the CADMÉE simulation, the Taylor
expansions, and the analytic continuation, in full, dashed, and
dash-dotted lines, respectively. b: Shapes of the interface at
different times (t = 0.25 ms, 1 ms and 1.75
ms).
Equation (5) gives a good estimate even for times beyond the
divergence of the perturbation series. This good agreement still holds
when the interface becomes multivalued (see Fig.
3b).
Another comparison has been made with an experiment done by Jacobs
and Krivets (2001). Figure
4 shows experimental results (circles) and the theoretical
result (dash-dotted line). For this experiment, the wave steepness is
a0 k = 0.23, the Mach number is equal to
1.3 and the two gases are air and SF6.
Growth of the Jacobs and Krivets (2001)
experiment (circles) versus
scaled time. Growth from the analytic continuation (dash-dotted
line).
Once again, analytic continuation of the nonlinear growth rates
obtained by the approximate perturbation method gives a very good
estimate of the experimental results. This good agreement still holds
in the intermediate nonlinear regime for values of
a(t)k larger than one.
5. CONCLUDING REMARKS
We have derived an approximate analytic continuation of the
perturbation series for the single-mode RM instability. We emphasize
that no parameter is needed to build this model. For all values of the
Atwood number, the results of this model cannot be distinguished from
those of the full perturbation method before their time of divergence.
After that time, the nonlinear growth rate obtained by this model has
been compared successfully with both numerical and experimental data up
to a(t)k = 5.5.
However, it should be noticed that the limit of this model as time
t tends to infinity gives a linear growth:
This behavior at large time disagrees with the
Tα or ln T time dependence often found
for highly nonlinear RM instabilities (see Prasad et al.,
2000, and references within). This
discrepancy comes either from the approximation and hypothesis leading
to the model or from the fact that we study only a single-mode
perturbation.
