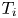1. Introduction
The need for fast computational methods in different areas of application, such as weather prediction, fluid dynamics, image and signal processing, optimization problems, large-scale interconnected systems, etc., has always been of great interest (see, e.g. [Reference Bertsekas and Tsitsiklis12]). This is simply due to the large numerical computations that are involved. Most of the problems that arise in these areas of application can be decomposed in such a way that the computations can be handled simultaneously by more powerful processors. This further led to the continuation of research on the development of parallel algorithms and high-efficient computing machines with multiprocessors, see, for example, [Reference Geer29].
The convex feasibility problem (CFP): find $x\in C=\cap _{i=1}^{n} F(T_i)$![]() , where $T_i:H\to H$
, where $T_i:H\to H$![]() , for each $i$
, for each $i$![]() , is an operator defined on a real Hilbert space $H$
, is an operator defined on a real Hilbert space $H$![]() , is a central task in mathematics. Such problems arise in different areas of application, such as road design [Reference Bauschke and Koch10], medical image reconstruction [Reference Elsner, Koltracht and Neumann28], signal processing, optimization problems, radiation therapy [Reference Censor, Elfving, Kopf and Bortfeld20], to mention but a few. There are many algorithms in the literature for approximating solutions of CFPs. One of the most commonly used algorithms is the projection algorithms that employ projections onto the underlying set, see, e.g. [Reference Bauschke and Borwein8, Reference Bauschke and Combettes9, Reference Cegielski14, Reference Cegielski, Reich and Zalas15, Reference Censor and Cegielski17, Reference Censor and Zenios18, Reference Censor, Chen, Combettes, Davidi and Herman21, Reference Combettes24, Reference Combettes25, Reference Herman32, Reference Masad and Reich40] and the references therein.The Krasnoselkii–Mann algorithm is often used when the underlying set is a finite intersection of fixed point sets of some non-expansive-type mappings, see, e.g. [Reference Browder and Petryshyn13, Reference Halpern30, Reference Kim and Xu33, Reference Lions34, Reference Mann37, Reference Marino and Xu38, Reference Reich42, Reference Reich43]. In an attempt to speed up the computation of algorithms, several authors have developed parallel algorithms for CFPs, see, e.g. [Reference Aharoni and Censor2, Reference Bauschke, Combettes and Kruk11, Reference Censor16, Reference Censor, Gordon and Gordon19]. The parallel algorithms, which can be run in a multiprocessor machine is, without doubt, better than the non-parallel algorithms that run in a machine with a single processor. This is simply because, for multiprocessor machines, the task can be distributed among the processors. However, in a case where the output of the processors needs to be synchronized before computing the next iterate, the master processor has to wait for the slowest processor to provide its output. A typical case of this is when the convex combination of the output from each processor is to be taken before moving to the next step. In essence, in synchronous parallel iterative algorithms, some of the processors will be idle for some time at each step. Moreover, if there is a failure of transmission from one of the processors, then the master processor will have to resend the last output for recomputation thereby delaying other processors. One way of preventing the problems associated with the synchronous method is via asynchronization. In asynchronous-parallel iterative algorithms, there is no need to wait for other processors in order to compute the next iterate. This method allows flexibility in such a way that a processor can use out-of-date information to compute the next output, see e.g., [Reference Zhimin, Yangyang, Ming and Wotao47]. The general method of approximating CFPs via synchronous parallel iterative algorithm can be put in the following form
, is a central task in mathematics. Such problems arise in different areas of application, such as road design [Reference Bauschke and Koch10], medical image reconstruction [Reference Elsner, Koltracht and Neumann28], signal processing, optimization problems, radiation therapy [Reference Censor, Elfving, Kopf and Bortfeld20], to mention but a few. There are many algorithms in the literature for approximating solutions of CFPs. One of the most commonly used algorithms is the projection algorithms that employ projections onto the underlying set, see, e.g. [Reference Bauschke and Borwein8, Reference Bauschke and Combettes9, Reference Cegielski14, Reference Cegielski, Reich and Zalas15, Reference Censor and Cegielski17, Reference Censor and Zenios18, Reference Censor, Chen, Combettes, Davidi and Herman21, Reference Combettes24, Reference Combettes25, Reference Herman32, Reference Masad and Reich40] and the references therein.The Krasnoselkii–Mann algorithm is often used when the underlying set is a finite intersection of fixed point sets of some non-expansive-type mappings, see, e.g. [Reference Browder and Petryshyn13, Reference Halpern30, Reference Kim and Xu33, Reference Lions34, Reference Mann37, Reference Marino and Xu38, Reference Reich42, Reference Reich43]. In an attempt to speed up the computation of algorithms, several authors have developed parallel algorithms for CFPs, see, e.g. [Reference Aharoni and Censor2, Reference Bauschke, Combettes and Kruk11, Reference Censor16, Reference Censor, Gordon and Gordon19]. The parallel algorithms, which can be run in a multiprocessor machine is, without doubt, better than the non-parallel algorithms that run in a machine with a single processor. This is simply because, for multiprocessor machines, the task can be distributed among the processors. However, in a case where the output of the processors needs to be synchronized before computing the next iterate, the master processor has to wait for the slowest processor to provide its output. A typical case of this is when the convex combination of the output from each processor is to be taken before moving to the next step. In essence, in synchronous parallel iterative algorithms, some of the processors will be idle for some time at each step. Moreover, if there is a failure of transmission from one of the processors, then the master processor will have to resend the last output for recomputation thereby delaying other processors. One way of preventing the problems associated with the synchronous method is via asynchronization. In asynchronous-parallel iterative algorithms, there is no need to wait for other processors in order to compute the next iterate. This method allows flexibility in such a way that a processor can use out-of-date information to compute the next output, see e.g., [Reference Zhimin, Yangyang, Ming and Wotao47]. The general method of approximating CFPs via synchronous parallel iterative algorithm can be put in the following form
where $F_n$![]() is a sequence of operators. However, the asynchronous version of 1.1 takes, in general, the following form:
is a sequence of operators. However, the asynchronous version of 1.1 takes, in general, the following form:
where $\tilde {x}^{n}$![]() is either $x^{n}$
is either $x^{n}$![]() or $x^{n-j}$
or $x^{n-j}$![]() for some $j\in \mathbb {N}$
for some $j\in \mathbb {N}$![]() , where $j$
, where $j$![]() is the delay amount of some processor. To fix ideas, suppose we have $p$
is the delay amount of some processor. To fix ideas, suppose we have $p$![]() processors and we set
processors and we set
to be the delay vector at each iteration step. Then, the $i^{th}$![]() component of the vector $J^{n}$
component of the vector $J^{n}$![]() gives the delay amount of the $i^{th}$
gives the delay amount of the $i^{th}$![]() processor. Moreover, suppose $\{i_n\}_{n\geq 1}\subset \mathbb {N}$
processor. Moreover, suppose $\{i_n\}_{n\geq 1}\subset \mathbb {N}$![]() , where $1\leq i_n\leq p$
, where $1\leq i_n\leq p$![]() , is an index sequence that gives information on whose output will be used to compute $x^{n+1}$
, is an index sequence that gives information on whose output will be used to compute $x^{n+1}$![]() . Then $\tilde {x}^{n}$
. Then $\tilde {x}^{n}$![]() is the last iterate sent to the $i_n^{th}$
is the last iterate sent to the $i_n^{th}$![]() processor, i.e., $\tilde {x}^{n}=x^{n-j_{i_n}^{n}}$
processor, i.e., $\tilde {x}^{n}=x^{n-j_{i_n}^{n}}$![]() . It is, however, worth mentioning that, while the asynchronous-parallel iterative algorithms have advantages over synchronous parallel iterative algorithms, they also have their own disadvantages. For instance, the asynchronous-parallel iterative algorithms are not easy to handle when it comes to convergence analysis and implementation compared to synchronous parallel iterative algorithms.
. It is, however, worth mentioning that, while the asynchronous-parallel iterative algorithms have advantages over synchronous parallel iterative algorithms, they also have their own disadvantages. For instance, the asynchronous-parallel iterative algorithms are not easy to handle when it comes to convergence analysis and implementation compared to synchronous parallel iterative algorithms.
The asynchronous-parallel iterative algorithm was first introduced by Chazan and Miranker [Reference Chazan and Miranker23] in 1969 to solve system of linear equations. Since then, many authors have successfully apply the method to solve problems in different areas, such as optimization [Reference Liu and Wright35, Reference Liu, Wright, Ré, Bittorf and Sridhar36, Reference Tai and Tseng44, Reference Zhang and Kwok46], nonlinear problems [Reference Bahi, Miellou and Rhofir4, Reference Baudet7], differential equations [Reference Aharoni and Barak1, Reference Amitai, Averbuch, Israeli and Itzikowitz3, Reference Chau, Spiteri, Guivarch and Boisson22, Reference Donzis and Aditya27] to mention but a few. Baudet [Reference Baudet7], in 1978, used totally asynchronous parallel iterative algorithm (in which arbitrary amount of delay is allowed without any bound) for $p$![]() -contractions (see, e.g. [Reference Zhimin, Yangyang, Ming and Wotao47]) for definition of $p$
-contractions (see, e.g. [Reference Zhimin, Yangyang, Ming and Wotao47]) for definition of $p$![]() -contractions). In [Reference Tseng, Bertsekas and Tsitsiklis45], Tseng et al. considered partially asynchronous parallel iterative algorithm (where the delay vectors are bounded from above by some non-negative number, say, $\rho$
-contractions). In [Reference Tseng, Bertsekas and Tsitsiklis45], Tseng et al. considered partially asynchronous parallel iterative algorithm (where the delay vectors are bounded from above by some non-negative number, say, $\rho$![]() ) for quasi-non-expansive mappings (see preliminaries below for definition). Recently, Zhimin et al. introduced ARock algorithm for approximation of fixed points of non-expansive mappings in Hilbert spaces. As opposed to the methods in [Reference Baudet7] and [Reference Tseng, Bertsekas and Tsitsiklis45] which assign coordinates in a deterministic manner, the ARock method is stochastic. More precisely, the ARock algorithm is following:
) for quasi-non-expansive mappings (see preliminaries below for definition). Recently, Zhimin et al. introduced ARock algorithm for approximation of fixed points of non-expansive mappings in Hilbert spaces. As opposed to the methods in [Reference Baudet7] and [Reference Tseng, Bertsekas and Tsitsiklis45] which assign coordinates in a deterministic manner, the ARock method is stochastic. More precisely, the ARock algorithm is following:
Algorithm 1: ARock: a framework for async-parallel coordinate updates

where $\mathcal {H}=H_1\times H_2\times H_3\ldots \times H_m$![]() , $S_{i_k}{x}_k=(0,\,\ldots,\,0,\,(Sx)_{i_k},\,0,\,\ldots,\,0)$
, $S_{i_k}{x}_k=(0,\,\ldots,\,0,\,(Sx)_{i_k},\,0,\,\ldots,\,0)$![]() .
.
Theorem 1.1 Zhimin et al. [ Reference Zhimin, Yangyang, Ming and Wotao47]. Let $T:\mathcal {H}\to \mathcal {H}$![]() be a non-expansive operator that has a fixed point. Let $(x^{k})_{k\geq 0}$
be a non-expansive operator that has a fixed point. Let $(x^{k})_{k\geq 0}$![]() be the sequence generated by Algorithm $1$
be the sequence generated by Algorithm $1$![]() with properly bounded step sizes $\eta _k$
with properly bounded step sizes $\eta _k$![]() . Then, with probability one, $(x^{k})_{k\geq 0}$
. Then, with probability one, $(x^{k})_{k\geq 0}$![]() converges weakly to a fixed point of $T$
converges weakly to a fixed point of $T$![]() . This convergence becomes strong if $\mathcal {H}$
. This convergence becomes strong if $\mathcal {H}$![]() has a finite dimension. In addition, if $T$
has a finite dimension. In addition, if $T$![]() is demicompact, then with probability one, $(x^{k})_{k\geq 0}$
is demicompact, then with probability one, $(x^{k})_{k\geq 0}$![]() converges strongly to a fixed point of $T$
converges strongly to a fixed point of $T$![]() . Furthermore, if $S\equiv I-T$
. Furthermore, if $S\equiv I-T$![]() is quasi-strongly monotone, then, T has a unique fixed point $x^{*}$
is quasi-strongly monotone, then, T has a unique fixed point $x^{*}$![]() , $(x^{k})_{k\geq 0}$
, $(x^{k})_{k\geq 0}$![]() converges strongly to $x^{*}$
converges strongly to $x^{*}$![]() with probability one, and $\mathbb {E}\|x^{k}-x^{*}\|^{2}$
with probability one, and $\mathbb {E}\|x^{k}-x^{*}\|^{2}$![]() converges to $0$
converges to $0$![]() at a linear rate.
at a linear rate.
More recently, Heaton and Censor [Reference Heaton and Censor31] introduced the asynchronous inertial algorithm (ASI) for non-expansive mappings and proved weak convergence result via the monotonicity of a sequence that includes classical error added to the error introduced from using out-of-date iterates. Consider a collection of $m$![]() non-expansive operators $\{T_i\}_{i=1}^{m}$
non-expansive operators $\{T_i\}_{i=1}^{m}$![]() on H with a common fixed point. Consider the CFP with $C=\cap _{i=1}^{m}F(T_i)$
on H with a common fixed point. Consider the CFP with $C=\cap _{i=1}^{m}F(T_i)$![]() , $i\in \{1,\,2,\,3,\,\ldots,\,m\}$
, $i\in \{1,\,2,\,3,\,\ldots,\,m\}$![]() . For each $i\in \{1,\,2,\,3,\,\ldots,\,m\}$
. For each $i\in \{1,\,2,\,3,\,\ldots,\,m\}$![]() , set $S_i=I-T_i$
, set $S_i=I-T_i$![]() , then the ASI algorithm is as follows:
, then the ASI algorithm is as follows:
Algorithm 2: Asynchronous Inertial Algorithm

They proved the following theorem:
Theorem 1.2 Heaton and Censor [Reference Heaton and Censor31]
Let $\{x^{k}\}_{k\in \mathbb {N}}$![]() be a sequence generated by the ASI algorithm and suppose Assumption $1$
be a sequence generated by the ASI algorithm and suppose Assumption $1$![]() holds. If there is an $\epsilon >0$
holds. If there is an $\epsilon >0$![]() such that
such that
then the sequence $\{x^{k}\}_{k\in \mathbb {N}}$![]() converges weakly to a common fixed point $x^{*}$
converges weakly to a common fixed point $x^{*}$![]() of the family $\{T_i\}_{i=1}^{m},$
of the family $\{T_i\}_{i=1}^{m},$![]() i.e.,
i.e.,
In this paper, we prove weak and strong convergence theorem (under additional mild condition) for the class of strict pseudo-contractions which properly contains the class of non-expansive operators considered in [Reference Heaton and Censor31]. More precisely, we prove the following theorem:
Theorem Let $T_i:H\longrightarrow H,\, \ i=1,\,2,\,3,\,\ldots,\,m$![]() be $k_i$
be $k_i$![]() -strictly pseudo-contractive mappings. Let $\{x_n\}$
-strictly pseudo-contractive mappings. Let $\{x_n\}$![]() be a sequence defined by $x^{0}\in H,$
be a sequence defined by $x^{0}\in H,$![]()

Suppose $\sup _{n\in \mathbb {N}}\|d^{n}\|_{\infty }\leq \rho$![]() for some $\rho \geq 1$
for some $\rho \geq 1$![]() and that
and that
for some $\epsilon _0>0,$![]() where $k=\displaystyle \max _{1\leq i\leq m}k_i$
where $k=\displaystyle \max _{1\leq i\leq m}k_i$![]() . Then, the sequence $\{x_n\}$
. Then, the sequence $\{x_n\}$![]() converges weakly to some point $x^{*}\in C=\cap _{i=1}^{n}F(T_i)\neq \emptyset$
converges weakly to some point $x^{*}\in C=\cap _{i=1}^{n}F(T_i)\neq \emptyset$![]() .
.
This class of operators allows some flexibility when data come with some noise in which the operator involved may fail to be non-expansive. Furthermore, we present the application of the ASI algorithm to solving convex minimization problems and Hammerstein integral equations.
2. Preliminaries
In this section, we give some definitions and lemmas that will be useful in the proof of our main results. In the sequel, we assume that $H$![]() is a real Hilbert space.
is a real Hilbert space.
Definition 2.1 Let $C$![]() be a non-empty subset of $H$
be a non-empty subset of $H$![]() . A map $T:C\longrightarrow C$
. A map $T:C\longrightarrow C$![]() is called
is called
(i) Non-expansive if $\|Tx-Ty\|\leq \|x-y\| \ \ \forall,\, \ x,\,y\in C.$

(ii) Quasi-non-expansive if $F(T)\neq \emptyset$
 and $\|Tx-y\|\leq \|x-y\| \ \ \forall,\, \ x\in C \ \mbox {and} \ y\in F(T),$
and $\|Tx-y\|\leq \|x-y\| \ \ \forall,\, \ x\in C \ \mbox {and} \ y\in F(T),$ where
\[ F(T)=\{y\in C:Ty=y\}. \]
where
\[ F(T)=\{y\in C:Ty=y\}. \]
(iii) $k$
 -strictly pseudo-contractive if there exists $k\in [0,\,1)$
-strictly pseudo-contractive if there exists $k\in [0,\,1)$ such that
\[ \|Tx-Ty\|\leq \|x-y\|+k\|(I-T)x-(I-T)y\| \ \ \forall, \ x,y\in C. \]
such that
\[ \|Tx-Ty\|\leq \|x-y\|+k\|(I-T)x-(I-T)y\| \ \ \forall, \ x,y\in C. \]
Remark 1 It is well known that the class of $k$![]() -strictly pseudo-contractive map properly contains the class of quasi-non-expansive maps and that of non-expansive maps. For example, the map $T:l_2\longrightarrow l_2$
-strictly pseudo-contractive map properly contains the class of quasi-non-expansive maps and that of non-expansive maps. For example, the map $T:l_2\longrightarrow l_2$![]() defined by $Tx=-{5}/{4}x$
defined by $Tx=-{5}/{4}x$![]() is not non-expansive. However, a simple calculation shows that
is not non-expansive. However, a simple calculation shows that
i.e., $T$![]() is ${1}/{9}$
is ${1}/{9}$![]() -strictly pseudo-contractive.
-strictly pseudo-contractive.
Definition 2.2 Let $C$![]() be a non-empty subset of $H$
be a non-empty subset of $H$![]() and $T:C\longrightarrow C$
and $T:C\longrightarrow C$![]() be a map. For a fixed $\alpha \in (0,\,1)$
be a map. For a fixed $\alpha \in (0,\,1)$![]() , the map $T_{\alpha }$
, the map $T_{\alpha }$![]() defined by
defined by
is called $\alpha$![]() -relaxation of the map $T$
-relaxation of the map $T$![]() .
.
It can be easily seen that $F(T)\neq \emptyset$![]() if and only if $F(T_{\alpha })\neq \emptyset$
if and only if $F(T_{\alpha })\neq \emptyset$![]() and that $F(T)=F(T_{\alpha })$
and that $F(T)=F(T_{\alpha })$![]() . If $T$
. If $T$![]() is non-expansive, then $T_{\alpha }$
is non-expansive, then $T_{\alpha }$![]() is also non-expansive, and in this case, $T_{\alpha }$
is also non-expansive, and in this case, $T_{\alpha }$![]() is called $\alpha$
is called $\alpha$![]() -averaged of $T$
-averaged of $T$![]() (see, e.g. [Reference Baillon, Bruck and Reich6]).
(see, e.g. [Reference Baillon, Bruck and Reich6]).
Lemma 2.3 Let $H$![]() be a real Hilbert space. Then the following identities hold
be a real Hilbert space. Then the following identities hold
(i) $\| \alpha x+(1-\alpha )y\|^{2}= \alpha \|x\|^{2}+(1-\alpha )\|y\|^{2}-\alpha (1-\alpha )\|x-y\|^{2}$
 .
.(ii) $\|x-y\|^{2}=\|x\|^{2}-2\langle x,\,y\rangle +\|y\|^{2}.$

Lemma 2.4 See, e.g. [Reference Marino and Xu38], proposition 2.1
Let $C$![]() be a non-empty closed convex subset of $H$
be a non-empty closed convex subset of $H$![]() and $T:C\longrightarrow C$
and $T:C\longrightarrow C$![]() be $k$
be $k$![]() -strictly pseudo-contractive map. Then,
-strictly pseudo-contractive map. Then,
(i) $T$
 is Lipschitz with the Lipschitz constant $\frac {1+k}{1-k},$
is Lipschitz with the Lipschitz constant $\frac {1+k}{1-k},$ i.e.,
\[ \|Tx-Ty\|\leq \frac{1+k}{1-k} \|x-y\|\ \ \forall, \quad x,y\in C. \]
i.e.,
\[ \|Tx-Ty\|\leq \frac{1+k}{1-k} \|x-y\|\ \ \forall, \quad x,y\in C. \]
(ii) The map $(I-T)$
 is demiclosed at $0,$
is demiclosed at $0,$ i.e., if $x_n\rightharpoonup x$
i.e., if $x_n\rightharpoonup x$ and $(I-T)x_n\rightarrow 0$
and $(I-T)x_n\rightarrow 0$ then $Tx=x$
then $Tx=x$ .
.
Lemma 2.5 See, e.g. [Reference Marino, Bruno and Erdal39], Lemma 2.6
Let $C$![]() be a non-empty closed convex subset of $H$
be a non-empty closed convex subset of $H$![]() and $T:C\longrightarrow C$
and $T:C\longrightarrow C$![]() be $k$
be $k$![]() -strictly pseudo-contractive map such that $F(T)\neq \emptyset$
-strictly pseudo-contractive map such that $F(T)\neq \emptyset$![]() . Then, the following inequality holds:
. Then, the following inequality holds:
Lemma 2.6 Let $T_i:H\longrightarrow H,$![]() $i=1,\,2,\,\ldots,\, n$
$i=1,\,2,\,\ldots,\, n$![]() be $k_i$
be $k_i$![]() -strictly pseudo-contractive maps such that $C=\cap _{i=1}^{n}F(T_i)\neq \emptyset$
-strictly pseudo-contractive maps such that $C=\cap _{i=1}^{n}F(T_i)\neq \emptyset$![]() . Let $\{x_n\}_{n\in \mathbb {N}}$
. Let $\{x_n\}_{n\in \mathbb {N}}$![]() be a sequence in $H$
be a sequence in $H$![]() such that $\|x_n-x^{*}\|$
such that $\|x_n-x^{*}\|$![]() converges for each $x^{*}\in C$
converges for each $x^{*}\in C$![]() and that $\|T_ix_n-x_n\|\to 0$
and that $\|T_ix_n-x_n\|\to 0$![]() for all $i=1,\,2,\,\ldots,\,n$
for all $i=1,\,2,\,\ldots,\,n$![]() , then the sequence $\{x_n\}_{n\in \mathbb {N}}$
, then the sequence $\{x_n\}_{n\in \mathbb {N}}$![]() converges weakly to a point in $C$
converges weakly to a point in $C$![]() .
.
Proof. We first observe that if $\{x_{n_k}\}_{k\in \mathbb {N}}$![]() is any subsequence of $\{x_n\}_{n\in \mathbb {N}}$
is any subsequence of $\{x_n\}_{n\in \mathbb {N}}$![]() that converges weakly to some point, say $x^{*}$
that converges weakly to some point, say $x^{*}$![]() , then, by lemma 2.4 (ii) $x^{*}\in C$
, then, by lemma 2.4 (ii) $x^{*}\in C$![]() . We now show that $\{x_n\}_{n\in \mathbb {N}}$
. We now show that $\{x_n\}_{n\in \mathbb {N}}$![]() has only one weak cluster point in $C$
has only one weak cluster point in $C$![]() from which the result will then follow.
from which the result will then follow.
Let $\{x_{n_k}\}_{k\in \mathbb {N}}$![]() and $\{x_{n_j}\}_{j\in \mathbb {N}}$
and $\{x_{n_j}\}_{j\in \mathbb {N}}$![]() be two subsequences of $\{x_n\}_{n\in \mathbb {N}}$
be two subsequences of $\{x_n\}_{n\in \mathbb {N}}$![]() such that $x_{n_k}\rightharpoonup p$
such that $x_{n_k}\rightharpoonup p$![]() and $x_{n_j}\rightharpoonup q$
and $x_{n_j}\rightharpoonup q$![]() , where $p,\,q\in C$
, where $p,\,q\in C$![]() (note that this is possible since the sequence $\{x_n\}_{n\in \mathbb {N}}$
(note that this is possible since the sequence $\{x_n\}_{n\in \mathbb {N}}$![]() is bounded). We show that $p=q.$
is bounded). We show that $p=q.$![]() We have that
We have that

From the assumption that $\|x_n-x^{*}\|$![]() converges for each $x^{*}\in C$
converges for each $x^{*}\in C$![]() we see $\lim _{n\to \infty }\langle x_n,\,p-q\rangle$
we see $\lim _{n\to \infty }\langle x_n,\,p-q\rangle$![]() exists. So that
exists. So that

Hence, $p=q$![]() . The proof is complete.
. The proof is complete.
Lemma 2.7 Let $C$![]() be a non-empty closed and convex subset of $H$
be a non-empty closed and convex subset of $H$![]() and $T:C\longrightarrow C$
and $T:C\longrightarrow C$![]() be a $k$
be a $k$![]() -strictly pseudo-contractive map. Then for $\alpha \in (0,\,1-k),$
-strictly pseudo-contractive map. Then for $\alpha \in (0,\,1-k),$![]() $T_{\alpha }$
$T_{\alpha }$![]() is a non-expansive map.
is a non-expansive map.
Proof. Using lemma 2.3 (i), Equation (2.1) and the fact that $T$![]() is $k$
is $k$![]() -strictly pseudo-contractive, we have
-strictly pseudo-contractive, we have

The result follows from the fact that $\alpha \in (0,\,1-k)$![]() .
.
3. Main results
We now state and prove our main theorem.
Theorem 3.1 Let $T_i:H\longrightarrow H,\, \ i=1,\,2,\,3,\,\ldots,\,m$![]() be $k_i$
be $k_i$![]() -strictly pseudo-contractive mappings. Let $\{x_n\}$
-strictly pseudo-contractive mappings. Let $\{x_n\}$![]() be a sequence defined by $x^{0}\in H,$
be a sequence defined by $x^{0}\in H,$![]()

Suppose $\sup _{n\in \mathbb {N}}\|d^{n}\|_{\infty }\leq \rho$![]() for some $\rho \geq 1$
for some $\rho \geq 1$![]() and that
and that
for some $\epsilon _0>0$![]() , where $k=\displaystyle \max _{1\leq i\leq m}k_i$
, where $k=\displaystyle \max _{1\leq i\leq m}k_i$![]() . Then, the sequence $\{x_n\}$
. Then, the sequence $\{x_n\}$![]() converges weakly to some point $x^{*}\in C=\cap _{i=1}^{n}F(T_i)\neq \emptyset$
converges weakly to some point $x^{*}\in C=\cap _{i=1}^{n}F(T_i)\neq \emptyset$![]() .
.
In Theorem (3.2), for each $n\in \mathbb {N}$![]() , $d^{n}$
, $d^{n}$![]() is the delay vector, $\{i_n\}$
is the delay vector, $\{i_n\}$![]() is an almost cyclic sequence on the set $\{1,\,2,\,3\ldots,\,m\}$
is an almost cyclic sequence on the set $\{1,\,2,\,3\ldots,\,m\}$![]() , $T_{i_n}$
, $T_{i_n}$![]() is the processor whose output will be used to compute $x^{n+1}$
is the processor whose output will be used to compute $x^{n+1}$![]() and finally, $\tilde {x}^{n}=x^{n}$
and finally, $\tilde {x}^{n}=x^{n}$![]() or $\tilde {x}^{n}=x^{n-j_{i_n}^{n}}$
or $\tilde {x}^{n}=x^{n-j_{i_n}^{n}}$![]() , where $j_{i_n}^{n}$
, where $j_{i_n}^{n}$![]() is the delay amount of the $i_n^{th}$
is the delay amount of the $i_n^{th}$![]() processor.
processor.
Remark 2 In Theorem (3.1), if we set $A_{i_n}=(I-T_{i_n})$![]() , then algorithm (3.1) becomes
, then algorithm (3.1) becomes

Proof of Theorem 3.3. We divide the proof into three steps:
Step 1. For any $x^{*}\in C=\cap _{i=1}^{n}F(T_i)$![]() , the following inequality holds:
, the following inequality holds:

Indeed, let $x^{*}\in C=\cap _{i=1}^{n}F(T_i)$![]() , then using Lemma 2.3 (ii), we have
, then using Lemma 2.3 (ii), we have

Using Lemma 2.5, we get

Also by using the fact that $d_{i_n}^{n}$![]() is the delay amount for the $i_n^{th}$
is the delay amount for the $i_n^{th}$![]() processor, and repeated application of the triangle inequality, we have
processor, and repeated application of the triangle inequality, we have

Using the fact that $2ab\leq \frac {1}{\gamma }a^{2}+\gamma b^{2}$![]() for any $a,\,b\in \mathbb {R}$
for any $a,\,b\in \mathbb {R}$![]() and $\gamma >0$
and $\gamma >0$![]() , we have
, we have


Substituting inequalities (3.6) and (3.8) in (3.5), we get the desired result.
Step 2. For any $x^{*}\in C=\cap _{i=1}^{n}F(T_i)$![]() the non-negative sequence $\{\beta _n\}_{n \in \mathbb {N}}$
the non-negative sequence $\{\beta _n\}_{n \in \mathbb {N}}$![]() defined by
defined by

is convergent, where $c_r=(1+\rho -r)+\epsilon _0,\, \ r=1,\,2,\,3\ldots,\, m+1$![]() .
.
Using inequality (3.4), we have

By changing the indexing variable and observing that $c_{r+1}+1=c_r$![]() , we have
, we have

Since $c_{\rho +1}=\epsilon _0$![]() and $c_1=\rho +\epsilon _0$
and $c_1=\rho +\epsilon _0$![]() we have that $\{\beta _n\}$
we have that $\{\beta _n\}$![]() is non-increasing. Thus, $\{\beta _n\}_{n \in \mathbb {N}}$
is non-increasing. Thus, $\{\beta _n\}_{n \in \mathbb {N}}$![]() converges.
converges.
Step 3. The sequences $\{\|x^{n}-x^{*}\|\}_{n \in \mathbb {N}}$![]() , $\{\|x^{n+1}-x^{n}\|\}_{n \in \mathbb {N}}$
, $\{\|x^{n+1}-x^{n}\|\}_{n \in \mathbb {N}}$![]() and $\{\|x^{n}-\tilde {x}^{n}\|\}_{n \in \mathbb {N}}$
and $\{\|x^{n}-\tilde {x}^{n}\|\}_{n \in \mathbb {N}}$![]() converge as $n\to \infty$
converge as $n\to \infty$![]() .
.
Indeed, from (3.11), we have that
so that
Using (3.9) and (3.13), we see that
Finally, we have

So that
Step 4. $\|T_ix^{n}-x^{n}\|\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() for all $i=1,\,2,\,3\ldots,\,m$
for all $i=1,\,2,\,3\ldots,\,m$![]() .
.
Let $i\in \{1,\,2,\,3\ldots,\,m\}$![]() and $T_i^{\alpha }$
and $T_i^{\alpha }$![]() be an $\alpha$
be an $\alpha$![]() -relaxation of $T_i$
-relaxation of $T_i$![]() . Let $s_n$
. Let $s_n$![]() be a sequence in $\mathbb {N}$
be a sequence in $\mathbb {N}$![]() such that $s_n$
such that $s_n$![]() is the smallest integer $\geq n$
is the smallest integer $\geq n$![]() with $i_{s_n}=i$
with $i_{s_n}=i$![]() . Then
. Then
Now,

In the last inequality, we have used the fact that $T_i^{\alpha _{s_n}}$![]() is non-expansive (Lemma 2.7). Using the fact that $\{i_n\}_{n\in \mathbb {N}}$
is non-expansive (Lemma 2.7). Using the fact that $\{i_n\}_{n\in \mathbb {N}}$![]() is an almost cyclic sequence on $\{1,\,2,\,3\ldots,\,m\}$
is an almost cyclic sequence on $\{1,\,2,\,3\ldots,\,m\}$![]() with almost cyclic index $N$
with almost cyclic index $N$![]() we have $\tilde {x}^{s_n}=x^{h}$
we have $\tilde {x}^{s_n}=x^{h}$![]() for some $n-\rho \leq h\leq s_n\leq n+N$
for some $n-\rho \leq h\leq s_n\leq n+N$![]() . Thus, from inequality (3.17) and repeated application of triangle inequality, we have
. Thus, from inequality (3.17) and repeated application of triangle inequality, we have

From inequalities (3.19) and (3.20), we have

Inequalities (3.17) and (3.21) further imply that

Applying (3.13), we see that $\|T_i^{\alpha _{s_n}}(x^{n})-x^{n}\|\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() .
.
Now
Therefore,
(3.14) combined with (3.24) implies that all the assumptions of Lemma 2.6 are satisfied. Hence the sequence $\{x^{n}\}_{n\in \mathbb {N}}$![]() converges weakly to some point in $C=\cap _{i=1}^{n}F(T_i)$
converges weakly to some point in $C=\cap _{i=1}^{n}F(T_i)$![]() . The proof is complete.
. The proof is complete.
Definition 3.2 see, e.g. [Reference Petryshyn41]
A map $T:H \longrightarrow H$![]() is said to be demicompact if it has the property that whenever a sequence $\{x_n\}$
is said to be demicompact if it has the property that whenever a sequence $\{x_n\}$![]() is bounded and the sequence $\{x_n-Tx_n\}$
is bounded and the sequence $\{x_n-Tx_n\}$![]() converges strongly, then there exists a subsequence of $\{x_n\}$
converges strongly, then there exists a subsequence of $\{x_n\}$![]() that converges strongly.
that converges strongly.
We now give the following strong convergence result.
Theorem 3.3 Let $T_i:H\longrightarrow H,\, \ i=1,\,2,\,3,\,\ldots,\,m$![]() be $k_i$
be $k_i$![]() -strictly pseudo-contractive mappings. Let $\{x_n\}$
-strictly pseudo-contractive mappings. Let $\{x_n\}$![]() be a sequence defined by $x^{0}\in H,$
be a sequence defined by $x^{0}\in H,$![]()

Suppose $\sup _{n\in \mathbb {N}}\|d^{n}\|_{\infty }\leq \rho$![]() for some $\rho \geq 1$
for some $\rho \geq 1$![]() and that
and that
for some $\epsilon _0>0,$![]() where $k=\displaystyle \max _{1\leq i\leq m}k_i$
where $k=\displaystyle \max _{1\leq i\leq m}k_i$![]() . Then, the sequence $\{x_n\}$
. Then, the sequence $\{x_n\}$![]() converges weakly to some point $x^{*}\in C=\cap _{i=1}^{n}F(T_i)\neq \emptyset$
converges weakly to some point $x^{*}\in C=\cap _{i=1}^{n}F(T_i)\neq \emptyset$![]() . Suppose in addition that $T_{i_0}$
. Suppose in addition that $T_{i_0}$![]() is demicompact for some $i_0\in \{i=1,\,2,\,3,\,\ldots,\,m\}$
is demicompact for some $i_0\in \{i=1,\,2,\,3,\,\ldots,\,m\}$![]() , then the sequence $\{x_n\}$
, then the sequence $\{x_n\}$![]() converges strongly to $x^{*}$
converges strongly to $x^{*}$![]() .
.
Proof. Suppose $T_{i_0}$![]() is demicompact for some $i_0\in \{i=1,\,2,\,3,\,\ldots,\,m\}$
is demicompact for some $i_0\in \{i=1,\,2,\,3,\,\ldots,\,m\}$![]() . Since we have, by Theorem 3.1 that $\{x_n\}$
. Since we have, by Theorem 3.1 that $\{x_n\}$![]() is bounded and $x_n-Tx_n \to 0$
is bounded and $x_n-Tx_n \to 0$![]() as $n\to \infty$
as $n\to \infty$![]() , then there exists a subsequence $\{x_{n_k}\}$
, then there exists a subsequence $\{x_{n_k}\}$![]() of $\{x_n\}$
of $\{x_n\}$![]() such that $x_{n_k}\to x^{*}$
such that $x_{n_k}\to x^{*}$![]() . Lemma 2.6 implies that $x^{*}\in C$
. Lemma 2.6 implies that $x^{*}\in C$![]() . Similarly, by Theorem 3.1, we have that $\|x_n-x^{*}\|$
. Similarly, by Theorem 3.1, we have that $\|x_n-x^{*}\|$![]() converges. Therefore, $x_n\to x^{*}$
converges. Therefore, $x_n\to x^{*}$![]() as $n\to \infty$
as $n\to \infty$![]() . The proof is complete.
. The proof is complete.
4. Applications
In this section, we also give the application of our main theorem to solving the convex minimization problem and Hammerstein integral equations.
4.1. Convex optimization
We first recall the following definition.
Definition 4.1 Let $A:H\longrightarrow H$![]() be a map. $A$
be a map. $A$![]() is called $\beta$
is called $\beta$![]() -inverse strongly monotone if for each $x,\,y\in H$
-inverse strongly monotone if for each $x,\,y\in H$![]() we have
we have
It is well known that a map $T$![]() is $k$
is $k$![]() -strictly pseudo-contractive if and only if the map $A:=I-T$
-strictly pseudo-contractive if and only if the map $A:=I-T$![]() is $\frac {1-k}{2}$
is $\frac {1-k}{2}$![]() -inverse strongly monotone and that $F(T)=N(A)$
-inverse strongly monotone and that $F(T)=N(A)$![]() where $N(A)=\{x\in H: Ax=0\}$
where $N(A)=\{x\in H: Ax=0\}$![]() (see, e.g. [Reference Browder and Petryshyn13]). We now give the following Lemma which is due to Baillon and Haddad [Reference Baillon and Haddad5].
(see, e.g. [Reference Browder and Petryshyn13]). We now give the following Lemma which is due to Baillon and Haddad [Reference Baillon and Haddad5].
Lemma 4.2 Baillon and Haddad [Reference Baillon and Haddad5]
Let $E$![]() be a Banach space. Suppose $f$
be a Banach space. Suppose $f$![]() is continuously Fréchet differentiable and convex function. If the gradient $\nabla f$
is continuously Fréchet differentiable and convex function. If the gradient $\nabla f$![]() of $f$
of $f$![]() is $\frac {1}{\alpha }$
is $\frac {1}{\alpha }$![]() -Lipschitz, then $\nabla f$
-Lipschitz, then $\nabla f$![]() is $\alpha$
is $\alpha$![]() -inverse strongly monotone.
-inverse strongly monotone.
Theorem 4.3 Let $H$![]() be a real Hilbert space and $f_i:H\longrightarrow \mathbb {R},$
be a real Hilbert space and $f_i:H\longrightarrow \mathbb {R},$![]() $i=1,\,2,\,3,\,\ldots,\, m$
$i=1,\,2,\,3,\,\ldots,\, m$![]() be continuously Fréchet differentiable and convex functions such that $\nabla f_i$
be continuously Fréchet differentiable and convex functions such that $\nabla f_i$![]() is $L_i$
is $L_i$![]() -Lipschitz for each $i=1,\,2,\,3,\,\ldots,\, m$
-Lipschitz for each $i=1,\,2,\,3,\,\ldots,\, m$![]() . Suppose that the set $C=\cap _{i=1}^{m} C_i\neq \emptyset,$
. Suppose that the set $C=\cap _{i=1}^{m} C_i\neq \emptyset,$![]() where $C_i=argmin_{x\in H}f_i(x)=\{x\in H: f(x)=\min _{x\in H}f(x)\}$
where $C_i=argmin_{x\in H}f_i(x)=\{x\in H: f(x)=\min _{x\in H}f(x)\}$![]() for each $i$
for each $i$![]() . Under the conditions of Theorem (3.1), the sequence generated by Algorithm (3.3) converges weakly to a point in $C$
. Under the conditions of Theorem (3.1), the sequence generated by Algorithm (3.3) converges weakly to a point in $C$![]() . Moreover, if $\nabla f_{i_0}$
. Moreover, if $\nabla f_{i_0}$![]() is demicompact for some $i_0$
is demicompact for some $i_0$![]() , then the sequence converges strongly to a point in $C$
, then the sequence converges strongly to a point in $C$![]() .
.
Proof. We simply use the fact that $\nabla f_i(x^{*})=0$![]() if and only if $x^{*}$
if and only if $x^{*}$![]() is a minimizer of the function $f_i$
is a minimizer of the function $f_i$![]() and the result follows immediately.
and the result follows immediately.
4.2. Hammerstein integral equations
Let $\Omega$![]() be a measurable and bounded subset of ${\mathbb {R}}^{n}$
be a measurable and bounded subset of ${\mathbb {R}}^{n}$![]() . A non-linear integral equation of Hammerstein type is one of the forms
. A non-linear integral equation of Hammerstein type is one of the forms
where $dy$![]() is a $\sigma$
is a $\sigma$![]() -finite measure. The function $k:\Omega \times \Omega \rightarrow \mathbb {R}$
-finite measure. The function $k:\Omega \times \Omega \rightarrow \mathbb {R}$![]() is the kernel of the equation and $f:\Omega \times \mathbb {R} \rightarrow \mathbb {R}$
is the kernel of the equation and $f:\Omega \times \mathbb {R} \rightarrow \mathbb {R}$![]() is a measurable real-valued function. The function $w$
is a measurable real-valued function. The function $w$![]() and the unknown function $u$
and the unknown function $u$![]() lie in a suitable Banach space of measurable real-valued functions, say, $\mathcal {F}(\Omega,\, \mathbb {R})$
lie in a suitable Banach space of measurable real-valued functions, say, $\mathcal {F}(\Omega,\, \mathbb {R})$![]() . If we define the operators $F:\mathcal {F}(\Omega,\, \mathbb {R})\rightarrow \mathcal {F}(\Omega,\, \mathbb {R})$
. If we define the operators $F:\mathcal {F}(\Omega,\, \mathbb {R})\rightarrow \mathcal {F}(\Omega,\, \mathbb {R})$![]() and $K:\mathcal {F}(\Omega,\, \mathbb {R})\rightarrow \mathcal {F}(\Omega,\, \mathbb {R})$
and $K:\mathcal {F}(\Omega,\, \mathbb {R})\rightarrow \mathcal {F}(\Omega,\, \mathbb {R})$![]() by
by
then (4.1) can easily be put in the abstract Hammerstein equation
where, without loss of generality, we have taken $w$![]() to be the zero map in $\mathcal {F}(\Omega,\, \mathbb {R})$
to be the zero map in $\mathcal {F}(\Omega,\, \mathbb {R})$![]() . We also recall that a map $A:H\longrightarrow H$
. We also recall that a map $A:H\longrightarrow H$![]() is called $\alpha$
is called $\alpha$![]() -strongly monotone if for each $x,\,y\in H$
-strongly monotone if for each $x,\,y\in H$![]() we have
we have
Now, let $E=H\times H$![]() with the inner product
with the inner product
and the norm
Define the map $T:E\longrightarrow E$![]() by
by
Then it is easy to see that $u^{*}\in H$![]() solves (4.3) if and only if $T(u^{*},\,v^{*})=(0,\,0)$
solves (4.3) if and only if $T(u^{*},\,v^{*})=(0,\,0)$![]() , where $v^{*}=KFu^{*}$
, where $v^{*}=KFu^{*}$![]() ; and that $T$
; and that $T$![]() is strongly monotone and Lipschitz whenever the maps $F$
is strongly monotone and Lipschitz whenever the maps $F$![]() and $K$
and $K$![]() are both strongly monotone and Lipschitz. It is also easy to verify that a Lipschitz strongly monotone map is inverse strongly monotone. We now give the following result for approximating a common solution of Hammerstein integral equations.
are both strongly monotone and Lipschitz. It is also easy to verify that a Lipschitz strongly monotone map is inverse strongly monotone. We now give the following result for approximating a common solution of Hammerstein integral equations.
Theorem 4.4 Let $H$![]() be a real Hilbert space and $F_i,\,K_i:H\longrightarrow H$
be a real Hilbert space and $F_i,\,K_i:H\longrightarrow H$![]() be $\eta _i$
be $\eta _i$![]() -strongly monotone and $L_i$
-strongly monotone and $L_i$![]() -Lipschitz maps for $i=1,\,2,\,3,\,\ldots,\, m$
-Lipschitz maps for $i=1,\,2,\,3,\,\ldots,\, m$![]() . Suppose that the set
. Suppose that the set
Then, under the conditions of Theorem (3.1), the sequence generated by Algorithm (3.3) converges weakly to a point in $\Omega$![]() .
.
Proof. Define the maps $A_i:E\longrightarrow E$![]() by $A_i(u,\,v)=(F_iu-v,\,K_iv+u)$
by $A_i(u,\,v)=(F_iu-v,\,K_iv+u)$![]() as in (4.4). Then, for each $i=1,\,2,\,3,\,\ldots,\, m$
as in (4.4). Then, for each $i=1,\,2,\,3,\,\ldots,\, m$![]() , $A_i$
, $A_i$![]() is inverse strongly monotone and the result follows.
is inverse strongly monotone and the result follows.
5. Conclusion
In this paper, we proved weak and strong convergence of the asynchronous inertial algorithm to a common fixed point of $k$![]() -strictly pseudo-contractive maps in Hilbert spaces. We also give application of our main result to solving convex minimization problems and Hammerstein integral equations. In future work, we shall concentrate on the implementation of the asynchronous inertial algorithm and also on the convergence of the algorithm for other classes of non-linear maps, such as pseudo-contractions, accretive and monotone maps (see e.g. [Reference Combettes and Eckstein26]).
-strictly pseudo-contractive maps in Hilbert spaces. We also give application of our main result to solving convex minimization problems and Hammerstein integral equations. In future work, we shall concentrate on the implementation of the asynchronous inertial algorithm and also on the convergence of the algorithm for other classes of non-linear maps, such as pseudo-contractions, accretive and monotone maps (see e.g. [Reference Combettes and Eckstein26]).